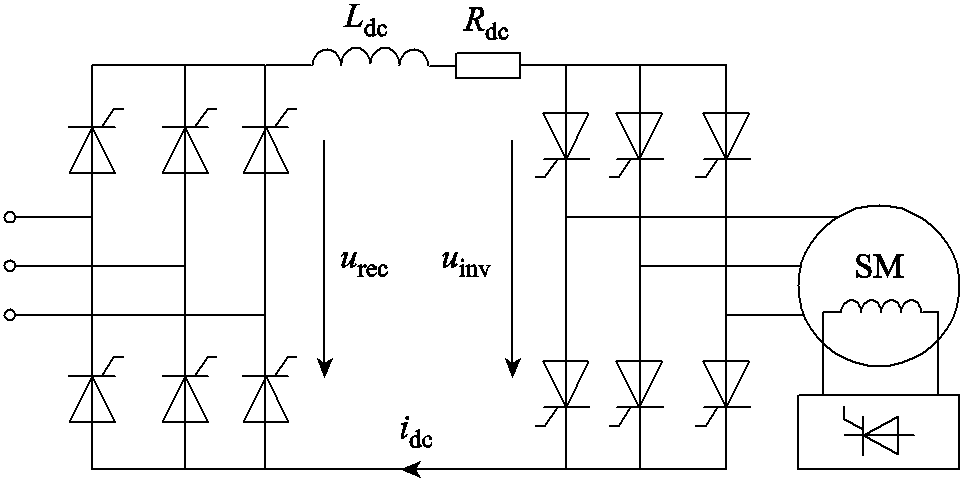
图1 LCI驱动器拓扑结构
Fig.1 Topology of LCI driver
摘要 负载换流逆变器（LCI）驱动电励磁同步电机控制系统广泛应用于中高压场合，在应对干扰和负载变化上，较大的系统惯性系数和较低的开关频率导致其动态响应性能欠佳。该文提出一种基于LCI驱动电励磁同步电机的无速度传感器模型预测控制方法。首先根据LCI的数学模型建立预测状态方程，同时给出合适的代价函数和约束条件；然后分析负载换相模式下的控制矢量模型，给出速度观测器的设计方法和参数选择依据，并针对负载变化对速度观测产生的影响进行分析和补偿。同时该观测器还能够同时实现逆变桥输入电压和端电压相位的观测；最后，通过3.75kW的LCI驱动电励磁同步电机实验平台对提出的无速度传感器模型预测控制方法进行实验验证。结果表明所提出的控制方法能够有效提升系统的动态响应性能，所设计的观测器具有可行性，速度观测结果在额定阶跃负载下误差小于13°。
关键词：负载换流逆变器 电励磁同步电机 无速度传感器 模型预测控制
负载换流逆变器（Load Commutated Inverter, LCI）驱动电励磁同步电机具有容量大、成本低、可靠性高和控制简单等特点，因此该驱动系统被广泛应用于高速精轧机、大型燃气轮机、抽水蓄能电站及其他风机泵类等中高压场合[1-4]。在高速精轧机的工况应用中，驱动系统需要在钢材加入后快速稳定在预定转速上，这就要求所采用的控制算法在负载快速变化时有着较好的动态响应特性。如果稳定转速效果不佳，会导致轧制钢材的堆积和产品加工失败。而好的动态响应能力能够有效减小变载时的速度变化，缩短速度恢复时间，从而直接提高成品率和钢品质量。在大型燃气轮机、抽水蓄能电站及其他风机泵类工况应用中，更高的动态响应速度能够使系统更好地应对干扰和负载变化，从而提高机组起动的成功率和系统的稳定性[5]。
模型预测控制由于建模难度低、鲁棒性和稳定性较高、动态响应性能好等优势逐渐开始取代传统控制方法。但它同时存在稳态波动大、计算量大等问题[6-10]。而LCI驱动电励磁同步电机系统惯性系数高，这可以抑制模型预测控制带来的稳态波动问题。由于LCI采用半控型晶闸管器件作为其电力电子器件，因此其控制频率通常仅为几百赫兹，不过较低的开关频率相比其他驱动系统来说，为算法在线运行留出了更充足的计算资源。文献[10-11]提出了一种基于LCI的模型预测控制方法，该方法采用多级控制，但只有部分采用了模型预测控制，因此所采用的模型预测控制实际应用效果受到了其他控制器的限制。
此外，传统的机械式传感器安装繁琐，难以保证其安装同轴度，可靠性也较低。在一些特殊工况下，如高温易爆和水下场合，甚至无法完成机械式传感器的安装。目前无传感器控制方法已有丰富的研究成果，但大多都集中在永磁同步电机、异步电机及开关磁阻电机等[12-15]。文献[16]设计了一种基于电励磁同步电机的速度观测器，但并未考虑负载变化给观测带来的影响。文献[17]设计了一种速度观测器，但负载换相模式给速度观测带来的影响未被考虑。
本文基于LCI驱动电励磁同步电机控制系统提出了一种无速度传感器模型预测控制方法。提出的单级模型预测控制方法能够避免多级控制带来的木桶效应，提高系统的动态响应性能，降低硬件成本并提高系统运行的可靠性。本文首先分析了LCI模型，推导了系统的预测状态方程，并给出相应的代价函数和参数约束。然后分析负载换流模式下的矢量模型，设计了一种适用于高速阶段的多参数观测器并给出了参数选择依据，同时针对负载换相模式运行特点和负载变化给观测带来的影响进行了补偿。最后通过3.75kW的LCI驱动电励磁同步电机实验平台对提出的无速度传感器模型预测控制方法进行了实验验证。
图1为LCI驱动器拓扑结构。该结构主要包括整流桥、逆变桥及平波电抗器三部分。图1中urec为整流输出电压，uinv为逆变输入电压，idc为直流母线电流，Ldc为平波电抗器电感，Rdc为直流母线等效电阻。
图1 LCI驱动器拓扑结构
Fig.1 Topology of LCI driver
以LCI回路建立等效电压模型，其表达式为
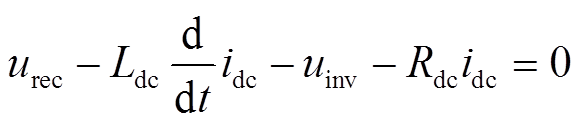（1）对于其中的三相全控整流桥来说，其输出电压与网侧电压的数学关系为
（2）式中，Us为网侧相电压有效值；α为整流桥的触发延迟角。
在LCI驱动器中，整流桥与逆变桥具有完全相同的拓扑结构，仅有能量流向相反。在控制策略上，整流和逆变通过改变触发延迟角即可实现相互切换。为了实现与整流桥相反的能量流向，逆变桥的触发延迟角需要大于90°。因此，逆变输入电压数学表达式可表示为
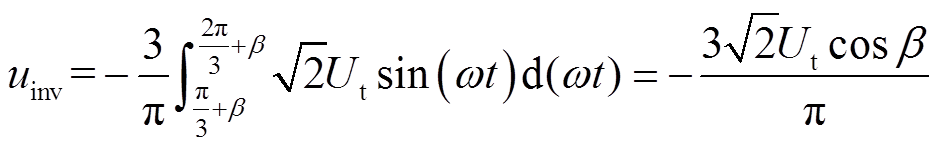（3）式中，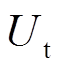
为电机端线电压
有效值；β为逆变桥的触发延迟角。
将式（2）和式（3）代入式（1）中，则LCI回路电压方程可表示为
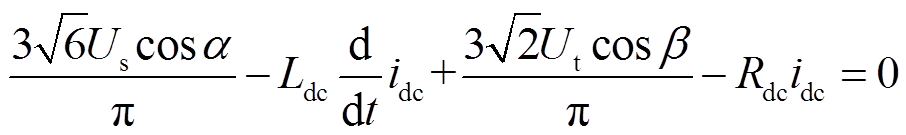（4）电机的机械运动方程为
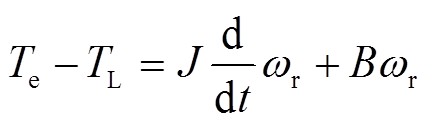（5）式中，Te为电机的电磁转矩；TL为负载转矩；J为轴系转动惯量；B为粘滞系数；ωr为转子的机械转速。
忽略逆变桥的能量损耗，电机的电磁转矩可以表示为
（6）
当电励磁同步电机采用恒励磁电流控制时，uinv/idc可近似为定值。将式（6）代入式（5）中，电机的机械运动可表示为
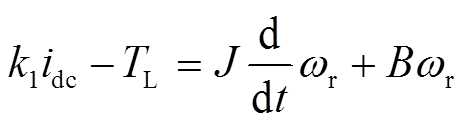（7）式中，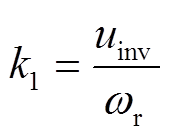
。
将式（4）与式（7）改写为标准的状态空间方程为
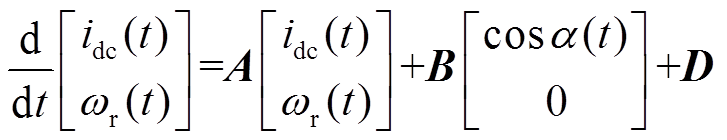（8）其中
控制周期ts很小，可认为有关系
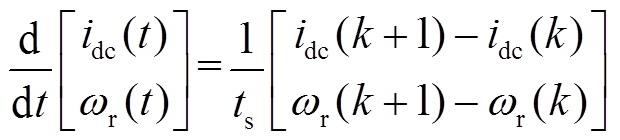（9）将式（9）代入式（8）后，可得到离散化的系统预测方程
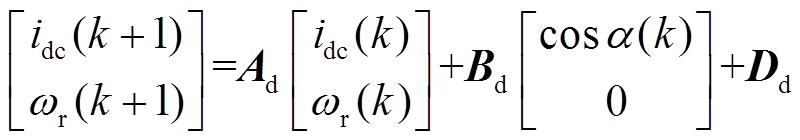（10）其中
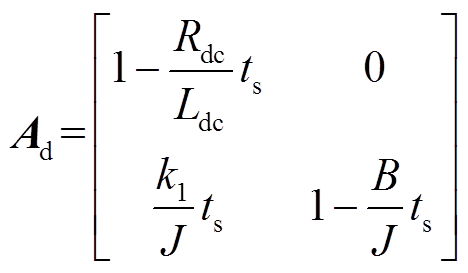
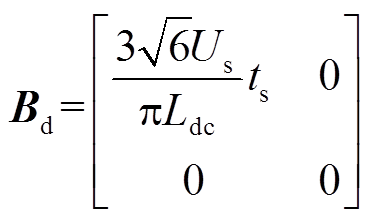
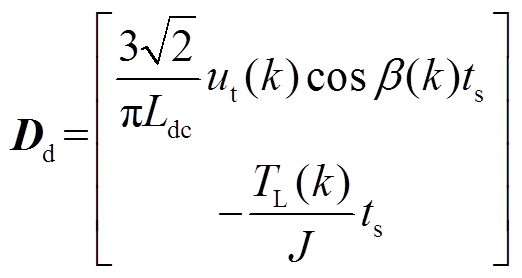
式（10）为k时刻的预测方程，将其与k-1时刻的预测方程做差，得到的增量式预测方程为
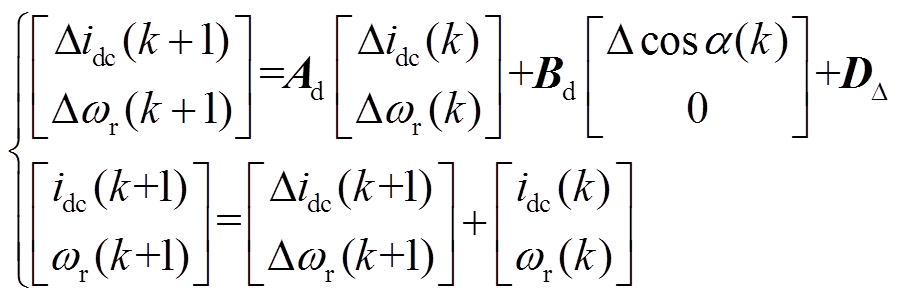（11）式中
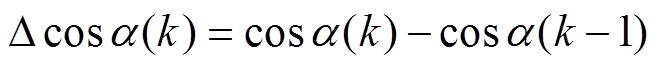
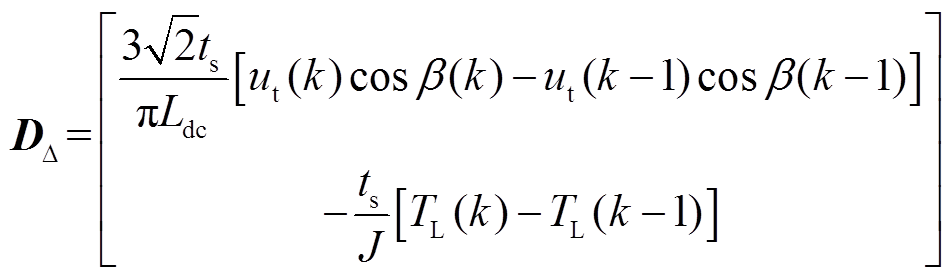
在一个控制周期ts内，认为负载转矩TL恒定不变，即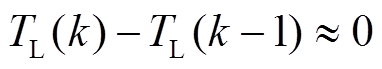
。
图2所示为基于LCI驱动电励磁同步电机的模型预测控制框图。模型预测控制的输入包括转速给定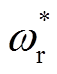
、超前换相角给定
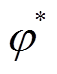、直流母线电流idc、电机端电压ut和实际转速
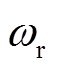，输出量为整流角的余弦值。其中，ut和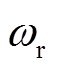是由观测器得到的，观测器的设计将在2.2节详细介绍。将模型预测控制应用于LCI驱动电励磁同步电机的目的在于提升系统的动态响应性能。但该系统中的励磁环节通常都有着很大的惯性系数，励磁调节滞后会大大降低系统的动态响应能力，因此励磁采用恒流控制方式。逆变采用恒超前换相角控制策略，该控制方式可以在保证逆变桥可靠换相的基础上，尽可能地提高LCI驱动器的功率因数。再结合观测得到的端电压相位，给出合适的逆变触发信号。整流控制则直接采用模型预测控制算法。
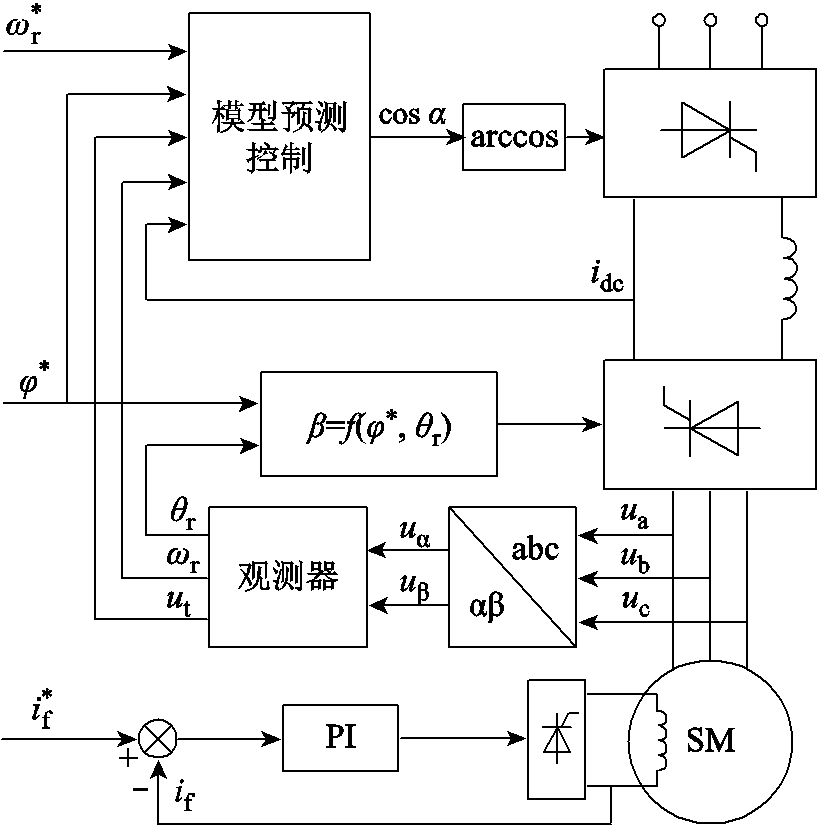
图2 模型预测控制框图
Fig.2 Block diagram of model predictive control
模型预测控制的一大优势是利用代价函数同时优化多个参数，因此代价函数的设计对系统的控制效果起着非常重要的作用。本文的控制算法是针对LCI驱动电励磁同步电机系统而设计的，为同时兼顾被控目标及系统可靠性，代价函数J设计为
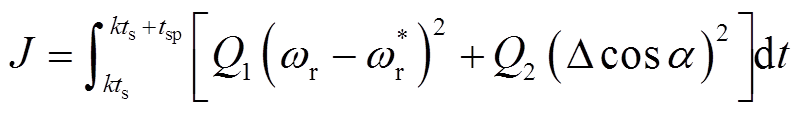（12）式中，tsp为预测控制时域长度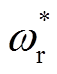；为电机的转速给定；Q1和Q2为被控量的权重因子。
由于ts很小，可以认为在一个控制周期内各参数值不变，则离散化的代价函数Jd可以表示为
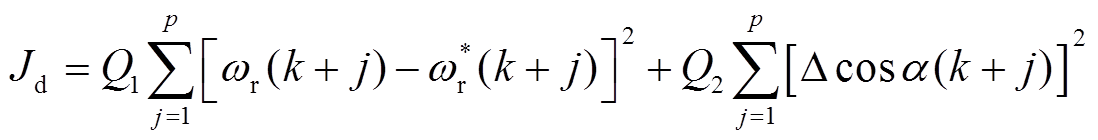（13）式中，p为预测步长。
从式（13）可以看出，算法要求速度差与整流角的变化量尽可能地小。但是，除了这些参数的软约束，还需要对系统中的部分变量进行硬约束，其硬约束表达式为
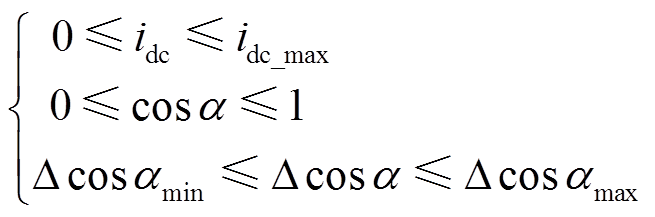（14）式中，下角标max和min分别代表参数的上限和下限。
为了降低硬件成本以及提高系统运行的可靠性，本文设计了一个适用于高速阶段的多参数观测器。从图2可以看出，基于LCI驱动电励磁同步电机的模型预测控制算法所需的速度和逆变输入电压均由观测器观测得到，无需使用速度传感器和额外的电压传感器。逆变桥的触发则利用观测到的端电压相位进行换相控制，也无需采用位置传感器。
图3为电励磁同步电机运行在负载换相模式下的矢量图。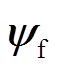
为励磁磁链，其方向仅由转子位置θe所决定，其表达式为
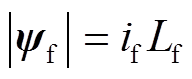（15）式中，Lf为励磁电感；if为励磁电流。
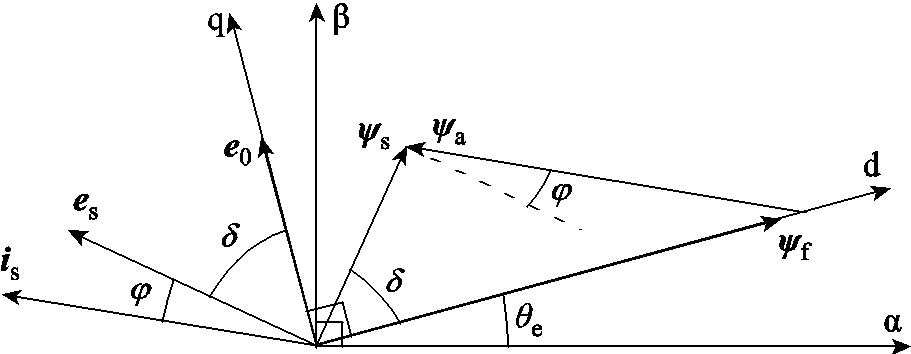
图3 电励磁同步电机负载换相模式矢量图
Fig.3 Vector diagram of electrically excited synchronous motor in natural commutation mode
空载时，励磁电流产生的磁场会在定子侧感生出空载反电动势e0。而当电机带载运行时，定子磁链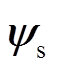
将超前于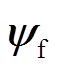一个角度δ，该角度为负载角。同时，带载反电动势es也将超前于空载反电动势e0负载角δ。如果直接根据电机三相端电压来观测速度，那么当负载变化时，随着负载角的改变，速度观测也会在变载时产生较大的偏差，从而影响LCI的可靠换相，降低系统可靠性。
在负载换相模式下，为了保证电机的可靠换相，必须保证定子电流is超前反电动势es一个角度φ。定子电流is与电枢磁链ψa数学关系为
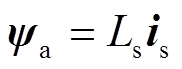（16）式中，Ls为定子电感。
定子电流可以通过如下表达式进行计算得到
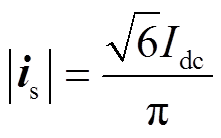（17）式中，Idc为直流母线电流平均值。
在图3中的磁链三角形中，根据余弦定理可以得到
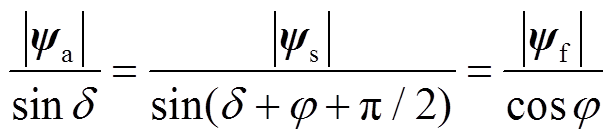（18）将式（15）~式（17）代入到式（18）中，可得负载角δ的计算表达式为
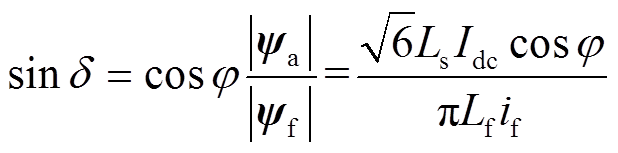（19）为了得到包含所需信息的正交信号，电机三相端电压首先需要进行3/2变换，将ABC三相静止坐标系下的电压信号转化为αβ0两相静止坐标系下的电压信号，其转换关系为
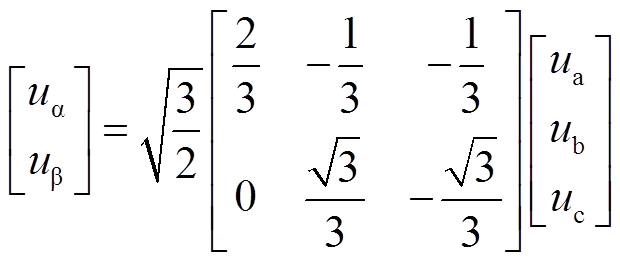（20）式中，ua、ub、uc为机端三相相电压；uα、uβ为两相静止坐标系下的机端电压。
图4为本文设计观测器的原理图。观测器由归一化环节、正交锁相环和速度校正三部分组成。采用锁相环作为观测器主体可以大大降低系统噪声对观测过程的干扰。
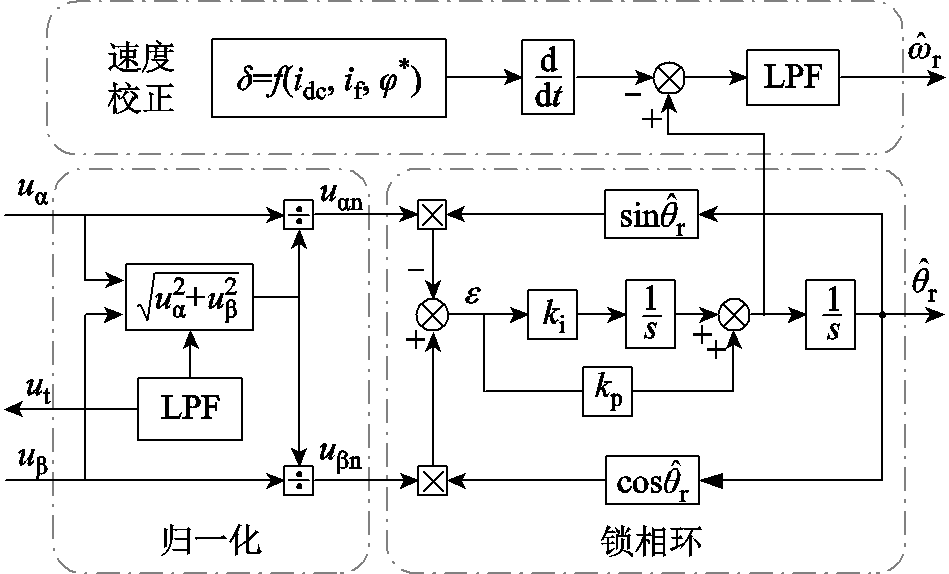
图4 观测器原理图
Fig.4 Schematic of the designed observer
由式（20）得到的正交信号uα、uβ的关系为
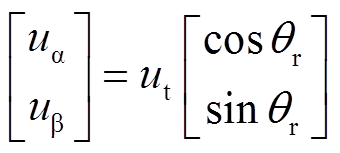（21）式中，θr为电机端电压相角。
根据式（21）易得出
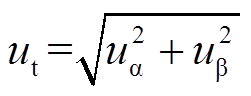（22）如果直接利用正交信号uα、uβ作为锁相环的输入，可得到表达式为
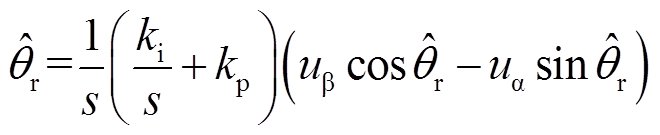（23）式中，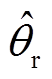
为电机端电压相位观测值；kp、ki分别为锁相环的比例增益和积分增益。
把式（21）代入式（23）可得关系式为
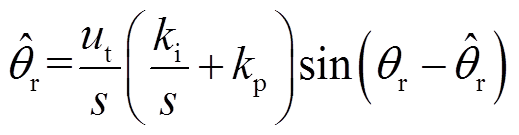（24）当锁相环进入稳态后，
和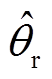的误差很小。可以认为
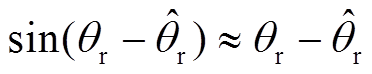。将该近似关系代入式（24）中后，可得到未进行归一化的正交锁相环传递函数为
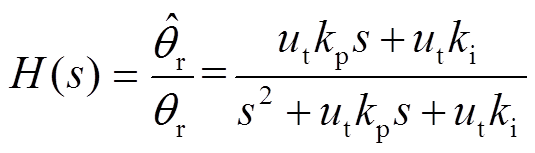（25）由式（25）可知，该锁相环的传递函数受参数ut的影响。这就导致逆变输入电压的变化会引起锁相环带宽的改变。图5为未归一化锁相环的幅频特性曲线。
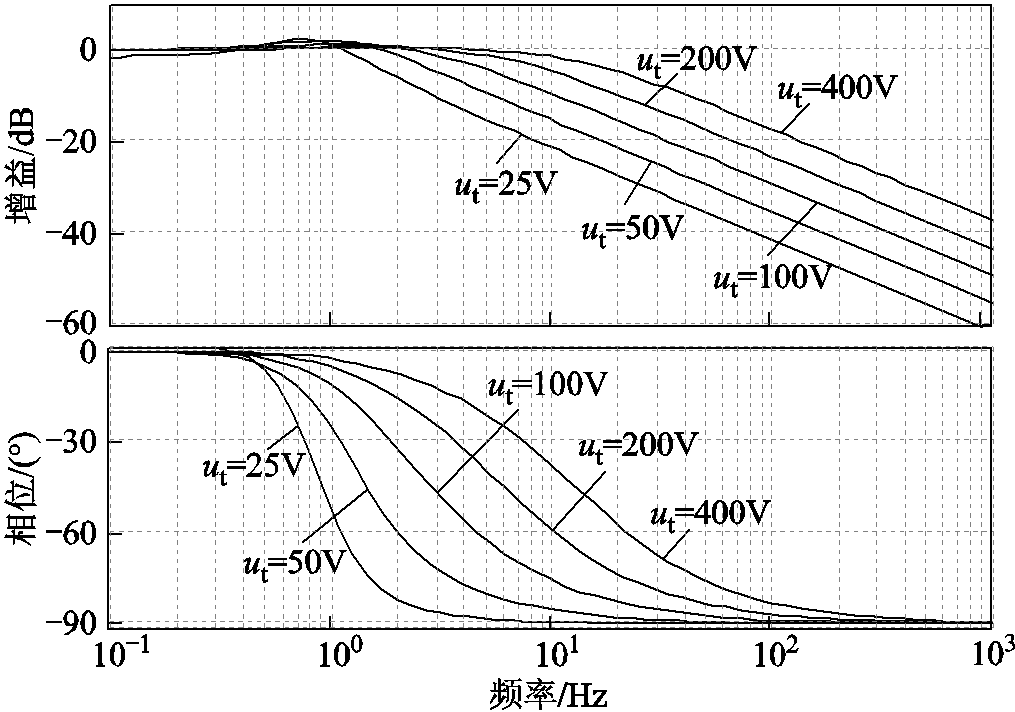
图5 未归一化锁相环的幅频特性
Fig.5 The frequency response of the PLL without normalization
为了避免观测器的带宽受系统参数的影响，正交信号uα、uβ在进入锁相环之前进行了归一化处理。归一化后的正交信号uα1、uβ1可表示为
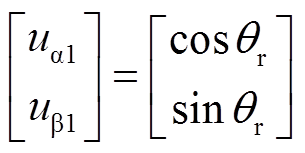（26）此时的锁相环传递函数可表示为
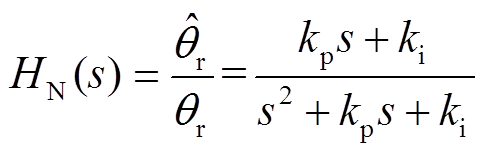（27）归一化后的观测器只受参数kp和ki的影响，因此选择合适的参数对提高观测器的性能至关重要。由式（27）可知，所设计的观测器为一个二阶锁相环。根据李雅普诺夫稳定判据，传递函数的两个极点应该位于复平面的左半区域。为了简化设计过程，直接令两个极点重合于实轴的负半轴，即有关系
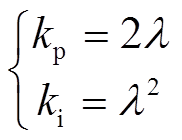（28）式中，λ为正定常实数。
当电机以加速度a运行时，所设计的二阶观测器会存在一个稳态误差θer，其数学关系为
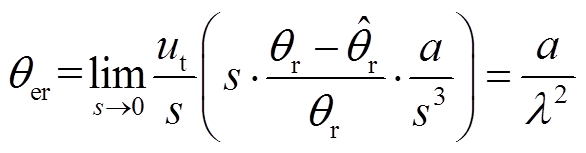（29）由式（29）可知，观测器的稳态误差与参数λ的选择有直接的关系，因此可以根据系统所允许的最大稳态误差来选择合适的参数，即
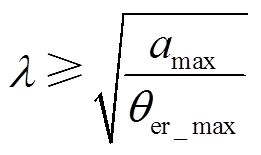（30）式中，amax为最大加速度；θer_max为系统所允许的最大稳态误差。
由于锁相环所得到的端电压相角速度与实际转速之间存在偏差，该偏差是由负载变化所引起的，因此需要对其进行校正。根据式（19）可以计算出负载角δ的实时值，对δ进行微分即可得到转速偏差值。所设计的观测器中锁相环本身具有低通性质，因此观测到的端电压相角θr可以直接输出。而观测到的ut和ωr则需要额外的低通滤波器（LPF）来避免系统噪声的干扰。由于ut和ωr均主要为直流量，一阶LPF即可满足要求。
图6所示为LCI驱动电励磁同步电机实验平台。本文提出的无速度传感器模型预测控制方法在该平台上进行实验验证。电励磁同步电机的基本参数如下：额定功率为3.75kW，额定电压为380V，额定电流6.45A，同步频率为50Hz，同步转速为1 500r/min，极对数为2。在本平台的LCI驱动系统中，整流侧、逆变侧均采用六脉动结构，励磁采用西门子直流变换器6RA80进行控制，数字处理器采用TMS320F-28377D双核DSP芯片。
图6 LCI驱动电励磁同步电机实验平台
Fig.6 The LCI-fed electrically excited synchronous motor experimental platform
图7所示为电机运行在负载变化下的转速观测结果。四次加载和卸载分别为25%、50%、75%和100%的额定负载。该实验设计可以测试空载及不同负载情况下的观测器效果及算法控制效果。加载和卸载均为阶跃情况，尽可能地模拟极端情况，测试观测器设计和控制算法的可行性上限。当驱动系统切换到负载换相模式下，速度观测结果迅速收敛。本文所设计的转速观测器考虑了负载换相运行模式下负载变化对观测结果产生的影响，相比未校正的转速估计误差，校正后的转速估计结果更加准确，负载的变化对观测影响更小。当负载恒定时，速度观测误差小于5°，随着负载的变化程度增加，瞬时的转速观测误差也逐渐增加。全程转速观测误差小于13°。图7说明本文提出的速度观测器设计具有可行性，在阶跃负载的情况下观测效果依旧较好。
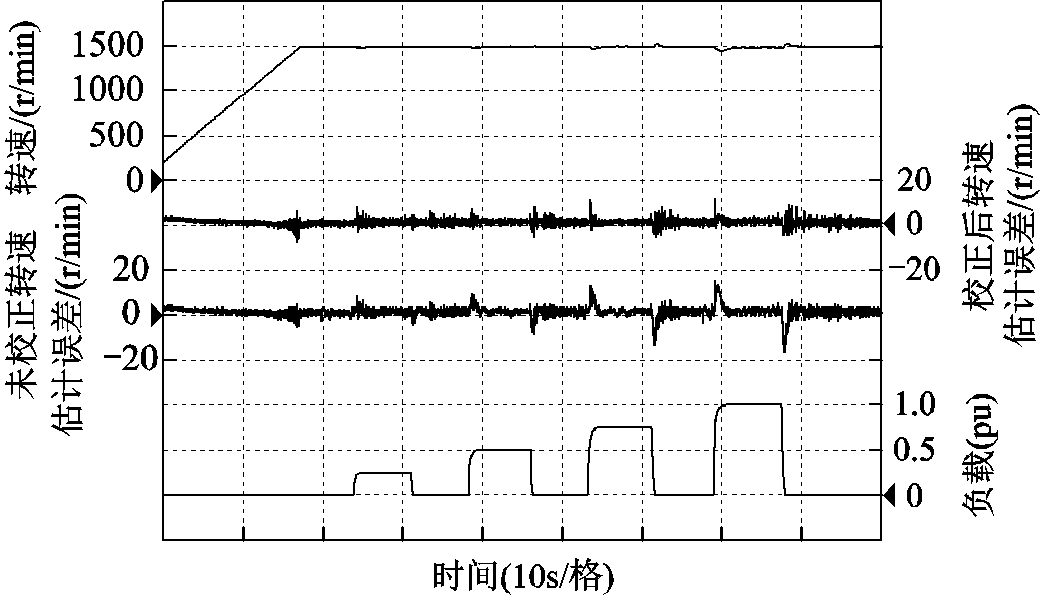
图7 变载速度观测结果
Fig.7 Observed speed results with variable load
图8a所示为无速度传感器变载PI控制波形。本实验采用PI算法为经典的速度外环-电流内环的双闭环PI控制。图8b和图8c分别为50%及100%变载下PI控制波形放大图。图9a所示为无速度传感器变载模型预测控制波形。图9b和图9c分别为50%及100%变载下模型预测控制波形放大图。图8和图9为一组对比实验，速度给定相同，电励磁同步电机均由静止匀速升速到额定转速，之后速度给定始终为额定值。负载变化均为25%、50%、75%和100%的额定阶跃负载。两组实验中均使用观测器的速度观测结果和端电压相位观测结果。端电压相位的观测结果直接影响LCI负载换相的可靠性，观测结果的不准确会导致换相失败。两组实验的可靠运行可以从侧面验证相位观测的准确性。
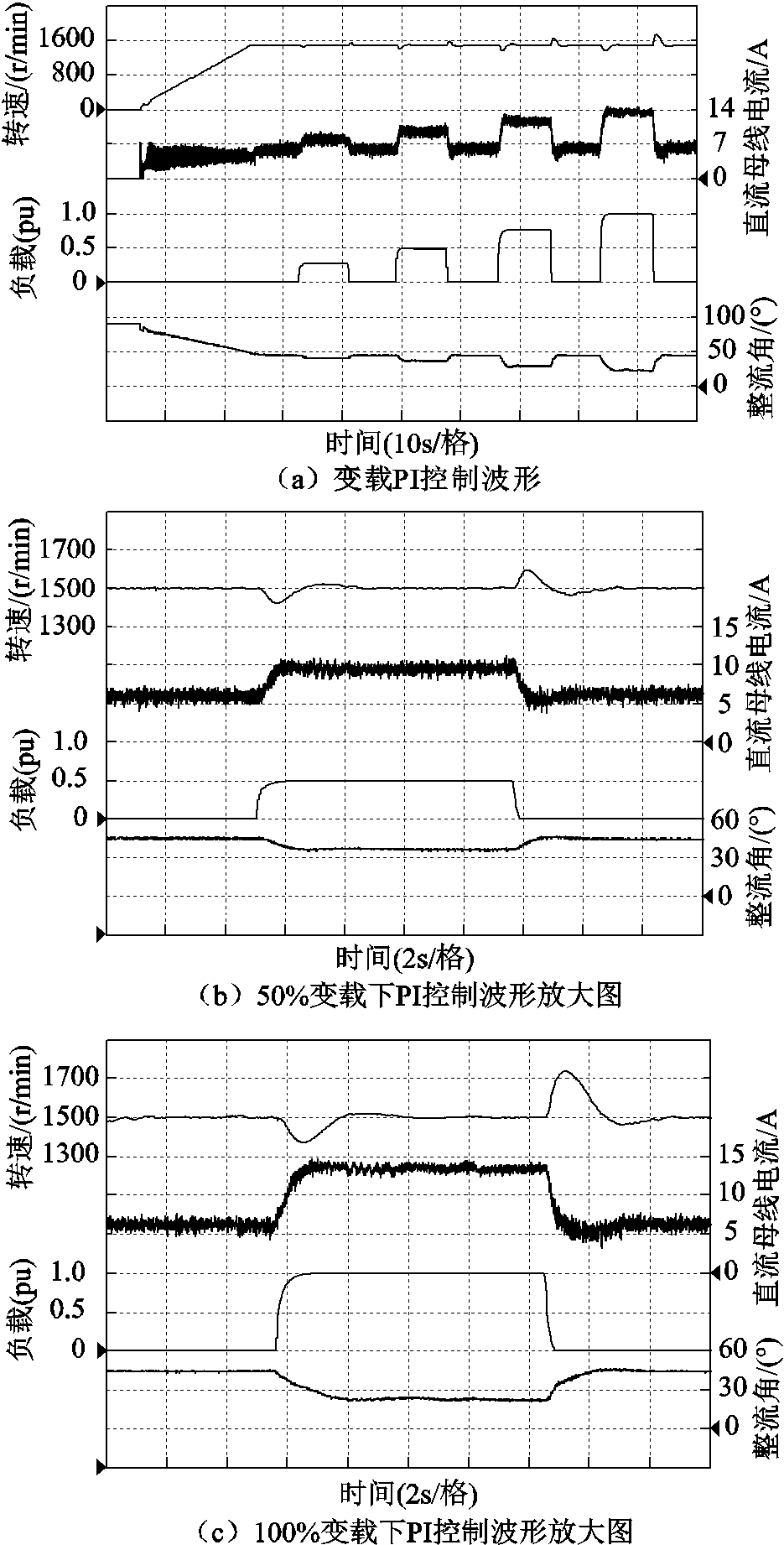
图8 无速度传感器PI控制波形
Fig.8 The waveforms of speed sensorless PI control
从图8b和图9b可知，在同为50%变载实验中，加载时，两次实验的最大速度跌落分别为85r/min和10r/min；卸载时，最大速度抬升分别为103r/min和13r/min。对比图8c和图9c，在同为100%的变载实验中，加载时，两种控制算法的最大速度跌落分别为141r/min和18r/min；卸载时，最大速度抬升分别为247r/min和24r/min。可以看出，本文提出的模型预测控制算法的动态响应效果远优于传统的PI控制。当负载变化时，模型预测控制算法可以更快地达到给定速度曲线，并且运行速度偏差更小。对比图8和图9还能发现，传统的PI控制由于动态响应速度有限，输出的整流角波形光滑，模型预测控制输出的整流角波动较PI更加明显。这也直接导致了模型预测控制下的直流母线电流波动较PI控制更为明显。但其在图9中所引起的速度波动并不明显，这是由于LCI为电流型逆变器，平波电抗可以大大抑制模型预测控制带来的稳态波动。此外，LCI驱动电励磁同步电机驱动系统通常用于中高压系统，其惯性系数很大，能够进一步抑制模型预测控制带来的稳态波动。在图9的模型预测控制实验中，算法使用了观测器观测到的端电压参数，这也能从侧面印证观测器的设计具有可行性。
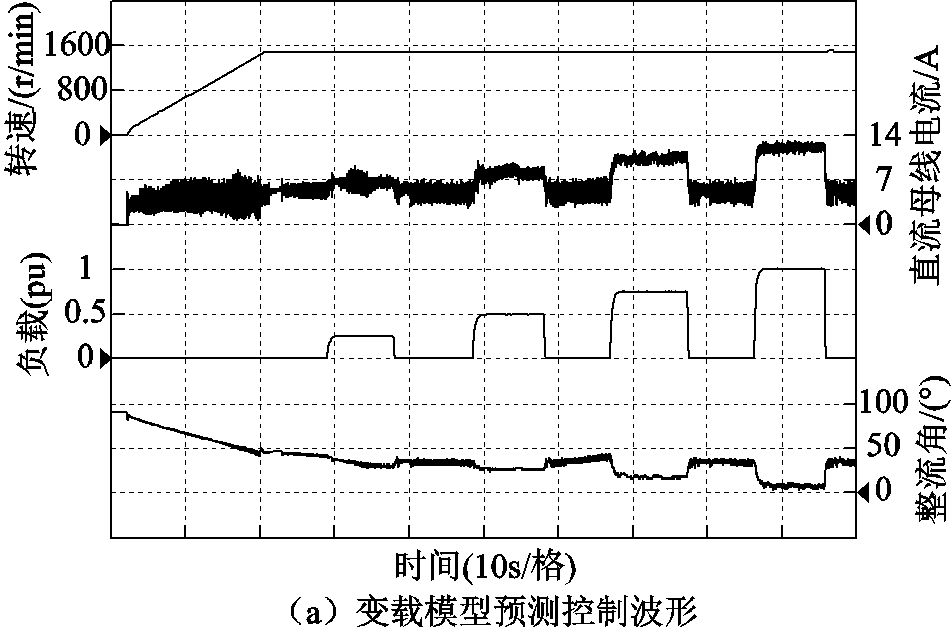
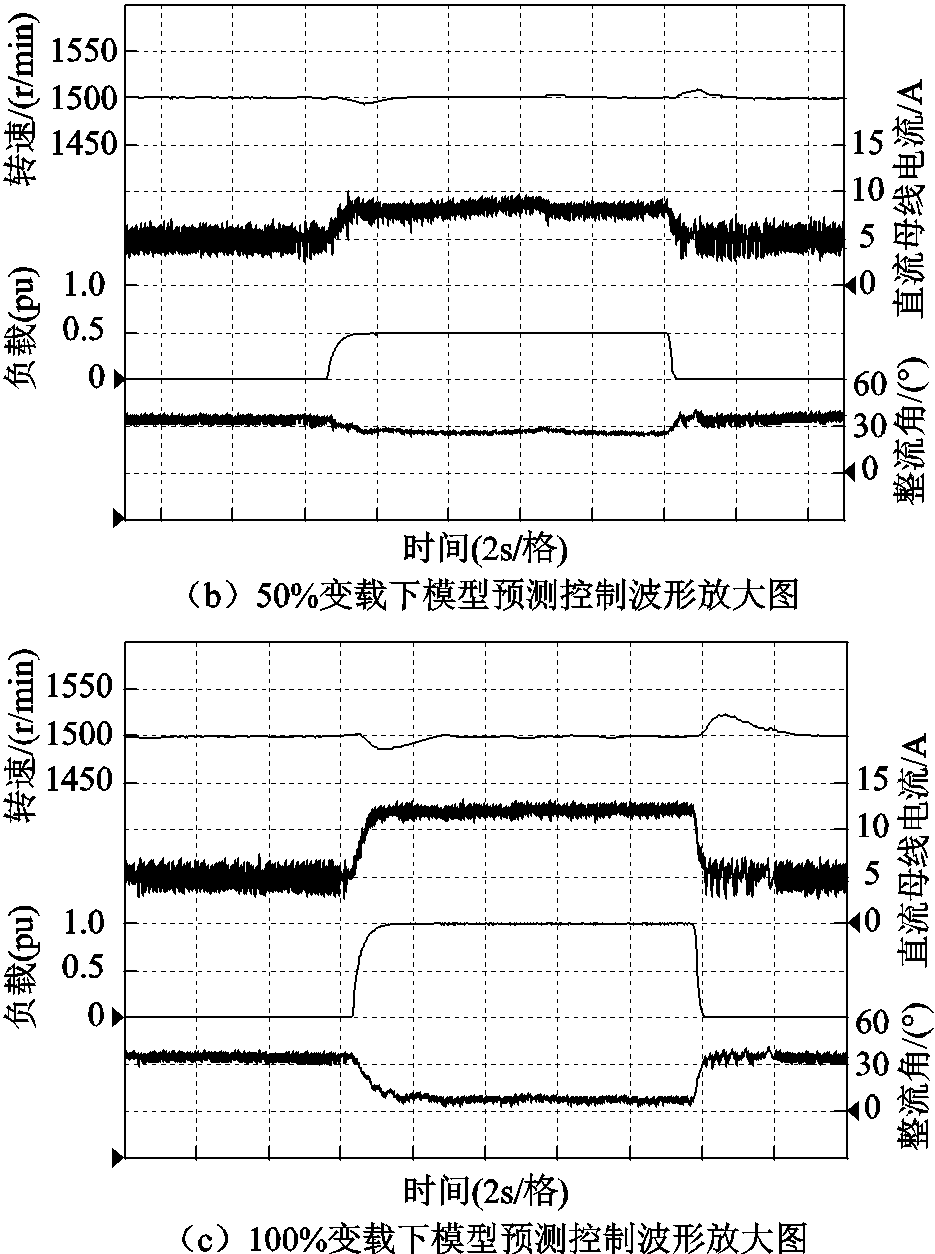
图9 无速度传感器模型预测控制波形
Fig.9 The waveforms of speed sensorless model predictive control
本文提出了一种基于LCI驱动电励磁同步电机的无速度传感器模型预测控制方法。跟据LCI的数学模型和电机运动方程建立了预测状态方程，并给出了合适的代价函数和约束条件。然后分析并设计了适用于负载换相模式下的速度观测器。分析了负载换相模式下的矢量模型，给出了速度观测的校正方法。该观测器还能同时观测逆变输入电压和端电压相位，在降低了系统硬件成本的同时也提高了系统的可靠性。分析并给出了观测器的参数设计依据。实验结果表明，本文提出的无传感器模型预测控制方法相比于PI控制具有更好动态响应特性。所设计的观测器具有可行性，速度观测结果在额定阶跃负载下，误差小于13°。
参考文献
[1] Kataoka T, Nishikata S. Transient performance analysis of self-controlled synchronous motors[J]. IEEE Transactions on Industry Applications, 1981, IA-17(2): 152-159.
[2] Besselmann T J, Almér S, Ferreau H J. Model predictive control of load-commutated inverter-fed synchronous machines[J]. IEEE Transactions on Power Electronics, 2016, 31(10): 7384-7393.
[3] Mohamadian S, Tessarolo A, Castellan S, et al. Steady-state simulation of LCI-fed synchronous motor drives through a computationally efficient algebraic method[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 452-470.
[4] 寇佳宝, 高强, 徐可, 等. 负载换相逆变器驱动电励磁同步电机静止及低速转子位置检测方法[J]. 电工技术学报, 2018, 33(24): 5670-5677. Kou Jiabao, Gao Qiang, Xu Ke, et al. Rotor position detection method at standstill or low speed for load commutated inverter-fed electrically excited synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5670-5677.
[5] Titus J, Hatua K. An asymmetric nine-phase induction motor for LCI-fed medium voltage drive applications[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 5047-5056.
[6] 林茂, 李颖晖, 吴辰, 等. 基于滑模模型参考自适应系统观测器的永磁同步电机预测控制[J]. 电工技术学报, 2017, 32(6): 156-163. Lin Mao, Li Yinghui, Wu Chen, et al. A model reference adaptive system based sliding mode observer for model predictive controlled permanent magnet synchronous motor drive[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 156-163.
[7] 刘珅, 高琳. 永磁同步电机的改进模型预测直接转矩控制[J]. 电机与控制学报, 2020, 24(1): 10-17. Liu Kun, Gao Lin. Improved model of predictive direct torque control for permanent magnet synchronous motor[J]. Electric Machines and Control, 2020, 24(1): 10-17.
[8] Ahmed A A, Koh B K, Lee Y I. A comparison of finite control set and continuous control set model predictive control schemes for speed control of induction motors[J]. IEEE Transactions on Industrial Informatics, 2018, 14(4): 1334-1346.
[9] Hu Yuansheng, Hu Cungang, Zhang Pinjia, et al. A novel hybrid seven-level converter for permanent magnet synchronous motor driving system based on model predictive control[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 389-396.
[10] Besselmann T J, Almér S, Ferreau H J. Model predictive control of load-commutated inverter-fed synchronous machines[J]. IEEE Transactions on Power Electronics, 2016, 31(10): 7384-7393.
[11] Besselmann T J, Van de moortel S, Almér S, et al. Model predictive control in the multi-megawatt range[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4641-4648.
[12] 赵远洋, 韩邦成, 陈宝栋. 基于霍尔矢量相位跟踪的永磁同步电机转子位置与速度估算方法[J]. 电工技术学报, 2019, 34(15): 3147-3157. Zhao Yuanyang, Han Bangcheng, Chen Baodong. Speed and rotor position estimation for PMSM based on hall vector phase-tracking[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3147-3157.
[13] Cai Jun, Liu Zeyuan, Zeng Yu. Aligned position estimation based fault-tolerant sensorless control strategy for SRM drives[J]. IEEE Transactions on Power Electronics, 2019, 34(8): 7754-7762.
[14] Xu Wei, Wang Lei, Liu Yi, et al. Improved rotor flux observer for sensorless control of PMSM with adaptive harmonic elimination and phase compensation[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(2): 151-159.
[15] 孙兴法, 聂子玲, 朱俊杰, 等. 基于低阶串行双扩展卡尔曼滤波的永磁直线同步电机无速度传感器控制策略[J]. 电工技术学报, 2018, 33(12): 2685-2694. Sun Xingfa, Nie Ziling, Zhu Junjie, et al. A speed sensorless control strategy for a permanent magnet linear synchronous motor based on low-order serial dual extended Kalman filters[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2685-2694.
[16] Hasegawa C, Nishikata S. A sensorless rotor position detecting method for self-controlled synchronous motors[C]//2008 International Conference on Electrical Machines and Systems, Wuhan, China, 2008: 1017-1021.
[17] Kou Jiabao, Gao Qiang, Xu Ke, et al. A sensorless rotor position estimation method based on the field current harmonic for an LCI-fed EESM[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 2561-2569.
Speed Sensorless Model Predictive Control for Load Commutated Inverter-Fed Electrically Excited Synchronous Motor
Abstract Load commutated inverter (LCI)-fed electrically excited synchronous motor control system is widely used in medium and high voltage industrial applications. In response to disturbances and load change, the system dynamic response performance is poor due to its large inertia coefficient and low switching frequency. A speed sensorless model predictive control method based on LCI-fed electrically excited synchronous motor is proposed in this paper. Firstly, the prediction equation of state is established according to the LCI model, and the appropriate cost function and constraint conditions are given. Then, the control vector model in load commutation mode is analyzed. The design method and parameter selection principle of designed speed observer are given, and the effect of load change on speed observation is analyzed and compensated. At the same time, the designed observer can observe the inverter input voltage and terminal voltage phase. Finally, the proposed speed sensorless model predictive control method is verified at a 3.75kW LCI-fed electrically excited synchronous motor experimental platform. The results show that the proposed control method can effectively improve the dynamic response performance of system, and the designed observer is feasible. The speed observation error is less than 13° with rated step load.
keywords：Load commutated inverter, electrically excited synchronous motor, speed sensorless, model predictive control
中图分类号：TM359.7
DOI：10.19595/j.cnki.1000-6753.tces.200753
国家重点研发计划（2017YFB0102301）和台达电力电子科教发展计划2018年重点项目（DREK2018003）资助。
收稿日期 2020-06-30
改稿日期 2020-09-16
寇佳宝 男，1990年生，博士研究生，研究方向为电励磁同步电机控制、无传感器控制技术。E-mail：koujiabao_hit@163.com
高 强 男，1964年生，博士，教授，博士生导师，研究方向为大功率交流传动控制、高温电力电子应用。E-mail：gq651@hit.edu.cn（通信作者）
（编辑 郭丽军）