（1）摘要 为避免转子位置角检测误差给永磁同步电动机调速系统带来的不利影响，提高系统的可靠性，提出一种等价于id=0的永磁同步电动机模型预测功率控制方法。该方法通过建立两相静止坐标系下的电机增量模型，使用枚举法对基本电压矢量作用下的电流进行预测，利用采样得到的电压及电流估计反电动势和转子侧瞬时功率值，然后通过功率价值函数选择最优电压矢量。所提方法无需使用高分辨率位置传感器检测转子位置角进行旋转坐标解耦变换，可降低系统的复杂度。电机增量模型无需使用永磁体磁链参数预测电流，降低了算法对电机参数变化的敏感度。实验对比了所提控制方法与直接功率控制的稳态功率波动、转矩波动和暂态响应速度等指标，证明了所提方法的有效性。
关键词：表贴式永磁同步电动机 两相静止坐标系 瞬时功率 预测控制
逆变器馈电的永磁同步电动机（Permanent Magnet Synchronous Motor, PMSM）具有功率密度高、效率高、转矩脉动小等特点，已广泛应用在航空航天、船舶电力推进、汽车与工业自动化等诸多领域[1]。目前比较成熟的控制方法是矢量控制（Field Oriented Control, FOC）和直接转矩控制（Direct Torque Control, DTC）。FOC使用转子磁链定向，引入坐标变换将定子电流解耦为转矩电流分量和励磁电流分量，拥有较好的稳态性能，但转子位置角检测精度将直接影响系统的性能[2]。DTC构造了相对独立的转矩滞环和磁链滞环结构，实现磁链和转矩的直接控制，但存在低速性能差、开关频率不固定等缺点。考虑到矢量控制与直接转矩控制存在的问题，各国学者开始寻求综合提升系统性能的控制方法，如鲁棒控制[3]、滑模控制[4]、模型预测控制[5-9]等。在这些先进的控制方法中，有限集模型预测控制因其实现简单，具有良好的动态性能而受到广泛的关注。
根据控制对象不同，有限集模型预测控制通常分为模型预测电流控制（Model Predictive Current Control, MPCC）[5-6]、模型预测转矩控制（Model Predictive Torque Control, MPTC）[7]、模型预测磁链控制（Model Predictive Flux Control, MPFC）[8]。基于电机的数学模型，MPCC预测逆变器每个开关状态下的电流响应，并选择可以将价值函数最小化的电压矢量作为最优电压矢量。与FOC相类似，MPCC的性能也依赖转子位置角检测的准确性。不同于MPCC，MPTC将价值函数中的dq轴电流替换为转矩与定子磁链，由于控制变量具有不同的量纲，需要引入权重系数，而当前权重系数的选取缺少明确的理论指导，设计过程复杂，不易得到最优值[9]。
随着瞬时功率理论的不断完善[10]，功率作为控制变量被应用于电机动态控制方法中[11-14]。文献[11]在永磁同步电动机开环I/f控制方案的基础上，通过电机的瞬时功率反馈值来调节电流矢量，实现电流矢量闭环。文献[12]通过控制电机输入瞬时有功无功功率来控制电机磁场和输出转矩，获得了快速的转矩动态响应和稳定的稳态转矩。文献[13]分析了逆变器输出功率与电磁转矩、定子磁场之间的关系，利用FOC坐标变换的思想，给定电机所需的有功功率与无功功率，计算所需电压矢量。该方法有效抑制了功率波动，但其功率给定机制相对复杂且与转子位置角采样精度有关。文献[14]借鉴DTC的思想，提出了基于开关表的直接功率控制方法（Direct Power Control, DPC），根据瞬时有功功率与无功功率滞环比较器的输出，查询开关表，选取合适的开关电压矢量，从而对瞬时功率进行直接控制以达到调速目的。直接功率控制形式简单，但会带来较大的功率波动。
为避免转子位置角检测不准对电机运行性能造成的影响，同时降低电机运行过程中的功率波动，本文应用瞬时功率理论对永磁同步电动机的能量传递过程进行分析，建立了两相静止坐标系下的电机增量模型，得到了转子侧功率在两相静止坐标系下的表达式，提出了一种永磁同步电动机模型预测功率控制方法（Model Predictive Power Control, MPPC）。该方法无需使用转子磁链定向，避免了旋转坐标变换，降低了系统的复杂度。使用增量预测模型，降低了系统对参数变化的敏感度。采用转子侧有功功率、无功功率作为被控对象，避免了因价值函数中控制对象量纲不同而设计权重系数。与传统的DPC方法相比，所提控制方法在电机运行过程中的功率波动更小。实验结果验证了该控制方法的有效性。
本文3s/2s变换采用恒功率变换，其变换矩阵为T1。
（1）式中，x可表示电压、电流及磁链。
假设磁路不饱和，空间磁场呈正弦分布，不计磁滞和涡流损耗影响，两相静止坐标系下表贴式永磁同步电动机的电压方程为
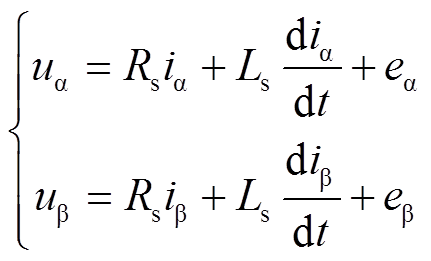（2）其中，反电动势表示为
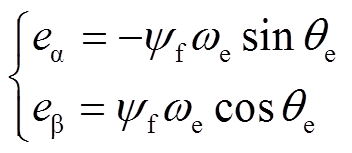（3）式中，uα、uβ分别为电机a、b轴定子电压；iα、iβ分别为电机a、b轴定子电流；eα、eβ分别为电机a、b轴反电动势；Rs、Ls分别为电机定子等效电阻和电感； yf为电机转子永磁体磁链；we和qe分别为电机电角速度和转子位置角。
根据瞬时功率理论，系统输入的有功功率与无功功率可表示为
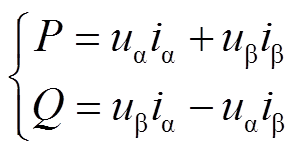（4）根据式（2）和式（4）可得功率表达式为
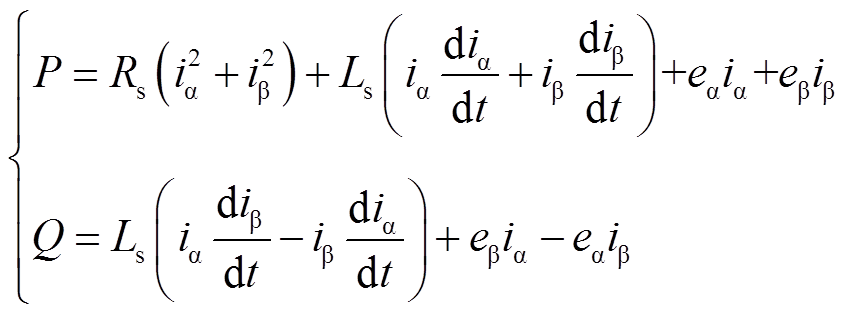（5）对式（5）进行分析，有功功率可分为三个部分：第一部分为定子电阻消耗的功率；第二部分为耦合磁场磁能变化的功率；第三部分为传递到转子侧的功率，即电磁功率。无功功率可分为两部分：第一部分为耦合磁场吸收的功率；第二部分为传递到转子侧的无功功率，即为励磁功率。由此可得传递到电机转子侧的功率表达式为
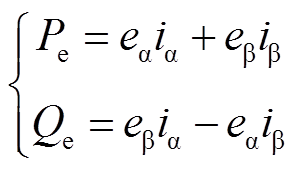（6）利用转子磁链进行定向，其变换矩阵为T2。
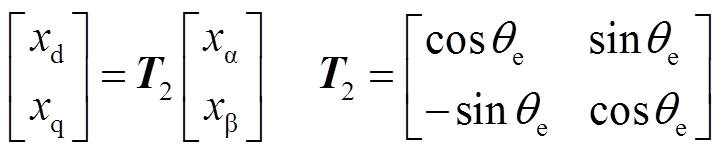（7）根据式（3）与式（7）可以得到
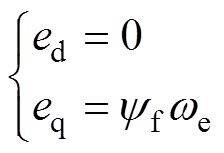（8）利用T2的逆矩阵，可以得到
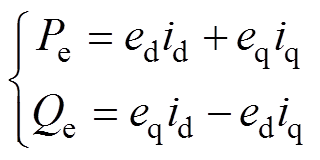（9）结合式（8）对式（9）进行分析，对于表贴式永磁同步电动机，当采用id=0的控制方法时，电机转子侧无功功率Qe为0，电机转子侧有功功率Pe与q轴电流iq呈线性对应关系。由此可见，静止坐标系下的转子侧无功功率给定值为0的控制方法与传统id=0的控制方法等价。
考虑数字控制系统时序控制中存在的一拍延迟的问题，利用前向欧拉法将式（2）离散化，得到电流的离散方程为
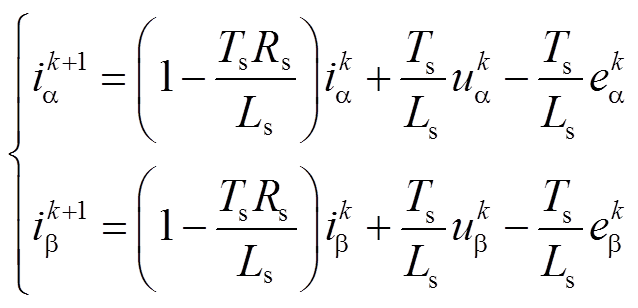（10）式中，
、
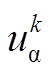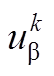和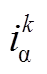
、
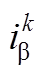分别为电机kTs时刻值经坐标变换得到的α、β轴定子电压和定子电流；
、
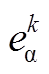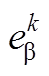为kTs时刻α、β轴反电动势分量；Ts为控制周期。同理可得
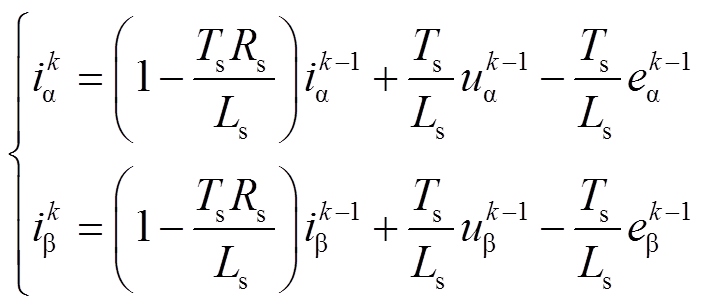（11）式中，
、
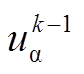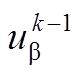和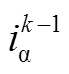
、
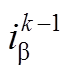分别为电机(k-1)Ts时刻α、β轴定子电压和定子电流；
、
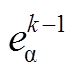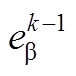为(k-1) Ts时刻拍α、β轴反电动势分量。由式（3）可知，反电动势与转子磁链幅值、电机转速成正比，而电机的机械时间常数远大于电磁时间常数，可近似认为在相邻控制周期反电动势保持不变，通过式（10）和式（11）得
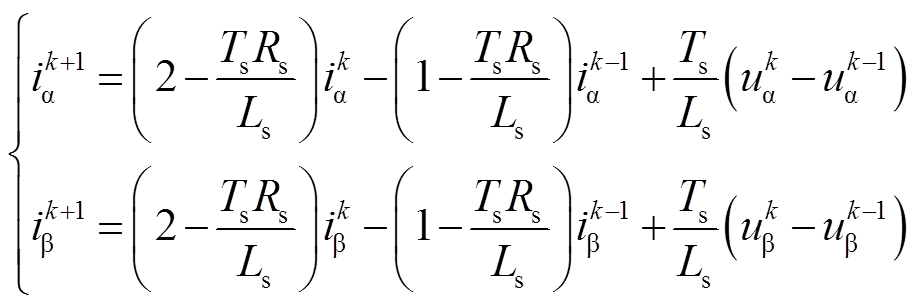（12）由于电机电流环控制周期一般在100μs左右，电机电阻在几百mΩ，电感在几到十几mH，RsTs/Ls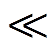
1[15]，式（12）可简化为
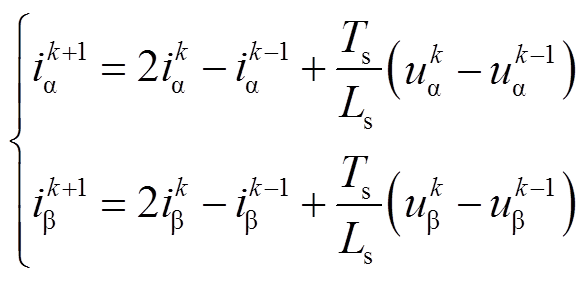（13）利用kTs及(k-1)Ts拍采样得到的电压和电流预测k+1拍的电流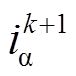
、
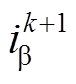，从而利用预测得到的（k+1）Ts的电流代替采样电流进行转子侧功率计算，补偿了数字控制系统存在的延迟。延迟补偿后，(k+2)Ts时刻的电流可以表示为
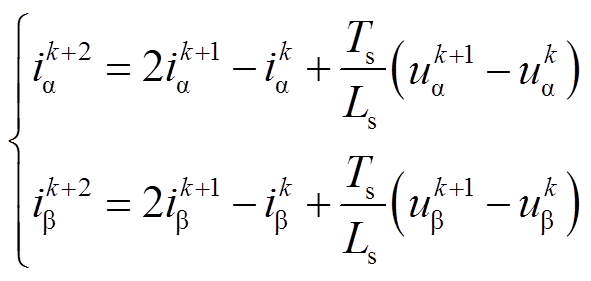（14）与传统电流预测方程式相比，利用式（14）对两相静止坐标系下电流进行预测，无需使用转子位置角计算反电动势，同时避免了使用定子电阻及转子磁链幅值，降低了系统对电机参数变化的敏感度。
根据瞬时功率理论得到电机转子侧功率离散方程为
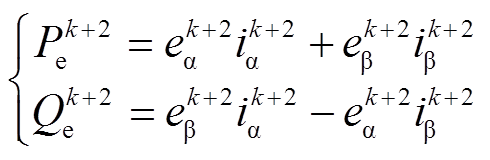（15）传统计算k+2拍反电动势的方法需使用电机转子永磁体磁链yf、电机电角速度we和转子位置角qe。当温度升高电机永磁体磁链参数会发生变化，导致估计转子侧功率与实际转子侧功率产生偏差。假设永磁体磁链参数变为标称值的λ倍，实际反电动势可表示为
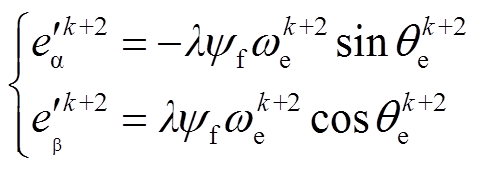（16）因为k+2拍电流使用增量模型进行预测，因此反电动势偏差并不会对电流预测值产生影响，根据式（15）、式（16）得到实际转子侧功率与估计转子侧功率的关系为
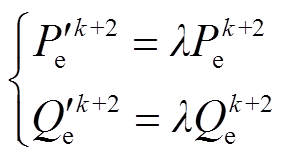（17）为避免永磁体磁链参数变化及转子位置角采样误差对系统带来的不利影响，利用电机电压方程对反电动势进行估计，根据式（11）可以得到
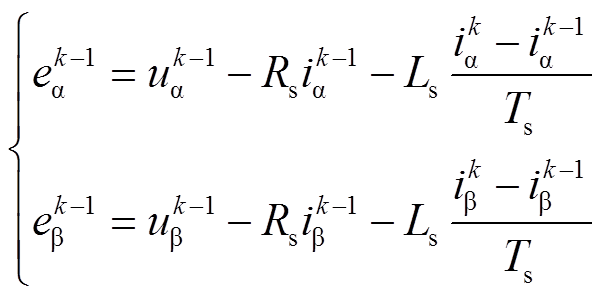（18）当采样频率为10kHz时，由于采样频率较高，可认为(k+2)Ts时刻的电角速度与永磁体磁链参数相对于(k-1)Ts时刻没有发生变化，但相对于(k-1)Ts时刻，(k+2)Ts时刻的转子位置角发生了3ωeTs的偏移。因此利用k-1拍反电动势估计k+2拍反电动势，需要将该角度偏移进行补偿，根据式（3）可知
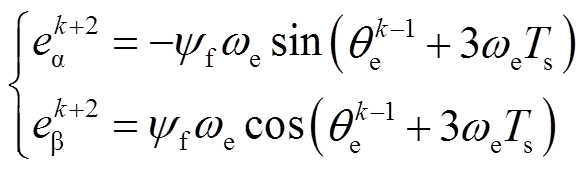（19）根据式（19）可以得到k+2时刻反电动势与k-1时刻反电动势之间的关系为
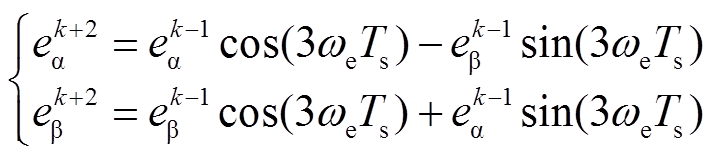（20）使用式（20）计算反电动势，无需利用永磁体磁链，降低了参数的敏感性，且不需要使用转子位置角及电机转速，避免了测量噪声给系统带来的不利影响。
转子侧有功功率给定值可由式（21）计算。
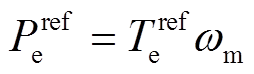（21）式中，Teref是由PI控制器产生的参考电磁转矩；ωm为机械角速度。转子侧无功功率给定Qeref为0。
利用价值函数来评估6个非零基本电压矢量及零矢量对有功功率和无功功率的控制效果，使价值函数值最小的电压矢量即为最优电压矢量。定义给定功率参考值与k+2时刻的预测功率值之间偏差值的2-范数为价值函数为
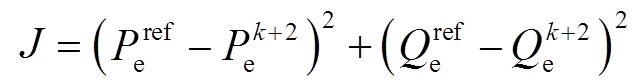（22）MPPC方法的结构框图如图1所示。MPPC的算法流程如图2所示。
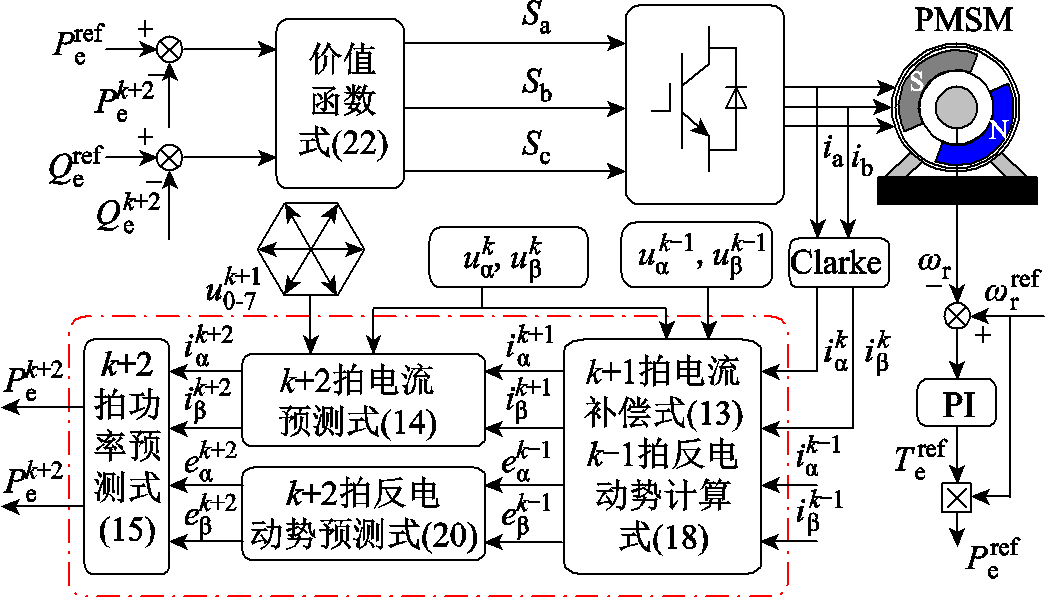
图1 MPPC结构框图
Fig.1 The diagram of MPPC control
首先利用k拍及k-1拍的定子电压和定子电流进行数字控制系统延迟补偿，得到k+1拍电流，随后预测基本电压矢量作用下k+2拍的电流、反电动势及功率，根据价值函数对预测结果进行评估并选出最优电压矢量在下一个控制周期发出。
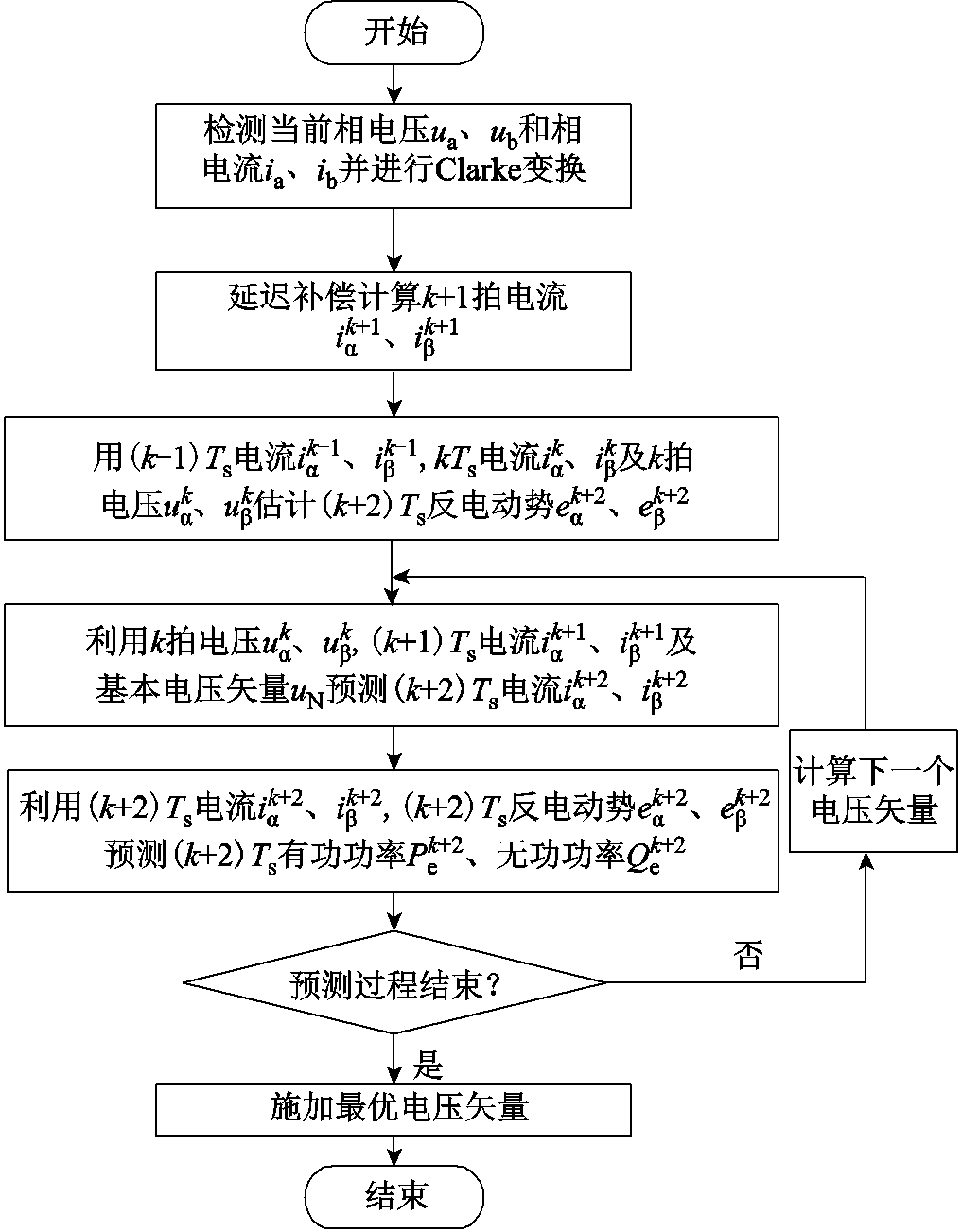
图2 MPPC控制算法流程
Fig.2 The flow chart of MPPC
使用5.5kW的永磁同步电动机进行实验研究，该电机的参数见表1。
表1 系统和控制参数
Tab.1 System and control parameters
参数数值 电机额定电压Ua/V380 电机额定功率P/kW5.5 直流母线电压Udc/V540 电机额定频率f/Hz50 电机极对数Np2 电机定子电阻Rs/Ω0.83 定子电感Ls/mH10.17 电机额定转矩T/(N·m)35 永磁体磁链ψf /Wb0.966 8
系统控制器使用数字控制器TMS320F28335，三相桥逆变器使用三菱公司的PM50RL1A060，电流传感器采用LEM15-NP，电压传感器采用LEM公司的LV25-P，实验环境如图3所示。实验中定子电流使用电流探头测得，其他变量由DA转换器输出到示波器上显示。系统采样频率为10kHz。
由于实验中无法直接改变电机永磁体参数，针对本文所提控制方法，在仿真环境下对永磁体磁链参数变化的鲁棒性进行验证。以模型预测功率控制方法为基础，将使用电机参数计算反电动势的方法与本文提出的反电动势估计方法进行对比，仿真所用参数与前文给出的电机参数完全相同。当电机运行在1 500r/min，负载转矩为15N·m的条件下，永磁体磁链参数分别变化为标称值的0.8倍、1.2倍，仿真结果如图4所示。
图3 永磁同步电动机实验平台
Fig.3 Permanent magnet synchronous motor experimental platform
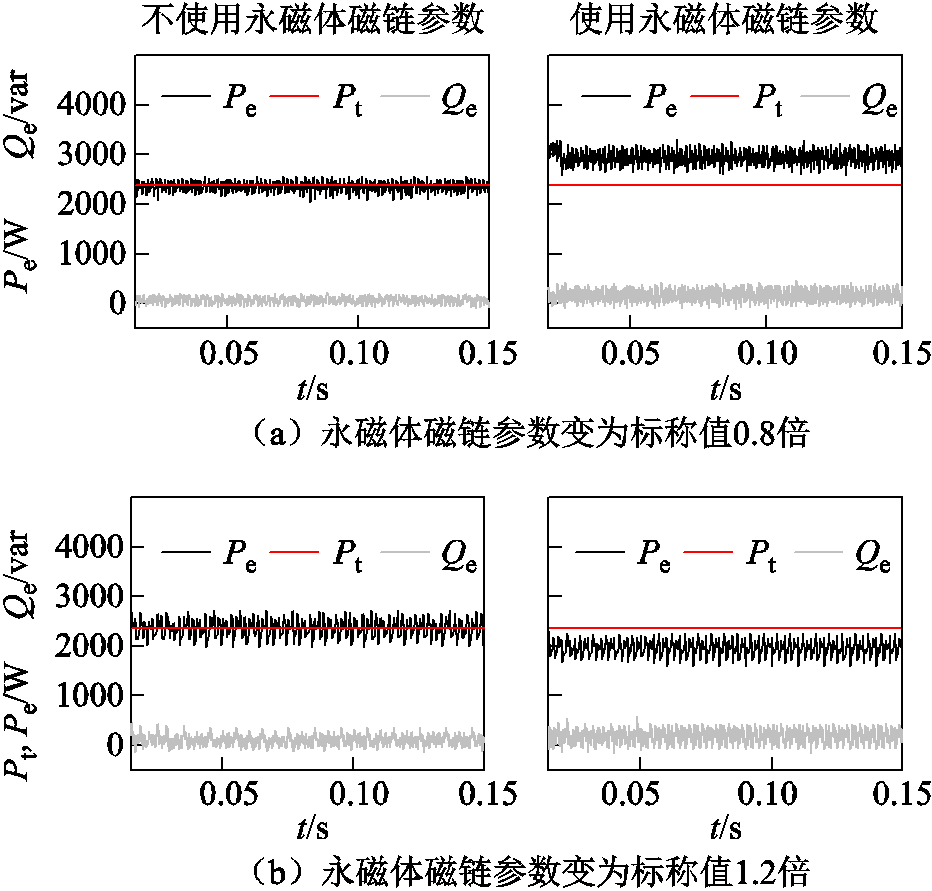
图4 参数变化影响
Fig.4 The impact of parameter changes
当电机稳定运行在1 500r/min、负载转矩为15N·m的条件下，电机电磁转矩等于负载转矩，理论上所需转子侧有功功率Pt为2 356kW。从仿真结果可以看出，当永磁体磁链参数变化为标称值的0.8倍、1.2倍后，使用电机参数估计反电动势导致电机转子侧有功功率无法跟踪功率理论值，且电机转子侧无功功率波动较大，而使用本文所提估计方法在永磁体参数发生变化后，转子侧功率仍能有效跟踪理论值，因为所提估计方法并不需要使用永磁体参数来估计反电动势，有效提高了系统的可靠性。同时，因为对电流、转速的估计都无需使用转子位置角，有效避免了转子位置角采样误差对控制系统的影响。
为了验证本文所提方法在功率波动抑制方面的表现，与传统的直接功率控制方法（Direct Power Control，DPC）[14]进行对比，测试条件为转速1 500r/min，负载转矩30N·m。实验结果如图5所示，其中，Pep-p表示有功功率峰-峰值，Qep-p表示无功功率峰-峰值，Tep-p表示电磁转矩峰-峰值。本文使用转矩纹波系数来评价电机稳态运行时转矩脉动，转矩纹波系数定义为
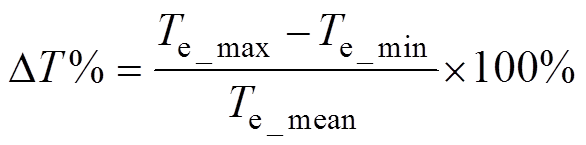（23）
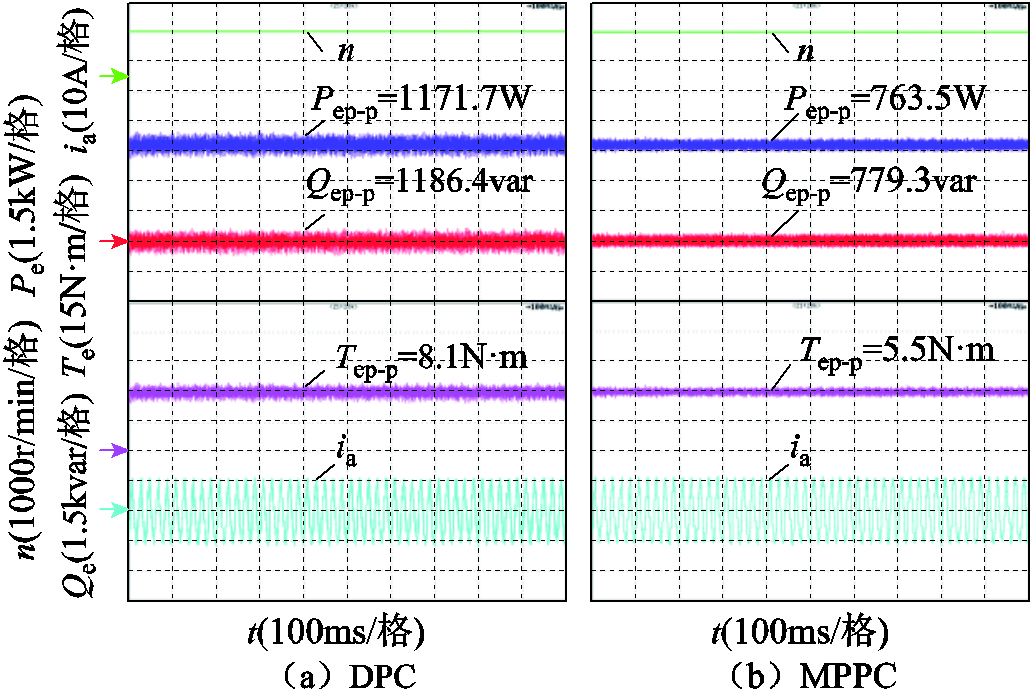
图5 1 500r/min和30N·m负载时稳态性能对比
Fig.5 Comparison of steady state performance with 1 500r/min and 30N·m
功率纹波系数ΔP%计算方法与转矩纹波系数ΔT%计算方法相同。
在稳态情况下，MPPC的转矩纹波系数ΔT%约为18.6%，DPC的转矩纹波系数ΔT%约为27.1%。与DPC相比，使用MPPC控制方法使转矩波动降低了约8.5%。
为进一步验证MPPC在抑制功率波动的能力，负载转矩为30N·m条件下，分别在300r/min、600r/min、900r/min和1 200r/min的条件下进行测试，其有功功率波动峰-峰值Pep-p、无功功率波动峰峰值Qep-p、功率纹波系数ΔP%如图6所示。
由图6可以看出，在不同转速的情况下，MPPC控制方法相对于DPC控制方法都有效降低了运行过程中的功率波动。相比DPC控制方法，使用MPPC控制方法的功率纹波系数ΔP%降低了约10%，验证了该方法在功率波动抑制方面的有效性。
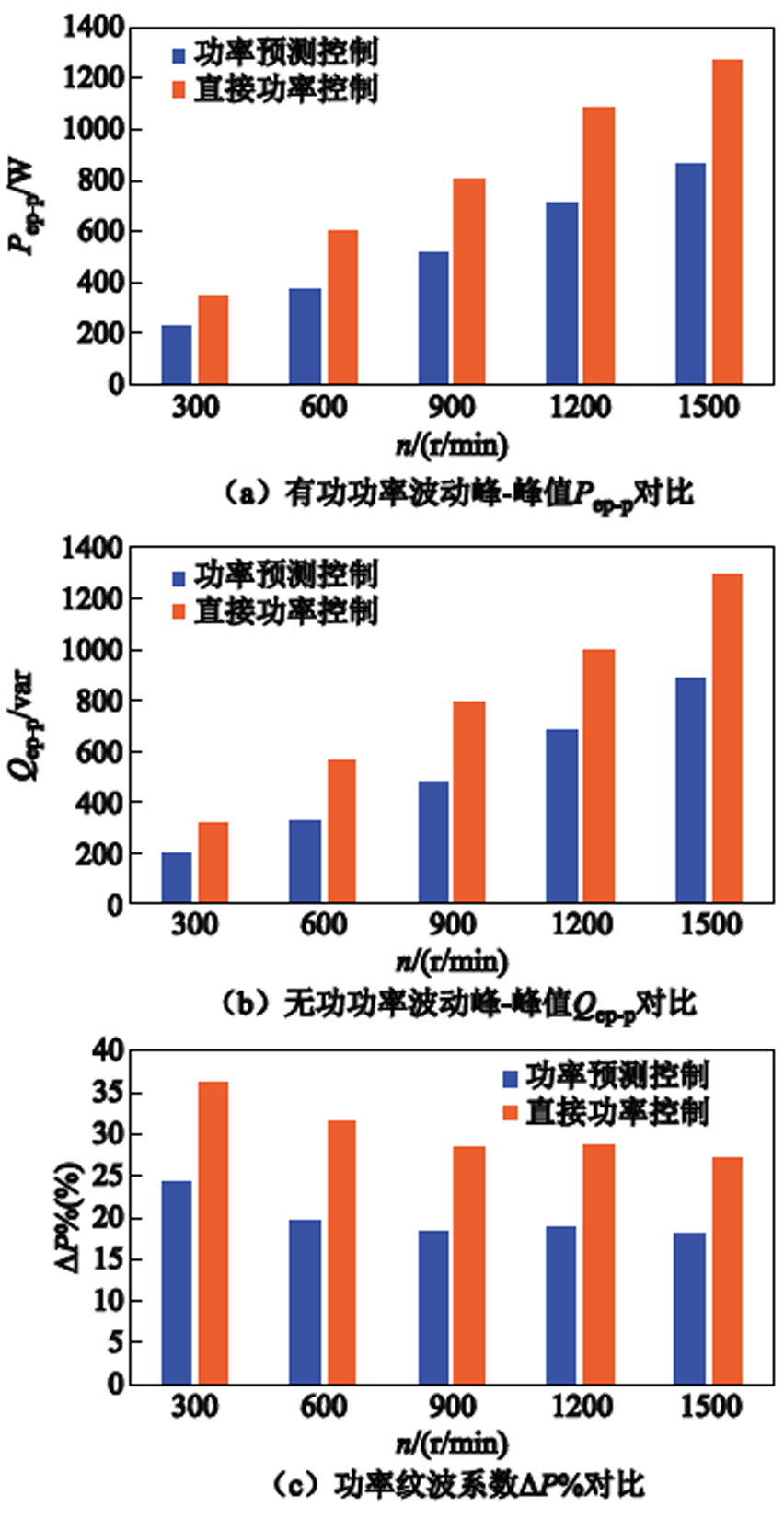
图6 不同转速下稳态性能对比
Fig.6 Comparison of steady state performance under different speeds
负载转矩为15N·m条件下，转速给定由500r/min阶跃为1 500r/min，其实验结果如图7所示。两种控制方法转速达到给定所需时间大约为0.43s。可见本文所提方法具有与DPC控制方法的动态调节时间大体相当，均具有良好的动态性能。但在加速过程中，MPPC的功率波动、转矩波动更小。
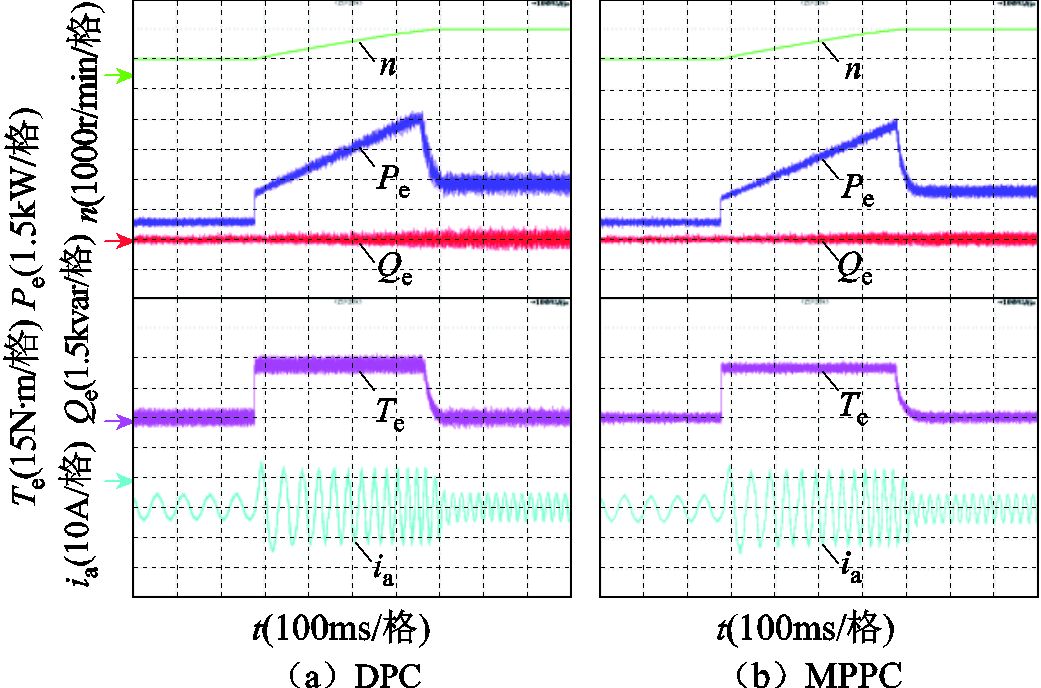
图7 MPPC与DPC转速突变实验对比
Fig.7 The speed step response comparison of MPPC and DPC
图8为转速为1 500r/min，负载转矩由15N·m突变为30N·m的实验波形对比。突加负载时两种控制方法均出现约90r/min的转速跌落，随后迅速回调，MPPC对负载转矩突变的响应速度几乎与DPC相同，但MPPC的功率波动、转矩波动更小。
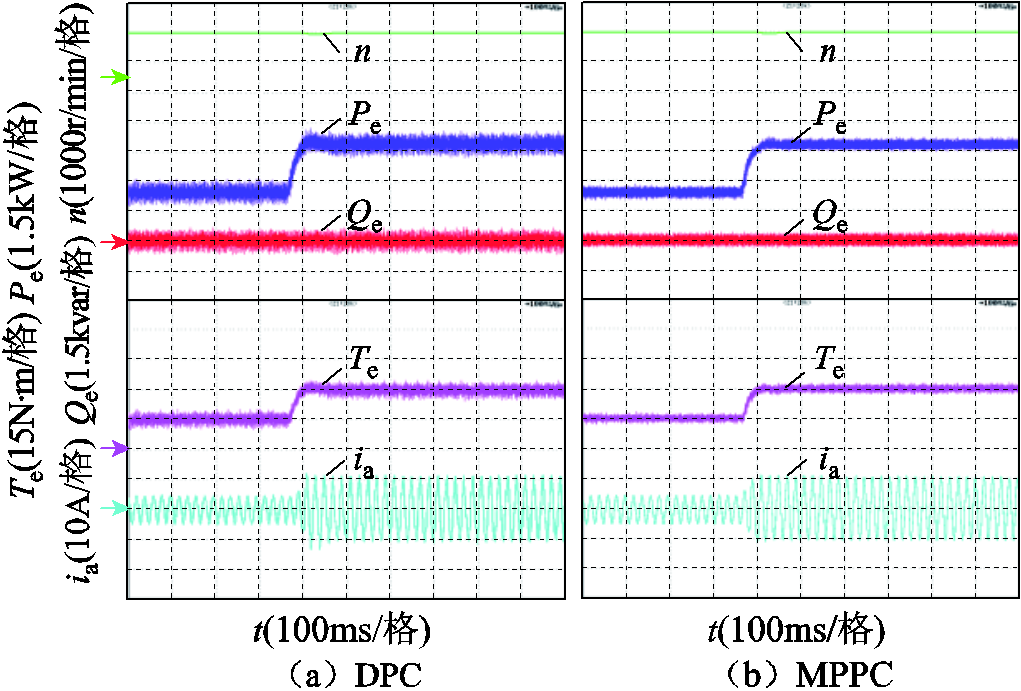
图8 MPPC与DPC转矩突变实验对比
Fig.8 The torque step response comparison of MPPC and DPC
将传统dq轴坐标系下模型预测电流控制方法（MPCC）、直接功率控制方法（DPC）、本文所提控制方法（MPPC）算法程序执行时间进行对比，对比结果见表2。
表2 不同控制方法程序执行时间
Tab.2 Program execution time of different control methods
控制方法程序执行时间/μs MPCC47 DPC28 MPPC31
可以看出直接功率控制方法与本文所提控制方法算法执行时间接近。相对于传统模型预测电流控制方法，本文所提控制方法将算法执行时间减小了34%，原因是本文所提控制方法在两相静止坐标系下执行，避免了枚举法选择最优电压矢量过程中频繁使用三角函数进行计算。这有利于后续在此控制方法的基础上加入电感参数辨识等算法，再次提高该控制方法的可靠性。
为减小转子位置角检测不准给电机性能带来的不利影响，本文提出了一种永磁同步电动机模型预测功率控制方法并得到以下结论：
1）本文提出的永磁同步电动机模型预测功率控制方法完全在两相静止坐标系下实现，无需使用转子位置角定向，避免了传统电流控制方法中转子位置角检测误差给系统性能带来的不利影响。
2）使用增量模型预测电流，无需使用转子位置角计算电机反电动势，降低了控制方法对参数变化的敏感度。
3）与传统直接功率控制方法相比，在不牺牲动态响应速度的情况下有效减小了电机运行的功率波动和转矩波动。
4）不同于传统模型预测转矩控制，以转子侧有功功率、无功功率作为控制对象，两者具有相同的量纲，无需为价值函数设计权重系数。
参考文献
[1] 张永昌, 杨海涛, 魏香龙. 基于快速矢量选择的永磁同步电机模型预测控制[J]. 电工技术学报, 2016, 31(6): 66-73.Zhang Yongchang, Yang Haitao, Wei Xianglong. Model predictive control of permanent magnet synchronous motors based on fast vector selection[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 66-73.
[2] 王海兵, 赵荣祥, 汤胜清, 等. 永磁同步电机位置检测偏差对驱动系统性能的影响[J]. 电工技术学报, 2018, 33(4): 910-918. Wang Haibing, Zhao Rongxiang, Tang Shengqing, et al. Research on the influence of the position detection error to the PMSM drive system[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 910-918.
[3] 侯利民, 申鹤松, 阎馨, 等. 永磁同步电机调速系统H_∞鲁棒控制[J]. 电工技术学报, 2019, 34(7): 1478-1487. Hou Limin, Shen Hesong, Yan Xin, et al. H_∞ Robust control of PMSM speed regulation system[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1478-1487.
[4] Peng Xiaoyan, Jia Mingfei, He Lei, et al. Fuzzy sliding mode control based on longitudinal force estimation for electro-mechanical braking systems using BLDC motor[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(1): 142-151.
[5] Zhang Yongchang, Xu Donglin, Liu Jiali, et al. Performance improvement of model predictive current control of permanent magnet synchronous motor drives[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3683-3695.
[6] Zhang Xiaoguang, Zhang Liang, Zhang Yongchang. Model predictive current control for PMSM drives with parameter robustness improvement[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1645-1657.
[7] 周湛清, 夏长亮, 陈炜, 等. 具有参数鲁棒性的永磁同步电机改进型预测转矩控制[J]. 电工技术学报, 2018, 33(5): 965-972. Zhou Zhanqing, Xia Changliang, Chen Wei, et al. Modified predictive torque control for PMSM drives with parameter robustness[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 965-972.
[8] Zheng Zhihao, Sun Dan. Model predictive flux control with cost function-based field weakening strategy for permanent magnet synchronous motor[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 2151-2159.
[9] 牛峰, 韩振铎, 黄晓艳, 等. 永磁同步电机模型预测磁链控制[J]. 电机与控制学报, 2019, 23(3): 38-45. Niu Feng, Han Zhenze, Huang Xiaoyan, et al. Model predictive flux control for permanent magnet synchronous motor[J]. Electric Machines and Control, 2017, 32(19): 1-10.
[10] Guo Xiaoqiang, Chen Weijian. Control of mutiple power inverters for more electronics power systems: a review[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(3): 255-263.
[11] 王萌, 杨家强, 张翔, 等. 一种表贴式永磁同步电机电流矢量闭环I/f控制方法[J]. 中国电机工程学报, 2015, 35(10): 2513-2521. Wang Meng, Yang Jiaqiang, Zhang Xiang, et al. An I/f control method with closed-loop regulation of current vector for surface permanent magnet synchronous motor drives[J]. Proceedings of the CSEE, 2015, 35(10): 2513-2521.
[12] 郑灼. 永磁同步电机瞬时功率控制[J]. 中国电机工程学报, 2007, 27(15): 38-42.Zheng Zhuo. Instantaneous power control of permanent magnet synchronous machine[J]. Proceedings of the CSEE，2007, 27(15): 38-42.
[13] 李昆鹏, 万健如, 朱琳. 永磁同步电机瞬时功率预测控制[J]. 电工技术学报, 2015, 24(10): 38-44. Li Kunpeng, Wan Jianru, Zhu Lin. Predictive instantaneous power control for permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2015, 24(10): 38-44.
[14] 储剑波, 胡育文, 黄文新, 等. 永磁同步电机直接功率控制基本原理[J]. 电工技术学报, 2009, 24(10): 21-26. Chu Jianbo, Hu Yuwen, Huang Wenxin, et al. Basic theory of direct power control for PMSM[J]. Transactions of China Electrotechnical Society, 2009, 24(10): 21-26.
[15] 王庚, 杨明, 牛里, 等. 永磁同步电机电流预测控制电流静差消除算法[J]. 中国电机工程学报, 2015, 35(10): 2544-2551. Wang Geng, Yang Ming, Niu Li, et al. A static current error elimination algorithm for PMSM predictive current control[J]. Proceedings of the CSEE, 2015, 35(10): 2544-2551.
Model Predictive Power Control of Permanent Magnet Synchronous Motor in Two-Phase Static Coordinate System
Abstract In order to avoid the adverse effect of rotor position detection error on permanent magnet synchronous motor (PMSM) speed control system and improve the reliability of the system, a model predictive power control method equivalent to the id=0 control method is proposed to improve the reliability of the system in this paper. Through the establishment of a motor incremental model in a two-phase stationary coordinate system, the enumeration method is used to predict the current under the action of the basic voltage vector, The sampled voltages and currents are used to estimate the back electromotive force and the instantaneous power on rotor side. Then, the cost function based on power are established to select the optimal voltage vector. The proposed method does not need to use a high-resolution position sensor to detect the rotor position angle for decoupling transformation of the rotating coordinate, which reduces the complexity of the system. The incremental model predicts currents without using permanent magnetic flux linkage parameters, which reduces the sensitivity of the algorithm to changes in the motor parameters. A comparative study between the proposed method and direct power control were conducted in terms of power ripples, torque ripples and dynamic response. The experimental results verify the effectiveness of the control method.
keywords：Surface-mounted permanent magnet synchronous motor(SPMSM), two-phase stationary coordinate system, instantaneous power, predictive control
中图分类号：TM351
DOI：10.19595/j.cnki.1000-6753.tces.200416
高技术船舶科研计划“高性能电动甲板吊机研制”资助项目。
收稿日期 2020-04-27
改稿日期 2020-07-03
姚绪梁 男，1969年生，博士，教授，研究方向为电力电子与电力传动、船舶电力推进技术。E-mail：yaoxuliang@hrbeu.edu.cn
王景芳 男，1984年生，博士，研究方向为大功率变流器的谐波抑制。E-mail：jingfangwang@hrbeu.edu.cn（通信作者）
（编辑 郭丽军）