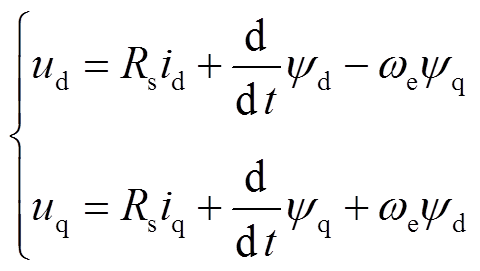（1）摘要 针对模型预测控制算法（MPC）在处理多目标多约束条件时权重系数设计问题，该文提出一种基于混沌变异的动态重组多种群粒子群算法（CDMSPSO）实现权重系数自整定。通过分析模型预测转矩控制（MPTC）代价函数，以两相旋转坐标系下电流误差方均根为参考，将降低转矩脉动和减小电流总谐波畸变（THD）作为主要控制目标，设计粒子群算法中粒子的目标函数。采用CDMSPSO算法，将整个种群划分为多个小的子粒子群，并以一定重组周期将粒子进行随机重组，然后随机选择一个子粒子群，以其中任一粒子为基础迭代生成混沌序列，并将新的混沌序列替代选择的子粒子群，实现粒子的混沌变异。仿真和实验结果验证了该方法能较好地解决权重系数整定问题，且稳态性能优异。
关键词：永磁同步电机 模型预测控制 权重系数 粒子群优化 动态重组 混沌变异
永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）因其结构简单、高效率、高功率密度和高功率因数等特点，在工业伺服等领域被广泛应用[1-3]。矢量控制算法因其级联式内外环比例积分（Proportional Integrate, PI）控制结构，带来参数设计及调制复杂等问题[4]。直接转矩控制具有结构简单、动态响应快等特点，但存在稳态性能差，转矩纹波大等不利因素[5]。
有限集模型预测控制策略（Finite Control Set Model Predictive Control, FCS-MPC）通过离散系统模型来预测系统的未来行为，设计代价函数对这些预测进行评估，得到系统的最优控制序列[6]。其具有原理简单、多变量控制和非线性约束易处理等优点，受到不少研究者的广泛关注[7-8]。
MPC中代价函数可包含多目标多约束条件[9]，在交流电机模型预测转矩控制（Model Predictive Torque Control, MPTC）中，代价函数通常包括电磁转矩误差和定子磁链误差[10]，也可包含开关频率等[11]。但是由于电磁转矩和定子磁链具有不同的量纲，需要设计合理的权重系数来实现对两者的同步优化控制[12]。文献[13]以优化转矩控制为主，构造包含权重系数的转矩误差方程，求解方程最小值时对应的权重系数作为优化权重系数，但该方法仅关注转矩控制效果，并未考虑电流质量。文献[14]采用转矩控制和磁链控制的级联结构，通过依次评估两个单独的代价函数来选择最佳的电压矢量，但该方法并未实现转矩和磁链的同步优化控制，且未包含电流限幅项。文献[15]分析了不同的电流误差权重系数下系统的性能，然后采用模糊控制算法动态调整权重系数，从而提高系统电流响应速度，优化开关频率，但是模糊控制推理规则需要先验知识来确定，模糊论域则需要通过实验确定大概范围。也有学者基于转矩和磁链无差拍的方法，将参考转矩和参考磁链转换为参考电压，构建电压代价函数取代传统的转矩和磁链代价函数，选择与参考电压误差最小的矢量作为最优电压矢量，从而消除了权重系数[10, 16]，但是由于在使用数学模型得到参考电压的过程中需要忽略模型中的电阻项，因此转换过程会降低对精度的要求。文献[17]中采用并行的预测转矩控制结构，将转矩误差和磁链误差设计为两个独立的代价函数，通过设置误差界限生成最优转矩控制电压矢量序列、最优磁链控制电压矢量序列和次优磁链控制电压矢量序列，以转矩误差最小为前提，根据转矩控制序列和磁链控制序列中的电压矢量择优选择输出电压矢量，达到消除权重系数的目的。但是该方法需要对不同情况下的电压序列进行分类讨论，在一定程度上增加了预测转矩控制算法的复杂性。
权重系数设计实则为参数优化问题，传统优化算法受限于基于梯度的模型连续、可导的要求。粒子群算法（Particle Swarm Optimization, PSO）是由Russell Eberhart和James Kennedy提出的一种模仿生物系统行为的群体智能优化算法[18]，该方法能够克服伺服系统中模型参数变化和非线性等不确定因素，在参数优化中得到了广泛应用[19-21]。
为了进一步优化权重系数的设计，本文提出一种基于粒子群算法的权重系数自整定策略，通过分析模型预测转矩控制中权重系数的设计原则，以两相旋转坐标系下电流误差的方均根作为参考，将降低转矩脉动和减小电流总谐波畸变率（Total Harmonic Distortion, THD）作为主要控制目标，设计了粒子群算法中粒子的目标函数，然后采用基于混沌变异的动态重组多种群粒子群算法整定权重系数，以加快算法的收敛速度，提高最优权重系数的搜索精度。仿真和实验结果表明，本文所提出的方法能够准确地获取合适的权重系数，在保证电磁转矩误差较小的同时，减小电流的总谐波畸变。
本文以表贴式PMSM为仿真和实验对象。假设电机的三相绕组对称且为星形联结，转子每相气隙磁动势呈正弦分布，忽略铁心饱和、涡流和磁滞损耗，则SPMSM在两相旋转坐标系下的定子电压方程为[2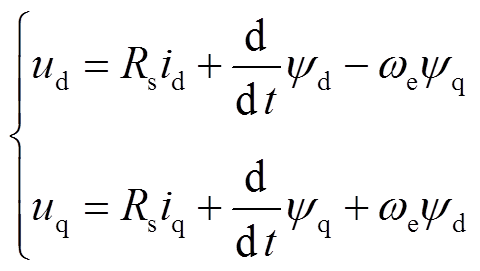1]
（1）定子磁链方程为
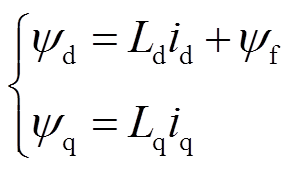（2）电磁转矩方程为
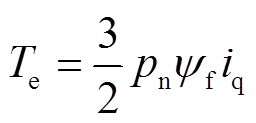（3）式中，ud、uq，id、iq和ψd、ψq分别为d、q轴定子电压、定子电流和定子磁链；Rs为定子电阻；ωe为电角速度；Ld、Lq分别为d、q轴定子电感；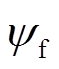
为永磁体磁链；Te为电磁转矩；
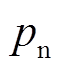为磁极对数。
永磁同步电机MPTC的控制原理框图如图1所示，转矩参考Te*由转速外环的PI控制器得到，磁链参考则是由转矩参考利用最大转矩电流比（Maximum Torque Per Ampere, MTPA）公式得到（见式（4））。将采样的三相电流实行坐标变换，根据当前时刻最优电压矢量、转速反馈对坐标变换后的电流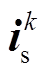
进行单步预测，得到下一时刻的电流
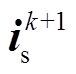，获得一拍的延时补偿。将8个电压矢量分别代入转矩和磁链的预测模型中，获得各个矢量作用下的预测转矩
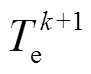和预测磁链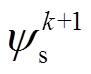
，将预测得到的转矩和磁链代入代价函数中，选取使代价函数最小的电压矢量作为最优电压矢量进行输出。
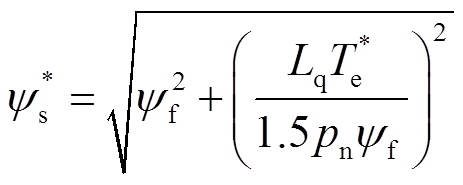（4）
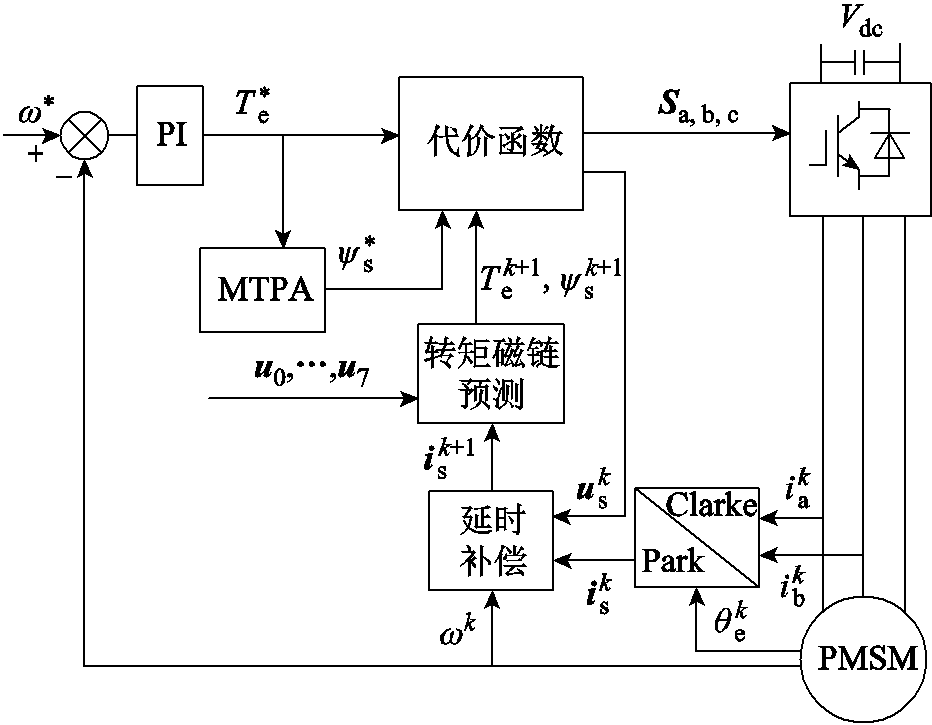
图1 MPTC控制原理图
Fig.1 Control diagram of MPTC control method
将式（2）代入式（1），永磁同步电机电压方程可表示为
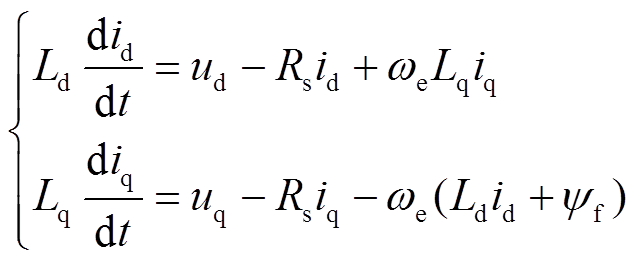（5）采用一阶欧拉公式对式（5）进行离散化可得电流预测模型为
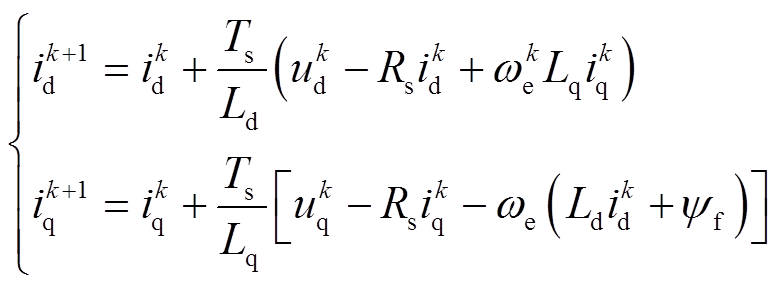（6）磁链预测模型为
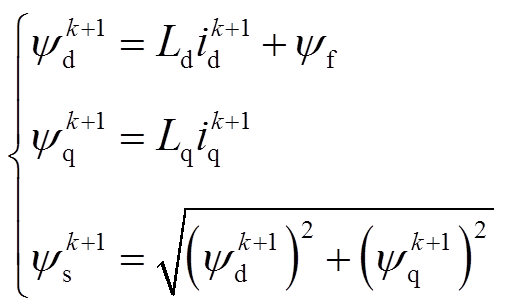（7）转矩预测模型为
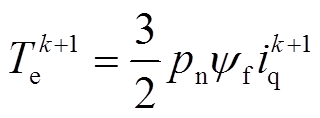（8）式中，Ts为采样周期。
在实际数字控制系统中，由于其存在一拍控制延迟，当前控制周期计算的最优电压矢量在下一时刻才能作用到系统中，从而使系统的控制性能变差。因此，在数字控制系统中有必要采用一拍的延迟补偿，即将当前时刻作用的电压矢量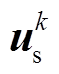
、采样电流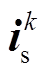代入式（6）中进行一步预测，得到的预测电流
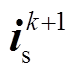替代采样电流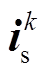完成后续的预测控制算法[22]。
由于一阶欧拉前向离散公式精度不高，因此本文采用二阶欧拉离散方法，主要包括欧拉前向积分公式和梯形积分公式，其离散表达式为
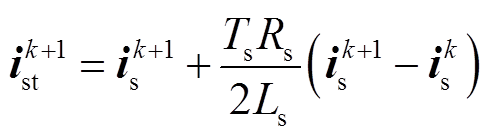（9）式中，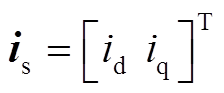
；
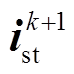为预测电流值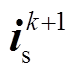；为前向欧拉算法积分部分的值，为预测电流的近似值。该方程等价于将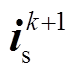作为初值的梯形积分法[10]。
MPTC主要是以电磁转矩和磁链的跟踪误差为控制目标，因此通常将代价函数设计为
（10）式中，Tn、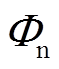
分别为额定转矩和额定磁通；λ为权重系数；
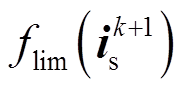为电流限幅项，满足条件
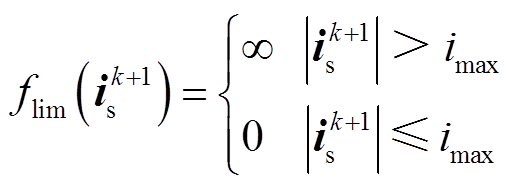（11）式中，imax为最大允许电流。
权重系数的设计通常采用与主要变量即电流误差相关的数据进行评估，如电流稳态误差方均根（Root Mean Square, RMS）或电流THD[22]。
MPTC中代价函数的权重系数用来调整转矩误差和磁链误差的控制比重，实际上也是间接地调整旋转坐标下电流id、iq误差的控制权重，将式（7）和式（8）代入式（10）中，得
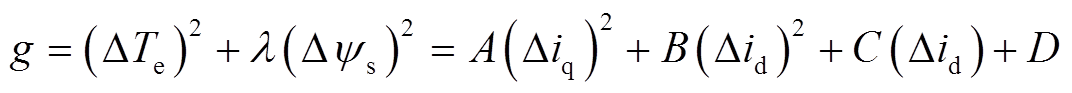（12）其中
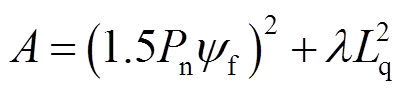
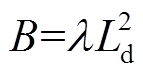
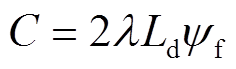
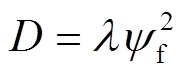
因此可以将电流id、iq的稳态误差方均根作为评价权重系数设计的依据。
PSO算法中每个粒子代表一个权重系数，由于用电流id、iq稳态误差的方均根评价权重系数，所以每个粒子的目标函数值应该由含有电流误差方均根的目标函数确定。由式（2）和式（3）可知，对于表贴式永磁同步电机，转矩主要由电流iq决定，而电流id的误差主要影响磁链误差的大小，因此可将目标函数设计为
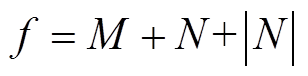（13）其中
M=rms(∆id)+δrms(∆iq) N=rms(∆iq)-rms(∆id)
式中，M项为电流id、iq的误差控制项，其作用是减小电流THD；δ为电流iq误差控制权重系数，仿真和实验表明该系数应尽量大，直至PSO算法收敛为寻优范围的最小值1；N+|N|项是保证使电流iq误差不大于电流id误差，使电流THD较小的同时，转矩误差应尽可能小。
传统粒子群算法中每个粒子的初始位置是随机分布的，在每次迭代中记录每个粒子的历史最优位置pBestk，及整个粒子群的全局最优位置gBestk，每次迭代完成后，粒子位置和速度根据式（14）更新。
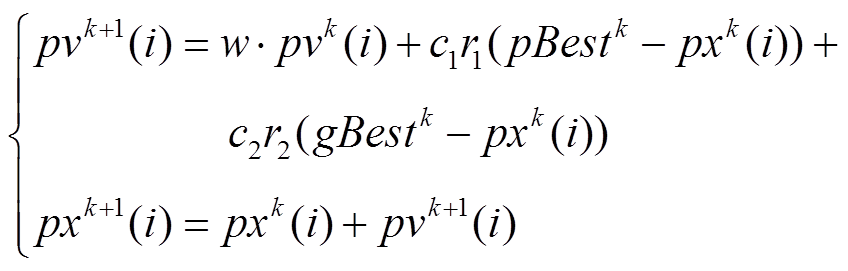（14）式中，pvk(i)、pxk(i)分别为粒子i在第k代的速度和位置；w为惯性权重系数；c1、c2分别为局部学习因子和全局学习因子；r1、r2为[0,1]之间的随机数。
将惯性权重系数w设置为从wmax=0.9到wmin=0.2线性下降[23]，见式（15）；c1、c2采用异步时变的设置方式，见式（16）。这种设置的目的是在优化初期加强全局搜索，而在搜索后期促使粒子收敛于全局最优解。
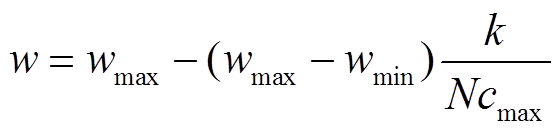（15）
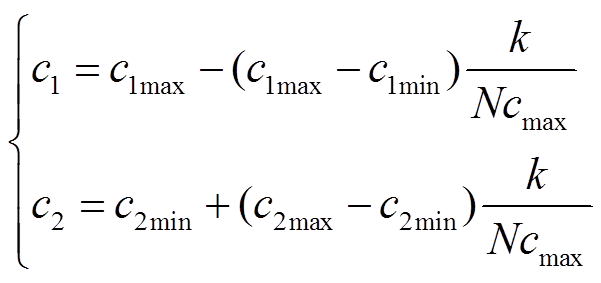（16）式中，k为迭代次数；Ncmax为最大迭代次数；c1max= c2max=2.5，c1min=c2min=0.5。
粒子群算法有较大邻域时，处理简单问题效果较好，邻域较小时，可更好地处理复杂问题[24]。2005年J. J. Liang等设计了采用动态重组的多种群粒子群算法（Dynamic Multi-swarm Particle Swarm Ptimizer, DMSPSO），使用小的粒子群解决复杂的问题，同时将小粒子群动态重组，以便粒子能在不同种群中交换信息，提高探索精度[25]。
在DMSPSO中，将整个粒子群分为多个小的子粒子群，每个子粒子群作为一个独立的种群进行寻优，然后以一定的重组周期P，将整个粒子群再次进行随机重组。DMSPSO的具体步骤如下：
（1）采用传统PSO算法初始化粒子群的参数，将粒子群进行随机重组。
（2）计算粒子的目标函数值。
（3）当迭代次数k＜0.9Ncmax时，采用式（17）更新粒子的速度和位置；否则，采用式（14）进行更新。
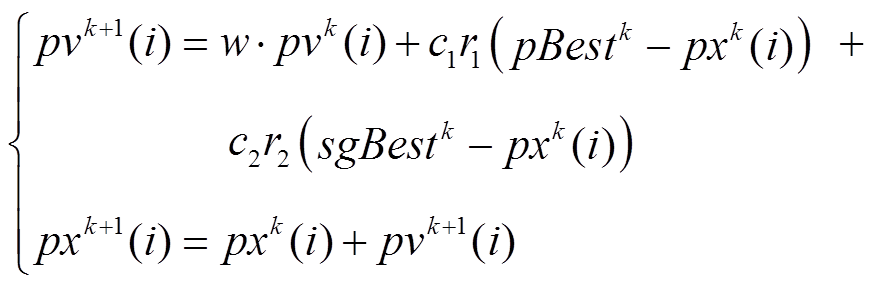（17）式中，sgBestk为每个子粒子群的全局最优值。
（4）如果满足mod(k,p)=0且k＜0.9Ncmax，则对粒子群进行随机重组；否则，不执行该步骤。
（5）返回到步骤（2）直到达到最大迭代次数。
混沌是一种在自然界广泛存在的非线性现象，具有随机性、遍历性、初始条件敏感性等特点，其在局部寻优中具有较优的性能。一个简单的混沌logistice方程为[26]
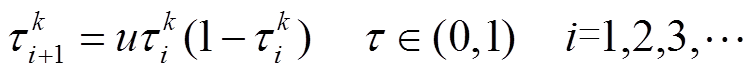（18）式中，t为混沌变量。当u介于3.56和4之间时，方程迭代的值变化最大，可完全进入混沌状态。
基于混沌变异的动态重组多种群粒子群算法的具体步骤如下：
（1）根据传统PSO算法初始化粒子群的参数，将粒子进行随机重组。
（2）计算每个粒子的目标函数值。
（3）当迭代次数k＜0.9Ncmax时，采用式（17）更新粒子的速度和位置；否则，采用式（14）进行更新。
（4）如果满足mod(k,p)=0且k＜0.9Ncmax，先将粒子群进行随机重组，然后随机选取一组子粒子群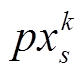
，对该子粒子群实行混沌变异：
①将子粒子群中的粒子映射到logistice方程的定义域(0,1)中，即
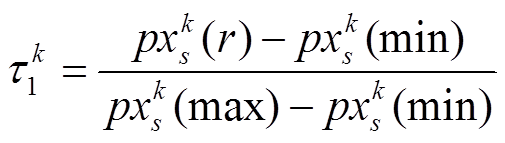（19）式中，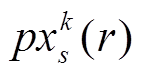
、
、
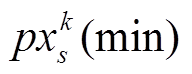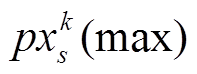分别为子粒子群s中的任一粒子、最小粒子和最大粒子。
②将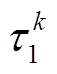
代入式（18）中，进行n次迭代，得到一个混沌序列
。
③将混沌序列映射到原粒子群空间中（式（20）），从而产生一个混沌变异的子粒子群，并用该粒子群替换原粒子群。
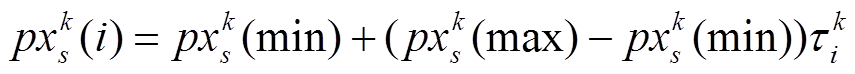（20）式中，i=1,2,…,n，n为该子粒子群中粒子个数。
否则，不执行该步骤。
（5）返回步骤（2），直至达到最大次数。
为了验证改进PSO算法的搜索速度和精度，在Matlab/Simulink的仿真环境中设计粒子群算法整定权重系数的永磁同步电机模型预测转矩控制（MPTC）的仿真模型，分别采用传统粒子群算法（CPSO）、动态重组的多种群粒子群算法（DMSPSO）、基于混沌变异的动态重组多种群粒子群算法（CDMSPSO）对MPTC中的权重系数进行整定，通过对比三种不同的粒子群算法验证改进算法的优越性和可行性。仿真和实验的电机参数见表1。
表1 仿真和实验的电机参数
Tab.1 Simulation and experimental parameters
参 数数 值 直流母线电压Udc/V512 额定转速Nr/(r/min)1 500 极对数pn4 相电阻Rs/Ω1.32 d、q轴电感Ld, Lq/mH13.6 转子磁链0.435 转动惯量J/(kg×m2)0.004 5 额定转矩Tn/(N×m)24
为了合理对比三种不同PSO算法的性能， CPSO、DMSPSO、CDMSPSO算法均采用动态惯性权重系数和异步更新的学习因子，如式（15）和式（16），总的粒子个数为15，每个粒子维度为1，寻优范围为[1,30]，最大迭代次数为150次。对于DMSPSO和CDMSPSO，子粒子群个数为5，粒子重组周期为5，在每次粒子重组后，CDMSPSO进行一次混沌变异。为了分析不同的电流iq误差控制比重对代价函数中权重系数的寻优结果的影响，仿真中设置了不同的目标函数权重系数δ为1、1.1、1.5和2，使用200个电流误差采样点计算RMS，然后计算每个粒子的目标函数值。权重系数整定时电机工况为1 000r/min，50%额定负载，仿真结果如图2所示。表2中列出了对于不同的目标函数控制权重δ，三种算法整定出的代价函数的最优权重系数λ，及其对应的电流THD。λ=1时电流的THD=11.10%。
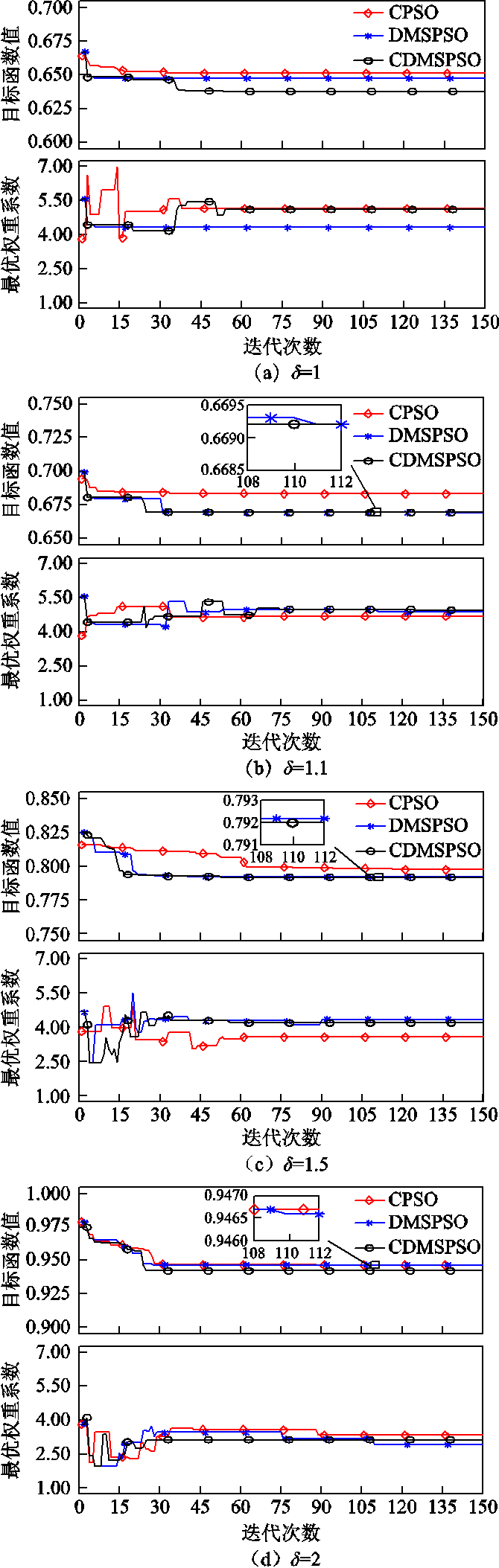
图2 在电机转速1000r/min，50%额定转矩下每代的目标函数值和最优权重系数
Fig.2 The objective function value and optimal weighting factors of each generation at 1000rpm and 50% rated torque
表2 权重系数整定和电流THD的仿真结果
Tab.2 Simulation results of weighting factors setting and current THD
δ方法λTHD(%) 1CPSO5.159.58 DMSPSO4.329.58 CDMSPSO5.119.60 1.1CPSO4.68 9.55 DMSPSO4.869.54 CDMSPSO4.969.56 1.5CPSO3.589.89 DMSPSO4.369.59 CDMSPSO4.219.59 2CPSO3.359.56 DMSPSO2.939.40 CDMSPSO3.149.45
由仿真结果图2可知，相比于CPSO、DMSPSO，CDMSPSO能在较少的迭代次数内快速收敛到使目标函数值较小的参数范围内，且最终整定出的参数使目标函数值更小，即寻优到的参数更优，因此CDMSPSO具有较快的收敛速度和探索精度。而表2中仿真结果表明，三种算法均能搜索到较优的权重系数，并且对于不同的目标函数的权重系数δ，三种算法整定的代价函数权重系数λ使电机的电流THD差小于0.5%。而对于预测转矩控制，其主要控制目标为转矩，所以在保证电流THD尽可能小的同时，其代价函数中转矩应该占有较大的控制比重，因此目标函数中应以电流iq的误差控制为主，即δ的值应该尽可能大。
为了验证采用PSO算法整定模型预测控制中权重系数的可行性，本文中结合Matlab和DSP进行实验平台验证。实验平台如图3所示，包括3.8kW驱动电机，3.8kW负载电机，以及由英飞凌 IGBT FF300R12ME4 模块和德州仪器TMS320F28379 MCU构成的驱动控制器。
考虑到PSO 算法运算量较大的问题，选择将其在Matlab/GUIDE设计的上位机中实现，将采样数据发送到上位机中，分别由三种PSO算法整定权重系数，而不用额外增加DSP的计算负担。实验验证系统的框图如图4所示。
图3 实验平台
Fig.3 Experiment platform of PMSM system
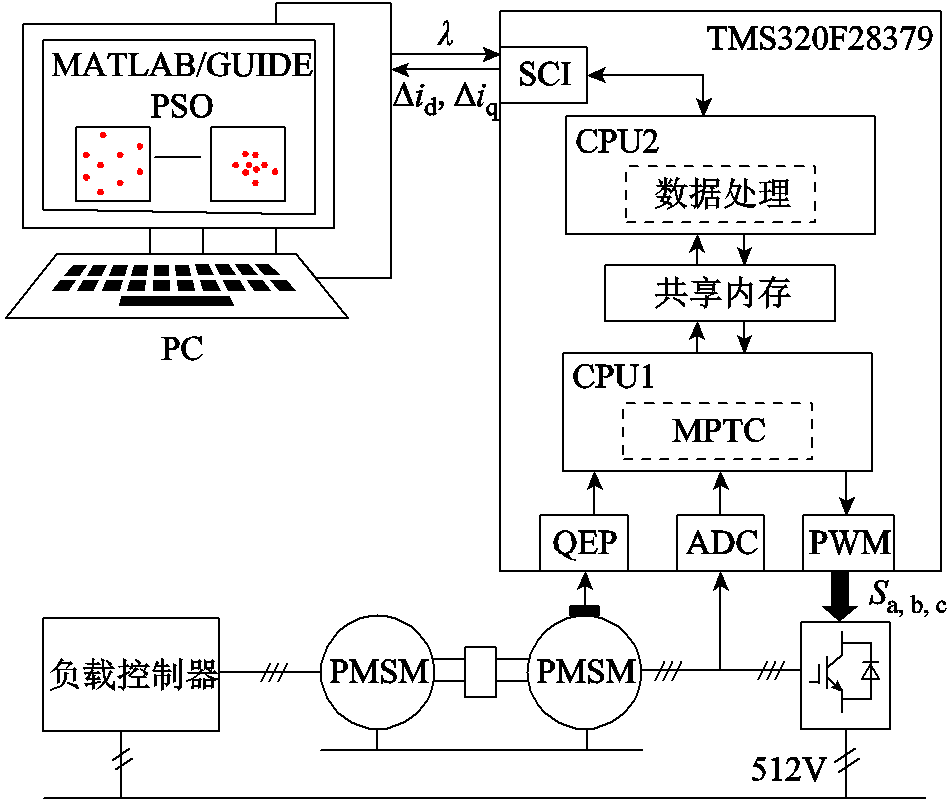
图4 实验验证系统框图
Fig.4 Block diagram of the experimental verification system
在实验中选取目标函数的权重系数δ为2，为了减少实验过程中权重系数整定的时间，在PSO算法运行中，如果全局最优值连续30代不变，则停止整定，将其作为最优权重系数给定到MPTC程序中，因此整定时间长短存在差异，同时由于受限于串联接口传输速度，所以整定时间相对较长。
由实验结果图5所示可知，三种算法CPSO、DMSPSO、CDMSPSO整定出的权重系数分别为3.72、3.41、3.27，对应的电流THD为3.23%、3.17%、2.49%，而当权重系数为1时，电机的电流THD为4.12%，因此将转矩误差和磁链误差标幺化后，尽管转矩误差较小，但是并不能得到好的电流控制效果，而采用三种PSO算法整定出的权重系数λ均能使电机具有较小的电流THD，相比之下，CDMSPSO整定得到的λ更小，即能使转矩波动更小，因此CDMSPSO相比CPSO、DMSPSO，在求解由问题定义的目标函数的最优解时，具有更好的寻优精度。
为验证所提方法的优越性，选取较新的级联式PTC[14]与文中所提方法进行对比。对比实验结果如图5d、图6所示，级联式PTC的电流THD为4.82%，采用所提方法整定权重系数后电流THD为2.49%，由此可知，虽然级联式PTC无需调整权重系数，但是该方法并不能实现控制目标的同步优化，相比级联式PTC，采用权重系数调整控制目标的控制比重，实现同步优化的方法具有更小的转矩脉动和更好的电流质量。
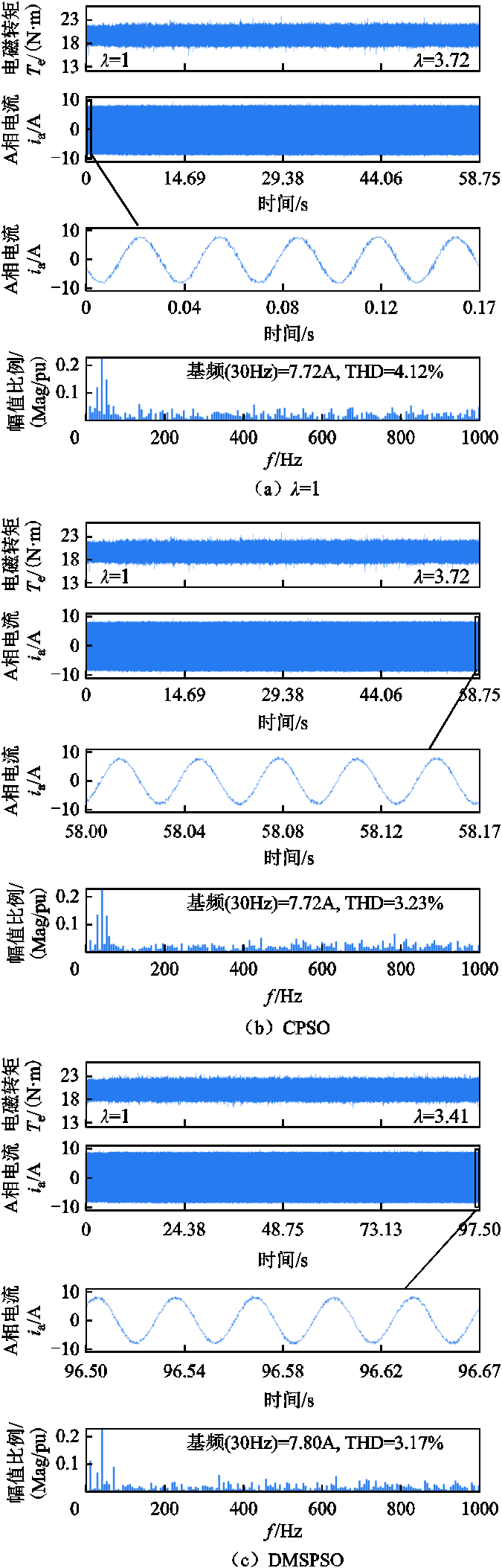
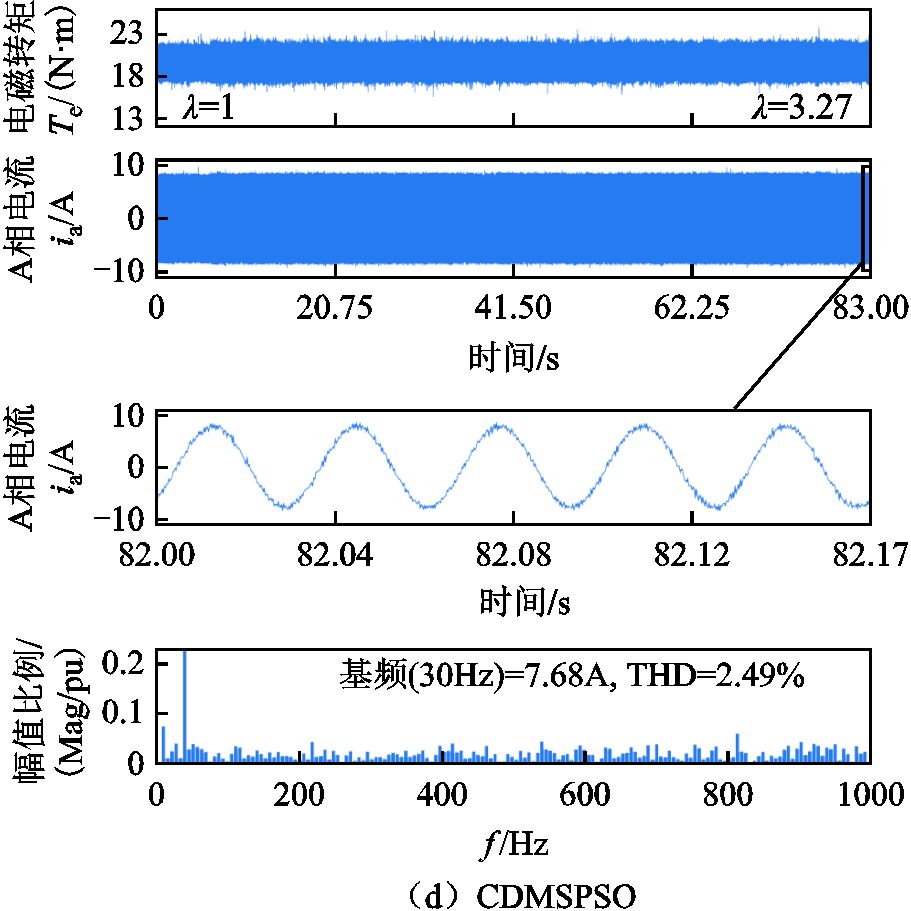
图5 转速450r/min，90%负载下，权重系数自整定过程的实验电流波形
Fig.5 The self-tunning process and experiment result of weighting factors under 450r/min and 90%load
图6 转速450r/min，90%负载下，级联式PTC的实验电流波形
Fig.6 The experiment results of cascade PTC under 450r/min and 90%load
为进一步验证系统动态性能，在额定转速、空载工况下整定的权重系数λ=2.13，并进行额定转速翻转测试，结果如图7所示，图8为转速450r/min下突加50%负载的实验波形，图8a和图8b分别为测试传统标幺化方法λ=1和λ=2.82时负载变化的处理效果，可知，在相同控制结构的系统中（外环为PI控制器，内环为PTC控制器），权重系数对其动态性能无较大影响，但是在所提方法整定出的权重系数下（λ=2.82），电流THD（4.94%）相比于λ=1时的电流THD（6.39%）更小。因此，整定出的权重系数在不影响系统动态性能的同时，可实现更好的电流控制效果。
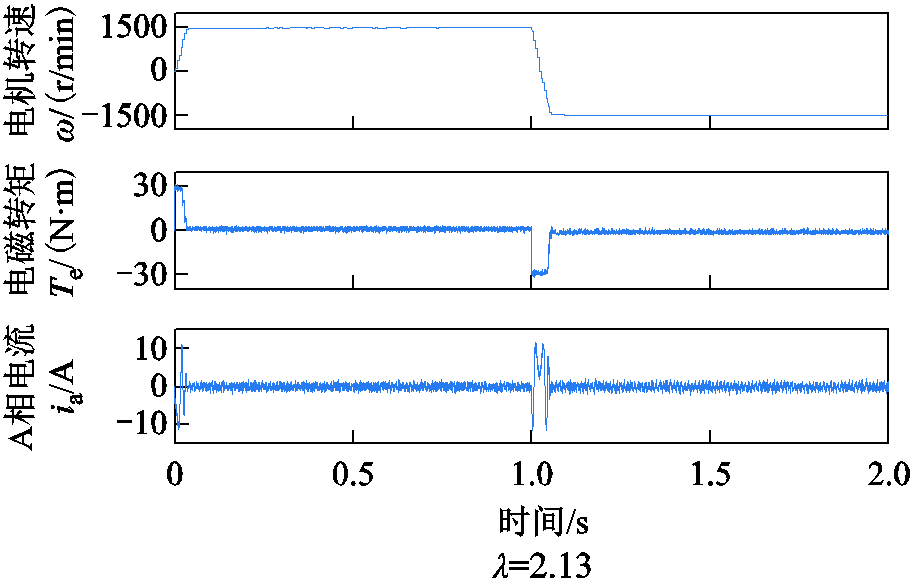
图7 额定转速下电机翻转实验波形
Fig.7 Experimental waveforms of PMSM speed reverse at rated speed
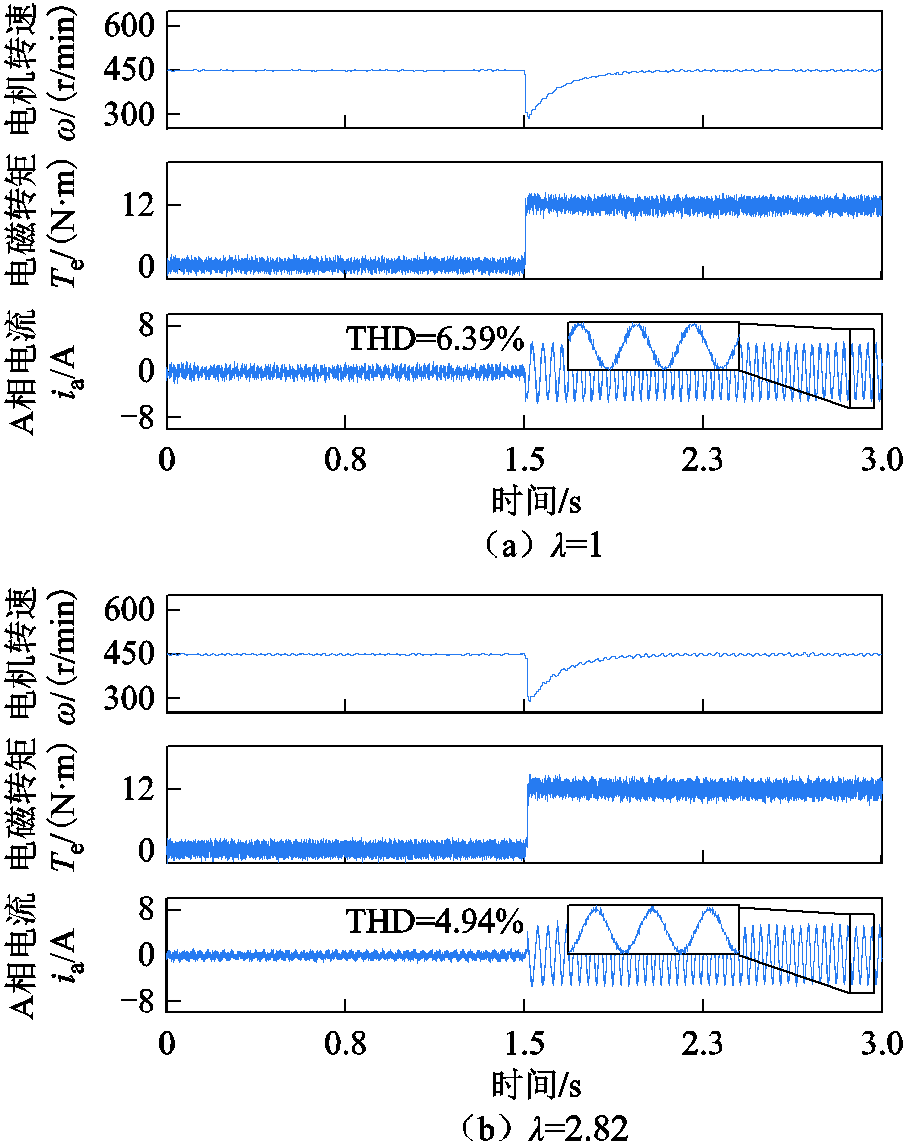
图8 转速450r/min下突加50%负载的实验波形
Fig.8 Experimental waveforms with step-changing load at 450r/min
图9给出了不同工况下，由CDMSPSO算法整定出的λ，为了减小实验中扰动带来的偶然因素影响，在每种工况下，用算法CDMSPSO对其进行5次的系数整定，然后将最小的三个系数取平均值作为最优权重系数。
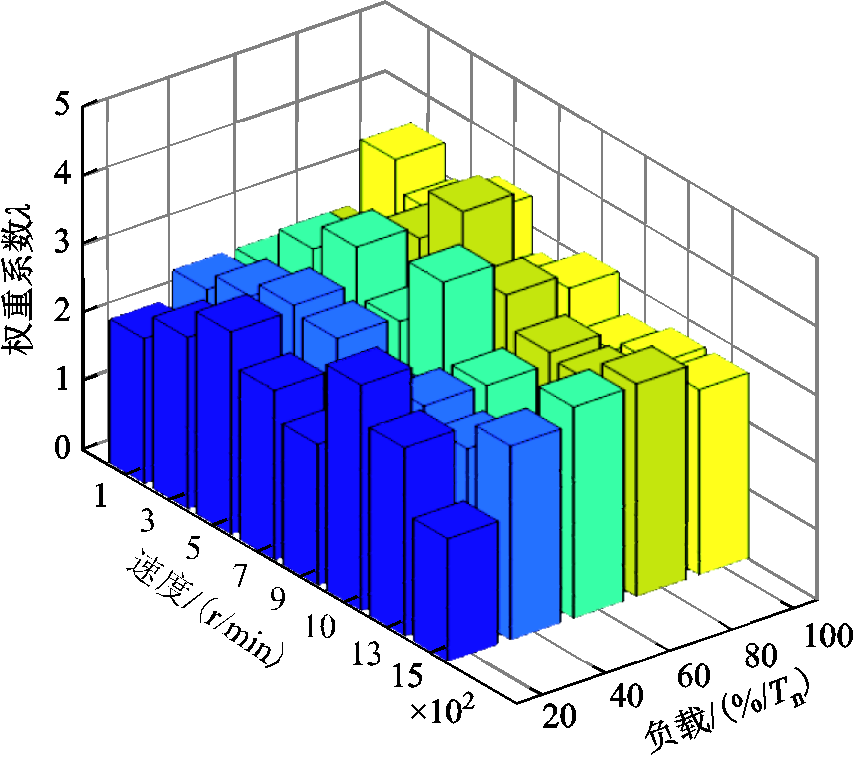
图9 不同工况下权重系数
Fig.9 The weighting factors under different working conditions
由图9 可知，如果只考虑系统的稳态性能，对于电机不同的工况，其权重系数的大小相差不大。但是在相同负载情况下，电机在中、低速时的磁链权重系数λ要比高速时的磁链权重系数λ大；而在相同转速时，重载下的磁链权重系数λ相对较大。
本文通过分析模型预测转矩控制中权重系数设计原则，将电流id、iq误差的方均根作为权重系数调整的依据，设计了粒子的目标函数，运用混沌变异的动态重组多种群粒子群算法对权重系数进行整定。该算法在传统的粒子群算法的基础上使用动态重组的粒子结构，结合混沌变异的更新策略，在全局探索性能、搜索精度、收敛速度上均有较好的效果。仿真及实验结果证明采用粒子群算法整定权重系数的可行性，并且得出CDMSPSO算法较CPSO、DMSPSO在权重系数整定中的优越性、可获得更优的电流控制质量结果。本文提出的模型预测控制权重系数设计方法可扩展应用于多电平多变量等复杂系统。
参考文献
[1] 陈炜, 曾思坷, 张国政, 等. 永磁同步电机改进型三矢量模型预测转矩控制[J]. 电工技术学报, 2018, 33(增刊2):420-426. Chen Wei, Zeng Sike, Zhang Guozheng, et al. Improved three-vector model predictive torque control of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 420-426.
[2] Aoyama M, Deng J. Visualization and quantitative evaluation of eddy current loss in bar-wound type permanent magnet synchronous motor for mild-hybrid vehicles[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(3): 269-278.
[3] 班斐, 连广坤, 陈彪, 等. 针对永磁同步电机的解耦预测转矩控制策略研究及其无位置传感器对比分析[J]. 电工技术学报, 2018, 33(增刊2): 401-410. Ban Fei, Lian Guangkun, Chen Biao, et al. Comparative analysis of sensorless control methods based on the decoupling predictive torque control strategy for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 401-410.
[4] 魏尧, 魏艳君, 马云飞, 等. 永磁同步电机转子位置的级联预测控制[J]. 电工技术学报, 2019, 34(1): 41-48. Wei Yao, Wei Yanjun, Ma Yunfei, et al. Cascade predictive control for rotor position of permanent magnet synchronous machines[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 41-48.
[5] 刘珅, 高琳. 永磁同步电机的改进模型预测直接转矩控制[J]. 电机与控制学报, 2020, 24(1): 10-17. Liu Shen, Gao Lin. Improved model of predictive direct torque control for permanent magnet synchronous motor[J]. Electric Machines and Control, 2020, 24(1): 10-17.
[6] Cortes P, Rodriguez J, Vargas R, et al. Cost function-based predictive control for power converters[C]// IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 2006: 2268-2273.
[7] 张永昌, 杨海涛. 感应电机模型预测磁链控制[J]. 中国电机工程学报, 2015, 35(3): 719-726. Zhang Yongchang, Yang Haitao. Model predictive flux control for induction motor drives[J]. Proceedings of the CSEE, 2015, 35(3): 719-726.
[8] 康劲松, 李旭东, 王硕. 计及参数误差的永磁同步电机最优虚拟矢量预测电流控制[J]. 电工技术学报, 2018, 33(24): 5731-5740. Kang Jinsong, Li Xudong, Wang Shuo. Optimal virtual vector predictive current control for permanent magnet synchronous motor considering parameter errors[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5731-5740.
[9] 郭磊磊, 金楠, 李琰琰, 等. 电压源逆变器虚拟矢量模型预测共模电压抑制方法[J]. 电工技术学报, 2020, 35(4): 839-849. Gou Lielie, Jin Nan, Li Yanyan, et al. Virtual vector based model predictive common-mode voltage reduction method for voltage source inverters[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 839-849.
[10] Zhang Xiaoguang, Hou Benshuai. Double vectors model predictive torque control without weighting factor based on voltage tracking error[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2368-2380.
[11] 李耀华, 秦辉, 苏锦仕, 等. 永磁同步电机模糊自适应变开关次数权重系数模型预测转矩控制[J]. 电机与控制学报, 2020, http://kns.cnki.net/kcms/ detail/23.1408.TM.20200117.1645.031.html. Li Yaohua, Qin Hui, Su Jinshi, et al. Model predictive torque control of permanent magnet synchronous motor based on adaptive dynamic weight coefficient using fuzzy control[J]. Electric Machines and Control,2020, http://kns.cnki.net/kcms/detail/23.1408.TM. 20200117. 1645.031.html
[12] Hadla H, Cruz S. Predictive stator flux and load angle control of synchronous reluctance motor drives operating in a wide speed range[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 6950-6959.
[13] Davari S A, Khaburi D A, Kennel R. An improved FCS-MPC algorithm for an induction motor with an imposed optimized weighting factor[J]. IEEE Transactions on Power Electronics, 2012, 27(3): 1540-1551.
[14] Norambuena M, Rodriguez J, Zhang Z, et al. A very simple strategy for high-quality performance of AC machines using model predictive control[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 794-800.
[15] 涂文聪, 骆光照, 刘卫国. 基于模糊动态代价函数的永磁同步电机有限控制集模型预测电流控制[J]. 电工技术学报, 2017, 32(16): 89-97. Tu Wencong, Luo Guangzhao, Liu Weiguo. Finite-control-set model predictive current control for permanent magnet synchronous motor based on dynamic cost function using fuzzy method[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 89-97.
[16] 张晓光, 张亮, 侯本帅. 永磁同步电机优化模型预测转矩控制[J]. 中国电机工程学报, 2017, 37(16): 4800-4809. Zhang Xiaoguang, Zhang Liang, Hou Benshuai. Improved model predictive torque control of permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2017, 37(16): 4800-4809.
[17] Wang Fengxiang, Xie Haotian, Chen Qing, et al. Parallel predictive torque control for induction machines without weighting factors[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1779-1788.
[18] Sandre-Hernandez O, Morales-Caporal R, Rangel-Magdaleno J, et al. Parameter identification of PMSMs using experimental measurements and a PSO algorithm[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(8): 2146-2154.
[19] Liu Zhaohua, Wei Hualiang, Li Xiaohua, et al. Global identification of electrical and mechanical parameters in PMSM drive based on dynamic self-learning PSO[J]. IEEE Transactions on Power Electronics, 2018,33(12): 10858-10871.
[20] Xu W, Ismail M M, Liu Yi, et al. Parameter optimization of adaptive flux-weakening strategy for permanent-magnet synchronous motor drives based on particle swarm algorithm[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 12128-12140.
[21] 刘细平, 胡卫平, 丁卫中, 等. 永磁同步电机多参数辨识方法研究[J]. 电工技术学报, 2020, 36(6): 1198-1207. Liu Xiping, Hu Weiping, Ding Weizhong, et al. Research on multi-parameter identification method of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 36(6): 1198-1207.
[22] Jose Rodriguez, Patricio Cortes. 功率变换器和电气传动的预测控制[M]. 陈一民, 周京华, 卫三民等译. 北京: 机械工业出版社, 2015.
[23] 黄凯, 郭永芳, 李志刚. 基于信息反馈粒子群的高精度锂离子电池模型参数辨识[J]. 电工技术学报, 2019, 34(增刊1): 378-387.Huang Kai, Guo Yongfang, Li Zhigang. High precision parameter identification of lithium-ion battery model based on feedback particle swarm optimization algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 378-387.
[24] Kennedy J. Small worlds and mega-minds: effects of neighborhood topology on particle swarm performance[C]// Proceedings of the 1999 Congress on Evolutionary Computation-CEC99(99TH8406), Washington DC, USA, 1999: 1931-1938.
[25] Liang J J, Suganthan P N. Dynamic multi-swarm particle swarm optimizer[C]// IEEE Swarm Intelligence Symposium, Pasadena, CA, USA, 2005: 124-129.
[26] 贾东立, 张家树, 张超. 基于混沌遗传算法的基元提取[J]. 西南交通大学学报, 2005, 40(4): 496-500. Jia Dongli, Zhang Jiashu, Zhang Chao. Geometric primetive extraction using chaos genetic algorithm[J]. Journal of Southwest Jiaotong University, 2005, 40(4): 496-500.
Weighting Factors Design of Model Predictive Control for Permanent Magnet Synchronous Machine Using Particle Swarm Optimization
Abstract In this paper, a dynamic recombined multi-population particle swarm optimization algorithm based on chaotic-mutation (CDMSPSO) is proposed to realize self-tuning of the weighting factors when model predictive control algorithm (MPC) is dealing with multi-objective and multi-constraint conditions. By analyzing the design principle of cost function in the model predictive torque control (MPTC), taking the root mean square of the current error in the two-phase rotating coordinate system as a reference, the objective function of particles in particle swarm optimization is designed with reducing the torque ripple and reducing the current total harmonic distortion (THD) as the main control objectives. The whole population was divided into several small sub-particle swarms by using CDMSPSO, and the particles were randomly recombined with a certain recombination period, then a random sub-particle swarm is selected and chaotic sequence is generated iteratively on the basis of any particle, and the selected sub-particle swarm is replaced by the new chaotic sequence to realize chaotic mutation of particles. Simulation and experimental results show that this method can solve the problem of weighting factors setting well and achieve excellent steady-state performance.
keywords：Permanent magnet synchronous motor, model predictive control, weighting factors, particle swarm optimization, dynamic recombination, chaotic mutation
中图分类号：TM341
DOI: 10.19595/j.cnki.1000-6753.tces.200752
国家自然科学基金项目（51877207）和中国科学院海西研究院“前瞻跨越”计划重大项目（CXZX-2018-Q01）资助。
收稿日期 2020-06-30
改稿日期 2020-07-25
李家祥 男，1996年生，硕士研究生，研究方向为电机控制和智能优化算法。E-mail：jiaxiang_li163@163.com
汪凤翔 男，1982年生，研究员，博士生导师，研究方向为电机驱动与电力电子。E-mail：fengxiang.wang@fjirsm.ac.cn（通信作者）
（编辑 郭丽军）