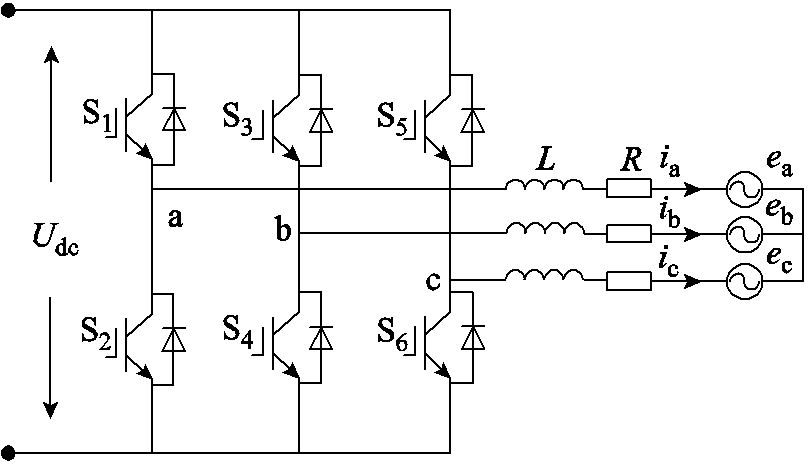
图1 两电平电压源逆变器拓扑结构
Fig.1 Topology of 2-level voltage source inverter
摘要 近年来，模型预测控制（MPC）以其良好的自适应性、鲁棒性等优越性能广泛应用于两电平电压源逆变器中。然而，常规的模型预测控制每个控制周期只使用1个电压矢量，导致电流谐波较大。为抑制电流谐波，提出一种双矢量调制模预测控制策略。首先，在每个控制周期同时使用两个电压矢量来跟踪目标矢量，且每个电压矢量的作用时间根据调制模型预测控制原理计算；其次，根据无差拍控制原理计算参考电压，并根据参考电压位置在每个控制周期仅需要选择三组电压矢量组合进行在线评估，从而得到最优电压矢量组合。最后，通过详细的理论分析，验证了所提双矢量调制模型预测控制策略的有效性。此外，该文研究还表明，所提策略还可用于控制其他类型的逆变器，如三相四开关逆变器。同时，所提方法可以获得和常规双矢量法类似的控制性能，且具有计算量小等优点。理论分析和实验结果验证了所提方法的有效性。
关键词：电压源逆变器 双矢量 调制模型预测控制 有效性证明
近年来，随着能源危机与环境污染等问题的不断加剧，可再生能源技术得到广泛研究和应用。作为电能转换的关键设备，两电平电压源逆变器已经广泛应用于光伏、风电等可再生能源系统中[1-5]。目前，两电平电压源逆变器主要的控制策略有矢量控制和直接功率控制，但矢量控制需要设计比例积分（PI）控制器和脉冲宽度调制（PWM）模块。虽然直接功率控制不需要设计PI和PWM模块，但其功率脉动较大。
为了简化控制策略、降低功率脉动，实现两电平电压源逆变器的最优控制，近年来，模型预测控制（Model Predictive Control, MPC）在电力电子领域得到广泛研究。2004年，J. Rodriguez教授在文献[6]中提出了一种应用于两电平电压源逆变器的模型预测控制策略。此后，许多学者开始研究改进的模型预测控制策略来减少计算量[7-8]、降低开关频率[9-10]，抑制共模电压[11-12]或减少电流谐波[13-24]。
目前，在模型预测控制系统中，常用的电流谐波抑制方法主要有两种：一种是直接增加采样频率，然而，采样频率的增加受计算量的限制；另一种是多矢量模型预测控制，即在每个控制周期同时应用多个电压矢量以提高预测控制精度。文献[13-16]在每个控制周期中同时使用两个电压矢量，因此，电流谐波得到抑制。文献[17-21]通过在每个控制周期中同时使用三个电压矢量，进一步降低了电流谐波。
对于上述多矢量模型预测控制策略，为了更好地提高控制性能，准确且快速地计算出每一个电压矢量的作用时间是极其重要的。目前，主要有两种计算电压矢量作用时间的方法：一种是基于无差拍控制原理矢量作用时间计算方法[13-21]；另一种被称为调制模型预测控制，其基本原理是假设每个电压矢量的作用时间与其价值函数成反比[22-23]。尽管使用第一种方法理论上可以准确地计算出电压矢量的作用时间，但其计算量较大，且易出现作用时间大于控制周期或小于零的不合理情况，导致在实际控制中也无法实现全局意义上的最优控制。由于实现简单、计算量小等优点，近年来，许多学者对调制模型预测控制进行了研究[22-23]。然而，虽然许多仿真及实验研究已经验证了调制模型预测控制的有效性，但很少有学者对调制模型预测控制的有效性进行理论分析和证明。由于假设电压矢量作用时间与价值函数成反比是没有严格理论依据的，因此需要进行详细的理论分析，以为调制模型预测控制提供可靠的理论支撑。
为了解决这一问题，本文针对两电平电压源逆变器设计了双矢量调制模型预测控制策略，并进行详细的理论分析和实验验证。
与常规的多矢量调制模型预测控制相比[22-23]，本文首次给出详细的理论分析，证明了所提双矢量法的有效性，从而为调制模型预测提供了坚实的理论支撑。与常规基于无差拍原理的双矢量法相比[16]，所提方法可以获得与其类似的动态稳态控制性能，但计算量更小。
此外，文中的研究进一步表明，本文所提方法还可以扩展到其他类型的逆变器，如三相四开关（Three-Phase Four-Switch, TPFS）逆变器。理论分析和实验结果均验证了其有效性。
两电平电压源逆变器拓扑结构如图1所示，图中，Udc为直流母线电压，L为滤波电感，R为滤波电感的寄生电阻，ea、eb、ec为负载反电动势，ia、ib、ic是逆变器输出三相电流。两电平电压源逆变器有8种不同的开关状态，可得8种对应的电压矢量，如图2所示。
图1 两电平电压源逆变器拓扑结构
Fig.1 Topology of 2-level voltage source inverter
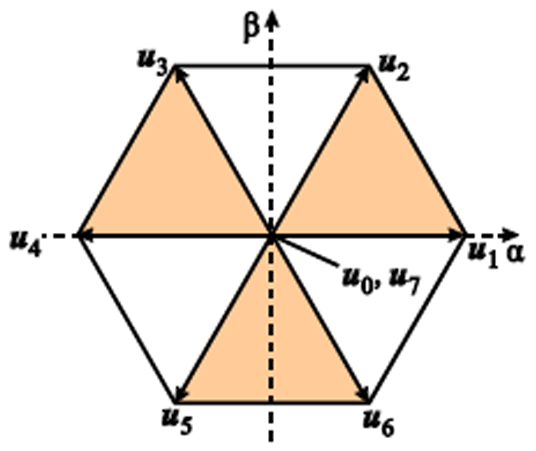
图2 电压矢量图
Fig.2 Diagram of voltage vectors
两电平电压源逆变器在αβ静止坐标系下的数学模型为
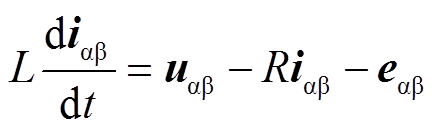（1）其中
uab=[ua ub]T iab=[ia ib]T eab=[ea eb]T
式中，uα、uβ分别为逆变器的输出电压的α、β轴分量；iα、iβ分别为逆变器的输出电流的α、β轴分量；eα、eβ分别为负载反电动势的α、β轴分量。
假设采样周期为T，将式（1）进行离散化可得
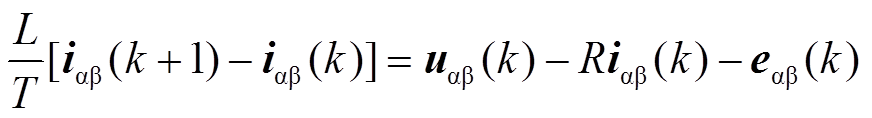（2）式中，x(k)为变量x在tk时刻的值；x(k+1)为变量x在tk+1时刻的值。
化简式（2）可以得到tk+1时刻电流预测表达式为
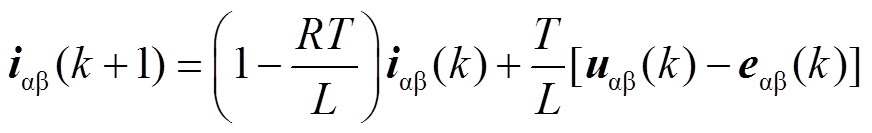（3）为了对模型预测控制策略的延迟进行补偿，可将上一周期最优电压矢量值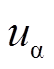
(k)和ub(k)代入式（3）计算得到tk+1时刻的预测电流值ia(k+1)和ib(k+1)。然后把图2中的8个电压矢量u(k+1)依次代入式（4）计算得到tk+2时刻的预测电流iab(k+2)为
（4）式中，x(k+2)为变量x在tk+2时刻的值。
当采样频率远高于负载反电动势频率时，可近似认为负载反电动势满足
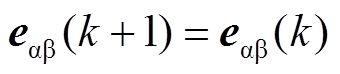（5）为了得到最优电压矢量，建立如式（6）所示的价值函数，以评估电流预测误差。将8种预测电流依次代入式（6）所示价值函数，通过比较可获得使价值函数最小的电压矢量作为最优电压矢量，并在下一周期将其应用于逆变器。
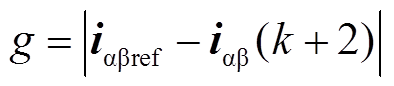（6）式中，iabref为给定的参考电流。
常规模型预测控制策略由于每个控制周期仅使用1个电压矢量，导致其电流谐波较大，针对该问题，本文研究并提出了一种双矢量调制模型预测控制策略。所提方法在每个控制周期同时使用两个电压矢量，从而减小了电流谐波。
为了减少计算量，本文基于无差拍控制原理，推导了参考电压uabref，即
（7）式中，uabref =[uaref ubref]T，uaref、ubref分别为α轴、β轴参考电压。
基于参考电压定义价值函数为
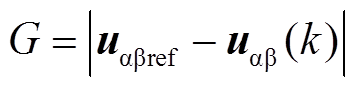（8）为了在每个控制周期同时施加两个电压矢量，本文根据逆变器8个基本电压矢量定义了12个电压矢量组合，分别为us1 (u0, u1)，us2(u0, u2)，us3(u0,u3)，us4(u0, u4)，us5(u0, u5)，us6(u0, u6)，us7(u1, u2)，us8(u2, u3)，us9(u3, u4)，us10(u4, u5)，us11(u5, u6)，us12(u6, u1)，如图3所示。
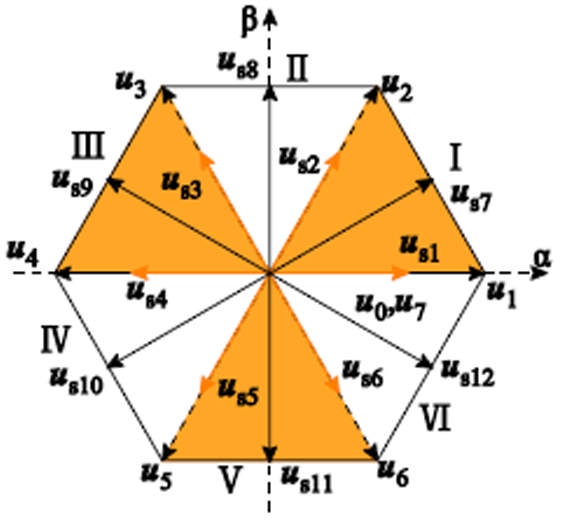
图3 电压矢量组合
Fig.3 Voltage vector combinations
12个电压矢量组合与基本电压矢量关系式为
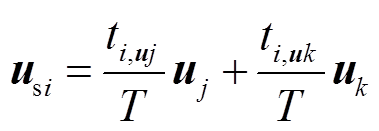（9）式中，ti,uj+ti,uk =T, ti,uj和ti,uk分别为uj和uk的作用时间；usi为合成电压矢量；uj、uk为基本电压矢量。
例如，us7为基本电压矢量u1、u2的组合,它们关系可以表示为
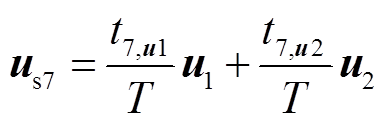（10）为了确定12个电压矢量组合的位置，首先需要计算12个电压矢量组合中每个电压矢量的作用时间。计算矢量作用时间的方法主要有两种：第一种是基于无差拍控制原理的矢量作用时间计算方法，该方法计算量较大，且易出现作用时间大于控制周期或小于零的不合理情况[16]；第二种被称为调制模型预测控制，它假定每个电压矢量的作用时间与其价值函数值成反比，这种方法简单且有效[22-23]，所以本文采用这种控制策略。
例如，t7,u1和t7,u2可以由式（11）计算得到。
（11）式中，G1和G2分别为u1和u2的价值函数值。
为了简化模型预测控制，根据图3，可将电压矢量平面平均分为六个扇区。当根据式（7）计算出参考电压后，可以很容易地获得其扇区位置，然后再根据该扇区位置选择三组电压矢量组合进行在线评估，从而可降低计算量。
图4给出了所提出控制策略的详细实现步骤，具体包括：
（1）根据逆变器的实际电流、参考电流和式（7）计算参考电压，并结合图3判断其所在扇区，进而进行电压矢量预选。
（2）将预选的电压矢量代入式（8）和式（11），计算每个电压矢量的作用时间，并根据式（9）进行电压矢量的合成。
（3）将合成的三个电压矢量组合代入式（8）进行评估，并选择1个最优矢量组合作用于逆变器。
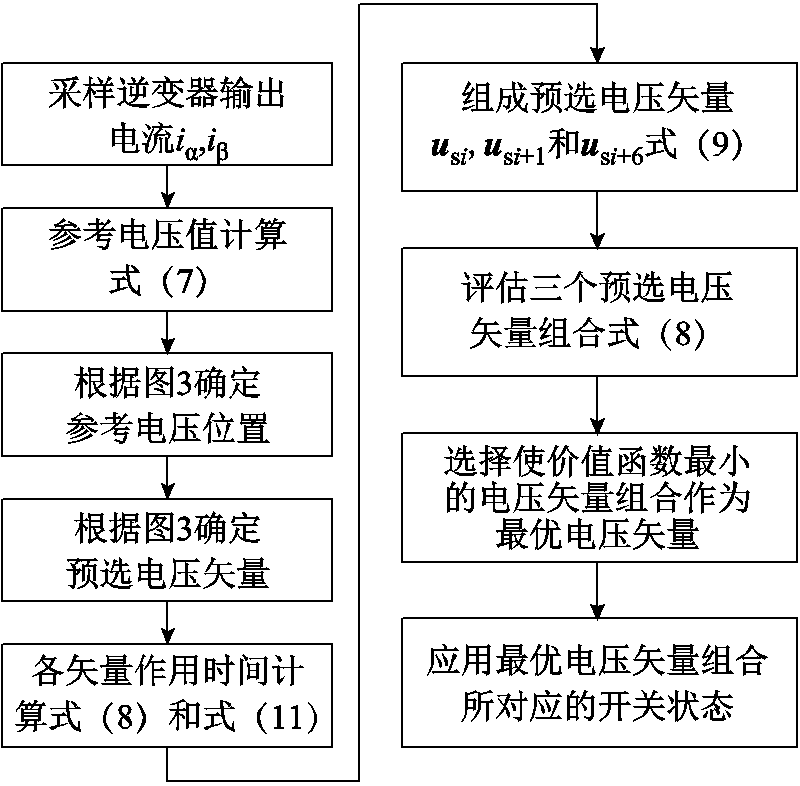
图4 所提控制策略实现步骤
Fig.4 Implementation steps of the proposed control strategy
近年来，关于调制模型预测控制有诸多研究[22-23]，然而，很少有论文在理论上证明其有效性。尽管当电压矢量的价值函数较大时，其作用时间应该较短，但它们成反比的假设仍然只是一种猜想，并没有严格的理论依据。为了证明所提双矢量调制模型预测控制策略的有效性，本文进行了详细的理论分析。调制模型预测控制策略有效性分析如图5所示，在此分析中，假定参考电压uref位于扇区Ⅰ。
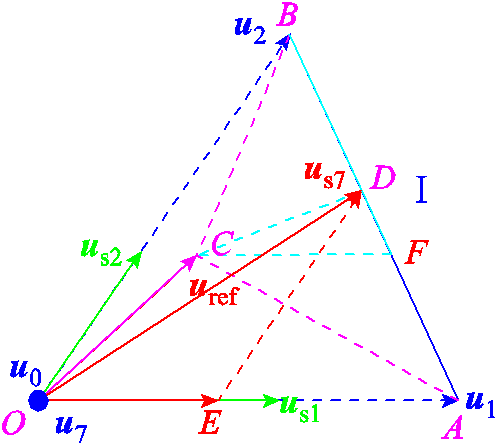
图5 调制模型预测控制策略有效性分析
Fig.5 Effectiveness analysis of the modulated model predictive control strategy
由图5所示，us7由u1和u2组合得到，满足式（10）。同时，由式（11）可知t7,u1和t7,u2满足
（12）结合式（10）和式（12）可得
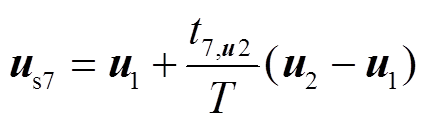（13）根据图5所示的几何关系，可得|AD|= t7,u2|u2-u1|/T，|BD|= t7,u1|u2-u1|/T。根据式（11）可得t7,u1/t7,u2=G2/G1。因此，可以推导出|BD|/|AD|= G2/G1。此外，根据式（8），很容易理解G1=|AC|，G2=|BC|。所以，|BD|/|AD|=|BC|/|AC|。
假设AB上有一点F，且|BC|=|BF|。由于|BC|+|AC|＞|AB|和|AB|=|BF|+|AF|，可得|AC|＞|AF|。因此，可以推导出
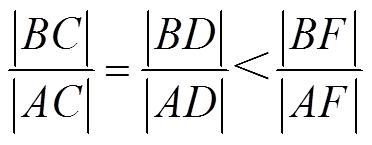（14）因为|BD|/|AD|＜|BF|/|AF|，所以点F必然位于线段AD上。
因为|BC|=|BF|，所以∠BCF=∠BFC。同时，因为∠CDB是三角形CDF的外角，所以∠CDB＞∠BFC。因此，∠CDB＞∠BCF。因为∠CBD＜p/3，所以∠BCF和∠BFC应大于p/3。因此，得出结论∠CDB＞p/3＞∠CBD。综上所述，由正弦定理得|BC|＞|CD|。因为|BC|是电压矢量u2的电压控制误差，|CD|是电压矢量组合us7的电压控制误差。所以，当采用us7来代替u2时，可以降低控制误差。
同理，可以推导出|AC|＞|CD|，这意味着us7的控制误差小于u1的控制误差。类似地，可以证明，us1的控制误差小于u0和u1，us2的控制误差小于u7和u2。因此，可以理解本文采用所定义的12个电压矢量组合代替8个基本电压矢量时是可以减小控制误差的。这也表明基于式（11）计算电压矢量作用时间是有效的，验证了文献[22-23]所提调制模型预测控制的正确性。因此，本文所提双矢量调制模型预测控制策略可以改善控制性能。
图5中，当参考电压的顶点C位于线段AB上时，G1=|AC|，G2=|BC|。同时，由上述推理可知，|BD|/|AD|= G2/G1，所以|BD|/|AD|=|BC|/|AC|，点C与点D重合，即参考电压矢量uref与合成电压矢量组合us7重合，此时，所提双矢量模型预测控制可实现最优控制。
同理，可以得到当参考电压的顶点C位于线段OB或线段OA上时，所提双矢量模型预测控制也可以实现最优控制。
然而，当参考电压位于其他区域时，本文所提方法无法实现最优控制。而在常规双矢量模型预测控制中[16]，虽然利用无差拍原理计算电压矢量作用时间可以在理论上达到最优控制，但却会出现电压矢量作用时间超出控制周期，或小于0的情况，从而降低了控制精度。所以常规双矢量模型预测控制也无法实现全局最优控制。后文的仿真结果表明，本文所提方法可以获得和常规方法类似的控制效果，但其计算量更小。
进一步研究表明，本文所提双矢量调制模型预测控制也可以用于控制其他类型的逆变器，如TPFS逆变器。以下进行详细分析。
图6为TPFS逆变器的拓扑结构，其中a相连接到直流侧电容中性点，该拓扑可作为三相六开关逆变器的容错结构。由于TPFS逆变器的直流电压的平衡控制已有很多方法[24]，本文假设直流中点电压是平衡的。平衡直流电压下的电压矢量为V1(0, 0)、V2(1, 0)、V3(1, 1)和V4(0, 1)，如图7a所示。
为了减小电流纹波，本文定义了如图7a所示的4组电压矢量组合，即Vs1(V1, V2)、Vs2(V2, V3)、Vs3(V3, V4)、Vs4(V4, V1)。在每个控制周期，4组电压矢量组合采用枚举的方式滚动优化，并选取使价值函数最小的电压矢量组合作为最优矢量对TPFS逆变器进行控制。同时，这里仍然采用式（11）计算这4组电压矢量组合中每个电压矢量的作用时间。
图6 TPFS逆变器拓扑
Fig.6 Topology of the TPFS inverter
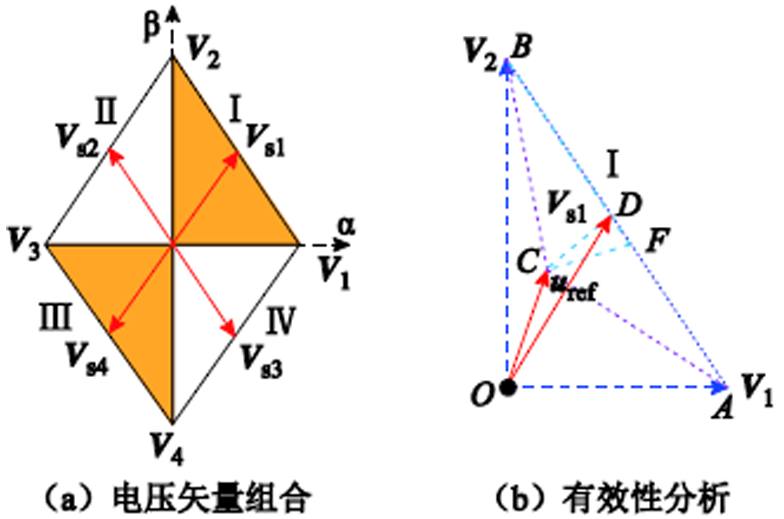
图7 TPFS逆变器电压矢量图
Fig.7 Voltage vector of the TPFS inverter
为了说明所提策略的理论扩展可行性，下面将从理论方面详细分析所提双矢量调制模型预测控制策略应用于TPFS逆变器的有效性。为了方便起见，将电压矢量平面平均分为四个扇区，如图7a所示。在此基础上，假设参考电压uref位于扇区Ⅰ。
如图7b所示，Vs1由矢量V1和矢量V2组合得到，根据式（9）可以得到
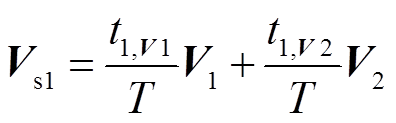（15）因为t1,V1+ t1,V2 =T，所以可得
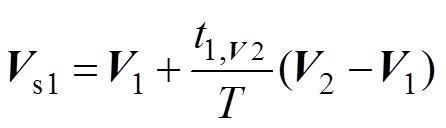（16）根据图8所示的矢量几何关系，可以看出
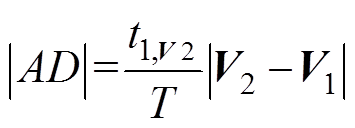（17）同理
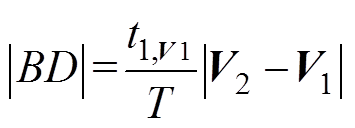（18）根据式（11）调制模型预测电压矢量作用时间计算方法，可以得出
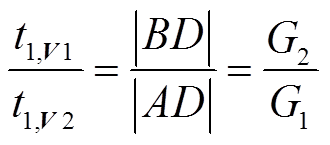（19）根据式（8）关于电压的价值函数可以得到G1=|AC|, G2=|BC|，因此可得
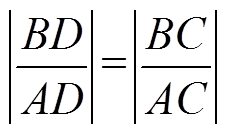（20）假设线段AB上存在一点F，满足|BC|=|BF|。则
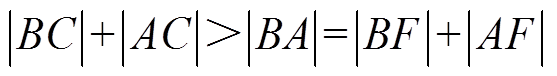（21）因为|BC|=|BF|，可以得到
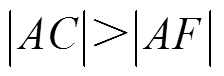（22）根据式（20）、式（21）和式（22），可以推导出
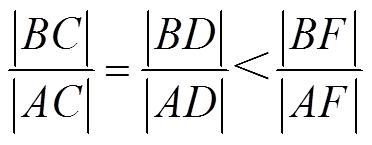（23）所以点F必须位于线段AD上。因为∠CDB为三角形CFD的一个外角，所以存在
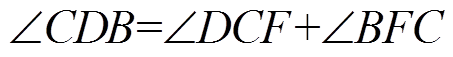（24）又因为∠BCF=∠BFC，所以
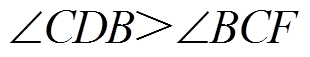（25）由三相四开关逆变器电压矢量关系可以得到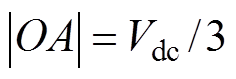
，
，考虑到∠OBD=arctan (|OA|/|OB|)=30°＞∠CBF，所以有
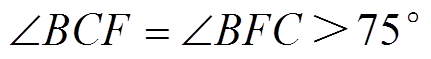（26）可以进一步得到
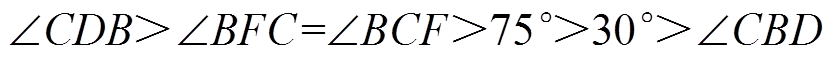（27）根据正弦定理可得|BC|＞|CD|，因为|CD|为电压矢量Vs1的控制误差，|BC|为电压矢量V2的控制误差，所以可以得出结论：采用合成电压矢量Vs1控制的误差小于使用单电压矢量V2的控制误差。同理也可以得到|AC|＞|CD|，即使用合成电压矢量Vs1的控制误差小于电压矢量V1的控制误差。
综上分析可见，双矢量调制模型预测控制的控制误差小于常规模型预测控制，且应用于TPFS逆变器时仍然适用。
为了进一步验证所提双矢量调制模型预测控制策略的有效性，搭建了Matlab/Simulink仿真模型和基于PE-PRO的两电平电压源逆变器实验平台，并进行对比研究，实验平台如图8所示。实验系统采用DSP28335作为主控制器。逆变器由IPM模块7MBP50RJ120组成。直流电压由APL-II双向直流电源提供。YOKOGAWA DLM4000系列示波器用于记录实验结果。仿真与实验系统参数见表1。
图8 实验平台
Fig.8 Experimental platform
表1 系统参数
Tab.1 System parameters
参数数值 直流电压Udc/V250 交流相电压峰值e/V150 滤波电感L/mH20 寄生电阻R/Ω0.05 采样周期T/ms66.67
为了验证所提双矢量调制模型预测控制利用与价值函数成反比计算单个电压矢量作用时间的准确性，图9a和图9b分别给出了参考电流从4A突增至8A时常规双矢量法[16]、所提双矢量模型预测控制策略的电流动态仿真结果。
图9 参考电流4A突增到8A仿真结果
Fig.9 Simulation results when the reference current is stepped up from 4A to 8A
由图9可知，两种方法的并网电流总谐波畸变率（Tolal Harmonic Distortion, THD）近似相等，且都具有良好的动态效果。这表明所提双矢量模型预测控制与常规双矢量法具有类似的控制效果，也验证了第3节理论分析的正确性。
表2给出了参考电流为8A时，常规模型预测控制、常规双矢量法和所提双矢量模型预测控制的定量比较结果。结果表明，相对于常规模型预测控制，由于控制误差的减小，开关频率的提高，常规双矢量与所提双矢量模型预测控制策略都可降低并网电流THD。但所提双矢量法程序执行时间比常规双矢量降低了3.9μs。与此同时，所提双矢量模型预测控制可以获得与常规双矢量法类似的控制效果。
表2 几种方法的定量比较
Tab.2 Quantitative comparison of the three methods control
常规MPC常规双矢量MPC所提双矢量MPC 采样频率/ kHz151515 平均开关频率/kHz3.466.946.94 THD(%)1.790.981.02 执行时间/μs21.9733.8629.96
为了进一步验证所提控制方法的有效性，采取第1节所介绍的常规模型预测控制策略作为对比方法，图10、图11分别给出了参考电流为3A和8A时常规模型预测控制与所提模型预测控制的对比实验结果。
由图10可知，当负载频率为50Hz、参考电流值为3A时，常规模型预测控制的电流THD为7.73%，而采用所提模型预测控制策略时，电流THD为4.94%。当参考电流值为8A时，使用常规模型预测控制与所提模型预测控制策略的电流THD分别为3.18%和2.33%，如图11所示。由此可见，相对于常规模型预测控制，本文所提模型预测控制策略电流稳态纹波明显减小。这就验证了所提控制策略的有效性，进而也验证了第3节理论分析的正确性。
图10 电流为3A时的实验结果
Fig.10 Experimental results when the current is 3A
图11 电流为8A时的实验结果
Fig.11 Experimental results when the current is 8A
为了进一步验证给定不同电流值、不同负载频率时本文所提控制策略的有效性，图12a和图12b分别给出了负载频率为50Hz和20Hz时常规模型预测控制与所提模型预测控制策略的电流THD曲线。
图12a表明，负载频率为50Hz时，本文所提模型预测控制策略的电流THD小于常规模型预测控制。当负载频率为20Hz时，图12b表明，本文所提模型预测控制策略效果也优于常规模型预测控制。这进一步验证了所提控制策略的有效性。
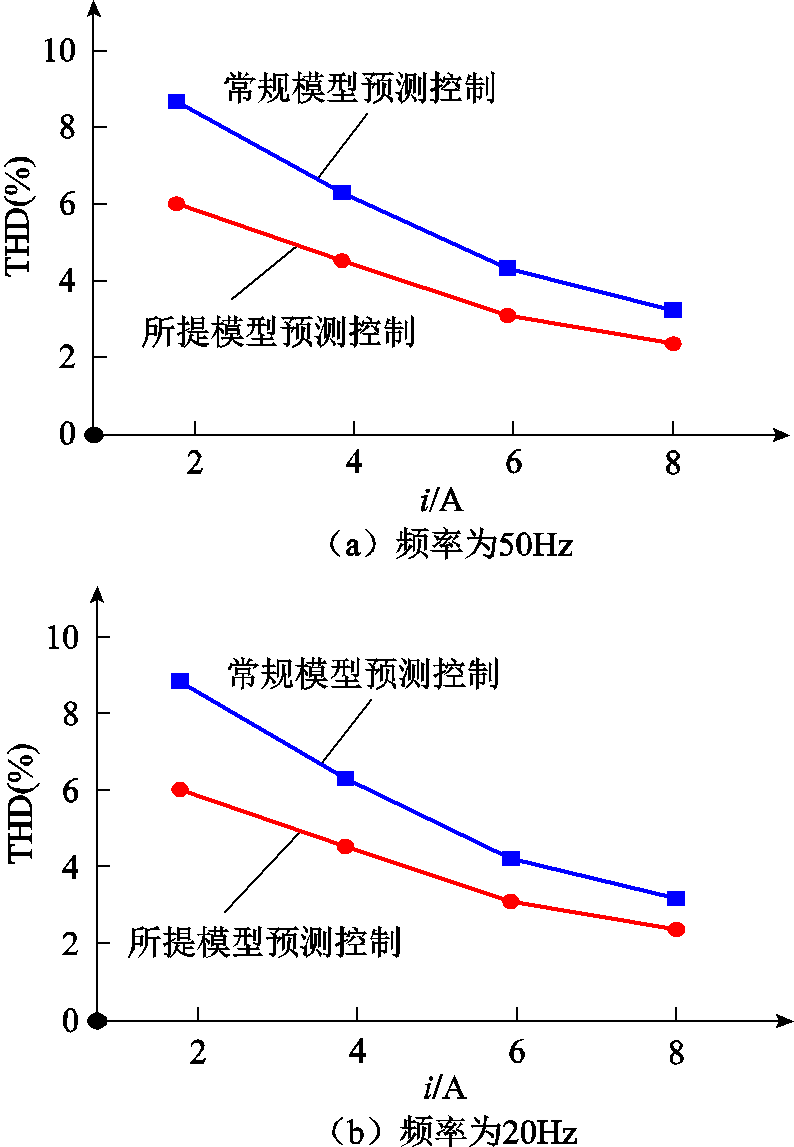
图12 电流THD
Fig.12 The current THD
为了测试所提控制策略的动态控制效果，本文进一步进行了动态对比实验研究。图13为负载频率为50Hz，参考电流值由3A突增到8A时的动态实验结果。图14为参考电流为8A，负载频率由20Hz突增到50Hz时的动态实验结果。
由图13可知，当参考电流值由3A突增到8A时，与常规模型预测控制相比，本文所提模型预测控制策略也具有良好的动态性能，且稳态电流THD仍然小于常规模型预测控制。当负载频率由20Hz突变到50Hz时，由图14可见，所提控制策略与常规控制策略均具有较好的动态特性，且所提控制策略的稳态电流THD仍然较小。这进一步表明，所提双矢量调制模型预测控制具有良好的动态性能和稳态性能，从而也证明了第3节理论分析的合理性。
图13 电流由3A突增为8A时的实验结果（50Hz）
Fig.13 Experimental results when the current is stepped up from 3A to 8A (50Hz)
图14 负载频率由20Hz突增为50Hz时的实验结果（8A）
Fig.14 Experimental results when the load frequency is stepped up from 20Hz to 50Hz (8A)
为了进一步验证所提模型预测控制策略的有效性，本文将其应用于TPFS逆变器，并进行了实验验证。实验参数与三相六开关逆变器一致，见表1。
图15为常规单矢量模型预测控制的实验结果，图16为本文所提模型预测控制的实验结果。在该实验中，负载频率为50Hz，参考电流为4A。由图15可见，常规模型预测控制方法的电流THD为10.7%。由图16可见，本文所提策略的电流THD减小为5.21%。因此，与常规模型预测控制相比，本文所提控制策略电流谐波明显减小，进一步验证了该控制策略的有效性。
图15 TPFS逆变器常规模型预测控制实验结果
Fig.15 Experimental results of the conventional model predictive control method for TPFS inverter
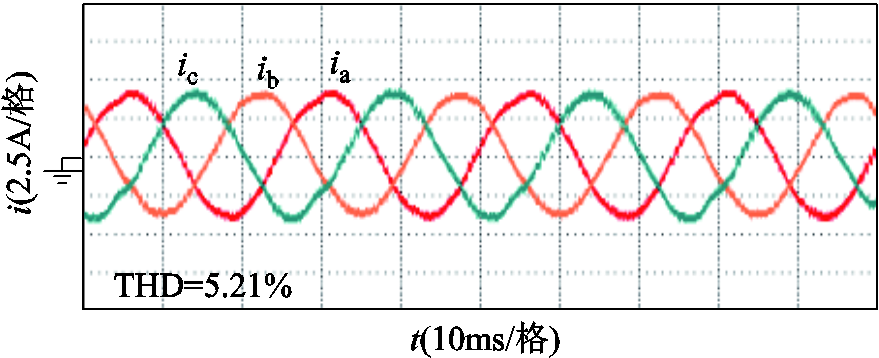
图16 TPFS逆变器双矢量调制模型预测控制实验结果
Fig.16 Experimental results of the two-vector modulated model predictive control method for TPFS inverter
为了降低常规模型预测控制的电流谐波，本文以两电平电压源逆变器为研究对象，提出了一种双矢量调制模型预测控制策略，并结合电压矢量的空间位置关系，首次从理论上证明了其有效性，从而为调制模型预测控制理论的应用提供了坚实的理论基础。同时，本文的进一步研究表明，所提双矢量调制模型预测控制还可以应用于其他类型的逆变器，如TPFS逆变器。此外，研究结果表明，本文所提方法与常规双矢量法具有类似的动稳态控制性能，且具有计算量低等优点。
在今后的研究工作中，还需要进一步深入研究本文所提双矢量调制模型预测控制的推广应用，使其可以应用到更多类型的逆变器中，如多电平逆变器，并从理论上证明其有效性。
参考文献
[1] Li Yu, Zhang Zhenbing, Li Kejun, et al. Predictive current control for voltage source inverters considering dead-time effect[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(1): 35-42.
[2] 万晓凤, 詹子录, 丁小华, 等. 基于虚拟同步发电机的多逆变器并联改进控制策略[J].电机与控制学报, 2020, 24(2): 118-127. Wan Xiaofeng, Zhan Zilu, Ding Xiaohua, et al. Improved control strategy of multi-inverter parallel based on virtual synchronous generator[J]. Electric Machines and Control, 2020, 24(2): 118-127.
[3] 谢文浩, 王建赜, 纪延超, 等. 一种LCL型并网逆变器的复合阻抗重塑方法[J].电机与控制学报, 2018, 22(10): 35-42. Xie Wenhao, Wang Jianze, Ji Yanchao, et al. Composite impedance reshaping method for LCL-type grid-tied inverter[J]. Electric Machines and Control, 2018, 22(10): 35-42.
[4] 杨超颖, 王金浩, 杨赟磊, 等. 不对称故障条件下并网光伏逆变器峰值电流抑制策略[J]. 电力系统保护与控制, 2018, 46(16): 103-111. Yang Chaoying, Wang Jinhao, Yang Yunlei, et al. Control strategy to suppress peak current for grid-connected photovoltaic inverter under ubbalanced voltage sags[J]. Power System Protection and Control, 2018, 46(16): 103-111.
[5] 晁凯云, 苗世洪, 刘子文, 等. 基于虚拟同步机控制的微电网稳定性分析[J]. 电力系统保护与控制, 2019, 47(3): 9-16. Chao Kaiyun, Miao Shihong, Liu Ziwen, et al. Stability analysis of microgrid based on virtual synchronous generator control[J]. Power System Protection and Control, 2019, 47(3): 9-16.
[6] Rodriguez J, Pontt J, Silva C A, et al. Predictive current control of a voltage source inverter[J]. IEEE Transactions on Industrial Electronics, 2007, 54(1): 495-503.
[7] 张永昌，杨海涛, 魏香龙, 等. 基于快速矢量选择的永磁同步电机模型预测控制[J]. 电工技术学报, 2016, 31(6): 66-73. Zhang Yongchang, Yang Haitao, Wei Xianglong, et al. Model predictive control of permanent magnet synchronous motors based on fast vector selection[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 66-73.
[8] Xia Changliang, Liu Tao, Shi Tingna, et al. A simplified finite-control-set model-predictive control for power converters[J]. IEEE Transactions on Industrial Informatics, 2014, 10(2): 991-1002.
[9] 姚骏, 刘瑞阔, 尹萧, 等. 永磁同步电机三矢量低开关频率模型预测控制研究[J]. 电工技术学报, 2018, 33(13): 2935-2945. Yao Jun, Liu Ruikuo, Yin Xiao, et al. Research on 3-vector model predictive control with low switching frequency of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 2935-2945.
[10] Liu Xing, Wang Dan, Peng Zhouhua. Cascade-free fuzzy finite-control-set model predictive control for nested neutral point-clamped converters with low switching frequency[J]. IEEE Transactions on Control Systems Technology, 2019, 27(5): 2237-2244.
[11] 郭磊磊, 金楠, 李琰琰, 等. 电压源逆变器虚拟矢量模型预测共模电压抑制方法[J]. 电工技术学报, 2020, 35(4): 839-849. Guo Leilei, Jin Nan, Li Yanyan, et al. Virtual vector based model predictive common-mode voltage reduction method for voltage source inverters[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 839-849.
[12] 陈素华. 有限集预测控制减少三相电压源逆变器共模漏电流方法[J]. 电力系统保护与控制, 2016, 44(22): 136-141. Chen Suhua. Finite set control model predictive control method to reduce common-mode leakage for three-phase voltage source inverter[J]. Power System Protection and Control, 2016, 44(22): 136-141.
[13] Song Zhan, Tian Yanjun, Chen Wei, et al. Predictive duty cycle control of three-phase active-front-end rectifiers[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 698-710.
[14] 云献睿, 周肖飞, 何凤有, 等. 基于电压误差判断的PMSM双矢量模型预测控制[J]. 电力电子技术, 2019, 53(1): 11-13. Yun Xianrui, Zhou Xiaofei, He Fengyou, et al. PMSM dual vector model predictive control based on voltage error judgment[J]. Power Electronics, 2019, 53(1): 11-13.
[15] Zhang Yongchang, Peng Yubin, Yang Haitao. Performance improvement of two-vectors-based model predictive control of PWM rectifier[J]. IEEE Transactions on Power Electronics, 2016, 31(8): 6016-6030.
[16] 徐艳平, 张保程, 周钦. 永磁同步电机双矢量模型预测电流控制[J]. 电工技术学报, 2017, 32(20): 222- 230. Xu Yanping, Zhang Baocheng, Zhou Qin. Two-vector based model predictive current control for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 222-230.
[17] 兰志勇, 王波, 徐琛, 等. 永磁同步电机新型三矢量模型预测电流控制[J]. 中国电机工程学报, 2018, 38(增刊1): 243-249. Lan Zhiyong, Wang Bo, Xu Chen, et al. A novel three-vector model predictive current control for permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2018, 38(S1): 243-249.
[18] 杨兴武, 牛梦娇, 李豪, 等. 基于开关状态函数计算的改进模型预测控制[J]. 电工技术学报, 2018, 33(20): 4834-4844. Yang Xingwu, Niu Mengjiao, Li Hao, et al. Improved model predictive control based on switching state function calculation[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4834-4844.
[19] 陈炜, 曾思珂, 张国政, 等. 永磁同步电机改进型三矢量模型预测转矩控制[J]. 电工技术学报, 2018, 33(增刊2): 420-426. Chen Wei, Zeng Sike, Zhang Guozheng, et al. Improved three-vector model predictive torque control of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 420-426.
[20] 丁雄, 林国庆. 三相并网逆变器的改进模型预测控制研究[J]. 电气技术, 2020, 21(3): 16-21. Ding Xiong, Lin Guoqing. Research on three-phase grid-connected inverter based on discrete space vector model predictive control[J]. Electrical Engineering, 2020, 21(3): 16-21.
[21] 徐艳平, 王极兵, 张保程, 等. 永磁同步电机三矢量模型预测电流控制[J]. 电工技术学报, 2018, 33(5): 980-988. Xu Yanping, Wang Jibing, Zhang Baocheng, et al. Three-vector-based model predictive current control for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 980-988.
[22] Yeoh S, Yang T, Tarisciotti L, et al. Permanent-magnet machine- based starter-generator system with modulated model predictive control[J]. IEEE Transactions on Transportation Electrification, 2017, 3(4): 878-890.
[23] Tarisciotti L, Zanchetta P, Watson A, et al. Modulated model predictive control for a three-phase active rectifier[J]. IEEE Transactions on Industry Applications, 2015, 51(2): 1610-1620.
[24] Zeng Zhiyong, Zhu Chong, Jin Xiaoliang, et al. Hybrid space vector modulation strategy for torque ripple minimization in three-phase four-switch inverter-fed PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2017, 64(3): 2122-2134.
Two-Vector-Based Modulated Model Predictive Control Method for 2-Level Voltage Source Inverters: Theoretical Analysis, Experimental Verification and Extension
Abstract In recent years, model predictive control (MPC) has been widely used to control 2-level voltage source inverters due to its adaptability and robustness. However, in conventional MPC system, only one voltage vector is used per control cycle, resulting in larger current harmonics. To suppress the current harmonics, a two-vector-based modulated MPC strategy is proposed. First, two voltage vectors are used simultaneously to track the target vector in each control period, and the operating time of each voltage vector is calculated based on the principle of modulated MPC. Second, the reference voltage is calculated according to the principle of dead-beat control, and based on the position of the reference voltage only three voltage vector combinations are selected and evaluated online per control period to get the optimal voltage vector combination. Finally, the effectiveness of the proposed two-vector-based modulated MPC strategy is verified by detailed theoretical analysis for the first time. Additionally, the study in this paper also shows that the proposed strategy can be utilized to control other types of inverters, such as three-phase four-switch inverter. Meanwhile, the method proposed in this paper can obtain a similar control performance with the conventional two-vector method, with the advantages of less computation, etc. Theoretical analysis and experimental results verify the effectiveness of the proposed method.
keywords：Voltage source inverters, two-vector, modulated model predictive control, effectiveness verification
中图分类号：TM464
DOI: 10.19595/j.cnki.1000-6753.tces.200309
国家自然科学基金（51607159，51707176）、河南省青年人才托举工程项目（2019HYTP021）、河南省重点研发与推广专项(科技攻关)项目（202102210103）和河南省高等学校重点科研项目（18A470020，20A470011）资助。
收稿日期 2020-03-28
改稿日期 2020-06-24
郭磊磊 男，1987年生，博士，讲师，硕士生导师，主要研究方向为新能源并网发电技术，永磁同步电机驱动控制。E-mail: 2006guoleilei@163.com
金 楠 男，1982年生，博士，教授，硕士生导师，主要研究方向为电能变换可靠性和模型预测控制。E-mail: Jinnan@zzuli.edu.cn（通信作者）
（编辑 郭丽军）