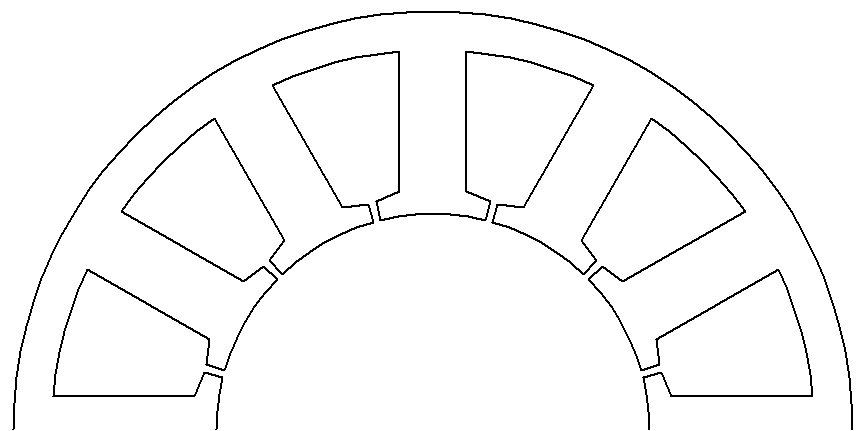
图1 双三相永磁容错电机定子
Fig.1 Stator of dual three-phase permanent magnet fault tolerant machine
摘要 为改善双三相永磁容错电机采用传统预测直接转矩控制(PDTC)时存在的权重系数整定困难、有限控制集元素数量多以及电压矢量滚动寻优时间长等问题,该文提出一种基于权重系数消除和有限控制集优化的快速PDTC。首先,根据无差拍直接转矩磁链控制思想,将评价函数中不同量纲的变量等效为相同量纲的电压矢量,消除了定子磁链权重系数;其次,基于永磁容错电机大电感的特点,提出仅选取零序电压为零的电压矢量或者所合成虚拟电压矢量作为有限控制集元素,不仅消除了零序权重系数,还将有限控制集中的元素从64个减少到19个,同时改善了零序电流的抑制效果;最后设计了一种可一次选出最优电压矢量的方法,避免了滚动寻优带来的计算负担。实验结果验证了所提PDTC的可行性和有效性。
关键词:双三相永磁容错电机 预测直接转矩控制(PDTC) 权重系数消除 有限控制集优化 快速电压矢量选择
双三相永磁电机属于多相永磁电机的一种,兼具永磁电机转矩平稳性好、转矩密度高以及多相电机控制自由度多、容错性能强的双重优势,在航空航天驱动及电力机车牵引等领域备受关注[1],这些场合对电机的容错能力要求较高,然而普通双三相永磁电机不具备短路容错能力。为使电机具备该能力,需将双三相永磁电机的定子槽设计为如图1所示的形状。图1电机槽口深而窄,通过大幅度地增大相绕组漏感来提升电机自感,以抑制短路电流;并且采用隔齿绕制各相绕组形式,实现磁隔离、热隔离及物理隔离[2],这类电机称为双三相永磁容错电机。

图1 双三相永磁容错电机定子
Fig.1 Stator of dual three-phase permanent magnet fault tolerant machine
此外,上述场合通常对电机的电磁转矩控制要求较高[3]。传统直接转矩控制(Direct Torque Control, DTC)因为其快速的转矩、磁链控制能力,可作为双三相永磁容错电机具有竞争力的驱动方案。但其缺点是采用了离线计算的最优开关表,未考虑不同转速、负载的影响,导致转矩脉动一般较大,同时双三相电机开关矢量多,最优开关矢量表构建困难,如果考虑零序电流抑制,情况更加复杂。
目前已有众多文献致力于优化DTC的上述缺点,其中,将有限控制集预测控制与DTC相结合被证明是有效方案之一[4]。形成的有限控制集预测直接转矩控制(Predictive Direct Torque Control, PDTC)不但保留了DTC的快速响应性,还在选择开关状态时考虑了转速、负载及零序分量的影响,同时仅需构建形式较为简单的评价函数,无需构建最优开关矢量表。但应用于双三相永磁容错电机时,PDTC仍然存在几点问题。
一是权重系数选取复杂。由于同时兼顾基波平面及零序平面多个不同变量的控制,需要引入多个权重系数,双三相永磁容错电机的权重系数整定更加困难[5]。对于权重系数的处理,文献[6]提出了基于模糊控制的权重系数在线整定方案,针对电机的不同运行状态,实时计算相应的权重系数;文献[7]则构造了二次型价值函数,成功地将多个权重系数整合成一个权重系数的求解。但这两种方案会进一步增加控制芯片的计算压力。因此,越来越多的学者主张消除权重系数,如文献[8-9]将对转矩和磁链的控制等效为对定子磁链的控制,由于等效控制目标的量纲相同,不再需要权重系数;文献[10]将评价函数设计为对转矩的控制;文献[11]则直接采用了电流预测控制,构建时只包含电流,也避免了权重系数的存在。但文献[8]不适用于凸极永磁电机,文献[9, 11]没有涉及零序电流的抑制。
二是双三相永磁容错电机有限控制集中元素数量较多。相比于三相电机只有8个电压矢量,双三相电机采用双三相逆变器驱动时,电压矢量增至64个,导致PDTC计算负担较重。文献[12]只选取了6个最大矢量进行合成,减少了有限控制集元素数量。文献[13]在六相异步电机驱动系统中采用了部分矢量合成的虚拟矢量,实现了减小计算负担的目的,但在一定程度上影响了电机性能。因此文献[5]在文献[13]基础上增加了虚拟矢量的个数,改善了电机转矩性能。而文献[14]为了抑制共模电压,选取了共模电压为零的矢量,矢量数量减少,但是降低了母线电压利用率。上述文献中的方案虽然精减了电压矢量,却牺牲了电机驱动系统的部分性能。
三是滚动优化循环次数多,计算负担大。预测控制采用了将有限控制集中元素滚动代入评价函数寻找最优值的方式,元素越多,滚动计算次数越多。通过扇区划分和对电压误差量的比较,文献[11]只需一次预测即可选出最优电压矢量;文献[15]通过划分区域优化了有限控制集,减少了满足条件的矢量,缩短了寻找最小价值函数值的时间。但文献[11, 15]未考虑零序电流的抑制。文献[8, 16]剔除了部分矢量,选择剩余的矢量建成了优化离线开关表,节省了计算时间,但仍然需要多次在线滚动计算,计算负担尚需进一步减小。
为解决上述问题,本文提出了一种基于权重系数消除和有限控制集优化的双三相永磁容错电机快速PDTC方法。首先,以数学模型更为一般的凸极式永磁电机为研究对象,利用无差拍直接转矩磁链控制思想,将预测变量等效为量纲一致的电压矢量,消除了定子磁链权重系数;其次,根据永磁容错电机漏感大的特点,仅选用零序电压为零的电压矢量或者合成虚拟电压矢量来抑制零序电流,消除了零序权重系数并优化了有限控制集中的元素;再次,提出了一种快速最优电压矢量选择方法。最后搭建了双三相永磁容错电机测试平台,实验结果表明所提策略有效可行。
双三相永磁容错电机驱动系统如图2所示。其中,ACE相和BDF相绕组负端分别连接成一个中性点N1和N2,A、B相之间相差60°,UDC为母线电压。参与机电能量转换的基波分量坐标系如图3所示,其中,A~F分别对应电机各相绕组轴线,αβ为两相静止坐标系,α轴与A相轴线位置重合,dq轴是与转子同步的两相旋转坐标系,其中,d轴与α轴之间电角度差为θr,xy为定子磁链定向坐标系,x与d轴夹角为电角度δ,即转矩角;与α轴夹角为电角度θs。另外,ψr、ψs、is、us分别为转子、定子磁链矢量、定子电流和电压矢量,其在不同轴上的投影分别用对应的下标表示,ωr为转子旋转角速度。
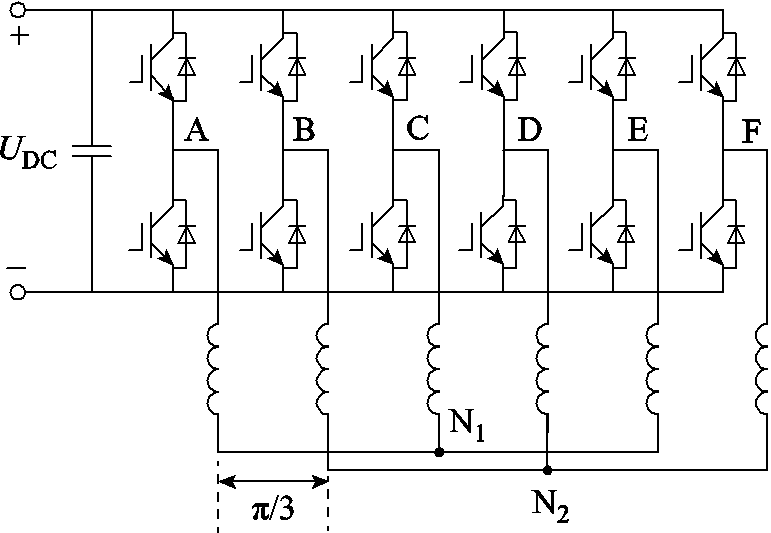
图2 双三相永磁容错电机驱动系统
Fig.2 Dual three-phase permanent magnet fault tolerant machine drive system
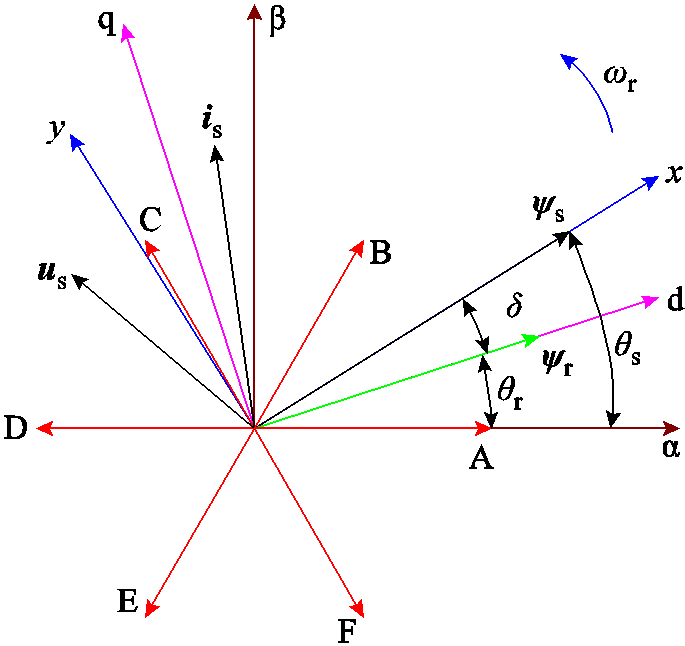
图3 基波分量坐标系
Fig.3 Coordinate definition of fundamental components
为了实现双三相永磁容错电机的解耦,根据矢量空间解耦理论推导得到解耦矩阵如式(1)所示[12]。矩阵的前两行对应参与能量转换的αβ轴分量,除此之外,还有4个零序分量,分别表示为z1~z4,这些分量不参与机电能量转换,但是会增加电机相电流的谐波含量和损耗,因此希望将其控制为0。
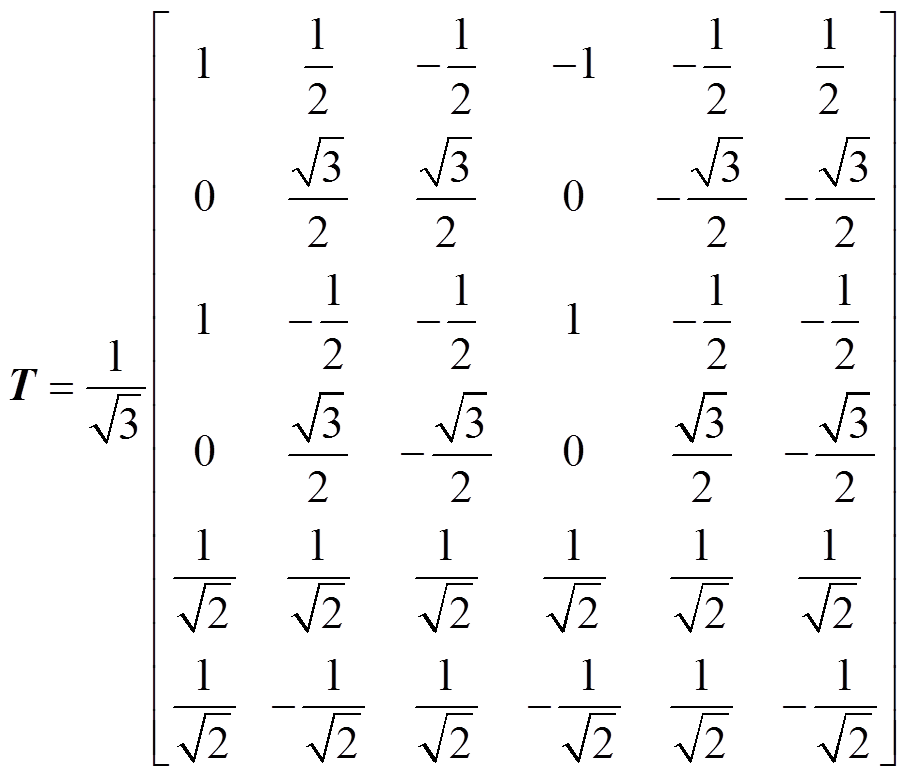 (1)
(1)dq轴下电机的磁链、电压和转矩方程分别为
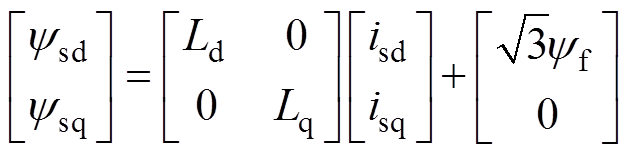 (2)
(2)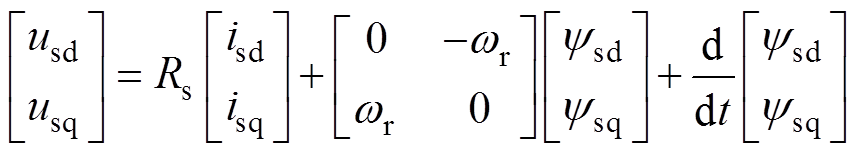 (3)
(3)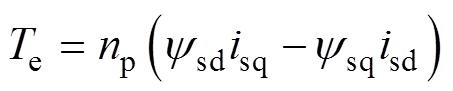 (4)
(4)式中,Ld、Lq分别为d、q轴电感;ψf为转子磁链;np为电机极对数。
零序分量的磁链和电压方程分别为
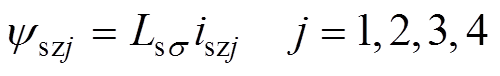 (5)
(5)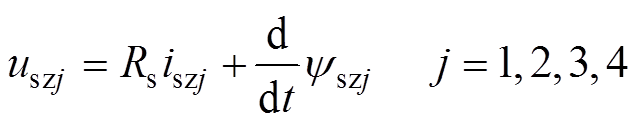 (6)
(6)式中,Lsσ为电机相绕组漏感;Rs为定子相绕组电阻;iszj、ψszj分别为零序电流和磁链分量,由于双三相电机采用双中性点的连接模式,ACE相和BDF相的相电流之和为零,由式(1)的最后两行可知,isz3和isz4自然为0,故只需要考虑将isz1和isz2控制为0。
按照传统PDTC思想,除对电机的转矩、磁链进行控制,根据1.1节的分析可知,还需要加入对isz1和isz2的抑制。因此评价函数为[5]
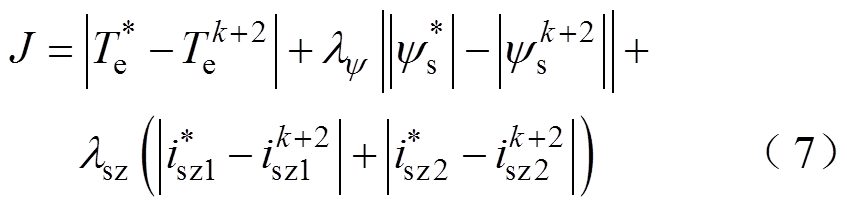
式中,λψ和λsz分别为定子磁链和零序权重系数。
当图1中六个桥臂分别取不同值时,可产生64个电压矢量,按照A~F从高到低进行二进制计数,它们在αβ平面及z1z2平面的电压分量分别如图4和图5所示。式(7)中,k+2时刻各电压开关量对应的转矩、磁链可根据当前时刻的状态量、式(2)~式(4)、图4及其他相关电机方程进行预测;而零序电流则根据式(5)、式(6)和图5进行预测。
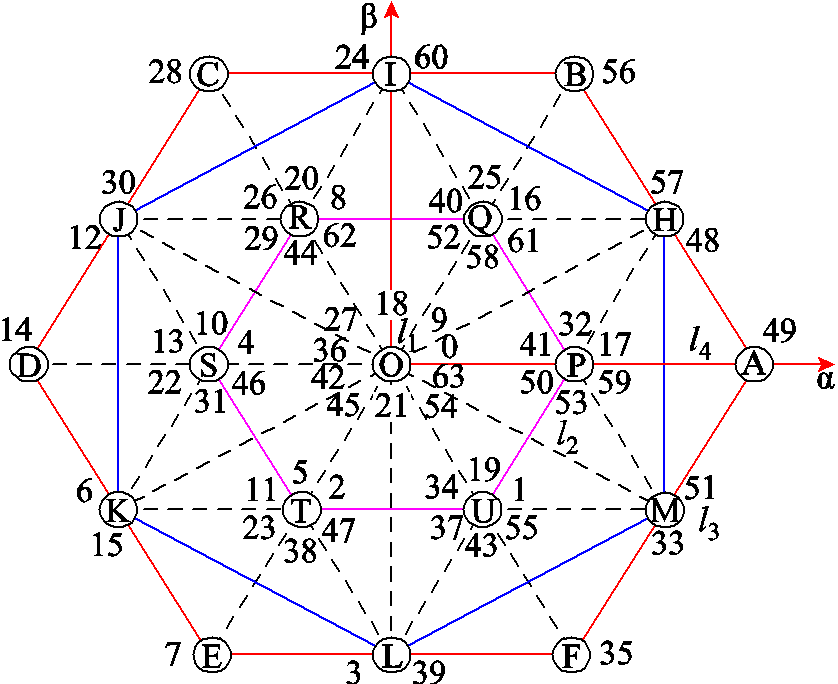
图4 αβ平面定子电压矢量图
Fig.4 The stator voltage vector on αβ plane
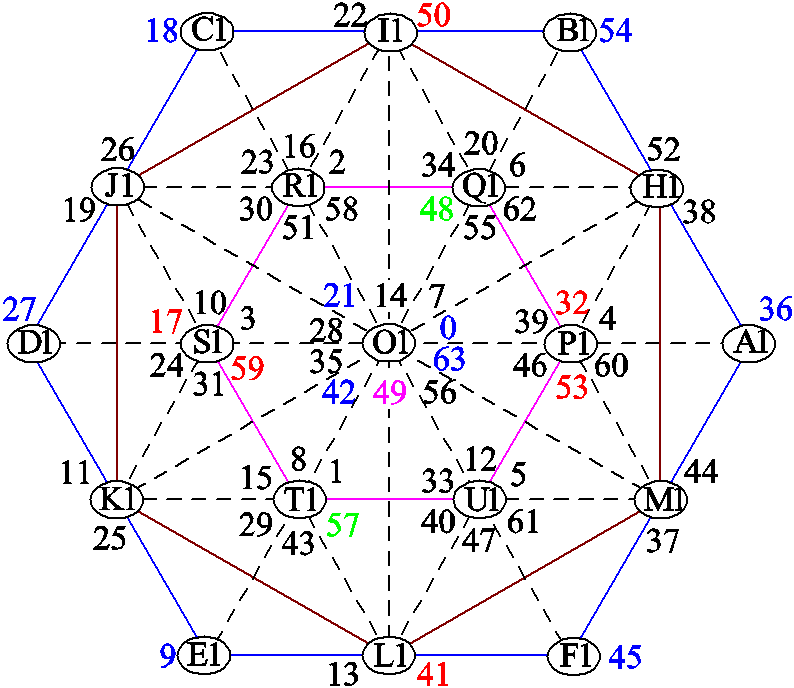
图5 z1z2平面定子电压矢量图
Fig.5 The stator voltage vector on z1z2 plane
传统PDTC虽然可以实现转矩、磁链及零序电流的控制,但存在问题有:①评价函数中不同量纲的变量较多,需要引入多个权重系数,使得本就复杂的权重系数选取更加困难;②有限控制集中元素数量较多,计算量大;③滚动寻优时循环次数多,计算负担重。为解决上述问题,本文提出了一种基于权重系数消除、有限控制集优化和快速电压矢量选择的PDTC。其中,1.3.1节给出了所提权重系数消除方案的第一步;1.3.2节给出了所提权重系数消除方案的第二步和有限控制集优化方案;1.3.3节给出了所提快速电压矢量选择方案。
1.3.1 定子磁链权重系数λψ消除
本节主要介绍所提权重系数消除方案的第一步,即优化评价函数中的评价变量,将不同量纲的变量等效为相同量纲的变量,达到消除λψ的目的。
将式(2)代入式(4)可以得到
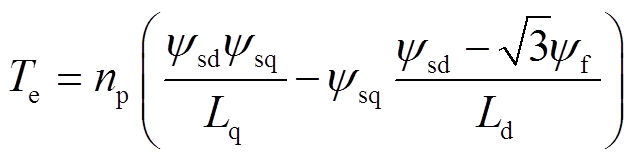 (8)
(8)而
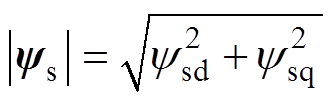 (9)
(9)因此,转矩和磁链均可表示为只与变量ψsd和ψsq相关的表达式,也就是说控制好d轴、q轴磁链,就等效于控制好了磁链幅值和转矩。而根据式(5),零序电流与零序磁链成正比,因此控制好零序磁链也等效于控制好了零序电流,故评价函数式(7)可等效为

式(10)中,评价函数中所有的量纲均为磁链,故只需要在dq轴磁链和零序磁链间引入一个零序权重系数λsz即可,从而消除了λψ,避免了多个权重系数的存在。式(10)的具有实现过程如下。
1)预测每个电压矢量在k+2时刻的d、q轴磁链
将式(3)离散化可知k+1时刻的d、q轴磁链为
 (11)
(11)式中,Ts为控制周期,且
 (12)
(12)通过式(2)得到k+1时刻的d、q轴电流分别为
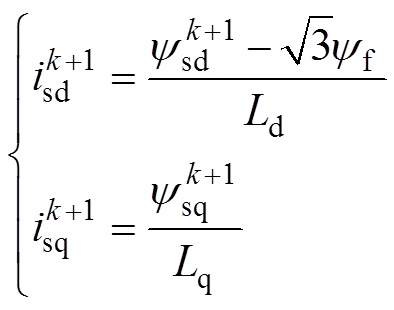 (13)
(13)类似式(11),推导得k+2时刻d、q轴磁链为
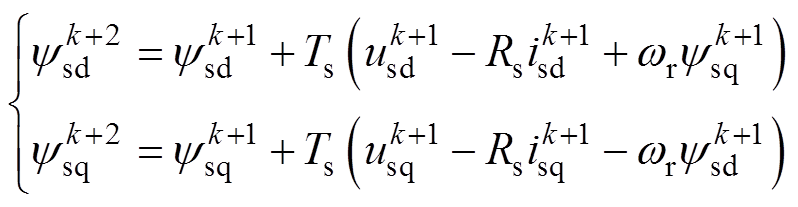 (14)
(14)2)预测每个电压矢量在k+2时刻的零序磁链
根据式(5)、式(6)得到k+1时刻零序实际磁链为
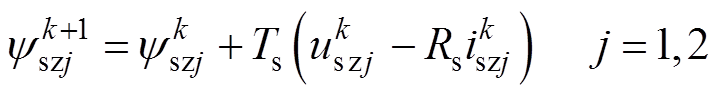 (15)
(15)将式(15)代入式(5)得到此时的零序电流为
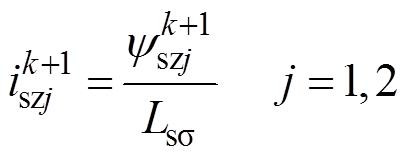 (16)
(16)类似式(15),得到k+2时刻零序实际磁链为
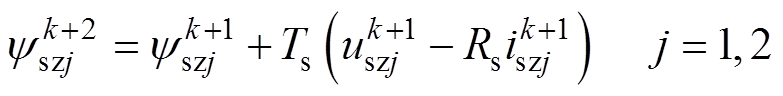 (17)
(17)3)求解d、q轴参考磁链
相比于k+2时刻d、q轴磁链预测值和零序磁链预测值容易求得,d、q轴磁链参考值却难以求得,这里给出了d、q轴参考磁链的求解。
根据图3可得
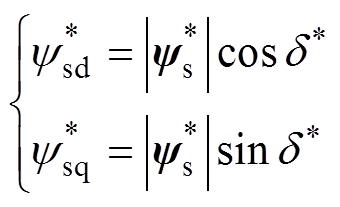 (18)
(18)故只需求出转矩角就能准确跟踪d、q轴磁链,而转矩角的表达式为[17]
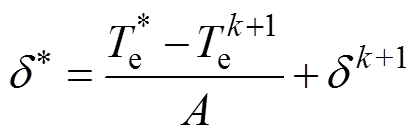 (19)
(19)其中
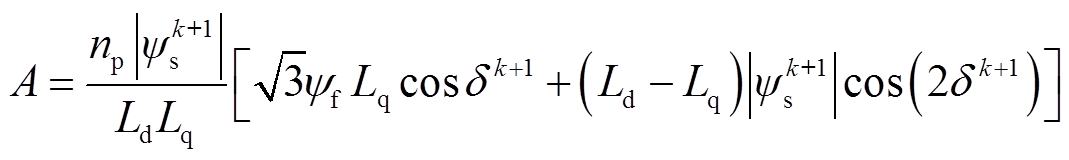 (20)
(20)而k+1时刻转矩、磁链幅值和转矩角分别为
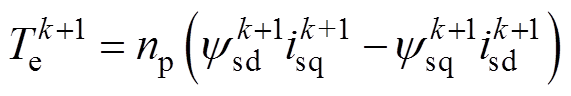 (21)
(21)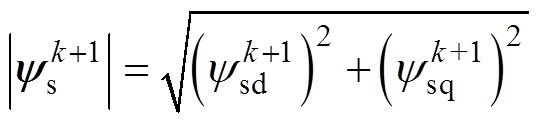 (22)
(22) (23)
(23)4)零序磁链参考值
根据式(5),零序电流与零序磁链成正比,故欲将零序电流控制为0,则零序磁链参考值应为0。
5)将各矢量对应的量代入评价函数滚动寻优
至此为式(10)的预测过程,其在消除λψ的过程中,考虑了电机凸极效应和电阻的影响,适用性更强。但缺点是:除预测每个开关矢量在下两个时刻对应的d、q轴磁链和零序磁链,还需要计算dq轴磁链参考值,计算负担重。而如果能将磁链预测转变为电压矢量的预测,然后直接与图4和图5中的电压矢量进行对比,将更加直接简便。具体过程如下。
对于基波平面,这里采用xy轴坐标系作为中间变量,根据无差拍直接转矩磁链控制思想得
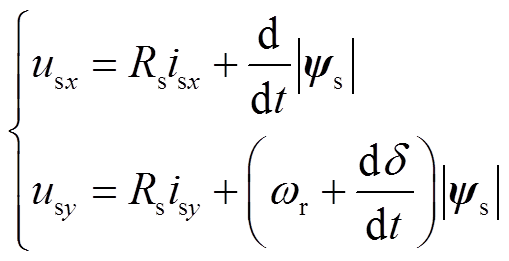 (24)
(24)离散化后得
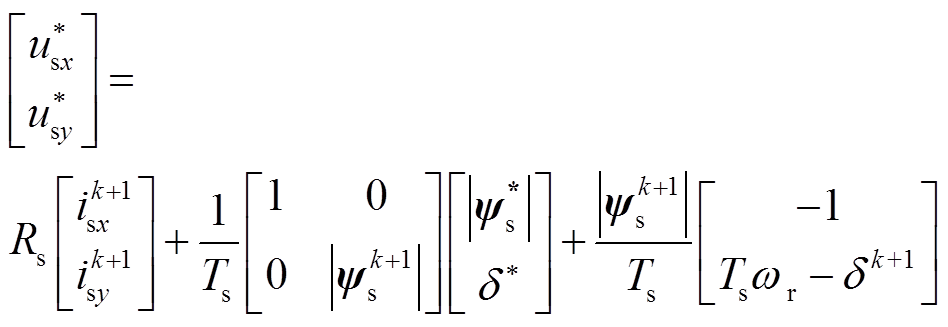 (25)
(25)其中
 (26)
(26)将式(11)~式(13)及式(19)~式(23)代入式(25)即可求出xy轴参考电压值,根据x、y轴电压与α、β轴电压的关系,求出α、β轴参考电压为
 (27)
(27)而αβ轴实际电压可根据图4得到。
对于零序平面,由式(5)与式(6)得
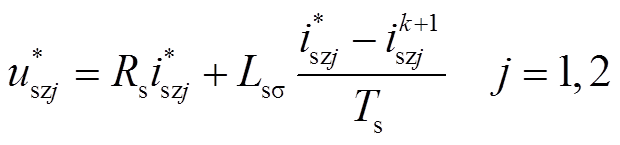 (28)
(28)式(28)中,目标零序电流为零;实际零序电压可由式(1)和图5得到。根据上述分析,设计评价函数为
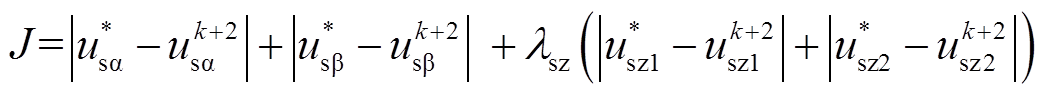 (29)
(29)与式(7)相比,评价函数式(29)不仅完成了评价变量量纲的统一,还成功地将预测变量等效为更直接的电压量,从而消除了权重系数λψ,简化了评价过程、减轻了计算负担。
1.3.2 零序权重系数λsz消除以及有限控制集优化
式(29)虽然实现了评价函数的优化和定子磁链权重系数λψ的消除,但仍然存在的问题是:①零序权重系数λsz依旧存在,仍需要对其进行复杂的整定;②需要将64个电压矢量代入,进行在线滚动寻优,计算负担重。本节将致力于解决以上两个问题。
1.3.1节通过统一变量量纲实现了λψ的消除,但由于控制目标重要程度不同,导致无法消除λsz。而从式(28)可知,为使实际零序电流为零,需将零序电压参考值设为0;而如果实际零序电压平均值也为0,则式(29)中后两项恒等于零,λsz就可以消除。根据式(6)构建如图6所示的零序电流iszj(j=1,2)等效电路,电路中仅包含了零序电压、相电阻和漏感。由图6可知,仅需使uszj在一个控制周期中的平均值为0,即可满足上述要求,而要使uszj平均值为0,可直接选择零序电压为0的电压矢量或者通过电压矢量合成的方式获得。
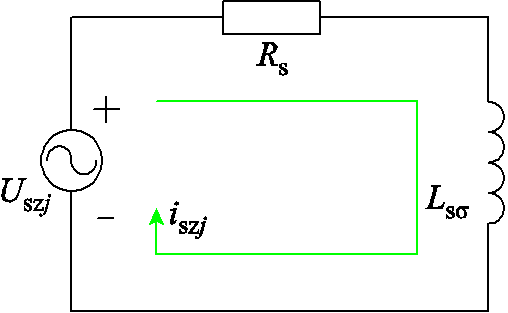
图6 零序电流等效电路
Fig.6 Equivalent circuit of zero-sequence current
具体方法为:在保证图4电压矢量图完整的前提下,在每个顶点上选取一个零序电压为零的电压矢量,或者两个零序电压方向相反的电压矢量合成零序电压为0的虚拟电压矢量,以抑制零序电流,从而消除λsz,此为权重系数消除方案的第二步。
文献[12]研究表明采用合成虚拟电压矢量时,死区及开关管的开通关断会产生不可控的电压矢量,虽然时间较短,伏秒积数值小,但由于普通电机零序电流环时间常数较小,故会产生较大的零序电流。而本文研究的是双三相永磁容错电机,大漏感导致其自感较大。正是由于这一特点,上述因素造成的零序电流数值较小,文献[12]所提的影响在本电机中无需考虑。因此双三相永磁容错电机可采用两矢量合成虚拟电压矢量的方法抑制零序电流。
同时基于上述分析,本文提出了双三相永磁容错电机的有限控制集优化方法。图4中虽然共有64个电压矢量,但是在αβ平面上只形成19种不同情况,按照幅值分为l1~l4四层。并且这19个点均存在零序电压为0的电压矢量,或者至少两个零序电压相反的电压矢量。其中,l1层只存在一个点,即O点,满足该点的矢量有10个,但是只有四个产生的零序电压为零,即编号为0、21、42、63的矢量,另外6个矢量产生的零序电压处于最外层,它们幅值相等,但两两方向相反(36与27,54与9,18与45分别相反);l2层存在6个点,即P、Q、R、S、T、U,每个点上有6个矢量,以P点为例,包含矢量17、32、41、50、53和59,矢量17、59的零序电压与32、53的零序电压大小相同,方向相反,矢量41与50的零序电压大小相等,方向相反;l3层也包括6个点,即H、I、J、K、L、M,每个点上有两个矢量,以H点为例,矢量48与57的零序电压大小相等,方向相反;而l4层同样有6个点,每个点上一个矢量,所有矢量产生的零序电压均为0。
根据上述分析,选出如图7所示的电压矢量组合作为有限控制集的元素,其中,l2和l3层所在六边形顶点上的电压矢量为两个实际矢量所合成的虚拟电压矢量。以顶点H上的电压矢量为例,其虚拟电压矢量由48和57合成,其余虚拟电压矢量的合成方式类似,这里不再赘述。
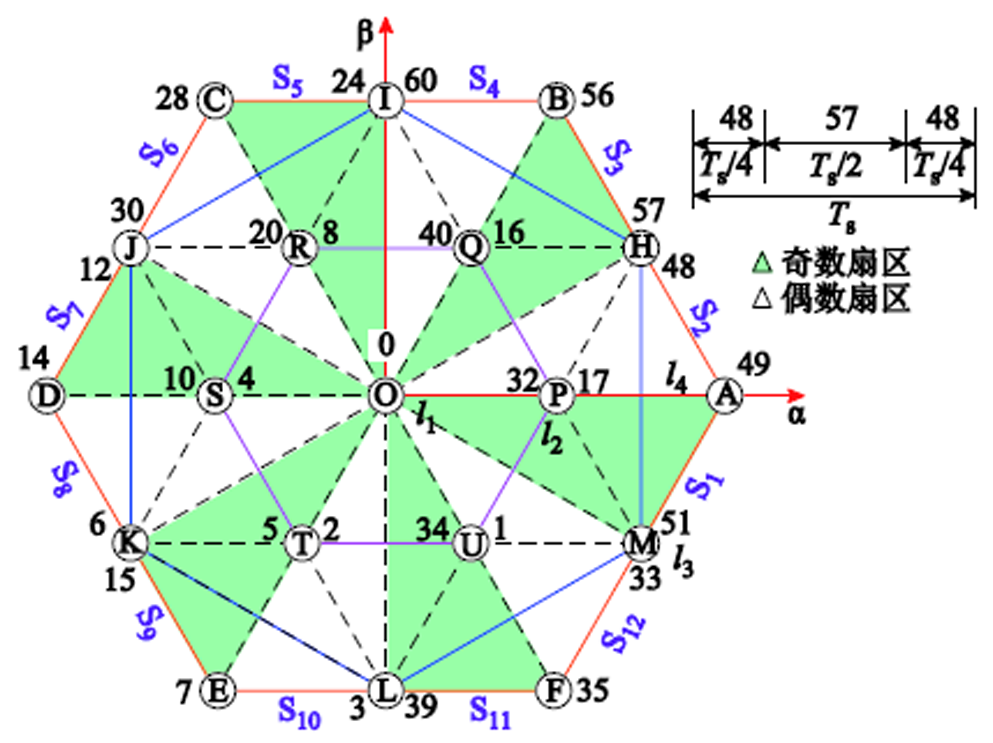
图7 优化后的αβ平面定子电压开关矢量图
Fig.7 The optimized stator voltage vector on αβ plane
采用本节所提的λsz消除和有限控制集优化方案后,只需要根据参考电压矢量的αβ分量在图7中的19个矢量组合中选择最适合的矢量组合即可同时实现转矩、磁链以及零序电流的控制,无需再遍历64个矢量,也可将评价函数简化为
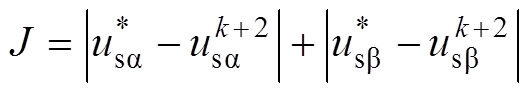 (30)
(30)与式(29)相比,式(30)中只存在αβ轴电压分量,为两个相同量纲、重要程度一致的变量,因此无需再引入任何权重系数,也就是说实现了权重系数的完全消除。此外,有限控制集的元素从64个缩减到19个,零序电流也可得到相应的抑制。
1.3.3 快速电压矢量选择
1.3.1节和1.3.2节所提策略解决了传统PDTC的前两个问题,但即使如此,在每个控制周期内仍然需要循环19次。为了进一步减小计算负担,本节提出了一种快速电压矢量选择方案。
如图7中所示,电压矢量被划分为12个扇区:S1~S12,每个扇区均包含l1~l4层一个点。如果按照扇区划分的方法,在确定参考电压矢量的扇区后,继续采用滚动寻优的方式寻找最优电压点,需要4次,仍然较多,本节旨在进一步减少寻优次数。
图7中,奇数扇区均可通过旋转的方式对应到扇区S1,而偶数扇区均可通过先旋转到扇区S2,再对称到扇区S1,因此所有扇区的寻优完全变换成了扇区S1的寻优。
再对扇区S1进行分区,如图8所示,两条虚线d1、d2将扇区1分为三个部分,其中,d1、d2分别为OP、PA的中垂线。参考电压终点落于d1左侧区域时,更靠近O点,此时应选择O点上的矢量;参考电压终点在d1与d2中间区域时更靠近P点或者M点,并且如果矢量在VX上侧,选择P点,在VX下侧,选择M点,其中VX为PM的中垂线;同样参考电压终点在d2右侧时,如果在XY上侧,选择A点,在XY下侧,选择M点,XY为AM的中垂线。因此不需要循环寻优,而只需要进行一次查找即可得到最优点,最后根据参考电压矢量实际所在扇区选出实际对应的点和矢量。
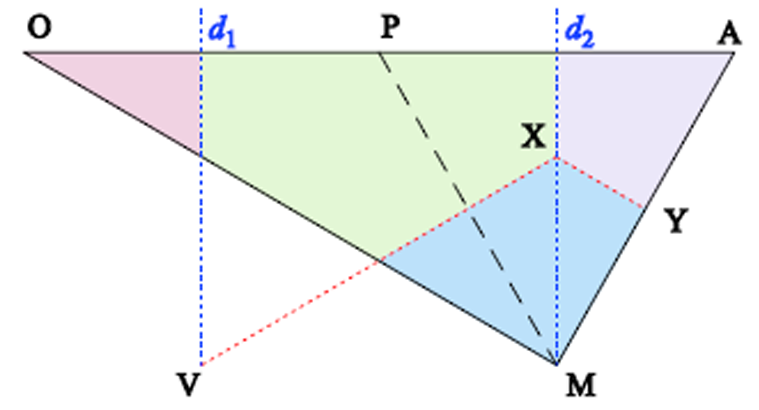
图8 快速电压矢量选择示意图
Fig.8 Schematic diagram of fast voltage vector selection
综上,快速电压矢量选择的步骤为:
1)根据参考电压矢量的αβ分量判断所处扇区。
2)求出参考电压矢量旋转到扇区S1时对应的αβ轴电压分量![]() 和
和![]() ,具体旋转关系式如下。
,具体旋转关系式如下。
当参考电压位于奇数扇区时(S为实际扇区)
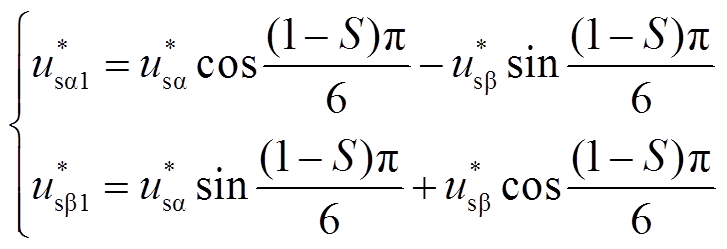 (31)
(31)参考电压位于偶数扇区时
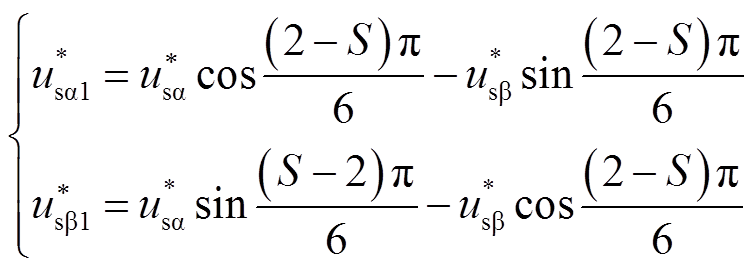 (32)
(32)3)根据转换后的αβ轴电压分量,确定其在扇区S1中对应的区域,选出最合适的点:其中,线d1、d2的α坐标分别为![]() 和
和![]() ;VX表达式为
;VX表达式为![]() ;XY表达式为
;XY表达式为![]() 。
。
(1) ,选择O点。
,选择O点。
(2) 且
且 ,选择P点。
,选择P点。
(3) 且
且![]() ,选择M点。
,选择M点。
(4)![]() 且
且![]() ,选择A点。
,选择A点。
(5)![]() 且
且![]() ,选择M点。
,选择M点。
4)根据实际所处扇区及所选点,选出实际对应点和矢量,具体关系见表1。
表1 扇区S1上的点与实际点和矢量的对应关系
Tab.1 The relationship between actual points and voltage vectors and points in S1
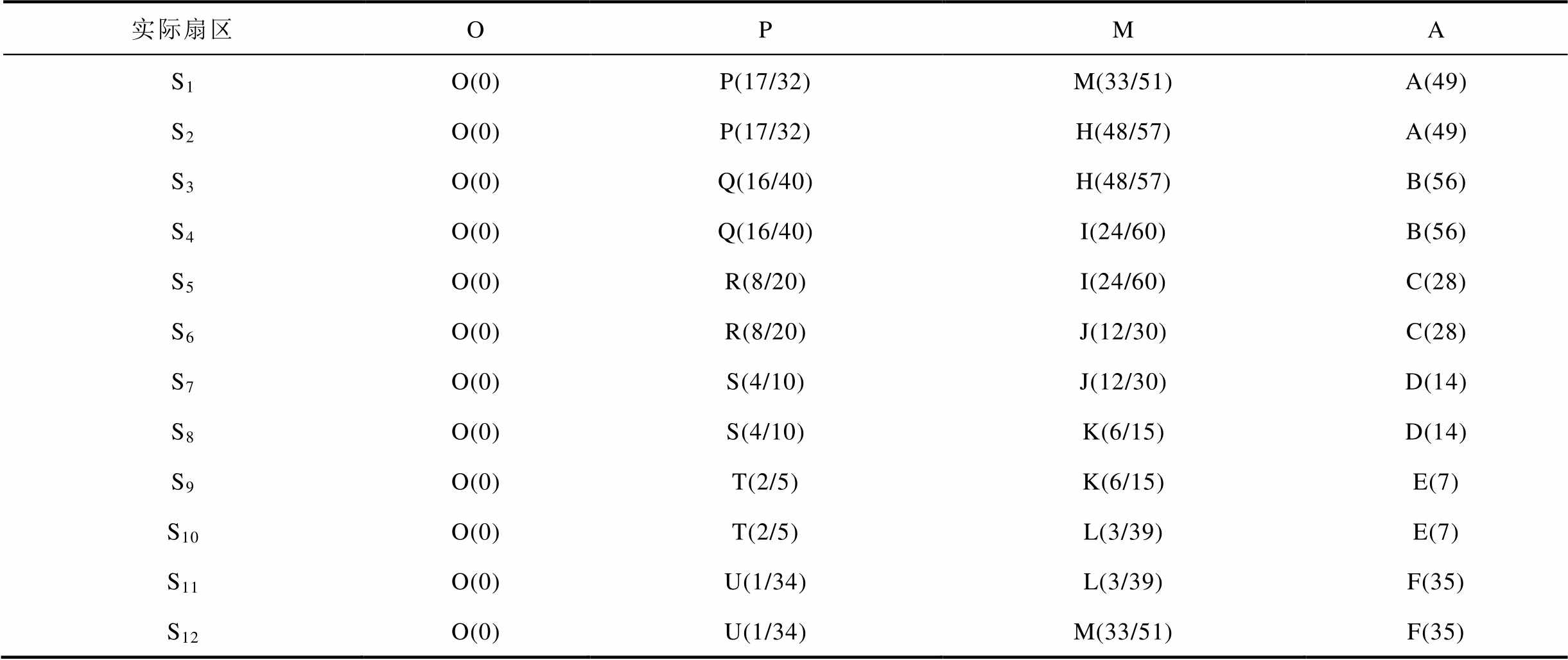
实际扇区OPMA S1O(0)P(17/32)M(33/51)A(49) S2O(0)P(17/32)H(48/57)A(49) S3O(0)Q(16/40)H(48/57)B(56) S4O(0)Q(16/40)I(24/60)B(56) S5O(0)R(8/20)I(24/60)C(28) S6O(0)R(8/20)J(12/30)C(28) S7O(0)S(4/10)J(12/30)D(14) S8O(0)S(4/10)K(6/15)D(14) S9O(0)T(2/5)K(6/15)E(7) S10O(0)T(2/5)L(3/39)E(7) S11O(0)U(1/34)L(3/39)F(35) S12O(0)U(1/34)M(33/51)F(35)
所提双三相永磁容错电机PDTC框图如图9所示。通过检测到的k时刻电流,坐标变换后代入式(2)中,计算得到k时刻dq轴磁链;根据k时刻实施的开关状态,得到相应的dq轴电压,与角速度一起代入式(11)中进行延时补偿,预测k+1时刻dq轴磁链及其幅值,结合式(13)可得k+1时刻电流,以式(21)计算k+1时刻转矩,采用式(23)得到此时的转矩角。系统外环为转速闭环,速度调节后计算出目标转矩,将目标转矩、给定磁链幅值,k+1时刻转矩、磁链、电流和转矩角,转子位置、转速,代入式(25)~式(27)得到定子α轴、β轴定子参考电压;最后根据定子参考电压判断扇区,采用快速方案选择矢量,进行矢量合成,从而控制整个系统。
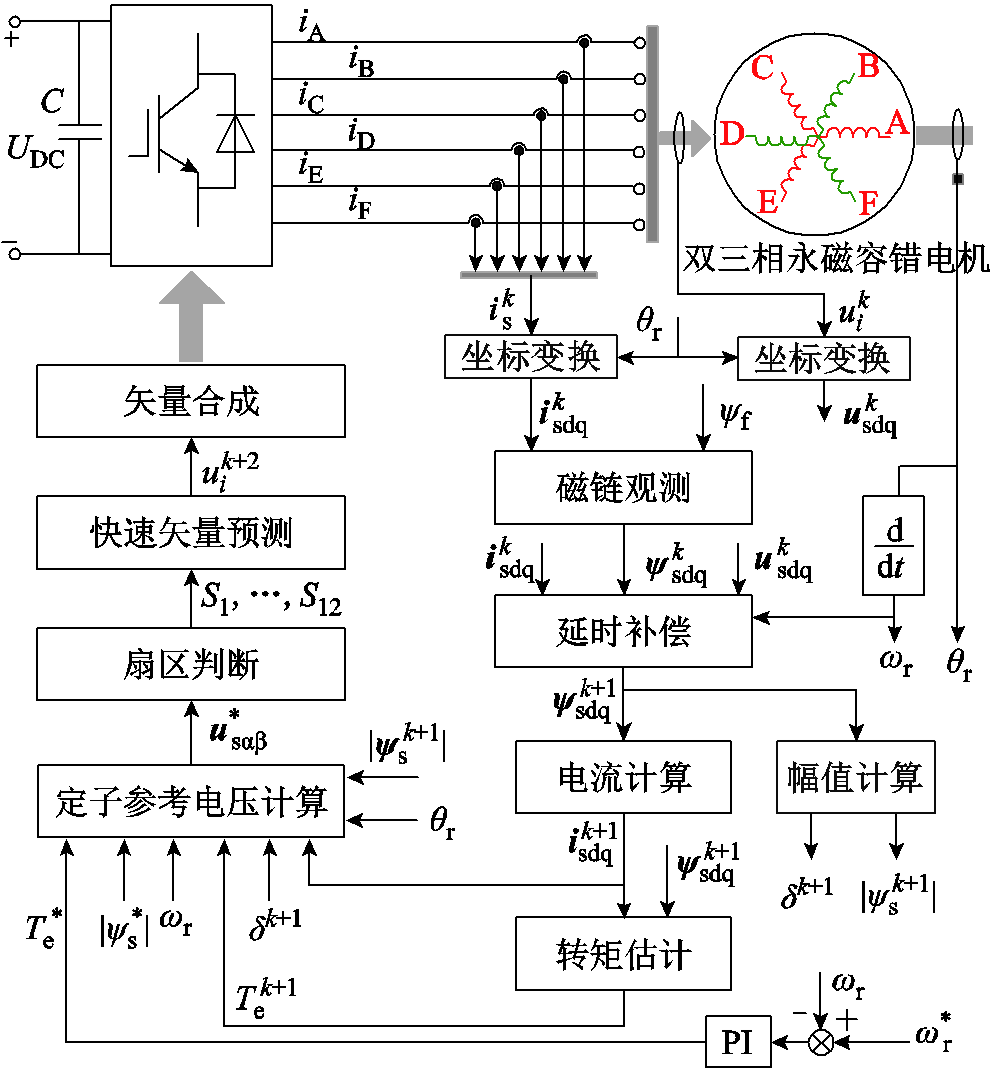
图9 双三相永磁容错电机PDTC驱动系统框图
Fig.9 PDTC of dual three-phase permanent magnet fault tolerant machine
本文所采用的双三相永磁容错电机部分参数见表2。基于该电机,搭建了如图10所示的实验平台。转子同轴安装了旋转变压器进行位置检测,负载电机为一异步电机,采用通用变频器驱动。所用双三相永磁容错电机的逆变器和控制单元分别如图10中③、④所示,逆变器直流母线电压100V,控制单元的控制周期为80μs。
表2 电机参数
Tab.2 Parameters of machine

参数数值 额定电流/ A7.8 额定转速/(r/min)1 000 极对数5 额定转矩/(N·m)5 相电阻/Ω0.21 d轴电感/mH2.078 q轴电感/mH2.151 转子磁链/Wb0.029 6

图10 实验平台
①—通用变频器 ②—加载平台 ③—逆变器 ④—控制单元
Fig.10 The experimental system
为充分研究系统的稳态性能,本文分别对具有所提定子磁链权重系数消除方案(以下称为PDTC1),具有所提定子磁链权重系数消除、零序权重系数消除和有限控制集优化方案(以下称为PDTC2)以及具有所提定子磁链权重系数消除、零序权重系数消除和有限控制集优化、快速电压矢量选择方案(以下称为PDTC3)的三种策略在200r/min、500r/min和1 000r/min下带额定负载进行了实验,三种策略的对比见表3。对于PDTC1,已根据λsz对转矩、磁链和零序电流的不同影响效果,为式(29)选择了合适的λsz。具体实验结果如图11~图13所示。
表3 三种控制策略对比
Tab.3 Comparisons of three control strategies

名称PDTC1PDTC2PDTC3 评价函数式(29)式(30)式(30) 权重系数个数100 有限控制集元素641919 寻优次数64191
上述实验结果显示,PDTC1在200r/min、500r/min和1 000r/min情况下均能实现对转矩转速的有效控制,表明所提定子磁链权重系数λψ消除方案可行有效,且稳定性较好。PDTC2的稳定运行则证明了所提零序权重系数消除方案的稳态性能,另外相比于PDTC1,PDTC2具有更小的零序电流,因此其相电流幅值更小,带载能力更强。同时对三种情况下的A相电流进行了谐波THD分析,结果如图13所示。同样,PDTC2的相电流谐波含量远低于PDTC1,说明所提选取零序电压为0的电压矢量或者合成虚拟电压矢量对抑制双三相永磁容错电机的零序电流作用明显。此外,PDTC2和PDTC3的转矩脉动小于PDTC1,则是因为式(30)相比于式(29)没有零序变量的预测,得到的αβ轴最优电压矢量更接近于αβ轴参考电压,对转矩磁链的控制效果更好,故转矩脉动更小。表4给出了三种策略的计算时长,PDTC2时长相比于PDTC1缩短了约23%,证明有限控制集优化策略可有效降低计算压力,而与PDTC2相比,PDTC3的零序电流、谐波含量与前者相当,但是计算时间比PDTC2又再次缩短了22%,体现了所提快速电压矢量选择方案的显著效果。
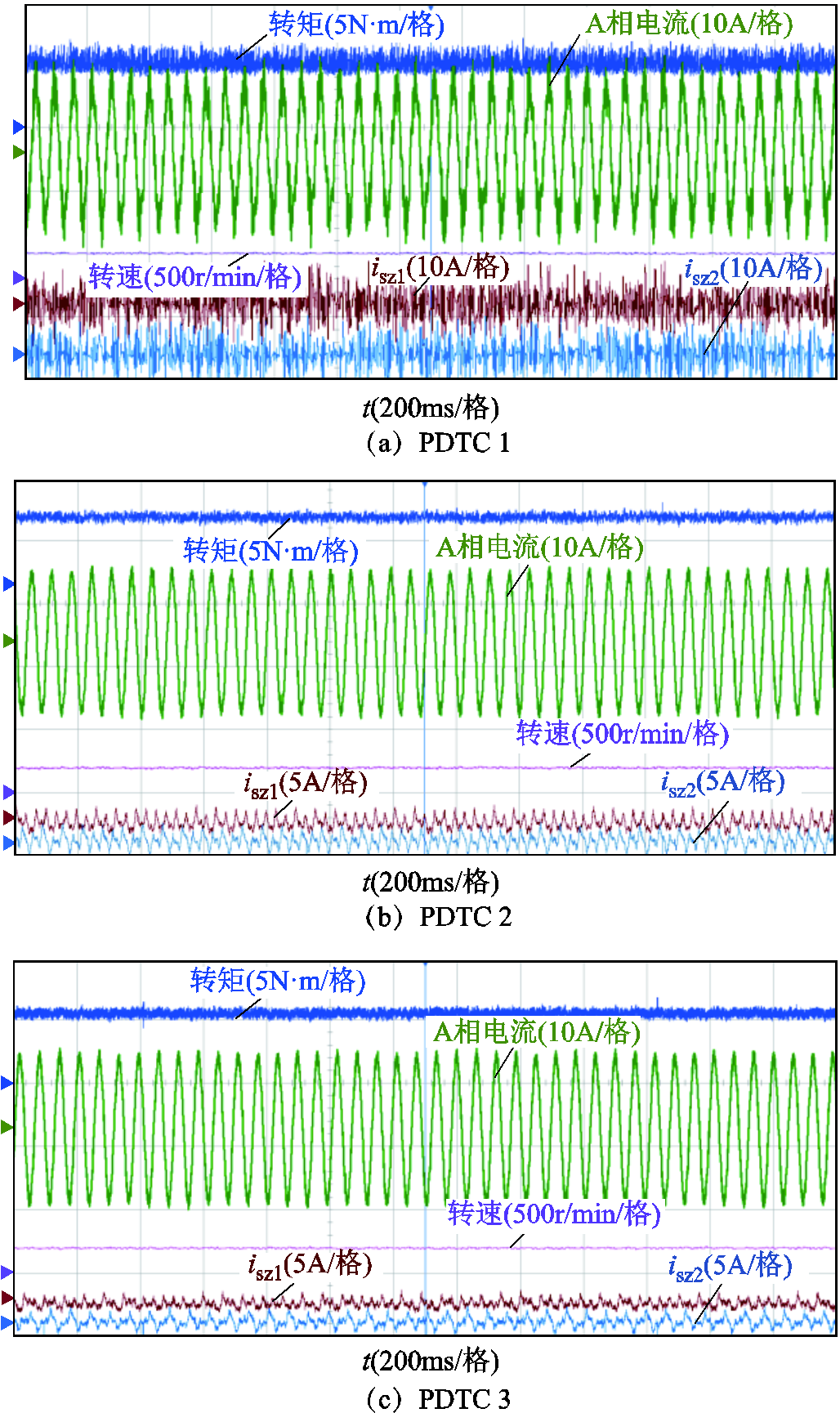
图11 200r/min稳态实验
Fig.11 Steady-state experiments at 200r/min
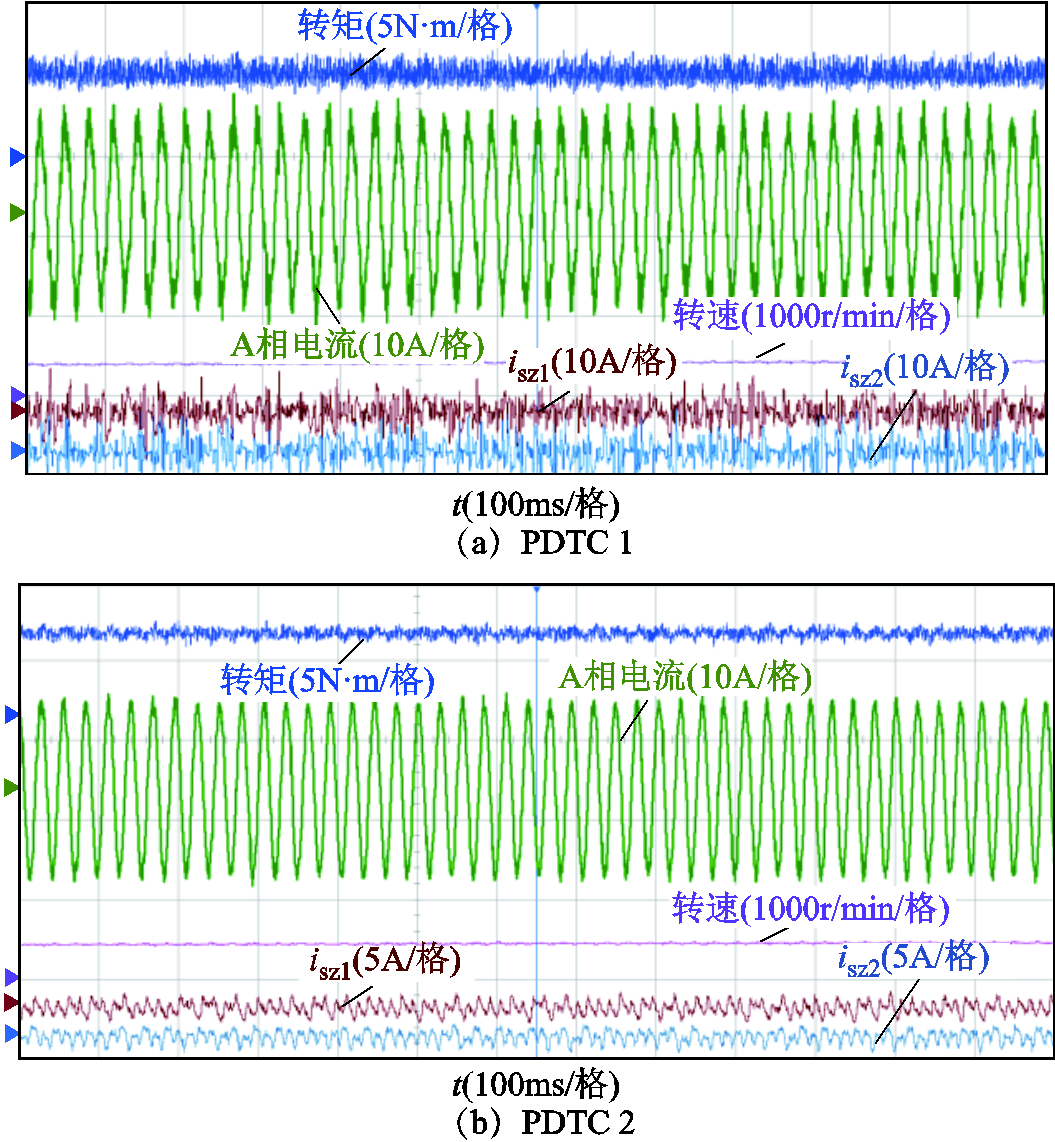
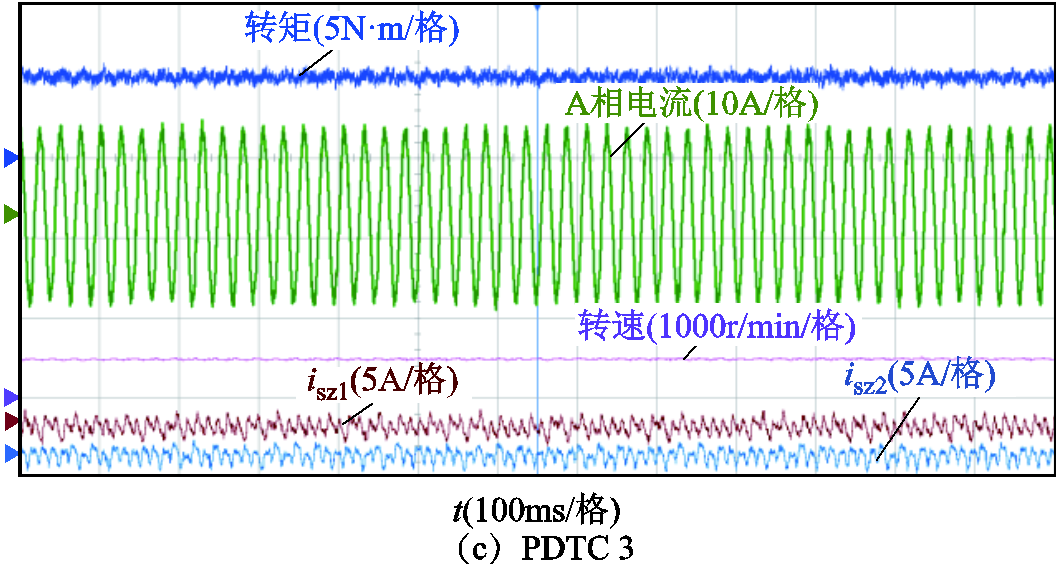
图12 500r/min稳态实验
Fig.12 Steady-state experiments at 500r/min

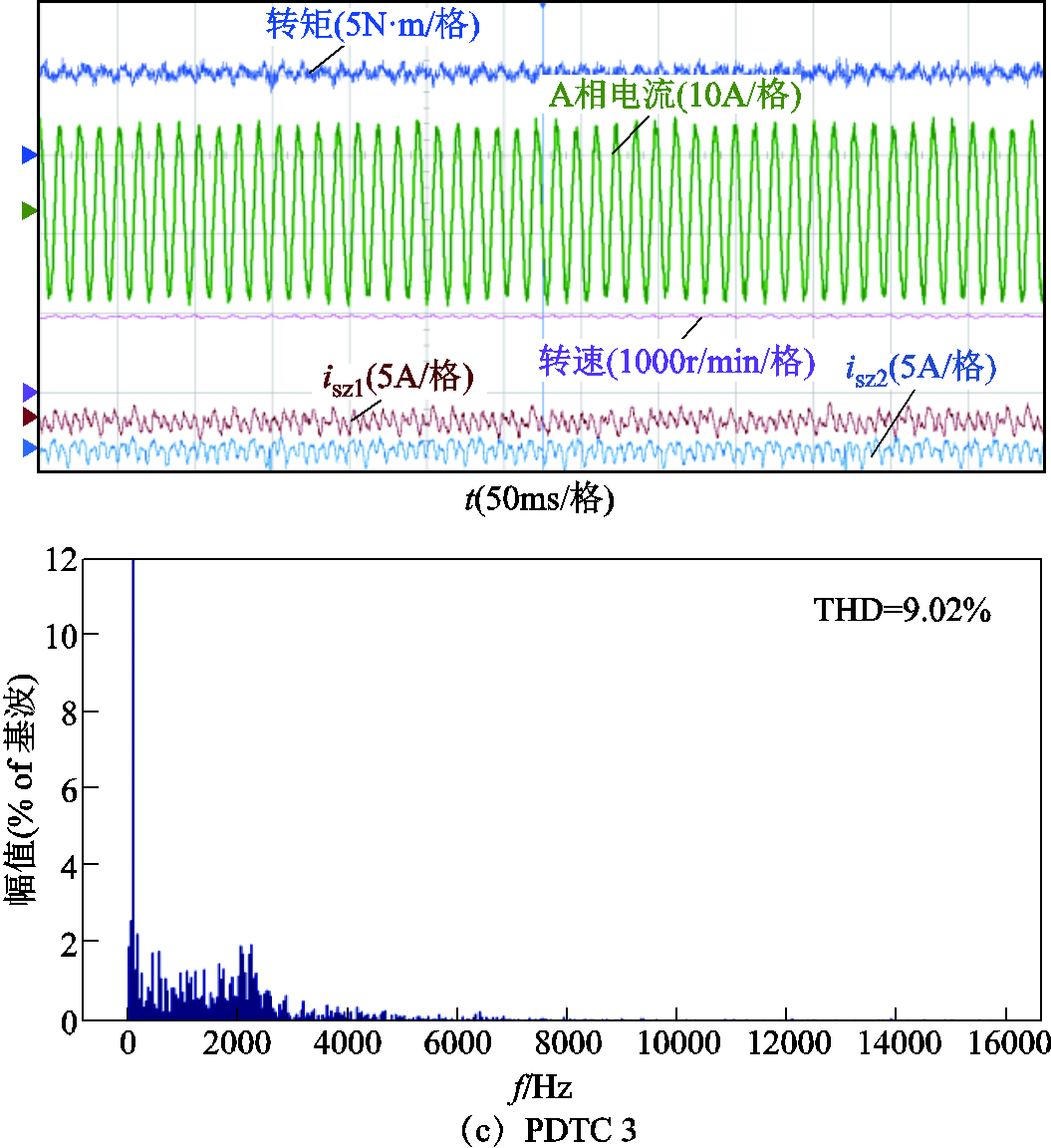
图13 1 000r/min稳态实验
Fig.13 Steady-state experiments at 1 000r/min
表4 计算时长对比
Tab.4 Comparison of computation burden

PDTC1PDTC2PDTC3 计算时长/μs75.3658.2745.35
为了验证所提策略的动态性能,进行了额定1 000r/min转速下的动态实验,如图14所示。负载电机从施加空载直接阶跃到施加额定负载。实验表明,三种策略均能快速地跟踪突变的负载,说明所提权重系数消除和有限控制集优化方案具有较好的动态性能。同时三种策略下零序电流均能稳定在0附近,且PDTC2和PDTC3相比于PDTC1零序电流更小,证明所提选取零序电压为0的电压矢量或者合成虚拟电压矢量减小零序电流策略在动态过程中也能保持对零序电流良好的抑制效果。

图14 1 000r/min动态性能实验
Fig.14 Load step experiments results at 1 000r/min
本文针对双三相永磁容错电机提出了一种基于权重系数消除和有限控制集优化的快速电压矢量选择预测直接转矩控制,并采用实验对所提策略进行了验证,结果表明:
1)所提定子磁链权重系数消除方案可将评价函数中的变量等效为量纲一致的电压矢量,并消除定子磁链权重系数λψ。
2)所提零序权重系数消除和有限控制集优化方案可成功消除零序权重系数λsz,免去繁琐的权重系数校正过程;优化有限控制集元素数量,减轻计算负担;并且可以有效地控制零序电流大小,具有较好的稳态以及动态性能。
3)所提快速电压矢量选择方案,省去了循环寻优过程,只需要一次即可找出最优的点和矢量,极大地节省了计算时间。
参考文献
[1] 魏永清, 康军, 曾海燕, 等. 十二相永磁电机驱动系统的容错控制策略[J]. 电工技术学报, 2019, 34(21): 4467-4473. Wei Yongqing, Kang Jun, Zeng Haiyan, et al. Fault-tolerant control strategy for twelve-phase permanent magnet synchronous motor propulsion system[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4467-4473.
[2] Jiang Xuefeng, Wang Shaoshuai, Li Qiang, et al. Design and optimization of dual-winding fault-tolerant permanent magnet motor[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(1): 45-53.
[3] 杨建飞, 曹伟, 李德才, 等. 两相导通无刷直流电机直接转矩控制零电压矢量特性分析[J]. 电工技术学报, 2019, 34(23): 4948-4956. Yang Jianfei, Cao Wei, Li Decai, et al. Analysis on zero voltage vector in two-phase conduction direct torque control of brushless DC motor[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4948-4956.
[4] 於锋, 朱晨光, 吴晓新, 等. 基于矢量分区的永磁同步电机三电平双矢量模型预测磁链控制[J]. 电工技术学报, 2020, 35(10):2130-2140. Yu Feng, Zhu Chenguang, Wu Xiaoxin, et al. Two-vector-based model predictive flux control of three-level based permanent magnet synchronous motor with sector subregion[J]. Transactions of China Electrotechnical Society, 2020, 35(10):2130-2140.
[5] Luo Yixiao, Liu Chunhua. Elimination of harmonic currents using a reference voltage vector based-model predictive control for a six-phase PMSM motor[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 6960-6972.
[6] 李耀华, 秦辉, 苏锦仕, 等. 永磁同步电机模糊自适应变开关次数权重系数模型预测转矩控制[J]. 电机与控制学报, 2020, http://kns.cnki.net/kcms/ detail/23.1408.TM20200117.1645.031.html. Li Yaohua, Qin Hui, Su Jinshi, et al. Model predictive torque control of permanent magnet synchronous motor based on adaptive dynamic weight coefficient using fuzzy control[J]. Electric Machines and Control, 2020, http://kns.cnki.net/kcms/ detail/23.1408. TM20200117. 1645.031.html.
[7] 史婷娜, 杨雨要, 周湛清, 等. 基于二次型价值函数的双电机转矩同步系统有限集模型预测控制[J]. 中国电机工程学报, 2019, 39(15): 4531-4541. Shi Tingna, Yang Yuyao, Zhou Zhanqing, et al. FCS-MPC for dual-motor torque synchronization system based on quadratic form cost function[J]. Proceedings of the CSEE, 2019, 39(15): 4531-4541.
[8] Luo Yixiao, Liu Chunhua. A flux constrained predictive control for a six-phase PMSM motor with lower complexity[J]. IEEE Transactions on Industrial Electronics, 2019, 66(7): 5081-5093.
[9] Zhang Yongchang, Yang Haitao. Model-predictive flux control of induction motor drives with switching instant optimization[J]. IEEE Transactions on Energy Conversion, 2015, 30(3): 1113-1122.
[10] 徐艳平, 李园园, 张保程, 等. 一种消除权重系数三矢量模型预测转矩控制[J]. 电工技术学报, 2018, 33(16): 3925-3934. Xu Yanping, Li Yuanyuan, Zhang Baocheng, et al. Three-vector based model predictive torque control of eliminating weighting factor[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3925-3934.
[11] 张永昌, 杨海涛, 魏香龙. 基于快速矢量选择的永磁同步电机模型预测控制[J]. 电工技术学报, 2016, 31(6): 66-73. Zhang Yongchang, Yang Haitao, Wei Xianglong. Model predictive control of permanent magnet synchronous motors based on fast vector selection[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 66-73.
[12] 周扬忠, 程明, 熊先云. 具有零序电流自矫正的六相永磁同步电机直接转矩控制[J]. 中国电机工程学报,2015, 35(10): 2504-2512. Zhou Yangzhong, Cheng Ming, Xiong Xianyun. Direct torque control for six-phase permanent magnet synchronous motor with zero-sequence current self-adjust[J]. Proceedings of the CSEE, 2015, 35(10): 2504-2512.
[13] Gonzalez-Prieto I, Duran M J, Aciego J J, et al. Model predictive control of six-phase induction motor drives using virtual voltage vectors[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 27-37.
[14] 徐质闲, 王政, 王学庆, 等. T型三电平双三相永磁同步电机驱动零共模电压模型预测控制[J]. 中国电机工程学报, 2020, 40(13): 4301-4310. Xu Zhixian, Wang Zheng, Wang Xueqing, et al. A predictive current control method for a T-type three-level dual three-phase PMSM with zero common-mode voltage[J]. Proceedings of the CSEE, 2020, 40(13): 4301-4310.
[15] 夏长亮, 仇旭东, 王志强, 等. 基于矢量作用时间的新型预测转矩控制[J]. 中国电机工程学报, 2016, 36(11): 3045-3053. Xia Changliang, Qiu Xudong, Wang Zhiqiang, et al. Predictive torque control based on optimal operating time of vector[J]. Proceedings of the CSEE, 2016, 36(11): 3045-3053.
[16] Huang Wentao, Hua Wei, Yin Fangbo, et al. Model predictive thrust force control of a linear flux-switching permanent magnet machine with voltage vectors selection and synthesis[J]. IEEE Transactions on Industrial Electronics, 2019, 66(6): 4956-4967.
[17] Lin Xiaogang, Huang Wenxin, Jiang Wen, et al. Deadbeat direct torque and flux control for permanent magnet synchronous motor based on stator flux oriented[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 5078-5092.
Fast Predictive Direct Torque Control of Dual Three-Phase Permanent Magnet Fault Tolerant Machine Based on Weighting Factor Elimination and Finite Control Set optimization
Abstract In this paper, a fast predictive direct torque control (PDTC) based on weighting factor elimination and finite control set optimization is presented. The weighing factors are removed and the number of elements in finite control set are reduced. The heavy computing burden of conventional PDTC for dual three-phase permanent magnet fault tolerant machine system are also released. Firstly, according to the deadbeat direct torque and flux control, the variables with different dimensions in the cost function are all equivalent to the voltage vectors, eliminating the weighting factor of stator flux. Then, based on the large flux leakage of permanent magnet fault tolerant machine, only the voltage vectors or virtual voltage vectors whose zero-sequence voltages are zero are selected as the elements of finite control set. As a result, the weighting factor of zero sequence is eliminated, and the elements number of finite control set is decreased from 64 to 19. Besides that, the zero-sequence currents are improved. Finally, a fast method which just needs one time to select the optimal voltage vector is designed. The experimental results verify the feasibility and effectiveness of proposed PDTC.
Keywords:Dual three-phase permanent magnet fault tolerant machine, predictive direct torque control (PDTC), weighting factor elimination, optimal finite control set, fast voltage vector selection
中图分类号:TM341
DOI:10.19595/j.cnki.1000-6753.tces.200762
国家自然科学基金(51777096)和江苏省研究生科研创新计划(KYCX18_0285)资助项目。
收稿日期2020-06-30
改稿日期 2020-09-10
赵 勇 男,1991年生,博士研究生,研究方向为永磁同步电机及其控制技术。E-mail:zhaoyong1105@nuaa.edu.cn(通信作者)
黄文新 男,1966年生,教授,博士生导师,研究方向为电机及其控制、新型风力发电技术、电能变换、航空电源等。E-mail:huangwx@nuaa.edu.cn
(编辑 郭丽军)