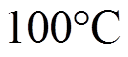 将引起磁链降低
将引起磁链降低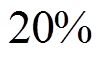 [11]。研究表明,电机发生参数摄动和失磁故障时将会导致FCS-MPC中的预测模型参数和实际参数有偏差,即发生模型失配现象而产生预测误差,甚至进一步错误选择最佳电压矢量而引起系统控制性能降低[12]。因此,在模型失配的情况下,为保持预测控制器良好的控制性能,实现对电机参数摄动的容错控制(Fault-Tolerant Control, FTC),已成为目前的研究热点。文献[13]提出基于补偿观测器的鲁棒容错预测电流控制方法,有效改善了电机参数摄动和永磁体失磁对电机安全运行的影响。
[11]。研究表明,电机发生参数摄动和失磁故障时将会导致FCS-MPC中的预测模型参数和实际参数有偏差,即发生模型失配现象而产生预测误差,甚至进一步错误选择最佳电压矢量而引起系统控制性能降低[12]。因此,在模型失配的情况下,为保持预测控制器良好的控制性能,实现对电机参数摄动的容错控制(Fault-Tolerant Control, FTC),已成为目前的研究热点。文献[13]提出基于补偿观测器的鲁棒容错预测电流控制方法,有效改善了电机参数摄动和永磁体失磁对电机安全运行的影响。摘要 针对传统有限集模型预测控制在电机发生参数摄动和永磁体失磁故障时模型失配导致系统性能下降的问题,提出一种用于永磁同步电机(PMSM)电流控制的有限集无模型容错预测控制方法。首先,考虑电机参数不确定性,依据永磁同步电机在参数摄动下的dq轴数学模型,建立基于系统输入和输出的永磁同步电机新型超局部模型。其次,基于新型超局部模型设计PMSM电流环的有限集无模型容错预测控制器,利用滑模观测器估计PMSM新型超局部模型中未知部分h。最后,与传统有限集模型预测控制方法进行实验结果对比,证明了所提方法对电机参数摄动和永磁体失磁故障具有容错性和鲁棒性。
关键词:永磁同步电机超局部模型有限集无模型容错预测控制参数摄动滑模观测器
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)驱动系统因其具有结构紧凑、高效率、动态性能优异等优点,目前已被广泛应用于工程实践中,例如电动汽车、机器人、轨道交通等领域[1]。作为经典控制方案的磁场定向控制采用电流内环速度外环的双闭环控制,在PMSM驱动系统中取得了高性能的控制效果。传统PI控制策略因其结构简单、便于工程应用等特点被广泛用作电机电流和转速控制器。但PI控制器有积分饱和等局限性,不符合高标准PMSM驱动系统的控制目标[2]。
在高精度、高性能的工程应用中,PMSM驱动控制系统要求转矩响应快且波动小,而电流环的动态响应与电磁转矩直接相关,即要求电流响应快速且波动小。因此,目前电机控制领域有很多高性能电流调节方案,如预测控制[3-4]、滑模控制[5]、神经网络控制[6]等。模型预测控制(Model Predictive Control,MPC)因其系统结构简单、响应快且易于实现非线性多目标控制等优势,成为电机控制领域的研究热点[7]。MPC主要分为连续状态下的模型预测控制(Continuous Control Set MPC, CCS-MPC)和离散状态下的有限控制集模型预测控制(Finite Control Set MPC, FCS-MPC)。FCS-MPC充分利用电力电子器件的开关离散特性,在所有可能的控制开关状态下,依据电机模型对系统状态的未来变化进行预测,并用表示系统性能要求的代价函数比较每个预测变量,选择使代价函数值最优的控制开关状态作为逆变器的控制信号。与CCS-MPC相比,FCS-MPC无需调制模块,运算量小且易于工程实现[8]。
与大部分依据模型的控制方法一样,FCS-MPC的良好性能建立在系统参数已知且稳定的基础上,所以有对参数变化较强敏感性等缺点[9]。因此,FCS-MPC策略的控制性能易受电机模型的电感、电阻、磁链等参数的影响。在实际工程应用中,PMSM运行工况多变,电阻、电感参数受到温度及其他因素影响而发生摄动,转子的永磁材料受到电磁、散热、机械等影响会出现失磁故障[10],运行环境温度每升高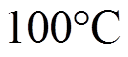 将引起磁链降低
将引起磁链降低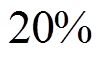 [11]。研究表明,电机发生参数摄动和失磁故障时将会导致FCS-MPC中的预测模型参数和实际参数有偏差,即发生模型失配现象而产生预测误差,甚至进一步错误选择最佳电压矢量而引起系统控制性能降低[12]。因此,在模型失配的情况下,为保持预测控制器良好的控制性能,实现对电机参数摄动的容错控制(Fault-Tolerant Control, FTC),已成为目前的研究热点。文献[13]提出基于补偿观测器的鲁棒容错预测电流控制方法,有效改善了电机参数摄动和永磁体失磁对电机安全运行的影响。
[11]。研究表明,电机发生参数摄动和失磁故障时将会导致FCS-MPC中的预测模型参数和实际参数有偏差,即发生模型失配现象而产生预测误差,甚至进一步错误选择最佳电压矢量而引起系统控制性能降低[12]。因此,在模型失配的情况下,为保持预测控制器良好的控制性能,实现对电机参数摄动的容错控制(Fault-Tolerant Control, FTC),已成为目前的研究热点。文献[13]提出基于补偿观测器的鲁棒容错预测电流控制方法,有效改善了电机参数摄动和永磁体失磁对电机安全运行的影响。
为了在保留FCS-MPC优点的同时解决参数敏感性的缺陷,国内外研究者基于参数辨识方法对参数敏感性问题进行改进[14-16]。这类方法旨在通过在线辨识实时的电机参数,如定子电阻、电感、永磁体磁链等,达到实时修正控制器参数的效果。然而,一方面,未建模的非线性因素,如逆变器死区[16]、磁路交叉耦合现象[17]等,会直接影响辨识结果的精度;另一方面,复杂的辨识算法还会增加FCS-MPC的计算量[18]。此外,文献[19]提出不采用传统电机模型,而是直接由相电流采样值的差分关系代替物理模型进行预测,实现无模型的FCS-MPC,该方法能实时调整电流变化率,但增加了对电流采样点时序和精度的要求。文献[20]提出一种根据工况筛选相邻数据的局部建模方法,即“Model-on-Demand”法,该方法可以提高预测性能,却增加了数据筛选阶段的运算量。
法国学者M. Fliess提出的无模型控制[21](Model-Free Control,MFC)为解决电机参数摄动和失磁故障的容错控制提供了新思路。MFC使用系统的输入和输出信息构造超局部模型,然后在该模型的基础上设计控制器,实现高性能控制。文献[22]将无模型控制中的反馈控制器设计为滑模变结构控制器,实现了电机在失磁故障下的容错控制。文献[23]将超局部模型应用在无差拍预测控制中,实现了无模型无差拍预测电流控制,但是其估计系统未知部分时运算量较大,也没有讨论电机参数变化对其控制性能的影响。
为了解决FCS-MPC模型失配问题,提升预测控制对电机参数变化的鲁棒性,将MFC与FCS-MPC相结合,提出了一种有限集无模型容错预测控制算法(Finite Control Set Model-Free Fault-Tolerant Predictive Control, FCS-MFFTPC),该方法无需已知电机的准确数学模型,实现了电机在出现参数摄动和失磁故障时容错控制的目的。首先分析PMSM在参数摄动情况下的数学模型,建立PMSM的新型超局部模型;其次,基于PMSM新型超局部离散模型设计FCS-MFFTPC电流控制器,改进传统FCS-MPC算法并减少了控制器对模型参数准确度的依赖性;然后设计离散滑模观测器实时在线观测新型超局部模型的未知部分,使预测模型与电机实际模型保持一致;最后通过实验平台,讨论参数摄动、失磁故障对传统FCS-MPC和FCS-MFFTPC的影响,验证了所设计FCS-MFFTPC方案的有效性,并与传统FCS-MPC进行对比,验证了所提方案的技术优势。
目前,在大部分研究中,有限集预测控制方案中的预测模型大多采用在标称参数下的理想数学模型。当忽略PMSM铁心饱和、损耗,不考虑参数摄动情况时,可以得到PMSM在dq坐标系下的理想数学模型为
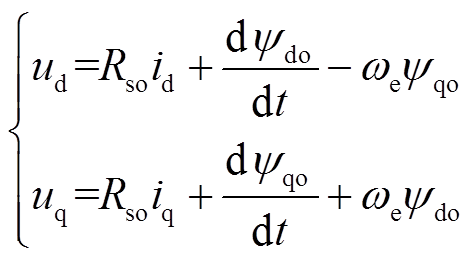 (1)
(1)其中,定子磁链方程为
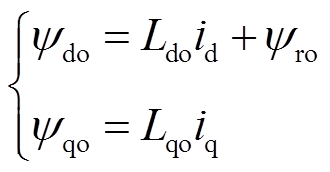 (2)
(2)式中,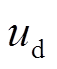 、
、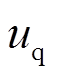 分别为定子d、q轴电压分量;
分别为定子d、q轴电压分量;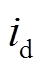 、
、 分别为定子d、q轴电流分量;
分别为定子d、q轴电流分量;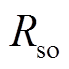 为定子相绕组电阻的标称值;
为定子相绕组电阻的标称值;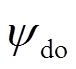 、
、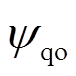 分别为定子在标称参数下的d、q轴磁链分量;
分别为定子在标称参数下的d、q轴磁链分量; 、
、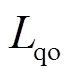 分别为定子绕组d、q轴电感的标称值,对于表贴式永磁同步电机(Surfaced-mounted PMSM,SPMSM)而言,
分别为定子绕组d、q轴电感的标称值,对于表贴式永磁同步电机(Surfaced-mounted PMSM,SPMSM)而言,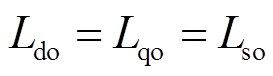 ;
;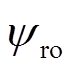 为转子磁链的标称值;
为转子磁链的标称值;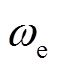 为转子电角速度。
为转子电角速度。
在实际运行工况下,由于温度及其他因素的影响,电阻和电感参数会出现摄动,转子永磁体会发生失磁故障。因此,在式(1)的前提下设计预测控制器的效果将受到影响。
为了确保控制器的良好性能,反映PMSM的实际运行情况,得到在参数摄动情况下PMSM的数学模型为
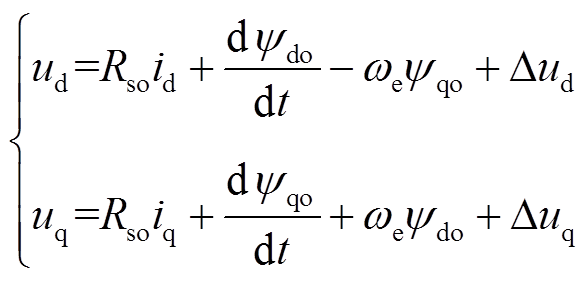 (3)
(3)式中,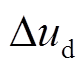 、
、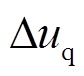 为电机参数变化引起的电压扰动量,即
为电机参数变化引起的电压扰动量,即
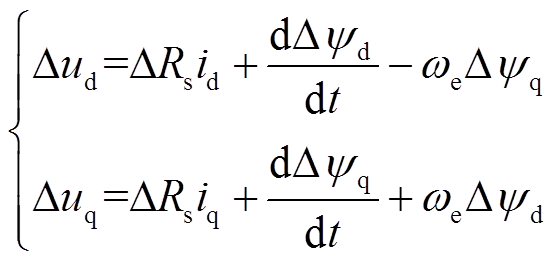 (4)
(4)其中,定子磁链变化量为
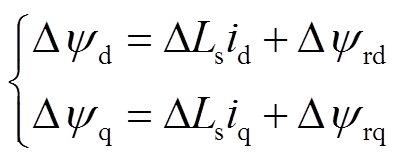 (5)
(5)式中,DRs、DLs分别为定子相电阻、电感的摄动值,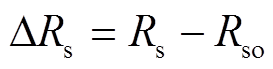 ,
,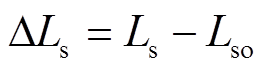 ;Dyd、Dyq分别为定子d、q轴磁链的摄动值,
;Dyd、Dyq分别为定子d、q轴磁链的摄动值,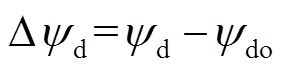 ,
,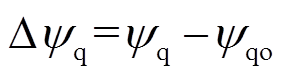 ;
;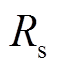 、
、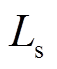 和
和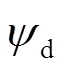 、
、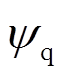 分别为电机定子相电阻、电感和d、q轴磁链的实际值;
分别为电机定子相电阻、电感和d、q轴磁链的实际值;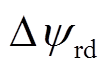 、
、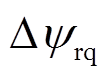 分别为发生失磁故障时转子磁链在d、q轴的摄动值。
分别为发生失磁故障时转子磁链在d、q轴的摄动值。
PMSM永磁体磁链的变化如图1所示[24],当PMSM出现失磁故障时,转子磁链矢量的大小和方向在一定范围内产生改变。大小由标称的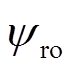 变化为实际的
变化为实际的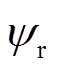 ,方向相对于电机磁场定向d轴方向存在偏差角
,方向相对于电机磁场定向d轴方向存在偏差角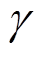 。相应的转子磁链方程为
。相应的转子磁链方程为
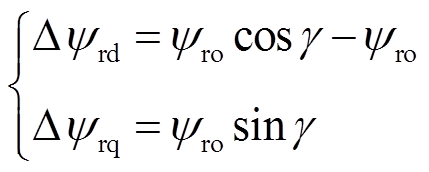 (6)
(6)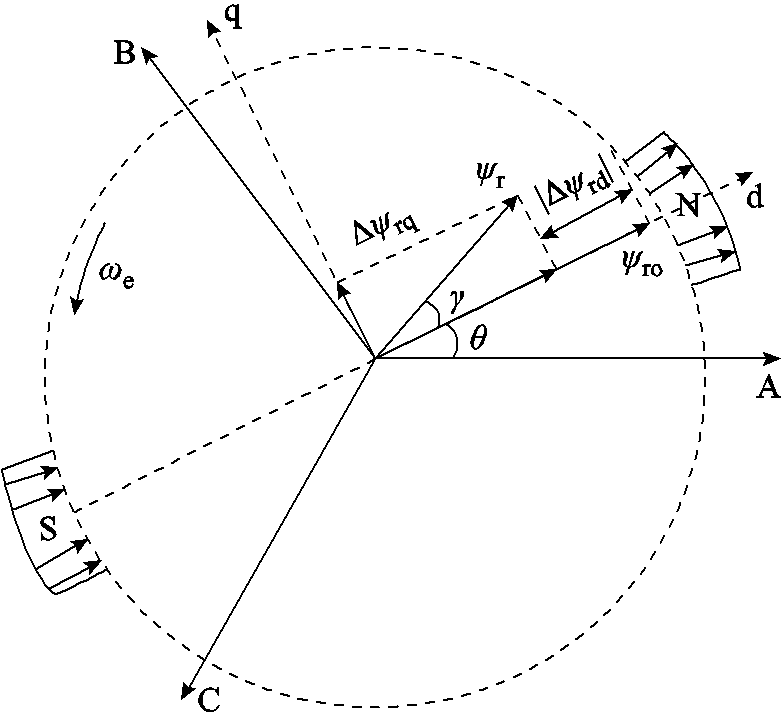
图1 PMSM永磁体磁链的变化
Fig.1 Variation of PM flux linkage in PMSM
考虑到在实际工程系统中,可以认为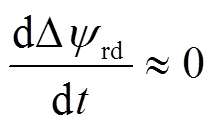 ,
,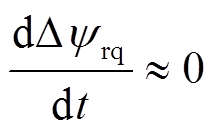 。将式(4)和式(5)代入式(3)中,选择定子d、q轴电流分量为系统状态变量,可得到PMSM在参数摄动和失磁故障下的状态方程为
。将式(4)和式(5)代入式(3)中,选择定子d、q轴电流分量为系统状态变量,可得到PMSM在参数摄动和失磁故障下的状态方程为
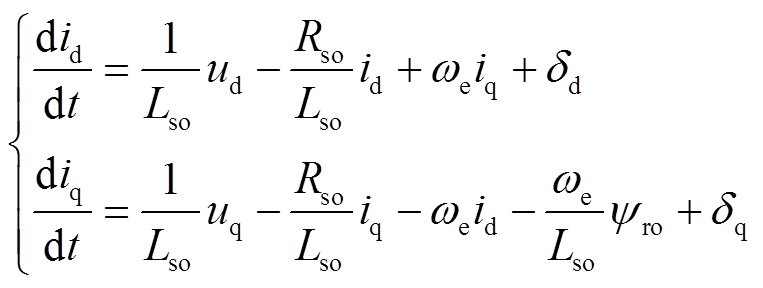 (7)
(7)式中,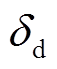 、
、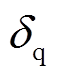 分别为d、q轴电流环扰动量,其具体表达式为
分别为d、q轴电流环扰动量,其具体表达式为
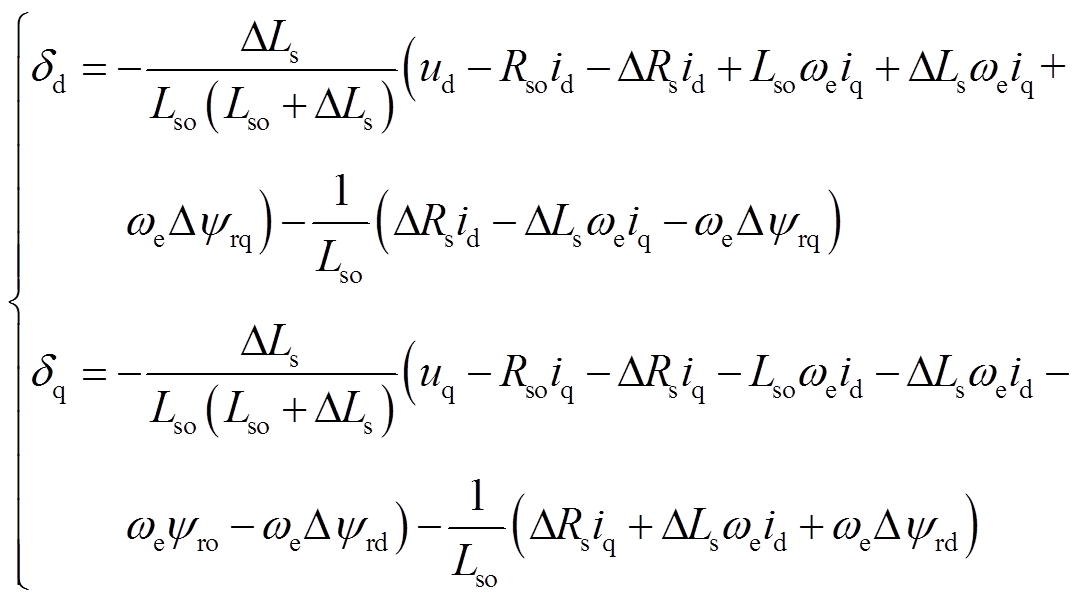 (8)
(8)SPMSM在dq坐标系下的电磁转矩方程为
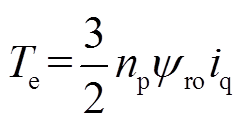 (9)
(9)式中,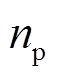 为极对数。
为极对数。
SPMSM在dq坐标系下的机械方程为
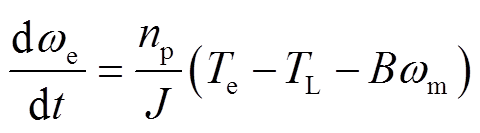 (10)
(10)式中,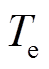 为PMSM输出的电磁转矩;
为PMSM输出的电磁转矩;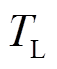 为负载转矩;
为负载转矩;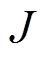 为转动惯量;
为转动惯量; 为转矩阻尼系数;
为转矩阻尼系数;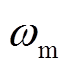 为转子机械角速度;
为转子机械角速度;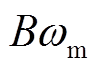 为阻尼转矩。
为阻尼转矩。
1.2.1 典型超局部模型
单输入单输出的非线性系统可用超局部模型表示为
 (11)
(11)式中,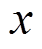 为系统的状态变量;
为系统的状态变量;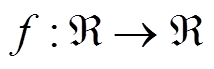 是只取决于
是只取决于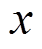 的未知非线性函数,满足Lipschitz有界性,包含有界扰动部分;
的未知非线性函数,满足Lipschitz有界性,包含有界扰动部分;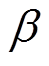 为非物理常数增益,使
为非物理常数增益,使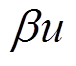 和
和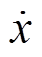 保持相同的数量级;
保持相同的数量级;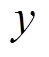 和
和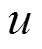 分别为系统的输出和控制输入。
分别为系统的输出和控制输入。
1.2.2 新型超局部模型
将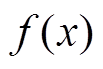 进一步表示为[25]
进一步表示为[25]
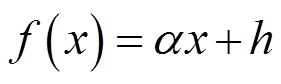 (12)
(12)式中,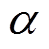 为系统状态增益;
为系统状态增益; 为未知的非线性部分,满足Lipschitz有界性和Lebesgue可测量性。
为未知的非线性部分,满足Lipschitz有界性和Lebesgue可测量性。
根据式(12),可以把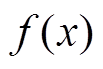 进一步分成线性部分和非线性部分。因此式(11)所示的系统可表示为新型超局部模型,即
进一步分成线性部分和非线性部分。因此式(11)所示的系统可表示为新型超局部模型,即
 (13)
(13)为了减少电流环对PMSM模型准确的依赖性,提高控制系统的容错能力,根据式(7)与式(13),构造电流环的新型超局部模型为
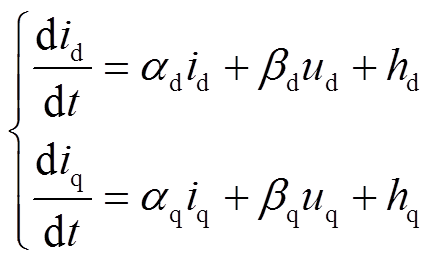 (14)
(14)式中,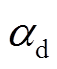 、
、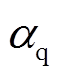 为待设计的电流系数;
为待设计的电流系数;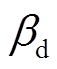 、
、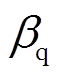 为待设计的电压系数;
为待设计的电压系数;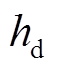 、
、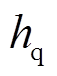 为未知部分,包括PMSM的已建模部分和扰动部分,满足Lipschitz有界条件且认为在控制周期足够小的情况下可以忽略其变化。
为未知部分,包括PMSM的已建模部分和扰动部分,满足Lipschitz有界条件且认为在控制周期足够小的情况下可以忽略其变化。
新型超局部模型表达式(14)改写为
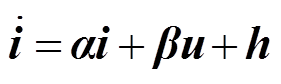 (15)
(15)其中
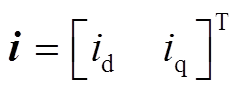
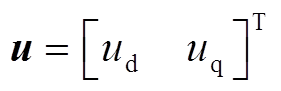
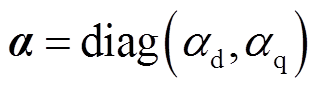
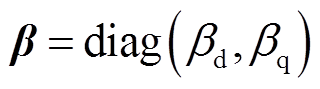
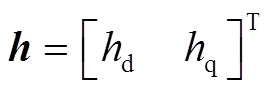
通过比较电机状态方程式(7)和新型超局部模型式(14),可以得到
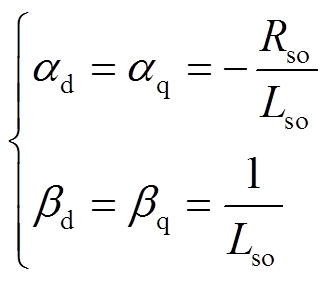 (16)
(16)需要指出的是,虽然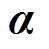 和
和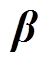 是预先设计的常数系数矩阵,但即使不是很精确,也可以通过调整h的值来保持良好的控制效果,因此不需要知道电机的准确参数,这是超局部模型的优点之一[26]。
是预先设计的常数系数矩阵,但即使不是很精确,也可以通过调整h的值来保持良好的控制效果,因此不需要知道电机的准确参数,这是超局部模型的优点之一[26]。
目前,传统的FCS-MPC算法利用PMSM在理想情况下的预测模型来预测电流的未来值。当电阻和电感等参数出现摄动,以及转子永磁体发生失磁故障时,如果继续采用此预测模型,将出现预测模型与真实模型失配等问题,使电机的运行性能降低。本文采用MFC思想中的超局部模型为预测模型,结合FCS-MPC的控制思路,提出FCS-MFFTPC算法。
FCS-MPC的预测模型采用被控制对象的离散化模型,被控量的预测值由系统输入输出关系计算得到。通常的连续模型离散化方式有前向欧拉法、预测-校正法、泰勒展开式等。这些离散方法都是用来拟合实际被控对象模型,以到达预期效果。
本文采用工程上常用的一阶前向欧拉法对电机模型离散化,有
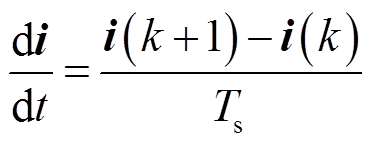 (17)
(17)式中,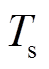 为采样周期,
为采样周期,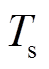 足够小时差分近似于微分。
足够小时差分近似于微分。
利用该方法离散化式(15),从而PMSM的离散状态方程为
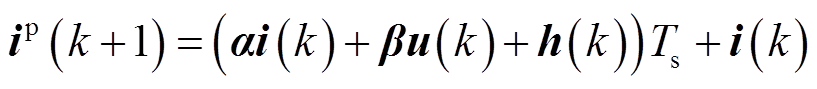 (18)
(18)其中
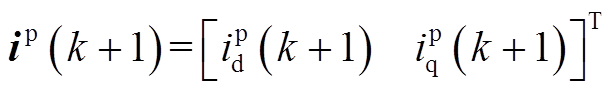
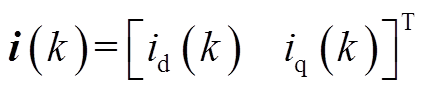
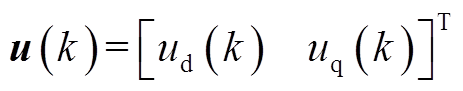
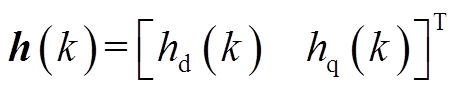
式中,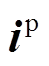 (k+1)为第
(k+1)为第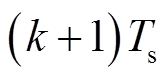 时刻的预测电流值。此外,
时刻的预测电流值。此外,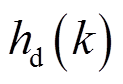 和
和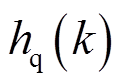 在每一个采样周期实时更新,包括了电机参数摄动和逆变器非线性引起的不确定部分。
在每一个采样周期实时更新,包括了电机参数摄动和逆变器非线性引起的不确定部分。
定义代价函数是FCS-MPC中一个重要的环节,表示期望达到的控制效果,而电流控制的目标是使实际电流接近参考电流,因此定义代价函数来衡量预测电流值与参考值之间的误差。代价函数为
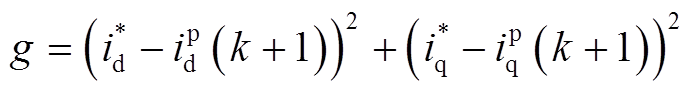 (19)
(19)式中,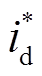 和
和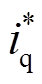 为参考电流值。实施
为参考电流值。实施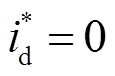 的电机控制策略,转矩电流参考值
的电机控制策略,转矩电流参考值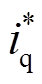 来自速度外环。
来自速度外环。
在两电平逆变器中共有8个基本电压矢量,包括6个非零电压矢量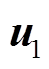 ,
, ,
,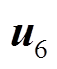 和2个零电压矢量
和2个零电压矢量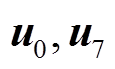 ,共提供7种不同的电压矢量
,共提供7种不同的电压矢量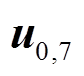 ,
, 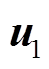 ,
,  ,
,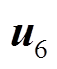 ,其开关状态与静止两相电压的关系见表1。
,其开关状态与静止两相电压的关系见表1。
 表示逆变器直流侧母线电压,
表示逆变器直流侧母线电压,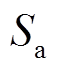 、
、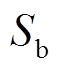 、
、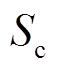 表示ABC三相桥臂的开关状态,当
表示ABC三相桥臂的开关状态,当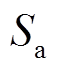 ,
, 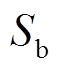 ,
, 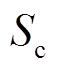 =1或
=1或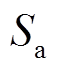 ,
, 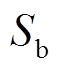 ,
, 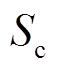 =0时表示上桥臂导通或关断,上、下桥臂的导通是互斥关系。通过查询表1,结合式(20)得到
=0时表示上桥臂导通或关断,上、下桥臂的导通是互斥关系。通过查询表1,结合式(20)得到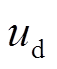 、
、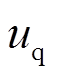 。
。
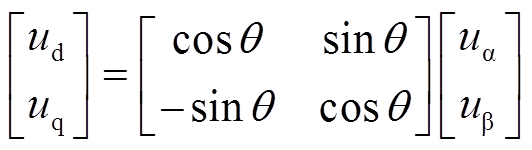 (20)
(20)式中,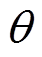 为转子电角度。
为转子电角度。
表1 开关状态表
Tab. 1 Switching state table
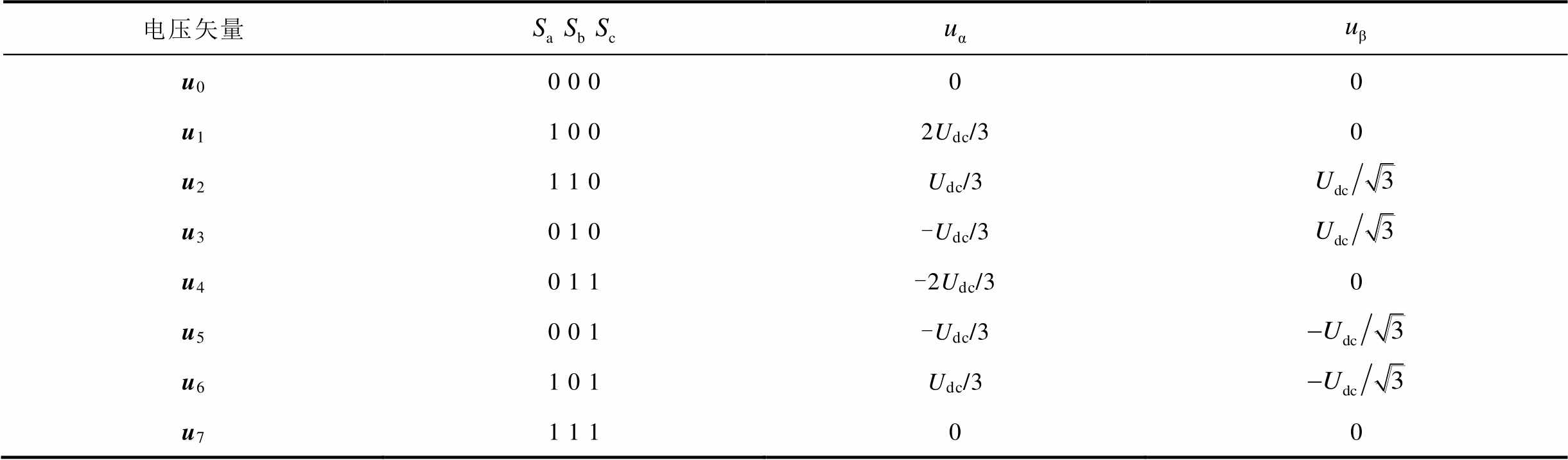
电压矢量 u00 0 000 u11 0 02Udc/30 u21 1 0Udc/3 u30 1 0-Udc/3 u40 1 1-2Udc/30 u50 0 1-Udc/3 u61 0 1Udc/3 u71 1 100
在离散控制系统中,实际输出电压与参考电压之间有一拍延时[27],即第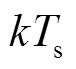 时刻选定的控制量,在第
时刻选定的控制量,在第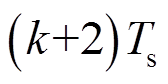 时刻才能应用,会造成系统动稳态性能降低的后果。为了弥补这一影响,本文采用基于“两步”运算的延时补偿方法对控制延迟进行补偿,即每个采样周期开始时,首先通过表1和式(20)将上一周期应用的最佳电压矢量(初始时刻采用零矢量进行初始化)转换得到对应的
时刻才能应用,会造成系统动稳态性能降低的后果。为了弥补这一影响,本文采用基于“两步”运算的延时补偿方法对控制延迟进行补偿,即每个采样周期开始时,首先通过表1和式(20)将上一周期应用的最佳电压矢量(初始时刻采用零矢量进行初始化)转换得到对应的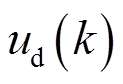 、
、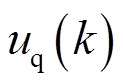 ,再将
,再将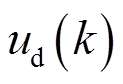 、
、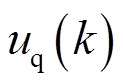 代入式(18)计算出第
代入式(18)计算出第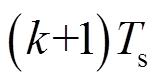 时刻的电流值,最后利用式(21)得到第
时刻的电流值,最后利用式(21)得到第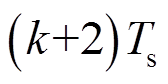 时刻的预测电流值,相应的电流预测表达式为
时刻的预测电流值,相应的电流预测表达式为
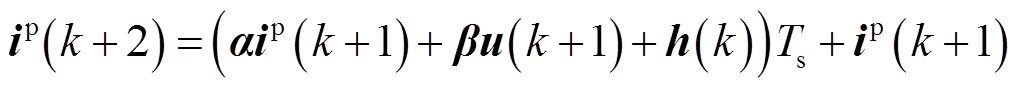 (21)
(21)相应的代价函数表达式改写为
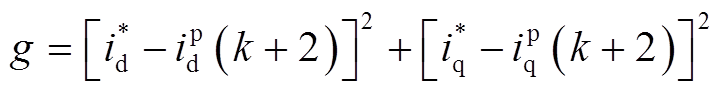 (22)
(22)将前述7种不同电压矢量的d、q轴电压代入式(21)中,预测第 时刻的电流值
时刻的电流值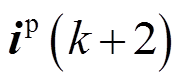 ;然后将
;然后将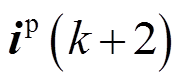 代入代价函数式(22)中;最后经过遍历寻优,选择使得式(22)最小的最佳电压矢量
代入代价函数式(22)中;最后经过遍历寻优,选择使得式(22)最小的最佳电压矢量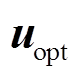 ,在第
,在第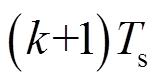 时刻将对应的开关状态
时刻将对应的开关状态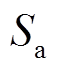 、
、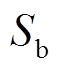 、
、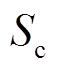 输入到逆变器,使得第
输入到逆变器,使得第 时刻电流达到
时刻电流达到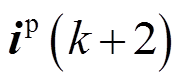 ,避免一拍延时对控制性能的影响。
,避免一拍延时对控制性能的影响。
由于u0和u7的代价函数值相等,将出现这两者均为uopt的情况,在切换控制信号时应按照减少损耗的要求来选取u0或u7,即如果上一时刻确定的电压矢量为u0、u1、u3、u5,则选择零电压矢量u0,反之选择u7,这样3组开关状态只需切换其中1组。
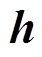
为实现良好的控制性能,对式(15)中未知部分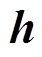 的准确估计至关重要。文献[28]采用了代数参数辨识技术对未知量进行估计,但是需要设置合理的采样窗口序列长度,存储大量的数据,增加系统运算负担。本文基于当前时刻的电压值和电流值,设计了式(23)滑模观测器来获取观测值
的准确估计至关重要。文献[28]采用了代数参数辨识技术对未知量进行估计,但是需要设置合理的采样窗口序列长度,存储大量的数据,增加系统运算负担。本文基于当前时刻的电压值和电流值,设计了式(23)滑模观测器来获取观测值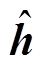 。
。
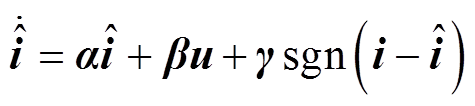 (23)
(23)式中,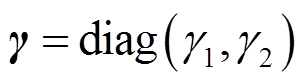 、
、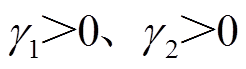 为待设计的参数;
为待设计的参数;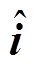 为
为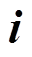 的观测值,
的观测值,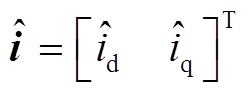 ;
;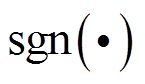 为符号函数。
为符号函数。
观测器误差定义为
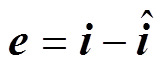 (24)
(24)式中,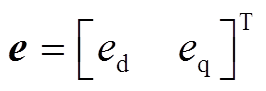 ,
,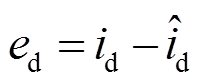 ,
,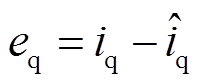 。
。
由式(15)和式(23)可得观测器误差方程为
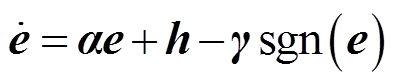 (25)
(25)选取电流误差变量e作为滑模面,则设计适当的矩阵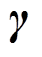 时,由式(25)确定的观测器误差方程将在有限时间内收敛到0。
时,由式(25)确定的观测器误差方程将在有限时间内收敛到0。
证明:选取正定函数V作为Lyapunov函数以证明其稳定性,即
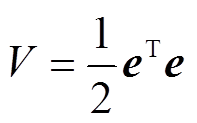 (26)
(26)对式(26)求导,并代入式(25)可得
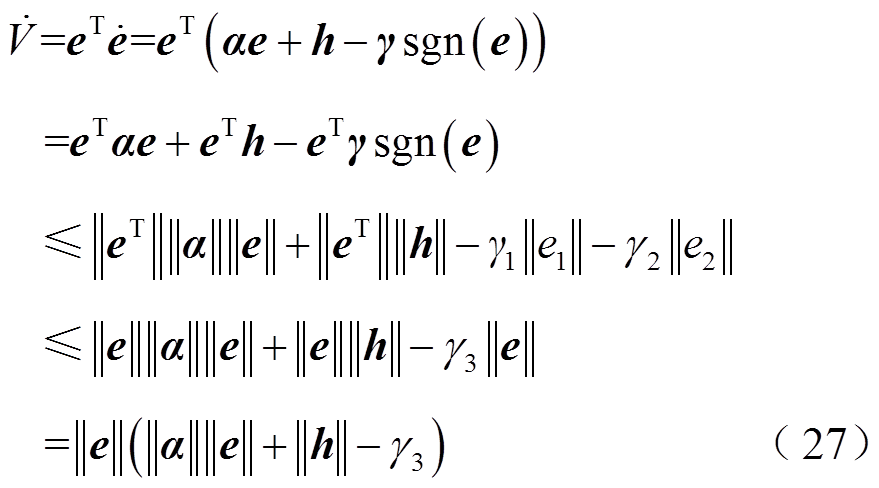
式中, 表示向量或矩阵的范数,
表示向量或矩阵的范数,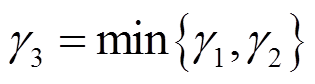 。
。
在式(27)中,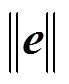 、
、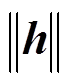 未知但在工程上认为有界。因此当设计
未知但在工程上认为有界。因此当设计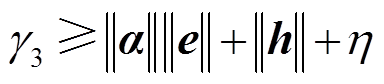 时,其中
时,其中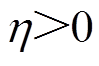 ,由式(27)可得
,由式(27)可得
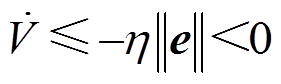 (28)
(28)根据Lyapunov稳定性判别准则和滑模可达条件,误差e会在有限时间内渐近收敛至0,由此可知观测器式(23)渐近稳定。
在实际的数字控制系统中,考虑到所设计的滑模观测器仅在离散时刻运行,因此推导出该观测器的离散形式。在采样周期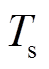 足够小时,式(23)的离散形式表示为
足够小时,式(23)的离散形式表示为
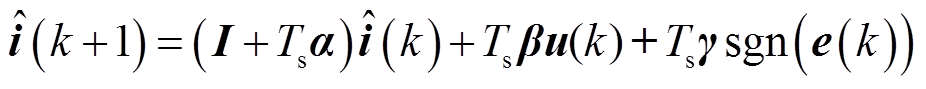 (29)
(29)式中,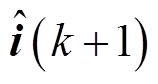 为
为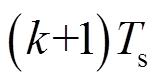 时刻的电流观测值,
时刻的电流观测值,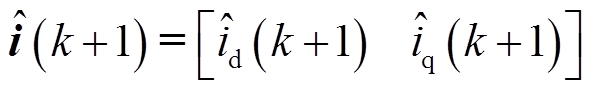 ;
;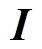 为单位矩阵。
为单位矩阵。
根据滑模等值原理,当系统状态运行到滑模面时有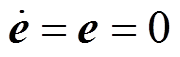 ,根据误差方程式(25)可得未知部分为
,根据误差方程式(25)可得未知部分为
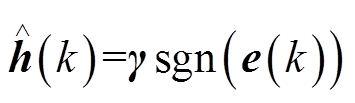 (30)
(30)本文采用开关切换的连续函数替换符号函数,实现削弱滑模运动抖振的目的,则式(30)可改写为
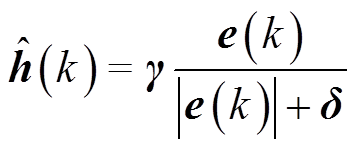 (31)
(31)式中,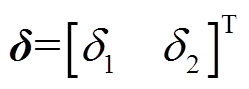 ,
,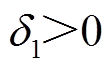 、
、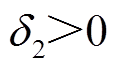 均是微小值。
均是微小值。
综上所述,本文所设计的FCS-MFFTPC算法的控制系统框图如图2所示。所提方法的控制流程如下:首先,由滑模观测器观测出PMSM已知部分和扰动部分的总和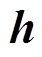 ,将其观测值
,将其观测值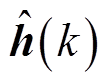 送入基于超局部模型的预测电流表达式(21)中;然后,经过遍历寻优,选择使代价函数最小的最佳电压矢量
送入基于超局部模型的预测电流表达式(21)中;然后,经过遍历寻优,选择使代价函数最小的最佳电压矢量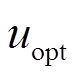 ;最后,将这一最佳电压矢量
;最后,将这一最佳电压矢量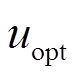 所对应的开关状态
所对应的开关状态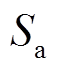 、
、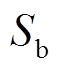 、
、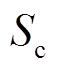 输出到逆变器,从而消除电流预测偏差,使电机能够容错运行。
输出到逆变器,从而消除电流预测偏差,使电机能够容错运行。
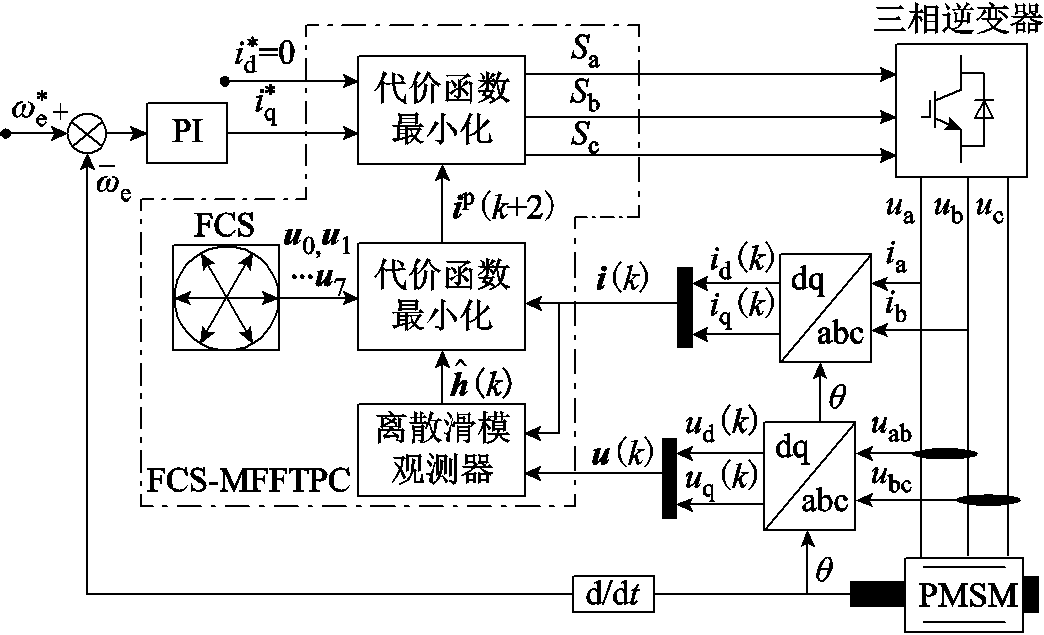
图2 FCS-MFFTPC控制系统框图
Fig.2 Block diagram of the FCS-MFFTPC control system
由于用实际电机模拟失磁故障比较困难,因此,本文使用RT-LAB来实现PMSM驱动系统的硬件在环仿真实验(Hardware-In-the-Loop Simulation,HILS),图3为本文采用的RT-LAB实验台。图4为PMSM控制系统RT-LAB硬件在环系统配置图。实验采用DSP控制器TMS320F2812,利用RT-LAB(OP5600)来构造PMSM及逆变器等系统其余部分。

图3 RT-LAB实验台
Fig.3 RT-LAB experiment platform
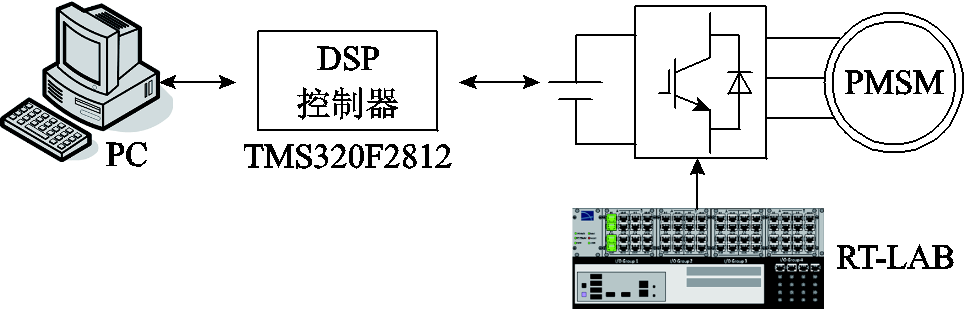
图4 RT-LAB硬件在环系统配置
Fig.4 Configuration of the RT-LAB HILS system
表2中列出了实验所用SPMSM的标称参数。实验采用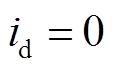 的控制策略,速度PI控制器提供q轴参考电流。采样周期
的控制策略,速度PI控制器提供q轴参考电流。采样周期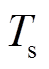 设置为
设置为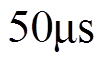 ,直流侧电压
,直流侧电压 为1 200V。速度环控制器比例系数P和积分系数I分别为100和3.5。此外,经实际调试,滑模观测器的系数设置为
为1 200V。速度环控制器比例系数P和积分系数I分别为100和3.5。此外,经实际调试,滑模观测器的系数设置为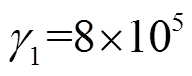 和
和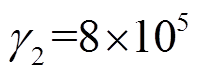 。新型超局部模型的系数设置为
。新型超局部模型的系数设置为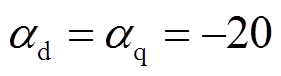 和
和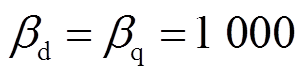 。
。
表2 SPMSM标称参数
Tab.2 Nominal parameters of SPMSM

参 数数 值 额定功率/125 额定转速/(r/min)2000 额定转矩/(N×m)800 定子绕组相电阻Rso/W0.02 极对数4 定子电感Lso/mH1 转子永磁体磁链0.892 转动惯量J/( kg×m2)1.57
为了验证所提出的控制方案的优点,实验条件设置为:给定转速为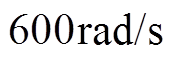 ;电机空载时起动,在0.2s时加到额定转矩
;电机空载时起动,在0.2s时加到额定转矩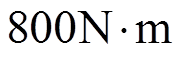 ;电机的内部参数不变,均为标称值。
;电机的内部参数不变,均为标称值。
图5和图6分别为PMSM在正常情况下即电机保持标称参数不变时,传统FCS-MPC和FCS-MFFTPC的实验结果。其中,图5a和图6a为d、q轴电流响应;图5b和图6b为输出转矩响应;图5c和图6c为转速响应;图6d为未知量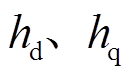 的观测值。
的观测值。
由图5和图6相比可见,FCS-MFFTPC与传统FCS-MPC具有相似的响应速度,在0.2s时转矩变化到额定转矩,q轴电流响应和转矩响应均能快速到达参考值。同时,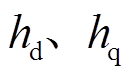 的观测值也在0.2s时发生相应的变化,为FCS-MFFTPC控制器提供了准确的预测模型。
的观测值也在0.2s时发生相应的变化,为FCS-MFFTPC控制器提供了准确的预测模型。
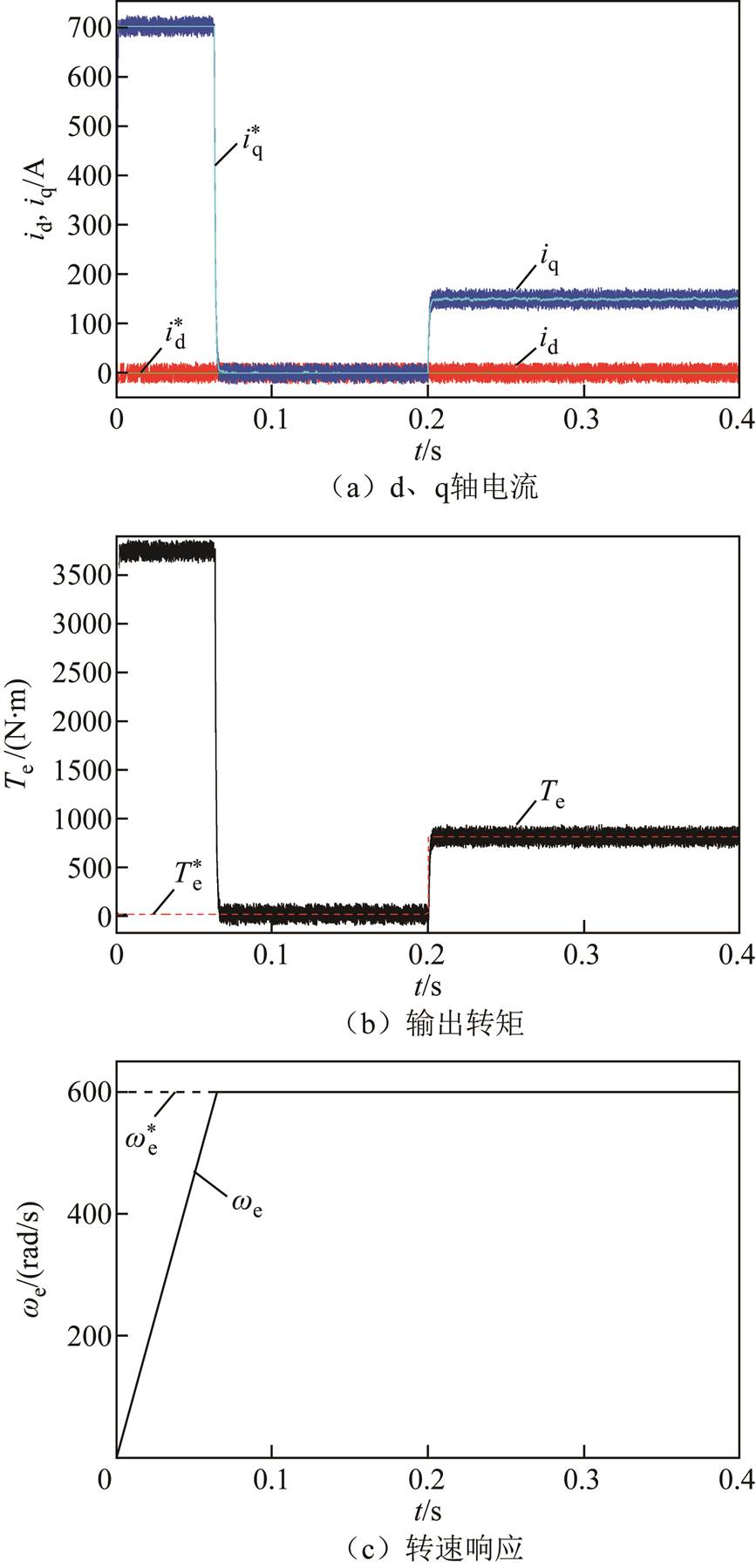
图5 传统FCS-MPC在正常情况下的实验结果
Fig.5 Experimental results of conventional FCS-MPC for normal conditions

图6 FCS-MFFTPC在正常情况下的实验结果
Fig.6 Experimental results of FCS-MFFTPC for normal conditions
由此可知,本文所提出的FCS-MFFTPC和传统FCS-MPC控制相比,虽然对传统控制算法做出了改变,但是并未影响到传统FCS-MPC在电机参数不变时的动态性能,保留了其快速响应能力这一优点。
为了比较两种控制方法在PMSM出现失磁故障情况下的控制性能,用转子磁链幅值及偏差角的阶跃性改变来表示故障情况。设置实验条件如下:参考转速为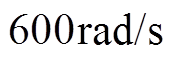 ;电机在零负载下起动,0.3s时加载至
;电机在零负载下起动,0.3s时加载至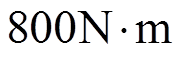 ;转子磁链初始值
;转子磁链初始值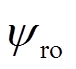 为
为 ,失磁偏差角
,失磁偏差角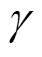 为
为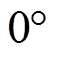 ;在0.1s时设置
;在0.1s时设置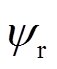 减小为
减小为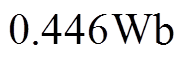 ,在0.2s时设置偏差角
,在0.2s时设置偏差角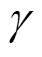 为
为 ,其他参数不变。
,其他参数不变。
图7和图8分别为PMSM发生失磁故障时,FCS-MFFTPC和传统FCS-MPC的实验结果。其中,图7a和图8a为d、q轴电流响应;图7b和图8b为输出转矩响应;图7c和图8c为转速响应;图8d为未知量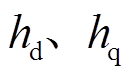 的观测值。
的观测值。
由图7和图8比较可知,在0.1s时永磁体磁链幅值发生变化,由传统FCS-MPC控制的d、q轴电流对给定值的跟踪出现偏差,响应转矩大于给定转矩,从而转速逐渐上升,而FCS-MFFTPC没有发生前述变化。在0.2s时永磁体磁链角发生变化,即幅值和角度同时变化,由传统FCS-MPC控制的d、q轴电流偏差更大,而FCS-MFFTPC控制的d、q轴始终保持不变。在0.3s时给定转矩为额定转矩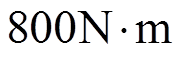 ,传统FCS-MPC在失磁故障下的q轴电流响应比FCS-MFFTPC较慢,同时出现电流偏差,FCS-MFFTPC的转矩响应比传统FCS-MPC更快。由图8d可知,当电机发生失磁故障时,未知量
,传统FCS-MPC在失磁故障下的q轴电流响应比FCS-MFFTPC较慢,同时出现电流偏差,FCS-MFFTPC的转矩响应比传统FCS-MPC更快。由图8d可知,当电机发生失磁故障时,未知量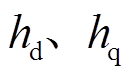 的观测值产生相应变化,达到实时更新预测模型的目的,实现了对失磁故障的容错控制。
的观测值产生相应变化,达到实时更新预测模型的目的,实现了对失磁故障的容错控制。
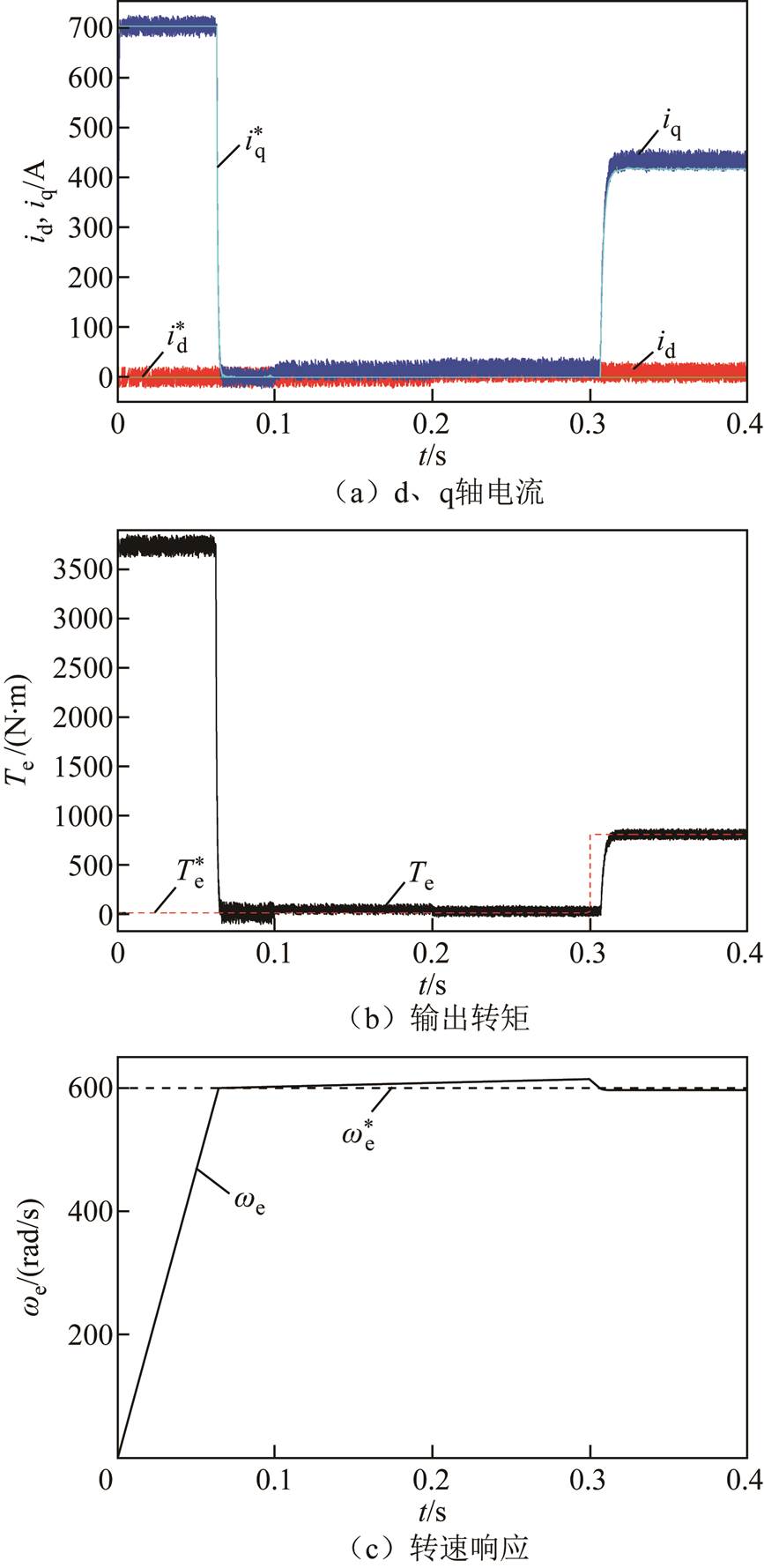
图7 传统FCS-MPC在失磁故障下的实验结果
Fig.7 Experimental results of conventional FCS-MPC for PM demagnetization
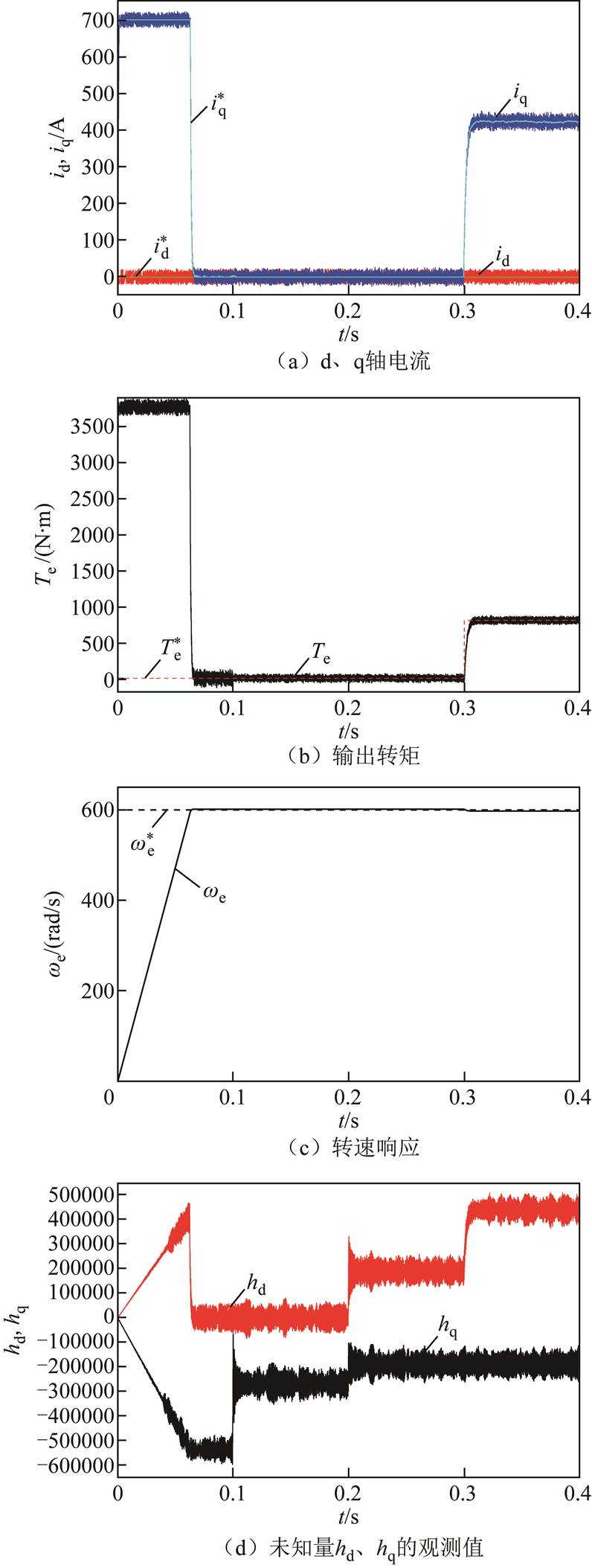
图8 FCS-MFFTPC在失磁故障下的实验结果
Fig.8 Experimental results of FCS-MFFTPC for PM demagnetization
为了进一步验证所提方法的鲁棒性,考虑失磁故障同时存在参数摄动情况下的控制性能。设置如下实验条件:参考转速为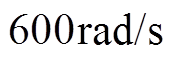 ;电机在零负载下起动,0.2s时加载至
;电机在零负载下起动,0.2s时加载至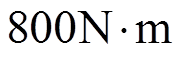 ;
;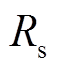 为
为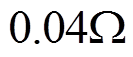 ;
;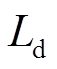 和
和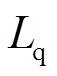 为
为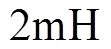 ,
,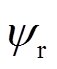 减小为
减小为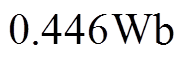 。
。
图9和图10分别为PMSM发生失磁故障同时存在电阻、电感等参数摄动情况下,传统FCS-MPC和FCS-MFFTPC的实验结果。其中,图9a和图10a为d、q轴电流响应;图9b和图10b为输出转矩响应;图9c和图10c为转速响应;图10d为未知量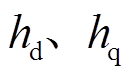 的观测值。
的观测值。
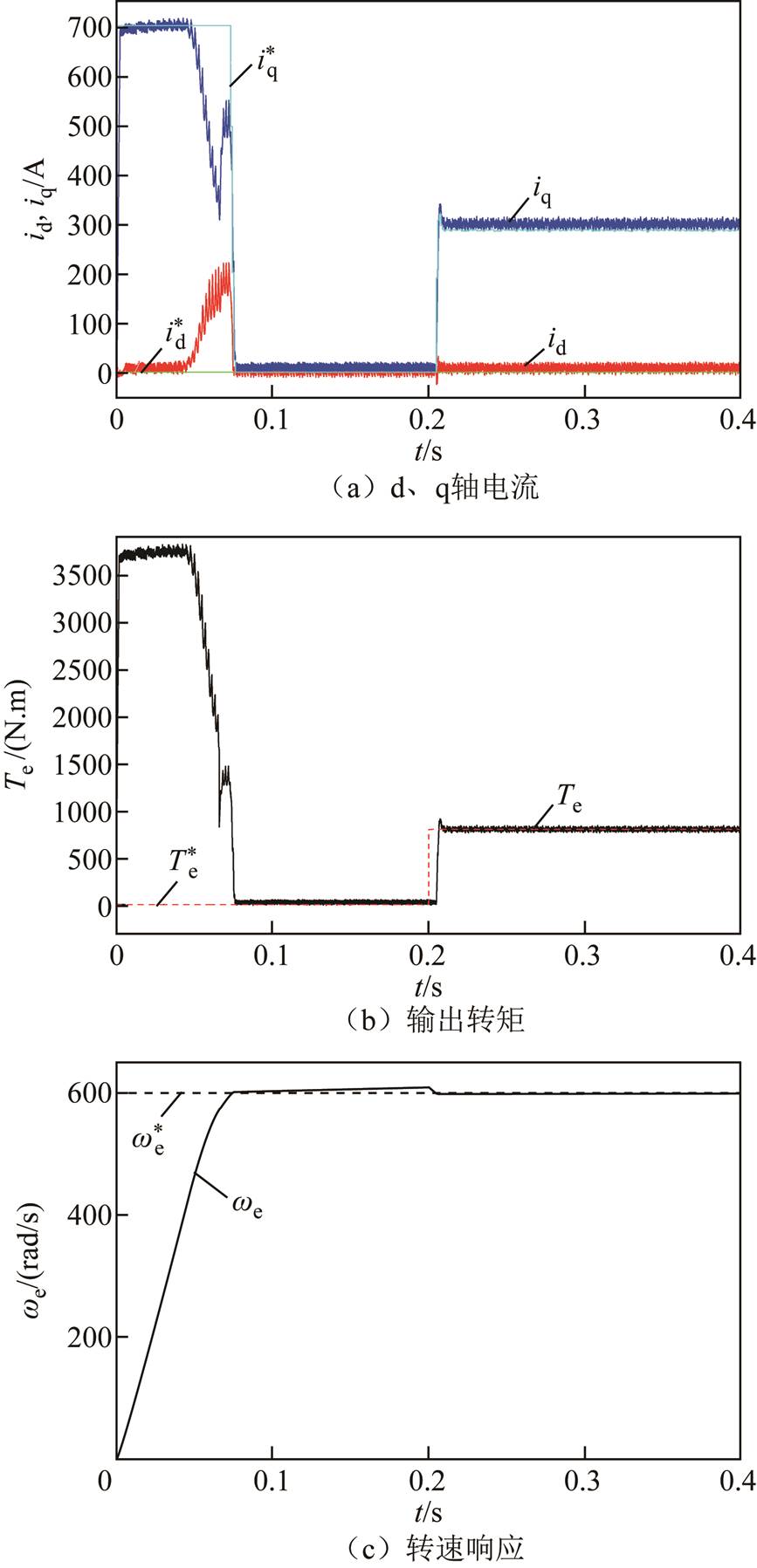
图9 传统FCS-MPC在失磁故障和参数摄动下的实验结果
Fig.9 Experimental results of conventional FCS-MPC for PM demagnetization and parameter perturbation
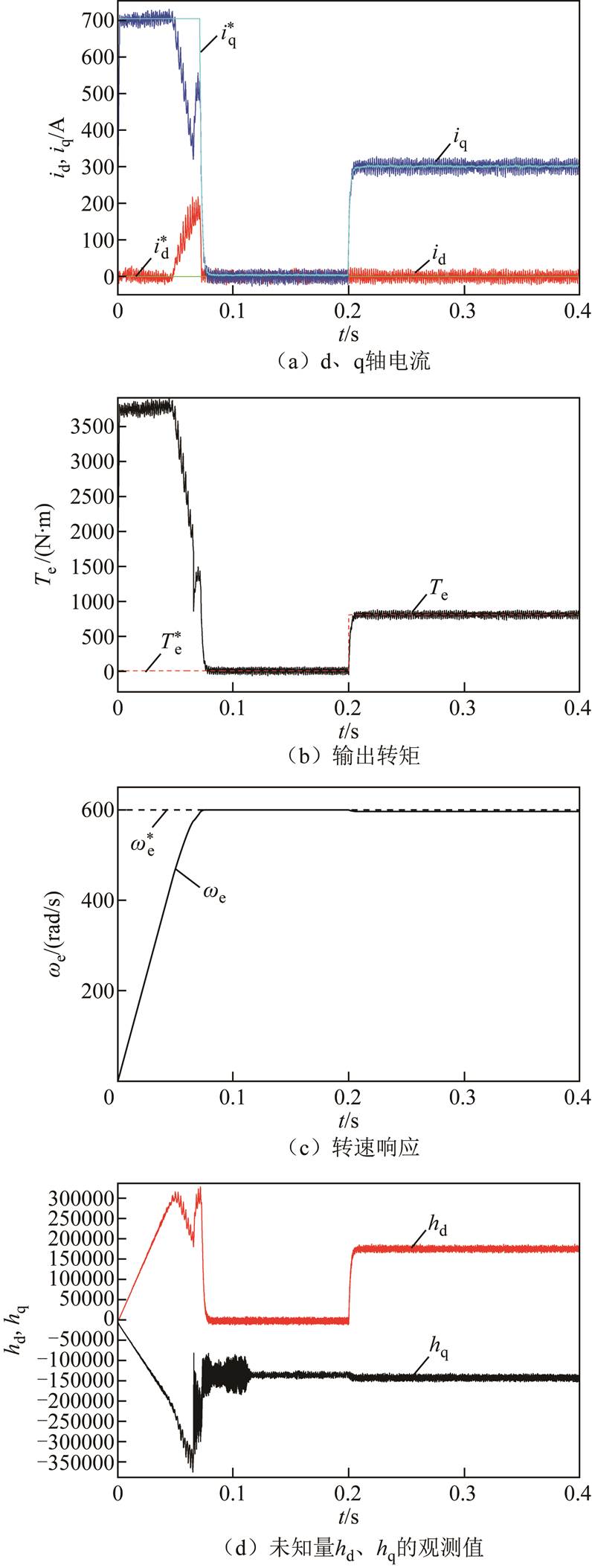
图10 FCS-MFFTPC在失磁故障和参数摄动下的实验结果
Fig.10 Experimental results of FCS-MFFTPC for PM demagnetization and parameter perturbation
由图9和图10比较可知,当电机出现失磁故障同时存在参数摄动时,传统FCS-MPC控制的d、q轴电流与参考电流存在偏差,输出转矩与负载转矩也存在偏差,导致转速不稳定,而FCS-MFFTPC的控制性能比较稳定。当加载到额定转矩时,传统FCS-MPC控制的q轴电流和输出转矩相比FCS-MFFTPC出现超调,且转矩响应慢,这说明FCS-MFFTPC的鲁棒性强于传统FCS-MPC。由图10d可知,FCS-MFFTPC所表现出的良好性能与未知量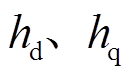 的准确估计密切相关。
的准确估计密切相关。
由实验结果可知,当电机在转子永磁体失磁故障和电阻、电感参数摄动的情况下,传统FCS-MPC的控制性能受到比较严重的影响,在相同负载转矩、转速条件下,电流稳态误差比FCS-MFFTPC更大,转矩响应更差。而FCS-MFFTPC控制的电流响应和模型匹配时一致,说明观测器观测未知量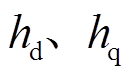 达到了实时修正预测模型的目的,实现了对参数摄动的鲁棒控制。再次证明了传统FCS-MPC是一种基于模型的控制方法,一旦存在一些未知扰动或非线性因素时,则该控制方法不能保证良好的控制性能。
达到了实时修正预测模型的目的,实现了对参数摄动的鲁棒控制。再次证明了传统FCS-MPC是一种基于模型的控制方法,一旦存在一些未知扰动或非线性因素时,则该控制方法不能保证良好的控制性能。
针对PMSM驱动系统运行在复杂多变的工况下存在参数摄动和失磁故障等不确定性问题而引起传统FCS-MPC方法预测模型与实际模型的失配现象,本文提出了一种有效的FCS-MFFTPC控制算法。该方法将无模型控制理论与有限集预测控制相结合,基于PMSM的新型超局部模型设计有限集无模型容错预测控制器。与传统FCS-MPC相比较,所提FCS-MFFTPC控制方法在电机发生参数摄动和失磁故障时的暂稳态性能更好、鲁棒性更强,且克服了FCS-MPC算法对模型参数准确的依赖性,实现了对电机参数摄动和失磁故障的容错控制。实验结果表明,FCS-MFFTPC既保留了传统FCS-MPC的快速响应能力,又改善了传统FCS-MPC在电机参数摄动时的暂稳态性能。
参考文献
[1] 张昌凡, 吴公平, 何静, 等. 一种永磁同步电机失磁故障容错预测控制算法[J]. 电工技术学报, 2017, 32(15): 100-110. Zhang Changfan, Wu Gongping, He Jing, et al. Fault-tolerant predictive control for demagnetization faults in permanent magnet synchronous machine[J]. Transactions of China Electrotechnical Society, 2017, 32(15): 100-110.
[2] Zhao Kaihui, Li Peng, Zhang Changfan, et al. Sliding mode observer-based current sensor fault reconstruction and unknown load disturbance estimation for PMSM drivens[J]. Sensors, 2017, 17(12): 2833.
[3] 赵凯辉, 陈跃, 张昌凡, 等. PMSM失磁故障的有限集模型预测容错控制[J]. 电子测量与仪器学报, 2019, 33(7): 79-87. Zhao Kaihui, Chen Yue, Zhang Changfan, et al. Finite-set model predictive fault control for demagnetization faults of permanent magnet synchronous motor drives[J]. Journal of Electronic Measurement and Instrumentation, 2019, 33(7): 79-87.
[4] 周湛清, 夏长亮, 陈炜, 等. 具有参数鲁棒性的永磁同步电机改进型预测转矩控制[J]. 电工技术学报, 2018, 33(5): 965-972. Zhou Zhanqing, Xia Changliang, Chen Wei, et al. Modified predictive torque control for PMSM drives with parameter robustness[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 965-972.
[5] 王要强, 冯玉涛, 秦明, 等. 表贴式永磁同步电机全阶滑模观测与控制策略[J]. 电工技术学报, 2018, 33(24): 5688-5699. Wang Yaoqian, Feng Yutao, Qin Ming, et al. Full-order sliding mode observation and control strategy for surface permanent magnet synchronous motor [J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5688-5699.
[6] 王硕, 康劲松. 一种基于自适应线性神经网络算法的永磁同步电机电流谐波提取和抑制方法[J]. 电工技术学报, 2019, 34(4): 654-663. Wang Shuo, Kang Jinsong. Harmonic extraction and suppression method of permanent magnet synchronous motor based on adaptive linear neural network[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 654-663.
[7] Cortes P, Kazmierkowski M P, Kennel R M, et al. Predictive control in power electronics and drives[J]. IEEE Transactions on Industrial Electronics, 2008, 55(12): 4312-4324.
[8] Vazquez S, Rodriguez J, Rivera M, et al. Model predictive control for power converters and drives: advances and trends[J]. IEEE Transactions on Industrial Electronics, 2017, 64(2): 935-947.
[9] Young H A, Perez M A, Rodriguez J. Analysis of finite-fontrol-set model predictive current control with model parameter mismatch in a three-phase inverter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3100-3107.
[10] Verkroost L, Druant J, Vansompel H, et al. Performance degradation of surface PMSMs with demagnetization defect under predictive current control[J]. Energies, 2019, 12(5): 782.
[11] 李红梅, 陈涛, 姚宏洋. 电动汽车PMSM退磁故障机理、诊断及发展[J]. 电工技术学报, 2013, 28(8): 276-284. Li Hongmei, Chen Tao, Yao Hongyang. Mechanism, diagnosis and development of demagnetization fault for PMSM in electric vehicle[J]. Transactions of China Electrotechnical Society, 2013, 28(8): 276-284.
[12] 李键, 牛峰, 黄晓艳, 等. 永磁同步电机有限控集模型预测电流控制预测误差分析[J]. 电机与控制学报, 2019, 23(4): 1-7. Li Jian, Niu Feng, Huang Xiaoyan, et al. Prediction error analysis of finite-control-set model predictive current control for PMSMs[J]. Electric Machines and Control, 2019, 23(4): 1-7.
[13] Zhang Changfan, Wu Gongping, Rong Fei, et al. Robust fault-tolerant predictive current control for permanent magnet synchronous motors considering demagnetization fault[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5324-5334.
[14] Zhang Xiaoguang, Zhang Liang, Zhang Yongchang. Model predictive current control for PMSM drives with parameter robustness improvement[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1645-1657.
[15] Nalakath S, Preindl M, Emadi A. Online multi-parameter estimation of interior permanent magnet motor drives with finite control set model predictive control[J]. IET Electric Power Applications, 2017, 11(5): 944-951.
[16] Chen Zhuoyi, Qiu Jianqi, Jin Mengjia. Adaptive finite-control-set model predictive current control for IPMSM drives with inductance variation[J]. IET Electric Power Applications, 2017, 11(5): 874-884.
[17] Yamazaki K, Kumagai M. Torque analysis of interior permanent-magnet synchronous motors by considering cross-magnetization: variation in torque components with permanent-magnet configurations[J]. IEEE Transactions on Industrial Electronics, 2014, 61(7): 3192-3201.
[18] Zhang Yongchang, Xu Donglin, Liu Jiali, et al. Performance improvement of model-predictive current control of permanent magnet synchronous motor drives[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3683-3695.
[19] Lin Chengkai, Yu Jente, Lai Yenshin, et al. Improved model-free predictive current control for synchronous reluctance motor drives[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3942-3953.
[20] Stenman A. Model-free predictive control[C]// Proceedings of the 38th IEEE Conference on Decision and Control, Phoenix, AZ, USA, 1999: 3712-3717.
[21] Fliess M, Join C. Model-free control[J]. International Journal of Control, 2013, 86(12): 2228-2252.
[22] 赵凯辉, 殷童欢, 张昌凡, 等. 永磁同步电机无模型滑模控制方法研究[J]. 电子测量与仪器学报, 2018, 32(4): 172-180. Zhao Kaihui, Yin Tonghuan, Zhang Changfan, et al. Research on model-free sliding mode control of permanent magnet synchronous motor[J]. Journal of Electronic Measurement and Instrumentation, 2018, 32(4): 172-180.
[23] Zhou Yanan, Li Hongmei, Zhang Hengguo. Model-free deadbeat predictive current control of a surface-mounted permanent magnet synchronous motor drive system[J]. Journal of Power Electronics, 2018, 18(1): 103-115.
[24] 肖曦, 张猛, 李永东. 永磁同步电机永磁体状况在线监测[J]. 中国电机工程学报, 2007, 27(24): 43-47. Xiao Xi, Zhang Meng, Li Yongdong. On-line estimation of permanent-magnet flux linkage ripple for PMSM[J]. Proceedings of the CSEE, 2007, 27(24): 43-47.
[25] Safaei A, Mahyuddin M N. Adaptive model-free control based on an ultra-local model with model-free parameter estimations for a generic SISO system[J]. IEEE Access, 2018, 6: 4266-4275.
[26] Zhang Yongchang, Jiang Tao, Jiao Jian. Model-free predictive current control of DFIG based on an extended state observer under unbalanced and distorted grid[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 8130-8139.
[27] 张永昌, 杨海涛, 魏香龙. 基于快速矢量选择的永磁同步电机模型预测控制[J]. 电工技术学报, 2016, 31(6): 66-73. Zhang Yongchang, Yang Haitao, Wei Xianglong. Model predictive control of permanent magnet synchronous motors based on fast vector selection[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 66-73.
[28] Wang Yuchen, Li Hongmei, Liu Rundong, et al. Modulated model-free predictive control with minimum switching losses for PMSM drive system[J]. IEEE Access, 2020, 8: 20942-20953.
Finite Control Set Model-Free Fault-Tolerant Predictive Control for Permanent Magnet Synchronous Motor
Abstract To solve the performance degradation of traditional finite control set model predictive control (FCS-MPC) for motor parameters perturbation and permanent magnet (PM) demagnetization faults, this paper proposes a finite control set model-free fault-tolerant predictive control (FCS-MFFTPC) method for permanent magnet synchronous motor (PMSM) current control. Firstly, considering the uncertainty of motor parameters, according to the dq axis mathematical model of PMSM under parameters perturbation, a novel ultra-local model of PMSM is established based on system input and output data. Secondly, based on the novel ultra-local model, a FCS-MFFTPC controller for PMSM current loop is designed. The sliding mode observer is used to estimate the unknown part h in the novel ultra-local model of PMSM. Finally, compared with the traditional FCS-MPC method, the experimental results show that the proposed method proves to be fault-tolerant and robust to motor parameters perturbation and PM demagnetization faults.
keywords:Permanent magnet synchronous motor, ultra-local model, finite control set model-free fault-tolerant predictive control, parameters perturbation, sliding mode observer
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.200389
国家自然科学基金(61773159)、湖南省自然科学基金(2020JJ6083, 2019JJ40072,2018JJ4066)和湖南省研究生科研创新项目(CX20190861)资助。
收稿日期 2020-04-20
改稿日期2020-09-27
赵凯辉 男,1973年生,博士,副教授,硕士生导师,研究方向为永磁同步电机智能控制及故障诊断。E-mail:zhaokaihui@hut.edu.cn
黄 刚 男,1979年生,博士,讲师,硕士生导师,研究方向为永磁同步电机故障诊断与容错控制。E-mail:12120@hut.edu.cn(通信作者)
(编辑 郭丽军)