图1 伪双极MMC-HVDC系统结构
Fig.1 Topology of Pseudo bipolar MMC-HVDC system
摘要 在基于模块化多电平换流器（MMC）的柔性直流输电系统中，高效可靠地识别线路故障是系统安全经济运行的重要保证之一。为快速可靠识别线路故障，提出一种基于交叉重叠差分（SOD）变换的区内外故障识别方法。首先分析MMC等效阻抗模型形成的物理边界对高频分量的衰减作用，当线路发生内部故障时，其故障电压起始变化陡峭、幅值大、长时窗时域波形有振荡；当线路发生外部故障时，其故障电压起始变化平缓、幅值小。其次利用交叉重叠差分对故障电压和故障电流进行变换，变换后的电压和电流信号相乘得到SP，定义K为SP绝对值的最大值，根据K值判断区内外故障。在PSCAD/EMTDC上搭建MMC-HVDC系统仿真模型，仿真结果表明，该方法能可靠准确地识别区内外故障，速动性好，具有较强的耐过渡电阻能力和适用性。
关键词：高压直流输电 模块化多电平换流器 物理边界 交叉重叠差分变换 故障特性分析 故障识别
模块化多电平换流器（Modular Multilevel Converter, MMC）是一种新型电压源型换流器拓扑结构[1]，该拓扑采用子模块级联的方式[2]，子模块由绝缘栅双极晶体管（Insulated Gate Bipolar Transistor，IGBT）和电容组成，可独立控制子模块投入和切除，与传统高压直流输电相比，不存在换相失败问题[3]，且MMC采用阶梯波调制方式[4]，输出的波形质量更高。目前我国在建的柔性直流输电工程大多采用MMC拓扑结构，基于MMC的柔性直流输电已成为直流输电领域的一个重要发展方向[5]。
为满足远距离、大容量的输电需求，使用架空线路成为柔性直流输电的一个趋势，但相比电缆线路，架空线路更容易发生故障，并且直流系统本身比交流系统的阻尼更小[6]，因此发生故障的概率更大。当直流输电线路发生故障时，换流站中子模块电容放电，在数毫秒内故障电流达到较大的过电流水平，这将严重威胁IGBT等换流站内部设备[7]。因此，快速有效地识别MMC-HVDC直流输电线路故障具有十分重要的意义。
针对柔性直流输电系统线路故障问题，国内外学者已经展开了广泛研究[8-10]。文献[11]分析了直流配电网故障后的零模网络，通过Hausdorff算法对区内外零模差动电流进行相似度比较，进而实现区内外故障识别。文献[12]利用直流线路电流固有模态能量熵构造直流侧故障判据，以区分直流侧故障和交流侧故障。文献[13]提出了基于电压变化率的故障识别方案，但该方法所能识别的最大电阻不超过150Ω，耐过渡电阻能力不强。文献[14]提出利用健全极MMC注入特征信号的直流线路故障性质判别方法，但该方法不适用于伪双极输电系统。文献[15]利用故障电流的初始上升率来进行故障识别，但没有进行可靠性和适用性分析。文献[16]提出了一种基于线路直流电抗器两侧电压小波变换细节系数幅值比的快速方向纵联识别判据，该方法能可靠识别区内外故障，但需要在线路两端加入平波电抗器，不具有普遍适用性。因此，亟待提出一种新型识别方法，能快速、可靠地识别MMC-HVDC输电线路故障。
本文针对柔性直流输电线路故障识别问题，分析了区内、区外故障的故障特性，并在此基础上提出了一种基于单端量的交叉重叠差分（Sequential Overlapping Derivative, SOD）变换线路故障识别方法，定义SP为经交叉重叠差分变换后的电压和电流信号的乘积，K为SP绝对值的最大值，根据K值判断区内外故障。最后在PSCAD/EMTDC中搭建仿真模型，验证得出该识别方法有较好的适用性。
伪双极MMC-HVDC系统结构如图1所示，阀组侧变压器采用三角形联结，无中性点，交流侧变压器采用星形联结，中性点采用直接接地方式。直流侧经大电阻接地，为直流线路正、负两极提供零电位参考点，且能对直流侧输出的电压起到钳位作用。图1中，M为线路量测点，f1、f2为线路内部故障，其中f1为正极接地故障，f2为双极短路故障，f3、f4为线路外部故障。
图1 伪双极MMC-HVDC系统结构
Fig.1 Topology of Pseudo bipolar MMC-HVDC system
MMC换流器的拓扑结构[17-20]如图2所示，图中uj和ij（j=a, b, c）分别为交流侧系统电压和电流；ujp、ujn分别为第j相的上、下桥臂的级联子模块输出的电压之和；ijp、ijn分别为第j相的上、下桥臂电流；uSM为子模块的输出电压；UC为电容电压；Udc为直流电压；Rs、R0分别为交流侧等效电阻和桥臂电阻，Ls、L0分别为交流侧等效电感和桥臂电感；C0为子模块电容。
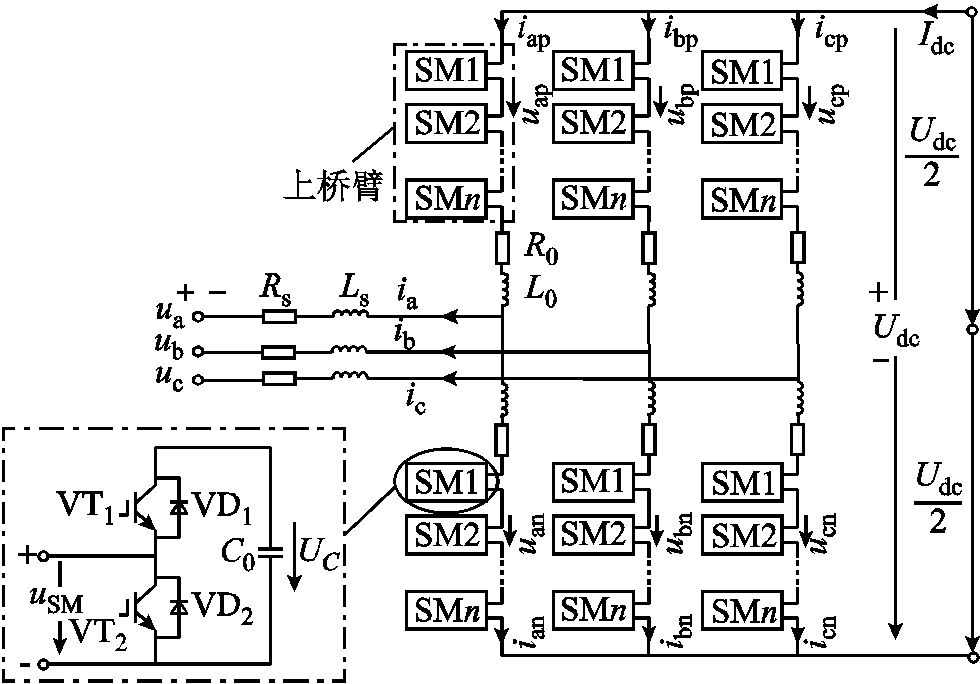
图2 MMC拓扑结构
Fig.2 Topology of MMC
对于a相，上、下桥臂分别满足KVL方程
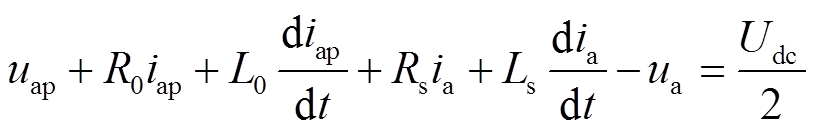（1）
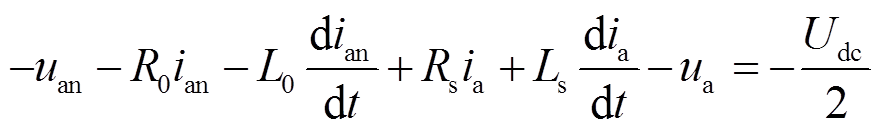（2）将式（1）和式（2）相减后再对a、b和c三相进行叠加可得
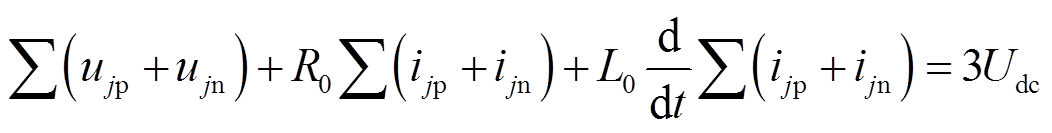（3）在图2所示的拓扑结构中有
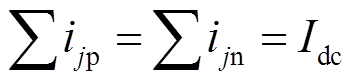（4）
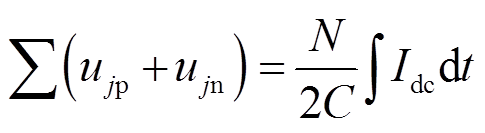（5）因此式（3）可以简化为
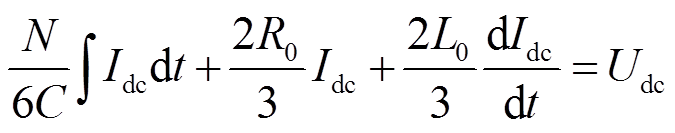（6）对式（6）进行正弦稳态分析得
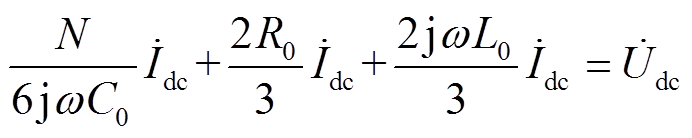（7）定义MMC直流侧阻抗[21]为
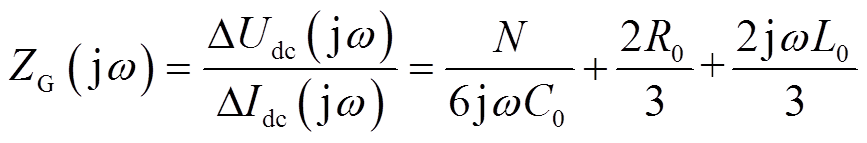（8）阻抗谐振频率为
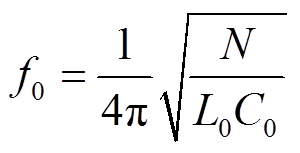（9）由式（6）可知，MMC直流侧可由电阻、电容和电感元件串联进行等效，其等效模型如图3所示。
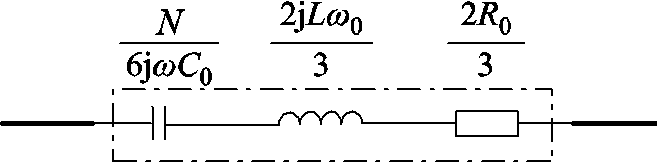
图3 MMC等效阻抗模型
Fig.3 Equivalent impedance model of the MMC
MMC直流输电系统中由于换流器子模块电容、桥臂电感和桥臂电阻的存在，使线路内部故障和线路外部故障时电压波形在线路保护测量点呈现特性不同。MMC中换流器子模块电容、桥臂电感和桥臂电阻构成的物理边界如图3所示，R0=0.005Ω，L0=50mH，C0=2 800µF，N=76。
根据物理边界的结构参数，分析得出其对地等值阻抗ZG的阻抗频率特性如图4所示。由图4可知，物理边界的谐振频率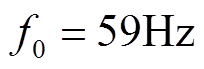
，当频率大于1kHz时，随着频率的增加，边界阻抗值线性增加，呈现感抗特性，该阶段边界对高频信号有一定的衰减作用。
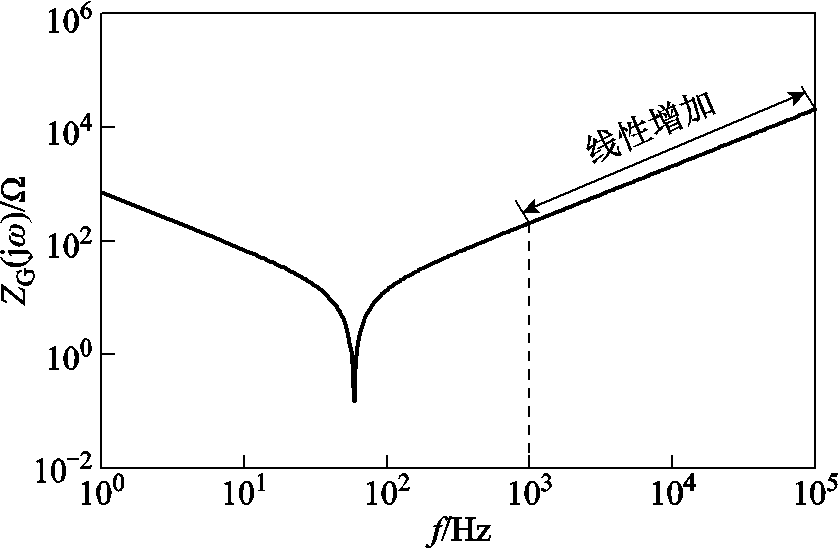
图4 MMC等效阻抗频率特性
Fig.4 Equivalent impedance frequency characteristic of the MMC
当f＞1kHz时，MMC等效阻抗形成的物理边界可视为纯电感，如图5所示。
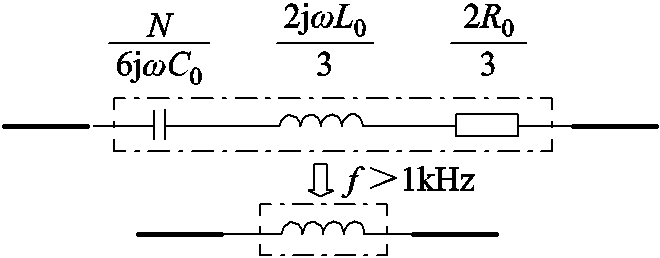
图5 MMC物理边界等效图
Fig.5 MMC physical boundary equivalent diagram
当发生单极接地故障f1时，故障通路示意图如图6所示，对地电位参考点发生变化[22]，由图6中的①变为②，考虑到输电线路的对地电容效应，接地点通过对地电容形成放电回路，直流侧出现接地电流。由于故障行波的流向为由故障点流向线路两侧，即先流过量测点M，再经过MMC模块形成的物理边界，因此量测点测量到的高频暂态分量大。
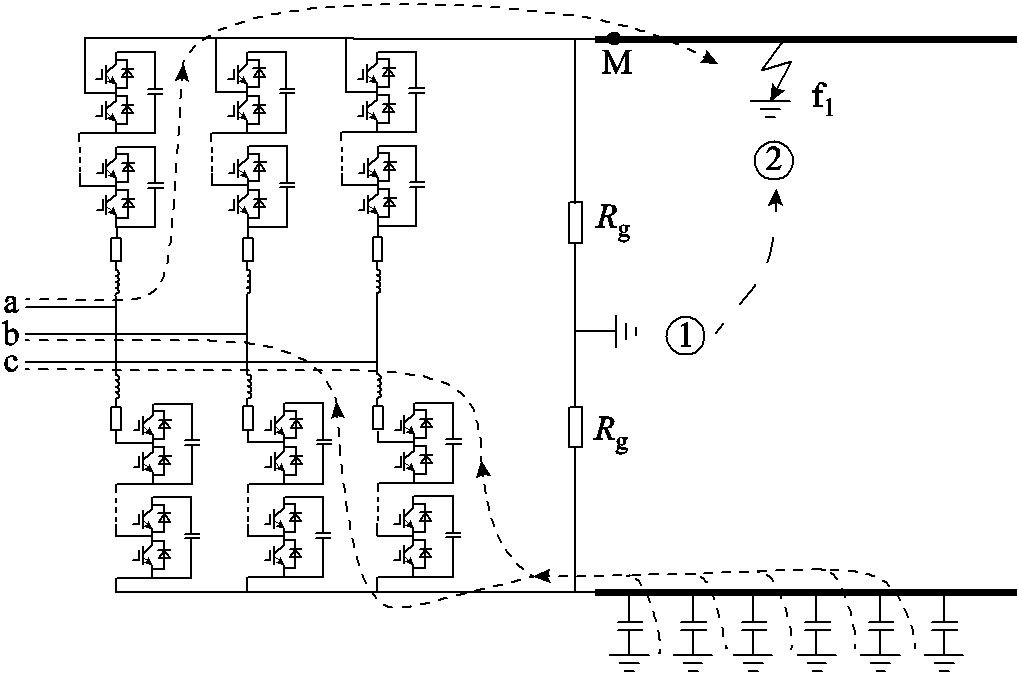
图6 单极接地故障通路示意图
Fig.6 Single pole line-to-ground fault path schematic diagram
当发生双极短路故障f2时，故障通路示意图如图7所示。与单极接地故障相似，其故障行波也先流过量测点，再经过MMC模块形成的物理边界，因此量测点测量到的高频暂态分量大。
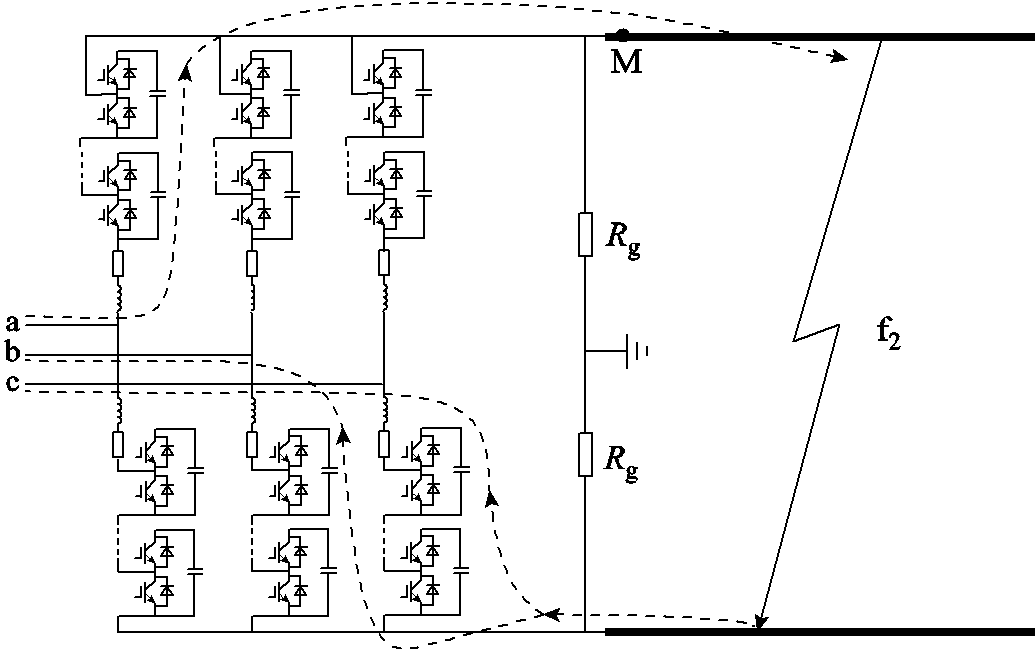
图7 双极短路故障通路示意图
Fig.7 Bipolar short circuit fault path schematic diagram
当发生区外故障f3时，故障通路如图8所示。由于故障行波由故障点流向线路两侧，即先流过MMC模块形成的物理边界，再经过量测点M，因此量测点测量到的高频暂态分量小。
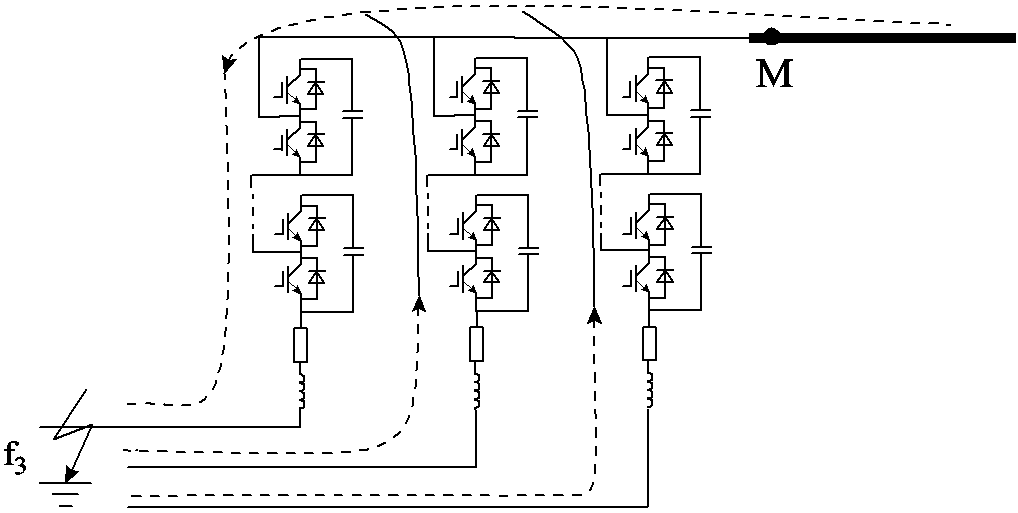
图8 交流侧单相接地故障通路示意图
Fig.8 AC side single phase ground fault path schematic diagram
根据以上分析，本文对MMC-HVDC系统的区内故障和区外故障进行仿真分析，采样频率为10kHz，为避开控制系统响应对暂态保护的影响，取故障后2ms时窗内的电压数据，量测端电压波形如图9和图10所示。
对比图9和图10可知，区内故障时，采样点之间的突变量较大；区外故障时，采样点之间的突变量较小。
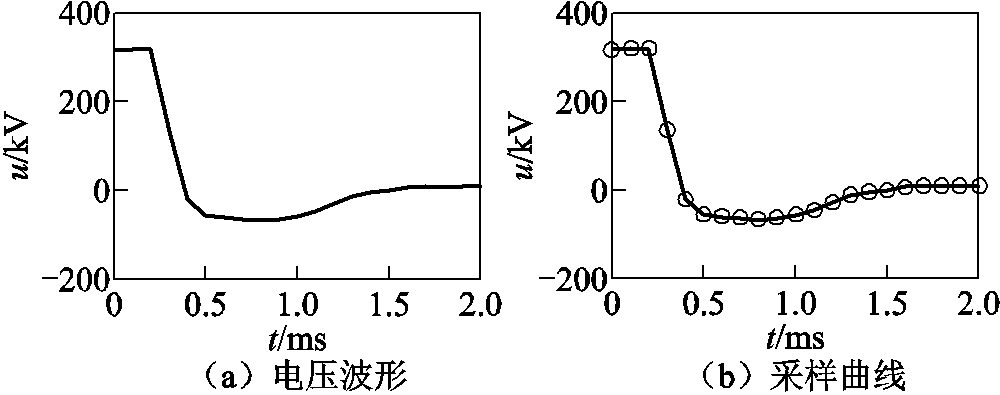
图9 区内故障时电压波形
Fig.9 Voltage waveform of internal fault
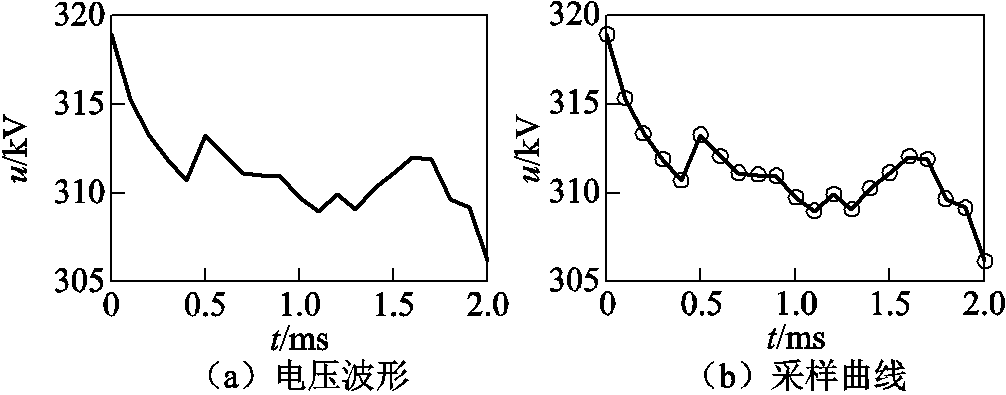
图10 区外故障时电压波形
Fig.10 Voltage waveforms of external fault
线路内部故障即区内故障时，故障信息没有经过换流器形成的边界，量测点的电压含有较高的高频分量，暂态行波的幅值和波头的陡度都较大，量测点的故障信息变化比较明显，采样点之间的突变量较大；线路外部故障即区外故障时，由于换流器形成的边界对高频分量有衰减作用，使线路量测点电压高频分量明显减少，暂态行波的幅值和波头的陡度相对较小，所以量测点的故障信息变化比较平缓，采样点之间的突变量较小。为进一步增大区内故障与区外故障时故障电压的差异，提高区分度，本文提出一种基于交叉重叠差分变换的故障识别算法。
交叉重叠差分变换属于一种差分运算，其本质是高阶差分，差分阶数越高[23]，得到的结果越能反映信号高频暂态量的特征及其突变方向，描述为
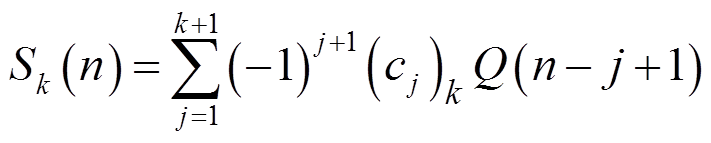（10）式中，k为差分的阶数；Sk(n)为信号的k阶差分；Q(n)为原始故障信号；n为瞬时采样点数，至少从k+1开始；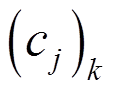
为SOD变换系数，其计算方法如下。
（1）SOD变换的第一个和最后一个系数相等，且为1，即
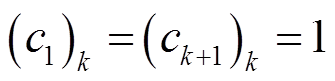（11）（2）SOD变换的第二个系数为SOD变换的阶数，即
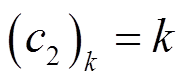（12）（3）SOD变换的其他系数可通过式(13)计算。
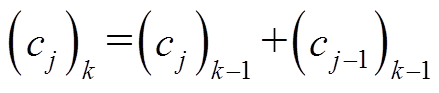（13）式中，SOD所有系数之和为0，即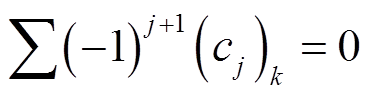
。
式（10）中n从k+1开始，每k+1个采样点进行一次运算，前k+1个采样点运算得出的数作为新集合的第一个数，依次往后顺延一个采样点重复之前的运算，可得出变换后的一组新数据，构成k阶SOD变换信号。根据式（10）计算出某样本数据1~5阶SOD变换后的值，如图11所示。当样本数据的大小均匀变化（变化量大于0）时，k(k＞1)阶SOD变换信号值均为0，如图11a所示；当样本数据的大小不均匀变化时，随着阶数的增加，SOD变换后信号各点之间的差值增大，如图11b所示。
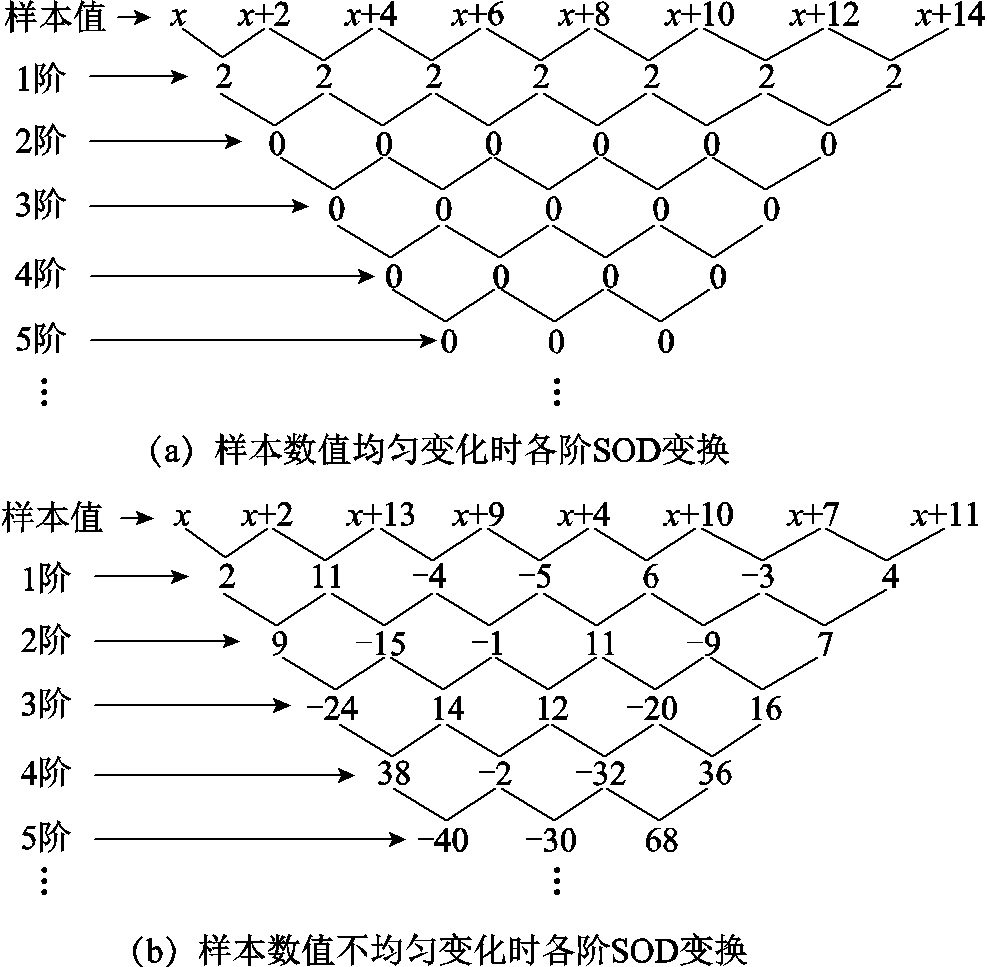
图11 样本数据1~5阶SOD变换
Fig.11 1~5 order SOD transformation of sample data
例如，对电压采样值进行四阶SOD变换，即
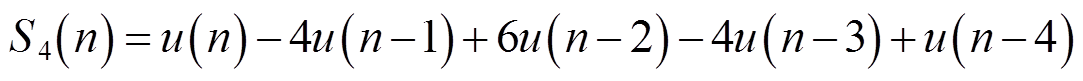（14）由式（14）可知，对电压原始信号的每个采样点乘相应的变换系数，一方面放大各个采样点之间的差异；另一方面各个采样点的变换系数正负交替，可看作每两个采样点先做一次差分计算，最后再作积分运算。SOD变换前后波形如图12所示。由图12可知，若电压信号中采样点之间的变化比较均匀，则差分计算后接近零值，压低了缓变量，即阻断直流稳态分量；若各个采样点之间的变化较大，则差分计算后变化量增大，即故障突变量更加明显，而积分运算则对全局的变化量有平缓的作用。
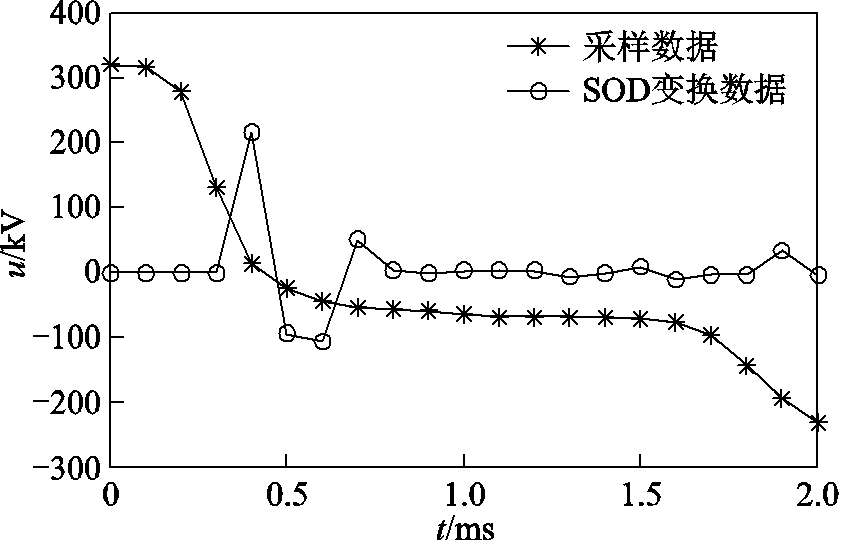
图12 SOD变换前后波形比较
Fig.12 Comparison of waveforms before and after SOD transformation
在故障暂态信号中，相比于低频分量，高频分量衰减得比较快，不利于分析。为凸显SOD变换的先进性，文中对故障原始信号和SOD变换之后的信号分别进行频谱分析，频谱如图13所示。由频谱分析结果可得，经SOD变换之后，原始信号的低频分量被抑制，高频分量被突出。
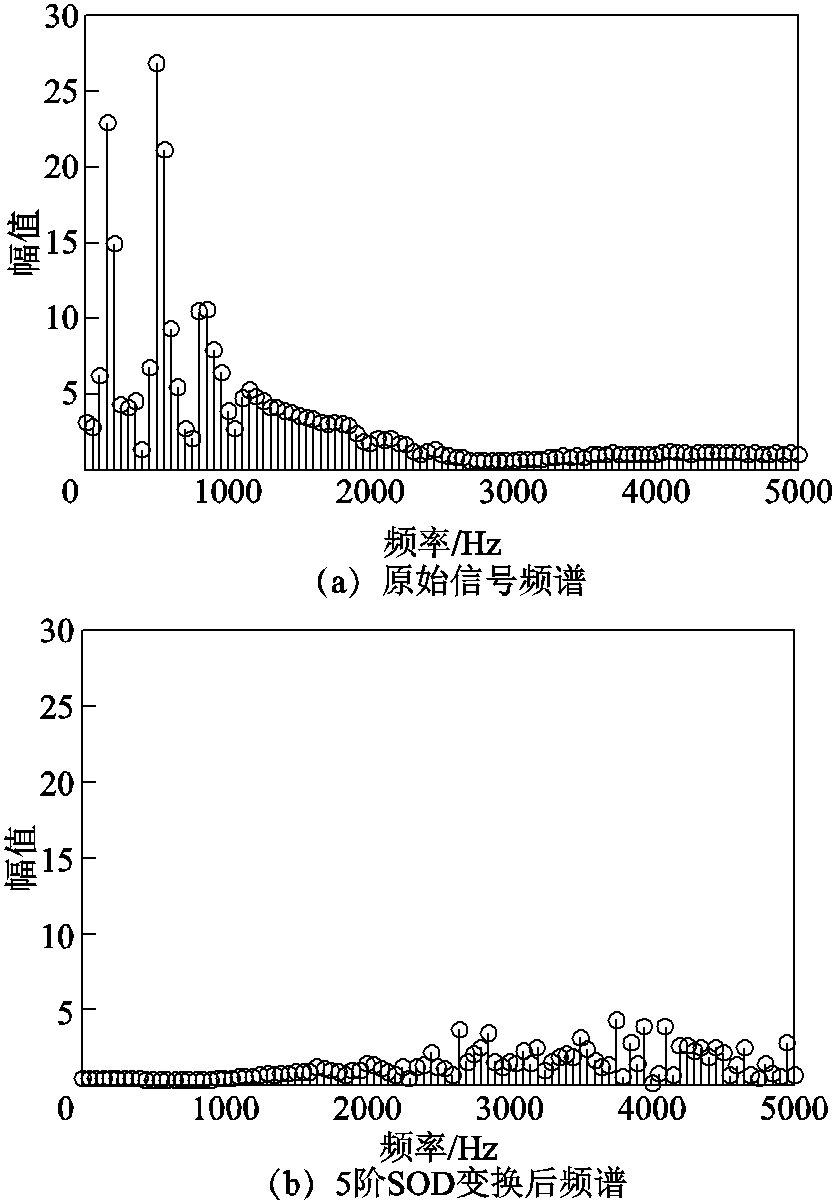
图13 原始电压及其SOD变换频谱图
Fig.13 Spectrums graph of original voltage and SOD transformation
正常运行时正极电压和电流不均匀变化但变化值较小，所以SOD变换之后均接近零值。图14a为正极接地故障时正极电压的原始信号，此时电压突变量较大。图14b为故障发生后5ms的电压1~5阶SOD变换的波形，当采样点之间的差值很小时，Sk(n)接近零值，变换后的波形幅值较小；当采样点之间的差值较大且不均匀变化时，变换后的波形幅值较大。
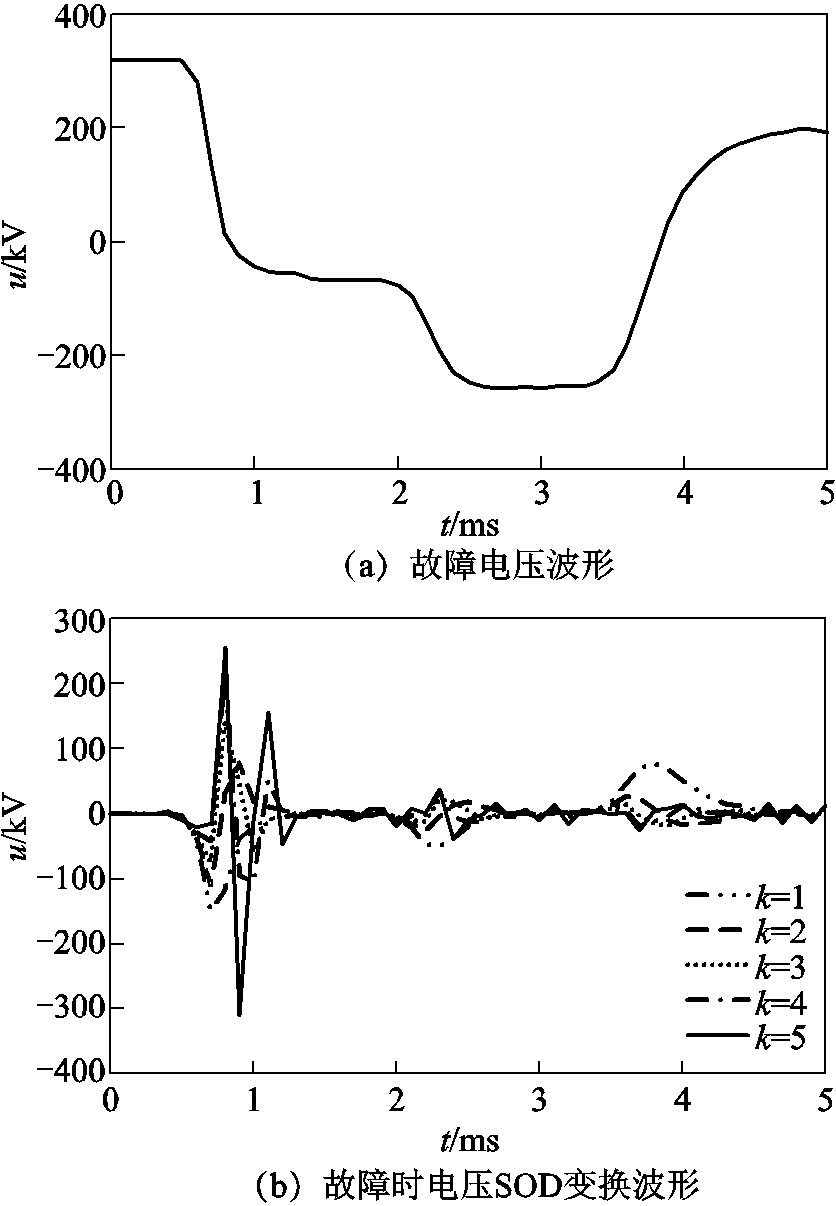
图14 故障电压及其SOD变换波形
Fig.14 Fault voltage and SOD transform waveforms
根据SOD变换理论及图14可得出，随着阶数k的增加，SOD变换系数增大且连续两个采样点的变换系数差值也增大，进而增大了突变量的幅值，因此差分阶数越高，波形幅值变化越明显。且随着阶数增加，其变换表达式越复杂，会增加计算负担和计算时间。在本文中四阶SOD变换即可满足需求，故选择四阶变换来进行后续分析。
在第2节中已经分析，由于直流线路两端换流器形成的物理边界的存在，当发生线路区内故障时，故障信号没有经过换流器形成的边界，量测点的电压含有较多的高频分量，暂态行波的幅值和波头的陡度都较大，所以量测点的故障信息变化比较明显，采样点之间的突变量较大。为尽可能地放大故障特征，增大区内、外故障的区分度，本文对故障电压和故障电流分别进行SOD变换得到Su(n)和Si(n)，并由其构成式（15），现定义K为SP绝对值的最大值，如式（16）所示，最后根据K值区分区内、区外故障。
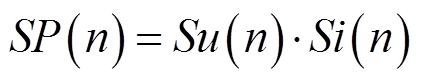（15）
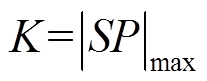（16）输电线路发生故障时，故障点产生的行波向线路两端传播，由于线路两端有换流器形成的物理边界使行波不断地发生折反射，该过程伴有能量的损耗，因此导致量测点的电压和电流出现严重的波动，如图15a和图15b所示。
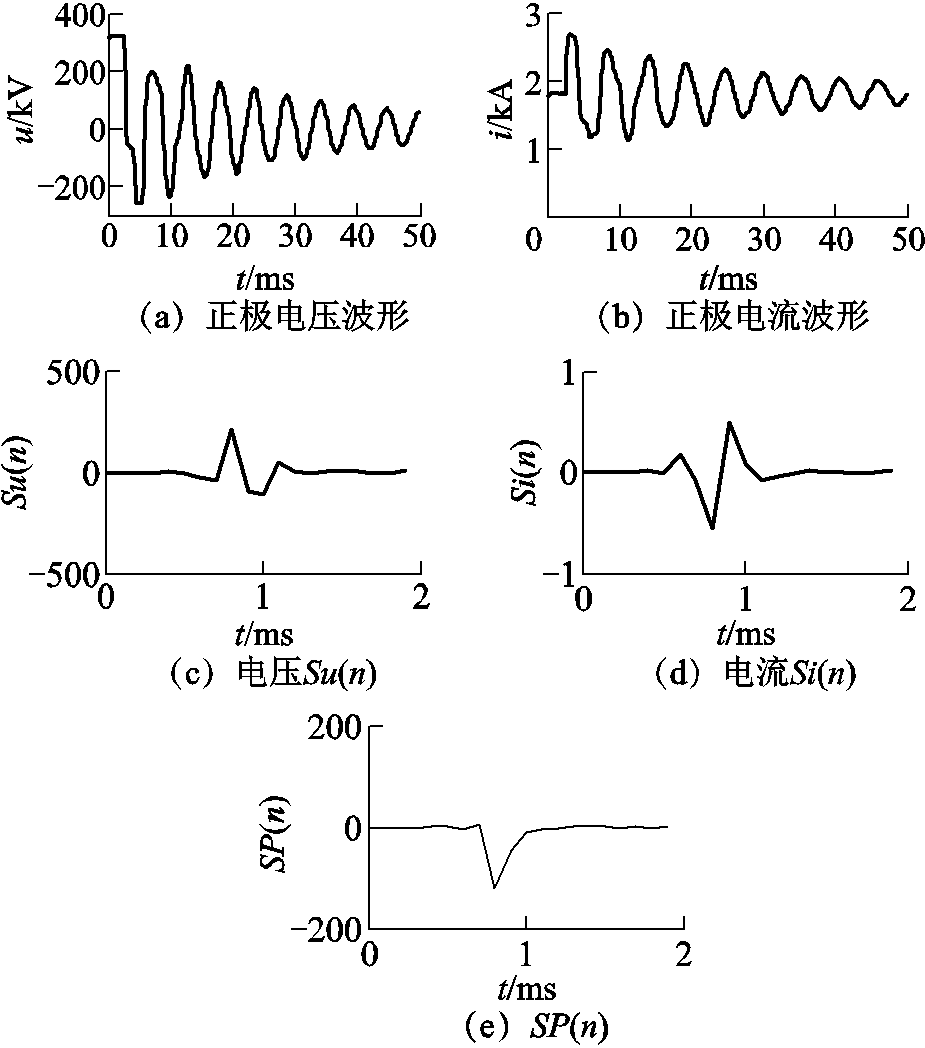
图15 正极接地故障时电压、电流SOD变换及其SP(n)
Fig.15 Voltage and current SOD transform and SP(n)waveforms，for positive pole line-to-ground fault
当发生正极接地故障时，正极接地故障时电压、电流SOD变换及其SP(n)如图15所示。由图15可知，故障信号没有经过换流器形成的边界，因此故障电压和电流中含有较多的高频分量，幅值和陡度变化比较大。在第3节SOD变换理论中指出，SOD变换增大了采样点的突变量且起到抑制低频突出高频的作用，当采样数据的数值突变量较大时，经SOD变换后突变量更加明显，所以区内故障时K值较大。
现在线路全长范围内遍历正极接地故障，得到不同过渡电阻情况下的K值，如图16所示。由图16可知，随着过渡电阻的增大，K值逐渐减小，当故障距离为400km，过渡电阻为300Ω时，K值达到最小值4.326。
当发生双极短路故障时，电压、电流SOD变换及其SP(n)如图17所示。由于故障信号没有经过换流器形成的边界，故障电压和电流中含有较多的高频分量，幅值和陡度变化比较大，因此K值较大。
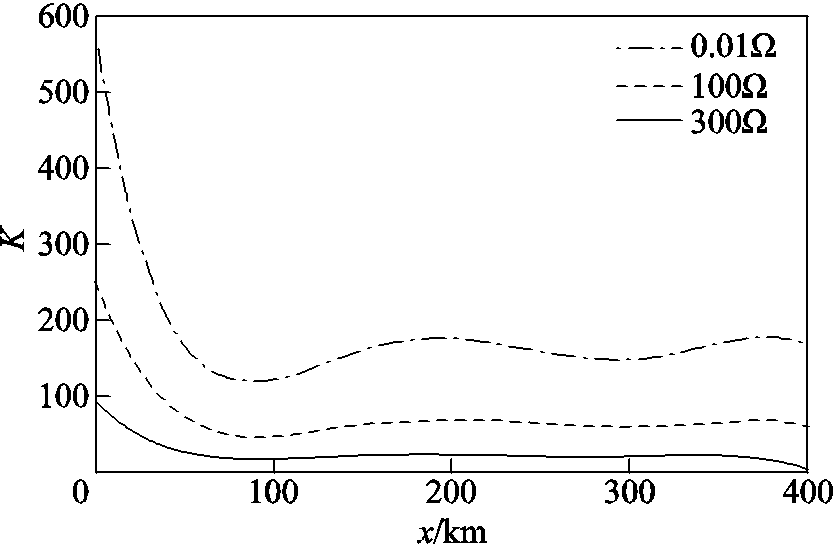
图16 正极接地故障时线路全长范围内K值
Fig.16 Positive pole line-to-ground fault K value within the full length of the line
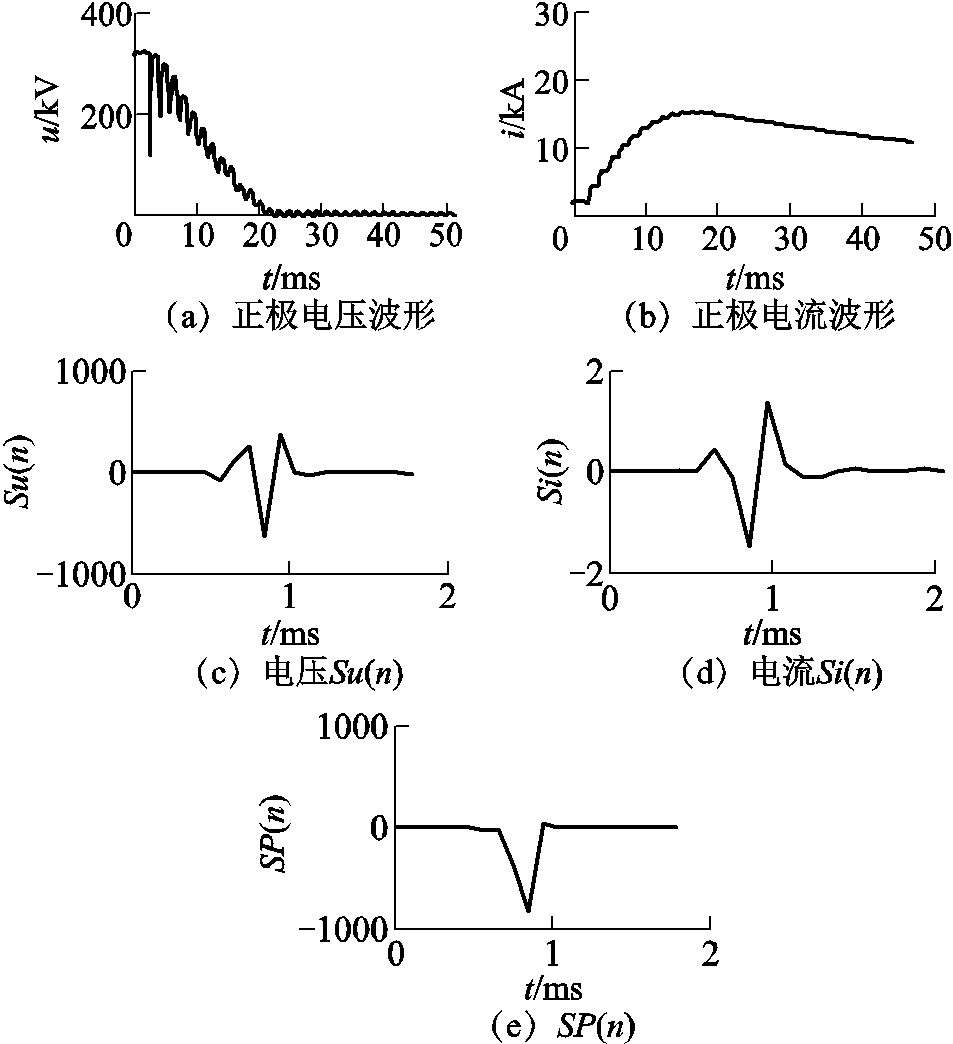
图17 双极短路故障时电压、电流SOD变换及其SP(n)
Fig.17 Voltage and current SOD transform and SP(n) waveforms，for pole-to-pole fault
在全线长范围内遍历双极短路故障（过渡电阻为0.01Ω），如图18所示。在相同故障位置，并且过渡电阻相同的条件下，与单极接地故障相比，双极短路时的K值较大。因此选用单极接地故障的K值最小值与区外故障时K值最大值进行区内外故障识别门槛值的整定。
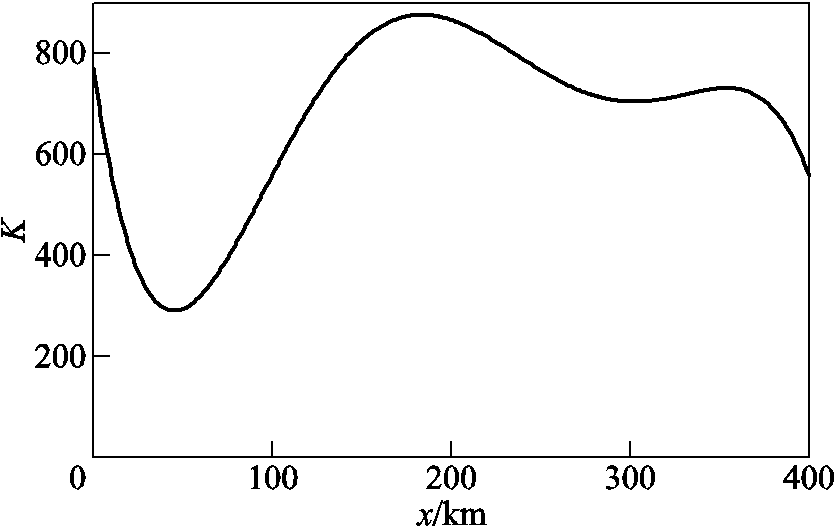
图18 双极短路故障时线路全长范围内K值
Fig.18 Bipolar short circuit fault K value within the full length of the line
当发生区外故障时，电压、电流SOD变换及其SP(n)如图19所示，换流器形成的边界对高频分量有衰减作用，暂态行波的幅值和波头的陡度相对较小，量测点的故障信息变化比较平缓，采样点之间的突变量较小。在第3节SOD变换理论中指出，当采样数据的数值均匀变化或者突变量较小时，经SOD变换后接近零值，即压低了缓变量，因此K值较小。
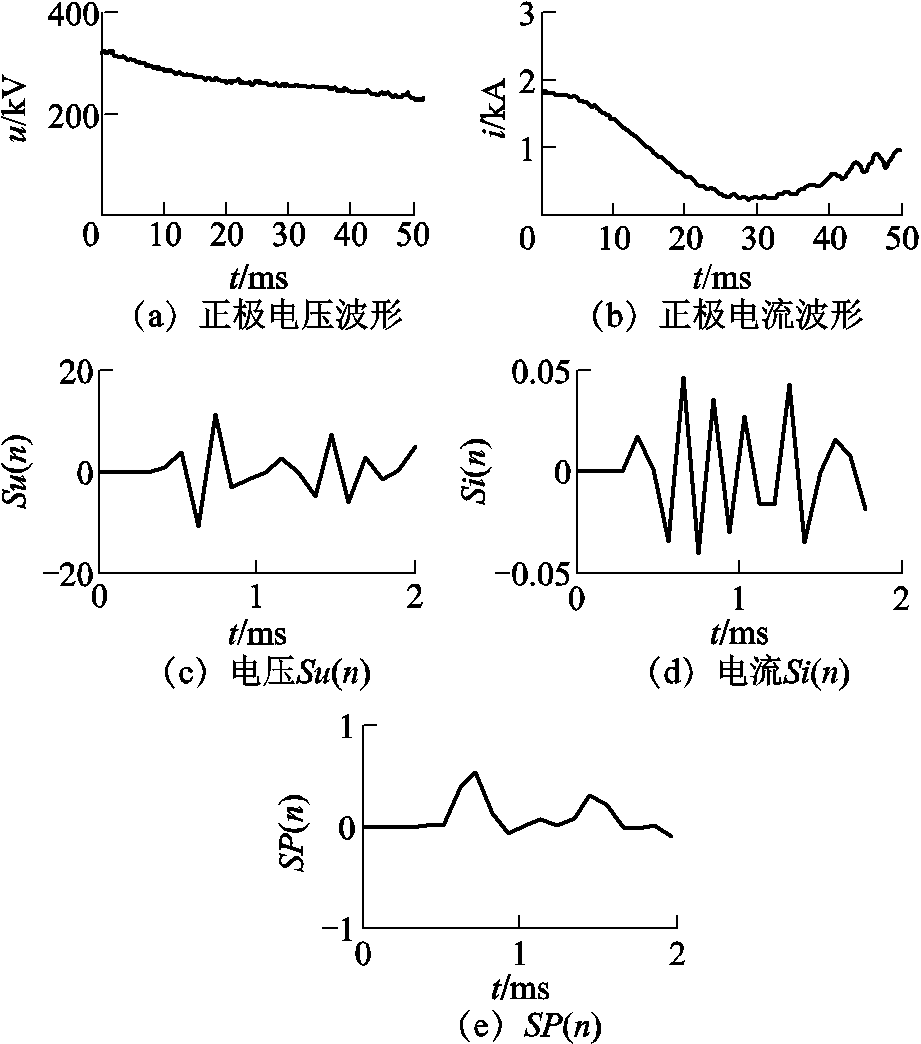
图19 交流侧故障时电压、电流SOD变换及其SP(n)
Fig.19 Voltage and current SOD transform and SP(n) waveforms, for AC system fault
对整流侧交流系统发生单相接地故障（AG）、两相短路故障（AB）、两相短路接地故障（ABG）及三相短路故障（ABC）时的电压和电流分别进行SOD变换，得到SP(n)如图20所示。可以看出，SP(n)值较小，其最大值K均小于1。
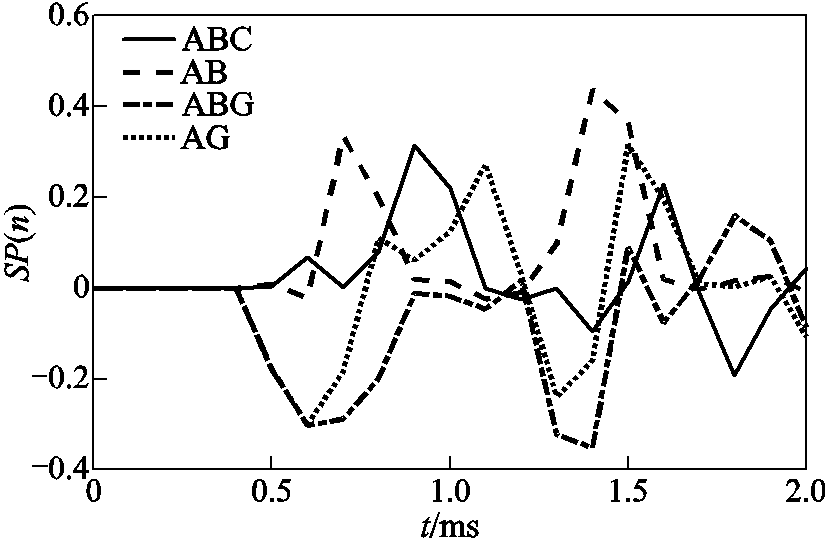
图20 整流侧交流系统故障时SP(n)
Fig.20 Rectifier-side AC system fault SP(n)
综上分析，当线路发生单极接地故障或发生双极短路故障时，K值较大；当交流侧发生故障时，K值较小。
本文的输电系统输电线路总长为400km，当故障距离为400km，过渡电阻为300Ω时，K值为4.326，记为Kmin，因此门槛值以Kmin来整定。初步给定区内外识别判据为：K≥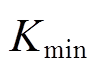
，则为区内故障；若K＜
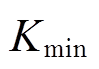，则为区外故障。
为提高判据的可靠性，考虑了实际因素、测量误差和一定的裕度，引入可靠系数Krel=1.2~1.3，具体分析如下。
考虑的实际因素包括过渡电阻、故障距离和采样率。
设正极线路接地故障距量测端为100km，采样率为10kHz，过渡电阻分别为0.01Ω、100Ω、300Ω，由量测端量测数据计算得到SP(n)，如图21所示。SP(n)的绝对值的最大值定义为K，由图21可知，随着过渡电阻的增加，K值逐渐减小。
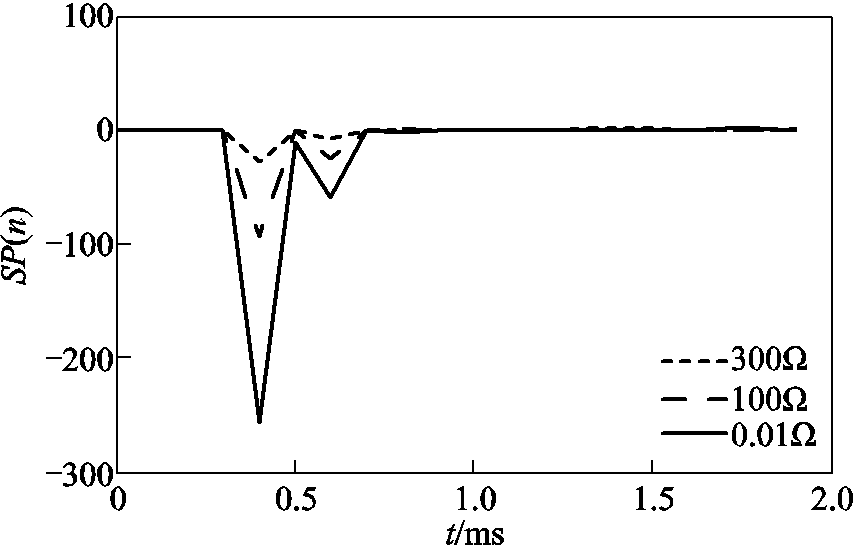
图21 不同过渡电阻下的SP(n)
Fig.21 SP(n) of different transition resistance
设正极线路接地故障过渡电阻为0.01Ω，采样率为10kHz，故障距离分别为20km、200km、380km，由量测端量测数据计算得到SP(n)，如图22所示。由图22可知，随着故障距离的增加，K值逐渐减小。
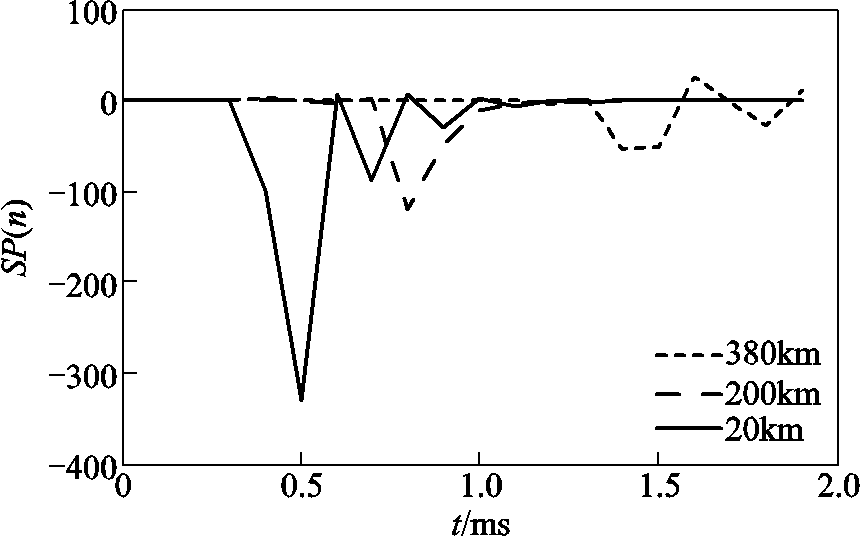
图22 不同故障距离下的SP(n)
Fig.22 SP(n) of different fault distances
设正极线路接地故障过渡电阻为0.01Ω，故障距离为100km，采样率分别为6.4kHz、10kHz、12.8kHz，由量测端量测数据计算得到SP(n)，如图23所示。由图23可知，随着采样率的增大，K值也逐渐增大。
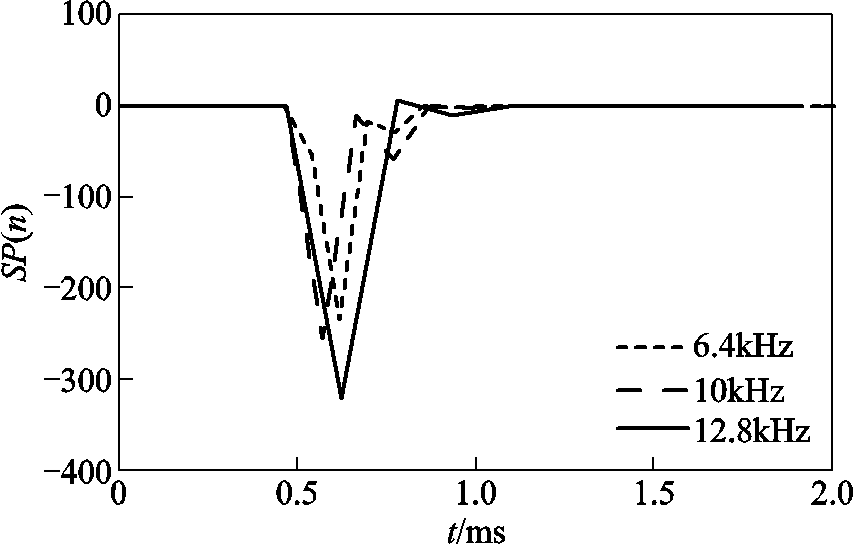
图23 不同采样率下的SP(n)
Fig.23 SP(n) of different sampling rates
考虑的测量误差：由于本文用故障电压和电流形成组合功率表达式SP(n)，考虑到量测端的电压和电流信号是一次电压和电流经过二次回路后产生的，电压和电流二次回路的传递函数的幅频特性和相频特性不一致[24]，因此电压和电流信号不同步，产生测量误差。文中增加了在区内最不利的故障情况（远端高阻）和区外最不利的故障情况（三相短路）下，电压和电流信号不同步时造成的误差对本文判据的影响，见表1。
表1 电压和电流不同步时的K值
Tab.1 K value when voltage and current are not synchronized
不同步采样点数K值 远端高阻ABC三相短路 05.711.34 19.481.26 25.091.01 34.960.86 49.200.68 58.070.38 61.800.57
由表1可知，由于采样点不同步，K值发生变化。当电压和电流的不同步采样点数小于等于5时，区内故障的K值均大于Kmin，区外故障的K值均小于Kmin；当电压和电流的不同步采样点数大于5时，该判据失效。
综上所述，考虑各种实际因素、测量误差和一定的裕度等，引入可靠系数Krel=1.2~1.3，因此本文中设置K的整定门槛值为
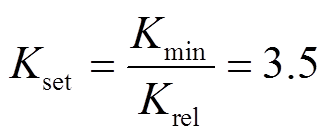
因此，甄别直流线路区内外故障的判据为：若K≥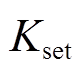
，则为区内故障；若K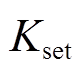＜则为区外故障。
基于交叉重叠差分变换的MMC-HVDC线路故障识别方法的流程如图24所示。
图24 故障识别流程
Fig.24 Flow chart of fault identification
在PSCAD/EMTDC中搭建伪双极仿真模型，验证本文提出的判据的有效性，其主要参数见表2。
表2 仿真系统的主要参数
Tab.2 Main parameters of simulation model
参数数值 交流系统额定电压/kV230 系统额定输送容量/(MV·A)1 200 额定直流电压/kV±320 额定直流电流/kA1.6 桥臂子模块数N76 子模块电容C/µF2 800 桥臂电感L/mH50 钳位电阻Rg/Ω104 架空线路长度/km400 架空线路电阻/(mΩ/km)10.61 架空线路电感/(mH/km)0.890 6
本文选取仿真采样率为10kHz，对线路正极接地故障、双极短路故障和交流侧故障进行仿真，截取故障后2ms时窗内的故障电压和电流数据分别进行四阶SOD变换获取Su(n)和Si(n)，并由其构成表达式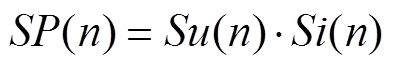
，定义K为SP绝对值的最大值，并根据K值判断区内外故障。在不同的故障类型、不同故障位置和不同过渡电阻情况下分别进行仿真对比，利用K值进行故障识别，得到相应的判断结果。
为验证该方法在不同故障类型下准确识别区内、区外故障，分别对输电线路发生普通故障、雷击故障、两端交流系统故障分别发生三相短路、两相短路和单相接地短路进行仿真，仿真结果见表3和表4。从仿真结果可看出，当发生不同故障类型时，该方法仍能准确识别区内故障和区外故障。
表3 输电线路不同故障类型的判断结果
Tab.3 Judgment results for different fault types in transmission lines
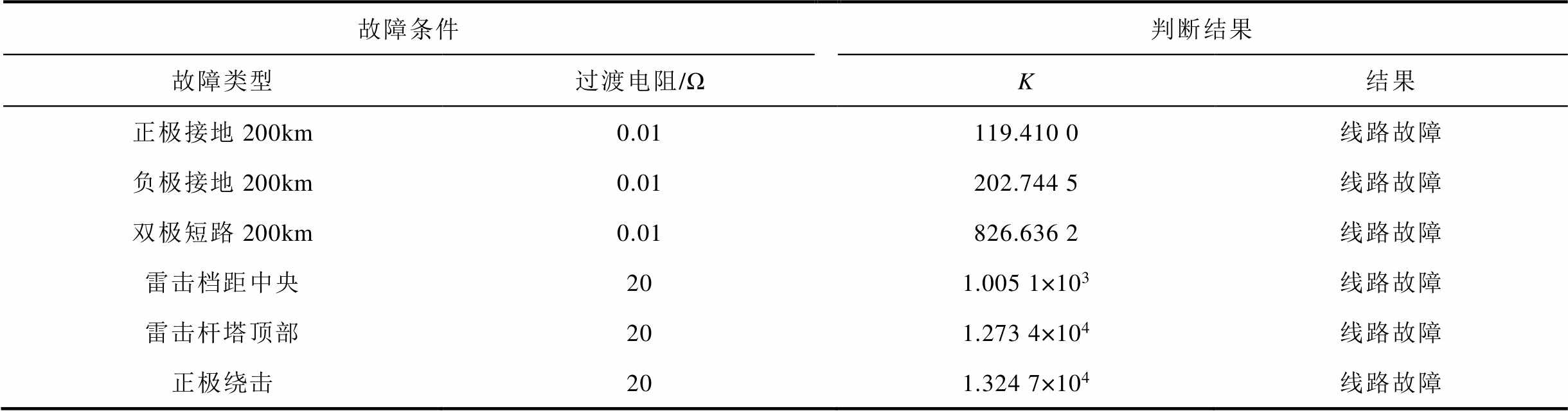
故障条件判断结果 故障类型过渡电阻/ΩK结果 正极接地200km0.01119.410 0线路故障 负极接地200km0.01202.744 5线路故障 双极短路200km0.01826.636 2线路故障 雷击档距中央201.005 1×103线路故障 雷击杆塔顶部201.273 4×104线路故障 正极绕击201.324 7×104线路故障
表4 交流系统不同故障类型的判断结果
Tab.4 Judgment results for different fault types in the AC system
故障条件判断结果 故障位置故障类型K结果 逆变侧交流系统故障ABC 1.336 2区外故障 AB 1.669 7区外故障 AG1.336 2区外故障
对输电线路分别发生正极接地故障、负极接地故障、双极短路故障和整流侧交流系统故障进行仿真验证，故障的过渡电阻分别设为0.01Ω、100Ω、200Ω、300Ω，仿真结果见表5，从仿真结果可以看出，该方法有一定的耐过渡电阻能力。
对输电线路分别发生正极接地故障、负极接地故障、双极短路故障和两端交流系统故障进行仿真分析，过渡电阻为0.01Ω；两端交流系统故障时，故障类型设置为三相短路，仿真结果见表6。从仿真结果可以看出，无论是近端故障还是远端故障，该方法均能正确识别区内故障和区外故障。
表5 不同过渡电阻的判断结果
Tab.5 Judgment results for different transition resistance
故障条件判断结果 故障位置（距M端）过渡电阻/ΩK结果 负极接地200km0.01202.744 5线路故障 10087.410 3线路故障 20043.784 2线路故障 30027.410 0线路故障 双极短路200km0.01826.636 2线路故障 100425.384 1线路故障 20076.683 1线路故障 300174.534 2线路故障 整流侧交流系统故障0.010.524 0区外故障 1001.023 8区外故障 2000.463 5区外故障 3000.313 6区外故障
表6 不同故障位置的判断结果
Tab.6 Judgment results for different fault locations
故障条件判断结果 故障位置（距M端）过渡电阻/ΩK结果 正极接地70km0.0165.832 2线路故障 负极接地20km0.01222.307 2线路故障 双极短路380km0.01705.551 3线路故障 逆变侧交流系统故障0.011.336 2区外故障
本文所提方法特点在于凸显故障特征，由此考虑此算法对真双极MMC-HVDC系统的区内外故障识别有一定的适应性。因此应用文中提出的区内外故障识别判据，针对真双极MMC-HVDC系统在全线长范围内遍历区内正极接地故障，其K值如图25所示，当故障距离为400km，过渡电阻为300Ω时，K值为5.738，大于整定值3.5，满足区内故障识别判据。
在真双极的整流侧和逆变侧交流系统设置不同类型的故障，故障判断结果见表7，K值均小于判据中的整定值3.5，满足区外故障识别判据。
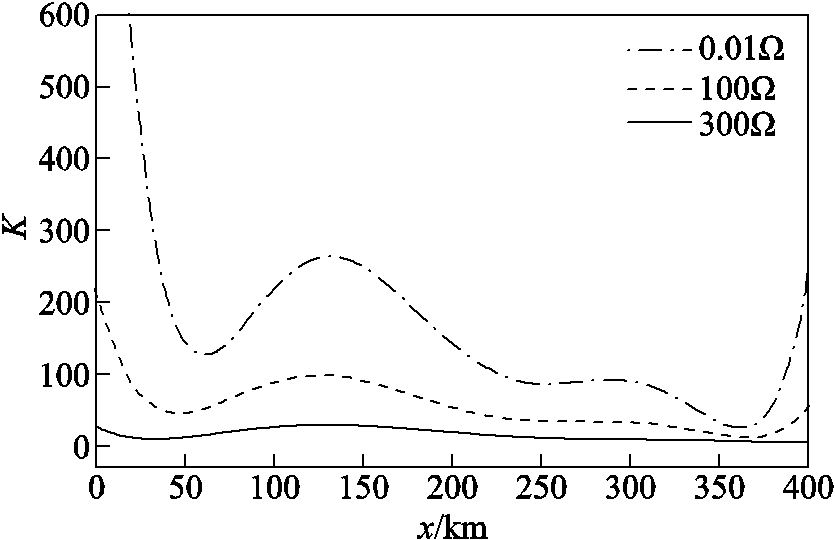
图25 线路全长范围内K值
Fig.25 K value within the full length of the line
表7 交流系统不同故障类型的判断结果
Tab.7 Judgment results for different fault types in the AC system
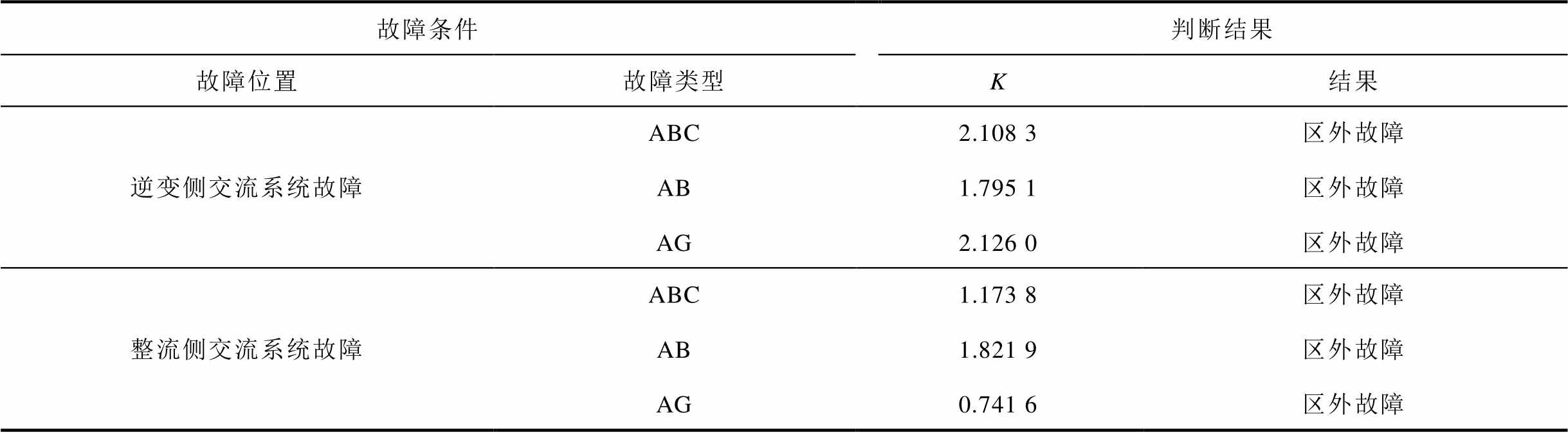
故障条件判断结果 故障位置故障类型K结果 逆变侧交流系统故障ABC 2.108 3区外故障 AB 1.795 1区外故障 AG 2.126 0区外故障 整流侧交流系统故障ABC 1.173 8区外故障 AB 1.821 9区外故障 AG 0.741 6区外故障
通过仿真分析可知，本文提出基于SOD变换的故障识别方法不仅适用于伪双极MMC-HVDC系统也适用于真双极MMC-HVDC系统，并有一定的耐过渡电阻能力，适用性较强。
于正极线路全长范围内遍历仿真接地故障。不同过渡电阻的SOD变换方法下的K值和电压变化率du/dt沿线分布分别如图26a和图26b所示。根据全线长范围内的遍历结果可以看出，随着过渡电阻和故障距离的增加，K值和du/dt值均减小。
现对相同故障条件下两种方法的遍历曲线进行波动性分析，标准差能反映一个数据集的离散程度，对两种方法下的遍历曲线分别求标准差，结果见表8。
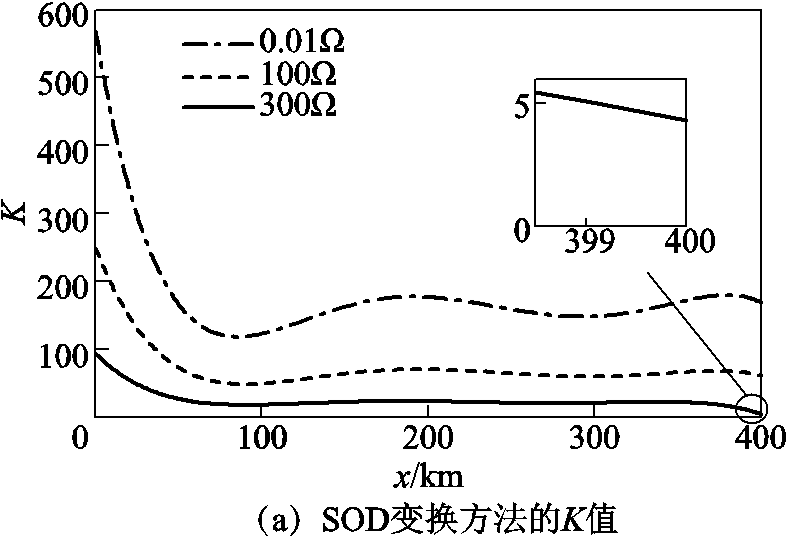
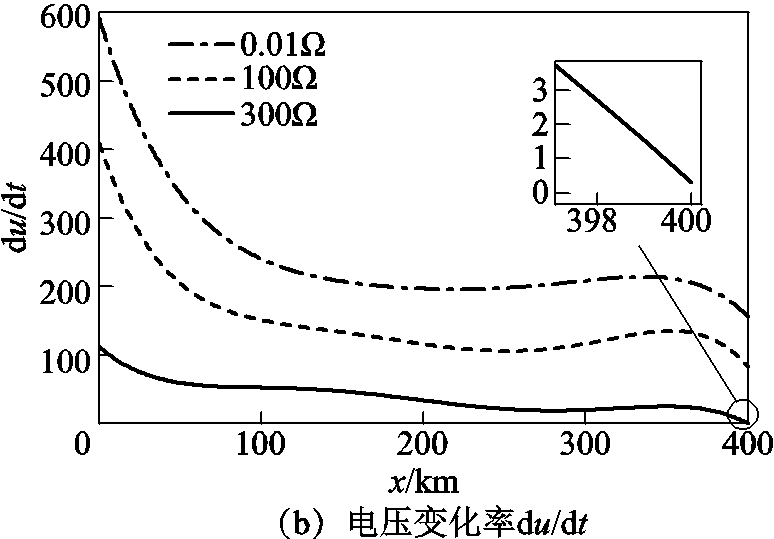
图26 SOD变换方法与电压变化率du/dt比较
Fig.26 Comparison of SOD transform method and voltage change rate du/dt
表8 SOD变换与du/dt方法比较
Tab.8 Comparison of SOD transformation and du/dt method
过渡电阻/Ω标准差 SODdu/dt 0.0171.455 186.191 7 10032.866 960.626 9 30013.169 621.265 4
由表8可知，在相同过渡电阻情况下du/dt方法的标准差都比SOD 算法的大，说明du/dt耐线长的能力弱于SOD算法，随着故障距离的增大，高频分量衰减，采用du/dt不能完全捕捉到高频信息，而采用SOD算法能够提取到更多的高频分量，因此其性能优于du/dt算法，即有更好的鲁棒性。
本文对MMC-HVDC系统的单极接地故障、双极短路故障和交流侧故障进行了故障特性分析，利用系统故障物理边界特点，对各种故障情况下的故障电压和故障电流分别作SOD变换，将变换后的电压和电流信号相乘得到SP，定义K为SP绝对值的最大值，并根据K值判断区内外故障，得出以下结论：
1）交叉重叠差分变换不仅能够增大突变量使故障特征更加明显，而且能抑制故障低频分量、突出高频分量更利于暂态分析。
2）本文采用故障后2ms时窗内的暂态信息，基本不受两端控制系统的影响。与基于双端电气量的故障识别方法相比，该方法仅使用单端电气量，不受两端通信延时的影响。
3）通过仿真分析，本文所提方法有很强的适用性，不仅适用于伪双极MMC-HVDC系统也适用于真双极MMC-HVDC系统，并且有较好的耐过渡电阻能力。
参考文献
[1] Marquardt R. Stronmrichterschaltungen mit verteilten erginesspeichern: German, DE10103031A1[P]. 2001-01-24.
[2] 徐政, 薛英林, 张哲任. 大容量架空线柔性直流输电关键技术及前景展望[J]. 中国电机工程学报. 2014, 34(29): 5051-5062. Xu Zheng, Xue Yinglin, Zhang Zheren.VSC-HVDC technology suitable for bulk power overhead line transmission[J]. Proceedings of the CSEE, 2014, 34(29): 5051-5062.
[3] 汤广福, 贺之渊, 庞辉. 柔性直流输电工程技术研究、应用及发展[J]. 电力系统自动化, 2013, 37(15): 3-14. Tang Guangfu, He Zhiyuan, Pang Hui. Research, application and development of VSC-HVDC engineering technology[J]. Automation of Electric Power Systems,2013, 37(15) :3-14.
[4] 张建坡, 赵成勇, 孙海峰, 等. 模块化多电平换流器改进拓扑结构及其应用[J]. 电工技术学报, 2014, 29(8): 173-179. Zhang Jianpo, Zhao Chengyong, Sun Haifeng, et al. Improved topology of modular multilevel converter and application[J]. Transactions of China Electrote-chnical Society, 2014, 29 (8): 173-179.
[5] 赵成勇, 许建中, 李探. 模块化多电平换流器直流输电建模技术[M]. 1版. 北京:中国电力出版社, 2017.
[6] 吴婧, 姚良忠, 王志冰, 等. 直流电网MMC拓扑及其直流故障电流阻断方法研究[J]. 中国电机工程学报, 2015, 35(11): 2681-2694. Wu Jing, Yao Liangzhong, Wang Zhibing,et al. The study of MMC topologies and their DC fault current blocking capacities in DC grid[J]. Proceedings of the CSEE, 2015, 35(11): 2681-2694.
[7] 张建坡, 赵成勇. MMC-HVDC直流侧故障特性仿真分析[J]. 电力自动化设备, 2014, 34(7): 32-37. Zhang Jianpo, Zhao Chengyong. Simulation and analysis of DC-link fault characteristics for MMC-HVDC[J]. Electric Power Automation Equipment, 2014, 34(7): 32-37.
[8] 宁连营, 邰能灵, 郑晓冬, 等. 基于自定义差分电流的MMC-HVDC输电线路纵联保护[J]. 电力系统自动化, 2017, 41(17): 87-93, 133. Ning Lianying, Tai Nengling, Zheng Xiaodong, et al. Pilot protection for MMC-HVDC transmission line based on custom difference current[J]. Automation of Electric Power Systems, 2017, 41(17): 87-93, 133.
[9] 罗永捷, 徐罗那, 熊小伏, 等. MMC-MTDC系统直流单极对地短路故障保护策略[J]. 电工技术学报, 2017, 32(1): 107-115. Luo Yongjie，Xu Luona，Xiong Xiaofu，et al. Pole-to-ground DC fault protection of MMC-MTDC systems[J]. Transactions of China Electrotechnical Society, 2013, 43(1): 98-106.
[10] 王帅, 毕天姝, 贾科. 基于小波时间熵的MMC-HVDC架空线路单极接地故障检测方法[J]. 电网技术, 2016, 40(7): 2179-2185. Wang Shuai, Bi Tianshu, Jia Ke. Wavelet entropy based single pole grounding fault detection approach for MMC-HVDC overhead lines[J]. Power System Technology, 2016, 40(7): 2179-2185.
[11] 戴志辉, 刘雪燕, 黄敏, 等. 基于相似度比较的环状柔直配电网线路单极接地故障保护[J]. 电力系统自动化, 2019, 43(23): 107-115. Dai Zhihui, Liu Xueyan, Huang Min, et al. Similarity comparison based single-pole grounding fault protection for line in ring-shaped flexible DC distribution network[J]. Automation of Electric Power Systems, 2019, 43(23): 107-115.
[12] 宁连营, 邰能灵, 郑晓冬, 等.基于单端暂态电流的MMC-HVDC输电线路保护方案研究[J]. 中国电机工程学报, 2017, 37(17): 5010-5017, 5220. Ning Lianying, Tai Nengling, Zheng Xiaodong, et al. Research on MMC-HVDC transmission line protection scheme based on one terminal transient current[J]. Proceedings of the CSEE, 2017, 37(17): 5010-5017, 5220.
[13] 张峻榤, 林卫星, 文劲宇. 基于直流电压变化率的直流电网直流故障保护[J]. 南方电网技术, 2017, 11(1): 14-22. Zhang Junjie,Lin Weixing ,Wen Jinyu. DC fault protection based on change rate of DC voltage in DC grid[J]. Southern Power System Technology, 2017, 11(1): 14-22.
[14] 宋国兵, 王婷, 张晨浩, 等. 利用健全极MMC注入特征信号的直流线路故障性质判别方法[J].电工技术学报, 2019, 34(5): 994-1003. Song Guobing, Wang Ting, Zhang Chenhao, et al. DC Line fault identification based on characteristic signal injection using the MMC of sound pole[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 994-1003.
[15] Ikhide M, Tennakoon S, Griffiths A, et al. Fault detection in multi-terminal modular multilevel Converter (MMC) based high voltage DC (HVDC) transmission system[C]//2015 50th International Universities Power Engineering Conference (UPEC), Stoke on Trent, UK, 2015: 10.1109/UPEC.2015.739887.
[16] 何佳伟, 李斌, 李晔, 等. 多端柔性直流电网快速方向纵联保护方案[J]. 中国电机工程学报, 2017, 37(23): 6878-6887, 7078. He Jiawei, Li Bin, Li Ye, et al.A fast directional pilot protection scheme for the MMC-based MTDC grid[J]. Proceedings of the CSEE, 2017, 37 (23): 6878-6887, 7078.
[17] 徐政. 柔性直流输电系统[M]. 2版. 北京: 机械工业出版社, 2016.
[18] 王奎, 郑泽东, 李永东. 基于新型模块化多电平变换器的五电平PWM整流器[J]. 电工技术学报. 2011, 26(5): 34-38. Wang Kui, Zheng Zedong, Li Yongdong. A five-level PWM rectifier based on new modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 34-38.
[19] 苏见燊, 郭敬东, 金涛. 柔性直流电网中直流故障特性分析及线路故障重启策略[J]. 电工技术学报, 2019, 34(增刊1): 352-359. Su Jianwei, Guo Jingdong, Jin Tao. Analysis of DC fault characteristics and line fault restart strategy in flexible DC grid[J]. Transactions of China Electrotec-hnical Society, 2019, 34(S1): 352-359.
[20] 姚骏, 谭义, 裴金鑫, 等. 模块化多电平变流器高压直流输电系统直流故障改进控制策略[J]. 电工技术学报, 2018, 33(14): 3306-3318. Yao Jun, Tan Yi, Pei Jinxin, et al. Improved DC fault control strategy for modular multilevel converter HVDC transmission system[J]. Transactions of China Electrotechnical Society, 2018, 33 (14): 3306-3318.
[21] 薛英林, 徐政, 张哲任, 等. MMC-HVDC换流器阻抗频率特性分析[J]. 中国电机工程学报, 2014, 34(24): 4040-4048. Xue Yinglin, Xu Zheng, Zhang Zheren, et al. Analysis of impedance frequency characteristics of MMC-HVDC converter[J]. Proceedings of the CSEE, 2014, 34(24): 4040-4048.
[22] 赵成勇, 陈晓芳, 曹春刚, 等. 模块化多电平换流器HVDC直流侧故障控制保护策略[J]. 电力系统自动化, 2011, 35(23): 82-87. Zhao Chengyong, Chen Xiaofang, Cao Chungang, et al. Control and protection strategies for MMC-HVDC under DC faults[J]. Automation of Electric Power Systems, 2011, 35(23): 82-87.
[23] Dina Mourad Hafez, Elsayed Hassan Shehab Eldin, Abdu Aziz Mahmoud Abdu Alaziz. A novel unit protective relaying concept based on current signal sequential overlapping derivative transform: Two sides fed transmission line application[J]. Ain Shams Engineering Journal, 2012, 3(3): 267-277.
[24] 董新洲, 雷傲宇, 汤兰西, 等. 行波特性分析及行波差动保护技术挑战与展望[J]. 电力系统自动化, 2018, 42(19): 184-191. Dong Xinzhou, Lei Aoyu, Tang Xilan, et al. Analysis of traveling wave characteristics and challenges and prospects of traveling wave differential protection technology[J]. Automation of Electric Power Systems, 2018, 42(19): 184-191.
Fault Identification Method of MMC-HVDC Line Based on Sequential Overlapping Derivative Transform
Abstract In the high voltage direct current transmission based on modular multilevel converter (MMC) system, identifying line faults efficiently and reliably was one of the important guarantees for the safe and economic operation of the system. In order to identify line faults quickly and reliably, an internal and external fault identification method based on sequential overlapping derivative(SOD) transform was proposed. This paper first analyzes the physical boundary formed by the MMC equivalent impedance model, which has a strong attenuation effect on high frequency components, the start voltage caused by the line fault changes steeply when amplitude is large and the time-domin waveform isshowen shaking violently;the the start voltage caused by the external fault changes gently and amplitude is small. Secondly, the SOD transformation is used to transform the fault voltage and current. The converted voltage and current signal are multiplied to obtain SP, and K is defined as the maximum value of the absolute value of SP, and the internal and external faults are determined according to the K value. The MMC-HVDC system simulation model is built on PSCAD/EMTDC. The simulation results show that the method , which has good quick action, certain resistance to transition resistance and strong applicability ,can reliably and accurately identify internal faults and external faults.
Keywords：HVDC, modular multilevel converter, physical boundary, sequential overlapping derivative transform, fault characteristic analysis, fault identification
中图分类号：TM723
DOI: 10.19595/j.cnki.1000-6753.tces.191546
国家自然科学基金（51807084、52037003）和云南省重大专项（202002AF080001）资助项目。
收稿日期 2019-11-22
改稿日期 2020-01-22
束洪春 男，1961年生，博士，教授，博士生导师，研究方向为电力系统新型继电保护与故障测距、故障录波、数字信号处理及DSP应用等。E-mail：kmshc@sina.com.cn
安 娜 女，1985年生，博士研究生，研究方向为输变电设备及自动化。E-mail：anna073000@163.com（通信作者）
（编辑 郭丽军）