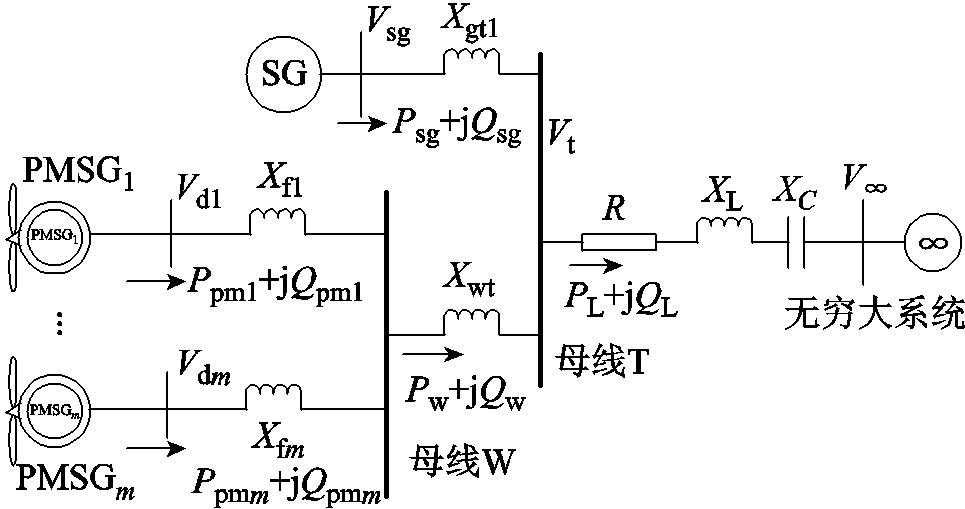
图1 直驱风机风电场并网等效系统
Fig.1 Equivalent system of PMSGs interfaced with AC power grid
摘要 随着新能源电力电子器件的广泛接入，电力系统次同步振荡问题的诱发机理越来越复杂。为了能够及时定位到诱发次同步振荡的机组并采取措施，基于深度迁移学习提出了一种次同步振荡源定位的方法。该方法首先依据开环模式谐振理论构建仿真系统，并在仿真系统中获取训练数据样本；其次，运用卷积神经网络（CNN）进行振荡源特征提取并建立训练定位模型；最后，通过迁移学习将训练模型迁移到实际系统，以实现定位模型的应用。为验证所提方法的有效性，设计了含直驱风机并网的电力系统的仿真系统测试算例。结果表明，该方法相比于传统的特征值分析方法，具有定位准确率高、在线应用方便等优势。该方法能够在较短时间内给出判别结果，为实现振荡源的在线识别奠定了基础。
关键词：开环模式谐振 次同步振荡 直驱风机 振荡源定位 机器学习
随着新能源电力电子器件的广泛接入，电力系统稳定性不断出现新的挑战。由早期报道的美国德克萨斯州风电场因风机与串补输电线路的交互作用而发生次同步振荡[1]，到2015年新疆哈密地区风电机组在无串补情况下发生的大规模次同步振荡[2]，风电场引发的次同步振荡问题层出不穷。电力系统次同步振荡问题影响范围广，已经危害到电力系统安全稳定运行，并且其诱发因素不确定，给采取抑制措施带来了较大的阻碍[3]。
次同步振荡问题最早始于1930年的由系统中容性负载或串补线路引发的电气谐振[4]，而后1970年至1971年，美国Mohave电厂因串补引发的振荡对两台同步机轴系造成了损坏，引发了广泛关注[5]。近年来，次同步振荡问题依旧是活跃的话题，诸多学者已经对新能源设备或电力电子器件，如风机[6]、统一潮流控制器[7]、静止同步补偿器[8]等展开了广泛的研究。这些研究主要包括：引发电力系统次同步振荡的机理，次同步振荡的抑制装置，附加阻尼控制策略等。其中，机理研究目前广泛使用的方法有阻抗法与模式法[9-10]。根据现有的机理分析，次同步振荡问题主要包括：次同步谐振[11-12]（Sub-Synchronous Resonance, SSR），次同步交互作用[13-14]（Sub-Synchronous Control Interaction, SSCI）以及由装置自身引起的次同步现象[15]（Sub-Synchronous Torsional Interaction, SSTI）。而次同步振荡抑制装置[16-17]以及附加阻尼控制策略[18-19]的研究是根据现有的机理分析进行的，例如，当风电场经柔性交流输电系统联网时，选择在柔性交流输电装置（如静止同步补偿器、可控串补、静止无功补偿器等）上附加阻尼控制[20]，或在风力发电机控制回路上附加阻尼控制[21]。但大规模的风电场通常含有成百上千台风机，其类型不尽相同，控制参数各异，在次同步振荡发生时很难从中确定要采取措施的风机。
在工程实际中，当次同步振荡发生时甚至发生前希望能够尽快地确定诱发的因素，定位诱发的元件，从而及时采取抑制措施，保证系统的安全稳定运行。因此，识别定位风电场并网系统中次同步振荡源机组至关重要[22]。其中次同步振荡源，是指引起次同步振荡的因素或元件，本文中特指由控制环节而引发系统次同步振荡的风电机组。近年来，由于新型次同步振荡问题[23]越来越突出，传统的模式分析法是通过闭环线性模型，根据系数矩阵计算并找到主导特征根，进而通过该主导特征根对应的参与因子找到引起模式改变的状态变量，确定振荡源[6]。但这种方法局限于离线分析，且通常系统的规模庞大，模式的计算耗时长。
目前已有学者开始基于广域测量系统（Wide Area Measurement System, WAMS）数据实现振荡源的识别定位，其中能量函数法的应用最为广泛，在低频振荡源识别定位方面获得了较大的成功[24-25]，但次同步振荡相较于低频振荡其频率范围更宽，振荡的诱发原因复杂多样，其振荡源定位的研究难度较大。文献[26]同样采用能量函数法研究了源最为明确的次同步强迫振荡扰动源的定位，但该方法仅针对具有阻尼环节的同步机采用能量函数进行了推导分析，而对于由于控制不当引发的风机次同步振荡的源定位未进行相关分析研究。文献[27]提供了根据次/超同步功率和阻抗确定SSCI源的三个标准，基于阻抗法对哈密风电系统的SSCI源实现了定位，但阻抗法本质上是一种数值算法，虽然能够实现振荡源定位，但需要根据量测数据在线构造模型，时间上存在较大延迟，很难实现在线应用，并且阻抗法计算时需首先进行频率分析从而确定谐振频率点，而谐振频率点的精确度会影响到次同步振荡模式的确定。文献[28]提出了基于传播路径匹配原理的多风电场汇集区域次同步振荡扰动源的定位方法，通过解析计算了次同步电流在系统中的传播规律，并与实际分布规律进行对比分析，确定引起振荡的主导风电场。该方法在计算时也需要先进行频率分析，这对于频率范围较宽的次同步振荡而言在时效及精度方面都会受到影响。此外，由于该方法在计算次同步电流在系统中的传播规律时是基于参数完全已知的确定系统，其模型采用线性化仿真模型，但实际系统在发生振荡时往往参数不能全部已知，且实际系统获得的数据由于噪声等原因与仿真系统差异较大，这可能会影响到该方法的实际应用可行性。
鉴于此，本文引入机器学习建立运行数据与振荡源的关系，提出一种风电场振荡源定位方法，从而实现通过运行数据快速定位到相关机组。该方法与上述数值方法相比有以下特点：①机器学习是以历史数据为基础的经验学习，通过离线学习模型，实现在线判断决策，在判断速度上具有明显的优势，在线应用的扩展上更具有优势；②机器学习是基于数据特征的学习方法，其框架结构决定了模型具有很强的抗噪性与鲁棒性；③机器学习的方法更加智能化，不受限于特定系统或模型，从数据直接提取特征，具有良好的迁移性与泛化性。
在本文的算例中，初步对一个简单的含直驱风机的电力系统由相互作用引发的次同步振荡问题进行了测试分析，结果表明，所提方法能够有效迁移训练模型，并达到较高的定位准确率。
考虑如图1所示的等效系统模型。假设直驱风电场用m台并联的直驱风机（Permanent Magnet Synchronous Generator, PMSG）模型表示，并连接于集中母线W上，设与之临近地区存在一个含有同步发电机（Synchronous Generator, SG）的火电机组，风电场与火电厂机组的功率汇集于母线T上，经过串联补偿线路接入交流主网（无穷大系统等效），形成风火打捆系统[6]。
图1 直驱风机风电场并网等效系统
Fig.1 Equivalent system of PMSGs interfaced with AC power grid
为建立上述系统的线性化闭环模型[6]，本文将图1中系统分为风机子系统与剩余子系统两部分，其中将被研究风机记为“风机子系统”，而其余部分记为“剩余子系统”。
风机子系统即在某一运行点下只考虑其中一台风机的动态方程，忽略系统中其他风机及电网的动态方程，风机子系统的状态空间方程为
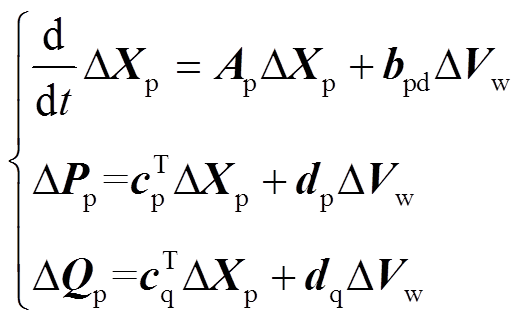（1）式中，Xp为风机所有状态变量组成的列向量，Xp=[xp1xp2 
xpm]T；Vw为风机并网点的机端输入电压幅值，Vw=[Vwd Vwq]T；Pp、Qp为输出变量，分别为风机向电力系统注入的有功功率和无功功率；Ap为状态矩阵；bpd为与Vw相关的输入矩阵；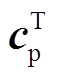
、dp、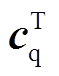
、dq为系数。
同理，在同一运行点下，忽略上述研究风机的动态方程，并将DPp、DQp作为输入变量，DVw作为输出变量，则剩余子系统的状态空间方程为
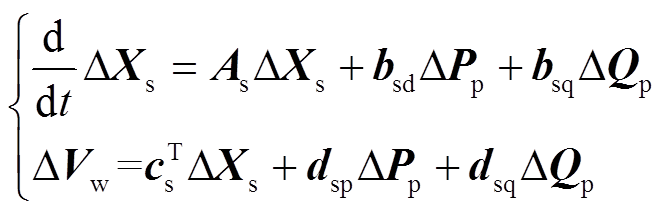（2）式中，Xs为剩余子系统所有状态变量组成的列向量；As为状态矩阵；bsd、bsq为与输入变量相关的输入矩阵；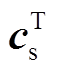
、dsp、dsq为系数。
如果在这一运行点下同时考虑“风机子系统”及“剩余子系统”，则构成风机并网的闭环互联系统，联立式（1）、式（2），可得闭环互联系统的状态方程为
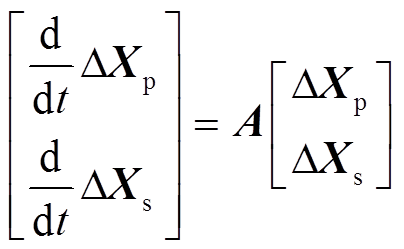（3）式中，A的详细表示见附录。
定义状态矩阵A的特征值
及相对应的左右特征向量wiT和vi为
（4）系统状态变量xi(t)和系统振荡模式变量zi(t)=zi(0)elt之间的关系为
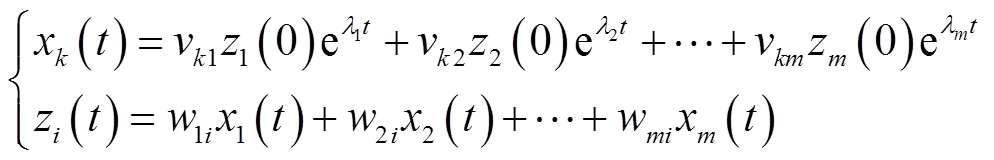（5）式中，vki为右特征向量矩阵的第k行第i列的元素；wki为左特征向量矩阵的第k行第i列元素。系统模式li的参与因子可由第i个模式在第k个状态变量的度量表示为
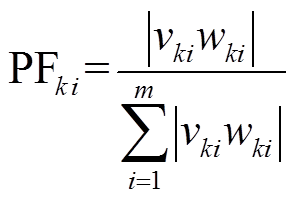（6）因此，参与因子PFki衡量了受第k个状态变量激励的第i个模式在该状态变量时域响应中的参与程度。
如果确定了系统的网架结构、系统中设备参数K以及运行点P0，就可得到电力系统的闭环模型，则参与因子与运行点之间的关系可表示为
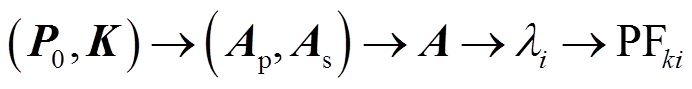（7）式中，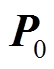
由量测有功功率P、量测无功功率Q、端电压V及相角
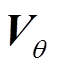构成。
由式（7）可知，给定设备参数以及运行点，采用数值的方法逐步计算能够得到系统的特征根与参与因子，且对于确定的一个P0有唯一的参与因子与之对应，即
（8）式中，f (×)为输入变量(P0, K)与输出变量PF之间的关系函数。然而，根据Galois定理可知，n（n＞4）阶矩阵的特征值无法代数求解，这意味着虽然能够数值求解式（7）中系数矩阵A并得到特征根，但不可能获得函数f的显式表达式。
综上可知，运行点P0和PFki之间的关系建模可以扩展为机器学习问题。记振荡源S为引起次同步振荡的元件，在本文中特指风电机组（PMSG机组编号）。由于该元件特性改变（或控制参数不合理等）能够诱发次同步振荡引起系统主导模式改变，通过参与因子分析可找到与该主导模式对应的状态变量。因此，振荡源S与参与因子以及运行点之间的关系可表示为
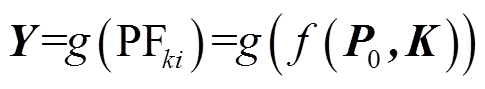（9）式中，Y为振荡源S的标签；g (×)为参与因子PF与振荡源标签之间的关系函数。
由式（9）可知，闭环互联系统中，风机向电力系统注入的有功功率和无功功率以及并网节点处的电压与闭环特征根有直接影响，因此量测并网节点处的有功功率、无功功率及电压能够表征闭环系统的稳定状态。根据训练数据，通过特征提取及拟合能够获得式（9）的关系函数，得到训练模型。特征提取与关系拟合通过卷积神经网络（Convolutional Neural Network, CNN）进行，其中卷积层由多个特征矩阵组成，用以提取输入数据的局部特征。特征矩阵与卷积核进行卷积运算得到下一层的新的特征矩阵，其计算公式为
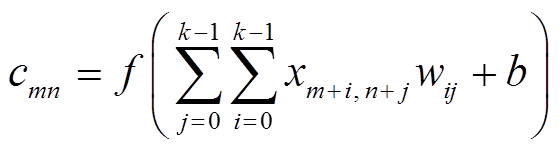（10）式中，xm+i，n+j为输入矩阵x的第m+i行、n+j列元素；cmn为输出矩阵c的第m行第n列元素；wij为k阶卷积核w的第i行第j列元素；b为偏置项；f为激活函数。
池化层的作用是将特征矩阵降维，池化过程与滤波过程类似，一方面对数据进行了降维，在保留主要特征的同时减小了计算量；另一方面，可以防止过拟合。且该过程是无参变换，不必进行参数的更新，本文采用均值池化，计算公式为
（11）式中，yab为输出矩阵y的第a行第b列元素；ca×p+i，b×p+j为输入矩阵c的第a×p+i行、b×p+j列元素。
经过多层卷积-池化网络后，将特征提取的结果展开为一维数组输入全连接层，经过Relu函数映射输出，由于本文研究次同步振荡源定位，因此在全连接层后增加一个softmax分类器，最终输出为机组标签。通过上述过程即可建立运行数据与振荡源之间的关系。
迁移学习[29]是将一个领域内学习到的知识应用到另一个相似的领域中，即采用机器学习算法将已有知识从源任务（Domain Task）迁移进目标任务（Target Task）。电力系统中稳态运行数据充足，而振荡失稳数据相对匮乏且价格昂贵，但由于稳态数据与不同振荡模式下的失稳数据差异较大，无法直接用于迁移学习，考虑到基于开环模式谐振理论离线仿真系统数据获取容易，因此采用仿真系统样本数据迁移学习实际系统数据的任务。
考虑迁移的方便性，本文的迁移学习采用模型迁移的方法。给定一个源域Ds及一个目标域Dt，对任意数据域都由其特征空间X及概率分布P(X)构成，即Ds={Xs, Ps(Xs)}, Dt={Xt, Pt(Xt)}。其中，s或t即源域或目标域。而域内的任务可描述为Ts={Ys, fs}, Tt={Yt, ft}。其中，Ys与Yt分别表示源域和目标域的标签空间，fs与ft分别表示源域和目标域的映射函数，或条件概率Qs(Ys|Xs)和Qt(Yt|Xt)。
假设源域与目标域的特征空间分布相同，而源域与目标域的标签空间分布不同，则迁移学习的目标是学习目标预测函数ft: Xt→Yt，在Dt上期望误差低，并满足Xs=Xt, Ys=Yt, Ps(Ys|Xs)¹Pt(Yt|Xt)及Qs(Ys|Xs)¹Qt(Yt|Xt)。深度迁移学习是指由〈Ds, Dt, Ts, Tt, f (·)〉确定的学习，其中函数f(·)是深度网络。
本文采用的是一种使用监督学方式的深度学习框架为CNN网络，因此，深度迁移模型及其构成如图2所示。
图2 迁移模型及其构成
Fig. 2 Diagram of transfer model and its composition
考虑到实际系统中振荡数据获取不易，因此，本文引入迁移学习，即在离线状态下训练仿真系统电气量并提取其特征，将该特征泛化到实际系统中。其中训练模型主要由CNN模型离线完成，迁移模型采用联合分布适配原则，最小化仿真系统与实际系统的差异。实际上，仿真系统与实际系统的概率分布并不相同，因此，迁移学习最关键的步骤是减小其与实际系统样本数据的概率分布差异。
设仿真系统为源域，实际系统为目标域，其中源域是有标签的系统，记为Ds={(X1,Y1),,(Xn,Yn)}；而目标域是无标签系统，记为Dt={Xn+1, , Xn+m}。
定义（联合分布适配[30-31]）：对于源域与目标域，满足Xs=Xt, Ys=Yt, P(Xs)¹P(Xt), Q(Ys|Xs) ¹Q(Yt|Xt)，找到一个特征分布T或者分类器函数f使其同时满足边缘分布差异最小化以及条件分布差异最小化，则分类器经源域训练后能够有效的泛化到目标域内。
其中边缘分布适配通过采用最大均值差异（Maximum Mean Discrepancy, MMD）[29]度量不同分布的适配程度，即
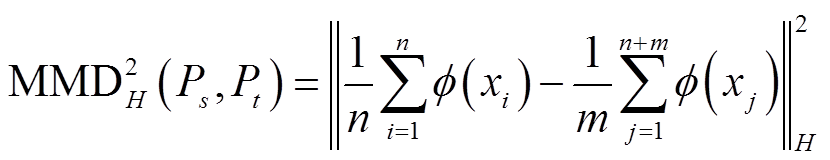（12）式中，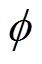
: X→H表示核空间中的无穷阶非线性特征映射。
条件适配中采用直推式学习，将源域中训练好的分类器应用到目标域，获得目标域的预标注，进而采用扩展MMD计算不同标签类别下的条件分布距离，有
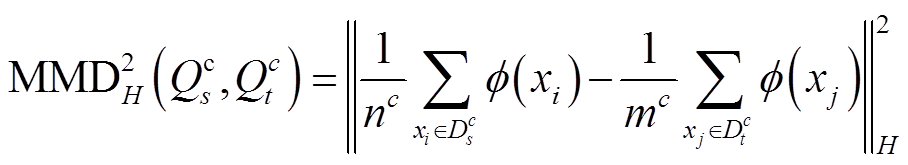（13）式中，Qc表示标签为c的条件分布；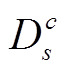
={Xi:Xi∈Ds，且Y(Xi)=c}表示源域中标签为c的样本构成的集合，Y(Xi)=c为源域中的实际标注。同理，
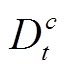={Xi: Xi∈Dt, 且Y∗(Xi)=c}表示目标域中预标注为c的样本构成的集合，Y∗(Xi)=c为目标域中的预测标注。nc与mc分别表示相应特征域内标签为c的数量。
联立式（12）、式（13），联合分布适配的正则项为
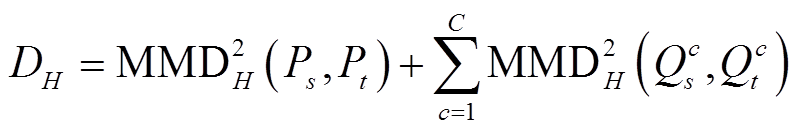（14）则通过最小化式（14），能够使边缘分布和条件分布各阶矩统计量都在无穷维H中进行适配。
综上所述，考虑联合分布适配的迁移模型学习框架形式为
（15）式中，f=wTf(x)表示预测输出函数，f：X®Y即迁移分类模型；K为与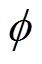对应的核函数，满足〈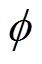(Xi), 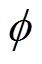(Xj)〉=K(Xi, Xj)；λ为正则系数；L为度量f对训练样本学习精度的损失函数，在此选L为交叉熵损失。
通过特征提取及迁移模型的构建过程来看，虽然由于特征提取不一定能够充分有效，仿真系统与实际系统样本分布存在差异，使得目标领域的标签的预测并不完全正确，但从概率统计角度来看，理论上能够在当前学习条件下得到理想的分类结果。
根据2.2节提出的定位模型，次同步振荡源定位采用离线学习与在线应用相结合的方法。仿真系统离线学习数据特征构建定位模型，实际系统在线应用定位方法，定位方法的具体实施过程如下：
1）系统构建。
（1）仿真系统的构建是将含直驱风电场并网的电力系统在Matlab中进行非线性仿真，其中并网接入无穷大系统。
（2）实际系统与仿真系统结构相似，参数不同，并且实际系统通常是一个风电场接入交流电网的系统。
2）数据准备。
（1）根据构建的仿真系统，设置不同的工况类型，并基于开环模式谐振理论，调节风机参数，使系统发生次同步振荡，采集所有风机并网端口处的电气量[P, Q, V, Vq] 构成数据样本Xs，并根据发生动态交互的风机编号，标注样本构造标签集Ys，最终形成训练样本Ds。采用交叉验证方法[32]划分k-1数据集作为训练数据集Dtrain，余下的一组作为验证数据集Dvalid。
（2）根据假设的仿真系统，设置不同的工况类型，调节运行点使所有运行点包含于仿真系统的运行点数据集内，同样地，采集电气量构成n组测试样本Dtk={(Xtk,Ytk)}, k=1,2,,n。
3）确定网络的结构与训练算法。本文离线与在线两个过程共包含两个网络，其中，训练网络采用CNN网络结构，其超参数设置主要包括输入、输出层，卷积层数量，卷积核相关参数。输入、输出层维数由步骤2）中变量的数量决定。经过多次试探，卷积核设置为5´5，池化核大小设置为2´2，网络建模效果较好。同时，采用Adam加速算法对网络进行训练。在线网络是训练网络训练完成后直接迁移出全连接层以及Softmax分类器外的网络，其全连接层以及分类器参数随机初始化。
4）参数更新。
（1）CNN网络部分，其损失函数是根据实际标签数据及网络分类器输出数据的期望计算的，并加入式（15）的正则项，其中参数计算时样本需要采用T-SNE降维进行处理[33]。每次按照梯度下降方式迭代，并更新CNN网络参数。
（2）在线应用网络是由离线训练网络迁移形成的，因此，在线应用网络在一段时间后，根据实际效果，对训练网络进行重新训练，更新训练模型。
5）算法的停止。
（1）对于训练网络，按上述流程进行一轮计算后，返回步骤1）调整k组数据集作为训练验证数据集的顺序，形成第j+1轮运算，直到验证数据误差达到预期目标，停止迭代，并保存模型。
（2）在线应用网络，在进行一次计算输出后即完成一次，直到达到设定次数，停止输出。
综合以上的实施流程，次同步振荡源定位方法的具体流程如图3所示。
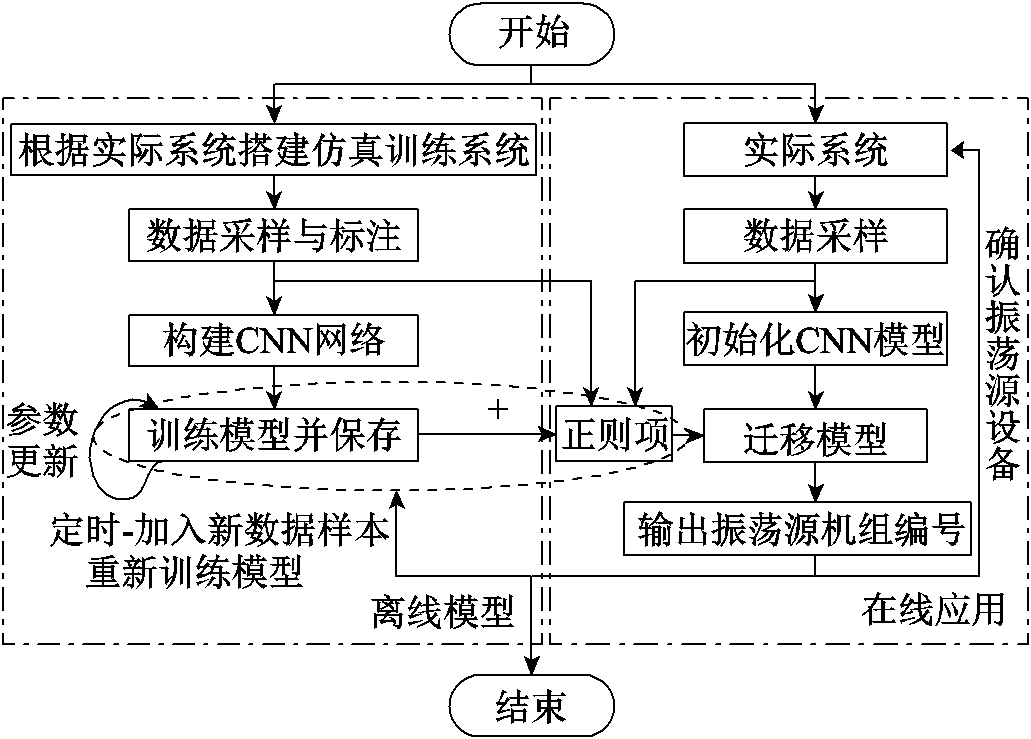
图3 次同步振荡源定位方法的具体流程
Fig. 3 Flow chart of subsynchronous oscillation source localization method
为了验证上述的方法可行性，本文设计算例针对风电场与同步机发生谐振时风电场中的振荡源进行定位。通过Matlab搭建了改进的IEEE第二标准系统仿真模拟产生数据样本，其系统结构如图4所示。仿真数据与实际的相量测量单元（Phasor Measurement Unit, PMU）量测数据会由于仿真系统模型参数的影响而存在明显差异，使得学习仿真样本得到的训练模型可能无法直接应用于实际系统，因此，在搭建仿真模型时，风机1的参数采用实际参数对仿真系统进行校准。采用Facebook公司发布的Pytorch0.4.1 框架搭建学习网络，并构建迁移学习的振荡源定位模型算法。
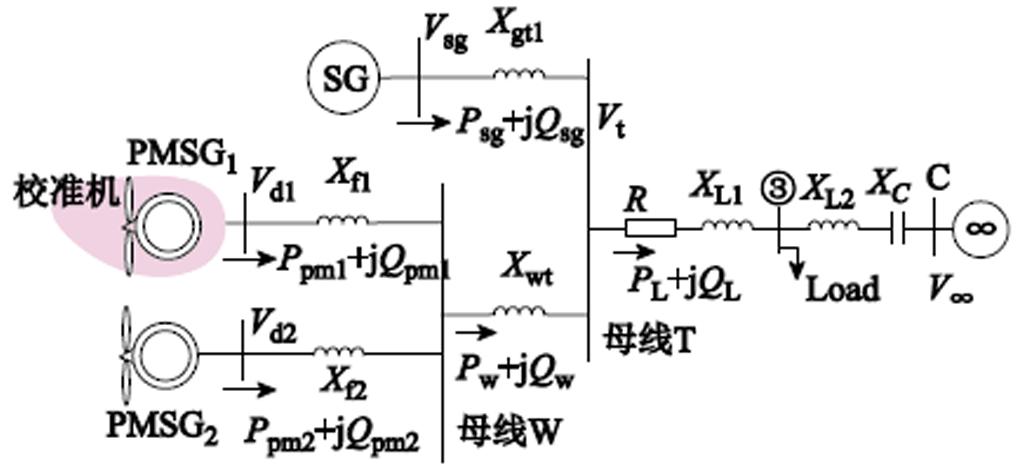
图4 搭建仿真系统结构
Fig.4 Structure of simulation system
训练样本质量的高低对振荡源定位结果至关重要。若不同的振荡源样本差异过大，其在空间中的分布会相距很远，不会出现重叠区域，这样算法就能很轻易地区分出不同的数据类别，造成各项指标均为100%的结果而无法显示算法的优劣。而在实际系统中，不同的运行点会影响模式的改变，不同的扰动可能使不同的振荡源数据样本相似，人工进行振荡源的识别无法在短时间内综合分析其不同模式波形的差别，而较难进行振荡源的定位。为了模拟实际中更加丰富的数据集样本，本文借鉴文献[34]系统稳定数据集生成方法，经过改进后应用于振荡源定位样本集生成。为了让数据集样本的分布更加合理，按照如下规则设置运行点、施加扰动，进行时域仿真：
1）依据开环模式谐振理论，逐步调整风机1与风机2的控制参数，使其分别与同步发电机轴系发生闭环次同步谐振，随机选取能够诱发谐振的参数形成仿真系统的初始设置。参数调整范围见附录。
2）当系统运行点在稳定运行时，设置风机1、风机2以及同步发电机输出有功总出力不变，而三台机组在额定功率按照同比增加或减少0~20%，得到若干运行点。
3）在节点3增加负荷，按系统负荷的30%~120%设置若干运行点。在所有运行点下进行时域仿真。
4）设置仿真的采样频率为2kHz，仿真时长为2s。暂态仿真，0.1s时在三台机组的出口随机施加70%~120%的功率扰动；随机设置节点3上接地导纳模拟短路故障，考虑所有扰动持续时间随机为0.01~0.1s后切除。
记录两台风机出口的有功功率P、无功功率Q、电压幅值V、电压相角Vq，以及该运行点下系统是否稳定和不稳定时参与谐振的风机标号。对所有获取的电气量进行去均值处理以及插值采样，形成样本数据集Xs={P1, Q1, V1, Vq1, P2, Q2, V2, Vq2}，根据对应状态下的参与因子与特征值，对数据集进行标注，稳定标注为0，风机1是振荡源标注为1，风机2是振荡源标注为2，形成与Xs相对应的标签数据集Ys。经过上述过程，共产生6 120组数据样本，剔除潮流不收敛的无效样本，最终得到4 690个有效样本数据。为了显示开环模式下数据样本的制作过程，给出所有数据样本的主导模式如图5所示。
图5 数据样本主导模式
Fig.5 Dominant mode of whole data samples
由图5可知，在不同运行工况下产生的数据样本可能出现系统振荡失稳的情况，也可能是稳定状态。
训练模型时，从样本数据集中随机选取80%作为训练样本，剩下20%作为验证样本。考虑到振荡源的定位还包括了系统的稳定性问题，数据集对应标签不仅包括了风机的位置标签{1,2}，还包括了没有振荡源系统稳定的情况，标签{0}，因此，在评价模型时，不仅要考虑其定位振荡源正确率，还要考虑其是否将振荡源样本判断为稳定样本的误判率，定义模型的定位精确指标Ac及稳定性综合评价指标F1为
（16）
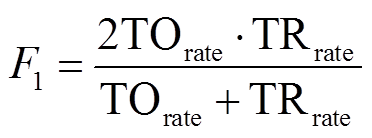（17）式中，TS为预测为非振荡源实际为非振荡源的数量；TO为预测为振荡源实际为振荡源的数量；FO为预测为振荡源实际为非振荡源的数量；FS为预测为非振荡源实际为振荡源的数量；TN1为预测与实际均是风机1为振荡源的数量；TN2为预测与实际均是风机2是振荡源的数量；指标TRrate为振荡源的查全率；TOrate为查准率。
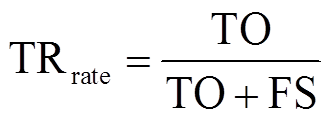（18）
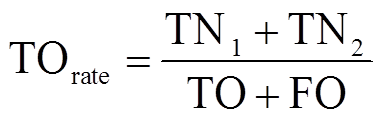（19）图6给出了模型各指标随迭代次数增加的曲线示意图。表1给出了迭代过程中训练模型的评价指标变化及训练用时。由训练结果可以看出在训练100次时，各指标准确率能达到90%左右，基本可进行初步定位。
表1 不同训练次数下的各指标与训练用时比较
Tab.1 Comparison of various indicators and training time under different training epoch
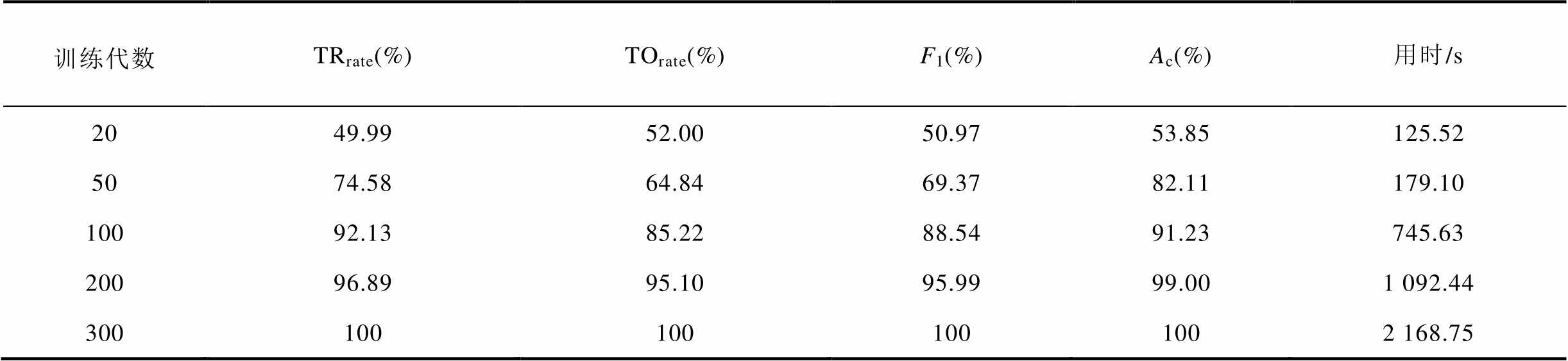
训练代数TRrate(%)TOrate(%)F1(%)Ac(%)用时/s 2049.9952.0050.9753.85125.52 5074.5864.8469.3782.11179.10 10092.1385.2288.5491.23745.63 20096.8995.1095.9999.001 092.44 3001001001001002 168.75
图6 模型各指标训练过程
Fig.6 Training process of each index of the model
考虑到实际系统数据获取不易，为了验证方法的可行性，假设含直驱风电场并网的电力系统接入一个交流系统来模拟实际系统与仿真系统的差异。实际系统中机组参数与仿真系统中所设置的参数不一致，会导致数据集出现偏差，但仿真系统中考虑了较宽的运行点运行范围来模拟实际系统运行状态，这样会尽可能使得振荡源与非振荡源在数据集分布特性上有一定规律可循。为了测试模型在实际系统的泛化能力，本文搭建测试系统如图7所示，其中将图4仿真系统中的无穷大系统换成交流系统。
图7 测试系统结构
Fig.7 Structure of test system
通常仿真系统无法做到与实际系统采用一致的参数，本文采用的仿真系统与测试系统参数设置见附录。由于训练模型时选择了较宽的运行范围，而实际系统可能运行点仅为训练模型中运行点的一部分，因此，本文通过图7的测试系统，产生位于训练模型运行点区域之内的运行点并进行时域仿真，形成测试数据集，模拟实际系统的量测数据。与训练样本的生成方式类似，生成测试数据样本集3组，每组含有200个样本。其中，样本数据集1在同一运行点下随机施加不同类型不同大小的扰动，共计200个样本；样本数据集2在同一种扰动下随机设置不同的出力与负荷，共产生200个不同的运行点；样本数据集3随机设置不同的运行点与不同的扰动200个。三组测试样本集的主导模式如图8所示。对比图5与图8可知，测试系统产生的三组测试样本集的主导模式包含于训练样本集模式范围内。
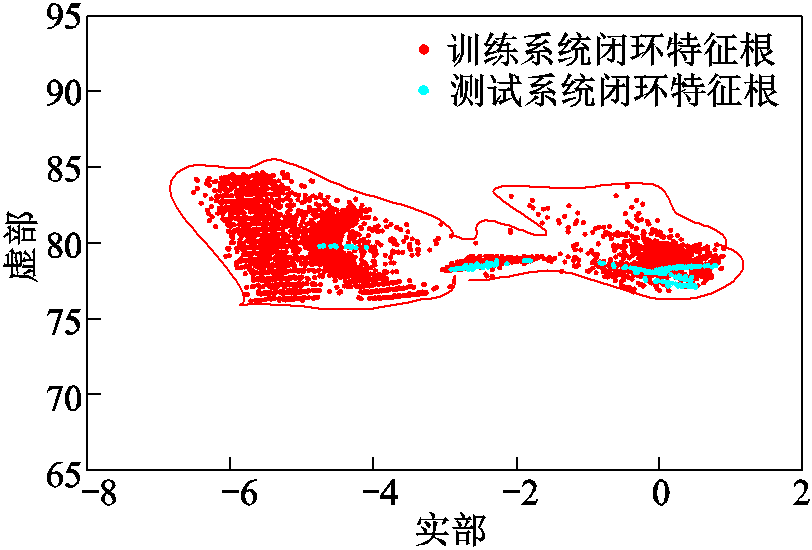
图8 测试样本与训练样本的主导模式
Fig.8 Dominant mode of training and testing samples
分别采用三组测试样本集对训练产生的模型进行泛化性测试，测试结果见表2。由表2结果可知，最终的定位准确率能达到90%以上，说明训练出的模型具有很高的泛化性，并且从测试总用时可以看出本文采用的机器学习进行定位的方法测试200个样本用时不到1s（约4ms /样本），能够实现快速定位。为了与阻抗法的时效性进行对比，测试了样本集3中第1个样本数据的Prony算法过程，用时0.2s，因此，数值算法与机器学习相比，由于需要进行频域分析，在时间上有明显的劣势。
表2 迁移模型测试结果
Tab.2 Test results of transfer model
验证样本TRrate(%)TOrate(%)F1(%)Ac(%)测试用时/s 样本集194.8586.6990.5991.050.92 样本集295.4989.7592.5393.220.80 样本集397.7687.0692.1192.980.76
3.4.1 卷积结构改变对模型精度的影响
卷积结构对模型的精度有重要的影响，为了测试训练模型卷积结构的稳定性，本节测试了在训练模型中增减卷积层对定位准确率的影响，如图9所示。
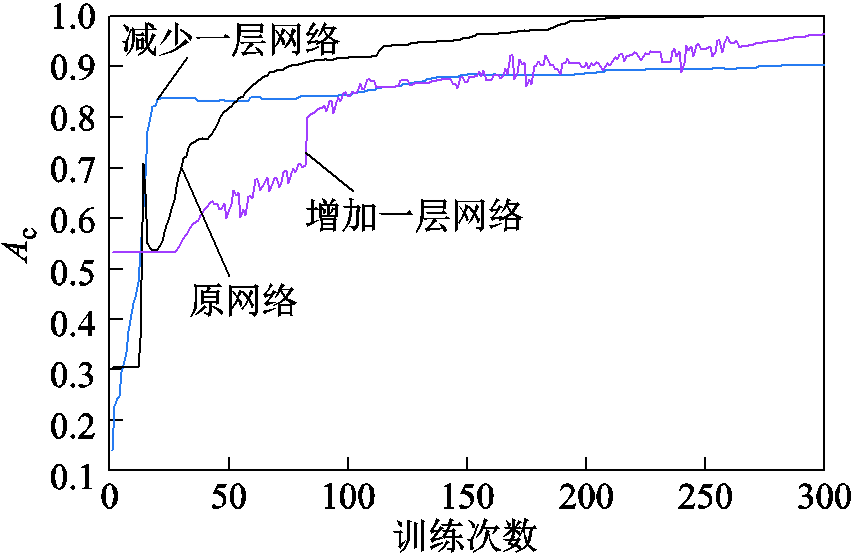
图9 增减卷积层对模型Ac指标影响
Fig.9 Effect of convolutional layers on Ac
如图9所示，增加一层卷积后，由于引入了一层未训练过的网络，其网络规模变大，训练需要经过更长的时间，并且较原网络准确率波动较大，需要更多迭代训练才能稳定收敛。而减少一层卷积后，定位准确率较原网络在训练初期上升更快，但由于减少卷积后弱化了网络特征的稳定提取能力，在稳定收敛性方面不如原网络，需要迭代训练更多次数才能够100%定位。总体而言，增减卷积网络层数对定位准确率影响较小，说明模型的鲁棒性良好，该种基于迁移学习的定位模型框架已经具有较稳定的特征提取能力。
3.4.2 训练模型正则项对迁移效果的影响
为了提高训练模型对实际系统的泛化能力，本文在训练模型时加入联合分布适配正则项，测试结果显示达到了较为理想的测试效果。为了验证加入联合分布适配正则项的迁移模型泛化能力更好，本节重新训练了不加正则项的训练模型，并将此模型直接迁移，进行测试。表3给出了两种方式下的测试指标对比。
表3 迁移模型测试结果
Tab.3 Test results of transfer model
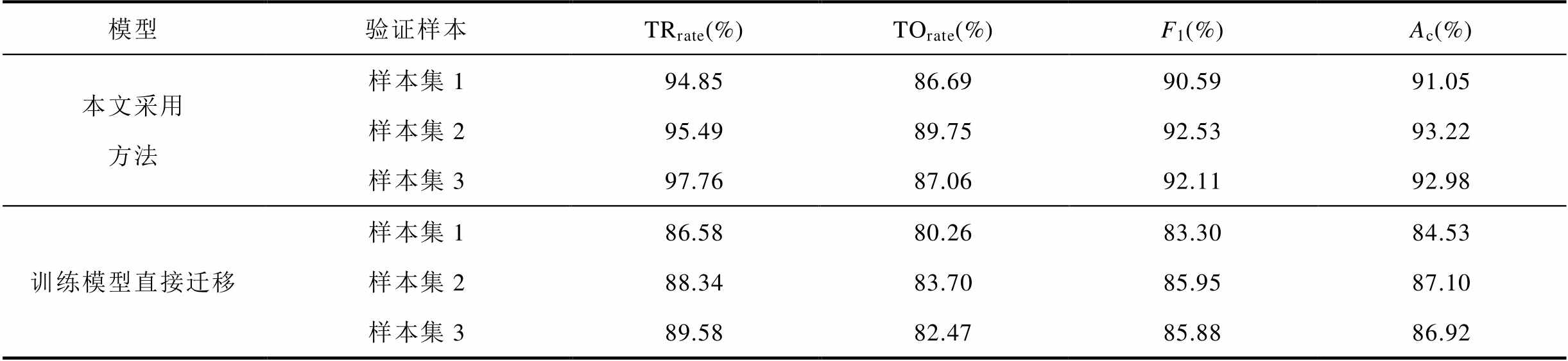
模型验证样本TRrate(%)TOrate(%)F1(%)Ac(%) 本文采用方法样本集194.8586.6990.5991.05 样本集295.4989.7592.5393.22 样本集397.7687.0692.1192.98 训练模型直接迁移样本集186.5880.2683.3084.53 样本集288.3483.7085.9587.10 样本集389.5882.4785.8886.92
从表3的结果可以看出，训练模型直接迁移的方法与本文采用的方法相比，其定位准确率较低，泛化效果较差。根据第2节提出的联合适配正则项计算方法可得仿真系统与实际系统的联合分布系数差异较大，当训练模型中不加入正则项直接迁移到实际系统中，无法克服这种差异对定位结果的影响。
3.4.3 噪声测试
实际系统的量测存在一定的噪声，且有些噪声不能有效地滤波，噪声可能会影响算法的性能。PMU的量测幅值误差能达到0.2%，但相位误差仍较大，在0.2°左右。据此，本文对测试样本3数据中统一增加20dB、30dB、40dB的高斯白噪声进行验证，验证结果见表4。与表2的测试结果相比，结果基本不受影响，这是由于：①CNN网络结构本身具有降噪功能；②对于时序序列的样本数据集，增加的噪声对样本整体的特征影响不大，只有对十分靠近稳定边界处的数据噪声可能有较大影响，而对于振荡源与非振荡源样本其本身具有相对明显的边界。
表4 样本含噪声测试结果
Tab.4 Noise sample test results
噪声/dBTRrate(%)TOrate(%)F1(%)Ac(%) 不含噪声97.7687.0692.1192.98 2097.5486.7691.8393.42 3096.8286.5791.4092.57 4095.1886.0390.3791.12
本文基于深度迁移学习提出了一种用于风电场振荡源定位的方法，该方法采用训练系统数据进行离线建模，并迁移到实际系统实现振荡源的及时定位。通过建立不同的仿真系统对所提出方法进行了验证分析，结果显示本文提出的次同步振荡源定位方法能够有效地将训练模型迁移到实际系统，并且在多工况下都能保证较高的准确率，具有较强的抗噪能力。相比于传统的稳定性分析，本文方法不需要进行大规模仿真建模，实现了通过量测数据进行识别定位；相比于阻抗法等需要在线构造学习模型的数值方法，本文提出的方法是以历史数据为基础的经验学习，通过离线学习模型，实现在线判断决策，在判断速度上具有明显的优势。这为实现振荡源的在线识别定位以及调控奠定了基础，对实现电力系统的智能化应用有重要意义。
综上所述，基于深度迁移学习的风电场次同步振荡源定位方法初步验证了人工智能技术在系统振荡源定位的应用可行性，但该方法在更加复杂的大型风电场中的表现有待进一步研究，应用深度迁移学习进行海量数据建模以及大型风电场的等效小系统构建是未来研究的重点。
1. 公式推导
根据式（1）、式（2）可得
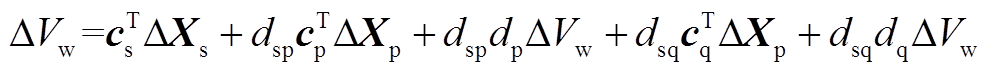（A1）将式（A1）代入式（1）可得
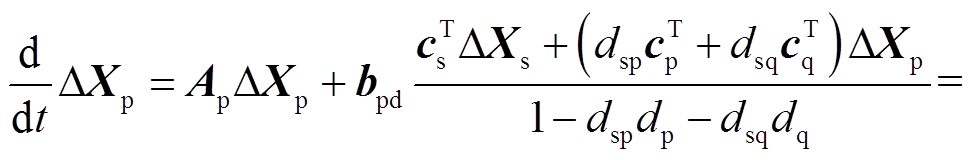
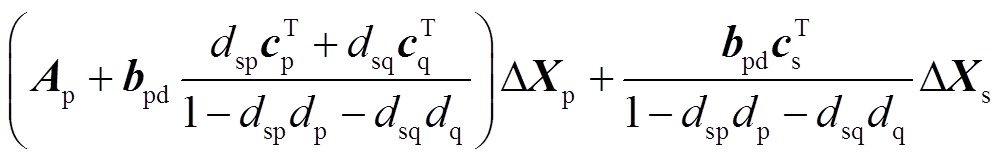（A2）同理，将式（A1）代入式（2）可得
由式（A2）和式（A3），式（5）中的矩阵A可写为
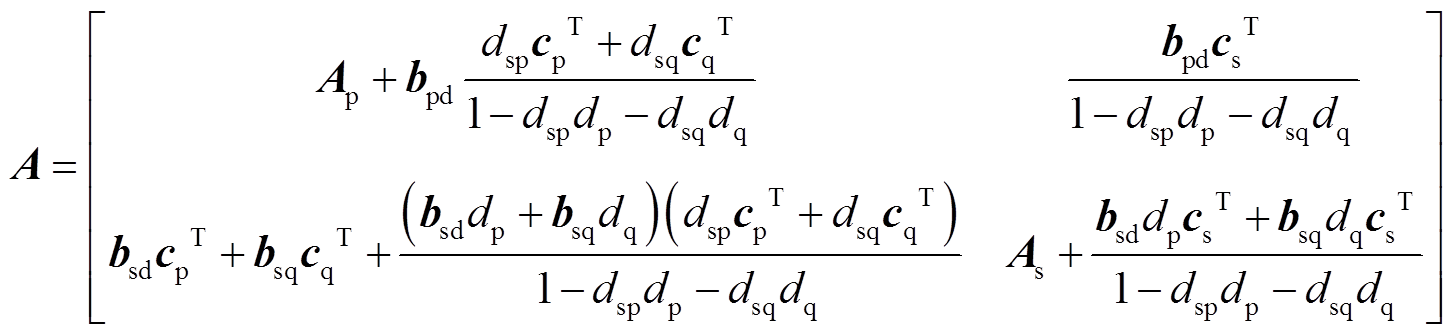
2. 仿真系统参数设置
附表1 仿真系统参数设置
App.Tab.1 Parameter configuration of simulation system （pu）
类别设备/参数名称数值 运行参数平衡机SG电压1.05 同步机SG输出有功（初始值）0.36~0.54(0.45) PMSG1输出有功（初始值）0.16~0.24(0.2) PMSG2输出有功（初始值）0.2~0.3(0.25) SG1及PMSG电压幅值1.0 控制参数PMSG1/ PMSG2 Vdc-Kp（初始值）20~30(28.2) PMSG1/ PMSG2 Vdc-Ki（初始值）400~550(450) PMSG1/ PMSG2 Vq-Kp470 PMSG1/ PMSG2 Vq-Ki800 PMSG1/ PMSG2 Id-Kp47 PMSG1/ PMSG2 Id-Ki85 PMSG1/ PMSG2 Iq-Kp（初始值）40~60(47) PMSG1/ PMSG2 Iq-Ki（初始值）0~100(85) 网络参数Xf1, Xf20.1 Xgt0.1 Xwt0.1 R0.01 XL0.2 其他参数SG1-阻尼系数5 SG2-阻尼系数20 Xd, Xq1 0.5 T¢d00.1
3. 测试系统参数设置
附表2 测试系统参数设置
App.Tab.2 Parameter configuration of test system （pu）
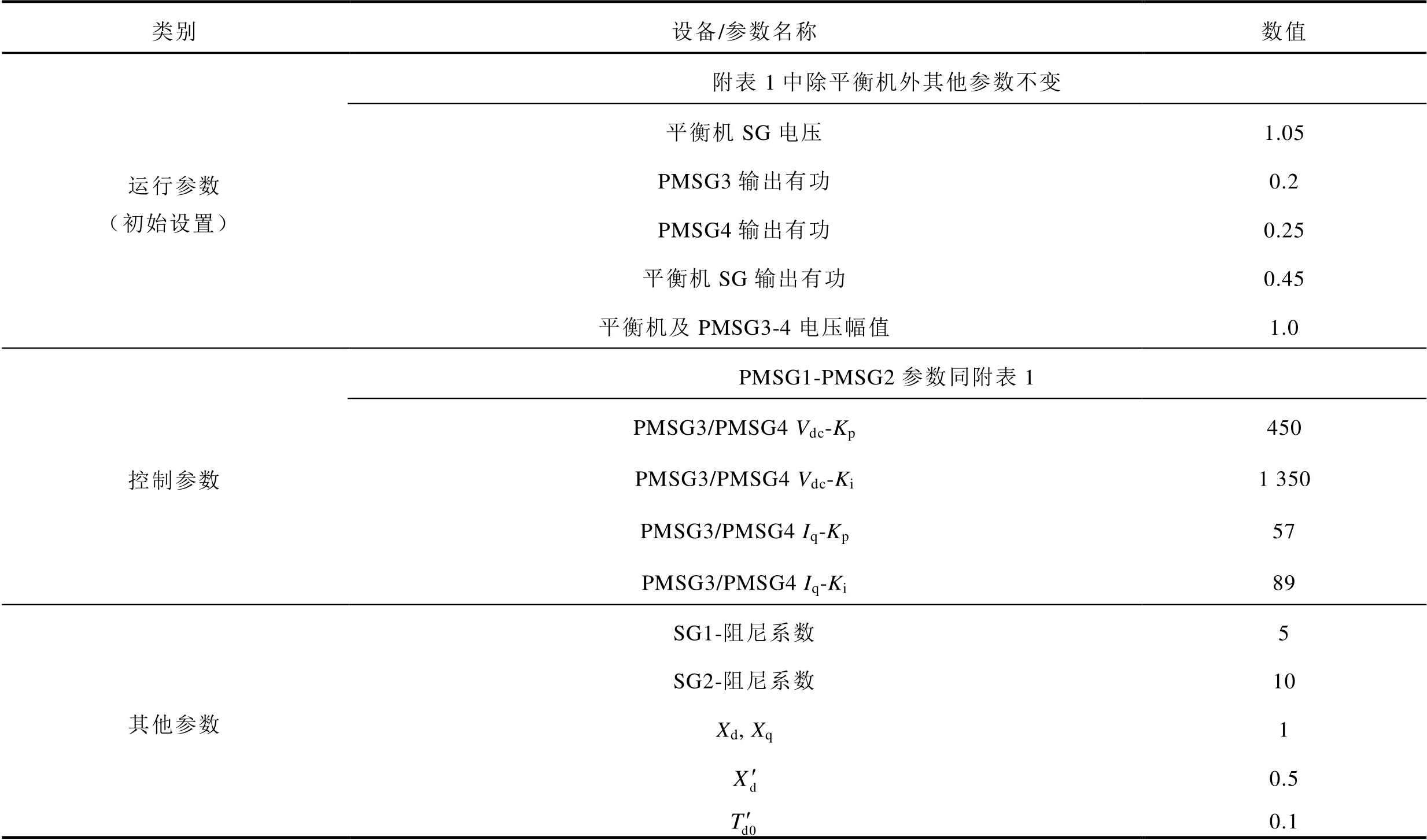
类别设备/参数名称数值 运行参数（初始设置）附表1中除平衡机外其他参数不变 平衡机SG电压1.05 PMSG3输出有功0.2 PMSG4输出有功0.25 平衡机SG输出有功0.45 平衡机及PMSG3-4电压幅值1.0 控制参数PMSG1-PMSG2参数同附表1 PMSG3/PMSG4 Vdc-Kp450 PMSG3/PMSG4 Vdc-Ki1 350 PMSG3/PMSG4 Iq-Kp57 PMSG3/PMSG4 Iq-Ki89 其他参数SG1-阻尼系数5 SG2-阻尼系数10 Xd, Xq1 0.5 0.1
参考文献
[1] 肖湘宁, 罗超, 廖坤玉. 新能源电力系统次同步振荡问题研究综述[J]. 电工技术学报, 2017, 32(6): 85-97. Xiao Xiangning, Luo Chao, Liao Kunyu. Review of the research on subsynchronous oscillation issues in electric power system with renewable energy sources[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 85-97.
[2] 谢小荣, 刘华坤, 贺静波, 等. 直驱风电机组风电场与交流电网相互作用引发次同步振荡的机理与特性分析[J]. 中国电机工程学报, 2016, 36(9): 2366-2372. Xie Xiaorong, Liu Huakun, He Jingbo, et al. Mechanism and characteristics of subsynchronous oscillation caused by the interaction between full-converter wind turbines and AC systems[J]. Proceedings of the CSEE, 2016, 36(9): 2366-2372.
[3] 张学广, 邱望明, 方冉, 等. 基于变流器改进控制的双馈风电机组SSO抑制方法[J/OL]. 电机与控制学报, 2020(2), https://doi.org/10.15938/j.emc.2020. 02.001.Zhang Xueguang, Qiu Wangming, Fang Ran, et al. SSO mitigation method of DFIG based on improved control of converter[J/OL]. Electric Machines and Control, 2020(2), https://doi.org/10.15938/j.emc.2020.02.001.
[4] 王伟胜, 张冲, 何国庆, 等. 大规模风电场并网系统次同步振荡研究综述[J]. 电网技术, 2017, 41(4): 1050-1060. Wang Weisheng, Zhang Chong, He Guoqing, et al. Overview of research on subsynchronous oscillations in large-scale wind farm integrated system[J]. Power System Technology, 2017, 41(4): 1050-1060.
[5] Du Wenjuan, Chen Xiao, Wang Haifeng, et al. Power system electromechanical oscillation modes as affected by dynamic interactions from grid-connected PMSGs for wind power generation[J]. IEEE Transactions on Sustainable Energy, 2017, 8(3): 1301-1312.
[6] 王洋, 杜文娟, 王海风. 基于开环子系统模式信息的次同步谐振机理研究[J].电工技术学报, 2019, 34(24): 5209-5220. Wang Yang, Du Wenjuan, Wang Haifeng. Mechanism study of subsynchronous resonance based on open-loop modal information[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5209-5220.
[7] 任必兴, 杜文娟, 王海风. UPFC与系统的强动态交互对机电振荡模式的影响[J]. 电工技术学报, 2018, 33(11): 2520-2534. Ren Bixing, Du Wenjuan, Wang Haifeng. Impact of strong dynamic interaction between UPFC and system on electromechanical oscillation mode[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2520-2534.
[8] 任必兴, 杜文娟, 王海风. 静止同步补偿器与直驱永磁风机的次同步控制交互研究[J]. 电工技术学报, 2018, 33(24): 5884-5896. Ren Bixing, Du Wenjuan, Wang Haifeng. Analysis on sub-synchronous control interaction between static synchronous compensator and permanent magnet synchronous generator[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5884-5896.
[9] Liu Huakun, Xie Xiaorong, Zhang Chuanyu, et al. Quantitative SSR analysis of series compensated DFIG-based wind farms using aggregated RLC circuit model[J]. IEEE Transactions on Power Systems, 2017, 32(1): 474-483.
[10] Du Wenjuan, Fu Qiang, Wang Haifeng, et al. Concept of modal repulsion for examining the subsynchronous oscillations caused by wind farms in power systems[J]. IEEE Transactions on Power Systems, 2019, 34(1): 518-526.
[11] Piyasinghe Lakshan, Miao Zhixin, Khazaei Javad, et al. Impedance model-based SSR analysis for TCSC compensated type-3 wind energy delivery systems[J]. IEEE Transactions on Sustainable Energy, 2015, 6(1):179-187.
[12] Xie Xiaorong, Liu Huakun, Han Yingduo. SEDC's ability to stabilize SSR: a case study on a practical series-compensated power system[J]. IEEE Transactions on Power Systems, 2014, 29(6): 3092-3101.
[13] 李鹏瀚, 王杰, 吴飞. 双馈风电机组次同步控制相互作用的反馈线性化滑模变结构抑制[J]. 电工技术学报, 2019, 34(17): 3661-3671. Li Penghan, Wang Jie, Wu Fei. Sub-synchronous control interaction mitigation for DFIGs by sliding mode control strategy based on feedback linearization[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3661-3671.
[14] Ren Wei, Larsen E. A refined frequency scan approach to sub-synchronous control interaction (SSCI) study of wind farms[J]. IEEE Transactions on Power Systems, 2016, 31(5): 3904-3912.
[15] Gao Benfeng, Hu Yunting, Song Ruihua, et al. Impact of DFIG-based wind farm integration on sub-synchronous torsional interaction between HVDC and thermal generators[J]. IET Generation, Transmission & Distribution, 2018, 12(7): 3913-3923.
[16] Mohammadpour H A, Santi E. SSR damping controller design and optimal placement in rotor-Side and grid-side converters of series-compensated DFIG-based wind farm[J]. IEEE Transactions on Sustainable Energy, 2015, 6(2): 388-399.
[17] Ghafouri M, Karaagac U, Mahseredjian J, et al. SSCI damping controller design for series-compensated DFIG-based wind parks considering implementation challenges[J]. IEEE Transactions on Power Systems, 2019, 34(4): 2644-2653.
[18] Zhang Jian, Xiao Xiangning, Zhang Peng, et al. Suppressing intermittent subsynchronous oscillation via subsynchronous modulation of reactive current[J]. IEEETransactions on Power Delivery, 2015, 30(5): 2321-2330.
[19] Moharana A, Varma R K, Seethapathy R. SSR alleviation by STATCOM in induction-generator-based wind farm connected to series compensated line[J]. IEEE Transactions on Sustainable Energy, 2014, 5(3): 947-957.
[20] El-Moursi M S, Bak-Jensen B, Abdel-Rahman M H. Novel STATCOM controller for mitigating SSR and damping power system oscillations in a series compensated wind park[J]. IEEE Transactions on Power Electronics, 2010, 25(2): 429-441.
[21] Fan Lingling, Miao Zhixin. Mitigating SSR using DFIG-based wind generation[J]. IEEE Transactions on Sustainable Energy, 2012, 3(3): 349-358.
[22] Chen Lei, Zhao Wei, Wang Fuping. An interharmonic phasor and frequency estimator for subsynchronous oscillation identification and monitoring[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(6): 1714-1723.
[23] 谢小荣, 刘华坤, 贺静波, 等. 电力系统新型振荡问题浅析[J].中国电机工程学报, 2018, 38(10): 2821-2828, 3133. Xie Xiaorong, Liu Huakun, He Jingbo, et al. On new oscillation issues of power systems[J]. Proceedings of the CSEE, 2018, 38(10): 2821-2828, 3133.
[24] 王茂海, 孙昊. 强迫功率振荡源的在线定位分析技术[J]. 中国电机工程学报, 2014, 34(34): 6209-6215. Wang Maohai, Sun Hao. An analysis method for forced power oscillation source detection[J]. Proceedings of the CSEE, 2014, 34(34): 6209-6215.
[25] Shu Yinbiao, Zhou Xiaoxin, Li Wenfeng. Analysis of low frequency oscillation and source location in power systems [J]. CSEE of Journal of Power and Energy Systems, 2018, 4(1): 58-66.
[26] 陈磊, 王文婕, 王茂海, 等. 利用暂态能量流的次同步强迫振荡扰动源定位及阻尼评估[J]. 电力系统自动化, 2016, 40(19): 1-8. Chen Lei, Wang Wenjie, Wang Maohai, et al. Disturbance source location of subsychronous forced oscillation and damping evaluation using transient energy flow[J]. Automation of Electric Power systems, 2016, 40(19): 1-8.
[27] Xie Xiaorong, Zhan Ying, Jan S, et al. Identifying the source of subsynchronous control interaction via wide-area monitoring of sub/super-synchronous power flows[J]. IEEE Transactions on Power Delivery, 2019, DOI: 10.1109/TPWRD.2019.2963336.
[28] 许璞轩. 风电汇集区域次同步频率分量的传播路径与扰动源定位研究[D]. 北京: 华北电力大学, 2018.
[29] Pan Sinno Jialin, Yang Qiang. A survey on transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10):1345-1359.
[30] Long Mingsheng, Wang Jianmin, Ding Guiguang, et al. Adaptation regularization: a general framework for transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(5): 1076-1089.
[31] 龙明盛. 迁移学习问题与方法研究[D]. 北京: 清华大学, 2014.
[32] 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016.
[33] George D, Joana N, Kampff A R. T-SNE visualization of large-scale neural recordings[J]. Neural Computation, 2018, 30(7): 1750-1774.
[34] Florian T, Andreas V, Robert E, et al. Efficient database generation for data-driven security assessment of power systems[J]. IEEE Transactions on Power Systems, 2019, DOI: 10.1109/TPWRS.2018. 2890769.
A Method of Locating the Power System Subsynchronous Oscillation Source Unit with Grid-Connected PMSG Using Deep Transfer Learning
Abstract With increasing penetration of new energy power electronic devices, the induced mechanism of the subsynchronous oscillation problem of power systems has become more complicated. In order to locate the unit that induces subsynchronous oscillation in time, a method for locating sub-synchronous oscillation sources based on deep transfer learning is proposed. The method first builds a simulation system based on the open-loop mode resonance theory, and obtains training data samples in the simulation system. Second, it uses convolutional neural networks(CNN) to extract the characteristics of the oscillation source and establish a training localization model. Finally, the training model is transferred to the actual situation through transfer learning, and to realize the application of the location model. In order to verify the effectiveness of the proposed method, this paper designs a simulation system example of a power system with direct-drive generators connected to the grid. The test results show that the proposed method has the advantages of high location accuracy and convenient online application, compared with the traditional eigenvalue analysis method. Besides, this method can give the identification result in a short time, which lay a foundation for realizing the online identification of the oscillation source.
keywords：Open loop mode resonance, subsynchronous oscillation (SSO), permanent magnet synchronous generator (PMSG), oscillation source localization, machine learning
中图分类号：TM712
DOI:10.19595/j.cnki.1000-6753.tces.191703
中央高校基本科研基金资助项目（YJ201654）。
收稿日期2019-12-06
改稿日期 2020-02-11
陈 剑 女，1992年生，博士研究生，研究方向为机器学习在电力系统中的应用、电力系统稳定性分析。E-mail：sdqzjane316@gmail.com
杜文娟 女，1979年生，教授，研究方向为电力系统稳定性理论与控制，柔性输电、大规模新能源接入电力系统的分析与控制。E-mail：ddwenjuan@qq.com（通信作者）
（编辑 赫蕾）