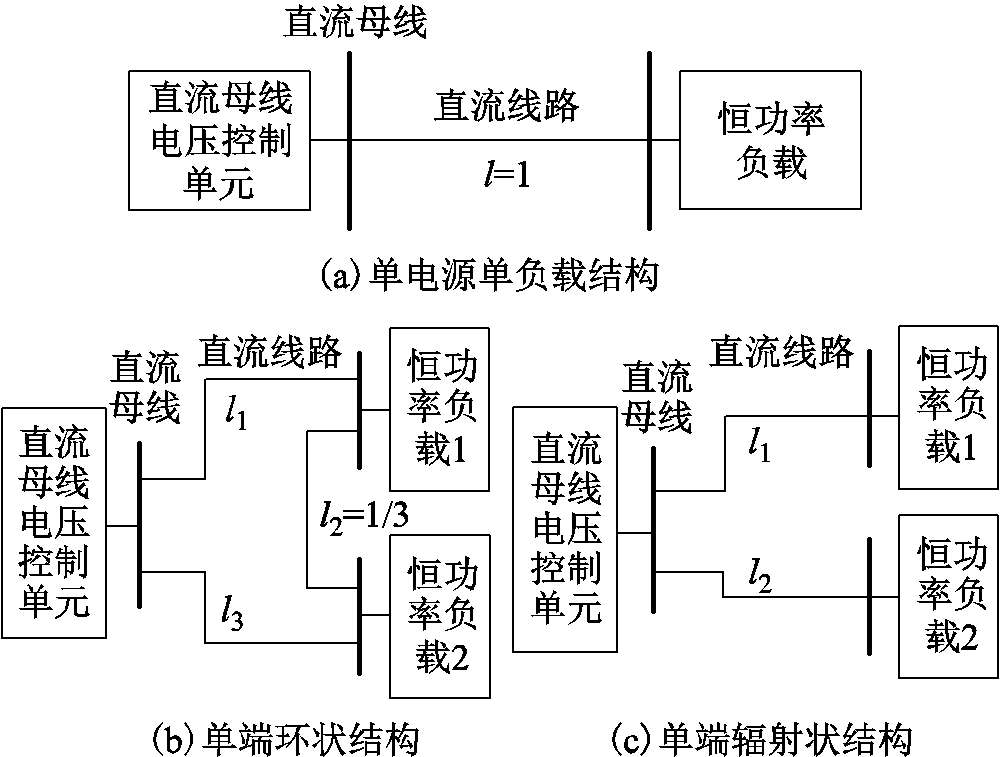
图1 不同网架结构的直流微电网
Fig.1 Different grid structures of DC microgrid
摘要 不同网架结构下的直流微电网系统是否具有稳定性差异尚不明确,亟需开展研究。针对该问题,建立几种典型网架结构下系统的小信号模型,并基于参与因子以及系统特征根的变化,研究不同网架结构下系统参数对系统稳定性的影响规律。结果显示,单独改变源侧控制器参数,不同网架结构下系统的稳定性基本一致,仅存在谐振频率的差异;单独改变负载侧控制器参数,仅影响与负载有关的振荡模态,且负载与线路基本不产生交互作用;单独改变线路参数,由于源网间的交互作用,不同系统间出现稳定性差异。最后,通过仿真验证了理论分析的正确性。
关键词:网架结构 小信号模型 参与因子法 根轨迹 稳定性
直流微电网作为分布式发电系统的重要组成部分,能够更高效可靠地接纳分布式电源。同时,直流微电网具有系统成本低、可靠性高、变换环节较少、损耗较低等优点,且不存在无功和相位等问题,具有广泛的应用前景[1-3]。
直流母线电压是衡量直流微电网稳定运行的唯一指标[4-6]。直流微电网的稳定性分析对直流微电网稳定可靠运行有重要作用[7]。文献[8]通过理论推导将多储能系统并联运行时的模型简化为单电源单负载模型,通过稳定性分析了不同系统参数下直流微电网的稳定性,并设计验证了直流微电网分级稳定控制策略。文献[9]分析了两端柔性直流输电系统的稳定性。文献[10]建立了向无源网络供电的双端柔性直流输电系统全局小信号模型,并通过灵敏度分析方法进行验证。文献[11]分析了在弱电网条件下,三相LCL逆变侧电流反馈并网逆变器的稳定性,提出了一种电压前馈控制策略以提高系统稳定性。文献[12]分析了下垂控制下模块化多电平换流器的稳定性。文献[13]分析了弱交流电网与柔性直流输电系统矢量控制环节交互作用对系统稳定性的影响。上述文献解决一些直流微电网各个换流器的稳定性问题,但多是将换流器间的连接方式简化为单母线或单电源单负载形式,然而不同网架结构的选择会影响系统潮流分布、保护配置、接地方式、稳定性、系统控制等方面[14-16]。不同网架结构下系统是否有稳定性差异则鲜有研究。
此外在直流微电网中,由于大量电力电子器件的接入,系统呈低惯性,对功率、电压波动较为敏感,严重影响系统的电能质量和稳定运行[17-18]。针对该问题,各国学者提出了不同的惯性控制策略来改善系统的电能质量。文献[19-20]基于虚拟同步发电机控制,提出了一种满足多约束条件的灵活虚拟惯性控制,通过灵敏度及根轨迹法分析了所提控制中关键参数对系统稳定性的影响规律。文献[21]通过模拟电容的工作原理,为直流微电网提供惯性支撑,并分析了主要控制参数的变化对系统稳定性的影响,提供了虚拟惯性系数的选取范围。
基于上述问题,本文针对不同网架结构下系统的稳定性差异展开研究。首先,建立不同网架结构下的系统小信号模型;其次,根据小信号模型得出各网架结构下系统的振荡模态,并根据参与因子法探究不同结构下各系统状态变量间的相互作用情况;再次,基于系统根轨迹研究了不同网架结构下源侧、负载侧以及线路参数变化对稳定性的影响规律;最后,通过Matlab时域仿真验证了理论分析的正确性。
本文主要针对单电源单负载、单端辐射及单端环状三种结构下的直流微电网系统展开研究,不同网架结构如图1所示。
直流母线电压控制单元由储能单元和双向DC-DC换流器等效而成[22],为了提高系统惯性,抑制直流母线电压波动,本文控制方式采用文献[21]中模拟电容工作原理的虚拟惯性控制。此外,为了便于分析,将直流母线电压控制单元简称为电源。
为了减小传输损耗和增大输送距离,一般母线电压等级都高于负载电压等级,通常需要Buck电路进行电压变换。为了维持负载电压恒定,一般采用定电压控制,因此直流负载可等效成恒功率负载。

图1 不同网架结构的直流微电网
Fig.1 Different grid structures of DC microgrid
为了突出不同网架结构的区别和减小由于参数不一致带来的分析误差,以单电源单负载结构为基准,规定其线路长度为1。其他两种结构的线路长度总和也为1,负载间的距离保持不变,对应的线路两侧分布电容总和也应相等。三种结构的恒功率负载总和应保持一致。为方便说明,将单电源单负载系统简称为系统1,单端环状系统简称为系统2,单端辐射状系统简称为系统3。
直流母线电压控制单元以维持直流母线电压和平衡微电网内功率波动为目的。为增强系统惯性,减小电压波动,本文采用虚拟惯性控制。控制原理为通过类比电容器充放电功率,控制换流器释放或吸收惯性功率。控制策略的表达式为[21]
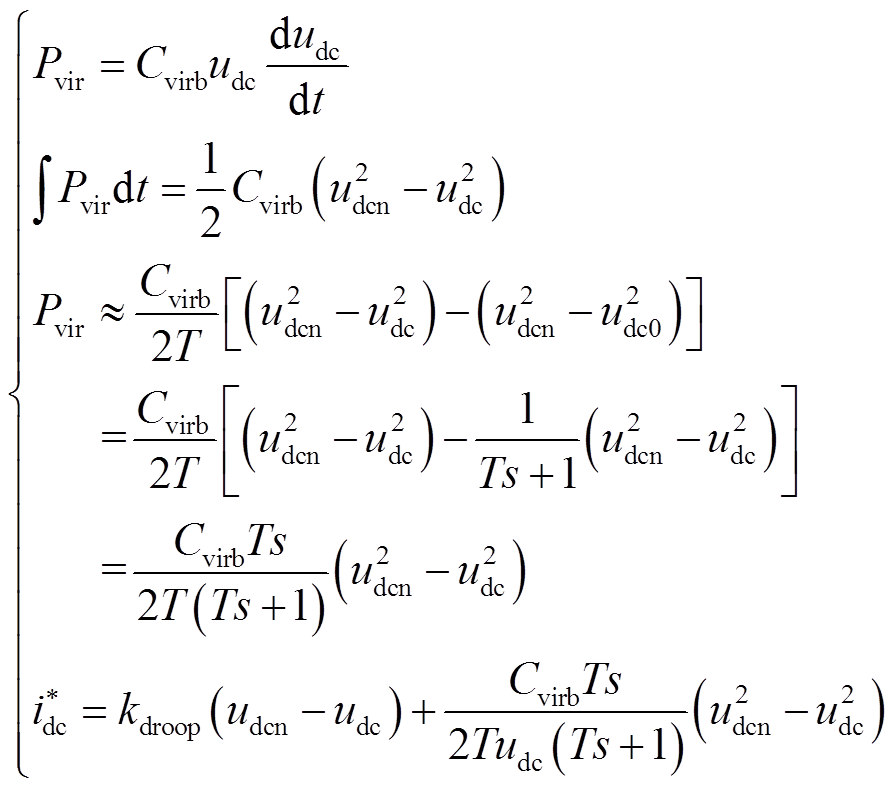 (1)
(1)式中,Pvir为虚拟惯性功率;udcn、udc和udc0分别为直流母线额定电压、换流器侧直流母线电压和前一时刻换流器侧直流母线电压;Cvirb为直流母线电压控制单元的虚拟惯性系数;kdroop为下垂系数;T为虚拟惯性控制的一阶惯性环节的时间常数;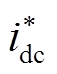 为换流器输出电流参考值。通过一阶惯性环节模拟直流母线额定电压和前一时刻换流器侧直流母线电压的二次方差。
为换流器输出电流参考值。通过一阶惯性环节模拟直流母线额定电压和前一时刻换流器侧直流母线电压的二次方差。
根据式(1)可得到虚拟惯性的控制框图如图2所示。
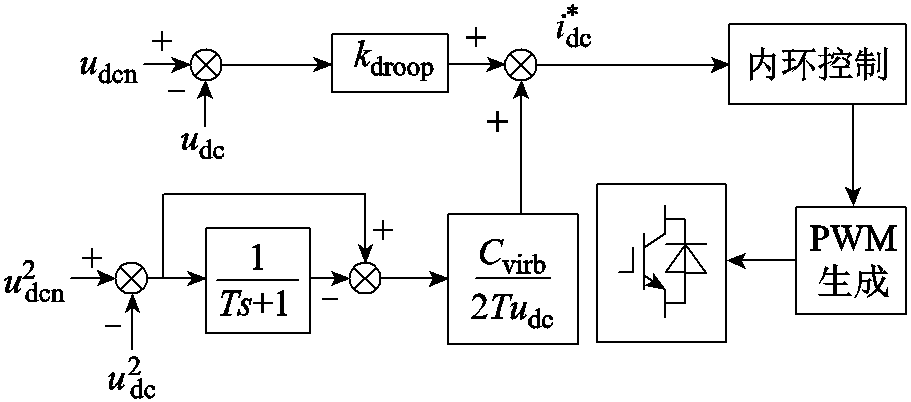
图2 虚拟惯性控制框图
Fig.2 Virtual inertia control block diagram
直流母线电压控制单元换流器采用双向DC-DC换流器,其电路如图3所示,其中,Rb、Lb分别为电源侧的寄生电阻和滤波电感;S1、S2为可控开关器件;Cb为换流器侧的支撑电容;ub、ib分别为电源的电压和输出电流;idc为换流器输出电流。
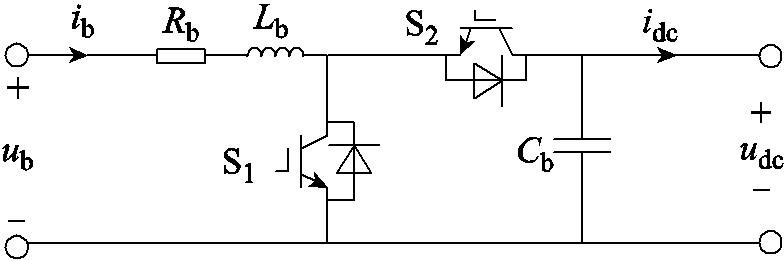
图3 双向DC-DC换流器电路
Fig.3 Circuit diagram of bidirectional DC-DC converter
根据图2、图3可以得到虚拟惯性控制下直流母线电压控制单元的状态空间平均模型为
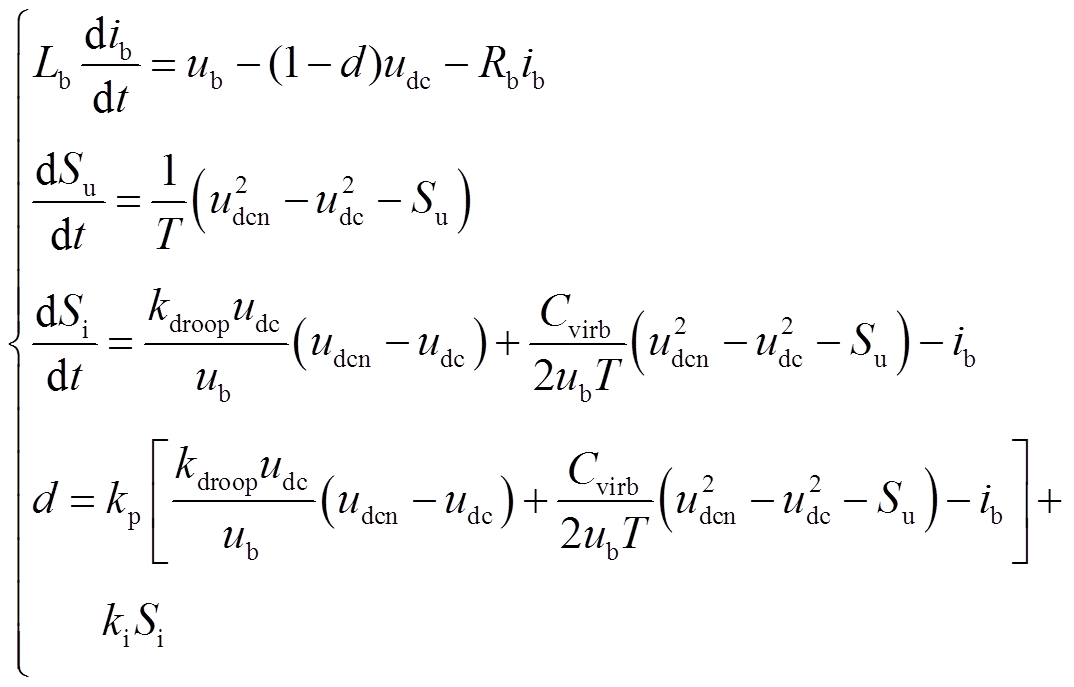 (2)
(2)式中,d为Boost模式下的占空比;Su为经一阶惯性环节后的额定直流电压和实际直流电压的二次方差;Si为内环PI环节的积分部分;kp和ki分别为PI环节的比例和积分系数。
将式(2)在稳态值附近线性化后,可得到直流母线电压控制单元的小信号模型,即
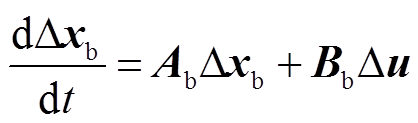 (3)
(3)式中,Δxb=[Δib ΔSu ΔSi]T;Δu=[Δudc]T;系数矩阵Ab、Bb详见附录。
恒功率负载由Buck电路接恒阻抗负载等效而成,其控制策略如图4所示。图中,udcL、uLN和uL分别为恒功率负载侧直流母线电压、恒功率负载的额定电压和实际电压;Cdc、CL和LL分别为直流母线侧的支撑电容以及LC滤波环节的滤波电容和滤波电感;RL为寄生电阻;PL为恒功率负载的功率;idcL为负载的输入电流,iL为换流器输出电流。
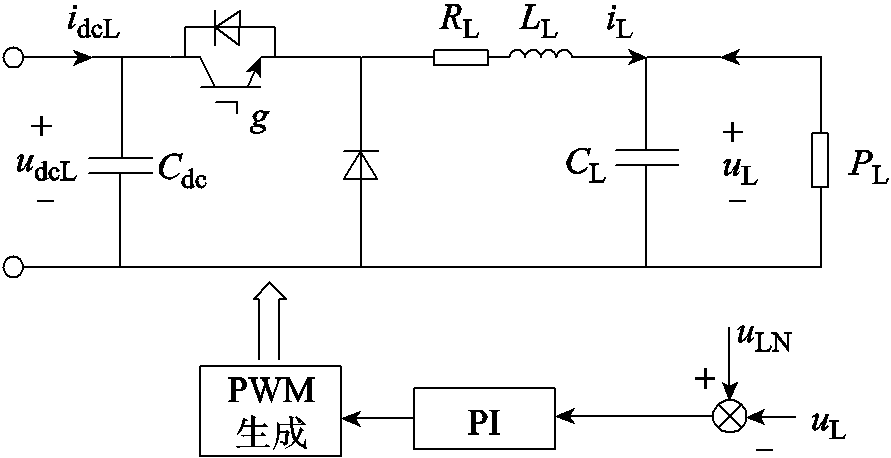
图4 恒功率负载控制策略
Fig.4 Constant power load control strategy chart
根据图4可以得到定电压控制下恒功率负载的状态空间平均模型为
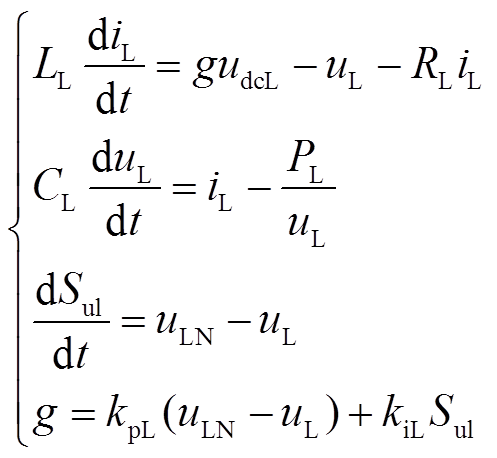 (4)
(4)式中,g为Buck模式下的占空比;Sul为PI环节的积分部分;kpL和kiL分别为恒功率负载控制PI环节的比例和积分系数。
将式(4)在稳态值附近线性化后,可得到恒功率负载的小信号模型,即
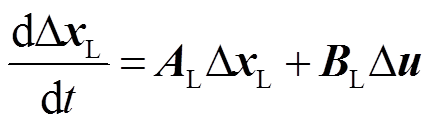 (5)
(5)式中,ΔxL=[ΔiL ΔuL ΔSul]T;Δu=[ΔudcL]T;系数矩阵AL、BL详见附录。
直流线路如图5所示。图中,ud1、ud2分别为直流线路两侧的直流电压;id1、id2分别为直流线路两侧的输入输出电流;Rd、Ld分别为直流线路的线路电阻和线路电感;Cd1、Cd2分别为直流线路两侧的分布电容;id为直流线路传输电流。
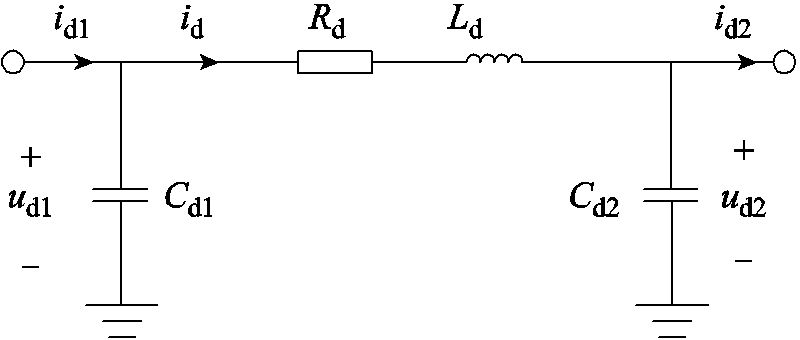
图5 直流线路
Fig.5 DC circuit diagram
根据图5可以得到直流线路的状态空间平均模型为
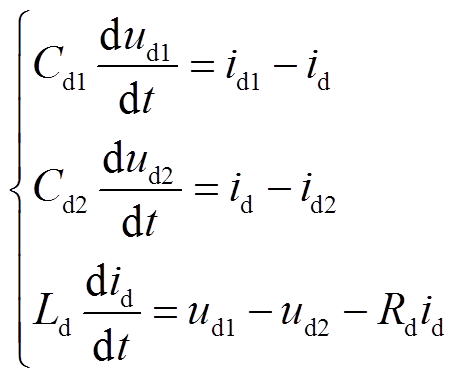 (6)
(6)将式(6)在稳态值附近线性化后,可得到直流线路的小信号模型,即
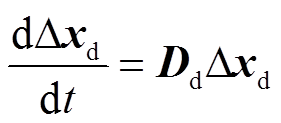 (7)
(7)式中,Δxd=[Δud1 Δud2 Δid]T;系数矩阵Dd详见附录。
由于线路的分布电容较小,为简化分析,可将直流线路的分布电容整合到换流器母线侧支撑电容中[7]。将图3~图5按照图1中不同网架结构形式连接就构成了直流微电网系统。
以图1a所示的单电源单负载结构为例,将图5中的Cd1并入图3中的Cb中,Cd2并入图4中的Cdc中,则根据图3~图5及式(6)可重新表示为
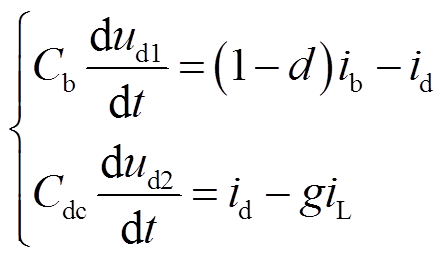 (8)
(8)将式(8)在稳态值附近线性化后,与式(3)、式(5)和式(7)联立后可得到系统1的小信号模型,即
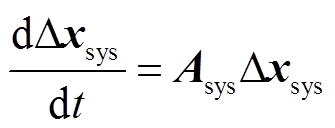 (9)
(9)式中,Δxsys=[Δxb ΔxL Δxd]T;系数矩阵Asys为
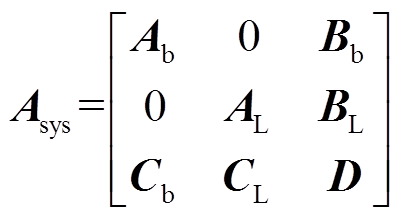
系数矩阵Cb、CL、D详见附录。
同理可列出系统2和系统3的小信号模型。详见附录。
直流微电网的系统参数见附表1。由式(9)可得,系统1有9个特征根,系统2有15个特征根,系统3有14个特征根。在附表1参数下,不同网架结构系统的特征根如图6所示,其相应的特征值分析见表1。
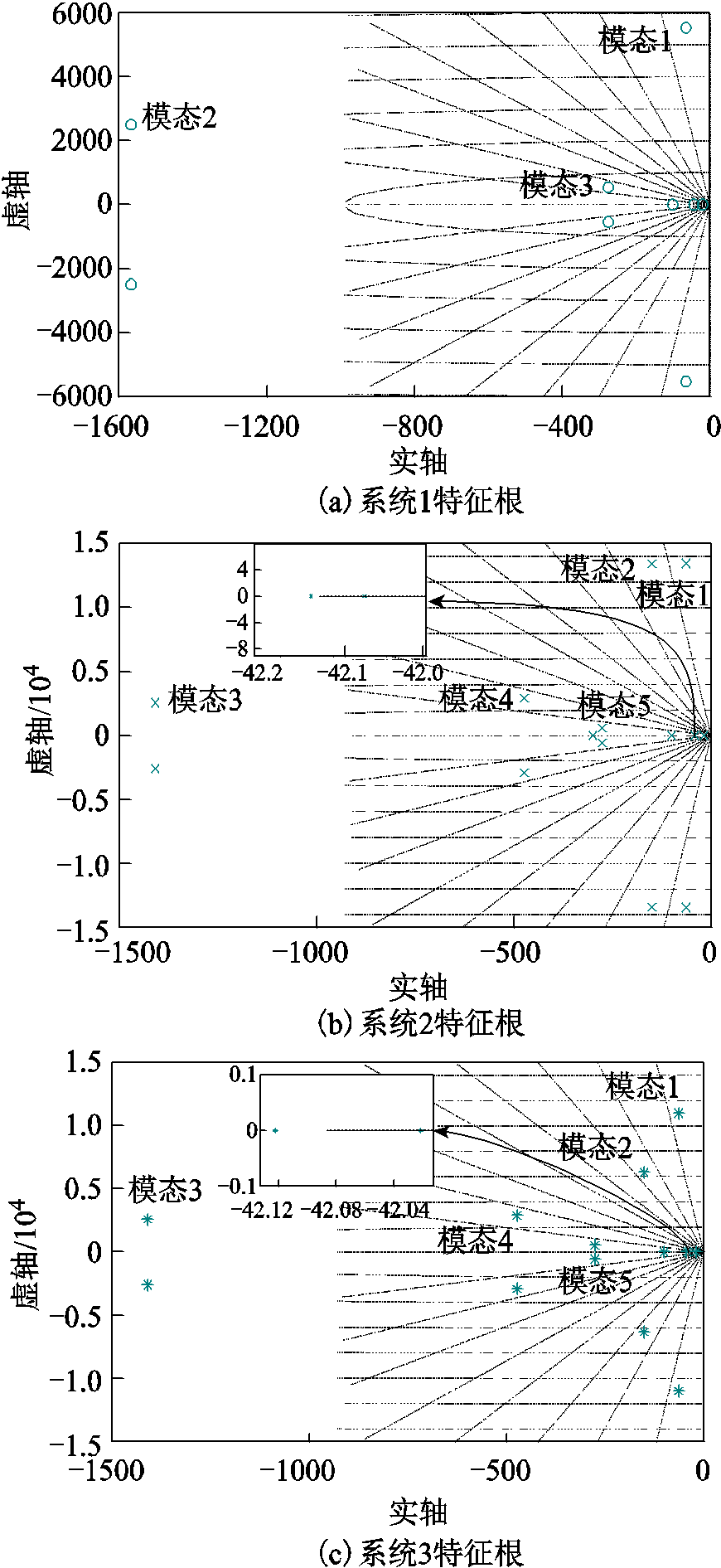
图6 不同网架结构系统的特征根
Fig.6 Characteristic roots of different grid structure systems
由图6可以看出,系统1共有三个振荡模态,其中主导模态为模态1;系统2有5个振荡模态,其中主导模态为模态1与模态2;系统3有5个振荡模态,其中主导模态为模态1与模态2。
表1 特征根分析
Tab.1 Eigenvalue analysis

系统模式特征根振荡频率/Hz阻尼比 系统1模态1-64.171±j5535.566881.0130.0116 模态2-1566.388±j2497.901397.5530.5313 模态3-274.275±j546.81787.0290.4483 系统2模态1-62.877±j13440.1322139.0630.0047 模态2-150.001±j13415.5752135.1550.0112 模态3-1410.185±j2586.156411.5990.4787 模态4-472.727±j2901.052461.7170.1608 模态5-275.551±j552.18687.8830.4465 系统3模态1-63.004±j10983.5191748.0810.0057 模态2-150.003±j6322.7901006.3030.0237 模态3-1410.183±j2586.154411.5990.4787 模态4-472.726±j2901.049461.7160.1608 模态5-275.425±j551.64687.7970.4467
为探究各系统中的振荡模态与状态变量之间的联系,本节通过参与因子法研究状态变量间的相互作用,参与因子的计算方法为[23]
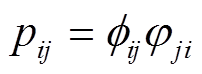 (10)
(10)式中,pij为第i个状态变量对模态j的影响水平;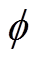 ij为系统状态矩阵的左特征向量中第i个元素;φji为系统状态矩阵的右特征向量中第i个元素。
ij为系统状态矩阵的左特征向量中第i个元素;φji为系统状态矩阵的右特征向量中第i个元素。
对三种系统分别进行参与因子分析,结果分别如图7~图9所示。
由参与因子分析可知,电源和线路有交互作用,改变线路参数将影响电源的稳定性,进而影响整个系统的稳定性。由于电源侧的直流母线电压和直流线路两侧电压ud1近似相等,因此改变电源的参数还将会影响线路模式的变化。负载模式由于只与负载相关的状态变量有关,当线路或者电源参数改变时,负载模式对应振荡模态应保持不变。
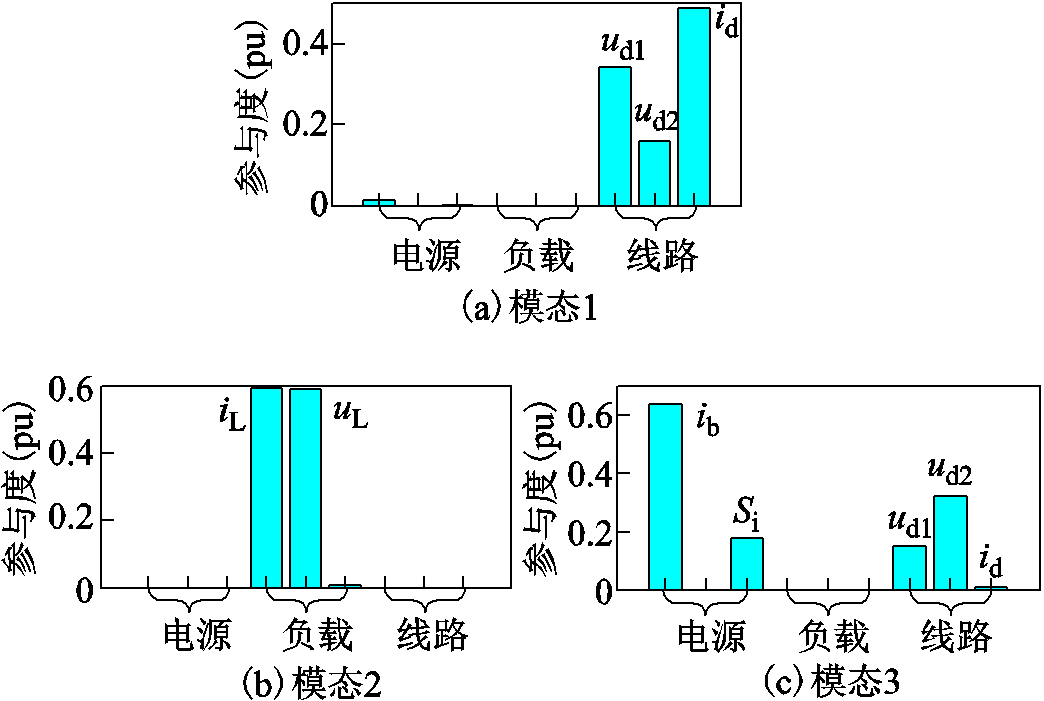
图7 系统1参与因子分析
Fig.7 System 1 participation factor analysis
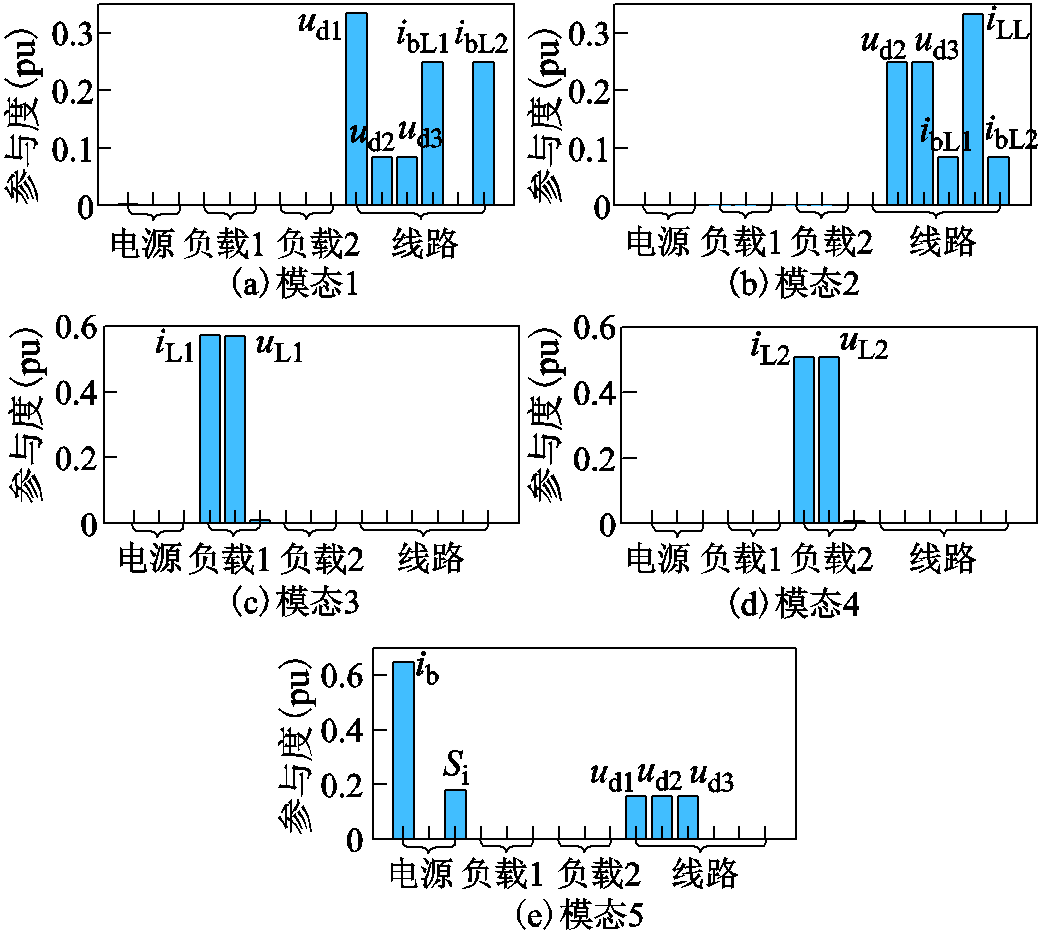
图8 系统2参与因子分析
Fig.8 System 2 participation factor analysis
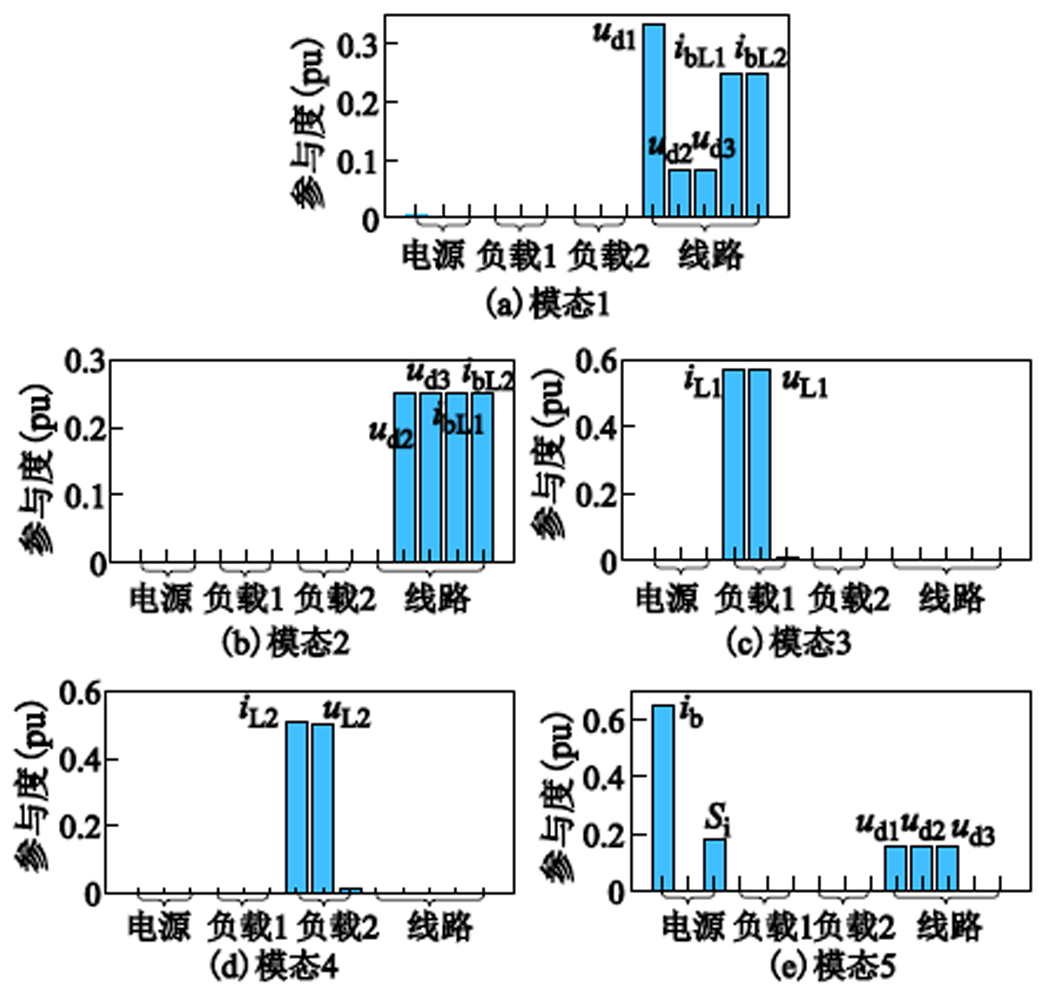
图9 系统3参与因子分析
Fig.9 System 3 participation factor analysis
本文所研究的直流微电网系统在附表1参数下均能稳定运行,因此以附表1参数为标况值,为验证3.2节中系统模态与状态变量之间的联系,并探究各系统参数对系统稳定性的影响。基于3.2节参与因子分析结果,重点研究电源控制器参数、恒功率负载控制器参数以及线路长度对系统稳定性的影响。
3.3.1 电源内环比例系数
电源内环比例系数由标况值的0.5倍增加至2.5倍,其他参数与附表1中保持一致。3个系统的特征根根轨迹如图10所示。
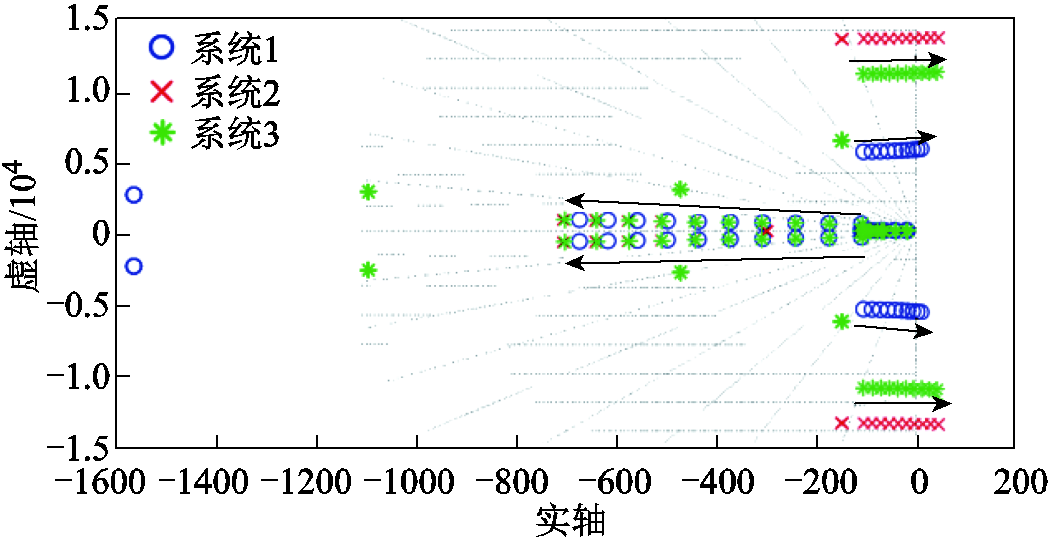
图10 电源内环比例系数的影响
Fig.10 The influence of power supply inner loop proportion coefficient
由图10可以看出,随着电源内环比例系数的增大,三个系统的模态1均向右移动,最后到达复平面的右半平面,系统失去稳定。电源-线路模式对应模态向左移动,其余模态基本不受影响,与参与因子分析的结果一致。改变电源控制器参数将会改变线路模式和电源-线路模式。增大电源内环比例系数将由线路模式对应模态导致系统失稳,减小电源内环比例系数将由电源-线路模式对应模态导致系统失稳,因此比例系数的取值有一定范围。不同网架结构间的稳定性差异主要体现在系统失稳时的谐振频率上。
3.3.2 电源内环积分系数
电源内环积分系数由标况值的1/10增加至10倍,其他参数与附表1中保持一致。3个系统的特征根根轨迹如图11所示。
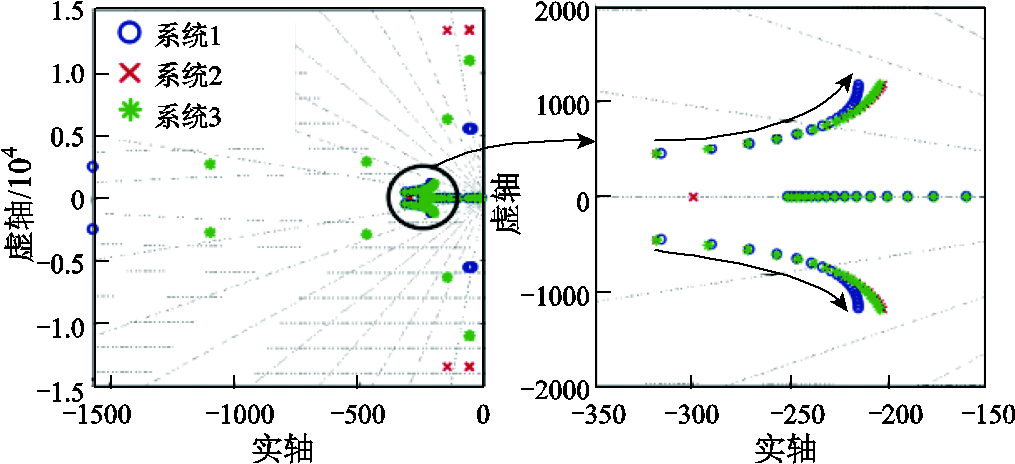
图11 电源内环积分系数的影响
Fig.11 The influence of the integral coefficient of the inner loop of the power supply
由图11可以看出,随着电源内环积分系数的增大,三个系统的电源-线路模式对应模态向右扩散,谐振频率升高。其余模态基本不受影响,与参与因子分析的结果一致。三个系统的电源-线路模式移动轨迹基本一致,表明电源内环积分主要影响电源自身稳定性。
3.3.3 恒功率负载控制器比例系数
恒功率负载控制器比例系数由0增至标况值的10倍,其他参数与附表1保持一致。3个系统的特征根根轨迹如图12所示。
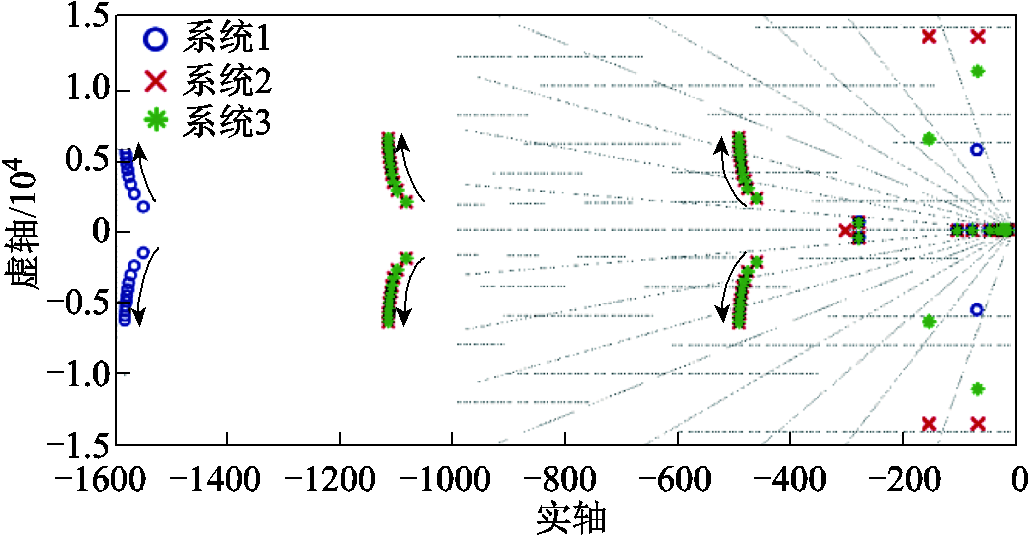
图12 恒功率负载控制器比例系数的影响
Fig.12 Proportional coefficient of constant power load controller
由图12可以看出,随着恒功率负载控制器比例系数的增大,三个系统的负载模式对应的模态均向远离实轴的方向移动,阻尼减小,谐振频率升高,系统稳定性减弱。其余模态基本不受影响,与参与因子分析的结果一致。改变恒功率负载控制器参数只会改变负载模式。对直流母线电压稳定性基本无影响。
3.3.4 恒功率负载控制器积分系数
恒功率负载控制器积分系数由标况值的1/10增加至10倍,其他参数与附表1中保持一致。3个系统的特征根根轨迹如图13所示。
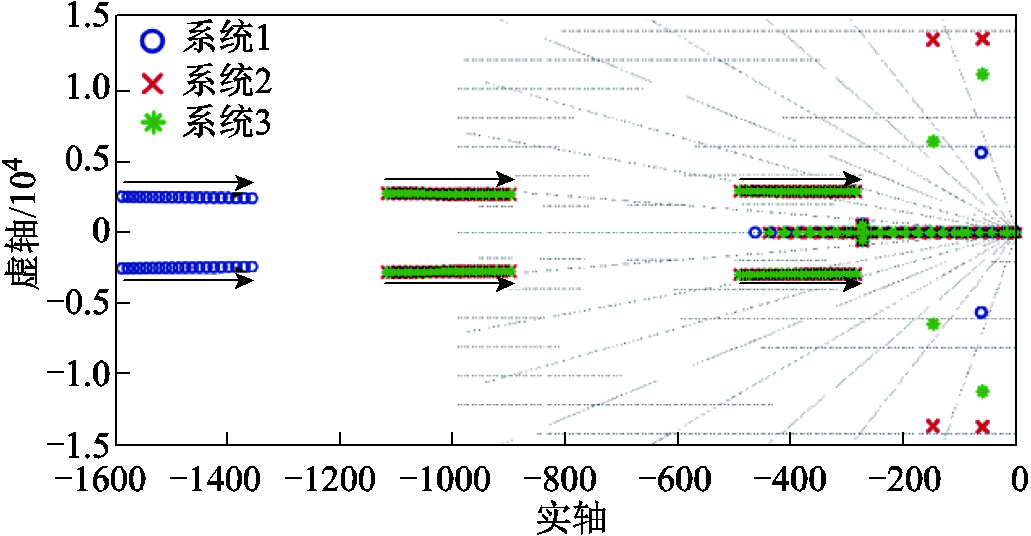
图13 恒功率负载控制器积分系数的影响
Fig.13 The influence of integral coefficient of constant power load controller
由图13可以看出,随着恒功率负载积分系数的增大,三个系统的负载模式对应模态向右平移收缩,谐振频率略微下降。其余模态基本不受影响,与参与因子分析的结果一致。
3.3.5 电源内环比例系数与线路参数
电源内环比例系数由标况值的1/5增加至2倍,线路总电感分别为标况值的1/2、标况值和标况值的2倍,其他参数与附表1保持一致。3个系统的特征根根轨迹如图14所示。
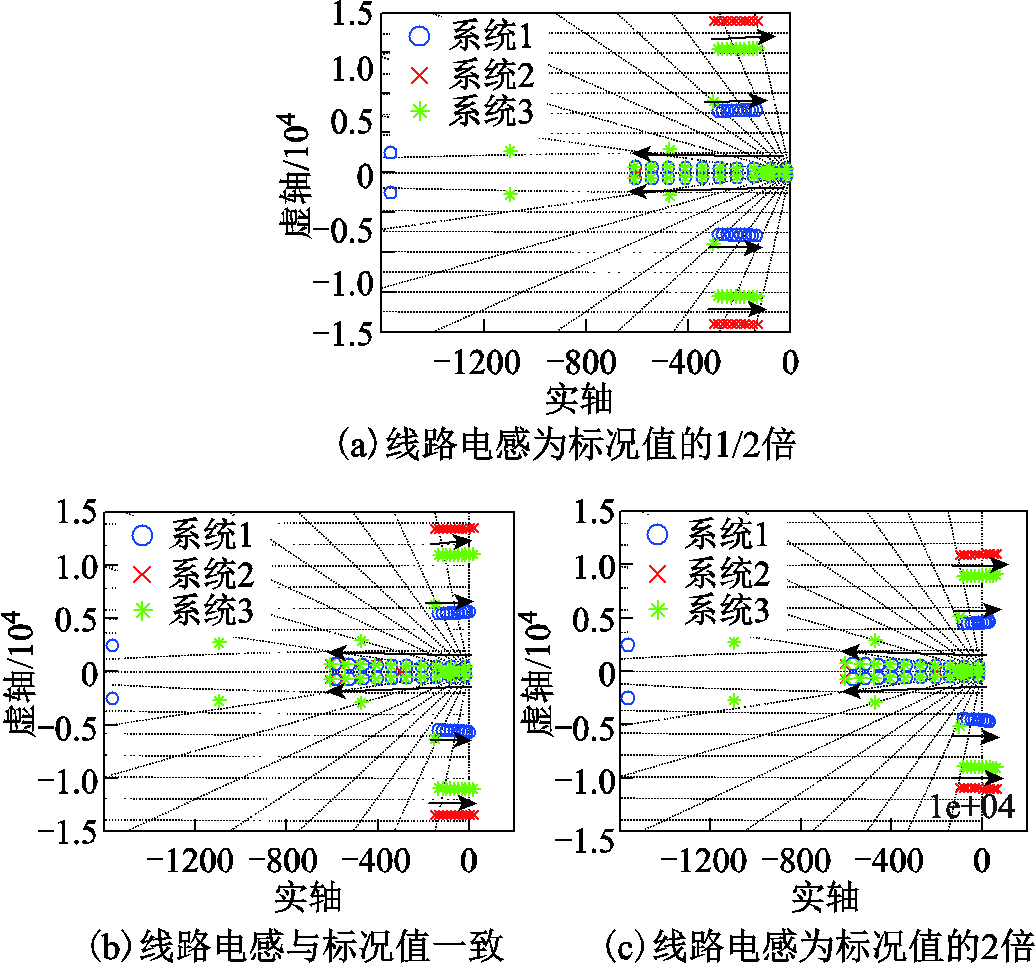
图14 电源内环比例系数与线路参数的影响
Fig.14 The influence of the proportion coefficient of the power supply inner loop and the line parameters
由图14可以看出,随着电源内环比例系数的增大,三个系统的特征根根轨迹与图10相似。增大线路电感不利于系统稳定性,模态1的振荡频率也随之降低;但电源-线路模式基本不受电感变化影响,表明线路电感主要影响线路模式。比较图14a、图14c可见,增大线路电感将缩小比例系数的稳定边界,降低系统的可靠性,考虑实际运行,输电线路的长度不能无限增加。
3.3.6 线路长度
按第1节假设,以系统1的线路长度为基准,且设线路总长度为1,改变系统2和3中蓄电池到达恒功率负载1的距离l1。对于系统2,假定两个负载的长度为总长度1/3且保持不变,为了使线路长度满足三角形三边定则,l1的长度应为1/6~1/2;同理,系统3中l1的长度应为1/3~2/3。具体推导见附录。3个系统的特征根根轨迹如图15、图16所示。
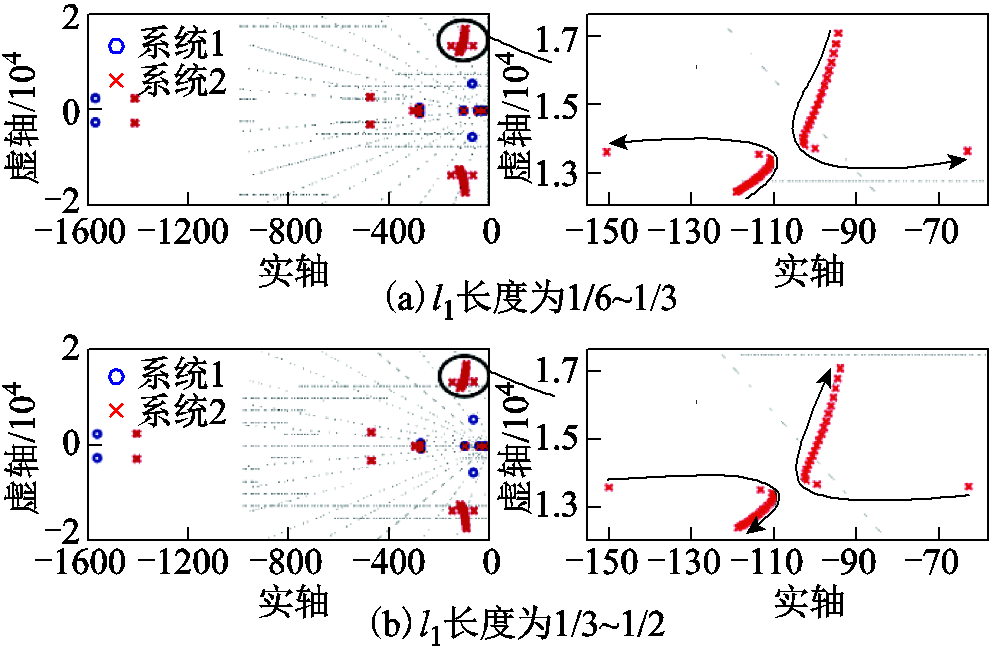
图15 系统2中l1长度的影响
Fig.15 The influence of l1 length in system 2
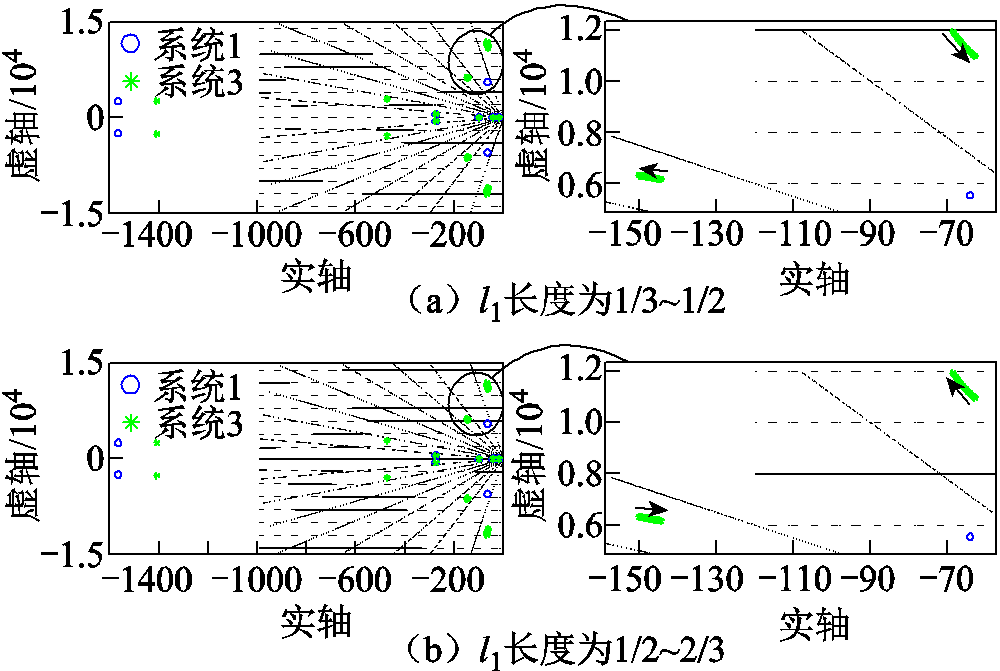
图16 系统3中l1长度的影响
Fig.16 The influence of l1 length in system 3
由图15可以看出,当l1的长度在1/6~1/3之间时,随着长度增加,系统2的模态1和模态2不断靠近,称此过程为吸引阶段,到达一定长度时,沿横轴相互排斥,当长度为1/3时,排斥距离到达顶峰,称此过程为排斥阶段;当距离从1/2~1/3时,随着长度减小,系统2的模态1和模态2处于吸引阶段,到达一定长度时,进入排斥阶段,当长度为1/3时,排斥距离到达顶峰。可见,由于环网的对称性,l1从1/6~1/3和从1/2~1/3有着相同的根轨迹,说明线路模式基本不受负荷大小的影响,只受电源和线路参数的影响。其中,当线路均匀分配时,系统1和系统2有着近似相同的稳定性。当线路不对称时,由于模态1和模态2的实部较为接近,系统的主导模态应有两对。模态1和模态2有相互吸引的趋势,对应的两组振荡频率也不断接近,当接近到一定程度时,两组频率相互叠加,大大增加了振荡的程度,反映到根轨迹中就是当模态1和模态2接近到一定程度时,突然沿横轴相互排斥,容易使系统失稳。
由图16可以看出,系统3与系统2有着相似的结论,但系统3中的线路模式变化程度远小于系统2,因此系统2对线路参数变化更敏感。
将线路总电感提高1倍后,使系统2的l1的长度由1/6增至1/3;系统3的l1的长度由1/3增至1/2。三个系统中线路模式对应特征根根轨迹如图17所示。
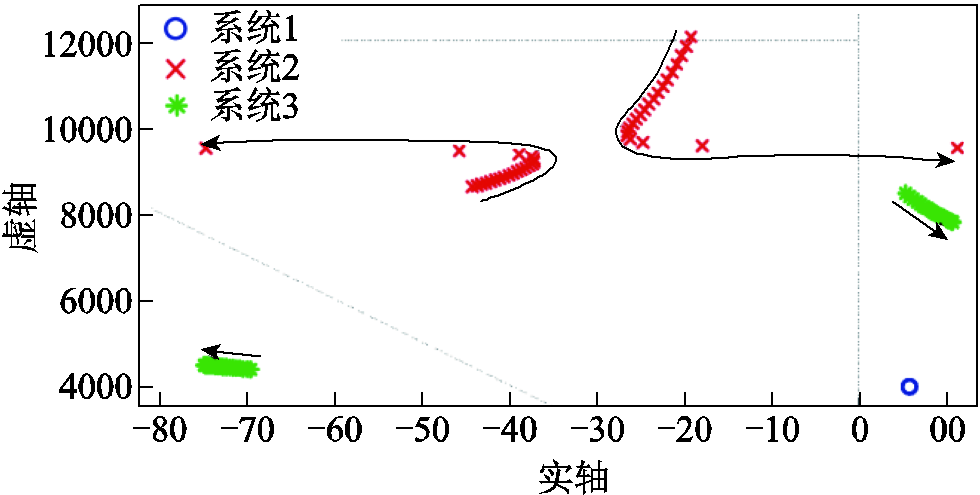
图17 线路长度的影响
Fig.17 Influence of line length
由图17可以看出,由于系统2对线路参数较为敏感,因此,当l1的长度接近线路总长度的1/3时,模态1和模态2由吸引阶段到达排斥阶段,此时仅需很小的线路参数变化,模态1的实部便能移动较长的距离,且越接近1/3,移动的距离便越长。而系统3中l1的长度越接近线路总长度的1/2,模态1移动的距离越短。当直流线路对称性较弱时,系统2仍可保持稳定,而系统1和系统3已经失稳。
根据上述的分析可以看出,导致不同网架结构的稳定性出现差异的主导模态是各系统的模态1。当直流线路具有高度对称性时,各系统的稳定性基本一致;当直流线路不对称时,由图17可知当l1较小时,系统2优于系统1和系统3。
为了验证上述分析的正确性,本文基于Matlab/Simulink软件搭建了图1所示不同网架结构的直流微电网模型。相关参数见附表1。
仿真条件与3.3节一致,系统1初始负荷为30kW,t=2s时,负荷突增20kW。系统2和系统3初始负荷为负载1和负载2各15kW,t=2s时,负载1负荷突增20kW。本文主要研究电源内环比例系数过大对系统稳定性的影响,因此电源内环比例系数分别取标况值和2.5倍标况值,以验证3.3节的结论。对应直流母线电压仿真图和3s时进行快速傅里叶变换(Fast Fourier Transform, FFT)的结果如图18所示。由图18可知,内环比例系数的增大使系统发生谐振,与3.3节分析结果一致。由FFT分析的谐振频率和表1可知,导致系统失稳的主导因素是模态1。由于网架结构的区别,三个系统在不同的频率发生谐振,仿真结果证明了理论分析的正确性。
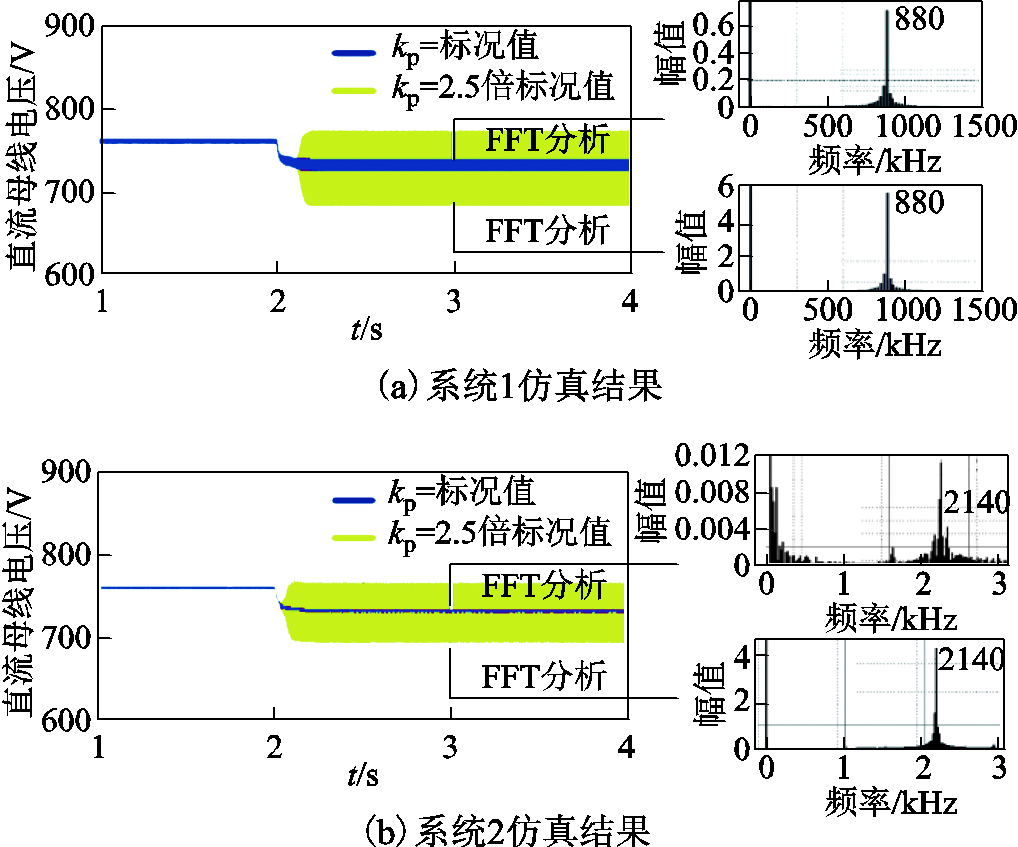

图18 内环比例变化时的仿真结果
Fig.18 Simulation results when the proportion of inner ring changes
仿真条件与4.1节一致。电源内环积分系数分别取0.1倍标况值、标况值和10倍标况值,以验证3.3节的结论。对应电源输出电流仿真图和3s时进行快速傅里叶分析的结果如图19所示。
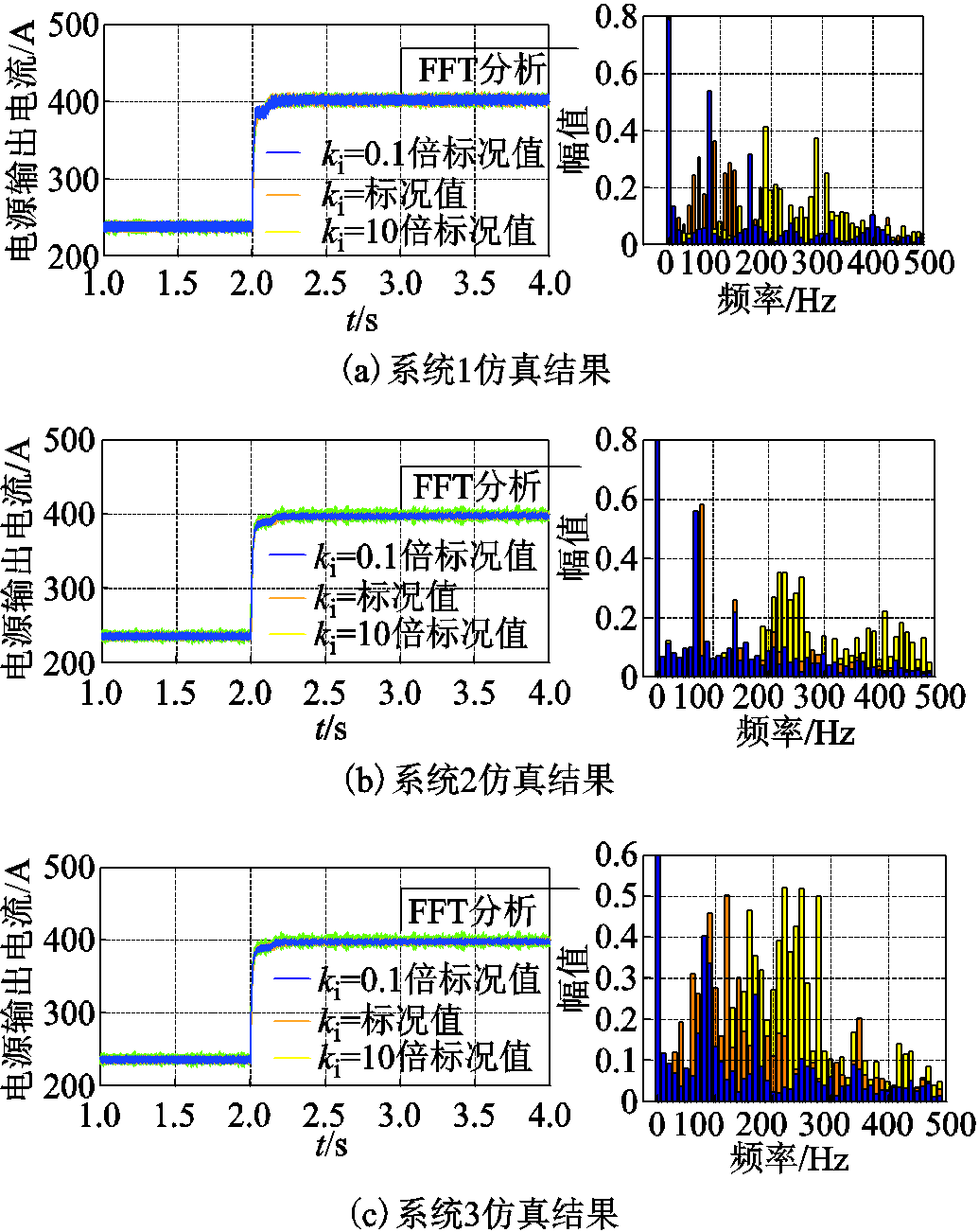
图19 内环积分变化时的仿真结果
Fig.19 Simulation results of inner loop integral changing
由图19可知,内环积分系数的增大使系统谐振频率升高,与3.3节分析结果一致。三个系统的谐振频率基本相同,仿真结果验证了电源内环积分主要影响电源自身稳定性。
仿真条件与4.1节一致。恒功率负载1比例系数分别取0和10倍标况值。对应负载电压仿真图和2s时进行快速傅里叶分析的结果如图20所示。
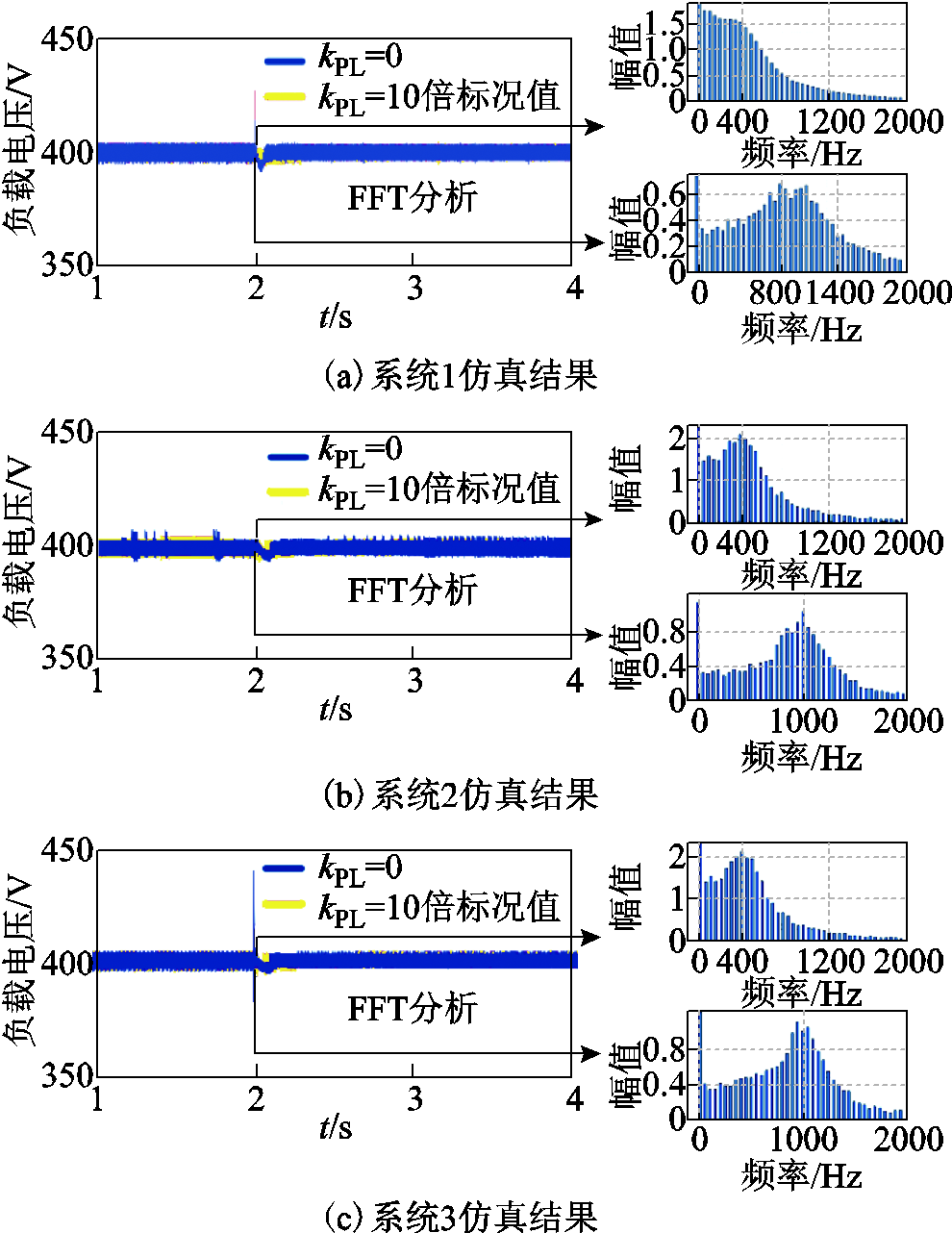
图20 恒功率负载比例系数变化时的仿真结果
Fig.20 Simulation results of constant power load proportion coefficient changes
如图20,由FFT分析得结果可知,增大恒功率负载比例系数使负载电压谐波频率升高,与3.3节分析结果一致。主导谐振的模态是负载模式,与参与因子分析结果一致。负载电压只与负载模式有关,联系图18、图19可知,负载模式与其他两组模式没有明显的交互关系。其他两组模式基本不受负载控制器参数影响。
仿真条件与4.1节一致。恒功率负载积分系数分别取0.1倍标况值、标况值和10倍标况值,以验证3.3节的结论。对应负载电压仿真图和3s时进行快速傅里叶分析的结果如图21所示。由图21可知,恒功率负载积分系数增大时,系统谐振频率基本无变化,与3.3节分析结果一致。积分系数过小时,系统到达稳态的时间变长,系统的动态特性变差。
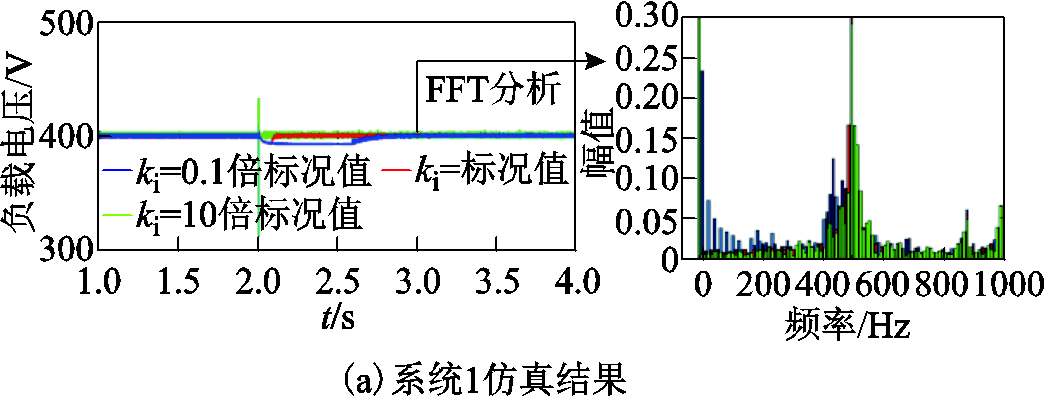
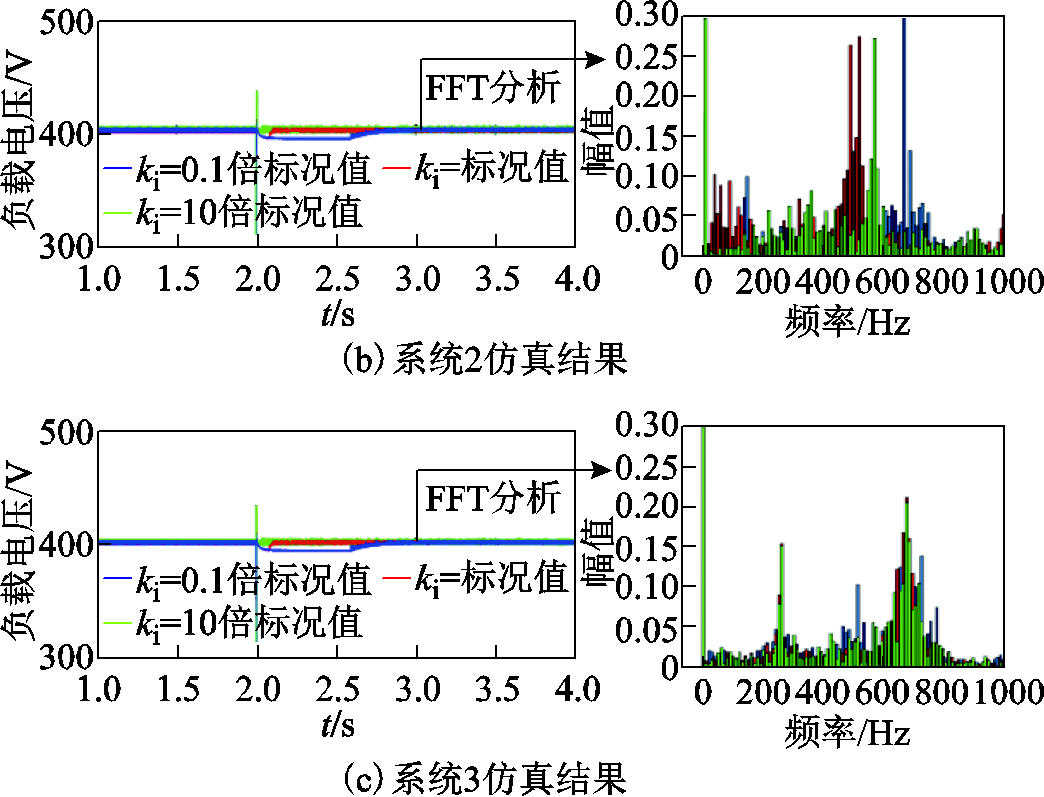
图21 恒功率负载积分系数变化时的仿真结果
Fig.21 Simulation results of constant power load integral coefficient changes
仿真条件与4.1节一致。工况1~5的电源内环比例系数和线路总电感分别取标况值的(1, 1)、(0.2, 0.5)、(0.2, 2)、(2, 0.5)和(2, 2)倍。对应仿真结果如图22所示。
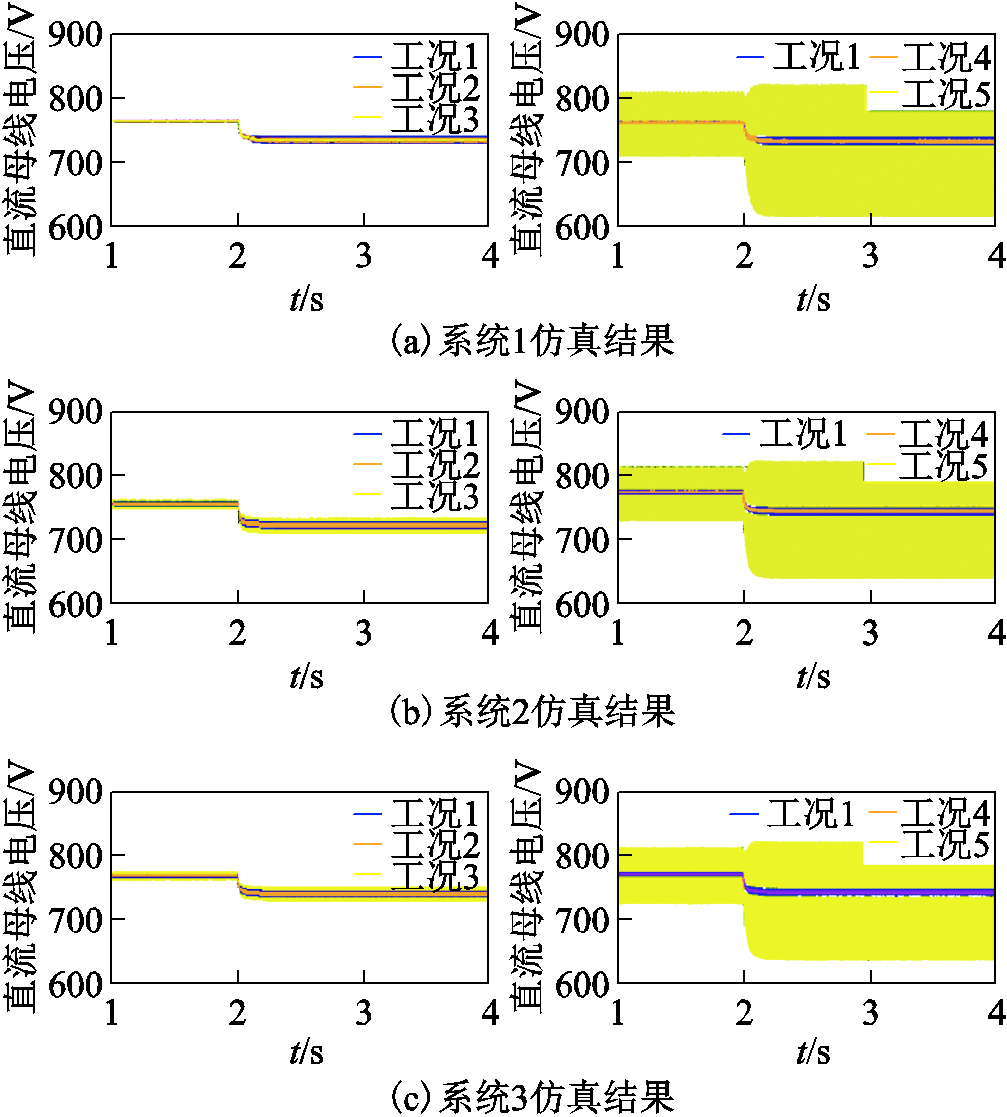
图22 电源比例系数和线路参数变化时的仿真结果
Fig.22 Simulation results of power supply ratio coefficient and line parameters changing
如图22,工况2和工况3指低内环比例系数条件下,不同线路电感的仿真工况。可见三个系统在对应工况下均能稳定运行,改变线路电感基本不会影响电源-线路模式;工况4和工况5指高内环比例系数条件下,不同线路电感的仿真工况。可见工况5系统失稳,工况4系统仍能保持稳定,增大线路电感会降低内环比例系数的最大稳定边界值,不利于系统的稳定。以上仿真结果验证了3.3节理论分析的结论。
仿真条件与4.1节一致,改变线路总电感至2倍标况值。系统2中l1的长度分别取总长度的1/6、1/3和1/2。系统3中l1的长度分别取总长度的1/3、1/2和2/3。对应直流母线电压仿真图和3s时进行快速傅里叶分析的结果如图23所示。
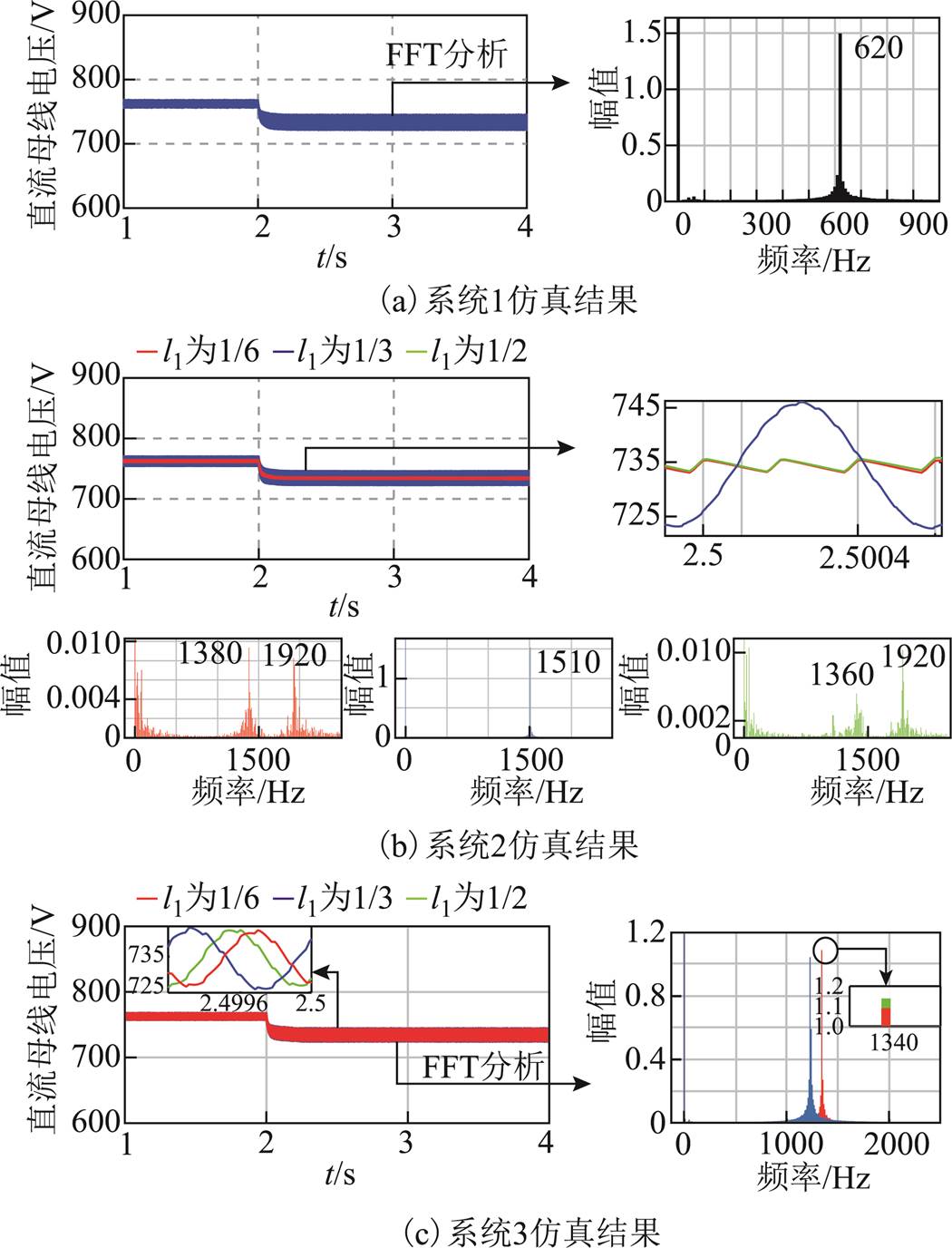
图23 l1变化时的仿真结果
Fig.23 Simulation results when l1 changes
由图23可以看出,系统1在线路总电感为2倍标况值时,发生谐振,谐振频率和系统1在仿真参数下模态1的振荡频率基本一致。系统2只在l1=1/3时发生谐振,谐振频率和系统2在仿真参数下模态1的振荡频率基本相同。当l1=1/6和l1=1/2时,直流母线电压波形基本一致,和3.3节分析结果一致,且直流母线电压主要受模态1和模态2两个模态影响。系统3在l1改变时均发生谐振,与3.3节特征根分析的结果一致,且当l1=1/3和l1=2/3时有相同的谐振频率。
本文通过构建不同网架结构下直流微电网的小信号模型,通过参与因子分析以及小信号稳定性的方法,探究了不同网架结构下直流微电网稳定性的差异,结论如下:
1)电源和直流线路存在交互作用,恒功率负载与直流线路基本不存在交互作用。
2)当线路对称时,控制器参数的变化对不同系统的影响基本一致,其区别仅在于系统失稳时的振荡频率不同。其中,单端环状结构系统振荡频率最高,单电源单负载系统振荡频率最低。当系统的网架结构不同但线路参数高度对称时,对不同网架结构系统的分析,都可等效为对单电源单负载结构的分析。
3)线路不对称时,当环状结构的线路模式对应振荡模态处于吸引阶段时,单端环状系统稳定性明显优于单电源单负载系统和单端辐射式系统。处于排斥阶段时,三个系统的稳定性基本一致。
1. 小信号模型
式(3)中,系数矩阵Ab、Bb分别为
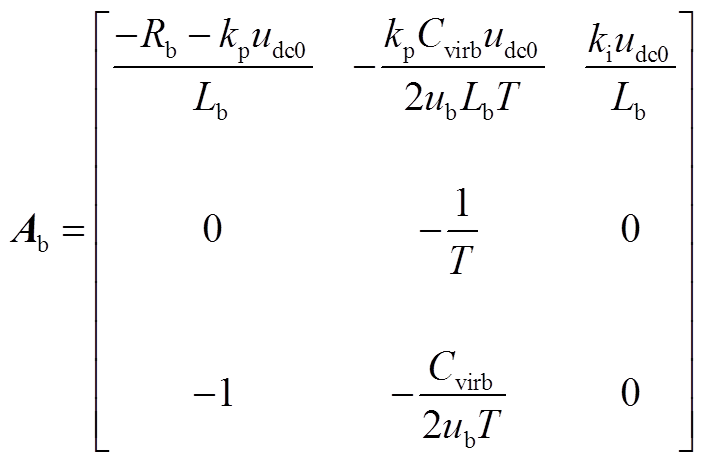 (A1)
(A1)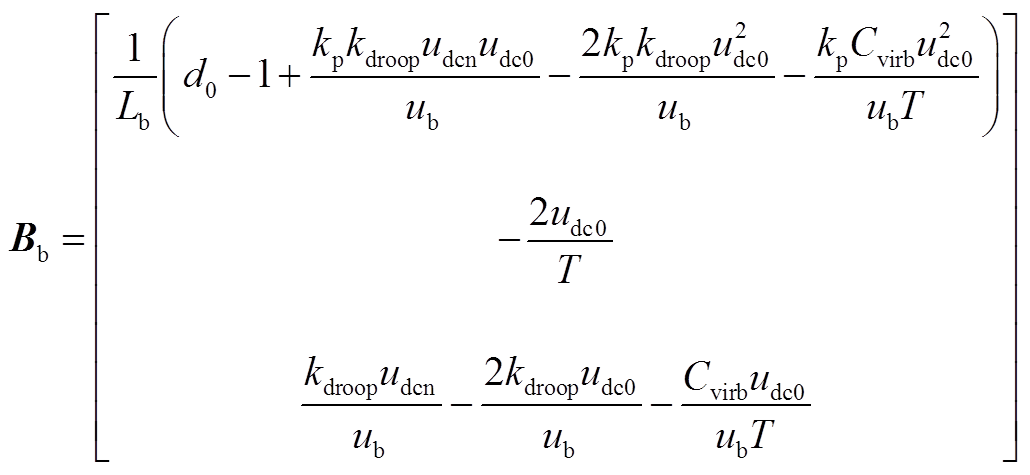 (A2)
(A2)式中,下标0代表对应状态变量的稳态值。
式(5)中,系数矩阵AL、BL、Dd分别为
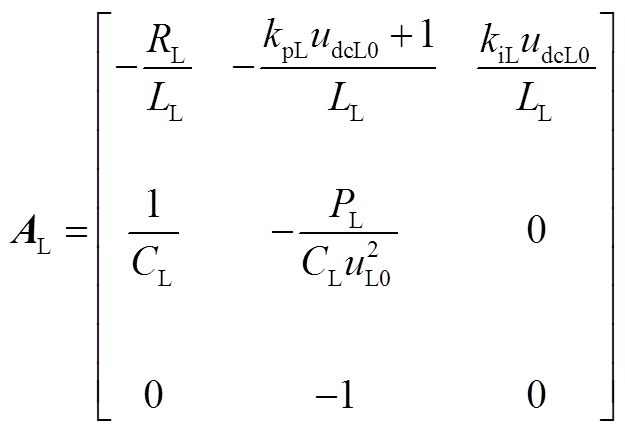 (A3)
(A3)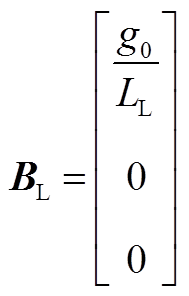 (A4)
(A4)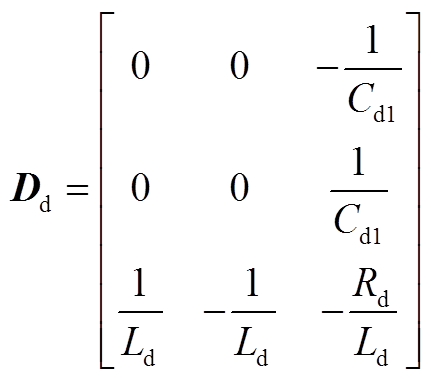 (A5)
(A5)式(9)中,系统1的系数矩阵Cb、CL、D分别为
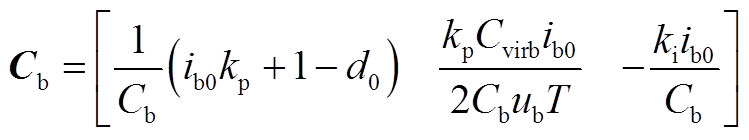 (A6)
(A6)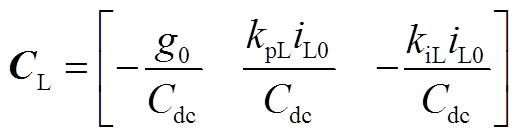 (A7)
(A7)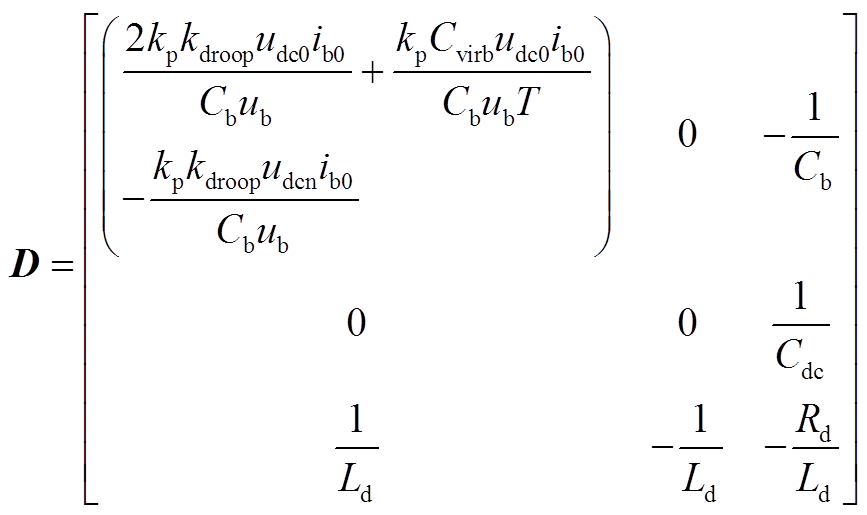 (A8)
(A8)系统2的系数矩阵Asys为
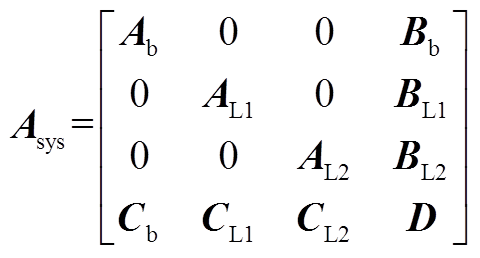 (A9)
(A9)AL1、AL2、BL1、BL2、CL1和CL2形式一样,参数由系统参数决定。不同系统主要区别在D阵构建上。系统2的D阵为
 (A10)
(A10)同理,系统3的D阵为
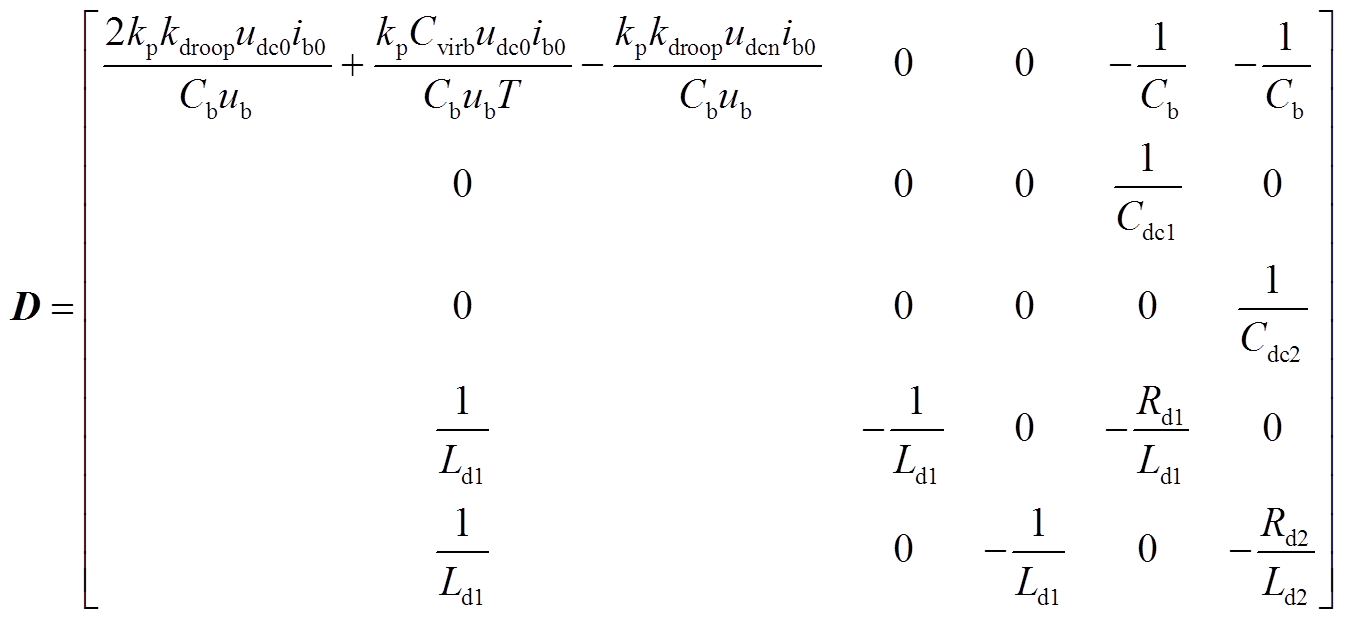 (A11)
(A11)2. 线路长度
对于系统2,有
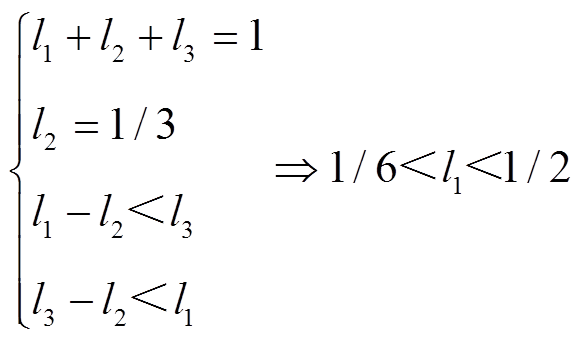 (A12)
(A12)对于系统3,有
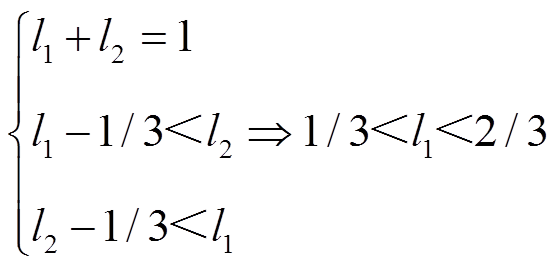 (A13)
(A13)3. 系统参数
附表1 系统参数
App.Tab.1 System parameter

项目参数 蓄电池额定电压ubn=120V,额定容量2000A·h 蓄电池侧支撑电容0.005F 虚拟惯性控制系数Cvirb=0.01,时间常数T=0.05,下垂系数kdroop=16/15 内环PI控制比例系数kp=0.0005,积分系数ki=0.1,开关频率10kHz 蓄电池侧线路参数Rb=0.001Ω,Lb=500μH 恒功率负载功率PL=50kW 恒功率负载1功率PL1=35kW 恒功率负载2功率PL2=15kW 恒功率负载PI控制比例系数kpL=0.001,积分系数kiL=0.1,开关频率10kHz 负载额定电压400V 负载侧线路参数RL=0.1Ω,LL=2mH,CL=100μF 负载侧支撑电容总和Cdc=0.01F 直流线路参数Rd=0.003Ω,Ld=10μH 直流母线额定电压udc=800V
参考文献
[1] 李霞林, 郭力, 王成山, 等. 直流微电网关键技术研究综述[J]. 中国电机工程学报, 2016, 36(1): 2-17. Li Xialin, Guo Li, Wang Chengshan, et al. Summary of research on key technologies of DC micro grid[J]. Proceedings of the CSEE, 2016, 36(1): 2-17.
[2] Xu Lie, Chen Dong. Control and operation of a DC microgrid with variable generation and energy storage[J]. IEEE Transactions on Power Delivery, 2011, 26(4): 2513-2522.
[3] Dragicevic T, Lu X, Vasquez J C, et al. DC microgrids part I: a review of control strategies and stabilization techniques[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 4876-4891.
[4] 贺悝, 李勇, 曹一家, 等. 考虑分布式储能参与的直流配电网电压柔性控制策略[J]. 电工技术学报, 2017, 32(10): 101-110. He Li, Li Yong, Cao Yijia, et al. Flexible voltage control strategy of DC distribution network considering distributed energy storage[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 101-110.
[5] 张国荣, 王新兵, 乔龙洋.直流微网中母线电压对直流负载影响[J]. 电力系统及其自动化, 2013, 35(2): 65-67. Zhang Guorong, Wang Xinbing, Qiao Longyang. The impact of bus voltage on the DC load for DC microgrid[J]. Automation of Electric Power Systems, 2013, 35(2): 65-67.
[6] 彭克, 陈佳佳, 徐丙垠, 等. 柔性直流配电系统稳定性及其控制关键问题[J]. 电力系统自动化, 2019, 43(23): 90-100, 115.Peng Ke, Chen Jiajia, Xu Bingyin, et al. Stability and control of flexible DC distribution system[J]. Automation of Electric Power Systems, 2019, 43(23): 90-100, 115.
[7] 张学, 裴玮, 邓卫, 等. 含恒功率负载的交直流混联配电系统稳定性分析[J]. 中国电机工程学报, 2017, 37(19): 5572-5582, 5834. Zhang Xue, Pei Wei, Deng Wei, et al. Stability analysis of AC-DC hybrid distribution system with constant power load[J]. Proceedings of the CSEE, 2017, 37(19): 5572-5582, 5834.
[8] 谢文强, 韩民晓, 严稳利, 等. 考虑恒功率负荷特性的直流微电网分级稳定控制策略[J]. 电工技术学报, 2019, 34(16): 3430-3443. Xie Wenqiang, Han Minxiao, Yan Wenli, et al. DC micro grid hierarchical stability control strategy considering constant power load characteristics[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3430-3443.
[9] 李国庆, 孙银锋, 吴学光. 柔性直流输电稳定性分析及控制参数整定[J]. 电工技术学报, 2017, 32(6): 231-239. Li Guoqing, Sun Yinfeng, Wu Xueguang. Stability analysis and control parameter setting of flexible DC transmission[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 231-239.
[10] 杨洁, 刘开培, 王东旭, 等. 向无源网络供电的双端柔性直流输电系统小信号稳定性分析[J]. 中国电机工程学报, 2015, 35(10): 2400-2408. Yang Jie, Liu kaipei, Wang Dongxu, et al. Small signal stability analysis of a two terminal flexible DC transmission system powered by a passive network[J]. Proceedings of the CSEE, 2015, 35(10): 2400-2408.
[11] 郑征, 黄旭, 杨明, 等. 弱电网下逆变侧电流反馈的并网逆变器稳定性分析及优化[J]. 电力系统保护与控制, 2019, 47(19): 31-37. Zheng Zheng, Huang Xu, Yang Ming, et al. Stability analysis and optimization of grid connected inverter with current feedback at inverter side under weak current network[J]. Power System Protection and Control, 2019, 47(19): 31-37.
[12] 吴蒙, 贺之渊, 阎发友, 等. 下垂控制对直流电网动态电压稳定性的影响分析[J]. 电力系统保护与控制, 2019, 47(10): 8-15. Wu Meng, He Zhiyuan, Yan Fayou, et al. Analysis of the influence of droop control on the dynamic voltage stability of DC power grid[J]. Power System Protection and Control, 2019, 47(10): 8-15.
[13] 邵冰冰, 赵书强, 高本锋, 等. 连接弱交流电网的VSC-HVDC失稳机理及判据研究[J]. 电工技术学报, 2019, 34(18): 3884-3896. Shao Bingbing, Zhao Shuqiang, Gao Benfeng, et al. Study on VSC-HVDC instability mechanism and criteria for weak AC power grid connection[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3884-3896.
[14] 韩民晓, 谢文强, 曹文远, 等. 中压直流配电网应用场景与系统设计[J]. 电力系统自动化, 2019, 43(23): 2-14, 89. Han Minxiao, Xie Wenqiang, Cao Wenyuan, et al. Application scenario and system design of medium voltage DC distribution network[J]. Automation of Electric Power Systems, 2019, 43(23): 2-14, 89.
[15] 吴鸣, 刘海涛, 陈文波, 等. 中低压直流配电系统的主动保护研究[J]. 中国电机工程学报, 2016, 36(4): 891-899. Wu Ming, Liu Haitao, Chen Wenbo, et al. Research on active protection of medium and low voltage DC distribution system[J]. Proceedings of the CSEE, 2016, 36(4): 891-899.
[16] 李蕊, 罗飞, 焦在滨. 中压直流配电系统接地方式研究[J]. 电网技术, 2018, 42(8): 2594-2603. Li Rui, Luo Fei, Jiao Zaibin. Study on the grounding mode of medium voltage DC distribution system[J]. Power System Technology, 2018, 42(8): 2594-2603.
[17] 万千, 夏成军, 管霖, 等. 含高渗透率分布式电源的独立微网的稳定性研究综述[J]. 电网技术, 2019, 43(2): 598-612. Wan Qian, Xia Chengjun, Guan Lin, et al. Summary of stability research on independent microgrid with high permeability distributed generation[J]. Power System Technology, 2019, 43(2): 598-612.
[18] 魏智宇, 彭克, 李海荣, 等. 电动汽车接入直流配电系统的稳定性及虚拟惯量控制[J]. 电力系统自动化, 2019, 43(24): 50-72. Wei Zhiyu, Peng Ke, Li Hailong, et al. Stability and virtual inertia control of electric vehicle connected to DC distribution system[J]. Automation of Electric Power Systems, 2019, 43(24): 50-72.
[19] 孟建辉, 彭嘉琳, 王毅, 等. 多约束下光储系统的灵活虚拟惯性控制方法[J]. 电工技术学报, 2019, 34(14): 3046-3058. Meng Jianhui, Peng Jialin, Wang Yi, et al. Flexible virtual inertial control method of optical storage system under multiple constraints[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 3046-3058.
[20] 孟建辉, 邹培根, 王毅, 等. 基于灵活虚拟惯性控制的直流微网小信号建模及参数分析[J]. 电工技术学报, 2019, 34(12): 2615-2626. Meng Jianhui, Zou Peigen, Wang Yi, et al. Small signal modeling and parameter analysis of DC microgrid based on flexible virtual inertial control[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2615-2626.
[21] 朱晓荣, 谢志云, 荆树志. 直流微电网虚拟惯性控制及其稳定性分析[J]. 电网技术, 2017, 41(12): 3884-3893. Zhu Xiaorong, Xie Zhiyun, Jing Shuzhi. Virtual inertia control and stability analysis of DC micro grid[J]. Power System Technology, 2017, 41(12): 3884-3893.
[22] 郭力, 冯怿彬, 李霞林, 等. 直流微电网稳定性分析及阻尼控制方法研究[J]. 中国电机工程学报, 2016, 36(4): 927-936. Guo Li, Feng Yibin, Li Xialin, et al. Study on stability analysis and damping control method of DC micro grid[J]. Proceedings of the CSEE, 2016, 36(4): 927-936.
[23] 苑宾, 李探, 许建中, 等. 联接弱交流电网MMC系统小信号稳定性分析[J]. 中国电机工程学报, 2017, 37(18): 5339-5349, 5533. Yuan Bin, Li Tan, Xu Jianzhong, et al. Small signal stability analysis of MMC system connected to weak AC power grid[J]. Proceedings of the CSEE, 2017, 37(18): 5339-5349, 5533.
Stability Analysis of DC Microgrid Based on Different Grid Structures
Abstract It is not clear whether the DC microgrid system with different grid structures has different stability, which needs to be studied. In order to solve this problem, the small signal models of several typical grid structures are established. Based on the change of participation factors and system characteristic roots, the influence of system parameters on system stability under different grid structures is studied. The results show that the stability of the system under different grid structures is basically the same with only the difference of resonance frequency when the parameters of the controller on the source side are changed alone; when the parameters of the controller on the load side are changed alone, only the oscillation modes related to the load are affected, and the load and the line basically have no interaction; when the parameters of the line are changed alone, due to the interaction between the source network, different systems appear Stability difference. Finally, the correctness of the theoretical analysis is verified by simulation.
keywords:Grid structure, small signal model, participation factor method, root locus, stability
中图分类号:TM712
DOI:10.19595/j.cnki.1000-6753.tces.191846
收稿日期2019-12-31
改稿日期2020-03-04
朱晓荣 女,1972年生,博士,副教授,研究方向为新能源发电及并网技术、电力系统分析等。E-mail:xiaorongzhu@ncepu.edu.cn(通信作者)
李 铮 男,1995年生,硕士研究生,研究方向为新能源发电技术。E-mail:727819580@qq.com
(编辑 赫蕾)