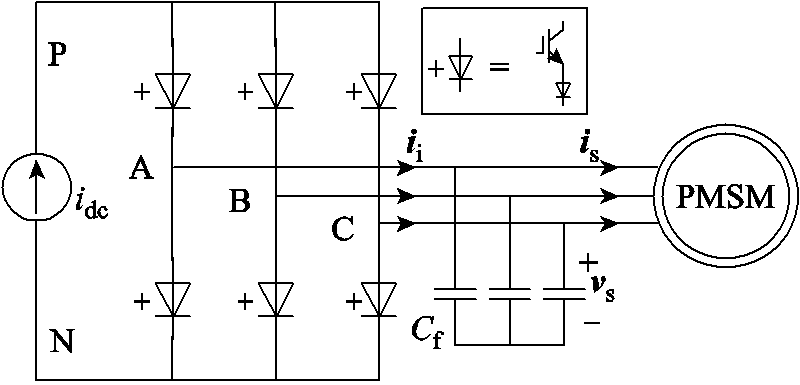
图1 电流源变流器永磁同步电机驱动系统拓扑结构
Fig.1 Power circuit of CSC fed PMSM drive system
摘要 电流源变流器输出电压平滑、具有天然短路保护能力,在长电缆驱动、中压驱动等场景得到广泛应用。电流源变流器的输出滤波电容与电机的电磁动力学方程构成二阶系统,存在天然的谐振频率,易失稳,因此对控制器的设计提出了严峻挑战。该文深入地分析了被控对象的数学模型,在不考虑控制变量和状态变量约束的条件下,理论上求解了可实现电磁转矩的无差拍控制的输入电压值,以此作为滤波电容电压的参考值。在此基础上,充分利用模型预测控制多目标全局优化的能力,将dq轴电流、输出电容电压和开关惩罚项包含在一个统一的代价函数中,提出一种计及全状态变量的预测转矩控制策略。所提的全状态变量预测转矩控制可有效抑制滤波电容和定子电感之间的能量振荡。在此基础上,通过理论分析和大量仿真数据获取采样频率和开关惩罚项权系数的设计准则,通过选取合理的开关惩罚项权系数,可实现开关频率和稳态控制性能的优化设计。最后,通过硬件在环(HiL)对所提控制策略进行了验证。测试结果表明,全变量预测转矩控制稳态转矩脉动小;在动态转换过程中,转矩响应速度快。
关键词:电流源变流器 直接预测转矩控制 永磁同步电机 大功率驱动
随着能源和环境问题日趋严峻,提升能效,促进节能减排,已成为全社会关注的焦点问题。相比传统燃气轮机,电机驱动转换效率高、排放低,是应对能源和环境问题的有效手段。其中,永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)因其高功率密度、低维护成本、高功率因数等突出优势备受关注[1-5]。近年来,永磁材料在磁和热性能上的突飞猛进使永磁同步电机的功率等级得以覆盖大功率的应用场景,其典型应用包括伺服驱动、电动汽车、泵类、压缩机和风机等负载[6-8]。
以油气产业的潜油电泵系统为代表,其主要由多级离心式潜油电泵和地面电机驱动系统组成。然而,连接地面驱动系统和井下潜油电机的动力线缆可长达数公里,如,挪威北海Otter油田的水上变频器通过23.4km的电缆为水下双电潜泵供电。电机驱动系统动力电缆的长度达到一定程度后,其寄生参数不可忽略。这会导致:①电能在线缆上的传输变为一个和时间、长度相关的波过程,进而在电机端造成反射过电压,并且线缆的各个参数之间有一个固有的谐振频率,当输入信号包含此频率谐波时会加剧过电压的问题;②由于电缆的电阻特性,电压基波信号会在长电缆上产生较大压降,进而造成电机端基波电压不足的问题[9-11]。以上两个问题为高性能远距离变频驱动系统的设计提出了严峻挑战[12-13]。
众所周知,电流源变流器(Current Source Converter, CSC)具有输出电压变化率(dV/dt)低的特点。具体而言,其端口电压必须经过电容滤波器后输出电能,经过滤波之后的电容电压高频成分大大降低,因此非常适合于长电缆驱动系统。此外,电流源变流器还具有结构简单、短路自保护能力、成本低等优点。功率器件的不断进步,同样促成了电流源变流器在中压驱动领域中的蓬勃发展。例如,在Rockwell的电流源中压驱动产品中采用了对称门极换流晶闸管(Symmetric Gate-Commutated Thyristor, SGCT)。鉴于电流源变流器的上述特点,使其在油气、矿产开采等长电缆驱动的应用场景相比电压源变流器具有显著优势,得到了广泛应用。
高性能电机控制策略是电流源变流器的核心技术,直接影响驱动系统的性能指标。众所周知,电流源变流器输出滤波电容的存在虽有效降低了电机端的dV/dt,但与此同时也导致转矩控制的动态性能下降。为了提升电磁转矩的动态响应能力,(线性)矢量控制(Field Oriented Control, FOC)和(非线性)直接转矩控制(Direct Torque Control, DTC)被先后提出,并在工业界得到广泛应用[14-15]。
矢量控制的基本思想是经过坐标变换将永磁电机定子电流分解为转矩分量(q轴)和励磁分量(d轴),通过对dq轴电流的解耦控制实现电机转矩的快速跟踪。为了将控制器输出的电流矢量调制为变流器的开关状态,需要嵌入脉宽调制(Pulse Width Modulator, PWM)单元。脉宽调制依赖伏(安)秒平衡机理,当开关频率远高于被控对象的时间常数时,稳态控制效果好。然而,对于大功率电流源变换器,其开关频率较低,MW级的中压驱动其开关频率甚至只有数百赫兹。在这样的应用场合,基于变流器平均开关模型的矢量控制的性能大打折扣。另一方面,电流源变流器驱动永磁同步电机的直接转矩控制可以通过类比电压源型直接转矩控制策略得出,其利用滞环比较器和电流开关矢量表格直接控制定子磁链幅值和电磁转矩,无需PWM调制器和坐标变换,并且可以获得更快的瞬态响应。但传统的直接转接控制存在转矩和磁链脉动大的缺点。
模型预测控制(Model Predictive Control, MPC)早在20世纪80年代被应用于电力电子与电机驱动领域[16-17],随着相关学者深入研究和实时控制器性能的大幅提升,在21世纪初得到长足发展。其中,有限控制集模型预测控制(Finite Control Set MPC, FCS-MPC)充分利用变流器功率开关组合具有有限个状态的特性,在每个采样周期内依据被控对象的数学模型预测状态变量在未来时刻的演变轨迹,并依据代价函数,直接选取最优开关状态。FCS-MPC可实现多目标控制,易于包含非线性约束条件,并充分利用变流器的物理极限,实现良好的稳态运行和快速的瞬态控制性能[18-21]。
FCS-MPC应用于电机驱动,根据控制目标不同可分为预测电流控制(Predictive Current Control, PCC)和预测转矩控制(Predictive Torque Control, PTC)[22-23]。通常直接控制电机的电磁转矩被认为是更加方便和直观的控制策略。虽然已有大量文献提出和改进了永磁同步电机和感应电机的预测转矩控制策略,但其主要应用于电压源变流器驱动系统中[24-25],关于电流源变流器驱动系统的预测转矩控制却鲜有文献深入研究。因此,电流源变流器驱动系统尚存在诸多关键科学问题,亟待解决。首先,电流源变流器的输出滤波电容与永磁同步电机的电磁动力学方程构成二阶系统,存在天然的谐振频率。当驱动系统内的谐波频率趋近于LC网络的谐振频率时,谐波电流会被进一步放大,进而导致输出转矩的振荡,甚至系统失稳。已经有诸多文献针对电流源滤波器谐振问题提出解决方案。其中,主流方法为无源阻尼法和有源阻尼法两种。无源阻尼法,即通过在电感支路串联电阻或电容支路并联电阻的方式抑制输出电流的振荡。该方法简单有效,但引入了额外的损耗,降低了变换器的转换效率。文献[26-27]提出了有源阻尼方法,通过在控制策略中增加相应的电流反馈环路,模拟并联在滤波电容上的等效电阻的阻尼特性,亦可取得良好的抑制振荡的效果。但该方法需要谐波检测和前馈回路等环节,实现和调试过程复杂。此外,对于大功率应用场景,开关频率必须严格限制,以降低开关损耗。为了实现低开关频率下高电流控制质量,文献[28]针对电流源驱动PMSM,提出了空间矢量调制和谐波消除相结合的调制策略,实现了大功率高速电机的高性能控制。但鲜有文献深入讨论电流源变流器采用预测控制时,开关频率的优化设计方法。最后,对于电流源变流器,由于滤波电容的存在使得其动态响应缓慢。因此,提升其动态响应是电流源变流器控制的另一项关键技术。
基于上述分析,本文提出一种针对电流源变流器永磁同步驱动系统的全状态变量预测转矩控制(Full State-Variable Predictive Torque Control, FSV-PTC)策略。所提方法通过同时控制输出转矩(定子电流)和滤波电容电压,并根据无差拍控制(Deadbeat Control)原理,解析计算得到滤波电容电压的参考值,以此有效抑制LC网络的谐振,显著减小输出转矩脉动,降低系统的电磁噪声。同时,由于在目标函数中添加了电容电压控制项,有助于在长电缆驱动应用场景中进一步降低供电端的谐波含量,进而减弱波反射的影响[10]。所提的FSV-PTC继承了预测控制天然的快速动态响应特性。在此基础上,本文深入分析了采样频率、开关惩罚项权系数和开关频率之间的关系,为电流源变流器预测控制的参数设计提供了理论依据。最后,在实时控制单元和功率模拟单元上对所提方法进行了硬件在环(Hardware in the Loop, HiL)验证,结果证明FSV-PTC在稳态输出转矩脉动抑制和动态转矩快速响应方面具有良好的控制性能。
电流源变流器永磁同步电机驱动系统的功率拓扑如图1所示,功率开关器件由具有反向电压阻断能力的SGCT或由IGBT与二极管串联组成。在此,直流侧采用理想电流源模拟直流平波电抗器。Cf为变流器的输出滤波电容,为感性负载提供续流回路的同时,可以滤除变流器侧电流的高频分量。定义ii=[iA iB iC]T为变流器侧电流矢量,vs=[vsA vsBvsC]T为输出电容电压矢量,is=[isA isB isC]T为输出电流矢量,即流经电机定子绕组的电流矢量。

图1 电流源变流器永磁同步电机驱动系统拓扑结构
Fig.1 Power circuit of CSC fed PMSM drive system
对变流器功率器件的开关函数定义为
 (1)
(1)式中,P为桥臂上侧功率开关;N为下侧功率开关。变流器侧的输出电流矢量ii可以根据开关状态和直流电流通过式(2)计算。
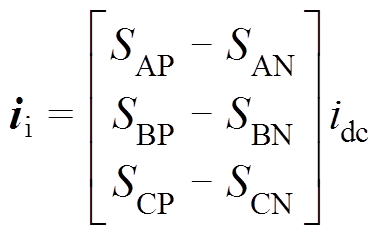 (2)
(2)对于电流源变流器,其直流侧为电流源属性,应避免选择使直流侧开路的开关组合状态;同时,交流侧由于输出电容的存在呈电压源属性,应避免选择使交流侧短路的开关组合状态。考虑到上述两个约束条件,共存在9个有效开关组合状态。定义控制矢量为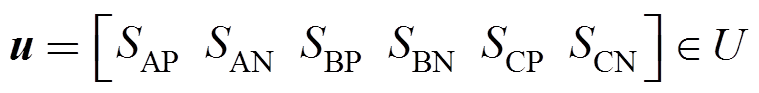 ,其有限控制集U的定义见表1。
,其有限控制集U的定义见表1。
表1 电流源变流器有限控制集开关表
Tab.1 Finite control set switching table of CSCs
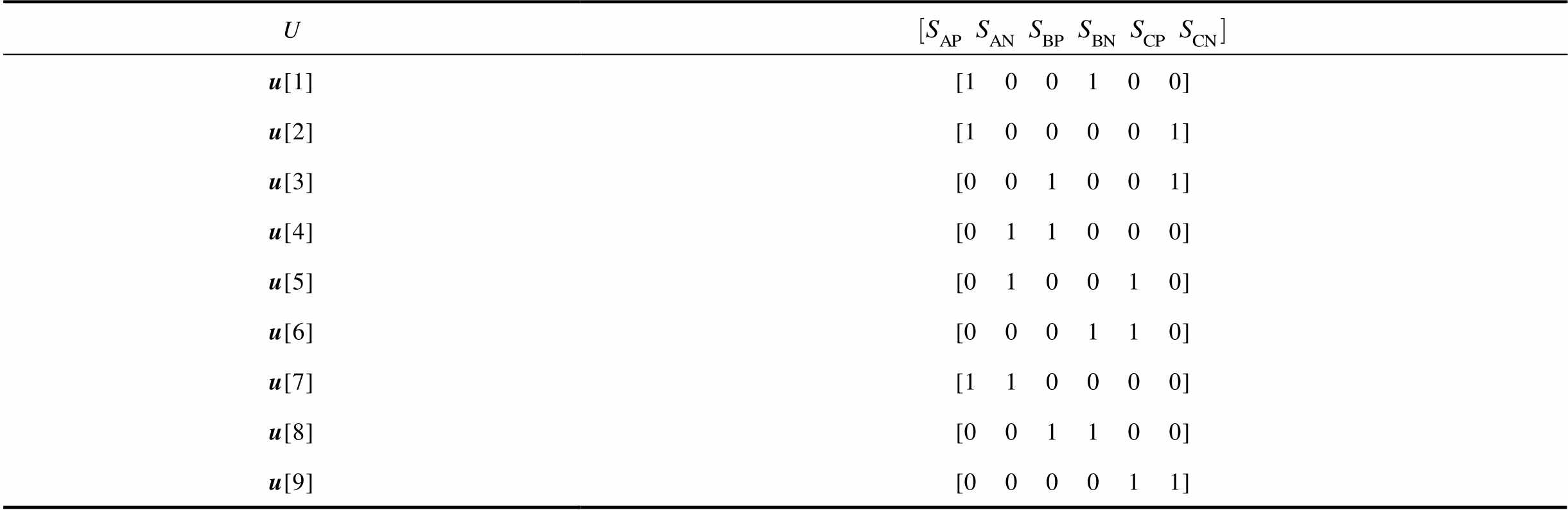
U u[1] [1 0 0 1 0 0] u[2] [1 0 0 0 0 1] u[3][0 0 1 0 0 1] u[4][0 1 1 0 0 0] u[5][0 1 0 0 1 0] u[6] [0 0 0 1 1 0] u[7] [1 1 0 0 0 0] u[8] [0 0 1 1 0 0] u[9] [0 0 0 0 1 1]
根据图1中各变量的定义,输出电容上的电压矢量vs的动力学方程可以描述为
 (3)
(3)至此,已建立电流源变流器及其输出电容在三相静止坐标系下的数学模型。注意到输出电容上的电压实际上是施加到PMSM定子电枢上的端电压。而对于PMSM的建模,当选取转子磁场定向的同步旋转坐标系(即dq坐标系)时,永磁体产生的磁链为投影到d轴的常量,模型得以简化。因此,将输出电容上的电压矢量vs通过坐标变换矩阵TABC-dq,得到dq坐标系下的电压矢量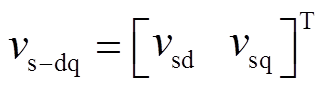 。
。
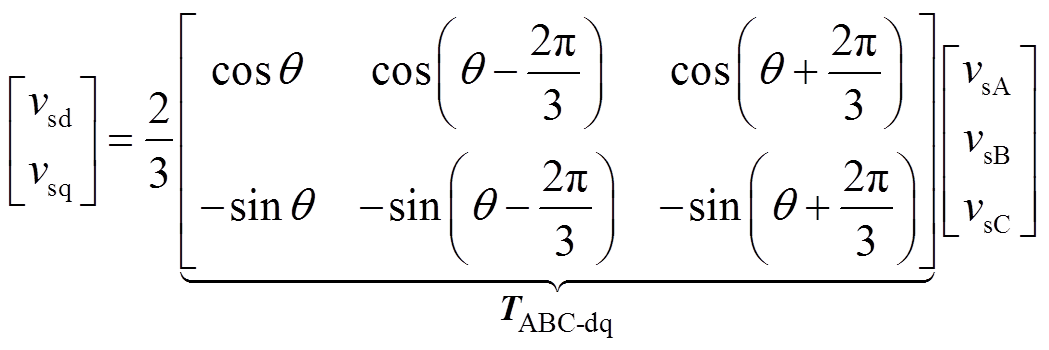 (4)
(4)式中,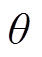 为转子磁链的电角度。
为转子磁链的电角度。
在dq坐标系下,连续时间域的PMSM电磁模型可表示为
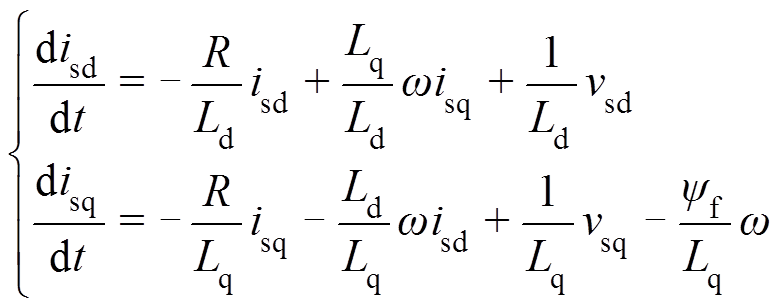 (5)
(5)式中,isd和isq分别为定子电流矢量is转换至dq坐标系下的d轴和q轴分量;ω为转子磁链的电角速度;Ld和Lq分别为d轴和q轴定子电感;R为单相定子绕组电阻;ψf为转子永磁体磁链。当Ld≠Lq时,通过控制isd为预设值,可实现单位电流最大转矩(Maximum Torque Per Ampere, MTPA)控制。为聚焦研究点,本文仅考虑Ld=Lq的情况。此时,电磁转矩的表达式为
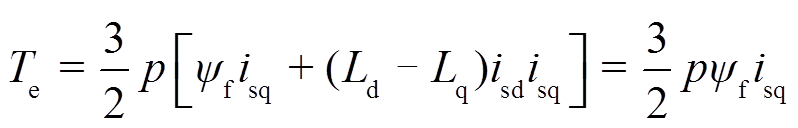 (6)
(6)式中,p为极对数。可见,此时d轴电流对电磁转矩无贡献。因此,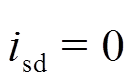 即可实现MTPA。
即可实现MTPA。
模型预测控制依赖离散时间域下被控对象的数学模型,以此对未来时刻的状态轨迹进行预测。对于采样周期远小于被控对象时间常数的情形,采用一阶Euler法可获得理想的离散化精度。首先,对式(3)进行离散化得到输出电容电压的预测公式为
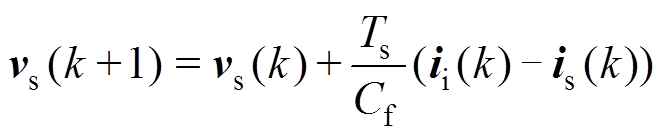 (7)
(7)式中,Ts为采样周期。经坐标变换得到dq坐标系下的电压矢量vs-dq(k+1)=[vsd(k+1) vsq(k+1)]T。然后,对式(5)进行一阶Euler离散化,得到定子电流的预测方程为
 (8)
(8)由此可得电磁转矩的预测方程为
 (9)
(9)本节将首先介绍基于电流源的预测转矩控制,在此基础上,提出全状态变量预测转矩控制。
电流源预测转矩控制框图如图2所示。其中,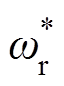 和ωr分别为转子机械角速度的参考值和测量值,ωr与ω存在如下关系:ω=pωr。对应地,
和ωr分别为转子机械角速度的参考值和测量值,ωr与ω存在如下关系:ω=pωr。对应地,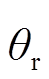 为转子的机械角度,
为转子的机械角度,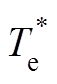 为转矩内环的参考值。转速外环通过线性PI控制器获得转矩参考值。内环的转矩跟踪则由预测转矩控制器通过直接触发功率开关实现。同时,预测转矩控制器将尽可能地降低开关频率。为实现上述控制目标,代价函数定义为
为转矩内环的参考值。转速外环通过线性PI控制器获得转矩参考值。内环的转矩跟踪则由预测转矩控制器通过直接触发功率开关实现。同时,预测转矩控制器将尽可能地降低开关频率。为实现上述控制目标,代价函数定义为
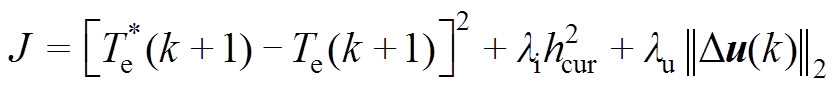 (10)
(10)式中,λi≥0和λu≥0为d轴电流和开关动作惩罚项对应的权系数。此外
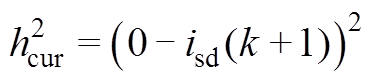 (11)
(11)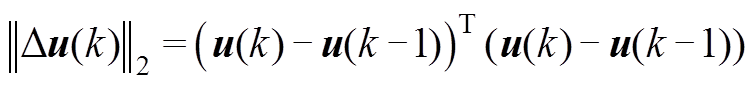 (12)
(12)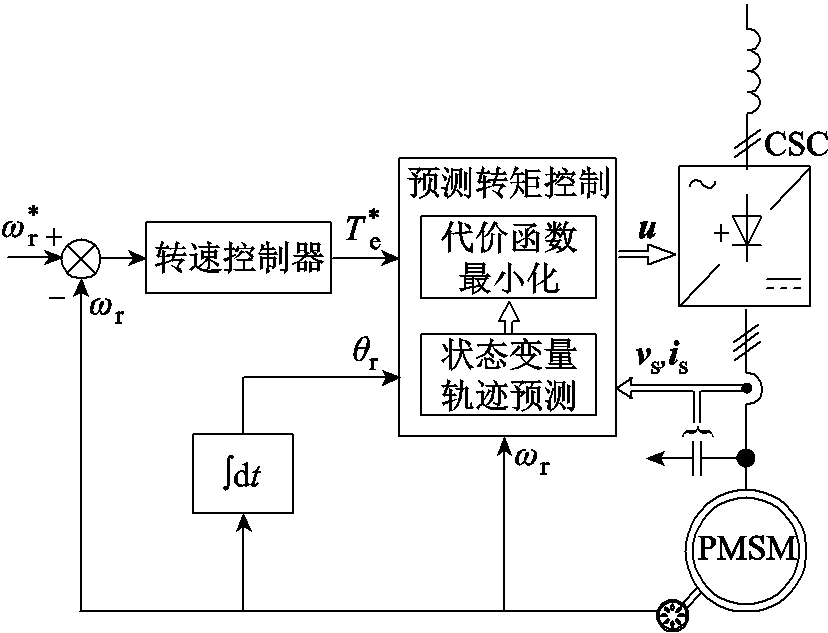
图2 电流源变流器永磁同步电机驱动系统转速外环及预测转矩控制内环结构框图
Fig.2 Predictive torque control of CSC fed PMSM drives
代价函数中共包含三项:第一项惩罚电磁转矩预测值与参考值之间的偏差;第二项惩罚d轴电流偏离零值的偏差,目的在于利用永磁体建立全部气隙磁场,实现MTPA控制;第三项为控制矢量u的增量的2-范数,以此限制开关频率。
至此,预测转矩控制可转换为最优化问题的一般形式:在满足式(7)~式(9)的前提下,寻找最优控制矢量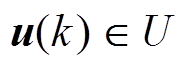 使得代价函数式(10)最小,即
使得代价函数式(10)最小,即
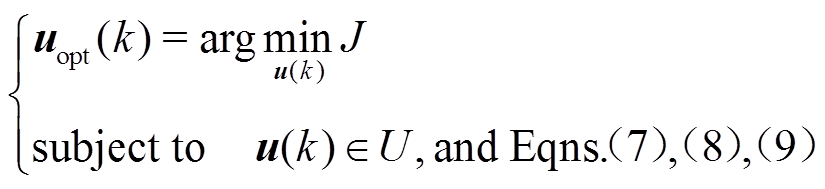 (13)
(13)如前文所述,滤波电容与定子绕组电感形成了LC网络。当谐波电流靠近LC网络的谐振频率时,会将谐波分量放大,甚至引起系统失稳。
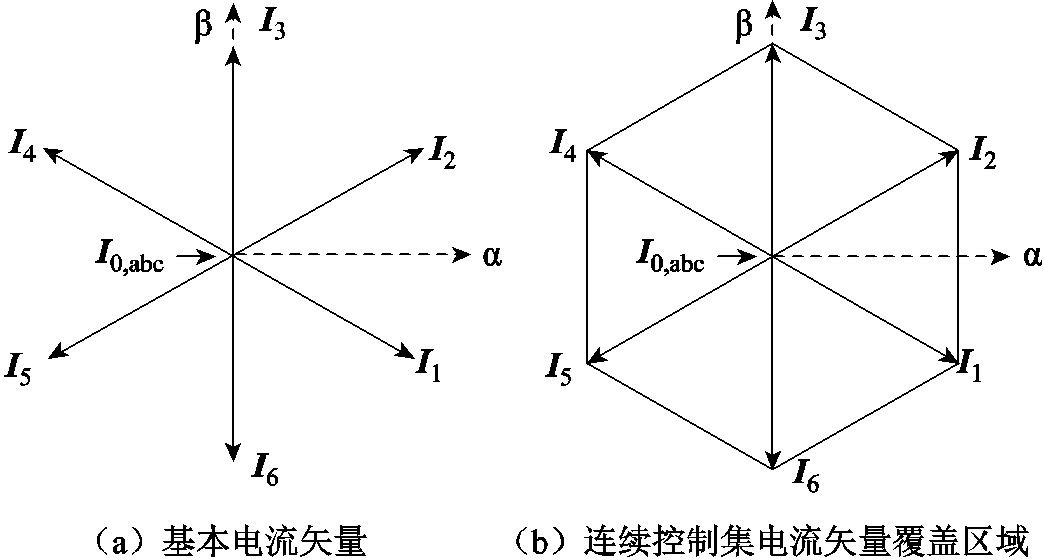
图3 电流源变流器开关状态对应的有效电流矢量
Fig.3 Current vector in α-βplane of a CSC
回顾预测转矩控制中代价函数J的定义,不难发现,该控制器仅对定子电流(转矩亦由定子电流唯一确定)进行控制,即仅控制系统输出变量。从状态空间的角度理解,同时控制滤波电容的电压和输出定子电流两个状态变量,有利于抑制无源部件之间的能量振荡,提升系统的稳定性。基于上述分析,并考虑模型预测控制具有多控制目标全局优化的能力,提出一种计及电流源驱动PMSM全状态变量的预测转矩控制策略,其代价函数定义为
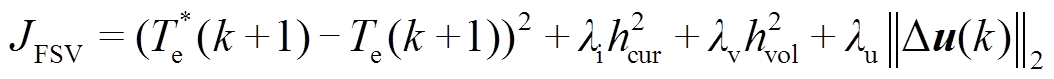 (14)
(14)其中
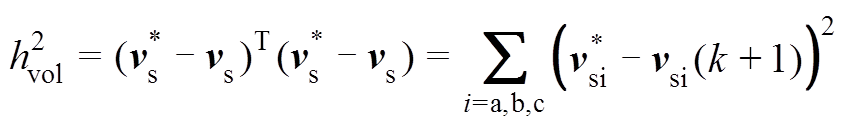
至此,关键问题转化为定义合理的电容电压矢量vs的参考值。现假设控制集为连续控制集,如,采用PWM调制,并忽略调制饱和效应,可得到等效连续控制集。该连续控制集映射到α-β平面的有效电流矢量为六边形覆盖的所有区域,见图3b。考察式(8),将其写成状态空间的形式,即
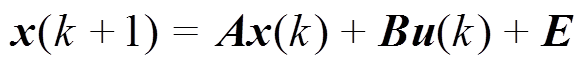 (15)
(15)其中
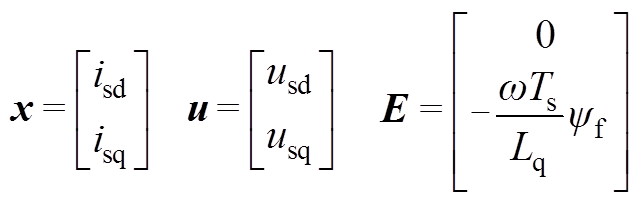
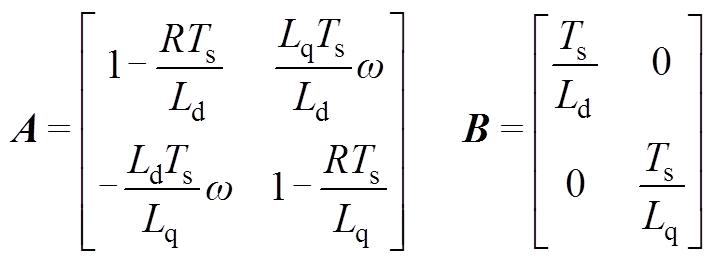
式中,矩阵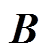 可逆,因此,在一个采样周期内,必然可以找到输入变量
可逆,因此,在一个采样周期内,必然可以找到输入变量
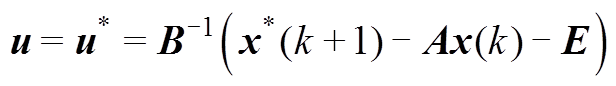 (16)
(16)满足关系
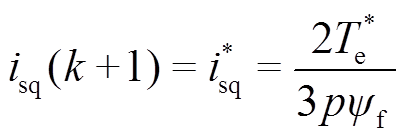 且
且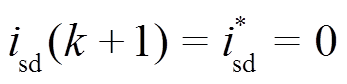 (17)
(17)因此,由式(16)可得电容电压在dq坐标系下的参考值为
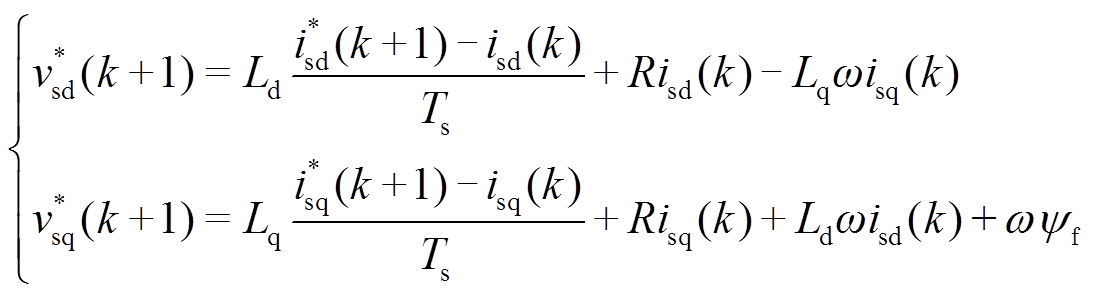 (18)
(18)通过Tabc-dq的逆变换可以得到电容电压在三相静止坐标系下的参考值为
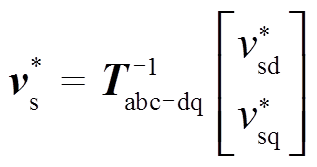 (19)
(19)权重系数的设计可依照如下原则确定:d、q轴电流具有同等重要性,应具有相同的权重系数。对于PMSM而言,转矩正比于q轴电流,即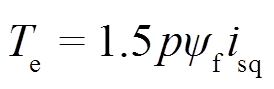 。由此,可确定电磁转矩与其他被控变量的权重关系。当电磁转矩Te对应的权重系数选取为1时,则d轴电流对应的权重系数计算式为
。由此,可确定电磁转矩与其他被控变量的权重关系。当电磁转矩Te对应的权重系数选取为1时,则d轴电流对应的权重系数计算式为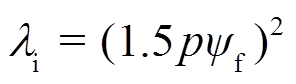 。从抑制功率环路振荡的角度,输出电流和滤波电容电压具有相同的重要性。因此,在对系统进行归一化处理后,二者应具有相同的权重系数。在国际单位制情况下,滤波电容电压项对应的权重系数为
。从抑制功率环路振荡的角度,输出电流和滤波电容电压具有相同的重要性。因此,在对系统进行归一化处理后,二者应具有相同的权重系数。在国际单位制情况下,滤波电容电压项对应的权重系数为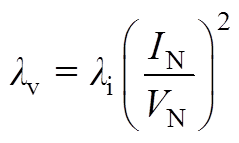 ,其中
,其中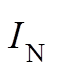 和
和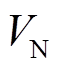 分别为被控电机的额定电流和额定电压。最后,全状态变量预测转矩控制可转换为最优化问题的一般形式,即
分别为被控电机的额定电流和额定电压。最后,全状态变量预测转矩控制可转换为最优化问题的一般形式,即
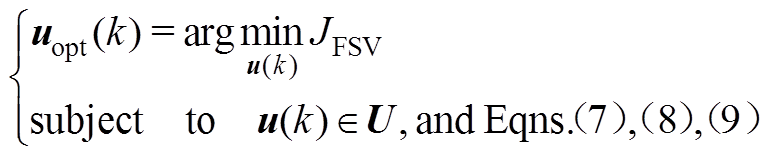 (20)
(20)在每个采样周期内枚举所有控制元素,可取得优化问题(20)的最优解,将获得uopt(k)直接作用到电流源变流器的功率开关。由于采样和数值计算造成一拍延时,通常采用补偿的手段进行算法优化,即算法向前滚动预测一拍。采用伪代码的形式,将全状态变量预测转矩控制总结为Algorithm 1。

Algorithm 1 全状态变量预测转矩控制 1.function FSVPTC()2. 初始化;3. 用式(8)计算,补偿一拍延时;4. 用式(17), 式(18)计算参考值:;5. for j=1:9 do6. 用式(2)计算,其中;7. 用式(7)计算;8. 通过坐标变换式(4)计算;9. 用式(8)计算;10. 用式(9)计算电磁转矩;11. 用式(13)计算代价函数;12. if then13. and;14. end if15. end for16. return ;17.end function
在文献[16]中已给出了FCS-MPC控制器的若干设计准则。本文结合具体应用场景,给出所提控制策略中两个关键参数的设计原则,即,权重系数和采样频率,以此确保系统性能的最优化。
众所周知,开关频率与功率器件的损耗直接相关。在大功率变流器运行过程中,开关频率必须进行严格的限制。在经典的带调制器的控制策略中,开关频率通常设计为固定值。但当采用模型预测控制时,开关频率随控制器参数和运行工况变化。因此,为了确保变流器运行在极限开关频率以下,必须分析影响开关频率的参数。
考察代价函数式(13),其中的开关动作惩罚项用以约束变流器的开关频率。当其对应的权系数较大时,开关动作将被严格约束,开关频率低;当其对应的权重系数较小时,开关动作约束减弱,开关频率高。假设将开关动作惩罚项对应的权重系数λu设置为零,即忽略开关动作对代价函数的影响,此时影响开关频率的唯一参数为采样频率,开关频率将被限定在采样频率的1/2以下。然而,当开关动作惩罚项的权重系数λu=0时,模型预测控制本质上等效为定量化无差拍控制(Quantized Deadbeat Controller)[16]。因此,必须通过合理设定λu,获取期望的开关频率。事实上,λu的选取还需考虑采样频率的影响。关于采样频率的设计,将在下节讨论。
在λu=0的前提下,开关频率fsw和采样频率fs理论上满足fsw<fs/2。更多实验数据表明,通常情况下fsw<fs/4。为了获得良好的控制性能,并且通过调整λu取得合理的开关频率,采样频率与开关频率之比fs/fsw应足够大,以使得功率开关可实现近似在任意时刻触发,类比于最优脉宽调制(Optimal Pulse Patten, OPP)的作用。同时,过高的采样率为实时计算提出了挑战。因此,需要在控制性能和控制器计算负担之间做出合理取舍。
针对大功率电流源驱永磁同步电机,通过多组离线仿真绘制图4a,图4a所示为在开关频率近似的情况下,不同fs下输出电流THD分布情况。由图4a可见,随着fs的升高,输出电流THD显著降低。图4b则更加直观地展示了采样周期分别为100μs和10μs,开关频率近似相等(约980Hz)时,定子电流的时域仿真波形。由于输出电容的存在,高次谐波分量得以滤除,定子电流在两种情况下均呈较高质量的正弦包络。但仍可观察到在采样率较高的情况下,定子电流更加光滑,高次谐波含量更低。
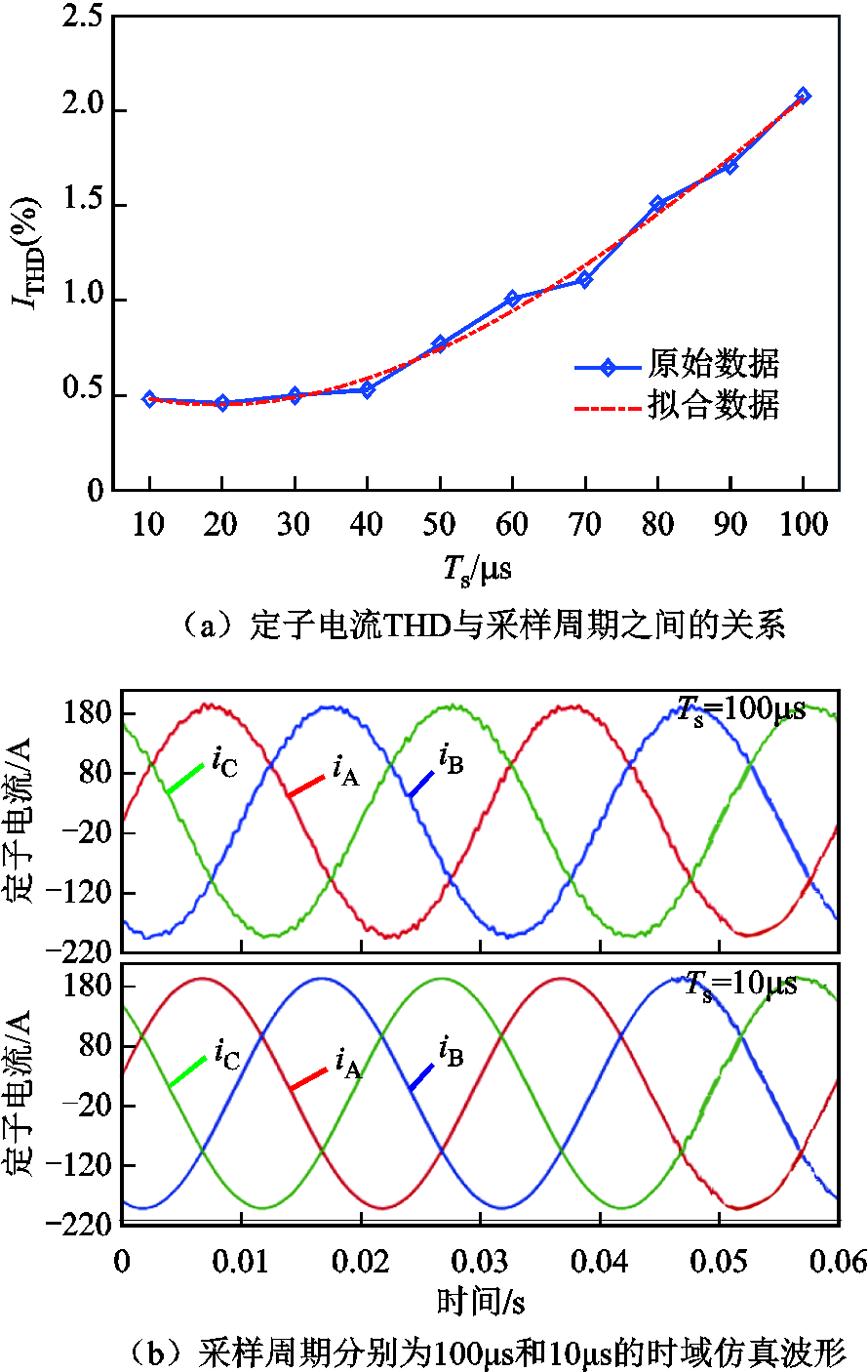
图4 定子电流THD与采样周期之间的关系曲线
Fig.4 Stator current THD as a function of sampling frequency at a switching frequency of fsw≈980Hz
结合文献[16],本文给出更一般性的结论:大功率应用场景,当开关频率严格限定在很低的水平时采样频率fs需比开关频率fsw高10倍,甚至两个数量级左右,通过合理选取λu,使得开关频率在期望值附近,以此获得最佳稳态效果。
本节对所提的FSV-PTC进行了效果验证和性能评估。在额定功率P=10kW的电流源驱动永磁同步电机测试平台上进行了硬件在环测试。测试平台采用Plexim公司推出的半实物模拟器。该半实物模拟器针对电力电子应用,进行了模型优化,可实现高离散化频率的系统级硬件在环测试,实物图如图5所示。永磁同步电机、电流源变流器和控制器的主要参数见表2。
首先,本节将考察所提控制策略的整体性能,为此设计了电机起动和反转运行的测试条件。
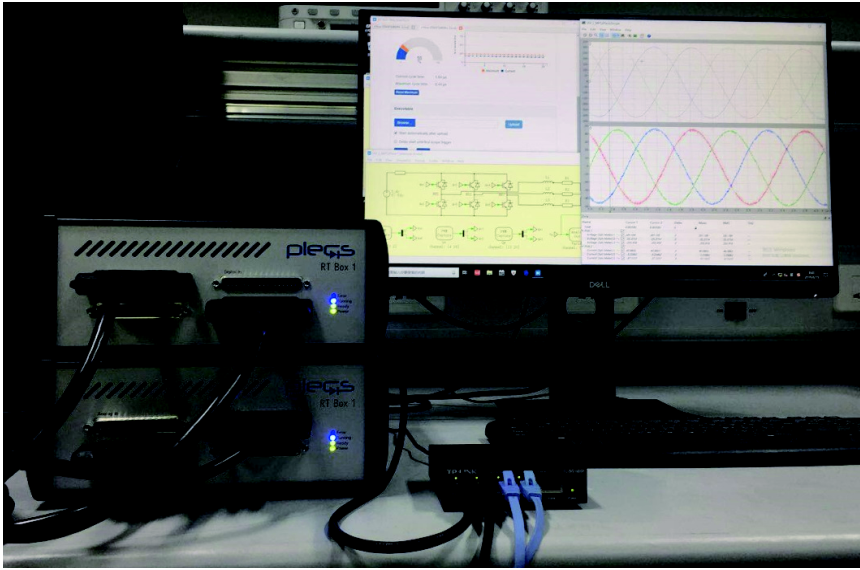
图5 硬件在环测试平台
Fig.5 Hardware in the loop test bench
表2 电流源变流器永磁同步电驱系统关键参数
Tab.2 Key parameters of CSC-fed PMSM drives

参数数值 采样周期Ts/μs13.2 直流母线电流Idc/A50 输出电容Cf/μF20 d轴电感Ld/mH19.5 q轴电感Lq/mH19.5 定子电阻R/Ω0.15 永磁磁通Φf/Wb0.427 极对数p3 转动惯量J/(N·m·s2)0.01 速度环PI参数Kp=0.5, Ki=100 权重系数λi=3.7, λv=0.06, λu=60
图6为所提控制策略的全局性能,包括了电机起动加速过程,恒速稳态过程和转速参考反向的追踪过程。图6从上到下分别为电机的电磁转矩、转速、定子电流、输出电容电压。外环的转速控制器采用抗饱和PI控制器,以减少速度超调。转速控制产生的电磁转矩的参考值,送入FSV-PTC单元,实现参考转矩的快速、精准的跟踪。
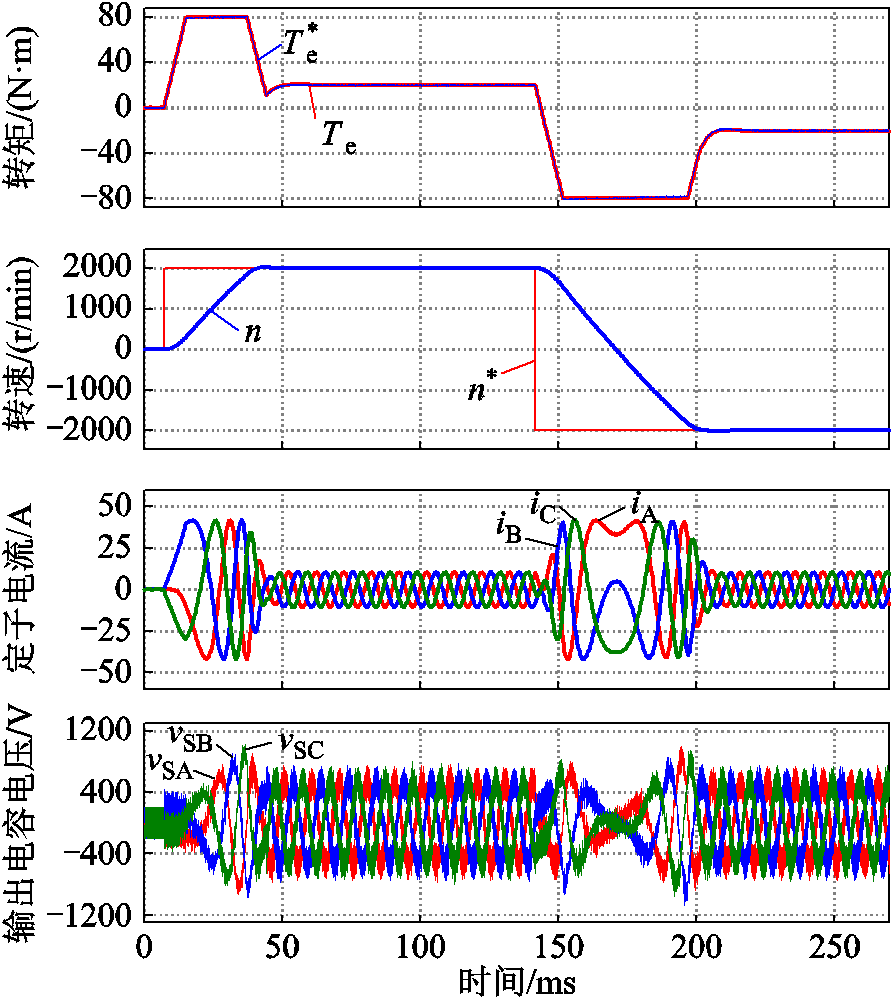
图6 全状态变量预测转矩控制全局控制性能
Fig.6 Overall system behavior of proposed FSV-PTC
电机在起动的过程中,负载转矩正比于转速的二次方。起动过程中,电磁转矩迅速响应并以最大转矩限幅值(80N·m)驱动电机加速。在电机转速升至额定转速时,电磁转矩迅速减小到负载转矩附近,以维持转速恒定。在经历一段时间的恒速运行后,参考转速跃变至负的额定转速。此时,电磁转矩迅速响应,以最大转矩限幅值(80N·m)驱动电机跟踪转速参考值,电机经历减速、反转的过程,最终在-2 000r/min的额定转速上稳定运行。
从全局效果看,电机转速可快速跟踪参考值,超调量小,稳速精度高。由于输出滤波电容的存在,电流源变流器输出电流平滑,高次谐波含量低,可有效降低电磁转矩脉动和电机的铁耗,提升效率。
如前文所述,电流源变流器的输出滤波电容与电机定子绕组存在固有谐振频率,通常需要无源阻尼或有源阻尼等手段对其进行抑制。所提FSV-MPC无需额外有源或无源阻尼技术,即可实现电磁转矩的高性能控制。此外,通过合理整定开关惩罚项的权重系数,可操控开关频率在期望值附近。
图7a为电机工作于满载,且λu=0,平均开关频率为4.01kHz的运行波形。由测试结果可见,定子电流呈正弦包络,电磁转矩脉动小。滤波电容电压存在一定高频谐波含量,其THD值为22.6%。相比输出电压呈高频方波的电压源变流器,电流源变流器的输出电压对电机而言,dV/dt较低,更加友好。
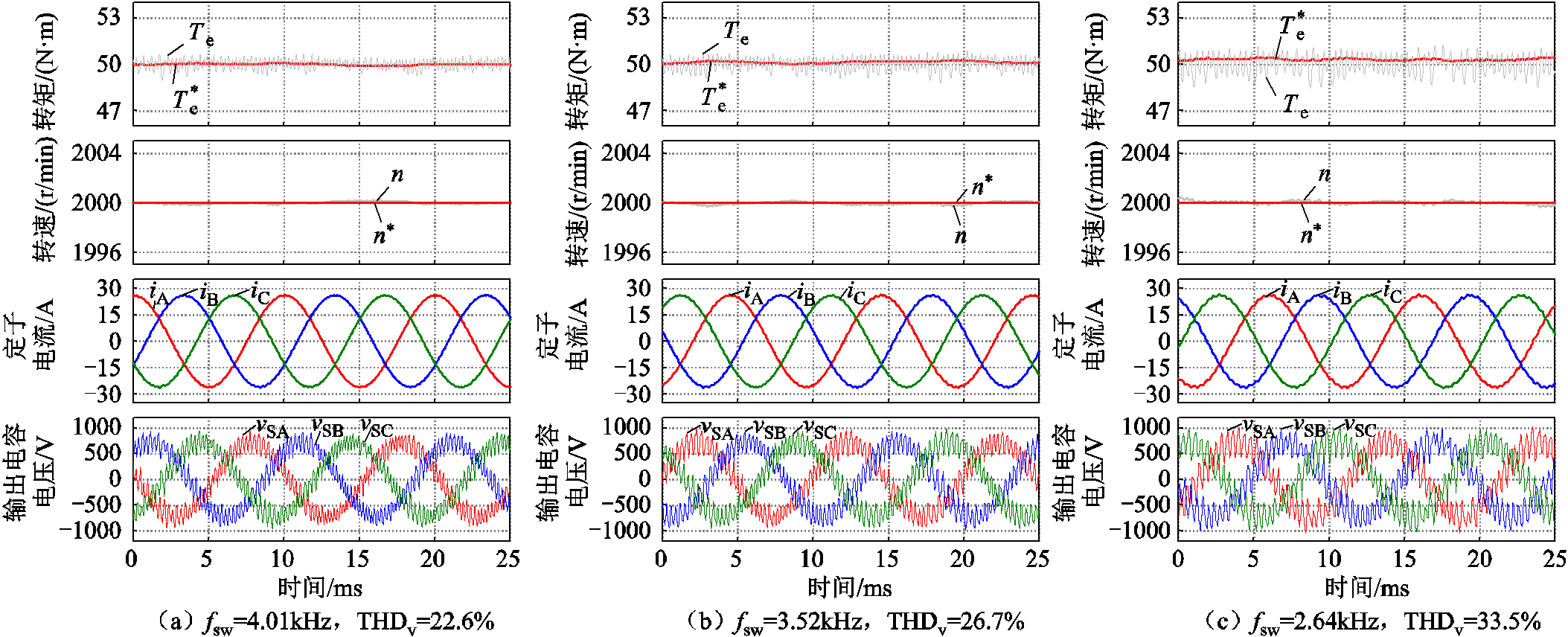
图7 不同开关频率下的稳态性能
Fig.7 Steady-state performance evaluation
图7b给出了所提FSV-MPC在λu=20,平均开关频率为3.52kHz的情况下的控制效果。结果表明,电磁转矩脉动略有增大,但仍具备良好的稳态控制效果。此时,输出电容电压的THD值为26.7%。进一步,在λu=80,平均开关频率为2.64kHz的情况下的测试结果如图7c所示。显然,电磁转矩脉动进一步增大,输出电容电压的THD值为33.5%。
需要指出的是,图7的对比结果中FSV-PTC通过开关惩罚项权重系数的调节,可以实现系统稳态性能和开关频率的有效控制。如前文介绍设计准则,应选较高的fs/fsw值,通过的合理选择确定开关频率,以此实现系统性能的最大化。
进一步,对所提方法和传统方法进行了对比测试。值得说明的是,为了对比公平,需调节开关惩罚项对应的权重系数,使其对应的平均开关频率近似相等,即避免开关惩罚项对系统性能评价的影响。图8给出了所提方法和传统方法对比性测试结果,其中图8a为所提的全状态变量预测控制,其电容电压THD为24.6%;图8b为传统预测控制,其电容电压THD为34.2%。由此可见,所提方法输出电容具有更好的稳态控制效果,滤波电容电压畸变显著降低,有效抑制了滤波电容和电机绕组电感之间的振荡。相应地,电机输出相电流更趋近于正弦,电磁转矩的脉动显著减小。
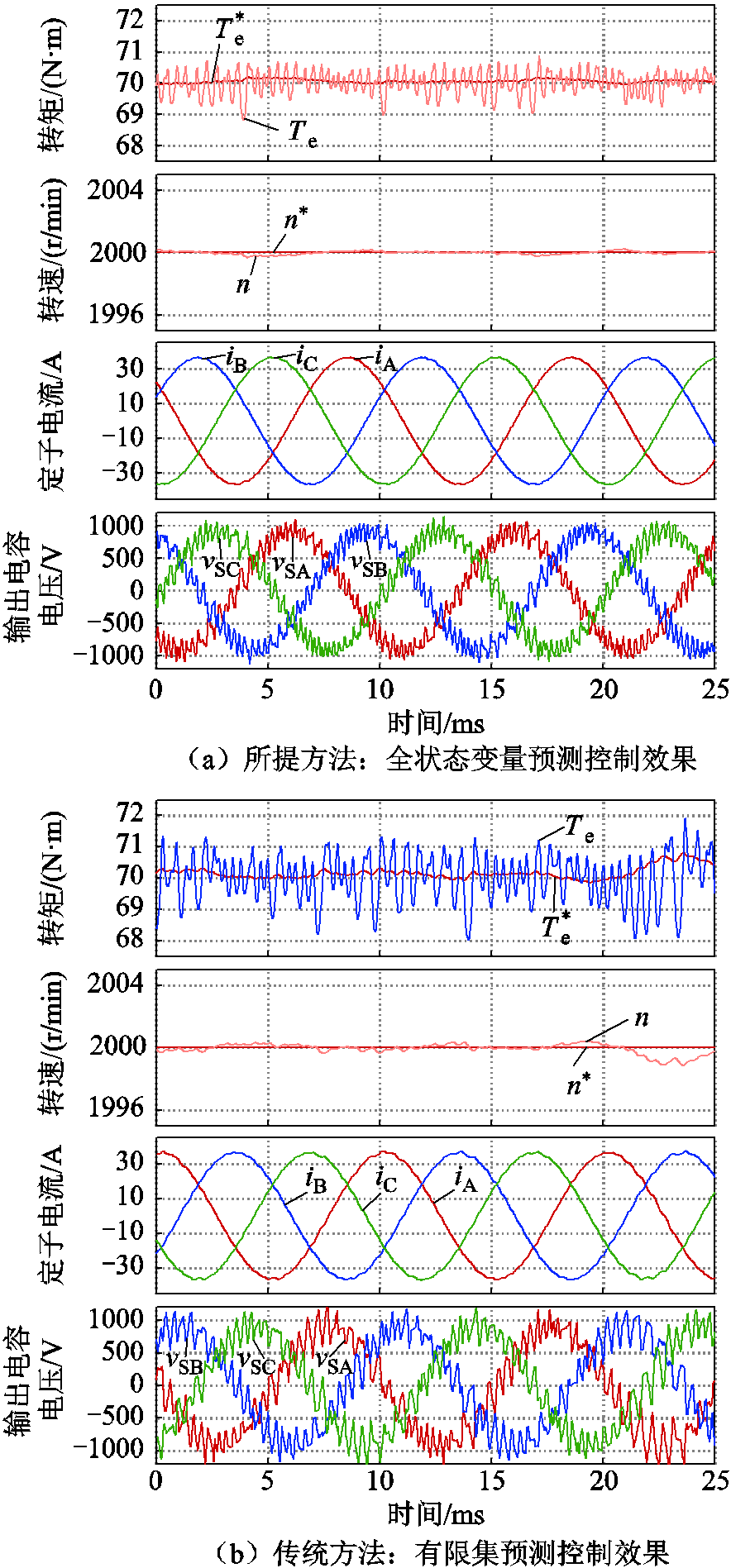
图8 所提方法与传统方法的对比性测试
Fig.8 Comparative study: FSV-MPC and FCS-MPC
本节考察负载转矩的动态响应,选取λu=20,转矩参考值在4ms从0N∙m发生阶跃变化至额定转矩50N∙m,得到全状态变量预测转矩控制转矩动态性能如图9所示。为了抑制电磁转矩的过冲,在参考值与FSV-PTC之间插入转矩参考变化率的限制模块,允许的最大变化率为40N∙m /ms。在转矩参考变化后,开关动作立即响应,快速驱动转矩分量(q轴)电流,迫使电磁转矩快速跟踪参考值,上升时间小于1.5ms。在动态过程中,虽然d轴电流存在小幅度波动,q轴存在小幅过冲,但dq轴电流总体上实现了良好的解耦控制。在16ms,转矩参考值由50N∙m突降至0N∙m,电磁转矩快速响应,下降时间小于1.5ms,动态过程与转矩突升的过程类似。
图10展示了在负载转矩突变时,电机转速和电磁转矩的响应能力。负载转矩在28ms左右发生阶跃,由-30N∙m跃变至70N∙m。在动态过程中,转速的波动使得速度环控制器产生相应的转矩参考值变化,进而使电磁转矩(定子电流)快速追踪新的参考值,重新将转速维持在参考值附近。在108ms左右,负载转矩再次由70N∙m跃变至-30N∙m,动态过程,转速波动范围小于10%。
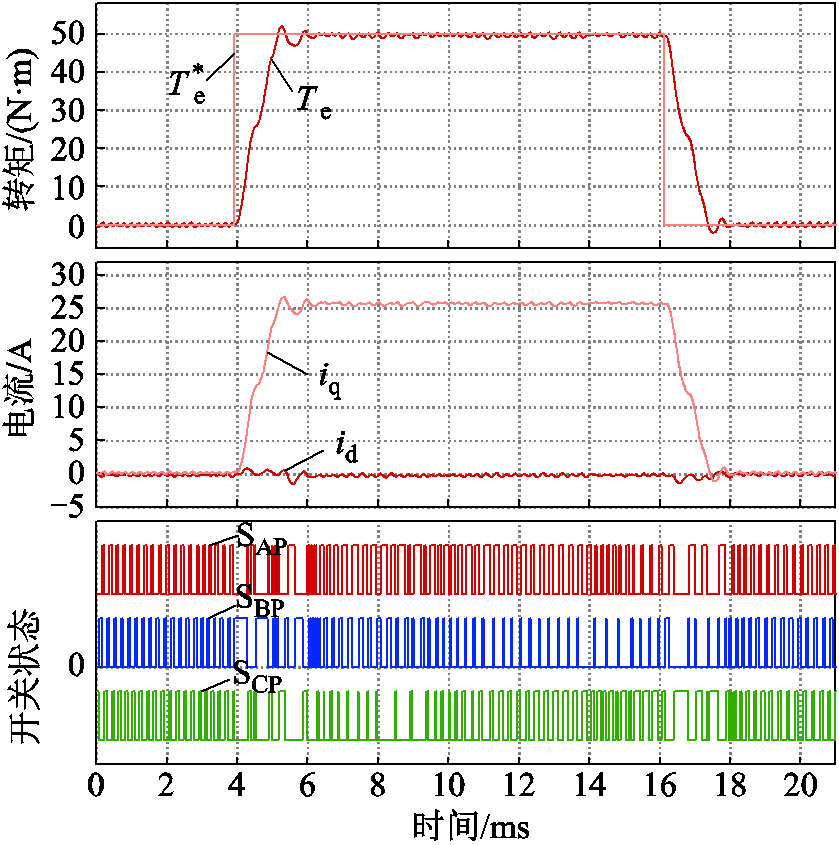
图9 全状态变量预测转矩控制转矩动态性能
Fig.9 Torque dynamic response evaluation of FSV-PTC
将全局图中的20~40ms和100~120ms区域放大,进一步考察动态过程。由图10可见,负载转矩突变瞬间,电容电压响应极快,所提FSV-PTC继承了PTC的固有特点,转矩响应极快。极高的转矩控制带宽可显著提高转速控制器的设计带宽,优化系统整体动态响应能力。这一解决方案有效克服了传统控制策略内外环路级联导致的系统整体动态性能差的缺陷。
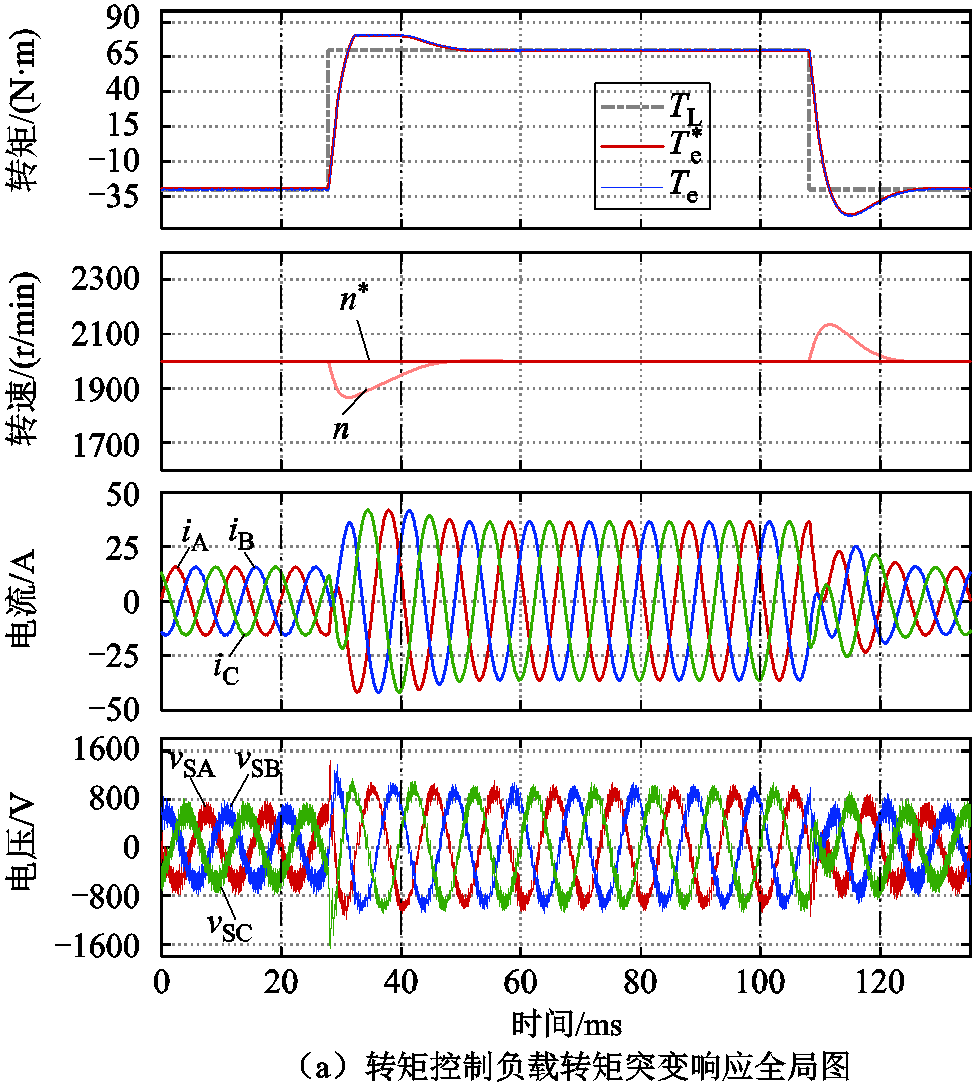
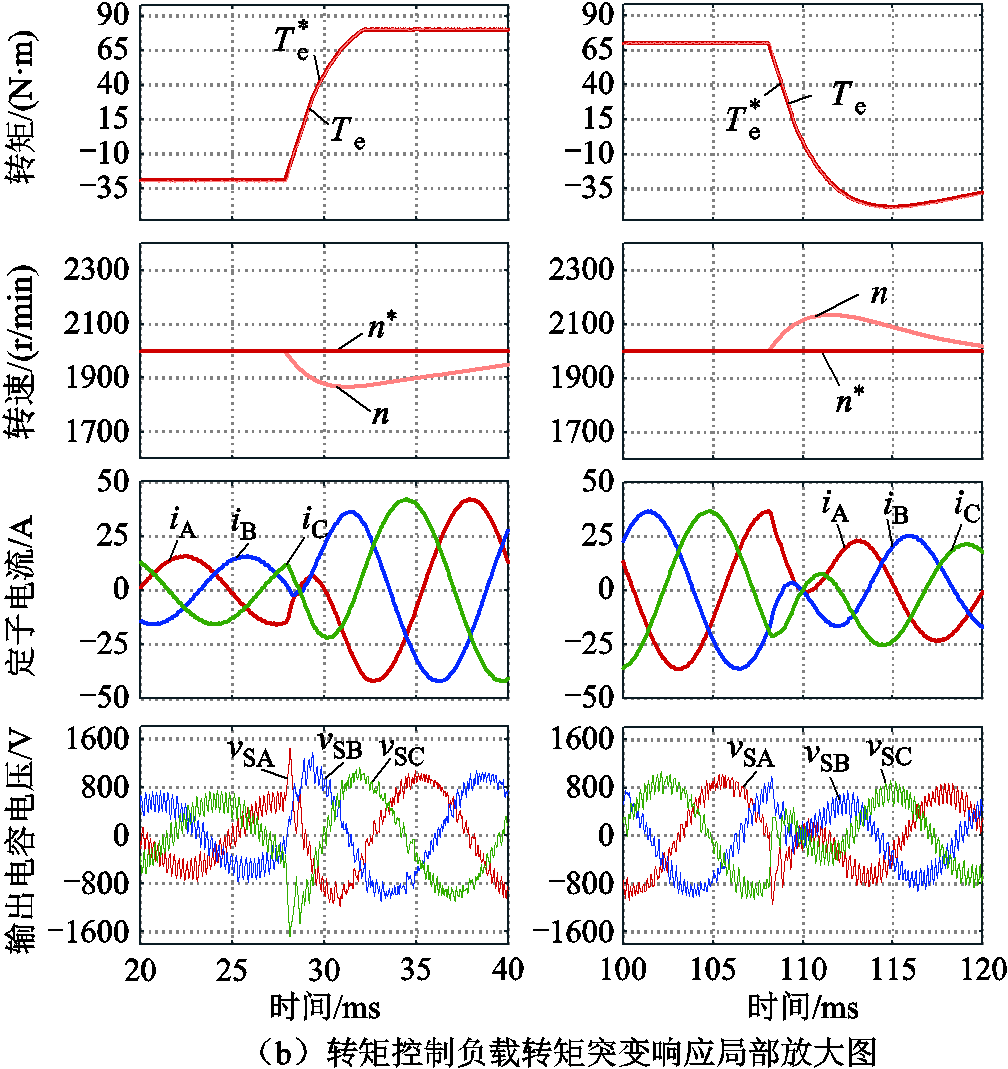
图10 全状态变量预测转矩控制负载转矩突变响应
Fig.10 Load torque response evaluation of FSV-PTC
本节进一步考察在预测模型和实际电机参数不匹配的条件下所提方法的控制性能。首先,在硬件在环仿真中,将被控对象中的滤波电容设定为额定值的85%,dq轴电感设定为额定值的90%,控制器参数设定为额定值。稳态下的测试结果如图11a所示。可见,在滤波电容和电机电感小于额定值的情况下,电机的转矩、转速仍然可以实现良好的跟踪效果。转矩的纹波相比准确模型的情形有所增大,输出电流及滤波电容电压的电能质量略有下降。在平均开关频率为4.05kHz的情况下,滤波电容THD值为26.2%。
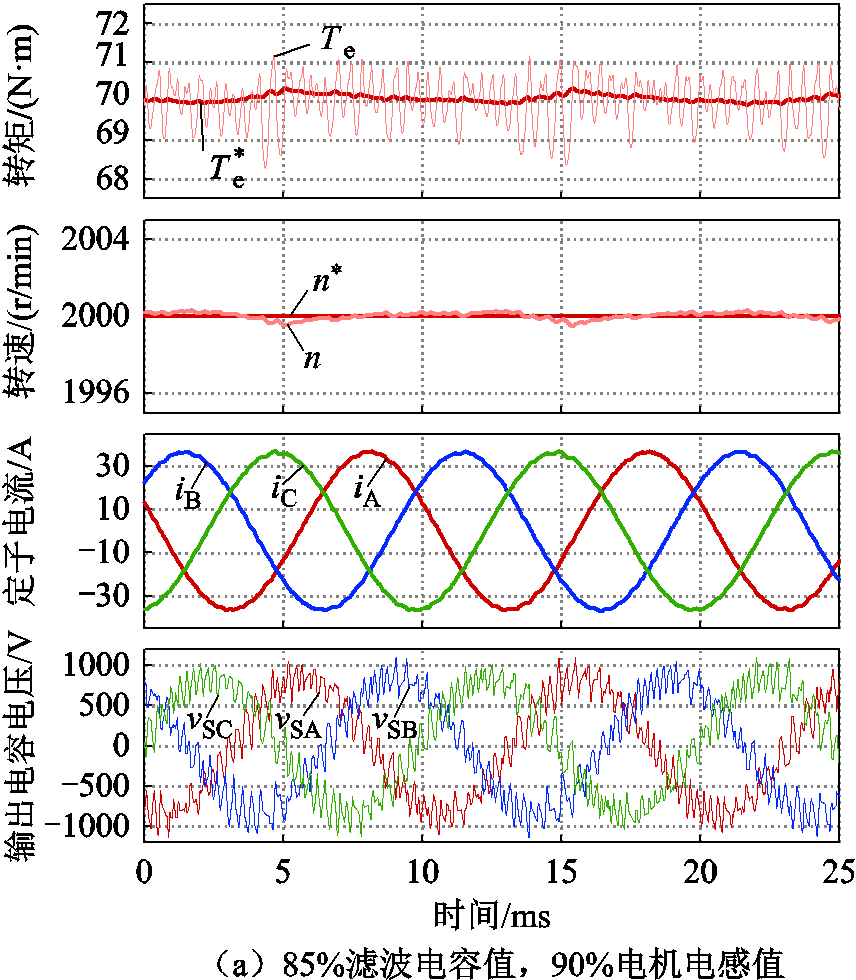
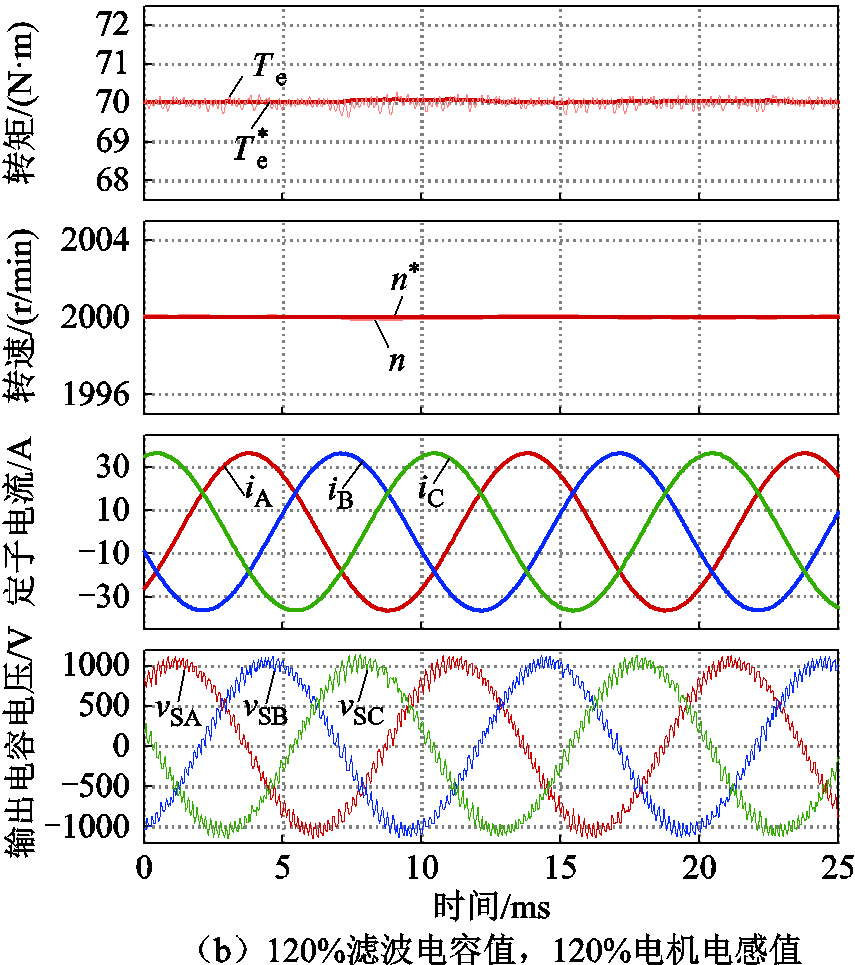
图11 模型参数鲁棒性测试
Fig.11 Evluation of model parameters robustness
进一步地,硬件在环仿真中将被控对象中的滤波电容设定为额定值的120%,dq轴电感设定为额定值的120%,控制器参数设定为额定值。稳态下的测试结果如图11b所示。可见,在滤波电容和电机电感大于额定值的情况下,电机的转矩、转速实现了更佳的跟踪效果。转矩的纹波相比准确模型的情形进一步下降,输出电流及滤波电容电压的电能质量有所提升。在平均开关频率为4.05kHz的情况下,滤波电容THD值为8.5%。这主要是因为滤波电容和电机绕组电感的增加有助于减小开关纹波,提升稳态性能。
由此可见,所提方法对于模型参数具有良好的鲁棒性,在预测模型参数与实际被控对象参数不匹配的情况下仍然可以实现良好的控制性能。在实际滤波电容和电机电感值增大的情况下,即使参数失配,稳态的控制性能依然提升显著。
本文针对电流源变流器永磁同步电机驱动系统,提出了一种计及全状态变量预测转矩控制策略。通过分析被控对象的数学模型,理论计算了电容电压的参考值。利用模型预测控制可实现多目标控制的能力,构建了由电磁转矩、d轴电流、输出电容电压和开关动作四个惩罚项组成的代价函数,取得了全局优化的效果,简化了传统控制器的级联结构。此外,通过理论分析结合仿真数据的方法,给出了开关动作惩罚项对应的权系数和采样频率的设计准则,以此确保系统性能最优。最后,通过硬件在环试验验证了所提方法的有效性。测试结果表明,所提控制策略具有快速的转矩动态响应,同时,可有效抑制滤波电容和定子电感之间的能量振荡,电磁转矩脉动低。本文所提的全变量预测转矩控制为电流源变流器电机驱动系统提供了一种极具潜力的高性能控制策略。因本文聚焦电流源变流器控制策略,尚未考虑长电缆模型影响,计及长电缆模型的控制策略将在后续工作中重点展开。
参考文献
[1] Preindl M, Bolognani S. Model predictive direct torque control with finite control set for PMSM drive systems, part 1: maximum torque per ampere operation[J]. IEEE Transactions on Industrial Informatics, 2013, 9(4): 1912-1921.
[2] Siami M, Khaburi D A, Rodriguez J. Torque ripple reduction of predictive torque control for PMSM drives with parameter mismatch[J]. IEEE Transactions on Power Electronics, 2017, 32(9): 7160-7168.
[3] 王硕, 康劲松. 一种基于自适应线性神经网络算法的永磁同步电机电流谐波提取和抑制方法[J]. 电工技术学报, 2019, 34(4): 654-663. Wang Shuo, Kang Jinsong. Harmonic extraction and suppression method of permanent magnet synchronous motor based on adaptive linear neural network[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 654-663.
[4] 甘志伟, 缪冬敏, 王云冲, 等. 宽转速范围永磁同步发电机系统稳压控制及参数优化[J]. 电工技术学报, 2020, 35(8): 1624-1633. Gan Zhiwei, Miao Dongmin, Wang Yunchong, et al. Voltage stabilization control and parameters optimization for wide-speed-range permanent magnet synchronous generator systems[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1624-1633.
[5] 李春艳, 王豫, 孟涛. 反凸极永磁同步电机弱磁特性分析[J]. 电工技术学报, 2019, 34(增刊2): 474-483. Li Chunyan, Wang Yu, Meng Tao. Research on flux weakening characteristics of a negative salient pole permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 474-483.
[6] 甘志伟, 缪冬敏, 王云冲, 等. 宽转速范围永磁同步发电机系统稳压控制及参数优化[J]. 电工技术学报, 2020, 35(8): 1624-1633.Gan Zhiwei, Miao Dongmin, Wang Yunchong, et al. Voltage stabilization control and parameters optimization for wide-speed-range permanent magnet synchronous generator systems[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1624-1633.
[7] 徐奇伟, 孙静, 杨云, 等. 用于混合动力车的复合结构永磁电机电磁优化设计[J]. 电工技术学报, 2020, 35(增刊1): 126-135. Xu Qiwei, Sun Jing, Yang Yun, et al. Electromagnetic optimization design of compound-structure permanent-magnet motor for hybrid electric vehicle[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 126-135.
[8] 王小飞, 代颖, 罗建. 基于流固耦合的车用永磁同步电机水道设计与温度场分析[J]. 电工技术学报, 2019, 34(增刊1): 22-29. Wang Xiaofei, Dai Ying, Luo Jian. Waterway design and temperature field analysis of vehicle permanent magnet synchronous motor based on fluid-solid coupling[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 22-29.
[9] He Jiangbiao, Gennadi Y S, Zhang Peng, et al. A review of mitigation methods for overvoltage in long-cable-fed PWM AC drives[C]//IEEE Energy Conversion Congress & Exposition, Phoenix, AZ, USA, 2011, DOI: 10.1109/ECCE.2011.6064054.
[10] 平朝春, 王艳红, 郭宏, 等. 水下大功率电机远距离变频驱动过电压问题分析[J]. 海洋工程装备与技术, 2019, 6(增刊1):160-165. Ping Zhaochun, Wang Yanhong, Guo Hong, et al. Analysis of the over-voltage problems of variable frequency drives long distance subsea high power motor system[J]. Ocean Engineering Equipment and Technology, 2019, 6(S1): 160-165.
[11] A von Jouanne, P. Enjeti W Gray. The effect of long motor leads on PWM inverter fed AC motor drive systems[C]//Proceeding of 1995 IEEE Applied Power Electronics Conference & Exposition-APEC, Dallas, TX, USA, 2002, DOI: 10.1109/APEC 1995.469081.
[12] Wang Zheng, Cheng Ming, Lang Yongqiang, et al. Active damping of LC resonance for interleaved CSC fed motor drives[C]//International Conference on Electrical Machines and Systems, ICEMS 2011, Beijing, China, 2011, DOI: 10.1109/ICEMS. 2011. 60 73944.
[13] Ding Li, Li Yunwei, Zargari N. Discrete-time SMO sensorless control of current source converter-fed PMSM drives with low switching frequency[J]. IEEE Transactions on Industrial Electronics, 2020, DOI: 10.1109/TIE.2020.2972433
[14] 张永昌, 杨海涛. 异步电机无速度传感器模型预测控制[J]. 中国电机工程学报, 2014, 34(15): 2422-2429. Zhang Yongchang, Yang Haitao. Model predictive control for speed sensorless induction motor drive[J]. Transactions of China Electrotechnical Society, 2014, 34(15): 2422-2429.
[15] Zhang Yongchang, Zhu Jianguo. Direct torque control of permanent magnet synchronous motor with reduced torque ripple and commutation frequency[J]. IEEE Transactions on Power Electronics, 2011, 26(1): 235-248.
[16] Karamanakos P, Geyer T. Guidelines for the design of finite control set model predictive controllers[J]. IEEE Transactions on Power Electronics, 2020, 35(7): 7434-7450.
[17] Rodriguez J, Kazmierkowski M P, Espinoza R, et al. State of the art of finite control set model predictive control in power electronics[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2): 1003-1016.
[18] Zhang Zhenbin, Wang Fengxiang, Sun Tongjing, et al. FPGA based experimental investigation of a quasi-centralized DMPC scheme for a back-to-back converter[J]. IEEE Transactions on Power Electronics, 2015:1-1.
[19] Zhang Zhenbin, Hackl C M, Kennel R. Computationally efficient DMPC for three-level NPC back-to-back converters in wind turbine systems with PMSG[J]. IEEE Transactions on Power Electronics, 2017, 32(10): 8018-8034.
[20] Wang Fengxiang, Li Shihua, Mei Xuezhu, et al. Model-based predictive direct control strategies for electrical drives: an experimental evaluation of PTC and PCC methods[J]. IEEE Transactions on Industrial Informatics, 2015, 11(3): 671-681.
[21] 徐艳平, 王极兵, 张保程, 等. 永磁同步电机三矢量模型预测电流控制[J]. 电工技术学报, 2018, 33(5): 980-988. Xu Yanping, Wang Jibing, Zhang Baocheng. Two-vector based model predictive current control for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 980-988.
[22] Zhang Yongchang, Yang Haitao. Two-vector-based model predictive torque control without weighting factors for induction motor drives[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1381-1390.
[23] Geyer T. Model predictive direct torque control: derivation and analysis of the state-feedback control law[J]. IEEE Transactions on Industry Applications, 2011, 49(5): 2146-2157.
[24] 齐昕, 周晓敏, 马祥华, 等. 感应电机预测控制改进算法[J]. 电机与控制学报, 2013, 17(3): 62-69. Qi Xin, Zhou Xiaomin, Ma Xianghua, et al. Improved predictive control algorithm for induction motors[J]. Electric Machines and Control, 2013, 17(3): 62-69.
[25] 张永昌, 杨海涛. 感应电机模型预测磁链控制[J]. 中国电机工程学报, 2015, 35(3): 719-726. Zhang Yongchang, Yang Haitao. Model predictive flux control for induction motor drives[J]. Transactions of China Electrotechnical Society, 2015, 35(3): 719-726.
[26] Wiseman J, Wu Bin. Active damping control of a high power PWM current source rectifier for line current THD reduction[J]. IEEE Transactions on Industrial Electronics, 2005, 52(3 ): 758-764.
[27] Rivera M, Rodriguez J, Wu Bin, et al. Current control for an indirect matrix converter with filter resonance mitigation[J]. IEEE Transactions on Industrial Electronics, 2012, 59(1): 71-79.
[28] Wang Zheng, Wu Bin, Xu Dewei, et al. A high-speed CSC based PMSM drive with a switching frequency of 420Hz[C]//IEEE International Symposium on Industrial Electronics, Bari, Italy, 2010, DOI: 10.1109/ ISIE.2010.5636615.
Abstract The current source converter (CSC) is widely used in long cable drives and medium voltage drives due to its friendly output voltage and short-circuits protection capability. The filter capacitor of the CSC and the electromagnetic dynamics equation of the motor constitute a second-order system, which has a natural resonance frequency. In this paper, the input variables are solved to achieve the deadbeat control performance based on the mathematical model of the control plant. Then, we put the dq-axis current, output capacitance voltage and switch penalty term in a unified cost function, and a predictive torque control (PTC) strategy with full state variables (FSV) is proposed. The proposed FSV-PTC can effectively suppress the energy oscillation between the filter capacitor and the stator inductance, and reduce the torque ripple. Moreover, the design criteria of sampling frequency and switch penalty weight factor is given. Finally, the control performance of the CSC-fed permanent magnet synchronous drive system is verified through hardware-in-the-loop (HiL) test. The test results show that the proposed FSV-PTC has a small steady-state torque ripple and fast torque response.
keywords:Current source converter, direct predictive torque control, permanent magnet synchronous motor, high power electric drives
中图分类号:TM346
10.19595/j.cnki.1000-6753.tces.200681
中海石油(中国)有限公司北京研究中心(CCL2019RCPS0268RSN),山东省重点研发计划(重大科技创新工程)(2019JZZY020805),国家自然科学基金面上项目(51977124),山东省自然青年基金(ZR2019QEE001)和江苏省自然科学基金(BK20190204)资助项目。
收稿日期 2020-06-19
改稿日期 2020-09-20
李 昱 男,1986年生,博士研究生,研究方向为电力电子与电力传动、智能微电网。E-mail:yu.li@mail.sdu.edu.cn
张祯滨 男,1984年生,教授,博士生导师,研究方向新能源、并网四象限变流系统、储能及混联微网、先进驱动。E-mail:zbz@sdu.edu.cn (通信作者)
(编辑 郭丽军)