图1 BROCKHAUS磁性能测量系统
Fig.1 BROCKHAUS measurements system
摘要 基于TEAM-P21c基准模型深入研究交直流混合激励下变压器中叠片式磁构件杂散损耗的数值模拟及实验验证方法。考虑空载、负载条件下线圈损耗的差异，提出一种基于实验确定结构件杂散损耗的改进方法。搭建硅钢叠片磁特性、损耗特性测量系统，提出可考虑偏置磁场影响的铁损模型，并用于计算三维漏磁场激励下的叠片式磁构件的杂散损耗。通过磁场、损耗的仿真与实验结果对比，验证了该文方法的有效性。最终基于仿真及测量结果，分析了直流偏置磁场对杂散损耗的影响，得到了交直流混合激励下导磁构件中附加损耗的分布及其对杂散损耗的影响。
关键词：TEAM-P21c基准模型 磁构件 杂散损耗 交直流混合激励 附加损耗
随着我国高压直流输电系统（High Voltage Direct Current, HVDC）的迅速发展和广泛应用，换流变压器作为系统中的关键电气设备，其损耗分布是设计过程中备受关注的问题之一。而换流变压器需经常工作在交直流混合激励下[1]，加剧了漏磁场和杂散损耗分布的不合理性，设备局部过热和运行故障的风险也随之增加，因此，磁构件损耗问题的研究面临着更严峻的挑战[2-3]。研究交直流混合激励条件下变压器磁构件中磁场及损耗分布情况，可在变压器的设计过程中采取有效措施以降低杂散损耗，对电网的安全稳定运行、产品设计和结构优化具有重要的理论价值。
为研究变压器结构件损耗模拟及局部过热问题，程志光博士提出了TEAM Problem 21基准族模型。基于这些基准模型，相关学者对三维涡流和杂散场损耗进行了大量的研究工作。程志光等研究了磁性能和电源频率的变化对硅钢片内部杂散损耗的影响[4-6]。C. Ragusa等研究了无取向硅钢片在偏磁激励下的损耗[7-8]。H. Hauser提出利用磁滞模型的方法计算杂散损耗[9]。朱占新等提出了用解析解和数值解相结合的方法计算电力变压器漏磁场和漏磁场损耗，计算分析了谐波激励下结构件的杂散损耗[10-11]。郑伟英等提出了一种子空间校正方法，有效地解决了硅钢叠片三维非线性涡流问题[12]。刘亚青等计算和分析了谐波磁化作用下绕组中的涡流损耗和结构件中的杂散场损耗[13-15]。赵志刚等指出交直流混合激励下可用直流磁化曲线描述材料的磁性能，提出基于改进后的损耗计算三项式模型[15-17]，通过瞬态场仿真求解激励线圈损耗，利用实验测量的模型总损耗减去相同工况下的线圈损耗仿真计算值，得到间接确定的电磁装备结构件中杂散损耗[18]。
上述研究中，仍有一些关键问题亟待进一步解决：①目前杂散损耗问题的研究多数为正弦激励条件，交直流混合激励下材料损耗数据测量难度增大而该方面研究却相对较少；②以往的研究未考虑空载状态和负载状态下线圈损耗的差异，给磁构件杂散损耗的确定带来一定误差；③交直流激励的改变对材料磁特性以及对应杂散损耗和附加损耗的影响规律有待深入研究。
本文在考虑激励线圈在负载和空载两种不同条件下损耗变化的前提下，改进了磁构件损耗的实验测定方法，提出一种有效、实用的交直流混合激励下损耗计算模型；基于TEAM-P21c基准模型，建立了三维交直流混合激励条件下硅钢叠片内部杂散损耗的实验平台，通过分别对比空间漏磁场与杂散损耗结果的计算值与测量值，验证了本文方法的有效性；通过分别改变交、直流分量研究二者对叠片式磁构件杂散损耗的影响；计算和分析了硅钢叠片作为磁构件时，叠片内附加损耗的分布及其对杂散损耗的影响。
为保证交直流混合激励下损耗的研究的准确性，本文采用BROCKHAUS磁性能测量系统中的爱泼斯坦方圈对交直流混合激励条件下磁构件的磁性能进行测量，测量系统如图1所示，其工作原理示意图如图2所示。
图1 BROCKHAUS磁性能测量系统
Fig.1 BROCKHAUS measurements system
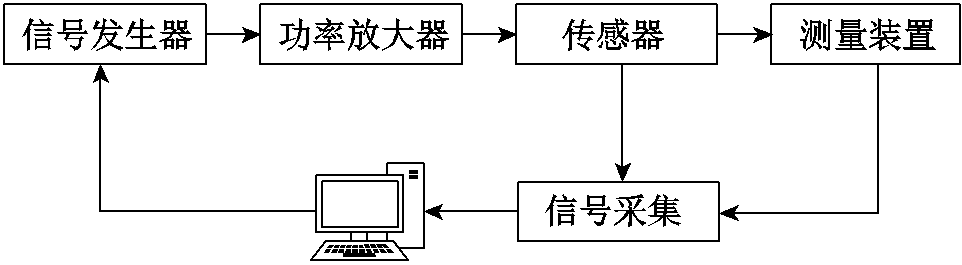
图2 BROCKHAUS工作原理示意图
Fig.2 BROCKHAUS working principle diagram
本文对5Hz、50Hz、100Hz及150Hz下，Hdc为20~600A/m的不同偏置磁场下的30P120硅钢叠片磁滞回线及损耗特性进行测量，并基于改进迭代法对测量结果进行处理[19]，部分结果如图3、图4所示。
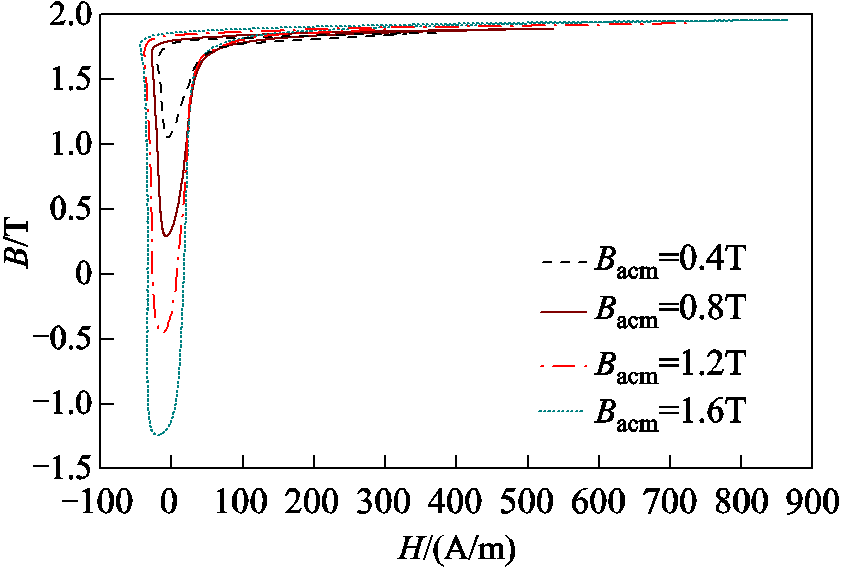
图3 直流偏磁磁滞回线族（Hdc=50A/m，f=50Hz）
Fig.3 DC-biasing magnetic hysteresis loops (Hdc=50A/m, f=50Hz)
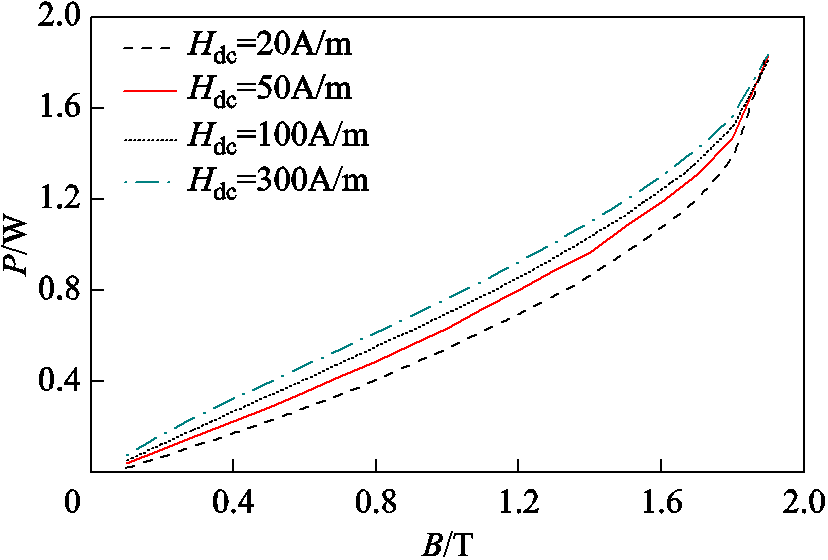
图4 不同直流偏磁场下的损耗曲线（f=50Hz）
Fig.4 Losses curves in different DC bias level (f=50Hz)
图3中Bacm为不同交流激励下对应的磁通密度的交流分量峰值。从图3可以看出，加入直流分量激励导致铁磁材料的磁滞回线出现较严重的畸变和不对称线性，从而影响其磁场及损耗。图4是交流频率为50Hz时，不同偏置磁场下硅钢叠片损耗特性曲线。从图4中可以看出，随着直流偏置磁场的增加，损耗呈现出显著增加的趋势。
综上所述，加入不同直流磁场强度分量将导致磁性材料的磁性能及损耗特性发生改变。在对磁构件进行损耗计算时，应采用相应激励下的损耗数据。由于直流分量的影响，以往正弦激励下的损耗模型的运用将受到限制。因此，本文在测量磁构件磁性能及损耗特性的基础上提出一种既便于实现，又能够保证准确性，适用于交直流混合激励下的铁损模型。
本文设总铁损Ps为[20-22]
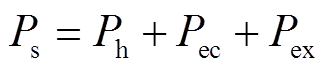（1）式中，Ph为磁滞损耗；Pec为涡流损耗；Pex为异常损耗。
由于磁滞损耗Ph在总损耗中所占比例较大[23]，因此磁滞损耗的计算准确性在较大程度上影响着铁损计算结果。当激励频率足够低时，磁滞损耗可从总铁损中得到，且通常认为磁滞损耗Ph与频率f呈正比[24]。针对交直流混合激励，本文采用式（2）对磁滞损耗进行模拟。
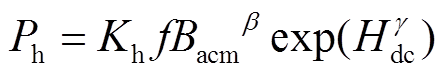（2）式中，Kh为与磁滞损耗相关的常系数；f为基波频率；Bacm为磁通密度的交流分量峰值；β为与Bacm相关的三次多项式指数；Hdc为外加直流磁场强度；γ为基于测量数据的待定系数。
在交直流混合激励下，由于磁滞回线的不对称性，将对磁滞损耗和杂散损耗产生较大影响。直流分量对磁滞损耗的影响在式（2）中具体表现为加入的直流磁场强度指数形式。同时，直流磁场强度的指数值为1时，对应于正弦激励下的损耗。
涡流损耗Pec与磁通密度B随时间的变化有关，与直流激励无关，因此交直流混合激励下的涡流损耗拟合与正弦激励条件下相同。
涡流损耗Pec可表示为[25]
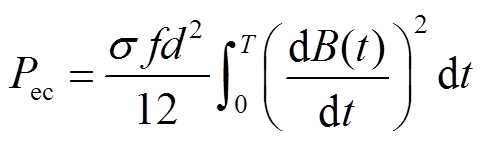（3）式中，σ为磁构件材料电导率；d为磁构件材料厚度；T为激励周期。
基于E. Barbisio[26]提出的异常损耗模型，异常损耗Pex与磁通密度对时间的导数dB(t)/dt有关，考虑直流激励影响，异常损耗Pex可表示为
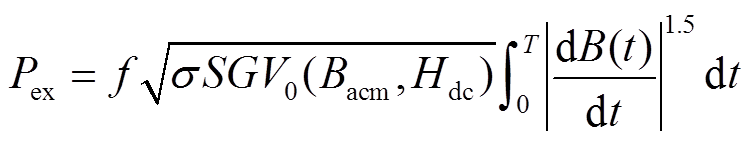（4）式中，G为无量纲系数，本文模型中G=0.135 6[27]；S为材料横截面积；V0为表征统计特征参数，其取值与磁通密度的交流分量峰值Bacm以及直流磁场强度Hdc有关，具体形式可表示为
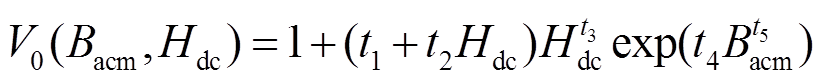（5）式中，ti (i=1,2,3,4,5)为根据实测数据拟合损耗曲线确定的参数；V0表征偏磁情况与正弦情况下比值关系，当直流磁场强度Hdc为0时，统计特征参数为1，此时异常损耗模型取决于交流磁密对时间的导数dB(t)/dt及磁构件参数。
如图5所示为不同直流偏磁条件下的磁滞损耗实验值与模型拟合对比结果。由图中可看出磁滞损耗Ph拟合结果与实验值较为吻合，验证了本文磁滞损耗模型的有效性与准确性。
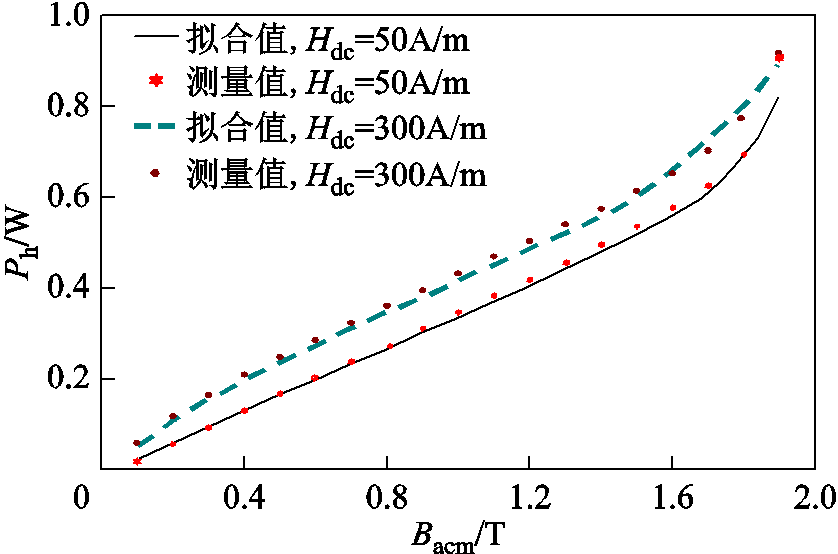
图5 交直流混合激励下拟合与测量磁滞损耗的对比
Fig.5 Comparison between fitted and measured hysteresis loss under AC-DC hybrid excitation
为验证式（5）中的异常损耗模型，测量的总损耗Ps减去测得的磁滞损耗Ph及计算出的涡流损耗Pec得到的基于实验确定的异常损耗Pex，与本文所提出模型拟合得到的异常损耗进行对比如图6所示，可看出二者具有较好的一致性。
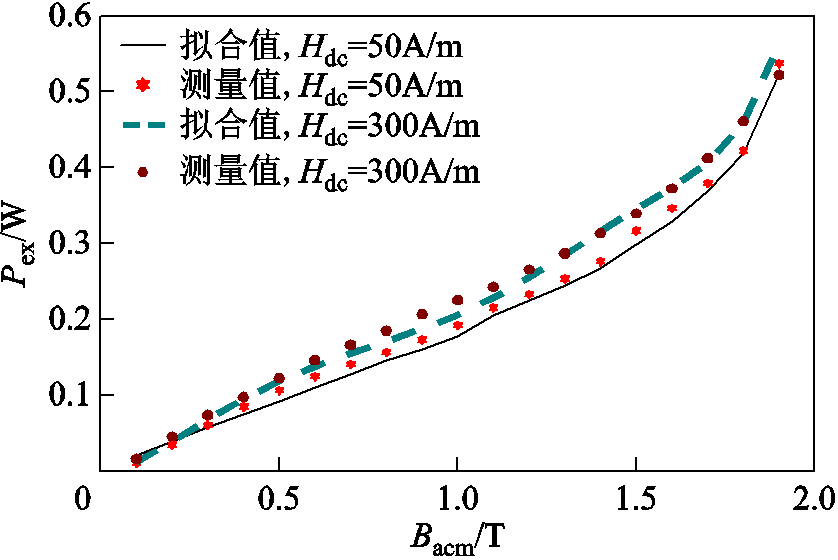
图6 交直流混合激励下拟合与测量异常损耗对比
Fig.6 Comparison between fitted and measured excess loss under AC-DC hybrid excitation
由式（2）~式（5）拟合得出总损耗Ps如图7所示，对比不同交直流混合激励下的总损耗Ps的拟合值与实测值。从图7中可知，实测数据与本文模型拟合较为一致，证明了所提出的损耗模型运用于交直流混合激励下的硅钢叠片损耗计算时的有效性与准确性。
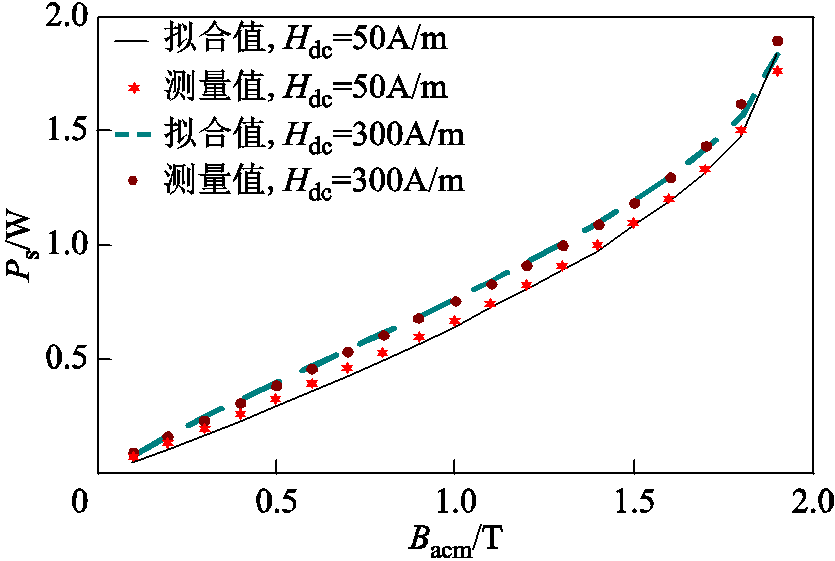
图7 交直流混合激励下模型拟合与实验损耗的对比
Fig.7 Comparison between modeled and measured loss under AC-DC hybrid excitation
TEAM-P21c基准族模型以电力变压器三维杂散损耗模拟为工程背景而提出，涵盖多项杂散损耗模拟技术[28-30]。为标准化交直流混合激励下的杂散场损耗模型验证，本文将所提出的损耗模型运用于TEAM-P21c基准模型中，对模型拟合结果进行验证分析。
本文使用的TEAM-P21c基准模型磁构件为20片30P120型取向硅钢叠片，每片尺寸为520mm× 360mm×0.3mm，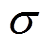
=2.22
106S/m。测量系统包括多功能发生器（NF WF1974）、功率放大器（NF 4520A）、功率分析仪（WT-3000E YOKAGAWA）等，基准模型和实验设备如图8所示。图9显示了基准模型的结构及其尺寸参数。在激励线圈中施加交直流混合激励进行实验测量。实验电路原理如图10所示。
图8 实验平台
Fig.8 Experimental platform
在图9的激励线圈中施加交直流混合激励，激励具体形式为
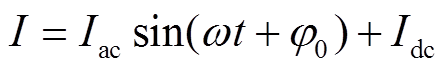（6）式中，ω为基波角频率；Iac为交流电流幅值；φ0为初始相位，本文中φ0=0；Idc为直流激励电流幅值。本文基波频率为50Hz。
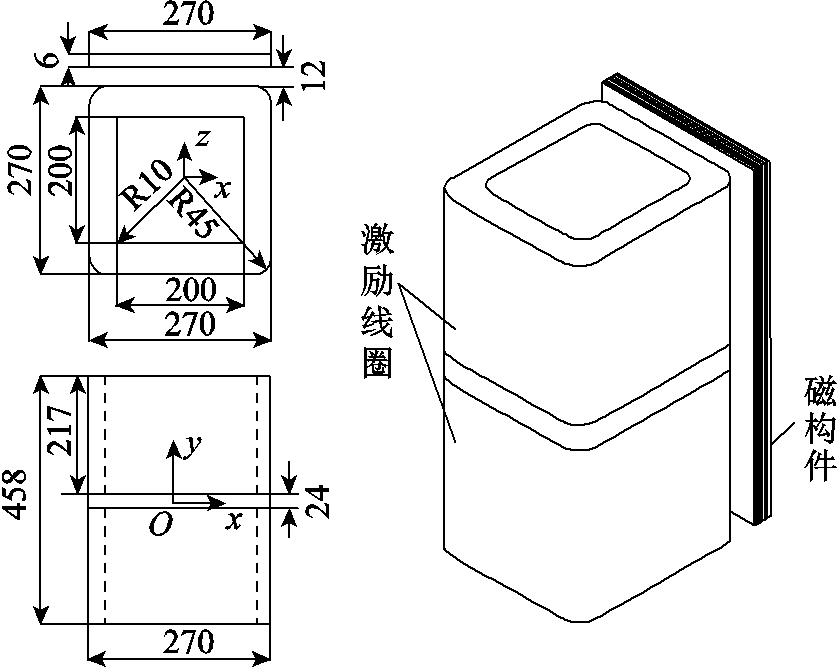
图9 TEAM-P21模型的结构及参数
Fig.9 Structure and parameters of TEAM-P21
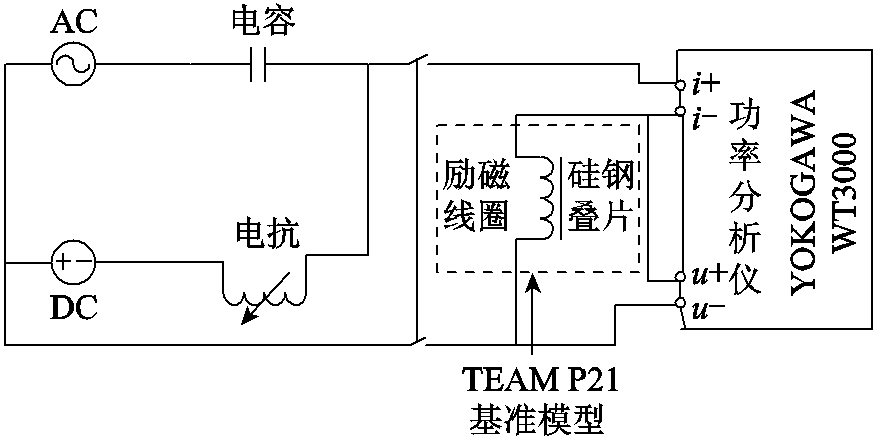
图10 实验接线图
Fig.10 Experimental circuit diagram
激励线圈中的涡流损耗是由漏磁场在导线中感应产生，因此涡流损耗的大小与线圈周围漏磁场的分布密切相关。不同工况下模型的二维磁通分布如图11所示。由图11可知，有无磁构件对激励线圈周围的磁场分布有着较大影响，因此空载、负载情况下不同漏磁场感应产生的线圈涡流损耗也将发生变化。
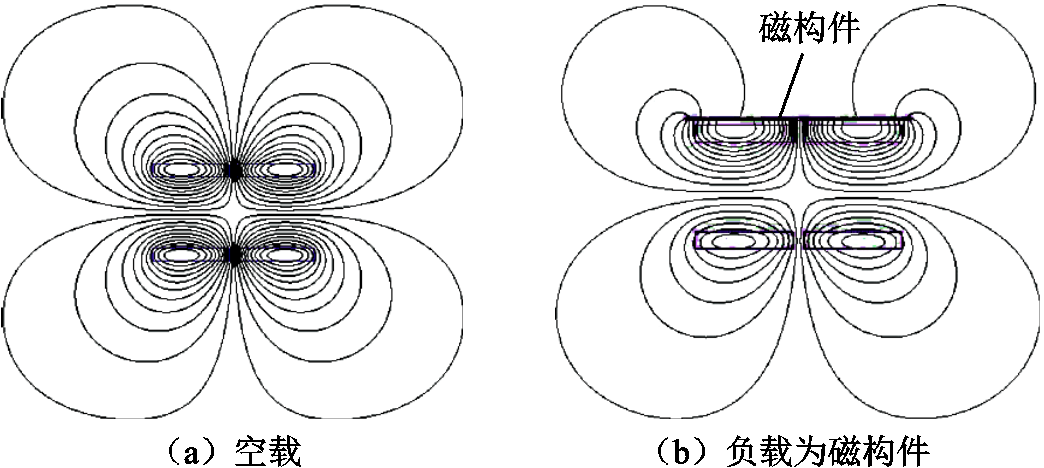
图11 不同工况下模型的二维磁通分布
Fig.11 2-D magnetic flux density distribution of the model under different conditions
传统的测量方法未考虑由于不同工况引起的漏磁通分布差异带来的影响[31]。本文在考虑空载、负载工况下激励线圈的损耗差异的前提下，对激励线圈进行精细化有限元建模计算，引入一个仿真中负载工况下线圈损耗相比空载工况下线圈损耗增加的比例，采用测量的负载工况下模型的总损耗减去用系数修正过的测量的空载工况下线圈的损耗得到磁构件杂散损耗的实验值。由此，改进的杂散损耗表示为
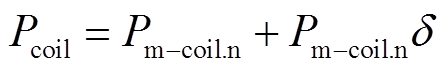（7）
（8）
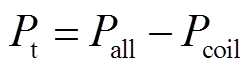（9）式中，Pcoil为负载条件下激励线圈实际损耗值；Pm-coil.n为测量的空载条件下激励线圈的损耗值；δ为仿真计算中负载工况下线圈损耗相比空载工况下线圈损耗增加的比例；Ps-coil为仿真中负载工况下的线圈损耗；Ps-coil.n为仿真中空载工况下的线圈损耗；Pt为磁构件杂散损耗；Pall为负载工况下测量的总损耗。
在实验中，为了保证负载工况下和空载工况下线圈的欧姆损耗不发生变化，需调整电压保持激励线圈内电流的有效值不变。
本文采用的改进的1/4精细化建模计算激励线圈损耗进行仿真，1/4精细化模型如图12所示。
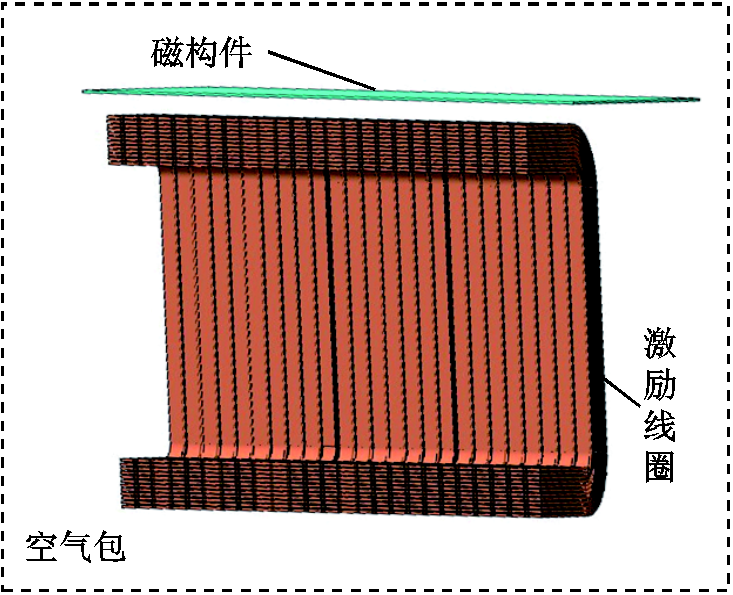
图12 1/4精细化模型图
Fig.12 One quarter model for simulation
基于以上改进方法，通过引入δ表示损耗比例，考虑了空负载工况下激励线圈的损耗差，借助精细化建模计算激励线圈损耗，可以基于实验得到更合理、更准确的磁构件杂散损耗。
图13给出了基于传统方法的磁构件杂散测量结果和仿真结果，也给出了基于改进方法的杂散测量结果。在交流激励Iac=10A叠加不同的直流激励Idc下，仿真所得损耗结果为Pcalc；传统方法得到的磁构件杂散损耗为Ptra，与Pcalc的相对误差为Δtra；本文改进方法得到的磁构件杂散损耗为Pimp，与Pcalc的相对误差为Δimp。对比可知，改进后测量结果与计算结果更接近，从而验证了本文基于实验改进的杂散损耗确定方法的有效性。
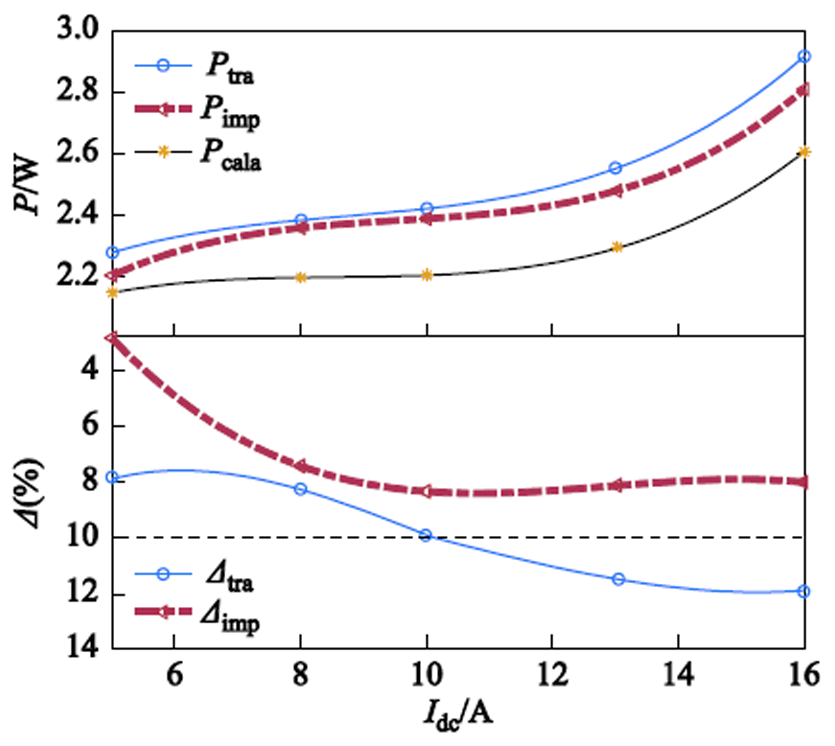
图13 改进前与改进后杂散损耗测量结果与计算结果误差对比
Fig.13 Comparison of stray-field loss between measurement and simulation in two different (improved and conventional) methods
本文考虑了材料的各向异性，对实际磁构件结构进行合理简化以减少三维建模仿真的计算量，针对硅钢叠片的建模方法如下：
由于靠近激励线圈的叠片损耗较大，在仿真建模时，需要对靠近激励线圈的硅钢片进行单片精细化建模。硅钢叠片建模如图14所示，仿真中针对靠近激励线圈侧前5片以及远离激励线圈后2片进行单片建模，视为三维涡流区；其余叠片整体进行整体化建模为一个实体块（bulk），视为二维涡流区。通过以上简化操作以降低计算代价。
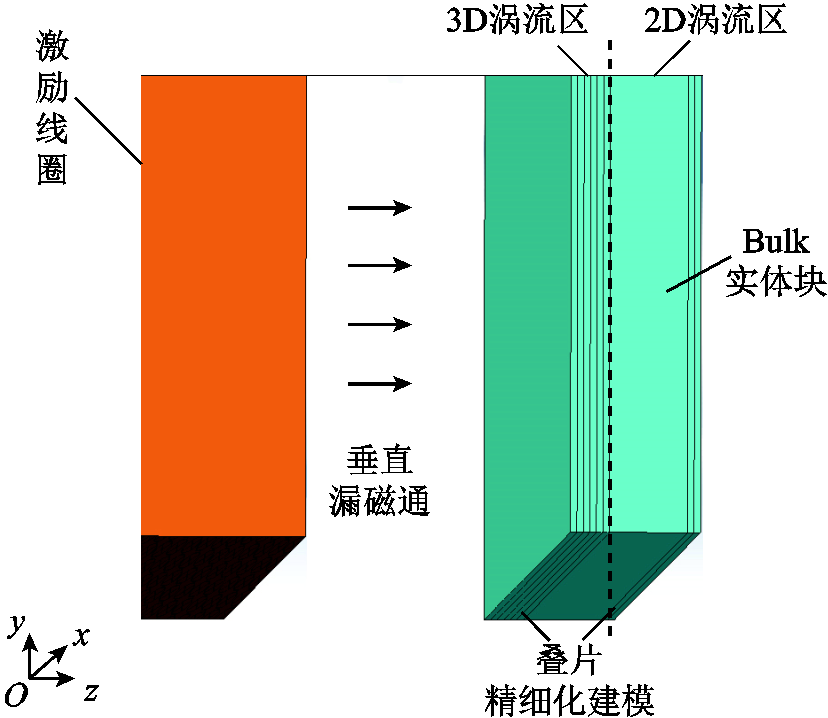
图14 硅钢叠片建模图
Fig.14 Model of silicon steel lamination
结合所建模型对电导率和磁导率分别进行设置，电导率σ在三维涡流区按各向异性处理，在二维涡流区将z方向的电导率σz设置为0。二维涡流区和三维涡流区的磁导率按式（10）进行设置[32]。
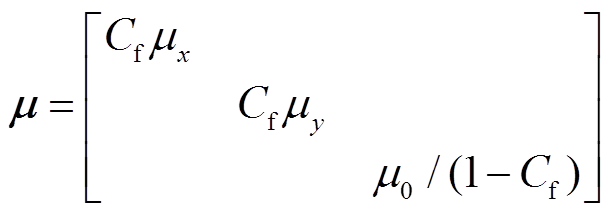（10）式中，μ为考虑叠片效应后的等效磁导率；Cf为叠片系数；μx、μy分别为x向（沿轧制方向）和y向（垂直轧制方向）的磁导率；μ0为真空磁导率。
将磁构件中的漏磁场和平均磁通密度的交流分量的计算结果与测量结果进行比较，以验证建模和模型计算的准确性。
使用高斯计测量硅钢叠片表面的漏磁场，测点分别为硅钢叠片上、下侧并紧贴叠片，从两个激励线圈中心位置（坐标y=0mm）开始，沿着叠片宽度中心线等间距各取23个点测量漏磁通，测点位置如图15所示。
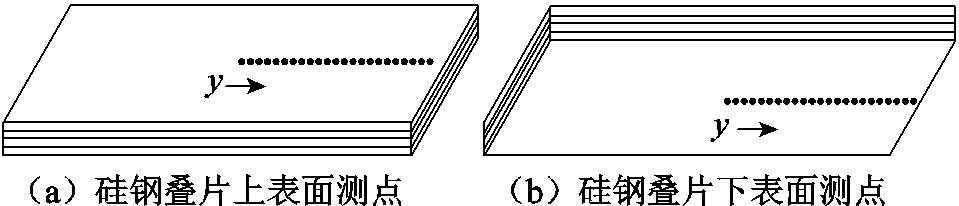
图15 测点布置图
Fig.15 Arrangement of measuring points
图16为在交直流混合激励下（Iac=20A，Idc=16A）仿真与测量的漏磁场的比较。对比结果表明，漏磁场仿真结果与测量结果较为一致，验证了仿真时模型磁场计算的准确性。
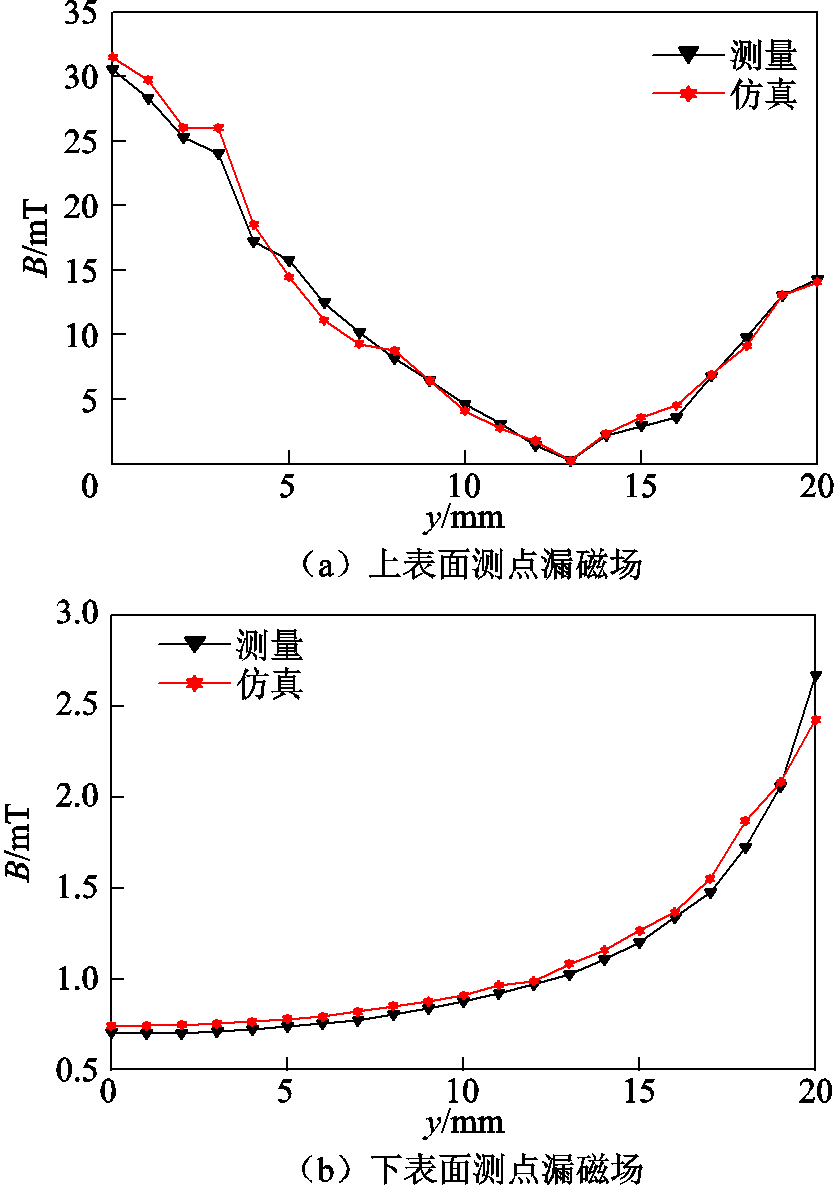
图16 硅钢叠片表面测点漏磁场
Fig.16 Magnetic flux density on the surface of silicon steel lamination
在交直流磁通同时存在的情况下，通过测量从混合磁通中提取直流磁通分量难以实现，因此本文基于电磁感应定律采用测量线圈得到叠片中平均磁通密度的交流分量。在硅钢叠片的指定位置上缠绕线径为0.1mm、匝数为20匝的漆包线，基于该位置的测量先得到交流感应电压，通过积分关系得出交链磁通的最大值，进而计算出硅钢叠片中的平均磁通密度Baverage，具体计算表达式为
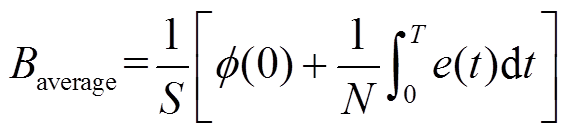（11）式中，e为交流感应电压；N为线圈匝数；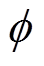
为感应磁通；S为线圈所在位置的有效截面积。
计算距激励线圈最近的四片及最远的一片硅钢片的平均磁通密度。在硅钢叠片的长边的四分之一处缠绕测量线圈，根据式（11）对所测电压进行平均磁通密度的计算，测量如图17所示。
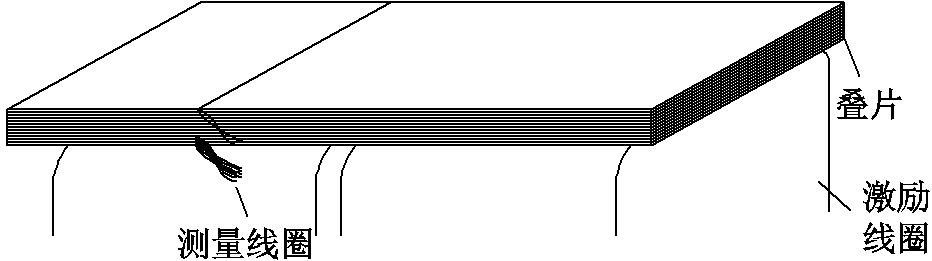
图17 平均磁通密度交流分量的测量
Fig.17 Average magnetic flux density measurement
交直流混合激励下，距激励线圈最近的硅钢片内部磁通密度的交流分量测量结果与仿真结果的对比如图18所示，由图中可看出，二者对比结果较为一致，验证了仿真时TEAM-P21c基准模型磁场分布的正确性。
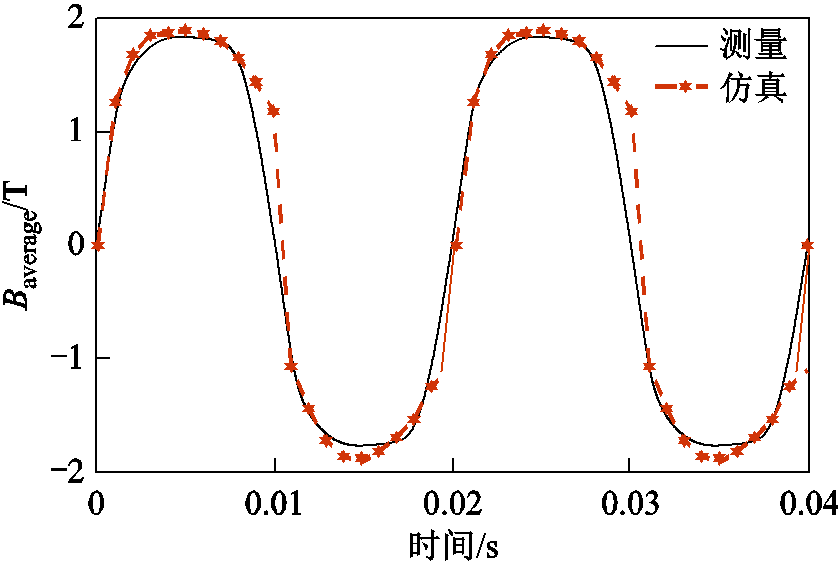
图18 硅钢片内部磁通密度的交流分量
Fig.18 Average AC flux density inside the silicon steel lamination
硅钢叠片作为磁构件时，垂直进入硅钢片的漏磁通产生的涡流损耗较大，将其中的损耗分为两部分，即总杂散损耗P可表示为
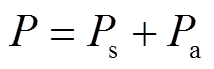（12）式中，Ps为根据式（1）的损耗模型计算的杂散损耗，也称标准铁损；Pa为垂直于硅钢叠片的直流偏磁通引起的额外铁损，可以根据上述简化模型和叠片材料特性的特殊处理计算得出[32]。
表1、表2为不同交直流混合激励下硅钢叠片内部杂散损耗。Pcalc为杂散损耗仿真值，Pt为测量的杂散损耗，Δ为相对误差。
表1 交直流混合激励下硅钢片的杂散损耗（Iac=10A）
Tab.1 Stray-field loss of laminations under AC-DC hybrid excitation (Iac=10A)
Idc/APt/WPcalc/WΔ（%） 02.1—— 52.209 32.144 72.92 82.368 12.194 37.34 102.398 82.201 68.22 162.830 52.606 97.90
表2 交直流混合激励下硅钢片的杂散损耗（Iac=20A）
Tab.2 Stray-field loss of laminations under AC-DC hybrid excitation (Iac=20A)
Idc/APt/WPcalc/WΔ（%） 010.7—— 516.523 517.600 1-6.52 816.784 115.282 4 8.95 1017.426 418.581 9-6.63 1619.290 320.517 9-6.36
从表1和表2的结果可以看出，杂散损耗实验值与仿真值较为吻合，验证了基于精细化建模计算激励线圈损耗方法的准确性和有效性。随着交流激励的增加，磁构件的杂散损耗显著增加。此外，当交流激励保持不变时，施加的直流激励的增加会导致磁构件内部杂散损耗的增加。
基于上述精细化建模，可得不同交直流混合激励下磁构件中各层叠片的附加损耗Pa。表3和表4分别展示了Iac=10A、Idc=10A和Iac=10A、Idc=16A时各层叠片内的附加损耗Pa和杂散损耗Ps。m表示硅钢叠片的层数序号，m=1和m=20分别为距离激励线圈最近和最远的硅钢片。
从表3、表4中可以看出，由于漏磁通垂直进入硅钢叠片而导致的附加铁损Pa主要分布在靠近激励线圈的前两片硅钢叠片上，并且随着叠片到激励线圈的距离增大而迅速减小。同时从表中数据可看出，单层硅钢片损耗和各硅钢片损耗总和中，附加损耗Pa占总损耗P比例均较大。除此之外，在交直流混合激励中，当交流分量不变时，直流分量的增大将导致附加损耗的增加，这是导致磁构件中总杂散损耗增加的重要原因之一。
表3 交直流混合激励下硅钢片的附加铁损（Iac=10A，Idc=10A）
Tab.3 The additional iron loss of silicon steel sheet under AC-DC hybrid excitations(Iac=10A, Idc=10A)
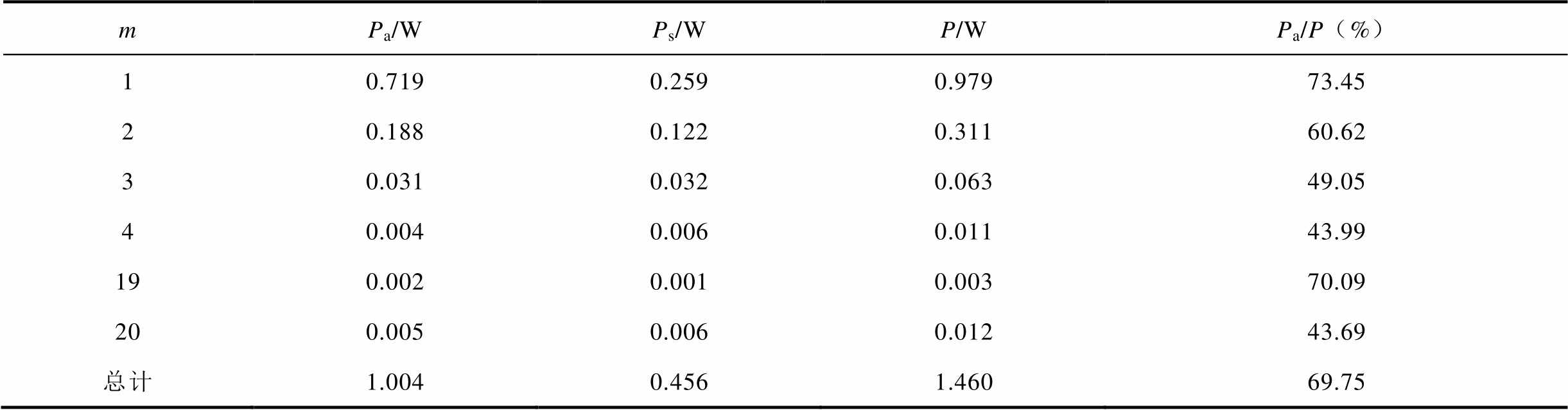
mPa/WPs/WP/WPa/P（%） 10.7190.2590.97973.45 20.1880.1220.31160.62 30.0310.0320.06349.05 40.0040.0060.01143.99 190.0020.0010.00370.09 200.0050.0060.01243.69 总计1.0040.4561.46069.75
表4 交直流混合激励下硅钢片的附加铁损（Iac=10A，Idc=16A）
Tab.4 The additional iron loss of silicon steel sheet under AC-DC hybrid excitations(Iac=10A, Idc=16A)
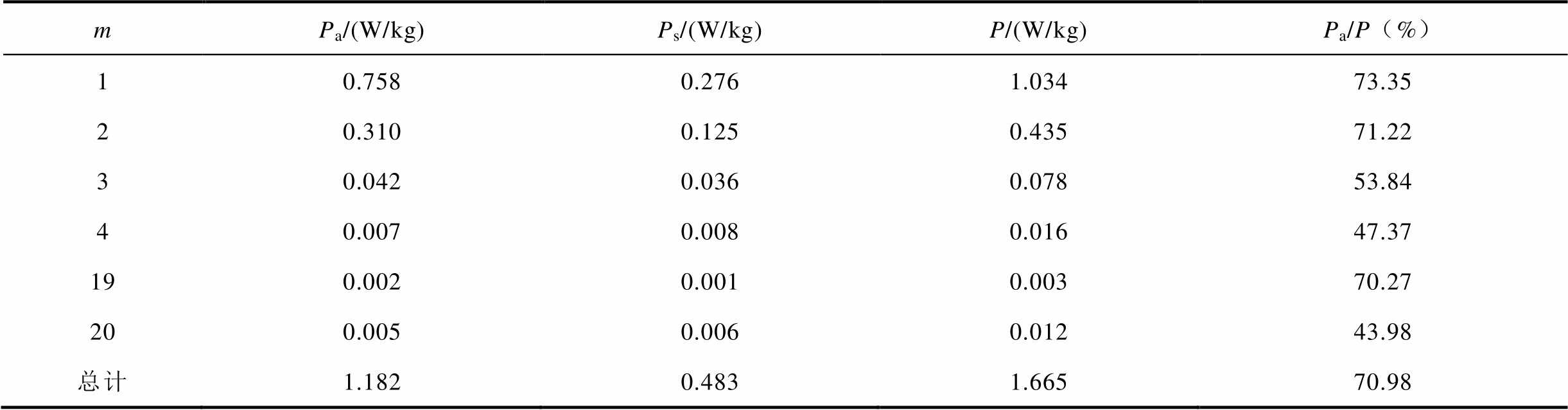
mPa/(W/kg)Ps/(W/kg)P/(W/kg)Pa/P（%） 10.7580.2761.03473.35 20.3100.1250.43571.22 30.0420.0360.07853.84 40.0070.0080.01647.37 190.0020.0010.00370.27 200.0050.0060.01243.98 总计1.1820.4831.66570.98
1）根据直流条件下铁损的特征，提出考虑偏置场影响的铁损分离模型，并将其应用于偏磁下三维杂散损耗的数值模拟及分析。
2）考虑空、负载下漏磁场不同对磁构件杂散损耗计算的影响，提出一种基于实验测量确定叠片式磁构件中的杂散损耗的改进方法，并通过精细化建模和媒质参数等效处理进行数值仿真，有效地提高了大型电力变压器的杂散损耗评估的准确性。
3）交直流混合激励下，随着交流激励增大，磁构件的杂散损耗明显增加；当交流激励不变时，增大直流激励将引起磁构件内杂散损耗的增大。
4）垂直进入叠片的漏磁通引起的附加损耗占杂散损耗比例较大，且主要分布在靠近激励线圈的两块硅钢叠片中，随着从激励线圈到叠片的距离迅速减小；交流激励不变时，直流激励的增大将导致附加损耗的增大。
参考文献
[1] 赵小军, 晋志明, 曹越芝, 等. 基于磁标量位的定点频域算法及其在叠片铁心偏磁问题中的应用[J]. 电工技术学报, 2019, 34(17): 3590-3598. Zhao Xiaojun, Jin Zhiming, Cao Yuezhi, et al. A fixed-point frequency domain method based on magnetic scalar potential and its application to the DC biased problem in the laminated core[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3590-3598.
[2] 朱占新, 谢德馨, 张艳丽. 大型电力变压器三维漏磁场与结构件损耗的时域分析[J]. 中国电机工程学报, 2012, 32(9): 156-160. Zhu Zhanxin, Xie Dexin, Zhang Yanli. Time domain analysis of 3D leakage magnetic fields and structural part losses of large power transformers[J]. Proceedings of the CSEE, 2012, 32(9): 156-160.
[3] 康丽, 张艳丽, 唐伟, 等. 基于变系数Steinmetz公式的直流偏磁下铁心损耗计算[J]. 电工技术学报, 2019, 34(增刊1): 1-6. Kang Li, Zhang Yanli, Tang Wei, et al. Calculation of core loss under DC bias based on the variable coefficient Steinmetz formula[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 1-6.
[4] Zhao Xiaojun, Meng Fanhui, Cheng Zhiguang, et al. Stray-field loss and flux distribution inside magnetic steel plate under harmonic excitation[J]. COMPEL- The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2017, 36(6): 1715-1728.
[5] Cheng Z, Takahashi N, Forghani B, et al. 3-D finite element modeling and validation of power frequency multishielding effect[J]. IEEE Transaction on Magnetics, 2012, 48(2): 243-246.
[6] Takahashi N, Sakura T, Cheng Z, Nonlinear analysis of eddy current and hysteresis losses of 3-D stray field loss model (problem 21)[J]. IEEE Transaction on Magnetics, 2001, 37(5): 3672-3675.
[7] Ragusa C, Zhao Hanyu, Appino C, et al. Loss decomposition in non-oriented steel sheets: the role of the classical losses[J]. IEEE Magnetics Letters, 2016, 7: 1-5.
[8] Olivier de la B, Ragusa C, Appino C, et al. Prediction of energy losses in soft magnetic materials under arbitrary induction waveforms and DC bias[J]. IEEE Transactions on Industrial Electronics, 2017, 64(3): 2522-2529.
[9] Hauser H. Energetic model of ferromagnetic hysteresis: Isotropic magnetization[J]. Journal of Applied Physics, 2004, 96(5): 2753-2767.
[10] Zhu Zhanxin, Xie Dexin, Wang Gang, et al. Computation of 3-D magnetic leakage field and stray losses in large power transformer[J]. IEEE Transaction on Magnetics, 2012, 48(2): 739-742.
[11] Yan Xiuke, Yu Xiangdong, Shen Min, et al. Research on calculating eddy-current loss in power transformer tank walls using finite-element method combined with analytical method[J]. IEEE Transaction on Magnetics, 2016, 52(3): 1-3.
[12] Zheng Weiying, Chen Xinhong. Subspace correction method for computing magnetic shields in large power transformers[J]. IEEE Transaction on Magnetics, 2015, 51(5): 1-6.
[13] Liu Jian, Huang Qianqiang, Liu Yaqing, et al. Calculation method of winding eddy-current losses for high-voltage direct current converter transformers[J]. IET Electric Power Applications, 2016, 10(6): 488-497.
[14] Elmoudi A, Lehtonen M, Nordman H. Corrected winding eddy-current harmonic loss factor for transformers subject to nonsinusoidal load currents[C]// 2005 IEEE Russia Power Tech, Petersburg, 2005: 1-6.
[15] Liu Yaqing, Zhang Dandan, Li Zhenbiao, et al. Study of the stray losses calculation in structural parts for HVDC converter transformers based on the TEAM Problem 21 family[J]. IEEE Transactions on Power Delivery, 2016, 31(2): 605-612.
[16] 赵志刚, 刘福贵, 程志光, 等. HVDC中直流偏磁电力变压器叠片铁心损耗及磁通分布[J]. 高电压技术, 2010, 36(9): 2346-2351. Zhao Zhigang, Liu Fugui, Cheng Zhiguang, et al. Loss and flux distribution of power transformers laminated core under DC-biased magnetization condition in HVDC[J]. High Voltage Engineering, 2010, 36(9): 2346-2351.
[17] 赵志刚, 刘佳, 郭莹, 等. 非正弦励磁环境磁性材料改进损耗模型的研究[J]. 电工技术学报, 2019, 34(13): 2693-2699. Zhao Zhigang, Liu Jia, Guo Ying, et al. Investigation on the improved loss model of magnetic materials under non-sinusoidal excitation environment[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2693-2699.
[18] 赵志刚, 刘福贵, 张晓晨, 等. 一种确定交直流混合激励电磁构件杂散损耗的有效方法[J]. 电工技术学报, 2017, 32(2): 95-101. Zhao Zhigang, Liu Fugui, Zhang Xiaochen, et al. Confident determination of stray-field loss in electro-magnetic components under AC-DC hybrid excitation[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 95-101.
[19] 赵小军, 李琳, 程志光, 等. 基于直流偏磁实验的叠片铁心磁化特性分析[J].电工技术学报, 2011, 26(1): 7-13. Zhao Xiaojun, Li Lin, Cheng zhiguang, et al. Analysis of magnetizing characteristic of laminated core based on the DC-biasing experiment[J]. Transactions of China Electrotechnical Society, 2011, 26(1): 7-13.
[20] Bertotti G. Physical interpretation of eddy current losses in ferromagnetic materials, I. theoretical considerations[J]. Journal of Applied Physics, 1985, 57(6): 2110-2117.
[21] Bertotti G. Physical interpretation of eddy current losses in ferromagnetic materials, II. analysis of experimental results[J]. Journal of Applied Physics, 1985, 57(6): 2118-2126.
[22] 张冬冬, 赵海森, 王义龙, 等. 用于电机损耗精细化分析的分段变系数铁耗计算模型[J]. 电工技术学报, 2016, 31(15): 16-24. Zhang Dongdong, Zhao Haisen, Wang Yilong, et al. A piecewise variable coefficient model for precise analysis on iron losses of electrical machines[J]. Transactions of China Electrotechnical Society, 2016, 31(15): 16-24.
[23] 刘刚, 孙立鹏, 王雪刚, 等. 正弦及谐波激励下的铁心损耗计算方法改进及仿真应用[J]. 电工技术学报, 2018, 33(21): 4909-4918. Liu Gang, Sun Lipeng, Wang Xuegang, et al. Improvement of core loss calculation method and simulation application under sinusoidal and harmonic excitations[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4909-4918.
[24] Fiorillo F, Novikov A. An improved approach to power losses in magnetic laminations under nonsinusoidal induction waveform[J]. IEEE Transaction on Magnetics, 1990, 26(3): 2904-2910.
[25] Boglietti A, Cavagnino A, Lazzari M, et al. Predicting iron losses in soft magnetic materials with arbitrary voltage supply: an engineering approach[J]. IEEE Transaction on Magnetics, 2003, 39(2): 981-989.
[26] Barbisio E, Fiorillo F, Ragusa C. Predicting loss in magnetic steels under arbitrary induction waveform and with minor hysteresis loops[J]. IEEE Transactions on Magnetics, 2004, 40(4): 1810-1819.
[27] 程志光, 高桥则雄, 博扎德·弗甘尼, 等. 电气工程电磁热场模拟与应用[M]. 北京: 科学出版社, 2009.
[28] Zheng Weiying, Chen Xinhong. Efficient finite element simulation for GO silicon steel laminations using inner-constrained laminar separation[J]. IEEE Transactions on Magnetics, 2012, 48(8): 2277-2283.
[29] 程志光, 刘涛, 范亚娜, 等. 基于TEAM P21三维杂散场问题建模仿真与验证[J]. 电工技术学报, 2014, 29(9): 194-203. Cheng Zhiguang, Liu Tao, Fan Yana, et al. TEAM P21-based validation of 3-D stray-field modeling and simulation[J]. Transactions of China Electrotechnical Society, 2014, 29(9): 194-203.
[30] Cheng Z, Takahashi N, Forghani B, et al. Extended progress in TEAM Problem 21 family[J]. COMPEL- The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2014, 33(1-2): 234-244.
[31] 李琳, 张元禄. 电力变压器三维漏磁场及铁芯拉板涡流损耗的计算[J]. 中国电机工程学报, 1999, 19(6): 34-37, 52. Li Lin, Zhang Yuanlu. Calculation of the 3D nonlinear magnetic field and eddy current loss of the plate in transformer[J]. Proceedings of the CSEE, 1999, 19(6): 34-37, 52.
[32] Cheng Z, Takahashi N, Forghani B, et al. 3-D finite element modeling and validation of power frequency multishielding effect[J]. IEEE Transaction on Magnetics, 2012, 48(2): 243-246.
Numerical Simulation and Experimental Verification of Stray Loss of Laminated Magnetic Components for Transformers under AC-DC Hybrid Excitation
Abstract Based on the TEAM-P21c benchmark model, the numerical simulation and experimental verification methods of the stray-field loss of laminated magnetic components in transformers under AC-DC hybrid excitation are thoroughly studied. For determining the stray-field loss of the structural part more accurately, an improved method based on experiments considering the difference of coil loss under no-load and load conditions is proposed. An enhanced measurement system based on TEAM-P21c for the magnetic and loss characteristics of silicon steel laminations was established. An iron loss model considering the influence of the DC-biased magnetic field was proposed, and it was used to calculate the stray-field loss of laminated magnetic components under the excitation of 3-D leakage magnetic field. By comparing the simulation and experimental results of the magnetic field and loss, the validity of this method is verified. Finally, based on the simulation and measurement results, the influence of the DC-biased magnetic field on the stray-field loss was analyzed. Hence, the distribution and effect on the stray-field loss of the additional loss in the magnetic component under the AC-DC hybrid excitation are obtained.
keywords：TEAM-P21c benchmark model, magnetic components, stray-filed loss, AC-DC hybrid excitation, additional iron loss
中图分类号：TM153
DOI: 10.19595/j.cnki.1000-6753.tces.191725
国家重点研发计划（2017YFB0902703）、国家自然科学基金（51777073）、河北省自然科学基金（E2017502061）和中央高校基本科研业务费（2019 MS078）资助项目。
收稿日期2019-12-12
改稿日期 2020-04-11
赵小军 男，1983年生，副教授，硕士生导师，研究方向电工材料磁性能测量与模拟技术，频域数值计算方法，变压器直流偏磁及振动噪声问题，多物理场耦合模型及计算方法。E-mail：zxjncepu@ncepu.edu.cn（通信作者）
曹越芝 女，1997年生，硕士研究生，研究方向为电磁场理论及其应用等。E-mail：black_csong@ncepu.edu.cn
（编辑 赫蕾）