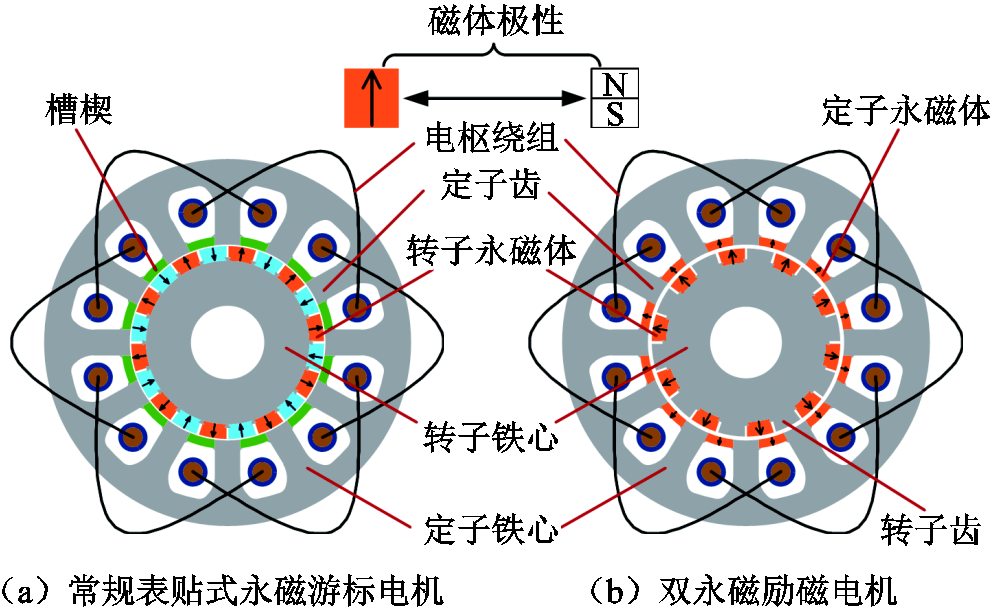
图1 两台电机结构示意图
Fig.1 Cross section of two machines
摘要 该文对比分析了两种典型的场调制型永磁电机,即常规永磁游标电机和双永磁励磁电机的性能和特点。首先介绍两种电机的结构,总结它们的结构特点;接着通过推导两种电机的一般性表达式,即空载反电动势及输出转矩,揭示两种电机的工作原理,比较“单向磁场调制效应”与“双向磁场调制效应”;最后利用有限元法对比分析两台电机的性能,验证一般性表达式的正确性。有限元仿真结果表明,在相同的尺寸、定子槽数、定子齿数、绕组极对数、转子磁体极对数、线圈匝数、绕组联结方式、电负荷、铜损耗及转速的条件下,双永磁励磁电机在永磁体用量、反电动势、转矩密度、单位磁体体积的转矩、功率因数及效率方面优于常规永磁游标电机。
关键词:磁场调制 永磁电机 转矩密度 游标电机
场调制型永磁电机(Field Modulated Permanent-Magnet Machine, FMPM)凭借其转矩密度大、效率高、无需配套机械齿轮箱使用等优点,在风力发电、电力船舶推进等低速大转矩直驱场合受到了许多专家学者的广泛关注[1-2]。
众所周知,集成磁性齿轮永磁电机(Integrated Magnetic Geared Permanent-Magnet Machine, IMGPM)[3]和常规永磁游标电机(Permanent-Magnet Vernier Machine, PMVM)[4-5]是两种最常见的场调制型永磁电机。与集成磁性齿轮永磁电机的多层气隙结构相比,常规永磁游标电机结构简单、制造难度小、成本低,更适合用于低速大转矩直驱应用领域。从结构上来看,常规永磁游标电机只有一套永磁体,且磁体与电枢绕组的极对数不相等;从运行原理来看,永磁游标电机基于“单向磁场调制效应(Unidirectional Field Modulation Effect, UFME)”工作。在该效应的作用下,永磁游标电机在气隙中调制出大量的磁场谐波。在这些极对数相等且转速相同的有效谐波的相互作用下,永磁游标电机实现了稳定的机电能量转换。
近些年来出现了一种新型场调制型永磁电机,文献[6]将其命名为“双永磁励磁电机(Dual Permanent-Magnet-Excited Machine, DPMEM)”。该电机的结构特点是只有一层气隙,结构简单;两套永磁体分别位于定子和转子上,且两套磁体的极对数和电枢绕组的极对数彼此互不相等。从工作原理来看,双永磁励磁电机在双向磁场调制效应(Bi-Directional Field Modulation Effect, BFME)的作用下,保证了两套磁体激发的磁场与电枢磁场有效耦合,从而实现了稳定的机电能量转换。文献[6-7]通过分析表明,双永磁励磁电机比它自身拓扑结构中所含的场调制型永磁电机能提供更大的转矩,这使其在低速大转矩领域成为一个有力的竞争者。
回顾现有文献关于永磁游标电机和双永磁励磁电机的研究情况,有关它们的研究工作主要集中在工作原理的揭示[4-6,8-13]、新型高性能电机拓扑结构的设计分析[14-22]、电机的优化分析[23-25]、电机的控制[26-32]、参数对性能的影响[33-34]以及各自不同拓扑结构之间的性能比较[35-38]。然而,几乎没有有关永磁游标电机和双永磁励磁电机之间性能对比分析的报道。
本文研究的目的在于对比分析两种典型的场调制型永磁电机,即常规永磁游标电机和双永磁励磁电机的性能和特点。为了公平比较,本文选择一台常规表贴式游标电机和一台看成由这台常规游标电机演化而来的双永磁励磁电机为研究对象。首先介绍两种电机的结构,总结其结构特点;其次通过推导两种电机的一般表达式,即空载反电动势及输出转矩,揭示两种电机的工作原理,比较总结“单向磁场调制效应”与“双向磁场调制效应”;接着利用有限元法(Finite Element Method, FEM)对比分析两台电机的性能,验证一般性表达式的正确性;最后得出一些结论。
常规表贴式游标电机的结构示意图如图1a所示。N极与S极交替排列的转子永磁体沿转子铁心圆周表面安装于转子铁心上,若转子永磁体数目为2Z2,则转子永磁体形成的极对数(Pole-Pair Number, PPN)为Z2。定子铁心设有Z1个定子齿和Z1个宽口定子槽,三相电枢绕组布置于定子槽中,环氧树脂材料制作的槽楔装于定子槽口以防绕组脱落。在文献[4]中,宽口槽定子铁心被T. A. Lipo教授解读为定子具有“齿极结构(Toothed-Pole Structure, TPS)”。这种齿极结构的作用类似于同轴磁性齿轮的调磁环,常规游标电机中的场调制效应(Field Modulation Effect, FME)由此而产生。

图1 两台电机结构示意图
Fig.1 Cross section of two machines
双永磁励磁电机的结构示意图如图1b所示。它可看作由图1a中的电机演变而来,具体而言,保留图1a中半数磁极相同的转子永磁体,另一半磁极相同的转子磁体换成转子齿,定子槽楔换成永磁体,这样便得到了图1b中所示的双永磁励磁电机。由图1b可以看出,该电机定、转子铁心均具有齿极结构,它们均能产生场调制效应;定、转子磁体分别插入定、转子槽中且所有磁体的极性都相同。特别说明,该电机每块磁体和其相邻的铁心齿构成一对磁极,由此方式构成的磁极被称为庶极(Consequent Pole, CP)[18],其中的铁心齿可看作“伪N极或伪S极”。因此,该电机定子槽数、定子齿数与定子磁体极对数均相等,为Z1;转子槽数、转子齿数与转子磁体极对数也都相等,为Z2。
小结:①常规表贴式PMVM只有一套磁体、一个齿极结构,而DPMEM有两套磁体(定子和转子磁体)、两个齿极结构;②DPMEM采用庶极方式,所有磁体极性相同,定转子磁体极对数与相应的定转子齿数目相同,确保了有效的磁场调制。
本节通过推导常规表贴式永磁游标电机和双永磁励磁电机的一般性表达式,即空载反电动势(Back Electromotive Force, Back EMF)和输出转矩,揭示两种电机的工作原理。
一般性表达式可以通过分析气隙磁动势(Magnetomotive Force, MMF)和气隙磁通密度得到。为便于分析,作如下假设:①定、转子铁心的磁阻和磁饱和忽略不计;②只考虑磁动势和磁导函数中的主要谐波,忽略气隙磁通密度中的高次谐波;③三相电枢绕组注入对称的正弦电流ix(x=A、B、C)如下:
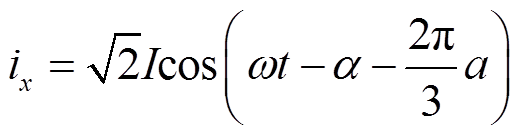 (1)
(1)式中,I为电流有效值;ω为电流角频率;a为电流相角;a=0,1,2,与A、B、C三相一一对应。
此外,这两种电机获得最大的输出转矩均遵循如下设计原则[4,38]。
 (2)
(2)式中,p为电枢绕组极对数。
永磁游标电机机械角度和轴的定义如图2所示,转子永磁磁动势的参考轴位于某块磁极中心线上,绕组磁动势的参考轴位于某个定子齿的中心线上。θs、θr、θm分别为绕组磁动势、转子永磁磁动势及转子转过的机械角度,它们满足的关系是θr=θs-θm,其中θm=ωrt,ωr为转子的机械角频率,单位为rad/s。
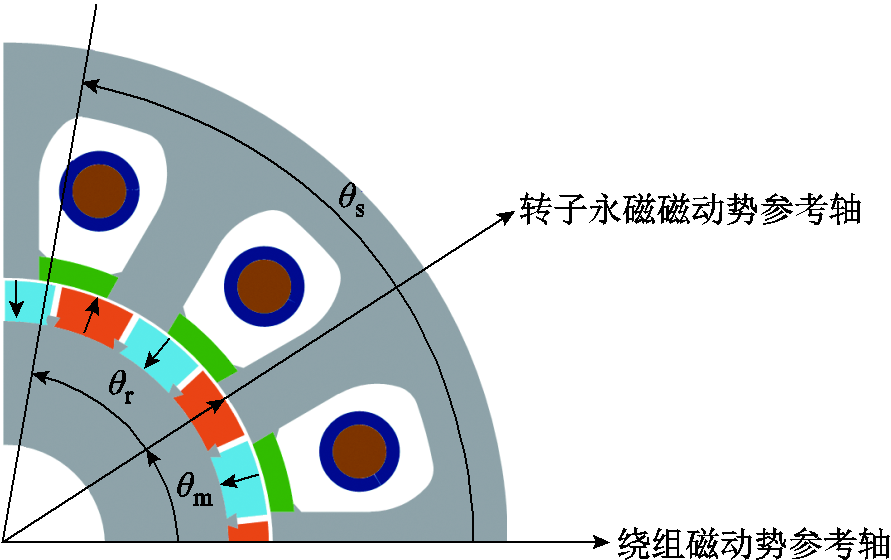
图2 永磁游标电机机械角度和轴的定义
Fig.2 Definition of mechanical angles and axises of PMVM
以转子永磁磁动势参考轴建立极坐标系,转子永磁磁动势可表示为
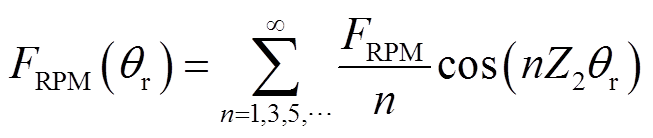 (3)
(3)式中,FRPM为转子永磁磁动势基波幅值;Z2为PMVM的转子磁体极对数。
将θr=θs-θm与θm=ωrt代入式(3),得到
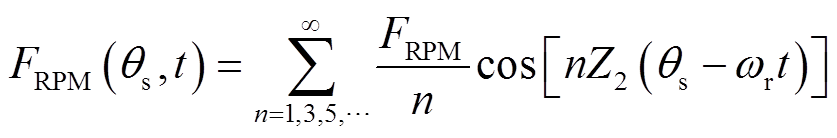 (4)
(4)由于绕组磁动势参考轴位于定子齿中心线上,由定子齿极结构引起的气隙磁导函数也可以用绕组磁动势参考轴建立的极坐标系表示为
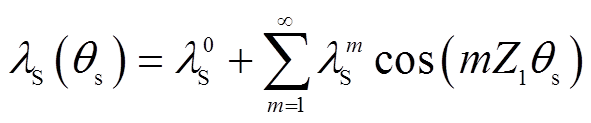 (5)
(5)式中,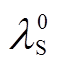 和
和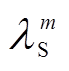 分别为PMVM中由定子齿极结构引起的气隙磁导的直流分量和m次谐波幅值。
分别为PMVM中由定子齿极结构引起的气隙磁导的直流分量和m次谐波幅值。
由式(4)与式(5)的乘积可以得到转子永磁体产生的气隙磁密。考虑到假设②,转子永磁体产生的气隙磁密可近似表示为
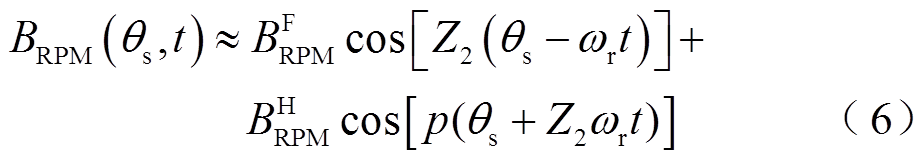
式中,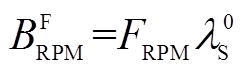 ,
,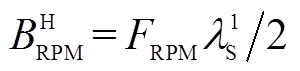 。
。
从式(6)可以看出,气隙中存在两个主要磁场谐波,即一个基波 和一个经定子齿极结构调制得到的谐波
和一个经定子齿极结构调制得到的谐波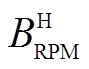 。永磁游标电机转子磁体在气隙产生的主要谐波如图3所示。从图3可以看出,这两个谐波的极对数不相等,转速也不同步。
。永磁游标电机转子磁体在气隙产生的主要谐波如图3所示。从图3可以看出,这两个谐波的极对数不相等,转速也不同步。
三相空载反电动势可以通过式(7)计算得到[5]。
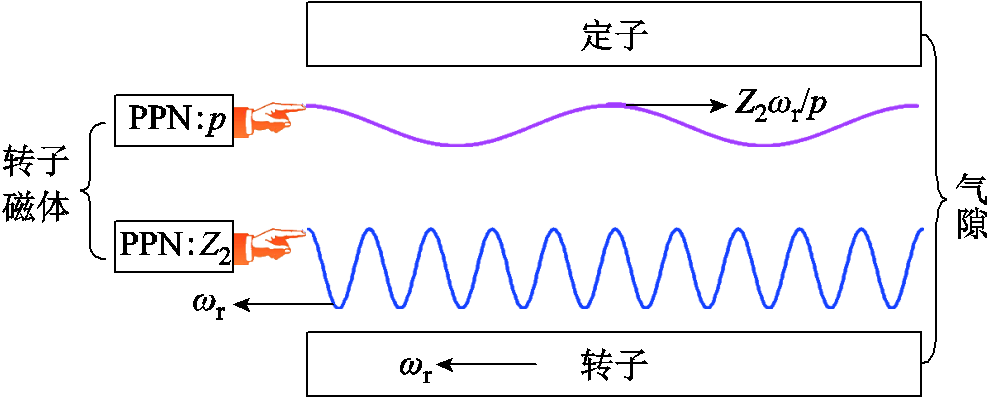
图3 永磁游标电机转子磁体在气隙产生的主要谐波
Fig.3 Dominant harmonics in air-gap generated by rotor PMs of PMVM
 (7)
(7)式中,x=A、B、C,代表A、B、C三相;Rg为气隙平均半径;l为电机轴向有效长度;Nx(θs)为三相绕组函数,表示为
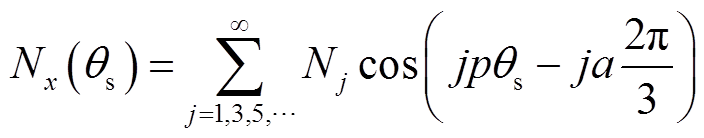 (8)
(8)式(8)中,Nj的计算式为
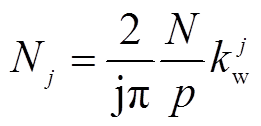 (9)
(9)式中,N为每相串联线圈总匝数; 为j次谐波绕组系数。
为j次谐波绕组系数。
将式(6)、式(8)和式(9)代入式(7),得到三相空载反电动势表达式为
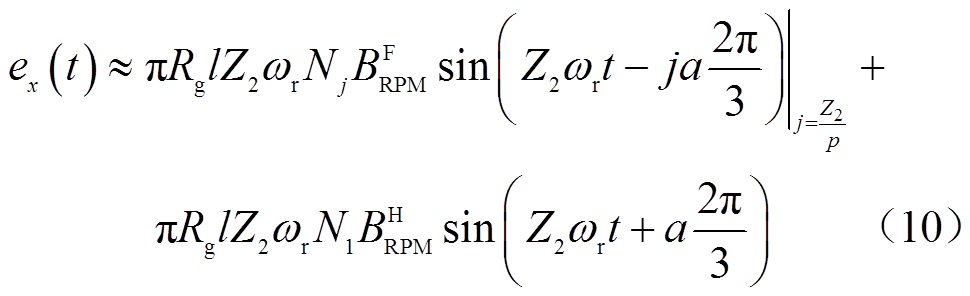
从式(10)可以看出,转子永磁体基波和谐波均对反电动势的产生作出了贡献。特别注意,虽然它们的极对数不相同,转速不同步,但是产生反电动势的频率相同。
电机输出转矩计算式为
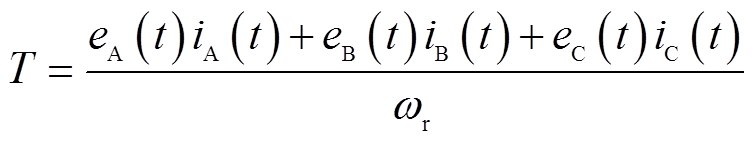 (11)
(11)将式(1)和式(10)代入式(11),得到输出转矩表达式为
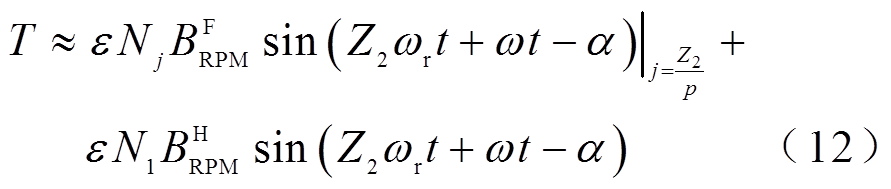
式中,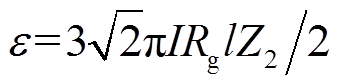 。
。
从式(12)可以看出,当电流的角频率ω与转子的机械角频率ωr满足式(13)时,电机输出稳定的转矩。
ω=-Z2ωr (13)
式中,“-”反映了转子转速方向与绕组旋转磁场方向相反。当a=-π/2,永磁游标电机输出最大转矩。
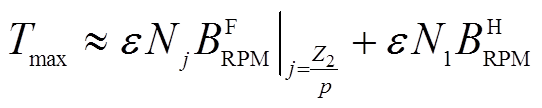 (14)
(14)显然,转子永磁体基波和谐波均对转矩的输出作出了贡献。
双永磁励磁电机的机械角度和轴的定义如图4所示,由于双永磁励磁电机采用庶极(CP),定子齿和转子齿可看成“伪N极”,则定、转子齿的中心线视为定转子永磁磁动势的参考轴。特别说明,为推导方便,定子永磁磁动势参考轴与绕组磁动势参考轴重合。比较图2和图4,不难发现各参考轴之间的机械角度关系也满足θr=θs-θm。
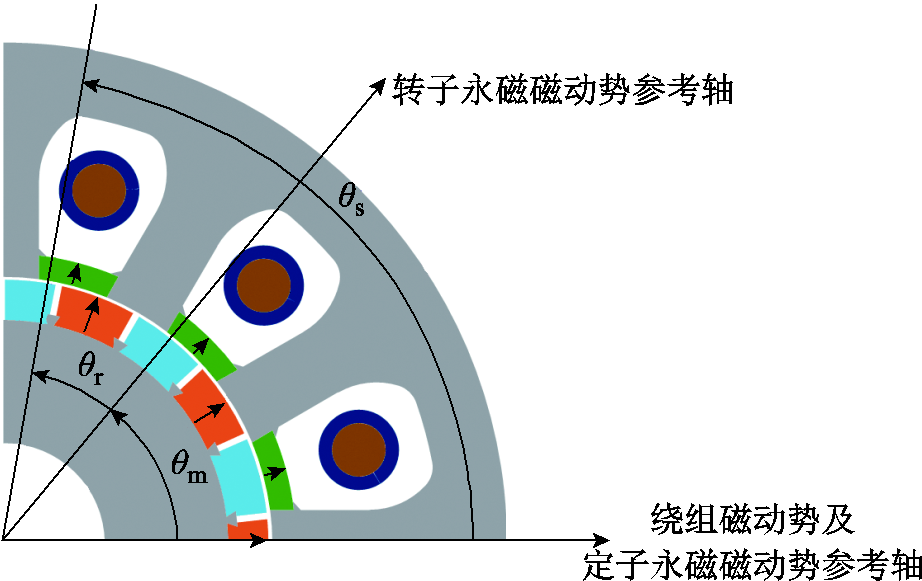
图4 双永磁励磁电机机械角度和轴的定义
Fig.4 Definition of mechanical angles and axises of DPMEM
以定子永磁磁动势参考轴建立极坐标系,定子永磁磁动势可表示为
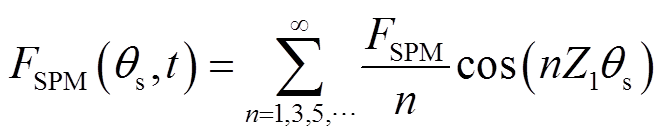 (15)
(15)式中,FSPM为定子永磁磁动势基波幅值;Z1为DPMEM的定子磁体极对数。
由于转子永磁磁动势参考轴位于转子齿中心线上,由转子齿极结构引起的气隙磁导函数也可以用转子永磁磁动势参考轴建立的极坐标系表示为
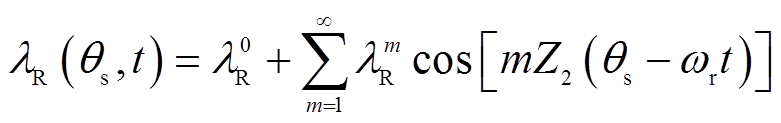 (16)
(16)式中,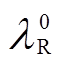 和
和 分别为DPMEM中由转子齿极结构引起的气隙磁导的直流分量和m次谐波幅值。
分别为DPMEM中由转子齿极结构引起的气隙磁导的直流分量和m次谐波幅值。
基于假设②,由式(15)与式(16)的乘积可以得到定子永磁体产生的主要气隙磁通密度,即
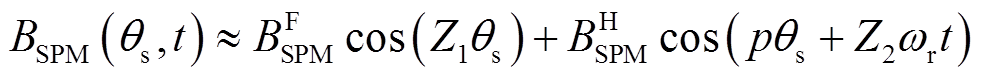 (17)
(17)式中,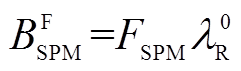 ,
,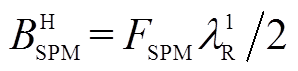 。
。
从式(17)可以看出,定子永磁体在气隙中提供了两个起主要作用的磁场谐波,即一个基波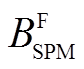 和一个经转子齿极结构调制得到的谐波
和一个经转子齿极结构调制得到的谐波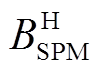 ,这两个谐波的极对数不相等,转速也不同步。需注意的是基波转速为零。此外,双永磁励磁电机转子上也有一套永磁体。根据图4定义的参考轴,推导出转子磁体在定子齿极结构作用下产生的气隙磁通密度表达式与式(6)相同。图5展示了双永磁励磁电机两套磁体在气隙产生的主要谐波。从图5可以看出,定转子磁体各提供了两个磁场谐波。
,这两个谐波的极对数不相等,转速也不同步。需注意的是基波转速为零。此外,双永磁励磁电机转子上也有一套永磁体。根据图4定义的参考轴,推导出转子磁体在定子齿极结构作用下产生的气隙磁通密度表达式与式(6)相同。图5展示了双永磁励磁电机两套磁体在气隙产生的主要谐波。从图5可以看出,定转子磁体各提供了两个磁场谐波。
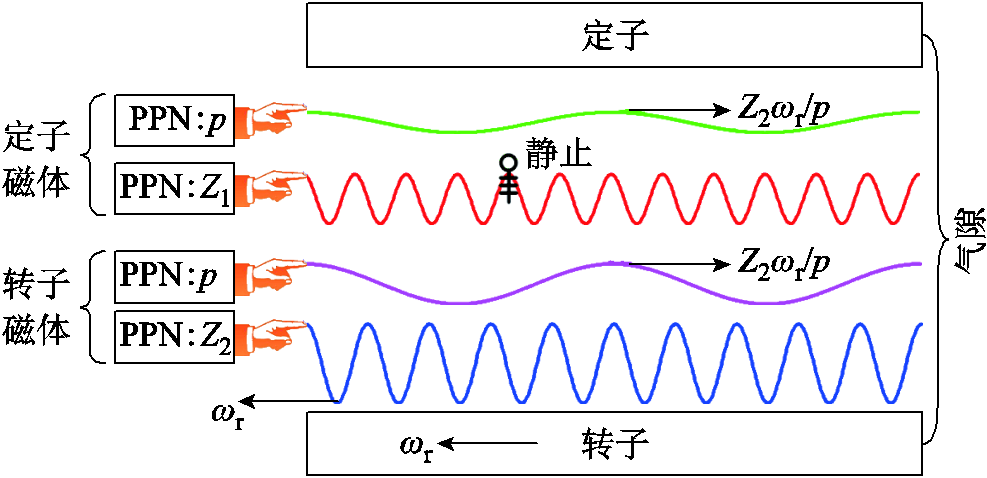
图5 双永磁励磁电机定转子磁体在气隙产生的主要谐波
Fig.5 Dominant harmonics in air-gap generated by stator and rotor PMs of DPMEM
将式(6)和式(17)相加代入式(7)得到双永磁励磁电机的三相反电动势表达式为
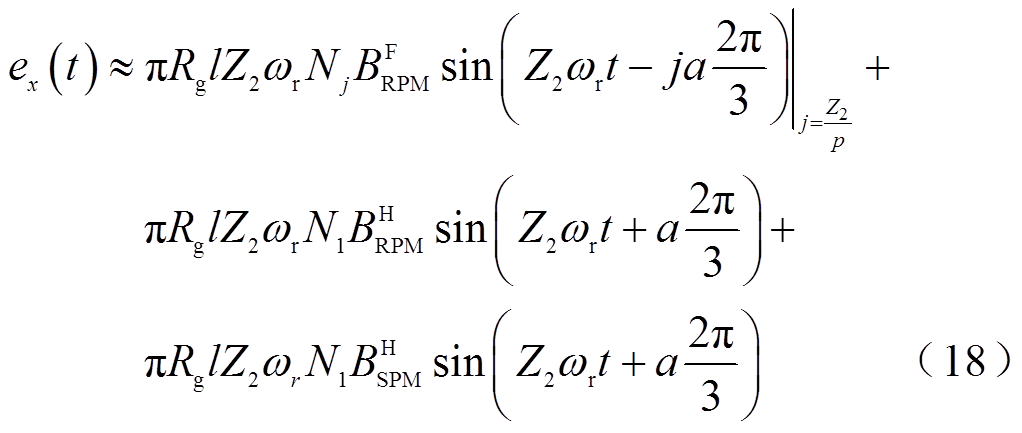
式中,第一项、第二项和第三项分别表示转子磁体基波、转子永磁磁场经定子齿极结构调制的谐波及定子永磁磁场经转子齿极结构调制的谐波产生的反电动势。然而,定子磁体基波磁通密度由于不随时间变化,没有产生反电动势。
将式(18)代入式(11)得到双永磁励磁电机输出转矩表达式,即
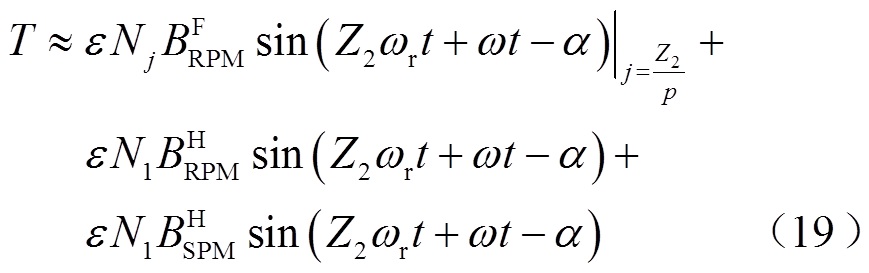
从式(19)可以得出,当ω与ωr满足式(13),双永磁励磁电机输出稳定的转矩。当a=-π/2,双永磁励磁电机输出最大转矩为
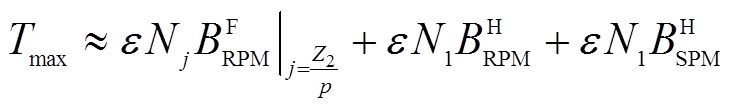 (20)
(20)由式(20)可知,转子磁体基波磁场、转子永磁磁场被调制的谐波磁场及定子永磁磁场被调制的谐波磁场均参与了转矩的输出。然而,定子磁体基波磁场对转矩的输出没有贡献。
1)场调制型永磁电机空载时,转子永磁磁场被定子齿极结构有效调制或定子永磁磁场被转子齿极结构有效调制的现象称为“单向磁场调制效应”;场调制型永磁电机空载时,转子永磁磁场被定子齿极结构有效调制,同时定子永磁磁场被转子齿极结构有效调制的现象称为“双向磁场调制效应”。本文研究的常规永磁游标电机属于前者,而双永磁励磁电机属于后者。
2)对比图3和图5可知,常规永磁游标电机在“单向磁场调制效应”的作用下,气隙中只有两个主要磁场谐波,而双永磁励磁电机在“双向磁场调制效应”的作用下,气隙中有四个主要磁场谐波。
3)对比式(10)与式(18)、式(14)与式(20)可知,双永磁励磁电机反电动势和输出转矩表达式均比永磁游标电机的多了一项,这意味着双永磁励磁电机提供的反电动势和转矩比永磁游标电机的要大。
4)由式(18)与式(19)可知,双永磁励磁电机定子永磁基波磁场由于静止不动,并未参与机电能量转换。
本节以一台常规表贴式永磁游标电机和一台由该游标电机演变而来的双永磁励磁电机为例(如图1所示),通过二维有限元法验证第2节推导的反电动势和输出转矩表达式,并对比两台电机的整体性能。特别强调,两台电机定子铁心和转子磁体尺寸参数、定子槽数和齿数、转子磁体和绕组极对数、线圈匝数、绕组联结方式及铁心和永磁体材料均相同,详细说明见表1。两台电机槽电动势星形图和绕组联结如图6所示。
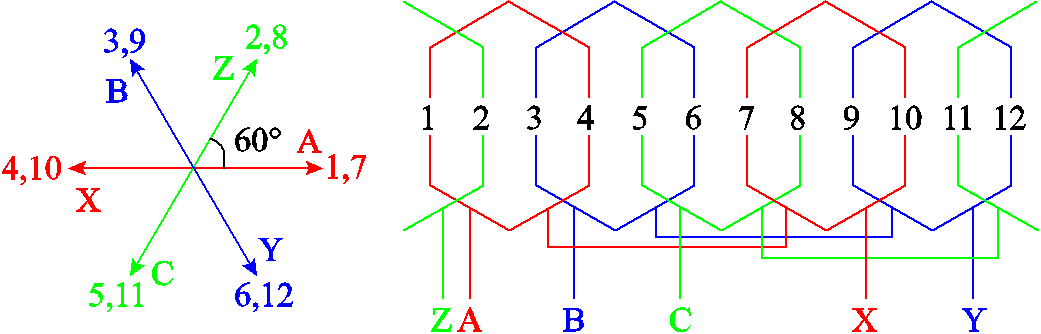
图6 槽电动势星形图和绕组联结图
Fig.6 Slot EMF star vectogram and winding connection
表1 两台电机说明
Tab.1 The specifications of two machines

参数数值 PMVMDPMEM 定子槽数Z11212 定子磁体极对数Z1—12 转子磁体极对数Z21010 绕组极对数p22 每个线圈匝数288288 相电阻Ra/Ω1.71 1.71 额定电流有效值I/ A3.14 3.14 额定转速/(r/min)120 120 磁体剩磁/T1.2 1.2 磁体相对磁导率1.051.05 磁体电阻率/(Ω·m)1.44´10-61.44´10-6 定转子铁心材料50H47050H470 定子铁心外径、内径/mm150, 80 150, 80 定子轭厚度/mm1010 定子磁体厚度/mm—3.5 气隙长度/mm0.60.6 转子磁体厚度/mm6 6 转子轭外径、内径/mm66.8, 3066.8, 30 轴向有效长度l/mm6060 气隙平均半径Rg/mm39.739.7 电机总体积V0/mm31.02´1061.02´106 磁体总体积V1/mm373 921.4 65 665.4
两台电机空载磁场分布如图7所示。尽管磁体极对数很多,但是在场调制效应的作用下都形成了2对极磁场谐波,如图7中包络线所示,且调制的谐波极对数与绕组的相同。从颜色来看,双永磁励磁电机调制的场谐波比常规永磁游标电机的要大。
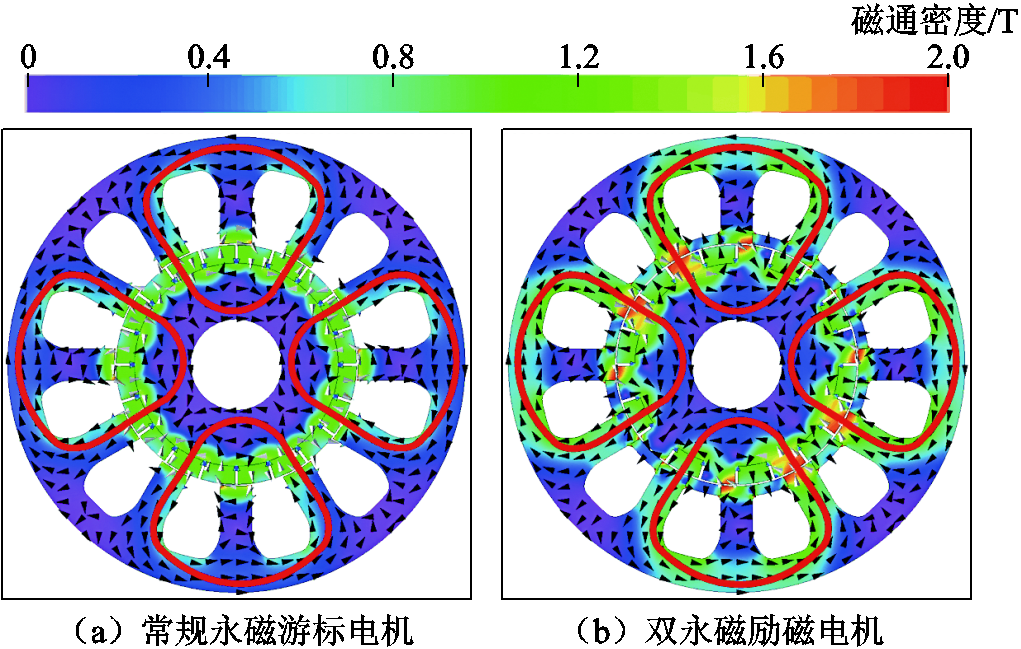
图7 两台电机空载磁场分布
Fig.7 No-load magnetic field distribution of two machines
两台电机永磁体单独作用时的气隙磁通密度波形及相应的谐波谱如图8所示。从图8可以看出,双永磁励磁电机在BFME作用下产生了四个主要谐波,而常规永磁游标电机只有两个,这与本文第2节的分析相吻合。
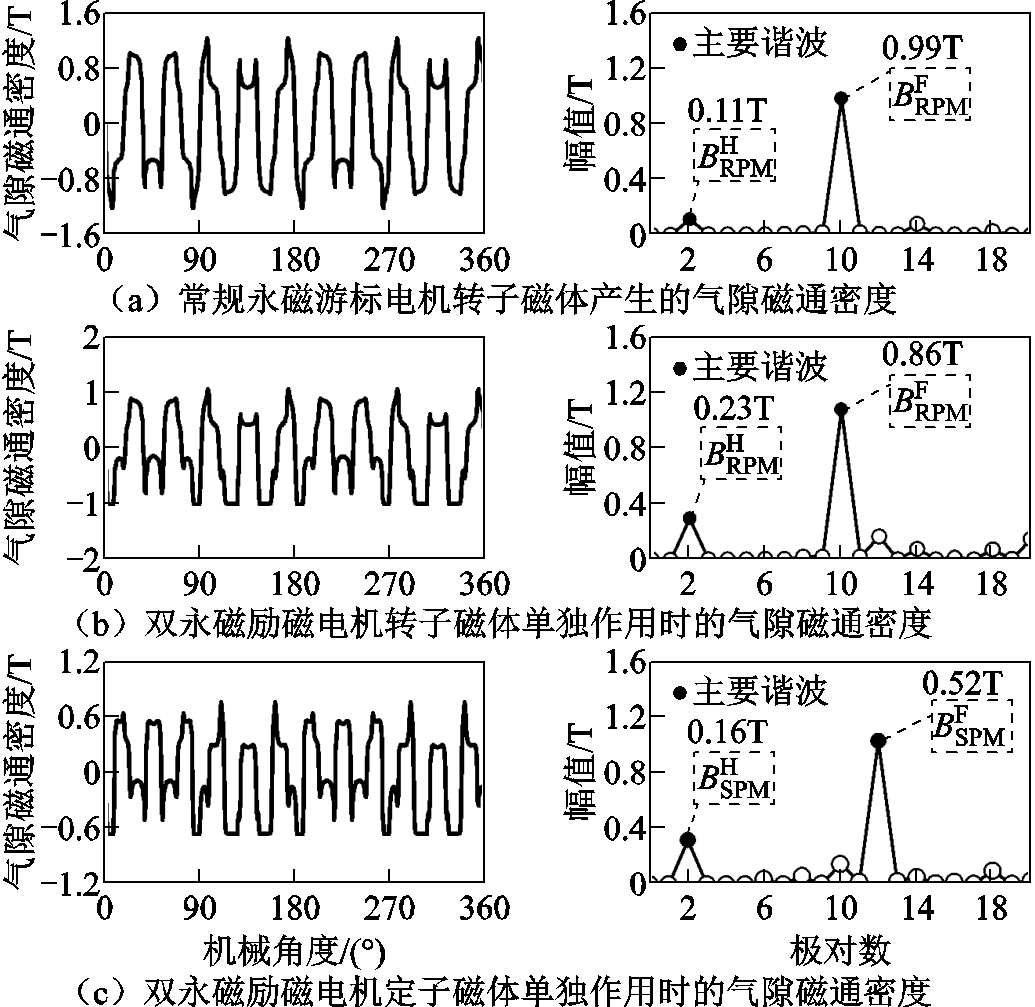
图8 气隙磁密波形及对应的谐波谱
Fig.8 Air-gap flux density waveforms and corresponding harmonic spectrum
两台电机的齿槽转矩波形如图9所示。显然,它们的齿槽转矩峰值非常接近。
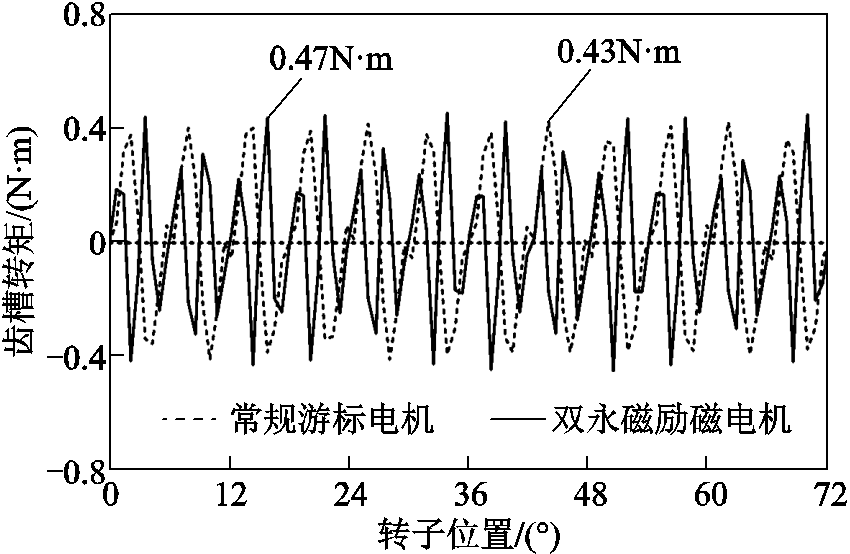
图9 齿槽转矩波形
Fig.9 Waveforms of cogging torque
两台电机仿真得到的三相反电动势波形如图10所示,可以看出在额定转速下,双永磁励磁电机的反电动势最大值比常规永磁游标电机的要大,几乎是它的两倍。将图8中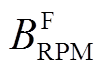 、
、 、
、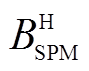 的数值及表1中相关数据分别代入式(10)和式(18),通过Matlab得到图10中的波形。分别对比图10a及图11a,图10b及图11b,可以看出仿真得到的反电动势最大值与公式计算的反电动势最大值相差不大,这证明了式(10)和式(18)的正确性。
的数值及表1中相关数据分别代入式(10)和式(18),通过Matlab得到图10中的波形。分别对比图10a及图11a,图10b及图11b,可以看出仿真得到的反电动势最大值与公式计算的反电动势最大值相差不大,这证明了式(10)和式(18)的正确性。

图10 仿真得到的反电动势波形
Fig.10 Back EMF waveforms obtained by simulation
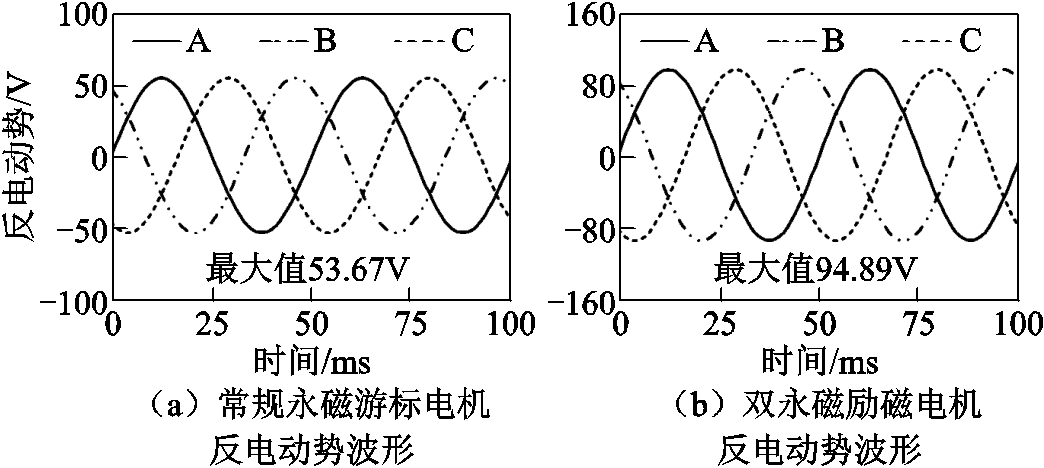
图11 通过公式得到的反电动势波形
Fig.11 Back EMF waveforms obtained by formula
两台电机电感波形如图12所示。可以看出,在相同绕组匝数和联结方式的情况下,双永磁励磁电机的自感(La)、互感(Mab)、直轴电感(Ld)及交轴电感(Lq)均比常规永磁游标电机的大。此外,各自的交直轴电感相差不大,对于PMVM而言,Ld≈Lq=93.63 mH;对于双永磁励磁电机而言,Ld≈Lq=161.81 mH,这也反映了两台电机的凸极效应不明显,可以忽略不计。
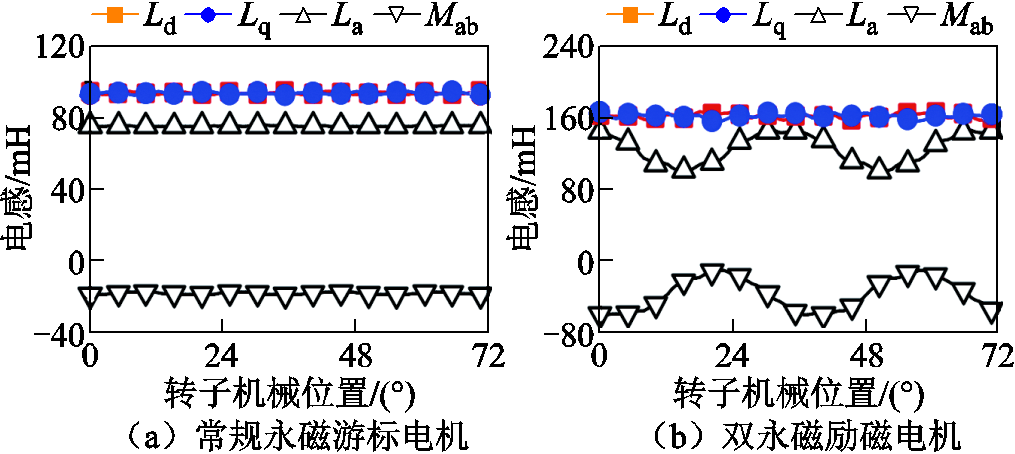
图12 电感波形
Fig.12 Inductance waveforms
转子转速为零,电流I=3.14 A时,两台电机转矩随电流相位变化的波形如图13所示。图中公式计算得到的波形是将图8中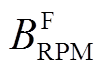 、
、 、
、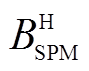 的数值及表1中相关数据分别代入到式(12)和式(19),通过Matlab得到的。由图13可以得出,在电负荷相同以及磁体用量小的情况下,双永磁励磁电机能够输出的最大转矩比常规永磁游标电机输出的最大转矩要大。对比两台电机各自仿真波形与通过公式计算得到的波形,发现结果相差不大,尤其是常规永磁游标电机的结果,这证明了式(12)和式(19)推导的正确性。双永磁励磁电机的结果相差略大是由铁心饱和所致。
的数值及表1中相关数据分别代入到式(12)和式(19),通过Matlab得到的。由图13可以得出,在电负荷相同以及磁体用量小的情况下,双永磁励磁电机能够输出的最大转矩比常规永磁游标电机输出的最大转矩要大。对比两台电机各自仿真波形与通过公式计算得到的波形,发现结果相差不大,尤其是常规永磁游标电机的结果,这证明了式(12)和式(19)推导的正确性。双永磁励磁电机的结果相差略大是由铁心饱和所致。

图13 转矩随电流相角变化波形
Fig.13 Torque versus current phase angle waveforms
两台电机在额定电流、额定转速下输出的最大转矩波形如图14所示。从图14可以得出:①双永磁励磁电机的转矩纹波比常规永磁游标电机的要大,但是平均转矩明显地高于常规永磁游标电机,高了约65%;②常规永磁游标电机和双永磁励磁电机的转矩密度分别为23.76kN×m/m3和39.10kN×m/m3,单位磁体体积的输出转矩分别为327.92kN·m/m3和607.47kN×m/m3。对比可知,双永磁励磁电机分别将转矩密度和单位磁体体积的转矩提高了65%和85%。
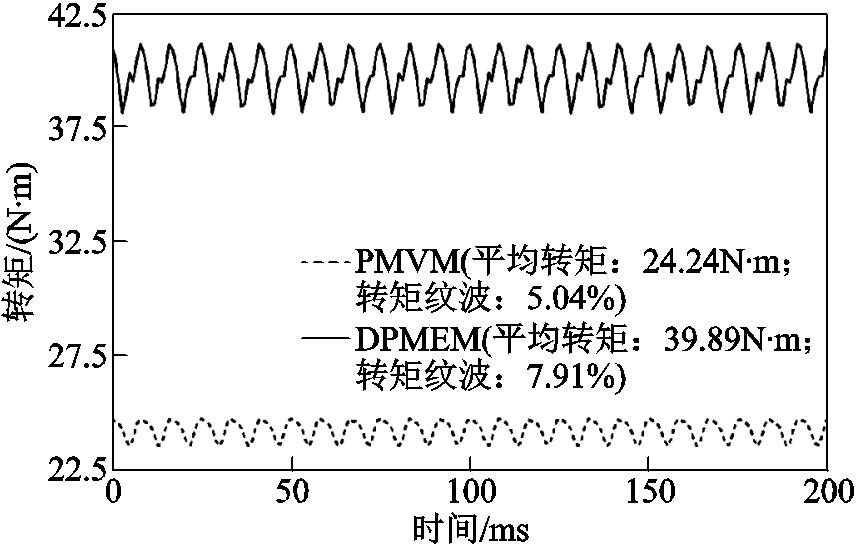
图14 额定输出转矩波形
Fig.14 Rated output torque waveforms
电机功率因数(Power Factor, PF)可以由式(21)计算。
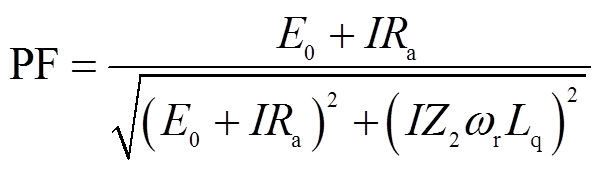 (21)
(21)式中,E0为反电动势有效值。这样计算得到双永磁励磁电机和常规永磁游标电机在额定状态下的功率因数分别为0.76和0.74。由此可知,尽管双永磁励磁电机的交、直轴电感约为常规永磁游标电机的1.73倍,但是功率因数并未显著减小,相反,由于较高的E0,功率因数略高于常规PMVM。
借助Jmag-designer有限元仿真工具得到两台电机额定状态下的损耗,见表2。从表2可以看出,双永磁励磁电机总的铁心损耗约为常规永磁游标电机的2.63倍。双永磁励磁电机总铁损比常规永磁游标电机大的主要原因是双永磁励磁电机定、转子铁心上均有永磁体,而它的定子铁心与常规永磁游标电机的完全一样,且等效气隙长度比常规永磁游标电机的要小得多,其铁心较常规永磁游标电机的更易饱和,尤其是定子铁心(磁场分布见图7,特别说明:铁心材料50H470的B-H曲线拐点处对应的磁通密度为1.4 T)。此外,对于两台电机各自而言,铁损主要集中在定子铁心上,其中双永磁励磁电机总的定子铁损占总铁损的比例为75%,而常规永磁游标电机占的比例为89%。
表2 两台在额定状态下的损耗
Tab.2 The losses of two machines at rated condition (单位:W)

类型损耗 PMVMDPMEM 定子铁心涡流损耗0.16 0.49 定子铁心磁滞损耗1.312.77 总的定子铁心损耗1.473.26 转子铁心涡流损耗0.040.32 转子铁心磁滞损耗0.140.76 总的转子铁心损耗0.181.08 总的铁心损耗Piron1.654.34 永磁体损耗PPM0.350.21 铜损耗PCu50.6350.63
在不考虑摩擦损耗、风阻和杂散损耗的情况下,电机的效率计算式为[34,37]
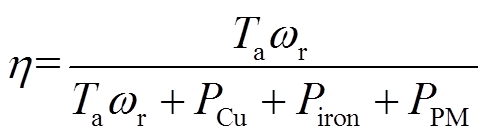 (22)
(22)式中,Ta和ωr分别为电机输出的平均转矩和转子的机械角频率(rad/s);PCu、Piron、PPM分别为铜损耗、总的铁心损耗以及永磁体损耗。将图14中的额定平均转矩,额定转速120 r/min对应的机械角频率以及表2中的相关损耗代入式(22),得到常规PMVM和DPMEM在额定状态下的效率,分别为85%和90%,显然,DPMEM将效率提高了5%。
电机磁体是否退磁可以通过比较磁体沿充磁方向的最小磁通密度与磁体退磁曲线拐点处的磁通密度来判断。若磁体沿充磁方向的最小磁通密度大于磁体退磁曲线拐点处的磁通密度,则磁体不会退磁;反之,磁体存在不可逆退磁风险。为了方便分析,根据表1磁体的剩磁和相对磁导率,可以认为磁体为稀土永磁体,其退磁曲线为线性,且拐点处的磁通密度为0。评估两台电机在额定状态下的退磁情况,只需比较两台电机磁体径向最小磁通密度与0的大小。通过有限元分析,得到常规永磁游标电机和双永磁游标电机磁体沿径向充磁的最小磁通密度,分别如图15a及图15b所示。由图15a可知,当转子转过一个电周期,磁体径向最小磁通密度始终大于0,因此,常规永磁游标电机的磁体在额定状态下不会出现退磁现象。从图15b可以看出,无论是定子磁体还是转子磁体,波形出现了部分径向最小磁通密度小于0的情况,这意味着在额定状态下,双永磁励磁电机的定子和转子磁体存在局部不可逆退磁的风险。此外,转子磁体的径向最小磁通密度与0的差值较小,这表明双永磁励磁电机的定子磁体比转子磁体更易出现退磁现象。
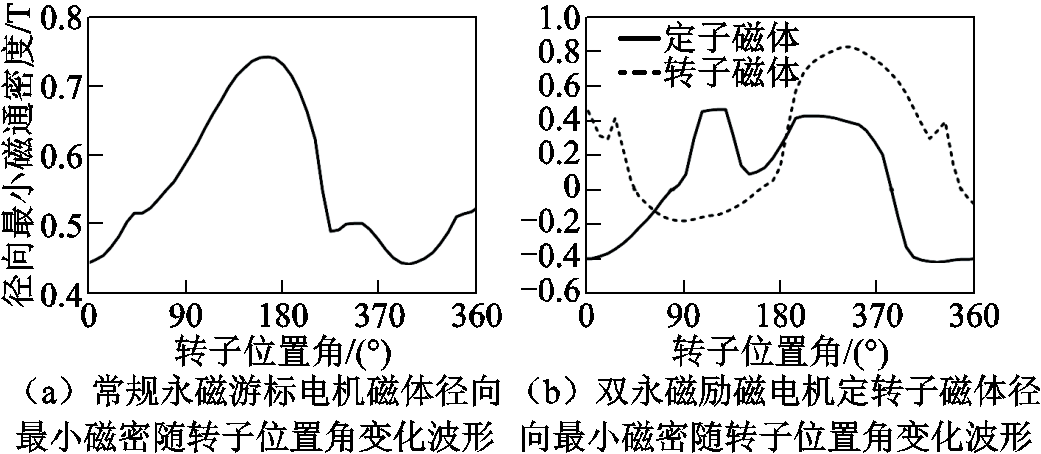
图15 最小磁通密度波形
Fig.15 Waveforms of minimum flux density
图16给出了双永磁励磁电机在额定状态下退磁最严重的定转子磁体退磁区域分布。图16由有限元仿真得到的磁场云图经过Matlab后处理得到。从图16可以看出,定子磁体退磁区域明显比转子磁体的要大。经计算,定、转子磁体退磁区域占各自整块磁体区域的比例分别为1.68%和0.18%。退磁区域所占比例很小,因此,双永磁励磁电机在额定状态下的退磁风险可以忽略不计。
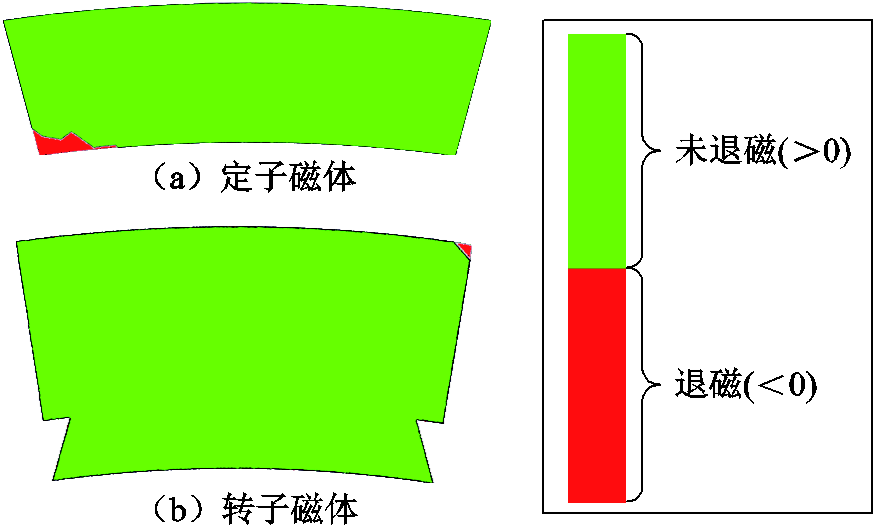
图16 额定状态下双永磁励磁电机中退磁最严重的定、转子磁体的退磁区域分布
Fig.16 Demagnetization region distribution of stator and rotor PMs with the worst demagnetization in the DPMEM at rated condition
本文对比分析了两种典型的场调制型永磁电机,即常规永磁游标电机和双永磁励磁电机的性能和特点,得到以下结论:
1)从结构上来看,常规表贴式PMVM只有一套磁体、一个齿极结构,而DPMEM有两套磁体、两个齿极结构;DPMEM磁体极对数的构成采用CP方式,所有磁体极性相同,定转子磁体极对数与相应的定转子齿数相同,确保了有效的磁场调制。
2)从工作原理来看,常规PMVM基于单向场调制效应,而DPMEM基于双向磁场调制效应。前者气隙有两个主要永磁谐波,而后者有四个主要永磁谐波。后者虽然有四个主要谐波,但是从反电动势和转矩表达式可以看出,实际参与机电能量转换的只有三个,即转子磁体基波和谐波、定子磁体谐波。
3)对比反电动势和转矩表达式可以得出,与UFME相比,BFME能够额外引入一个定子永磁谐波。这是DPMEM反电动势和转矩高于常规PMVM的原因。尽管BFME引入了一套定子永磁体,但是DPMEM磁体用量比常规PMVM的少,减少了11.17%。
4)仿真结果表明常规PMVM及DPMEM一般性表达式推导的正确性。仿真结果还表明DPMEM在磁体用量、反电动势、功率因数、效率、转矩密度及单位磁体体积的转矩方面优于常规PMVM。与常规PMVM比较而言,DPMEM的磁体用量减少了11.17%,反电动势增加了一倍,转矩密度、效率及单位磁体体积的转矩分别提高了65%、5%及85%。
5)DPMEM的铁损比常规PMVM的大,主要原因是双永磁励磁电机定、转子铁心上均有永磁体,其铁心较常规永磁游标电机的更易饱和。对于它们各自而言,铁损都集中在定子铁心上。
6)双永磁励磁电机定、转子虽然都有齿极结构,但是交直轴电感很接近,凸极效应很小,可以忽略不计。
7)在额定状态下,常规PMVM不存在退磁风险,而DPMEM存在局部退磁风险。但经评估发现,退磁最严重的定、转子磁体,退磁区域占整个磁体区域的比例很小,因此,DPMEM在额定状态下的退磁风险可以忽略不计。
参考文献
[1] 鲍晓华, 刘佶炜, 孙跃, 等. 低速大转矩永磁直驱电机研究综述与展望[J]. 电工技术学报, 2019, 34(6): 1148-1160. Bao Xiaohua, Liu Jiwei, Sun Yue, et al. Review and prospect of low-speed high-torque permanent magnet machines[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1148-1160.
[2] Li Xianglin, Chau K T, Cheng Ming, et al. Performance analysis of a flux-concentrating field-modulated permanent-magnet machine for direct-drive applications[J]. IEEE Transactions on Magnetics, 2015, 51(5): 1-11.
[3] Jian Linni, Chau K T, Jiang Jianzhong. A magnetic-geared outer-rotor permanent-magnet brushless machine for wind power generation[J]. IEEE Transactions on Industry Applications, 2009, 45(3): 954-962.
[4] Toba A, Lipo T A. Generic torque-maximizing design methodology of surface permanent-magnet vernier machine[J]. IEEE Transactions on Industry Applications, 2000, 36(6): 1539-1546.
[5] Li Dawei, Qu Ronghai, Li Jian, et al. Analysis of torque capability and quality in vernier permanent magnet machines[J]. IEEE Transactions on Industry Applications, 2016, 52(1): 125-135.
[6] Jian Linni, Shi Yujun, Liu Cheng, et al. A novel dual-permanent-magnet-excited machine for low-speed large-torque applications[J]. IEEE Transactions on Magnetics, 2013, 49(5): 2381-2384.
[7] Zhao Wenxiang, Sun Xiaojin, Ji Jinghua, et al. Design and analysis of new vernier permanent-magnet machine with improved torque capability[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4): 1-5.
[8] Jiang Shan, Liu Guohai, Zhao Wenxiang, et al. Modeling and analysis of spoke-type permanent magnet vernier machine based on equivalent magnetic network method[J]. Chinese Journal of Electrical Engineering, 2018, 4(2): 96-103.
[9] 张进, 张秋菊. 同极内嵌式永磁游标电机电磁性能分析[J]. 电机与控制学报, 2020, 24(4): 158-164. Zhang Jin, Zhang Qiuju. Electromagnetic performances analysis of a consequent-pole interior permanent magnet vernier machine[J]. Electric Machines and Control, 2020, 24(4): 158-164.
[10] Kim B, Lipo T A. Operation and design principles of a PM vernier motor[J]. IEEE Transactions on Industry Applications, 2014, 50(6): 3656-3663.
[11] Liu Guohai, Jiang Shan, Zhao Wenxiang, et al. Modular reluctance network simulation of a linear permanent magnet vernier machine using new mesh generation methods[J]. IEEE Transactions on Industrial Electronics, 2017, 64(7): 5323-5332.
[12] 杨玉波, 刘国鹏, 陈鹏, 等. 基于子域法的游标混合电机电磁性能解析计算[J]. 电机与控制学报, 2019, 23(9): 9-17, 25. Yang Yubo, Liu Guopeng, Chen Peng, et al. Electromagnetic performance investigation of vernier hybrid machine[J]. Electric Machines and Control, 2019, 23(9): 9-17, 25.
[13] Liu Guohai, Jiang Shan, Zhao Wenxiang, et al. A new modeling approach for permanent magnet vernier machine with modulation effect consideration[J]. IEEE Transactions on Magnetics, 2017, 53(1): 1-12.
[14] Xu Liang, Liu Guohai, Zhao Wenxiang, et al. Hybrid stator design of fault-tolerant permanent-magnet vernier machines for direct drive applications[J]. IEEE Transactions on Industrial Electronics, 2017, 64(1): 179-190.
[15] 梁子漪, 曲荣海, 李大伟, 等. 一种交替极切向励磁游标永磁电机的分析与设计[J]. 电工技术学报, 2020, 35(15): 3173-3181. Liang Ziyi, Qu Ronghai, Li Dawei, et al. Analysis of a consequent-pole spoke-array vernier permanent magnet machine[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3173-3181.
[16] 李岱岩, 白保东, 杨晨, 等. 基于调磁块阵列的永磁游标电机研究[J]. 电工技术学报, 2018, 33(增刊2): 359-366. Li Daiyan, Bai Baodong, Yang Chen, et al. Study of permanent magnet vernier machine by using magnetic tuning block array[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 359-366.
[17] Shi Chaojie, Qu Ronghai, Gao Yuting, et al. Design and analysis of an interior permanent magnet linear vernier machine[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.
[18] Li Dawei, Qu Ronghai, Li Jian, et al. Consequent-pole toroidal-winding outer-rotor vernier permanent-magnet machines[J]. IEEE Transactions on Industry Applications, 2015, 51(6): 4470-4481.
[19] Shi Yujun, Jian Linni. A novel dual-permanent-magnet-excited machine with flux strengthening effect for low-speed large-torque applications[J]. Energies, 2018, 11(1): 1-17.
[20] Liang Ziyi, Gao Yuting, Li Dawei, et al. Design of a novel dual flux modulation machine with consequent-pole spoke-array permanent magnets in both stator and rotor[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(1): 73-81.
[21] Wang Qingsong, Niu Shuangxia. A novel hybrid-excited dual-PM machine with bidirectional flux modulation[J]. IEEE Transactions on Energy Conversion, 2017, 32(2): 424-435.
[22] Xie Kangfu, Li Dawei, Qu Ronghai, et al. A novel permanent magnet vernier machine with Halbach array magnets in stator slot opening[J]. IEEE Transactions on Magnetics, 2017, 53(6): 1-5.
[23] Xu Liang, Zhao Wenxiang, Liu Guohai, et al. Design optimization of a spoke-type permanent-magnet vernier machine for torque density and power factor improvement[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3446-3456.
[24] Siddiqi M R, Kffaliq S, Kwon J W, et al. Optimal design of dual stator spoke type vernier machine considering armature winding placement[J]. International Journal of Applied Electromagnetics and Mechanics, 2019, 59(3): 921-930.
[25] Jian Linni, Shi Yujun, Wei Jin, et al. Design optimization and analysis of a dual-permanent-magnet-excited machine using response surface methodology[J]. Energies, 2015, 8(9): 10127-10140.
[26] 陈晓, 赵文祥, 吉敬华, 等. 考虑边端效应的双边直线永磁游标电机模型预测电流控制[J]. 电工技术学报, 2019, 34(1): 53-61. Chen Xiao, Zhao Wenxiang, Ji Jinghua, et al. Model predictive current control of double-side linear vernier permanent magnet machines considering end effect[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 53-61.
[27] 陈浩, 和阳, 赵文祥, 等. 基于占空比调制的五相容错永磁游标电机直接转矩控制[J]. 电工技术学报, 2020, 35(5): 1055-1064. Chen Hao, He Yang, Zhao Wenxiang, et al. Direct torque control of five-phase fault-tolerant permanent magnet vernier motor based on duty cycle modulation [J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1055-1064.
[28] Zhao Wenxiang, Gu Chenyu, Chen Qian, et al. Remedial phase-angle control of a five-phase fault-tolerant permanent-magnet vernier machine with short-circuit fault[J]. CES Transactions on Electrical Machines and Systems, 2017, 1(1): 83-88.
[29] 刘国海, 杨欣宇, 徐亮, 等. 五相永磁容错型游标电机弱磁特性研究[J]. 电工技术学报, 2017, 32(19): 52-61. Liu Guohai, Yang Xinyu, Xu Liang, et al. Research on flux-weakening performances for five-phase fault-tolerant permanent-magnet vernier motors[J]. Transactions of China Electrotechnical Society, 2017, 32(19): 52-61.
[30] 陈仲华, 赵文祥, 张建, 等. 高推力永磁游标直线电机的开放式绕组SVPWM控制[J]. 电工技术学报, 2016, 30(增刊2): 216-224. Chen Zhonghua, Zhao Wenxiang, Zhang Jian, et al. SVPWM control for dual two-level inverter fed open-end winding high thrust permanent magnet vernier linear motor[J]. Transactions of China Electrotechnical Society, 2016, 29(S2): 216-224.
[31] 矫帅, 赵文祥, 邱先群, 等. 基于改进式反电动势法的直线游标永磁电机无位置传感器控制[J]. 电工技术学报, 2016, 31(增刊2): 242-248. Jiao Shuai, Zhao Wenxiang, Qiu Xianqun, et al. Sensorless control of linear permanent magnet vernier motor based on improved stator back EMF[J]. Transactions of China Electrotechnical Society, 2016, 31(S2): 242-248.
[32] Niu Shuangxia, Ho S L, Fu W N. A novel stator and rotor dual PM vernier motor with space vector pulse width modulation[J]. IEEE Transactions on Magnetics, 2014, 50(2): 805-808.
[33] Wu Leilei, Qu Ronghai, Li Dawei, et al. Influence of pole ratio and winding pole numbers on performances and optimal Design parameters of surface permanent magnet vernier machines[J]. IEEE Transactions on Industry Applications, 2015, 51(5): 3707-3715.
[34] Shi Yujun, Wei Jin, Deng Zhengxing, et al. Design and analysis of a dual-permanent-magnet-excited machine for low-speed large-torque applications[J]. Journal of Electronic Materials, 2019, 48(3): 1400-1411.
[35] Yu Yanlei, Chai Feng, Pei Yulong, et al. Comparisons of torque performance in surface-mounted PM vernier machines with different stator tooth topologies[J]. IEEE Transactions on Industry Applications, 2019, 55(4): 3671-3684.
[36] Zou Tianjie, Li Dawei, Ru Ronghai, et al. Performance comparison of surface and spoke-type flux-modulation machines with different pole ratios[J]. IEEE Transactions on Magnetics, 2017, 53(6): 1-5.
[37] Xu Liang, Liu Guohai, Zhao Wenxiang, et al. Quantitative comparison of integral and fractional slot permanent magnet vernier motors[J]. IEEE Transactions on Energy Conversion, 2015, 30(4): 1483-1495.
[38] Shi Yujun, Niu Shuangxia, Wei Jin, et al. Comparison between dual-permanent-magnet-excited machines with fewer stator poles and fewer rotor poles[J]. IEEE Transactions on Magnetics, 2015, 51(3): 1-4.
Comparative Analysis of Two Typical Field Modulated Permanent-Magnet Machines
Abstract In this paper, the performance and characteristics of two typical field modulated permanent-magnet machines (FMPMs), i.e. regular permanent-magnet vernier machine (PMVM) and dual permanent-magnet-excited machine (DPMEM), were compared and analyzed. Firstly, the structures of the two machines were introduced and their structural characteristics were summarized. Next, by deducing the general expressions of the two machines, i.e. no-load back electromotive force (EMF) and output torque, their working principles were revealed, and the “unidirectional field modulation effect (UFME)” and “bi-directional field modulation effect (BFME)” were compared. Finally, by finite element method (FEM), the performance of two machines was compared and analyzed, and the correctness of the general expressions was verified. The results of FEM simulation show that under the same size, number of stator slots and stator teeth, pole-pair number (PPN) of windings and rotor permanent magnets (PMs), turns of each coil, winding connection, electric load, copper loss and rotational speed, the DPMEM is superior to the regularPMVM in terms of PM consumption, back EMF, torque density, torque per unit volume of magnet, power factor and efficiency.
keywords:Field modulated, permanent magnet machine, torque density, vernier machine
中图分类号:TM351
DOI:10.19595/j.cnki.1000-6753.tces.191108
深圳市科技创新委员会项目(ZDSYS201604291912175),澳门科学技术发展基金(FDCT/040/2017/A1)和澳门大学研究委员会项目(MYRG2017-00158-FST)和深圳市稳定支持面上项目(2020ZDZX3002)资助。
收稿日期 2019-08-30
改稿日期 2019-12-19
石玉君 男,1986年生,博士研究生,研究方向为新型永磁电机的设计、优化与控制。E-mail:shiyj3@mail.sustech.edu.cn
蹇林旎 男,1983年生,副教授,博士生导师,研究方向为电机及其驱动系统、电动汽车与电网能量交互、智能微电网、电动汽车无线充电技术与新能源产业发展规划。E-mail:jianln@sustech.edu.cn(通信作者)
(编辑 郭丽军)