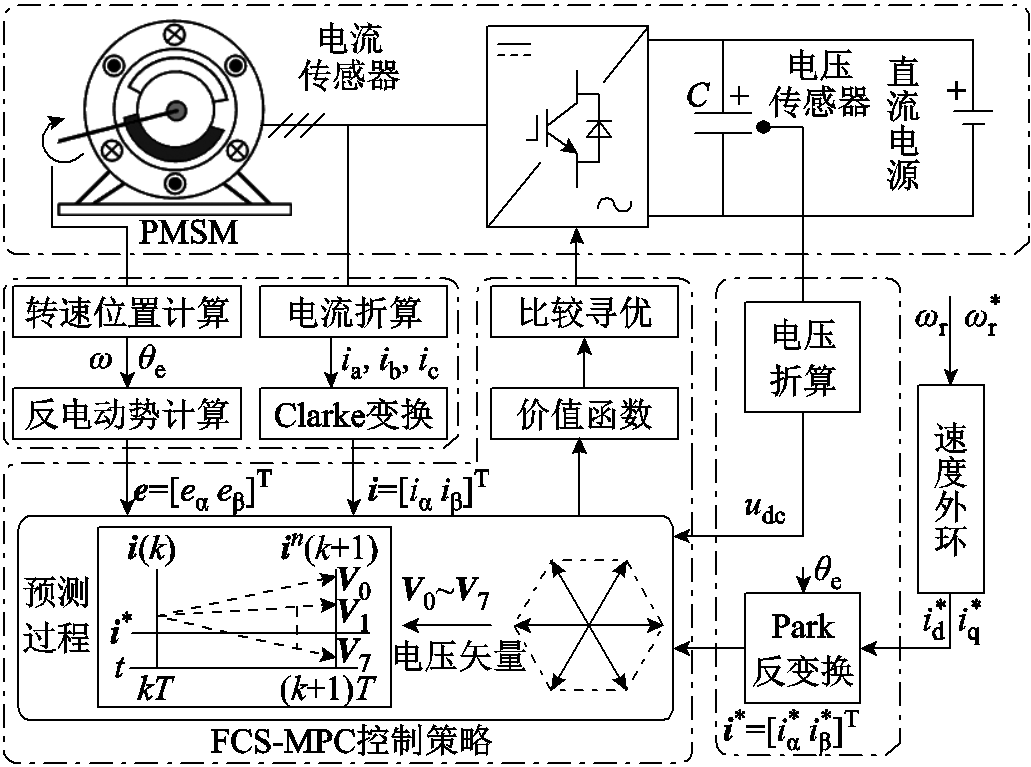
图1 FCS-MPC控制策略结构图
Fig.1 Structure diagram of FCS-MPC control strategy
摘要 有限集模型预测控制算法存在较长程序执行时间与较短控制周期之间的矛盾，算法执行效率低于传统线性控制算法，进而影响开关频率与控制精度的进一步提高。针对此问题，结合近几年微控制器在多核心领域的发展，以永磁同步电机为被控对象，提出一种基于多核并行计算的有限集模型预测控制策略。由于算法对数据、时序依赖度高，与微控制器中多核心独立运行特点相矛盾，为此，该文设计了双核、四核控制策略架构，并提出数据交换策略和动态标志位。通过搭建实验系统，对所提方法的动稳态性能、附加约束兼容性、程序执行时间进行分析对比，证明了所提方法能够在保持原算法控制性能和控制特点的基础上，有效降低算法执行时间。
关键词：永磁同步电机 有限集模型预测控制 多核心 并行计算
在过去的十几年中，有限集模型预测控制（Finite Control Set Model Predictive Control, FCS-MPC）算法发展迅速，并在电力电子变换器、电机驱动以及可再生能源等领域得到了国内外学者的广泛关注。与传统的线性控制策略相比，FCS-MPC具有诸如内部解耦、动态性能好、易于加入非线性约束等优点[1-4]。
但是，相比传统线性控制算法，FCS-MPC算法需要更大的计算量[5]。其原因在于：①FCS-MPC算法的实现依赖被控对象数学模型的精确描述，计算过程较为复杂[6]；②FCS-MPC算法需要对变流器所能输出的所有电压矢量的作用效果进行分别预测，相应的迭代计算过程将大幅增加计算量[7]；③FCS-MPC算法在寻优过程中，价值函数计算及结果之间的比较过程需要耗费较大计算量[8]。
与传统线性控制算法相比，FCS-MPC不采用脉宽调制方法，其开关频率不恒定。因此，为了达到相近的稳态控制效果，FCS-MPC算法的控制周期必须小于传统线性控制算法。在基于两电平逆变器的永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）驱动系统中，FCS-MPC算法的控制周期接近传统线性控制算法的六分之一[9]，造成了FCS-MPC算法中较长程序执行时间与较短控制周期之间的矛盾。目前，在绝大多数FCS-MPC研究成果中，系统控制周期大于10μs，平均开关频率一般不高于10kHz [10]。与之相比，基于脉宽调制技术的线性控制算法，在采用绝缘栅双极型晶体管（Insulated Gate Bipolar Transistor, IGBT）的电压源型逆变器中开关频率可达15kHz。随着微处理器和半导体技术的发展，特别是宽禁带半导体（氮化镓和碳化硅）的应用，高性能电机驱动系统的开关频率可达20kHz甚至更高，这意味着FCS-MPC算法的程序执行时间已成为限制其性能提升的瓶颈[11]。算法执行时间过长将不利于控制频率的提高，造成定子电流误差无法得到及时修正，从而降低电机的稳态控制精度。
为了解决这一问题，相关研究主要分为两个方向：①在软件上简化FCS-MPC算法；②在硬件上提高FCS-MPC的算法执行效率。针对软件方面的简化，最近几年，一些FCS-MPC简化方法相继被提出。文献[12]通过对空间电压矢量进行分区，减少预测过程中候选矢量的数量，从而缩短程序运行时间。文献[13]通过预测式的等效变换和电压矢量的分区，简化了预测过程和电压矢量寻优过程。文献[14]通过将李雅普诺夫原理引入扇区分区方法中，消除了不需要的电压矢量，简化了算法控制结构。对于其他类型的拓扑结构，一些学者针对六相电机或双三相电机，采用电压矢量筛选法、查表法、预测式转化法等方法简化了算法结构和参数整定复杂度[15-16]。
上述针对FCS-MPC的简化方法虽然降低了算法复杂度，减少了计算时间，但是存在几个问题：
（1）大多数简化算法成立的前提基于一些假定，例如：假设定子磁链在控制周期内保持不变，或直轴电流保持为零等[17-18]。此类假定将造成简化算法与原算法不完全等效。特别是在电机处于弱磁控制模式下，直轴电流通常不为零，导致简化算法的前提假设不成立，从而影响算法的控制性能。
（2）部分算法对预测过程和价值函数进行了变换，从而简化了算法结构。然而，由于缺少原算法与简化算法之间的关联性推导，无法证明简化算法与原算法完全等效，同时无法确定简化算法能够保持原算法的所有特性。例如在文献[19]中，简化算法将转矩与磁链预测过程转换成单一的磁链预测过程，有效降低了算法复杂度，但简化过程忽略了转矩、磁链权值的调节作用，造成简化算法失去了原算法中调节转矩、磁链占比重的特性。因此，简化算法与原算法并非完全等效。
（3）许多简化算法没有证明其对附加约束的兼容性，当原算法中加入附加约束时，无法确定简化算法能够达到相同的控制效果。部分文献仅给出了针对个别附加约束的简化方法，但是，当存在其他附加约束时，不能确定简化方法仍然适用，即无法证明简化算法对其附加约束的普适性[20]。
由于FCS-MPC简化方法存在一定的局限性，部分学者转而研究在硬件上对FCS-MPC算法的执行效率进行优化。其中，现场可编程门阵列（Field Programmable Gate Array, FPGA）可根据编程代码生成逻辑门结构，从而实现芯片内逻辑功能的重构。由于FPGA内的逻辑门可以并行工作，因此可实现FCS-MPC算法的并行计算，减少算法执行时间。目前，国外已有少量论文进行了相关研究[21-23]。
尽管FPGA可以实现FCS-MPC的并行计算，但是，目前大部分电机驱动系统仍采用微控制器（Micro Control Unit, MCU）或数字信号处理器（Digital Signal Processor, DSP）作为其控制核心。相比FPGA，MCU集成了大量外围设备，并在电机实时控制方面进行了特定优化，具有更好的性能/成本优势。另外，MCU在编程难易程度和程序可移植性方面也有一定优势，因此，短期内FPGA难以在实时控制方面取代MCU的地位。近几年，随着MCU的发展，多核心MCU逐渐出现，使其计算性能成倍提高。然而，与FPGA架构不同，多核心MCU中各个核心是独立编程与运行的，其设计初衷是让各核心完成不同的任务，例如双核心分别完成电机控制和上位机通信，或双核心分别完成交-直-交变流器中的整流侧控制和逆变侧控制[24]。相关控制的特点在于，各核心的控制算法之间不存在数据依赖，或存在数据依赖但对时序依赖度较弱。由于FCS-MPC的各步骤紧密相连，相邻步骤间存在很强的数据和时序依赖度，难以分成两个独立运行的控制策略，如何在多核心MCU中实现FCS-MPC并行计算，是一个亟待解决的问题。目前，针对多核心MCU的FCS-MPC并行控制策略在国内外相关领域还未曾提及。考虑程序执行时间已成为限制FCS-MPC性能提升的瓶颈，而新兴的多核心MCU可以达到更高的计算性能，具有提高FCS-MPC算法执行速度的潜力，结合具有高开关速度的宽禁带半导体技术，有利于降低电流谐波和转矩脉动，提升电机系统的控制性能。因此，研究多核MCU中FCS-MPC并行计算实现方法具有一定的实际意义。
本文以德州仪器公司的TMS320F28379D为硬件平台，研究“双CPU+双CLA”架构下FCS-MPC算法的并行计算实现方法。通过对算法各个环节的数据依赖度分析，实现控制策略的分割，构建了双核、四核并行计算下的FCS-MPC控制流程。为保证FCS-MPC并行计算的时序正确性，提出了两阶段数据交换策略和动态标志位方法。最后，实验分为三部分：①通过动态稳态性能评估和附加约束兼容性测试，证明并行控制策略能够保持FCS-MPC算法的控制性能和特性；②分析并行控制策略对程序执行效率的提升效果；③分析并行控制策略运行于更短控制周期时的控制精度，证明所提方法的可行性和有效性。
基于FCS-MPC的永磁同步电机驱动系统控制策略结构如图1所示。
图1 FCS-MPC控制策略结构图
Fig.1 Structure diagram of FCS-MPC control strategy
图1中可以看到，FCS-MPC主要实现永磁同步电机的电流内环控制，而速度外环控制器可由包括线性控制在内的其他控制方法实现。虽然FCS-MPC减少了复杂的旋转坐标变换，但由于其对电机状态变量的依赖度较高，需要进行反电动势计算、Clarke变换、Park反变换以获得预测过程的输入量。FCS-MPC控制策略主要由预测过程、价值函数、比较寻优三个部分组成，其理论基础分析如下。
在静止坐标系下，表贴式永磁同步电机的电压平衡方程可以表示为
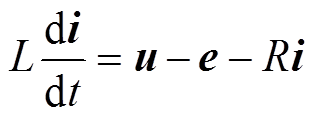（1）式中，R、L分别为电机定子电阻与定子电感；i为定子电流矢量，i=[iαiβ]T；e为定子反电动势矢量，e=[eαeβ]T；u为逆变器输出电压，u=[uαuβ]T，对于逆变器所有的8种开关状态S0~S7，u的取值对应8种电压矢量V0~V7，其数值与直流侧电压udc相关。
图1中FCS-MPC的预测过程对应电流预测式。根据前向欧拉法，电流预测式由式（1）得到，即
（2）式中，T为控制周期；i(k)为kT时刻的电流矢量测量值；in(k+1)为(k+1)T时刻的电流矢量预测值。
FCS-MPC的核心思想是：通过预测电压矢量V0~V7对电流的作用效果，筛选出距离电流参考值i*（其中i*=[i* αi* β]T）最近的电流预测值in(k+1)，并将所对应最优电压矢量Vo的开关状态输出至逆变器。在寻优过程之前，需要构建价值函数对各个预测值进行评估，有
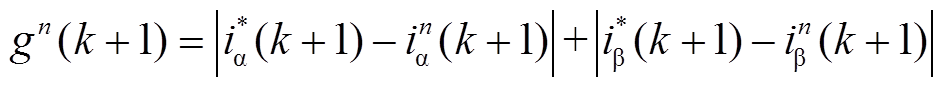（3）最优电压矢量为
式中，argmin gn(k+1)为最小gn(k+1)值对应的电压矢量Vn。
在每一个控制周期，FCS-MPC将电压矢量V0~V7代入电流预测式（式（2）），并采用价值函数对所有电流预测结果进行评估和比较，使价值函数达到最小值的电压矢量将作为最优矢量输出至逆变器。其控制流程如图2所示。
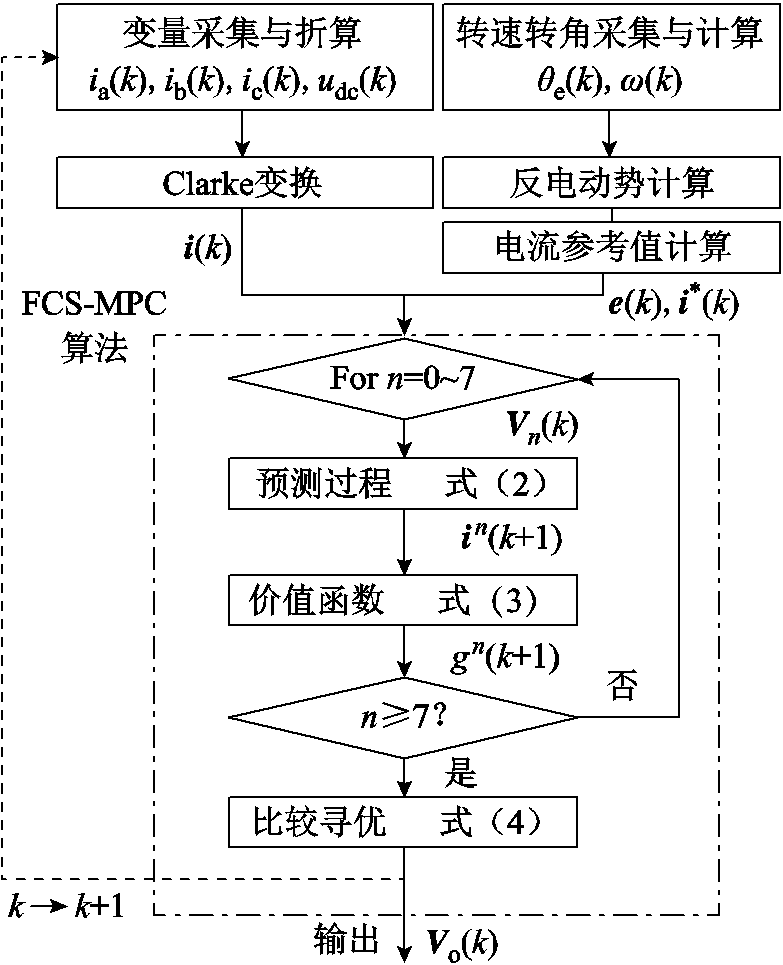
图2 FCS-MPC控制流程
Fig.2 Control flow chart of FCS-MPC
TMS320F28379D微控制器共有两个32位处理核心，即CPU1和CPU2，每个核心均可提供 200MHz的处理性能；除此之外，微控制器具有两个可编程控制律加速器（Control Law Accelerator CLA），即CPU1.CLA1和CPU2.CLA1，CLA是一种独立的32位浮点处理器，运行速度与主CPU相同。多核架构如图3所示。
图3 TMS320F28379D微控制器多核架构
Fig.3 Multi-core architecture of TMS320F28379D
图3中可以看到，CPU1与CPU2之间存在多种数据交换模式，即IPC模块、全局共享内存、MSG内存。由于CPU1与CPU2同时读写同一数据区域会产生冲突问题，三种交换模式均包含内存读写权限，例如在MSG内存中，CPU1→CPU2 MSG内存允许CPU1进行读写操作，但禁止CPU2进行写入操作；相反，CPU2→CPU1 MSG内存允许CPU2进行读写操作，但禁止CPU1进行写入操作。考虑IPC模块中的仲裁机制较为复杂，影响数据交换速度。而全局共享内存需要CPU1预先进行寄存器配置，且CPU2没有配置权限。与之相比，CPU1与CPU2之间的MSG内存具有结构简单，无需预先配置的优点，通过合理设计数据交换策略，能够实现更高的数据交换速度。与上述情况类似，CPU与CLA之间主要采用MSG内存进行数据交换，需要注意的是，两个CLA核心之间不能直接进行数据交换。
FCS-MPC单核顺序控制策略的流程如图4所示。
图4 FCS-MPC单核顺序控制策略
Fig.4 FCS-MPC single-core sequential control strategy
由图4可以看到，单核顺序控制存在三个特点：
（1）各个步骤顺序执行（部分步骤旁标注了该步骤所输出的变量）。当获得预测过程所需的所有变量时，控制流程将依次进入FCS-MPC算法的预测过程、价值函数、比较寻优三个步骤（也称为预测、评估、寻优）。此过程中，控制算法将对V0~V7进行逐个预测、评估、寻优，最终得到最优电压矢量。
（2）通过观察各个步骤可以看到，大部分步骤存在依赖关系，即前一个步骤完成之后，才能进行下一步骤。例如，Clarke变换必须在A-D转换、电压电流折算之后进行；另一方面，部分步骤之间不存在依赖关系，例如A-D转换与eQEP模块可以同时运行，同理，Clarke变换与反电动势计算可以同时进行，因为它们之间不存在变量依赖关系。
（3）在FCS-MPC算法对V0~V7进行逐个预测、价值函数计算的两个阶段中，8个电压矢量没有先后顺序要求，它们之间没有时序依赖关系。
通过分析FCS-MPC中各步骤的数据依赖关系，可以为算法分割提供一定依据。然而，FCS-MPC内部对数据和时序的依赖度高，难以分割出彼此独立运行的各个部分。因此，如何建立各核心之间的数据联系，设计数据交换对象、交换次数及交换时间点是一个需要解决的问题。
将单核顺序控制策略中不存在依赖关系的流程分别分配给CPU1与CPU2；同时，将针对V0~V7的预测过程、价值函数、比较寻优过程进行均分，分别分配给CPU1与CPU2，可以得到FCS-MPC双核并行控制策略，其流程如图5所示。
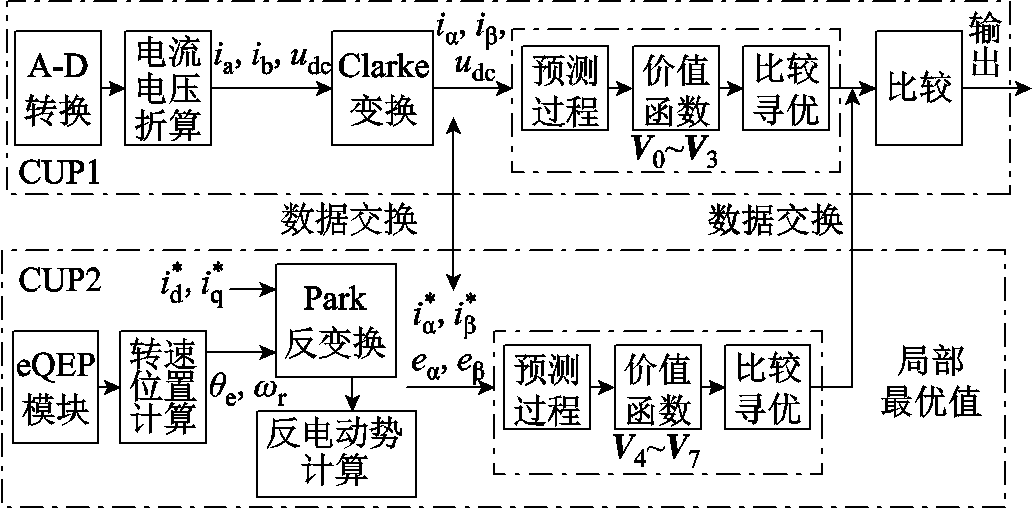
图5 FCS-MPC双核并行控制策略
Fig.5 FCS-MPC dual-core parallel control strategy
由图5可以看到，与单核顺序控制策略不同，双核并行控制策略中需要进行数据交换，以保证各处理核心中预测、评估、寻优过程的正常进行。其中，第一次数据交换发生在预测过程执行之前，在此过程中，CPU1将A-D转换→电流电压折算→ Clarke变换过程所得到udc、iα、iβ传输至CPU2。与此同时，CPU2需要将eQEP模块→转速位置计算→ Park反变换→反电动势计算过程得到的i* α、i* β、eα、eβ传输至CPU1中。第二次数据交换发生在各处理核心完成预测、评估、寻优过程之后，在此过程中， CPU2将其得到的局部最优电压矢量发送至CPU1中，以便CPU1将两核心分别得到的局部最优值电压矢量进行对比，从而得到最终输出的电压矢量。
在双核并行控制策略的基础上，将部分电压矢量的预测、评估、寻优过程分配到CLA核心中，从而实现“双CPU+双CLA”的四核并行控制策略。
图6 FCS-MPC四核并行控制策略
Fig.6 FCS-MPC four-core parallel control strategy
由图6所示的流程中可以看到，在CPU1与CPU2完成数据交换后，CPU1.CLA1与CPU2. CLA1分别从各自对应的CPU核心中获取预测过程所需的变量值，并针对所负责的电压矢量，逐步实现预测过程、价值函数、比较寻优的相应计算，从而使FCS-MPC执行效率得到进一步优化。当CLA核心获得局部最优电压矢量时，需要在CPU1与CPU2进行第二次数据交换前，将最优值传输至各自对应CPU。可以看到相比双核并行控制策略，四核并行控制策略增加了CPU与CLA之间的数据交换。
在并行计算策略中，CPU1、CPU2以及所对应的CLA核心彼此独立，各核心内的控制算法顺序执行。然而，由于缺乏时序控制机制，无法保证预测、评估、寻优过程中数据的同步性。本文设计了一种数据交换策略，在保证数据完整性的基础上，保持多核并行计算的时序正确。以避免某些核心在其他核心未完成相应计算之前，过早地进行数据交换，进而将上一控制周期的变量用于本控制周期的计算中，最终导致预测误差以及控制偏差的情况出现。
与2.3节对应，数据交换分为两个阶段进行，分别处于FCS-MPC算法的前后，如图7所示。
图7 CPU1和CPU2的数据交换策略
（注：“P”代表数据传输完成）
Fig.7 Data exchange strategy between CPU1 and CPU2
CPU1与CPU2不能直接传输数据，而是通过MSG内存间接传输数据；同时，考虑到2.1节中所述的两种MSG内存在读写权限上的差异，在数据交换策略的设计中：①收发数据过程必须选择特定的MSG内存；②通过设置标志位以确保CPU1与CPU2按照一定时序进行数据交换。其中，F1：第一阶段CPU1→CPU2数据传输完成的标志位；F2：第一阶段CPU2→CPU1数据传输完成的标志位；F3：第二阶段CPU2→CPU1数据传输完成的标志位。
在第一阶段中，CPU1向CPU1→CPU2 MSG内存发送变量udc、iα、iβ之后，将F1标志位赋值为P；与此同时，CPU2不断地对F1标志位进行检查，当检测到F1=P时，即判别CPU1已完成数据发送，并据此读取MSG内存的相应变量udc、iα、iβ。当CPU2读取变量后，将变量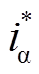
、
、
、
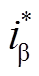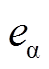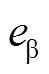发送至CPU2→CPU1 MSG内存中，并将F2标志位赋值为P；另一方面，在CPU1完成数据发送后，将不断地对F2标志位进行检查，当检测到F2=P时，即判别CPU2已完成数据发送，并据此读取MSG内存的相应变量i* α、i* β、eα、eβ。
在第二阶段中，当CPU2获得局部最优电压矢量后，将矢量序号和相应的价值函数计算结果发送到CPU2→CPU1 MSG内存中，并将F3标志位赋值为P；另一方面，在CPU1计算得到局部最优电压矢量后，不断地对F3标志位进行检查，当检测到F3=P时，将读取最优值，并进行最终比较和输出。
由上述过程可以看到，采用标志位可以保证CPU1与CPU2在每个控制周期中，利用最新采集的电机状态量，同步地对电机未来状态进行预测、评估、寻优。反之，如果没有标志位对交换过程进行时序控制，在第一阶段中，CPU1或CPU2可能在没有接收到对方数据的情况下，提前进行预测；在第二阶段中，CPU1可能在CPU2未获得局部最优电压矢量的情况下，提前进行最终比较与输出。这两种情况均会造成FCS-MPC控制误差，以至影响整个电机控制系统的稳定性。
由图中可以看到，当两个阶段完成之后，标志位F1、F2、F3均赋值为P，由于P在此控制周期中的意义为数据传输完成，因此在下一个控制周期开始前，必须将标志位F1、F2、F3复位。但是，在双核系统中，CPU1和CPU2只对各自的MSG内存具有写入权限，因此将所有标志位复位需要CPU1与CPU2之间进行多次数据传输和判断，这将在一定程度上增加算法的复杂性。为解决这一问题，本文设计了一种动态标志位，即
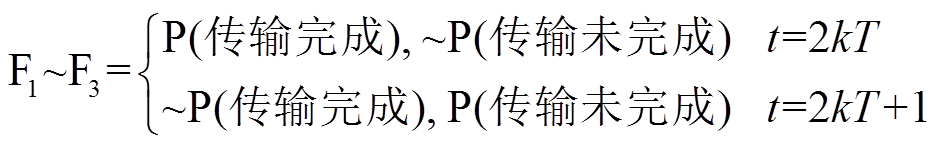（5）式中，“~P”表示对变量P进行取反运算，即“非运算”。
可以看到，F1、F2、F3的对应数值的意义是随着控制周期交替变化的。在t=2kT控制周期结束时，F1,F2,F3=P，意味着数据交换的两个阶段均已完成，而在下一控制周期的起始，即t=2kT+1时，F1, F2,F3=P表示两次数据交换均未完成。通过标志位赋值意义的动态交替转换，简化了相应的标志位复位过程。
图8显示了动态标志位复位方法与传统标志位复位方法的区别。
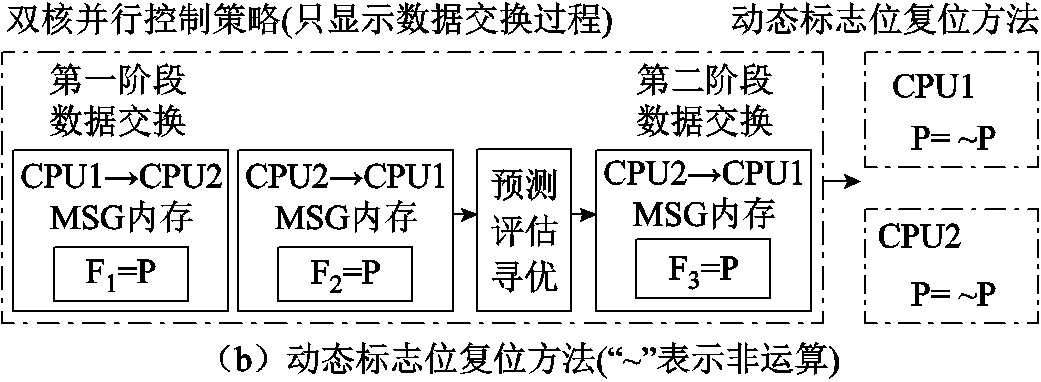
图8 传统标志位复位方法与动态标志位复位方法
Fig.8 Traditional flag reset method and dynamic flag reset method
图8中可以看到，传统标志位复位方法中，标志位F1必须先于F2、F3进行复位，否则可能造成CPU1未完成第二阶段数据交换时，CPU2对F3提前复位，造成控制时序错误。为此，标志位复位过程存在大量MSG内存的读写与标志位检测过程，这些过程均会造成一定的延迟，影响算法执行效率。与之相比，在动态标志位复位方法中，各核心只需要对变量P进行取反运算，算法简单，基本无延迟。
与CPU之间数据交换策略类似，CPU与CLA之间的数据交换同样分为两个阶段。所不同的是，两个阶段的数据传输方向均是单向的，另外，数据交换策略采用预设标志位与中断标志位相结合的方法保证时序正确性。以CPU1与CLA1之间的数据交换为例，相应的交换策略如图9所示。
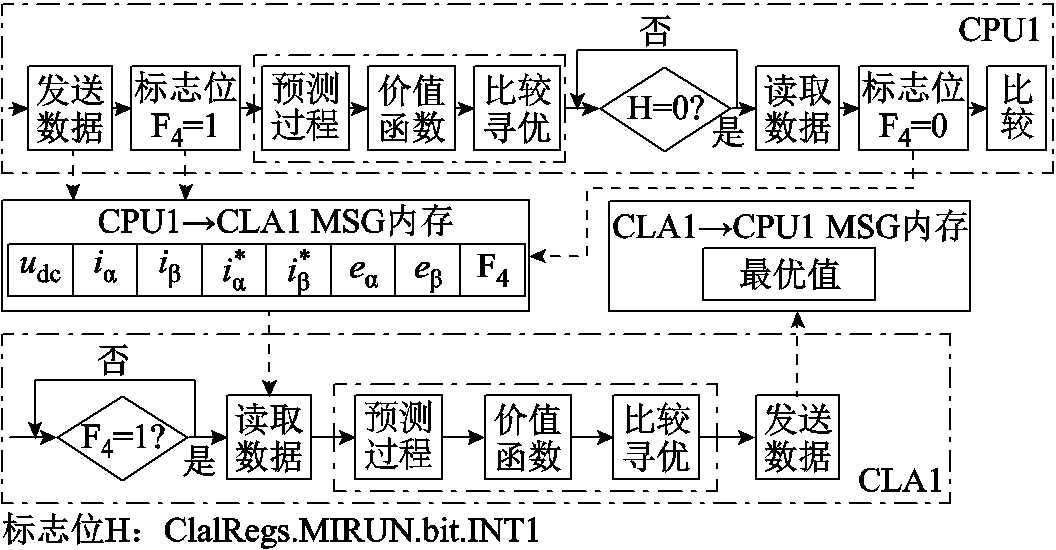
图9 CPU1和CLA1的数据交换策略
Fig.9 Data exchange strategy between CPU1 and CLA1
在第一阶段数据交换过程完成时，CPU1将预测过程所需的变量udc、iα、iβ、i* α、i* β、eα、eβ发送至CPU1→CLA1 MSG内存，并将其中预先设置的标志位F4赋值为1。与此同时，CLA1不断地检查标志位F4，当检测到F4=1时，则意味着数据传输已完成，CLA1将逐个读取变量。在此之后，CPU1与CLA1执行各自所分配电压矢量的预测、评估、寻优过程，并得到局部最优值。在控制算法进入数据交换的第二阶段之前，CLA1将发送局部最优值至CLA1→CPU1 MSG内存，而CPU1将不断地检查标志位H，以判断CLA1是否完成数据传输，当标志位H为0时，CPU1将读取MSG内存中的局部最优值，将标志位F4复位为0，并进行局部最优值的比较过程。标志位H为中断标志位Cla1Regs. MIRUN.bit.INT1，当CLA1程序执行完成后，该标志位将由1转变为0，因此可以将其作为CLA1数据发送完成的标志。
基于代码生成技术的实验平台如图10所示。
图10 实验平台
Fig.10 Experiment platform
图10中，控制器为德州仪器的浮点型微控制器TMS320F28379D。电机驱动单元基于氮化镓半桥功率元件LMG5200，能够实现更高的功率密度和开关频率。被测电机与负载电机均为表贴式永磁同步电机，集成1 000脉冲/圈正交编码器，相应的电机参数见表1。另外，系统的控制周期T=20μs。
表1 电机参数
Tab.1 Motor parameters
参数数值 额定转速ωN/(r/min)3 000 额定电流IN/A7.7 最大直流侧电压Vmax/V60 额定转矩TN/(N×m)0.423 7 额定功率PN/W133 极对数p4 定子相电阻R/Ω0.345 反电动势常数ke/[V/(103r/min)]6.64 定子相电感L/mH0.366 逆变器直流电压udc/V24~48
基于代码生成技术，构建多核并行计算的FCS-MPC控制策略，相应的开发环境与图形化程序结构（以CPU1为例）如图11所示。为了补偿FCS-MPC的计算过程造成的单位控制周期的延迟，控制程序中加入了延迟补偿算法[25]。
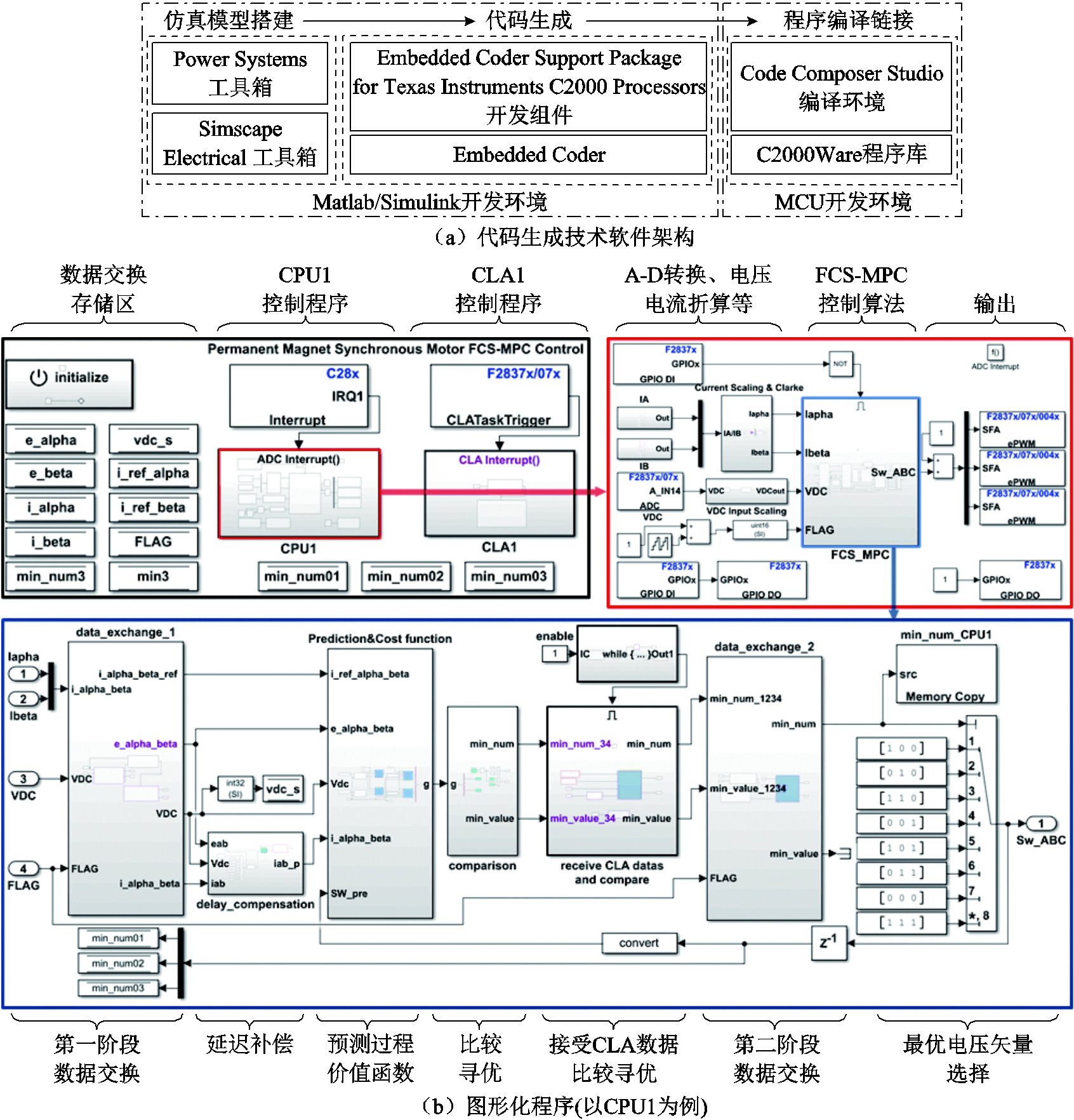
图11 基于代码生成技术的开发环境与图形化程序
Fig.11 Develop platform and graphics program based on code generation technology
直流侧电压udc=48V，定子电流参考值由3A阶跃到6A，相应的定子电流波形如图12所示。
通过对图12a和图12b进行对比，可以看到，四核并行控制策略的电流谐波含量、电流阶跃时间基本与单核顺序控制相一致，这意味着并行控制保持了FCS-MPC的动稳态性能。
在永磁同步电机中，常见的附加约束有开关频率约束与共模电压约束。其中，开关频率的高低直接影响电机逆变器的开关损耗和散热温度；共模电压直接影响电机的中性点绝缘性和电磁兼容性。
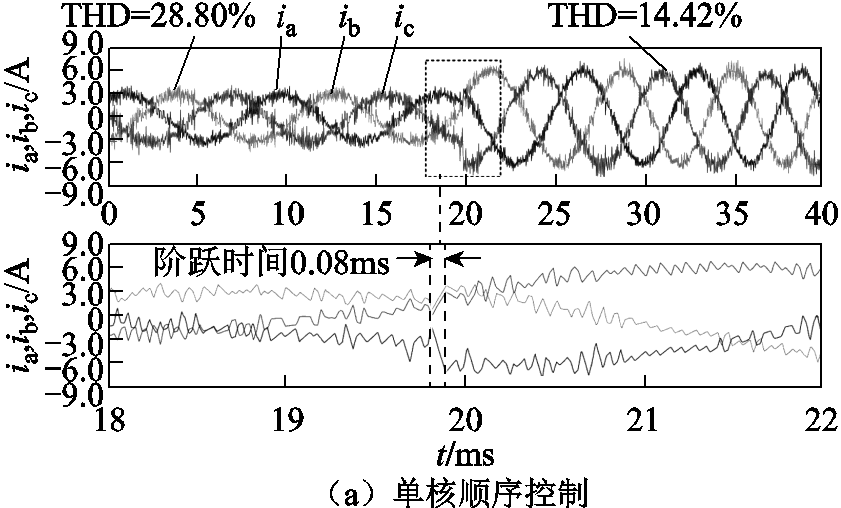
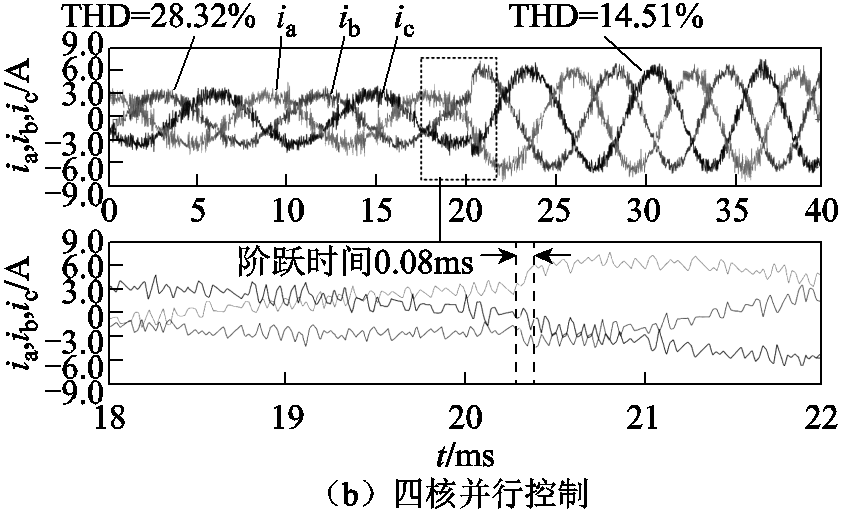
图12 三相定子电流波形
Fig.12 Three-phase stator current waveforms
为评估四核并行控制策略对附加约束的兼容性，设置udc=36V，定子电流参考值为5A。当加入开关频率约束时，FCS-MPC的价值函数变为
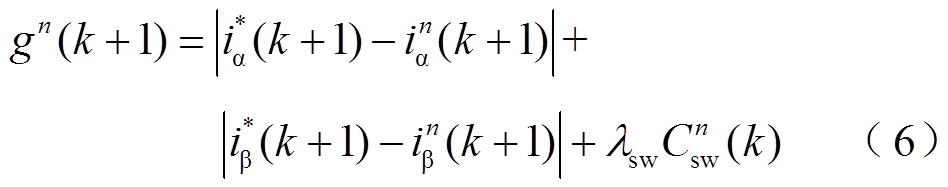
式中，
为附加的开关频率约束项，其中
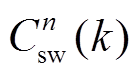为(k-1)T~(k+1)T时间段内，两个相邻控制周期间的桥臂开关状态切换次数。例如，若(k-1)T~kT时间段开关状态(SaSbSc)=(101)，kT~(k+1)T时间段开关状态(SaSbSc)=(011)，则表示a相桥臂与b相桥臂对应的开关状态各切换了一次，即
。
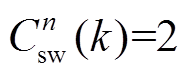定子电流及各控制周期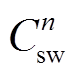
值如图13所示。
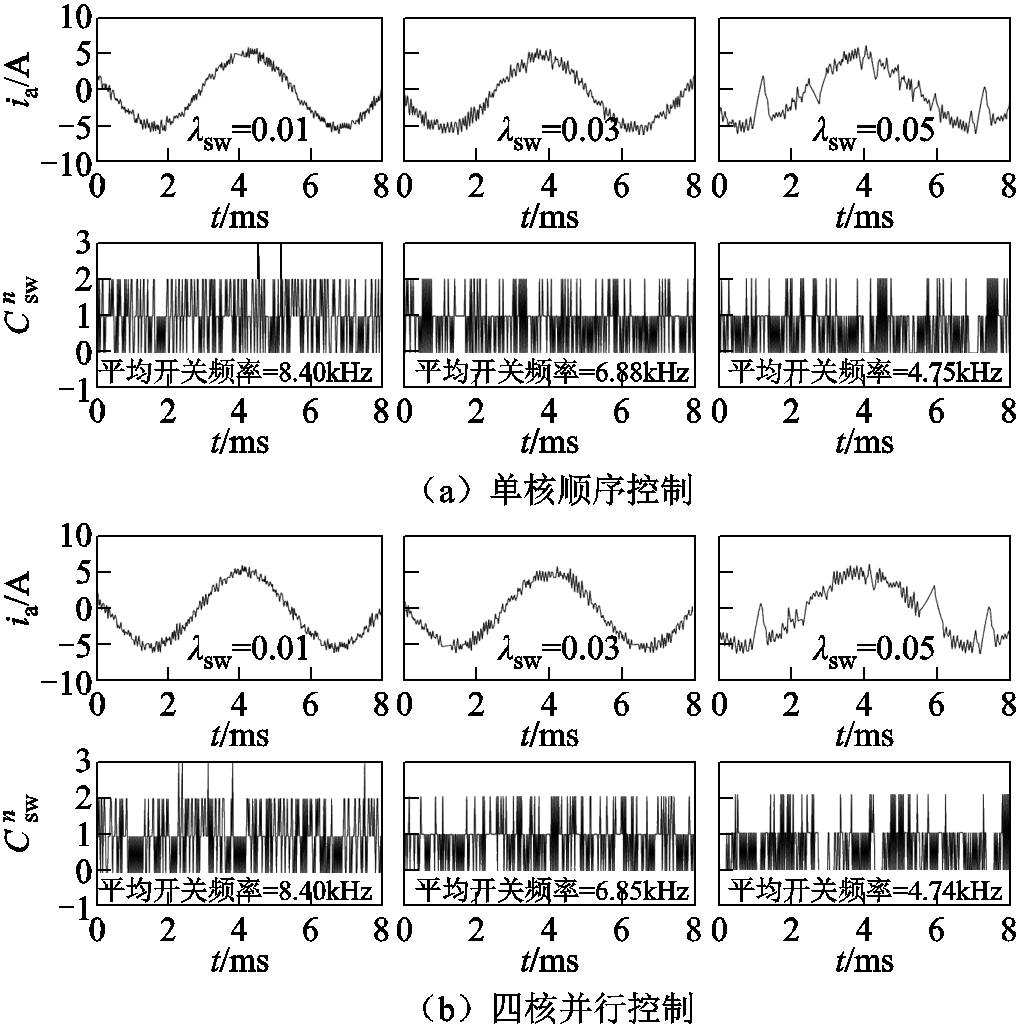
图13 定子电流与开关切换次数波形
Fig.13 Waveforms of stator currents and power device switching times
图13中，平均开关频率由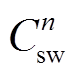计算得到。随着λsw逐渐增大，桥臂开关状态切换次数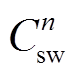的变动范围逐渐缩小，而平均开关频率也随之减小。当λsw=0.05时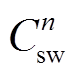，值主要集中于0~1范围内，而平均开关频率减小至4.7kHz。与之相对，定子电流的畸变率随着λsw的增大而逐渐上升，表明电流约束与开关频率约束存在互相制约的关系。对比图13a与图13b可知，四核并行控制方法在定子电流波形、开关状态切换次数、平均开关频率方面的实验结果与单核顺序控制方法基本保持一致。
在加入开关频率约束的基础上，进一步加入共模电压约束，FCS-MPC的价值函数变为
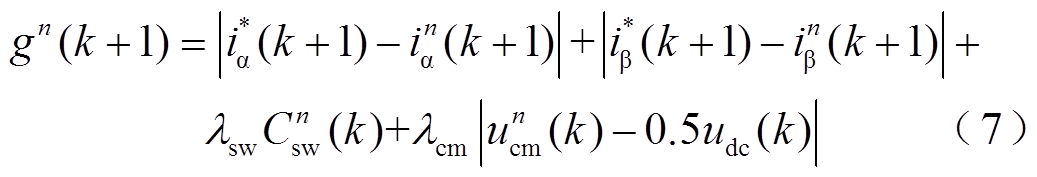
式中，
为共模电压，为
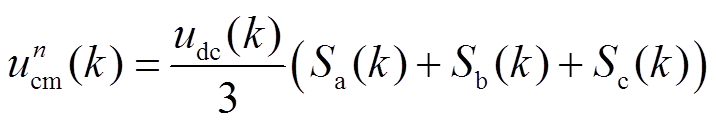（8）设置开关频率约束λsw=0.01，共模电压约束λcm分别设为0.05、0.3、0.5，记录定子电流与共模电压的波形，如图14所示。
图14 定子电流与共模电压波形
Fig.14 Stator current and common mode voltage waveforms
从图14中可以看到，随着共模电压约束λcm的逐渐增大，共模电压ucm的变动范围逐渐缩小，表明共模电压逐渐得到抑制。与之相对，定子电流畸变率随着λcm增大而逐渐上升，表明电流约束与共模电压约束存在互相制约关系。对比图14a与图14b可知，四核并行控制方法在定子电流、共模电压的实验结果与单核顺序控制方法基本保持一致。
对比图13和图14实验结果，可验证单核顺序控制与四核并行控制在附加约束兼容性上是一致的。
对于附加上述两种约束的FCS-MPC算法，图15显示了单核顺序控制、双核并行控制，及四核并行控制的程序执行时间测量结果。
从图15中可以看到，在单核顺序控制中，FCS-MPC所对应的模型预测、价值函数计算、比较寻优过程在程序执行时间中所占比重最大（约62%）。当采用双核并行控制时，上述过程在各个核心中的执行时间下降了近50%；而在四核并行控制中，该过程的执行时间得到了进一步的下降。与此同时，相比单核顺序控制，并行控制方法通过把不存在依赖关系的步骤（1）与步骤（2）分摊到CPU1与CPU2中分别执行，进一步减少了计算时间。另外，由于并行控制依赖数据交换过程，相关的通信和时序等待时间将消耗额外程序执行时间，这将对进一步降低程序执行时间产生影响。
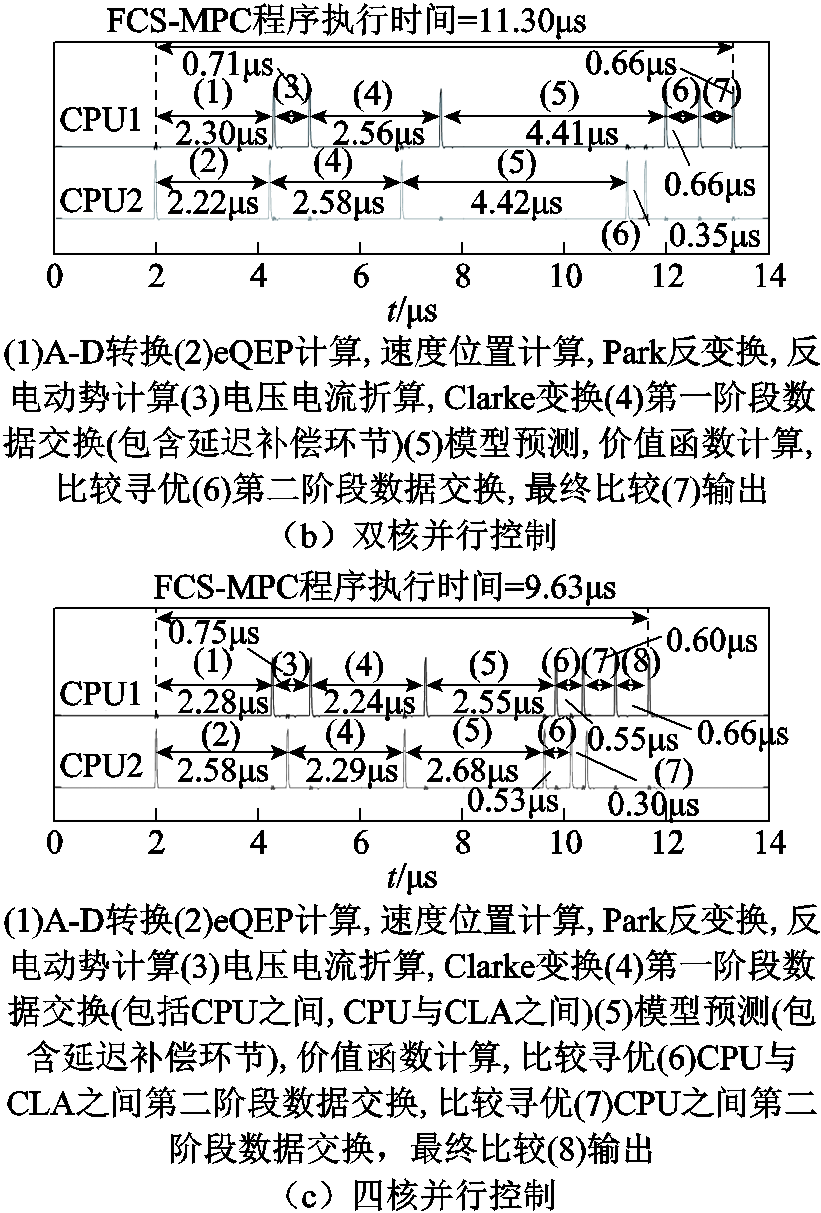
图15 FCS-MPC各个步骤执行时间
Fig.15 Execution time of each step in FCS-MPC
通过对各计算步骤进行合理分配，采用四核并行控制的FCS-MPC算法可将程序执行时间降低到低于10μs。通过分析各步骤的执行时间，可以预见，随着多核微控制器的发展以及核心间通信带宽的增加，基于并行计算的FCS-MPC算法仍有较大的程序执行效率提升空间。
对于低压高速永磁同步电机，定子电感相对较小，定子电流频率较高，FCS-MPC算法需要更小的控制周期以保持电流控制效果。设置udc=36V，图16显示了四核并行控制与单核顺序控制在不同控制周期下的定子电流稳态波形以及相应的开关频率、电流谐波分析结果。
从图16中可以看到，相比单核顺序控制，四核并行控制可以将控制周期缩短至10μs，从而实现更为平滑的定子电流波形和更低的总谐波失真率（Total Harmonic Distortion, THD）。由于两种方法的控制周期不同，为方便对比，开关切换次数由针状图表示。通过对比可知，多核并行控制能够让处理器可以运行于更高控制频率上，逆变器的平均开关频率为20.83kHz，与高性能线性控制策略相一致，从而实现更为精细的电流控制，有效抑制电流谐波。
图16 不同控制周期下定子电流波形对比
Fig.16 Comparison of stator current waveforms under different control periods
图17显示了四核并行控制与单核顺序控制在不同控制周期下的定子电流暂态响应波形。图17中，电流幅值由3A阶跃到5A。
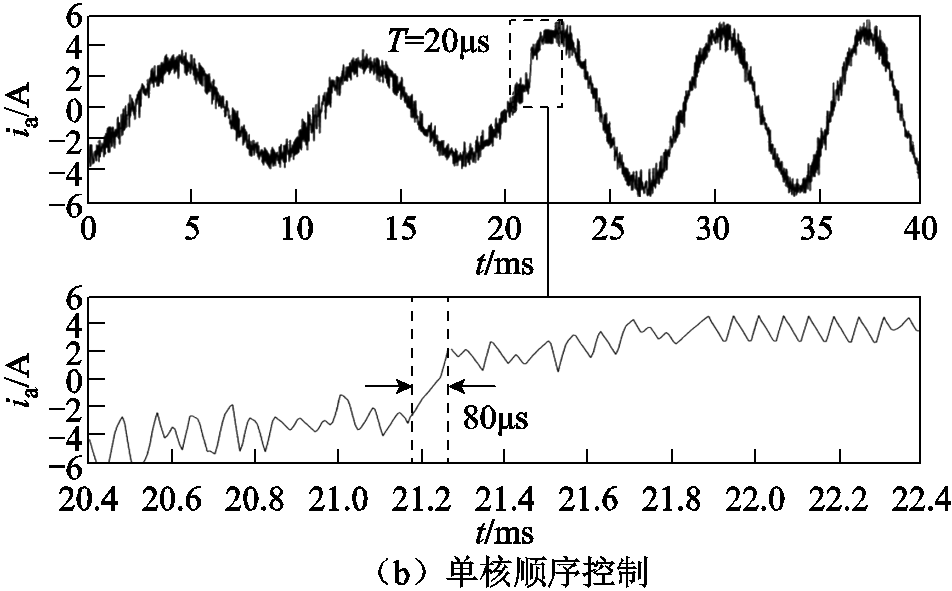
图17 不同控制周期下定子电流暂态响应速度对比
Fig.17 Comparison of current transient response speed under different control periods
由图17中可以看到，相比单核顺序控制，四核并行控制方法在电流阶跃过程中具有更快的响应速度，这主要是因为四核并行控制方法能够实现更短的控制周期，进而达到更快的电流控制速度。
图18显示了四核并行控制与单核顺序控制在不同控制周期下的电磁转矩纹波对比。
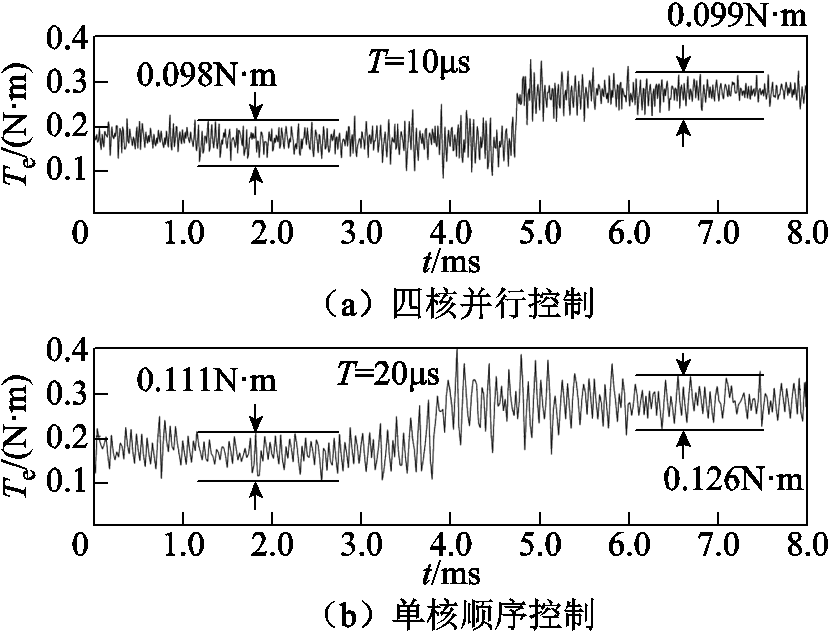
图18 不同控制周期下电磁转矩纹波对比
Fig.18 Comparison of electrical torque ripple under different control periods
由图18中可以看到，四核并行控制方法具有更低的电磁转矩纹波，同时可以看到，在电流幅值发生阶跃时，四核并行控制所对应的电磁转矩动态响应速度更快。
四核并行控制方法有利于提高定子电流的动、稳态性能，同时能够有效地抑制转矩波动，提高转矩响应速度。在未来的发展中，有利于FCS-MPC应用于具有高开关频率的宽禁带半导体开关元件中。
本文针对永磁同步电机驱动系统，提出了一种基于多核并行计算的FCS-MPC控制策略。其中，针对新型微控制器TMS320F28379D的双CPU+双CLA架构以及FCS-MPC的算法结构特点，分别构建了双核、四核并行控制策略，并设计了数据交换策略和动态标志位方法。实验结果表明，通过将FCS-MPC算法的各个部分合理分配到微控制器的各核心，可以在保持原算法控制性能和控制特点的基础上，有效降低算法的执行时间。有利于进一步缩短FCS-MPC算法的控制周期，提高开关频率和控制精度。相比FPGA方法，该方法基于多核微控制器，具有更为成熟的电机系统软硬件开发环境和更低的开发难度，为改善FCS-MPC程序执行效率提供了一条新思路。
参考文献
[1] Vazquez S, Rodriguez J, Rivera M, et al. Model predictive control for power converters and drives: advances and trends[J]. IEEE Transactions on Industrial Electronics, 2016, 64(2): 935-947.
[2] 陈卓易, 邱建琪, 金孟加. 内置式永磁同步电机无位置传感器自适应集总电动势模型预测控制[J]. 电工技术学报, 2018, 33(24): 5659-5669. Chen Zhuoyi, Qiu Jianqi, Jin Mengjia.Sensorless adaptive lumped electromotive-force model predictive control of interior permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5659-5669.
[3] 姚骏, 刘瑞阔, 尹潇. 永磁同步电机三矢量低开关频率模型预测控制研究[J]. 电工技术学报, 2018, 33(13): 2935-2945. Yao Jun, Liu Ruikuo,Yin Xiao. Research on 3-vector model predictive control with low switching frequency of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 2935-2945.
[4] 苗磊, 张勇军, 童朝南, 等. 基于模型预测直接转矩控制的永磁同步发电机效率优化研究[J]. 电工技术学报, 2018, 33(15): 3535-3546. Miao Lei, Zhang Yongjun, Tong Chaonan, et al. Efficiency optimization of permanent magnet synchronous generators based on model predictive direct torque control[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3535-3546.
[5] Shen Kun, Feng Jianghua, Zhang Jing. Finite control set model predictive control with feedback correction for power converters[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(3): 312-319.
[6] 陈卓易, 邱建琪, 金孟加. 永磁同步电机有限集无参数模型预测控制[J]. 电机与控制学报, 2019, 23(1): 19-26. Chen Zhuoyi, Qiu Jianqi, Jin Mengjia.Finite control set nonparametric model predictive control for permanent magnet synchronous machines[J]. Electric Machines and Control Application, 2019, 23(1): 19- 26.
[7] 杨兴武, 牛梦娇, 李豪, 等. 基于开关状态函数计算的改进模型预测控制[J]. 电工技术学报, 2018, 33(20): 4834-4844. Yang Xingwu, Niu Mengjiao, Li Hao, et al. Improved model predictive control based on switching state function calculation[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4834-4844.
[8] 於锋, 朱晨光, 吴晓新, 等. 基于矢量分区的永磁同步电机三电平双矢量模型预测磁链控制[J]. 电工技术学报, 2020, 35(10): 2130-2140. Yu Feng, Zhu Chenguang, Wu Xiaoxin, et al. Two-vector-based model predictive flux control of three-level based permanent magnet synchronous motor with sector subregion[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2130-2140.
[9] Zhou Zhanqing, Xia Changliang, Yan Yan. Torque ripple minimization of predictive torque control for PMSM with extended control set[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 6930-6939.
[10] Rodriguez J, Kazmierkowski M P, Espinoza J R, et al. State of the art of finite control set model predictive control in power electronics[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2): 1003-1016.
[11] Shirabe K, Swamy M, Kang J K, et al. Advantages of high frequency PWM in AC motor drive applications[C]// IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, USA, 2012: 2977-2984.
[12] Liu Tao, Cai Yan, Song Zhanfeng. Simplified predictive torque control for surface-mounted PMSM based on equivalent transformation and partition method[J]. IEEE Access, 2020, 8(1): 35048-35062.
[13] Xia Changliang, Liu Tao, Shi Tingna, et al. A simplified finite-control-set model-predictive control for power converters[J]. IEEE Transactions on Industrial Informatics, 2014, 10(2): 991-1002.
[14] Liu Xing, Wang Dan, Peng Zhouhua. A computationally efficient FCS-MPC method without weighting factors for NNPCs with optimal duty cycle control[J]. IEEE/ASME Transactions on Mechatronics, 2018, 23(5): 2503-2514.
[15] Luo Yixiao, Liu Chunhua. A flux constrained predictive control for a six-phase PMSM motor with lower complexity[J]. IEEE Transactions on Industrial Electronics, 2019, 66(7): 5081-5093.
[16] Luo Yixiao, Liu Chunhua. Model predictive control for a six-phase PMSM motor with a reduced-dimension cost function[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2):969-979.
[17] Sun Chong, Sun Dan, Zheng Zhihao, et al. Simplified model predictive control for dual inverter-fed open-winding permanent magnet synchronous motor[J]. IEEE Transactions on Energy Conversion, 2018, 33(4): 1846-1854.
[18] Xiao Meng, Shi Tingna, Gu Xin, et al. Simplified predictive torque control for permanent magnet synchronous motor with discrete duty cycle control[J]. IET Electric Power Applications, 2019, 13(3): 294-301.
[19] Kodumur M R E, Kunisetti V P K, Kumar T V. Enhanced predictive torque control for open end winding induction motor drive without weighting factor assignment[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 503-513.
[20] 李耀华, 师浩浩, 孟祥臻. 表面式永磁同步电机直接转矩控制系统简化预测控制策略[J]. 电机与控制学报, 2020, 24(4): 96-103. Li Yaohua, Shi Haohao, Meng Xiangzhen. Simplified predictive control for direct torque control of surface permanent magnet synchronous motor[J]. Electric Machines and Control Application, 2020, 24(4): 96-103.
[21] Zhang Zhenbin, Li Zhen, Kazmierkowski M P, et al. Robust predictive control of three-level NPC back-to-back power converter PMSG wind turbine systems with revised predictions[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9588-9598.
[22] Gulbudak O, Santi E. FPGA-based model predictive controller for direct matrix converter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4560-4570.
[23] Zhang Zhenbin, Wang Fengxiang, Sun Tongjing, et al. FPGA-based experimental investigation of a quasi-centralized model predictive control for back-to-back converters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 662-674.
[24] Akin B, Bhardwaj M, Choudhury S. An integrated implementation of two-phase interleaved PFC and dual motor drive using single MCU with CLA[J]. IEEE Transactions on Industrial Informatics, 2013, 9(4): 2082-2091.
[25] Cortes P, Rodriguez J, Silva C, et al. Delay compensation in model predictive current control of a three-phase inverter[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 1323-1325.
Finite Control Set Model Predictive Control of Permanent Magnet Synchronous Motor Based on Multi-Core Parallel Computing
Abstract Finite control set model predictive control (FCS-MPC) has a contradiction between long program execution time and short control period, and its algorithm execution efficiency is lower than the traditional linear control algorithm, which further affect the improvement of the switching frequency and control accuracy. In order to solve this problem, combined with the development of multi-core microcontrollers in recent years, this paper proposed a multi-core parallel computing based FCS-MPC strategy for permanent magnet synchronous motor. FCS-MPC has a high dependence on data and timing, which contradicts the independent characteristics of multi-core microcontrollers. This paper designed the dual-core and quad-core control architectures, and proposed the data exchange strategy and dynamic flags. With the experimental system, the transient and steady state performance, the additional constraint compatibility, and the program execution time of the proposed method were analyzed and compared. It is proved that the proposed method can effectively reduce the execution time of FCS-MPC strategy while maintaining the performance and characteristics of the original algorithm.
keywords：Permanent magnet synchronous motor (PMSM), finite control set model predictive control (FCS-MPC), multi-core, parallel computing
中图分类号：TM351; TM341
DOI: 10.19595/j.cnki.1000-6753.tces.200717
国家自然科学基金（51807139）、天津市自然科学基金（19JCQNJC03600）和天津工业大学学位与研究生教育改革项目（Y20180108）资助。
收稿日期 2020-06-28
改稿日期 2020-07-29
刘 涛 男，1984年生，博士，讲师，研究方向为电机系统及其控制。E-mail：taoliu@tju.edu.cn（通信作者）
习金玉 男，1996年生，硕士研究生，研究方向为电机系统及其控制。E-mail：xjy@tiangong.edu.cn
（编辑 郭丽军）