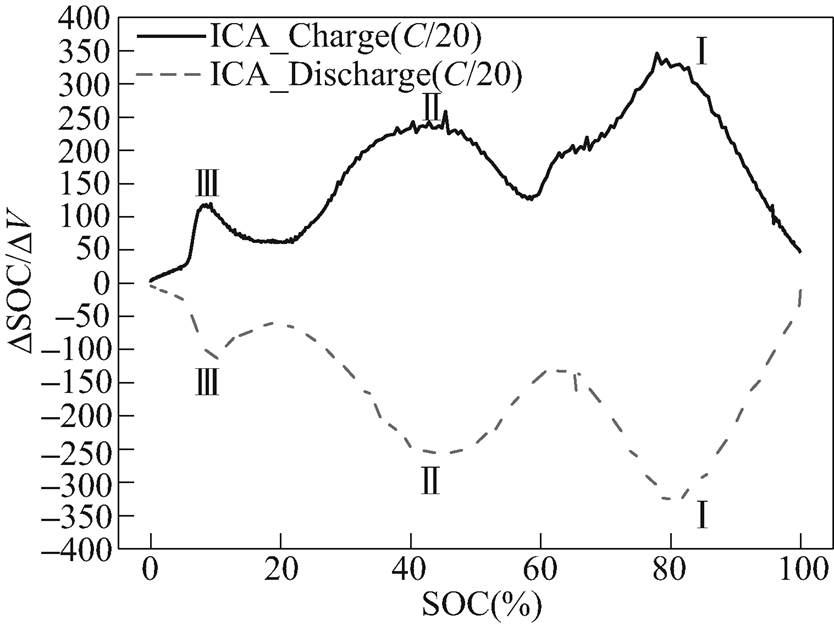
图1 容量增量曲线
Fig.1 Capacity increment curves
摘要 锂离子电池在不同容量区间和不同工况应力下使用衰退性能不同。该文以复合材料锂离子电池为研究对象,基于电化学相变机理对循环区间进行划分,在分区间和全区间分别完成了累计吞吐量600次的循环测试。基于不同容量区间循环过程性能衰退结果,采用回归分析法建立锂离子电池的特征参量相关性模型,包含累积容量衰退率的相关性、累积内阻衰退率的相关性和二者之间的相关性,得到模型的拟合优度均在95%以上。进一步地,将模型推广到更宽的温度范围,量化分析了模型的适用性。结果表明:在不同温度下,累积容量衰退率的相关模型适用性很强,但累积内阻相关模型和两参量之间相关模型的适用性较弱。不同衰退路径下容量和内阻的演变规律,为锂离子电池的使用区间选择提供了依据,也为不同条件下的衰退预测提供了新思路。
关键词:锂离子电池 循环区间 衰退路径 相关性 温度适用性
目前,电动汽车逐渐已成为汽车产业的重要发展方向。动力电池是电动汽车主要能量来源,决定着电动汽车的续航里程、动力性、经济性和安全 性[1-2],而使用过程中表现出来的性能衰退一直是制约电动汽车发展的关键因素[3]。对电池衰退特性的研究通常包括衰退路径划分、衰退轨迹预测以及衰退机理分析等[3-4]。现阶段国内外多位学者对锂电池的循环区间进行了研究[4-5]。文献[6]以纯电动公交车锂离子电池的使用条件控制为研究目标,在分析了北京奥运会纯电动公交车首批电池运行数据后,发现电池在不同荷电状态(State of Charge, SOC)区间循环使用后的容量衰退速率存在差异。文献[7]尝试以放电深度(Depth of Discharge, DOD)和初始SOC为变量,根据电动汽车实际使用情况将不同的DOD与初始SOC进行组合,划分一系列循环区间进行研究。文献[8]在进行锂离子电池健康状态(State of Health,SOH)的相关研究中,提取了城市混合动力汽车典型运行工况,设计了不同SOC区间的循环实验,并将进行深入研究。但以上研究大多忽略了锂离子电池在实际运行过程中存在的不同反应阶段,没有从机理上去划分动力电池的反应区间。锂离子电池的相变过程能够反映出非常丰富的特征信息,与电池的多个参数具有非常高的关联性。采用容量增量分析(Incremental Capacity Analysis, ICA)曲线能将传统充放电电压曲线上涉及电池相变的电压平台转化成能明确识别的峰[9-10],建立电池外特性和内部电化学特性的对应关系。本文基于被测电池的IC曲线划分了三个相变区间,加上全区间,共计四个区间,并对此进行了测试。基于测试数据能够分析电池在单个相变区间循环工作时,相关参数随循环次数的演变规律,同时进一步建立分区间参数与全区间参数的关系。
容量和内阻是锂离子电池性能衰退过程中两个主要的表征参数,其对电池的功率、能量等参数的估计和控制策略的制定有重要影响[11-12]。
目前,研究人员对锂离子电池衰退后的性能表现进行了多角度的研究。文献[13]对不同衰退路径下的锂离子电池进行低温应力测试,来探究低温衰退结果与循环衰退之间存在的映射关系。文献[14]对退运电池的性能衰退规律进行了总结分析,但没有基于确定的衰退路径。随着研究的不断深入,研究人员开始将容量和内阻两个参数放置在一起讨论。文献[15]从电池组的角度出发,针对某一工况下的循环测试数据,采用一元线性拟合的方式描述了电池容量及内阻的变化趋势。文献[16-17]以综述的形式描述了容量和内阻的分析对锂离子电池性能衰退研究的意义。文献[18]采用统计学的方式分析锂离子电池在循环过程中的容量衰退和内阻变化,Anthony Barre等在实车运行的基础上设计了复杂的工况,变量包括实车运行经度、纬度、海拔、环境温度、电池温度、电压、电流等25个参数,实验周期长达23个月,实际容量衰退至额定容量的88%,内阻增长至初始值的115%[18]。综合上述研究发现,如何把容量和内阻结合起来,采用两个参数“打包”表征电池的SOH,目前还没有成熟的方法。而且,电池循环衰退后性能表现的相关性问题的定量分析现有文献也很少涉及。
因此,本文采用回归分析法研究不同衰退路径下累积容量衰退率的相关性、累积内阻衰退率的相关性和二者之间的相关性,以及其结果在不同环境温度下的适用性等规律。
本文通过划分不同的SOC循环区间对锂离子电池进行老化试验,同时设定温度和倍率为两个加速参数。现阶段大部分研究没有从机理上去划分动力电池的反应区间,不利于本质上去分析锂离子电池的性能衰退。容量增量分析法的优点是将传统充放电电压曲线上涉及电池相变的电压平台转化成容量增量曲线上能明确识别的DQ/DV峰。由于容量增量曲线比传统充放电曲线具有更高的敏感性,因此能通过监测和分析这些DQ/DV峰随环境和工况的变化以及不同老化程度的演变过程,得到电池电化学特性变化的关键信息,建立电池外特性和内部电化学特性的对应关系[19]。将传统容量增量曲线转化为以SOC为横坐标,DSOC/DV为纵坐标的容量增量曲线[19-20],得到如图1所示的容量增量曲线。由图中显示的峰Ⅰ、峰Ⅱ、峰Ⅲ,可以将电池循环区间划分为A区间(0~20%SOC),B区间(20%~60%SOC),C区间(60%~100%SOC),以及D区间(0~100%SOC)。

图1 容量增量曲线
Fig.1 Capacity increment curves
本文测试平台如图2所示,包括主控计算机、充放电设备、温箱及被测电池。充放电设备选用美国Arbin公司的BT2000单体测试设备及其数据采集系统,电压采集精度为±0.02%FSR(FSR指满量程),电流采集精度为±0.1%FSR,最小计数时间间隔为10ms,最小计数电压间隔为1mV。这里选取8块同一批次的35A·h三元锰酸锂复合材料锂离子电池,分别标记为1~8号,在测试过程中,为避免试验结果的偶然性,每组均有两块电池。分析讨论试验结果以每组一块电池为例,相同现象不再赘述。其中1号、5号电池工作在A区间,2号、6号电池工作在B区间,3号、7号电池工作在C区间,4号、8号电池工作在D区间。试验内容包括循环衰退测试和性能测试。相关测试方案的制定参照了35A·h锂离子电池产品规格书及USABC和743两个标准。

图2 试验平台
Fig.2 Experimental platform
本文研究选取的动力电池最大允许充电电流为3C,最大放电电流为8C;充电允许温度范围为-10~+40℃,放电允许温度范围为-20~+55℃。基于上述信息,考虑到国内大部分城市温度上限为40℃左右,且保证其在允许应力下实现正常衰退,设置循环电流为2C,循环温度为40℃。为在不同区间进行准确地对比分析,要保证各区间电池的循环吞吐量一致,即工作在D区间的电池完成1个循环,工作在A区间的电池需完成5个循环。本文对循环次数的定量描述均以D区间为准,全周期共完成600次循环。为避免频繁进行性能测试对试验造成干扰,每100次循环进行一次性能测试。8块电池分组情况及试验条件见表1。
表1 循环区间分组情况
Tab.1 Cycle range grouping

电池区间SOC范围(%)温度/℃倍率 1号、5号A0~20402C 2号、6号B20~60 3号、7号C60~100 4号、8号D0~100
本文主要探究锂离子电池容量和内阻的衰退特性,因此确定容量和内阻为主要测算参数。同时在性能测试过程中选定三个温度点,分别为15℃、25℃和40℃。不同温度性能测试中间搁置12h,以确保电池实际温度稳定在目标温度。
本研究采用C/3电流对电池的容量进行测试;采用近似混合脉冲功率性能测试(the Hybrid Pulse Power Characteristic, HPPC)方式,放电脉冲2C,充电脉冲3C/2,利用公式R=DU/DI来测算电池的内阻值。具体测试流程如图3所示。
3.1.1 容量衰退
在不同循环区间下,锂离子电池容量衰退结果存在一定差异,且差异性随着循环次数的增加而愈发明显,容量衰退的速率随循环次数的增加也明显加快。不同循环区间容量保持量如图4所示和不同循环区间累积容量衰退率如图5所示。由图可见,A、B区间电池容量基本随循环次数的增加缓慢降低;C、D区间电池在400次左右循环时累积容量衰退量大致相同,但D区间电池变化比较规律,基本呈抛物线型衰减,C区间电池在循环开始时衰退率较大,但随循环次数增加而逐渐放缓;400次循环以后,四个不同区间电池容量的衰退规律逐渐明显,D区间衰退速度最快,A区间最慢,整体衰退速度为D区间>C区间>B区间>A区间。
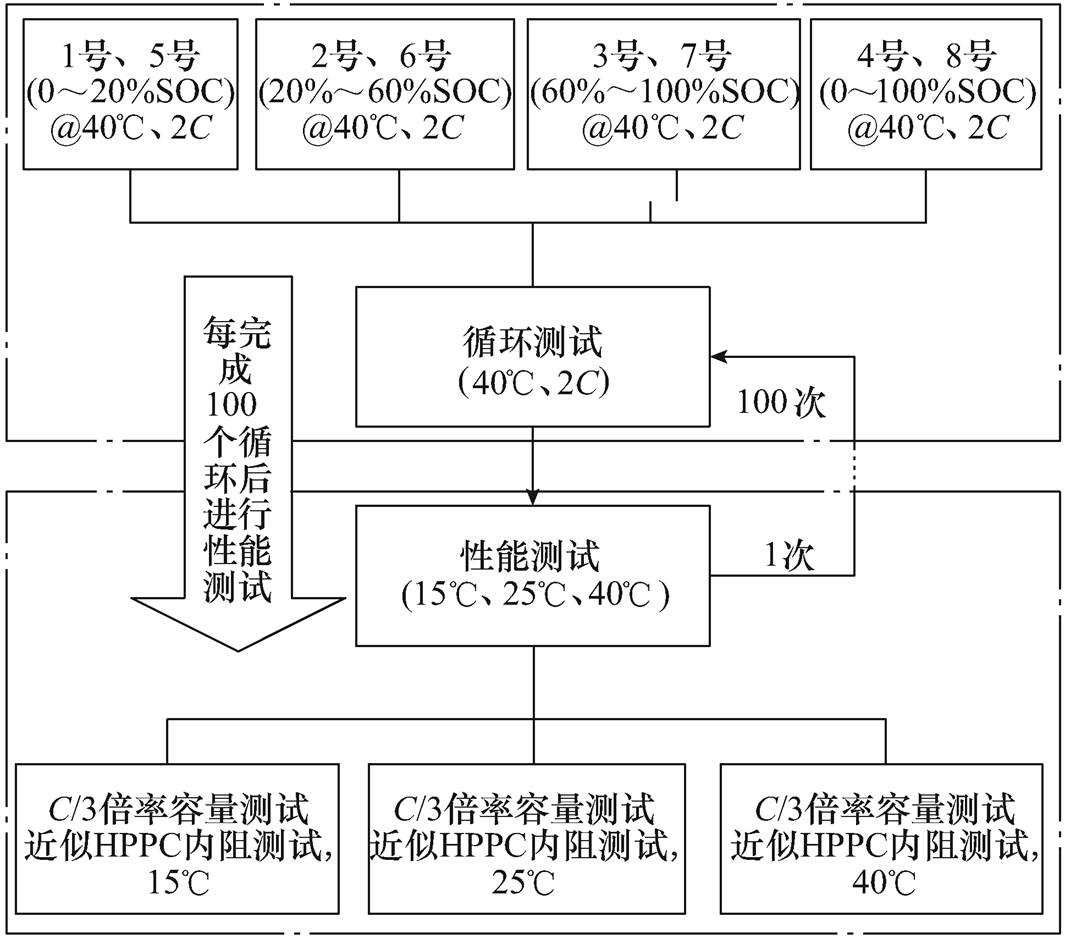
图3 测试流程
Fig.3 Test flow chart
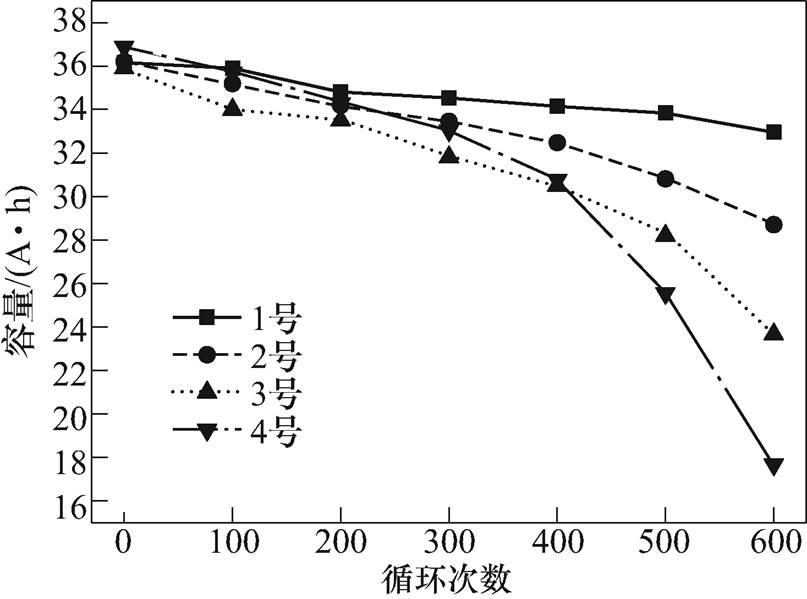
图4 不同循环区间容量保持量
Fig.4 Holding capacity for different cycle ranges
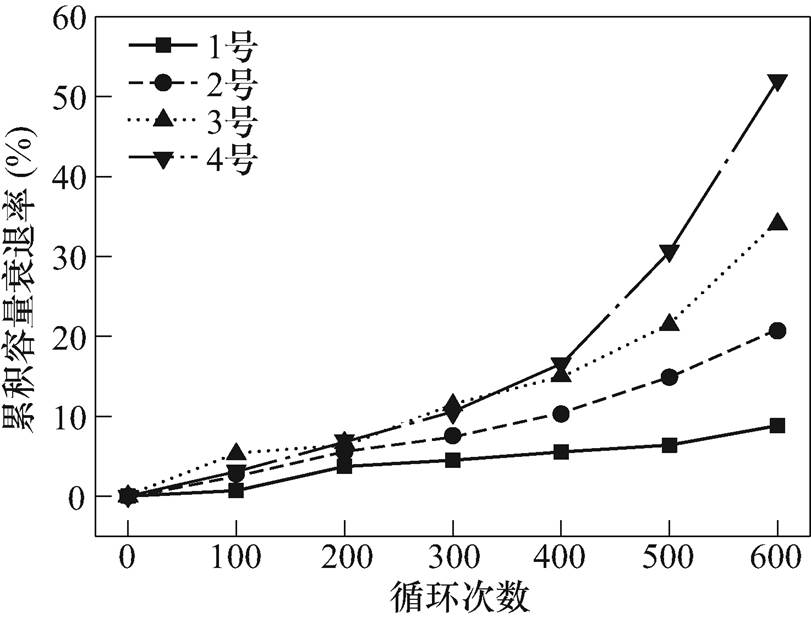
图5 不同循环区间累积容量衰退率
Fig.5 The rate of accumulate capacity degradation for different cycle ranges
3.1.2 内阻变化
试验在充放电方向上共测定了13个SOC点(0%、5%、10%、20%、30%、40%、50%、60%、70%、80%、90%、95%、100%)的放电内阻,在计算内阻值时,针对某一特定SOC点的分析往往不能很好地控制测试误差对数据结果的干扰,故本文研究的集总内阻值采用较为平缓的20%~80%SOC区域的平均值。不同循环区间内阻变化如图6所示和不同循环区间累积内阻变化率如图7所示,在各区间循环的电池内阻初期均有减小,整体表现为先减小后增大的趋势[12]。同样地,A、B区间电池内阻在整个循环过程处于比较缓慢的变化;在400次循环之前,C、D区间电池内阻变化较为平缓,400次循环以后开始出现快速增加的趋势,D区间电池整体处于比较规律的近似指数型变化。通过分析可知,每个循环区间的容量和内阻随循环次数的增加,变化规律具有一定的关联性。此外,400次左右循环后C、D区间的容量和内阻均发生了衰退加速的现象,经过分析发现这两个区间均经历了恒压充电过程,电池承受的电压应力较大,电池内部结构遭到破坏。另外,循环试验是在40℃,相当于加大了温度应力,因此衰退速率加快出现在了400次,如果温度低一些,试验设计中不含恒压充电过程或恒压结束的电流条件设得高一些、恒压过程短一些,循环衰退速率加快的点会适当延后,大于400次。
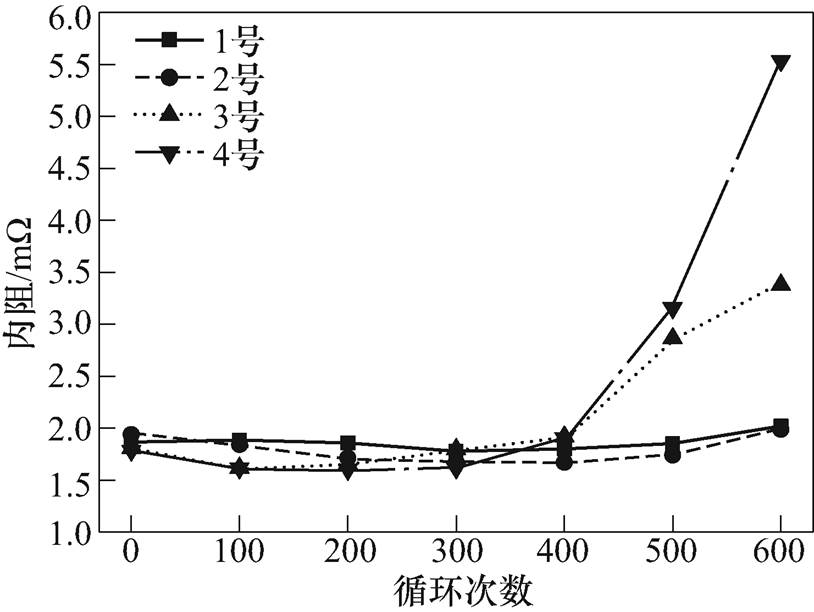
图6 不同循环区间内阻变化
Fig.6 Internal resistance change for different cycle ranges
通过对不同区间电池容量及内阻的变化分析,初步发现累积容量衰退率和累积内阻变化率在不同区间循环的结果具有类似的变化趋势。首先从数值上分析全区间的衰退结果是否为各分区间的简单叠加;进而再通过多元线性回归的方式进行拟合,通过函数模型来描述性能的相关性。
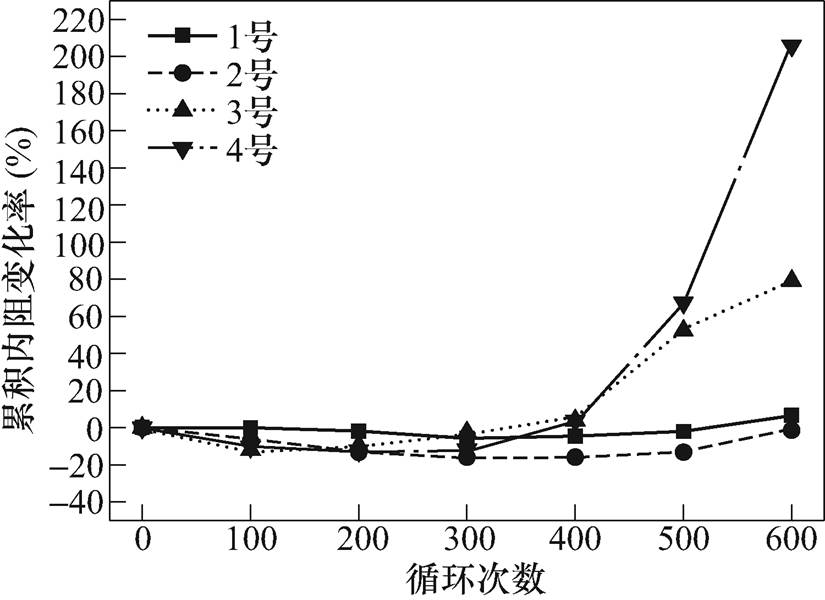
图7 不同循环区间累积内阻变化率
Fig.7 The rate of internal resistance change for different cycle ranges
3.2.1 全区间与分区间累积衰退对比
由于在试验过程中每个区间保持了相同的吞吐量,即每个循环区间的实际充放电量是相同的,所以在简单叠加过程中应按一定的加权使得各分区间吞吐量的和等于全区间吞吐量,即
 (1)
(1)式中,Acr、Bcr、Ccr为自变量,分别代表各区间容量和内阻的变化率;Ds为因变量表示简单叠加的结果。A、B、C区间容量衰退率及内阻变化率之和与D区间实际变化的对比如图8、图9所示。可以看出,在数值上各区间与全区间不是简单的叠加关系,再分别应用多元线性回归对衰退结果进行拟合。
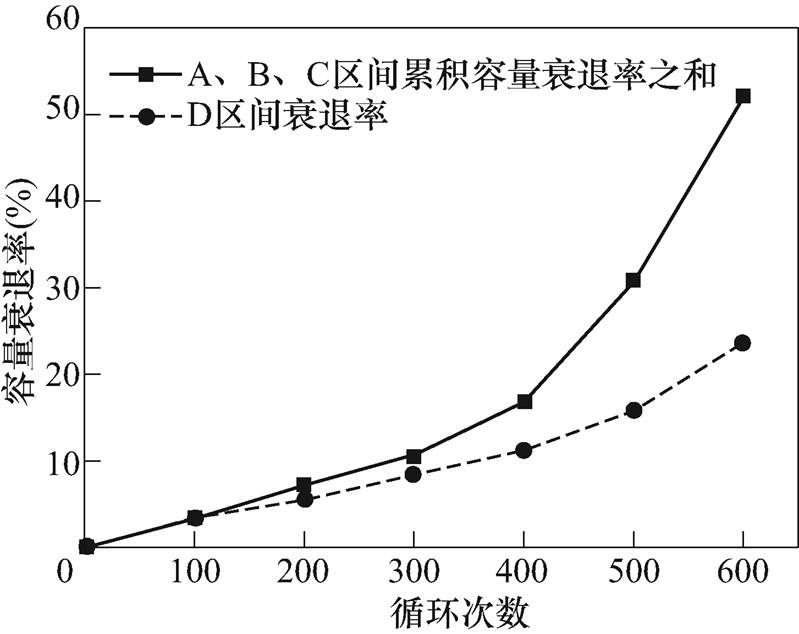
图8 A、B、C区间容量衰退率之和与D区间的关系
Fig.8 The relation between the simple sum of A, B, C and D
3.2.2 容量相关性
运用多元线性回归法对A、B、C、D区间衰退结果进行分析,其中Ac、Bc、Cc为自变量,Dfc为因变量,函数关系为
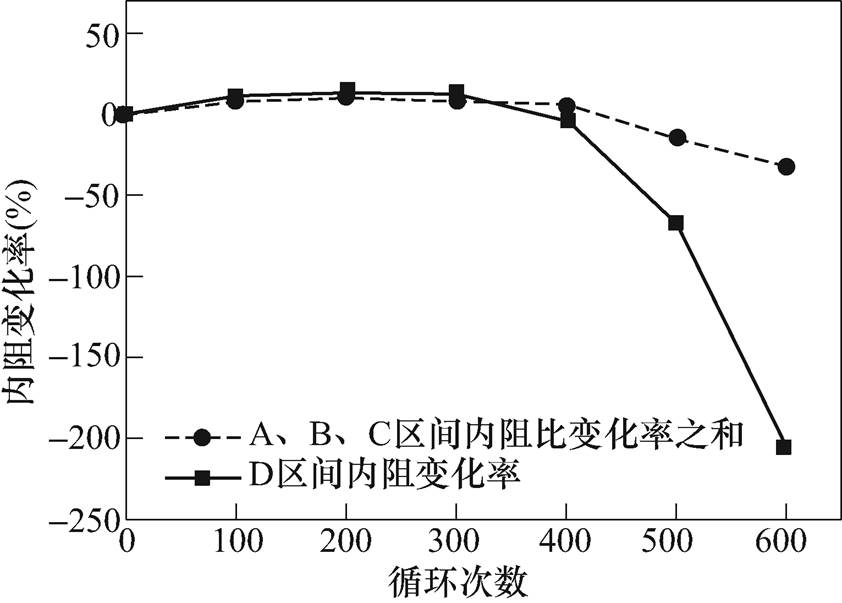
图9 A、B、C区间内阻变化率之和与D区间的关系
Fig.9 The relation between the simple sum of A, B, C and D
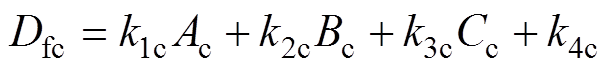 (2)
(2)图10是由式(2)得到的累积容量衰退率的多元线性拟合结果。表2为多元线性回归分析得到的拟合参数,k1c、k2c、k3c、k4c分别为待拟合系数;Multiple R为复相关系数,用来衡量自变量与因变量之间相关程度的大小;R-square为拟合优度,它体现了回归模型中自变量的变异在因变量的变异中所占比例,其值介于0~1之间,1代表所有数据点都完美落在了回归线上,0则说明没有任何关系;Adjusted R-square为避免由于变量个数增加对拟合优度产生影响而经过调整的R-square;Significance F是对模型整体的方差检验,描述自变量影响的显著程度。此处,R=0.992,表明它们之间存在高度相关性;R-square=0.985,Adjusted R-square值为0.969,拟合优度较高;Significance F值为0.003,小于显著性水平0.05,即该回归方程回归效果显著。
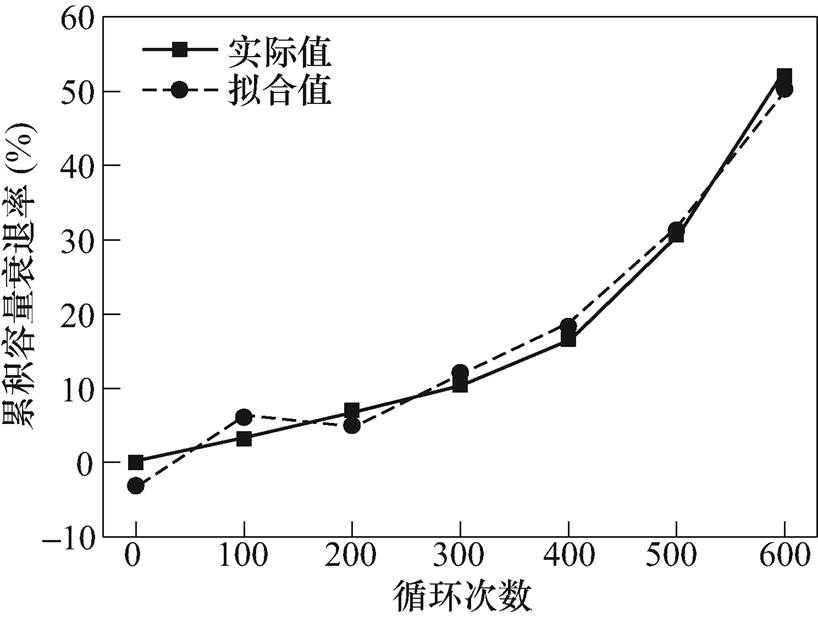
图10 累计容量衰退多元线性拟合结果
Fig.10 Accumulate capacity degradation rate and multiple linear fitting results
3.2.3 内阻相关性
运用多元线性回归法对累积内阻变化率进行拟合,同样Ar、Br、Cr为自变量,Dfr为因变量。函数关系为
表2 累积容量衰退期率多元线性回归得到的拟合参数
Tab.2 Multiple linear fitting parameters of accumulate capacity degradation rate

拟合参数数 值 k1c-2.347 k2c1.531 k3c1.245 k4c-0.031 Multiple R0.992 R-square0.985 Adjusted R-square0.969 Significance F0.003
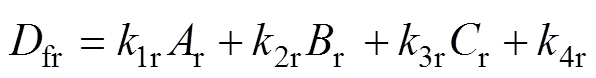 (3)
(3)图11是由式(3)得到的累积内阻变化率多元线性拟合结果,表3为多元线性回归分析得到的拟合参数。可以看到参数Multiple R值为0.985,Signi- ficance F值为0.008,说明采用多元线性回归模型来描述不同循环区间内阻变化率相关性具有较好的效果。
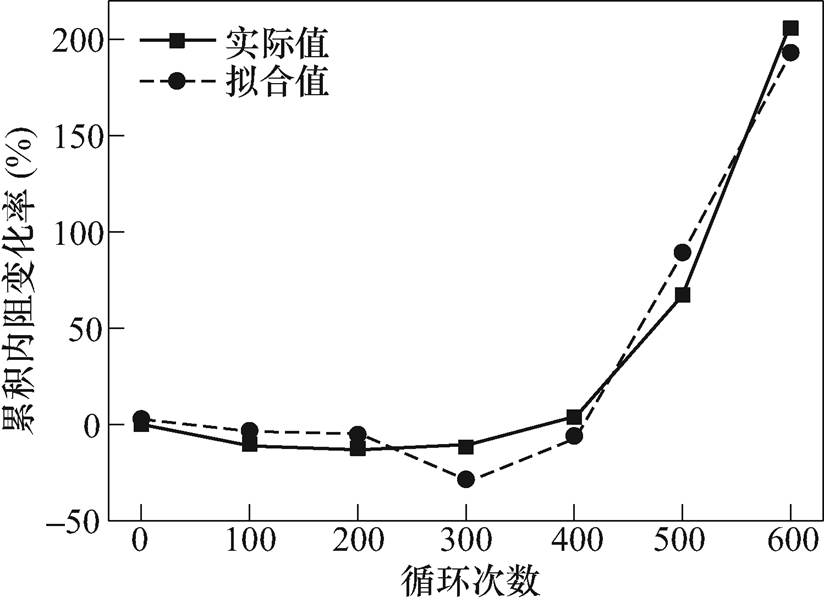
图11 累积内阻变化率多元线性拟合结果
Fig.11 Accumulate internal resistance change rate and multiple linear fitting results
表3 累积内阻变化率多元线性拟合参数
Tab.3 Multiple linear fitting parameters of accumulate internal resistance change rate

拟合参数数 值 k1r9.823 k1r-1.891 k3r1.561 k4r0.029 Multiple R0.985 R-square0.971 Adjusted R-square0.942 Significance F0.008
3.2.4 残差分析
残差是指因变量实际值和通过回归线得到的估计值之间的差,残差分析是多元线性回归模型拟合后模型诊断的必须步骤,主要包含三方面内容。首先,残差应该随机分布在0附近,没有具体的模式。如果残差呈现出一些能很好定义的模式,如线性趋势、U形等,那么说明其他的函数形式更适合拟合该数据,图12为针对累积容量衰退率和累积内阻变化率进行多元线性回归的残差,可以看出残差分布没有明显规律。其次,残差应该服从正态分布,通过残差直方图进行验证,如图13所示。最后,残差应该相互独立,通过德宾-沃森检验统计量(Durbin- Watson statistic, DW)进行分析,这是一个序次残差之差的二次方和与所有残差二次方和的比率,其值在1.5~2.5之间表示非自相关。通过计算得到容量的DW值为2.421,内阻的DW的值为2.478,其值均在1.5~2.5之间,表示通过多元线性回归分析得到的残差均相互独立。从以上分析可知模型选取比较合适。
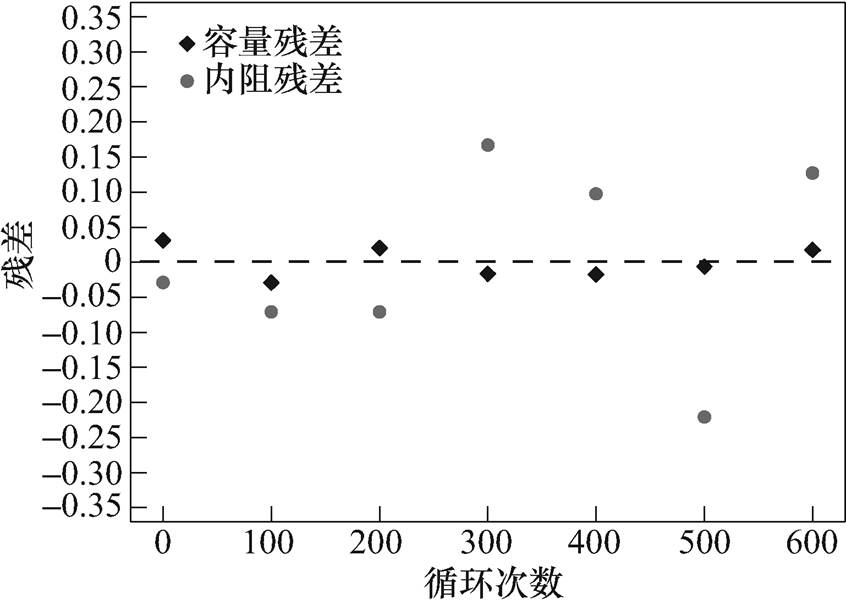
图12 多元线性回归的残差
Fig.12 Residuals for multiple linear regression
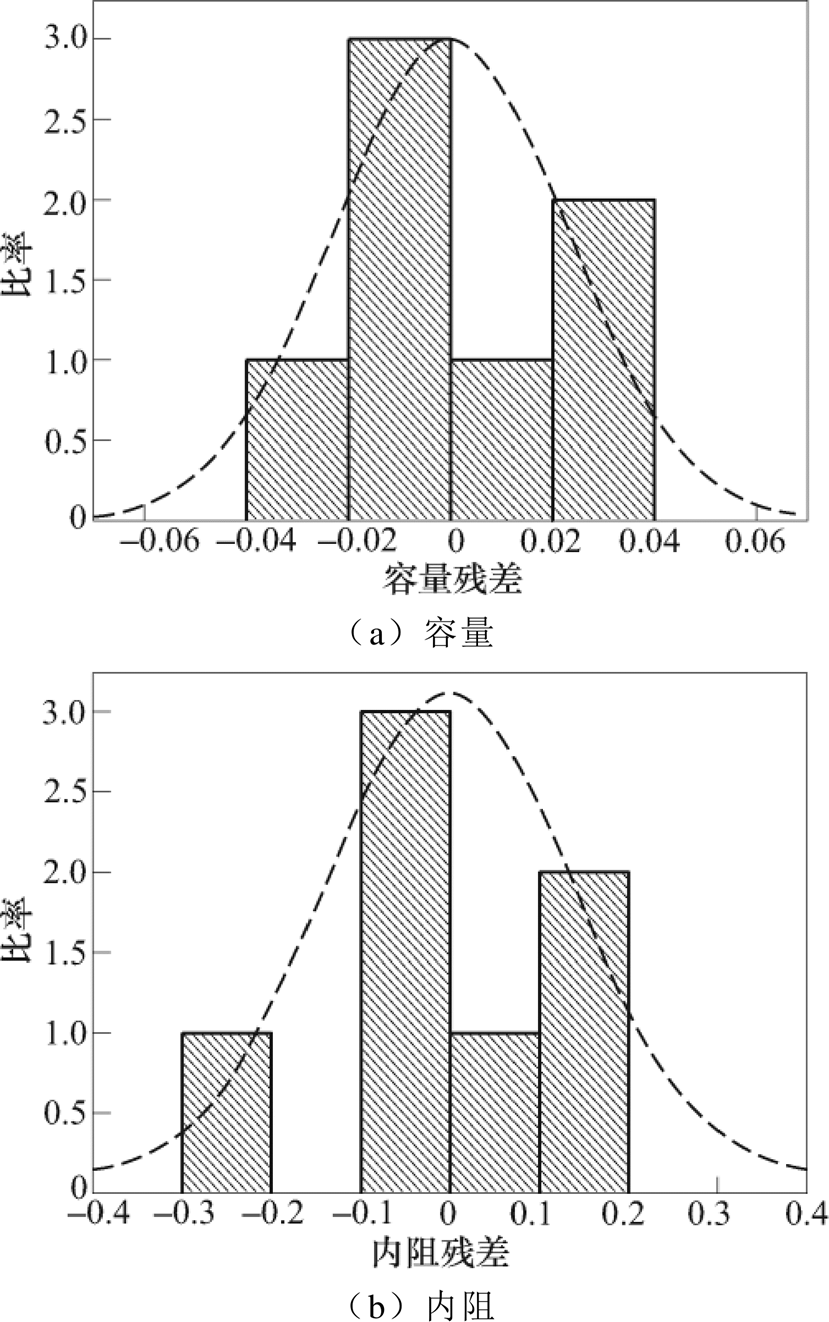
图13 残差直方图
Fig.13 Residual histogram
3.3.1 容量和内阻变化特性
相同循环区间的锂离子电池经过600次循环后容量和内阻的变化结果如图14所示,以虚线将内阻减小和内阻增大两个阶段分开。首先从机理上分析容量和内阻在性能衰退过程中的相关性。1号电池容量衰退存在“急—缓—急”三个阶段:第一个“急”对应固态电解质界面(Solid Electrolyte Interface, SEI)膜建立与稳定过程导致的容量快速衰退阶段,实际上对应的也是虚线的左半部,内阻由于SEI膜的建立过程出现了一定程度上的减小;“缓”对应的是活性锂离子减少造成的相对平缓的衰退,内阻在这个阶段也是相对平缓的增加;第二个“急”对应加速衰退阶段,内阻在这个阶段大幅增加,推测这个阶段造成容量加速衰退的原因与造成内阻增加的原因是相同的。3号电池的衰退模型与1号电池类似,但衰退程度较深。第一个阶段很短,100次循环后就进入了内阻增加的阶段,400次循环后内阻大幅增加,容量加速衰退。
2号电池和4号电池衰退模式与上述内容存在一定差异,最明显的是其容量衰退曲线趋势直接呈指数下降。内阻方面,2号电池内阻存在较长时间的减小且程度最深,推测同样是由SEI膜建立与稳定过程导致的,但对应容量衰退曲线无法找到相应阶段,猜想其容量衰退的前两个阶段融合到了一起。4号电池趋势与2号类似,其最为明显的特点是400次循环后内阻大幅度增加对应的容量大幅度衰退。综上所述,本文划分出了锂离子电池性能衰退的三个阶段:SEI膜建立与稳定阶段,对应容量快速衰退,内阻一定程度上的减小;缓慢的线性衰退阶段,对应容量线性衰退,内阻线性增加,但其斜率均较小;加速衰退阶段,对应容量加速衰退,内阻大幅度增加。

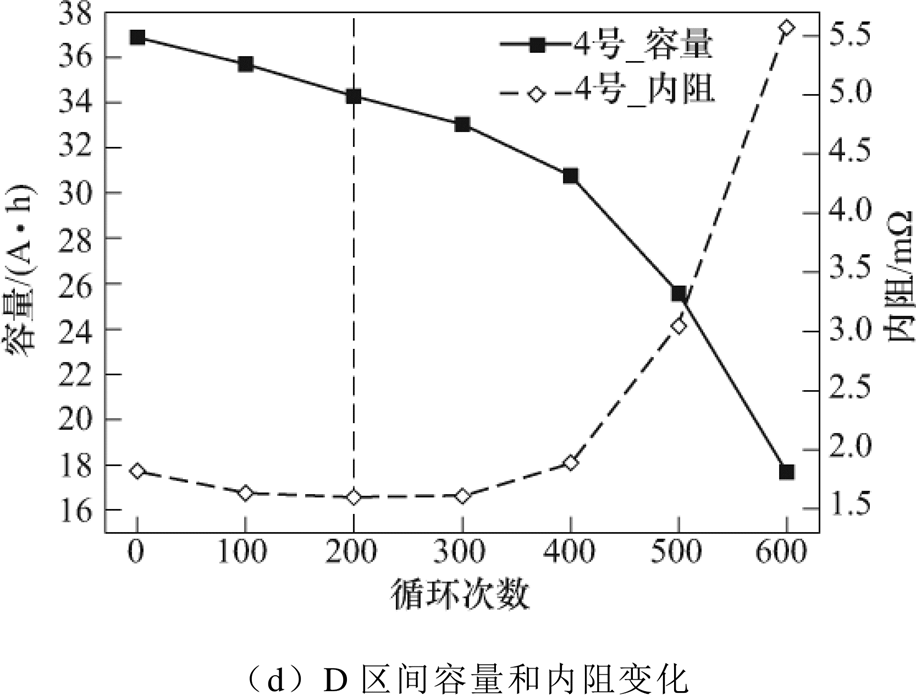
图14 A、B、C、D区间容量和内阻相关性分析
Fig.14 Correlation analysis of the capacity and internal resistance of A、B、C、D
3.3.2 容量与内阻变化相关性分析
采用回归分析法找到其相关性的数学表达式。对于锂离子电池全生命周期而言,第一阶段较短且内阻出现与整体趋势相反的现象,故在进行回归分析时舍弃第一阶段,对第二、第三阶段进行研究。分别以累积内阻增加率和累积容量衰退率为目标参数,对25℃下的数据进行处理得到的结果为
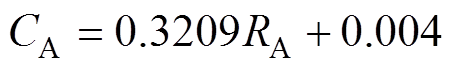 (4)
(4)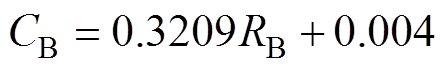 (5)
(5)
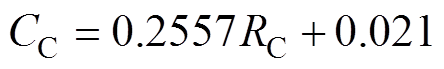 (6)
(6)
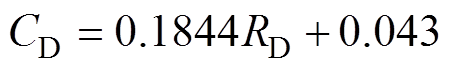 (7)
(7)式中,Cx为因变量;Rx为自变量,x=A, B, C, D。表4为回归结果的拟合参数。表4中增加了两个评价参数,SSE为误差二次方和,RMSE为方均根(标准值),两者越接近零表示拟合效果越好。
表4 回归结果的拟合参数
Tab.4 Basic parameters of linear regression analysis

电池斜率截距SSERMSER-squareAdjusted R-square 1号0.320 90.0043.3×10-50.0040.970 40.955 6 2号0.472 50.0321.3×10-50.003 70.996 40.992 8 3号0.255 70.020 70.003 860.031 040.940 30.925 4 4号0.184 40.043 40.004 830.040 10.969 30.959
3.4.1 不同区间性能相关模型的温度适用性
为了分析相关模型的温度适用性,将15℃和40℃环境下分区间累积容量衰退率和累积内阻增加率的数据分别代入式(2)、式(3)中,多元线性回归在不同温度下的拟合结果如图15所示。
利用25℃下的模型,在不同温度下全区间累积容量衰退率依然保持较高的预测精度,除起始点外,15℃环境下最大偏差为2.47%,40℃环境下最大偏差为2.41%。因此,累积容量衰退率的相关模型温度适用性较高。但观察图15b,累积内阻变化率在不同温度下的预测结果偏差较大,尤其是40℃环境下,各循环点预测准确性均较低。分析其原因,主要是由于锂离子电池的内阻对温度十分敏感,在不同温度下内阻值波动较大。
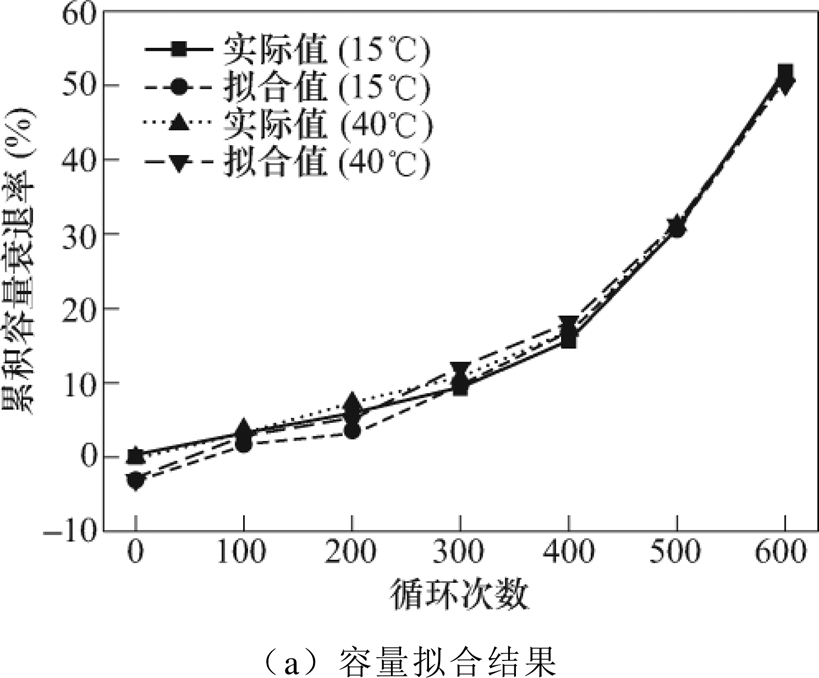
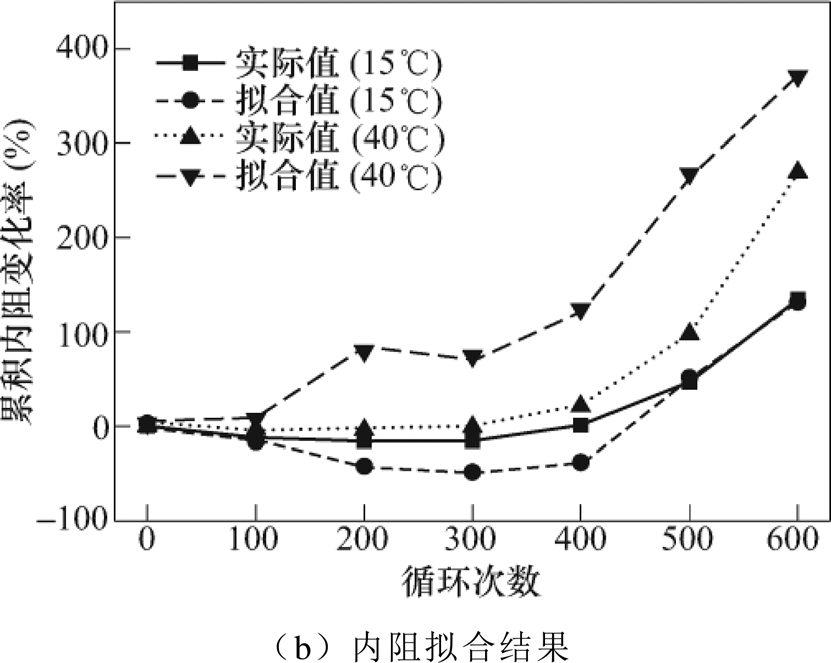
图15 多元线性回归在不同温度下的拟合结果
Fig.15 Fitting results of multiple linear regression at different temperatures
3.4.2 同区间性能相关模型的温度适用性
25℃下同区间累积容量衰退率和累积内阻变化率的相关模型如式(4)~式(7)所示,将15℃及40℃下得到的性能测试数据代入以上模型,得到容量与内阻变化率相关性的温度适用性分析如图16所示,不同温度下性能参数的实际值与拟合值均有一定的差异。15℃下最大误差超过10%,40℃下有10%左右的误差,因此可以看出各循环区间的电池累积容量衰退率与累积内阻增加率相关模型的适用性较弱。


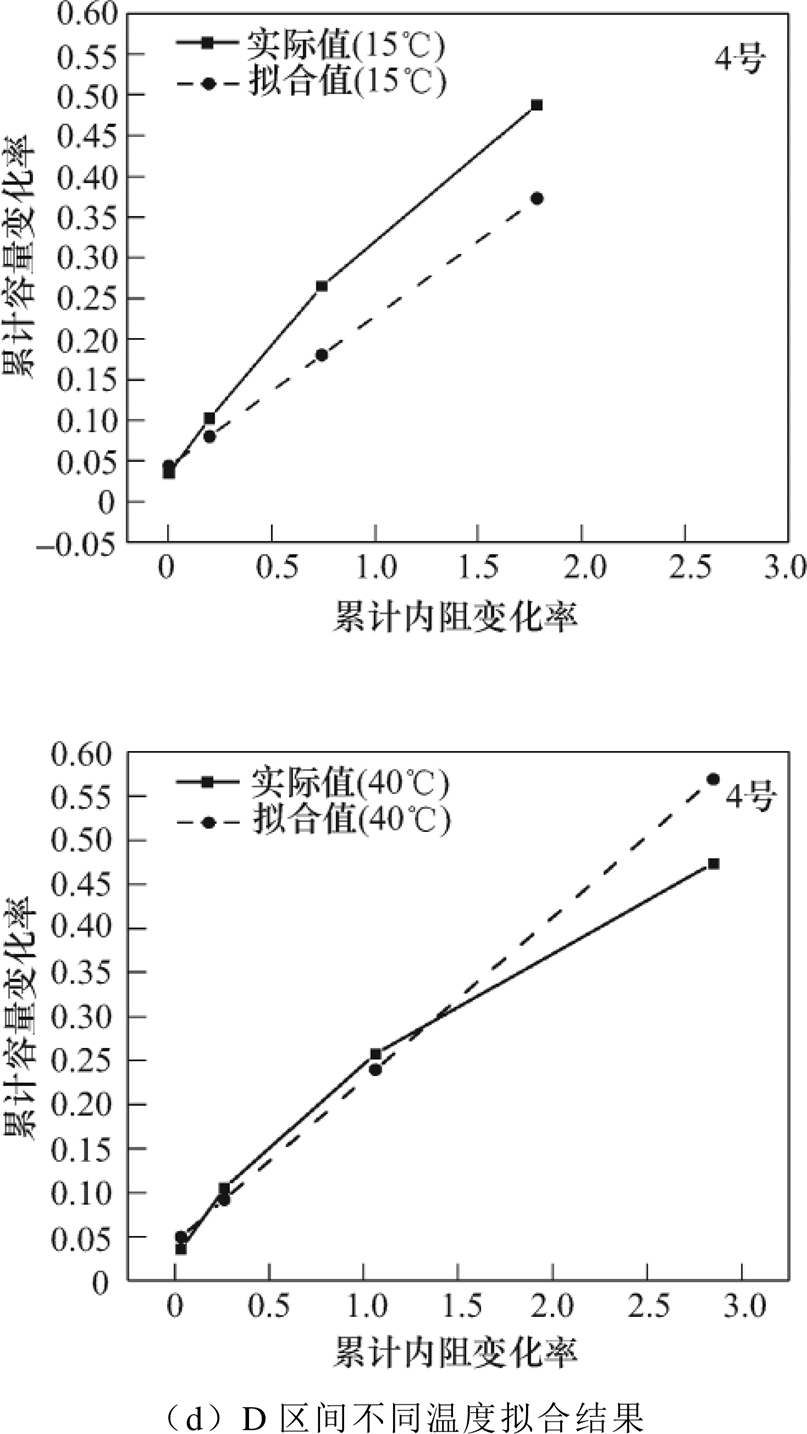
图16 容量与内阻变化率相关性的温度适用性分析
Fig.16 Temperature applicability analysis of the correlation between the rate of change of internal resistance and capacity
本文基于容量增量曲线对电池循环区间进行划分。通过设计合理的循环试验及性能测试方式,得到了锂离子电池性能衰退的结果,对不同衰退路径下电池容量及内阻的衰退规律进行了研究。
采用多元线性拟合的方式分析了A、B、C区间与D区间累积容量衰退率和累积内阻变化率的相关性,得到的拟合曲线其拟合优度基本在0.95以上。在不同温度下,累积容量衰退率的相关模型有较好的适用性,对于多元线性拟合结果,在15℃环境下拟合值与实际值之间最大偏差为2.47%,40℃环境下最大偏差为2.41%;但累积内阻变化率的模型适用性较弱。此外,分析了每个循环区间下容量及内阻的变化规律的特性,从“急—缓—急”三个阶段分析了两者变化相关性的内部机理;同时利用线性拟合分段描述了两者的线性关系,拟合优度均在0.94以上,经验证二者的相关性在不同温度下适用性较弱。这些相关性规律的研究,为锂离子电池的使用区间选择和电池衰退预测提供了参考依据。
参考文献
[1] 刘伟龙, 王丽芳, 廖承林, 等. 充电模态下电动汽车动力电池模型辨识[J]. 电工技术学报, 2017, 32(11): 198-207.
Liu Weilong, Wang Lifang, Liao Chenglin, et al. Model identification of electric vehicle power battery in charging mode[J]. Transactions of China Electro- technical Society, 2017, 32(11): 198-207.
[2] Li Xiaoyu, Wang Zhenpo. A novel fault diagnosis method for lithium-ion battery packs of electric vehicles[J]. Measurement, 2018, 116: 402-411.
[3] Gao Yang, Jiang Jiuchun, Zhang Caiping, et al. Lithium-ion battery aging mechanisms and life model under different charging stresses[J]. Journal of Power Sources, 2017, 356: 103-114.
[4] Ma Zeyu, Jiang Jiuchun, Shi Wei, et al. Investigation of path dependence in commercial lithium-ion cells for pure electric bus applications: aging mechanism identification[J]. Journal of Power Sources, 2015, 274: 29-40.
[5] Ouyang Minggao, Feng Xuning, Han Xuebing. A dynamic capacity degradation model and its appli- cations considering varying load for a large format Li-ion battery[J]. Applied Energy, 2016, 165: 48-59.
[6] 龚敏明, 时玮, 张言茹, 等. 纯电动公交车锂离子动力电池的使用条件控制[J]. 吉林大学学报, 2014, 44(4): 1081-1087.
Gong Minming, Shi Wei, Zhang Yanru, et al. The condition control of pure electric bus lithium ion power battery[J]. Journal of Jilin University, 2014, 44(4): 1081-1087.
[7] Long Lam, Pavol Bauer. Practical capacity fading model for Li-ion battery cells in electric vehicles[J]. IEEE Transactions on Power Electronics, 2012, 28(12): 5910-5918.
[8] Jens Groot. State-of-health estimation of Li-ion batteries: cycle life test methods[D]. Goteborg: Chalmers University of Technology, 2012.
[9] 薛楠, 孙丙香, 白恺, 等. 基于容量增量分析的复合材料锂电池分区间循环衰退机理[J]. 电工技术学报, 2017, 32(13): 145-152.
Xue Nan, Sun Bingxiang, Bai kai, et al. Different state of charge range cycle degradation mechanism of composite material lithium-ion batteries based on incremental capacity analysis[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 145- 152.
[10] Li Xiaoyu, Wang Zhenpo, Zhang Lei, et al. State- of-health estimation for Li-ion batteries by combing the incremental capacity analysis method with grey relational analysis[J]. Journal of Power Sources, 2019, 410-411: 106-114.
[11] 王震坡, 孙逢春, 林程. 不一致性对动力电池组使用寿命影响的分析[J]. 北京理工大学学报, 2006(7): 577-580.
Wang Zhenpo, Sun Fengchun, Lin Cheng. Analysis of the impact of inconsistency on the service life of power battery[J]. Journal of Beijing Institute of Technology, 2006(7): 577-580.
[12] 王立业, 王丽芳, 刘伟龙. 基于容量差的电动汽车主动均衡控制策略研究[J]. 电工电能新技术, 2017, 36(11): 44-50.
Wang Liye, Wang Lifang, Liu Weilong. Research on active balance control strategy of electric vehicle based on capacity difference[J]. New Technology of Electrical Power, 2017, 36(11): 44-50.
[13] 孙丙香, 姜久春, 韩智强, 等. 基于不同衰退路径下的锂离子动力电池低温应力差异性[J]. 电工技术学报, 2016, 31(10): 159-167.
Sun Bingxiang, Jiang Jiuchun, Han Zhiqiang, et al. The lithium-ion battery low temperature stress based on different degradation paths[J]. Transactions of China Electrotechnical Society, 2016, 31(10): 159- 167.
[14] 刘道坦, 范茂松. 退运电动汽车动力电池性能测试与分析[J]. 电源技术, 2016, 40(3): 532-535.
Liu Daotan, Fan Maosong. Performance test and analysis of the power battery of the returned electric vehicle[J]. Power Source Technology, 2016, 40(3): 532-535.
[15] 林成涛, 李腾, 田光宇, 等. 电动汽车用锂离子动力电池的寿命试验[J]. 电池, 2010, 40(1): 23-26.
Lin Chengtao, Li Teng, Tian Guangyu, et al. Life test of lithium-ion power battery for electric vehicle[J]. Bettery, 2010, 40(1): 23-26.
[16] Anthony Barre, Benjamin Deguilhem, Sebastien Grolleau, et al. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications[J]. Journal of Power Sources, 2013(241): 680-689.
[17] Bharath Pattipati, Chaitanya Sankavaram, Krishna R Pattipati. System identification and estimation frame- work for pivotal automotive battery management system characteristics[J]. IEEE Transactions on systems, 2011, 41(6): 869-884.
[18] Anthony Barre, Frederic Suard, Mathias Gerard, et al. Statistical analysis for understanding and predicting battery degradations in real-life electric vehicle use[J]. Journal of Power Sources, 2014, 245: 846- 856.
[19] 马泽宇, 姜久春, 张维戈, 等. 锂离子动力电池热老化的路径依赖性研究[J]. 电工技术学报, 2014, 29(5): 221-227.
Ma Zeyu, Jiang Jiuchun, Zhang Weige, et al. Path dependence of thermal aging of Li-ion power battery[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 221-227.
[20] 马泽宇, 姜久春, 王占国, 等. 基于容量增量分析的石墨负极磷酸铁锂电池SOC估算方法研究[J]. 汽车工程, 2014, 36(12): 1439-1444.
Ma Zeyu, Jiang Jiuchun, Wang Zhanguo, et al. A research on SOC estimation for LiFePO4 battery with graphite negative electrode based on incremental capacity analysis[J]. Automotive Engineering, 2014, 36(12): 1439-1444.
Performance Correlation and Temperature Applicability of Li-ion Batteries under Different Range Degradation Paths
Abstract The performance of li-ion battery is different under different capacity ranges and stress conditions. In this paper, lithium ion battery of composite material was taken as the research object, and the cycle range was divided based on the electrochemical phase change mechanism. A total throughput of 600 cycle tests was performed in the divided ranges and the whole range. Based on the performance degradation results in the cycle of different capacity ranges, the regression parameter analysis method was used to establish the characteristic parameter correlation model of lithium ion battery, including the correlation of cumulative capacity degradation rate, the correlation of cumulative internal resistance degradation rate and the correlation between them. The fitting goodness of the models are above 95%. Furthermore, the models were extended to a wider temperature range, and the applicability of the models was quantitatively analyzed. The results show that the correlation model of cumulative capacity degradation rate is very applicable at different temperatures. However, the applicability of the cumulative internal resistance correlation model and the correlation model between the two parameters are weak. The evolution law of internal resistance and capacity under different degradation paths provides a basis for the selection of the cycle range of li-ion batteries, and also provides a new idea for degradation prediction under different conditions.
keywords:Lithium-ion battery, cycle range, degradation path, correlation, thermal applicability
中图分类号:TM911
DOI: 10.19595/j.cnki.1000-6753.tces.190300
国家重点研发计划(2018YFB0104400)和国家自然科学基金重点基金(61633015)资助项目。
收稿日期 2019-03-25
改稿日期 2019-11-14
孙丙香 女,1979年生,副教授,博士生导师,研究方向为动力电池成组应用技术。E-mail: bxsun@bjtu.edu.cn(通信作者)
刘 佳 男,1994年生,硕士研究生,研究方向为动力电池成组应用技术。E-mail: 17121466@bjtu.edu.cn
(编辑 陈 诚)