基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法
李超然 肖 飞 樊亚翔 杨国润 唐 欣
(舰船综合电力技术国防科技重点实验室(海军工程大学) 武汉 430033)
摘要 锂离子电池作为重要的储能元件,其荷电状态(SOC)直接影响所在系统的运行状态。为了实现对锂离子电池SOC的精确估算,提出一种基于门控循环单元神经网络(GRU-RNN)和Huber-M估计鲁棒卡尔曼滤波(HKF)融合方法的锂离子电池SOC估算模型。该方法利用Huber-M估计改进卡尔曼滤波器的鲁棒性,并将基于GRU-RNN所估算的锂离子电池SOC值作为改进卡尔曼滤波器的观测量。在两组锂离子电池数据集上分别进行锂离子电池SOC估算实验。实验结果表明,基于GRU-RNN和HKF融合方法的锂离子电池SOC估算模型不仅能够准确地实现锂离子电池SOC估算,而且能够降低测量误差及异常值对估算结果的影响,使锂离子电池SOC估算结果快速且精确收敛。
关键词:锂电池 荷电状态 门控循环单元神经网络 卡尔曼滤波
0 引言
在现代化电力系统中,储能装备所起到的作用越来越重要,其意义主要包括:削峰填谷,实现电力系统能量灵活的管理和应用;提高电力系统可靠性,在故障时提供临时电能支撑;改善电能质量和特性;满足高能量大功率用电设备需求。常见的储能方式包括抽水储能、压缩空气储能、飞轮储能、超级电容储能、超导磁储能、铅酸电池储能、锂离子电池储能等[1]。其中,锂离子电池因其高能量密度、高功率密度、清洁可靠等优点,已经在便携式电子设备、电动车辆和固定储能装置中获得了广泛应用[2]。
作为储能分系统中的重要储能元件,锂离子电池的运行状态对电力系统能源调配策略非常重要,因此,需要获取锂离子电池状态信息并对其进行管理[3-4]。其中,荷电状态(State of Charge, SOC)是锂离子电池重要的状态信息之一,其被定义为剩余电量与额定电量之比,用来衡量锂离子电池中可用的电量,代表锂离子电池的续航能力,类似于汽车“油表”的功能[5-7]。
然而,锂离子电池SOC无法通过仪器测量直接获取,需要通过仪器测量电压、电流、温度等间接进行估算。而由于锂离子电池的时变性、非线性以及电化学反应的不确定性等因素,电压、电流、温度与SOC之间的关系变得难以刻画,使得锂离子电池SOC获取成为一大难题。为了解决以上问题,研究人员提出了大量锂离子电池SOC估算方法,主要分为安时积分法[8]、开路电压法[9]、电化学阻抗法[10]、基于模型的方法[11-14]、数据驱动的方法[16-18]和融合方法[19-22]。其中,安时积分法根据电量的定义对电流连续检测并进行积分得到电池释放或吸收的电量,虽然被广泛应用,但其无法获取初始SOC,需要结合其他方法使用。开路电压法通过观察电池开路电压(Open Circuit Voltage, OCV),利用开路电压和SOC之间的关系获得SOC,但充电和放电阶段OCV-SOC的关系曲线不一致且中间段曲线平缓,不易于SOC辨识。另外,还需要将电池长时间静置才可以获得稳定的开路电压,因此开路电压法无法满足SOC实时在线的估算需求。电化学阻抗法则是通过测量电池交流内阻获取SOC,但电池交流内阻受外部环境影响较大,且阻值难以测量,该方法一般适用于实验室研究,无法应用到实际中。基于模型的方法采用观测器或滤波器框架,将电池SOC作为状态量,并将安时积分法和电池模型分别作为状态方程和观测方程,通过观测方程获得的结果进行递推式修正状态量,进一步实现电池SOC估算。常见的观测器和滤波器包括卡尔曼滤波器[11]、粒子滤波器[12]、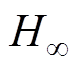 观测器[13]、滑模观测器[14]等,采用的电池模型主要包括电化学模型、等效电路模型、热模型和拟合模型等[15]。虽然基于模型的方法能够实现锂离子电池SOC估算,但是电池内部复杂的化学反应和动态变化的外部环境,使得难以建立准确的电池模型。此外,基于模型的方法需要花费较大的计算资源对模型参数不断进行辨识,这在一定程度上限制了该类方法的应用。数据驱动的方法通过机器学习算法来学习电池外部可观测量和SOC之间复杂的非线性关系,避免了对锂离子电池内部机理和模型的精确研究,在电池SOC估算中也得到了广泛应用。这类方法主要采用支持向量机[16]、模糊逻 辑[17]、神经网络[18]等机器学习方法。对于数据驱动的方法而言,SOC估算结果与训练集的选取有关,训练集与所应用的电池工况越相似,则锂离子电池SOC估算结果越准确。融合模型将上述方法中的两种或多种进行组合,以弥补单一方法的缺陷并保留各自优势,目前也得到了广泛应用。这类方法的融合形式主要以数据驱动方法与滤波方法结合以及滤波方法自身结合为主,包括支持向量机与卡尔曼滤波方法结合[19]、模糊控制与卡尔曼滤波结合[20]、神经网络与卡尔曼滤波结合[21]、粒子滤波与卡尔曼滤波结合[22]等。文献[19]将最小二乘支持向量机作为卡尔曼滤波方法的观测方程,提出一种融合支持向量机和卡尔曼滤波的SOC估计算法。类似地,文献[20]提出了一种结合模糊控制与卡尔曼滤波的锂离子电池SOC估算模型,该融合模型相对于基于传统卡尔曼滤波的锂离子电池SOC估算模型,提高了在实际应用中的鲁棒性。文献[21]将人工神经网络和双扩展卡尔曼滤波器进行结合,提出了一种能够同时实现锂离子电池SOC和电池健康状态(State of Health, SOH)估算的方法。文献[22]采用一种结合扩展卡尔曼滤波和粒子滤波的多滤波器实现锂离子电池SOC估算,与基于单滤波器的估算方法相比,该方法能够更好地跟踪和预测SOC。
观测器[13]、滑模观测器[14]等,采用的电池模型主要包括电化学模型、等效电路模型、热模型和拟合模型等[15]。虽然基于模型的方法能够实现锂离子电池SOC估算,但是电池内部复杂的化学反应和动态变化的外部环境,使得难以建立准确的电池模型。此外,基于模型的方法需要花费较大的计算资源对模型参数不断进行辨识,这在一定程度上限制了该类方法的应用。数据驱动的方法通过机器学习算法来学习电池外部可观测量和SOC之间复杂的非线性关系,避免了对锂离子电池内部机理和模型的精确研究,在电池SOC估算中也得到了广泛应用。这类方法主要采用支持向量机[16]、模糊逻 辑[17]、神经网络[18]等机器学习方法。对于数据驱动的方法而言,SOC估算结果与训练集的选取有关,训练集与所应用的电池工况越相似,则锂离子电池SOC估算结果越准确。融合模型将上述方法中的两种或多种进行组合,以弥补单一方法的缺陷并保留各自优势,目前也得到了广泛应用。这类方法的融合形式主要以数据驱动方法与滤波方法结合以及滤波方法自身结合为主,包括支持向量机与卡尔曼滤波方法结合[19]、模糊控制与卡尔曼滤波结合[20]、神经网络与卡尔曼滤波结合[21]、粒子滤波与卡尔曼滤波结合[22]等。文献[19]将最小二乘支持向量机作为卡尔曼滤波方法的观测方程,提出一种融合支持向量机和卡尔曼滤波的SOC估计算法。类似地,文献[20]提出了一种结合模糊控制与卡尔曼滤波的锂离子电池SOC估算模型,该融合模型相对于基于传统卡尔曼滤波的锂离子电池SOC估算模型,提高了在实际应用中的鲁棒性。文献[21]将人工神经网络和双扩展卡尔曼滤波器进行结合,提出了一种能够同时实现锂离子电池SOC和电池健康状态(State of Health, SOH)估算的方法。文献[22]采用一种结合扩展卡尔曼滤波和粒子滤波的多滤波器实现锂离子电池SOC估算,与基于单滤波器的估算方法相比,该方法能够更好地跟踪和预测SOC。
综上所述,以数据驱动与滤波方法结合的融合模型,一方面能够利用数据驱动的方法表示非线性关系且易于实现,另一方面能够结合滤波方法迭代收敛的特性实时修正模型输出,目前已经成为实现锂离子电池SOC估算的有效方法。但以上方法由于未考虑时序因素的影响,因而无法较好地处理时间递归问题。
对于锂离子电池而言,SOC是时变状态量,其历史状态对当前状态的影响是无法忽视的。另外,为了实现锂离子电池SOC的精确估计,算法必须对噪声具有鲁棒性。因此,本文对卡尔曼滤波器进行鲁棒性改进,并在改进卡尔曼滤波方法的框架下,分别引入安时积分法和考虑时序因素影响的循环神经网络,提出了一种基于门控循环单元神经网络(Recurrent Neural Network with Gated Recurrent Unit, GRU-RNN)和Huber-M估计鲁棒卡尔曼滤波(Huber-M Robust Kalman Filter, HKF)融合方法的锂离子电池SOC估算模型,对动态工况下的锂离子电池SOC进行估算。该方法在Huber-M估计鲁棒卡尔曼滤波方法的基础上,将安时积分法所使用的库仑计量公式作为状态方程,并将基于GRU-RNN的锂离子电池SOC估算结果作为观测量,从而实现了锂离子电池SOC的估算,整体研究思路如图1所示。该方法具有以下优点:①GRU-RNN能够考虑时序因素对于锂离子电池SOC的影响,具有较高的估算精度,同时能为HKF的状态方程提供准确的初始值,使滤波算法更快地收敛;②HKF能够提高GRU-RNN的鲁棒性,降低电压、电流、温度传感器测量误差和偶发性测量异常值以及SOC初始误差对锂离子电池SOC估算精度影响,进一步提升模型估算精度;③库仑计量公式是对锂离子电池SOC随时间变化过程的描述,采用库仑计量公式作为锂离子电池状态方程,即使GRU-RNN的估算结果出现较大误差,依然能够保证最终锂离子电池SOC估算结果的精确性。最后,通过对一组公开的锂离子电池数据集和一组实测锂离子电池数据集进行实验,验证了该模型的有效性。
1 门控循环单元神经网络
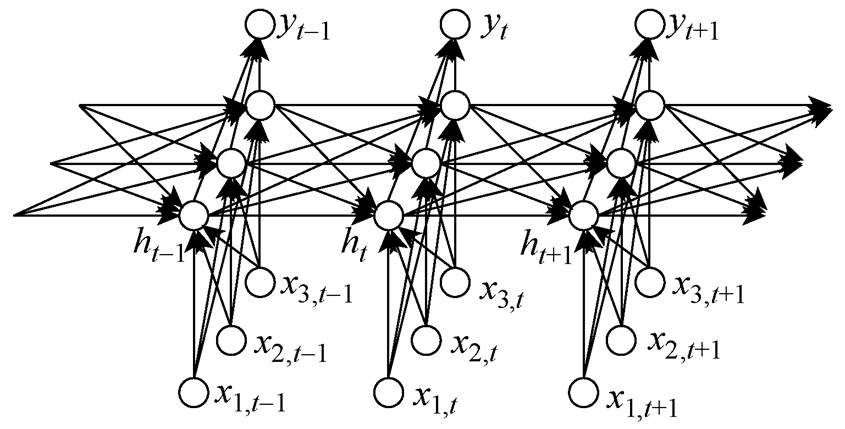
循环神经网络(Recurrent Neural Network, RNN)因其神经元可以通过内部组件保存之前的输入信息,并将其应用到后续神经网络中,已被广泛应用于解决时间序列数据问题,如语音识别和故障预 测[23-26],其结构如图2所示。
然而,RNN因梯度爆炸和梯度消失而只能处理较短的时序问题。解决梯度爆炸和梯度消失的办法主要包括合理设置初始参数、使用relu函数替代sigmoid函数和tanh函数作为激活函数以及对RNN的隐藏层节点进行改进。其中,改进RNN的隐藏层节点是最常用的做法,如长短期记忆循环神经网络(Long Short Term Memory RNN, LSTM-RNN)和带有门控循环单元(Gated Recurrent Unit, GRU)的GRU-RNN。其中,与LSTM-RNN相比,GRU-RNN采用了更简单的结构和更少的参数,并且在更小的数据集上优于LSTM-RNN[27],因此本文选取GRU- RNN作为研究对象。
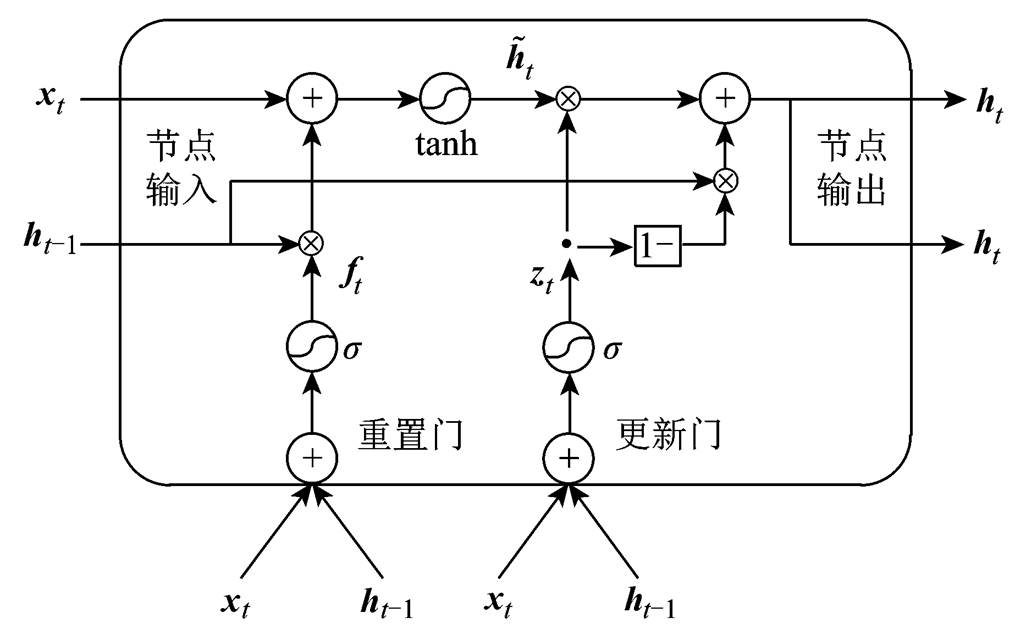
GRU-RNN是RNN的优化,与RNN同样具有图2所示的链式结构,且采用包含更新门(update gate)和重置门(reset gate)等结构的门控循环单元,并将单元状态与输出合并为一个状态,实现了神经元中信息的控制与传递,如图3所示。其中,更新门决定了前一时刻状态对当前时刻状态的影响程度,重置门决定了当前输入与前一时刻状态的结合程度。
由图3可以得出GRU-RNN获得隐藏层输出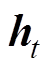 的计算公式为
的计算公式为
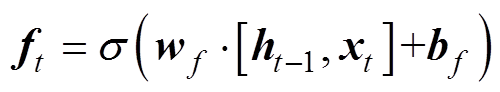 (2)
(2)
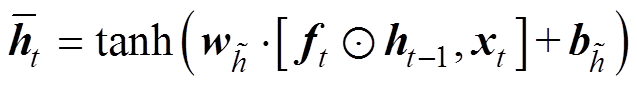 (3)
(3)
式中,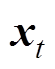 、
、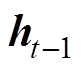 、
、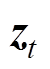 、
、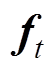 分别为GRU-RNN隐藏层节点的输入、输出、更新门输出以及重置门输出,输入
分别为GRU-RNN隐藏层节点的输入、输出、更新门输出以及重置门输出,输入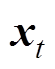 和前一时刻隐藏层输出
和前一时刻隐藏层输出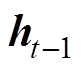 共同决定过程量
共同决定过程量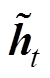 ;
;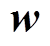 和
和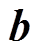 分别为训练所获得的权重参数和偏置参数,其中
分别为训练所获得的权重参数和偏置参数,其中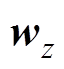 和
和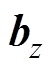 、
、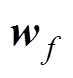 和
和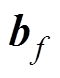 、
、 和
和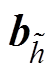 分别为计算更新门输出、重置门输出、过程量所需的权重参数和偏置参数;
分别为计算更新门输出、重置门输出、过程量所需的权重参数和偏置参数; 表示矩阵对应位置元素相乘;
表示矩阵对应位置元素相乘;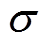 和tanh分别代表sigmoid函数和双曲正切函数。
和tanh分别代表sigmoid函数和双曲正切函数。
2 Huber-M鲁棒卡尔曼滤波
由于电压、电流、温度传感器存在一定范围的测量误差或偶发性测量异常值,并且该误差或异常值会通过GRU-RNN直接传递至SOC估算结果中,从而导致瞬时SOC估计误差增大。本节将GRU- RNN估计所得的SOC作为观测方程,为了消除观测方程中的误差,提高算法的鲁棒性,采用Huber-M估计对卡尔曼滤波的观测方程进行改进。下面首先介绍卡尔曼滤波的原理,然后在此基础上给出了Huber-M估计的推导过程,得到Huber-M估计鲁棒卡尔曼滤波。
卡尔曼滤波器(Kalman Filter, KF)是一种递归滤波器,利用输出值和输入值的递推,来计算和更新状态的最小方均误差估计值,其关键过程是状态方程和量测方程的建立。假设线性离散时间动态系统的状态方程和观测方程可以表示为
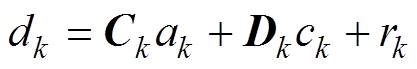 (6)
(6)
式中,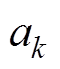 为系统的状态量;
为系统的状态量;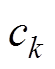 为系统的输入量;
为系统的输入量;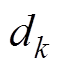 为系统的输出量;
为系统的输出量;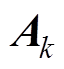 为状态转移矩阵;
为状态转移矩阵;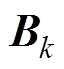 为控制输入矩阵;
为控制输入矩阵; 为系统的观测矩阵;
为系统的观测矩阵;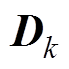 为控制输出矩阵;
为控制输出矩阵;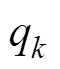 和
和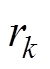 分别为相互独立且均服从于高斯白噪声的系统噪声和观测噪声,并分别构成了矩阵
分别为相互独立且均服从于高斯白噪声的系统噪声和观测噪声,并分别构成了矩阵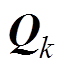 和
和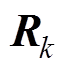 。
。
卡尔曼滤波算法的基本递推公式如下。
状态估计的时间更新为
计算误差协方差矩阵为
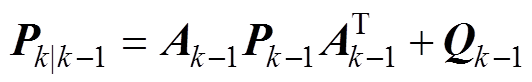 (8)
(8)
计算卡尔曼增益为
计算状态估计的量测更新为
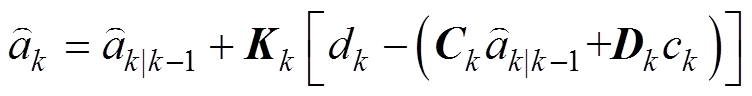 (10)
(10)
计算误差协方差矩阵的量测更新为
式中,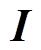 为单位矩阵。
为单位矩阵。
然而,卡尔曼滤波方法在滤波过程中必须满足量测噪声符合高斯分布的假设条件,而非高斯量测噪声分布将导致滤波器鲁棒性变差,甚至导致滤波发散。因此,本文利用Huber-M估计将标准卡尔曼滤波观测更新步骤更改为关于预测状态和观测值之间的线性回归问题,从而实现对标准卡尔曼滤波的鲁棒化,得到Huber-M估计鲁棒卡尔曼滤波。
首先定义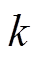 时刻的状态预测误差为
时刻的状态预测误差为
式中,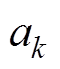 为
为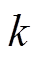 时刻状态真实值;
时刻状态真实值;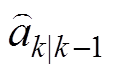 为
为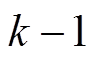 时刻对
时刻对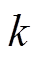 时刻状态的估算先验值。
时刻状态的估算先验值。
结合式(6)可以构造线性回归问题为
定义矩阵
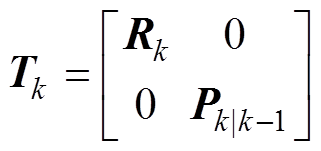 (14)
(14)
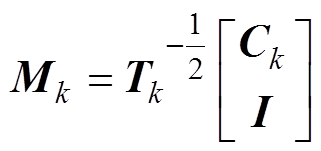 (16)
(16)
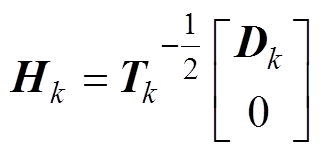 (17)
(17)
则式(13)可以转换为
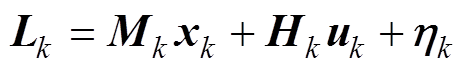 (19)
(19)
定义Huber-M估计的代价函数为
式中,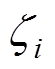 为残差向量
为残差向量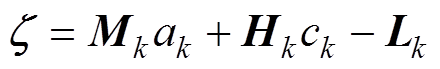 的第
的第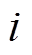 个分量;
个分量;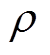 为Huber函数,可表示为
为Huber函数,可表示为
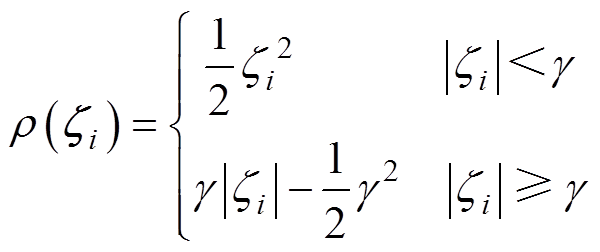 (21)
(21)
式中,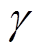 为调节参数(tuning parameter)。若Huber函数
为调节参数(tuning parameter)。若Huber函数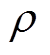 可以对
可以对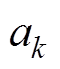 求导,则可以通过对残差向量求偏导的方法确定代价函数的极小值,如式(22)所示。
求导,则可以通过对残差向量求偏导的方法确定代价函数的极小值,如式(22)所示。
其中,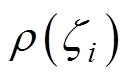 满足
满足
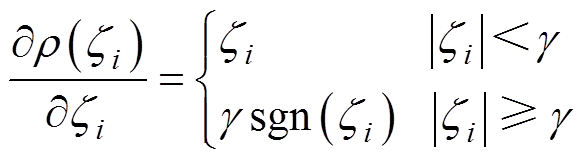 (23)
(23)
定义函数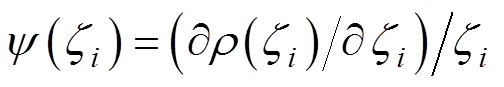 和矩阵
和矩阵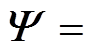
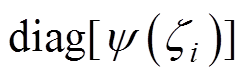 ,并将
,并将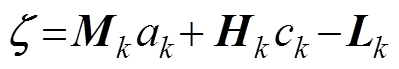 代入式(22)可得
代入式(22)可得
进一步展开后可得
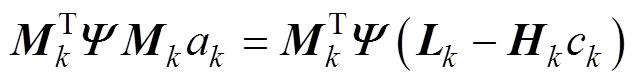 (25)
(25)
其迭代解可以表示为
式中,上标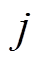 表示迭代次数。Huber迭代过程所得收敛结果为系统状态的后验估计值
表示迭代次数。Huber迭代过程所得收敛结果为系统状态的后验估计值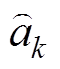 ,同时矩阵
,同时矩阵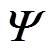 中的元素均为非增元素,因此该迭代方法收敛。最后,后验的状态误差协方差矩阵
中的元素均为非增元素,因此该迭代方法收敛。最后,后验的状态误差协方差矩阵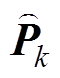 可以由以上收敛状态得到的矩阵
可以由以上收敛状态得到的矩阵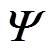 来计算得到,即
来计算得到,即
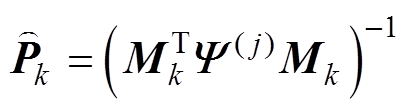 (27)
(27)
将上述预测状态和观测值之间的线性回归问题引入卡尔曼滤波算法观测方程的更新之中,便能得到Huber-M估计鲁棒卡尔曼滤波。
3 基于GRU-RNN和HKF融合方法的锂电池SOC估算模型
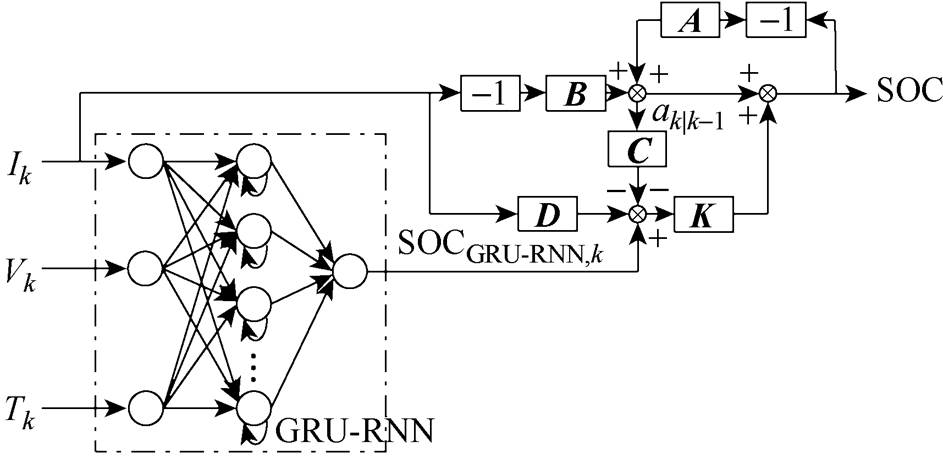
本文提出的基于GRU-RNN和HKF融合方法所建立的锂离子电池SOC估算模型如图4所示。
该模型首先通过GRU-RNN将锂离子电池电流、电压、温度映射至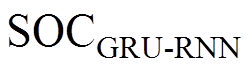 。GRU-RNN强大的非线性拟合能力能够在复杂条件下提取锂离子电池特性,准确得出观测电流、电压、温度和SOC之间的联系。但电流、电压、温度传感器不可避免地存在观测误差,以上误差将通过GRU-RNN直接影响SOC估计结果,造成SOC估计误差增大。图4中所示的锂离子电池SOC估算模型在GRU-RNN方法的基础上结合HKF方法,从而减少噪声或其他不确定因素的影响,以获得更加准确的SOC估算结果。
。GRU-RNN强大的非线性拟合能力能够在复杂条件下提取锂离子电池特性,准确得出观测电流、电压、温度和SOC之间的联系。但电流、电压、温度传感器不可避免地存在观测误差,以上误差将通过GRU-RNN直接影响SOC估计结果,造成SOC估计误差增大。图4中所示的锂离子电池SOC估算模型在GRU-RNN方法的基础上结合HKF方法,从而减少噪声或其他不确定因素的影响,以获得更加准确的SOC估算结果。
如图4所示,GRU-RNN由3个输入节点、1个全连接层和1个输出节点构成,其输入为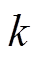 时刻的电流
时刻的电流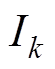 、电压
、电压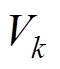 、温度
、温度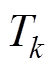 ,输出为
,输出为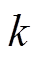 时刻的GRU- RNN估算量
时刻的GRU- RNN估算量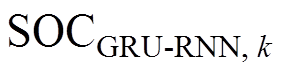 ,并将其作为HKF中的观测量,即
,并将其作为HKF中的观测量,即
将锂离子电池库仑计量过程作为描述锂离子电池充放电过程的状态方程,即
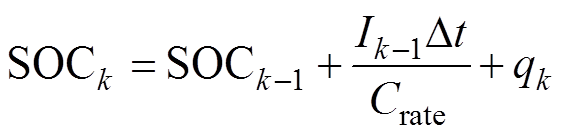 (29)
(29)
式中,Crate为电池的容量;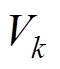 、
、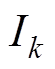 、
、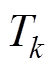 分别为电池在
分别为电池在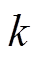 时刻的电压、电流和温度;
时刻的电压、电流和温度;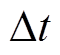 为采样时间间隔;
为采样时间间隔;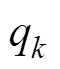 和
和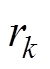 为系统的噪声;
为系统的噪声;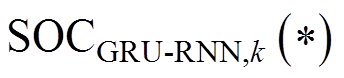 为GRU-RNN模型的输出。参考式(5)和式(6),
为GRU-RNN模型的输出。参考式(5)和式(6),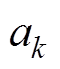 即为
即为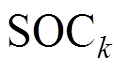 ,
,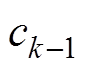 为
为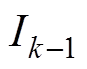 ,
,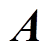 和
和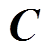 均为单位矩阵,
均为单位矩阵,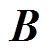 为
为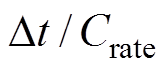 ,
,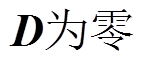 矩阵,
矩阵,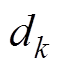 为
为 。该方法本质上是在Huber-M估计鲁棒卡尔曼滤波方法的基础上,将库仑计量公式作为状态方程,并将基于GRU- RNN的锂离子电池SOC估算结果作为观测量,从而实现了锂离子电池SOC的估算。其中,GRU-RNN所使用的变量包括电压
。该方法本质上是在Huber-M估计鲁棒卡尔曼滤波方法的基础上,将库仑计量公式作为状态方程,并将基于GRU- RNN的锂离子电池SOC估算结果作为观测量,从而实现了锂离子电池SOC的估算。其中,GRU-RNN所使用的变量包括电压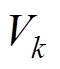 、电流
、电流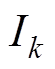 、温度
、温度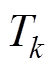 ,如式(28)中的
,如式(28)中的 所示;HKF所使用的变量包括SOC、电流
所示;HKF所使用的变量包括SOC、电流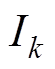 、采样时间间隔
、采样时间间隔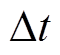 ,如式(29)所示。
,如式(29)所示。
基于GRU-RNN和HKF融合方法所建立的锂离子电池SOC估算具体流程如下:
(1)设置GRU-RNN结构和参数。设置神经网络输入层、隐藏层、输出层神经元结构,确定激活函数、损失函数、优化算法、评价函数,设置计算步长、迭代次数、采样间隔等超参数,初始化网络权重和偏置。
(2)训练并验证GRU-RNN。将训练集和验证集输入到GRU-RNN网络中,迭代优化网络参数,直到满足步骤(1)中所设置的条件。
(3)确定GRU-RNN参数。将步骤(2)中所获得的权重和偏置保留,作为神经网络的参数,得到GRU-RNN。
(4)初始估计。步骤(3)中所得GRU-RNN将初始电流、电压、温度映射至初始SOC,并将该值作为估计值的初始值,计算误差协方差。
(5)时间更新。根据式(7)和式(8)计算SOC估计先验值和估计误差协方差矩阵。
(6)引入Huber-M估计。定义式(14)~式(18),建立线性回归问题如式(19)所示。
(7)量测方程更新。按照式(28)计算下一时刻的量测方程预测值。按照式(20)定义代价函数并求解极小值。然后通过式(26)计算得到SOC后验估计值,并通过式(27)计算得到状态后验估计误差协方差矩阵。
(8)重复执行步骤(5)~步骤(7),所获得的估计值即为基于GRU-RNN和HKF融合方法所建立的锂离子电池SOC估算结果。
基于GRU-RNN和HKF的融合方法:一方面能够通过HKF强化GRU-RNN的鲁棒性,提高模型抗干扰能力;另一方面,GRU-RNN能够为HKF提供准确的初始值,使滤波算法更快且更准确地收敛。
4 电池测试数据
本文分别通过Panasonic 18650PF锂离子电池和国内某公司提供的磷酸铁锂离子电池测试数据,验证本文所提出的基于GRU-RNN和HKF融合方法的锂离子电池SOC估算模型的有效性。
4.1 Panasonic 18650PF锂离子电池测试数据集
Panasonic 18650PF锂离子电池数据集[28]是由加拿大马克马斯特大学自动化所收集。所测试的Panasonic 18650PF锂离子电池参数见表1。Panasonic 18650PF锂离子电池分别在0℃、10℃、25℃三个不同温度下进行了九种电动汽车驾驶工况下的测试,包括Cycle 1、Cycle 2、Cycle 3、Cycle 4、US06、HWFET、UDDS、LA92、Neural Network (NN)。其中,US06、HWFET、UDDS、LA92是电动汽车常见的四种驾驶工况,而Cycle 1、Cycle 2、Cycle 3、Cycle 4、NN是由US06、HWFET、UDDS、LA92随机混合组成的。测试过程中所记录的数据包括时间、锂离子电池端电压、电流、放电量、功率、能量、电池壳体温度、温箱温度等。数据采样频率为10Hz,Panasonic 18650PF锂离子电池数据集共包含约500万个采样点,因此其总共包含约500万组锂离子电池测试数据。其中,一组数据由一个采样点所记录的端电压、电流、放电量、功率、能量、电池壳体温度、温箱温度等组成,本文所用到的数据包括端电压、电流、放电量、电池壳体温度等,其中,电流、端电压、电池壳体温度分别对应式(28)中 的
的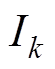 、
、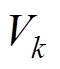 、
、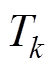 ,放电量按照式(29)以库仑计量公式由电流对时间的积分获得,并基于该值按照SOC定义计算并记录用于实验对比的实测SOC。另外,该数据集所使用的采样时间间隔
,放电量按照式(29)以库仑计量公式由电流对时间的积分获得,并基于该值按照SOC定义计算并记录用于实验对比的实测SOC。另外,该数据集所使用的采样时间间隔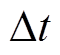 为0.1s。
为0.1s。
表1 Panasonic 18650PF锂离子电池参数
Tab.1 Parameters of Panasonic 18650PF
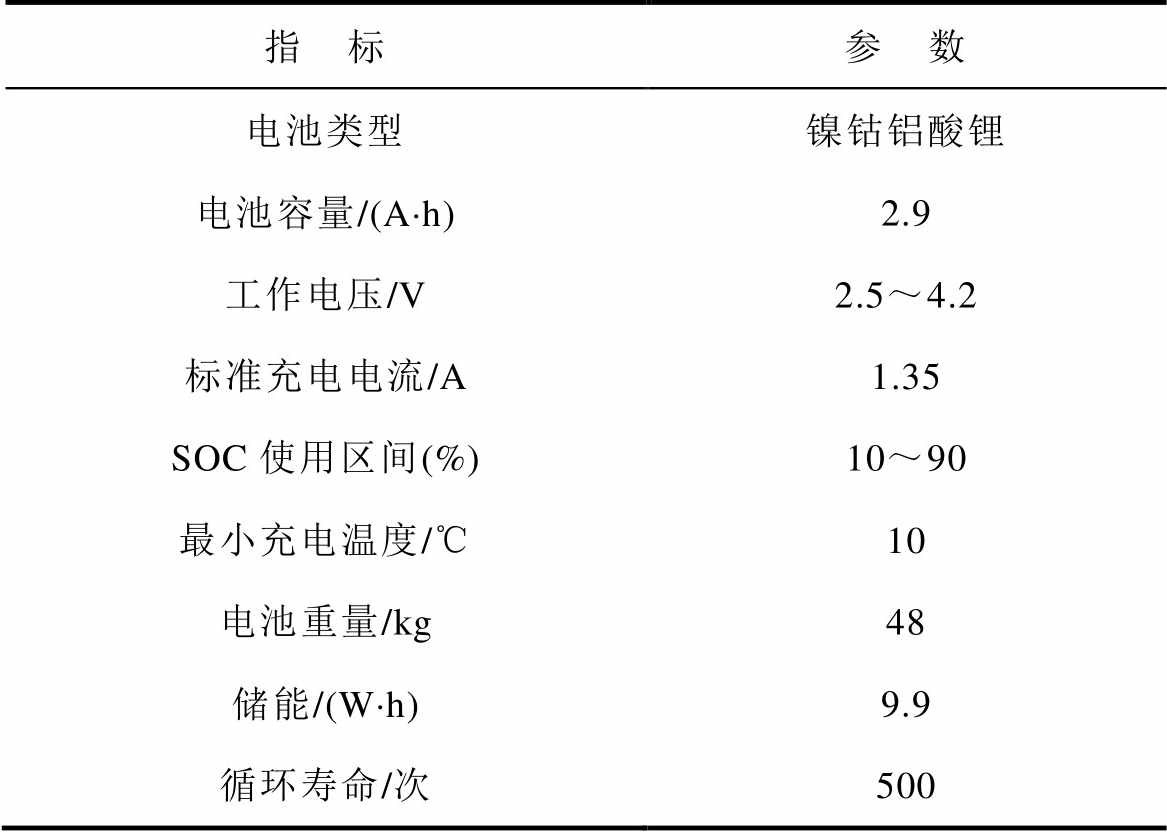
指 标参 数 电池类型镍钴铝酸锂 电池容量/(A×h)2.9 工作电压/V2.5~4.2 标准充电电流/A1.35 SOC使用区间(%)10~90 最小充电温度/℃10 电池重量/kg48 储能/(W×h)9.9 循环寿命/次500
4.2 锂离子电池大倍率脉冲放电测试数据集
锂离子电池大倍率脉冲放电测试数据集是由本课题组测试并收集。测试所用的国内某公司提供的18A·h锂离子电池参数见表2。锂离子电池大倍率脉冲放电测试首先使锂离子电池以1C恒流充电至最大额定电压,然后保持恒压充电,直至电流减小为0.01A后静置1h。接下来在0℃、25℃、45℃三个不同温度下,以30C的放电倍率使被测锂离子电池连续脉冲放电160次(放电深度DOD约为66.7%),其中一个脉冲周期包括0.5s的恒流放电过程和0.1s的静置过程。测试过程中,数据记录仪以100Hz的采样频率记录时间、锂离子电池端电压、电流、放电量、功率、能量、电池壳体温度、温箱温度等。所使用的数据同4.1节相同,分别为端电压、电流、放电量、电池壳体温度等,以上数据与式(28)和式(29)的对应关系与4.1节中一致。
表2 18A·h锂离子电池参数
Tab.2 Parameters of 18Ah lithium battery
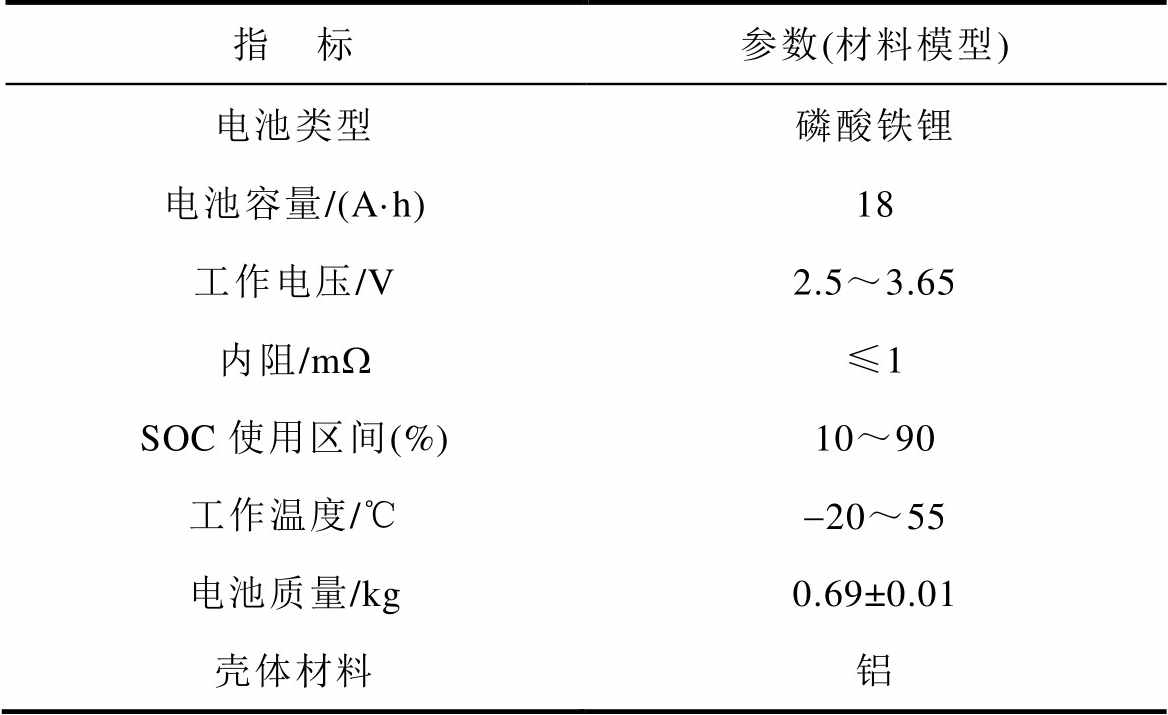
指 标参数(材料模型) 电池类型磷酸铁锂 电池容量/(A·h)18 工作电压/V2.5~3.65 内阻/mW≤1 SOC使用区间(%)10~90 工作温度/℃-20~55 电池质量/kg0.69±0.01 壳体材料铝
4.3 数据集归一化
数据集的归一化(Normalization)是将数据按照比例缩放至特定的区间,使神经网络在处理数据集时能够不受单位和量级的影响,从而提高神经网络的鲁棒性和收敛速度。本文在将数据集输入锂离子电池SOC估算模型之前,按照式(30)进行数据归一化处理。
式中,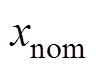 为归一化后的数据;
为归一化后的数据;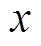 为原始数据;
为原始数据;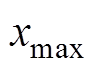 和
和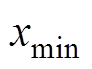 为原始数据中最大值和最小值。归一化后的数据处于区间[-1, 1]。
为原始数据中最大值和最小值。归一化后的数据处于区间[-1, 1]。
5 实验结果与分析
为了验证所提出的基于GRU-RNN和HKF融合方法的锂离子电池SOC估算模型的有效性,本小节分别在Panasonic 18650PF锂离子电池测试数据集和锂离子电池大倍率脉冲放电测试数据集上进行 实验。
5.1 实验设置
本实验所采用的软硬件包括CPU(Intel Core i7- 8700k 3.2GHz)、GPU(NVIDIA GeForce GTX 1070Ti 8GB)和RAM内存(16GB)、Linux操作系统和Keras环境。基于GRU-RNN和HKF融合方法所建立的锂离子电池SOC估算模型中,所采用的GRU-RNN在两个锂离子电池测试数据集测试上所采用的参数设置通过实验对比确定,相关实验对比工作见参考文献[29],具体参数设置见表3。其中,计算步长指循环神经网络单个输入样本的时序数据长度,采样间隔指循环神经网络相邻两个输入样本之间的时序间隔。
表3 GRU-RNN超参数设置
Tab.3 Hyperparameters of GRU-RNN

指标Panasonic 18650PF锂离子电池测试数据集锂离子电池大倍率脉冲放电测试数据集 输入节点33 隐藏节点1 000100 输出节点11 激活函数Sigmoid函数/双曲正切函数Sigmoid函数/双曲正切函数 损失函数MAEMAE 优化算法AdamAdam 评价函数MAE/MAX/RMSEMAE/MAX/RMSE 计算步长1 000100 迭代次数10030 采样间隔501
表3中,平均绝对值误差(Mean Absolute Error, MAE)、最大误差(Max Error, MAX)和方均根误差(Root Mean Squared Error, RMSE)的表达式分别为
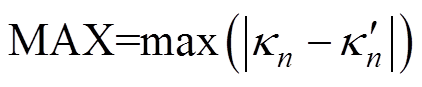 (32)
(32)
 (33)
(33)
式中,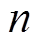 为样本序列,共有
为样本序列,共有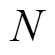 个样本序列;
个样本序列;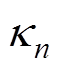 和
和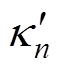 分别为估算值和实际值。
分别为估算值和实际值。
5.2 结果与分析
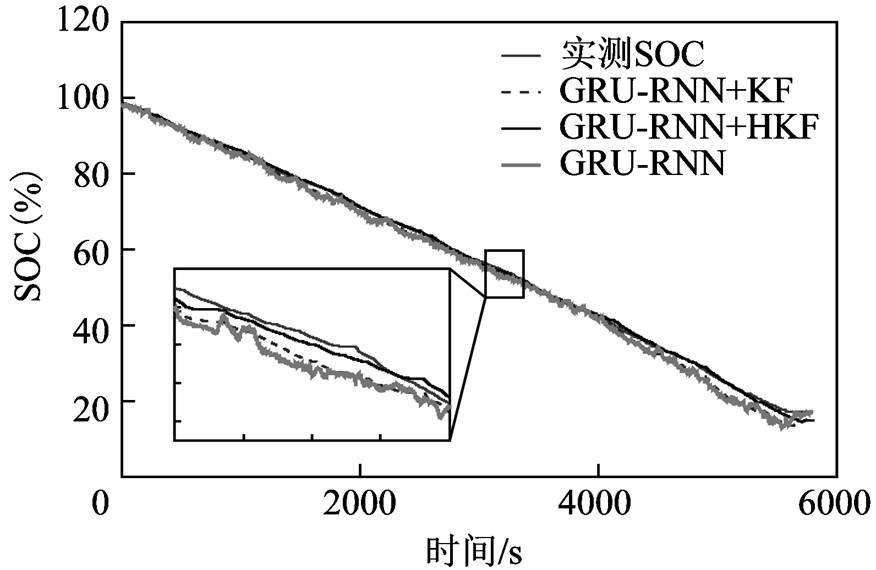
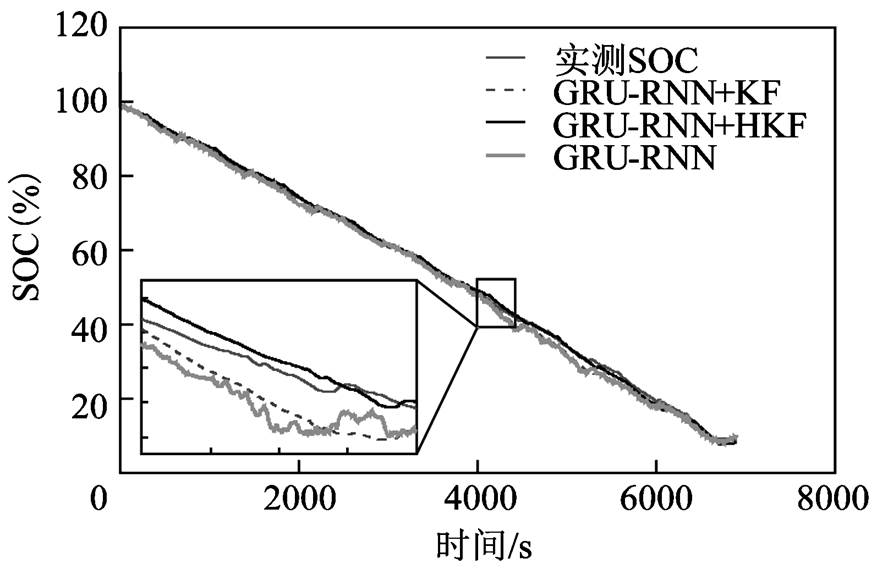
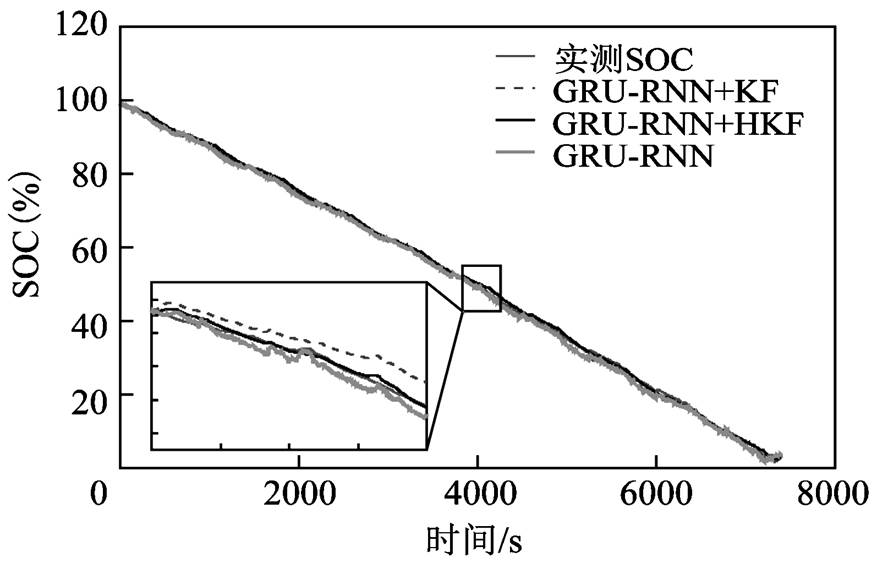
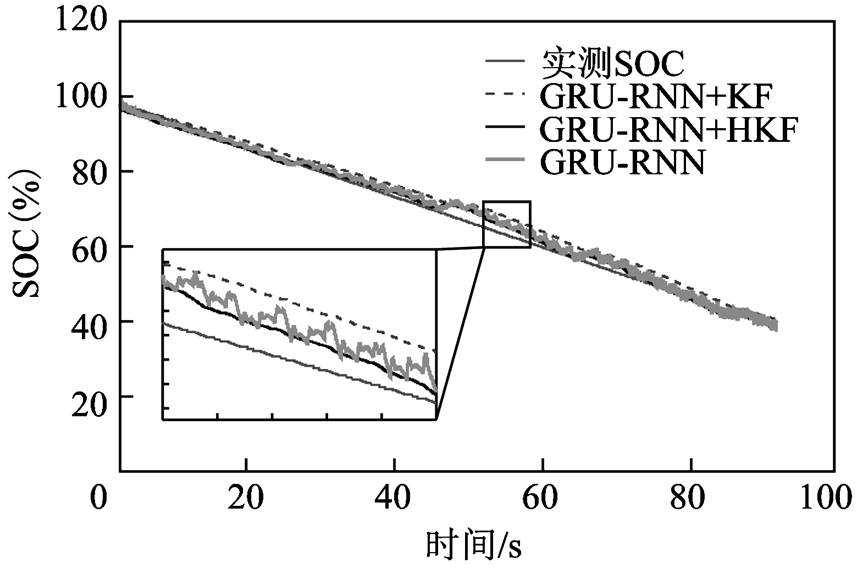
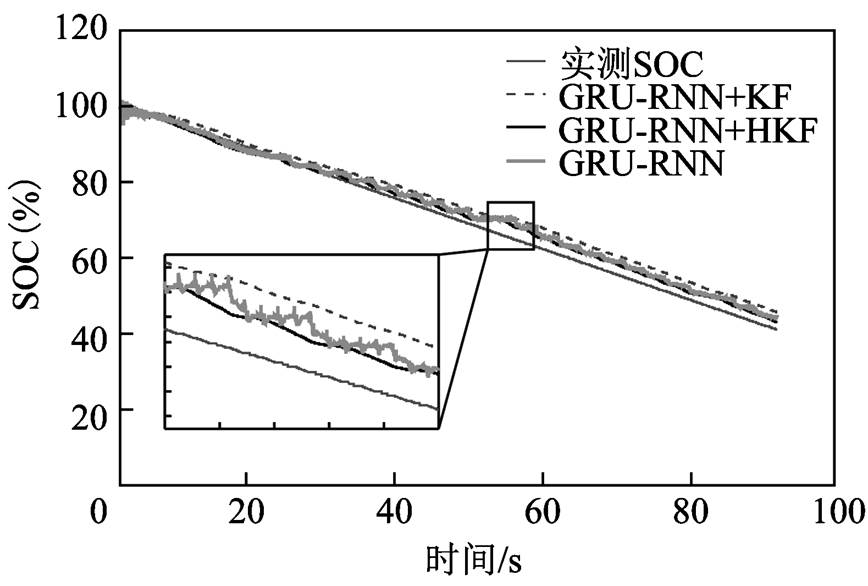
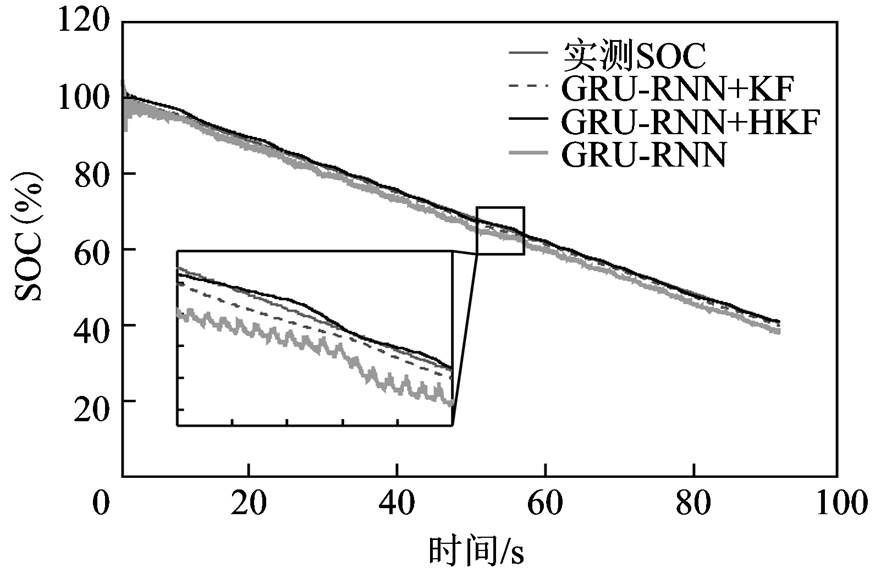
对于Panasonic 18650PF锂离子电池测试数据集,实验将0℃、10℃、25℃三种不同环境温度的Cycle 1、Cycle 2、Cycle 3、Cycle 4和NN工况下的锂离子电池测试数据作为锂离子电池SOC估算模型的训练数据,将三种不同环境温度的HWFET工况下的锂离子电池测试数据作为测试数据。所提出的锂离子电池SOC估算模型在0℃、10℃、25℃环境温度的HWFET工况下的SOC估算结果如图5~图7所示。对于锂离子电池大倍率脉冲放电测试数据集,实验所使用的训练数据和测试数据分别采集于同一环境温度下两款相同的锂离子电池。所提出的锂离子电池SOC估算模型在0℃、25℃、45℃环境温度的大倍率脉冲工况下的SOC估算结果如图8~图10所示。
通过分析图5~图10,可以发现基于GRU-RNN的锂离子电池SOC估算曲线存在明显抖动,其原因在于GRU-RNN将电压、电流、温度传感器的测量误差映射至SOC估算结果之中,导致存在瞬时SOC估计误差。基于神经网络和卡尔曼滤波融合方法的锂离子电池SOC估算模型能够降低神经网络输入中测量误差对于SOC估算的影响,相对于仅基于神经网络方法的锂离子电池SOC估算模型具有更高的估算精度。其中HKF由于Huber-M估计的存在,相对于传统卡尔曼滤波方法具有更强的鲁棒性,因此基于GRU-RNN和HKF融合方法的锂离子电池SOC估算模型具有更高的SOC估算精度。另外,从SOC估算曲线可以看出,当所设置的初始SOC估算值与SOC实际值存在偏差时,锂离子电池SOC估算模型能够很快将SOC估算值收敛至实际值附近。
为了定量分析图5~图10的SOC估算结果,利用5.1小节设置的评价函数进行描述,见表4。可以看出,所提出的基于GRU-RNN和HKF融合方法的锂离子电池SOC估算模型能够精确实现SOC估算,且模型性能评价函数MAE和MAX从小到大依次为本文所提出的基于GRU-RNN和HKF融合方法的锂离子电池SOC估算模型、基于GRU-RNN和KF的锂离子电池SOC估算模型、基于GRU-RNN的锂离子电池SOC估算模型,说明采用神经网络结合卡尔曼滤波的融合方法具有更高的SOC估算精度,能够减小神经网络输入中测量误差对于SOC估算的影响,且本文引入的Huber-M估计能够提升估算模型的鲁棒性,从而进一步提升SOC估算精度。三个温度下Panasonic 18650PF锂离子电池测试数据集和锂离子电池大倍率脉冲放电测试数据集上的最大MAE分别为0.56%和1.78%,最大MAX分别为2.39%和4.12%,最大RMSE分别为0.7%和2.01%,相对于基于GRU-RNN的锂离子电池SOC估算模型分别下降了0.89%、0.35%,6.25%、4.69%,1.11%、0.49%;相对于基于GRU-RNN+KF的锂离子电池SOC估算模型分别下降了0.71%、1.57%,3.14%、1.62%,0.9%、1.72%,验证了基于GRU-RNN和HKF融合方法的锂离子电池SOC估算模型的有效性和优势。
表4 锂离子电池SOC估算模型对比结果
Tab.4 Comparison results of Lithium-ion battery SOC estimation models
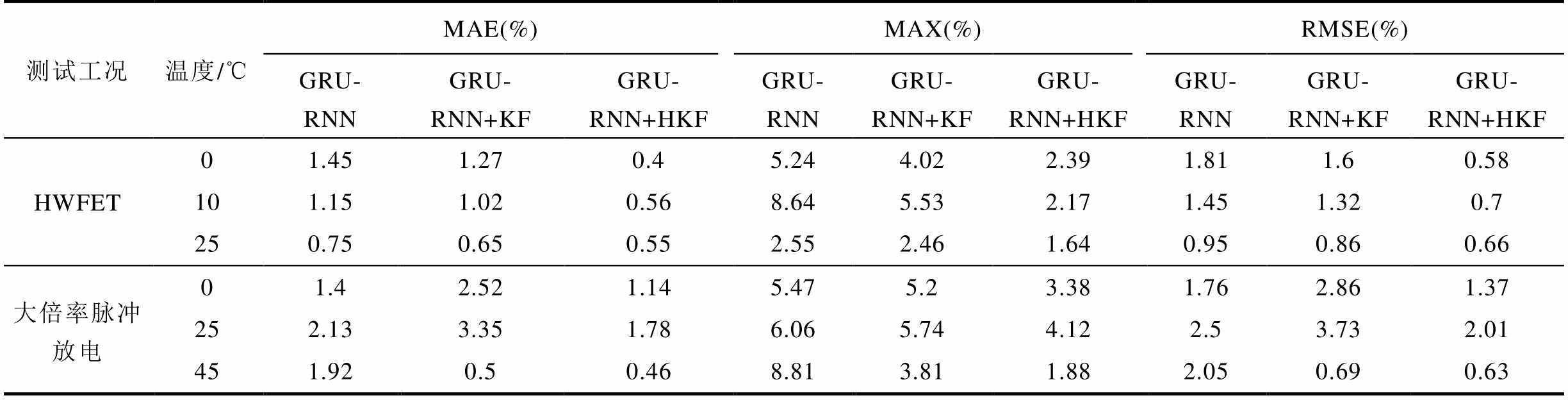
测试工况温度/℃MAE(%)MAX(%)RMSE(%) GRU- RNNGRU- RNN+KFGRU- RNN+HKFGRU- RNNGRU- RNN+KFGRU- RNN+HKFGRU- RNNGRU- RNN+KFGRU- RNN+HKF HWFET01.451.270.45.244.022.391.811.60.58 101.151.020.568.645.532.171.451.320.7 250.750.650.552.552.461.640.950.860.66 大倍率脉冲放电01.42.521.145.475.23.381.762.861.37 252.133.351.786.065.744.122.53.732.01 451.920.50.468.813.811.882.050.690.63
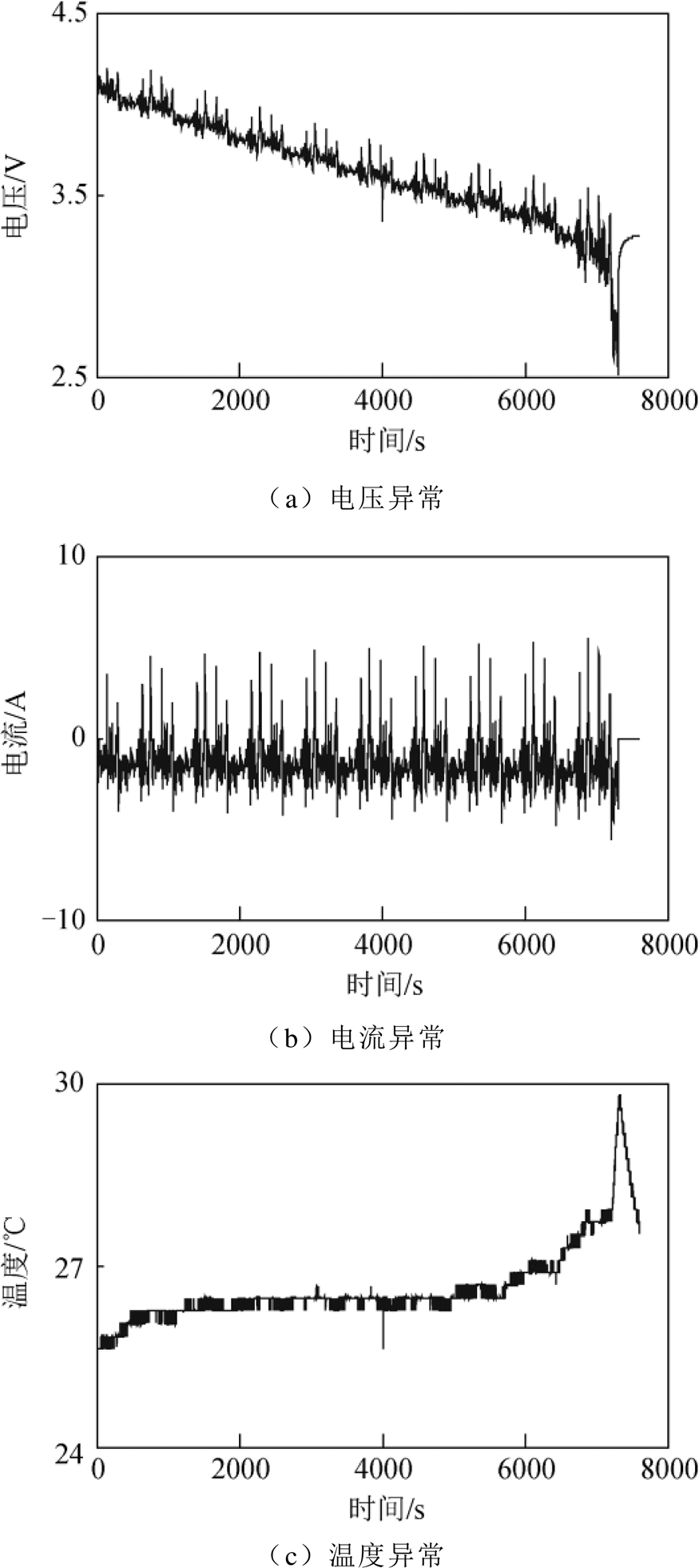
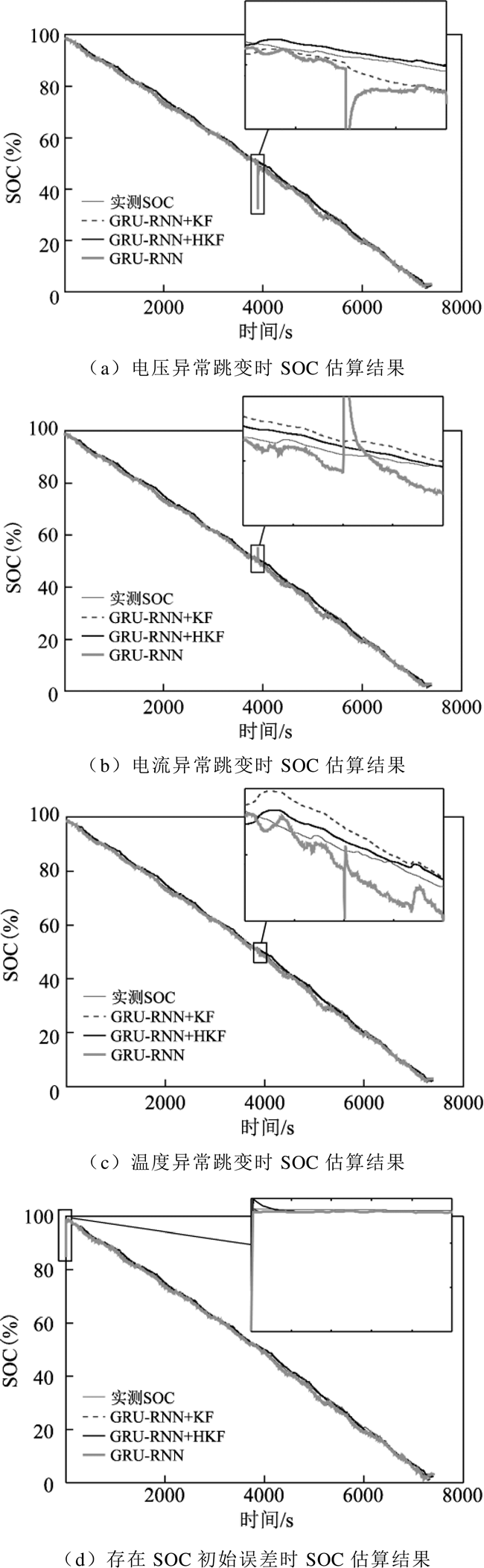
电压、电流、温度传感器除了存在一定范围的测量误差,还会存在偶发性测量异常值,测量误差和异常值均影响SOC估算模型的性能。上述实验已经证明了本文提出的基于GRU-RNN和HKF融合方法的锂离子电池SOC估算模型降低电压、电流、温度传感器测量误差对SOC估算精度影响的能力。为了证明该方法还能同时检测并处理偶发性测量异常值,在传感器测量的电压、电流、温度存在偶发性测量异常值的情况下,采用本文提出的模型进行锂离子电池SOC估算。本实验中假设电压、电流、温度传感器分别存在如图11所示的偶发性异常跳变,其中跳变发生时刻为第4 000s,跳变幅值为25℃环境温度HWFET工况下电压、电流、温度最大值与最小值间差值的15%。另外,在实际应用中,不能保证锂离子电池的初始状态为满充状态,初始SOC是未知的。为了分析SOC初始误差对估算模型的影响,本实验中假设SOC初始值为85%,即SOC初始值误差为15%。
基于GRU-RNN和HKF融合方法的锂离子电池SOC估算模型、基于GRU-RNN和KF的锂离子电池SOC估算模型、基于GRU-RNN的锂离子电池SOC估算模型在25℃环境温度HWFET工况下的SOC估算结果如图12所示。在图12a~图12c中,当传感器测量的电压、电流、温度出现偶发性测量异常值时,基于GRU-RNN的锂离子电池SOC估算模型随即出现异常值,说明该模型不具备鲁棒性。而基于神经网络和卡尔曼滤波融合方法的锂离子电池SOC估算模型变化不大,均能检测并处理该异常值,但是从图12a~图12c中可以看出,基于GRU- RNN和HKF融合方法的锂离子电池SOC估算模型基本不受影响,而基于GRU-RNN和KF融合方法的锂离子电池SOC估算模型结果存在跳变,说明基于GRU-RNN和HKF融合方法的锂离子电池SOC估算模型具有很强的鲁棒性,能够检测并处理偶发性测量异常值。在图12d中可以看出,以85%的未知SOC初始值(即SOC初始值误差为15%)开始锂离子电池SOC估算,三种模型几乎均能从下一个采样点就能收敛到正确的SOC值,完全不受未知SOC初始误差影响,这是因为这三种基于GRU- RNN的模型的输入中不包含SOC,SOC初始误差影响无法影响模型对SOC的估算。综上所述,本文所提出的基于GRU-RNN和HKF融合方法的锂离子电池SOC估算模型对电压、电流、温度异常值以及SOC初始误差具有很强的鲁棒性。
6 结论
基于融合模型的锂离子电池SOC估算模型将两种或多种进行组合,能够弥补单一方法的缺陷并保留各自优势。本文针对动态工况下的锂离子电池SOC估算问题,考虑时序因素对锂离子电池SOC估算的影响,提出一种结合卡尔曼滤波器和循环神经网络的融合锂离子电池SOC估算模型,并在六种锂离子电池运行工况和三种异常工况下验证了模型的精确性和鲁棒性。实验结果表明,该模型在三个温度下Panasonic 18650PF锂离子电池测试数据集和锂离子电池大倍率脉冲放电测试数据集上的最大MAE分别为0.56%和1.78%,最大MAX分别为2.39%和4.12%,最大RMSE分别为0.7%和2.01%。该模型将GRU-RNN和HKF进行融合,一方面能够通过HKF强化GRU-RNN的鲁棒性,降低电压、电流、温度传感器噪声和异常值以及SOC初始误差对锂离子电池SOC估算精度的影响;另一方面,GRU-RNN能够为HKF提供准确的初始值,使滤波算法更快地收敛。另外,由于HKF的状态方程采用库仑计量公式,即使GRU-RNN出现较大误差,依然能够保证锂离子电池SOC估算精度。下一步将针对该算法的实用性进行研究并在装置中进行实际应用。此外,还可以在当前增加算法鲁棒性的基础上,进一步考虑算法自适应能力的提升,研究一种自适应且鲁棒的SOC估算方法,从而使算法对不同电池对象和使用工况的变化具有自适应能力。
参考文献
[1] 李建林, 马会萌, 惠东. 储能技术融合分布式可再生能源的现状及发展趋势[J]. 电工技术学报, 2016, 31(14): 1-10.
Li Jianlin, Ma Huimeng, Hui Dong. Present deve- lopment condition and trends of energy storage technology in the integration of distributed renewable energy[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 1-10.
[2] Dunn B, Kamath H, Tarascon J M. Electrical energy storage for the grid: a battery of choices[J]. Science, 2011, 334(6058): 928-935.
[3] 李保恩, 李献伟, 毋炳鑫. 基于储能SOC状态的微电网能量优化调度策略研究[J]. 电力系统保护与控制, 2017, 45(11): 108-114.
Li Baoen, Li Xianwei, Wu Bingxin. Research on energy optimal dispatching strategy for microgrid based on battery SOC[J]. Power System Protection and Control, 2017, 45(11): 108-114.
[4] 范兴明, 王超, 张鑫, 等. 基于增量学习相关向量机的锂离子电池SOC预测方法[J]. 电工技术学报, 2019, 34(13): 2700-2708.
Fan Xingming, Wang Chao, Zhang Xin, et al. A prediction method of Li-ion batteries SOC based on incremental learning relevance vector machine[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2700-2708.
[5] 谷苗, 夏超英, 田聪颖. 基于综合型卡尔曼滤波的锂离子电池荷电状态估算[J]. 电工技术学报, 2019, 34(2): 419-426.
Gu Miao, Xia Chaoying, Tian Congying. Li-ion battery state of charge estimation based on com- prehensive Kalman filter[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 419-426.
[6] 谢长君, 费亚龙, 曾春年, 等. 基于无迹粒子滤波的车载锂离子电池状态估计[J]. 电工技术学报, 2018, 33(17): 3958-3964.
Xie Changjun, Fei Yalong, Zeng Chunnian, et al. State of charge estimation of lithium-ion battery using unscented particle filter vehicle[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(17): 3958-3964.
[7] 刘芳, 马杰, 苏卫星, 等. 基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J]. 电工技术学报, 2020, 35(4): 698-707.
Liu Fang, Ma Jie, Su Weixing, et al. State of charge estimation method of electric vehicle power battery life cycle based on auto regression extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35 (4): 698-707.
[8] Zheng Yuejiu, Ouyang Minggao, Lu Languang, et al. Cell state-of-charge inconsistency estimation for LiFePO4 battery pack in hybrid electric vehicles using mean-difference model[J]. Applied Energy, 2013, 111: 571-580.
[9] Hou Chaoyong,Yang Shuili, Hu Juan, et al. A study of SOC estimation algorithm for energy storage lithium battery pack based on information fusion technology[C]//International Conference on Power System Technology, Chengdu, 2014, DOI: 10.1109/ powercon.2014.6993645.
[10] Xu Jun, Mi Chunting Chris, Cao Binggang, et al. A new method to estimate the state of charge of lithium- ion batteries based on the battery impedance model[J]. Journal of Power Sources, 2013, 233: 277-284.
[11] 孙国强, 任佳琦, 成乐祥, 等. 基于分数阶阻抗模型的磷酸铁锂电池荷电状态估计[J]. 电力系统自动化, 2018, 42(23): 57-63.
Sun Guoqiang, Ren Jiaqi, Cheng Lexiang, et al. State of charge estimation of LiFePO4 battery based on fractional-order impedance model[J]. Automation of Electric Power Systems, 2018, 42(23): 57-63.
[12] Ye Min, Guo Hui, Cao Binggang. A model-based adaptive state of charge estimator for a lithium-ion battery using an improved adaptive particle filter[J]. Applied Energy, 2017, 190: 740-748.
[13] Li Xue, Jiang Jiuchun, Zhang Caiping, et al. Effects analysis of model parameters uncertainties on battery SOC estimation using H-infinity observer[C]//IEEE 23rd International Symposium on Industrial Electro- nics, Istanbul, Turkey, 2014, DOI: 10.1109/ISIE. 2014.6864862.
[14] Xiong Binyu, Zhao Jiyun, Su Yixin, et al. State of charge estimation of vanadium redox flow battery based on sliding mode observer and dynamic model including capacity fading factor[J]. IEEE Transa- ctions on Sustainable Energy, 2017, 8(4): 1658-1667.
[15] 季迎旭, 王明旺. 动力电池建模与应用综述[J]. 电源技术, 2016, 40(3): 740-742.
Ji Yingxu, Wang Mingwang. Review in power battery modeling and application[J]. Chinese Journal of Power Sources, 2016, 40(3): 740-742.
[16] Hu J N, Hu J J, Lin H B, et al. State-of-charge estimation for battery management system using optimized support vector machine for regression[J]. Journal of Power Sources, 2014, 269: 682-693.
[17] Malkhandi S. Fuzzy logic-based learning system and estimation of state-of-charge of lead-acid battery[J]. Engineering Applications of Artificial Intelligence, 2006, 19(5): 479-485.
[18] Guo Yifeng, Zhao Zeshuang, Huang Limin, et al. SOC estimation of lithium battery based on improved BP neural network[C]//8th International Conference on Applied Energy, Beijing, 2017: 4153-4158.
[19] 赵天意, 彭喜元, 彭宇, 等. 改进卡尔曼滤波的融合型锂离子电池SOC估计方法[J]. 仪器仪表学报, 2016, 37(7): 1441-1448.
Zhao Tianyi, Peng Xiyuan, Peng Yu, et al. Lithium- ion battery SOC estimation method with fusion improved Kalman filter algorithm[J]. Chinese Journal of Scientific Instrument, 2016, 37(7): 1441-1448.
[20] 林程, 张潇华, 熊瑞. 基于模糊卡尔曼滤波算法的动力电池SOC估计[J]. 电源技术, 2016, 40(9): 1836- 1883.
Lin Cheng, Zhang Xiaohua, Xiong Rui. State of charge estimation for power lithium-ion batteries based on fuzzy Kalman filtering algorithm[J]. Chinese Journal of Power Sources, 2016, 40(9): 1836-1883.
[21] Bai Guangxing, Wang Pingfeng, Hu Chao, et al. A generic model-free approach for lithium-ion battery health management[J]. Applied Energy, 2014, 135: 247-260.
[22] Wang Yujie, Zhang Chenbin, Chen Zonghai. State- of-charge estimation of lithium-ion batteries based on multiple filters method[J]. Energy Procedia, 2015, 75: 2635-2640.
[23] Sak H, Senior A, Rao K, et al. Learning acoustic frame labeling for speech recognition with recurrent neural networks[C]//IEEE International Conference on Acoustics, Speech and Signal Processing, Brisbane, 2015, DOI: 10.1109/ICASSP.2015.7178778.
[24] Pigou L, Aäron V D O, Dieleman S, et al. Beyond temporal pooling: Recurrence and temporal convo- lutions for gesture recognition in video[J]. Inter- national Journal of Computer Vision, 2015: 1-10.
[25] Xu Chang, Wang Gang, Liu Xiaoguang, et al. Health status assessment and failure prediction for hard drives with recurrent neural networks[J]. IEEE Transactions on Computers, 2016, 65(11): 3502-3508.
[26] Marcella C, Lorenzo B, Giuseppe S, et al. Predicting human eye fixations via an LSTM-based saliency attentive model[J]. IEEE Transactions on Image Processing, 2018, 27(10): 5142-5154.
[27] Chung J, Gulcehre C, Cho K, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[J]. ArXiv, 2014: 1412.3555.
[28] Chemali E, Kollmeyer P J, Preindl M, et al. State- of-charge estimation of Li-ion batteries using deep neural networks: a machine learning approach[J]. Journal of Power Sources, 2018, 400: 242-255.
[29] Li Chaoran, Xiao Fi, Fan Yaxiang. An approach to state of charge estimation of lithium-ion batteries based on recurrent neural networks with gated recurrent unit[J]. Energies, 2019, 12(9): 1592.
A Hybrid Approach to Lithium-Ion Battery SOC Estimation Based on Recurrent Neural Network with Gated Recurrent Unit and Huber-M Robust Kalman Filter
Li Chaoran Xiao Fei Fan Yaxiang Yang Guorun Tang Xin
(National Key Laboratory of Science and Technology on Vessel Integrated Power System Naval University of Engineering Wuhan 430033 China)
Abstract As one of the most important energy storage devices, lithium-ion (Li-ion) batteries has been widely used. Accurate and robust state of charge (SOC) estimation of lithium-ion battery is a challenging task in battery management system. In this paper, based on the recurrent neural network with gated recurrent unit (Li-ion), a new hybird model is proposed for SOC estimation. Huber-M estimation is used to improve the robustness of traditional Kalman filter and the output of the GRU-RNN is utilized as the observation of the improved Kalman filter. The performance of proposed methods is evaluated by two experimental datasets. We demonstrate the proposed method achieves satisfactory performance, as well as performs strong robustness against influence of measurement errors and outliers.
keywords:Lithium-ion battery, state of charge, recurrent neural network with gated recurrent unit, Kalman filter
中图分类号:TM912
DOI: 10.19595/j.cnki.1000-6753.tces.190547
国防科技创新特区资助项目。
收稿日期 2019-05-07
改稿日期 2019-09-16
作者简介
李超然 男,1992年生,博士研究生,研究方向为大功率储能技术、深度学习。E-mail: lichaoranhg@163.com
樊亚翔 男,1989年生,博士,助理研究员,研究方向为深度学习、状态监测及故障诊断。E-mail: fanyaxiang@126.com(通信作者)
(编辑 郭丽军)
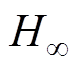 观测器[13]、滑模观测器[14]等,采用的电池模型主要包括电化学模型、等效电路模型、热模型和拟合模型等[15]。虽然基于模型的方法能够实现锂离子电池SOC估算,但是电池内部复杂的化学反应和动态变化的外部环境,使得难以建立准确的电池模型。此外,基于模型的方法需要花费较大的计算资源对模型参数不断进行辨识,这在一定程度上限制了该类方法的应用。数据驱动的方法通过机器学习算法来学习电池外部可观测量和SOC之间复杂的非线性关系,避免了对锂离子电池内部机理和模型的精确研究,在电池SOC估算中也得到了广泛应用。这类方法主要采用支持向量机[16]、模糊逻 辑[17]、神经网络[18]等机器学习方法。对于数据驱动的方法而言,SOC估算结果与训练集的选取有关,训练集与所应用的电池工况越相似,则锂离子电池SOC估算结果越准确。融合模型将上述方法中的两种或多种进行组合,以弥补单一方法的缺陷并保留各自优势,目前也得到了广泛应用。这类方法的融合形式主要以数据驱动方法与滤波方法结合以及滤波方法自身结合为主,包括支持向量机与卡尔曼滤波方法结合[19]、模糊控制与卡尔曼滤波结合[20]、神经网络与卡尔曼滤波结合[21]、粒子滤波与卡尔曼滤波结合[22]等。文献[19]将最小二乘支持向量机作为卡尔曼滤波方法的观测方程,提出一种融合支持向量机和卡尔曼滤波的SOC估计算法。类似地,文献[20]提出了一种结合模糊控制与卡尔曼滤波的锂离子电池SOC估算模型,该融合模型相对于基于传统卡尔曼滤波的锂离子电池SOC估算模型,提高了在实际应用中的鲁棒性。文献[21]将人工神经网络和双扩展卡尔曼滤波器进行结合,提出了一种能够同时实现锂离子电池SOC和电池健康状态(State of Health, SOH)估算的方法。文献[22]采用一种结合扩展卡尔曼滤波和粒子滤波的多滤波器实现锂离子电池SOC估算,与基于单滤波器的估算方法相比,该方法能够更好地跟踪和预测SOC。
观测器[13]、滑模观测器[14]等,采用的电池模型主要包括电化学模型、等效电路模型、热模型和拟合模型等[15]。虽然基于模型的方法能够实现锂离子电池SOC估算,但是电池内部复杂的化学反应和动态变化的外部环境,使得难以建立准确的电池模型。此外,基于模型的方法需要花费较大的计算资源对模型参数不断进行辨识,这在一定程度上限制了该类方法的应用。数据驱动的方法通过机器学习算法来学习电池外部可观测量和SOC之间复杂的非线性关系,避免了对锂离子电池内部机理和模型的精确研究,在电池SOC估算中也得到了广泛应用。这类方法主要采用支持向量机[16]、模糊逻 辑[17]、神经网络[18]等机器学习方法。对于数据驱动的方法而言,SOC估算结果与训练集的选取有关,训练集与所应用的电池工况越相似,则锂离子电池SOC估算结果越准确。融合模型将上述方法中的两种或多种进行组合,以弥补单一方法的缺陷并保留各自优势,目前也得到了广泛应用。这类方法的融合形式主要以数据驱动方法与滤波方法结合以及滤波方法自身结合为主,包括支持向量机与卡尔曼滤波方法结合[19]、模糊控制与卡尔曼滤波结合[20]、神经网络与卡尔曼滤波结合[21]、粒子滤波与卡尔曼滤波结合[22]等。文献[19]将最小二乘支持向量机作为卡尔曼滤波方法的观测方程,提出一种融合支持向量机和卡尔曼滤波的SOC估计算法。类似地,文献[20]提出了一种结合模糊控制与卡尔曼滤波的锂离子电池SOC估算模型,该融合模型相对于基于传统卡尔曼滤波的锂离子电池SOC估算模型,提高了在实际应用中的鲁棒性。文献[21]将人工神经网络和双扩展卡尔曼滤波器进行结合,提出了一种能够同时实现锂离子电池SOC和电池健康状态(State of Health, SOH)估算的方法。文献[22]采用一种结合扩展卡尔曼滤波和粒子滤波的多滤波器实现锂离子电池SOC估算,与基于单滤波器的估算方法相比,该方法能够更好地跟踪和预测SOC。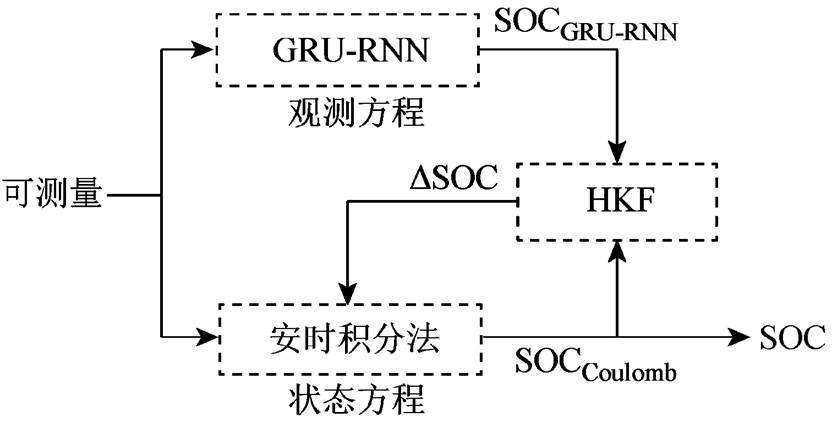
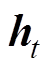 的计算公式为
的计算公式为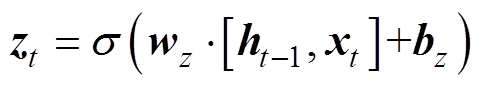 (1)
(1)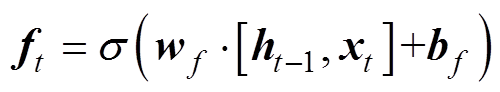 (2)
(2)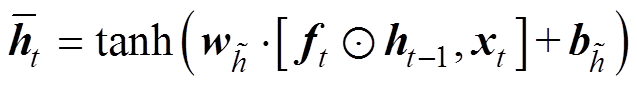 (3)
(3)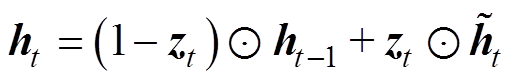 (4)
(4)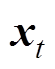 、
、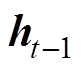 、
、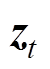 、
、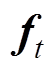 分别为GRU-RNN隐藏层节点的输入、输出、更新门输出以及重置门输出,输入
分别为GRU-RNN隐藏层节点的输入、输出、更新门输出以及重置门输出,输入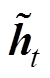 ;
;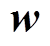 和
和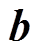 分别为训练所获得的权重参数和偏置参数,其中
分别为训练所获得的权重参数和偏置参数,其中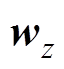 和
和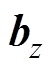 、
、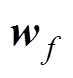 和
和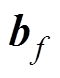 、
、 和
和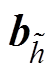 分别为计算更新门输出、重置门输出、过程量所需的权重参数和偏置参数;
分别为计算更新门输出、重置门输出、过程量所需的权重参数和偏置参数; 表示矩阵对应位置元素相乘;
表示矩阵对应位置元素相乘;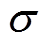 和tanh分别代表sigmoid函数和双曲正切函数。
和tanh分别代表sigmoid函数和双曲正切函数。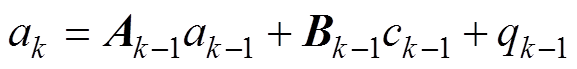 (5)
(5)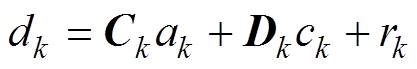 (6)
(6)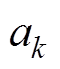 为系统的状态量;
为系统的状态量;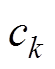 为系统的输入量;
为系统的输入量;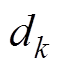 为系统的输出量;
为系统的输出量;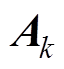 为状态转移矩阵;
为状态转移矩阵;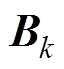 为控制输入矩阵;
为控制输入矩阵; 为系统的观测矩阵;
为系统的观测矩阵;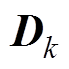 为控制输出矩阵;
为控制输出矩阵;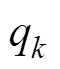 和
和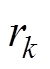 分别为相互独立且均服从于高斯白噪声的系统噪声和观测噪声,并分别构成了矩阵
分别为相互独立且均服从于高斯白噪声的系统噪声和观测噪声,并分别构成了矩阵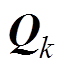 和
和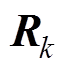 。
。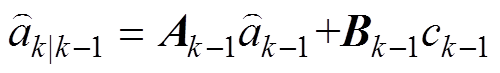 (7)
(7)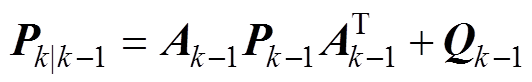 (8)
(8)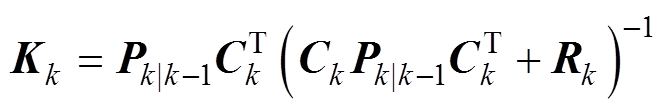 (9)
(9)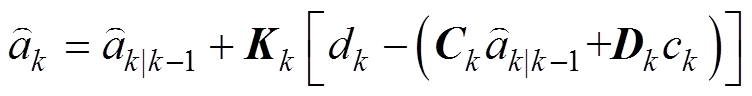 (10)
(10)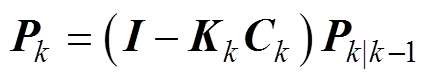 (11)
(11)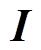 为单位矩阵。
为单位矩阵。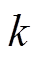 时刻的状态预测误差为
时刻的状态预测误差为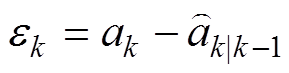 (12)
(12)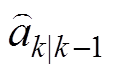 为
为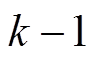 时刻对
时刻对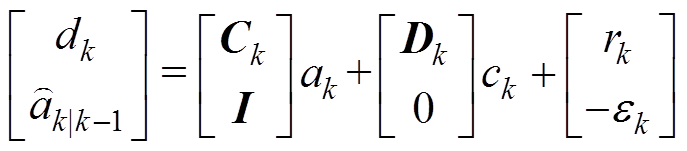 (13)
(13)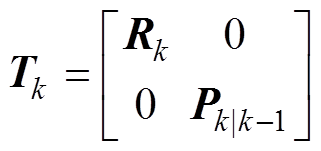 (14)
(14)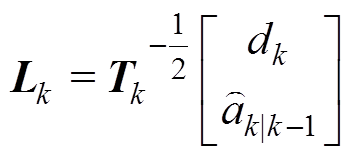 (15)
(15)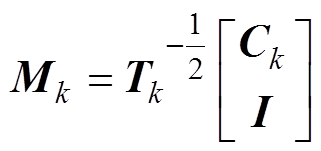 (16)
(16)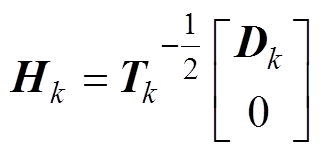 (17)
(17)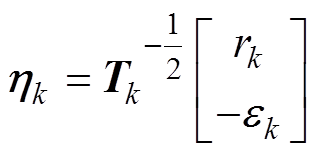 (18)
(18)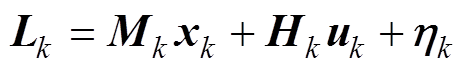 (19)
(19)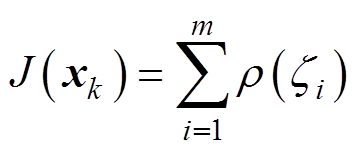 (20)
(20)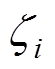 为残差向量
为残差向量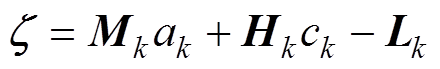 的第
的第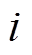 个分量;
个分量;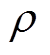 为Huber函数,可表示为
为Huber函数,可表示为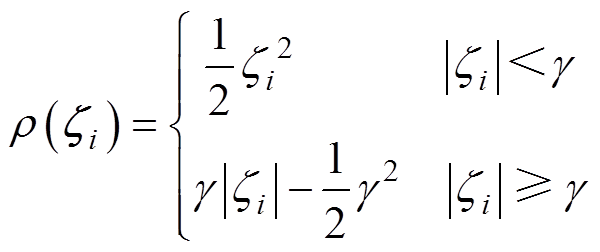 (21)
(21)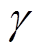 为调节参数(tuning parameter)。若Huber函数
为调节参数(tuning parameter)。若Huber函数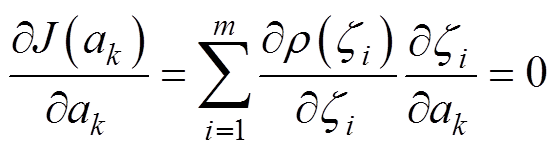 (22)
(22)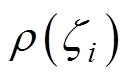 满足
满足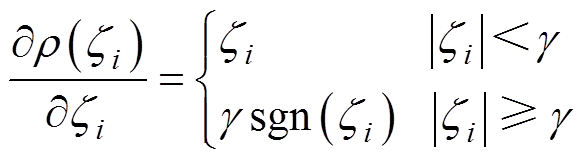 (23)
(23)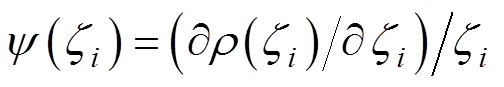 和矩阵
和矩阵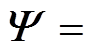
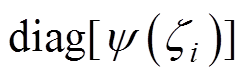 ,并将
,并将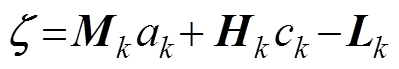 代入式(22)可得
代入式(22)可得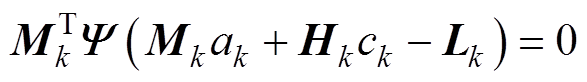 (24)
(24)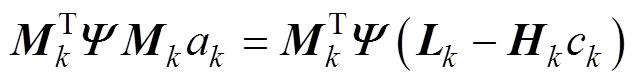 (25)
(25)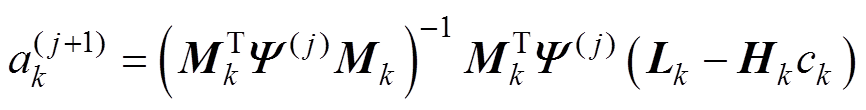 (26)
(26)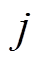 表示迭代次数。Huber迭代过程所得收敛结果为系统状态的后验估计值
表示迭代次数。Huber迭代过程所得收敛结果为系统状态的后验估计值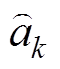 ,同时矩阵
,同时矩阵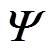 中的元素均为非增元素,因此该迭代方法收敛。最后,后验的状态误差协方差矩阵
中的元素均为非增元素,因此该迭代方法收敛。最后,后验的状态误差协方差矩阵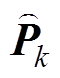 可以由以上收敛状态得到的矩阵
可以由以上收敛状态得到的矩阵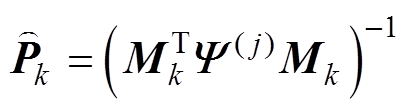 (27)
(27)
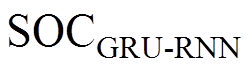 。GRU-RNN强大的非线性拟合能力能够在复杂条件下提取锂离子电池特性,准确得出观测电流、电压、温度和SOC之间的联系。但电流、电压、温度传感器不可避免地存在观测误差,以上误差将通过GRU-RNN直接影响SOC估计结果,造成SOC估计误差增大。图4中所示的锂离子电池SOC估算模型在GRU-RNN方法的基础上结合HKF方法,从而减少噪声或其他不确定因素的影响,以获得更加准确的SOC估算结果。
。GRU-RNN强大的非线性拟合能力能够在复杂条件下提取锂离子电池特性,准确得出观测电流、电压、温度和SOC之间的联系。但电流、电压、温度传感器不可避免地存在观测误差,以上误差将通过GRU-RNN直接影响SOC估计结果,造成SOC估计误差增大。图4中所示的锂离子电池SOC估算模型在GRU-RNN方法的基础上结合HKF方法,从而减少噪声或其他不确定因素的影响,以获得更加准确的SOC估算结果。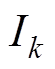 、电压
、电压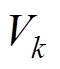 、温度
、温度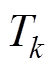 ,输出为
,输出为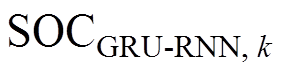 ,并将其作为HKF中的观测量,即
,并将其作为HKF中的观测量,即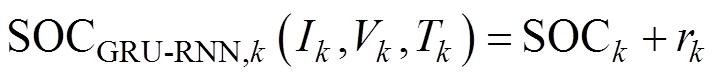 (28)
(28)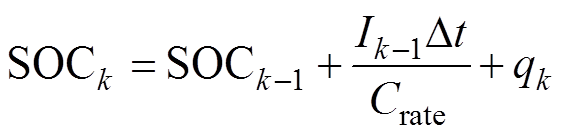 (29)
(29)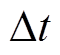 为采样时间间隔;
为采样时间间隔;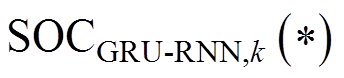 为GRU-RNN模型的输出。参考式(5)和式(6),
为GRU-RNN模型的输出。参考式(5)和式(6),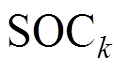 ,
,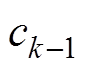 为
为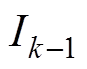 ,
,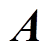 和
和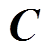 均为单位矩阵,
均为单位矩阵,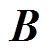 为
为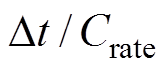 ,
,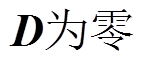 矩阵,
矩阵, 。该方法本质上是在Huber-M估计鲁棒卡尔曼滤波方法的基础上,将库仑计量公式作为状态方程,并将基于GRU- RNN的锂离子电池SOC估算结果作为观测量,从而实现了锂离子电池SOC的估算。其中,GRU-RNN所使用的变量包括电压
。该方法本质上是在Huber-M估计鲁棒卡尔曼滤波方法的基础上,将库仑计量公式作为状态方程,并将基于GRU- RNN的锂离子电池SOC估算结果作为观测量,从而实现了锂离子电池SOC的估算。其中,GRU-RNN所使用的变量包括电压

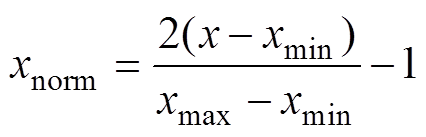 (30)
(30)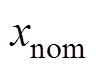 为归一化后的数据;
为归一化后的数据;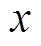 为原始数据;
为原始数据;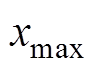 和
和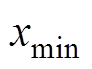 为原始数据中最大值和最小值。归一化后的数据处于区间[-1, 1]。
为原始数据中最大值和最小值。归一化后的数据处于区间[-1, 1]。
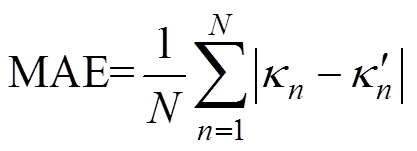 (31)
(31)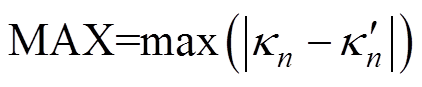 (32)
(32) (33)
(33)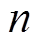 为样本序列,共有
为样本序列,共有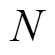 个样本序列;
个样本序列;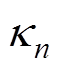 和
和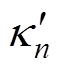 分别为估算值和实际值。
分别为估算值和实际值。