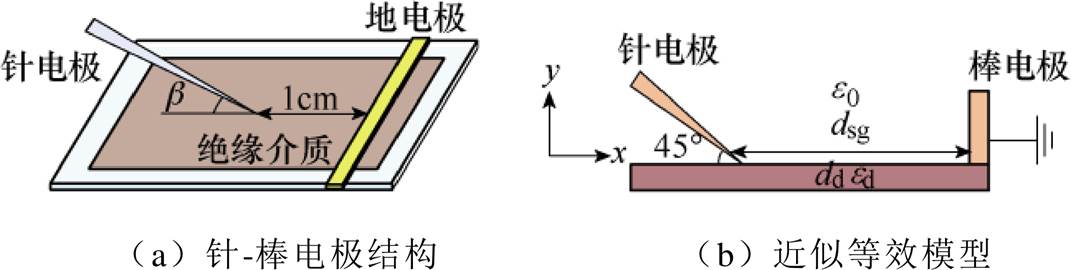
图1 针-棒电极结构及其近似等效模型
Fig.1 Schematic of needle-bar electrode system and simulation model
摘要 沿面放电是导致高频电力变压器气-固绝缘系统失效的主要原因之一。为研究空气-聚酰亚胺界面放电发展过程，该文基于流体动力学理论，通过对粒子输运方程、泊松方程和等离子化学反应的耦合表征，并充分考虑带电粒子在绝缘介质表面的反应过程和累积条件，建立了负极性脉冲电应力下空气-聚酰亚胺沿面放电等离子体模型。模型采用简化反应集定义空气放电涉及的粒子反应，模型复杂程度大幅降低。为避免求解过程中粒子密度出现负值，采用对数形式有限元法求解所建模型，实现了针-棒电极结构下1cm间隙沿面放电发展过程的动态模拟，得到了放电过程中带电粒子密度、表面电荷密度及电场分布等参量的时空演化规律，并通过实验从放电发展形态和表面电荷累积两方面验证了模型可靠性。基于该仿真模型，进一步探究了沿面放电的影响因素，结果表明，沿面放电平均传播速度与温度正相关，与气压负相关；界面二次电子发射系数越大，放电发展越迅速，表面电荷积聚越严重。
关键词：沿面放电 流体模型 等离子体 电荷密度 电场分布 放电发展速度
高频电力变压器作为一种变换方式灵活、控制性能优越的新型输变电设备，在电力牵引、分布式能源并网等领域具有广阔的应用前景[1]。高频电力变压器主要采用空气-聚酰亚胺（Polyimide, PI）绝缘系统[2]，由于其体积小，结构紧凑，长期承受上升时间短、幅值大的高频电应力[3-4]，运行环境较传统变压器恶劣，更易在绝缘薄弱处诱发局部放电或沿面放电，进而造成聚酰亚胺在高频强场下老化甚至过早失效，且随着变压器容量和电压等级的提升，绝缘问题更加突出[5]。
高频电力设备的稳定运行很大程度上取决于其绝缘水平，而气-固交界面是绝缘的薄弱环节，随着超/特高压输电的发展，沿面放电已成为导致高频电力设备气-固绝缘系统失效、危害电力系统安全的重要原因之一[6]。受现有实验手段的限制，沿面放电过程中带电粒子分布与电场畸变情况难以实时测量，放电过程的微观机制无法完全明晰。随着计算机运算与存储能力的飞跃和数值模拟方法的发展，气体放电过程中电场、电荷分布等微观参数的仿真成为可能。目前气体放电模拟多集中在针-板电极空气间隙放电[7-8]及平板电极间介质阻挡放电（Dielectric Barrier Discharge, DBD）[9-10]。相较于沿面放电，空气间隙放电无需考虑固体绝缘介质对放电过程的影响，而DBD是在一定条件下产生大面积、高能量密度的低温等离子体，并未在两电极之间形成贯穿性放电通道。当前沿面放电过程的模拟还处于探索阶段，Ho-Young Lee等运用电流体动力学（Electro- Hydro Dynamics,EHD）方法模拟了针-棒电极结构下液-固绝缘系统沿面放电过程，计算了放电传播速度[11]；S. Singh等基于流体动力学理论，考虑阻挡介质内部的电荷输运过程，模拟了固体介质阻挡层对针-板电极间空气放电发展过程的影响[12]；文献[13]基于流体动力学理论，建立了两相体沿面放电数值模型，针对表面染污和固体颗粒堆积两种情况，研究了壁电荷和表面电导率对沿面放电发展的影响。另有一些学者将流体动力学理论与放电过程中的等离子体反应结合，如李清泉等采用流体扩散方程，考虑8种粒子、16种放电粒子化学反应对沿面型DBD进行了二维仿真[14]；刘春香等考虑12种粒子、31种化学反应建立了N2/O2环境中沿面放电等离子体模型，获得了表面电荷等微观参量的分布规律[15]。这些研究都取得了一定的进展，但电极结构多局限于沿面型DBD（线状或梳状电极分布于介质板两侧）和平板电极，而高频电力变压器沿面放电多发生在极不均匀电场下，且长期承受脉冲应力，因此有必要开展脉冲应力下针-棒电极结构沿面放电仿真研究。另外，空气组分复杂致使放电过程中粒子间反应多达数百种，如何将空气放电过程涉及的化学反应合理简化仍需进一步探究。
本文针对高频电力变压器匝间绝缘沿面放电问题，建立针-棒电极结构下沿面放电非平衡等离子体模型。该模型以流体动力学理论为基础，采用反应集形式定义空气放电过程中的化学反应，使建模和求解均得到大幅简化，实现了针-棒电极结构下空气-聚酰亚胺沿面放电发展过程的动态模拟，获得了表面电荷等微观参量的时空分布规律，并进一步探究了环境及材料特性对沿面放电过程的影响。本文研究结果提供了一种针对沿面放电行为的定量分析手段，可为高频电力变压器绝缘系统设计提供有效指导，促进其向大容量、高可靠性发展。
目前高频电力变压器匝间切向电应力的沿面放电模拟主要采用针-板[16]和针-棒[17]两种电极结构。针-板电极结构中较强的法向分量容易引发绝缘介质内部局部放电，导致绝缘介质纵向击穿。而针-棒模型可通过调节针电极倾斜角度b 改变切向和法向电场分布，灵活控制沿面放电发展速度，便于放电过程观测。因此，本文选择针-棒电极结构模拟高频变匝间绝缘沿面放电行为。针-棒电极结构及其近似等效模型如图1所示。经试验，针电极与PI表面夹角为45°时，绝缘表面存在足够的切向电场分量促使沿面放电发展，同时法向电场不会导致绝缘热击穿。高频变压器电压频率的提高会显著缩小变压器的体积和重量，尖端沿面放电距离处于厘米级别，目前模拟高频变压器匝间绝缘沿面放电的实验也大多采用1～2cm间隙[18-19]，综合考虑高频变压器结构及沿面放电距离对放电起始电压与放电速度的影响，针尖与棒电极之间放电间隙dsg=1cm。实验表明，针-棒电极结构下聚酰亚胺沿面放电轨迹近似为直线型，等离子体通道主要沿针尖到地电极间的垂线发展[20]。为降低模型复杂程度，本文采用图1b所示二维模型近似等效针-棒电极结构。针电极直径2mm，尖端曲率半径6mm，棒电极规格：长×宽×高= 50mm×5mm×6mm。聚酰亚胺薄膜厚度dd=125mm，空气介电常数e0=1，PI介电常数ed=3.7。
图1 针-棒电极结构及其近似等效模型
Fig.1 Schematic of needle-bar electrode system and simulation model
沿面放电过程仿真不仅需要准确描述气体放电过程，还需考虑绝缘介质的影响。传统流体模型将电子、正负离子的连续性方程与泊松方程耦合，描述带电粒子在电场下的碰撞、扩散和漂移过程以及带电粒子产生的自洽场，实现带电粒子的产生、输运和消失过程的模拟。但传统流体方程只考虑了光电离导致的二次电子崩过程，不包含沿面放电过程中高能粒子轰击材料表面导致的二次电子发射过程。因此，需在传统流体方程基础上，添加材料表面二次电子发射作为电子源项。
电子传输过程通常由Boltzmann方程描述，玻耳兹曼方程为6维相空间非局部连续性方程，难以实现高效求解。通过乘以加权函数并在速度空间上积分，玻耳兹曼方程可以近似表示为流体方程，将电子传输过程简化为三维时间依赖性问题。
忽略外电场造成的电子对流，电子输运方程为
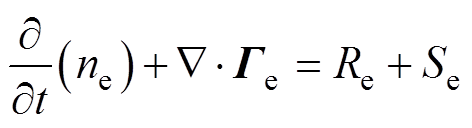（1）
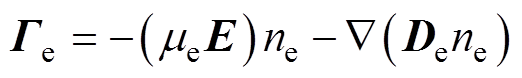（2）
式中，ne为电子密度；Ge为电子通量；Re为由等离子体反应及绝缘介质表面反应决定的电子源项；me为电子迁移率；De为电子扩散系数；E为电场强度；Se为光电离项，用三指数亥姆霍兹方程组近似代替传统积分模型，具体表达式及参数取值来自文献[21]。
电子能量方程为
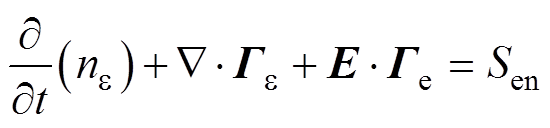（3）
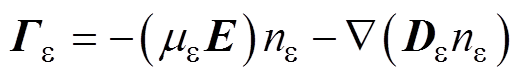（4）
式中，ne 为电子能量密度；Ge 为电子能量通量；Sen为非弹性碰撞中电子损失或获得的能量；me 和De分别为电子能量迁移率和电子能扩散系数。根据Einstein公式，电子迁移系数me、电子扩散系数De、电子能量迁移系数me、电子能量扩散系数De 之间满足De=meTe、me=5/3me、De=meTe，其中，me=3.74× 1024(1021E)-0.22(V·m·s)-1[22]；Te为电子温度，且Te= 2/3eave，eave为平均电子能量。
式（1）和式（3）中的源项Re和Sen由等离子体化学反应确定。假设有M（M=M1+M2）种反应会导致电子数密度变化，有P（P=P1+P2）种反应表征电子-中性粒子之间的非弹性碰撞。当反应速率系数给定时，Re和Sen可分别表示为
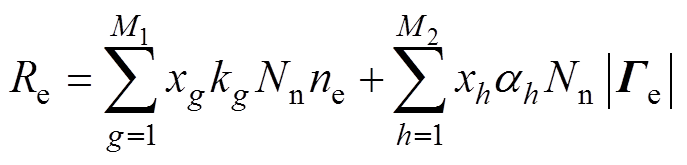（5）
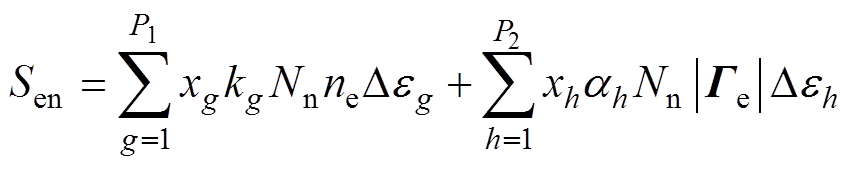（6）
式中，xg、xh分别为参与反应g、h的摩尔分数；kg和ah分别为反应g、h的速率系数和汤森系数；Nn为中性粒子数密度；Deg和Deh分别为反应g、h的能量损失。
放电过程中质量较大的非电子物质视为重粒子，用多组分扩散方程描述为
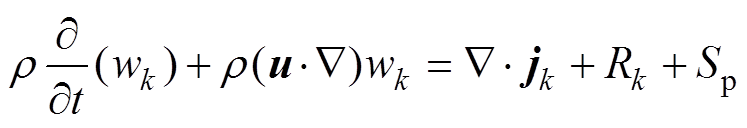（7）式中，k为物质种类，k=1, 2, 3,…, K；r 为混合物密度；wk为物质k的质量分数；u为平均流体速度；Rk为物质k的变化速率；jk为扩散流矢量；Sp为光电离项，只存在于正离子扩散方程中，负离子及中性粒子扩散方程中此项为0。
电场通过泊松方程计算
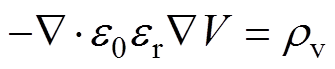（8）
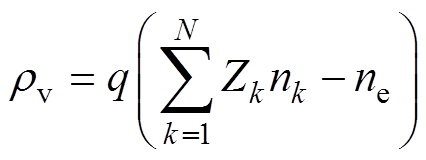（9）
式中，rv为空间电荷密度；q为元电荷；Zk为物质k所带电荷数；nk为物质k的密度；V为空间电动势。
空气作为一种混合气体，其放电涉及的等离子体反应非常复杂，包含数十种粒子及数百个化学反应[23]。考虑到本模型主要研究沿面放电发展演化动态过程，并不关心某种反应具体情况，采用反应集代替种类繁多的粒子来描述放电过程以便降低模型复杂度。
本文所建模型考虑的等离子体反应见表1，不再将氮气和氧气参与的反应单独处理，而是统一用物种A来代替，A可以电离成正离子p，也可以附着电子形成负离子n。
表1 空气放电化学反应
Tab.1 Collisions and reactions modeled
编号反应方程反应类型反应速率系数 1e+A=>p+2e电离反应— 2e+A=>n附着反应— 3e+2A=>n+A三体附着反应2×10-41×(300/Te)×NA2 4e+p=>A电子-正离子复合反应5×10-14 5n+p=>2A正-负离子复合— 反应5×10-12—
表1中，NA为阿伏伽德罗常数，三体反应（三个粒子间反应）速率系数单位为m6/s，二体反应速率系数单位为m3/s。
电离和附着反应速率通过汤森系数给定，三体附着反应、电子-正离子及正-负离子复合反应由速率系数确定。简化空气组分N2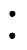
O2=4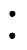1，利用氮气、氧气横截面数据[24]，用玻耳兹曼两项近似方法求取汤森系数[25]，如图2所示。
绝缘介质对放电过程的影响主要考虑两方面：①带电粒子在绝缘材料表面发生反应，并贡献二次电子；②电荷在绝缘材料表面累积，改变电场分布[15]。根据文献[26]对绝缘介质表面反应的处理，假设带电粒子与绝缘介质表面接触时将电荷传递给介质表面，离子全部转化为中性粒子，粘附系数设置为1。
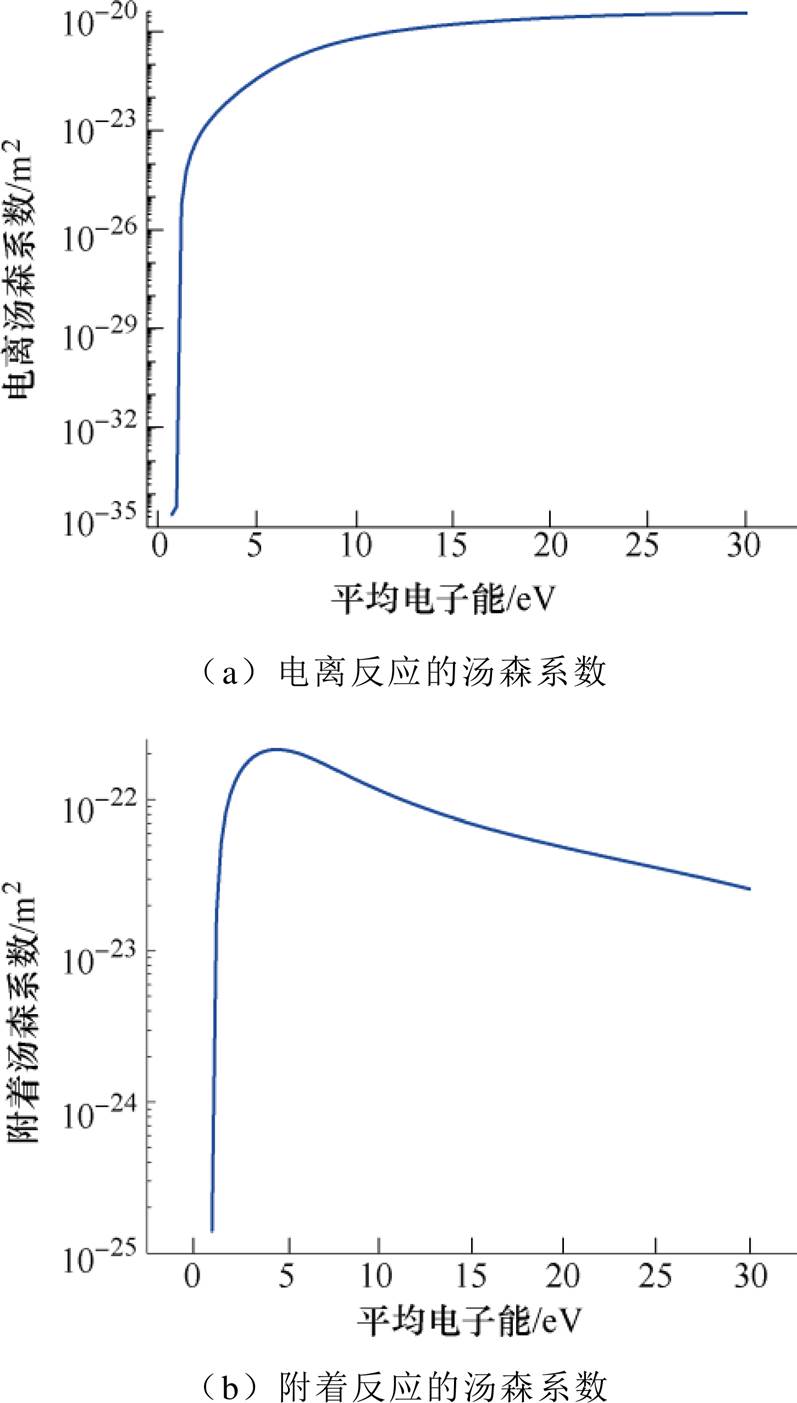
图2 电离和附着反应的汤森系数
Fig.2 Townsend coefficients for ionization and attachment reaction
1.4.1 壁面边界
反应壁上电子密度及能量变化主要来源于热运动、电迁移及以及二次电子发射。与纯空气间隙放电模拟不同，沿面放电过程需要考虑的二次电子发射包括两方面：一是正离子撞击高压针电极，引起的阴极二次电子发射；二是高能粒子轰击材料表面导致的二次电子发射。电子密度和电子能量密度的通量边界为
（10）
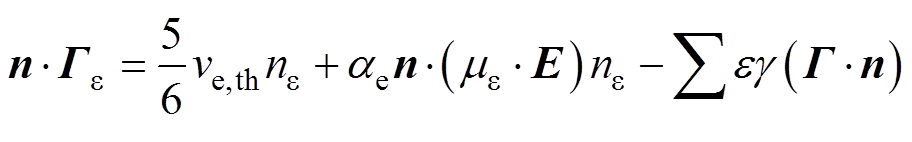（11）
式中，n为气体间隙指向电极及介质的法向量；等号右侧第一项为热运动作用下电子在壁面消失/反弹导致的电子数量及能量变化，ve,th为电子热运动速度；第二项为电迁移项，系数ae取值与电场强度方向有关，考虑本文施加脉冲电应力为负极性，在棒电极处ae取值为1，针电极处为0；第三项为二次电子发射导致的电子数量及能量增益，g 为二次电子发射系数，e 为二次电子平均能量。阴极二次电子发射参考纯空气间隙放电模拟[7]设置为0.004，参照介质阻挡放电模拟[9-10]对二次电子发射的描述，并综合考虑聚酰亚胺的二次电子发射能力，设置PI表面g=0.5；二次电子平均能e =2.5eV。
重物质k的通量边界只考虑漂移和热运动，假设包含l =1, 2,…, L种表面反应，k=1, 2,…, K种重粒子，则
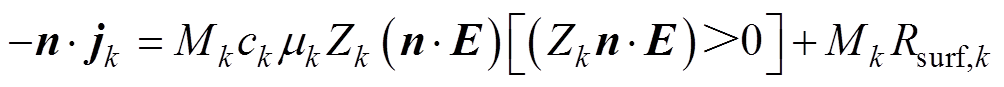（12）其中
（13）
反应i的速率常数为
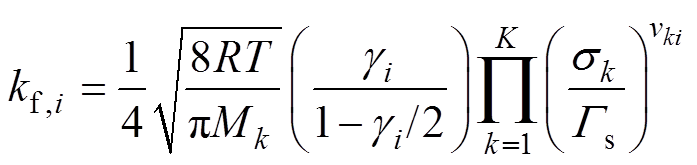（14）式中，Gs为表面原位总浓度；gi为反应i的粘附系数，介于0～1之间；Mk、ck、mk和Zk分别为物质k的摩尔分子质量、摩尔浓度、迁移系数和电荷数；sqrt(8RT/pMk)为物质k的热运动速度，R为通用气体常数，T为气体温度；sk为放电特征长度；vki为化学计量矩阵；qi为反应i的表面反应速率；Rsurf,k为物质k的表面反应总速率。
1.4.2 表面电荷累积
放电过程中，绝缘介质表面会积累电荷，导致介质分界面两侧电位移矢量不连续，表面电荷累积边界条件[27]为
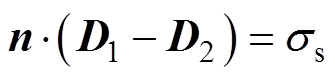（15）式中，D1、D2分别为空气和介质侧的电位移矢量；ss为表面电荷密度，可以通过流过PI表面的电流对时间积分得到
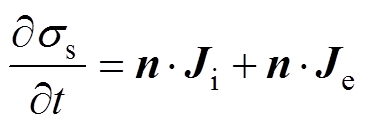（16）
式中，n·Ji、n·Je分别为壁上总离子流密度和总电子流密度的法向分量。
经大量仿真结果分析，针电极施加脉冲的重复率、峰值、脉宽不同时，对放电发展快慢均存在一定影响，但总体而言，重复脉冲下沿面放电走势以及放电发展过程中电场强度、电子密度等微观参数的时空演化规律与幅值足够大、上升时间足够短的单脉冲放电行为无较大差异。为更直观简洁地展现沿面放电动态演化过程，本文选择了幅值大、上升时间短的单个脉冲进行了沿面放电动态模拟，外施电压波形如图3所示，峰值为-20kV，脉宽60ns，频率为1 000kHz。棒电极接地，其余边界设置为绝缘边界。模型基于多物理场仿真软件COMSOL Multiphysics求解，计算网格共划分为146 543个单元，采用非均匀网格划分，放电发展区域，即气-固交界区域网格剖分最细，单元尺寸控制在30mm以下，对计算结果影响较小的区域采用较大的网格尺寸，最大网格单元不超过150mm，在保证计算精度的同时减小计算量，提升计算速度。另外，为避免求解过程中粒子浓度出现负值，采用对数形式有限元法进行求解。环境条件设置为20℃和1 atm（1atm= 1.013×105Pa），沿面放电模型计算流程如图4所示。
图3 外施电压波形
Fig.3 Applied voltage waveform
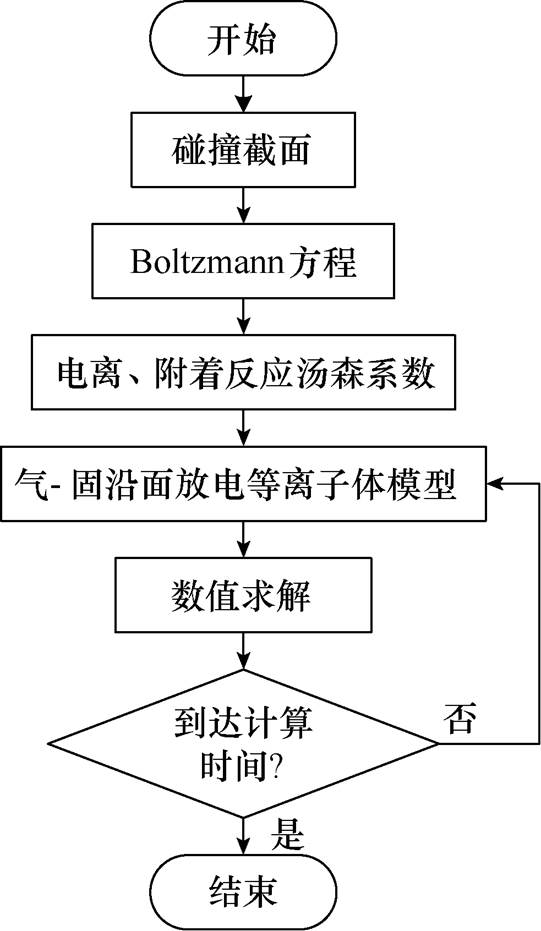
图4 沿面放电模型计算流程
Fig.4 Calculation process for surface discharge model
沿面放电过程中放电区域电场强度及电子密度分布可以直观展现放电发展过程，对放电机理的明晰具有重要意义。沿面放电发展演化动态过程如图5所示。由图5可知，放电初期电场最大值出现在针电极附近，强电场使针电极附近区域电离出大量电子，电子在电场作用下向棒电极运动，由于电子运动速度比正离子快，正离子将滞留在电离区域，加强与针电极之间的电场，针电极附近碰撞电离加剧，促使放电向前发展。根据空间电荷对电场分布的影响程度，可将整个放电过程划分为三个阶段：①电子崩发展阶段（0～8ns），此阶段空间电荷对电场的影响可以忽略，电子数目急剧增大，由1010m-3量级增加到1017m-3量级，8ns时电子崩发展到距针电极0.40mm处，此时的电子密度峰值约为7.93× 1017m-3，接近文献[28]计算得到的电子崩转化为流注的临界密度值1.0×1018m-3；②电子崩向流注发展阶段（8～9ns），这一阶段电子密度虽达到临界值，但对空间电场的影响依旧较小；③流注发展阶段（9～16ns），此阶段空间电荷继续畸变电场，电场强度最大区域向前发展，推动绝缘材料表面的等离子体通道逐渐向地电极延伸，最终在16ns时刻贯穿两电极。
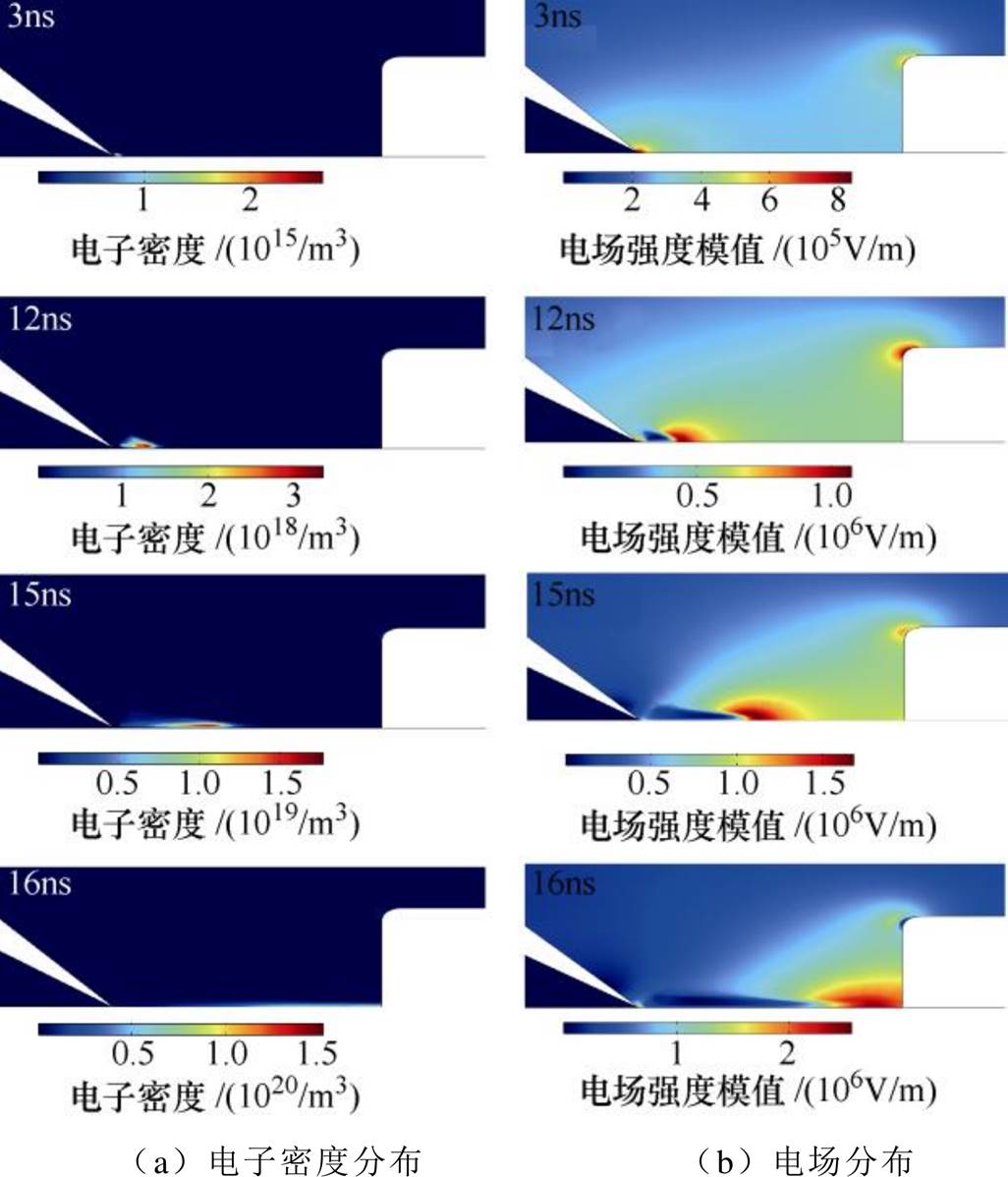
图5 沿面放电发展演化动态过程
Fig.5 Evolution of the surface discharge
图6和图7展示了放电过程中绝缘材料表面电子密度及表面电场强度动态分布，可以看到两者展现了较好的对应性，沿面流注发展过程中，绝缘材料表面电子密度及电场强度在整个放电区域内均呈增大趋势，且电子密度极大值总是出现在电场强度极大值附近，这是因为强电场导致电离更剧烈，电子密度更高。每一时刻电子密度与电场强度极大值均出现在针电极附近及流注头部，且随流注发展逐渐增大。
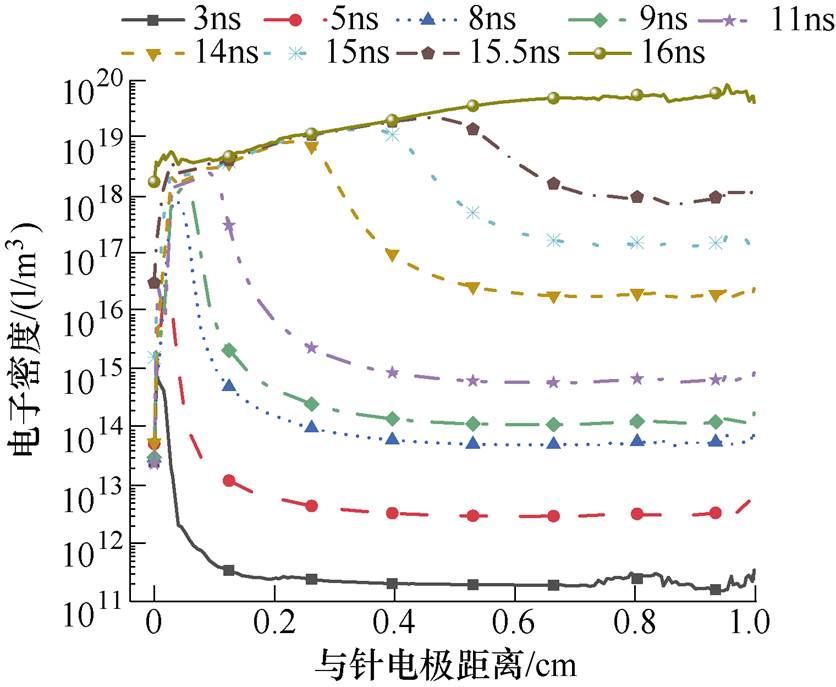
图6 绝缘材料表面电子密度动态分布
Fig.6 Dynamic distribution of electron density on insulation surface
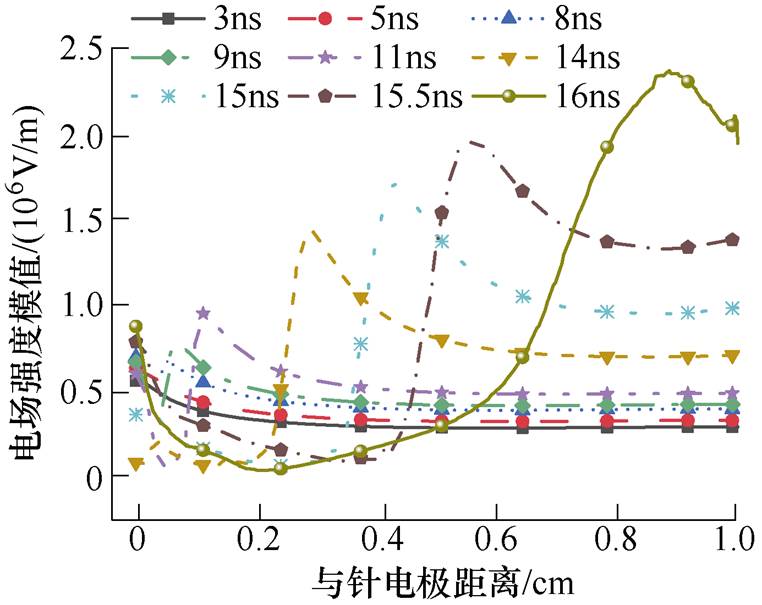
图7 绝缘材料表面电场强度动态分布
Fig.7 Dynamic distribution of electric field strength on insulation surface
针电极附近电子密度较高，一方面由于电极结构不对称导致针电极附近形成强场区；另一方面空间电荷的存在使针电极附近电场强度进一步增大，外电场与空间电荷场叠加形成的复合场达到约10kV/cm，强电场导致针电极附近碰撞电离剧烈，产生大量电子。流注头部电子密度高，一方面因为随着等离子体通道延伸，绝缘间隙逐渐变短，且外加电压不断增加，电场强度增大；另一方面因为空间电荷畸变外电场使流注头部前方电场继续增大，电离加剧，电子密度增加。
图8为沿面放电发展过程中正负离子实时密度动态分布。由图可见，正离子密度分布规律与电子密度分布类似，这主要是因为两者主要来源均为碰撞电离。和正离子相比，任意时刻负离子密度不存在很明显的尖峰，而是相对均匀地广泛存在于等离子体通道内。负离子主要由电子和中性分子附着形成，因此负离子大量存在于电子密度高的区域，但整体而言，负离子密度比正离子小1～2个数量级，这是因为：①在强电场作用下电离为主要反应，产生大量正离子；②强电场作用下电子运动速度快，难以被氧气分子捕获形成负离子；③在等离子体通道内电场强度较低，负离子容易与周围大量存在的正离子发生复合反应致使密度降低。
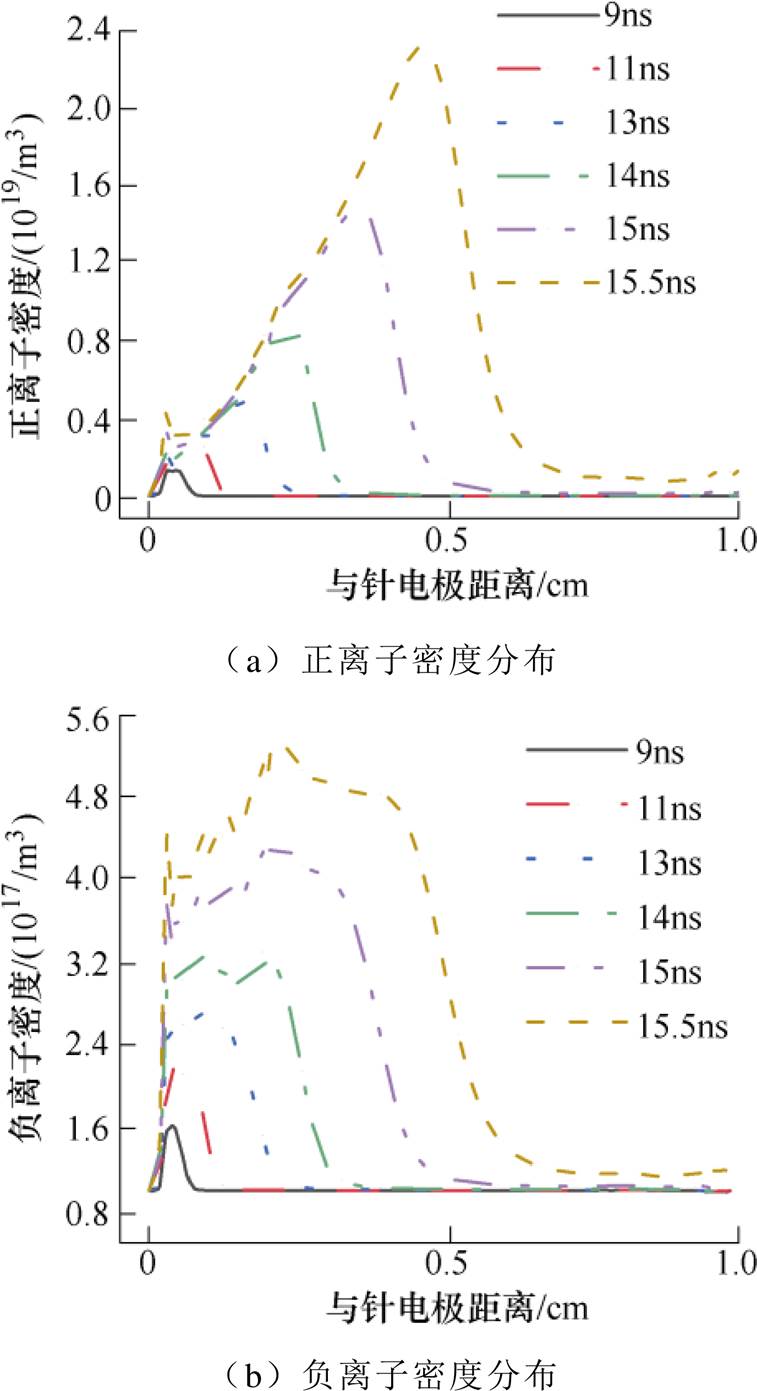
图8 绝缘材料表面正负离子密度动态分布
Fig.8 Dynamic distribution of positive and negative ion density
电子由空间电场获得能量，通过与重粒子碰撞等过程完成能量传递。电子温度是电子能量的表征，研究其分布对于了解放电过程中碰撞电离、复合等过程以及能量转移速率具有重要作用。沿面放电过程中不同时刻的电子温度分布如图9所示。电场强度越大，电子获得的能量越多，电子温度也就越高，因此电子温度最大值也出现在流注头部。放电过程中流注头部电子温度基本维持在5～6eV，而流注内部电子温度较低，这是由于等离子体通道内部电子与各粒子碰撞频繁，导致电子能量大量损失。
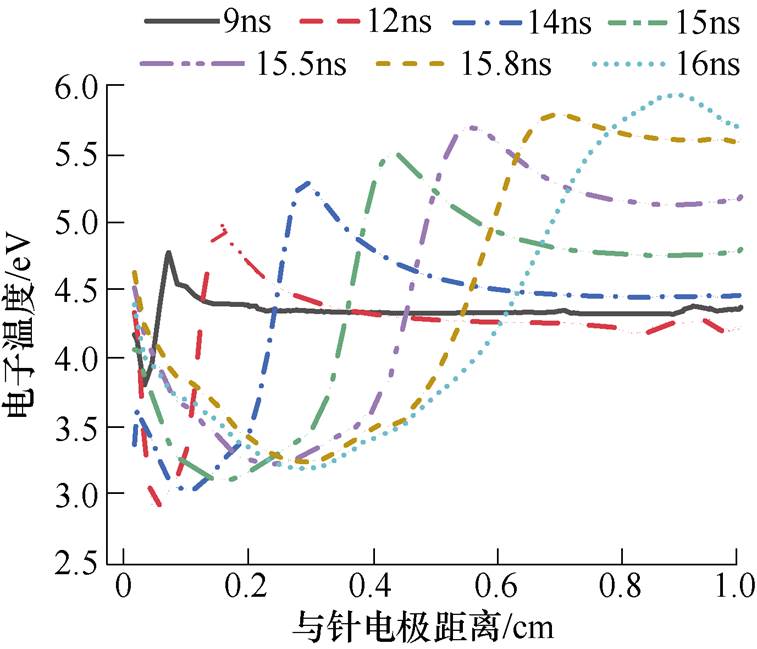
图9 电子温度分布
Fig.9 Electron temperature distribution
平行于绝缘材料表面取y =0.03cm的截线得到放电区域空间电荷密度分布如图10所示。随着沿面流注的发展，空间电荷量整体呈增大趋势，且主要集中在流注头部，而流注通道内部电荷量很少，这与流注理论相符。由图10可见，流注头部出现正负电荷中心分离，一方面由于电子和正离子的迁移速率不同，另一方面由于外电场作用对电子和正离子牵引方向不同。观察发现针电极附近也出现了少量正电荷，这是由于针电极附近电离剧烈，大量正离子产生，且正离子在电场作用下向阴极附近迁移，而阴极鞘对负离子的排斥作用导致负离子密度很小，最终针电极附近呈现正电属性；以13ns时刻为分界线，针电极附近正电荷量呈现先增加后减少的规律，在流注发展前期（13ns之前）不断增加，主要因为电场强度增大，电离剧烈；13ns之后针电极附近正电荷积聚量反而减小，猜测由于等离子体通道不断向前发展，流注头部与针电极间距离增大，导致流注头部正电荷在电场作用下的迁移对针电极附近正电荷积聚的贡献越发微弱，且针电极附近虽然电离较剧烈，但产生的正离子在电场作用下迅速与针电极碰撞消失并发射二次电子，进一步导致了正电荷量的减小。
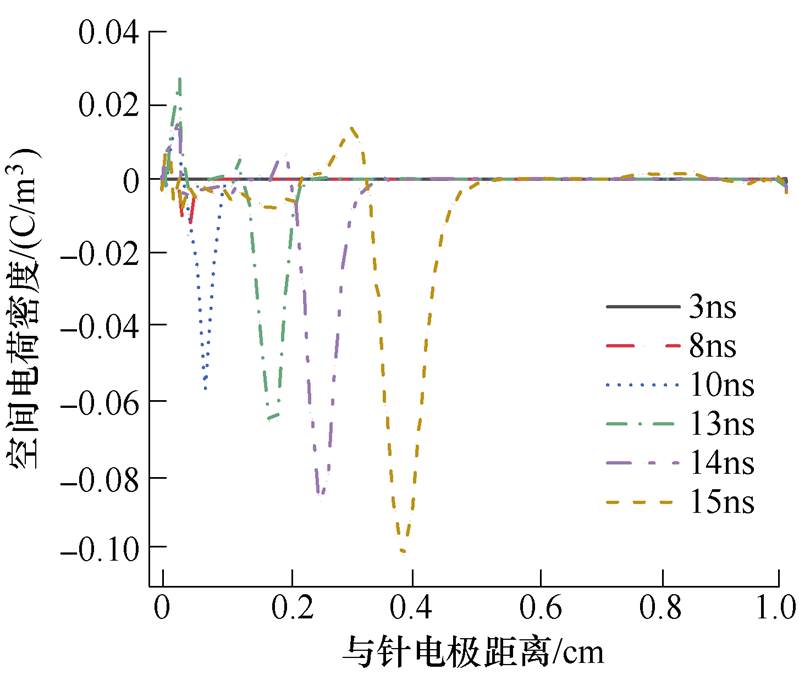
图10 空间电荷密度分布
Fig.10 Space charge density distribution
表面电荷积聚会改变空间电场分布，进而影响沿面放电过程，仿真得到的绝缘材料表面电荷密度分布曲线如图11所示。绝缘材料表面积聚负极性电荷，随着沿面流注的发展，绝缘材料表面负电荷积聚量不断增加，且高密度电荷区域逐渐由针电极向地电极发展。沿面放电发展过程中绝缘材料表面积聚的平均电荷密度如图12所示，可以看到流注发展阶段（9ns之后）表面电荷积聚速率迅速增大，到16ns时，表面平均电荷密度达到-1.11mC/m2。
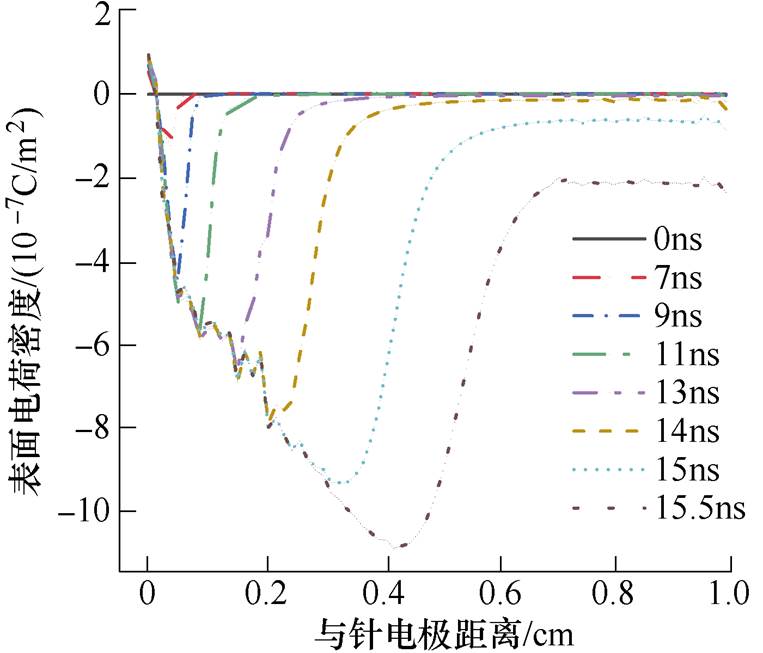
图11 绝缘材料表面电荷密度分布
Fig.11 Surface charge density distribution
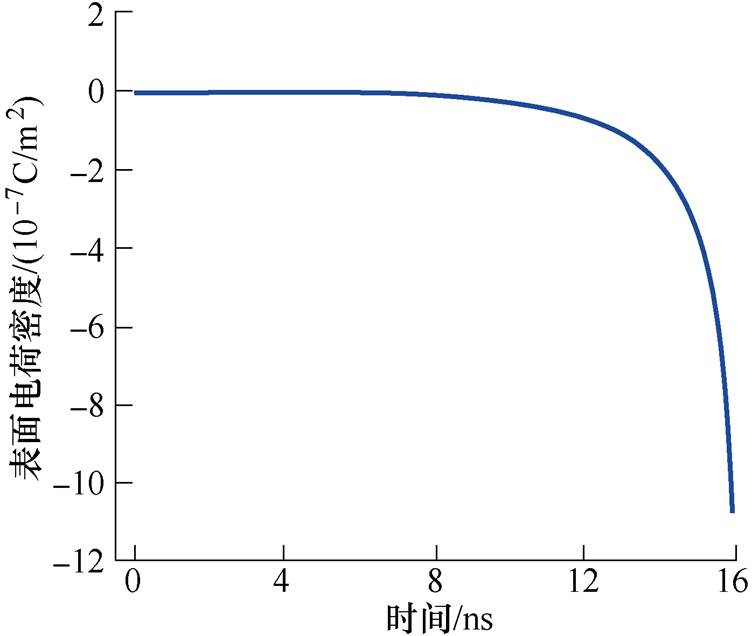
图12 绝缘材料表面平均电荷密度
Fig.12 Evolution of average surface charge density
为验证模型可靠性，采用针-棒电极结构进行大气压下空气-聚酰亚胺沿面放电实验，由于仿真条件下放电过程非常迅速，现有实验条件难以准确捕捉放电进程，且表面电荷分布目前难以实现实时在线测量。为准确捕捉放电过程，有效控制放电不同发展阶段，以获得表面电荷分布随放电发展的变化，实验中选择降低电压和频率（降低电压峰值至11kV，频率为20kHz）控制放电发展速度，保证沿面放电持续发展直至最后闪络，整个过程可以持续数小时，通过安装在放电区域上方的摄像机对沿面放电形态进行连续记录。将放电起始至闪络的整个时段定义为沿面寿命L，取沿面寿命的20%、60%、80%及100%节点，将沿面放电发展过程划分为第一至第四阶段，分别对应仿真（L=16ns）中3.2ns（20%）、9.6ns（60%）、12.8ns（80%）及16ns（100%）时刻。在沿面放电基础上，利用反馈式静电探头及Trek Model 347静电电压表对每个放电阶段结束后PI薄膜表面电荷分布进行离线测量。沿面放电发展过程实验和仿真对比如图13所示，由图13可知，随着沿面放电的不断发展，等离子体通道沿PI薄膜表面由针尖逐渐向棒电极延伸，最终贯穿两电极，形成闪络电弧。且放电轨迹近似呈直线型，验证了模型降维的合理性。图14和图15为实测的沿面放电发展不同阶段PI表面电荷积聚的情况，图14表面电荷测量范围为针尖附近边长1.5cm的正方形区域，图15为针尖到棒电极垂线上表面电荷累积的变化情况。可以看出，PI表面积聚负极性电荷，且针尖附近为高密度区域，随着放电发展，电荷分布范围由针电极向棒电极延伸，表面电荷密度由-0.2mC/m2增大至-1.39mC/m2。图14和图15的实测结果与图11所示的仿真结果相比，呈现的表面电荷分布规律及量级基本一致，表明了仿真结果的正确性。
图13 沿面放电发展过程实验和仿真对比
Fig.13 Comparison of the experimental and numerical results for evolution of surface discharge
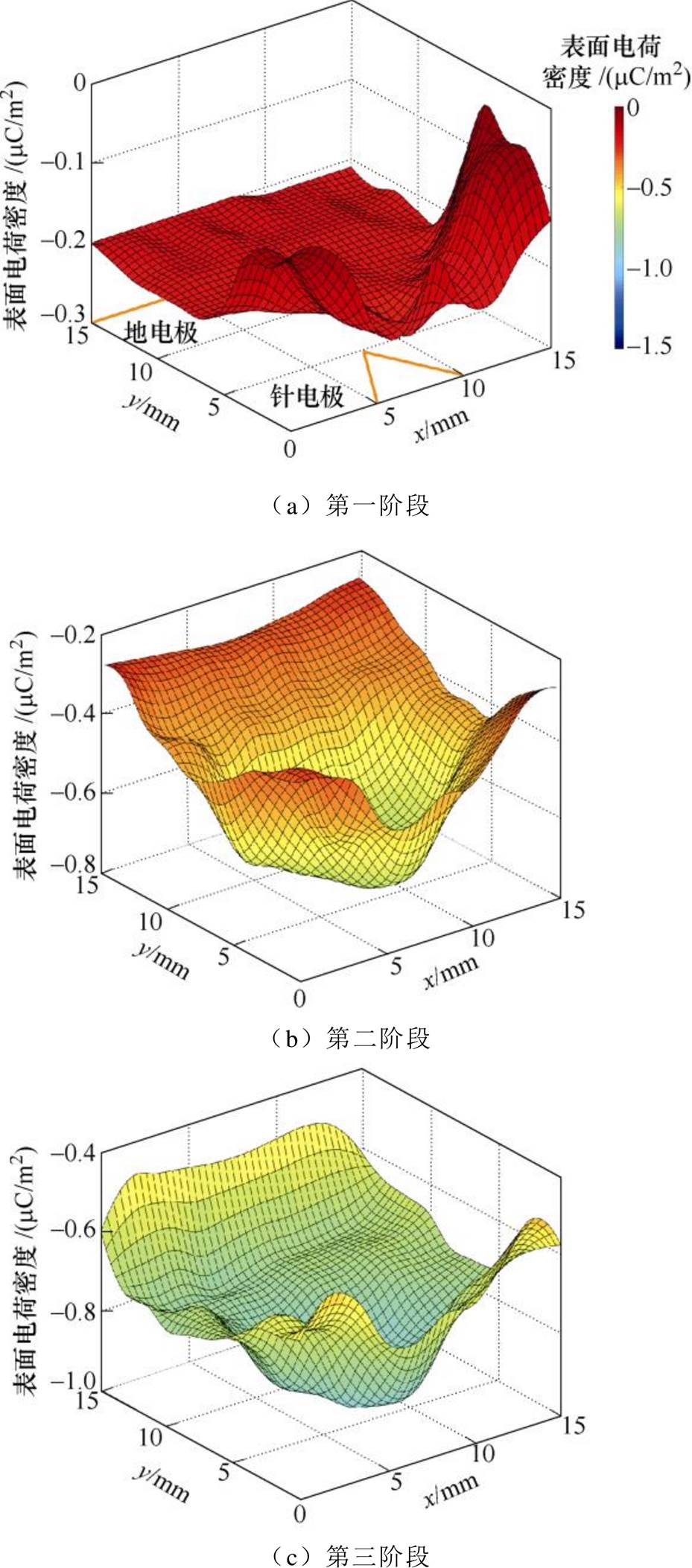
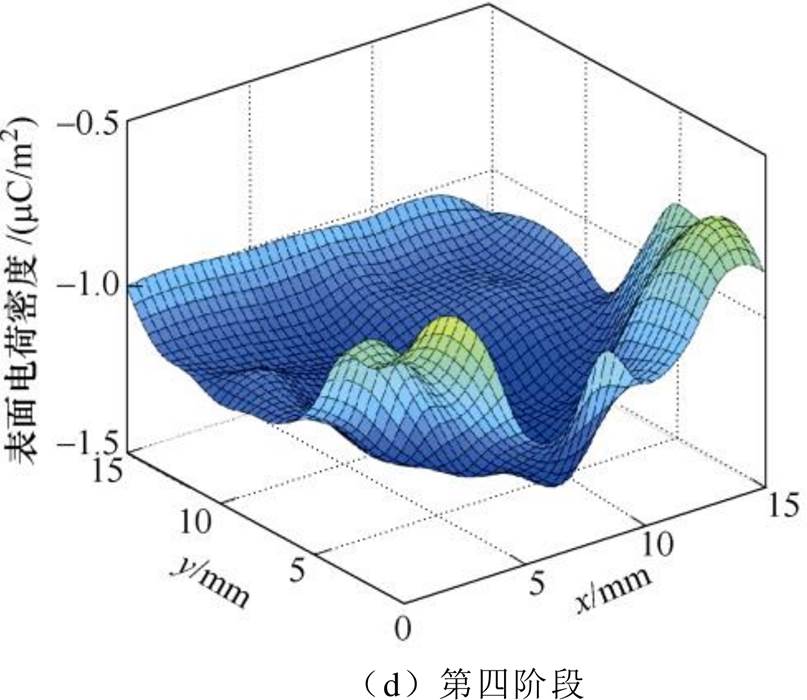
图14 放电发展不同阶段表面电荷密度
Fig.14 Surface charge distribution at different stages
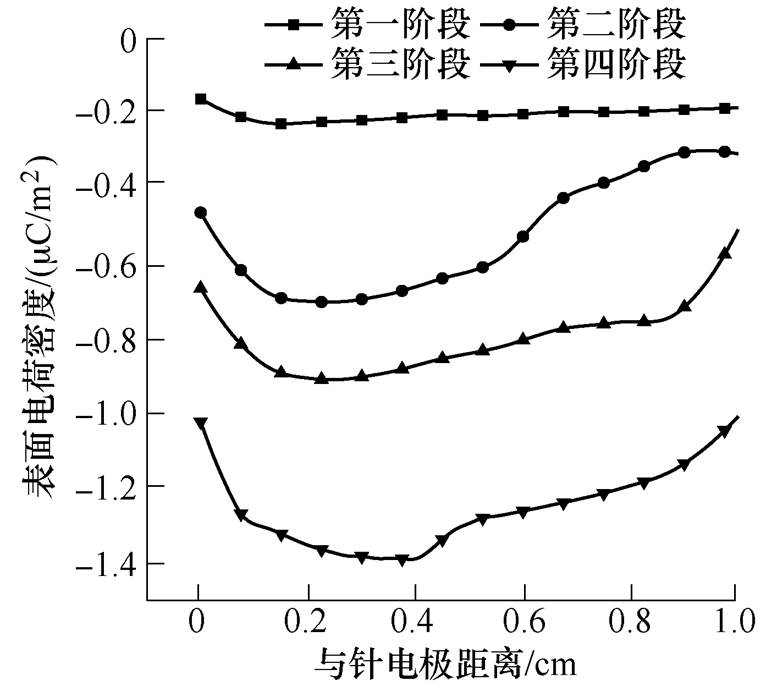
图15 针-棒电极间轴线表面电荷累积
Fig.15 Surface charge distribution along axis
沿面放电发展速度与流注通道前方电场强度关系密切，电场越强，放电发展速度越快[29]，流注通道前方电场强度由背景电场强度与空间电荷及表面电荷产生的附加电场强度叠加形成。图16给出了不同时刻放电发展速度与流注通道前方切向电场强度变化，随着沿面放电发展，切向电场强度不断增大，且增长速率越来越大。取任意时刻t0，分别记t0-Dt, t0+Dt时刻流注头部位置为s1和s2，则放电发展速度v=(s2-s1)/(2Dt)。观察沿面放电发展速度随时间的变化情况，发现在电子崩发展阶段，沿面放电发展速度较小，低于105m/s；电子崩向流注转化阶段，速度增幅较明显，量级在105m/s；流注发展阶段，前期（9～14ns）速度稳步增长，14ns之后急剧增大，达到106m/s，与文献[15]仿真结果量级一致。图17更直观地展现了沿面放电发展速度v与流注头部切向电场Et的关系，所用拟合函数v=2.975×10-16×|Et|3.518。文献[30]实验结果表明，绝缘材料表面流注“沿面”分量速度随外加电场增大而显著增大，与本文仿真结果规律一致。
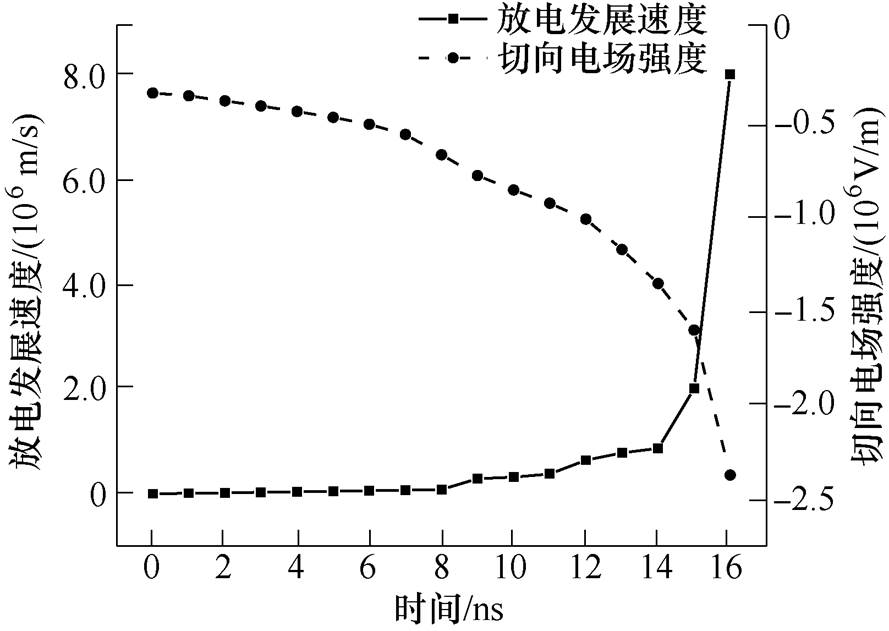
图16 不同时刻放电发展速度与切向电场强度的变化
Fig.16 Surface discharge propagation velocity and tangential electric field strength
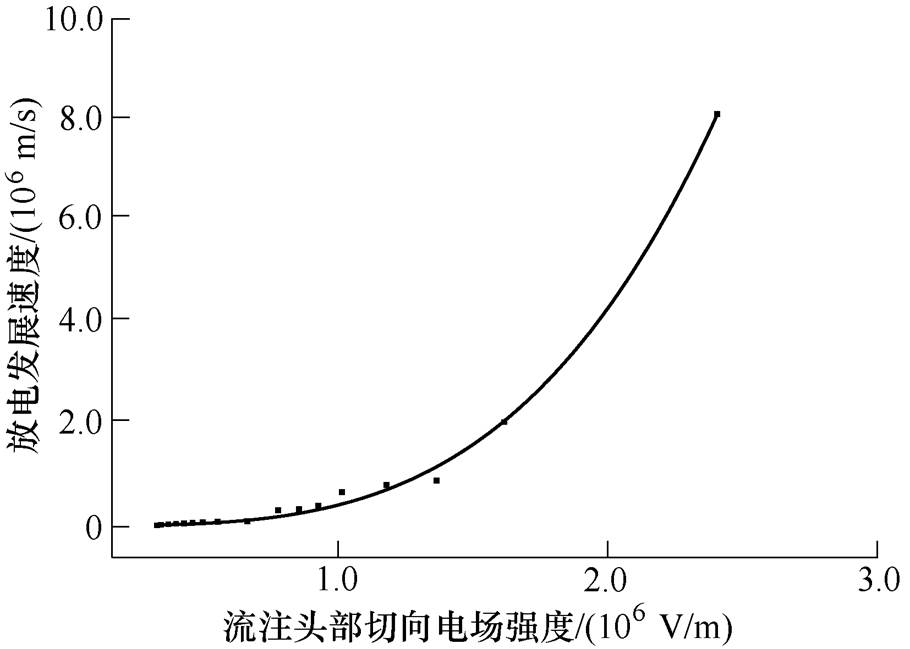
图17 放电发展速度随流注头部切向电场强度的变化
Fig.17 Relationship between surface discharge propagation velocity and tangential electric field strength of streamer head
温度T、气压P对沿面放电过程中电子密度动态分布的影响如图18和图19所示。图18选取了6ns、9ns、13ns分别作为电子崩、电子崩转流注、流注发展三个阶段的代表，发现环境温度对任一时刻电子密度峰值大小及出现位置均有影响，温度越高，同一时刻电子密度越大且等离子体通道发展越远。
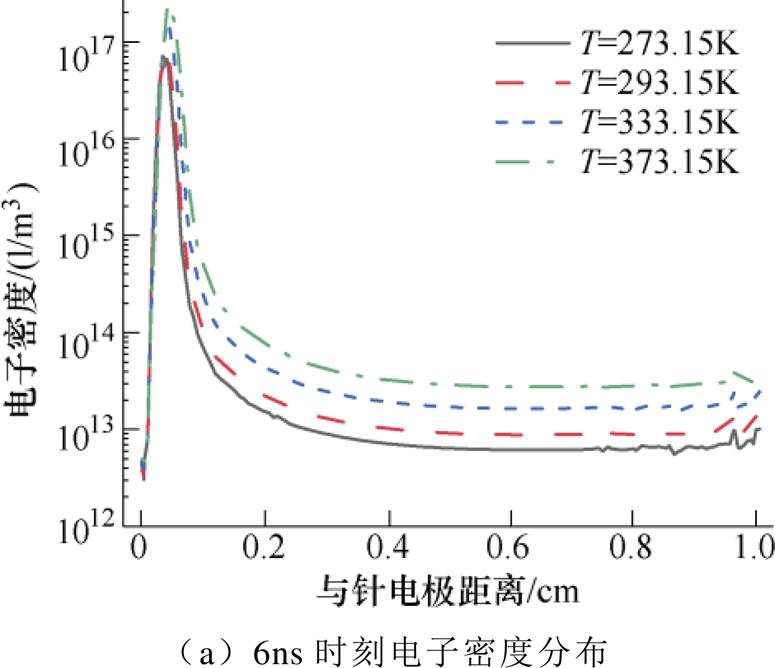
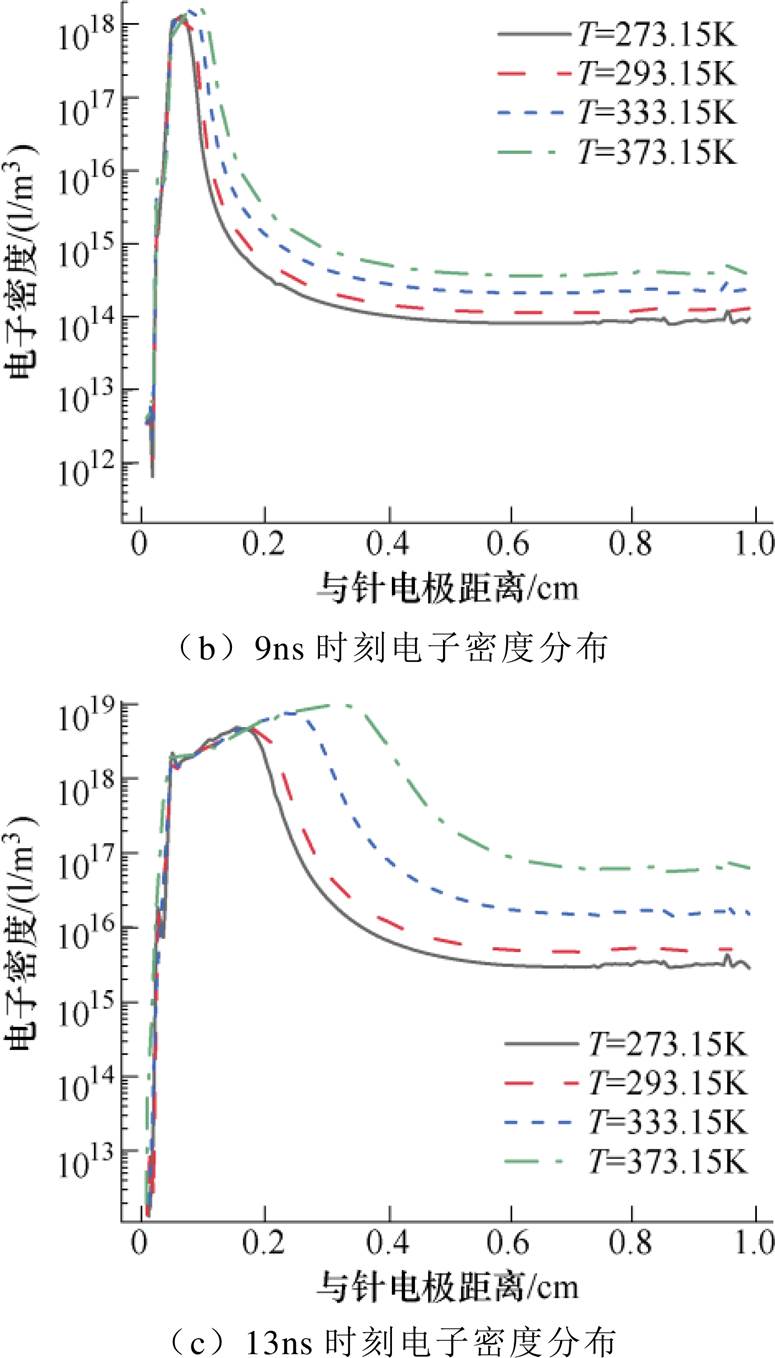
图18 温度对电子密度动态分布的影响
Fig.18 Effect of temperature on the electron density distribution
图18表明，随着温度升高，放电发展的平均速度增大，等离子体通道贯穿两电极的时间变短，这是因为温度升高，带电粒子的迁移速率和扩散速率都会增大，从而导致碰撞电离过程加剧，加快了放电发展进程。温度及气压对放电发展速度的影响如图20所示。结合图19和图20可见，气压升高不利于沿面放电发展，放电发展的平均速度减小，等离子体通道贯穿两极的时间逐渐变长，这是由于气压增大导致中性粒子数增加，电子平均自由程缩短，不利于碰撞电离的发生。文献[31]的研究同样表明，气压越高，流注传播速度越小，与本文结论一致。
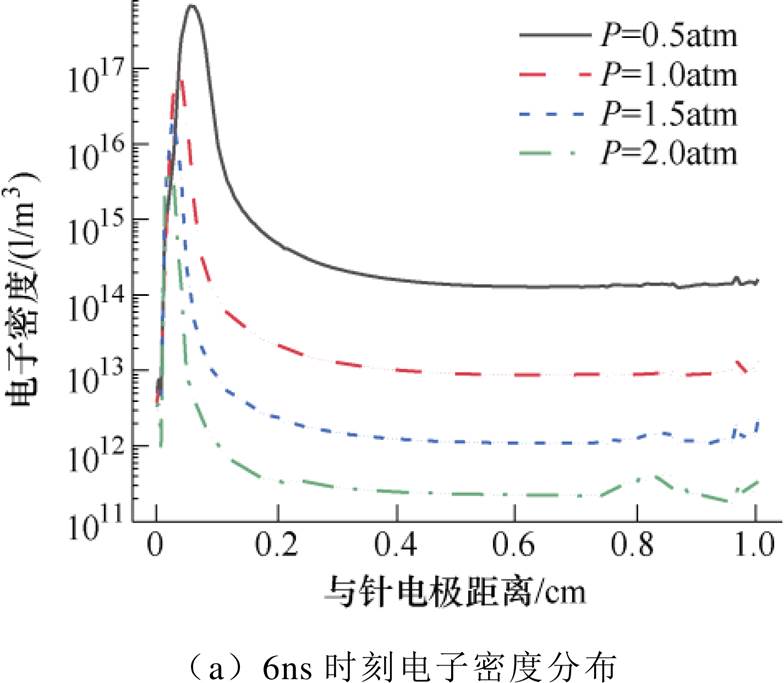
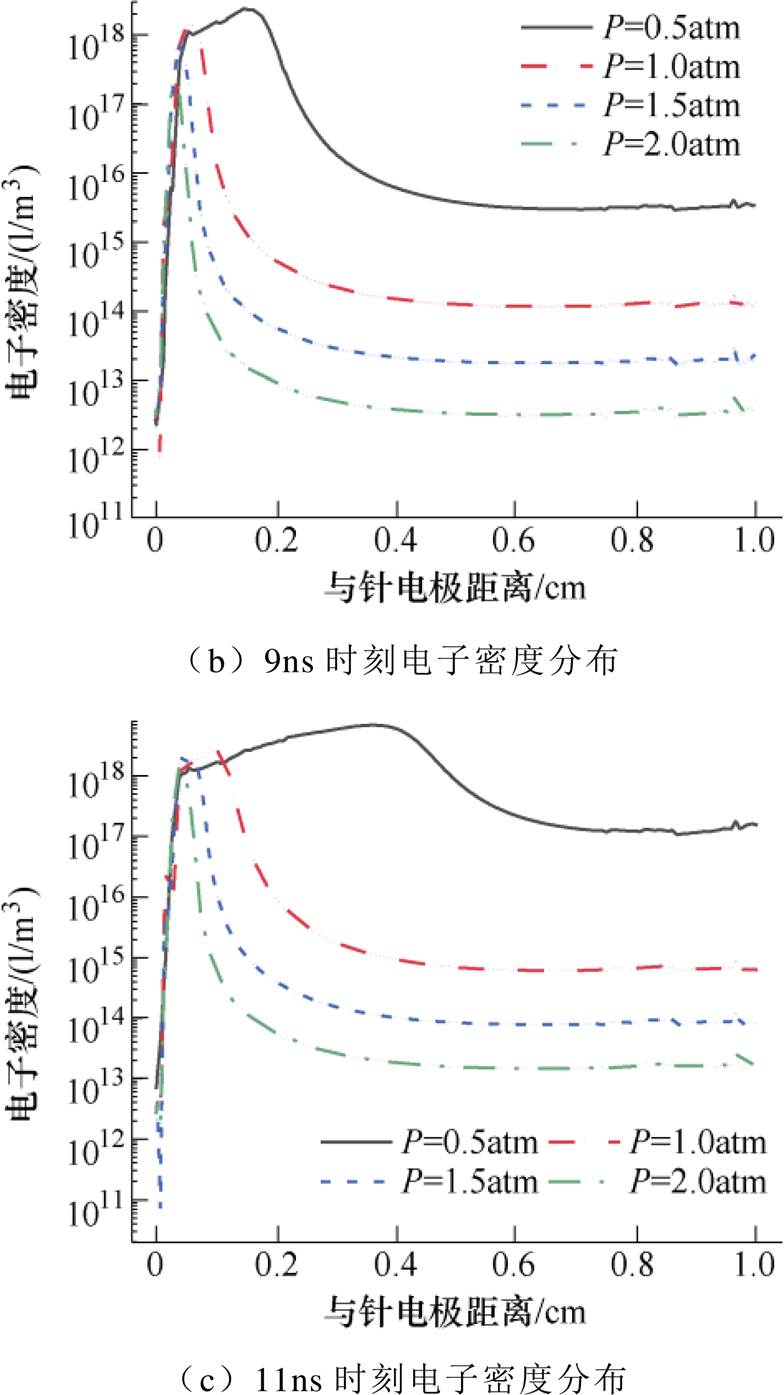
图19 气压对电子密度动态分布的影响
Fig.19 Effect of air pressure on the electron density distribution
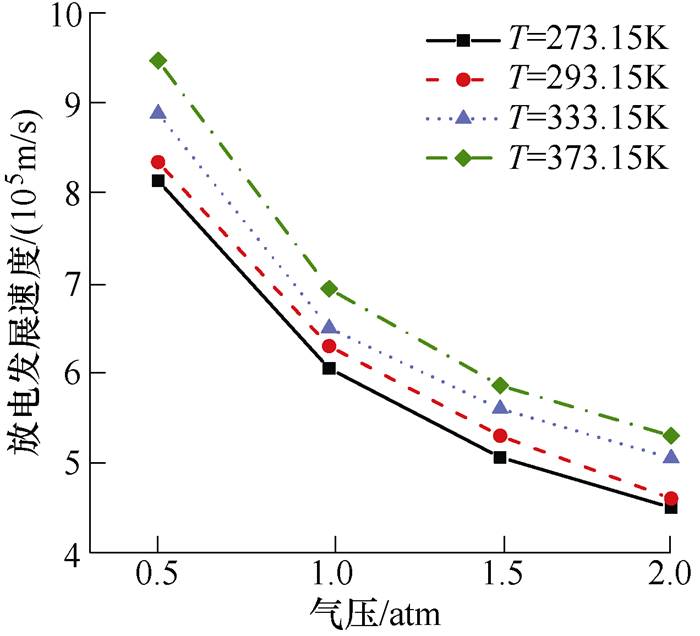
图20 温度及气压对放电发展速度的影响
Fig.20 Effect of temperature and pressure on discharge propagation velocity
高频电压下趋肤效应和邻近效应更显著，变压器铁心损耗、绕组铜耗、绝缘材料介质损耗以及功率器件的开关损耗等，都将远远高于工频电压，导致变压器产热严重、运行温度升高。运行经验表明，高频电力设备的局部温度可达150～200℃，温升在加速绝缘老化的同时，也会促进沿面放电发展，而放电活动又会使局部温度进一步升高，因此及时有效的散热措施对保证高频变安全稳定运行是非常必要的。由仿真结论可知，气压升高对抑制沿面放电同样有效，但气压受实际运行环境制约很大，调控气压不易实现。
介质表面特性是影响沿面放电发展的重要因素。聚酰亚胺二次电子发射与诸多因素有关，如电子入射角度、电子能量等，综合已经发表的实验数据[32]，聚酰亚胺二次电子发射系数大致处于0.2～2.5范围内；另外，考虑到可以通过材料改性来降低其二次电子发射系数[33]，达到提高闪络电压的目的，在PI二次电子发射系数大致范围内选取g值分别为0.05、0.2、0.5及2时来观察放电发展过程的变化。界面二次电子发射对电子密度动态分布的影响如图21所示。可以看出，随着二次电子发射系数增大，同一时刻电子密度峰值增大且等离子体通道发展加快。二次电子发射系数越大，自由电子越多，放电越剧烈，等离子体通道发展越迅速。二次电子发射对表面电荷累积的影响如图22所示，展示了g值分别为0.05、0.2、0.5、2时，0～16ns过程中平均表面电荷积聚情况，结合图22可知，随着沿面放电的发展，平均表面电荷密度不断增加，且进入流注发展阶段之后表面电荷积聚速率迅速增大。另外，二次电子发射系数越大，表面电荷积聚越严重，与文献[34]实验结果呈现的规律一致。
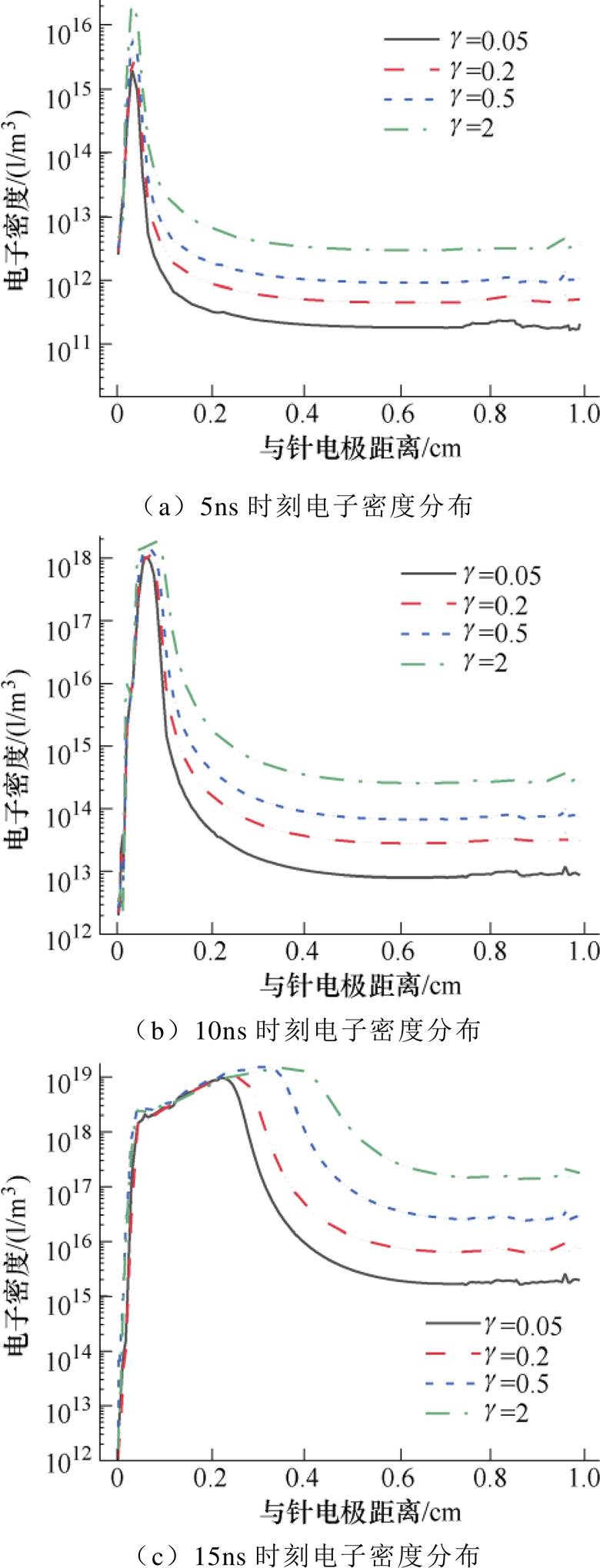
图21 界面二次电子发射对电子密度动态分布的影响
Fig.21 Effect of secondary electron emission coefficient on the electron density distribution
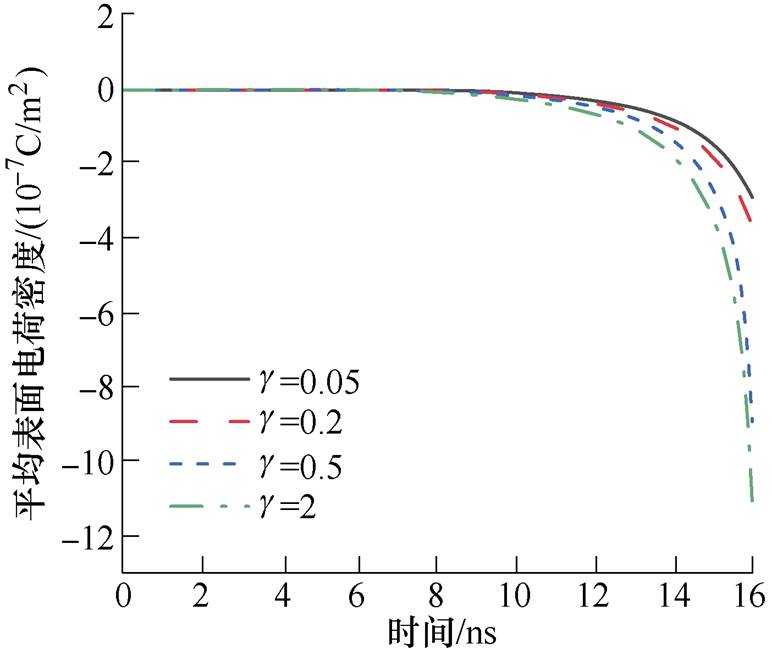
图22 二次电子发射对表面电荷累积的影响
Fig.22 Average surface charge accumulation under different secondary electron emission coefficients
因此，在进行高频绝缘设计时，为避免沿面闪络的发生，应优先选择二次电子发射系数较小的绝缘材料；或者可以通过表面改性减小绝缘材料二次电子发射系数，抑制沿面放电的发展进程，提高绝缘寿命，促进高频变向大容量高可靠性方向发展。
本文采用针-棒电极结构模拟高频电力变压器匝间绝缘沿面放电缺陷，建立了空气-聚酰亚胺界面放电非平衡态等离子体模型，实现了针-棒电极结构下1cm间隙沿面放电发展过程的动态模拟，得到了电场、粒子密度、空间及表面电荷密度等微观参量的时空演化规律，基于本文建立的针-棒电极结构1cm间隙沿面放电模型，所得结论如下：
1）空气作为一种混合气体，建立起完备的等离子体反应体系极其困难，借鉴流体动力学模型思想，采用反应集形式描述空气放电过程中的化学反应，大大降低了等离子体建模难度。
2）沿面放电过程包含电子崩、电子崩转流注以及流注发展三个阶段；放电初期电子数量迅速增加且集中在针电极附近，随着放电发展，流注头部产生大量电子，等离子体通道向地电极延伸，最终贯穿两电极时，电子密度达到1020m-3量级。
3）负极性脉冲应力下，绝缘介质表面积聚负极性电荷，电荷分布范围由针电极向地电极延伸，且平均累积电荷量及累积速率随着沿面放电发展不断增加。
4）温度升高，沿面放电发展平均速度增加，等离子体通道贯穿两电极的时间变短；气压升高则不利于沿面放电发展；二次电子发射系数越大，等离子体通道发展越迅速，且表面电荷积聚越严重。
5）本文所建立数值模型可用于分析纳秒脉冲下空气-固体绝缘系统厘米级间隙沿面放电/流注/闪络发展过程，弥补实验观测手段的不足。如何能在更大时间尺度（ms级甚至ms级）和空间尺度（分米级甚至米级）范围内应用数值仿真方法，值得进一步深入研究。
参考文献
[1] 李子欣, 高范强, 赵聪, 等. 电力电子变压器技术研究综述[J]. 中国电机工程学报, 2018, 38(5): 1274-1289.
Li Zixin, Gao Fanqiang, Zhao Cong, et al. Research review of power electronic transformer techno- logies[J]. Proceedings of the CSEE, 2018, 38(5): 1274-1289.
[2] Qin Hengsi, Kimball J W. Solid-state transformer architecture using AC-AC dual-active-bridge con- verter[J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 3720-3730.
[3] 张明锐, 刘金辉, 金鑫. 应用于智能微网的SVPWM固态变压器研究[J]. 电工技术学报, 2012, 27(1): 90-97.
Zhang Mingrui, Liu Jinhui, Jin Xin. Research on the SVPWM solid state transformer applied[J]. Transa- ctions of China Electrotechnical Society, 2012, 27(1): 90-97.
[4] 陈彬, 李琳, 赵志斌. 典型非正弦电压波激励下高频磁心损耗(英文)[J]. 电工技术学报, 2018, 33(8): 1696-1704.
Chen Bin, Li Lin, Zhao Zhibin. Magnetic core losses under high-frequency typical non-sinusoidal voltage magnetization[J]. Transactions of China Electro- technical Society, 2018, 33(8): 1696-1704.
[5] Liu Tao, Li Qingmin, Dong Guojing, et al. Multi- factor model for lifetime prediction of polymers used as insulation material in high frequency electrical equipment[J]. Polymer Testing, 2019, 73: 193-199.
[6] 张开放, 张黎, 李宗蔚, 等. 高频正弦电应力下气-固绝缘沿面放电现象及特征分析[J]. 电工技术学报, 2019, 34(15): 3275-3284.
Zhang Kaifang, Zhang Li, Li Zongwei, et al. Analysis of the phenomena and characteristics of gas-solid insulation surface discharge under high frequency sinusoidal electrical stress[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3275-3284.
[7] Lu Binxian, Sun Hongyu. The role of photoionization in negative corona discharge[J]. Aip Advances, 2016, 6(9): 095111.
[8] 彭庆军, 司马文霞, 杨庆, 等. 初始电子浓度对空气中针板间隙正极性流注放电的影响[J]. 高电压技术, 2013, 39(1): 37-43.
Peng Qingjun, Sima Wenxia, Yang Qing, et al. Influence of initial electron concentration on positive streamer discharge in pin-plate air gap[J]. High Voltage Engineering, 2013, 39(1): 37-43.
[9] 姚聪伟, 常正实, 张冠军, 等. 大气压氩气介质阻挡放电等离子体特性变化的一维仿真[J]. 高电压技术, 2015, 41(6): 2084-2092.
Yao Congwei, Chang Zhengshi, Zhang Guanjun, et al. One-dimensional simulation of evolution characteri- stics of dielectric barrier discharge in atmospheric pressure argon[J]. High Voltage Engineering, 2015, 41(6): 2084-2092.
[10] Barjasteh A, Eslami E, Morshedian N. Experimental investigation and numerical modeling of the effect of voltage parameters on the characteristics of low- pressure argon dielectric barrier discharges[J]. Physics of Plasmas, 2015(22): 073508.
[11] Lee H Y, Kang I M, Lee S H. Fully coupled finite element analysis for surface discharge on solid insulation in dielectric liquid with experimental validation[J]. IEEE Transactions on Magnetics, 2016, 52(3): 1-4.
[12] Singh S, Serdyuk Y V, Summer R. Streamer pro- pagation in hybrid gas-solid insulation[C]//IEEE Conference on Electrical Insulation and Dielectric Phenomena, Ann Arbor, MI, USA, 2015: 387-390.
[13] 陈田. 两相体沿面放电研究[D]. 武汉: 华中科技大学, 2015.
[14] 李清泉, 许光可, 房新振, 等. 沿面型介质阻挡放电的数值仿真计算[J]. 高电压技术, 2012, 38(7): 1548-1555.
Li Qingquan, Xu Guangke, Fang Xinzhen, et al. Numerical simulation of surface dielectric barrier discharge[J]. High Voltage Engineering, 2012, 38(7): 1548-1555.
[15] 司马文霞, 刘春香, 杨鸣, 等. 沿绝缘介质表面的气体放电等离子体模型[J]. 中国电机工程学报, 2017, 37(9): 278-287.
Sima Wenxia, Liu Chunxiang, Yang Ming, et al. Plasma model of gas discharge along the dielectric surface[J]. Proceedings of the CSEE, 2017, 37(9): 278- 287.
[16] Dervos C, Bourkas P D, Kayafas E A, et al. Enhanced partial discharges due to temperature increase in the combined system of a solid-liquid dielectric[J]. IEEE Transactions on Electrical Insulation, 1990, 25(3): 469-474.
[17] 鲁杨飞, 李庆民, 刘涛, 等. 高频电压下表面电荷分布对沿面放电发展过程的影响[J]. 电工技术学报, 2018, 33(13): 3059-3070.
Lu Yangfei, Li Qingmin, Liu Tao, et al. Effect of surface charge on the surface discharge evolution for polyimide under high frequency voltage[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(13): 3059-3070.
[18] Dai Jie, Wang Zhongdong, Jarman P. Creepage discharge on insulation barriers in aged power transformers[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2010, 17(4): 1327-1335.
[19] 赵义焜, 张国强, 郭润睿, 等. 变压器耐高温型匝间绝缘材料的放电特性研究[J]. 电工电能新技术, 2019, 38(3): 1-9.
Zhao Yikun, Zhang Guoqiang, Guo Runrui, et al. Study on discharge characteristics of heat resistant inter-turn insulation materials in power trans- formers[J]. Advanced Technology of Electrical Engineering and Energy, 2019, 38(3): 1-9.
[20] 刘涛, 韩帅, 李庆民, 等. 频变电应力下高频电力变压器绝缘沿面放电形态及发展过程[J]. 电工技术学报, 2016, 31(19): 199-207.
Liu Tao, Han Shuai, Li Qingmin, et al. Patterns and development of the surface discharge of high frequency power transformer insulation under frequency-dependent electric stress[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 199-207.
[21] Bourdon A, Pasko V P, Liu N Y, et al. Efficient models for photoionization produced by non-thermal gas discharges in air based on radiative transfer and the Helmholtz equations[J]. Plasma Sources Science and Technology, 2007, 16(3): 656-678.
[22] Kulikovsky A A. Positive streamer between parallel plate electrodes in atmospheric pressure air[J]. Journal of Physics D: Applied Physics, 1997, 30(3): 441-450.
[23] Tsai J H, Hsu C M, Hsu C C. Numerical simulation of downstream kinetics of an atmospheric pressure nitrogen plasma jet using laminar, modified laminar, and turbulent models[J]. Plasma Chemistry and Plasma Processing, 2013, 33(6): 1121-1135.
[24] Plasma data exchange project[EB/OL]. 2018[2019-01-23]. http://www.lxcat.laplace.univ-tlse.fr.
[25] Hagelaar G J M, Pitchford L C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models[J]. Plasma Sources Science and Technology, 2005, 14(4): 722-733.
[26] Liu Xinghua, He Wei, Yang Fan, et al. Numerical simulation and experimental validation of direct current air corona discharge under atmospheric pressure[J]. Chinese Physics B, 2012, 21(7): 75201.
[27] 王泽忠, 全玉生, 卢斌先. 工程电磁场[M]. 北京: 清华大学出版社, 2011.
[28] 郑殿春. 气体放电数值仿真方法[M]. 北京: 科学出版社, 2016.
[29] 梁曦东, 陈昌渔, 周远翔. 高电压工程[M]. 北京: 清华大学出版社, 2003.
[30] 孟晓波, 梅红伟, 陈昌龙, 等. 绝缘介质表面流注发展特性的机理研究[J]. 中国电机工程学报, 2013, 33(22): 155-165.
Meng Xiaobo, Mei Hongwei, Chen Changlong, et al. Research on characteristics of streamer propagation along insulation surfaces[J]. Proceedings of the CSEE, 2013, 33(22): 155-165.
[31] 孟晓波, 梅红伟, 陈昌龙, 等. 气压与湿度对绝缘介质表面流注发展特性影响的试验研究[J]. 中国电机工程学报, 2014, 34(12): 1938-1947.
Meng Xiaobo, Mei Hongwei, Chen Changlong, et al. Experimental research on influences of air pressure and humidity on characteristics of streamer pro- pagation along insulation surfaces[J]. Proceedings of the CSEE, 2014, 34(12): 1938-1947.
[32] 翁明, 胡天存, 曹猛, 等. 电子入射角度对聚酰亚胺二次电子发射系数的影响[J]. 物理学报, 2015, 64(15): 456-462.
Weng Ming, Hu Tiancun, Cao Meng, et al. Effects of electron incident angle on the secondary electron yield for polyimide[J]. Acta Physica Sinica, 2015, 64(15): 456-462.
[33] 张博, 乌江, 郑晓泉. 改性聚酰亚胺表面稳定性与真空直流沿面闪络抑制方法研究[J]. 电工技术学报, 2019, 34(13): 2846-2853.
Zhang Bo, Wu Jiang, Zheng Xiaoquan. Study of the surface stability of modified polyimide and the suppression method of surface flashover under DC voltage in vacuum[J]. Transactions of China Electro- technical Society, 2019, 34(13): 2846-2853.
[34] 孙泽来. 纳秒脉冲下真空沿面放电的二次电子发射机制研究[D]. 北京: 华北电力大学, 2016.
Numerical Simulation for Surface Discharge of Air-Polyimide Insulation under Pulsed Electrical Stress
Abstract Surface discharge is one of the main reasons for the failure of the gas-solid insulation system of high-frequency power transformers. In order to investigate the evolution process of surface discharge, a simplified but effective set of reactions was used to describe all the particle reactions in air discharges. On this basis, a numerical model for discharge along air-polyimide surface was proposed with fluid dynamic theory, in which the transport equations of different particles, Poisson equation and plasma chemistry reactions in the discharge gap or channel were involved, along with the reaction process and accumulation of the charged particles on the dielectric surface. Then, the surface discharge evolution under the needle-to-bar electrode with 1cm gap was investigated by simulations. Distribution and variation of particle density, surface charge density and electric field versus discharge time were obtained. The reliability of the model was verified by experiments from the aspects of discharge development morphology and surface charge accumulation. Accordingly, the influence of temperature, gas pressure and secondary electron emission on surface discharge was also studied and revealed. The results indicate that the discharge propagation velocity is positively correlated with temperature, and negatively correlated with air pressure. The larger the secondary electron emission coefficient, the faster the discharge develops and the more the surface charge accumulates.
keywords：Surface discharge, fluid model, plasma, charge density, electric field distribution, discharge propagation velocity
中图分类号：TM433
DOI: 10.19595/j.cnki.1000-6753.tces.190289
国家自然科学基金资助项目（51929701，51737005）。
收稿日期2019-03-19
改稿日期 2019-06-29
董国静 女，1995年生，硕士研究生，研究方向为高频绝缘与放电物理。E-mail: guojingdong0920@163.com
李庆民 男，1968年生，教授，博士生导师，研究方向为高电压与绝缘技术、放电物理等。E-mail: lqmeee@ncepu.edu.cn（通信作者）
（编辑 崔文静）