 (1)
(1)摘要 由于分布式能源(DERs)在配电网的渗透率不断提高以及电力改革对售电侧的放开,充分发挥需求侧资源的灵活性变得愈加重要。该文以电动汽车(EV)和暖通空调(HVAC)两种典型的需求侧资源为例,在计及设备的物理特性和人为、环境因素的影响下,采用极端能量场景方法建立通用虚拟电池(VB)模型用于刻画其资源的灵活性。在此基础上,进一步针对交互平台参与日前电力市场情况提出了日前优化调度模型。仿真算例表明基于通用VB模型的日前优化调度可以分配日前调度计划及备用容量。此外,通过仿真验证了所提模型的有效性,并结合算例结果分析了其在运算效率与信息安全方面的优越性。
关键词:需求侧资源灵活性 交互平台 通用虚拟电池模型 日前优化调度 备用容量
随着分布式能源(Distributed Energy Resources, DERs)在配电网渗透率的不断提高以及电力市场改革售电侧的放开,电力系统运行方式从传统的电源追踪负荷转变为源-网-荷-储互动协调运行方式,使能源供应向着清洁、低碳、分布式方向转型[1-2]。但由于高比例的DERs具有间歇性、不确定性以及传统发电机组占比的逐步降低造成系统中可提供的灵活性资源容量受到限制,由此使得系统在局部时段的灵活性严重不足,进一步导致其对灵活性需求的大幅度提升[3]。因此目前需要充分发挥其他资源灵活性潜力,实现多时间尺度的灵活性平衡。
针对上述问题,需求侧资源,包括电动汽车(Electric Vehicle, EV)、储能设施(Energy Storage System, ESS)、热泵、温控负荷(Temperature Control Loads, TCLs)等在技术可靠性以及运行经济性上可以代替发电侧提供灵活性平衡,给用户和电网带来经济收益[4]。但需求侧资源由于分散于系统结构底层导致其对市场的电价信号相对“绝缘”、参与优化调度能力明显不足,同时具有容量小、规模大、种类繁多等特点。因此要想充分发挥这些资源的灵活性就必须进行整合与量化[5]。目前,整合手段主要分为直接控制策略和间接控制策略。其中前者以微电网、虚拟电厂、负荷聚集商(aggregator)作为整合主体参与批发市场,并在市场出清后分摊收益[6-9];后者则引入市场竞争,一般通过交互平台以价格或智能合约作为信号激励用户,把灵活性以商品的形式整合到市场运行当中[4-5, 10]。
然而,DERs的规模不断扩大造成对基于常规的量化模型的整合单元在进行优化求解时出现“维数灾”问题,进一步增加了计算成本[11]。文献[12-13]采用基于基础系统概率特性的集群资源灵活性刻画方法来描述商业楼宇的灵活性。相比于上述从上至下的描述方式,一种由下至上,即从单元设备灵活性进行描述并进行整合的方法用于表征多种类型资源灵活性更具有优势[14]。文献[15]提出多面体(polytopes)的半平面表征形式(Half-plane representation,H-表达),并与传统的基于顶点表征形式(Vertex repress- entation,V-表达)建模表征资源灵活性对比,具有更高的计算效率,但是仍难以应对大规模集中式求解。在此基础上,一些学者分别采用外、内逼近的方法对polytopes[11, 16]、zonotopes[14]以及半定约束[17]所描述的资源灵活性进行改造,以牺牲准确性为前提有效地解决上述表征模型在处理大规模设备时运算乏力的问题。然而,资源的灵活性是多时间尺度的,文献[11-17]均无法提前刻画多时间尺度的资源灵活性来评估参与辅助服务市场制定备用容量方案。文献[18-19]通过找到平均功率值作为基准建立商业和居民型暖通空调(Heating Ventilating and Air Conditioning, HVAC)的通用虚拟电池(Virtual Battery, VB)模型。基于此,aggregator可以在参与日前批发市场的同时提供辅助服务以获取收益,其刻画得到时移的功率、电能边界通用整合形式可以有效地降低大规模运算的复杂性。文献[20-21]采用通用VB模型分别描述了单辆EV与集群EV的灵活性,并分别平抑风力发电的不确定性和参与市场竞价。但EV模型并未考虑Vehicle-to-Grid以及可以同时参与多个市场。
综上所述,本文以集群EV与TCLs作为需求侧资源中储能单元与似储能单元的典型资源,综合考虑其物理特性、自然与人为影响因素,建立通用VB模型用于表征其灵活性。基于此,提出应用于交互平台的日前优化调度模型,以评估资源灵活性参与日前能量与辅助服务市场的经济收益与制定调度计划。最后,通过算例对比分析验证了通用VB模型的有效性,并结合算例结果与运行模式从信息安全和运算效率上说明了提出模型的优越性。
通用VB模型是一种采用一套标准的电池参数描述需求侧资源灵活性的量化方法,其中需求侧资源包括储能单元,如EV、ESS,也可以是似储能资源,如HVAC等温控负荷以及热泵,其形式如下
 (1)
(1)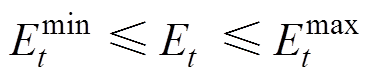 (2)
(2)
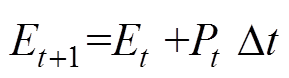 (3)
(3)
式中,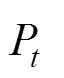 和
和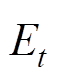 分别为t时段通用VB模型的功率、电能变量;
分别为t时段通用VB模型的功率、电能变量;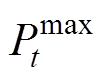 与
与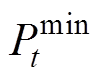 分别为通用VB模型的功率的上、下限;
分别为通用VB模型的功率的上、下限;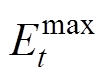 与
与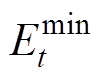 分别为通用VB模型能量的上、下限;
分别为通用VB模型能量的上、下限;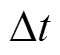 为时段。从调度层级方面,相比于对单元级设备的功率可行域直接采用闵可夫斯基求和,VB模型通过一个整合的功率可行域表征集群的资源灵活性可以大大减少优化求解过程中决策变量、等式、不等式约束个数,解决了多个决策变量之间的耦合关系给计算带来的复杂性,有效地简化了优化求解大规模设备的计算负担,同时其整合形式可以在合理的运行框架下降低用户用电信息暴露的风险[5]。此外,其简明、通用的外表征特性也可应用于评估事前对电网提供辅助服务的收益及其灵活性的可视化展示。本节以考虑V2G的EV以及HVAC分别作为储能与似储能单元的典型资源,并对其通用VB建模展开研究。
为时段。从调度层级方面,相比于对单元级设备的功率可行域直接采用闵可夫斯基求和,VB模型通过一个整合的功率可行域表征集群的资源灵活性可以大大减少优化求解过程中决策变量、等式、不等式约束个数,解决了多个决策变量之间的耦合关系给计算带来的复杂性,有效地简化了优化求解大规模设备的计算负担,同时其整合形式可以在合理的运行框架下降低用户用电信息暴露的风险[5]。此外,其简明、通用的外表征特性也可应用于评估事前对电网提供辅助服务的收益及其灵活性的可视化展示。本节以考虑V2G的EV以及HVAC分别作为储能与似储能单元的典型资源,并对其通用VB建模展开研究。
1.1.1 单辆EV的VB模型
本节以EV代表储能单元为例展开分析。EV功率可行域不仅受电池自身功率限制影响,也受到电能限制影响。这里采用图示法,以k和k+1两个时段进行对比分析,EV电能对功率影响如图1所示。
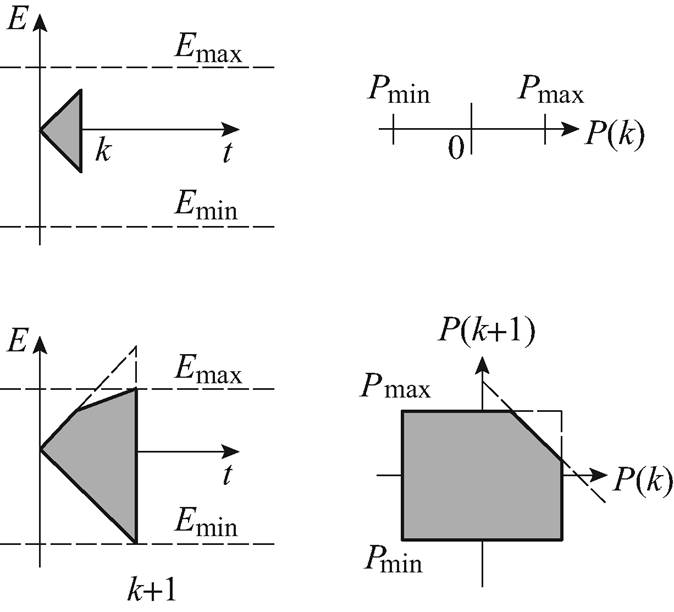
图1 EV电能对功率影响
Fig.1 Diagram of EV energy effect on its power
图1中,灰色区域为资源的功率可行域范围,虚线代表电能对的功率限制间接受电池容量限制。因此本文通过极端场景能量分析方法,综合考虑充电桩的信息、车主信息以及EV的信息,建立VB模型对V2G的EV灵活性进行量化,EV的VB建模原理如图2所示。
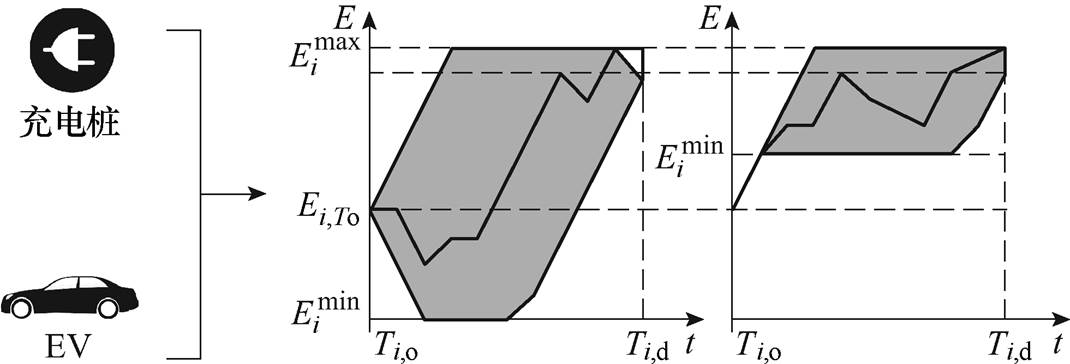
(a)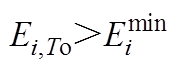 (b)
(b)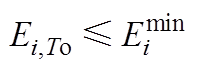
图2 EV的VB建模原理
Fig.2 VB modeling principle of EV
图2中,通过比较第i辆EV并网的初始容量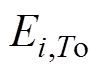 以及电池容量上、下限
以及电池容量上、下限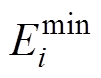 、
、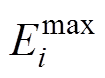 可以把EV的功率可行域分成a、b两种情景。由情景a可知其能量上、下限由式(4)~式(7)得到,而情景b在
可以把EV的功率可行域分成a、b两种情景。由情景a可知其能量上、下限由式(4)~式(7)得到,而情景b在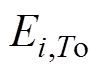 小于允许电池容量下限时EVi认为不具有灵活性,其功率可行域则通过式(4)与式(6)生成。考虑能量范围影响对应时段的功率上、下界,分别如式(8)、式(9)所示。
小于允许电池容量下限时EVi认为不具有灵活性,其功率可行域则通过式(4)与式(6)生成。考虑能量范围影响对应时段的功率上、下界,分别如式(8)、式(9)所示。
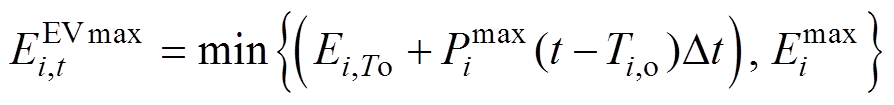
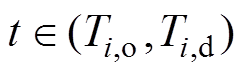 (4)
(4)
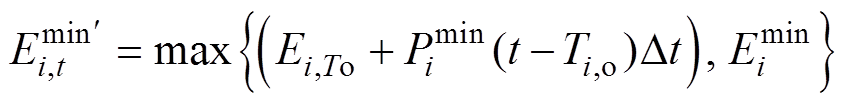
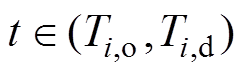 (5)
(5)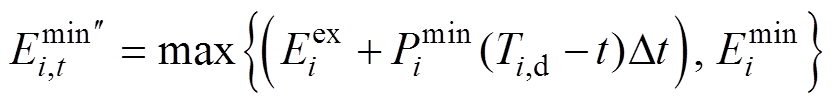
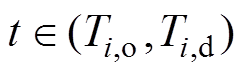 (6)
(6)
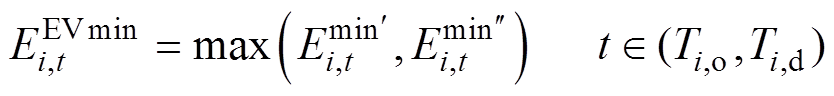 (7)
(7)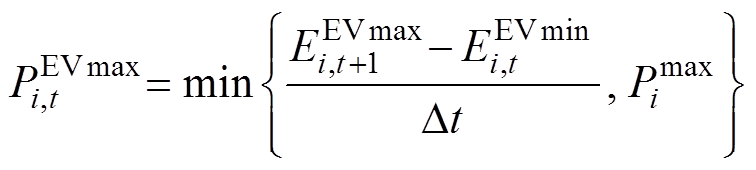
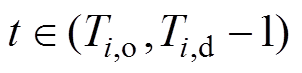 (8)
(8)
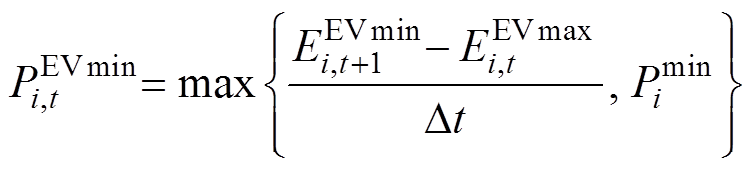
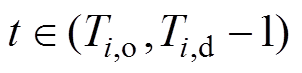 (9)
(9)
式中,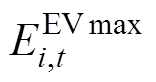 、
、 和
和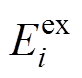 分别为在t时段第i 辆车的最大、最小能量值以及车主期望离网时的能量值;Ti,o与Ti,d分别为EV并网与离网的时段;
分别为在t时段第i 辆车的最大、最小能量值以及车主期望离网时的能量值;Ti,o与Ti,d分别为EV并网与离网的时段;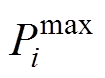 与
与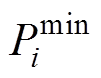 分别为考虑充电桩的充放电效率基础上第i辆车的充放功率最大值和最小值;
分别为考虑充电桩的充放电效率基础上第i辆车的充放功率最大值和最小值;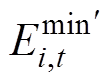 、
、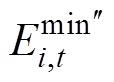 分别是由离网时段向前推的能量下限与并网时段向后推的能量下限;
分别是由离网时段向前推的能量下限与并网时段向后推的能量下限;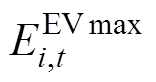 与
与 分别为在t时段第i辆车的功率上、下限。由此得
分别为在t时段第i辆车的功率上、下限。由此得
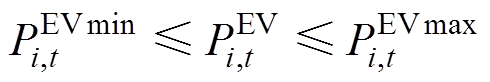 (10)
(10)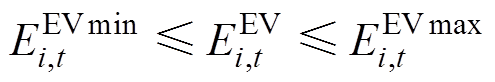 (11)
(11)
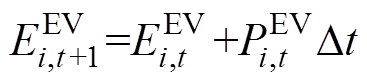 (12)
(12)
式中,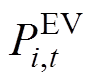 为第i辆EV在t时段的功率;
为第i辆EV在t时段的功率;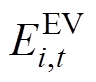 为第i辆EV在t时段的电能,二者都为决策变量。
为第i辆EV在t时段的电能,二者都为决策变量。
1.1.2 集群EV的VB模型
由单元EV的功率、电能刻画边界分别进行求和可以表征集群EV的灵活性,其整合的功率、电能刻画边界[22]分别为
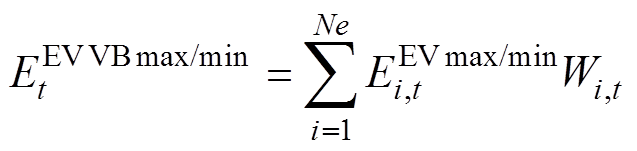 (13)
(13)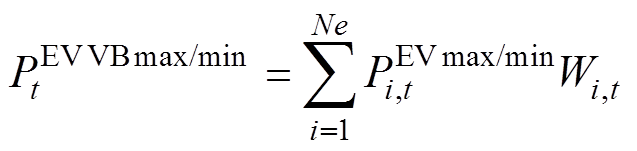 (14)
(14)
式中,Ne为集群EV的数量;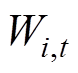 为第i辆车在t时段的并网情况,取值为0或1。由闵氏求和可知对于式(13)、式(14)这种边界闵氏求和表达方式,实际上扩大了功率可行域的范围,因此这种外逼进的方法可以称为进行松弛的精确闵可夫斯基求和方法,但对于集群EV总功率表达是准确的。此外,第i辆EV会在并网与离网时段使并网的集群EV的VB模型的电能值发生阶跃现象,其电能变化为
为第i辆车在t时段的并网情况,取值为0或1。由闵氏求和可知对于式(13)、式(14)这种边界闵氏求和表达方式,实际上扩大了功率可行域的范围,因此这种外逼进的方法可以称为进行松弛的精确闵可夫斯基求和方法,但对于集群EV总功率表达是准确的。此外,第i辆EV会在并网与离网时段使并网的集群EV的VB模型的电能值发生阶跃现象,其电能变化为
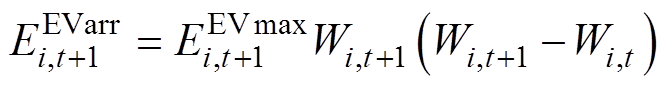 (15)
(15)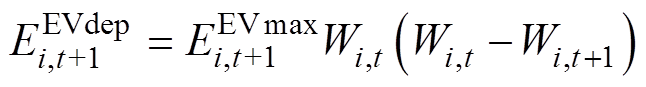 (16)
(16)
式中,计及Ne辆EV并网和离网对VB模型的电能影响,其形式为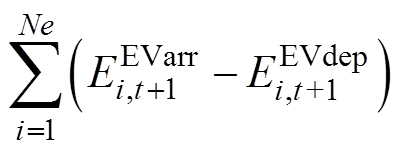 ,即展开式(17)用于修正集群EV的VB模型。
,即展开式(17)用于修正集群EV的VB模型。
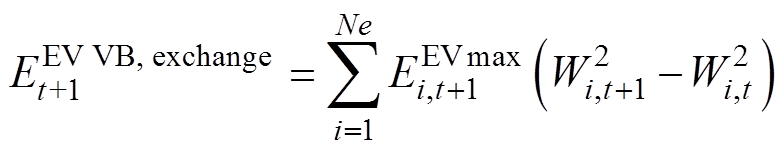 (17)
(17)由此得到集群EV的VB模型为
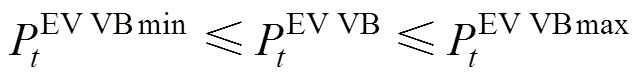 (18)
(18)
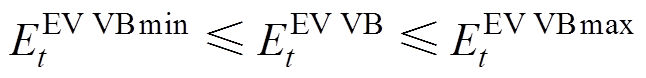 (19)
(19)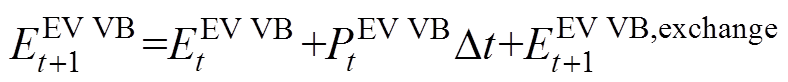 (20)
(20)
式中,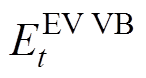 、
、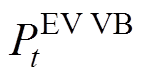 分别为集群EV的VB模型的电能与功率变量。
分别为集群EV的VB模型的电能与功率变量。
TCLs的机理模型本身并不是电池模型,然而其物理特性与电池模型存在相似的特性,因此二者的数学模型本质上是相同的,即温度范围对其出力影响如图1所示。本节以目前在TCLs中占有重要比例的HVAC来说明。
1.2.1 单位HVAC的VB建模及原理
HVAC通常采用一阶常微分方程描述温度变化的热力学等效模型,经过离散化处理后t时段其温度与功率之间的关系为
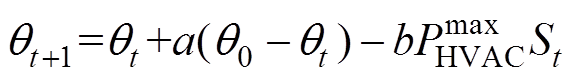 (21)
(21)式中,a =1/(RC),R为热阻,C为热容;b=COP/C,COP为能效系数; 为空调用电功率;
为空调用电功率;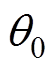 为环境温度;qt为t时段的室内温度;St为1/0开关。这里忽略了热辐射、室内热源等干扰因素。v时段室内温度的拓展方程为
为环境温度;qt为t时段的室内温度;St为1/0开关。这里忽略了热辐射、室内热源等干扰因素。v时段室内温度的拓展方程为
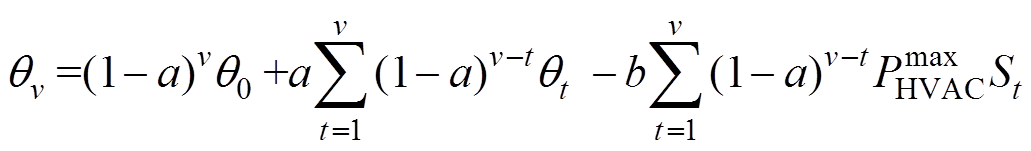 (22)
(22)
由于存在温度死区,温度qt约束为
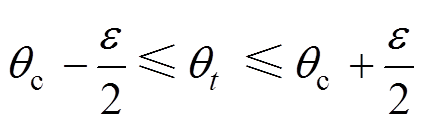 (23)
(23)式中,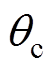 为空调设定温度;
为空调设定温度;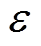 为温度死区宽度。把式(22)代入式(23)得不等式为
为温度死区宽度。把式(22)代入式(23)得不等式为
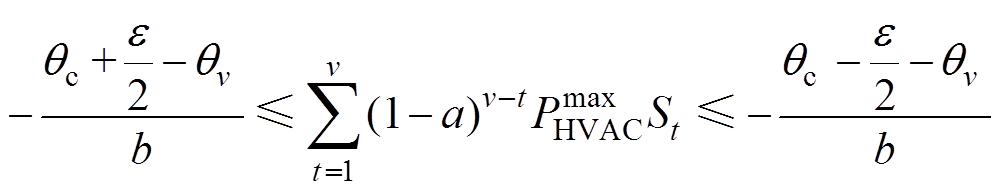 (24)
(24)
式中,在对于集群HVAC的建模过程中可以把离散功率变量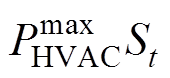 换成连续变量
换成连续变量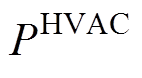 [18],约束为
[18],约束为
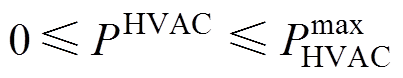 (25)
(25)由式(22)~式(24)可知,建立单元HVAC的VB模型要依据室内温度范围、室外温度变化以及HVAC物理特性、楼宇建筑属性等因素,VB模型建立原理如图3所示。一方面,将室内温度上限、下限与电池容量的下限、上限等效;另一方面,将室内温度到达用户舒适度上限与电池电能耗尽等效,将室内温度到达用户舒适度下限与电池电能充满等效。例如,以环境温度高于室内温度为前提,由约束式(22)可知HVAC制冷量做功,使室内温度降低,即相当于VB模型电能上升;当环境温度高于室内温度时,根据热力学第二定律,物体两端的温度差使热量从高温流向低温,使室内温度上升,即减少VB模型的电能。进一步地,为了更好地比拟电池,文献[19]证明了式(26)中的功率可以很好地接近于在考虑占空比的HVAC混合模型中求解得到的平均功率,因此可以作为在VB模型中衡量电池充放电的功率基准值,当大于基准值时,代表充电;反之,则为放电。
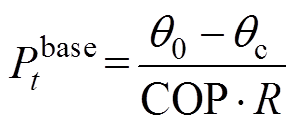 (26)
(26)
对于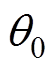 造成室内温度的影响,等效于VB中的自损耗,由消散系数确定
造成室内温度的影响,等效于VB中的自损耗,由消散系数确定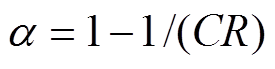 ,由此得到单位HVAC的VB模型的荷电状态约束为
,由此得到单位HVAC的VB模型的荷电状态约束为
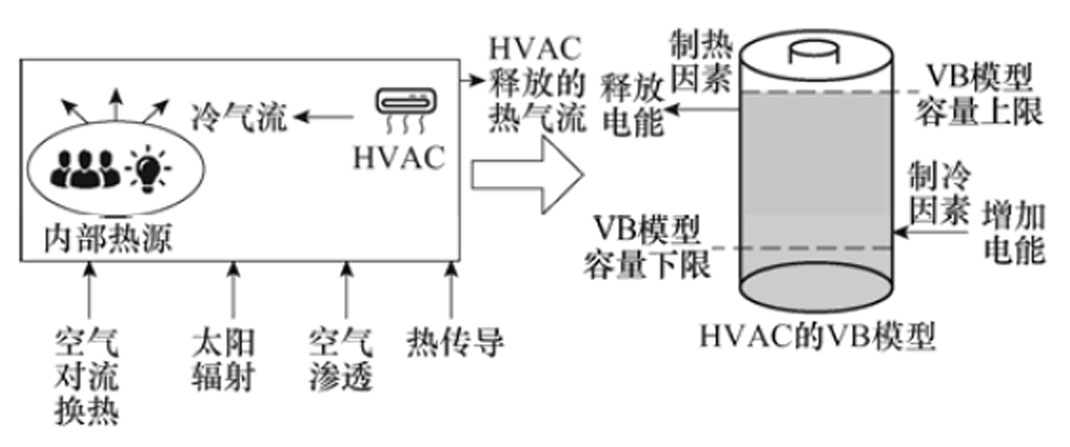
图3 HVAC的VB建模原理
Fig.3 VB modeling principle of HVAC
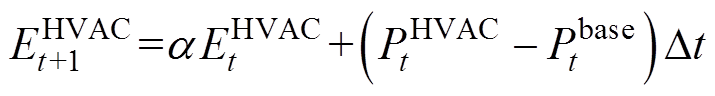 (27)
(27)1.2.2 集群HVAC的VB模型
基于1.2.1节中对单位HVAC建立VB模型原理的叙述,可以进一步拓展到对集群HVAC资源叙述。本节选用基于优化的求解方法[19],用于刻画极端场景确定边界。首先,由于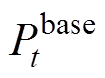 的选择尤为重要,这里假设
的选择尤为重要,这里假设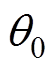 已知,采用二次范数形式,即式(28)作为优化目标确定室内温度尽可能地逼近
已知,采用二次范数形式,即式(28)作为优化目标确定室内温度尽可能地逼近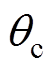 ,并计及一阶等效模型约束式(21)、功率约束式(25)以及用户舒适范围约束,即
,并计及一阶等效模型约束式(21)、功率约束式(25)以及用户舒适范围约束,即
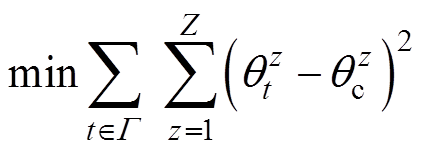 (28)
(28)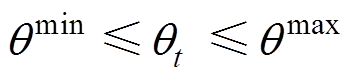 (29)
(29)
式中,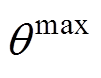 、
、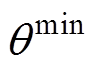 分别为用户舒适度上、下限;
分别为用户舒适度上、下限;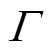 为可控时段,本文设定为6h;z为第z个区域,共Z个区域。由优化目标式(30)、式(31)分别求得集群HVAC的实际功率上、下限和保持室内温度处于上下限需要的功率上、下限,其中约束仍然是式(21)、式(25)和式(29)。
为可控时段,本文设定为6h;z为第z个区域,共Z个区域。由优化目标式(30)、式(31)分别求得集群HVAC的实际功率上、下限和保持室内温度处于上下限需要的功率上、下限,其中约束仍然是式(21)、式(25)和式(29)。
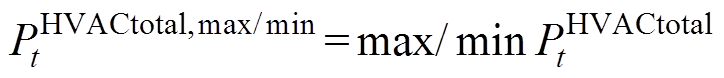 (30)
(30)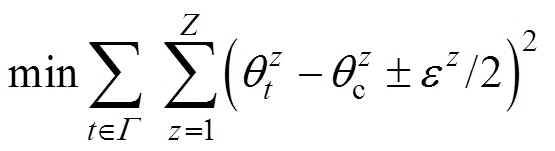 (31)
(31)
式中,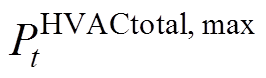 与
与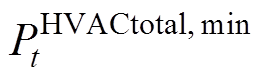 分别为HVAC的功率上、下限;式(31)可求解维持qt在最小值或最大值时的功率,即维持VB模型能量处于上限与下限的功率值,分别由
分别为HVAC的功率上、下限;式(31)可求解维持qt在最小值或最大值时的功率,即维持VB模型能量处于上限与下限的功率值,分别由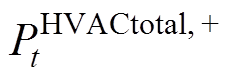 、
、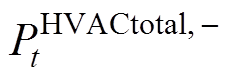 表示。由此可得VB模型的充、放电功率上、下限分别为
表示。由此可得VB模型的充、放电功率上、下限分别为
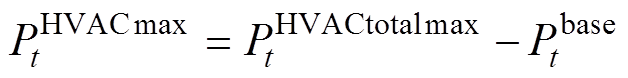 (32)
(32) (33)
(33)
分别以整个可控时段的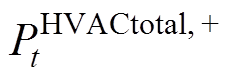 、
、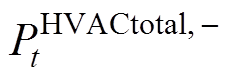 的平均功率求解HVAC的VB模型的能量上、下限,即
的平均功率求解HVAC的VB模型的能量上、下限,即
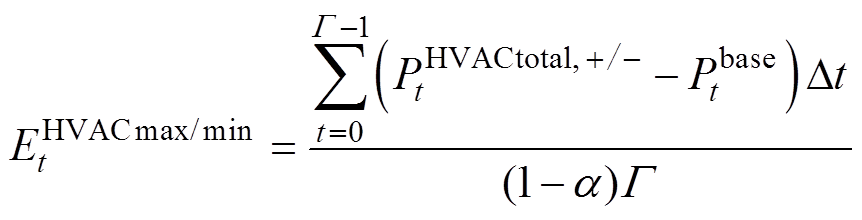 (34)
(34)由此得到集群HVAC的VB模型为
 (35)
(35)
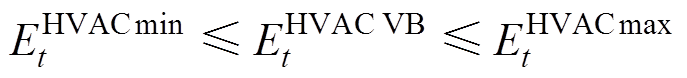 (36)
(36) (37)
(37)
式中, 、
、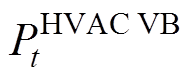 分别为集群HVAC的VB模型的电能与功率变量;
分别为集群HVAC的VB模型的电能与功率变量;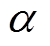 可以取z个区域的消散系数的平均值。上述方法对于其他的TCLs,如热水器和热泵等资源,由于存在死区温度区间及时耦特性,仍然与电池模型存在相似性,因此实际上仍可以采用通用VB模型对其灵活性进行刻画,在此不再赘述。
可以取z个区域的消散系数的平均值。上述方法对于其他的TCLs,如热水器和热泵等资源,由于存在死区温度区间及时耦特性,仍然与电池模型存在相似性,因此实际上仍可以采用通用VB模型对其灵活性进行刻画,在此不再赘述。
本文借鉴北欧电力市场,以文献[5, 23]制定的配售分离环境下的运行框架为基础,在可交易能源系统中构建了交互平台参与日前电力市场,如图4所示。其中交互平台负责收集资源信息并通过通用VB模型刻画集群的资源灵活性,最终作为资源代理参与日前电力市场。输电系统运营商(Trans- mission System Operator, TSO)负责网络安全校验,最终由日前电力市场确定出清价格并发布给交互平台。
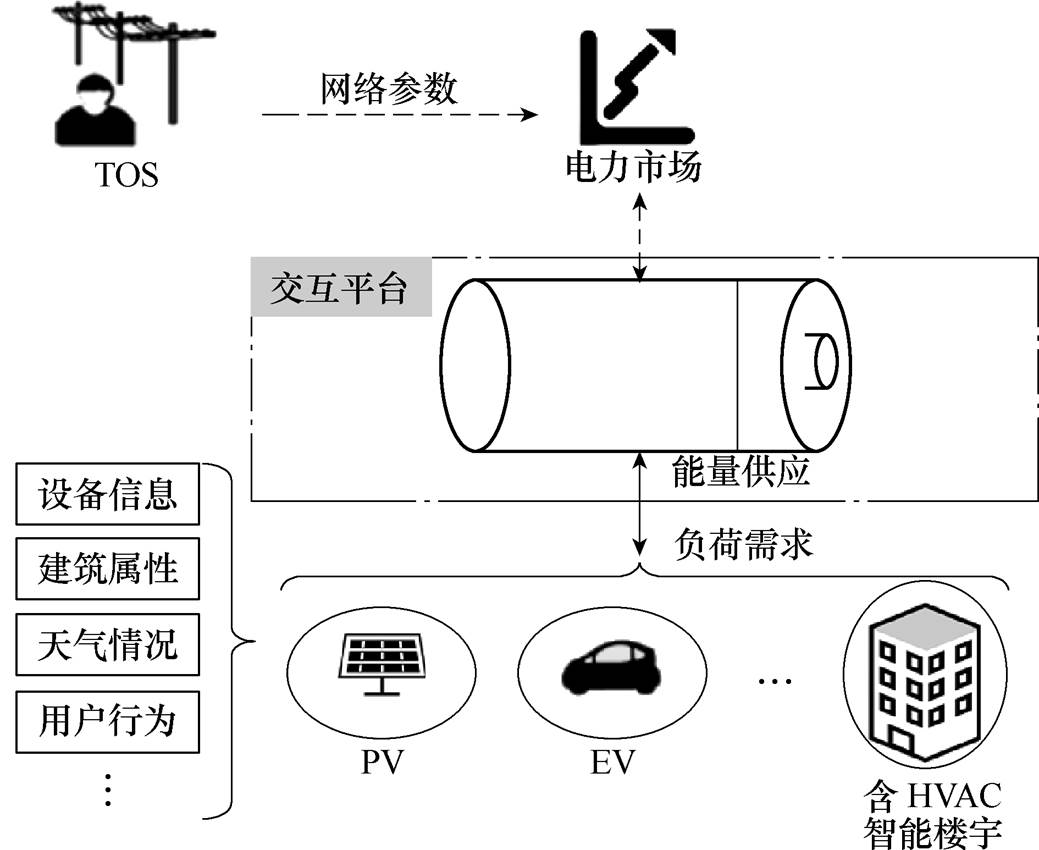
图4 基于交互平台的市场运行框架
Fig.4 Transactive platform to participate in the electricity market operational framework
需求侧资源的灵活性从多时间尺度划分,可以分为调度灵活性和上、下调节灵活性。在日前优化调度模型中调度灵活性主要体现在调度出力,调节灵活性则体现在备用容量。因此交互平台是在考虑资源的用电需求为前提,目标是实现日前优化调度费用最少并在参与日前辅助服务市场中获得最大经济收益,表示如下
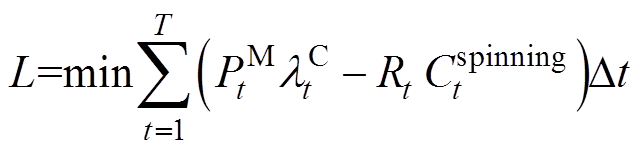 (38)
(38)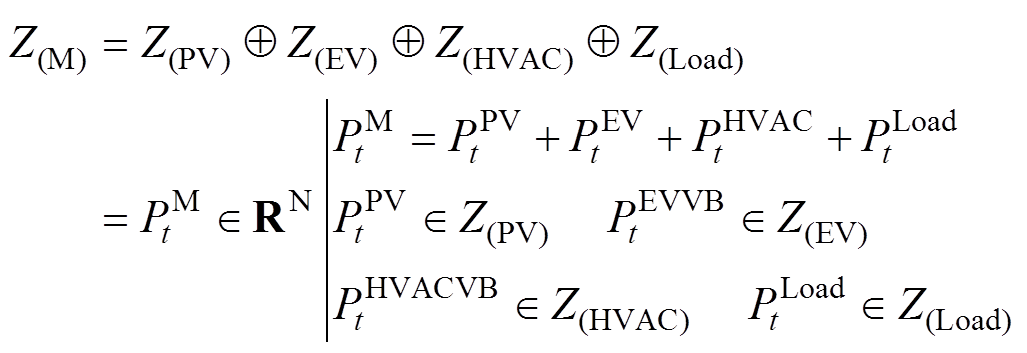 (39)
(39)
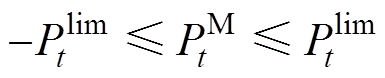 (40)
(40)
式中,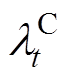 、
、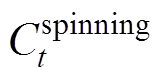 分别为日前电力市场出清电价和旋转备用容量价格,根据交互平台的容量大小以及文章主旨,在此假设二者均为已知常数,可由历史数据得到,以便于交互平台评估参与日前电力市场制定调度方案;
分别为日前电力市场出清电价和旋转备用容量价格,根据交互平台的容量大小以及文章主旨,在此假设二者均为已知常数,可由历史数据得到,以便于交互平台评估参与日前电力市场制定调度方案;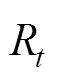 为旋转备用容量;
为旋转备用容量;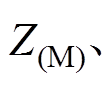
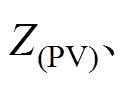
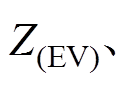
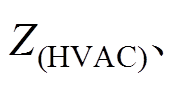
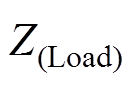 分别是整合的所有资源、集群PV、集群EV、集群HVAC与日用负荷的功率可行域集合。其对应整合的功率值为
分别是整合的所有资源、集群PV、集群EV、集群HVAC与日用负荷的功率可行域集合。其对应整合的功率值为 、
、 、
、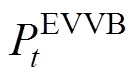 、
、 、
、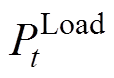 ;
;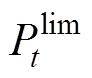 为交互平台的限制功率;T为一天总时段数。由于在本文中日前阶段不考虑通过切断PV提供灵活性,
为交互平台的限制功率;T为一天总时段数。由于在本文中日前阶段不考虑通过切断PV提供灵活性,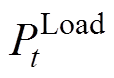 和
和 都假设为常数。
都假设为常数。
显然,评估交互平台的日前能量需求和灵活性参与日前电力市场制定优化调度计划是一个协调优化问题,既需要考虑购买能量的成本也要考虑提供辅助服务获得的收益。因此,首先交互平台需要把资源分成灵活性资源与非灵活性资源;其次,灵活性资源必须作为统一整体进行分析。即在文中要实现对集群的EV和HVAC进行整合。由于资源的功率可行域同时由功率与电能限制决定,即不能直接通过对决策变量(功率)、状态变量(电能)进行直接闵氏求和实现对资源灵活性的整合[12],因此,整合的对象应该是集合,其资源灵活性可行集描述为
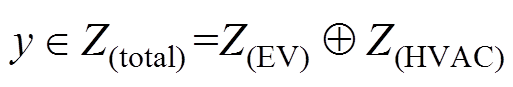 (41)
(41)在实时阶段中资源的灵活性作为备用容量可以参与调频辅助服务,由于调频备用对电能的需求很小,因此在日前调度模型中可以忽略其能量在时间耦合上带来的限制[20]。同时,其实时阶段中系统的变化难以预测,因此这里仅考虑得到日前优化调度结果后实时阶段的可参与辅助调频服务的备用容量的时域分布与裕度情况。基于此,旋转备用容量及预留的上下调节的备用容量约束为
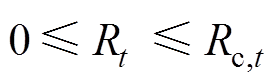 (42)
(42)
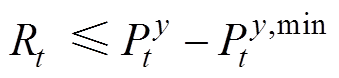 (43)
(43)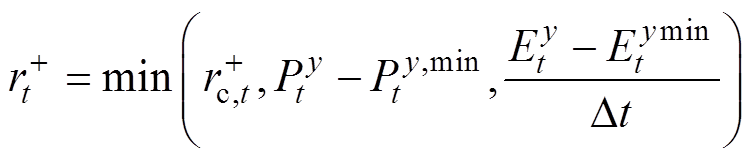 (44)
(44)
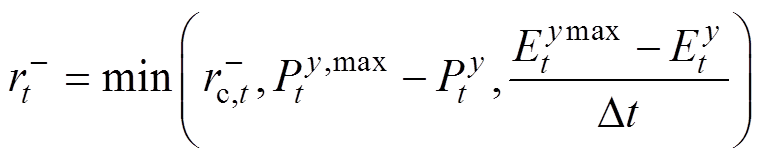 (45)
(45)
式中,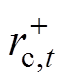 、
、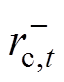 分别为提供调频备用时规定的容量限制上、下限;
分别为提供调频备用时规定的容量限制上、下限;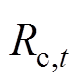 为提供旋转备用容量时规定的容量限制上限;
为提供旋转备用容量时规定的容量限制上限;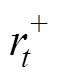 、
、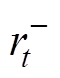 分别为参与调频服务上、下调节备用容量的范围,这里以日前调度计划功率为准;式(42)、式(43)为由资源灵活性确定的旋转备用容量限制;
分别为参与调频服务上、下调节备用容量的范围,这里以日前调度计划功率为准;式(42)、式(43)为由资源灵活性确定的旋转备用容量限制;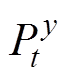 为整合灵活性资源的调度功率;
为整合灵活性资源的调度功率;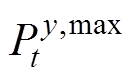 、
、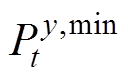 分别为整合灵活性资源的功率上、下限;
分别为整合灵活性资源的功率上、下限; 、
、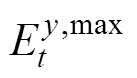 、
、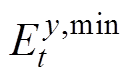 分别为整合灵活性资源的能量值及其上、下限。此外,旋转备用具有时间耦合特性,因此旋转备用容量的多时间尺度的能量限制必须考虑,其表达式为
分别为整合灵活性资源的能量值及其上、下限。此外,旋转备用具有时间耦合特性,因此旋转备用容量的多时间尺度的能量限制必须考虑,其表达式为
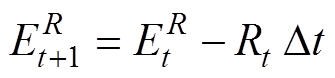 (46)
(46)式中,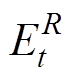 为旋转备用容量造成的电能变化值,其初始状态为0。其上、下限约束为
为旋转备用容量造成的电能变化值,其初始状态为0。其上、下限约束为
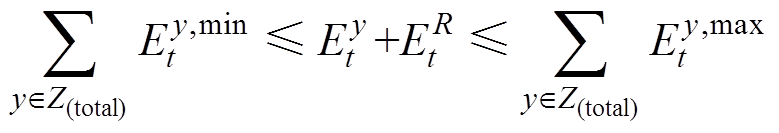 (47)
(47)
式中, 应满足初始与结束时段的能量值相等。
应满足初始与结束时段的能量值相等。
本文在Matlab2015a平台下通过YALMIP工具箱调用CPELX12.6求解器对算例进行求解,其中将一天分为T=96个时段,以15min为一个时间步长。对于日前电价以及备用容量价格,本文借鉴于国外电力市场对需求侧资源备用价格的制定情况[4, 19],所制定的曲线如图5所示。对于备用容量限制均为200kW。仿真算例中EV、HVAC数量分别为200辆和200台。EV以BYD E6为例,电池容量为64kW·h,充放电功率限制为6.5kW,运行中电池容量范围为[0.1, 1]kW·h。HVAC的可用时段假设为全天,COP为2.5,制冷功率上限为3kW,死区温度设为[-0.5, 0.5]℃,用户舒适度范围为[19, 25]℃。其他随机变量参数服从的分布函数情况见表1(表中热容、热阻为便于运算给出经单位换算的参数值),并基于蒙特卡洛法模拟生成相应的场景,进一步在通用的VB模型中把行为习惯、物理参数、天气情况、建筑材料属性等因素综合考虑。天气状况及光伏出力情况选用典型的夏季场景,如图6所示。交互平台限制功率设为1 500kW。
表1 随机参数分布情况
Tab.1 Distribution function situation obeyed by stochastic parameters
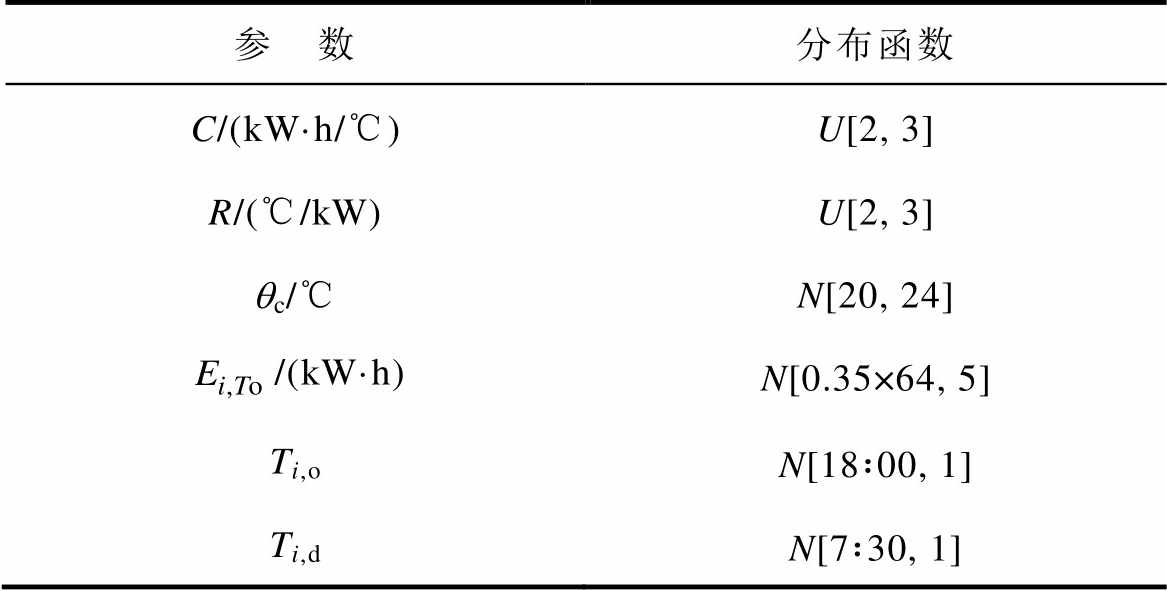
参 数分布函数 C/(kW·h/℃)U[2, 3] R/(℃/kW)U[2, 3] qc/℃N[20, 24] /(kW·h)N[0.35×64, 5] Ti,oN[18:00, 1] Ti,dN[7:30, 1]
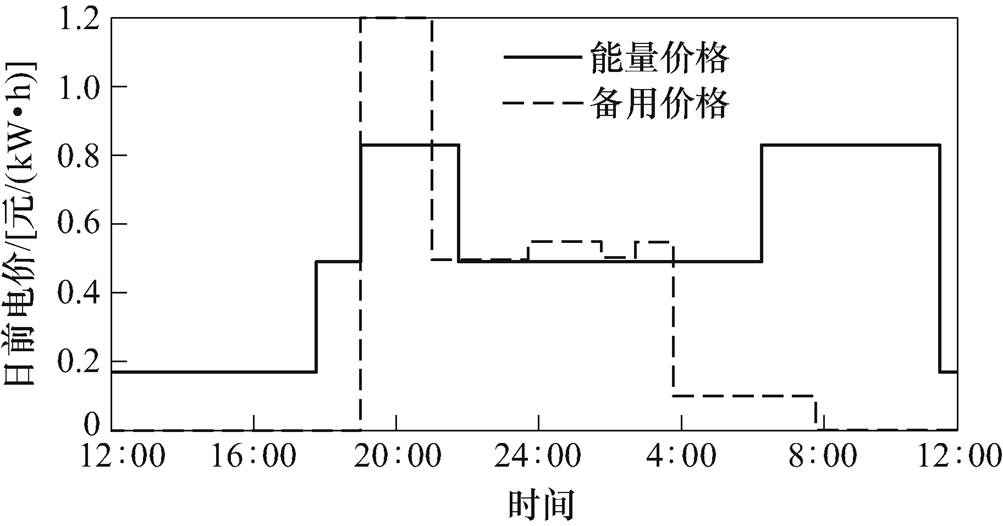
图5 日前市场出清价格
Fig.5 Clearing price set from the wholesale market
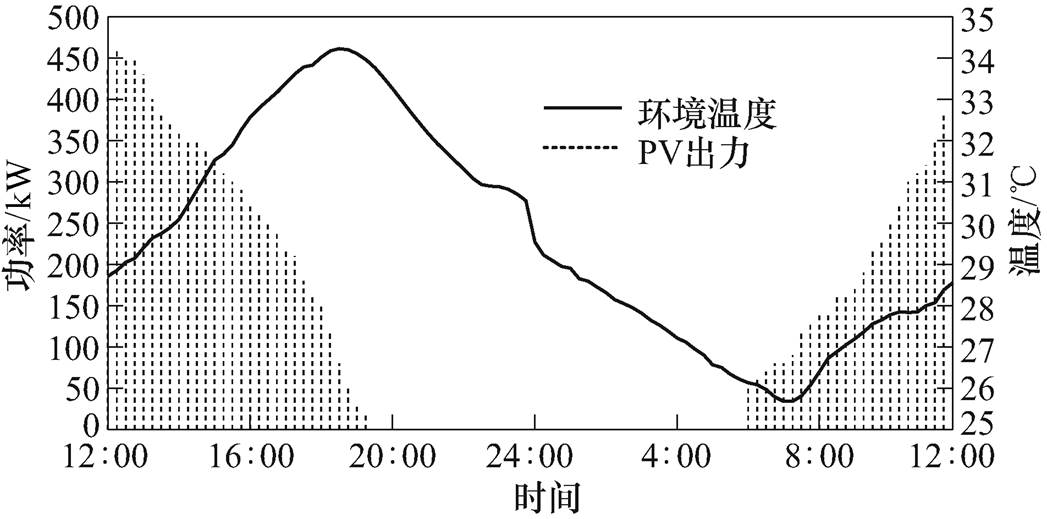
图6 光伏出力与温度曲线
Fig.6 PV output and ambient temperature curves
在此要说明两点:①本文重在描述如何基于VB模型刻画DERs的灵活性,因此未涉及不确定性问题,然而需求侧资源灵活性量化中用户行为、环境等因素带来的不确定性已经成为目前电力市场运行中必须考虑的问题[24],事实上,多场景法、鲁棒优化以及采用数据驱动等方法都可以与提出的模型结合来降低由于实时与日前的不平衡偏差量对成本的影响[25-27];②本文的VB模型可采用由下至上的描述方式对资源灵活性进行刻画,因此可用于描述参数不同的异质DERs设备的灵活性。但这种建模方法显然对数据测量装置有更高的要求,不仅要测量、采集数据并要对其进行进一步加工处理。而从另一个角度来看提出的方法也适用于通过对信息采集中心得到的数据采用概率统计的方法进行处理,得到相关的数据特征,最后实现由上至下的需求侧资源负荷建模[12]。两个角度的建模方法侧重点不同,因此应用的场景也不一样[28]。
为了验证提出的VB模型的有效性,本文在基于3.1节提供的参数生成的相同场景环境下,对比了常规模型与提出的VB模型所得的优化调度结果。优化目标函数设定如下
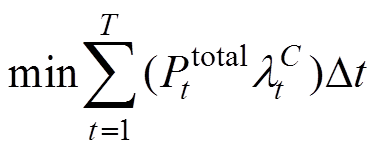 (48)
(48)式中, 为集群EV或HVAC的总调度功率。EV的通用VB模型为式(18)~式(20),其常规模型为式(10)~式(12)。要强调的是常规模型实际上与更接近于普遍的V-表达形式的标准模型[8, 23],都是基于多面体集合得到的不同表达形式,因此实际上二者在应用于优化调度时得到的结果是相同 的[15]。对于HVAC的平均功率值,本文分别采用模型一:室内温度与HVAC出力线性关系式(26);模型二:VB建模中采用优化方法以式(28)为目标确定的基准功率;模型三:分别由式(21)、式(25)和式(48)组成的一阶等效热参数模型进行对比验证分析。
为集群EV或HVAC的总调度功率。EV的通用VB模型为式(18)~式(20),其常规模型为式(10)~式(12)。要强调的是常规模型实际上与更接近于普遍的V-表达形式的标准模型[8, 23],都是基于多面体集合得到的不同表达形式,因此实际上二者在应用于优化调度时得到的结果是相同 的[15]。对于HVAC的平均功率值,本文分别采用模型一:室内温度与HVAC出力线性关系式(26);模型二:VB建模中采用优化方法以式(28)为目标确定的基准功率;模型三:分别由式(21)、式(25)和式(48)组成的一阶等效热参数模型进行对比验证分析。
 (49)
(49)
式中,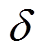 为一个非常小的正数。式(49)的目的是在采用稳态模型中让温度尽量接近于qc而忽略电价影响,等效于一般提出的考虑占空比的HVAC混合模型[19]。HVAC调度结果对比分别采用本文提出的通用VB模型式(35)~式(37),以及一阶等效热参数模型式(21)、式(23)及式(25)作为常规模型进行结果对比。
为一个非常小的正数。式(49)的目的是在采用稳态模型中让温度尽量接近于qc而忽略电价影响,等效于一般提出的考虑占空比的HVAC混合模型[19]。HVAC调度结果对比分别采用本文提出的通用VB模型式(35)~式(37),以及一阶等效热参数模型式(21)、式(23)及式(25)作为常规模型进行结果对比。
集群EV的功率、电能对比如图7所示。图7a、图7b为集群EV的功率及电能的对比情况。可以看出在随机参数模拟生成的相同场景下通过对极端能量边界进行闵氏求和得到的集群EV的VB模型,应用于优化调度求解所得到的结果与常规模型得到的调度结果一致,说明外逼近的刻画方法对于整合的功率结果是相同的。同时通用VB模型以一个整合的决策变量代替设备变量,可以大幅度减少决策变量,因此适用于面对大规模设备优化求解问题,同时可以降低计算机内存需求,从而降低运算成本。从边界形式来看,其刻画方式采用的是具有时移的功率、电能边界,因此在向上层提供资源信息时是通过建立整合的通用VB模型,以一套标准的电池参数形式进行上报,可以避免直接把用户资源全部信息上报,对于用户信息起到一定保护作用。
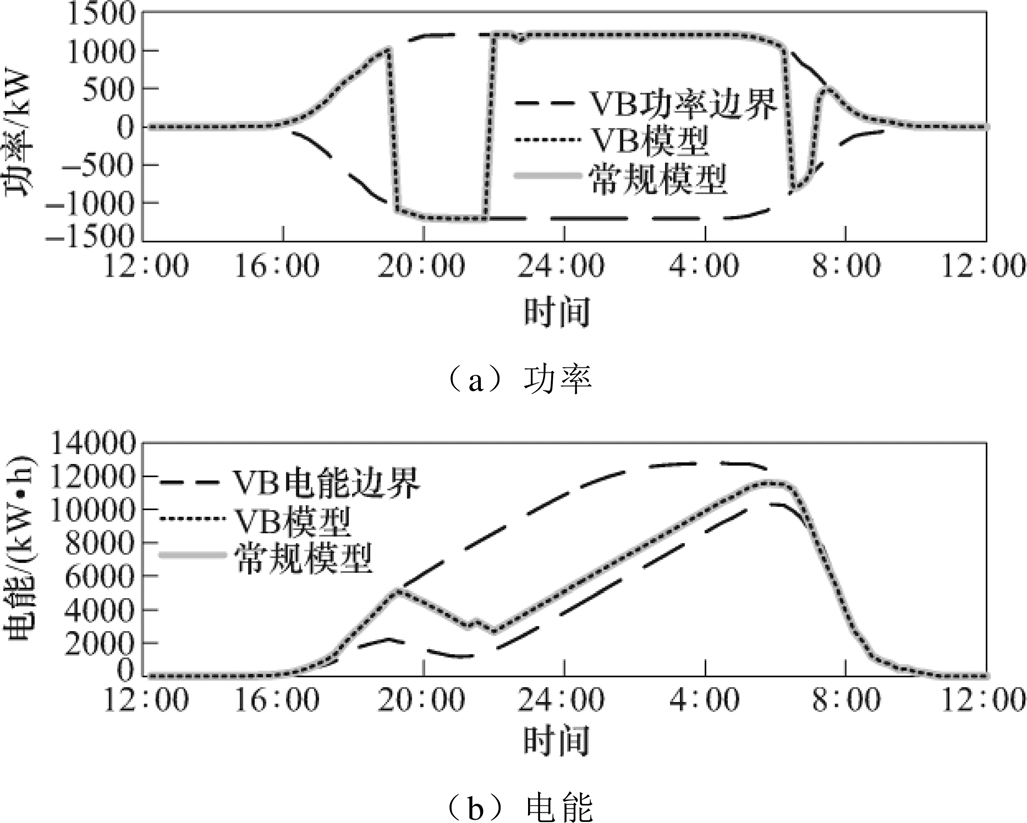
图7 集群EV的功率、电能对比
Fig.7 Power and energy state comparisons of VB model for aggregated EVs
图8为采用三种不同模型对设定温度恒定的HVAC进行优化调度。可知三种仿真结果相近,证实了以平均功率作为基准功率搭建HVAC的通用VB模型的方法是合理的。由一阶等效热参数模型与提出的通用VB模型参与优化调度得到的结果如图9所示,可知二者的结果相近,但同样存在差异。这是因为通用VB模型建模过程中,初始温度的选取会影响能量边界的取值,能量边界的求法为多时段的平均值,从而间接影响了结果。而常规模型不考虑开关占空比等因素影响,仅有功率、温度约束来确定调度结果。此外,提出的通用VB模型在信息与运算效率角度的优越性与EV的通用VB模型描述相同,在此不再赘述。
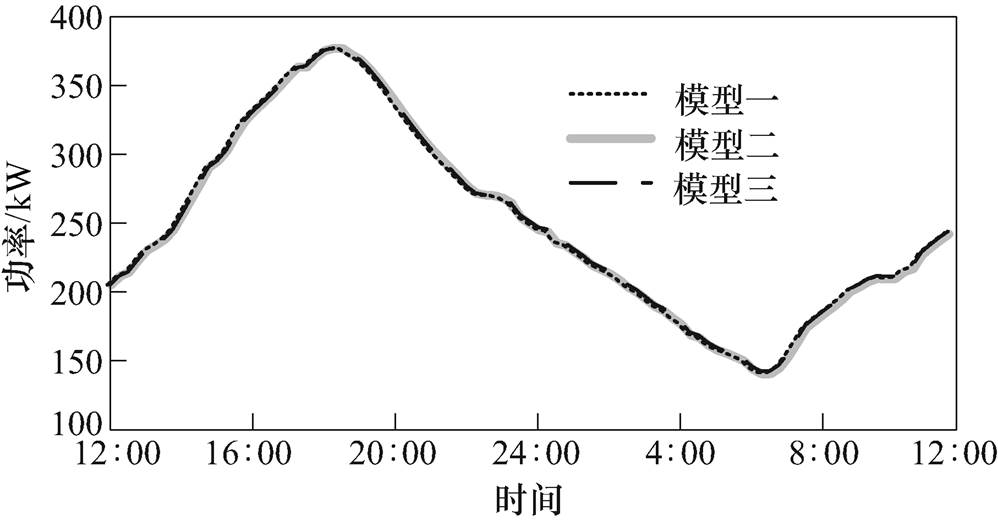
图8 集群HVAC的平均功率对比
Fig.8 Average power comparison of VB model for aggregated HVACs
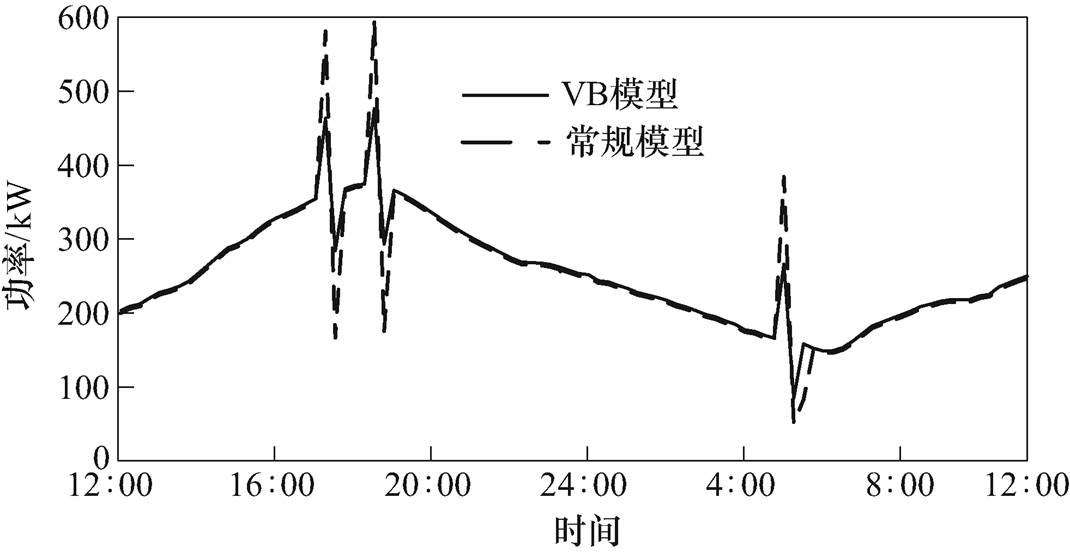
图9 集群HVAC的调度功率对比
Fig.9 Power comparison of VB model for aggregated HVACs
这里对HVAC响应电价过程稍加描述。由于优化目标是实现用电费用最少,因此,对于HVAC而言,用电功率尽可能最小,室内温度尽量保持在死区范围的上限,即在VB模型的电能下边界上。而遇到电价时段交替的地方,HVAC会尽量在电价低的时段多用电,在电价高的时段少用电。对于VB模型的电能情况则表现为电能值上升,在电价平稳后继续保持在电能下边界。
图10分别给出了不同死区宽度对HVAC调度功率的影响。首先,由优化目标式(28)、式(29)知通用VB模型的电能边界与死区温度相关,而其功率边界与死区温度无关。因此实际边界是固定的。其次,虽然增大死区宽度会扩大通用VB模型的电能上、下限,但通用VB模型响应电价的能力随着死区温度范围的扩大而逐渐减小,且实际功率值在逐渐下降。实际上,这与上述对响应电价的描述是一致的。空调出力使室内温度维持在死区温度上限,这说明它是受电能下边界影响的,因此随着下边界不断下降导致实际功率下降。同时死区范围的增大,实际上相当于室内的温度范围增大。当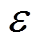 >3时,对于图10中整个VB模型功率区间都是可行范围,因此功率一直处于VB模型功率的下边界而不再由VB模型的电能下界决定。
>3时,对于图10中整个VB模型功率区间都是可行范围,因此功率一直处于VB模型功率的下边界而不再由VB模型的电能下界决定。
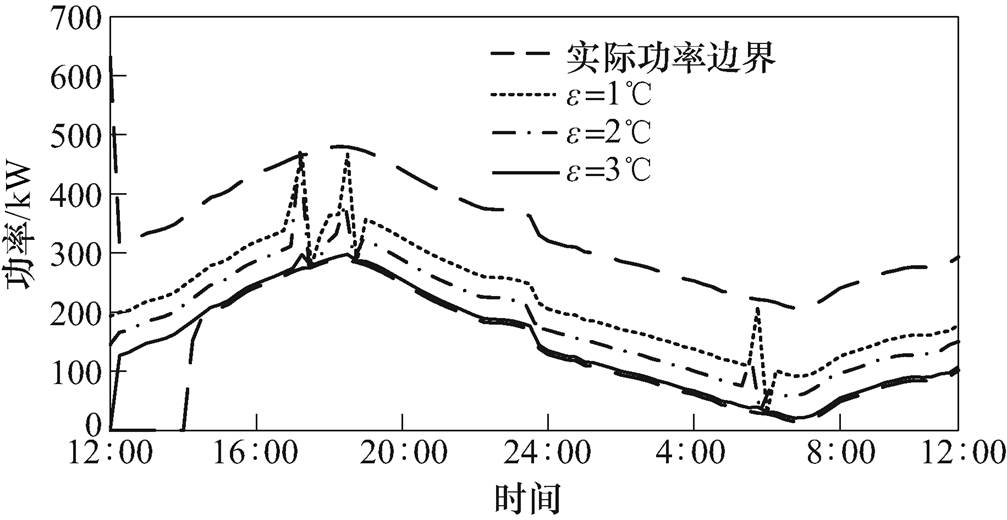
图10 不同死区宽度对HVAC调度功率的影响
Fig.10 Impact of different temperature bands on HVAC scheduling power
多种资源的优化调度分布情况如图11所示。图11为交互平台通过收集固定负荷、PV、EV、HVAC资源信息并接受电力市场电价引导得到的优化调度结果。EV在并网时段16:00~8:00,响应电价,并在高峰电价时段18:30~21:00进行放电获取收益。而另一高峰时段7:00~8:00期间,由于大量EV已经开始并网,因此集群EV的放电能力受到了限制。而对于HVAC,显然是整体趋势与外界环境温度相关。同时,HVAC只在电价发生交替的时段19:00、6:00左右,出力发生了明显的变化。这是因为HVAC会尽量选择在低电价时段多用电,在高电价时段少用电,既保证室内温度维持在死区温度范围内,又使用电费用最低。从总功率曲线来看,由于EV充、放电功率值与容量较大,因此在相同规模下,HVAC的调度效果明显不如EV,从总功率来看整合的灵活性资源具有较强的调度灵活性。对于备用容量,通过备用价格的引导,在20:00~21:00以及24:00~1:30时段,分别提供旋转备用容量,从而体现DERs调节的灵活性。
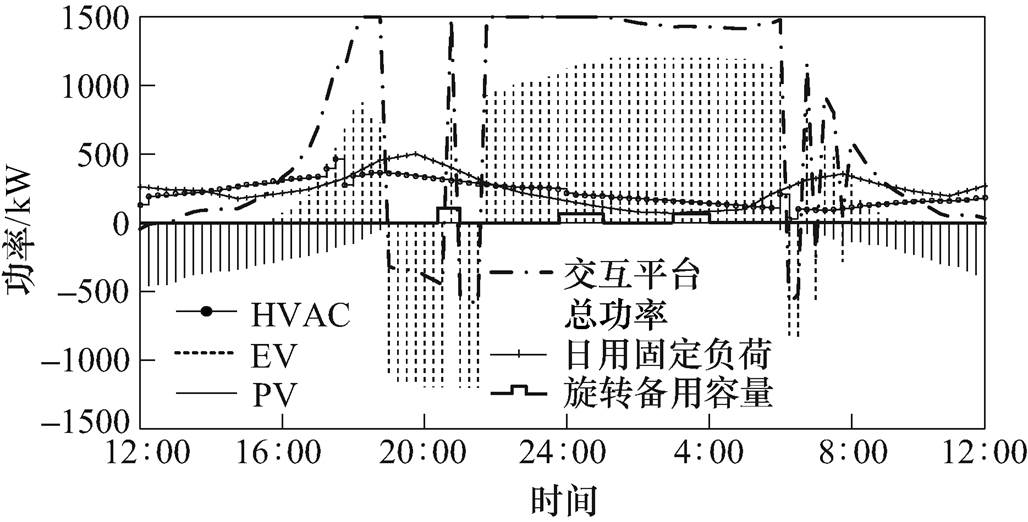
图11 多种资源的优化调度分布情况
Fig.11 Power distribution of a variety of resources
集群的EV、HVAC以及对应整合的灵活性资源的备用容量对应的电能变化情况如图12所示。由图12a、图12b可知其电能的变化趋势与图11对应的功率变化情况是相同的。要强调的是图12c的电能趋势与图12a中集群EV的趋势相近的原因是本文EV电池容量大,而HVAC由于死区宽度导致其可调度容量有限,进而限制其电能上、下边界,因此对整体资源的电能边界影响较小。此外,由于本文中对旋转备用容量设定限制较小,因此从整合的能量值来看,其曲线仍属于电能上、下边界之间,但与未考虑备用容量的电能值曲线接近。

图12 VB模型的电能情况
Fig.12 Energy state of VB model for aggregated EVs and HVACs
EV、HVAC资源的灵活性还可以体现在提供上、下调节功率上,实时阶段参与调频等辅助服务,并获取收益。由于实时阶段过程中功率调节时间较快,因此在本文以15min为时间步长的日前优化调度中仅给出其可以调节的时域分布与容量大小,可参与调频的上、下调节备用容量分布情况如图13所示。对于需求侧资源,由于削减负荷相当于增大发电,因此把在实时阶段中可以减少的功率作为上调节备用容量,下调节备用容量则正相反。
随着高比例DERs在配电网的接入,如何整合、量化分散的需求侧资源灵活性是市场运营商在优化求解时面临的重要挑战。本文首先采用通用化的VB模型对集群的EV、HVAC资源的灵活性进行量化描述,其模型可兼顾单位灵活性资源设备的物理特性、建筑材料属性以及环境、人为因素。其次,基于建立的VB模型,构建需求侧资源参与日前能源市场与辅助服务市场的优化调度模型。通过算例仿真分析得到以下结论:
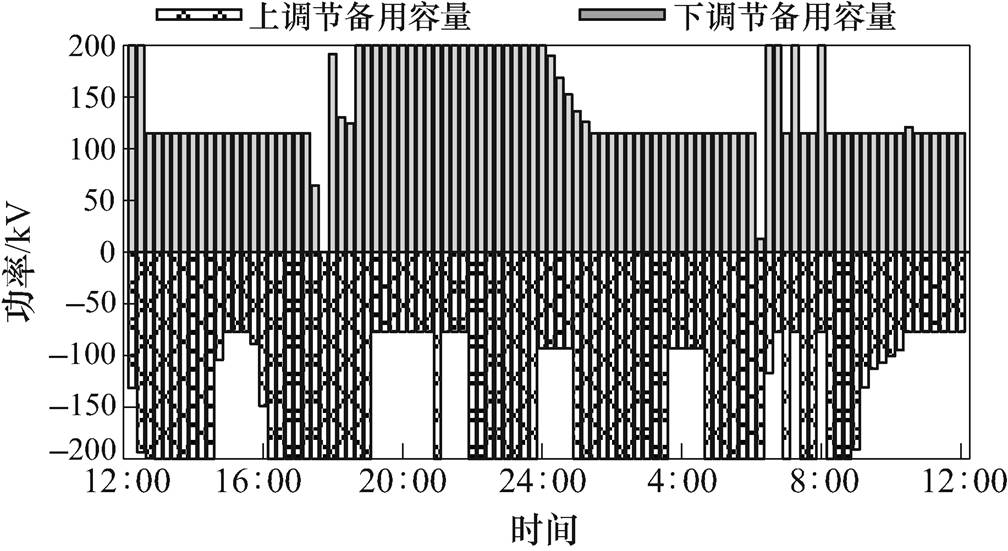
图13 可参与调频的上下调节备用容量分布情况
Fig.13 Distribution of the up and down reserve capacity for frequency support
1)基于通用VB模型刻画的需求侧资源的灵活性可用于制订日前调度计划及旋转备用容量计划,并给出实时调频辅助服务的备用容量的时域分布与裕度。
2)分别通过与常规的EV、HVAC模型对比,证实了通用VB模型应用于优化调度中的有效性。从交互平台的调度结果来看整合的DERs具有很强的调度灵活性,其在多时间尺度上提供备用容量进行调节,进一步降低了交互平台的调度成本。
3)从优越性角度分析,VB模型的整合变量大幅度减少了决策变量数,改善了目前存在的运算效率问题;在售电侧放开的电改背景下,以一套标准的电池参数形式用于表征集群灵活性资源信息方面与以往调度过程中需获取全部调度信息相比,降低了信息暴露的风险。
4)与HVAC相比,相同规模的EV具有更强的调度灵活性。此外,虽然增大死区宽度会扩大HVAC通用VB模型的电能上、下限,但从结果来看死区范围不断扩大会导致降低VB模型对电价的响应能力。
在计及EV充放电效率时的实际功率与电网调度功率并不相同。对于相同效率参数的集群EV,本文提出的VB通用模型仍然可以准确地表征其功率可行域,但对于效率参数不同的集群EV,基于VB模型的优化问题求解结果存在误差,具有局限性[26]。
此外,需求侧资源的灵活性具有物理、时间、价值等多维属性,同时受人为、环境、设备特性等多重影响,因此通用VB建模仍然需要进一步研究:①资源带来的不确定性问题不可忽视,应考虑随机优化、鲁棒优化或结合数据驱动进行建模;②应将VB模型与潮流、安全约束等系统运行条件以及市场运行机制纳入多主体协调运行的优化调度策略;③从稳定性、可靠性、安全性及经济性角度出发,需求侧资源整合成的VB模型可用于规划问题中实现选址定容。
参考文献
[1] 肖云鹏, 王锡凡, 王秀丽, 等. 面向高比例可再生能源的电力市场研究综述[J]. 中国电机工程学报, 2018, 38(3): 663-674.
Xiao Yunpeng, Wang Xifan, Wang Xiuli, et al. Review on electricity market towards high proportion of renewable energy[J]. Proceedings of the CSEE, 2018, 38(3): 663-674.
[2] 王成山, 李鹏, 于浩. 智能配电网的新形态及其灵活性特征分析与应用[J]. 电力系统自动化, 2018, 42(10): 13-21.
Wang Chengshan, Li Peng, Yu Hao. Development and characteristic analysis of flexibility in smart distribution network[J]. Automation of Electric Power Systems, 2018, 42(10): 13-21.
[3] 鲁宗相, 李海波, 乔颖. 高比例可再生能源并网的电力系统灵活性评价与平衡机理[J]. 中国电机工程学报, 2017, 37(1): 13-24.
Lu Zongxiang, Li Haibo, Qiao Ying. Flexibility evaluation and supply/demand balance principle of power system with high-penetration renewable electricity[J]. Proceedings of the CSEE, 2017, 37(1): 13-24.
[4] Hanif S, Massier T, Gooi H B, et al. Cost optimal integration of flexible buildings in congested distribution grids[J]. IEEE Transactions on Power Systems, 2017, 32(3): 2254-2266.
[5] 胡俊杰, 王坤宇, 艾欣, 等. 交互能源: 实现电力能源系统平衡的有效机制[J]. 中国电机工程学报, 2019, 39(4): 953-965.
Hu Junjie, Wang Kunyu, Ai Xin, et al. Transactive energy: an effective mechanism for balancing electric energy system[J]. Proceedings of the CSEE, 2019, 39(4): 953-965.
[6] 赵波, 汪湘晋, 张雪松, 等. 考虑需求侧响应及不确定性的微电网双层优化配置方法[J]. 电工技术学报, 2018, 33(14): 3284-3295.
Zhao Bo, Wang Xiangjin, Zhang Xuesong, et al. Two-layer method of microgrid optimal sizing con- sidering demand-side response and uncertainties[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3284-3295.
[7] 祖其武, 牛玉刚, 邹媛媛, 等. 基于弹性负荷分时调度和多电源联合供电的微网经济运行[J]. 电力系统保护与控制, 2018, 46(4): 214-223.
Zu Qiwu, Niu Yugang, Zou Yuanyuan, et al. Economic operation of mircrogrid based on elastic load sub-period dispatch and combined power supply of multiple energy[J]. Power System Protection and Control, 2018, 46(4): 214-223.
[8] 徐建军, 王保娥, 闫丽梅, 等. 混合能源协同控制的智能家庭能源优化控制策略[J]. 电工技术学报, 2017, 32(12): 214-223.
Xu Jianjun, Wang Baoe, Yan Limei, et al. The strategy of the smart home energy optimization control of the hybrid energy coordinated control[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 214-223.
[9] 卢锦玲, 於慧敏. 考虑风电相依结构的虚拟发电厂内部资源随机调度策略[J]. 电工技术学报, 2017, 32(17): 67-74.
Lu Jinling, Yu Huimin. Stochastic scheduling strategy of resources in virtual power plant con- sidering wind power dependence structure[J]. Transactions of China Electrotechnical Society, 2017, 32(17): 67-74.
[10] 平健, 陈思捷, 张宁, 等. 基于智能合约的配电网去中心化交易机制[J]. 中国电机工程学报, 2017, 37(13): 3682-3690.
Ping Jian, Chen Sijie, Zhang Ning, et al. Decentra- lized transactive mechanism in distribution network based on smart contract[J]. Proceedings of the CSEE, 2017, 37(13): 3682-3690.
[11] Barot S, Taylor J A. A concise, approximate representation of a collection of loads described by polytopes[J]. International Journal of Electrical Power & Energy Systems, 2017, 84: 55-63.
[12] Sajjad I, Chicco G, Napoli R. Definitions of demand flexibility for aggregate residential loads[J]. IEEE Transactions on Smart Grid, 2016, 7(6): 2633-2643.
[13] 李亚平, 姚建国, 雍太有, 等. 居民温控负荷聚合功率及响应潜力评估方法研究[J]. 中国电机工程学报, 2017, 37(19): 5519-5528.
Li Yaping, Yao Jianguo, Yong Taiyou, et al. Estimation approach to aggregated power and response potential of residential thermostatically controlled loads[J]. Proceedings of the CSEE, 2017, 37(19): 5519-5528.
[14] Müller F L, Szabó J, Sundström O, et al. Aggregation and disaggregation of energetic flexibility from distributed energy resources[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 1205-1214.
[15] Trangbaek K, Bendtsen J. Exact constraint aggre- gation with applications to smart grids and resource distribution[C]//51st Annual Conference on Decision and Control (CDC), Maui, USA, 2012: 4181-4186.
[16] Zhao Lin, Zhang Wei, Hao He, et al. A geometric approach to aggregate flexibility modeling of thermo- statically controlled loads[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4721-4731.
[17] Barot S, Taylor J A. An outer approximation of the Minkowski sum of convex conic sets with application to demand response[C]//55th Conference on Decision and Control (CDC), Las Vegas, USA, 2016: 4233- 4238.
[18] Hao He, Somani A, Lian Jianming, et al. Generalized aggregation and coordination of residential loads in a smart community[C]//2015 IEEE International Con- ference on Smart Grid Communications (Smart Grid Comm), Miami, USA, 2015: 67-72.
[19] Hao He, Wu Di, Lian Jianming, et al. Optimal coordination of building loads and energy storage for power grid and end user services[J]. IEEE Transa- ctions on Smart Grid, 2018, 4(2): 4335-4345.
[20] Mathieu J L, Vayá M G, Andersson G. Uncertainty in the flexibility of aggregations of demand response resources[C]//Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 2013: 8052- 8057.
[21] 占恺峤, 胡泽春, 宋永华, 等. 含新能源接入的电动汽车有序充电分层控制策略[J]. 电网技术, 2016, 40(12): 3689-3695.
Zhan Kaiqiao, Hu Zechun, Song Yonghua, et al. Electric vehicle coordinated charging hierarchical control strategy considering renewable energy generation integration[J]. Power System Technology, 2016, 40(12): 3689-3695.
[22] Ulbig A, Andersson G. Analyzing operational flexibi- lity of electric power systems[J]. International Journal of Electrical Power & Energy Systems, 2015, 72: 155-164.
[23] 吴界辰, 艾欣, 张艳, 等. 配售分离环境下高比例分布式能源园区电能日前优化调度[J]. 电网技术, 2018, 42(6): 1709-1717.
Wu Jiechen, Ai Xin, Zhang Yan, et al. Day-ahead optimal scheduling for high penetration of distributed energy resources in community under separated distribution and retail operational environment[J]. Power System Technology, 2018, 42(6): 1709-1717.
[24] 王毅, 张宁, 康重庆, 等. 电力用户行为模型: 基本概念与研究框架[J]. 电工技术学报, 2019, 34(10): 2056-2068.
Wang Yi, Zhang Ning, Kang Chongqing, et al. Electrical consumer behavior model:basic concept and research framework[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2056-2068.
[25] Margellos K, Goulart P, Lygeros J. On the road between robust optimization and the scenario approach for chance constrained optimization pro- blems[J]. IEEE Transactions on Automatic Control, 2014, 59(8): 2258-2263.
[26] 吴界辰, 艾欣, 胡俊杰, 等. 计及不确定因素的需求侧灵活性资源优化调度[J]. 电力系统自动化, 2019, 43(14): 73-80, 89.
Wu Jiechen, Ai Xin, Hu Junjie, et al. Optimal schedule of demand side flexible resource under uncertainty[J]. Automation of Electric Power Systems, 2019, 43(14): 73-80, 89.
[27] Wang Andong, Li Rongling, You Shi. Development of a data driven approach to explore the energy flexibility potential of building clusters[J]. Applied Energy, 2018: 89-100.
[28] Arif A, Wang Zhaoyu, Wang Jianhui, et al. Load modeling-a review[J]. IEEE Transactions on Smart Grid, 2018, 9(6): 5986-5999.
Methods for Characterizing Flexibilities from Demand-Side Resources and Their Applications in the Day-Ahead Optimal Scheduling
Abstract Due to the increasing penetration of distributed energy resources (DERs) in the distribution network and the electricity market reform which allows demand side resources to participate in the electricity market, the leverage of flexibilities from demand-side resources has attracted more and more attentions. This paper takes electric vehicle (EV) and heating ventilating & air conditioning (HVAC) as the typical demand-side resources. Considering the physical characteristics of equipment, the behaviors of occupants and environmental factors, a generalized virtual battery model (VB) is established for characterizing the flexibilities using an extreme energy circumstance method. On this basis, a day-ahead optimal scheduling model is developed for the transactive platform to participate in the wholesale market. The numerical results show that the energy schedule and reserve capacity can be determined by the general VB model. In addition, the proposed model is verified by simulation, and its superiority in terms of computational efficiency and information security is analyzed.
keywords:Flexibilities from demand-side resources, transactive platform, generalized virtual battery model, day-ahead optimal scheduling, reserve capacity
中图分类号:TM769
DOI: 10.19595/j.cnki.1000-6753.tces.190400
国家重点研发计划(2016YFB0900500)、国家自然科学基金(51877078)和北京市自然科学基金(3182037)资助项目。
收稿日期 2019-04-11
改稿日期 2019-08-25
吴界辰 男,1991年生,博士研究生,主要研究方向为新能源电力系统及负荷建模技术。E-mail: wjcncepu@foxmail.com
胡俊杰 男,1986年生,副教授,硕士生导师,主要研究方向为新能源电力系统及微电网。E-mail: junjiehu@ncepu.edu.cn(通信作者)
(编辑 陈 诚)