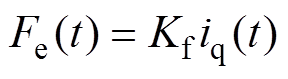 (1)
(1)摘要 为解决永磁直线同步电机(PMLSM)运行过程中对参数变化、外部扰动和摩擦力等不确定性因素敏感的问题,提出一种动态边界层全局互补滑模控制(GCSMC)方法。首先建立含有不确定性因素在内的PMLSM数学模型。然后利用广义滑模面和互补滑模面相结合的方式设计互补滑模控制器,来抑制不确定性因素对系统的影响,进而削弱抖振,但其边界层厚度值恒定不变,致使系统状态轨迹只能在边界层范围内收敛。为此,采用新型饱和函数来设计全局互补滑模控制器,以实现边界层的动态变化,使边界层厚度值随状态轨迹的变化而减小直至收敛到切换平面上,进一步提高了系统在边界层内的鲁棒性。实验结果表明该方法既改善了系统跟踪性能,又保证了系统的全局鲁棒性。
关键词:永磁直线同步电机 不确定性因素 动态边界层 全局互补滑模控制 鲁棒性
永磁直线同步电机(Permanent Magnet Linear Synchronous Motor, PMLSM)取消了传统的“旋转电机+滚珠丝杠”的结构,无需齿轮箱、链条等中间传动环节,可实现无间隙传动[1-2]。PMLSM具有噪声低、效率高、磨损小、精度高等优点,已经广泛应用于半导体、医疗、数控加工乃至军事等行业[3]。但由于省去丝杠传动方式,使PMLSM对参数变化、外部扰动和摩擦力等不确定性因素十分敏感,这些不确定性直接作用于PMLSM的动子上,极大地影响了动子运动[4]。因此,抑制这些不确定性因素对系统的影响对改善高速高精伺服性能具有十分重要的意义。
由于PMLSM伺服系统要求电机在不确定性因素影响下仍具有良好的位置跟踪性能,传统比例-谐振控制、反推控制等方法在一些应用场合无法满足控制要求[5]。近年来,滑模控制作为一种非线性、强鲁棒控制方法得到国内外学者的关注[6]。针对PMLSM这一非线性、强耦合伺服系统,滑模控制具有极大的优越性,当系统到达滑动模态时,系统状态不再受参数变化、外部扰动等不确定性因素的影响,从而可保证系统的强鲁棒性,但抖振问题的存在影响了滑模控制在实际电机控制中的广泛应 用[7-8]。因此,削弱抖振是确保滑模控制性能最为关键的步骤。文献[9]提出一种基于卡尔曼滤波器的自适应滑模控制方法,利用卡尔曼滤波降低测量噪声和系统抖振,但滑模控制指数趋近律中符号函数的切换动作仍会对系统稳态造成影响。文献[10]利用径向基神经网络的输出量替代滑模控制中的切换控制律,极大地削弱了抖振,减小了系统超调量,但径向基神经网络容易陷入局部最优解,严重时将导致系统无法收敛至稳定状态。文献[11]在传统滑模面的基础上设计互补滑模面,并利用饱和函数实现边界层控制,削弱了抖振,提高了跟踪精度,但互补滑模控制(Complementary Sliding Mode Control, CSMC)中,边界层厚度和切换增益的值需依照经验不断调试获得,且由于饱和函数恒定不变,导致系统轨迹只能收敛到边界层内,降低了系统在切换平面上的鲁棒性。文献[12]对CSMC加以改进,将新型自适应PI饱和函数应用于CSMC中,解决了边界层厚度增加时系统无法保证稳态误差的问题,但是此自适应算法的设计及稳定性证明过程较为 复杂。
为此,本文提出动态边界层全局互补滑模控制(Global Complementary Sliding Mode Control, GCSMC)方法。GCSMC采用新型饱和函数代替CSMC中恒定不变的饱和函数,可实现边界层厚度的动态控制,不但可以削弱抖振,还能使边界层厚度随系统状态轨迹的收敛而逐渐减小到零,解决CSMC方法在边界层内鲁棒性差的问题,从而改善系统的全局鲁棒性和控制精准性。实验结果表明,动态边界层GCSMC方法切实可行,可明显提高系统的位置跟踪性能和鲁棒性能。
对PMLSM伺服系统进行矢量控制,在id=0的条件下,电磁推力方程简化为
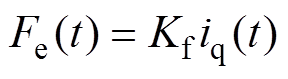 (1)
(1)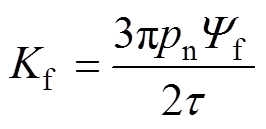 (2)
(2)
式中, 为电磁推力;
为电磁推力;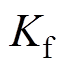 为电磁推力系数;
为电磁推力系数;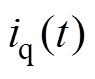 为q轴电流;
为q轴电流;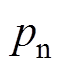 为极对数;
为极对数;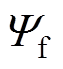 为基波磁链;
为基波磁链;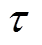 为极距。
为极距。
PMLSM运动方程为
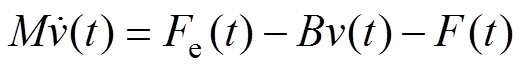 (3)
(3)式中,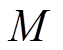 为动子质量;
为动子质量;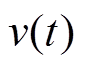 为动子速度;
为动子速度;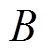 为黏滞摩擦因数;
为黏滞摩擦因数;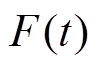 为系统扰动,包括参数变化、外部扰动和摩擦力等。若使系统具有良好的控制性能,必须设计行之有效的方法削弱
为系统扰动,包括参数变化、外部扰动和摩擦力等。若使系统具有良好的控制性能,必须设计行之有效的方法削弱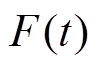 对系统的影响。
对系统的影响。
若忽略参数变化、外部扰动和摩擦力等不确定因素对PMLSM伺服系统的影响,即 时,可将式(3)改写为
时,可将式(3)改写为
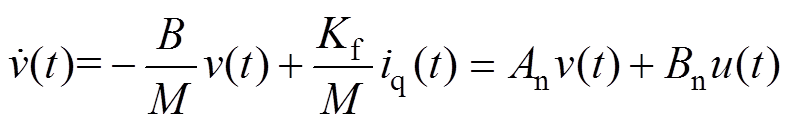 (4)
(4)式中,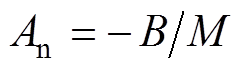 ;
;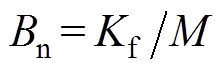 ;
;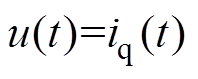 为系统控制输入。
为系统控制输入。
若考虑不确定性因素对系统的影响,即在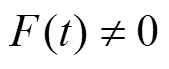 的情况下,式(3)可改写为
的情况下,式(3)可改写为

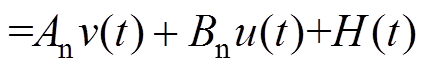 (5)
(5)
 (6)
(6)
式中,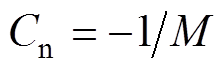 ;
;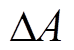 、
、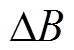 和
和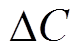 为由系统参数
为由系统参数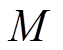 和
和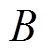 引起的不确定性;
引起的不确定性;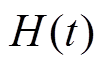 为总不确定性因素,且定义
为总不确定性因素,且定义 ,
,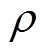 为正常数,是
为正常数,是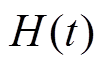 的上界,同时也作为CSMC和GCSMC的切换增益。
的上界,同时也作为CSMC和GCSMC的切换增益。
为使PMLSM伺服系统在受不确定性因素影响情况下,动子位置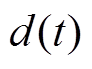 仍可以精准跟踪给定位置
仍可以精准跟踪给定位置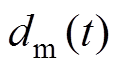 ,提出动态边界层GCSMC方法保证系统实现高精度强鲁棒控制性能。基于GCSMC的PMLSM伺服系统框图如图1所示。
,提出动态边界层GCSMC方法保证系统实现高精度强鲁棒控制性能。基于GCSMC的PMLSM伺服系统框图如图1所示。
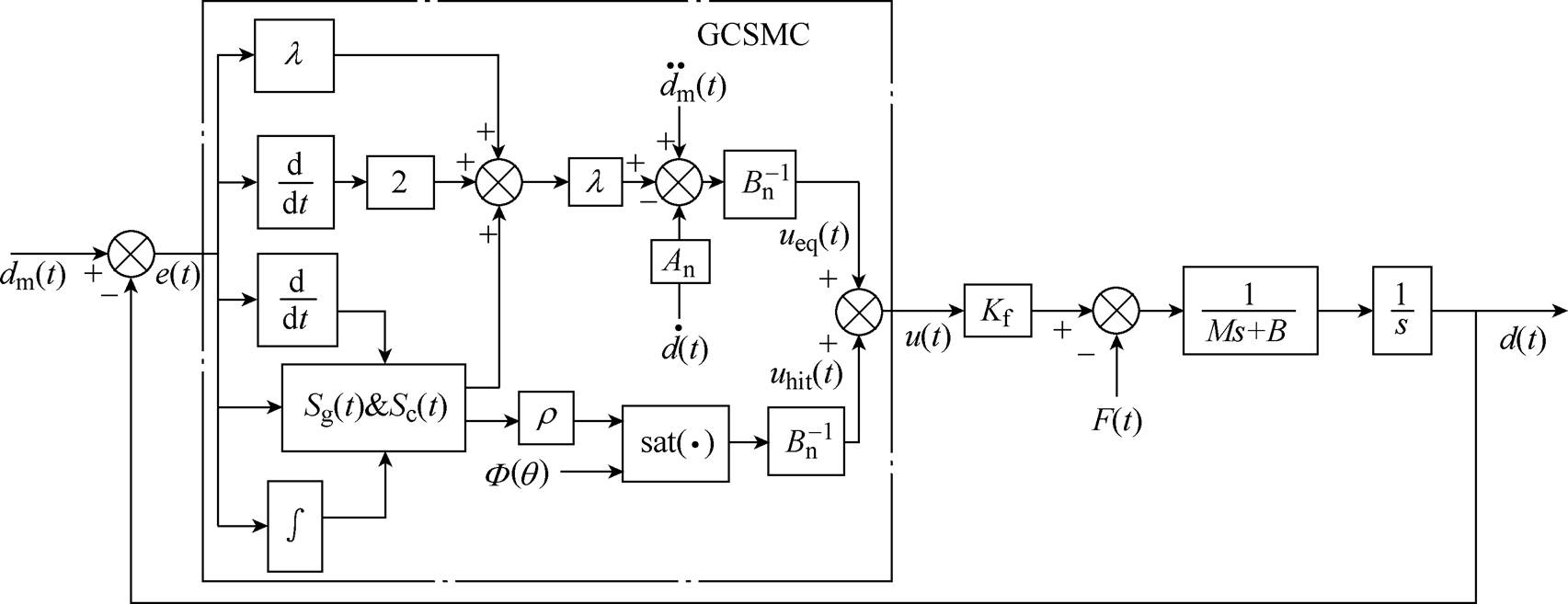
图1 基于GCSMC的PMLSM伺服系统框图
Fig.1 Block diagram of PMLSM servol system based on GCSMC
定义PMLSM的位置跟踪误差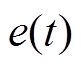 为
为
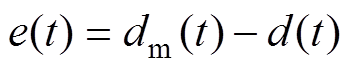 (7)
(7)GCSMC的设计过程主要包括两个相对独立的部分:滑模面设计和控制律设计。在设计滑模面时,需保证系统状态轨迹于有限时间收敛到切换平面上或边界层内,使滑动模态渐近稳定[13]。设计广义滑模面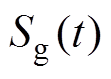 和互补滑模面
和互补滑模面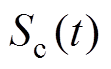 分别为
分别为
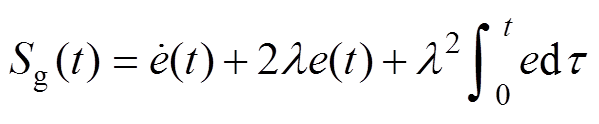 (8)
(8)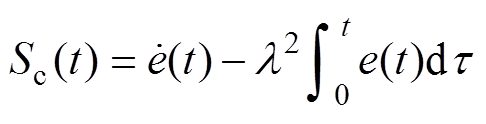 (9)
(9)
式中,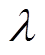 为正常数。
为正常数。
由式(8)和式(9)可得两个滑模面之间的关系为
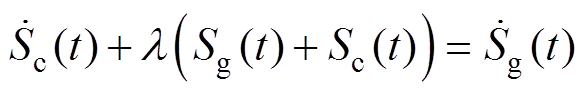 (10)
(10)为保证系统的稳定性,设计CSMC的控制律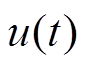 表示为
表示为
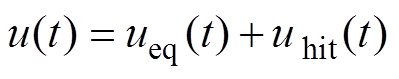 (11)
(11)
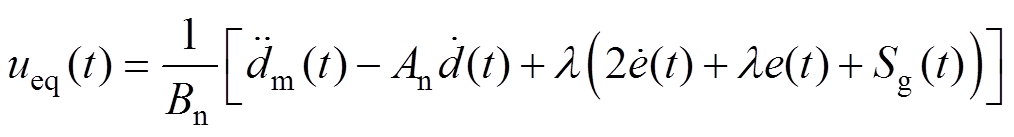 (12)
(12)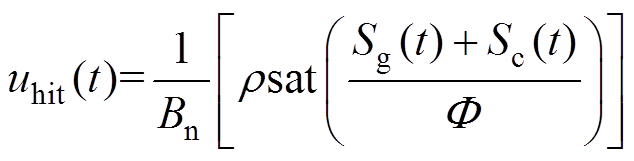 (13)
(13)
式中,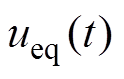 为等效控制律;
为等效控制律;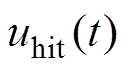 为切换控制律;
为切换控制律;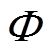 为边界层厚度值;sat(∙)为饱和函数。由式(11)可以看出,
为边界层厚度值;sat(∙)为饱和函数。由式(11)可以看出,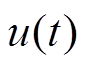 包括
包括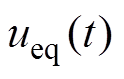 和
和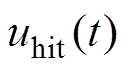 两部分,设计
两部分,设计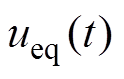 时针对理想情况下确定性系统无外加干扰,设计
时针对理想情况下确定性系统无外加干扰,设计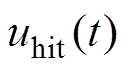 时针对不确定性系统有外加干扰。GCSMC结构框图如图1中点画线框所示。
时针对不确定性系统有外加干扰。GCSMC结构框图如图1中点画线框所示。
定义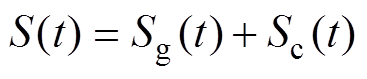 为两个滑模面之和,则传统sat(∙)可表示为
为两个滑模面之和,则传统sat(∙)可表示为
 (14)
(14)对式(14)加以简化,可改写为
 (15)
(15)
由式(15)可以看出,采用传统饱和函数的CSMC中两个边界层分别为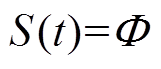 和
和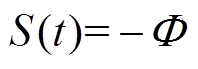 。就含有不确定性因素的PMLSM伺服系统而言,选取
。就含有不确定性因素的PMLSM伺服系统而言,选取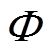 值过小,对于削弱抖振效果不大;
值过小,对于削弱抖振效果不大;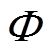 值过大,削弱抖振的同时会产生稳态误差从而影响控制精度[14]。CSMC中边界层图示如图2所示。
值过大,削弱抖振的同时会产生稳态误差从而影响控制精度[14]。CSMC中边界层图示如图2所示。
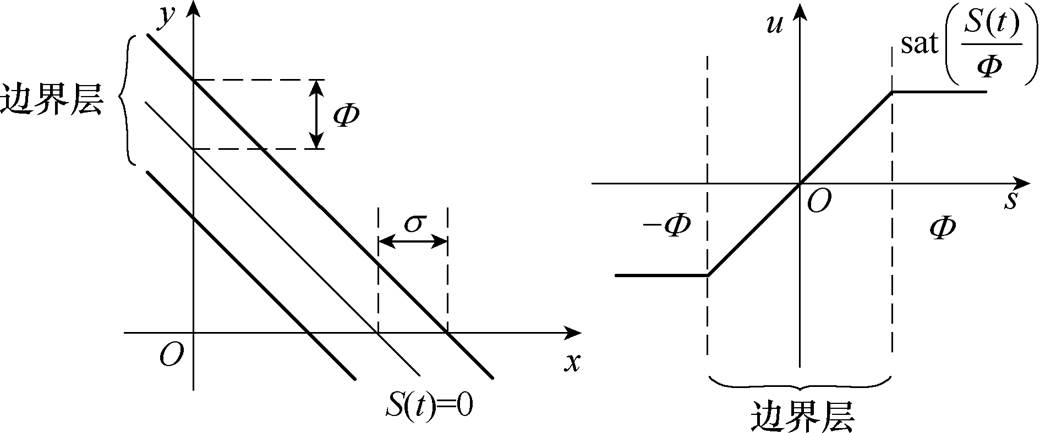
图2 边界层图示
Fig.2 Diagram of boundary layer
图2中,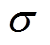 为边界层宽度。从图2可知,边界
为边界层宽度。从图2可知,边界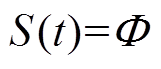 和
和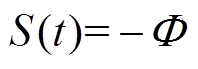 处于切换平面
处于切换平面 的两侧,由于该边界层内采用的是线性控制,这样就会使系统状态轨迹在有限时间内无法收敛到
的两侧,由于该边界层内采用的是线性控制,这样就会使系统状态轨迹在有限时间内无法收敛到 上,而是在边界层厚度内,即
上,而是在边界层厚度内,即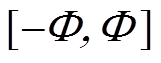 区间内保持稳定,这就使系统在切换平面上的鲁棒性降低,也就是系统状态轨迹的到达过程不具有全局鲁棒性[15]。因此,必须设计新型饱和函数使系统实现动态边界层控制,使边界层厚度能随系统状态的变化而逐渐变窄,最终收敛至切换平面上。
区间内保持稳定,这就使系统在切换平面上的鲁棒性降低,也就是系统状态轨迹的到达过程不具有全局鲁棒性[15]。因此,必须设计新型饱和函数使系统实现动态边界层控制,使边界层厚度能随系统状态的变化而逐渐变窄,最终收敛至切换平面上。
为设计新型饱和函数使边界层厚度随着系统状态轨迹变化,定义新型饱和函数为
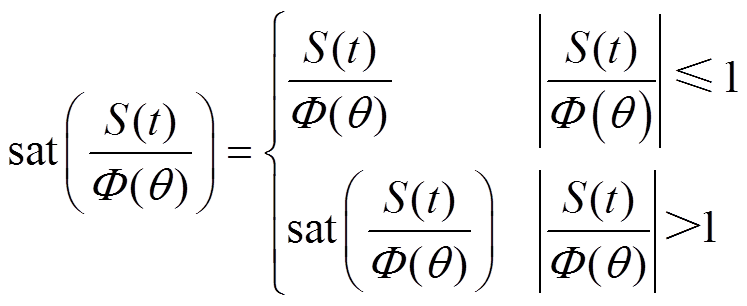 (16)
(16)式中,定义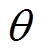 为接近角,是状态轨迹和切换平面两者间的夹角。动态边界层图示如图3所示。
为接近角,是状态轨迹和切换平面两者间的夹角。动态边界层图示如图3所示。
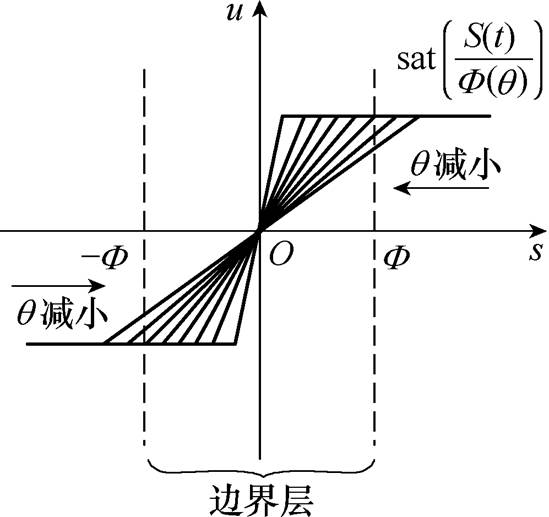
图3 动态边界层图示
Fig.3 Diagram of dynamic boundary layer
由图3可看出,边界层厚度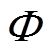 是一个与
是一个与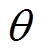 相关的动态变量,两者之间关系为
相关的动态变量,两者之间关系为
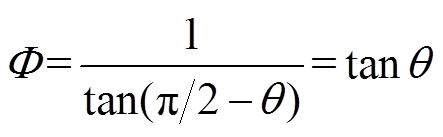 (17)
(17)当系统状态轨迹到达边界层内时,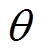 会逐渐减小,
会逐渐减小, 的斜率会增加,使边界层趋近于切换平面
的斜率会增加,使边界层趋近于切换平面 ,当
,当 ,
, 的斜率无限增大,从而使新型饱和函数达到渐近稳定状 态,即
的斜率无限增大,从而使新型饱和函数达到渐近稳定状 态,即
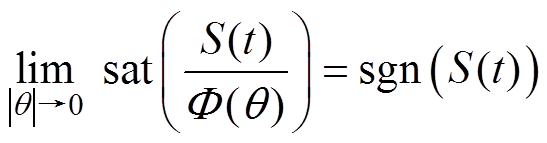 (18)
(18)
由式(18)可以看出,新型饱和函数近似于符号函数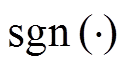 却又不同于
却又不同于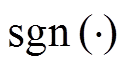 ,这就使新型饱和函数同时具有离散型符号函数和连续型饱和函数的优点。因此,采用式(16)中的新型饱和函数
,这就使新型饱和函数同时具有离散型符号函数和连续型饱和函数的优点。因此,采用式(16)中的新型饱和函数 替换传统饱和函数
替换传统饱和函数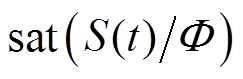 并应用于CSMC中构成GCSMC方法,可以有效地削弱系统抖振,解决CSMC中边界层厚度值不变,系统轨迹无法渐近收敛到切换平面上的问题,从而提高系统的全局鲁棒性。
并应用于CSMC中构成GCSMC方法,可以有效地削弱系统抖振,解决CSMC中边界层厚度值不变,系统轨迹无法渐近收敛到切换平面上的问题,从而提高系统的全局鲁棒性。
为证明GCSMC的稳定性,选择Lyapunov函数为
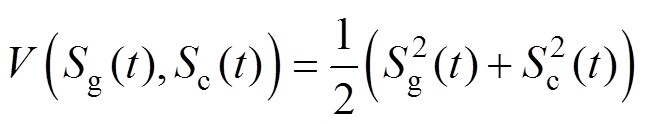 (19)
(19)为确保系统稳定,需保证边界层外的状态轨迹能够于有限时间内到达边界层。因此,需对边界层外的状态点,即在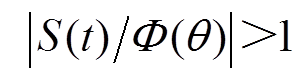 的情况下进行稳定性分析。
的情况下进行稳定性分析。
由图3可以看出,当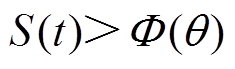 时,有
时,有 。对Lyapunov函数求导并结合式(8)~式(13)得
。对Lyapunov函数求导并结合式(8)~式(13)得

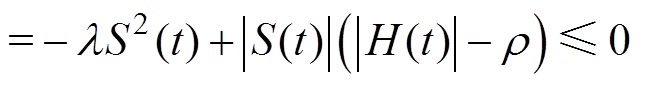 (20)
(20)
当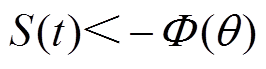 时,有
时,有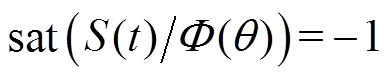 。对Lyapunov函数求导并结合式(8)~式(13)得
。对Lyapunov函数求导并结合式(8)~式(13)得
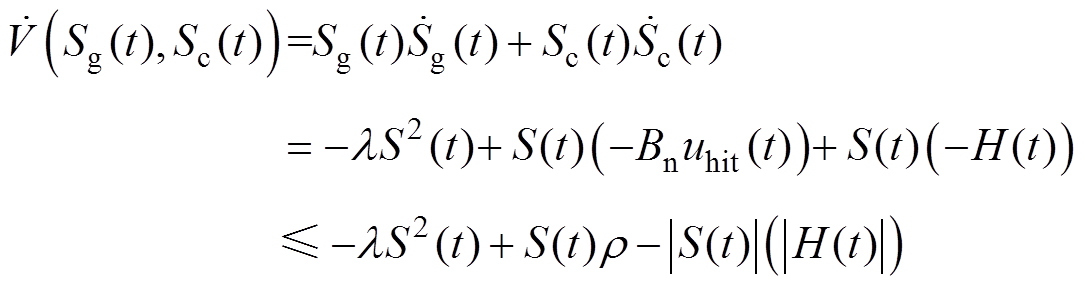
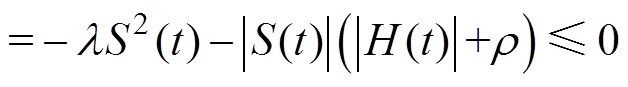 (21)
(21)
由于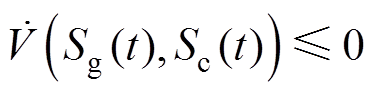 ,系统满足Lyapunov稳定性条件,这确保了系统任意位置的状态轨迹都可以在有限时间内到达边界层直至到达切换平面,保证了系统的稳定性。
,系统满足Lyapunov稳定性条件,这确保了系统任意位置的状态轨迹都可以在有限时间内到达边界层直至到达切换平面,保证了系统的稳定性。
基于DSP的PMLSM伺服控制系统硬件结构如图4所示。该系统主要包括PMLSM、PC+TMS320 F2812A DSP运算控制单元、IPM主回路功率变换单元、整流逆变模块、直线光栅位置传感器以及动子电流检测传感器等。基于DSP的PMLSM伺服系统实验平台如图5所示。
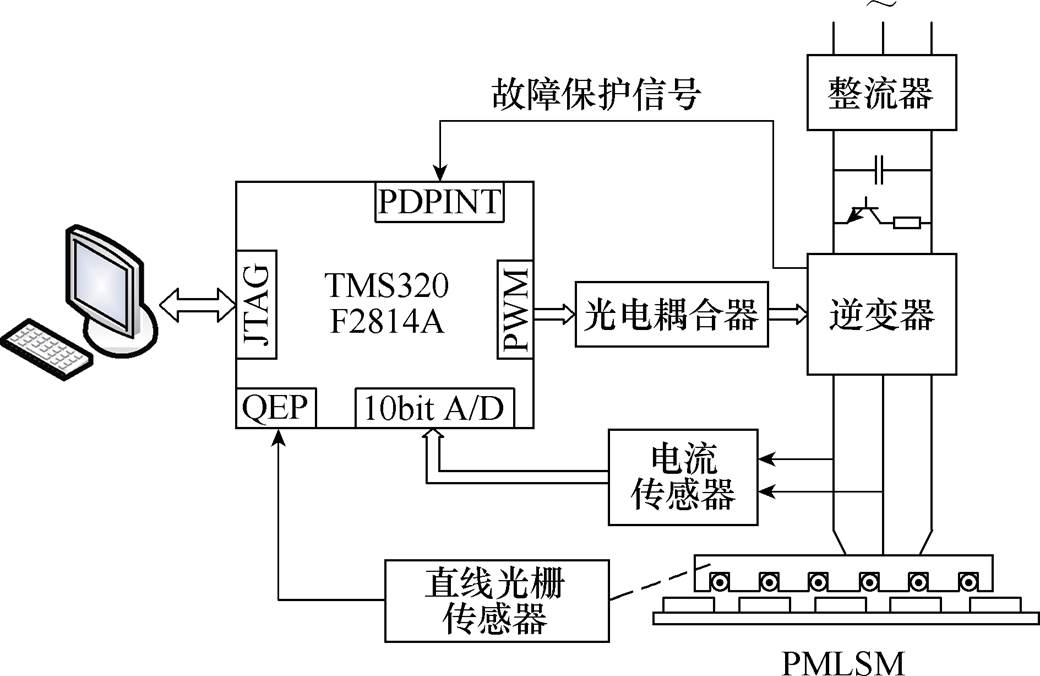
图4 基于DSP的PMLSM伺服系统硬件结构
Fig.4 Hardware structure diagram of PMLSM servo system based on DSP

图5 基于DSP的PMLSM伺服系统实验平台
Fig.5 Experiment platform of PMLSM servo system based on DSP
为验证所提出的控制方法的可行性,实验中将采用CSMC和GCSMC两种方法进行对比分析。PMLSM的参数选择为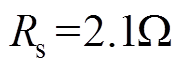 ,
,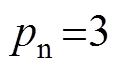 ,
,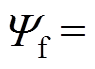
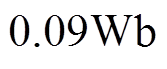 ,
,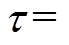
![]() ,
, ,
,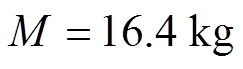 ,
,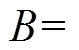
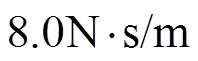 。在CSMC中,选取参数
。在CSMC中,选取参数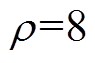 ,
,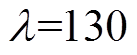 ,
,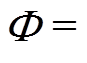
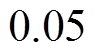 。在GCSMC中,选取参数
。在GCSMC中,选取参数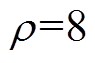 ,
,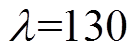 ,
,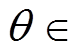
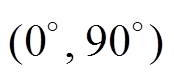 。
。
对系统给定幅值为1mm的阶跃信号,两种控制方法下的PMLSM伺服系统位置跟踪曲线如图6所示。从系统响应初期可以看出,在CSMC方法下,系统约在0.05s达到稳态,而GCSMC方法下响应时间约为0.03s,两种控制方法下均没有明显超调。为验证GCSMC方法的鲁棒性,在0.5s时对系统突加50N阶跃干扰。通过0.5~0.7s时两种控制方法下的位置跟踪曲线放大细节图对比可看出,在CSMC方法下电机在受到干扰时位置曲线出现明显波动,稳定时误差约为1.2~3.5mm,而GCSMC控制下的PMLSM在受到外界干扰时曲线并未出现明显波动,从而可以证明较CSMC相比,GCSMC方法具有更强的抗干扰能力。
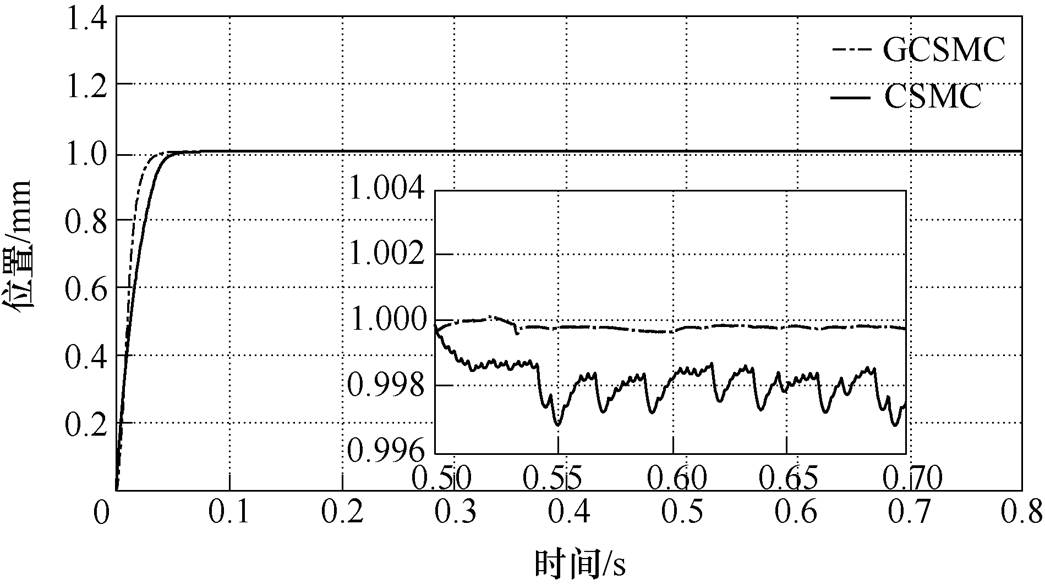
图6 阶跃信号下PMLSM位置跟踪曲线
Fig.6 Position tracking curves of PMLSM under step signal
对系统给定幅值为10mm,周期为p 的正弦信号以验证GCSMC的动态跟踪性能。图7为正弦信号下基于CSMC和GCSMC的PMLSM位置跟踪误差曲线。对比图7a和图7b可以看出,在CSMC方法下位置误差约在-5.0~5.5mm之间波动,而在GCSMC方法下PMLSM位置误差约在-1.2~1.5mm之间变化,且位置跟踪误差曲线更为平滑。另外,对比图8中两种控制方法下的控制输入u曲线可看出,图8b的GCSMC方法控制曲线较为平滑,这是由于GCSMC将传统的饱和函数替换为带有接近角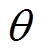 的新型饱和函数,可使边界层厚度值随状态轨迹的变化而减小直至收敛到切换平面上,进一步提高系统在边界层内的鲁棒性。尽管曲线仍有小幅度抖振,但同CSMC控制输入相比,具有更为优异的控制性能。因此,GCSMC方法可抑制不确定性因素对PMLSM伺服系统的影响,提高系统的跟踪性和鲁棒性。
的新型饱和函数,可使边界层厚度值随状态轨迹的变化而减小直至收敛到切换平面上,进一步提高系统在边界层内的鲁棒性。尽管曲线仍有小幅度抖振,但同CSMC控制输入相比,具有更为优异的控制性能。因此,GCSMC方法可抑制不确定性因素对PMLSM伺服系统的影响,提高系统的跟踪性和鲁棒性。
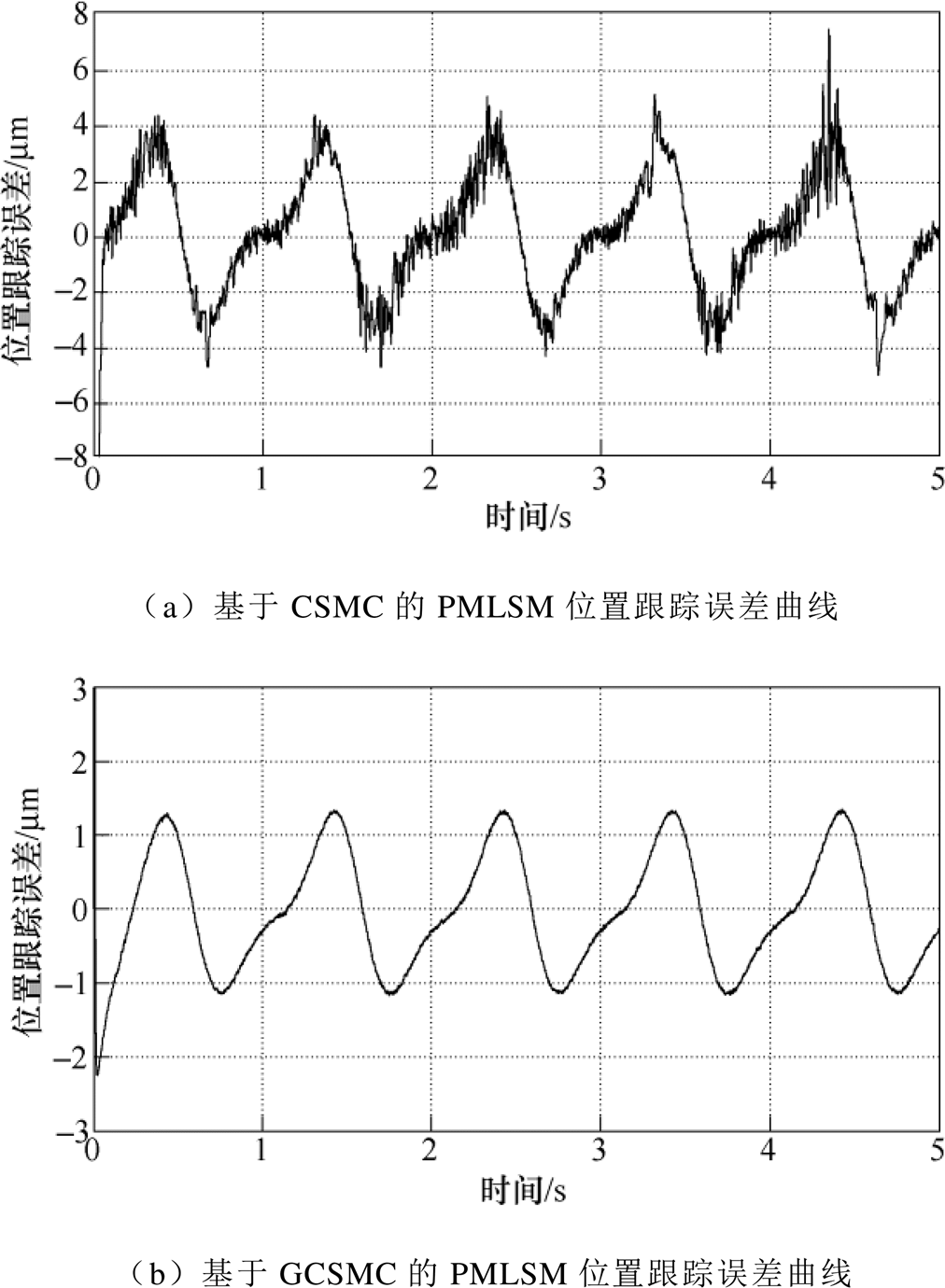
图7 正弦信号下位置跟踪误差曲线
Fig.7 Position tracking error curves under sinusoidal signal
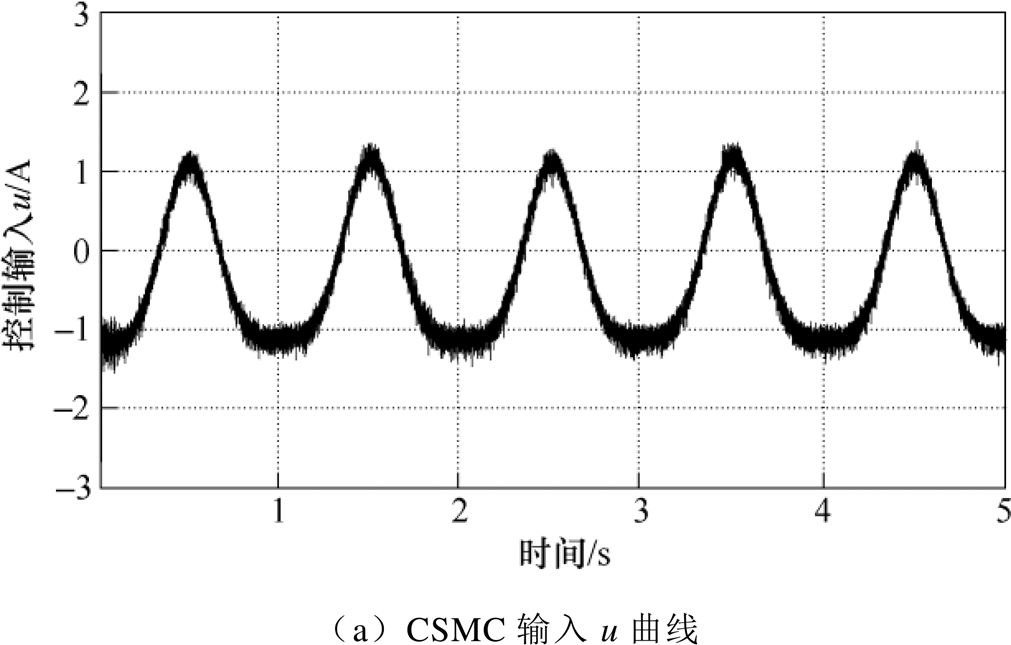

图8 控制输入u曲线
Fig.8 Control input u curves
针对PMLSM伺服系统中存在不确定因素而影响系统控制性能的问题,采用一种动态边界层GCSMC方法。GCSMC采用新型饱和函数实现边界层的动态控制,有效地解决了CSMC中恒定饱和函数使系统状态轨迹只能收敛于边界层内而无法到达切换平面的问题,削弱了抖振,提高了系统的鲁棒性。实验结果表明,与CSMC相比,GCSMC明显提高了系统的位置跟踪精度并保证了系统全局鲁棒性,可满足高精度快响应的伺服加工性能要求。
参考文献
[1] 武志涛, 杨永辉. 一种永磁直线电机驱动X-Y平台精密轮廓跟踪控制策略[J]. 电工技术学报, 2018, 33(17): 4037-4043.
Wu Zhitao, Yang Yonghui. A precise contour tracking control method for X-Y table driven by permanent magnet linear motors[J]. Transactions of China Elec- trotechnical Society, 2018, 33(17): 4037-4043.
[2] 智淑亚, 吴洪兵. 数控进给伺服系统摩擦补偿控制仿真[J]. 沈阳工业大学学报, 2019, 41(4): 361-365.
Zhi Shuya, Wu Hongbing. Simulation of friction compensation control of NC feed servo system[J]. Journal of Shenyang University of Technology, 2019, 41(4): 361-365.
[3] 朱国昕, 雷鸣凯, 赵希梅. 永磁同步电机伺服系统自适应迭代学习控制[J]. 沈阳工业大学学报, 2018, 40(1): 6-11.
Zhu Guoxin, Lei Mingkai, Zhao Ximei. Adaptive iterative learning control for permanent magnet synchronous motor servo system[J]. Journal of Shenyang University of Technology, 2018, 40(1): 6-11.
[4] 尹忠刚, 白聪, 杜超, 等. 基于内模干扰观测器的永磁同步直线电机无差拍电流预测控制方法[J]. 电工技术学报, 2018, 33(24): 5741-5750.
Yin Zhonggang, Bai Cong, Du Chao, et al. Deadbeat predictive current control for permanent magnet linear synchronous motor based on internal model disturbance observer[J]. Transactions of China Elec- trotechnical Society, 2018, 33(24): 5741-5750.
[5] 赵希梅, 武文斌, 朱国昕. 一种基于PLDOB的PMLSM伺服系统长期稳定运行的方法[J]. 电机与控制学报, 2018, 22(5): 110-116.
Zhao Ximei, Wu Wenbin, Zhu Guoxin. Method of PMLSM servo system long-term stable operation based on periodic learning disturbance observer[J]. Electric Machines and Control, 2018, 22(5): 110-116.
[6] 侯利民, 王巍. 表面式永磁同步电机无源非奇异快速终端滑模控制[J]. 电工技术学报, 2014, 29(11): 45-52.
Hou Limin, Wang Wei. Passivity-based control and nonsingular fast terminal sliding mode control for SPMSM[J]. Transaction of China Electrotechnical Society, 2014, 29(11): 45-52.
[7] Kazraji S M, Soflayi R B, Sharifian M B B. Sliding- mode observer for speed and position sensorless control of linear-PMSM[J]. Electrical Control & Communication Engineering, 2014, 5(1): 20-26.
[8] 赵希梅, 金鸿雁. 基于Elman神经网络的永磁直线同步电机互补滑模控制[J]. 电工技术学报, 2018, 33(5): 973-979.
Zhao Ximei, Jin Hongyan. Complementary sliding mode control for permanent magnet linear synchronous motor based on Elman neural network[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(5): 973-979.
[9] 邓永停, 李洪文, 王建立, 等. 基于卡尔曼滤波器的交流伺服系统自适应滑模控制[J]. 光学精密工程, 2014, 22(8): 2088-2095.
Deng Yongting, Li Hongwen, Wang Jianli, et al. Adaptive sliding mode control for AC servo system based on Kalman filter[J]. Optics and Precision Engineering, 2014, 22(8): 2088-2095.
[10] 楚远征, 鞠鹏, 杨阳, 等. 永磁同步电机的滑模抗饱和控制策略[J]. 信息与控制, 2017, 46(6): 732- 737.
Chu Yuanzheng, Ju Peng, Yang Yang, et al. Sliding mode control strategy with anti-windup for permanent magnet synchronous motor[J]. Information and Control, 2017, 46(6): 732-737.
[11] 赵希梅, 赵久威. 精密直驱龙门系统的交叉耦合互补滑模控制[J]. 电工技术学报, 2015, 30(11): 7-12.
Zhao Ximei, Zhao Jiuwei. Cross-coupled comple- mentary sliding mode control for precision direct- drive gantry system[J]. Transaction of China Elec- trotechnical Society, 2015, 30(11): 7-12.
[12] Lin C K, Fu L C, Liu T H, et al. Passivity-based adaptive complementary PI sliding-mode speed controller for synchronous reluctance motor using predictive current control[C]//American Control Conference, USA, 2012: 1168-1173.
[13] 黄宴委, 刘喆怡, 熊少华, 等. 基于二阶终端滑模优化的电流环滑模控制[J]. 电机与控制学报, 2018, 22(3): 74-81.
Huang Yanwei, Liu Zheyi, Xiong Shaohua, et al. Sliding mode control for current loop by second order terminal sliding mode[J]. Electric Machines and Control, 2018, 22(3): 74-81.
[14] Repecho V, Biel D, Arias A, et al. Fixed switching period discrete-time sliding mode current control of a PMSM[J]. IEEE Transactions on Industrial Elec- tronics, 2017, 65(3): 2039-2048.
[15] 金鸿章, 罗延明, 肖真, 等. 抑制滑模抖振的新型饱和函数法研究[J]. 哈尔滨工程大学学报, 2007, 28(3): 288-291.
Jin Hongzhang, Luo Yanming, Xiao Zhen, et al. Investigation of a novel method of saturation function for chattering reduction of sliding mode control[J]. Journal of Harbin Engineering University, 2007, 28(3): 288-291.
Dynamic Boundary Layer Global Complementary Sliding Mode Control for Permanent Magnet Linear Synchronous Motor
Abstract In order to solve the problem that permanent magnet linear synchronous motor (PMLSM) is sensitive to uncertainty factors such as parameter variations, external disturbances and frictions, a dynamic boundary layer global complementary sliding mode control (GCSMC) method was proposed. Firstly, the mathematical model of PMLSM including uncertainty factors was established. Then a complementary sliding mode controller was designed by combining generalized sliding mode surface with complementary sliding mode surface to suppress the influence of uncertainty factors on the system and then weaken the chattering. However, the thickness of boundary layer is constant, so the state trajectory of the system can only converge within the boundary layer. Therefore, a new saturation function was used to design a global complementary sliding mode controller to realize the dynamic change of boundary layer, which can reduce the boundary layer thickness with the change of state trajectory until it converges to the switching surface, thereby further improving the robustness of the system in the boundary layer. The experimental results show that the method not only improves the tracking performance, but also guarantees the global robustness of the system.
keywords:Permanent magnet linear synchronous motor, uncertainty factors, dynamic boundary layer, global complementary sliding mode control, robustness
中图分类号:TP273; TM351
DOI: 10.19595/j.cnki.1000-6753.tces.181972
辽宁省自然科学基金计划重点项目(20170540677)和辽宁省教育厅科学技术研究项目(LQGD2017025)资助。
收稿日期2018-12-28
改稿日期 2019-07-05
金鸿雁 女,1993年生,博士研究生,研究方向为电机控制、智能控制等。E-mail: jinhongyanch@163.com
赵希梅 女,1979年生,教授,博士生导师,研究方向为电机控制、机器人控制、智能控制等。E-mail: zhaoxm_sut@163.com(通信作者)
(编辑 赵 鹏)