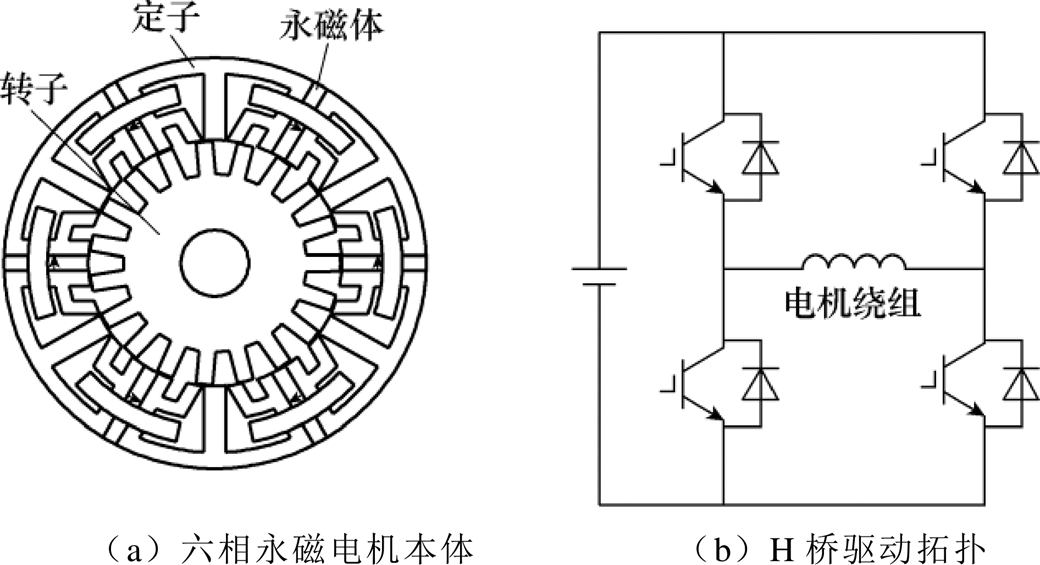
图1 6/19容错型永磁磁通切换电机及驱动拓扑
Fig.1 6/19 FTFSPM motor and its drive topology
摘要 为了提高容错型永磁磁通切换(FTFSPM)电机驱动系统的可靠性,该文从定子磁链幅值恒定角度对电机绕组开路及短路组合故障进行分析。对绕组正常电流缺失及短路电流扰动进行磁链补偿,从而实现对电机的容错控制。然而转速的动态性能受到传统直接转矩控制中转速环PI参数的影响,因此,该文提出基于转矩冲量平衡控制的直接转矩控制策略,利用动态过程前后转矩冲量值不变,推导系统发送前进矢量与后退矢量的作用时间,使得电机在组合故障容错后的转速动态性能达到最优。通过仿真和实验实现了电机在开路及短路组合故障下的转矩冲量平衡控制,并对不同组合故障下的动态响应进行比较,验证了所提算法的正确性与有效性。
关键词:容错型永磁磁通切换电机 绕组开路及短路组合故障 容错 转矩冲量平衡控制
由于容错型永磁磁通切换(Fault Tolerant Flux Switching Permanent Magnet, FTFSPM)电机既具有一般永磁电机的特点(体积小、功率密度高等),又具有开关磁阻电机的高可靠性和故障容错性能,因此在电动汽车、风力发电、航空航天等要求高可靠性场合具有较大的应用潜力[1-5]。若再结合相应的故障容错控制算法,可使整个电机驱动系统具有较好的容错能力,满足高输出性能的要求[6-8]。
常见的电机故障类型主要分为电机相开路故障、相短路故障。短路故障相较于开路故障更为严重,在短路电流的扰动作用以及故障相转矩缺失的情况下,电机输出转矩脉动增大,系统的性能明显降低[9-10]。然而在电机实际运行的过程中,会出现更为复杂的开路及短路组合故障,此时电机运行在不对称状态,为了实现系统在组合故障下的稳定运行,对其容错控制策略的研究显得尤为关键[11-12]。
目前已有文献[13-24]分别对电机绕组的开路、短路故障下的容错控制策略进行了单独的研究,包括谐波电流注入法[13-16]、非对称空间电压矢量脉宽调制法[17-19]、容错电流控制策略[20-21]和前馈补偿 法[22-24]。通过上述容错控制策略可有效地改善电机在开路或短路故障状态下的稳态性能及动态性能,但对于电机在开路及短路组合故障情况下提高系统动稳态性能的相关文献相对较少。文献[25-26]针对电机驱动器开关的开路及短路组合故障,提出了电压补偿控制方法,从而有效地抑制了转矩脉动,使得电机在故障状态下具有良好的稳态性能,但对电机绕组的开路及短路组合故障容错尚未进行研究。文献[27]针对永磁电机的开路及短路组合故障,根据功率守恒原则,提出了一种最优电流直接控制策略,实现了转矩脉动最小化输出,提高了电机故障状态下的容错性能,但转速外环采用PI调节,使其无法实现最快的动态跟踪。文献[28]基于矢量控制,提出了一种统一容错矢量控制策略,有效地抑制了电机相开路和相短路组合故障导致的推力脉动,改善了电机故障状态下的稳态性能和动态性能,但系统的动态响应过程仍然受到多个电流环PI参数的影响,无法达到理论上的最优控制。文献[29]同样基于矢量控制,针对永磁电机绕组的开路与短路组合故障,提出了电流矢量容错控制策略,从而获得最优输出转矩并有效地降低了电机组合故障下的转矩脉动,但由于转速PI参数的影响,导致电机在故障情况下的动态性能不理想。文献[30-32]提出了最优转矩控制策略,同时结合拉格朗日等数学优化方法,提高了系统的容错性能,使得电机在绕组开路及短路组合故障下无脉动运行,虽然系统的电流环采用PID进行调节,相较于PI调节器,微分控制器在一定程度上能够改善被控量的动态性能,但很难实现最优控制[33-34]。
PI与PID调节都是一个线性调节的过程,比例环节会产生一定的静态误差,且过大的比例系数会引起系统振荡,甚至不稳定;积分环节会对误差不断积分,直至稳态误差接近于零,从而导致动态过程的滞后及超调;微分环节会使得系统对扰动的抑制能力减弱[35-39]。因此为了优化电机的动态过程,本文提出了组合故障下基于转矩冲量平衡控制的直接转矩控制策略(Direct Torque Control strategy based on Torque Impulse Balance Control, TIBC- DTC)。它的实现方式主要为:首先,在直接转矩控制(Direct Torque Control, DTC)策略下对电机绕组的开路及短路组合故障进行静态特性补偿,从而实现对电机的容错控制,保证电机在故障状态下的稳定运行;其次,建立了组合故障下的转矩冲量平衡方程,在不同组合故障下比较了空间电压矢量的差异,并分析了磁链补偿的不同对电机转矩角调节能力的影响,给出了电机在不同组合故障下TIBC-DTC的实现方式,同时结合电机的运动方程,比较得出了在不同开路与短路组合故障下系统采用TIBC-DTC进行动态调节时间长短的一般规律。本文以6/19容错型永磁磁通切换电机作为实验样机,通过仿真和实验验证了该控制算法的有效性以及不同组合故障下动态性能的差异。
本文研究的6/19容错型永磁磁通切换电机及结构拓扑如图1a所示。电机的转子采用多齿结构,有利于输出功率的提高及转矩脉动的减少;定子为六相绕组,提高了系统控制的自由度,从而有利于实现对电机的故障容错控制。此外,电机的六相绕组为集中绕组,均采用独立H桥驱动,以实现相绕组之间的电气隔离,如图1b所示。

图1 6/19容错型永磁磁通切换电机及驱动拓扑
Fig.1 6/19 FTFSPM motor and its drive topology
通过对六组H桥开关状态进行不同的组合,可得到逆变器输出空间电压矢量为
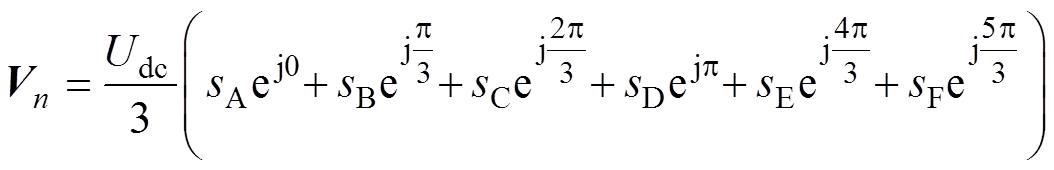 (1)
(1)式中,Vn为六相电压构成的电压矢量;n的取值范围为1~6;Udc为直流母线电压幅值;sj为各开关管的导通状态,sj的取值范围为-1、0、1,j为电机的相数,j =A~F。
为了实现FTFSPM电机在不同开路及短路组合故障下的TIBC-DTC,首先需要对电机进行静态特性补偿,保障电机在组合故障下能够稳定地运行。
与单相开路、短路故障不同,组合故障必须考虑在缺相电流及短路电流共同作用下对定子磁链幅值的影响,具体实施方案如下。
根据坐标变换原理,电机绕组输入的六相对称电流iA~iF在两相静止坐标系下表达式分别为
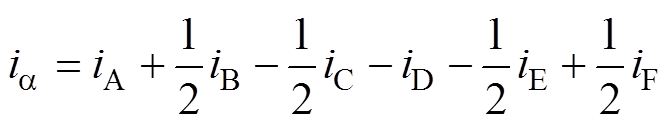 (2)
(2)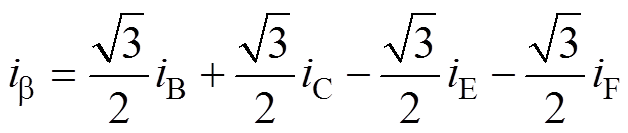 (3)
(3)
式中,ia、ib 分别为a、b 轴下的电流。
当电机的m相绕组发生开路故障,n相绕组发生短路故障时,对应故障相绕组电流im-open、in-short分别为
 (4)
(4)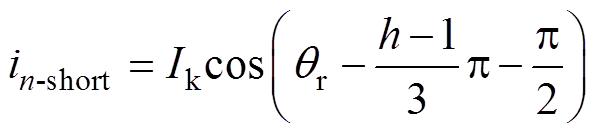 (5)
(5)
式中,Ik为短路电流幅值;qr为转子电角度;h的取值范围为1~6分别对应于A~F相。
由于组合故障类型不同,a、b 轴的电流均可能发生变化,而电压ua、ub 不变,则a、b坐标下的磁链值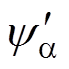 、
、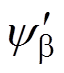 分别为
分别为
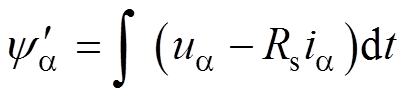 (6)
(6)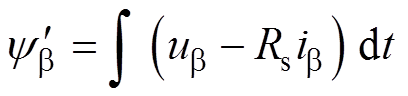 (7)
(7)
式中,Rs为定子电阻。
对6/19容错型永磁磁通切换电机而言,故障相对健康相没有影响,其余相磁链仍为正常值,为了保持其定子磁链幅值恒定,需要对缺失的磁链进行补偿。
为了消除传统的纯积分计算定子磁链所带来直流偏移等影响,可直接利用电流及永磁磁链得到各相绕组相定子磁链矢量的幅值ysj为
 (8)
(8)式中,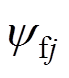 为各相永磁磁链幅值;L为绕组电感。
为各相永磁磁链幅值;L为绕组电感。
当电机绕组发生组合故障时,为了使总的定子磁链幅值保持不变,根据k时刻电磁转矩的误差,经PI调节后得到下一个控制周期定子磁链的变化角度Dd(k+1),同时结合k时刻定子磁链幅值ys(k)以及定子磁链角qs即可得到下一个控制周期各相绕组定子磁链的给定幅值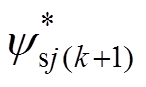 为
为
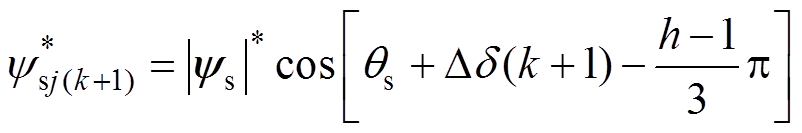 (9)
(9)式中,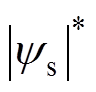 为给定总磁链幅值。
为给定总磁链幅值。
永磁磁通切换电机定子磁链控制矢量如图2 所示。

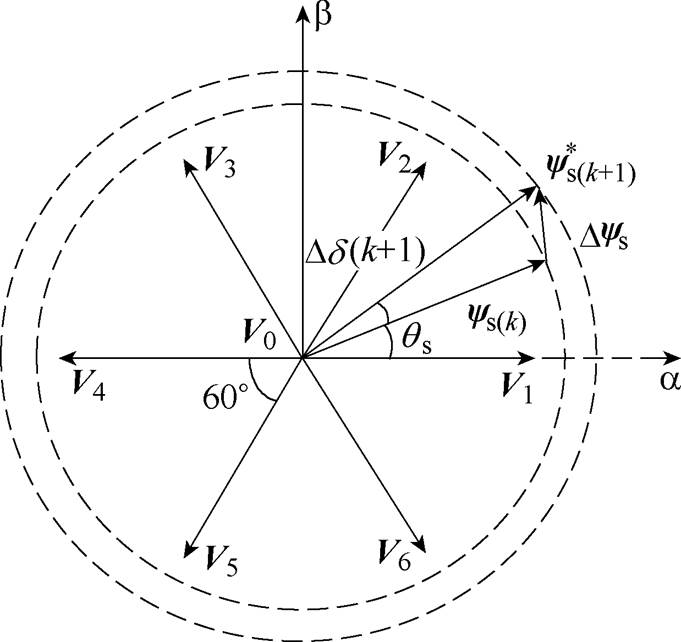
图2 永磁磁通切换电机定子磁链控制矢量
Fig.2 The stator flux control vector of FSPM motor
当电机绕组同时发生m相开路与n相短路故障时,需要补偿的定子磁链幅值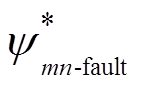 为
为
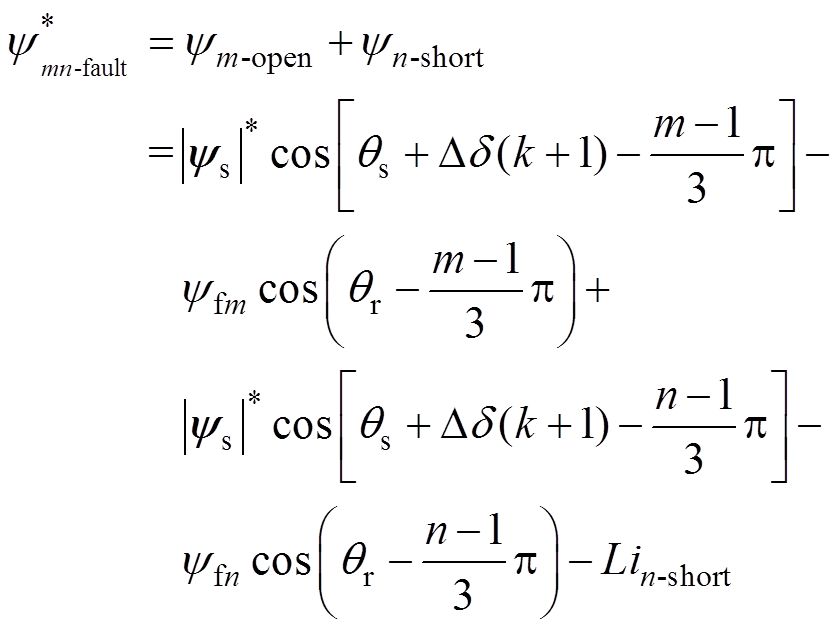 (10)
(10)式中,ym-open、yn-short分别为m相开路、n相短路故障所需补偿的定子磁链值;yfm、yfn分别为m相、n相绕组所对应的永磁磁链幅值。
根据故障相的相对位置不同,各相磁链分布可以分为六种情况,电机两相故障时各相磁链矢量分布如图3所示。
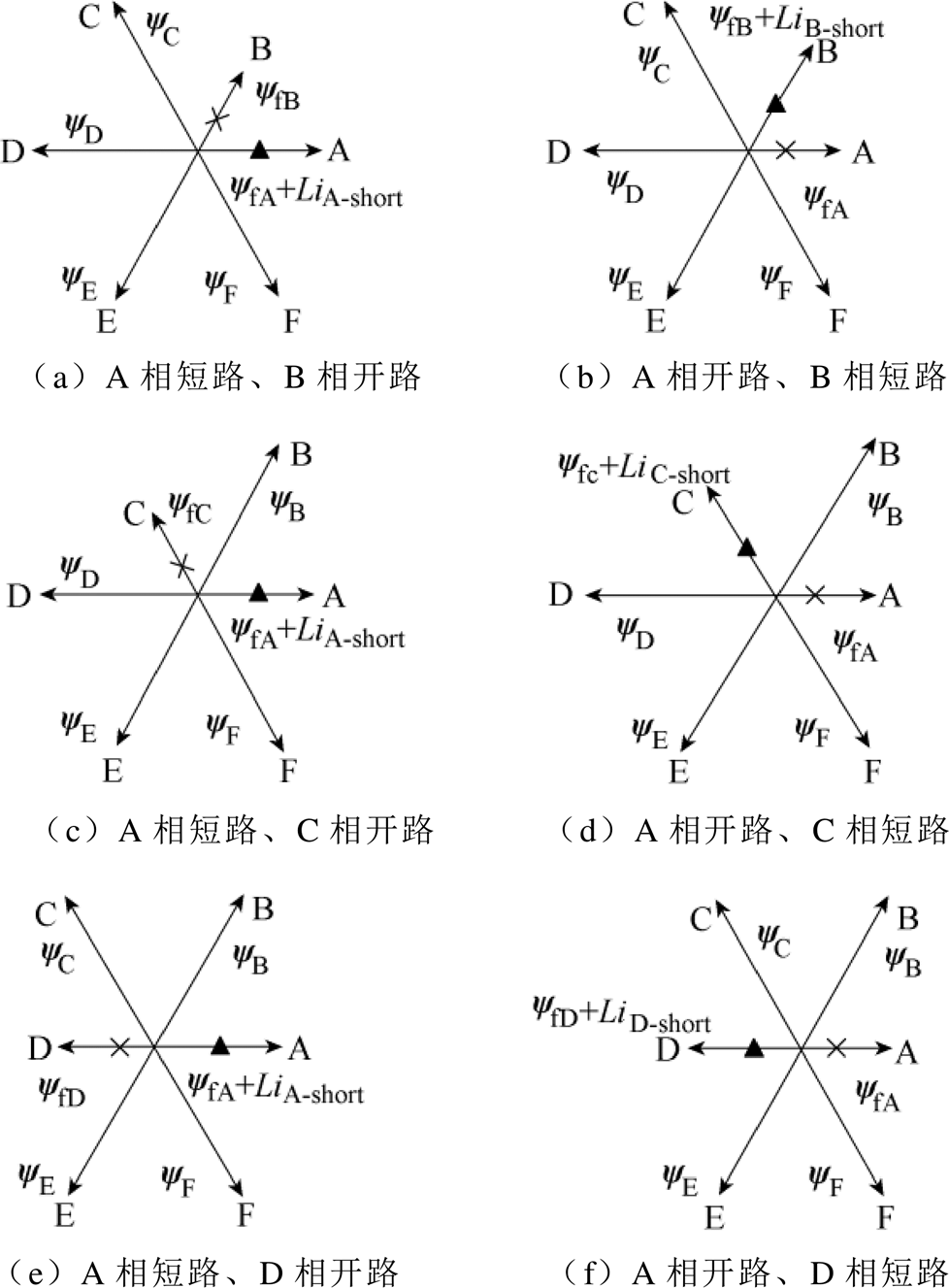
图3 电机两相故障时各相磁链矢量分布
Fig.3 Vector distribution of magnetic flux of each phase when two-phase faults occur
以A相短路、B相开路组合故障为例进行分析,其所对应的补偿分布见表1,其余的组合故障情况以此类推。
在负载突变情况下,系统采用DTC容错后的动态响应波形如图4所示。可以看出在上述补偿控制策略之后,电机可以实现组合故障下的稳定运行,但转速的动态性能受到PI控制器的影响,需要经过多次调节才能达到收敛。为了克服电机动态调节过程中线性控制的不足,提出了电机绕组开路及短路组合故障下的TIBC-DTC。
表1 A相短路、B相开路时磁链补偿分布
Tab.1 The compensation of flux under A phase short-circuit and B phase open-circuit

六相绕组两相故障时磁链幅值补偿磁链幅值补偿后磁链幅值 A— B— CyC-yA-shortyC-yA-short DyD-yB-openyD-yB-open EyE-yA-shortyE-yA-short FyF-yB-openyF-yB-open
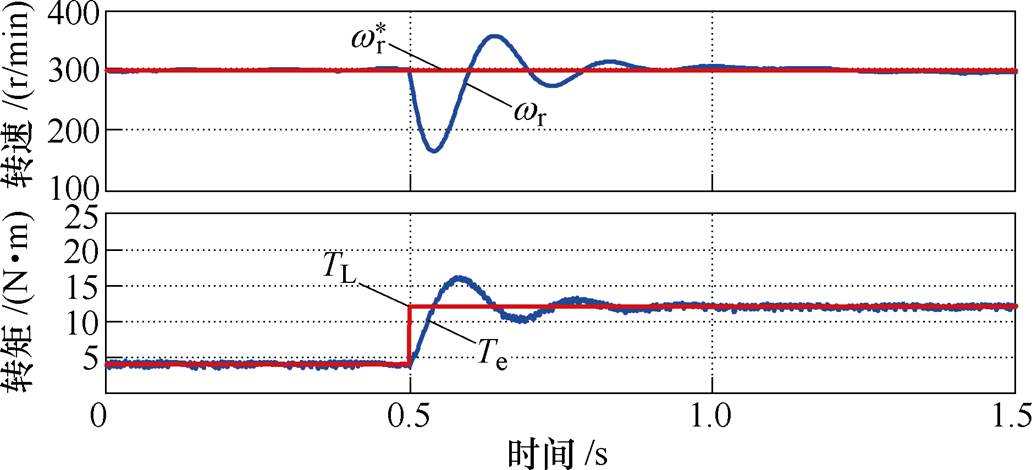
图4 基于DTC容错后的电机动态响应波形
Fig.4 Dynamic response waveforms of motor after fault tolerance based on DTC
图5给出了在电机绕组组合故障下突加负载时,系统采用TIBC-DTC的动态响应波形。图5中,在t0时刻,负载转矩TL发生突变,突变量为DTL;在t0~t2内,电磁转矩误差信号t =1,逆变器发送前进矢量,使得电磁转矩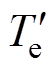 以最快的速度增加;在t2~t3内,t =0,逆变器发送后退矢量,使得电磁转矩以最快的速度减少。若选取合适的t2,可以使得阴影部分的面积满足A1=A2+A3,则电磁转矩
以最快的速度增加;在t2~t3内,t =0,逆变器发送后退矢量,使得电磁转矩以最快的速度减少。若选取合适的t2,可以使得阴影部分的面积满足A1=A2+A3,则电磁转矩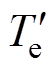 仅与转速n经过一次调节在t3时刻同时达到收敛。此时,转速的动态调节时间最短,达到理论上的最快速度控制。
仅与转速n经过一次调节在t3时刻同时达到收敛。此时,转速的动态调节时间最短,达到理论上的最快速度控制。
为了满足电机在突加负载前后转速保持不变,电机的电磁转矩冲量与负载转矩冲量应相等,即
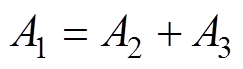 (11)
(11)当电机在m相开路和n相短路组合故障下突加负载时,总的电磁转矩Te为
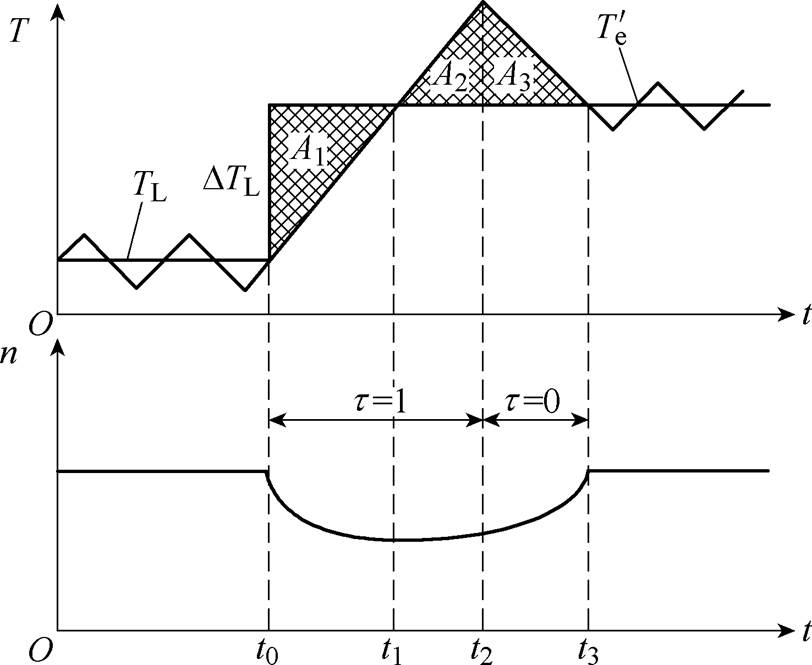
图5 电机突加负载过程中动态响应波形
Fig.5 Dynamic response waveform during motor sudden load
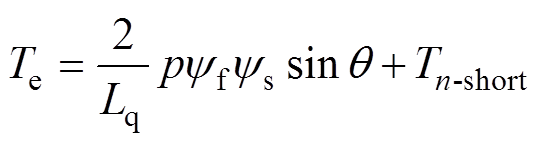 (12)
(12)式中,Lq为q轴等效电感;p为极对数;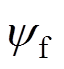 为永磁磁链幅值;ys为定子磁链幅值;q为转矩角;Tn-short为n相短路电流的扰动转矩,表达式为
为永磁磁链幅值;ys为定子磁链幅值;q为转矩角;Tn-short为n相短路电流的扰动转矩,表达式为
 (13)
(13)
那么剩余健康相电磁转矩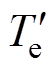 的表达式为
的表达式为
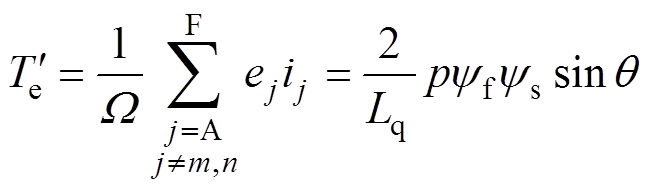 (14)
(14)式中,W 为电机转子机械角速度;ej、ij分别为j相所对应的瞬时电压、电流。
当电机绕组发生组合故障时,通过上述的容错控制算法可以使定子磁链幅值保持恒定,则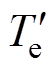 与sinq呈正比。曲线sinq的斜率k1、k2在上升及下降时间段内可分别表示为
与sinq呈正比。曲线sinq的斜率k1、k2在上升及下降时间段内可分别表示为
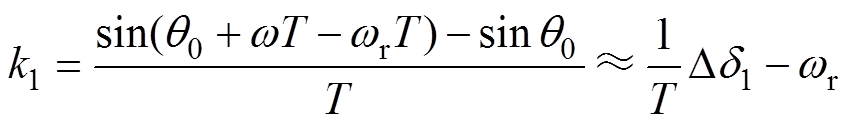 (15)
(15)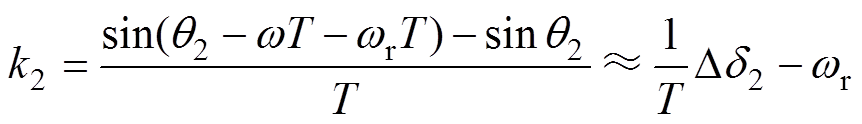 (16)
(16)
式中,q0为t0时刻的转矩角;q2为t2时刻的转矩角;T为控制器的中断周期;w 为电机定子磁链旋转的同步角速度;wr为电机转子的电角速度;Dd1、Dd2分别为定子磁链在前进矢量、后退矢量作用下一个中断周期T内改变的角度。
当电机发生m相开路与n相短路组合故障时,根据定子磁链所在扇区位置S不同,可以分别得到定子磁链在下一个中断周期T内需要改变的角度Dd1、Dd2见表2。具体推导和求解过程见附录。
从而进一步得到组合故障下定子磁链补偿值,使定子磁链幅值保持不变,在提高电机故障容错能力的同时,转速的动态性能达到最优控制。
表2 不同组合故障下定子磁链下一中断周期改变的角度
Tab.2 Angle of change of next interruption period of the stator flux linkage under different combined faults

mnSDd1Dd2 ABⅠ, Ⅱ, Ⅳ, Ⅴ Ⅲ, Ⅵ ACⅠ, Ⅲ, Ⅳ, Ⅵ Ⅱ, Ⅴ ADⅠ~Ⅵ
基于TIBC-DTC的系统控制框图如图6所示。
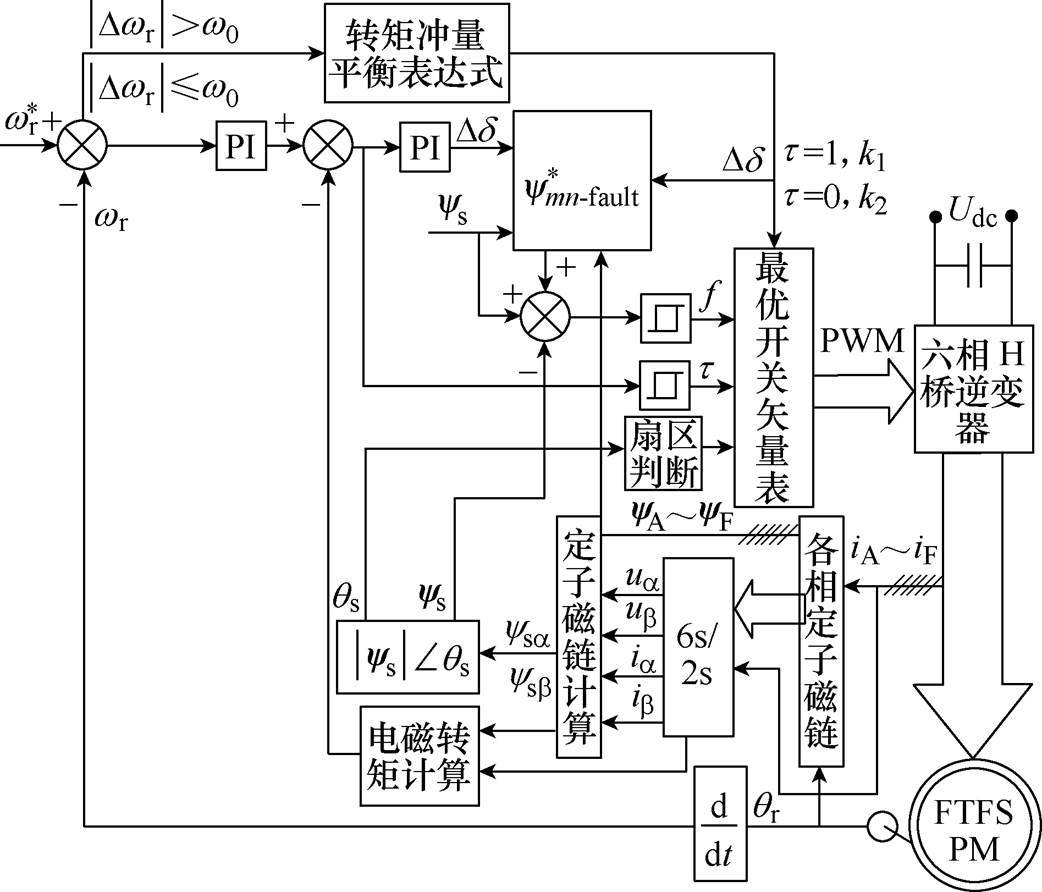
图6 基于TIBC-DTC的FTFSPM电机系统控制框图
Fig.6 Control block diagram of FTFSPM motor system based on TIBC-DTC
基于转矩冲量平衡控制思想,推导出电机绕组在不同组合故障下实现方式见表3。
当定子磁链幅值ys为定值时,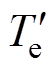 与sinq呈正比,电机输出总的转矩斜率在上升及下降阶段内可以分别近似地等效成k1、k2。根据不同组合故障下定子磁链所在扇区S的位置,选择表3所示的转矩斜率。
与sinq呈正比,电机输出总的转矩斜率在上升及下降阶段内可以分别近似地等效成k1、k2。根据不同组合故障下定子磁链所在扇区S的位置,选择表3所示的转矩斜率。
根据式(11)~式(16),可得转矩冲量平衡方程为
表3 不同组合故障下基于转矩冲量平衡控制思想的实现方式
Tab.3 Implementation of the idea based on torque impulse balance control under different combination faults

mnSk1k2 ABⅠ, Ⅱ, Ⅳ, Ⅴ Ⅲ, Ⅵ ACⅠ, Ⅲ, Ⅳ, Ⅵ Ⅱ, Ⅴ ADⅠ~Ⅵ
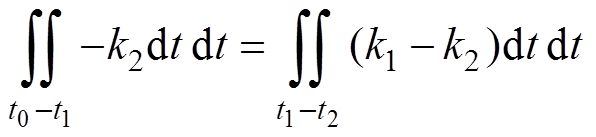 (17)
(17)通过式(17)可以求得电机在负载突加动态过程中所需要施加的前进矢量和后退矢量的时间以及切换时刻t2,从而实现动态过程的快速调节。
由图5可以看出
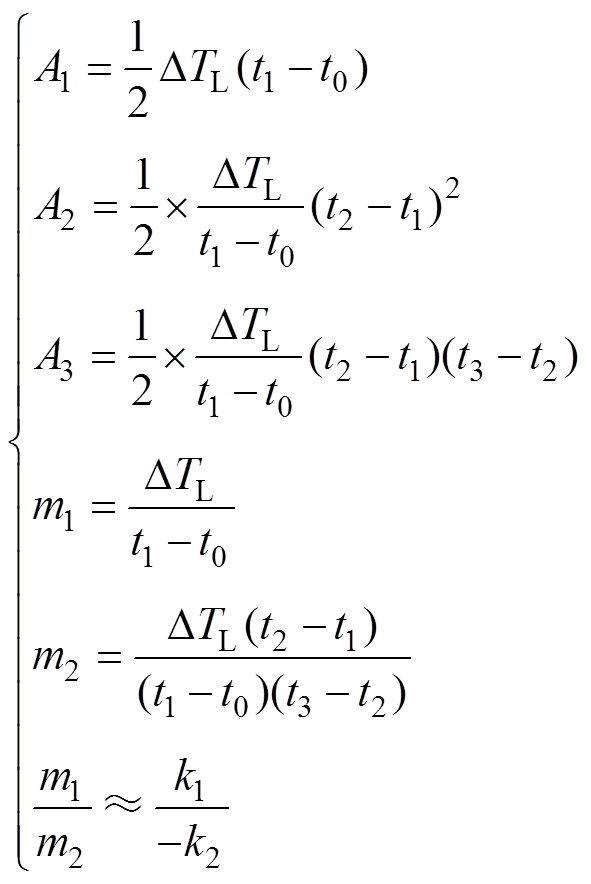 (18)
(18)式中,DTL负载转矩突变量。
那么动态调节的总时间DT为
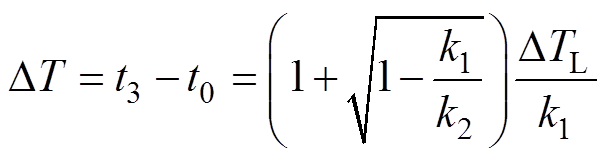 (19)
(19)电机m相绕组开路与n相绕组短路组合故障下的动态响应时间见表4。从表4可以看出,不同组合故障下的平均动态调节时间DTave同正常运行下的动态调节时间DTnormal相比为1 2.25
2.25 2.25
2.25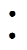 3.01。
3.01。
表4 不同组合故障下动态响应时间
Tab.4 Dynamic response time under different combined faults
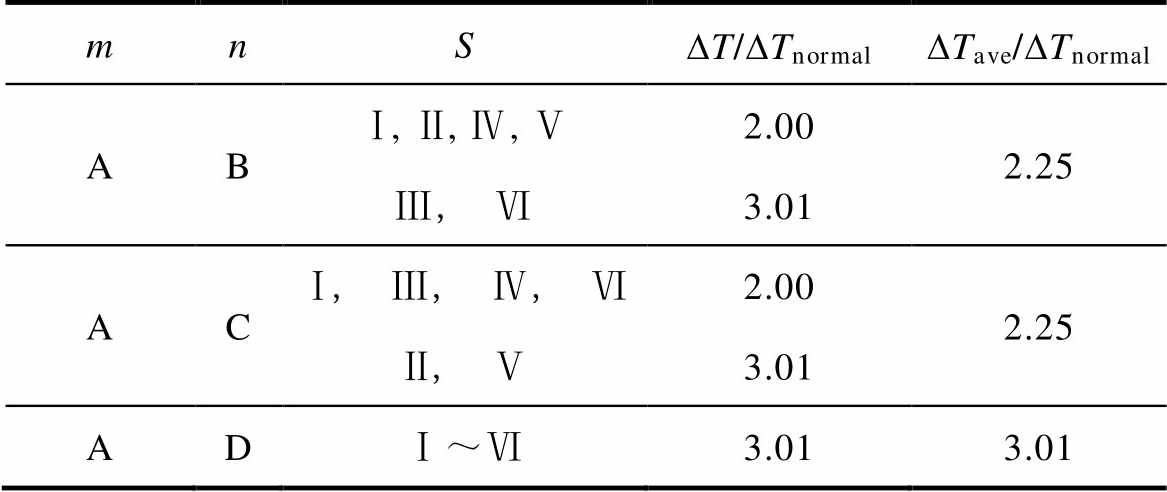
mnSDT/DTnormalDTave/DTnormal ABⅠ, Ⅱ, Ⅳ, Ⅴ2.002.25 Ⅲ, Ⅵ3.01 ACⅠ, Ⅲ, Ⅳ, Ⅵ2.002.25 Ⅱ, Ⅴ3.01 ADⅠ~Ⅵ3.013.01
在Matlab/Simulink仿真软件中,系统采用TIBC- DTC实现了电机绕组开路及短路组合故障下的动态过程调节,从而验证了算法的正确性。仿真参数见表5。
首先,在电机绕组开路及短路组合故障下,系统采用DTC容错后的仿真波形如图7所示。由图7可以看出,通过补偿控制策略,转速和转矩都能够达到跟踪给定的效果。
表5 仿真参数
Tab.5 Simulation parameters

参 数数 值 额定转速/(r/min)300 额定定子磁链/Wb0.06 额定转子磁链/Wb0.004 4 直流母线电压/V100
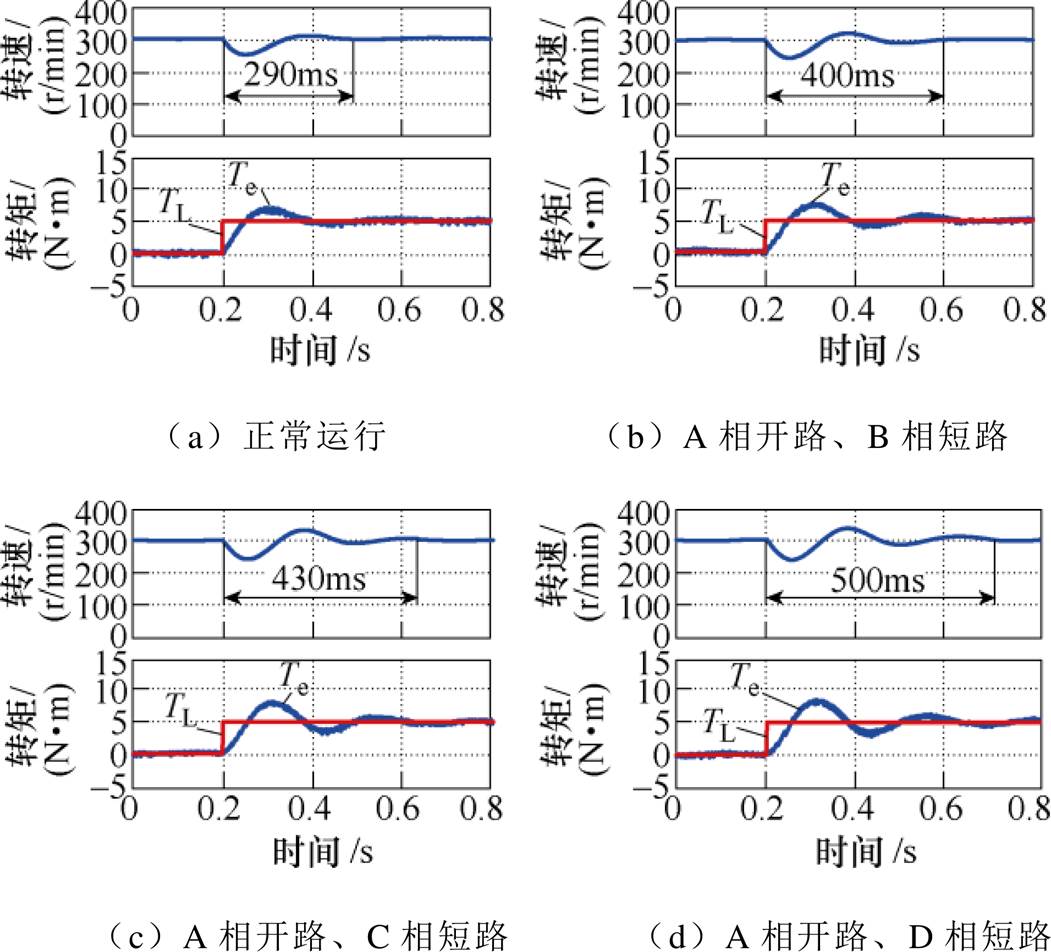
图7 电机组合故障下基于DTC容错后的仿真波形
Fig.7 Simulation waveforms based on DTC fault tolerance under motor combination fault
其次,在实现电机容错运行的基础上,系统采用TIBC-DTC进行动态调节,在t =0.2s时,给电机突加5N·m的负载,其仿真波形如图8所示。
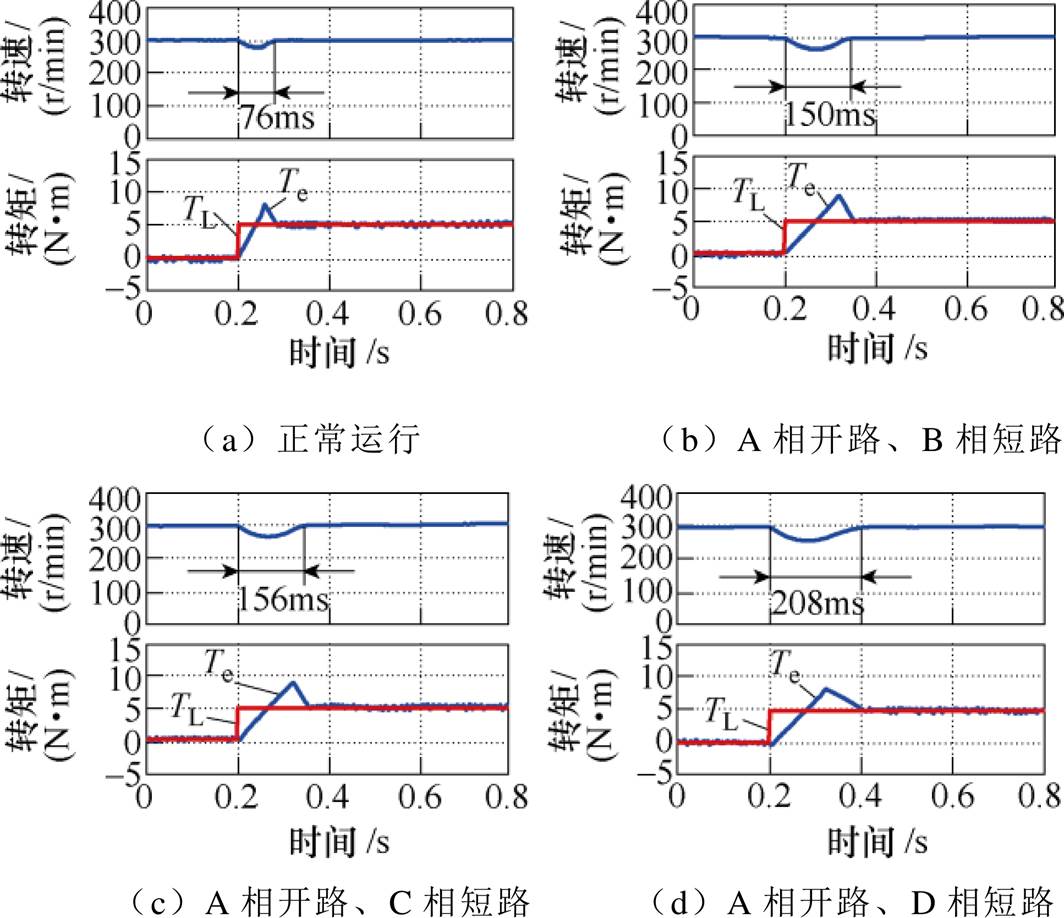
图8 电机组合故障容错后基于TIBC-DTC的仿真波形
Fig.8 Simulation waveforms based on TIBC-DTC after fault tolerance of motor combination fault
当电机绕组发生不同开路及短路组合故障时,基于DTC与TIBC-DTC的动态响应时间见表6。可以看出,相较于DTC,系统采用TIBC-DTC的动态调节过程得到了优化。从横向角度进行比较,在同样采用TIBC-DTC时,重构后的空间电压矢量对电机转矩角的调节作用越强,系统的动态调节时间越短,与前文理论分析的结果一致。
表6 不同开路及短路组合故障下动态响应时间
Tab.6 Dynamic response time under different open and short circuit combined faults
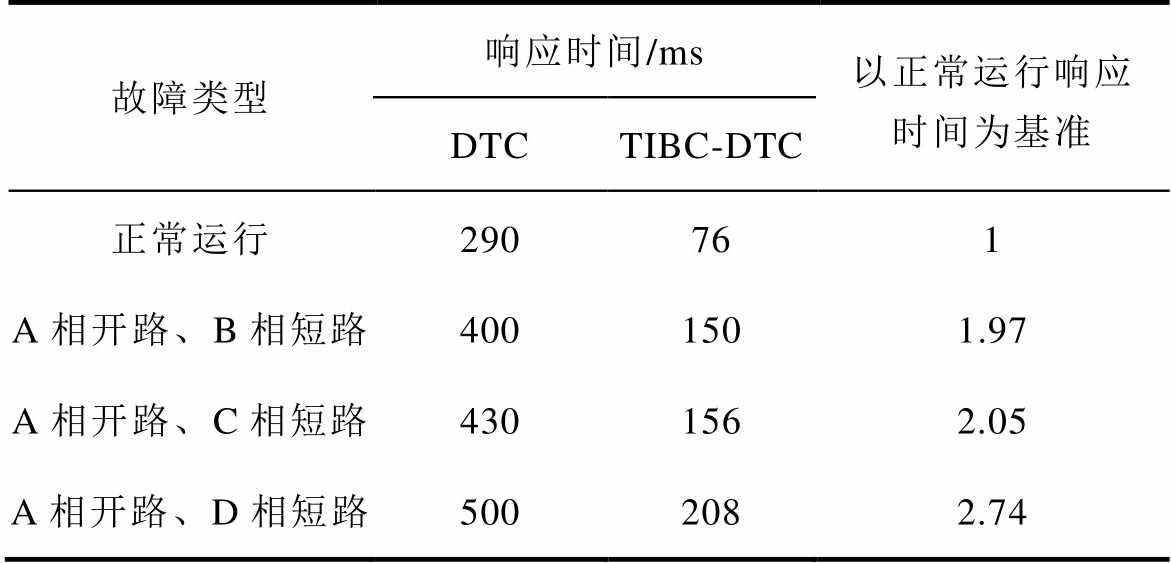
故障类型响应时间/ms以正常运行响应时间为基准 DTCTIBC-DTC 正常运行290761 A相开路、B相短路4001501.97 A相开路、C相短路4301562.05 A相开路、D相短路5002082.74
基于6/19容错型永磁磁通切换电机实验平台,在电机绕组发生开路及短路组合故障情况下对TIBC-DTC算法的有效性进行验证。实验平台如图9所示。

图9 实验平台
Fig.9 Experimental platform
3.2.1 组合故障下的容错控制实验
当电机绕组发生m相开路与n相短路组合(以A相开路、B相短路,A相开路、C相短路及A相开路、D相短路为例)故障时,对容错控制策略进行实验验证。图10为故障补偿前电机的转速与转矩实验波形,转矩波动峰峰值分别为3.6N·m、4N·m和5.8N·m;图11为故障补偿后电机的转速与转矩实验波形,可以看出转矩脉动得到了抑制,从而实现电机故障后的稳定运行。
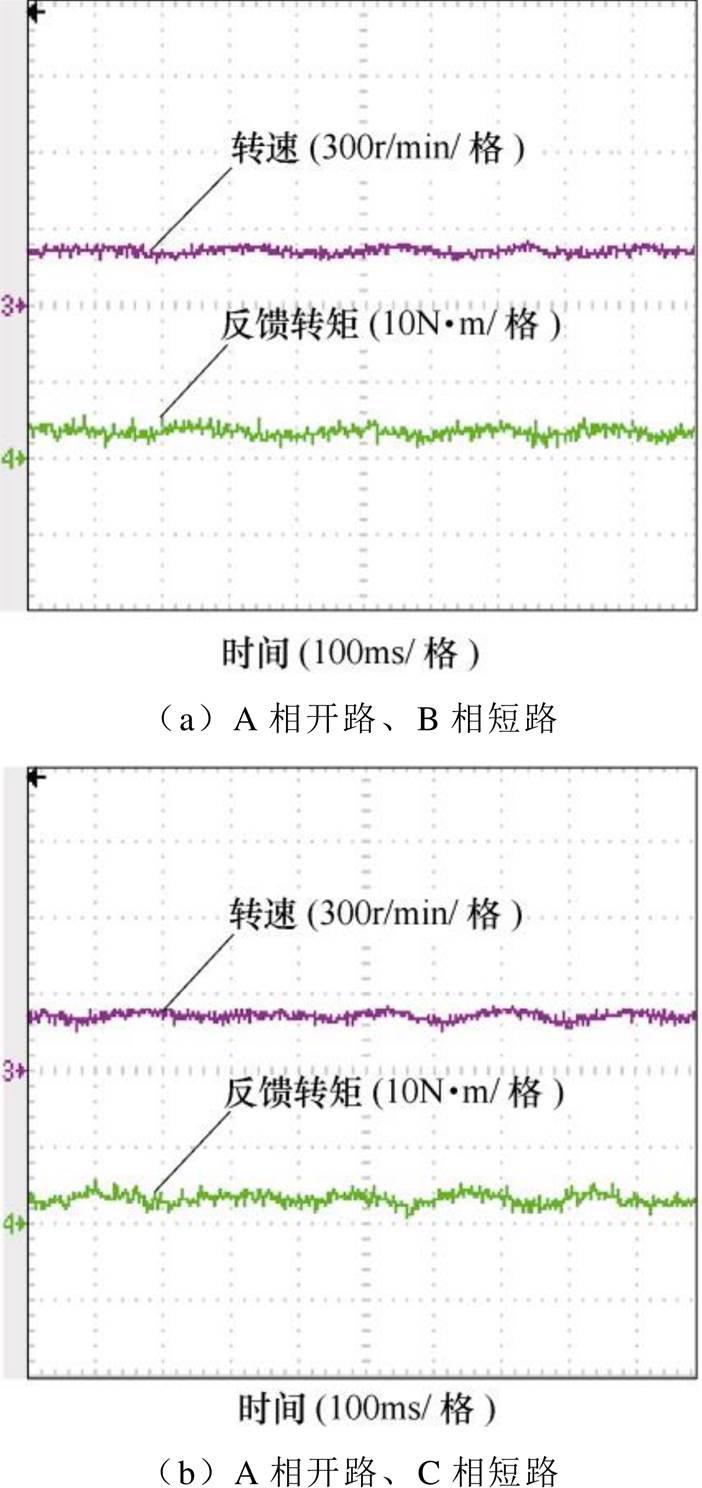
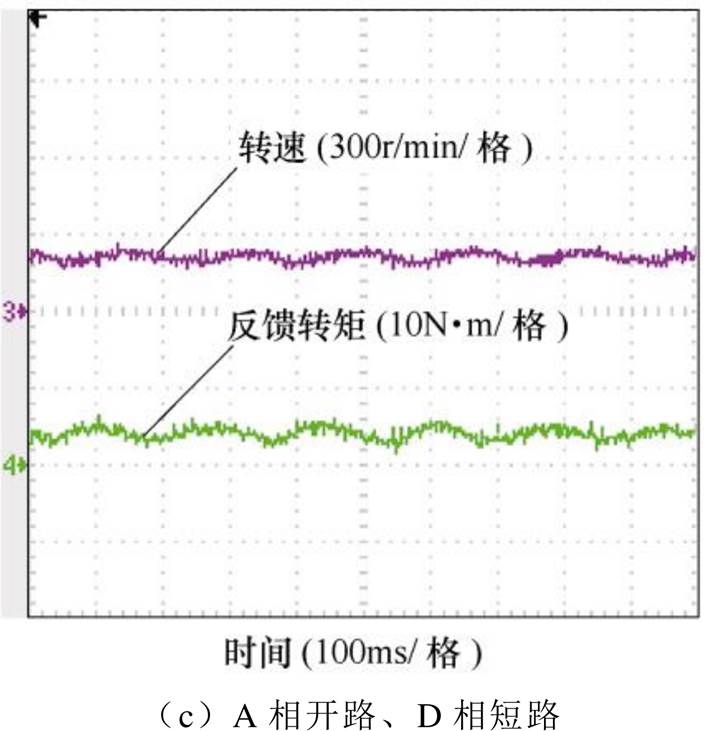
图10 故障补偿前的实验波形
Fig.10 Experiment waveforms before fault compensation
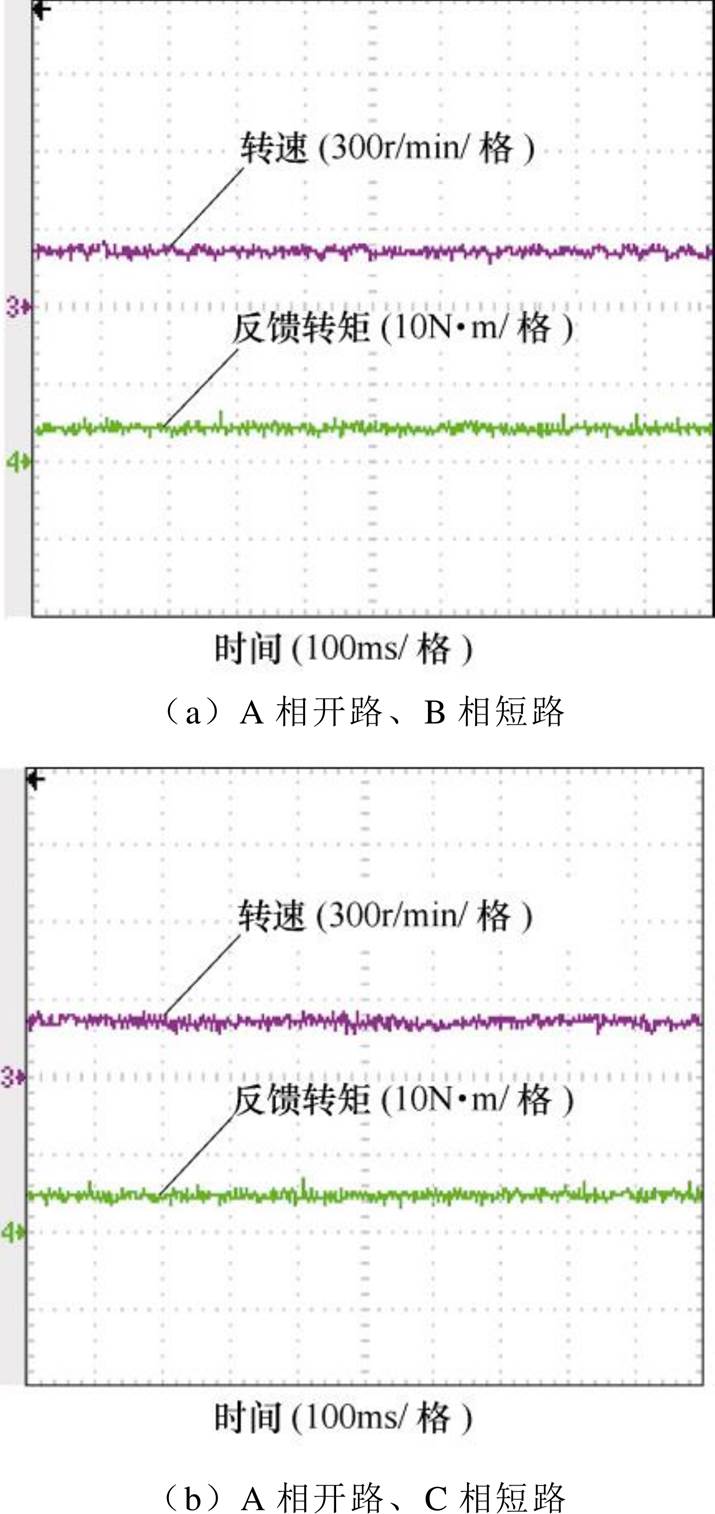
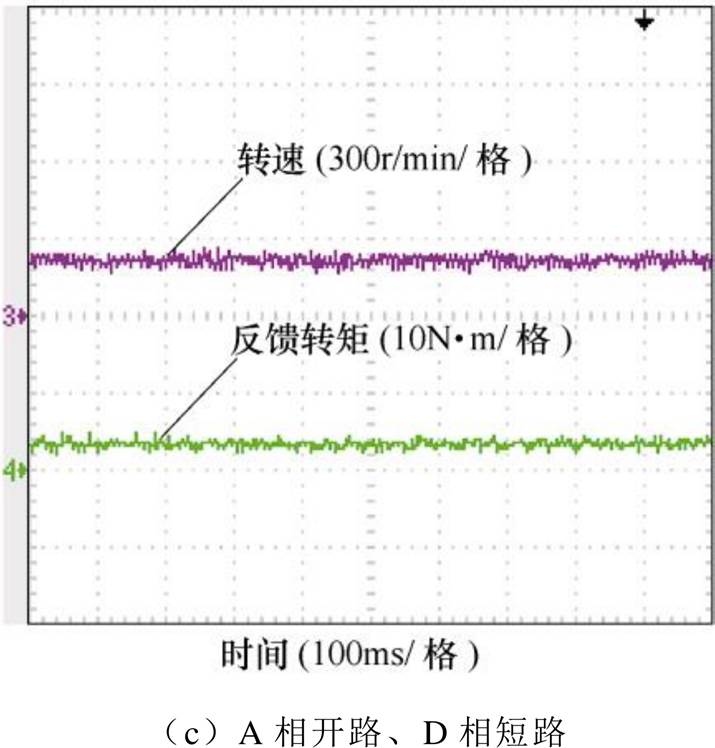
图11 故障补偿后的实验波形
Fig.11 Experiment waveforms after fault compensation
3.2.2 组合故障下突加负载实验
当电机绕组发生m相开路与n相短路组合(以A相开路、B相短路,A相开路、C相短路及A相开路、D相短路为例)故障时,通过上述容错控制可以实现组合故障下的稳定运行,在此基础上,进行突加负载实验。基于DTC的动态响应过程如图12所示,其转速与转矩都能够得到较好地跟踪,整个动态调节时间分别为300ms、300ms和350ms。
图13为电机在同等情况下采用TIBC-DTC的动态响应实验波形。整个动态过程的响应时间分别为200ms、210ms和270ms,与传统的DTC相比,转速的动态响应时间提高了23%~33%,动态性能得到了较大地提升,从而验证了TIBC-DTC的正确性。
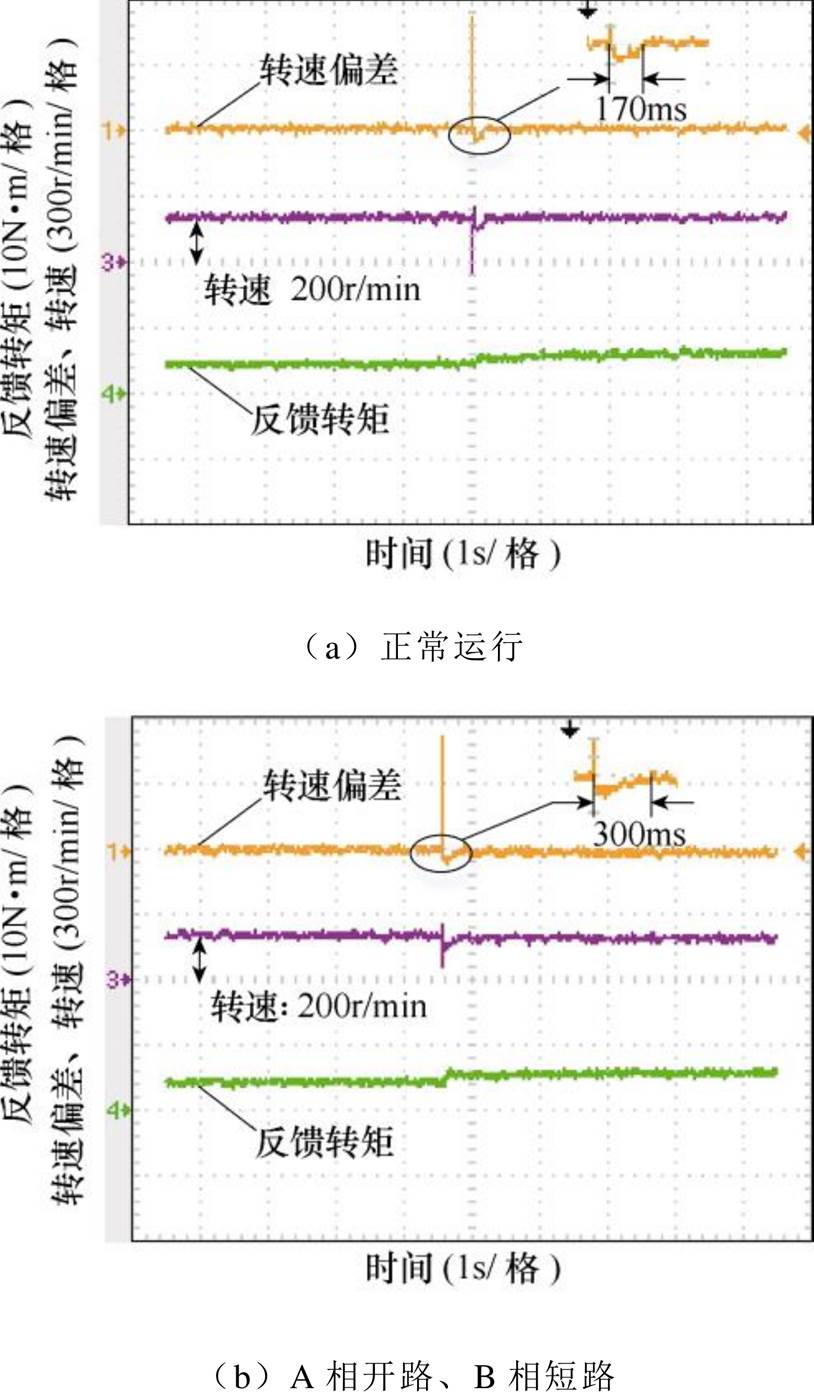

图12 基于DTC的动态响应实验波形
Fig.12 Experimental waveforms of dynamic response based on DTC
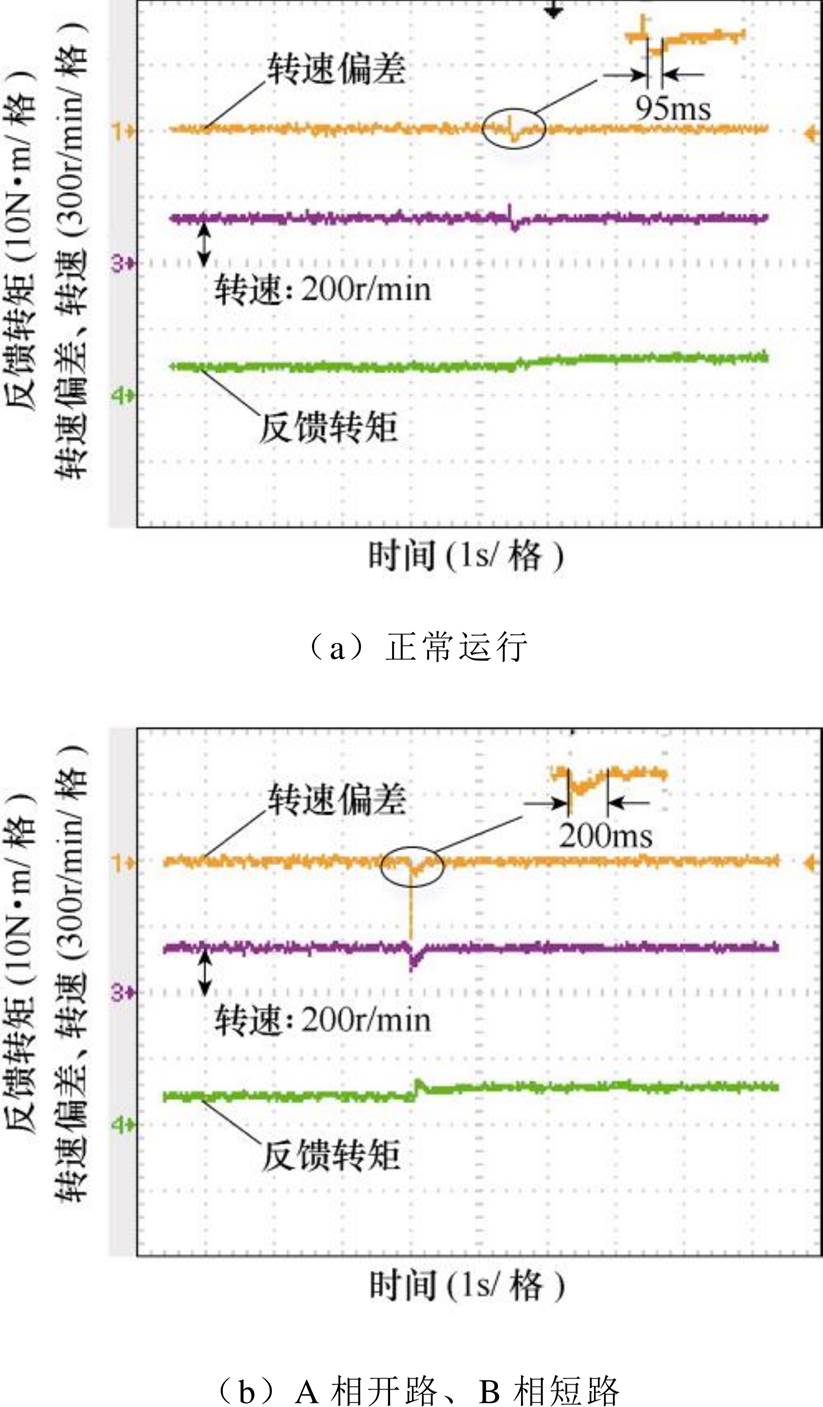
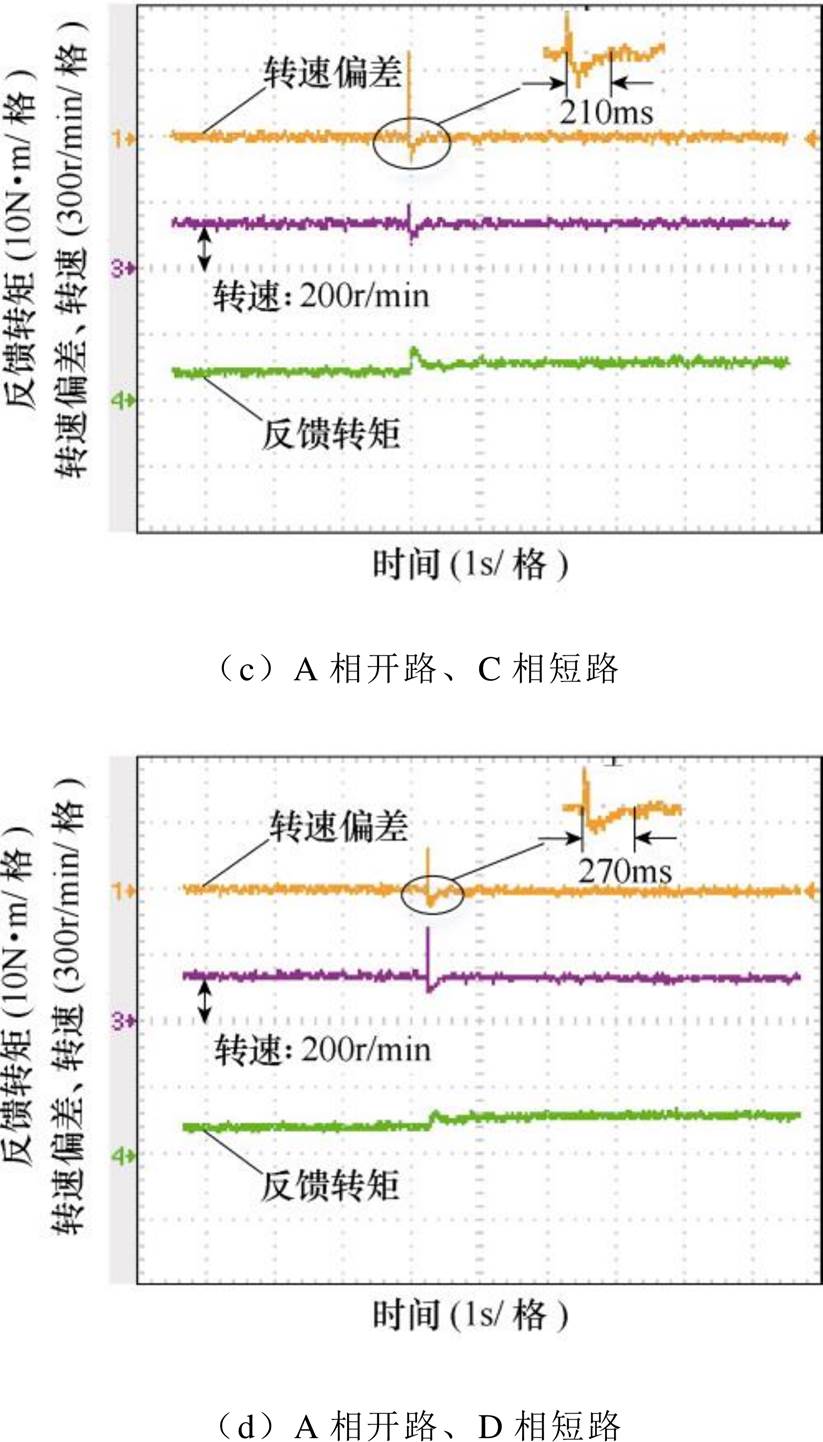
图13 基于TIBC-DTC的动态响应实验波形
Fig.13 Experimental waveforms of dynamic response based on TIBC-DTC
图14从理论、仿真与实验角度对电机绕组处于开路及短路组合故障情况下基于TIBC-DTC的动态调节时间(以正常运行的动态调节时间为基准)进行了对比。可以看出,当电机绕组发生m相开路与n相短路故障时,采用TIBC-DTC的动态响应时间仿真与实验得到的结果与理论分析的趋势一致。
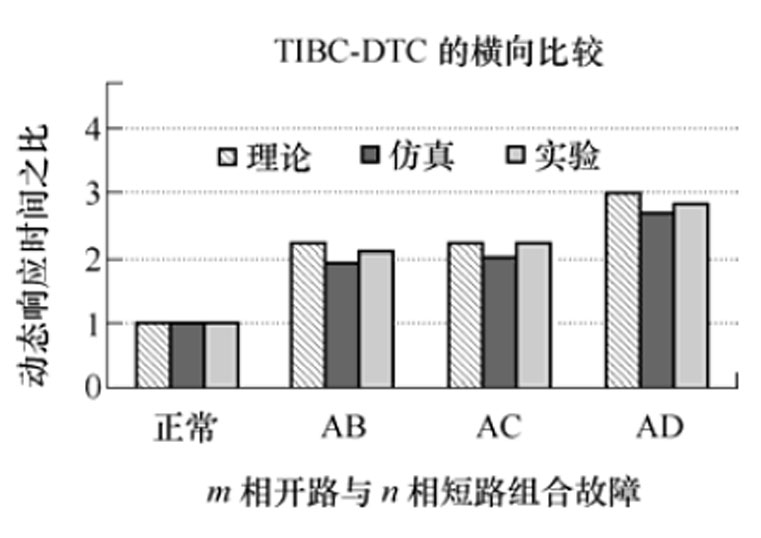
图14 基于TIBC-DTC的动态调节时间横向比较
Fig.14 Horizontal comparison histogram of dynamic adjustment time based on TIBC-DTC
本文针对容错型永磁磁通切换电机m相开路与n相短路组合故障下基于转矩冲量平衡控制的直接转矩控制策略进行研究。得到如下结论:
1)实现了组合故障下的基于转矩冲量平衡控制的直接转矩控制策略,与传统的直接转矩控制策略相比,提高了电机的动态性能。从维持定子磁链幅值恒定的角度出发,通过正常相对故障相缺失磁链进行补偿及空间电压矢量的重构,推导了不同组合故障下系统前进矢量和后退矢量的作用时间,实现组合故障下的动态性能最优。
2)在1)的基础上,横向比较了电机在不同组合故障下基于转矩冲量平衡控制思想的系统动态调节时间。通过建立组合故障下转矩冲量平衡控制方程,同时结合运动方程比较得出了系统动态调节时间的一般规律。在电机两相绕组发生开路及短路组合故障稳态运行的情况下,正常相合成的空间电压矢量对电机转矩角的调节作用越强,系统的动态响应时间越短。
A相开路与B相短路故障下的空间电压矢量如附图1所示。由附图1可以看出,当电机发生A相开路与B相短路故障时,此时定子磁链处于Ⅰ扇区,通过前进矢量V2与V3的交替作用,在一个中断周期T内,定子磁链在切线方向上改变量为
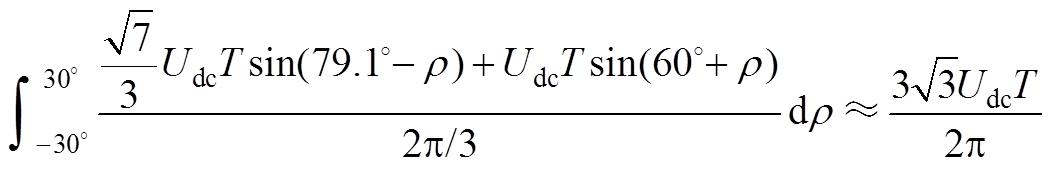 (A1)
(A1)同样地,在后退矢量V5与V6的交替作用下,定子磁链在切向方向上改变量为
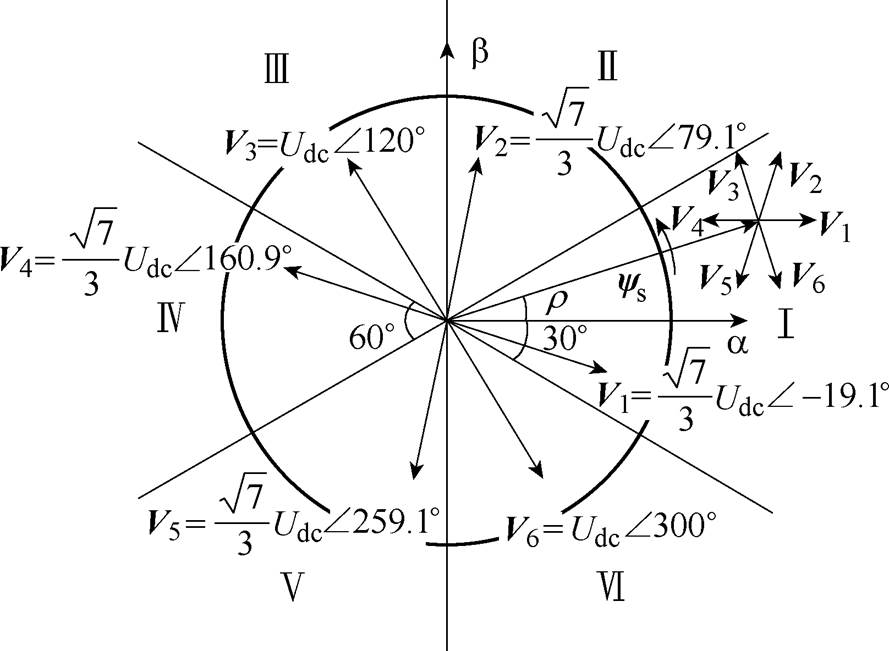
附图1 A相开路与B相短路故障下的空间电压矢量
App.Fig.1 Space voltage vector under A phase open circuit and B phase short circuit fault
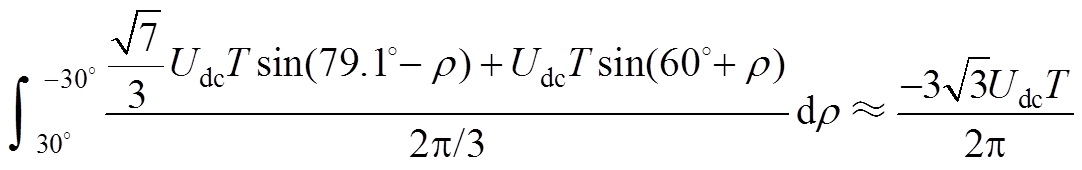 (A2)
(A2)当定子磁链位于扇区Ⅱ~Ⅵ时,通过选择相应的前进矢量进行交替作用,那么在一个中断周期内,其在切线方向改变量为
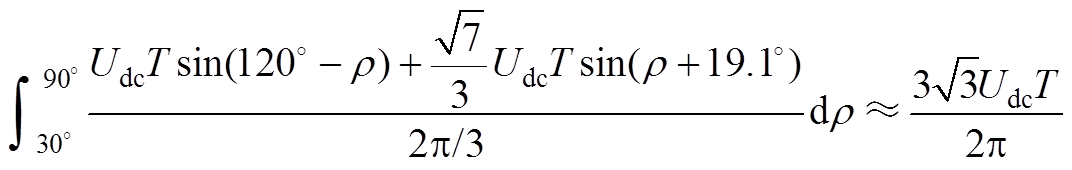 (A3)
(A3)
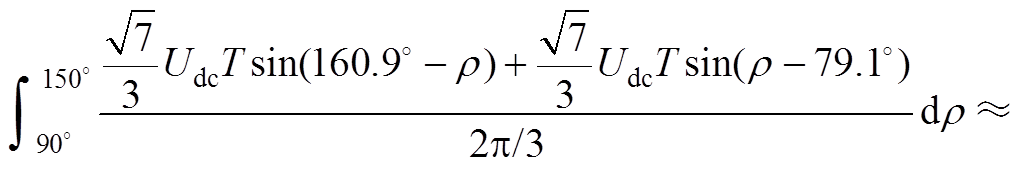
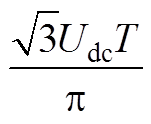 (A4)
(A4)
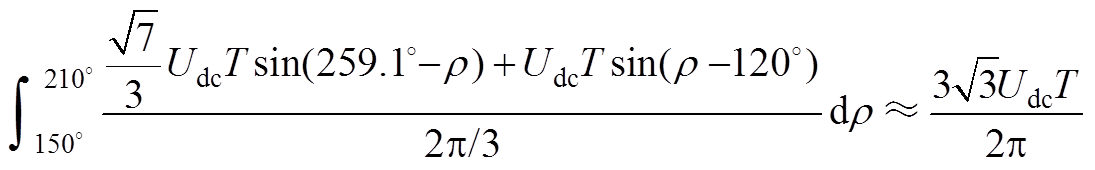 (A5)
(A5)
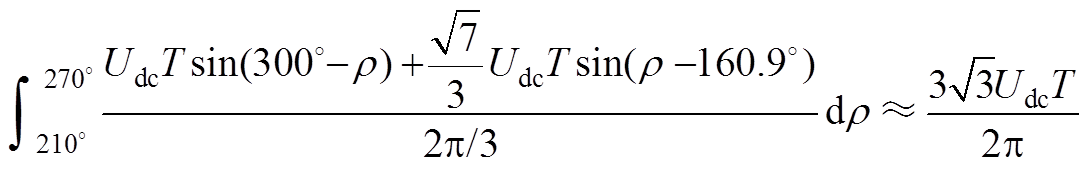 (A6)
(A6)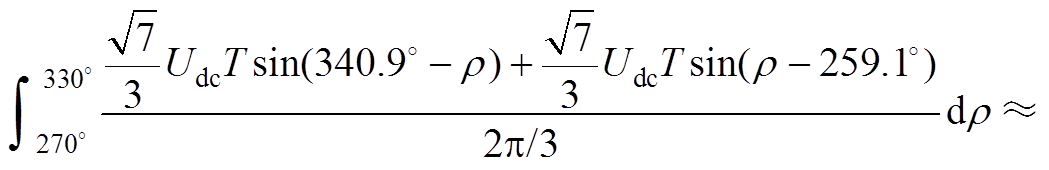
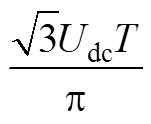 (A7)
(A7)
通过选择相应的后退矢量,定子磁链在切线方向上改变量分别为
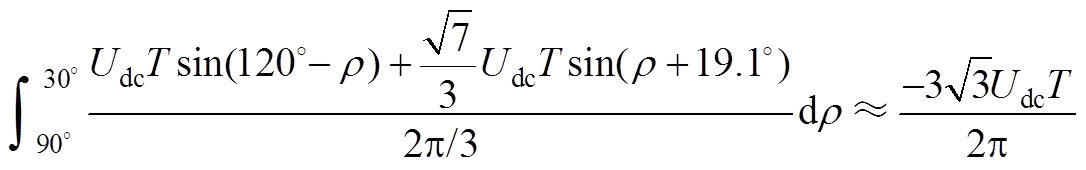 (A8)
(A8)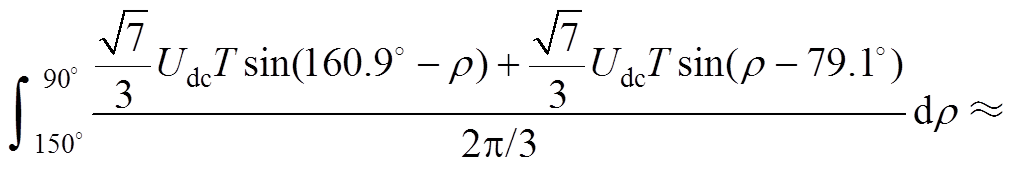
 (A9)
(A9)
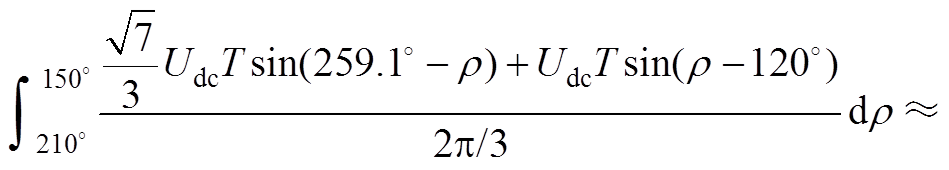
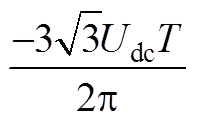 (A10)
(A10)
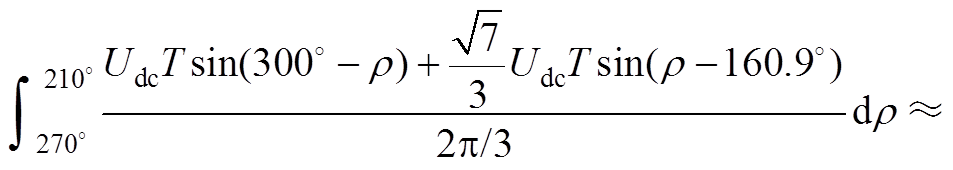
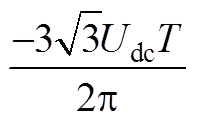 (A11)
(A11)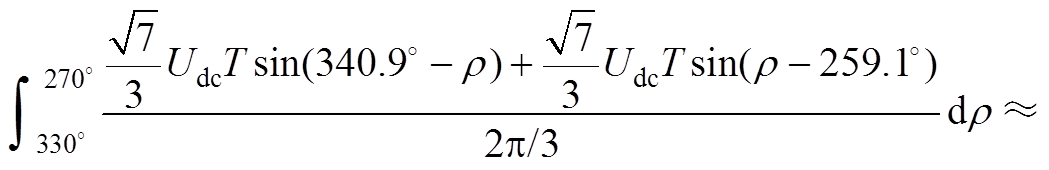
 (A12)
(A12)
由此可以得出在一个中断周期内处于扇区Ⅰ、Ⅱ、Ⅳ和Ⅴ的定子磁链在前进矢量、后退矢量的作用下改变的角度Dd1、Dd2分别为
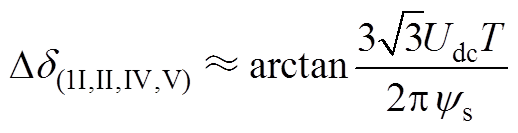 (A13)
(A13)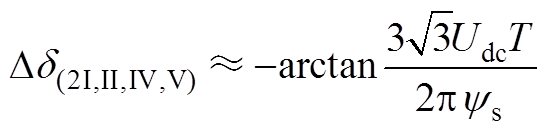 (A14)
(A14)
当其在扇区Ⅲ和Ⅵ时,改变的角度Dd1、Dd2分别为
 (A15)
(A15)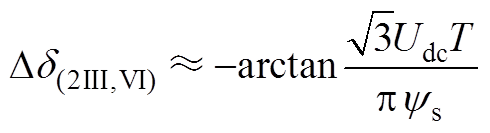 (A16)
(A16)
当电机绕组发生A相开路与C相短路、A相开路与D相短路故障时,由式(1)可以得出不同组合故障下的空间电压矢量见附表1。
当电机绕组发生A相开路与C相短路、A相开路与D相短路组合故障时,根据定子磁链所在的扇区S选择相应的前进矢量、后退矢量,类似于A相开路与B相短路组合故障的求解过程,可以得到在一个中断周期T内定子磁链改变的角度。由于篇幅限制,此处不再赘述。
附表1 m相开路与n相短路组合故障下的空间电压矢量
App.Tab.1 Space voltage vector under combined fault of m-phase open fault and n-phase short circuit

组合故障类型空间电压矢量幅值相位/(°) A相开路、C相短路V1Udc/319.1 V2Udc60 V3Udc/3100.9 V4Udc/3199.1 V5Udc240 V6Udc/3280.9 A相开路、D相短路V12Udc/30 V22Udc/360 V32Udc/3120 V42Udc/3180 V52Udc/3240 V62Udc/3300
参考文献
[1] Petrica Taras, Li Guangjin, Zhu Ziqiang. Com- parative study of fault-tolerant switched-flux permanent- magnet machines[J]. IEEE Transactions on Industrial Electronics, 2017, 64(3): 1939-1948.
[2] Vincenzo Madonna, Paolo Giangrande, Chris Gerada, et al. Thermal analysis of fault-tolerant electrical machines for more electric aircraft applications[J]. The Journal of Engineering, 2018, 2018(13): 461- 467.
[3] Dongsu Lee, Austin Jin, Byung-Hoon Min, et al. Optimisation method to maximise torque density of high-speed slotless permanent magnet synchronous machine in aerospace applications[J]. IET Electric Power Applications, 2018, 12(8): 1075-1081.
[4] 黄文涛, 花为, 於锋. 考虑定位力矩补偿的磁通切换永磁电机模型预测转矩控制方法[J]. 电工技术学报, 2017, 32(15): 27-33.
Huang Wentao, Hua Wei, Yu Feng. A model predictive torque control scheme for flux-switching permanent magnet machines with cogging torque compensation[J]. Transactions of China Electro- technical Society, 2017, 32(15): 27-33.
[5] Athanasios G Sarigiannidis, Minos E Beniakar, Panagiotis E Kakosimos, et al. Fault tolerant design of fractional slot winding permanent magnet aerospace actuator[J]. IEEE Transactions on Trans- portation Electrification, 2016, 2(3): 380-390.
[6] 谢德娥, 王宇, 邓智泉. 考虑反电动势2次谐波的容错型磁通切换电机开路及短路故障控制策略[J]. 电工技术学报, 2016, 31(14): 130-138.
Xie De’e, Wang Yu, Deng Zhiquan. Fault-tolerant control strategy for fault tolerant flux-switching motor with one phase open or short considering second harmonic back-electromotive force[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(14): 130-138.
[7] 於锋, 程明, 田朱杰, 等. 九相磁通切换电机主动缺相运行控制策略[J]. 电工技术学报, 2019, 34(8): 1626-1635.
Yu Feng, Cheng Ming, Tian Zhujie, et al. Active phase-deficient control of a nine-phase flux- switching permanent magnet machine[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(8): 1626-1635.
[8] Huang Wentao, Hua Wei, Chen Fuyang, et al. Model predictive current control of open-circuit fault- tolerant five-phase flux-switching permanent magnet motor drives[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(4): 1840-1849.
[9] Hang Jun, Ding Shichuan, Zhang Jianzhong, et al. Detection of interturn short-circuit fault for PMSM with simple fault indicator[J]. IEEE Transactions on Energy Conversion, 2016, 31(4): 1697-1699.
[10] Cui Ronghua, Fan Ying, Li Chenxue. On-line inter- turn short-circuit fault diagnosis and torque ripple minimization control strategy based on ow five-phase BFTHE-IPM[J]. IEEE Transactions on Energy Con- version, 2018, 33(4): 2200-2209.
[11] Ali Mohammadpour, Leila Persa. Global fault- tolerant control technique for multiphase permanent- magnet machines[J]. IEEE Transactions on Industrial Electronics, 2015, 51(1): 178-186.
[12] Bhaskar Sen, Wang Jiabin. Stationary frame fault- tolerant current control of polyphase permanent- magnet machines under open-circuit and short-circuit faults[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 4684-4696.
[13] Liu Guohai, Lin Zhipeng, Zhao WenXiang, et al. Third harmonic current injection in fault-tolerant five-phase performance-magnet motor drive[J]. IEEE Transactions on Power Electronics, 2018, 33(8): 6970-6979.
[14] Yu Feng, Cheng Ming, Chau K T. Controllability and performance of a nine-phase FSPM motor under severe five open-phase fault conditions[J]. IEEE Transactions on Energy Conversion, 2016, 31(1): 323-332.
[15] Ignacio Gonzalez-Prieto, Mario J Duran, Federico J Barrero. Fault-tolerant control of six-phase induction motor drives with variable current injection[J]. IEEE Transactions on Power Electronics, 2017, 32(10): 7894-7903.
[16] Huang Qiuliang, Chen Yong, Xu Li. Fault-tolerant control strategy for five-phase PMSM with third- harmonic current injection[J]. IEEE Access, 2018, 6: 58501-58509.
[17] Liu Guohai, Qu Li, Zhao Wenxiang, et al. Com- parison of two SVPWM control strategies of five- phase fault-tolerant permanent-magnet motor[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6621-6630.
[18] Zhang Li, Fan Ying, Cui Ronghua, et al. Fault- tolerant direct torque control of five-phase FTFSCW- IPM motor based on analogous three-phase SVPWM for electric vehicle applications[J]. IEEE Transa- ctions on Vehicular Technology, 2018, 67(2): 910- 919.
[19] Chen Qian, Liu Guohai, Zhao Wenxiang, et al. Asymmetrical SVPWM fault-tolerant control of five- phase PM brushless motors[J]. IEEE Transactions on Energy Conversion, 2017, 32(1): 12-22.
[20] 匡志, 杜博超, 徐浩, 等. 十五相永磁同步电机的驱动控制与容错运行[J]. 电工技术学报, 2019, 34(13): 2734-2743.
Kuang Zhi, Du Bochao, Xu Hao, et al. Drive control and fault-tolerant operation of fifteen phase permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2734-2743.
[21] Christoph M Hackl, Urs Pecha, Korbinian Schechner. Modeling and control of permanent-magnet synch- ronous generators under open-switch converter faults[J]. IEEE Transactions on Power Electronics, 2019, 34(3): 2966-2979.
[22] Zhou Huawei, Liu Guohai, Zhao Wenxiang, et al. Dynamic performance improvement of five-phase permanent-magnet motor with short-circuit fault[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 145-155.
[23] 方敏, 周新秀, 刘刚. 三相永磁同步电机断相容错控制[J]. 电工技术学报, 2018, 33(13): 2972-2981.
Fang Min, Zhou Xinxiu, Liu Gang. Fault-tolerant control strategy for three-phase permanent magnet synchronous motor in case of one phase open- circuit[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 2972-2981.
[24] Alberto Berzoy, Osama A Mohammed, Jose Restrepo. Analysis of the impact of stator induction short- circuit faults on induction machines driven by direct torque control[J]. IEEE Transactions on Energy Conversion, 2018, 33(3): 1463-1474.
[25] Wang Zheng, Wang Xueqing, Cheng Ming, et al. Comprehensive investigation on remedial operation of switch faults for dual three-phase PMSM drives fed by T-3L inverters[J]. IEEE Transactions on Industrial Electronics, 2018, 65(6): 4574-4587.
[26] Masoud Farhadi, Majid Tahmasbi Fard, Mehdi Abapour, et al. DC-AC converter-fed induction motor drive with fault-tolerant capability under open-and short-circuit switch fauilures[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1609-1621.
[27] 郝振洋, 胡育文, 黄文新, 等. 永磁容错电机最优电流直接控制策略[J]. 中国电机工程学报, 2011, 31(6): 46-51.
Hao Zhenyang, Hu Yuwen, Huang Wenxin, et al. Optimal current direct control strategy for fault tolerant permanent magnet motor[J]. Proceedings of the CSEE, 2011, 31(6): 46-51.
[28] 周华伟, 周城, 刘国海, 等. 五相圆筒永磁电机统一容错矢量控制[J]. 中国电机工程学报, 2019, 39(5): 1479-1487.
Zhou Huawei, Zhou Cheng, Liu Guohai, et al. A unified fault-tolerant vector control for tubular permanent motors[J]. Proceedings of the CSEE, 39(5): 1479-1487.
[29] Zhu Jingwei, Bai Hongfen, Wang Xia, et al. Current vector control strategy in a dual-winding fault- tolerant permanent magnet motor drive[J]. IEEE Transactions on Energy Conversion, 2018, 33(4): 2191-2199.
[30] Guo Hong, Xu Jinquan, Chen Ye-Hwa. Robust control of fault-tolerant permanent-magnet synch- ronous motor for aerospace application with guaranteed fault switch process[J]. IEEE Transa- ctions on Industrial Electronics, 2015, 62(12): 7309-7321.
[31] Ede J D, Atallah K, Wang Jiabin, et al. Effect of optimal torque control on rotor loss of fault-tolerant performance-magnet brushless machines[J]. IEEE Transactions on Magnetics, 2002, 38(5): 3291- 3293.
[32] Wang Jiabin, Atallah K, Howe D. Optimal torque control of fault-tolerant permanent magnet brushless machines[J]. IEEE Transactions on Magnetics, 2003, 39(5): 2962-2964.
[33] Wang Junsheng, Yang Guanghong. Data-driven output- feedback fault-tolerant compensation control for digital PID control systems with unknown dynamics[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11): 7029-7039.
[34] 潘泽跃, 程健, 吴嘉珉, 等. 基于FPGA广义预测比例-积分-微分控制在特种电源中的应用[J]. 电工技术学报, 2018, 33(10): 2376-2382.
Pan Zeyue, Cheng Jian, Wu Jiamin, et al. The application of generalized predictive proportion- integration-differentiation control in special power supply based on FPGA[J]. Transactions of China Electrotechnical Society, 2018, 33(10): 2376-2382.
[35] Eric Meyer, Liu Yanfei. Digital charge balance controller with an auxiliary circuit for improved unloading transient performance of Buck converters[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 357-370.
[36] 陈虹, 赵明星, 赵海艳, 等. 三相逆变器的随机双PID组合优化方法[J]. 电机与控制学报, 2018, 22(10): 1-9.
Chen Hong, Zhao Mingxing, Zhao Haiyan, et al. Combinatorial optimization control strategy for a three-phase inverter with random double PID[J]. Electric Machines and Control, 2018, 22(10): 1-9.
[37] 郜羚, 王宇, 王子禹. 基于单周期控制的三输入绕组开放式永磁发电机系统动态性能[J]. 电工技术学报, 2016, 31(增刊1): 76-84.
Gao Ling, Wang Yu, Wang Ziyu. Dynamic perfor- mance of a three input open winding generator system based on one cycle control[J]. Transactions of China Electrotechnical Society, 2016, 31(S1): 76- 84.
[38] Sheng Tiantian, Wang Xiaolin, Zhang Julia, et al. Torque-ripple mitigation for brushless DC machine drive system using one-cycle average torque control[J]. IEEE Transactions on Industrial Electronics, 2015, 62(4): 2114-2122.
[39] 赵熙临, 林震宇, 付波, 等. 预测优化PID方法在含风电电力系统AGC中的应用[J]. 电力系统及其自动化学报, 2019, 31(3): 16-22.
Zhao Xilin, Lin Zhenyu, Fu Bo, et al. Application of predictive optimization PID method to AGC of power system with wind power[J]. Proceedings of the CSU- EPSA, 2019, 31(3): 16-22.
Research on Torque Impulse Balance Control Strategy of Fault Tolerant Flux Switching Permanent Magnetic Motor under Combined Open and Short Circuit Faults
Abstract In order to improve the reliability of the fault tolerant flux switching permanent magnet (FTFSPM) machine drive system, the open and short circuit combination faults of the motor windings are analyzed from the perspective of constant amplitude of stator flux linkage. The flux linkage compensation is performed for the normal current loss of the winding and short-circuit current disturbance, thereby achieving fault-tolerant control of the motor. However, the dynamic performance of the speed is affected by the PI parameters of the speed loop in the traditional direct torque control. Hence, a direct torque control strategy based on the torque impulse balance control is proposed. According to the principle that the value of the torque impulse is balanced, the response time of the system to send the forward vector and the back vector is derived, so that the dynamic performance of the motor after the fault tolerance of the combined fault is optimized. The torque impulse balance control of the motor under the combined faults is realized by simulation and experiments. The dynamic response under different combined faults is compared, and the validity and effectiveness of the proposed algorithm are verified.
keywords:Fault tolerant flux switching permanent magnet motor, open and short circuit combination faults of winding, fault-tolerant, torque impulse balance control
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.190309
国家自然科学基金(51741705,51977107)、台达电力电子科教发展计划(DREG2018014)和中央高校基本科研业务费(XAC18083,XCA18154-04)资助项目。
收稿日期 2019-03-25
改稿日期 2019-07-08
顾 惠 男,1995年生,硕士研究生,研究方向为容错型永磁磁通切换电机控制。E-mail: 18351987976@163.com
王 宇 男,1982年生,副教授,硕士生导师,研究方向为磁通切换型电机、交流电机先进控制技术、新能源发电系统以及起动发电系统。E-mail: wanghaohao@nuaa.edu.cn(通信作者)
(编辑 陈 诚)