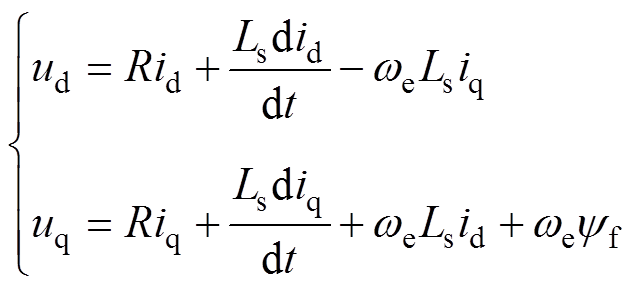（1）式中，ud、uq分别为d、q轴电压分量；id、iq分别为d、q轴电流分量；Ls为定子电感；R为定子电阻；we为角速度；yf为永磁体磁链。根据式（1）可得永磁电机电流环控制模型，如图1所示。
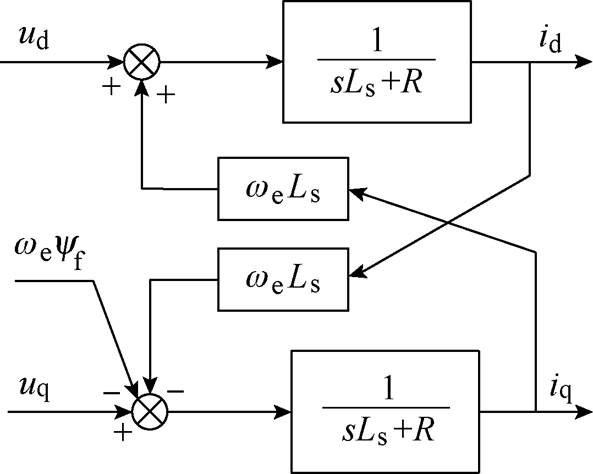
图1 永磁电机数学模型
Fig.1 Mathematical model of permanent magnet motor
摘要 高性能永磁电机伺服系统需要快速的电流响应，数字控制系统中的延时环节会制约电流环动态性能。为此，该文推导了矢量控制系统中主要延时环节的数学模型并分析其不利影响；在此基础上，引入Smith预估算法，针对永磁电机电流环的高动态响应要求，提出一种Smith预估电流控制器，给出该电流控制器的设计过程及实现方法，并讨论了电机参数敏感性。仿真与实验结果表明，所提控制策略正确有效，而且能对控制系统的延时环节进行较好补偿，可有效改善电流环动态性能，进而有助于提高伺服系统整体性能。
关键词：永磁电机 电流控制器 Smith预估控制
高端装备制造是近年来我国产业转型升级的重要领域，高性能伺服系统是其中的重点之一，也越来越受到重视[1-2]。永磁同步电机具有转矩惯量比大、功率因数和功率密度较高等优点，被广泛用于自动化制造、智能机器人、航空航天、船舶舰艇等领域的伺服系统，因此研究高性能永磁电机伺服系统对国民经济和国防建设都具有重要意义和价值[3-4]。
上述领域的伺服系统往往要求电机调速范围宽、转矩脉动小，所以永磁电机伺服系统通常采用矢量控制[5]。在矢量控制为基础的三环控制结构中，作为最内环的电流环是影响永磁电机伺服系统运行性能的一个关键环节，因而关于电流环的优化设计也是当前高性能永磁电机伺服系统的研究热点之一[6]。
高性能永磁伺服系统要求电流环具有高动态响应能力[7-8]。在如何提高电流环动态性能的问题上，目前已有大量研究，总结起来，主要有以下几个方面：第一，对电机运行过程中的非理想因素进行建模，在此基础上进行控制器参数整定[9-11]，该方法主要适合用于特定的被控对象，应用范围不太广泛；第二，优化电流控制时序以缩短控制周期[12-13]，这种方法建立在硬件性能的基础上，会增加成本；第三，采用基于先进控制理论的控制方法，这种方法适用性较强，且对硬件没有特殊要求，近年来受到了广泛关注[14]。从现有的研究来看，预测控制就是其中一种行之有效且具有较好应用前景的控制方 法[14]。所谓预测控制是指，基于被控对象数学模型，将被控对象的预测计算值补偿到实际闭环反馈中，进而达到改善控制性能的目的[14]。针对不同的应用场合，许多学者研究了不同的提高电流环动态性能的预测控制算法。例如，文献[15]针对电机参数扰动的问题，提出一种基于复合观测器的预测电流控制算法，该方法具有较好的参数鲁棒性；文献[16]提出一种基于广义预测控制和非线性扰动观测器的电流单环控制方法，有效改善了负载扰动情况下电流环动态性能；文献[17]提出一种适用于低开关频率的电流预测控制算法，在大功率、低开关频率的应用场合也可获得较好的电流动态响应。
数字控制被广泛采用于伺服系统中，而数字控制有离散性，会造成控制过程中的延时[18]，如采样、运算、逆变器响应等环节。针对这种现象有较多补偿方法，如复矢量法可减小延时造成的电流耦合现象[19-20]，重复控制法可以减小延时造成的周期性波 动[21-22]。尽管前文已指出预测控制能有效改善不同应用场合下电流环动态性能[15-17]，但是这些研究均不是专门针对数字控制系统的延时影响而开展的。
在现有预测控制中，Smith预估控制是解决数字控制系统中延时问题的一种有效方法，而且它在电气控制系统中已有一些研究。例如，文献[23]将Smith预估控制与神经网络比例-积分（PI）控制结合，提出了一种基于延时补偿的电网谐波电流信号跟踪方法，得到了较好的谐波治理效果；文献[24]研究了电压型逆变器计算延时的不利影响，对比了前馈补偿控制和Smith预估控制在解决这一问题上的效果，并指出Smith预估控制的优势；文献[25]将Smith预估器应用于微电网功率控制中，解决了信号传输过程中的延时问题。另外，针对永磁电机伺服系统，也有学者引入Smith预估控制来改善系统性能。例如，文献[26]指出扰动和延时会导致误差累积，在此基础上提出一种基于Smith预估和性能加权函数的控制方案，有效减小了位置跟踪误差；文献[27]针对可能存在的模型参数误差讨论了Smith预估控制策略对电机参数的鲁棒性，就具体的参数误差给出了Smith预估控制策略的适用范围；文献[28]提出一种参数自适应的Smith预估控制策略，通过观测电机参数对预估参数进行修正。上述研究很好地证明了Smith预估控制的优势，不过它们并未涉及永磁伺服系统的电流环动态性能 改善。
电流环的动态性能是其实现永磁电机伺服系统高性能控制的重要基础和前提，它同样受数字控制系统中各延时环节影响。为解决此问题，本文将Smith预估算法引入到永磁电机伺服系统的电流控制中，探索高动态响应的电流控制方法。首先，推导永磁电机矢量控制系统中主要延时环节的数学模型，通过频域分析指出了延时环节带来的不利影响；在此基础上，基于Smith预估控制思想提出一种电流环高动态响应控制策略，并给出它的关键参数设计方法及实现措施；最后，开展仿真和实验研究，对所提控制策略的正确性和有效性进行了详细验证。
本文所研究的Smith预估控制是以被控对象的数学模型为基础进行的，因此有必要先对永磁电机矢量控制系统的数学模型进行分析。
永磁电机在两相旋转坐标系下的电压方程为
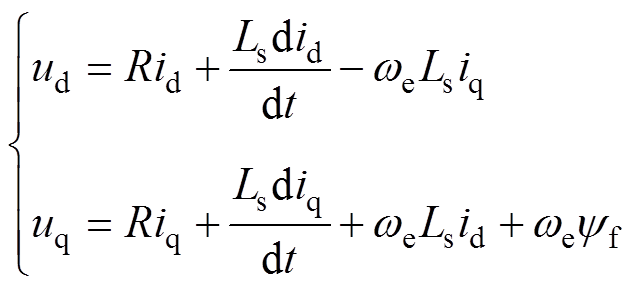（1）式中，ud、uq分别为d、q轴电压分量；id、iq分别为d、q轴电流分量；Ls为定子电感；R为定子电阻；we为角速度；yf为永磁体磁链。根据式（1）可得永磁电机电流环控制模型，如图1所示。
图1 永磁电机数学模型
Fig.1 Mathematical model of permanent magnet motor
在中低速运行状态下交直轴电流近似解耦，可认为是两个具有相同表达形式的独立变量[2]，故其电压电流开环传递函数可表示为
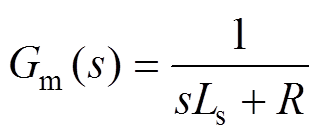（2）式（2）表明，在矢量控制系统中，永磁电机可近似为一个与电机电阻和电感参数有关的惯性系统。
图2是永磁电机电流控制器数学模型，其中iref为电流控制器的给定输入值，ifed为实际电流值。
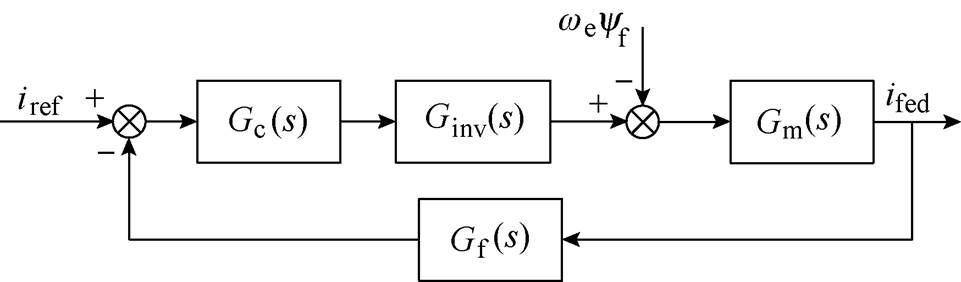
图2 永磁电机电流控制器数学模型
Fig.2 Mathematical model of current loop for permanent magnet motor
图2中，Ginv(s)为逆变器等效传递函数，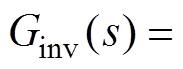
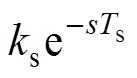，其中，ks为逆变器等效增益，Ts为逆变器控制周期，取其离散数字系统的控制周期。Gf (s)为采样环节的等效传递函数，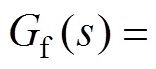
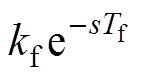，其中，kf为采样等效增益，Tf为与滤波深度和控制周期有关的滤波时间常数，在工程应用中，一般为控制周期的5～10倍[9]。Gc(s)为电流控制器传递函数，例如，结构较为简单的PI控制器可表示为
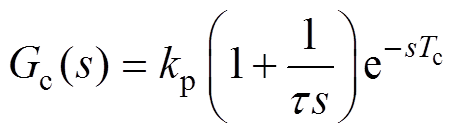（3）式中，kp为比例系数；t 为积分时间常数；Tc为对应的控制器计算时间。
Gm(s)为永磁电机等效传递函数，由式（2）给出。
在1.2节的基础上，电流环开环传递函数可表示为
（4）式中，K为电流环开环等效增益，K=kpkskf/(Rt )；Td为等效延时常数，Td=Ts+Tf+Tc；te为被控电机电气时间常数，te=Ls/R。
传统PI控制一般采用零极点对消的设计方法将系统开环传递函数校正为I型系统[29]。其闭环传递函数为
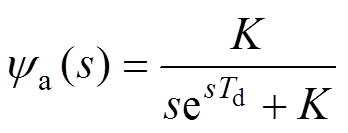（5）式（5）表明，控制系统中的延时环节会在闭环传递函数分母引入纯延时项，对闭环极点产生一定影响。
Td远小于K，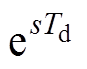
可用一个一阶微分环节近似表示，则式（5）可进一步表示为
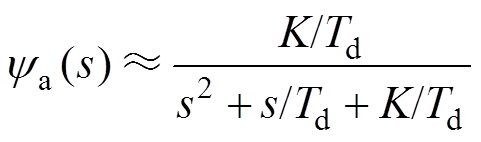（6）式（6）表明，考虑了延时环节的闭环传递函数可近似等效于典型二阶系统，其中，延时时间Td以及系统开环增益K之间的关系为KTd=1/4x2，系统阻尼比为x。阻尼比x 和延时时间Td与开环增益K的乘积密切相关。开环增益K不变的情况下，根据二阶系统动态响应特性，延时时间Td增大会导致阻尼比x 减小，系统动态响应过程振荡增大，调节时间变长。
阻尼比x 的二次方与KTd的值成反比，阻尼比通常取0.7附近，以兼顾动态响应快速性与稳定性[9]，在这一取值附近，系统阻尼比x 对KTd的变化较为敏感，延时时间Td会对系统阻尼特性造成较大影响。
计算得到电流环的频域特性为
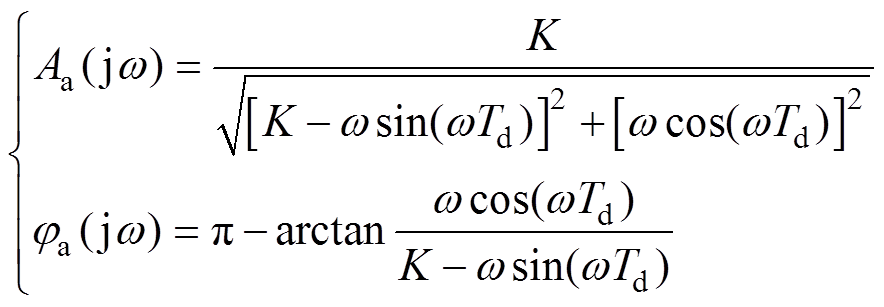（7）式中，Aa(jw)为幅频特性函数；ja(jw)为相频特性 函数。
设系统对数增益下降到-3dB时的频率为wA，相位滞后达到p/2时的频率为wj，二者均与延时时间常数Td有关。
根据式（7）计算wATd、wjTd和KTd之间的关系。
其中，wATd与KTd的关系为
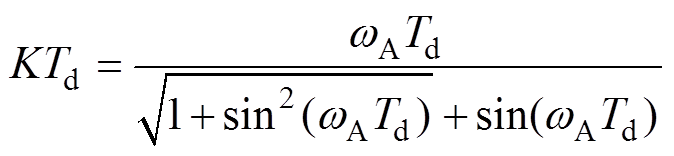（8）wjTd与KTd的关系为
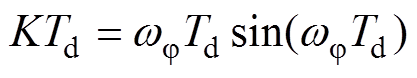（9）
根据动态响应快速性与平稳性的要求，通常使阻尼比x 取0.7左右，即KTd在这一取值范围附近，wA和wj 都随着KTd增加而增大，且与Td为反比关系。KTd取值约为0.5。
由本节传递函数模型的分析可知，延时环节对动态响应特性与带宽均有较为显著的影响。主要体现在以下两个方面：
（1）延时影响二阶系统的阻尼特性，过大的延时导致阻尼比较小，动态过程中的超调与振荡加剧。
（2）在一定范围内带宽与延时成反比，延时会使动态响应速度减慢。
在传统PI控制器中，调节比例系数与积分系数的比值，使得对应的零点抵消由电机参数产生的大时间常数极点。延时环节在控制上表现为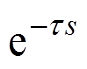
的形式，PI控制器无法对这样的纯延时环节进行有效处理[30]，难以针对延时过程进行较为有效的改善。
第2节分析指出，数字控制系统中存在纯延时环节，会对电流环动态性能造成不利影响，需加以抑制。
在图2的基础上加入Smith预估控制，如图3所示。点画线框中则为Smith预估控制环节，包括两个部分：Gs(s)表示被控对象的数学模型，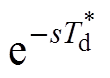
则为预估器矫正延时传递函数。
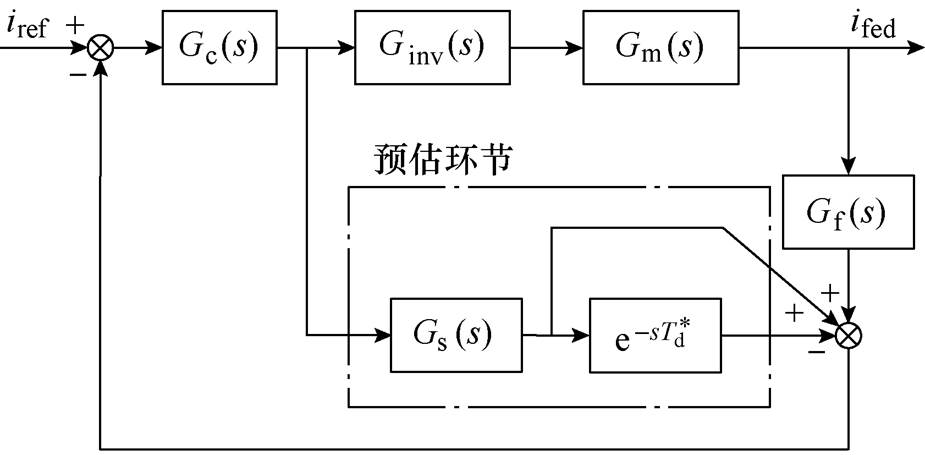
图3 电流环Smith预估控制基本原理
Fig.3 Smith predictive control principle of current loop
加入点画线框所示的Smith预估控制环节后，闭环传递函数变为
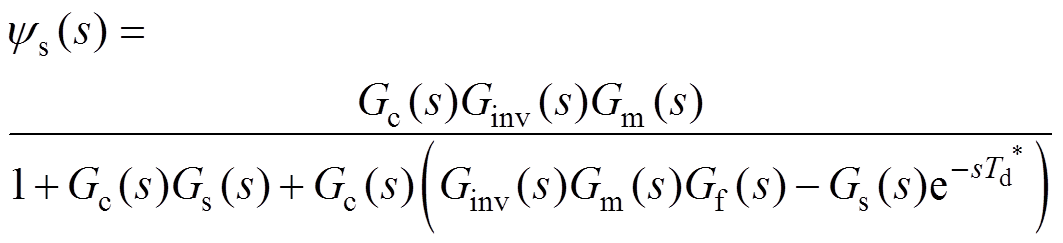（10）其中，Ginv(s)Gm(s)Gf (s)项包含被控电机模型与延时环节。当Smith预估控制环节中的被控对象数学模型与延时校正函数与之相匹配时，式（10）简化为
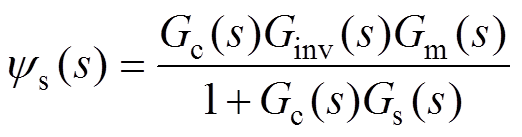（11）
式（11）表明，闭环传递函数特征方程中不再含有纯延时环节，即控制延时不再对闭环系统的稳定性产生显著影响。
将Smith预估控制应用于永磁电机电流控制中，如图4所示。
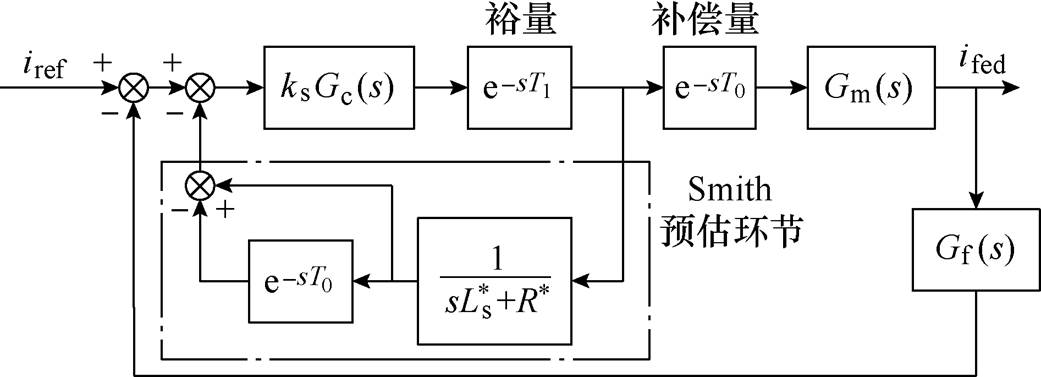
图4 基于Smith预估控制的电流控制框图
Fig.4 Current control block diagram based on Smith prediction
在电流负反馈基础上引入Smith预估控制环节，对延时进行补偿。由3.1节分析可知，该方法可抵消被控对象中的时间滞后环节，改善电流响应速度和动态性能。
图4中，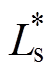
、R*分别为电机预估模型的电感和电阻参数。预估环节包括电机预估模型的传递函数和预估延时补偿时间，在模型匹配较为理想的情况下，1/(
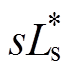+R*)=1/(sLs+R)。
在实际工程应用中，由于存在一些非理想因素影响与电机运行过程中的参数变化，难以做到完全的补偿。为使控制器运行平稳，应对系统延时进行部分的补偿，留有相应裕量。将总延时时间分为两个部分，即Td=T0+T1，其中，补偿量T0一般取电流环控制周期Ts的整数倍为宜，即取T0=nTs，留有裕量T1[18]。
电流环的开环传递函数可表示为
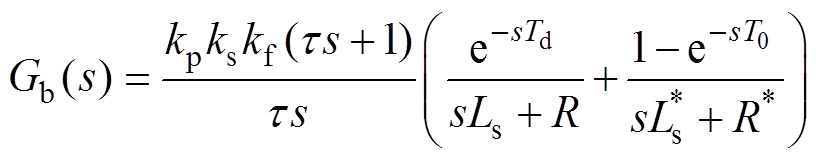（12）同样令系统开环增益K=kpkskf/(Rτ)，简化得与式（8）和式（9）类似的闭环频域特性关系式，有
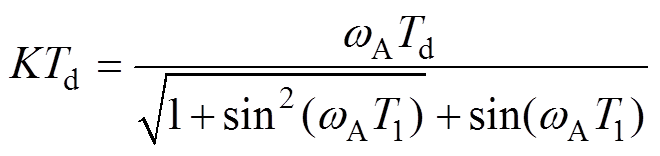（13）
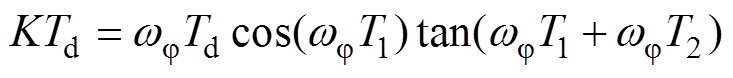（14）由本节的频域特性分析可知，在系统比例增益KT1取值为0.5左右时整体动态响应效果较好，引入Smith预估控制后，系统延时环节得到较好的补偿，等效延时时间减小。在式（13）与式（14）中，KTd＞KT1≈0.5，在保持系统阻尼特性基本不变的情况下，系统比例增益范围增大，闭环带宽有效增加。
在永磁电机矢量控制系统中采用基于Smith预估控制的永磁电机电流控制器，如图5所示。
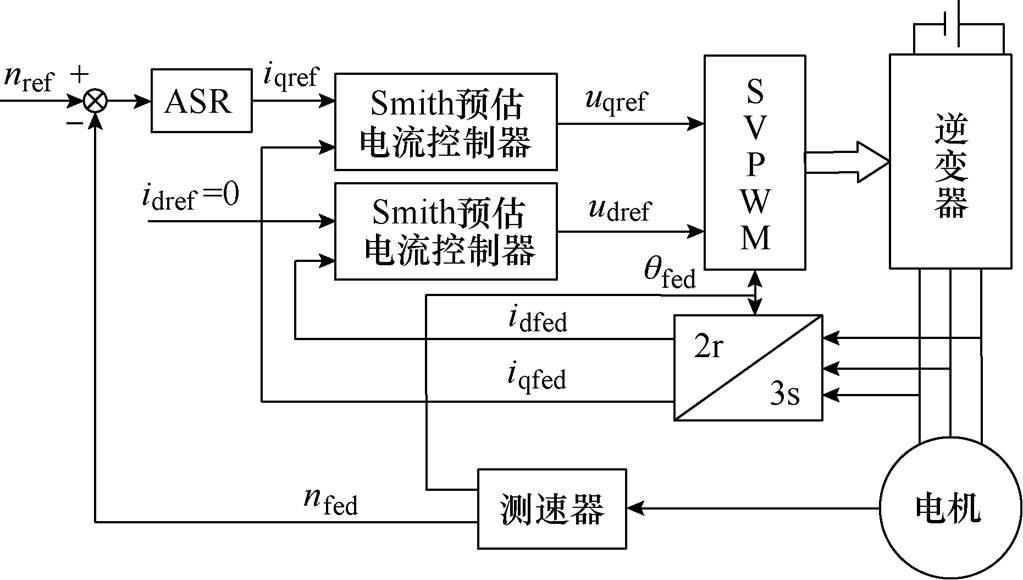
图5 基于Smith预估电流控制器的永磁电机矢量控制策略
Fig.5 Vector control with current loop using Smith predictor
图5中，nref为转速给定值，nfed和qfed分别是电机测速器测得的电机转速与位置，ASR为速度控制器，输出为iq给定值。
第2节在连续时间情况下讨论了延时环节对永磁电机矢量控制中电流环的影响，本节研究了电流环Smith预估控制参数设计，这里需要对控制方法进行离散化以便进行微处理器的数字编程，首先需要对图4中的Smith预估控制部分进行离散域建模。
离散域的Smith预估控制算法如图6所示。
图6 Smith预估控制离散域框图
Fig.6 Smith predictive control diagram in discrete domain
具体实现过程如下：将第k-1个控制周期计算得到的参考电压U(k-1)进行保存；在第k个周期输入Smith预估器，对本周期电流控制结果进行预估得到Ip(k)，然后将预估结果与本周期反馈电流叠加作为最终的反馈量DIp(k)，参与输出电压的计算。其中参考电压U(k-1)和Ip(k)的数量关系为
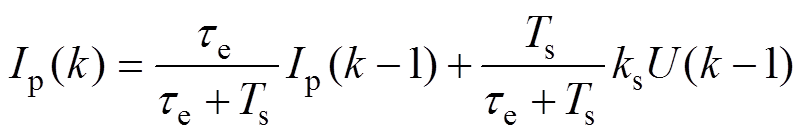（15）预估补偿是一个纯延时环节，在离散域中即可等效为对时间的差分项，有
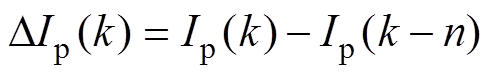（16）
通过上述离散处理后，控制器结构较为简单，计算量小，易于实现。
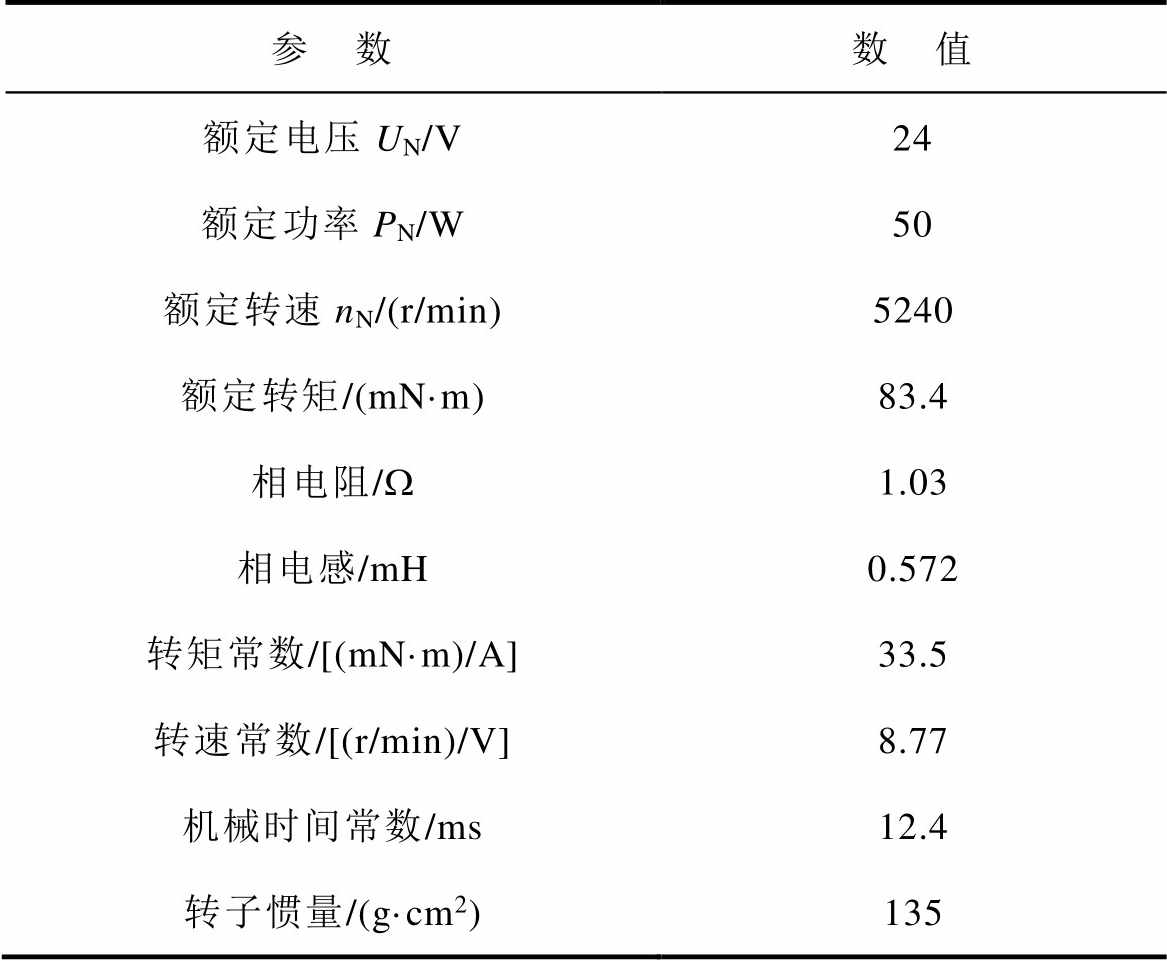
在Matlab/Simulink仿真环境中搭建永磁电机矢量控制模型，其参数见表1。开关频率为fc=10kHz。
表1 永磁电机仿真参数
Tab.1 Simulation parameters of the permanent magnet motor
参 数数 值 额定电压UN/V24 额定功率PN/W50 额定转速nN/(r/min)5240 额定转矩/(mN·m)83.4 相电阻/W1.03 相电感/mH0.572 转矩常数/[(mN·m)/A]33.5 转速常数/[(r/min)/V]8.77 机械时间常数/ms12.4 转子惯量/(g·cm2)135
图7为永磁电机电流环在Smith预估控制与普通PI调节闭环幅频和相频特性的仿真。可以看出，系统幅值截止频率wA和相位截止频率wj 随着等效延时时间的减小而增大。这表明，采用Smith预测控制后闭环带宽增加，系统的动态响应性能得到了有效提高。
图8为仿真Smith预估控制与普通PI调节的电流阶跃响应对比以及在不同的延时矫正参数下Smith预估控制效果对比。在本文所设计Smith预估控制中，延时矫正参数T0代表了Smith预估控制算法作用的效果，当该参数为零时等同于并未采用Smith预估控制的普通PI调节，在T0等于系统延时时间的情况下则等同于对延时环节理想的完全补偿。图8中4个子图分别对应Smith预估控制矫正延时参数T0不同取值时的情况。
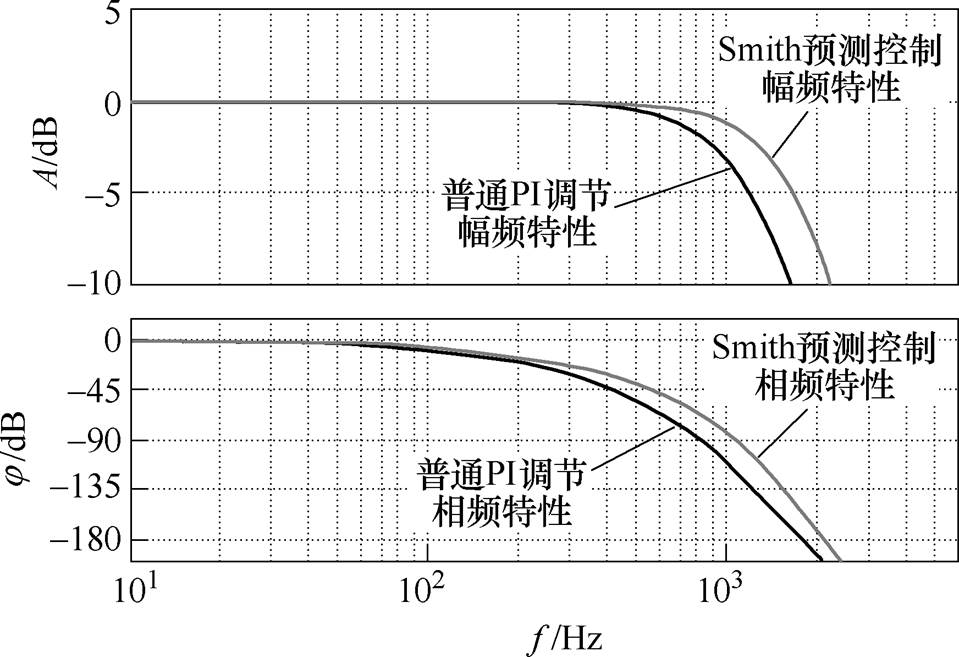
图7 Smith预估控制与普通PI调节闭环幅频与相频特性对比
Fig.7 Comparison of amplitude-frequency and phase-frequency characteristics between Smith predictive control and PI regulation of closed loop
图8a的矫正延时参数较小，Smith预估控制的作用不强，与普通PI调节的区别不大。图8b表示，随着矫正延时参数变大，系统振荡显著减弱，电流动态响应性能有所改善。图8c表明，在矫正延时参数较理想的匹配系统延时的情况下，Smith预估控制可以有效改善动态性能。由图8d可看出，矫正延时参数过大也会导致动态响应不稳定，故实际应用中应如3.1节所述保留一定裕量。
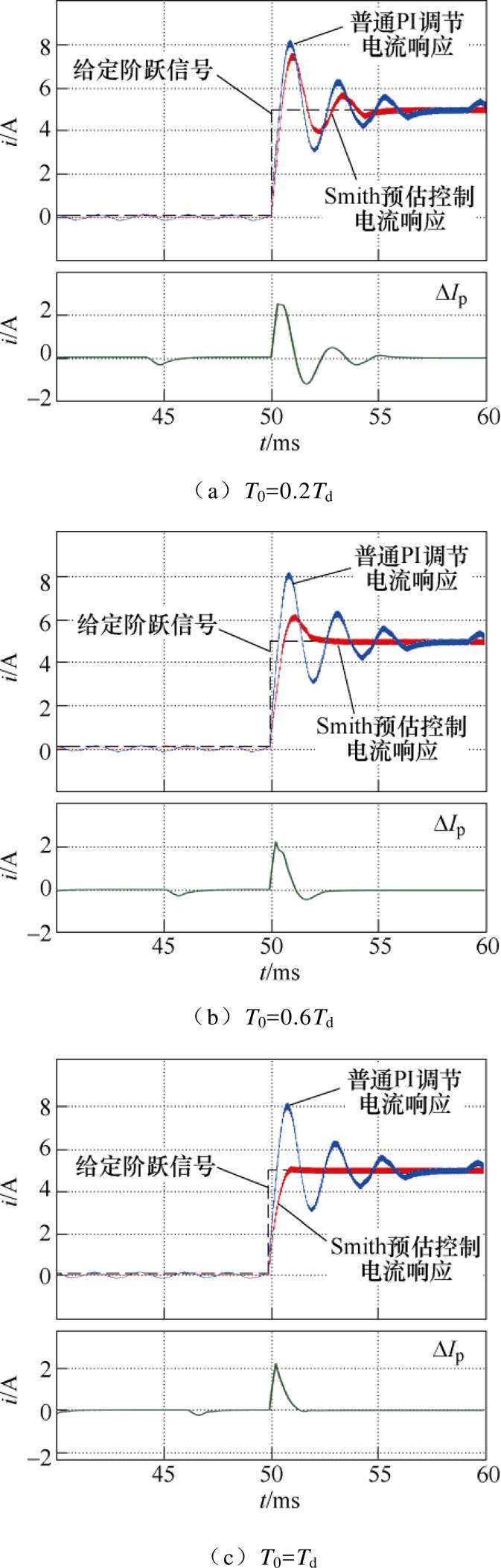
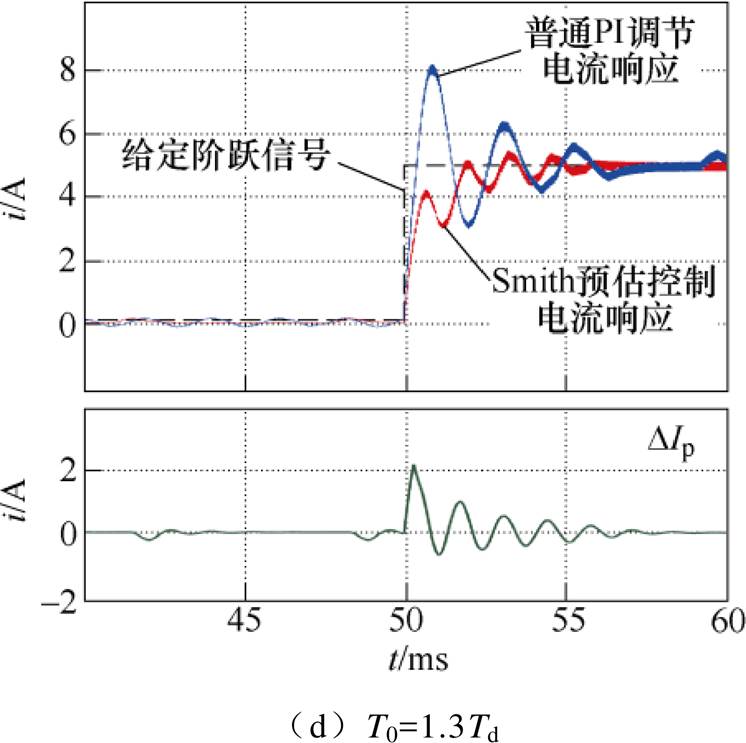
图8 Smith预估控制与普通PI调节电流阶跃响应对比
Fig.8 Comparison of Smith predictive control and PI regulated current on step response
电机运行过程中，电机参数会随着环境状态发生变化。就一般伺服应用场合而言，电感和电阻参数会发生约20%的变化[31]。
图9为Smith电流预估器在理想状态下和电机参数存在误差情况下电流阶跃响应对比。
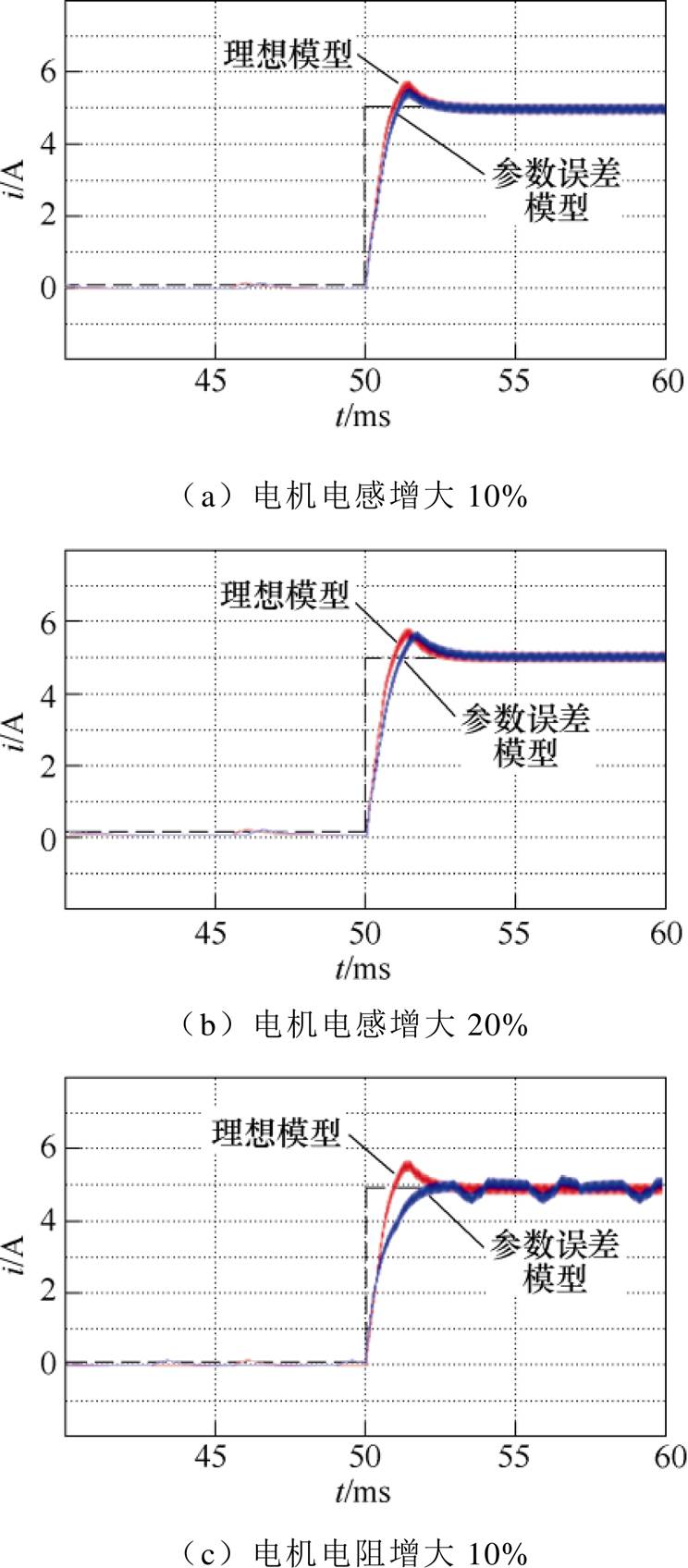
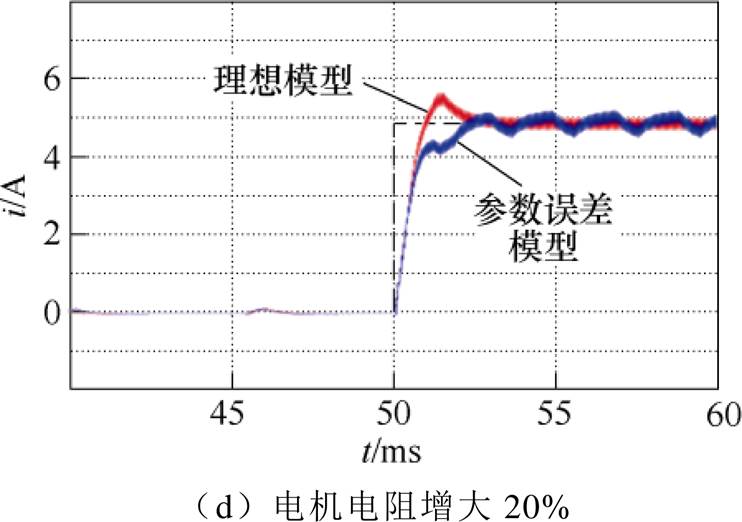
图9 理想模型与参数误差模型电流阶跃响应对比
Fig.9 Comparison of current step response between ideal model and parameter error model
由仿真结果可见，电机电感参数对电流动态响应效果影响较小，电感参数误差对控制效果影响不大；电机电阻参数变化对控制效果有一定影响，电阻参数误差会使电流响应速度减慢，预测补偿量因参数误差而产生偏差，导致动态过程出现周期性的波动。
本文所提出的控制策略受电机电感参数变化影响较小，电机电阻参数的变化会导致动态过程出现小幅周期性波动。在电机正常运行过程中，本文所提出的控制策略在电机参数小幅变化的情况下仍然可以保持较好的效果。
在以TMS320F28335为核心的永磁电机矢量控制实验平台上进行了实验验证。电机参数与仿真相同。
图10为电流阶跃响应实验波形，1s时刻id给定值从-5A阶跃到5A。
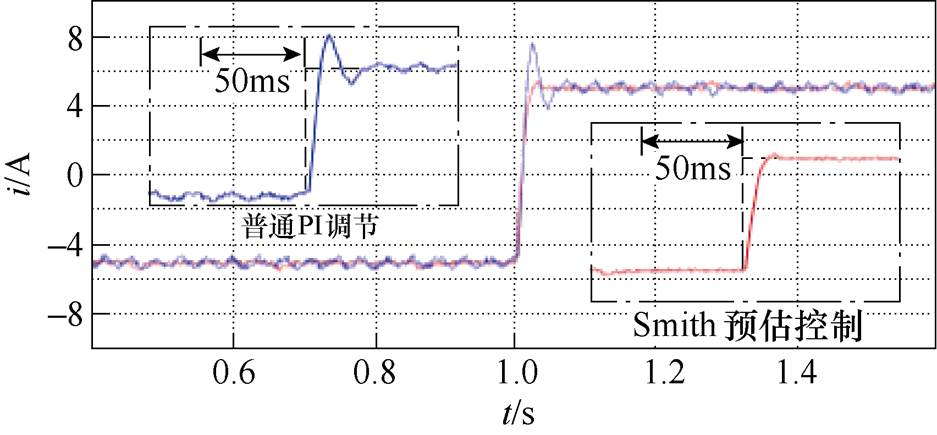
图10 电流阶跃响应实验对比
Fig.10 Experimental comparison of current step response
在阶跃信号跟踪过程中，普通PI调节的电流响应受延时环节影响，动态过程呈现振荡衰减的小阻尼特性，而采用Smith预估控制的电流动态响应保持了较为平稳的阶跃响应性能，表明采用本文所提出的控制方法可以在保持较快响应速度的基础上使电流动态响应过程较为平稳。
图11和图12分别为普通PI调节和Smith预估控制在电机起动动态过程中，电机转速-电流给定-电流反馈值的实验波形。在电机达到额定速度后，本文提出的Smith预估控制的比普通PI调节的振荡调整时间更短，在具有较为平稳的电流响应波形的同时更快地使电机重新运行在稳定状态。
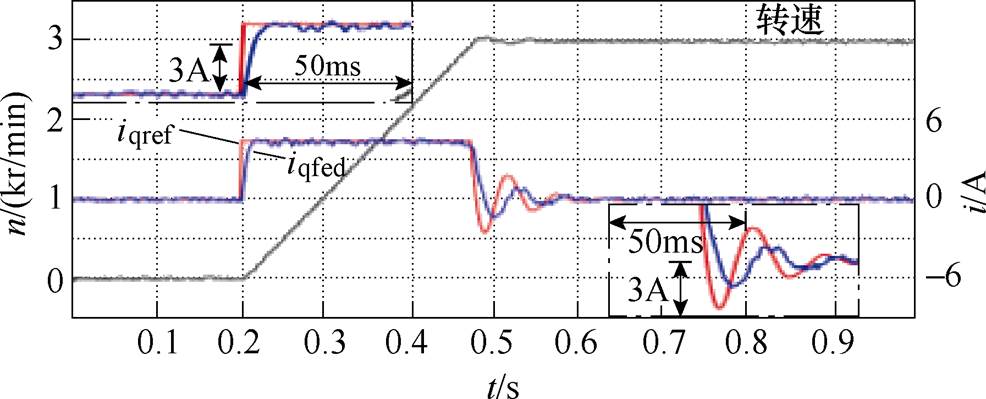
图11 普通PI调节起动过程
Fig.11 Starting process of PI regulation
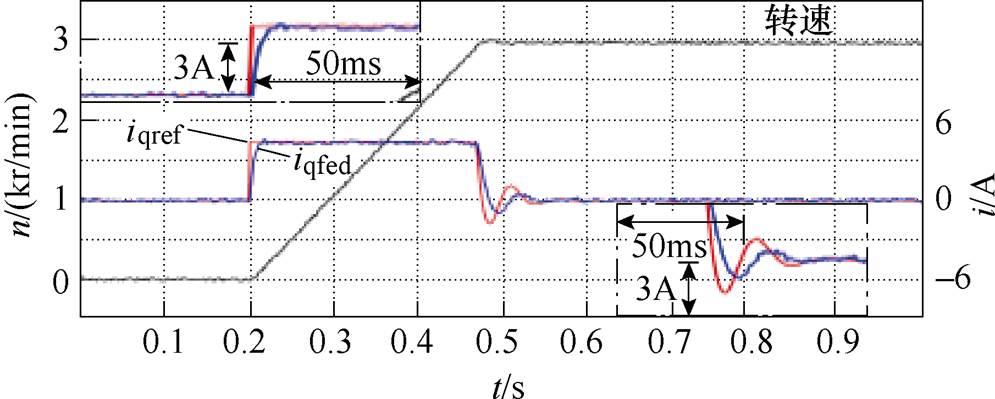
图12 Smith预估控制起动过程
Fig.12 Starting process of Smith predictor
普通PI调节无法对延时环节进行校正，数字控制的延时会制约普通PI调节的动态响应性能，仅靠PI参数优化无法兼顾动态响应稳定性与快速性。本文所提出优化控制策略可抑制延时的不利影响，实验和仿真结果均表明，在合理的参数设计下，采用本文所述的Smith预估控制方法可有效改善电流动态响应性能。
永磁电机伺服系统对电流环的动态响应性能要求较高，而数字控制系统中的延时环节会对动态响应性能造成不利影响。本文引入Smith预估控制算法，提出一种永磁电机电流环高动态响应控制策略，并给出相关参数的设计过程，以及机器编程的离散化实现方法。在控制系统数学模型中，延时环节会使阻尼比减小，动态过程振荡加剧；闭环带宽与延时时间成反比，减小等效延时时间可扩展闭环带宽。普通PI调节无法对闭环特征方程中的纯延时项进行校正，采用本文所提出的Smith预估控制策略能对延时环节进行补偿。仿真和实验结果均表明，相比普通PI调节，本文所提出的控制方法在动态过程中能更快速平稳地跟随给定电流的变化，有效提高电流环动态响应性能。
参考文献
[1] 文思奇, 林荣文, 黄李威. 进给伺服系统的PID参数整定[J]. 电气技术, 2018, 19(2): 66-70.
Wen Siqi, Lin Rongwen, Huang Liwei. PID parameter tuning of feed servo system[J]. Electrical Engineering, 2018, 19(2): 66-70.
[2] 周小壮. 高性能交流伺服控制系统的研究[D]. 广州: 华南理工大学, 2017.
[3] Wang Lesan, Wang Mingyan, Guo Ben, et al. Analysis and design of a speed controller for electric load simulators[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7413-7422.
[4] 杨明, 曹佳, 徐殿国. 基于输入整形技术的交流伺服系统抖动抑制[J]. 电工技术学报, 2018, 33(21): 4980-4986.
Yang Ming, Cao Jia, Xu Dianguo. Suppression of vibration of AC servo system based on input shaping technique[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4980-4986.
[5] 张尘. 高性能关节电机伺服控制器的设计[D]. 成都: 电子科技大学, 2018.
[6] 马伟明, 王东, 程思为, 等. 高性能电机系共同的共性基础科学问题与技术发展前沿[J]. 中国电机工程学报, 2016, 36(18): 2025-2035.
Ma Weiming, Wang Dong, Cheng Siwei, et al. Common basic scientific problems and development of leading-edge technology of high performance motor system[J]. Proceedings of the CSEE, 2016, 36(18): 2025-2035.
[7] Cheng Ming, Yu Feng, Chau K T, et al. Dynamic performance evaluation of a nine-phase flux- switching permanent-magnet motor drive with model predictive control[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4539-4549.
[8] 王要强, 冯玉涛, 秦明, 等. 表贴式永磁同步电机全阶滑模观测与控制策略[J]. 电工技术学报, 2018, 33(24): 5688-5699.
Wang Yaoqiang, Feng Yutao, Qin Ming, et al. Full- order sliding mode observation and control strategy for surface permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5688-5699.
[9] 王莉娜, 朱鸿悦, 杨宗军. 永磁同步电机调速系统PI控制器参数整定方法[J]. 电工技术学报, 2014, 29(5): 104-117.
Wang Lina, Zhu Hongyue, Yang Zongjun. Tuning method for PI controllers of PMSM driving system[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 104-117.
[10] 王爽, 冯坚栋, 丁雪, 等. 基于最优开环截止频率学习的永磁伺服PI控制器参数整定方法[J]. 电工技术学报, 2017, 32(21): 44-54.
Wang Shuang, Feng Jiandong, Ding Xue, et al. PI controllers tuning method of permanent magnet servo system based on optimal open-loop cut-off frequency learning[J]. Transactions of China Electrotechnical Society, 2017, 32(21): 44-54.
[11] Xia Changliang, Ji Bingnan, Yan Yan. Smooth speed control for low-speed high-torque permanent-magnet synchronous motor using proportional-integral-resonant controller[J]. IEEE Transactions on Industrial Elec- tronics, 2015, 62(4): 2123-2134.
[12] 苏玲宏. 基于FPGA的高性能永磁同步电机电流控制器研究[D]. 武汉: 华中科技大学, 2014.
[13] 伍庆. 基于FPGA的交流伺服系统电流环设计[D]. 武汉: 华中科技大学, 2013.
[14] 王东文, 李崇坚, 吴尧, 等. 永磁同步电机的模型预测电流控制器研究[J]. 电工技术学报, 2014, 29(增刊1): 73-79.
Wang Dongwen, Li Chongjian, Wu Yao, et al. Model predictive current control scheme for permanent magnet synchronous motors[J]. Transactions of China Electro- technical Society, 2014, 29(S1): 73-79.
[15] Zhang Changfan, Wu Gongping, Rong Fei, et al. Robust fault-tolerant predictive current control for permanent magnet synchronous motors considering demagnetization fault[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5324-5334.
[16] 刘旭东, 李珂, 张奇, 等. 基于非线性扰动观测器的永磁同步电机单环预测控制[J]. 中国电机工程学报, 2018, 38(7): 2153-2162.
Liu Xudong, Li Ke, Zhang Qi, et al. Single-loop predictive control of PMSM based on nonlinear disturbance observers[J]. Proceedings of the CSEE, 2018, 38(7): 2153-2162.
[17] 姚骏, 刘瑞阔, 尹潇. 永磁同步电机三矢量低开关频率预测控制研究[J]. 电工技术学报, 2018, 33(13): 2935-2945.
Yao Jun, Liu Ruikuo, Yin Xiao. Research on 3-vector model predictive control with low switching frequency of permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(13): 2935-2945.
[18] 孙大南, 刁利军, 刘志刚. 交流传动矢量控制系统时延补偿[J]. 电工技术学报, 2011, 26(5): 138-145.
Sun Danan, Diao Lijun, Liu Zhigang. Time-delay compensation about AC drive vector control system[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 138-145.
[19] 赵雷廷, 刁利军, 张哲, 等. 低开关频率下异步电机电流环的数字控制[J]. 中国电机工程学报, 2014, 34(24): 3456-3466.
Zhao Leiting, Diao Lijun, Zhang Zhe, et al. Discrete- time current controller for induction motors at low switching frequency[J]. Proceedings of the CSEE, 2014, 34(24): 3456-3466.
[20] 吴为, 丁信忠, 严彩忠. 基于复矢量的电流环解耦控制方法研究[J]. 中国电机工程学报, 2017, 37(14): 4184-4191.
Wu Wei, Ding Xinzhong, Yan Caizhong. Research on control method of current loop decoupling based on complex vector[J]. Proceedings of the CSEE, 2017, 37(14): 4184-4191.
[21] 胡晨. 三电平有源电力滤波器数字电流环控制算法研究[D]. 成都: 电子科技大学, 2015.
[22] 李帅, 孙立志, 刘兴亚, 等. 永磁同步电机电流谐波抑制策略[J]. 电工技术学报, 2019, 34(增刊1): 87-96.
Li Shuai, Sun Lizhi, Liu Xingya, et al. Current harmonics suppression strategies of permanent magnet synchronous motor[J]. Transactions of China Elec- trotechnical Society, 2019, 34(S1): 87-96.
[23] 庄建煌, 陈永华, 黄少敏, 等. 基于延时补偿的电网谐波电流信号跟踪控制方法研究[J]. 机电工程, 2016, 33(9): 1125-1129.
Zhuang Jianhuang, Chen Yonghua, Huang Shaomin, et al. Tracking control method of power network harmonic current signal based on time delay compensation[J]. Journal of Mechanical & Electrical Engineering, 2016, 33(9): 1125-1129.
[24] Bosio Federico de, Ribeiro Luiz A de S, Francisco D Freijedo, et al. Discrete-time domain modeling of voltage source inverters in standalone applications: enhancement of regulators performance by means of Smith predictor[J]. IEEE Transactions on Industrial Electronics, 2017, 33(10): 8100-8114.
[25] Constanza Ahumada, Roberto Cárdenas, Doris Sáez, et al. Secondary control strategies for frequency restoration in islanded microgrids with consideration of communication delays[J]. IEEE Transactions on Smart Grid, 2016, 7(3): 1430-1441.
[26] 赵希梅, 马志军, 朱国昕. 基于Smith预估和性能加权函数的永磁直线同步电机鲁棒迭代学习控制[J]. 电工技术学报, 2016, 31(19): 142-146.
Zhao Ximei, Ma Zhijun, Zhu Guoxin. Robust iterative learning control for PMLSM based on Smith predictor and performance weighting function[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 142-146.
[27] 段秀东. 交流永磁同步电机高性能电流控制策略研究[D]. 武汉: 华中科技大学, 2015.
[28] Zhang Qiao, Shen Anwen, Tong Qiaoling, et al. Predictive control for a permanent magnet synchronous motor using automatic tuning smith-predictor with optimal parameter mismatch[C]//2008 International Conference on Electrical Machines and Systems, Wuhan, 2008: 1520-1525.
[29] 王斌, 王跃, 郭伟, 等. 基于定子磁链降阶状态观测的永磁同步电机无差拍直接转矩控制系统[J]. 电工技术学报, 2014, 29(3): 160-171.
Wang Bin, Wang Yue, Guo Wei, et al. Deadbeat direct torque control of permanent magnet synchronous motor based on reduced order stator flux observer[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 160-171.
[30] 贺明智, 许建平, 游小杰, 等. 环路延时对数字峰值电压控制开关变换器瞬态性能的影响[J]. 中国电机工程学报, 2009, 28(6): 1-7.
He Mingzhi, Xu Jianping, You Xiaojie, et al. Time delay effect on transient performance of digital peak voltage controlled switching converter[J]. Pro- ceedings of the CSEE, 2009, 28(6): 1-7.
[31] 周湛清, 夏长亮, 陈炜, 等. 具有参数鲁棒性的永磁同步电机改进型预测转矩控制[J]. 电工技术学报, 2018, 33(5): 965-972.
Zhou Zhanqing, Xia Changliang, Chen Wei, et al. Modified predictive torque control for PMSM drives with parameter robustness[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 965-972.
High-Dynamic-Response Current Loop Control Strategy of Permanent Magnet Motor Based on Smith Predictor
Abstract High performance permanent magnet motor servo system needs fast current response. The delay link in digital control system will restrict the dynamic performance of current loop. For this reason, this paper deduces the mathematical model of the delay link in vector control system and analyses its adverse effects. Accordingly, Smith predictive method is introduced, and a Smith predictive current controller is proposed for the high dynamic response requirements of the current loop. The design process and implementation method of the current controller are given, and the sensitivity of motor parameters is discussed. The simulation and experimental results show that the proposed control strategy is correct and effective. It can compensate the delay link of the control system, improve the dynamic performance of the current loop effectively, and then improve the overall performance of the servo system.
keywords：Permanent magnet motor, current controller, Smith predictive control
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.190280
国家自然科学基金（51507079）、中央高校基本科研业务费（NS2018025）和中国博士后科学基金（2016T90454）资助项目。
收稿日期 2019-03-17
改稿日期 2019-06-06
潘子昊 男，1996年生，硕士研究生，研究方向为电力电子与电力传动。E-mail: panzihao@nuaa.edu.cn
卜飞飞 男，1984年生，博士，副教授，研究方向为航空电源、新能源发电、电机及其控制等。E-mail: bufeifei1984@163.com（通信作者）
（编辑 崔文静）