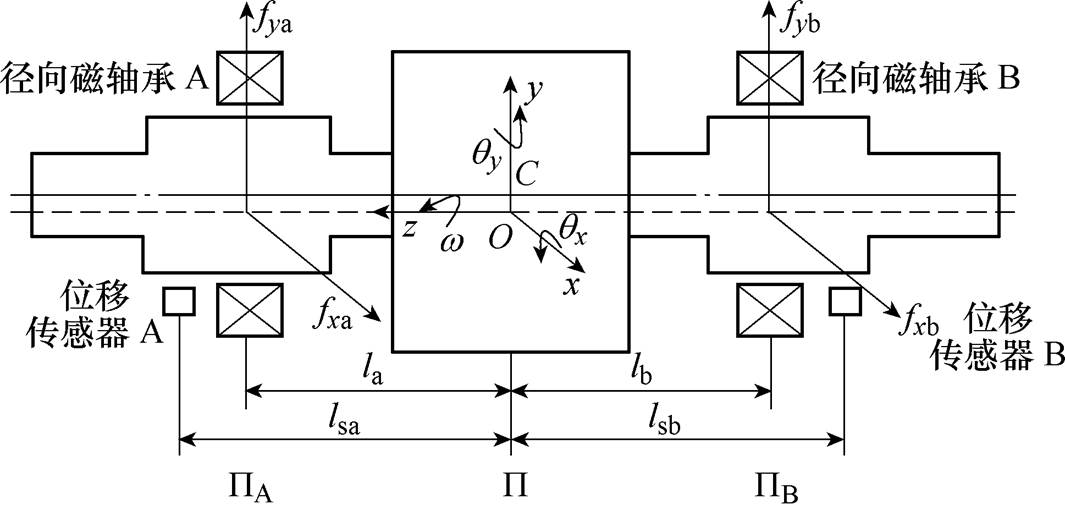
图1 磁悬浮高速电机转子结构
Fig.1 Rotor structure of magnetically levitated high-speed motor
摘要 该文针对磁悬浮高速电机的不平衡振动,提出一种基于自适应变步长最小均方误差(LMS)算法的不平衡补偿方法。首先,通过分析步长和频率对LMS算法特性的影响,给出合适的步长计算公式。之后,利用基于变步长LMS算法的自适应滤波器,在线识别转子位移信号中与转速同频的振动分量,并通过反馈对转子的同频振动进行不平衡补偿,以实现最小位移控制。然后,利用广义根轨迹法分析了引入不平衡补偿后转子系统的闭环稳定性。通过切换步长符号,实现转子系统在全转速范围内的闭环稳定运行。最后,分别在频率匹配、频率失配、存在噪声和恒加速四个条件下,将该方法应用于四自由度转子的仿真模型中,并且在磁悬浮高速电机实验平台上进行了相关实验。仿真和实验结果均表明,该方法能够有效地抑制转子的不平衡振动。
关键词:磁悬浮高速电机 不平衡补偿 最小均方误差 根轨迹
采用主动电磁轴承(Active Magnetic Bearings, AMBs)的高速电机,其额定转速可达每分钟几万转甚至十几万转,在输出功率相同时,其体积远小于常规电机,所以在气体压缩机、制冷机、涡轮分子泵、飞轮储能等领域得到了广泛应用[1-2]。
由于材料、加工精度及工作变形等原因,转子存在一定的不平衡。旋转过程中,转子不平衡产生的不平衡力引起转子的不平衡振动,不仅影响了转子的运行精度,还降低了系统的可靠性,所以必须对转子的不平衡振动进行有效的控制。
根据控制目标,刚性转子系统的不平衡振动控制可分为自动平衡控制和不平衡补偿两种方式[3-4]。
自动平衡控制是通过抵消或过滤传感器输出信号中的不平衡位移信号,使控制器不对该信号产生控制力,从而令转子绕其惯性轴旋转。B. Shafai等提出了一种称为“自适应力平衡(Adaptive Forced Balancing, AFB)”的控制方法,通过AFB补偿器,输出转速同频补偿信号,抵消传感器输出信号中的转速同频量,从而令控制器不产生对转速同频信号的响应[5]。R. Herzog等将广义窄带陷波器用于磁悬浮转子不平衡振动的控制中,利用某一转速下的灵敏度矩阵来计算该转速下的陷波器参数[6]。孙岩桦等利用Herzog算法进行了实验,并证明了算法在很大的转速范围内均具有良好的效果[7]。K. Nonami等提出一种基于尝试-调整方法的不平衡振动控制方法[8]。F. Betschon等通过增益调度自适应控制,获得转子不平衡量参数,进行自动平衡[9]。K. Y. Lum等提出通过某一转速下辨识得到的不平衡量参数,在全转速范围内对转子不平衡振动进行补偿[10]。A. Rundell等[11]、A. Mohamed等[12]分别采用滑模控制及Q参数化法实现自动平衡控制。韩邦成等设计了滑模变结构扰动观测器,对同频不平衡扰动力和力矩进行补偿[13]。蒋科坚等通过检测在施加试探性激振信号后电流中转速同频信号分量的幅值和相位的变化,直接获取不平衡干扰的Fourier系数,从而得到精确的补偿信号[14]。Zheng Shiqiang等将前馈控制策略与自适应陷波器相结合,分别补偿不平衡振动力中的位移刚度力分量和电流刚度力分量,实现自动平衡控制[15]。自动平衡法虽然可以减小电流或者电磁力,但无法完全抑制转子位移信号中的同频分量,不适应对转子位移精度要求较高的场合。
不平衡补偿是通过一定的算法产生一个与不平衡力大小相等、方向相反的控制力,抵消了不平衡力的作用效果,从而强迫转子绕其几何轴旋转。 J. Setiawan等利用偏置电流激励识别不平衡力,令转子绕几何轴高精度旋转,但只适用于转速变化不大的情况[16]。A. Matras等将自适应扰动抑制方法应用于磁悬浮转子系统中,在恒定频率下取得了明显的控制效果,但选取一个合理的权重矩阵比较困难,并且算法的收敛速度有待提高[17]。H. Chiacchiarini等将迭代学习算法应用于不平衡补偿中,并将采用遗忘因子和采用非因果低通滤波器这两种方法的效果进行对比,发现后者更优[18]。龙亚文等利用混合灵敏度H∞控制策略,设计鲁棒控制器,对柔性转子系统进行振动控制[19]。蒋科坚等提出了一种基于振动识别的自适应不平衡振动补偿控制方法,但该方法比较复杂,对硬件要求高[20]。R. Nezamabadi等通过H∞鲁棒控制来产生不平衡补偿力,但控制器阶次较高,不易实现[21]。
本文将自适应变步长最小均方误差(Least Mean Square, LMS)算法应用于磁悬浮高速电机转子系统的不平衡补偿控制中。首先,分析了不同步长和不同频率对于LMS算法特性的影响,选用了特定的步长计算公式,并与另外两种不同步长选择方法的LMS算法的效果进行比较。然后,采用广义根轨迹法分析了加入LMS算法后转子系统的闭环稳定性,证明了在电机运行至刚体临界转速附近时,只要切换步长的符号,就能保证刚性转子在全转速范围内的稳定运行。之后,通过仿真,分别在频率的匹配及失配、白噪声干扰以及恒加速运行等条件下,对本文采用的基于自适应变步长LMS算法的不平衡补偿方法的效果进行验证。最后,在磁悬浮高速电机平台上对于该方法的有效性进行了实验验证。
本文研究的磁悬浮高速电机转子的结构如图1所示。轴对称转子的轴向由一对永磁轴承支承,径向由两个电磁轴承支承。由于转子的工作转速远低于转子的弯曲临界转速,所以转子可以简化为一个四自由度的刚性转子系统。

图1 磁悬浮高速电机转子结构
Fig.1 Rotor structure of magnetically levitated high-speed motor
假设两端电磁轴承A和B的中心平面分别为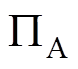 和
和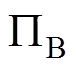 。平衡转子的质心为C,由于对称性,质心C必位于转子几何中心线上,过
。平衡转子的质心为C,由于对称性,质心C必位于转子几何中心线上,过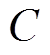 点做平行于平面
点做平行于平面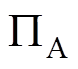 和
和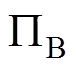 的平面
的平面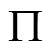 ,它与定子几何中心线交于O点。设
,它与定子几何中心线交于O点。设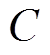 点到平面
点到平面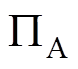 和
和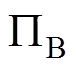 的距离分别为
的距离分别为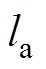 和
和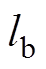 ,平面
,平面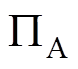 和
和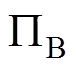 之间的距离为
之间的距离为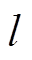 。
。
建立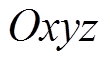 固定坐标系,其中
固定坐标系,其中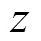 方向为转子轴向,x方向为转子径向水平方向,y方向为径向竖直方向,
方向为转子轴向,x方向为转子径向水平方向,y方向为径向竖直方向,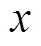 、
、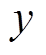 和
和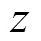 遵循右手定则。那么,就可以用转子质心在
遵循右手定则。那么,就可以用转子质心在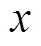 和
和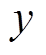 方向的平动位移(x, y)和转子绕
方向的平动位移(x, y)和转子绕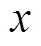 及
及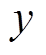 轴的角位移(
轴的角位移(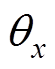 ,
,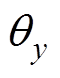 )来具体描述转子的径向运动状态。
)来具体描述转子的径向运动状态。
不平衡的转子模型,可以看作是在平衡转子模型的基础上,叠加一个不平衡质量,且叠加的不平衡质量的位置必不在原质心C点处。假设叠加的转子不平衡质量在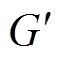 点位置,
点位置,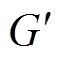 在转子几何中心平面
在转子几何中心平面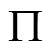 内的投影为
内的投影为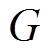 ,在
,在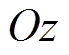 轴上的投影长度为
轴上的投影长度为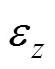 ,
,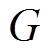 点到
点到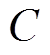 点的偏心距为
点的偏心距为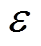 。
。
为了便于描述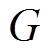 点在转子几何中心平面
点在转子几何中心平面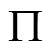 内的运动,以
内的运动,以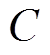 为原点,建立
为原点,建立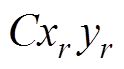 旋转坐标系,并设其旋转速度为
旋转坐标系,并设其旋转速度为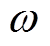 。当
。当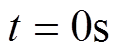 时,令旋转坐标系
时,令旋转坐标系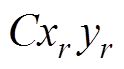 的
的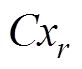 轴与
轴与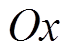 轴平行,并设此时CG与
轴平行,并设此时CG与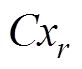 轴的夹角为
轴的夹角为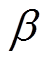 。那么,当
。那么,当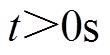 时,旋转坐标系
时,旋转坐标系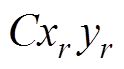 的
的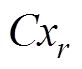 轴与
轴与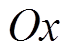 轴之间的夹角变为
轴之间的夹角变为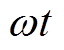 ,
,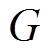 点相对于C点在
点相对于C点在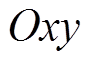 静止坐标系下的相位为
静止坐标系下的相位为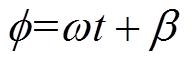 ,如图2所示。
,如图2所示。
为了建立径向四自由度磁悬浮高速电机转子系统的动力学方程,假设:①转子附加不平衡质量与转子的质量相比很小,不足以影响转子质心位置的偏移,于是不平衡转子的质心仍然在C点,不平衡转子的运动状态仍然用平衡转子质心C点的广义坐标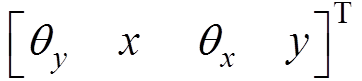 来描述;②由于轴对称,刚性转子绕x轴和绕y轴的转动惯量相同;③两端的电磁轴承A和B与位移传感器A和B不在同一个平面上内。
来描述;②由于轴对称,刚性转子绕x轴和绕y轴的转动惯量相同;③两端的电磁轴承A和B与位移传感器A和B不在同一个平面上内。
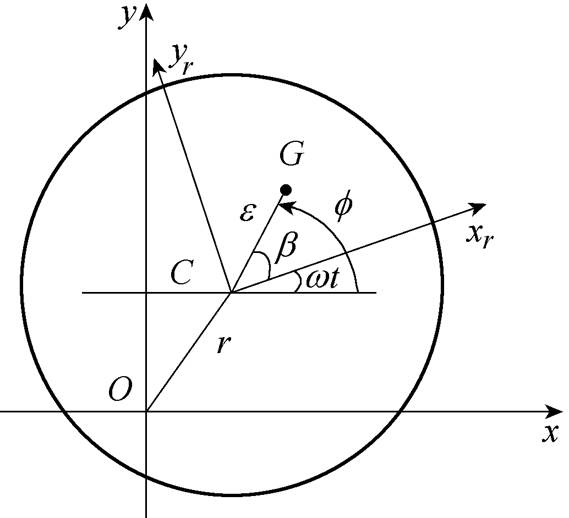
图2 转子截面示意图
Fig.2 Schematic diagram of rotor section
利用转子动力学理论,可以得到磁悬浮高速电机转子系统在变速运动过程中的运动微分方程为
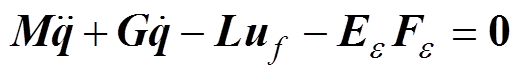 (1)
(1)其中
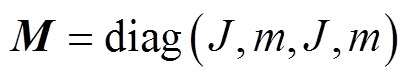
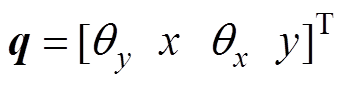
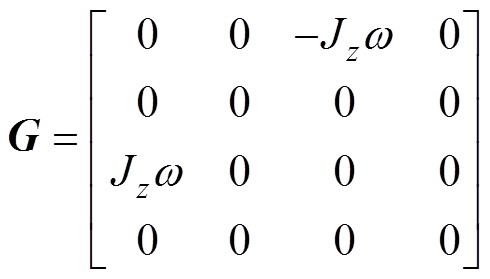
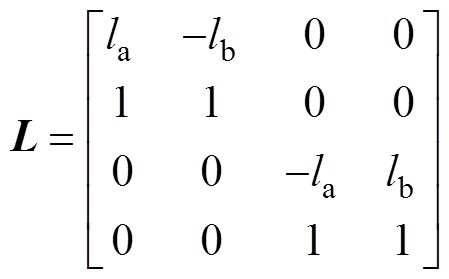
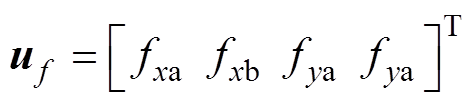
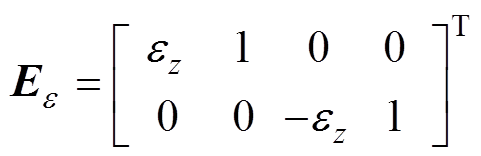
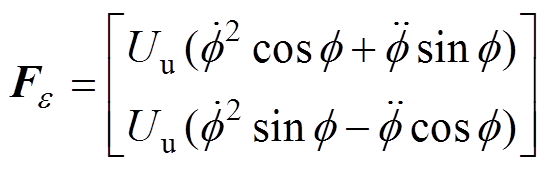
式中,m为转子的质量;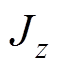 及J分别为转子绕
及J分别为转子绕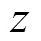 轴及绕
轴及绕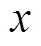 轴(
轴(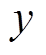 轴)的转动惯量;
轴)的转动惯量;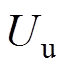 为不平衡量,通常为不平衡质量
为不平衡量,通常为不平衡质量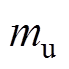 与偏心距
与偏心距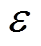 的乘积,即
的乘积,即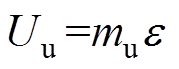 ;也可以用转子质量与等效转子质量的偏心量
;也可以用转子质量与等效转子质量的偏心量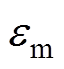 的乘积来表示,即
的乘积来表示,即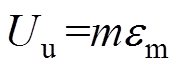 ;
;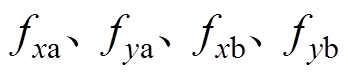 分别为电磁轴承A和B在
分别为电磁轴承A和B在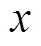 及
及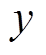 方向上的电磁力。
方向上的电磁力。
可见,转子的不平衡将导致高速电机转子系统产生同频振动,因此需要对不平衡位移进行补偿以抑制转速同频振动。
图3为基于LMS算法的自适应滤波器的结构。其中,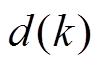 为输入信号,包含需要滤去的特定频率的正弦信号;
为输入信号,包含需要滤去的特定频率的正弦信号;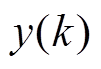 为输出信号,包括
为输出信号,包括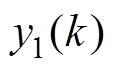 和
和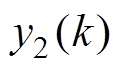 两个分量;
两个分量;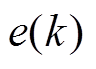 为误差信号;
为误差信号;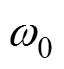 为算法的滤波角频率;
为算法的滤波角频率;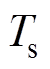 为采样周期。
为采样周期。
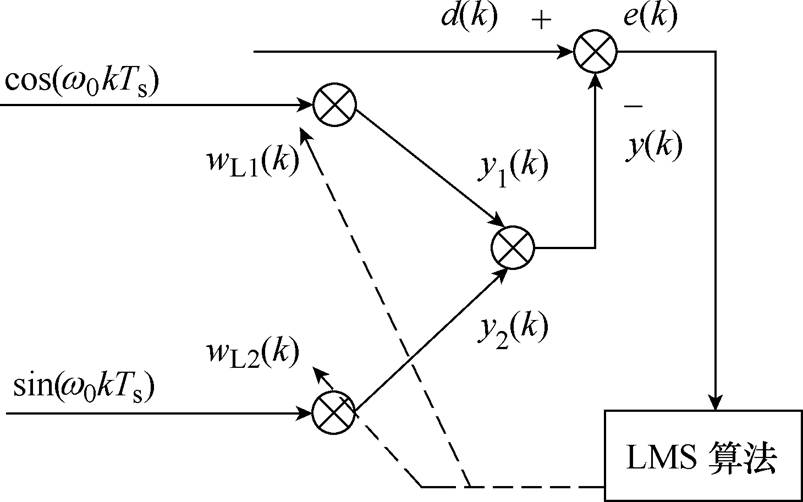
图3 基于LMS算法的自适应滤波器结构
Fig.3 Structure of adaptive filter based on LMS algorithm
则有
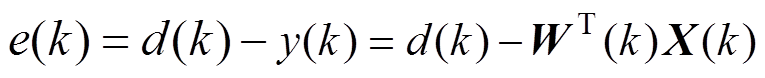 (2)
(2)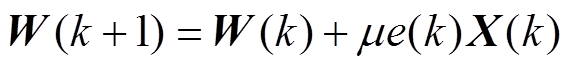 (3)
(3)
式中,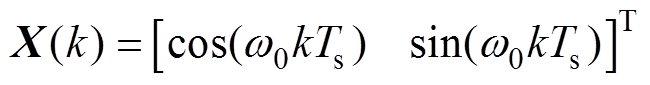 为算法的输入向量;
为算法的输入向量;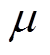 为步长;
为步长;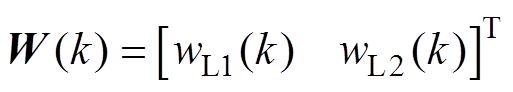 为权向量,其中,
为权向量,其中,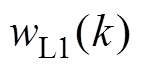 和
和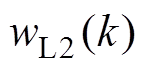 分别为
分别为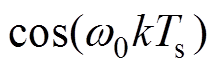 和
和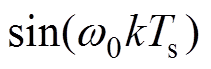 的幅值。
的幅值。
利用z变换可以得到从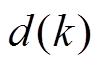 到
到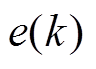 的脉冲传递函数为
的脉冲传递函数为
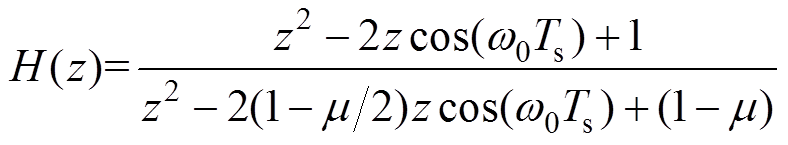 (4)
(4)由式(4)可知,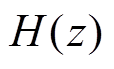 的零点为
的零点为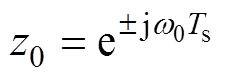 。可知,对于
。可知,对于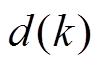 中角频率为
中角频率为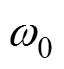 的正弦信号分量,相对应的
的正弦信号分量,相对应的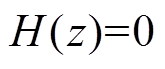 ,这表明LMS算法可以完全滤去输入信号中角频率与
,这表明LMS算法可以完全滤去输入信号中角频率与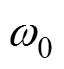 相同的正弦信号分量。
相同的正弦信号分量。
当采样周期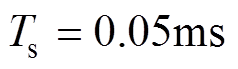 (以下所有仿真和实验均在该采样周期下进行)时,在同一输入信号频率
(以下所有仿真和实验均在该采样周期下进行)时,在同一输入信号频率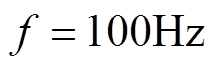 下不同步长对LMS算法效果的影响如图4所示,在同一步长
下不同步长对LMS算法效果的影响如图4所示,在同一步长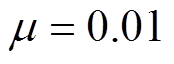 下不同频率对LMS算法效果的影响如图5所示。
下不同频率对LMS算法效果的影响如图5所示。
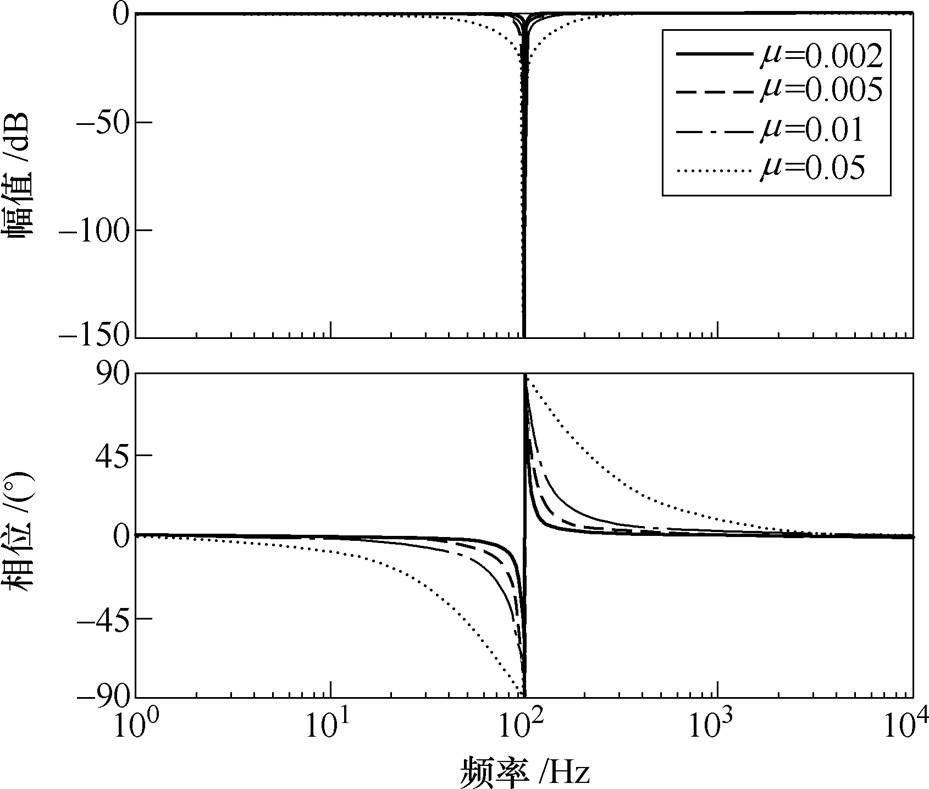
图4 不同步长对LMS算法特性的影响
Fig.4 Influence of different step sizes on LMS
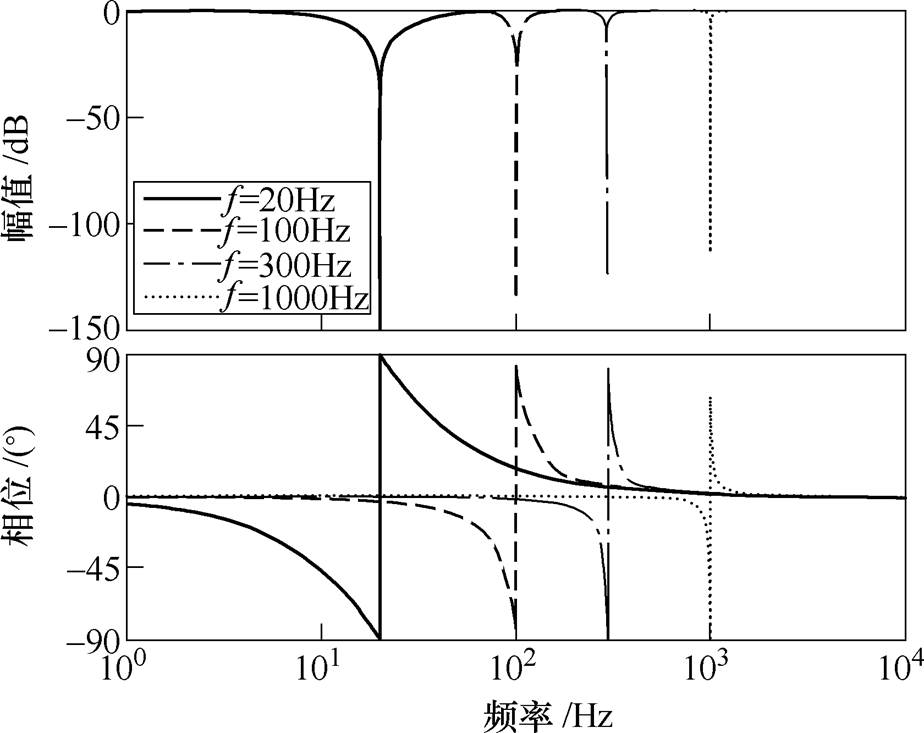
图5 相同步长不同频率下的频率特性
Fig.5 Frequency characteristics with the same step size at different frequencies
图4和图5均表明,LMS算法效果实际上与陷波器类似。由图4可知,步长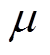 太大会导致陷波深度过深,陷波范围太大,系统容易失稳。而步长
太大会导致陷波深度过深,陷波范围太大,系统容易失稳。而步长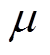 太小会导致陷波效果不理想,收敛速度太慢。因此,在固定频率下,步长
太小会导致陷波效果不理想,收敛速度太慢。因此,在固定频率下,步长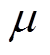 要合适,既不能太大,也不能太小。由图5可知,当
要合适,既不能太大,也不能太小。由图5可知,当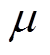 相同时,随着频率的增大,陷波深度不断降低,说明固定步长不适合应用在需要滤去的信号频率在大范围变化的场合。而在磁悬浮高速电机中的不平衡振动信号与转速同频,当转速改变时,就必须采用变步长的LMS算法,使步长
相同时,随着频率的增大,陷波深度不断降低,说明固定步长不适合应用在需要滤去的信号频率在大范围变化的场合。而在磁悬浮高速电机中的不平衡振动信号与转速同频,当转速改变时,就必须采用变步长的LMS算法,使步长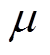 随频率的增大而适当增加,以补偿频率的增大对于陷波质量的不利影响。
随频率的增大而适当增加,以补偿频率的增大对于陷波质量的不利影响。
对于变步长的LMS算法,步长有不同的选择方法。高辉等对步长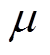 进行改进,采用的步长[22]为
进行改进,采用的步长[22]为
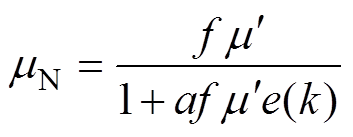 (5)
(5)式中,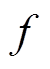 为转动频率;
为转动频率;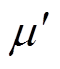 为一个非常小的正参数;
为一个非常小的正参数;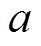 为一个恒定正参数。这样选择步长存在两个问题:一是
为一个恒定正参数。这样选择步长存在两个问题:一是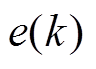 的正负会在很大程度上影响
的正负会在很大程度上影响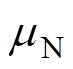 的大小。当
的大小。当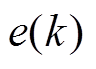 为正时,
为正时,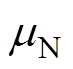 <
<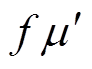 ;当
;当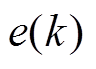 为负时,
为负时,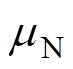 >
>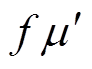 。那么,当
。那么,当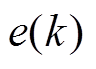 在零点附近上下波动时,
在零点附近上下波动时,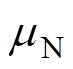 时大时小,算法的收敛速度还有待于进一步提高。二是步长
时大时小,算法的收敛速度还有待于进一步提高。二是步长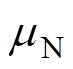 中有两个参数,调整起来比较复杂。
中有两个参数,调整起来比较复杂。
为了解决上述的问题,本文选择的步长为
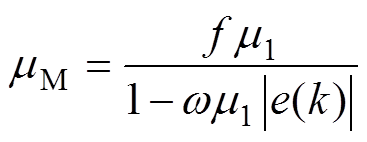 (6)
(6)式中,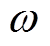 为转速;
为转速;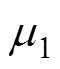 为一个很小的正数。
为一个很小的正数。
图6和图7展示了在频率匹配情况下,定步长LMS算法、高辉等的算法以及本文算法在输入信号频率分别为100Hz和300Hz时的误差响应曲线。其中,取输入正弦信号的幅值为1,定步长LMS算法的步长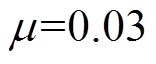 ,高辉等的算法中
,高辉等的算法中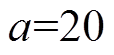 ,
,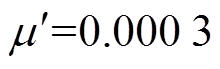 ,本文算法中
,本文算法中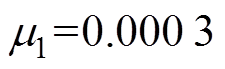 。结果表明,定步长LMS算法不适应输入信号频率变化的场合,高辉等的算法和本文算法均能适应频率变化,而本文算法在收敛过程中的幅值变化更小,收敛速度更快,具有明显优势。
。结果表明,定步长LMS算法不适应输入信号频率变化的场合,高辉等的算法和本文算法均能适应频率变化,而本文算法在收敛过程中的幅值变化更小,收敛速度更快,具有明显优势。
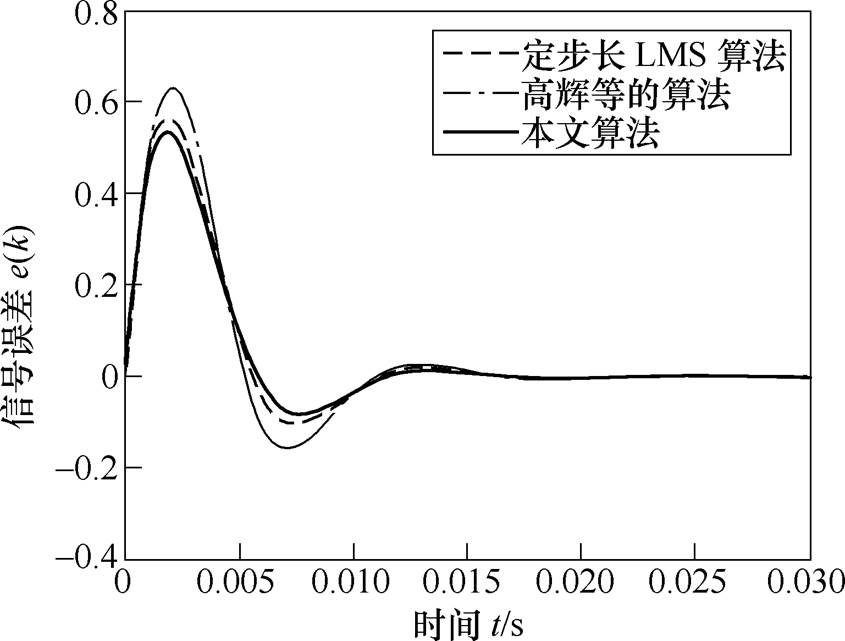
图6 在输入信号频率为100Hz时不同算法的响应对比
Fig.6 Response comparison of different algorithms when the input frequency is 100Hz
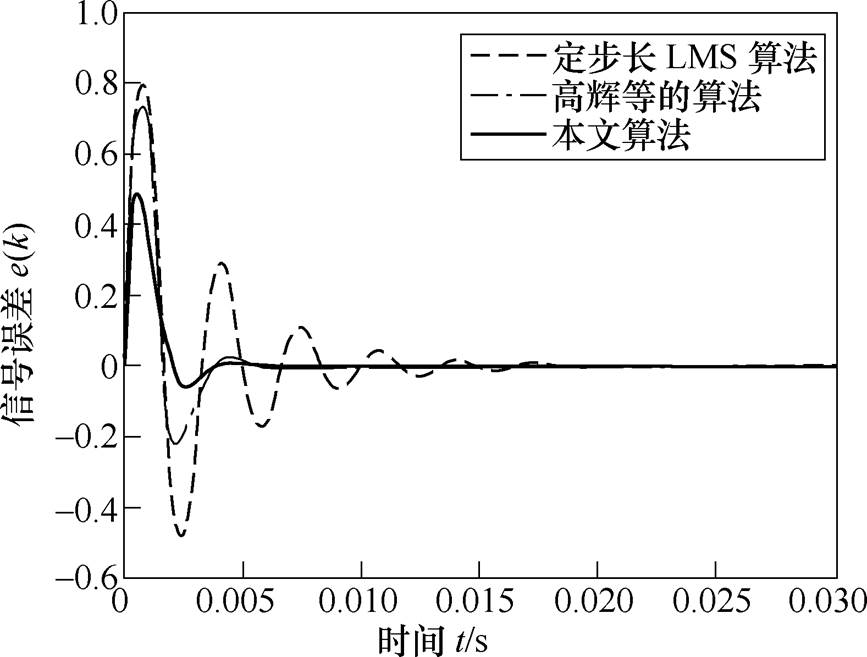
图7 在输入信号频率为300Hz时不同算法的响应对比
Fig.7 Response comparison of different algorithms when the input frequency is 300Hz
图8为基于自适应变步长LMS算法的磁悬浮高速电机转子系统不平衡补偿控制的结构框图。其原理为:首先,通过基于变步长LMS算法的自适应滤波器,获得与转速同频的位移信号。之后,通过控制器、功率放大器和执行器,产生与转速同频的控制力。该力与转子不平衡力相抵消,使转子的同频振动位移最终趋近于零。
图8中,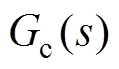 为PID主控制器的传递函数;
为PID主控制器的传递函数;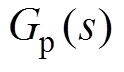 为功率放大器的传递函数;
为功率放大器的传递函数;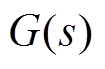 为磁悬浮转子系统的传递函数;
为磁悬浮转子系统的传递函数;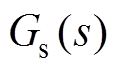 为位移传感器的传递函数。
为位移传感器的传递函数。
在系统采用最常见的PID控制的情况下,PID控制器的传递函数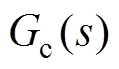 可以表述为
可以表述为
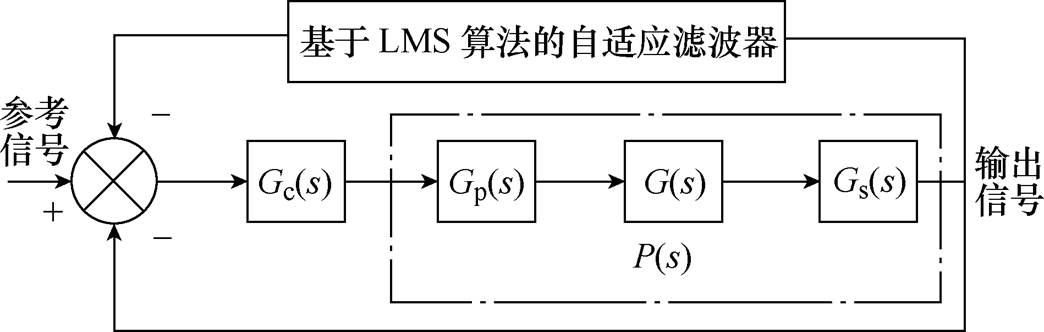
图8 基于自适应变步长LMS算法的不平衡补偿
Fig.8 Unbalance compensation based on an adaptive variable step size LMS algorithm
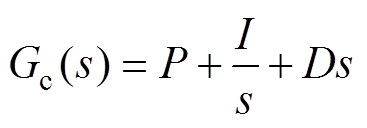 (7)
(7)式中,P、I、D分别为PID控制器的比例、微分、积分控制系数。
如果不考虑功率放大器及传感器的动态特性,它们均视为一阶线性系统,其传递函数分别为
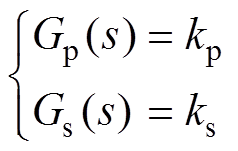 (8)
(8)式中,kp和ks分别为功率放大器及传感器的放大系数。
磁悬浮转子系统的传递函数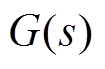 为
为
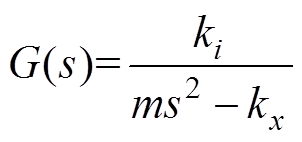 (9)
(9)式中,ki和kx分别为电磁轴承的电流刚度系数和位移刚度系数。
最后得到磁悬浮转子系统的传递函数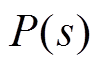 为
为
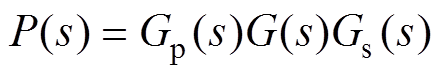 (10)
(10)图9展示了步长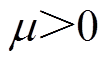 时,以转速
时,以转速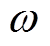 为变量的闭环系统的根轨迹。可见,闭环系统共有五条根轨迹分支,离虚轴较近的两条分支为主导根轨迹。
为变量的闭环系统的根轨迹。可见,闭环系统共有五条根轨迹分支,离虚轴较近的两条分支为主导根轨迹。
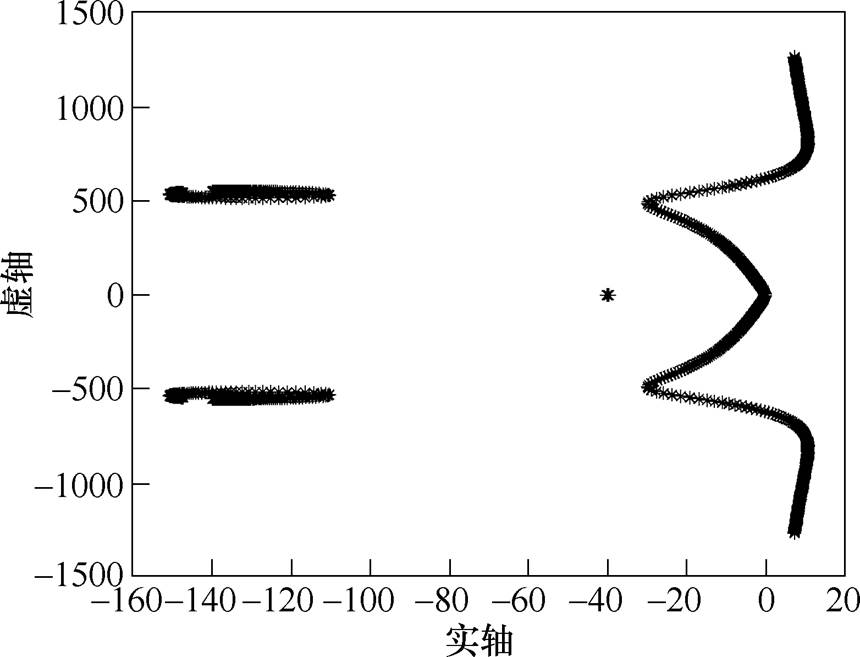
图9 步长为正时闭环系统的根轨迹
Fig.9 The root locus of closed loop system when the step size is positive
图10展示了系统的主导根轨迹。随着转速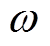 的增大,主导根轨迹从s左半平面穿越虚轴进入s右半平面,闭环系统失稳。可见,在应用基于自适应变步长LMS算法的不平衡补偿控制方法中,若步长一直取正值,转子系统无法在比刚体临界转速更高的速度下稳定运行。
的增大,主导根轨迹从s左半平面穿越虚轴进入s右半平面,闭环系统失稳。可见,在应用基于自适应变步长LMS算法的不平衡补偿控制方法中,若步长一直取正值,转子系统无法在比刚体临界转速更高的速度下稳定运行。
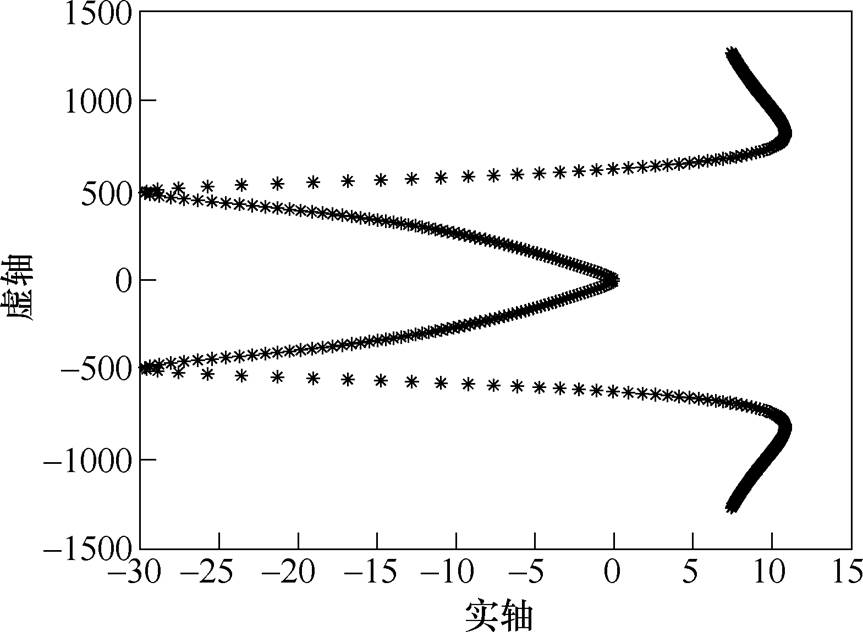
图10 步长为正时闭环系统的主导根轨迹
Fig.10 The major root locus of closed loop system when the step size is positive
由式(4)可知,步长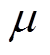 的大小不会改变基于LMS算法的自适应滤波器的传递函数的零点,因此算法对同频量仍具有滤除的作用。取步长
的大小不会改变基于LMS算法的自适应滤波器的传递函数的零点,因此算法对同频量仍具有滤除的作用。取步长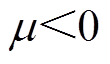 ,闭环系统的主导根轨迹如图11所示。可知,仅仅采用负步长的基于自适应变步长LMS算法的不平衡补偿控制,无法令闭环系统在比刚体临界转速更低的速度下运行。
,闭环系统的主导根轨迹如图11所示。可知,仅仅采用负步长的基于自适应变步长LMS算法的不平衡补偿控制,无法令闭环系统在比刚体临界转速更低的速度下运行。
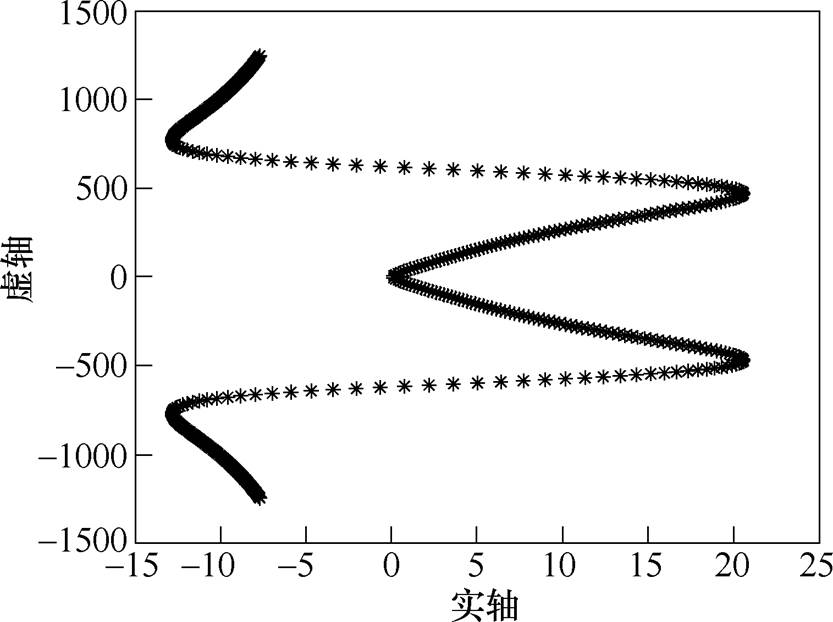
图11 步长为负时闭环系统的主导根轨迹
Fig.11 The major root locus of closed loop system when the step size is negative
由于固定符号的步长无法满足转子系统在整个转速范围内的闭环稳定性,本文提出切换步长符号的方法,用以实现基于自适应变步长LMS算法的不平衡补偿控制在全转速范围内均能够稳定运行。具体的切换规律为:当转速低于转子的刚体临界转速时,取步长为正;当转速高于转子的刚体临界转速时,取步长为负;当转速位于转子的刚体临界转速附近时,取步长为零。
应用切换步长符号的方法后,闭环系统的主导根轨迹如图12所示。可见主导根轨迹均位于s左半平面,闭环系统是稳定的。
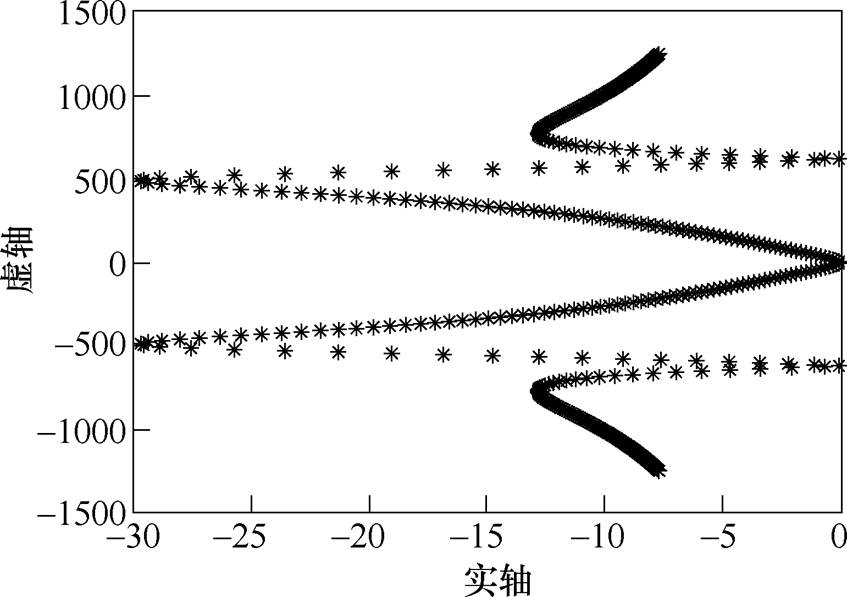
图12 应用切换步长符号的方法后的主导根轨迹
Fig.12 The major root locus under the varying step-size sign strategy
通过转子系统闭环根轨迹分析,可知转子系统的刚体临界转速对应的频率在85Hz附近。下面分别在亚临界和超临界区进行仿真分析。仿真中转子系统的各项参数见表1。
表1 磁悬浮高速电机转子系统的各项参数
Tab.1 Parameters of magnetically levitated high-speed motor rotor system

参 数数 值 转子质量m/kg18.09 转子绕x轴和y轴的转动惯量J/(kg·m2)0.2 转子绕z轴的转动惯量Jz/(kg·m2)0.02 A端到中心平面距离la/m0.13 B端到中心平面距离lb/m0.13 单边理想气隙c0/mm0.35 电磁轴承电流刚度系数ki/(N/A)577.96 电磁轴承位移刚度系数kx/(N/m)2.75×106
当转子的旋转频率分别为60Hz及150Hz时,在0.2s时分别开启基于正、负步长的自适应变步长LMS算法的不平衡补偿控制,转子A端的位移响应仿真结果如图13所示。其中,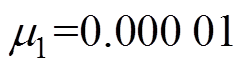 。结果表明,开启不平衡补偿控制后,转子A端的振动位移能够被迅速抑制。
。结果表明,开启不平衡补偿控制后,转子A端的振动位移能够被迅速抑制。
取转子频率为150Hz时,进行频率失配性能仿真,失配误差频率分别为148Hz、148.5Hz、149Hz、151Hz、151.5Hz及152Hz。在0.2s时开启基于自适应变步长LMS算法的不平衡补偿控制,转子A端的位移响应仿真结果分别如图14~图16所示,其中,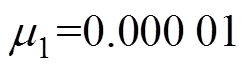 。
。
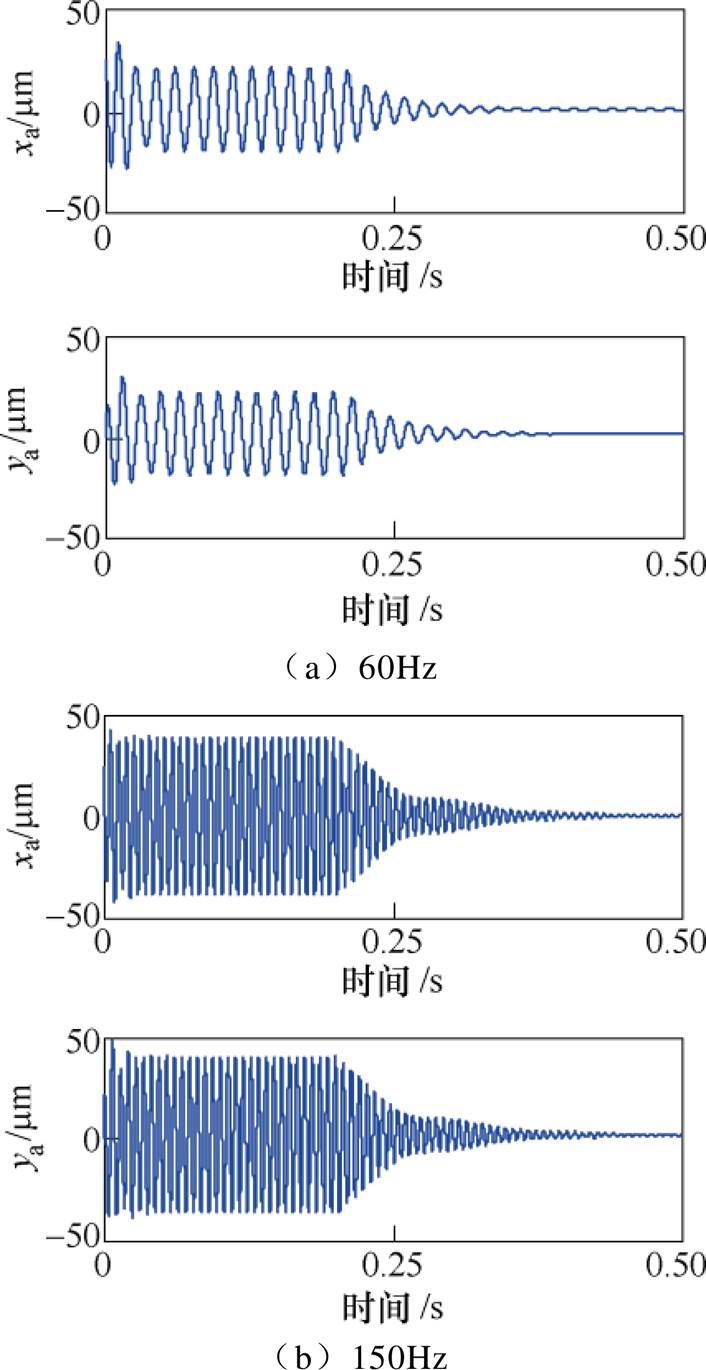
图13 转子A端的位移响应
Fig.13 Displacement response at A side
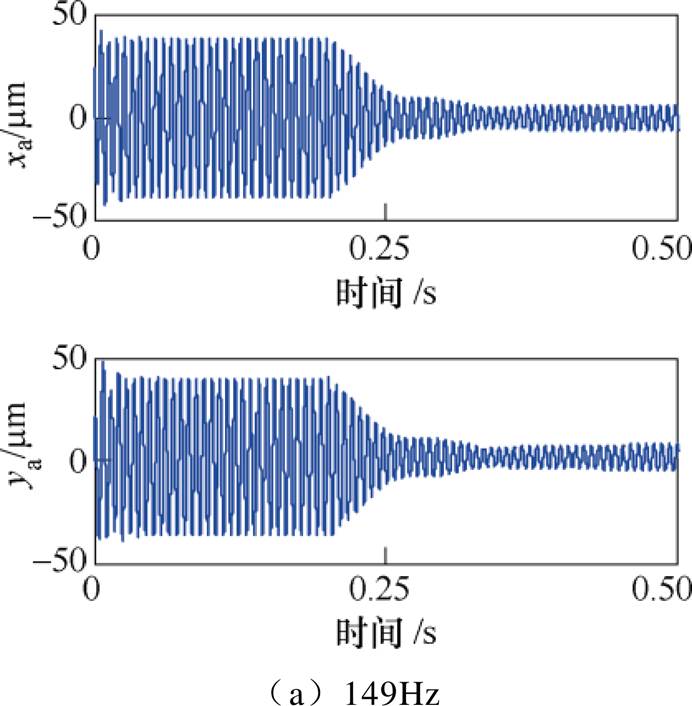
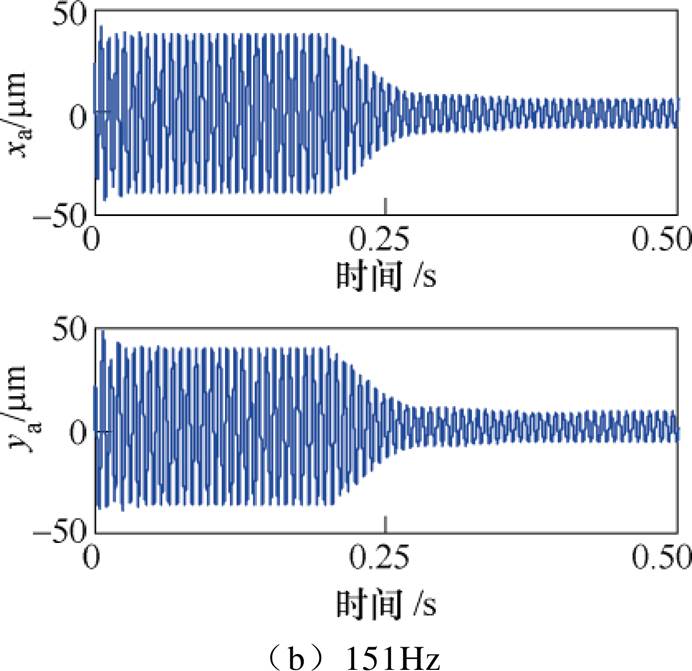
图14 频率误差为1Hz时转子A端的位移响应
Fig.14 Displacement response at A side with a frequency error of 1Hz
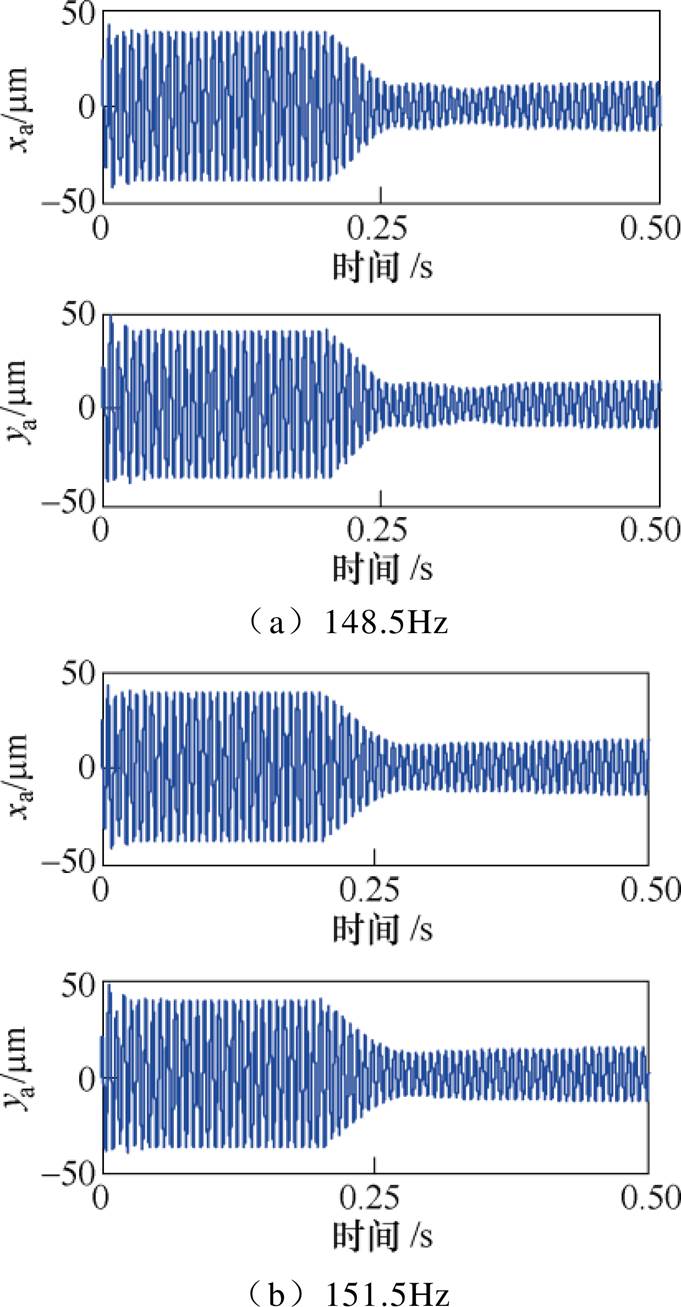
图15 频率误差为1.5Hz时转子A端的位移响应
Fig.15 Displacement response at A side with a frequency error of 1.5Hz
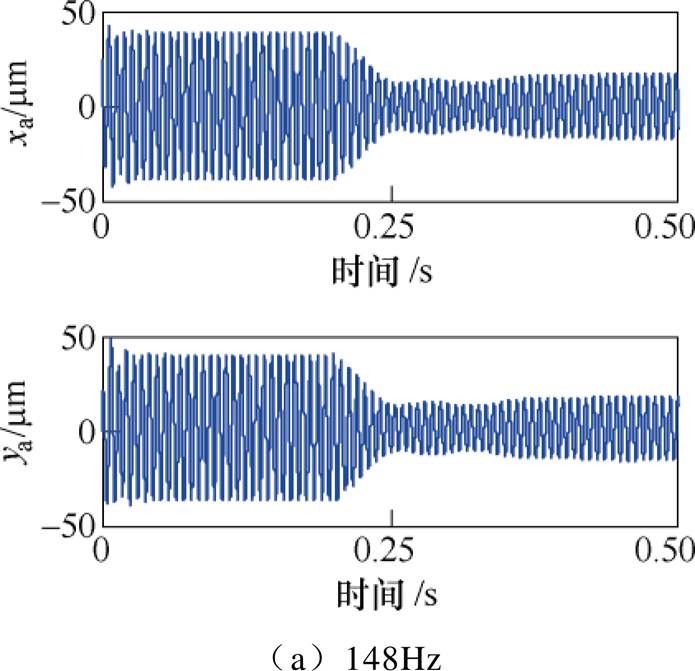
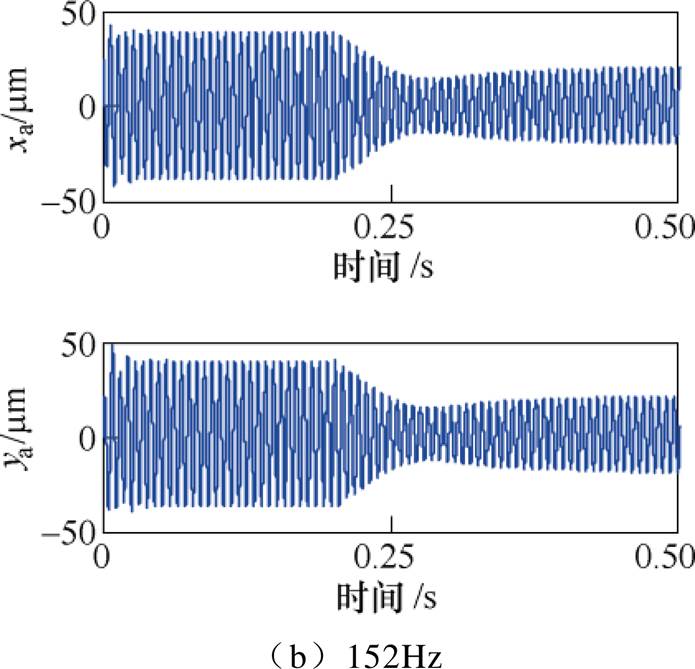
图16 频率误差为2Hz时转子A端的位移响应
Fig.16 Displacement response at A side with a frequency error of 2Hz
结果表明,采用基于自适应变步长LMS算法不平衡补偿方法,当失配频率误差为1Hz时,转子位移减小了约85%;当失配频率误差为1.5Hz时,转子位移减小了约70%;当失配频率误差为2Hz时,转子位移减小了约50%。在一定频率误差范围内,采用基于自适应变步长LMS算法的不平衡补偿,依然能够较好地抑制同频振动。
取转子的旋转频率为150Hz时,分别加入信噪比SNR=2、4、10、20的白噪声干扰。采用基于自适应变步长LMS算法的不平衡补偿控制前后,转子A端的位移响应如图17所示。
结果表明,基于自适应变步长LMS算法的不平衡补偿控制方法在一定噪声干扰下也能保证收敛,转子同频振动位移依然能够被快速抑制。
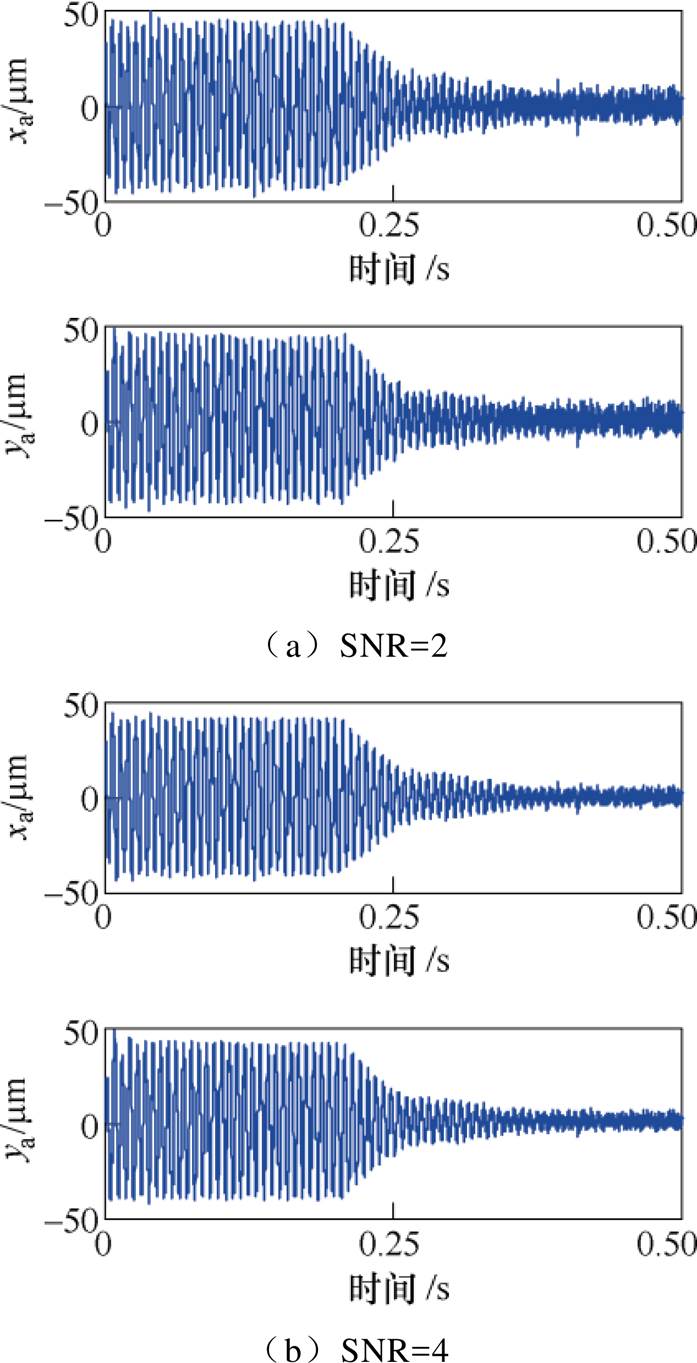
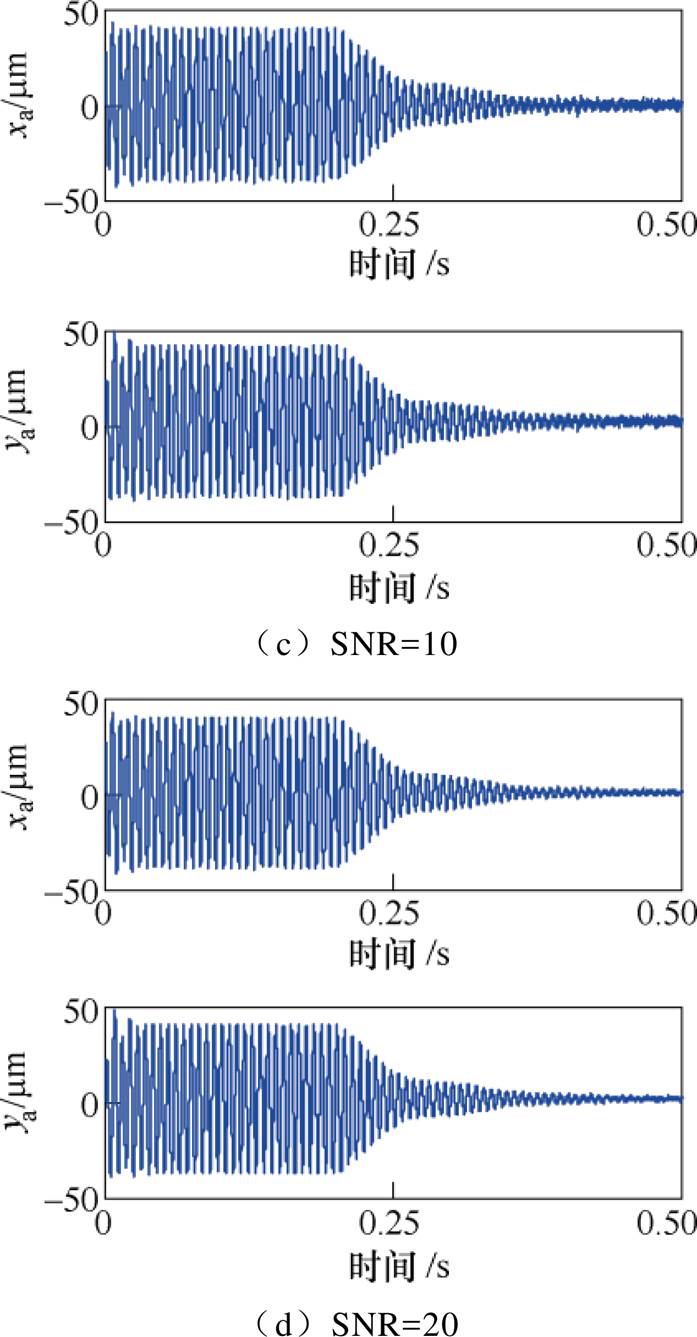
图17 不同噪声水平下转子A端的位移响应
Fig.17 Displacement response at A side with different SNRs
为了验证算法在转子恒加速过程中的效果,在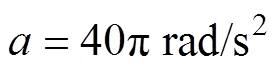 的恒加速条件下,采用基于自适应变步长LMS算法来进行不平衡补偿控制,仿真结果如图18所示。
的恒加速条件下,采用基于自适应变步长LMS算法来进行不平衡补偿控制,仿真结果如图18所示。
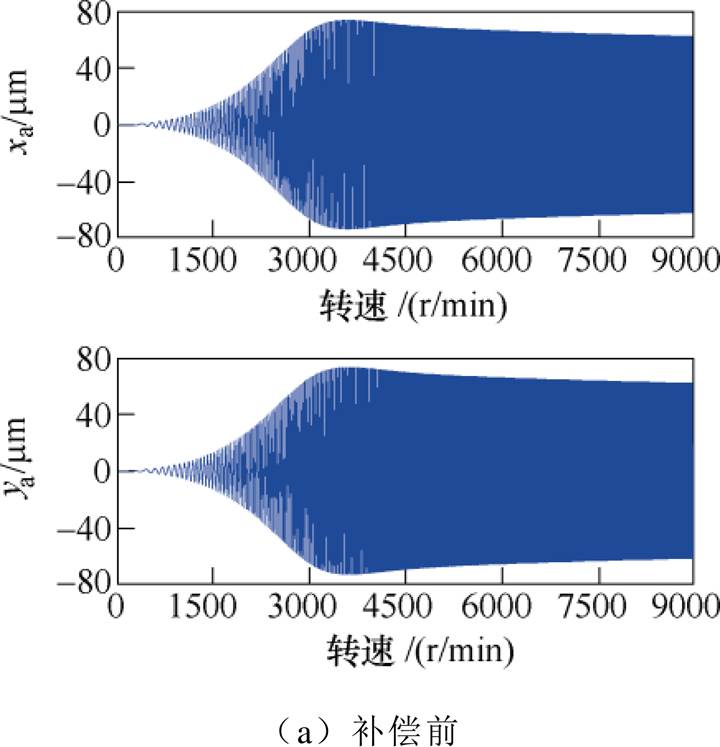
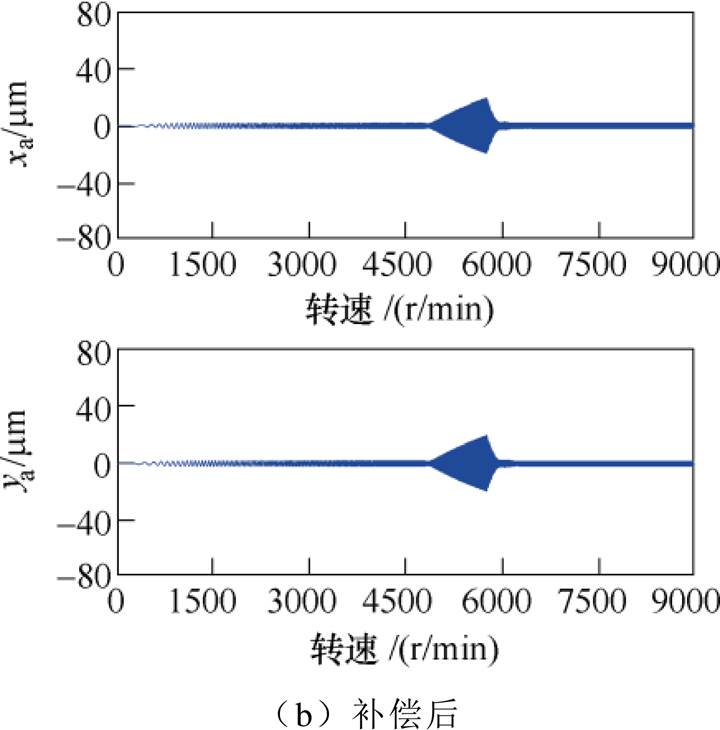
图18 恒加速条件下加入补偿前后转子A端的位移响应
Fig.18 Displacement response under constant acceleration at A side before and after compensation
可见,在采用基于自适应变步长LMS算法的不平衡补偿控制前,转子振动位移很大,最大值接近0.08mm;在采用基于自适应变步长LMS算法的不平衡补偿控制后,转子的不平衡振动得到了很好的抑制。虽然转子运行到临界转速附近时振动位移会略有增大,但位移最大值不超过0.02mm。
相关实验是在如图19所示额定功率为75kW、额定转速为24 000r/min的磁悬浮高速电机实验平台上进行的。磁悬浮转子系统主要由dSPACE控制平台、上位机、开关功放、测速模块以及电涡流位移传感器等组成。由于转子在0~9 000r/min转速范围内振动比较明显,所以这里主要给出在这个区间的试验结果。

图19 磁悬浮高速电机转子系统试验平台
Fig.19 Magnetically levitated high-speed motor rotor system test platform
为了设备安全起见,首先进行转子静态悬浮条件下的在线模拟调试。
为了在在线模拟调试中考虑转子不平衡力的影响,试验中不平衡力通过采用外加激励的方式来模拟,也就是通过控制器在转子水平及垂直方向加入与转速同频的正弦及余弦激励信号,模拟转子在转动时产生的同频不平衡力。
图20显示了模拟转速分别为3 600r/min及9 000r/min时,采用基于自适应变步长LMS算法的不平衡补偿前(左图)后(右图),转子A端的运动轨迹。可知,加入采用基于自适应变步长LMS算法的不平衡补偿控制后,转子振动被明显地抑制。
恒加速运行条件下,不平衡补偿控制前后转子的振动信号瀑布图如图21所示。可知,在恒加速条件下,采用基于自适应变步长LMS算法的不平衡补偿后,不平衡振动得到了有效的抑制,特别是在两个刚体临界转速附近。
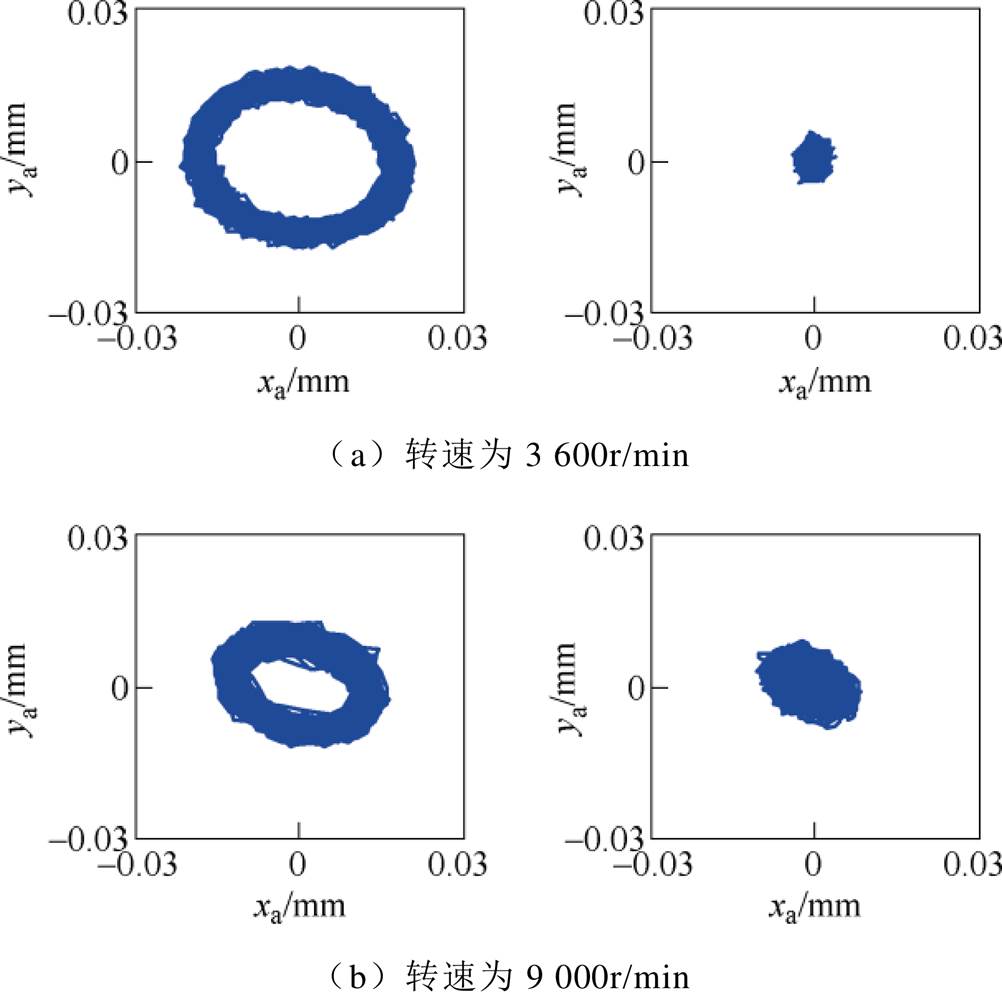
图20 加补偿前后在线模拟调试结果
Fig.20 Online simulation results before and after compensation
在确认在线模拟调试的结果与仿真结论相符后,在磁悬浮高速电机实验平台上进行旋转实验。
不平衡补偿控制前后转子的振动信号瀑布图如图22所示。采用不平衡补偿控制前,转速在5 200r/min时,转子A端在x方向和y方向上的振幅已经达到了0.09mm。若继续加速,转子可能会因振动过大而与保护轴承发生碰撞。采用不平衡补偿控制后,电机转子能够以较小的振动顺利穿越刚体临界转速,最高转速可以达到24 000r/min。在整个转速范围内,A端x方向上最大振幅不超过0.022mm,振动幅值减小约76%。
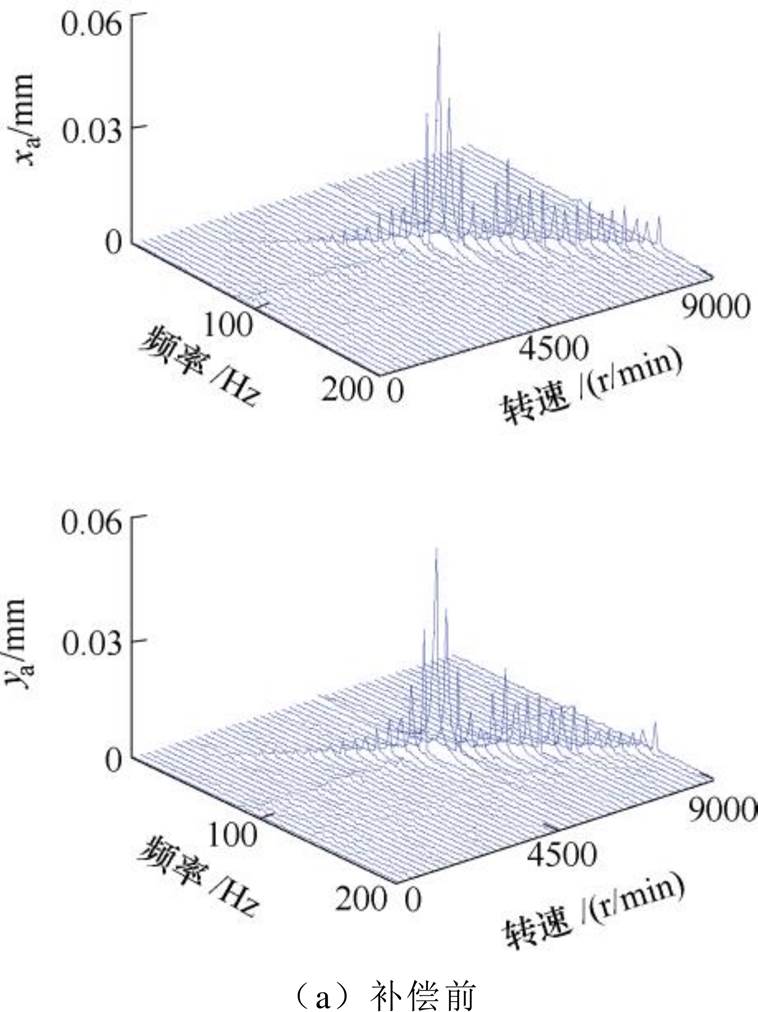
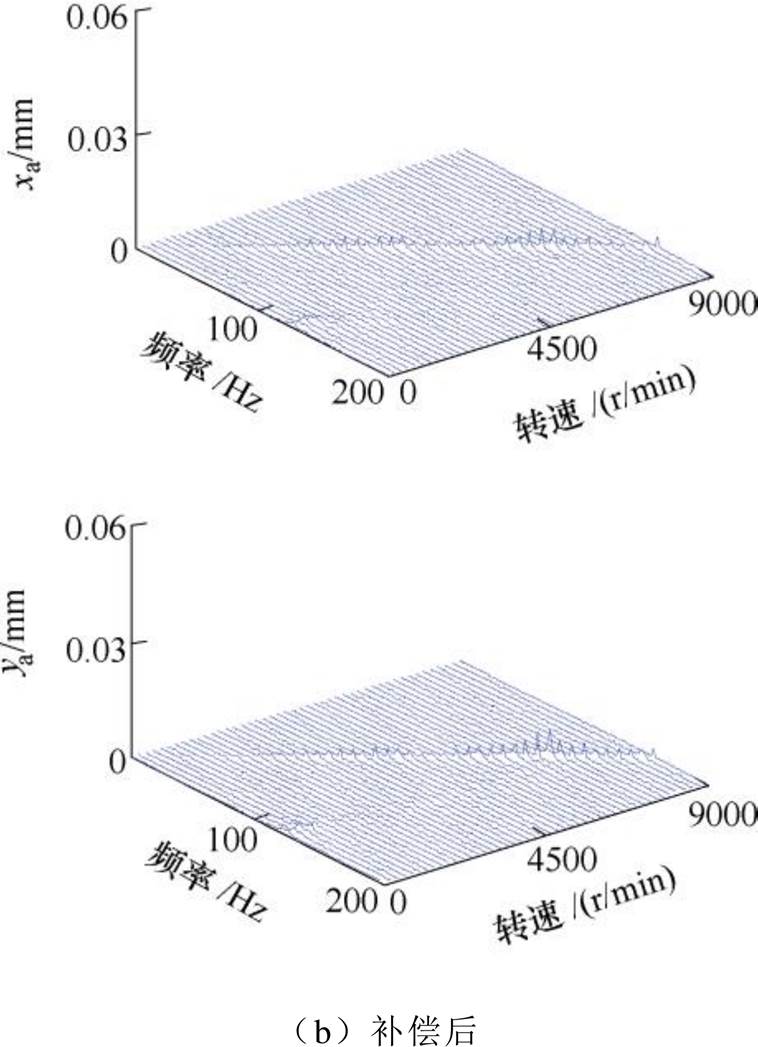
图21 补偿前后在线模拟调试A端振动信号瀑布图
Fig.21 Vibration signal waterfall of online simulation at A side before and after compensation
本文针对磁悬浮高速电机转子系统,提出了一种基于自适应变步长LMS算法的滤波器在线识别位移信号中的同频分量,通过反馈产生同频控制力以抵消转子的不平衡力,从而实现不平衡补偿控制的策略,通过切换步长符号,保证了转子系统在整个转速范围内的闭环稳定运行。仿真和实验结果表明,所提出的基于自适应变步长LMS算法的转子不平衡补偿方法能够有效地抑制转子的不平衡振动。
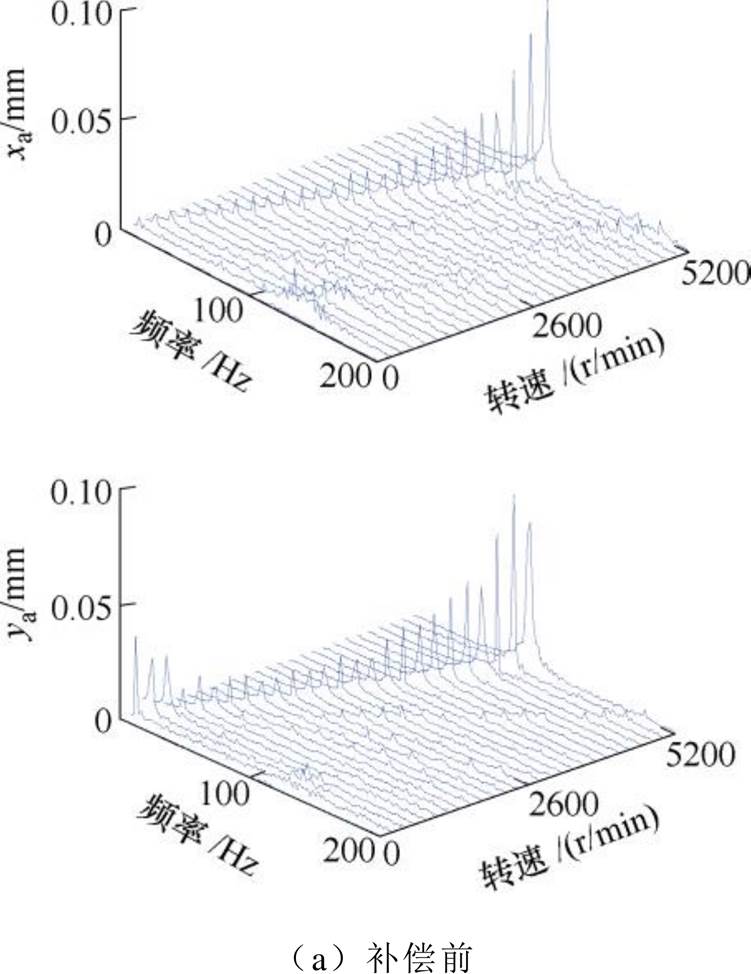
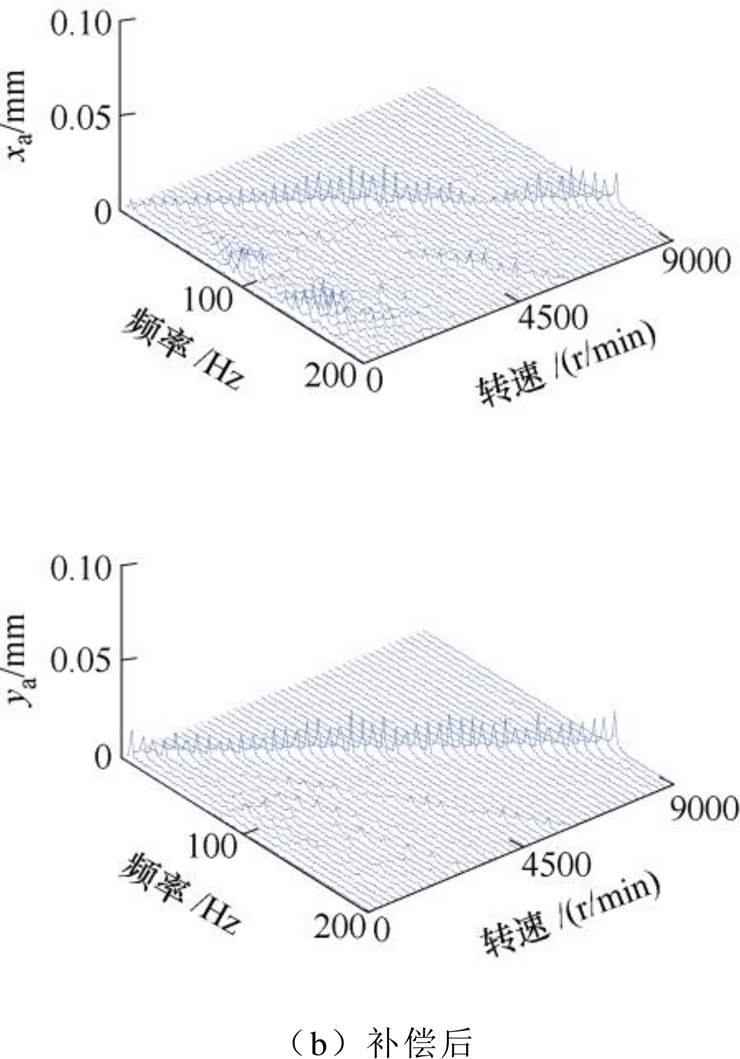
图22 补偿前后实验时A端的振动信号瀑布图
Fig.22 Vibration signal waterfall of experiment at A side before and after compensation
参考文献
[1] 于洁, 祝长生, 余忠磊. 考虑涡流的自传感主动电磁轴承转子位置估计策略[J]. 电工技术学报, 2018, 33(9): 1946-1956.
Yu Jie, Zhu Changsheng, Yu Zhonglei. Rotor position estimation strategy for self-sensing active magnetic bearing considering eddy currents[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 1946-1956.
[2] 陈亮亮, 祝长生, 王忠博. 基于逆系统解耦的电磁轴承飞轮转子系统二自由度控制[J]. 电工技术学报, 2017, 32(23): 100-114.
Chen Liangliang, Zhu Changsheng, Wang Zhongbo. Two-degree-of-freedom control for active magnetic bearing flywheel rotor system based on inverse system decoupling[J]. Transactions of China Electro- technical Society, 2017, 32(23): 100-114.
[3] 陈杰, 邓智泉, 杨艳. 无轴承开关磁阻电机质量偏心振动补偿[J]. 电工技术学报, 2016, 31(18): 13-20.
Chen Jie, Deng Zhiquan, Yang Yan. Compensation of mass eccentricity for a bearingless switched relu- ctance motor[J]. Transactions of China Electro- technical Society, 2016, 31(18): 13-20.
[4] Schweitzer G, Maslen E. Magnetic bearings: theory, design and application to rotating machinery[M]. Berlin: Springer, 2009.
[5] Shafai B, Beale S, Larocca P, et al. Magnetic bearing control systems and adaptive forced balancing[J]. IEEE Control Systems, 1994, 14(2): 4-13.
[6] Herzog R, Buhler P, Gahler C, et al. Unbalance compensation using generalized notch filters in the multivariable feedback of magnetic bearings[J]. IEEE Transactions on Control Systems Technology, 1996, 4(5): 580-586.
[7] 孙岩桦, 罗岷, 虞烈. 基于自适应陷波器的电磁轴承不平衡补偿方法[J]. 振动工程学报, 2000, 13(4): 610-615.
Sun Yanhua, Luo Min, Yu Lie. Unbalance com- pensation based on adaptive notch filter to active magnetic bearings[J]. Journal of Vibration Engin- eering, 2000, 13(4): 610-615.
[8] Nonami K, Qifu F, Ueyama H. Unbalance vibration control of magnetic bearing systems using adaptive algorithm with disturbance frequency estimation[J]. JSME International Journal, 2008, 41(2): 220- 226.
[9] Betschon F, Knospe C R. Reducing magnetic bearing currents via gain scheduled adaptive control[J]. IEEE/ASME Transactions on Mechatronics, 2001, 6(4): 437-443.
[10] Lum K Y, Coppola V T, Bernstein D S. Adaptive autocentering control for an active magnetic bearing supporting a rotor with unknown mass imbalance[J]. IEEE Transactions on Control Systems Technology, 1996, 4(5): 587-597.
[11] Rundell A, Drakunov S, Decarlo R. A sliding mode observer and controller for stabilization of rotational motion of a vertical shaft magnetic bearing[J]. IEEE Transactions on Control Systems Technology, 1996, 4(5): 598-608.
[12] Mohamed A, Ilene B. Imbalance compensation and automatic balancing in magnetic bearing systems using the Q-parameterization theory[C]//Proceedings of American Control Conference, Baltimore, Maryland, USA, 1994: 2952-2957.
[13] 韩邦成, 崔华, 汤恩琼. 基于滑模扰动观测器的磁轴承主动振动控制[J]. 光学精密工程, 2012, 20(3): 563-570.
Han Bangcheng, Cui Hua, Tang Enqiong. Vibration suppression of magnetic bearing based on sliding mode disturbance observer[J]. Optics and Precision Engineering, 2012, 20(3): 563-570.
[14] 蒋科坚, 祝长生. 基于不平衡识别的主动电磁轴承转子系统自动平衡[J]. 振动工程学报, 2009, 22(6): 559-564.
Jiang Kejian, Zhu Changsheng. Auto balance of active magnetic bearings for rotor support system by means of unbalance identification[J]. Journal of Vibration Engineering, 2009, 22(6): 559-564.
[15] Zheng Shiqiang, Feng Rui. Feedforward com- pensation control of rotor imbalance for high-speed magnetically suspended centrifugal compressors using a novel adaptive notch filter[J]. Journal of Sound and Vibration, 2016, 366: 1-14.
[16] Setiawan J, Mukherjee R, Maslen E. Synchronous disturbance compensation in active magnetic bearings using bias current excitation[C]//Proceedings of IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Como, Italy, 2001: 707- 712.
[17] Matras A, Flowers G, Fuentes R, et al. Suppression of persistent rotor vibrations using adaptive tech- niques[J]. Journal of Vibration and Acoustics, 2003, 128(6): 682-689.
[18] Chiacchiarini H, Mandolesi P. Unbalance compen- sation for active magnetic bearings using ILC[C]// Proceedings of IEEE International Conference on Control Applications, Mexico City, Mexico, 2001: 58-63.
[19] 龙亚文, 谢振宇, 徐欣. 磁悬浮轴承H∞ 鲁棒控制策略研究[J]. 振动与冲击, 2013, 32(23): 115-120.
Long Yawen, Xie Zhenyu, Xu Xin. H∞ robust control strategy for an active magnetic bearing[J]. Journal of Vibration and Shock, 2013, 32(23): 115-120.
[20] 蒋科坚, 祝长生. 主动电磁轴承转子系统自适应不平衡补偿控制[J]. 浙江大学学报: 工学版, 2011, 45(3): 503-509.
Jiang Kejian, Zhu Changsheng. Adaptive unbalance compensation control of active magnetic bearing sup- porting rotor system[J]. Journal of Zhejiang University: Engineering Science, 2011, 45(3): 503-509.
[21] Nezamabadi R, Poshtan J, Jahed-Motlagh M. Robust control design to imbalance compensation and automatic balancing of magnetic bearings[C]// Proceedings of IEEE International Conference on Industrial Technology, Mumbai, India, 2006: 1093- 1098.
[22] 高辉, 徐龙祥. LMS类算法在磁轴承滤波补偿中的应用分析[J]. 中国机械工程, 2011, 22(1): 9-14.
Gao Hui, Xu Longxiang. Analysis of kinds of LMS algorithms in application of filtering compensation for magnetic bearings[J]. China Mechanical Engin- eering, 2011, 22(1): 9-14.
Unbalance Compensation for Magnetically Levitated High-Speed Motors Based on Adaptive Variable Step Size Least Mean Square Algorithm
Abstract For unbalance vibration in magnetically levitated high-speed motors, a modified adaptive variable step-size least mean square (LMS) algorithm was proposed to achieve unbalance compensation. Firstly, a formula to get appropriate step size was given by analyzing the influence of step size and frequency on the characteristics of LMS algorithm. Then, with the help of an adaptive filter based on variable step-size LMS algorithm, the minimum displacement control was achieved by online identifying speed-frequency component in displacement signal and adding feedback control. In addition, the stability of closed-loop system was analyzed using generalized root locus. In order to achieve unbalance compensation within the whole speed range, a varying step-size sign strategy was used. Finally, the proposed method was applied to the simulation model of four-degree-of-freedom rotor under the four conditions of frequency matching, frequency mismatching, noise existing and constant acceleration, and relevant experiments were carried out on the magnetically levitated high-speed motor rotor system test platform. Simulation and experimental results show that the proposed method can effectively suppress the imbalance synchronous vibration.
keywords:Magnetically levitated high-speed motor, unbalance compensation, least mean square (LMS), root locus
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.190386
国家自然科学基金(116320154)和国家重点研发计划(2018YF0905500)资助项目。
收稿日期2019-04-08
改稿日期 2019-08-22
周天豪 男,1996年生,博士研究生,研究方向为高速转子系统振动主动控制。E-mail: zhouth419@163.com
祝长生 男,1963年生,教授,博士生导师,研究方向为转子系统动力学、高速电机及飞轮储能等。E-mail: zhu_zhang@zju.edu.cn(通信作者)
(编辑 赵 鹏)