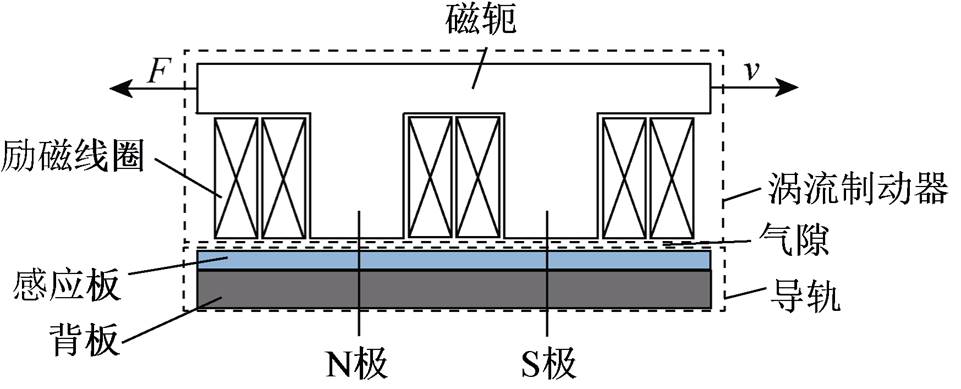
图1 涡流制动装置原理图
Fig.1 Schematic diagram of eddy-current braking device
摘要 涡流制动系统对于磁悬浮列车安全运行至关重要。该文采用子域法解析得到速度（包括超高速）、励磁电流、气隙长度、感应板厚度和电导率等参数与涡流制动力之间的解析式。在二维坐标系下建立解析模型，以磁矢位为求解变量，在解析模型各个子域内列写泊松方程，并结合各子域之间的边界条件求得气隙内的磁通密度表达式，进而得到涡流装置所受涡流制动力的表达式。利用有限元仿真证明了解析计算的正确性，并探究超高速下磁浮列车应用涡流制动系统的可行性。使用解析计算对涡流制动力进行参数分析，得到优化超高速涡流制动系统的方法。相比于仿真分析，解析计算能够反映涡流制动力产生机理并具有节省计算时间的优点。
关键词：超高速磁浮 涡流制动力 子域法 解析计算 有限元仿真 参数分析
涡流制动是高速磁浮列车在紧急制动情况下使用的重要制动系统，因此确保涡流制动系统的安全可靠十分关键[1]。涡流制动装置的制动力与列车速度、制动器励磁电流、制动器与感应板之间气隙长度、感应板厚度和电导率等变量存在复杂的关系，其中涡流制动力与速度之间的关系尤为重要，因为它是列车运行控制系统判断列车运行状态的重要依据。由于制动力是涡流器的主要性能指标，多位学者在这方面做了一些研究工作，文献[2]从Maxwell方程出发，推导得到涡流制动力特性方程，分析了速度、励磁电流和气隙长度对制动力的影响，然而特性方程计算过程做了大量简化，准确性较低；文献[3]采用有限元计算方法对涡流制动力进行分析，但结论只是定性地介绍了制动力与速度、励磁电流、感应板电导率和磁导率之间的关系；Marc T. Thompson虽然给出了计算涡流制动力的经验公式，并分析了涡流制动力随速度变化的特性[4]，但是只是针对较低速下涡流制动力的特性进行分析；在文献[5]中，作者推导了涡流制动力解析表达式，并给出了峰值制动力与临界速度点的表达式，但作者是针对永磁涡流制动进行的分析；文献[6]利用等效磁路法以及几何计算法对涡流制动试验平台进行了设计，并利用电磁场理论和有限元仿真对涡流制动力进行了计算，但其计算分析是针对旋转模型。文献[7]采用磁等效电路法、子域法和有限元法对一种新型混合励磁线性涡流制动器进行了研究；文献[8]提出了一种计算鼓式涡流制动器制动力的新方法，表明当感应板的电导率降低时，涡流制动器产生的最大转矩点会向高速移动；文献[9-10]利用子域法通过分子域处理，列写各子域内的微分方程，结合模型的边界条件对永磁电机模型进行准确计算，并通过有限元法验证了解析计算的正确性。
目前，涡流制动力的研究主要针对中低速运动装置，对于速度超过600km/h（166.7m/s）的超高速磁浮运动装置，由于速度高且磁场变化复杂，鲜有文献探究其应用的可行性及其涡流制动力的变化特性。此外，超高速使得涡流制动试验平台的设计、制造非常困难，涡流制动装置不仅速度高而且体积大、制造成本高，通过实际样机得到的实验结果来验证并改进设计方案的做法不容易实现。故在超高速磁浮涡流实际装置制造前需对制动力与各变量之间的关系有较为准确的定量分析，以指导装置的设计调整，由此说明了本文研究工作的重要性。
本文重点分析涡流装置在高速及超高速 （≥400km/h）下涡流制动力的特性。通过二维电磁场理论推导出涡流制动力与速度、励磁电流、气隙长度、感应板厚度及电导率之间的关系式，并用卡特系数对气隙长度进行修正，给出解析计算结果。然后利用有限元仿真软件建立二维仿真模型对涡流制动力进行仿真计算，以验证理论公式的正确性、解析计算结果的准确度以及高速下应用涡流制动的可行性，之后通过参数分析提出改进高速及超高速下涡流制动力性能的方法。与有限元仿真相比，利用求解得到的涡流制动力解析式进行不同工况下制动力的计算，计算速度快，能节省大量的时间和计算资源，可作为分析设计高速及超高速下涡流制动系统的有效工具。
涡流制动原理图如图1所示，涡流制动系统由涡流制动器、导轨以及两者之间的气隙组成。涡流制动器由磁轭、磁极以及励磁线圈组成，涡流制动器的N极、S极交替排列；导轨由感应板及背板组成，其中背板起到支撑感应板以及闭合磁路的作用。当涡流制动器与导轨做相对运动时，将在感应板上产生随时间变化的磁感应强度，根据电磁感应定理，时变的磁感应强度将在导电的感应板内感应出涡流。涡流磁场与励磁磁场叠加使得励磁磁场发生畸变，在运行方向上涡流制动器的前端部分的磁场被削弱，后端的磁场被加强，在与运行方向相反的方向上形成一个水平分力F，即为涡流制动力[11-12]。
图1 涡流制动装置原理图
Fig.1 Schematic diagram of eddy-current braking device
下面利用子域法[13-17]并根据电磁场理论公式以及涡流制动装置各个区域的边界条件进行涡流制动力解析式的推导。
由于子域法只能对二维模型进行求解，在此忽略涡流制动装置的横向端部效应进行二维等效。图2为涡流制动一对极下二维简化模型，区域Ⅰ为涡流制动器，分为铁心以及励磁线圈，铁心材料为导磁钢，励磁线圈材料为铜；区域Ⅱ由气隙与气隙上方的感应板组成，感应板采用非铁磁的导电材料；区域Ⅲ为导磁背板，材料为硅钢叠片。并给出假设：①铁磁区域Ⅰ、Ⅲ的相对磁导率为无穷大[18]；②忽略区域Ⅲ内涡流的影响；③感应板的相对磁导率为1，且不考虑感应板涡流的趋肤效应；④区域Ⅰ中的励磁电流等效为区域Ⅰ与区域Ⅱ分界面上的线电流密度[19]，且线电流均匀分布在该分界面的薄层中。
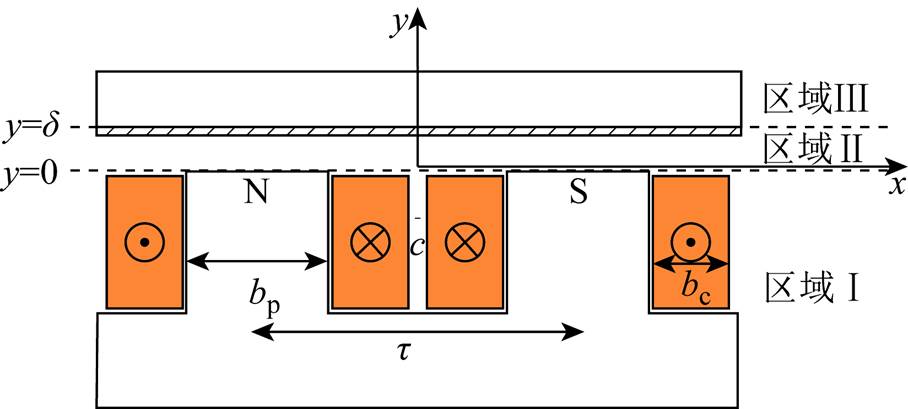
图2 涡流制动二维简化模型
Fig.2 Two-dimensional simplified model of eddy current braking
图2中，d 为气隙长度，t 为制动器极距，bp为制动器磁极宽度，bc为励磁线圈宽度，c为两相邻线圈间距离。
因为在二维平面内求解，所以区域Ⅰ、Ⅱ、Ⅲ的磁通密度B只有x和y方向的分量，即
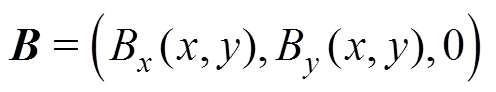（1）为了求解磁通密度B的表达式，需要引入磁矢位A作为待求场函数[20-21]，上述三个区域内泊松方程的一般表达形式为
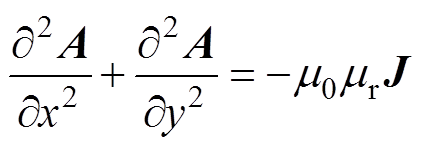（2）
式中，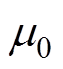
为真空磁导率；
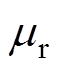为材料的相对磁导率；J为电流密度矢量。
在整个求解区域中电流密度J只有z方向分量，即
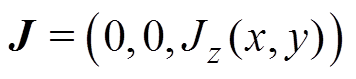（3）因而整个求解区域的磁矢位A也只有z方向分量，即
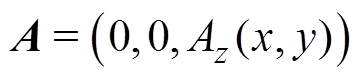（4）
根据分离变量法得到磁矢位A在z方向分量的表达式为[22]
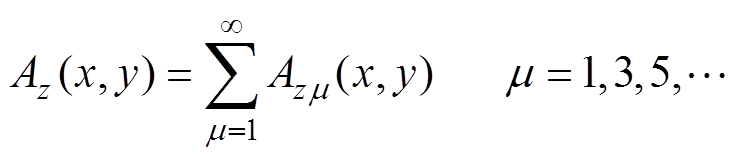（5）
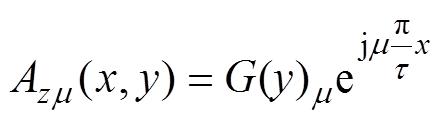（6）
式中，m 为谐波次数；G(y)m 为待求的y的函数；j为虚数单位；t 为极距。
在图2中，假设④虽然对区域Ⅰ中的磁通密度计算结果有影响，但不影响区域Ⅱ与Ⅲ中的磁通密度，可确保涡流制动力求解结果的正确性。同时把感应板内的涡流作为区域Ⅱ与区域Ⅲ边界条件的线电流密度考虑。
可认为区域Ⅰ、Ⅱ、Ⅲ都没有电流源，因此对于整个求解区域来说，泊松方程式（2）变为拉普拉斯方程，把式（6）代入式（2）中得
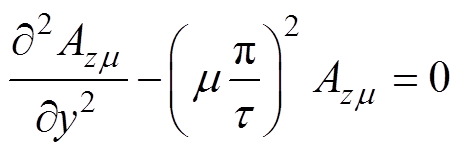（7）根据式（7）解得整个求解区域的磁矢位的m 次谐波表达式为
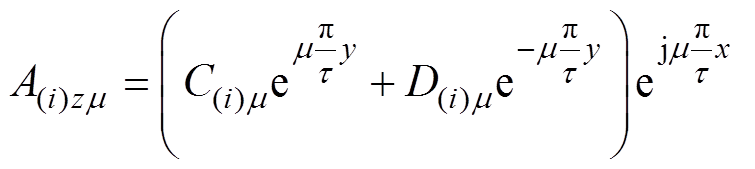（8）
式中，C(i)m、D(i)m 为待求常数，i代表区域编号，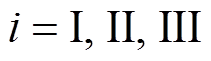
。
根据式（8）可得整个求解区域磁通密度B在x、y方向上的m 次谐波表达式为
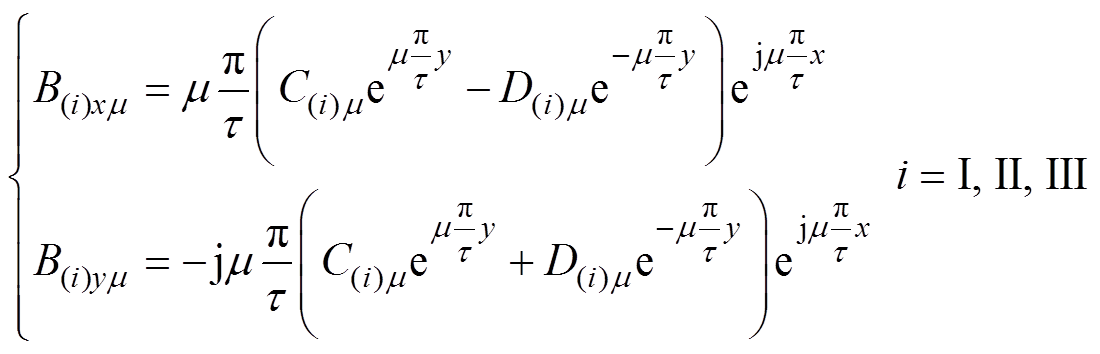（9）为求解式（9）中的待求常数，需对磁场边界条件进行分析，磁场中不同区域分界面上的衔接条件为
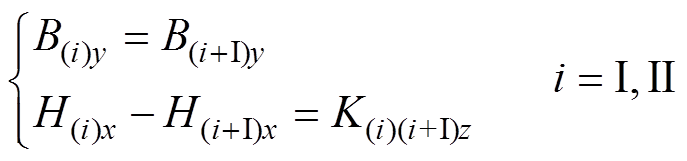（10）式中，By为磁通密度的法向分量；Hx为磁场强度的切向分量；Kz为区域分界面上线电流密度的z向 分量。
下面分析区域Ⅰ与区域Ⅱ分界面、区域Ⅱ与区域Ⅲ分界面的边界条件。
1.3.1 区域Ⅰ与区域Ⅱ分界面线电流密度
上面提到，在图2中区域Ⅰ的励磁电流可按磁势相等原则等效为区域Ⅰ与区域Ⅱ分界面线电流密度，其分布曲线如图3所示。
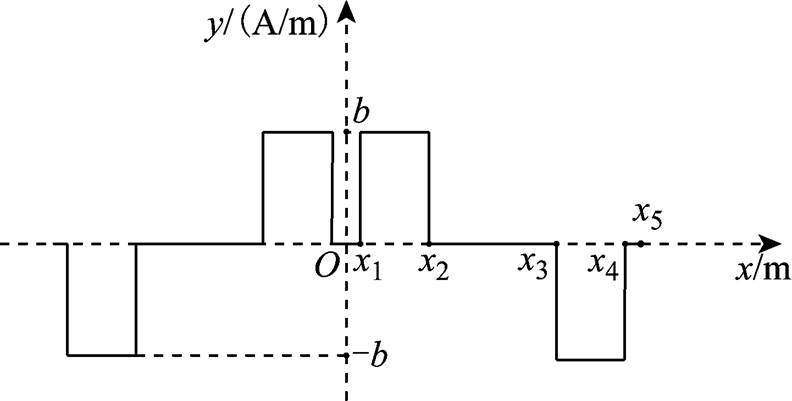
图3 区域Ⅰ与区域Ⅱ分界面线电流密度分布曲线
Fig.3 Curve of linear current density distribution on the interface between region Ⅰ and region Ⅱ
图3中曲线的横坐标表达式见表1。
表1 图3横坐标表达式
Tab.1 Expressions of horizontal coordinate in Fig.3
参 数表达式 x1c/2 x2c/2+bc x3t-(c/2+bc) x4t-c/2 x5t
对图3中的线电流密度曲线进行傅里叶分解，表达式中只有奇次分量，即
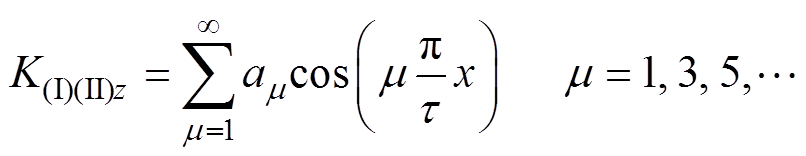（11）其中
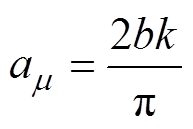（12）
线电流密度常数b与励磁线圈电流密度J、励磁线圈截面积S、线圈槽满率kf、励磁线圈宽度bc的关系为
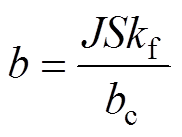（13）设k为线电流密度分布系数，k可写成
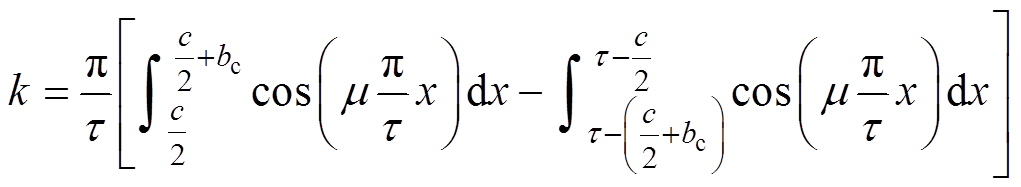（14）
根据式（11），且为计算方便，得区域Ⅰ与区域Ⅱ分界面线电流密度的m 次谐波表达式为
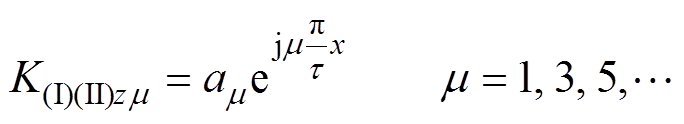（15）1.3.2 区域Ⅱ与区域Ⅲ分界面线电流密度
根据磁路中欧姆定律
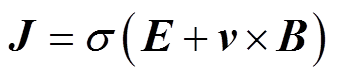（16）式中，s 为感应板电导率；E为电场强度矢量；v为导轨与涡流制动器之间相对速度。
由于在感应板中只有运动电动势，没有感应电动势，且感应板内的涡流近似等效为区域Ⅱ与区域Ⅲ分界面的线电流密度，则在区域Ⅱ与区域Ⅲ分界面y=d 处的线电流密度的m 次谐波表达式为
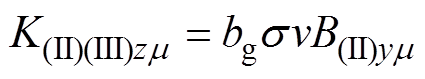（17）式中，bg为感应板厚度。
结合式（9）、式（10）、式（15）、式（17）求得在区域Ⅱ与区域Ⅲ分界面y=d 处x方向与y方向的磁通密度m 次谐波为
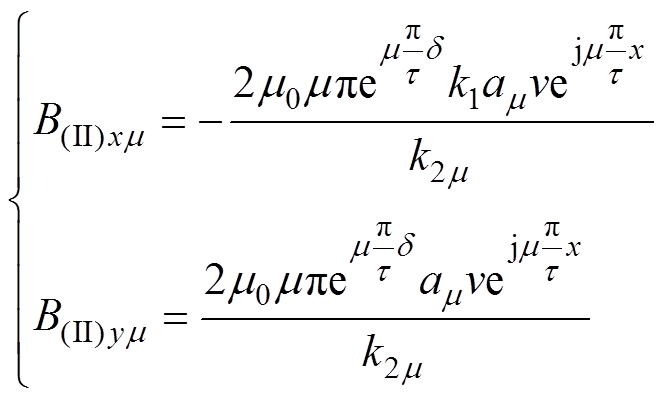（18）式中，k1、k2m 为相应系数，表达式为
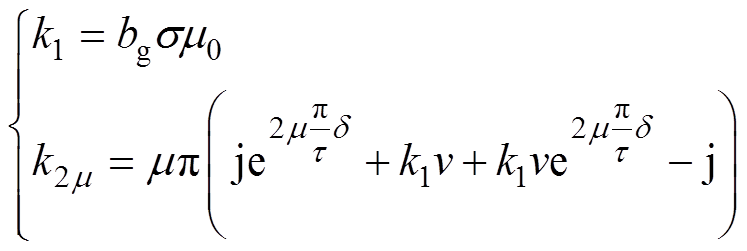（19）
根据麦克斯韦张力公式[23-24]得到感应板所受的涡流制动力的m 次谐波分量为
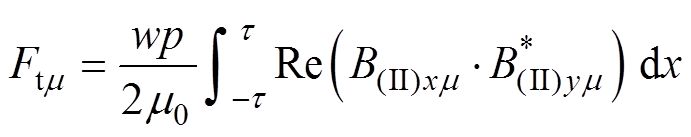（20）式中，“*”表示共轭。
计算得涡流制动力的m次谐波表达式为
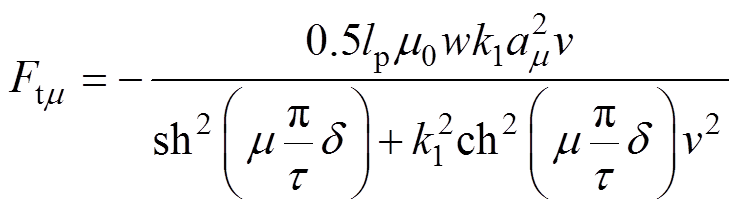（21）式中，lp为涡流制动器总长，lp=2pt，p为极对数；w为涡流制动器垂直纸面深度。则总制动力为
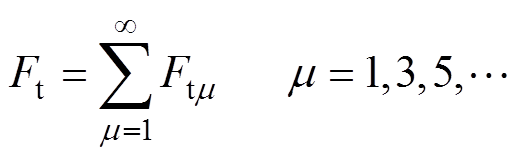（22）
由此本文得到了涡流制动力与速度、励磁电流、气隙长度、感应板厚度和电导率以及涡流制动器结构尺寸的解析式。
由于定子开槽，需要用卡特系数kC对气隙宽度进行修正[25]，修正后的气隙长度为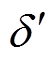
等于kC与d 之积，其中卡特系数为
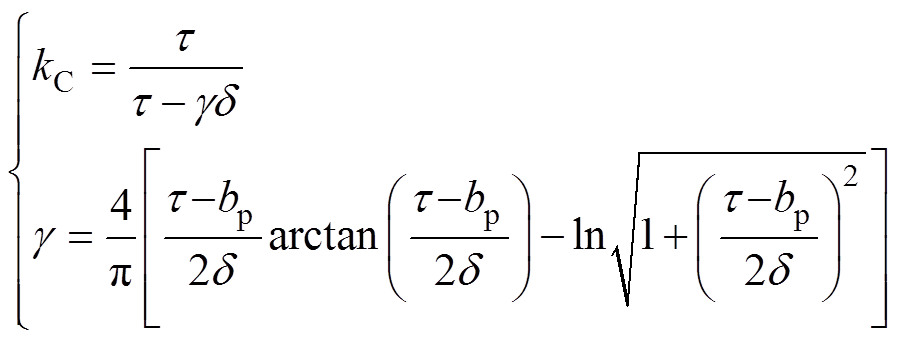（23）在解析计算时使用修正后的气隙长度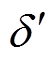与有限元仿真计算时的气隙长度更为相符。
根据目前实验室某磁浮项目（以下简称项目）的需求，在有限元仿真软件Ansoft Maxwell中里建立涡流制动二维仿真模型，利用有限元仿真结果验证理论计算结果的正确性，表2为模型在额定工况下的输入参数。
表2 模型额定工况参数
Tab.2 Rated operating parameters of model
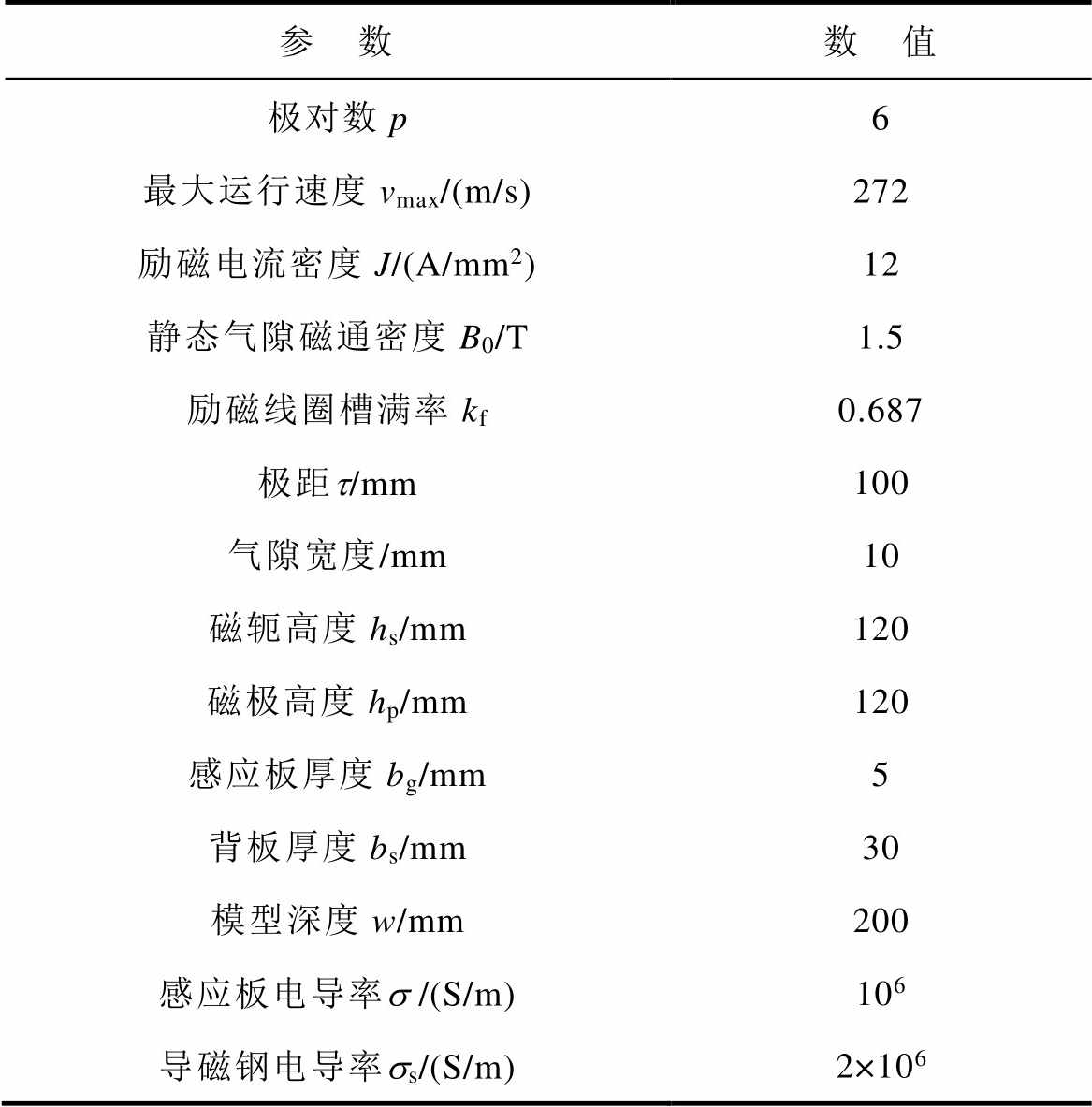
参 数数 值 极对数p6 最大运行速度vmax/(m/s)272 励磁电流密度J/(A/mm2)12 静态气隙磁通密度B0/T1.5 励磁线圈槽满率kf0.687 极距t/mm100 气隙宽度/mm10 磁轭高度hs/mm120 磁极高度hp/mm120 感应板厚度bg/mm5 背板厚度bs/mm30 模型深度w/mm200 感应板电导率s /(S/m)106 导磁钢电导率ss/(S/m)2×106
根据表2所给出的模型基本参数，利用等效磁路法[26]计算单个闭合磁路中总磁动势为
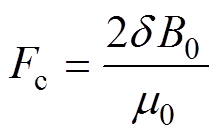（24）根据励磁线圈电流密度以及槽满率计算励磁线圈的横截面积
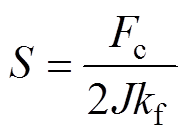（25）
进而求得励磁线圈以及磁极的有关尺寸，计算得到的模型有关参数见表3。
表3 模型计算参数
Tab.3 Calculation parameters of the model
参 数数 值 励磁线圈截面积S/mm21 759.5 磁极宽度bp/mm69.6 励磁线圈高度hc/mm115 励磁线圈宽度bc/mm15.3
根据表2、表3设计得到涡流制动有限元仿真模型如图4所示。
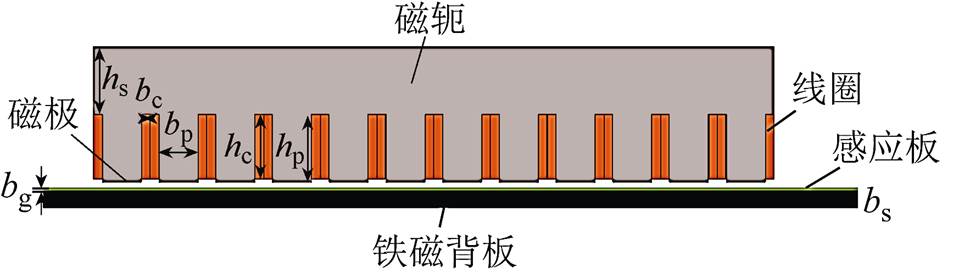
图4 涡流制动有限元仿真模型
Fig.4 Finite-element simulation model of eddy current braking
在图4中，上方为涡流制动器，其中磁轭和磁极选用导磁钢（型号为steel_1008）。励磁线圈采用铜线圈；下方为导轨，感应板采用非铁磁的导电材料，为减小背板内的涡流损耗，其材料采用硅钢片（型号为35WW270），且考虑其中磁饱和的影响。在有限元仿真软件里采用瞬态求解器仿真，涡流制动器以一定的速度相对轨道运动。由于采用二维有限元仿真模型，在仿真过程中没有考虑模型的横向端部效应。
根据上述模型额定工况，在有限元仿真软件中进行动态模型求解，仿真速度的步长为15m/s，且根据项目需求，模型运行的最大速度为272m/s（对应0.8Ma）。
为验证在解析计算中假设忽略背板内的涡流损耗具有合理性，现分别计算在本文重点研究的速度范围内，涡流制动器高速运行时的下限速度110m/s和超高速运行时的上限速度272m/s这两个速度点的感应板以及背板的涡流分布情况。经有限元计算，110m/s时，背板中涡流损耗为总损耗（背板中涡流损耗与感应板中涡流损耗之和）的4.22%；272m/s时，背板中涡流损耗为总损耗的2.17%。由此可以看出，在以上两种边界情况下，背板中涡流损耗占总损耗不足5%，因此为简化计算，在解析计算时忽略背板内的涡流影响具有合理性。
接下来分析背板的饱和情况，图5得到了仿真模型在110m/s时的磁通密度分布云图。
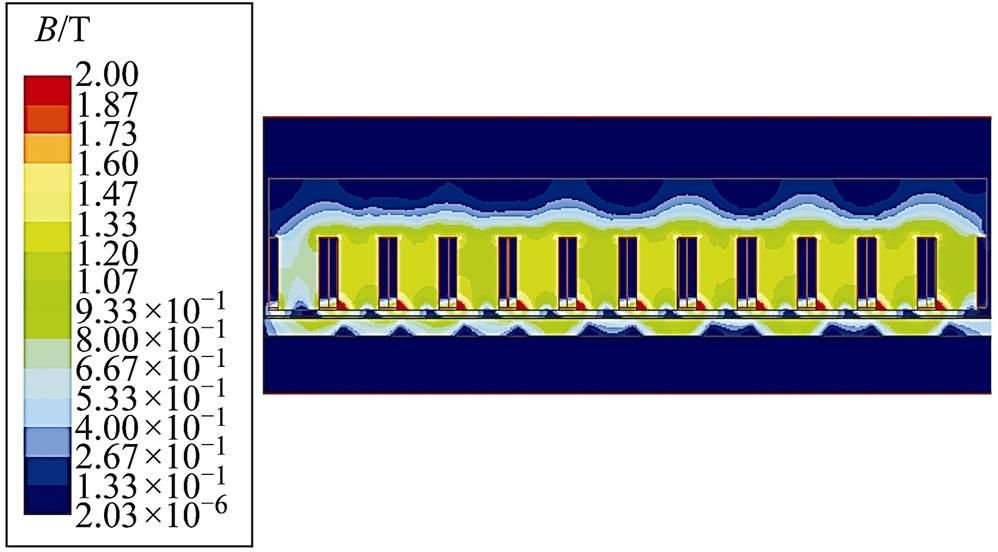
图5 110m/s时仿真模型磁通密度分布云图
Fig.5 Distribution field diagram of magnetic density distribution of simulation model at 110m/s
在图5中，背板中磁通密度的最大值约为0.98T，结合背板材料属性可以看出背板并未达到饱和。同时随着速度的增加，由于受背板内涡流趋肤效应的影响，背板内的磁通密度会变得越来越小，因此在高速以及超高速下背板基本不受磁饱和的影响，这里与解析计算中假设背板的相对磁导率为无穷大 一致。
图6得到涡流制动力随速度变化的解析解与仿真解对比曲线。
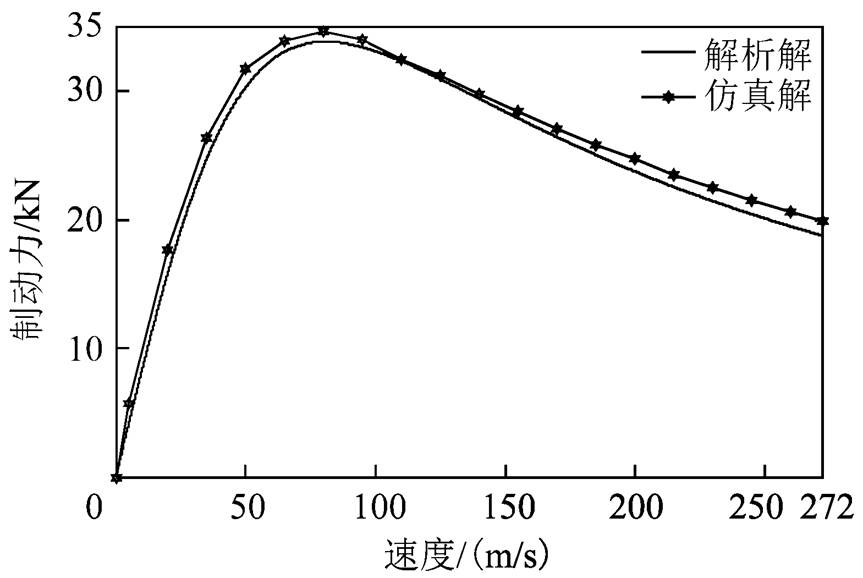
图6 涡流制动力随速度变化曲线
Fig.6 Curves of eddy current braking force varying with speed
从图6可以看出，理论计算结果与仿真结果基本吻合，同时涡流制动力随着速度的增加先快速上升，然后缓慢下降，在90m/s处达到涡流制动力的最大值。并且发现在超高速（≥600km/h，约为167m/s）下涡流制动力虽有所下降，也可保持相对较高的数值，相比其他传统制动方式，涡流制动方便且操控性好，验证了磁浮列车在超高速下应用涡流制动的可行性。但仿真解略高于解析解，这是由于在解析计算中忽略了感应板涡流的趋肤效应、背板饱和以及背板内涡流的影响，使得解析计算时涡流磁场有所减弱，从而导致涡流制动力的解析计算值低于仿真值。根据图6，在高速及超高速下解析解与仿真解的最大误差为-5.68%，误差在合理的范围内。综上，理论推导正确，计算结果准确度高，下面利用式（22）进行涡流制动力的参数分析。
本节根据涡流制动力解析式（22）分析励磁电流、气隙长度、感应板厚度和电导率对涡流制动力的影响。对以上参数一一进行分析，思路为选定某一参数为变量，其他参数均采用额定工况数值。根据图6，可大致认为110m/s这个速度点是制动力开始下降的临界点，同时也是高速段的起始速度点，为使得涡流制动系统在较大制动力下进行参数分析，并且考虑到在高速及超高速下任何速度点进行参数分析的效果是等效的，由此选定参数分析时涡流制动器的仿真速度为110m/s。
保证其他参数为额定工况的数值，改变涡流制动器励磁线圈中励磁电流密度J的数值来分析涡流制动力随励磁电流的变化情况，其中励磁电流密度J的仿真范围为8～14A/mm2，仿真步长为1A/mm2。根据式（12）和式（13）可知，式（22）变为涡流制动力随励磁电流密度J的二次函数表达式Ft(J)。图7给出了制动力随励磁电流密度变化的解析解与仿真解曲线。
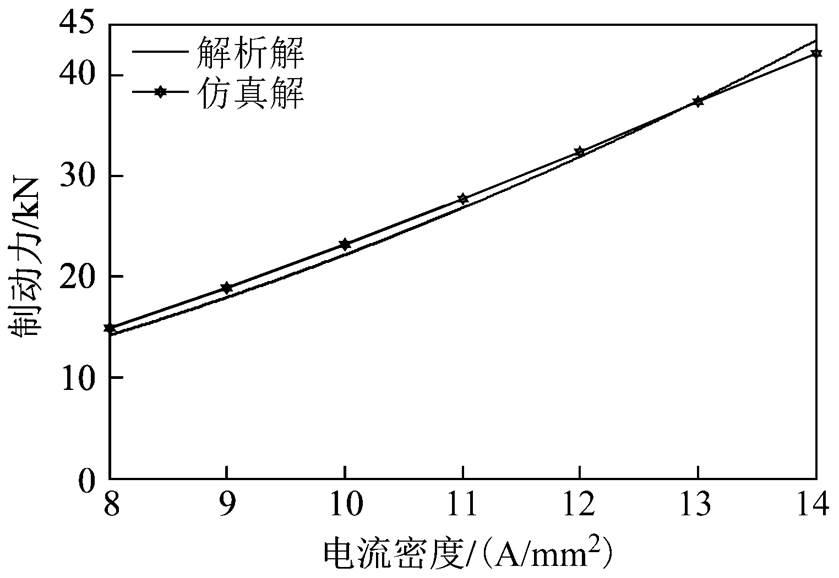
图7 涡流制动力随励磁电密变化曲线
Fig.7 Curves of eddy current braking force varying with exciting current density
从图7可以看出，涡流制动力随励磁电流密度成二次函数增长，仿真解在8～12A/mm2范围内略高于解析解，在12～14A/mm2范围内略低于解析解，仿真解与解析最大误差为5.57%，理论计算结果与仿真结果基本吻合。
分析气隙长度对涡流制动力的影响也是保证其他参数为额定工况的数值，改变气隙长度研究涡流制动力随气隙长度的变化情况，气隙长度选取的仿真范围为7～13mm，仿真步长为1mm。式（22）变为制动力随气隙长度d 的表达式Ft(d)，图8给出了制动力随气隙长度变化的解析解与仿真解曲线。
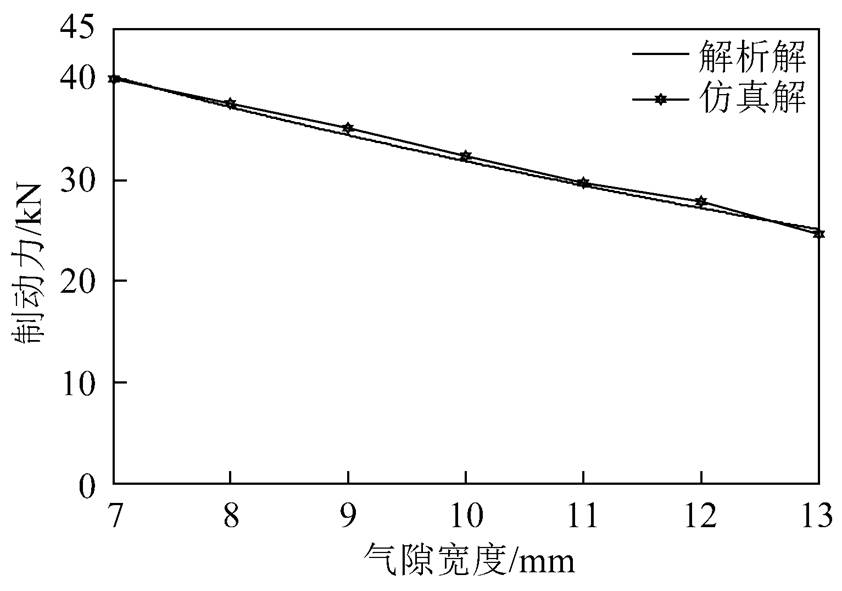
图8 涡流制动力随气隙长度变化曲线
Fig.8 Curves of eddy current braking force varying with air-gap length
从图8中可以看出，涡流制动力随气隙长度的增加不断下降，考虑到实际工况，同时参考项目中磁浮列车悬浮气隙长度，涡流制动气隙长度选为10mm较为合适。解析解与仿真解基本吻合，但仿真解总体略高于解析解，仿真解与解析解的最大误差为2.49%。
同理分析感应板厚度对涡流制动力的影响，选取感应板厚度的仿真范围为2～8mm，仿真步长同样为1mm。式（22）变为涡流制动力随感应板厚度bg的表达式Ft(bg)，图9为制动力随感应板厚度变化的解析解与仿真解曲线。
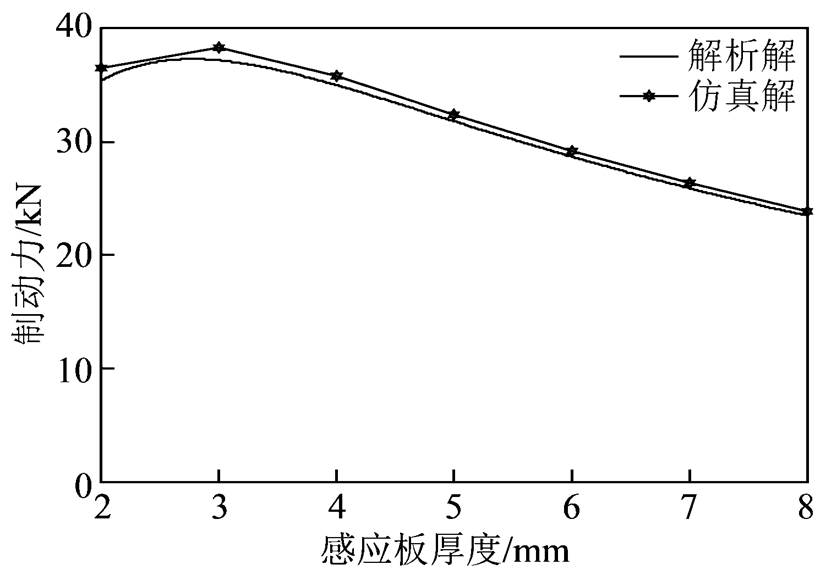
图9 涡流制动力随感应板厚度变化曲线
Fig.9 Curves of eddy current braking force varying with induction plate thickness
从图9可以看出，解析解与仿真解曲线的趋势基本一致，仿真解总体略高于解析解，仿真解与解析解的最大误差为3.16%。根据涡流制动力随感应板厚度bg的表达式Ft(bg)，求得Ft(bg)的峰值制动力对应的感应板厚度为2.79mm，因此在此额定工况下，选择该厚度的感应板能够获得最大的涡流制 动力。
分析感应板电导率对涡流制动力的影响，选取感应板电导率在105～2×107S/m范围内的若干值进行有限元仿真。式（22）变为涡流制动力随感应板电导率s 的表达式Ft(s )。图10为制动力随感应板电导率变化的解析解与仿真解曲线。
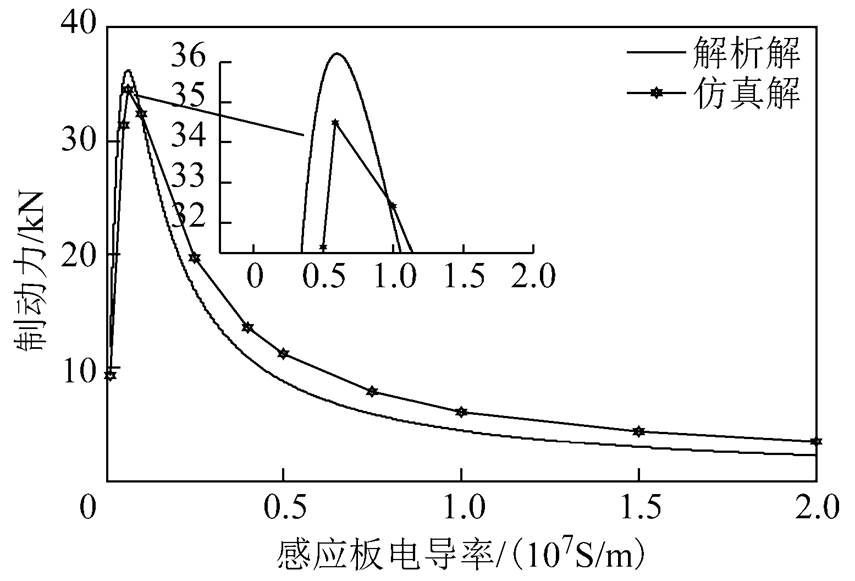
图10 涡流制动力随感应板电导率变化曲线
Fig.10 Curves of eddy current braking force varying with induction plate conductivity
从图10可以看出，仿真解与解析解的总体趋势一致，但在高电导率的范围106～2×107S/m内，仿真解高于解析解，且两者的误差相差较大。根据涡流制动力随感应板电导率s 的表达式Ft(s )及其曲线，在此工况下选择电导率在5×105～106S/m范围内的非铁磁感应板材料能够很好地提高涡流制 动力。
通过以上参数分析，解析计算与有限元仿真的正确性得到了相互验证，并得到了高速及超高速下提高涡流制动力性能的方法。
本文利用解析计算得出适用于高速及超高速下涡流制动力随各个参数变化的解析式，并根据实验项目需求选定额定参数利用有限元仿真软件对理论计算结果进行验证，经过验证对比发现理论计算结果与仿真结果基本吻合，证明了理论计算结果的正确性。并且本文利用计算得出的涡流制动力解析式对励磁电流、气隙长度、感应板厚度和感应板电导率进行参数分析，给出了高速下提高涡流制动力的方法。
同时本文发现在高速及超高速下涡流制动出力较大，为高速及超高速下磁浮列车使用涡流制动系统以及涡流装置的设计提供了参考。
参考文献
[1] 张涛, 刘欣, 凤莫丽, 等. 磁悬浮高速电机系统建模与控制[J]. 电机与控制学报, 2018, 22(4): 98-104.
Zhang Tao, Liu Xin, Feng Moli, et al. Modeling and control of magnetic suspension high-speed motor[J]. Electric Machines and Control, 2018, 22(4): 98-104.
[2] 郭其一, 陈鹏, 骆廷勇, 等. 基于解析法的涡流制动电磁机理研究[J]. 机车电传动, 2006(1): 30-32.
Guo Qiyi, Chen Peng, Luo Tingyong, et al. Study on electromagnetic mechanism in eddy current brake (ECB) based on analytical method[J]. Electric Drive for Locomotives, 2006(1): 30-32.
[3] 朱仙福, 张秀荣. 高速列车轨道涡流制动的制动力分析与计算[J]. 上海铁道大学学报, 1996(4): 1-8.
Zhu Xianfu, Zhang Xiurong. Analysis and calculation of braking force on rail eddy current braking of high speed trains[J]. Journal of Shanghai Teidao Univer- sity: Natural Science, 1996(4): 1-8.
[4] Marc T. Thompson. Practical issues in the use of NdFeB permanent magnets in maglev, motors, bearings and eddy current brakes[J]. Proceedings of the IEEE, 2009, 97(11): 1758-1767.
[5] Edwards J D, Jayawant B V, Dawson W R C, et al. Permanent-magnet linear eddy-current brake with a nonmagnetic reaction plate[J]. IEE Proceedings- Electric Power Applications, 1999, 146(6): 627-631.
[6] Reza Yazdanpanah, Mojtaba Mirsalim. Axial-flux wound-excitation eddy-current brakes: analytical study and parametric modeling[J]. IEEE Transactions on Magnetics, 2014, 50(6): 8000710.
[7] Kou Baoquan, Jin Yinxi, Lu Zhang, et al. Characteristic analysis and control of a hybrid excitation linear eddy current brake[J]. Energies, 2015, 8(7): 7441-7464.
[8] Cho Sooyoung, Liu Huaicong, Han Woong Ahn, et al. Eddy current brake with a two-layer structure: calculation and characterization of braking perfor- mance[J]. IEEE Transactions on Magnetics., 2017, 53(11): 8110205.
[9] Xue Zhiqiang, Li Huaishu, Zhou Yu, et al. Analytical prediction and optimization of cogging torque in surface-mounted permanent magnet machines with modified particle swarm optimization[J]. IEEE Transactions on Industrial Electronics, 2017, 64(12): 9795-9805.
[10] Zhou Yu, Li Huaishu, Meng Guangwei, et al. Analytical calculation of magnetic field and cogging torque in surface-mounted permanent-magnet machines accounting for any eccentric rotor shape[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3438-3447.
[11] Cho S, Liu H, Lee J, et al. Design and analysis of the eddy current brake with the winding change[J]. Journal of Magnetics, 2017, 22(1): 23-28.
[12] 邓妮. 磁浮列车涡流制动系统建模及紧急制动控制策略的研究[D]. 杭州: 浙江大学, 2006.
[13] 郭保成, 黄允凯, 彭飞, 等. Halbach阵列盘式永磁电机的解析计算[J]. 中国电机工程学报, 2019, 39(1): 289-295, 343.
Guo Baocheng, Huang Yunkai, Peng Fei, et al. An analytical model for axial flux permanent magnet machines with Halbach array[J]. Proceedings of the CSEE, 2019, 39(1): 289-295, 343.
[14] 郑迪, 王大志, 于林鑫, 等. 盘式永磁涡流驱动器的电磁-温度耦合解析模型[J]. 电工技术学报, 2019, 34(11): 2315-2323.
Zheng Di, Wang Dazhi, Yu Linxin, et al. Electromagnetic-thermal analytical model of axial- flux permanent magnet eddy current driver[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2315-2323.
[15] 孙权贵, 邓智泉, 张忠明. 基于齿槽效应的高速永磁电机转子涡流损耗解析计算[J]. 电工技术学报, 2018, 33(9): 1994-2004.
Sun Quangui, Deng Zhiquan, Zhang Zhongming. Analytical calculation of rotor eddy current losses in high speed permanent magnet machines accounting for influence of slot opening[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 1994- 2004.
[16] 杨玉波, 刘国鹏, 陈鹏, 等. 基于子域法的游标混合电机电磁性能解析计算[J]. 电机与控制学报, 2019, 23(9): 9-17, 25.
Yang Yubo, Liu Guopeng, Chen Peng, et al. Electro- magnetic performance investigation of vernier hybrid machine[J]. Electric Machines and Control, 2019, 23(9): 9-17, 25.
[17] Paudel N, Bird J Z. General 2-D steady-state force and power equations for a traveling time-varying magnetic source above a conductive plate[J]. IEEE Transactions on Magnetics, 2012, 48(1): 95-100.
[18] 张守首, 郭思源. 考虑分段斜极和磁性槽楔的永磁同步电机磁场解析方法[J]. 电工技术学报, 2019, 34(1): 11-22.
Zhang Shoushou, Guo Siyuan. Analytical magnetic field method of permanent magnet synchronous machine considering step-skewed magnets and magnetic slot wedge[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 11-22.
[19] 杨通. 高速大推力直线感应电机的电磁理论与设计研究[D]. 武汉: 华中科技大学, 2010.
[20] 杜超, 孟大伟. 基于场路结合法的电磁弹射用新型永磁直线同步电机的研究[J]. 电机与控制学报, 2019, 23(9): 65-74.
Du Chao, Meng Dawei. Investigation of permanent magnet linear synchronous motor for electromagnetic launch based on field-circuit combined method[J]. Electric Machines and Control, 2019, 23(9): 65-74.
[21] 李节宝, 井立兵, 周晓燕, 等. 表贴式永磁无刷电机直接解析计算方法[J]. 电工技术学报, 2012, 27(11): 83-88.
Li Jiebao, Jing Libing, Zhou Xiaoyan, et al. Exact analytical method for surface-mounted permanent- magnet brushless motors[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 83-88.
[22] Liu Z J, Vourdas A, Binns K J. Magnetic field and eddy current losses in linear and rotating permanent magnet machines with a large number of poles[J]. Science Measurement & Technology IEE Proceedings A, 1991, 138(138): 289-294.
[23] 阎秀恪, 谢德馨, 高彰燮, 等. 电磁力有限元分析中麦克斯韦应力法的积分路径选取的研究[J]. 电工技术学报, 2003, 18(5): 32-36.
Yan Xiuke, Xie Dexin, Gao Zhangxie, et al. Research on integration path selection of Maxwell stress tensor method used in electromagnetic force FEM analysis[J]. Transactions of China Electrotechnical Society, 2003, 18(5): 32-36.
[24] 王峰, 吴志强, 李亚杰, 等. 开关磁阻电机转子径向电磁合力的解析建模[J]. 电工技术学报, 2019, 34(5): 934-945.
Wang Feng, Wu Zhiqiang, Li Yajie, et al. Analytical modeling of rotor radial electromagnetic force in switched reluctance motor[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 934-945.
[25] Ion B, Syed A N. The induction machine design handbook[M]. 2nd ed. Boca Raton, FL: CRC Press, 2010.
[26] 孙玉坤, 于丰源, 袁野, 等. 一种混合双定子磁悬浮开关磁阻电机[J]. 电工技术学报, 2019, 34(1): 1-10.
Sun Yukun, Yu Fengyuan, Yuan Ye, et al. A hybrid double stator bearingless switched reluctance motor[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 1-10.
Analytical Calculation of Braking Force of Super High Speed Maglev Eddy Current Device
Abstract The eddy-current braking system (ECBS) is vital to the safe operation of a high-speed maglev. This paper used the subdomain method for the analytic calculation of the expression of the eddy-current braking force that is related to parameters, such as speed (or super high speed), exciting current, air-gap length, induction plate thickness and conductivity. An analytical model was established in the 2-D coordinate system. With the magnetic vector potential as a variable, each subdomain of the model could be expressed by Poisson equations. In combination with the expression of air-gap flux density obtained according to the boundary condition between two adjacent subdomains, it is possible to derive the expression of eddy-current braking force. The results of finite-element simulation show that the analytic calculation is correct, and the feasibility of the ECBS to be used in the superhighspeed maglev is explored. The analytic calculation used for the parametric analysis of braking force is a good way of optimizing the superhighspeed ECBS. Compared with the simulation analysis, the analytic calculation can reflect the mechanism of eddy-current braking force and have the advantage of time-saving calculation.
keywords：Super high speed maglev, eddy-current braking force, subdomain method, analytic calculation, finite-element simulation, parametric analysis
中图分类号：TM153+.3
DOI: 10.19595/j.cnki.1000-6753.tces.190568
国家自然科学基金资助项目（51677092，51907093）。
收稿日期 2019-05-14
改稿日期 2019-12-08
郑晓钦 女，1985年生，博士，讲师，硕士生导师，研究方向为多相电机及其系统的分析与控制。E-mail: zhengxiaoqin619@sina.com
吴新振 男，1964年生，博士，教授，博士生导师，研究方向为电机系统设计分析与控制。E-mail: wuxinzhen8l@163.com（通信作者）
（编辑 郭丽军）