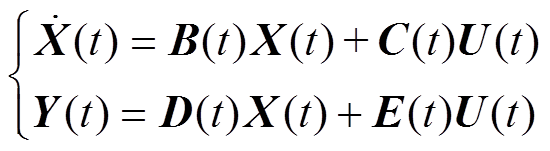（1）摘要 针对变压器遭受到直流扰动时的铁心振动问题，建立单相双绕组变压器与三相三柱式Yd变压器的直流扰动振动模型。基于电磁耦合原理辨识绕组电流；构建振动谐响应模型研究振动特性，对不同直流扰动时的变压器电磁特性进行仿真计算；分析在直流影响下绕组异常电流和铁心振动加速度的变化特性，并总结其规律。搭建变压器交直流混杂动模实验平台，分别对绕组电流和铁心振动信号进行辨识和采集，并与仿真结果进行对比，证明了该文方法的正确性和有效性。
关键词：变压器 直流偏磁 异常电流 铁心振动 谐响应
直流扰动会对交流电网中的电力变压器设备产生影响，变压器的运行可靠性直接关系到电力系统的安全稳定[1-6]。（准）直流流入变压器会造成铁心正负半周励磁不对称，致使变压器出现半波饱和，进而产生严重的磁致伸缩效应[7-9]，导致铁心饱和、振动加剧、铁心松动[10-12]。因此，铁心-绕组构件抗直流扰动能力已成为变压器设计及运行所关注的重要方面[13-14]。
目前，已有学者针对变压器铁心振动问题开展研究工作。文献[15]通过实验研究了变压器直流偏磁对磁致伸缩特性的影响，并测量了铁心不同位置的空载振动，但未考虑负载情况。文献[16]建立了三维磁-机械强耦合数值模型，计算了三相变压器空载条件下的磁场和铁心振动位移。文献[17]同时考虑磁致伸缩及麦克斯韦力的影响，仿真分析不同激励下变压器铁心振动。文献[18]分析了变压器铁心的磁致伸缩应变特性。综上所述，研究人员针对变压器磁致伸缩振动模型进行了深入研究，但在建模过程中铁磁材料各向同性、泊松比等参数获取困 难[19]。而且实际工程中10kV以上的大型变压器铁心均封闭在变压器箱体内，无法在内部铁心加装传感器以量测振动数据。虽然可以在变压器箱体外测量振动信号，但由于其内部的电磁屏蔽装置导致所测量的外部振动数据无法准确地反映内部铁心振动情况。故本文对直流扰动下绕组电流的异常变化进行研究，以此表征铁心振动情况。
本文针对交直流混杂环境下变压器电磁振动问题，建立单相和三相变压器直流扰动振动模型，基于电磁耦合原理建立交直流混杂模式状态方程。构建振动谐响应模型，研究直流扰动对铁心振动的影响。对空载与满载运行模式下遭受不同直流扰动的变压器进行仿真计算，探索绕组异常电流与铁心振动的变化情况和规律。搭建变压器动模实验平台，量测一次绕组电流，同时在线监测变压器铁心振动信号，并与仿真结果进行对比。
变压器交直流混杂电磁耦合状态方程为
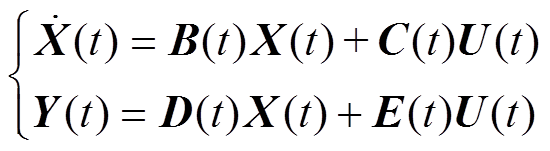（1）式中，X(t)为系统状态变量，包含电流矩阵i和电感矩阵L；U(t)为系统输入变量，包括交流电压激励、直流扰动电压列向量以及负载变量；Y(t)为输出变量，主要包含电路参量与磁场场量；B(t)、C(t)、D(t)、E(t)为系数矩阵。该状态方程包含电路与磁场两部分，其求解过程通过时域磁场-电路间接耦合实现。
假设某时刻的绕组电流已知，可以采用基于矢量磁位A的能量平衡有限元法（Energy Balance Finite Element Method, EBFEM）计算该时刻的时域电感矩阵。磁场模型为
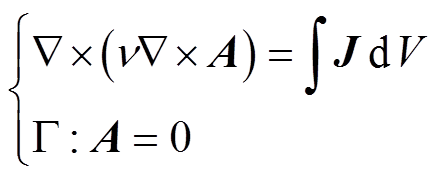（2）式中，n 为磁阻率；J为电流密度矢量，表示绕组激励电流的分布情况。
磁场模型通过Galerkin余量公式求解
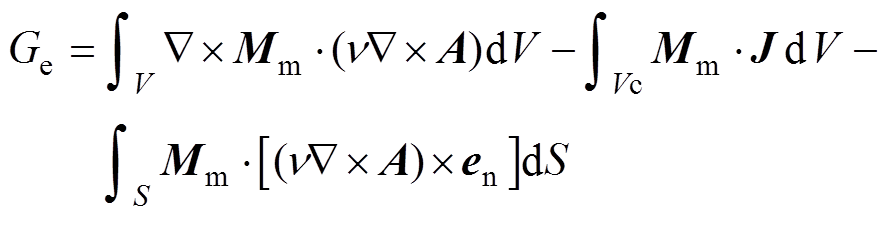（3）式中，Ge为Galerkin余量；{Mm}为权函数序列，权函数与基函数相同。对式（3）进行推导，得到
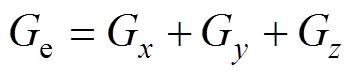（4）
将加权余量方程离散形成代数方程组，求解可得A，进而计算磁场场量B、H等。
根据能量平衡法，由系统能量计算时域电感。在单相双绕组变压器中令某一时刻一次、二次绕组电流变化为dih、diq（h, q =1, 2）。可将变压器的电磁能量变化与状态变量关联，得到
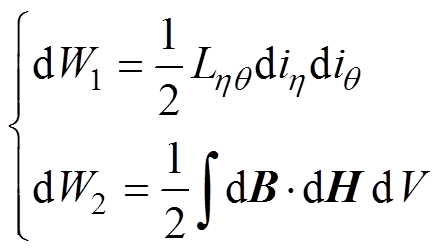（5）由能量守恒可联立式（5）中方程计算时域电感，以作为电路模型的状态变量。
计算三相三柱式变压器电感参数时则需要考虑一次、二次侧任意两绕组的电流变化，但电感计算原理同上。
由计算得到的电感参数回馈电路模型可以计算绕组电流。单相双绕组变压器直流扰动若从一次侧注入，其电路模型如图1所示。
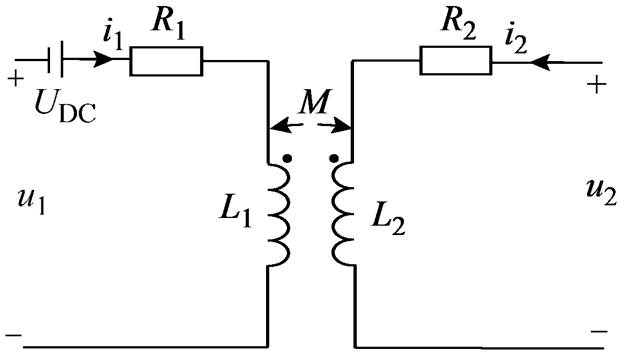
图1 单相双绕组变压器
Fig.1 Single-phase double-winding transformer
变压器基本回路方程为
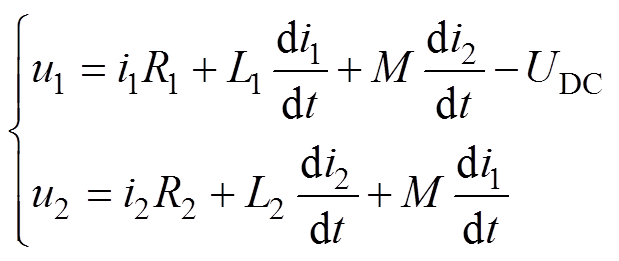（6）式中，i1、i2分别为一、二次绕组电流；u1、u2分别为一次、二次绕组电压；L1、L2为自感；M为互感；R1、R2分别为一次、二次绕组电阻；UDC为直流电压。
三相三柱式Yd联结变压器直流扰动模型如图2所示。图2中，iA、iB、iC为高压侧绕组电流，ia、ib、ic为低压侧端口电流，ia1、ib1、ic1为低压侧三角形联结绕组电流；LA、LB、LC为一次侧自感，La、Lb、Lc为二次侧自感；MAx、MBx、MCx（x =a1, b1, c1）为一次侧互感，Maz、Mbz、Mcz（z =A, B, C）为二次侧互感（具体电路参数意义及推导过程详见附录）；r1、r2为绕组电阻，uA、uB、uC为高压侧电压，ua、ub、uc为低压侧电压，icn为低压侧环流。
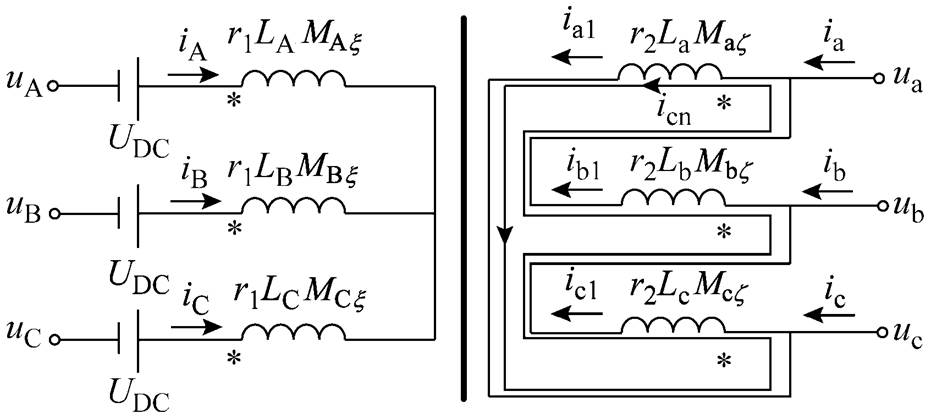
图2 Yd联结变压器直流扰动电路模型
Fig.2 DC disturbance circuit model of Yd transformer
推导Yd联结变压器时域电路微分方程，并忽略各绕组自身漏感[20]，则有
（7）式中，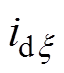
为A、B、C三相互感相互影响所产生的电流增量；
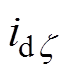为a、b、c三相互感相互影响所产生的电流增量。
若tk时刻的电感参数已知，可代入电路微分方程，利用改进欧拉法（IEu），由绕组电流ik计算下一时刻的电流为
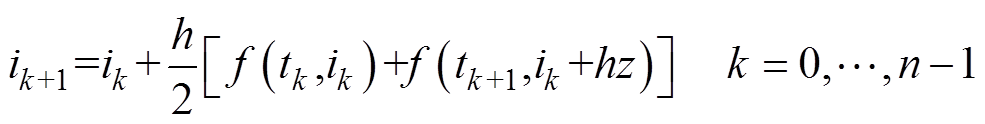（8）式中，h为步长；z为步长内的分段计算斜率。将时域电流作为磁场模型的状态变量。
基于电磁耦合的状态方程求解原理如下：
（1）利用能量平衡有限元法计算磁场模型的电感参数，回馈电路模型计算下一时刻电流。
（2）将电路模型计算得到的时域电流作为磁场模型下一次磁场求解的输入变量。
在磁场中，电力变压器铁心硅钢片将受到磁致伸缩力的影响而产生振动。去掉外加磁场后，磁致伸缩效应会消除，硅钢片恢复原有的形状尺寸，因此可将磁致伸缩力视为弹性力学问题。当弹性体的每一个截面的变形、应力与z方向无关时，可看作平面应变问题，应力和应变的关系为
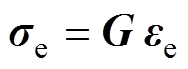（9）
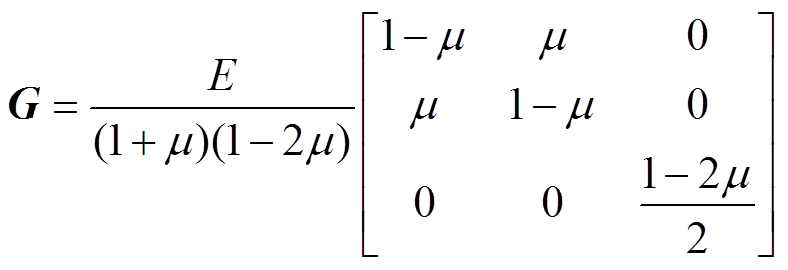（10）
式中，se为单元应力；ee为单元应变；G为弹性矩阵；m 为泊松比；E为杨氏模量。
根据虚位移原理[21]，节点力在虚位移上所做的虚功等于弹性体内应力在需应变上所做的虚功，可得到单元磁致伸缩力为
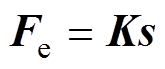（11）式中，Fe为单元等效磁致伸缩力；K为单元机械刚度；s为单元位移向量。
铁心在电磁力激励下的振动满足动力方程[22]
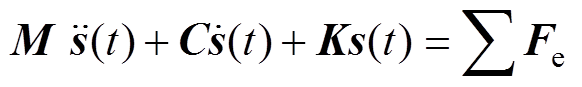（12）式中，M为模型质量矩阵；C为模型阻尼矩阵。
对铁心所受的电磁力进行傅里叶变换，即可得到各谐波分量，将其作为简谐激励源，进行稳态结构谐响应振动分析。考虑材料刚度与简谐激励的频率，受力谐响应原理为
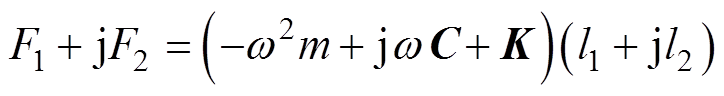（13）式中，w 为简谐激励的角频率；l为振动位移，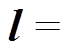
。
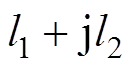根据振动位移可计算振动加速度g为
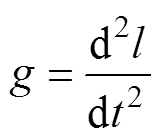（14）变压器振动谐响应原理如图3所示。
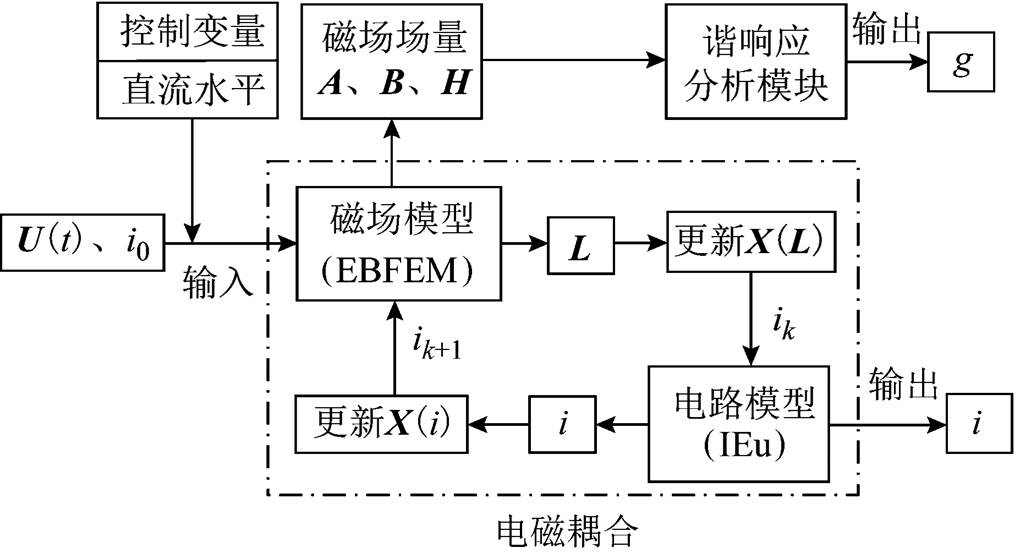
图3 振动谐响应原理
Fig.3 Vibration harmonic response principle
对220V单相双绕组实验变压器进行建模仿真，铁心硅钢片型号为Z10，具体参数见表1。
表1 单相双绕组变压器参数
Tab.1 Single-phase two windings transformer parameters
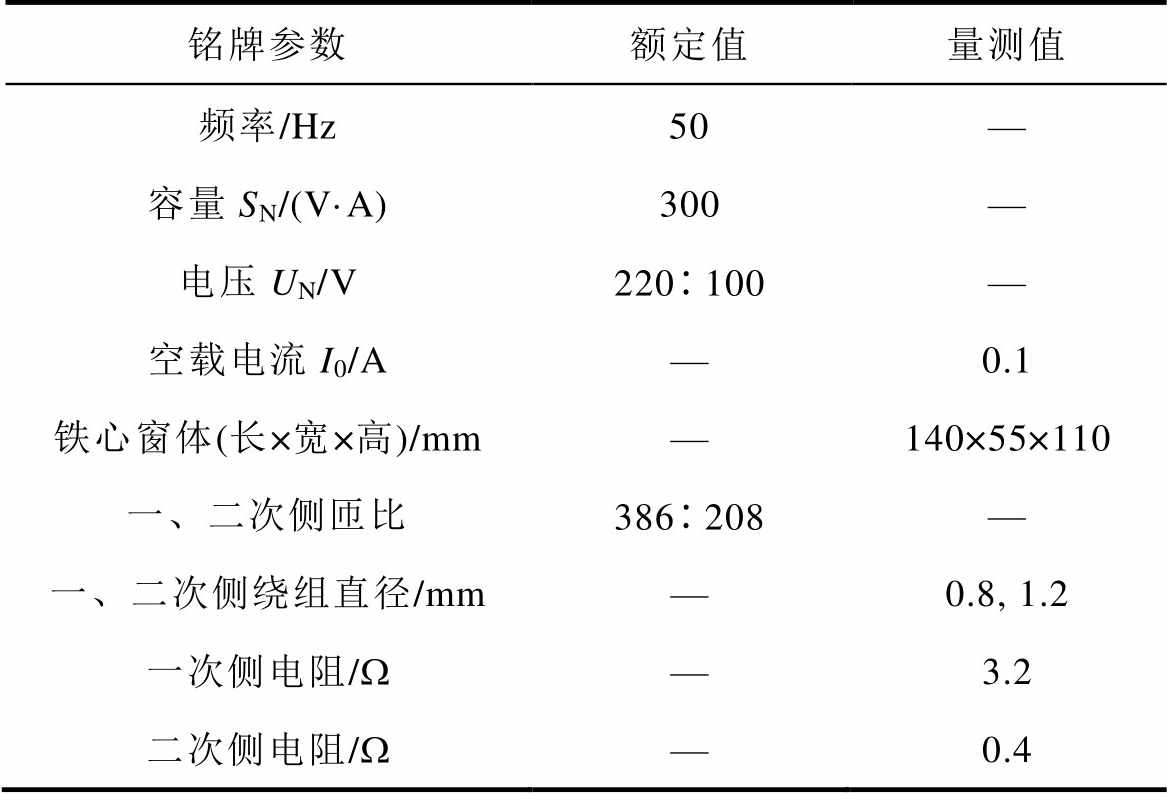
铭牌参数额定值量测值 频率/Hz50— 容量SN/(V·A)300— 电压UN/V220100— 空载电流I0/A—0.1 铁心窗体(长×宽×高)/mm—140×55×110 一、二次侧匝比386208— 一、二次侧绕组直径/mm—0.8, 1.2 一次侧电阻/W—3.2 二次侧电阻/W—0.4
一次侧所接直流源产生的直流电流为IDC（IDC= aI0），a 为直流水平系数，表征直流扰动大小。分别对a =0、1.0、2.0、3.0四种直流扰动下的变压器运行模式进行仿真，单相变压器空载电流与励磁电流的有效值与最大值见表2。
表2 单相变压器空载电流与励磁电流
Tab.2 No-load current and excitation current of single-phase transformer
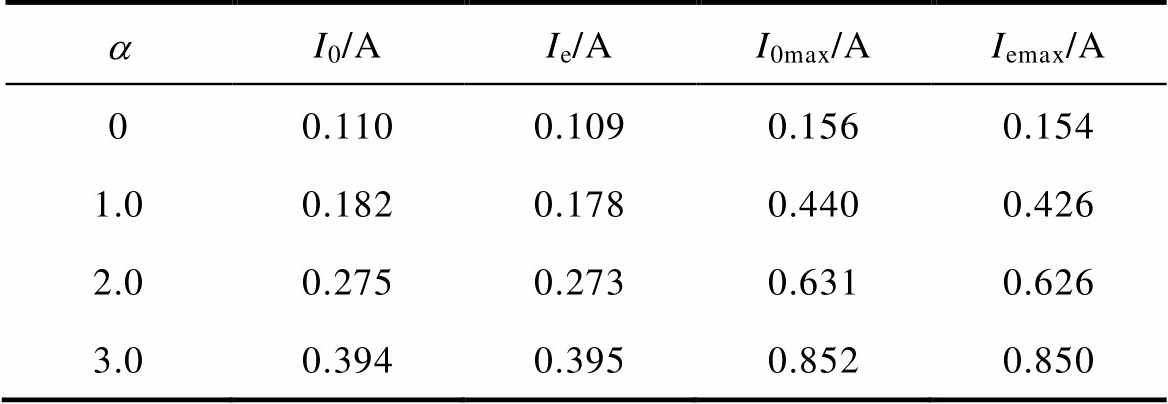
aI0/AIe/AI0max/AIemax/A 00.1100.1090.1560.154 1.00.1820.1780.4400.426 2.00.2750.2730.6310.626 3.00.3940.3950.8520.850
由表2可知变压器空载运行时绕组电流与励磁电流基本相同，通过对绕组电流的辨识可以有效表征变压器内部励磁电流的变化情况，进而对变压器励磁饱和状态进行分析。
空载与满载运行下变压器一次绕组电流波形仿真结果如图4所示。
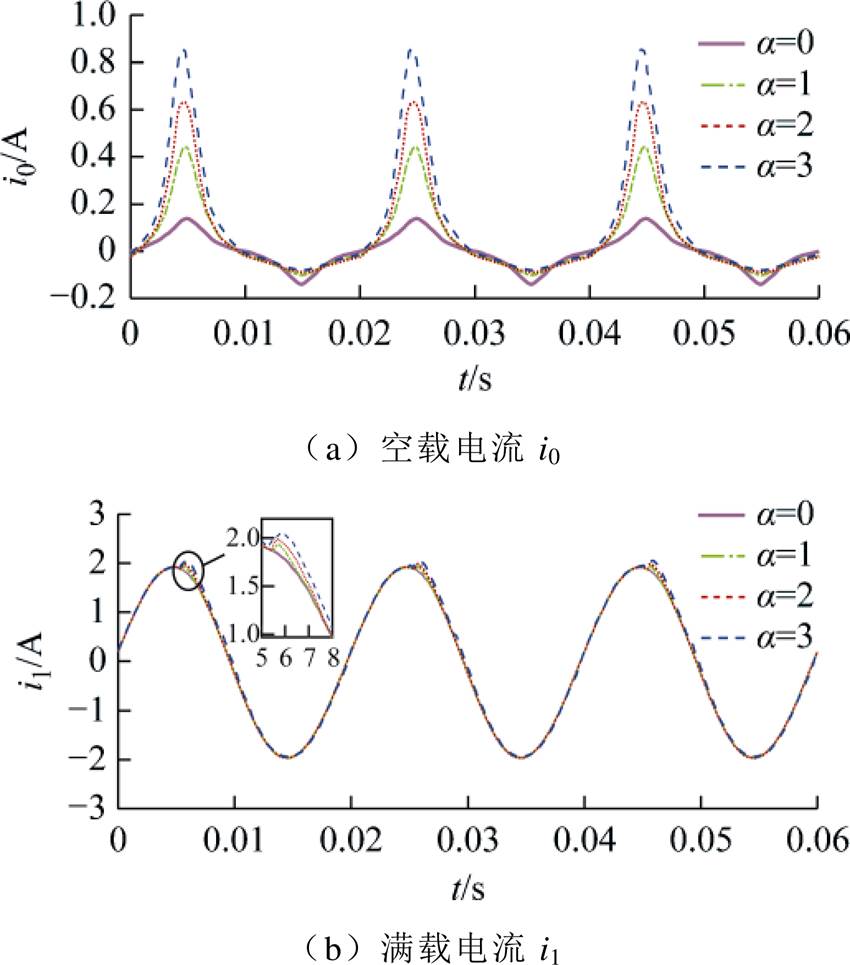
图4 不同直流扰动下单相变压器一次侧电流仿真结果
Fig.4 Simulation results of primary current of single-phase transformer under different DC
变压器空载运行时绕组电流与励磁电流基本相同。变压器正常运行时空载电流i0的波峰、波谷区域均表示变压器励磁处于饱和状态，零点附近区域表示励磁处于不饱和状态。在交直流混杂模式下，励磁饱和，i0畸变，波形呈现“半波畸变、半波衰减”的现象。满载运行时由于满载电流i1数值较大，随着直流扰动程度加深，畸变并不明显。
仿真计算各典型测试点如图5所示。在不同条件下的振动加速度，电气-振动异常特征信息见表3。
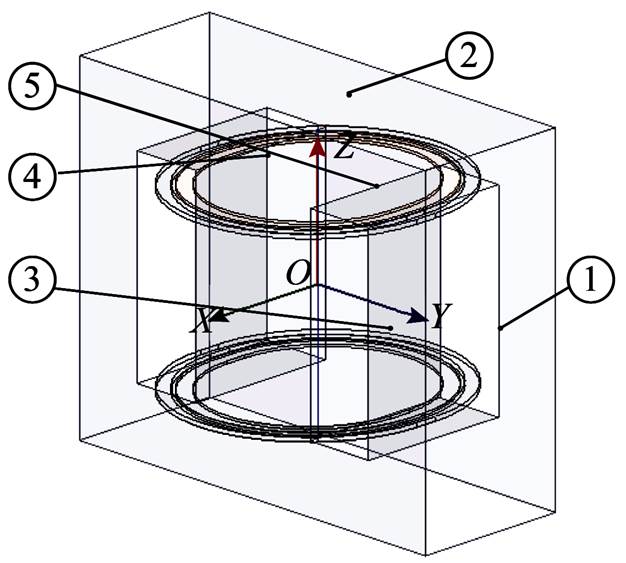
图5 单相变压器振动测试点分布
Fig.5 Testing points distribution of single-phase transformer
当发生直流扰动时，各测试点的振动加速度均随直流扰动程度的升高而增大。其中，测试点1、3、4、5的振动幅度明显大于测试点2，表明变压器铁心沿主磁通垂直方向发生的振动大于沿其平行方向的振动。对比测试点3、5可以发现铁心柱的振动幅度大于旁轭。结合图4、表3可以看出，直流扰动下一次侧空载电流畸变明显，电流有效值变化幅度大；而满载运行时一次电流变化较小，说明在空载运行时通过对一次电流的辨识可以有效表征铁心的振动情况。
表3 不同条件下单相变压器振动加速度仿真结果
Tab.3 Simulation results of vibration acceleration of single-phase transformer under different conditions
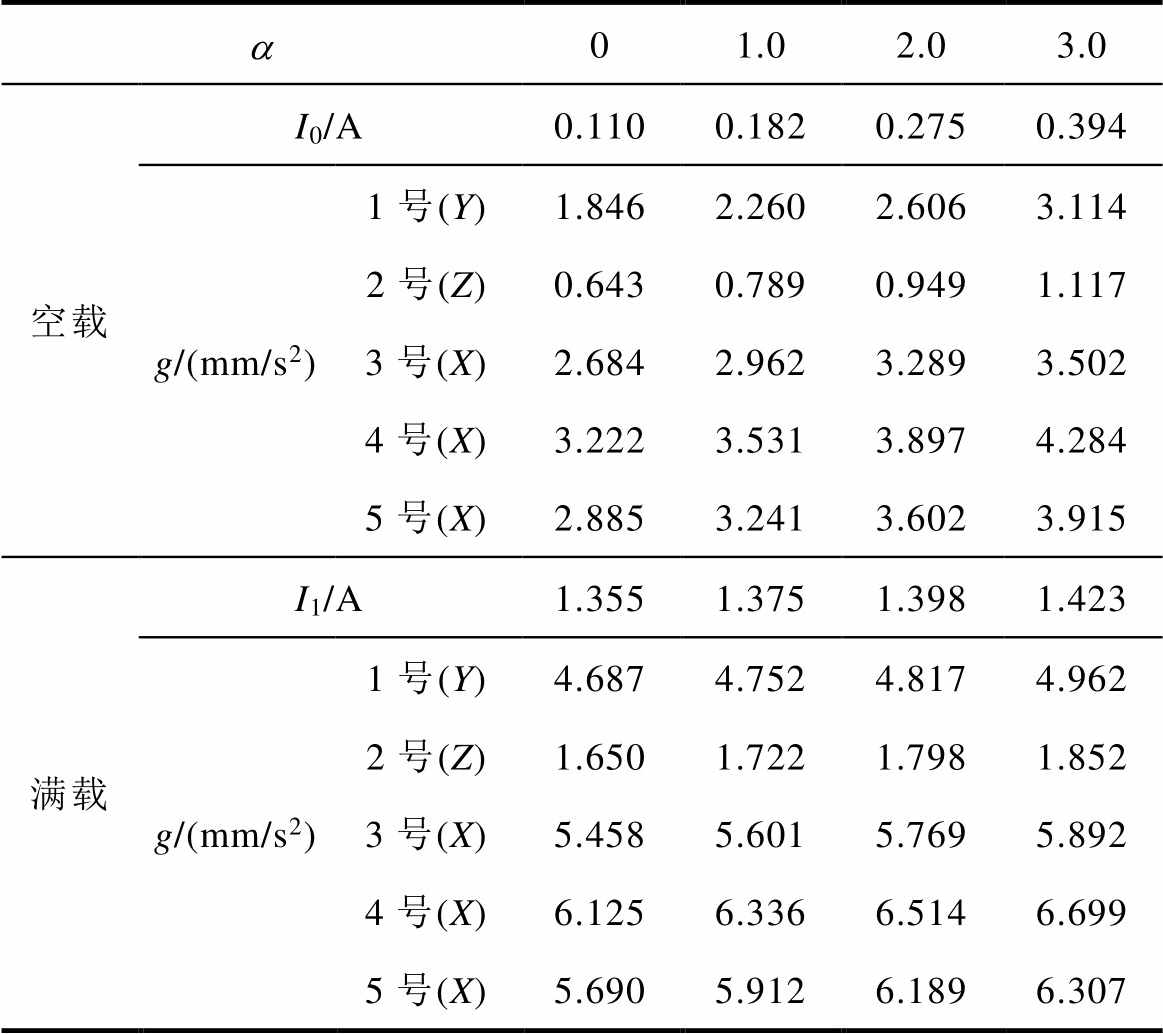
a01.02.03.0 空载I0/A0.1100.1820.2750.394 g/(mm/s2)1号(Y)1.8462.2602.6063.114 2号(Z)0.6430.7890.9491.117 3号(X)2.6842.9623.2893.502 4号(X)3.2223.5313.8974.284 5号(X)2.8853.2413.6023.915 满载I1/A1.3551.3751.3981.423 g/(mm/s2)1号(Y)4.6874.7524.8174.962 2号(Z)1.6501.7221.7981.852 3号(X)5.4585.6015.7695.892 4号(X)6.1256.3366.5146.699 5号(X)5.6905.9126.1896.307
对测试点的振动加速度进行快速傅里叶变换（Fast Fourier Transformation, FFT），在1kHz范围内分析其频谱，结果如图6所示（以空载运行条件下的1、2、3号测试点为例）。
无直流注入时，铁心振动频谱中出现偶次谐波分量，分析其原因是由于磁滞伸缩效应所引起。铁心磁致伸缩变化周期为电源周期的0.5倍，故磁致伸缩引起的铁心振动是以2倍电源频率为基频（100Hz）[23-24]。随着直流扰动增大，振动信号的各次谐波分量都呈现上升规律，且低频分量（≤500Hz）所占比重较大。其中，振动信号频谱在100Hz处的变化最为剧烈，说明直流扰动对铁心振动的基频分量影响较大。
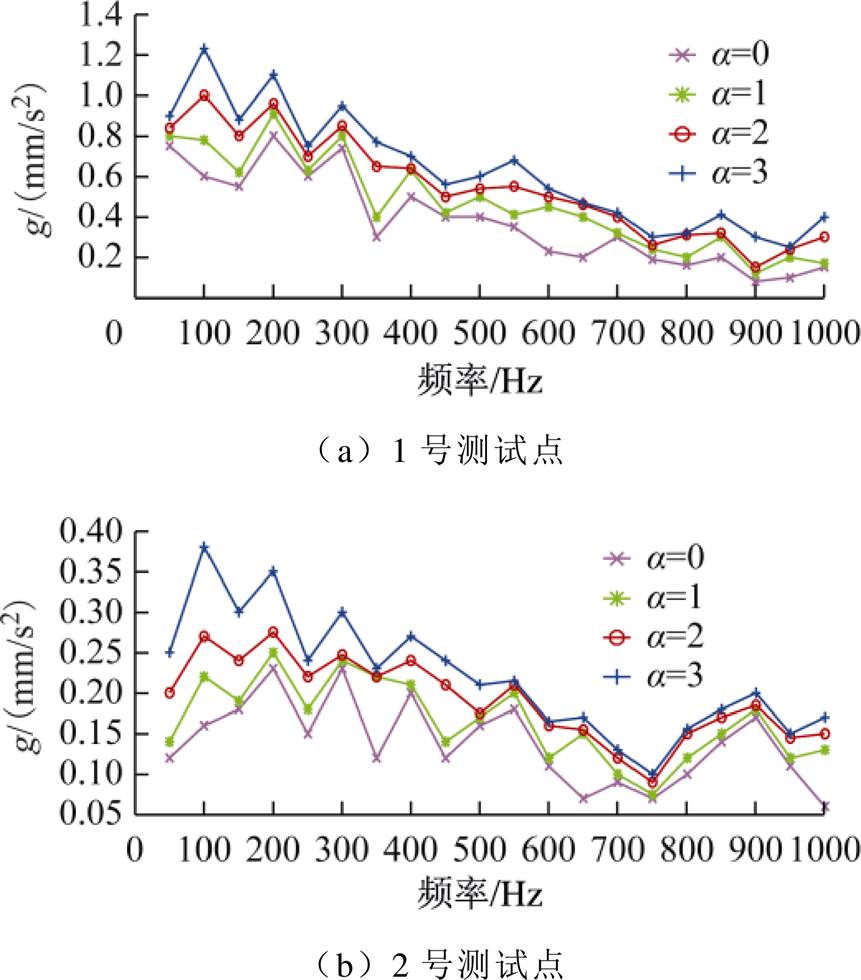
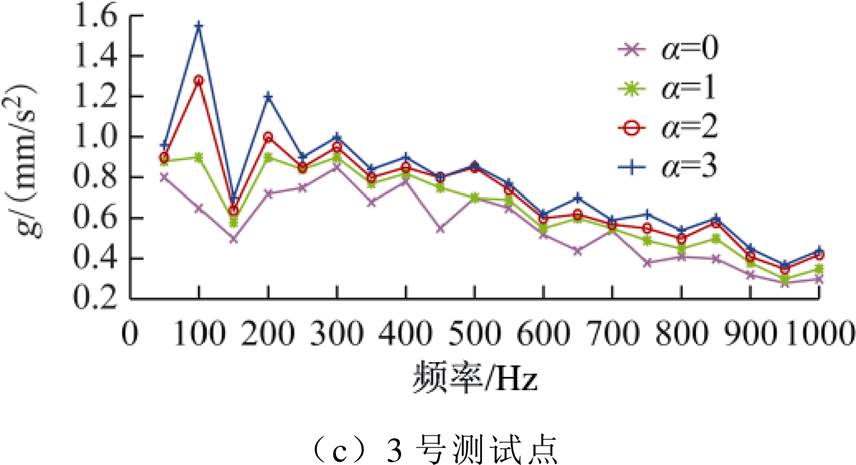
图6 单相变压器仿真振动频谱图
Fig.6 Simulation vibration spectrum of single-phase transformer
根据实际三相三柱式Yd变压器BSS-1000V·A建立仿真模型（具体参数见表4），为了与单相变压器对比，铁心硅钢片型号为Z10。在一次侧接入直流电流源模拟直流扰动，分析其直流扰动电磁特性。
表4 三相变压器参数
Tab.4 Three-phase transformer parameters
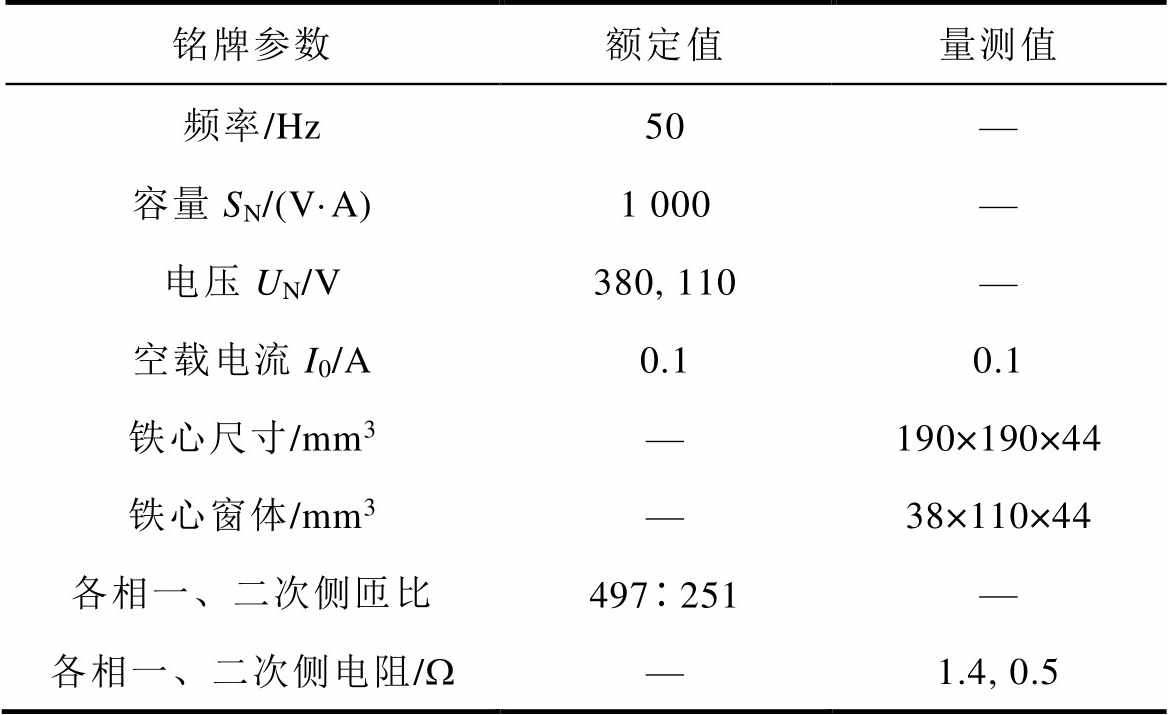
铭牌参数额定值量测值 频率/Hz50— 容量SN/(V·A)1 000— 电压UN/V380, 110— 空载电流I0/A0.10.1 铁心尺寸/mm3—190×190×44 铁心窗体/mm3—38×110×44 各相一、二次侧匝比497251— 各相一、二次侧电阻/W—1.4, 0.5
考虑三相对称性，以A相为例，一次绕组空载电流iA0和满载电流iA波形如图7所示。
无直流扰动时iA0与iA均为正弦波，注入直流后iA0畸变严重且扰动越大波形畸变幅度越大，而iA轻微畸变，与单相双绕组变压器变化情况相似。
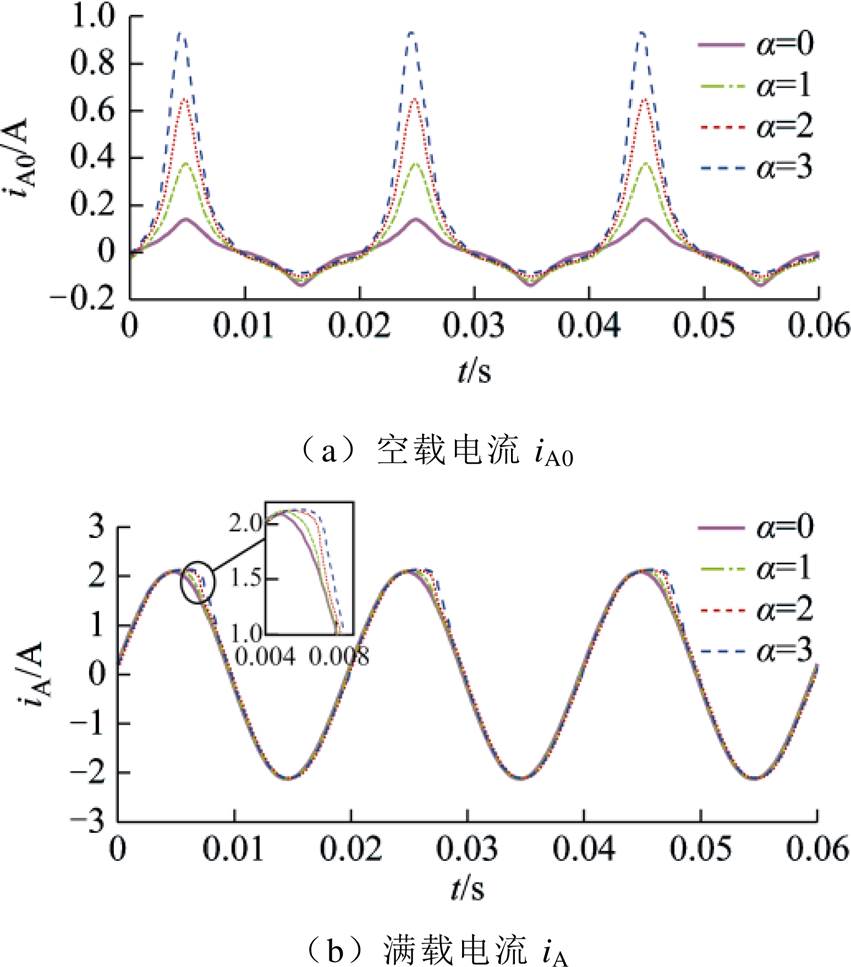
图7 不同直流扰动下三相变压器一次侧电流仿真结果
Fig.7 Simulation results of primary current of three-phase transformer under different DC
选取如图8所示具有代表性测试点，计算不同条件下的振动加速度，结果见表5。
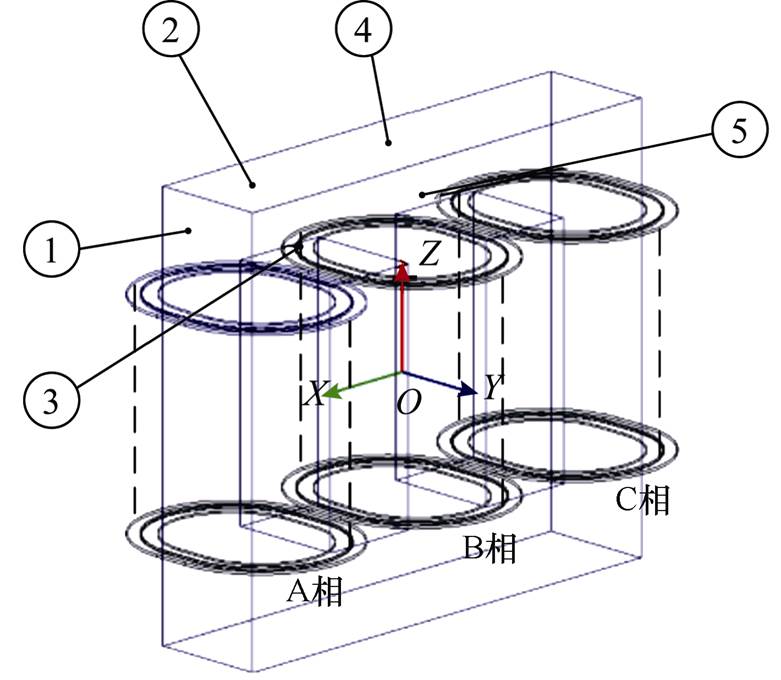
图8 三相变压器振动测试点分布
Fig.8 Testing points distribution of three-phase transformer
表5 不同条件下三相变压器振动加速度仿真结果
Tab.5 Simulation results of vibration acceleration of three-phase transformer under different conditions
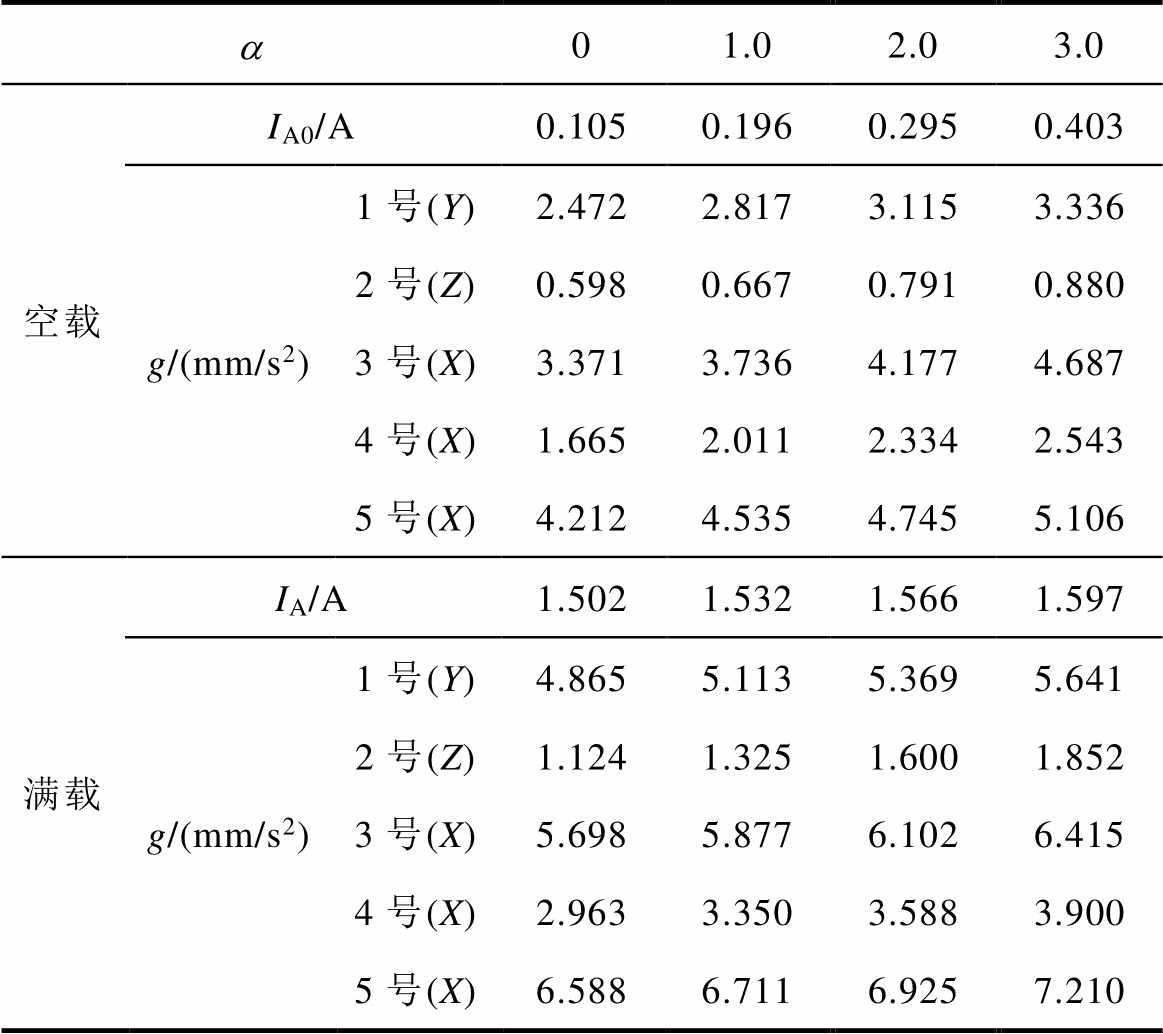
a01.02.03.0 空载IA0/A0.1050.1960.2950.403 g/(mm/s2)1号(Y)2.4722.8173.1153.336 2号(Z)0.5980.6670.7910.880 3号(X)3.3713.7364.1774.687 4号(X)1.6652.0112.3342.543 5号(X)4.2124.5354.7455.106 满载IA/A1.5021.5321.5661.597 g/(mm/s2)1号(Y)4.8655.1135.3695.641 2号(Z)1.1241.3251.6001.852 3号(X)5.6985.8776.1026.415 4号(X)2.9633.3503.5883.900 5号(X)6.5886.7116.9257.210
发生直流扰动时，5个测试点的振动加速度均随直流扰动程度的升高而增大。其中，测试点2、4的振动幅度明显小于测试点1、3、5，表明变压器铁心沿主磁通垂直方向发生的振动大于沿其平行方向的振动；测试点5的振动加速度强于测试点3，可以看出B相铁心柱的振动强于A、C相，分析其原因主要是B相铁心柱中磁通密度大于A、C相[25]，导致由磁致伸缩引起的铁心振动更为剧烈。结合图7与表5，空载运行时iA0波形与有效值变化明显；满载运行时iA只发生轻微变化，与单相变压器所得规律一致。
对振动加速度进行FFT分析，在1kHz范围内分析空载条件下测试点1、2、3的振动频谱，结果如图9所示。
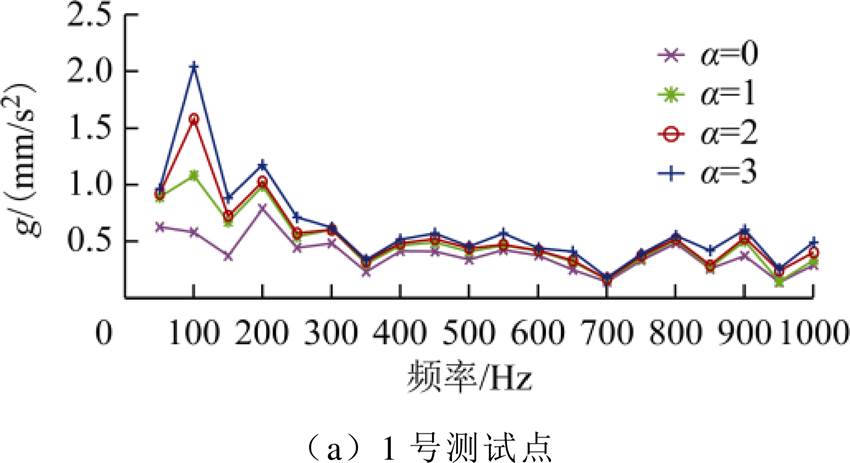
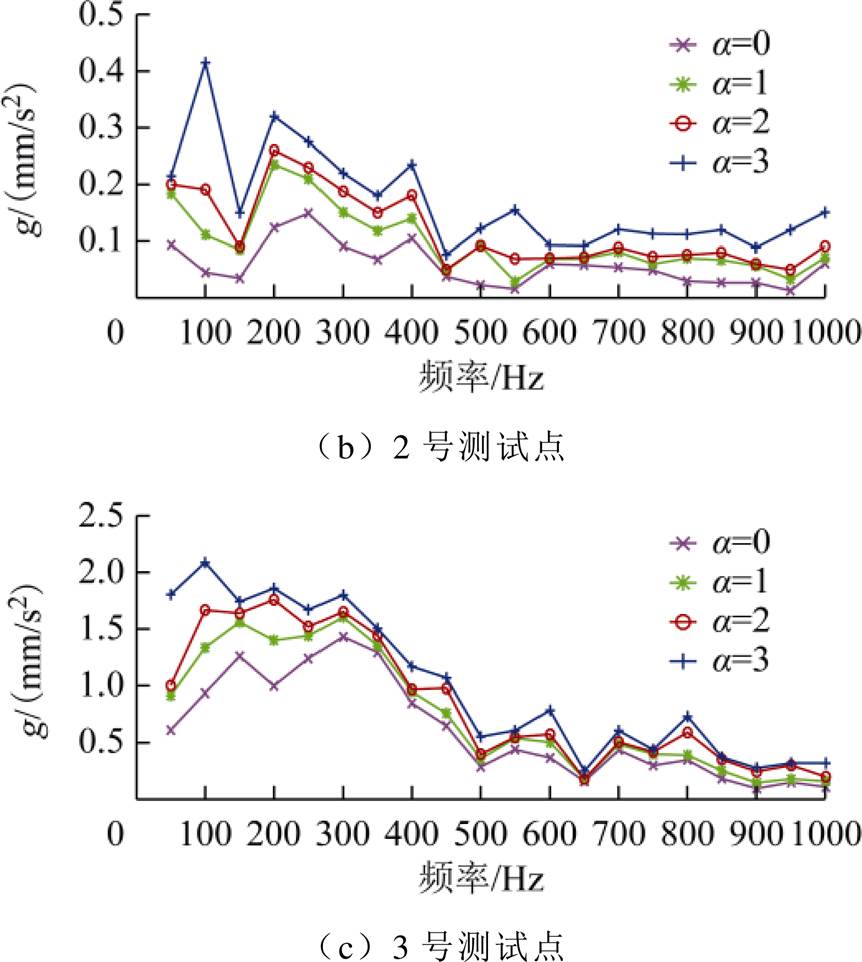
图9 三相变压器仿真振动频谱图
Fig.9 Simulation vibration spectrum of three-phase transformer
随着直流扰动增大，振动信号的各次谐波分量都呈现上升规律；振动频谱中低频分量所占比重较大，且n×100Hz（n=1, 2, 3, 4, 5）信号变化较为明显，铁心振动信号频谱在100Hz处变化最为剧烈。通过研究变压器交直流混杂运行时的振动特性，得出以下结论：
（1）直流水平升高时，铁心振动加剧，振动信号垂直主磁通方向的分量强于平行方向的分量；单相变压器铁心柱的振动强于旁轭，三相变压器B相铁心柱的振动强于A、C相；振动频谱中低频分量所占比重较大，且振动基频的变化最为剧烈。
（2）空载运行时，随着直流水平升高，一次侧空载电流畸变明显，电流有效值变化较大，通过对电流的辨识可以有效表征铁心的振动情况；满载运行时，由于电流幅值较大故变化不明显。
针对交直流混杂运行下的变压器振动问题，搭建模块化动模实验平台，具体实验步骤如下：
（1）在电压调节模块中调节调压器T1，使得施加在变压器一次侧的电压达到额定值。
（2）在直流注入模块闭合直流支路开关S，通过调节滑动变阻器Rd来改变直流电压源UDC注入直流的大小。
（3）通过电流监测模块记录电流波形。
（4）在振动监测模块采用压电加速度传感器JF2100-T监测铁心振动情况，采样频率为5kHz，灵敏度为20mV/g，振动量测点的选择与仿真计算中的测试点分布保持一致。
实验时将传感器触头吸附于变压器铁心不同位置，对振动加速度进行监测。基本工作原理为：压电式加速度传感器是以压电材料为转换元件，当加速度发生变化时压电元件受力也随之变化，将加速度输入转换成与之成正比的电信号输出，并通过计算机中的在线监测软件记录实时加速度。
搭建220V单相变压器动模实验平台，实验变压器参数见表1。振动量测点的选择与仿真计算中的测试点分布保持一致，实验平台如图10a所示，接线原理如图10b所示。
不同条件下一次绕组电流i0、i1如图11所示。无直流扰动时，i0、i1为正弦波，添加直流扰动后，两者均发生畸变，电流有效值见表6。其中空载电流畸变明显呈现尖顶波，而满载电流由于本身数值较大，导致畸变不明显，实验结果与仿真波形相符。不同条件下的振动加速度见表6，空载运行条件下1、2、3号测试点的振动加速度频谱如图12所示。
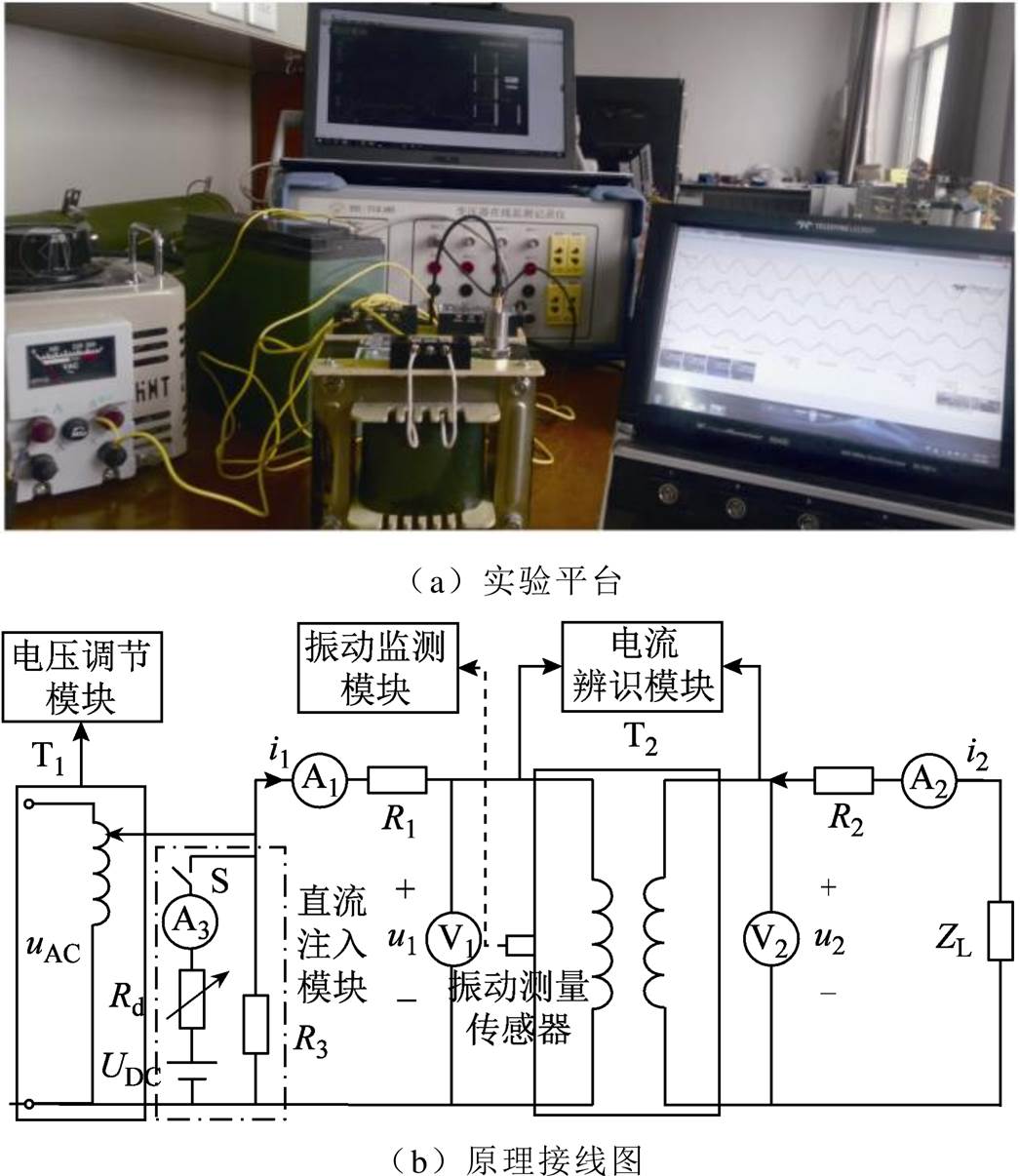
图10 实验接线图
Fig.10 Wiring diagram of experiment
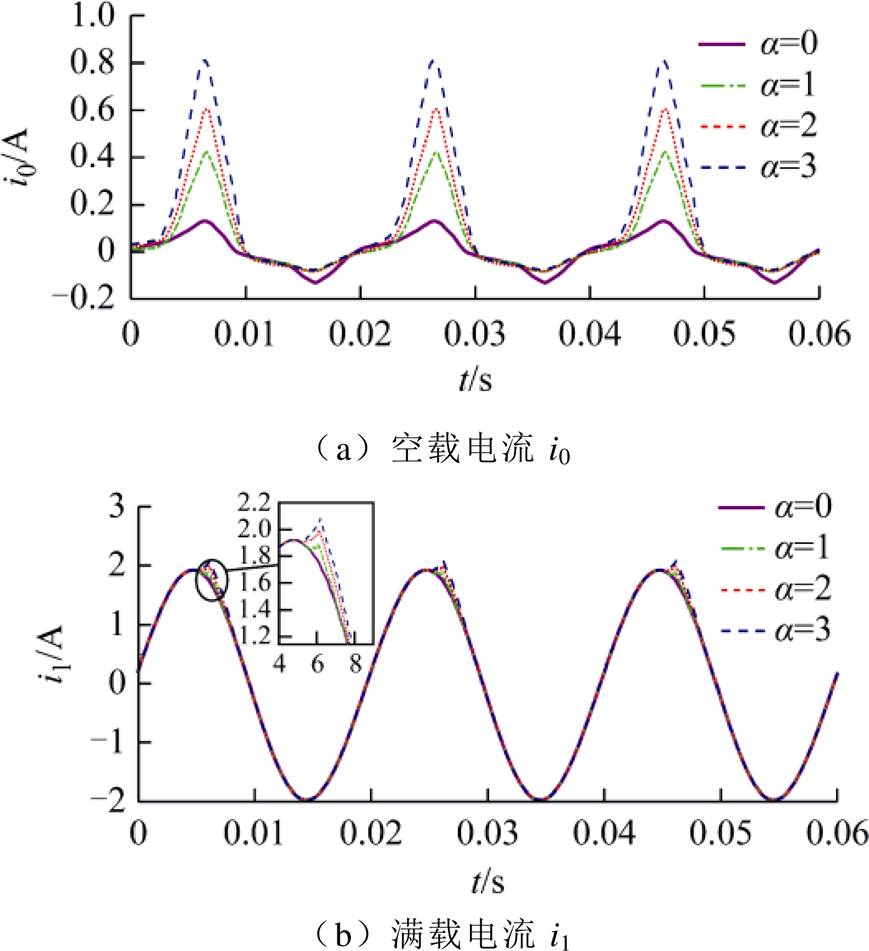
图11 不同直流扰动下单相变压器一次侧电流实验结果
Fig.11 Experimental results of primary current of single-phase transformer under different DC
表6 不同条件下单相变压器振动加速度实验结果
Tab.6 Experimental results of vibration acceleration of single-phase transformer under different conditions
a01.02.03.0 空载I0/A0.0980.1900.2810.390 g/(mm/s2)1号(Y)1.8122.2062.4982.900 2号(Z)0.5880.7110.9011.133 3号(X)2.3302.5882.9643.221 4号(X)2.9123.2013.4103.890 5号(X)2.5802.9143.1623.492 满载I1/A1.3401.3681.3941.425 g/(mm/s2)1号(Y)4.4584.6324.7904.910 2号(Z)1.6121.6951.8001.848 3号(X)4.9205.1565.3455.599 4号(X)5.9116.3206.5986.715 5号(X)5.3695.5525.7706.011
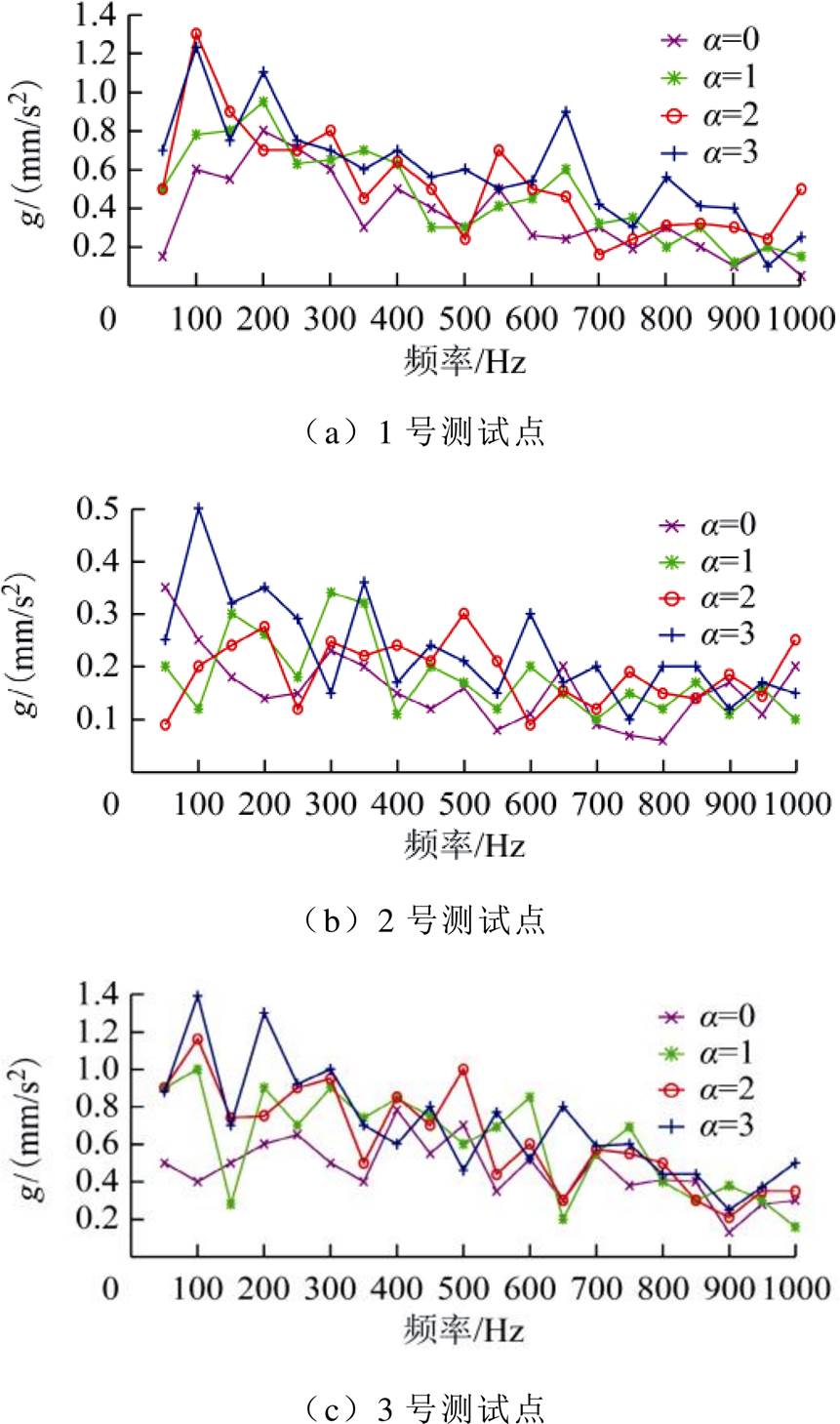
图12 单相变压器实验振动频谱图
Fig.12 Experimental vibration spectrum of single-phase transformer
随着直流水平的升高，铁心各测试点的振动加速度逐渐增强，且测试点1、3、4、5的振动加速度明显大于测试点2；测试点4的振动加速度强于测试点5，表明铁心柱的振动更为剧烈；振动频谱图中各次谐波分量均呈逐步上升的趋势，且振动基频受直流扰动影响最为明显；空载运行条件下随着直流水平的升高空载电流幅值变化明显，铁心振动也更为剧烈，通过对空载电流的辨识可以有效表征铁心振动情况，实验结果与仿真结果一致。同时，满载运行下随着a 的增大，噪声增强，铁心振动变得更为剧烈，当a 增至3.0时已发生局部过热。
搭建Yd变压器动模实验平台（如图13a所示）对上述所得结论进行验证，实验变压器参数见表4。振动量测点的选择与仿真计算中的测试点分布保持一致，实验接线如图13b所示。
以A相为例，iA0、iA的实验波形如图14所示。
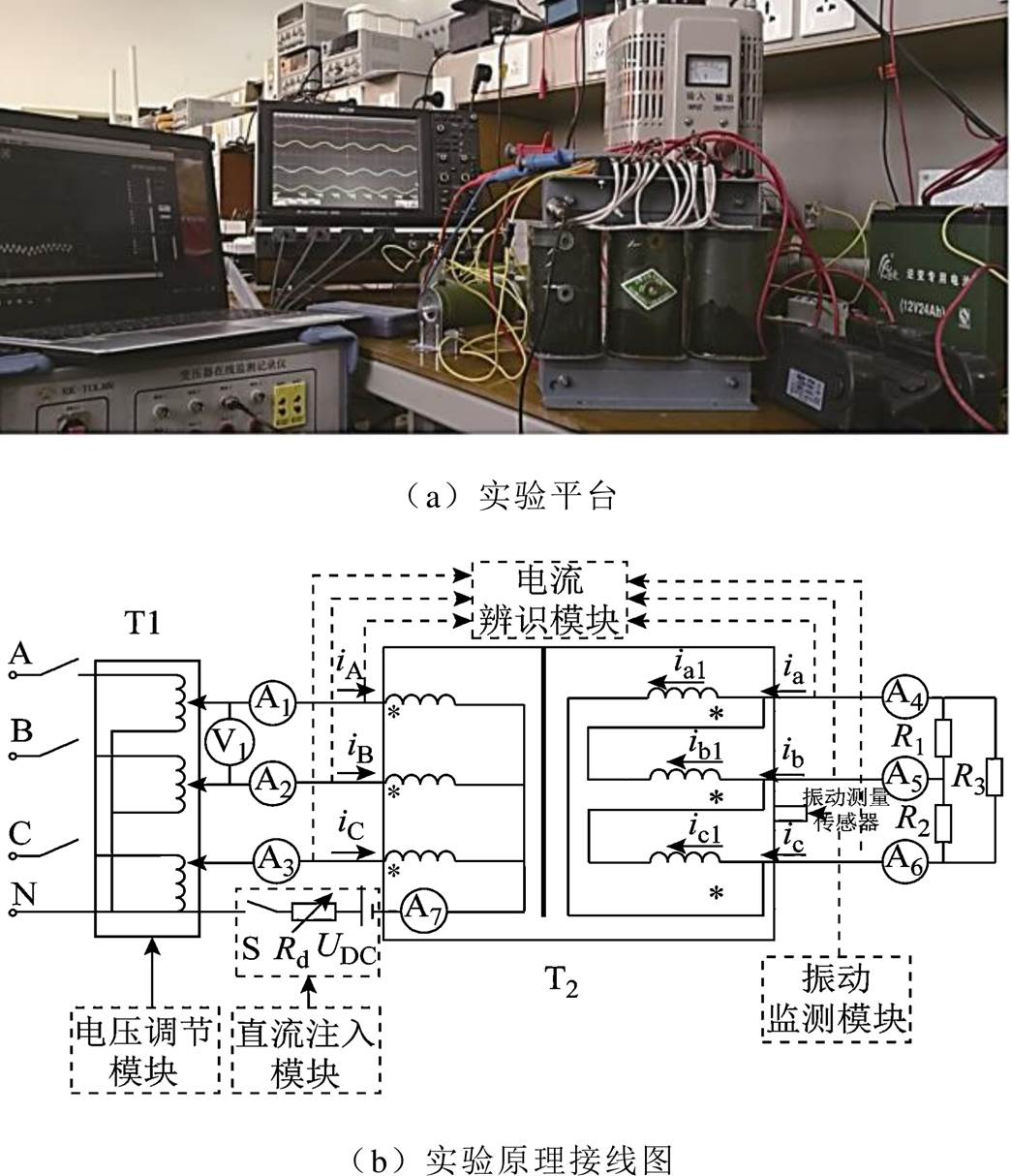
图13 实验接线图
Fig.13 Wiring diagram of experiment
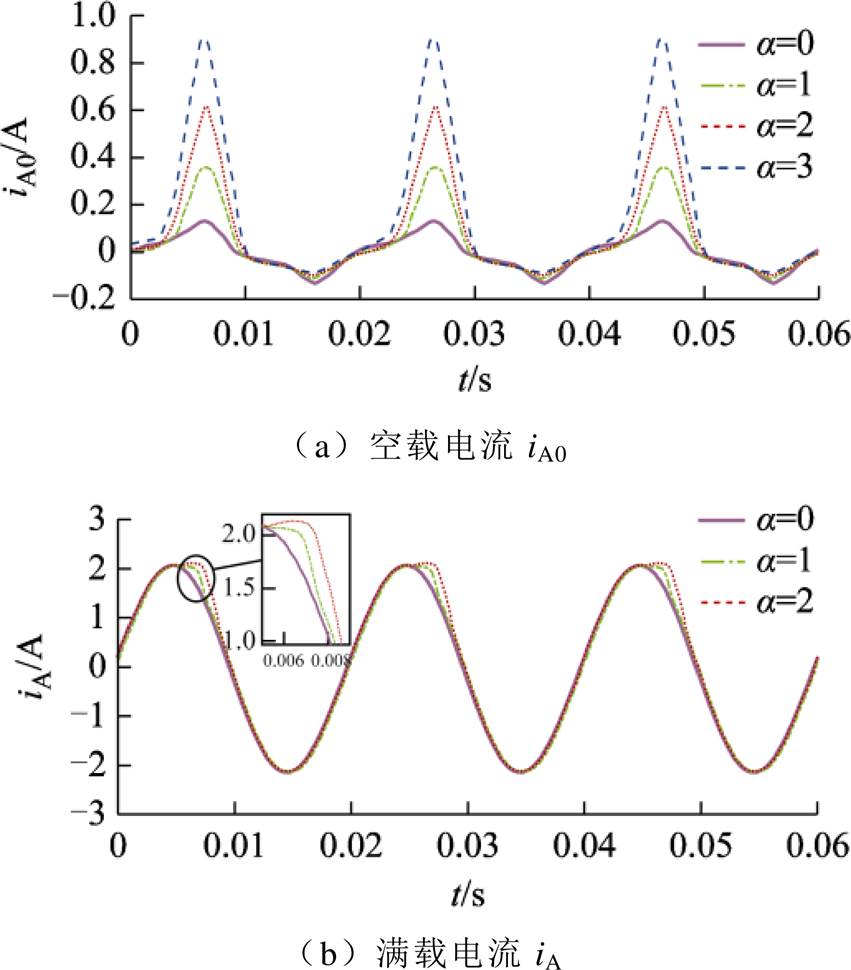
图14 不同直流扰动下三相变压器一次侧电流实验结果
Fig.14 Experimental results of primary current of three-phase transformer under different DC
与图6进行对比可知，仿真计算结果与实验量测数据基本相同，验证了所采用的电流辨识方法的正确性；在满载实验中当a 增至2.5时变压器已出现明显振动，并伴随绝缘烧毁现象。
通过振动监测模块对铁心振动信号进行采集，结果见表7，空载运行下1、2、3号测试点的振动频谱如图15所示。
表7 不同条件下三相变压器振动加速度实验结果
Tab.7 Experimental results of vibration acceleration of three-phase transformer under different conditions
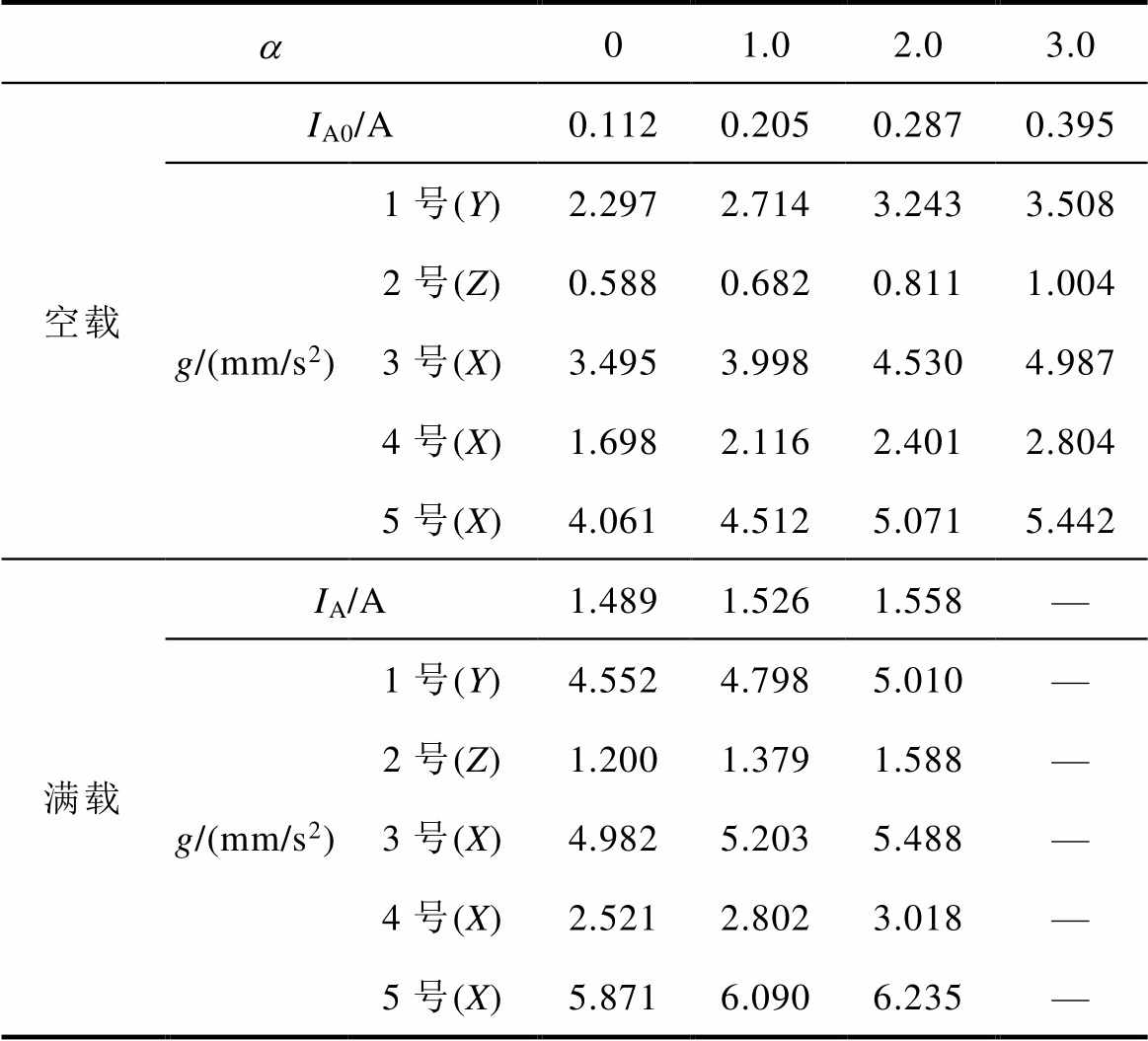
a01.02.03.0 空载IA0/A0.1120.2050.2870.395 g/(mm/s2)1号(Y)2.2972.7143.2433.508 2号(Z)0.5880.6820.8111.004 3号(X)3.4953.9984.5304.987 4号(X)1.6982.1162.4012.804 5号(X)4.0614.5125.0715.442 满载IA/A1.4891.5261.558— g/(mm/s2)1号(Y)4.5524.7985.010— 2号(Z)1.2001.3791.588— 3号(X)4.9825.2035.488— 4号(X)2.5212.8023.018— 5号(X)5.8716.0906.235—
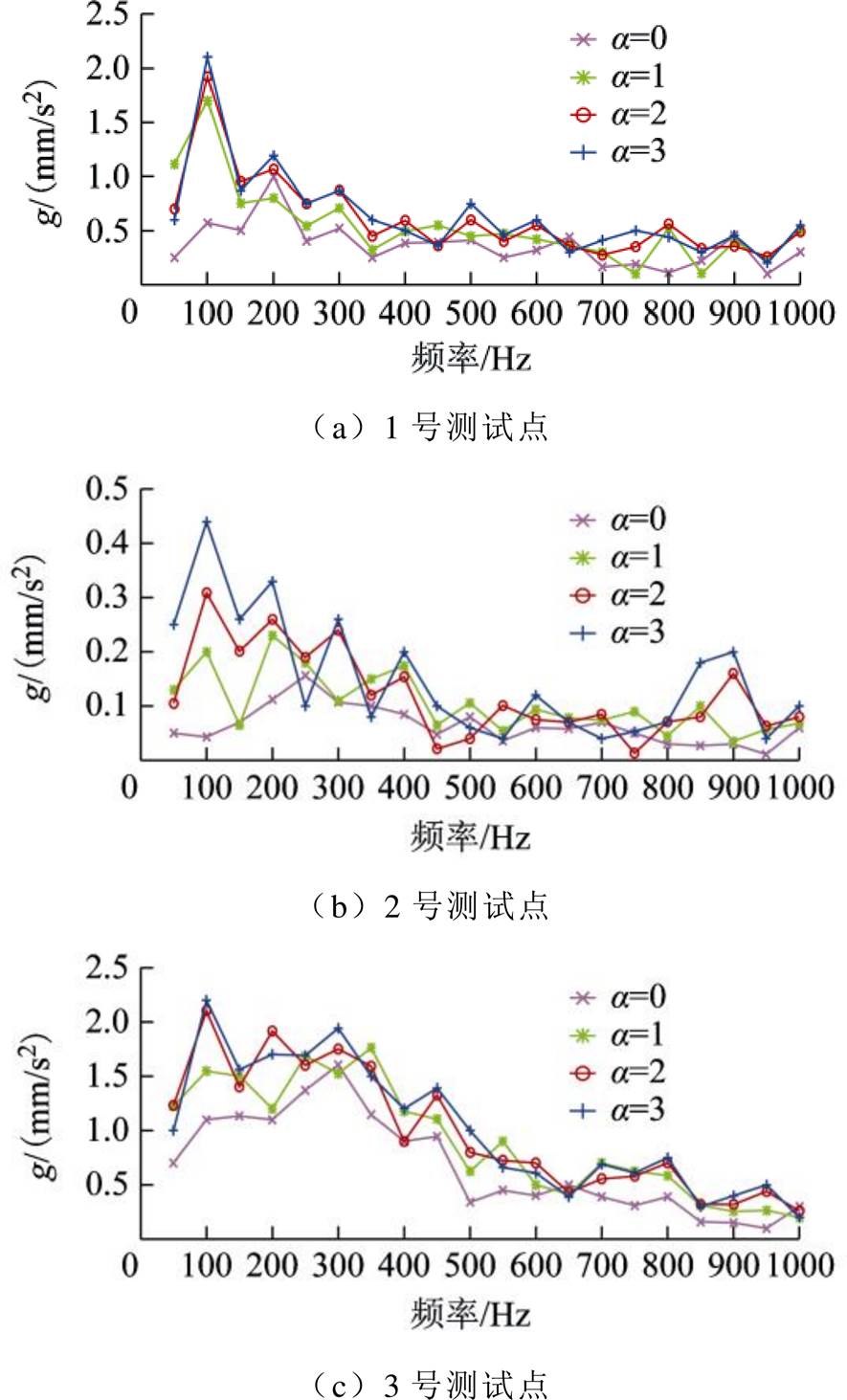
图15 三相变压器实验振动频谱图
Fig.15 Experimental vibration spectrum of three-phase transformer
结合表7，图15、直流扰动下测试点的振幅加剧（主要集中于前500Hz）；随着直流水平升高，振动加速度的频谱幅值呈现增长的趋势，且测试点5的振动强于测试点3。实验量测各点振动加速度及其频谱的变化规律与仿真结果基本一致。
为进一步验证仿真结果的正确性，对单相双绕组变压器及三相三柱式变压器的仿真与实验误差进行分析，结果见表8和表9。
表8 单相变压器仿真与实验误差
Tab.8 Simulation and experimental error of single-phase transformer
a01.02.03.0 空载I0/A10.94.42.21.0 g误差(%)1号(Y)1.82.44.16.9 2号(Z)8.59.95.11.4 3号(X)13.112.69.98.0 4号(X)9.69.312.59.2 5号(X)10.510.112.210.8 满载I1/A1.10.50.30.1 g误差(%)1号(Y)4.92.50.61.0 2号(Z)2.31.60.10.2 3号(X)9.97.97.35.0 4号(X)3.50.31.30.2 5号(X)5.66.16.84.7
表9 三相三柱式变压器仿真与实验误差
Tab.9 Simulation and experimental error of three-phase three-limb transformer
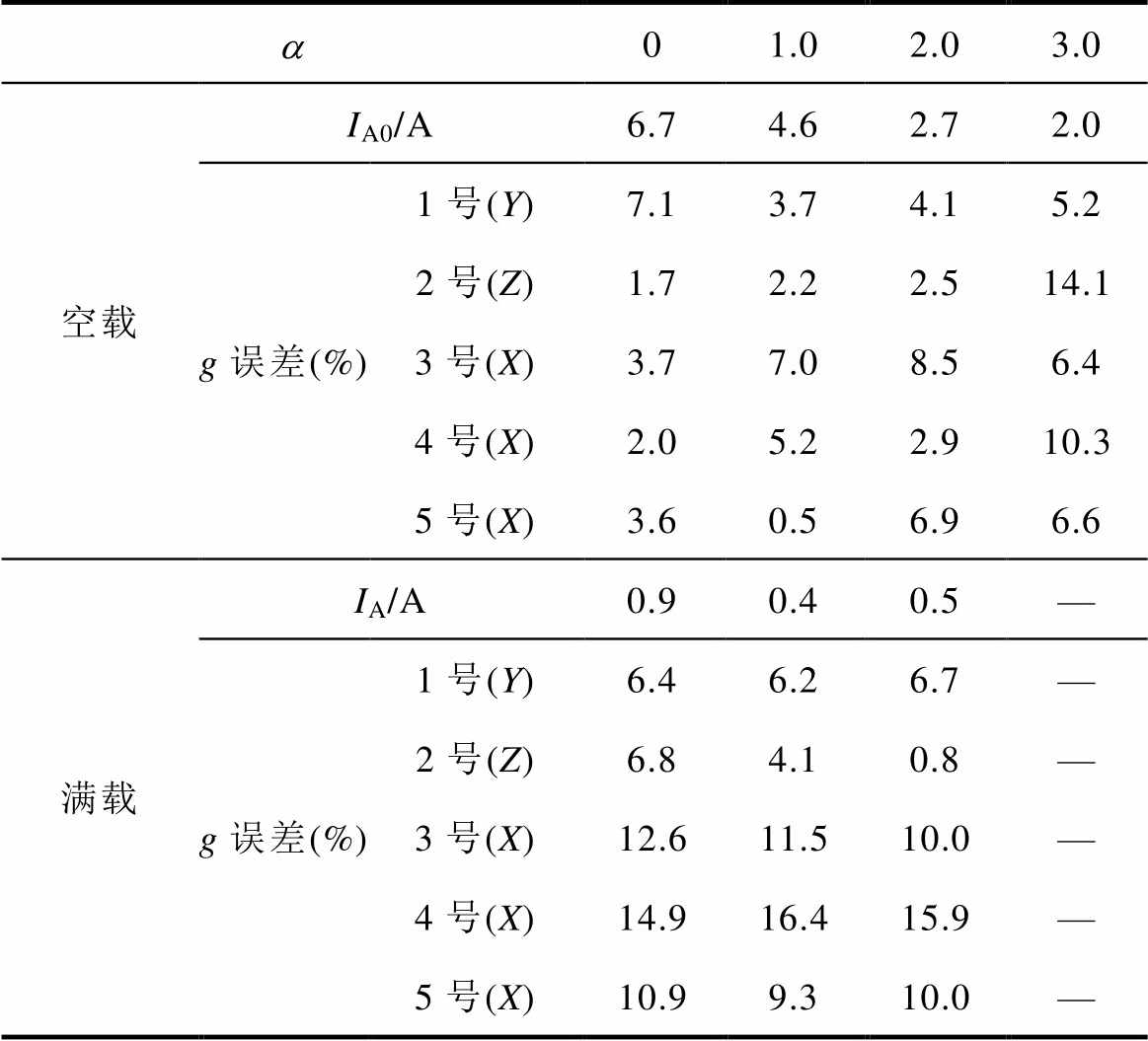
a01.02.03.0 空载IA0/A6.74.62.72.0 g误差(%)1号(Y)7.13.74.15.2 2号(Z)1.72.22.514.1 3号(X)3.77.08.56.4 4号(X)2.05.22.910.3 5号(X)3.60.56.96.6 满载IA/A0.90.40.5— g误差(%)1号(Y)6.46.26.7— 2号(Z)6.84.10.8— 3号(X)12.611.510.0— 4号(X)14.916.415.9— 5号(X)10.99.310.0—
由表8和表9可知，电流及振动加速度的仿真计算与实验量测数据间存在一定误差，分析其原因主要是由于实际变压器受到夹件、拉板等构件的约束以及量测过程中存在的误差，同时在仿真计算中并未考虑变压器本身的剩磁影响。实验数据与仿真数据的基本变化趋势与规律均保持一致，且大部分数据的误差均在10%以内，验证了仿真结果的正确性及本文所提方法的有效性。
研究变压器交直流混杂运行时的电流变化情况与铁心振动特性，得出以下结论：
1）基于电磁耦合原理建立单相双绕组变压器与三相三柱式变压器的直流扰动振动模型，该模型能够有效地计算变压器绕组电流和铁心振动加速度。通过对比仿真结果和实验数据，验证了该模型的正确性。
2）随着直流水平a 升高，铁心振动加剧；单相变压器铁心柱的振动强于旁轭，三相变压器B相铁心柱的振动强于A、C相；振动频谱中低频分量 （≤500Hz）所占比重较大且基频分量受直流的影响最为明显。满载运行条件下当a 达到3.0时单相变压器已出现局部过热，而当a 增至2.5时三相变压器已出现明显振动并伴随绝缘烧毁现象，对比表明单相变压器的抗直流扰动能力更强。
3）空载运行条件下，随着a 的升高绕组电流畸变明显，有效值变化较大，可以通过空载电流的变化情况表征铁心振动；满载运行条件下，由于绕组电流数值较大，随着a 的升高变化并不明显，故无法表征铁心振动。
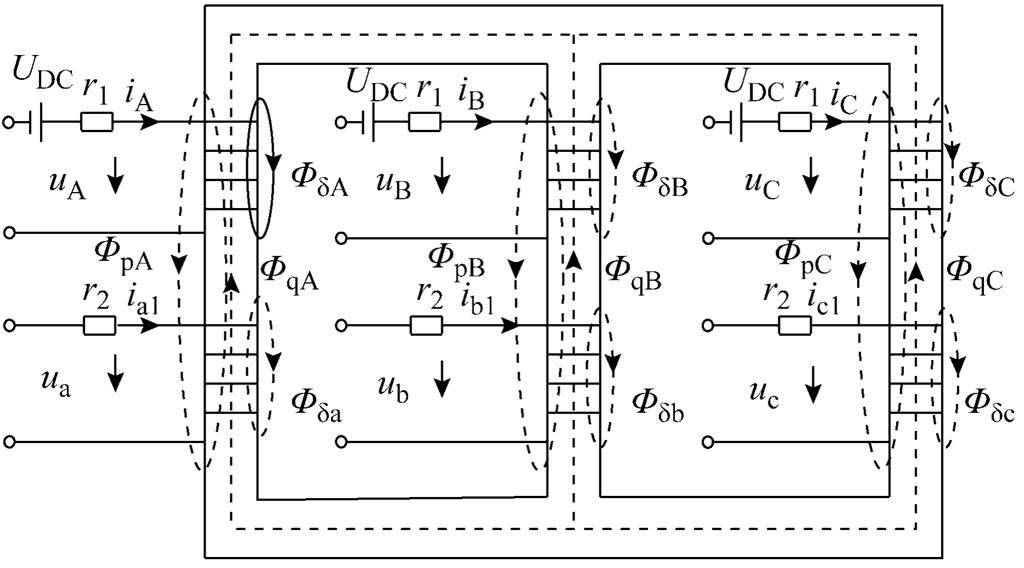
三相三柱式变压器交直流混杂运行时内部电磁关系如附图1所示。
附图1 三相三柱式变压器电磁关系
App.Fig.1 Electromagnetic relationship of three-phase three-limb transformer
附图1中为了区分高、低压绕组产生的磁通效应，将对应线圈分离表示。其中，ux、ix（x=a1, b1, c1）为二次侧各绕组的端电压和绕组电流；uz、iz（z =Α, B, C）为一次侧各绕组的端电压和绕组电流。
高、低压绕组匝数为n1、n2，每个绕组所交链的磁通可以分为三部分：①Fd 为只交链一个绕组的漏磁通；②Fp为同时交链各心柱上两个绕组的漏磁通；③Fq为同时交链所有绕组的主磁通，即完全在铁心构成闭合回路的磁通。
Fp和Fq同时交链每个心柱上的两个绕组，可将两侧参数归算到一次侧，则一次绕组端电压可表示为
（A1）式中，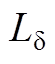
为一次绕组漏感；id为归算后的各心柱绕组差流，其表达式为
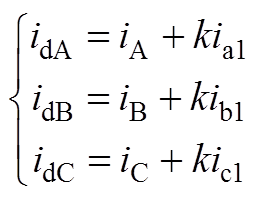（A2）
式中，k=n1/n2。
以A相为例，各电感参数的物理意义为
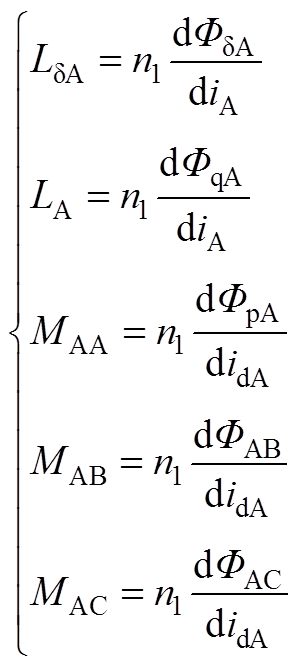（A3）参考文献
[1] Chen Dezhi, Feng Zhiyu, Wang Qingpeng, et al. Study of analysis and experiment for ability to withstand DC bias in power transformers[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-6.
[2] 张荣伦, 王帅, 穆海宝, 等. 大型电力变压器损耗带电测试技术研究[J]. 电工技术学报, 2019, 34(4): 683-692.
Zhang Ronglun, Wang Shuai, Mu Haibao, et al. The on-site method for the loss characteristic in power transformer[J]. Transactions of China Electro- technical Society, 2019, 34(4): 683-692.
[3] 张大宁, 刘孝为, 詹江杨, 等. 变压器油纸绝缘频域介电谱的虚部分析[J]. 电工技术学报, 2019, 34(4): 847-854.
Zhang Daning, Li Xiaowei, Zhan Jiangyang, et al. Analysis of imaginary part of frequency domain spectroscopy for oil-paper insulation transformer[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 847-854.
[4] 王建元, 梁惠娟, 康爱民. 国内电力变压器局部放电超声波定位研究进展[J]. 东北电力大学学报, 2019, 39(2): 10-14.
Wang Jianyuan, Liang Huijuan, Kang Aimin. Researches of power transformer partial discharge location using ultrasonic method in China[J]. Journal of Northeast Electric Power University, 2019, 39(2): 10-14.
[5] 曹文斌, 尹项根, 王育学, 等. 高阻抗变压器涌流的特殊性比较分析[J]. 电力系统自动化, 2019, 43(16): 141-150.
Cao Wenbin, Yin Xianggen, Wang Yuxue, et al. Analysis of the particularity of inrush current in high impedance transformer[J]. Automation of Electric Power System, 2019, 43(16): 141-150.
[6] 王祯, 尹项根, 陈玉, 等. 配电变压器集成式混合补偿系统[J]. 电力系统自动化, 2019, 43(11): 152- 160, 190.
Wang Zhen, Yin Xianggen, Chen Yu, et al. Integrated hybrid compensation system for distribution trans- former[J]. Automation of Electric Power System, 2019, 43(11): 152-160, 190.
[7] 刘春明, 王璇, 刘连光, 等. 考虑海岸效应影响的电网地磁感应电流的计算方法[J]. 中国电机工程学报, 2016, 36(22): 6059-6066.
Liu Chunming, Wang Xuan, Liu Lianguang, et al. Calculation method of geomagnetically induced currents in the power grid considering the influence of the coast effect[J]. Proceedings of the CSEE, 2016, 36(22): 6059-6066.
[8] 陈志伟, 白保东, 陈德志, 等. 电力变压器直流偏磁现象形成机理及一种抑制措施的研究[J]. 电工技术学报, 2015, 30(14): 208-214.
Chen Zhiwei, Bai Baodong, Chen Dezhi, et al. Research on the formation mechanism and suppression method of transformer DC bias[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 208- 214.
[9] Liu Chunming, Li Xiaohan, Li Xinjie. Simulating the vibration increase of the transformer iron core due to the DC bias[J]. International Journal of Applied Electromagnetics and Mechanics, 2017, 55(3): 423- 433.
[10] 王洋, 刘志珍. 基于Jiles Atherton磁滞理论的直流偏磁下铁心损耗预测[J]. 中国电机工程学报, 2017, 37(1): 313-323.
Wang Yang, Liu Zhizhen. The forecasting method of core loss under DC bias based on the jiles atherton hysteresis theory[J]. Proceedings of the CSEE, 2017, 37(1): 313-323.
[11] 张黎, 王国政, 董攀婷, 等. 基于磁致伸缩本征特性的晶粒取向性变压器铁心振动模型[J]. 中国电机工程学报, 2016, 36(14): 3990-4001.
Zhang Li, Wang Guozheng, Dong Panting, et al. Study on the vibration of grain-oriented transformer core based on the intrinsic characteristics[J]. Pro- ceedings of the CSEE, 2016, 36(14): 3990-4001.
[12] 王帅兵, 李琳, 赵小军, 等. 定点时间周期有限元法及其在变压器直流偏磁特性分析中的应用[J]. 中国电机工程学报, 2017, 37(17): 5198-5205.
Wang Shuaibing, Li Lin, Zhao Xiaojun, et al. Fixed-point time-periodic finite element method and its application for DC bias characteristics of trans- former[J]. Proceedings of the CSEE, 2017, 37(17): 5198-5205.
[13] Saburo T, Hayaki M, Tomova H, et al. Imaging of magnetic nanoparticles using a second harmonic of magnetization with DC bias field[J]. IEEE Transa- ctions on Magnetics, 2015, 51(2): 1-4.
[14] 潘超, 金明权, 蔡国伟, 等. 基于变压器励磁电流辨识的直流失稳与抑制策略[J]. 电工技术学报, 2018, 33(18): 4267-4276.
Pan Chao, Jin Mingquan, Cai Guowei, et al. DC instability and suppression strategy of transformer based on exciting-current identification[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(18): 4267-4276.
[15] 王佳音, 白保东, 刘宏亮. 直流偏磁对变压器振动噪声的影响[J]. 电工技术学报, 2015, 30(8): 56-61.
Wang Jiayin, Bai Baodong, Liu Hongliang. Research on vibration and noise of transformers under DC bias[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 56-61.
[16] 祝丽花, 杨庆新, 闫荣格, 等. 考虑磁致伸缩效应电力变压器振动噪声的研究[J]. 电工技术学报, 2013, 28(4): 1-6, 19.
Zhu Lihua, Yang Qingxin, Yan Rongge, et al. Research on vibration and noise of power tansformer cores including magnetostriction effects[J]. Transa- ctions of China Electrotechnical Society, 2013, 28(4): 1-6, 19.
[17] 张鹏宁, 李琳, 程志光, 等. 并联电抗器与变压器模型铁心振动仿真与试验对比[J]. 电工技术学报, 2018, 33(22): 5273-5281.
Zhang Pengning, Li Lin, Cheng Zhiguang, et al. Vibration simulation and experiment comparison of shunt reactor and transformer model core[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5273-5281.
[18] 高沛, 王丰华, 苏磊, 等. 直流偏磁下电力变压器的振动特性[J]. 电网技术, 2014, 38(6): 1536-1541.
Gao Pei, Wang Fenghua, Su Lei, et al. Analysis on vibration characteristics of power transformer under DC bias[J]. Power System Technology, 2014, 38(6): 1536-1541.
[19] 李长云, 郝爱东, 娄禹. 直流偏磁条件下电力变压器振动特性研究进展[J]. 电力自动化设备, 2018, 38(6): 215-223.
Li Changyun, Hao Aidong, Lou Yu. Status and progress of research on transformer vibration characteristics with DC bias[J]. Electric Power Automation Equipment, 2018, 38(6): 215-223.
[20] 索南加乐, 许立强, 焦在滨, 等. 基于磁路特征的三相三柱式变压器励磁参数识别[J]. 中国电机工程学报, 2011, 31(19): 97-104.
Suonan Jiale, Xu Liqiang, Jiao Zaibin, et al. Identification method for excitation inductances of three-phase three-limb transformer based on characteristics of magnetic circuit[J]. Proceedings of the CSEE, 2011, 31(19): 97-104.
[21] 李世芸, 肖正明. 弹性力学及有限元[M]. 北京: 机械工业出版社, 2015.
[22] 王丰华, 段若晨, 耿超, 等. 基于“磁-机械”耦合场理论的电力变压器绕组振动特性研究[J]. 中国电机工程学报, 2016, 36(9): 2555-2562.
Wang Fenghua, Duan Ruochen, Geng Chao, et al. Research of vibration characteristics of power transformer winding based on magnetic-mechanical coupling field theory[J]. Proceedings of the CSEE, 2016, 36(9): 2555-2562.
[23] 祝丽花, 王斌, 刘松, 等. 不同负载对干式变压器电磁振动的影响分析[J]. 电工技术学报, 2018, 33(7): 1599-1606.
Zhu Lihua, Wang Bin, Liu Song, et al. Research on electromagnetic vibration of dry type transformer under different types of load[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1599- 1606.
[24] 汪金刚, 毛凯, 段旭, 等. 直流偏磁下的变压器振动仿真与试验[J]. 电机与控制学报, 2015, 19(1): 58-67.
Wang Jingang, Mao Kai, Duan Xu, et al. Simulation and test of transformer vibration under DC[J]. Electric Machines and Control, 2015, 19(1): 58-67.
[25] 邓涛, 舒群力, 杨李栋, 等. 特高压变压器空载直流偏磁电磁特性计算[J]. 变压器, 2018, 55(10): 14-18.
Deng Tao, Shu Qunli, Yang Lidong, et al. Calculation of electromagnetic characteristics of no-load DC-bias in UHV transformer[J]. Transformer, 2018, 55(10): 14-18.
Research on Characterization of Core Vibration by Abnormal Current of DC Bias Transformer
Abstract DC disturbance vibration model of single-phase transformer and three-phase three- limb Yd transformer are established according to core vibration problem of transformer disturbed by DC. Winding current is identified based on electromagnetic coupling principle, and vibration harmonic response model was constructed to research vibration characteristics. Electromagnetic characteristics of transformer under different DC levels are simulated. Variation characteristics of winding abnormal current and core vibration acceleration under the influence of DC are analyzed, and summarizing rule. AC/DC hybrid dynamic model experimental platform of transformer is built to identify and collect the winding current and core vibration signals respectively. Experimental data are compared with simulation results to verify the correctness and effectiveness of the proposed method.
keywords：Transformer, DC bias, abnormal current, core vibration, harmonic response
中图分类号：TM41
DOI: 10.19595/j.cnki.1000-6753.tces.190248
吉林省科技发展计划（20190303007SF）和国家自然科学基金（51507027）资助项目。
收稿日期 2019-03-12
改稿日期 2019-05-15
潘 超 男，1981年生，博士，副教授，研究方向为电力系统稳定与电磁兼容。E-mail: 31563018@qq.com
苏 昊 男，1994年生，硕士研究生，研究方向电力变压器直流偏磁振动效应。E-mail: 379272394@qq.com（通信作者）
（编辑 郭丽军）