图1 八磁极径向电磁轴承结构
Fig.1 Structure of radial AMB with eight magnetic poles
摘要 电磁场分布特性的准确分析与计算是电磁轴承性能优化的基础,而目前电磁轴承磁场分析时较少同时考虑涡流和铁心磁导率的非线性这两个因素的影响。因此,该文利用指数方程拟合硅钢片的磁化曲线来考虑磁导率的非线性,引入动态相对磁导率来计及涡流对磁场的影响。建立了计及磁极边缘效应、定转子铁心磁阻、铁心磁导率非线性、涡流及实时控制电流在内的径向电磁轴承非线性等效磁路模型。采用该模型计算转子具有静态位移0.1mm时电磁轴承的气隙磁场分布,与有限元仿真结果吻合较好,在磁极正对处的气隙磁通密度的误差基本在3%以内。并分析了转子周期振动导致的铁心涡流对气隙磁通及电磁力的影响,考虑涡流后,磁通及电磁力都有一定程度的衰减,并且转子振动频率越高,衰减越大。
关键词:电磁轴承 等效磁路法 磁导率非线性 涡流 转子振动
电磁轴承(Active Magnetic Bearing, AMB)是利用电磁力将转子稳定悬浮在给定位置的一种高性能机电一体化轴承,与传统的机械轴承相比,其具有无接触、无需润滑、无磨损、转速高、功耗低、维护简单等优点,因而在飞轮储能、高速机床、鼓风机、涡轮分子泵等高速旋转设备上得到了广泛应用,尤其在真空、超净、超高速、航空航天、核能等场合,其具有不可替代的优势[1-2]。
电磁场建模和分析一直是电磁轴承领域的重要研究内容,准确的磁场分析是电磁轴承结构设计与优化、承载力计算和铁心损耗分析的基础。目前,国内外不少学者针对电磁轴承磁场建模方法进行了持续研究。文献[3]通过建立的等效磁路模型对径向电磁轴承进行了结构优化设计,但未考虑磁极边缘效应和材料磁导率的非线性。文献[4]基于材料磁导率的非线性,建立了电磁轴承的非线性等效磁路模型,并用于分析轴承承载力,但并未涉及涡流对磁场的影响。文献[5]的研究结果表明,计及磁通边缘效应建立的等效磁路模型具有更高的准确性。文献[6-8]建立磁路模型对混合磁轴承的磁场分布和承载力进行分析。文献[9]在分析三磁极交流混合磁轴承的悬浮力时,建立了计及边缘效应的等效磁路模型,但未考虑材料磁导率的非线性和涡流的影响。文献[10]针对三磁极电磁轴承,以转子偏心量为摄动量,利用摄动法求解不同磁场区域的拉普拉斯方程和泊松方程,计算轴承偏心时的电磁力,其计算结果与有限元仿真结果吻合较好,但其计算过程较为复杂,在电磁轴承磁场分析中使用较少。文献[11]通过建立的磁阻网络模型,对交变电流激励下的径向电磁轴承的损耗进行了分析,但其磁阻计算并未考虑涡流和铁磁材料饱和因素的影响,误差较大。文献[12]针对轴向电磁轴承,建立了考虑涡流影响的磁路模型,并用于分析轴承动态刚度,并未考虑材料磁导率的非线性。
由于质量不平衡或在外界激励力的作用下,磁悬浮转子旋转时不可避免地会产生径向振动,导致铁心在交变磁场作用下产生涡流,从而影响电磁轴承的磁场分布。而现有的研究较少考虑转子振动导致的涡流对磁场分布的影响。
本文将在考虑材料磁导率的非线性以及磁极边缘效应的基础上,采用等效相对磁导率来考虑涡流的影响,建立径向电磁轴承的非线性等效磁路模型,并根据此模型,针对0.35mm硅钢片叠成的八磁极径向电磁轴承,分析转子径向振动导致的涡流对电磁轴承的磁场分布及电磁力的影响。
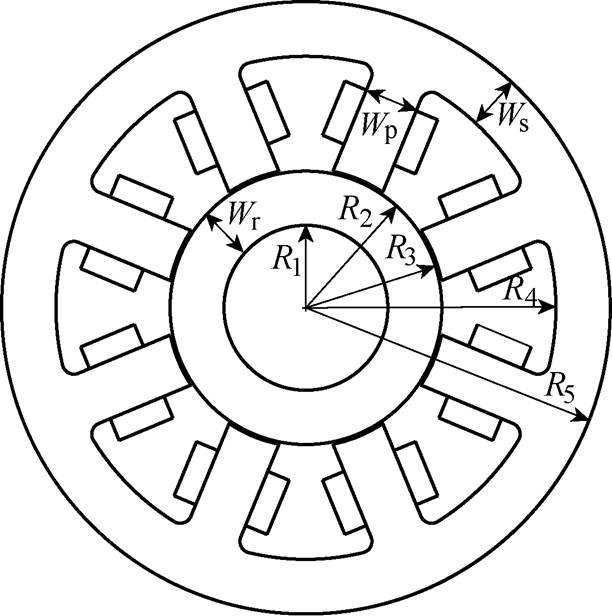
以如图1所示的八磁极径向电磁轴承为例,研究电磁场建模方法,电磁轴承任一对磁极的结构如图2所示。

图1 八磁极径向电磁轴承结构
Fig.1 Structure of radial AMB with eight magnetic poles
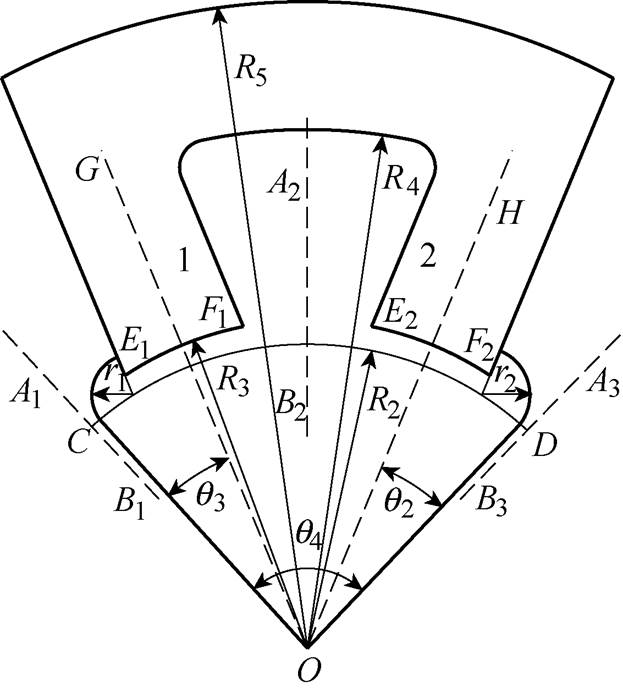
图2 任一对磁极的结构
Fig.2 Structure diagram of any pair of magnetic poles
当转子处于中心位置(平衡点)时,任一个定子磁极与转子之间的正对气隙处的气隙磁阻为
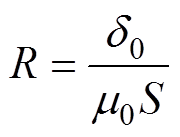 (1)
(1)式中,d0为电磁轴承悬浮气隙长度;S为一个磁极的有效横截面积;m0为真空磁导率。
电磁轴承实际运行时,转子通常会偏离平衡点,在平衡点附近振动,此时气隙的周向分布将会变得不均匀,本文主要针对此种情况下的气隙磁阻进行建模。
为了考虑边缘效应,根据磁场分割法,可将磁极处的磁通划分为7个部分,如图3所示,1为磁极端面正对区域,2~7为边缘区域。这些区域磁通之和为定子磁极中的总磁通。
图3 边缘效应磁通分布
Fig.3 Distribution of edge effect flux
1.1.1 定子磁极端面正对气隙处的主气隙磁导
当转子振动偏离平衡位置时,磁极和转子表面不再是等距的,此时可以采用微元积分法计算气隙磁导[13]。根据磁动势相等条件下,磁通总是沿磁阻最小的路径流通的原理,求出磁极表面的某个微元到转子表面的最短距离即为磁通的最短流通路径,利用微元法即可得出转子偏离平衡位置后磁极正对气隙所对应的气隙磁导。转子具有位移时定子磁极与转子表面几何关系如图4所示,EF为平衡位置处的转子表面,GH为偏离平衡点后转子表面,AB为相应的定子磁极面,O1为定子磁极圆心,也为坐标原点,O2为转子偏离平衡点后的圆心,坐标为(![]() ,
,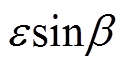 ),其中,e 为O1和O2之间的距离,b 为O1O2与x轴正向之间的夹角。CD为转子表面与定子磁极面之间的线段,需要求出CD的最短长度。CD的长度L为
),其中,e 为O1和O2之间的距离,b 为O1O2与x轴正向之间的夹角。CD为转子表面与定子磁极面之间的线段,需要求出CD的最短长度。CD的长度L为
 (2)
(2)式中,R2为转子半径;R3为定子半径;q1为O2D与x轴之间的夹角。
由 可得,当
可得,当
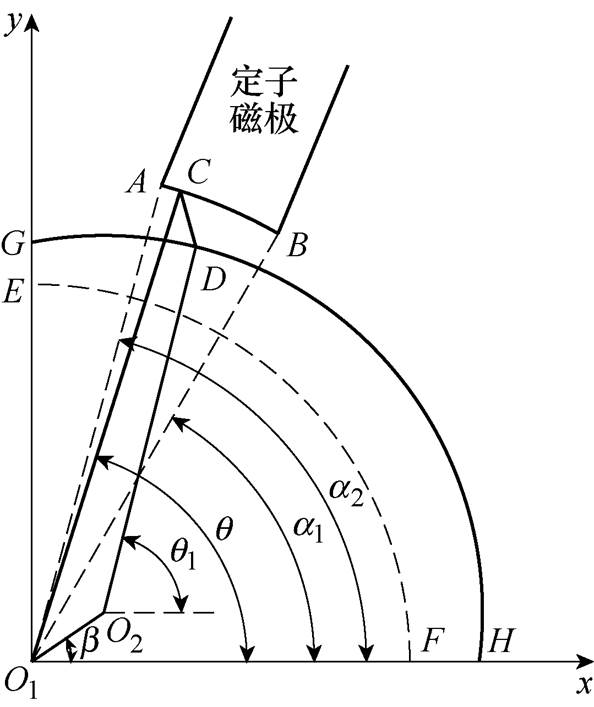
图4 转子具有位移时定子磁极与转子表面几何关系
Fig.4 Schematic diagram of geometric relationship between stator pole and rotor surface with rotor vibration displacement
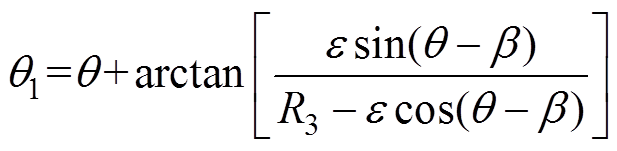 (3)
(3)时,CD长度L最短,且为
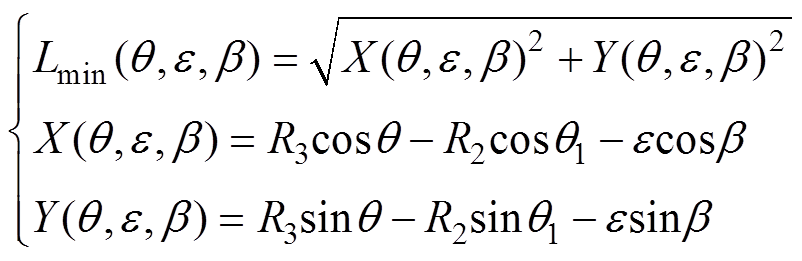 (4)
(4)
由微元法可得图3中磁极端面1正对处的气隙磁导为
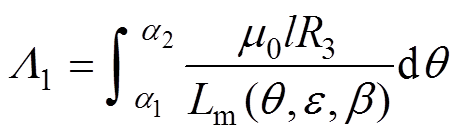 (5)
(5)式中,a1、a2分别为定子磁极的起始角和终止角;l为电磁轴承的轴向长度。
1.1.2 磁极的边缘气隙磁导
为了简化边缘气隙磁导的计算,假设如下:
(1)由于转子表面周长远大于定子磁极弧长,因此在计算边缘气隙磁导时假设磁极端面与转子表面均为平面,且同一磁极下的气隙长度近似相等,等于磁极中心线处的气隙长度。
(2)假定磁极边缘效应划分的区域为标准的圆柱体或球体。
(3)忽略磁极与磁极之间的漏磁。
气隙磁导的计算公式为
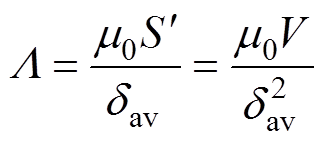 (6)
(6)式中,dav为平均气隙长度;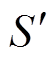 为磁通横截面积;V为磁通流通区域的体积。
为磁通横截面积;V为磁通流通区域的体积。
区域2、6为1/4圆柱体,其磁导分别为L2、L6;区域3、7为1/4空心圆柱体,磁导分别为L3、L7;区域4为1/8实心球体,磁导为L4;区域5为1/8空心球体,磁导为L5。根据式(6)可计算给出各部分的气隙磁导分别为
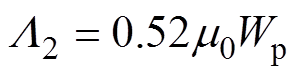 (7)
(7)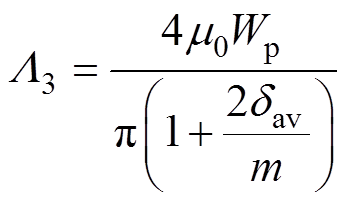 (8)
(8)
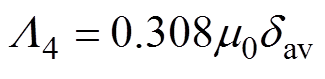 (9)
(9)
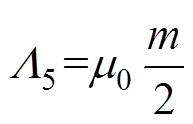 (10)
(10) (11)
(11)
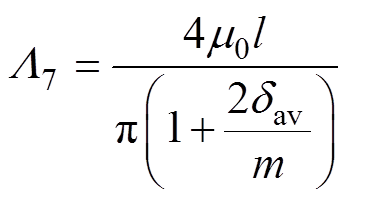 (12)
(12)
式中,Wp为磁极宽度;m为边缘磁通沿磁极径向分布长度,其值取磁极中心线对应气隙长度的1~2倍[14],本文取2,磁极中心线对应的气隙值可以由式(3)和式(4)计算得出。
考虑边缘效应的单个磁极的气隙总磁导为
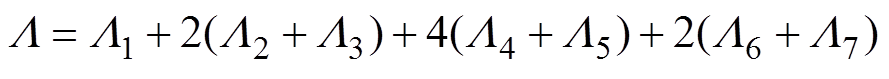 (13)
(13)目前,大多数文献中针对电磁轴承所建立的等效磁路模型,通常只考虑一对磁极正对的转子磁阻,而很少考虑边缘磁通的那部分转子磁阻。
如图2所示,A1B1、A2B2、A3B3分别为磁极分界线,OG、OH分别为磁极中心线,CD为转子外表面,E1F1、E2F2为定子磁极端面。设r为考虑边缘效应时磁极上边缘磁通的跨越半径,则r1=d1+m1,r2=d2+m2,其中d1、d2分别为磁极1和磁极2中心线对应的气隙长度,q3=arctan[(m+d1+Wp/2)/R2],q2=arctan[(m+d2+Wp/2)/R2]。由此可得,考虑磁极边缘效应时,磁极1和磁极2对应的转子角度为q4。进而可以计算转子铁心磁导为
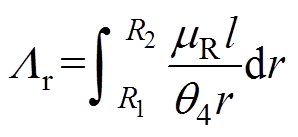 (14)
(14)式中,R1为轴半径;mR为转子铁心的磁导率。
定子磁轭和磁极的铁心磁阻分别为
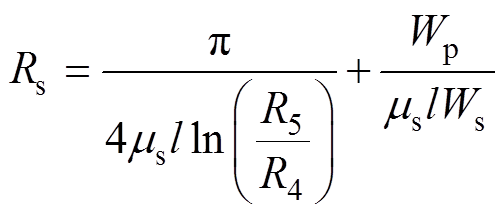 (15)
(15)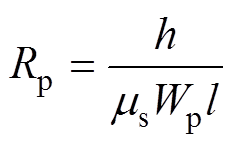 (16)
(16)
磁极对与相邻磁极对之间定子磁轭磁阻为
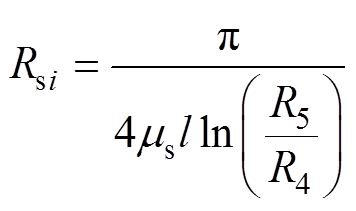 (17)
(17)式中,R4为定子中径;R5为转子外径;ms为定子铁心的磁导率;h为磁极径向长度;i=1,…, 4。
1.2.1 铁心材料磁导率的非线性
为了更准确地计算电磁轴承的磁场,在模型中需要考虑定子和转子铁心材料磁导率的非线性。电磁轴承的定转子铁心材料通常均采用硅钢片叠片结构,在实际工程应用中,软磁材料的外磁场强度一般在0~7 000A/m[4],在这个范围内,对定子、转子铁心材料的磁化曲线进行非线性拟合可以反映材料的非线性。目前,拟合近似B-H曲线多采用幂方程[4]、指数方程、多项式以及分段线性方程[15]、正切方程[16]等。指数方程拟合效果较好、计算简单,因此本文采用指数方程进行拟合。WG35WW250硅钢片的磁化曲线以及非线性拟合曲线如图5所示,相应的拟合方程为
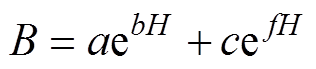 (18)
(18)式中,a=1.43 1;b=2.588×10-5;c=-1.561;f = -0.013 58。
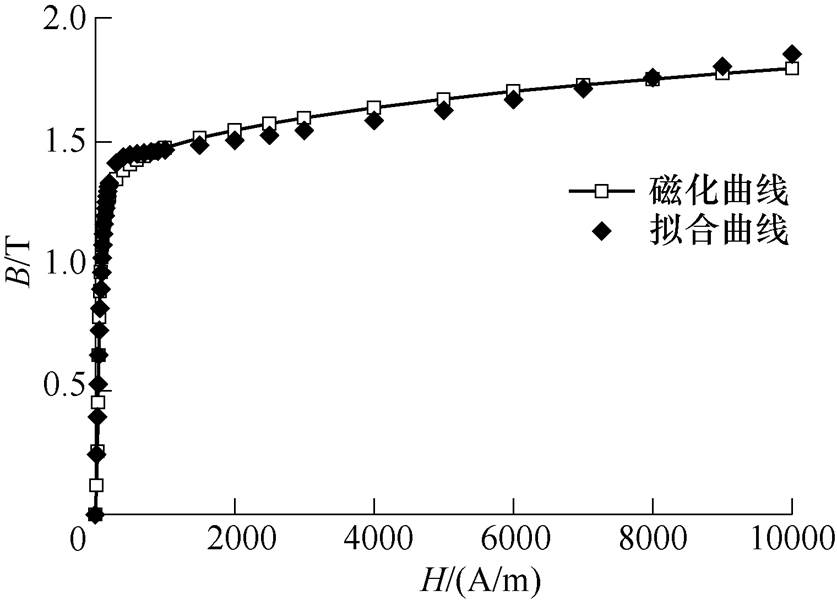
图5 硅钢片B-H曲线及其拟合曲线
Fig.5 B-H curve and its fitting curve of silicon steels
1.2.2 涡流对铁心磁阻的影响
当转子径向振动时,由于线圈电流的交变作用,会在定转子铁心中产生涡流,进而影响磁场的分布特征。为了减小涡流,电磁轴承一般采用硅钢片叠片结构,在频率较低时,涡流对磁场的影响比较小;但当频率较高时,涡流对磁场具有显著影响。有学者为了考虑涡流的影响,引入了动态相对磁导 率[17-18],有
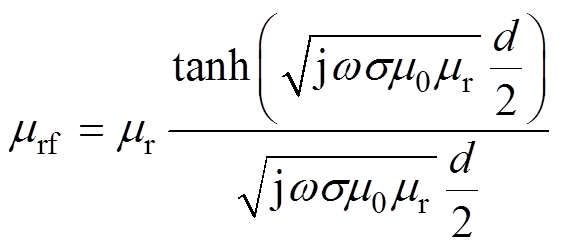 (19)
(19)式中,mr为铁心的静态相对磁导率;w 为磁通变化频率;s 为电导率;d为硅钢片厚度,根据工业界磁悬浮轴承常用硅钢片厚度,本文中硅钢片的厚度取为0.35mm。
动态相对磁导率随频率的变化关系如图6所示,动态相对磁导率是一个随频率变化的复数,随着频率的增加,幅值不断减小,其相位也随之产生滞后,在频率较低时,动态相对磁导率变化并不明显。将式(19)代入铁心磁阻计算式(14)~式(17)中,在一定程度上可以计及涡流对定、转子铁心磁阻的影响。
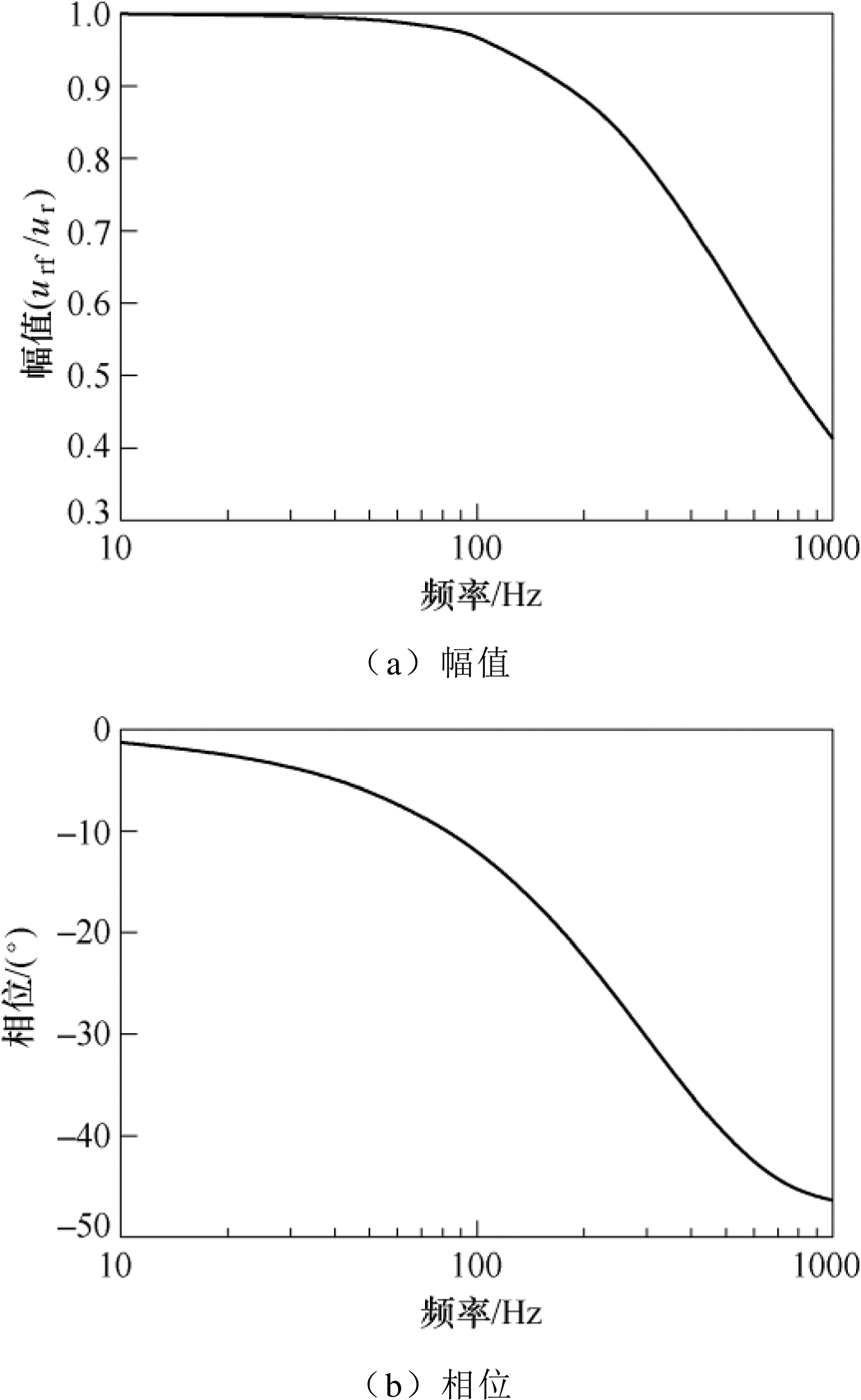
图6 动态相对磁导率随频率的变化关系
Fig.6 Dynamic relative permeability versus frequency
根据以上计算出的磁导,求出相应的磁阻为
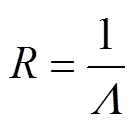 (20)
(20)建立的八磁极径向电磁轴承的磁路模型如图7所示,图中,N为线圈匝数;iy+、iy-、ix+、ix-分别为y+、y-、x+、x-方向对应的线圈电流;Rsy+、Rsy-、Rsx+、Rsx-、Rry+、Rry-、Rrx+、Rrx-分别为y+、y-、x+、x-方向的定子磁轭和转子铁心的等效磁阻;Rg1y+、Rg2y+、Rg3y-、Rg4y-、Rg5x-、Rg6x-、Rg7x+、Rg8x+分别为y+、y-、x-、x+方向包含边缘磁阻在内的总气隙磁阻;Rpy+、Rpy-、Rpx+、Rpx-分别为y+、y-、x+、x-方向的定子磁极铁心的等效磁阻。
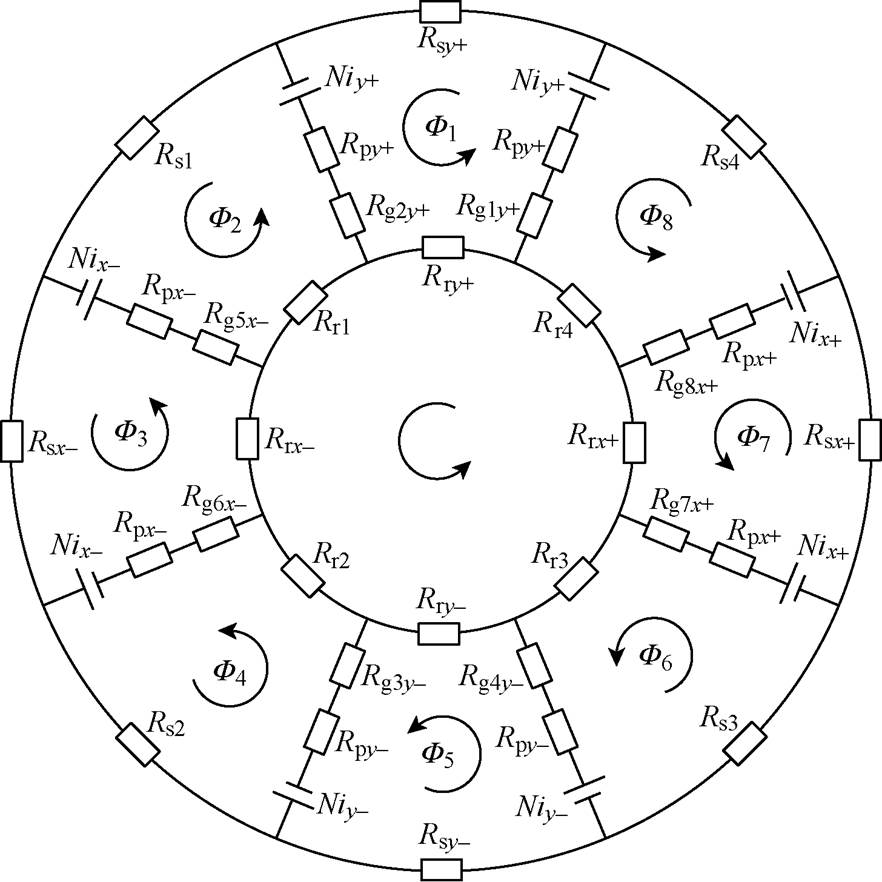
图7 径向电磁轴承等效磁路模型
Fig.7 Equivalent magnetic circuit of radial AMB
由此可得施加控制电流后磁路方程为
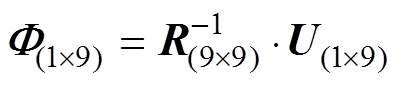 (21)
(21)其中

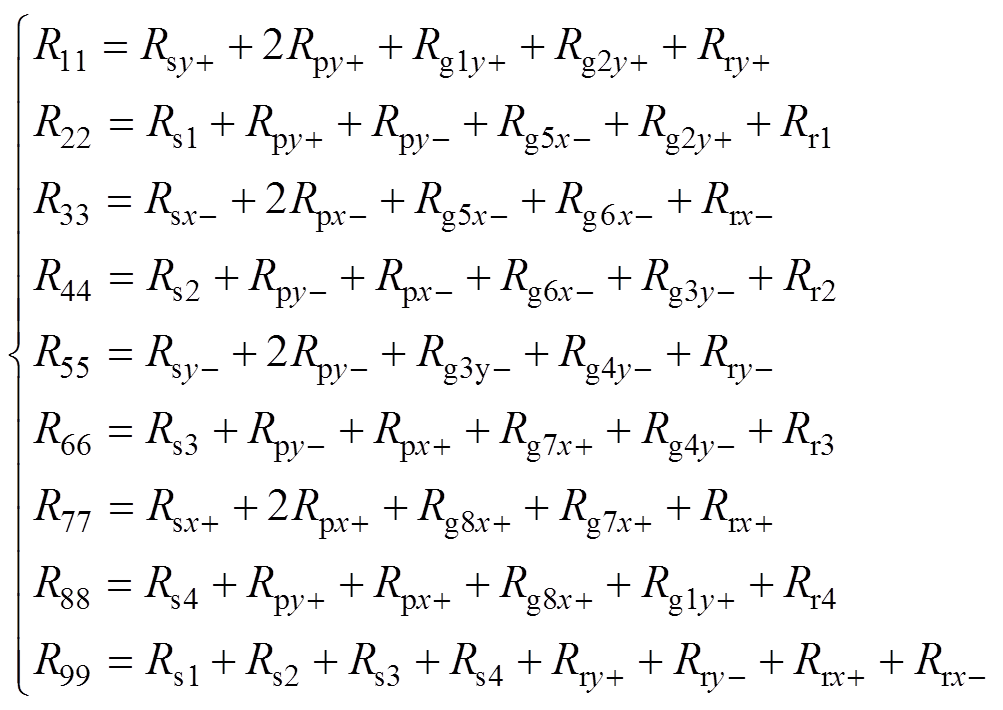
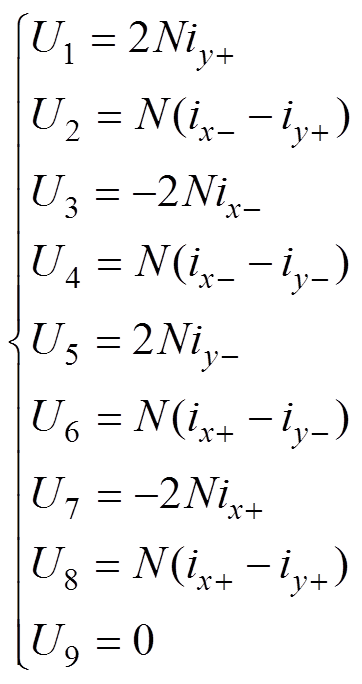
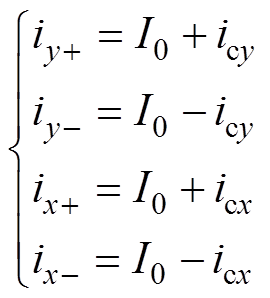
忽略转子的重力作用,在理想情况下,转子处于平衡位置时,8个定子磁极的气隙均相等,定子线圈中的电流均相等且为偏置电流I0。以y方向振动为例,当转子向y+方向振动时,y+方向的气隙减小,y-方向的气隙增大,控制系统将改变线圈电流,以减小y+方向的电磁力,增加y-方向的电磁力,形成一个使转子回到平衡位置的恢复力,基本控制框图如图8所示。Gc为控制器传递函数,GA为功率放大器的增益,Gs为位移传感器的增益,Us为位移传感器输出电压信号,U0为转子处于平衡位置时传感器输出电压信号,Ur为电压误差。线圈电流与位移的关系[19]为
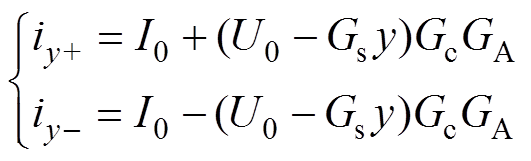 (22)
(22)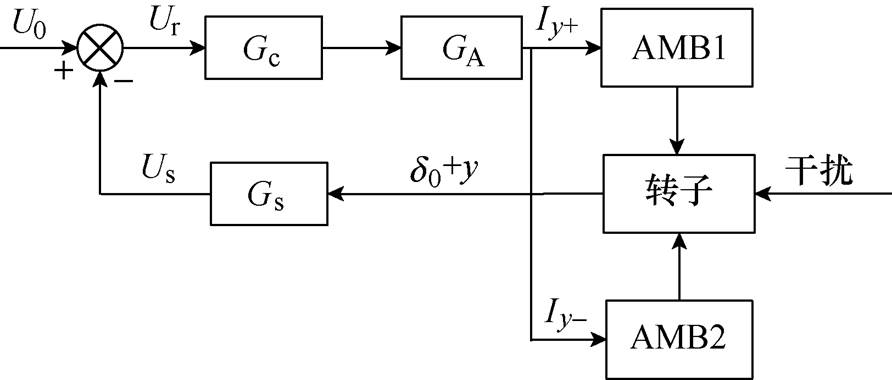
图8 电磁轴承基本控制框图
Fig.8 Basic control block diagram of AMB
以目前电磁轴承常用的PID控制器为例,其传递函数的一般形式为Gc=kp+ki/s+kds/(1+tfs),其中kp为比例系数;ki为积分系数;kd为微分系数;tf为微分反馈时间常数。设转子具有y方向径向振动y= Aycos(wt+j),其中Ay为振幅;w 为振动角频率;w= 2pf;f为振动频率;j 为初相位,本文取j =0。
结合式(21)和式(22),即可求解出径向电磁轴承磁路中的磁通。由于该方程组为非线性方程组,因此采用逐步迭代的方法进行求解,具体迭代步骤如图9所示,其中D 为计算精度,t 为迭代步长。
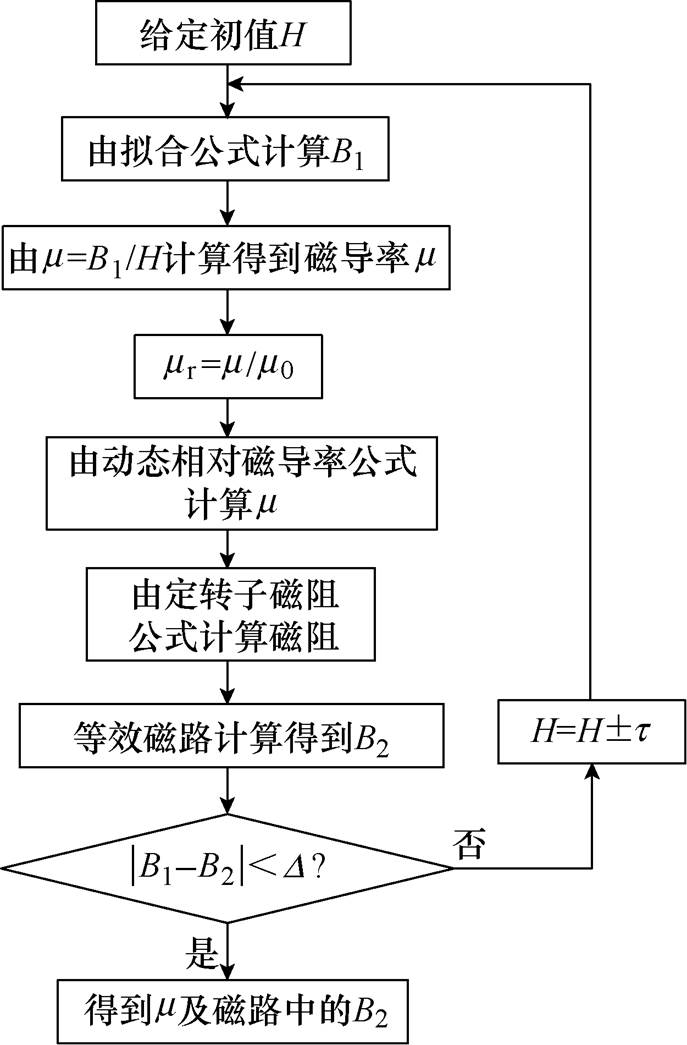
图9 非线性磁路方程求解迭代步骤
Fig.9 Iterative steps for solving nonlinear magnetic circuit equations
由式(21)和式(22)可计算出气隙处对应的磁压降为Ug,进而计算出磁极正对应的气隙平均磁通密度为
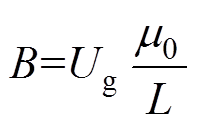 (23)
(23)求解出磁路中的磁通后,可计算出转子振动时,作用在转子上的y方向的电磁力为
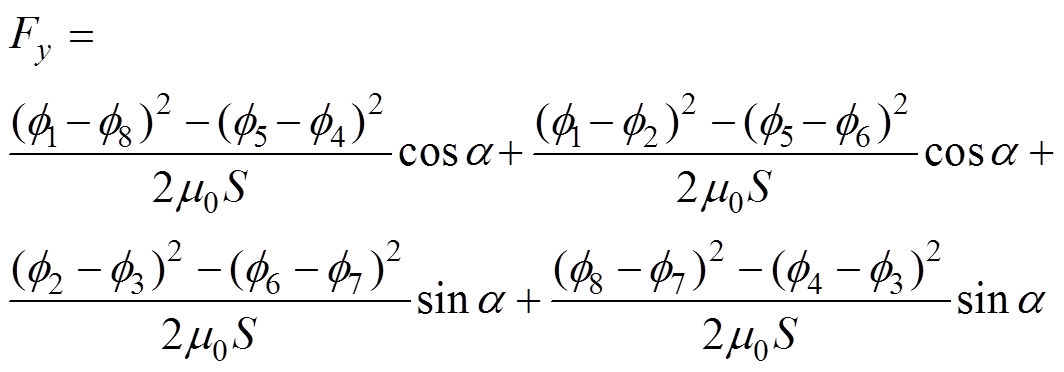 (24)
(24)
式中,a =p/8;S为考虑边缘磁通的磁极端面面积。
针对如图10和表1所示参数的径向电磁轴承,采用本文所建立的等效磁路模型来计算其磁场分布特征,并与电磁场有限元仿真软件给出的结果进行对比,来检验所建等效磁路模型的有效性和准确性。图11为在有限元软件中建立的径向电磁轴承三维模型。该电磁轴承的控制参数见表2,转子径向振动的振幅Ay=0.2mm。
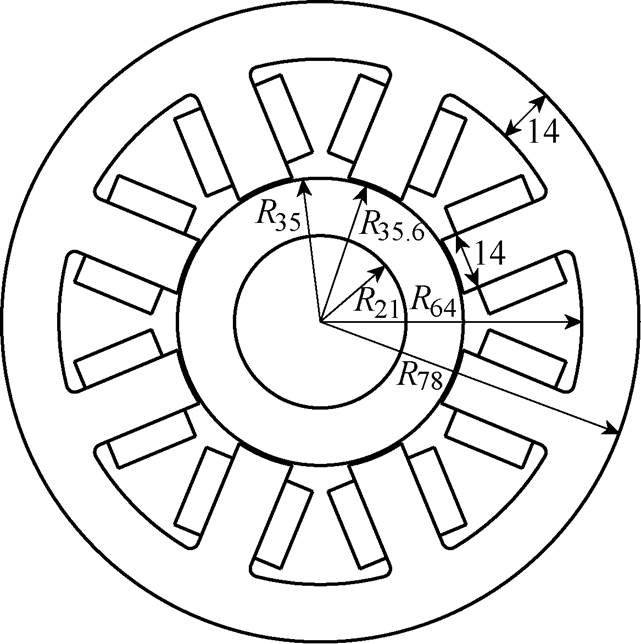
图10 某个电磁轴承结构
Fig.10 Structure of an AMB
表1 电磁轴承的参数
Tab.1 Parameters table of AMB
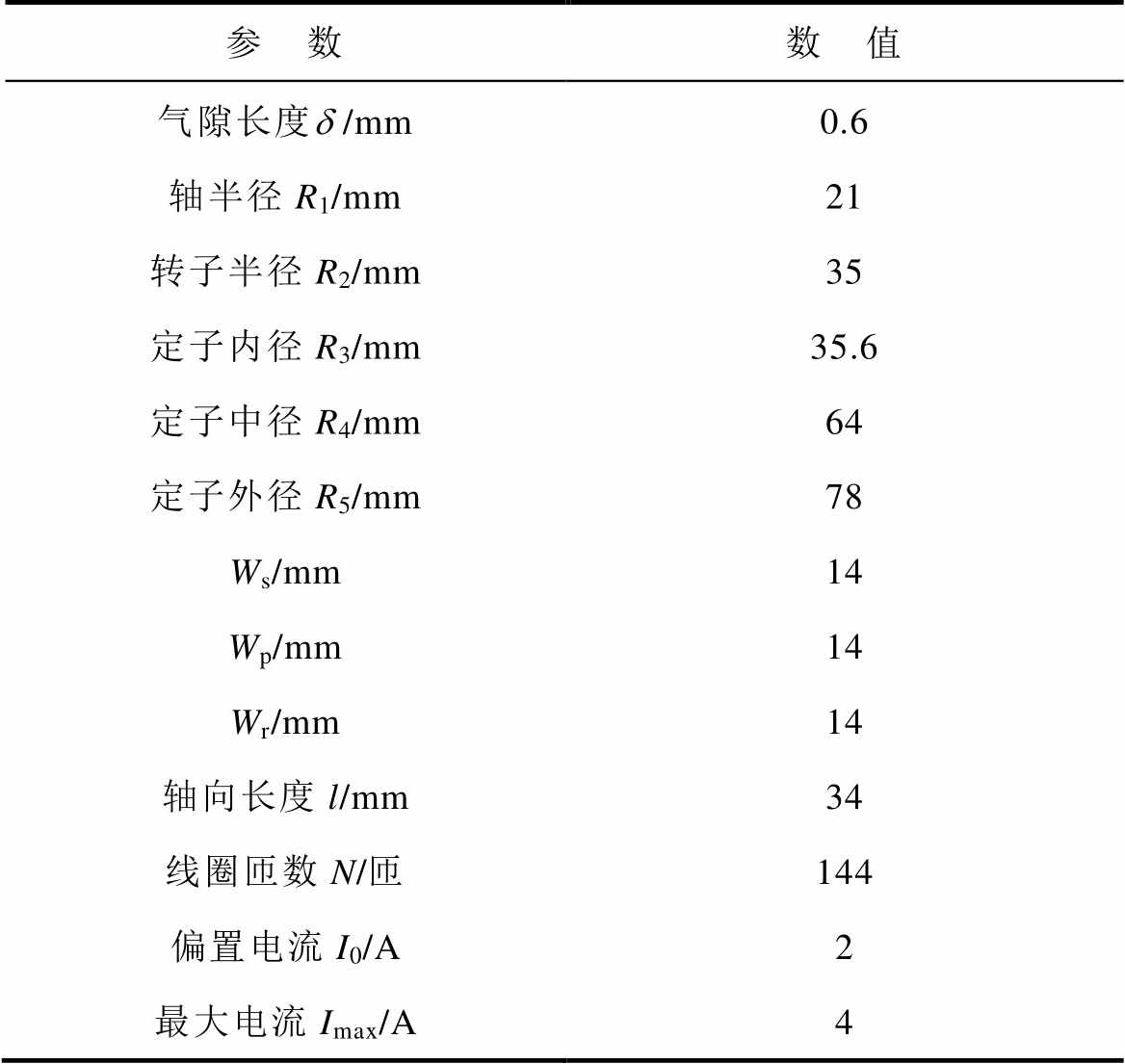
参 数数 值 气隙长度d/mm0.6 轴半径R1/mm21 转子半径R2/mm35 定子内径R3/mm35.6 定子中径R4/mm64 定子外径R5/mm78 Ws/mm14 Wp/mm14 Wr/mm14 轴向长度l/mm34 线圈匝数N/匝144 偏置电流I0/A2 最大电流Imax/A4
图11 径向电磁轴承三维模型
Fig.11 Three-dimensional model of radial AMB
由于电磁轴承结构具有对称性,本文仅研究转子沿y方向振动时的磁场分布。
表2 电磁轴承控制参数
Tab.2 Control parameters of AMB
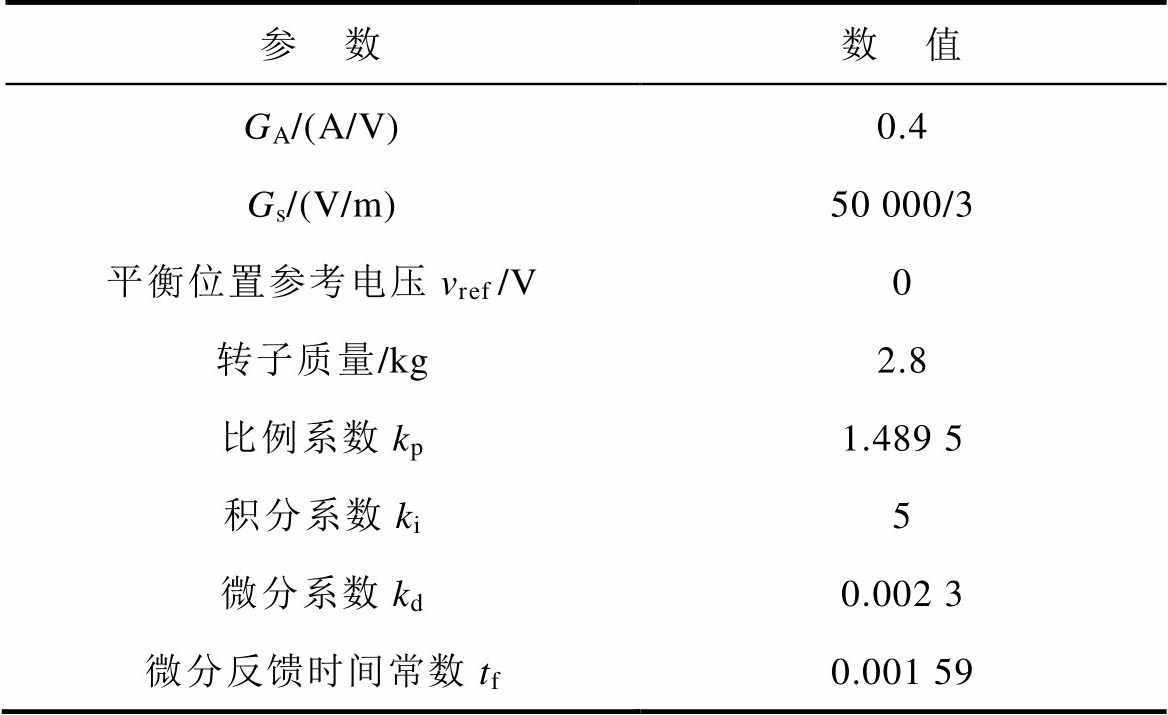
参 数数 值 GA/(A/V)0.4 Gs/(V/m)50 000/3 平衡位置参考电压vref/V0 转子质量/kg2.8 比例系数kp1.489 5 积分系数ki5 微分系数kd0.002 3 微分反馈时间常数tf0.001 59
根据非线性等效磁路模型(Nonlinear Equivalent Magnetic Circuit Model, NEMC)和有限元法(Finite Element Method, FEM)计算了转子在径向y+方向具有静态位移0.1mm,且y+方向线圈电流为0.916 4A,y-方向线圈电流为3.083 6A时,y+和y-方向各一对磁极对应的气隙的磁通密度分布,分别如图12a和图12b所示。在磁极端面正对气隙处,两种方法的计算结果之间的相对误差如图13a和图13b所示,由于结构的对称性,此处仅计算了一个磁极处的误差。可见,非线性等效磁路法在计算磁极端面正对处的气隙磁通密度时具有较高的准确性,与有限元法之间的误差基本不超过3%,验证了非线性等效磁路法的准确性。

图12 气隙磁通密度计算结果对比
Fig.12 Comparison of calculation results of air gap magnetic flux density
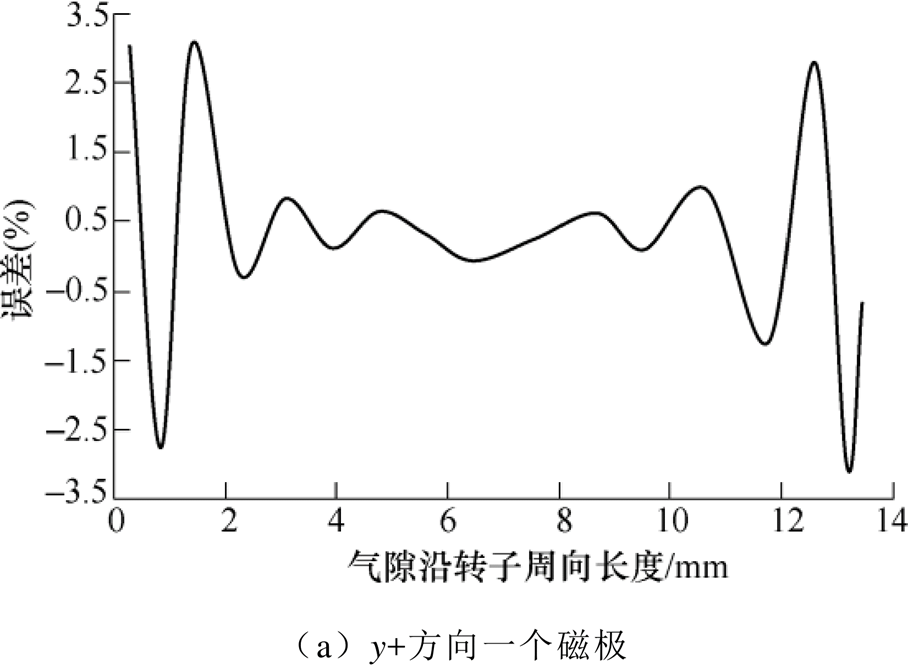
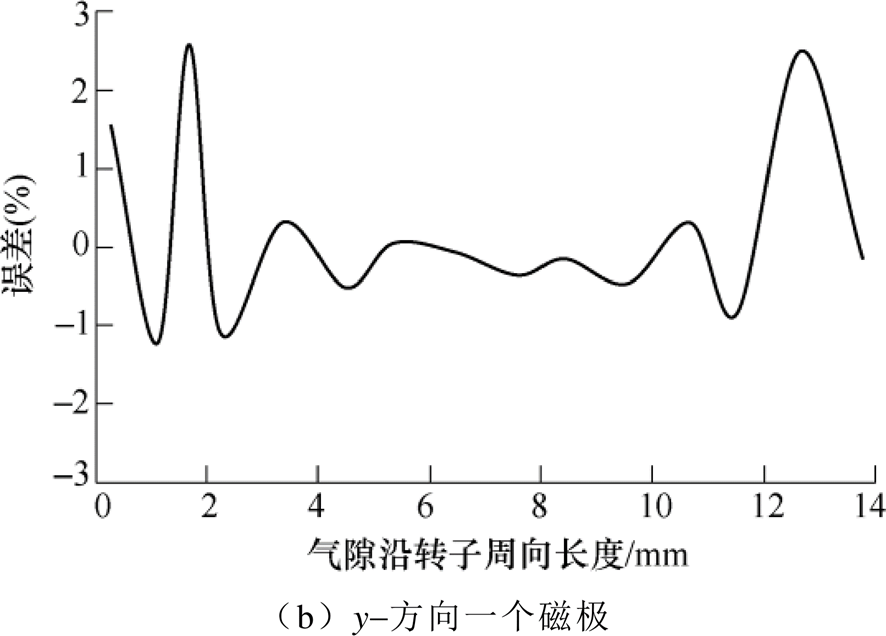
图13 主磁极处气隙磁通密度计算相对误差
Fig.13 The relative error of air-gap magnetic flux density between FEM and NEMC in the main magnetic pole
电磁轴承转子沿径向振动时,由于控制电流的交变,会在定转子铁心中产生交变磁场,从而产生涡流,影响磁场的分布,因此,径向磁悬浮轴承通常采用硅钢片叠片结构来减小涡流。本文以工业界磁悬浮轴承常用的0.35mm厚的硅钢片构成的八磁极径向电磁轴承为例,分析涡流对轴承磁场的影响。
由于目前的电磁场有限元软件暂不能分析转子振动时,电磁轴承的磁场分布及电磁力,因而本文主要从理论上探索转子振动时的涡流对电磁轴承磁场及电磁力的影响。
根据建立的非线性等效磁路模型,计算了转子沿径向y方向振动(振幅为0.2mm),在100Hz、1 000Hz和2 000Hz三种振动频率下,考虑涡流影响与不考虑涡流影响时,y+和y-方向气隙磁通随转子振动位移的变化关系,如图14所示。可以看出,不考虑涡流时,三种振动频率的磁通随转子振动位移的变化曲线几乎重合,但由于控制电流不同,其磁通又存在一定的差别。考虑涡流的影响后,随着振动频率的增加,磁通会出现一定程度的衰减,在频率较低时,涡流的影响并不明显;但随着频率的增加,涡流的影响越来越大。在y+方向,频率为2 000Hz,转子振动位移为-0.2mm时,受涡流的影响,磁通的衰减约为2.34%。

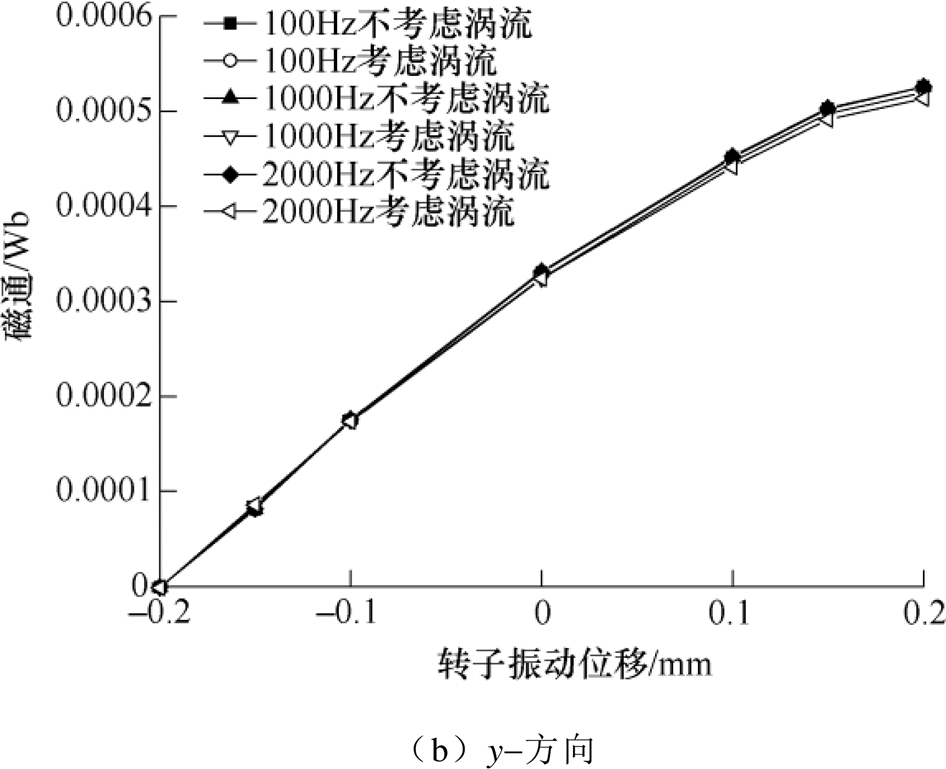
图14 不同频率考虑涡流影响与不考虑涡流影响时,y方向磁通随振动位移变化
Fig.14 Magnetic flux versus vibration displacement in y direction at different frequencys when considering eddy current effect or not
图15给出了不同频率下,考虑涡流影响与不考虑涡流影响,y方向电磁力随转子振动位移的变化关系。可以看出,相较于不考虑涡流影响情况,在计及涡流影响后,电磁力会出现一定程度的削减,与不考虑涡流时的相对偏差如图16所示。可以看出,振动频率为100Hz时,电磁力几乎不受涡流的影响;振动频率为1 000Hz时,电磁力衰减约3%;振动频率为2 000Hz时,电磁力衰减约5.5%,最大衰减为6.81%。因此,涡流对电磁力的削减作用会随振动频率的增加而增大。
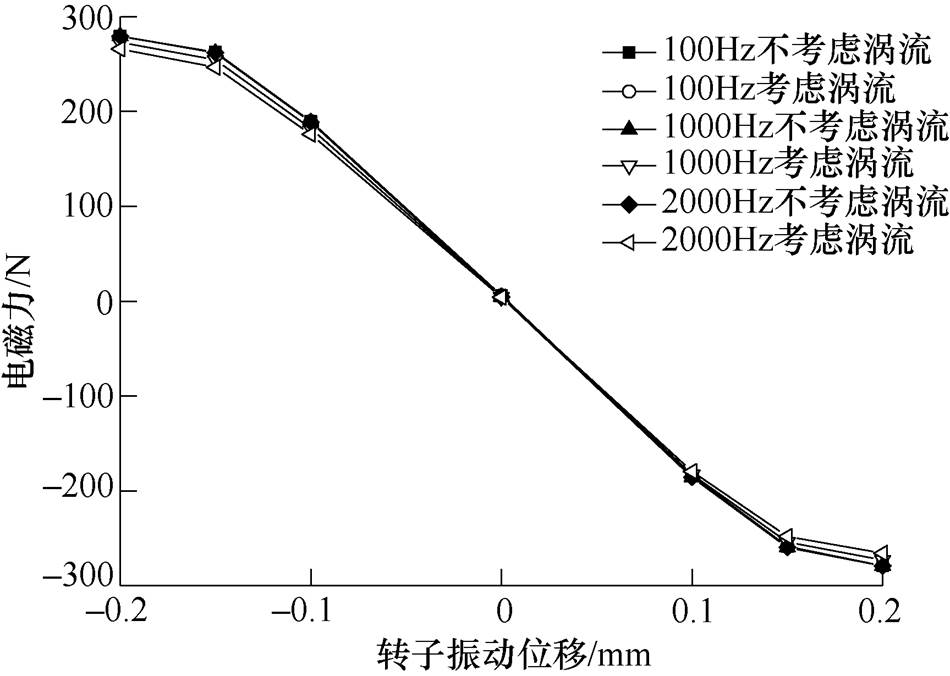
图15 不同频率考虑涡流影响与不考虑涡流影响时,y方向电磁力随振动位移变化
Fig.15 Electromagnetic force versus vibration displacement in y direction at different frequencys when considering eddy current effect or not
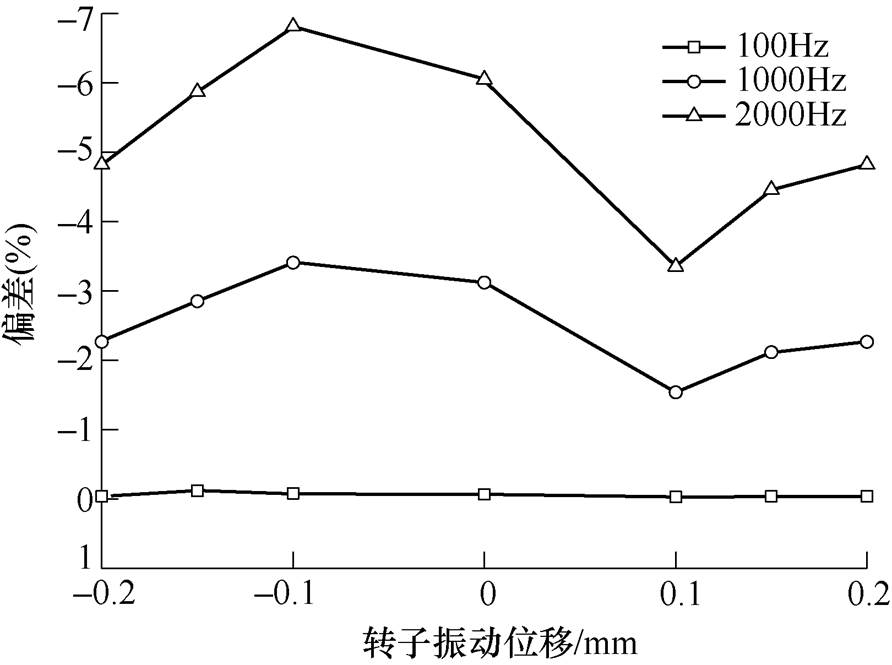
图16 不同频率考虑涡流与不考虑涡流影响电磁力偏差
Fig.16 Error of electromagnetic force at different frequencys when considering eddy current or not
在考虑铁心材料磁导率的非线性以及磁极的边缘效应的基础上,采用动态相对磁导率考虑涡流的影响,同时考虑定子线圈电流随转子振动位移的变化关系,建立了计及定转子铁心磁阻及气隙磁阻在内的径向电磁轴承非线性等效磁路模型。并以转子具有静态位移0.1mm的径向电磁轴承为例,分别采用所建立的非线性等效磁路法和有限元法计算了磁极端面正对处的气隙磁通密度,两种方法的计算误差基本不超过3%,验证了所建模型的准确性。
由于目前商用有限元软件并不能分析转子振动情况下电磁轴承的磁场,因此,本文建立相应的理论模型,从理论上对转子振动情况下的由0.35mm硅钢片叠成的径向电磁轴承的磁场进行研究,分析了转子振动引起的铁心涡流对电磁轴承磁场和电磁力的影响。与不考虑涡流时的模型相比,考虑涡流的影响后,磁通及电磁力都有一定程度的衰减,并且转子振动频率越高,衰减越大。在本文的例子中,转子振动频率达到2 000Hz时,电磁力衰减在5.5%左右。
电磁轴承系统实际运行时,随着转速的升高,转子铁心中磁通的交变频率也快速增加,再加上磁滞因素和定子槽的影响,转子铁心中的磁场分布也会出现较大的畸变,涡流分布也会更加不均匀。如果再考虑转子旋转时的振动对电磁轴承磁场分布的影响,将是更难的问题。
参考文献
[1] Schweitzer G, Maslen E H. Magnetic bearings: theory, design, and application to rotating machinery[M]. BeHin: Springer-Verlag Berlin and Heidelberg, 2009.
[2] 张维煜, 朱熀秋, 袁野. 磁悬浮轴承应用发展及关键技术综述[J]. 电工技术学报, 2015, 30(12): 12-20.
Zhang Weiyu, Zhu Huangqiu, Yuan Ye. Study on key technologies and applications of magnetic bearings[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 12-20.
[3] Le Yun, Fang Jiancheng. Design and optimization of a radial magnetic bearing for high-speed motor with flexible rotor[J]. IEEE Transactions on Magnetics, 2015, 51(6): 1-13.
[4] Wang Dongxiong, Wang Nianxian, Ye Chun, et al. Research on analytical bearing capacity model of active magnetic bearings based on magnetic satur- ation[J]. IET Electric Power Applications, 2017, 11(9): 1548-1557.
[5] 张云鹏, 薛博文, 刘淑琴, 等. 基于气隙磁通边缘效应的轴向混合磁轴承承载力解析计算[J]. 电机与控制学报, 2014, 18(9): 54-59, 67.
Zhang Yunpeng, Xue Bowen, Liu Shuqin, et al. Calculation of electromagnetic force of axial hybrid magnetic bearing based on fringe effect of magnetic flux[J]. Electric Machines and Control, 2014, 18(9): 54-59, 67.
[6] 张云鹏, 刘淑琴, 李红伟, 等. 基于磁路分析的周向混合磁轴承径向承载力解析计算[J]. 电工技术学报, 2012, 27(5): 137-142.
Zhang Yunpeng, Liu Shuqin, Li Hongwei, et al. Calculation of radial electromagnetic force of axial hybrid magnetic bearing based on magnetic circuit analysis[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 137-142.
[7] 赵旭升, 邓智泉. 永磁偏置径向磁轴承的原理分析与参数设计[J]. 电工技术学报, 2011, 26(11): 127-134.
Zhao Xusheng, Deng Zhiquan. Principle analysis and parameter design of permanent magnet[J]. Transa- ctions of China Electrotechnical Society, 2011, 26(11): 127-134.
[8] 吴磊涛, 王东, 苏振中, 等. 异极式永磁偏置径向磁轴承的建模与实验[J].电工技术学报, 2018, 33(5): 1051-1057.
Wu Leitao, Wang Dong, Su Zhenzhong, et al. Modeling and experiment of permanent magnetic biased radial heter-polar magnetic bearing[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1051-1057.
[9] 朱熀秋, 丁书玲. 计及边缘效应的交流混合磁轴承建模[J]. 中国电机工程学报, 2016, 36(23): 6528- 6535.
Zhu Huangqiu, Ding Shuling. Modeling for AC hybrid magnetic bearings considering edge effect[J]. Proceedings of the CSEE, 2016, 36(23): 6528-6535.
[10] Fariba S, Akbar R, Mohammad M. 2D analytical model for heteropolar active magnetic bearings considering eccentricity[J]. IET Electric Power Applications, 2018, 12(5): 614-626.
[11] Aleksei R, Alexander S. Losses estimation and modelling in active magnetic bearings[C]//IEEE Sixteenth European conference on Power Electronics and Applications, Lappeenranta, Finland, 2014: 1-8.
[12] Sun Yanhua, Yick-Sing Ho. Dynamic stiffnesses of active magnetic thrust bearing including eddy- current effects[J]. IEEE Transaction on Magnetics, 2009, 45(1): 139-149.
[13] 董宏林, 闫颖鑫, 王科俊, 等. 径向电磁轴承气隙磁阻近似计算方法分析[J]. 机械工程学报, 2007, 43(8): 43-47.
Dong Honglin, Yan Yingxin, Wang Kejun, et al. Analysis of approximate calculation method for air gap reluctance of radial magnetic bearings[J]. Chinese Journal of Mechanical Engineering, 2007, 43(8): 43-47.
[14] 林其壬, 赵佑民. 磁路设计原理[M]. 北京: 机械工业出版社, 1987.
[15] Kang K, Palazzolo A. Homopolar magnetic bearing saturation effects on rotating machinery vibration[J]. IEEE Transactiions on Magnetics, 2012, 48(6): 984- 1994.
[16] Jalal N. A generalized dynamical model for trans- formers with saturation and hysteresis effects[J]. Mathematical and Computer Modelling of Dynamical Systems, 2013, 19(1): 51-66.
[17] Meeker D C, Maslen E H. An augmented circuit model for magnetic bearings including eddy currents, fringing, and leakage[J]. IEEE Transactions on Magnetics, 1996, 32(4): 3219-3227.
[18] Le Yun, Fang Jiancheng. Dynamic circuit model of a radial magnetic bearing with permanent magnet bias and laminated cores[J]. International Journal of Applied Electromagnetics and Mechanics, 2014, 46(1): 43-60.
[19] 高辉, 徐龙祥. 主动磁悬浮轴承系统拍振现象分析[J]. 机械工程学报, 2011, 47(13): 104-112.
Gao Hui, Xu Longxiang. Analysis of beat vibration for active magnetic bearing system[J]. Journal of Mechanical Engineering, 2011, 47(13): 104-112.
Equivalent Magnetic Circuit Modeling of Radial Active Magnetic Bearing Considering Material Nonlinearity and Eddy Current Effects
Abstract The accurate analysis and calculation of the electromagnetic field distribution characteristics are the basis for the performance optimization of active magnetic bearing (AMB). At present, the influence of eddy current and the nonlinearity of material permeability were rarely both considered in the magnetic field analysis of AMB. Therefore, the exponential equation was used to fit the magnetization curve of the silicon steel sheet to consider the nonlinearity of magnetic permeability of the material, the dynamic relative magnetic permeability was introduced to account for the influence of the eddy current. Then a nonlinear equivalent magnetic circuit model (NEMC) of radial AMB was established with the edge effect, stator and rotor core reluctance, nonlinear magnetic permeability, eddy current influence and real-time control current. Using this model, the magnetic field distribution in the air-gap was calculated when the rotor had a static displacement of 0.1mm. The results are in good agreement with the finite element simulation (FEM) results, and the relative error in the opposite of magnetic poles is basically less than 3%. In addition, the influence of eddy current caused by rotor period vibration on magnetic flux and electromagnetic force was analyzed. After considering the eddy current, the magnetic flux and the electromagnetic force decrease, and the higher the vibration frequency, the greater the attenuation.
keywords:Active magnetic bearing, equivalent magnetic circuit, nonlinearity of permeability, eddy current, rotor vibration
中图分类号:TM14
DOI: 10.19595/j.cnki.1000-6753.tces.190359
收稿日期2019-04-01
改稿日期 2019-08-29
叶品州 男,1995年生,硕士研究生,研究方向为磁力轴承理论与应用。E-mail: 1542518829@qq.com
李红伟 男,1979年生,博士,讲师,硕士生导师,研究方向为磁力轴承理论与应用。E-mail: lhw08@sdu.edu.cn(通信作者)
(编辑 崔文静)