图1 直流偏磁磁性能测量系统
Fig.1 Measuring system for DC-biasing magnetic property
摘要 基于Preisach磁滞模型，提出了面向非对称磁滞回线模拟的参数辨识方法，并应用于取向硅钢片的静态及动态磁滞特性模拟。通过实验获得取向硅钢片静态直流偏磁极限磁滞回线，利用数值方法生成具有非对称特征的一阶回转曲线，进而建立直流偏磁条件下的Everett函数。对静态下的直流偏磁磁滞回线进行拟合，通过与实验结果的对比，验证了该文方法的有效性。进一步考虑直流偏磁磁场和交流磁通密度峰值对异常损耗的影响，构建直流偏磁动态磁滞模型，实现了直流偏磁条件下取向硅钢片损耗特性的模拟，分析了直流偏磁对不同类型损耗的影响。
关键词：直流偏磁 Preisach模型 损耗分离 磁滞特性 损耗特性
电工软磁材料在电力系统电工装备中的应用具有非常重要的意义。大型电机、变压器、电抗器等设备的铁心，通常都是由硅钢片叠制而成，工作时通常运行在工频正弦交变激励下[1]。然而由于直流输电的发展及大量电力电子器件在输电系统中的广泛应用[2-4]，变压器经常运行在直流偏磁条件下，由取向硅钢片叠制而成的铁心将会呈现出非常复杂的非线性、非对称磁滞特性，当直流偏磁加剧时，磁滞回线面积增加、损耗增大，从而对变压器的正常运行造成严重的危害[5-6]。因此对直流偏磁条件下电工软磁材料的磁滞及损耗特性进行精确模拟，将对考虑偏磁影响下的硅钢片制备及变压器优化设计具有重要的意义[7]。
用于软磁材料磁滞特性模拟的有Jiles-Atherton（J-A）模型、Energetic模型、E&S模型以及Preisach模型等。J-A模型具有相对明确的物理意义，通过较少的参数，实现对标量和矢量磁特性的模拟[8-11]，与有限元结合可以实现考虑磁滞效应的非线性磁场计算与分析[12]；Energetic模型则是根据铁磁材料能量最小化原理提出，因为含有更多的参数，一般具有较好的拟合精度[13-14]；E&S模型专门针对二维矢量磁特性而提出，基于该模型的研究、改进以及非线性场的计算等均取得了一些进展[15-16]；Preisach模型的模拟精度较高，可用于高频正弦及谐波激励下的磁滞特性模拟，也能够与数值计算相结合[17-20]，但参数辨识过程较为复杂，不易掌握和实现。以上各模型中，Preisach模型的输出值与输入值及输入的历史相关，基于一阶回转曲线，建立Everett函数，实现模型的参数辨识；而其他模型大都要基于测定的磁滞回线，采用一定的优化算法得到拟合参数，在磁特性较为复杂时，不易得到合适的参数，且模型的预测能力相对较弱。
目前为止，利用磁滞模型对直流偏磁条件下磁滞特性进行模拟的研究工作还较为少见，其原因主要在于大部分磁滞模型在开始提出时，只针对正弦激励下对称的磁滞回线，而直流偏磁磁滞回线具有显著的不对称性，很难进行有效且准确的模拟。对现有模型进行改进，或者提出新的有效磁滞模型，对非对称激励下的磁滞及损耗特性进行模拟，成为软磁材料磁性能模拟工作中亟待解决的问题。
本文采用德国BROCKHAUS磁性能测量系统，获得了取向硅钢片在直流偏磁条件下的磁滞与损耗特性。基于测量得到的非对称静态极限磁滞回线，采用数值方法生成一阶回转曲线，建立Everett函数，实现Preisach模型的参数辨识。进一步考虑直流偏磁程度和交流磁通密度峰值对异常损耗的影响，得到了直流偏磁动态磁滞模型。将仿真结果与实验结果相比较，验证了本文方法的有效性和准确性。
采用德国BROCKHAUS磁性能测量系统中的单片测量仪对型号为B27R095的取向硅钢片在直流偏磁条件下的磁滞及损耗特性进行测量。测量设备如图1所示。通过系统电源和两个不同的绕组，实现硅钢片的偏磁激励。在两个绕组中的交流绕组上施加工频50Hz的交流激励，直流绕组上施加不同直流电流，从而实现直流磁场强度Hdc为不同值的直流偏磁激励。表1给出了实验中所用磁性能测量系统的主要参数，相关场量的测量精度可以达到0.1%。实验中所测样片的尺寸为100mm×500mm。
图1 直流偏磁磁性能测量系统
Fig.1 Measuring system for DC-biasing magnetic property
表1 测量系统的主要参数
Tab.1 Some key parameters of the measuring system
主要测量参数可测量范围 H/(A/m)1～10 000 B/T0.001～2 频率/Hz3～20 000
为获得硅钢片在静态下的直流偏磁磁滞特性，应使得系统激励为理想的直流激励，然而，一方面理想的直流测量需要大量的时间，效率很低；另一方面在磁滞特性测量中理想的直流激励难以实现。因此，首先在实验中设定系统交流激励的频率为4Hz，直流磁场强度Hdc分别设定为25A/m和50A/m，测量得到取向硅钢片的磁滞回线及损耗，将其近似作为静态直流偏磁磁性能；然后再设定系统交流激励的频率为50Hz，测量得到取向硅钢片的动态直流偏磁磁滞及损耗特性。
由于测量系统不能直接获取硅钢片中磁通密度的直流分量，因此本文采用迭代法[21]计算得到不同偏磁情况下磁通密度直流分量。激励磁感应强度交流分量峰值Bacm分别为0.5T、0.8T、1.0T、1.3T、1.6T，4Hz和50Hz正弦基波叠加直流偏磁量为50A/m时的静态和动态直流偏磁磁滞回线族分别如图2和图3所示。激励为50Hz正弦基波叠加不同直流偏磁量时硅钢片的损耗曲线如图4所示。
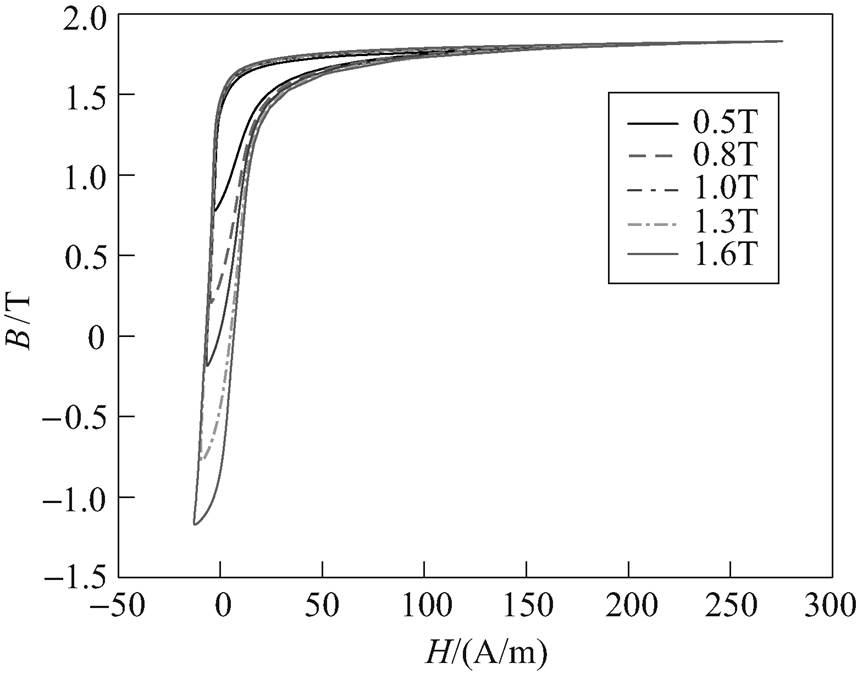
图2 静态直流偏磁磁滞回线族（f =4Hz）
Fig.2 Static DC-biasing magnetic hysteresis loops ( f =4Hz)
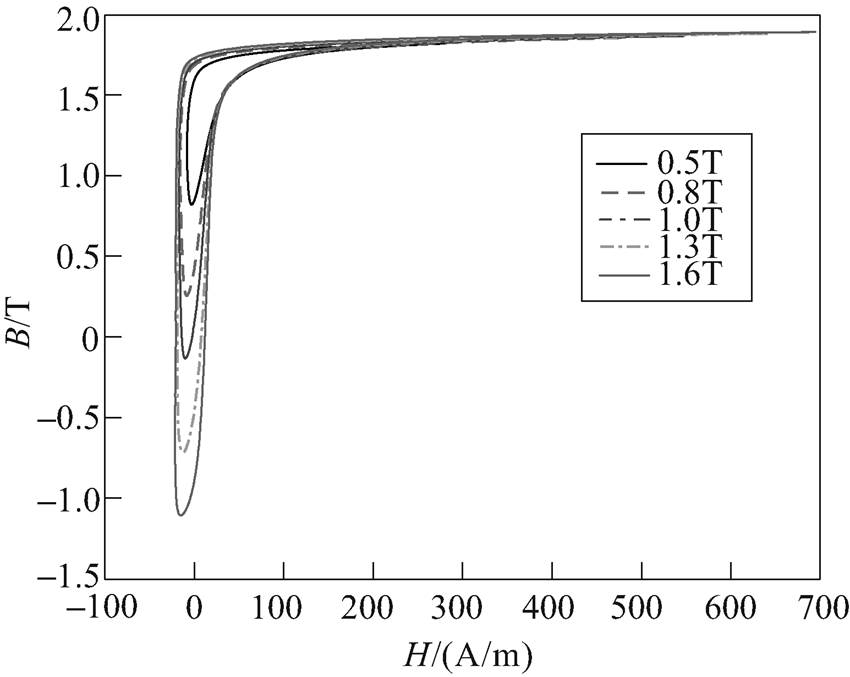
图3 动态直流偏磁磁滞回线族（f =50Hz）
Fig.3 Dynamic DC-biasing magnetic hysteresis loops ( f =50Hz)
借助Preisach模型拟合静态偏磁磁滞特性的一般思路为：先根据直流偏磁情况下非对称的极限磁滞回线，利用数值的方法得到非对称的一阶回转曲线，进而生成非对称的Everett函数，最后实现模型。因此，模型实现的关键在于如何利用直流偏磁情况下测量的极限磁滞回线的数据生成非对称的一阶回转曲线。
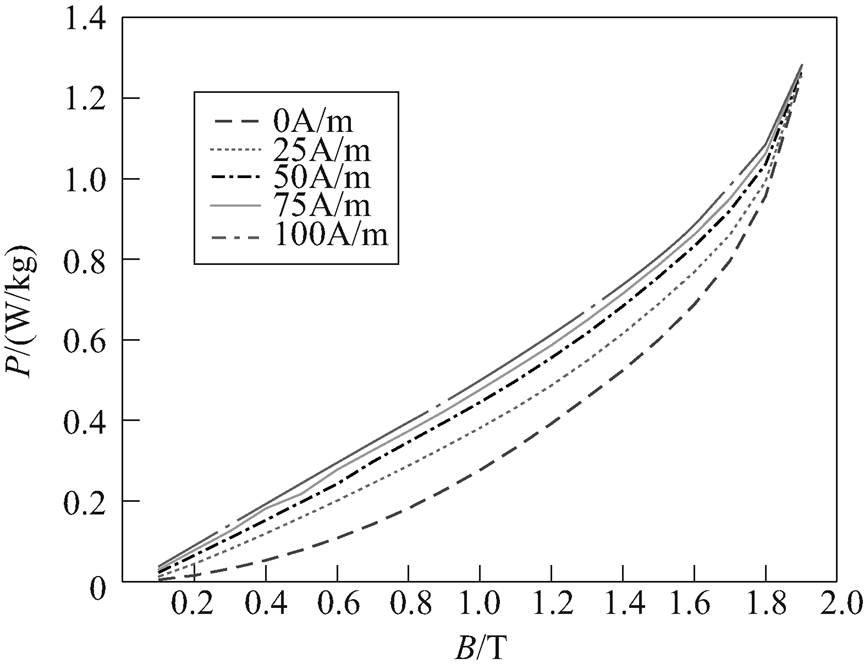
图4 不同直流偏磁量下的损耗曲线
Fig.4 Losses curves in different DC bias level
要建立Preisach磁滞模型，首先要得到材料的一阶回转曲线。对比有、无偏磁条件下的磁滞回线可知，无偏磁条件下的一阶回转曲线与直流偏磁条件下的一阶回转曲线明显不同，因此如何获得直流偏磁下的一阶回转曲线，是建立Everett函数，实现直流偏磁磁滞模型参数辨识的关键。
E. Dlala提出了基于对称的极限磁滞回线生成一阶回转曲线的数值方法，但是该方法具有局限性，即不能基于非对称的极限磁滞回线生成一阶回转曲线[22]。S. E. Zirka提出了另一种不同的数值方法，并将其应用于无偏磁下软磁材料的磁滞与损耗特性模拟[23]。通过本文研究发现，这种新的一阶回转曲线的数值生成方法具有更佳的泛化能力和更广的适用范围，能够用于非对称一阶回转曲线的生成。本文将采用该方法构造直流偏磁一阶回转曲线。
图5所示为一条起始于直流偏磁极限磁滞回线下降支的一阶回转曲线R-P-N-T的生成，它起始于点R，终止于极限磁滞回线的饱和点T，即直流偏磁极限磁滞回线的上升支Ha0（B）和下降支Hd0（B）在该点处重合。该一阶回转曲线的构造过程如下。
首先根据起始点R处的磁感应强度BR确定上升支与下降支间水平宽度DHrev和从点R到点T的垂直距离DBrev，有
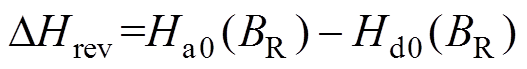（1）
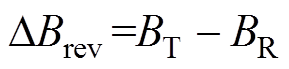（2）
式中，BT为极限磁滞回线饱和点T处的磁感应强度值。
然后在[BR, BT]区间内任取一点BP，其对应的磁场强度HP为
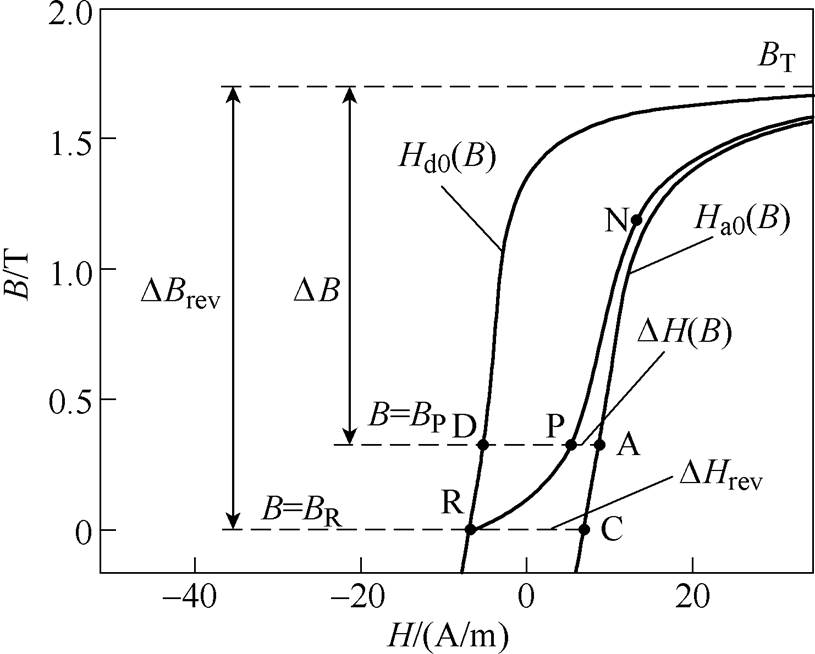
图5 基于偏磁极限磁滞回线的一阶回转曲线R-P-N-T构造
Fig.5 The construction of first order reversal curve R-P-N-Tbased on DC-biasing major hysteresis loop
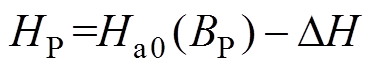（3）式中，DH为点P到点A的距离。DH[22]进一步可以写成
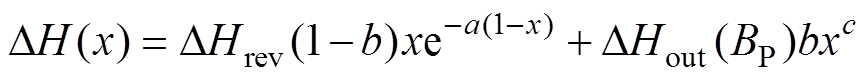（4）
（5）式中，DHout为P点对应的极限磁滞回线水平宽度（即图5中D-A段的长度）；DB为点P到点T的垂直距离；a、b、c（a＞0，0＜b＜1，c＞0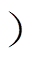
各参数值可采用文献中给定的值[22]，对不同的软磁材料具有较强的通用性。
通过1.2小节的实验，可测量得到Bacm=1.9T，Hdc=50A/m时的静态直流偏磁极限磁滞回线，采用以上提到的数值方法生成起始点位于上升支的下降的一阶回转曲线（First Order Reversal Curves, FORCs），如图6所示。进而可以得到逆Everett函数E(bu, bv)，如图7所示。
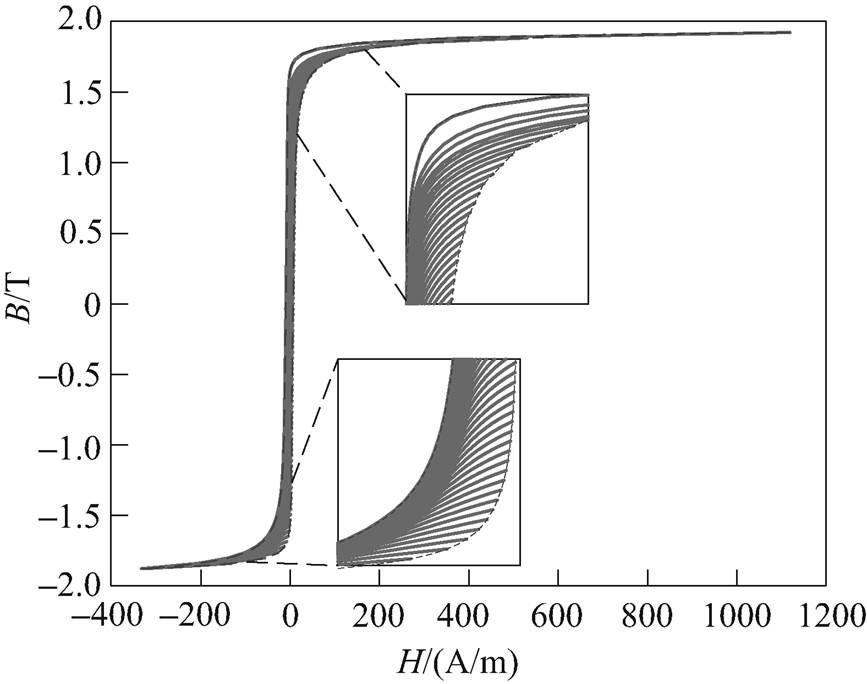
图6 下降的一阶回转曲线
Fig.6 The descending FORCs
基于非对称的逆Everett函数建立Preisach磁滞模型，对Bacm=1.0T，Hdc=50A/m和Bacm=1.2T，Hdc= 25A/m两种不同偏磁情况下的静态直流偏磁磁滞回线进行拟合，图8、图9给出了仿真结果与实验结果对比。其中，虚线和实线分别代表基于非对称一阶回转曲线和对称一阶回转曲线拟合的结果。
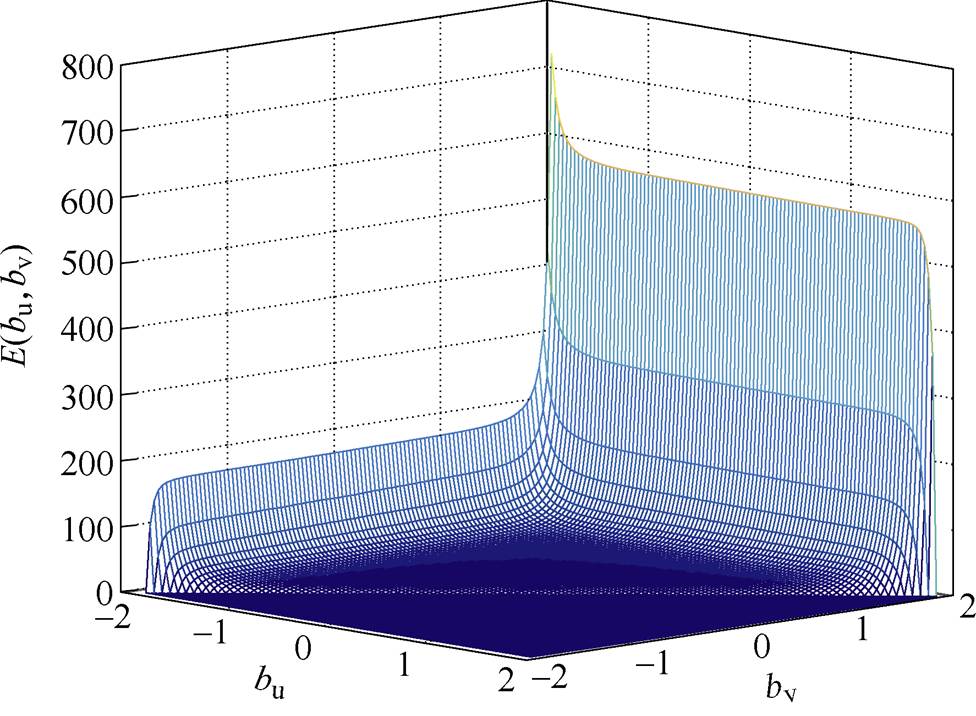
图7 逆Everett函数
Fig.7 Inverted Everett function
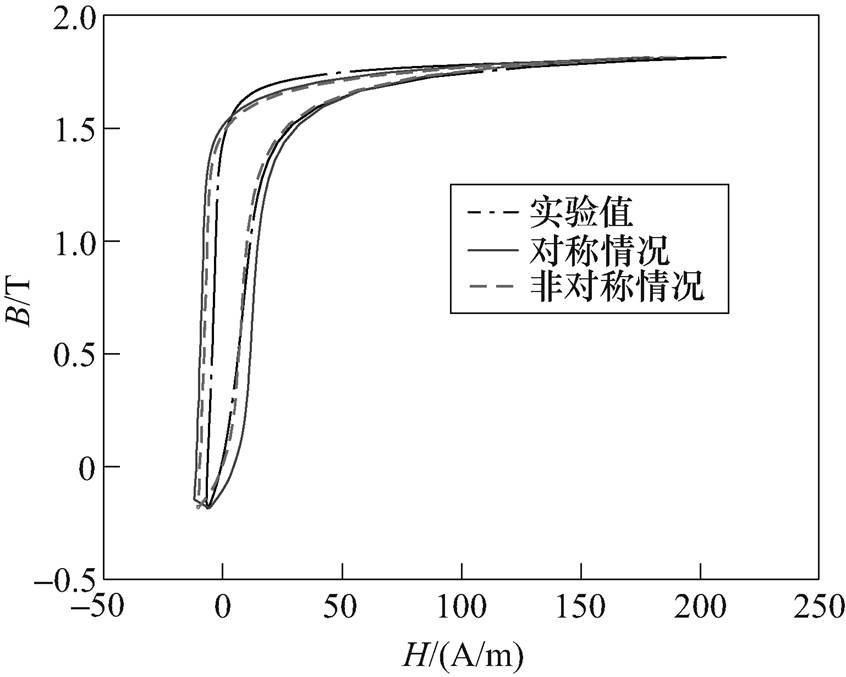
图8 Bacm=1.0T, Hdc=50A/m磁滞回线测量与拟合对比
Fig.8 Comparison between measured static hysteresis loop with simulated one with Bacm=1.0T and Hdc=50A/m
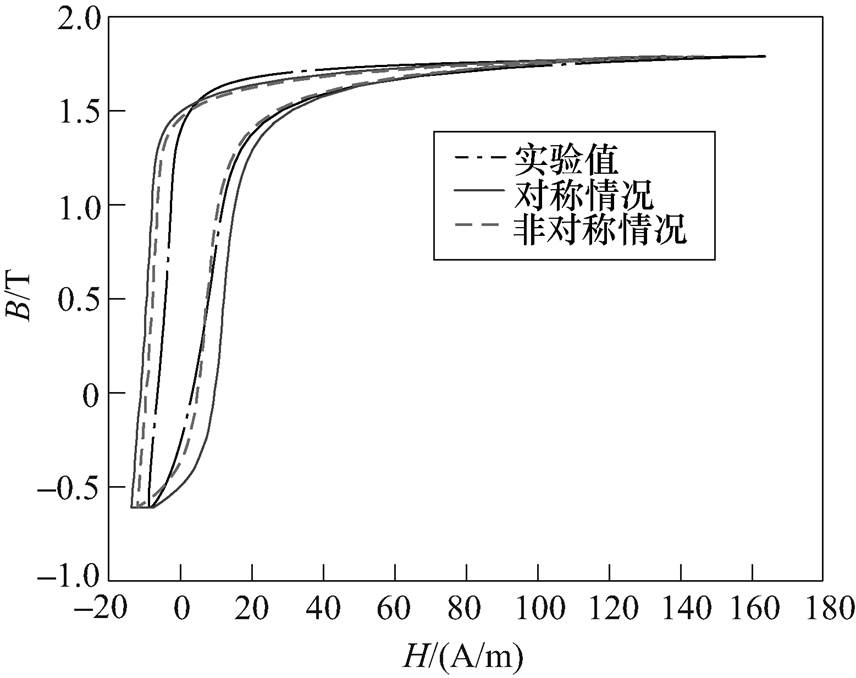
图9 Bacm=1.2T, Hdc=25A/m磁滞回线测量与拟合对比
Fig.9 Comparison between measured static hysteresis loop with simulated one with Bacm=1.2T and Hdc=25A/m
由于图8和图9在饱和区域，测量值和拟合值对比不明显。因此，在表2和表3中，分别给出在饱和区域附近拟合值和实验值的具体数值对比。其中，Hmea为磁场强度测量值，H1为基于非对称一阶回转曲线得到的拟合值，H2为基于对称一阶回转曲线的拟合值。
表2 Bacm=1.0T, Hdc=50A/m时磁滞回线饱和段拟合值和实验值对比
Tab.2 Comparison between measured H and simulated ones with Bacm=1.0T and Hdc=50A/m in saturation region
B/THmea/(A/m)H1/(A/m)H2/(A/m) 1.814 7210.52189.85178.35 1.814 3207.42188.55177.51 1.813 4202.42185.27175.39 1.812 2197.16181.49172.96 1.811 0192.08177.48170.37
表3 Bacm=1.2T, Hdc=25A/m时磁滞回线饱和段拟合值和实验值对比
Tab.3 Comparison between measured H and simulated ones with Bacm=1.2T and Hdc=25A/m in saturation region
B/THmea/(A/m)H1/(A/m)H2/(A/m) 1.789 1163.55146.53135.74 1.788 0159.59144.49133.31 1.786 4154.05141.72130.02 1.784 7148.13138.57126.29 1.783 0142.37135.68123.65
为了进一步论证此方法能更加准确地模拟静态直流偏磁磁滞特性，表4给出了Hdc=25A/m时，静态磁滞损耗拟合值和实验值的对比。其中，Pmea为静态磁滞损耗测量值；P1和P2分别为基于非对称一阶回转曲线和对称一阶回转曲线进行参数辨识时，静态磁滞损耗的拟合值；Dr为两者相对误差之差。由表4可以看出，基于非对称一阶回转曲线进行参数辨识时，静态损耗模拟的精度提高了40%以上。
表4 Hdc=25A/m时静态磁滞损耗拟合值和实验值对比
Tab.4 Comparison between measured static hysteresis losses and simulated ones with Hdc=25A/m
Bacm/TPmea/(W/kg)P1/(W/kg)P2/(W/kg)Dr(%) 0.60.008 20.009 40.013 448.78 0.80.011 50.013 10.018 443.48 1.00.014 70.016 70.023 445.58 1.20.018 40.019 80.027 843.48 1.40.022 80.024 90.034 240.79
从图8、图9和表2～表4的对比结果看出，本文基于非对称一阶回转曲线的拟合结果较基于对称一阶回转曲线的拟合结果更为准确，因为图7所示逆Everett函数考虑了直流偏磁磁滞特性的非对称特征。可知，本文提出的方法能够更加准确地模拟硅钢片在直流偏磁情况下的静态磁滞特性。
传统的计算铁心损耗的经验公式认为，在工频条件下，时间周期T范围内每单位体积硅钢片的总损耗由磁滞损耗Ph、涡流损耗Pcl和异常损耗Pex相加得到[23]。E. Dlala等由场量和能量间的关系，基于场分离技术，将动态下的磁场强度H分为三个部分[24-25]，有
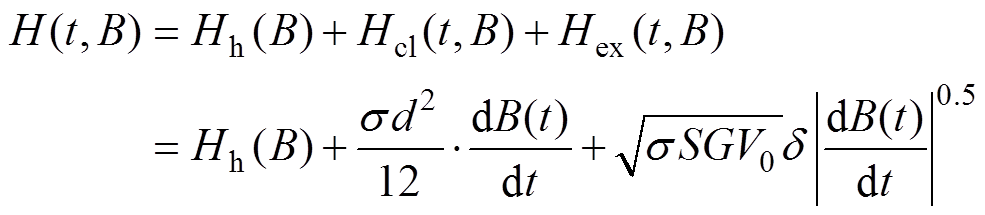（6）式中，Hh、Hcl和Hex分别为磁滞损耗Ph、涡流损耗Pcl和异常损耗Pex相对应的磁场强度分量；d为叠片厚度；s 为材料电导率；S为叠片的横截面积；G为无量纲系数，G=0.135 6；d =sign(dB/dt)=±1，取决于磁感应强度B随时间变化的曲线是上升还是下降；V0为一个和磁场值有关的需要拟合的系数，其用来描述材料的微观结构特征，在直流偏磁情况下，V0是激励磁感应强度交流分量峰值Bacm和直流偏置量Hdc的函数。
由式（6）可知，涡流损耗与直流偏磁量无关，只与B的变化率有关，可以直接由式（6）中的第二项计算；第三项，即与异常损耗相对应的磁场强度Hex则需要同时考虑Hdc、Bacm的影响。因此需要对式（6）中的异常损耗的参数V0进行提取。
由3.1节的分析可知，异常损耗对应的磁场强度为
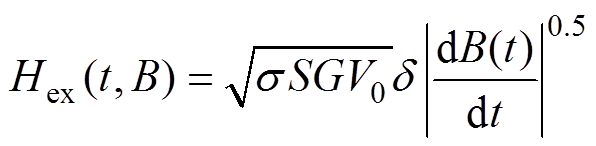（7）计算Hex的关键在于准确拟合函数V0（Bacm, Hdc）。在本文当中，借助实验数据提取一系列V0值，在分析V0（Bacm, Hdc）随Bacm和Hdc变化规律的基础上，通过数值拟合的方法确定V0（Bacm, Hdc）与变量Bacm、Hdc之间的函数关系式。表5给出了不同Bacm及Hdc下提取的参数V0值。
表5 不同Hdc和Bacm下提取的V0值
Tab.5 Parameter V0 extracted under different Hdc and Bacm
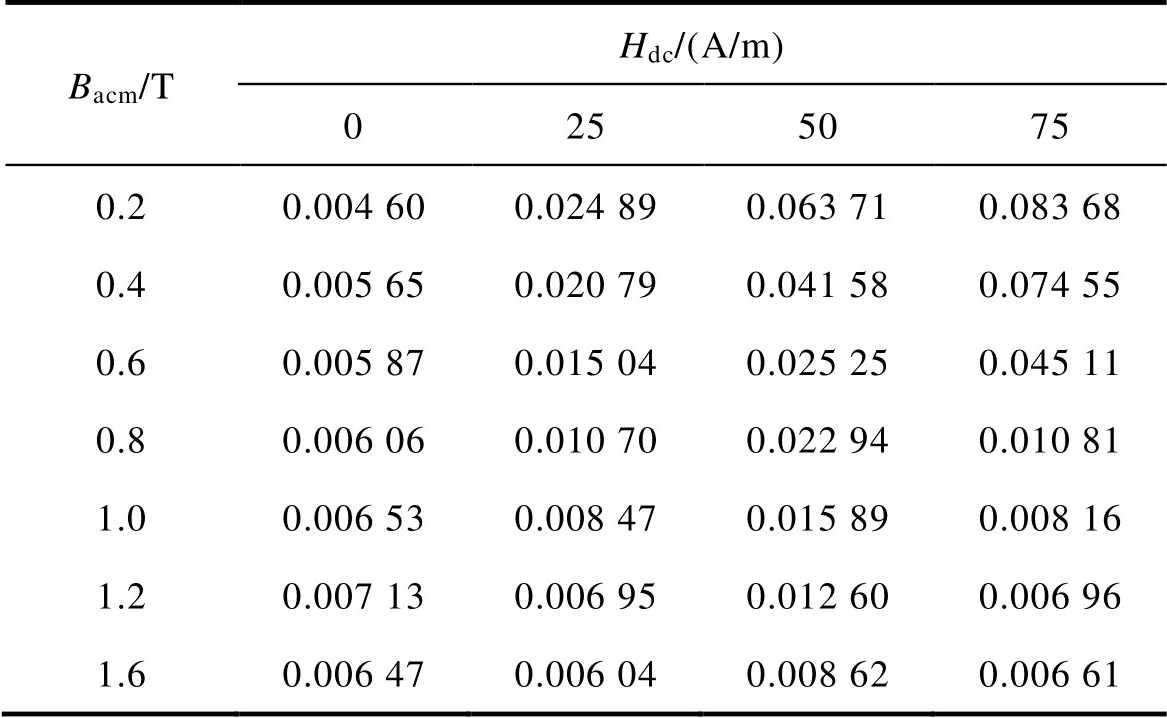
Bacm/THdc/(A/m) 0255075 0.20.004 600.024 890.063 710.083 68 0.40.005 650.020 790.041 580.074 55 0.60.005 870.015 040.025 250.045 11 0.80.006 060.010 700.022 940.010 81 1.00.006 530.008 470.015 890.008 16 1.20.007 130.006 950.012 600.006 96 1.60.006 470.006 040.008 620.006 61
从表5中V0的提取值可以看出，当磁感应强度交流分量峰值Bacm不变时，直流偏磁量Hdc越大，参数V0的值越大。此外，当磁感应强度交流分量峰值Bacm越大时，V0对Hdc的敏感程度越低。根据以上特点，文献[25-26]选用有理函数作为参数V0（Bacm, Hdc）的函数拟合公式，虽然简单但计算精度不高。因此本文选用高斯函数作为V0的函数拟合公式，给出V0的函数表达式为
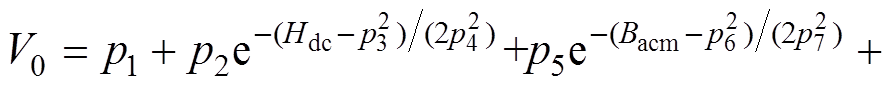
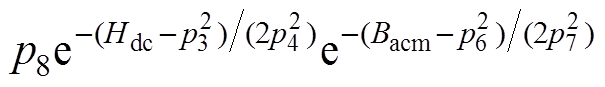（8）
式中，p1～p8为待拟合的系数。在本文当中，p1～p8的值分别为0.007 6、0.000 6、86.575 1、40.122 6、-0.012 3、0.196 5、0.304 0、0.095 0。
表6给出直流偏磁量Hdc=25A/m时，不同交流磁通密度峰值Bacm下，V0计算值和实验值的对比。其中，V0m为实验结果，V0c为计算结果。通过表6可以看出，计算值和实验值较为吻合，相对误差控制在10%以内，具有较高的计算精度。由此说明了V0的函数表达式可以满足计算要求。
表6 Hdc=25A/m时V0计算值和实验值对比
Tab.6 Comparison between measured V0 and calculated ones with Hdc=25A/m
Bacm/TV0mV0c相对误差(%) 0.30.023 8580.023 732-0.53 0.50.016 6220.018 0358.51 0.70.013 2080.012 040-8.84 0.90.009 5990.008 906-7.22 1.10.007 5900.007 9464.69
利用损耗分离模型，对型号为B27R095的硅钢片在直流偏磁情况下动态磁滞回线进行拟合。直流偏磁磁场Hdc=50A/m，磁感应强度交流分量峰值Bacm=0.5T、Bacm=0.9T及Bacm=1.5T时拟合的动态磁滞回线与实验结果对比如图10所示。直流偏磁磁场Hdc=25A/m，磁感应强度交流分量峰值Bacm=0.7T、Bacm=1.1T及Bacm=1.7T时拟合的动态磁滞回线与实验结果对比如图11所示。
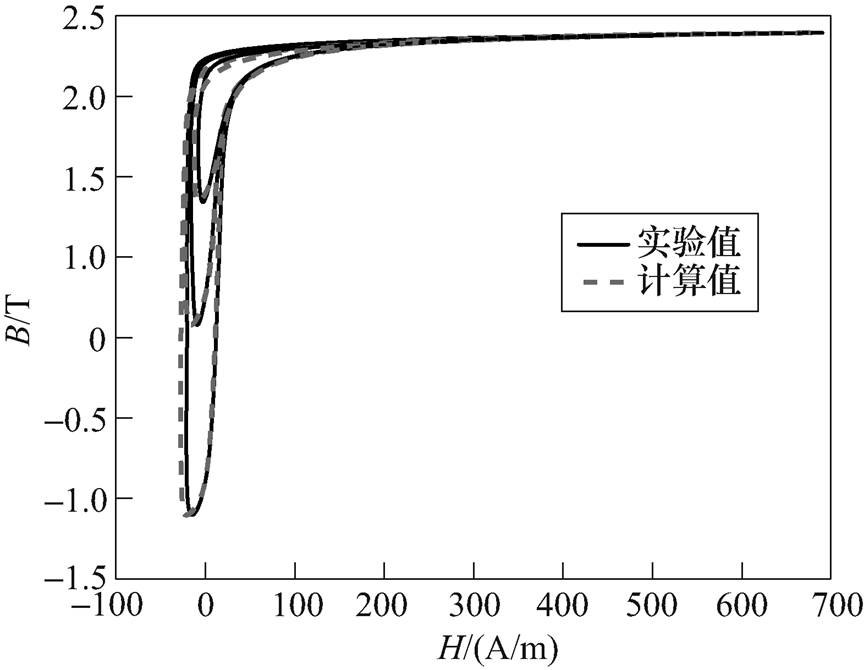
图10 Hdc=50A/m，Bacm不同时动态磁滞回线测量与拟合对比
Fig.10 Comparison between measured dynamic hysteresis curves with simulated ones in different Bacm with Hdc=50A/m
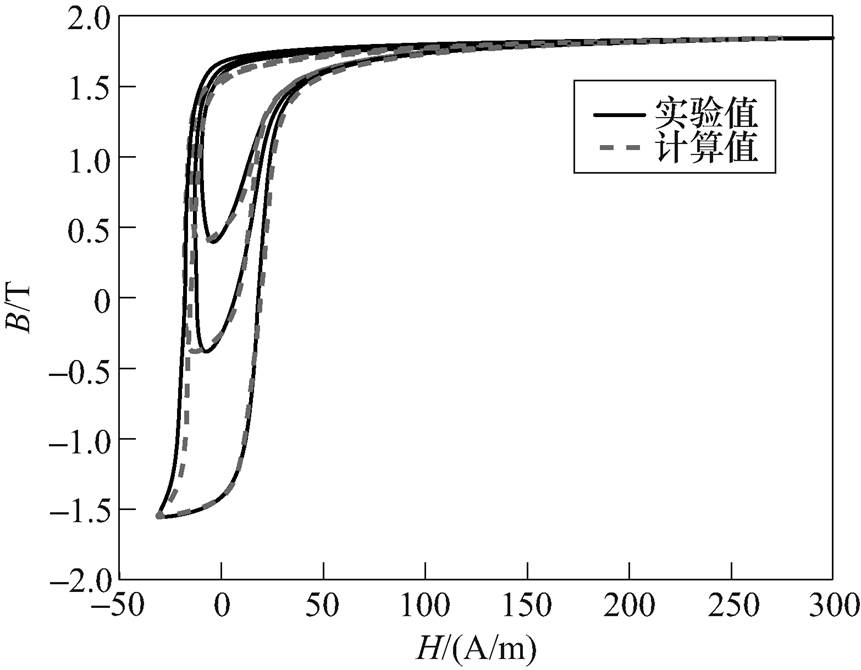
图11 Hdc=25A/m，Bacm不同时动态磁滞回线测量与拟合对比
Fig.11 Comparison between measured dynamic hysteresis curves with simulated ones in different Bacm with Hdc=25A/m
可以看出，利用损耗分离模型拟合时，拟合的动态磁滞回线与测量结果基本一致。进一步说明，本文算法可以对硅钢片在直流偏磁情况下的动态磁滞特性进行比较准确的计算
利用损耗分离模型，对型号为B27R095的硅钢片，在偏磁激励下进行损耗分离计算。直流偏磁磁场Hdc=50A/m和25A/m时，测量损耗Pt、计算损耗P、磁滞损耗Ph、涡流损耗Pcl和异常损耗Pex分别如图12和图13所示。
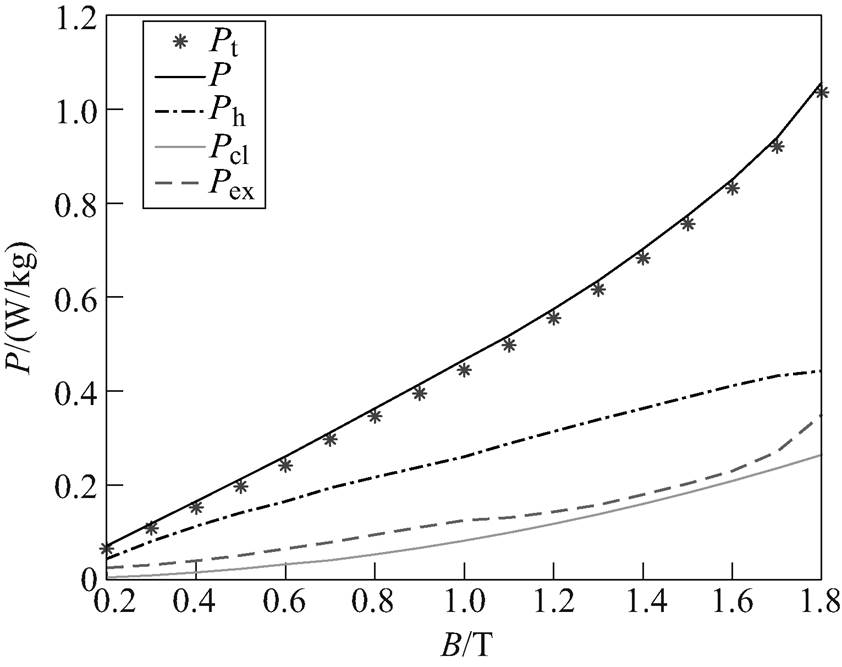
图12 Hdc=50A/m硅钢片损耗分离情况
Fig.12 Results of loss separation with Hdc=50A/m
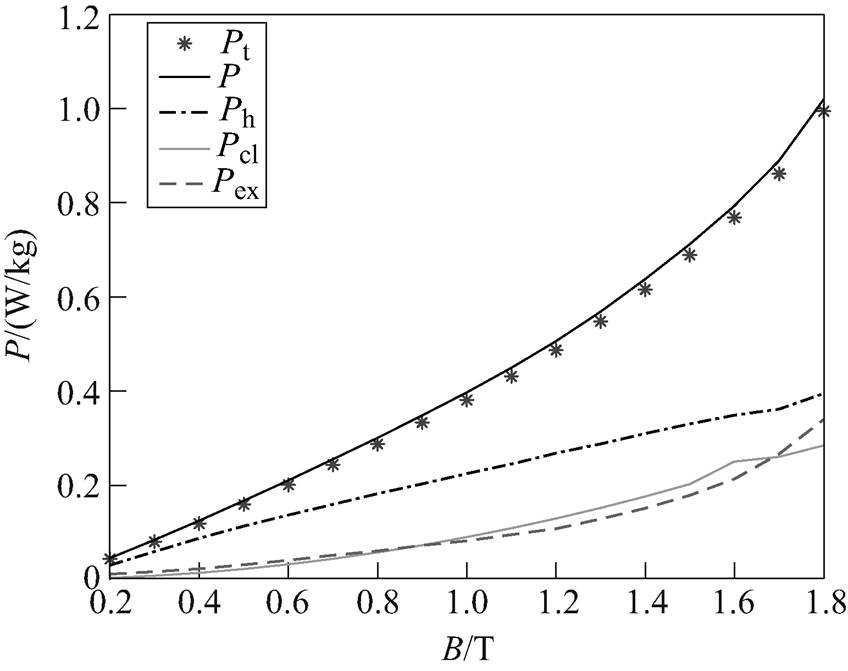
图13 Hdc=25A/m硅钢片损耗分离情况
Fig.13 Results of loss separation with Hdc=25A/m
由图12和图13可以看出，偏磁激励下，利用损耗分离模型可以较为准确地计算出总损耗。在频率为50Hz时，铁耗的三个分量中静态磁滞损耗所占比重最大，且三个分量均随磁感应强度交流分量峰值Bacm的增大而增大。
不同偏磁量下，静态磁滞损耗、涡流损耗以及异常损耗的对比分别如图14～图16所示。分析可知，静态磁滞损耗不仅与交流磁通密度的峰值Bacm有关，还与所加的直流偏磁量Hdc有关，静态磁滞损耗随Bacm和Hdc增大而增多。涡流损耗仅与交流磁通密度的峰值Bacm有关，随着Bacm的增大而增大，直流偏磁量Hdc对涡流损耗的影响不大。当交流磁通密度峰值Bacm较小时，异常损耗随着偏磁量的增加而增加；当Bacm较大时，随着Bacm的增大，异常损耗将趋于一致，究其原因，随着Bacm值越大，V0随Hdc的变化将不明显。
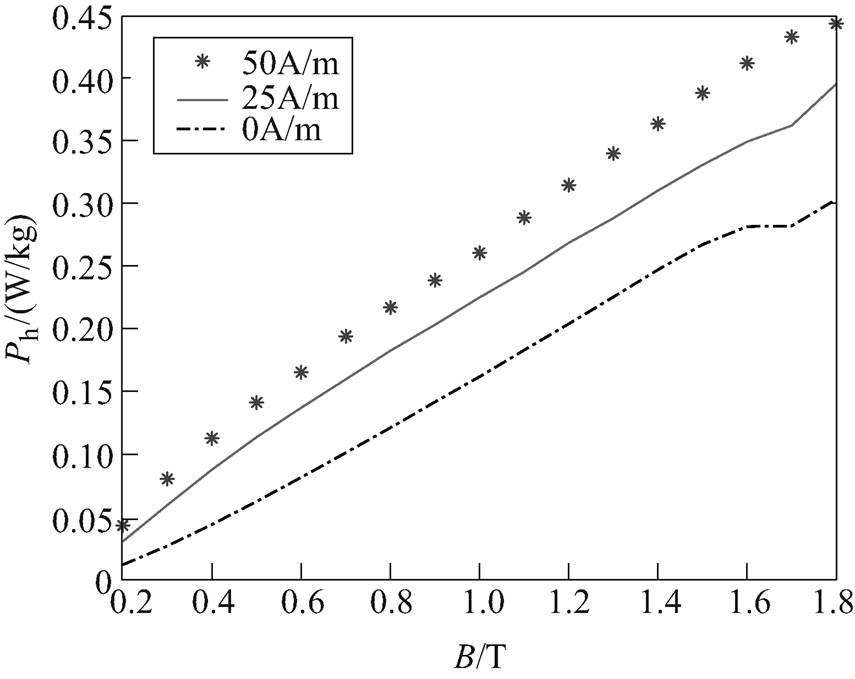
图14 不同直流偏磁量下的磁滞损耗
Fig.14 Hysteresis losses under different DC bias condition
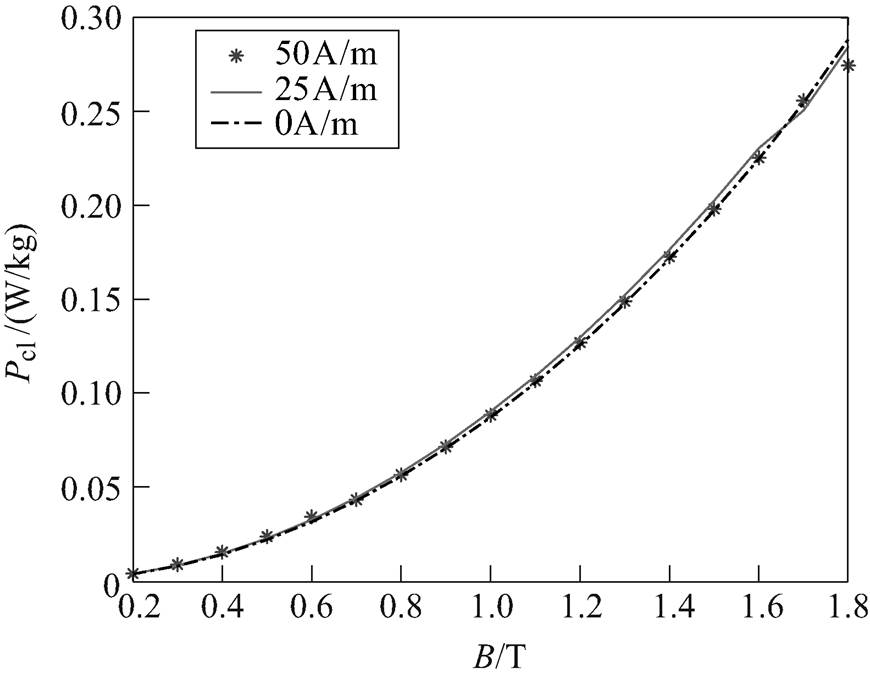
图15 不同直流偏磁量下的涡流损耗
Fig.15 Eddy-current losses under different DC bias condition
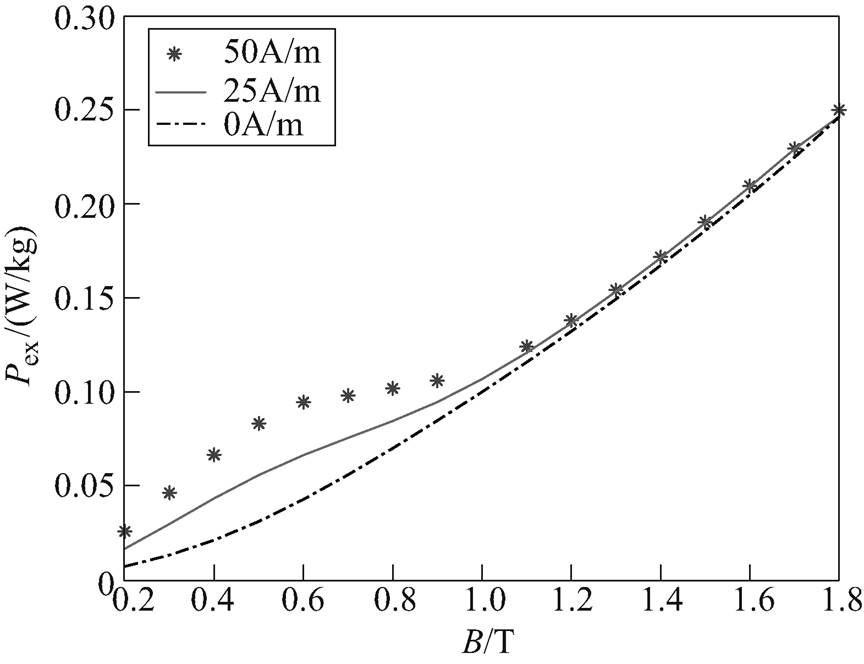
图16 不同直流偏磁量下的异常损耗
Fig.16 Excess losses under different DC bias condition
1）基于非对称极限磁滞回线生成偏磁下的一阶回转曲线，实现Preisach磁滞模型的参数辨识，能够更加准确地模拟直流偏磁磁滞特性。
2）考虑直流偏磁磁场和交流磁通密度峰值对异常损耗的影响，构造异常损耗中相关参数的函数式，基于实验结果进行参数提取，实现了直流偏磁条件下异常损耗的准确模拟。
3）直流偏磁条件下，不同偏磁下的涡流损耗相同，即直流偏磁对涡流损耗没有影响；静态磁滞损耗随偏磁程度的增加而不断增大；交流磁通密度峰值较低时，异常损耗随偏磁量程度的增大而增大，交流磁通密度峰值较高时，不同偏磁下的异常损耗趋于一致。
4）本文所提出的数值模拟方法适用于其他任意非对称磁滞特性的模拟，不仅限于直流偏磁。但是直流偏磁对总损耗及不同类型损耗的影响规律，可能因硅钢片类型的不同而不同，需要结合实验进行深入分析，从而为材料生产和应用提供重要参考。
参考文献
[1] 程志光, 高生, 李琳. 电气工程涡流问题的分析与验证[M]. 北京: 高等教育出版社, 2000.
[2] 江鹏, 李敬, 张群, 等. 基于A-l混合单元法的静磁场数值求解[J]. 电工技术学报, 2018, 33(5): 1167-1176.
Jiang Peng, Li Jing, Zhang Qun, et al. Numerical simulation for magnetostatic problems based on A-l mixed finite element method[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1167- 1176.
[3] 胡静竹, 刘涤尘, 廖清芬, 等. 基于有限元法的变压器电磁振动噪声分析[J]. 电工技术学报, 2016, 31(15): 81-88.
Hu Jingzhu, Liu Dichen, Liao Qingfen, et al. Analysis of transformer electromagnetic vibration noise based on finite element method[J]. Transactions of China Electrotechnical Society, 2016, 31(15): 81-88.
[4] 赵小军, 李琳, 程志光, 等. 应用谐波平衡有限元法的变压器直流偏磁现象分析[J]. 中国电机工程学报, 2010, 30(21): 103-108.
Zhao Xiaojun, Li Lin, Cheng Zhiguang, et al. Analysis of the DC bias phenomenon in transformers based on harmonic-balanced finite element method[J]. Proceedings of the CSEE, 2010, 30(21): 103-108.
[5] 王佳音, 白保东, 刘宏亮, 等. 直流偏磁对变压器振动噪声的影响[J]. 电工技术学报, 2015, 30(8): 56-61.
Wang Jiayin, Bai Baodong, Liu Hongliang, et al. Research on vibration and noise of transformers under DC bias[J]. Transactions of China Electro- technical Society, 2015, 30(8): 56-61.
[6] 康丽, 张艳丽, 唐伟, 等. 基于变系数Steinmetz公式的直流偏磁下铁心损耗计算[J]. 电工技术学报, 2019, 34(增刊1): 1-6.
Kang Li, Zhang Yanli, Tang Wei, et al. Calculation of core loss under DC bias based on the variable coefficient steinmetz formula[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 1-6.
[7] 陈彬, 李琳, 赵志斌. 典型非正弦电压波激励下高频磁心损耗[J]. 电工技术学报, 2018, 33(8): 1696- 1704.
Chen Bin, Li Lin, Zhao Zhibin. Magnetic core losses under high-frequency typical non-sinusoidal voltage magnetization[J]. Transactions of China Electro- technical Society, 2018, 33(8): 1696-1704.
[8] 刘任, 李琳, 王亚琦, 等. 基于随机性与确定性混合优化算法的Jiles-Atherton磁滞模型参数提取[J]. 电工技术学报, 2019, 34(11): 2260-2268.
Liu Ren, Li Lin, Wang Yaqi, et al. Parameter extraction for Jiles-Atherton hysteresis model based on the hybrid technique of stochastic and deter- ministic optimization algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2260- 2268.
[9] Beatrice C, Appino C, De La Barrière O, et al. Broadband magnetic losses in Fe-Si and Fe-Co laminations[J]. IEEE Transactions on Magnetics, 2014, 50(4): 1-4.
[10] Hamada S, Louai F Z, Nait-Said N, et al. Dynamic hysteresis modeling including skin effect using diffusion equation model[J]. Journal of Magnetism & Magnetic Materials, 2016, 410: 137-143.
[11] 白保东, 赵晓旋, 陈德志, 等. 基于J-A模型对直流偏磁条件下变压器励磁电流的模拟及实验研究[J]. 电工技术学报, 2013, 28(增刊2): 162-166.
Bai Baodong, Zhao Xiaoxuan, Chen Dezhi, et al. Simulation and experiment research on transformer excitation current under DC magnetic bias based on J-A model[J]. Transactions of China Electrotechnical Society, 2013, 28(S2): 162-166.
[12] 李阳. 基于动态J-A磁滞模型直流偏磁下的变压器铁损计算[D]. 天津: 天津工业大学, 2018.
[13] 刘任, 李琳. 基于场分离技术与损耗统计理论的动态Energetic磁滞模型[J]. 中国电机工程学报, 2019, 39(21): 6412-6419.
Liu Ren, Li Lin. Dynamic Energetic hysteresis model based on field separation approach and statistical theory of losses[J]. Proceedings of the CSEE, 2019, 39(21): 6412-6419.
[14] Hauser H. Energetic model of ferromagnetic hysteresis 2: magnetization calculations of (110)[001] FeSi sheets by statistic domain behavior [J]. Journal of Applied Physics, 1995, 77(6): 2625-2633.
[15] 刘洋, 张艳丽, 谢德馨, 等. 考虑硅钢片二维矢量磁特性的复数E&S模型[J]. 中国电机工程学报, 2012, 32(3): 144-149, 3.
Liu Yang, Zhang Yanli, Xie Dexin, et al. A complex E&S model considering 2D vector magnetic pro- perties of silicon steel sheet[J]. Proceedings of the CSEE, 2012, 32(3): 144-149, 3.
[16] Enokizono M, Shimoji H, Horibe T. Loss evaluation of induction motor by using magnetic hysteresis E&S model[J]. IEEE Transaction on Magnetic, 2002, 38(5): 2379-2381.
[17] Dlala E. Efficient algorithms for the inclusion of the Preisach hysteresis model in nonlinear finite-element methods[J]. IEEE Transaction on Magnetic, 2011, 47(2): 395-408.
[18] Hussain S, Lowther D A. An efficient implementation of the classical Preisach model[J]. IEEE Transaction on Magnetic, 2018, 54(3): 1-4.
[19] 段娜娜, 徐伟杰, 李永建, 等. 基于极限磁滞回线法的软磁复合材料磁特性模拟[J]. 电工技术学报, 2018, 33(20): 4739-4745.
Duan Nana, Xu Weijie, Li Yongjian, et al. Elec- tromagnetic property modeling of the soft magnetic composite material based on the limiting loop method[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4739-4745.
[20] Mayergoyz I D. Mathematical model of hysteresis and their applications[M]. New York: Academic Press, 2003.
[21] 赵小军. 基于谐波平衡有限元法的变压器直流偏磁特性研究[D]. 北京: 华北电力大学, 2011.
[22] Zirka S E, Moroz Y I, Harrison R G, et al. Inverse hysteresis models for transient simulation[J]. IEEE Transactions on Power Delivery, 2014, 29(2): 552- 559.
[23] Bertotti G. Hysteresis in magnetism[M]. San Diego: Acedemic, 1998.
[24] Dlala E. A simplified iron loss model for laminated magnetic cores[J]. IEEE Transaction on Magnetic, 2008, 44(11): 3169-3172.
[25] 刘任, 李琳. 基于损耗统计理论与J-A磁滞模型的直流偏磁下磁性材料损耗计算方法[J]. 高电压技术, 2019, 45(12): 4062-4069.
Liu Ren, Li Lin. Loss prediction of magnetic material under DC bias based on the statistical theory of losses and Jiles-Atherton hysteresis model[J]. High Voltage Engineering, 2019, 45(12): 4062-4069.
[26] Wang Xiaohui, Thomas D W P, Sumner M, et al. Characteristics of Jiles-Atherton model parameters and their application to inrush current simulation[J]. IEEE Transaction on Magnetic, 2008, 44(3): 340-345.
Hysteretic and Loss Modeling of Silicon Steel Sheet under the DC Biased Magnetization Based on the Preisach Model
Abstract Based on the Preisach model, a parameter identification method for simulating asymmetric hysteresis loops is proposed and applied to the simulation of static and dynamic hysteresis characteristics of grain-oriented (GO) silicon steel sheet. Due to the asymmetry of curves under the DC bias, an algorithm was presented to create asymmetrical first order reversal curves (FORCs) according to the experimental data of major hysteresis loop measured in DC-bias condition, and the corresponding Everett function was established. The static hysteresis curves were simulated by the Preisach model. The consistency between the simulated results and the measured ones verified the proposed method. Finally, the DC-biasing dynamic hysteresis model was constructed considering the influence of DC bias magnetic field and AC magnetic flux peak on excess loss. In addition, the loss characteristics of GO silicon steel sheet under DC bias condition were simulated. The influence of DC bias on different types of losses was analyzed.
keywords：DC bias, Preisach model, loss separation, hysteresis, loss characteristics
中图分类号：TM153
DOI: 10.19595/j.cnki.1000-6753.tces.190603
国家重点研发计划（2017YFB0902703）、国家自然科学基金项目（51777073）、河北省自然科学基金项目（E2017502061）和中央高校基本科研业务费（2019MS078）资助。
收稿日期2019-05-16
改稿日期 2019-08-25
赵小军 男，1983年生，博士，副教授，硕士生导师，研究方向为电工材料磁性能测量与模拟技术、频域数值计算方法、变压器直流偏磁及振动噪声问题、多物理场耦合模型及计算方法。E-mail: zxjncepu@ncepu.edu.cn（通信作者）
刘小娜 女，1995年生，硕士研究生，研究方向为软磁材料磁滞及损耗特性的测量与数值模拟。E-mail: 15733228939@126.com
（编辑 崔文静）