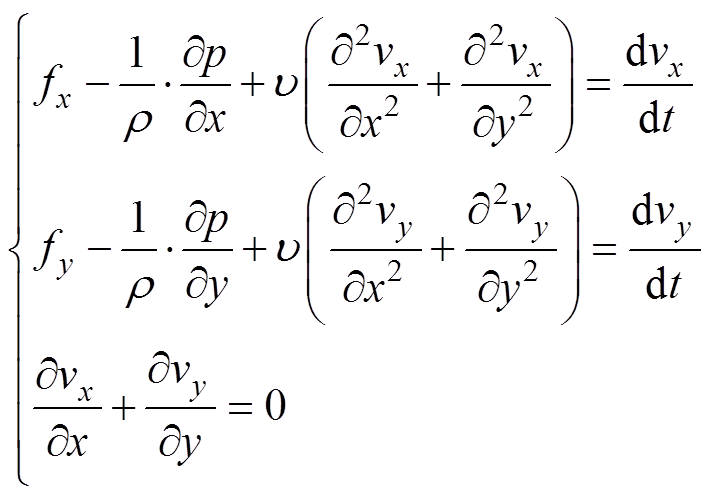（1）摘要 输电线路导线覆冰是电力系统最严重的自然灾害之一，研究导线覆冰的数值计算方法，建立仿真平台，不仅可以科学地预测导线覆冰增长，并且能大量减少自然覆冰观测工作量。但是已有的数学模型和仿真计算方法都回避了导线覆冰扭转这一自然现象，从而不能有效模拟实际覆冰增长。该文基于导线覆冰形成机理，加入导线覆冰扭转因素，提出导线扭转的数学模型，借助C语言编写仿真模拟程序，实现导线覆冰动态增长的数值模拟过程。仿真结果表明，导线覆冰增长是一个伴随扭转的动态过程，距离杆塔距离、档距、风速、液态水滴直径大小均对扭转角度大小有影响。在重庆大学雪峰山自然覆冰试验基地，验证了该文所提出的数值模拟方法的科 学性。
关键词：导线覆冰 扭转 数学模型 动态增长
随着全球气候变化，极端气候频繁出现，输电线路冰雪灾害时有发生。输电线路导线作为电力系统能量的传输部分，发生严重覆冰会引起杆塔变形、倒塔、导线断股等危害，给电网可靠性带来极大的威胁。世界各国电力领域的研究机构和学者不断开展导线覆冰研究，其中包括形成机理研究、导线覆冰模型提出和仿真计算，在很多方面取得了一定的成果与突破，但是由于导线覆冰机理的复杂性与其影响因素的多样性，现有的仿真计算模型均不能有效计算、预测实际的自然覆冰增长过程[1-4]。
目前已有的导线覆冰计算模型，可以概括为经验模型、理论模型和物理模型。经验模型是根据试验与现场覆冰数据，覆冰结果与气象参数相对比分析，从而总结出一定的导线覆冰模型，例如Kuoiwa模型、Lenhard模型、Imai模型、Chaine-Skeates模型、Mc Comber-Govoni模型和湖南回归模型[5-11]。这类模型往往简单地适用于某一特定环境下，若改变其他参数将不再适用。导线覆冰主要包括导线捕获过冷却水滴与过冷却水滴冻结，研究者主要考虑这两个方面，建立理论模型，例如Goodwin导线覆冰干增长模型和鲍尔格斯道夫模型[12-13]，此类模型过于理想化，从而丧失其科学性。考虑到导线覆冰的碰撞系数、捕获系数等因素，研究者Makkonen提出了导线覆冰时变模型[13]，设定导线覆冰总是呈圆筒形增长，随着导线覆冰的发展，覆冰导线外径增大，但是在实际导线覆冰过程中，在不同的区域，覆冰表面捕获的水滴数量不同，也就是碰撞率不同，这种情况下导线表面各处的覆冰就变得不均匀，而这种不均匀的表面又进一步使气流扰动加强，使得碰撞率的差异进一步扩大，经过一定时间后，导线表面形成覆冰形状。文献[13]采用边界元法和边界层理论，提出了覆冰导线流场计算方法，采用拉格朗日数值计算水滴撞击导线，并将冰形的表面粗糙度纳入仿真计算，从而提出导线无扭转覆冰过程的仿真计算方法。此计算方法在原有的模型基础上有了较大的改善和发展，能适用于部分覆冰较少的情况。
在实际的导线覆冰过程中，空气中的过冷却水滴随着气流运动，与导线表面发生碰撞，当有足够的冻结核时，过冷却水滴在导线表面冻结，剩余部分流失或者在表面形成水膜。过冷却水滴在导线表面冻结，覆冰首先在导线迎风侧增长，在短期内风向不发生急剧变化，则导线覆冰厚度继续在迎风侧不规则增长。当覆冰达到一定厚度后，在偏心覆冰扭矩作用下，覆冰导线发生扭转。当覆冰导线继续扭转，一段时间后，导线表面覆冰呈圆筒形或者椭圆形。当覆冰导线不足以扭转时，导线表面覆冰则一直在迎风侧发展，最终呈常见的翼型覆冰。上述现象即为输电线路导线覆冰过程中常见的扭转现象，这是覆冰过程中必然存在的物理过程。导线覆冰扭转是一复杂的物理过程，现有的仿真计算模型并不能有效地对导线覆冰进行科学的计算，其难点在于如何针对覆冰导线扭转进行计算，而其扭转过程影响了整个导线流场，需要不断更新边界重新计算在现有的模型和仿真计算中。
本文基于导线覆冰形成机理，提出导线扭转的数学模型，借助C语言编写仿真模拟程序，实现导线覆冰动态增长的数值模拟过程。通过仿真计算结果，得出导线覆冰扭转动态增长过程、导线覆冰质量与冰形变化，分析距离杆塔距离、档距、风速、液态水滴直径大小对导线覆冰扭转角度的影响。最后，在重庆大学雪峰山自然覆冰试验基地，采用一段档距为80m的LGJ-500/35导线进行自然覆冰试验，验证本文所提出的数值模拟方法的科学性。
导线周围流场是覆冰的重要影响因素，由N-S（Navier-Stokes）方程，把导线周围流场当作粘性不可压缩流体，从而根据其运动方程，计算得到导线周围空气流场的速度分布，其数学表达式为
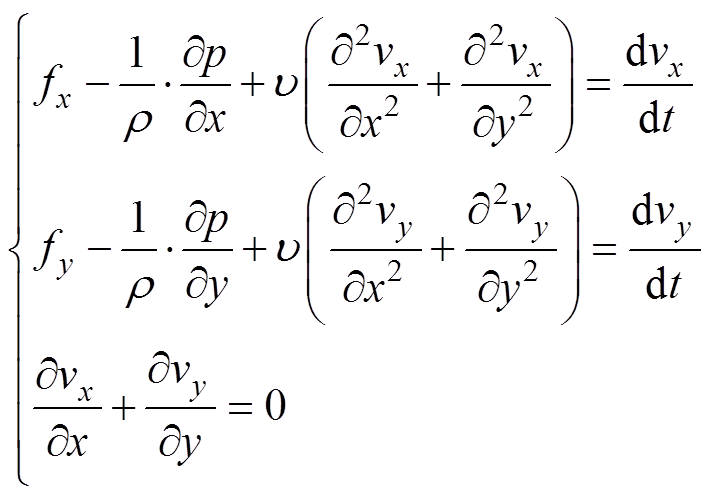（1）式中，r 为空气流场密度（g/cm³）；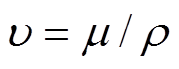
，m 为动力粘性系数；p为空气流场压强（Pa）；fx为空气流场在x轴方向的所受力（N）；fy为空气流场在y轴方向的所受力（N）；vx为空气流场在x轴方向的速度分量（m/s）；vy为空气流场在y轴方向的速度分量（m/s）。
空气中液态水滴轨迹计算可以借助标准四阶龙格-库塔法进行微分方程联立计算求解[13]，其主要方法为
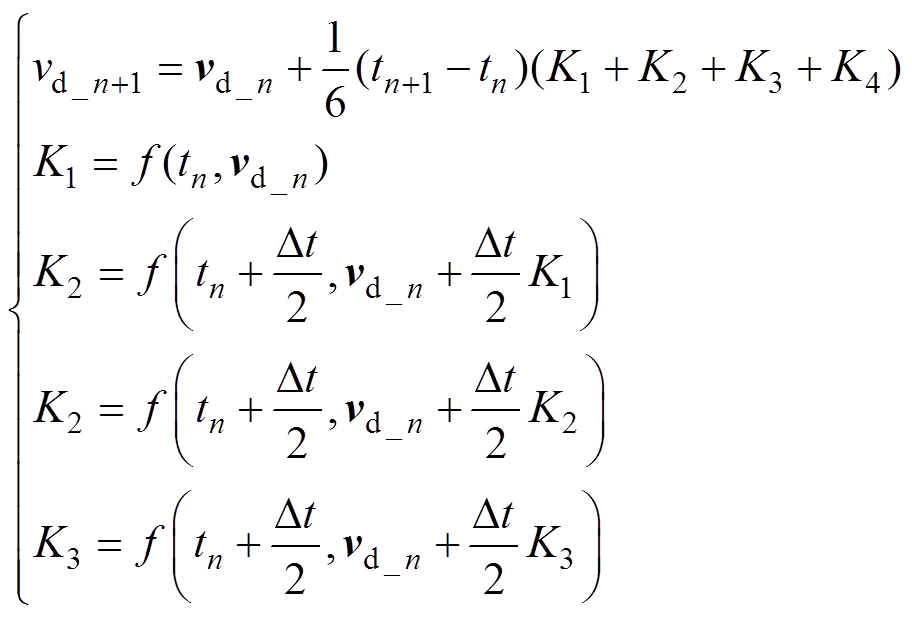（2）
式中，νd_n和νd_n+1分别为当前时刻tn和下一时刻tn+1的水滴速度；K1、K2、K3和K4为四阶计算系数。
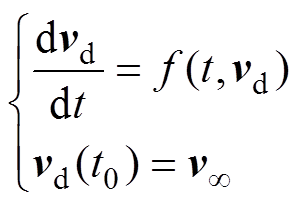（3）式中，vd为水滴运动速度矢量；vd（t0）为t0时刻水滴运动速度（m/s）；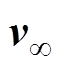
为无穷大时刻水滴运动速度（m/s）。
在得出水滴在x轴、y轴上的速度分量后，接着求解水滴在下一个时刻的所在位置，可表示为
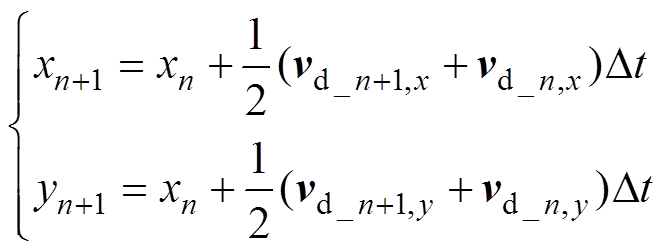（4）在实际的空气中，液态水滴直径大小的分布是分散的。在实际的导线覆冰计算中，引入液态水滴中值体积直径（Median Volume Diameter, MVD），从而简单地表示空气中液态水滴直径大小，以简化导线覆冰计算过程。
导线覆冰过程的冻结过程，也是一个热力学平衡过程。在导线表面或者冰层表面，水滴的冻结有着多种能量的变化与平衡关系。将覆冰导线划分成多个覆冰单元，其必须遵守能量守恒和质量守恒两个基本的物理定律[14-15]，可描述为
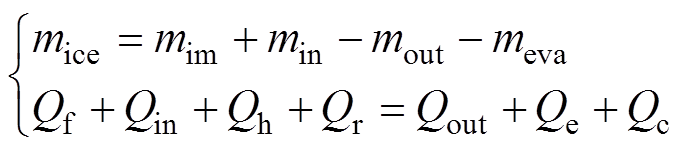（5）式中，mice为导线表面覆冰质量大小（kg）；min为液态水流入这一微元的质量（kg）；mout为流出液态水流出这一微元的质量大小（kg）；meva为所蒸发的液态水质量大小（kg）；mim为空气中液态水与导线碰撞部分的质量大小（kg）；Qf为液态水滴冻结所放出的热量（J）；Qin为流出覆冰微元的热量（J）；Qh为液态水滴与导线碰撞的释放的热量（J）；Qr为气流与导线表面摩擦发出的热量（J）；Qout为从覆冰微元流出的热量（J）；Qe为过冷却水滴蒸发所需热量（J）；Qc为空气对流换热量（J）。
在本文仿真计算中，导线长度设置为L，将导线等间隔取9个节点，取样代表整段导线覆冰情况。由于导线不同位置覆冰形状和距离导线悬挂点距离是一个三维空间，为了有效地描述不同节点处导线覆冰形状，采用直角坐标表示导线节点位置结合的三位坐标，x、y轴表示覆冰截面，z表示导线某点到杆塔的距离大小。导线扭转角度受两个因素影响：一是导线的扭转刚度，这由导线自身机械参数决定；二是覆冰节点与杆塔之间的距离。在一定的导线刚度下，导线扭转角度是与离杆塔距离和时间的关系函数，因此本文用a (z, t)表示导线z点在t时刻的扭转角度大小。
设置导线不同位置随时间变化的表面覆冰位置为
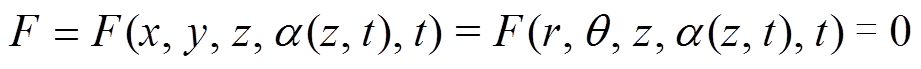（6）为简化变量，将变量无量纲化处理，有
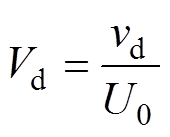
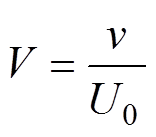
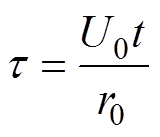
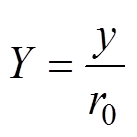
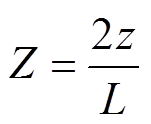
式中，U0为液态水滴的运动速度（m/s）；V为无量纲风速；vd为无量纲液态水滴的运动速度；t 为无量纲时间；x, y, z分别为覆冰切面的横坐标、纵坐标和距离杆塔位置（m）；r0为裸导线半径（m）；L为档距（m）。
用无量纲化变量代替原有变量，则上述导线表面覆冰位置可表示为
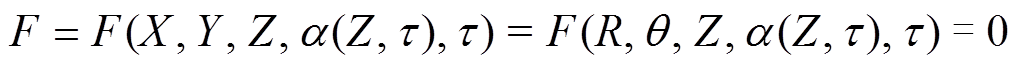（7）先对导线覆冰质量进行计算，有
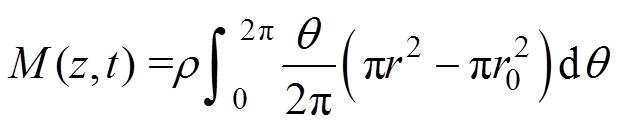（8）
归一化处理后可表示为
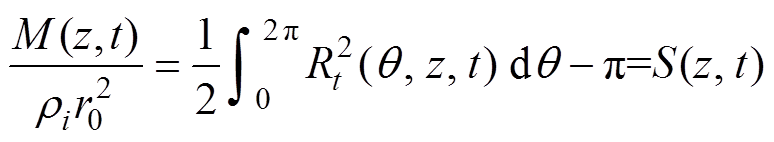（9）式中，M为覆冰质量（kg）；r 为导线覆冰密度（kg/m3）；ri为导线覆冰微元密度（kg/m³）；r为覆冰边界半径（m）；Rt为覆冰导线半径的时间函数（m）；Rt为覆冰导线直径R的函数（m）；S为覆冰导线截面积（m2）。
通过极坐标将直角坐标转换，则导线表面覆冰位置可表示为
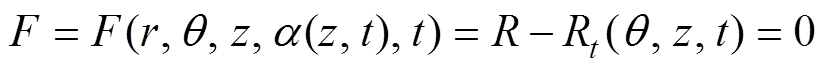（10）根据重心计算公式，在无量纲杆塔距离Z为定值时，覆冰导线的重心坐标为
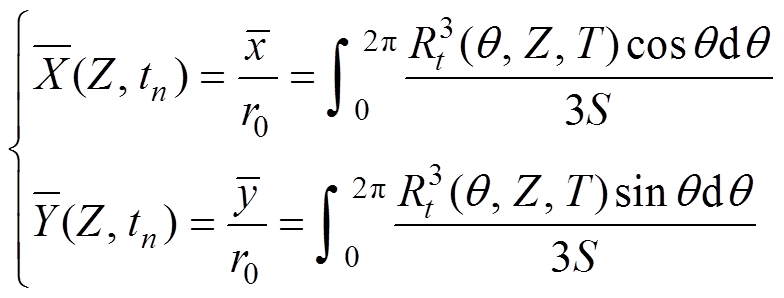（11）
为了简化表达，将覆冰导线直径和坐标化为
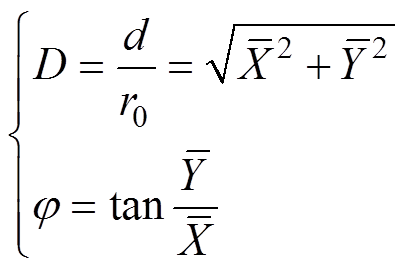（12）设a (z, t)为t时刻与导线悬挂点的距离z处的覆冰扭转大小，在任何时间，覆冰导线扭转角度与冰扭力矩的关系都必须满足方程，定义QR(z, t)为
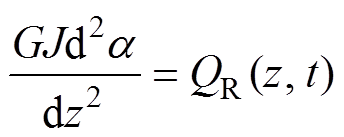（13）
式中，G为导线的扭转弹性模量（MPa）；J为导线的扭转极惯矩（mW）。
导线在悬挂点的扭转角度始终为零，任一时刻，在确定的导线档距下，覆冰导线扭转角度是一定值，得出边界条件为
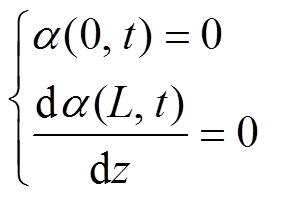（14）导线覆冰在一段时间内处于稳定状态，达到扭转条件的冰厚才扭转，用数学描述为(tn, tn+Dt)不扭转。在一个扭转状态到来前，在Dtn内导线不发生扭转，也就是说导线在同一个方向上覆冰增长。为了描述覆冰导线冰扭力矩的大小，可表达为
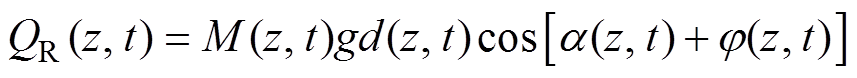（15）
将其进行归一化，得出
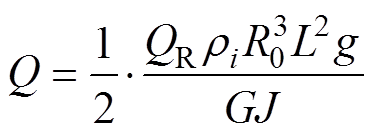（16）代入上述方程，则可将覆冰导线扭转方程改写为
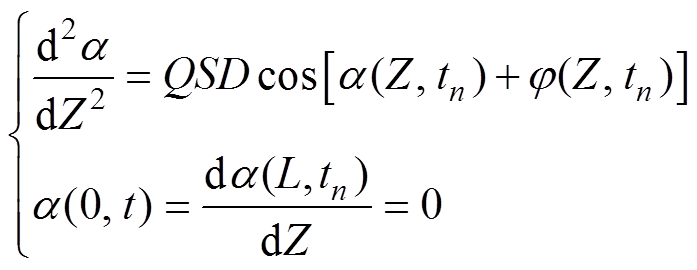（17）
式中，a 为扭转角度（°）；Q为归一化扭转力矩；S为覆冰截面积（m2）；D为覆冰导线直径（m）。
将式（17）改写为准线性方程，有
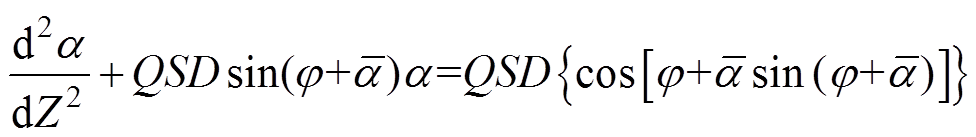（18）根据标准中心差分格式，得出覆冰导线扭转角度矩阵为
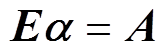
式中，E为三对角矩阵，有
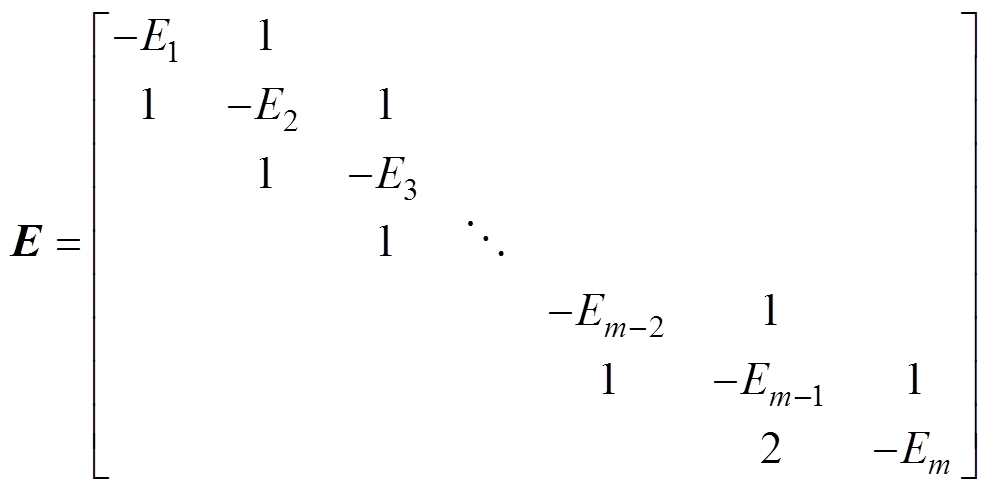（19）式中，
。
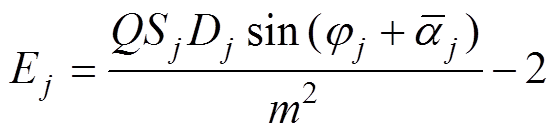（20）
基于导线覆冰形成机理，和上述所提出的导线覆冰扭转的数学模型，借助C语言编写仿真模拟程序，实现导线覆冰动态增长的数值模拟过程。
导线覆冰在一段时间内总是处于稳定状态，在达到扭转条件的冰厚才扭转，用数学描述为(t, t+Dt)不扭转。把t+Dt时刻的导线覆冰形状导出，重新计算导线周围流场和覆冰导线此时的扭转，在达到下一个扭转状态前，导线位置保持稳定，在原有的覆冰形状下不扭转继续覆冰。反复导出上一时间导线覆冰参数，多次迭代运算，这一过程重复进行到导线覆冰结束，计算出导线所取节点任何时间的导线表面覆冰重量、覆冰形状与扭转角度，其模拟仿真计算流程如图1所示。
本文的数值模拟取时间步长为15min，前文提及导线看做对称导线，因此9个节点只需对5个节点数值模拟。
2.2.1 水滴运动轨迹和覆冰圆相对关系
当气流把空气中的过冷却水滴吹落在导线表面与之发生碰撞后，导线表面沿迎风侧覆冰增长，偏心覆冰进而产生扭矩，当覆冰扭转大小超过临界值时，覆冰导线发生扭转，扭转后的覆冰导线边界发生变化，从而致使空气中的过冷却水滴与导线表面冰层的碰撞位置发生变化，导致下一个阶段导线覆冰发生变化。因此研究覆冰导线扭转特性时，对水滴运动轨迹和覆冰圆相对关系的研究必不可少。
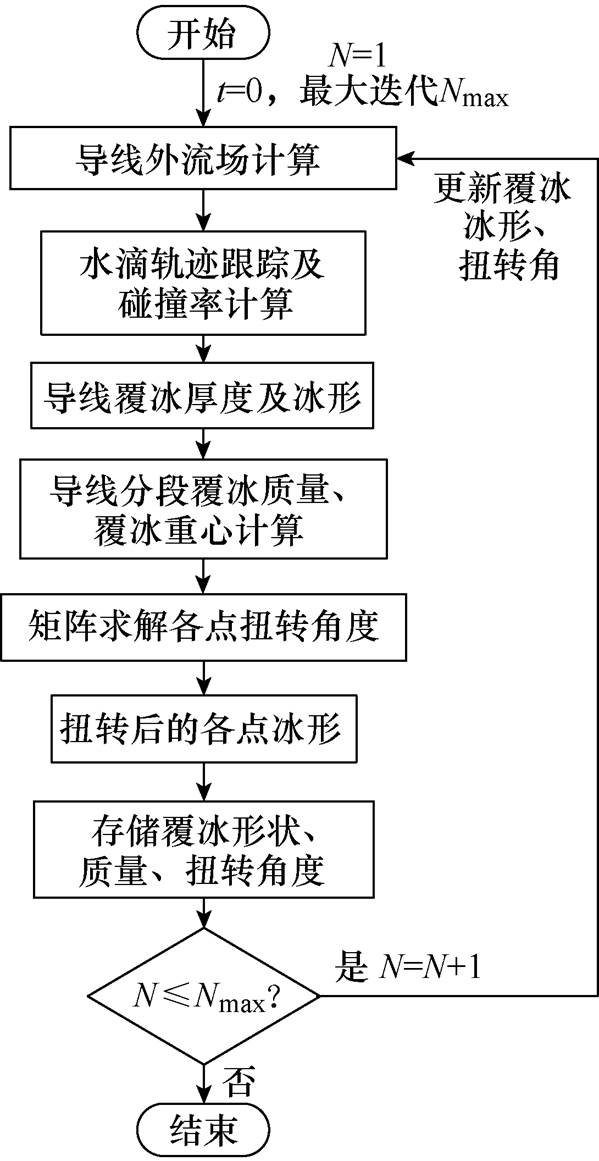
图1 导线覆冰数值计算流程
Fig.1 Numerical simulation process of conductor icing
本节以导线直径为30mm、风速为10m/s、液态水滴直径中值为20mm、档距为400m为例，取节点5作为研究对象，通过仿真计算结果，取第1、6、11、16和22个时间步长的水滴运动轨迹，得出如图2所示的水滴运动轨迹和覆冰圆相对关系。与如图3所示的不考虑导线扭转时的水滴运动轨迹进行对比分析。
图2中，横纵坐标为各点到导线轴心的距离，线条表示空气中过冷却水滴运动轨迹，不规则小圆构成图形是导线覆冰表面边界。通过仿真计算结果可知，随着导线覆冰的增长，导线表面边界发生变化，从而空气的过冷却水滴运动轨迹发生变化，在整个导线覆冰过程中，过冷却水滴运动轨迹与覆冰圆之间的关系处于动态变化中，不能简单地处理为如图3中的导线不扭转的导线单侧覆冰，这与导线自然覆冰结果相悖。
图2 导线扭转覆冰水滴运动轨迹
Fig.2 Conductor twisting ice droplets movement track
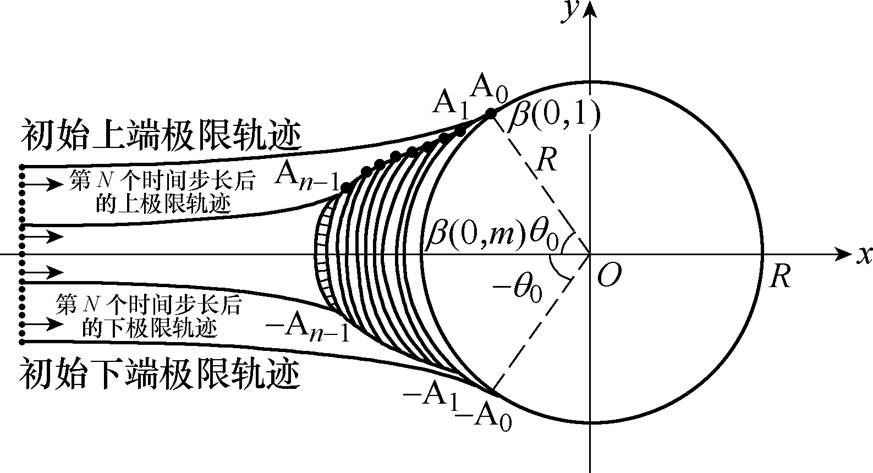
图3 导线无扭转覆冰水滴运动轨迹
Fig.3 Conductor no twisting ice droplets movement track
2.2.2 不同节点冰形变化
已有的研究为简化计算，将导线自然覆冰中的扭转因素忽略，从而得出如图4所示的导线不扭转覆冰冰形变化结果。本文以导线直径为30mm、风速为10m/s、液态水滴中值直径为20mm、档距为80m为例，通过本文提出的导线覆冰数值模拟，分别计算了5个节点的22个时间步长的导线覆冰冰形变化过程，如图5所示。
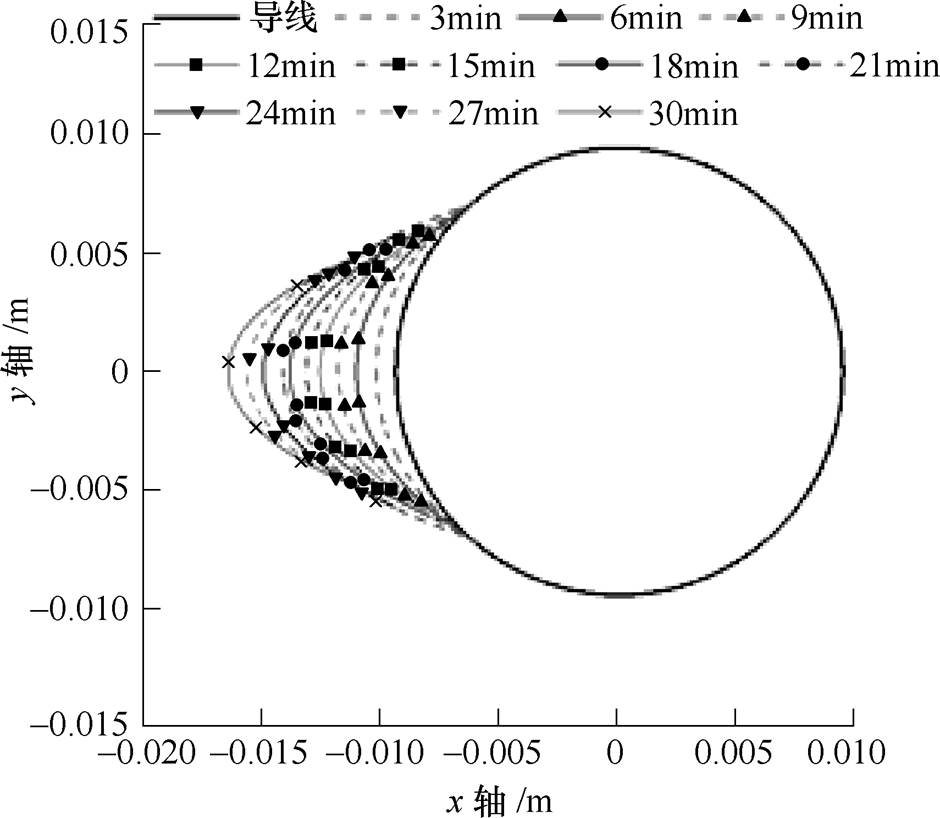
图4 导线不扭转覆冰冰形变化
Fig.4 Conductor does not twist and change the ice shape
当气流把空气中的过冷却水滴吹落在导线表面与之发生碰撞后，导线表面沿迎风侧覆冰增长，偏心覆冰产生扭矩，当覆冰扭转大小超过临界值时，覆冰导线发生扭转，导致下一个阶段导线覆冰发生变化，在新的冰形下继续覆冰，依次重复这一过程到覆冰结束。本文的数值模拟实现了导线覆冰动态增长这一过程，大大提高了导线覆冰模拟的准确性。
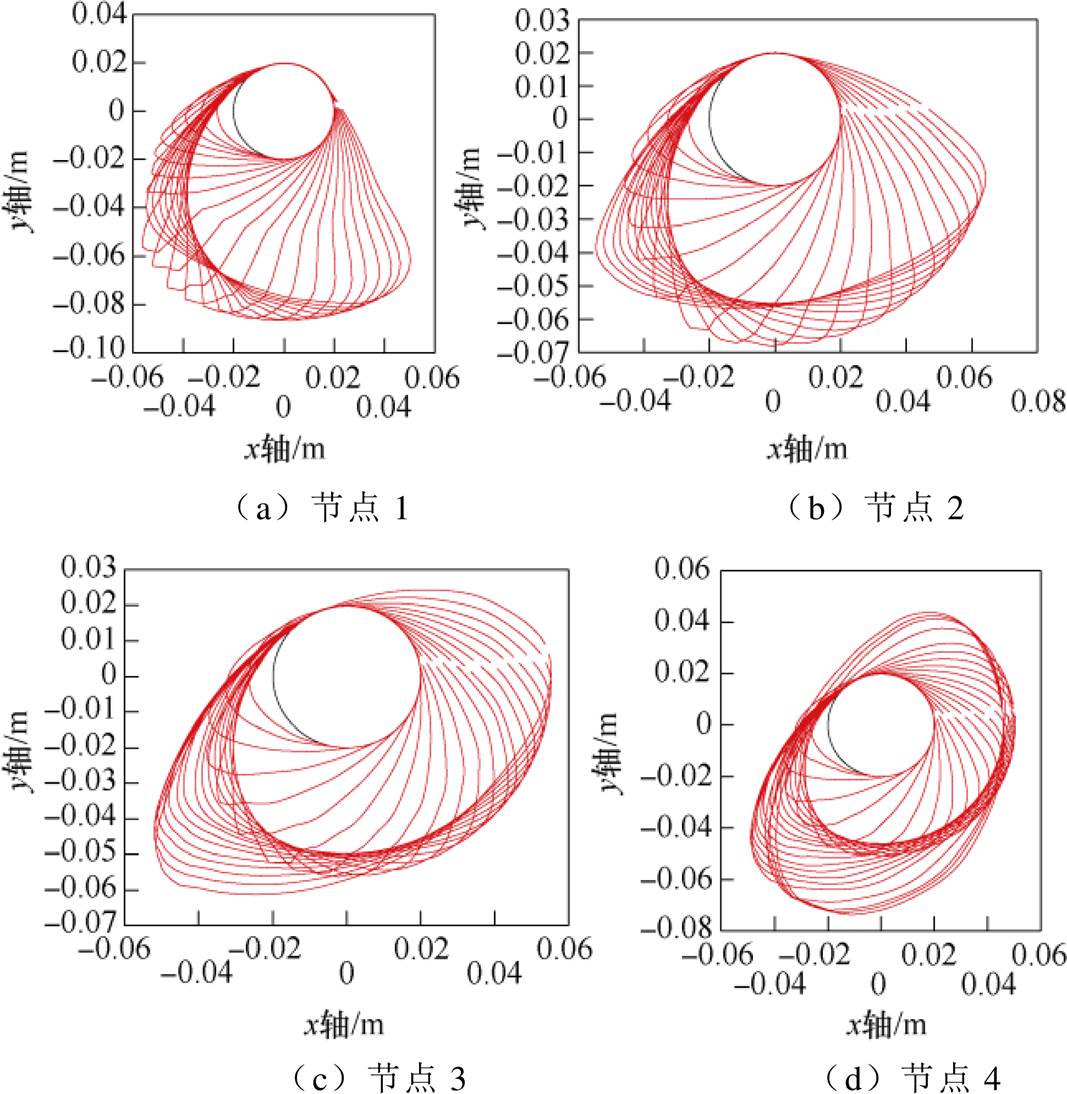
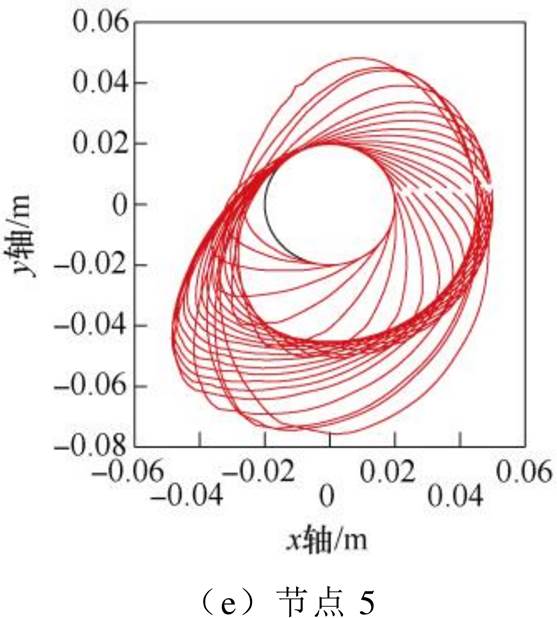
图5 导线覆冰扭转不同节点冰形变化
Fig.5 Changes of ice shape in different node
2.2.3 不同节点的扭转特性
根据仿真计算结果，以导线直径为30mm、风速为10m/s、液态水滴中值直径为20mm，档距为80m为例，绘制5个节点的覆冰导线扭转角度大小随覆冰时间的变化关系，如图6所示。
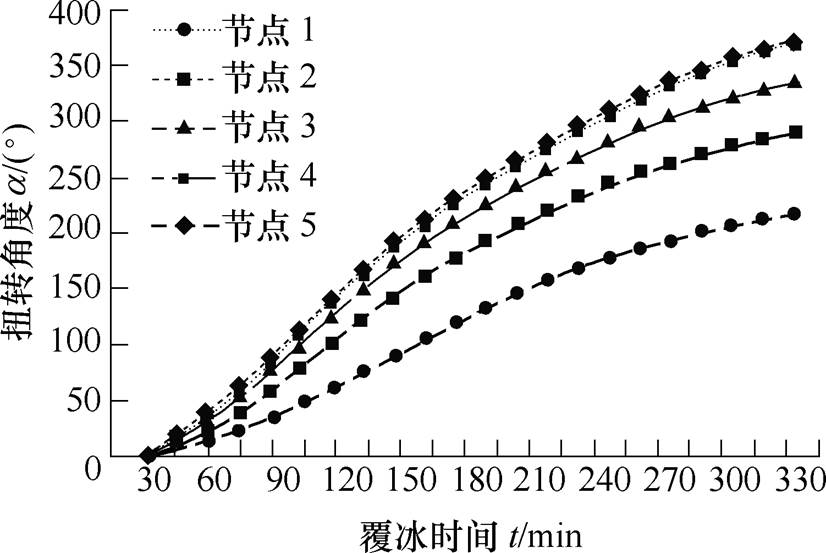
图6 不同覆冰节点扭转特性
Fig.6 Twisting characteristics of conductor icing indifferent icing nodes
根据仿真结果分析，随着覆冰的增长，导线扭转角度也不断增加，扭转角度增加的速度在减缓。根据计算结果，5个节点的扭转角度依次增大，且增大的幅度在减少，即覆冰导线距离杆塔越远，扭转角度越大，这与自然覆冰现象一致，其原因是距离越远，导线的抗扭转力矩越小，覆冰导线扭转更严重。
2.2.4 覆冰质量变化
导线覆冰质量是仿真计算的重要内容，通过本文所提出的数值模拟方法，冰重变化如图7所示。
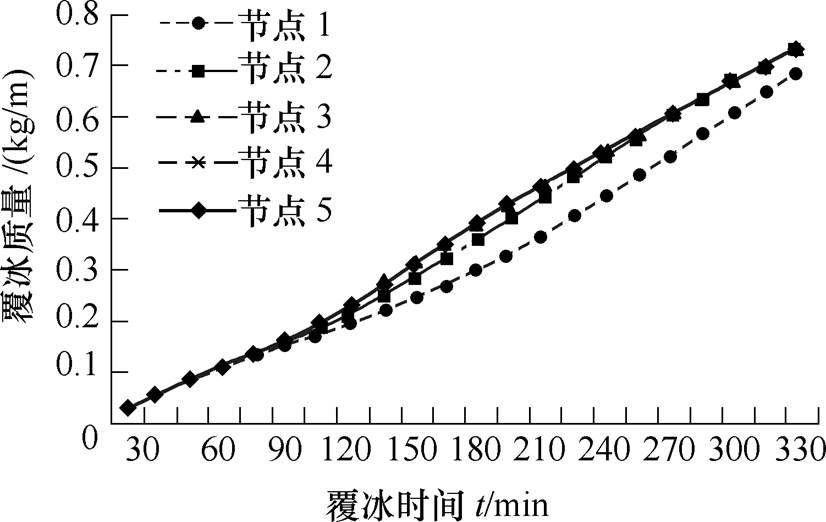
图7 冰重变化
Fig.7 Ice amount changing
根据仿真结果可知，覆冰质量随着覆冰时间增加而增长，节点2、3、4和5处的单位长度覆冰质量极为相近，节点1的单位长度覆冰质量略小于其余4个节点，但通过计算，最大覆冰质量差值仅为9.1%，根据2.2.3小节，随着覆冰时间增加，5个节点处扭转角度差值大，但单位长度覆冰质量差别很小，可得出导线覆冰质量与导线悬挂点距离关系甚小，与扭转角度无关。
2.2.5 不同导线档距下的扭转特性
在工程实际中，不同的线路档距大小不一，为研究档距大小对导线覆冰扭转角度影响，设置导线直径为30mm、风速为10m/s、液态水滴中值直径为20mm、计算得出档距分别为80m、320m和1 200m情况下，节点5的导线覆冰扭转角度变化如图8所示。
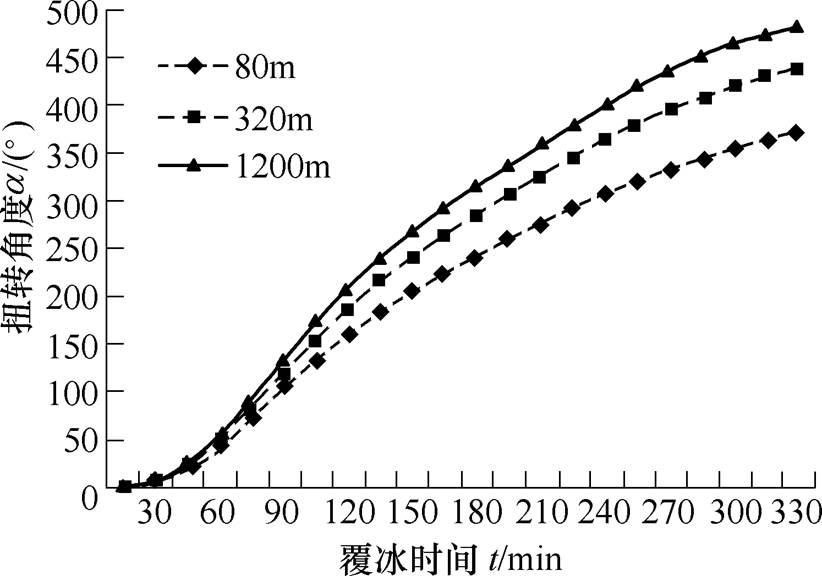
图8 不同档距导线覆冰扭转特性
Fig.8 Twisting characteristics of conductor icing with different tower span
根据仿真计算结果，在同一节点，输电线路档距越大导线扭转角度越大，这与2.2.3小节中得出的距离杆塔越远的节点，扭转角度越大的原因一致。
2.2.6 不同风速下的扭转特性
覆冰环境参数对导线覆冰有巨大影响，本文设置导线直径为30mm、档距为80m、液态水滴中值直径为20mm，对比分析5m/s、10m/s和15m/s三种风速下导线覆冰扭转角度变化，如图9所示。
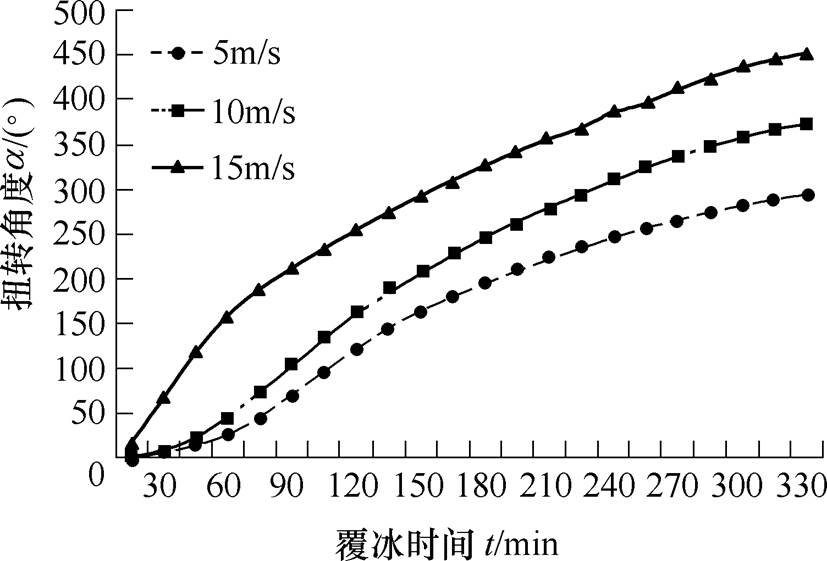
图9 不同风速导线覆冰扭转特性
Fig.9 Twisting characteristics of conductor icing with different wind speed
根据仿真结果分析，风速越大，导线覆冰扭转角度越大。根据导线覆冰基本原理，风速越大，碰撞系数越大，覆冰增长越快，冰扭力矩在更短的时间内扭转临界值，因此扭转更严重。
2.2.7 不同液态水直径下的扭转特性
本文设置导线直径为30mm、档距为80m、风速为10m/s，对比液态水滴中值直径分别为10mm、20mm和30mm时导线覆冰扭转角度变化，如图10所示。
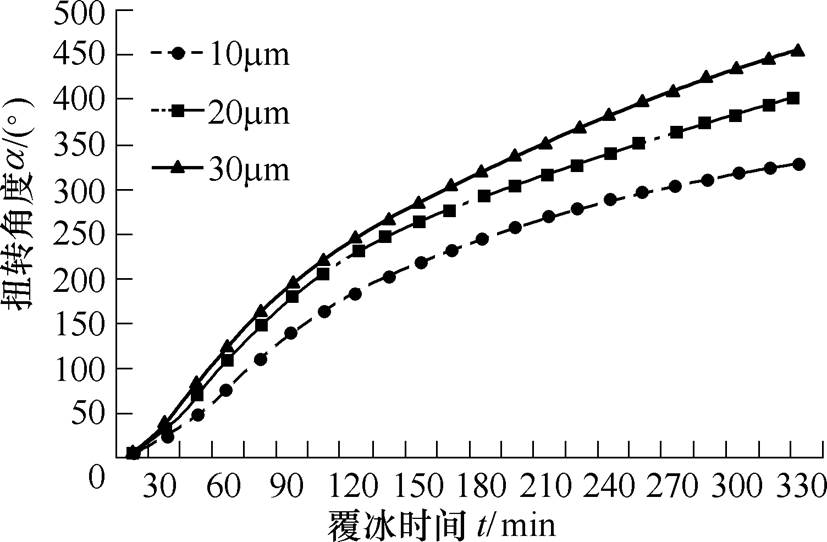
图10 不同液态水滴直径导线覆冰扭转特性
Fig.10 Twisting characteristics of conductor icing with different liquid droplet diameter
根据仿真结果可知，液态水滴中值直径越大，覆冰导线扭转角度越大。其原因是，液态水滴中值直径越大，其所受惯性力越大，更多的水滴随着气流与导线发生碰撞，因此其覆冰速率大，达到扭转临界值所需时间更短，覆冰导线扭转也就更加严重。
试验在重庆大学雪峰山自然覆冰试验基地开展，其全景如图11a所示。该自然覆冰试验站海拔1 400m，属于典型的微地形、微气象覆冰区，历史最大雨凇覆冰厚度超过500mm，最大风速可达25m/s，年覆冰时间大于60天。基地有两架距离80m的雨凇塔，可布置多种直径和类型的试验线段，如图11b所示。
图11 雪峰山自然覆冰试验基地
Fig.11 Xuefeng mountain natural icing test base
为监测导线覆冰气象环境参数，试验采用芬兰Vaisala公司的温湿压一体计测量覆冰环境温度与湿度，如图12a所示。采用旋转多导体积冰器监测空气中的水滴中值直径和液态水滴含量，如图12b所示。在两架雨凇塔的试验线段中，采用一段档距为80m的LGJ-500/35单导线进行自然覆冰试验，为方便测量扭转角度，每间隔8m处的位置用铁丝扎紧导线并与地面垂直，如图12c所示。
图12 气象条件测量设备
Fig.12 Meteorological parameters measuring equipment
在自然覆冰试验中，测量的工作量巨大，且覆冰时间间隔短，覆冰量变化小的情况下，测量误差较大。为了增加测量结果可靠性，测量时间间隔采用0.5h，取1、3和5三个节点，即分别离雨凇架固定点8m、24m和40m处用角度测量仪测量扭转角度。在铁丝标记处，测量覆冰导线扭转角度，取5cm长度导线测量覆冰重量，折算到单位长度覆冰质量，测量结果如图13所示。根据温湿压一体计和旋转多导体积冰器测量结果，显示该冰期内液态水滴中值直径为20mm、平均风速为10m/s，自然覆冰试验结果与本文数值模拟计算结果进行对比分析，如图14和图15所示。
图13 导线自然覆冰试验
Fig.13 Natural ice test of conductor
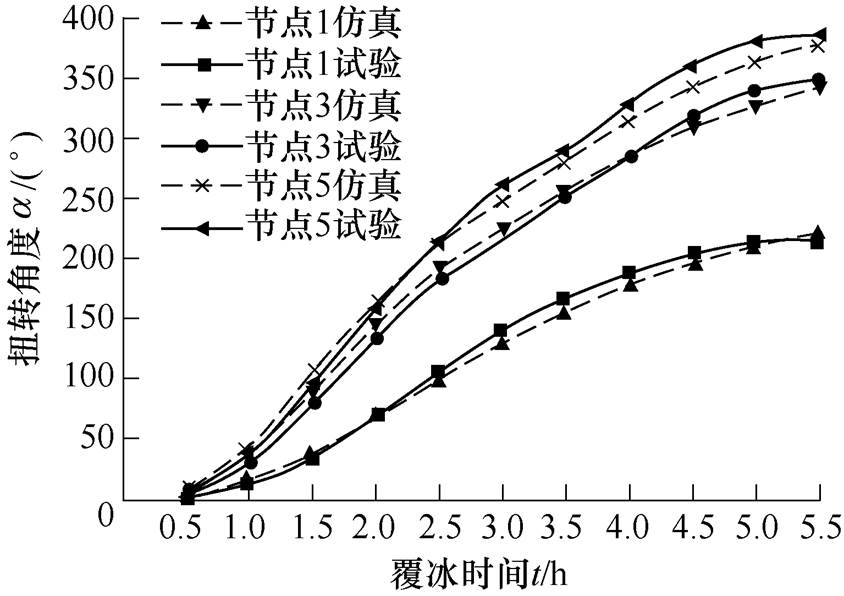
图14 扭转角度自然观测与仿真计算结果对比
Fig.14 Comparison of natural observation and simulation results of torsion angle
根据重庆大学雪峰山自然覆冰试验结果与本文提出的仿真模拟计算方法得出的结果，对比分析结果见表1，由表可知，节点1、3、5的扭转角度最大误差分别为8.75%、7.49%、8.15%，最大平均误差为5.02%；而覆冰质量最大误差分别为9.34%、6.18%、7.56%，最大平均误差为4.83%。自然覆冰试验与数值模拟计算出的导线覆冰扭转角度和质量均在误差允许范围之内，因此可以认定本文所提出的导线覆冰数值模拟方法与自然覆冰结果吻合度较高，本文所提出的数值计算方法是有效的。
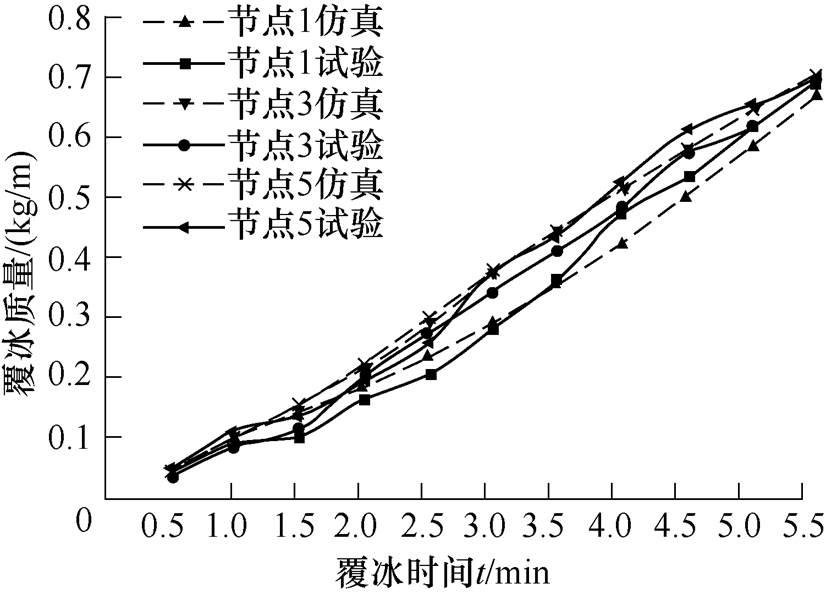
图15 覆冰重量自然观测与仿真计算结果对比
Fig.15 Comparison of natural observation and simulation results of icing amount
表1 仿真计算误差
Tab.1 Simulation calculation error
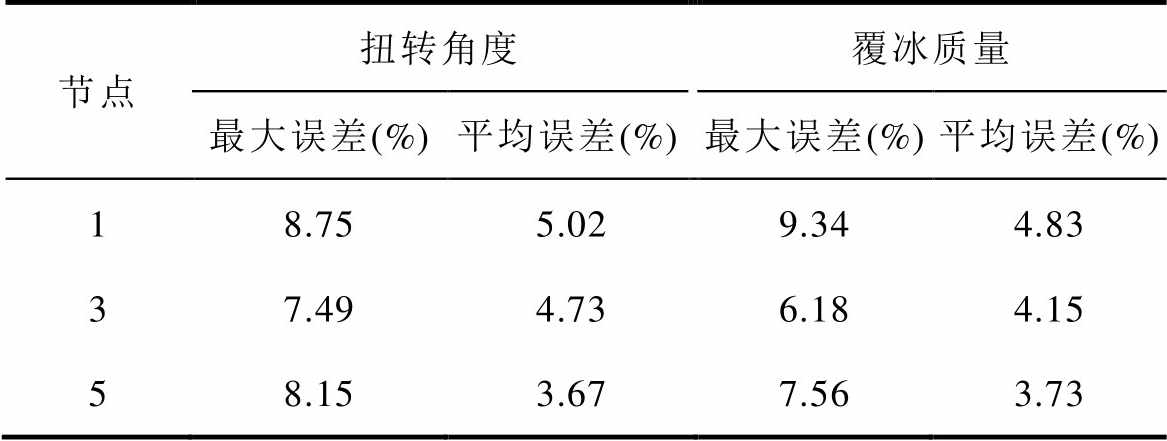
节点扭转角度覆冰质量 最大误差(%)平均误差(%)最大误差(%)平均误差(%) 18.755.029.344.83 37.494.736.184.15 58.153.677.563.73
本文结合热力学、流体力学与材料力学理论，阐明了导线扭转是输电线路覆冰增长的一个重要因素，建立了输电线路导线覆冰扭转数学模型，提出了导线覆冰扭转数值模拟方法，通过自然覆冰试验与数值仿真计算结果对比分析得出以下结论：
1）导线覆冰是一个动态增长的过程，导线扭转是导线覆冰的重要特性之一，在计算覆冰模型和仿真计算中，不考虑扭转大大降低了其合理性和准确性。
2）距离杆塔越远档距越大，风速和液态水滴中值直径越大，覆冰导线扭转越严重，但导线覆冰扭转对覆冰重量影响可以忽略不计。
3）本文所提出的数值模拟计算结果的冰形与覆冰量和自然覆冰试验结果吻合度较高，验证了本文所提出的数值模拟方法的科学性。
参考文献
[1] 蒋兴良, 易辉. 输电线路覆冰及防护[M]. 北京: 中国电力出版社, 2002.
[2] 韩兴波, 蒋兴良, 毕聪来, 等. 基于分散型旋转圆导体的覆冰参数预测[J]. 电工技术学报, 2019, 34(5): 1096-1105.
Han Xingbo, Jiang Xingliang, Bi Conglai, et al. Prediction of icing environment parameters based on decentralized rotating conductors[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1096- 1105.
[3] 蒋兴良, 张志劲, 胡琴, 等. 再次面临电网冰雪灾害的反思与思考[J]. 高电压技术, 2018(2): 6-9.
Jiang Xingliang, Zhang Zhijin, Hu Qin, et al. Thinkings on the restrike of ice and snow disaster to the power grid[J]. High Voltage Engineering, 2018(2): 6-9.
[4] 张志劲, 黄海舟, 蒋兴良. 复合绝缘子雾凇覆冰厚度预测模型[J]. 电工技术学报, 2014, 29(6): 318- 325.
Zhang Zhijin, Huang Haizhou, Jiang Xingliang, et al. Model for predicting thickness of rime accreted on composite insulators[J]. Transactions of China Elec- trotechnical Society, 2014, 29(6): 318-325.
[5] Imai. Studies on ice accretion[J]. Researches on Snow and Ice, 1953, 3(1): 35-34.
[6] Lenhard R W. An indirect method for estimating the weight of glaze on wires[J]. Bull Amer Meteor Soc, 1955, 36(3): 1-5.
[7] Kuroiwa D. Icing and snow accretion on electric wires[R]. U.S. Army Cold Regions Research and Engineering Laboratory, 1965: 1-10.
[8] Chaine P M, Casfonguay G. New approach to radial ice thichness concept applied to bundle-like con- ductors[R]. Industial Metecrology Study, Enwiron- ment Canada, 1974.
[9] Jones K F. A simple model for freezing rain ice loads[J]. Atmospheric Research, 1998, 46(1-2): 87-97.
[10] 廖玉芳, 段丽洁. 湖南电线覆冰厚度估算模型研究[J]. 大气科学学报, 2010, 33(4): 395-400.
Liao Yufang, Duan Lijie. Study on estimation model of wire icing thickness in Hunan province[J]. Transactions of Atmospheric Sciences, 2010, 33(4): 395-400.
[11] Langmuir I, Blodgett K. A mathematical investi- gation of water droplet trajectories[R]. Army Air Force Technical Report, 1946: 5418.
[12] 汪泉霖. 输电线路导线无扭转覆冰过程的仿真实验方法研究[D]. 重庆: 重庆大学, 2018.
[13] 梁曦东, 李雨佳, 张轶博, 等. 输电导线的覆冰时变仿真模型[J]. 高电压技术, 2014, 40(2): 336-343.
Liang Xidong, Li Yujia, Zhang Yibo, et al. Time- dependent simulation model of ice accretion on transmission line[J]. High Voltage Engineering, 2014, 40(2): 336-343.
[14] 蒋兴良, 姜方义, 汪泉霖, 等. 基于最优时间步长模型的输电导线雾凇覆冰预测[J]. 电工技术学报, 2018, 33(18): 4408-4418.
Jiang Xingliang, Jiang Fangyi, Wang Quanlin, et al. Prediction of rime accretion on transmission line based on optimal time step model[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4408- 4418.
[15] 张暕, 何青. 输电线路覆冰时导线表面形状对碰撞系数的影响[J]. 电工技术学报, 2016, 31(13): 209- 217.
Zhang Jian, He Qing. Influence of conductor surface shape on collision coefficient during transmission line icing[J]. Transactions of China Electrotechnical Society, 2016, 31(13): 209-217.
Numerical Simulation of Torsion Characteristics of Transmission Line Conductor
Abstract Conductor icing of overhead transmission line is one of the most serious natural disasters in power systems. Studying the numerical simulation method of conductor icing and establishing a simulation platform can not only predict the growth of conductor icing scientifically, but also greatly reduce the work of field observation. However, the existing mathematical models and simulation calculation methods all ignore the torsion of conductor in icing process, so the actual ice accretion process cannot be simulated accurately and effectively. In this paper, based on the formation mechanism of conductor icing, the twisting factor is taken into account, and then the mathematical model of conductor torsion is proposed. Meanwhile, the simulation program is written by C language to realize the numerical simulation process of dynamic conductor icing growth. The simulation results show that the conductor icing growth is a dynamic process with torsion. At the same time, the distance from the tower, the span, the wind speed, and the diameter of the liquid droplets all have great influence on the torsion angle. The numerical simulation method proposed is verified at the Xuefeng-mountain Natural Icing Test Base of Chongqing University.
keywords：Conductor icing, torsion, mathematical model, dynamic growth
中图分类号：TM85
DOI: 10.19595/j.cnki.1000-6753.tces.190181
国家自然科学基金重点项目（51637002）、国家创新研究群体基金（51321063）和国家电网公司总部科技项目（521999180006）资助。
收稿日期2019-02-22
改稿日期 2019-04-03
蒋兴良 男，1961年生，教授，博士生导师，研究方向为高电压绝缘技术、气体放电以及输电线路覆冰及防护。E-mail: xljiang@cqu.edu.cn
侯乐东 男，1993年生，硕士研究生，研究方向为输电线路导线覆冰。E-mail: 412035833@qq.com（通信作者）
（编辑 崔文静）