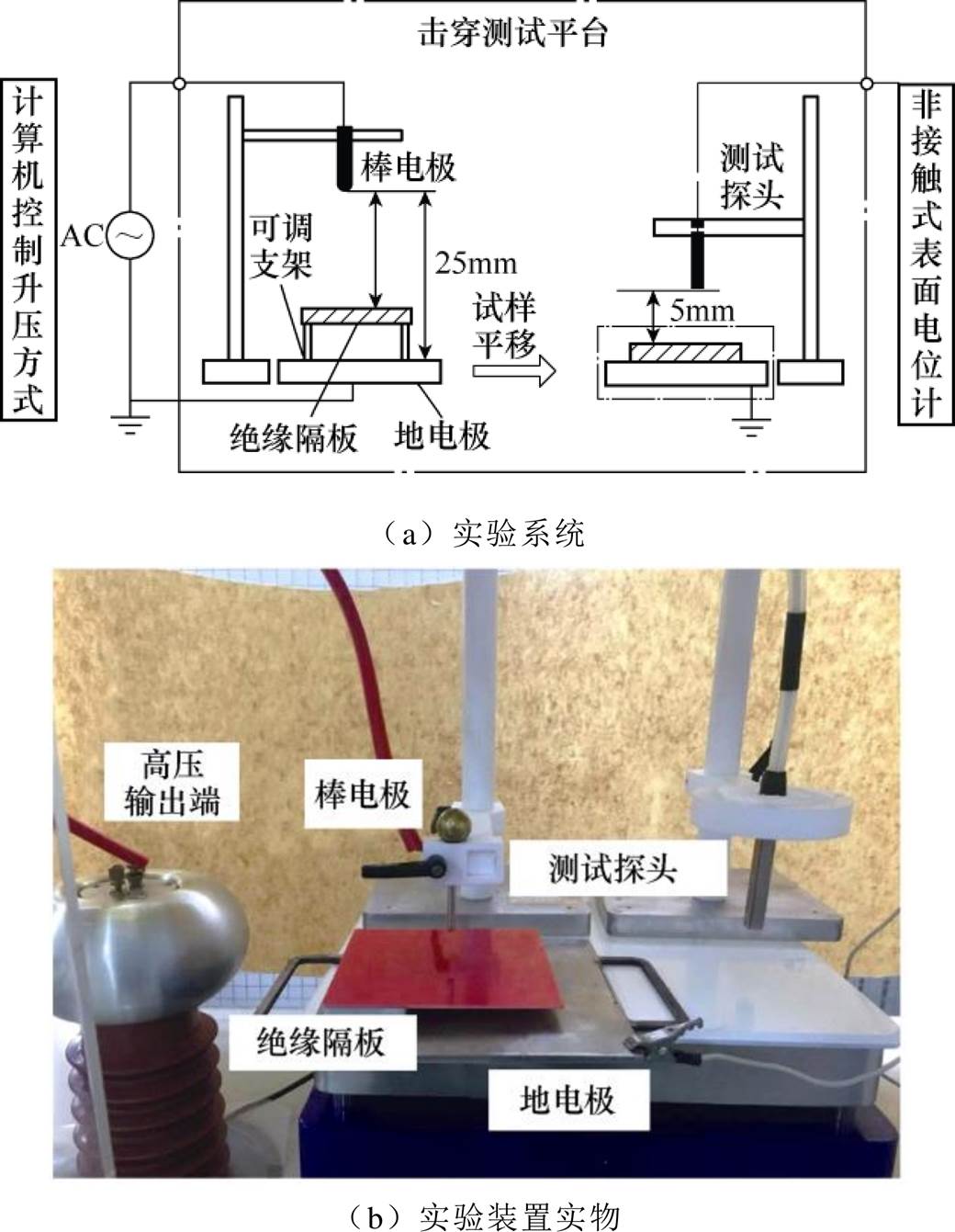
图1 实验系统示意图
Fig.1 Schematic diagram of experimental setup
摘要 在空间有限的高压箱内部,通过合理引入绝缘隔板,可显著提高整个系统的绝缘性能。该文研究聚酯玻璃毡板(GPO-3)尺寸、位置和厚度对“棒-隔板-地电极”工频击穿特性的影响;采用非接触式表面电位计,研究放电后隔板表面残余电荷衰减特性。实验结果表明,GPO-3隔板的增加会阻止电晕层的发展,“棒-隔板-地电极”系统的击穿电压最大可提高至原来的1.91倍。当隔板厚度超过约6mm时,击穿电压增幅较小;工频电压下间隙放电后,GPO-3表面存在明显的残余电荷,且滞留时间较长,放电后GPO-3的表面电位为3 856V,衰减1h后仍为239V。基于Simmons理论,计算材料表面陷阱分布,发现GPO-3表面残余电荷密度峰值为1.59×1019/m3和8.87×1018/m3,对应陷阱能级约为1.0eV,深陷阱是导致隔板表面电荷积聚的主要原因。该文可为工程设计中绝缘隔板的设计提供理论和实验依据。
关键词:“棒-板”空气间隙 绝缘隔板 工频击穿电压 表面残余电荷 表面陷阱分布
动车组车顶高压断路器、高压隔离开关等设备容易因受到外界污秽、冰雪、沙尘、高低温等环境因素影响,而导致设备的绝缘部分发生沿面放电或体击穿故障。采用高压箱将各类高压设备进行密封保护[1],可以有效地减少外界因素的干扰。设计中,由于车顶空间有限,要求高压箱尺寸不宜过大。在有限的空间内部,高压箱内部高压母排和金属底板之间容易发生气体放电,通过在高压母排和金属底板之间合理地引入绝缘隔板,可以提高整个系统的绝缘性能。
已有较多工作研究了SF6或空气中不均匀电场下电晕放电特性[2-6],气压、环境温度、湿度等对电晕放电和流注放电特性的影响[7-9],以及绝缘隔板对直流、交流和冲击电压的影响[10-16]。M. Rezinkina等研究了通过改变尖端高度、曲率半径和电极极性,其尖端周围电场分布对电晕放电的影响[15]。A. Kara等采用“棒-板”电极,研究了不同尺寸硅橡胶和聚氯乙烯的直流击穿电压,发现随着隔板尺寸(直径37.5~150mm)的增加,直流击穿电压升高[11]。郑跃胜等采用“棒-板”电极研究了片状复合材料(Sheet Molding Compound, SMC)隔板尺寸对空气间隙工频耐压特性的影响,发现隔板的引入大大地提高了整个间隙的击穿电压,当隔板尺寸较大(16cm× 16cm)时,击穿电压最大可提高到原来的2.32倍[13]。
工程应用中,绝缘隔板的设计需要综合考虑绝缘材料的选取、尺寸、厚度和安装位置等因素,已有研究工作侧重于上述某一因素。目前,绝缘隔板材料、尺寸、位置和厚度等综合因素对工频击穿电压的影响有待深入研究,尤其是对放电后隔板表面残余电荷的情况缺乏定量研究。实际应用中,根据外部电压的大小,研究棒-板间隙不同放电程度,比如,轻微间歇性电弧、持续性电弧通道等。当棒-板间隙仅发生轻微放电或仅产生电晕时,短时间内并不影响设备的正常运行,但放电导致的绝缘隔板表面残余电荷会影响后续放电过程,因此,开展放电后的电荷残余分析有助于深入认识放电机理和发展过程。
聚酯玻璃毡板(GPO-3)因具有优良的耐电弧性、耐热性、阻燃性和机械性能,而成为动车组车顶高压箱的隔板材料。本文考虑动车组车顶高压箱隔板的实际应用,以GPO-3为研究对象,通过改变隔板尺寸、“棒-隔板”间距和隔板厚度,采用程控击穿测试仪实验研究上述因素对“棒-隔板-地电极”工频气隙击穿特性的影响;采用非接触式表面电位计测量放电后隔板表面电位,并基于Simmons理论,研究放电后隔板表面电荷衰减特性,计算隔板表面陷阱分布,进而分析“棒-隔板-地电极”系统的放电机理。
棒-板空气间隙工频击穿测试实验系统示意图如图1所示。系统主要由程序加压控制单元、非接触式表面电位测试单元、棒-板电极、绝缘隔板等组成,实验系统如图1a所示,实验装置实物如图1b所示。研究GPO-3在不同条件(尺寸、位置和厚度)下对棒-板空气间隙工频击穿特性的影响。四种隔板尺寸分别裁剪为:5cm×5cm、10cm×10cm、15cm× 15cm和20cm×20cm;六种隔板厚度分别为0.5mm、2mm、4mm、6mm、8mm和10mm;地电极尺寸为20cm×20cm;棒电极距离地电极尺寸固定为25mm;绝缘隔板与棒电极之间的间距可以调整,最大间距可为25mm。
依据IEC 60243-1:1998开展击穿测试,升压方式为连续升压,速率为1.0kV/s,环境温度为25℃,环境湿度为60%。为避免放电后材料表面残余电荷的影响,加快表面电荷消散,每次间隙放电后,采用无水乙醇清洁试样表面,并放入烘箱20min。保持实验条件不变,相同尺寸的试样被重复测试5~10次,采用误差棒表示击穿电压分布。

图1 实验系统示意图
Fig.1 Schematic diagram of experimental setup
为了探索棒-板间隙放电之后,绝缘隔板表面残余电荷的衰减特性,搭建了表面电位测试平台,采用Trek非接触式表面电位计测量放电后隔板表面电位,表面电位计测试最大量程为±20kV。当棒-板间隙发生放电后,迅速将隔板移动至测试探头正下方,距离约为5mm,并开启表面电位计主机,采用计算机记录击穿后1h内隔板的表面电位数据。
图2给出了GPO-3工频击穿电压随尺寸的变化。实验中,GPO-3厚度为2mm;隔板与棒电极的间距固定为10mm;四种隔板尺寸分别为5cm×5cm、10cm×10cm、15cm×15cm、20cm×20cm;实验中,棒电极与地电极的距离保持为25mm。
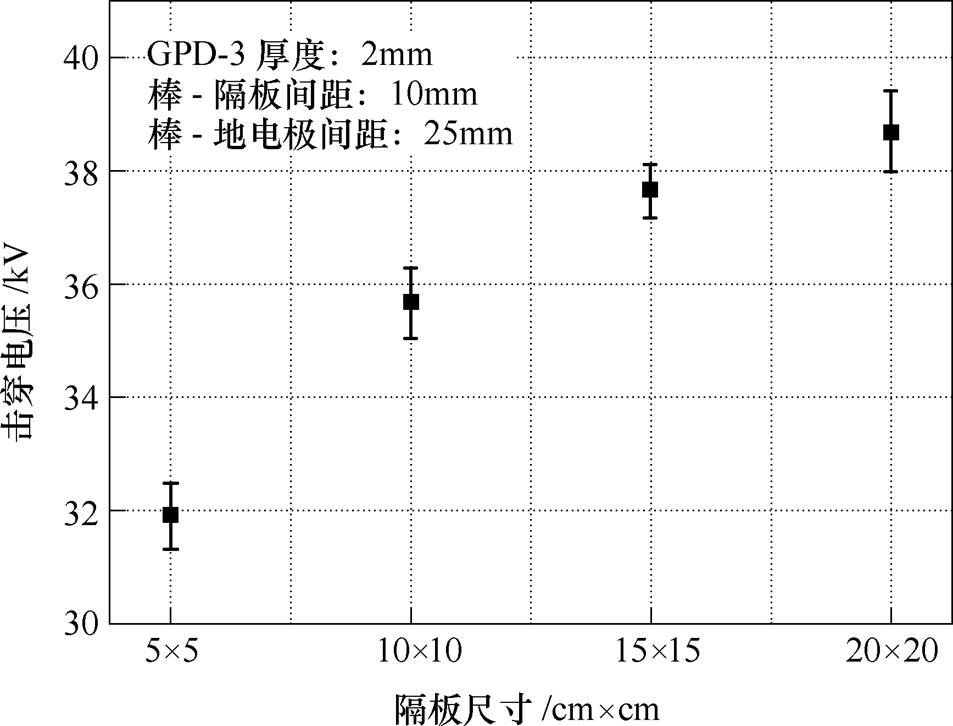
图2 击穿电压随隔板尺寸的变化
Fig.2 Breakdown voltage versus size of barrier
在放置绝缘隔板前,首次测试“棒-地电极”空气间隙的击穿电压为20.26kV。由图2可以看出,在棒电极和地电极之间,增加不同尺寸的绝缘隔板后,击穿电压均明显升高。尺寸为20cm×20cm的GPO-3隔板,击穿电压为38.68kV,是原来的1.91倍。这是由于尺寸的增加会延长放电路径,从而导致击穿电压升高。
根据气体放电理论[14],不均匀电场作用下放电总是起始于曲率半径较小的电极,对于正极性的棒电极,电子崩中的电子会迅速进入棒电极,而正离子由于运动速度慢则会聚集在棒电极附近形成空间电荷,加强放电区的外部空间的电场,随着外施电压的增加,电晕层向地电极扩展最终导致击穿。绝缘隔板的增加会阻挡电晕层的扩展,从而提高击穿电压。当自持放电发生时,电弧会首先由电场集中的棒电极达到正下方的隔板表面,进而沿着隔板向边缘发展,随着隔板尺寸增大,电弧发展的路径延长,从而提高击穿电压。
图3给出了GPO-3工频击穿电压随“棒-隔板”间距的变化。实验中,GPO-3厚度为2mm;隔板尺寸固定为10cm×10cm;“棒-隔板”间距分别为5mm、10mm、15mm、20mm和23mm;实验中,棒电极与地电极的距离保持为25mm。
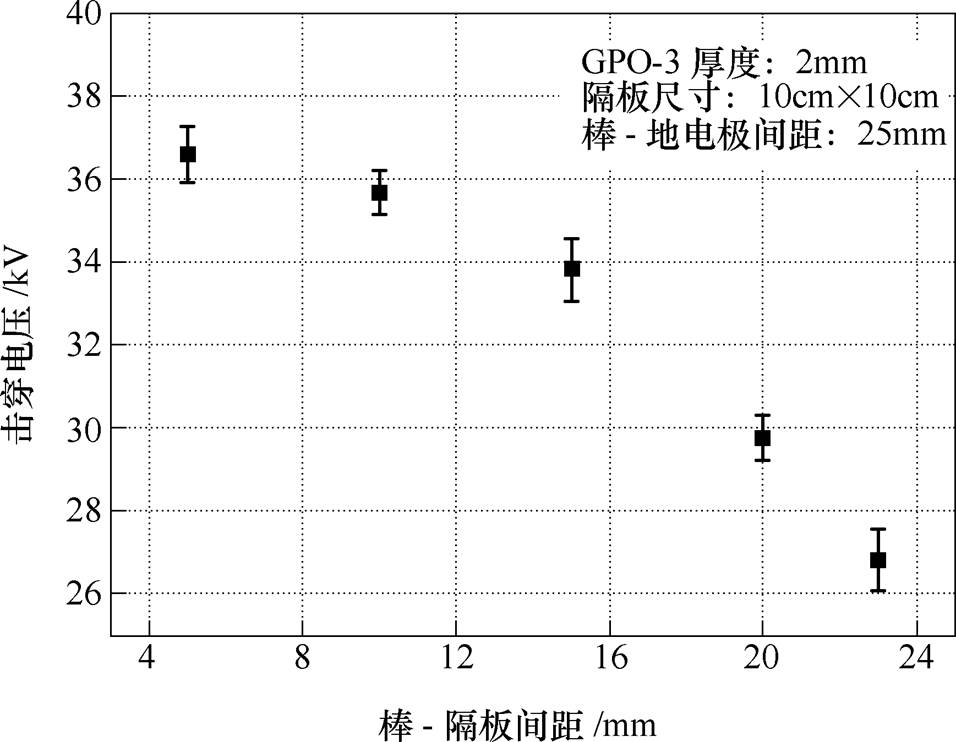
图3 击穿电压随“棒-隔板”间距的变化
Fig.3 Breakdown voltage versus distance between rod electrode and barrier
由图3可知,随着“棒-隔板”间距的增加,击穿电压逐渐降低,说明隔板越靠近棒电极,击穿电压越高。当间距增加至23mm时,即将2mm的GPO-3直接放置于地电极上方,GPO-3的击穿电压降低为26.80kV。分析认为绝缘隔板距离棒电极越近,在自持放电发生前,由于棒-地电极之间隔板的引入,隔断了棒电极穿过空气介质到达地电极的放电路径,阻止了电晕向地电极蔓延,从而提高击穿电压。棒-隔板距离越近,隔板阻止空气放电路径越早,击穿电压提高越明显。
图4给出了六种厚度的绝缘隔板工频击穿电压随厚度的变化。实验中,隔板尺寸固定为10cm× 10cm;“棒-隔板”间距为10mm;六种厚度分别为0.5mm、2mm、4mm、6mm、8mm和10mm。实验中保持棒电极与地电极的距离不变,为25mm。

图4 击穿电压随隔板厚度的变化
Fig.4 Breakdown voltage versus thickness of barrier
由图4可知,随着隔板厚度的增加,系统的击穿电压升高,对于较薄的试样,电压增加较明显,但当厚度超过一定数值时,击穿电压增加的幅度较小。对于0.5mm厚的GPO-3,击穿电压为34.10kV,当厚度增加为4mm时,击穿电压为37.76kV,是原来的1.11倍;但当厚度超过约6mm时,击穿电压增加幅度较小。分析认为这是由于在一定放电能量下会导致较薄的试样易发生体击穿,而厚试样则主要发生沿面放电。采用三维超景深视频数码显微镜对放电痕迹进行观察,发现,对于较薄的试样(0.5mm),很容易发生体击穿,试样被穿透,大多数试样存在明显的放电痕迹,厚度0.5mm GPO-3隔板的放电痕迹如图5所示。而对于较厚的隔板,则主要发生沿面放电,随着厚度的进一步增加,并不会影响沿面放电路径的发展。由于动车组车顶高压箱质量受限,在保证电气绝缘性能的情况下,应尽可能选取较薄的绝缘隔板。
为了探索“棒-绝缘隔板-地电极”间隙放电后,绝缘隔板表面残余电荷的衰减特性,采用非接触式表面电位计测量放电后隔板的表面电位,测量时间为1h。实验中,隔板尺寸为10cm×10cm;厚度为2mm;“棒-绝缘隔板”间距10mm。图6给出了GPO-3表面电位随时间的衰减曲线。
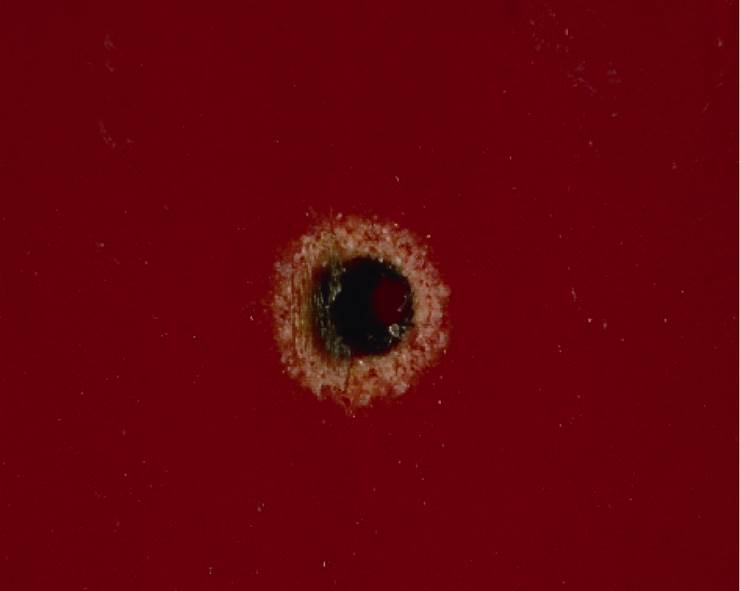
图5 厚度0.5mm GPO-3隔板的放电痕迹
Fig.5 Discharge trace of GPO-3 with 0.5mm
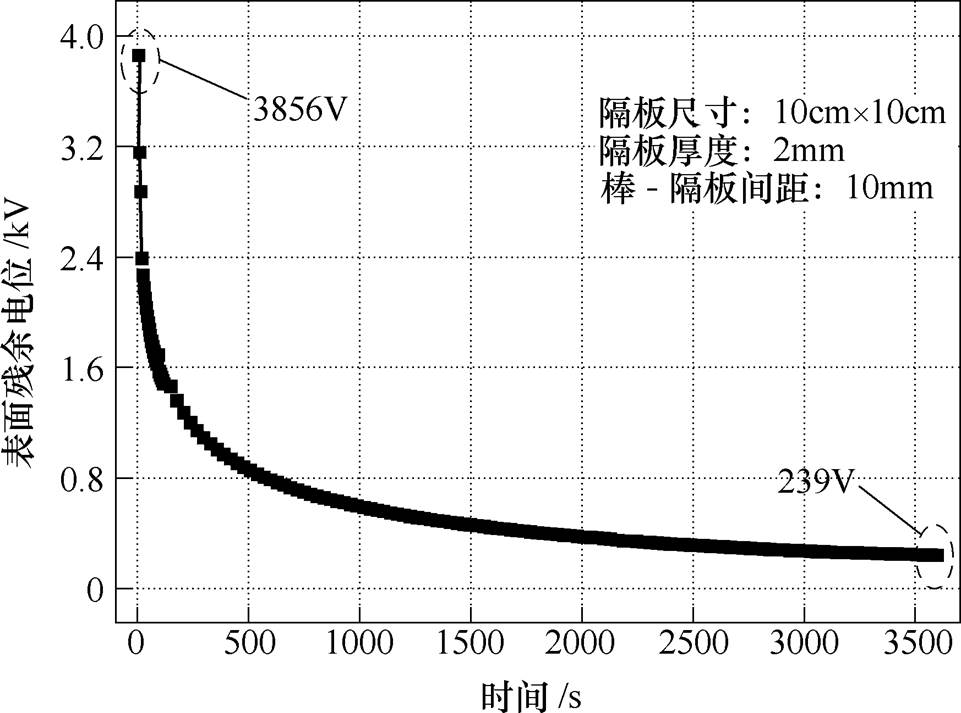
图6 击穿之后隔板表面电位衰减曲线
Fig.6 Surface potential decay curve of barrier after breakdown
由图6可知,工频击穿发生后,材料表面存在明显的残余电荷,表面电位达到几kV,实际中表面电位更高,并且这部分电荷在材料表面滞留时间较长,在1h之后,仍存在几百伏的表面电位。GPO-3的初始表面电位为3 856V,放电停止1h后,GPO-3的表面电位仍为239V,实际初始表面电位更高。因为实验过程中,放电停止后,因试样的移动和表面电位计的启动需要一定时间,大约10s,而无法采集到数据,但实际材料的表面电位在撤去电压后的瞬间衰减非常迅速[18]。该现象与材料的表面陷阱特性有关系。
放电发生后,部分电荷会聚集在材料表面大约1~2mm的位置[18-19],这部分电荷被隔板表面的陷阱捕获,滞留在材料表面,从而反映出较高的表面电位。假设介质内部存在双重能级陷阱,即深陷阱和浅陷阱。被能级较浅的陷阱捕获的电荷可以在较短时间内迅速脱陷,表现为表面电位衰减速率较快;而能级较深的陷阱电荷,需要克服更大的势垒,停滞在陷阱中心的时间较长。深陷阱电荷数量决定了表面电位趋于平衡时的电位值,陷阱能级决定了电位衰减平衡时间。在放电发生后的初期(大约200s),表面电位衰减较快,这是因为被较浅陷阱能级捕获的电荷,可以在短时间内获得能量脱离陷阱中心,重新成为自由电荷。研究表明,陷阱能级为0.1eV时的滞留时间大约为1×10-12s[20-21];而对于被较深陷阱能级捕获的陷阱,在材料内部滞留时间更长。
本文基于Simmons理论[18, 21-23],计算介质表面陷阱参数。单位时间内陷阱热发射电子概率en为
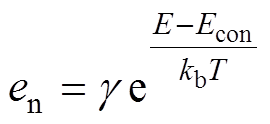 (1)
(1)式中,g 是热电子振动频率;kb是玻耳兹曼常数;T是热力学温度;E是陷阱能级;Econ是导带底部对应能级。
定义函数Gn(E,t),表达式为
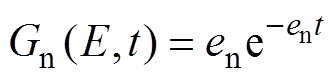 (2)
(2)Gn(E,t)函数决定了任意时刻电子陷阱能级对电流的贡献权重,当E=Em时,Em为t时刻的陷阱能级,Gn(E,t)取最大值。
求解微分方程,可以得到陷阱能级为
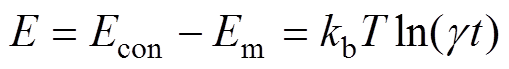 (3)
(3)棒-板间隙放电后电荷主要分布于厚度为d 的隔板表面,由高斯定理可得出介质表面电位Vs为
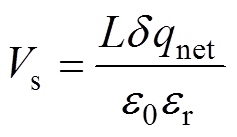 (4)
(4)
式中,L为介质厚度;d 为隔板表面积聚电荷厚度;qnet为隔板表面积聚电荷密度;e0为真空介电常数;er为绝缘隔板材料的相对介电常数。
陷阱密度表达式为
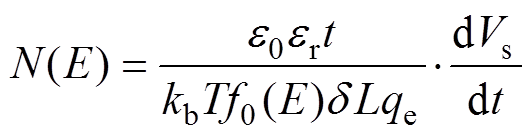 (5)
(5)式中,N(E)是陷阱能级E对应的陷阱密度;f0(E)是陷阱初始占有率;qe是电子电量。
将测量得到的表面电位数据代入式(5),通过求解微分方程,可以得到材料表面陷阱参数分布,隔板表面陷阱分布谱图如图7所示。其中,GPO-3相对介电常数通过宽频介电谱系统Concept80测量得到,频率为1kHz,室温下GPO-3的相对介电常数为3.69。
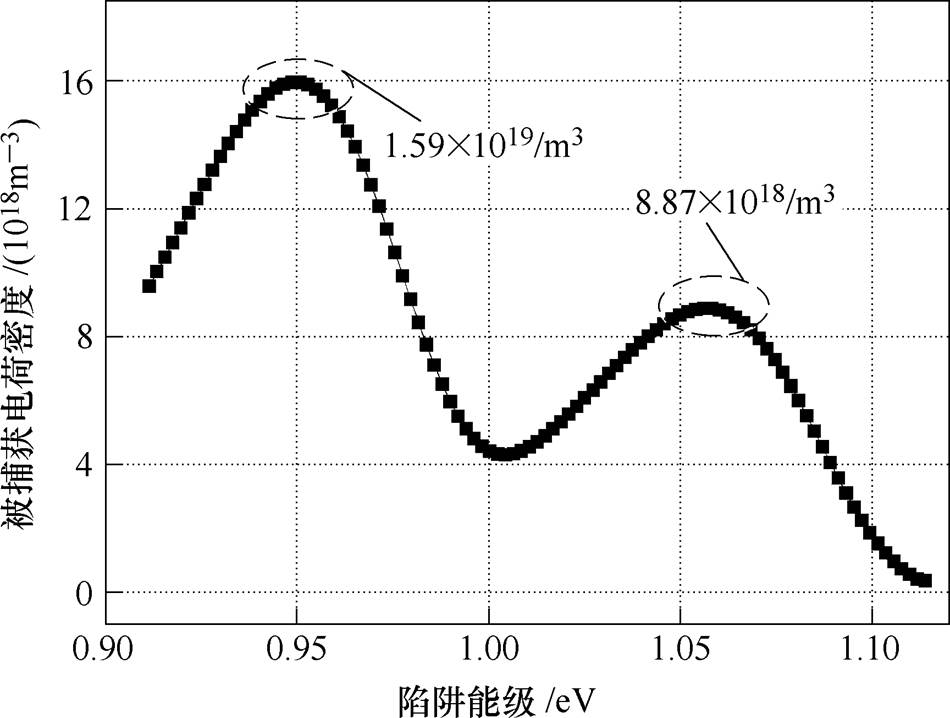
图7 隔板表面陷阱分布谱图
Fig.7 Surface trap distributions of barrier
分析图7可知,GPO-3表面陷阱能级为0.90~1.11eV,存在两个被捕获残余电荷密度峰值,该能级范围属于深陷阱的范畴[18-19]。GPO-3表面残余电荷密度峰值为1.59×1019/m3和8.87×1018/m3,对应陷阱能级分别为0.95eV和1.06eV,隔板表面深陷阱数量较多,是导致隔板表面容易积聚电荷,且滞留时间较长的原因。因此,工程设计中,需要合理选取绝缘隔板的材料。本文采用非接触式表面电位计,定量研究隔板表面残余电荷特性的方法,可用于探索放电后绝缘材料特性及放电发展过程。
隔板表面残余电荷会影响后续电晕和击穿过程,电晕起始电压和击穿电压的变化取决于棒电极极性、隔板表面电荷极性以及棒-板间距。初步分析认为,当隔板表面积聚正电荷时,这部分电荷形成的电场会削弱正极性棒电极附近的电场,提高电晕起始电压;同时会削弱“棒-隔板”空间的电场,增加“隔板-地电极”之间空间电场。“棒-隔板-地电极”击穿电压的升高或降低取决于“棒-隔板”间距和“隔板-地电极”间距。“棒-隔板”间距越小,隔板表面残余电荷对电晕起始电压和击穿电压的影响越大。
实验结果表明,合理设置绝缘隔板可以显著地提高棒-板空气间隙的击穿电压,绝缘隔板的尺寸、“棒-隔板”间距、厚度和材料表面特性均会影响击穿电压。结合实验结果,下面将重点讨论上述因素对击穿电压的影响机理。对极不均匀电场,空气间隙的工频击穿一般发生在正半周[17]。图8为“棒电极-绝缘隔板-地电极”间隙放电示意图。
放电路径主要取决于隔板尺寸,实验观察发现,当尺寸隔板较小(5cm×5cm)时,相比隔板中心来说,由于其边缘存在毛刺、不平整等缺陷,电弧会沿最短路径直接达到隔板边缘,然后向地电极发展,放电后可以明显地观察到隔板边缘有烧蚀痕迹,而表面无明显痕迹。当尺寸较大(15cm×15cm)时,多数情况下放电路径会沿着棒电极顶部向下发展至隔板,然后沿着隔板达到边缘,最后向地电极发展。因此,随着隔板尺寸的增大,放电路径延长,从而提高击穿电压。在自持放电前,随着外施电压的升高,棒电极附近电晕层逐渐向地电极蔓延,隔板的增加阻止电晕层的发展。隔板距离棒电极越近,在自持放电发生前,越早阻止电晕层向地电极发展,从而提高击穿电压,所以随着棒-隔板间距的减小,击穿电压不断提高。
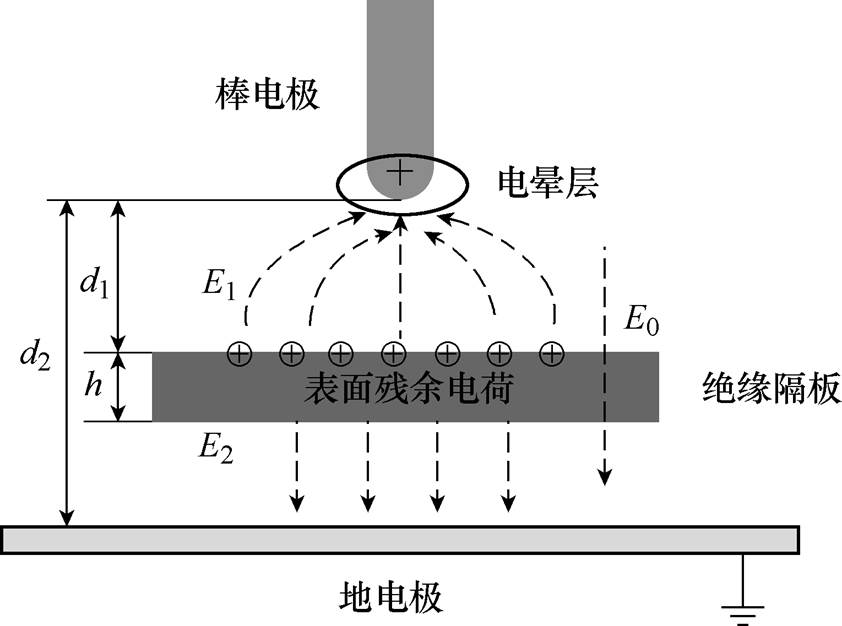
图8 隔板表面残余电荷对原电场的影响示意图
Fig.8 Effect of surface residual charges in the barrier on the initial electric field
表面电位测试结果表明,击穿后隔板表面存在明显的残余电荷,GPO-3的表面电位为3 856V,且这部分电荷在材料表面滞留时间长达1h。分析认为,隔板表面电荷会影响棒电极附近的电场、“棒-隔板”空间的电场和“隔板-地电极”空间的电场,进而影响击穿电压(见图8)。当隔板表面存在正电荷时,这部分电荷形成的局部电场会削弱棒电极附近,从而提高电晕起始电压;同时会削弱“棒-隔板”空间的电场,增加“隔板-地电极”空间电场,由此引起的击穿电压变化需要考虑“棒-隔板”间距和“隔板-地电极”间距两方面的因素:一方面,“棒-隔板”空间电场的降低会阻止电晕层的发展,提高击穿电压;另一方面,“隔板-地电极”空间电场的增加,会使到达隔板的电弧迅速向地电极蔓延,降低击穿电压。后续将通过“棒-绝缘板-地电极”间隙粒子场动态仿真,研究电晕和击穿起始、发展过程中电荷动态迁移过程。
工程设计中需要综合参照实验结果和实际故障反馈数据,合理选择绝缘隔板材料、尺寸和位置。实验表明,放电后隔板表面会长时间滞留较高的表面电位,这部分电荷将形成局部电场,改变棒电极和“棒-板”空间的电场分布,进而影响电晕起始电压和击穿电压。工程应用中,棒-板间隙电晕起始电压和击穿电压受多种因素影响,包括环境温度、湿度、电极形状、隔板尺寸、位置、厚度以及隔板表面状态等,定量研究隔板表面残余电荷对电晕起始电荷和击穿电压的影响,确定合适的绝缘隔板材料和合理的绝缘隔板尺寸,需要进行大量的实验探索。
实验得到GPO-3隔板尺寸、位置和厚度对“棒-隔板-地电极”工频击穿特性的影响规律;采用非接触式表面电位,定量研究了放电后隔板表面电荷衰减特性,采用Simmons理论,计算得到隔板表面陷阱分布,分析了“棒-板”间隙放电过程。主要结论如下:
1)GPO-3隔板尺寸的增加将阻止电晕层的发展,在本文设定实验条件下,“棒-隔板-地电极”系统的击穿电压最高可提高至原来的1.91倍。此外,隔板距离棒电极越近,间隙击穿电压越高。
2)随着隔板厚度的增加,系统的击穿电压升高,对于较薄(0.5~4mm)的试样,电压增加较明显;当超过一定厚度(约6mm)时,击穿电压增加的幅度较小。对放电痕迹进行观察发现,较薄的试样容易发生体击穿,而厚试样则主要发生沿面放电,随着厚度的进一步增加,对沿面放电路径的改革并不显著。在保证绝缘性能的情况下,选取较薄的隔板,有利于减轻产品质量。
3)采用非接触式表面电位计,定量研究隔板表面残余电荷特性。工频电压下“棒-隔板-地电极”间隙击穿后,GPO-3表面存在明显的残余电荷,且滞留时间较长,放电后GPO-3的表面电位为3 856V,衰减1h后,仍为239V。进一步分析,GPO-3表面陷阱能级约为1.0eV,表面残余电荷密度峰值为1.59× 1019/m3和8.87×1018/m3,深陷阱数量较多是导致隔板表面容易积聚电荷,且滞留时间较长的原因。
参考文献
[1] 张国芹. 车顶高压箱安装结构: 中国, CN 104882805 A[P]. 2015-09-02.
[2] Bian Xingming, Wang Liming, Macalpine J M K, et al. Positive corona inception voltages and corona currents for air at various pressures and humilities[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2010, 17(1): 63-70.
[3] 付洋洋, 罗海云, 邹晓兵, 等. 棒-板电极下缩比气隙辉光放电相似性的仿真研究[J]. 物理学报, 2014, 63(9): 288-295.
Fu Yangyang, Luo Haiyun, Zou Xiaobing, et al. Simulation on similarity law of glow discharge in scale-down gaps of rod-plane electrode configu- ration[J]. Chinese Journal of Physics, 2014, 63(9): 288-295.
[4] 舒胜文, 刘畅, 阮江军. 棒-板电极正直流电晕起始判据对比[J]. 武汉大学学报, 2015, 48(6): 836-841, 847.
Shu Shengwen, Liu Chang, Ruan Jiangjun. Com- parative of positive DC corona inception criteriafor a road-plane electrode[J]. Engineering Journal of Wuhan University, 2015, 48(6): 836-841, 847.
[5] 廖瑞金, 伍飞飞, 刘康淋, 等. 棒-板电极直流负电晕放电脉冲过程中的电子特性研究[J]. 电工技术学报, 2015, 30(10): 319-329.
Liao Ruijin, Wu Feifei, Liu Kanglin, et al. Simulation of characteristics of electrons during a pulse cycle in bar-plate DC negative corona discharge[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(10): 319-329.
[6] 文韬, 张乔根, 郭璨, 等. 冲击电压下SF6棒-板间隙放电极性效应的反转现象[J]. 高电压技术, 2015, 41(1): 275-281.
Wen Tao, Zhang Qiaogen, Guo Can, et al. Reversal phenomenon of discharge polarity effect in SF6 rod-plate gap under impulse voltages[J]. High Voltage Engineering, 2015, 41(1): 275-281.
[7] 杨亚奇, 李卫国. 低气压直流电压下流注放电特性与极性效应的反转[J]. 电工技术学报, 2018, 33(13): 3083-3088.
Yang Yaqi, Li Weiguo. DC streamer discharge characteristics and the reversion of polarity effect under low pressure condition[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3083-3088.
[8] 周远翔, 周仲柳, 郭绍伟, 等. 基于脉冲电流法的低频与工频电压下油中电晕放电特性对比研究[J]. 电工技术学报, 2019, 34(1): 160-169.
Zhou Yuanxiang, Zhou Zhongliu, Guo Shaowei, et al. Comparison of the characteristics of corona discharge in the oil under low and power frequency voltage by impulse-current method[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 160-169.
[9] 胡琴, 何高辉, 彭华东, 等, 高湿条件下基于凝露分布模型的导线电晕起始电压预测[J]. 电工技术学报, 2018, 33(7): 1634-1640.
Hu Qin, He Gaohui, Peng Huadong, et al. Prediction of conductor corona onset voltage based on condensation-distribution model under high humidity conditions[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1634-1640.
[10] Kang H, Na J B, Chung Y D, et al. Experimental study on the barrier effects in gaseous Helium for the insulation design of a high voltage SFCL[J]. IEEE Transactions on Applied Superconductivity, 2011, 21(3): 1328-1331.
[11] Kara A, Onal E, Kalenderli O, et al. The effect of insulating barriers on AC breakdown voltage in inhomogeneous field[C]//IEEE Mediterranean Elec- trotechnical Conference (MELECON), Benalmádena, Spain, 2006: 1206-1208.
[12] Sebo S A, Kahler J, Hutchins S. et al. The effect of insulating sheets in various gaps-the study of AC breakdown voltages and barrier factors[C]//11th International Symposium on High Voltage Engin- eering, London, UK, 1999: 144-147.
[13] 郑跃胜, 陈雍, 钟小燕, 等. 隔板尺寸对棒-板空气绝缘间隙工频耐压特性的影响[J]. 高电压技术, 2018, 44(1): 195-200.
Zheng Yuesheng, Chen Yong, Zhong Xiaoyan, et al. Effects of barrier dimensions on AC withstand characteristics of air insulated rod-plane gaps[J]. High Voltage Engineering, 2018, 44(1): 195-200.
[14] Kara A, Kalenderli O, Mardikyan K. DC breakdown voltage characteristics of small air gaps with insulating barriers in non-uniform field[C]//Inter- national Conference on High Voltage Engineering and Application, New Orleans, Louisiana, 2010: 425-428.
[15] Rezinkina M, Rezinkin O, D'Alessandro F, et al. Experimental and modelling study of the dependence of corona discharge on electrode geometry and ambient electric field[J]. Journal of Electrostatics, 2017, 87: 79-85.
[16] Wilkins R, Lang M, Allison M. Effect of insulating barriers in arc flash testing[J]. IEEE Transactions on Industry Applications, 2008, 44(5): 1354-1359.
[17] 施围, 邱毓昌, 张乔根. 高电压工程基础[M]. 北京: 机械工业出版社, 2006.
[18] Li Guochang, Li Shengtao, Pan Shaoming, et al. Dynamic charge transport characteristics in polyimide surface and surface layer under low-energy electron radiation[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(4): 2393-2403.
[19] Shen Wenwei, Mu Haibao, Zhang Guanjun, et al. Identification of electron and hole trap based on isothermal surface potential decay model[J]. Journal of Applied Physics, 2013, 113(8): 083706.
[20] Meunier M, Quirke N. Molecular modeling of electron trapping in polymer insulators[J]. The Journal of Chemical Physics, 2000, 113: 369-376.
[21] Meunier M, Quirke N, Aslanides A. Molecular modeling of electron traps in polymer insulators: chemical defects and impurities[J]. The Journal of Chemical Physics, 2001, 115: 2876-2881.
[22] Simmons J G, Tam M C. Theory of isothermal currents and the direct determination of trap parameters in semiconductors and insulators con- taining arbitrary trap distributions[J]. Physical Review B, 1973, 7(8): 3706-3713.
[23] 杨百屯, 屠德民, 刘耀南. 等温电荷理论及其检测固体介质中的陷阱分布[J]. 应用科学学报, 1992(3): 233-240.
Yang Baitun, Tu Demin, Liu Yaonan. Theory of isothermal charge and direct determination of trap distributions in solid dielectrics[J]. Journal of Applied Sciences, 1992(3): 233-240.
Influence of GPO-3 Barrier on AC Breakdown Voltage of Rod-Plane Gaps and Surface Residual Charge Characteristics
Abstract The insulation performance of the whole system can be greatly improved by introducing the insulation barrier. The effects of size, position and thickness of insulation barrier on ac breakdown voltage were studied. Furthermore, the surface residual charge properties on the barrier after discharge were measured by non-contact surface potentiometer. The experimental results indicate that the breakdown voltage of the system increases up to 1.91 times. When the thickness exceeds about 6mm, the increase of breakdown voltage is not obvious. Obvious residual charges can be observed on the barrier after breakdown, while the surface potential of GPO-3 reaches 3 856V after breakdown and reduces to 239V after 1h. The peak density of surface charges on GPO-3 are 1.59×1019/m3 and 8.87×1018/m3 respectively, and the trap level is about 1.0eV. This paper can provide a reference for the design of the insulation barrier.
keywords:Rod-plane air gap, insulation barrier, AC breakdown voltage, surface residual charge, surface trap distribution
中图分类号:TM853
DOI: 10.19595/j.cnki.1000-6753.tces.190186
山东省自然科学基金(ZR2018BEE029)和青岛市应用基础研究专项(18-2-2-23-jch)资助项目。
收稿日期 2019-02-25
改稿日期 2019-08-21
昝海斌 男,1972年生,高级工程师,研究方向为轨道交通领域车辆用高压及辅助电气系统。E-mail: zanhaibin@126.com
李国倡 男,1985年生,博士,副教授,硕士生导师,研究方向为电力设备绝缘材料与绝缘技术、多场耦合下绝缘部件电场仿真与结构优化。E-mail: Lgc@qust.edu.cn(通信作者)
(编辑 陈 诚)