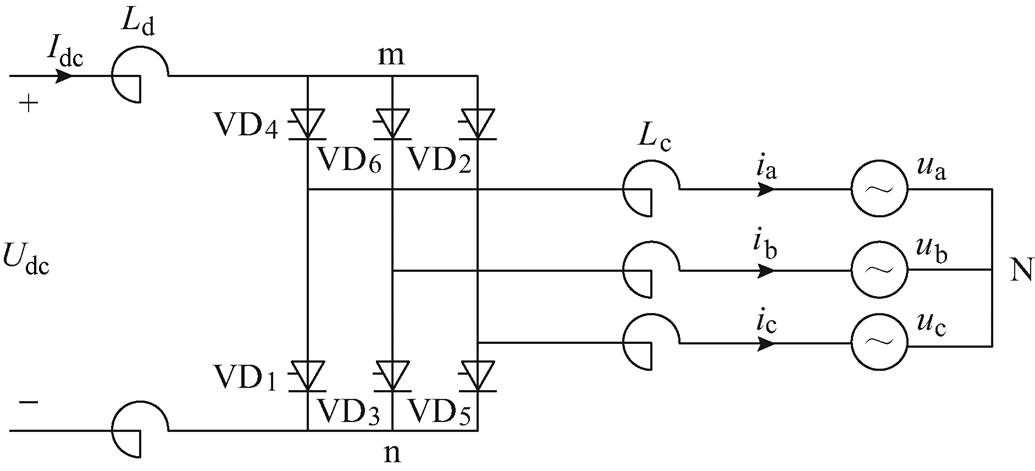
图1 HVDC逆变站换流器结构
Fig.1 HVDC inverter station inverter structure diagram
摘要 在多馈入高压直流系统(MIDC)中,逆变站换相失败的相互影响是引发换相失败传递的重要因素。该文详细分析逆变站换相失败期间的暂态特性,并根据开关函数模型及动态相量理论推导直流系统向交流系统注入的换相失败分量;进而研究在交流系统故障及换相失败双重影响下各逆变站换相电压的解析计算方法;在此基础上,通过对比各换流阀的最大换相面积与其关断所需的最小换相面积,提出针对多馈入高压直流系统的换相失败判断分析方法;最后,通过所建多馈入高压直流系统模型的仿真结果,验证了该文方法的有效性。
关键词:多馈入高压直流系统 相互影响 换相失败 开关函数 换相面积
高压直流输电(High Voltage Direct Current, HVDC)在远距离大容量输电、非同步电网互联等领域具有独特的技术经济优势[1-2]。随着我国“西电东送”、“全国联网”战略的全面实施,直流输电技术已得到了广泛应用[3-4]。目前,华东电网与南方电网已形成多馈入交直流系统[5-7],湖北电网也逐渐呈现出多电压等级、送受端并存的特点。交直流互联电网的相互影响日益严重,电网的运行特性更趋复杂[8]。由交流系统接地故障所产生电压暂降会导致多回特高压常规直流逆变站换流母线电压下降,从而进一步导致直流系统换相失败甚至闭锁。而特高压直流换相失败/闭锁给受端电网带来的有功和无功冲击则进一步导致受端交流电网的各类安全稳定问题,甚至出现复杂的连锁故障模式。在此情况下,亟需深入研究交直流互联电网的相互影响机理。
为衡量多馈入高压直流输电系统中逆变站间相互作用的强弱,CIGRE WG B4-41工作组提出多馈入交互作用因子(Multi-Infeed Interaction Factor, MIIF)以衡量换流站相互作用强度[9-10]。文献[11]基于换相失败免疫因子指标(Commutation Failure Immunity Index, CFII),研究了多馈入高压直流输电系统中各逆变站的当地换相失败免疫能力与同时换相失败免疫能力。文献[12]将MIIF进行推广应用,推导出临界交直流系统耦合作用因子,以判断受端交流系统故障是否会引发多馈入高压直流系统换相失败。上述研究仅从稳态分析的角度研究了交流系统故障对直流系统换相过程的影响,而未对直流系统换相失败的相互影响进行分析。实际上,换相失败是暂态过程,某回直流系统发生换相失败会给其他直流系统带来明显的电压扰动,可能造成换相失败的进一步传递。
部分学者从换相失败期间的无功特性展开研究:文献[13]对逆变站暂态无功特性的研究表明,换相失败期间,直流系统会从受端系统额外吸收一定的无功功率;文献[14]指出换相失败所造成的无功冲击,会造成其他换流母线电压的进一步跌落,进而引发其他直流系统发生换相失败。然而,对直流系统换相失败期间暂态无功特性的研究尚缺乏理论支撑,难以进行解析表达。部分学者通过建立开关函数模型分析逆变站电压、电流的暂态特性:文献[15]根据换相失败后换流阀通断状态的改变,研究了换相失败期间逆变侧交流电压及电流开关函数的变化规律;文献[16]基于动态相量理论和开关函数方法,研究了换相失败期间直流系统注入交流电网等值工频电流的暂态特性。这些研究只针对逆变站换相失败期间的暂态特性进行分析,而未进一步研究在多馈入高压直流系统中换相失败的相互影响机理。文献[17]虽进一步推导了换相失败分量对其他逆变站换相电压的影响,但只得到电压扰动在某些情况下更为严重的定性结论,难以衡量其他逆变站是否会发生换相失败。
本文旨在研究考虑换相失败相互影响的多馈入高压直流系统换相失败判断方法。首先根据开关函数模型及动态相量理论推导了换相失败期间直流系统向交流系统额外注入的换相失败分量;随后分析了在交流系统接地故障及换相失败双重影响下,逆变站换流母线电压的变化规律;最后根据各逆变站换流母线电压的解析表达式,计算复杂扰动情况下各换流阀的最大换相面积,通过与换流阀关断所需的最小换相面积对比,从而判断多馈入高压直流输电系统中各回逆变站是否发生换相失败。基于PSCAD的算例仿真表明,本文所提方法具有更高的准确性。
图1所示为HVDC逆变站换流器结构。

图1 HVDC逆变站换流器结构
Fig.1 HVDC inverter station inverter structure diagram
图1中,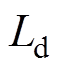 为直流系统平波电抗器电感;
为直流系统平波电抗器电感;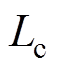 为每相等值换相电抗器电感;m和n为逆变器的共阳极点与共阴极点;N为交流系统电压的参考点位;
为每相等值换相电抗器电感;m和n为逆变器的共阳极点与共阴极点;N为交流系统电压的参考点位;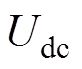 为换流站直流电压;
为换流站直流电压;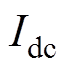 为换流站直流电流;
为换流站直流电流;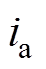 、
、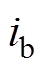 、
、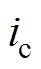 为换流器出口侧三相交流电流;
为换流器出口侧三相交流电流;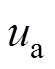 、
、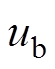 、
、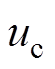 为三相交流电压。
为三相交流电压。
根据换流器工作原理,直流电压及电流可视为交流三相电压及电流被开关函数调制的结果[15]。按照开关函数和调制理论的定义,LCC-HVDC系统交直流两侧的电压和电流可表示为
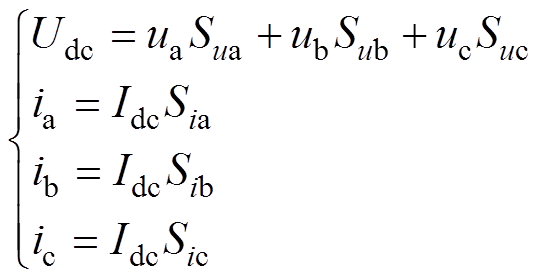 (1)
(1)式中,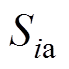 、
、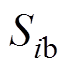 、
、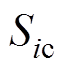 为三相电流的开关函数;
为三相电流的开关函数;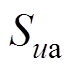 、
、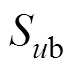 、
、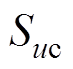 为三相电压的开关函数。开关函数的取值由各阀臂的导通情况确定,并满足
为三相电压的开关函数。开关函数的取值由各阀臂的导通情况确定,并满足
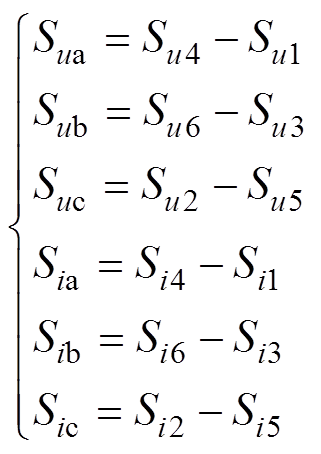 (2)
(2)
式中,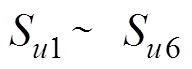 分别为换流器6个阀臂电压的开关函数;
分别为换流器6个阀臂电压的开关函数;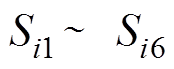 分别为换流器6个阀臂电流的开关函数。通过调制开关函数,可模拟直流系统在不同运行状态下的换相过程。在此基础上,对开关函数进行傅里叶分析,可对直流系统交流侧的暂态特性进行定量研究。
分别为换流器6个阀臂电流的开关函数。通过调制开关函数,可模拟直流系统在不同运行状态下的换相过程。在此基础上,对开关函数进行傅里叶分析,可对直流系统交流侧的暂态特性进行定量研究。
基于开关函数来描述逆变站的换相过程,其示意图如图2所示。正常情况下各换流阀及交流侧各相电流的开关函数如图2a所示。当发生换相失败时,换流阀的导通顺序被打乱,逆变站对交流系统的注入电流也发生改变,呈现出复杂的暂态特性。为准确衡量逆变站换相失败对交流系统的冲击作用,下面将利用开关函数对换相失败期间直流系统的暂态过程进行分析。

图2 逆变站换相过程示意图
Fig.2 Schematic diagram of commutation process of inverter station
不妨假设换相失败发生于阀1向阀3的换相过程,各换流阀及交流侧各相电流的开关函数如图2b所示。
P3时刻,阀3被触发,因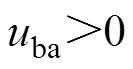 ,直流电流逐渐由阀1向阀3转移。由于换相电压下降、过零点偏移等因素造成换相面积不足,当
,直流电流逐渐由阀1向阀3转移。由于换相电压下降、过零点偏移等因素造成换相面积不足,当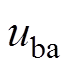 过零点时,阀1未完成去游离过程,无法可靠关断。随后,因
过零点时,阀1未完成去游离过程,无法可靠关断。随后,因 ,阀1重新导通,阀3电流减小直至关断,即发生了阀3向阀1的倒换相。
,阀1重新导通,阀3电流减小直至关断,即发生了阀3向阀1的倒换相。
P4时刻,阀4被触发导通,开始阀2到阀4的换相过程。由于阀1与阀4同时导通,直流侧形成短路通路,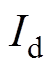 迅速增大,同时交流系统等效开路。在此过程中直流电流对交流系统的注入电流减小为0。
迅速增大,同时交流系统等效开路。在此过程中直流电流对交流系统的注入电流减小为0。
P5时刻,阀5被触发,因其承受反向电压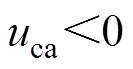 ,所以无法正常导通,交流系统仍视为开路。
,所以无法正常导通,交流系统仍视为开路。
P6时刻,阀6承受电压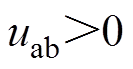 ,电流开始由阀4向阀6转移。若换相成功,则导通顺序恢复正常。但在直流侧短路期间,由于直流电流大幅增加,很可能导致阀4向阀6的换相失败。在此过程中,交流系统的a、b两相通过阀4与阀6形成两相短路,短路电流受
,电流开始由阀4向阀6转移。若换相成功,则导通顺序恢复正常。但在直流侧短路期间,由于直流电流大幅增加,很可能导致阀4向阀6的换相失败。在此过程中,交流系统的a、b两相通过阀4与阀6形成两相短路,短路电流受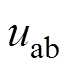 影响,先增大后减小,直到完成阀6到阀4的倒换相。在不考虑电压波形畸变、换相电感初始状态影响的理想情况下,a、b两相短路电流的等效幅值与逆变站正常运行情况下的直流电流
影响,先增大后减小,直到完成阀6到阀4的倒换相。在不考虑电压波形畸变、换相电感初始状态影响的理想情况下,a、b两相短路电流的等效幅值与逆变站正常运行情况下的直流电流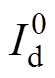 相近。
相近。
阀6向阀4倒换相完成后,直流系统仍等效短路,向交流系统的注入电流降为零。换相过程依次类推,直至阀1或阀4关断,直流系统恢复正常导通顺序。
通过对比正常换相过程与换相失败期间直流系统对交流系统的电流注入量,可得换相失败期间直流系统向交流系统注入电流的变化量,即换相失败分量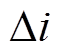 。对交流系统而言,直流系统换相失败期间的暂态特性,相当于在原正常电流波形的基础上额外叠加
。对交流系统而言,直流系统换相失败期间的暂态特性,相当于在原正常电流波形的基础上额外叠加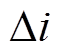 这一扰动激励源。
这一扰动激励源。
以阀4导通时刻作为起始时段,交流系统各相的换相失败分量所对应的开关函数为
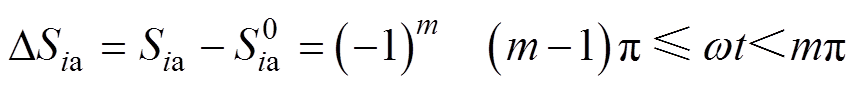 (3)
(3)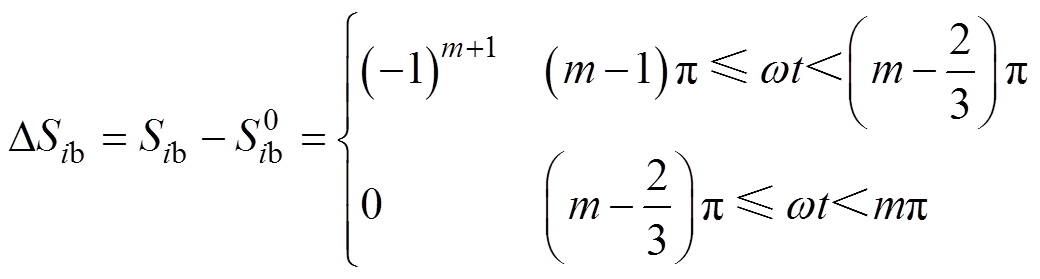 (4)
(4)
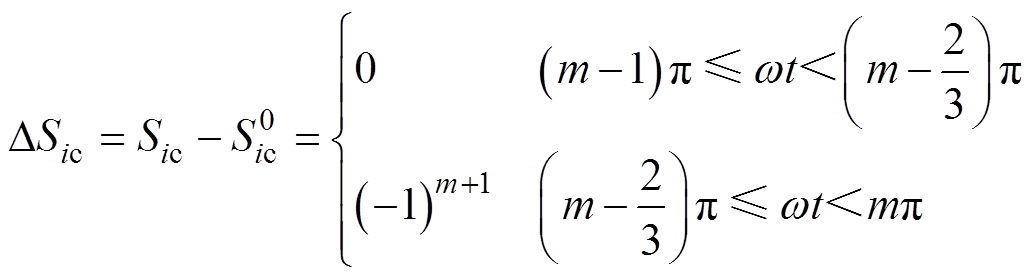 (5)
(5)
对应于换流变压器交流系统侧的三相电流为
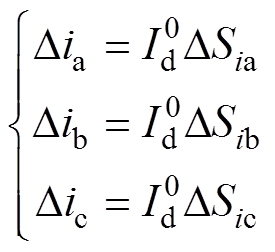 (6)
(6)根据动态相量理论[18-19],对于任意非正弦信号,均可在任意区间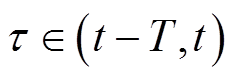 将其展开为时变傅里叶级数,以分析其暂态过程,其中T为工频周期。
将其展开为时变傅里叶级数,以分析其暂态过程,其中T为工频周期。
由傅里叶级数计算推导换相失败分量的各阶动态相量为
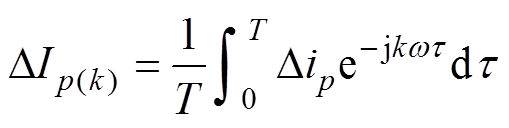 (7)
(7)式中,w 为动态相量分析的基准频率, ;p为交流系统三相值,
;p为交流系统三相值,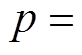
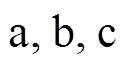 ;
;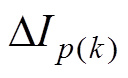 为换相失败分量的第k阶(k≥1)动态相量。从而可得
为换相失败分量的第k阶(k≥1)动态相量。从而可得
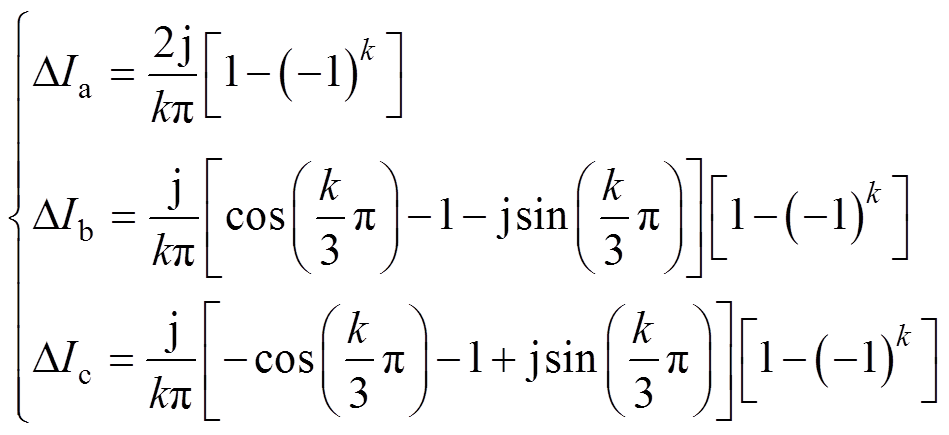 (8)
(8)
考虑到单桥逆变站滤波器对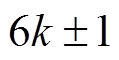 次谐波的抑制作用与换流变压器的电压比,换相失败分量向交流系统实际注入的电流为
次谐波的抑制作用与换流变压器的电压比,换相失败分量向交流系统实际注入的电流为
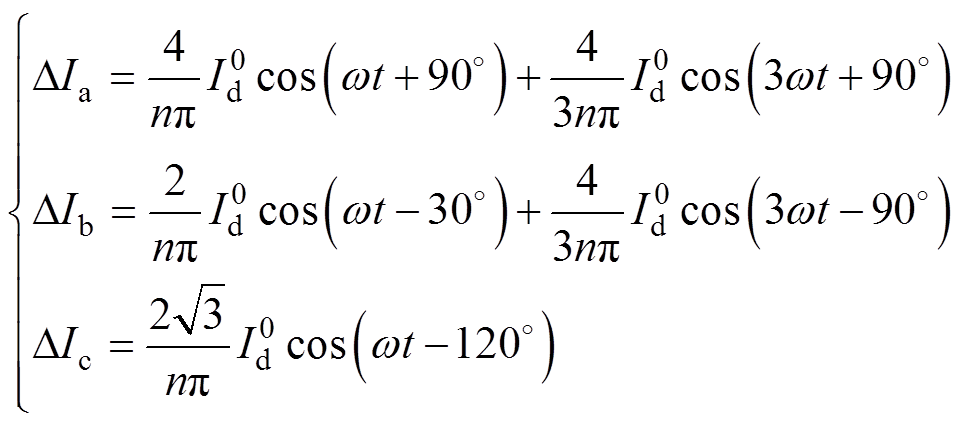 (9)
(9)式中,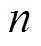 为换流变压器的电压比。根据傅里叶分析结果可知,a、b、c三相的换相失败分量不对称且含有较多的谐波成分。由此造成交流系统电压波形畸变,进而对同一落点的其他逆变站产生影响。
为换流变压器的电压比。根据傅里叶分析结果可知,a、b、c三相的换相失败分量不对称且含有较多的谐波成分。由此造成交流系统电压波形畸变,进而对同一落点的其他逆变站产生影响。
同理可得,正常换相情况下直流系统向交流系统的注入电流为
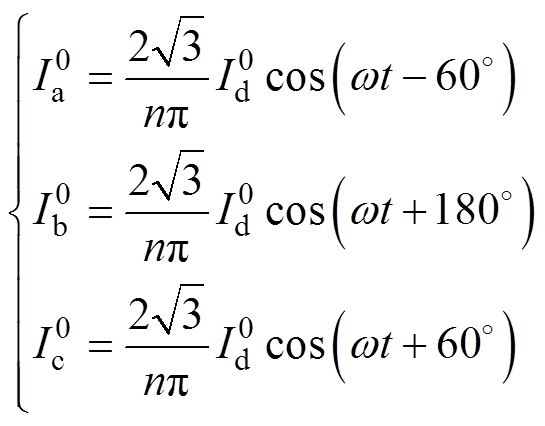 (10)
(10)为研究多馈入高压直流系统中换相失败的相互影响机理,需对换相失败后各逆变站换相电压的变化情况进行研究。以双馈入高压直流系统作为分析对象,其网架结构如图3所示。
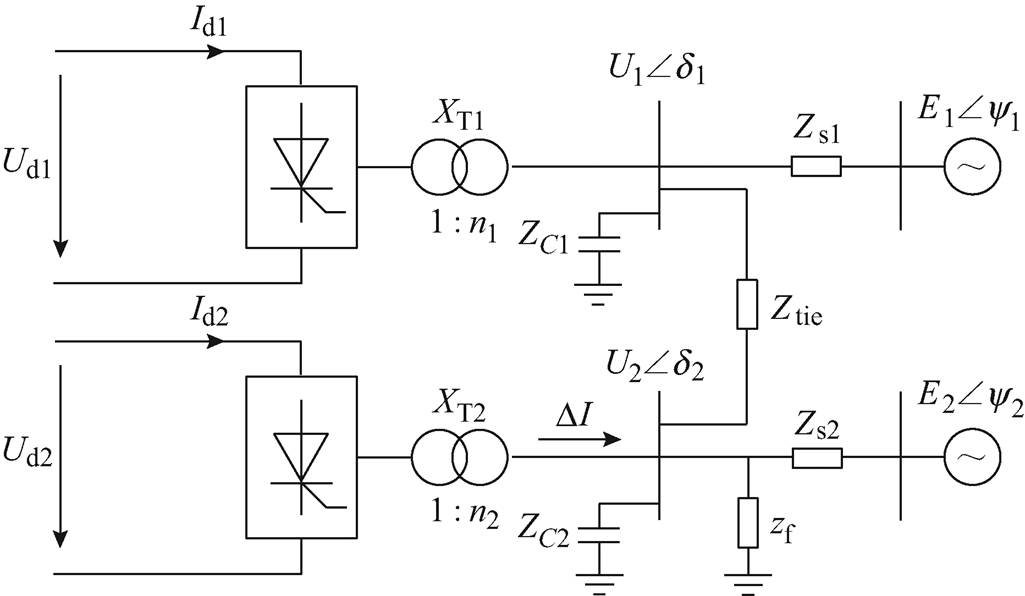
图3 双馈入高压直流系统模型
Fig.3 The model of dual-infeed high-voltage DC system
图3中,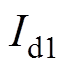 、
、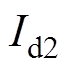 、
、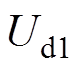 、
、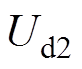 分别为两回直流系统的直流电流及直流电压;
分别为两回直流系统的直流电流及直流电压;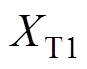 与
与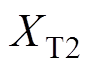 为换流变压器电抗;
为换流变压器电抗;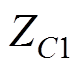 与
与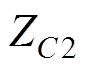 为滤波器及并联无功补偿电容器的阻抗;
为滤波器及并联无功补偿电容器的阻抗;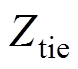 为换流母线的联络阻抗;
为换流母线的联络阻抗;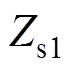 与
与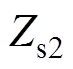 为逆变站交流系统的等值阻抗;
为逆变站交流系统的等值阻抗;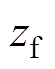 为逆变站2换流母线发生三相接地故障时的接地阻抗,反映交流系统故障的严重程度;
为逆变站2换流母线发生三相接地故障时的接地阻抗,反映交流系统故障的严重程度;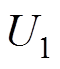 与
与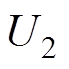 为换流母线电压,
为换流母线电压, 与
与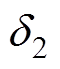 为换流母线电压的相位;
为换流母线电压的相位;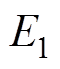 与
与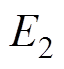 为逆变侧交流系统等值电动势,
为逆变侧交流系统等值电动势,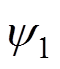 与
与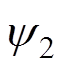 为等值电源的相位;
为等值电源的相位;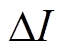 为逆变站2换相失败期间向交流系统注入的换相失败分量。
为逆变站2换相失败期间向交流系统注入的换相失败分量。
正常情况下2号逆变站向交流系统注入三相电流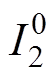 超前于1号换流母线相电压
超前于1号换流母线相电压 的相位差为
的相位差为
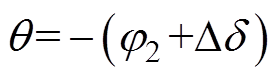 (11)
(11)式中,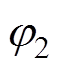 为2号逆变站换流变压器出口处交流电压超前于注入交流电流的相位差,即2号逆变站的功率因数角;
为2号逆变站换流变压器出口处交流电压超前于注入交流电流的相位差,即2号逆变站的功率因数角;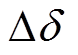 为1号逆变站换流母线电压超前于已换相失败逆变站换流母线电压的相位差,
为1号逆变站换流母线电压超前于已换相失败逆变站换流母线电压的相位差,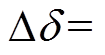
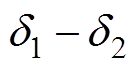 。
。
对于图3所示的双馈入高压直流系统,假设在2号换流母线发生三相接地故障后,2号逆变站首先发生换相失败。现对2号逆变站换相失败期间,1号换流母线的电压变化规律进行分析。易知,1号换流母线的电压受交流系统接地故障与换相失败分量的双重影响,下文首先分析由接地故障引起的电压暂降。
根据文献[11-12],当2号换流母线发生三相接地故障时,1号换流母线的电压变化量为
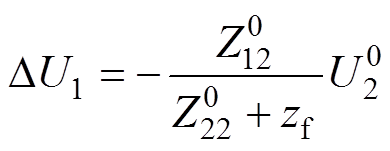 (12)
(12)式中,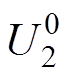 为交流系统故障前2号换流母线的电压;
为交流系统故障前2号换流母线的电压;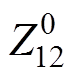 为交流系统故障前节点阻抗矩阵
为交流系统故障前节点阻抗矩阵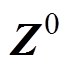 中两条换流母线间的互阻抗;
中两条换流母线间的互阻抗;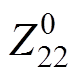 为2号换流母线的等值自阻抗。考虑到交流系统等值阻抗中感性成分占优,且正常运行时各馈入节点电压的标幺值近似相等,可认为接地故障发生后,1号换流母线仅发生了幅值上的变化,即
为2号换流母线的等值自阻抗。考虑到交流系统等值阻抗中感性成分占优,且正常运行时各馈入节点电压的标幺值近似相等,可认为接地故障发生后,1号换流母线仅发生了幅值上的变化,即
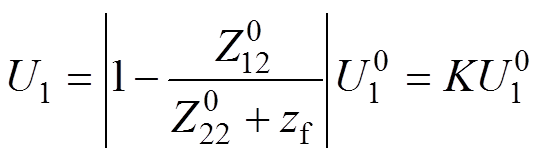 (13)
(13)
式中, 为交流系统故障前1号换流母线的电压;
为交流系统故障前1号换流母线的电压;
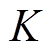 为接地故障后换流母线电压的比例系数。
为接地故障后换流母线电压的比例系数。
由换相失败分量引起的电压波动除工频成分外还包括3次谐波分量,需分别根据接地故障发生后系统的等效网络进行分析。
对于换相失败分量中的工频成分,其在1号换流母线处引起的电压波动为
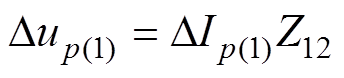 (14)
(14)对于换相失败分量中的3次谐波成分,其在1号换流母线处引起的电压波动为
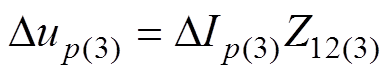 (15)
(15)
式中, 与
与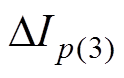 分别为换相失败分量中的工频分量与3次谐波分量;
分别为换相失败分量中的工频分量与3次谐波分量;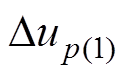 与
与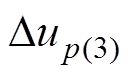 分别为由换相失败分量引起的1号换流母线处电压波动的工频分量与3次谐波分量;
分别为由换相失败分量引起的1号换流母线处电压波动的工频分量与3次谐波分量; 与
与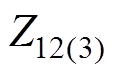 分别为发生接地故障后交流系统工频节点阻抗矩阵Z与3次谐波节点阻抗矩阵Z(3)中两回换流母线间的互阻抗。
分别为发生接地故障后交流系统工频节点阻抗矩阵Z与3次谐波节点阻抗矩阵Z(3)中两回换流母线间的互阻抗。
2号逆变站发生换相失败后,1号逆变站的换相电压受交流系统故障与换相失败分量的共同影响。结合前文分析,得到1号换流母线处的三相电压为
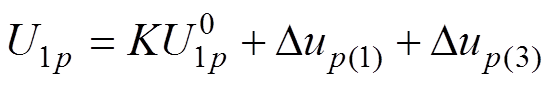 (16)
(16)结合式(13)~式(16),可得1号换流母线处三相电压的解析表达式为
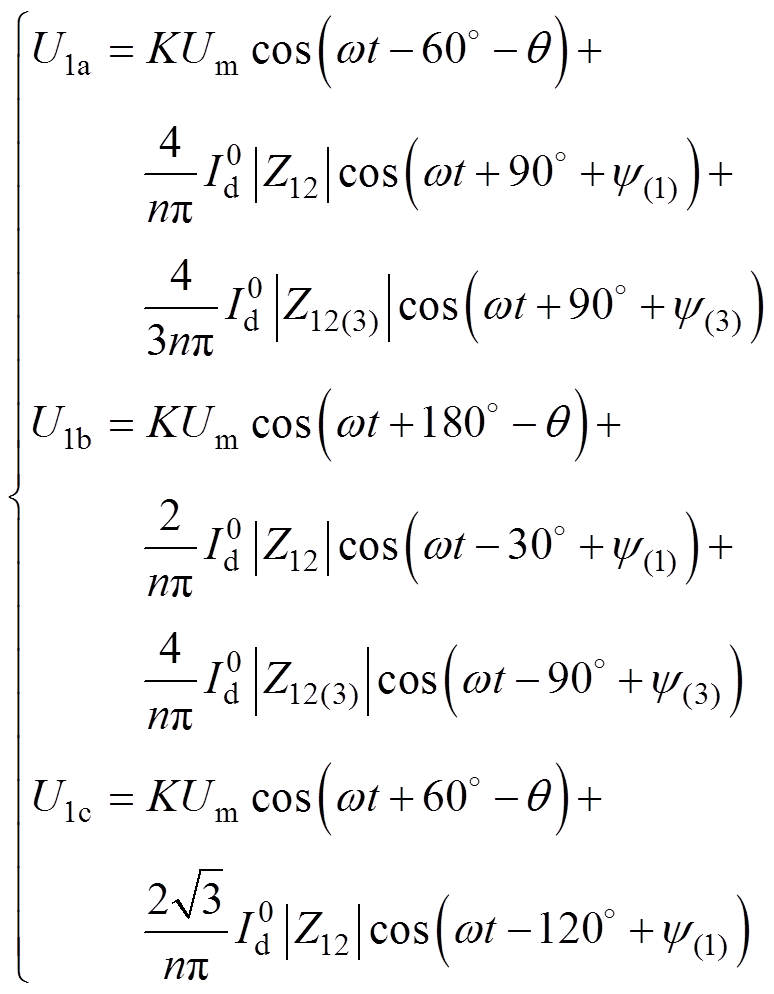 (17)
(17)
式中,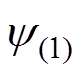 与
与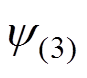 分别为
分别为 与
与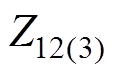 的阻抗角。当接地阻抗变小时,两回换流母线间的互阻抗减小,故障点对换相失败分量的分流作用随之增强,从而由换相失败分量而导致的1号换流母线的电压波动减小。但与此同时,由交流系统故障而导致的1号换流母线处的电压暂降也会增大,同样会导致换相失败发生。为准确衡量直流系统对这两类扰动的免疫能力,需分析直流系统的等效换相面积。
的阻抗角。当接地阻抗变小时,两回换流母线间的互阻抗减小,故障点对换相失败分量的分流作用随之增强,从而由换相失败分量而导致的1号换流母线的电压波动减小。但与此同时,由交流系统故障而导致的1号换流母线处的电压暂降也会增大,同样会导致换相失败发生。为准确衡量直流系统对这两类扰动的免疫能力,需分析直流系统的等效换相面积。
当直流系统对称稳定运行时,各换流阀在换相过程满足
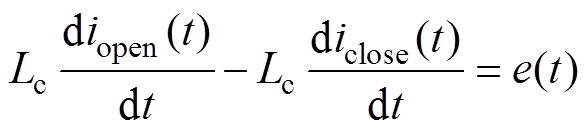 (18)
(18)式中,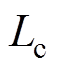 为逆变侧等值换相电感;
为逆变侧等值换相电感;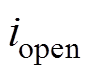 与
与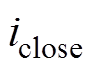 分别为将要导通、关断阀上流过的电流;
分别为将要导通、关断阀上流过的电流; 为两阀臂所承受的换相电压,对应于换流变阀侧线电压。对式(18)积分可得
为两阀臂所承受的换相电压,对应于换流变阀侧线电压。对式(18)积分可得
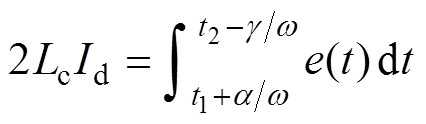 (19)
(19)式中,等式左侧为完成换相过程所需的最小换相面积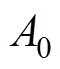 ;等式右侧,
;等式右侧,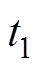 为欲导通阀的触发时刻,滞后于
为欲导通阀的触发时刻,滞后于 上一过零点
上一过零点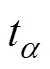 一个a 角;
一个a 角;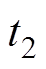 为换相完成时刻,超前于
为换相完成时刻,超前于 下一过零点
下一过零点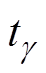 一个g 角;
一个g 角;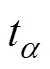 、
、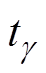 分别为触发延迟角与关断角在一个工频周期内所对应的时间。
分别为触发延迟角与关断角在一个工频周期内所对应的时间。
换相失败出现的最直接原因是换相过程所预留的关断角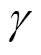 小于晶闸管关断所需的最小关断角
小于晶闸管关断所需的最小关断角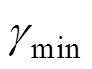 。根据1号换流母线处三相电压的解析表达式,可计算换相电压所能提供的最大换相面积(以阀1为例)。换相过程与换相面积示意图如图4所示,其中
。根据1号换流母线处三相电压的解析表达式,可计算换相电压所能提供的最大换相面积(以阀1为例)。换相过程与换相面积示意图如图4所示,其中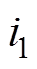 为流过阀1的电流。
为流过阀1的电流。
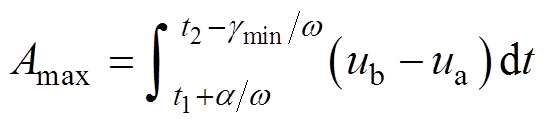 (20)
(20)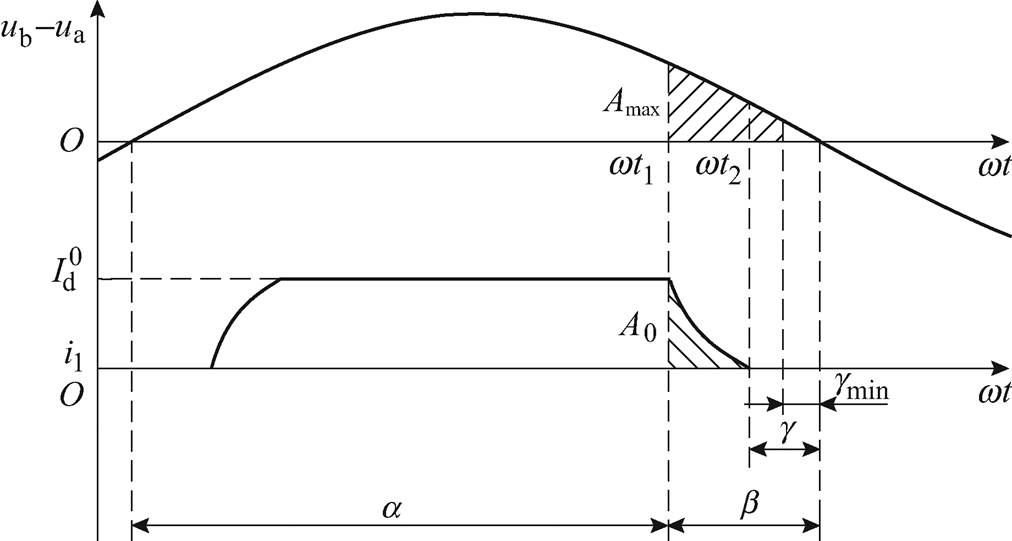
图4 换相过程及换相面积示意图
Fig.4 The diagram of commutation process and commutation area
已有研究表明[20],在逆变站直流侧形成短路通路前,直流电流上升幅度较小,可近似认为逆变侧直流电流是在直流侧形成短路后才开始变化的。从而在判断1号逆变站是否发生换相失败时,认为其所需的最小换相面积保持不变。根据1号换流母线处的三相电压分析1号逆变站在扰动影响下各换流阀的最大换相面积,当某一阀的最大换相面积 时即认为1号逆变站会发生换相失败。
时即认为1号逆变站会发生换相失败。
对复杂多馈入系统的分析与双馈入高压系统相似,不同的是发生多回逆变站换相失败时,需同时考虑多个换相失败激励源对逆变站换相电压的影响。利用换相失败期间换相电压的解析表达式,可方便地计算各逆变站换相面积的变化情况,从而实现对换相失败的准确判断。其计算流程如下:
(1)计算由交流系统故障所引发的各换流母线电压下降幅度,通过对比换相过程所需的最小换相电压,得到仅受交流故障影响便发生同时换相失败的逆变站集合。
(2)选取换相失败集合中某一逆变站为基准逆变站,设定其发生阀1到阀3的换相失败(或其他任意换相过程)。根据各换流母线间的电压夹角,推算同一时刻下其他各回逆变站发生换相失败的阀。
(3)计算换相失败集合中各逆变站的换相失败分量,并推算未发生换相失败逆变站的换流母线电压的变化情况,最终得到其对应的最大换相面积,进而实现对各逆变站换相失败的判断。
以双馈入高压直流系统为例验证考虑换相失败相互影响的多馈入高压直流系统换相失败判断方法。本文基于CIGRE标准测试系统[21]搭建了如图3所示的双馈入高压直流系统。仿真系统主要参数见表1。
表1 仿真系统主要参数
Tab.1 Main parameters of simulation system

参 数数 值 换流母线额定线电压/kV230 LCC额定直流电压/kV500 LCC额定直流电流/kA2 换流变压器电压比422.84kV230kV 换流变压器短路阻抗(pu)0.18 换流变压器容量/(MV·A)1 196 交流系统短路比2.5
两回直流系统参数整定相同,稳定运行条件下,两回直流系统换流母线的电压相位差为零,逆变侧触发角为142°。在算例调节过程中,换流母线联络阻抗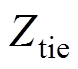 的阻抗角保持为80.5°,接地故障考虑三相对称电感性接地的情况。通过调节联络阻抗与接地电感的幅值可分析多馈入直流系统在不同运行条件下换相失败的相互影响能力及发生换相失败的逆变站。
的阻抗角保持为80.5°,接地故障考虑三相对称电感性接地的情况。通过调节联络阻抗与接地电感的幅值可分析多馈入直流系统在不同运行条件下换相失败的相互影响能力及发生换相失败的逆变站。
图5为两回直流输电系统发生换相失败期间关断角的仿真波形。2号逆变站首先发生换相失败,经一定时间后,1号逆变站在交流系统故障与换相失败分量的双重作用下发生换相失败,即两回逆变站发生了非同时的换相失败。仿真结果验证了多馈入高压直流系统中存在换相失败的相互影响作用。
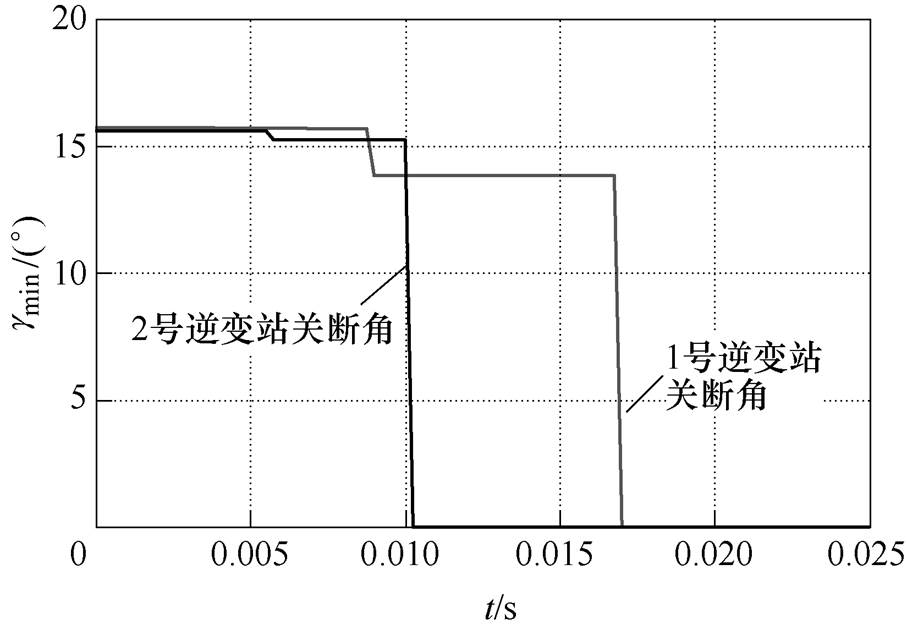
图5 两回逆变站关断角的仿真波形
Fig.5 Simulation waveforms of extinction angle of two inverter stations
图6给出了逆变站在正常换相过程与换相失败过程中对交流系统的注入电流(电流已做标幺值处理)。图6b所示的换相过程,首先发生阀1到阀3的换相失败,经历3次换相失败后,直流系统的导通顺序恢复正常。对比正常换相过程与换相失败期间的电流波形,可得换相失败期间直流系统向交流系统注入的换相失败分量,如图6c所示。
对比图6c与图2b可知,换相失败分量的仿真计算结果与理论相符,两者差异主要由换相过程引起。另外,在交流系统等效相间短路期间,因换相电感初始状态的差异及换相电压的畸变,交流系统向换流器注入的短路电流会略大于直流系统的额定电流,从而给换相失败分量带来误差。但误差幅值较小,且存在时间较短,对换流母线电压的影响能力有限。因此,基于换相失败分量可较好地表征直流系统换相失败期间的暂态特性。
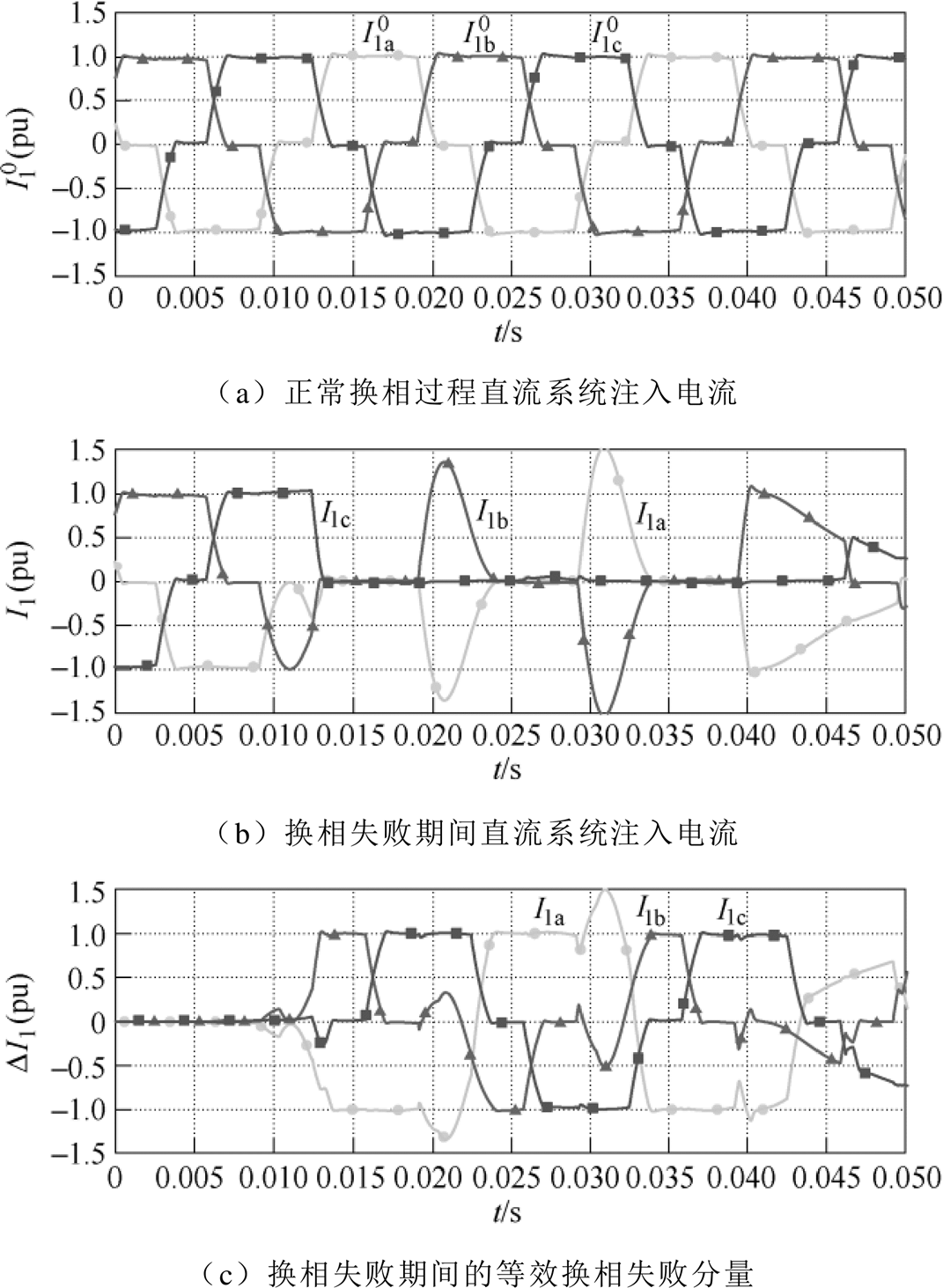
图6 不同情况下直流系统向交流系统注入电流的仿真波形
Fig.6 Simulation waveforms of current injection from DC system to ac system under different conditions
图7为联络阻抗取0.1(pu)且考虑换相失败分量影响时,1号逆变站各换流阀在不同接地阻抗下最大换相面积与所需换相面积的比值。图7中实线为仅考虑交流系统接地故障时,1号逆变站换相能力随接地阻抗的变化曲线。
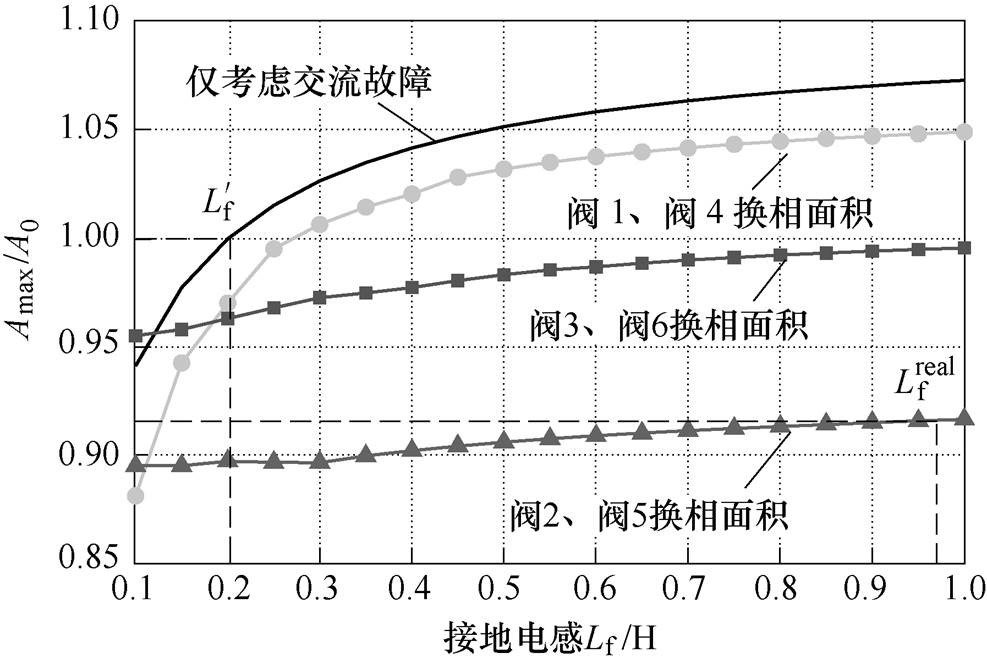
图7 联络阻抗为0.1(pu)时各换流阀换相面积随接地电感的变化规律
Fig.7 The commutation area of each converter valve under different grounding inductance when Ztie=0.1(pu)
取同一接地阻抗下各换流阀换相面积的最小值,即反映了1号逆变站对交流系统故障及换相失败分量的免疫能力。可以发现,在考虑换相失败相互影响时,不论接地阻抗取值多少,2号逆变站换相失败必然会引起1号逆变站发生换相失败;而在仅考虑交流系统故障作用时,当接地电感小于0.2H时才会引起1号逆变站发生换相失败。为验证分析结果,在已有模型基础上去除接地阻抗,并设定在2号逆变站阀1到阀3换相的过程中,令换流变阀侧交流系统的a相与直流系统共阴极点发生短时金属性短路,等效于阀1的持续导通过程,从而模拟2号逆变站换相失败的情况。仿真结果表明,此时1号逆变站会跟随2号逆变站发生换相失败,这也说明本文理论分析的准确性。根据仿真计算结果,当接地电感为0.98H时,2号逆变站发生换相失败,1号逆变站也随之发生换相失败。即此时两回直流输电系统对2号换流母线处接地故障的免疫能力一致,两直流系统具有强耦合性。
此外,受换相失败分量不对称且含谐波的影响,1号逆变站各换流阀的换相面积存在较大差别,部分阀的换相面积可能比仅考虑交流系统故障影响时有所上升,但逆变站整体的换相能力大幅下降。在2号逆变站发生阀1到阀3换相失败的情况下,1号逆变站阀2与阀5的换相面积下降最为明显,其对应的换相电压 受换相失败分量的影响也最为严重。
受换相失败分量的影响也最为严重。
图8为联络阻抗取0.2(pu)时,1号逆变站各换流阀换相面积随接地电感的变化规律。
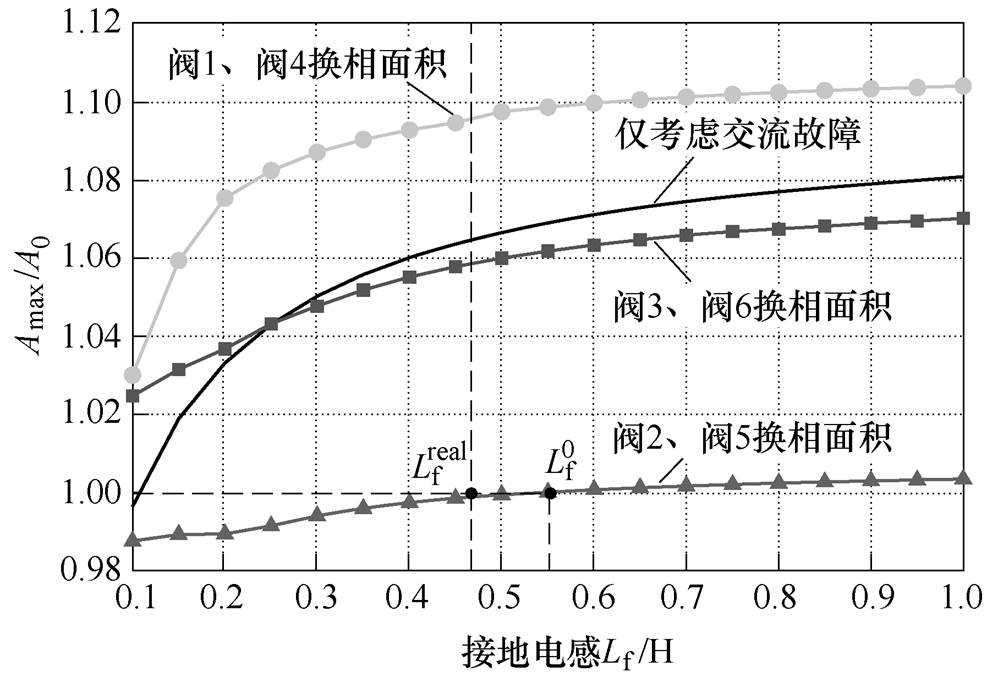
图8 联络阻抗为0.2(pu)时各换流阀换相面积随接地电感的变化规律
Fig.8 The commutation area of each converter valve under different grounding inductance when Ztie=0.2(pu)
根据本文理论分析结果,引起1号逆变站发生换相失败的临界接地电感为0.55H,PSCAD循环仿真的结果表明临界接地电感为0.47H。而在仅考虑交流系统接地故障影响时,只有当接地电感下降至约0.1H时才会引起1号逆变站换相失败。显然本文的分析结果更为准确。
图9为联络阻抗取0.2(pu)且接地电感为0.8H时,各换流阀换相面积随两逆变站关联相位差的变化规律。
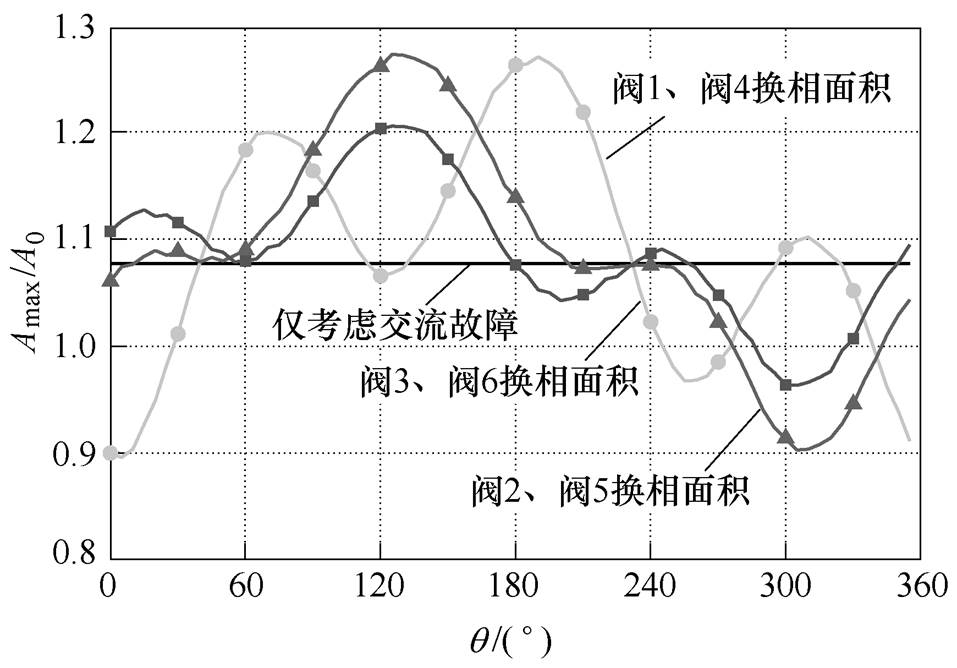
图9 各换流阀换相面积随关联相位差的变化规律
Fig.9 The commutation area of each converter valve under different relative phase angle difference
由图9可知,考虑换相失败分量影响时,1号逆变站各换流阀的换相面积受关联相位差的影响较大。在某些情况下,换相失败分量甚至会有利于1号逆变站的正常换相。但在实际工程中[22],逆变站换流器的无功消耗约为有功功率的40%~60%,对应于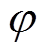 为
为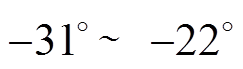 ,且两换流母线之间的电压相位差不会超过
,且两换流母线之间的电压相位差不会超过 。因此,在多馈入高压直流系统中,各逆变站的换流母线电压与换相失败逆变站注入电流的关联相位差
。因此,在多馈入高压直流系统中,各逆变站的换流母线电压与换相失败逆变站注入电流的关联相位差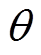 的变化范围为
的变化范围为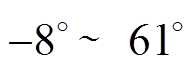 。从而在实际工程中,换相失败分量会对其他逆变站的换相过程带来负面影响。
。从而在实际工程中,换相失败分量会对其他逆变站的换相过程带来负面影响。
构建如图10所示的三馈入高压直流系统,以验证本文方法在更多馈入高压直流系统中的适用性。其中,三回直流系统的参数整定与表1一致,换流母线联络阻抗的阻抗角保持为80.5°;Ztie12=0.1(pu)为换流母线1与换流母线2间的联络阻抗;Ztie13= 0.2(pu)为换流母线1与换流母线3间的联络阻抗;Ztie23=0.1(pu)为换流母线2与换流母线3间的联络 阻抗。
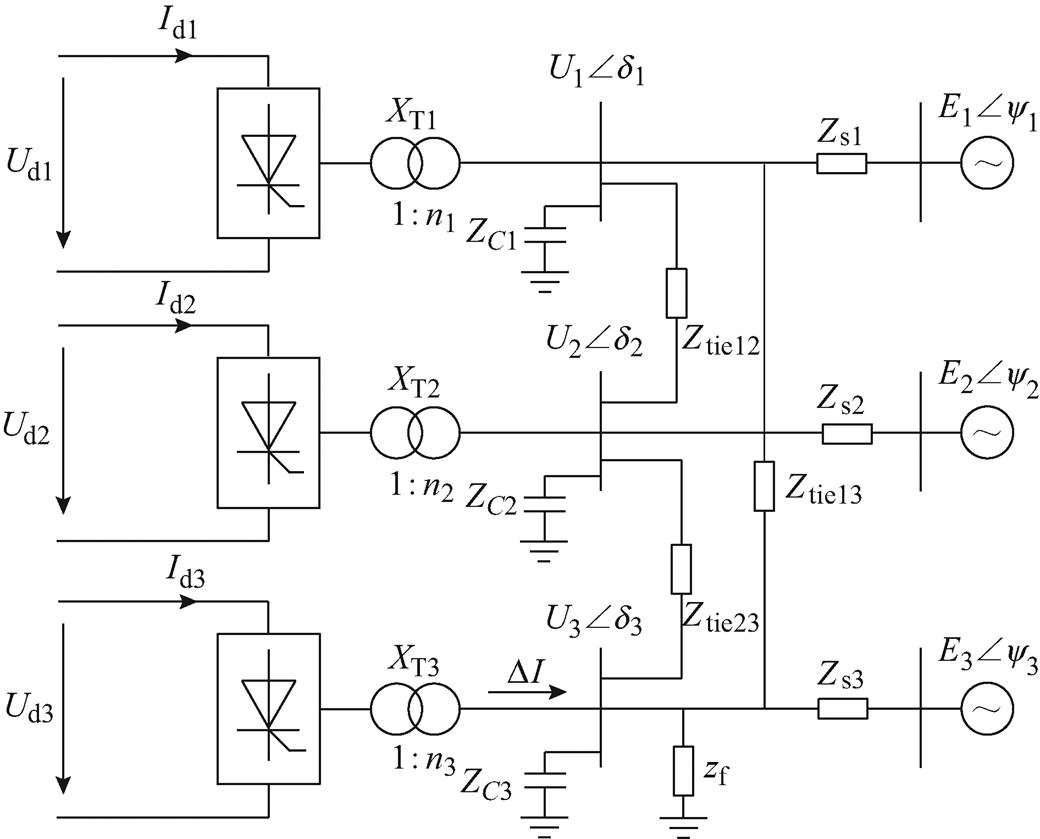
图10 三馈入高压直流系统模型
Fig.10 The model of three-infeed AC-DC system
通过计算不同接地阻抗下2号逆变站与3号逆变站各换流阀的最大换相面积,从而判断其是否会发生换相失败,并研究其换相失败临界接地电感。图11与图12分别展示了1号逆变站与2号逆变站各换流阀换相能力随接地阻抗的变化规律。
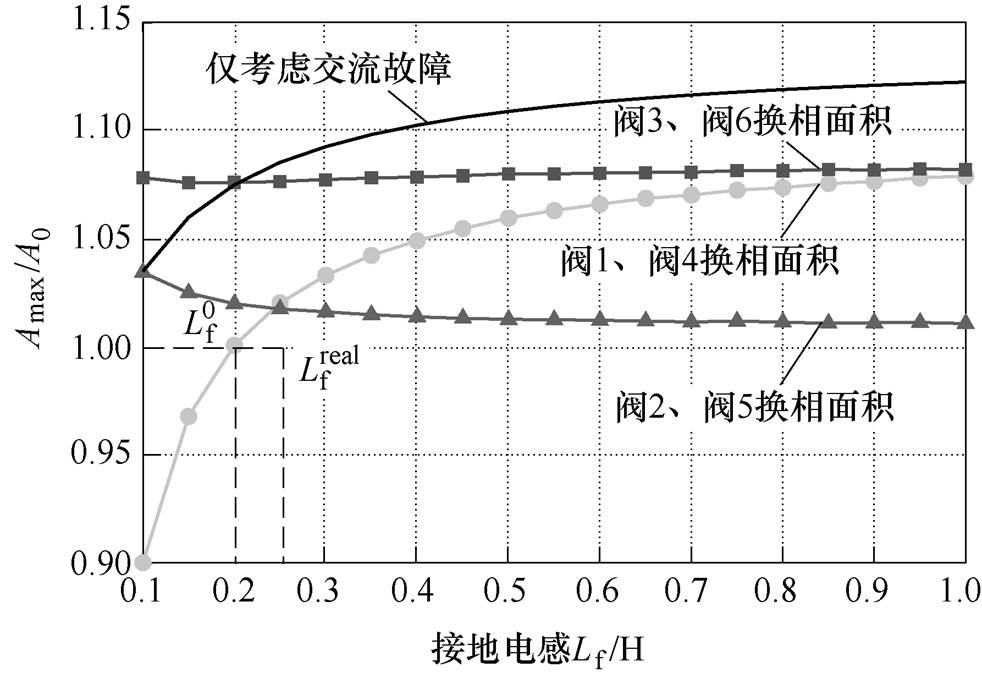
图11 1号逆变站各换流阀换相面积随接地电感的变化规律
Fig.11 The commutation area of each converter valve under different grounding inductance in inverter station 1
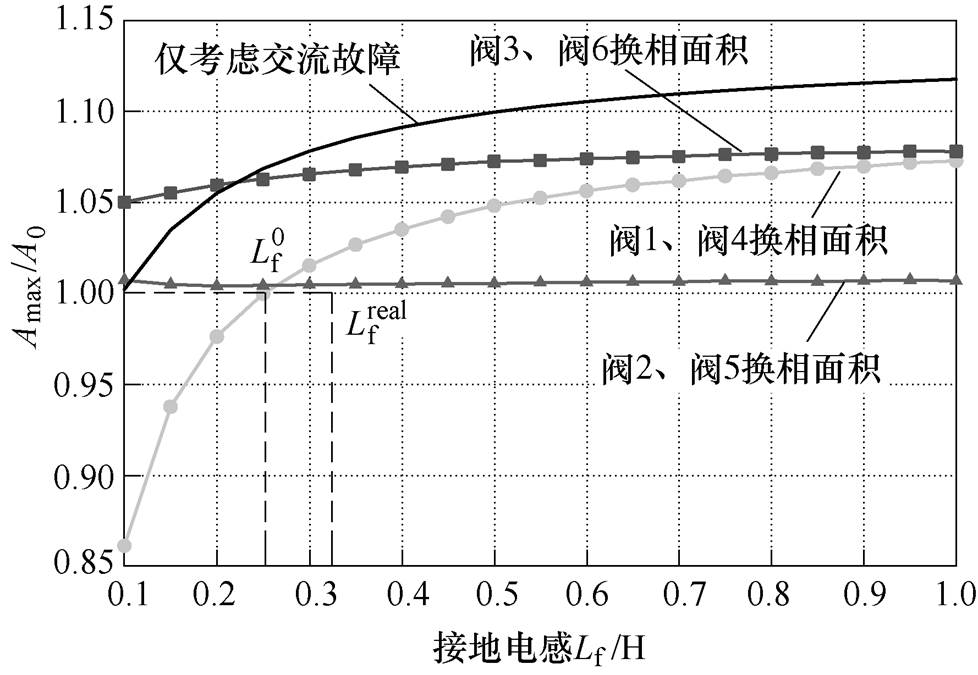
图12 2号逆变站各换流阀换相面积随接地电感的变化规律
Fig.12 The commutation area of each converter valve under different grounding inductance in inverter station 2
根据本文理论分析结果,引起1号逆变站发生换相失败的临界接地电感为0.2H,引起2号逆变站发生换相失败的临界接地电感为0.25H;基于PSCAD循环仿真的结果表明,1号逆变站的实际临界接地电感为0.24H,2号逆变站的实际临界接地电感为0.32H,而在仅考虑交流系统故障影响时,1号逆变站与2号逆变站的临界接地电感均小于0.1H。本文的理论分析结果均比仅考虑交流系统故障影响时更为准确,说明本文所提换相失败判断方法在更多馈入高压直流系统中同样有效。
针对多馈入高压直流系统中换相失败的相互影响问题,本文研究了逆变站换相失败期间的暂态电流特性,在此基础上分析了换相失败分量对换流母线电压及换相面积的影响机理,并进一步提出了逆变站换相失败判断方法。得出以下结论:
1)逆变站换相失败期间,其向交流系统额外注入的换相失败分量具有三相不对称、含大量3次谐波的特性,使交流系统电压发生严重畸变,进而引起电气距离较近的其他逆变站发生换相失败。在实际工程中,考虑多馈入高压直流系统换相失败的相互影响,有助于准确评估逆变站对换相失败的免疫水平,为避免发生连锁故障提供指导意见。
2)受多馈入高压直流系统中部分逆变站换相失败分量的影响,同一落点的其他逆变站各换流阀的最大换相面积存在较大差异,部分阀的换相面积增加,但逆变站的整体换相能力下降。
3)考虑多馈入高压直流系统中逆变站换相失败分量影响时,同一落点的其他逆变站各换流阀的换相面积受关联相位差的影响较大。但在实际工程中,换相失败分量只会对其他逆变站的换相过程带来负面影响。
参考文献
[1] 王增平, 刘席洋, 李林泽, 等. 多馈入直流输电系统换相失败边界条件[J]. 电工技术学报, 2017, 32(10): 12-19.
Wang Zengping, Liu Xiyang, Li Linze, et al. Boun- dary conditions of commutation failure in multi- infeed HVDC systems[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 12-19.
[2] 武文, 吴学智, 荆龙, 等. 适用于多端直流输电系统的模块化多端口直流潮流控制器[J]. 电工技术学报, 2019, 34(3): 539-551.
Wu Wen, Wu Xuezhi, Jing Long, et al. A modular multi-port DC power flow controller for multi- terminal DC transmission system[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 539-551.
[3] 王增超, 郑俊超, 曾耿晖, 等. 基于高压直流换流站站域信息的交流线路距离保护方法[J]. 电力系统保护与控制, 2019, 47(1): 101-107.
Wang Zengchao, Zheng Junchao, Zeng Genghui, et al. A distance protection method for AC transmission lines based on substation area information in HVDC convertor station[J]. Power System Protection and Control, 2019, 47(1): 101-107.
[4] 郭名文, 樊艳芳, 耿山, 等. 特高压直流接地极周边断裂结构对地表电位分布的影响研究[J]. 电力系统保护与控制, 2019, 47(2): 73-79.
Guo Mingwen, Fan Yanfang, Geng Shan, et al. Study on the effect of fracture structure adjacent to ground electrodes of UHVDC power transmission lines on earth surface potential distribution[J]. Power System Protection and Control, 2019, 47(2): 73-79.
[5] 王玲, 文俊, 李亚男, 等. 谐波对多馈入直流输电系统换相失败的影响[J]. 电工技术学报, 2017, 32(3): 27-34.
Wang Ling, Wen Jun, Li Yanan, et al. The harmonic effects on commutation faliure of multi-infeed direct current transmission systems[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 27-34.
[6] 蔡国伟, 史一明, 杨德友. 基于节点聚类分簇的多馈入直流落点筛选方法[J]. 电工技术学报, 2017, 32(9): 140-148.
Cai Guowei, Shi Yiming, Yang Deyou. Multi-infeed DC terminal location selection method based on clustering nodes[J]. Transactions of China Electro- technical Society, 2017, 32(9): 140-148.
[7] 王少辉, 唐飞, 向农. 华东电网多直流同时换相失败仿真分析[J]. 电力系统保护与控制, 2017, 45(12): 16-21.
Wang Shaohui, Tang Fei, Xiang Nong. Commutation failure simulation analysis of east China power grid multiple HVDC lines[J]. Power System Protection and Control, 2017, 45(12): 16-21.
[8] 刘子文, 冉晓洪, 苗世洪. 基于广域测量系统的交直流系统Markov切换控制器设计[J]. 电工技术学报, 2017, 32(10): 241-251.
Liu Ziwen, Ran Xiaohong, Miao Shihong. Design of Markov switching controller of AC-DC power system based on wide area measurement system[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(10): 241-251.
[9] CIGRE Working Group B4.41. Systems with multiple DC infeed[R]. Paris: CIGRE, 2008.
[10] Nayak R N , Sasmal R P , Sehgal Y K , et al. AC/DC interactions in multi-infeed HVDC scheme: a case study[J]. Power India Conference, 2006, 11: 25-28.
[11] 肖浩, 朱佳, 李银红, 等. 多馈入直流系统换相失败免疫水平快速确定方法研究[J]. 中国电机工程学报, 2015, 35(11): 2711-2717.
Xiao Hao, Zhu Jia, Li Yinhong, et al. Study on rapid determination method of commutation failure immunity levels for multi-infeed HVDC transmission systems[J]. Proceedings of the CSEE, 2015, 35(11): 2711-2717.
[12] 邵瑶, 汤涌. 一种快速评估多馈入直流系统换相失败风险的方法[J]. 中国电机工程学报, 2017, 37(12): 3429-3436.
Shao Yao, Tang Yong. A fast assessment method for evaluating commutation failure risk of multi-infeed HVDC systems[J]. Proceedings of the CSEE, 2017, 37(12): 3429-3436.
[13] 屠竞哲, 张健, 曾兵, 等. 直流换相失败及恢复过程暂态无功特性及控制参数影响[J]. 高电压技术, 2017, 43(7): 2131-2139.
Tu Jingzhe, Zhang Jian, Zeng Bing, et al. HVDC transient reactive power characteristics and impact of control system parameters during commutation failure and recovery[J]. High Voltage Engineering, 2017, 43(7): 2131-2139.
[14] 王晶, 梁志峰, 江木, 等. 多馈入直流同时换相失败案例分析及仿真计算[J]. 电力系统自动化, 2015, 39(4): 141-146.
Wang Jing, Liang Zhifeng, Jiang Mu, et al. Case analysis and simulation of commutation failure in multi-infeed HVDC transmission systems[J]. Auto- mation of Electric Power Systems, 2015, 39(4): 141-146.
[15] 王超. 考虑换相失败的换流站开关函数模型[D]. 北京: 华北电力大学, 2012.
[16] 王童辉, 贾科, 毕天姝, 等. 基于动态相量理论的高压直流系统换相失败暂态特性[J]. 电力系统自动化, 2018, 42(23): 78-85.
Wang Tonghui, Jia Ke, Bi Tianshu, et al. Transient characteristics of commutation failure of HVDC system based on dynamic phasor theory[J]. Auto- mation of Electric Power Systems, 2018, 42(23): 78-85.
[17] 刘羽超. 多馈入直流输电换相失败机理分析与防御措施研究[D]. 北京: 华北电力大学, 2015.
[18] 夏黄蓉, 韩民晓, 姚蜀军, 等. 模块化多电平换流器动态相量建模[J]. 电工技术学报, 2015, 30(增刊2): 120-127.
Xia Huangrong, Han Minxiao, Yao Shujun, et al. Dynamic phasor modeling of simplified modular multilevel converter[J]. Transactions of China Elec- trotechnical Society, 2015, 30(S2): 120-127.
[19] 戚庆茹, 焦连伟, 严正, 等. 高压直流输电动态相量建模与仿真[J]. 中国电机工程学报, 2003, 23(12): 28-32.
Qi Qingru, Jiao Lianwei, Yan Zheng, et al. Modeling and simulation of HVDC with dynamic phasors[J]. Proceedings of the CSEE, 2003, 23(12): 28-32.
[20] 刘俊磊, 王钢, 李海锋, 等. HVDC系统换相失败对交流电网继电保护影响的机理分析[J]. 中国电机工程学报, 2013, 33(19): 111-118.
Liu Junlei, Wang Gang, Li Haifeng, et al. Mechanism analysis of HVDC commutation failure influence on AC power network relay protection[J]. Proceedings of the CSEE, 2013, 33(19): 111-118.
[21] Faruque M O, Zhang Yuyan, Dinavahi V. Detailed modeling of CIGRE HVDC benchmark system using PSCAD/EMTDC and PSB/SIMULINK[J]. IEEE Transa- ctions on Power Delivery, 2006, 21(1): 378-387.
[22] 刘济豪, 郭春义, 刘羽超, 等. 基于无功潮流分析的多馈入直流输电耦合作用[J]. 电力系统自动化, 2014, 38(13): 153-159.
Liu Jihao, Guo Chunyi, Liu Yuchao, et al. Coupling effect in multi-infeed direct current transmission system based on reactive power flow analysis[J]. Automation of Electric Power Systems, 2014, 38(13): 153-159.
Commutation Failure Judgment Method for Multi-Infeed HVDC Systems Considering the Interaction of Commutation Failures
Abstract In the multi-infeed high-voltage DC system (MIDC), the interaction among inverter stations is an important factor that triggers the propagation of commutation failure. In this paper, the transient characteristics of inverter station during commutation failure are analyzed in detail, and the commutation failure component is derived by the switching function model and the dynamic phasor theory. Then, the analytical calculation method is studied to reflect the commutation voltage of each inverter station, considering the mutual influence of AC system fault and commutation failure. On this basis, by comparing the maximum commutation area of each converter valve with the minimum commutation area required for turning off, a commutation failure judgement method is proposed. Finally, the simulation results verify the proposed method.
keywords:Multi-infeed high-voltage DC system, mutual influence, commutation failure, switching function, commutation area
中图分类号:TM721
DOI: 10.19595/j.cnki.1000-6753.tces.190143
国网湖北省电力有限公司经济技术研究院科技资助项目(SGHBJY00JHJS1800026)。
收稿日期 2019-02-03
改稿日期 2019-04-27
许汉平 男,1969年生,硕士,研究方向为电力系统运行及控制。E-mail: xuhping@sina.com
杨炜晨 男,1995年生,博士研究生,研究方向为直流输电运行与控制。E-mail: yangwc@hust.edu.cn(通信作者)
(编辑 陈 诚)