图1 CDSM-MMC双极故障各阶段等效电路
Fig.1 Equivalent circuits of CDSM-MMC in different stage
摘要 柔性直流配电系统中,直流故障通常导致全网换流器自身闭锁保护速动(2~5ms),保护需要利用有限、时变的故障信息快速、准确地识别故障区域,跳开相应故障隔离开关快速恢复供电。因此,基于时变的故障暂态信号,研究快速、准确识别故障区域的保护是直流配电系统发展的迫切需求。该文提出一种基于故障全电流相关性检验的柔性直流配电线路纵联保护。该方法以故障发生后线路两侧电流波形形变特征、极性特征的规律变化为基础,通过t检验(假设检验的一种)算法对两侧全电流信号进行相关性检验,即对两侧全电流信号的幅值大小、方向、极性、突变特性进行统一描述,进而构造保护动作判据。所提方法优点在于无需固定频段特征提取,无需特征绝对值及瞬时幅值的比较,因此避免了常规利用暂态信号的保护受过渡电阻、线路分布式电容、噪声的影响。通过物理实验与仿真结果表明所提保护能较好地满足直流配电系统对保护速动性与选择性的需求,具有一定的应用前景。
关键词:柔性直流配电系统 故障电流特征 相关性检验 t检验算法 故障判别
柔性直流配电系统可以高效地接入光伏等分布式电源与直流负荷,灵活控制功率,且已受到国内外配电网研究的广泛关注[1-3]。然而,由于直流配电系统配电支路多,无法大量配置直流断路器,目前工程上使用自清除型换流器隔离故障,其快速闭锁导致整个直流电网失电,因此如何利用极短时间内的暂态、时变数据有选择性地识别故障区域并快速隔离故障,以便减少系统停电时间,成为保障柔性直流配电系统安全可靠运行的关键技术[4-6]。
目前柔性直流系统的保护借鉴了高压直流的保护策略,主保护通常配有行波保护、电流微分保护、电流差动保护,此外还配置直流过电压保护和直流电压不平衡保护[7-8]。行波保护动作速度快,不受电流互感器饱和及长线路分布式电容等因素影响,但发生较大电阻故障时故障灵敏度不足。因此鉴于现有行波保护的不足,文献[9]提出利用正、反向行波幅值特点构成的行波纵联方向保护。文献[10]利用小波分解重构的电流行波构成差动保护,但由于直流配电系统的直流线路相对较短,行波保护受限于线路长度,因此不适用于直流配电系统。而电流微分保护同样受过渡电阻的影响,可能会导致保护不正确动作,因此针对电流微分保护受过渡电阻影响的问题,文献[11]给出了利用电流二次微分识别过渡电阻的方法,但电流的二次微分受噪声的影响比较严重,直接影响到保护的可靠性,所以难以应用到直流配电系统中。关于电流差动保护,虽具有较好的耐故障电阻能力,但易受分布电容的影响,只能通过长延时来躲过分布式电容影响,考虑到换流器故障闭锁时间短,目前很难设置有效时延。因此为解决电流差动保护因受线路分布电容的影响而存在延时的问题,文献[12]利用电流突变量的极性构成纵联保护,该方法简单、可靠,但要求双端数据同步性高。
综上,由于故障特性的时变和非线性特征,同时现场运行情况下往往故障特征更为复杂,大多数现有直流线路保护在满足柔性直流配电系统线路保护需求同时无法兼顾噪声、分布电容、通信延时、过渡电阻等因素的影响。因此,本文在分析柔性直流配电系统直流线路区、内外故障暂态特征的基础上,根据故障后故障线路两侧暂态电流存在的内在联系及波形规律变化,提出了一种基于故障全电流相关性检验的柔性直流配电线路纵联保护。该算法对线路两侧全电流信号进行假设检验,利用t检验算法检验直流线路两侧电流的相关性,即对两侧全电流信号的幅值大小、方向、极性、突变特性进行统一描述,进而构造了保护动作判据。与现有利用暂态信号的电流差动以及利用电流极性特征构成的保护方法相比,所提方法不受线路分布电容影响,故障判别的可靠性与快速性较高;同时具有较强的抗噪声的能力。最后通过物理实验与仿真结果验证了所提保护的动作性能。
直流线路故障后全网所有换流器闭锁,将导致全网失电,因此保护的目的是要快速切除故障,实现系统供电恢复。为了提高直流系统供电可靠性,考虑直流保护出口时间、快速开关动作时间和换流站恢复时间之和小于10ms(配网中停电时间在10ms以下的不计入停电时间,只算是电压闪动[13]),因此研究快速、准确地识别故障区域的直流线路保护至关重要。
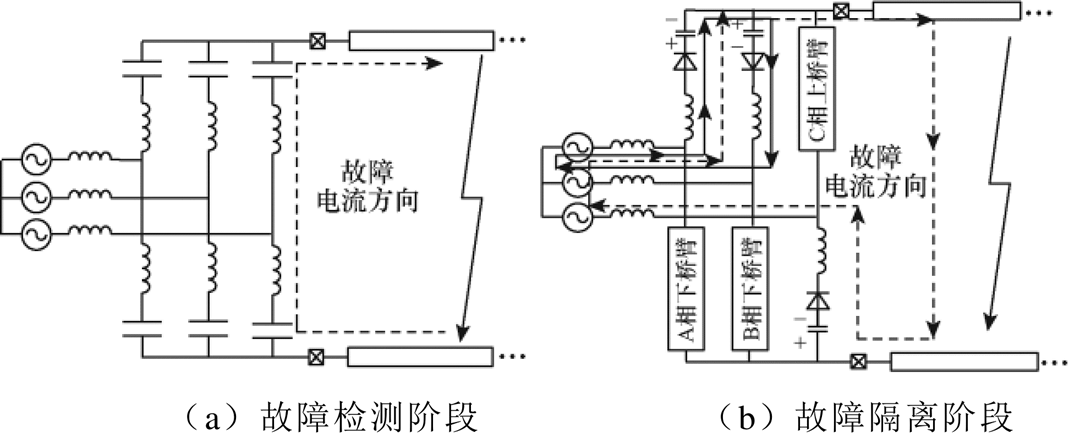
目前直流配电系统的实际工程都是电缆线路双极运行,由于直流配电系统的接地方式一般为高阻接地,单极接地故障不会引起严重过电流,系统可以持续运行一段时间,同时对于保护无过高的速动性要求。为此,本文的故障分析及所提保护主要关注双极短路故障。以钳位双子模块型模块化多电平变换器(Clamp Double Sub-Module-Modular Multilevel Converter, CDSM-MMC)作为换流器的直流双极故障发展过程可分为故障检测和故障隔离两个阶段。CDSM-MMC双极故障各阶段等效电路如图1所示。

图1 CDSM-MMC双极故障各阶段等效电路
Fig.1 Equivalent circuits of CDSM-MMC in different stage
关于故障检测阶段,当发生直流双极短路故障时,CDSM-MMC子模块内的电容首先向故障点快速放电,如图1a所示。此阶段故障电流主要是子模块电容的放电电流[14]。故障发生瞬间,在假设每个桥臂投入子模块数量一样的情况下,其电路可等效为二阶振荡电路且为欠阻尼响应。
关于故障隔离阶段,在发生直流双极短路故障后,故障电流迅速增大且达到换流器中IGBT本体保护的定值,即换流器快速闭锁。换流器闭锁后,由于二极管的钳位作用,换流器的短路电流通路分为两种情况,如图1b所示。换流器内部的子模块电容以串联/并联形式接入到故障电流流通路径当中,会给故障回路提供反向电动势,此时短路电流将被阻断[15-17]。系统中所有的能量都因CDSM-MMC的特殊拓扑结构而被迫馈入到子模块的电容里,使得直流侧故障电流下降至零,最终隔离故障。
由于换流器在故障隔离阶段的直流侧故障电流为零,不能为保护提供有效的故障信息。因此,下文的故障特征分析主要针对换流器闭锁前的故障电流信息。
本文以图2所示的简易双端直流配电系统示意图为例进行区内外故障电流特征分析。规定电流的正方向为母线流向线路,当直流线路发生双极故障时,线路两侧故障电流存在内在联系且波形形变特征具有规律性。
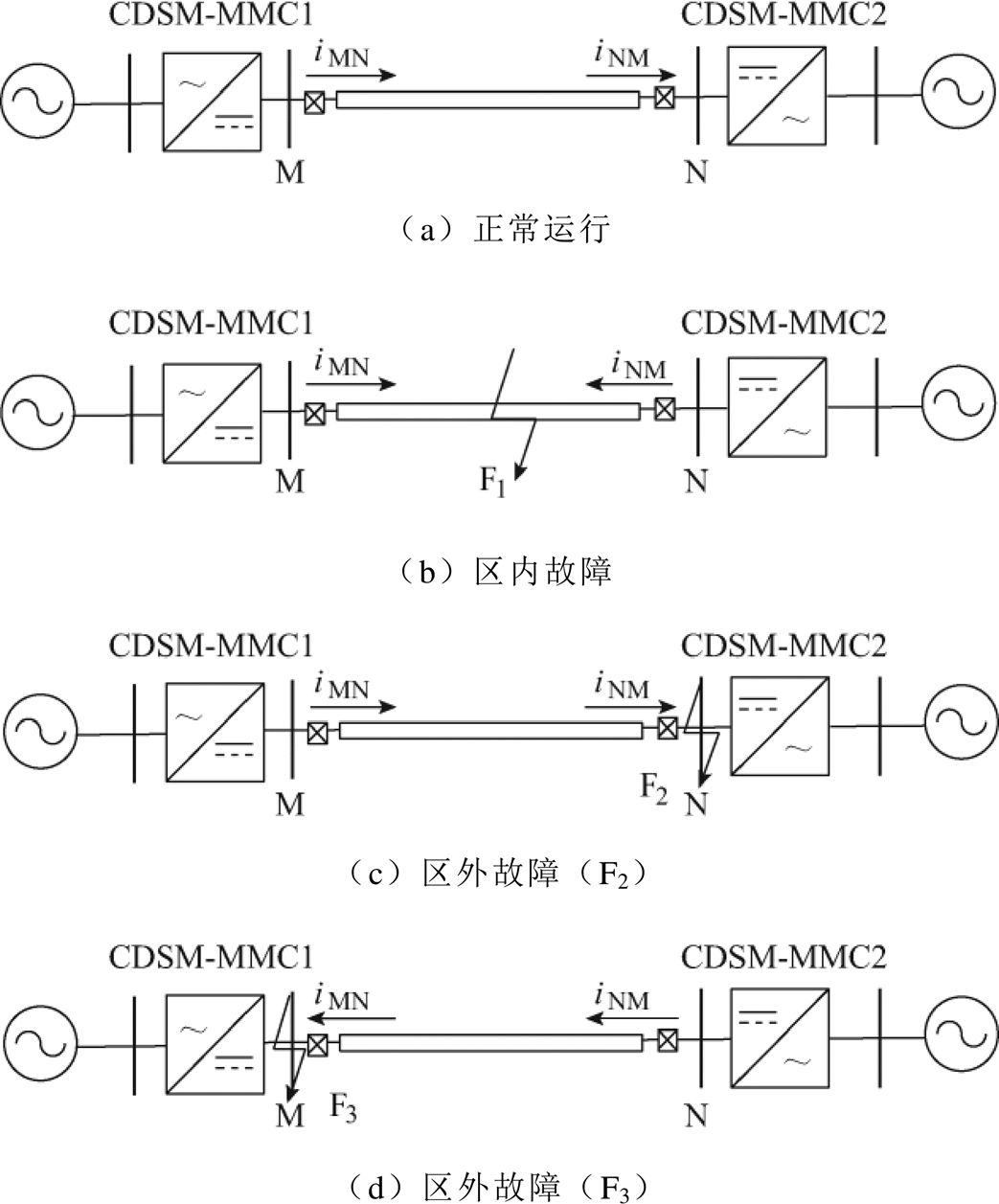
图2 双端直流配电系统示意图
Fig.2 Schematic diagram of DC distribution system
在正常运行状态下,负荷电流为穿越性电流,如图2a所示。因为直流电流没有相位,只有极性,所以电流流向与正方向相同为正极性,流向与正方向相反为负极性。正常运行状态下,所测得两端电流的极性都是一正一负,并不存在电流波形形变,均可看作一条直线,即两侧电流从物理意义(极性)、波形上都相对独立且呈反相关性。
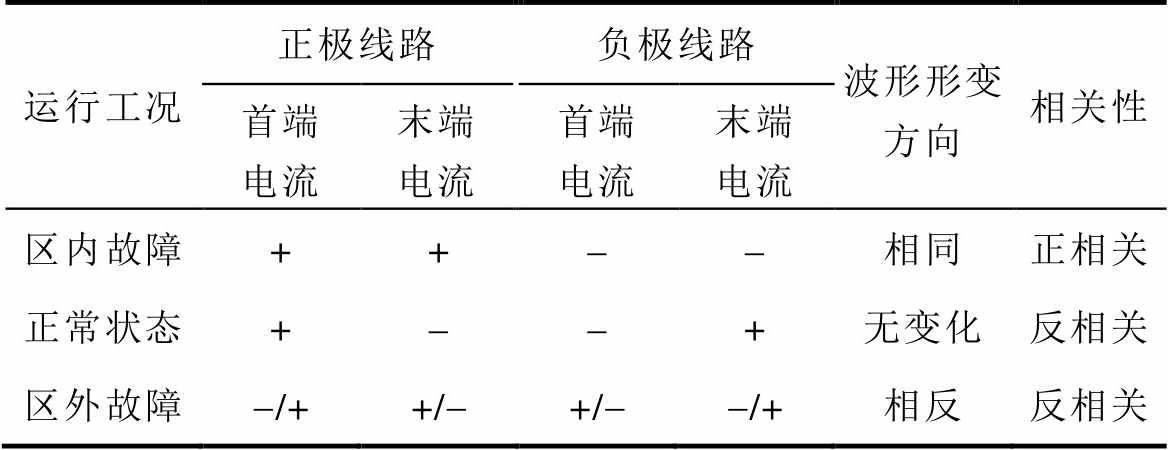
当F1发生故障时,如图2b所示,直流线路两端测得故障电流iMN、iNM都流向故障点F1,此时两侧故障电流的极性均为正,存在电流波形形变,其波形形变方向相同。所以从物理意义(极性)、波形的变化规律角度出发,区内故障时两侧电流呈正相关。当区外发生故障时,如图2c和图2d所示,故障电流为穿越性电流,正极线路两端电流极性为一正一负,负极线路两端电流极性也是一正一负,此时故障电流波形虽然存在形变,但其形变方向相反,即两侧电流的物理意义(极性)、波形变化都呈反相关。综上所述,故障线路两侧故障电流特征见表1。
表1 故障线路两侧故障电流特征
Tab.1 Characteristics of two sides current
运行工况正极线路负极线路波形形变方向相关性 首端电流末端电流首端电流末端电流 区内故障++--相同正相关 正常状态+--+无变化反相关 区外故障-/++/-+/--/+相反反相关
本文基于上述理论分析,提出常规的方向纵联保护、极性纵联保护,但考虑外界影响(如过渡电阻、通信延时、线路分布式电容、噪声等)时可能会存在误动或拒动的情况。因此,本文以区内外故障电流波形形变特征和极性变化特征为保护原理的物理依据,通过检验两侧电流的相关性构造保护新原理。
相关性是指对两个或多个具备相关性的变量元素进行分析,从而衡量两个变量的相关密切程度,源于统计学。目前常用的相关性分析方法是假设检验。在电力系统中,故障位置(回路中线路分布式电容不同)、过渡电阻、测量误差、噪声一直是影响常规直流保护正确动作的重要因素,因此为解决这些问题,本文提出利用t检验(假设检验方法的一种)的方法检验直流线路两端电流的相关性,进而避开使用受上述因素影响的传统电流特征(幅值、方向、极性等),最终构建保护判据。
t检验是假设检验的一种,用t分布理论推导差异发生的概率,从而比较两个数据样本平均数的差异是否显著[18-19],换句话说,就是检验两个数据样本是否存在联系,即相关性。其整个检验过程分为三个步骤:
(1)建立假设H,确定检验水准a(又称置信度,一般取0.05),因此假设:①H=0,两组独立数据正相关;②H=1,两组独立数据反相关。
建立的假设是为了验证两个独立样本是否来自同一分布,其H的结果是判断假设是否成立,即验证两者独立数据的相关性。
(2)计算检验统计量t,其公式为
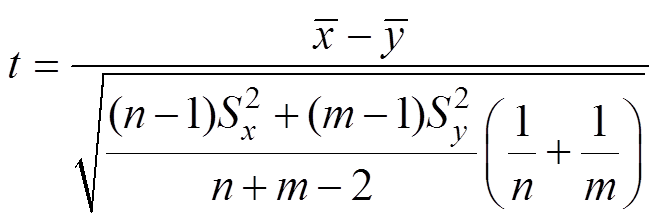 (1)
(1)式中,分子表示两个样本均值的差值;x和y分别为两组样本的采样值,即两侧电流的采样值,其表示形式应为x={x1, x2, x3,…, xn},y={y1, y2, y3,…, yn};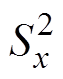 和
和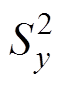 分别表示两个样本的方差;n和m为样本数量,即两侧电流的采样点数量,可以认为m=n。
分别表示两个样本的方差;n和m为样本数量,即两侧电流的采样点数量,可以认为m=n。
(3)通过临界t值表进行查找,利用t值确定P值。临界t值表是统计学中一个非常常见且固定的数据表,详见附表3。附表3中自由度的计算公式为u=n-1,n表示数据的采样样本数。查表时注意自由度u的选择,最终确定P值后做出推断结论。由于所提保护的采样频率是10kHz,数据窗长是0.5ms(5个采样点),因此本文只需要对比自由度为4时的P值即可。
P值表示概率的大小,如果P>0.05则接受H=0的假设并拒绝H=1的假设,说明两个独立数据样本来自同一分布,具有相同的均值,即证明了两者数据呈正相关;若P<0.05则接受H=1的假设并拒绝H=0的假设,表明两个独立数据样本不是来自同一分布,无相同均值,即证明了两者数据呈反相关。
通过对t检验算法的描述,可知该算法能够有效检验两个独立变量的相关性,同时根据区内外故障特征分析可知故障时故障线路两端暂态电流存在物理联系(极性)和规律性的波形变化特征,即可以利用t检验算法检验故障后直流线路两侧暂态电流的相关性。因此,依据2.1节的检验步骤(3)可知,当H=0时证明两侧暂态电流呈正相关,即发生区内故障;当H=1时则证明两侧暂态电流呈反相关,即发生区外故障。因此,保护判据可以依据1和0之间的显著差异而构造,即
 (2)
(2)式中,H为假设检验结果值。
为了确保所提保护在柔性直流换流站启动过程、正常运行模式切换过程、暂态引起振荡等条件下不误动,将保护整体实现方案设计成由保护启动、故障检测与识别两部分组成。保护动作流程如图3所示。
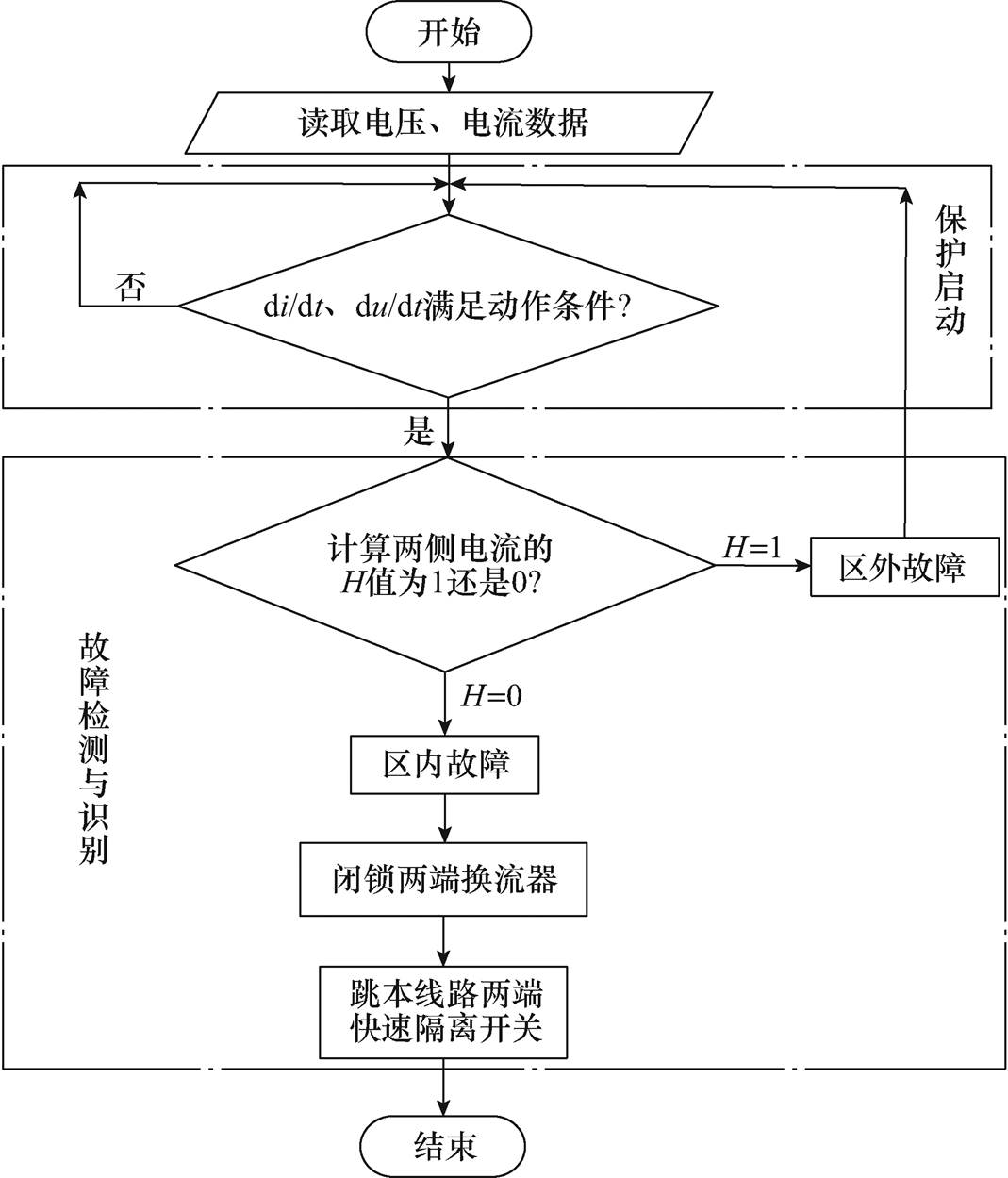
图3 保护动作流程
Fig.3 Flow chart of the proposed protection operation
(1)配置di/dt、du/dt作为保护方案的启动判据,形成保护启动部分。当系统发生故障时,电流迅速上升。di/dt就是利用短路情况和正常运行情况下电流变化率的差异特征来确定故障的发生。其启动门限值应大于直流线路负荷电流上升率的最大值,即包含了直流换流站启动过程、正常运行模式切换两种情况,以免出现误判的情况。
(2)保护装置启动后,直流线路两侧采集故障后一个窗长(0.5ms)的电流,然后利用t检验的方法检验两侧电流的相关性,其结果为H值,为了确保所提保护在暂态引起振荡条件下不误动,故障检测时需要连续满足判据3次才能最终确认是故障 发生。
(3)计算结果根据式(2)的设定,判定直流线路的故障区域。若H=0,则认为是区内故障,随即闭锁两侧换流站,清除故障电流,最后跳开相应直流线路上的快速隔离开关,以隔离故障;若结果H=1,则认为是区外故障,保护复归。
利用物理硬件实验平台验证所提保护的正确性,低压柔性直流物理硬件实验平台如图4所示。物理硬件实验平台为两电平拓扑的双端低压直流系统。该系统直流额定电压为800V,额定功率为10kW。直流线路分别由3个0.1mH的电感和3个0.06W 的电阻模拟;直流并联电容器为1 260mF;交流侧换流电抗器为12.5mH。测量点设置在直流线路的两端,其采样频率为1.6kHz。直流故障利用接触器和一个5W 的电阻模拟,以确保设备的安全。整个物理实验系统被安装在两个屏柜里,其电路如图4b所示。
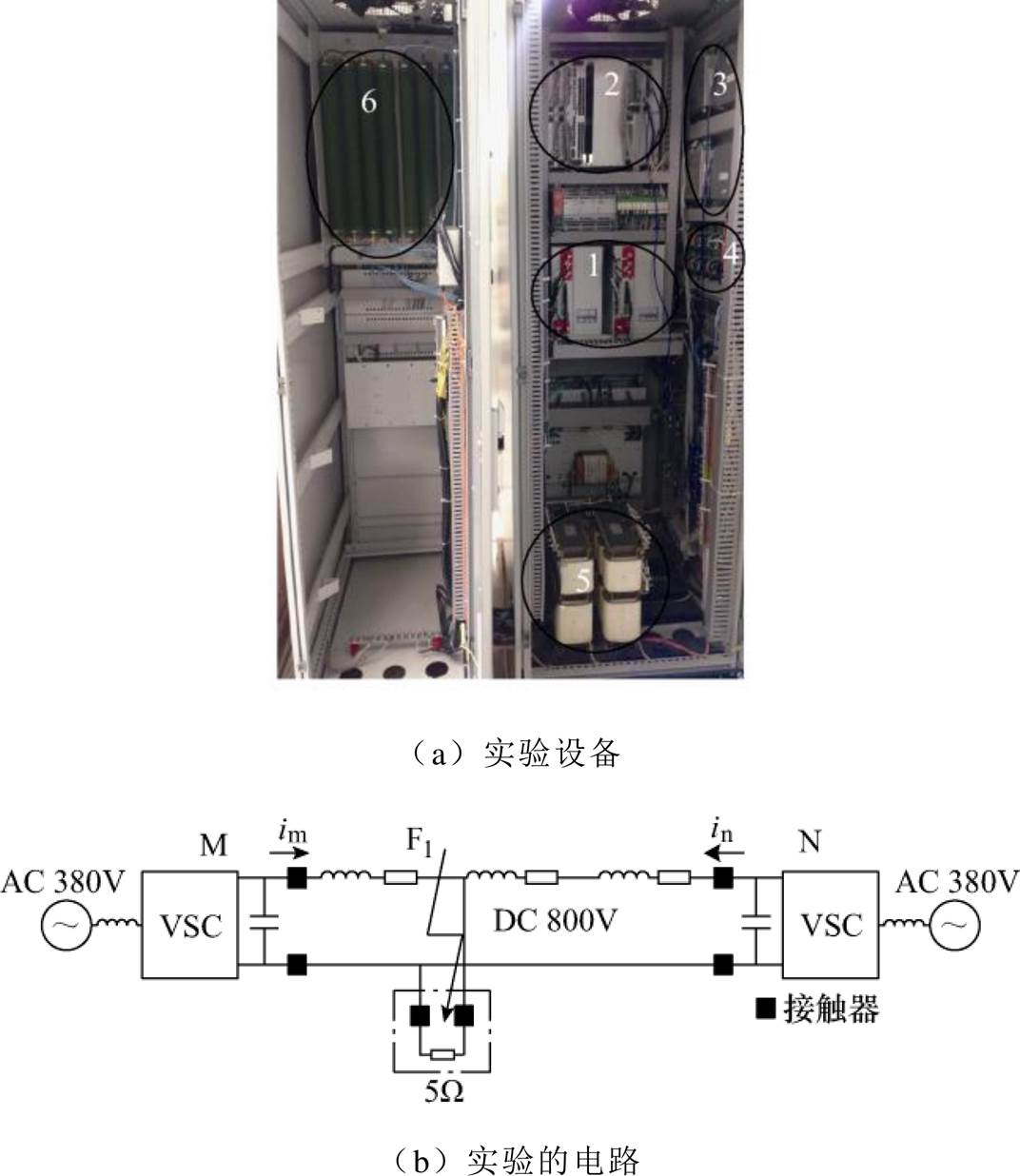
图4 低压柔性直流物理硬件实验平台
1—两电平换流器 2—开关控制器 3—测量单元 4—霍尔传感器 5—电感 6—电阻
Fig.4 Scaled-down hardware test bed of low voltage flexible DC system
在实验中,直流系统的两端都通过两电平换流器与380V交流电源相联。M端换流器设置为定直流电压控制,N端换流器为定有功功率控制。正常负荷电流从M端流向N端,实验波形及结果如图5所示。故障点设置在F1处,两端测量的电流波形如图5a所示。
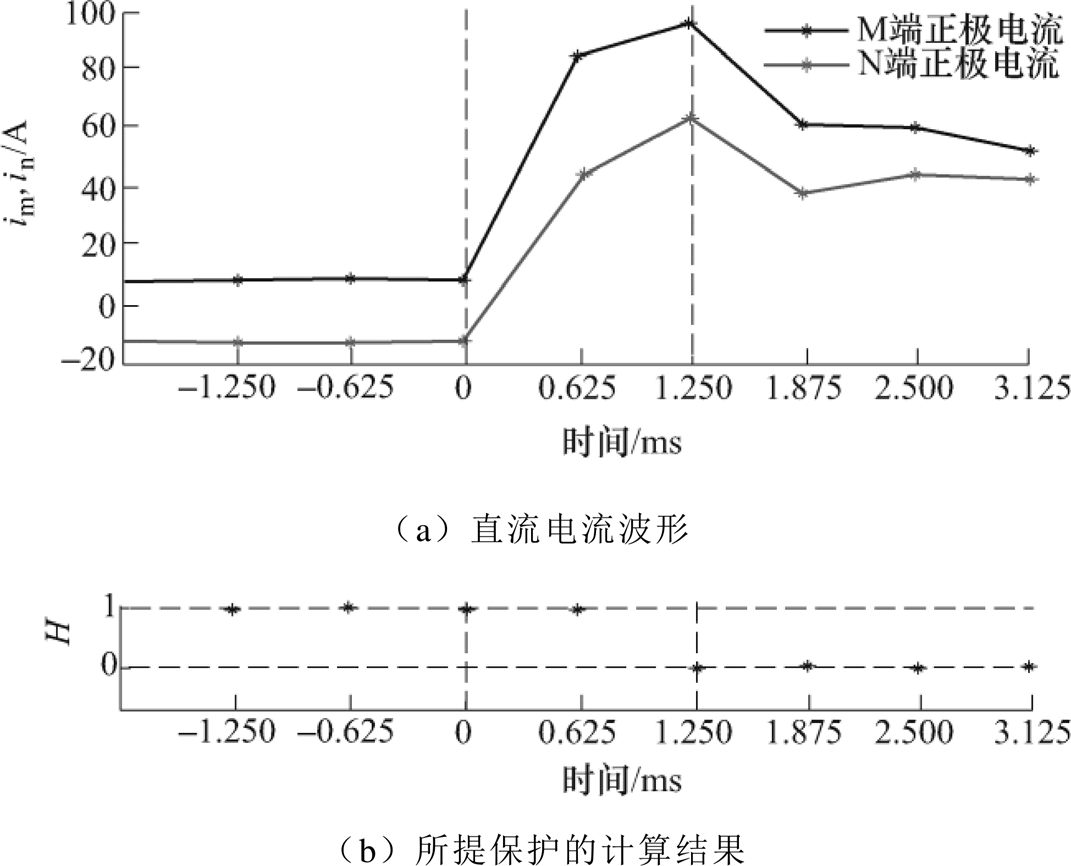
图5 实验波形及结果
Fig.5 Experiment waveforms and results
从图5a中可知,正常运行状态(t<0ms 下,M端电流为正,N端电流为负,无电流波形形态变化,即两侧电流反相关。故障后(t>0ms),两端电流都迅速上升且波形形变方向一致,即两侧电流正相关。无论故障前后,两端电流波形的形变特征、极性特征与理论分析均一致,验证了上文分析的正确性。将测量数据在Matlab中利用t检验算法进行假设检验,其数据窗长为1.25ms(每3个采样点计算1次相关性),如图5b所示,从图中可以看出故障后(t>0ms)1.25ms,H=0(故障后两个采样点),则两侧电流正相关。这不仅验证所提保护的准确性,同时也证明了所提保护具有较好的速动性。
下,M端电流为正,N端电流为负,无电流波形形态变化,即两侧电流反相关。故障后(t>0ms),两端电流都迅速上升且波形形变方向一致,即两侧电流正相关。无论故障前后,两端电流波形的形变特征、极性特征与理论分析均一致,验证了上文分析的正确性。将测量数据在Matlab中利用t检验算法进行假设检验,其数据窗长为1.25ms(每3个采样点计算1次相关性),如图5b所示,从图中可以看出故障后(t>0ms)1.25ms,H=0(故障后两个采样点),则两侧电流正相关。这不仅验证所提保护的准确性,同时也证明了所提保护具有较好的速动性。
由于物理硬件的实验平台系统架构相对简单,重在验证保护对于实际故障时的适应性,从而验证保护理论的正确性,无法全面评估所提保护的性能,因此本文在PSCAD/EMTDC中搭建如图6所示的±10kV柔性直流配电系统示意图,以进一步验证保护性能,其具体参数见附录中附表1和附表2。该仿真以测量点1、2作为所提保护的测试对象,采样频率设为10kHz,窗长为0.5ms。图6中,F1、F3表示区外双极短路故障,F2表示区内双极短路故障。
在区内F2处设置双极短路故障,故障发生时刻为0.8s,以正极两端所测电流为例,区内F2双极故障下两侧正极电流波形如图7所示。故障瞬间,故障线路两端所测电流i12、i21迅速上升且波形形变方向与极性一致,如图7a所示;而区外两条非故障的直流线路电流波形虽也发生形变,但如第1节的理论分析,其两端电流波形形变方向与极性都相反,如图7b的电流i63、i36和图7c的电流i54、i45所示。

图6 直流配电系统示意图
Fig.6 Schematic diagram of DC distribution system
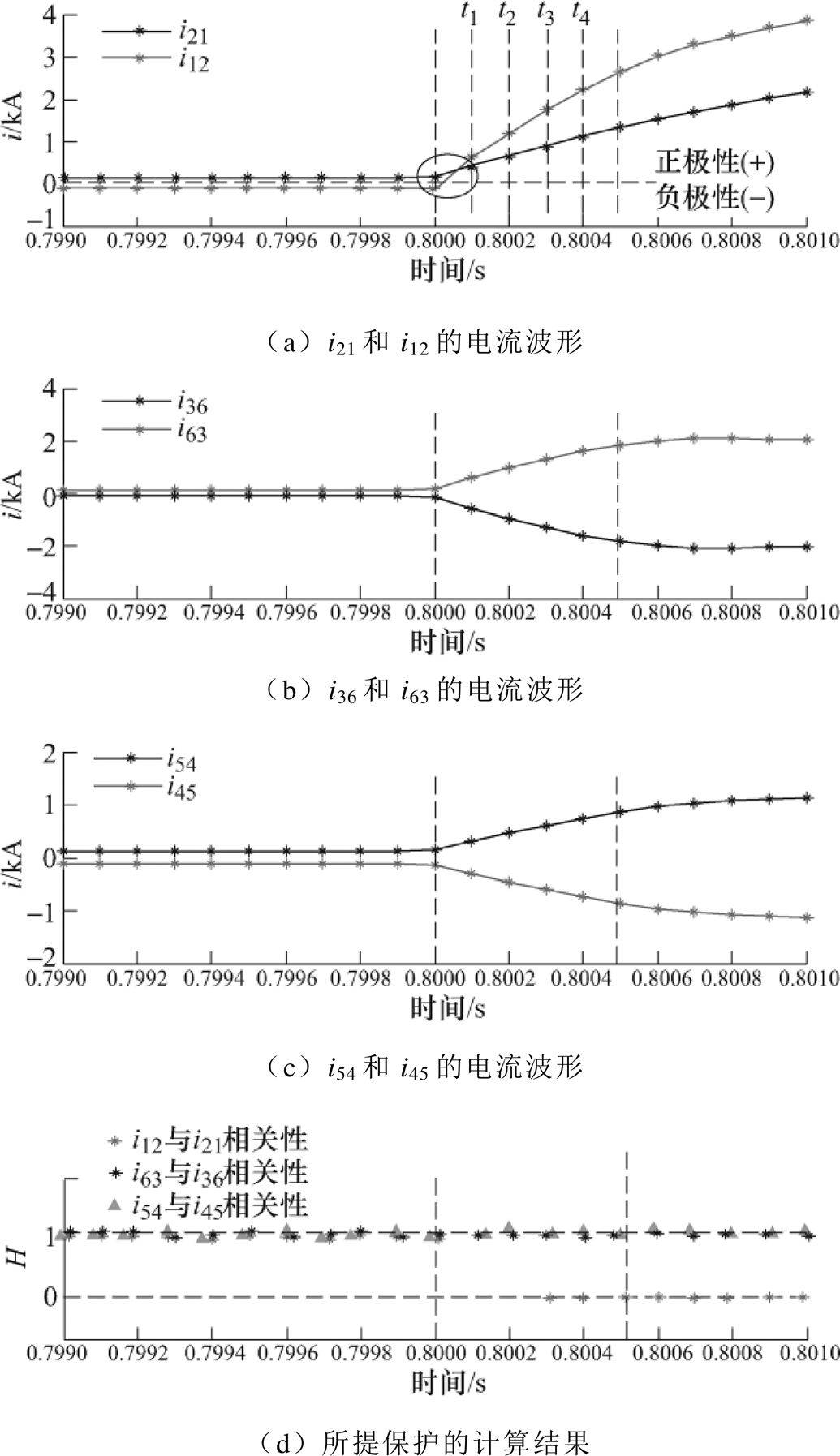
图7 区内F2双极故障下两侧正极电流波形
Fig.7 Current wave of two sides for internal pole-pole fault F2
故障后0.5ms,区内两侧保护通过H值的结果识别出区内故障,如图7d中i12与i21相关性所示,其H值为0,满足区内故障的判据,验证了所提保护的速动性与可靠性。图7d中i54与i45相关性和i63与i36相关性数值为非故障线路所检测的H值结果,其值一直为1,反映了非故障线路两端电流反相关。
4.2.1 过渡电阻的影响
为分析过渡电阻故障的影响,设置故障时的过渡电阻为5W、10W、15W 和20W。表2给出了F1处发生上述过渡电阻时的H值。
表2 F1过渡电阻故障时的两端电流的相关性
Tab.2 Correlation of two sides for pole-pole fault F1 with different high resistances
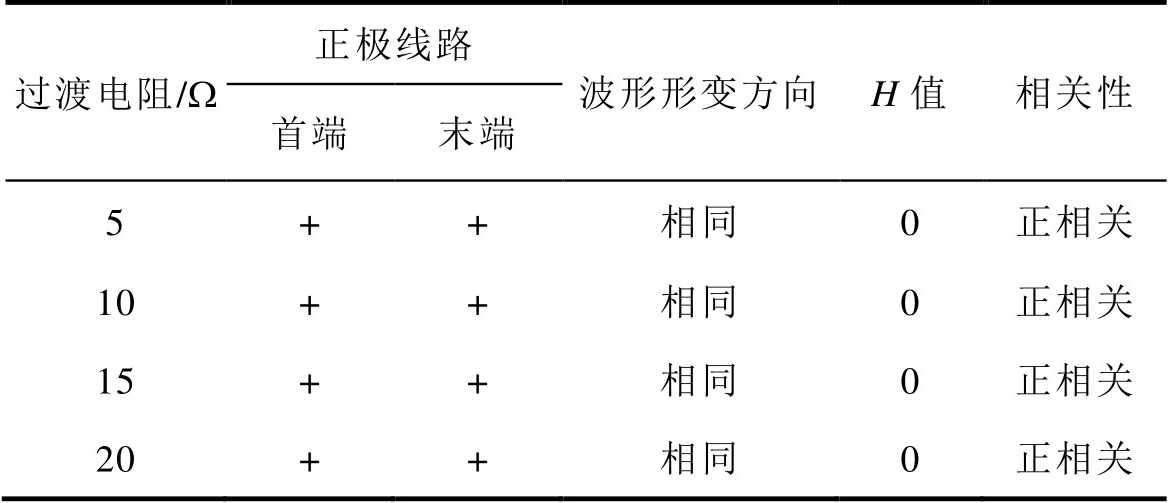
过渡电阻/W正极线路波形形变方向H值相关性 首端末端 5++相同0正相关 10++相同0正相关 15++相同0正相关 20++相同0正相关
由表2可知,四种过渡电阻下均满足假设H=0,即正相关的假设成立,保护可以有效可靠地动作,从而验证了所提保护具有很强的耐受过渡电阻能力。与常规基于电流变化率故障判别方法相比,所提方法的抗过渡电阻能力较高,主要因为所提保护动作性能由两侧暂态电流的相关性决定,并不直接依赖于故障电流的大小。而基于电流变化率故障判别方法受过渡电阻影响且整定时需要对绝对值大小、正负进行故障区域判断[11]。
4.2.2 线路分布式电容的影响
直流线路内部发生故障后,以单个p 型线路为例的线路分布电容充放电过程故障回路如图8所示。
从图8中可以看出,整个过程分为四种:两个电容同时放电、两个电容同时充电、两个电容一个放电(充电)一个充电(放电)。因此,根据图8中四种充放电过程,可写出4个公式分别为

图8 线路分布电容充放电过程的故障回路
Fig.8 Fault circuit of charging or discharging process of distributed capacitance
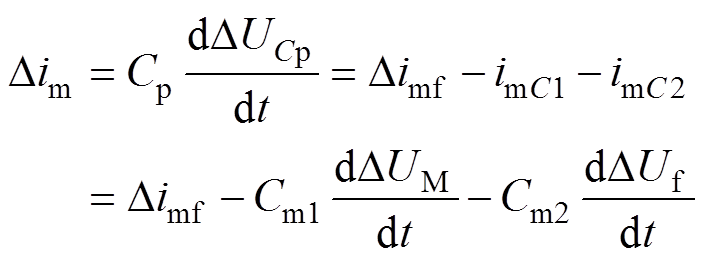 (3)
(3)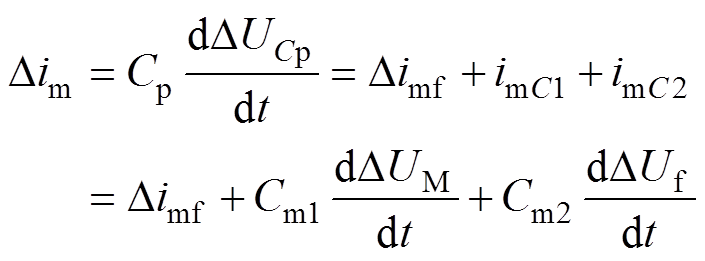 (4)
(4)
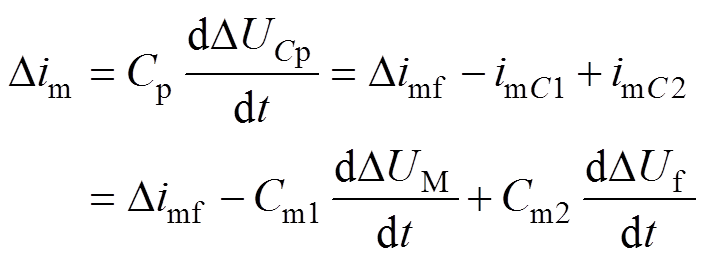 (5)
(5)
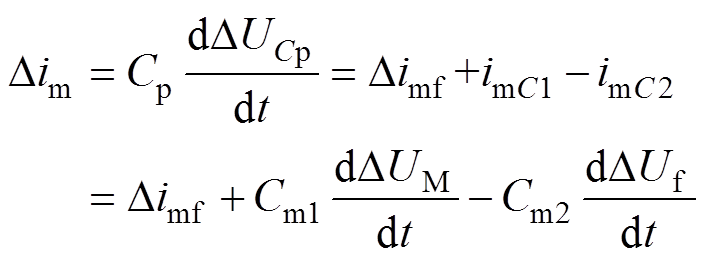 (6)
(6)式中,DUCp为换流器等效电容压降;DUM为测量点M的压降;DUf为故障点压降;im为M端所测的电流;imC为线路分布式电容电流;imf为故障点故障电流;imCp为换流器放电电流;Cp为换流器内部等效电容;Cm、Cn为线路分布式电容;Rm、Lm和Rn、Ln分别为M端和N端距离故障点的阻抗。根据式(3)~式(6)综合分析可知,直流线路内部发生故障后,分布式电容的暂态电流特性(充放电过程)会直接造成直流暂态电流波动。尤其当多个p型线路串联时,充放电电流通路较多,过程更为复杂且无法直接利用数学模型解析出直流暂态电流波动规律。
以F1处故障为例,将线路分布式电容增大到原来10倍,分布式电容增大时F1故障的两侧电流波形如图9所示,F1双极故障下不同分布式电容的相关性结果如图10所示。
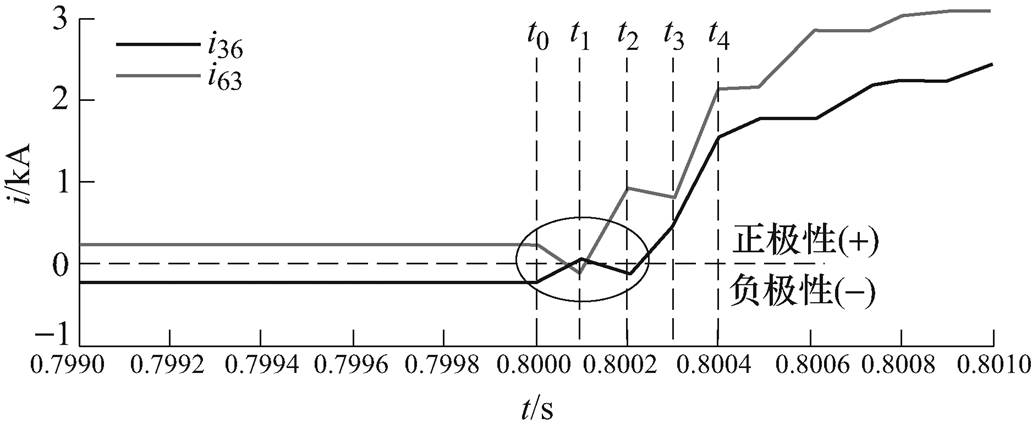
图9 分布式电容增大时F1故障的两侧电流波形
Fig.9 Current waveforms of two sides under the five times line distributed capacitance when the F1 fault
故障时(区内故障)由于负荷电流的影响,在故障初始存在一个过渡过程,如图9中t0~t1区间的i36所示。因此,传统以正负极性确定方向的纵联保护通常会将保护动作门槛设为额定电流的1.2~1.5倍[12],以避免稳定运行时负荷电流较小或没有负荷电流时出现零漂现象导致的保护误动。从图9中看出两侧电流在t0~t2段出现振荡且电流方向、极性均相反,此时可能会导致极性纵联保护无法达到动作门槛,降低了动作可靠性。综上,故障后分布式电容的暂态电流特性会造成传统以正负极性确定方向的纵联保护动作性能下降。
假设t0~t4区间受分布式电容影响后的数据为x={x0, x1, x2, x3, x4},y={k0x0, k1x1, k2x2, k3x3, k4x4}并将其代入式(1)计算检验统计量t为
 (7)
(7)F1双极故障下不同分布式电容的相关性结果如图10所示。在假设检验的过程中,计算检验统计量t时是将两侧原始的采集数据(电流)进行取均值、方差处理后才进行计算的,因此减小了原始采样数据的幅值波动(分布式电容影响),使其数据归一化,同时没有影响两组独立数据的整体变化趋势。从图10的计算结果可知,故障后两端暂态电流的H值均为0,非故障线路H值均为1,因此保护可以正确动作,即线路分布式电容不会影响所提保护的结果。
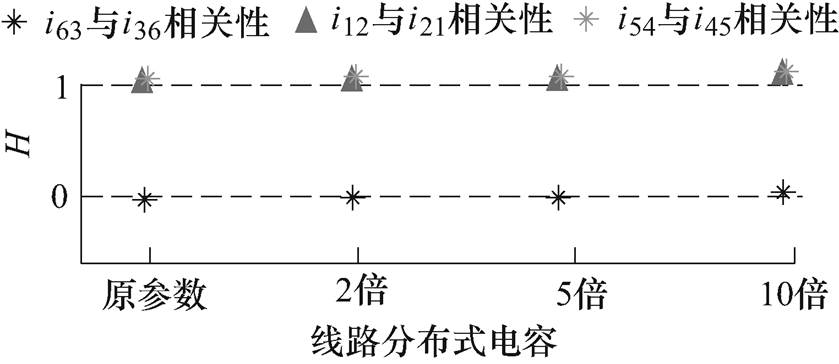
图10 F1双极故障下不同分布式电容的相关性结果
Fig.10 Correlation results of pole-pole fault F1 with different line distributed capacitance
4.2.3 通信延时的影响
在实际工程应用中,双端量测量一般采用的同步方法是乒乓对时法。乒乓对时法的同步精度与收发信道的传输时差有关。由于直流保护的采样频率通常为10kHz,换流器闭锁时间在故障后的2~5ms,除去继电器动作时间是3ms,留给保护CPU计算的数据仅有1ms左右,即10个采样点。因此,本文考虑了最大通信延时0.3ms,即延时3个采样点。常规的差动保护需要连续满足判据4次(4个采样点)后保护才可以出口,而由于通信延时的影响,保护判据可能无法满足连续判别4次。
为测试所提保护原理在较大同步误差下的性能,表3给出了不同通信延时情况下F2处故障时的保护算法测试结果,所有测试都没有进行通信再同步。可见,对于不同的通信延时,电流相关性检验的保护可以准确判别故障位置。其原因在于所提保护主要是利用故障发生后故障线路两侧电流波形形变特征、极性特征存在规律变化为基础,通过t检验算法对两侧全电流信号进行相关性检验并构造了保护动作判据。换句话说,故障后两侧电流的大小、方向、极性、突变特性都可用相关性理论进行统一描述,刻画的是两侧电流波形整体的变化趋势。虽然通信延时导致两侧电流的幅值不对应,但两侧电流波形的整体变化趋势并没有发生改变。因此所提保护提升了对于数据较短的暂态故障电流利用效率,在一定程度上不受通信延时的影响。
表3 不同通信延时保护测试结果
Tab.3 Test results of protections under synchronization error

故障位置通信延时/ msH值 i12与i21i36与i63i54与i45 F20.11(区外故障)0(区内故障)1(区外故障) 0.21(区外故障)0(区内故障)1(区外故障) 0.31(区外故障)0(区内故障)1(区外故障)
4.2.4 噪声的影响
在故障电流中分别加入20dB、40dB和60dB的白噪声[21],测试所提保护的抗噪声能力。同样以故障点F1双极短路故障为例,测试结果见表4。从表4可知,在不同噪声下,所提保护计算的H值均为0,即保护可以正确动作。
表4 不同噪声下F1故障时的两端电流的相关性
Tab.4 Correlation of two sides for pole-pole fault F1 under different noise
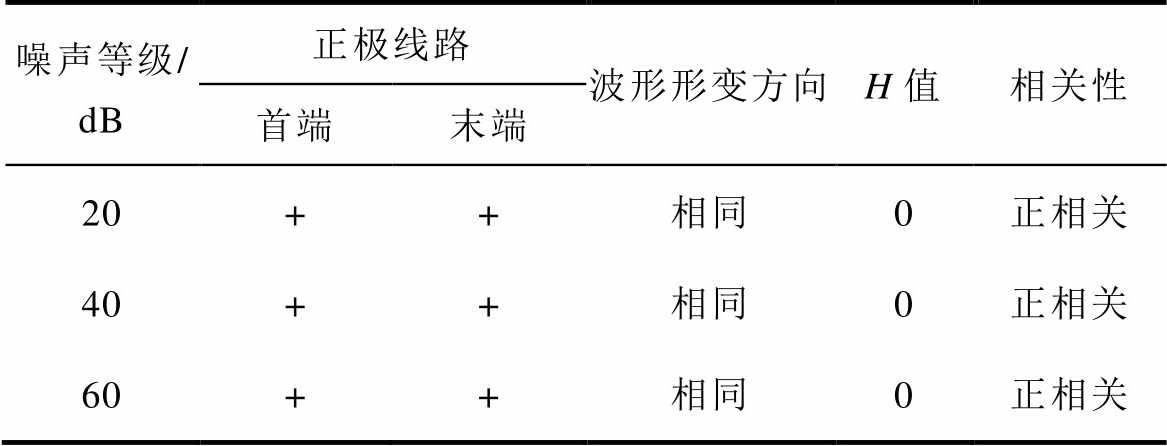
噪声等级/dB正极线路波形形变方向H值相关性 首端末端 20++相同0正相关 40++相同0正相关 60++相同0正相关
F1双极故障下两侧正极电流波形(含噪声)如图11所示。由于噪声的等级是以信噪比决定,信噪比越小,噪声越大。所以20dB的噪声在直流系统中是最严重情况[20]。因此本文给出20dB噪声下的仿真结果。从图11b中可以得知,噪声会影响直流暂态电流波形形变,使其幅值、方向和极性发生波动。尤其是对于采用电流突变特征的保护影响最大,在实际工程应用当中,计算故障电流的突变特性大多采用电流差分的方法,即Di(t)=i(t)-i(t0),其中t0是系统稳定运行时的电流。假设采样数据点i(t)恰巧是噪声点,那么计算出的Di(t)是不准确的,可能会引起保护的误动或者拒动。
而从图11d可以看出,故障发生0.3ms后H值为0,保护算法仍能可靠识别故障,验证了所提方法相比于传统的纵联保护具有较强的抗噪声能力。本保护原理是通过检验线路两端故障电流的相关性判别故障,在保护计算过程中,计算检验统计量t时是将两侧采集的原始数据(电流)进行一定的数学运算(取均值、算方差等),减小了原始采样数据的幅值波动(噪声影响),使其数据归一化,同时没有影响两组独立数据的整体变化趋势,极大地降低了噪声导致的采样数据幅值波动的情况,因此理论上不会影响保护的正确动作。
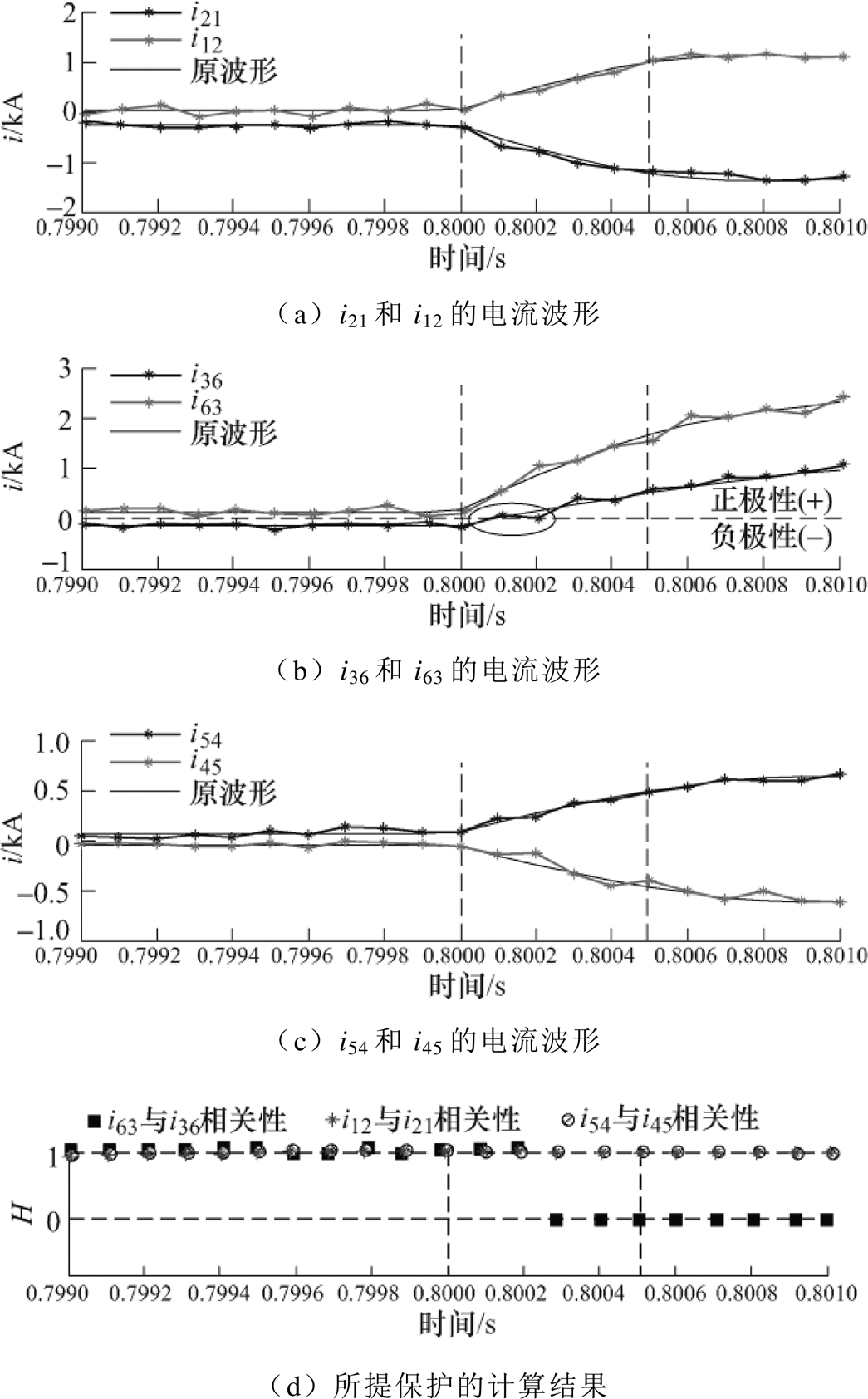
图11 F1双极故障下两侧正极电流波形(含噪声)
Fig.11 Current waveforms of two sides for fault F1 (noise)
4.2.5 CT误差的影响
关于电流互感器(Current Transformer, CT)测量误差,实际应用中电流互感器对直流电流进行采样后,使用嵌入式数字继电器中的模数转换器将其转换为数字形式,然后进行计算。因此,在互感器测量电流的过程中,测量装置的安装或配线不当、周围环境条件的变化等因素都会造成测量数据出现误差。但根据保护级电流互感器的技术要求,电流互感器的测量误差最大不得超过10%。因此,为了分析CT误差对该保护原理的影响,在仿真波形中添加了10%的随机误差,CT测量误差下F1故障时的两端电流的相关性见表5。
由表5可知,不同CT测量误差下均满足假设H=0,即正相关的假设成立,保护可以有效可靠地动作,从而验证了所提保护不受CT测量误差的影响。在幅值误差为10%时,虽然波形会产生畸变,但只能影响幅值的变化,而所提保护原理是通过检验线路两端故障电流的相关性判别故障,与幅值无关。因此理论上不会影响保护的正确动作。
表5 CT测量误差下F1故障时的两端电流的相关性
Tab.5 Correlation of two sides for pole-pole fault F1 under measurement error of CT

随机测量误差(%)正极线路波形形变方向H值相关性 首端末端 0++相同0正相关 2++相同0正相关 5++相同0正相关 10++相同0正相关
为了进一步验证所提保护不受CT饱和的影响,本文假设区内F1故障时存在一端的CT发生饱和(持续饱和状态),区内F1双极故障下一端CT饱和时H值计算结果如图12a所示。从图12a中看出,当故障0.3ms后,测量电流i63的CT发生饱和现象(虚线),与未饱和(实线)的电流i63相比,其幅值变小且成平顶状态,但变化方向与极性相同,波形整体变化趋势没有发生变化。因此,当CT饱和时不会影响相关性的计算,其结果如图12b所示,在故障后0.3ms后,H值依然变为0,即保护可以正确动作。其主要原因在于本文提出的方法主要是刻画两侧电流波形整体的变化趋势。虽然直流CT饱和后会影响全电流的幅值,但两侧电流的整体波形变化趋势不会变化。因此本文所提方法不受CT饱和的影响。
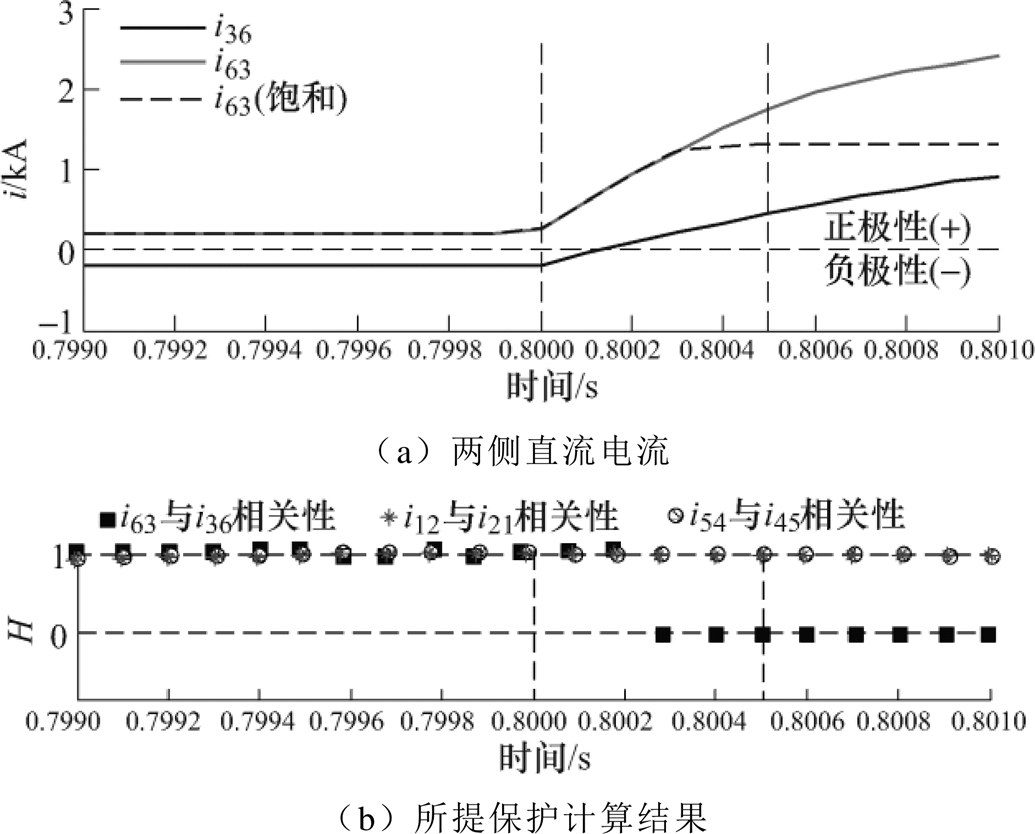
图12 区内F1双极故障下一端CT饱和时H值计算结果
Fig.12 H values of internal pole-pole fault F1 under saturation of one current transformer
本文提出了一种基于故障全电流相关性检验的柔性直流配电线路纵联保护。通过t检验(假设检验的一种)算法对两侧全电流信号进行相关性检验,即对两侧全电流信号的幅值大小、方向、极性、突变特性进行统一描述,进而构造了保护动作判据。经物理实验与数字仿真验证结果表明所提保护具有以下优点:
1)该方法满足柔性直流配电系统的保护需求,解决了现有直流线路保护很难同时满足不受线路长短、过渡电阻、线路分布式电容、噪声、通信延时的影响。
2)与传统电流差动、方向(极性)纵联保护相比,该原理不受分布式电容、通信弱同步的影响,可靠性较高且不需要在保护测量处增加方向元件。
3)与常规电流突变量保护相比,具有抗大过渡电阻故障的能力。
4)当面对多端且复杂的直流配电系统时,可根据系统拓扑结构的保护需求与单端量保护相互配合,形成整体的保护方案,所提保护有较好的适应性。
本文所研究柔性直流配电系统中,换流器和直流线路参数分别见附表1、附表2。2个AC-DC变换环节均采用具有直流故障电流隔离能力的CDSM-MMC,其中CDSM-MMC1和CDSM-MMC2的元件参数相同,具体如下:桥臂电抗为15mH,子模块电容为300mF,电平数为五。2个DC-DC变换环节均采用基于双主动全桥(Dual- Active Bridge, DAB)串并联的直流固态换流器(DC Solid State Transformer, DCSST),拓扑结构如附图1所示。其中,DC-DC1和DC-DC2的元件参数相同,具体如下:高压侧电容为500mF,低压侧电容为150mF,高频变压器额定频率和漏感分别为2 200Hz和12mH。附表3为临界值t。
附表1 换流器参数
App.Tab.1 Parameters of converters
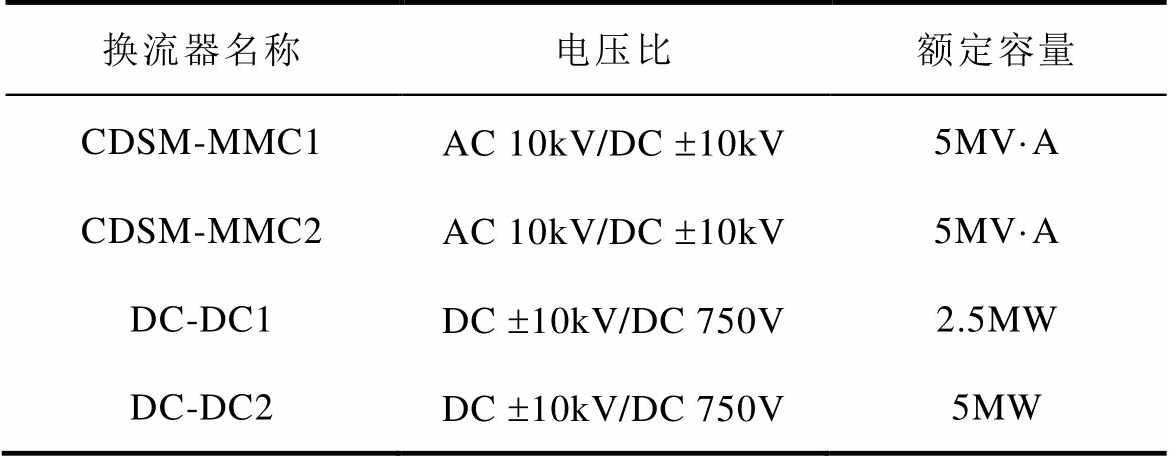
换流器名称电压比额定容量 CDSM-MMC1AC 10kV/DC ±10kV5MV·A CDSM-MMC2AC 10kV/DC ±10kV5MV·A DC-DC1DC ±10kV/DC 750V2.5MW DC-DC2DC ±10kV/DC 750V5MW
附表2 直流线路参数
App.Tab.2 Parameters of DC lines
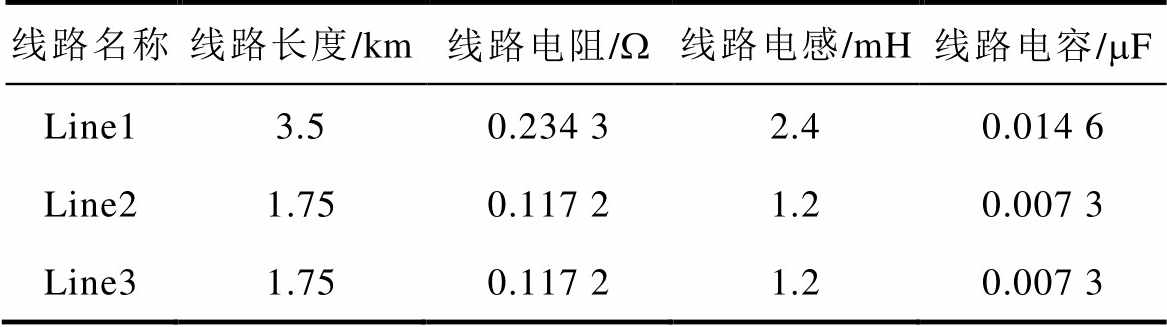
线路名称线路长度/km线路电阻/W线路电感/mH线路电容/mF Line13.50.234 32.40.014 6 Line21.750.117 21.20.007 3 Line31.750.117 21.20.007 3
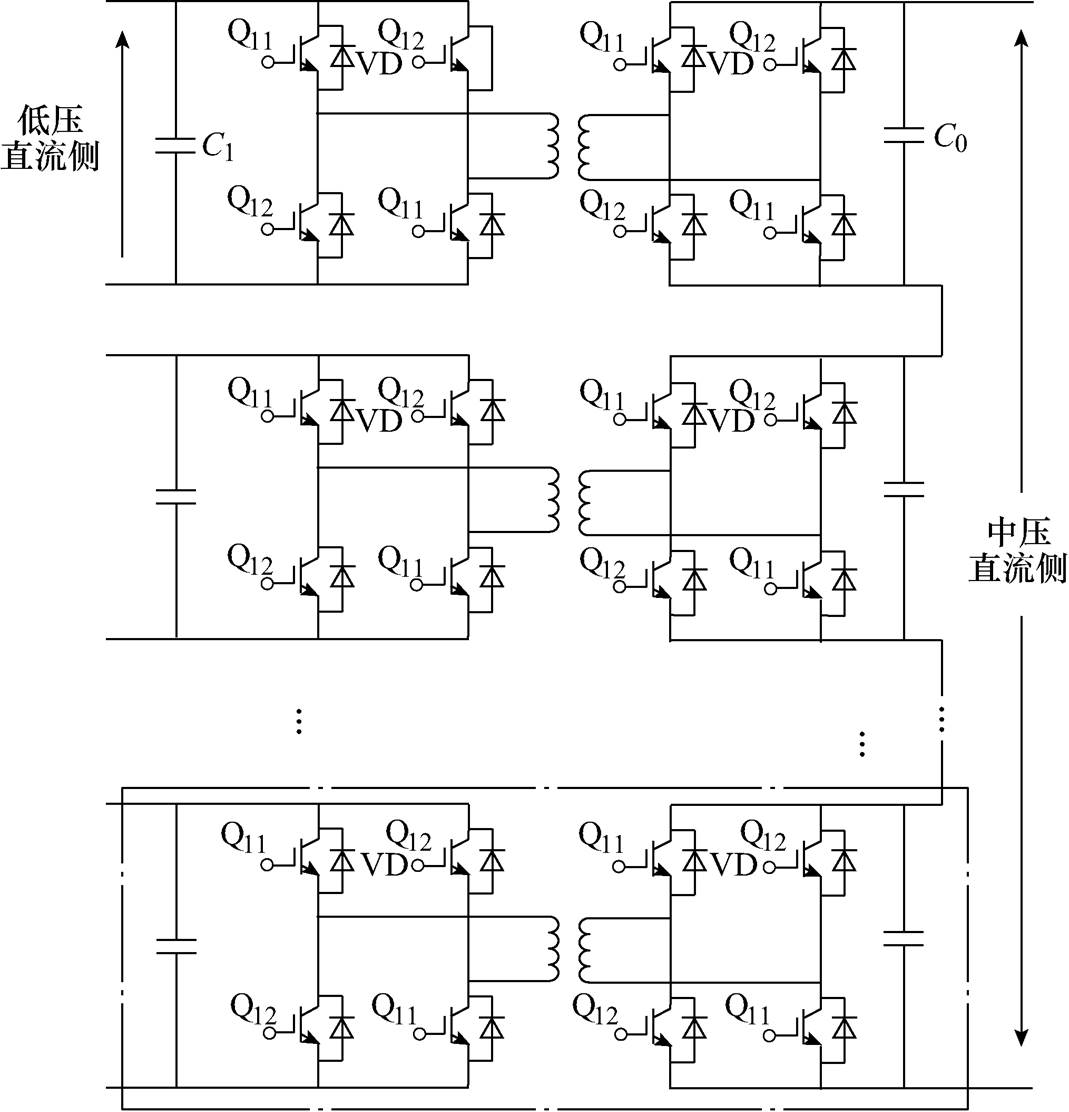
附图1 DAB型直流固态换流器拓扑结构
App.Fig.1 Topology of DCSST
附表3 临界值t
App.Tab.3 t critical value
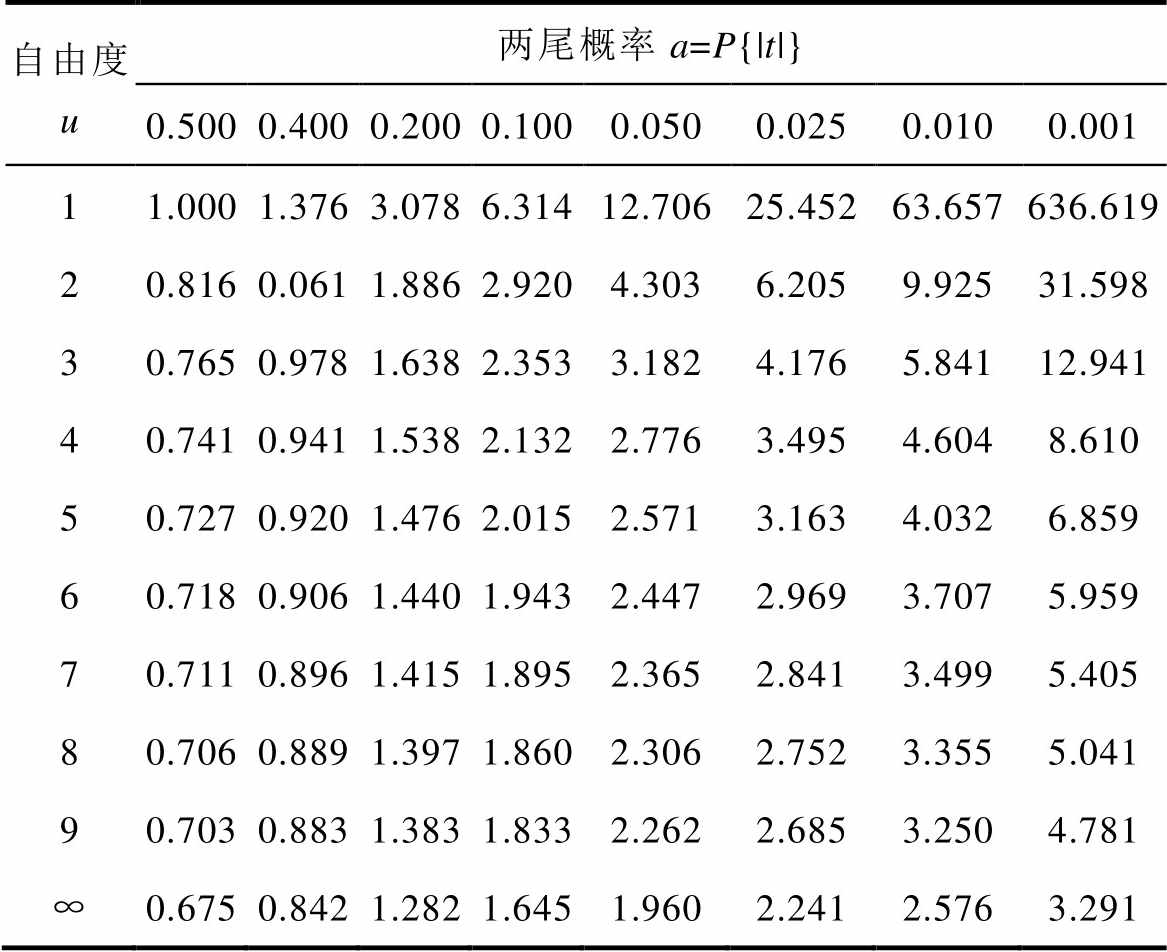
自由度u两尾概率a=P{|t|} 0.5000.4000.2000.1000.0500.0250.0100.001 11.0001.3763.0786.31412.70625.45263.657636.619 20.8160.0611.8862.9204.3036.2059.92531.598 30.7650.9781.6382.3533.1824.1765.84112.941 40.7410.9411.5382.1322.7763.4954.6048.610 50.7270.9201.4762.0152.5713.1634.0326.859 60.7180.9061.4401.9432.4472.9693.7075.959 70.7110.8961.4151.8952.3652.8413.4995.405 80.7060.8891.3971.8602.3062.7523.3555.041 90.7030.8831.3831.8332.2622.6853.2504.781 ∞0.6750.8421.2821.6451.9602.2412.5763.291
参考文献
[1] 肖湘宁, 廖坤玉, 唐松浩, 等. 配电网电力电子化的发展和超高次谐波新问题[J]. 电工技术学报, 2018, 33(4): 707-720.
Xiao Xiangning, Liao Kunyu, Tang Songhao, et al. Development of power-electronized distribution grids and the new supraharmonics issues[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 707- 720.
[2] Monadi M, Zamani M A, Candela J I, et al. Protection of AC and DC distribution systems embedding distributed energy resources: a com- parative review and analysis[J]. Renewable and Sustainable Energy Reviews, 2015, 51: 1578-1593.
[3] 戴志辉, 葛红波, 严思齐, 等. 柔性直流配电网故障分析[J]. 电工技术学报, 2018, 33(8): 1863-1874.
Dai Zhihui, Ge Hongbo, Yan Siqi, et al. Fault analysis of flxible DC distribution system[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(8): 1863-1874.
[4] 苏见燊, 郭敬东, 金涛. 柔性直流电网中直流故障特性分析及线路故障重启策略[J]. 电工技术学报, 2019, 34(增刊1): 352-359.
Su Jianshen, Guo Jingdong, Jin Tao. DC fault characteristics and line fault recovery strategy in flexible DC power network[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 352-359.
[5] Zheng Xiaodong, Tai Nengling, Wu Z, et al. Harmonic current protection scheme for voltage source converter-based high-voltage direct current transmission system[C]//Power & Energy Society General Meeting, Denver, CO, 2015, DOI: 10.1109/ PESGM.2015.7285723.
[6] 郭贤珊, 李探, 李高望, 等. 张北柔性直流电网换流阀故障穿越策略与保护定值优化[J]. 电力系统自动化, 2018, 42(24): 196-202.
Guo Xianshan, Li Tan, Li Gaowang, et al. Fault ride-through strategy and protection setting optimi- zation of converter valve for Zhangbei VSC-HVDC grid[J]. Automation of Electric Power Systems, 2018, 42(24): 196-202.
[7] 汤广福. 基于电压源换流器的高压直流输电技[M]. 北京: 中国电力出版社, 2010.
[8] 于洋, 孙学锋, 高鹏, 等. 高压直流输电线路暂态保护分析与展望[J]. 电力系统保护与控制, 2015, 43(22): 127-133.
Yu Yang, Sun Xuefeng, Gao Peng, et al. Analysis and prospect on transient protection for HVDC trans- mission lines[J]. Power System Protection and Control, 2015, 43(22): 127-133.
[9] 张颖, 邰能灵, 徐斌. 高压直流线路纵联行波方向保护[J]. 电力系统自动化, 2012, 36(21): 77-80.
Zhang Ying, Tai Nengling, Xu Bin. Travelling wave based pilot directional protection for HVDC line[J]. Automation of Electric Power Systems, 2012, 36(21): 77-80.
[10] 孔飞, 张保会, 王艳婷. 基于行波波形相关性分析的直流输电线路纵联保护方案[J]. 电力系统自动化, 2014, 38(20): 108-114.
Kong Fei, Zhang Baohui, Wang Yanting. A new pilot protection scheme for HVDC transmission lines based on waveform correlation analysis of traveling wave[J]. Automation of Electric Power Systems, 2014, 38(20): 108-114.
[11] Meghwani A, Srivastava S, Chakrabarti S. A non-unit protection scheme for DC microgrid based on local measurements[J]. IEEE Transactions on Power Delivery, 2017, 32(1): 172-181.
[12] 高淑萍, 索南加乐, 宋国兵. 利用电流突变特性的高压直流输电线路纵联保护新原理[J]. 电力系统自动化, 2011, 35(5): 52-56.
Gao Shuping, Suonan Jiale, Song Guobing. A new pilot protection principle for HVDC transmission lines based on current fault component[J]. Auto- mation of Electric Power Systems, 2011, 35(5): 52-56.
[13] 杨帆. 谈GB/T 30137-2013《电能质量电压暂降与短时中断》的贯彻 访中国电力科学研究院教授级高工林海雪[J]. 电气应用, 2015, 34(11): 6-9.
Yang Fan. Discussion on power quality-voltage dips and short interruptions (GB/T 30137-2013)[J]. Electrotechnical Application, 2015, 34(11): 6-9.
[14] 范志华, 苗世洪, 刘子文, 等. 模块化多电平换流器子模块故障特性分析与解耦控制策略[J]. 电工技术学报, 2018, 33(16): 3707-3718.
Fan Zhihua, Miao Shihong, Liu Ziwen, et al. Modular multilevel converter sub-module fault characteristics analysis and decoupling control strategy[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(16): 3707-3718.
[15] 蔡静, 董新洲. 高压直流输电线路故障清除及恢复策略研究综述[J]. 电力系统自动化, 2019, 43(11): 181-190.
Cai Jing, Dong Xinzhou. Overview on research of fault clearing and recovery strategy for HVDC transmission lines[J]. Automation of Electric Power Systems, 2019, 43(11): 181-190.
[16] 丁然, 梅军, 管州, 等. 适用于MMC型直流变压器的直流故障主动限流控制方法[J]. 电力系统自动化, 2018, 42(21): 131-142.
Ding Ran, Meijun, Guan Zhou, et al. Active current limiting control method for DC fault of MMC based DC transformer[J]. Automation of Electric Power Systems, 2018, 42(21): 131-142.
[17] 郝瑞祥, 杨晓峰, 薛尧, 等. 一种具有直流故障限流能力的模块化多电平换流器[J]. 电工技术学报, 2017, 32(6): 172-180.
Hao Ruixiang, Yang Xiaofeng, Xue Yao, et al. A novel modular multilevel converter with DC fault current limiting capability[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 172-180.
[18] 张良圣, 倪永年. t检验法用于评价中药色谱指纹图谱的相似度[J]. 分析科学学报, 2007, 23(5): 511- 514.
Zhang Liangsheng, Ni Yongnian. Application of t-test method to similarity analysis of chromato- graphic fingerprint of herbal medicine[J]. Journal of Analytical Science, 2007, 23(5): 511-514.
[19] 申希平, 丁建生, 李娟生, 等. 在SPSS中利用均数和标准差做两独立样本t检验[J]. 现代预防医学, 2007(21): 4066-4067, 4069.
Shen Xiping, Ding Jiansheng, Li Juansheng, et al. 2- independent-samples t-test undertaking by the means of mean and standard deviation in SPSS[J]. Modern Preventive Medicine, 2007(21): 4066-4067, 4069.
[20] Carrica D, Benedetti M, Petrocelli R. Random sampling applied to the measurement of a DC signal immersed in noise[J]. IEEE Transactions on Instru- mentation & Measurement, 2001, 50(5): 1319-1323.
Pilot Protection for Flexible-DC Distribution Line Based on Correlation Test of DC Current
Abstract Because the converter is fast blocking (2~5ms) when DC line fault occurs in flexible DC distribution system, limited time and data with time-varying are available for fault area estimation. Therefore, quick fault detection and isolation of faulty section are desired in DC distribution system, which can accelerate the process of clear fault and decrease the system restoration time. This paper proposed a new pilot protection for flexible-DC distribution line based on correlation test of DC current. Based on the fault current characteristics, the t-test was adopted to calculate the correlation of transient, and then the criterion was constructed. The method uniformly describes the magnitude, direction, polarity and abrupt characteristics of total current signals on both sides, avoiding the influence of transition resistance, distributed capacitance and noise on the protection of transient signals. Hardware test and simulation results show that the proposed protection can identify internal faults with good reliability and high sensitivity, which is feasible for industry application.
keywords:Flexible DC distribution line, fault current characteristics, correlation test, t-test algorithm, fault identification
中图分类号:TM771
DOI: 10.19595/j.cnki.1000-6753.tces.190185
国家重点研发计划基金(2018YFB0904104)和国家电网公司科技项目(SGHB0000KXJS1800685)资助。
收稿日期 2019-02-25
改稿日期 2019-09-11
王聪博 男,1990年生,博士研究生,研究方向为柔性直流配电系统保护与控制。E-mail: wangcongbo107@163.com
贾 科 男,1986年生,教授,博士生导师,研究方向为电力系统保护与控制、新型配电网故障定位与系统自我恢复。E-mail: ke.jia@ncepu.edu.cn(通信作者)
(编辑 陈 诚)