 (1)
(1)摘要 该文基于模域回路中波的传播特性与频率特性研究混合线路中电缆与架空线不同比例下重合闸过电压幅值和主导频率的变化规律。通过电报方程得到相模转换的变换矩阵,计算了模域中各回路的电压传播常数。并采用电磁暂态仿真软件(EMTP)建立10kV配网非对称结构的混合线路模型,研究了不同比例的混合线路统计过电压变化规律。结果表明,随着电缆占比的增加,暂态电压的变化并非单调下降,而是出现极小值。基于模域回路的分析结果与EMTP计算结果相符。由于传播常数不受线路长度影响,当线路总长度变化时,可采用同样的方法分析不同比例混合线路的重合闸过电压变化。
关键词:电缆-架空线混合线路 重合闸过电压 模域回路 传播常数 主导频率
随着城市现代化建设步伐加快,配电线路电缆化率的要求不断提高,城市架空线路(Overhead Line, OHL)改地下电缆线路已经成为一种必然的发展趋势。由于早期建设了大量的架空线路,因此在改造过程中,配电网中必然会出现大量的电缆与架空线混合线路[1]。虽然电缆绝缘为固体绝缘材料,发生故障时多为永久性故障[2],并且重合闸操作会带来高幅值的操作过电压和短路电流冲击。但是为提高供电可靠性,在国网公司的福建、上海等地,和南方电网公司的广州、深圳等地,配网混合线路仍投入自动重合闸,并取得了一定效果[1]。但对于重合过程给设备可能带来的冲击未进行深入研究。
虽然10kV配电网电压等级较低,系统过电压耐受水平较高,但是近年来根据某市供电局报告,10kV系统曾多次发生由于操作冲击导致的电缆线路故障,甚至引起沟道起火[3]。电缆附件在安装过程中,容易产生多种微小缺陷,正常运行过程中受电、热的影响,缺陷会进一步发展[4]。当存在细微缺陷的影响,电缆线路在断路器操作过程中,高频暂态冲击电压的多次作用会造成线路的绝缘耐受能力大幅下降,对附件造成损伤[3, 5]。奥尔堡大学的F. Silva等通过研究指出,电压波在线路上来回地折反射,每次暂态过程中包含了数十次的冲击电压,因此实际线路在其服役周期内可能承受上万次的电压冲击作用[6]。徐龙等指出,10kV电缆附件在多次操作冲击作用后,进行局放测试时,缺陷处的放电量会急剧上升。以上的研究表明操作冲击对电缆线路绝缘劣化有着关键的影响,因此,研究电缆线路中的操作冲击电压的波形特征具有非常重要的意义[3]。
国内的学者对配电网混合线路重合闸的研究大多集中于故障定位、故障测距及自适应重合闸等[7-12]。电力规划部门和电力运行部门在设计、操作配电网电缆的时候,往往没有进行必要的过电压校核计算,也没有采取任何预防过电压的措施[13]。在重合闸的电磁暂态过程中,过电压冲击对电网设备绝缘产生威胁,并影响合闸后输电线路的正常运行。国内学者对于电缆及其混合线路中暂态过电压的研究多侧重于高压远距离输电线路上的雷电冲击、工频过电压以及分合闸时的过电压[14-19],对配电网混合线路重合闸过电压特性需要更深入的研究。
在输电线路电磁暂态过程中,电磁波的传播特性直接受输电线路的阻抗、导纳参数影响[20-21]。架空线与电缆的阻抗、导纳参数差异明显,因此两类线路的比例会影响电磁暂态过程。文献[14-15]中,H. Khalilnezhad等运用统计方法研究了混合线路过电压,但是对过电压的变化规律尚需要深入研究和机理上的解释。本文立足于模域回路理论,分析各独立回路的传播特性,在线路阻抗、导纳参数及电压波的传播过程的基础上,对配电网不同比例的混合线路中暂态过电压变化规律进行分析。研究结果不仅可应用于配电网,同样适用更高电压等级的混合线路,进一步完善了混合线路暂态冲击电压的特性研究。
本文首先简要介绍了输电线路中波的传播特性,引出电缆和架空线各自的模域回路及其电压波传播常数。然后在电磁暂态仿真软件(Electro-Magnetic Transients Program, EMTP)中建立了混合线路的电磁暂态模型,基于统计值研究了不同线路结构的过电压累积概率,并得到了统计过电压呈现出的规律。最后,结合暂态电压的主导频率以及第1节中的模域回路理论,从电压波的传播特性角度对不同线路比例下的受电端暂态过电压的波形特征变化规律进行了详细分析。
以电路理论为基础,输电线路上电压、电流的传播特性是描述波过程的基础理论。本节通过频域电报方程,引出电缆与架空线在模域中的独立回路,并计算得到各回路的传播常数。
在电缆系统中,频域下的电报方程可转化为式(1)和式(2)的形式[22]。当计及线路单位长度电阻R与电导G时,方程可考虑传输线的损耗。当仅考虑线路电压与电流随长度的变化关系时,将式(1)和式(2)对x进行二阶求导以及变量替换,可得如式(3)和式(4)所示的二阶微分方程[23]。
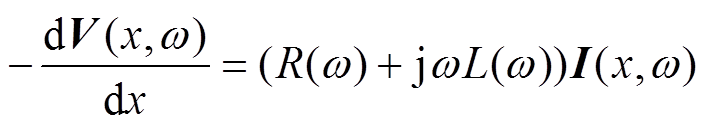 (1)
(1)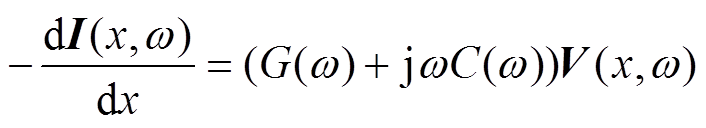 (2)
(2)
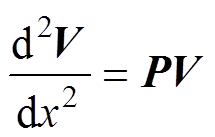
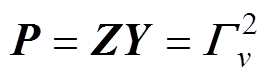 (3)
(3)
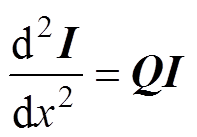
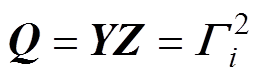 (4)
(4)式中,V为在距离x处的n维电压向量;I为该处的n维电流向量;w 为角频率;L、C分别为电感、电容;n为一个传输系统中所包含的n个金属导体;Z、Y为n×n的线路单位长度的阻抗与导纳矩阵;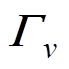 为输电线路上电压波的传播常数;
为输电线路上电压波的传播常数;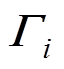 为电流波传播常数。由式(1)~式(4)可得,输电线路电压、电流的传播特性由线路的阻抗和导纳参数决定。
为电流波传播常数。由式(1)~式(4)可得,输电线路电压、电流的传播特性由线路的阻抗和导纳参数决定。
通常10kV架空线路不架设避雷线,且三相导线中仅含传输电能的金属铝导体,因此架空线的阻抗、导纳为3×3矩阵。电缆线路结构中含有金属护层或者铠装,从而形成一个维度大于3的多导体系统。无论是架空线还是电缆,其阻抗、导纳参数均取决线路的空间分布、物理几何尺寸以及绝缘材料和敷设环境的电气特性。图1所示为配电网混合线路中三芯管型电缆与架空线路的物理几何参数。需要注意,由于10kV三芯电缆内部仅含线芯铜导体和外层铠装,故Z、Y均为4×4的方阵。
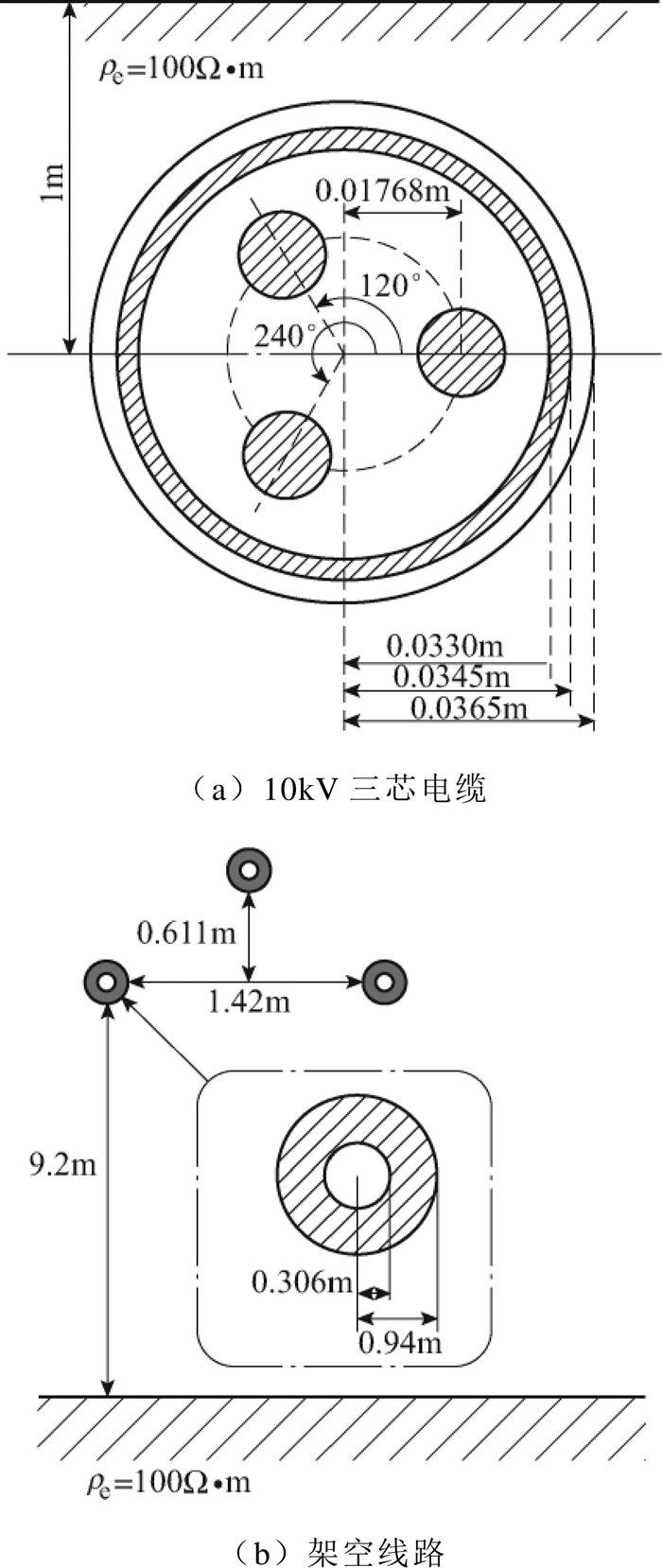
图1 10kV混合线路模型
Fig.1 Model of 10kV hybrid line
由式(1)和式(2)可知,线路Z、Y均为频率为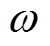 的函数。在EMTP中,J. Marti模型可模拟线路的频变特性,在架空线路中得到了广泛应用。但是电缆线路采用J. Marti模型可能会存在计算收敛性问题,因此常采用固定频率的Bergeron模型[21, 24-25]。通常重合闸过电压的频率范围高达20kHz[26],不同计算频率下的零序阻抗的频率特性如图2所示。从图中可知,在10kHz下线路零序参数与精确PI模型的拟合度最高。为精确模拟高频下的线路暂态行为,线路参数的计算频率设定为10kHz。
的函数。在EMTP中,J. Marti模型可模拟线路的频变特性,在架空线路中得到了广泛应用。但是电缆线路采用J. Marti模型可能会存在计算收敛性问题,因此常采用固定频率的Bergeron模型[21, 24-25]。通常重合闸过电压的频率范围高达20kHz[26],不同计算频率下的零序阻抗的频率特性如图2所示。从图中可知,在10kHz下线路零序参数与精确PI模型的拟合度最高。为精确模拟高频下的线路暂态行为,线路参数的计算频率设定为10kHz。
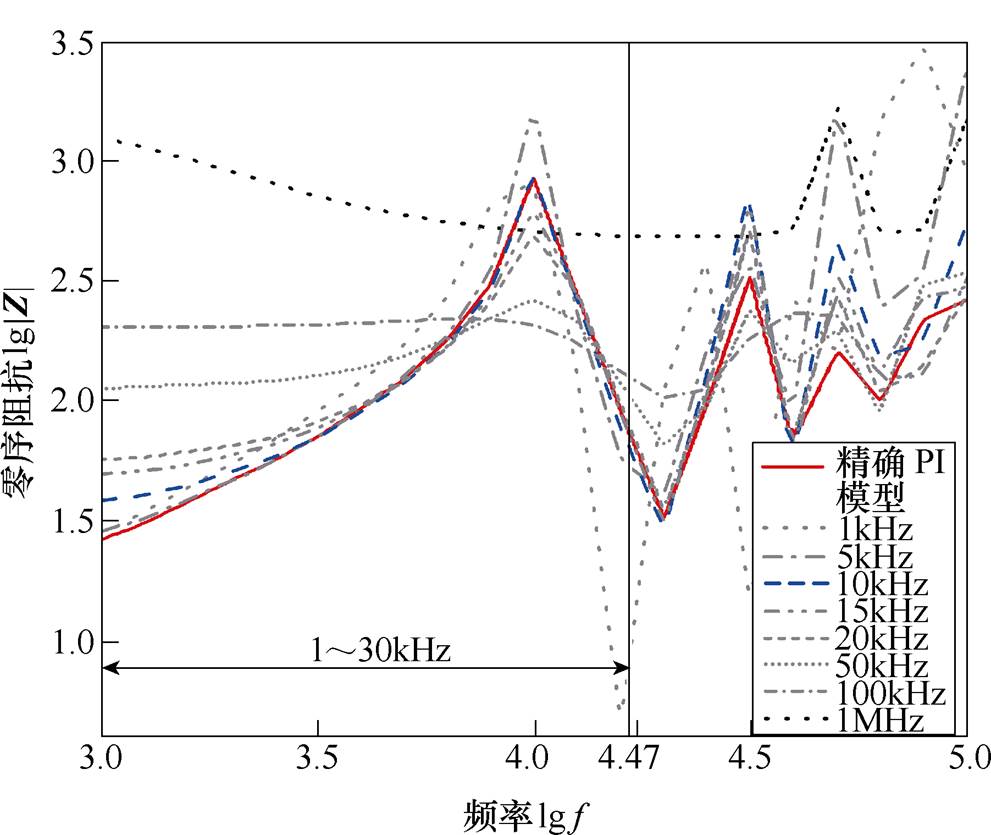
图2 不同计算频率下的零序阻抗频率特性
Fig.2 Frequency characteristic of zero sequence impedance in different calculating frequency
在多导体传输系统中,由于导体间的电磁耦合,多维度的参数矩阵Z、Y为满阵,非对角元素不为0。在矩阵为非对角阵的条件下,无法直接得到传播常数[23]。而将矩阵的特征值理论应用到参数变换中时,可以对矩阵P、Q进行对角化,将相互耦合的多导体系统转换为多个相互独立的回路,如图3、图4所示。与对称分量法或卡伦鲍厄变化相似,三相电压或电流均可表示为各独立回路电压、电流的叠加[20-27]。
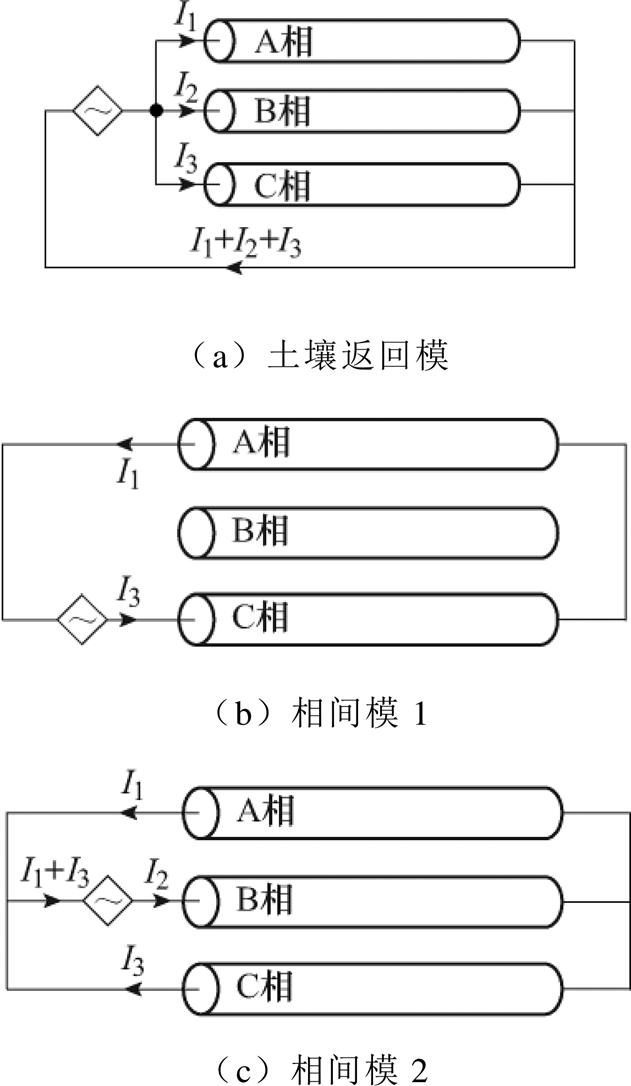
图3 架空线路模域回路
Fig.3 Return circuits of OHL in modal domain
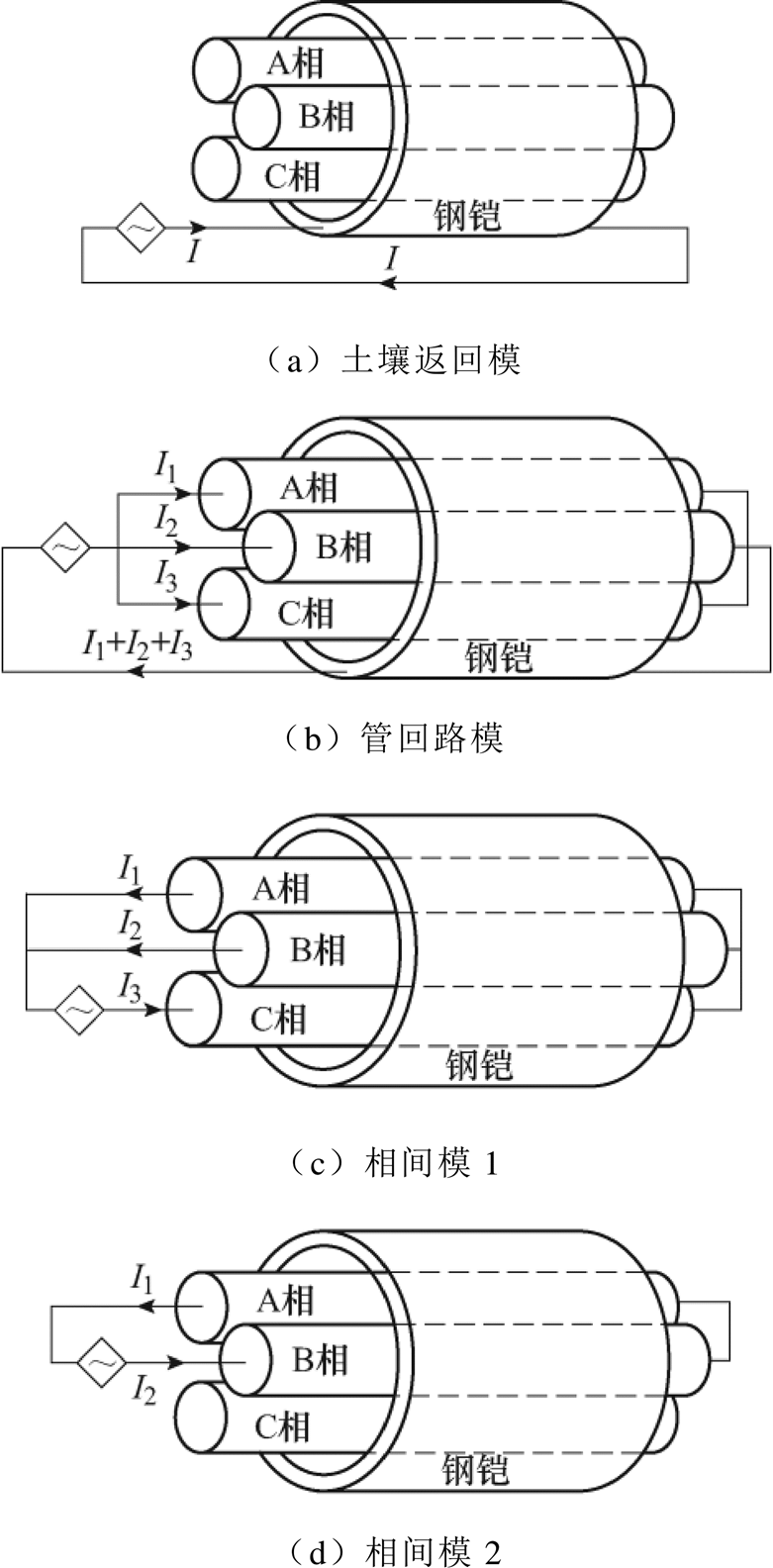
图4 管形电缆模域回路
Fig.4 Return circuits of pipe-type cable in modal domain
定义 为矩阵
为矩阵 的特征向量矩阵,
的特征向量矩阵,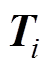 为
为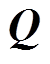 的特征向量矩阵,则可得
的特征向量矩阵,则可得
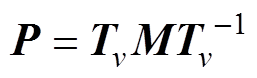 (5)
(5)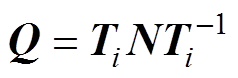 (6)
(6)
式中,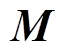 、
、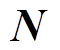 为矩阵P、Q的特征值矩阵,注意此时的
为矩阵P、Q的特征值矩阵,注意此时的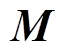 、
、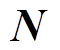 为对角阵。
为对角阵。
运用式(5)和式(6),将非对角阵P、Q转化为对角阵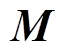 、
、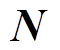 。这一过程中,用到的变换矩阵分为
。这一过程中,用到的变换矩阵分为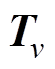 、
、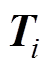 。定义式(3)和式(4)中的V、I均为相域下(三相系统)的电压和电流向量。通过变换矩阵
。定义式(3)和式(4)中的V、I均为相域下(三相系统)的电压和电流向量。通过变换矩阵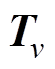 、
、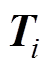 ,可得模域下的电压向量v、电流向量i[27]分别为
,可得模域下的电压向量v、电流向量i[27]分别为
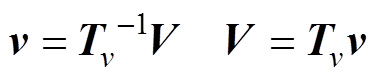 (7)
(7)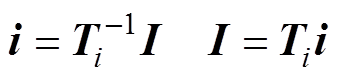 (8)
(8)
将式(5)~式(8)代入式(3)和式(4),可得模域下的电报方程,如式(9)和式(10)所示。方程中的对角阵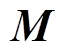 、
、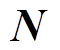 表明,多相耦合的传输线路已被转化为模域中相互独立的回路。
表明,多相耦合的传输线路已被转化为模域中相互独立的回路。
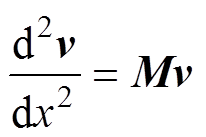 (9)
(9)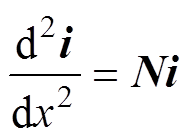 (10)
(10)
从式(3)~式(6)可见,变换矩阵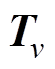 、
、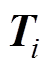 由传输线路的阻抗、导纳参数Z、Y决定。
由传输线路的阻抗、导纳参数Z、Y决定。
根据架空线、电缆参数,可计算得到架空线与电缆线路的变换矩阵,并可确定各回路电流的通路。变换矩阵中各元素均为复数,且具有频变特性。随着频率的增大,变换矩阵中元素的角度会逐渐趋于180°,因此各复数元素的虚部近似为0[6]。
1.3.1 架空线模域回路
式(11)为架空线路的变换矩阵,模域中架空线存在三个相互独立的回路。
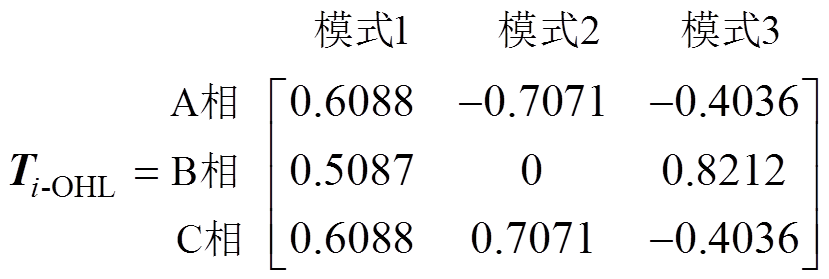 (11)
(11)通过矩阵的第一列(模式1)可得土壤返回模的电流通路,三相的各个元素均为正值,表明电流从三相线路注入,如图3a所示。注入的电流通过土壤返回,故为土壤返回模。
通过矩阵的第二列(模式2)可得相间模1的电流回路,C相和A相的矩阵元素互为相反数,且C相元素为正,表明电流从C相注入,通过A相返回,如图3b所示。
通过矩阵的第三列(模式3)可得相间模2的电流回路。其中,B相元素为正,A、C相元素为负。并且,B相元素数值等于A、C相元素数值绝对值之和。因此,相间模2表示电流从B相注入,通过A、C相返回,对应图3c所示的电流回路。在模式2和模式3中,电流仅在三相导体之间构成回路,故称为相间模。
1.3.2 电缆模域回路
与架空线不同,电缆由于自身结构中含有除线芯导体外的金属导体(护层、铠装),因而电流会通过护层或铠装构成回路,增加了模域中的电流回路数目。如式(12)所示,对于三芯电缆,模域中存在四个回路。
 (12)
(12)通过矩阵的第一列(模式1)可看出土壤返回模的电流回路。其中,A、B和C相元素均为0,钢铠的对应元素为正值,表明电流从钢铠注入,通过土壤返回,对应图4a所示的电流回路。
由于钢铠的屏蔽,三相电流通过钢铠导体返回,如式(12)第二列(模式2)所示。A、B和C三相元素均为正值,钢铠的对应元素为负值,且A、B和C三相元素的和等于钢铠元素的绝对值。以上元素的数值关系表明,电流从三相导体被注入,通过钢铠返回,构成管回路模,对应图4b所示的电流通路。
通过式(12)第三列(模式3)可得相间模式1的电流回路。C相元素为正,B和C相元素为负值,且C相元素值等于B、C相元素绝对值之和。以上关系表明电流通过C相注入,从A、B相返回,对应图4c所示的电流回路。
通过式(12)第四列(模式4)可得相间模式2的电流回路。C相元素为0,A和B相元素互为相反数,且绝对值相等。电流从B相注入,通过A相导体返回,对应图4d所示的回路。
1.3.3 传播常数
由式(5)和式(6)可知,矩阵M、N为对角矩阵,其二次方根即为模域中各回路的传播常数。采用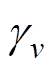 表示各回路电压传播常数;
表示各回路电压传播常数;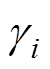 表示回路电流的传播常数。尽管矩阵P、Q不同,但是对角化后的传播常数矩阵
表示回路电流的传播常数。尽管矩阵P、Q不同,但是对角化后的传播常数矩阵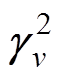 、
、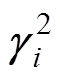 中各元素相同,因此文中电压、电流的传播常数均由
中各元素相同,因此文中电压、电流的传播常数均由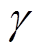 表示。传播常数
表示。传播常数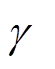 的实部
的实部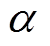 为衰减常数,虚部
为衰减常数,虚部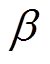 为相位常数,即
为相位常数,即
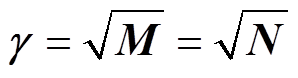 (13)
(13)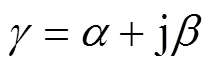 (14)
(14)
通过相位常数,计算各个回路的传播速度[23]为
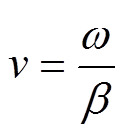 (15)
(15)分别使用架空线与电缆的阻抗、导纳参数,计算得到模域下各回路的传播常数,见表1。
表1 混合线路模域回路传播常数
Tab.1 The propagation constant of return circuit along hybrid line

输电线路传播回路衰减常数/(dB/km)传播速度/(m/ms) 架空线土壤返回模0.013 1257.08 相间模10.001 2298.21 相间模20.001 2297.92 电缆土壤返回模0.244 619.70 管回路模0.084 2176.25 相间模10.028 8180.76 相间模20.028 8180.76
本文基于陕西省的典型10kV配电网结构,在EMTP中建立了混合线路的电磁暂态模型,如图5所示。由于EMTP的计算结果可以精确反映线路上的电压电流传播特性,故将其作为本文研究混合线路电磁暂态过程的仿真计算平台[28]。
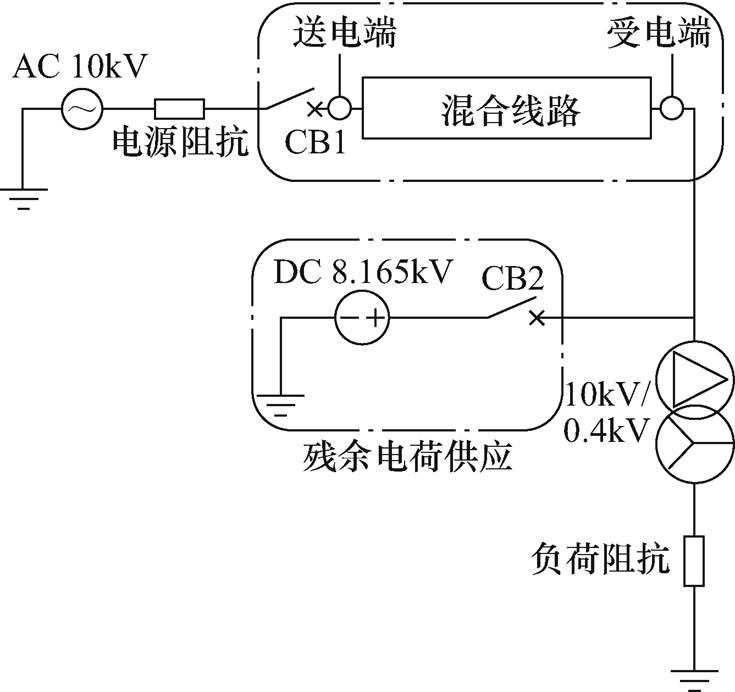
图5 10kV混合线路模型
Fig.5 The simulation model of 10kV hybrid line
如图5所示,混合线路中的电缆在暂态计算中采用Bergeron模型,计算频率为10kHz,架空线采用线路参数随频率变化的J. Marti模型,混合线路总长度为2km。重合闸下的暂态过电压与正常合闸时的区别在于线路中的残余电荷,当残余电荷的极性与合闸时电源电压的极性相反时,会产生更严重的电磁能量振荡。本文模型中考虑残余电荷产生的电压为100%相电压,故在线路末端接入负极性8.165kV的直流电源表示残余电荷的作用[24]。
电网公司规定10kV配电网短路电流不超过20kA[29],其对应电源内电感设置为1mH。实际中配网线路仅在送电端存在断路器,故线路受电端直接与配电变压器及负荷相连。断路器CB1采用统计开关,从而可以得到重合闸时的过电压统计值。受电端的配电变压器额定容量选择为一般的630kV·A,对应的空载以及短路试验数据可根据国家标准GB/T 6451—2015确定[30]。尽管线路末端带有负荷,但为了计算更为严重的过电压值,模型中考虑的负荷容量仅为变压器额定容量的20%。功率因数为0.95,对应的负荷阻抗为(1.088+j0.358)W。
混合线路中,线路的结构与位置会影响受电端的暂态过电压。典型位置结构为图6所示的非对称结构,线路1和线路2分别为两类不同的线路。文献[15]通过统计分析指出,非对称结构的混合线路过电压相比于对称结构线路的过电压更严重[14-15],因此本文将非对称结构作为研究重点,纯电缆、架空线路结构作为统计分析的对比和验证。
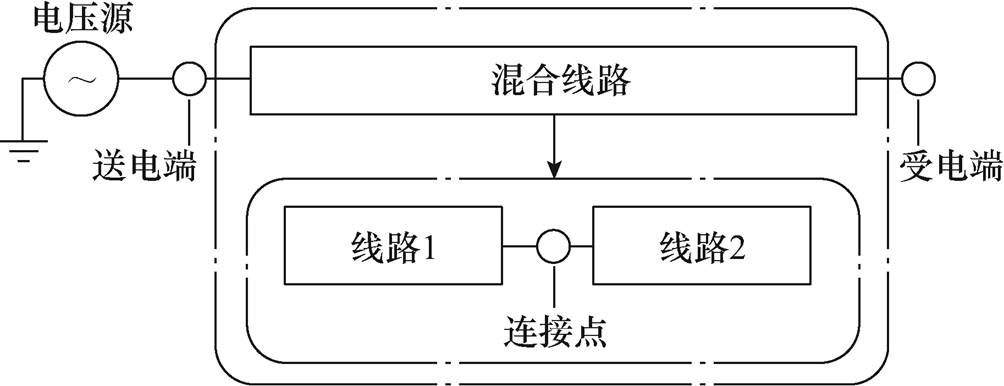
图6 典型非对称混合线路位置
Fig.6 The typical asymmetric structure of hybrid line
研究采用的电缆、架空线的波阻抗计算结果分别为92.19W、494.53W。基于式(16)中的电压波折返射关系,可得当线路1为电缆,线路2为架空线时,受电端节点会产生更严重的暂态过电压。
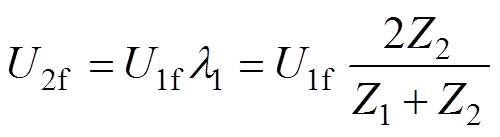 (16)
(16)式中,U1f为在第一段线路上的前行电压波;U2f为在第二段线路上的前行电压波;l1为折射系数;Z1和Z2分别为第一段和第二段线路的波阻抗。
基于上述模型,首先计算不同线路比例的重合闸过电压的统计值,得到不同比例混合线路暂态过电压的变化规律。断路器动作100次,混合线路与纯线路的暂态过电压累积概率曲线如图7所示。
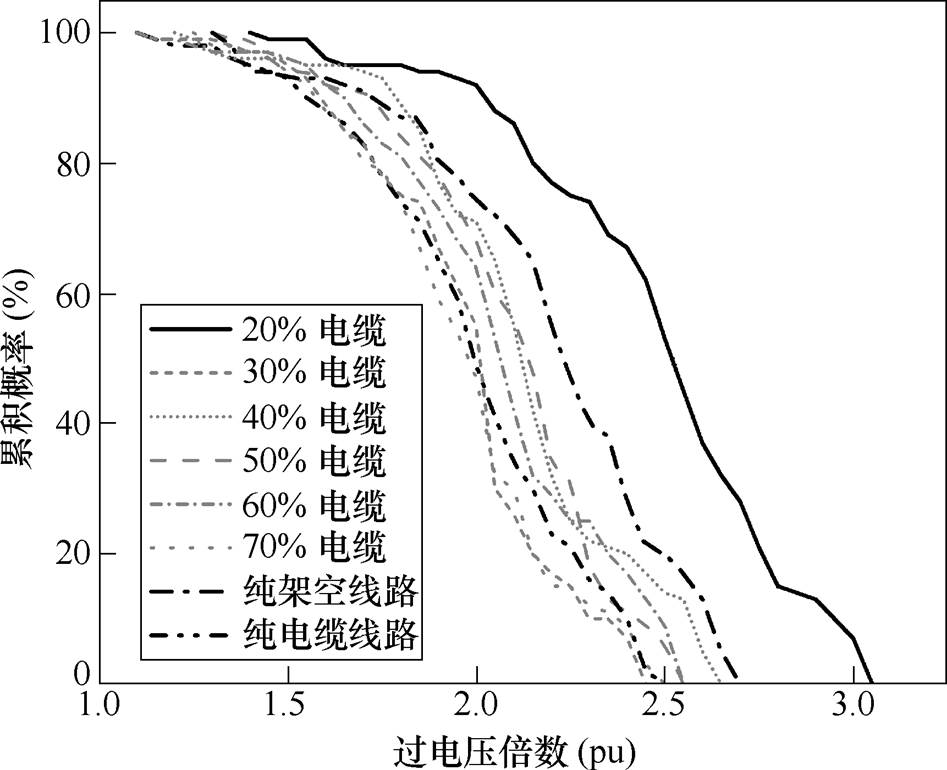
图7 重合闸过电压累积概率曲线
Fig.7 Cumulative probablity of reclosing overvoltage
从图7可得,与纯线路相比,在不同比例的混合线路中,更高幅值过电压出现的概率会有较大差异。并且,对于总长度为2km的混合线路,在电缆占比为20%时,不同倍数过电压的累积概率均大于其余情况。需要注意,20%不是定值,其与比例的取值细化程度有关,且并非适用所有线路,应该根据具体的线路长度具体分析,采用lcable表示电缆线路长度,lOHL表示架空线路长度。
进一步计算不同比例的混合线路统计值的变化规律,如图8所示。很明显,随着混合线路中电缆占比的增加,重合闸过电压的各个统计值总体呈下降趋势。但是当lcable lOHL=600
lOHL=600 1 400时,最大值、平均值和2%统计过电压值均出现极小值点,这时最大值和2%值均为2.45(pu)。当架空线所占比例最大时,受电端电压最大值和2%值为3.05(pu)。
1 400时,最大值、平均值和2%统计过电压值均出现极小值点,这时最大值和2%值均为2.45(pu)。当架空线所占比例最大时,受电端电压最大值和2%值为3.05(pu)。
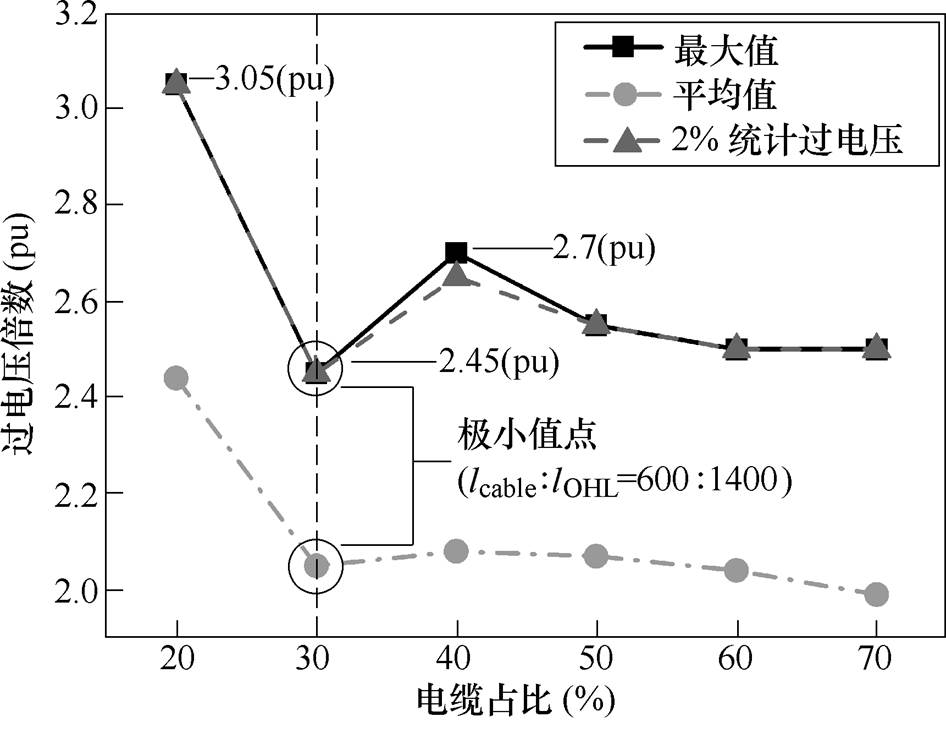
图8 受电端暂态过电压统计值变化
Fig.8 Statistical values of overvoltage at receiving end
通过图8可得,混合线路受电端的暂态过电压并非随架空线或电缆的变化而单调递减。电压波在不同的输电线路上的传播特性不同,并且混合线路比例的改变会直接影响电压波的传播过程。因此下文将根据电压波的传播特性与频率特性,分析混合线路中电缆与架空线的比例对过电压的影响。
如引言所述,应用特征值理论可将多相耦合的多导体回路转换为模域中相互独立的回路,并可得各回路的传播常数,每一相电压可认为是不同模域回路电压的叠加。考虑断路器的合闸不同期性,架空线路的过电压在暂态过程中由土壤返回模电压主导,即主导模;相间模电压波的传播速度较快,叠加在土壤返回模电压上,故其为传播模[20-21]。
混合线路为电缆在前、架空线在后的非对称结构,即图6中线路1为电缆,线路2为架空线,线路总长均为2km。
3.2.1 主导频率特性
过电压的主导频率对应暂态过电压波形的振荡周期。根据上述统计值,选取幅值最大时的电压波形,应用傅里叶变换或频率扫描,得到不同线路比例下的过电压主导频率,如图9所示。
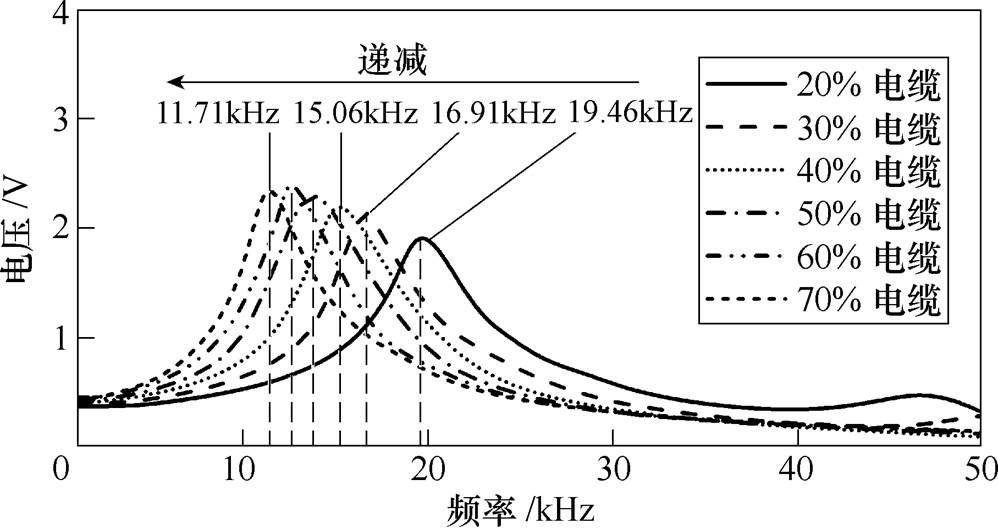
图9 暂态过电压频率特性
Fig.9 Frequency characteristic of transient overvoltage
通过图9中的数据可得,当电缆占比为20%时,主导频率最大为19.46kHz,70%电缆的电压主导频率为11.71kHz。随着电缆占比增加,受电端暂态过电压的主导频率呈递减趋势。
3.2.2 波形变化规律
通过图8统计值的变化可得,暂态过电压并没有随混合线路中架空线长度的减少呈单调递减。当lcable lOHL=600
lOHL=600 1 400时,暂态过电压出现极小值。图10~图12分别描述了电缆占比分别为20%、30%、40%的连接点与受电端处的A相电压。
1 400时,暂态过电压出现极小值。图10~图12分别描述了电缆占比分别为20%、30%、40%的连接点与受电端处的A相电压。
1)电缆20%~架空线80%
从图10可得,电压波经过前端的电缆线路后,在40.001 7ms时,连接点处的电压开始上升。经过5.4ms后,架空线受电端电压开始上升,因此传播模电压经过5.4ms从架空线的首端传播到末端。表1中计算结果表明,架空线相间模的传播速度为298m/ms。由于架空线长度为1 600m,可计算得单次传播时间为5.37ms,故对应图中两节点电压起始的时间差值。因此认为经过5.4ms相间模电压波可在架空线上传递一次,再经过同样的时间(5.4ms)相间模电压波传递回架空线首端。从40.007 1ms开始经过10.8ms,在40.017 9ms处相间模电压波(第2波)再一次回到架空线路末端(受电端)。
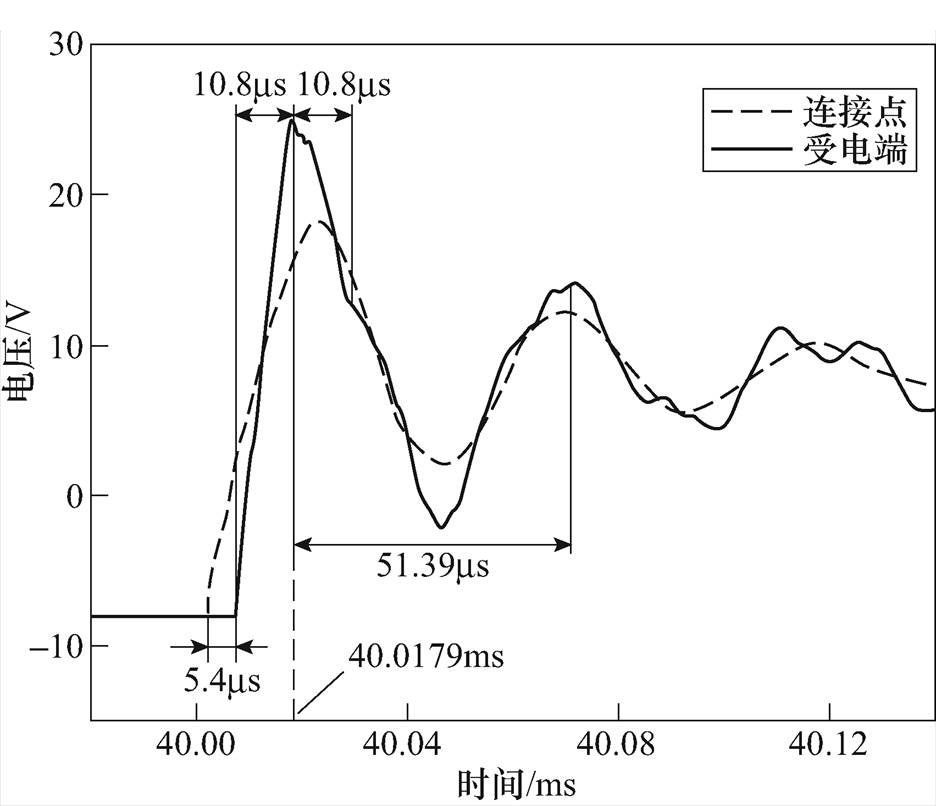
图10 lcable lOHL=400
lOHL=400 1 600时连接点与受电端电压
1 600时连接点与受电端电压
Fig.10 Voltage at joint and receiving end when lcable lOHL=400
lOHL=400 1 600
1 600
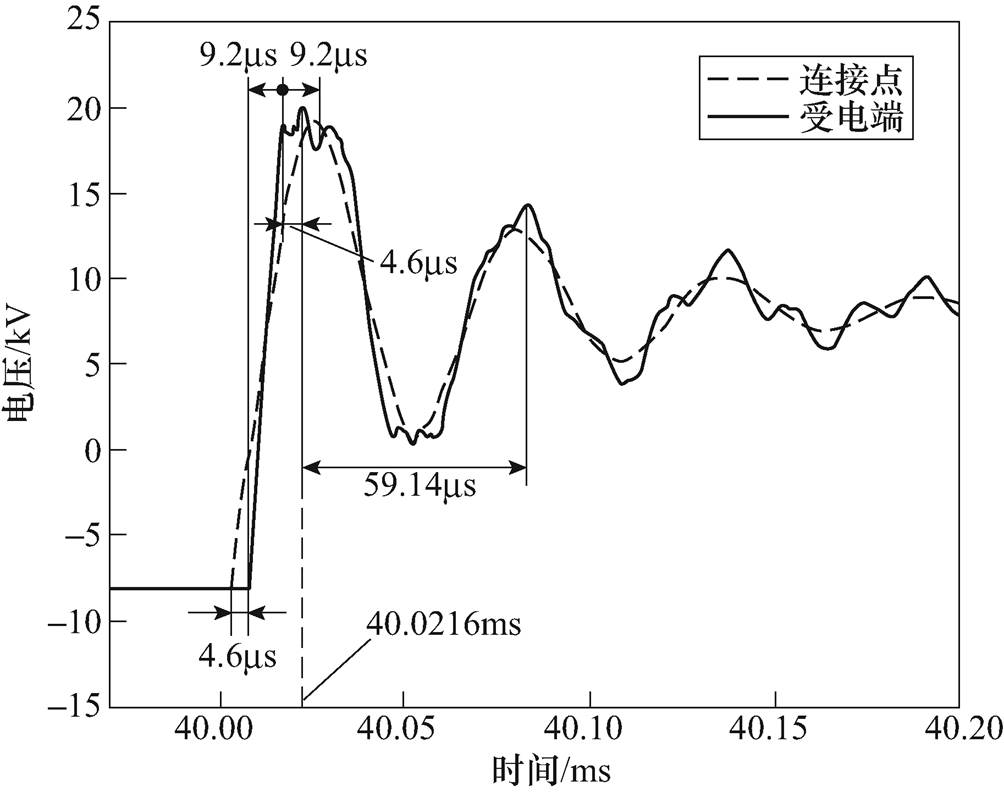
图11 lcable lOHL=600
lOHL=600 1 400时连接点与受电端电压
1 400时连接点与受电端电压
Fig.11 Voltage at joint and receiving end when lcable lOHL=600
lOHL=600 1 400
1 400

图12 lcable lOHL=800
lOHL=800 1 200时连接点与受电端电压
1 200时连接点与受电端电压
Fig.12 Voltage at joint and receiving end when lcable lOHL=800
lOHL=800 1 200
1 200
从图9可得,当lcable lOHL=400
lOHL=400 1 600时,暂态电压主导频率为19.46kHz。若假设主导模电压,即土壤返回模,为正弦波形,则该波形周期可通过主导频率估算[20],结果为51.39ms,对应图10中两电压峰值点间隔。在40.017 9ms处,主导模电压取得极大值。同时,传播模电压(第2波)到达受电端,两者叠加产生严重的暂态过电压。考虑线路中残余电荷的作用,暂态电压超过3.0(pu)。从图10中还可看出,当相间模电压波第3次回到受电端时,电压波形的下降速度得到缓和。
1 600时,暂态电压主导频率为19.46kHz。若假设主导模电压,即土壤返回模,为正弦波形,则该波形周期可通过主导频率估算[20],结果为51.39ms,对应图10中两电压峰值点间隔。在40.017 9ms处,主导模电压取得极大值。同时,传播模电压(第2波)到达受电端,两者叠加产生严重的暂态过电压。考虑线路中残余电荷的作用,暂态电压超过3.0(pu)。从图10中还可看出,当相间模电压波第3次回到受电端时,电压波形的下降速度得到缓和。
2)电缆30%~架空线70%
由于线路长度不影响波的传播常数,当混合线路中架空线路长度减小时,传播时间会减小。如 图11所示,由两节点电压起始时间差可得传播模电压波从架空线首端传到受电端用时4.6ms。由传播速度可得相间模电压波传播时间为4.69ms。当线路长度减少,电压波的传播时间减小。每经过9.2ms,电压波再次返回到线路受电端。
另一方面,由于线路受电端暂态电压的主导频率为16.91kHz,故土壤返回模电压的周期近似为59.14ms。如图11所示,两个电压峰值点之间的时间间隔为59.14ms,并且可得土壤返回模电压在40.021 6ms时达到峰值。当相间模电压波(第2波)到达受电端时会引起波形的畸变出现一个峰值,但此时土壤返回模电压并为达到极大值。再经过4.6ms土壤返回模电压达到极大值,但这时相间模电压恰好传回架空线路首端。故与图10所示的情况相比,这时产生的电压最大值下降。
3)电缆40%~架空线60%
如图12所示,两节点处电压起始时间差值近似为4ms,通过传播速度易计算得相间模传播时间为4.03ms。因此可认为从40.003ms起经过4ms,相间模电压波(第1波)到达受电端,并且每经过8ms电压波再次到达受电端。
当lcable lOHL=800
lOHL=800 1 200时,受电端暂态电压主导频率为15.05kHz,对应的周期时间近似为66.4ms,符合图12中两电压峰值点间隔。自连接点处40.003ms起,经过4+8×3=28ms后,即40.031ms时,相间模电压第4次回到受电端,并且和主导模电压极大值叠加。因此和30%电缆占比下的暂态电压相比,此时电压最大值会更大。但由于传播模的电压波在传播过程会发生衰减,故暂态电压最大值会小于电缆占比为20%时的最大值。应用同样的分析方法,可进一步对其余线路比例下的过电压波形进行分析。
1 200时,受电端暂态电压主导频率为15.05kHz,对应的周期时间近似为66.4ms,符合图12中两电压峰值点间隔。自连接点处40.003ms起,经过4+8×3=28ms后,即40.031ms时,相间模电压第4次回到受电端,并且和主导模电压极大值叠加。因此和30%电缆占比下的暂态电压相比,此时电压最大值会更大。但由于传播模的电压波在传播过程会发生衰减,故暂态电压最大值会小于电缆占比为20%时的最大值。应用同样的分析方法,可进一步对其余线路比例下的过电压波形进行分析。
通过上述分析可得,暂态电压的最大幅值受模域回路电压的叠加时刻影响,改变混合线路中电缆与架空线路的比例可影响传播模电压的传播时间。并且在不同比例的混合线路中,受电端处过电压的主导频率差别较大。从而不同比例混合线路的过电压最大值产生较大差异,且其变化并不单调。主导模与传播模电压值受电源侧能量供给影响,而线路长度则会影响波的传递时间与叠加时刻。在实际中,对于不同长度的混合线路,均可应用同样的方法分析暂态过电压最大值的变化。
本文基于EMTP平台,从模域回路电压波传播特性角度研究了在不同比例线路下的配电网混合线路重合闸过电压变化特性。
1)不同比例的混合线路中,过电压的累积概率差异显著。且与纯线路相比,在电缆占比较低的混合线路中出现高幅值过电压的概率更大。
2)随着电缆占比的增加,过电压最大值、平均值、2%值非单调变化,且均出现极小值。
3)混合线路中不同线路比例的暂态电压主导频率差异明显。随电缆占比增加,暂态过电压的主导频率呈递减趋势,过电压的振荡周期递增。
4)根据模域回路电压在主导频率与传播速度上的差异,对混合线路重合闸过电压随电缆占比的变化规律与极小值点出现的原因进行了分析。
对暂态过电压的波形特征及频率特性的分析,为研究操作冲击对电缆绝缘缺陷的发展及配网混合线路重合闸策略的制定具有重要的指导意义。
参考文献
[1] 江南, 谢聿琳, 侯俊平, 等. 电缆架空线混合线路重合闸投切方式[J]. 电力系统自动化, 2010, 34(3): 112-115.
Jiang Nan, Xie Yulin, Hou Junping, et al. Reclosing mode of cable-overhead mixed lines[J]. Automation of Electric Power Systems, 2010, 34(3): 112-115.
[2] 于景丰, 赵锋. 电力电缆实用技术[M]. 北京: 中国水利水电出版社, 2003.
[3] 徐龙, 赵艾萱, 李嘉明, 等. 多次操作冲击对含刀痕缺陷10kV电缆终端局部放电特性的影响[J]. 高电压技术, 2020, 46(2): 673-681.
Xu Long, Zhao Aixuan, Li Jiaming, et al. Effects of multiple switching impulses on the partial discharge characteristics of 10kV cable termination with knife incision[J]. High Voltage Engineering, 2020, 46(2): 673-681.
[4] 周凯, 李旭涛, 黄华勇, 等. 电缆终端安装刀痕缺陷的局部放电特性分析[J]. 电力系统保护与控制, 2013, 41(10): 104-110.
Zhou Kai, Li Xutao, Huang Huayong, et al. Analysis of partial discharge characteristics for installing cutting defects in cable terminations[J]. Power System Protection & Control, 2013, 41(10): 104-110.
[5] Cao Linfeng, Zanwar A, Grzybowski S. Electrical aging phenomena of power cables aged by switching impulses[J]. High Voltage Engineering, 2013, 39(8): 1911-1918.
[6] Silva F F D, Bak C L. Electromagnetic transients in power cables[M]. London: Springer, 2013.
[7] 周念成, 肖舒严, 虞殷树, 等. 基于质心频率和BP神经网络的配网故障测距[J]. 电工技术学报, 2018, 33(17): 4154-4166.
Zhou Niancheng, Xiao Shuyan, Yu Yinshu, et al. Fault location in distribution networks based on controid frequency and BP neural networks[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4154-4166.
[8] 罗勋华, 黄纯, 江亚群, 等. 基于电压内积的带并联电抗器输电线路单相自适应重合闸[J]. 电工技术学报, 2017, 32(11): 17-25.
Luo Xunhua, Huang Chun, Jiang Yaqun, et al. A voltage inner product based approach for single- phase adaptive reclosure on transmission line with shunt reactors[J]. Transactions of China Electro- technical Society, 2017, 32(11): 17-25.
[9] 罗勋华, 黄纯, 潘志敏, 等. 基于序分量无功功率的单相自适应重合闸[J]. 电工技术学报, 2016, 31(11): 149-156.
Luo Xunhua, Huang Chun, Pan Zhimin, et al. Single- phase adaptive reclosure based on reactive power of sequence components[J]. Transactions of China Electrotechnical Society, 2016, 31(11): 149-156.
[10] 沈军, 李超群, 朱晓彤, 等. 高压电缆—架空线混合线路重合闸新判据[J]. 电力系统自动化, 2012, 36(13): 97-100.
Shen Jun, Li Chaoqun, Zhu Xiaotong, et al. New reclosing criterion for hybrid lines of high-voltage cables and pole lines[J]. Automation of Electric Power Systems, 2012, 36(13): 97-100.
[11] 刘顺桂, 李勋, 张宏钊, 等. 一种采用时间判别法的混合线路故障行波定位方法[J]. 电力系统保护与控制, 2017, 45(1): 41-46.
Liu Shungui, Li Xun, Zhang Hongzhao, et al. A traveling wave fault location method of hybrid line using time discrimination[J]. Power System Pro- tection & Control, 2017, 45(1): 41-46.
[12] 束洪春, 彭仕欣. 基于短窗数据S变换能量的缆-线混合配电网络故障选线方法[J]. 电工技术学报, 2009, 24(10): 152-159.
Shu Hongchun, Peng Shixin. A fault line detection algorithm for distribution network of overhead line and underground cable mixed lines using S-transform energy from short window data[J]. Transactions of China Electrotechnical Society, 2009, 24(10): 152- 159.
[13] 曹珍崇, 杨学昌, 郅啸, 等. 电缆配电网操作过电压的计算与分析[J]. 清华大学学报: 自然科学版, 2007, 47(4): 466-469.
Cao Zhenchong, Yang Xuechang, Zhi Xiao, et al. Calculation and analysis of operating overvoltage in cable distribution network[J]. Journal of Tsinghua University: Science and Technology, 2007, 47(4): 466-469.
[14] Khalilnezhad H, Popov M, Bos J A, et al. Investi- gation of statistical distribution of energization overvoltages in 380kV hybrid OHL-cable systems[C]// The International Conference on Power Systems Transients, Seoul, 2017: 1-6.
[15] Khalilnezhad H, Popov M, Bos J A, et al. Statistical analysis of energization overvoltages in EHV hybrid OHL-cable systems[J]. IEEE Transactions on Power Delivery, 2018, 33(6): 2765-2775.
[16] 赵丹丹, 张嘉旻, 黄华, 等. 220kV城市电缆及混合线路过电压及绝缘配合研究[J]. 华东电力, 2012, 40(2): 114-118.
Zhao Dandan, Zhang Jiamin, Huang Hua, et al. Overvoltage and insulation coordination of 220kV urban cable and hybrid lines[J]. East China Electric Power, 2012, 40(2): 114-118.
[17] 肖翔, 张小青, 李聪. 风电机组雷电过电压的仿真分析[J]. 电工技术学报, 2015, 30(24): 237-244.
Xiao Xiang, Zhang Xiaoqing, Li Cong. Simulation analysis on overvoltage in wind turbines by lightning stroke[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 237-244.
[18] 张帆, 段雄英, 吕洋, 等. 选相投切特高压线路及对其操作冲击绝缘的影响[J]. 电工技术学报, 2018, 33(5): 1151-1157.
Zhang Fan, Duan Xiongying, Lü Yang, et al. Controlled switching UHV line and its effect on line switching impulse insulation[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1151- 1157.
[19] 徐曙, 李勋, 黄荣辉, 等. 架空线-电缆混合输电线路工频过电压分布特性[J]. 山东理工大学学报: 自然科学版, 2017, 31(5): 51-54.
Xu Shu, Li Xun, Huang Ronghui, et al. Research on power frequency overvoltage distribution property along hybrid transmission line[J]. Journal of Shandong University of Technology: Natural Science Edition, 2017, 31(5): 51-54.
[20] Ohno T, Ametani A, Bak C L, et al. Analysis of statistical distributions of energization overvoltages of EHV cables[C]//The International Conference on Power Systems Transients, Vancouver, 2013: 1-7.
[21] Ohno T. Dynamic study on the 400kV 60km kyndbyværket-asnæsværket line[D]. Aalborg: Aalborg University, 2012.
[22] Wedepohl L M. Application of matrix methods to the solution of traveling wave phenomena in polyphase system[J]. Proceedings of the Institution of Electrical Engineers, 1963, 110(12): 2200-2212.
[23] Ametani A. Wave propagation characteristics of cables[J]. IEEE Transactions on Power Apparatus & Systems, 1980, 99(2): 499-505.
[24] Ghassemi F. Effect of trapped charges on cable SVL failure[J]. Electric Power Systems Research, 2014, 115: 18-25.
[25] Ghassemi F, Dennis S, Ainsley A, et al. 275kV cable discharge field measurement and analysis of SVLs chain failure using ATP[J]. Electric Power Systems Research, 2018, 161: 95-102.
[26] 施围, 郭洁. 电力系统过电压计算[M]. 北京: 高等教育出版社, 2006.
[27] Noualy J P, Roy G L. Wave-propagation modes on high-voltage cables[J]. IEEE Transactions on Power Apparatus & Systems, 1977, 96(1): 158-165.
[28] Dommel H W. EMTP theory book[M]. Vancouver: MicroTran Power System Analysis Corp, 1996.
[29] 文锋, 秦丝, 王琦, 等. 广州供电局中低压电网设备技术原则[R]. 中国南方电网, 2013.
[30] 章忠国, 刘爽, 姜益民, 等. GB/T 6451—2015 油浸式电力变压器技术参数和要求[S]. 北京: 中国标准出版社, 2015.
Analysis of Reclosing Overvoltage in Cable-Overhead Line Hybrid Line Based on Return Circuit Theory in Modal Domain
Abstract The amplitude and dominant frequency characteristics of reclosing overvoltage with different cable proportions in cable-overhead hybrid line were studied based on the wave propagation in modal domain. The propagation constants of 10kV cable and overhead line (OHL) in modal domain circuit were obtained through modal transformation. Using electro-magnetic transients program (EMTP), an asymmetrical line model was established, and the variation tendency of statistical overvoltage under different cable proportions was investigated. The results show that statistical values vary non-monotonically and a minimum value appears when the cable proportion increases. The results based on voltage propagation in modal domain are consistent with those calculated by EMTP. This method can also be applied in hybrid lines with different proportions since the propagation constants are not influenced.
keywords:Cable-overhead line hybrid line, reclosing overvoltage, return circuit in modal domain, propagation constants, dominant frequency
中图分类号:TM861
DOI: 10.19595/j.cnki.1000-6753.tces.190132
国家电网总部科技项目(5226SX1600U9)和国家自然科学基金项目(51577150)资助。
收稿日期2019-01-30
改稿日期 2019-07-08
李嘉明 男,1995年生,硕士研究生,研究方向为电力系统暂态过电压仿真计算。E-mail: ljmlightclouds@163.com
邓军波 男,1976年生,副教授,博士生导师,研究方向为电力系统暂态过电压仿真计算、电缆绝缘状态及载流量评估和气体绝缘中的沿面放电测量。E-mail: dengjb@mail.xjtu.edu.cn(通信作者)
(编辑 赵 鹏)