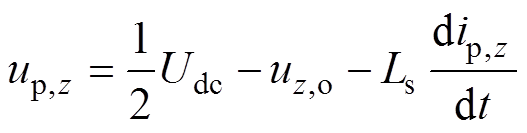 (1)
(1)摘要 最近电平-脉宽调制(NL-PWM)适用于中压模块化多电平换流器(MMC),较最近电平调制(NLM)可大幅减少谐波电流。NL-PWM通过电压排序实现桥臂子模块均压,均压切换设置在阶梯波跳变点,可减少额外的开关切换,但也限制了均压频率,影响了均压效果。PWM开关频率较高,在其开关点进行均压切换可大幅提高均压频率。现有NL-PWM方法基于三角载波,其开关点随参考电压变化,不便于均压控制的实施。该文提出非倍频和倍频的基于锯齿载波的NL-PWM方法,锯齿载波具有固定的跳变点便于均压控制。分析了所提调制的谐波特性,研究表明,采用倍频锯齿载波NL-PWM方法可在降低开关频率的同时保证良好的均压效果与输出电能质量。此外,所提调制亦可避免功率开关的窄脉冲。仿真与实验研究验证了理论分析的正确性。
关键词:中压模块化多电平换流器 最近电平-脉宽调制 锯齿载波 开关频率 窄脉冲
模块化多电平换流器(Modular Multilevel Con- verter, MMC)[1]被广泛应用于直流输电、电力电子变压器和可再生能源发电之中[2-7]。MMC具有高度模块化的特点,便于电压和功率的扩展。此外,模块化结构可实现子模块冗余,从而提高系统可靠性。
在10kV及以下电压等级的中压电网中,MMC可以提供中压直流母线,组建直流配电网,中压直流母线为集中式可再生能源发电提供了良好的并网接口[7];也可应用于MMC型电力电子变压器,组建交直流配电网[8]。与高压MMC不同,中压MMC子模块数量较少,采用高压MMC常用的最近电平调制(Nearest Level Modulation, NLM)[9]会导致电压跟踪误差大、谐波电流畸变率高。
适用于MMC的调制方法较多,典型的有:基于载波的移相调制(Carrier Phase Shift PWM, CPS- PWM)[10]和层叠调制(Carrier Level Shift PWM, CLS-PWM)[11];基于无载波的NLM和空间矢量调制(Space Vector PWM, SVPWM)[12];基于载波+无载波结合的NL-PWM[13]。基于载波的调制方法中,CPS-PWM因其等效开关频率高、开关频率分布均衡得到了广泛的研究[14-15]。相较于CPS-PWM,NLM采用阶梯波逼近正弦参考电压,通过电压排序实现子模块均压,具有开关频率较低和均压控制简单的优势,适用于高压场合,也得到了广泛的研 究[16-17]。针对中压场合子模块数较少的特点,文献[13]提出了最近电平-脉宽调制(Nearest Level Pulse Width Modulation, NL-PWM),该调制继承了NLM的优势,又具有PWM低频谐波含量较少的特点,在中压场合具有良好的应用前景。
NL-PWM和NLM的子模块均压方法类似,均基于电压排序法[18]。该方法在每个均压控制周期对桥臂子模块电压进行采样与排序,根据电压高低顺序和桥臂电流方向决定子模块的输出电平。为了尽可能地减少子模块均压切换造成的开关频率增加,均压切换可设置于阶梯波的跳变点[13],但这也限制了均压频率,影响了均压效果。这种情况下,为了达到良好的均压效果需要较大的子模块电容。鉴于NL-PWM含有PWM,其开关频率相对较高,若在其开关点进行均压切换,则可大幅提高均压频率。然而,现有的NL-PWM方法基于三角载波,其PWM开关点随参考电压变化使得相邻两个开/关点的时间间隔也是变化的,故留给均压控制的时间也是变化的,不利于均压控制的实施。
针对以上问题,本文提出了基于锯齿载波的NL- PWM方法,锯齿载波在每个周期中均具有固定的跳变点,可获得固定的开通或关断时刻,便于均压控制的周期性实施。分析了基于锯齿载波的NL-PWM的谐波特性,研究了提高其等效开关频率的方法,提出了减少均压产生的额外开关频率的子模块均压方法,并通过仿真与实验对理论分析进行了验证。
本节简要介绍MMC的拓扑、原理和NL-PWM的原理与实施方法。
基于半桥子模块的三相MMC拓扑如图1所示,每相有2个桥臂,每个桥臂有N个半桥子模块SM和1个电感Ls,交流母线为a、b、c,直流母线为P、N。
根据KVL可得桥臂电压满足
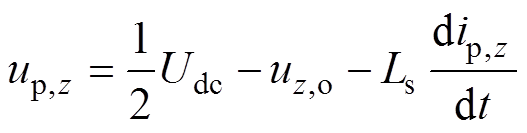 (1)
(1)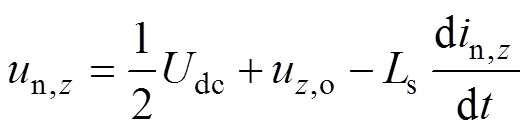 (2)
(2)
式中,up,z、un,z和uz,o分别为上、下桥臂电压和相电压,z=a, b, c;ip,z和in,z分别为上、下桥臂电流;Udc为直流母线电压。
可得,交流侧相电压和稳态直流电压为
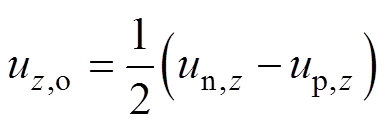 (3)
(3)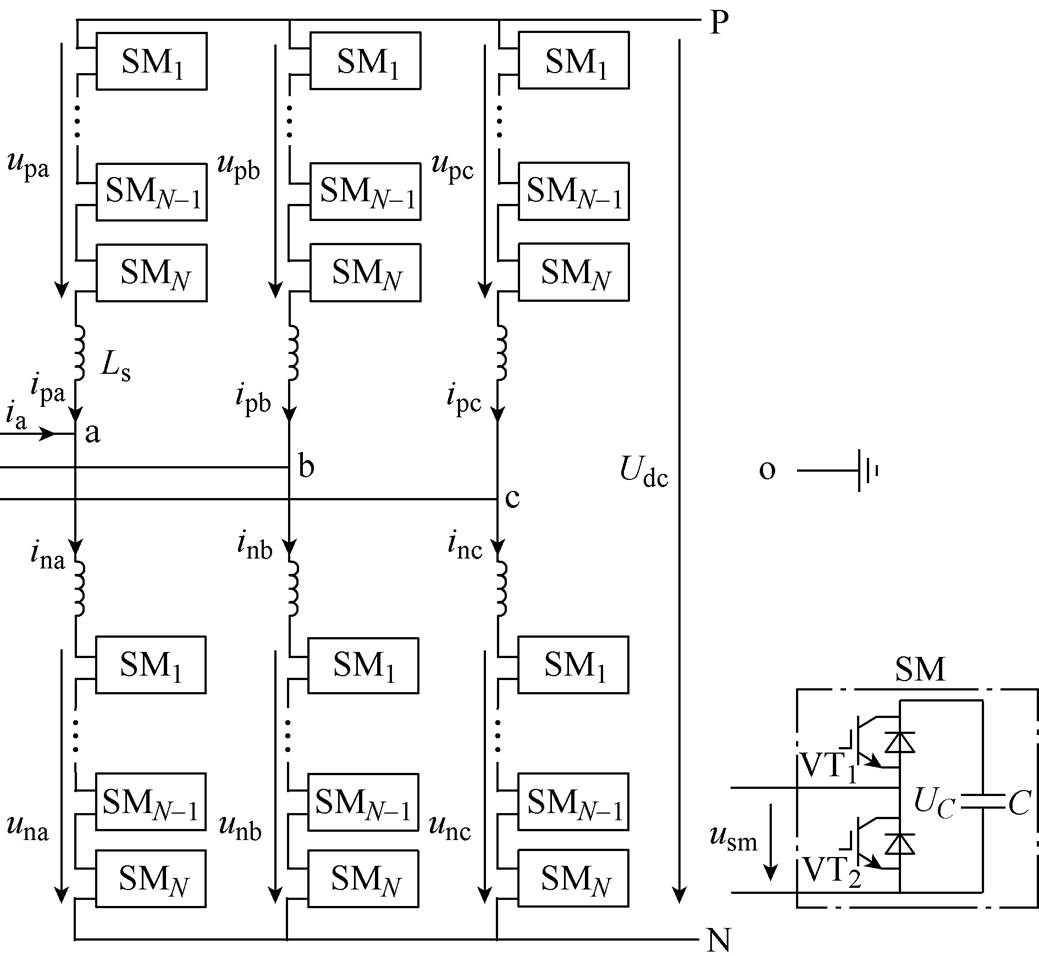
图1 MMC拓扑
Fig.1 Topology of MMC
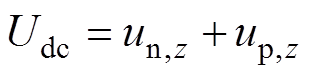 (4)
(4)NL-PWM是NLM与PWM的结合。桥臂中N-1个子模块输出阶梯波,1个子模块输出PWM。以子模块额定电压为基准值,N=6时,下桥臂电压波形如图2所示。根据文献[13]所述,当桥臂电流大于等于零时,电压较高的子模块投入,电压较低的子模块旁路,而电压靠中的子模块输出PWM电压;当桥臂电流小于零时,电压较低的子模块投入,电压较高的子模块旁路,电压靠中的子模块输出PWM电压。通过上述方法即可实现子模块均压和PWM与阶梯波输出的分配。
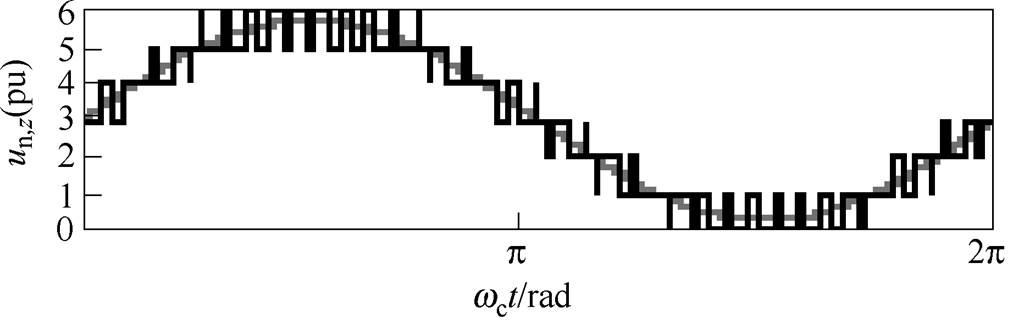
图2 下桥臂电压
Fig.2 Voltage of lower bridge arm
NL-PWM的具体实施方法如下所示。
上、下桥臂阶梯波电压表达式为
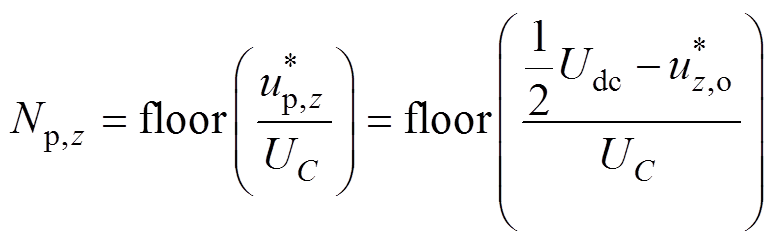
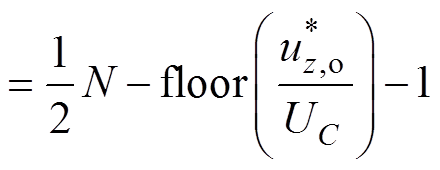 (5)
(5)
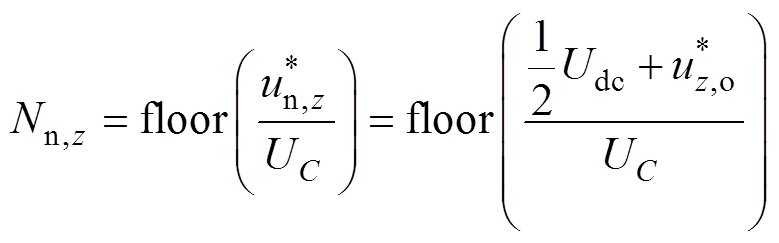
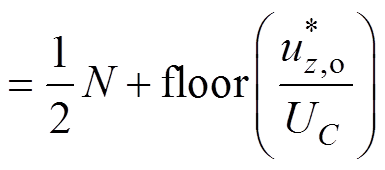 (6)
(6)式中, 、
、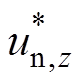 和
和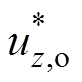 分别为上、下桥臂参考电压和相参考电压;UC为子模块直流电压。
分别为上、下桥臂参考电压和相参考电压;UC为子模块直流电压。
上、下桥臂PWM参考电压表达式为
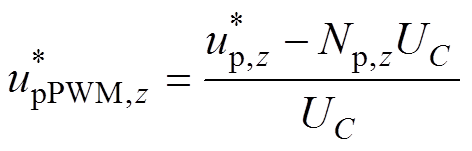
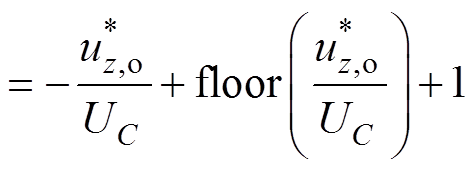 (7)
(7)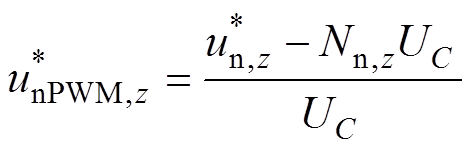
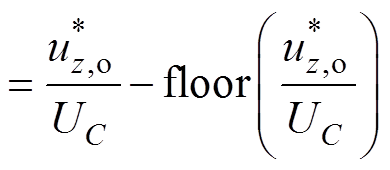 (8)
(8)
根据式(4)~式(8)可得直流电压为
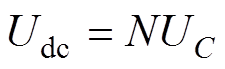 (9)
(9)根据以上分析可得桥臂PWM参考电压和阶梯波电压如图3所示。
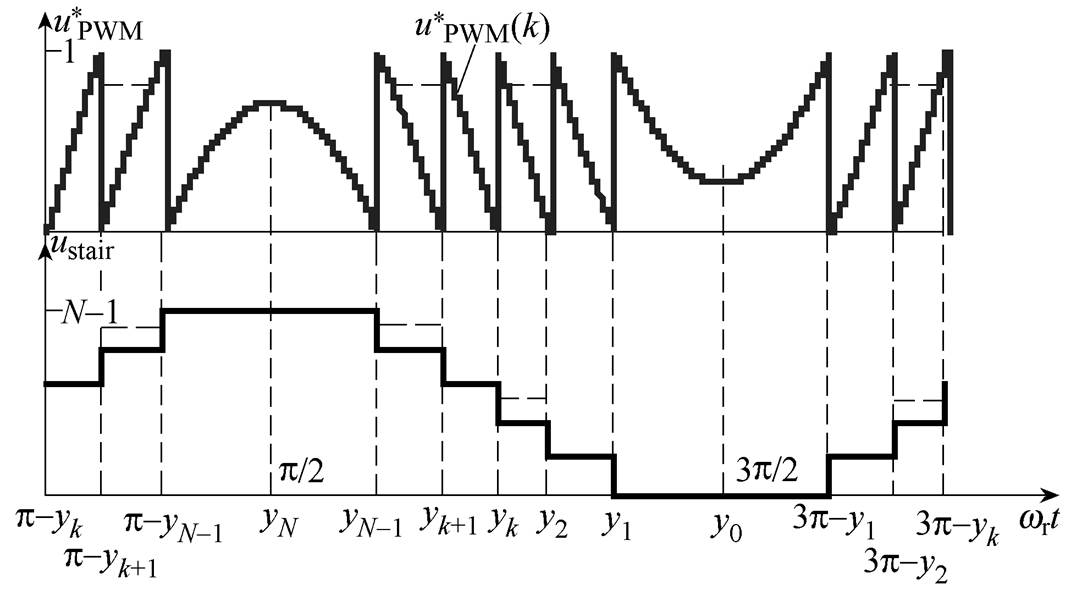
图3 PWM参考电压和阶梯波电压
Fig.3 PWM reference voltage and stair-wave voltage
图3中,阶梯波电压有0~N-1共N个电平,PWM参考电压每周期具有2(N-1)个间断点。由图3可得,第k段PWM参考电压的表达式为
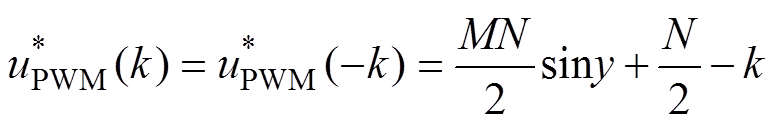
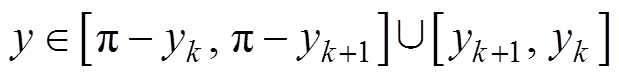
 (10)
(10)
式中,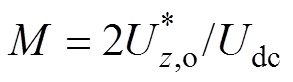 ,
,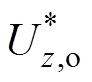 为
为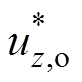 的峰值。
的峰值。
图3中阶梯波跳变点的表达式为
 (11)
(11)以上即为NL-PWM实施方法,可为后文研究基于锯齿载波的NL-PWM的谐波特性奠定基础。
文献[13]中,PWM载波为三角波,因此PWM开关点随参考电压变化不便于均压控制的实施。文献[13]将均压切换设置在了阶梯波跳变点,这限制了均压频率。为此,后文提出了基于锯齿载波的NL-PWM方法解决这一问题。
为解决基于三角载波的PWM,其输出的开关点随参考电压变化的问题,本文将锯齿载波应用于NL-PWM。本节提出了非倍频和倍频的锯齿载波NL-PWM方法,并分析比较了二者的谐波特性。
2.1.1 非倍频法
在非倍频法下,相电压中最低次中心谐波的频率为载波频率(理论分析详见2.2.1节),此时上、下桥臂的锯齿载波关于纵轴镜像对称。由式(7)和式(8)可得,同一时刻上下桥臂的PWM参考电压之和为1。综上可得,上下桥臂PWM载波和参考电压如图4所示。
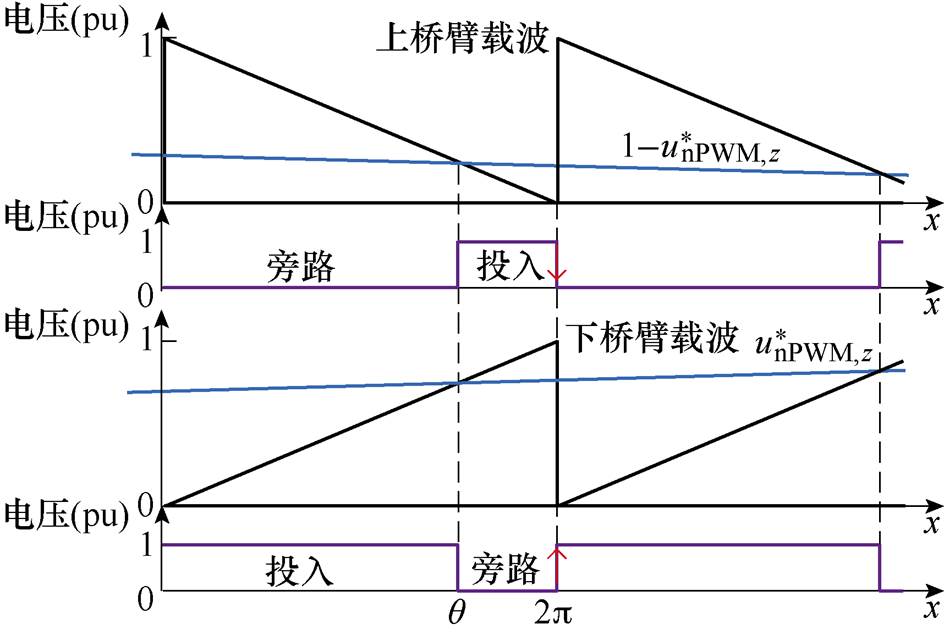
图4 非倍频法上下桥臂PWM载波与参考电压
Fig.4 PWM carrier and reference voltage of upper and lower bridge arms under non-frequency-doubling method
图4中,上、下桥臂的PWM输出电压表达式为
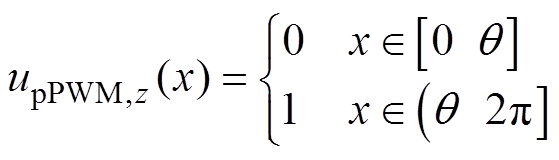 (12)
(12)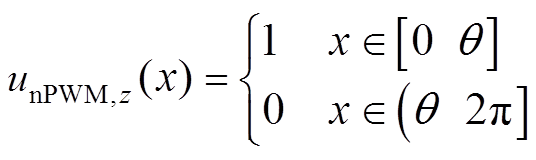 (13)
(13)
由图4可知,上下桥臂的PWM波在同一时刻发生跳变,同时由式(3)可知,相电压输出为下、上桥臂电压之差的一半,因此,非倍频法相电压PWM输出在一个PWM周期中仅开关一次,故其最低次中心谐波频率为载波频率。
2.1.2 倍频法
在倍频法下,相电压中最低次中心谐波的频率为两倍载波频率,且无载波频率的奇次谐波(理论分析详见2.2.2节),此时上下桥臂三角载波在图4基础上相对平移180°,而参考电压保持不变,如图5所示。
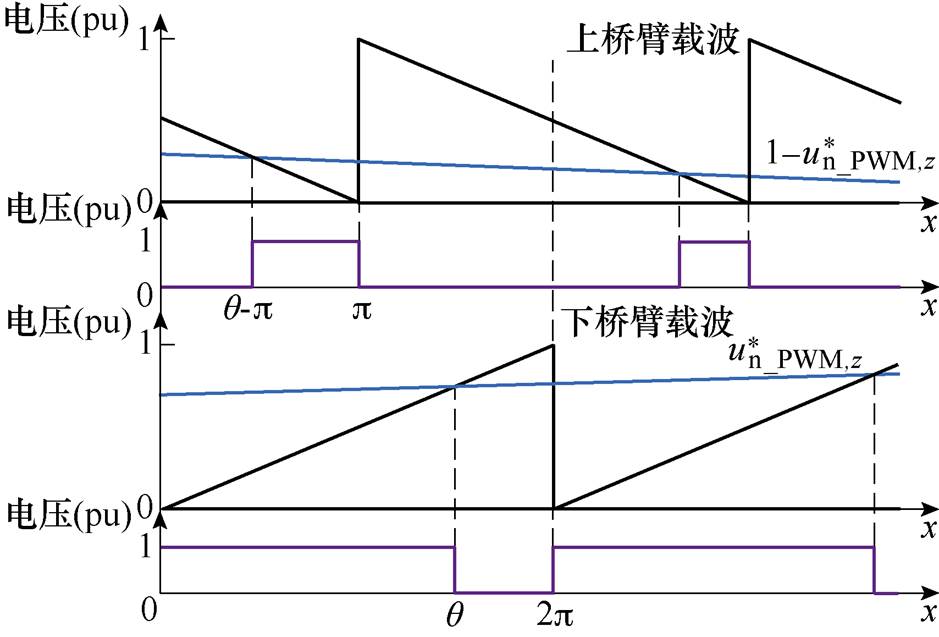
图5 倍频法上下桥臂PWM载波与参考电压
Fig.5 PWM carrier and reference voltage of upper and lower bridge arms under frequency-doubling method
图5中,上、下桥臂的PWM输出电压表达式为
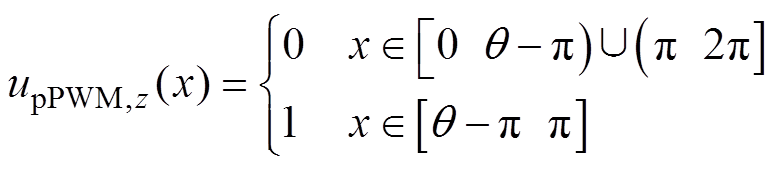 (14)
(14)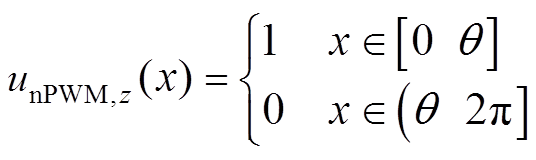 (15)
(15)
由图5可知,上下桥臂的PWM跳变点相差180°,因此倍频法相电压PWM输出在一个PWM周期中开关两次,故其最低次中心谐波频率为两倍载波 频率。
2.2.1 非倍频法谐波特性
不考虑子模块电容电压波动,根据双傅里叶变换法,以a相下桥臂为例,可得PWM电压分解[19]为
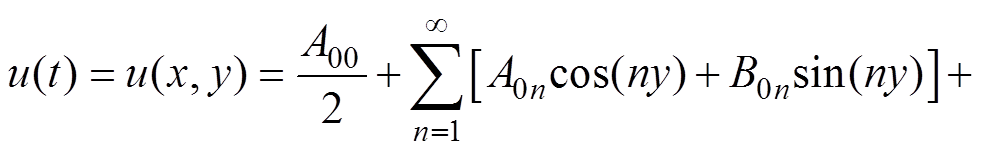
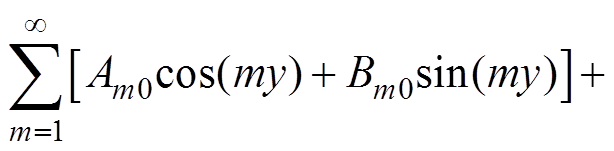
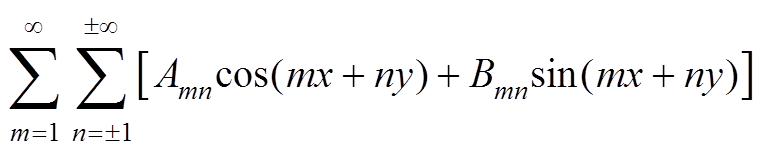
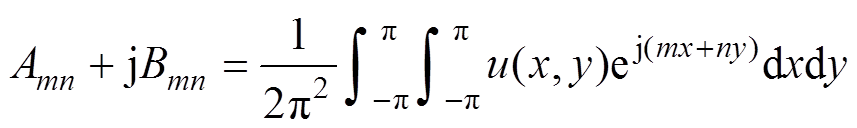 (16)
(16)式中,x=wct,y=wrt,wc、wr分别为载波和调制波频率。
根据式(10)、式(11)、式(13)和式(16)可得,锯齿载波NL-PWM桥臂PWM输出电压的傅里叶系数为
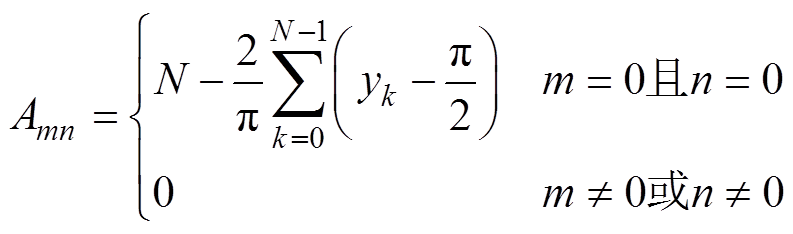 (17)
(17)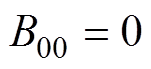 (18)
(18)
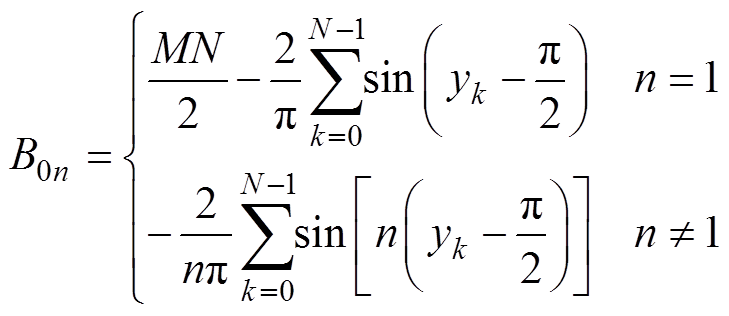 (19)
(19)
1)当mN为偶数时
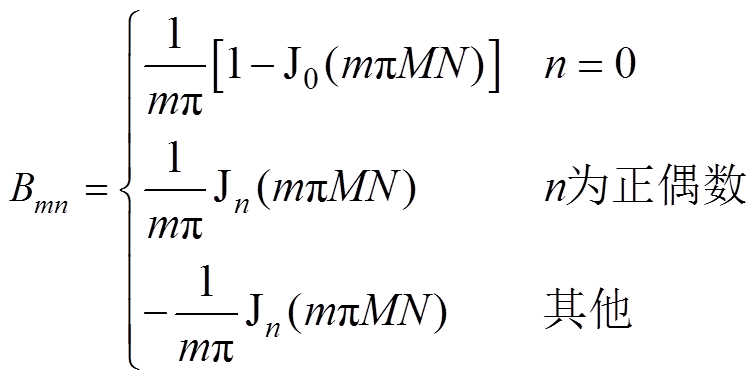 (20)
(20)式中,Jn(x)为n阶贝塞尔函数。
2)当mN为奇数时
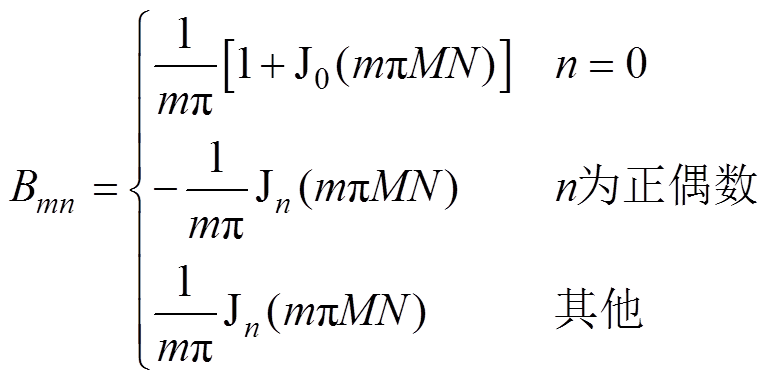 (21)
(21)阶梯波电压的傅里叶级数可由文献[13]得到
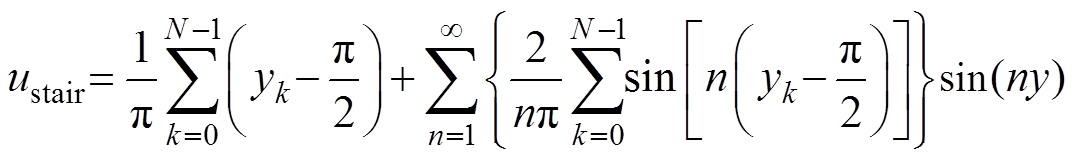 (22)
(22)
根据式(16)~式(22)可得下桥臂电压的傅里叶级数为

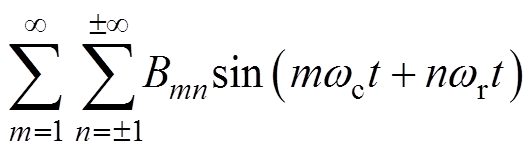 (23)
(23)
同理,根据上桥臂参考电压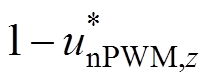 和式(13),可得上桥臂电压的傅里叶级数为
和式(13),可得上桥臂电压的傅里叶级数为
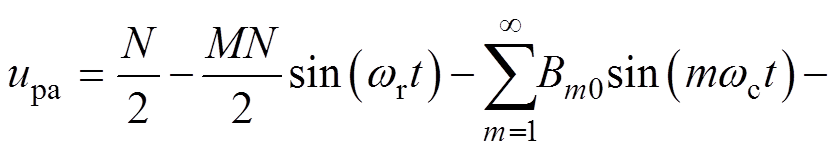
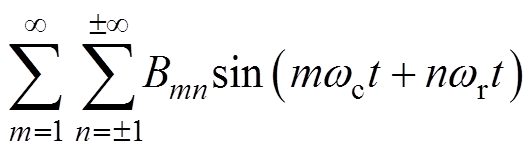 (24)
(24)
根据式(23)、式(24)可得a相相电压的傅里叶级数为
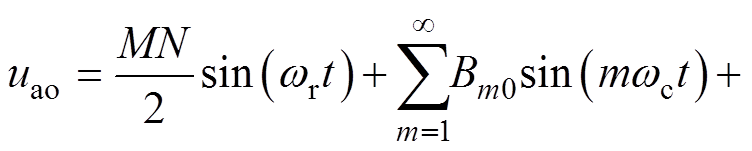
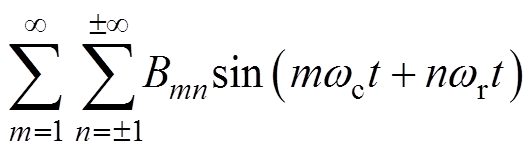 (25)
(25)
由式(25)可知,锯齿载波NL-PWM的相电压含有载波频率及其倍频的谐波以及所有边带谐波,相比文献[13]中三角载波NL-PWM的相电压不含m为奇数、n为偶数的边带谐波和m为偶数、n为奇数的边带谐波,锯齿载波NL-PWM的相电压边带谐波更丰富。
同理,b相相电压的傅里叶级数为
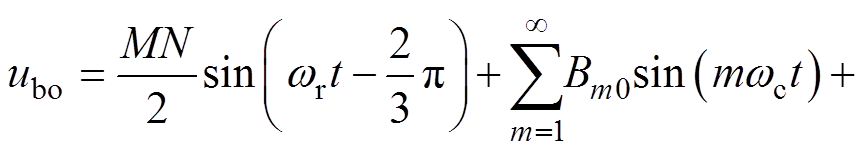
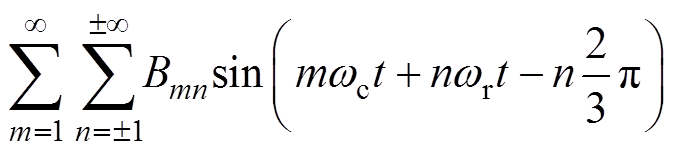 (26)
(26)
由式(25)、式(26)可得线电压傅里叶级数为
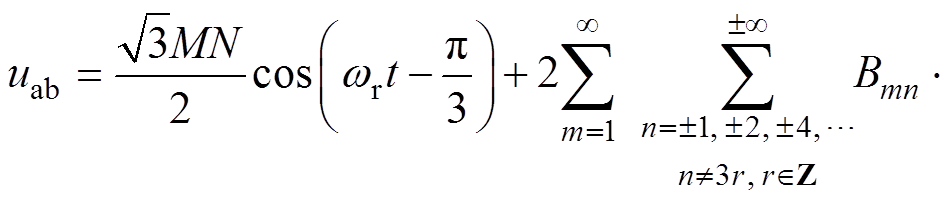
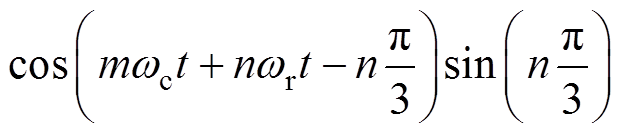 (27)
(27)
由式(27)可知,锯齿载波NL-PWM的线电压不含载波频率及其倍频的谐波与n=3r,r∈Z的边带谐波。
综上所述,非倍频锯齿载波NL-PWM较丰富的边带谐波使其输出电压谐波较三角载波NL-PWM更多。
2.2.2 倍频法谐波特性
由图4和图5可知,倍频法与非倍频法区别为上下桥臂载波移相。后文以下桥臂载波不变、上桥臂载波移相180°为例进行分析。
下桥臂电压傅里叶级数同式(23),傅里叶系数同式(17)~式(21);根据式(14),同理可得上桥臂电压的傅里叶级数同式(24),而傅里叶系数为
(1)m为偶数:上下桥臂傅里叶系数相等。
(2)m为奇数:上下桥臂傅里叶系数互为相反数。
由以上分析可知,倍频法上桥臂电压中,载波频率谐波、载波频率奇数次倍频谐波以及二者的边带谐波,其相位均与下桥臂相同,故相电压不含上述谐波,有
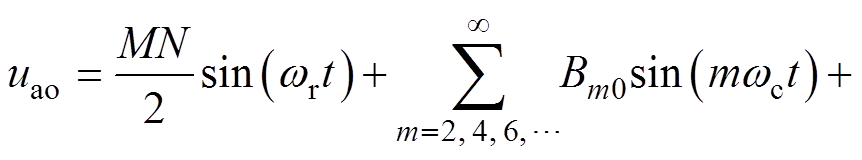
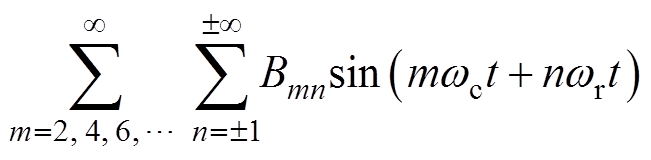 (28)
(28)
同理,线电压傅里叶级数为
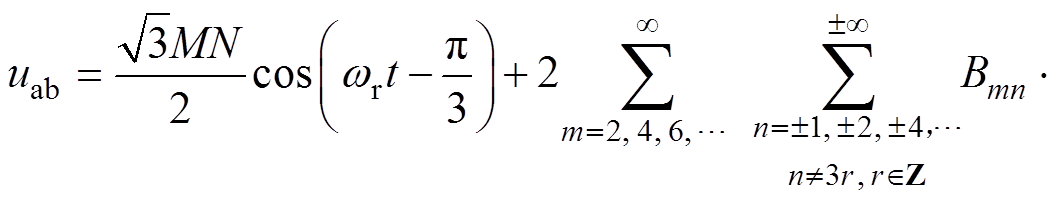
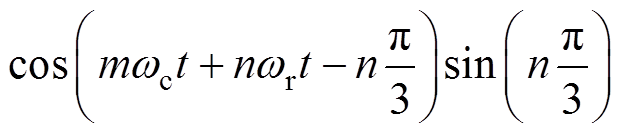 (29)
(29)
由式(29)可知,倍频锯齿载波NL-PWM的线电压不含载波频率及其奇数次倍频谐波以及二者的边带谐波,同时不含n=3r,r∈Z的边带谐波。
当N=3、M=0.84、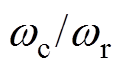 =39时,非倍频三角载波NL-PWM[13]、倍频三角载波NL-PWM[20]、非倍频锯齿载波NL-PWM和倍频锯齿载波NL-PWM的线电压频谱分别如图6a~图6d所示。
=39时,非倍频三角载波NL-PWM[13]、倍频三角载波NL-PWM[20]、非倍频锯齿载波NL-PWM和倍频锯齿载波NL-PWM的线电压频谱分别如图6a~图6d所示。
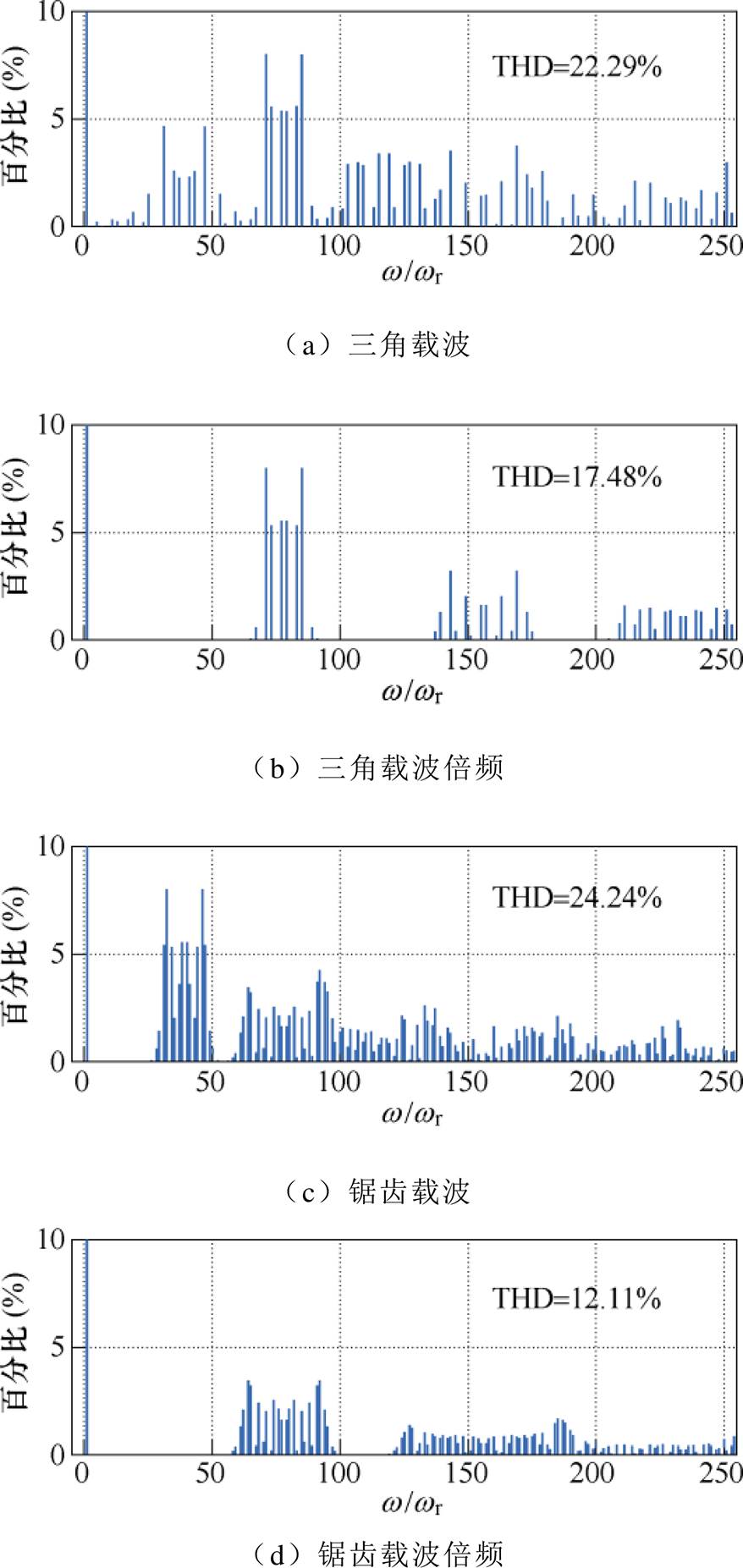
图6 四种调制的线电压频谱与THD
Fig.6 Spectrums and THDs of line voltages under the four modulation methods
对比图6a和图6c可知,非倍频三角载波NL- PWM较非倍频锯齿载波NL-PWM具有较低的总谐波畸变率(Total Harmonic Distortion, THD),但其边带衰减较慢,具有一定的低次谐波;对比图6b和图6d可知,倍频锯齿载波NL-PWM较倍频三角载波NL-PWM具有更低的THD和谐波幅值,具有更良好的输出电压质量。
NL-PWM通过电压排序和桥臂电流方向判断调整桥臂子模块输出电平从而实现其均压。锯齿载波NL-PWM由于锯齿载波具有固定的跳变沿(调制比大于0且小于1时),因此可利用该跳变点进行均压切换,以降低子模块由于均压切换产生的额外开关频率。但如图4所示,锯齿载波仅有固定的上升沿或下降沿,因此只能减少部分切换模式的额外开关次数。
同一时刻至多3个子模块参与均压切换的子模块切换模式如图7所示。若均压切换设置在锯齿载波跳变点,子模块的基本切换模式及其对额外开关次数的影响见表1。其他复杂切换模式或更多子模块参与的切换模式,其结果均可由表1所示模式组合得到。特殊地,表1中,切换模式1,2和3,4包含阶梯波电平变动,其额外开关次数排除了阶梯波和PWM波二者带来的开关次数,上述情况均不增加额外开关次数。

图7 子模块的均压切换模式
Fig.7 Voltage-balancing rotating modes of SM
由以上分析可知,基于锯齿载波的NL-PWM在至多3个子模块参与均压切换的情况下,仅四(28.57%)种情况不能减少额外开关次数、十(71.43%)种情况可避免额外开关。对于文献[13]所提将均压切换设置在阶梯波跳变点的情况,其相关结果见表1,区别为均压频率较低;对于均压切换既不在阶梯波跳变点,也不在锯齿载波跳变点的情况,其额外开关次数等于参与均压切换的子模块数的一半。以上分析仅针对至多3个子模块参与均压切换的情况,若同一时刻存在更多的子模块参与均压切换,则必然带来更多的额外开关动作。然而,在阶梯波跳变点触发情况下,两次均压控制时间较短,期间子模块电压变化不大,同一时刻参与均压切换的子模块较少。
表1 子模块的切换模式及其对额外开关次数的影响
Tab.1 SM’s basic rotating modes and its affect to the additional counts of switching

切换模式额外开关次数 1, 4+0.50 2, 30+0.5 5, 6+1+1 1, 200 3, 400 1, 2, 5+10 3, 4, 60+1
除对额外开关次数的影响,不同均压切换触发时刻所具有的特点见表2,其中fr=wr/(2p),fc=wc/(2p)。最大均压频率方面:定时触发频率最灵活,但无法减少额外开关次数;阶梯波跳变点触发可减少额外开关次数,但最大均压频率较低;而锯齿载波跳变点触发在减少额外开关次数的同时具有较高的最大均压频率。窄脉冲[21]方面,来源有三:①PWM窄脉冲;②阶梯波电平变化与PWM电平变化时间相隔较近且作用于同一子模块;③均压切换与阶梯波电平变化或PWM电平变化的时间相隔较近且作用于同一子模块。定时触发和阶梯波跳变点触发均可因来源①~③产生窄脉冲。锯齿载波跳变点触发由于均压切换在锯齿波跳变时刻,该时刻在每个PWM周期中是固定的,故可设置阶梯波采样点与均压切换时刻重合或者具有近1个控制周期的时间间隔,从而避免来源③产生的窄脉冲;将PWM输出子模块的切换时刻限制在锯齿波跳变点,可避免来源②产生的窄脉冲;参考电压限幅可避免来源①的窄脉冲。由以上分析可知,锯齿载波跳变点触发可避免窄脉冲。
表2 不同均压切换触发时刻的特点
Tab.2 Characteristics of different triggers of voltage-balancing rotating

均压切换触发时刻最大均压频率窄脉冲 定时∞存在 阶梯波跳变点2(N-1)fr存在 锯齿载波跳变点fc可避免
综上所述,本文提出的锯齿载波NL-PWM的均压方法如图8所示,图中,Td为延时,略大于DSP计算单元从执行子模块电压采样到逻辑器件接收到子模块电压顺序和输出电平所用的时长。
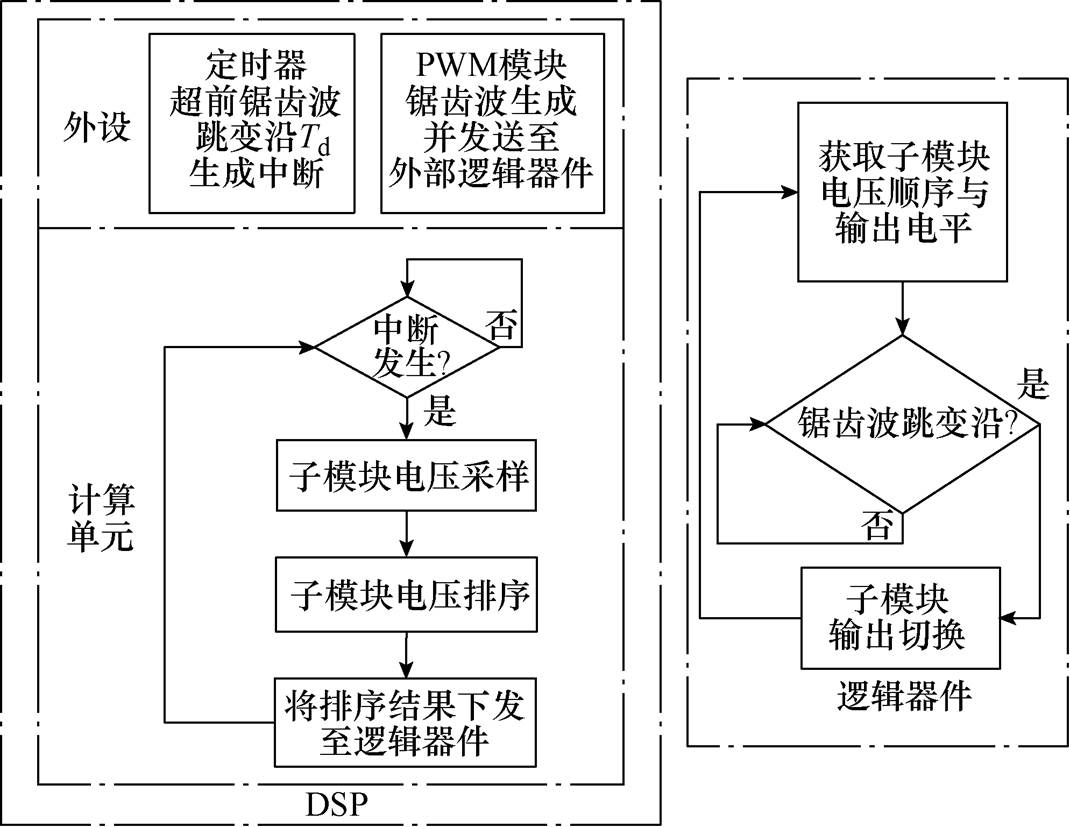
图8 锯齿载波NL-PWM的均压方法
Fig.8 Voltage-balancing method for sawtooth-carrier based NL-PWM
本文在PSCAD/EMTDC中建立了如图1所示的MMC仿真模型,模型参数见表3。仿真模型中,MMC交流侧连接交流电网,直流侧连接直流负载。
表3 仿真模型参数
Tab.3 Parameters of simulation model

参 数数 值 直流母线电压Udc/kV19.5 直流负载功率PN/kW1 000 桥臂子模块数N3 桥臂电感Ls/mH69 子模块电容C/mF220 子模块电压UC/kV6.5 交流电网电压Ug/kV10 交流电网频率fr/Hz50 调制比M0.84 PWM载波频率fc/Hz1 950 功率因数1 死区/ms5
图9a、图9b分别为锯齿载波NL-PWM和倍频锯齿载波NL-PWM的线电压频谱与THD仿真结果。对比图9与图6可知,仿真结果与理论分析基本相符。仿真中设置的5ms死区使得仿真结果在低频段出现了少许谐波,理论分析与仿真结果THD的误差小于4.8%。

图9 线电压频谱与THD仿真结果
Fig.9 Simulation results of spectrums and THDs of line voltages
图10为四种调制的电网电流及其THD(1~39次谐波)。对比图10a和图10c可知,在非倍频的情况下,锯齿载波NL-PWM的低频段谐波含量更丰富,在开关频率较低时,将会有更多的谐波电流满足THD计算范围,因而三角载波NL-PWM具有更低的电流THD;对比图10b与图10d可知,在倍频的情况下,锯齿载波NL-PWM具有更低的电流THD,与理论分析相符。
图11为四种均压切换触发模式下的子模块电压仿真结果。图中,Uband为子模块电压最大离散宽度,fb为平均到每个功率开关的由均压切换产生的额外开关频率,是通过功率开关平均开关频率减去其平均分担的PWM和阶梯波开关频率得到的。对比图11a和图11c可知,在Uband同为84V时,采用锯齿载波跳变点触发较采用定时触发可减少81.4%的额外开关频率;对比图11b和图11d可知,在额外开关频率相近的情况下,采用锯齿载波跳变点触发较采用阶梯波跳变点触发可减少约87.1%的Uband,具有良好的均压效果。
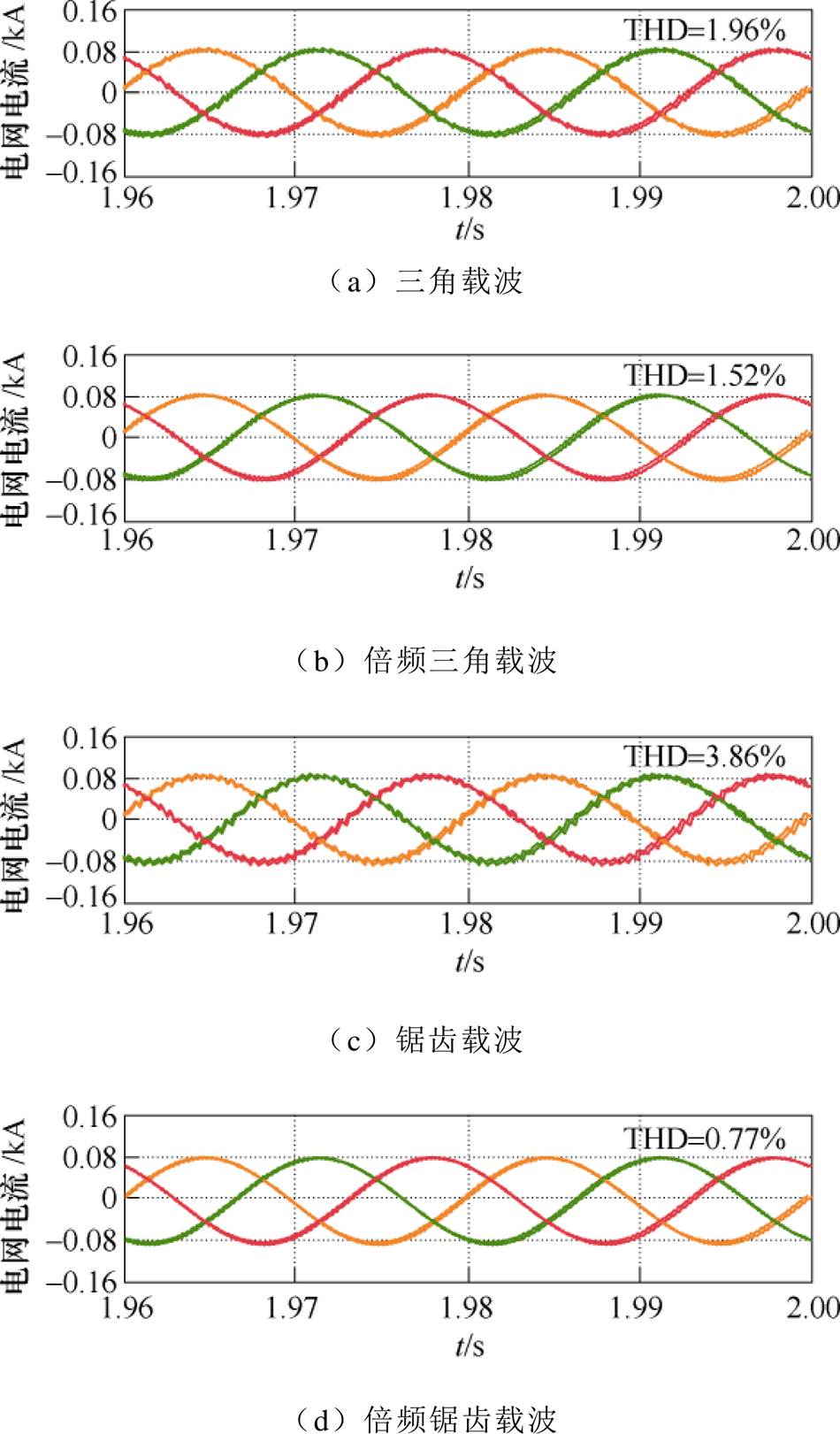
图10 四种调制的电网电流及其THD仿真结果
Fig.10 Simulation results of grid-side currents and their THDs of four modulation methods
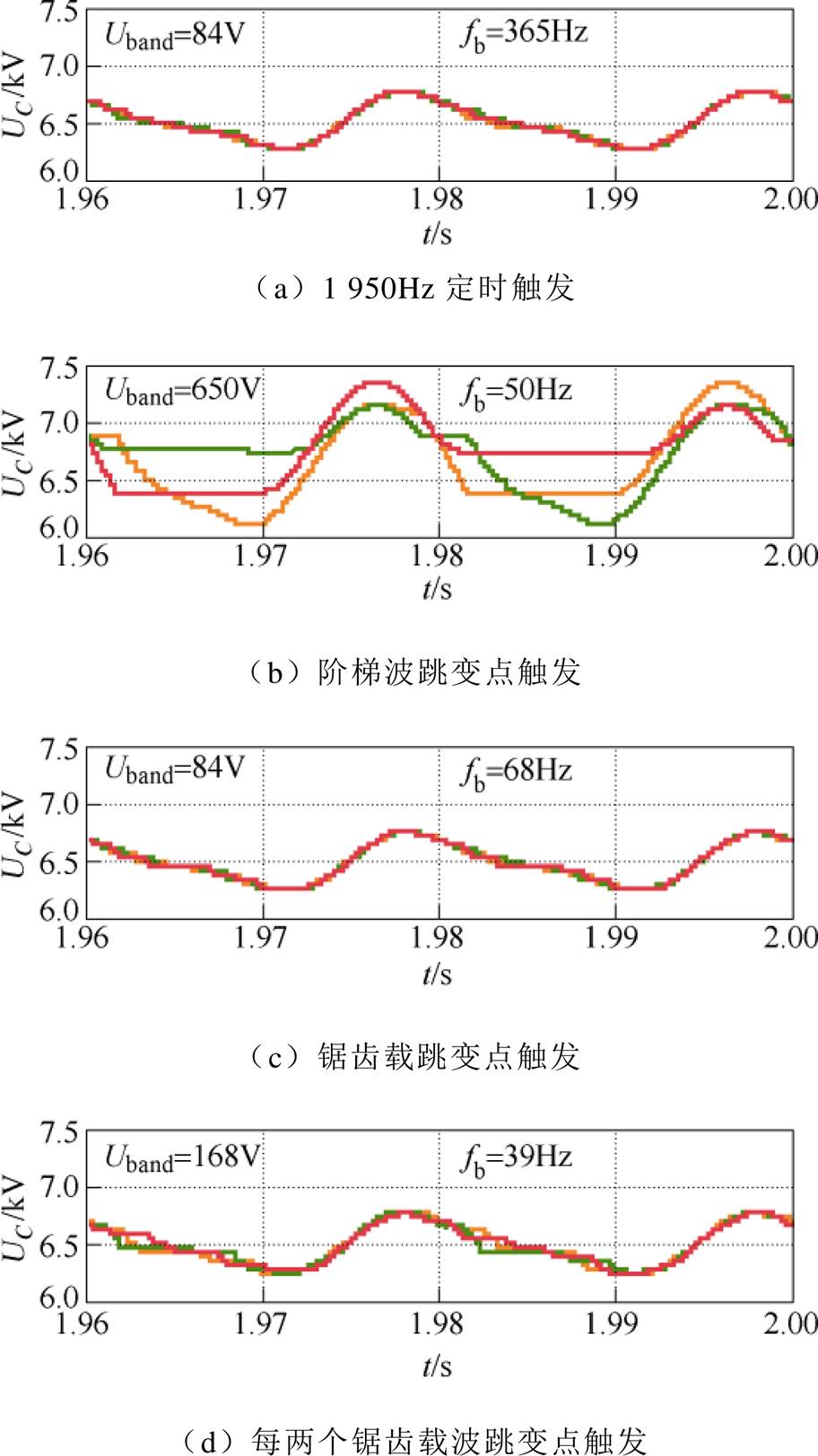
图11 四种均压切换触发模式下的子模块电压
Fig.11 Simulation results of voltage-balancing effects with different triggers of voltage-balancing rotating
图12为锯齿载波跳变点触发情况下的载波、调制波与子模块触发脉冲仿真结果。如图所示,t =t1前,SM2负责输出PWM波;t =t1,在锯齿载波上升沿,PWM输出切换至SM1,此时SM1和SM2虽进行了均压切换,但仅SM1存在开关动作,SM1的切换模式符合表1所示模式3,该模式下均压切换不增加开关次数。
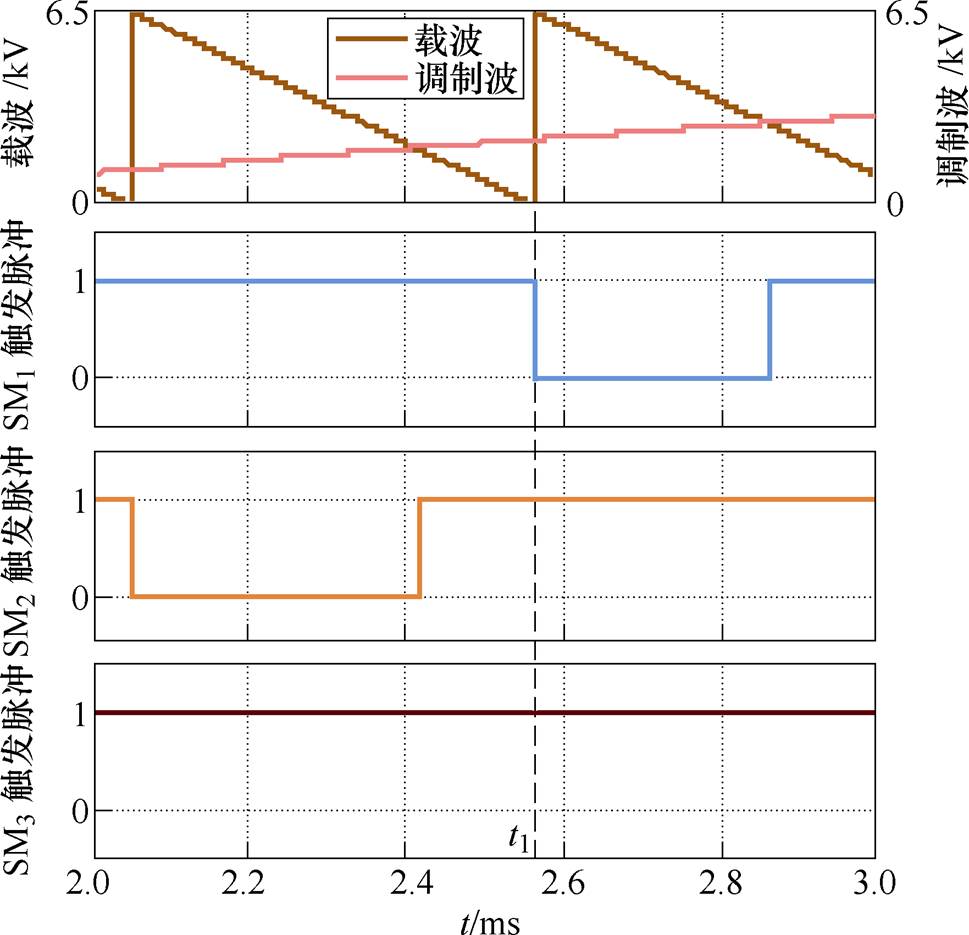
图12 锯齿载波跳变点触发情况下的载波、调制波与子模块触发脉冲仿真结果
Fig.12 Simulation results of carrier wave, modulation wave, and SM gate signals triggered at the edges of sawtooth carrier
图13为三种不同均压切换触发模式下,桥臂所有功率开关每秒发生的脉冲宽度小于5ms的窄脉冲次数仿真结果。由图13可知,窄脉冲主要由第3节所述原因③产生,采用锯齿载波跳变点触发能有效避免窄脉冲。
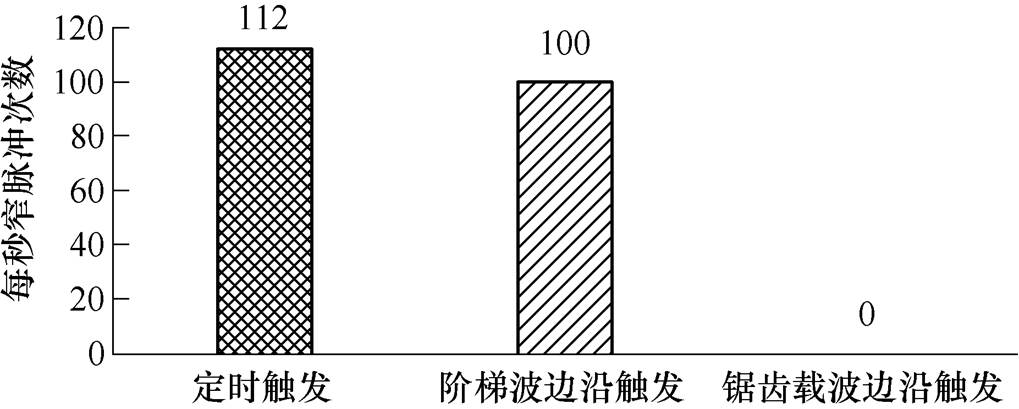
图13 不同均压切换触发模式下的桥臂每秒窄脉冲次数
Fig.13 Simulation results of every second bridge-arm narrow pulse count with different triggers of voltage-balancing rotating
根据图1所示拓扑搭建如图14所示的MMC样机进行实验验证,样机参数见表4。实验中,MMC交流侧连接交流电网,直流侧连接直流负载。

图14 MMC 样机
Fig.14 Prototype of MMC
表4 样机参数
Tab.4 Parameters of prototype

参 数数 值 直流母线电压Udc/kV1.95 直流负载功率PN/kW100 桥臂子模块数N3 桥臂电感Ls/mH6.9 子模块电容C/mF2 200 子模块电压UC/kV0.65 交流电网电压Ug/kV1 交流电网频率fr/Hz50 调制比M0.84 PWM载波频率fc/Hz1 950 功率因数1 死区/ms5
图15a、图15b分别为非倍频锯齿载波NL-PWM和倍频锯齿载波NL-PWM的线电压频谱与THD的实验结果。对比图15、图9与图6可知,实验结果与仿真和理论分析结果基本相符。
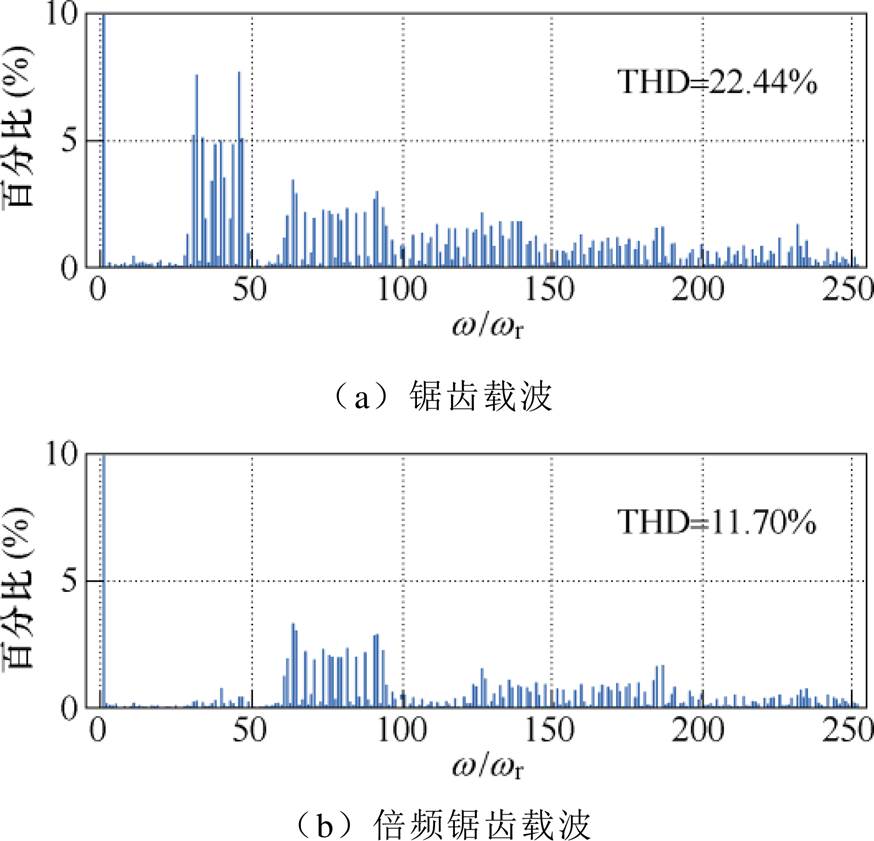
图15 线电压频谱与THD实验结果
Fig.15 Experimental results of spectrums and THDs of line voltages
图16为锯齿载波跳变点触发情况下PWM比较器输出(不含死区)与子模块触发脉冲(含死区)实验结果。如图16所示,t =t1前,SM2负责输出PWM波;t =t1,在锯齿载波上升沿PWM输出切换至SM3,此时,SM2和SM3虽进行了均压切换,但仅SM3存在开关动作,SM3的切换模式符合表1所示模式3,该模式下均压切换不增加开关次数。上述结果与仿真结果相符,证明所提调制可降低开关频率。
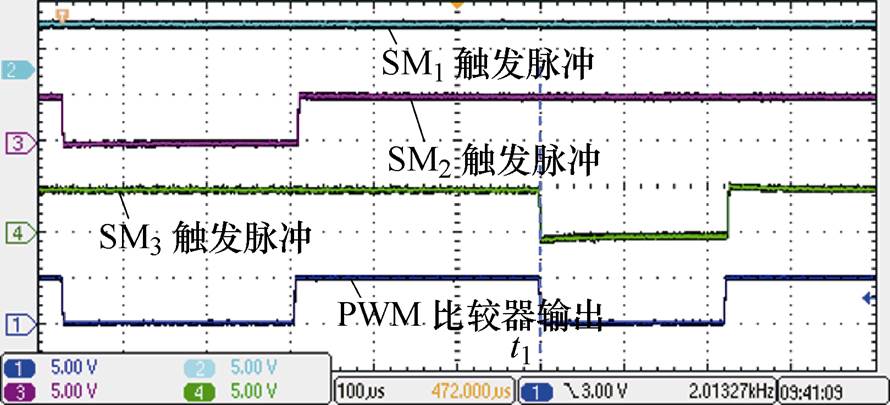
图16 锯齿载波跳变点触发情况下PWM比较器输出与子模块触发脉冲实验结果
Fig.16 Experimental results of PWM-comparator output and SM trigger signals triggered at the edge of sawtooth carrier
图17为三相交流电网电流实验结果。图17a~图17d中,电流THD分别为1.86%、1.45%、3.79%和0.72%。实验结果表明,基于非倍频三角载波的NL-PWM较基于非倍频锯齿载波的NL-PWM输出电流质量更好,而基于倍频锯齿载波的NL-PWM具有最优的输出电流质量,该结论与理论分析和仿真结果相符。

图17 三相交流电流实验结果
Fig.17 Experimental results of three-phase AC currents
图18为上桥臂子模块电容电压实验结果。实验中采用锯齿载波跳变点触发,3个子模块电容电压的均压效果良好。本文样机与文献[13]样机以额定功率标幺后,具有相近的桥臂电容储能。本文子模块电压最大离散宽度约40V(0.06(pu)),较文献[13]在阶梯波跳变点触发所得0.2(pu)结果有较大改善。
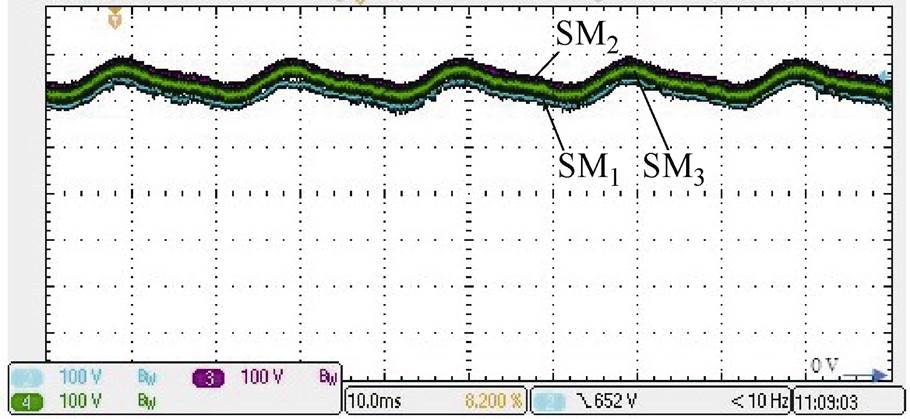
图18 上桥臂子模块电容电压实验结果(CH2:SM1;CH3:SM2;CH4:SM3)
Fig.18 Experimental results of SM capacitor voltages of upper bridge-arm
NL-PWM方法适用于子模块数较少的中压MMC,本文在现有基于三角载波的NL-PWM方法基础上,提出了非倍频和倍频的基于锯齿载波的NL-PWM方法。锯齿载波具有固定的跳变沿,可在其跳变点进行子模均压切换,以减少由于子模块均压切换而产生的额外开关次数,从而降低开关频率。在本文研究案例中,当子模块电压离散宽度相同时,所提调制及其均压方法较定时触发均压切换的NL- PWM可减少约81.4%的额外开关频率;当开关频率相近时,所提调制及其均压方法较阶梯波跳变点触发均压切换的NL-PWM可减少约87.1%的子模块电压离散宽度。此外,本文所提调制方法亦可避免均压切换产生的功率器件窄脉冲。通过分析对比基于不同载波的NL-PWM的谐波特性,本文研究表明,倍频锯齿载波NL-PWM方法可在降低开关频率的同时保证良好的均压效果与输出电能质量。倍频调制下,每相投入的子模块数具有时变性,需适当增大桥臂电感以抑制相间高频环流。
参考文献
[1] Lesnicar A, Marquardt R. An innovative modular multilevel converter topology suitable for a wide power range[C]//IEEE Power Technology Conference, Bologna, Italy, 2003: 1-6.
[2] 尹太元, 王跃, 段国朝, 等. 基于零直流电压控制的混合型MMC-HVDC直流短路故障穿越策略[J]. 电工技术学报, 2019, 34(增刊1): 343-351.
Yin Taiyuan, Wang Yue, Duan Guochao, et al. Zero DC voltage control based DC fault ride-through strategy for hybrid modular multilevel converter in HVDC[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 343-351.
[3] 王一凡, 赵成勇, 郭春义. 双馈风电场孤岛经模块化多电平换流器直流输电并网系统小信号稳定性分析与振荡抑制方法[J]. 电工技术学报, 2019, 34(10): 2116-2129.
Wang Yifan, Zhao Chengyong, Guo Chunyi. Small signal stability and oscillation suppression method for islanded double fed induction generator-based wind farm integrated by modular multilevel converter based HVDC system[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2116-2129.
[4] 李子欣, 王平, 楚遵方, 等. 面向中高压智能配电网的电力电子变压器研究[J]. 电网技术, 2013, 37(9): 2592-2601.
Li Zixin, Wang Ping, Chu Zunfang, et al. Research on medium- and high-voltage smart distribution grid oriented power electronic transformer[J]. Power System Technology, 2013, 37(9): 2592-2601.
[5] Briz F, López M, Rodríguez A, et al. MMC based SST[C]//IEEE 13th International Conference on Industrial Informatics (INDIN), Cambridge, 2015: 1591-1598.
[6] Pacheco J, Honório D, Oliveira D. An AC-DC isolated MMC-based structure suitable for MV SST traction applications[J]. IEEE Access, 2019, 7: 106395- 106406.
[7] Jing L, Xu Cai, Molinas M. Optimal design of controller parameters for improving the stability of MMC-HVDC for wind farm integration[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(1): 40-53.
[8] 赵争鸣, 冯高辉, 袁立强, 等. 电能路由器的发展及其关键技术[J]. 中国电机工程学报, 2017, 37(13): 3823-3834.
Zhao Zhengming, Feng Gaohui, Yuan Liqiang, et al. The development and key technologies of electric energy router[J]. Proceedings of the CSEE, 2017, 37(13): 3823-3834.
[9] Hu Pengfei, Jiang Daozhuo. A level-increased nearest level modulation method for modular multilevel converters[J]. IEEE Transactions on Power Electro- nics, 2015, 30(4): 1836-1842.
[10] Wang Kun, Deng Yan, Peng Hao, et al. An improved CPS-PWM scheme-based voltage balancing strategy for MMC with fundamental frequency sorting algorithm[J]. IEEE Transactions on Industrial Elec- tronics, 2019, 66(3): 2387-2397.
[11] 白志红, 周玉虎. 模块化多电平换流器的载波层叠脉宽调制策略分析与改进[J]. 电力系统自动化, 2018, 42(21): 139-144.
Bai Zhihong, Zhou Yuhu. Analysis and improvement on carrier level-shifted pulse width modulation strategy for modular multilevel converter[J]. Auto- mation of Electric Power Systems, 2018, 42(21): 139-144.
[12] Deng Yi, Wang Yebin, Teo K H, et al. Optimized control of the modular multilevel converter based on space vector modulation[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 5697-5711.
[13] Wang Yi, Hu Can, Ding Ruoyu, et al. A nearest level PWM method for the MMC in DC distribution grids[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9209-9218.
[14] Choi J, Han B, Kim H. New scheme of phase-shifted carrier PWM for modular multilevel converter with redundancy submodules[J]. IEEE Transactions on Power Delivery, 2016, 31(1): 407-409.
[15] Tariq M, Meraj M, Azeem A, et al. Evaluation of level-shifted and phase-shifted PWM schemes for seven level single-phase packed U cell inverter[J]. CPSS Transactions on Power Electronics and Applications, 2018, 3(3): 232-242.
[16] Deng Yi, Harley R G. Space-vector versus nearest- level pulse width modulation for multilevel con- verters[J]. IEEE Transactions on Power Electronics, 2015, 30(6): 2962-2974.
[17] Lin Lei, Lin Yizhe, He Zhen, et al. Improved nearest-level modulation for a modular multilevel converter with a lower submodule number[J]. IEEE Transactions on Power Electronics, 2016, 31(8): 5369-5377.
[18] 苟锐锋, 赵方舟, 肖国春, 等. 基于修正优化归并排序的MMC电容均压策略[J]. 中国电机工程学报, 2017, 37(1): 251-261.
Gou Ruifeng, Zhao Fangzhou, Xiao Guochun, et al. A capacitor voltage balancing strategy for MMC based on optimized merge sort[J]. Proceedings of the CSEE, 2017, 37(1): 251-261.
[19] Li Yufei, Wang Yue, Li Q Ben. Generalized theory of phase-shifted carrier PWM for cascaded H-bridge converters and modular multilevel converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(2): 589-605.
[20] Hagiwara M, Maeda R, Akagi H. Control and analysis of the modular multilevel cascade converter based on double-star chopper-cells (MMCC-DSCC)[J]. IEEE Transactions on Power Electronics, 2011, 26(6): 1649-1658.
[21] 李敏裕, 马晓军, 魏曙光, 等. 三电平虚拟空间矢量脉宽调制算法窄脉冲抑制研究[J]. 电工技术学报, 2018, 33(14): 3264-3273.
Li Minyu, Ma Xiaojun, Wei Shuguang, et al. Research on narrow pulse suppression of three-level virtual space vector pulse width modulation algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3264-3273.
A Reduced-Switching Frequency NL-PWM Method Based on Sawtooth Carrier for Medium Voltage Modular Multilevel Converter
Abstract The nearest level pulse width modulation (NL-PWM) is suitable for the medium voltage modular multilevel converters (MMCs), which can greatly reduce the current distortion compared with the nearest level modulation (NLM). The NL-PWM achieves bridge-arm sub-module voltage balancing by the sorting algorithm. The implementation of the voltage-balancing rotating at each edge of the stair wave can reduce extra switching, but it also limits the balancing frequency and consequently affects the balancing effect. Since the switching frequency of PWM is relatively high, conducting the voltage-balancing rotating at the edges of PWM wave can greatly increase the balancing frequency. The state-of-the-art NL-PWM is based on triangle carrier, and its switching point varies with the reference voltage, which is not convenient for the implementation of the voltage-balancing control. In this paper, a non-frequency-doubling and a frequency-doubling NL-PWM methods based on sawtooth-carrier are proposed. The sawtooth wave has fixed edges to facilitate the voltage-balancing control. The hormonic characteristics of the proposed modulations are analyzed. It is shown that the frequency-doubling sawtooth-carrier based NL-PWM method can ensure both good voltage-balancing effect and output power quality while reducing the switching frequency. Besides, the proposed modulation can also avoid narrow pulse of power switches. Simulation and experiments verify the correctness of the theoretical analysis.
keywords:Medium voltage modular multilevel converter, nearest level pulse width modulation (NL-PWM), sawtooth carrier, switching frequency, narrow pulse
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.190182
北京市自然科学基金项目(3172036)和新能源电力系统国家重点实验室(华北电力大学)自主研究课题(LAPS2019-20)资助。
收稿日期2019-02-23
改稿日期 2019-09-18
张雪垠 男,1992年生,博士研究生,研究方向为多电平换流器和电力电子变压器等。E-mail: elec_zhang@foxmail.com(通信作者)
徐永海 男,1966年生,博士,教授,博士生导师,研究方向为电能质量分析与控制技术、电力电子变压器和新能源电力系统等。E-mail: yonghaixu@263.net
(编辑 崔文静)