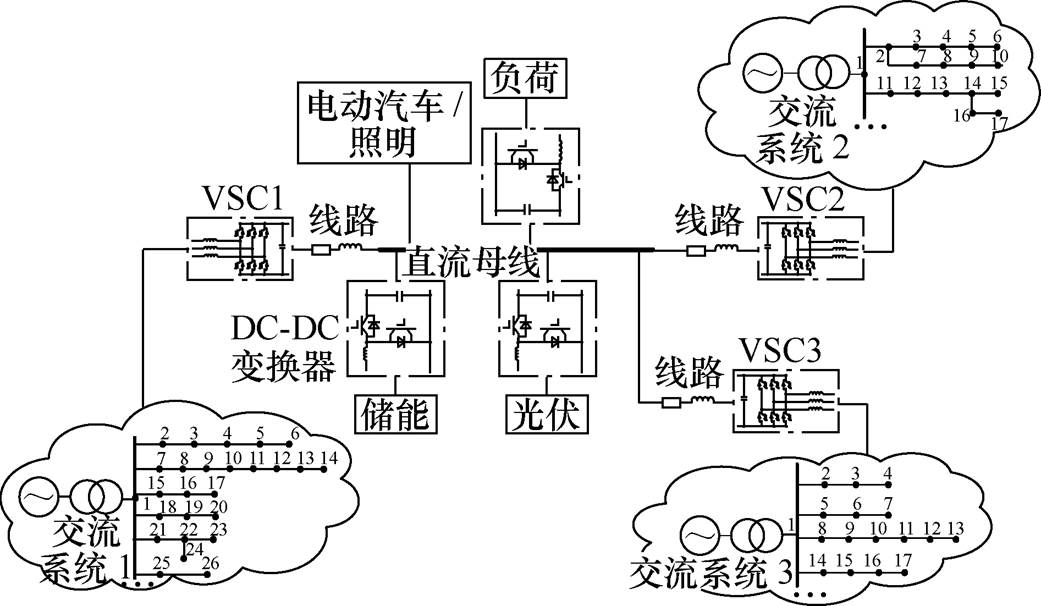
图1 三端MTDC系统典型结构
Fig.1 Typical structure of three-terminal DC system
摘要 集成优化是多端直流(MTDC)系统的关键技术之一。该文面向低压三端直流系统提出一种提升运行边界的集成参数优化配置方法。首先建立三端MTDC系统等效电路及其特性模型,分析集成参数对系统运行边界的影响;然后,以稳定区域与设计区域的面积差最小、集成成本最低为优化目标,提出集成参数多目标优化模型。最后采用第二代非支配排序遗传算法(NSGA-II)对模型求解帕累托(Pareto)最优解集,并通过模糊聚类算法筛选出集成参数优化配置方案。对算例进行仿真分析,研究结果表明,所提方法有效可行,能够在保障系统经济性的前提下,显著提升三端MTDC系统运行边界。
关键词:多端直流 系统集成 参数配置 运行边界 多目标优化
随着大规模分布式可再生能源接入电网,对系统的灵活接入和有效管控提出了新的挑战和更高的要求,而直流系统接入可以减少变换环节、提高整体运行效率的优势日益凸显,光伏、风电等分布式能源以直流方式聚集实施灵活接入成为新的发展趋势。与此同时,电动汽车(Electric Vehicle, EV)、储能装置、LED照明等直流设备的广泛使用[1-3],对供需双方迫切的技术与应用需求进一步推动了低压直流配电系统的迅速发展[4]。
基于多端直流(Multi-Terminal DC, MTDC)构建的交直流混合配电系统可以实现灵活组网,在多个交直流电压等级集成分布式可再生能源,实现灵活安全接入,提高能源利用效率、增强系统控制能力、在更大范围实现互联互补、充分消纳可再生能源已成为未来电网的重要形态之一[5],目前学者们对此已经开展了诸多研究,如未来可再生电能输送与管理系统(Future Renewable Electric Energy Delivery and Management System, FREEDM)[6],欧洲通用灵活电力管理系统(Universal and Flexible Power Management System, UNIFLX)[7]以及深圳市宝龙工业城多端直流配电系统[8]。
MTDC系统的可靠运行依赖所接入的多类型电力电子变换器,包含承担直流网与交流网之间潮流控制的AC-DC换流装置,以及承担不同直流电压等级转换的DC-DC 变换器[9-10]。值得注意的是,当系统采用主从控制模式时,运行于功率调度方式的AC-DC换流装置以及DC-DC 变换器将与恒功率负载(Constant Power Load, CPL)呈现负阻抗特性[11];当直流电压偏离稳态点时,负阻抗特性会进一步加剧直流电压的波动,严重时会导致直流网的不稳定,影响整个系统的安全运行[12-13]。这也意味着,在负阻抗特性的影响下,AC-DC换流装置的传送功率不能进行任意调节,实际的运行容量可能低于或大幅度低于装置的设计容量,这也意味着MTDC系统的直流网内源-网-荷-储等多类型变流设备进行集成时,设计的系统运行边界将随之收缩,相应地降低了系统的技术经济性。
另一方面,电力电子变流设备对高可靠性、高功率密度的需求日益凸出,小型化和轻量化的变流设备对于MTDC系统集成而言具有较强优势。由于变流设备内部的开关管、滤波器等的体积、质量跟所采用的器件类型息息相关,因此在体积、质量的应用需求驱动下,SiC功率器件[14]、金属薄膜电容[15]等逐步得以应用。较之采用传统器件,变流设备的整体成本相应也将随之增加。
综上所述,MTDC系统集成时将面临运行边界受限和集成成本增加两方面问题,如何既降低集成成本又有效提升系统运行边界已成为整体集成的关键技术之一。本文针对三端MTDC系统多类型变流设备集成问题,提出一种提升系统运行边界的集成参数优化配置方法,在保障系统经济性的前提下,通过对各设备直流侧电容等关键参数进行配置优化,进而提升系统运行边界以及各端之间的功率互济能力,并进行相应的分析计算与仿真研究。
三端MTDC系统的典型结构如图1所示,在交流系统中通过集成MTDC(包括多个换流装置与直流网),进而形成多端互济互联结构,这样依赖可控的分布式能源、灵活的直流多端互联拓扑以及精准的多端协调控制,可以将多个交流系统之间的潮流经直流网进行互济均衡,使得整体具有更宽范围的功率分担能力和供电能力。图1中三个电压源型换流站(Voltage-Source Converter, VSC),VSC1、VSC2、VSC3的交流侧分别接入交流系统1、交流系统2与交流系统3,而直流侧则经一定长度的线路接入直流母线。直流网可集成接入风电、光伏等可再生能源、储能系统以及直流负载等,当设备电压的等级与直流母线电压等级不匹配时可配置DC-DC变换器进行转换。

图1 三端MTDC系统典型结构
Fig.1 Typical structure of three-terminal DC system
当三端MTDC系统采用主从控制模式时,如VSC1作为主站,采用定直流电压控制方式,其直流侧电容通常高裕度配置,以增强系统抗扰动能力、支撑直流网的电压恒定;VSC2、VSC3、储能系统则采用功率调度方式。忽略电力电子变流设备的功率损耗,则系统的等效电路如图2所示。
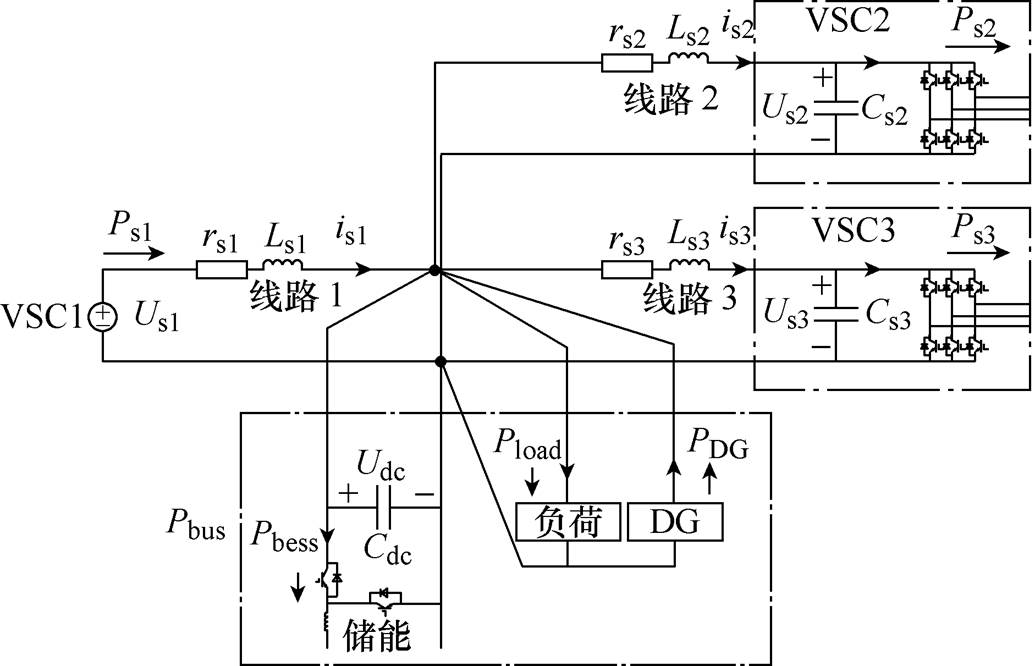
图2 系统等效电路
Fig.2 System equivalent circuit
图2中,主站通过直流线路rs1、Ls1连接直流母线,VSC2、VSC3分别通过直流线路rs2、Ls2,直流线路rs3、Ls3连接直流母线;Us1、is1分别表示主站的直流侧电压与线路电流,作为主站,Us1通常可视为恒定。Us2、is2、Cs2以及Ps2分别表示VSC2的直流侧电压、线路电流、直流侧电容以及传送功率;Us3、is3、Cs3以及Ps3分别表示VSC3的直流侧电压、线路电流、直流侧电容以及传送功率;Udc、Cdc分别表示直流母线电压、储能直流侧电容;Pbess、Pload、PDG分别表示储能功率、负荷功率、分布式电源功率。直流母线等效负荷功率Pbus为
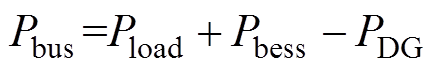 (1)
(1)在多个交流系统中集成MTDC时,VSC、直流母线等的空间位置通常与现有系统中实际的直流负荷、交流负荷等关键节点的分布息息相关,在一定的系统结构和负荷分布下,设计的各VSC与直流母线的距离相对固定,此时集成优化的主要对象为各VSC设备直流侧电容等关键参数。
针对如图2所示的MTDC系统建立等效电路方程,并进行线性化,推导可得
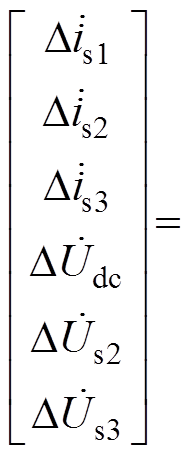
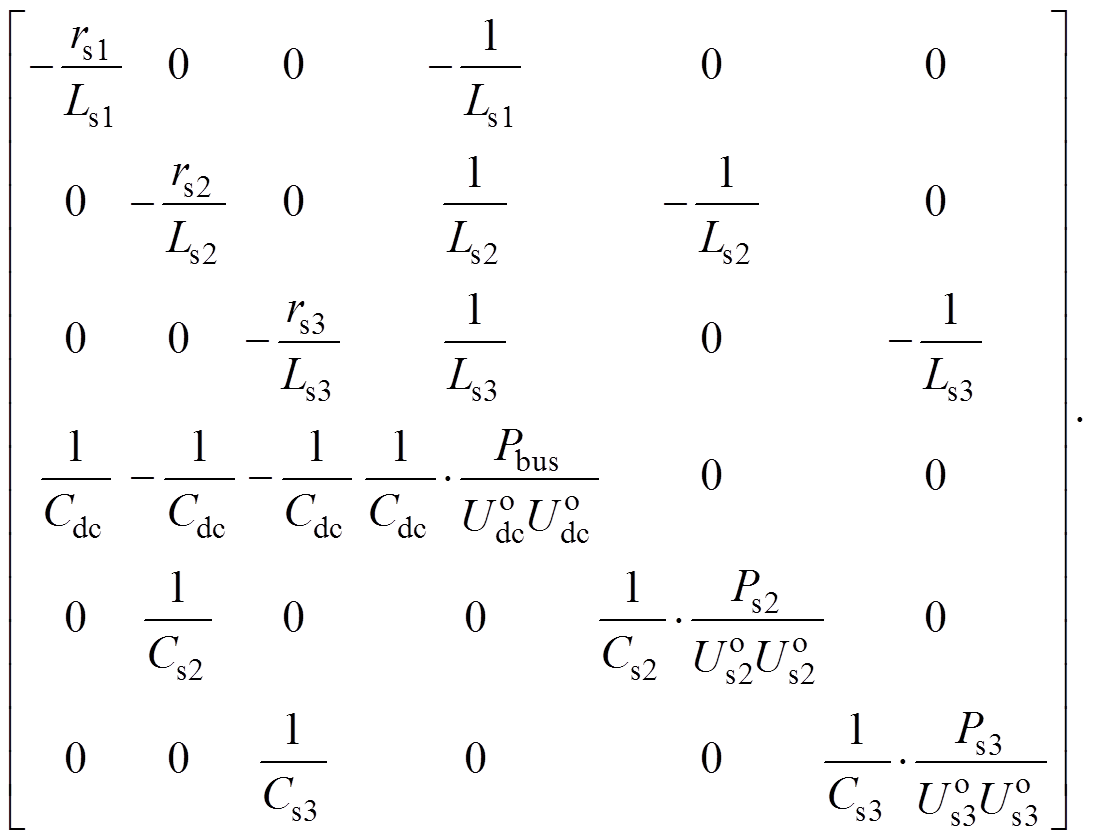
 (2)
(2)
式中,上标o代表物理量的稳态值。由式(2)可知,在直流线路距离和直流网电压等级一定的情况下,VSC2、VSC3的传送功率以及直流母线等效负荷功率与Cdc、Cs2、Cs3存在一定的耦合关系。依据式(2)绘制如图3所示的MTDC系统运行边界,其原理为:在给定一组运行点时,采用式(2)求解系统特征根(或主导特征根),如果特征根进入复平面右半平面,系统将进入失稳区域,按照上述判定依据通过循环扫描各运行点,进而可以确定由稳定运行点形成的区域及失稳区域,两者之间的边界确定为系统运行边界。其中系统参数见表1(表中直流网电压等级为DC 800V,主站设计的额定容量Pvsc1,rated为1.5MW,VSC2设计的额定容量Pvsc2,rated和VSC3 设计的额定容量Pvsc3,rated均为500kW,储能设计的额定容量Pbess,rated为100kW,直流母线等效负荷功率统计分布为-50~200kW)。
由于Ps2和Ps3接受功率调度运行时,两者的负阻抗特性将直接影响到系统的运行边界。这也意味着当其中一方功率变化时,为了能够保持系统稳定,另一方此时相应的最大允许交互功率也将发生变化;反之亦然。扫描Ps2和Ps3各运行功率后可形成系统的运行边界及稳定区域如图3所示。由图3a可知,在不同的Pbus下,Ps2和Ps3两者形成的稳定区域也会发生变化,在Pbus=-50kW情况下,其稳定区域面积最大,随着输出功率Pbus逐步减少至0或者吸收功率逐步增加,两者形成的稳定区域不断收缩,且边界的收缩趋势均一致,在Pbus= 200kW时,其稳定区域面积最小,如图3b所示。
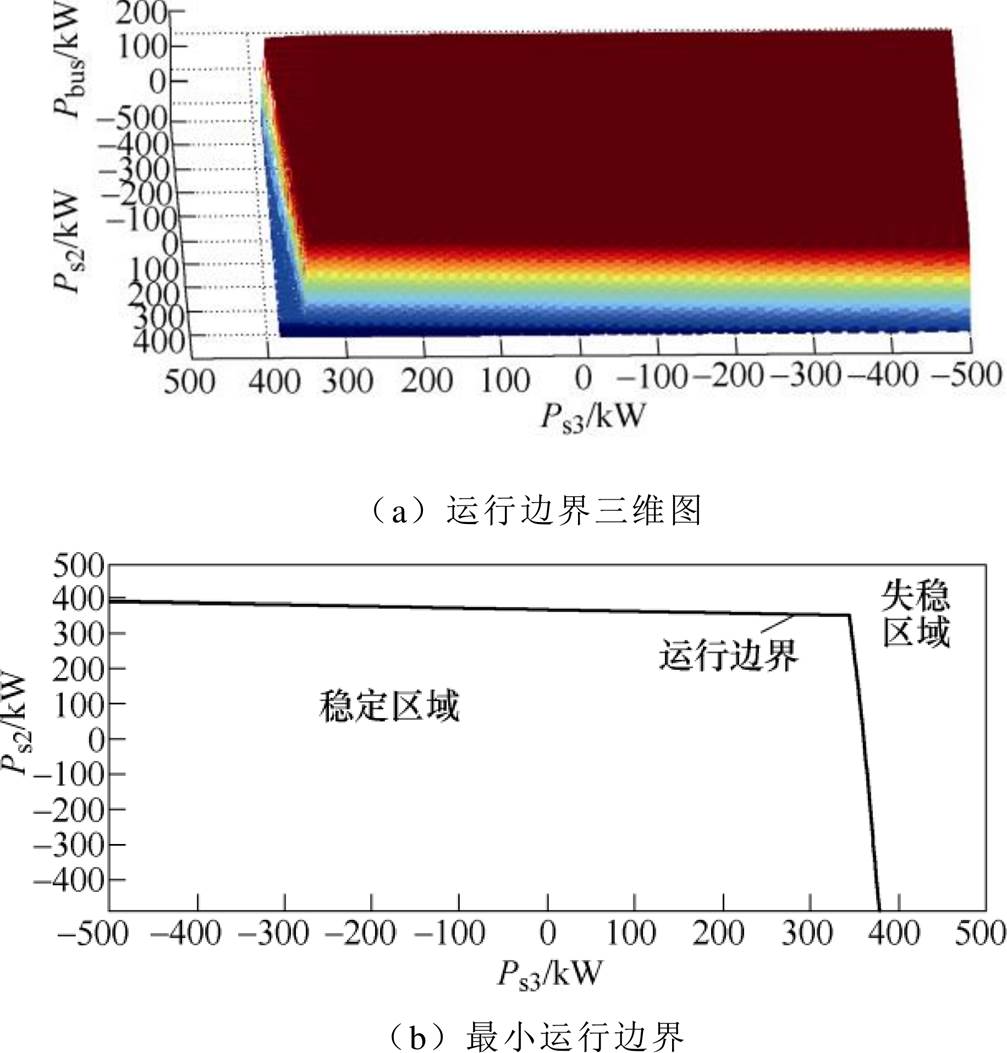
图3 系统运行边界
Fig.3 System operational boundary
表1 系统参数
Tab.1 System parameters

参 数数 值参 数数 值 rs1/W0.005 5rs2/W0.018 2 Ls1/mH0.014 7Ls2/mH0.049 0 Cdc/mF1 200 (经验值)Cs2/mF1 500 (经验值) Us1/VDC 800rs3/W0.045 5 Pvsc1,rated/kW1 500Ls3/mH0.122 5 Pvsc2,rated/kW500Cs3/mF1 500 (经验值) Pvsc3,rated/kW500线路1/km0.06 Pbess,rated/kW100线路2/km0.2 Pbus/kW-50~200线路3/km0.5
图4描述了Pbus=200kW时,本文采用的等效模型与三端MTDC详细模型对应的系统运行边界比较(其中,三端MTDC详细模型如式(A6)所示)。由图4可知,两种模型下的系统运行边界近似重合,相互之间的差值较小,最高误差不超过0.6%。由此可见,等效模型在一定程度上具有较高的准确度,能够刻画系统的运行边界。
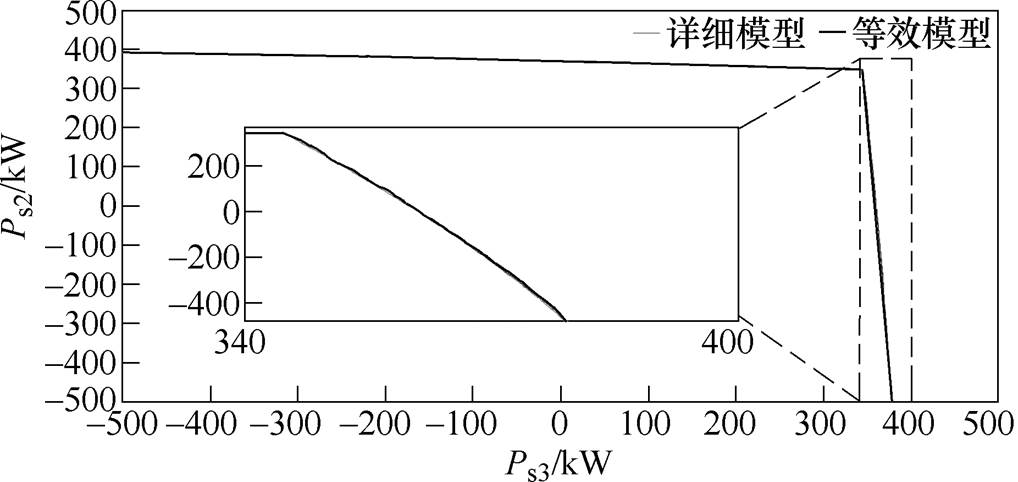
图4 详细模型与等效模型的运行边界比较
Fig.4 Comparison of operational boundary between the detailed model and equivalent model
依据图2所示的三端MTDC系统结构,利用Matlab/Simulink搭建对应的仿真模型,具体参数见表1。设置图3b中对应的运行点Ps3=300kW、Ps2= 330kW变化至Ps3=300kW、Ps2=360kW,此时直流母线电压Udc的仿真结果如图5所示。
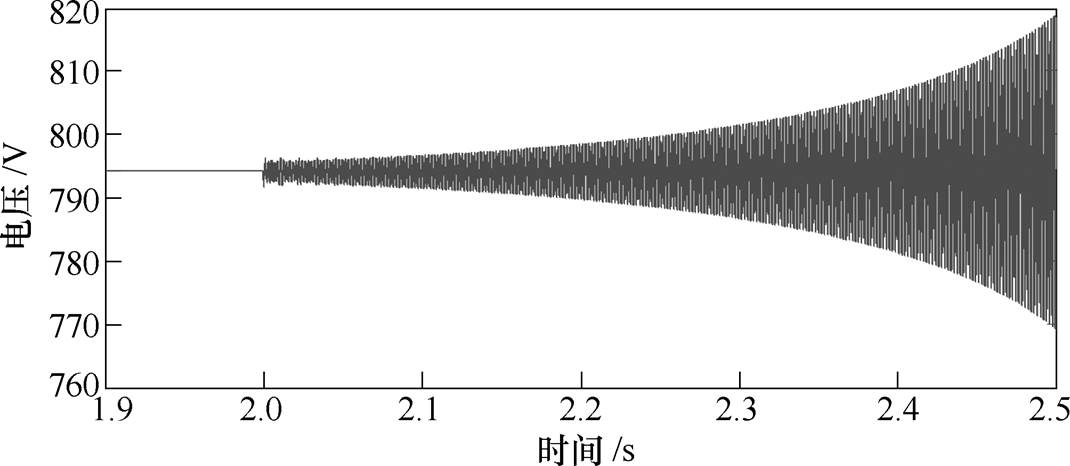
图5 Ps2=330kW变化至Ps2=360kW的仿真结果(Ps3=300kW)
Fig.5 Simulation results by changing Ps2 from 330kW to 360kW (Ps3=300kW)
由图5结果可知,当t =20s运行点发生变化时,直流母线电压出现发散振荡,直至电压失稳。由图3b可知,运行点Ps3=300kW、Ps2=330kW虽接近运行边界,但仍处于稳定区域,而Ps3=300kW、Ps2= 360kW已经越过运行边界,进入失稳区域。仿真结果与理论分析结果相吻合。
在MTDC系统集成设计中,需要全面考虑系统的各种运行工况,尤其是极值情况如稳定区域面积最小情况下,依然能够保证系统的安全运行。选取Pbus=200kW情况下的系统运行边界进行分析(下同),由式(2)可知,系统的运行边界与Cdc、Cs2、Cs3等关键参数存在一定的耦合关系,图6描述了针对表1所述系统参数,分别改变Cdc、Cs2及Cs3时对应的运行边界变化情况。
由图6a可知,储能直流侧电容Cdc从1 000mF变化至1 500mF时,系统运行边界相应扩大,但变化较小。储能接入直流母线后,其Cdc变化对距离直流母线一定线路长度的VSC2与VSC3而言,改变运行边界的能力相对有限。
由图6b可知,VSC2的Cs2从1 200mF变化至1 800mF时,系统运行边界相应扩大,变化显著且两侧边界的变化趋势一致;由图6c可知,VSC3的Cs3从1 200mF变化至1 800mF时,其上侧边界不断降低,而右侧边界则不断扩大。

图6 Cdc, Cs2以及Cs3变化下的系统运行边界
Fig.6 System operational boundary by changing Cdc, Cs2 and Cs3
由此可见,受到系统结构和线路参数的共同影响,分布在不同位置、具有相同容量的VSC,即使其直流侧电容在相同范围变化情况下,各自对系统运行边界的影响也不尽相同,尤其是Cs3对运行边界的影响更为复杂。
不同的Cdc、Cs2及Cs3配置将直接影响到MTDC系统的运行边界,过高的配置能够保障运行边界满足设计需求,但会相应地增加集成成本;而偏低配置虽然降低了集成成本,但无法保证运行边界满足既定的设计需求。因此,本文提出一种兼顾系统经济性并提升系统运行边界的集成参数优化配置方法,由于运行边界和经济性属于不同维度,故采用多目标优化方法。建立的集成参数多目标优化模 型为
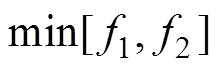 (3)
(3)1)优化目标1:集成成本最低,即通过优化Cdc、Cs2及Cs3等参数配置,在提升系统运行边界的同时,使得系统的设备集成成本最小,目标函数为
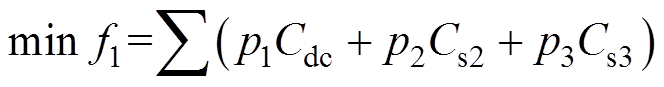 (4)
(4)式中,p1、p2、p3分别为储能的直流侧电容价格(元/mF)、VSC2的直流侧电容价格(元/mF)和VSC3的直流侧电容价格(元/mF)。
2)优化目标2:稳定区域与设计区域的面积差最小,即通过对各设备直流侧电容等关键参数进行配置优化,最大化系统稳定区域,进而显著扩大系统运行边界、提升各端之间的功率互济能力,目标函数为
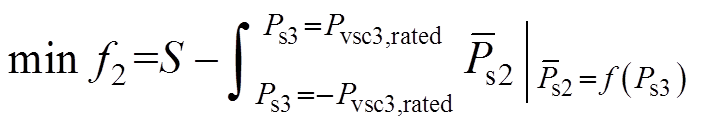 (5)
(5)式中,S为系统稳定运行的设计区域,如理想状态下VSC2与VSC3实现四象限的满容量运行,则S= 1 000kW×1 000kW。 为当前系统参数下Ps3一定时对应的VSC2最大允许交互功率(即运行边界上的点),该数值跟随Ps3变化而变化,以
为当前系统参数下Ps3一定时对应的VSC2最大允许交互功率(即运行边界上的点),该数值跟随Ps3变化而变化,以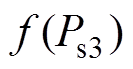 表示,其值由式(2)求解系统特征根且判断特征根是否进入复平面右半平面来决定。通过积分方式近似拟合稳定区域的面积,稳定区域与设计区域的面积差越小,意味着系统的稳定区域面积越大,当f2=0时,MTDC系统的稳定区域完全满足设计需求。
表示,其值由式(2)求解系统特征根且判断特征根是否进入复平面右半平面来决定。通过积分方式近似拟合稳定区域的面积,稳定区域与设计区域的面积差越小,意味着系统的稳定区域面积越大,当f2=0时,MTDC系统的稳定区域完全满足设计需求。
1)VSC运行功率约束
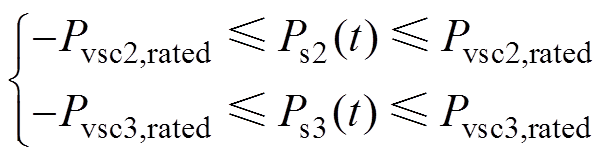 (6)
(6)式中,Ps2(t)为第t次计算中的VSC2传送功率;Ps3(t)为第t次计算中的VSC3传送功率。
2)直流潮流约束
 (7)
(7)式中,Ui(t)、Uj(t)分别为第t次计算中直流节点i、节点j的电压值;Yij为节点i和节点j间的电导。
3)节点电压约束
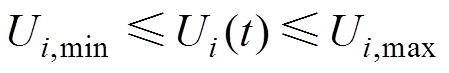 (8)
(8)式中,直流节点i包括直流母线、VSC2直流侧、VSC3直流侧等;Ui,min和Ui,max为节点i的电压值允许下限和电压值允许上限。
4)边界约束
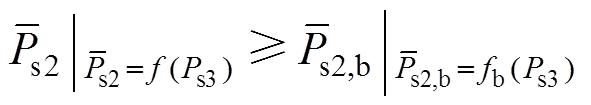 (9)
(9)式中,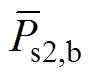 为初始条件下(见表1系统参数)Ps3一定时对应的VSC2最大允许交互功率(见图3b中运行边界上的点),求解方式同
为初始条件下(见表1系统参数)Ps3一定时对应的VSC2最大允许交互功率(见图3b中运行边界上的点),求解方式同 ;fb(Ps3)表示
;fb(Ps3)表示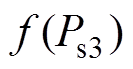 基于初始条件进行求解。表1中的Cdc、Cs2、Cs3为经验值,基于上述经验值可绘制如图3b所示的运行边界,在此基础上对Cdc、Cs2、Cs3进行优化时,每种组合下对应的上边界、右边界各自整体应不低于图3b所示初始条件下的上边界和右边界,进而保障参数优化后的系统稳定区域面积不低于图3b所示初始条件下的稳定区域面积,有效地提升了系统的运行边界。
基于初始条件进行求解。表1中的Cdc、Cs2、Cs3为经验值,基于上述经验值可绘制如图3b所示的运行边界,在此基础上对Cdc、Cs2、Cs3进行优化时,每种组合下对应的上边界、右边界各自整体应不低于图3b所示初始条件下的上边界和右边界,进而保障参数优化后的系统稳定区域面积不低于图3b所示初始条件下的稳定区域面积,有效地提升了系统的运行边界。
5)电容值约束
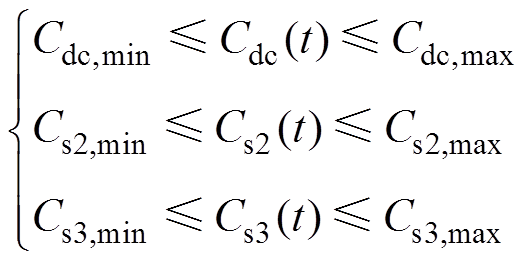 (10)
(10)式中,Cdc(t)、Cs2(t)、Cs3(t)分别为第t次计算中储能、VSC2、VSC3的直流侧电容;下标min代表各自电容值的下限;下标max代表各自电容值的上限。
多目标优化问题中,目标间常常具有冲突性,如优化集成参数时某一目标的优化可能会导致其他目标性能的降低:当集成参数电容值的配置降低时,集成成本相应下降,系统的经济性目标得以优化,但相应地会造成系统稳定运行区域缩小,导致其与设计区域的面积差这一目标性能降低。本文选择智能优化算法对多目标问题进行求解,得到多目标优化模型的Pareto前沿,同时针对给出的最优解集,通过筛选得到更加符合需求的优化解。
本文所建立的多目标优化模型具有非线性、约束复杂的特点,第二代非支配排序遗传算法(Non- dominated Sorting and Sharing Genetic Algorithm, NSGA-Ⅱ)通过快速非支配排序能够降低计算的复杂度,具有很好的全局寻优能力,同时能够保证Pareto前沿的均匀性和多样性,适合该模型的求 解[16]。基于NSGA-Ⅱ算法的多目标优化模型求解流程如图7所示。
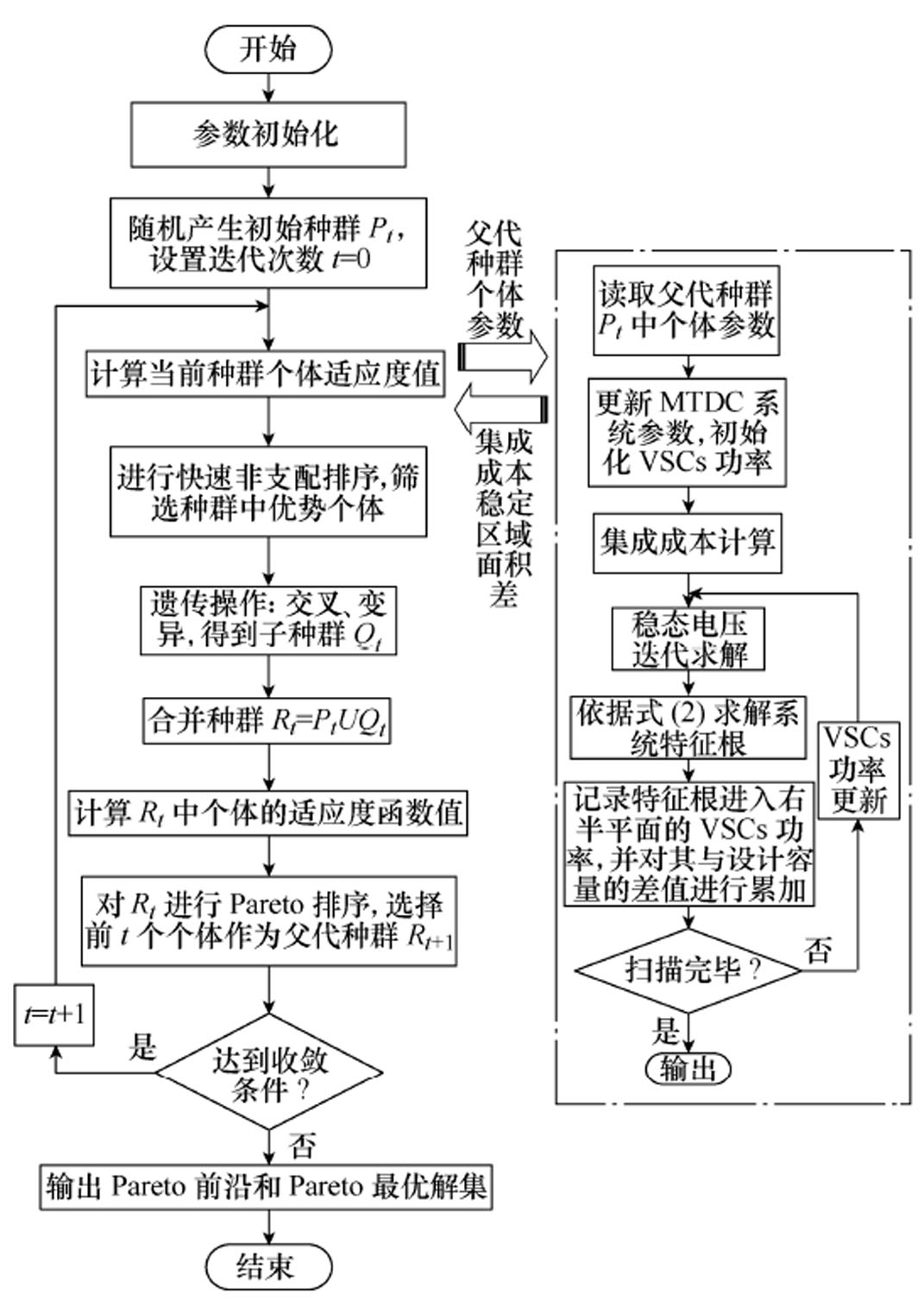
图7 多目标优化模型求解流程
Fig.7 Solving process for multi-objective optimization model
基于NSGA-Ⅱ得到Pareto前沿和Pareto最优解集之后,通过模糊聚类算法筛选出符合需求的最优解[17]。设定多目标各自的权重,并对Pareto前沿的两个目标函数值进行去量纲的隶属度计算,得到每组两个目标函数值的隶属度后结合设定权重进行综合隶属度操作,搜索最大值对应的解即为优化解。
以图2所示三端MTDC系统为研究对象,其系统参数见表1。设定Udc、Us2、Us3的电压值允许下限为DC 760V,电压值允许上限为DC 840V;储能、VSC2、VSC3的直流侧电容均选用高性能金属薄膜电容模块,折合价格p1=p2=p3=2 250元/mF,Cdc,min= 0.8mF,Cdc,max=2mF,Cs2,min=Cs3,min=1mF,Cs2,max= Cs3,max=3mF。通过NSGA-Ⅱ和稳定区域计算对系统进行优化求解,得到的Pareto前沿如图8所示。
1)侧重集成成本情况下的参数配置
设定优化目标1的权重为0.6,优化目标2的权重为0.4,此时图8所示Pareto前沿中优化解为Cdc=855mF,Cs2=1 840mF,Cs3=1 475mF,在此配置下MTDC系统侧重集成成本的系统运行边界如图9所示。在此优化的集成参数下,系统集成成本约为9 380元,低于系统按照初始条件(见表1系统参数)配置时的集成成本9 450元,与此同时,系统运行边界较之初始条件配置时有一定程度的提升,尤其是上边界,其整体提升约20%。由图9可知,通过本文的集成参数优化配置方法并筛选优化解,能够以低于经验值设计时的集成成本来获取更好的系统稳定区域。
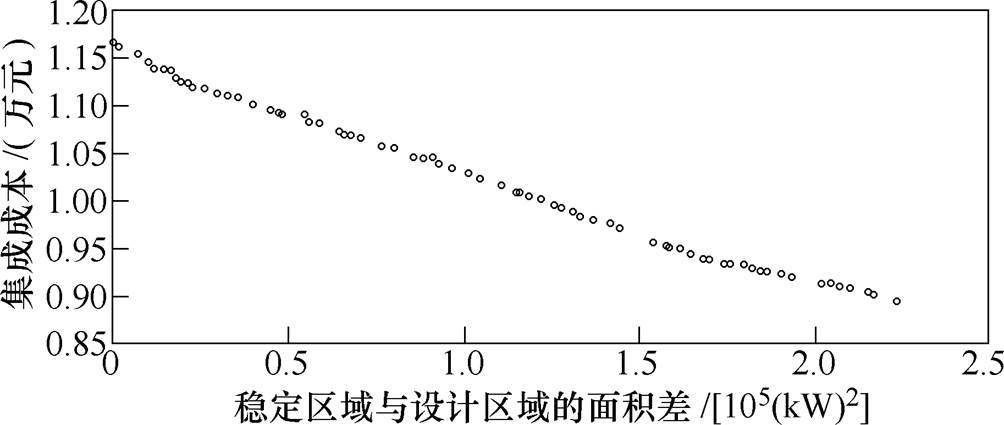
图8 Pareto前沿
Fig.8 Pareto frontier
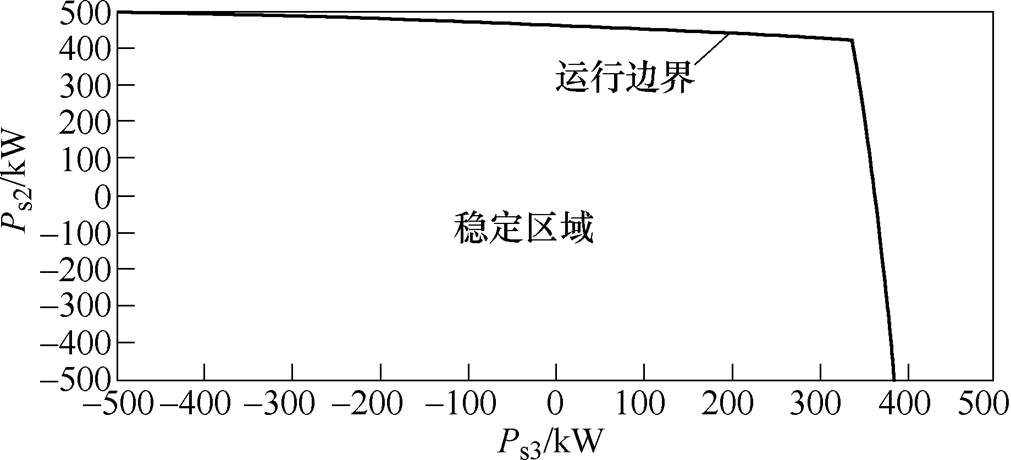
图9 侧重集成成本的系统运行边界
Fig.9 System operational boundary that focuses on the integration costs
2)侧重稳定区域情况下的参数配置
设定优化目标1的权重为0.4,优化目标2的权重为0.6,此时图8所示Pareto前沿中优化解为Cdc= 857mF,Cs2=2 065mF,Cs3=2 137mF,在此配置下系统侧重稳定区域的系统运行边界如图10所示。
在此优化的集成参数下,系统集成成本约为11 382元,高于初始条件配置时的集成成本,与此同时,系统运行边界较之初始条件配置时有全面的提升,上边界和右边界均接近设计容量,稳定区域面积较之初始条件配置时增加约25%,这意味着系统各端之间的功率互济能力显著增强。以2.2节中运行点Ps3=300kW、Ps2=330kW为例,对应的Ps2最大允许交互功率从初始条件配置时的350kW提升至480kW,提升幅度约40%。这也意味着通过集成参数的优化配置,系统运行边界显著提升,原本失稳的运行工作点可以保持稳定。
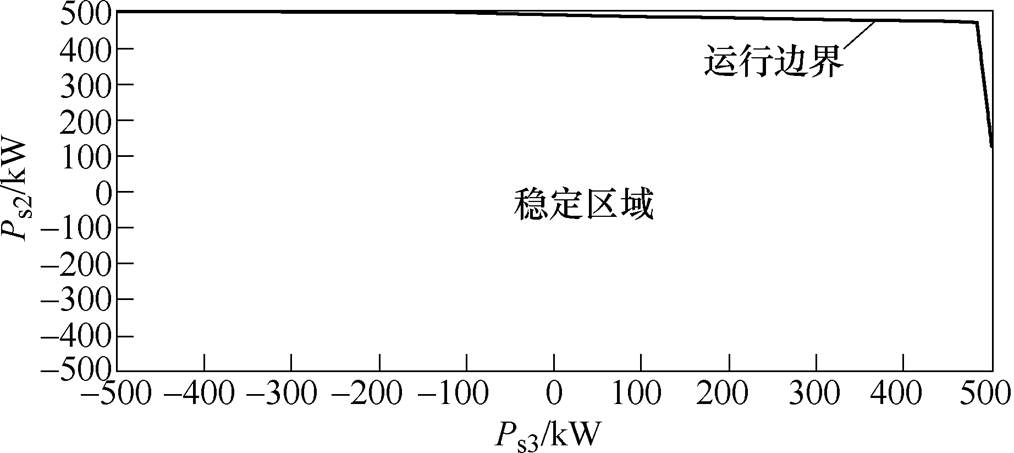
图10 侧重稳定区域的系统运行边界
Fig.10 System operational boundary that focuses on the stable area
利用2.2节构建的仿真模型(具体参数见表1),更新Cdc、Cs2、Cs3后,设置运行点Ps3=300kW、Ps2= 330kW变化至Ps3=300kW、Ps2=360kW,以及Ps3= 300kW、Ps2=480kW,此时直流母线电压Udc的仿真结果如图11所示。
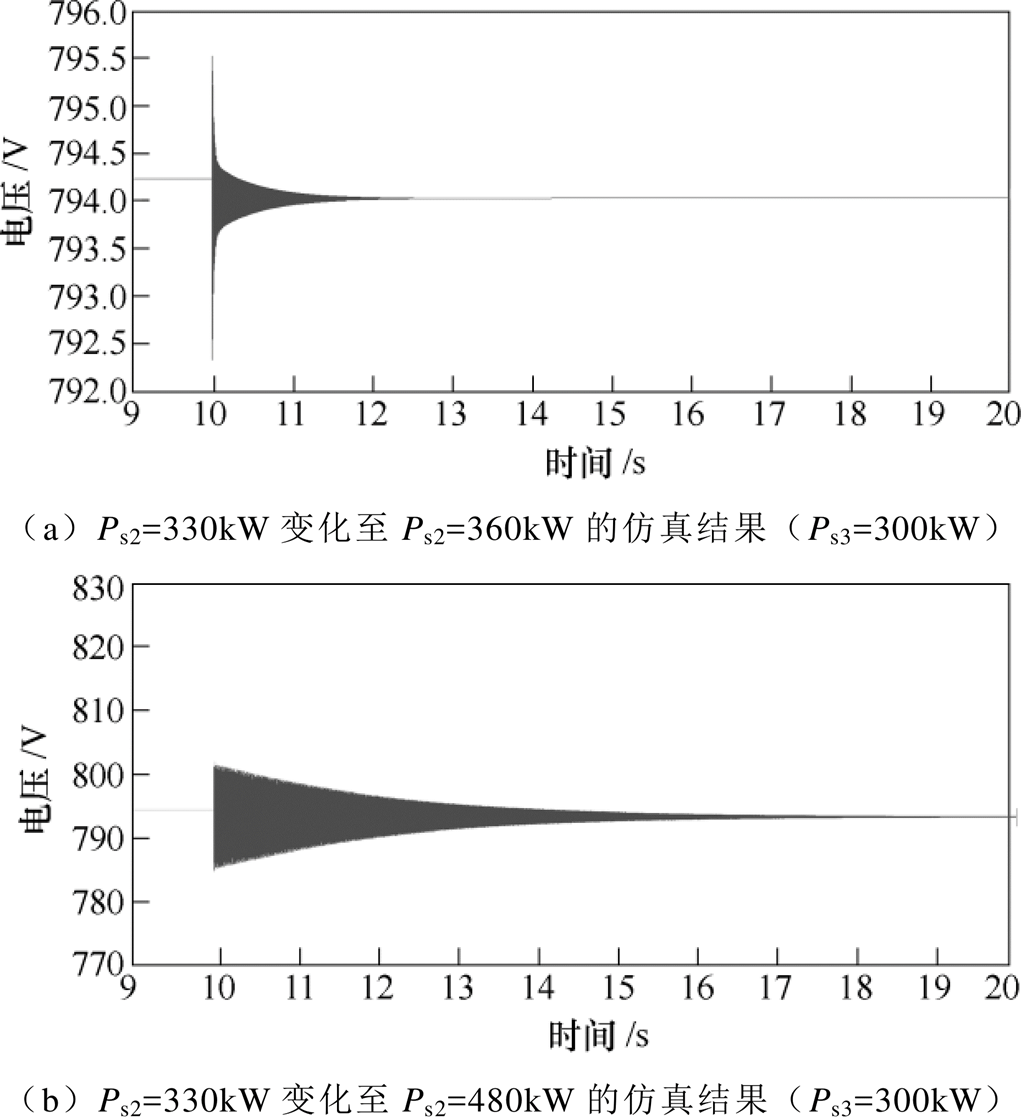
图11 Ps2变化时的仿真结果
Fig.11 Simulation results by changing Ps2
由图5可知,在参数优化配置前Ps3=300kW、Ps2=360kW处于失稳区域,当参数优化配置后,原本失稳的工作点Ps3=300kW、Ps2=360kW进入稳定区域。结合图11a可知,当t =10s运行点调整时,直流母线电压经过小幅的振荡调整,能够快速恢复稳定。
参数优化配置后,Ps3=300kW对应的Ps2最大允许交互功率提升至480kW左右,图11b描述了当t =10s运行点变化至运行边界上的Ps3=300kW、Ps2= 480kW时的仿真曲线。可以看出直流母线电压出现了较为明显的振荡,但经过短时调节仍然可以保持稳定。
综上可知,因为侧重稳定区域,Pareto最优解集中筛选的优化解将更注重优化目标2,即考虑稳定区域与设计区域的面积差优于集成成本,这样在增加较小的集成成本的同时,能够显著扩展系统稳定区域。
3)满足设计要求的参数配置
由图8可知,当考虑稳定区域与设计区域的面积差最小,即式(5)中f2=0时,此时系统的稳定区域完全满足设计需求。图8 Pareto前沿中对应横坐标零点处的优化解为Cdc=861mF,Cs2=2 113mF,Cs3=2 207mF,在此配置下系统稳定区域面积为1 000kW×1 000kW,VSC2与VSC3能够实现四象限的满容量运行。此时系统的优化集成成本约为11 657元。这也意味着通过本文的集成参数优化配置方法,能够获取满足设计需求MTDC系统稳定区域的以及集成成本最小的Cdc、Cs2、Cs3等关键参数,从而有效地指导面向低压多端直流运行边界提升的集成参数优化配置。
本文构建了三端MTDC系统等效模型,分析了关键变流设备包括VSC、储能的直流侧电容等集成参数对系统运行边界的影响,并提出了一种集成参数优化配置方法,通过对各电容值的优化配置,在保障系统经济性的同时有效地提升了系统运行边界,进而增强各端之间的功率互济能力。主要结论包括:
1)在系统结构、直流线路距离和直流网电压等级一定的情况下,VSC、储能等变流设备直流侧电容参数主导系统运行边界,且各电容值对系统运行边界的影响各异。
2)针对各电容依据经验值配置的原有方案,通过集成参数优化配置方法,可以有效地改善系统集成成本,并实现对原有系统运行边界的较大幅度提升。
3)通过对各个优化目标选取不同的权重,可实现多种应用需求下的集成参数优化配置,在保障系统经济性的同时满足MTDC系统的多种运行能力需求。
第i个VSC换流站的等效电路如附图1所示。附图1中,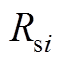 、
、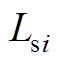 表示第i个VSC换流站交流侧等效电阻、等效电感;
表示第i个VSC换流站交流侧等效电阻、等效电感; 、
、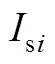 、
、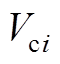 表示第i个VSC换流站交流侧的并网点电压、并网电流、输出电压;
表示第i个VSC换流站交流侧的并网点电压、并网电流、输出电压;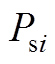 、
、 表示第i个VSC换流站交流侧有功功率、无功功率;
表示第i个VSC换流站交流侧有功功率、无功功率;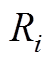 、
、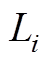 、
、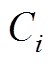 表示第i个VSC换流站直流侧线路电阻、线路电感、直流侧电容;
表示第i个VSC换流站直流侧线路电阻、线路电感、直流侧电容;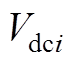 、
、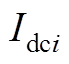 、
、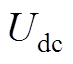 、
、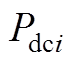 表示第i个VSC换流站直流侧输出电压、直流电流、直流母线电压以及直流功率。
表示第i个VSC换流站直流侧输出电压、直流电流、直流母线电压以及直流功率。
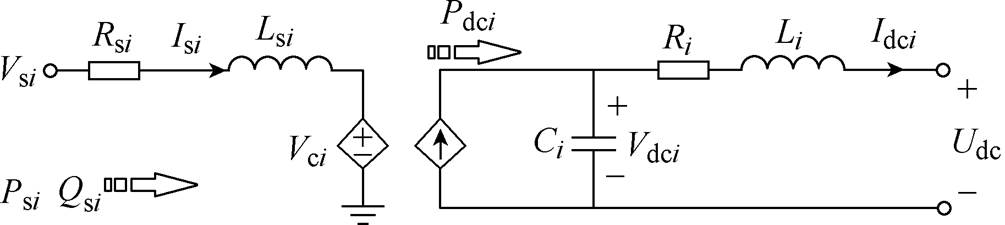
附图1 换流站等效电路
App.Fig.1 Equivalent circuit of VSC
dq坐标系下系统稳态方程满足
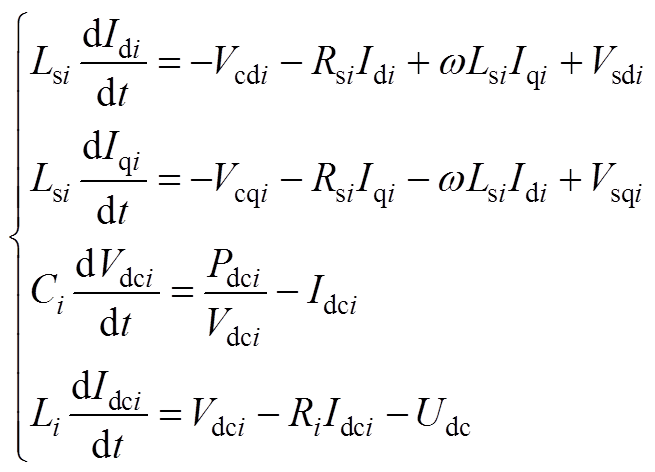 (A1)
(A1)式中, 、
、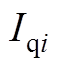 为
为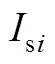 的d、q轴分量;
的d、q轴分量;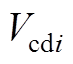 、
、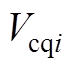 为
为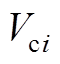 的d、q轴分量;
的d、q轴分量;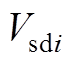 、
、 为
为 的d、q轴分量。两侧功率满足
的d、q轴分量。两侧功率满足
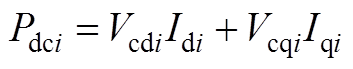 (A2)
(A2)
第i个VSC换流站采用的控制器结构如附图2所示。
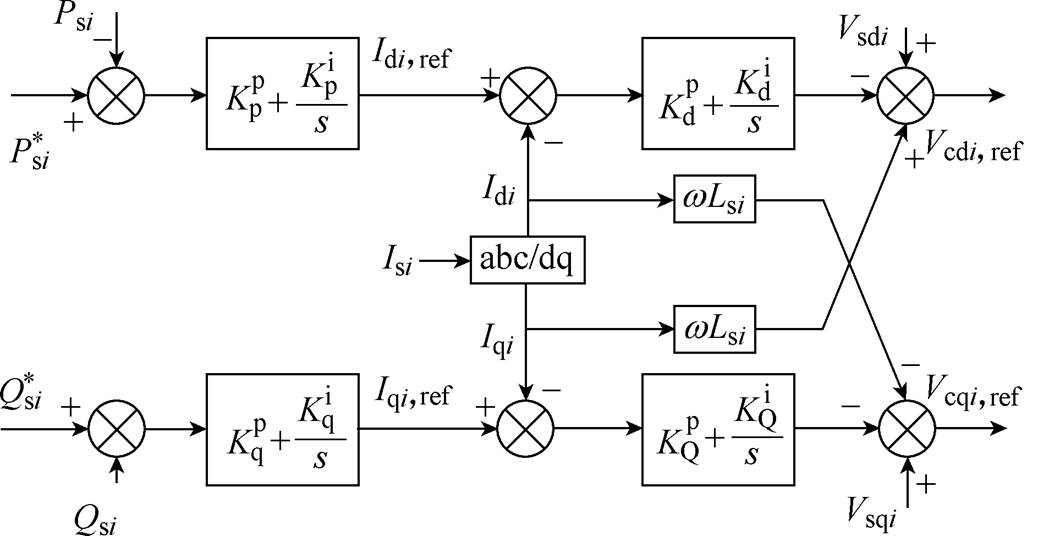
附图2 VSC换流站双闭环控制器
App.Fig.2 Double closed loop controlleds of VSC
图中,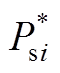 、
、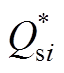 分别表示
分别表示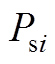 、
、 的参考值;
的参考值;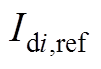 、
、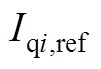 分别表示
分别表示 、
、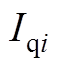 的参考值;
的参考值;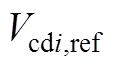 、
、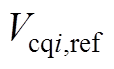 分别表示
分别表示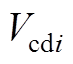 、
、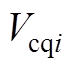 的参考值;
的参考值;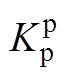 、
、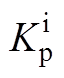 表示有功功率的外环控制器PI参数;
表示有功功率的外环控制器PI参数;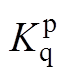 、
、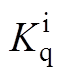 表示无功功率的外环控制器PI参数;
表示无功功率的外环控制器PI参数;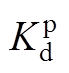 、
、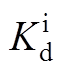 表示有功电流的内环控制器PI参数;
表示有功电流的内环控制器PI参数;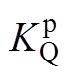 、
、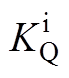 表示无功电流的内环控制器PI参数。
表示无功电流的内环控制器PI参数。
设定
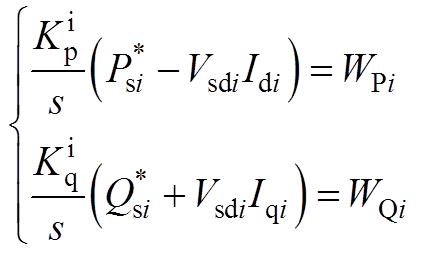 (A3)
(A3)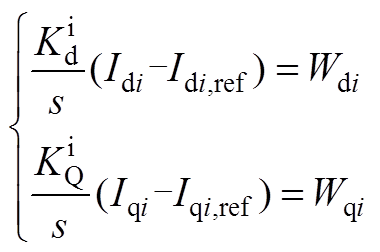 (A4)
(A4)
结合式(A1)~式(A4)建立第i个VSC换流站小信号模型,表示为
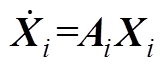 (A5)
(A5)式中,状态变量为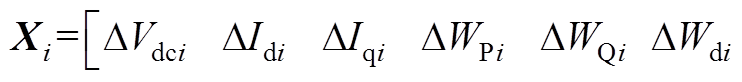
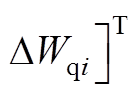 。
。
三端MTDC系统等效电路简化如附图3所示。
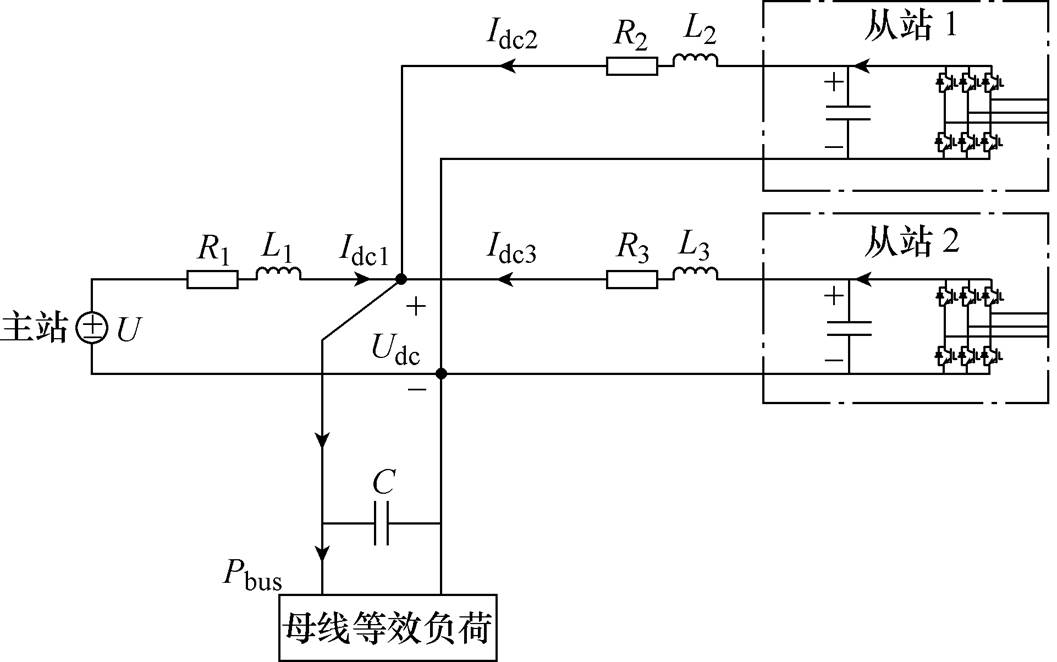
附图3 三端MTDC系统等效电路
App.Fig.3 Equivalent circuit of three-terminal DC system
附图3中,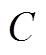 为直流母线等效电容。结合三条线路的电阻、电感以及直流母线等效电容的稳态表达式,推导可获取系统的小信号模型满足
为直流母线等效电容。结合三条线路的电阻、电感以及直流母线等效电容的稳态表达式,推导可获取系统的小信号模型满足
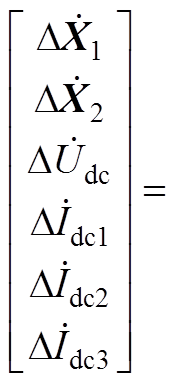

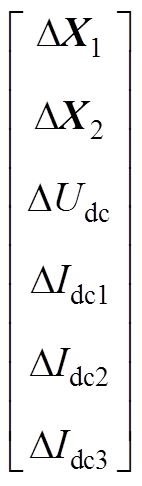 (A6)
(A6)
其中
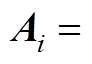


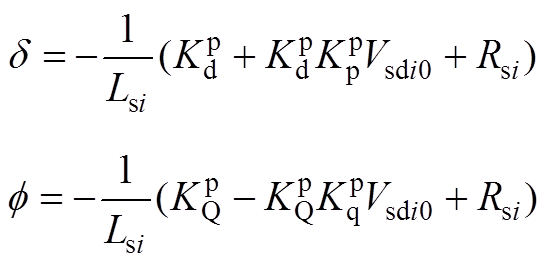
式中,变量下标“0”表示为该变量的稳态值。
附图3所示三端MTDC系统等效电路的参数见附表1。
附表1 三端MTDC系统参数
App.Tab.1 System prameters of three-terminal DC system

参 数数 值参 数数 值 /W0/mH2 /W0/mH2 /W0.005 5/mH0.014 7 /W0.018 2/mH0.049 0 /W0.045 5/mH0.122 5 /mF1 200/mF1 500 /mF1 500/V800 DC /(rad/s)314
附图3所示三端MTDC系统控制器参数见附表2。
附表2 控制器参数
App.Tab.2 Controller parameters
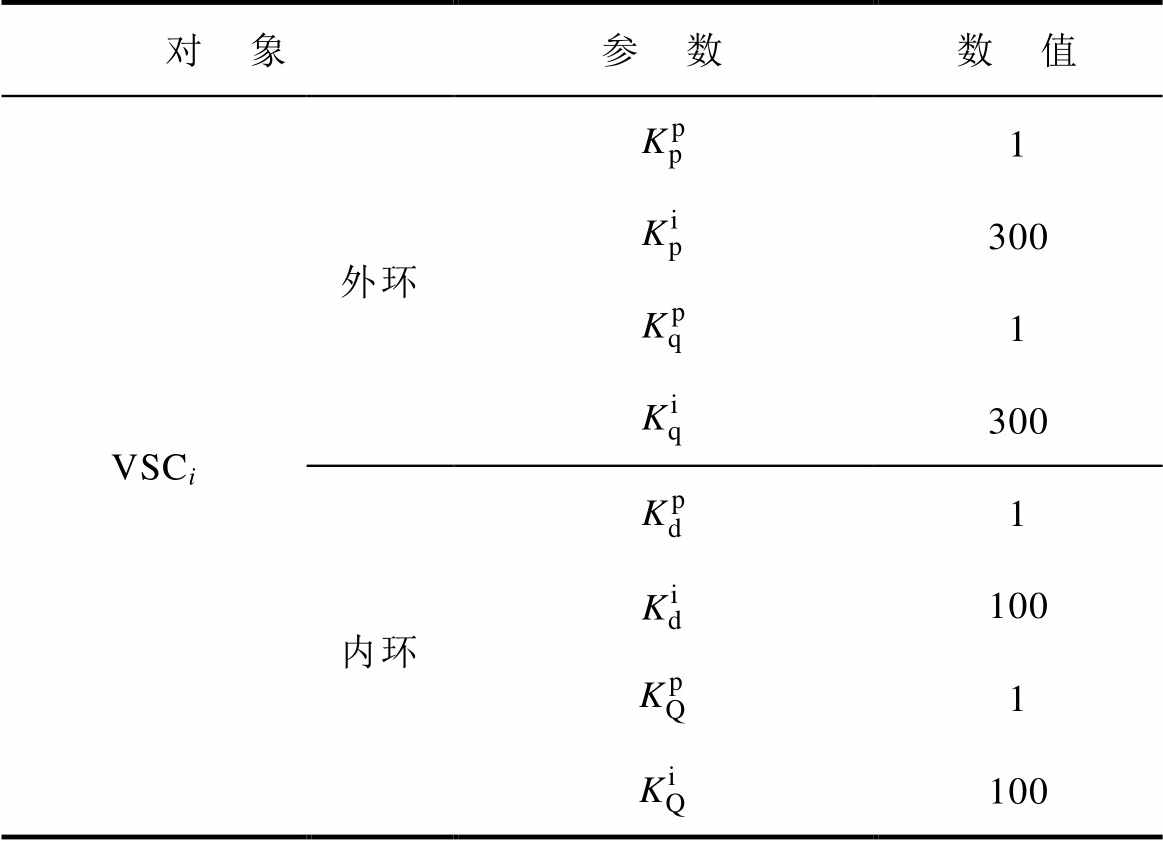
对 象参 数数 值 VSCi外环1 300 1 300 内环1 100 1 100
参考文献
[1] 李佳琪, 陈健, 张文, 等. 高渗透率光伏配电网中电池储能系统综合运行控制策略[J]. 电工技术学报, 2019, 34(2): 437-446.
Li Jiaqi, Chen Jian, Zhang Wen, et al. Integrated control strategy for battery energy storage systems in distribution networks with high photovoltaic penetr- ation[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 437-446.
[2] 张勇军, 刘子文, 宋伟伟, 等. 直流配电系统的组网技术及其应用[J]. 电力系统自动化, 2019, 43(23): 39-49.
Zhang Yongjun, Liu Ziwen, Song Weiwei, et al. Networking technology and its application of DC distribution system[J]. Automation of Electric Power Systems, 2019, 43(23): 39-49.
[3] 付菊霞, 陈洁, 滕扬新, 等. 基于集合经验模态分解的风电混合储能系统能量管理协调控制策略[J]. 电工技术学报, 2019, 34(10): 2038-2046.
Fu Juxia, Chen Jie, Teng Yangxin, et al. Energy management coordination control strategy for wind power hybrid energy storage system based on EEMD[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2038-2046.
[4] 谈竹奎, 徐玉韬, 班国邦, 等. 基于主从控制的交直流混合微电网多模式运行与切换策略[J]. 电气技术, 2018, 19(9): 60-64.
Tan Zhukui, Xu Yutao, Ban Guobang, et al. Multi- mode operation and transition for hybrid AC-DC microgrid based on master-slave control[J]. Electrical Engineering, 2018, 19(9): 60-64.
[5] 吴红斌, 杨超, 陈煜, 等. 基于电压源型换流器的多端直流配电网潮流计算[J]. 电力系统自动化, 2018, 42(11): 79-85.
Wu Hongbin, Yang Chao, Chen Yu, et al. VSC based power flow calculation of multi-terminal DC distri- bution network[J]. Automation of Electric Power Systems, 2018, 42(11): 79-85.
[6] Andrade A M S S, Schuch L, Martins M L D S. High step-u PV module integrated converter for PV energy harvest in FREEDM systems[J]. IEEE Transactions on Industry Applications, 2017, 53(2): 1138-1148.
[7] Bifaretti S, Zanchetta P, Watson A, et al. Advanced power electronic conversion and control system for universal and flexible power management[J]. IEEE Transactions on Smart Grid, 2011, 2(2): 231-243.
[8] 刘国伟, 赵宇明, 袁志昌, 等. 深圳柔性直流配电示范工程技术方案研究[J]. 南方电网技术, 2016, 10(4): 1-7.
Liu Guowei, Zhao Yuming, Yuan Zhichang, et al. Study on demonstration project technical scheme of VSC-DC distribution system in Shenzhen[J]. Sou- thern Power System Technology, 2016, 10(4): 1-7.
[9] 李微, 周雪松, 马幼捷, 等. 三端口直流微网母线电压控制器及多目标控制[J]. 电工技术学报, 2019, 34(1): 92-102.
Li Wei, Zhou Xuesong, Ma Youjie, et al. Three-port DC microgrid bus voltage controller and multi- objective control[J]. Transactions of China Electro- technical Society, 2019, 34(1): 92-102.
[10] 黄云辉, 宋泽凡, 唐金锐, 等. 连接弱电网的并网变换器直流电压时间尺度稳定器的设计与分析[J]. 电工技术学报, 2018, 33(增刊1): 189-196.
Huang Yunhui, Song Zefan, Tang Jinrui, et al. Design and analysis of DC-link voltage stabilizer for voltage source converter as connected to weak grid[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 189-196.
[11] Rahimi A M, Emadi A. Active damping in DC/DC power electronic converters: a novel method to overcome the problems of constant power loads[J]. IEEE Transactions on Industrial Electronics, 2009, 56(5): 1428-1439.
[12] Kongpan A, Theppanom S, Serhiy B, et al. Adaptive stabilization of uncontrolled rectifier based AC-DC power systems feeding constant power loads[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8927-8935.
[13] Ali E, Alireza K, Claudio H, et al. Constant power loads and negative impedance instability in auto- motive systems: definition, modeling, stability, and control of power electronic converters and motor drives[J]. IEEE Transactions on Vehicular Tech- nology, 2006, 55(4): 1112-1125.
[14] 倪喜军. 高压SiC器件在FREEDM系统中的应用[J]. 电源学报, 2016, 14(4): 139-146.
Ni Xijun. High voltage SiC device applied to FREEDM systems center[J]. Journal of Power Supply, 2016, 14(4): 139-146.
[15] 蔡晓燕, 许敬涛, 刘继茂, 等. 光伏逆变器中DC- link电容的选型计算[J]. 电力电子技术, 2012, 46(4): 43-44.
Cai Xiaoyan, Xu Jingtao, Liu Jimao, et al. Analytic calculation of the DC-link capacitor for PV inver- ters[J]. Power Electronics, 2012, 46(4): 43-44.
[16] Jeyadevi S, Baskar S, Babulal C K, et al. Solving multi-objective optimal reactive power dispatch using modified NSGA-II[J]. International Journal of Electrical Power & Energy Systems, 2011, 33(2): 219-228.
[17] Agrawal S, Panigrahi B K, Tiwari M K. Multio- bjective particle swarm algorithm with fuzzy clustering for electrical power dispatch[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(5): 529-541.
Research on Integrated Parameter Optimization Configuration for Operational Boundary Improvement of Three-Multi-Terminal DC System
Abstract Integration optimization is one of the key technologies for multi-terminal DC (MTDC) system. In this paper, an integrated parameter optimization configuration method for improving operational boundary is proposed for the three-terminal DC system. Firstly, the equivalent circuit and its characteristic model of MTDC system are established, and the influence of integrated parameters on system operational boundary is analyzed. Secondly, an integrated parameter multi-objective optimization model is proposed with the optimization goals of the smallest acreage difference between the stable area and the design area, and the lowest integration cost. Finally, the Pareto optimal solution set is solved by the NSGA-II algorithm, and the integrated parameter optimization configuration scheme is selected by the fuzzy clustering algorithm. The simulation analysis shows that the proposed method is effective and feasible, which can significantly improve the operational boundary of MTDC system while ensuring the system economics.
keywords:Multi-terminal DC, system integration, parameter configuration, operational boundary, multi-objective optimization
中图分类号:TM71
DOI: 10.19595/j.cnki.1000-6753.tces.190196
国家科技部重点研发专项(2017YFB0903300)、中国科学院洁净能源先导科技专项(XDA 21050100)和中科院前沿科学重点研究(QYZDB- SSW-JSC024)资助项目。
收稿日期 2019-02-28
改稿日期 2019-09-29
邓 卫 男,1983年生,博士,副研究员,研究方向为交直流系统稳定性分析与稳定控制技术等。E-mail: dengwei@mail.iee.ac.cn(通信作者)
裴 玮 男,1982年生,博士,研究员,研究方向为分布式发电、微电网与交直流混联配电技术等。E-mail: peiwei@mail.iee.ac.cn
(编辑 陈 诚)