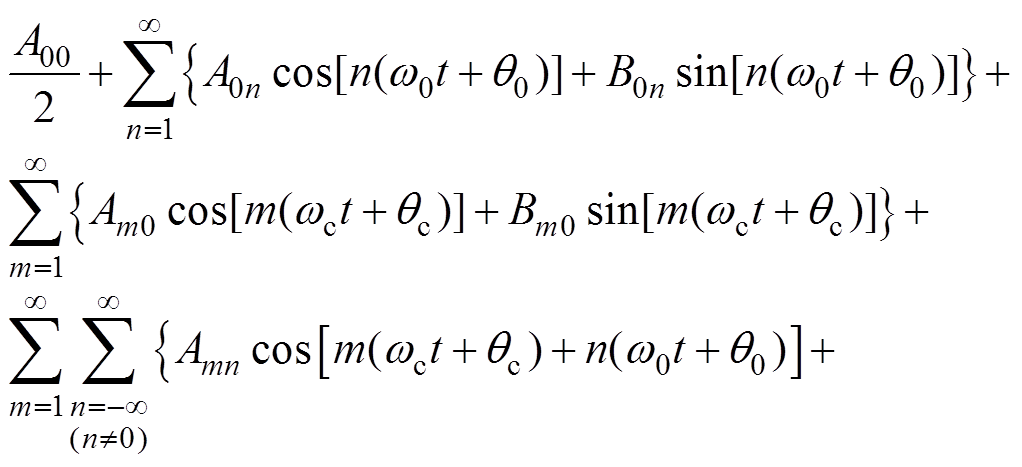
摘要 随着多电与全电飞机的大量应用，对航空静止变流器（ASI）的功率容量提出了更高的要求，也越来越多地采用模块化串、并联方式实现功率扩容，并结合载波移相调制进一步降低系统的开关频率谐波成分。但是在机载场合组合模块间的参数不平衡，以及基于模拟电路的控制方式，致使控制信号中易叠加额外低频或直流偏置扰动，导致ASI输入、输出侧叠加额外的谐波成分，对航空电源系统运行的稳定性与可靠性造成影响。该文基于桥臂输出电压谐波分布模型，采用双重傅里叶分析与指数函数分析相结合的方法，在考虑扰动分量这一非理想条件下，对模块化载波移相串、并联ASI的输入、输出谐波分布进行分析与比较，揭示了模块化组合式ASI的谐波分布特性。最后通过仿真和实验验证了理论分析的正确性。
关键词：交错并联 级联逆变器 双重傅里叶分析 谐波分布
基于高频链拓扑的航空静止变流器（Aeronautical Static Inverter, ASI）广泛应用于机载电源系统[1]。随着多电与全电飞机的出现，航空中频交流负载对ASI的功率容量提出了越来越高的要求，但是受限于功率开关器件的功率容量，需要通过拓扑结构的改进以适应扩容需要，如多电平结构与多模块并联结构[2]。传统的多电平方式需要额外的嵌位器件，影响可靠性，因此ASI适宜采用级（串）联型拓 扑[3]，但是该拓扑在提供有功功率时每个模块需要独立的直流电源，导致出现拓扑、前级变压器结构更为复杂，器件数量增多等问题[4]。因此，多模块并联方式也大量应用在ASI场合[5-6]，其能够通过载波交错优化谐波成分，多个并联模块之间还能够互为冗余，提高可靠性[7]，但均流控制较为复杂[8]。
ASI装置往往采用基于模拟电路的控制方式以及PID控制算法，此时串、并联模块之间存在主、控制电路参数不一致的问题；而且在航空电源系统中存在由发电机、二次电源以及电磁兼容问题导致的不同频率成分的扰动[9]，如文献[10]提到系统中其他静止变流器引入二次谐波成分等问题。上述问题导致不同模块的控制信号叠加不同频率成分的扰动分量，其中由于被动滤波装置对低频及直流成分的滤除效果较差，从而造成较大影响。
现有谐波分析方法多针对理想状态进行，如文献[11]主要研究了基于理想载波移相的H桥单元级联拓扑在不同调制方式下的谐波特性，提供了该类调制方式拓扑的分类依据，并一定程度上考虑了死区因素的影响；文献[12]则在理想的移相调制方式下比较了三电平与五电平H桥级联逆变器的谐波特性与总谐波畸变率（Total Harmonic Distortion, THD）分布；文献[13-14]通过建立交错并联桥臂谐波成分模型，分析了该方式下三相逆变器输出侧与并联桥臂环流中的谐波成分，并得到了最佳移相角度的选择依据；文献[15]在航空中频地面电源中采用基于载波移相的并联拓扑，并通过分析得到详细的谐波分布数据；文献[16]分析了理想载波相移方式对输入、输出侧谐波的影响。但上述文献缺少控制信号中叠加了低频、直流扰动时的分析，且很少对基于载波移相调制的模块化串联与并联这种拓扑的比较。因此本文重点对模块化载波移相串、并联ASI在不同调制策略下的输入、输出谐波分布进行分析与比较，揭示模块化ASI非理想工作状态下的谐波分布特性。
本文首先建立基本的桥臂输出电压谐波特征模型，并分析了单极性倍频调制方式的谐波特性；然后分析了基于载波移相的模块化串联、并联结构逆变器，在非理想状态下，低频与直流偏置扰动成分对输入、输出侧谐波分布的影响，总结两种调制方式下的ASI输入、输出谐波分布规律。在理论分析基础上结合了仿真分析与验证，最后通过实验验证分析的正确性。
为了分析ASI模块化串、并联拓扑的谐波分布规律，从最基本的桥臂单元入手。本文的串并联设计对象所采用的控制策略都是基于正弦-三角波调制的自然点采样方式。
桥式逆变器在SPWM调制下桥臂输出电压可以应用双重傅里叶积分对输入、输出谐波进行表述，得到桥臂输出电压谐波组成的表达式[17]为
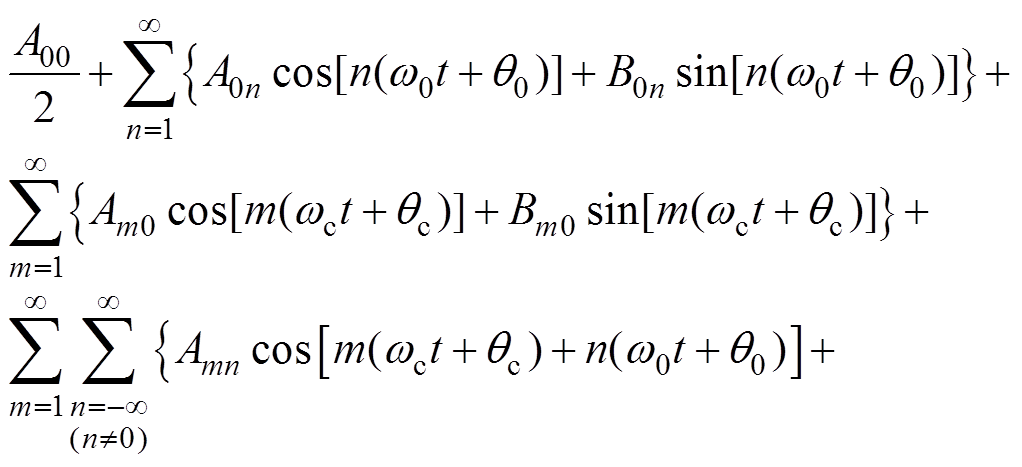
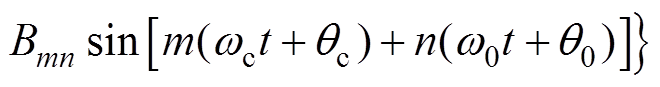（1）
式中，wc为桥臂输出电压载波角频率；qc为桥臂输出电压载波成分初始相位；w0为桥臂输出电压基波角频率；q0为桥臂输出电压基波成分初始相位；Amn、Bmn分别为桥臂输出电压双重傅里叶表达式余弦、正弦系数。第一行表示直流分量、基波分量（当n=1时）以及基带谐波分量；第二行表示载波谐波分量；第三、四行表示载波谐波频率上叠加的基波频率边带谐波分量。依据该表达式，能够分析由单元桥臂组成的各类拓扑的谐波成分。
将由两个开关管组成的桥臂看作基本桥臂单元，单个桥臂拓扑如图1所示。
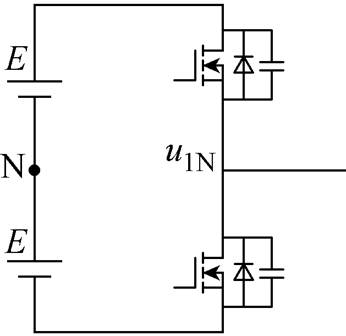
图1 单个桥臂拓扑
Fig.1 Topology of single bridge
假设调制波频率远小于载波频率，M为电压调制比，E为输入直流电压，三角载波幅值为1，若忽略调制信号中的直流分量等非理想因素，得到桥臂输出电压表达式为
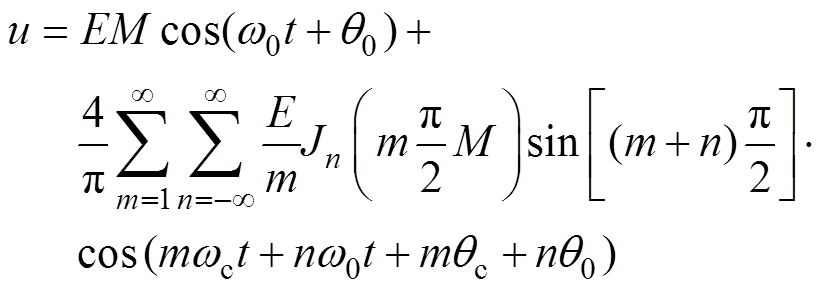（2）式中，Jn(x)为n阶贝塞尔函数。桥臂单元输出电压的谐波次数为mwc+nw0。从而，可以采用两组反相的调制波与同一组载波交截生成开关脉冲信号。根据式（2）可以得到全桥两组桥臂的中点电压u1N与u2N的表达式分别为
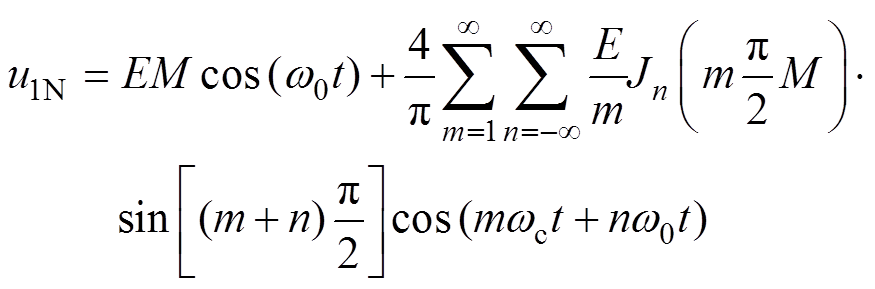（3）
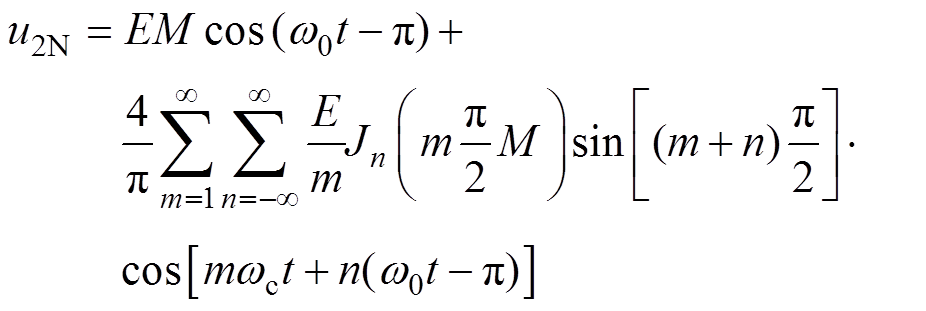（4）基于单极性倍频的SPWM调制H桥单元输出电压的谐波组成由两个桥臂的中点电压之差决定，因此能够得到
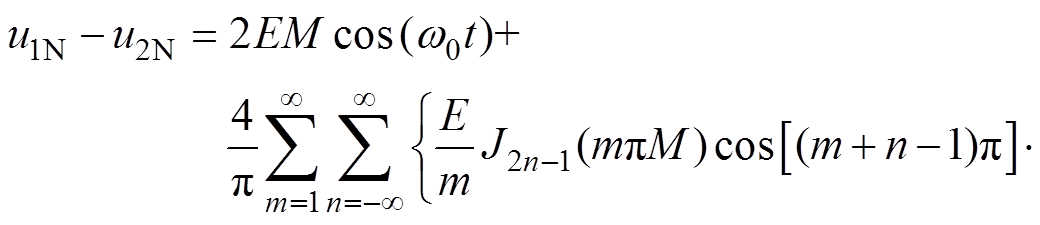
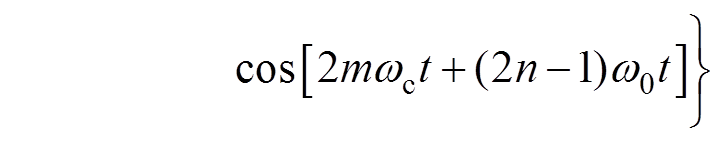（5）此时，当式（3）和式（4）中m为奇数，n必须为偶数才能保证sin[(m+n)p/2]≠0；当n为偶数时，式（3）与式（4）中的cos[mwct+n(w0t-p)]这一谐波分量相等，因此能够相互抵消。此时结合式（5），输出电压谐波中奇次载波谐波频率（wc, 3wc, 5wc, …）的成分被消除，也消除了偶次载波谐波上叠加的偶次基波边带谐波。
根据式（2），桥臂输出端对于输入直流母线中点N的电压u1N能够分解为不同次数的谐波成分。该电位成分理想状态下是由基波及其谐波、以及载波及其谐波成分组成的，其谐波成分频率可以统一表达为mwc+nw0形式。假设Umn1为桥臂输出端对于输入直流母线中点N的电压u1N中频率为mwc+ nw0谐波成分的幅值，uu1_mn为频率为mwc+nw0、幅值为Umn1的周期谐波分量，则uu1_mn表达式为
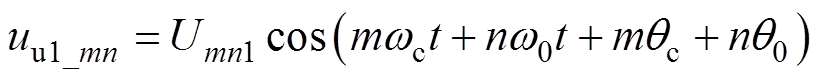（6）假设iL(t)为逆变器输出滤波电感电流，输入电压为理想直流电压2E，则倍频H桥单元中一个半桥的输入电流对应的谐波分量iin1_mn表达式为
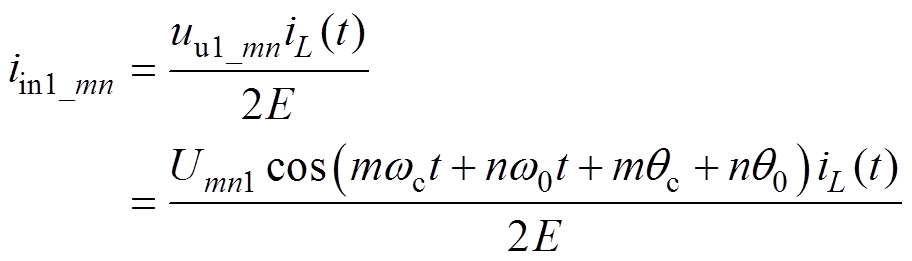（7）
基于单极性倍频SPWM调制的H桥单元由两组半桥单元构成，半桥单元之间载波相移角度为p，因而能够由式（7）推导得到第二组半桥产生的输入电流对应谐波分量iin2_mn的表达式为
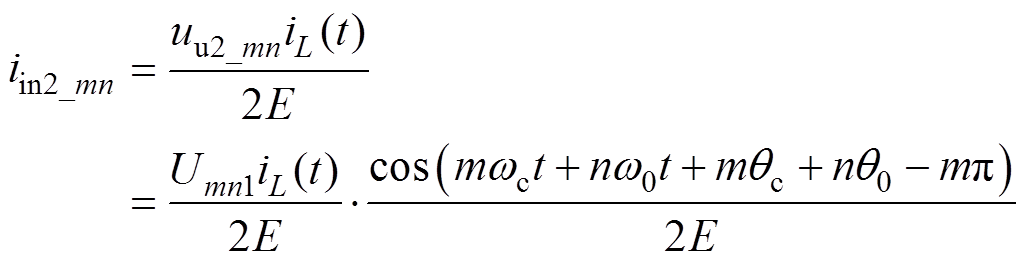（8）结合式（7）和式（8）得到输入电流谐波成分iin_mn表达式为
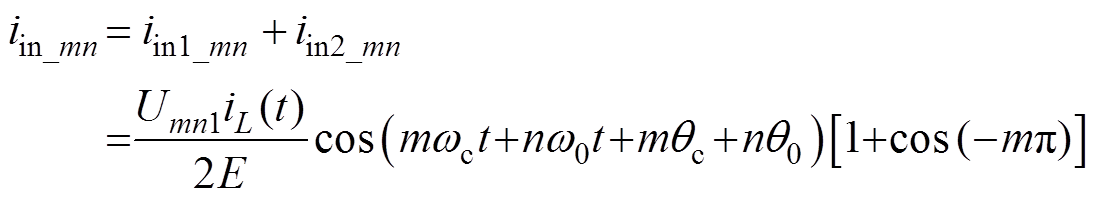（9）
根据式（9），当m为奇数时，输入侧频率成分为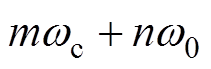
的谐波成分。iin_mn=0，因此奇次载波频率谐波成分被消除，基于倍频调制的H桥逆变单元输入谐波组成等效于提升了一倍载波频率。
但实际模拟控制电路中由于环路基准信号、运放输出的偏置以及器件开关时间的不一致等非理想因素，会导致调制信号叠加极低频分量或直流分量，为了简化分析流程，将极低频分量在若干个开关周期中等效为直流分量作为注入信号进行分析。
udc为若干个周期的直流成分扰动，且其与载波交截后在桥臂输出点产生的是一系列等宽周期脉冲，并假设载波初始角度qc=0，Um为调制波直流分量在桥臂输出电压中叠加的第m次载波谐波成分的幅值，其由输入电压、直流分量调制比决定。直流分量在桥臂输出电压导致的谐波成分ur(t)可采用周期性波形傅里叶分解表达，有
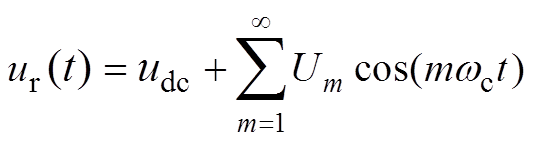（10）当倍频H桥两组桥臂单元采用同一个调制波、载波反相的调制方式，调制波中的直流成分在两个桥臂单元输出端产生的成分等效为等幅且反相，从而能够由式（10）得到
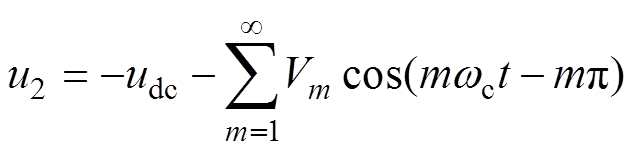（11）
式中，u2为另一组桥臂中载波移相后调制信号直流分量导致的谐波成分；Vm为调制波中直流分量导致的第一组桥臂输出电压中第m次载波谐波成分的 幅值。
根据式（9）得到输出电压谐波成分表达式为
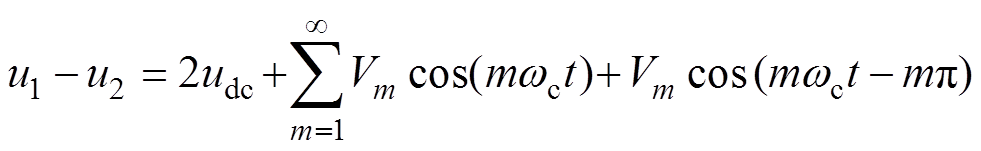
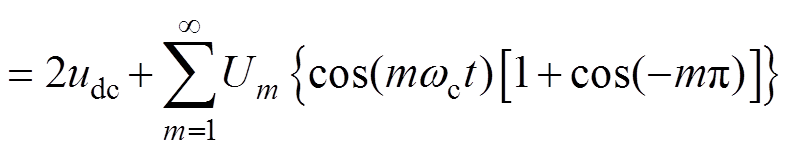（12）
可见，当考虑调制信号低频或直流分量的影响时，其输出信号将会叠加2k次载波谐波成分（k为包含0的正整数），这与倍频调制的效果是一致的，但是根据式（12）中的2udc成分，直流扰动会导致输出信号在若干个开关周期的偏置。
本文主要针对桥式拓扑在非理想情况下的谐波分布进行研究，因此仿真验证采用开环方式。
输入电压为180V，以保证ASI场合常用的115V/ 400Hz输出，为了模拟ASI场合的模拟控制电路电压特征（通常为5V或15V供电），开关信号采用幅值为4V的正弦波与幅值为5.5V的载波交截产生，参考本文图15a实验平台参数，设置模型输出滤波电感与滤波电容分别为60mH与10mF，开关频率为30kHz，负载电阻为8W。当在调制信号中叠加0.5V的直流分量后，输出滤波电感电流的谐波分布如图2所示。
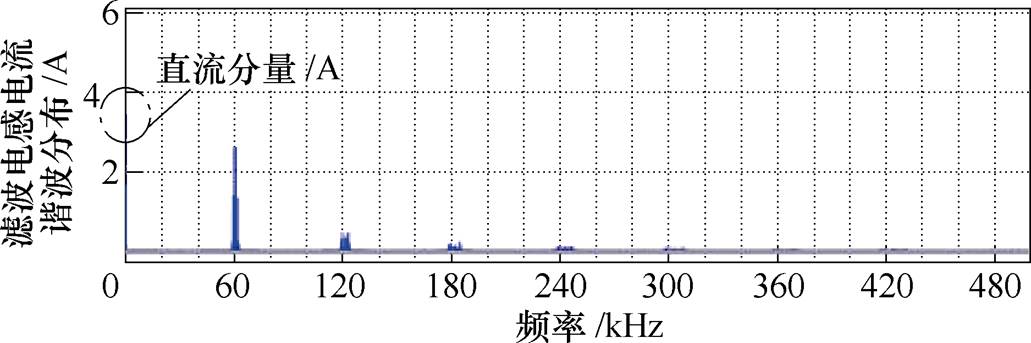
图2 调制信号叠加直流分量后倍频调制H桥电流谐波分布
Fig.2 Current harmonic distribution of double-frequency modulated H-bridge after the DC component injected into modulated signal
输出侧的载波谐波成分分布表明等效开关频率提高了一倍（60kHz），但是叠加了较大的直流成分，仿真结果与式（12）所得到的分析结果是一致的。
图3为两个H桥单元级联型（输出串联型）逆变器，该逆变器输出电压谐波成分由各H桥单元输出电压之和的谐波成分决定。u1N、u2N、u3N、u4N分别为四组桥臂输出中点-输入中点电压。
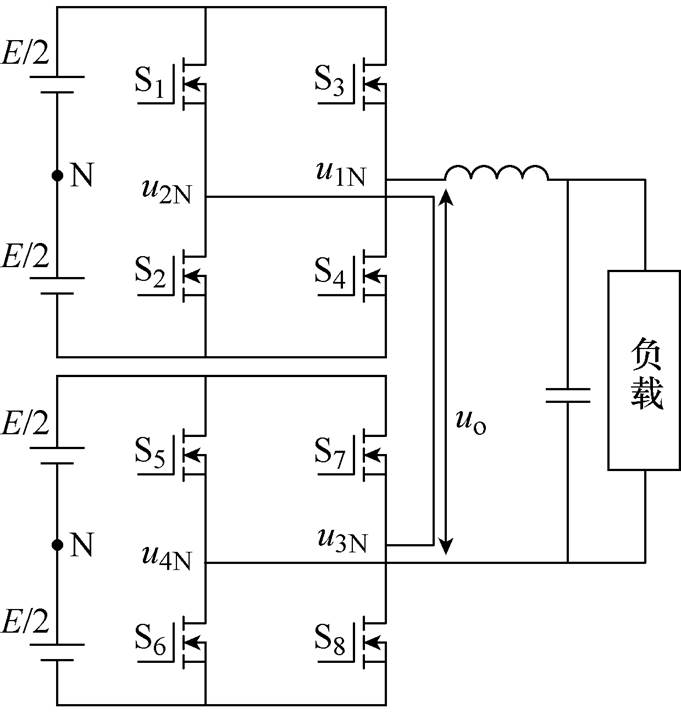
图3 单相两个H桥单元级联拓扑
Fig.3 Cascaded inverter with two H-bridge units
u12、u34分别为串联拓扑两个H桥单元输出桥臂电压，结合图3，有
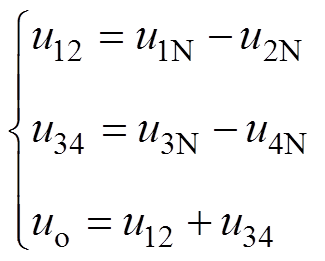（13）当H桥单元工作在单极性倍频调制方式时，输出电压u12、u34的最大、最小值可以分别为2E与-2E，此时输出电平数为2N+1五电平（2E, E, 0, -E, -2E）。
两个倍频调制H桥单元级联方式可以采用四列互差p/2的载波信号，产生8组开关信号控制8个开关管，实现级联桥臂的五电平输出；也可以采用两个幅值相等、相位差为p/2的三角载波T1、T2分别和两个相位相反的正弦调制信号交割。
因此，若采用x个H桥单元载波移相级联，每个H桥单元内部工作在单极性倍频SPWM调制方式，则需要N个相移为2p/N的载波信号。以两单元输出串（级）联为例，串联H桥单元之间相移角度为-p/2，调制波的相移为零；每个H桥单元工作在单极性倍频调制模式。从而由式（13）可以得到
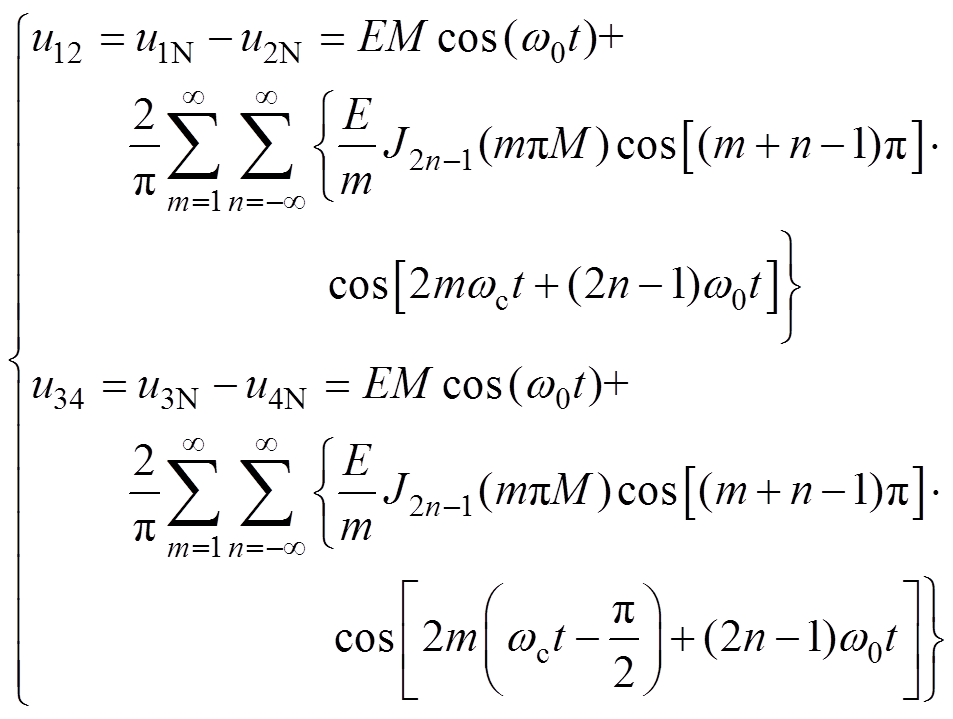（14）并得到输出串联后输出电压uo表达式为
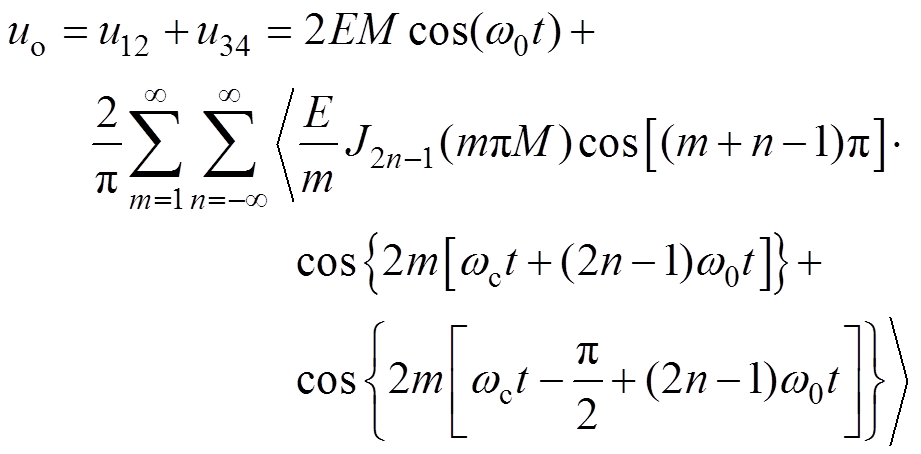（15）
由式（15）可得，当m不为0或偶数时，式（15）中谐波成分表达部分有
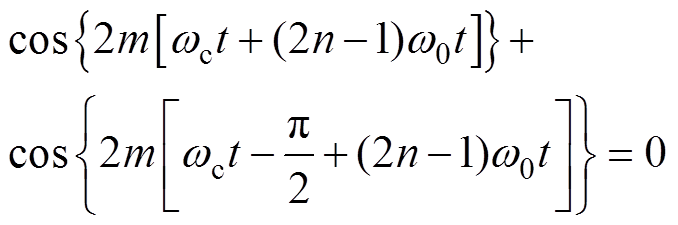（16）因此根据式（16）结果，基于载波相移的两H桥输出串联型SPWM逆变器输出电压uo中只存在频率为4mwc±(2n-1)（m、n =1, 2, 3,…）、w0的谐波，此时，式（15）又可表达为
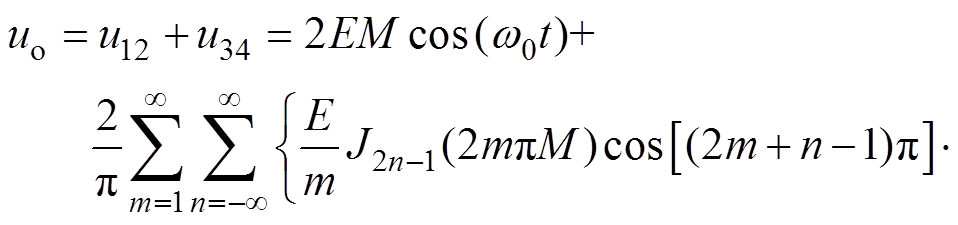
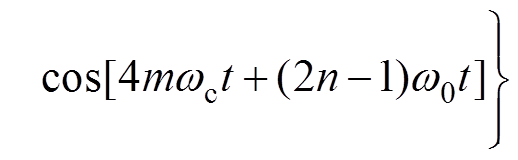（17）表明输出最低次谐波频率等效提高为4倍开关频率，且不存在偶数倍基波频率的载波边带谐波，这有助于减小输出滤波器的体积重量。若级联H桥逆变器输出串联N个单元，则等效开关频率为2N倍开关管的开关频率，因此级联单元数越多所需逆变器输出滤波器也越小。
针对本节拓扑的输入侧谐波成分分析，多个H桥单元输出串联组成的级联型逆变器，其每个单元采用独立的输入直流电源，因此每个直流电源等效于连接了单极性倍频SPWM调制逆变单元。此时H桥级联输入侧电流的谐波分析可参考第1节的分析结果，即每个H桥单元输入侧电流谐波成分最低次谐波频率为两倍载波频率，也等效提高了两倍功率管开关频率。
假设串联拓扑一组H桥单元的载波的初始相位qc=0，有
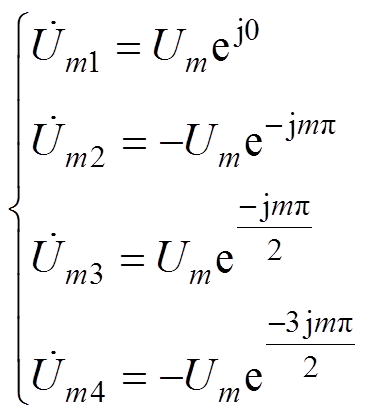（18）式中，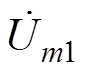
、
、
、
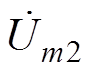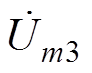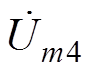分别为4个桥臂单元频率为mwc的幅值相量。由式（18）可见，调制信号中的直流分量对输出侧谐波的影响由式（19）所示的项决定。
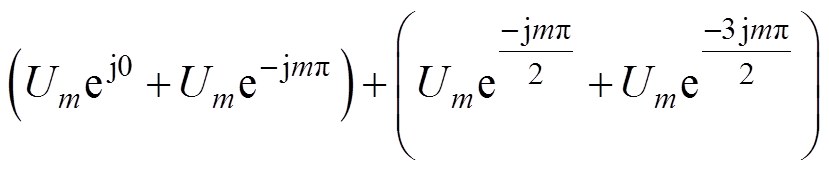（19）
式中，各括号中的分量能够两两抵消。因此两个H桥输出串联拓扑中串联单元共用一个调制信号时，调制信号中的直流分量不会导致输出侧叠加额外的载波谐波成分，这也是模块化串联型扩容方式在非理想状态下的优势。
对两H桥单元组成的载波移相级联型单相逆变器进行Saber仿真，仿真模型根据1kV·A样机电路结构参数进行设置。输出电压为115V/400Hz，两个单元输入电压独立且幅值均为90V，开关频率30kHz，输出电感80mH，输出滤波电容10mF，负载功率1kV·A，仿真波形如图4所示。因为需要考察直流分量对谐波成分的影响，且基波成分与直流成分频率较为接近，影响观测，因此在绘制谐波分布图时滤除基波频率成分。
如图4a所示，级联后桥臂输出电压uo工作在五电平状态。对输出端串联后的逆变器的桥臂输出电压和输入侧电流仿真结果进行傅里叶分析，如图4b所示，谐波分布表明两单元级联状态下输出侧谐波成分对应的等效开关频率为原来的4倍，输入电流谐波成分主要为载波频率的偶数倍谐波成分。
图4 理想情况下两H桥单元输出串联逆变器仿真波形
Fig.4 Simulation waveform of cascaded inverter with two H-bridge units under ideal conditions
在该仿真模型的调制信号中注入5 000个开关周期的0.5V直流分量，得到仿真波形如图5所示。
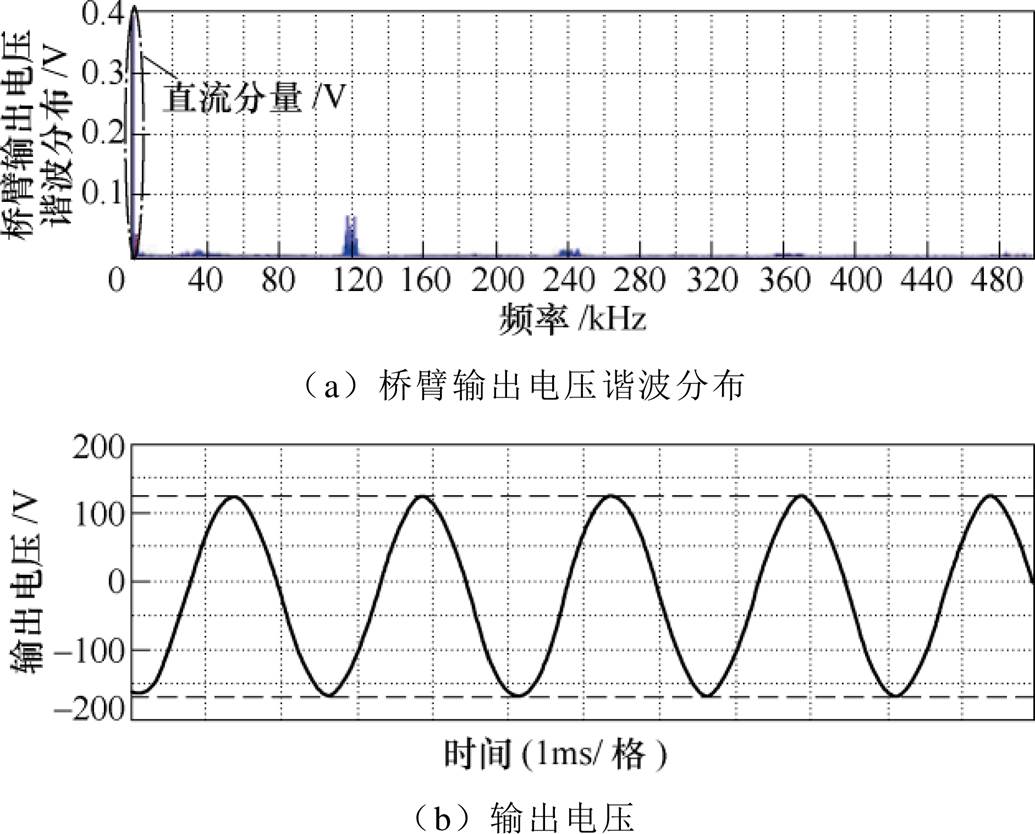
图5 调制信号叠加直流分量后仿真波形
Fig.5 Simulation waveforms of cascaded inverter under non-ideal conditions
桥臂输出电压谐波分布如图5a所示，对比图4b，其载波谐波分布与未注入直流分量时是一致的，因此式（19）表明，未影响载波谐波分布，但是依然会在若干个开关周期中增加直流成分。如图5b所示，该直流成分会导致短时间内输出电压的偏置。
以图6所示两组半桥逆变单元交错并联拓扑为例，经过两个输出桥臂在滤波电感之后共输出母线并联，输入端采用共直流母线并联方式。
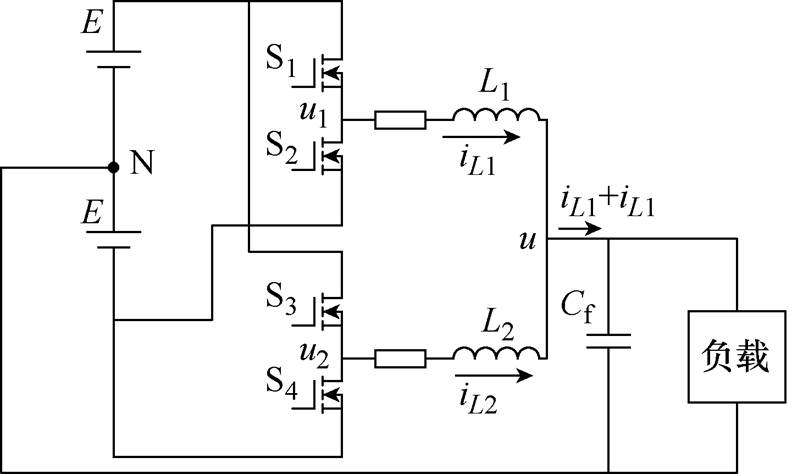
图6 两半桥逆变单元共输入输出交错并联拓扑
Fig.6 Common input and output paralleled inverter topology with two half-bridge units
假设图6拓扑中，T1与T2分别为两并联桥臂载波信号，两信号之间移相角度为k。载波信号分别与其并联单元调制信号比较生成桥臂上下管的开关脉冲信号，理想情况下并联桥臂的调制信号波形一致。交错并联后可以显著减小输出电流iL1+iL2的脉动，电感电流中的脉动电流大多以环流形式存在于并联桥臂之间，从而有效降低了输出信号的谐波含量。
假设载波与调制波初始相位qc、q0为零，变量Umn为图6中u1点电压谐波组成表达式中频率为mwc+nw0的谐波分量幅值。此时并联单元二的载波T2相移了k 角度，各次谐波幅值保持不变，则桥臂二输出电压对中点N的电压uu2中频率为mwc+nw0的谐波成分幅值相量表达式为Umne-jmk。
为了分析简便，假设图6中输出电压uu为理想的正弦波，不包含高频谐波成分；并假设并联桥臂间滤波电感感值及其寄生参数一致，此时输出电流iL1+iL2中频率为mwc+nw0的谐波成分幅值可以由并联桥臂输出信号之和来决定，假设两个并联桥臂对频率为mwc+nw0的阻抗为Zmn，则iL1+iL2中频率为mwc+nw0的幅值相量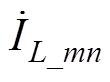
为
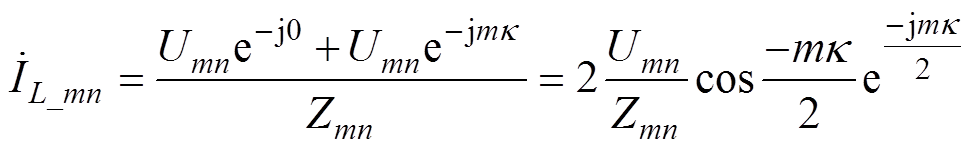（20）由式（20）可得，若k 角度为p 或者-p，偶数次载波谐波成分的幅值为0，即最低次谐波频率为两倍开关频率。同理，当相移角度为p/2时，能够抑制载波频率的4k+2次频率成分，如2、6、10次成分。此时最低次谐波频率为1倍开关频率。因此两个单元并联时载波相移p 为最佳角度。此时采用载波交错方式所滤除的谐波成分以环流形式存在（见图7中iac），而不流经输出侧电路。
假设并联单元数量为x时，移相角度采用2p/N能够最大程度地滤除谐波成分。此时输出电压中最低次谐波频率为2x倍开关频率。因此交错并联方式能够提高等效开关频率。
当采用载波移相方式时，并联单元的输入侧电流的相位将由交错角度k 所决定，此时部分谐波电流不会由iin提供，而是以环流成分形式存在于并联单元之间，具体分析如下：
交错并联方式能够在不改变iin1与iin2平均值的情况下，降低输入电流iin的谐波含量。假设交错角度为k，根据式（11）得到输入侧谐波组成是由输出侧电流iL，与并联公共点对输入中点电压中m次载波谐波以及n次基波谐波的谐波成分幅值Umn决定的，假设iL为理想正弦波（忽略谐波成分，且两路相等），输入谐波成分表达式为
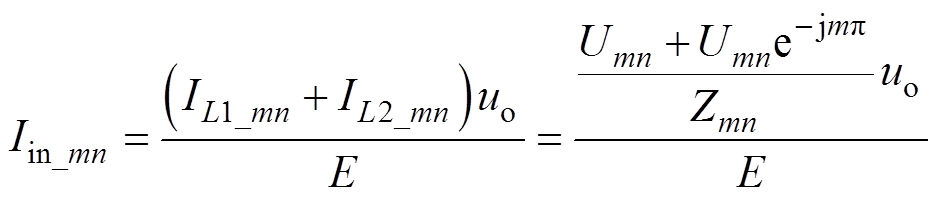
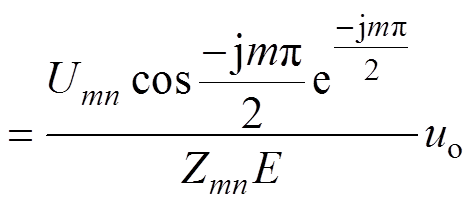（21）
此时，输入电流谐波只保留了偶数次载波频率成分。因此将基于交错并联半桥逆变单元采用共输入直流母线连接时，能够在并联单元之间形成环流通路，通过输入侧环流的形式降低输入电流的谐波成分，这有利于降低直流母线侧电容，提高整机功率密度与可靠性。
以两单元共输入连接为例，此时，输出交错并联，其输入侧环流路径如图7所示，输入侧电流iin为并联单元输入侧电流iin1与iin2之和。
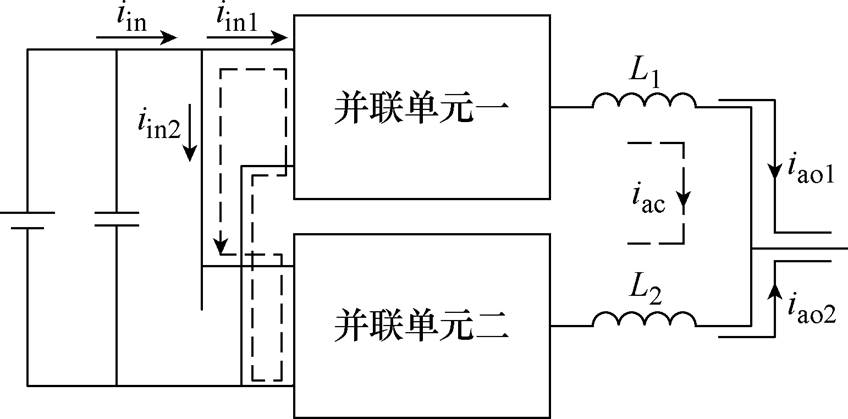
图7 两逆变单元交错并联输入侧谐波环流示意图
Fig.7 Schematic figure of circulating current caused by interleaving parallel topology
在图7中，当一组并联半桥的调制信号包含直流成分的扰动，并假设并联桥臂包含相等的寄生电阻，因为输出电压中的直流分量为两个桥臂输出的直流分量之和，所以闭环控制下的理想结果是输出电压中直流分量为0（即两个桥臂输出的直流分量之和为0），此时若一组桥臂调制信号中出现若干个开关周期的直流分量，理想控制条件下另一组桥臂会产生与之幅值相等相位相反的该分量。假设Um1、Um2、Um3、Um4为4个桥臂单元频率为mwc的幅值，载波初始相位为0，则有两个并联桥臂输出脉冲电压中调制信号直流分量导致的成分分别为
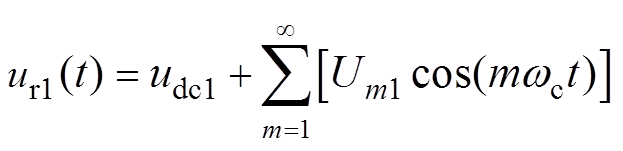（22）
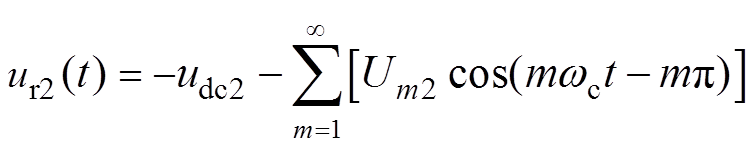（23）
当udc1-udc2=0，则输出电压不存在偏置。根据第1节的分析方法，假设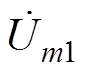
、
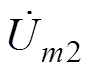分别为两个并联桥臂单元频率为mwc的幅值相量，当输出电压为理想正弦波时，两个并联单元的直流分量幅值相等相位相反，载波移相角度为-p，输出电压中直流分量导致的载波谐波成分可以表示为
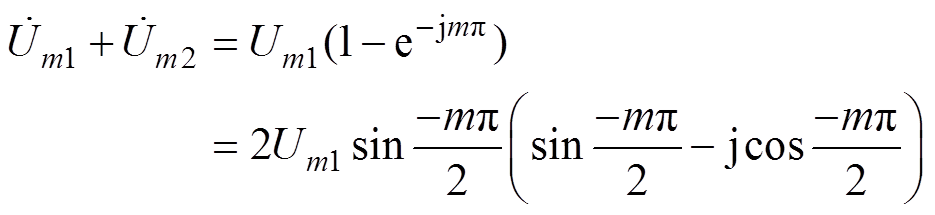
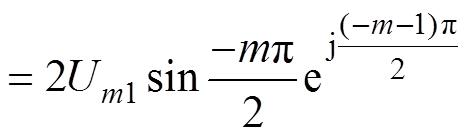（24）
式（24）表明，直流分量会导致输出信号中叠加2k+1次的谐波成分，即调制波中直流分量尽管不会导致输出电压偏置，但是将在输出电压中出现1倍频的载波谐波含量。
但当交错并联拓扑采用共输入输出母线连接方式时，需要通过控制策略抑制环流的影响，其每一组并联桥臂需要独立的调制信号。此时每组调制信号中直流成分的大小未必相等，其与环路参数、功率管开关时间等一系列因素有关。当并联单元桥臂输出电压的直流分量幅值不等时，udc1-udc2≠0，此时输出电压中包含直流分量导致的偏置。假设第二组并联半桥输出电压中直流分量导致的频率为mwc的幅值相量为
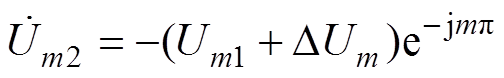（25）则根据式（25）可得
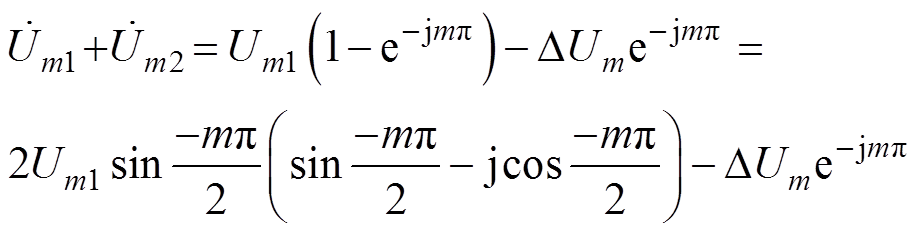（26）
可知，当并联单元调制信号中直流分量不平衡时，输出信号中会叠加奇次与偶次谐波成分。
当采用4个半桥单元交错并联时，调制信号叠加直流分量后，与两组半桥交错并联假设方式一致得到4个并联半桥频率为mwc的幅值为Um1、Um2、Um3、Um4，幅值相量为、、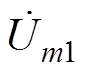
、
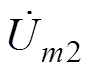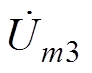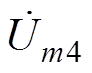，若考虑不平衡情况，则可得
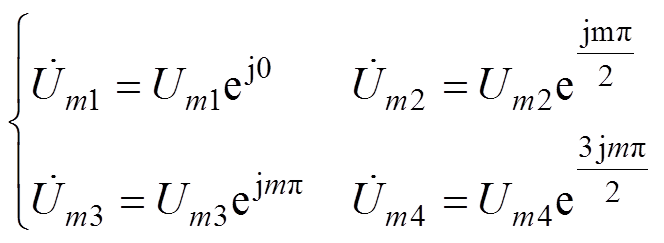（27）从而可得
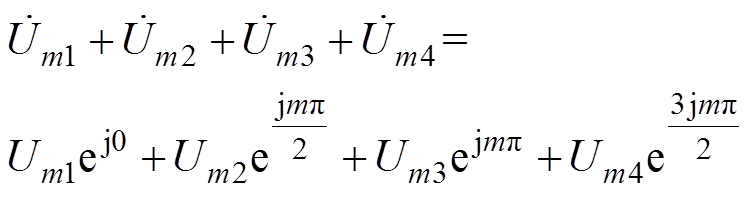（28）
假设存在以下关系
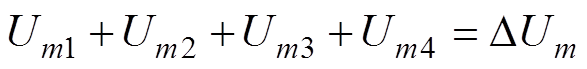（29）将式（27）代入（29），可得
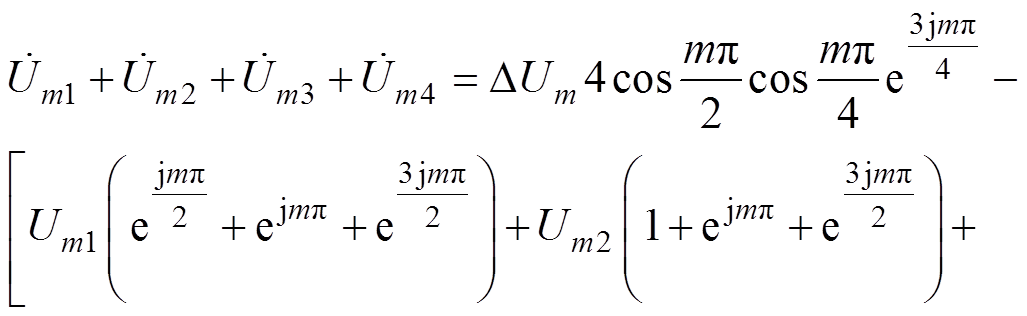
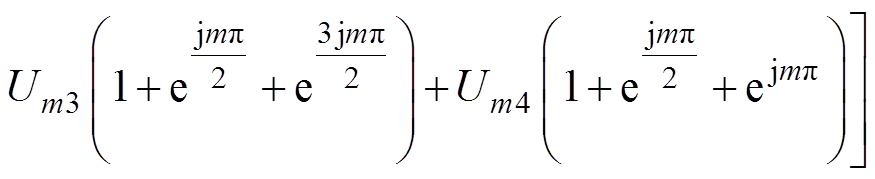（30）由式（30）可见，在分析直流分量对4个半桥交错并联的输出谐波成分影响时，要分两种情况讨论。分析过程如下：
（1）当Um1=Um2=Um3=Um4，此时得到
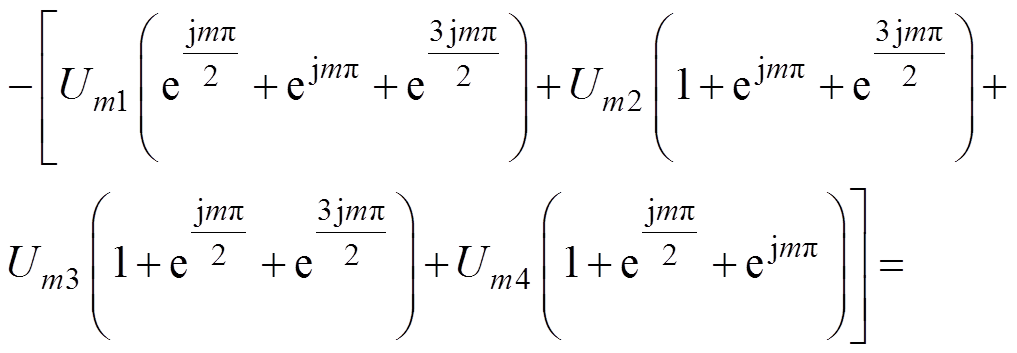
（31）
调制信号的直流成分在输出侧仅叠加4k次载波谐波成分，对输出电压谐波分布不构成影响。且此时DUm≠0，此时根据式（31）第二行可知，输出侧的偏置使输出侧叠加4k次谐波成分。上述成分与4个半桥交错并联时调制信号不包含直流偏置时的输出侧载波谐波成分是一致的。
（2）当输出电压不包含若干周期的直流偏置扰动时，即式（30）中DUm=0，此时必定不满足Um1= Um2=Um3=Um4，则调制波直流分量导致的输出侧谐波成分由式（30）第二、三行的项决定，该部分谐波成分包含所有次数的谐波分量。在实际4个桥臂交错并联拓扑中，因为共直流母线并联时需要均流控制，一般各并联单元设有独立的电流环，且采用共电流基准的方法来抑制环流，通常无法满足Um1= Um2=Um3=Um4，因此需要在实际中提高并联单元的一致性或抑制控制电路的偏置，避免调制信号中低频与直流成分在输出侧叠加额外的载波谐波成分。
若将交错并联半桥逆变器单元各增加一组桥臂，得到两个H桥单元的交错并联拓扑。此时，单极性倍频调制方式工作的H桥单元的等效开关频率提高了一倍，此处研究基于倍频调制的H桥单元交错并联时的谐波分布情况，分析以图8拓扑为例。假设图8中4个桥臂输出滤波电感及其寄生参数一致，Z1、Z2分别为4个桥臂输出侧阻抗、负载与输出滤波电容组成的网络阻抗；u1N、u2N、u3N、u4N为拓扑中4个桥臂对输入中点的瞬时电压。
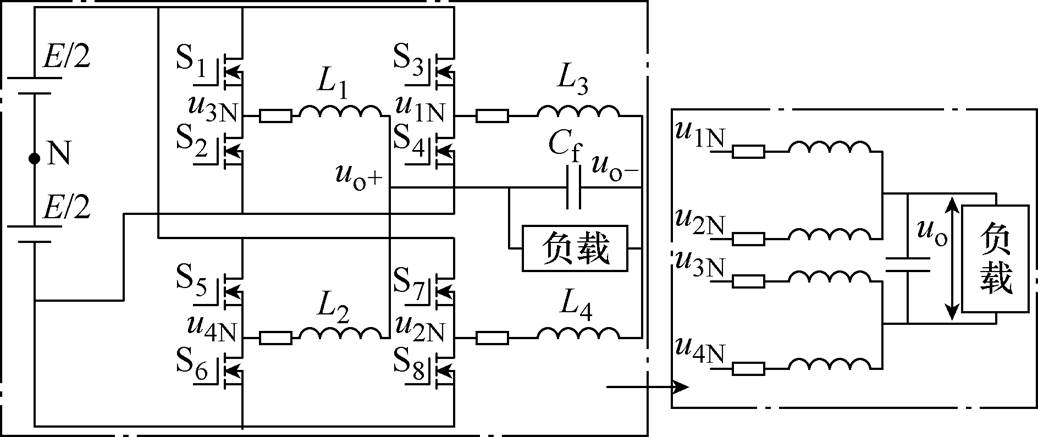
图8 两个倍频调制H桥单元交错并联拓扑
Fig.8 Interleaving paralleled inverter topology consists of two multiplier-frequency modulation H-bridge
输出电压为uo，uo+、uo- 为输出侧两端对输入中点的电压，结合图8，能够得到
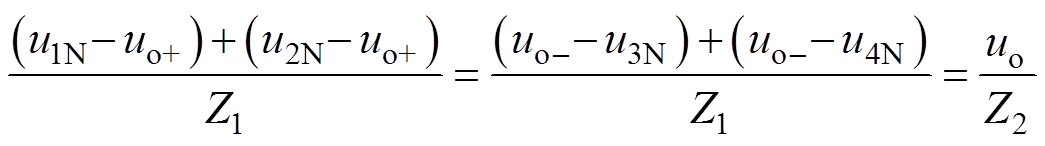（32）从而根据式（32）得到
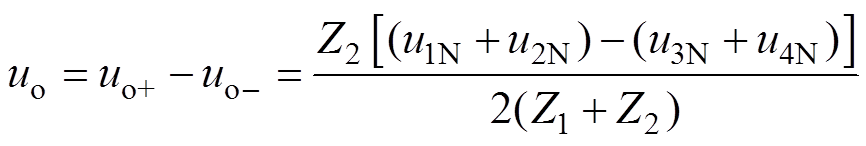（33）
uo可由式(u1N+u2N)-(u3N+u4N)表示。在分析该拓扑输出电压的谐波成分时采用与2或4组半桥交错并联类似的分析方法。假设图8中交错并联单元之间交错角度为k，载波初始相位为零。假设一组桥臂频率为mwc+nw0谐波成分的电压幅值为Umn，则得到图8中其他3个桥臂频率为mwc+nw0谐波成分电压幅值的表达式为
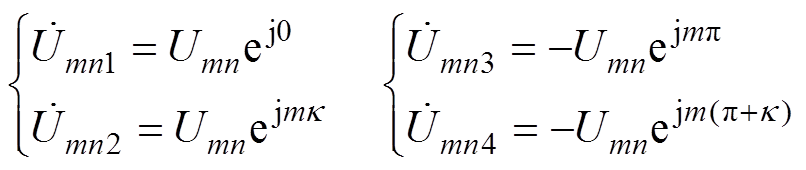（34）根据式（34），输出端的谐波成分为
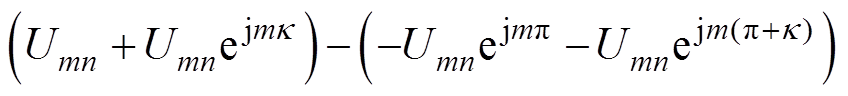（35）
由式（35）能够推导得到
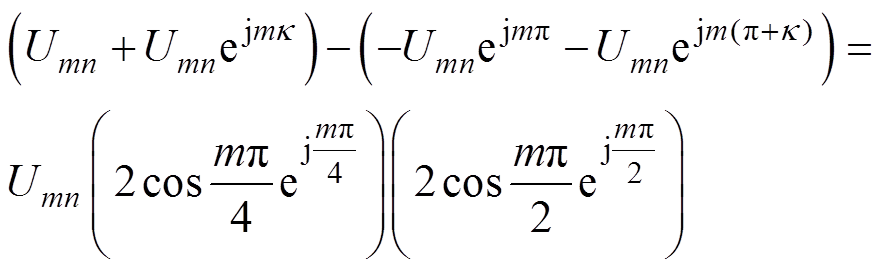（36）基于单极性倍频调制的H桥交错并联（交错角度为p/2）仅保留了m=4k的载波谐波成分，即对低次谐波频率为4倍载波频率，等效功率管开关频率为原来的4倍。因此，进一步推广对于x台倍频调制的H桥单元进行交错并联扩容时，应当将载波交错角度设置为p/x，以达到等效开关频率提高为原频率4倍的目的。其输入侧谐波成分也等效于提高为2N倍等效开关频率。此外，若取输出端为u1N的桥臂为例，其桥臂电感电流瞬时值表示为
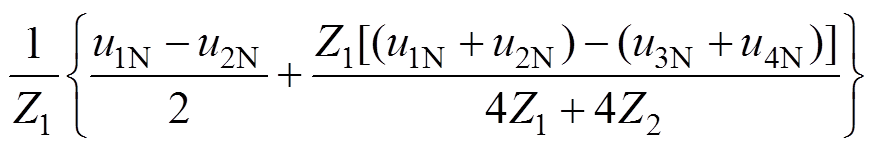（37）
一个桥臂的电感电流谐波组成除了输出电流谐波成分外，还包含了与其并联的另一组桥臂与之产生的环流成分（即(u1N-u2N)/2），因为最佳交错角度为p/2，则该环流成分包含载波频率奇数和偶数次谐波，因此倍频调制H桥单元采用p/2角度进行交错并联，虽然输出侧最低次谐波为载波频率的4倍，但是其每个并联桥臂电感电流谐波含1倍频的载波谐波，无法保持单台H桥倍频时两倍等效开关频率的效果。
假设一个桥臂中调制波直流成分导致的频率为mwc谐波成分的幅值为Vm1，则可以得到两个倍频H桥交错并联拓扑中4个桥臂调制波直流成分导致的谐波成分幅值表达式为
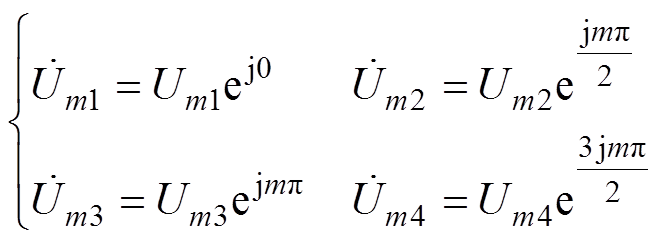（38）此时假设存在以下关系
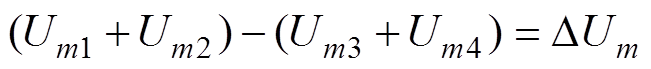（39）
将式（38）代入式（39）可得
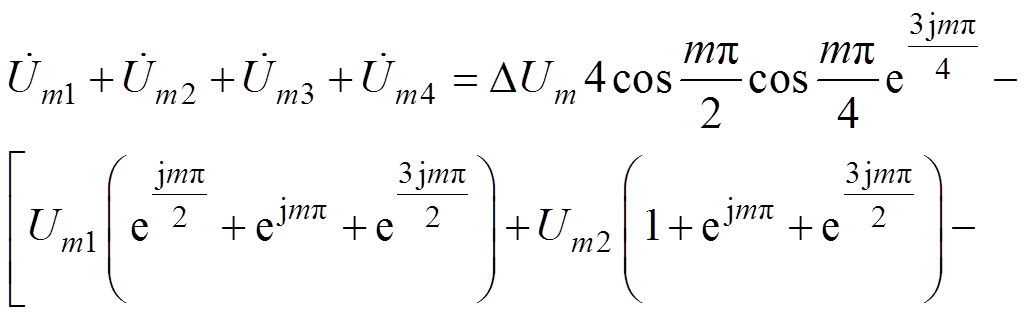
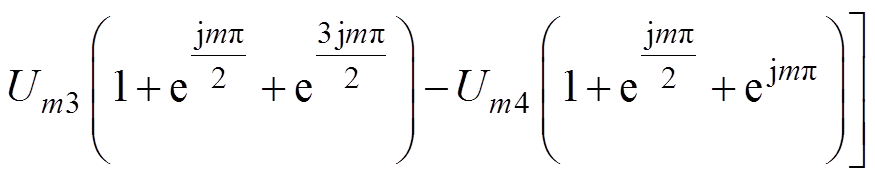（40）
可见，当Um1=Um2=Um3=Um4，4个桥臂调制信号中直流分量对输出侧载波谐波成分的影响与4个半桥交错并联的输出侧谐波组成一致。
为了便于分析，假设存在以下关系
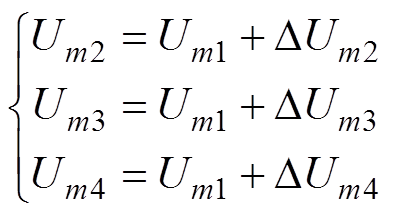（41）并将式（41）代入式（40）可以得到
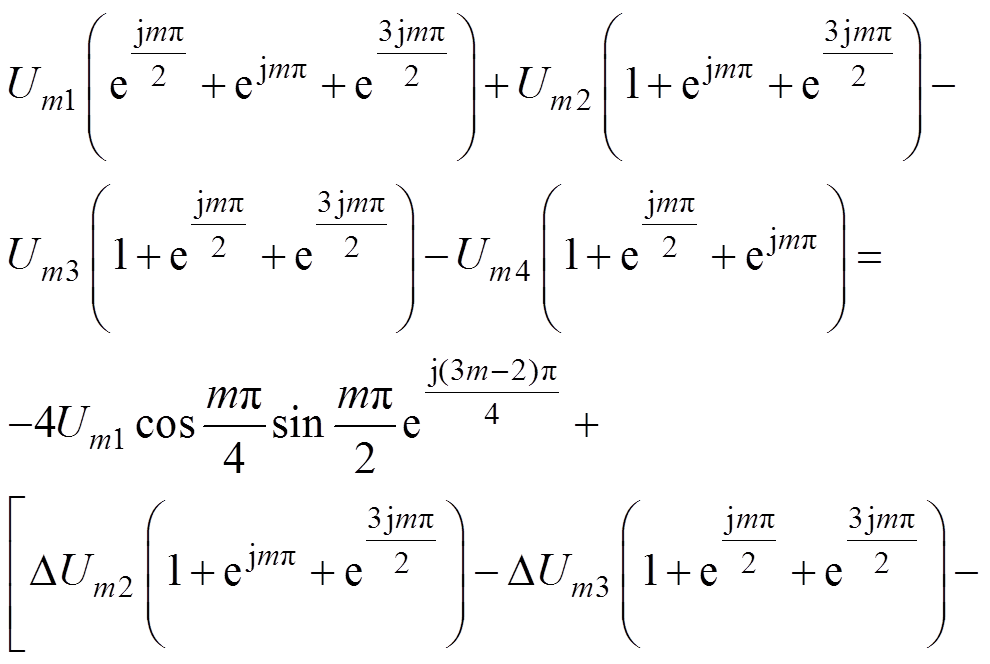
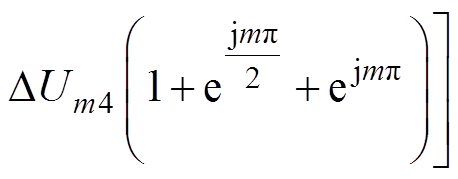（42）式中，第四、五行的项会引入奇数次载波谐波成分，这一点与第2节中所分析的4个桥臂交错并联方式下是不同的（之前调制信号叠加同样的直流成分4个半桥交错并联不仅引入奇次，也会引入偶次成分）。
应用Saber仿真软件对两、四组半桥逆变单元共输入、输出交错并联拓扑进行仿真。输出电压为115V/400Hz，并联单元共用输入电压独立且幅值均为180V，开关频率为30kHz，交错角度为2p/N，额定功率为3kV·A。输出滤波电感设置为150mH，输出滤波电容设为20mF。仿真波形分别如图9～图12所示。
图9a为第四组仿真波形为两个桥臂之间环流的波形。此时输入、输出谐波分布如图9b所示，谐波主要是2k次载波谐波成分，证明了式（20）和式（21）相关分析的正确性。此时如图9c所示，并联桥臂叠加了2k+1次载波谐波成分的环流，证明式（24）相关分析的正确性。
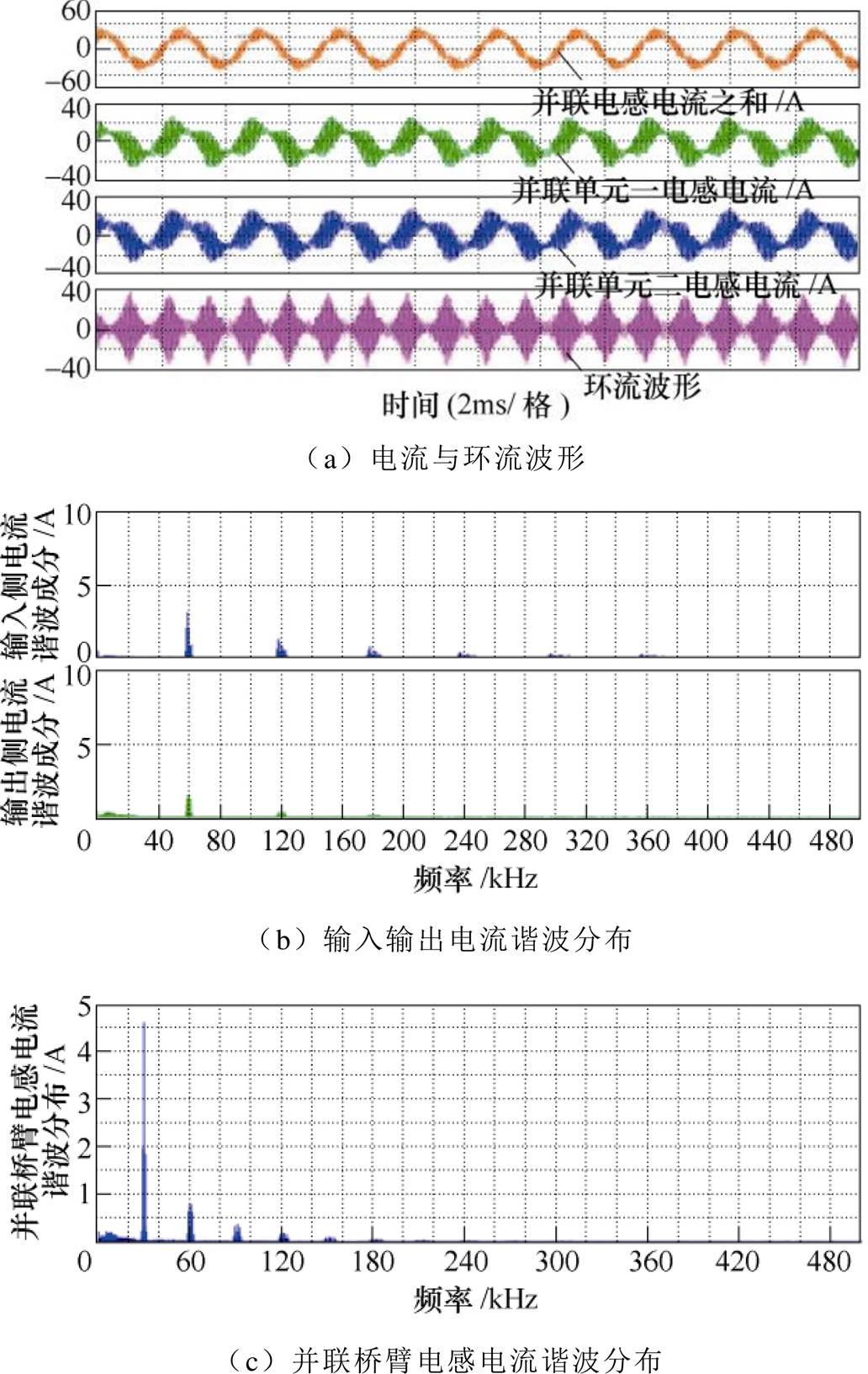
图9 理想情况下两个半桥单元交错并联仿真波形
Fig.9 Simulation waveforms of two half-bridge interleaving paralleled topology with ideal conditions
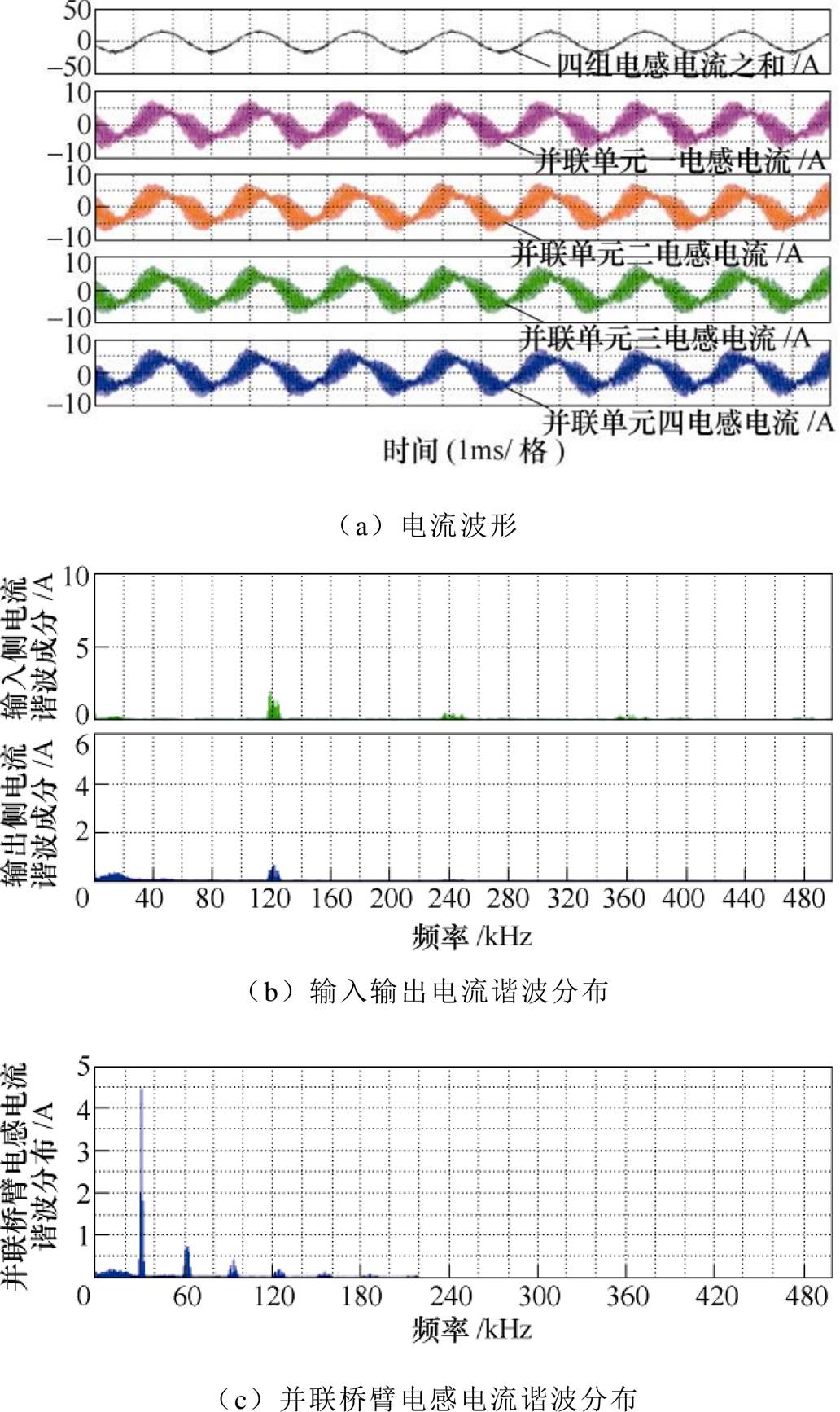
图10 理想情况下4个半桥单元交错并联开环仿真波形
Fig.10 Simulation waveforms of four half-bridge interleaving paralleled topology with ideal conditions
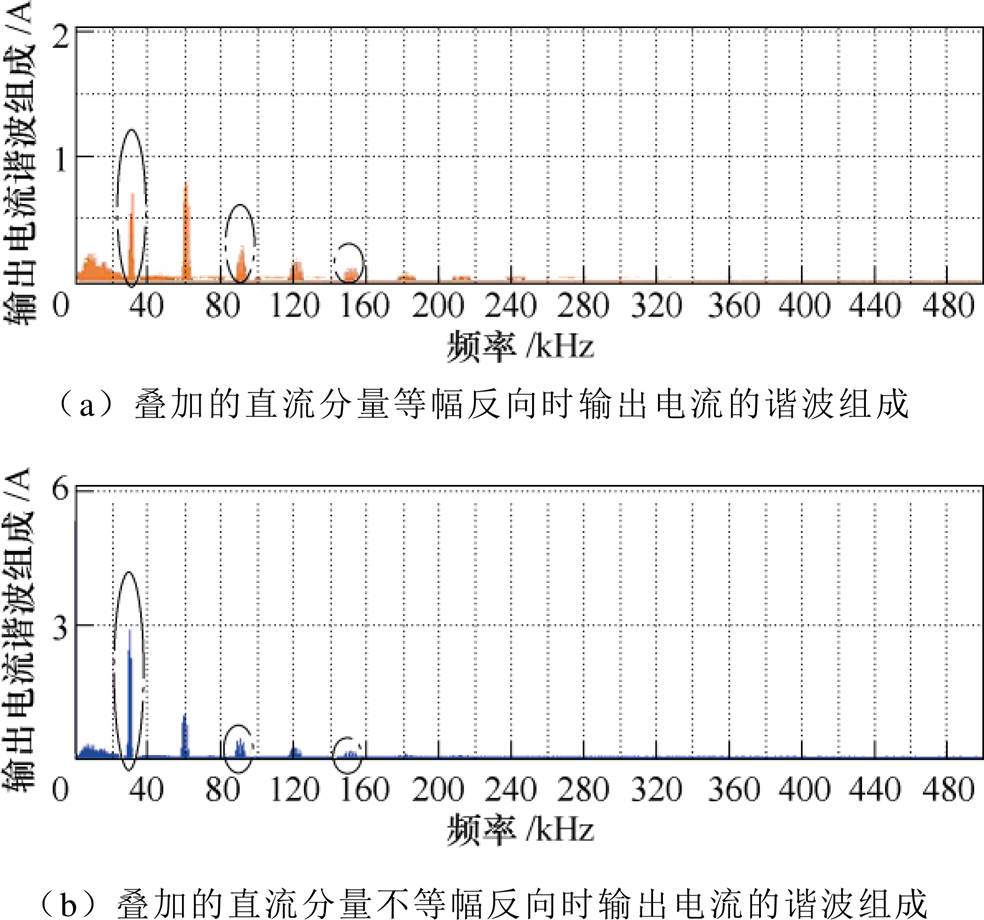
图11 调制信号引入直流分量后两个半桥单元交错并联仿真波形
Fig.11 Simulation waveforms of two half-bridge interleaving paralleled topology with non-ideal conditions
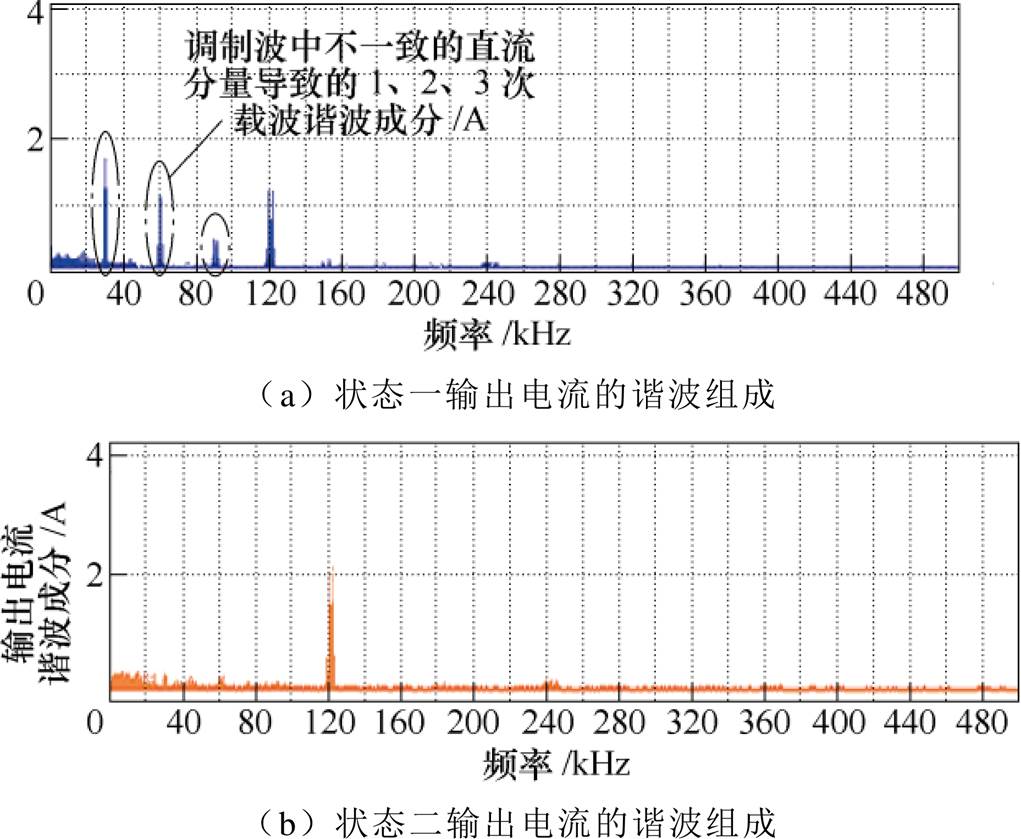
图12 调制信号引入直流分量后4个半桥单元交错并联仿真波形
Fig.12 Simulation waveforms of four half-bridge interleaving paralleled topology with non-ideal conditions
当交错并联单元数量增加到4时，仿真波形如图10所示，根据图10b仿真结果，输入输出电流的主要谐波成分为4k次载波谐波。如图10c所示，并联桥臂电感电流叠加了1、2、3次载波谐波环流成分。图10结果验证了式（27）～式（30）相关分析的正确性。
本文还对调制波中直流成分对输出谐波分布的影响进行了分析，因此在仿真模型中并联桥臂的调制波中注入直流分量进行验证，不同情况下输出侧谐波分布如图11和图12所示。
当两个并联桥臂调制波加入的直流分量幅值相反且绝对值也不等时，如图11b所示，输出侧谐波除增加了奇次谐波成分外还叠加了直流偏置成分（仿真中通过并联桥臂串联寄生电阻保证直流成分不会引起环流的累积）。如图11c所示，并联桥臂电感电流叠加了直流成分。
为考察4个半桥交错并联时调制信号中的直流分量对输出侧载波谐波成分的影响，在4个桥臂的调制信号中分别加入两种状态的直流分量进行仿真。
（1）状态一：一组桥臂调制信号加入0.5V的直流分量，另外三组桥臂调制信号加入-0.1V、-0.1V、-0.3V，仿真结果如图12a所示，4个桥臂不相等的调制波直流分量导致了输出侧叠加了很大的1、2、3次载波谐波。
（2）状态二：四组桥臂都加入直流分量0.3V进行仿真，仿真结果如图12b所示。此时输出侧除叠加了直流偏置导致的直流偏置成分外，最低次载波谐波依然为4倍的载波谐波成分。上述结果验证式（30）和式（31）相关分析的正确性。
图13为两组基于倍频SPWM调制的H桥单元交错并联仿真波形，交错角度为p/2。输出电流谐波主要由4k次载波谐波成分组成，等效提高为4倍功率管开关频率。
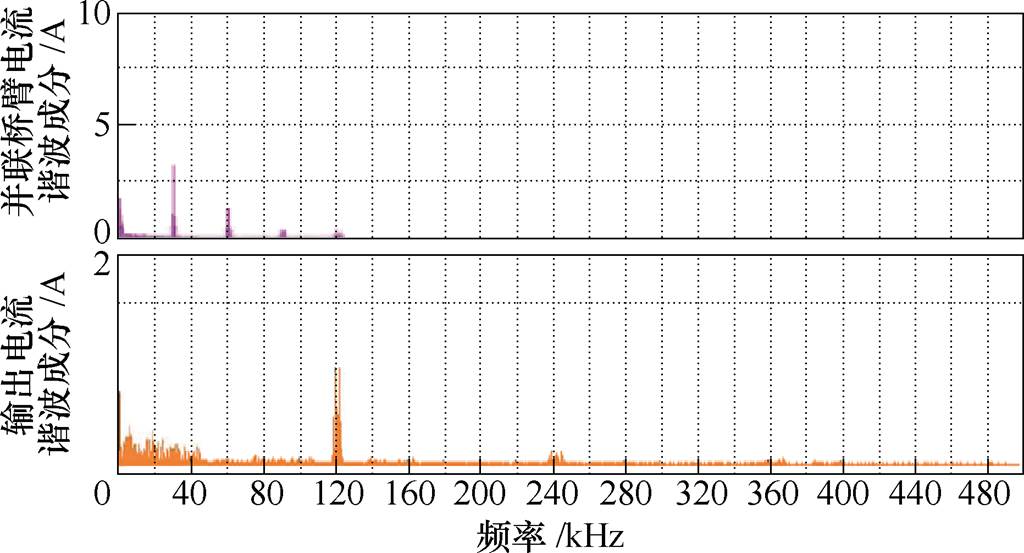
图13 理想情况下两个倍频H桥交错并联仿真结果
Fig.13 Simulation results of two multiplier-frequency H-bridge interleaving paralleled topology with ideal conditions
此时在仿真模型的4个桥臂调制波中叠加平衡或不平衡直流成分，为了验证式（38）～式（42）相关分析的正确性，采用两种直流分量叠加方法分别仿真：
（1）方法一：对第一组并联桥臂分别叠加0.3V、-0.3V，第二组并联桥臂分别叠加0.4V、-0.4V，仿真结果如图14a所示，输出侧在4倍载波谐波成分基础上还叠加了奇数次载波谐波成分。
（2）方法二：对第一组并联桥臂分别叠加0.4V、-0.6V，第二组并联桥臂分别叠加0.5V、-0.2V，仿真结果如图14b所示，与图14a比较，其增加了偶次载波谐波以及直流偏置成分。
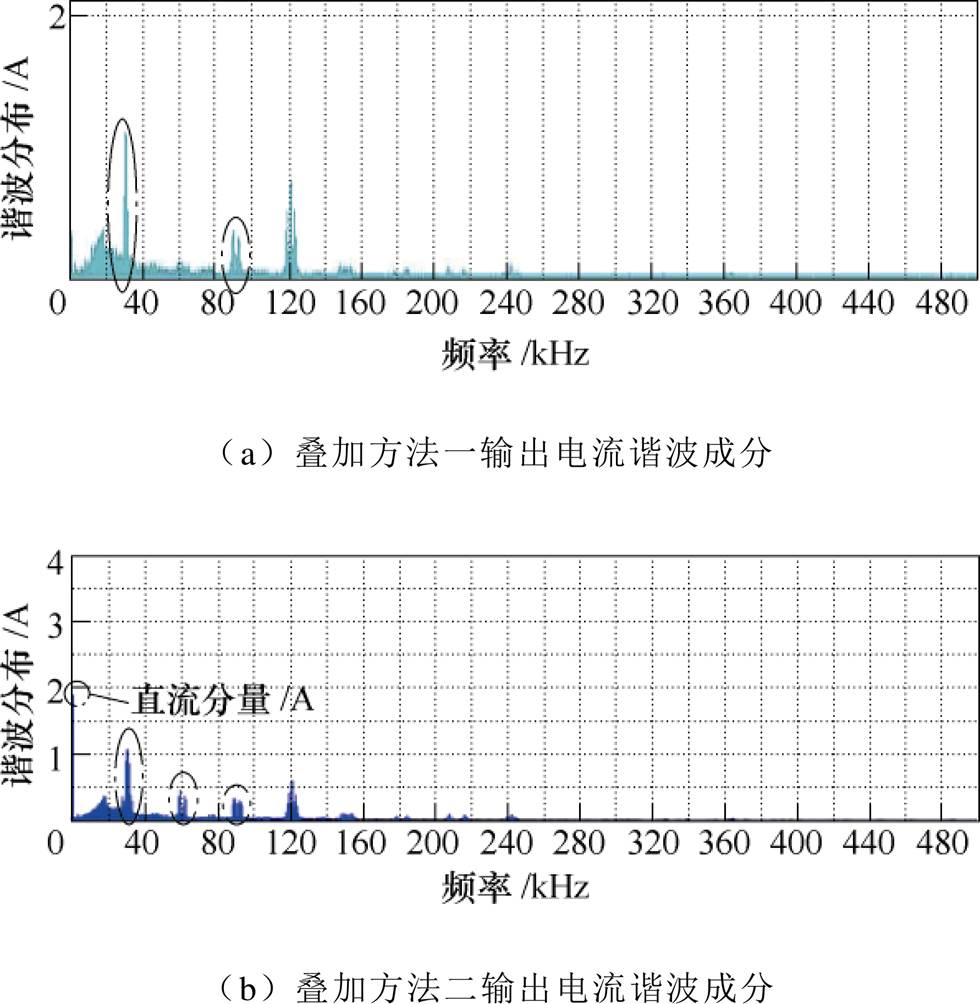
图14 调制信号包含直流分量时两个倍频H桥交错并联仿真结果
Fig.14 Simulation results of two multiplier-frequency H-bridge interleaving paralleled topology with non-ideal conditions
为了验证本文分析的正确性，分别在实验室搭建的模块化串联与模块化并联实验平台进行实验验证，两组实验平台分别如图15a和图15b所示。样机参数与第2、3节仿真参数一致。
图15 实验平台
Fig.15 Experiment platform
图16所示为逆变器在满载条件下输出电压和负载电流波形。由图16可见，输出电压和负载电流能够保持良好的稳态特性，且载波谐波含量较小。
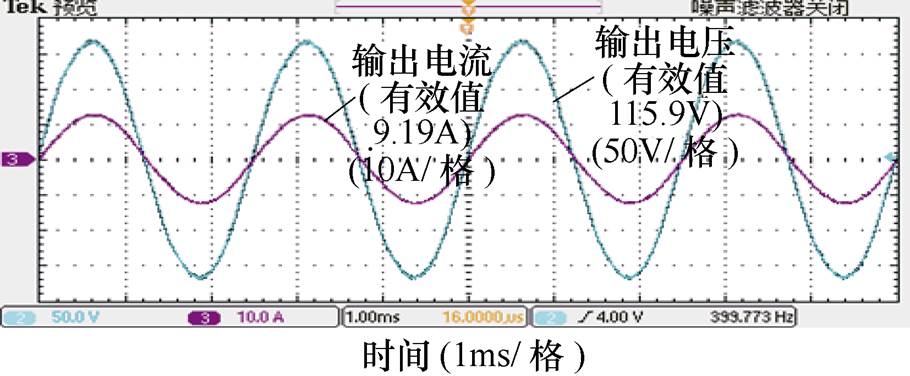
图16 两H桥输出串联满载1kV·A输出电压、电流波形
Fig.16 Experiment waveforms of output voltage and current of cascaded inverter
串联桥臂输出电压与电感电流实验波形如图17所示，串联桥臂输出电压为五电平形式，该波形与图4仿真波形以及分析结果是一致的。
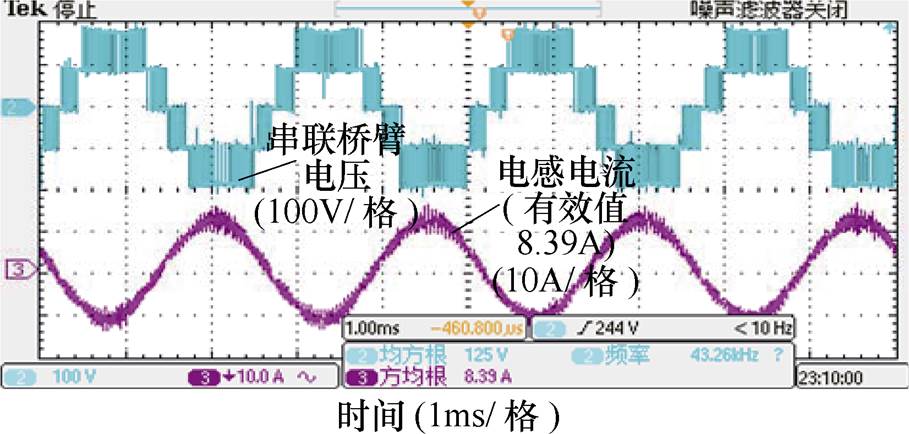
图17 串联桥臂输出电压与电感电流实验波形
Fig.17 Experiment waveforms of leg voltage and inductor current of cascaded inverter
对图15a中的多桥臂交错并联实验平台的载波进行移相，当并联桥臂数量为2时，移相角度为p，从而实现交错并联。实验平台参数与第2.3节仿真实验参数一致，实验波形如图18所示。根据图18a～图18c实验结果，各并联桥臂之间采用共电压外环，独立电流内环的分布式均流控制方式能够实现良好的均流效果。图18d、图18e分别为该实验电路在空载、满载切换瞬间并联桥臂的电感电流波形与输入电压波形，样机具备良好的动态性能。
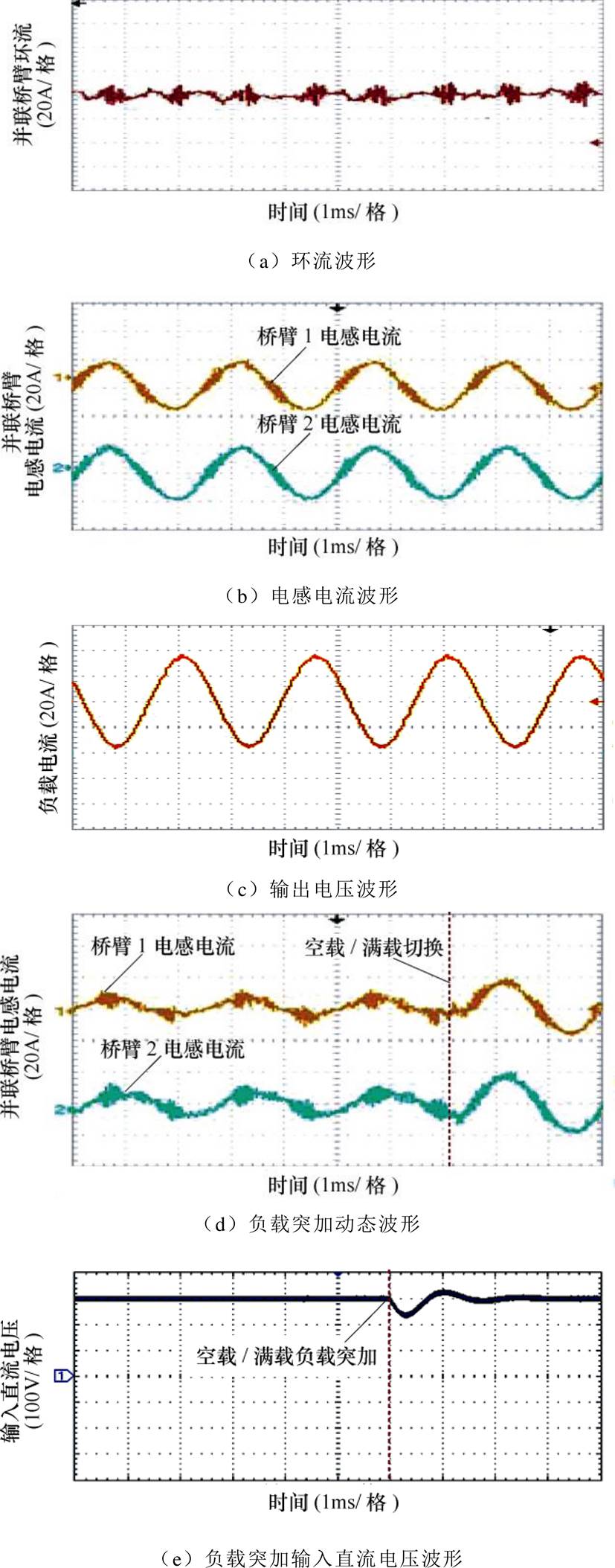
图18 移相角度为p 时的实验波形
Fig.18 Experiment waveforms of interleaving parallel inverter when phase shift of carrier waveform is p
为了进一步比较不同移相角度对桥臂波形的影响，进行了移相角度为p/2的实验，实验结果如图19所示。比较图19b与图18c中的输出电流波形，表明在非最佳移相角度下，输出电流的谐波明显增大。
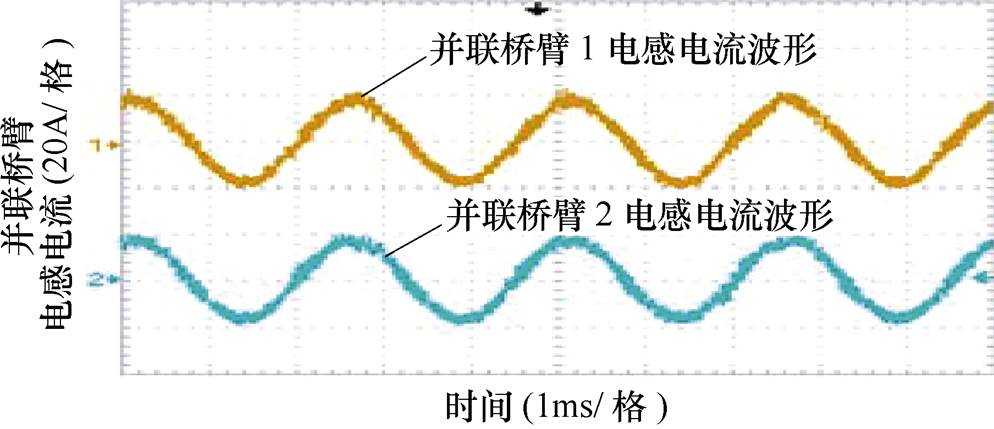
图19 移相角度为p/2时的实验波形
Fig.19 Experiment waveforms of interleaving parallel inverter when phase shift of carrier waveforms is p/2
实验验证最后采用在控制信号中叠加共地低频（5Hz）信号源的方式模拟本文所分析的非理想工作状态，实验采用Tektronix PA3000功率分析仪对逆变器的输入、输出侧的谐波分析验证本文的分析结果。谐波成分测试结果见表1，实验数据对应了图5、图11、图12仿真结果，进一步验证了分析的正确性。
本文主要针对基于载波相移的单相输出多模块串、并联扩容方式的谐波规律进行分析。根据第1～第3节的分析，当所有拓扑的组成单元开关频率一致时，要得到与x个基于单极性倍频调制的H桥输出串联拓扑等效的开关频率，需要x个采用倍频调制的全桥或2x个半桥逆变器采用载波移相的交错并联方式组合而等效。从而得到几种单相拓扑关系，见表2。
表1 几种拓扑输出电流谐波分布测试结果
Tab.1 Output current harmonic distribution test results
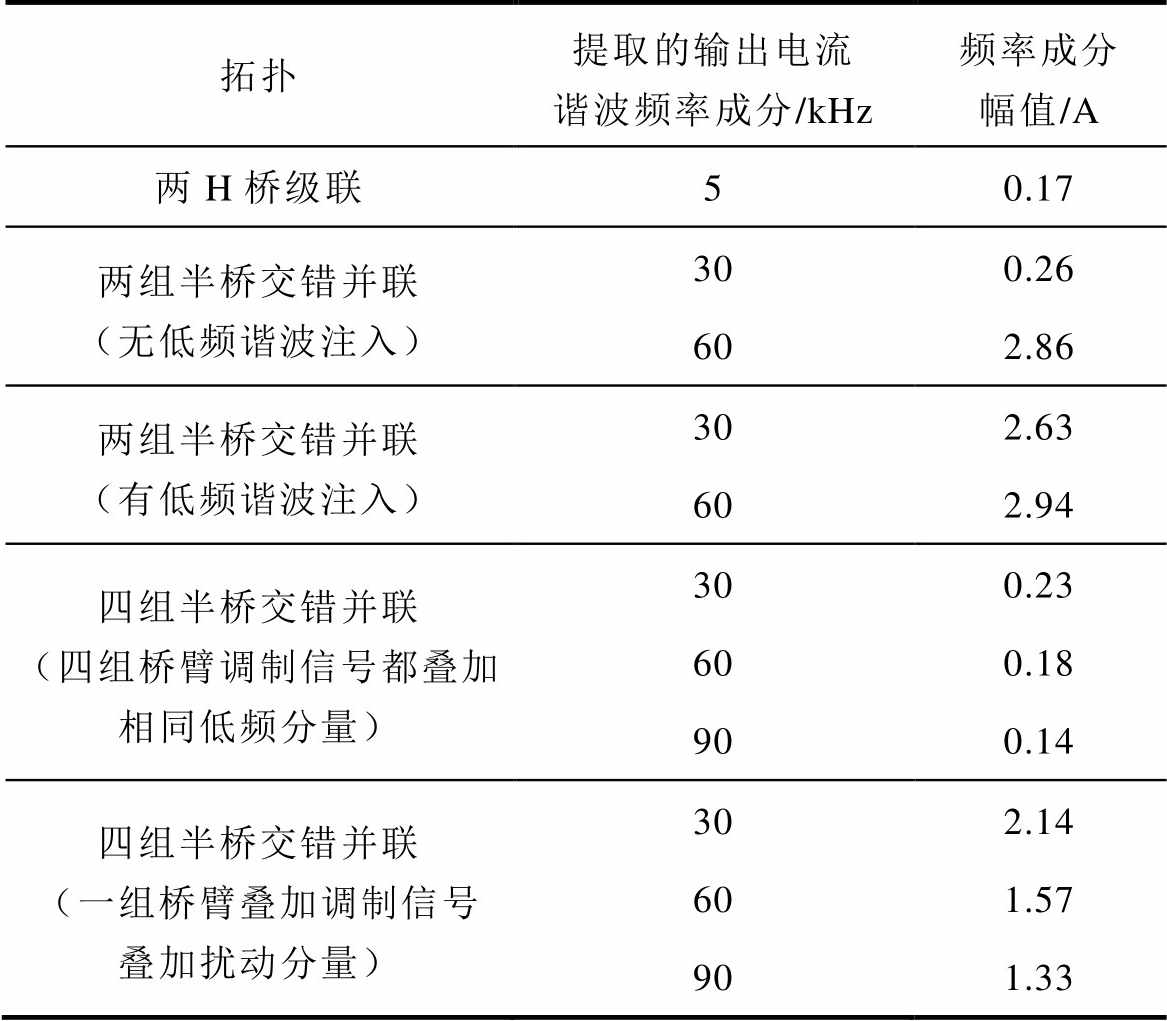
拓扑提取的输出电流谐波频率成分/kHz频率成分幅值/A 两H桥级联50.17 两组半桥交错并联（无低频谐波注入）30600.262.86 两组半桥交错并联（有低频谐波注入）30602.632.94 四组半桥交错并联（四组桥臂调制信号都叠加相同低频分量）3060900.230.180.14 四组半桥交错并联（一组桥臂叠加调制信号叠加扰动分量）3060902.141.571.33
表2 单相扩容拓扑比较
Tab.2 Single-phase expansion topology comparison
拓扑单元数量开关管数量开关管电压应力开关管电流应力独立电源数量 H桥级联x4xE/22Ix 全桥交错并联x4x2EI/21 半桥交错并联2x4xEI1
在保证输出总谐波含量不变的前提下，基于载波移相的H桥级联单相拓扑与交错并联拓扑相比，在综合滤波器数量、电压应力两个方面具有优势，但是其每个单元需要独立的输入侧直流电源，增加了前级高频隔离DC-DC变换器拓扑的复杂程度。若采取交错并联的半桥或者全桥拓扑，需要对并联单元采取均流措施，采集多个电感电流及闭环控制增加了控制系统的复杂程度。此外，根据第3节的分析，在交错并联拓扑中，由于每个桥臂控制环路独立设计，每个桥臂的调制波不同，因此调制波中的直流或低频分量扰动会增加输出电压的谐波含量。因此对单相ASI来说，两个倍频H桥级联具有一定的优势。而在输入输出电压等级较低但电流等级较高的场合，更适宜采用交错并联全桥与半桥拓扑。
参考文献
[1] 马海啸, 邵宇, 龚春英, 等. 三相四桥臂逆变器的非数字化控制策略[J]. 电工技术学报, 2016, 29(12): 26-32.
Ma Haixiao, Shao Yu, Gong Chunying, et al. Non- digital control strategy of three-phase four-leg inverter[J]. Transactions of China Electrotechnical Society, 2016, 29(12): 26-32.
[2] 张方华, 龚春英, 邓翔. 航空静止变流器的研究综述[J]. 南京航空航天大学学报, 2014, 46(1): 19-26.
Zhang Fanghua, Gong Chunying, Deng Xiang. Review of aeronautic static inverter[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2014, 46(1): 19-26.
[3] 何凯益, 任磊, 邓翔, 等. 混合H桥级联逆变器的优化调制[J]. 电工技术学报, 2016, 31(14): 193- 200.
He Kaiyi, Ren Lei, Deng Xiang, et al. Modified modulation of H-bridge hybrid cascaded inverters[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 193-200.
[4] 陈仲, 许亚明, 袁涛. 一种基于载波层叠脉宽调制的倍频调制方法[J]. 电工技术学报, 2018, 33(10): 2334-2344.
Chen Zhong, Xu Yaming, Yuan Tao. A double frequency modulation method based on the level- shifted pulse width modulation[J]. Transactions of China Electrotechnical Society, 2018, 33(10): 2334- 2344.
[5] 陈杰, 赵冰, 陈新, 等. 不平衡负载条件下三相四线制并联逆变器的下垂控制[J]. 电工技术学报, 2018, 33(20): 4790-4801.
Chen Jie, Zhao Bing, Chen Xin, et al. Research on droop control of three-phase four-wire parallel inverters under unbalanced load condition[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(20): 4790-4801.
[6] Fang Tianzhi, Shen Le, He Wei. Distributed control and redundant technique to achieve superior reliability for fully modular input-series-output- parallel inverter system[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 723-735.
[7] Avila D M A, Cougo B, Meynard T. Reconfigurable parallel interleaved three-phase inverter for aeronautical applications[C]//2012 Electrical Systems for Aircraft, Railway and Ship Propulsion, Bologna, Italy, 2012: 1-4.
[8] 龙江涛, 蔡环宇, 何昕东, 等. 基于平均功率控制的中频逆变器主从并联系统研究[J]. 电源学报, 2015, 13(2): 1-9.
Long Jiangtao, Cai Huanyu, He Xindong, et al. Research on master-slave paralleled middle-frequency inverters’ system based on average power control strategies[J]. Journal of Power Supply, 2015, 13(2): 1-9.
[9] 董培俊. 中频逆变器及其直流母线谐波抑制技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.
[10] 陈仲, 汪昌友, 陈淼. 航空静止变流器的输入纹波电流特性研究[J]. 中国电机工程学报, 2012, 32(27): 154-161.
Chen Zhong, Wang Changyou, Chen Miao. Analysis on input ripple current characteristics of aviation static inverters[J]. Proceedings of the CSEE, 2012, 32(27): 154-161.
[11] Li Yufei, Wang Yue, Li Ben Q. Generalized theory of phase-shifted carrier PWM for cascaded H-bridge converters and modular multilevel converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(2): 589-605.
[12] Rajesh B, Dr Manjesh. Comparison of harmonics and THD suppression with three and 5 level multilevel inverter-cascaded H-bridge[C]//2016 International Conference on Circuit, Power and Computing Technologies, Nagercoil, India, 2016: 1-6.
[13] Zhang Di, Wang Fred, Burgos Rolando, et al. Impact of interleaving on AC passive somponents of paralleled three-phase voltage-source converters[J]. IEEE Transactions on Industry Applications, 2010, 46(3): 1042-1054.
[14] Bao Xianwen, Zhuo Fang, Liu Baoquan, et al. Suppressing switching frequency circulating current in parallel inverters with carrier phase-shifted SPWM technique[C]//2012 IEEE International Symposium on Industrial Electronics, Hangzhou, China, 2012: 555-559.
[15] Mastromauro R A, Stasi S, Gervasio F, et al. A ground power unit based on paralleled interleaved inverters for a more-electric-aircraft[C]//2014 Inter- national Symposium on Power Electronics, Electrical Drives, Automation and Motion, Ischia, Italy, 2014: 216-221.
[16] Shin Dongsul, Lee Jong-Pil, Yoo Dong-Wook, et al. Stability improvement of interleaved voltage source inverters employing coupled inductors for grid- connected applications[J]. IEEE Transactions on Industry Electronics, 2015, 62(10): 6014-6023.
[17] 陈仲, 许亚明, 袁涛, 等. 级联型逆变器载波循环功率均衡控制方法及比较[J]. 电工技术学报, 2018, 33(20): 4802-4812.
Chen Zhong, Xu Yaming, Yuan Tao, et al. Power balance control methods and comparative study using carrier rotation technique for the cascaded inverter[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4802-4812.
Abstract With the larger scale application of multi-electric and all-electric aircraft, higher requirements are put forward on the power capacity of aeronautical static inverter (ASI), and more power expansion is realized by modular series and parallel methods. The expansion mode combined with carrier phase shift modulation can further reduce the switching frequency harmonic components of the system. However, the parameter imbalance between the modular modules on the airborne occasion and the control mode based on the analog circuit cause additional low frequency or DC offset disturbances in control signals, resulting in superimposing unconventional harmonic components on the input and output sides of the ASI. In this paper, based on the double-Fourier analysis and exponential function model of bridge voltage, the input and output harmonic distributions of modular series and parallel ASI are performed under non-ideal conditions. Analysis and comparison reveal the harmonic distribution characteristics of the modular ASI. Finally, the correctness of theoretical analysis is verified by simulation and experiment.
keywords：Interleaving parallel, cascaded inverter, double-Fourier analysis, harmonic distribution
中图分类号：TM614; TM76
DOI: 10.19595/j.cnki.1000-6753.tces.190140
江苏省自然科学基金青年项目（BK20160894）和中央高校基本科研业务费项目（2018CDQYZDH0039）资助。
收稿日期2019-01-30
改稿日期 2019-08-02
陈轶涵 男，1982年生，讲师，博士，主要研究方向为功率电子变换技术与航空电源系统技术等。E-mail: cyh@njupt.edu.cn
陈家伟 男，1986年生，特聘研究员，博士，主要研究方向为新能源发电技术和电网控制技术等。E-mail: echenjw@cqu.edu.cn（通信作者）
（编辑 崔文静）