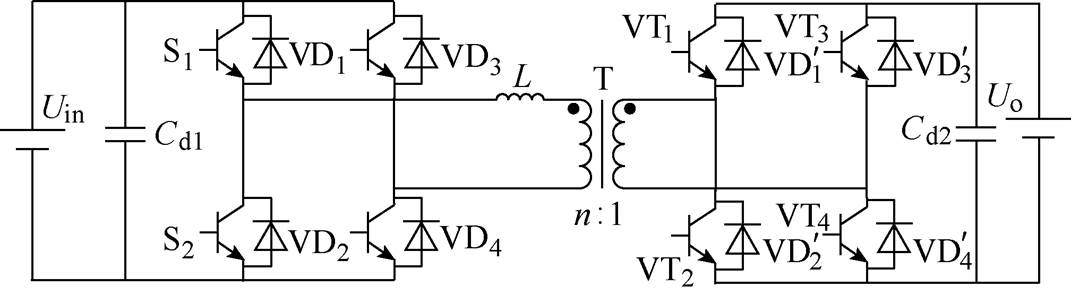
图1 传统两电平全桥隔离型双向DC-DC变换器
Fig.1 Traditional two level bidirectional full bridge isolated DC-DC converter
摘要 针对三电平半桥隔离型双向DC-DC变换器，提出了一种双PWM与移相结合控制（DPWMPS）的方法。通过对该控制工作原理进行分析，并以变压器两侧电压的相对位置为依据，归纳出系统运行的12种工作模式，并推导出每一种工作模式下的功率传输特性。在此基础上，该文提出一种电感最小峰值电流控制方法，能在电压配比m≤1的情况下实现稳态电感峰值电流全局最优。最后搭建实验平台，通过实验结果证明了该算法的正确性和有效性。
关键词：双PWM与移相结合控制 三电平半桥隔离型双向DC-DC变换器 工作模式 最小峰值电流控制
随着环境污染等问题日益突出，太阳能、风能发电、储能以及电动汽车等绿色可再生能源技术的发展越来越受到人们的关注[1-6]。对于上述应用场合，实现能量的双向流动至关重要，而隔离型双向DC-DC变换器除了能实现能量的双向流动之外，还具有功率密度高、输入输出电气隔离、易实现软开关等优点[7-11]。
传统的两电平全桥隔离型双向DC-DC变换器由两个H桥组成，其拓扑如图1所示[7]。
图1 传统两电平全桥隔离型双向DC-DC变换器
Fig.1 Traditional two level bidirectional full bridge isolated DC-DC converter
如图1所示，两电平全桥隔离型双向DC-DC变换器在运行过程中变压器两侧H桥结构中的功率器件处于关断状态时，其两端电压为整个输入或输出电压，电压应力较大，对器件耐压等级要求较高，这不利于提高系统功率密度和降低系统成本。针对该问题，可将三电平结构引入变压器两侧来替代两电平H桥结构，降低功率器件在关断时承受的电压应力。
在移相控制中，单移相控制（Single Phase Shift, SPS）应用最为广泛[7, 9]。该方法通过改变变压器两侧电压之间的相位差来控制功率传输方向及大小，控制简单，易实现，但是功率器件的电流应力和回流功率较大，而且只有一个控制自由度，灵活性低，系统可优化空间小。为了提高系统性能，有学者研究了拓展移相（Extended Phase Shift, EPS）控制[11-15]。该方法在保留变压器两侧电压之间移相角的同时，在一次侧或者二次侧H桥的两个桥臂的控制信号之间增加了一个移相角来控制系统传输功率的大小和方向。与SPS控制相比，EPS控制回流功率较小，控制自由度为两个，控制灵活性较高。为了对EPS进一步实现优化，又有学者对双重移相（Dual Phase Shift, DPS）控制进行了深入的研究[16-17]。DPS控制时在控制变压器两侧电压的移相角的同时，分别在变压器两侧H桥中加入一个相同的内移相角。在DPS控制的基础上，TPS（Triple Phase Shift, TPS）控制近年来引起了人们的关注[18-19]。TPS控制与DPS控制类似，只是在变压器两侧采用了不同的内移相角。因此DPS控制本质上是TPS控制的一种特例。与EPS控制相比，采用TPS控制，系统的回流功率和功率器件的电流应力都进一步减小，系统控制的自由度增加到3个，控制的灵活性也进一步提高。但是可以看出，从SPS控制到TPS控制，需要控制的变量逐渐增加，控制越来越复杂，实现难度较大。
由于SPS控制中电流应力较大，针对该问题，文献[20]研究了对SPS控制方法下的电流优化策略。文献[21]提出在EPS控制下其中一种工作模式的电流应力优化控制策略。文献[22]提出在DPS控制下其中一种工作模式的电流应力优化策略。文献[23]对TPS控制下其中一种工作模式的电流策略进行了研究。但是，无论是EPS控制、DPS控制还是TPS控制都具有多种工作模式，而已有的文献都只对其中某种特定的工作模式进行优化，因此所提出的电流优化方法都只属于局部优化结果，并没有达到该控制方法下的全局最优。
本文对三电平半桥隔离型双向DC-DC变换器进行详细研究，提出一种通过改变变压器两侧功率器件的占空比来进行控制的双PWM与移相结合（Dual-PWM- Phase-Shift, DPWMPS）的控制方法。通过直接改变功率器件的占空比和变压器两侧电压之间的移相角来进行控制。对系统在运行时的等效电路进行分析，将系统的运行模式进行完整的分类和研究，分析了所有工作模式的功率特性。在此技术上提出在m≤1时的最小峰值电流控制算法来实现系统峰值电流的全局最优。最后搭建实验平台，通过实验验证了本文所提方法的正确性和有效性。
三电平半桥隔离型双向DC-DC变换器的主电路如图2所示。Uin表示输入电压，Uo表示输出电压，n表示变压器的电压比，U1为变压器一次侧端电压，U2为变压器二次侧端电压，L表示辅助电感和变压器漏感折合之后的等效电感，iL表示等效电感电流，io表示输出电流，Cd1、Cd2表示变换器一次侧电容，Cd3、Cd4表示二次侧支撑电容。
本文中采用DPWMPS控制，功率器件驱动信号采用S1和S3信号互补，S2和S4信号互补，通过改变功率器件导通的占空比来控制变压器一次电压U1。在变压器二次侧半桥中功率器件的驱动信号采用T1和T3信号互补，T2和T4信号互补，通过改变功率器件导通的占空比来控制变压器二次电压U2。然后通过控制U1和U2之间的移相角来控制系统传输功率的大小和方向。该控制方法有多种工作模式，其中一种工作模式的控制原理如图3所示。图3中，T表示半个开关周期，D1、D2分别表示U1和U2的占空比，iL表示电感电流，f 表示变压器两侧电压移相角的电角度差除以180°（此时图中的f 为正）。
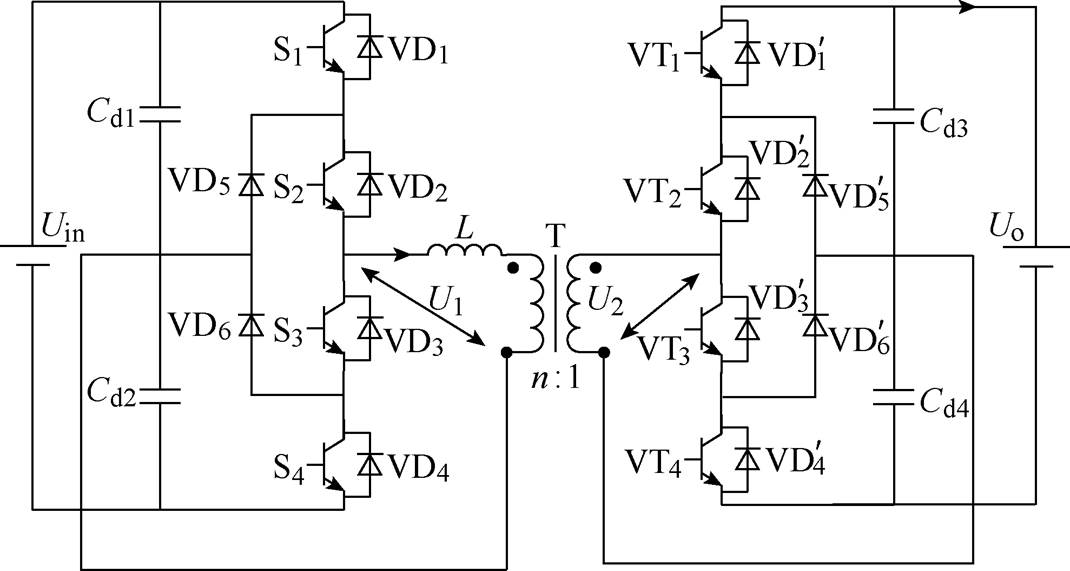
图2 三电平半桥隔离型双向DC-DC变换器
Fig.2 Three level half bridge isolated bidirectional DC-DC converter
图3 DPWMPS控制下模式A示意图
Fig.3 Schematic diagram of working mode A with DPWMPScontrol
从图3中可以看出，相比TPS控制而言，DPWMPS控制在实际中只需对变压器两侧半桥中的功率器件占空比、变压器两侧电压U1和U2之间的移相角进行控制，不用对内移相角进行控制，从而降低了系统的控制难度。
根据图3可知，D1、D2和f 的取值范围为
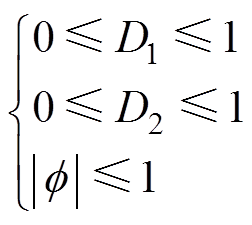（1）从图3可以看出，在系统运行过程中DPWMPS控制可以通过D1、D2和f 三个自由度来对传输功率进行控制。对于指定的传输功率来说，D1、D2和f理论上可以有无穷多个组合来进行控制，这时可以根据U1与U2的相对位置来对系统工作模式进行划分，一共可得到12种工作模式。由于分析方法基本相同，在此以其中三种工作模式为例进行分析。
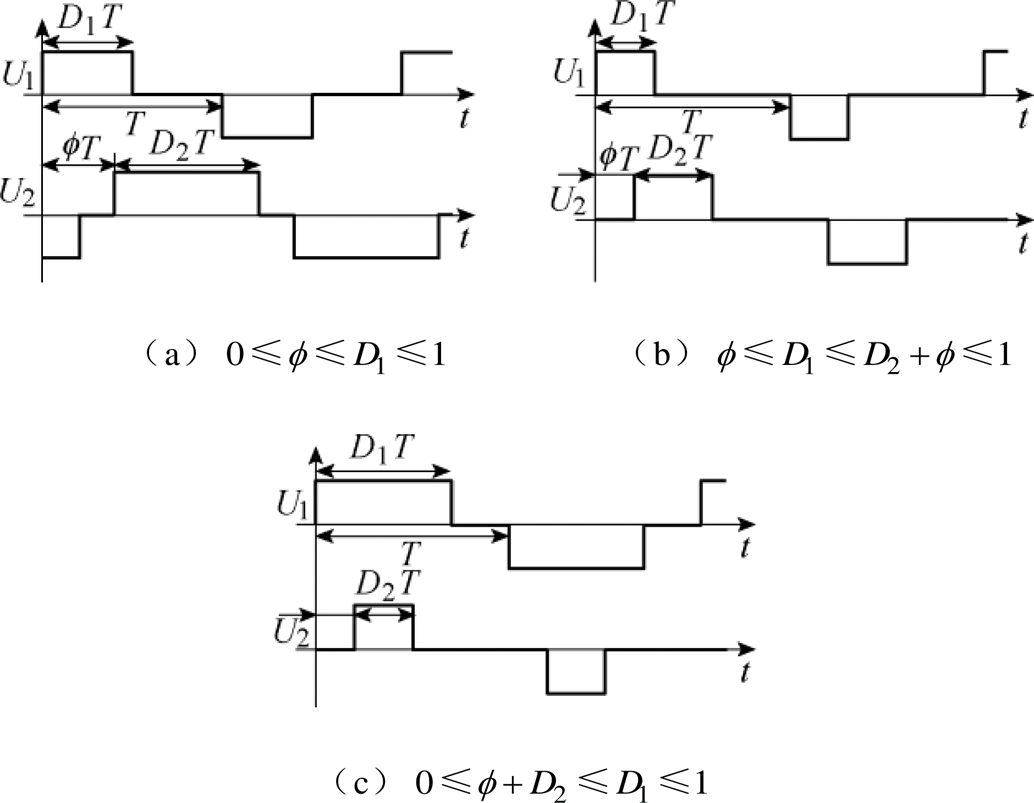
图4 U1与U2的三种波形
Fig.4 Three typical waveforms of U1 and U2
在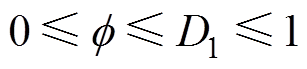
的情况下，U2上升沿在U1上升沿与下降沿之间。当U2下降沿处于T之后，此时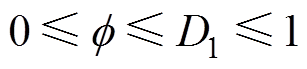，且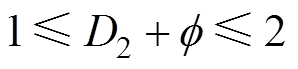
，如图4a所示。当U2下降沿处于U1下降沿与T之间，此时
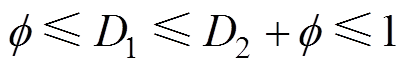，如图4b所示。当U2下降沿处于U1下降沿之前，此时
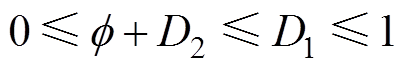，如图4c所示。按此分析方法得到系统的12种工作模式见表1。
每种工作模式的传输功率计算公式都不一样，但是分析方法是相同的。在此以图3所示的模式A为例进行分析。
表1 12种工作模式下D1、D2和f的取值范围
Tab.1 The range of D1、D2 and f for twelve kinds of working modes
D1、D2和f 取值工作模式 0≤f ≤D1≤1且1≤D2+f ≤2A 0≤f ≤D1≤D2+f ≤1B 0≤f ≤D2+f ≤D1≤1C 0≤D1≤f ≤1且1+D1≤D2+f ≤2D 0≤D1≤f ≤1且0≤D2+f ≤1+D1E 0≤D1≤f ≤1且0≤D2+f ≤1F 0≤-f ≤D2≤1且1≤D2-f ≤2G 0≤-f ≤D2≤D1-f ≤1H 0≤-f ≤D1-f ≤D2≤1I 0≤D2≤-f ≤1且1+D2≤D1-f ≤2J 0≤D2≤-f ≤1且1≤D1-f ≤1+D2K 0≤D2≤-f ≤1且0≤D1-f ≤1L
由于稳态情况下iL为半周期对称波形，在此只对前iL半周期进行分析。在前半周期中，模式A的5种模态的等效电路图如图5所示。
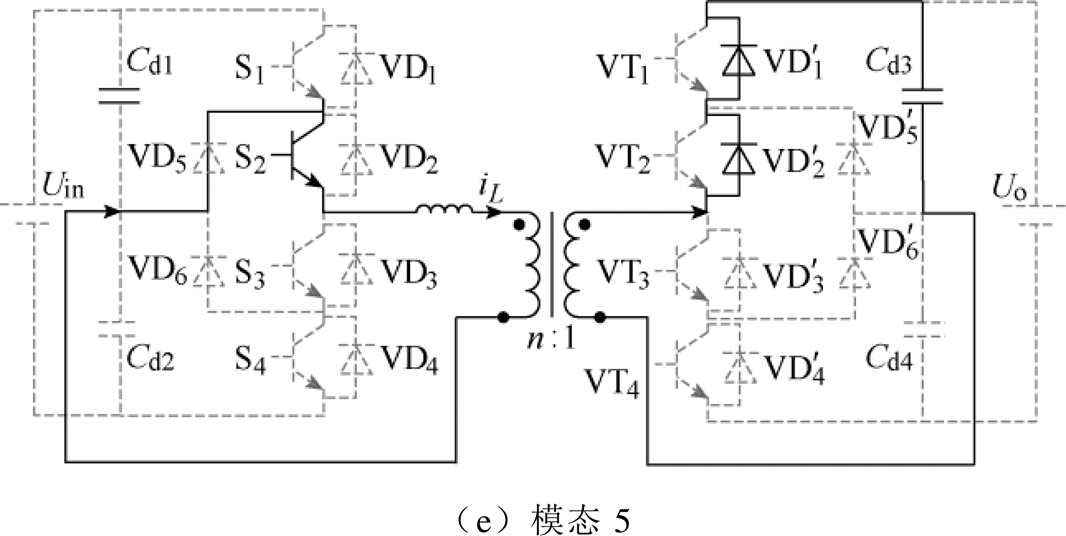
图5 模式A下5种工作模态
Fig.5 The five typical operational modes of working mode A
（1）模态1（t0～t1）：t0时刻S3、S4关断，S1、S2导通，此时电感电流方向为负，变压器一次电流通过VD1和VD2。变压器二次电流通过
和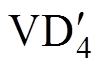
，电感上的电压为(Uin+nUo)/2。在t0～t1的过程中，电感电流iL为
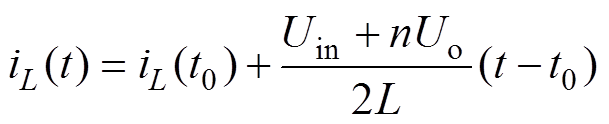（2）（2）模态2（t1～t2）：t1时刻，电感电流方向为正。电感电流在变压器一次侧通过S1、S2，在变压器二次侧通过VT3和VT4，在该时段中，电感电压为(Uin+nUo)/2。在t1～t2的过程中电感电流继续增加，其计算公式为
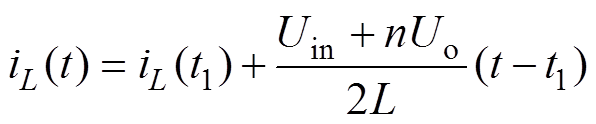（3）
（3）模态3（t2～t3）：t2时刻开关管VT2、VT3开通，电感电流在变压器二次侧通过VT3和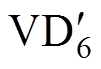
。在该时段中，电感电压为Uin/2，在t2～t3的过程中,电感电流继续上升，其计算公式为
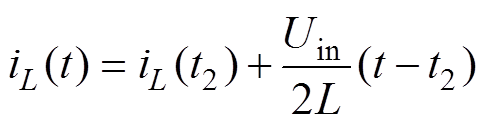（4）（4）模态4（t3～t4）：t3时刻VT3、VT4关断，VT1、VT2开通。此时电感电流方向为正，电感电流在变压器一次侧通过S1和S2，在变压器二次侧流过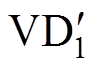
和
。在该时段中，电感电压为(Uin-nUo)/2，电感电流开始下降，电流计算公式为
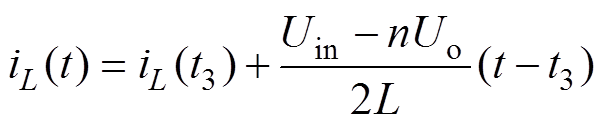（5）
（5）模态5（t4～t5）：t4时刻开关管VT2关断，VT4导通，变压器一次电流流经S2和VD5。变压器二次电流流过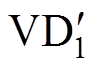和。在该时段中，电感电压为-nUo/2，电感电流继续下降，其计算公式为
（6）由于在稳态情况下，电感电流具有对称性，则有
（7）
解式（2）～式（7），则有
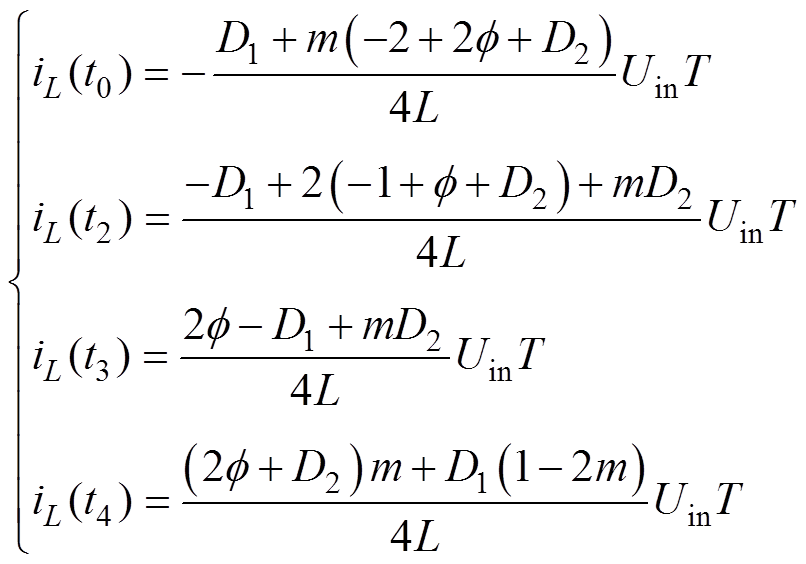（8）式中，m为电压配比，且m=nUo/Uin。
根据前面的分析，可以得到系统在模式A下传输功率的计算公式为
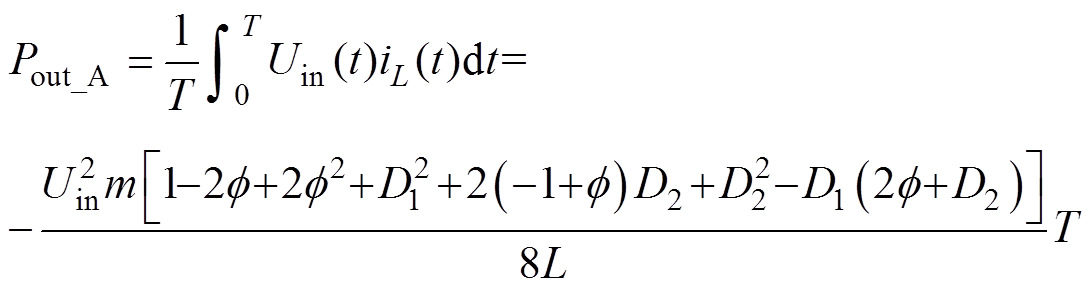（9）按照同样的方法可求得12种工作模式的传输功率表达式。进一步分析可知，系统工作在模式A时有最大传输功率，其计算公式为
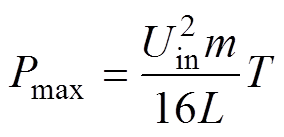（10）
用Pmax对式（9）进行标幺化处理得到模式A标幺化的传输功率计算公式为
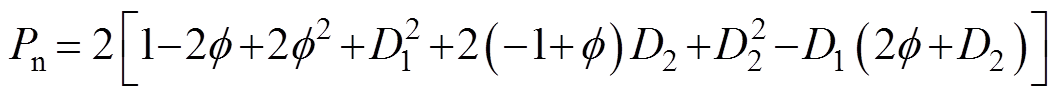（11）同理可求得12种工作模式标幺后传输功率的计算公式见表2。
表2 12种工作模式下传输功率表达式
Tab.2 The range of D1, D2 and f for twelve working modes
传输功率Pn模式Pn范围(pu) A[0, 1] B[0, 2/3] C[-1/2, 1/2] D[-1/2, 1/2] E[0, 2/3] F[0, 1/2] G[-1, 0] H[-2/3, 0] I[-1/2, 1/2] J[-1/2, 1/2] K[-2/3, 0] L[-1/2, 0]
根据表2可得到D1、D2和f 与传输功率Pn之间的关系如图6所示。
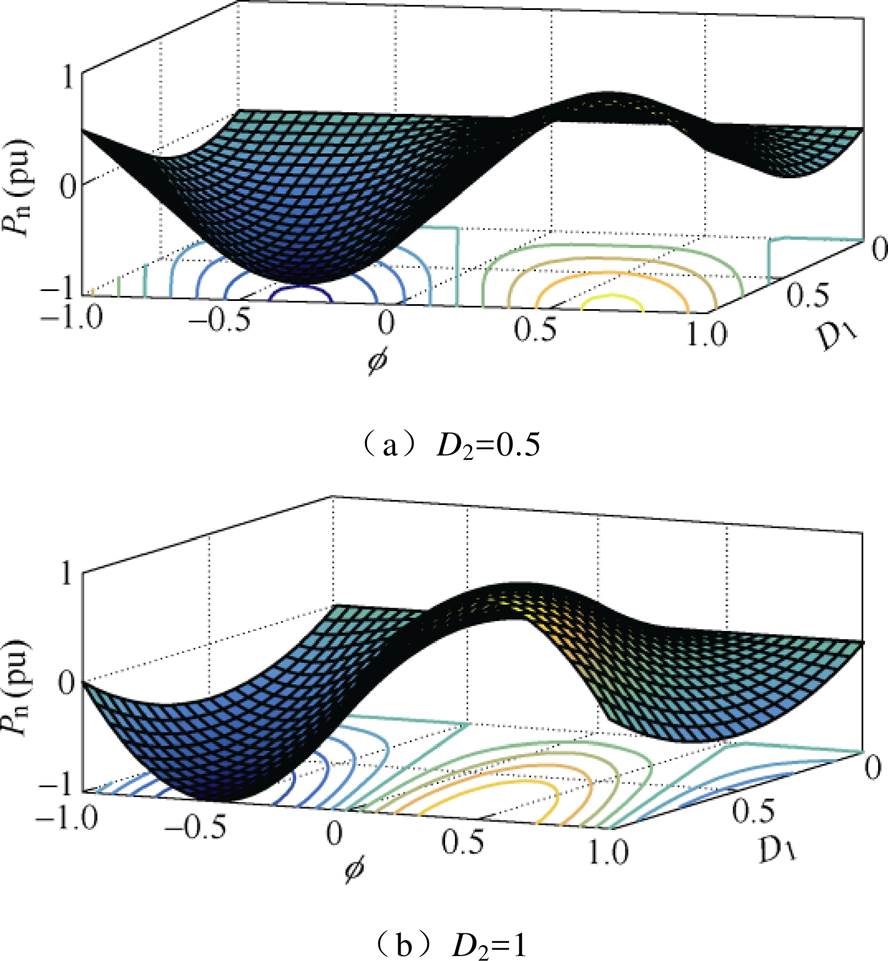
图6 DPWMPS控制下的功率传输特性
Fig.6 The transmission power of DPWMPS control
结合表1、表2和图6可以看出，D1、D2和f与传输功率Pn之间的关系具有以下特点：①f ≥0与f ＜0时的功率传输范围具有对称性，如模式A与模式G；②正向和反向传输的最大功率为受到D2限制，当D2=1时，系统可输出最大传输功率为±1；③在指定的输出功率下，可以由D1、D2和f 的多种组合来达到指定的传输功率；④在某一种具体的工作模式下，传输功率范围也有所不同；⑤传输功率为正的工作模式和传输功率为负的工作模式在运行空间和功率传输范围上具有对称性（如模式A与模式G对称，模式B与模式H对称）。
当系统运行时，电感电流iL的峰值电流是系统功率器件的最大值，由于iL为半周期对称波形，只用对前半周期进行分析即可，所以当系统运行在模式A的情况下时，峰值电流对应图3中的iL(t4)。峰值电流增大不仅使功率器件的导通损耗增加，也会使变压器的铜损增加，从而降低系统效率。因此，系统在指定的输出功率下，需要对峰值电流进行优化。由于三电平半桥隔离型双向DC-DC变换器的拓扑结构具有对称性，传输功率的方向和大小也具有对称性，因此为了简化分析，在此仅对传输功率为正的情况进行分析。
在前面的分析中可知，当系统输出功率一定时，有多种工作模式可供选择，但是在实际运行过程中不同工作模式的峰值电流不同。以模式A和模式B为例，如图7所示，当传输功率相同的时候，模式B的峰值电流小于模式A。这是因为系统只有在U1U2＞0时功率才会由源端向负载端直接传输功率。当U1U2≤0时，不能直接进行传输功率，只能暂时储存在电感L上。在相同时内，要传输相同的功率，U1U2≤0的时间越长，能量直接传输的时间越少，电感储存的能量越多，其峰值电流就越大。由于模式A的U1U2≤0时间要比模式B长，因此其峰值电流大于模式B的峰值电流。
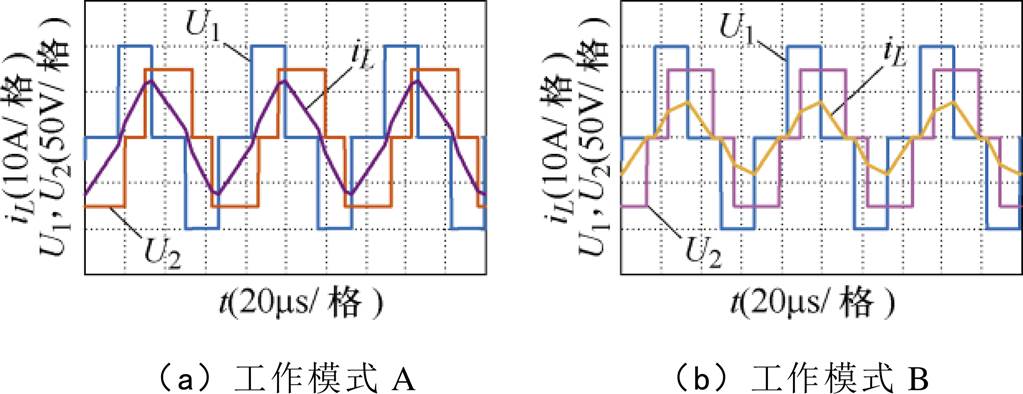
图7 Pn=0.5(pu)时两种工作模式对比
Fig.7 Comparison of two working modes when Pn=0.5(pu)
为了简化分析的工作量，可先找出在指定传输功率下峰值电较小的工作模式，然后对这些工作模式进行分析，最终得到全局峰值电流最小的控制方法。当传输功率为正时，根据表2可知，可选择的工作模式有模式A～模式F以及模式I和模式J这八种。但是其中模式D～模式F以及模式J在功率传输过程中始终有U1U2≤0，按照之前的分析，在指定的传输功率下，这几种工作模式的峰值电流较大，因此只需对模式A～模式C，以及模式I这四种工作模式分析即可。
按式（8）的分析方法，将四种工作模式的峰值电流ipmin计算公式进行总结并用TUin/4L进行标幺，见表3。
表3 功率正向传输时各个工作模式ipmin计算公式
Tab.3 ipmin of each working mode when power transmits forward
峰值电流计算公式模式Pn范围 A[0, 1] B[0, 2/3] C[-1/2, 1/2] I[-1/2, 1/2]
通常情况下，需要对四种工作模式建立拉格朗日方程进行优化求解，然后再将四种工作模式下的最小峰值电流进行比较。但是模式C与模式I的运行范围并非由凸集，所以不能满足拉格朗日方程。因此可以利用数值解找出四种工作模式在不同的Pn和m下的最小峰值电流进行比较，进一步找到峰值电流较小的工作模式进行分析。
结合表2和表3，得到四种工作模式在不同的Pn和m下的最小峰值电流ipmin对比如图8所示。
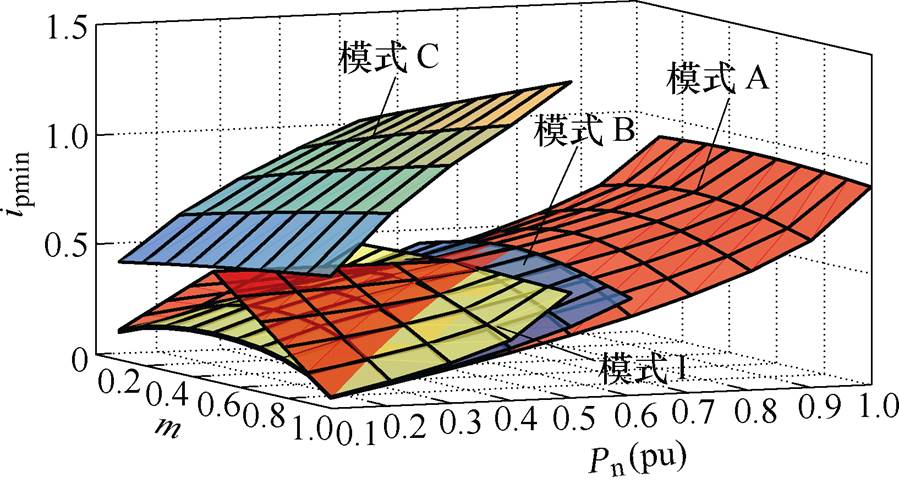
图8 四种工作模式最小峰值电流ipmin对比
Fig.8 Comparison of ipmin of four working modes
从图8中可以看出，在Pn和m不同的情况下，当传输功率较大时，工作模式A的最小峰值电流最小，此时可以让系统工作在工作模式A。当传输功率较小时，工作模式B和工作模式I的最小峰值电流较小，为了更好地分析，将两种工作模式的最小峰值电流进行比较，如图9所示。
从图9可以看出，工作模式B的最小峰值电流总是小于工作模式I的最小峰值电流，因此，在传输功率较小时，可以让系统工作在工作模式B。综合以上分析，要得到系统的全局最小峰值电流，只需要对工作模式A与工作模式B进行分析即可。
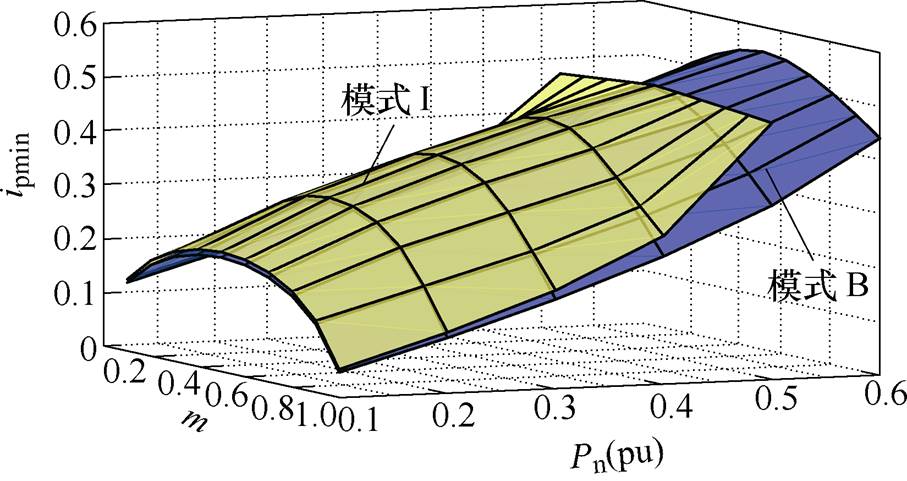
图9 工作模式B和工作模式I最小峰值电流ipmin对比
Fig.9 Comparison of ipmin of working mode B and working mode I
首先对工作模式A进行分析。结合表2和表3对模式A采用拉格朗日乘数法进行求解，可以得到D1、D2和f 的计算公式为
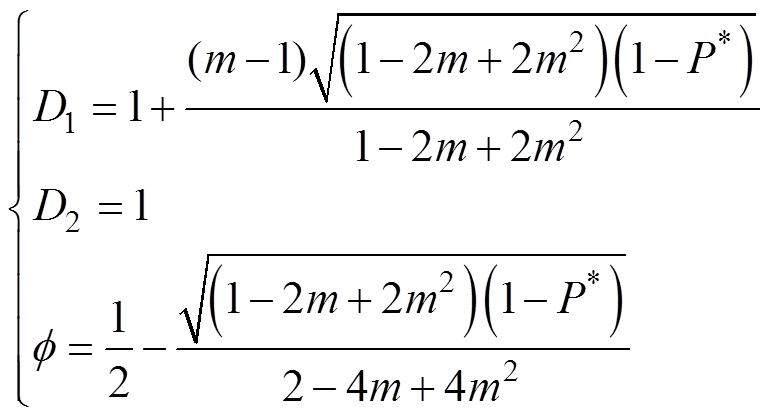（12）式中，P*为指定传输功率。
根据表1有工作模式A下D1、D2和f 的关系为0≤f ≤D1≤1且1≤D2+f ≤2，将式（12）带入该关系式中，进一步求出P*的范围为
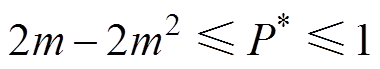（13）按照同样的方法可以求出系统在工作模式B下D1、D2和f 的计算公式为
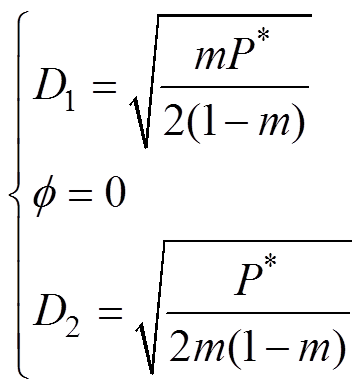（14）
根据表1有工作模式B下D1、D2和f 的关系为0≤f ≤D1≤D2+f ≤1，将式（14）带入该关系式中，进一步求出P*的范围为
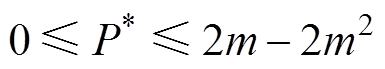（15）本文采用的闭环控制策略如图10所示。在实际控制中对Uin、Uo和io进行采样，计算电压配比m和传输功率P*的值，然后判断得到系统应该运行的工作模式，再根据式（12）或式（14）进行计算，剩下变量（f 或D1）通过PI控制器进行调节，提高系统的抗干扰能力。
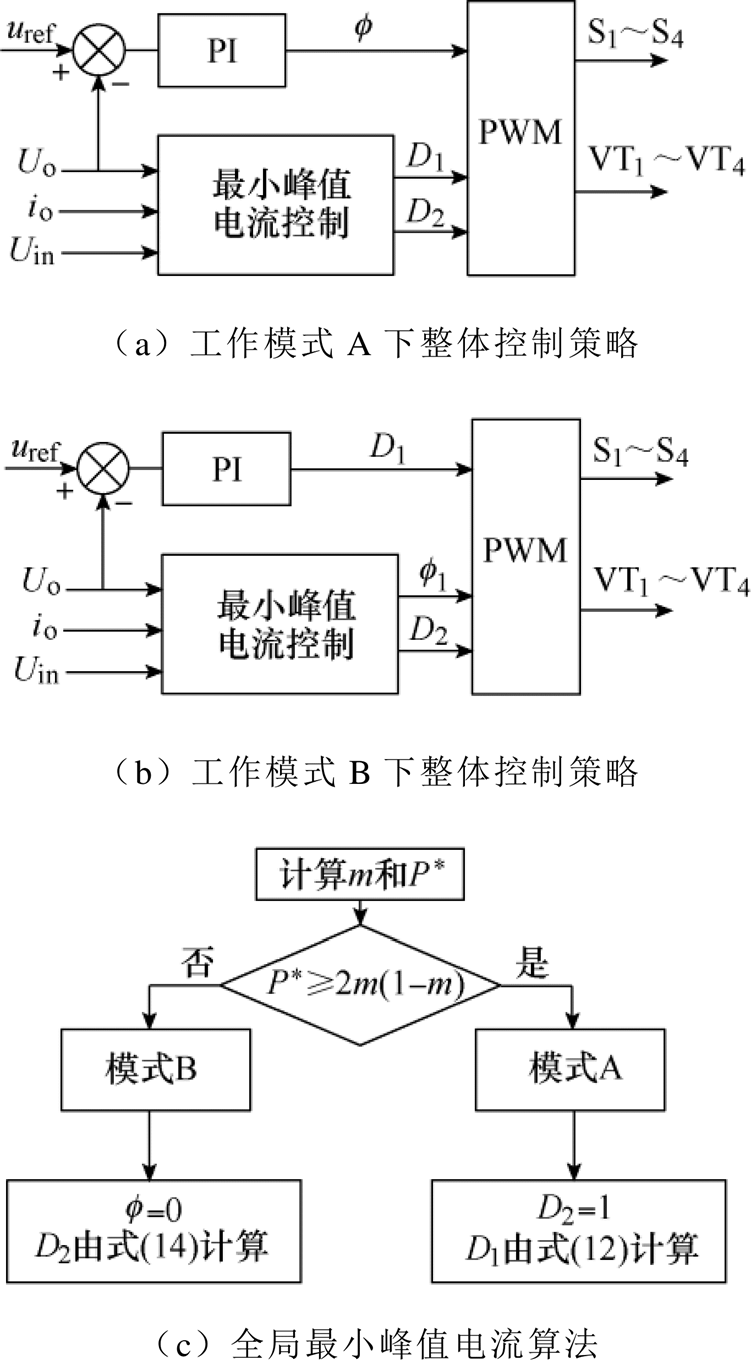
图10 全局最小峰值电流控制框图
Fig.10 The diagram of global minimum peak current control
本文以TI公司的TMS320F28335为控制器搭建实验平台如图11所示，平台主要参数见表4。
图11 实验平台
Fig.11 The experimental platform
图12为DPWMPS控制下工作模式A和工作模式F的实验波形。从图中可以看出，在相同的工作模式下，也能输出不同的功率。
表4 实验平台参数
Tab.4 Parameters of experimental platform
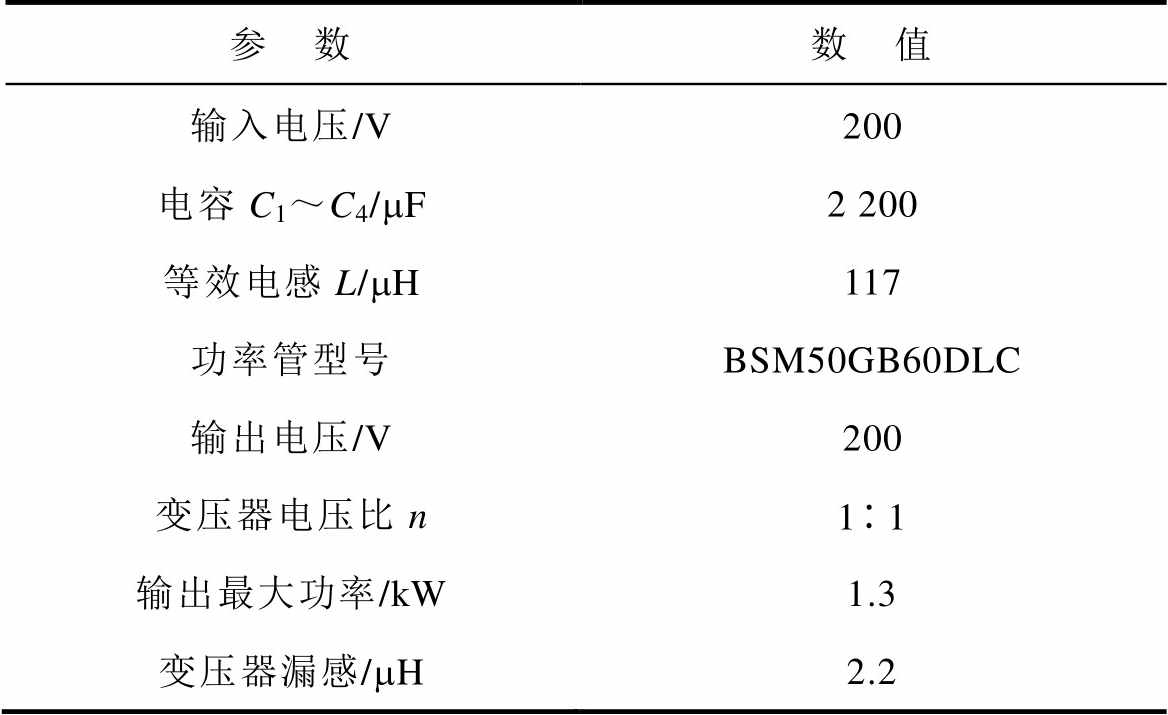
参 数数 值 输入电压/V200 电容C1～C4/mF2 200 等效电感L/mH117 功率管型号BSM50GB60DLC 输出电压/V200 变压器电压比n11 输出最大功率/kW1.3 变压器漏感/mH2.2
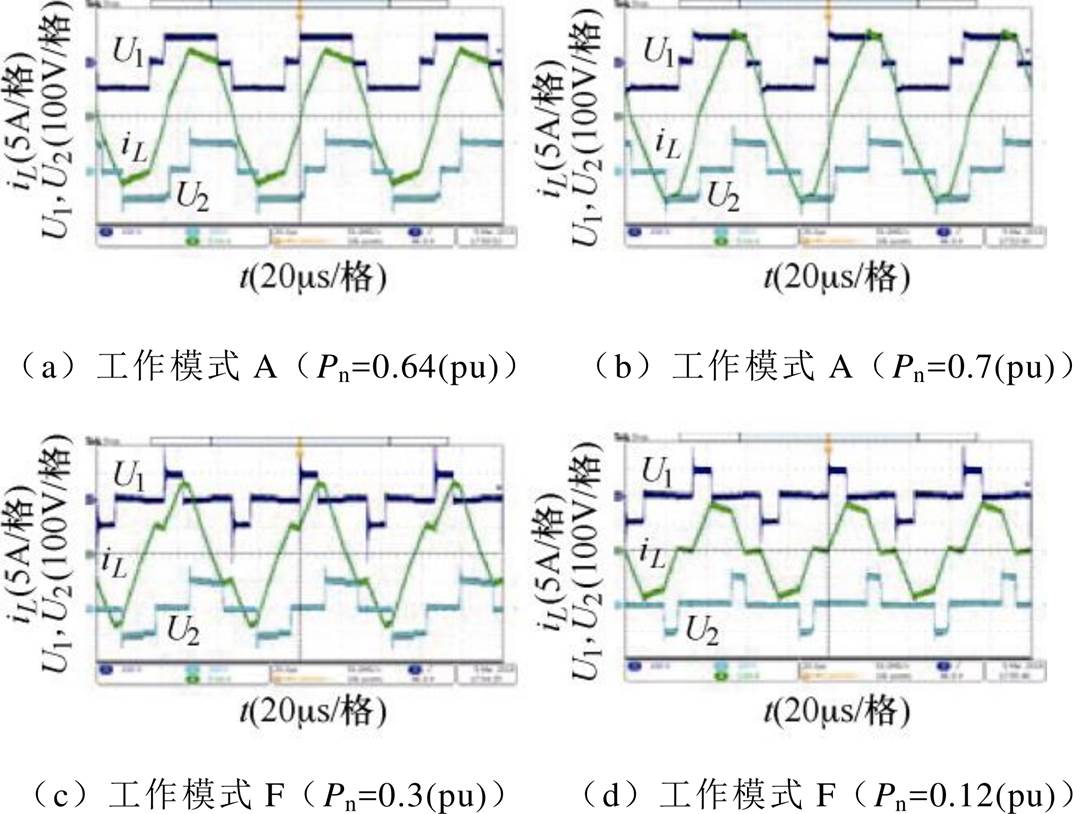
图12 DPWMPS控制下的两种工作模式
Fig.12 Two working modes under the PWMPS control
图13为Pn=0.4(pu)时，DPWMPS控制下四种工作模式的实验波形。从图中可以看出，在Pn相同的情况下，也可以通过选择不同的工作模式来实现。
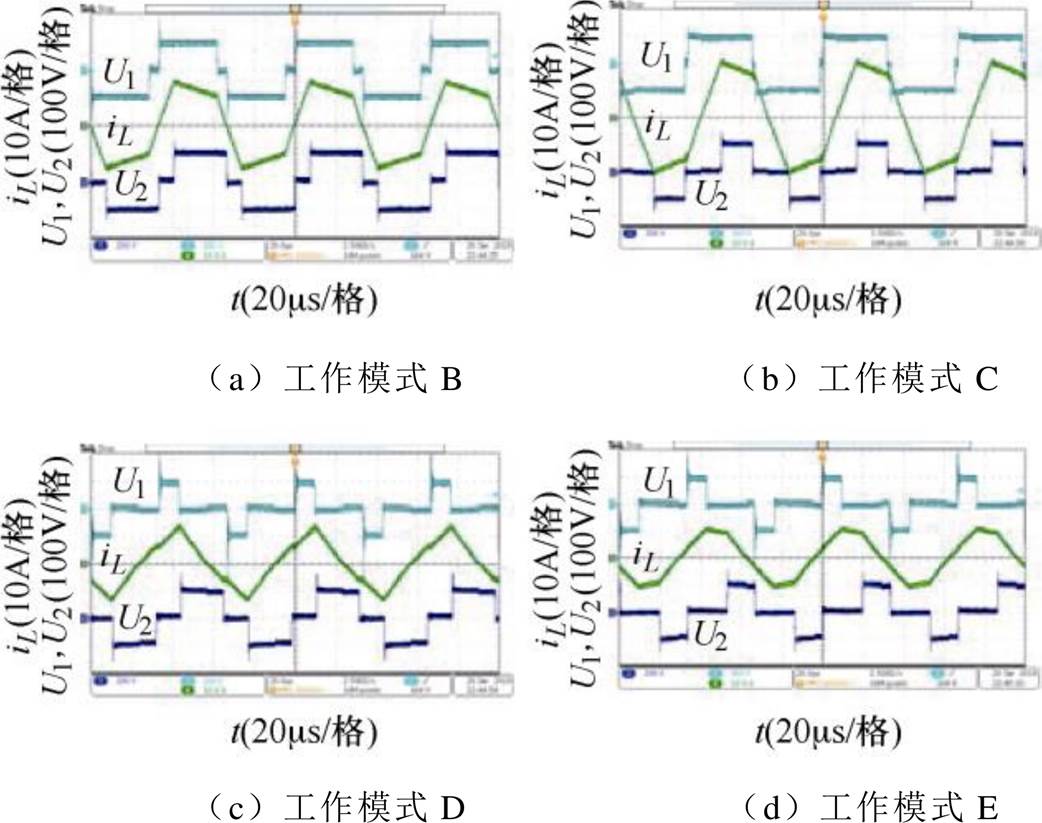
图13 Pn=0.4(pu)时DPWMPS控制下的四种工作模式
Fig.13 Four working modes with the DPWMPS control when Pn=0.4(pu)
结合图12和图13可以看出，在实验中，DPWMPS控制在相同的工作模式下能输出不同功率。在传输相同功率的情况下也能选择多种工作模式，控制灵活性较强，与之前的理论分析相同。
图14为当m=1，Pn=0.3(pu)时，采用最小峰值电流算法与其他工作模式下电感电流iL实验波形。根据图10的分析可以得到，此时最小峰值电流算法让系统工作在模式A。从图中可以看出，工作模式A的峰值电流是所有模式中最小的，与之前的理论分析相同。
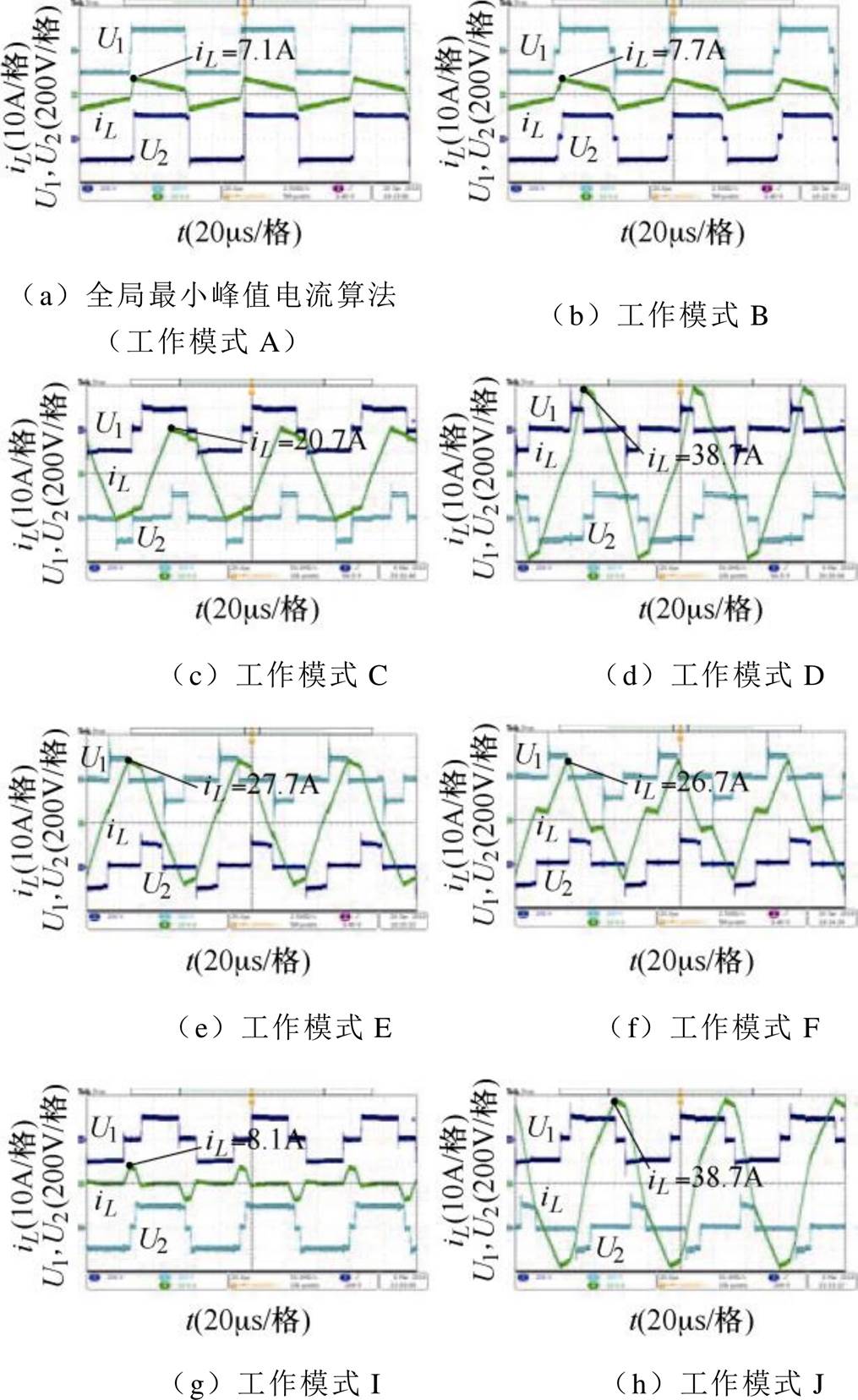
图14 m=1，Pn=0.3(pu)时全局最小峰值电流算法与其他工作模式实验
Fig.14 The experiments of global minimum peak current control and other working mode when m=1 and Pn=0.3(pu)
图15为当m=0.5，Pn=0.3(pu)时，采用最小峰值电流算法与其他工作模式下电感电流iL实验波形。此时最小峰值电流算法让系统工作在模式B。从图中可以看出，工作模式B的峰值电流是所有模式中最小的，与之前的理论分析相同。
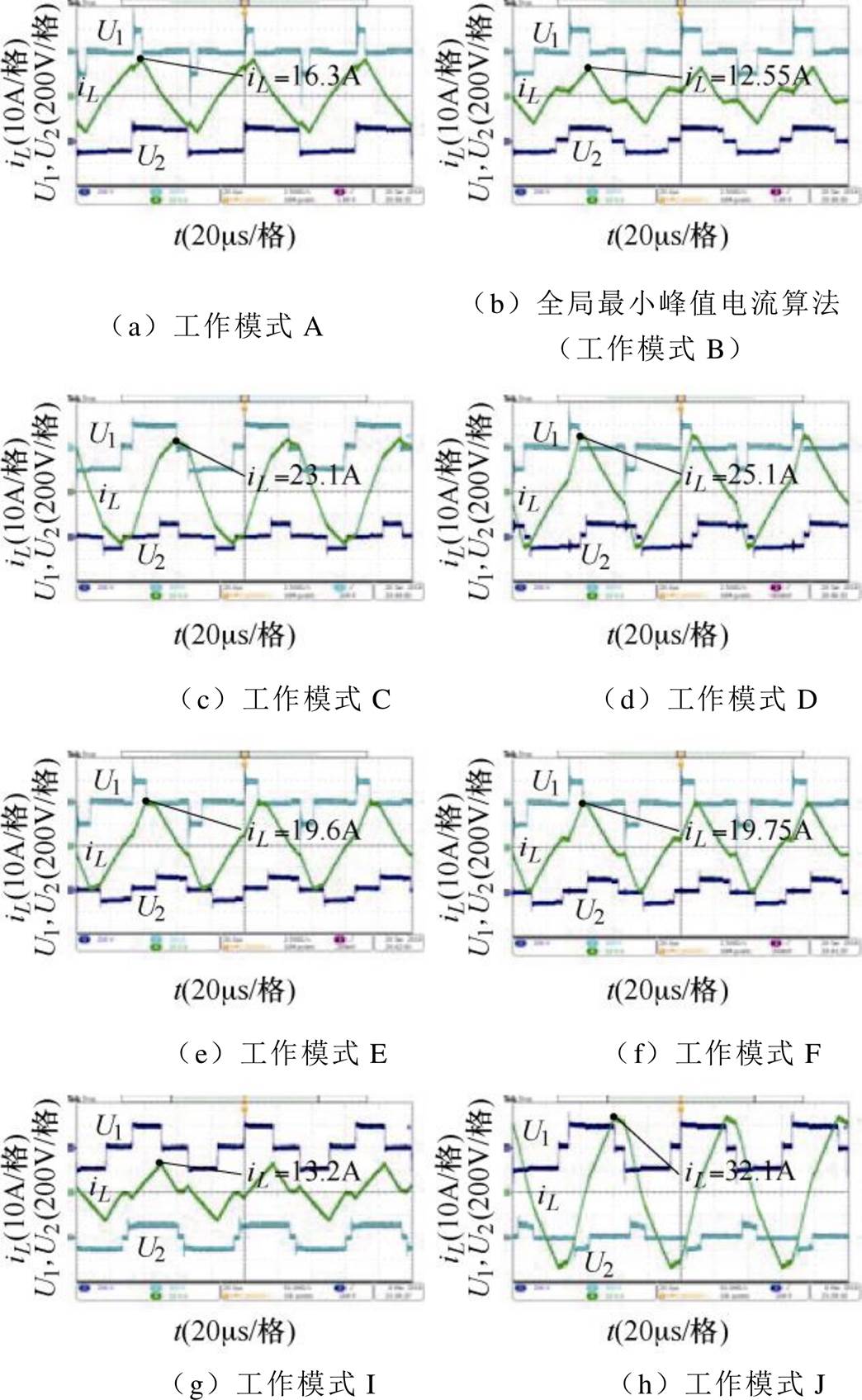
图15 m=0.5，Pn=0.3(pu)时全局最小峰值电流算法与其他工作模式实验
Fig.15 The experiments of global minimum peak current control and other working mode when m=0.5 and Pn=0.3(pu)
图16为当m=1时，四种控制方法的效率曲线。从图中可以看出，与传统TPS控制相比，DPPS控制效率略高于TPS控制。此外，本文所提的全局峰值电流最优控制效率在四种控制方法中效率最高。
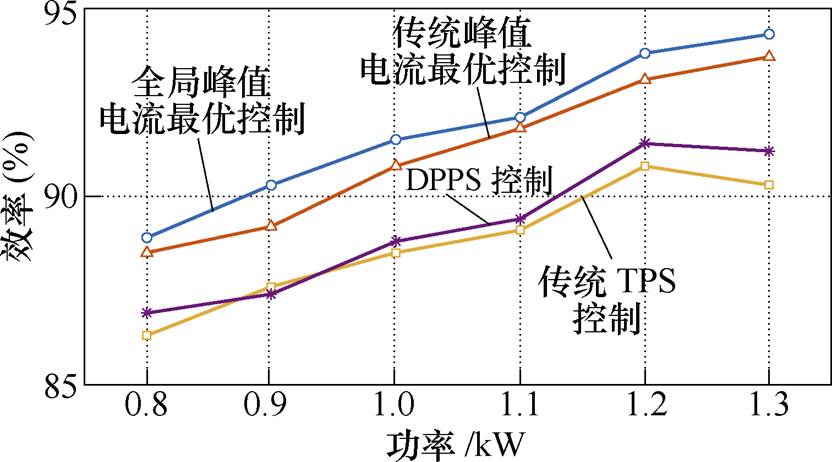
图16 四种控制方法效率对比
Fig.16 Efficiency comparison of four control methods
结合图14～图16可以看出，实验结果与理论分析一致，证明了该算法的正确性与有效性。此外，全局最小峰值电流控制方法的思路同样适用于m＞1的情况。m＞1的不同为：当m＞1时，等效电感上的电压同样为(Uin-nUo)/2，但是由于m＞1，此时电感电流变化方向为正（m≤1时电感电流方向为负），因此每种模式下的电感峰值电流计算公式会有所不同。但可按本文的分析思路得到m＞1时的全局最小峰值电流控制方法。由于文章篇幅有限，在此不进行详细分析。
本文以三电平半桥隔离型双向DC-DC变换器为研究对象，对DPWMPS控制方法进行研究，将该控制方法划分为12种不同的工作模式，并分析和推导了各种工作模式下的功率传输特性。在此基础上，提出了一种全局最小峰值电流控制方法。最后通过实验验证得出以下结论：
1）本文提出的DPWMPS控制在指定输出功率时，可以选择多种工作模式。此外，在同一种工作模式下也可输出不同的功率，控制灵活性较强。
2）本文提出的最小峰值电流算法在m≤1的情况下能有效减小稳态时电感的峰值电流，降低系统功率器件的电流应力。
参考文献
[1] 孙孝峰, 吴晓颖, 申彦峰, 等. 一种全功率范围零电压开通的电流型双向隔离DC-DC变换器[J]. 电工技术学报, 2018, 33(10): 2282-2292.
Sun Xiaofeng, Wu Xiaoying, Shen Yanfeng, et al. A novel current-fed bidirectional isolated DC-DC converter with full-operating-range ZVS[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(10): 2282-2292.
[2] Mohsenian-Rad H, Davoudi A. Towards building an optimal demand response framework for DC distri- bution networks[J]. IEEE Transactions on Smart Grid, 2014, 5(5): 2626-2634.
[3] 肖智明, 陈启宏, 张立炎. 电动汽车双向DC-DC变换器约束模型预测控制研究[J]. 电工技术学报, 2018, 33(增刊2): 489-498.
Xiao Zhiming, Chen Qihong, Zhang Liyan. Con- strained model predictive control for bidirectional DC- DC converter of electric vehicles[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 489- 498.
[4] 沙广林, 王聪, 程红, 等. 移相控制的双有源桥DC-DC变换器统一相量分析法[J]. 电工技术学报, 2017, 32(18): 175-185.
Sha Guanglin, Wang Cong, Cheng Hong, et al. Unified phasor analytical method for bi-directional dual-active-bridge DC-DC converter under phase- shift control[J]. Transactions of China Electro- technical Society, 2017, 32(18): 175-185.
[5] 刘宿城, 甘洋洋, 刘晓东, 等. 超级电容接口双向DC-DC变换器的电压快恢复控制策略[J]. 电工技术学报, 2018, 33(23): 5496-5508.
Liu Sucheng, Gan Yangyang, Liu Xiaodong, et al. Fast voltage recovery control strategy for super- capacitor interfacing bidirectional DC-DC converter[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5496-5508.
[6] 刘舒, 李正力, 王翼, 等. 含分布式发电的微电网中储能装置容量优化配置[J]. 电力系统保护与控制, 2016, 44(3): 78-84.
Liu Shu, Li Zhengli, Wang Yi, et al. Optimal capacity allocation of energy storage in micro-grid with distributed generation[J]. Power System Protection and Control, 2016, 44(3): 78-84.
[7] Inoue S, Akagi H. A bidirectional DC-DC converter for an energy storage system with galvanic isola- tion[J]. IEEE Transactions on Power Electronics, 2007, 22(6): 2299-2306.
[8] De Doncker R W A A, Divan D M, Kheraluwala M H. A three-phase soft-switched high-power-density DC/DC converter for high-power applications[J]. IEEE Transactions on Industry Applications, 1991, 27(1): 63-73.
[9] Kheraluwala M H, Gascoigne R W, Divan D M, et al. Performance characterization of a high-power dual active bridge DC-to-DC converter[J]. IEEE Transa- ctions on Industry Applications, 1992, 28(6): 1294- 1301.
[10] 殷晓东, 罗登, 李祖勇, 等. 一种双向隔离DC-DC变换器二次纹波电压抑制方法[J]. 电工技术学报, 2018, 33(6): 1356-1363.
Yin Xiaodong, Luo Deng, Li Zuyong, et al. A second-order ripple voltage suppression algorithm of bidirectional isolation DC-DC converter[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(6): 1356-1363.
[11] Oggier G G, Ordonez M, Galvez J M, et al. Fast transient boundary control and steady-state operation of the dual active bridge converter using the natural switching surface[J]. IEEE Transactions on Power Electronics, 2013, 29(2): 946-957.
[12] Hua Bai, Chris Mi. Eliminate reactive power and increase system efficiency of isolated bidirectional dual-active-bridge DC-DC converters using novel dual-phase-shift control[J]. IEEE Transactions on Power Electronics, 2008, 23(6): 2905-2914.
[13] Demetriades G D, Nee H P. Characterization of the dual-active bridge topology for high-power appli- cations employing a duty-cycle modulation[C]//IEEE Power Electronics Specialists Conference, Rhodes, Greece, 2008: 2791-2798.
[14] Zhang Zhe, Thomsen O C, Andersen M A E, et al. Analysis and design of bi-directional DC-DC converter in extended run time DC UPS system based on fuel cell and supercapacitor[C]//IEEE Applied Power Electronics Conference & Exposition, DC, USA, 2009: 714-719.
[15] Zhou Haihua, Khambadkone A M. Hybrid modu- lation for dual-active-bridge bidirectional converter with extended power range for ultracapacitor appli- cation[J]. IEEE Transactions on Industry Appli- cations, 2008, 45(4): 1434-1442.
[16] 王聪, 沙广林, 王俊, 等. 基于双重移相控制的双有源桥DC-DC变换器的软开关[J]. 电工技术学报, 2015, 30(12): 106-113.
Wang Cong, Sha Guanglin, Wang Jun, et al. The analysis of zero voltage switching dual active bridge DC-DC converters based on dual-phase-shifting control[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 106-113.
[17] Zhao Biao, Song Qiang, Liu Wenhua. Power characterization of isolated bidirectional dual-active- bridge DC-DC converter with dual-phase-shift control[J]. IEEE Transactions on Power Electronics, 2012, 27(9): 4172-4176.
[18] 谷庆, 袁立强, 聂金铜, 等. 基于开关组合规律的双有源桥DC-DC变换器传输功率特性[J]. 电工技术学报, 2017, 32(13): 69-79.
Gu Qing, Yuan Liqiang, Nie Jintong, et al. Trans- mission power characteristics of dual-active-bridge DC-DC converter based on the switching com- bination rules[J]. Transactions of China Electro- technical Society, 2017, 32(13): 69-79.
[19] 谷泓杰, 江道灼, 尹瑞, 等. 基于三重移相的双向全桥DC-DC功率特性分析[J]. 中国电力, 2016, 49(7): 122-127.
Gu Hongjie, Jiang Daozhuo, Yin Rui, et al. An analysis of the power characteristics of bidirectional full-bridge DC-DC converter under triple-phase-shift control[J]. Electric Power, 2016, 49(7): 122-127.
[20] Yazdani F, Zolghadri M. Design of dual active bridge isolated bi-directional DC converter based on current stresss optimization[C]//Power Electronics, Drive Systems & Technologies Conference, Mashhad, Iran, 2017: 247-252.
[21] Zhao Biao, Yu Qingguang, Sun Weixin. Extended- phase-shift control of isolated bidirectional DC-DC converter for power distribution in microgrid[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4667-4680.
[22] Zhao Biao, Song Qiang, Liu Wenhua, et al. Current- stress-optimized switching strategy of isolated bidirectional DC-DC converter with dual-phase-shift control[J]. IEEE Transactions on Industrial Electro- nics, 2013, 60(10): 4458-4467.
[23] Huang Jun, Wang Yue, Li Zhuoqiang, et al. Unified triple-phase-shift control to minimize current stress and achieve full soft-switching of isolated bidirectional DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4169-4179.
Global Minimum Peak Current Control of the Three Level Isolated Half-Bridge Bi-Directional DC-DC Converters with PWM-Phase-Shifting Control
Abstract This paper proposed a dual-PWM-phase-shift (DPWMPS) control method for three-level half-bridge isolated bidirectional DC-DC converter. Based on the analysis of the working principle of the method and the relative position of the voltages on both sides of the transformer, 12 operating modes of the system are concluded, and the power transmission characteristics of each mode are deduced. On this basis, a method of inductance minimum peak current control is proposed. This method achieves the global optimization of inductance peak current under the condition of voltage ratio m≤1. Finally, an experimental platform is built and the experimental results show that the algorithm is correct and effective.
keywords：Dual-PWM-phase-shift, three-level half-bridge isolated bidirectional DC-DC converter, working modes, minimum peak current control
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.190241
北京市科学技术委员会重点资助项目（D171100005317003）。
收稿日期2019-03-07
改稿日期 2019-08-26
杨 超 男，1988年生，博士研究生，研究方向为电力电子变流器技术及应用。E-mail: yangchao@mail.iee.ac.cn
许海平 男，1973年生，研究员，博士生导师，研究方向为电力电子技术、交流电机与变频调速、电动汽车等。E-mail: hpxu@mail.iee.ac.cn（通信作者）
（编辑 崔文静）