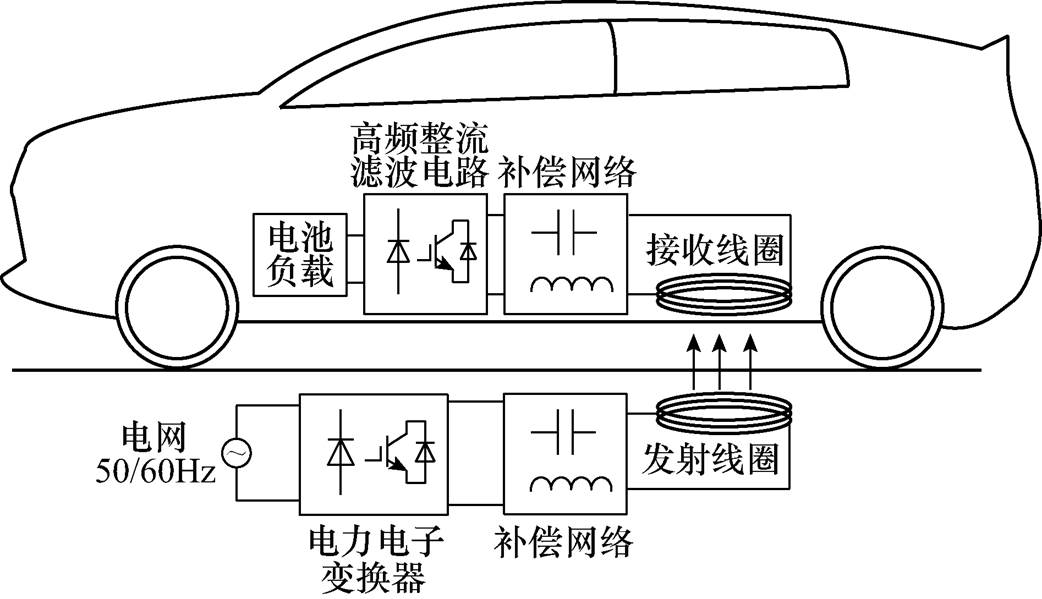
图1 典型电动汽车无线充电系统结构
Fig.1 Typical wireless charging system for EV
摘要 电动汽车静态无线充电技术以其操作方便、安全灵活和维护成本低等优点,受到了越来越多的关注。该文从磁耦合机构、补偿网络、电力电子变换器以及系统建模与优化控制等方面对电动汽车静态无线充电的关键技术进行了详细分析,指出了电动汽车无线充电技术亟待解决的问题,并讨论了今后的发展趋势,旨在为电动汽车静态无线充电技术的研究提供方向。
关键词:电动汽车 静态无线充电 磁耦合结构 系统建模 鲁棒性控制
为促进节能减排、减少汽车尾气排放、防治大气污染,电动汽车(Electric Vehicles, EV)成为了世界各国大力推广的新型交通工具,但由于电池容量的限制,导致电动汽车续航里程短,充电问题一直是制约电动汽车发展的主要瓶颈问题之一。随着无线电能传输技术的发展,基于磁场耦合式[1]电动汽车静态无线充电技术受到了越来越多的关注,相比于传统的有线充电系统,无线充电系统没有电气连接,具有操作方便、维护成本低、防水防尘、可实现全自动充电过程等优点。
典型的电动汽车静态无线充电系统结构如图1所示[2],包括电力电子变换器、原边补偿网络、发射线圈、接收线圈、副边补偿网络、高频整流滤波电路和电池负载等部分。近年来,国内外学者和研究机构对基于磁场耦合式的电动汽车静态无线充电技术已开展了大量的研究,然而,随着研究的深入,仍有许多关键问题需要解决。本文详细分析了基于磁场耦合式电动汽车静态无线充电的关键技术,主要包括磁耦合机构、补偿网络及其特性、电力电子变换器以及系统建模与优化控制等方面,并指出了电动汽车静态无线充电技术亟待解决的问题,为电动汽车静态无线充电技术未来的研究提供方向。

图1 典型电动汽车无线充电系统结构
Fig.1 Typical wireless charging system for EV
磁耦合机构是无线充电系统中原、副边能量耦合的关键元件,当前磁耦合机构的研究主要侧重在提高线圈之间耦合、提高抗偏移能力、减小线圈体积、减少成本等方面。对于磁耦合机构的研究,国外主要有新西兰奥克兰大学、美国橡树岭国家实验室、韩国高等科学技术学院、日本琦玉大学、密歇根大学等研究机构。
新西兰奥克兰大学的Boys J. T. 教授团队研究并提出了多种应用于电动汽车静态无线充电系统的磁耦合机构,如图2所示。2010年,该团队提出了Flux pipe型线圈,如图2a所示,此种线圈采用双线圈的结构,在电路上两线圈并联连接,在磁路上两线圈产生的磁通成串联的特点,即磁通从一个线圈穿入再从另一个线圈穿出,有效地提高了水平抗偏移的能力[3]。但此耦合机构为螺线管型线圈,漏磁较大,不利于屏蔽,当采用铝板屏蔽时,会影响到磁场分布[4],且磁通利用率较低,因而系统效率较低。2011年,该团队对平面圆形线圈进行了优化,尤其对磁心的数量、形状以及分布进行了研究与对比,得到了如图2b所示的最佳方案,有效减少了磁心的用量,减轻了线圈质量,提高了效率,实现了2~5kW的功率传输[5]。但圆形线圈产生的磁场高度有限,因此,2013年该团队又提出了一种由单根导线绕制的准双线圈结构,DD(double D)型线圈,此种线圈左右线圈的绕向相反,若左边由内向外顺时针绕制,则右边由外向内逆时针绕制,旨在让中间相邻导线的电流流向相同,使得两线圈中心磁通加强,有效提高了磁场的高度,大约是线圈长度的一半[6],提高了线圈之间耦合和抗偏移能力,另外磁场仅分布在线圈单侧,相比于磁场分布于两侧的螺线管型线圈,DD型线圈能有效提高磁场利用率,提高系统效率,而且也能降低金属屏蔽对系统的影响。文献[7]基于DD型线圈搭建了一套8kW的无线充电系统,在传输距离20cm的情况下,实现了95.66%的传输效率,在横向偏移30cm的情况下依旧能保持95.39%的高效率。但DD型线圈由于其磁场呈并联平行分布的特点,不能与单线圈混用,此外当线圈偏移超过约34%的时候存在磁场零点[6]。因此在DD型线圈的基础上,该团队又提出一种DDQ(DD-quadrature)型线圈,如图2d所示,并将DD型线圈作为发射线圈,将DDQ型线圈作为接收线圈,该种组合的磁耦合机构有效解决了磁场零点的问题,且充电区域是同尺寸的单线圈圆形磁耦合机构的5倍[6],但也带来用铜量增加、需要两路整流电路等缺点,导致系统损耗增大。为此,Zaheer A. 提出了一种BP(bipolar)型线圈,相比于DDQ型线圈,在实现与其类似功能的情况下,减少了25.17%的用铜量[8]。2017年7月,该团队又提出一种TP(tripolar)型线圈,进一步提高了线圈的抗偏移能力,但该结构需要复杂的控制[9]。
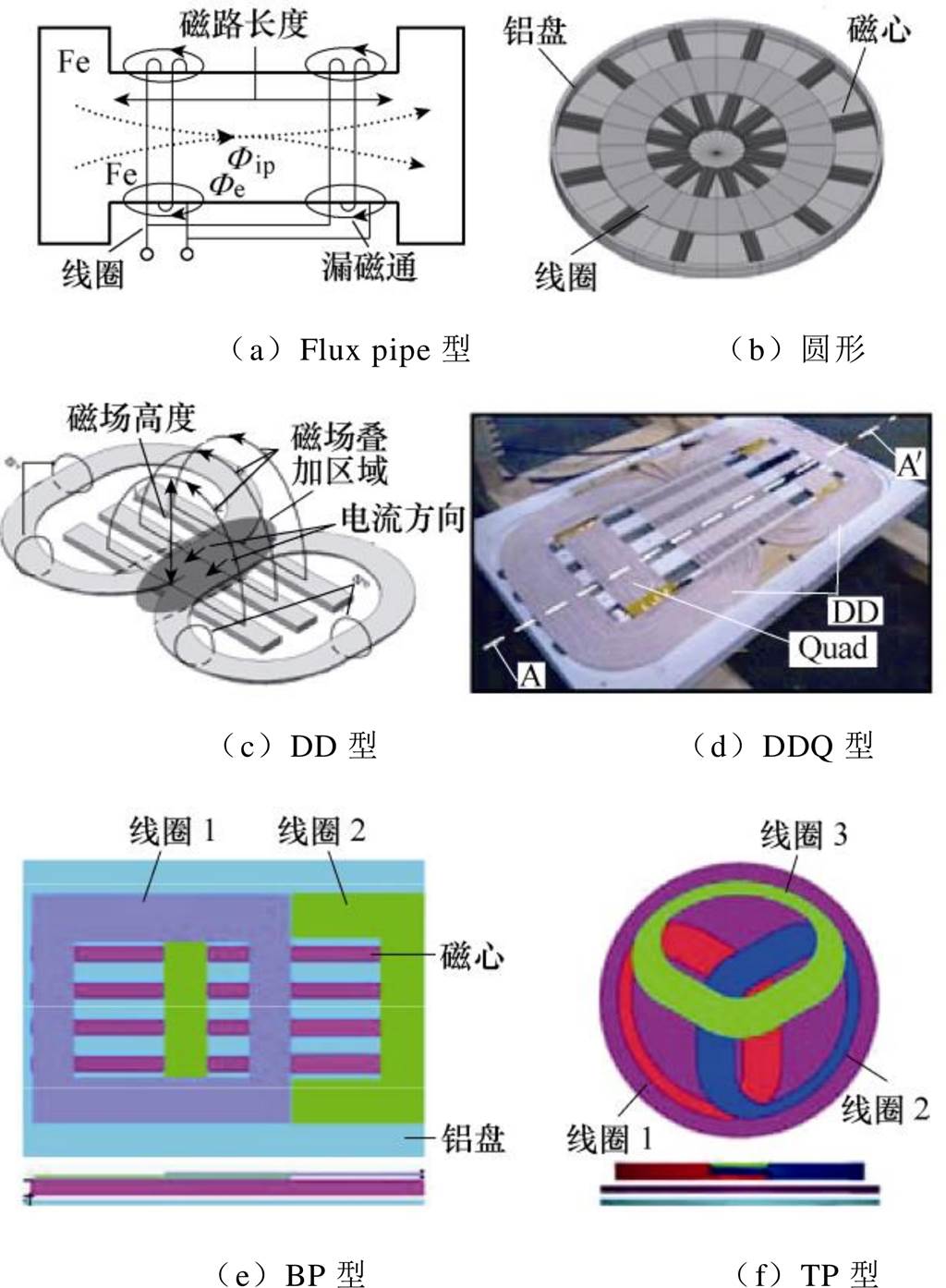
图2 奥克兰大学提出的线圈结构
Fig.2 The coil structures proposed by the University of Auckland
韩国高等科学技术学院团队在2014年提出了三线圈的耦合机构[10],如图3a所示。该结构的特点是发射线圈由两个嵌套的线圈构成,即在大线圈内嵌套一个小线圈,增加的小线圈一方面增强了发射线圈和接收线圈之间的耦合程度;另一方面可以避免频率分裂现象。文献[10]提出的磁耦合机构的发射线圈大线圈的谐振频率为85kHz,小线圈的谐振频率为110kHz,接收线圈的谐振频率为85kHz,系统开关频率设置为100kHz,通过这样的设置有效避免了频率分裂,实现了能量的高效传输,传输效率高达95.57%。同年Chun T. Rim教授团队提出了大小线圈(asymmetrical coils),如图3b所示,提高了线圈的抗偏移能力[11],但此结构体积较大。除静态无线充电用线圈外,韩国高等科学技术学院团队对电动汽车动态无线充电用线圈也进行了很深入的研究[12-15]。
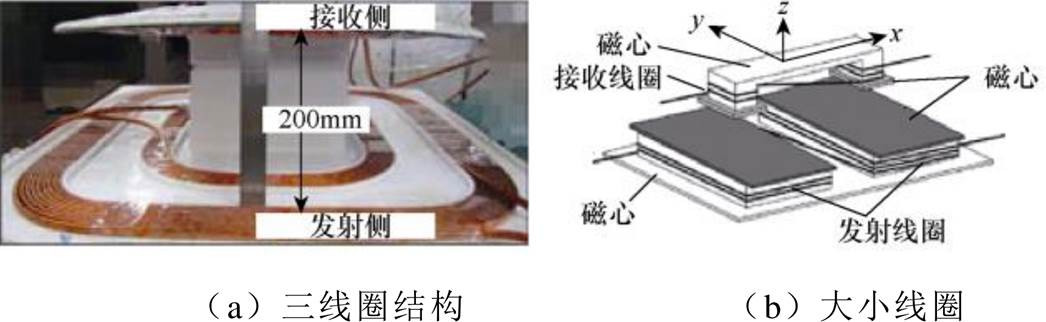
图3 韩国高等科学技术学院提出的线圈结构
Fig.3 The coil structures proposed by Korea Advanced Institute of Science and Technology
另外日本埼玉大学在2012年提出了H型线圈如图4所示[16-17]。H型线圈结构磁场分布在线圈两侧,该线圈的主要优势为结构紧凑,偏移容忍度高,但此结构与Flux pipe型一样,都属于双边绕组[2],存在较大的漏磁,而且H型线圈用铜量也很大,不利于系统效率的提高。密歇根大学Chris Mi教授团队在2015年研究了磁心的形状、位置数量对DD型线圈和矩形线圈耦合系数的影响,并分析了线圈位置正对和存在偏移时,DD型线圈和矩形线圈的兼容性[18]。该团队还分析了系统工作时线圈漏磁的情况,并建立了模型。

图4 H型线圈结构
Fig.4 The H-shaped coil structure
国内针对静态无线充电系统的磁耦合机构也开展了较多的研究,如图5所示。2015年,重庆大学孙跃教授团队在DD型线圈的基础上设计了一种DLDD(double layer double D)型线圈,即双层DD型线圈的线圈结构,并设计了相应的磁心结构[19],哈尔滨工业大学朱春波教授团队设计了平面W形磁耦合机构[20],天津工业大学杨庆新教授团队设计了盘式并绕线圈[21]。东南大学黄学良教授团队提出了一种平面盘式圆形线圈的优化与设计方法,综合考虑了线圈的半径、匝数以及谐振频率等因素[22]。

图5 国内各高校、研究机构的磁耦合机构
Fig.5 The magnetic couplers proposed by domestic universities and research institutions
表1总结了常用磁耦合机构的优缺点[3-6,8,23-24],旨在为电动汽车静态无线充电系统磁耦合机构的研究提供一定的指导。总体上,相比于单线圈结构,多线圈结构在抗偏移、传输距离等方面更具优势,但相应的也会增加用铜量,结构和控制等也更为复杂;相比于单边绕组结构,螺线管型等双边绕组,磁场利用率较低、漏磁较大,会导致系统效率的降低[25],可根据具体应用场合选择合适的磁耦合机构。
无线充电系统中由于传输线圈之间耦合小,通常需要加入补偿网络又称谐振网络以改善系统特性。补偿网络的选择需要考虑以下几点[26]:
(1)系统性能。加入补偿网络的主要目的就是要减小输入视在功率、提高系统传输效率和输出功率。
(2)负载特性。根据需求实现系统输出电压或电流与负载解耦,即具有恒流或恒压特性。
(3)系统稳定性。在强耦合区域内,磁场式无线充电系统中存在频率分岔现象,即在等效输入阻抗虚部为零对应的角频率存在多值现象,若采用零相位控制,即输入阻抗为纯电阻的控制方式,在系统参数变化的情况下,会出现控制器在多个角频率之间跳变,系统无法稳定工作,而系统稳定条件取决于负载品质因数和补偿网络。
(4)抗干扰能力。补偿网络参数与耦合系数、负载之间的关系。
表1 主要磁耦合机构特性
Tab.1 The characteristics of magnetic coupler

类别形状特征 圆形广泛应用于电动汽车无线充电各方向偏移容忍度一致,即无方向性当水平偏移大约线圈直径40%,互感系数存在零点[6]圆形线圈相比于同尺寸的其他线圈,在气隙间距和偏移度相同的情况下耦合系数小,当气隙间距是线圈直径1/4时,耦合系数大约为0.2[4,6] 方形扩大了磁通耦合范围,减小了边缘漏磁较圆形线圈具有更好的横向偏移容忍度,轻便集成制造方便 空间螺旋形小巧、轻便纵向偏移容忍度高磁场分布于线圈两侧,不利于屏蔽磁通利用率低,漏磁较大,导致系统效率降低 Flux pipe水平偏移容忍度高,耦合系数与圆形线圈相当磁场高度大约为接收线圈长度的一半[3-4]磁场分布于线圈两侧,不利于屏蔽磁通利用率低,漏磁较大,导致系统效率降低 DD型磁场仅分布于线圈一面,极大的减小了背面漏磁,提高了系统效率相比于圆、方形单线圈具有更好的横向偏移能力磁场高度是圆形线圈的2倍,与H型线圈相当,大约为线圈长度的一半,更适合于气隙间距大的场合沿y轴侧向偏移能力较好,但沿x轴偏移大约34%时存在耦合系数零点[6]由于产生的是并联磁通,不能与平面单线圈混用 DDQ型在DD型线圈的基础上增加了Q线圈在x、y轴方向都具有高的偏移容忍度,可以与平面单线圈混用作为发射线圈需要两个逆变电路,作为接收线圈需要两个整流电路,结构较复杂,增加了系统损耗用铜量多,损耗增加 BP型具有与DDQ型线圈类似的优点,但用铜量减少了25.17%[8]作为发射线圈需要两个逆变电路,作为接收需要两个整流电路需要位置和磁链传感器以及复杂的控制策略旋转偏移容忍度差,角度偏移30°,耦合系数降低13%[23]
目前根据谐振电容与谐振电感的连接方式,主要有串联(Series, S)补偿,并联(Parallel, P)补偿,串并联(LCL)以及在此基础上衍生的补偿网络。基本的补偿结构有四种(SS、SP、PS、PP),如图6所示,图中M为线圈之间的互感;L1、R1、L2、R2分别为发射线圈、接收线圈的电感和等效内阻;C1、C2分别为原边和副边的补偿电容;RL为等效负载电阻;vs为正弦电压源。已有大量文献对四种基本补偿结构的参数设计、特性和系统稳定性等方面进行了全面的分析[26-33]。设系统的工作频率为w,表2给出了在无功全补偿情况下(即无论接收线圈采用串联补偿还是并联补偿结构,接收线圈补偿电容都设计满足谐振条件,再使系统输入阻抗满足纯电阻特性)原边谐振电容和输入阻抗的表达式。
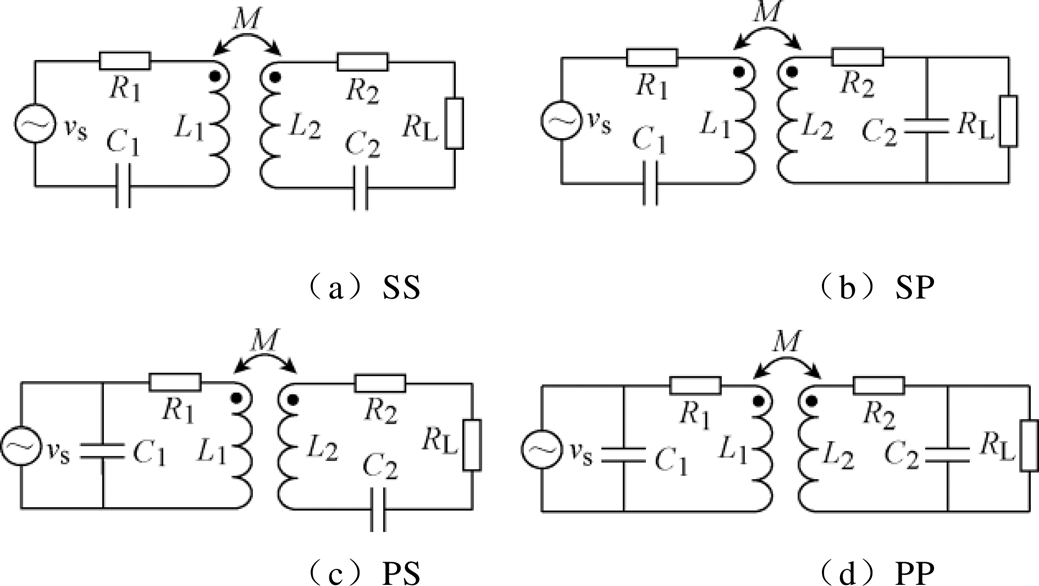
图6 四种基本补偿网络
Fig.6 The four basic compensation networks
表2 基本补偿网络特性
Tab.2 The characteristics of four basic compensation networks

拓扑类型原边补偿电容C1输入阻抗 SS SP PS PP
由表2可得以下结论:
(1)SS型补偿结构。原边补偿电容C1的值与线圈之间的互感和负载无关,可用于原、副边存在相对运动的场合,且即使在耦合系数较小情况下也能实现能量的高效率传输,但在轻载或空载时,SS型输入阻抗仅为原边线圈的寄生电阻,存在潜在危险。
(2)SP型补偿结构。原边补偿电容C1的值与原、副边线圈的互感相关,且M值越大C1也越大,因此SP拓扑结构适合于原、副边相对静止和负载变化较大的系统。与SS型类似,在空载情况下,输入阻抗仅为原边线圈的寄生电阻,需采取限流措施。
(3)PP和PS补偿结构。原边补偿电容C1既受原、副边线圈耦合系统的影响,同时也受负载的影响,因此原边采取并联补偿的拓扑结构更适合于原、副边相对静止且负载相对固定的系统。
针对频率分岔现象,表3给出了在四种基本补偿网络下系统稳定的条件,表3中w0为线圈的固有频率[27]。
表3 四种基本补偿网络下系统稳定条件
Tab.3 System stability conditions under four basic compensation networks
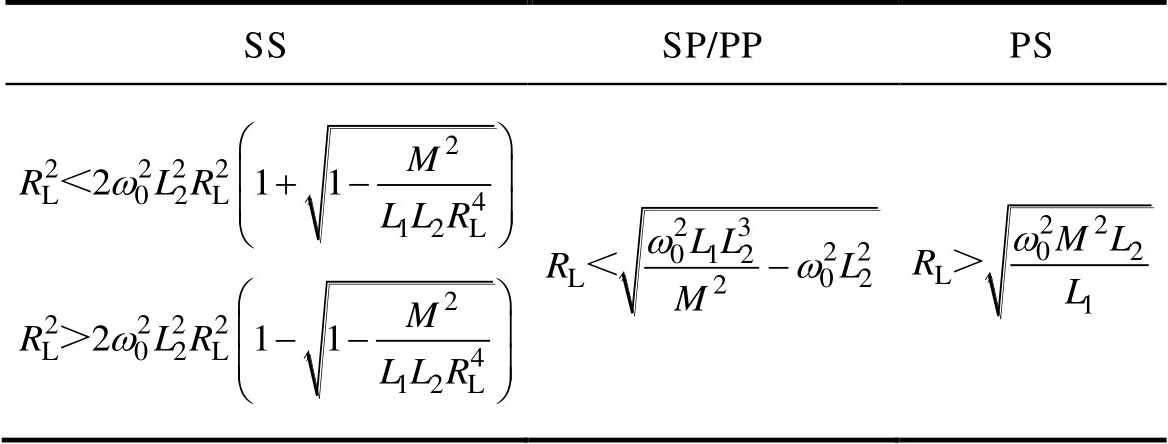
SSSP/PPPS
另外根据输入电源种类的不同,即电压源(Voltage, V)或电流源(Current, I),又可将四种基本电路拓扑分为八类,分别为I-SS、I-SP、I-PP、I-PS、V-SS、V-SP、V-PP、V-PS拓扑,文献[26]对八类特性进行了详细分析。表4给出了考虑不同指标时,八类拓扑的最优工作频率w,表4中,Q1= wL1/R1,Q2=wL2/R2分别为发射线圈和接收线圈的品质因数,QL为负载品质因数,当采用串联补偿时QL=wL2/RL,当采用并联补偿时QL=RL/wL2。由表4可知,系统工作在最大传输效率,当线圈品质因数远大于1时,八类拓扑工作频率都为副边谐振频率w2;当输入为电流源时,最大传输效率与最大输出功率的工作频率相同,都为副边谐振频率w2,而在输入为电压源时,V-PP、V-PS拓扑最大输出功率工作在其他频率。此外文献[26]也考虑了八类拓扑在不同指标下,最优工作频率对耦合系数的敏感度,对于最大传输效率而言只有I-SS、I-PS、V-SS、V-PS拓扑的工作频率完全不受耦合系数影响,对于最大输出功率I-SP、V-SS、I-SS拓扑工作频率对耦合系数不敏感,此外在恒压输出下耦合系数对I-SS拓扑最优工作频率无影响,在恒流输出下I-SP、I-PS、V-SS拓扑工作频率跟耦合系数无关。
表4 八种基本拓扑结构考虑不同目标下的最优工作频率
Tab.4 The optimal operating frequency of eight basic topologies under considering the different targets

指标最大传输效率最大输出功率①恒流输出①恒压输出① I-SS②④不存在 I-SP③不存在 I-PS② I-PP③ V-SS② V-SP② V-PS②不存在 V-PP③不存在
注:![]()
 。①:忽略线圈内阻;②:
。①:忽略线圈内阻;②: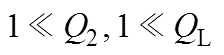 ;③:
;③: ;④:
;④: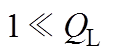 。
。
除了四种基本补偿结构外,SPS、LCL、LCC、CLC、CCL等复合型高阶拓扑结构也受到了广泛的关注[34-46],图7所示为常用的几种高阶补偿网络,图中,Lf1、Lf2、Cf1、Cf2分别为原边和副边的谐振电感和谐振电容。

图7 高阶补偿网络
Fig.7 The high-order compensation networks
SPS型拓扑结构,结合了SS型拓扑和PS型拓扑结构的特点,实现了输出功率与传输线圈耦合系数之间的解耦,具有较强的抗偏移能力[39-40]。LCL型补偿拓扑,用于原边补偿时可以实现原边线圈电流与负载、耦合系数解耦,产生恒定的原边线圈电流[38,47-48],在输入电压恒定、且忽略线圈内阻情况下,LCL-S型结构可以实现电压、电流增益与负载之间解耦,并在副边产生与负载无关的恒压源[47,49],而LCL-P型拓扑和LCL-LCL型拓扑则可以在副边产生与负载无关的恒流源[38-49],文献[38]将LCL- LCL型拓扑应用于多负载无线充电系统中,实现了良好的效果。LCL型补偿的缺点是外加的电感值大,增加了成本和体积[40]。为减小体积与成本,文献[40-41]提出了LCC-LCC型拓扑并将其应用在了电动汽车无线充电系统中,LCC-LCC型拓扑补偿网络的谐振频率与负载和耦合系数无关,系统可以工作在固定的频率,且发射线圈电流和输出电流也与负载无关,另外通过对补偿网络参数设计LCC型拓扑能够实现ZVS,实现极高的系统效率。实际上LCC型拓扑经过变化可以等效成LCL型拓扑[40,48],图8为LCC补偿拓扑原边等效电路,副边类似,图8中,M1为补偿电感与发射线圈之间的互感,Zref为等效反射阻抗,Lf1e、Cf1e、L1e分别为等效变换后的补偿电感、补偿电容和发射线圈电感。所以当系统工作在谐振频率时S-LCC、LCC-S、LCC-P、LCC-LCC拓扑负载特性与S-LCL、LCL-S、LCL-P、LCL-LCL拓扑一致[48]。
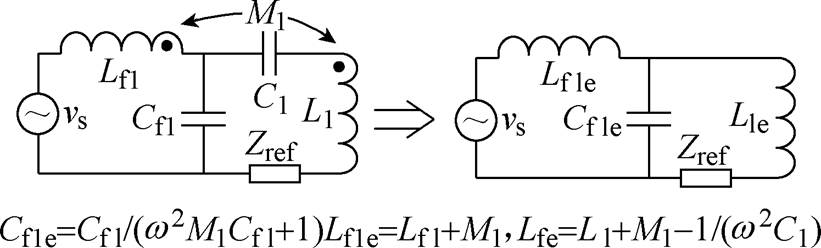
图8 LCC补偿网络等效电路
Fig.8 The equivalent circuit of LCC topology
表5[38,41,48-49]列出了在输入电压、互感M恒定并忽略线圈内阻的情况下,各种补偿网络的输出特性及工作条件。不同的补偿拓扑有其各自的优缺点,对系统的传输特性影响也各不相同,可根据负载的充电需求选择合适的拓扑结构以获得更好的传输性能。
表5 补偿网络输出特性及其工作条件
Tab.5 The output characteristics and working conditions of compensation network
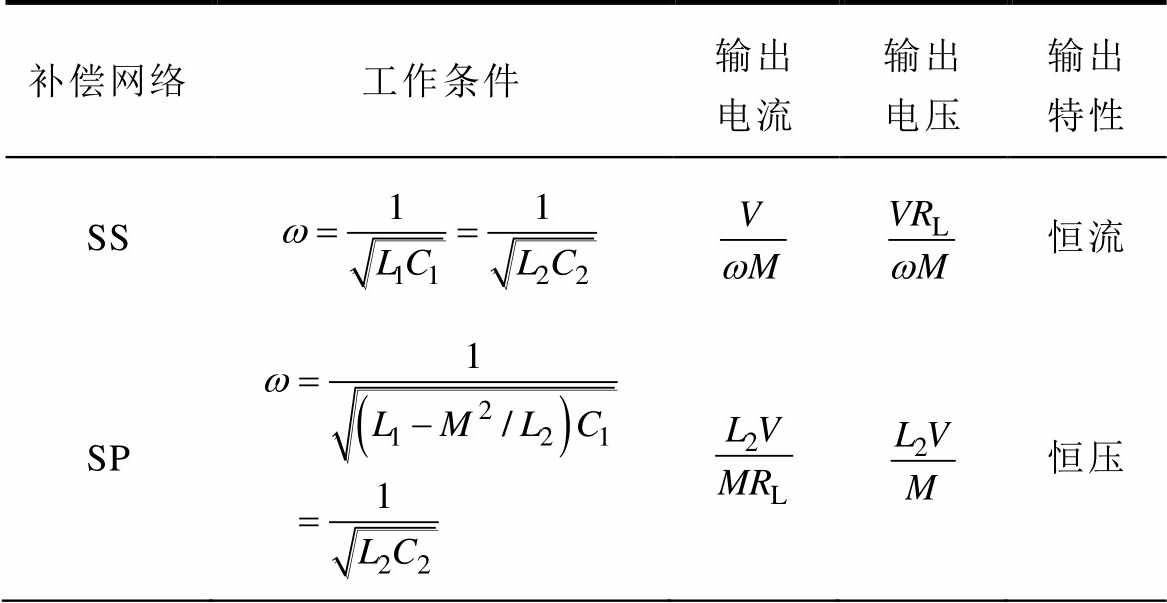
补偿网络工作条件输出电流输出电压输出特性 SS恒流 SP恒压
(续)

补偿网络工作条件输出电流输出电压输出特性 S-LCL恒压 LCL-S恒压 LCL-P恒流 LCL-LCL恒流 LCC-LCC恒流
注:V为输入正弦交流电源有效值。
在大多数工业应用场合,通常只能获得工频的交流电,所以对于电动汽车无线充电系统而言,功率变换器需要把50/60Hz的交流电变换成几十kHz的高频交流电。主要有两种实现方式:
(1)通过两级变换器级联。首先将50/60Hz的交流电整流成直流电,再通过高频逆变器将直流电转变成高频交流电,即AC-DC-AC,此种方式容易控制输入电流,实现单位功率因数,但变换器级联数增加,效率降低。
(2)通过单级变换器。直接实现50/60Hz交流电到高频交流电的转变,即AC-AC,此种方式主要的难点在于需要通过一级变压器实现多目标的控制,包括负载功率需求、输入侧功率因数校正、逆变器软开关等,优点则是去掉了直流侧的大电容、减少了开关器件,提高了系统效率。
目前AC-DC-AC变换器仍是电动汽车无线充电系统中应用最为广泛的结构,图9是典型的电动汽车无线充电用AC-DC-AC变换器结构框图。
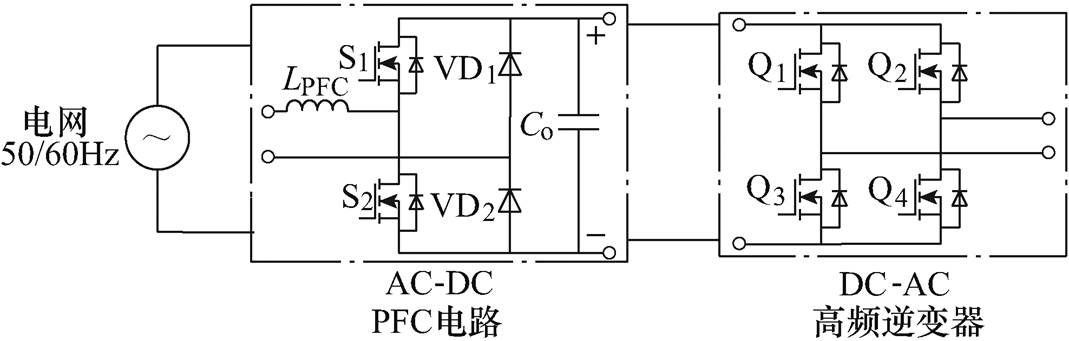
图9 电动汽车无线充电用AC-DC-AC变换器结构框图
Fig.9 Block diagram of a AC-DC-AC converter for wireless charging of EV
首先,第一级是单位功率因数校正电路,实现整流和调压,第二级是高频逆变电路,为发射线圈提供高频电源,通过这种结构可以很容易实现对电源侧功率因数、输出功率、软开关等多目标的控制。
近年来AC-AC变换器的研究也受到了广大研究者的关注。Hao Leo Li等提出一个基于自由振荡和能量注入控制的AC-AC变换器,省去DC环节,减少了变换器的开关应力、功率损耗和电磁干 扰,同时实现了器件的零电流关断(Zero Current Switching, ZCS),但是在输入工频交流电源过零点,谐振电流会大幅减小[50]。文献[51]提出了基于SiC器件的AC-AC变换器,通过移相控制的方式直接将三相工频电源转换成高频电源,减少了半导体器件的数量,仅需四个双向开关,但由于半导体器件工作在硬开关,承受的电压应力高,此拓扑不适合于大功率场合[4]。文献[52]则通过变频控制的方式实现AC-AC变换,并控制所有开关器件工作于软开关状态,减少了开关损耗和电磁干扰。文献[53]提出了应用于双向无线电能传输的AC-AC变换器,实现了1kW的功率传输,整机效率达到89.6%。另外文献[54-57]也对AC-AC变换器进行了研究,但以上变换器都是Buck型变换器,无法实现输入侧电流的直接控制,导致系统输入侧功率因数低[58],为此文献[58]提出Boost型单级AC-AC变换器,实现了单位功率因数。而文献[59]提出的AC-AC谐振变换器结合了Boost PFC电路和DC-AC高频逆变的特点,具有较高的功率因数,此外由于两级 电路共用两个开关器件,减少了开关器件的个 数,同时实现了器件的零电压开通(Zero Voltage Switching, ZVS),但当负载为恒流性质时,随着输出功率的增加系统将失去ZVS条件,且此拓扑直流侧仍需要大电容,另外系统参数是在耦合系数和负载均固定的情况下设计的,动态过程需要进一步深入研究[59]。表6对当前主要的AC-AC变换器的特性进行了总结。
表6 AC-AC变换器控制方式及其特性
Tab.6 The control method and characteristic of AC-AC converter
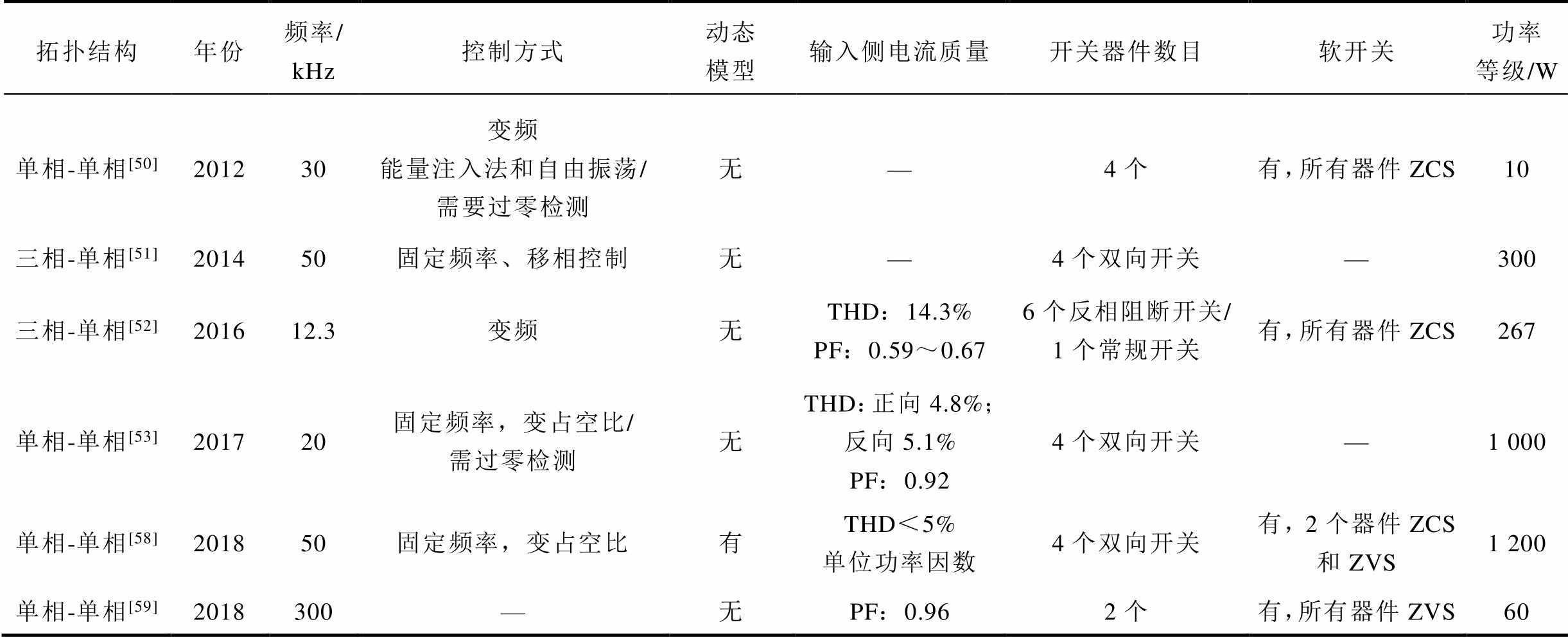
拓扑结构年份频率/ kHz控制方式动态模型输入侧电流质量开关器件数目软开关功率等级/W 单相-单相[50]201230变频能量注入法和自由振荡/需要过零检测无—4个有,所有器件ZCS10 三相-单相[51]201450固定频率、移相控制无—4个双向开关—300 三相-单相[52]201612.3变频无THD:14.3%PF:0.59~0.676个反相阻断开关/ 1个常规开关有,所有器件ZCS267 单相-单相[53]201720固定频率,变占空比/需过零检测无THD:正向4.8%;反向5.1%PF:0.924个双向开关—1 000 单相-单相[58]201850固定频率,变占空比有THD<5%单位功率因数4个双向开关有,2个器件ZCS和ZVS1 200 单相-单相[59]2018300—无PF:0.962个有,所有器件ZVS60
国内外对磁场耦合式无线充电系统模型的建立主要基于电路理论[27]和耦合模理论[60-61]。电路建模方法以电压、电流为变量,物理概念清晰,易于掌握,适用于低频和集中参数电路的分析与设计[62];耦合模理论以储能元件上电压、电流为复变量,在数学上属于微扰分析的一种形式[63],能够反映能量传递的本质和过程,耦合模型源于光学中光的传递规律,2007年MIT将其引入无线电能传输系统的分析中[60],是一种近似的建模方法,在一些复杂系统建模中更具优势。在一定条件下,耦合模型和电路模型可以互相等效[63-64]。
按照描述系统的稳态特性和暂态特性,可将系统模型分为稳态模型和动态模型。稳态模型通常被用于在稳定条件下,分析系统的传输特性以及设计、优化系统的参数。文献[65]中利用电路理论推导了在全补偿以及发射、接收线圈单独补偿等情况下,四种基本补偿拓扑结构的感应式无线充电系统传输效率和输出功率的表达式,分析了频率分岔现象以及互感、负载对最大输出功率和传输效率的影响,得到了最大输出功率下的互感和传输效率,见表7。由表7可知,无论哪种补偿方式,SS、SP型系统在输出功率最大时,传输效率仅为50%,而PS、PP型传输效率通常可达90%以上,但输出功率较小,设计时需综合考虑输出功率与传输效率。另外,文献[66]分析了谐振式无线充电系统原、副边线圈固有频率变化对系统效率的影响,并提出了通过发射功率源同步跟踪发射电路固有频率的方法,避免了系统的失谐。文献[67]基于互感模型分析了谐振式无线充电系统的频率分裂特性,并提出在过耦合区内,通过频率跟踪的方法实现对系统输出功率的调节。文献[68-69]通过进一步分析得到,在两线圈结构中,只有输出功率存在频率分裂现象,而传输效率无频率分裂现象。文献[70-71]则分别借助基于互感理论和耦合模理论的稳态模型,分析了四线圈结构系统的频率分裂现象,得到了系统的临界耦合条件。总体来说,稳态模型比较直观和简单,在分析一些对动态响应要求不高的场合较为适合。
表7 最大输出功率下的互感和传输效率
Tab.7 The mutual inductance and efficiency under maximum output power

系统最大功率时的互感传输效率 系统无功全补偿发射、接收线圈单独无功补偿系统无功全补偿发射、接收线圈单独无功补偿 SS型50%50% SP型50%50% PP型 PS型
在电动汽车无线充电实际应用中存在起动、停机、负载突变等一系列复杂的暂态行为,另外开关器件的开通与关断、电池等效电阻的变化等使系统还具有非线性特性[2],此时稳态模型不再适用,建立动态模型有助于对系统的暂态行为进行分析与控制,提高系统的鲁棒性。一个理想的动态模型应该是连续、线性、时不变和简洁的[72]。目前通常是利用微分方程来描述系统的动态行为,再借助一些特殊方法对系统建模。对于无线充电系统动态模型的建立可类比电力电子变换器的建模过程,如图10所示。可统一阐述为以下几步[72]:首先通过短时傅里叶变换将系统从不连续时变瞬态模型转化为连续的时不变大信号模型,常用的短时傅里叶变换方法包括:状态空间平均(State Space Averaging, SSA)法[73]、广义状态空间平均(Generalized State Space Averaging, GSSA)法[74]、扩展函数描述(Extended Describing Function, EDF)法[75]和动态向量变换法[72]。由于大信号模型是非线性的,通常还需进行线性化处理,以得到线性时不变小信号模型,应用较为广泛的线性化方法主要是基于小信号扰动[74]和雅可比矩阵方程[76]。虽然多数情况下最终是为了得到小信号模型,但大信号模型更有利于对于把控系统整体行为和非线性控制。
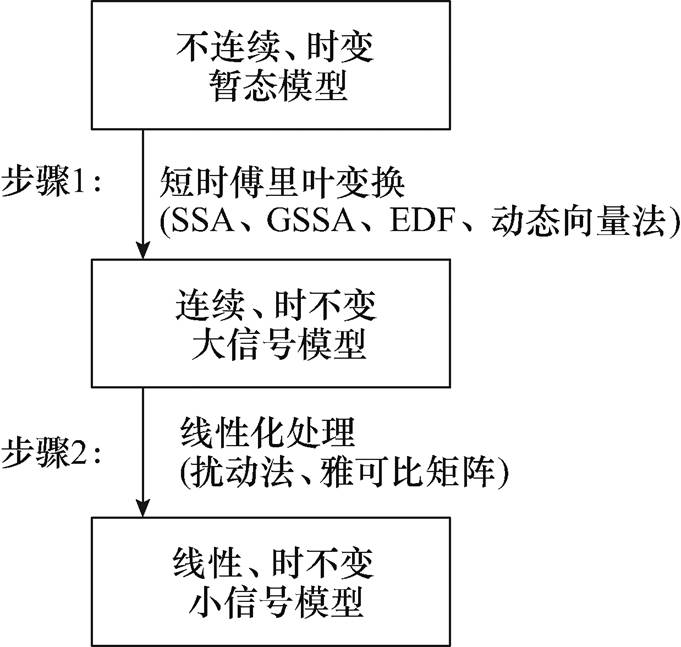
图10 系统动态模型的一般建模过程
Fig.10 General modeling process of dynamic model
现有研究对于无线充电系统动态模型的建立也有了一定的成果,文献[73]基于状态空间平均法建立了双向无线供电系统的动态模型,所提出的模型可实现对系统动态行为的准确预测,但文中未考虑系统中的非线性器件,无法得到解析式。文献[74]首先基于广义状态空间法建立了系统的大信号模型,在此基础上,利用扰动法建立了小信号模型,并应用于系统控制,提高了负载电压的动态响应。文献[77]利用Laplace向量变换法建立了系统的大信号模型,分析了系统对负载变化和输出电容变化瞬态响应。但相比于稳态模型,这些动态模型的阶数往往较高,文献[78]利用耦合模和平均化思想使系统阶次得到降低。文献[72]则基于动态向量法建立了系统的动态模型,并借助S域方程近似表达系统的线性部分,降低了系统模型的阶次。
总之,精确的模型是分析系统稳态特性和动态特性的基础,是实现系统优化设计与鲁棒性控制的前提,因此,有必要对系统模型进行进一步的研究与完善。
由于电动汽车无线充电应用场合比较复杂,系统参数容易受到环境影响,且在无线充电过程中,电池等效电阻会发生变化,另外受用户停车位置的影响,原、副边线圈的耦合系数也很容易偏移设定值,因此有必要对系统进行优化与控制,保证系统能稳定运行于最佳状态。
目前对于电动汽车静态无线充电系统,系统优化与能量传输鲁棒性控制的目标主要集中在以下几点:①实现最大效率点跟踪;②实现输出功率的控制与优化;③实现恒压/恒流控制;④提高系统的抗干扰能力等。常用的能量传输的鲁棒控制方法可分为:原边控制、副边控制和双边控制[4]。控制的实现方法一般又可分为基于DC-DC变换器的控制、基于高频逆变器的变频控制、基于高频逆变器或有源整流桥的移相控制等几类。基于DC-DC变换器控制简单可靠、适应性强,但增加了系统的成本、体积、复杂性和损耗;变频与移相控制无需增加额外的硬件电路,但变频控制较为复杂,且频率变化范围需满足相关标准,移相控制可能带来硬开关、直流电压纹波大等问题[79]。不同的控制方法各有利弊,需根据具体情况选择合适的方法。以下针对几种常见状况,对现有的系统优化与控制方法进行一个总结。
针对负载变化的情况,文献[80]采用原边控制策略,基于移相全桥电路,利用比例-积分(PI)控制对移相角进行调节,实现了恒压、恒流控制,控制过程仅用到原边信息。文献[81]采用副边控制的方法,基于极点配置法设计了PI控制器,对副边侧的有源整流桥和DC-DC变换器进行控制,同时实现了功率调节以及最大效率跟踪,且无需原、副边通信,但只在“整流模式”下才能实现最大效率跟踪,因而系统的平均效率较低。文献[82]采用双边控制策略,在原边前级和副边后级均加入了DC-DC变换器,通过调节副边DC-DC变换器的占空比改变等效电阻,以实现最大效率阻抗匹配,同时将输出电压以无线通信的方式传到原边,再通过原边DC-DC变换器对半桥逆变器的输入电压进行调节维持副边输出电压恒定,即同时实现了输出电压的恒定控制和效率的提升,但由于需要通信,系统成本较高且可靠性较低。因此,文献[83]提出了双边无通信控制策略,原边采用全桥结构,副边采用半有源桥结构,副边基于PI控制对半有源桥的移相角进行调节,以实现输出电流恒定,同时原边利用扰动观测法对逆变器进行移相控制,通过检测输入电流的最小值,来实现系统的最大效率跟踪,整个控制过程无需原、副边通信。但上述文献所提出的控制方法都是基于耦合系数已知的前提。
针对负载和耦合系数都变化的情况,文献[84]采用原边控制的方法,基于逆变器前级的DC-DC变换器对原边线圈电流大小进行控制,实现了系统最大效率跟踪以及恒定的输出电压,但需要原、副边的通信。文献[85]采用双边控制,原理与文献[82]类似,都是基于对原边前级和副边后级DC-DC变换器的控制,来实现最大效率跟踪,但文献[85]提出了耦合系数在线测量的方法,克服了控制策略对耦合系数的依赖,但依然需要原、副边通信。文献[79]基于双有源半桥结构,原、副边均采用Delta- sigma控制器产生脉冲密度调制信号来控制有源半桥,实现最大效率跟踪,该方法不仅免去了原、副边通信,而且双侧均实现了软开关。
针对失谐的情况,文献[86]分析了系统的失谐机理,提出基于自适应PI控制的可变模全数字锁相环的频率跟踪控制方法,实现了频率的快速跟踪。文献[87]提出通过控制副边单相有源整流桥的移相角和脉冲宽度来调整等效负载阻抗的实部和虚部的方法,调节虚部抵消失谐带来的电抗,调节实部以跟踪最大效率,原边侧通过PI控制器调节逆变器的驱动脉宽,实现输出电压的恒定。
此外,滑模控制器[88-89]、H∞控制器[90-93]等方法也被用来提高系统的动态响应。其中,文献[89]提出原边侧利用基于爬山搜索的相位控制来寻找输入电流的最小值,副边侧采用离散滑模控制器对DC- DC变换器控制的方法,实现了快速的最大效率跟踪和恒压控制,控制器框图[89]如图11所示。文献[92]对感应耦合电能传输系统高阶滑模控制算法进行了深入研究,实现了输出电压的鲁棒控制。文献[90]和文献[91]分别针对CLC型和π型谐振感应电能传输系统,应用广义状态空间平均法,建立了系统的扰动模型,并基于频域设计了H∞控制器,实现了系统的输出鲁棒控制,反馈控制框图[91]如图12所示。
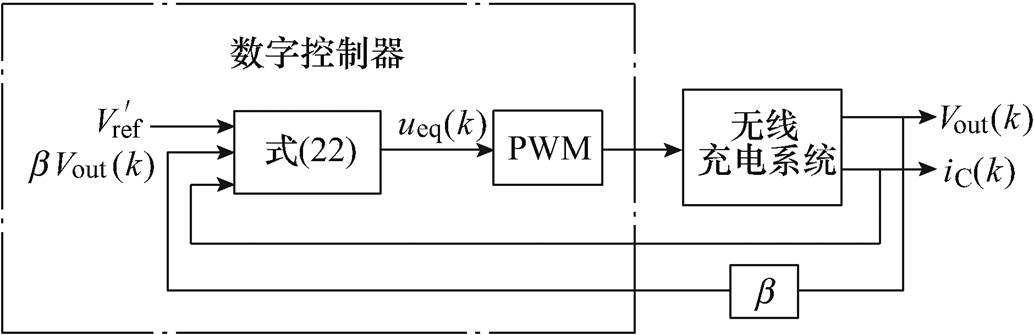
图11 离散滑模控制器框图
Fig.11 Control block diagram of the DSMC for WPT system
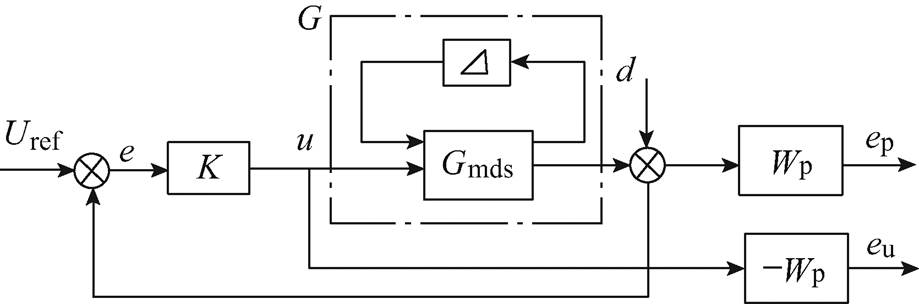
图12 混合灵敏度H∞输出反馈控制框图
Fig.12 Output feedback H∞ control scheme with mixed sensitivity
但总体来说,目前对于静态无线电能传输的控制策略大多数还是基于稳态模型,而电动汽车无线充电系统在应对一些突发情况时,通常要求有较快的动态响应,如何结合系统的动态模型,加强系统多参数摄动下的快速鲁棒性控制、实现系统优化、提升系统动态响应,具有重要意义。
综合国内外电动汽车静态无线充电技术的研究现状,可以看出,该项技术在各方面都已经得到了较为充分的研究,但仍有不少问题尚待解决。主要表现在以下几个方面:
(1)系统的抗偏移能力。如何提升系统抗偏移能力,一直是电动汽车无线充电技术的研究热点。在实际应用中,受用户停车位置的影响,系统原、副边线圈的相对位置会在一定范围内变化,造成耦合系数的变化,这就要求系统必须具备较强的抗偏移能力。目前主要是通过磁耦合机构的设计或系统闭环控制等方式提高系统的抗偏移能力,但这些技术层面上的方式改善效果有限,因此,有必要从机理上寻求突破。近年来提出的基于宇称-时间对称(Parity-Time Symmetry, PTS)原理的无线电能传输技术能在一定范围内实现恒定的输出功率和效率,而与耦合系数无关[76,94],另外基于分数阶电路的无线电能传输技术也展示了优良的特性[95-97],将这些新型的无线电能传输技术应用于电动汽车无线充电上,有望进一步提升系统的抗偏移能力。
(2)系统的环境敏感度。电动汽车无线充电应用场合较为复杂,系统线圈内阻、谐振频率等固有参数容易受到外界环境的影响而发生变化,尤其是汽车金属机身等对于线圈内阻、固有频率的影响较大,而谐振式无线输电技术对于固有频率的变化又十分敏感,目前关于金属物对谐振频率的影响通常是采用铁氧体等磁性材料进行屏蔽,或是通过电容矩阵、变频控制进行频率跟踪等方式进行改善,但这些无疑增加了系统的体积、质量与成本,如何提高系统抗谐振频率等固有参数变化的能力,降低系统对环境的敏感度,从原理上提出更加先进、经济有效的方法,仍然是电动汽车无线充电技术未来重要的研究方向之一。
(3)系统结构的优化。传统电动汽车无线充电系统的结构多是基于多级变换器,如AC-DC-AC变换器等,且通常会加入DC-DC变换器对系统进行功率调节等,但这增加了系统的体积与成本,降低了系统的整体效率。优化系统结构,研究高性能的AC-AC等电力电子变换器,减少系统变换器的级联数,利用控制策略以替代DC-DC变换器对系统功率等的调节,将更有利于系统性能的整体提升。
(4)系统动态模型的建立与鲁棒性控制。在电动汽车无线充电系统的实际应用中,通常需要实现快速的起、停机等操作,另外开关器件的开通与关断、电池等效电阻的变化等也给系统带来了复杂的非线性特性,这些都给系统的稳定性造成了较大的威胁。但当前对于无线充电系统特性的分析与控制,大都是基于系统的稳态模型,对于系统暂态响应、非线性特性的分析还较为缺乏。建立系统精确的动态模型并提出相应的控制策略,对系统动态行为进行控制,提升系统的稳定性,是今后的研究方向 之一。
本文从磁耦合机构、补偿网络、电力电子变换器以及系统的建模与特性、优化与控制等方面对基于磁耦合式的电动车无线充电的关键技术问题进行了总结与归纳,并指出了该项技术有待解决的问题以及未来的研究发展方向,可以看到,电动汽车静态无线充电技术已得到广泛的研究,并取得了一定的进展,但仍有许多关键技术有待解决,如系统抗偏移能力、对环境的敏感度问题、系统结构的优化设计以及稳定性控制等。目前电动汽车静态无线充电技术的研究正处在攻坚克难的阶段,仍需进一步完善和应用现有理论,乃至原理上的创新与突破。
参考文献
[1] 赵争鸣, 张艺明, 陈凯楠. 磁耦合谐振式无线电能传输技术新进展[J]. 中国电机工程学报, 2013, 33(3): 1-13.
Zhao Zhengming, Zhang Yiming, Chen Kainan. New progress of magnetically-coupled resonant wireless power transfer technology[J]. Proceedings of the CSEE, 2013, 33(3): 1-13.
[2] 赵争鸣, 刘方, 陈凯楠. 电动汽车无线充电技术研究综述[J]. 电工技术学报, 2016, 31(20): 30-40.
Zhao Zhengming, Liu Fang, Chen Kainan. New progress of wireless charging technology for electric vehicles[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 30-40.
[3] Budhia M, Covic G, Boys J. A new IPT magnetic coupler for electric vehicle charging systems[C]// IECON 36th Annual Conference on IEEE Industrial Electronics Society, Glendale, 2010: 2487-2492.
[4] Patil D, Mcdonough M K, Miller J M, et al. Wireless power transfer for vehicular applications: overview and challenges[J]. IEEE Transactions on Trans- portation Electrification, 2018, 4(1): 3-37.
[5] Budhia M, Covic G A, Boys J T. Design and optimization of circular magnetic structures for lumped inductive power transfer systems[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3096-3108.
[6] Budhia M, Boys J T, Covic G A, et al. Development of a single-sided flux magnetic coupler for electric vehicle IPT charging systems[J]. IEEE Transactions on Industrial Electronics, 2013, 60(1): 318-328.
[7] Nguyen T, Li S, Li W, et al. Feasibility study on bipolar pads for efficient wireless power chargers[C]// IEEE Applied Power Electronics Conference and Exposition (APEC), Fort Worth, 2014: 1676-1682.
[8] Zaheer A, Kacprzak D, Covic G A. A bipolar receiver pad in a lumped IPT system for electric vehicle charging applications[C]//IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, 2012: 283-290.
[9] Kim S, Covic G A, Boys J T. Tripolar pad for inductive power transfer systems for EV charging[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5045-5057.
[10] Moon S, Kim B, Cho S, et al. Analysis and design of a wireless power transfer system with an intermediate coil for high efficiency[J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 5861-5870.
[11] Choi S Y, Huh J, Lee W Y, et al. Asymmetric coil sets for wireless stationary EV chargers with large Lateral tolerance by dominant field analysis[J]. IEEE Transactions on Power Electronics, 2014, 29(12): 6406-6420.
[12] Ahn S, Pak J, Song T, et al. Low frequency electromagnetic field reduction techniques for the on- line electric vehicle (OLEV)[C]//IEEE International Symposium on Electromagnetic Compatibility, Fort Lauderdale, 2010: 625-630.
[13] Park C, Lee S, Jeong S Y, et al.Uniform power I-type inductive power transfer system with DQ power supply rails for on-line electric vehicles[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6446-6455.
[14] Lee W Y, Huh J, Choi S Y, et al. Finite-width magnetic mirror models of mono and dual coils for wireless electric vehicles[J]. IEEE Transactions on Power Electronics, 2013, 28(3): 1413-1428.
[15] Shin J, Shin S, Kim Y, et al. Design and implementation of shaped magnetic-resonance-based wireless power transfer system for roadway-powered moving electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2014, 61(3): 1179-1192.
[16] Chigira M, Nagatsuka Y, Kaneko Y, et al. Small-size light-weight transformer with new core structure for contactless electric vehicle power transfer system[C]// IEEE Energy Conversion Congress and Exposition, Phoenix, 2011: 260-266.
[17] Takanashi H, Sato Y, Kaneko Y, et al. A large air gap 3kW wireless power transfer system for electric vehicles[C]//IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, 2012: 269-274.
[18] Zhang Wei, White J C, Abraham A M, et al. Loosely coupled transformer structure and interoperability study for EV wireless charging systems[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6356-6367.
[19] 胡超. 电动汽车无线供电电磁耦合机构能效特性及优化方法研究[D]. 重庆: 重庆大学, 2015.
[20] 陈振伟. 电动汽车非接触充电系统用松耦合变压器设计与实现[D]. 哈尔滨: 哈尔滨工业大学, 2014.
[21] 张献, 杨庆新, 崔玉龙, 等. 大功率无线电能传输系统能量发射线圈设计、优化与验证[J]. 电工技术学报, 2013, 28(10): 12-18.
Zhang Xian, Yang Qingxin, Cui Yulong, et al. Design optimization and verification on the power transmitting coil in the high-power wireless power transmission system[J]. Transactions of China Elec- trotechnical Society, 2013, 28(10): 12-18.
[22] 谭林林, 黄学良, 赵俊锋, 等. 一种无线电能传输系统的盘式谐振器优化设计[J]. 电工技术学报, 2013, 28(8): 1-6.
Tan Linlin, Huang Xueliang, Zhao Junfeng, et al. Optimization design for disc resonators of a wireless power transmission system[J]. Transactions of China Electrotechnical Society, 2013, 28(8): 1-6.
[23] Wei Ni, Collings I B, Xin Wang, et al. Radio alignment for inductive charging of electric vehicles[J]. IEEE Transactions on Industrial Informatics, 2015, 11(2): 427-440.
[24] Ahmad A, Alam M S, Chabaan R. A comprehensive review of wireless charging technologies for electric vehicles[J]. IEEE Transactions on Transportation Electrification, 2018, 4(1): 38-63.
[25] Bi Z, Kan T, Mi C C, et al. A review of wireless power transfer for electric vehicles: prospects to enhance sustainable mobility[J]. Applied Energy, 2016, 179: 413-425.
[26] Sohn Y H, Choi B H, Lee E S, et al. General unified analyses of two-capacitor inductive power transfer systems: equivalence of current-source ss and sp compensations[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6030-6045.
[27] Wang C S, Covic G A, Stielau O H. Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems[J]. IEEE Transactions on Industrial Electronics, 2004, 51(1): 148-157.
[28] 周雯琪, 马皓, 何湘宁. 感应耦合电能传输系统不同补偿拓扑的研究[J]. 电工技术学报, 2009, 24(1): 133-139.
Zhou Wenqi, Ma Hao, He Xiangning. Investigation on different compensation topologies in inductively coupled power transfer system[J]. Transactions of China Electrotechnical Society, 2009, 24(1): 133-139.
[29] 孙跃, 夏晨阳, 戴欣, 等. 感应耦合电能传输系统互感耦合参数的分析与优化[J]. 中国电机工程学报, 2010, 30(33): 44-50.
Sun Yue, Xia Chenyang, Dai Xin, et al. Analysis and optimization of mutual inductance for inductively coupled power transfer system[J]. Proceedings of the CSEE, 2010, 30(33): 44-50.
[30] 李阳, 董维豪, 杨庆新, 等. 过耦合无线电能传输功率降低机理与提高方法[J]. 电工技术学报, 2018, 33(14): 3177-3184.
Li Yang, Dong Weihao, Yang Qingxin, et al. Mechanism of power decreasing and improvement method for wireless power transfer system in over coupled regime[J]. Transactions of China Electro- technical Society, 2018, 33(14): 3177-3184.
[31] Aditya K, Williamson S S. Comparative study of series-series and series-parallel compensation topo- logies for electric vehicle charging[C]//IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, 2014: 426-430.
[32] 孙跃, 廖志娟, 叶兆虹, 等. 基于振动理论的MCR-WPT系统频率分裂特性研究[J]. 电工技术学报, 2018, 33(13): 3140-3148.
Sun Yue, Liao Zhijuan, Ye Zhaohong, et al. Research on frequency splitting characteristic of MCR-WPT systems based on vibration theory[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3140- 3148.
[33] Feng Hao, Cai Tao, Duan Shanxu, et al. A dual- side-detuned series-series compensated resonant converter for wide charging region in a wireless power transfer system[J]. IEEE Transactions on Industrial Electronics, 2018, 65(3): 2177-2188.
[34] Wang C S, Covic G A, Stielau O H. Investigating an LCL load resonant inverter for inductive power transfer applications[J]. IEEE Transactions on Power Electronics, 2004, 19(4): 995-1002.
[35] Borage M, Tiwari S, Kotaiah S. Analysis and design of an LCL-T resonant converter as a constant-current power supply[J]. IEEE Transactions on Industrial Electronics, 2005, 52(6): 1547-1554.
[36] Kissin M, Huang C, Covic G A, et al. Detection of the tuned point of a fixed-frequency LCL resonant power supply[J]. IEEE Transactions on Power Electronics, 2009, 24(4): 1140-1143.
[37] Keeling N A, Covic G A, Boys J T. A unity-power- factor IPT pickup for high-power applications[J]. IEEE Transactions on Industrial Electronics, 2010, 57(2): 744-751.
[38] Madawala U K, Thrimawithana D J. A bidirectional inductive power interface for electric vehicles in V2G systems[J]. IEEE Transactions on Industrial Elec- tronics, 2011, 58(10): 4789-4796.
[39] Villa J L, Sallan J, Sanz Osorio J F, et al. High-misalignment tolerant compensation topology for ICPT systems[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 945-951.
[40] Li Weihan, Zhao Han, Li Siqi, et al. Integrated LCC compensation topology for wireless charger in electric and plug-in electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4215-4225.
[41] Li Siqi, Li Weihan, Deng Junjun, et al. A double- sided LCC compensation network and its tuning method for wireless power transfer[J]. IEEE Transactions on Vehicular Technology, 2015, 64(6): 2261-2273.
[42] Zhang Wei, Mi C C. Compensation topologies of high- power wireless power transfer systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(6): 4768-4778.
[43] Kan T, Nguyen T, White J C, et al. A new integration method for an electric vehicle wireless charging system using LCC compensation topology: analysis and design[J]. IEEE Transactions on Power Electronics, 2017, 32(2): 1638-1650.
[44] Samanta S, Rathore A K. A new current-fed CLC transmitter and LC receiver topology for inductive wireless power transfer application: analysis, design, and experimental results[J]. IEEE Transactions on Transportation Electrification, 2015, 1(4): 357-368.
[45] Wang Yijie, Yao Yousu, Liu Xiaosheng, et al. S/CLC compensation topology analysis and circular coil design for wireless power transfer[J]. IEEE Transactions on Transportation Electrification, 2017, 3(2): 496-507.
[46] Kan Tianze, Lu Fei, Nguyen T, et al. Integrated coil design for EV wireless charging systems using LCC compensation topology[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9231-9241.
[47] 周豪, 姚钢, 赵子玉, 等. 基于LCL谐振型感应耦合电能传输系统[J]. 中国电机工程学报, 2013, 33(33): 9-16.
Zhou Hao, Yao Gang, Zhao Ziyu, et al. LCL resonant inductively coupled power transfer systems[J]. Proceedings of the CSEE, 2013, 33(33): 9-16.
[48] Liu Fong, Zhang Yiming, Chen Kainan, et al. A comparative study of load characteristics of resonance types in wireless transmission systems[C]// IEEE Asia-Pacific International Symposium on Electromagnetic Compatibility (APEMC), Shenzhen, 2016: 203-206.
[49] Qu Xiaohui, Han Hongdou, Wong Siu-chang, et al. Hybrid IPT topologies with constant current or constant voltage output for battery charging appli- cations[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6329-6337.
[50] Li H L, Hu A P, Covic G A. A direct AC-AC converter for inductive power-transfer systems[J]. IEEE Transactions on Power Electronics, 2012, 27(2): 661-668.
[51] Xuan Bac N, Vilathgamuwa D M, Madawala U K. A SiC-based matrix converter topology for inductive power transfer system[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4029-4038.
[52] Moghaddami M, Anzalchi A, Sarwat A I. Single- stage three-phase AC-AC matrix converter for inductive power transfer systems[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6613-6622.
[53] Weerasinghe S, Madawala U K, Thrimawithana D J. A matrix converter-based bidirectional contactless grid interface[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 1755-1766.
[54] Kusumah P P, Kyyra J. Minimizing coil power loss in a direct AC/AC converter-based contactless electric vehicle charger[C]//IEEE 19th European Conference on Power Electronics and Applications (EPE'17 ECCE Europe), Warsaw, 2017: 1-10.
[55] Kusumah F P, Kyyra J. Bi-directional power transfer of a contactless electric vehicle charger using direct three-phase to single-phase AC/AC converter[C]// IEEE 20th European Conference on Power Electro- nics and Applications (EPE'18 ECCE Europe), Riga, 2018: 1-10.
[56] Kusumah F P, Vuorsalo S, Kyyra J. A direct three-phase to single-phase AC/AC converter for contactless electric vehicle charger[C]//2015 17th European Conference on Power Electronics and Applications (EPE'15 ECCE-Europe), Geneva, 2015: 1-10.
[57] Kusumah F P, Vuorsalo S, Kyyra J. Components selection of a direct three-phase to single-phase AC/AC converter for a contactless electric vehicle charger[C]//The18th European Conference on Power Electronics and Applications (EPE'16 ECCE Europe), Karlsruhe, 2016: 1-10.
[58] Samanta S, Rathore A K. A new inductive power transfer topology using direct AC-AC converter with active source current waveshaping[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(7): 5565-5577.
[59] 黄雅琪. 应用于无线输电系统的单相单级AC-AC谐振变换器[D]. 广州: 华南理工大学, 2018.
[60] Kurs A, Karalis A, Moffatt R, et al. Wireless power transfer via strongly coupled magnetic resonances[J]. Science, 2007, 317(5834): 83-86.
[61] Li Hongchang, Wang Kangping, Huang Lang, et al. Dynamic modeling based on coupled modes for wireless power transfer systems[J]. IEEE Transa- ctions on Power Electronics, 2015, 30(11): 6245- 6253.
[62] 疏许健, 张波. 感应耦合无线电能传输系统的能量法模型及特性分析[J]. 电力系统自动化, 2017, 41(2): 28-32.
Shu Xujian, Zhang Bo. Energy model and characteri- stic analysis for inductively coupled power transfer system[J]. Automation of Electric Power Systems, 2017, 41(2): 28-32.
[63] 黄学良, 曹伟杰, 周亚龙, 等. 磁耦合谐振系统中的两种模型对比探究[J]. 电工技术学报, 2013, 28(增刊2): 13-17.
Huang Xueliang, Cao Weijie, Zhou Yalong, et al. Comparative study on the two kinds of models in the technology of magnetic coupling resonance system[J]. Transactions of China Electrotechnical Society, 2013, 28(S2): 13-17.
[64] Kiani M, Ghovanloo M. The circuit theory behind coupled-mode magnetic resonance-based wireless power transmission[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2012, 59(9): 2065- 2074.
[65] 张波, 黄润鸿, 疏许健. 无线电能传输原理[M]. 北京: 科学出版社, 2018.
[66] 傅文珍, 张波, 丘东元. 频率跟踪式谐振耦合电能无线传输系统研究[J]. 变频器世界, 2009(8): 41-46.
Fu Wenzhen, Zhang Bo, Qiu Dongyuan. Study on frequence-tracking wireless power transfer system by resonant coupling[J]. The World of Inverters, 2009(8): 41-46.
[67] Sample A P, Meyer D A, Smith J R. Analysis, experimental results, and range adaptation of magnetically coupled resonators for wireless power transfer[J]. IEEE Transactions on Industrial Electro- nics, 2011, 58(2): 544-554.
[68] Zhang Yiming, Zhao Zhengming. Frequency splitting analysis of two-coil resonant wireless power transfer[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13: 400-402.
[69] Huang Runhong, Zhang Bo, Qiu Dongyuan, et al. Frequency splitting phenomena of magnetic resonant coupling wireless power transfer[J]. IEEE Transa- ctions on Magnetics, 2014, 50(11): 1-4.
[70] Zhang Yiming, Zhao Zhengming, Chen Kainan. Frequency-splitting analysis of four-coil resonant wireless power transfer[J]. IEEE Transactions on Industry Applications, 2014, 50(4): 2436-2445.
[71] 张献, 杨庆新, 陈海燕, 等. 电磁耦合谐振式传能系统的频率分裂特性研究[J]. 中国电机工程学报, 2012, 32(9): 167-173.
Zhang Xian, Yang Qingxin, Chen Haiyan, et al. Research on characteristics of frequency splitting in electromagnetic[J]. Proceedings of the CSEE, 2012, 32(9): 167-173.
[72] Li Hongchang, Fang J, Tang Y. Dynamic phasor- based reduced order models of wireless power transfer systems[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6245-6253.
[73] Swain A K, Neath M J, Madawala U K, et al. A dynamic multivariable state-space model for bidirectional inductive power transfer systems[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4772-4780.
[74] 林天仁, 李勇, 麦瑞坤. 基于LCL-S拓扑的感应电能传输系统的建模与控制方法[J]. 电工技术学报, 2018, 33(1): 104-111.
Lin Tianren, Li Yong, Mai Ruikun. Modeling and control method of inductive power transfer system based on LCL-S topology[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 104-111.
[75] Zahid Z U, Dalala Z, Lai J. Small-signal modeling of series-series compensated induction power transfer system[C]//IEEE Applied Power Electronics Con- ference and Exposition (APEC), Fort Worth, 2014: 2847-2853.
[76] Zhou Jiali, Zhang Bo, Xiao Wenxun, et al. Nonlinear parity-time-symmetric model for constant efficiency wireless power transfer: application to a drone-in- flight wireless charging platform[J]. IEEE Transa- ctions on Industrial Electronics, 2019, 66(5): 4097- 4107.
[77] Lee S, Choi B, Rim C T. Dynamics characterization of the inductive power transfer system for online electric vehicles by Laplace phasor transform[J]. IEEE Transactions on Power Electronics, 2013, 28(12): 5902-5909.
[78] Li Hongchang, Wang Kangping, Huang Long, et al. Dynamic modeling based on coupled modes for wireless power transfer systems[J]. IEEE Transa- ctions on Power Electronics, 2015, 30(11): 6245- 6253.
[79] Li Hongchang, Fang Jingyang, Chen Shuxin, et al. Pulse density modulation for maximum efficiency point tracking of wireless power transfer systems[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5492-5501.
[80] Song Kai, Li Zhenjie, Jiang Jinhai, et al. Constant current/voltage charging operation for series-series and series-parallel compensated wireless power transfer systems employing primary-side controller[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 8065-8080.
[81] Lovison G, Sato M, Imura T, et al. Secondary- side-only simultaneous power and efficiency control for two converters in wireless power transfer system[C]// IEEE IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, 2015: 4824-4829.
[82] Li Hongchang, Li Jie, Wang Kongping, et al. A maximum efficiency point tracking control scheme for wireless power transfer systems using magnetic resonant coupling[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3998-4008.
[83] Li Zhenjie, Song Kai, Jiang Jinhai, et al. Constant current charging and maximum efficiency tracking control scheme for supercapacitor wireless charging[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 9088-9100.
[84] Yeo T, Kwon D, Khang S, et al. Design of maximum efficiency tracking control scheme for closed-loop wireless power charging system employing series resonant tank[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 471-478.
[85] Dai Xin, Li Xiaofei, Li Yanling, et al. Maximum efficiency tracking for wireless power transfer systems with dynamic coupling coefficient estimation[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5005-5015.
[86] 刘帼巾, 李义鑫, 崔玉龙, 等. 基于FPGA的磁耦合谐振式无线电能传输频率跟踪控制[J]. 电工技术学报, 2018, 33(14): 3185-3193.
Liu Guojin, Li Yixin, Cui Yulong, et al, Frequency tracking control of wireless power transfer via magnetic resonance coupling based on FPGA[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3185-3193.
[87] Mai Raikun, Liu Yeyan, Li Yong, et al. An active-rectifier-based maximum efficiency tracking method using an additional measurement coil for wireless power transfer[J]. IEEE Transactions on Power Electronics, 2018, 33(1): 716-728.
[88] Ling R, Wang L, Sun Y, et al. A second-order sliding-mode controller for inductively coupled power transfer systems[C]//IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, 2017: 6497-6503.
[89] Yang Yun, Zhong Wenxing, Kiratipongvoot S, et al. Dynamic improvement of series–series compensated wireless power transfer systems using discrete sliding mode control[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 6351-6360.
[90] 戴欣, 余奎, 孙跃. CLC谐振型感应电能传输系统的H∞ 控制[J]. 中国电机工程学报, 2010, 30(30): 47-54.
Dai Xin, Yu Kui, Sun Yue. Study on H∞ control method for CLC resonant inductive power transfer system[J]. Proceedings of the CSEE, 2010, 30(30): 47-54.
[91] 戴欣, 周继昆, 孙跃. 具有频率不确定性的p 型谐振感应电能传输系统H∞控制方法[J]. 中国电机工程学报, 2011, 31(30): 45-53.
Dai Xin, Zhou Jikun, Sun Yue. H∞ Control method with frequency uncertainty for p type resonant inductive power transfer system[J]. Proceedings of the CSEE, 2011, 31(30): 45-53.
[92] 王理智. 感应耦合电能传输系统高阶滑模控制算法的研究[D]. 重庆: 重庆大学, 2017.
[93] 罗博, 陈丽华, 李勇, 等. 基于滑模控制的感应耦合电能传输系统输出电压控制研究[J]. 电工技术学报, 2017, 32(23): 235-242.
Luo Bo, Chen Lihua, Li Yong, et al. Investigation of output voltage control for the inductive power transfer system based on sliding mode control theory[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 235-242.
[94] Assawaworrarit S, Yu Xiaofang, Fan Shanhui. Robust wireless power transfer using a nonlinear parity- time-symmetric circuit[J]. Nature, 2017, 546(7658): 387-390.
[95] 疏许健, 张波. 降低整数阶无线电能传输谐振频率的分数阶方法[J]. 电工技术学报, 2017, 32(18): 83-89.
Shu Xujian, Zhang Bo. A fractional-order method to reduce the resonant frequency of integer-order wireless power transmission system[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 83-89.
[96] Jiang Yanwei, Zhang Bo. High-power fractional- order capacitor with 1<a<2 based on power converter[J]. IEEE Transactions on Industrial Electronics, 2018, 65(4): 3157-3164.
[97] Shu Xujian, Zhang Bo. The effect of fractional orders on the transmission power and efficiency of fractional-order wireless power transmission system[J]. Energies, 2018, 11(7): 1774-1782.
Overview of Static Wireless Charging Technology for Electric Vehicles:Part Ⅱ
Abstract Static wireless charging technology for electric vehicles (EV) have aroused extensive attention due to its safety and convenient. The key technologies of wireless charging of EV are analyzed in detail from the aspects of magnetic coupler, compensation networks, power electronics converters, and system modeling-optimization-robust control methods. In addition, hot issues and the future of static wireless charging technology for EV were discussed, aiming to point the way for the research of static wireless charging technology for EV.
keywords:Electric vehicles, static wireless charging technology, magnetic coupler, system modeling, robust control
中图分类号:TM724
DOI: 10.19595/j.cnki.1000-6753.tces.190107
国家自然科学基金重点资助项目(51437005)。
收稿日期 219-01-25
改稿日期 2019-05-27
吴理豪 男,1994年生,博士,研究方向为电力电子与电力传动。E-mail: epwulh@mail.scut.edu.cn
张 波 男,1962年生,教授,博士生导师,研究方向为电力电子与电力传动。E-mail: epbzhang@scut.edu.cn(通信作者)
(编辑 陈 诚)