 在d、q轴旋转坐标系中的定子电压方程为
在d、q轴旋转坐标系中的定子电压方程为摘要 为解决传统电压前馈解耦控制对电机参数敏感、抗扰性差的问题,该文提出一种基于滑模观测器的电流偏差解耦控制方法。通过计算偏差解耦控制电流的耦合项,发现相对于传统电压前馈解耦,偏差解耦的耦合项简单且易于控制,解决了传统电压前馈解耦控制解耦效果不理想的问题。通过电流滑模观测器的跟踪特性,将定子电流的估计值作为状态变量,反馈到系统输入端,用以补偿定子电流误差值。该方法不仅对电流环实现更好的补偿控制,还实现d、q轴电流完全解耦,保证系统动态响应速度,提高了系统的抗扰性。通过仿真和实验证明所提出控制器的有效性。
关键词:永磁同步电机 电压前馈解耦控制 电流偏差解耦控制 电流滑模观测器
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)以其高功率密度、高效率、高可靠性等优点在电动汽车上得到了广泛应用[1-2]。永磁同步电机是一个非线性强耦合多变量系统,PI矢量控制方法在永磁同步电机控制系统受到内部参数摄动及外部干扰时,不能满足高性能控制要求。因此,PMSM的控制策略向智能化发展。
PMSM采用空间矢量控制(Space Vector Pulse Width Modulation, SVPWM)后,经过坐标变换交、直轴电压平衡方程之间虽实现了静态解耦,但并没有消除动态耦合项,在电机高速运行时这一耦合项会严重影响交、直轴之间的独立控制,使系统控制效果变差,且在电感参数变化时的动态过程中表现尤其明显。因此有必要对d、q轴电流进行解耦处理。传统的电压前馈解耦控制(Voltage Feed-forward Decoupling Control, VFDC)利用反馈电流和转速计算出耦合部分并补偿至交、直轴的电压,实现了电压的完全解耦控制。VFDC提高了系统的动态特性,但它对电机参数有很强的依赖性,在系统低开关频率运行时,性能稳定性不足[3]。基于内模控制原理的电流解耦控制[4]本质上是VFDC,解耦效果较理想,对参数摄动具有较强的鲁棒性。但系统调节过程中会出现振荡现象。基于偏差电流计算前馈电压解耦控制策略[5]是内模控制方法的一种演变,不过同样存在内模控制的不足。复矢量电流调节器[6]能消除d、q轴电流耦合,动态性能较好,但对外部扰动鲁棒性较弱。文献[7]用神经网络的方法对系统不确定性进行在线辨识,进而用于前向补偿;通过模糊控制提高了控制系统的鲁棒性,有效地实现永磁同步电机的动态解耦控制。文献[8]采用电流偏差解耦控制(Current Deviation Decoupling Control, CDDC)来实现d、q轴间的电流解耦,但从控制方法上看,这只能算是一种理想的静态解耦控制。当电感实际值与估算值之间存在偏差时,解耦补偿量不能完全抵消实际耦合量,导致解耦不彻底。
观测器补偿控制具有结构简单又能有效抑制系统参数摄动和干扰的特点,在运动控制领域得到广泛应用。文献[9]在电流PI控制器的基础上,利用内模控制原理设计观测器,实现电流补偿控制。文献[10]利用电机本体的参考模型构造滑模面,设计速度观测器,以改善位置和速度估计精度,并提高系统的鲁棒性。文献[11]提出一种对滑模面积分构造一个简单的系统参数不确定观测器补偿滑模控制量完成对电流的滑模鲁棒控制。文献[12]为获得精确的电流观测值,通过低通滤波器滤除观测器输出的高频失真信号。文献[13]分别在连续和离散系统提出在PI解耦控制器下,构造李雅普诺夫函数设计电流误差观测器实现电流鲁棒控制。文献[14]将未知测量噪声和外部扰动作用作为扩张状态变量进行观测,观测值可以有效地补偿风电机组虚拟惯量,更好地抑制电网频率波动。文献[15]通过Elman神经网络估计器对不确定性因素进行估计,代替滑模控制中的切换控制,改善系统跟踪性能,进一步提高滑模控制的鲁棒性。文献[16]以锁相环计算位置信号为参考,自适应调节带通截止频率,利用滤波器滤除反电动势中的大量抖振和谐波。锁相环根据基波反电动势计算出转子速度和位置,有效地提高了表贴式永磁同步电机速度和位置观测性能。文献[17]利用自适应控制观测和补偿系统参数变化和外部扰动等因素的影响,并进行实时估计。这些方法从各自不同的角度提高了PMSM系统性能,但是无论是速度控制还是电流控制,都很好地利用观测器的跟踪特性,对控制量进行补偿控制,有效的抑制干扰量。
本文针对PMSM运行时电感参数随着外界环境、运行条件的变化而变化,控制器的电感估计值与实际值失配,解耦补偿不能完全抵消实际耦合量,提出一种基于电流滑模观测器(Current Sliding Mode Observer, CSMO)的电流偏差解耦控制方法。将d、q轴电流耦合和电感参数变化引起的电压误差量视为扰动,利用电流滑模观测器的跟踪特性,补偿电压误差值,实现对电流环更好的补偿控制。通过计算CDDC-CSMO算法耦合项,发现其多项式远小于CDDC、VFDC耦合多项式。该方法有效克服解耦效果受电感参数变化的影响,其解耦效果优于CDDC、VFDC算法,使系统具有较强的鲁棒性。
本文 在d、q轴旋转坐标系中的定子电压方程为
在d、q轴旋转坐标系中的定子电压方程为
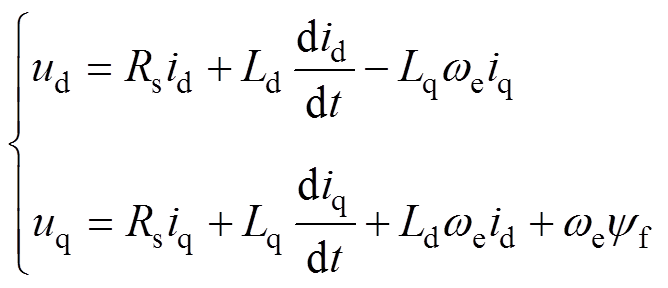 (1)
(1)式中, 、
、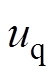 分别为d、q轴电压;
分别为d、q轴电压;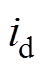 、
、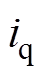 分别为d、q轴电流;
分别为d、q轴电流;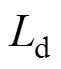 、
、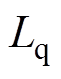 分别为d、q轴电感;
分别为d、q轴电感;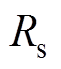 为定子相电阻;
为定子相电阻;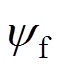 为转子永磁体磁链;
为转子永磁体磁链;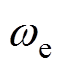 为转子电角速度。
为转子电角速度。
电磁转矩方程为
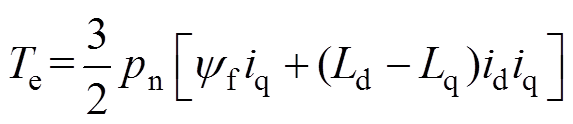 (2)
(2)运动方程为
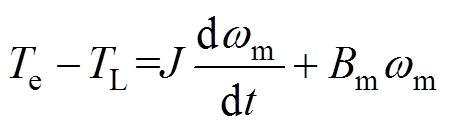 (3)
(3)
式中,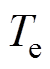 为电磁转矩;
为电磁转矩;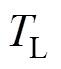 为负载转矩;pn为极对数;
为负载转矩;pn为极对数;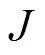 为系统的等效转动惯量;
为系统的等效转动惯量;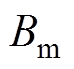 为摩擦转矩系数;
为摩擦转矩系数;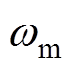 为转子机械角速度。
为转子机械角速度。
按照PMSM定子电压平衡方程,VFDC通过引入交、直轴电流的耦合量作为补偿,进而解除id、iq之间的耦合,实现电流的完全控制,其结构框图如图1所示。
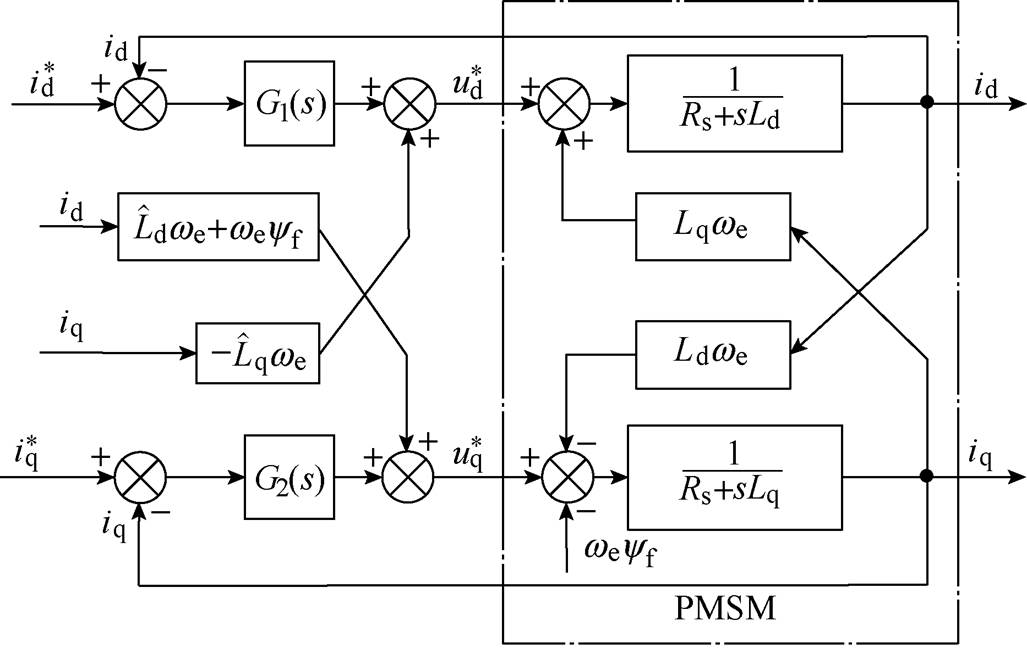
图1 电压前馈解耦控制框图
Fig.1 Structure diagram of voltage feedforward decouple controller
图1中,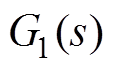 和
和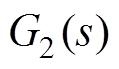 为PI控制器的传递函数,
为PI控制器的传递函数,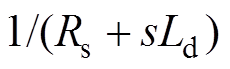 和
和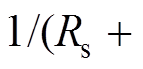
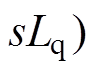 分别为d、q轴被控对象数学模型;
分别为d、q轴被控对象数学模型;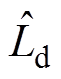 、
、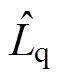 分别为d、q轴解耦控制器参数,通常选取电机正常运行时电感参数
分别为d、q轴解耦控制器参数,通常选取电机正常运行时电感参数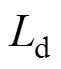 、
、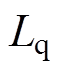 。电机电流的反馈值id、iq与给定值
。电机电流的反馈值id、iq与给定值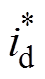 、
、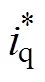 相比较,将误差经电流PI控制器调节,加上补偿量后输出方程为
相比较,将误差经电流PI控制器调节,加上补偿量后输出方程为
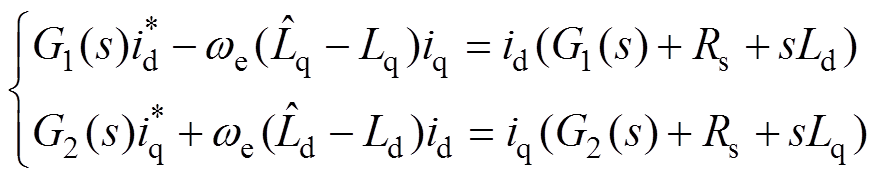 (4)
(4)由式(4)可以推导出d、q轴电流耦合方程为
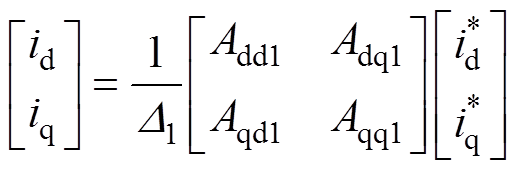 (5)
(5)
其中
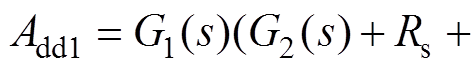
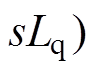
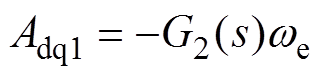
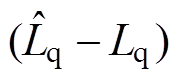
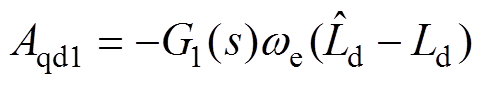
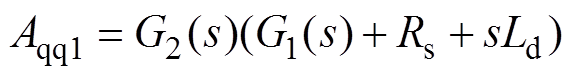
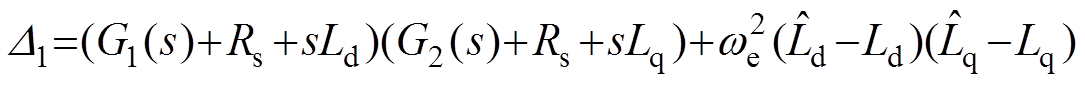
式中,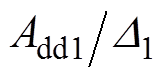 和
和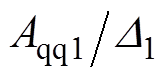 分别为d、q轴电流控制器的比例系数;
分别为d、q轴电流控制器的比例系数;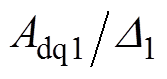 和
和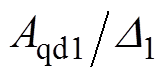 分别为d、q轴电流控制器的耦合系数。
分别为d、q轴电流控制器的耦合系数。
由式(5)的耦合系数可知,只有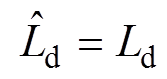 ,
,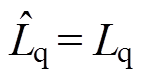 时,控制器才能实现完全解耦补偿。
时,控制器才能实现完全解耦补偿。
PMSM在正常运行时,当电感电流很大接近饱和时,电感值发生变化,一旦电感估计值与实际值失配,会使解耦不完全,系统存在耦合量。因此,VFDC方式在某些条件下并不能实现电流的独立控制。
CDDC将控制电流的给定值和反馈值的偏差生成调节电压,叠加在电流PI控制器生成的给定电压上,从而抵消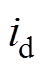 和
和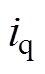 之间的耦合量,完全解除了
之间的耦合量,完全解除了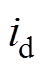 和
和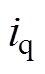 之间的耦合。电流偏差解耦控制器框图如图2所示。图中,除电流PI控制器传递函数
之间的耦合。电流偏差解耦控制器框图如图2所示。图中,除电流PI控制器传递函数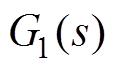 、
、 外,还需要偏差解耦控制器
外,还需要偏差解耦控制器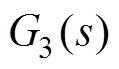 和
和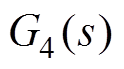 。
。
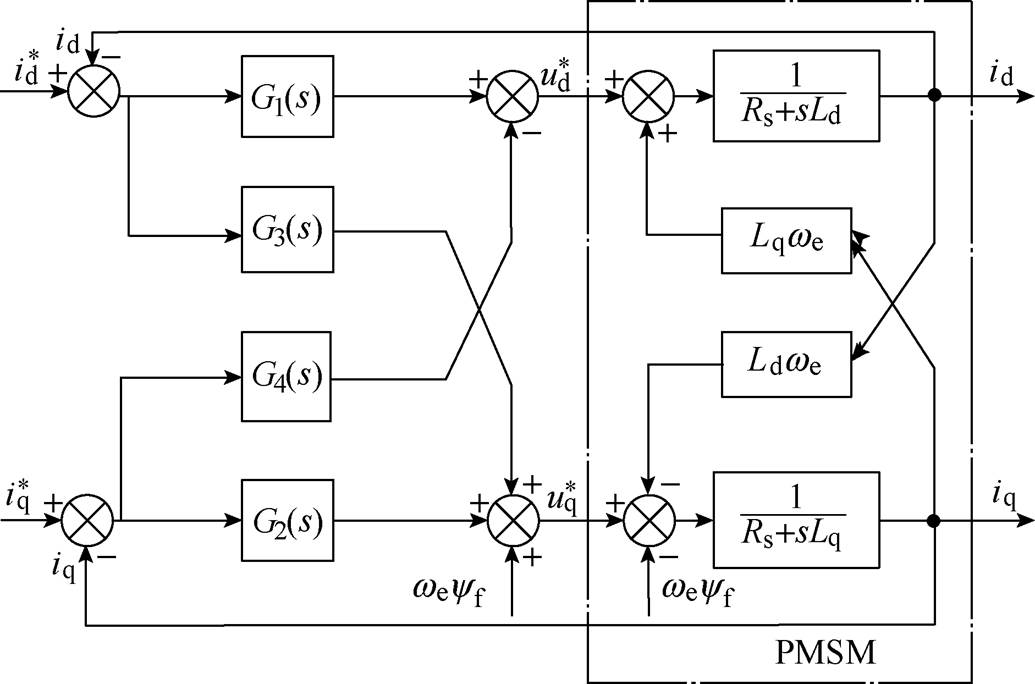
图2 电流偏差解耦控制框图
Fig.2 Structure diagram of current deviation decouple controller
由图2可得控制方程为
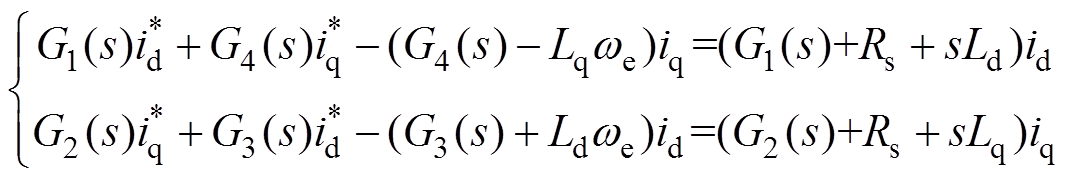 (6)
(6)式(6)整理可得
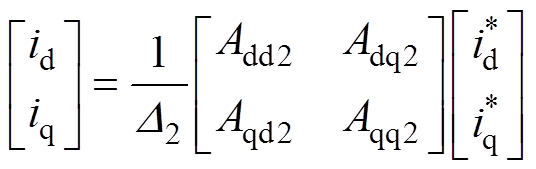 (7)
(7)
其中
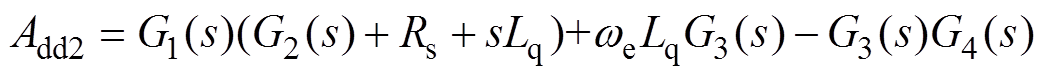
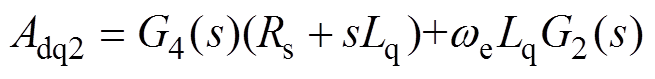
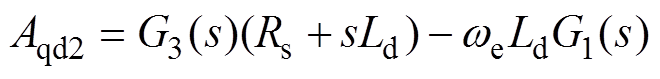
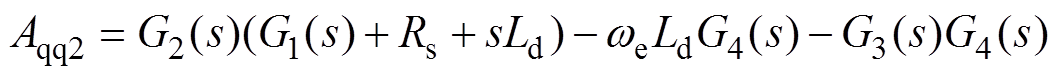
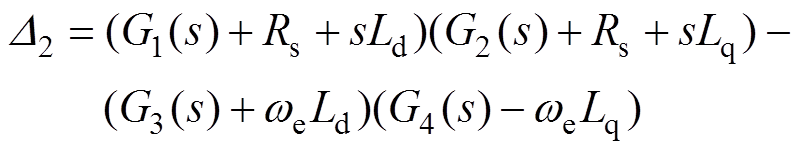
式中,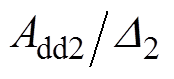 和
和 分别为d、q轴电流控制器的比例系数;
分别为d、q轴电流控制器的比例系数;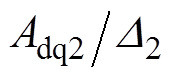 和
和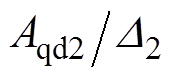 分别为d、q轴电流控制器的耦合系数。
分别为d、q轴电流控制器的耦合系数。
当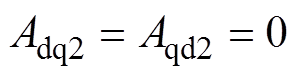 时,实现系统完全解耦,可解得解耦控制器传递函数G4(s)为
时,实现系统完全解耦,可解得解耦控制器传递函数G4(s)为
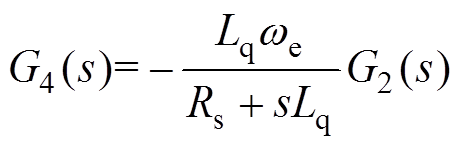 (8)
(8)同理可解得
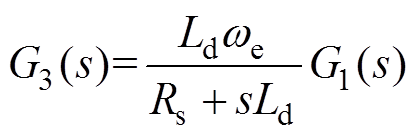 (9)
(9)
将解耦控制器的引出点后移,同时将式(8)、式(9)中控制器的电机参数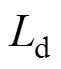 、
、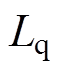 用估计值
用估计值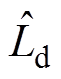 、
、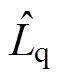 代替,所用估计值为电机正常运行时电感参数。在实际永磁同步电机控制系统中,由于温度的影响,定子电阻变化率一般在0~10%以内,电阻值的变化对解耦控制影响不大,本文暂不考虑电机电阻变化对解耦控制的影响。等效电流偏差解耦控制框图如图3所示。
代替,所用估计值为电机正常运行时电感参数。在实际永磁同步电机控制系统中,由于温度的影响,定子电阻变化率一般在0~10%以内,电阻值的变化对解耦控制影响不大,本文暂不考虑电机电阻变化对解耦控制的影响。等效电流偏差解耦控制框图如图3所示。
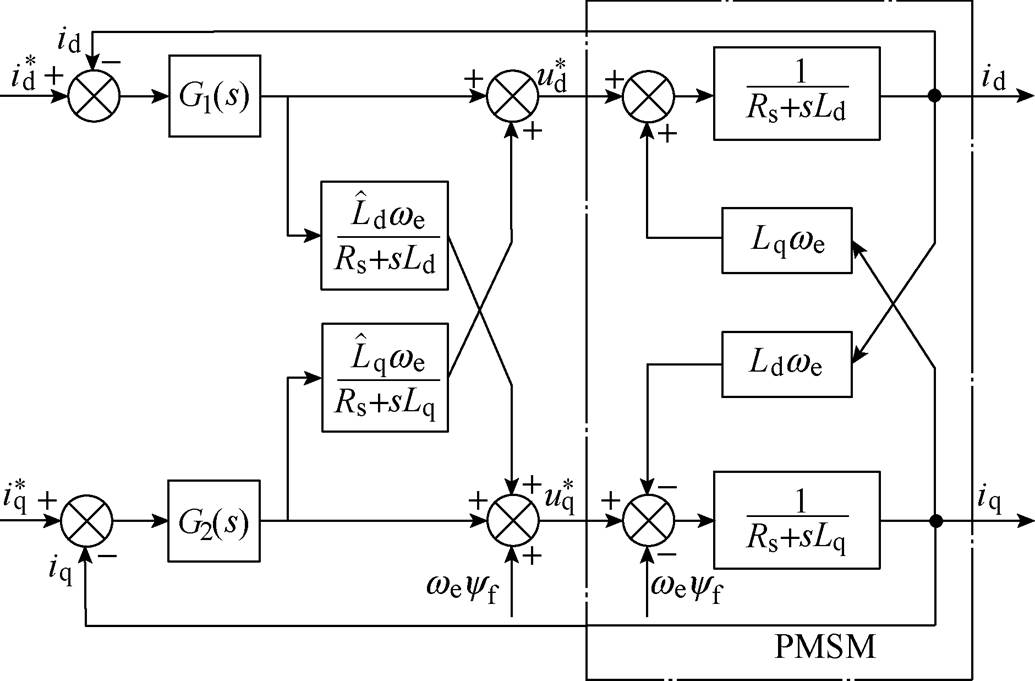
图3 等效电流偏差解耦控制框图
Fig.3 Structure diagram of equivalent current deviation decouple controller
从上述运算过程及图3可以看出,偏差解耦将电机电流的反馈值id、iq与给定值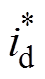 、
、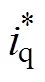 相比较,然后将误差经解耦控制器调节后叠加到输出电压中。由式(8)、式(9)的控制器传递函数可知,只有
相比较,然后将误差经解耦控制器调节后叠加到输出电压中。由式(8)、式(9)的控制器传递函数可知,只有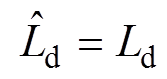 ,
,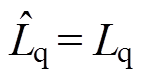 时,d、q轴间的电流耦合能被完全消除;当
时,d、q轴间的电流耦合能被完全消除;当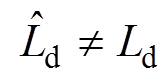 ,
,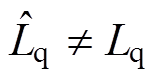 时,
时,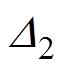 始终大于
始终大于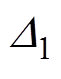 ,
, 总是小于
总是小于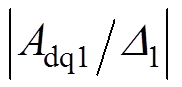 ,表明电流偏差解耦控制效果受电感参数变化的影响要小于电压前馈解耦控制,解耦效果要优于电压前馈解耦控制,但始终存在电流耦合。
,表明电流偏差解耦控制效果受电感参数变化的影响要小于电压前馈解耦控制,解耦效果要优于电压前馈解耦控制,但始终存在电流耦合。
由式(1)可知系统模型的准确度过于依赖其参数。对于电流环控制系统,将定子d、q轴电流定义为状态变量,其状态空间方程为
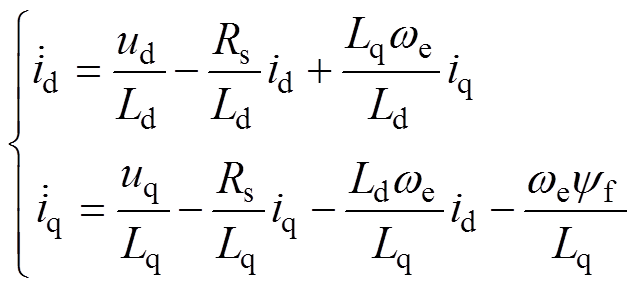 (10)
(10)通过本文第2节可知,CDDC参数取决于电机额定参数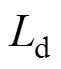 、
、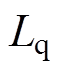 、
、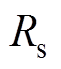 和
和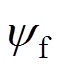 。由于电机运行情况改变,电机参数发生变化及干扰等不确定因素发生,CDDC无法很好地完全补偿解耦。本文通过设计一个电流滑模观测器,估计定子电流估计值
。由于电机运行情况改变,电机参数发生变化及干扰等不确定因素发生,CDDC无法很好地完全补偿解耦。本文通过设计一个电流滑模观测器,估计定子电流估计值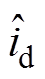 和
和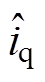 ,对电流实行更好的补偿控制。
,对电流实行更好的补偿控制。
将定子d、q轴电流作为观测对象,根据式(10)建立滑模观测器估计方程为
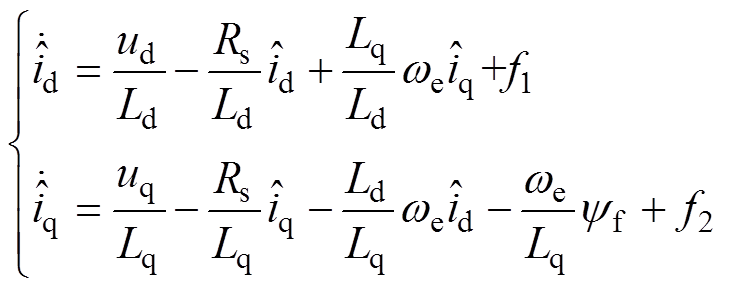 (11)
(11)电流滑模观测器控制律为
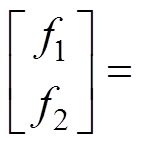
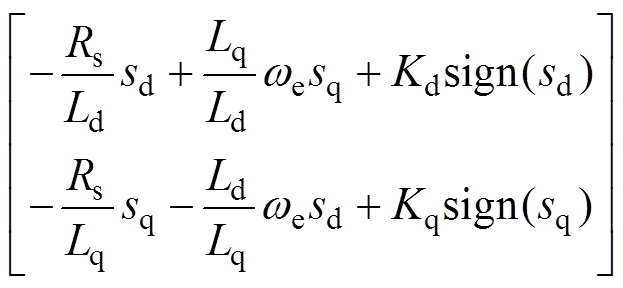 (12)
(12)
式中,Kd、Kq分别为d、q轴滑模增益;sign(x)为符号函数:x≥0,sign(x)=1;x<0,sign(x)=-1。
定义关于电流误差值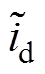 、
、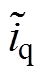 的滑模面为
的滑模面为
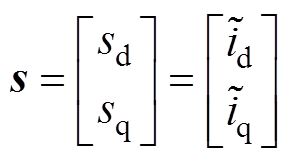 (13)
(13)式中,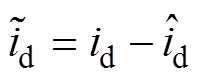 ;
;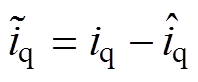 。
。
本文选择指数趋近律,表示为
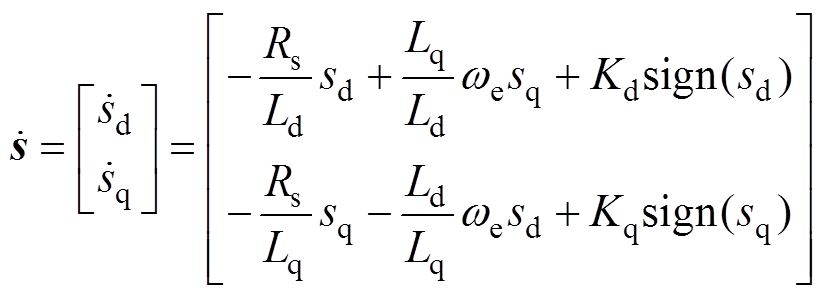 (14)
(14)按照李雅普诺夫稳定性条件,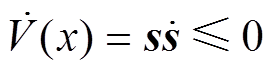 ,从可达性条件以及式(11)~式(13)可以看出
,从可达性条件以及式(11)~式(13)可以看出
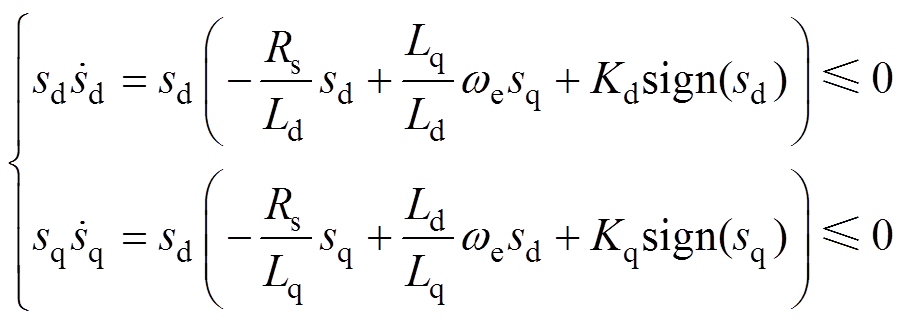 (15)
(15)只要保证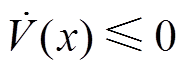 ,即可保证系统渐近稳定,则
,即可保证系统渐近稳定,则
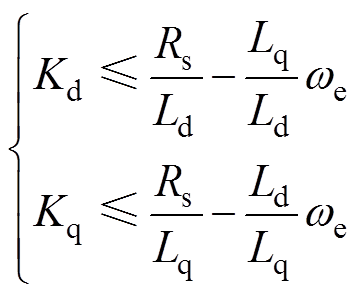 (16)
(16)
所以,只要选取适当的Kd、Kq值,系统渐近稳定,满足滑模运行条件,实现滑模观测。
根据式(10)~式(15),可得出系统电流滑模观测器的结构框图如图4所示。
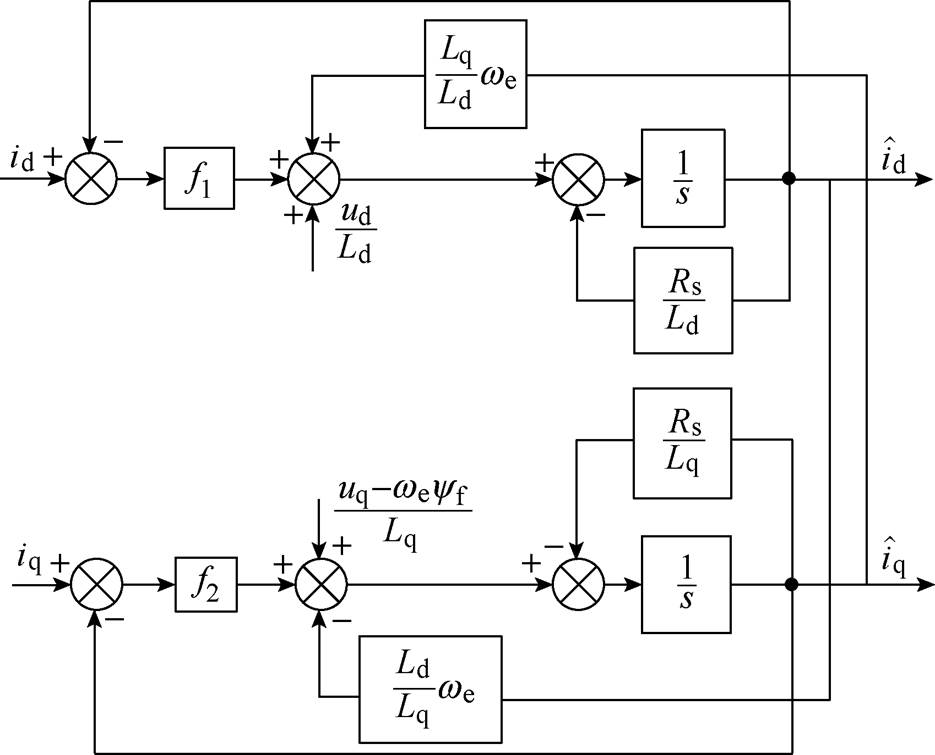
图4 系统电流滑模观测器结构框图
Fig.4 Structure diagram of current sliding mode observer
利用CSMO对d、q轴电流进行实时估算,并把估算电压量作为补偿信号反馈到逆变器输入端,以抵消扰动对系统输出的影响。
根据电流滑模观测器等效结构框图4可得控制方程为
 (17)
(17)根据式(6)及式(17),可得CDDC-CSMO的控制方程为
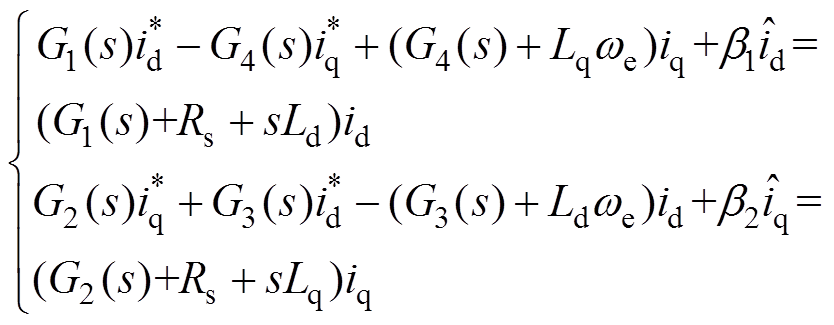 (18)
(18)
式中,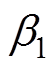 、
、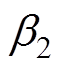 分别为d、q轴电流补偿系数。
分别为d、q轴电流补偿系数。
整理式(18)可得
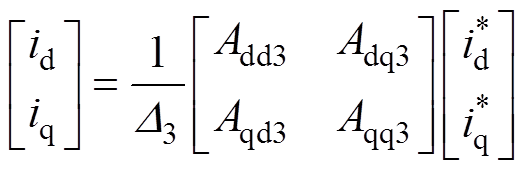 (19)
(19)其中

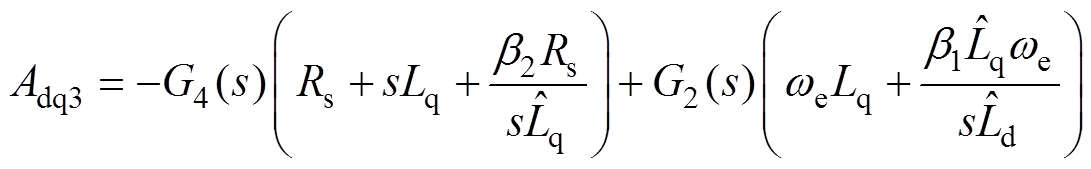
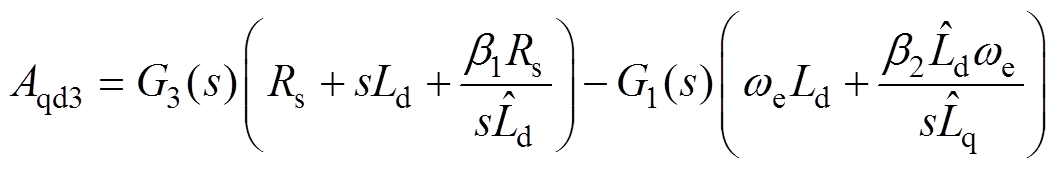
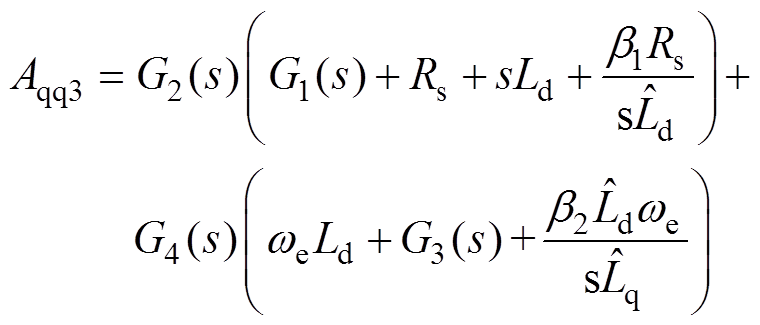
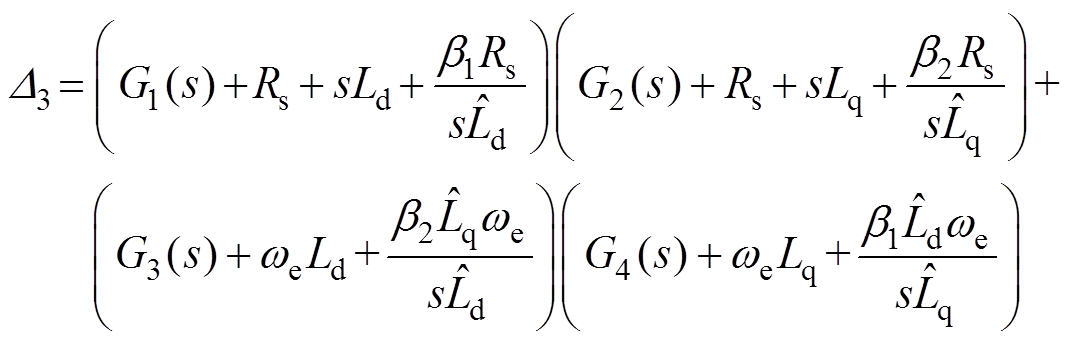
式中,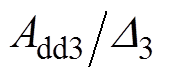 和
和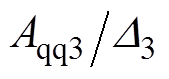 分别为d、q轴电流控制器的比例系数;
分别为d、q轴电流控制器的比例系数;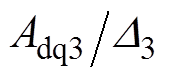 和
和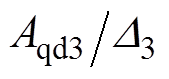 分别为d、q轴电流控制器的耦合系数。
分别为d、q轴电流控制器的耦合系数。
只有当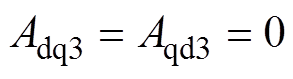 ,实现系统完全解耦,可解得等效解耦控制器传递函数G4(s)、G3(s)为
,实现系统完全解耦,可解得等效解耦控制器传递函数G4(s)、G3(s)为
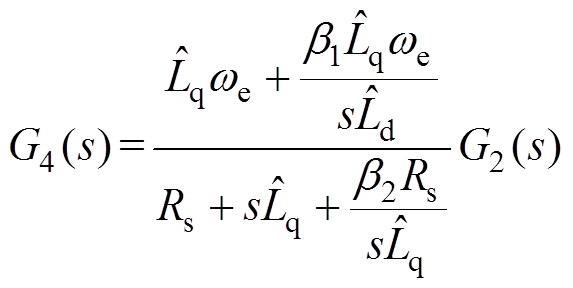 (20)
(20)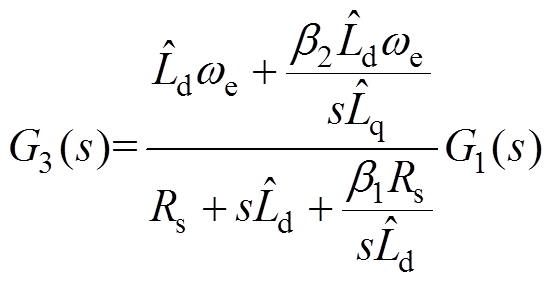 (21)
(21)
当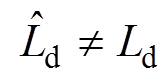 ,
,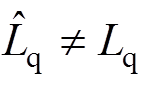 时,
时,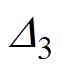 始终大于
始终大于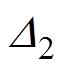 ,
,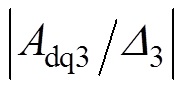 总是小于
总是小于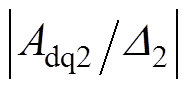 ,表明加入电流滑模观测器后的电流偏差解耦控制效果受电感参数变化的影响要小于电流偏差解耦控制,解耦效果要优于电流偏差解耦控制。
,表明加入电流滑模观测器后的电流偏差解耦控制效果受电感参数变化的影响要小于电流偏差解耦控制,解耦效果要优于电流偏差解耦控制。
解耦算法的灵敏度是指解耦算法对单位电感变化所致的电流耦合响应的变化程度。通过耦合系数对电感变化的灵敏度大小,可以判断各算法之间鲁棒性的强弱。
式(22)~式(24)分别为VFDC、CDDC和CDDC-CSMO算法灵敏度。
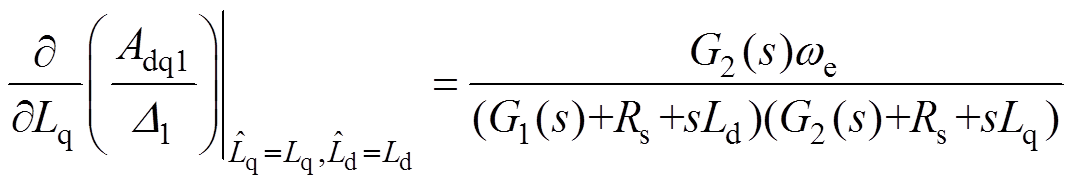 (22)
(22)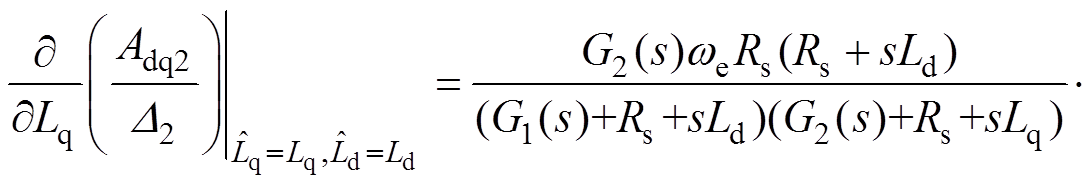
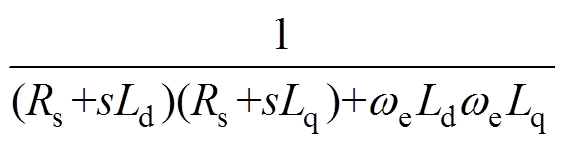 (23)
(23)
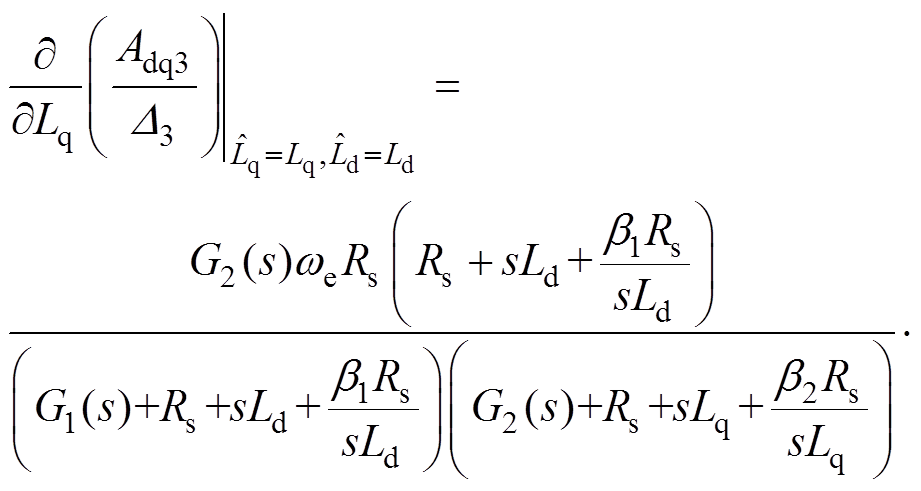
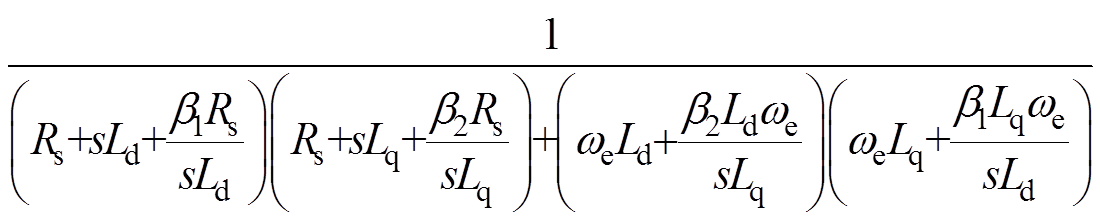 (24)
(24)
将式(24)与式(23)相减,其值小于零。由此可知,CDDC-CSMO的灵敏度比CDDC的灵敏度小,这表明加入CSMO后提高了系统对电感参数变化的鲁棒性。当电感参数变化时,CDDC-CSMO有着更好的电流解耦效果。
根据式(23)及式(22)可以得出,CDDC对电感参数变化的鲁棒性强于VFDC。验证了第2节通过解电流控制方程耦合项的方法,求得CDDC电流解耦效果要优于VFDC的准确性。
在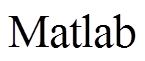 软件的环境下建立
软件的环境下建立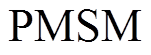 控制系统的仿真模型。输出功率为
控制系统的仿真模型。输出功率为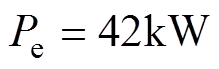 ,额定转速为
,额定转速为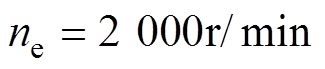 ,额定转矩为
,额定转矩为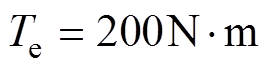 ,定子相电阻
,定子相电阻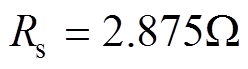 ,
, ,
,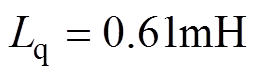 ,永磁体磁链
,永磁体磁链 ,极对数
,极对数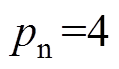 ,转动惯量
,转动惯量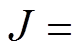
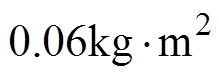 。直流电压
。直流电压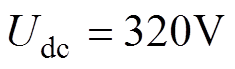 ,采样周期为Ts= 0.000 1s,仿真时间为1s。
,采样周期为Ts= 0.000 1s,仿真时间为1s。
基于滑模观测器的永磁同步电机电流偏差解耦控制系统框图如图5所示。永磁同步电机控制系统框图中控制器主要由速度控制器、电流控制器、滑模观测器、Park变换器、Park逆变换器、Clarke变换器、SVPWM模块、转子位置和速度检测模块、以及永磁同步电机环节组成。其中,电流控制器采用电流偏差解耦控制器,通过计算给定与反馈的误差,求出直接量和耦合量作为前馈给交、直轴电压输入,以实现解耦,提高系统鲁棒性。为了解决电感参数变化带来的动态解耦不完全,本文利用式(17)~式(19),将电流滑模观测器观测值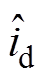 、
、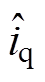 前馈补偿至电流偏差解耦控制器输出端,用于补偿解耦控制的耦合量,实现对电流环更好的补偿控制,使系统具有良好的动态特性。
前馈补偿至电流偏差解耦控制器输出端,用于补偿解耦控制的耦合量,实现对电流环更好的补偿控制,使系统具有良好的动态特性。
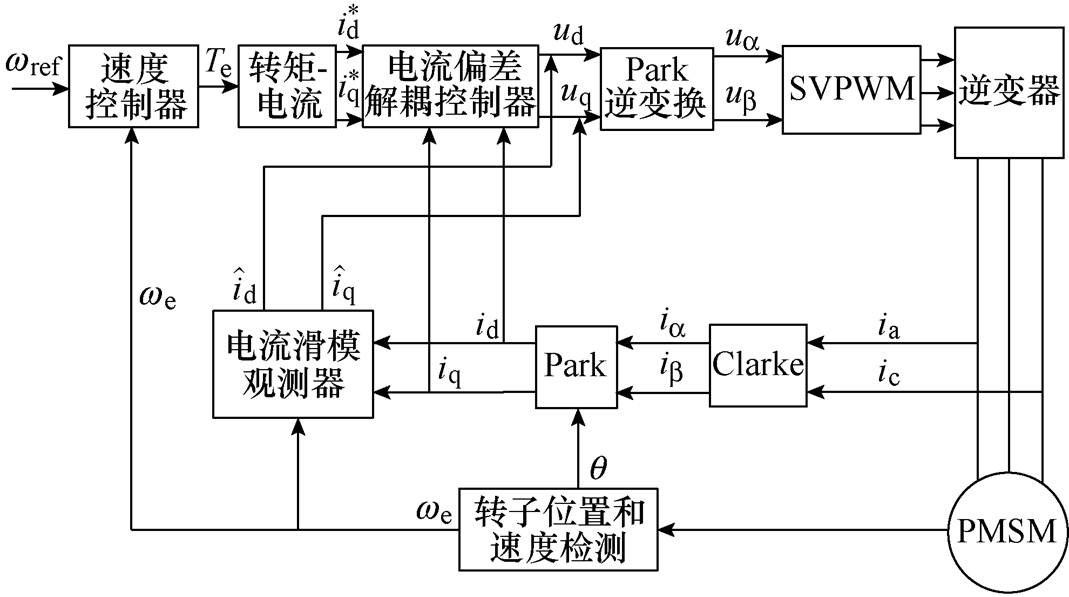
图5 永磁同步电机控制框图
Fig.5 Structure diagram of PMSM controller
图6和图7为不同解耦方法d、q轴电流动态响应仿真曲线。给定转速指令始终为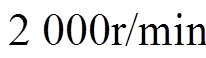 ,负载转矩为
,负载转矩为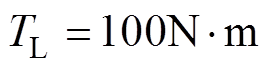 ,在
,在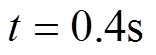 时刻突加负载转矩至
时刻突加负载转矩至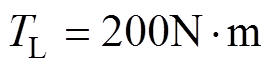 。在
。在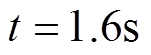 时刻突减负载转矩至
时刻突减负载转矩至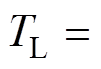
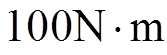 。当电机电感参数变化时,动态过程中d、q轴电流相互影响。当两种电感参数不完全匹配时,因动态解耦不完全产生不同程度的波形振荡。
。当电机电感参数变化时,动态过程中d、q轴电流相互影响。当两种电感参数不完全匹配时,因动态解耦不完全产生不同程度的波形振荡。
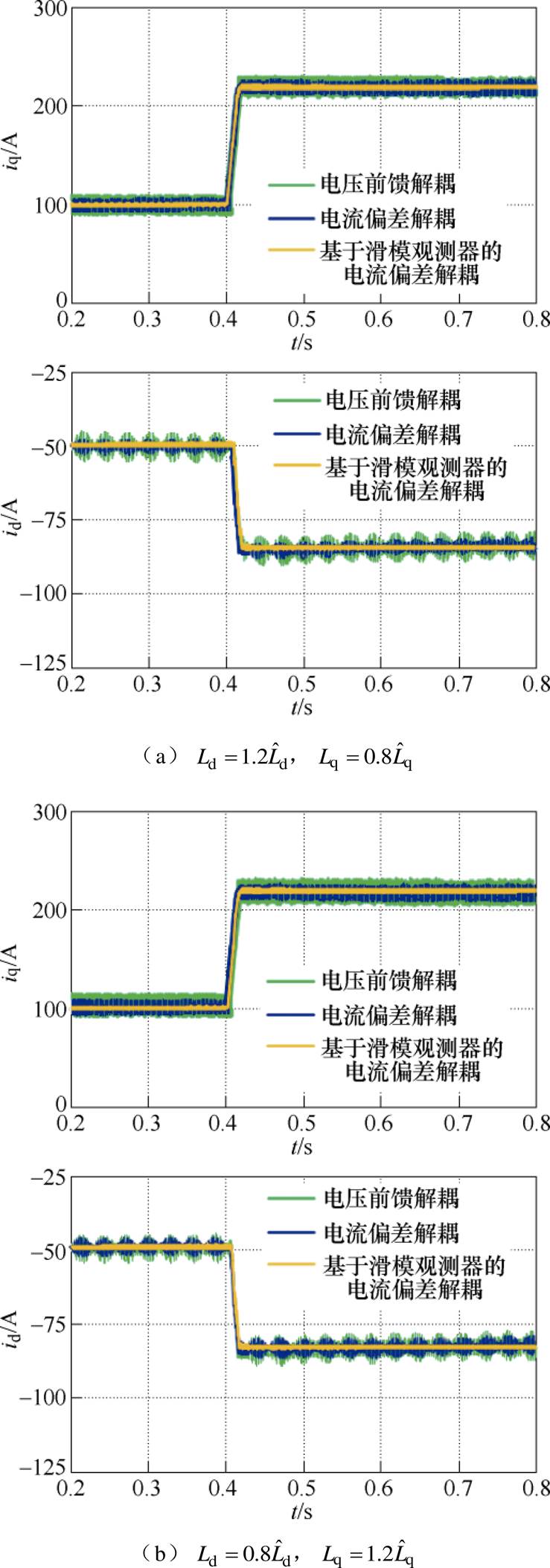
图6 突加负载动态响应仿真曲线
Fig.6 Responses of the loading simulation
仿真结果同时也证明了三种解耦控制的灵敏度的大小。电流偏差解耦的波形振荡幅值要小于电压前馈解耦。而采用基于电流滑模观测器的电流偏差解耦控制对电机参数变化的敏感度大大降低,不论电感值是否变化,CDDC-CSMO控制下,电流保持稳定,具有良好的动态解耦效果和较强的鲁棒性。
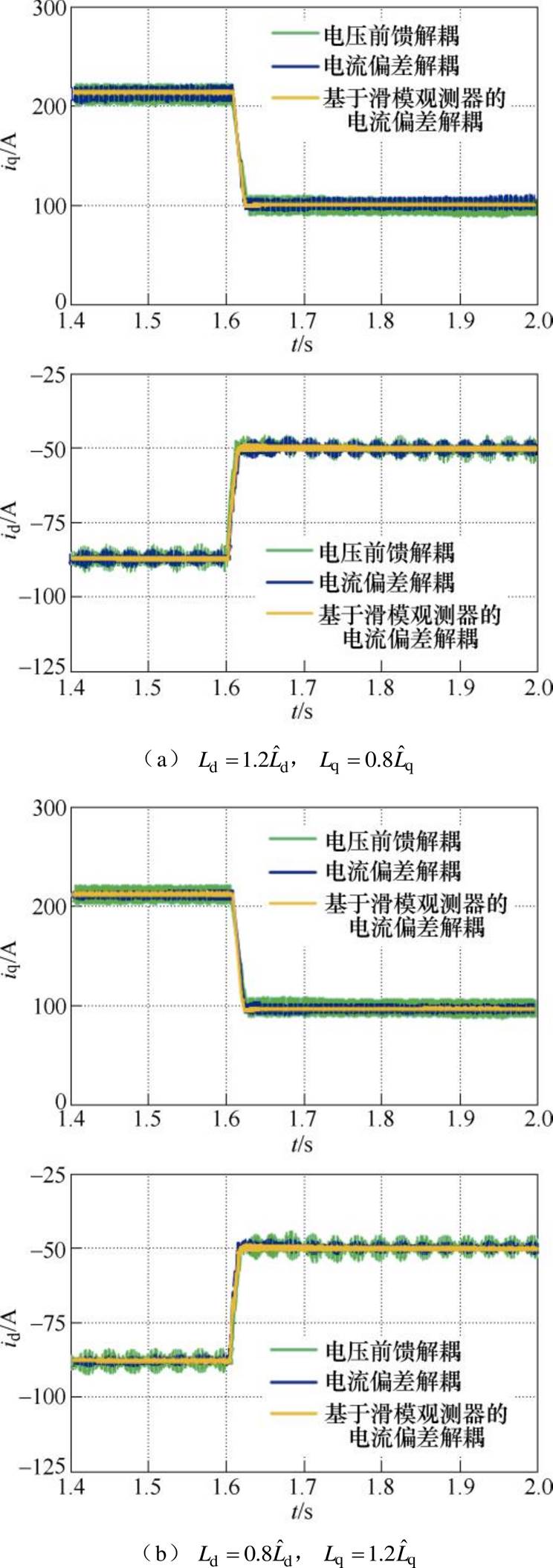
图7 突减负载动态响应仿真曲线
Fig.7 Responses of the unloading simulation
台架实验参数与系统仿真参数一致。电流滑模观测器实验参数如下:滑模增益系数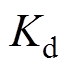 =0.01;
=0.01;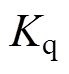 =1.0。电流PI控制器参数如下:q轴电流控制器比例系数为2.0;积分系数为0.003;d轴电流控制器比例系数为0.8;积分系数为0.003。其中,id、iq由10位D/A输出。图8~图13为电压前馈解耦控制器,电流偏差解耦控制器,以及基于电流滑模观测器的电流偏差解耦控制对负载扰动响应的对比曲线,给定速度指令
=1.0。电流PI控制器参数如下:q轴电流控制器比例系数为2.0;积分系数为0.003;d轴电流控制器比例系数为0.8;积分系数为0.003。其中,id、iq由10位D/A输出。图8~图13为电压前馈解耦控制器,电流偏差解耦控制器,以及基于电流滑模观测器的电流偏差解耦控制对负载扰动响应的对比曲线,给定速度指令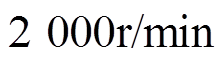 ,负载转矩为
,负载转矩为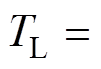
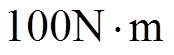 ,
,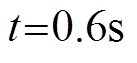 时突加负载至
时突加负载至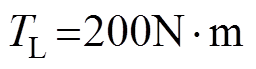 ,
,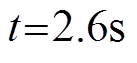 时突减负载至
时突减负载至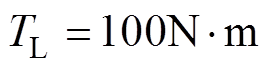 。
。
采用VFDC时系统突加负载的电流响应如图8所示。当两种电机电感参数变化时,VFDC电流响应时间较长,d、q轴电流间存在较大的稳态振荡。当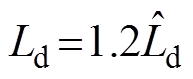 ,
,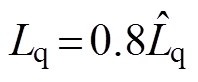 时,d、q轴电流的调节时间约为400ms;当
时,d、q轴电流的调节时间约为400ms;当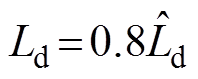 ,
, 时,d、q轴电流需要经过440ms调节达到稳态。
时,d、q轴电流需要经过440ms调节达到稳态。
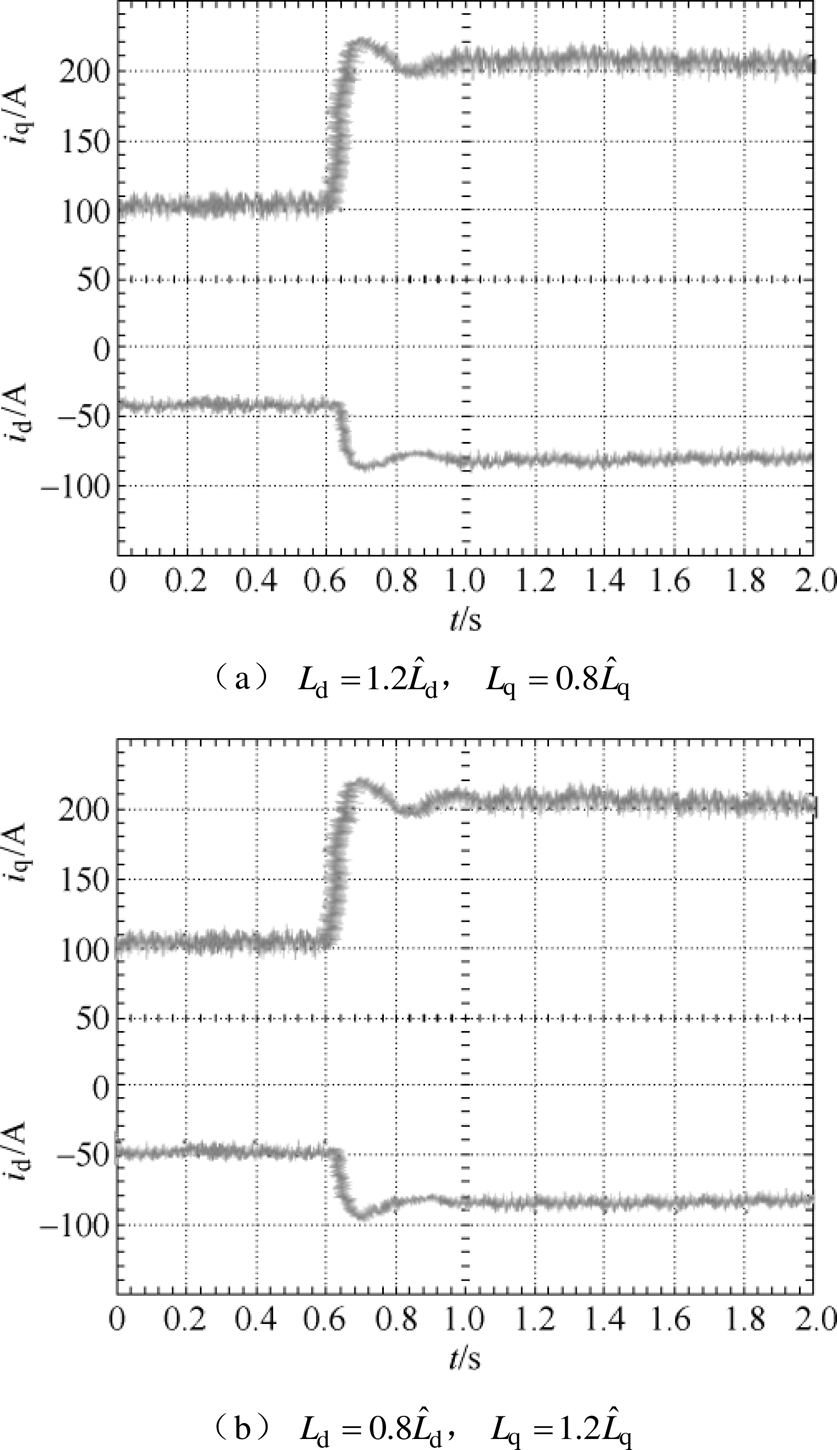
图8 突加负载电流动态响应实验波形(VFDC)
Fig.8 Response of the loading experiment waveforms (VFDC)
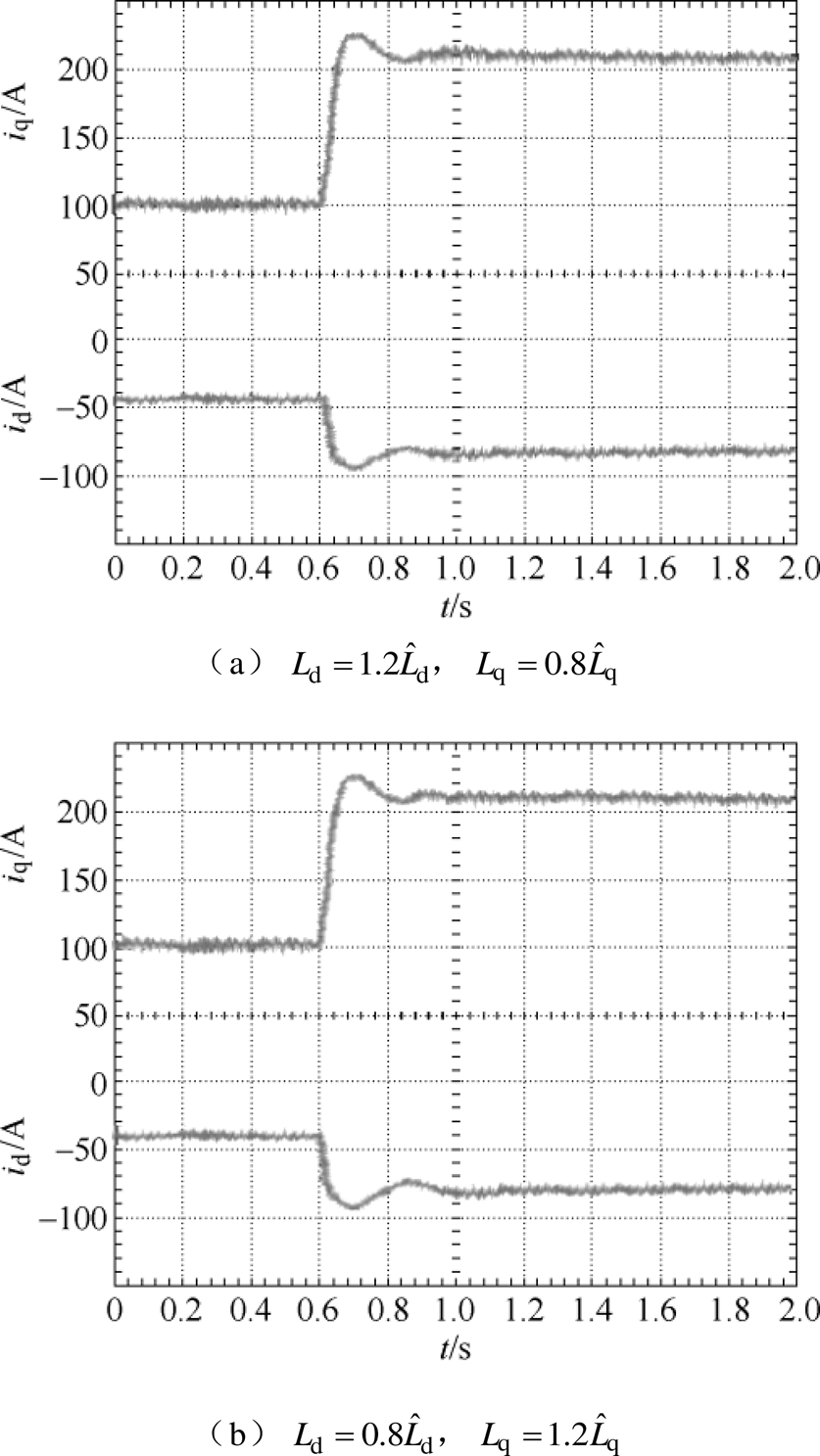
图9 突加负载电流动态响应实验波形(CDDC)
Fig.9 Response of the loading experiment waveforms (CDDC)
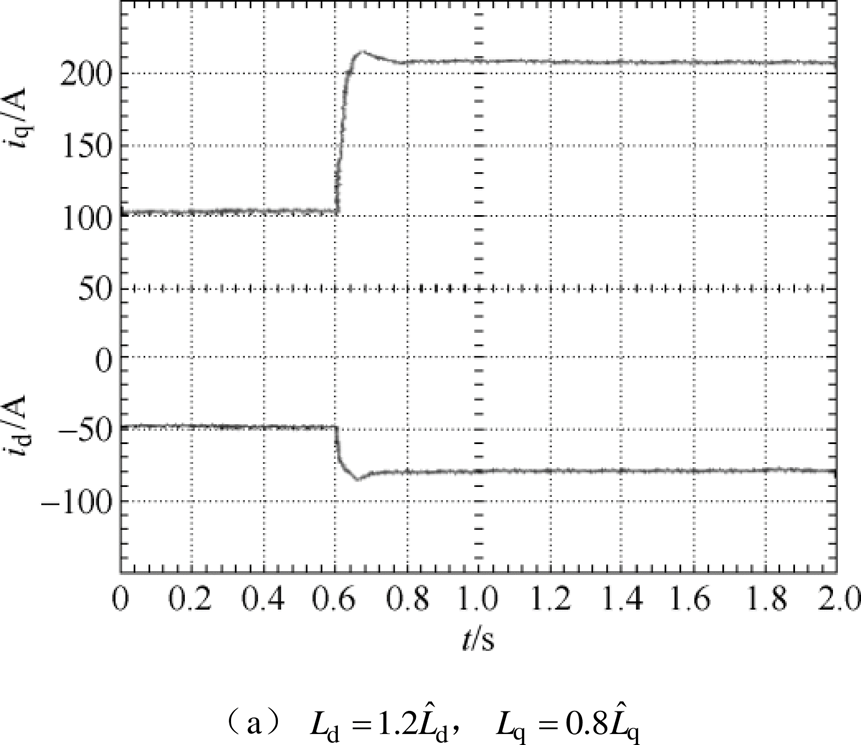
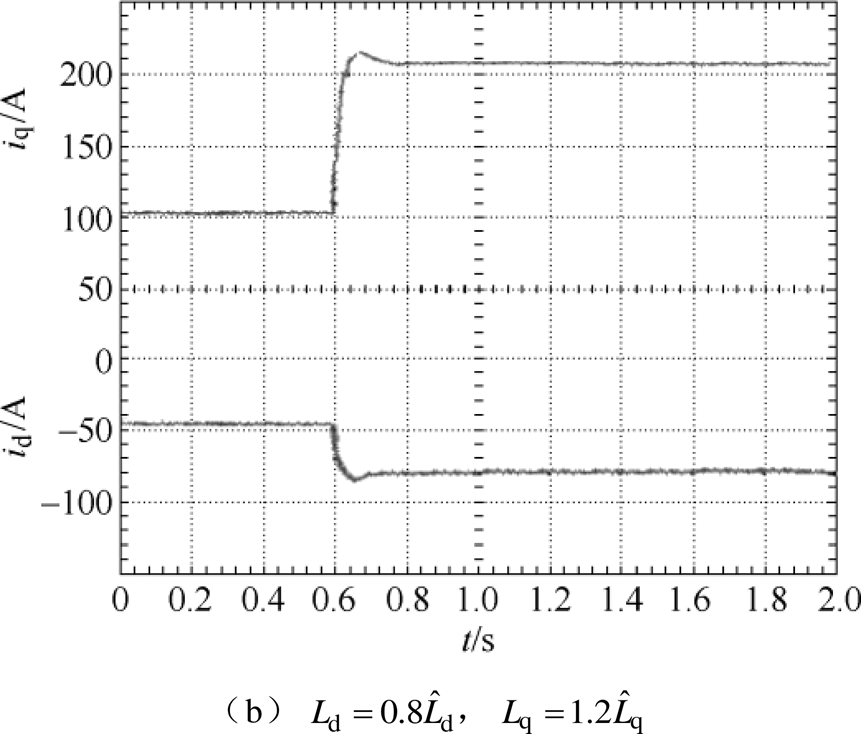
图10 突加负载电流动态响应实验波形(CDDC-CSMO)
Fig.10 Response of the loading experiment waveforms (CDDC-CSMO)
采用CDDC时系统突加负载的电流响应如图9所示。当两种电机电感参数变化时,CDDC电流响应时间较VFDC短,波动小于VFDC。当电感参数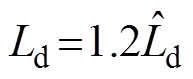 ,
,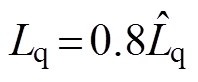 时,d、q轴电流的调节时间约为380ms;当
时,d、q轴电流的调节时间约为380ms;当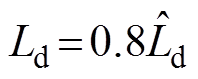 ,
, 时,d、q轴电流的调节时间约为400ms。CDDC虽然未完全实现d、q轴的电流解耦控制,但已经降低了d、q轴相互作用,并对电感参数变化有一定抗扰性。
时,d、q轴电流的调节时间约为400ms。CDDC虽然未完全实现d、q轴的电流解耦控制,但已经降低了d、q轴相互作用,并对电感参数变化有一定抗扰性。

图11 突减负载电流动态响应实验波形(VFDC)
Fig.11 Response of the unloading experiment waveforms (VFDC)
采用CDDC-CSMO时系统突加负载的电流响应如图10所示。当两种电机电感参数发生变化时,CDDC-CSMO电流响应时间较CDDC短,d、q轴电流的调节时间大约为210ms。不论电感参数是否变化,d、q轴电流间几乎不存在耦合波动,表明该方法对电感参数变化有较强的鲁棒性。
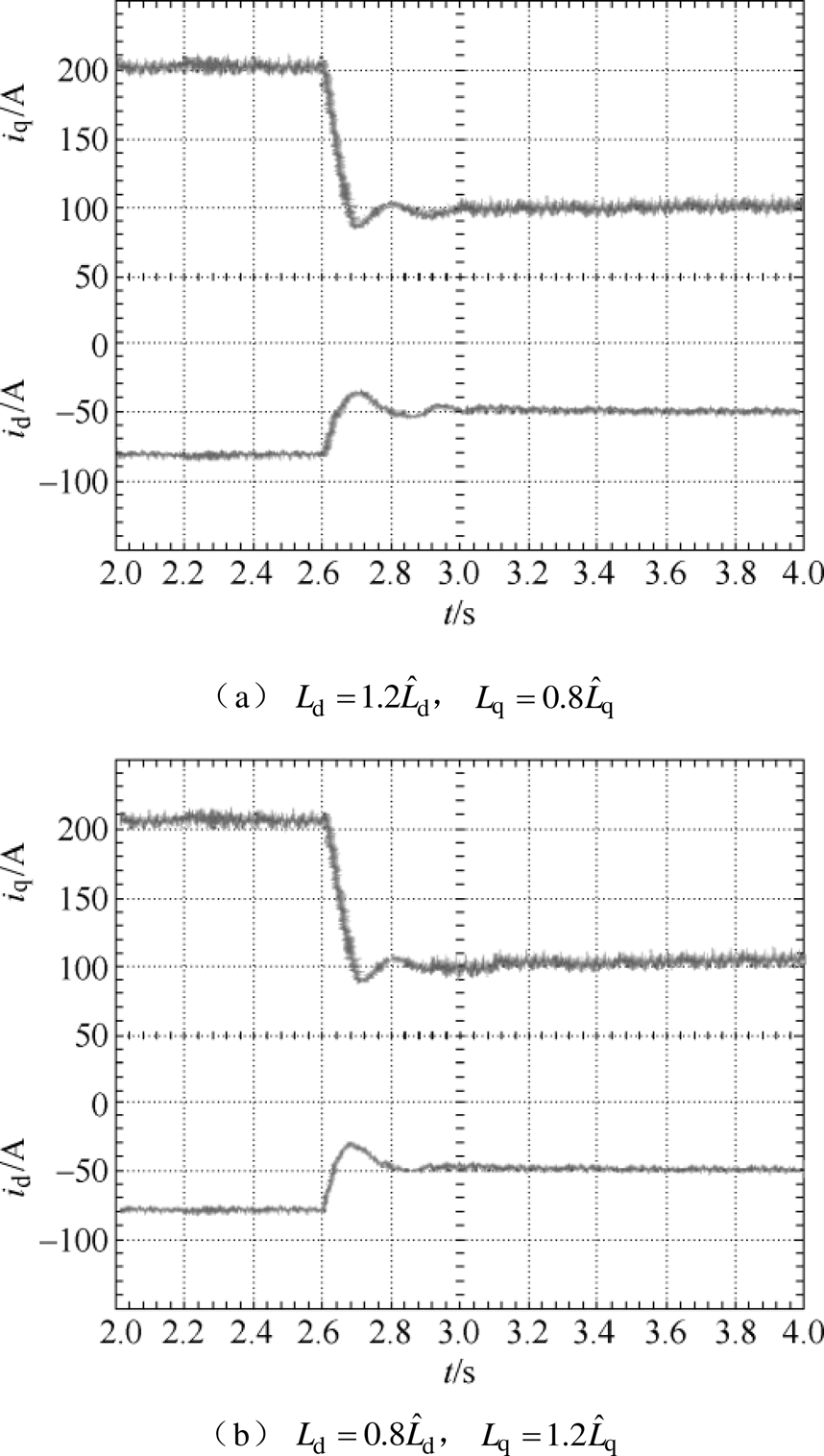
图12 突减负载电流动态响应实验波形(CDDC)
Fig.12 Response of the unloading experiment waveforms (CDDC)
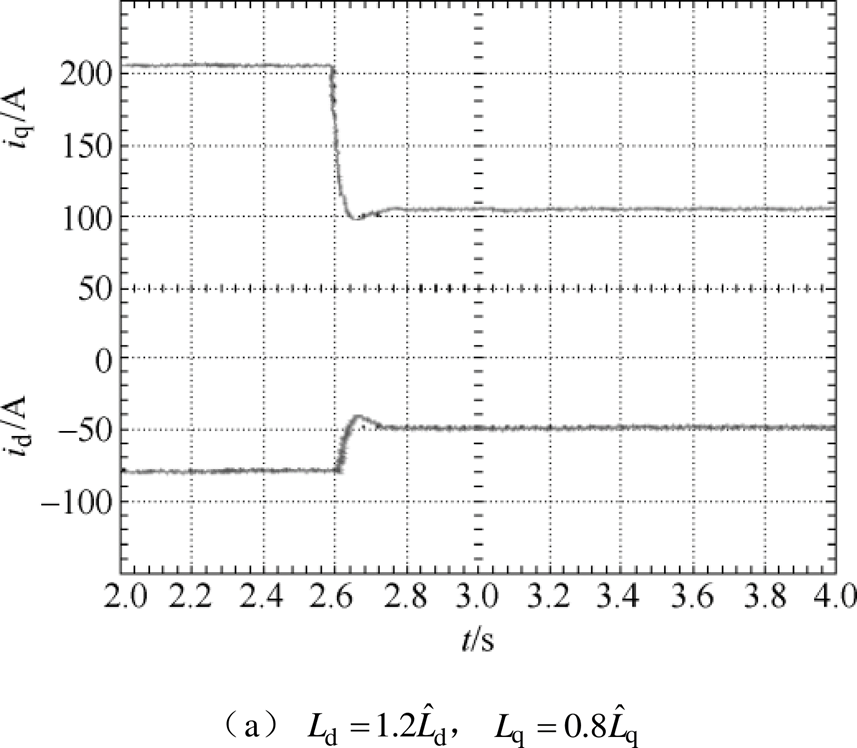

图13 突减负载电流动态响应实验波形(CDDC-CSMO)
Fig.13 Response of the unloading experiment waveforms (CDDC-CSMO)
图11~图13分别为采用VFDC、CDDC和CDDC- CSMO时系统突减负载的电流响应。从图中可以看出,CDDC-CSMO对负载干扰的响应情况要明显好于前两者,一方面由于负载突变造成响应时间明显缩短;另一方面由于耦合造成的电流波动明显减小。这是由于加入电流滑模观测器的电流偏差解耦控制器消除d、q轴电流的相互耦合,改善系统动态性能,提高了系统对电感参数变化的鲁棒性。电感参数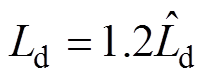 ,
,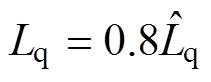 ,要比电感参数
,要比电感参数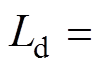
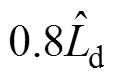 ,
,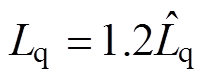 调节时间略长。
调节时间略长。
本文提出一种基于滑模观测器的永磁同步电机电流偏差解耦控制的方法。电流偏差解耦控制利用d、q轴空间状态方程,构造其耦合项多项式,有效降低了d、q轴电流间相互影响。利用滑模观测器对定子电流的跟踪特性,将定子电流的观测值反馈到系统输入端,用以补偿电流误差值,解决了偏差解耦控制与被控对象失配条件下,d、q轴之间仍有耦合项,解耦补偿不完全的现象。通过仿真与实验表明,该方法有效消除了d、q轴电流之间的相互耦合,改善了系统动态特性,提高了系统在整个动态范围内对电机参数干扰的鲁棒性。
参考文献
[1] Apoorva A, Kensuke S, Brent S G, et al. Variable flux permanent magnet synchronous machine (VF- PMSM) design methodologies to meet electric vehicle traction requirements with reduced losses[J]. IEEE Transaction on Industry Applications, 2017, 53(5): 4318-4326.
[2] Suneel K K, Michael D, Hamid R K, et al. A robust observer based sensor fault tolerant control for PMSM in electric vehicles[J]. IEEE Transaction on Industrial Electronics, 2016, 56(4): 1538-1545.
[3] 王伟华, 穆嘉毅, 符容, 等. 混合动力汽车凸极式永磁同步电机电流解耦控制[J]. 吉林大学学报: 工学版, 2017, 47(3): 693-700.
Wang Weihua, Mu Jiayi, Fu Rong, et al. Current decouple control of salient pole permanent magnet synchronous motor for hybrid electric vehicle[J]. Journal of Jilin University: Engineering and Tech- nology Edition, 2017, 47(3): 693-700.
[4] Song Shuai, Sun Ling. Research on the internal modal decouping control of VSC-MTDC[J]. The Journal of Engineering, 2019, 16: 3359-3364.
[5] 周志刚. 一种感应电机的解耦控制方法[J]. 中国电机工程学报, 2003, 23(2): 121-125.
Zhou Zhigang. A induction motor decouple control method[J]. Proceedings of the CSEE, 2003, 23(2): 121-125.
[6] Briz F, Degner M W, Lorenz R D. Analysis and design of current regulators using complex vectors[J]. IEEE Transactions on Industry Applications, 2000, 36(3): 817-825.
[7] Xia Changliang, Guo Chen, Shi Tingna. A neural- network-identifier and fuzzy-controller-based algorithm for dynamic decoupling control of permanent-magnet spherical motor[J]. IEEE Transactions on Industrial Electronics, 2010, 57(8): 2868-2878.
[8] 李春鹏, 贲洪奇, 刘博, 等. 采用扰动观测器的偏差解耦控制方法[J]. 中国电机工程学报, 2015, 35(22): 5859-5868.
Li Chunpeng, Ben Hongqi, Liu Bo, et al. Deviation decouple control method based on disturbance observer[J]. Proceedings of the CSEE, 2015, 35(22): 5859-5868.
[9] 黄宴委, 熊少华. 基于内模控制的永磁同步电机电流环观测器设计[J]. 中国电机工程学报, 2016, 36(11): 3070-3075.
Huang Yanwei, Xiong Shaohua. An internal model control-based observer for current loops in permanent magnet synchronous motors[J]. Proceedings of the CSEE, 2016, 36(11): 3070-3075.
[10] 林茂, 李颖晖, 吴辰, 等. 基于滑模模型参考自适应系统观测器的永磁同步电机预测控制[J]. 电工技术学报, 2017, 32(6): 156-163.
Lin Mao, Li Yinghui, Wu Chen, et al. A model reference adaptive system based sliding mode observer for model predictive controlled magnet synchronous motor drive[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 156-163.
[11] Liu Xudong, Yu Haisheng, Yu Jinpeng, et al. Combined speed and current terminal sliding mode control with nonlinear disturbance observer for PMSM drive[J]. IEEE Access, 2018, 6: 29594-29601.
[12] 钟泽航, 杨俊华. 双馈风力发电机转子电流滑模变结构观测器运行研究[J]. 微特电机, 2016, 7(44): 72-76.
Zhong Zehang, Yang Junhua. Operation of DFIG rotor current observer based on sliding mode variable structure controller[J]. Small & Special Electrical Machines, 2016, 7(44): 72-76.
[13] Yasser A R I M, Ehab F E S. A current control scheme with an adaptive internal model for torque ripple minimization and robust current regulation in PMSM drive systems[J]. IEEE Transactions on Energy Conversion, 2008, 23(1): 92-100.
[14] 王晓东, 李凯凯, 刘颖明, 等. 基于状态观测器的风电机组单机储能系统虚拟惯量控制[J]. 电工技术学报, 2018, 33(6): 1257-1264.
Wang Xiaodong, Li Kaikai, Liu Yingming, et al. Virtual inertia control of energy storage system in wind turbine based extended state observer[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1257-1264.
[15] 赵希梅, 金鸿雁. 基于Elman神经网络的永磁直线同步电机互补滑模控制[J]. 电工技术学报, 2018, 33(5): 973-979.
Zhao Ximei, Jin Hongyan. Complementary sliding mode control for permanent magnet linear synchronous motor based on Elman neural network[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(5): 973-979.
[16] 陈勇, 高玉文, 陈章勇. 一种自适应同步滤波器和正交锁相环相结合的滑模观测器[J]. 电工技术学报, 2018, 33(2): 265-273.
Chen Yong, Gao Yuwen, Chen Zhangyong. A sliding mode observer based on combination of adaptive synchronization filter and quadrature phase locked loop[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 265-273.
[17] 赵希梅, 王晨光. 永磁直线同步电机的自适应增量滑模控制[J]. 电工技术学报, 2017, 32(11): 111-117.
Zhao Ximei, Wang Chenguang. Adaptive incremental sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Elec- trotechnical Society, 2017, 32(11): 111-117.
Current Deviation Decoupling Control with a Sliding Mode Observer for Permanent Magnet Synchronous Motor
Abstract In this paper, a permanent magnet synchronous motor current controller based on a sliding mode observer is proposed for improving the robustness to parameter perturbations and load disturbances. By calculating the current deviation decoupling control coupling term, it is found that the deviation decoupling coupling term is simple compared with the conventional voltage feed-forward decoupling. It solves the unsatisfactory decoupling effect of the conventional voltage feed-forward decoupling control. Through the tracking characteristics of the current sliding mode observer, the estimated value of the stator current is taken as a state variable and fed back to the system input terminal to compensate the current error value. This method not only achieves better compensation control for the current loop, but also completely decouples the d and q axis currents, ensuring the dynamic response speed of the system and improving the immunity of the system. The proposed controller is found to be more effective than the conventional controller through simulations and experiments.
keywords:Permanent magnet synchronous motor (PMSM), voltage feed-forward decoupling control (VFDC), current deviation decoupling control (CDDC), current sliding mode observer (CSMO)
中图分类号:TM341
DOI: 10.19595/j.cnki.1000-6753.tces.181585
黑龙江省自然科学基金资助项目(E2017053)。
收稿日期 2018-10-08
改稿日期 2018-12-24
刘宇博 男,1989年生,博士研究生,研究方向为新能源汽车充电系统及电机驱动控制。E-mail: yubo_ryan@yahoo.com(通信作者)
王旭东 男,1958年生,博士,教授,博士生导师,研究方向为汽车工程与汽车电子的理论研究与实践、混合动力系统研究与利用。E-mail: wxd6158@163.com
(编辑 赵 鹏)