（1）摘要 针对开关磁阻电机（SRM）电感特殊点无位置控制方法受磁饱和的影响，导致三相电感交点（即特殊点）偏移使位置估计不准确的问题，提出了带有误差补偿的电感特殊点无位置控制方法。该方法针对交点偏移提出了补偿策略，在不同负载转矩下分别测量了电感曲线交点所对应的角度，并采用傅里叶拟合建立了负载转矩与角度的函数关系，进而推算出要补偿的角度误差。在磁饱和的情况下，通过误差补偿来减小交点偏移导致的误差，使位置估计更加准确。为了验证所提算法的有效性和正确性，以一台三相12/8极SRM为控制对象，对新方案和传统方案分别进行了仿真和实验。结果表明，新方案有效地减小了交点偏移导致的误差，使转子位置估计更加 准确。
关键词：开关磁阻电机 无位置控制 转子位置 磁饱和
开关磁阻电机（Switched Reluctance Motor, SRM）具有结构简单、成本低、调速范围广、可靠性高等优势，在电动汽车及航空工业等领域具有重要的应用价值[1-2]。对于SRM控制系统，准确的位置信息是实现SRM可靠运行的必要前提。在目前应用中，大多采用机械式位置传感器来获取位置信息，不仅成本高而且增加系统的复杂性；另外在一些高温、高粉尘等恶劣的环境下无法使用，极大地限制了SRM的应用领域。因此，研究精准、实用的无位置传感器技术具有重要的意义[3]。
近20年来，国内外学者针对如何准确的估计转子位置进行了广泛研究，并提出了一些控制方法，这些方法通过相绕组的电流、电压、磁链或者电感信息来估算出转子位置。有学者利用神经网络来训练样本数据，建立磁链、转子位置、电流之间非线性关系来实现无位置运行[4-6]，该方法不需要考虑电机复杂的电磁关系，但需要准确的数据和大量的训练时间，且实时性较差。部分学者提出磁链查表法，通过建立转子位置、电流、磁链之间的三维表格，并利用查表法得到转子位置[7-9]。这种方法基于实测样机数据而建立，准确度较高，但该方法需要预先存储大量的数据，占用内存。因此，文献[10-11]提出了简化磁链法，该方法只需预先存储换相点的磁链值就可以实现无位置运行，大大减小了内存，但降低了精度。由于电感和电机电流与磁链的非线性映射关系，部分学者提出利用电感辨识电机位置的方法。文献[12]提出了电感线性区模型法，该方法利用三相电感逻辑关系来辨识电感线性区，并通过建立电感和角度关系的数学模型来计算转子位置。在文献[13-14]的基础上，文献[15]在通过计算相电流的斜率差来获取相电感信息，再通过设置电感的阈值点对电感进行分区来选择导通相实现无位置运行。文献[16]提出了电感分区式无位置传感器技术，该方法利用电感随转子位置变化而周期性变化的特点，对电感进行分区并通过逻辑关系来辨识转子位置区间，发出对应的位置脉冲信号，进而估算转子位置。文献[15-16]提出的无位置控制技术均没有考虑到磁饱和对位置估计产生的影响，由于SRM在实际运行中，相绕组通常工作在磁饱和状态下，具有很强的非线性。若不考虑磁饱和影响，文献[12]会导致线性区电感发生偏移，文献[15]会导致电感阈值点发生改变，文献[16]会导致电感分区发生改变，因此最终都会使转子位置估计不准确，电机不能可靠运行。
因此，针对磁饱和影响导致无位置控制技术估计误差变大的问题，文献[17]提出了改进的电感分区式无位置传感器技术。该方法虽然从数学角度求出了受磁饱和影响导致的角度误差，但在电机带载运行或负载突变时，电感曲线会发生畸变，所选取的线性区域会发生改变，仍然具有一定的局限性。文献[18]提出了基于特殊位置点的无位置控制策略，该方法将受磁饱和影响较大的交点忽略，只利用受磁饱和影响较小的点来估计转子位置，有效地减小了估计误差，但是由于用来估计转子位置的特殊位置点变少，在转速较低或者转速不稳定的情况下，会使算法的准确度降低。文献[19]采用函数拟合来获取交点角度和电流的关系，并根据实际采样电流值来计算交点的位置实现无位置运行，但该方法容易受电流采样不准的影响使转子位置估计不准确，需要较高精度的电流传感器。
本文在传统电感特殊点无位置控制方法的基础上，针对电机实际运行时受磁饱和影响导致电感曲线交点偏移的问题，提出了新的改进策略。该方法只需在不同负载转矩下测量交点所对应的角度，并采用傅里叶拟合来建立负载转矩和角度的函数关系，进而推算出要补偿的角度误差。当负载转矩为零或者较小时，采用传统方法估计位置；当负载转矩变大时，采用改进后的方法对误差角度进行补偿，进而使位置估计更加准确。仿真和实验结果表明，SRM在稳态运行、带载运行、转矩突变的情况下，该方法均能够提高传统估计方法的精度。
本文选用三相12/8极SRM作为整个系统的控制对象，传统的“准线性”模型对于磁链的分段线性化处理未能充分表征相磁链（或相电感）原有的非线性特性，为了实现高精度控制，必须建立电机的非线性模型。SRM的基本方程包括电路方程、机械方程和运动方程，即
（1）其中
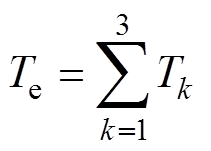
式中，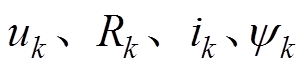
分别为电机定子第
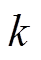相绕的电压、电阻、电流和磁链；
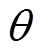为电机转子转过的角度；
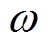为电机角速度；
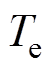为总电磁转矩；
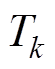为相电磁转矩；
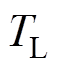为电机负载转矩；
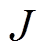为电机转动惯量；
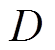为黏性摩擦因数。
SRM的第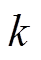相电感的表达式为
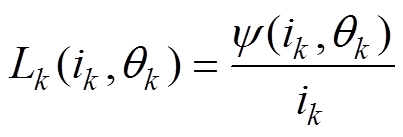（2）式中，qk为第k相电感对应的角度；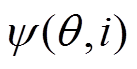
为电机磁链。
根据虚位移原理，SRM在任一运行点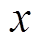
处的瞬时转矩方程可以表示为
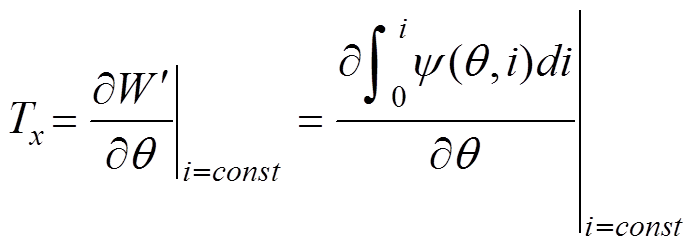（3）式中，
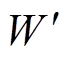为磁共能。
本文通过堵转实验测得电机的磁链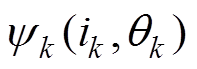
和转矩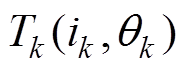
特性，再根据SRM的基本方程搭建本体仿真模型。图1a为堵转实验平台，图1b为实验所测得的SRM非线性磁链特性曲线图。图2为搭建的A相本体仿真模型，该模型中SRM的电感
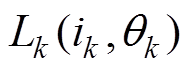和转矩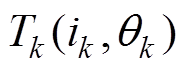特性数据表是由实验测得的磁链特性数据并根据式（2）和式（3）推导得来的。
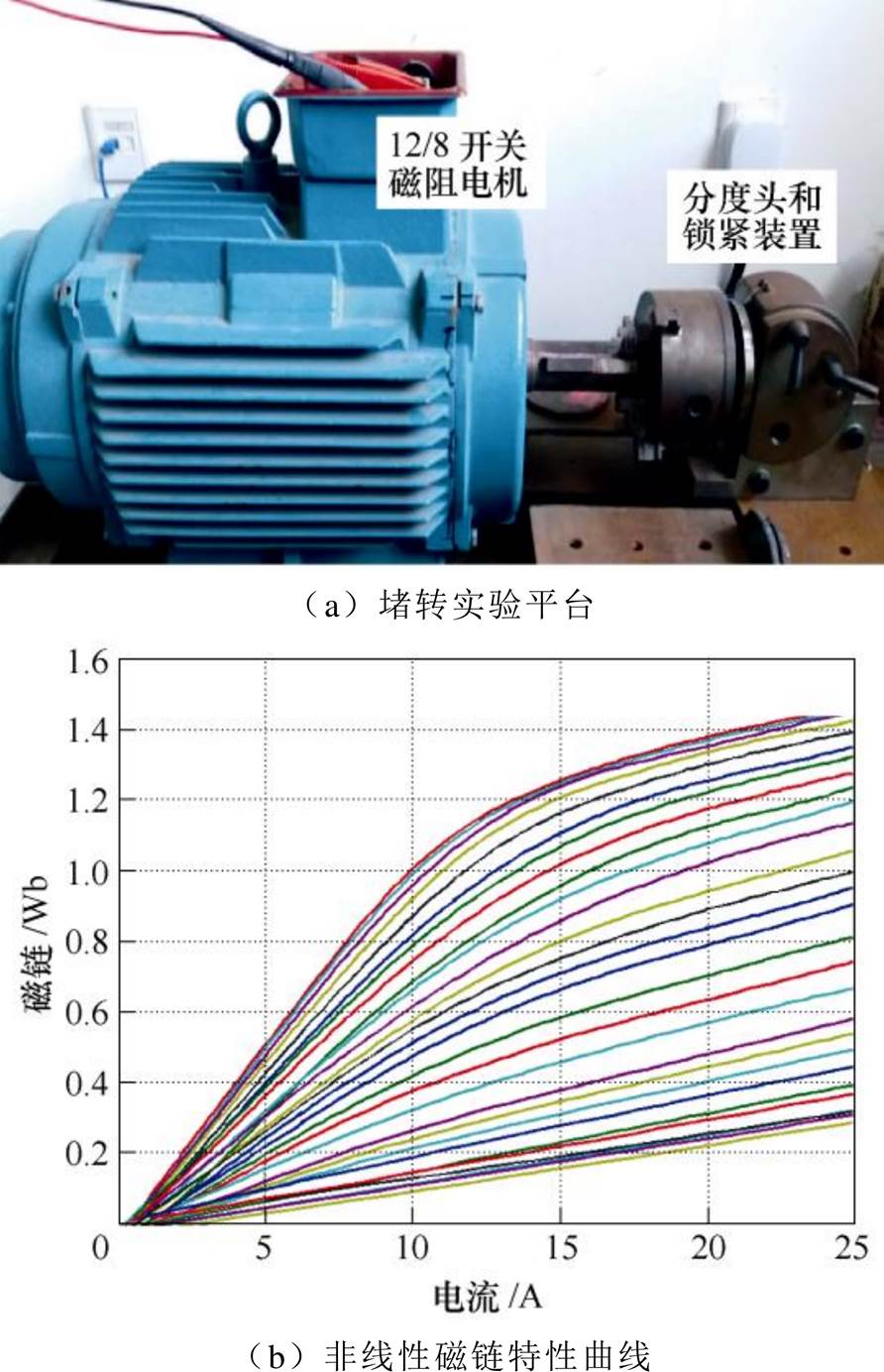
图1 堵转实验平台和磁链特性曲线
Fig.1 Platform of locked rotor test and flux curves of SRM
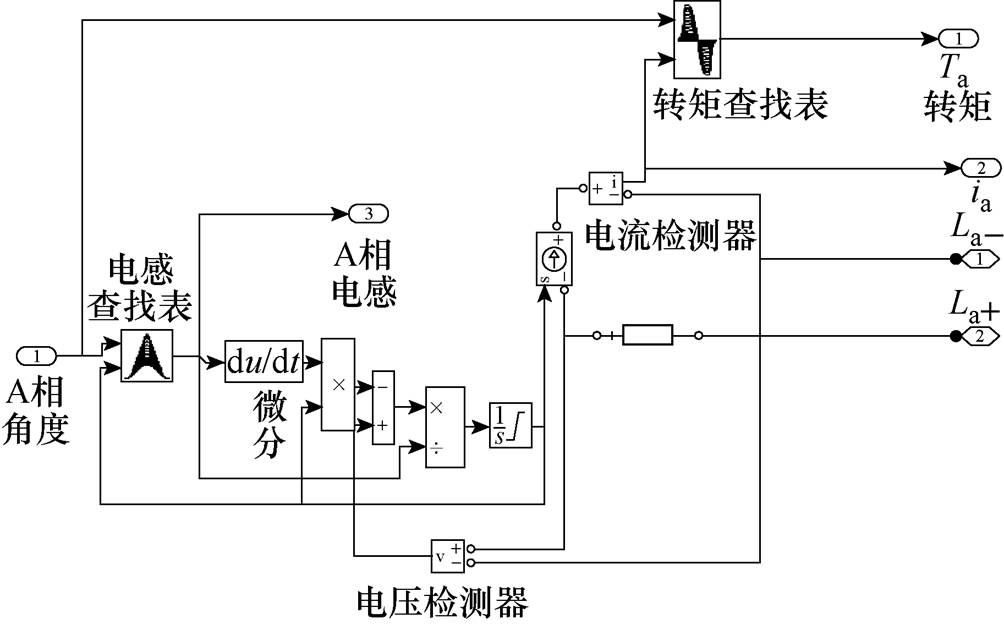
图2 SRM本体仿真模型（A相）
Fig.2 Simulation model of SRM（A-phase）
SRM各相绕组的电感随转子位置的变化而周期性变化，在电机运行时，向非导通相注入高频脉冲即可获取全周期电感信息。以三相12/8极SRM为例，若不考虑磁饱和影响，三相电感的交点示意图如图3所示。在B相电感的一个机械周期45°内，共有6个交点，相邻两个交点间隔的角度为7.5°，6个交点分别对应6个不同的角度，其中B相与C相相交于点1，对应B相的角度为7.5°；A相与B相相交于点2，对应的角度为15°。以此类推，交点3～交点6分别对应的角度为22.5°、30°、37.5°和45°。因此，电机每转一圈就有48个特殊位置点，可以通过48个交点来实时估算电机转速和转子位置角。
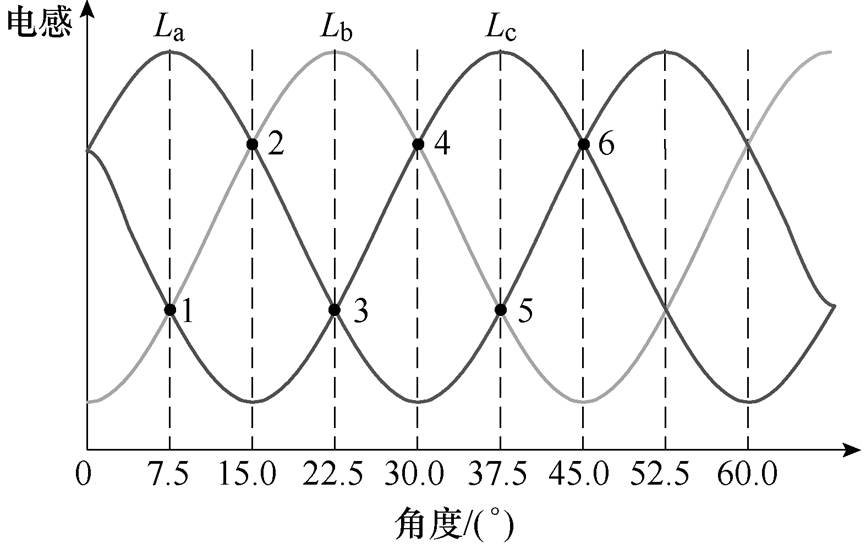
图3 三相电感交点示意图（忽略磁饱和）
Fig.3 Diagram of three-phase inductance intersection points (ignoring magnetic saturation)
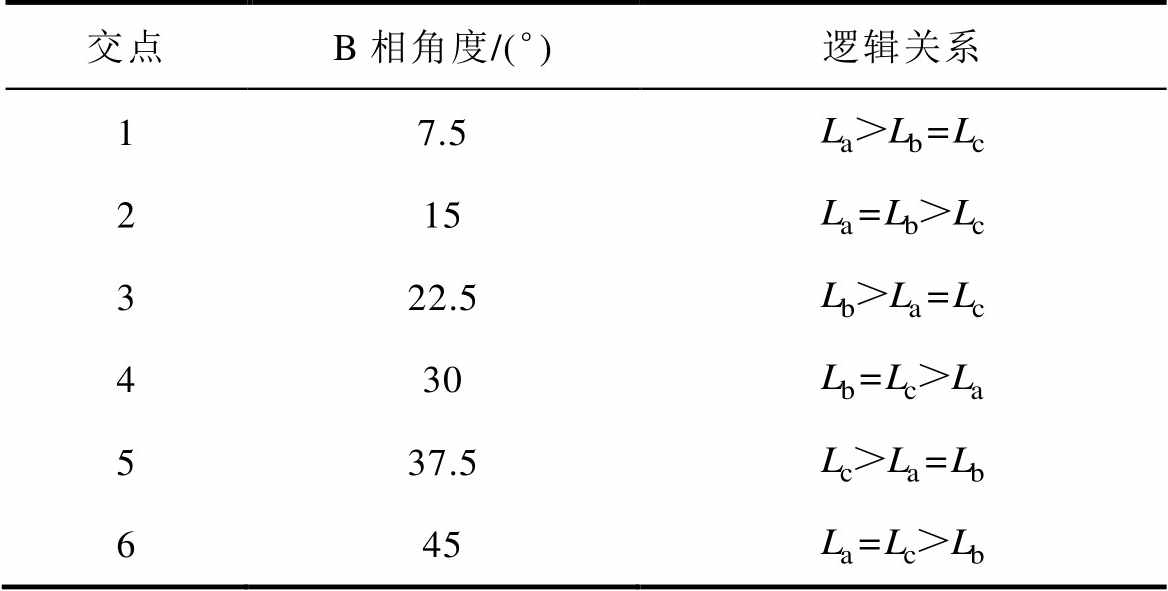
经分析，电感交点对应的角度和逻辑关系是一一对应的，如交点1对应的B相角度为7.5°，对应的电感逻辑关系为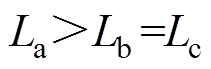
，以此类推，每个交点对应的角度和逻辑关系见表1。在电机运行时，当检测到交点对应的逻辑关系时，就发出一个位置脉冲信号，因此在一个45°周期中，共发出6个位置脉冲信号分别对应6个交点位置。
表1 交点对应的角度和逻辑关系（忽略磁饱和）
Tab.1 The angle and logical relationship of intersection points (ignoring magnetic saturation)
交点B相角度/(°)逻辑关系 17.5 215 322.5 430 537.5 645
角度计算原理示意图如图4所示，通过检测交点对应的逻辑关系来获取位置脉冲信号，再通过式（4）和式（5）来实时地估算SRM的转速和转子位置，实现无位置运行。因此在忽略磁饱和的情况下，相邻2个交点之间的B相角度计算公式详见表2。
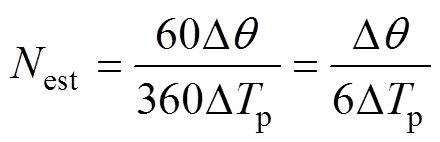（4）
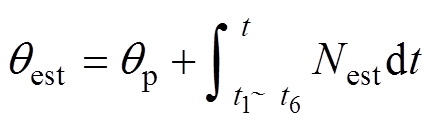（5）
式中，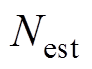
为估算的实时转速（r/min）；
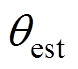为估算的转子位置角（°）；
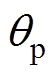为交点所对应的转子位置角（°）；
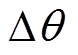为两个脉冲信号间隔的角度（12/8极SRM电机
7.5°）；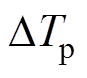
为两个脉冲信号的时间间隔（s）；
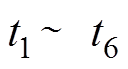为交点1～6对应的时刻（s）；
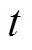为任意时刻（s）。
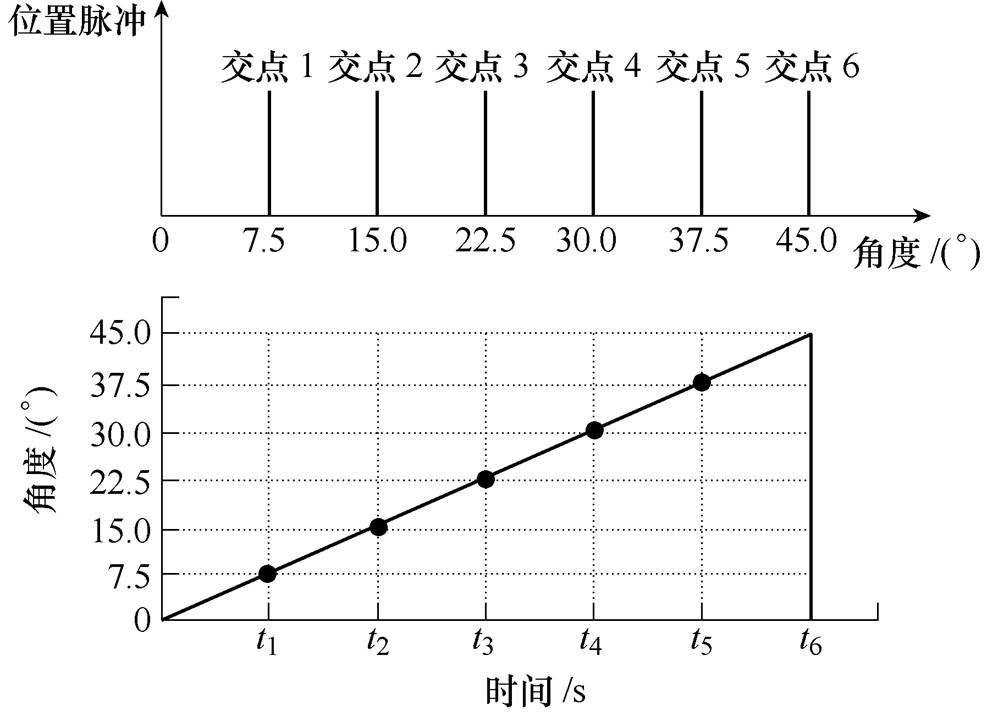
图4 角度计算原理示意图
Fig.4 Diagram of angle calculation principle
在SRM实际运行时，为了获得较大的转矩，电机通常工作在磁饱和状态，具有很强的非线性。随着负载转矩的增加磁路逐渐饱和，电感曲线会出现向下偏移的趋势，在一个电感周期内，三相电感曲线的6个交点会发生偏移，此时再利用交点来估计转子位置又将会出现较大的误差。
表2 两个交点之间的角度计算（忽略磁饱和）
Tab.2 Angle calculation between adjacent intersection points (ignoring magnetic saturation)
交 点B相角度计算 交点1和2间 交点2和3间 交点3和4间 交点4和5间 交点5和6间 交点6和1间
三相电感交点示意图如图5所示，当负载转矩为零或者较小时（即相电流较小时），电感曲线处于非饱和状态，三相电感曲线交点的偏移较小，用特殊点法来估计转子位置误差较小，可以忽略不计；然而，当负载转矩不断增大时（即相电流变大时），电感曲线逐渐向下偏移，由非饱和进入饱和状态，在这种情况下交点的偏移较大，利用传统特殊点法来估计转子位置会产生较大的误差。如图5所示，在磁饱和的情况下，交点1、3、5的角度偏差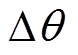（）较小，可以忽略不计；而交点2、4、6的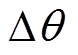较大，如果仍利用交点2、4、6来估计转子位置，将会产生非常大的估计误差。
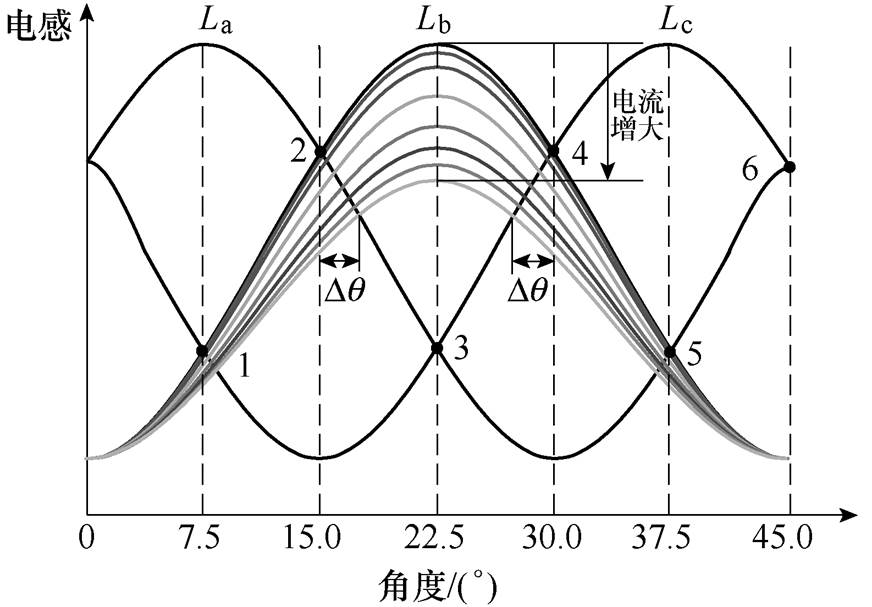
图5 三相电感交点示意图（考虑磁饱和）
Fig.5 Diagram of three-phase inductance intersection points (ignoring magnetic saturation)
为了验证SRM实际运行时，随负载转矩的增加，电感曲线会由非饱和进入饱和状态，且受磁饱和影响交点会发生偏移的现象，在电流斩波控制（Chopped Current Control, CCC）下，对12/8极SRM进行了仿真。在其他条件不变的情况下，将电机的负载转矩依次设定为15N·m、45N·m和75N·m，则电感曲线交点的仿真结果分别如图6a～图6c所示，交点2、4、6在不同负载下对应的角度如图7所示。
图6 不同负载下三相电感交点的示意图
Fig.6 Diagram of three-phase inductance intersection points under different loads
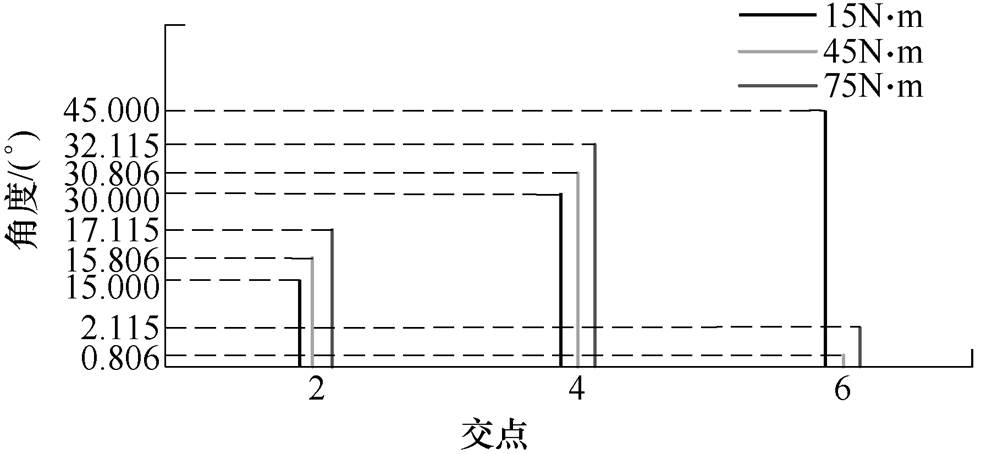
图7 交点2, 4, 6在不同负载下对应的位置角度
Fig.7 Diagram of angles corresponding to intersection points 2, 4, 6 under different loads
如图7所示，随着负载从15N·m增加到75N·m，交点2对应的角度将从15°逐渐偏移到17.115°，在不同的负载转矩下，交点对应的角度会有所不同，但角度变化具有一定的规律性。因此本文将负载转矩的变化作为自变量，交点角度的变化作为因变量，建立函数关系。通过函数关系就可以求得不同负载下交点2所对应的角度，再与非饱和状态下交点2的角度（15°）进行作差，求得要补偿的误差角度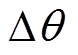。在磁饱和情况下，当检测到交点2时将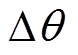补偿进去，再经计算得到实时的转速和位置角度，就可以消除磁饱和影响产生的误差，提高位置估计的精度。
本文采用12/8极SRM的额定转矩为95.5N·m，在其他条件相同的情况下，将负载转矩分别设定为15N·m、30N·m、45N·m、60N·m、75N·m、90N·m，并依次测得交点2所对应的角度，表3为在不同负载下测得的采样点的坐标。
表3 不同负载下交点2的坐标
Tab.3 Coordinates of intersection points 2 under different loads
负载转矩/(N·m)交点2坐标 15（15, 15） 30（30, 15.275） 45（45, 15.806） 60（60, 16.422） 75（75, 17.115） 90（90, 17.687）
对这6个采样点进行函数拟合，图8是不同拟合方式下的误差曲线。由图8可知，一次傅里叶拟合和三次多项式拟合的误差基本一致，且均满足要求。本文选择一次傅里叶拟合，拟合的函数表达 式为
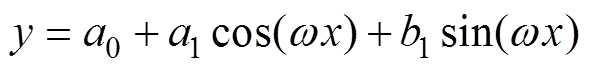（6）式中，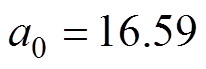
；
；
；
。
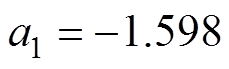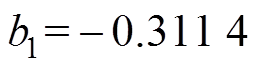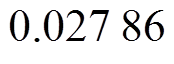因此，当负载不断增大时，可以根据式（6）计算出交点2所对应的角度（即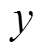
值），进而得到误差角度
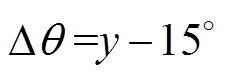，同理，交点4和6的误差角度与交点2相同。由以上分析，在磁饱和的情况下，当检测到交点2、4、6时，将角度误差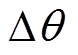补偿进去，交点1、3、5受磁饱和影响非常小，不需要误差补偿。因此，相邻2个交点之间的B相角度计算公式见表4。
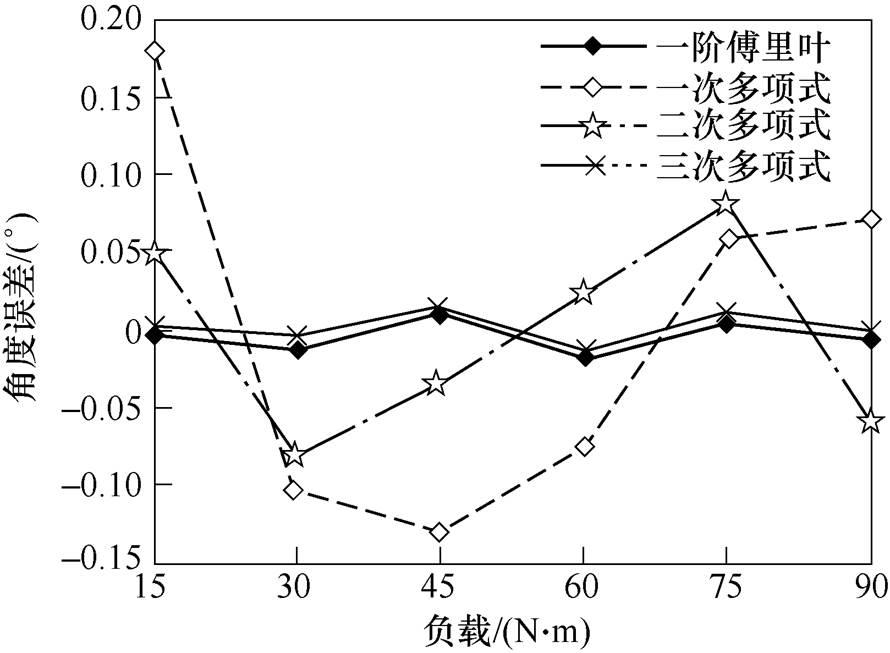
图8 不同拟合方式下的误差曲线
Fig.8 Diagram of error curves under different fitting modes
表4 两个交点之间的角度计算（考虑磁饱和）
Tab.4 Angle calculation between adjacent intersection points (considering magnetic saturation)
交 点B相角度计算 交点1和2间 交点2和3间 交点3和4间 交点4和5间 交点5和6间 交点6和1间
为了验证所提改进策略的正确性，根据堵转实验数据，在Matlab/Simulink环境下搭建了SRM的本体仿真模型，对传统特殊点无位置方法和改进后的方法分别进行了仿真。电机的参数见表5，采用电流斩波控制方式，在给定条件不变的情况下（导通相序为A—B—C—A；开通角为0°，关断角为19°），不断加大电机的负载转矩，让电感由非饱和进入饱和状态，并对比了传统和改进后两种方法的仿真结果。
传统无位置方法的仿真结果如图9所示，当SRM的负载转矩为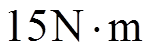
时，绕组电流在10A左右，由图1可知，当电流在10A以下，磁链均属于非饱和区域，此时电感曲线的交点几乎不发生偏移，不需要进行误差补偿，用传统方法估计转子位置非常准确，误差在0.04°以内。
表5 SRM样机参数
Tab.5 The parameters of prototype SRM
参 数数 值 定、转子极对数12/8 功率/kW15 额定转矩/(N·m)95.5 额定转速/(r/min)1 500 定子电阻/W0.6 转动惯量/(kg·m2)0.01 摩擦因数0.005
图9 传统无位置方法的仿真结果（负载15N·m，转速1 500r/min）
Fig.9 Simulation results of traditional sensorless method (TL=15N·m, n=1 500r/min)
传统和改进型无位置方法的仿真结果如图10所示，当负载加大到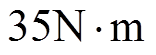
时，电感曲线已经进入饱和状态，由传统方法的仿真结果可以看出，估计角度误差由0.04°（非饱和）增大到了0.5°；由改进后方法的仿真结果可以看出，即便加大了电机的负载导致交点发生偏移，但经过误差补偿位置估计仍然很准确，其误差在0.09°以内。
传统和改进型无位置方法的仿真结果如图11所示，为了验证算法的稳定性，在0.12s时刻，让负载转矩由30N·m突增到45N·m，由仿真结果可以看出，当负载为30N·m时（即0.12s之前），传统方法的估计误差在0.3°以内，而改进后方法的误差非常小，在0.05°以内；当负载转矩由突增到恢复稳定的时间内（即0.12～0.134s），由于电感曲线发生了畸变，导致估计误差增大，传统方法和改进后方法的误差都在1°左右，但由于这段时间非常短且很快能够恢复稳定，所以这个过程的误差可以不考虑；当负载突增到45N·m并稳定后（即0.134s之后），传统方法的估计误差由0.3°增大到1°，然而改进后方法的误差由0.05°增大到0.1°，误差仍然非常的小。
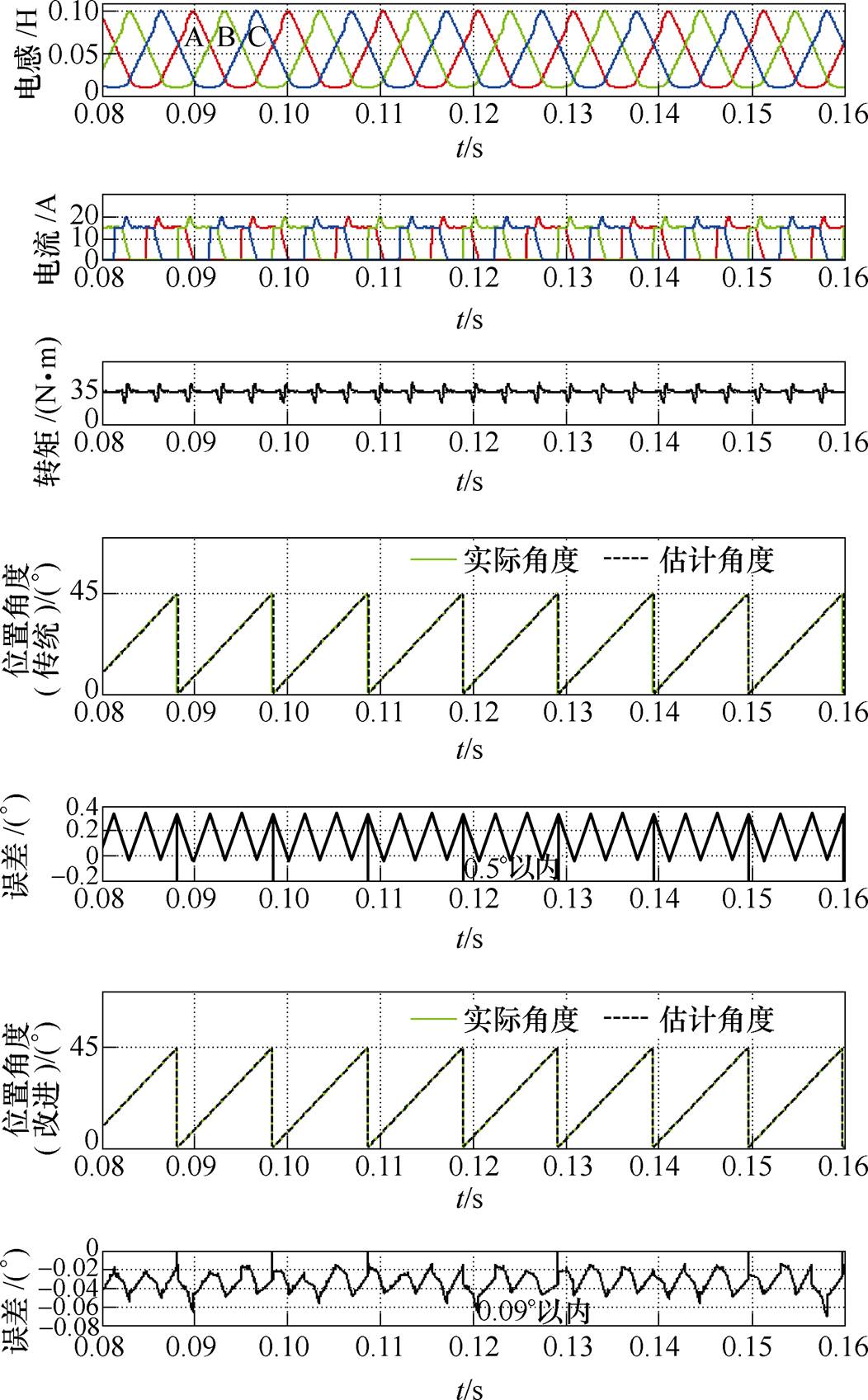
图10 传统和改进型无位置方法的仿真结果（负载35N·m，转速750r/min）
Fig.10 Simulation results of traditional and modified sensorless method (TL=35N·m, n=750r/min)
为了验证所提改进策略的可行性，搭建了SRM控制实验平台如图12所示。该平台用两块智能功率模块搭建不对称半桥功率变换器，以TMS320F2812芯片为控制核心，一台12/8极SRM为控制对象。
基于图12所示的SRM实验平台，在CCC算法下搭建了无位置控制系统，控制原理如图13所示。该系统采用双闭环控制，外环采用PI控制的转速调节器（Automatic Speed Regulator, ASR），内环采用CCC控制的电流调节器（Automatic Current Regulator, ACR）。首先通过AD采样获得SRM的三相电压值和电流值，再经过计算得到实时的三相电感值，根据表1进行逻辑关系比较，当检测到交点所对应的逻辑关系时，就发出位置脉冲信号，实验采用磁粉制动器对电机进行加载，将转矩传感器传出的转矩信号送入DSP并经过ADC采样来获取SRM所加负载转矩值，再根据拟合式（6）求出误差角度，最终根据脉冲信号和要补偿的误差角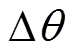
，依据表4的计算公式估算实时的转子位置。
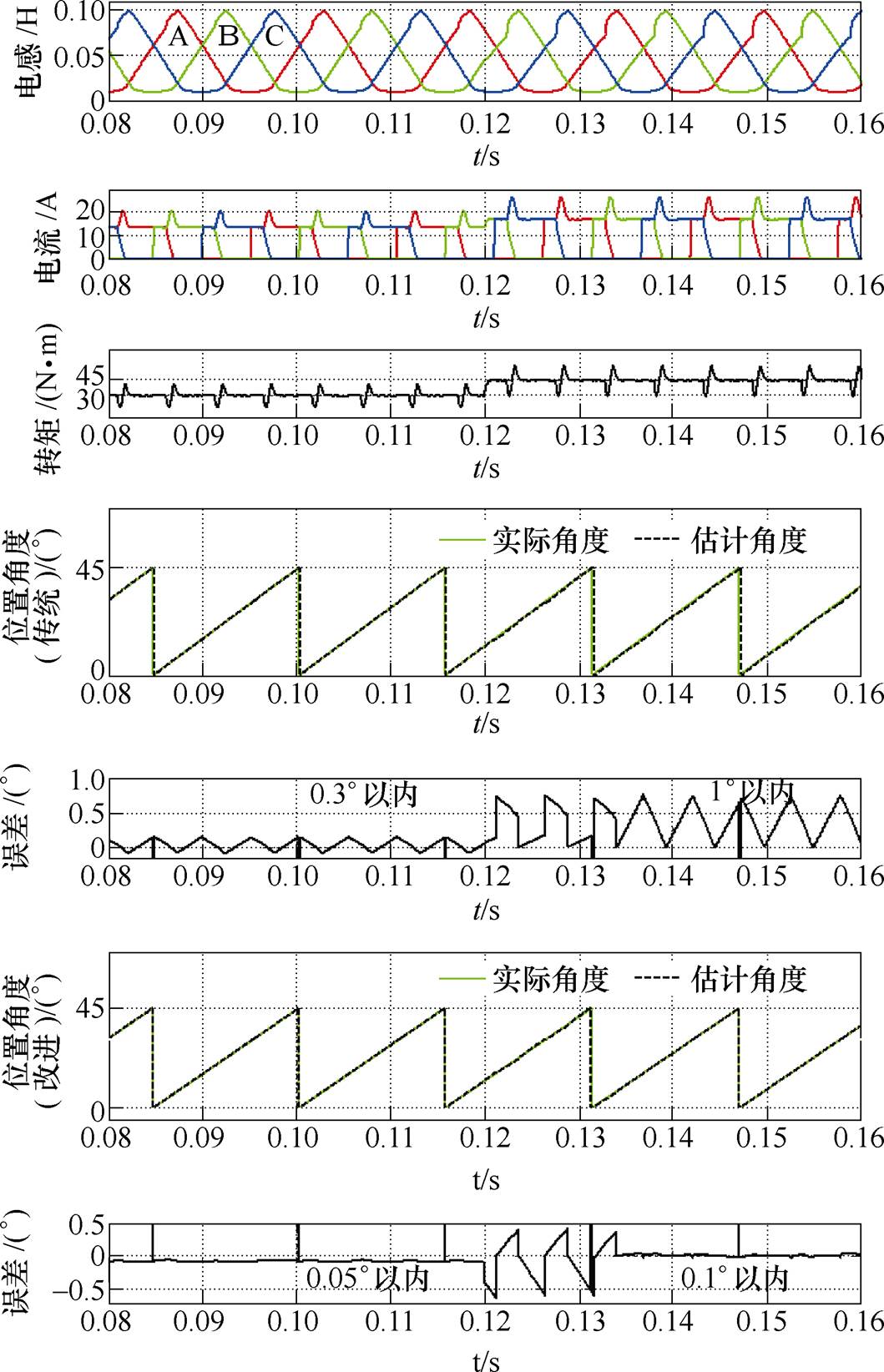
图11 传统和改进型无位置方法的仿真结果（负载由30N·m跳变到45N·m，转速500r/min）
Fig.11 Simulation results of traditional and modified sensorless method (30N·m→45N·m, n=500r/min)
图12 SRM实验平台
Fig.12 Experiment platform of SRM
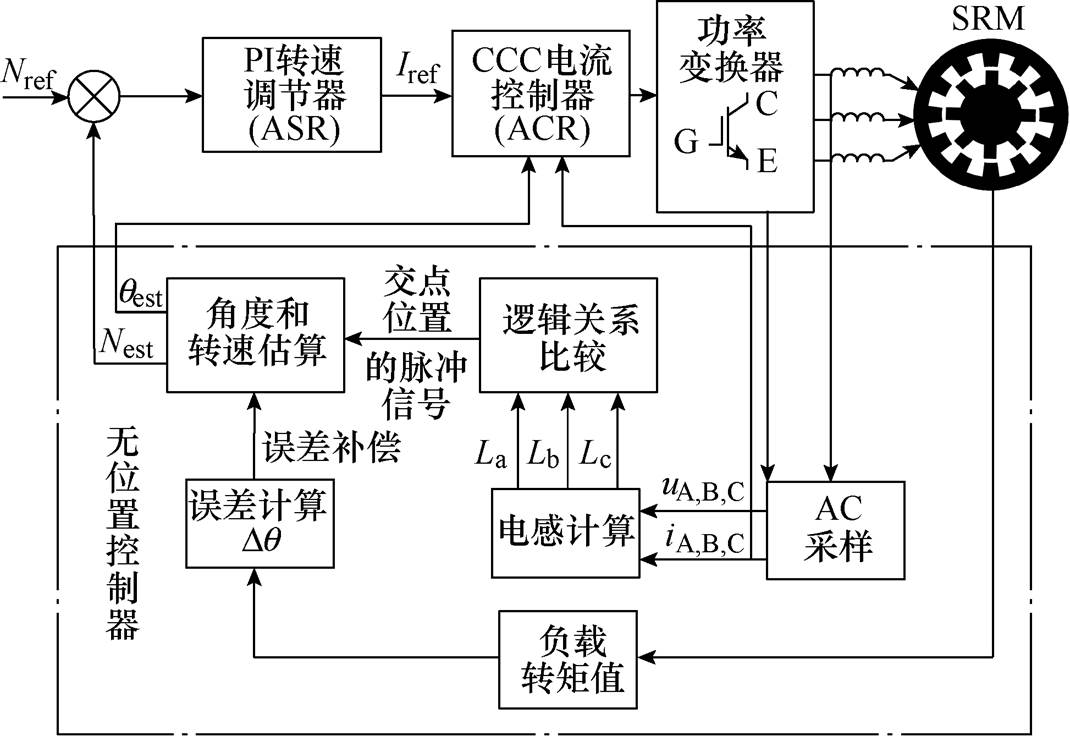
图13 SRM无位置控制系统原理图
Fig.13 Principle diagram of SRM sensorless control system
当SRM运行条件，开通角为0°，关断角为19°，负载转矩为15N·m，转速为1 500r/min时，图14为B相电流、负载转矩、实际角度、估计角度的实验波形图。电机运行在轻载的条件下，三相电感曲线的交点几乎不发生偏移，不需要误差补偿，利用传统方法估计的转子位置准确，误差在0.8°以内。
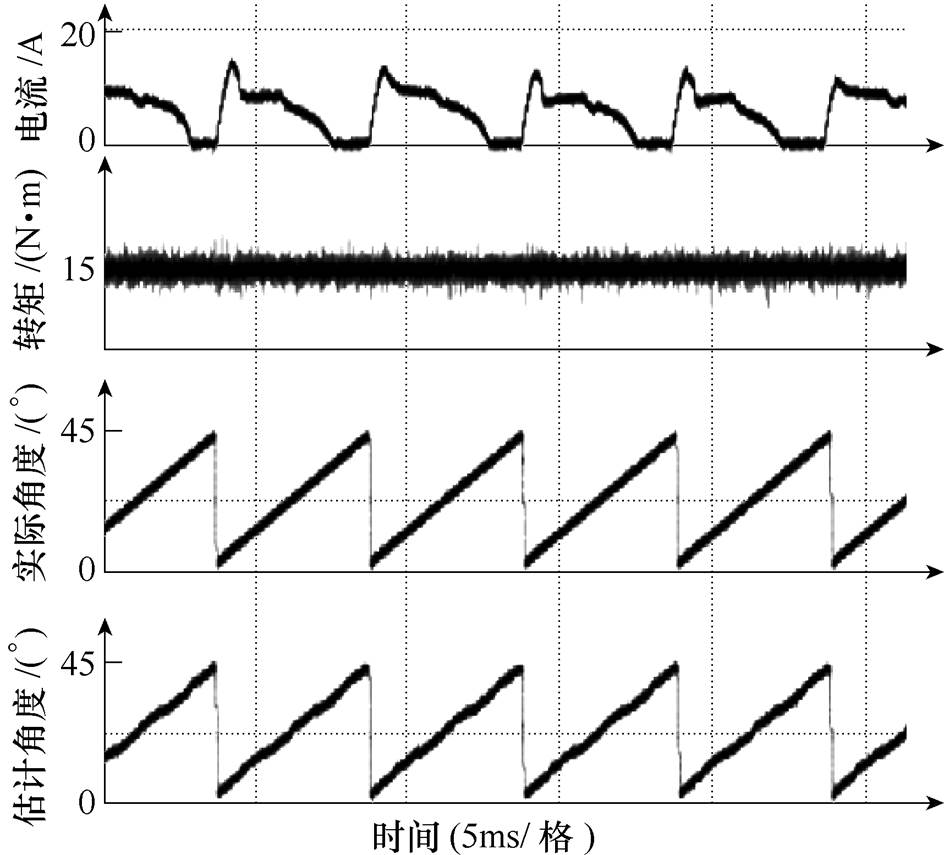
图14 传统无位置方法实验结果（负载15N·m，转速1 500r/min）
Fig.14 Experimental results of traditional sensorless method (TL=15N·m, n=1 500r/min)
当增加电机的负载转矩为35N·m，开通、关断角不变，转速为750r/min时，分别对传统和改进后的方法进行了实验，图15为实验结果对比，图16为与之对应的一个电周期每间隔3°位置的误差曲线。图15a为传统方法的实验波形，由图可知，SRM工作在重载条件下，电机运行在磁饱和状态，此时三相电感曲线的交点受磁饱和影响发生偏移导致估计误差增大。在图16a中可以知道，传统的误差在2.5°以内。图15b所示为改进后算法的实验波形，由图可知，经过误差补偿后，改进后的算法有效地减小了估计误差，结合图16b可知，误差在1°以内，实验结果验证了改进算法的有效性。
图15 传统和改进后实验结果对比（负载35N·m，转速750r/min）
Fig.15 Experimental results of traditional and modified sensorless method (TL=35N·m, n=750r/min)
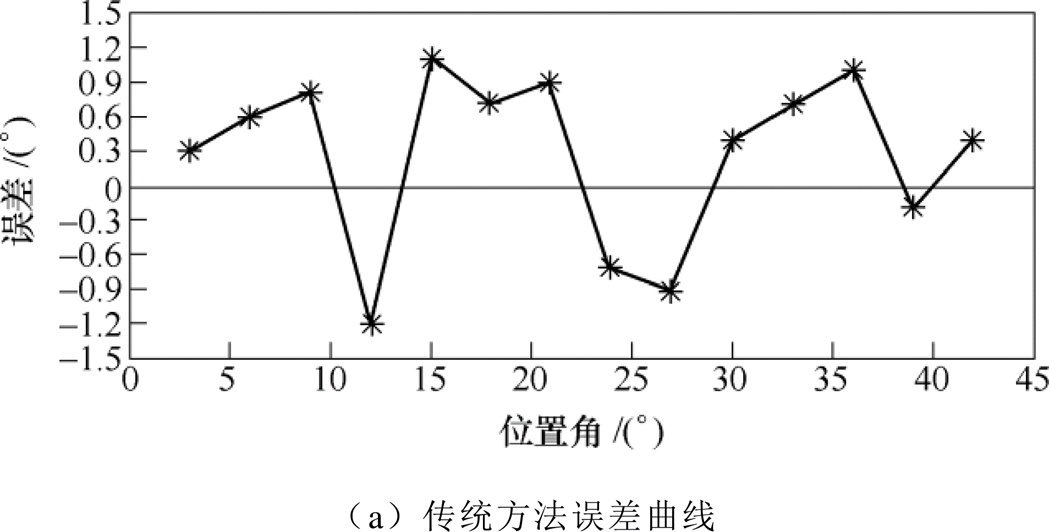
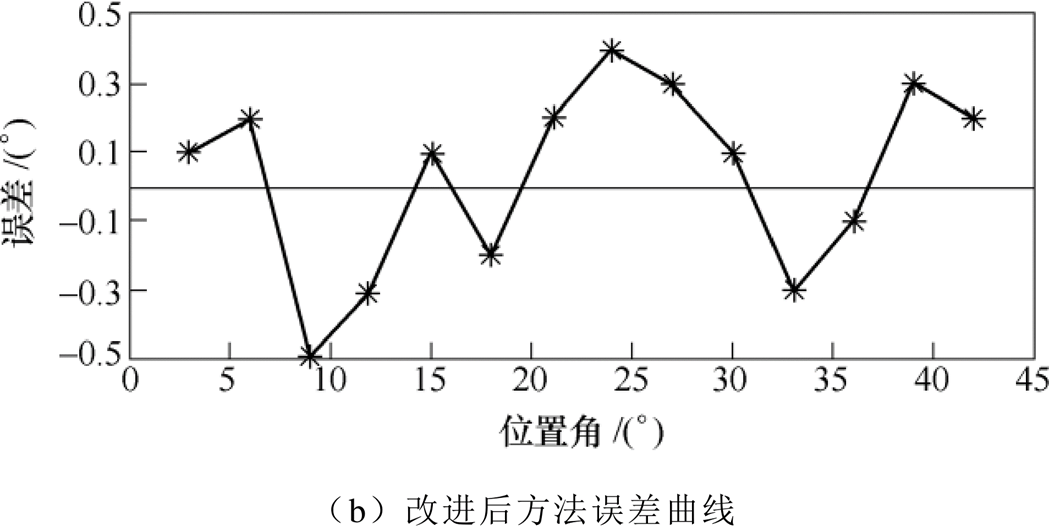
图16 传统和改进后误差曲线对比
Fig.16 Error curve results of traditional and modified sensorless method
为了验证改进后算法的稳定性，让电机的负载转矩从30N·m跳变到45N·m，开通、关断角保持不变，转速为500r/min时，对改进后的算法进行了实验，图17为三相电流、负载转矩、实际角度、估计角度的实验波形。由图可知，在负载转矩突变的情况下，该算法估计的转子位置能够很好地跟踪实际位置，具有很好的可靠性，且跳变前后估计误差未明显增大，均在1°以内。
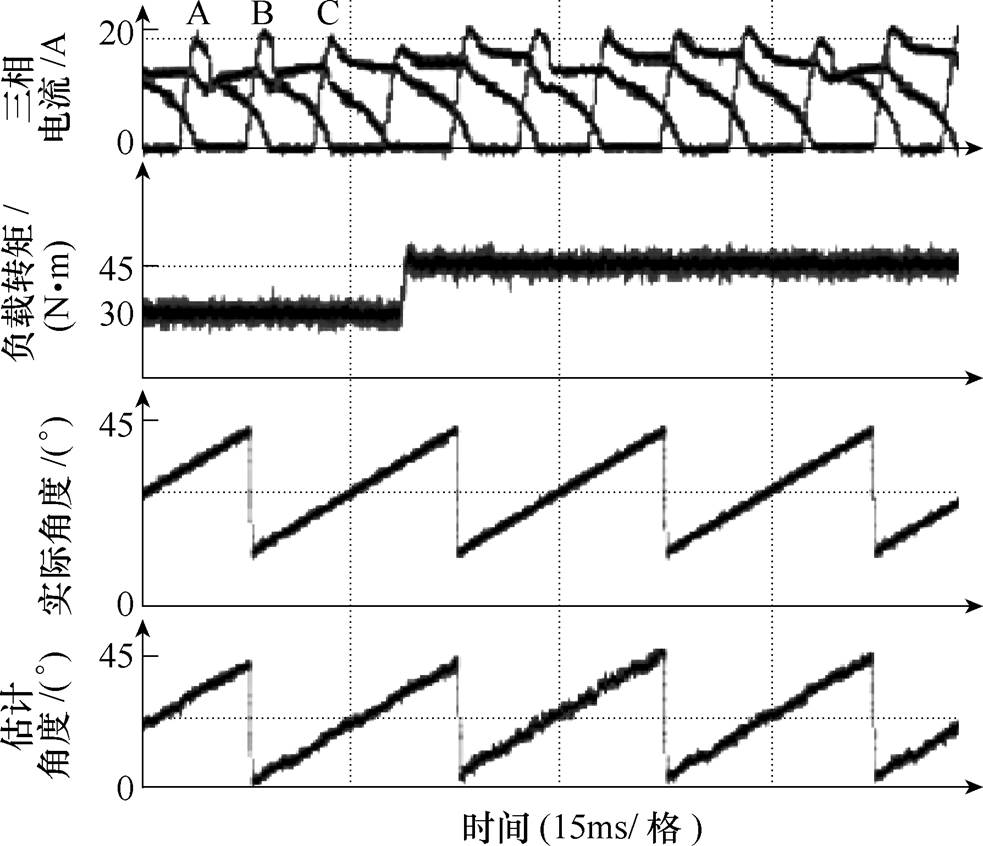
图17 改进后无位置方法实验结果（负载30N·m→45N·m，转速500r/min）
Fig.17 Experimental results of modified sensorless method (30N·m→45N·m, n=500r/min)
本文针对SRM受磁饱和影响导致三相电感交点偏移后位置估计不准确的问题，在不同负载转矩下分别测得交点所对应的角度，并利用傅里叶拟合建立角度与负载转矩的函数关系，进而求得交点偏移的误差角度，对其进行误差补偿，使位置估计更加准确。在一台三相12/8极SRM上对比分析了传统与改进后方法的仿真和实验，结果表明：
1）该方法与传统方法相比，经过误差补偿使位置估计更加准确，可有效地抑制磁饱和的影响。
2）针对运行在轻载、重载、负载跳变、中低速的情况下，该方法估计的位置均能很好地跟踪实际位置，实现无位置运行，具有较好的稳定性，可满足多数工业驱动要求。
3）在一个45°电感的机械周期，共检测6个特殊位置点，具有较高的精度。该方法适合于中低速运行，当运行在高速情况时，脉冲时间间隔的缩短可能会导致其中某个位置点未检测到，但并不影响下一时刻的位置估计，电机也能正常运行，具有一定的容错性和可靠性。
参考文献
[1] Hu Kaiwei, Chen Yenyang, Liaw Changming. A reversible position sensorless controlled switched- reluctance motor drive with adaptive and intuitive commutation tunings[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3781-3793.
[2] Song Shoujun, Ge Lefei, Zhang Zhihui. Accurate position estimation of SRM based on optimal interval selection and linear regression analysis[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3467-3478.
[3] Guo Haijiao, Takahashi M, Tadadaaki Watanabe J. A new sensorless drive method of switched reluctance motors based on motor's magnetic characteristics[J]. IEEE Transactions on Magnetics, 2001, 37(4): 2831- 2833.
[4] Xu Longya, Wang Chuanyang. Accurate rotor position detection and sensorless control for SRM for super- high speed operation[J]. IEEE Transactions on Power Electronics, 2002, 17(5): 757-763.
[5] 夏长亮, 王明超, 史婷娜, 等. 基于神经网络的开关磁阻电机无位置传感器控制[J]. 中国电机工程学报, 2005, 25(13): 123-128.
Xia Changliang, Wang Mingchao, Shi Tingna, et al. Position sensorless control for switched recluctance motors using neural network[J]. Proceedings of the CESS, 2005, 25(13): 123-128.
[6] Cai Yan, Wang Yu, Xu Hainan, et al. Research on rotor position model for switched reluctance motor using neural network[J]. IEEE/ASME Transactions on Mechatronics, 2018, 23(6): 2762-2773.
[7] 曾辉, 杨向宇. 带位置误差校正的开关磁阻电机电流梯度法[J]. 电机与控制学报, 2019, 23(4): 83-89.
Zeng Hui, Yang Xiangyu. Position sensorless control of switched reluctance motor using wavelet neural networks[J]. Electric Machines and Control, 2019, 23(4): 83-89.
[8] Lyons J P, Macminn S R, Preston M. Flux-current methods for SRM rotor position estimation[C]// Industry Applications Society, Dearborn, MI, USA, 1991: 482-487.
[9] Koblara T, Sorandaru C, Musuroi S, et al. A low voltage sensorless switched reluctance motor drive using flux linkage method[C]//International Con- ference on Optimization of Electrical and Electronic Equipment, Basov, Romania, 2010: 665-672.
[10] 张磊, 刘闯, 韩守义. 基于一种新型磁链模型开关磁阻电机无位置传感器技术[J]. 电机与控制学报, 2018, 22(7): 27-34.
Zhang Lei, Liu Chuang, Hang Shouyi. Sensorless technology of switched reluctance motor based on a new flux model[J]. Electric Machines and Control, 2018, 22(7): 27-34.
[11] 李珍国, 李彩红, 阚志忠, 等. 基于改进型简化磁链法的开关磁阻电机无位置传感器速度控制[J]. 电工技术学报, 2011, 26(6): 62-66.
Li Zhenguo, Li Caihong, Kan Zhizhong, et al. Switched reluctance motor sensorless speed control based on the improved simplified flux method[J]. Transactions of China Electrotechnical Society, 2011, 26(6): 62-66.
[12] 蔡骏, 邓智泉. 基于电感线性区模型的开关磁阻电机无位置传感器技术[J]. 中国电机工程学报, 2012, 32(15): 114-123.
Cai Jun, Deng Zhiquan. Sensorless control of switched reluctance motors based on phase inductance model in linear regions[J]. Proceedings of the CESS, 2012, 32(15): 114-123.
[13] 邵杰, 邓智泉, 胡荣光, 等. 基于改进脉冲注入开关磁阻电机无位置传感器技术[J]. 电工技术学报, 2015, 30(21): 147-153.
Shao Jie, Deng Zhiquan, Hu Rongguang, et al. An improved sensorless driving method of switched reluctance motors using impressed voltage pulse[J]. Transactions of China Electrotechnical Society, 2015, 30(21): 147-153
[14] 李景男, 王旭东, 周永勤. 基于两相脉冲激励的开关磁阻电动机无位置传感器转子位置检测[J]. 电机与控制学报, 2002, 6(1): 6-9.
Li Jingnan, Wang Xudong, Zhou Yongqin. Sensor- less rotor position detection of SRM based on voltage pulses to two phase[J]. Electric Machines and Control, 2002, 6(1): 6-9.
[15] 蔡骏, 邓智泉. 基于全周期电感法的开关磁阻电机无位置传感器控制技术[J]. 电工技术学报, 2013, 28(2): 145-154.
Cai Jun, Deng Zhiquan. Sensorless control of switched reluctance motors based on full-cycle inductance method[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 145-154.
[16] 周竟成, 王晓琳, 邓智泉, 等. 开关磁阻电机的电感分区式无位置传感器技术[J]. 电工技术学报, 2012, 27(7): 34-40.
Zhou Jingcheng, Wang Xiaolin, Deng Zhiquan, et al. The position sensorless technology of switched reluctance motor based on the regional comparison of three-phase inductance[J]. Transactions of China Electrotechnical Society, 2012, 27(7): 34-40.
[17] 刘勇智, 宋金龙, 周政, 等. 改进电感分区式SRM位置传感器研究[J]. 电力电子技术, 2016, 50(7): 66-69.
Liu Yongzhi, Song Jinlong, Zhou Zheng, et al. Sensor- less control of SRM based on improved regional comparison three-phase inductance[J]. Power Elec- tronics, 2016, 50(7): 66-69.
[18] 李孟秋, 陈欣, 任修勇, 等. 基于典型位置电感的开关磁阻电机无位置传感器控制策略[J]. 中国电机工程学报, 2017, 37(13): 3901-3908.
Li Mengqiu, Chen Xin, Ren Xiuyong, et al. Sensor- less control of switched reluctance motors based on typical position of three-phase inductances[J]. Pro- ceedings of the CSEE, 2017, 37(13): 3901-3908.
[19] 蔡辉, 王辉, 李孟秋, 等. 考虑饱和电感特性的开关磁阻电机的无位置传感器控制方法[J]. 电工技术学报, 2018, 33(12): 2723-2734.
Cai Hui, Wang Hui, Li Mengqiu, et al. Position sensorless control of switched reluctance motors con-sidering the magnetic saturation[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2723- 2734.
Rotor Position Detection and Error Compensation of Switched Reluctance Motor Based on Special Inductance Position
Abstract In sensorless control of the Switched Reluctance Motor (SRM) based on special position of inductance, inductance intersection point is affected by the magnetic saturation, which will cause inaccurate position estimation. To solve this problem, a control method with error compensation and an improved strategy for intersection offset are proposed. Under different load torques, angles of the intersections of inductance curves are measured. The function relationship between load torque and angle is established by Fourier fitting, then the angle error to be compensated is deduced. In the case of magnetic saturation, the error resulted from intersection offset can be reduced by error compensation to make position estimation more accurate. A three-phase 12/8 pole SRM was designed to verify the proposed method. The simulation and experimental results show that in the case of magnetic saturation, the new method can effectively reduce the error and estimate the rotor position more accurately.
keywords：Switched reluctance motors, sensorless control, rotor position, magnetic saturation
中图分类号：TM352
DOI: 10.19595/j.cnki.1000-6753.tces.190041
国家自然科学基金（51407021）和辽宁省科技创新基金（2018J12GX039）资助项目。
收稿日期 2019-01-16
改稿日期 2019-09-18
许爱德 女，1974年生，教授，硕士生导师，研究方向为电机统及其控制。E-mail: aidexu@dlmu.edu.cn
朱景伟 男，1963年生，教授，博士生导师，研究方向为电机本体设计及其系统控制。E-mail: zjwdl@dlmu.edu.cn（通信作者）
（编辑 赵 鹏）