图1 4极23槽环形绕组无刷直流电机
Fig.1 The structure of 4-pole, 23-slot CWBLDC motor
摘要 环形绕组无刷直流电机（CWBLDC）是一种多相且定子绕组环形连接的电机，由于反电动势的方波度更高，其转矩密度较传统三相无刷直流电机更大，通过极、槽数合理设计的分数槽绕组能够有效地抑制电机的转矩脉动。并且，CWBLDC所需的功率元器件数目较多的特点在多相大容量舰船电力推进系统的应用中不是缺点。针对相数较多、运行过程系统网络拓扑不断变化的难点，该文以并联支路电流为模型变量，利用拓扑的周期变换特性建立CWBLDC的数学模型，通过场路耦合仿真与原理样机实验验证了建模思路与模型分析结果的正确性。所建立的数学模型有助于深入理解包括换向过程的电机运行原理，快速得到电机的稳态性能，便于确定电机设计参数较不同参数选取对电机性能的影响。
关键词：无刷直流电机 多相环形绕组 分数槽绕组 负载换向 解析模型 拓扑周期变换
永磁电机的励磁绕组由高磁能积的稀土永磁材料所代替，其效率更高、结构更灵活，因而正逐步替代先进感应电机成为舰船电力推进（electric propulsion）系统的首选，并已在中小容量（10MW以内）范围内得到应用[1-4]。中大容量电力推进系统需要推进电机具有更高的功率与转矩密度，军事舰船还需要推进电机尽可能好的振动噪声性能，这对大容量、高转矩密度、低振动噪声的永磁推进电机提出了更高需求。
无刷直流电机（Brushless DC motor, BLDC）采用方波电流供电，方波气隙磁通密度能够充分利用铁心材料，因此BLDC比永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）的转矩密度更大，采用Six-step方波运行方式[5]，还可以有效地避免高频脉宽调制（Pulse Width Modulation, PWM）方式对电机容量提升的限制。但BLDC的换相转矩脉动较大[6-8]，因而限制了在高性能电力推进领域的应用。
针对BLDC的换相转矩脉动抑制方法几乎全部从控制角度出发[9-16]，如重叠换相法[10-11]、PWM_ ON_PWM法[13-14]、电流滞环控制法[18]等。一方面难以彻底消除换相的影响；另一方面增加了系统的复杂度。
环形绕组无刷直流电机（Circular Winding Brushless DC motor, CWBLDC）从电机拓扑角度出发来抑制转矩脉动，是一种多相、定子绕组环形连接的电机[17-21]。CWBLDC反电动势的方波度更高，能够提高电机的转矩密度，采取分数槽绕组结构能有效地抑制电机的转矩脉动[17]，适合在大容量舰船电力推进系统应用。
CWBLDC采用功率半导体器件代替有刷直流电机机械换向器，绕组电流方向的改变是电机正常运行的前提（下文统一采用“换向”指代这一过程）。由于采用负载换向方法[21]，换向相位决定了绕组相电流的波形，将直接影响电机的转矩输出能力、功率因数和换向过程的转矩脉动，因此需建立电机的数学模型，详细分析绕组电流的换向过程。
传统三相BLDC的驱动电路采用全控器件及反并联二极管，器件强迫关断的同时二极管提供绕组续流回路以实现BLDC换相[22-24]，这种建模方法不适用于绕组结构和换向方式不同的CWBLDC。若使用场路耦合仿真方法分析电机性能，仿真时长将使得参数扫描不具有可行性，也不便于分析换向的物理过程。很多文献对于多相环形绕组结构的相关研究较少[25-28]，且多停留在概念与原理研究阶段，并没有深入分析多相环形绕组的一般性工作原理，更没有建立物理意义明确、快速精确的数学模型。文献[19]在电路仿真软件Plecs中建立了动态数学模型，适应于分析系统的动态性能，但计算时间较解析方法依然很长，难以应用于设计阶段对电机参数的优化。因此，本文将建立多相环形绕组无刷直流电机的解析数学模型，首先介绍CWBLDC的基本结构与工作方式；其次介绍CWBLDC的建模过程；接着介绍数学模型参数的确定方法；最后验证数学模型的准确性。
4极23槽CWBLDC的基本结构如图1a所示，定子上的23槽绕组（同时也是23相绕组）首尾连接成环形，每一相绕组两端均由一对开关桥臂连接至直流输入电源，电机的驱动换向电路结构如图1b所示。图中，VDH1表示1相绕组左侧上桥臂开关，VDL1表示1相绕组左侧下桥臂开关，其他开关器件按此规则编号。
图1 4极23槽环形绕组无刷直流电机
Fig.1 The structure of 4-pole, 23-slot CWBLDC motor
同传统有刷直流电机的工作原理一致，为了持续输出方向恒定的稳定转矩，相绕组轴线与转子轴线重合时需改变电流方向。图2为转子转过单个槽距的运行情况。图2a中，1相绕组轴线与永磁体d轴正半轴轴线对齐，为了继续输出正向转矩，1相绕组电流方向改变；永磁体转子转过1/4个槽距后，7相绕组轴线与永磁体d轴负半轴轴线对齐，为了继续输出正向转矩，7相绕组电流方向改变。随着永磁体转子继续旋转，13相与19相绕组电流相继改变方向。
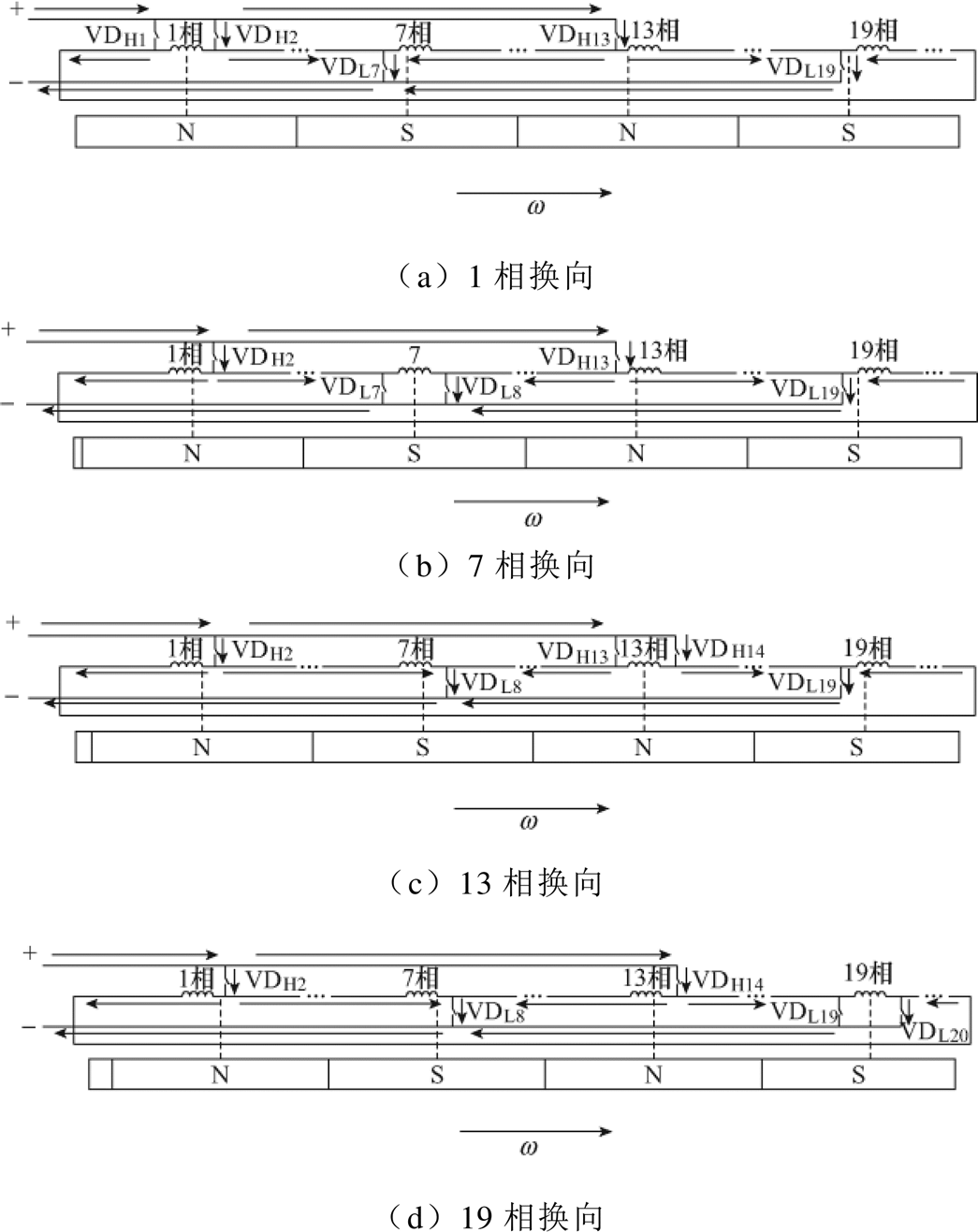
图2 单个槽距的运行情况
Fig.2 Operation for slot bitch
由此可知4极23槽CWBLDC转子转过一个槽距换向4次，没有绕组换向时，驱动换向电路的高压侧与低压侧各有2个功率开关导通，各相绕组将被分为4条并联支路。
换向与功率开关的成功关断是电机正常运行的关键。环形绕组无刷直流电机采用一种负载换向方法，它类似于大容量同步电机的负载换向方法，功率开关能够实现零电流关断，从而避免换向过程的电压尖峰。
图3以第1相绕组的换向过程为例说明了负载换向过程。
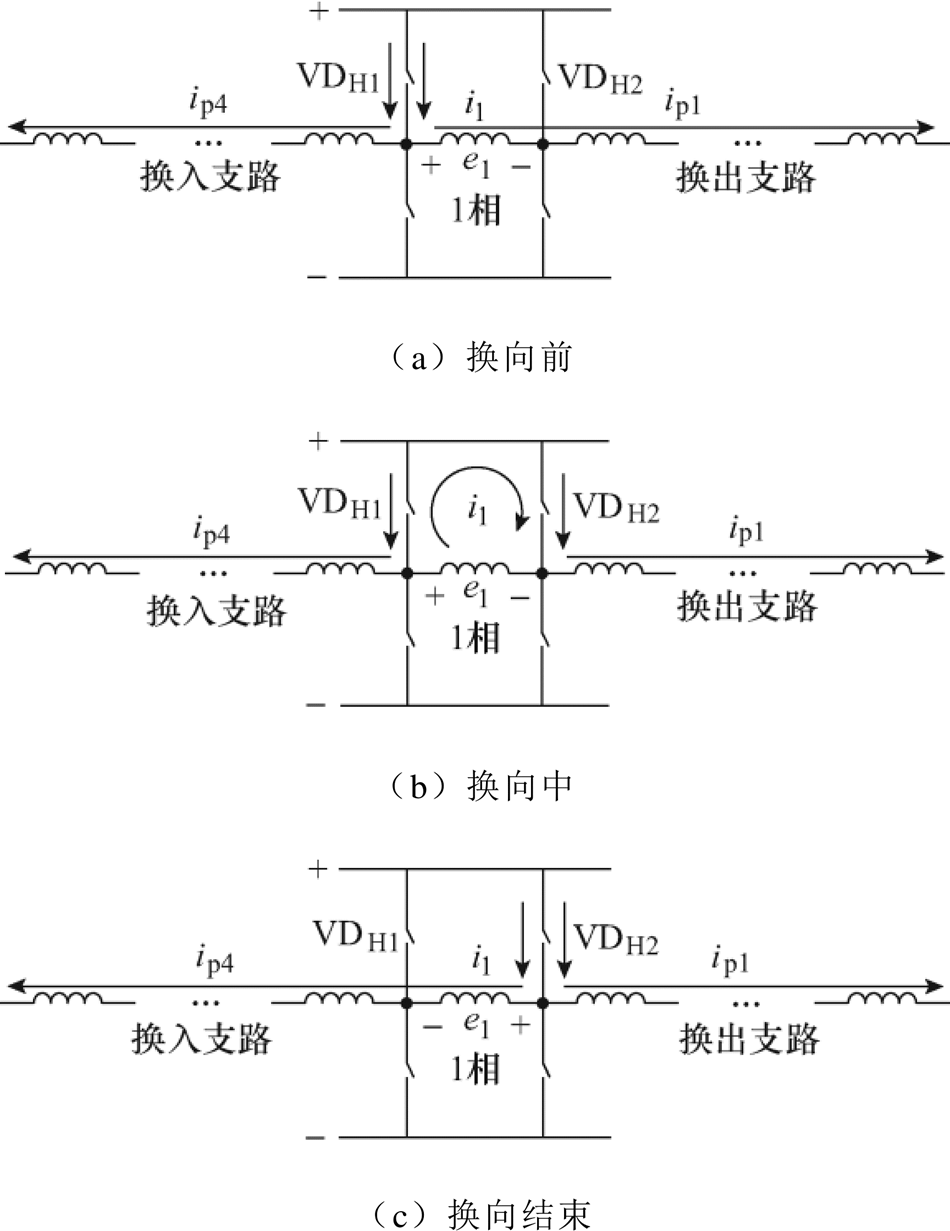
图3 负载换向方法
Fig.3 Load commutation method
换向前：图3a为换向前状态，支路p1与p4的电流由VDH1流入，1相电流i1与换出支路p1电流ip1相等。
换向中：由于转子永磁体d轴正半轴轴线接近1相绕组轴线，反电动势e1的极性会发生变化，在极性改变之前提前导通VDH2，1相绕组两开关短路。电流i1在e1的作用下换向，同时流过VDH1的电流减小，流过VDH2的电流增大，如图3b所示。
换向结束：i1反向增大与换入支路p4的电流ip4相等时，流过VDH1的电流为零，此时将VDH1关断，支路p1与p4的电流全部由VDH2流入，换向过程结束，如图3c所示。
可以看出负载换向方法的特点是提前导通下一状态的功率开关，换向中绕组两端的功率开关同时导通，当流过功率器件的电流为零后关断。
CWBLDC相数较多，互感参数多且无法解耦；相绕组的换向导致电机系统网络拓扑不断变化，这些都给电机的建模带来了困难。
本文以4极23槽分数槽绕组为对象研究建模过程，但所提出的建模方法也适用于整数槽绕组。
2.1.1 以并联支路电流为变量
4极23槽电机在非换向过程被分为4条或5条并联支路（换向相被短路后形成单独的支路），若以并联支路电流为数学模型的变量，变量数将大大减少，这简化了CWBLDC数学模型的复杂度。需要注意的是，此时并联支路的等效自感与等效互感需根据具体拓扑的相绕组连接关系推导，后文将具体介绍推导过程。
2.1.2 拓扑切换条件
系统网络拓扑切换的触发事件为开始换向和换向结束，以1相换向过程为例说明。图3b中导通VDH2是换向开始时刻，并时刻提前于反电动势过零的时间是可控量；图3c中电流i1与ip4相等时，换向结束时刻，可在分析过程中不断判断i1=ip4是否成立。
2.1.3 拓扑的周期变换特性
电机拓扑不断变化，若不能从中寻找规律，那么每一种拓扑都需要建立相应的微分方程，庞大的工作量将使建模难以实现。
电机转子转过一个槽距，4条并联支路各有一相绕组换向，4次换向结束后电机的拓扑结构与初始状态相同，只是各相绕组位置移动了一位。因此电机拓扑的变化是以一个槽距为周期的，分析这一周期后作周期延拓就可以得到完整的稳态性能。下一节将给出一个槽距内的电机系统网络拓扑，建立相应的微分方程组。
图4依次给出了4极23槽电机在一个槽距的8个系统网络拓扑。图4中，p1、p2、p3、p4为电机系统的4条并联支路，ip1、ip2、ip3、ip4为它们各自的电流，i1～i23为各相绕组电流。
电机经历了图4中的8个拓扑后，第2相绕组将开始换向，其换向的电机系统网络拓扑结构与图4a相同，只是各相绕组的位置移动了一位，因此4极23槽CWBLDC的运行就是这8个拓扑的不断循环。这8组拓扑所对应的微分方程组为
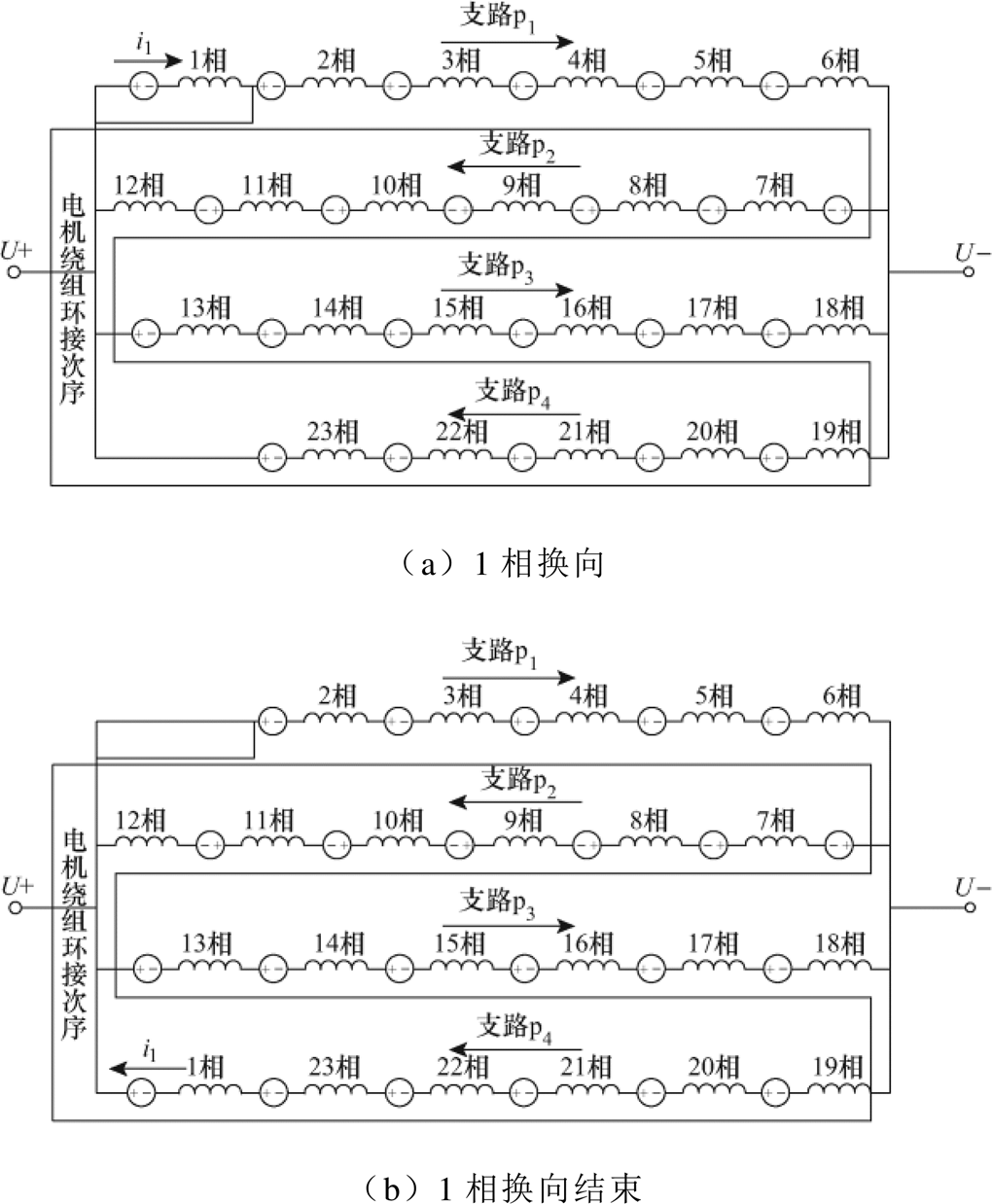
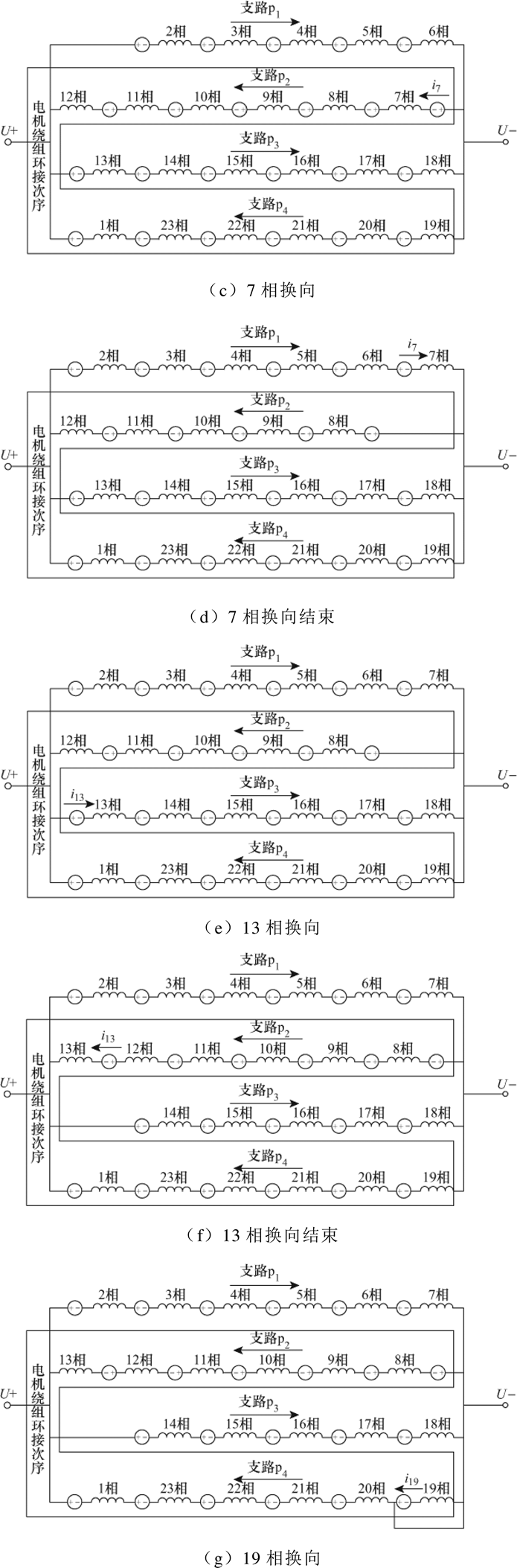
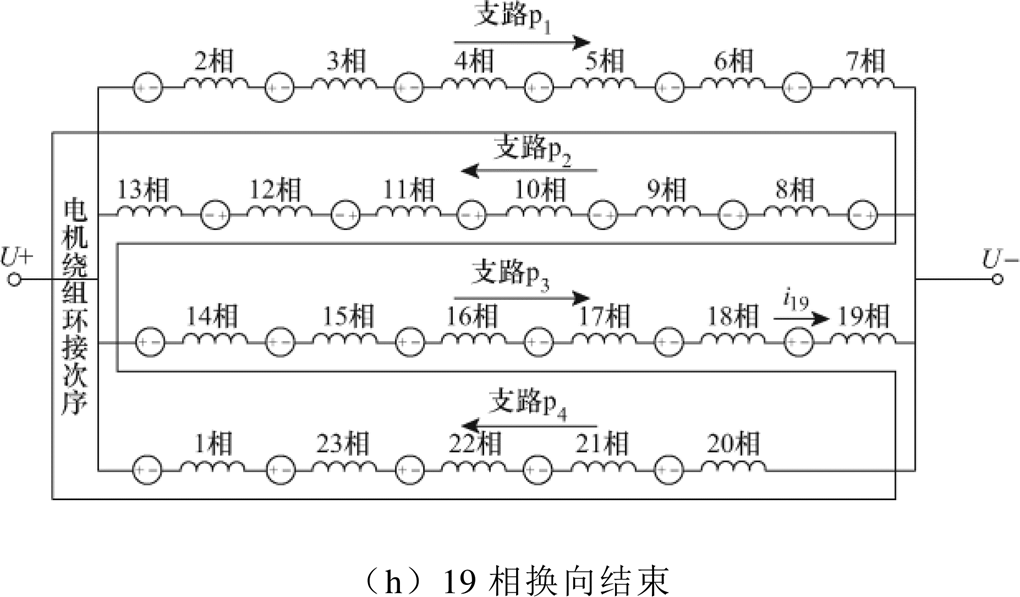
图4 4极23槽电机的系统网络拓扑
Fig.4 Topologies of 4-pole, 23-slot CWBLDC motor
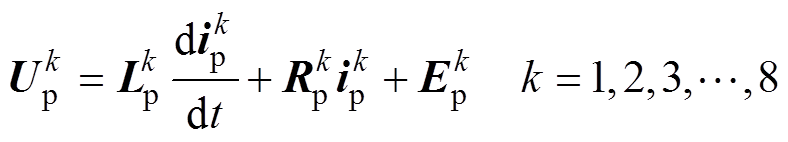（1）式中，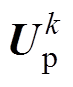
为各拓扑的支路端电压矢量；
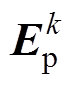为各拓扑的支路反电动势矢量；
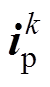为各拓扑的支路电流矢量；
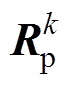为各拓扑的支路电阻矩阵；
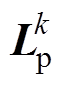为各拓扑的支路等效电感矩阵；上标k是拓扑编号；下标p表示微分方程是以支路电流为基础建立的。
利用龙格库塔（Runge-Kutta）数值方法求解微分方程组，并按2.1.2节所述的条件切换拓扑，便可以得到电机在一个槽距内各支路电流的解。
在得到图4所有拓扑各支路电流后，需进一步获得一个完整电周期的相电流。已知电机转子转过一个槽距后各相绕组位置移动一位，因此转过23个槽距后各相绕组回到最初的位置，电机系统网络拓扑再次切换为如图4a所示，所有相绕组在拓扑中的位置也经历了一个变化周期，即一个完整的电周期内图4的8个网络拓扑将循环23次。
为得到相电流的完整波形，只需将该相绕组在这23次循环周期所在的支路电流按时间组合在一起即可。以18相为例，前5次循环周期位于支路p3；第6次循环周期由支路p3换入支路p2；第7～11次位于支路p2；第12次由支路p2换入支路p1；第13～17次位于支路p1；第18次由支路p1换入支路p4；第19～22次位于支路p4；第23次由支路p4换入支路p3，回到最初的位置。假设Tn为第n次循环开始的时间，则18相的周期电流可以表示为
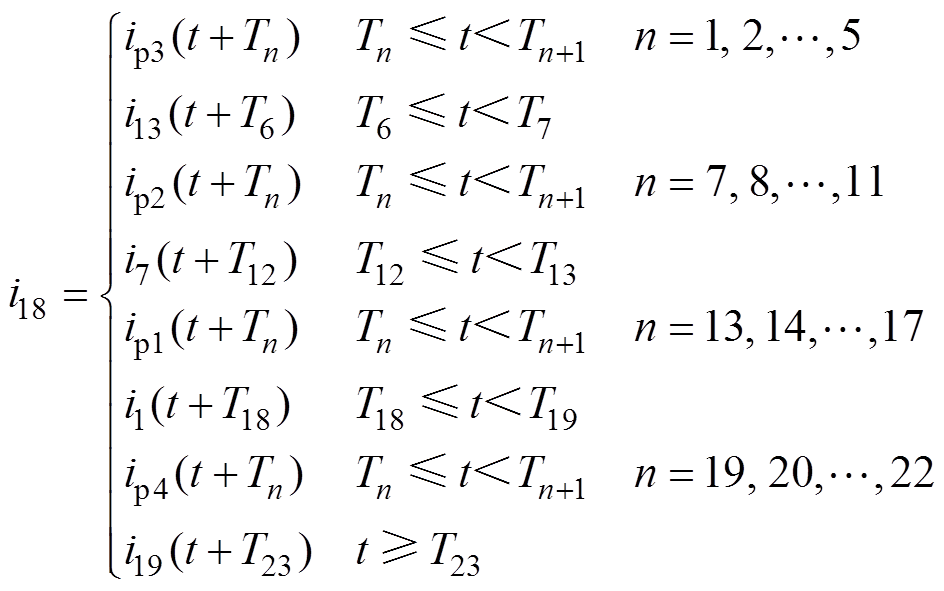（2）式中，n为图4中8个网络拓扑的循环次数编号。
忽略负载电枢反应磁场对永磁磁场的影响，将傅里叶级数拟合的电机实测空载反电动势波形作为数学模型的输入。傅里叶级数的表达式为
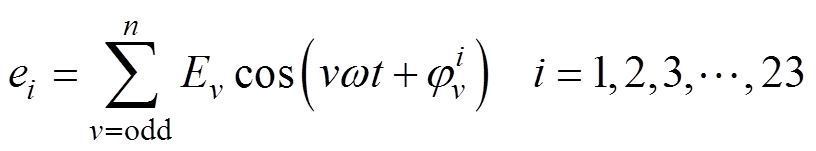（3）式中，ei是第i相反电动势的傅里叶级数；v为谐波次数；Ev为v次谐波分量的幅值；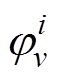
为第i相反电动势的v次谐波分量的相位；w 为电机角速度。
支路由不同的相绕组串联组成，因此电感矩阵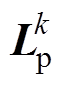可以由相绕组的电感矩阵计算。23相绕组的电感矩阵为
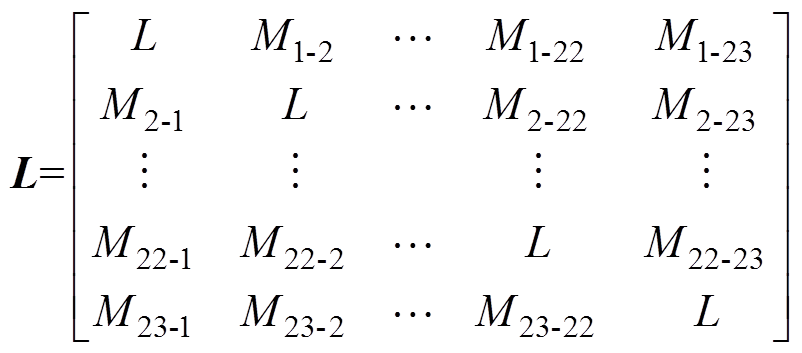（4）式中，L为相绕组自感；M1-2为1相绕组与2相绕组的互感，其余互感按此规则编号。相绕组的自感与互感可由绕组函数推导，本文不作详细介绍。
图4a所示拓扑中，式（1）中的支路电感矩阵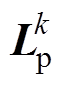（k=1）为
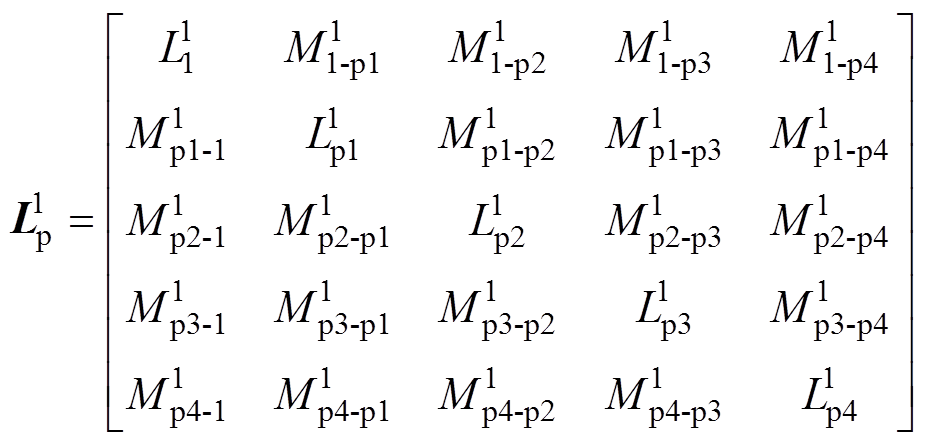（5）式中，下标表示支路相或换向相，如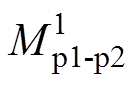
为支路p1与支路p2的等效互感；
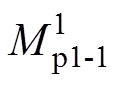为支路p1与此时的换向相绕组的等效互感。明确支路拓扑后便能计算支路电感与互感，下面计算以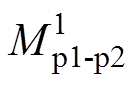为例，并说明计算过程。
支路p1由2、3、4、5、6相绕组串联组成，支路p2由7、8、9、10、11、12相绕组串联组成，在支路p2的电流作用下，支路p1所感应的磁链为
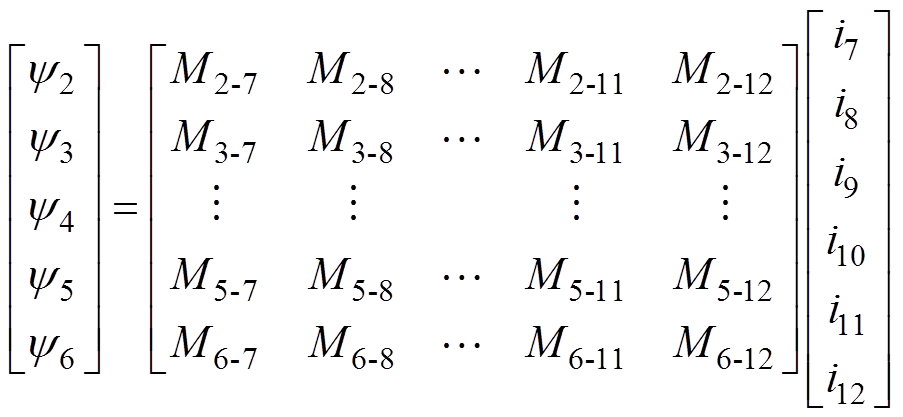（6）式中，y2, y3,…,y6分别为2, 3,…,6相绕组的磁链。
由于p2支路的各相电流相等，则等效互感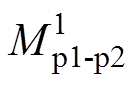为
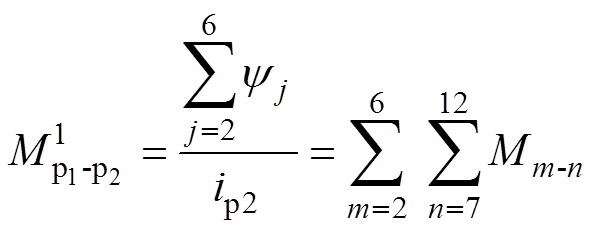（7）其他支路等效电感的计算方法相同，不再赘述。
以一台4极23槽CWBLDC的实际参数为例依次求解8个拓扑的微分方程组，图5是转子转过一个槽距内各支路电流与换向相的反电动势波形，图中可以观察到相电流在反电动势的作用下改变方向。
按式（2）得到相电压和电流波形如图6所示，负载换向的原理决定了相电流的相位必然较反电动势提前，电机始终具有超前的功率因数。
本文通过场路耦合仿真与原理样机的实验来验证数学模型的准确性。
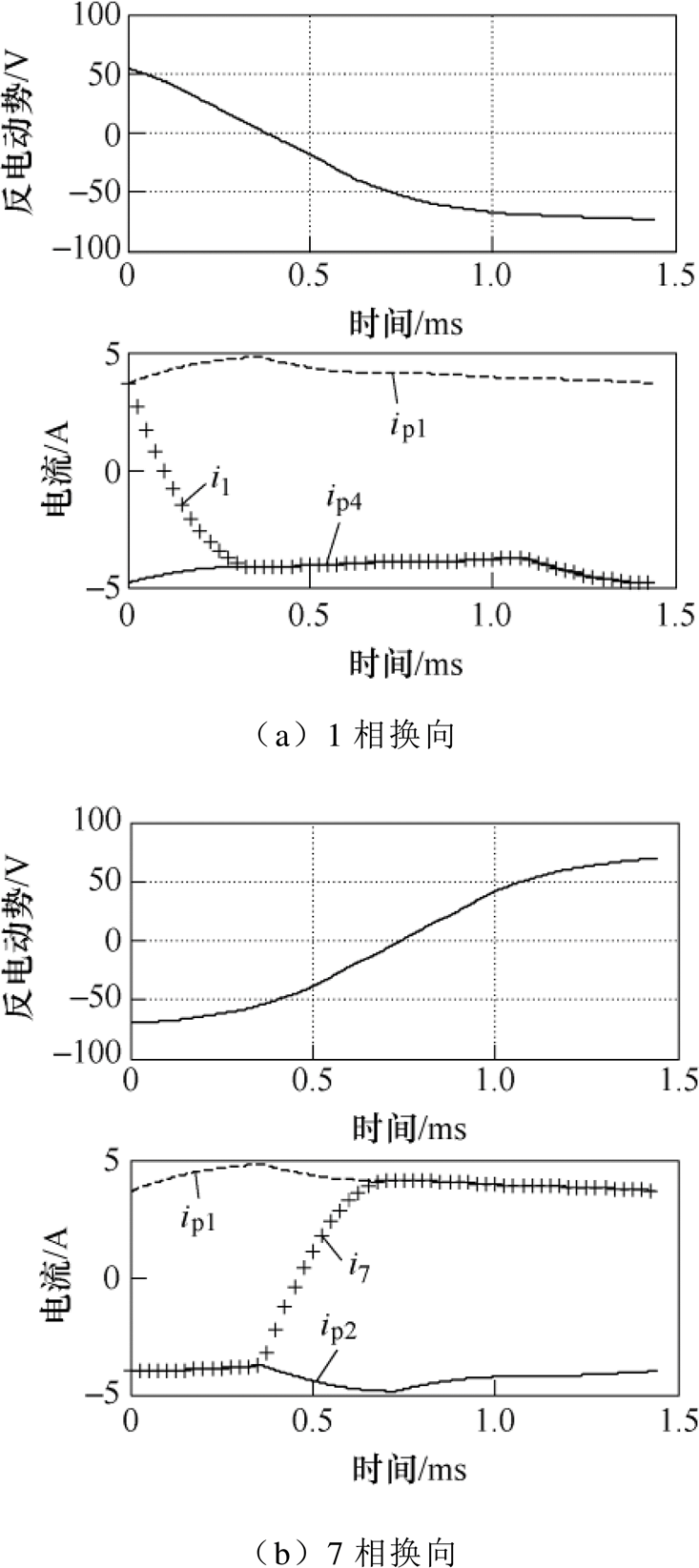
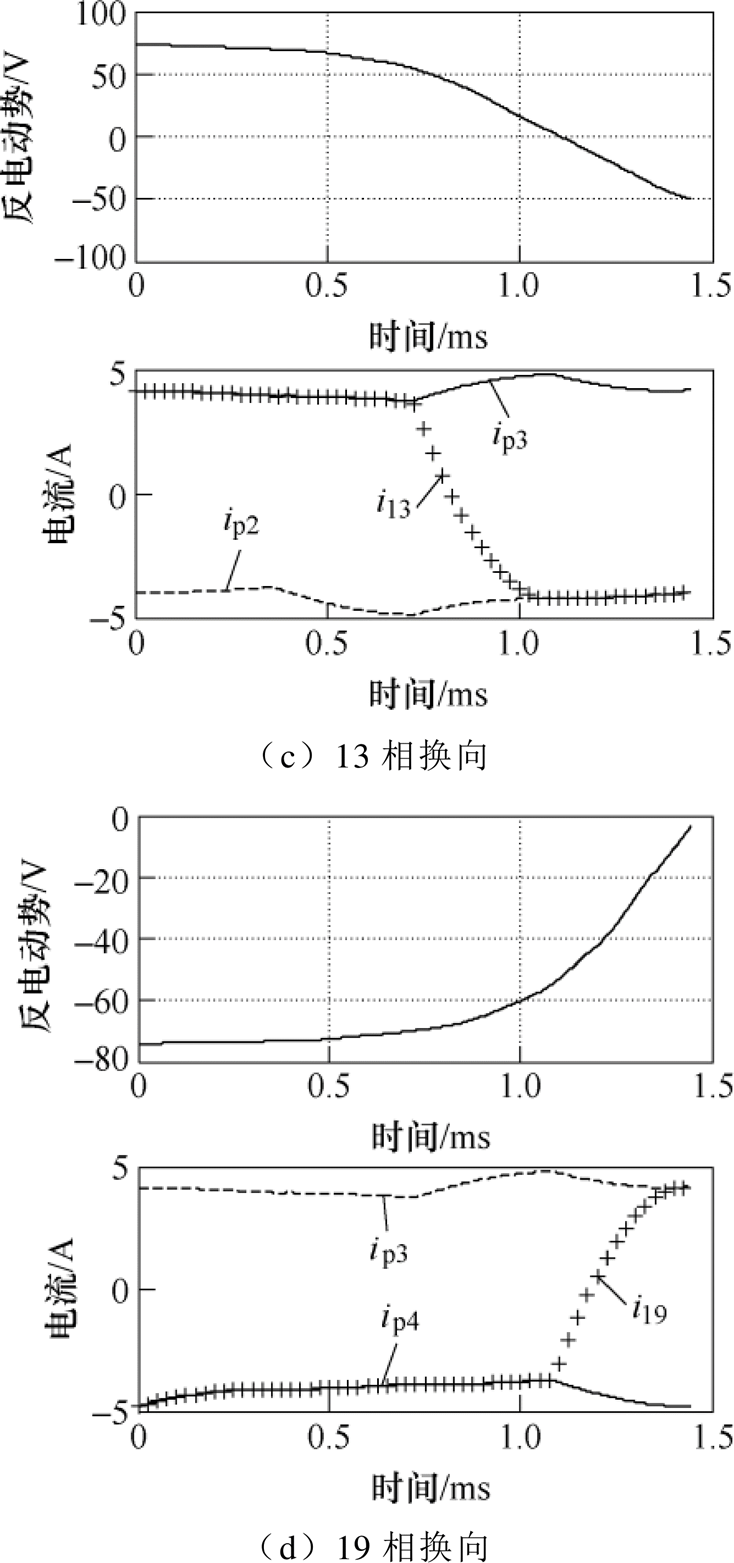
图5 支路电流波形
Fig.5 Currents in circuit branches
场路耦合仿真通过数据接口结合电磁场模型与驱动电路模型，能够准确地分析电机与驱动电路之间的相互作用，可信度较高。本文采用Maxwell 16.0建立电机的电磁场模型，采用Simplorer 11.0建立驱动电路模型。
本文采用的实验样机是一台8极46槽CWBLDC，它由2个4极23槽单元电机组成，图7为原理样机以及实验平台，表1是原理样机CWBLDC参数。
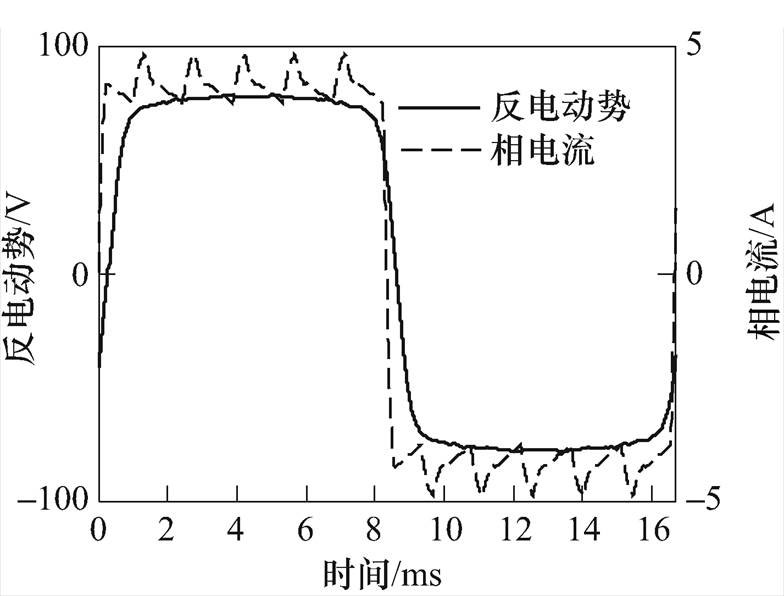
图6 相反电动势和电流波形
Fig.6 Back EMF and phase current waveforms
图7 原理样机实验平台
Fig.7 Experimental prototype CWBLDC motor
表1 CWBLDC样机参数
Tab.1 The parameters of prototype CWBLDC motor
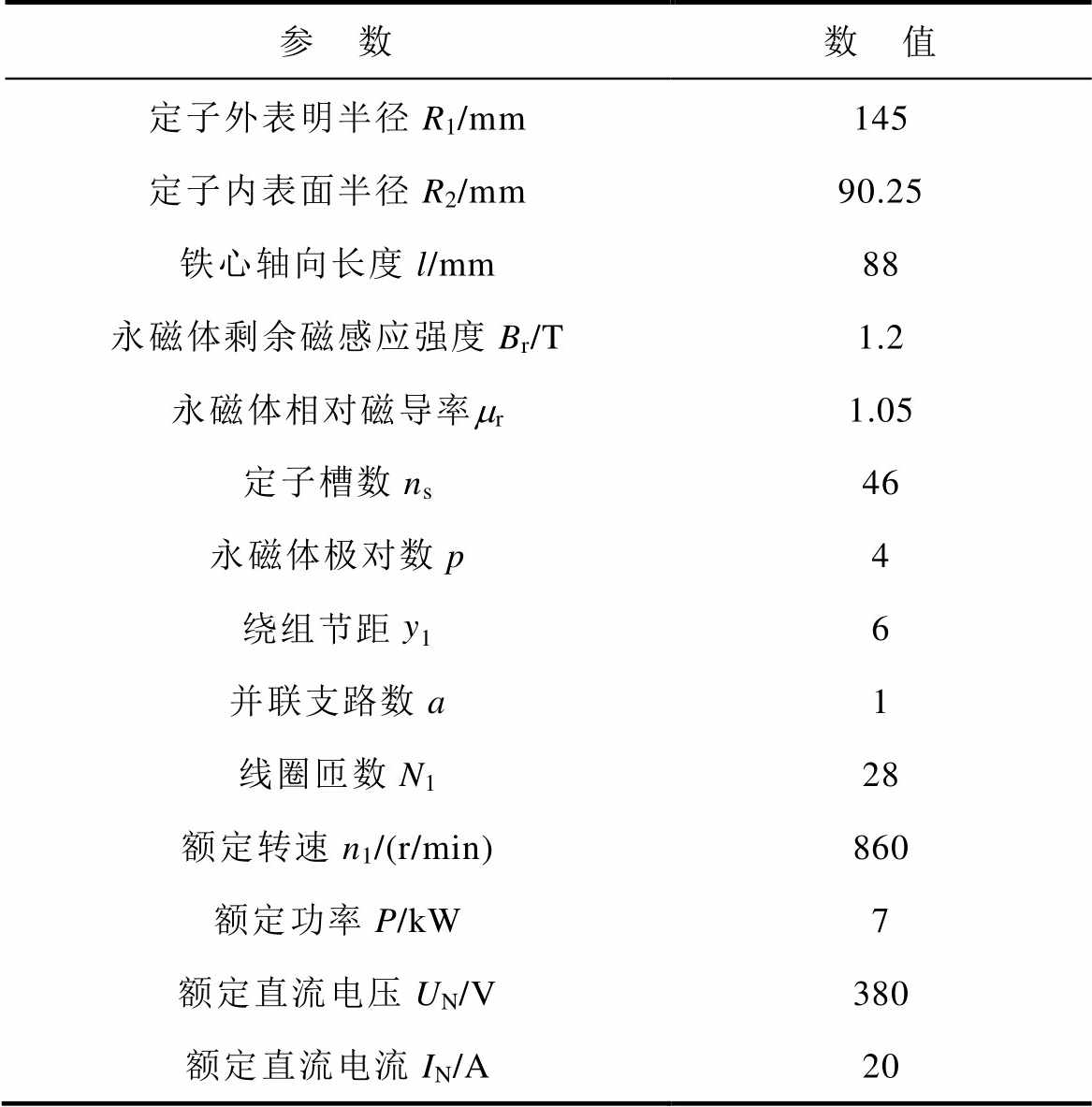
参 数数 值 定子外表明半径R1/mm145 定子内表面半径R2/mm90.25 铁心轴向长度l/mm88 永磁体剩余磁感应强度Br/T1.2 永磁体相对磁导率mr1.05 定子槽数ns46 永磁体极对数p4 绕组节距y16 并联支路数a1 线圈匝数N128 额定转速n1/(r/min)860 额定功率P/kW7 额定直流电压UN/V380 额定直流电流IN/A20
为充分验证所建立的CWBLDC数学模型，在轻载到额定负载取4个工况点，图8为数学模型计算结果、场路耦合仿真结果、实验结果对比的相电流波形。CWBLDC与有刷直流电机类似，控制直流母线电压的负载实现调速，由于系统负载为纯电阻，因此直流电压与直流电流为线性关系。
图8显示，无论是一个电周期的电流波形还是一个槽距内的电流纹波，数学模型的计算结果与场路耦合仿真结果基本一致。
实验测试结果与数学模型、场路耦合仿真结果在电周期尺度上基本一致，纹波上有较小的差别，这是由于数学模型与场路耦合仿真没有考虑驱动电路中如吸收电容等分散电路参数的影响。
实验结果证明建模思路正确，模型计算精度高，因此所建立的数学模型能够准确地分析CWBLDC。
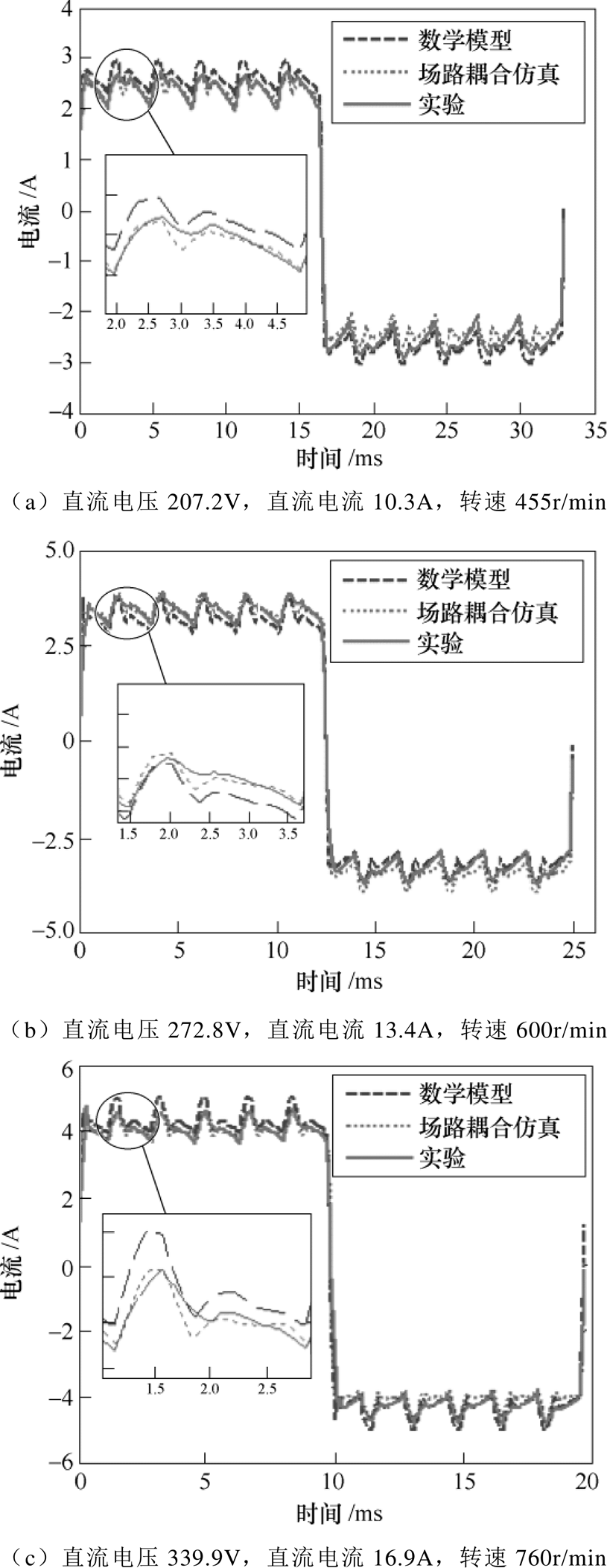
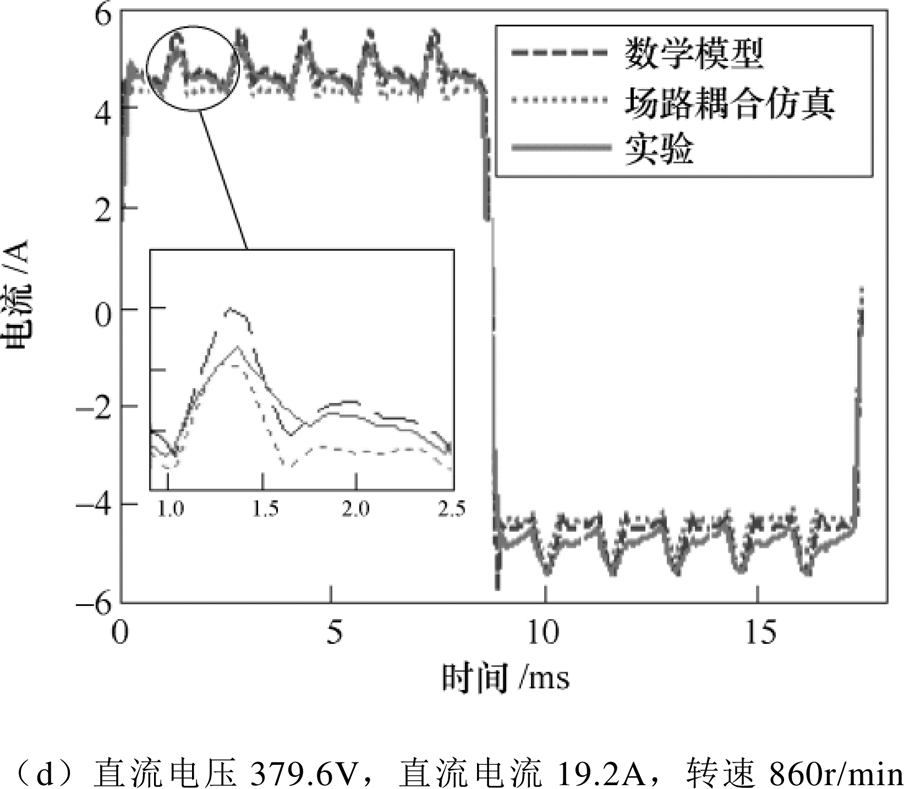
图8 数学模型、场路耦合仿真和实验结果对比
Fig.8 Analytical, field-circuit couple simulation and experiment results
由于分数槽绕组环形绕组无刷直流电机的相数多、相间互感关系复杂、运行中电机系统网络拓扑不断变化，因此常规的建模方法工作量过大，甚至无法实现。本文以并联支路电流为模型变量，利用拓扑的周期变换大大简化了建模过程。场路耦合仿真及原理样机实验表明建模思路正确，电机性能的计算结果准确。
该数学模型主要特点是计算速度快，分析时间远远小于场路耦合仿真的耗时。负载换向是否成功取决于提前导通下一功率开关（见1.2节SH2）的时间，不断摸索这一参数使得场路耦合仿真耗时严重。以4极23槽CWBLDC的稳态分析为例，场路耦合仿真的计算时间约为20h，数学模型的分析时间仅需约30s。因此该数学模型十分适用于电机设计，能够迅速比较不同设计的稳态性能。另外，将该数学模型作适当的拓展，结合如Matlab/Simulink等系统仿真软件，也能服务于动态性能分析与调速策略研究。
本文所提出的建模思路不仅适用于CWBLDC，对于相数较多、存在自关断功率器件、拓扑不断变化的其他复杂电机系统也同样适用，是一种可行、通用的建模思路。
参考文献
[1] Lewis C. The advanced induction motor[C]//2002 IEEE Power Engineering Society Summer Meeting, Chicago, 2002: 250-253.
[2] 王东, 吴新振, 马伟明, 等. 非正弦供电十五相感应电机气隙磁势分析[J]. 中国电机工程学报, 2009, 29(15): 88-94.
Wang Dong, Wu Xinzhen, Ma Weiming, et al. Air- gap MMF analysis of fifteen-phase induction motor with non-sinusoidal supply[J]. Proceedings of the CSEE, 2009, 29(15): 88-94.
[3] Thongam J S, Tarbouchi M, Okou A F, et al. Trends in naval ship propulsion drive motor techno- logy[C]//2013 IEEE Electrical Power & Energy Conference (EPEC), Halifax, 2013: 1-5.
[4] 姚文龙, 张均东, 张桂臣. 吊舱推进电机及其关键技术发展综述[J]. 电工技术学报, 2012, 27(3): 35-49.
Yao Wenlong, Zhang Jundong, Zhang Guichen. Development of the propulsion motor and its key technologies for ship podded system[J]. Transactions of China Electrotechnical Society, 2012, 27(3): 35-49.
[5] Laszlo Huber, Misha Kumar. Performance com- parison of three-step and six-step PWM in average- current-controlled three-phase six-switch Boost PFC rectifier[J]. IEEE Transactions on Power Electronics, 2016, 31(10): 7264-7272.
[6] Carlson R, Lajoie-Mazenc M, Fagundes J C D S. Analysis of torque ripple due to phase commutation in brushless DC machines[J]. IEEE Transactions on Industry Applications, 1992, 28(3): 632-638.
[7] 朱俊杰, 刘浩然, 蒋峰, 等. 无刷直流电机转矩脉动抑制系统的新型拓扑研究[J]. 电工技术学报, 2018, 33(17): 4060-4068.
Zhu Junjie, Liu Haoran, Jiang Feng, et al. A new topology research on torque ripple suppression system of brushless motor[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4060-4068.
[8] 王培侠, 姜卫东, 王金平, 等. 基于电流滞环控制的无刷直流电机多状态换相转矩脉动抑制方法[J]. 电工技术学报, 2018, 33(22): 5261-5271.
Wang Peixia, Jiang Weidong, Wang Jinping, et al. A current hysteresis control method for brushless DC motor in multi-state with commutation torque ripple reduction[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5261-5271.
[9] Jahns T M, Soong W L. Pulsating torque mini- mization techniques for permanent magnet AC motor drives-a review[J]. IEEE Transactions on Industrial Electronics, 1996, 43(2): 321-330.
[10] Murai Y, Kawase Y, Ohashi K, et al. Torque ripple improvement for brushless DC miniature motors[J]. IEEE Transactions on Industry Applications, 1989, 25(3): 441-450.
[11] 盛田田, 王晓琳, 顾聪, 等. 一种使用重叠换相法的无刷直流电机平均转矩控制[J]. 中国电机工程学报, 2015, 35(15): 3939-3947.
Sheng Tiantian, Wang Xiaolin, Gu Cong, et al. An average torque control method for brushless DC motors using overlap commutation strategy[J]. Proceedings of the CSEE, 2015, 35(15): 3939-3947.
[12] 林平, 韦鲲, 张仲超. 新型无刷直流电机换相转矩脉动的抑制控制方法[J]. 中国电机工程学报, 2006, 26(3): 153-158.
Lin Ping, Wei Kun, Zhang Zhongchao. A novel control scheme to suppress the commutation torque ripple in BLDCM[J]. Proceedings of the CSEE, 2006, 26(3): 153-158.
[13] Fang Jiandeng, Li Huitao, Han Bangcheng. Torque ripple reduction in BLDC torque motor with nonideal back EMF[J]. IEEE Transactions on Power Elec- tronics, 2012, 27(11): 4630-4637.
[14] 姜卫东, 黄辉, 王培侠, 等. 基于图解法的无刷直流电机抑制换相转矩脉动的方法[J]. 中国电机工程学报, 2016, 36(15): 4258-4266.
Jiang Weidong, Huang Hui, Wang Peixia, et al. A control method to suppress the commutation torque ripple of brushless DC motors based on the graphical method[J]. Proceedings of the CSEE, 2016, 36(15): 4258-4266.
[15] 夏鲲, 董斌, 卢晶. 一种基于电流反馈的分段式PWM控制无刷直流电机转矩波动抑制方法[J]. 电工技术学报, 2017, 32(17): 172-179.
Xia Kun, Dong Bin, Lu Jing. Research on hybrid PWM control method with current feedback for torque-ripple reduction in BLDCM[J]. Transactions of China Electrotechnical Society, 2017, 32(17): 172-179.
[16] 史婷娜, 李聪, 姜国凯, 等. 基于无模型预测控制的无刷直流电机换相转矩波动抑制策略[J]. 电工技术学报, 2016, 31(15): 54-61.
Shi Tingna, Li Cong, Jiang Guokai, et al. Model free predictive control method to suppress commutation torque ripple for brushless DC motor[J]. Transactions of China Electrotechnical Society, 2016, 31(15): 54-61.
[17] Wang Dong, Lin Huangda, Cheng Siwei, et al. A novel circular winding brushless DC (CWBLDC) machine with low torque ripple[C]//41st Annual Conference of the IEEE Industrial Electronics Society (IECON 2015), Yokohama, 2015: 1585-1591.
[18] Lin Huangda, Cheng Siwei, Wang Dong, et al. Load commutation of the circular winding brushless DC machine (CWBLDC)[C]//41st Annual Conference of the IEEE Industrial Electronics Society (IECON 2015), Yokohama, 2015: 2741-2746.
[19] Cheng Siwei, Zhang Qinghu, Jia Zhewu. Dynamic modeling of the circular winding brushless DC (CWBLDC) machine[C]//2016 IEEE 8th Inter- national Power Electronics and Motion Control Conference, Hefei, 2016: 2741-2746.
[20] Zhang Qinghu, Cheng Siwei, Wang Dong. Multiob- jective design optimization of high-power circular winding brushless DC motor[J]. IEEE Transactions on Industrial Electronics, 2018, 65(2): 1740-1750.
[21] 林黄达, 王东, 程思为, 等. 环形绕组无刷直流电机负载换向的解析模型[J]. 电工技术学报, 2017, 32(9): 40-47.
Lin Huangda, Wang Dong, Cheng Siwei, et al. Analytical model of load commutation of the circular winding brushless DC machine[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 40-47.
[22] Krishnan R. 永磁无刷电机及其驱动技术[M]. 北京: 机械工业出版社, 2014.
[23] 李鲲鹏, 胡虏生, 黄允凯. 计及绕组电感的永磁无刷直流电动机电路模型及其分析[J]. 中国电机工程学报, 2004, 24(1): 76-80.
Li Kunpeng, Hu Qiansheng, Huang Yunkai. The circuit model of the permanent-magnet brushless DC motor allowing for its windings inductances and its analysis[J]. Proceedings of the CSEE, 2004, 24(1): 76-80.
[24] 姜卫东, 廖玉茗, 王培侠, 等. 减小无刷直流电机换相转矩波动和换相时间的协调控制方法[J]. 中国电机工程学报, 2017, 37(7): 2120-2130.
Jiang Weidong, Liao Yuming, Wang Peixia, et al. A corporative control method to reduce commutation torque ripple and commutation time for brushless DC motor[J]. Proceedings of the CSEE, 2017, 37(7): 2120-2130.
[25] Chan C C, Jiang Jianzhong, Chen G H, et al. A novel polyphase multipole square-wave permanent magnet motor drive for electric vehicles[J]. IEEE Transa- ctions on Industry Applications, 1994, 30(5): 1258- 1266.
[26] Chan C C, Chau K T, Jiang Jianzhong, et al. Novel permanent magnet motor drives for electric vehicles[J]. IEEE Transactions on Industrial Electronics, 1996, 43(2): 331-339.
[27] Zhu Li, Jiang Shuzhong, Jiang Jianzhong, et al. A new simplex wave winding permanent-magnet brushless DC machine[J]. IEEE Transactions on Magnetics, 2011, 47(1): 252-259.
[28] Zhu Li, Jiang Shuzhong, Jiang Jianzhong, et al. Speed range extension for simplex wave winding permanent-magnet brushless DC machine[J]. IEEE Transactions on Magnetics, 2013, 49(2): 890-897.
Analytical Modeling of the Circular Winding Brushless DC Motor under Load Commutation
Abstract The circular winding brushless DC motor (CWBLDC) is a brushless DC motor, but a multiphase winding of the motor is connected in a unique polygon or circular fashion. The CWBLDC motor has higher torque density due to larger width of electromotive force (EMF) trapezoidal wave. Combined with well-designed fractional-slot winding, the motor can dramatically reduce the commutation torque ripple, which is suitable for electric propulsion systems of high power rating ships despite more power semiconductor devices required. Different from the conventional three-phase BLDC motor, the circuit topologies transform with the rotor rotation. Transformation period of topologies reduces the modeling complexity. Field-circuit couple simulations and experimental results verify the model. The model is helpful to understand the operation principle of CWBLDC motor. It can quickly analyze the steady-state performance, which is suitable for parameters determination in CWBLDC motor design.
keywords：Brushless DC motor, multiphase circular winding, fractional-slot winding, load commutation, analytical modeling, topology periodic change
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.190220
国家重点基础研究发展计划项目（973计划）（2013CB035601）和国家自然科学基金项目（51507181）资助。
收稿日期 2019-03-05
改稿日期 2019-11-08
林黄达 男，1986年生，博士，讲师，研究方向为电力推进技术。E-mail: linhuangda_2015@163.com
程思为 男，1985年生，副教授，研究方向为电力推进、独立电源系统等。E-mail: siwei_cheng@sina.com（通信作者）
（编辑 陈 诚）