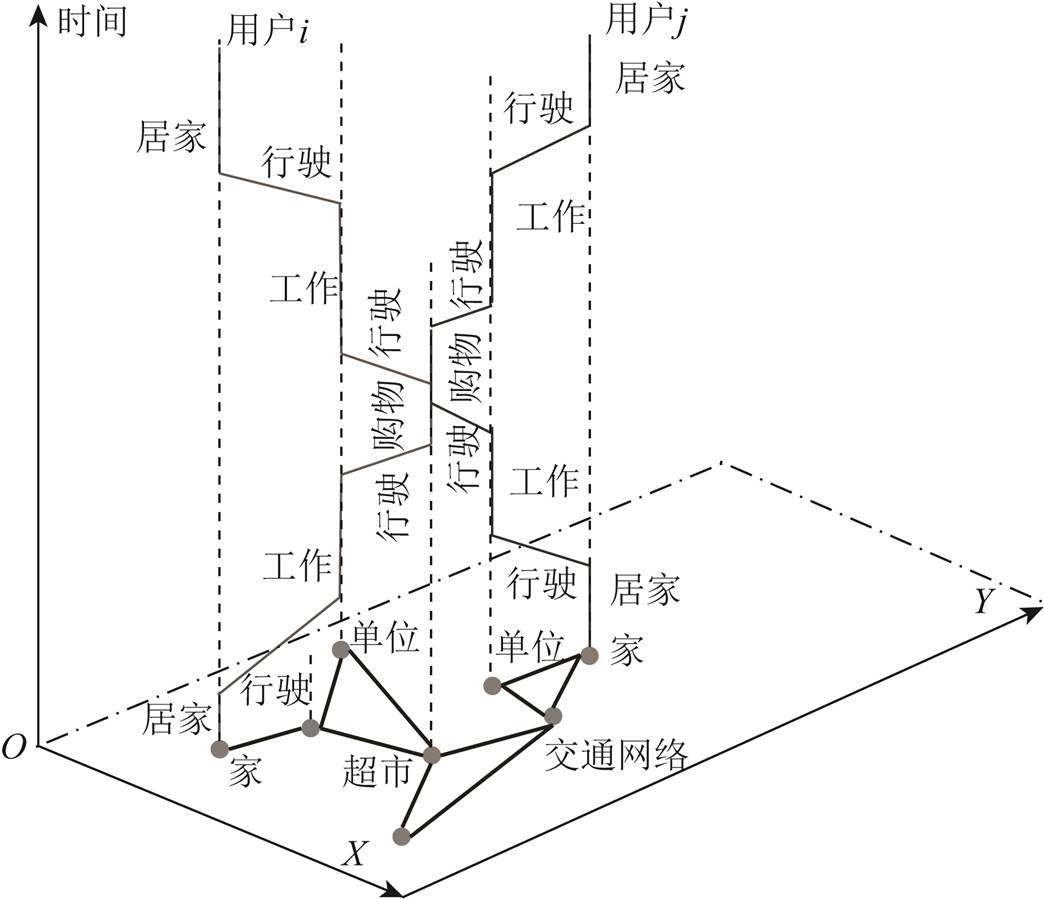
图1 用户的活动行为三维时空表达
Fig.1 Three-dimensional space-time representation of activity behaviors
摘要 电动汽车的时空行为包括时空转移行为和时空充电行为。如何对电动汽车时空行为进行精确建模已成为大规模电动汽车与电网进行有效互动的关键。该文引入活动分析法将出行行为理解为活动的派生行为，建立用户一天中不同活动-出行链间的时空转移关系；基于累计前景理论描述了用户在活动-出行链中的出行方式、出行路径、出发时刻选择上的有限理性心理；在此基础上考虑交通网络的动态特性和电动汽车的充电特性，研究了电动汽车在每条活动-出行链上的时空分布特性和充电特性；并在典型网络（Nguyen-Dupius网络）中对不同用户心理、电动汽车占比、充电站服务能力约束下的电动汽车时空转移和充电特性进行算例分析。计算结果表明所提方法能够更加合理地刻画用户选择心理及描述电动汽车用户时空行为，且发现电动汽车占比和充电站服务能力均对其有较大影响。
关键词：电动汽车时空行为 活动分析法 有限理性 累积前景理论 动态交通分配模型
电动汽车（Electric Vehicle, EV）作为一种绿色出行工具，替代燃料汽车成为未来主要交通工具已是时代发展的趋势[1]。然而，大规模电动汽车的出行及充放电势必给城市交通和电网的协调发展带来巨大挑战[2-4]，不仅会造成交通堵塞，还可能带来电能质量、电网稳定性恶化等影响[5-7]。因此，准确把握电动汽车时空行为是满足城市居民出行需求和保证电网安全经济运行的基础。
电动汽车时空行为指的是时空转移行为和时空充电行为，其中时空转移行为包括不同出行（链）之间的转移关系和电动汽车在每条出行（链）中的时空分布特性，属于用户行为研究范畴，涉及交通科学、心理学及电气学科等多领域。传统用户行为研究经历了从集计研究方法到非集计研究方法的发展过程。集计方法难以分析用户出行选择的真正原因[8]。从20世纪60年代开始对用户行为研究进入了非集计阶段，研究主要集中在数学模型的构建，先后建立了分析用户决策行为的多项Logit模型和树状分对数Logit模型[9-10]。F.S.Chapin结合经济学中的最大效用理论，对城市居民出行进行了相关研究，证明了用户的出行规律受社会经济影响较大[11]。但这些数学模型均遵循效用最大化理论，其假设人为完全理性，而现实中人们往往并不按照效用理论的预测结果行事。M. Allias悖论[12]、D. Ellsberg悖论等[13]行为经济学均对人的完全理性假设提出了质疑，且Logit模型不能很好地反映单次出行中出行发生、方式选择、出行分布等之间的密切联系及相互依赖性。
国内外针对电动汽车时空行为建模已经做了初步研究，主要集中在集计统计学分析方法、仿真分析方法和完全理性假设分析。在集计统计学分析方法上，文献[14-17]分别根据统计调查数据或跟踪测量数据对电动汽车出行和充电行为的特征量进行了拟合分析，包括出行起始时刻、出行时间、充电起始时刻、充电时间等；在仿真分析上，文献[18]提出了基于Agent-元胞自动机的电动汽车充电需求时空分布动态演化模型，对电动汽车的行驶行为和路径规划进行了仿真研究；在完全理性假设分析上，文献[19-20]基于效用最大化原则提出了电动汽车充电消费决策模型。这些研究工作均没有考虑实际情况中电动汽车用户的充电、出行等行为的不完全理性，将影响对电动汽车充电负荷的精确建模。
本文通过分析用户决策心理及交通流量分配规律，提出了一种电动汽车时空行为特性描述方法。将电动汽车的时空行为分为活动链之间的转移行为和在活动链上的转移行为。首先引入活动分析法，考虑用户行为的时空约束，将用户一天的出行活动在三维空间中进行表达；将用户每日活动进行分类，基于贝叶斯法分析了用户不同活动-出行链之间的转移关系；研究了每条活动-出行链上的转移行为，考虑用户在出行方式、出发时刻及出行路径选择之间的相互联系和有限理性心理，基于累计前景理论提出了用户感知满意的出行三参考点规则及出行选择模型；最后，计及交通网的动态特性和电动汽车充电特性，结合动态交通分配模型分析了电动汽车在活动-出行链上的时空分布特征，得出了电动汽车每日出行次数、充电次数等的变化规律。
活动分析法[21]采用日活动链将个人一天中所有活动和出行连接起来，系统反映出行的活动和出行安排之间的内部联系，描述所有出行之间相互依赖关系以及活动出行的时空约束。图1为用户一天中的活动行为三维时空表达。
图1 用户的活动行为三维时空表达
Fig.1 Three-dimensional space-time representation of activity behaviors
由图1可知，用户的活动出行行为在时空上均是连续的，每条活动-出行链的起点和活动时间必受历史活动-出行链的影响。对每位活动者，描述其一天的行为属性包括参与活动的次数、活动类型、活动地点、出发时刻、活动持续时间及活动的出行时间和出行方式。如果第i个用户一天的活动安排次数为n，活动-出行模式表示为ATPi，有
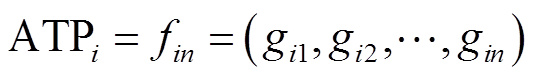（1）式中，gij为第i个用户参与的第j个活动的特征集合；fin为一整天的活动-出行模式。
根据S. Reichman等对人的活动需求研究，个体参与的活动分为必要活动和灵活选择活动两大类，如工作出行为必要活动，购物、交友为灵活选择活动[22]。考虑到用户的ATP每天都在变化，各种不同的模式都可能以一定的概率出现。从概率论的角度，每项活动发生的概率等于之前发生活动的条件概率。
若用户的第j个活动为第一类活动，则该活动发生的概率为
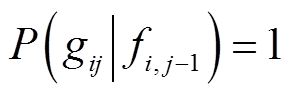（2）式中，fi,j-1为用户i参加第j个活动前的历史活动-出行模式。
若用户的第j个活动为第二类活动，假设用户i对所要参与的该活动的到达时间可接受上限为Tj，用户可供选择的出行方式有m类，用户选用第k类出行方式出行到达活动地点的最早时刻、最早时刻置信度为θ的上限分别为Tjk、Tjkθ。
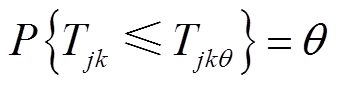（3）则用户所有出行方式的最早到达时间上限最小值为Tjmin，有Tjmin =min{Tjkθ, k∈m}，那么该活动发生的概率为
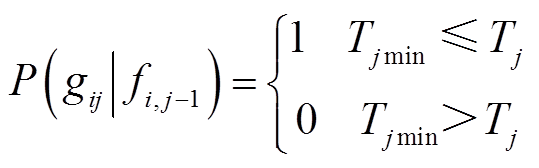（4）
根据贝叶斯理论及式（2）、式（4）可知，用户参与第j项活动（第j条活动-出行链产生）的概率为
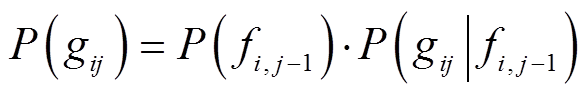（5）用户在活动-出行链上的时空转移取决于其对出行方式、出发时刻、出行路径的选择。有限理性指的是一方面由于人的认知能力有限，决策者不可能掌握全部信息，仅能根据掌握的部分信息对结果进行感知；另一方面，决策者在决策中往往追求“满意”标准，而非最优标准。
累计前景理论[23]考虑用户的有限理性，将用户的选择决策行为分为编辑和评价两个阶段。在编辑阶段用户基于对当前路网信息的认知进行编译，综合各种约束条件设定该次出行的参考点，根据不同出行的属性将其相对于参考点定义为“收益”和“损失”，并且形成关于“收益”和“损失”的主观概率权重（或决策权重）；在评价阶段，用户将“收益”和“损失”与主观概率权重相结合，形成对不同出行选择的感知效用。该过程体现了用户有限理性的第一个方面。
设一种选择的前景Pro出现结果xi的概率为pi，用户制定参考点x0的概率为p0。将可能出现的结果xi按照升序排列为x-r ≤x-(r-1)≤
≤x-1≤x0≤x1≤≤xq-1≤xq，则累计前景理论的模型可表示为
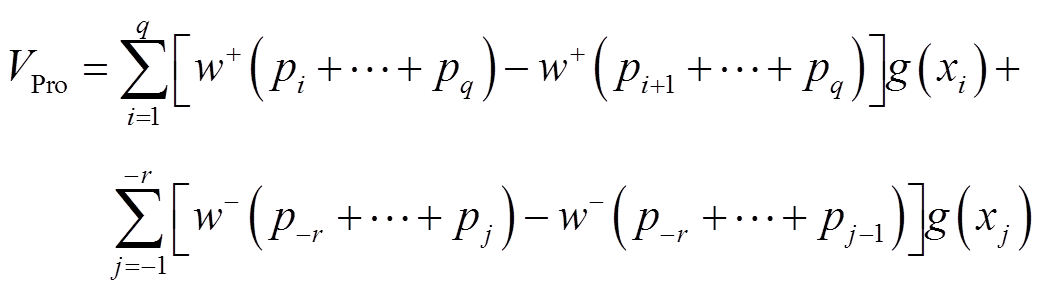（6）式中，VPro为用户的感知效用；g(xi)为结果xi的价值函数；w+(·)、w-(·)分别为收益和损失的概率权重函数。
考虑到结果xi发生概率的连续性，将选择结果的概率分布函数F(x)引入式（6）中，用户的感知效用，即累计前景为
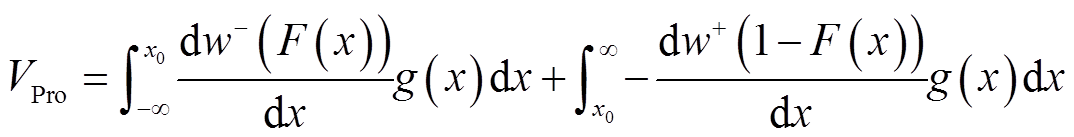（7） 根据经济学中D. Kahneman和A.Tversky等[24]研究者对价值函数和决策权重的研究，在参考点附近人们的风险偏好会发生逆转，面对收益倾向于风险厌恶，面对损失倾向于风险追求；面对等额的收益和损失，对损失的规避程度大于对收益的偏爱程度；越远离参考点，收益或损失的边际变化对人们心理影响越小；人们往往高估小概率事件，低估大概率事件。由此得出了描述决策者有限理性的“S”型价值函数和倒“S”型的决策函数，如图2所示。
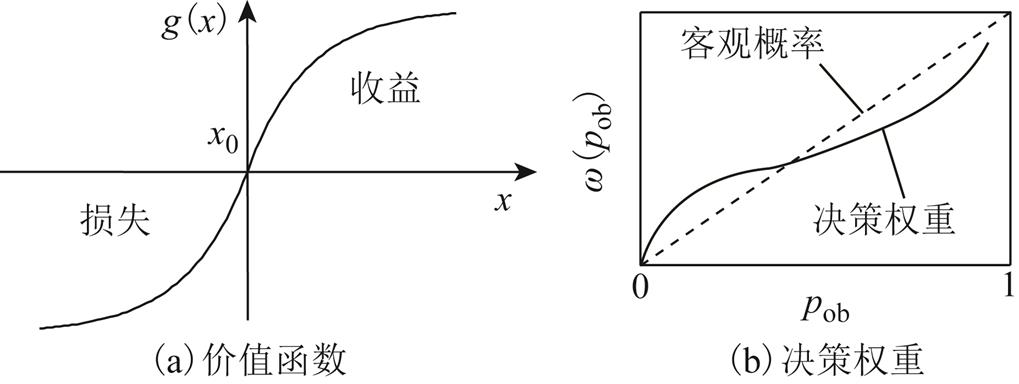
图2 用户价值函数和决策权重
Fig.2 Value function and weighting function of user
价值函数和决策权重可表示为
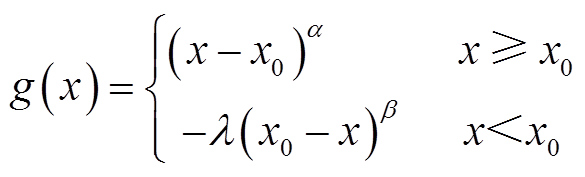（8）
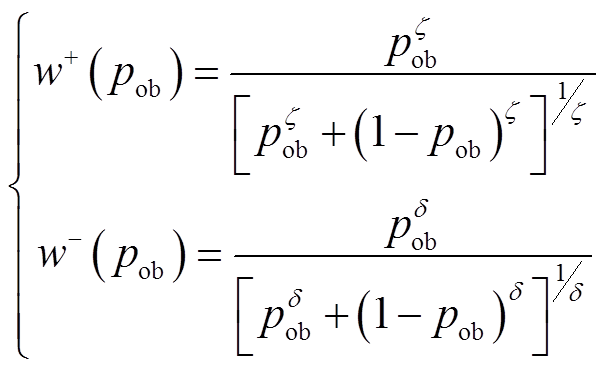（9）
式中，α、β和λ(0＜α,β＜1,λ≥1)反映了用户对风险的偏好水平，值越大表示决策者对于风险（收益或损失）的敏感性递减程度越小，决策者对风险越敏感；参数ζ和δ决定了倒“S”型决策函数的弯曲程度；pob为选择结果发生的客观概率。
通过式（6）~式（9）可描述决策者对某一选择的感知效用。
由2.1节可知，参考点选取是影响感知效用的重要参数之一，而实际中用户在出行方式、出发时刻和出行路径的选择上相互制约，故在进行参考点选取时必须同时考虑三者的影响。R.C.Jou等[25]在基于前景理论研究工作出行的出发时刻选择问题时，提出了以“可以接受的最早到达时刻TE”和“工作开始时刻TW”作为价值函数的两个参考点，出行者在这两个参照点之间到达将获得“收益”，否则为“损失”；在两个参考点之间存在一个“期望的最佳到达时刻TO”，出行者在TO到达获得“收益”最大，如图3所示。
本文在此基础上建立三个参考点设立规则：①将TE和TW作为出发时刻选择的参考点；②将TO作为路径选择的参考点，到达时刻离TO越近收益越大；③由文献[26]研究可知，出行者进行出行选择的最重要准则是行程时间，且出行者倾向于选择更具有可靠性的出行方式，故可将出行时间设定为出行方式的参考点。
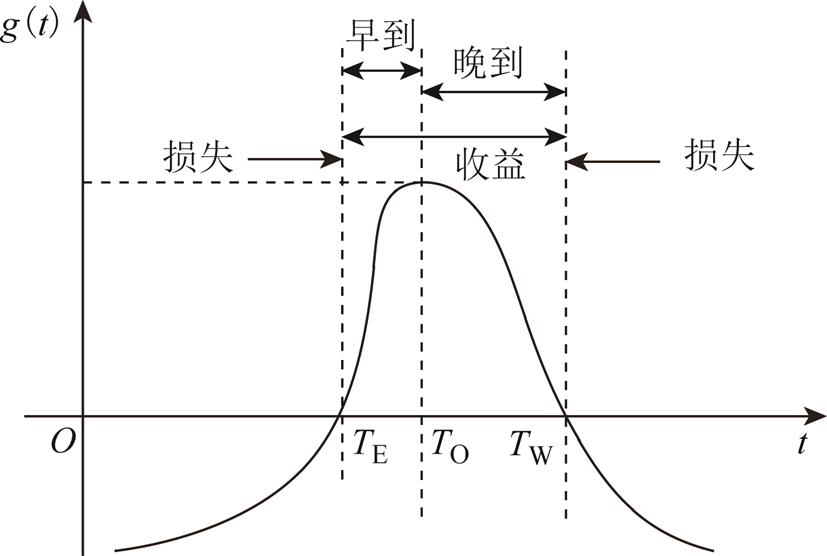
图3 出行者到达活动地点的价值函数
Fig.3 Value function of arrival time
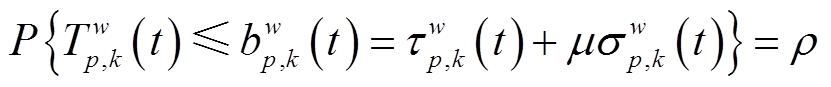（10）
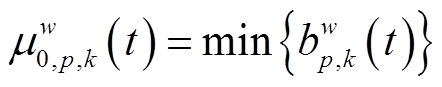（11）
式中，T w p,k(t)、bw p,k(t)和μw 0,p,k(t)分别为t时刻路径p上选用第k种出行方式的行程时间、出行时间预算及行程时间参考点；τw p,k(t)、σw p,k(t)分别为T w p,k(t)的期望和标准差；w为所有起讫点（Origin and Destination, OD）对集合；ρ为置信度；μ体现了活动出行者对风险的偏好程度。
将三个参考点代入式（8）可得出行方式选择、路径选择、早到和晚到的价值函数。进而由式（7）可得行程时间为连续分布下，时刻t在p路径上选择出行方式k的前景φw p,k(t)、时刻t第k种出行方式选择路径p的前景vw p,k(t)、早到前景ψw p,k,E(t)和晚到前景ψw p,k,L(t)，其中早到和晚到前景可统称为到达前景ψw p,k(t)。
活动者在出行过程中将根据不同出行方式、出发时刻及出行路径前景进行出行选择。为了更好地体现用户有限理性的第二个方面，采用选择概率的方法进行出行选择描述。设γw k(t)、ηw p(t)和μw(t)分别为时刻t出行者选择出行方式k、选择路径p及选择出行的概率，则出行者的选择行为可表示为
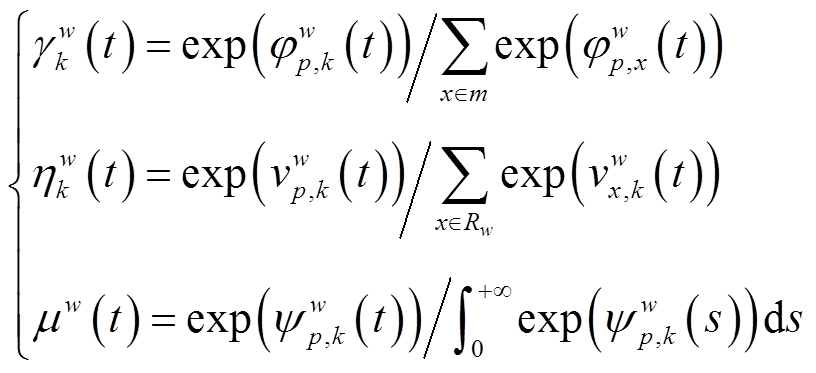（12）式中，Rw为所有可用路径集合。
通过分析三个参考点下的出行选择价值函数和决策权重函数可知，出行方式、路径、出发时刻的选择前景均为行程时间的函数，为此需对不同选择下的行程时间进行求解。考虑实际中主要出行方式有公共交通、私家车和出租车，且当用户选用出租车时用户决策行为与私家车类似，故可将出租车归为私家车进行研究。
3.1.1 行程时间计算
私家车包含燃油私家车和电动私家车。设燃油私家车、电动私家车以及公共交通分别为第1、2、3种出行方式。由于公共交通路线固定且有专用车道，受其他交通工具影响较小，其行程时间可通过路程与平均速度得到。
定义电动汽车的可用路径为一条不包括环，且可无需充电或通过中途充电到达目的地的路径。
对于私家车，根据交通领域经典模型建立路段行驶时间。
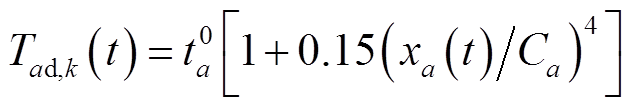（13）式中，Tad,k(t)为t时刻私家车在路段a上的行驶时间，k=1为燃油汽车，k=2为电动汽车；t0 a为路段a的自由行驶时间；Ca为路段a的通行能力；xa(t)为时刻t路段a上的流量。
计及电动汽车的充电时间，私家车路径行程时间（行驶时间与充电时间之和）可表示为
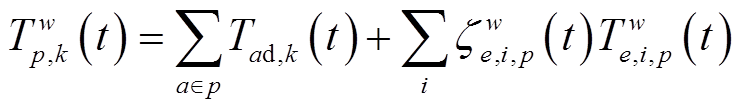（14）式中，T w e,i,p(t)为电动汽车e在节点i上的充电时间；ξ w e,i,p(t)为充电相关系数，若充电其值为1，反之为0。相似地，路径行程时间的期望和方差可以采用行驶时间和充电时间的期望及方差进行表示。
同时，路段行驶时间和充电时间方差采用变异系数描述。
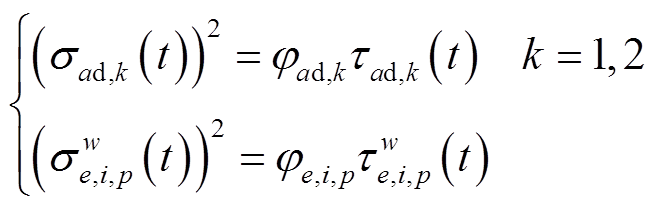（15）式中，τad,k(t)和(σad,k(t))2分别为私家车t时刻在路段a上的行驶时间期望和方差；τ w e,i,p(t)和(σ w e,i,p(t))2分别为电动汽车e在节点i上的充电时间期望和方差；φad,k 、φe,i,p为变异系数，φad,k, φe,i,p ≥0。
3.1.2 电动汽车充电模型
一般地，电动汽车通常在三种情况下产生充电行为：①在行程中，当剩余电量无法满足剩余里程行驶要求；②在活动地点电动汽车剩余电量低于阈值；③最后一次日活动结束归家后选择充满电。则t时刻电动汽车e在路径p上的节点i处的充电时间期望为
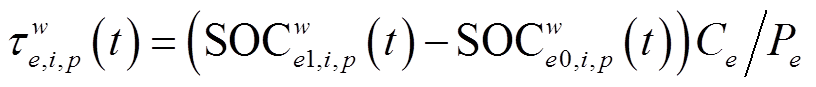（16）式中，SOC w e0,i,p(t)为t时刻电动汽车e的剩余电量；SOC w e1,i,p(t)为其充电完成后的电量；Ce为电动汽车e的电池容量，其充电功率可视为定值Pe。
考虑电动汽车用户的里程焦虑心理，在每个充电节点i上，电动汽车充电电量应满足
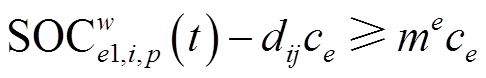（17）式中，me为电动汽车e的焦虑里程；ce为电动汽车e的耗电率；在路径p上，与节点i相邻的下一个充电节点或路径终点为j，两节点间的距离为di,j。
电动汽车同时在节点i上的充电数量应不大于充电桩数量，设节点i处的充电桩数为Ci，有
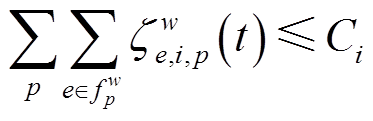（18）电动汽车在活动地点产生充电需求的条件为
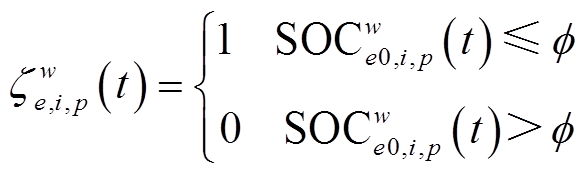（19）
式中，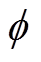
为电动汽车在活动地点产生充电需求的阈值，考虑到电池放电深度对电池寿命的影响，本文设置为0.3[27]。
在活动地点充电后，电动汽车的剩余电量为
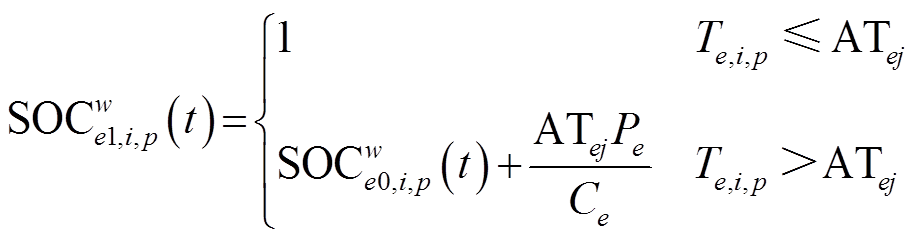（20）式中，Te,i,p为电动汽车充满电所需要的时间，Te,i,p= Ce (1-SOC w e0,i,p(t))/Pe；ATej为电动汽车e的用户参与活动j的持续时间。
3.1.3 含电动汽车的交通分配模型
3.1.1节和3.1.2节对各交通工具的行程时间进行了分析，可知电动汽车的行程时间包括充电时间和行驶时间，且其行驶时间是路径流量的函数，故需要对私家车在交通网中的流量分配进行研究。建立动态交通均衡模型为
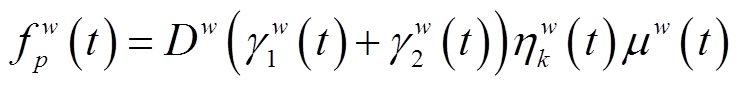（21）式中，f w p (t)为可用路径p上的流量；Dw为出行需求量。需要满足约束条件
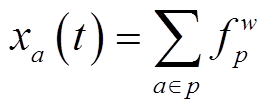（22）
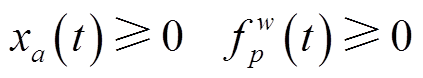（23）式（22）和式（23）分别为流量守恒和非负约束条件。
通过式（12）~式（23）建立了考虑活动出行者在出行方式、出行路径及出发时刻选择有限理性下的时空分布模型。
考虑到用户选择与交通流量的耦合性，以及动态交通分配问题的非对称性，无法找到与式（21）相对应的数学模型。通过变分不等式将式（21）转换为其等价模型，等价于在任意时刻的路径流量f w*p (t)，使得式（24）成立。
记式（21）的可行集为Ωw，令
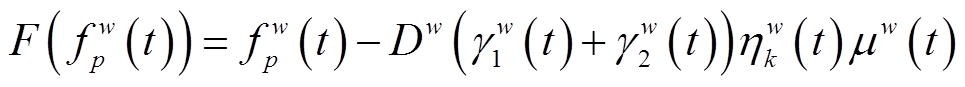（25）
对于实际出行需求Dw均有界，且F(f w p (t))在Ωw上为连续函数，故式（24）的解存在。
首先，基于路径搜索技术将所有无环路径设为初始可用路径集合。设计连续平均法(Method of Successive Average, MSA）进行出行方式、出发时刻、出行路径选择问题求解，具体求解算法步骤如图4中的流程所示。
为了得到电动汽车时空行为规律，本文以Nguyen-Dupius网络为研究对象，其网络结构如图5所示，相关参数见附表1。
根据T. Schwanen等采用大量股票市场及出行行为的研究[28]，式（8）和式（9）中的参数可取α=β=0.88，λ=2.25，ζ=0.61，δ=0.69，迭代收敛条件ε=0.01。充电站的充电变异系数取为0.3。
设置电动汽车每日上班出行时为满电状态，以Nissan Leaf为例，其电池容量为24kW∙h，每100km耗电量为30kW∙h，充电功率设定为平均值7.3kW，用户的焦虑里程为20km。设TW为期望到达时刻上限，TO为最佳期望到达时刻，TO=TW-15 min，最早到达时刻为TE=TW-30 min。规定公共交通的平均行驶速度为35km/h。
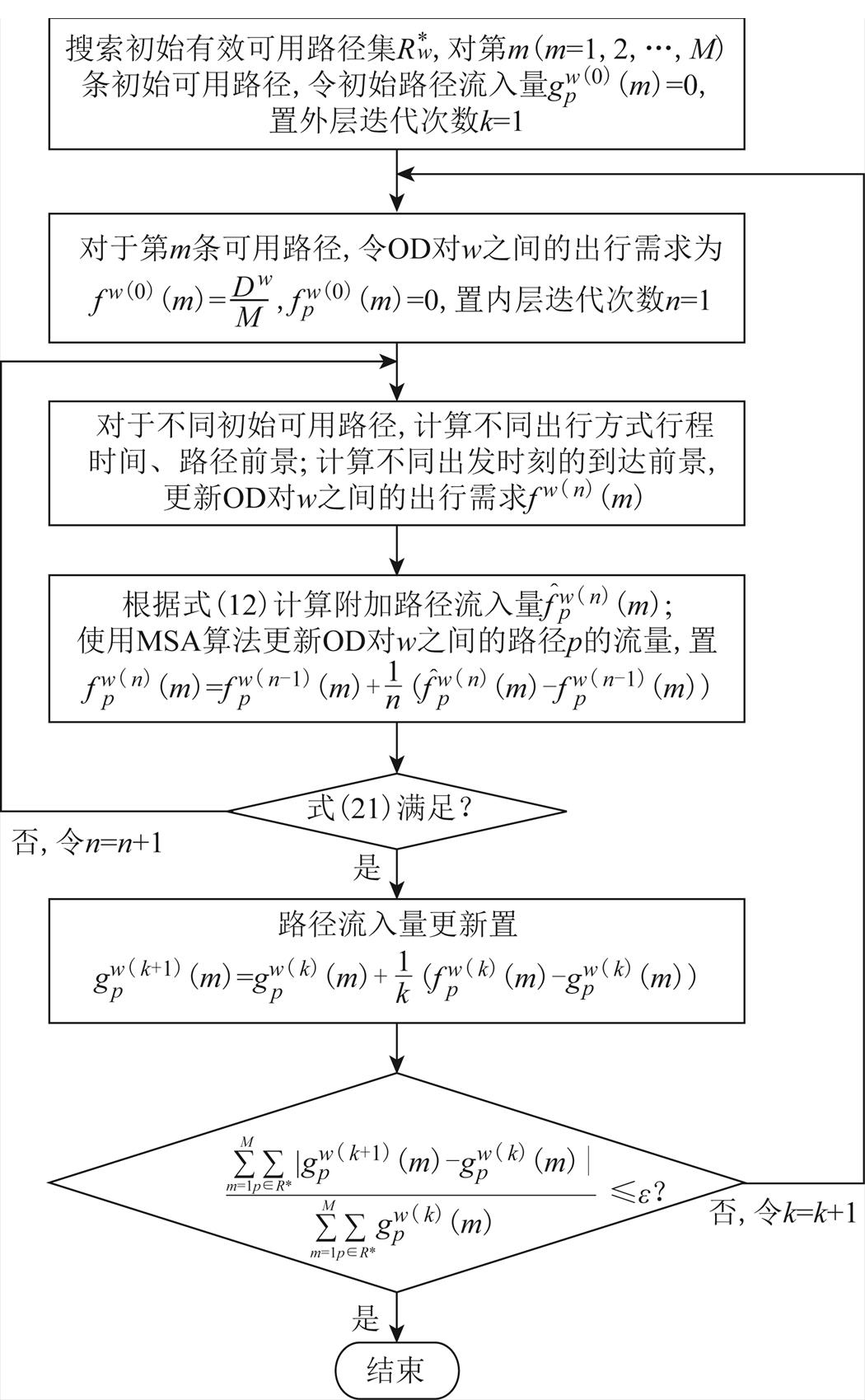
图4 模型求解算法
Fig.4 Solution of the model
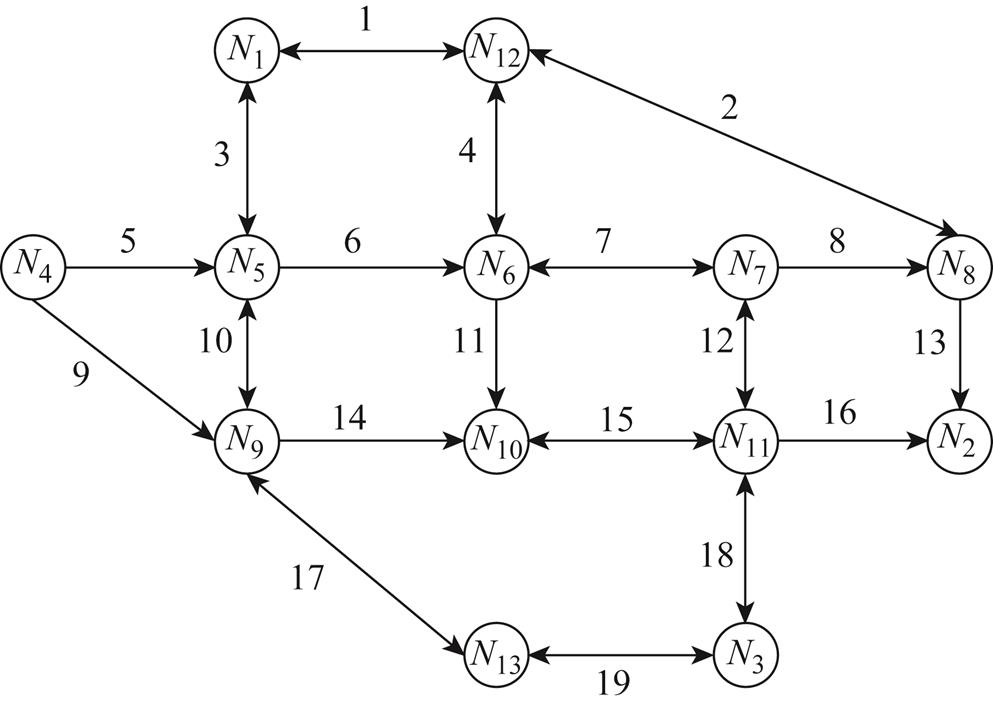
图5 Nguyen-Dupius交通网络
Fig.5 Topology of Nguyen-Dupius traffic network
选取居民早出行上班为研究对象，设置所有出行均为电动汽车，出行总需求为10 000。假定用户居家地点为节点N1，工作地点为节点N3，最早出行时间为7:00am，工作时间为9:30am和9:00am，分别为场景A和B。私家车可用路径见表1，其中，选择路径2和5的电动汽车需要在节点N11进行充电，且不考虑充电站服务能力限制，即认为所有节点均具有充足的充电桩。分别采用本文所提方法和基于完全理性假设的Wardrop交通均衡模型[29]进行电动汽车转移行为研究。各路径上的交通流量分配情况如图6所示。
表1 私家车可用路径
Tab.1 The available paths of private cars
路径123456 路段1-4-7- 12-181-4-11- 15-183-6-7- 12-183-6-11- 15-183-10-14- 15-183-10- 17-19
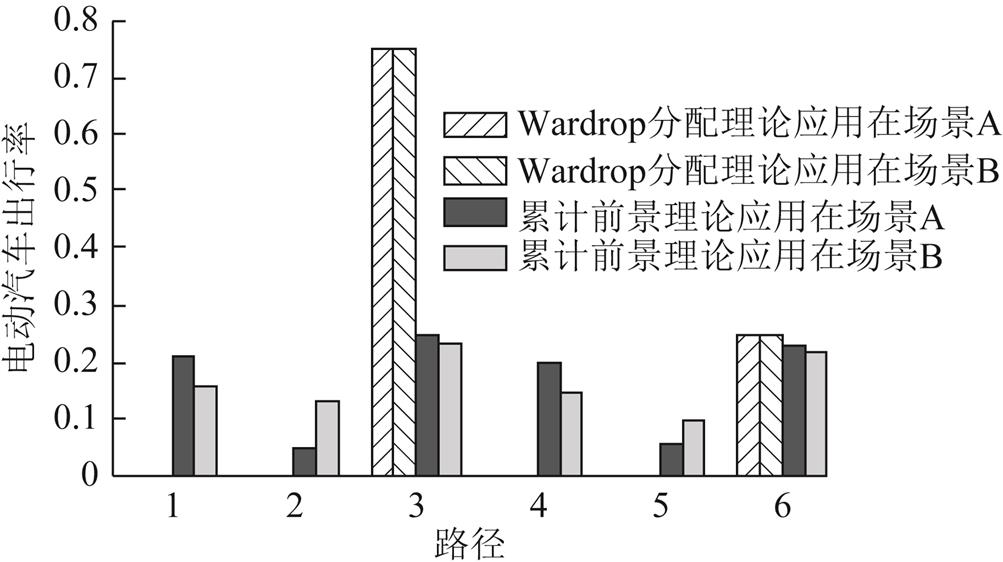
图6 不同模型下场景A、B交通流量分配情况
Fig.6 The traffic distribution of EVs in scenarios A and B
Wardrop交通均衡模型认为在道路的利用者都确切知道网络的交通状态并试图选择最短径路时，网络将会达到平衡状态，此时各条被使用的路径具有相等而且最小的行程时间；其余行驶时间大于或等于最小行程时间的路径将不被选择。由图6可得如下结论：
1）采用Wardrop交通均衡模型时，在A和B两种场景中电动汽车选择行为相同，即仅路径3和路径6被选择且两种场景中路径上的电动汽车出行率相等。
2）对于本文所提的电动汽车时空行为模型，不同的场景条件和参考点将使电动汽车在路径选择上发生改变，虽然每条路径均有电动汽车选择出行，但路径上的电动汽车的出行率有较大差别，如在A、B场景中路径5上的电动汽车出行率分别为0.06和0.1。
在实际的出行过程中，当出行者可以利用的时间较长时，出行者会表现出“风险规避”的行为，选择保险较高的路径。当出行者必须在短时间内到达目的地时，将显示为“风险寻求”。出行者可利用时间较短时，虽然路径1、2、4、5的风险非常高，但是出行者在寻求风险的心理中仍然会选择这些路径。因此，在前景不确定的选择中，基于累积前景理论的选择模型能够更合理地描述出行者的决策过程。
4.2.1 不同电动汽车占比下的电动汽车出行路径和出发时刻选择分析
在场景B的基础上设置公共交通路线为1-4-11-15-18和3-10-17-19，对不同电动汽车占比、充电站约束下的用户出行方式、电动汽车出行路径、电动汽车出发时刻等选择行为进行研究。设置4组场景，场景1中所有私家车均为纯电动汽车，场景2~4中电动汽车与燃油汽车比例分别为3:1、2:1、1:1。在场景1~4中的路径流量分配情况如图7所示。
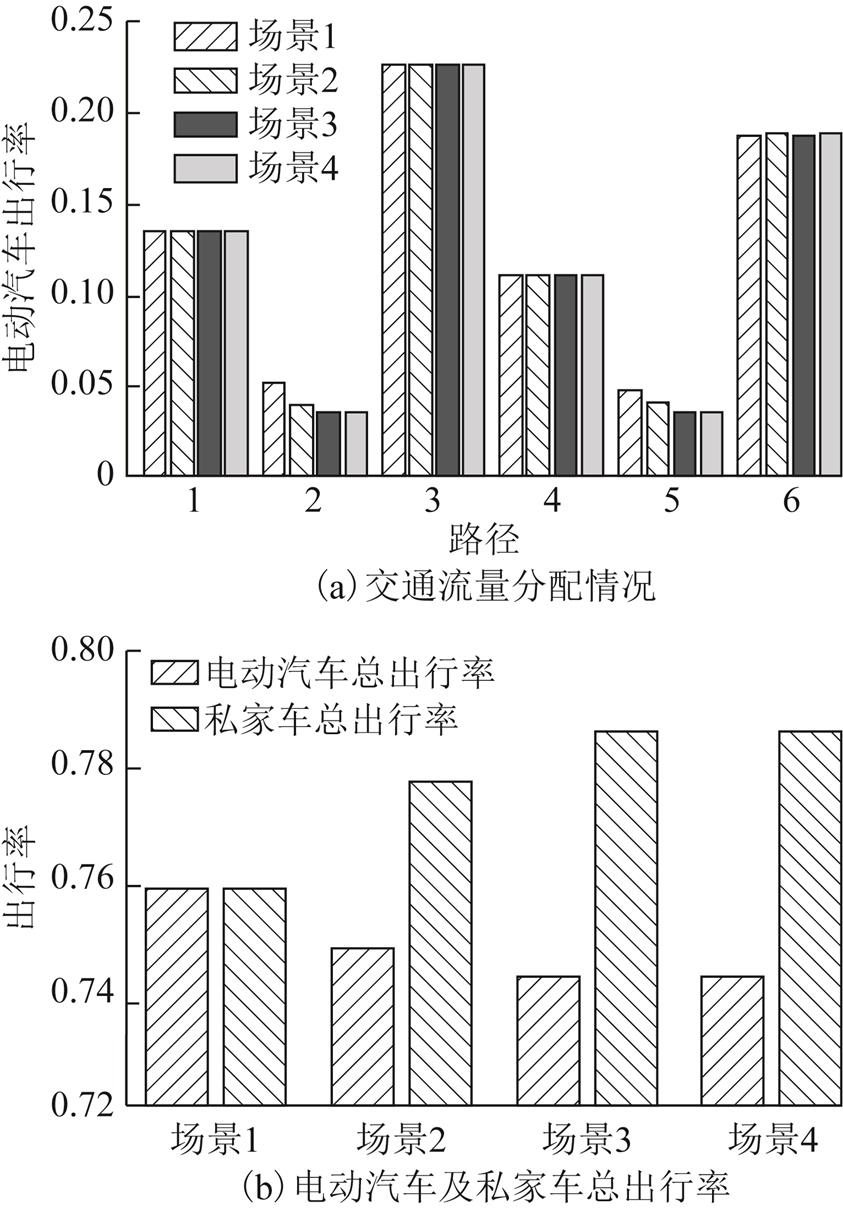
图7 场景1~4交通流量分配及电动汽车出行率
Fig. 7 The traffic distribution and the trip rate of EVs in scenarios 1 to 4
分析图7可知：
1）对于电动汽车需要中途充电的路径（如路径2、5），当燃油汽车占比增加时，路径上电动汽车出行率先减小后达到稳定。其主要原因为燃油汽车无需考虑充电时间，当燃油汽车占比增加时，相比于使用电动汽车，用户选择燃油汽车出行的意愿较强，导致该路径流量和行程时间增加，从而减弱了电动汽车用户的出行意愿；当燃油汽车占比的增加使得
路径流量达到路径通行能力限值时，路径出行时间达到最大，路径出行总量将达到稳定，燃油汽车占比的增加不再影响电动汽车出行率，如场景4中电动汽车的出行率与场景3相同。
2）对于电动汽车无需中途充电的路径（如路径1、3、4、6），路径流量及该路径上电动汽车出行率不受电动汽车占比影响，因为在该路径上电动汽车无需考虑充电时间，此时电动汽车的驾驶行为与燃油汽车相似。
3）电动汽车占比的减小虽然使得电动汽车出行率降低，但私家车总出行率将增加。
在场景1~4中，电动汽车用户在不同路径上进行出发时刻选择，以路径1和路径2为例，其出发时刻选择结果如图8所示。
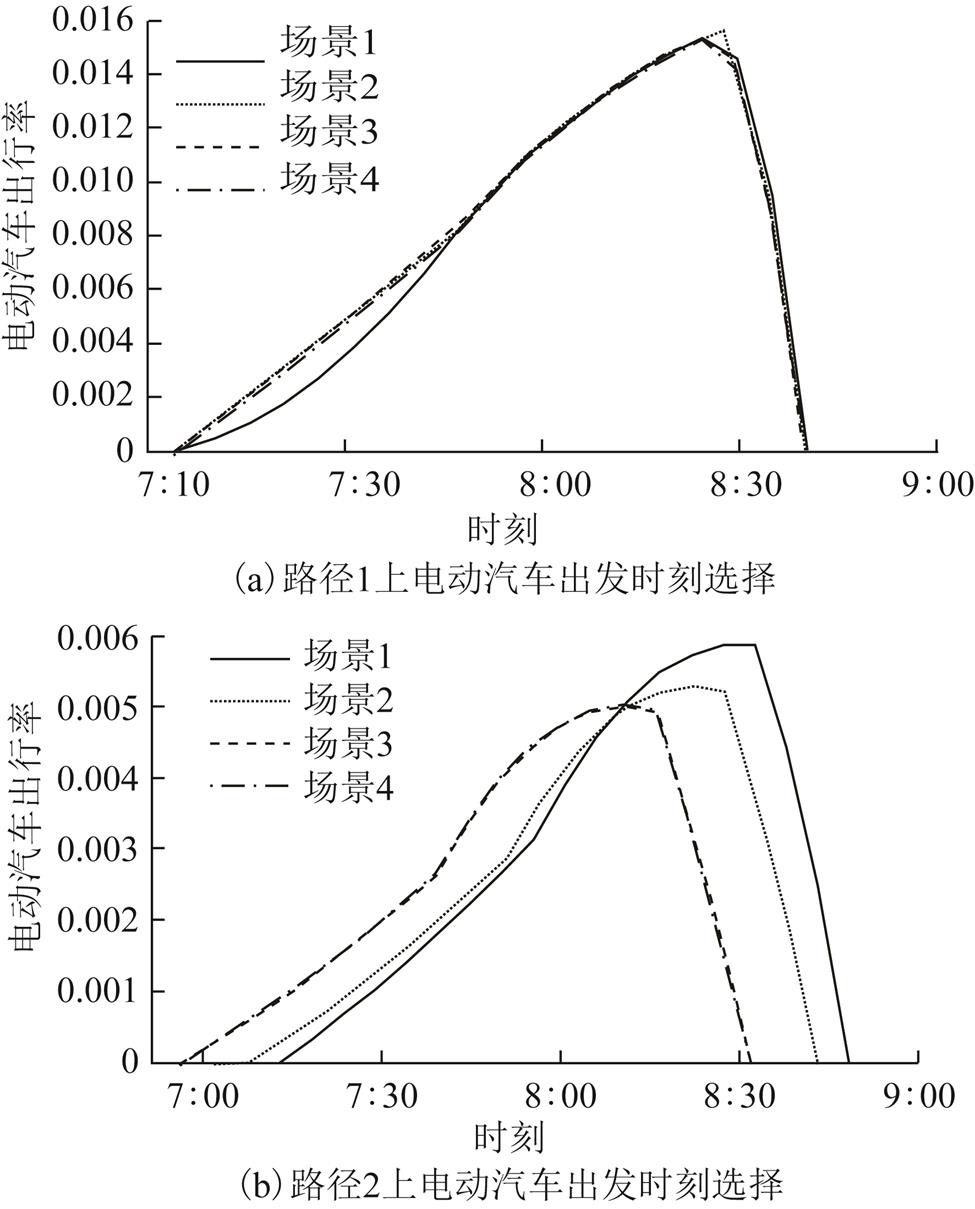
图8 场景1~4下电动汽车出发时刻选择
Fig.8 Departure time of EVs in scenarios 1 to 4
图8中四种场景下路径1上的电动汽车出发时刻曲线产生重叠，同时路径2上的电动汽车出发时刻曲线在场景3和4下出现重叠。从图8中可得出如下结论：
1）在电动汽车无需中途充电的路径上，由于电动汽车占比变化不影响其流量，电动汽车的出发时刻不受影响。
2）在电动汽车需要中途充电的路径上，燃油汽车比例增加将导致该路径上的流量逐渐增加后趋于稳定，使得该路径上的电动汽车行程时间增加，电动汽车的整体出发时刻将提前。当燃油汽车比例增加使得路径流量达到通行能力限值时电动汽车出发时刻将达到稳定，如场景4中的电动汽车出发时刻相比场景3无变化。
通过对电动汽车出发时刻和路径选择分析可得电动汽车在活动-出行链上的时空分布，如8:00am时场景1下的电动汽车在交通网中的分布如图9所示。
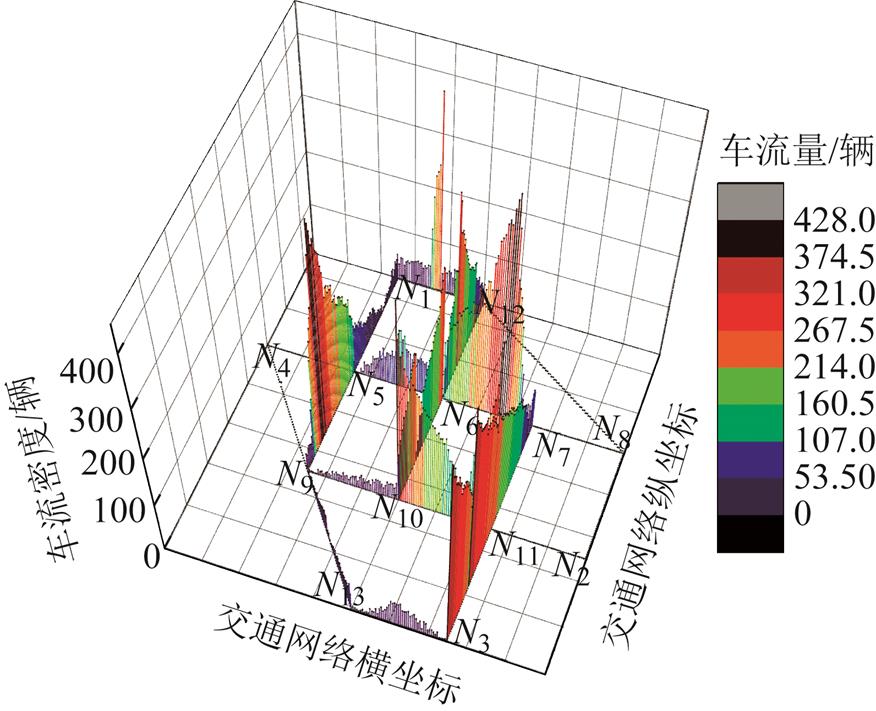
图9 8:00am场景1下电动汽车分布情况
Fig.9 The distribution of EVs in traffic network in scenario 1 at 8:00am
4.2.2 充电站服务能力约束下的电动汽车出行路径和出发时刻选择分析
通过电动汽车出发时刻分析可得场景1下路径2和5上同时刻出行的电动汽车的最大数量。考虑充电站充电服务能力，在场景1的基础上设置如下场景：节点N11上的充电桩数量分别为场景1下同时刻最大充电电动汽车数量的80%、40%、20%，分别对应场景5~7，得到各路径上的流量如图10所示。图10表明，考虑充电站服务能力限制，即充电桩数量减少时，需要中途充电的路径上的电动汽车出行率将降低，部分出行向无需中途充电的路径上转移，且交通网中电动汽车的总出行率减小。
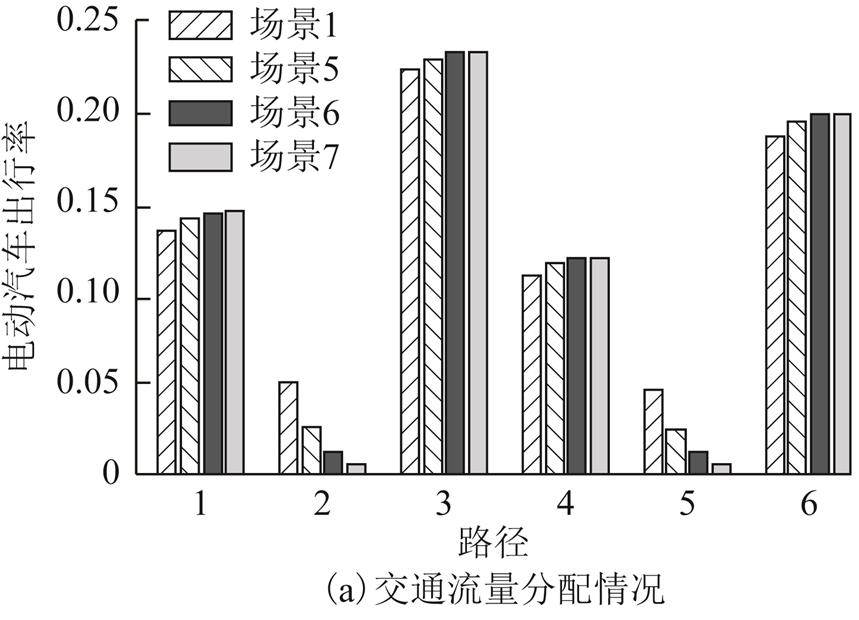
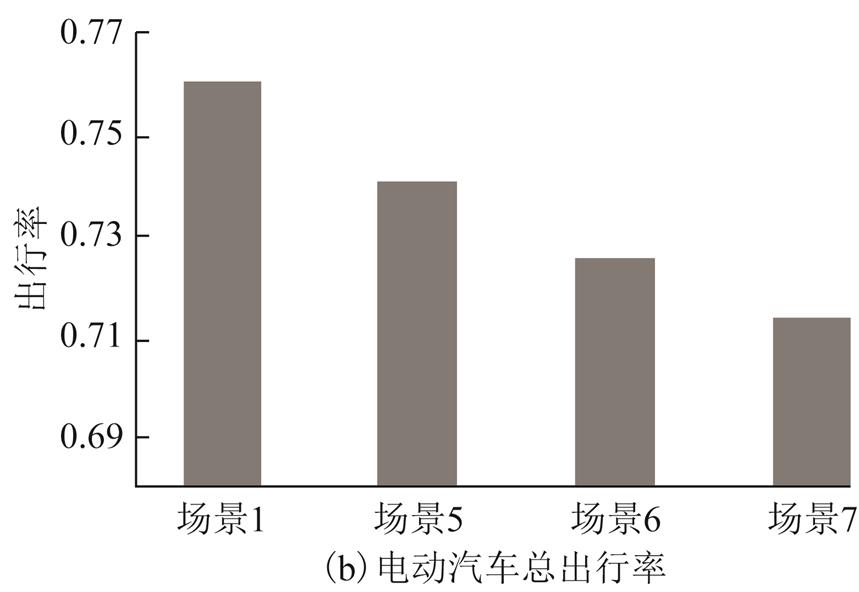
图10 场景5~7交通流量分配及电动汽车出行率
Fig.10 The traffic distribution and the trip rate of EVs in scenarios 5 to 7
仍以路径1、2为例，其用户出发时刻选择结果如图11所示。
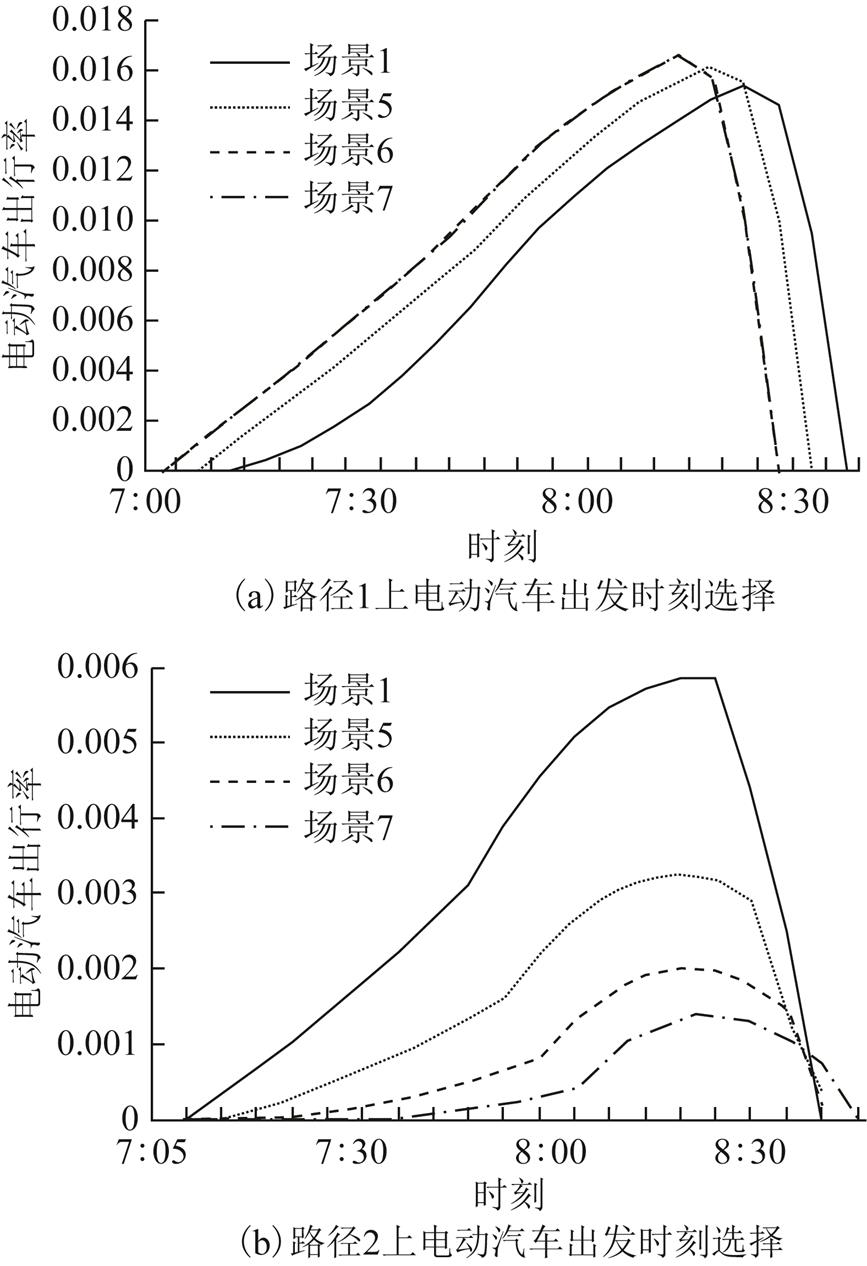
图11 场景5~7下电动汽车出发时刻选择
Fig.11 Departure time of EVs in scenarios 5 to 7
图11中场景6和7下路径1上的电动汽车出发时刻曲线出现重叠。结合图10和图11可得如下结论：
1）考虑充电站服务能力的限制，即充电桩数量减少时，由于路径流量减小，行程时间减短，中途需要进行充电的路径上的电动汽车出发时刻有较大延迟。
2）由于部分电动汽车出行向中途无需充电的路径上转移，其道路行程时间增加，使得用户在该路径上为了躲避拥堵提前出发时刻。
同样可得电动汽车在活动-出行链上的时空分布规律，8:00am时场景7下的电动汽车在交通网中的分布如图12所示。
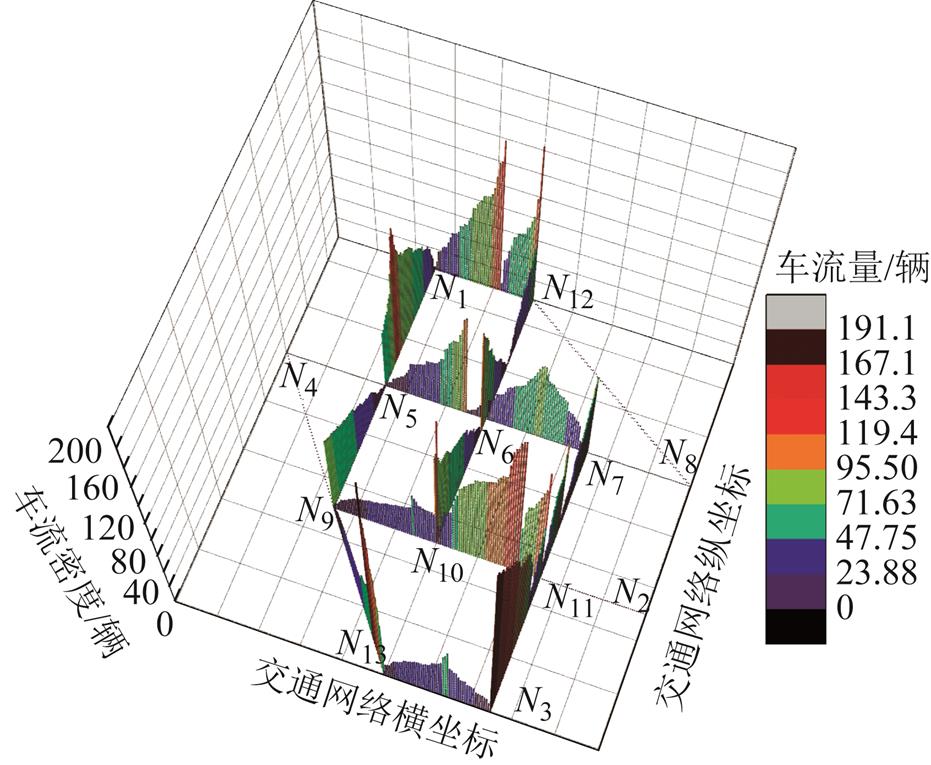
图12 8:00am场景7下电动汽车分布情况
Fig.12 The distribution of EVs in traffic network in scenario 7 at 8:00am
以居民日活动周期为研究范围，以活动者日常典型出行活动[30]（包括工作出行、购物、交往活动及归家等典型活动）为研究对象，研究电动汽车每日出行次数和充电次数。
仍假定用户居家地点为节点N1，工作地点为节点N3，上午上班时间为9:00am，中午下班时间为11:00am，下午上班时间为2:00pm，下午下班时间为5:00pm，下班到家期望时间上限为7:30pm；购物地点为节点N10，期望最佳购物时间上限为12:00am；下班交友活动地点为节点N7，期望到达时间上限为5:45pm。
4.3.1 不同电动汽车占比下的电动汽车每日出行次数及充电次数分析
在场景1~4的电动汽车占比下，分别对不同活动的出行需求进行交通流量分配分析，得到电动汽车每日出行次数与充电次数如图13所示。
从图13可知，随着电动汽车占比的降低，电动汽车平均出行次数和充电次数将逐渐减少。结合图7分析原因为：在电动汽车无需中途充电的路径上燃油汽车占比的增加不影响电动汽车行为；而在电动汽车需要中途充电的路径上燃油汽车占比的增加加大了电动汽车的行程时间，导致电动汽车在该路径及整个交通网络中的出行率和行驶里程的降低，进而降低了电动汽车每日平均充电次数。
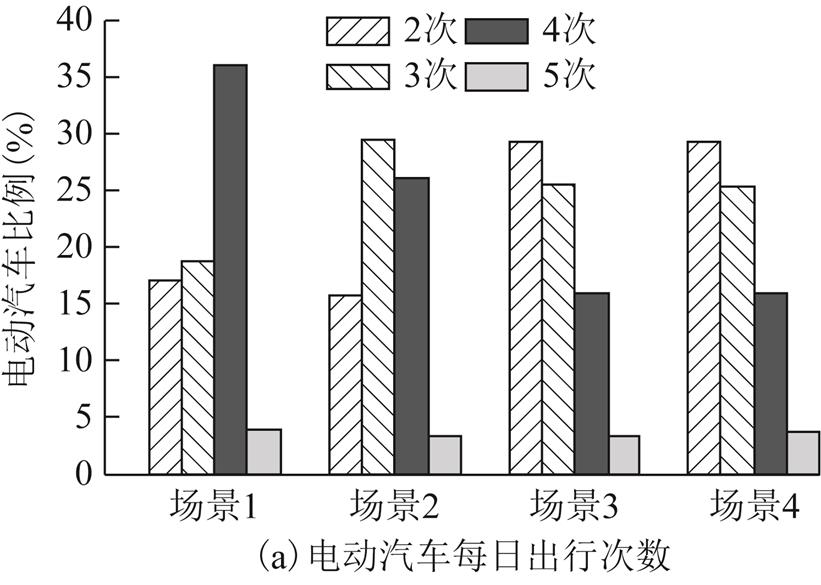
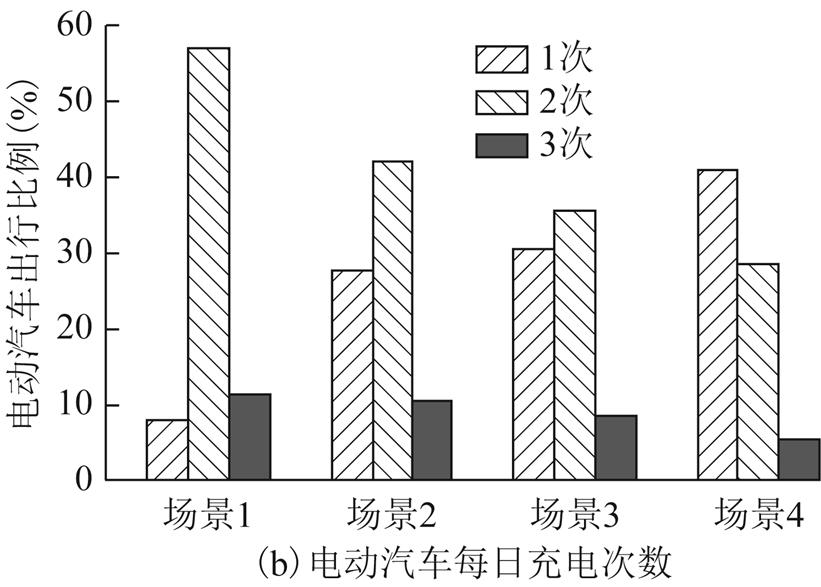
图13 场景1~4下电动汽车出行次数及充电次数
Fig.13 The daily trip frequency and charge frequency of EVs in scenarios 1 to 4
4.3.2 充电站服务能力约束下的电动汽车每日出行次数及充电次数分析
在场景1的基础上首先得出充电站无约束时用户每次活动出行中电动汽车在不同路径上的出发时刻选择情况，分别设置充电节点上的充电站服务能力为同时刻最大充电电动汽车数量的80%、40%、20%，作为场景8~10，得到不同充电站约束下的电动汽车每日出行次数与充电次数，如图14所示。
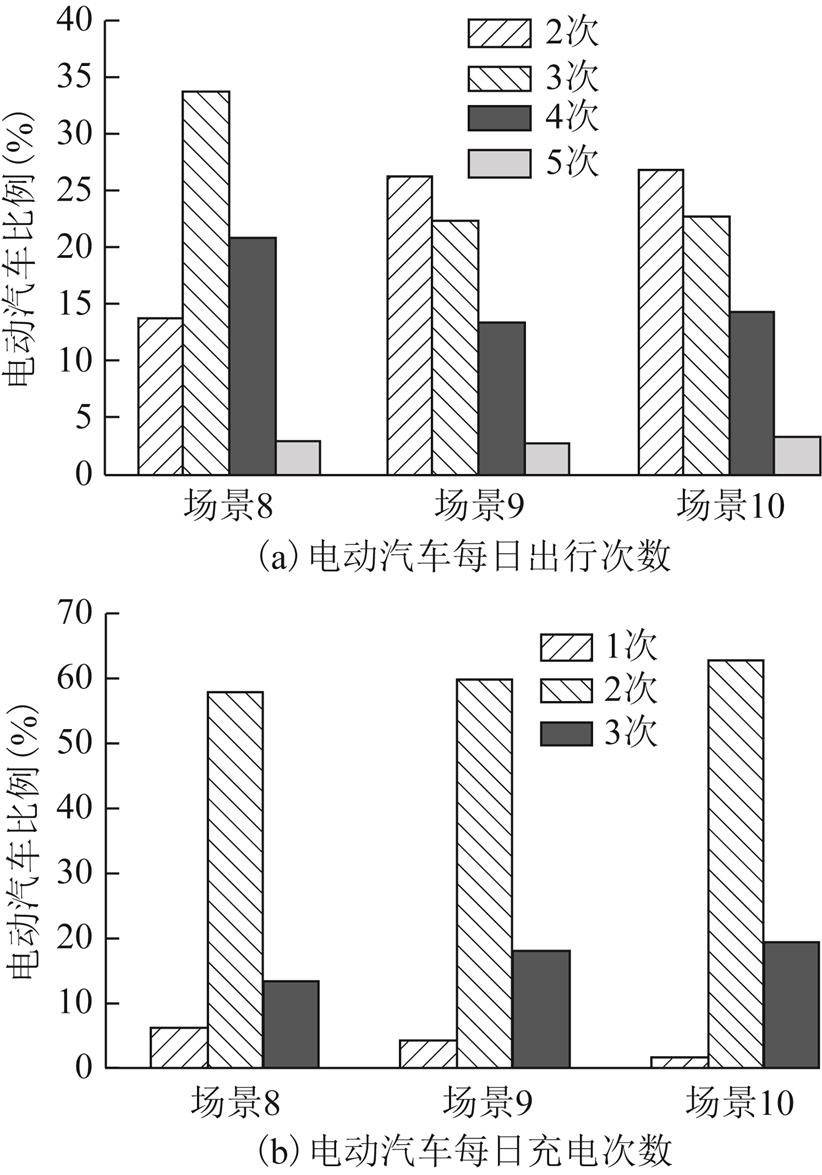
图14 场景8~10下电动汽车出行次数及充电次数
Fig.14 The daily trip frequency and charge frequency of EVs in scenarios 8 to 10
图14显示，随着充电站服务能力下降，电动汽车每日平均出行次数将逐渐降低，而电动汽车每日平均充电次数反而增加。结合图10可知其原因为当充电站服务能力下降时，电动汽车需要进行中途充电的路径上的流量减小且部分向电动汽车无需进行中途充电的路径上转移，增加了该路径上的行程时间，使得用户总体出行率降低，从而减少了电动汽车每日平均出行次数；由于充电站服务能力的限制，导致部分电动汽车出行改变路径选择计划，增加了电动汽车行程，进而引起电动汽车每日平均充电次数的增加。
本文首先通过活动分析法将用户的出行行为看作活动的派生行为，基于贝叶斯理论分析了用户不同活动-出行链之间的时空转移关系；然后，考虑用户在每条活动-出行链上转移行为的有限理性心理，基于累计前景理论建立了用户的出行方式、出发时刻和出行路径选择模型；在此基础上，考虑交通网络的动态特性和电动汽车的充电特性对电动汽车在活动-出行链上的时空转移规律和充电规律进行了研究。通过仿真分析可得出如下结论：
1）电动汽车的时空行为特性受多重因素的影响，不同条件下的用户行为特性会有较大差异，本文所提方法能够更加合理地描述不同场景下的电动汽车时空行为特性。
2）电动汽车占比的变化对电动汽车无需中途充电的路径流量和出发时刻无影响；对于电动汽车需要中途充电的路径，电动汽车占比的降低将使得该路径上的电动汽车出行率降低而出发时刻提前；同时电动汽车每日平均出行次数和充电次数将逐渐减少。
3）随着充电站服务能力的下降，电动汽车在需要中途充电的路径上的出行率降低，出发时刻推迟；无需中途充电的路径上出发时刻提前；电动汽车每日平均出行次数的降低，但将引起电动汽车每日平均充电次数的增加。
文中考虑用户具有相似的参考点选择标准，即用户的“同质化”，为本文的不足之处；同时，在用户选择决策模型中仅考虑了时间成本，对于电动汽车而言，不同的时空电价是否会对其出行行为产生影响未进行考虑。后续研究工作将围绕用户的“异质化”、不同时空电价以及交通故障或交通管制产生的拥堵情况对电动汽车时空行为的影响展开进一步工作。
附 录
附表1 Nguyen-Dupius交通网络参数
App.Fig.1 Parameters of Nguyen-Dupius traffic network
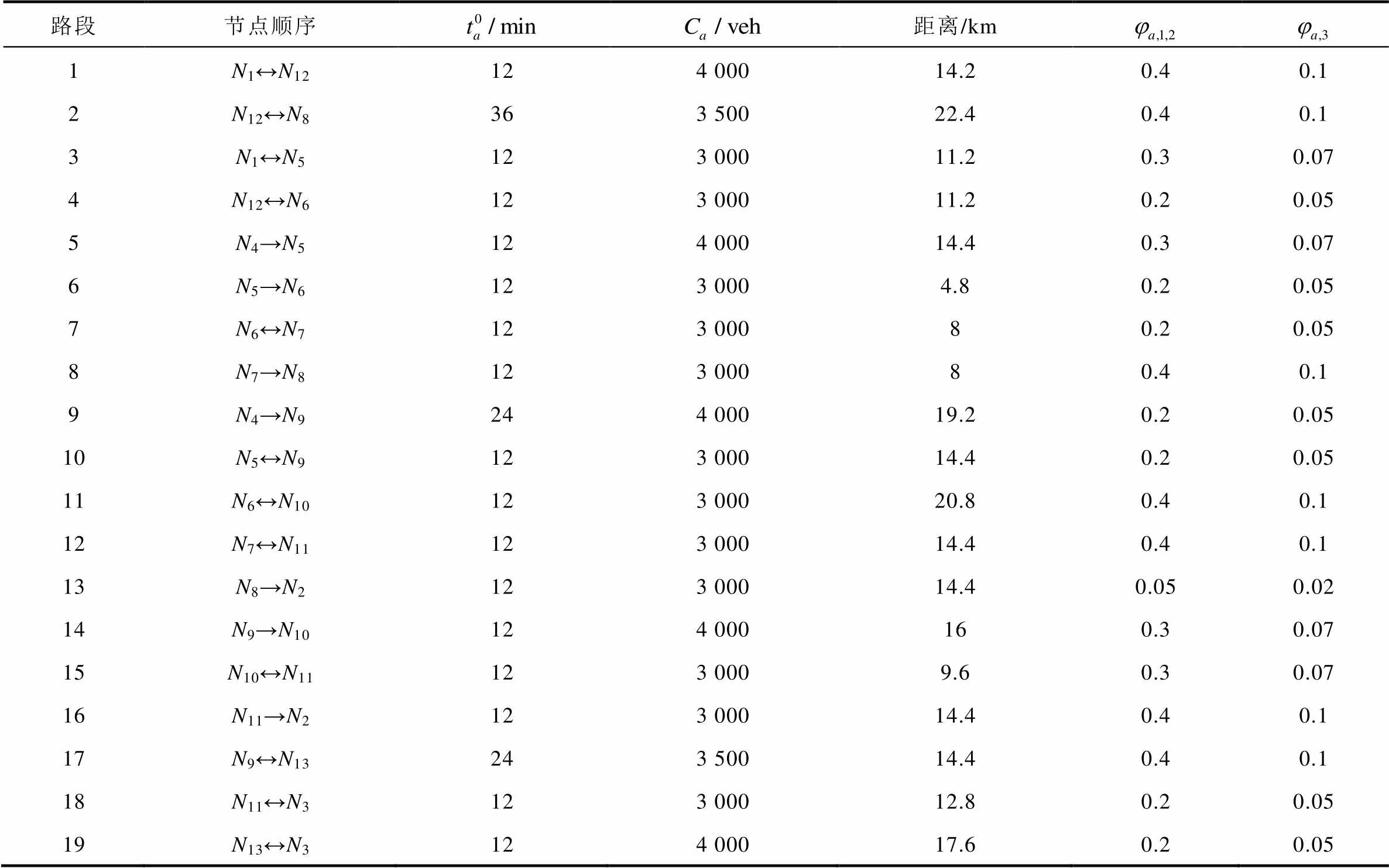
路段节点顺序距离/km 1N1↔N12124 00014.20.40.1 2N12↔N8363 50022.40.40.1 3N1↔N5123 00011.20.30.07 4N12↔N6123 00011.20.20.05 5N4→N5124 00014.40.30.07 6N5→N6123 0004.80.20.05 7N6↔N7123 00080.20.05 8N7→N8123 00080.40.1 9N4→N9244 00019.20.20.05 10N5↔N9123 00014.40.20.05 11N6↔N10123 00020.80.40.1 12N7↔N11123 00014.40.40.1 13N8→N2123 00014.40.050.02 14N9→N10124 000160.30.07 15N10↔N11123 0009.60.30.07 16N11→N2123 00014.40.40.1 17N9↔N13243 50014.40.40.1 18N11↔N3123 00012.80.20.05 19N13↔N3124 00017.60.20.05
参考文献
[1] 杨晓东, 张有兵, 蒋杨昌, 等. 微电网下考虑分布式电源消纳的电动汽车互动响应控制策略[J]. 电工技术学报, 2018, 33(2): 390-400. Yang Xiaodong, Zhang Youbing, Jiang Yangchang, et al. Renewable energy accommodation-based strategy for electric vehicle considering dynamic interaction in microgrid[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 390-400.
[2] 黄小庆, 陈颉, 谢啟波, 等. 用户充电选择对电网充电调度的影响[J]. 电工技术学报, 2018, 33(13): 3002-3011. Huang Xiaoqing, Chen Wei, Xie Qibo, et al. The influence of users’ charging selection on charging schedule power grid[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3002-3011.
[3] 张晨彧, 丁明, 张晶晶. 基于交通出行矩阵的私家车充电负荷时空分布预测[J]. 电工技术学报, 2017, 32(1): 78-87. Zhang Chenyu, Ding Ming, Zhang Jingjing. A temporal and spatial distribution forecasting of private car charging load based on origin-destination matrix[J]. Transactions of China Electrotechnical Society, 2017, 32(1): 78-87.
[4] 王毅, 谷亿, 丁壮, 等. 基于模糊熵和集成学习的电动汽车充电需求预测[J]. 电力系统自动化, 2020, 44(03): 114-124. Wang Yi, Gu Yi, Ding Zhuang, et al. Charging demand forecasting of electric vehicle based on empirical mode decomposition-fuzzy entropy and ensemble learning[J]. Automation of Electric Power Systems, 2020, 44(03): 114-124.
[5] 茆美琴, 陈强, 丁勇, 等. 基于模块化多电平换流器的电动汽车集群与智能电网集成系统参数优化设计[J]. 电工技术学报, 2018, 33(16): 3802-3810. Mao Meiqin, Chen Qiang, Ding Yong, et al. Parameters optimization design for MMC-based EV fleet integrated into smart grid[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3802-3810.
[6] Gomez J C, Morcos M M. Impact of EV battery chargers on the power quality of distribution systems[J]. IEEE Transactions on Power Delivery, 2003, 18(3): 975-981.
[7] 杨田, 刘晓明, 吴其, 等. 电动汽车充电站选址对电压稳定影响的研究[J]. 电力系统保护与控制, 2018, 46(5): 31-37． Yang Tian, Liu Xiaoming, Wu Qi, et al. Research on impacts of electric vehicle charging station location on voltage stability[J]. Power System Protection and Control, 2018, 46(5): 31-37．
[8] Ben-Akiva M, Lerman S R. Discrete choice analysis: theory and application analysis[M]. Cambridge, Massachusetts: MIT Press, 1985.
[9] Lu Xuedong, Eric I P. Socio-demographics, activity participation and travel behavior[J]. Transportation Research A, 1999, 33(1): 1-18.
[10] Bath C R. A model of post home-arrival activity participation behavior[J]. Transportation Research B, 1998, 32(1): 387-400.
[11] Chapin F S. Human time allocation in the city [C]// Human Activity and Time Geography, London, 1978, 2: 13-26.
[12] Allais M, Hagen O E. Expected utility hypothesis and the allias paradox[M]. Dordreche, Holland: D. Reidel Publishing Co. 1979．
[13] Ellsberg D. Risk, ambiguity and the savage axioms[J]. Quaterly Journal of Economics, 1961, 75(4): 643-669.
[14] 田立亭, 史双龙, 贾卓. 电动汽车充电功率需求的统计学建模方法[J]. 电网技术, 2010, 34(11): 126-130.Tian Liting, Shi Shuanglong, Jia Zhuo. A statistical model for charging power demand of electric vehicles[J]. Power System Technology, 2010, 34(11): 126-130.
[15] 杨波, 陈卫, 文明浩, 等. 电动汽车充电站的概率负荷建模[J]. 电力系统自动化, 2014, 38(16): 67-73.Yang Bo, Chen Wei, Wen Minghao, et al. Probabilistic load modelling of electric vehicle charging stations[J]. Automation of Electric Power Systems, 2014, 38(16): 67-73.
[16] 李含玉, 杜兆斌, 陈丽丹, 等. 基于出行模拟的电动汽车充电负荷预测模型及V2G 评估[J]. 电力系统自动化, 2019, 43(21): 88-96. Li Hanyu, Du Zhaobin, Chen Lidan, et al. Trip simulation based charging load forecasting model and vehicle-to-grid evaluation of electric vehicles[J]. Automation of Electric Power Systems, 2019, 43(21) : 88-96.
[17] 姜欣, 冯永涛, 熊虎, 等. 基于出行概率矩阵的电动汽车充电站规划[J]. 电工技术学报, 2019, 34(增刊1): 272-281. Jiang Xin, Feng Yongtao, Xiong Hu, et al. Electric vehicle charging station planning based on travel probability matrix[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 272-281.
[18] 苏舒, 林湘宁, 张宏志, 等. 电动汽车充电需求时空分布动态演化模型[J]. 中国电机工程学报, 2017, 37(16): 4618-4629, 4887. Su Shu, Lin Xiangning, Zhang Hongzhi, et al. Spatial and temporal distribution model of electric vehicle charging demand[J]. Proceedings of the CSEE, 2017, 37(16): 4618-4629, 4887.
[19] 周翔, 陈杰军, 谢培元, 等. 基于效用最大化原则的电动汽车充电站负荷特性分析方法[J]. 电测与仪表, 2018, 55(4): 1-8. Zhou Xiang, Chen Jiejun, Xie Peiyuan, et al. Load demand analysing method for electric vehicle charging station based on the principle of maximizing utility[J]. Electrical Measurement & Instrumentation, 2018, 55(4): 1-8.
[20] Weckx S, D’Hulst R, Claessens B, et al. Multiagent charging of electric vehicles respecting distribution transformer loading and voltage limits[J]. IEEE Transactions on Smart Grid, 2014, 5(6): 2857-2867.
[21] Rasouli S, Timmermans H J P. Activity-based models of travel demand: promises, progress and prospects[J]. International Journal of Urban Sciences, 2014, 18(1): 31-60.
[22] Reichman S. Travel adjustments and life styles: a behavioural approach[M]. Lexington, MA: Lexington Books, 1976.
[23] He Xuedong, Zhou Xunyu. Portfolio choice under cumulative prospect theory: an analytical treatment[J]. Social Science Electronic Publishing, 2011, 57(57): 315-331.
[24] Kahneman D, Tversky A. Prospect theory: an analysis of decision under risk[J]. Econometrica, 1979, 47(2): 263-292.
[25] Jou R C, Kitamura R, Weng M C, et al. Dynamic commuter departure time choice under uncertainty[J]. Transportation Research Part A, 2008, 42(5): 774-783.
[26] Bekhor S, Ben-Akiva M E, Ramming M S. Estimating route choice models for large urban networks [C]//The 9th World Conference on Transport Research, Seoul, Korea, 2001: 23-30.
[27] Zhou Chengke, Qian Kejun, Allan M, et al. Modelling of the cost of EV battery wear due to V2G application in power systems[J]. IEEE Transactions on Energy Conversion, 2011, 26(4): 1041-1050.
[28] Schwanen T, Ettema D. Coping with unreliable transportation when collecting children: examining parents’ behaviour with cumulative prospect theory[J]. Transportation Research Part A, 2009, 43(5): 511-525.
[29] Pietrabissa A, Suraci V. Wardrop equilibrium on time-varying graphs[J]. Automatica, 2017, 84: 159-165.
[30] 武汉市统计局. 武汉统计年鉴[J]. 北京: 中国统计出版社, 2018.
Research on Spatiotemporal Behavior of Electric Vehicles Considering the Users’ Bounded Rationality
Abstract The spatiotemporal behavior of electric vehicles (EVs) includes spatiotemporal transfer behavior and charging behavior. The accurate modeling of the spatiotemporal behavior of EVs has become the key to the effective interaction between large-scale EVs and power grid. The idea of activity-based analysis to understand the travel behavior as the activity derived behavior was applied in the paper, and the transfer relationship between different activity chains was established. Based on the cumulative prospect theory, the bounded rationality psychology of users in the choice of travel mode, travel path and departure time was described. Considering the dynamic characteristics of traffic network and the charging characteristics of EVs, the spatiotemporal distribution characteristics of EVs on each activity chain were studied. Finally, the Dupius network, a typical traffic network, was used to study the spatiotemporal transfer and charging behavior characteristics of EVs with different users’ psychologies, proportions of EVs and service capabilities of charging stations. The simulation results show that the proposed method can more reasonably describe the users' choice psychology and the spatiotemporal behavior, and it is found that the proportion of EVs and the service capacity of charging station have great effect on them.
keywords：Electric vehicles spatiotemporal behavior, activity-based analysis, bounded rationality, cumulative prospect theory, dynamic traffic assignment model
DOI:10.19595/j.cnki.1000-6753.tces.190475
中图分类号：TM714
吴赋章 男，1991年生，博士研究生，研究方向为新能源接入、电动汽车运行调度。E-mail：wufuzhangwfz@163.com
杨 军 男，1977年生，教授，博士生导师，研究方向为电力系统运行与控制、电动汽车、新能源接入技术。E-mail：JYang@whu.edu.cn（通信作者）
国家自然科学基金（51977154）、国家重点研发计划（2017YFB0902904）和教育部人文社会科学研究青年基金（17YJCZH212）资助。
收稿日期 2019-04-23
改稿日期 2019-07-30
（编辑 赫蕾）