Tab.1 Terminologies of FA and PV system

萤火虫算法光伏系统 萤火虫位置横坐标为电压,纵坐标为功率 萤火虫间距由萤火虫位置计算得到的笛卡尔距离 吸引度萤火虫间距的指数函数 萤火虫亮度功率值 最亮萤火虫亮度全局最大功率值
摘要 光伏阵列处于阴影条件下时,其P-U曲线呈现出较为复杂的多峰值特性,如果不能快速、准确地实现最大功率点跟踪,将会造成大量的能量损失。因此,研究可靠的最大功率跟踪控制算法,确保光伏系统在阴影条件下仍可以输出最大功率值已成为日益热门的课题。该文提出了一种免疫萤火虫(IFA)算法,通过建立疫苗库缩短算法收敛时间,利用免疫补充及时排除不良个体的影响,同时改进萤火虫的运动方程,缩小稳态振荡。在静态及动态环境下的仿真结果表明,免疫萤火虫算法能够在不同的局部阴影条件(PSC)下准确地跟踪到全局最大功率点,与传统的FA算法相比,IFA具有更快的收敛速度,且电压和功率的振荡得到了有效抑制。
关键词:光伏阵列 萤火虫算法 最大功率点跟踪 局部阴影条件
理想情况下,光伏阵列中的光伏电池工作在相同的温度和太阳辐射下,此时光伏阵列的P-U曲线呈现单峰特性,最大功率点跟踪(Maximum Power Point Tracking, MPPT)可通过传统的最大功率点跟踪方法,如扰动观测法、爬山法和增量电导法等来实现[1-3]。然而,在局部阴影条件(Partial Shading Conditions, PSC)下,部分光伏电池两端电压将由正变负,从而导致热斑效应,影响光伏阵列的正常工作。为避免这种情况,常在多个光伏电池两端并联旁路二极管,及时短路处于热斑效应下的光伏电池。但这带来了另一个问题,即旁路二极管可能会导致光伏阵列的P-U特性在局部阴影条件下呈现出复杂的多峰特征[4-6]。在这种情况下,传统的最大功率点跟踪算法需要花费大量的时间来确定最大功率点的位置,从而导致大量的能量损失。
光伏系统通常采用软件、硬件两种方法来消除或减弱阴影效应的影响。硬件方案主要包括电路补偿和重构。电路补偿方法采用附加电路消除多个峰值,使得P-U特性在PSC下仍然显示出单峰值特性,此时可采用传统的MPPT方法来实现最大功率点跟踪[7-8]。但是,附加电路增加了系统的复杂性,且不能灵活地适应不同结构的光伏阵列。文献[9-10]中提出了一种光伏系统电路重构的方法,该方法利用开关,重新连接光伏阵列中的每个光伏组件,将处于相同太阳辐照度下的光伏电池串联起来,从而减弱了PSC下的光伏电池对整个光伏阵列的负面影响。但硬件方案往往会大大提高系统配置的复杂性和成本,所以通常不被采用,也不是当下研究的热点[11]。
软件方法可以大致分为三类。第一类是群体智能算法,如粒子群优化(Particle Swarm Optimization, PSO)算法[12]、人工蜂群算法[13]、混沌改进猫群(Chaos Improved Cat Swarm Optimization, CICSO)算法等[14]。群体智能算法的优势在于无论P-U特性如何,它们都能准确跟踪到MPP。但是,群体智能算法的实现更加复杂,初始点难以控制,对算法结果影响很大。第二类算法通常采用逐渐缩小搜索间隔的方法来完成全局最大功率点(Global Maximum Power Point, GMPP)的搜索,例如DIRECT算法[15],以及基于Fibonacci数列的MPPT算法[16]。与其他方法相比,这两种方法在收敛速度方面没有显著优势,并且算法最终可能收敛在局部最优点。第三类是基于传统算法的改进MPPT方法。此类方法利用PSC下光伏阵列P-U曲线的峰值点分布特性来跟踪GMPP,且可以较为容易地实现。文献[17]利用局部阴影下光伏阵列最大功率点电流与短路电流之间近似的比例关系,提出一种三步骤的全局最大功率点跟踪算法,提高了算法跟踪速度。文献[18-19]认为P-U曲线中的峰值通常位于开路电压的80%处,基于此提出了一种改进的增量电导算法。
2007年,X. S. Yang等开发了一种名为萤火虫算法(Firefly Algorithm, FA)的智能算法[20]。K. Sundareswaran等在2014年利用萤火虫算法实现了PSC下光伏阵列的MPPT[21],结果表明该算法具有比PSO和扰动观察法(P&O)更好的性能。然而,利用FA算法进行最大功率跟踪时,仍然存在一些算法上的缺陷,例如,萤火虫的位置更新高度依赖于优秀的个体,个体间距过大可能会导致低亮度萤火虫移动速度较慢,使得算法收敛速度降低。此外,如果步长系数α的取值较大,则运动方程中的自由步长α(rand-1/2)将可能带来较大的功率和电压振荡,导致算法在首次收敛后又重新退出收敛状态。但如果步长系数α的取值较小,则难以有效地探索高亮度萤火虫的附近区域。
为此,本文提出利用疫苗库缩小初始种群分布范围,使大多数萤火虫更加集中,从而萤火虫将更容易接受周围优秀个体的影响;同时利用免疫补充及时消除不良个体的影响;其次,本文引入了新的运动方程,将原有FA迭代方程中的自由步长α(rand-1/2)替换为与间距r正相关的变步长函数,以此确保低亮度的萤火虫可以有效地探测高亮度萤火虫附近的区域。
因此本文提出的免疫萤火虫(Immune Firefly Algorithm, IFA)算法与传统FA算法相比不仅算法收敛速度更快,而且稳态振荡得到了有效削弱。
FA将空间各点看成萤火虫,利用发光强的萤火虫会吸引发光弱的萤火虫的特点,在萤火虫移动的过程中,完成位置的迭代,从而找出最优位置,完成寻优过程。传统FA算法的提出是基于以下三个假设:
1)种群所有的萤火虫没有性别之分,任意一只萤火虫都会被其他亮度更高的萤火虫吸引。
2)萤火虫的吸引力与其亮度成正比,且亮度随距离的增加而减小。
3)萤火虫的亮度由目标函数决定。
当FA算法应用于光伏系统的MPPT时,算法中的各项术语对照关系见表1。
表1 术语对照表
Tab.1 Terminologies of FA and PV system

萤火虫算法光伏系统 萤火虫位置横坐标为电压,纵坐标为功率 萤火虫间距由萤火虫位置计算得到的笛卡尔距离 吸引度萤火虫间距的指数函数 萤火虫亮度功率值 最亮萤火虫亮度全局最大功率值
在FA算法中,每只萤火虫相互吸引度β可以定量表示为
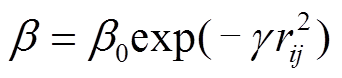 (1)
(1)式中,β0为r=0时的初始吸引度,通常设定为1;r为两个萤火虫之间的笛卡尔距离;γ为吸收系数。萤火虫i和萤火虫j之间的笛卡尔距离为
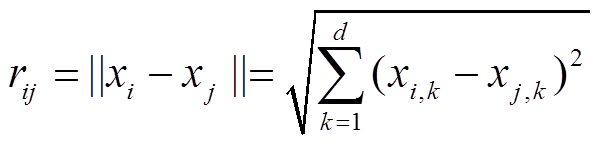 (2)
(2)
式中,xi,k和xj,k分别为第i和第j萤火虫空间坐标的第k个分量。在二维坐标系中,有
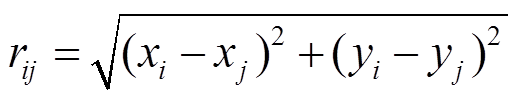 (3)
(3)如果萤火虫i被亮度更高的萤火虫j所吸引,那么萤火虫i的位置可由式(4)更新得到。
 (4)
(4)
式中,α为区间[0, 1]上的常数;rand为[0, 1]内的随机数;xi(t)和xj(t)分别为当前时刻第i和第j个萤火虫的位置;xi(t+1)为更新后的新位置。
图1为FA算法应用于MPPT时的执行步骤。首先,初始化所有萤火虫的位置,并将萤火虫的数量设置为n,n为正整数。之后计算萤火虫i和j的功率
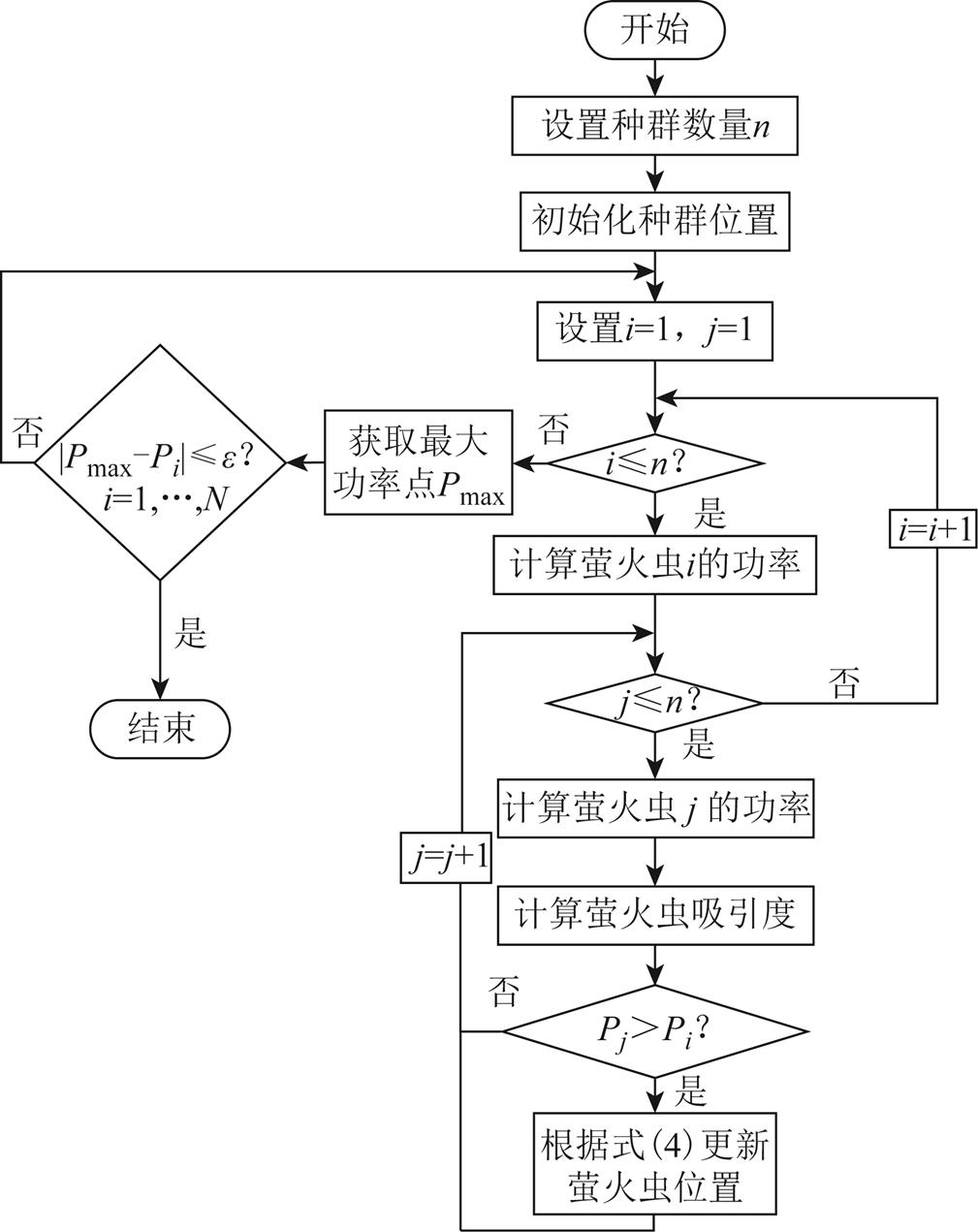
图1 萤火虫算法流程
Fig.1 FA algorithm flow chart
水平Pi、Pj,再判断是否存在Pi>Pj,若不等式成立,则第j个萤火虫的位置将由式(4)更新。当算法运行至i=n时,对所有萤火虫进行排序以获得最大功率值Pmax。最后,利用式(5)判断算法是否收敛。
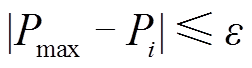 (5)
(5)式中,ε为收敛阈值;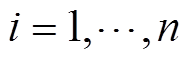 。
。
疫苗库的工作原理是,系统定期进行免疫应答,根据应答获得的数据生成抗体,从而建立疫苗数据库。
为了缩短收敛时间,本文提出通过建立疫苗库来缩小初始种群分布范围,使大多数萤火虫更加集中。因此,萤火虫将更容易接受周围优秀个体的影响。为了建立疫苗数据库,需要记录先前搜索的全局最大功率点,将它们分配到疫苗库中。疫苗库优化算法的步骤如下。
假设在疫苗库中存在的历史GMPP数量为m。Gmin和Gmax分别代表最小和最大的电压值。如图2所示,利用支持向量机(Support Vector Machine, SVM)最大化几何边缘,找到历史GMPP中相邻数据的最大间隔并以相邻数据的平均值作为划分区域的依据,以此将疫苗数据库划分为三个区域,Gmin和Gmax分别是a区的下限和c区的上限。
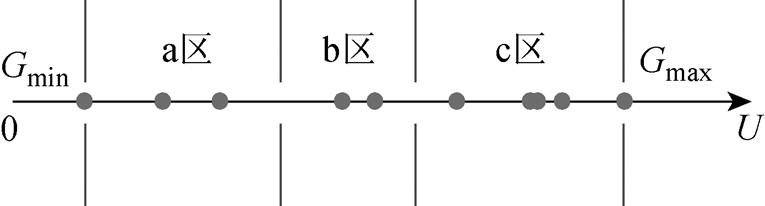
图2 利用支持向量机将疫苗数据库划分为三个区域
Fig.2 Using SVM to divide vaccine data-base into three regions
计算a区、b区和c区的历史GMPP数量,分别设置为Na、Nb、Nc。由此,萤火虫种群在区域a、b和c上的初始分布可由式(6)计算。
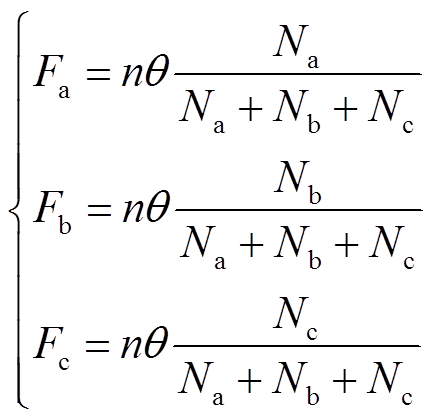 (6)
(6)式中,n为萤火虫种群数量;q为区间[0,1]上的常数;Fa、Fb和Fc分别为萤火虫种群在区域a、b和c上的初始分布数量。考虑到最大功率点可能出现在Gmin~Gmax之外,因而并不是种群中所有萤火虫都由疫苗库确定初始位置,仅有总数为nq的萤火虫由式(6)确定位置,除Fa、Fb和Fc外,剩余的萤火虫数量为n(1-q),随机分布在a、b和c区域外,即区域[0,Gmin]和[Gmax,Umax],其中Umax表示萤火虫个体能取得的最大电压值。
q较为合适的取值区间为0.6~0.8,若q>0.8,则Gmin~Gmax外分布的萤火虫数量较少,可能错过最大功率点所在的区间;若q<0.6,那么免疫库在算法中的作用将被大大削弱,算法收敛时间也随之延长。
疫苗库内的数据不是一成不变的,在IFA运行结束后,疫苗库需要及时更新,加入最新的GMPP,替换在数值上与之最接近的历史GMPP。
为了减小FA的稳态振荡,将式(4)中的不确定变量α(rand-1/2)替换掉,从而得到如式(7)所示的新的迭代公式。
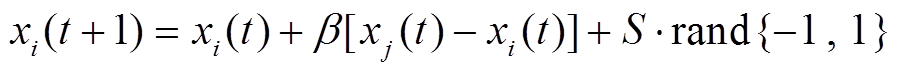 (7)
(7)式中,rand{-1,1}表示在集合{-1,1}中随机取到的值,-1和1被取值的概率均为50%。此外,步长函数S定义为
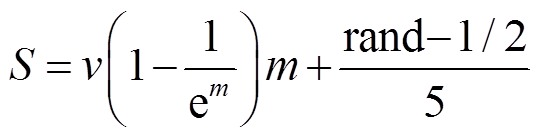 (8)
(8)
式中,v为常数;(rand-1/2)/5为振荡步长,防止两萤火虫相聚较近时步长函数的取值过小,无法有效探索附近区间;m的定义为
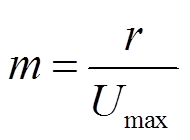 (9)
(9) 上述公式在计算时均为无量纲数值。在不同v的取值下,步长函数S的图形如图3所示。
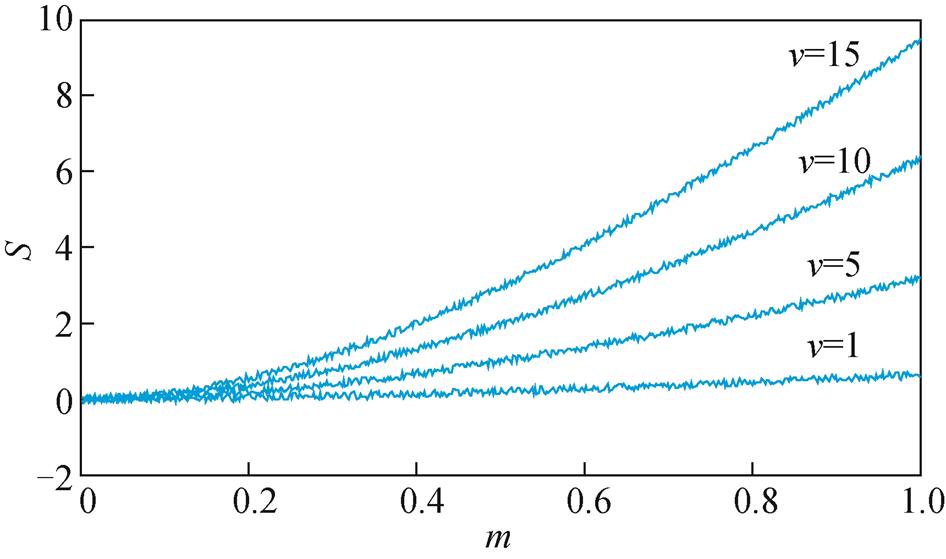
图3 v=1、5、10、15时的步长函数S
Fig.3 Image of S function when v=1,5,10,15
由图3可知,假如萤火虫相距较远,则S取值较大,低亮度的萤火虫可以有效地探测高亮度萤火虫的附近区域。如果萤火虫相距较近,则S值较小,确保算法收敛后的稳态振荡在合理范围内。同时设置S的上限阈值为10,假如某些情况下S的计算结果大于10,则取值为10。
在FA算法中,如果两个萤火虫之间的距离较大,则b的取值将非常小,导致在算法运行过程中,可能出现以下情况:大多数萤火虫聚集在一个小范围区域,而某些低亮度的萤火虫因距离高亮度萤火虫较远所以几乎保持原位不动,使得算法迟迟不能进入收敛状态。通过免疫补充操作,即从萤火虫中剔除亮度最低个体,补充新个体,则可以有效杜绝上述情况的发生。免疫补充操作的具体步骤如下。
对所有萤火虫进行排序,得到Pmax后,利用Gmin~Gmax区域内随机产生的若干只萤火虫,替换原有种群中相同数量的萤火虫。
设替换的萤火虫数量为mn,n为萤火虫种群数量,m为[0,1]上的疫苗系数。若m<0.2,那么位置较差的萤火虫可能需要多次免疫补充操作才能完全清除;若m>0.5,那么IFA的执行时间将会被大大延长。所以疫苗系数m较为合理取值范围应该为0.2~0.5。此外被替换的萤火虫应满足以下条件:①被替换的萤火虫的亮度比其他萤火虫低;②此时,式(5)不成立,且满足式(5)的萤火虫数量为大于或等于(1-m)n。
图4总结了IFA的执行步骤,虚线框内的部分表示IFA和FA之间的区别。
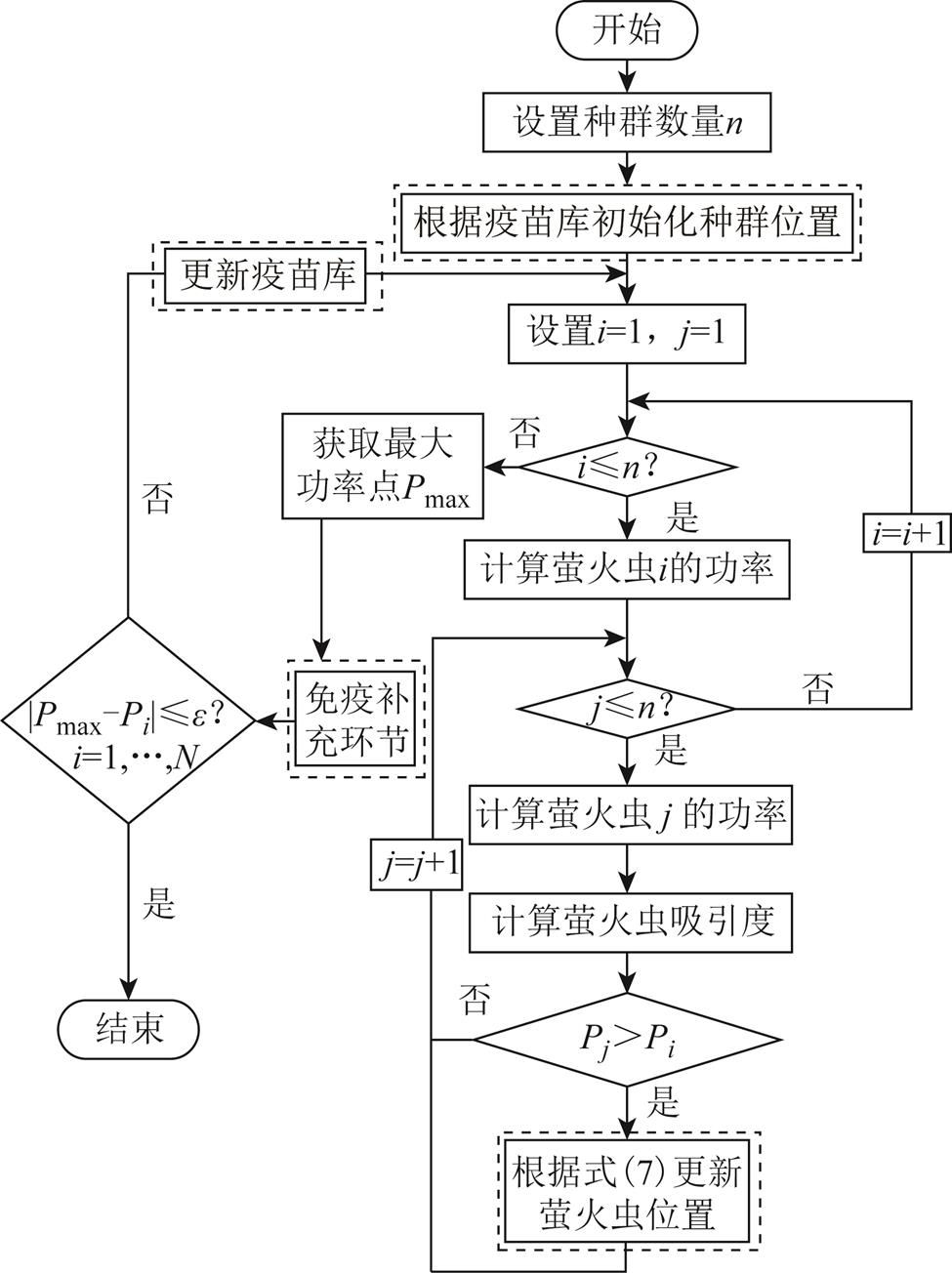
图4 免疫萤火虫算法流程
Fig.4 Flow chart of IFA
表2为IFA参数设置,光伏阵列容量为50kW,开路电压为880V,最大功率点电压为730V。设疫苗库中存在10个历史GMPP,分别是200.2V、248.5V、386.3V、522.2V、564.55V、609.7V、622.09V、700.7V、730.0V和807.8V。历史GMPP均为设置不同辐照度条件时,利用本文所搭建的光伏模型运行得到的数据。
表2 IFA算法参数设置
Tab.2 Parameter setting of IFA algorithm

参数数值 n10 g10-8 β01 a0.5 v5 q0.6 m0.2 ε5
本文将在3.2节、3.3节分别研究IFA和FA在静态及动态环境下的算法性能。在实际情况中,光伏阵列最大功率点出现的位置是不确定的,因而本文针对图5所示的三种不同静态条件,即最大功率点出现在左侧、中间及右侧位置三种情况进行最大功率点跟踪,以此说明即使最大功率点出现在不同的位置,IFA都能够实现GMPPT。
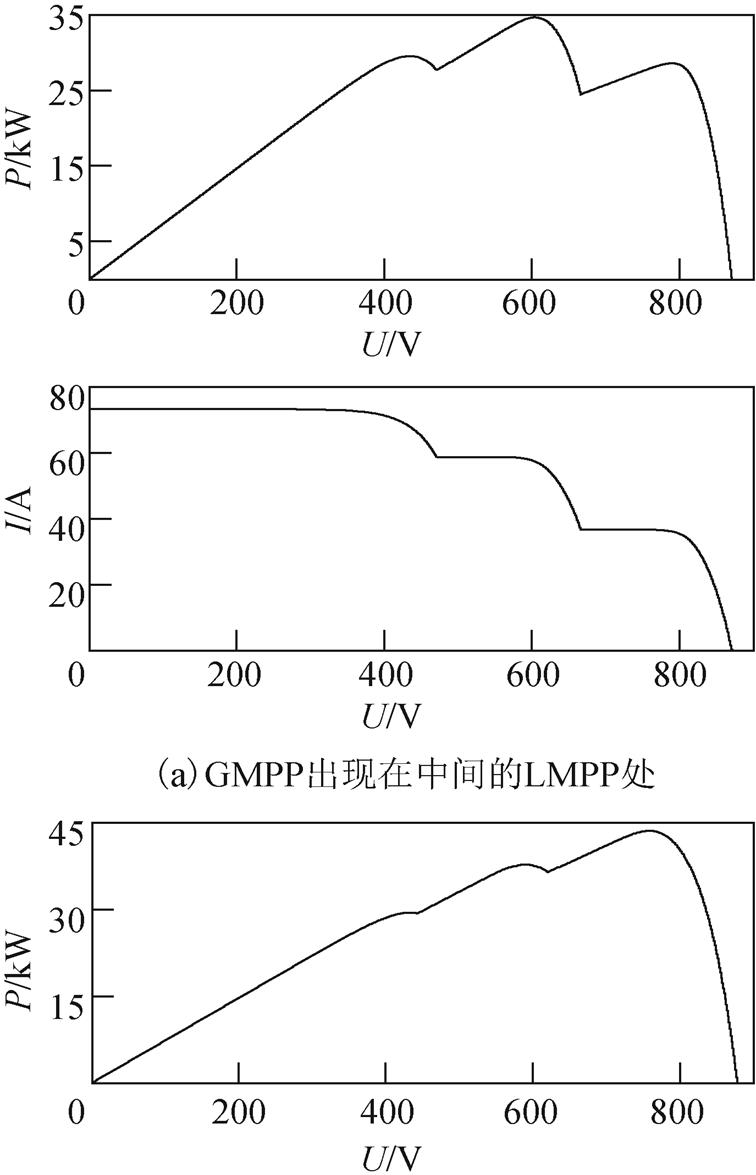
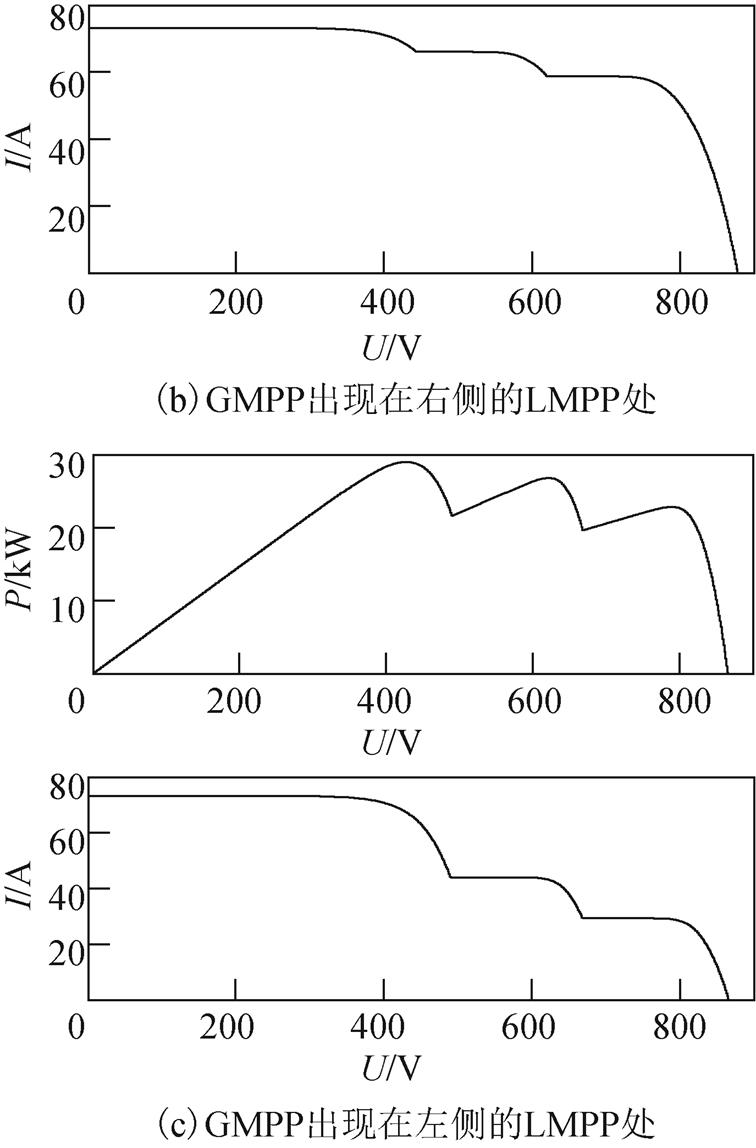
图5 阴影条件下不同的P-U特性曲线
Fig.5 Different P-U curves under various shading
1)案例1:如图5a所示,图中共有3个局部最大功率点(Local Maximum Power Point, LMPP),GMPP出现在P-U曲线的第2个LMPP处。图6和图7分别为GMPP在中间时IFA和FA的电压和功率波形。图6显示了当IFA应用于MPPT时的电压和功率波形。从图6的电压曲线可以看出,IFA从开始到收敛明显快于FA,仅需要39步就可以跟踪到GMPP,这个过程耗时0.49s。前10步代表萤火虫种群正在初始化其位置,之后,每只萤火虫根据其他萤火虫的亮度更新其位置。

图6 GMPP在中间时IFA电压、功率波形
Fig.6 Voltage and power waveforms of IFA if GMPP occurs at middle
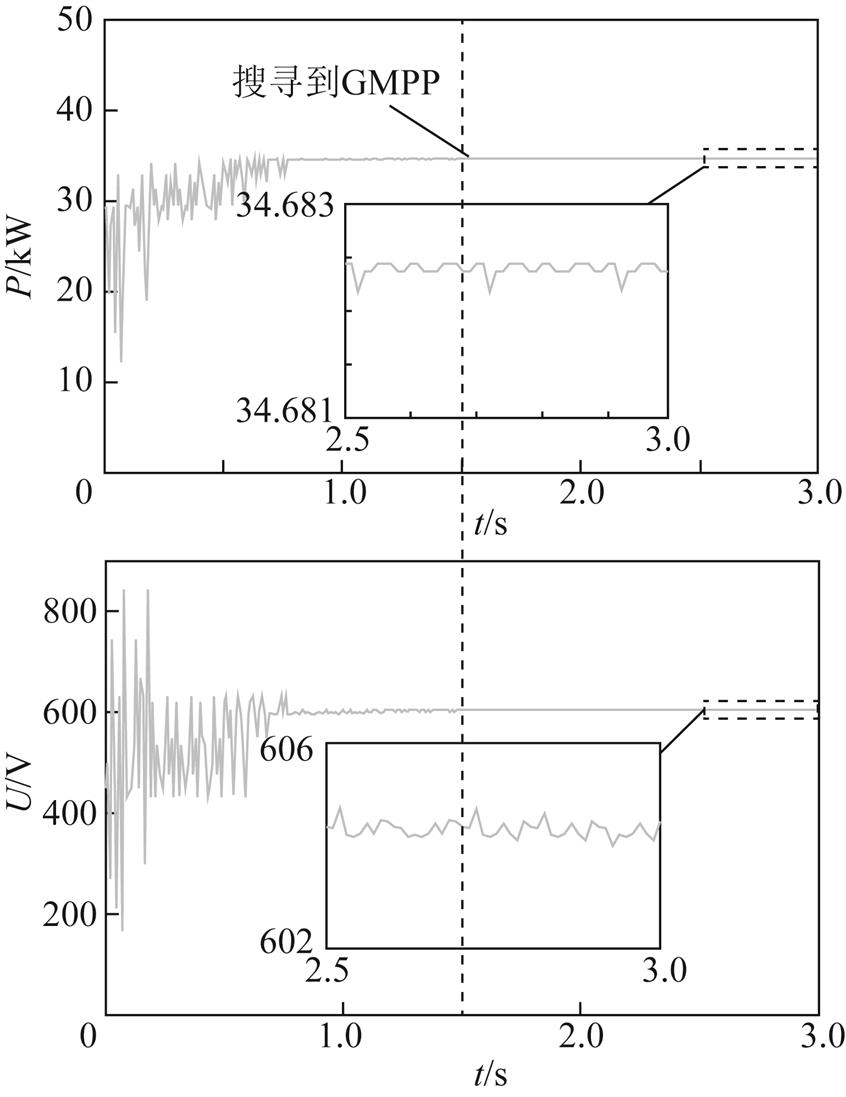
图7 GMPP在中间时FA电压、功率波形
Fig.7 Voltage and power waveforms of FA if GMPP occurs at middle
和IFA相比,FA需要149步(即1.76s)才能跟踪到GMPP。由于IFA利用疫苗库缩小初始分布区域,而且免疫补充操作确保了萤火虫中的每个个体都能发挥作用,因此IFA收敛时间更短。
除了缩短收敛时间外,IFA还可以抑制算法的稳态振荡。如图6和图7所示,虚线框部分表示算法收敛后输出功率的波动。结果表明,变步长函数S能有效地减小收敛后输出功率的振荡。在本案例中,GMPP在电压为604.5V时取得,因此,应将604.5V添加到疫苗数据库中,并去掉与之最接近的疫苗609.7V。
2)案例2:如图5b所示,图中共有3个LMPP,GMPP出现在P-U曲线最右边的LMPP处。图8和图9分别为GMPP在右侧时IFA和FA得到的电压和功率波形。图8为IFA应用于MPPT时的电压和功率波形。如图8所示,IFA搜寻到GMPP需要31步(即0.45s)。图9为FA应用MPPT时的电压和功率波形,FA搜寻到GMPP需要223步(即2.6s)。类似于案例1,在案例2中,IFA带来的稳态振荡依然小于传统的FA算法。
案例3:对于图5c中P-U的波形(GMPP出现在P-U曲线的最左侧),IFA和FA应用于MPPT时的电压、功率波形类似于案例1和案例2。
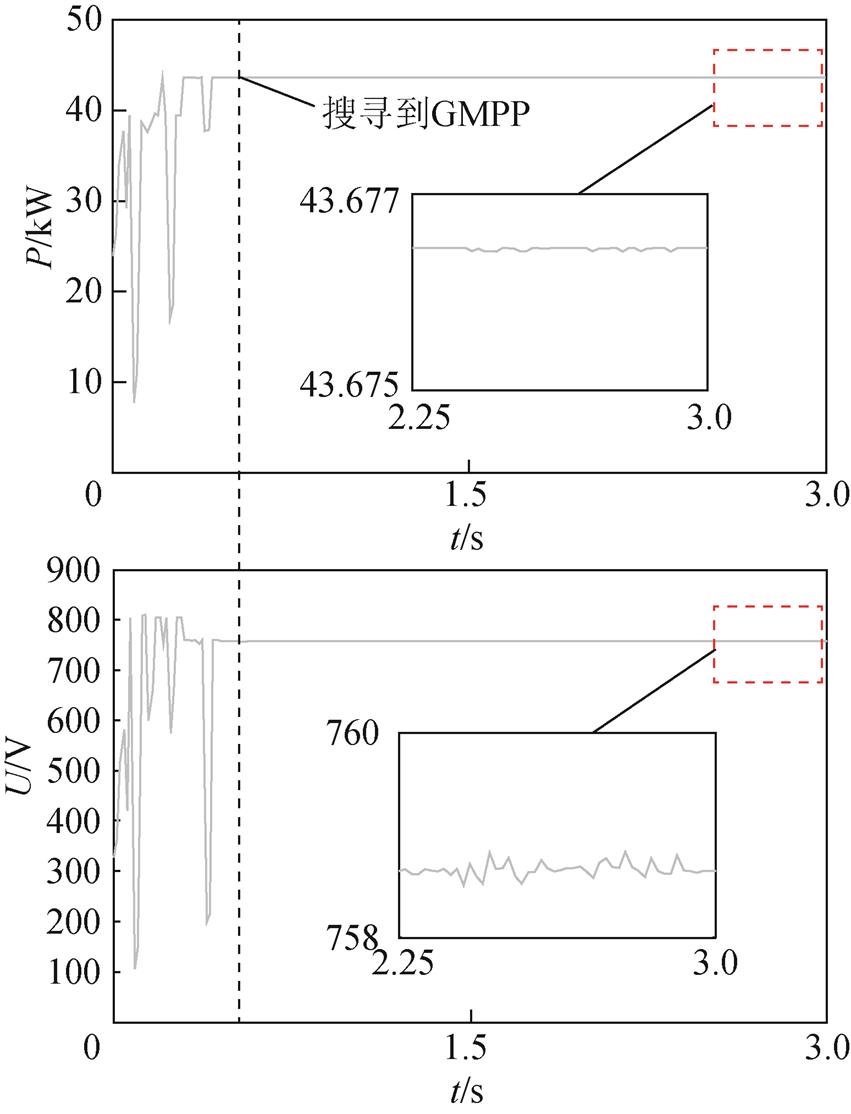
图8 GMPP在右侧时IFA电压、功率波形
Fig.8 Voltage and power waveforms of IFA if GMPP occurs at right
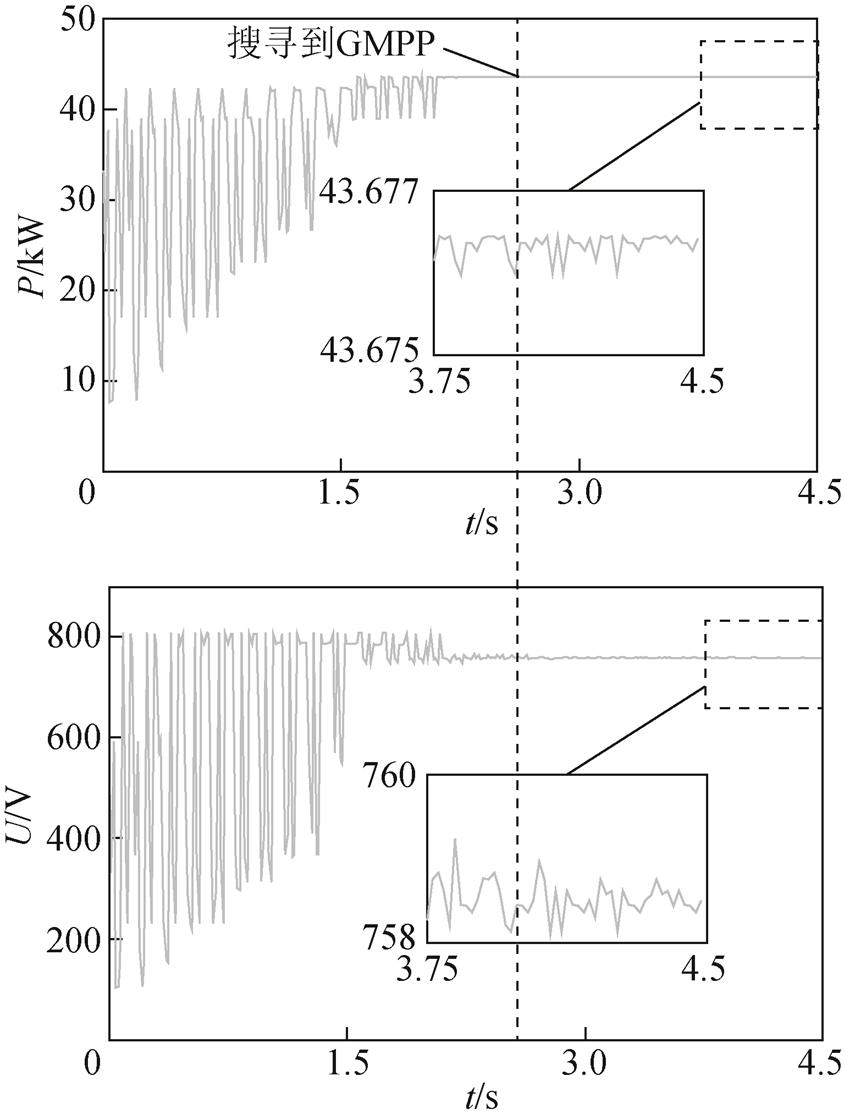
图9 GMPP在右侧时FA电压、功率波形
Fig.9 Voltage and power waveforms of FA if GMPP occurs at right
在案例2和案例3中,GMPP分别在电压为758.6V和427.8V时取得。因此,疫苗数据库中的原有疫苗730.0V和386.3V应被替换为758.6V和427.8V。
此外,对于IFA和FA这类群体智能算法,因为种群的初始位置是完全随机的,所以每次运行的收敛时间都会略有不同。因此,在上述三种不同的PSC下,运行IFA和FA各10次并记录各自的收敛时间。
由表3可知,在不同的阴影条件下,IFA跟踪GMPP的时间总是比FA短。
表3 IFA和FA算法收敛时间
Tab.3 Convergence time of FA and IFA (单位:s)

案例收敛时间 IFAFA 1最快0.210.60 最慢0.501.56 平均0.330.97 2最快0.390.95 最慢0.571.67 平均0.451.18 3最快0.270.79 最慢0.381.26 平均0.310.96
此外,以式(10)计算IFA及FA在收敛后的平均功率振荡区间。
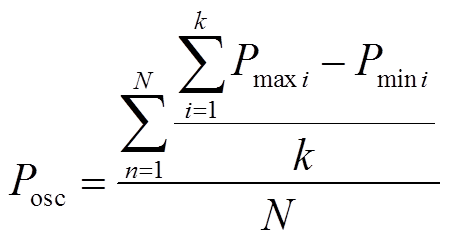 (10)
(10)式中,Pmaxi和Pmini分别为收敛后MPPT算法在每一次迭代中跟踪到的最大及最小功率值;k为算法收敛后的迭代次数;N为算法运行次数,本节中N的取值为10,同时设置算法最大迭代次数为30次。计算结果见表4。
表4 IFA和FA平均功率振荡区间
Tab.4 Average power oscillation interval of FA and IFA

案例Posc/W IFAFA 10.421.07 20.691.16 30.451.22
由表3可知IFA的跟踪速度几乎是FA的3倍(平均快2.8倍)。因此,即使在太阳辐照度变化较快的情况下,IFA仍然可以跟踪到GMPP。对于上面的三种不同PSC,FA的平均跟踪时间约为1.03s,而IFA的跟踪时间为0.36s。因此,如果PV阵列的环境变化频率超过0.5s,IFA仍然可以确保输出最大功率,而FA则不可以。此外,在实际情况中,光伏阵列可能工作在连续变化的PSC下,因此有必要探索IFA在动态环境下的跟踪能力。
如果光伏阵列工作在动态环境中,MPPT算法需要在适当的时候重启,重启条件为
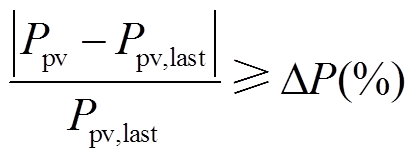 (11)
(11)式中,Ppv,last为上一次迭代完成时的GMPP功率;ΔP(%)通常设置为5%[22]。
在动态案例中,必须考虑两种情形,在第一种情形中,阴影条件发生突变,P-U曲线在极短的时间内发生显著变化,此时需要重新启动MPPT算法。
第二种情形是光伏系统所处的动态环境在连续的变化过程中,例如,云层的移动引起太阳辐照度的增加或减少。为模拟上述情形,设置P-U曲线的变化序列如图10所示。在这种情况下,MPPT算法将不会重新启动。
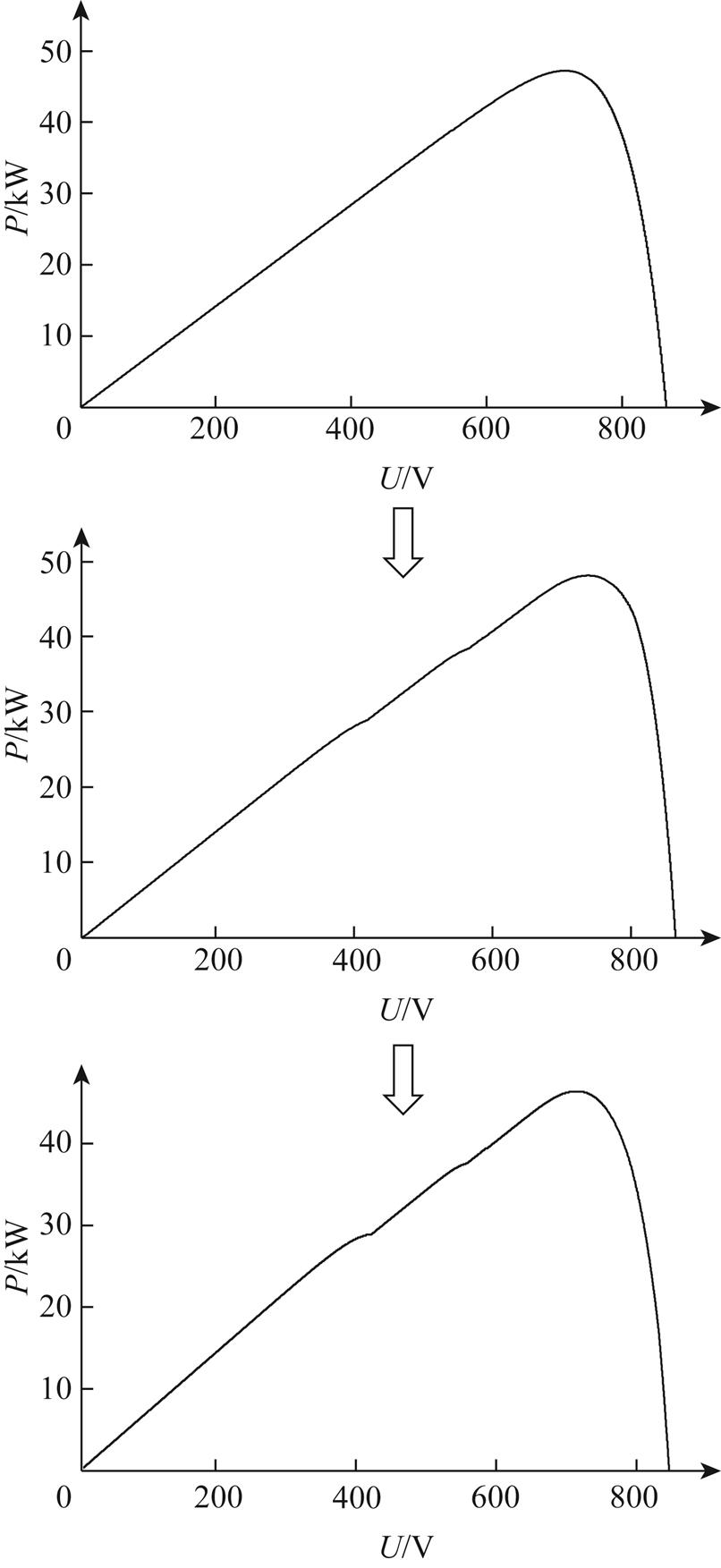
图10 渐变PSC下P-U特性变化顺序
Fig.10 Changing sequence of P-U characteristics under gradual PSC
情形1:图11为第一种情形下IFA和FA应用于MPPT时的跟踪结果。P-U特性分别在2s和3s时从图5b变为图5c。在P-U特性改变前,两种算法都成功跟踪到了GMPP。与3.2节中的案例类似,IFA跟踪到GMPP需要的时间比FA更短,且在P-U特性发生变化后,IFA仍然比FA更快搜索到GMPP。
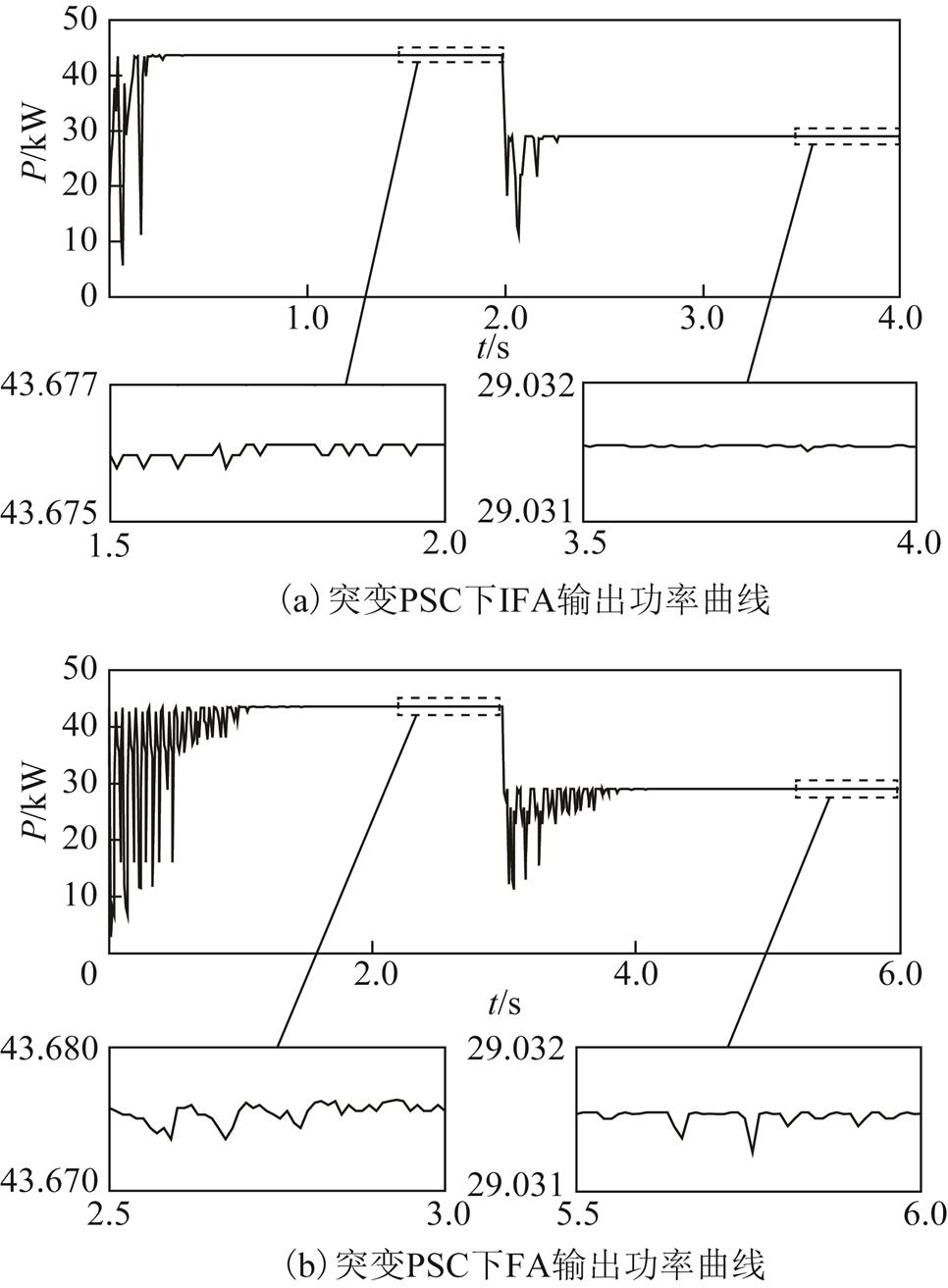
图11 突变PSC下IFA和FA输出功率曲线
Fig.11 Power curves of IFA and FA under sudden change PSC
情形2:PSC连续变化。此时需要注意的是,对于MPPT算法,处于合理的数值范围内的稳态振荡是必须要有的,否则,当PSC更改且算法不满足重启条件时,将无法找到新的MPP。
图12和图13分别为渐变PSC下,IFA和FA的跟踪结果,阴影模式分别在第3s和第6s发生改变。因为式(11)在此情形下一直不成立,所以IFA和FA都不会重启。如图12和图13所示,IFA和FA都可以成功地跟踪GMPP。然而,从图中可以看出,与FA相比,在PSC改变后,IFA的功率波动更小。此外,在PSC变化后FA搜寻到的最大功率值略低于实际的GMPP。
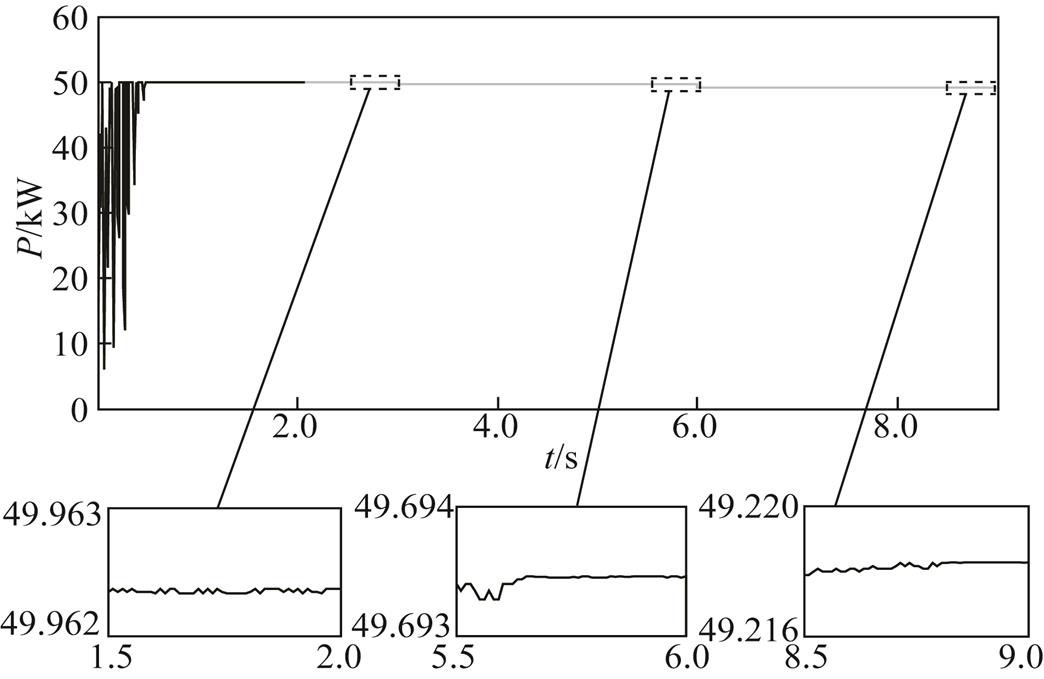
图12 渐变PSC下IFA输出功率曲线
Fig.12 Power waveform of IFA under gradual change PSC
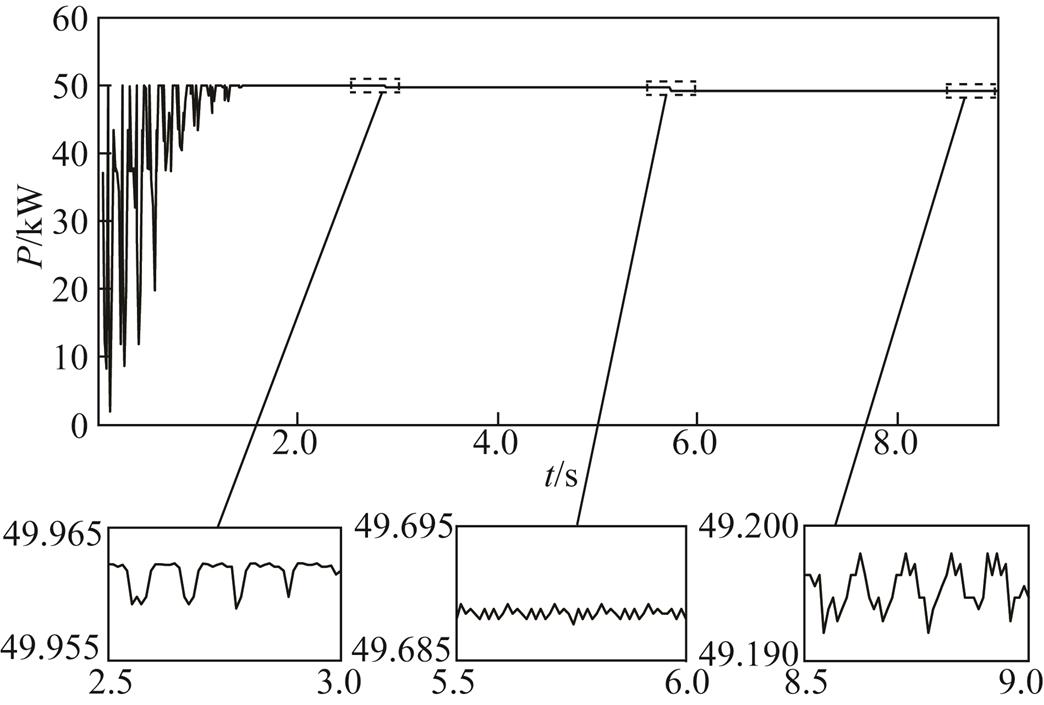
图13 渐变PSC下FA输出功率曲线
Fig.13 Power waveform of FA under gradual change PSC
本文提出了一种光伏系统的最大功率点跟踪算法IFA。该方法改进了传统FA算法的运动方程,增加了疫苗库和免疫补充环节,因此,IFA可以大大缩短算法的收敛时间,减少迭代步骤并减弱稳态振荡。多种静态及动态环境下的仿真结果表明,与FA算法相比,IFA的收敛时间仅为其1/3左右,因此,当辐照度发生快速变化时,IFA的动态性能与FA相比更优越。此外,当PSC发生突变时,IFA能比FA更快、更准确地找到最大功率点。
参考文献
[1] 商立群, 朱伟伟. 基于全局学习自适应细菌觅食算法的光伏系统全局最大功率点跟踪方法[J]. 电工技术学报, 2019, 34(12): 2606-2614. Shang Liqun, Zhu Weiwei. Photovoltaic system global maximum power point tracking method based on the global learning adaptive bacteria foraging algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2606-2614.
[2] 郑堃, 周林, 张前进, 等. 数字控制下光伏并网逆变器稳定性分析及参数优化设计[J]. 电工技术学报, 2018, 33(8): 1802-1813. Zheng Kun, Zhou Lin, Zhang Qianjin, et al. Stability analysis and parameter optimization design of photovoltaic grid-connected inverter under digital control[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1802-1813.
[3] 薛鹏飞, 周海芳, 王明军, 等. 基于FPA的光伏发电全局MPPT算法的研究[J]. 电气技术, 2017, 18(5): 1-5, 11. Xue Pengfei, Zhou Haifang, Wang Mingjun, et al. Research of global MPPT algorithm of photovoltaic generation system based on FPA[J]. Electrical Engineering, 2017, 18(5): 1-5, 11.
[4] 赵书强, 王明雨, 胡永强, 等. 基于不确定理论的光伏出力研究[J]. 电工技术学报, 2015, 30(16): 213-220. Zhao Shuqiang, Wang Mingyu, Hu Yongqiang, et al. Research on the prediction of PV output based on uncertainty theory[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 213-220.
[5] 杜进, 王睿驰, 王志鹍, 等. 并联型单开关管光伏组件优化器的研究与设计[J]. 电工技术学报, 2017, 32(24): 184-192, 213. Du Jin, Wang Reichi, Wang Zhikun, et al. Design and analysis of a parallel single-switch panel-integrated PV optimizer[J]. Transactions of China Electrotechnical Society, 2017, 32(24): 184-192, 213.
[6] 赖昌伟, 黎静华, 陈博, 等. 光伏发电出力预测技术研究综述[J]. 电工技术学报, 2019, 34(6): 1201-1217. Lai Changwei, Li Jinghua, Chen Bo, et al. Review of photovoltaic power output prediction technology[J]. Transactions of China Electrotechnical, 2019, 34(6): 1201-1217.
[7] 杨德友, 崔冬晓, 蔡国伟. 基于云控制器的燃料电池最大功率跟踪策略[J]. 电工技术学报, 2018, 33(14): 3362-3370. Yang Deyou, Cui Dongxiao, Cai Guowei. A maximum power point tracking technology for fuel cells using cloud model based intelligent controller[J]. Transactions of China Electrotechnical, 2018, 33(14): 3362-3370.
[8] Karatepe E, Hiyama T, Boztepe M, et al. Voltage based power compensation system for photovoltaic generation system under partially shaded insolation conditions[J]. Energy Convers. Manage, 2008, 49(8): 2307-2316.
[9] Sharma P, Argarwal V. Exact maximum power point tracking of grid-connected partially shaded PV source using current compensation concept[J]. IEEE Transactions on Power Electronics, 2014, 29(9): 4684-4692.
[10] El-Dein M Z S, Kazerani M, Salama M M A. Optimal photovoltaic array reconfiguration to reduce partial shading losses[J]. IEEE Transactions on Sustainable Energy, 2013, 4(1): 145-153.
[11] Koutroulis E, Blaabjerg F. A new technique for tracking the global maximum power point of PV arrays operating under partial shading conditions[J]. IEEE Journal of Photovoltaics, 2012, 2(2): 184-190.
[12] 朱艳伟, 石新春, 但扬清, 等. 粒子群优化算法在光伏阵列多峰最大功率点跟踪中的应用[J]. 中国电机工程学报, 2012, 32(4): 42-48. Zhu Yanwei, Shi Xinchun, Dan Yangqing, et al. Application of PSO algorithm in global MPPT for PV array[J]. Proceedings of the CSEE, 2012, 32(4): 42-48.
[13] 盛四清, 陈玉良, 张晶晶. 基于差分进化人工蜂群算法的光伏最大功率跟踪策略研究[J]. 电力系统保护与控制, 2018, 46(11): 23-29. Sheng Siqing, Chen Yuliang, Zhang Jingjing. Research on maximum power point tracking strategy based on differential evolution artificial bee colony algorithm of photovoltaic system[J]. Power System Protection and Control, 2018, 46(11): 23-29.
[14] 聂晓华, 王薇. 混沌改进猫群算法及其在光伏MPPT中的应用[J].中国电机工程学报, 2016, 36(22): 6103-6110. Nie Xiaohua, Wang Wei. Chaos improved cat swarm optimization and its application in the PV MPPT[J]. Proceedings of the CSEE, 2016, 36(22): 6103-6110.
[15] Nguyen T L, Low K S. A global maximum power point tracking scheme employing DIRECT search algorithm for photovoltaic systems[J]. IEEE Transactions on Industrial Electronics, 2010, 57(10): 3456-3467.
[16] Ahmed N A, Miyatake M. A novel maximum power point tracking for photovoltaic applications under partially shaded insolation conditions[J]. Electric Power System Research, 2008, 78(5): 777-784.
[17] 王云平, 李颖, 阮新波. 基于局部阴影下光伏阵列电流特性的最大功率点跟踪算法[J]. 电工技术学报, 2016, 31(14): 201-210. Wang Yunping, Li Ying, Ruan Xinbo. Maximum power point tracking algorithm for photovoltaic array under partial shading based on current property[J]. Transaction of China Electrotechnical Society, 2016, 31(14): 201-210.
[18] Patel H, Agarwal V. Maximum power point tracking scheme for PV systems operating under partially shaded conditions[J]. IEEE Transactions on Industrial Electronics, 2008, 55(4): 1689-1698.
[19] Tey K S, Mekhilef S. Modified incremental conductance algorithm for photovoltaic system under partial shading conditions and load variation[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5384-5392.
[20] Yang X S. Nature-inspired metaheuristic algorithms[M]. Cambridge: Luniver Press, 2008.
[21] Sundareswaran K, Peddapati S, Palani S. MPPT of PV systems under partial shaded conditions through a colony of flashing fireflies[J]. IEEE Transactions on Energy Conversion, 2014, 29(2): 463-472.
[22] Femia N, Petrone G, Spagnuolo G, et al. Optimization of perturb and observe maximum power point tracking method[J]. IEEE Transactions on Power Electronics, 2005, 20(4): 963-973.
Application of Immune Firefly Algorithms in Photovoltaic Array Maximum Power Point Tracking
Abstract The P-U curves exhibit complex multiple-peak characteristics if PV arrays operate under various partial shading conditions (PSC). In that case, if the maximum power point tracking can not be achieved quickly and accurately, it will lead to a large amount of energy loss. Therefore, it has become a hot topic to research a reliable maximum power tracking control algorithm to ensure that the PV system can still output maximum power under PSCs. In this paper, an immune firefly algorithm (IFA) is proposed, which utilizes vaccine data-base to shorten the convergence time of the algorithm and eliminates the influence of bad individuals in time by immune replenishment operation, in addition, IFA can reduce the steady-state oscillation by the improved motion equation. The simulations in static and dynamic environments verify that the immune firefly algorithm can track the global point under various partial shading conditions. Compared with conventional FA, IFA has faster convergence speed, and can effectively restrain the oscillation of voltage and power.
keywords:Potovoltaic (PV), firefly algorithm (FA), maximum power point tracking (MPPT), partial shading conditions (PSC)
DOI:10.19595/j.cnki.1000-6753.tces.190760
中图分类号:TM615
张明锐 男,1971年生,教授,博士生导师,研究方向为分布式发电与微网技术、电力系统能量管理与优化运行、轨道交通牵引供电系统。E-mail:zmr@tongji.edu.cn(通信作者)
陈喆旸 男,1995年生,硕士研究生,研究方向为光伏发电最大功率跟踪。E-mail:1343683145@qq.com
国家科技支撑计划资助项目(2015BAG19B02)。
收稿日期2019-06-25
改稿日期 2019-09-09
(编辑 赫蕾)