图1 孤岛微电网系统结构
Fig.1 Island microgrid system structure diagram
摘要 孤岛微电网无大电网支撑,源-荷电力电子装备间强交互耦合,易发生高频振荡等稳定性问题。对此,提出了一种离网源脉宽调制(PWM)逆变器的阻抗重构控制方法,可提高离网源PWM逆变器的输出序阻抗在高频处的相位,增加系统阻尼,能有效抑制系统高频振荡。采用谐波线性化方法,建立离网源PWM逆变器的小信号宽频带正、负序阻抗模型。为了进一步分析孤岛系统的源-荷交互稳定性,建立负荷PWM整流器的正、负序阻抗模型。然后,根据所建宽频带正、负序阻抗模型和Nyquist稳定性判据分析了控制方法、负荷类型、负荷功率大小对孤岛微电网系统稳定性的影响,揭示了孤岛微电网中源PWM逆变器与负荷PWM整流器型负荷交互发生高频振荡的本质原因:在高频处孤岛逆变器的输出阻抗具有负电阻值容性阻抗特性,而PWM整流器型负荷的输入阻抗为感性,导致系统阻抗比不满足稳定判据。所提阻抗重构控制方法,通过增加电压反馈支路,以改善孤岛逆变器在高频处的相位特性,增加系统阻尼,提高系统稳定性。最后,实验验证了本文分析的正确性。
关键词:孤岛微电网 小信号序阻抗建模 交互耦合 高频振荡抑制
微电网能够充分促进可再生能源的大规模接入,实现对本地负荷高可靠供给,使传统电网向智能电网过渡,且已得到长足发展[1-4]。微电网既可以运行于并网模式也可以运行于孤岛模式[5-6],当微电网运行于孤岛模式时,由于没有大电网的支撑,系统中源电力电子装备与负荷电力电子装备间强交互耦合,易发生高频振荡等稳定性问题,严重影响到孤岛微电网的安全稳定运行。
抑制电力电子系统振荡问题的方法主要分为两种:无源阻尼法[7-9]和有源阻尼法[10-15]。无源阻尼法是在电力电子系统中加入无源阻尼支路,抑制系统中存在的谐振尖峰,从而保证了系统的稳定,但是该方法会带来额外的功率损耗,降低系统效率;有源阻尼法是通过电压或电流反馈控制,等效地在系统中增加并联或串联的阻尼支路,从而调节源变换器的输出阻抗或负荷变换器的输入阻抗,使得级联系统的等效环路增益满足Nyquist稳定性判据[16],该虚拟阻尼支路不会引入额外的功率损耗。文献[10-16]的有源阻尼法是解决直流系统中的振荡问题,由于交流和直流系统中变换器的拓扑与控制器的差异,该方法难以直接应用到孤岛微电网系统中。
针对交流系统的振荡问题,文献[17]提出了四种不同形式的虚拟电阻控制,等效地在脉宽调制(Pulse Width Modulation, PWM)逆变器的LC输出滤波器上串联或者并联电阻,可有效抑制系统振荡。文献[18]分析了基于电容电流反馈的有源阻尼控制,并给出了相应的控制参数设计方法。文献[19-20]对比分析了不间断电源(Uninterrupted Power Supply, UPS)逆变系统采用单环电压控制、有源阻尼电压控制和带前馈的有源阻尼控制三种不同控制方式的控制性能。其中,带前馈的有源阻尼控制不仅能够有效抑制振荡,还能减小有源阻尼带来的控制相位滞后。但文献[18-20]研究的对象都是单相或三相的并网逆变器系统,抑制的主要是强网与逆变器之间的振荡问题。文献[21]考虑了数字控制延迟的影响,提出了基于电容电流反馈的有源阻尼控制的参数设计方法,可提高系统振荡抑制性能,但仅分析和解决PWM逆变器在空载下或带线性负荷下的稳定性问题。而孤岛微电网系统中的源和负荷都是电力电子装备,传统的双环控制策略[17-21]已难以抑制该系统中振荡问题[22-23]。
针对所研究的孤岛微电网系统,需要建立孤岛微电网中的源PWM逆变器和负荷PWM整流器的序阻抗模型。文献[24]在abc静止坐标系下,建立了并网逆变器的序阻抗模型,并分析验证了模型的正确性。文献[25]建立了并网逆变器在dq坐标轴下的阻抗,分析了其与电网之间交互的稳定性。文献[26]建立了恒功率负载下的平衡三相交流系统的dq轴阻抗,分析锁相环和电流环对系统稳定性的影响。现有的研究中,所建立的均是单一并网逆变器的正负序阻抗模型,而对三相离网逆变器的正负序阻抗建模还未见报道。目前采用谐波线性化方法对一个孤岛离网系统的正、负序阻抗进行建模也未见报道。而且,在正、负序阻抗视角下,对三相离网逆变器和负荷整流器进行交互稳定性分析更是少有研究。
本文首先采用谐波线性化方法,建立了三相离网源PWM逆变器正负序阻抗模型,在已有的整流器阻抗模型研究基础上,对比分析了系统中源PWM逆变器的输出序阻抗特性和负荷PWM整流器的输入序阻抗特性,且分析两者在系统中的交互稳定,并加入阻抗重构控制来修正所建立的三相离网源PWM逆变器模型,使其拥有优良的输出阻抗特性。然后,基于所建序阻抗模型和Nyquist稳定判据分析负荷类型、负荷功率大小对孤岛微电网系统稳定性的影响,揭示了源PWM逆变器与负荷PWM整流器交互发生高频振荡的本质原因:在高频处,源PWM逆变器的容性输出阻抗与负荷PWM整流器的感性输出阻抗不匹配。在传统的双环控制策略的基础上,加入了源PWM逆变器的阻抗重构控制,提高了源PWM逆变器的输出序阻抗在高频处的相位,本质上增加了系统阻尼,可有效抑制孤岛微电网系统高频振荡。最后,实验验证了本文分析的正确性。
图1所示为本文所研究微电网的结构图,当并网开关断开时,微电网运行于孤岛模式。从图1可知,孤岛微电网系统是一个高度电力电子化的系统,源-荷电力电子装备之间的交互作用明显,易引发系统振荡问题。为了更好地研究孤岛微电网系统中源-荷电力电子装备之间的小信号稳定性问题,需对图1中的孤岛微电网系统进行简化。新能源通过变换器以及储能(储能接在新能源发电的直流侧,图中未画出)能够共同维持直流侧电压稳定,因此可将它们用理想直流电压源代替;考虑最恶劣的情况,假设所有的交、直流负荷都是通过电力电子变换器进行供电的;交、直流负载最终都是通过PWM整流器接入到交流母线。由于多源PWM逆变器的输出阻抗或多负荷PWM整流器的输入阻抗可以聚合成一个输出阻抗或者输入阻抗[27]。因此在研究稳定性时,可将所有的电源用一个源PWM逆变器代替;所有的负荷可以用一个负荷PWM整流器代替。简化后的孤岛微电网系统结构及控制框图如图2所示。

图1 孤岛微电网系统结构
Fig.1 Island microgrid system structure diagram

图2 孤岛微电网系统简化结构及控制框图
Fig.2 Simplified structure and control block diagram of island microgrid system
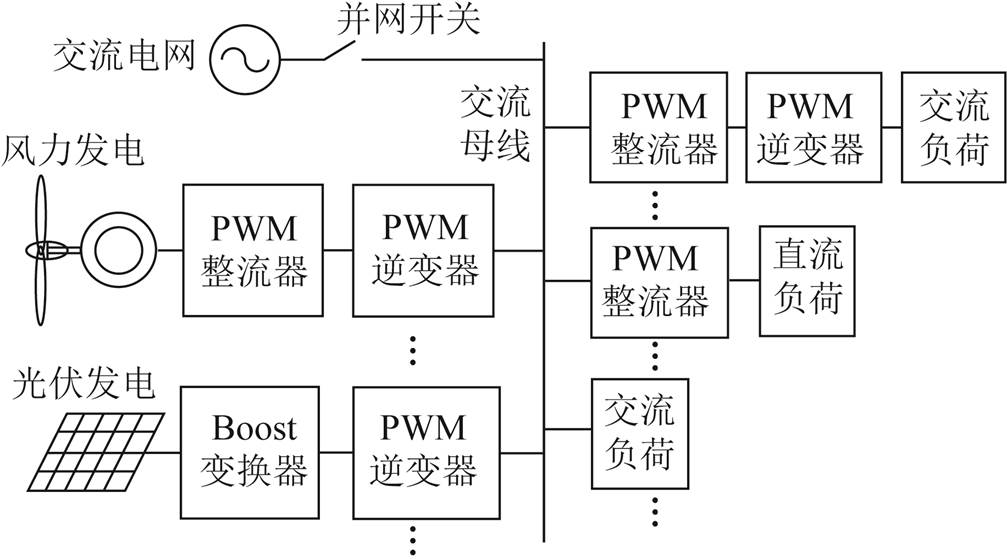
针对孤岛系统的高频振荡问题,提出了一种源PWM逆变器采用输出电压外环、电感电流内环的双闭环控制外加阻抗重构控制,如图2b所示。其中,输出电压外环包括负荷电流前馈及滤波电容电流解耦控制,电感电流内环包括输出电压前馈、滤波电感电压解耦控制和阻抗重构控制,控制方程分别为
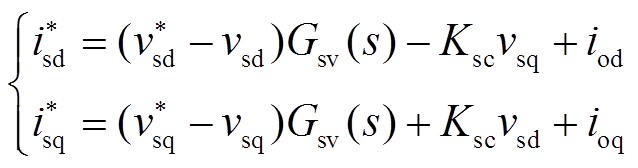 (1)
(1) (2)
(2)
式中,vsd、vsq分别为源PWM逆变器三相输出电压vsa、vsb、vsc在同步旋转坐标系下的d轴和q轴分量;iod、ioq分别为源PWM逆变器三相输出电流ioa、iob、ioc在同步旋转坐标系下的d轴和q轴分量;isd、isq分别为源PWM逆变器滤波电感电流isa、isb、isc在同步旋转坐标系下的d轴和q轴分量;v* sd、v* sq分别为vsd、vsq的指令;i* sd、i* sq分别为isd、isq的指令;csd、csq分别为源PWM逆变器三相调制波csa、csb、csc在同步旋转坐标系下的d轴和q轴分量;Lsf为源PWM逆变器的滤波电感;rsf、Csf分别为滤波电感的寄生电阻、滤波电容;Ksc为滤波电容电流解耦系数,Ksc=ωlCsf,ωl为基波角频率;KsL为滤波电感电压解耦系数,KsL=ωlLsf/(Vsdc/2);Ksff为前馈系数,Ksff=1/(Vsdc/2);kd、ωd分别为阻抗重构控制环节的高通滤波器的增益和截止角频率;Gsv(s)、Gsi(s)分别为源PWM逆变器的电压环和电流环的PI控制器,Gsv(s)=kp_sv+ki_sv/s,Gsi(s)=kp_si+ki_si/s。
负荷PWM整流器采用直流输出电压外环、电感电流内环的双闭环控制,如图2c所示。电压环和电流环的控制方程分别为
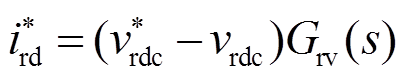 (3)
(3)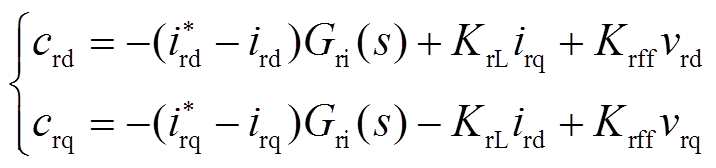 (4)
(4)
式中,vrdc、v* rdc分别为负荷PWM整流器的直流侧电压及其指令;vrd、vrq分别为负荷PWM整流器三相输入电压vra、vrb、vrc在同步旋转坐标系下的d轴、q轴分量;ird、irq分别为负荷PWM整流器滤波电感电流ira、irb、irc在同步旋转坐标系下的d轴、q轴分量;i* rd、i* rq分别为ird、irq的指令;crd、crq分别为负荷PWM整流器三相调制波(cra、crb、crc)在同步旋转坐标系下的d轴、q轴分量;Lrf、rrf分别为负荷PWM整流器的滤波电感及其寄生电阻;KrL为滤波电感电压解耦系数,KrL=ωlLrf/(Vrdc/2);Krff为前馈系数,Krff=1/(Vrdc/2);Grv(s)、Gri(s)分别为负荷PWM整流器的电压环、电流环的PI控制器,Grv(s)=kp_rv+ki_rv/s,Gri(s)=kp_ri+ki_ri/s。
源PWM逆变器和负荷PWM整流器中,从三相静止坐标系到两相同步旋转坐标系的变换矩阵T(θ)为
 (5)
(5)从两相同步旋转坐标系到三相静止坐标系的变换矩阵T-1(θ)为
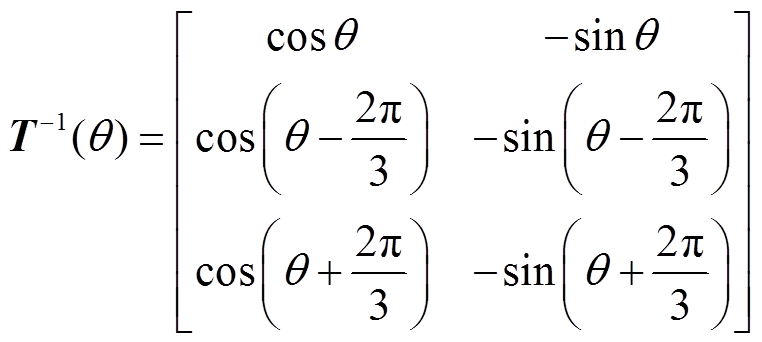 (6)
(6)
式中,θ在源PWM逆变器中用θs替代,θs由给定角频率ωs积分得到;θ在负荷PWM整流器用θPLL替代,θPLL由同步旋转坐标系下的锁相环(Phase Locked Loop, PLL)控制得到,其表达式为
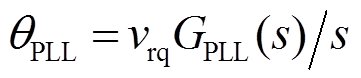 (7)
(7)式中,GPLL(s)为负荷PWM整流器中锁相环的PI控制器,GPLL(s)=kp_PLL+ki_PLL/s。
本文采用谐波线性化方法,推导出源PWM逆变器的正、负序输出阻抗模型。在时域中,加入正、负序小信号扰动后,源PWM逆变器的A相输出电压和输出电流为

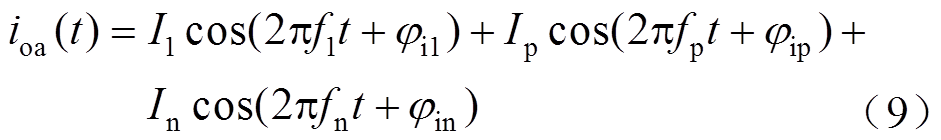
式中,V1、Vp和Vn分别为基波电压、正序扰动电压和负序扰动电压的峰值;I1、Ip和In分别为基波电流、正序扰动电流响应和负序扰动电流响应的峰值;f1、fp和fn分别为基波频率、正序扰动频率和负序扰动频率;φvp、φvn分别为正序扰动电压和负序扰动电压的初相角;φi1、φip和φin分别为基波电流、正序扰动电流响应和负序扰动电流响应的初相角。在频域中,电压vsa和电流ioa分别为
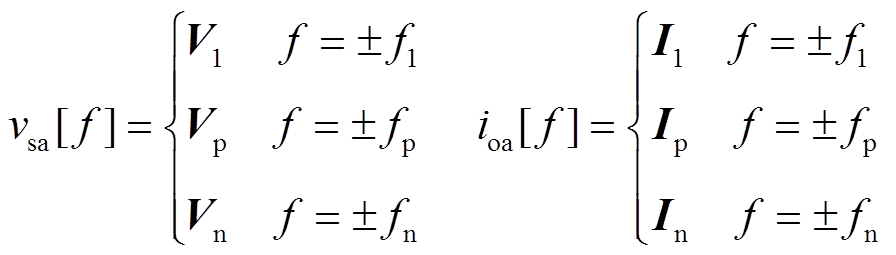 (10)
(10)式中,V1=V1/2;Vp=(Vp/2)e±jφvp;Vn=(Vn/2)e±jφvn;I1=(I1/2)e±jφi1;Ip=(Ip/2)e±jφip;In=(In/2)e±jφin。
由图2可知,源PWM逆变器的内电动势、输出电压、输出电流和滤波电容电流的关系为
 (11)
(11)式中,esa、esb和esc为源PWM逆变器的三相内电动势;ica、icb和icc为源PWM逆变器的三相滤波电容电流。
当系统三相对称时,可得同步旋转坐标系下源PWM逆变器的输出电压和输出电流的频域表达式为
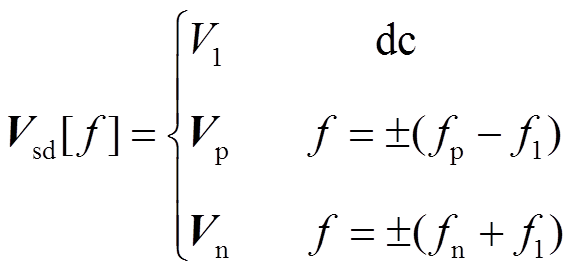 (12)
(12) (13)
(13)
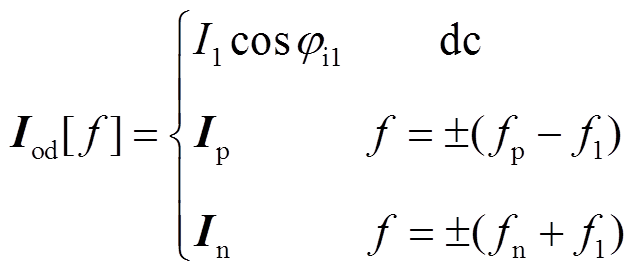 (14)
(14)
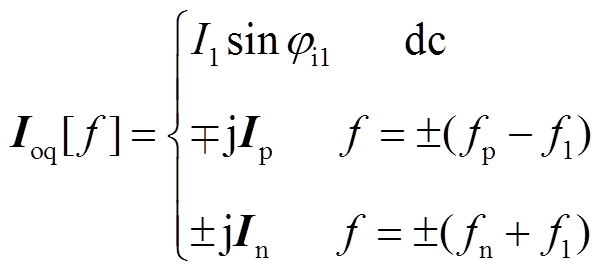 (15)
(15)同步旋转坐标系下滤波电容电流icd和icq的频域表达式为
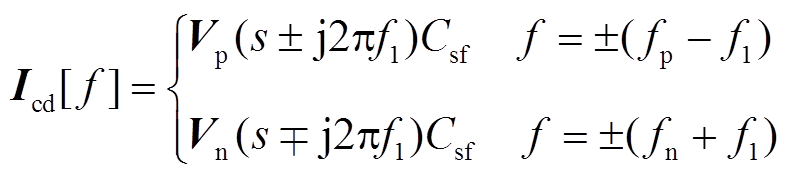 (16)
(16)
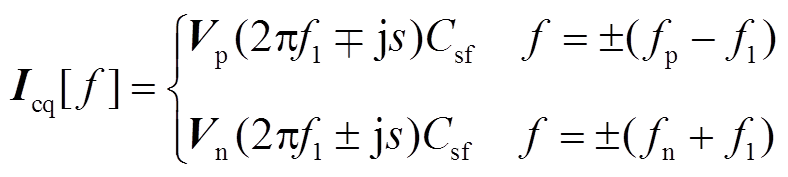 (17)
(17)根据基尔霍夫电流定律,由式(14)~式(17)可求得源逆变器输出电流isd和isq的频域表达式为
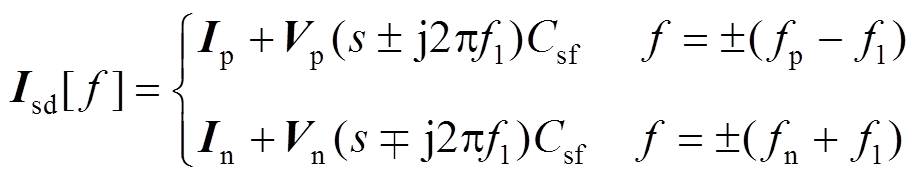 (18)
(18)
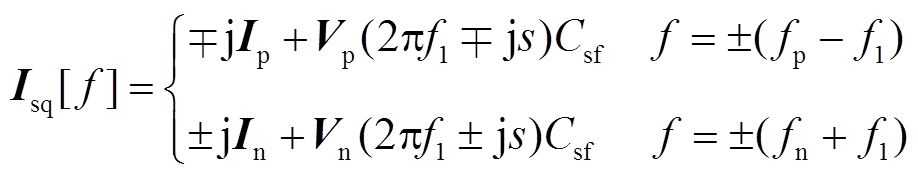 (19)
(19)然后将式(12)~式(15)代入式(1),可得i* sd和i* sq在频域的表达式为
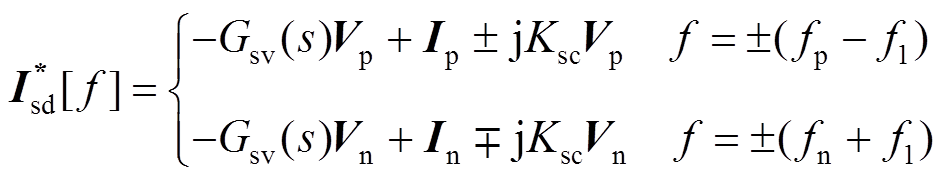 (20)
(20)
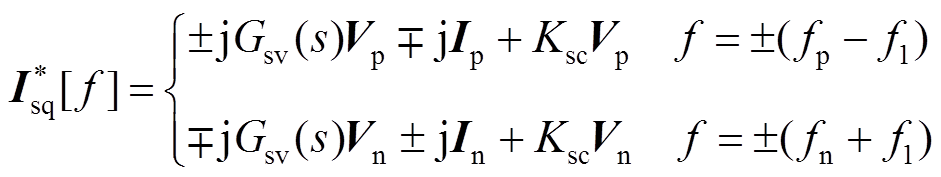 (21)
(21)将式(14)~式(17)代入式(2),可得csd和csq在频域的表达式为
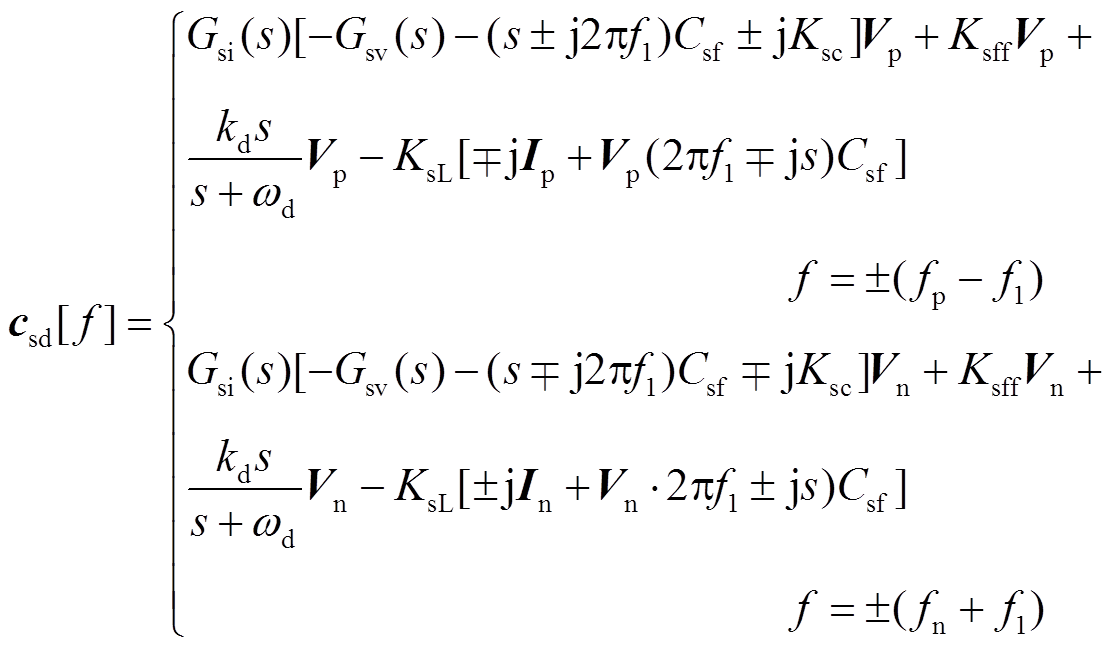 (22)
(22)
 (23)
(23)csa、csb和csc的表达式可由反Park变换得到,其表示为
 (24)
(24)
根据式(22)~式(24)和频域卷积定理并忽略在f=±(fp−2f1)和f=±(fn+2f1)的非线性耦合,可求出csa在频域中的表达式为
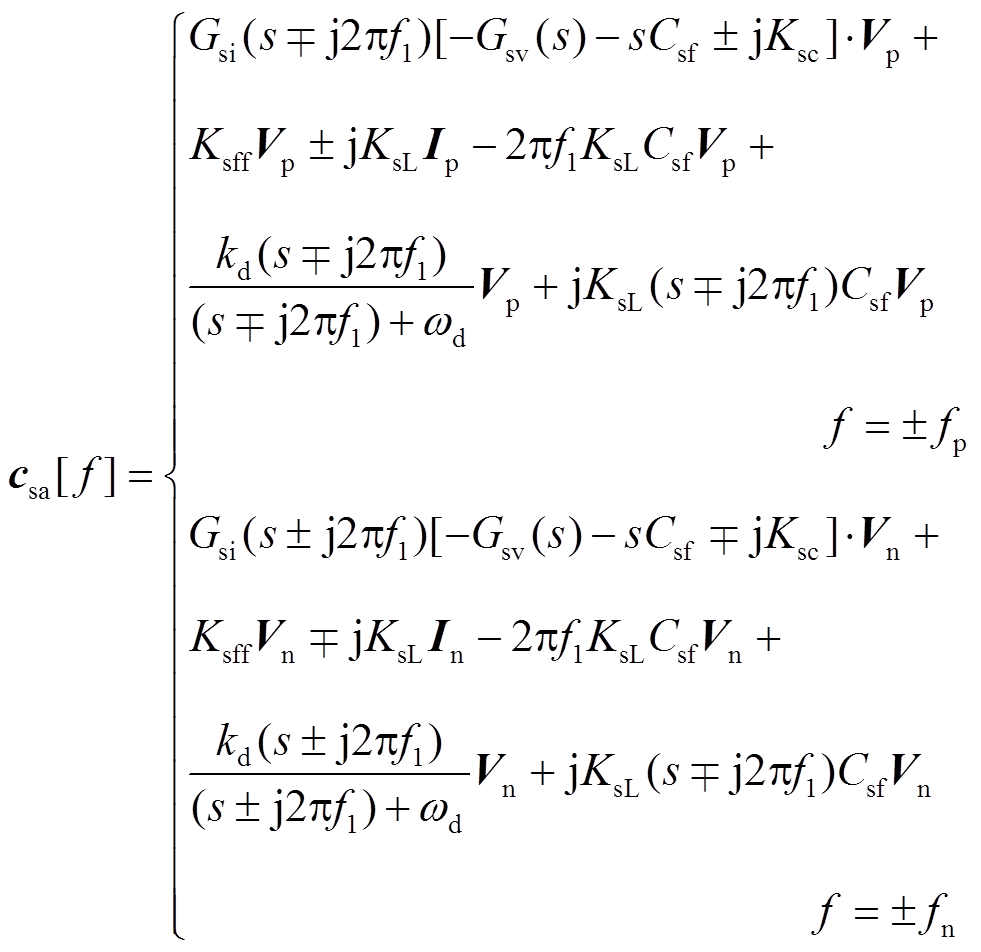 (25)
(25) 考虑信号采样和PWM的延时,将式(10)和式(14)~式(17)代入式(11)中,可以得到加上阻抗重构控制的源PWM逆变器的频域正、负序阻抗为
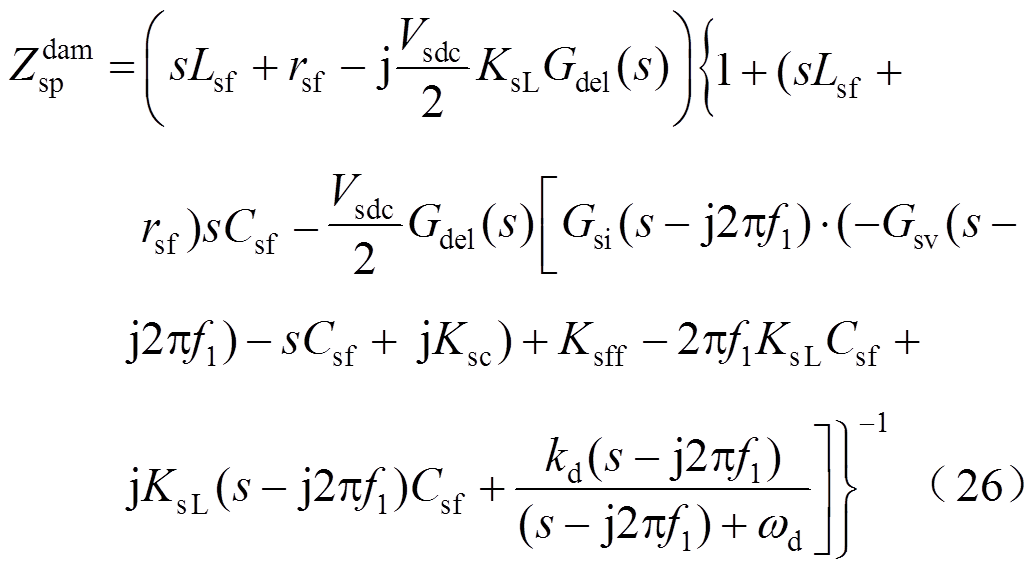
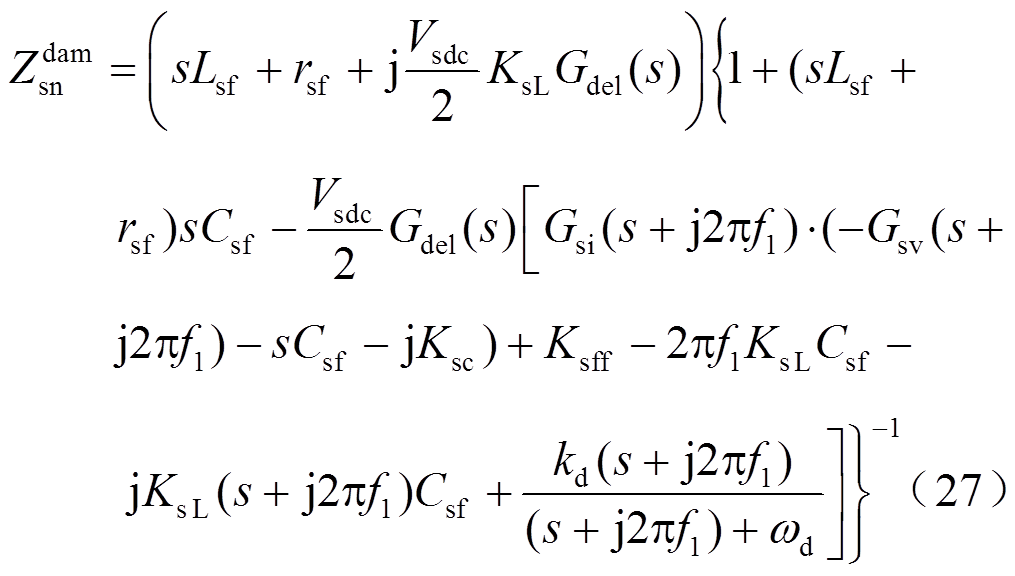
式中,Gdel(s)为信号采样和PWM的延时传递函数,Gdel(s)=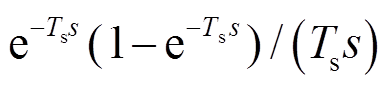 ,Ts为PWM开关周期。
,Ts为PWM开关周期。
当源PWM逆变器无阻抗重构控制时,仿照本节的推导方法,可以得到无阻抗重构控制的源PWM逆变器的频域正、负序阻抗为
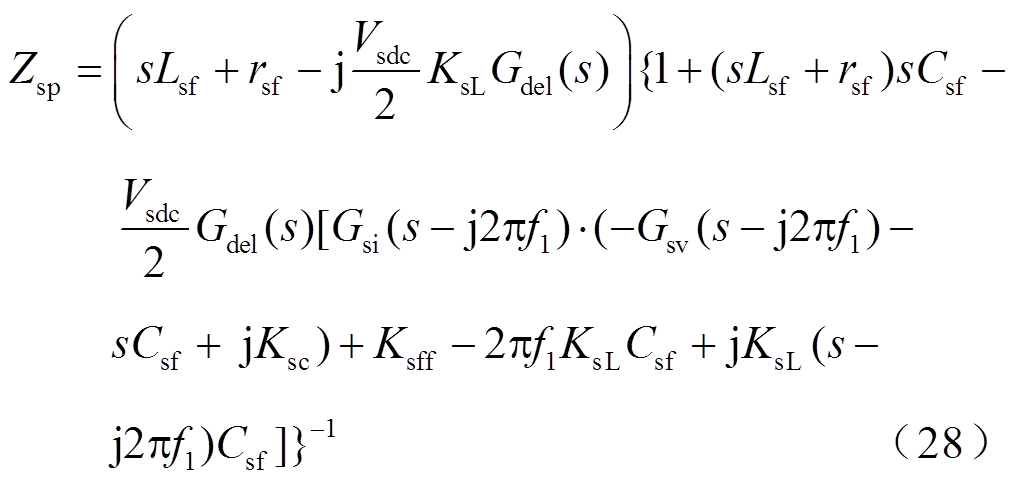
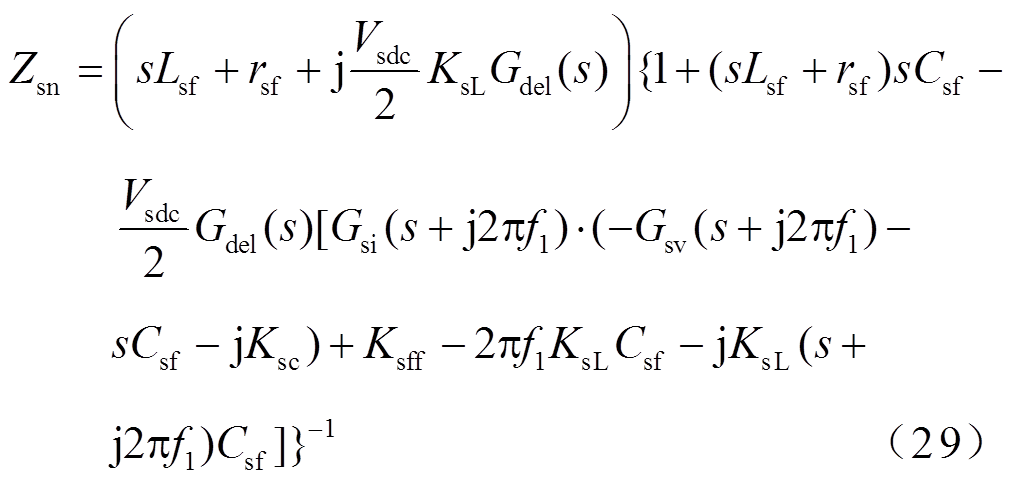
本文所研究源PWM逆变器的系统参数见表1,源PWM逆变器的额定功率PN为40kW,开关频率为5kHz,其控制参数参照文献[28]设计。图3和图4所示分别为没有阻抗重构控制和有阻抗重构控制下,不同输出功率下源PWM逆变器的正、负序输出阻抗特性及其仿真测量结果。图中,实线表示式(26)、式(28)所建正序阻抗,虚线代表式(27)、式(29)所建负序阻抗模型。从图中可知,阻抗测量结果和所建的阻抗模型能够很好地吻合,证明了源PWM逆变器序阻抗建模的正确性。
表1 源PWM逆变器的系统参数
Tab.1 System parameters of supply PWM inverter

参数数值参数数值 PN/kW40wd/rad4 000π Vsdc/V700Csf/μF40 V1/V311rsf/Ω0.01 ω1/rad100πkp_sv0.025 ωs/rad100πki_sv4.71 Lsf/mH1.6kp_si0.017 Ksc0.012 56ki_si0.106 KsL0.001 44fss/kHz5 kd0.005Ksff0.002 8
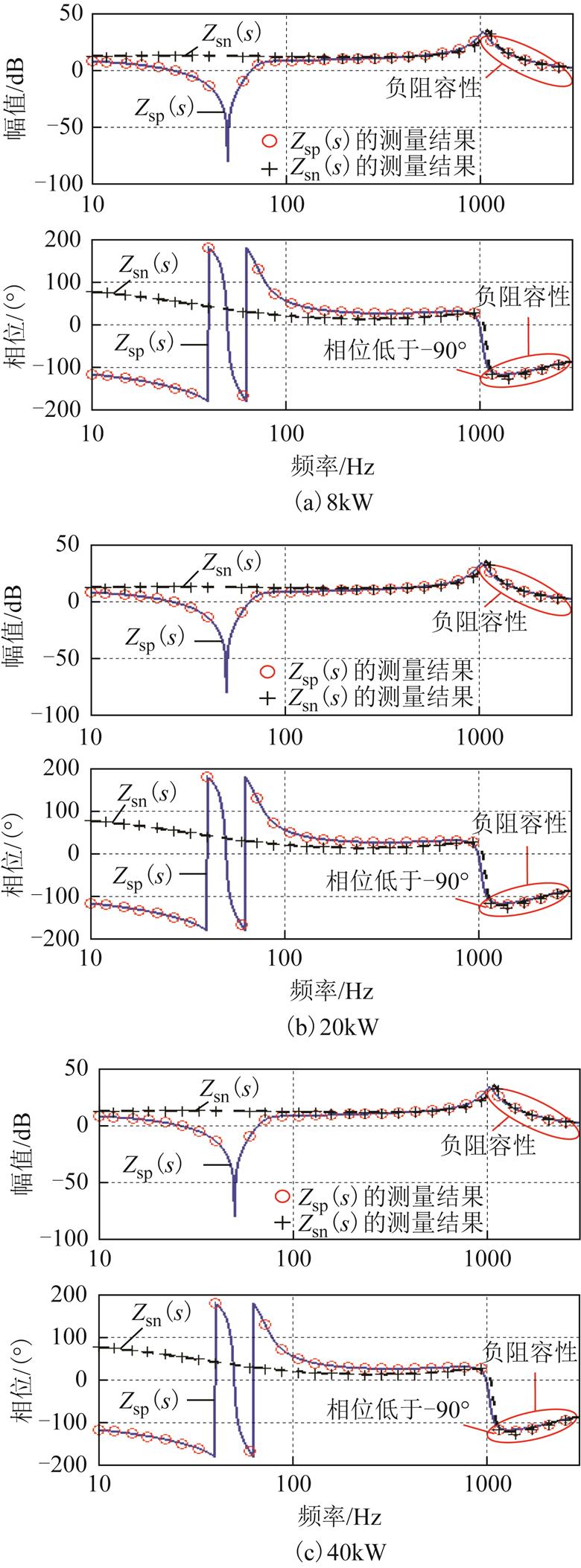
图3 不同输出功率下源PWM逆变器无阻抗重构控制的正、负序输出阻抗特性及其仿真测量结果
Fig.3 Positive and negative sequence output impedance characteristics and simulation measurement results of source PWM inverter without impedance reconstruction under different output powers
负荷PWM整流器的正、负序阻抗模型参照文献[24]进行过推导,该正、负序阻抗模型分别如式(30)和式(31)所示,负荷PWM整流器的系统参数见表2。图5所示为负荷PWM整流器的正、负序阻抗的幅频特性曲线及其仿真测量

图4 不同输出功率下源PWM逆变器有阻抗重构控制的正、负序输出阻抗特性及其仿真测量结果
Fig.4 Positive and negative sequence output impedance characteristics and simulation measurement results of source PWM inverter with impedance reconstruction under different output powers
结果。图中,实线和虚线分别表示负荷PWM整流器的正、负序阻抗模型。从图中可知,阻抗测量结果和该阻抗模型能够很好地吻合,证明了所建立的负荷PWM整流器正、负序阻抗模型的正确性。
表2 负荷PWM整流器的系统参数
Tab.2 System parameters of load PWM rectifier

参数数值参数数值 PN/kW40Krff0.002 86 vrdc/V700ki_PLL10.998 8 Lrf/mH3kp_PLL0.265 9 rrf/Ω0.001kp_ri0.017 kd0.002 7ki_ri0.106 V1/V311fsr/kHz5
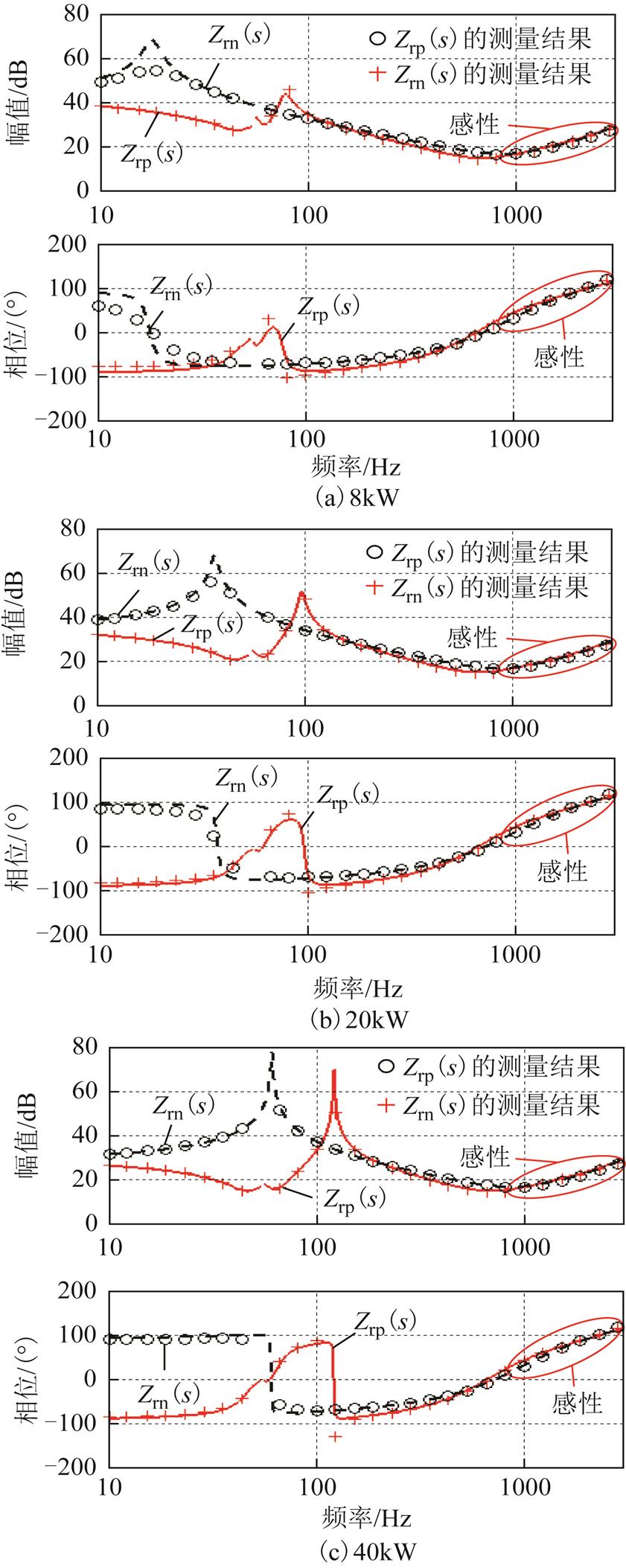
图5 不同输入功率下负荷PWM整流器的正、负序输入阻抗特性及其仿真测量结果
Fig.5 Positive and negative sequence input impedance characteristics of load PWM rectifiers with different input powers and their simulation measurements
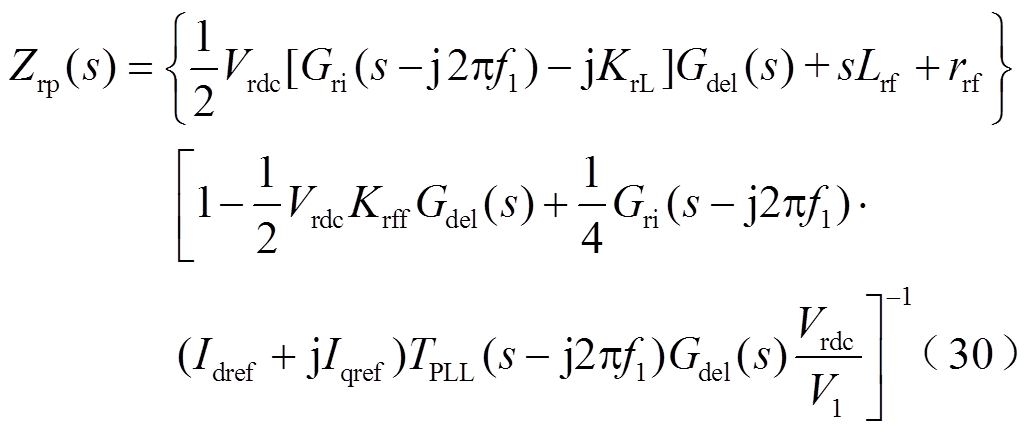
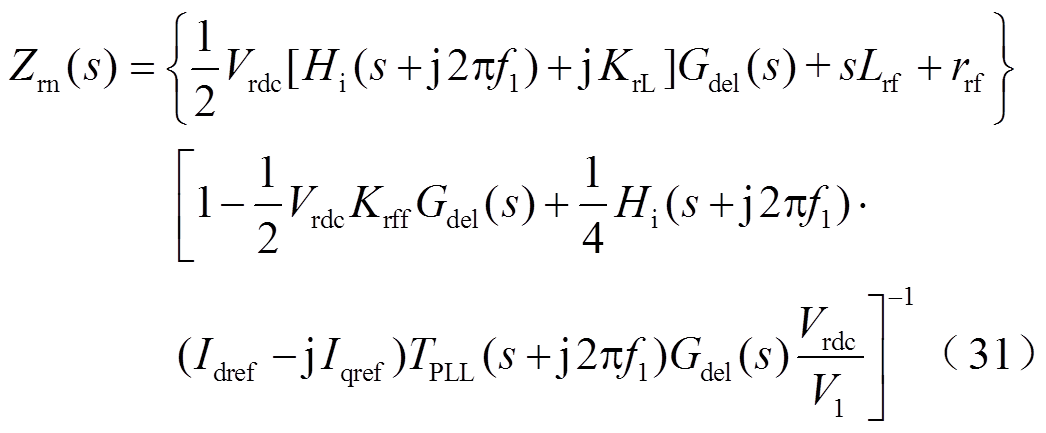
式中,TPLL(s)=V1HPLL(s)/(1+V1HPLL(s)),HPLL(s)= GPLL(s)/s;Idref和Iqref分别为ird和irq的指令值。
由图3~图5可得到源PWM逆变器和负荷PWM整流器的序阻抗有如下特性:
1)因为源PWM逆变器不存在锁相环,所以同步旋转坐标变换中不会产生非线性。因而,其正、负序阻抗特性均不受输出功率的影响,基本上不受运行工况的影响,且在高频段,其正、负序阻抗特性几乎一致。
2)负荷PWM整流器的正、负序阻抗特性在中低频段受输入功率影响较大。而在高频段,不同功率下负荷PWM整流器的正、负序阻抗特性均趋于一致。
3)在中低频段,源PWM逆变器的正、负序阻抗幅值分别都远小于负荷PWM整流器的正、负阻抗幅值。这是因为源PWM逆变器的外端口特性表现为电压源,等效输出正、负序阻抗小;负荷PWM整流器的外端口特性表现为电流源,等效输出正、负序阻抗大。
4)在高频段,无阻抗重构控制的源PWM逆变器的正序阻抗主要呈容性,且其电阻分量为负电阻,相位低于-90°;而负荷PWM整流器正序阻抗呈感性,其电阻分量为正电阻。当源PWM逆变器与负荷PWM整流器的正序阻抗在高频段相交,且相交处源PWM逆变器正序阻抗的负电阻大于负荷PWM整流器正序阻抗中的正电阻时,整个孤岛微电网系统的电阻为负,此时,将会引发系统负阻尼LC电磁振荡,且该振荡不需要振荡源。类似地,源PWM逆变器的负序阻抗特性为负阻值容性,负荷PWM整流器的负序阻抗特性为正阻值感性,两者负序阻抗幅值在高频处有交点,且交点处相位差低于-180°,两者负序阻抗出现不匹配的问题。而阻
抗重构控制的引入,使得源PWM逆变器的输出正、负序阻抗在高频段的相位均得到显著提高,明显高于-90°,其正、负序阻抗分别与负荷PWM整流器正、负序阻抗幅值交点处的相位差均远大于-180°。从本质上看,源-荷两侧相位差的提高是因为阻抗重构控制增加了系统的阻尼,破坏了源PWM整流器与负荷PWM整流器发生高频振荡的条件,能有效地抑制振荡,提高了孤岛微电网系统的稳定性。
源PWM逆变器加入阻抗重构控制后的控制结构框图如图6所示,在源PWM逆变器传统双闭环控制基础上增加了一个振荡抑制控制环,可改变源PWM逆变器高频处的阻抗特性,提高源PWM逆变器的输出序阻抗在高频处的相位,其中,kpwm为桥路PWM等效增益。
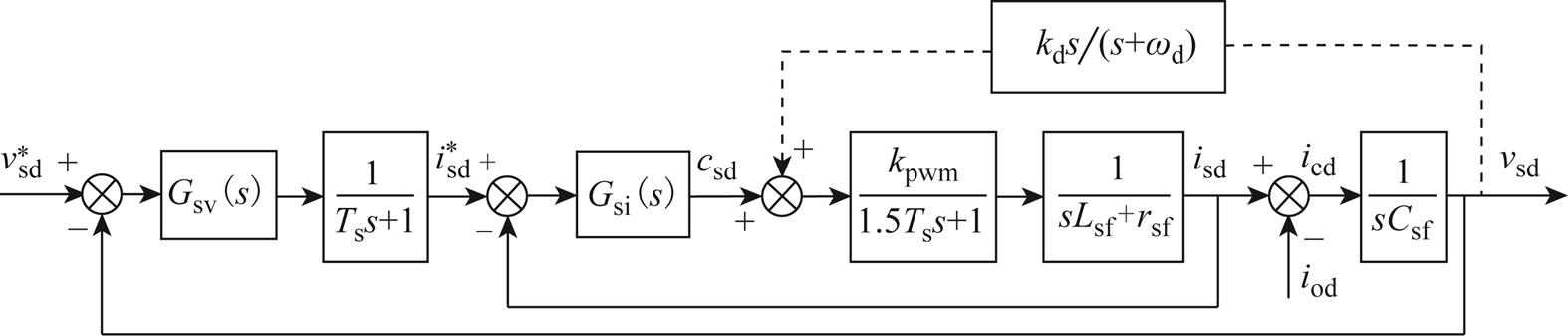
图6 源PWM逆变器的阻抗重构控制结构框图
Fig.6 Block diagram of impedance reconstruction control of source PWM inverter
为了验证源PWM逆变器采用所提阻抗重构控制后的闭环控制系统仍然是稳定的,可推导图6所示框图的电压闭环传递函数为
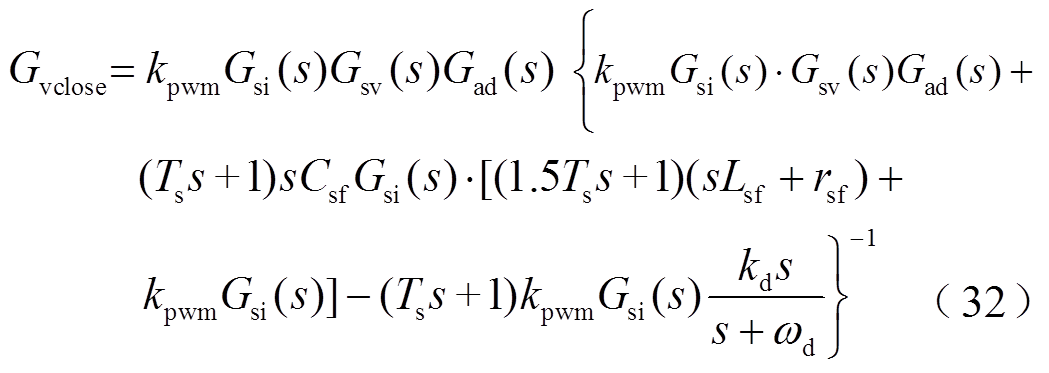
根据式(32)的电压闭环传递函数可求其闭环极点图,如图7所示。源PWM逆变器采用阻抗重构控制后,其闭环传递函数的所有极点均在负半平面里,源PWM逆变器自身稳定。
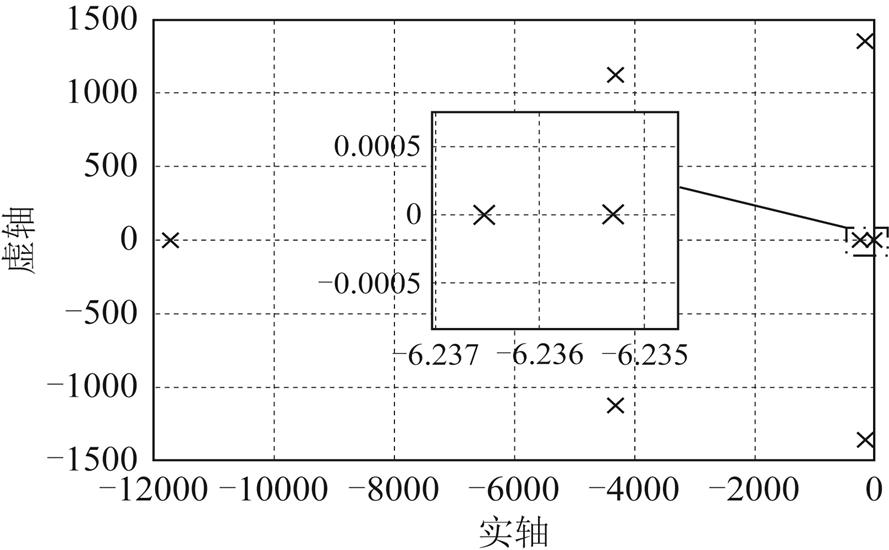
图7 采用阻抗重构控制的源PWM逆变器闭环极点图
Fig.7 Closed-loop pole diagram of source PWM inverter with impedance reconstruction control
孤岛微电网系统的小信号描述如图8所示。从交流端口看过去,源PWM逆变器可以看作电压源,用戴维南等效电路表示;负荷PWM整流器可以看作电流源,用诺顿等效电路表示。源PWM逆变器与负荷PWM整流器所构成级联系统的交互稳定性可采用Nyquist稳定判据分析系统的阻抗比。由于源PWM逆变器的外特性可看作电压源,负荷PWM整流器的外特性可看作电流源,因此根据阻抗稳定性判据,用于判稳的阻抗比[29]是源PWM逆变器的输出阻抗除以负荷PWM整流器的输入阻抗。
 (33)
(33)式中,IRp(s)、IRn(s)分别用于判稳的正、负序阻抗比。
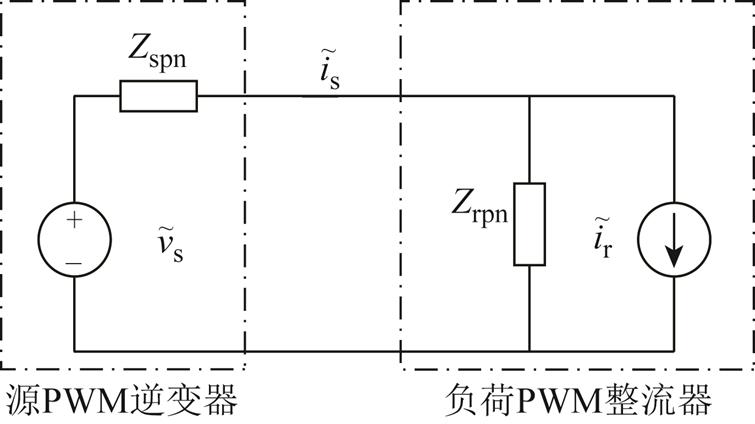
图8 孤岛微电网系统的小信号描述
Fig.8 Small signal description of island microgrid system
假设用纯电阻负荷代替负荷PWM整流器,则在不同功率下,无阻抗重构控制时,源-荷阻抗比IRp(s)、IRn(s)的Nyquist图如图9所示。图中,IRp(s)和IRn(s)的Nyquist图分别用实线和虚线表示。通过极点计算发现用纯电阻负荷代替负荷PWM整流器时,IRp(s)和IRn(s)都没有在正半平面的极点。从图9可知,在不同负荷功率下,源-荷阻抗比IRp(s)、IRn(s)的Nyquist曲线都未包围 (-1,j0)点,系统稳定。因此,源PWM逆变器带纯电阻负载时,源PWM逆变器采用传统双闭环控制可以维持孤岛微电网系统的稳定。虽然源PWM逆变器的输出接了LC滤波器,但传统双闭环控制中的电流内环可等效为有源阻尼控制,能有效抑制系统振荡。
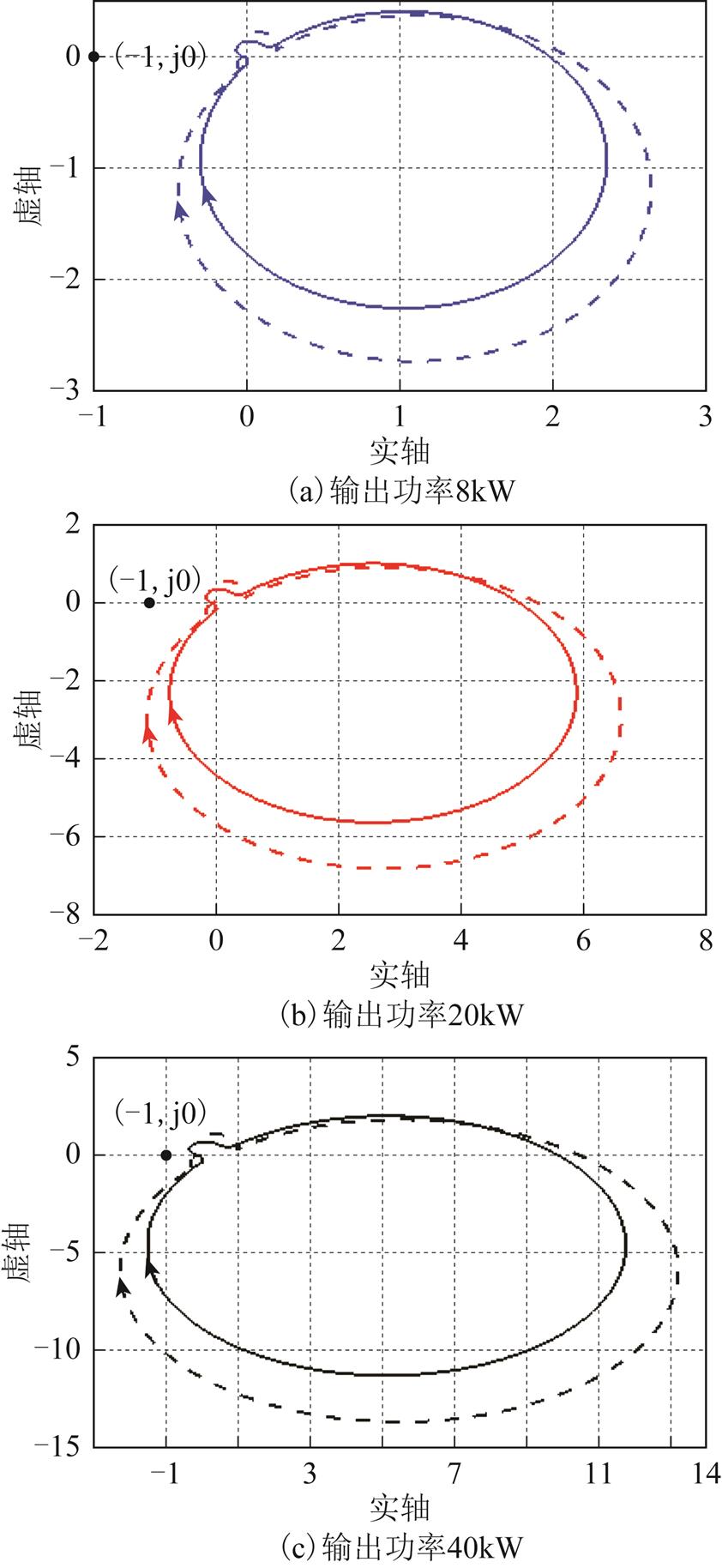
图9 无阻抗重构控制的源PWM逆变器带阻性负载下,不同输出功率IRp(s)和IRn(s)的Nyquist图
Fig.9 Nyquist plots of IRp(s) and IRn(s) without impedance reconstructionwith different output power under resistive load
在无阻抗重构控制的情况下,当源PWM逆变器所接负荷为负荷PWM整流器时,分别画出不同功率下的IRp(s)、IRn(s)的Nyquist图,如图10所示。同样地,通过极点计算发现此时IRp(s)和IRn(s)也都没有在正半平面的极点。图中,IRp(s)和IRn(s)的Nyquist图分别用实线和虚线表示。从图10可知,在不同的输出功率下,源-荷阻抗比IRp(s)、IRn(s)的Nyquist曲线均包围(-1, j0)点,系统不稳定。因此,源PWM逆变器接负荷PWM整流器时,如果源PWM逆变器仅采用传统双闭环控制,难以维持孤岛微电网系统的稳定。
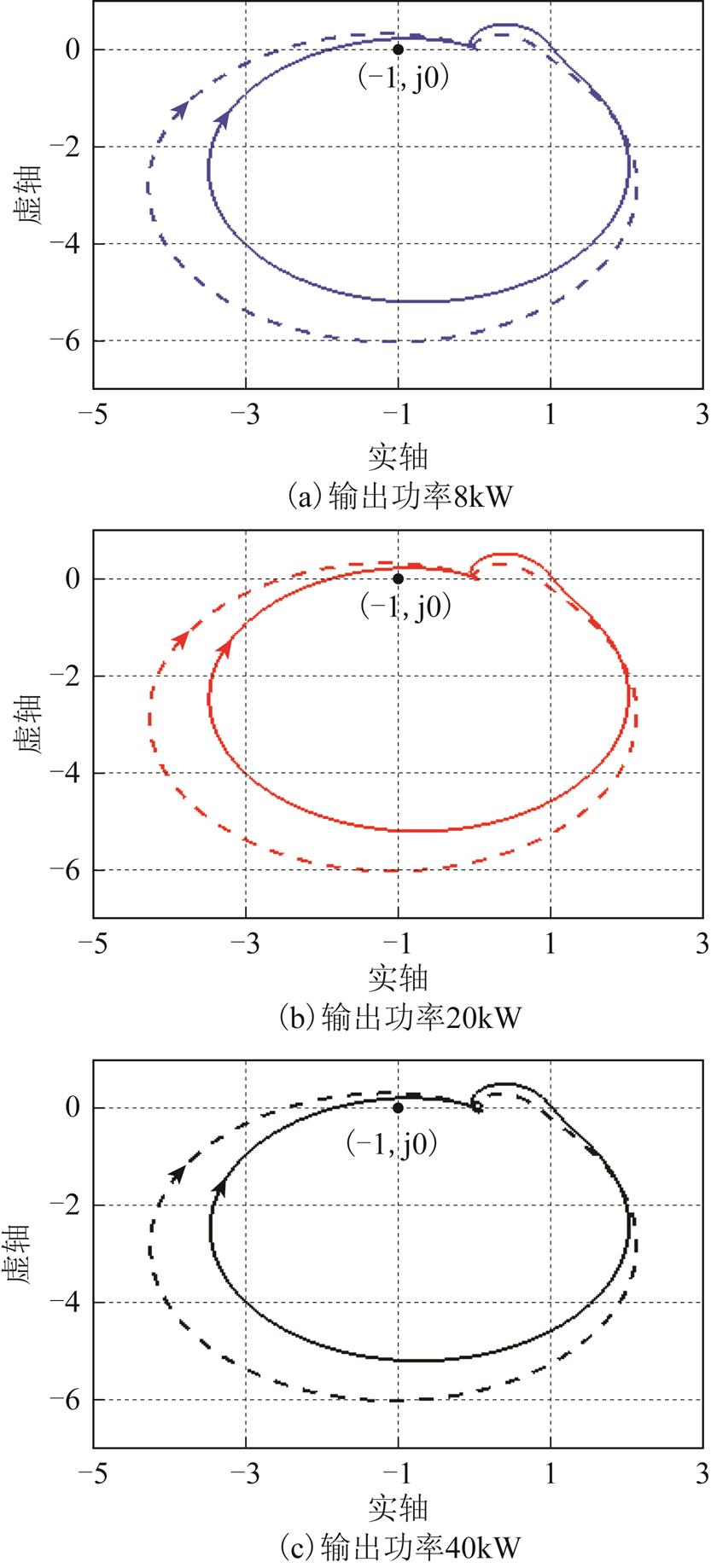
图10 无阻抗重构控制的源PWM逆变器带负荷PWM整流器下,不同输出功率IRp(s)和IRn(s)的Nyquist图
Fig.10 Nyquist plots of IRp(s) and IRn(s)without impedance reconstructionwith different output power under PWM rectifier load
图11为在加入阻抗重构控制后,源PWM逆变器带不同功率下的纯阻性负载的阻抗比IRp(s)以及IRn(s)的Nyquist图,IRp(s)和IRn(s)分别用实线和虚线表示。通过极点计算发现IRp(s)和IRn(s)都没有在正半平面的极点。图11中的Nyquist曲线均不包围(-1, j0)点,所以,系统在不同的功率下,均稳定。与图9相比,不同的输出功率下,图11的Nyquist曲线均更远离(-1, j0)点。相较之下,加入阻抗重构下的源逆变器,在带纯阻性负载时,系统更为稳定。
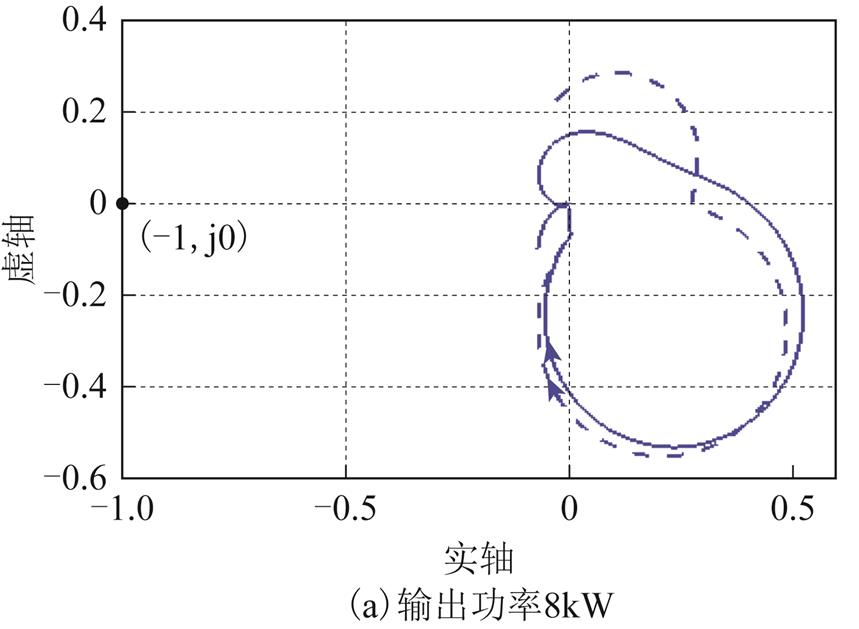
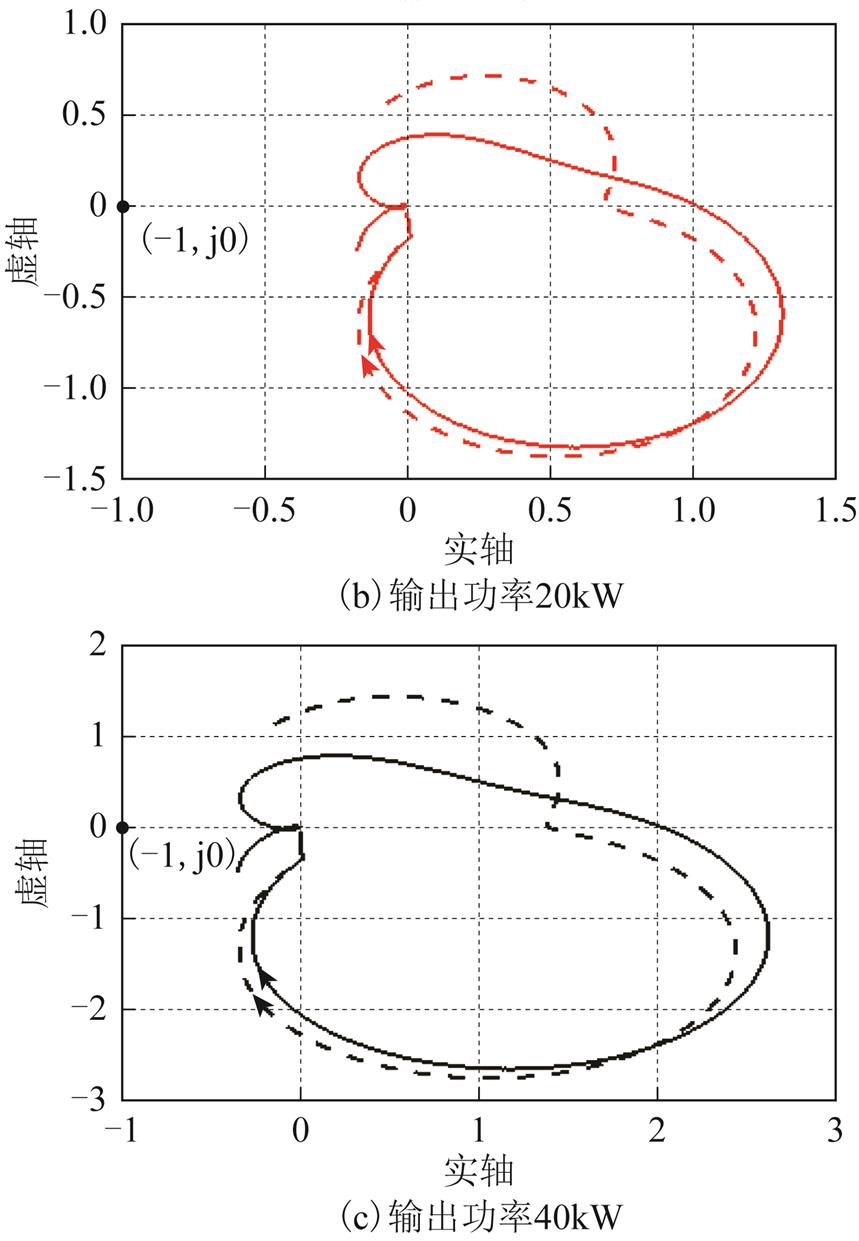
图11 加入阻抗重构控制后,带阻性负载下,不同输出功率IRp(s)和IRn(s)的Nyquist图
Fig.11 Nyquist diagram ofIRp(s) and IRn(s) with different output power under resistive load using impedance reconfiguration control
同样地,通过极点计算发现,在加入阻抗重构控制后带负荷PWM整流器时IRp(s)和IRn(s)都没有在正半平面的极点。图12中,IRp(s)和IRn(s)的Nyquist图分别用实线和虚线表示。由图12可知,在不同的输出功率下,源PWM逆变器带负荷PWM整流器负载的IRp(s)和IRn(s)的Nyquist曲线均不包围(-1, j0)点,系统稳定。与图10相比,在加入了阻抗重构控制后,系统由不稳定变为稳定。此变化说明了在加入了阻抗重构控制后,提高了源PWM逆变器的输出序阻抗在高频处的相位,使得源PWM逆变器与负荷PWM整流器的阻抗可以更好的匹配,可有效地抑制系统高频振荡。
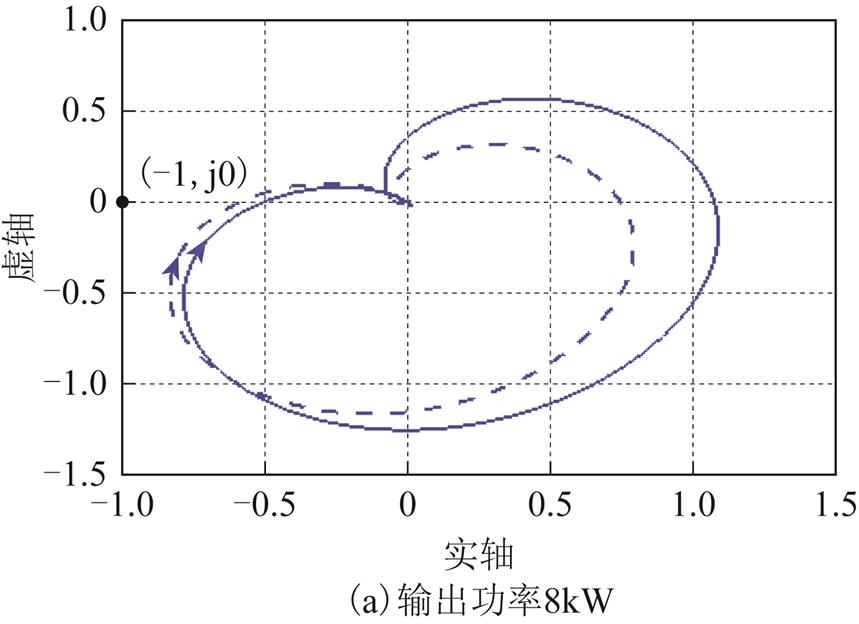
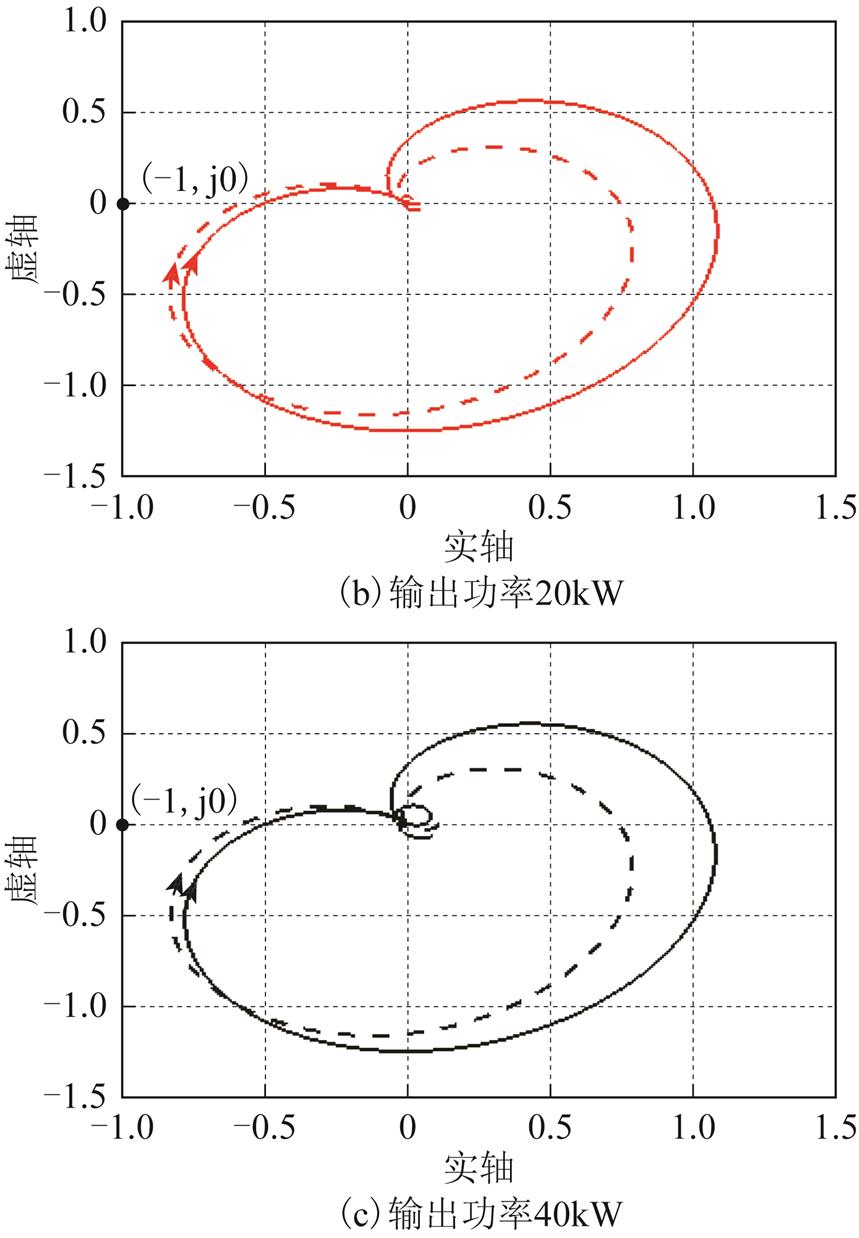
图12 加入阻抗重构控制后,带负荷PWM整流器下,不同输出功率IRp(s)和IRn(s)的Nyquist图
Fig.12 Nyquist diagram of IRp(s) and IRn(s) with different output power under PWM rectifier load using impedance reconfiguration control
为了验证本文分析方法和结论的正确性,搭建了如图13所示源PWM逆变器带负荷PWM整流器的实验平台。源PWM逆变器和负荷PWM整流器的系统参数分别见表1和表2。

图13 源PWM逆变器带负荷PWM整流器实验平台
Fig.13 Source PWM inverter experimental platform with load PWM rectifiter
图14和图15所示分别为不同功率切换下,孤岛源PWM逆变器分别带纯阻性负载和负荷PWM整流器时输出交流端口电压与电流的实验结果。源逆变器带纯阻性负荷时,不同功率下的输出电压与电流均稳定;而当负荷为PWM整流器时,源PWM逆变器的输出电压与电流出现严重的高频振荡。
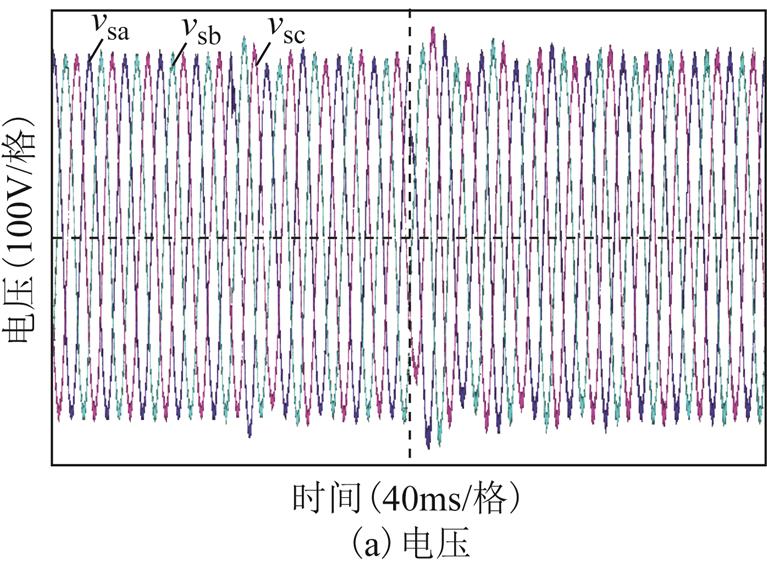

图14 无阻抗重构控制,不同输出功率切换下,源PWM逆变器带纯阻性负载的实验结果
Fig.14 Experimental results of source PWM inverters without impedance reconstructionwith resistive loads with output power switching
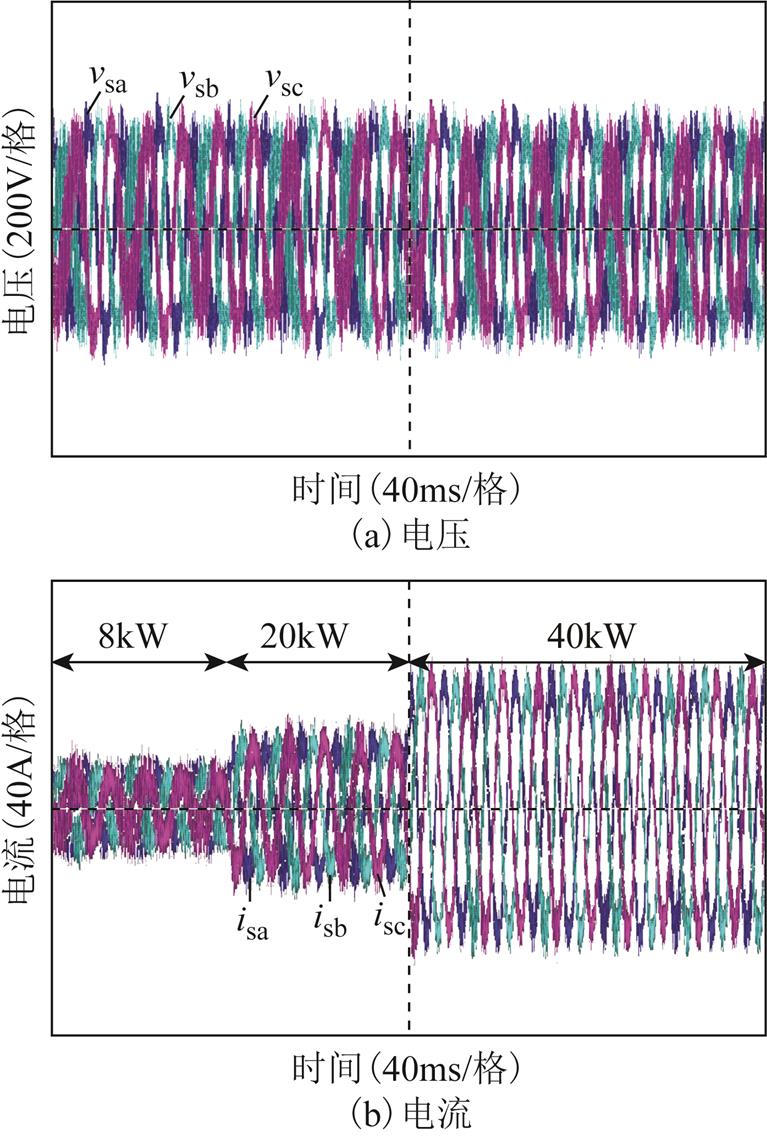
图15 无阻抗重构控制,不同输出功率切换下,源逆变器带负荷PWM整流器的实验结果
Fig.15 Experimental results of source inverter without impedance reconstructionwith load PWM rectifier with output power switching
图16和图17分别为源PWM逆变器采用本文所提出的阻抗重构控制后,不同功率切换下分别带纯阻性负载和负荷PWM整流器时输出交流端口电压与电流的实验结果。在加入阻抗重构后,源逆变器带纯阻性负荷时,不同功率下的输出电压和电流依然稳定;当负荷为PWM整流器时,源PWM逆变器的输出电压和电流的高频振荡得到了有效的抑制。因此,源PWM逆变器采用所提阻抗重构控制后,在不同特性负荷下,不同功率下,都能有效维持孤岛微电网系统的稳定。

图16 加入阻抗重构控制后,不同输出功率切换下,源逆变器带纯阻性负载的实验结果
Fig.16 The experimental results of source inverter with resistive load under with output power switching using impedance reconfiguration control
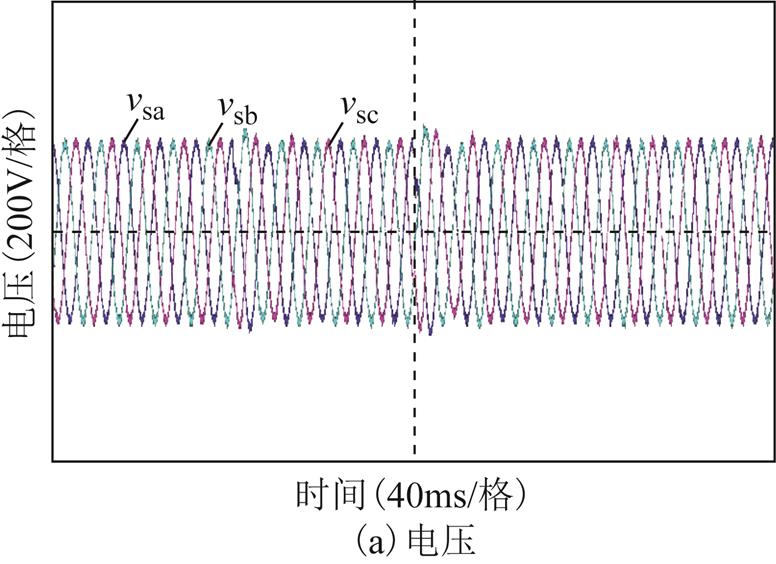
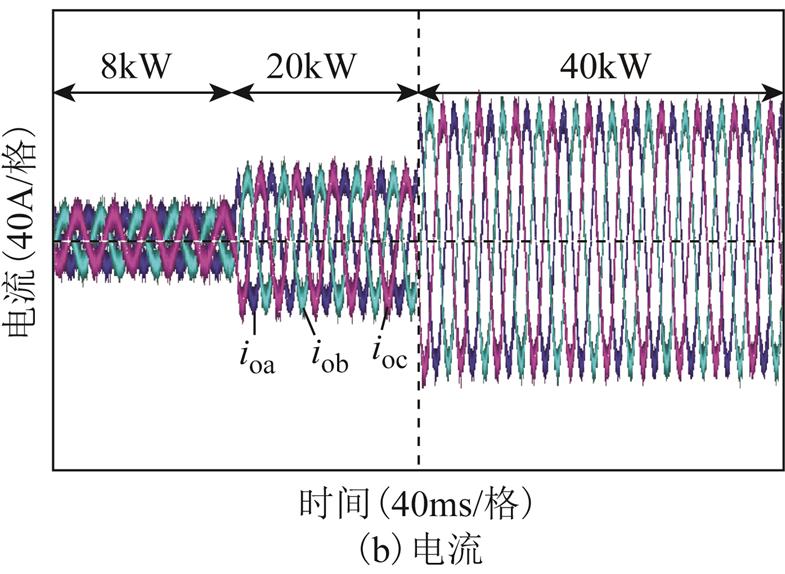
图17 加入阻抗重构控制后,不同输出功率切换下,源逆变器带负荷PWM整流器的实验结果
Fig.17 The experimental results of source inverter with load PWM rectifier with output power switching using impedance reconfiguration control
在电力电子装备强交互耦合的孤岛微电网系统中,易发生高频振荡等稳定性问题。对此,本文采用谐波线性化方法建立了孤岛微电网系统的小信号正、负序阻抗模型。基于所建序阻抗模型分析了孤岛微电网系统的振荡机理,并在传统双闭环控制方法的基础上,提出了源PWM逆变器的阻抗重构控制,可有效地抑制孤岛微电网系统高频振荡。本文可得出以下结论:
1)源PWM逆变器由于无锁相环存在,其输出阻抗不受稳定运行工作点的影响;而负荷PWM整流器由于存在锁相环这个非线性环节,其输入正、负序阻抗受稳定运行工作点的影响。
2)当采用传统双闭环控制时,源PWM逆变器带不同功率电阻负荷时都能稳定运行,但当接负荷PWM整流器时就会发生高频振荡问题。
3)孤岛微电网系统发生高频振荡的本质原因为:在高频处,源PWM逆变器的正、负序输出阻抗均具有负电阻值容性阻抗特性,负荷PWM整流器的输入正、负序阻抗都呈感性,两者交互时,会发生串联谐振,而此时孤岛微电网整体阻尼小于零,整个系统将发生串联高频振荡。对此,本文提出了源PWM逆变器的阻抗重构控制,该控制方法分别提高了源PWM逆变器的输出正、负序阻抗在高频处的相位,使得源PWM逆变器与负荷PWM整流器的正、负阻抗相交点的相位差都远大于-180°,从而增加孤岛微电网系统的阻尼,可有效抑制孤岛微电网系统高频振荡。
参考文献
[1] 张建华, 史佳琪, 郑德化, 等. 微电网运行与控制IEC标准进展与分析[J]. 电力系统自动化, 2018, 42(24): 1-14. Zhang Jianhua, Shi Jiaqi, Zheng Dehua, et al. Progress and analysis of IEC standards for microgrid operation and control[J] .Automation of Electric Power Systems, 2018, 42 (24): 1-14.
[2] 赵梓杉, 蒙志全, 章雷其, 等. 含异构分布式电源的微电网无功功率分散分层控制策略[J]. 电力系统自动化, 2019, 43(11): 59-72. Zhao Zishan, Meng Zhiquan, Zhang Leiqi, et al. Reactive power decentralized and hierarchical control strategy for microgrids with heterogeneous distributed power sources[J]. Automation of Electric Power Systems, 2019, 43 (11): 59-72.
[3] 陈杰, 刘名凹, 陈新, 等. 基于下垂控制的逆变器无线并联与环流抑制技术[J]. 电工技术学报, 2018, 33(7): 1450-1460. Chen Jie, Liu Mingwa, Chen Xin, et al. Inverter wireless parallel and circulating current suppression technology based on droop control[J]. Journal of Electrical Engineering and Technology, 2018, 33(7): 1450-1460.
[4] 伍文华, 陈燕东, 罗安, 等. 一种直流微网双向并网变换器虚拟惯性控制策略[J]. 中国电机工程学报, 2017, 37(2): 360-371. Wu Wenhua, Chen Yandong, Luo An, et al. A virtual inertia control strategy for bidirectional grid- connected converters in DC micro-grids[J]. Proceedings of the CSEE, 2017, 37(2): 360-371.
[5] 刘欣博, 高卓. 考虑恒功率负载与储能单元动态特性的直流微电网系统大信号稳定性分析[J]. 电工技术学报, 2019, 34(增刊1): 292-299. Liu Xinbo, Gao Zhuo. Large signal stability analysis of DC microgrid system considering the dynamic characteristics of constant power load and energy storage unit[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 292-299.
[6] 滕昌鹏, 王玉斌, 周博恺, 等. 含恒功率负载的直流微网大信号稳定性分析[J]. 电工技术学报, 2019, 34(5): 973-982. Teng Changpeng, Wang Yubin, Zhou Bokai, et al. Analysis of large signal stability of DC microgrid with constant power load[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 973-982.
[7] Cespedes M, Lei Xing, Sun Jian. Constant-power load system stabilization by passive damping[J]. IEEE Transactions on Power Electronics, 2011, 26(7): 1832-1836.
[8] 刘宝泉, 郭华, 朱一昕, 等. 三相变流器无源阻尼型LCL滤波器的分析与设计[J]. 电工技术学报, 2017, 32(2): 195-205. Liu Baoquan, Guo Hua, Zhu Yixin, et al. Analysis and design of three-phase converter passive damping LCL filter[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 195-205.
[9] 朱晓娟, 胡海涛, 陶海东, 等. 光伏并网系统的谐波不稳定产生机理及影响规律[J]. 电工技术学报, 2017, 32(10): 33-41. Zhu Xiaojuan, Hu Haitao, Tao Haidong, et al. Generation mechanism and influence law of harmonic instability in photovoltaic grid-connected systems[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 33-41.
[10] Wu Mingfei, Lu D D C. A novel stabilization method of LC input filter with constant power loads without load performance compromise in DC microgrids[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4552-4562.
[11] 郭力, 冯怿彬, 李霞林, 等. 直流微电网稳定性分析及阻尼控制方法研究[J]. 中国电机工程学报, 2016, 36(4): 927-936. Guo Li, Feng Yibin, Li Xialin, et al. Stability analysis and research of active damping method for DC microgrids[J]. Proceedings of the CSEE, 2016, 36(4): 927-936.
[12] 胡辉勇, 王晓明, 于淼, 等. 主从控制下直流微电网稳定性分析及有源阻尼控制方法[J]. 电网技术, 2017, 41(8): 2664-2673. Hu Huiyong, Wang Xiaoming, Yu Miao, et al. Stability analysis and active damping control for master-slave controlled DC microgrid[J]. Power System Technology, 2017, 41(8): 2664-2673.
[13] Hamzeh M, Ghafouri M, Karimi H, et al. Power oscillations damping in DC microgrids[J]. IEEE Transactions on Energy Conversion, 2016, 31(3): 970-980.
[14] 刘晓东, 胡勇, 方炜, 等. 直流微电网节点阻抗特性与系统稳定性分析[J]. 电网技术, 2015, 39(12): 3463-3469. Liu Xiaodong, Hu Yong, Fang Wei, et al. Analysis of node impedance characteristics and stability in DC microgrids[J]. Power System Technology, 2015, 39(12): 3463-3469.
[15] 季宇, 王东旭, 吴红斌, 等. 提高直流微电网稳定性的有源阻尼方法[J]. 电工技术学报, 2018, 33(2): 370-379. Ji Yu, Wang Dongxu, Wu Hongbin, et al. The active damping method for improving the stability of DC microgrid[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 370-379.
[16] Riccobono A, Santi E. Comprehensive review of stability criteria for DC power distribution systems[J]. IEEE Transactions on Industrial Applications, 2014, 50(5): 3525-3535.
[17] Dahono P Y, Bahar Y, Sato Y, et al. Damping of transient oscillations on the output LC filter of PWM inverters by using a virtual resistor[C]//4th IEEE International Conference on Power Electronics and Drive Systems Denpasar, Indonesia, 2001: 403-407.
[18] Adapa A, John V. Virtual resistor based active damping of LC filter in standalone voltage source inverter[C]//2018 IEEE Applied Power Electronics Conference and Exposition, San Antonio, USA, 2018: 1834-1840.
[19] Singh S, Choudhuri S. Active damping control with a feed forward loop for single-phase UPS inverter system: a comparative study[C]//2015 International Conference on Energy Economics and Environment, Greater Noida, India, 2015: 1-5.
[20] Li Yunwei. Control and resonance damping of voltage-sourceand current-source converters with LC filters[J]. IEEE Transactions on Industrial Electronics, 2009, 56(5): 1511-1521.
[21] Geng Yiwen, Yun Yang, Chen Ruicheng, et al. Parameters design and optimization for LC-type off-grid inverters with inductor-current feedback active damping[J]. IEEE Transactions on Industrial Electronics, 2018, 33(1): 703-715.
[22] Wen Bo, Boroyevich D, Burgos R, et al. Modeling the output impedance of three-phase uninterruptible power supply in d-q frame[C]//2014 IEEE Energy Conversion Congress and Exposition(ECCE), Pennsylvania, USA, 2014: 163-169.
[23] Shi Hongtao, Zhuo Fang, Zhang Dong, et al. Modeling, analysis, and measurement of impedance for three-phase AC distributed power system[C]//2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pennsylvania, USA, 2014: 4635-4639.
[24] Cespedes M, Sun Jian. Impedance modeling and analysis of grid-connected voltage-source converters[J]. IEEE Transactions on Power Electronics, 29(3): 1254-1261.
[25] Wen Bo, Boroyevich D, Burgos R, et al. Analysis of D-Q small-signal impedance of grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 675-687.
[26] Wen Bo, Boroyevich D, Mattavelli P, et al. Experimental verification of the generalized nyquist stability criterion for balanced three-phase AC systems in the presence of constant power loads[C]//2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, 2012: 3926-3933.
[27] Qian Qiang, Xie Shaojun, Huang Liuliu, et al. Harmonic suppression and stability enhancement for parallel multiple grid-connected inverters based on passive inverter output impedance[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 7587-7598.
[28] 张中锋. 微网逆变器的下垂控制策略研究[D]. 南京: 南京航空航天大学, 2013.
[29] Sun Jian. Impedance-based stability criterion for grid-connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078.
Sequence Impedance Modeling and High-Frequency Oscillation Suppression Method for Island Microgrid
Abstract The isolatedisland microgrid has no large grid support, and the source-load power electronic equipment is strongly interactively coupled, which is prone to stability problems such as high frequency oscillation. In this regard, the impedance reconstruction control method of the isolated island inverter is proposed, which can improve the phase of the output sequence impedance of the isolated island inverter at high frequency, increase system damping and effectively suppress the high frequency oscillation of the system. A small-signal wideband positive and negative sequence impedance model of the off-grid source PWM inverter is established by using the harmonic linearization method. In order to further analyze the interaction stability of the island system, the positive and negative sequence impedance model of the load PWM rectifier is established. Then, according to the established impedance model and Nyquist stability criterion, the influence of control method, load type and load power on the stability of the isolated island microgrid system is analyzed. The essential reason for the high frequency oscillation of the isolated island inverter and the PWM rectifier type load interaction in the island microgrid is revealed: the output impedance of the isolated island inverter is negatively resistive-capacitive at high frequency, and the input impedance of the PWM rectifier type load is Inductive, causing the system impedance ratio not to meet the stability criteria. The proposed impedance reconstruction control method can improve the phase characteristics of the isolated island inverter at high frequencies and increase the stability of the system by adding the voltage feedback branch.Finally, the experiment verifies the correctness of the analysis in this paper.
keywords:Isolated island microgrid, small signal sequence impedance modeling, interaction coupling, high frequency oscillation suppression
DOI:10.19595/j.cnki.1000-6753.tces.190456
中图分类号:TM464
刘津铭 男,1995年生,硕士研究生,研究方向为新能源发电装备建模及其振荡抑制。E-mail:1602501151@qq.com
陈燕东 男,1979年生,教授,博士生导师,研究方向为分布式发电、微电网控制、电能质量控制。E-mail:yandong_chen@hnu.edu.cn(通信000作者)
国家自然科学基金项目(51577056, 51707061)和博士后创新人才支持计划(BX20180095, BX20190109)资助。
收稿日期2019-04-22
改稿日期 2019-09-29
(编辑 赫蕾)