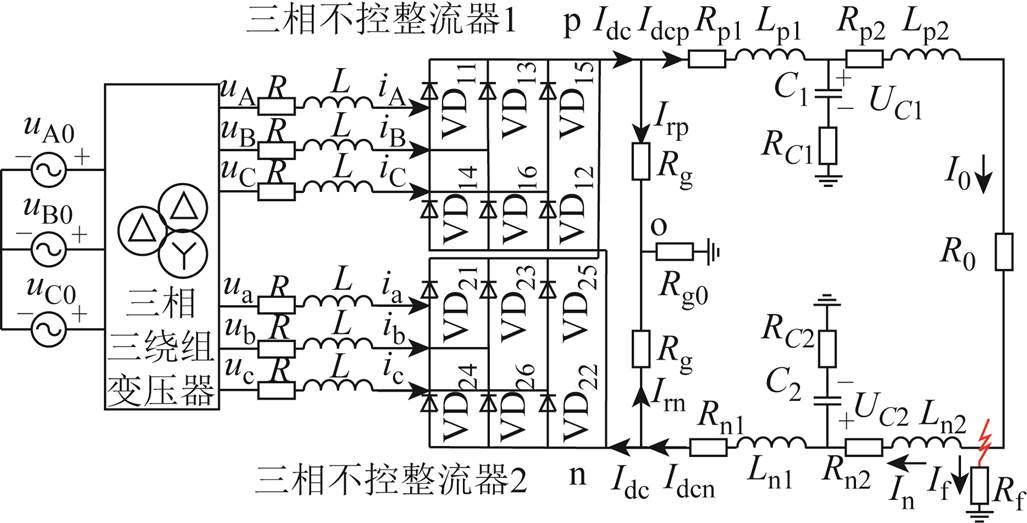
图1 十二脉波不控整流器供电直流系统原理
Fig.1 Schematic diagram of DC system powered by twelve-pulse diode rectifier
摘要 高阻接地的十二脉波不控整流器已广泛应用于船舶、飞机等独立电力系统。这类独立电力系统的十二脉波不控整流器发生单极接地短路时,因二极管导通组合多、暂态过程复杂且时间短,导致其单极接地短路的动态特性难以数学建模。针对该问题,提出一种基于开关函数、谐波平衡原理的动态数学建模方法,建立了十二脉波不控整流器在直流单极接地短路时的大信号数学模型,该模型具有非线性状态方程组形式。通过与物理实验进行对比,证明所提出的建模方法和数学模型的有效性,该模型可准确反映十二脉波不控整流器接地短路暂态特性和短路前、后的稳态平均值特性。
关键词:十二脉波不控整流器 直流单极接地短路 大信号模型 开关函数 谐波平衡原理
多脉波不控整流器以其低成本、易实现、高可靠性等优势在船舶、飞机等独立电力系统中得到广泛应用[1-2]。目前直流电力系统或交直流混合电力系统的接地技术研究不够深入,接地特性分析仍面临许多挑战。多脉波不控整流器的二极管数量及其导通组合多、二极管导通与关断时刻不受控,对于由其供电的舰船、飞机等独立电力系统,当发生直流单极接地短路时,短路暂态过程复杂且时间极短,导致其单极接地短路的动态数学建模非常困难,只能依赖时域仿真进行接地短路特性分析,无法掌握其动态特性的影响因素与变化规律。因此,有必要开展多脉波不控整流器单极接地短路动态数学建模研究,为独立电力系统的接地方式制定、接地短路特性分析与接地保护设计提供模型基础。
针对多脉波不控整流器的接地短路建模分析,目前国内外研究成果主要可以分为两类:
1)时域仿真建模。文献[3]针对由十二脉波不控整流器与三相逆变器级联构成的系统,仿真分析了不同位置发生接地短路时的共模电压和短路电流特性;文献[4]建立了三相交流发电机、三相不控整流器、三相逆变器三者级联系统的时域仿真模型,分析了交、直流侧接地短路引起的系统电压偏置,波形畸变和三次谐波;文献[5]针对典型船用中压直流系统,仿真计算了不同接地方式下发生接地短路时的暂态短路电流和过电压特性,分析了系统参数对故障特性的影响;文献[6-7]通过仿真对比,分析了基于模块化多电平变换器(Modular Multilevel Converter, MMC)的柔性直流输电系统、基于MMC的环状直流配网在不同接地方式下的接地故障特征;文献[8]运用仿真研究了真、伪双极MMC-HVDC系统直流单极接地故障时子模块电容放电机制,短路路径及桥臂电流变化特性;文献[9-11]仿真计算了直流系统单极接地故障时的故障电压、故障电流等电气特性,研究了该系统接地故障定位与保护方法。然而,这些时域仿真方法只能对系统在事先设定的接地短路情况的特性进行数值计算,无法定量掌握系统接地短路动态特性的影响因素与变化规律。
2)面向大电网的长时间尺度接地短路动态数学模型研究。文献[12]将高压直流输电系统中换流器模块简化为恒压源,利用序分量法求得单极接地故障下健全极的电压表达式,其结论可用于分析过电压峰值及沿线分布与系统端部结构、线路参数等因素之间的关系,并不能准确反映系统接地故障时的暂态波形;文献[13-15]中将基于电压源型换流器(Voltage Source Converter, VSC)的直流输电系统直流侧单极接地故障过程分成直流侧电容放电、网侧电流回馈、电压恢复三个阶段,分析了各阶段电路特征并建立了分阶段数学模型;文献[16-17]分析了MMC-MTDC系统和VSC-MTDC系统发生直流单极接地短路故障时故障电流流通路径,通过建立等效电路,得到故障电流及子模块电容电压等物理量的解析变化。上述面向大电网的直流输电接地建模中未对开关器件的开关过程进行暂态数学建模,主要是基于故障时刻电路特征进行了等效处理,未建立接地故障全过程的统一数学模型。同时,这些研究对象均没有涉及二极管数量和导通过程更复杂的双六脉波不控整流器并联组成的十二脉波不控整流器,而由其构成的小规模独立电力系统在系统结构及参数上与大电网相比均存在很大差异。
本文以直流侧经高阻接地的十二脉波不控整流器为研究对象,采用开关函数法和谐波平衡原理,建立了其统一的直流单极接地短路故障前、故障暂态过程和故障后的动态数学模型,在实验室构建了物理实验系统,实验证明了所建立模型可以很好地反映十二脉波不控整流器供电的直流系统单极接地短路动态特性,验证了所建立数学模型的准确性。
直流侧经高阻接地的十二脉波不控整流器如图1所示。三相交流市电电源通过二次侧分别为星形和三角形联结的三相三绕组变压器,形成线电压幅值相等、相位相差π/6的两组三相电源,经两个三相不控整流桥直流侧并联形成十二脉波不控整流器。

图1 十二脉波不控整流器供电直流系统原理
Fig.1 Schematic diagram of DC system powered by twelve-pulse diode rectifier
假设图1变压器二次侧两套三相绕组相电压表达式为uA=Vmsin(ωt),ua=Vmsin(ωt+π/6),其中,Vm为电源电压幅值,ω=2πf,f为工频频率。假设变压器参数对称,其输出两套三相绕组相电压严格相差2π/3。该系统接地方式采用直流正负极经等值电阻接地,考虑该系统的直流侧线路参数和对地分布电容。本文以电阻负载为例进行研究,方法可拓展至阻感负载、电动机负载等场合。
根据电路结构及二极管工作原理,在不考虑图1中交流侧线路参数的理想情况下,某一时刻十二脉波整流器直流侧输出电压等于上、下两个三相桥中交流电源线电压最大值,此时电路中最大线电压对应的两个桥臂导通,一个工频周期中每个桥臂的两个相邻导通角之间相差π/6。由于交流侧电感的影响,在由一个三相桥的两相切换至另一个三相桥的两相时会出现两个三相桥中同时有两相工作的换相过程,此换相重叠角用μ表示。μ由直流侧电流、交流电源电压及交流侧电感共同决定,在交流侧电源电压及交流侧电感为定值时,换相重叠角随负载的改变而改变,电路会出现两种不同的换相方式:①当μ≤π/6时,换相过程发生在上、下三相桥之间,由一个三相桥的两相换相至另一个三相桥的两相,半个工频周期内十二脉波不控整流器的12种二极管导通模态见表1;②当μ>π/6时,同一桥臂的前一个导通角内流过的电流未降到零就开始进入后一个导通角,从整体上来看,此时上下两个三相桥独立工作,换相过程在各自三相桥内进行,此时各自三相桥内的换相重叠角用δ表示。当δ≤π/6时电路中有4个或5个二极管同时工作,此时半个工频周期内十二脉波不控整流器的12种二极管导通模态见表2;当π/6<δ≤π/3时电路中有5个或6个二极管同时工作[18],此时半个工频周期内十二脉波不控整流器的12种二极管导通模态见表3。
表1 μ≤π/6时半个周波内整流器中二极管导通模态
Tab.1 Diodes conduction modes of the rectifier in half of line-frequency period when μ≤π/6

区间三相不控整流器1导通的二极管三相不控整流器2导通的二极管 T1VD15、VD16VD21、VD26 T2无VD21、VD26 T3VD11、VD16VD21、VD26 T4VD11、VD16无 T5VD11、VD16VD21、VD22 T6无VD21、VD22 T7VD11、VD12VD21、VD22 T8VD11、VD12无 T9VD11、VD12VD23、VD22 T10无VD23、VD22 T11VD13、VD12VD23、VD22 T12VD13、VD12无
表2 μ>π/6,𝛿≤π/6时半个周波内二极管导通模态
Tab.2 Diodes conduction modes in half of line-frequency period when μ>π/6 and𝛿≤π/6

区间三相不控整流器1导通的二极管三相不控整流器2导通的二极管 T1VD15、VD16VD21、VD25、VD26 T2VD15、VD16VD21、VD26 T3VD11、VD15、VD16VD21、VD26 T4VD11、VD16VD21、VD26 T5VD11、VD16VD21、VD22、VD26 T6VD11、VD16VD21、VD22 T7VD11、VD12、VD16VD21、VD22 T8VD11、VD12VD21、VD22 T9VD11、VD12VD21、VD23、VD22 T10VD11、VD12VD23、VD22 T11VD11、VD13、VD12VD23、VD22 T12VD13、VD12VD23、VD22
表3μ>π/6,π/6<𝛿≤π/3时半个周波内二极管导通模态
Tab.3 Diodes conduction modes in half of line-frequency period when μ>π/6and π/6<𝛿≤π/3

区间三相不控整流器1导通的二极管三相不控整流器2导通的二极管 T1VD14、VD16、VD15VD21、VD26、VD25 T2VD15、VD16VD21、VD26、VD25 T3VD11、VD16、VD15VD21、VD26、VD25 T4VD11、VD16、VD15VD21、VD26 T5VD11、VD16、VD15VD21、VD26、VD22 T6VD11、VD16VD21、VD26、VD22 T7VD11、VD16、VD12VD21、VD26、VD22 T8VD11、VD16、VD12VD21、VD22 T9VD11、VD16、VD12VD21、VD23、VD22 T10VD11、VD12VD21、VD23、VD22 T11VD11、VD13、VD12VD21、VD23、VD22 T12VD11、VD13、VD12VD23、VD22
当电路负载较小,满足μ≤π/6时,换相在上、下三相桥之间进行,在从一个三相桥的两相向另一个三相桥的两相切换的过程中会出现两个三相桥同时有两相导通的换相状态。此时电路工作情况如图2所示。根据电路工作情况,结合开关函数建模的基本原理,建立如图2所示的开关函数。建模时忽略电流脉波影响,认为换相电流为整流器输出电流的平均值。图中,当SA(或Sa)=1或0.5时,A相(或a相)上桥臂导通、下桥臂关断,其中SA(或Sa)=0.5为换相状态;当SA(或Sa)=-1或-0.5时,A相(或a相)下桥臂导通,上桥臂关断,其中SA(或Sa)=-0.5为换相状态。其余相开关函数按与A相(或a相)的相位关系左右平移2π/3得到。
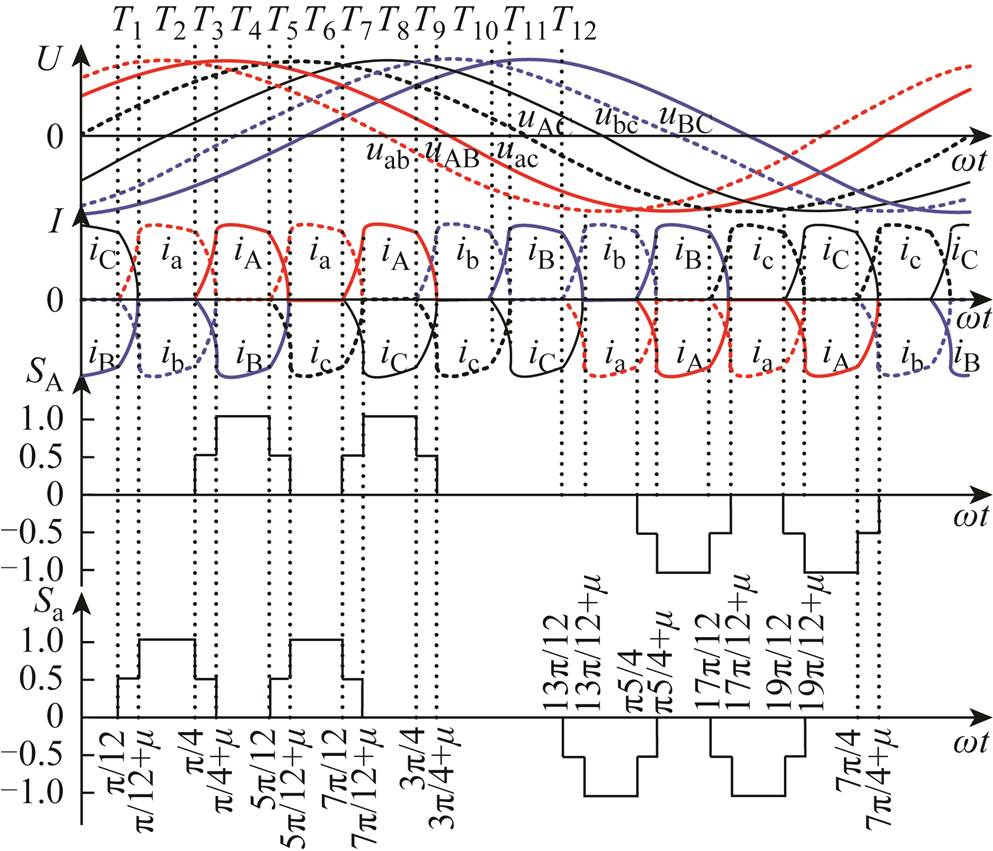
图2 μ≤π/6时交流电压电流波形及开关函数
Fig.2 AC side voltage and current waveforms and switch functions when μ≤π/6
令
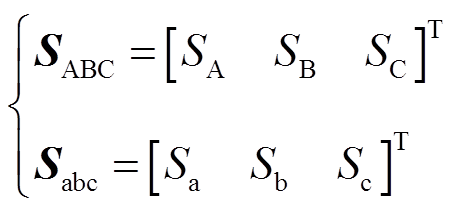 (1)
(1)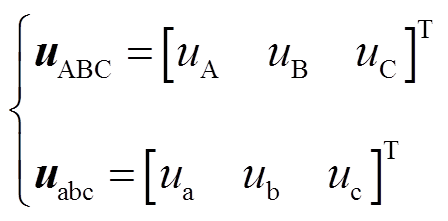 (2)
(2)
图1所示电路中p、n节点的电压满足
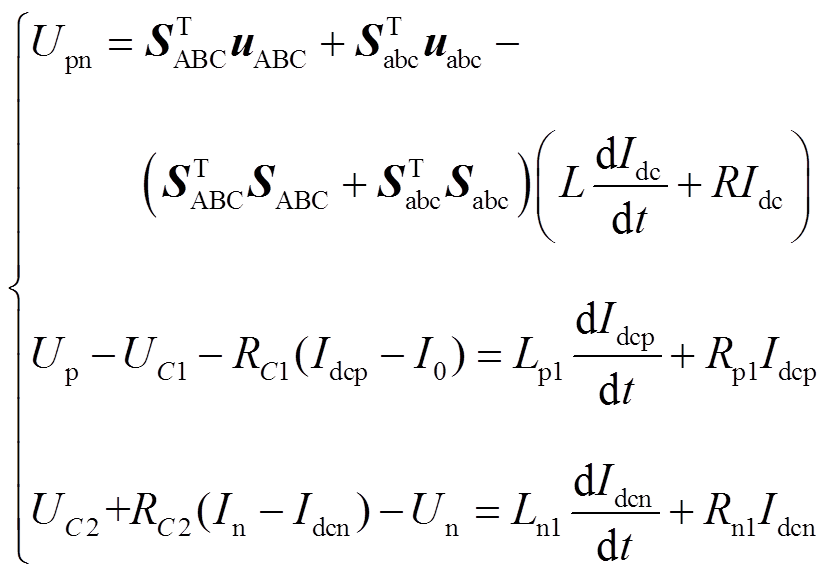 (3)
(3)式中,Up和Un分别为节点p、n对地电压;Upn为节点p、n之间电压即直流侧正负极电压;UC1和UC2分别为正极和负极对地分布电容两端电压。
并联等值接地电阻中的电流Irp和Irn满足
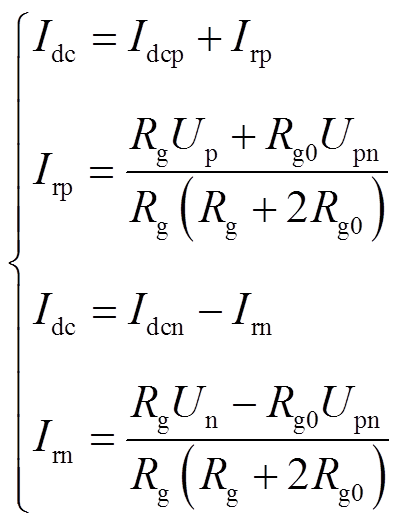 (4)
(4)由电路结构可得并联等值接地电阻两端p、n节点之间电压满足
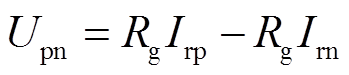 (5)
(5)
联立式(3)中的第一式、式(4)中第一、第三式及式(5)可得到Idc的微分方程;将式(3)中第二式及式(5)代入到式(4)第一、二式可得到Idcp的微分方程;将式(3)中第三式及式(5)代入到式(4)第三、四式可得到Idcn的微分方程;其余各状态变量的方程按照电路的基本关系列写。得到系统开关函数模型如式(6)所示,接地电阻Rf在系统正常工作时取无穷大,在接地短路时为实际接地短路电阻值。
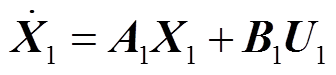 (6)
(6)其中
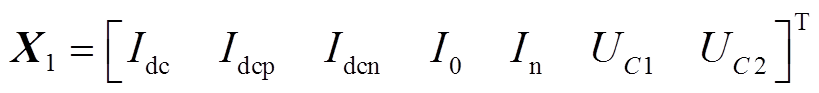
式中,A1、B1、U1见附录。
将开关函数进行傅里叶级数展开,得
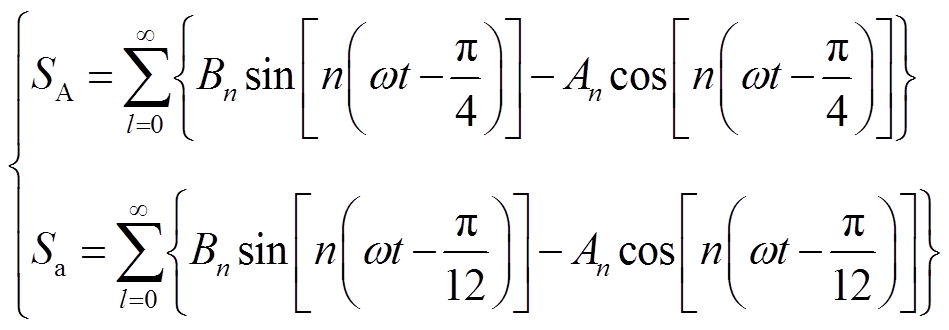 (7)
(7)其中
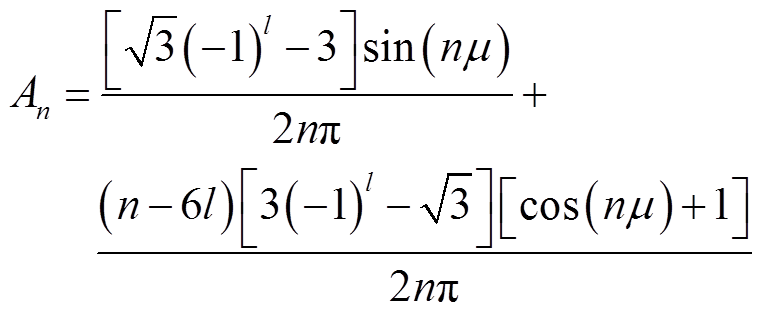
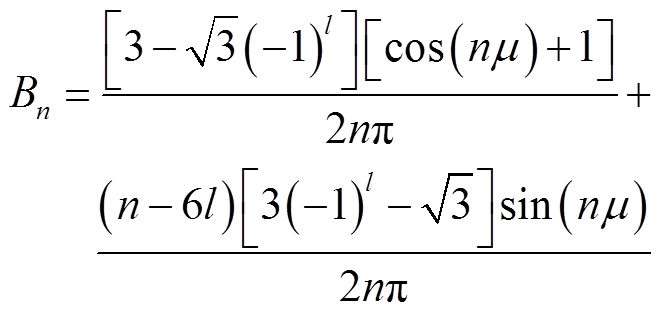
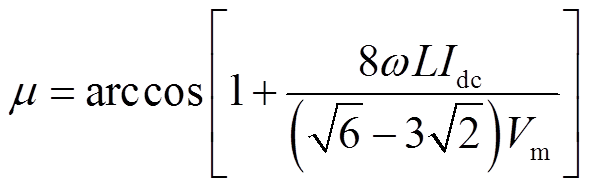
式中,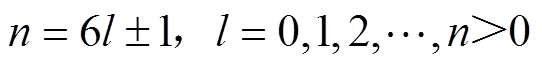 。
。
当负载增加使得μ>π/6时,电路的工作方式将发生很大改变。此时十二相不控整流器中将至少有4个二极管同时导通。从整体上来看,上下两个三相桥独立工作,换相过程在各自三相桥内进行。
为简化模型且能够有效反映系统特性,建模时忽略电流脉波影响,将换相电流认定为整流器直流侧输出电流的一半。根据以上分析的电路特性,建立图3所示的开关函数。图中SA和Sa的数值代表的物理意义同图2。其余各相的开关函数同样按与A相(或a相)的相位关系左右平移2π/3得到。

图3 μ>π/6时交流电压电流波形及开关函数
Fig.3 AC side voltage and current waveforms and switch functions when μ>π/6
按照与1.2节中同样的方法定义开关函数和电压状态变量。此种工作方式下除正负极间的电压表达式与1.2节中时的表达式不一样之外,其余各变量之间的关系均相同。
由
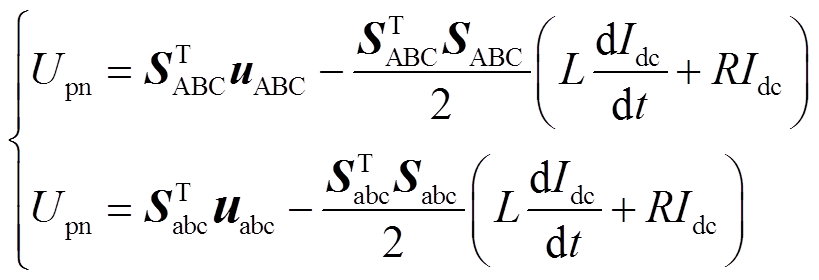
推出整流器直流侧输出电压

再利用1.2节中相同的建模分析方法对系统接地短路故障情况进行建模。得到系统开关函数模型如式(9)所示。此开关函数模型可以描述μ>π/6时𝛿≤π/6和π/6<𝛿≤π/3两种电路工作状态。
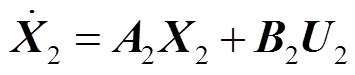 (9)
(9)其中
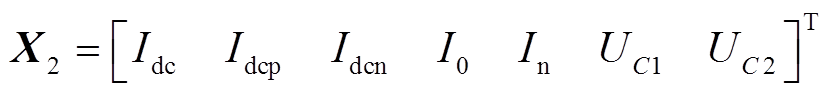
式中,A2、B2、U2见附录。
将开关函数进行傅里叶级数展开,得
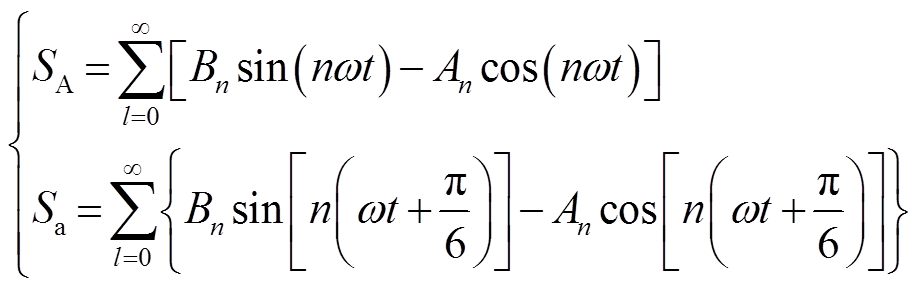 (10)
(10)式中
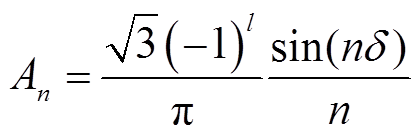
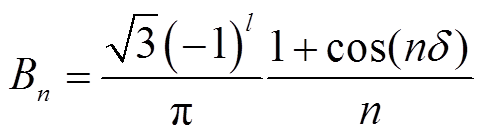
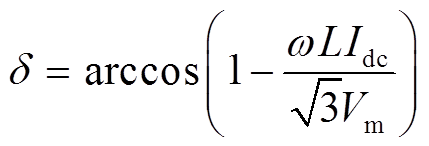
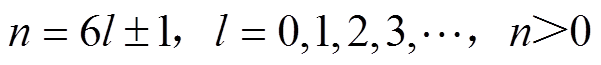
对系统进行谐波分析,图1所示的十二脉波不控整流器直流侧各电气量只存在直流量和12的倍数次谐波[19-20]。因十二脉波不控整流器直流侧输出电压脉波中12次倍频谐波分量相较于直流分量很小,且接地短路故障的暂态过程时间很短,其对接地短路暂态特性的影响很小,故只考虑直流分量即能够反映系统直流侧接地短路动态特性。
将两种工况的开关函数傅里叶级数一阶展开式、交流侧电压表达式与直流侧各电气量的直流分量分别代入各自开关函数模型中,根据谐波平衡原理,等号两边同次谐波项的系数相等[21-22],推导出μ≤π/6工况下7阶微分代数方程组形式的大信号数学模型如式(11)所示;μ>π/6工况下的数学模型中状态变量Idc0的微分方程如式(12)、其余状态变量的微分方程同式(11)。式(11)、式(12)中各电气量的直流分量可反映两种工况下各电气量的接地短路暂态特性及接地短路前、后的稳态平均值特性。
 (11)
(11)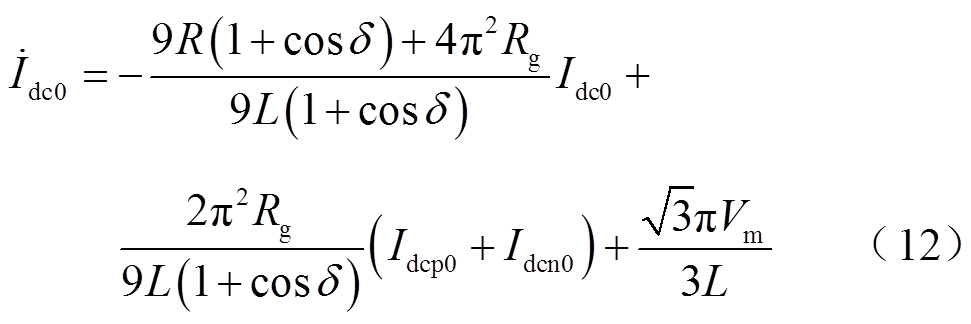
式中,下标0表示各电气量的直流分量。
为验证上述模型的正确性,在实验室搭建了25kV·A十二脉波不控整流器供电实验系统,如图4所示,其电路同图1。采用三相市电供电,各设备参数见表4(利用LCR测试仪测量得到)。

图4 十二脉波不控整流器供电实验系统
Fig.4 Experimental platform of twelve-pulse diode rectifier power supply system
表4 实验系统组成设备参数
Tab.4 Devices parameters of experimental platform

参数数值 交流侧(由变压器漏磁参数等效)R/Ω0.838 L/mH4.00 直流侧Lp1/µH374.0 Rp1/Ω0.002 Lp2/µH393.0 Rp2/Ω0.002 Ln1/µH379.0 Rn1/Ω0.002 Ln2/µH362.0 Rn2/Ω0.002 并联等值电阻Rg/Ω2000 并联等值电阻中点对地电阻Rg0/Ω2.60 正极对地分布电容C1/µF0.220 负极对地分布电容C2/µF0.221 正极对地分布电容支路对地电阻RC1/Ω2.80 负极对地分布电容支路对地电阻RC2/Ω2.80
实验时实测变压器二次侧输出线电压有效值为765V;结合实验室的接地极参数,发生接地短路时接地电阻Rf约为2.6Ω;实验时通过改变负载来改变整流器的直流侧输出电流,从而对两种换相重叠角情况下的数学模型分别进行验证。
算例1:负载电阻约为178Ω,此时换相重叠角为µ=0.331 4rad(即19°),满足µ≤π/6的工况条件,实验结果如图5所示。
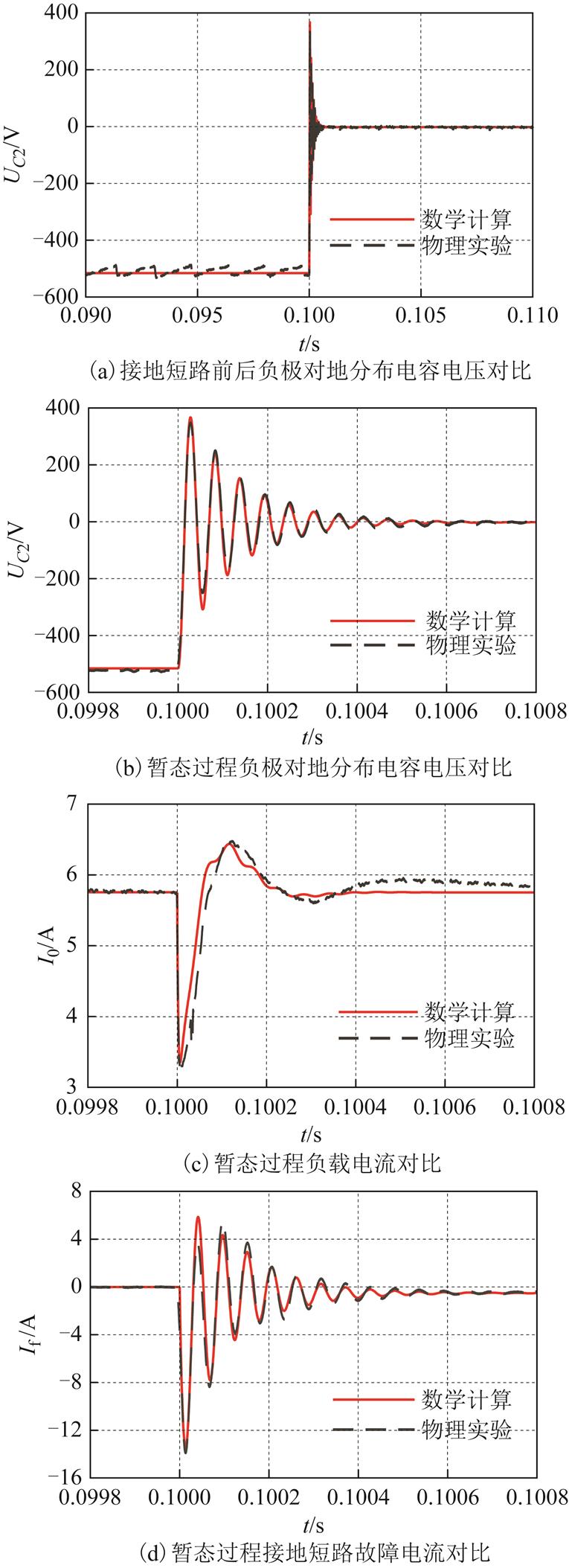
图5 μ≤π/6时数学模型与物理实验结果对比
Fig.5 Comparison between mathematical model and experiment when μ≤π/6
算例2:负载电阻约为49Ω。此时电路中µ的公式计算结果为0.617 1rad(即35°),各三相桥内部换相重叠角δ=0.219 0rad(即13°),满足μ>π/6的工况条件,实验结果如图6所示。
从数学模型求解结果与物理实验结果对比来看,数学模型求解结果与物理实验结果吻合较好,准确反映了单极接地短路时的动态特性。因此,所建数学模型对描述十二脉波不控整流器直流侧单极接地短路暂态特性是适用的。
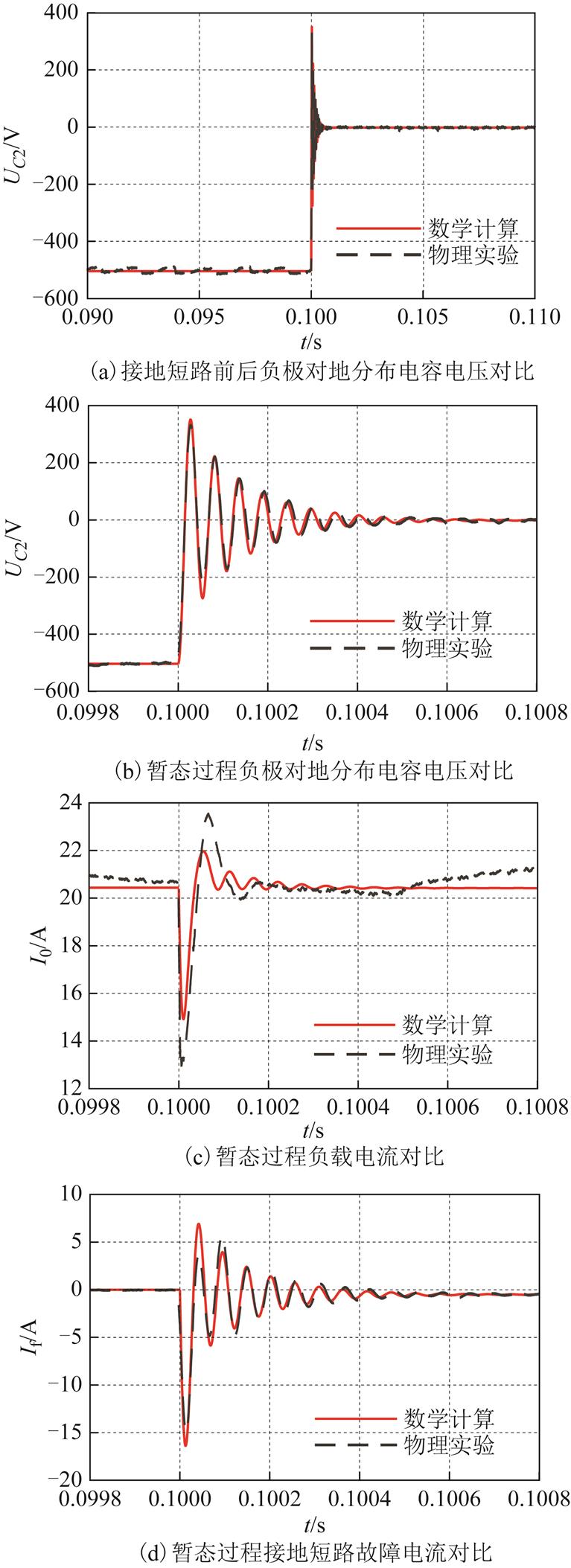
图6 μ>π/6时数学模型与物理实验结果对比
Fig.6 Comparison between mathematical model and experiment when μ>π/6
本文针对双六脉波不控整流器直流侧并联组成的十二脉波不控整流器,采用开关函数结合谐波平衡原理的方法,建立了其直流侧单极接地短路的动态数学模型,模型具有非线性状态方程组形式。经物理实验验证,该模型可以很好地反映系统直流侧单极接地短路暂态特性和接地短路发生前后的稳态平均值特性。所提数学建模分析方法解决了多脉波不控整流器的短时间尺度接地特性数学建模难题;所建模型适用于多脉波不控整流器供电的小型独立电力系统,并且可推广应用于其他形式的多脉波不控整流器以及多脉波不控整流器供电系统的接地特性建模分析。
附 录
本文建立的十二脉波不控整流器两种工况下直流单极接地短路的开关函数模型中A1、B1、U1及A2、B2、U2分别如式(A1)~式(A6)所示。
 (A1)
(A1)式中
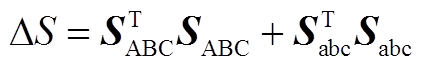
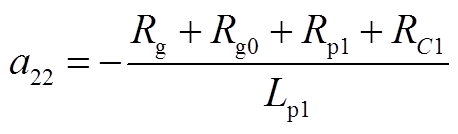
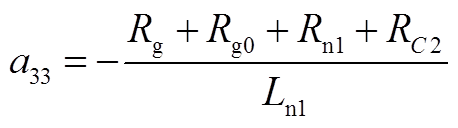

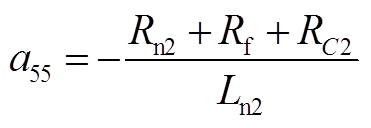
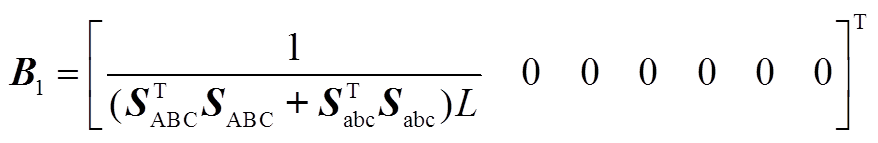 (A2)
(A2)
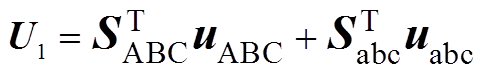 (A3)
(A3)A2矩阵的首行为
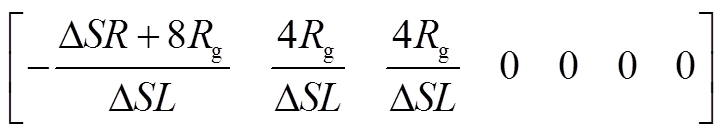 (A4)
(A4)
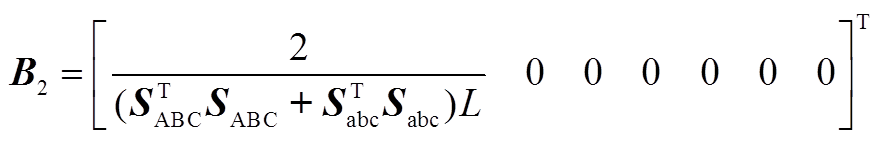 (A5)
(A5)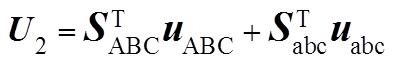 (A6)
(A6)
参考文献
[1] 孟凡刚, 杨世彦, 杨威. 多脉波整流技术综述[J]. 电力自动化设备, 2012, 32(2): 9-22. Meng Fangang, Yang Shiyan, Yang Wei. Overview of multiplex rectification technology[J]. Power Automation Equipment, 2012, 32(2): 9-22.
[2] 马伟明. 电力集成技术[J]. 电工技术学报, 2005, 20(1): 16-20. Ma Weiming. Power system integration technique[J]. Transaction of China Electrotechnical Society, 2005, 20(1): 16-20.
[3] Jacobson B, Walker J. Grounding considerations for DC and mixed DC and AC power systems[J]. Naval Engineers Journal, 2007, 119(2): 49-62.
[4] Infante D. Guiding the selection of physical experiments for the validation of a model designed to study grounding in dc distribution systems[D]. Gainesville: University of Florida, 2011.
[5] Wang Yunchao, Yu Zhanqing, He Jinliang, et al. Performance of shipboard medium-voltage DC system of various grounding modes under monopole ground fault[J]. IEEE Transactions on Industry Applications, 2015, 51(6): 5002-5009.
[6] 赵西贝, 许建中, 卢铁兵, 等. 采用架空线的MMC-HVDC单极接地过电压分析[J]. 电力系统自动化, 2018, 42(7): 44-49.Zhao Xibei, Xu Jianzhong, Lu Tiebing, et al. Overvoltage Analysis on Overhead Line based MMC-HVDC System under Single-pole-to-ground[J]. Automation of Electric Power Systems, 2018, 42(7): 44-49.
[7] 戴志辉, 黄敏, 苏怀波. 基于MMC的环状直流配网在不同接地方式下的故障特性分析[J]. 电力系统保护与控制, 2019, 47(1): 1-10. Dai Zhihui, Huang Min, Su Huaibo. Analysis on fault characteristics of MMC-based ring DC distribution networks under different grounding modes[J]. Power System Protection and Control, 2019, 47(1): 1-10.
[8] 陈继开, 孙川, 李国庆, 等. 双极MMC-HVDC系统直流故障特性研究[J]. 电工技术学报, 2017, 32(10): 53-60. Chen Jikai, Sun Chuan, Li Guoqing, et al. Study on characteristics of DC fault in bipolar MMC-HVDC system[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 53-60.
[9] 徐铭铭, 肖立业, 林良真. 直流配电网单极接地故障定位方法[J]. 电工电能新技术, 2015, 34(11): 55-62. Xu Mingming, Xiao Liye, Lin Liangzhen. Unipolar grounding fault location method for DC distribution network[J]. Advanced Technology of Electrical Engineering and Energy, 2015, 34 (11): 55-62.
[10] 孙刚, 时伯年, 赵宇明, 等. 基于MMC的柔性直流配电网故障定位及保护配置研究[J]. 电力系统保护与控制, 2015, 43(22): 127-133. Sun Gang, Shi Bonian, Zhao Yuming, et al. Research on the fault location method and protection configuration strategy of MMC based DC distribution grid[J]. Power System Protection and Control, 2015, 43(22): 127-133.
[11] 张青云, 马凡, 江汉红. 经电阻接地的直流电力系统接地故障保护方法[J]. 船电技术, 2015, 35(8): 1-5.Zhang Qingyun, Ma Fan, Jiang Hanhong. A method of grounding fault protection in DC power system with grounding resistance[J]. Marine Electric, 2015, 35(8): 1-5.
[12] Kimback E W. Transient overvoltages caused by monopolar ground fault on bipolar DC line: theory and simlation[J]. IEEE Transactions on power Apparatus and Systems, 1970, PAS-89(4): 584-592.
[13] 张紫光, 付媛, 王毅. 基于VSC的直流电网输电线路单极接地故障分析[J]. 现代电力, 2017, 34(1): 82-88. Zhang Ziguang, Fu Yuan, Wang Yi. Pole-to-ground fault analysis of transmission lines in VSC based DC power grids[J]. Modern Electric Power, 2017, 34(1): 82-88.
[14] 戴志辉, 葛红波, 严思齐, 等. 柔性直流配电网故障分析[J]. 电工技术学报, 2018, 33(8): 1863-1874.Dai Zhihui, Ge Hongbo, Yan Siqi, et al. Fault analysis of flexible DC distribution system[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1863-1874.
[15] Yang Jin, Fletcher J E, O'Reilly J. Short-circuit and ground fault analyses and location in VSC-based DC network cables[J]. IEEE Transactions on Industrial Electronics, 2012, 59(10): 3827-3837.
[16] 罗永捷, 徐罗那, 熊小伏, 等. MMC-MTDC系统直流单极对地短路故障保护策略[J]. 电工技术学报, 2017, 32(增刊1): 98-106. Luo Yongjie, Xu Luona, Xiong Xiaofu, et al. Pole-to-ground DC fault protection of MMC-MTDC systems[J]. Transactions of China Electrotechnical Society, 2017, 32(S1): 98-106.
[17] 汪楠楠, 姜崇学, 王佳成, 等. 采用直流断路器的对称单极多端柔性直流故障清除策略[J]. 电力系统自动化, 2019, 43(06): 181-189.Wang Nannan, Jiang Chongxue, Wang Jiacheng, et al.Fault Elimination Strategy of Symmetric Single-pole VSC-MTDC Based on DC Circuit Breaker, Automation of Electric Power Systems, 2019, 43(06): 181-189.
[18] Han Liqiu, Wang Jiabin, Howe D. State-space average modelling of 6- and 12-pulse diode rectifiers[C]// IEEE European Conference on Power Electronics and Applications, Aalborg, Denmark, 2007: 5047-5056.
[19] 王宇. 基于Matlab/Simulink的12脉波整流电路谐波分析[J]. 电气技术, 2013, 14(10): 25-27. Wang Yu. Analysis for 12-pulse rectifier on Matlab/Simulink[J]. Electrical Engineering, 2013, 14(10): 25-27.
[20] 秦萌涛, 宋文武, 黄琛. 舰用12脉波整流器直流侧谐波分析[J]. 舰船科学技术, 2015, 37(2): 101-106. Qin Mengtao, Song Wenwu, Huang Chen. Harmonic analysis of 12-pulse rectifier for ship at the DC side[J]. Ship Science and Technology, 2015, 37(2): 101-106.
[21] Zhang Gaifan, Ma Weiming. Transient analysis of synchronous machines[M]. Wuhan: Hubei Science and Technology Press, 2001.
[22] 赵小军, 张晓欣, 李慧奇, 等. 基于谐波平衡法的变压器直流偏磁电路-磁路频域耦合模型[J]. 电工技术学报, 2014, 29(9): 211-218. Zhao Xiaojun, Zhang Xiaoxin, Li Huiqi, et al. Frequency Domain Coupled Model between Magnetic and Electric Circuits of DC Biased Transformers by Harmonic Balance Method[J]. Transactions of China Electrotechnical Society. 2014, 29(9): 211-218.
Dynamic Mathematical Model of Twelve-Pulse Diode Rectifier with Pole-to-Ground DC Fault
Abstract Twelve-pulse diode rectifiers with high-resistance grounding type have been widely used in various isolated power systems such as ship and aircraft. It is hard to model the dynamic behavior of pole-to-ground(P-to-G) DC fault of twelve-pulse diode rectifier because of many diode conduction combinations, complex and short transient process. In order to solve this problem, a dynamic mathematical modeling approach based on switch function and principle of harmonic balance is proposed. A large signal mathematical model of twelve-pulse diode rectifier with P-to-G DC fault is established, which is in the form of a set of non-linear state equations. The proposed modeling method is validated through comparison of mathematical model and physical experiment. The mathematical model is effective and can accurately reflect the transient behavior of P-to-G DC fault and the steady-state average characteristics before and after the P-to-G DC fault.
keywords:Twelve-pulse diode rectifier, pole-to-ground DC fault, large signal model, switch function, principle of harmonic balance
DOI:10.19595/j.cnki.1000-6753.tces.190417
中图分类号:TM744
李 春 男,1993年生,硕士研究生,研究方向为电力系统建模与仿真。E-mail:lichun_0204@outlook.com
马 凡 男,1984年生,研究员,博士生导师,研究方向为舰船综合电力系统的建模与仿真、保护与稳定性。E-mail:mafan0803@163.com(通信作者)
国家自然科学基金项目(51607185,51877211)和国防973项目(613294)资助。
收稿日期 2019-04-12
改稿日期 2019-06-17
(编辑 赫蕾)