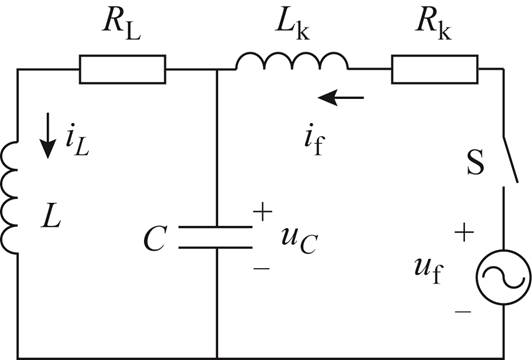
图1 谐振接地系统单相接地故障等效电路
Fig.1 Transient model of single-phase grounding fault of resonant grounding system
摘要 系统对地电容的准确测量涉及消弧线圈容量配置、补偿度调整、故障点残流控制等一系列问题。该文利用谐振接地系统单相接地故障等效电路，分析了故障点熄弧后的电气特征，发现熄弧后暂态过程为消弧线圈电感与对地电容之间的欠阻尼串联谐振过程，可利用其谐振频率与衰减因子等参数计算系统失谐度，再根据补偿电感（含消弧线圈及接地变零序电感）可计算得到系统对地电容或电容电流。该方法的误差与谐振频率、衰减因子及补偿电感的误差有关，但主要取决于补偿电感误差。利用仿真和实际故障数据验证了该方法的有效性与准确度。作为被动测量方法，该方法不需要外加任何专用设备或调整现有设备运行状态，安全性高。
关键词：谐振接地系统 电容电流测量 熄弧 暂态 失谐度
谐振接地（中性点经消弧线圈接地）系统中对地电容（系统对地电容电流）的测量非常关键。若系统对地电容测量不准确，则可能使消弧线圈容量配置不合理、失谐度过大或过小，进一步导致接地故障点残流过大影响熄弧效果或者导致欠补偿运行，也可能产生谐振或拍频等现象引起较为严重的过电压[1-2]，加重故障危害程度。除此之外，系统对地电容作为系统参数，对如谐波治理[3]、保护动作[4]、故障检测[5]、无功补偿[6-7]等多种问题将有影响。
现有系统对地电容测量多采用主动测量方法，如信号注入法[8-11]、偏置法[12-13]、中性点阻抗法[14-17]等。其中，信号注入法包括两频率法、三频率法、扫频法等不同方法，均通过在电压互感器（TV）二次侧注入电流信号，并测量开口三角侧电压，计算得到系统对地电容，测量精度依赖注入电流的幅值与选取的频率；偏置法包括偏置阻抗法、偏置电容法等不同方法，主要通过改变系统中性点电位，并利用电压、电流与系统对地电容之间的约束关系，得到系统对地电容，该方法操作相对复杂，且由于需要利用一次设备进行作业，具有一定的安全隐患；中性点阻抗法是通过改变中性点阻抗，并多次测量中性点电压幅值，计算得到系统对地电容电流，该方法需要对中性点阻抗合理取值，且对系统不对称度与失谐度等参数有所依赖。以上各种主动测量方法在配置合理、测量准确的情况下均能得到准确结果，但由于均存在不同方面的缺陷，测量准确性受到限制。因此，有必要寻找一种成本低、操作简单易于实现的测量方法作为补充或辅助。
单相接地故障时，系统暂态过程是一个在故障点虚拟电源激励下的零状态响应[18]，而故障点电弧熄灭后，系统暂态过程是一个非零状态下的零输入响应，且熄弧后的暂态过程仅和补偿电感（含消弧线圈电感、接地变零序电感、主变零序电感）、系统对地电容以及系统等效电阻有关，与故障点状态（如过渡电阻大小、电弧稳定程度等）无关，即熄弧后的暂态过程可反映消弧线圈电感值与对地电容值之间的约束关系。因此，在消弧线圈电感值已知的情况下，可以根据熄弧后暂态电气量计算系统对地电容。
本文利用谐振接地系统单相接地故障等效电路，对接地故障熄弧后的母线零序电压、中性点电流等电气量的暂态特征进行分析，给出暂态谐振频率、衰减因子等参数与系统失谐度间的约束关系，提出一种利用熄弧后电气量特征的对地电容电流测量方法，并对该方法的误差进行分析。最后利用仿真和现场实际故障数据对方法进行了验证。
图1为谐振接地系统单相接地故障的等效电路。其中，L为补偿电感，为消弧线圈零序电感、接地变压器零序电感与主变压器零序电感之和；RL为熄弧后恢复过程中系统等效有功损耗电阻，包括消弧线圈及接地变压器的零序电阻；电容C为系统中所有线路零序电容之和，uC为其两端电压，即为母线零序（零模）电压；Lk为故障点到母线之间线路的零模与线模参数及主变线模等效电感之和；Rk为故障点到母线之间线路的零模与线模参数、主变线模参数及故障点过渡电阻的等效电阻之和；虚拟电源uf=Umsin(w0t+f)，-f为故障相接地瞬间电源电动势相角，Um为电源电压幅值，w0为工频角频率；if为故障点电流。
图1 谐振接地系统单相接地故障等效电路
Fig.1 Transient model of single-phase grounding fault of resonant grounding system
当故障点电流过零熄弧，即开关S断开时，图1模型可用于分析熄弧后电气量特征。
对图1开关S断开后的电路列写常系数微分方程为
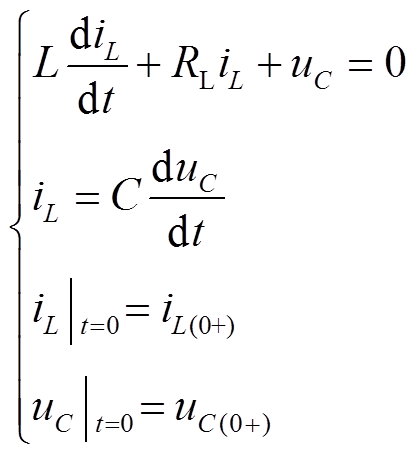（1）式中，uC(0+)为电弧熄灭时零序电压瞬时值；iL(0+)为熄弧时消弧线圈中电流瞬时值。
由于经消弧线圈接地系统中有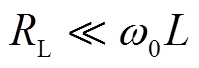
，求解式（1）可得零序电压uC为
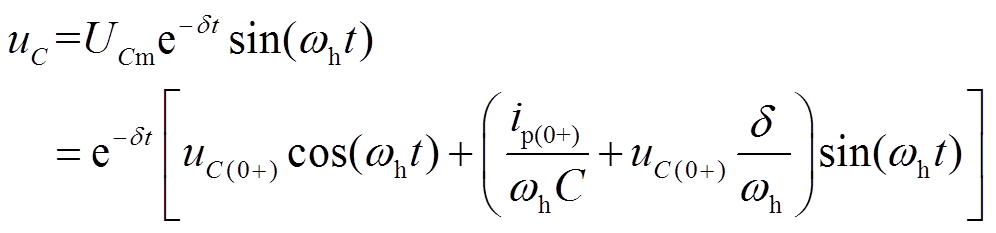（2）消弧线圈电流iL为
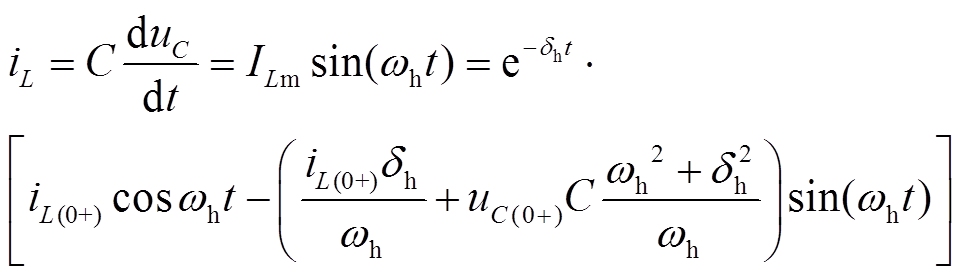（3）
式中，衰减因子d为
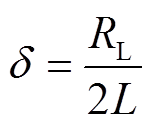（4）谐振角频率wh为
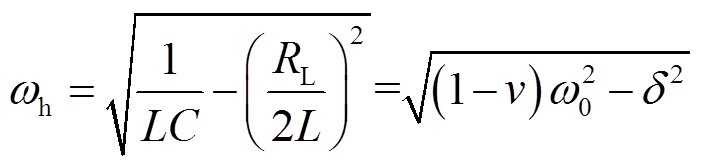（5）
失谐度v为
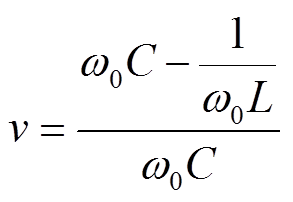（6）可以看出，衰减因子d及谐振角频率wh与uC(0+)、iL(0+)等量无关，仅与L、C等参数有关。
通过对式（2）及式（3）进行推导，可以得到零序电压暂态量幅值UCm为
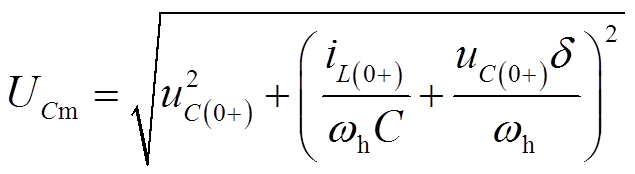（7）消弧线圈电流暂态量幅值为
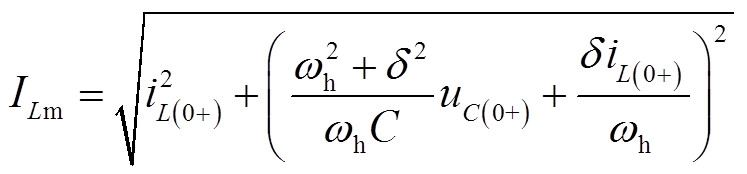（8）
可以得到补偿回路总能量W'与以上两个衰减信号幅值之间的关系为
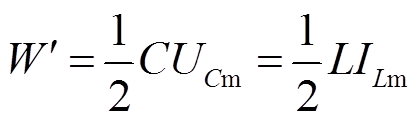（9）该能量大小等于熄弧时刻补偿回路所储存的能量大小。
燃弧期间，由图1可知，电容两端稳态电压（即零序电压）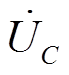
为
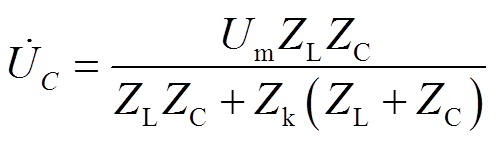（10）式中，ZL为补偿阻抗，ZL=R+jw0L；ZC为对地容抗，ZC=1/(jw0C)；Zk为线路阻抗，Zk=Rk+jw0Lk。对于特定系统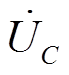，变化主要受Rk变化（主要为过渡电阻的变化）影响。
燃弧期间，任意时刻的补偿电感支路与对地电容所储存的总能量W为
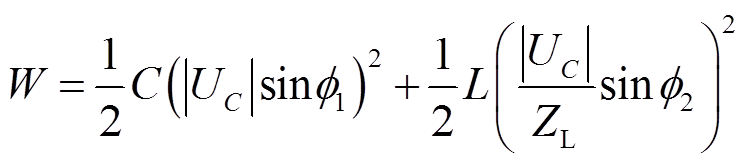（11）式中，f1为该时刻零序电压相角；f2为补偿电感支路电流相角。f1和f2相差约为90°。
显然，当发生电弧熄灭时，补偿回路能量W'等于该时刻能量W的大小，而后者将取决于零序电压的大小。结合式（10），对于同一个系统而言，W'将主要受过渡电阻影响。对于低阻接地故障，W'足够大，能够保证零序电压、中性点电流等电气量幅值足够大，从而满足测量要求；而当过渡电阻过高时，则会使零序电压、中性点电流等信号的幅值过小，从而难以保证测量精度。
失谐度v为-8%和-60%的10kV谐振接地系统发生金属性接地故障，电弧熄灭后零序电压uC与消弧线圈电流iL恢复过程如图2所示，t =0为熄弧时刻。
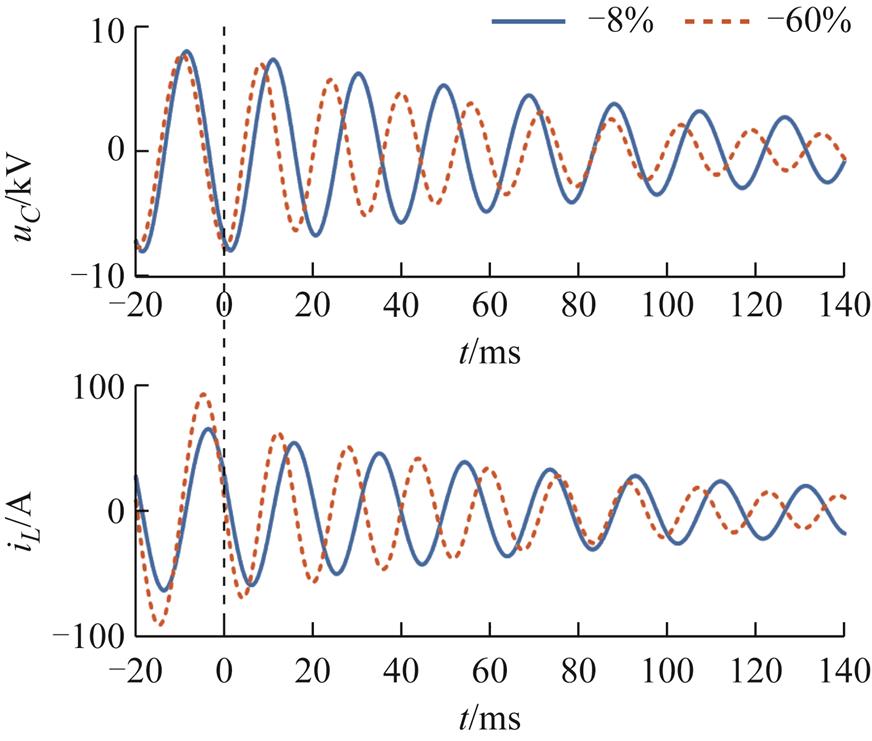
图2 谐振接地系统熄弧后暂态过程
Fig.2 Transient process after arc extinguishing in the resonance grounding system
可以看出，熄弧后的零序电压与消弧线圈电流均为衰减的正弦分量。各波形对应的参数见表1。
表1 谐振接地系统熄弧后波形信息
Tab.1 Information of waveform after arc extinguishing in the resonance grounding system
失谐度幅值频率/Hz衰减因子/s-1相位/(°) -8%电压8.098kV51.93 8.58243.90 电流69.84A51.938.57155.93 -60%电压7.833kV63.18 12.72261.20 电流73.06A63.1812.72174.99
同一个系统中，uC超前iL约90°，衰减速度一致。对比两个失谐度不同的系统，当失谐度绝对值较小时，谐振频率与工频接近，而当其值较大时，谐振频率将增大，与工频有明显差异。同时，在过补偿状态下失谐度绝对值较大时，补偿电感相对减小，零序电压幅值有所降低，但消弧线圈电流幅值有所上升。
由式（5）可以得到失谐度为
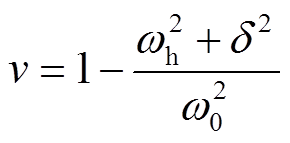（12）即可以根据熄弧后暂态过程的谐振角频率、衰减因子计算得到当前系统的失谐度。
由于补偿电感值已知，可根据式（6）中对地电容C与补偿电感L的关系
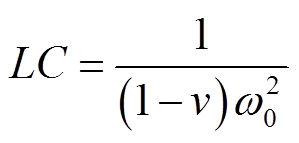（13）得到
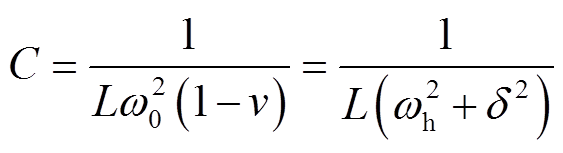（14）
进一步可得到系统对地电容电流为
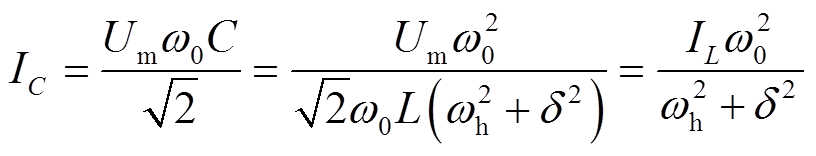（15）式中，IL为金属性接地时消弧线圈电流有效值。该值为额定电压条件下计算所得电容电流，可按照式（16）计算。
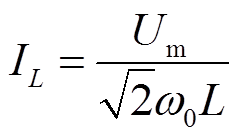（16）
由式（16）可知，IL的值将取决于L的大小。而由图1可知，L的值主要包括消弧线圈电感、主变压器和接地变压器等设备的零模电感，这些参数较易获得。
由式（15）可知，电容电流测量结果的误差取决于补偿电感L、谐振频率wh及衰减因子d的测量误差。
利用泰勒级数展开[19]可以得到系统对地电容的测量绝对误差为
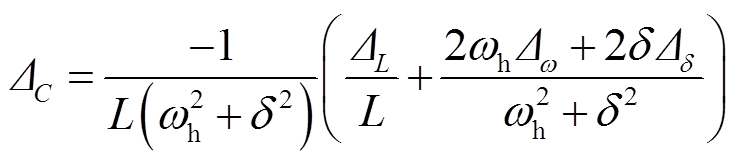（17）系统对地电容的相对误差为
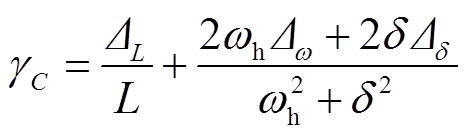（18）
式中，DL为补偿电感的绝对误差；Dw为谐振角频率的绝对误差；Dd为衰减因子的绝对误差。
失谐度v一般取为负值或较小正值（即过补偿或由于装置配置不正确导致的欠补偿）；wh的取值一般接近或大于工频角频率w0（100prad/s）；而d的取值一般为5~20s-1。显然，wh在数值上远大于d。因此，由式（17）及式（18），衰减因子误差对系统对地电容误差的影响较小，可以仅考虑补偿电感L与谐振角频率wh误差。
此时，式（17）与式（18）可以近似表示为
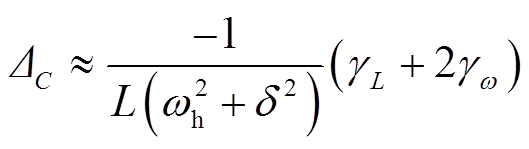（19）
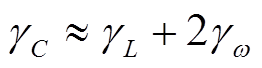（20）
式中，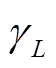
、
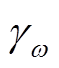分别为补偿电感与谐振角频率的相对误差。
可以看出，测量时系统对地电容的绝对误差或相对误差都仅与补偿电感和谐振频率的相对误差有关，而与绝对误差无关。同时，当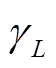与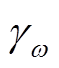数值上相等时，后者对系统对地电容电流误差的影响是前者的2倍。
由消弧线圈的相关标准（GB/T 1094.6—2011）可知，接地变压器与消弧线圈组合时的零序阻抗测量误差在最小位置时应在5%以内，在其他位置时应在10%以内，该误差可以近似看作是补偿电感的误差。但在实际中，消弧线圈设备所记录的电感值精度远高于该标准，一般在1%以内。
由电力系统的电能质量相关标准（GB/T 15945—2008）可知，系统频率的测量绝对误差应不大于0.01Hz。假设系统失谐度在-60%（消弧线圈容量选择过大，使补偿电感过小）和40%（消弧线圈容量选择过小，使补偿电感过大）之间变换，对应熄弧后的零序电气量谐振频率可在39.2~ 63.2Hz范围内变化。若测量误差为0.01Hz，可以得到其相对误差应在0.16%~ 0.25%范围内。根据式（20），则会给系统电容的测量误差带来0.32%~ 0.5%的影响。
虽然式（19）及式（20）中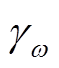的系数为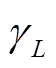的系数的2倍，但考虑实际情况，前者的相对误差在数值上远小于后者。因此，利用本文方法测量系统对地电容或系统电容电流时，误差受到补偿电感误差的影响较大。
由以上分析可知，通过测量故障消失后零序电压uC或消弧线圈电流iL的衰减因子d与谐振角频率wh，结合补偿电感L，即可确定电容C（即系统中所有线路零序电容之和）的大小，并可以进一步得到系统电容电流的大小。而在一般情况下，由于wh相对d较大，在计算过程中可以忽略d，仅测量wh即可得到较为准确的结果。
利用Matlab/Simulink搭建谐振接地系统进行仿真模拟，电压等级为10kV，共8条出线，包含电缆线路、架空线路与混合线路，其结构如图3所示。其中，不同线路类型的参数见表2，Rxu、Lxu、Cxu分别为分布参数电阻、电感、电容。
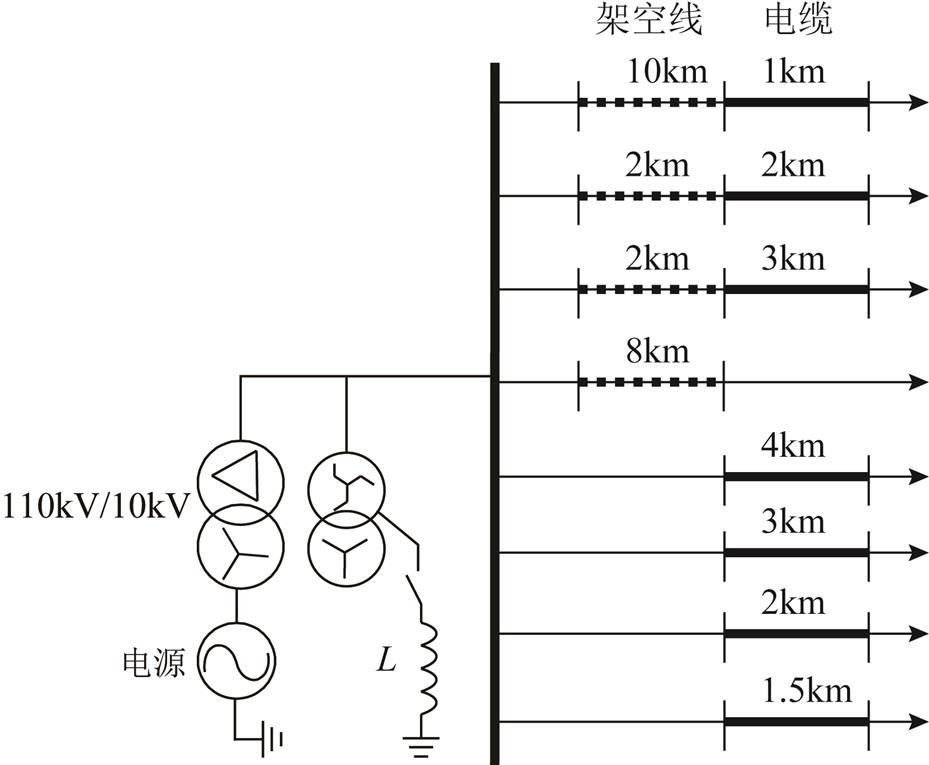
图3 谐振接地系统仿真结构
Fig.3 Simulation structure of resonance grounding system
系统对地电容为7.85mF，对应10kV系统电容电流为42.68A。通过改变消弧线圈电感值来改变系统失谐度，利用最小二乘矩阵束算法[20]得到谐振频率f（f=wh/2p）以及衰减因子d，补偿电感L仅取3倍消弧线圈电感，得到表3中前三列结果。
表2 架空线及电缆线路分布参数
Tab.2 Distribution parameters of overhead lines and cable lines
参数数值 架空线电缆 零序R0u/(Ω/km)0.346 00.797 0 L0u/(mH/km)4.7870.956 3 C0u/(μF/km)0.004 0350.470 0 正序R1u/(Ω/km)0.121 00.079 70 L1u/(mH/km)1.0190.273 9 C1u/(μF/km)0.011 480.470 0
表3 补偿电感不同时系统参数及熄弧后信息仿真结果
Tab.3 System parameters and simulation results of information after arc extinguishing for different compensation inductances
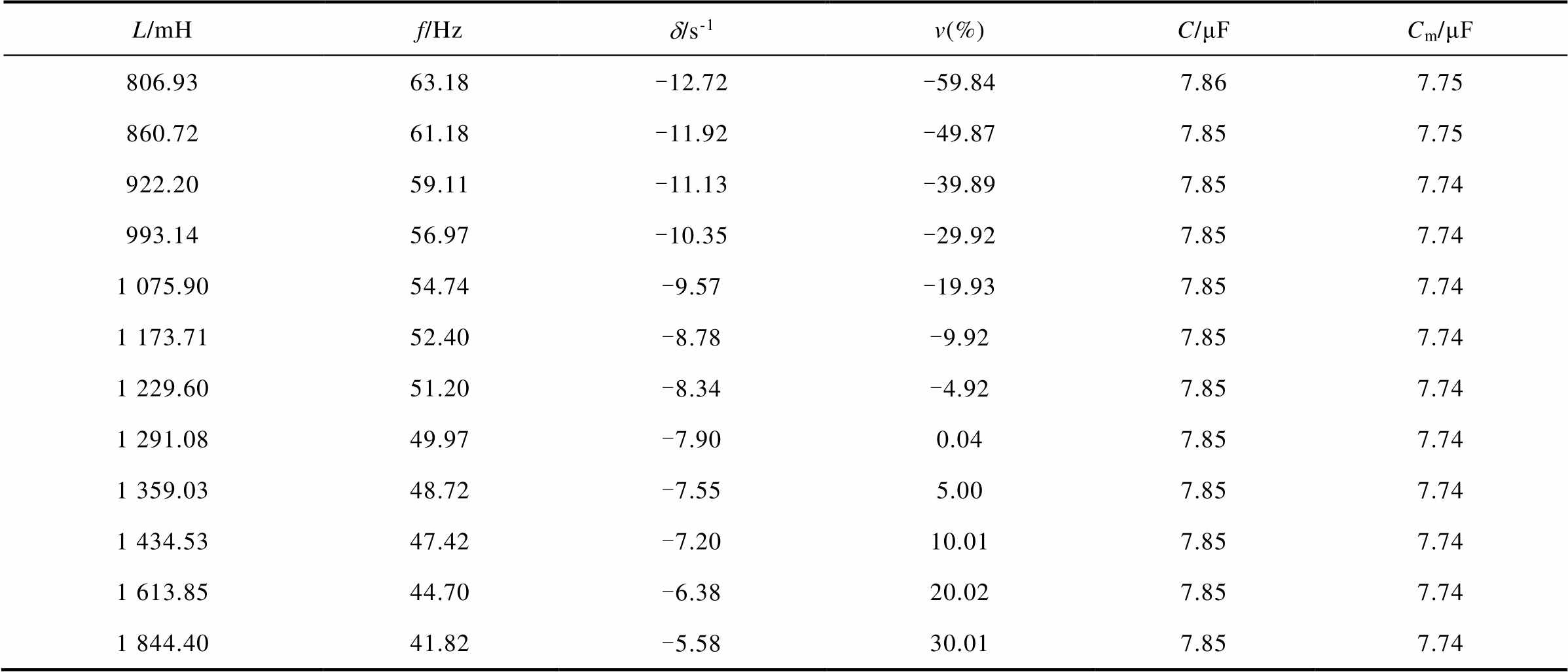
L/mHf/Hzd/s-1v(%)C/μFCm/μF 806.9363.18-12.72-59.847.867.75 860.7261.18-11.92-49.877.857.75 922.2059.11-11.13-39.897.857.74 993.1456.97-10.35-29.927.857.74 1 075.9054.74-9.57-19.937.857.74 1 173.7152.40-8.78-9.927.857.74 1 229.6051.20-8.34-4.927.857.74 1 291.0849.97-7.900.047.857.74 1 359.0348.72-7.555.007.857.74 1 434.5347.42-7.2010.017.857.74 1 613.8544.70-6.3820.027.857.74 1 844.4041.82-5.5830.017.857.74
根据表3中前三列测量内容，可以计算得到后三列所示结果。其中v为失谐度，利用式（12）准确计算结果；C为利用表3并结合式（15）计算所得结果；Cm为各参数存在误差的情况下所得结果，补偿电感相对误差1%，频率相对误差为0.2%，衰减因子相对误差为5%。
可以计算得到C与Cm之间的相对误差均为1.39%，接近1.4%，即补偿电感1%的相对误差与2倍频率相对误差之和，而与衰减因子的相对误差相差较大。
保持消弧线圈电感为350mH不变，即补偿电感为1.05H，通过改变各出线长度来改变系统电容电流，从而改变失谐度v。对地电容不同时系统参数及熄弧后信息仿真结果见表4，其中Cs为系统实际对地电容。
结合已知的补偿电感，利用表4中的频率与衰减因子，可以得到表4中的失谐度v与电容C，Cm为各参数存在误差得计算结果，各误差情况与表3相同。
表4 对地电容不同时系统参数及熄弧后信息仿真结果
Tab.4 System parameters and simulation results of information after arc extinguishing for different capacitances to ground
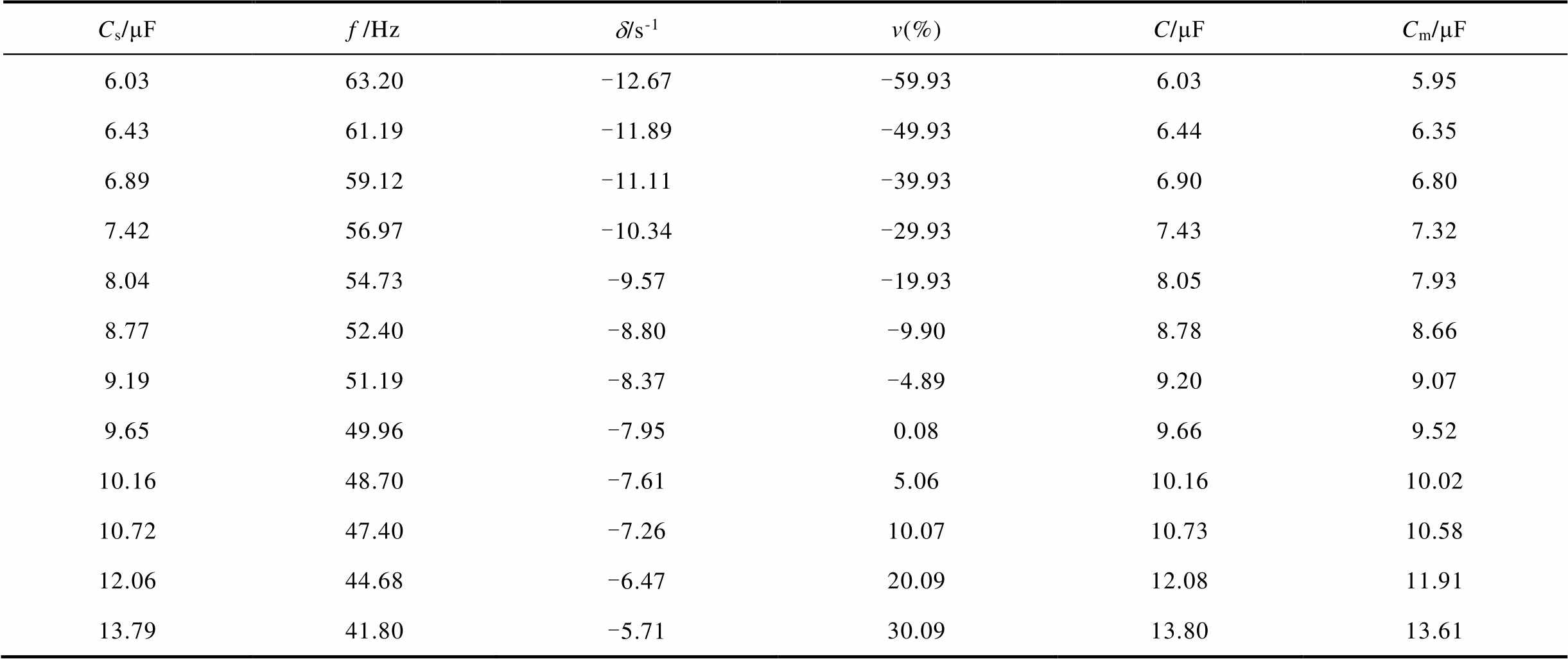
Cs/μFf /Hzd/s-1v(%)C/μFCm/μF 6.0363.20-12.67-59.936.035.95 6.4361.19-11.89-49.936.446.35 6.8959.12-11.11-39.936.906.80 7.4256.97-10.34-29.937.437.32 8.0454.73-9.57-19.938.057.93 8.7752.40-8.80-9.908.788.66 9.1951.19-8.37-4.899.209.07 9.6549.96-7.950.089.669.52 10.1648.70-7.615.0610.1610.02 10.7247.40-7.2610.0710.7310.58 12.0644.68-6.4720.0912.0811.91 13.7941.80-5.7130.0913.8013.61
同样，可以计算得到C与Cm之间的相对误差均为1.39%，接近1.4%，即补偿电感1%的相对误差与2倍频率相对误差之和，而与衰减因子的相对误差相差较大。
由以上结果可以看出，在补偿电感的变化或系统对地电容变化造成失谐度不同的情况下，均可以利用本文所提方法对系统电容（系统电容电流）进行准确测量。同时，虽然衰减因子误差取值最大，但衰减因子的数值较小，因此对测量结果的误差影响较小；而补偿电感的测量误差较大，频率的测量误差较小，使得计算得到的系统对地电容的误差更接近于补偿电感的误差。
实验系统为35kV，现场记录电容电流为9.3A，消弧线圈补偿电流为13.7A，补偿后的残流为4.4A，可以计算的失谐度为-47.3%。图4所示熄弧后恢复阶段零序电压谐振频率为60.7Hz，计算出该系统消弧线圈失谐度为-47.4%，根据消弧线圈电流可以计算得到电容电流为9.3A，与记录数据基本相符。
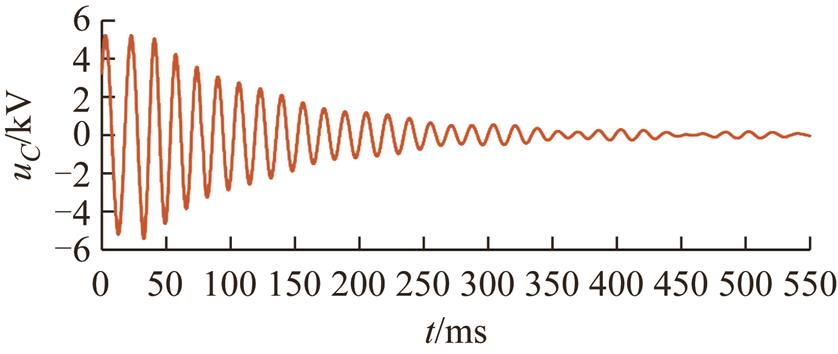
图4 谐振接地系统熄弧后零序电压恢复过程实际录波
Fig.4 Reality waveform of recovery process of resonance grounding system after arc extinguishing
在谐振接地系统中，单相接地故障的故障点熄弧后，系统进入恢复过程。此时，母线零序电压与中性点电流等电气量是逐渐衰减的正弦信号，且其谐振频率不同于工频。该过程的谐振频率、衰减因子等参数与系统的失谐度具有确定的约束关系。因此，可以通过测量熄弧后暂态电气量的谐振频率与衰减因子，计算得到系统失谐度，结合补偿电感参数或中性点电流，即可得到系统对地电容或系统电容电流大小，且对于一般情况，可忽略衰减因子，即可得到较为准确结果。
该方法可以在不增添专用电容电流测量设备的情况下，仅依靠已有电压互感器或电流互感器等测量设备，对系统对地电容进行测量。但该方法需要接地故障的发生作为先决条件，为补偿电感及系统对地电容提供能量，故仅能作为一种辅助测量方法，用以补充验证已有方法的准确性或在发生接地故障后为消弧线圈的校正提供反馈信息，使消弧线圈的校正工作形成闭环。
参考文献
[1] 曲轶龙. 全补偿消弧线圈及其控制方法的研究[D].北京: 华北电力大学, 2008.
[2] 何颋. 自动调谐消弧线圈投入引起谐振过电压的原因[J]. 高电压技术, 2007, 33(9): 216-217.He Ting. The cause of resonant overvoltage caused by auto-tuned arc suppression coil input[J]. High Voltage Engineering, 2007, 33(9): 216-217.
[3] 赵仁德, 李乾, 徐海亮, 等. 脉冲宽度调制并网变换器电网背景谐波电流的抑制[J]. 电工技术学报, 2018, 33(增刊2): 558-566.Zhao Rende, Li Qian, Xu Hailiang, et al. Grid background harmonic current suppression for grid-connected PWM converters[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 558-556.
[4] 吴继维, 童晓阳, 廖小君, 等. 基于零序差动阻抗的输电线路保护新原理研究[J]. 电力系统保护与控制, 2017, 45(10): 11-17. Wu Jiwei, Tong Xiaoyang, Liao Xiaojun, et al. Transmission line protection principle based on zero sequence differential impedance[J]. Power System Protection and Control, 2017, 45(10): 11-17.
[5] 贾清泉, 王振宇, 王宁, 等. 基于参数辨识的消弧线圈接地电网单相接地故障测距方法[J]. 电工技术学报, 2016, 31(23): 77-85.Jia Qingquan, Wang Zhenyu, Wang Ning, et al. A single-phase-to-ground fault locating algorithm for arc-suppression-coil earthed power distribution systems based on parameter estimation[J]. Transactions of China Electrotechnical Society, 2016, 31(23): 77-85.
[6] 周兴达, 陆帅. 一种基于消弧线圈和静止同步补偿器协同作用的配电网消弧结构与方法[J]. 电工技术学报, 2019, 34(6): 1251-1262.Zhou Xingda, Lu Shuai. An arc-suppression method based on the coordinated operation of the petersen coil and the static synchronous compensator in distribution networks[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1251-1262.
[7] 朱建鑫, 胡海兵, 陆道荣, 等. 应用于级联STATCOM的高精度低成本全FPGA实时仿真模型研究[J]. 电工技术学报, 2019, 34(4): 777-785. Zhu Jianxin, Hu Haibing, Lu Daorong, et al. The research on fully FPGA-based real-time simulation with high fidelity and low cost for the cascaded STATCOM[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 777-785.
[8] 曾祥君, 刘张磊, 马洪江, 等. 配电网电容电流实时测量技术[J]. 电力系统自动化, 2008, 32(3): 61-65.Zeng Xiangjun, Liu Zhanglei, Ma Hongjiang, et al. A capacitive current real-time measuring technique for distribution networks[J]. Automation of Electric Power Systems, 2008, 32(3): 61-65.
[9] 宋晓燕, 孙岩洲, 宋紫嫣, 等. 基于零序PT二次侧注入信号的配电网电容电流测量新方法[J]. 电力系统保护与控制, 2014, 42(19): 134-138.Song Xiaoyan, Sun Yanzhou, Song Ziyan, et al. A new method of distribution network capacitive current measurement based on injecting signals into the secondary side of the zero sequence PT[J]. Power System Protection and Control, 2014, 42(19): 134-138.
[10] 周求宽, 姚骏, 刘衍, 等. 基于三频率法的配电网电容电流测量新方法[J]. 电测与仪表, 2017, 54(10): 44-49.Zhou Qiukuan, Yao Jun, Liu Yan, et al. A new method to measure capacitance current in distribution network based on three-frequency method[J]. Electrical Measurement ＆ Instrumentation, 2017, 54(10): 44-49.
[11] 刘力, 孙结中. 一种测量配电网电容电流的新方法[J]. 电网技术, 2001, 26(5): 63-65.Liu Li, Sun Jiezhong. A newmethod to measure capacitance current in distribution network[J]. Power System Technology, 2001, 26(5): 63-65.
[12] 李景禄, 周羽生, 唐跃进. 偏置电容法电容电流测量的应用经验[J]. 电力自动化设备, 2004, 24(2): 99-100.Li Jinglu, Zhou Yusheng, Tang Yuejin. Application experiences of capacitive current measuring with partially installing capacitor[J]. Electric Power Automation Equipment, 2004, 24(2): 99-100.
[13] 李晓波, 苗晓鹏, 桑振华, 等. 基于偏置阻抗法的配电网电容电流测量新方法[J]. 电力系统保护与控制, 2014, 42(4): 22-26.Li Xiaobo, Miao Xiaopeng. Sang Zhenhua, et al. A new capacitive current measurement method of the distribution network based on bias impedance[J]. Power System Protection and Control, 2014, 42(4): 22-26.
[14] 刘宝稳, 李晓波. 基于失谐量的消弧线圈跟踪调谐方法[J]. 电力系统保护与控制, 2013, 41(5): 6-9. Liu Baowen, Li Xiaobo. New type of automatic tuning arc-suppression coil based on detuning size[J]. Power System Protection and Control, 2013, 41(5): 6-9.
[15] 靳维, 袁朋生, 张洋, 等. 基于调整中性点接地阻抗的配电网电容电流测量方法[J]. 电力系统保护与控制, 2015, 43(7): 37-41. Jin Wei, Yuan Pengsheng, Zhang Yang, et al. A method of measuring capacitive current in distribution network based on adjusting the neutral grounding impedance[J]. Power System Protection and Control, 2015, 43(7): 37-41.
[16] 贺良华, 葛来, 孙宝金. 基于谐振频率预测模型的配电网电容电流测量方法[J]. 电力系统自动化, 2018, 42(2): 143-147.He Lianghua, Ge Lai, Sun Baojin. Capitcitivc current measuring methml for distribution networks based on resonant frequency prediction model[J]. Automation of Electric Power Systems, 2018, 42(2): 143-147.
[17] 闫腾飞, 李康, 李晓波, 等. 基于牛顿—拉夫逊法的配电网电容电流测量新方法[J]. 电力系统保护与控制, 2017, 45(7): 1-5. Yan Tengfei, Li Kang, Li Xiaobo, et al. A new capacitive current measurement method of distribution network based on Newton-Raphson method[J]. Power System Protection and Control, 2017, 45(7): 1-5.
[18] 薛永端, 李娟, 陈筱薷, 等. 谐振接地系统高阻接地故障暂态选线与过渡电阻辨识[J]. 中国电机工程学报, 2017, 37(17): 5037-5048. Xue Yongduan, Li Juan, Chen Xiaoru, et al. Faulty feeder selection and transition resistance identification of high impedance fault in a resonant grounding system using transient signals[J]. Proceedings of the CSEE, 2017, 37(17): 5037-5048.
[19] 廖小兵, 刘开培, 张亚超, 等. 基于区间泰勒展开的不确定性潮流分析[J]. 电工技术学报, 2018, 33(4): 750-758.Liao Xiaobing, Liu Kaipei, Zhang Yachao, et al. Uncertain power flow analysis based on interval taylor expansion[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 750-758.
[20] 康小宁, 屈亚军, 焦在滨, 等. 基于最小二乘矩阵束算法的工频分量提取方法[J]. 电力系统自动化, 2014, 38(21): 66-70.Kang Xiaoning, Qu Yajun, Jiao Zaibin, et al. Power-frequency phasor extraction based on least square matrix pencil algorithm[J]. Automation of Electric Power Systems, 2014, 38(21): 66-70.
Measuring Method of Capacitance to Ground in Resonant Grounding System Based on Transient Information after Arc Extinguishing
Abstract Accurate measurement of capacitance to ground of the system involves a series of problems such as capacity allocation of arc suppression coil, compensation adjustment, control of residual current at fault point, etc. By using the equivalent circuit of single-phase grounding fault in resonant grounding system, the electrical characteristics of the fault point after arc extinguishing are analyzed. It is found that the transient process after arc extinguishing is the underdamped series resonance process between the inductance of arc suppression coil and the capacitance to ground. The system detuning degree can be calculated by the parameters of resonance frequency and damping factor. Then the capacitance or capacitance current of the system can be calculated according to compensation inductance, which includes zero-sequence inductance of arc suppression coil and grounding transformer. The error of this method is related to the error of resonance frequency, damping factor and compensation inductance. But it mainly depends on the error of compensation inductance. The validity and accuracy of the method are verified by simulation and field data. As a passive measurement method, this method needs no special equipment or adjustment of the operation status of existing equipment, it has high security and provides a new idea for capacitive current measurement of resonant grounding system.
keywords：Resonant grounding system, capacitance current measurement, arc extinguishing, transient, detuning degree
DOI:10.19595/j.cnki.1000-6753.tces.191178
中图分类号：TM930.1
薛永端 男，1970年生，博士，教授，博士生导师，研究方向为配电网故障检测。E-mail：xueyd70@126.com（通信000作者）
李 广 男，1994年生，硕士研究生，研究方向为配电网故障检测。E-mail：lig2017@126.com
国家自然科学基金资助项目（51477184）。
收稿日期 2019-09-17
改稿日期 2019-12-17
（编辑 赫蕾）