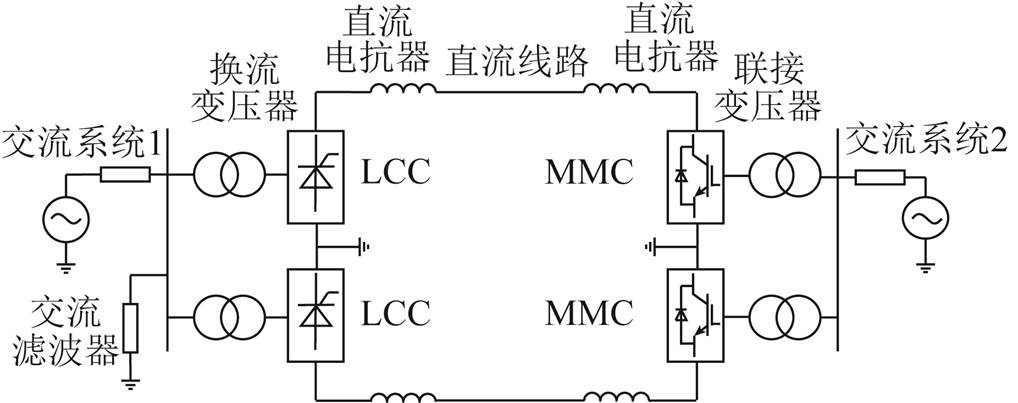
图1 LCC-MMC型混合直流输电系统结构
Fig.1 Diagram of LCC-MMC hybrid HVDC system
摘要 针对换相换流器(LLC)-模块化多电平换流器(MMC)型混合直流输电系统在联接极弱受端交流系统时容易出现的系统小信号失稳现象,提出一种附加频率-电压阻尼控制(SFVDC)。该控制方法基于逆变站模块化多电平换流器锁相环的角频率偏差信息产生附加直流电压阻尼分量,引入外环定直流电压控制器中,用以抑制极弱受端交流系统时LCC-MMC型混合直流输电系统的小信号失稳现象,从而提升系统的小信号稳定性。结果表明,所提出的SFVDC方法能够有效地抑制极弱受端交流系统下容易出现的系统小信号失稳现象,降低了系统稳定运行对于受端交流系统强度的要求,同时能够保证系统在较大的功率扰动下也具有良好的动态响应特性,在受端交流系统故障情况下具有良好的故障恢复特性。
关键词:电网换相换流器 模块化多电平换流器 混合直流输电系统 附加频率-电压阻尼控制 弱受端交流系统 小信号稳定性
电网换相换流器高压直流输电(Line Commutated Converter based HVDC, LCC-HVDC)已被广泛应用于远距离大容量输电等场合[1]。然而,LCC-HVDC系统也有一些缺点,如逆变侧易发生换相失败、无功功率需求大等[2],这些缺点在一定程度上制约了其在特定场景下的应用,尤其是弱或极弱受端交流系统场合。
模块化多电平换流器高压直流输电(Modular Multilevel Converter based HVDC, MMC-HVDC)采用全控器件,不存在换相失败问题,同时具有开关频率较低、无需交流滤波器等优点,成为柔性直流输电首选拓扑,在风电场并网、异步联网、城市供电等场合也得到了很多应用[3-4]。然而,与相同容量和电压等级的LCC-HVDC相比,MMC-HVDC系统的投资成本和运行损耗较高,同样在一定程度上制约着其在某些场景下的应用。
整流侧为LCC、逆变侧为MMC的LCC-MMC型混合直流输电系统结合了两类换流器的优势[5-8],不仅解决了LCC-HVDC系统逆变侧的换相失败问题,而且同MMC-HVDC系统相比在一定程度上降低了投资成本,因此具有广阔的工程应用前景。目前,南方电网公司在建的乌东德混合三端直流输电工程,其整流侧为LCC换流站,两个逆变侧为MMC换流站[9],即是混合两端系统的进一步扩展。
目前,已有诸多学者对LCC-MMC型混合直流输电系统展开了研究。文献[10-11]建立了LCC-MMC型混合直流输电系统模型,并对其控制策略进行了研究;文献[12-14]分析了LCC-MMC型混合直流输电系统的故障特征并提出了相应的故障穿越控制策略和输送功率提升策略;文献[15]研究了具有故障穿越功能的子模块混合型LCC-MMC混合直流输电系统的启动控制策略;文献[16]建立了LCC-MMC型混合直流输电系统的小信号模型并分析了其小信号稳定性,结果表明,当逆变侧MMC换流站连接极弱交流系统时,系统易发生小信号失稳现象,而这与该混合直流输电系统逆变侧采用MMC使其应用于弱甚至极弱交流系统场景的目标相悖,因而在一定程度上限制了该类型混合直流输电的应用范围。因此,有必要对提高LCC-MMC型混合直流输电系统在弱甚至极弱受端交流系统场景下稳定性的控制方法展开研究。
目前,已有诸多文献研究了VSC-HVDC及MMC-HVDC系统在接弱交流系统时的小信号稳定性[17-24],其中部分文献指出锁相环在弱交流系统下的动态特性对系统稳定性有关键影响作用[17-23],并提出了多种改进控制方法来提高系统的稳定性,例如改进电流矢量控制[17]、虚拟母线控制[18]、功率同步控制[19]及改进锁相环模型[21]等,为本文的研究工作提供了有价值的思路。然而以上研究仅能够反映MMC拓扑下系统的小信号稳定性,目前对于LCC-MMC型混合直流输电系统的小信号稳定性研究及改进控制方法研究还很少,有必要进行深入探讨。
本文针对LCC-MMC型混合直流输电系统在联接极弱受端交流系统时容易出现的系统小信号失稳现象,提出了一种附加频率-电压阻尼控制(Supplementary Frequency-Voltage Damping Control, SFVDC)方法。该方法基于逆变站MMC锁相环的输出角频率偏差信息产生附加直流电压阻尼分量,引入外环定直流电压控制器中。首先,建立含SFVDC的LCC-MMC型混合直流输电系统小信号模型并验证了其正确性;然后,研究SFVDC对系统小信号稳定性的影响,验证了极弱受端交流系统下SFVDC的有效性;最后,研究极弱受端交流系统下含SFVDC系统在较大功率扰动时的动态响应特性及其在受端交流系统故障情况下的暂态响应特性。结果表明,所提出的SFVDC能够有效抑制极弱受端交流系统下容易出现的系统小信号失稳现象,降低系统稳定运行对于受端交流系统强度的要求,同时能够保证系统在较大功率扰动下具有良好的动态响应特性,在受端交流系统故障情况下具有良好的故障恢复特性。
LCC-MMC型混合直流输电系统整流侧采用LCC换流站,逆变侧采用MMC换流站,系统结构如图1所示,等效原理如图2所示。图2中各变量的物理意义与文献[16]基本相同,故在正文中不赘述,见附表1。本文以单极系统为例进行系统小信号稳定性分析,其结论同样适用于双极系统。

图1 LCC-MMC型混合直流输电系统结构
Fig.1 Diagram of LCC-MMC hybrid HVDC system

图2 LCC-MMC型混合直流输电系统原理图
Fig.2 Schematic diagram of LCC-MMC hybrid HVDC system
图3所示为LCC-MMC型混合直流输电系统控制结构图。图3a、图3d分别为LCC和MMC的锁相环,其中w0为额定角频率,w1(w2)为LCC(MMC)锁相环输出角频率,θ1(θ2)为LCC(MMC)锁相环输出相角;图3b为LCC定直流电流控制器,其中Idcref_1、Idc_1、Idcm_1分别为LCC直流电流指令值、实际值及测量值,b和a分别为LCC的触发超前角和触发延迟角;图3c为本文所提出的附加频率-阻尼控制(SFVDC),将在2.1节中详细介绍;图3e为MMC环流抑制控制器(Circulating Current Suppression Controller, CCSC),其中Icird_2、Icirq_2(Ucird_2、Ucirq_2)分别为桥臂二倍频环流(二倍频修正电压)的d轴、q轴分量,2w2Larm为前馈补偿耦合项;图3f为电流矢量控制器(Vector Current Control, VCC),其中Udcref_2、Udc_2分别为MMC直流电压的参考值和实际值,Utref_2、Utm分别为MMC交流电压的参考值和测量值,Idref、Iqref分别为内环控制器的d、q轴电流参考值,Isdm_2、Isqm_2(Utdm_2、Utqm_2)分别为MMC交流侧电流(电压)的d、q轴分量经过一阶滤波得到的测量量,w2Leq为前馈补偿耦合项,Ucd、Ucq分别为MMC交流侧电压参考值的d、q轴分量。
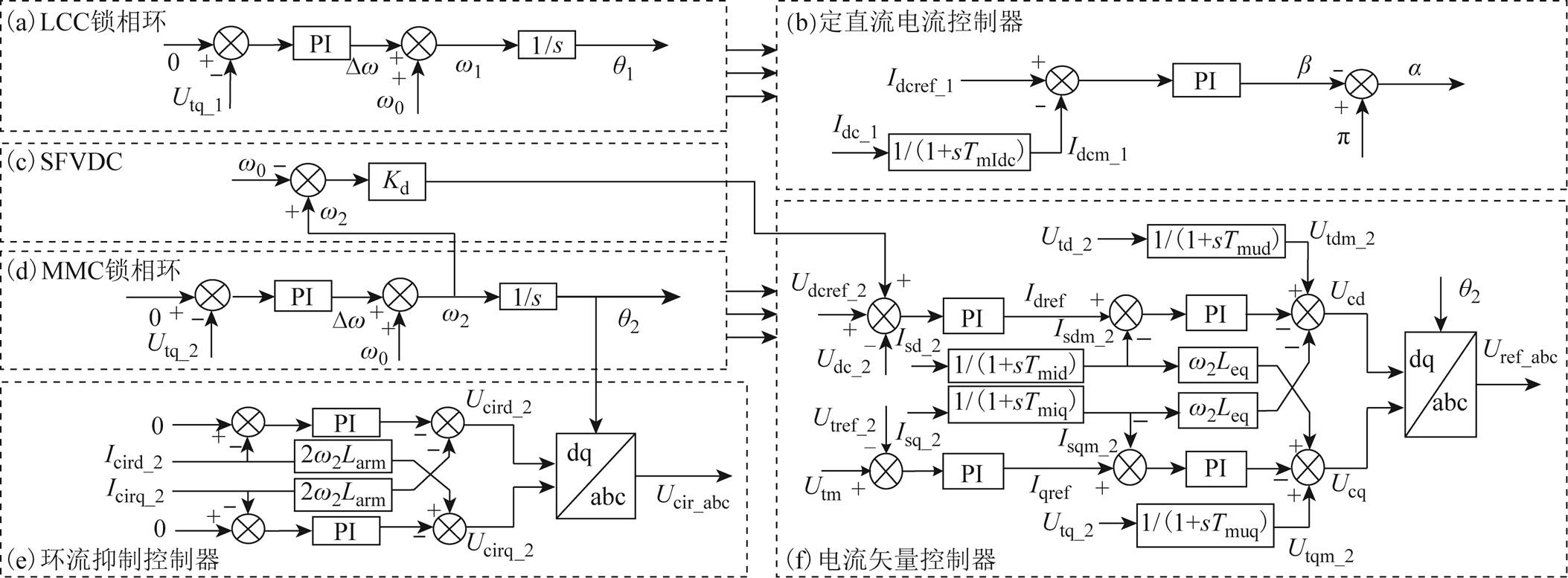
图3 LCC-MMC型混合直流输电系统控制框图
Fig.3 Control system block diagram of LCC-MMC hybrid HVDC system
LCC-MMC型混合直流输电系统参数见表1~表3。整流侧LCC所联交流系统短路比(Short-Circuit Ratio, SCR)SCR1=3.0,逆变侧MMC所联接交流系统短路比SCR2=1.5。
LCC-MMC型混合直流输电系统的状态空间模型主要包含LCC换流站、MMC换流站、交流系统、直流系统和控制系统。LCC换流站控制系统包括锁相环和定直流电流控制器;MMC换流站控制系统包括锁相环、电流矢量控制器(采用定直流电压和定交流电压控制)及环流抑制控制器。
表1 LCC系统参数
Tab.1 Parameters of LCC system

参数数值 额定交流母线电压/kV345 交流系统短路比SCR13.0∠85° 额定容量/MW1 000 换流变压器漏抗(pu)0.18 锁相环KpPLL_1=10, KiPLL_1=50 定直流电流控制器KpIdc=1, KiIdc=100 电流测量时间常数/msTmIdc=5
表2 MMC系统参数
Tab.2 Parameters of MMC system

参数数值 交流系统短路比SCR21.5∠85° 额定容量/MW1 000 换流变压器漏抗(pu)0.15 桥臂电感/H桥臂电阻/Ω0.0551 桥臂子模块数量200 子模块电容/F0.01 锁相环KpPLL_2=10, KiPLL_2=50 外环定直流电压控制器KpUdc=3, KiUdc=150 外环定交流电压控制器KpUac=1, KiUac=150 内环d轴电流控制器Kp1=0.5, Ki1=5 内环q轴电流控制器Kp2=0.5, Ki2=5 环流抑制控制器Kpcir=0.1, Kicir=10 电压测量时间常数/msTmud=Tmuq=2 电流测量时间常数/msTmid=Tmiq=0.2
表3 直流系统参数
Tab.3 Parameters of DC system

参数数值 额定直流电压/kV500 LCC直流电抗器/H0.3 线路长度/km500 线路单位长度电阻/(W/km)0.012 7 线路单位长度电感/(mH/km)0.88 线路单位长度电容/(μF/km)0.013
MMC锁相环结构如图3d所示,定义锁相环输出相角为
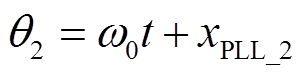 (1)
(1)式中,xPLL_2为锁相环输出角频率与额定角频率偏差的积分。MMC锁相环状态空间方程为
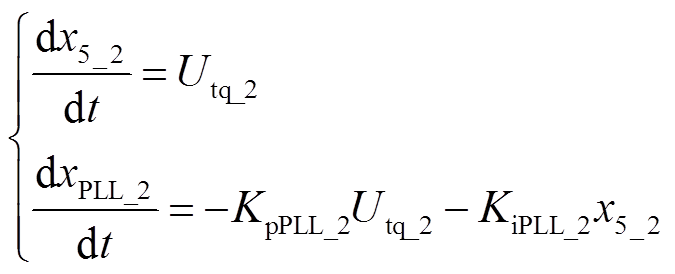 (2)
(2)
式中,x5_2为MMC锁相环的积分状态变量;Utq_2为MMC交流母线电压q轴分量;KpPLL_2、KiPLL_2为锁相环的PI参数。
MMC外环定直流电压控制器结构如图3f所示,其状态空间方程为
 (3)
(3)式中,Udcref为外环定直流电压参考值;Udc_2为MMC直流侧电压实际值;Idref为内环d轴电流控制器指令值;KpUdc、KiUdc为定直流电压控制器的PI参数;x3_2为外环定直流电压控制的积分状态变量。
式(1)~ 式(3)仅对附加频率-电压阻尼控制(详见2.1节)所涉及的部分状态空间模型进行介绍,模型其余部分在文献[16]中已有较为详细的描述,故不再详细展开。对状态空间模型在平衡点处进行线性化,即可得到混合直流输电系统的小信号模型,其形式为
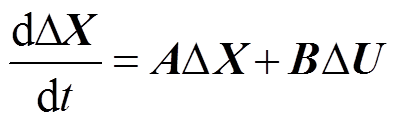 (4)
(4)式中,A为45×45阶系统状态矩阵;B为45×3阶输入矩阵;X为状态变量;U为输入变量。受篇幅限制,此处不再给出矩阵A、B的详细表达式。
基于式(4)所示的小信号模型,本节分析了联接极弱受端交流系统时系统的小信号稳定性。初始状态时,混合直流输电系统运行于表1~表3所示的额定运行工况。保持其他参数不变,将逆变侧MMC所联交流系统短路比SCR2由1.5减小至0.95,系统的根轨迹如图4所示。
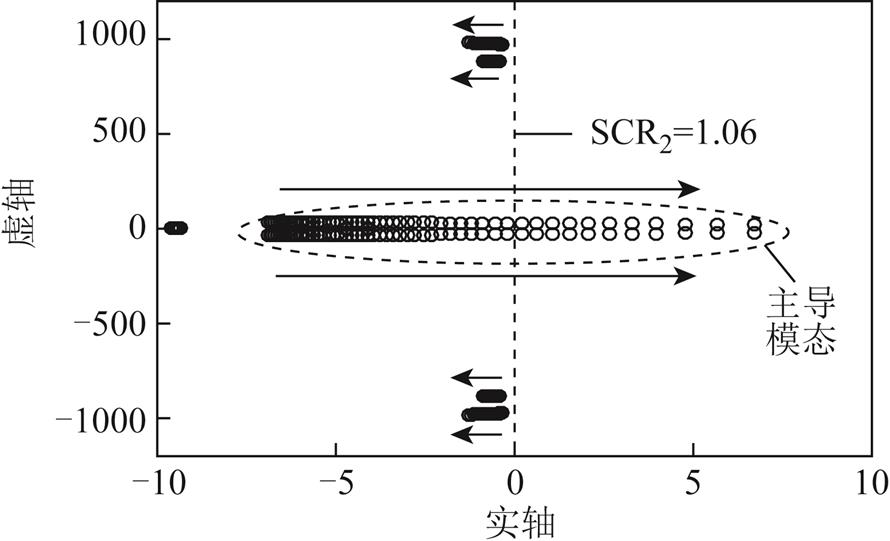
图4 交流系统短路比SCR2由1.5减小至0.95时系统的根轨迹
Fig.4 Eigenvalue locus of the system with SCR2 variation (1.5→0.95)
由图4可知,SCR2减小过程中,主导模态逐渐靠近虚轴,系统稳定性逐渐减弱,当SCR2<1.06时,主导模态穿越虚轴进入复平面的右半平面,系统出现小信号失稳现象。因此,能够使系统稳定运行的SCR2的最小值为1.06,即逆变侧MMC所联交流系统的临界短路比为SCR2min=1.06。
为验证以上特征根分析结果,基于PSCAD仿真平台进行如下仿真研究:初始时,系统运行于额定运行工况,2.0s<t<3.0s时,SCR2由1.5斜坡下降至1.0,此过程中系统传输有功功率响应如图5所示。由图5可知,SCR2降低至1.0后,系统有功功率逐渐振荡发散,说明LCC-MMC型混合直流输电系统在联接极弱受端交流系统时容易出现小信号失稳现象,同时验证了临界短路比SCR2min=1.06的正确性。
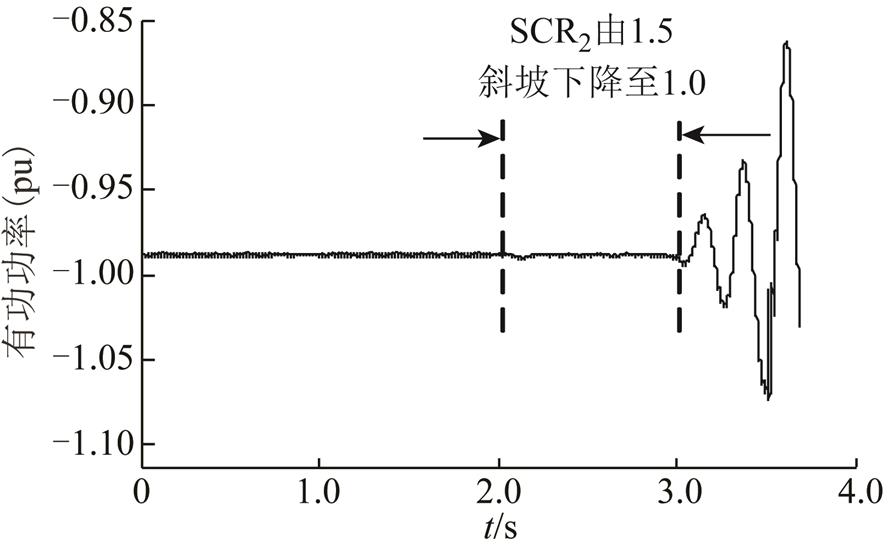
图5 交流系统短路比SCR2变化时系统有功功率响应
Fig.5 Active power response with SCR2 variation
基于1.2节的分析结果,本节进一步对图4所示的导致系统发散的主导模态进行参与因子分析。以参与程度最高的状态变量为基准,对各状态变量的参与程度进行标幺化,得到了SCR2为临界值1.06时各状态变量的参与度柱形图,如图6所示。
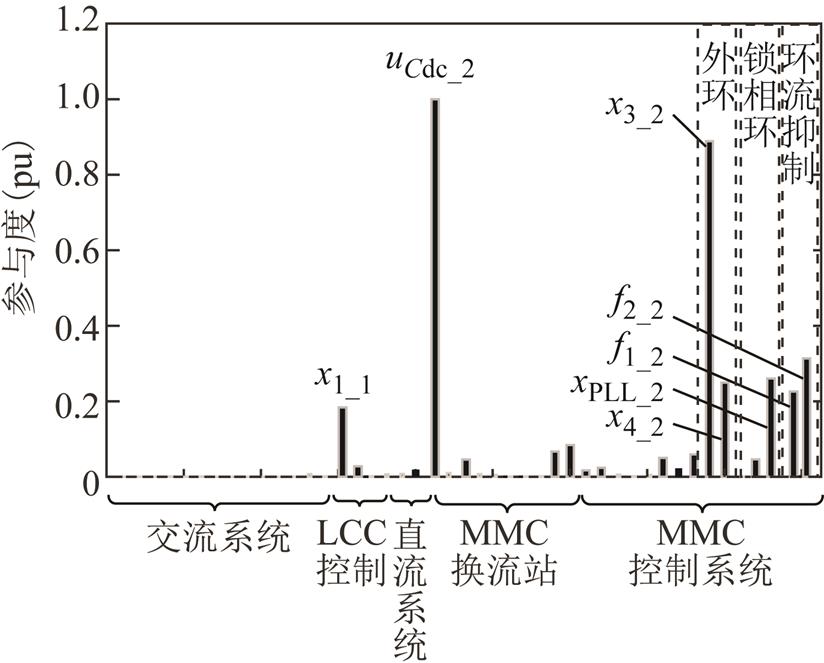
图6 SCR2=1.06时状态变量参与度柱形图(临界稳定状态)
Fig.6 Participation column diagram of state variables in SCR2=1.06(critical stable state)
由图6可知,SCR2=1.06时导致系统发散的主导模态中,参与程度较高的状态变量来源于LCC定电流控制、MMC换流站子模块电容电压直流分量和MMC控制系统,各主要参与状态变量及物理意义见表4。
表4 SCR2=1.06时主要参与状态变量及其物理意义
Tab.4 Major participation state variables and their physical meanings in SCR2=1.06

主要参与状态变量参与度(pu)物理意义 x1_10.185LCC定电流控制 1.0子模块电容电压直流分量 x3_20.891MMC外环定直流电压控制 x4_20.249MMC外环定交流电压控制 xPLL_20.254MMC换流站锁相环 f1_20.24MMC环流抑制控制(d轴) f2_20.328MMC环流抑制控制(q轴)
综合考虑如下两个方面:①锁相环作为主电路和控制系统的主要桥梁,通过锁相为控制系统提供参考频率和相位,其弱系统下的动态特性对系统稳定性有关键影响[17-22];②MMC的定直流电压控制是混合系统有功功率平衡和稳定传输的基础,因此将从MMC定直流电压控制器和锁相环的角度出发,来提高混合系统的小信号稳定性。
基于上述分析,本文提出了附加频率-电压阻尼控制(Supplementary Frequency-Voltage Damping Control, SFVDC),其原理如图3c所示。该控制引入附加阻尼系数Kd,将其与逆变站MMC锁相环的输出角频率偏差值相乘,产生附加直流电压阻尼分量,引入到MMC换流站外环定直流电压控制器中,用以抑制极弱受端交流系统场景下出现的系统小信号失稳现象,提升LCC-MMC型混合直流输电系统的小信号稳定性。
由图3c可知,建立含SFVDC的LCC-MMC型混合直流输电系统小信号模型,仅需将式(3)所示的MMC外环定直流电压控制的状态空间方程修改为
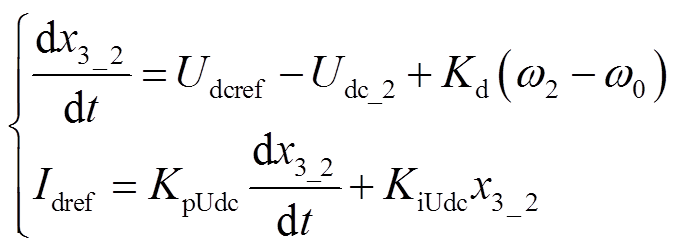 (5)
(5)式中,Kd为附加阻尼系数;w2为MMC锁相环输出角频率,即为式(1)中锁相环输出相角θ2的微分。
将包含式(5)的LCC-MMC型混合直流输电系统的状态空间模型在特定运行点处线性化后即可得到含SFVDC的系统小信号模型。
为了验证含SFVDC的LCC-MMC型混合直流输电系统小信号模型的正确性,在整流侧LCC直流电流参考值Idcref阶跃时,对比了基于Matlab小信号模型和基于PSCAD详细电磁暂态模型的动态响应特性。
系统初始时运行于额定工况,附加阻尼系数Kd=0.5;t=3.0s时,LCC直流电流参考值Idcref从1.0(pu)阶跃至0.95(pu);t=4.0s时,Idcref从0.95(pu)阶跃至1.0(pu)。此过程中系统动态响应对比结果如图7所示。由图7可知,基于Matlab小信号模型(SSM)和基于PSCAD详细电磁暂态模型(EMT)的动态响应具有良好的一致性,验证了含SFVDC的系统小信号模型的正确性。
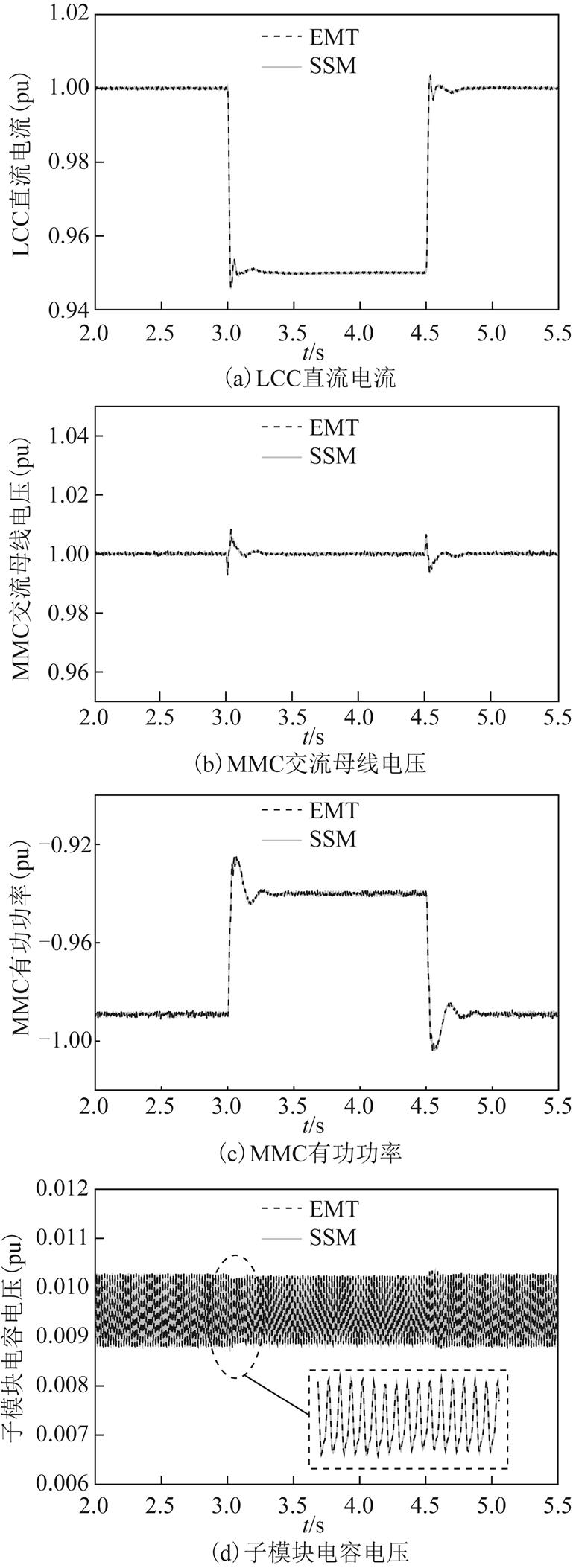
图7 系统在Idcref阶跃下的动态响应特性对比
Fig.7 Comparison of dynamic responses characteristics of the system under Idcref step
本节基于2.2节所述的含SFVDC的系统小信号模型,首先研究了极弱受端交流系统场景下SFVDC对系统小信号稳定性的影响;然后基于PSCAD电磁暂态模型,验证了极弱受端交流系统场景下SFVDC对提升系统小信号稳定性的有效性;最后分析了SFVDC对受端交流系统临界短路比的影响。
由1.2节分析可知,未投入SFVDC时,系统在联接极弱受端交流系统时(SCR2<1.06)出现小信号失稳现象。为了研究极弱受端交流系统下SFVDC对系统小信号稳定性的影响,现以SCR2=1.0为例,分析投入SFVDC前后系统特征根的变化。
阻尼系数Kd由0增大至5时,系统的根轨迹如图8所示。由图8可知,系统未投入SFVDC时(Kd=0),模态21(下文中表5所示)的特征根处于右半平面,系统不能稳定运行。投入SFVDC后,随着Kd的增大,模态21向负实轴方向移动,当Kd>1.90时,模态21穿越虚轴进入左半平面,系统稳定运行;与此同时,模态9(下文中表5所示)向实轴正方向移动,Kd>4.14时,模态9穿越虚轴进入右半平面,系统失稳。

图8 Kd变化时系统的根轨迹(SCR2=1.0)
Fig.8 Eigenvalue locus of the system with Kd variation (SCR2=1.0)
上述结果表明,在极弱受端交流系统下,SFVDC的投入可以提升系统的小信号稳定性,同时在本文的算例中附加阻尼系数Kd有一定的取值范围(1.90<Kd<4.15)。若Kd过小,SFVDC所提供的附加阻尼较小,无法充分发挥其作用;若Kd过大,可能出现新的不稳定模态,从而诱发LCC-MMC型混合直流输电系统的失稳现象。
为了进一步分析极弱受端交流系统下SFVDC的有效性,当SCR2=1.0时,对以下两个案例进行模态对比研究:Case1 混合直流输电系统未投入SFVDC(Kd=0);Case2 混合直流输电系统投入SFVDC(Kd=3.0),模态对比结果见表5。表5给出了系统各个模态的特征根、振荡频率及阻尼比,SCR2=1.0时导致系统失稳的主导模态为模态21。
表5 SCR2=1.0时投入SFVDC前后系统模态对比
Tab.5 Comparison of system modes before and after SFVDC put into use in SCR2=1.0

模态Case 1(Kd=0)Case 2(Kd=3) 特征根振荡频率/Hz阻尼比特征根振荡频率/Hz阻尼比 1-9 996.70.01.00-9 992.20.01.00 2-3 243.8±j5 515.9877.90.51-3 243.8±j5 515.9877.90.51 3-3 102.8±j4 734.3753.50.55-3 102.8±j4 734.3753.50.55 4-4 885.9±j55.88.91.00-4 879.8±j42.46.81.00 5-500.7±j1 767.1281.20.27-500.7±j1 767.0281.20.27 6-467.8±j1 081.6172.10.40-467.8±j1 081.6172.10.40 7-101.9±j1 056.0168.10.10-101.9±j1 055.9168.00.10 8-1.0±j978.9155.80.00-1.0±j978.9155.80.00 9-0.8±j881.3140.30.00-0.2±j881.0140.20.00 10-24.9±j749.9119.40.03-24.7±j750.0119.40.03 11-35.4±j392.362.40.09-37.8±j393.462.60.10 12-15.3±j381.660.70.04-16.2±j381.260.70.04 13-135.2±j278.144.30.44-133.0±j284.245.20.42 14-20.5±j298.647.50.07-29.2±j317.850.60.09 15-43.8±j314.250.00.14-43.8±j314.250.00.14 16-83.6±j149.023.70.49-86.1±j154.024.50.49 17-78.5±j113.618.10.57-79.4±j112.217.90.58 18-116.30.01.00-116.60.01.00 19-84.40.01.00-86.20.01.00 20-29.6±j35.65.70.64-27.2±j31.95.10.65 212.6±j27.24.3-0.10-1.5±j22.73.60.07 22-4.7±j4.90.80.69-4.5±j5.90.90.61 23-4.1±j4.90.80.64-4.7±j4.90.80.70 24-11.60.01.00-12.00.01.00 25-9.50.01.00-9.40.01.00
由表5可知,Case1中模态21阻尼比为负值(-0.10),系统不能稳定运行且振荡频率为4.3Hz;Case2中模态21的阻尼比为正值(0.07),系统可以稳定运行。由上述分析可知,在极弱受端交流系统下,SFVDC的投入可以增强系统阻尼,有效提升系统的小信号稳定性。
为了验证3.1节的理论分析结果,本节基于PSCAD电磁暂态模型进行以下仿真研究:t=0s时,系统运行于表1~表3所示的额定运行工况,此时系统未投入SFVDC;2.0s<t<3.0s时,SCR2由1.5逐渐下降至1.0;t=3.5s时投入SFVDC控制,附加阻尼系数Kd=3.0。此过程中系统动态响应特性如图9所示。
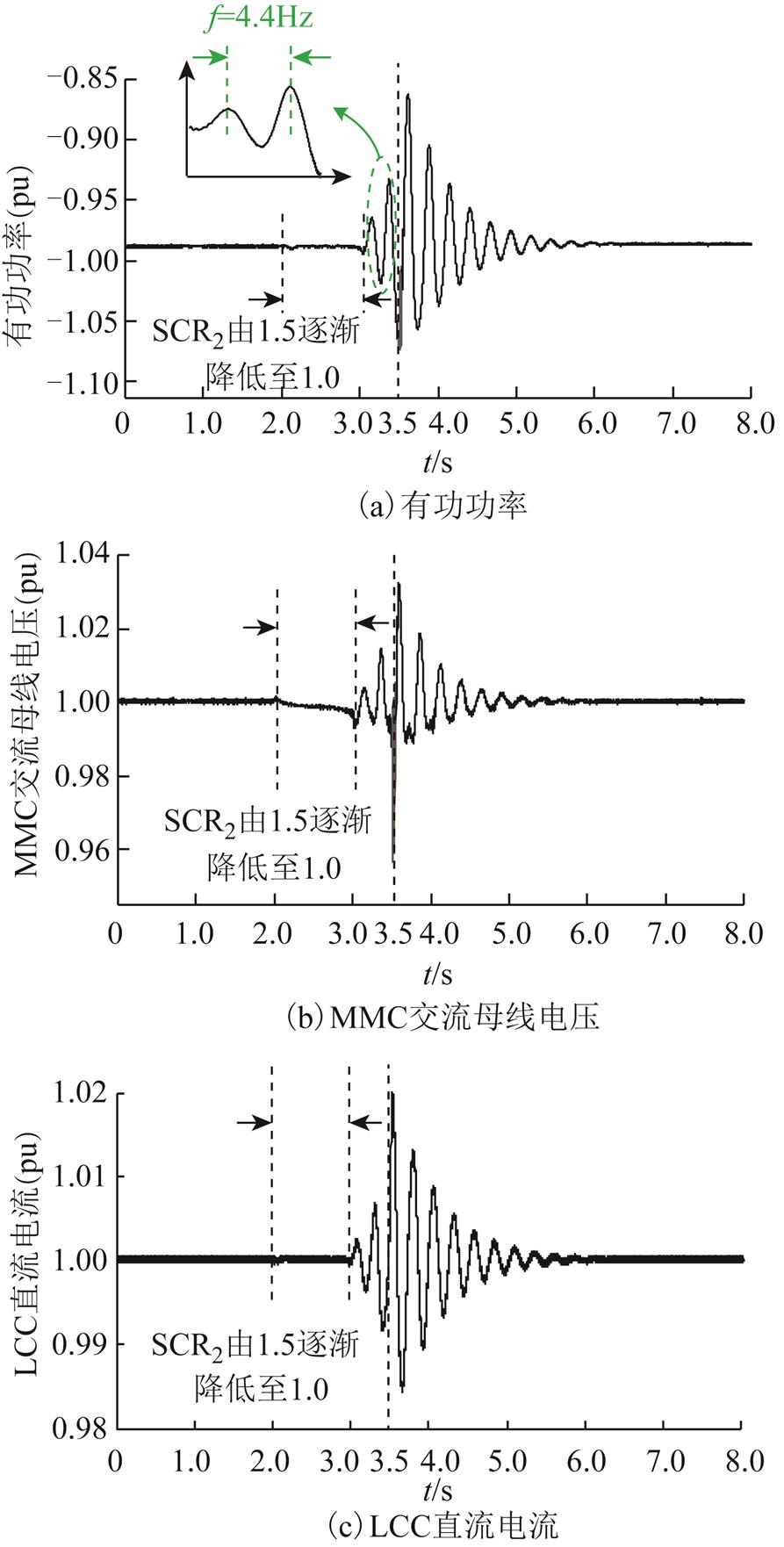
图9 SCR=1.0时系统动态响应特性
Fig.9 Dynamic responses characteristics of the system in SCR=1.0
由图9可知,未投入SFVDC时,SCR2降低至1.0后,系统有功功率、MMC交流母线电压和LCC直流电流逐渐振荡失稳,振荡频率为4.4Hz,与表5中模态21的振荡频率(4.3Hz)一致;投入SFVDC后系统逐渐振荡收敛并恢复稳定运行状态。由此说明本文所提SFVDC可有效抑制极弱受端交流系统场景下容易出现的系统小信号失稳现象,验证了本文所提控制对于提高系统小信号稳定性的有效性。
LCC-MMC型混合直流输电系统受端交流系统所允许的最小短路比(即临界短路比SCR2min)越低,表明系统在联接弱受端交流系统时保持稳定运行的能力越强。为了研究所提出的SFVDC方法对受端交流系统临界短路比的影响,在投入SFVDC时逐渐改变附加阻尼系数Kd,观察SCR2min随Kd的变化趋势,其结果如图10所示。

图10 Kd变化时的SCR2min
Fig.10 SCR2min with Kd variation
由图10可知,在Kd由0变化至4的过程中,SCR2min随着Kd的增大而有所降低(ΔSCR2min=0.1)。同时可以观察到,点A(0,1.06)表明,系统未投入SFVDC时SCR2min=1.06,与1.2节图4的分析结果吻合;点B(1.91,1.0)表明,Kd增加至1.91时,SCR2min可以降低至1.0,此结果与3.1节图8的分析结果一致,因此进一步验证了前述特征根结果的正确性。
以上结果表明,SFVDC能够降低受端交流系统临界短路比SCR2min,使得系统能够在联接更弱的受端交流系统时仍保持稳定运行,降低了系统稳定运行对于受端交流系统强度的要求。
本节研究了在极弱受端交流系统下(SCR2=1.0),投入SFVDC控制后LCC-MMC型混合直流系统在较大有功功率扰动下的动态响应特性。基于PSCAD电磁暂态模型进行以下仿真研究:初始时,系统稳定运行于SCR2=1.0,Kd=3.0工况,需要注意的是,若不投入SFVDC,系统无法在SCR2=1.0的工况下稳定运行;接着对整流侧 LCC 直流电流参考值Idcref进行阶跃设置,见表6,以此模拟系统中的有功功率扰动。Idcref阶跃过程中系统的动态响应特性如图11所示。
表6 SCR2=1.0时仿真验证的阶跃设置
Tab.6 Step setting of simulation validation in SCR2=1.0

时间/s直流电流参考值Idcref 1.0从1.0(pu)阶跃至0.75(pu) 2.0从0.75(pu)阶跃至0.50(pu) 4.0从0.50(pu)阶跃至0.60(pu) 5.0从0.60(pu)阶跃至0.70(pu) 6.0从0.70(pu)阶跃至0.85(pu)
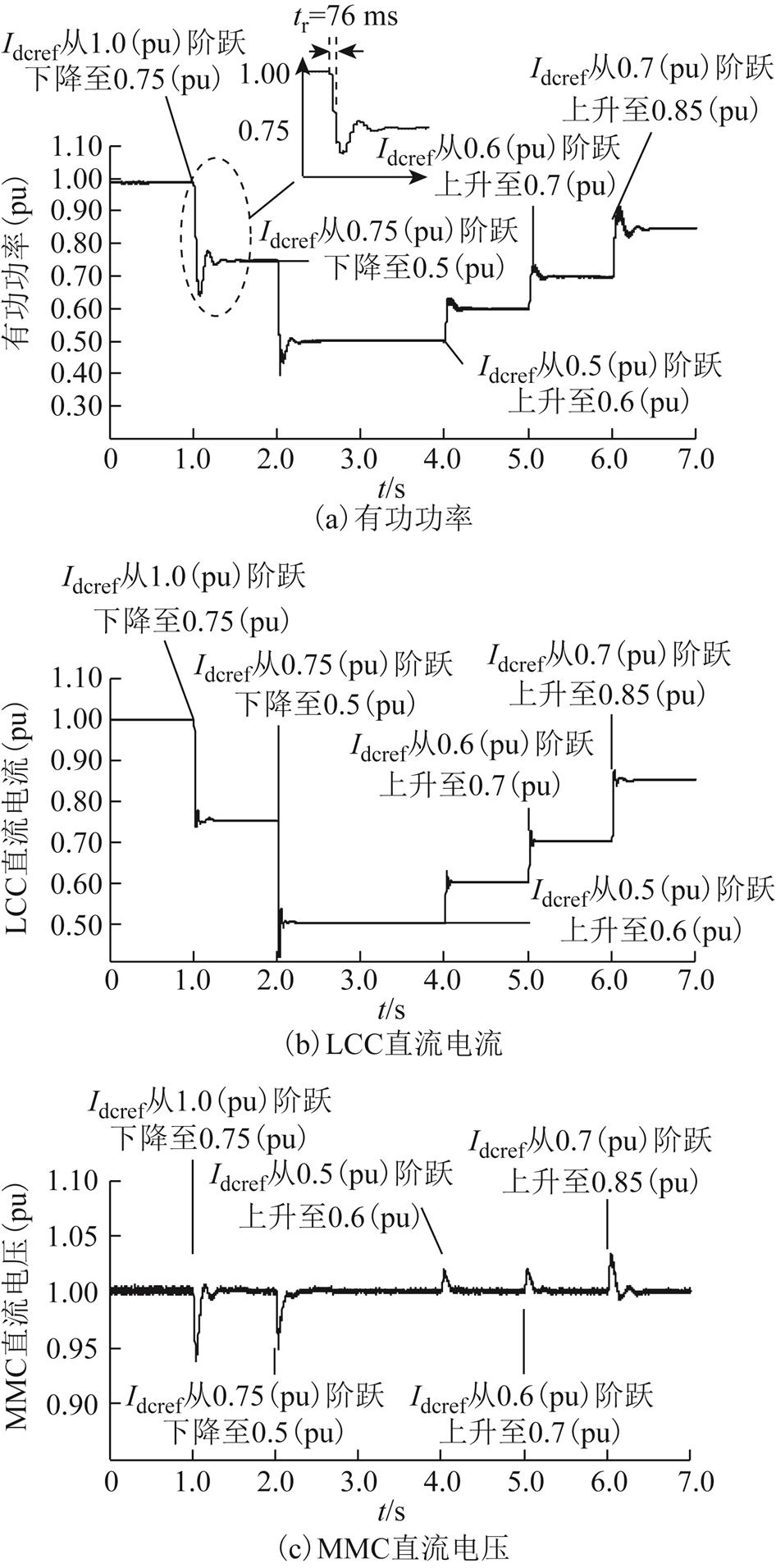
图11 SCR2=1.0时系统在Idcref阶跃下的动态响应特性
Fig.11 Dynamic response characteristics of the system under Idcref step in SCR2=1.0
由图11可知,t=1.0s时Idcref由1.0(pu)阶跃下降至0.75(pu)后,系统传输有功功率能够在较短时间内过渡到新的稳定状态(上升时间为tr=76ms),动态响应特性良好,同时可以观察到LCC直流电流响应和MMC直流电压响应均具有良好的动态特性。
同样地,在其他时刻Idcref进行阶跃后,系统均能够迅速且平稳地过渡到新的稳定运行状态。以上结果表明,在极弱受端交流系统(SCR2=1.0)情况下,含SFVDC的LCC-MMC型混合直流输电系统在有功功率大扰动下仍能够稳定运行,且具有良好的动态响应特性。
本节研究了在受端交流系统故障情况下含SFVDC的LCC-MMC型混合直流系统的暂态响应特性。基于PSCAD电磁暂态模型进行以下仿真研究:初始时,系统运行额定工况,SFVDC处于投入状态(Kd=3.0);t=0.2s时MMC换流站交流母线处发生单相(A相)直接接地短路故障,故障持续时间为0.1s,随后故障清除。上述过程中系统的暂态响应特性如图12所示。

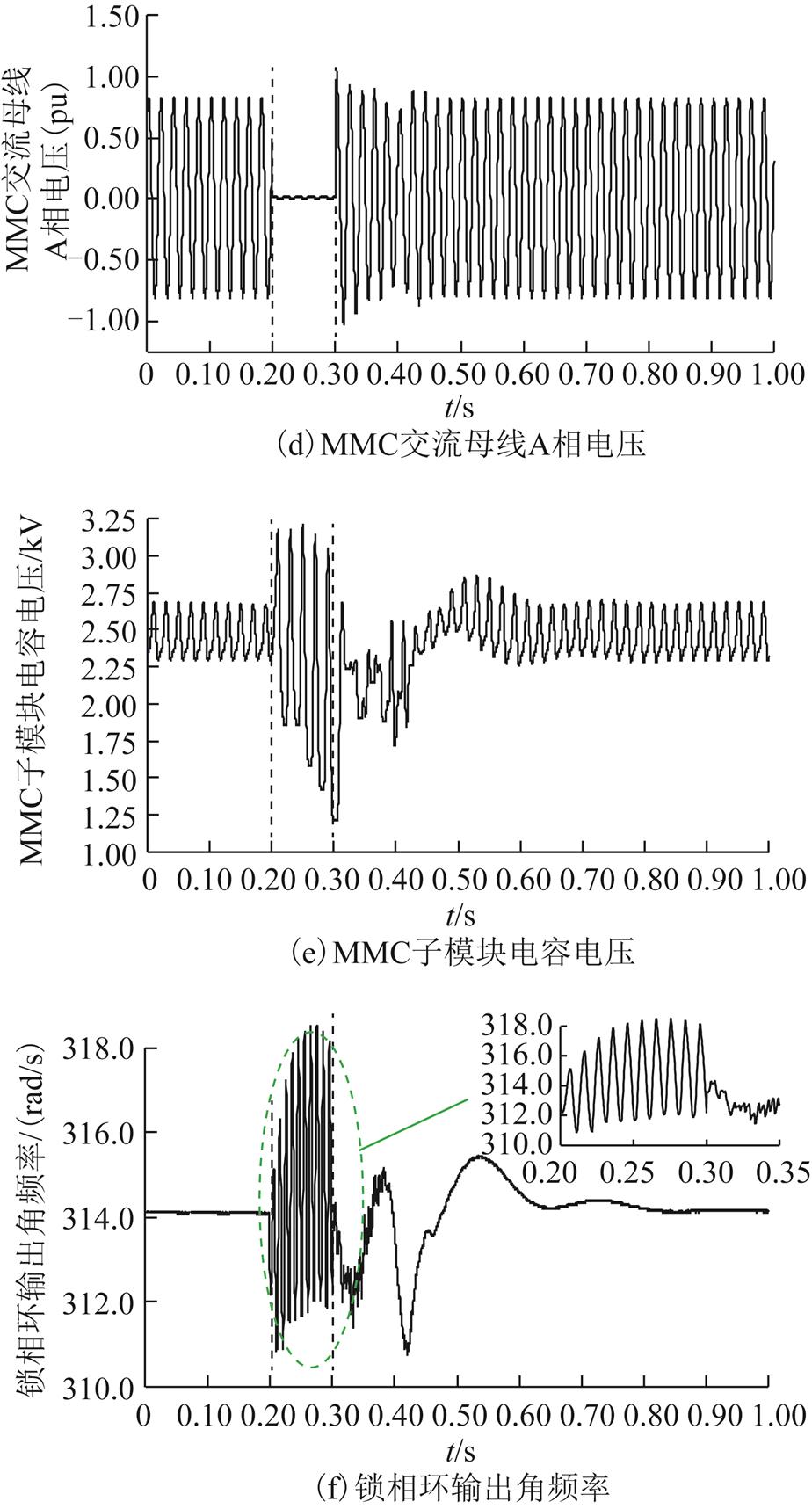
图12 系统在受端交流母线单相直接接地故障下的暂态响应特性
Fig.12 Transient response characteristics of the system under single-phase to ground fault at receiving AC bus
由图12可知,t=0.2s时发生A相直接接地短路故障后,交流母线A相电压迅速降低至零,LCC直流电流最大值为1.2(pu),MMC直流电压最大值为1.2(pu),MMC子模块电容电压最大值为3.2kV。故障清除后,系统传输有功功率在180ms内即可恢复至0.9(pu),表明含SFVDC的LCC-MMC型混合直流输电系统具有良好的故障恢复特性。
本文针对LCC-MMC型混合直流输电系统在联接极弱受端交流系统时容易发生的系统小信号失稳现象,首先提出了附加频率-电压阻尼控制(SFVDC),建立了含SFVDC的LCC-MMC型混合直流输电系统小信号模型并验证了其正确性;然后,研究了SFVDC对于系统小信号稳定性的影响,验证了极弱受端交流系统下SFVDC的有效性;最后,研究了极弱受端交流系统下含SFVDC系统在较大有功功率扰动下的动态特性及其在受端交流系统故障情况下的暂态响应特性。所得主要结论如下:
1)所提出的SFVDC能够增强系统的阻尼比,有效地抑制联接极弱受端交流系统时系统的小信号失稳现象,提升LCC-MMC型混合直流输电系统的小信号稳定性。
2)所提出的SFVDC能够降低受端交流系统临界短路比,使得系统能够在联接更弱的受端交流系统时保持稳定运行,降低了系统稳定运行对于受端交流系统强度的要求。
3)在极弱受端交流系统下,含SFVDC的LCC-MMC型混合直流输电系统在较大有功功率扰动下仍能够稳定运行,且具有良好的动态响应特性。
4)在受端交流系统故障情况下,含SFVDC的LCC-MMC型混合直流输电系统具有良好的故障恢复特性。
附 录
附表1 图2中各变量及其物理意义
App.Tab.1 Variables in Fig.2 and their physical meanings

变量物理意义 us_1(us_2)交流系统1(交流系统2)电网电压 Ls_1,Rs_1(Ls_2,Rs_2)交流系统1(交流系统2)戴维南等效电感和电阻 ut_1(Utd_1,Utq_1),ut_2(Utd_2,Utq_2)LCC、MMC公共连接点电压 LT_1,RT_1(LT_2,RT_2)换流变压器(联接变压器)的等效电感和电阻 is_1(Isd_1,Isq_1),is_2(Isd_2,Isq_2)交流系统1、交流系统2的电流 iv(Ivd_1,Ivq_1)LCC换流站出口的交流电流 Ldc_1(Ldc_2)LCC换流站平波电抗器(MMC换流站限流电抗器) Loh_1,Roh_1(Loh_2,Roh_2)直流线路等效电感和电阻 Coh直流线路等效电容 Idc_1(Idc_2)LCC(MMC)换流站直流电流 Udc_2MMC换流站直流电压 UCdc直流线路等效电容电压
参考文献
[1] 赵畹君. 高压直流输电工程技术[M]. 2版. 北京: 中国电力出版社, 2011.
[2] Son H I, Kim H M. An algorithm for effective mitigation of commutation failure in high voltage direct current systems[J]. IEEE Transactions on Power Delivery, 2016, 31(4): 1437 - 1446.
[3] Nami A, Liang J, Dijkhuizen F, et al. Modular multilevel converters for HVDC applications: review on converter cells and functionalities[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 18-36.
[4] Dekka A, Wu B, Fuentes R L, et al. Evolution of topologies, modeling, control schemes, and applications of modular multilevel converters[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2017, 5(4): 1631-1656.
[5] 肖湘宁, 李伟, 罗超, 等. 特高压直流孤岛运行特性与稳定控制研究综述[J]. 电工技术学报, 2017, 32(10): 1-11. Xiao Xiangning, Li Wei, Luo Chao, et al. Survey on operational characteristics and stability control of ultra-HVDC transmission system in islanded mode[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 1-11.
[6] 徐殿国, 刘瑜超, 武健. 多端直流输电系统控制研究综述[J]. 电工技术学报, 2015, 30(17): 1-12. Xu Dianguo, Liu Yuchao, Wu Jian. Review on control strategies of multi-terminal direct current transmission system[J]. Transactions of China Electrotechnical Society, 2015, 30(17): 1-12.
[7] 姚骏, 谭义, 裴金鑫, 等. 模块化多电平变流器高压直流输电系统直流故障改进控制策略[J]. 电工技术学报, 2018, 33(14): 3306-3318. Yao Jun, Tan Yi, Pei Jinxin, et al. Improved control strategy for DC fault in modular multi-level converter HVDC system[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3306-3318.
[8] 李建国, 刘文华, 王久和, 等. 基于LCC和双钳位MMC混联高压直流输电的实验[J]. 电工技术学报, 2018, 33(16): 3677-3685. Li Jianguo, Liu Wenhua, Wang Jiuhe, et al. Experiment of hybrid high voltage direct current transmission based on LCC and clamp double sub module MMC[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3677-3685.
[9] 饶宏, 洪潮, 周保荣, 等. 乌东德特高压多端直流工程受端采用柔性直流对多直流集中馈入问题的改善作用研究[J]. 南方电网技术, 2017, 11(3): 1-5. Rao Hong, Hong Chao, Zhou Baorong, et al. Study on improvement of VSC-HVDC at inverter side of Wudongde multi-terminal UHVDC for the problem of centralized multi-infeed HVDC[J]. Southern Power System Technology, 2017, 11(3): 1-5.
[10] 陈凌云, 程改红, 邵冲, 等. LCC-MMC型三端混合直流输电系统控制策略研究[J]. 高压电器, 2018, 54(7): 146-152. Chen Lingyun, Cheng Gaihong, Shao Chong, et al. Research on control strategy for a 3-terminal LCC-MMC HVDC transmission system[J]. High Voltage Apparatus, 2018, 54(7): 146-152.
[11] 卢雨涵. LCC-MMC型混合直流输电系统的建模与控制策略研究[D]. 武汉: 湖北工业大学, 2018.
[12] 时伯年, 洪潮, 张野, 等. LCC-MMC三端混合直流输电系统整流站交流故障穿越协调控制策略[J]. 南方电网技术, 2017, 11(7): 11-18. Shi Bonian, Hong Chao, Zhang Ye, et al. Rectifier side AC fault ride-through coordination control strategy for three-terminal LCC-MMC hybrid HVDC system[J]. Southern Power System Technology, 2017, 11(7): 11-18.
[13] 蔡宜君, 文明浩, 陈玉, 等. LCC-MMC混合直流输电系统整流侧故障穿越控制策略[J]. 电力系统保护与控制, 2018, 46(14): 1-8. Cai Yijun, Wen Minghao, Chenyu, et al. Control strategy of LCC-MMC hybrid HVDC system under rectifier side fault[J]. Power System Protection and Control, 2018, 46(14): 1-8.
[14] 时伯年, 洪潮, 孙刚, 等. 交流不对称故障下的LCC-MMC混合直流系统输送功率提升策略研究[J]. 电力系统保护与控制, 2017, 45(20): 73-78. Shi Bonian, Hong Chao, Sun Gang, et al. Research on power transmission enhancement strategy of LCC-MMC hybrid HVDC system under AC symmetric fault[J]. Power System Protection and Control, 2017, 45(20): 73-78.
[15] 杨洋, 王瑶, 李浩涛, 等. 子模块混合型LCC-MMC混合直流输电系统的启动控制策略[J]. 电力系统保护与控制, 2018, 46(8): 58-64. Yang Yang, Wang Yao, Li Haotao, et al. Start-up control strategies for the cell-hybrid LCC-MMC hybrid HVDC system[J]. Power System Protection and Control, 2018, 46(8): 58-64.
[16] 郭春义, 殷子寒, 王烨, 等. LCC-MMC型混合直流输电系统小干扰动态模型[J]. 中国电机工程学报, 2018, 38(16): 4705-4714, 4975. Guo Chunyi, Yin Zihan, Wang Ye, et al. Small-signal dynamic model of LCC-MMC hybrid HVDC system[J]. Proceedings of the CSEE, 2018, 38(16): 4705-4714, 4975.
[17] Egea-Alvarez A, Fekriasl S, Hassan F, et al. Advanced vector control for voltage source converters connected to weak grids[J]. IEEE Transactions on Power Systems, 2015, 30(6): 3072-3081.
[18] Arani M F M, Mohamed A R I. Analysis and performance enhancement of vector-controlled VSC in HVDC links connected to very weak grids[J]. IEEE Transactions on Power Systems, 2017, 32(1): 684-693..
[19] Zhang L, Harnefors L, Nee H P. Power-synchronization control of grid-connected voltage-source converters[J]. IEEE Transactions on Power Systems, 2010, 25(2): 809-820.
[20] 苑宾, 李探, 许建中, 等. 联接弱交流电网MMC系统小信号稳定性分析[J]. 中国电机工程学报, 2017, 37(18): 5339-5349, 5533. Yuan Bin, Li Tan, Xu Jianzhong, et al. Small-signal stability analysis of modular multilevel converter connected to a weak AC system[J]. Proceedings of the CSEE, 2017, 37(18): 5339-5349, 5533.
[21] 喻悦箫, 刘天琪, 王顺亮, 等. 基于平均值模型的双端MMC-HVDC系统小信号建模[J]. 中国电机工程学报, 2018, 38(10): 2999-3006, 3150. Yu Yuexiao, Liu Tianqi, Wang Shunliang, et al. Small signal modeling of two-terminal MMC-HVDC based on AVM model[J]. Proceedings of the CSEE, 2018, 38(10): 2999-3006, 3150.
[22] 李探, 赵成勇, Gole A M. MMC-HVDC内部谐波模态识别及其稳定性分析[J]. 中国电机工程学报, 2017, 37(8): 2185-2196. Li Tan, Zhao Chengyong, Gole A M. Identification and stability analysis of the internal harmonic modes of the MMC-HVDC system[J]. Proceedings of the CSEE, 2017, 37(8): 2185-2196.
[23] 马燕峰, 刘海航, 俞人楠, 等. 考虑锁相环的双馈风力发电机组无源控制[J]. 电工技术学报, 2017, 32(24): 224-232. Ma Yanfeng, Liu Haihang, Yu Rennan, et al. Passivity-based control for doubly-fed induction generator considering the phase-locked loop[J]. Transactions of China Electrotechnical Society, 2017, 32(24): 224-232.
[24] 邵冰冰, 赵书强, 高本锋, 等. 连接弱交流电网的VSC-HVDC失稳机理及判据研究[J]. 电工技术学报, 2019, 34(18): 3884-3896. Shao Bingbing, Zhao Shuqiang, Gao Benfeng, et al. Instability mechanism and criterion analysis of VSC-HVDC connected to the weak AC power grid[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3884-3896.
Supplementary Frequency-Voltage Damping Control for LCC-MMC Hybrid HVDC System Connected to Extremely Weak Receiving AC Grid
Abstract In this paper, a novel supplementary frequency-voltage damping control (SFVDC) is proposed to suppress the small-signal instability of line commutated converter-modular multilevel converter (LCC-MMC) hybrid HVDC system under extremely weak receiving AC grid. The proposed control approach generates supplementary DC voltage damping component based on the angular frequency deviation from the phase-locked loop (PLL) of MMC station, and the component is then introduced into the outer loop constant DC voltage controller. The proposed control is used to suppress the small-signal instability of the LCC-MMC hybrid HVDC system connected to extremely weak receiving AC grid, so as to improve the small-signal stability of the system. The results show that the proposed SFVDC method can effectively suppress the small-signal instability under extremely weak receiving AC grid and reduce the requirements of the receiving AC grid strength for stable operation. In addition, the good dynamic responses of the system were also obtained under large power disturbance and single-phase to ground fault at receiving AC bus.
keywords:Line commutated converter (LCC), modular multilevel converter (MMC), hybrid HVDC system, supplementary frequency-voltage damping control (SFVDC), weak receiving AC grid, small-signal stability
DOI:10.19595/j.cnki.1000-6753.tces.190525
中图分类号:TM712; TM722
王燕宁 女,1996年生,硕士研究生,研究方向为直流输电等。E-mail:wangyanning913@163.com
郭春义 男,1984年生,博士,副教授,博士生导师,研究方向为直流输电、FACTS等。E-mail:chunyiguo@outlook.com(通信000作者)
国家自然科学基金(51877077)、国家电网公司总部科技项目(±800kV特高压柔性直流输电换流阀和控制保护关键技术研究)资助。
收稿日期2019-05-06
改稿日期2019-06-03
(编辑 赫蕾)