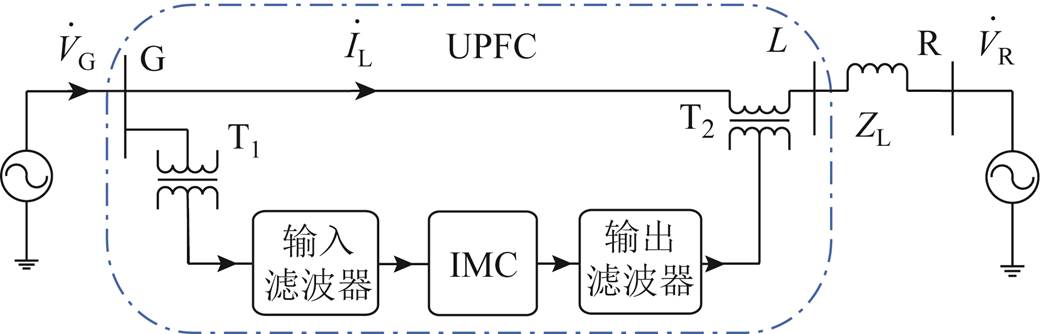
图1 两节点网络IMC-UPFC原理
Fig.1 The IMC-UPFC schematic diagram in two-bus transmission network
摘要 考虑到现有基于双级矩阵变换器的统一潮流控制器(IMC-UPFC)并联侧无功功率范围的受限问题,提出一种基于模型预测控制(MPC)的IMC-UPFC并联侧无功范围扩展方案。论文推导了IMC-UPFC串联侧线路电流预测模型和并联侧无功预测模型,建立了以控制线路潮流和扩展并联侧无功范围为目标的综合代价函数,通过合理地选取使综合代价函数最小化的IMC的最优开关状态,以达到其控制目标。MPC控制策略具备算法简单及无需额外设置调制规则等优势。两节点网络IMC-UPFC的Matlab/Simulink仿真对比结果表明,所提IMC-UPFC的MPC控制策略有效地扩大了IMC-UPFC并联侧无功范围,进一步证实了该方案的合理性与有效性。
关键词:双级矩阵变换器 统一潮流控制器 模型预测控制 并联侧无功扩展
近年来,随着电力系统的快速发展,降低输电系统投资成本、提升输电系统的传输容量、增强电力系统的安全可靠性能和改善电力系统的暂态稳定性[1-3]成为现代输电系统发展的方向之一,柔性交流输电系统(Flexible AC Transmission Systems, FACTS)也因此受到广泛的关注,得到大力发展。
作为极具潜力、功能强大且灵活通用的FACTS设备之一——统一潮流控制器(Unified Power Flow Controller, UPFC)在现代电力系统潮流控制中展现出良好的动态性能[4-6]。传统的UPFC由两个“背靠背”式连接的“AC-DC”换流器及中间直流电容器组成,而这两个换流器分别通过耦合变压器接入电力系统[7-9]。矩阵变换器(Matrix Converter, MC)是一种新型四象限功率变换器,具有正弦输入/输出电流波形、输入功率因数可控、无需中间直流电容以及功率可双向流动的特点。因此,基于MC的UPFC具备更多优势,譬如:成本降低、体积与质量减小、寿命延长和可靠性增强等,也越来越受到重视[10-12]。MC因省却了中间直流电容,在简化UPFC物理结构和节约设备投资成本的同时仍然保证了其功能的实现,这对于UPFC的研究与应用具有重要意义。
目前,有关UPFC的研究大多聚焦在控制问题。已有的控制方案有多种,其中大多是传统的线性控制策略。文献[9,13-14]提出了一种基于dq坐标系的串、并联侧解耦控制器,可较好地控制线路潮流。文献[15-16]提出一种模糊控制策略,与常规PI控制相比,该方法具有更强的鲁棒性。在文献[9]的基础上,文献[17]提出一种基于状态反馈线性化的非线性控制策略,可以更好地适应系统运行点的大范围变化,能更显著地提高系统故障后的暂态稳定性。
与传统UPFC相比,基于MC的UPFC没有中间储能环节,使其并联侧无功生成机理有着独特的特点。研究表明,MC-UPFC的并联侧无功控制能力与其串联侧的工作状态有关,不仅如此,它还与MC的调制策略存在密切联系。目前,有关MC-UPFC的研究主要集中在潮流控制器的设计和无功控制策略方面。文献[10]提出一种基于单级矩阵变换器-统一潮流控制器(DMC-UPFC)的直接功率控制((Direct Power Control, DPC)方案,该方案较常规PI控制稳定性更好,响应更快。文献[11]提出了DMC-UPFC的线性滑模控制器的设计方案,进一步增强了系统的鲁棒性。然而,这一类方案的研究对象均为DMC,也未考虑UPFC的并联侧无功控制范围。文献[12]提出基于双级矩阵变换器-统一潮流控制器(IMC-UPFC)的dq解耦控制策略,但也并未对UPFC并联侧控制方案与并联侧无功控制范围进行研究。文献[18]提出了基于IMC-UPFC的模型预测控制策略,但该预测控制主要用在潮流控制方面而未涉及系统的并联侧无功生成能力。文献[19]提出了一种基于数学构造法的DMC输入无功扩大方案,与常规SVM调制策略相比,该方案输入侧无功控制范围显著提升。文献[20]提出两种扩大双级矩阵变换器输入侧无功控制范围的调制策略。以上两篇文献对MC的输入无功功率进行了深入分析,但缺乏对输入无功功率应用方面的讨论。
针对IMC-UPFC的潮流控制和并联侧无功功率范围受限问题,本文提出了一种基于模型预测控制的IMC-UPFC并联侧无功控制范围扩展方案。该方案既可实现线路潮流稳态控制,又可显著扩大IMC-UPFC的并联侧无功功率调节范围,为IMC-UPFC提供了一个良好的运行方案。
两节点网络IMC-UPFC的原理如图1所示。IMC-UPFC主要由IMC、输入/输出滤波器及串/并联变压器组成。IMC-UPFC的逆变级通过串联耦合变压器T2(电压比为1∶1)向输电网络注入幅值和相位可调的电压控制线路潮流,该部分等同于静止同步串联补偿器(Static Synchronous Series Compensator, SSSC);而整流级则通过并联的耦合变压器T1(电压比为1∶1)向系统注入或吸收输入无功功率,这部分可等价为并联静止无功补偿器。

图1 两节点网络IMC-UPFC原理
Fig.1 The IMC-UPFC schematic diagram in two-bus transmission network
若忽略输入/输出滤波器的影响,IMC-UPFC的单相等效电路如图2所示,其中IMC的逆变级可等效为受控电压源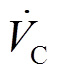 ,整流级可等效为受控电流源
,整流级可等效为受控电流源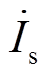 。
。
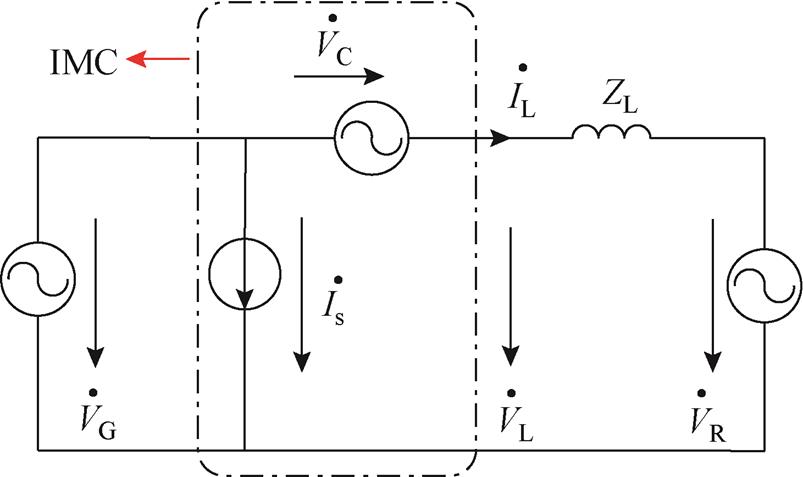
图2 IMC-UPFC单相等效电路
Fig.2 Single-phase equivalent circuit of IMC-UPFC
根据图2,电压平衡方程可描述为
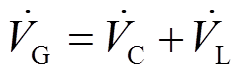 (1)
(1)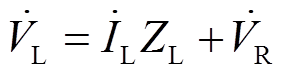 (2)
(2)
式中,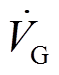 、
、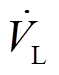 、
、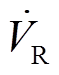 、
、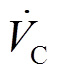 及
及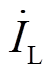 分别为节点G、节点L、节点R、IMC-UPFC串联侧注入电压相量及线路电流相量;
分别为节点G、节点L、节点R、IMC-UPFC串联侧注入电压相量及线路电流相量;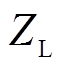 为线路阻抗。
为线路阻抗。
线路节点G处流向传输线路的视在功率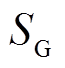 可表示为
可表示为
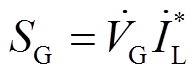 (3)
(3)式中,上标“*”表示复共轭。
联立式(1)~式(3),假设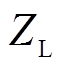 呈纯感性,可得节点G处传输的有功功率
呈纯感性,可得节点G处传输的有功功率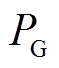 与无功功率
与无功功率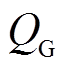 分别为
分别为
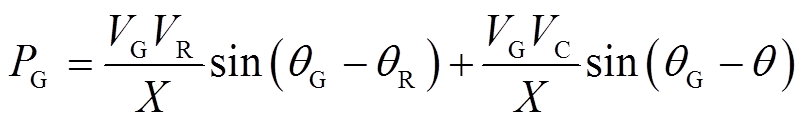 (4)
(4)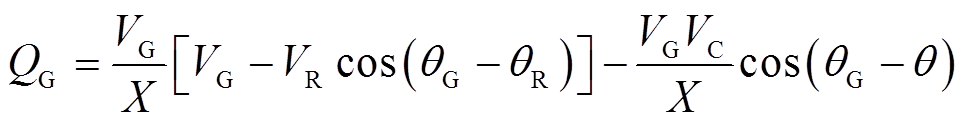 (5)
(5)
式中,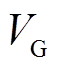 、
、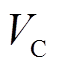 、
、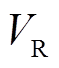 及角度
及角度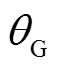 、
、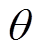 、
、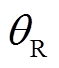 分别为相量
分别为相量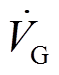 、
、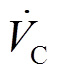 、
、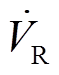 的幅值和相角;
的幅值和相角;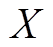 为线路感抗。可以看出,式(4)和式(5)第二项的贡献均来自于受控电压源,即通过控制
为线路感抗。可以看出,式(4)和式(5)第二项的贡献均来自于受控电压源,即通过控制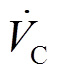 可灵活控制线路潮流。
可灵活控制线路潮流。
根据图1,线路节点G处流向IMC-UPFC并联侧的视在功率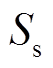 可表示为
可表示为
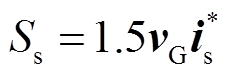 (6)
(6)式中,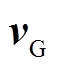 与
与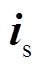 分别为节点G电压与并联侧电流的空间矢量。同理,IMC-UPFC串联侧发出的视在功率
分别为节点G电压与并联侧电流的空间矢量。同理,IMC-UPFC串联侧发出的视在功率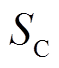 为
为
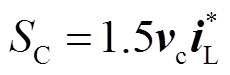 (7)
(7)
式中,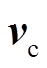 与
与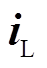 分别为串联侧注入电压与线路电流的空间矢量。
分别为串联侧注入电压与线路电流的空间矢量。
若采用传统空间矢量调制[21],忽略输入滤波器的影响以及开关损耗,IMC-UPFC并联侧无功可表示为
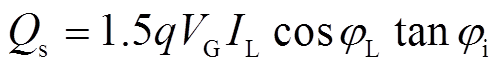 (8)
(8)式中,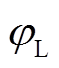 为
为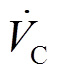 与
与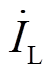 之间的夹角;
之间的夹角;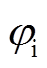 为IMC整流级功率因数角,
为IMC整流级功率因数角,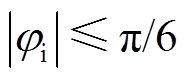 ;
; 为矩阵变换器的电压传输比,可表示为
为矩阵变换器的电压传输比,可表示为
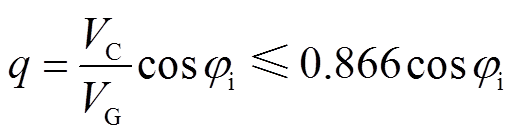 (9)
(9)
根据式(4)、式(5)和式(8)可知,欲调节线路潮流,IMC-UPFC存在两个自由度,其一为串联侧电压,其二为并联侧电流。通常串联侧电压起主要作用,但有时也需要充分利用并联侧无功功率的补偿能力来调节节点G的电压。
然而,由式(8)可知,并联侧无功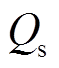 和IMC电压传输比、输出负载角
和IMC电压传输比、输出负载角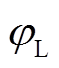 及输入功率因数角
及输入功率因数角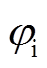 有关,且相互之间存在复杂约束。因此,并联侧无功控制这一自由度在传统调制策略下可发挥的空间不大。为此,本文将提出一种无需调制策略的模型预测控制方案,充分挖掘并联侧无功的控制范围,进一步提升IMC-UPFC的性能。
有关,且相互之间存在复杂约束。因此,并联侧无功控制这一自由度在传统调制策略下可发挥的空间不大。为此,本文将提出一种无需调制策略的模型预测控制方案,充分挖掘并联侧无功的控制范围,进一步提升IMC-UPFC的性能。
IMC-UPFC的整体拓扑如图3所示。输入/输出滤波器均采用二阶LCR结构,前者用来消除输入谐波电流、维持输入电压稳定;后者则是抑制输出电流/电压谐波。
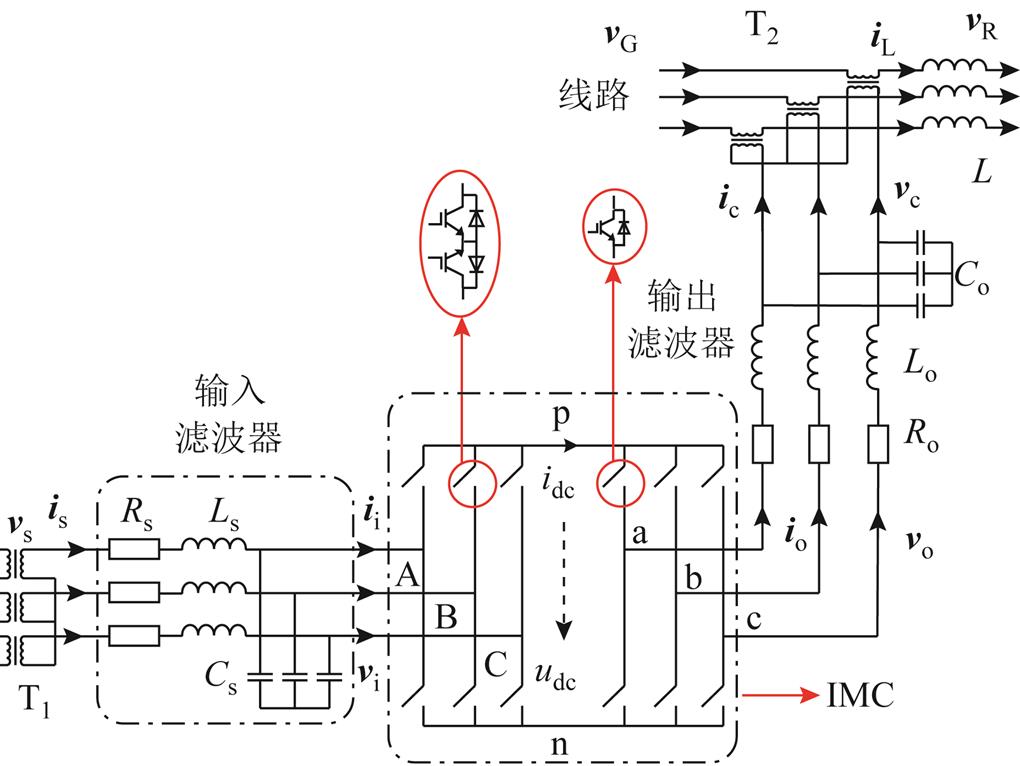
图3 IMC-UPFC整体拓扑
Fig.3 Overall topology of IMC-UPFC
根据图3,可得到IMC-UPFC串联侧的数学模型为
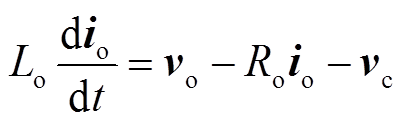 (10)
(10)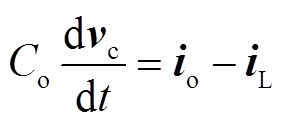 (11)
(11)
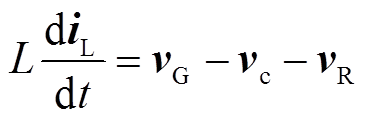 (12)
(12)
式中,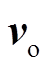 与
与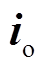 分别为IMC输出电压与电流的空间矢量;
分别为IMC输出电压与电流的空间矢量;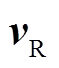 为节点R电压空间矢量;
为节点R电压空间矢量;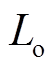 、
、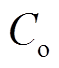 、
、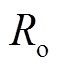 分别为输出滤波器的滤波电感、滤波电容和漏感电阻;
分别为输出滤波器的滤波电感、滤波电容和漏感电阻;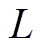 为线路电感。
为线路电感。
同理,根据图3,可得IMC-UPFC并联侧的数学模型为
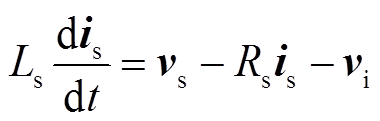 (13)
(13)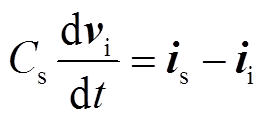 (14)
(14)
式中,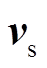 、
、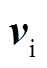 、
、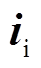 分别为并联侧输入电压、IMC输入电压和电流的空间矢量;
分别为并联侧输入电压、IMC输入电压和电流的空间矢量;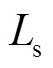 、
、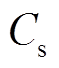 、
、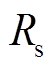 分别为输入滤波器的滤波电感、滤波电容及漏感电阻。
分别为输入滤波器的滤波电感、滤波电容及漏感电阻。
为了保证IMC能够安全稳定运行,IMC的功率开关必须满足以下约束:任意输入两相之间不能短路;任意输出相不能开路;中间直流电压必须上正下负。
IMC的整流级和逆变级开关矩阵可写成
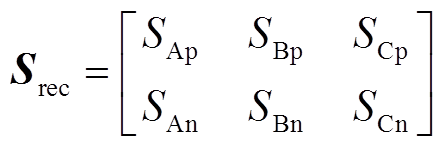 (15)
(15)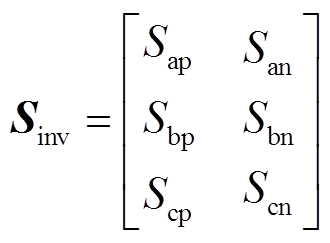 (16)
(16)
式中,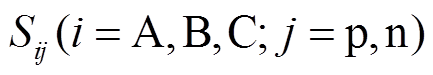 为整流级开关矩阵的开关状态;
为整流级开关矩阵的开关状态;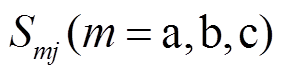 为逆变级开关矩阵的开关状态。开关的闭合与断开状态分别以1和0表示,同时,要服从运行约束:
为逆变级开关矩阵的开关状态。开关的闭合与断开状态分别以1和0表示,同时,要服从运行约束: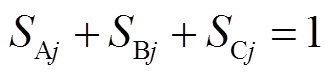 ;
;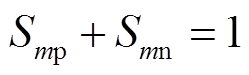 。
。
整流级共有3´3(9)种开关状态,见附表1;逆变侧共有2´2´2(8)种开关状态,见附表2。值得注意的是,为避免中间直流电压上负下正导致逆变级发生短路,整流级在任一控制周期仅需考虑三种有效的开关状态(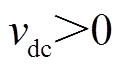 ),因此,IMC实际有3´8(24)种有效的开关状态。
),因此,IMC实际有3´8(24)种有效的开关状态。
中间直流电压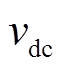 与电流
与电流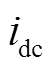 可写为
可写为
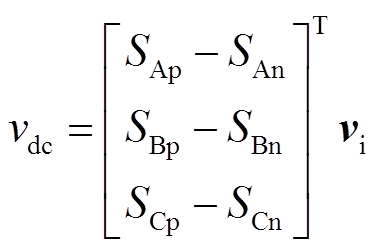 (17)
(17)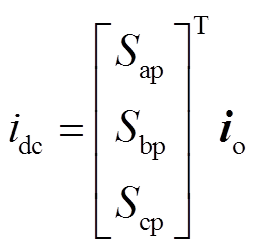 (18)
(18)
根据IMC的拓扑结构,可知IMC的输入输出关系为
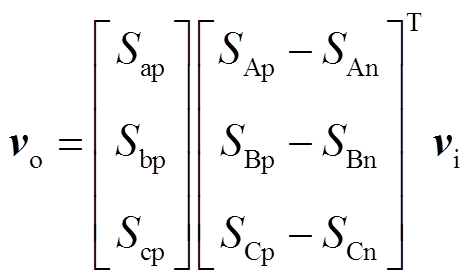 (19)
(19)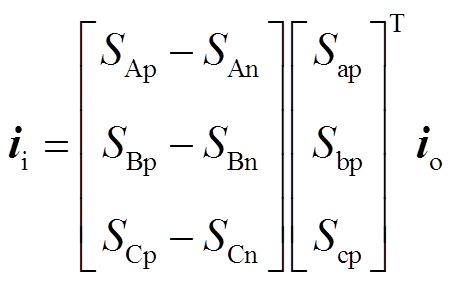 (20)
(20)
IMC-UPFC系统的控制目标为:①通过串联侧获得稳定线路潮流;②通过并联侧提供尽可能多的无功。本文采用模型预测控制策略,通过在任一控制周期最小化代价函数,选择最优开关状态实现控制目标,控制框图如图4所示。
根据线路潮流参考值(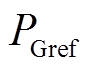 ,
,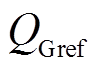 ),可以得出线路电流给定值
),可以得出线路电流给定值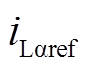 和
和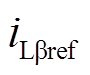 为
为
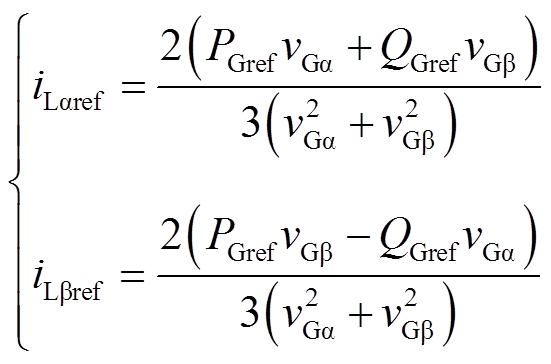 (21)
(21)式中,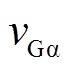 和
和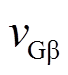 分别为节点G电压
分别为节点G电压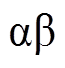 分量。为减少计算量,文中均将相应三相电量转换为两相
分量。为减少计算量,文中均将相应三相电量转换为两相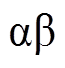 分量。
分量。
并联侧无功参考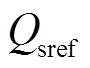 则先以传统SVM调制策略下IMC-UPFC的并联侧无功的范围为基础,然后适当进行增大。
则先以传统SVM调制策略下IMC-UPFC的并联侧无功的范围为基础,然后适当进行增大。
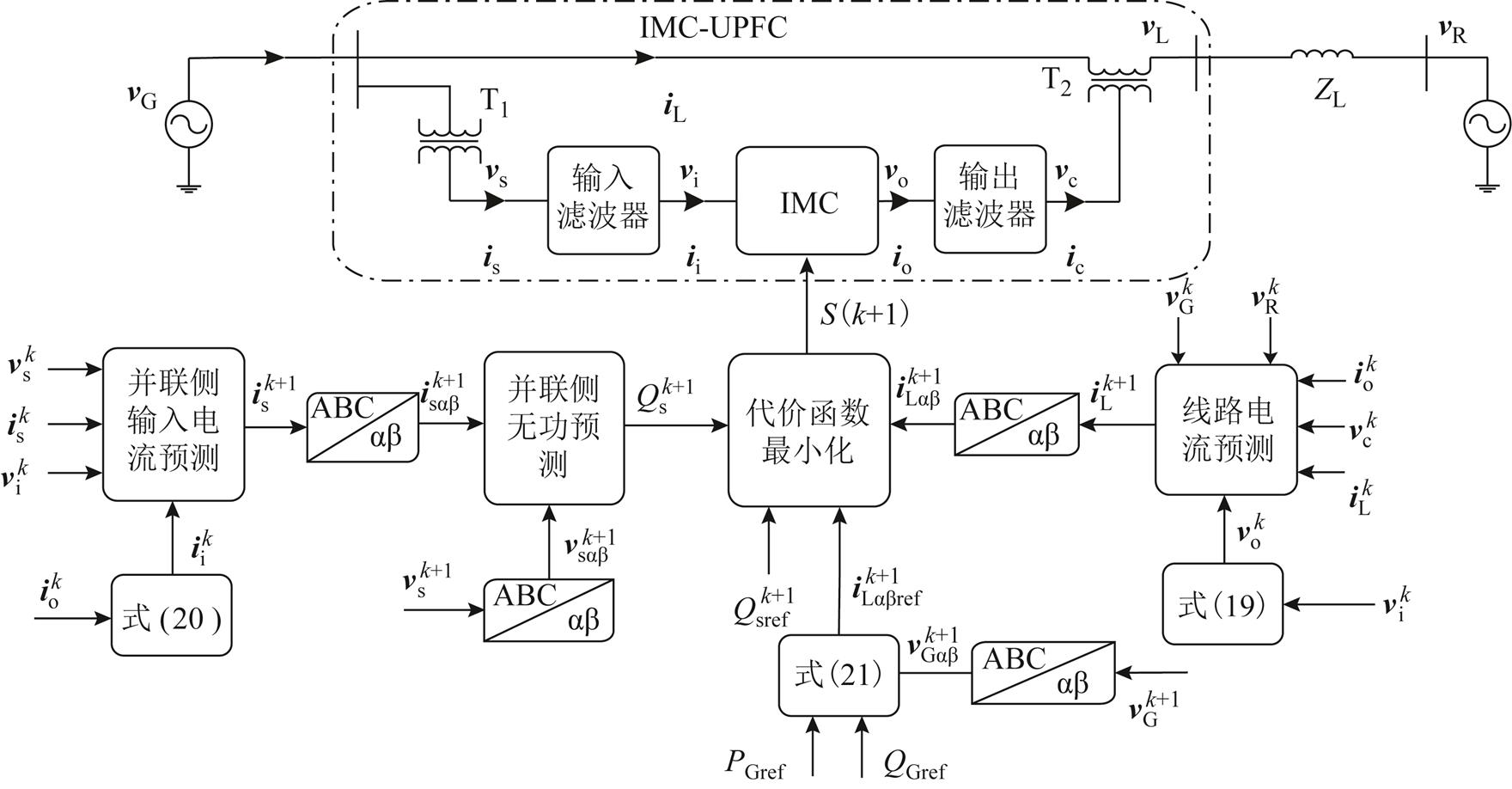
图4 IMC-UPFC模型预测控制原理
Fig.4 Block diagram of model predictive control for IMC-UPFC
欲使IMC-UPFC在MPC控制策略下安全稳定运行,代价函数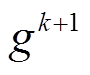 须囊括IMC-UPFC线路电流及并联侧无功的跟踪误差,即
须囊括IMC-UPFC线路电流及并联侧无功的跟踪误差,即
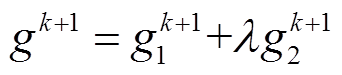 (22)
(22)其中
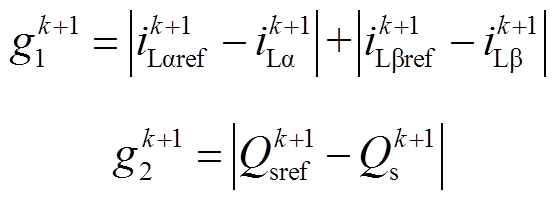
式中,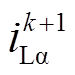 、
、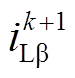 及
及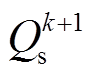 分别为各量在第k+1个控制周期的预测量;l为代价函数的权重系数,主要用于均衡线路电流与并联侧无功的相对重要程度。为了统一量纲,l的单位为
分别为各量在第k+1个控制周期的预测量;l为代价函数的权重系数,主要用于均衡线路电流与并联侧无功的相对重要程度。为了统一量纲,l的单位为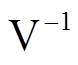 ,主要由线路电流参考、并联侧无功功率参考以及它们之间的相对重要程度m决定。
,主要由线路电流参考、并联侧无功功率参考以及它们之间的相对重要程度m决定。
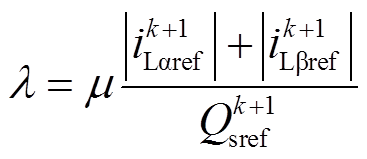
若线路电流和并联侧无功同等重要,则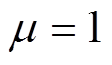 ;若考虑线路潮流的重要性更高,也即线路电流的重要性更高,那么
;若考虑线路潮流的重要性更高,也即线路电流的重要性更高,那么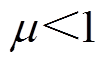 ;反之,若更重视并联侧无功的重要性,则
;反之,若更重视并联侧无功的重要性,则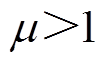 。
。
为了得到相关变量的预测量,应先推导出系统的离散模型。首先,依据式(10)~式(12),可以得到其连续时间的状态空间表达式为
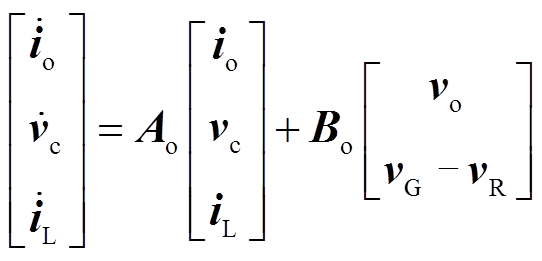 (23)
(23)其中
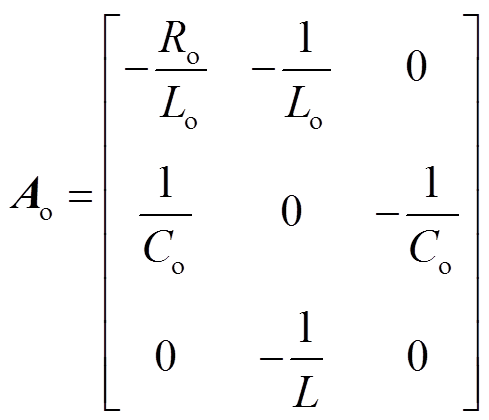
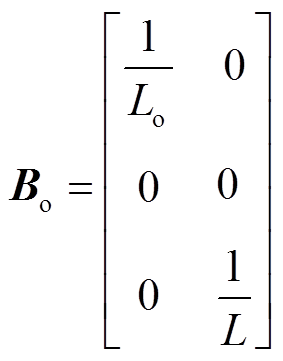
然后,假定采样时间为Ts,应用零阶保持器,相应离散状态空间模型可写为
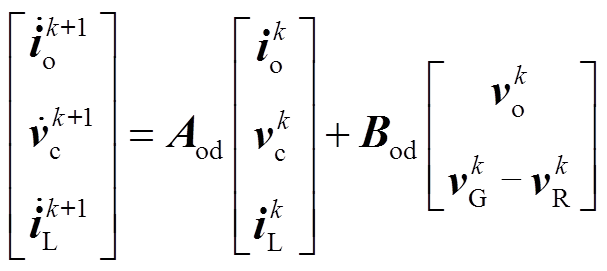 (24)
(24)其中
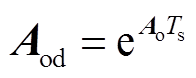
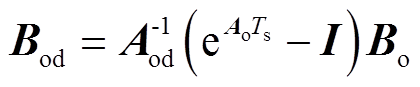
依据式(24),可得到IMC线路电流的预测值为
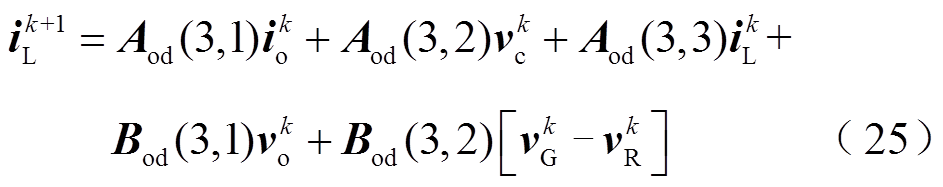
式中,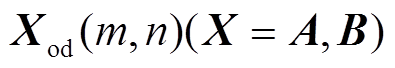 为参数矩阵
为参数矩阵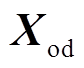 的第m行、第n列的元素;
的第m行、第n列的元素;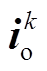 、
、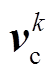 、
、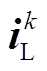 、
、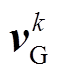 和
和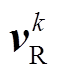 分别为各变量在第k采样瞬间的测量值;
分别为各变量在第k采样瞬间的测量值;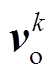 为不同开关状态下的IMC输出电压。
为不同开关状态下的IMC输出电压。
与串联侧类似,根据式(13)、式(14),可得到相应连续时间的状态空间表达式为
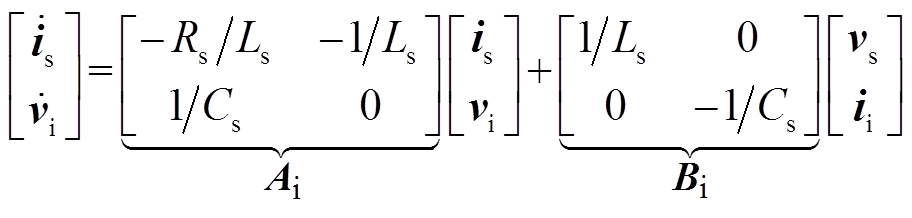 (26)
(26)采用同样的方式将式(26)离散化,可得
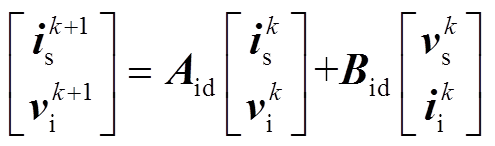 (27)
(27)
因此,从节点G端流入IMC的电流预测值为
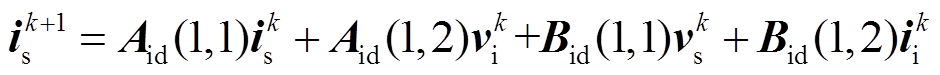 (28)
(28)式中,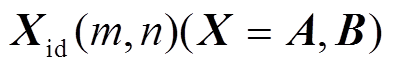 为参数矩阵
为参数矩阵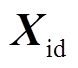 的第m行、第n列的元素;
的第m行、第n列的元素;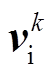 、
、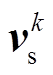 、
、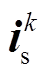 分别为各变量在第k采样瞬间的测量值;
分别为各变量在第k采样瞬间的测量值;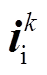 为每个开关状态下的IMC输入电流。
为每个开关状态下的IMC输入电流。
采取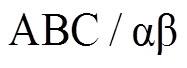 坐标变换后,可计算并联侧无功在第k+1个控制周期的预测值
坐标变换后,可计算并联侧无功在第k+1个控制周期的预测值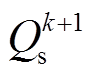 为
为
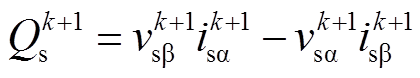 (29)
(29)考虑到采样频率(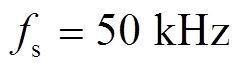 )远高于电网频率(
)远高于电网频率(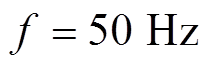 ),故可认为
),故可认为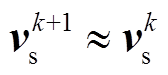 。值得注意的是,采样频率过高会增加系统的计算负担,过低则会影响线路电流波形质量[22-24],同时考虑到矩阵变换器在有限集预测控制中的平均开关频率约等于采样频率的1/6[25],本文折中选取采样频率
。值得注意的是,采样频率过高会增加系统的计算负担,过低则会影响线路电流波形质量[22-24],同时考虑到矩阵变换器在有限集预测控制中的平均开关频率约等于采样频率的1/6[25],本文折中选取采样频率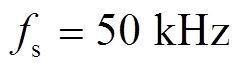 。
。
目前,IMC输入无功特性的研究主要集中于调制算法,其中空间矢量调制算法应用较为广泛。由于IMC中间直流电压需要满足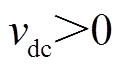 这一约束,使得输入功率因数角
这一约束,使得输入功率因数角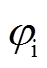 只能在[-p/6,p/6]范围内调节,导致输入无功的可调节范围有限。
只能在[-p/6,p/6]范围内调节,导致输入无功的可调节范围有限。
文献[21]提出一种“矢量倒置法”,在整流与逆变级同时采用“相反矢量”代替“原矢量”,以此来完成空间矢量算法的合成,进而使得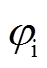 的控制范围扩展为[-p/2,p/2],极大地提高了IMC的输入无功控制能力。
的控制范围扩展为[-p/2,p/2],极大地提高了IMC的输入无功控制能力。
考虑到输入滤波器主要用于滤除IMC开关切换导致的高频谐波,截止频率较高,电感和电容值较小;此外,滤波器吸收(产生的)无功往往被限制在一个较小数值。相对系统并联侧的无功能力,滤波器对并联侧无功的影响可以忽略。因此,通过采用“矢量倒置法”的空间矢量调制算法,可以获取IMC-UPFC并联侧输入无功最大值的表达式[19]为
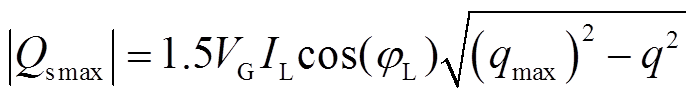 (30)
(30)式中,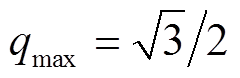 。
。
为了更直观地了解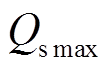 的范围,依据式(30)可以绘出其变化范围如图5所示。从三维图中可以看出,
的范围,依据式(30)可以绘出其变化范围如图5所示。从三维图中可以看出,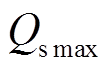 与IMC输出功率因数以及电压传输比相关。电压传输比越大,
与IMC输出功率因数以及电压传输比相关。电压传输比越大,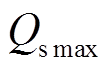 越小;输出功率因数角越大,
越小;输出功率因数角越大,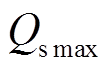 越小。
越小。
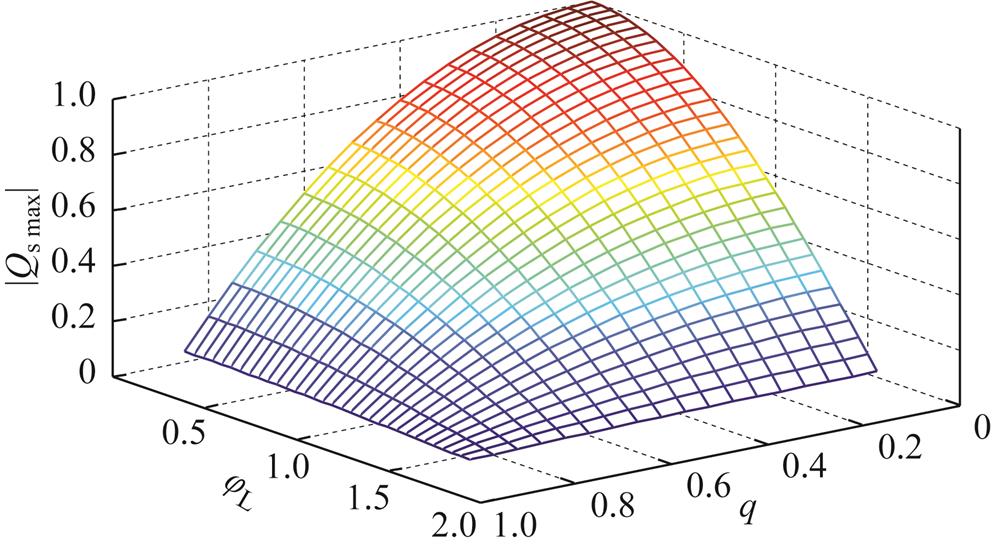
图5 改进的SVM调制策略下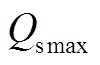 随
随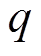 、
、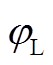 变化的三维立体图
变化的三维立体图
Fig.5 3-D diagrams of 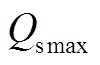 for different q and
for different q and 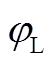 in the improved SVM
in the improved SVM
IMC-UPFC的MPC控制策略无需调制算法,而是通过最小化代价函数选择最优开关状态,实现控制线路潮流以及扩展IMC并联侧无功范围的目的。因而,该MPC控制策略无法像传统调制算法那样直接得出IMC-UPFC并联侧无功最大值的解析表达式。但通过大量离线训练,可在确保线路电流波形质量的前提下获取各运行条件下的并联侧无功范围。
为了验证文中所提并联侧无功扩展方法的有效性,本节主要针对两节点低压网络的IMC-UPFC进行Matlab/Simulink数值仿真。依据图4所示控制原理,搭建了相应的仿真模型,并在相同运行条件下,分别对PI控制策略(传统SVM调制)和MPC控制策略产生的并联侧无功进行仿真分析。
仿真详细参数设置见附表3。其中,两个耦合变压器T1、T2的电压比均设置为220V/220V,容量为50kW;系统频率f=50Hz;线路阻抗给定为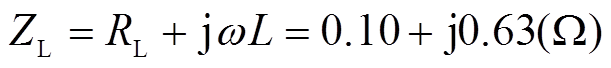 。
。
线路潮流初始值为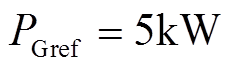 ,
,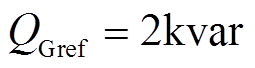 ,0.3s时刻线路潮流无功变化
,0.3s时刻线路潮流无功变化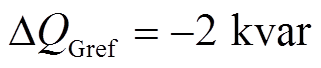 。图6a为常规PI与MPC控制策略的并联侧A相电流波形;图6b为两种策略下节点G流向线路的有功功率和无功功率波形曲线;图6c是两种策略下系统的并联侧无功功率波形曲线。
。图6a为常规PI与MPC控制策略的并联侧A相电流波形;图6b为两种策略下节点G流向线路的有功功率和无功功率波形曲线;图6c是两种策略下系统的并联侧无功功率波形曲线。

图6 MPC与PI策略下IMC-UPFC系统响应(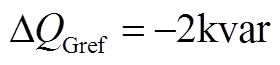 )
)
Fig.6 The response of IMC-UPFC with MPC and PI method(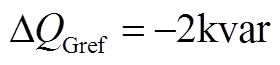 )
)
由图6a和图6c可知,在相同条件下,MPC控制策略产生的并联侧相电流幅值与无功均要大于采用常规PI控制策略的情况;依据图6b可知,两种策略产生的线路潮流均能达到其参考值并保持稳定,且几乎无差别,同时MPC策略下系统的动态性能更好。
为了进一步验证MPC控制策略可靠性,现考虑线路潮流参考值不同时系统所产生的响应。假定线路潮流初始参考值不变,0.3s时线路潮流有功功率变化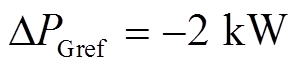 。图7a为PI与MPC控制策略的并联侧A相电流波形,图7b为两种策略下节点G流向线路的有功功率和无功功率波形曲线,图7c为两种策略下系统的并联侧无功功率波形曲线。
。图7a为PI与MPC控制策略的并联侧A相电流波形,图7b为两种策略下节点G流向线路的有功功率和无功功率波形曲线,图7c为两种策略下系统的并联侧无功功率波形曲线。
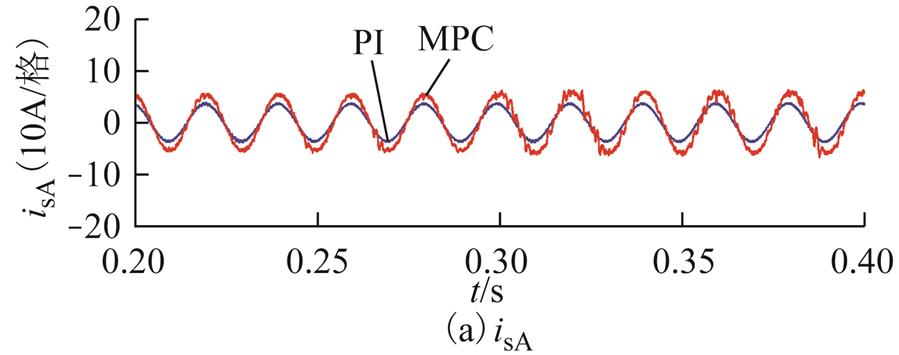
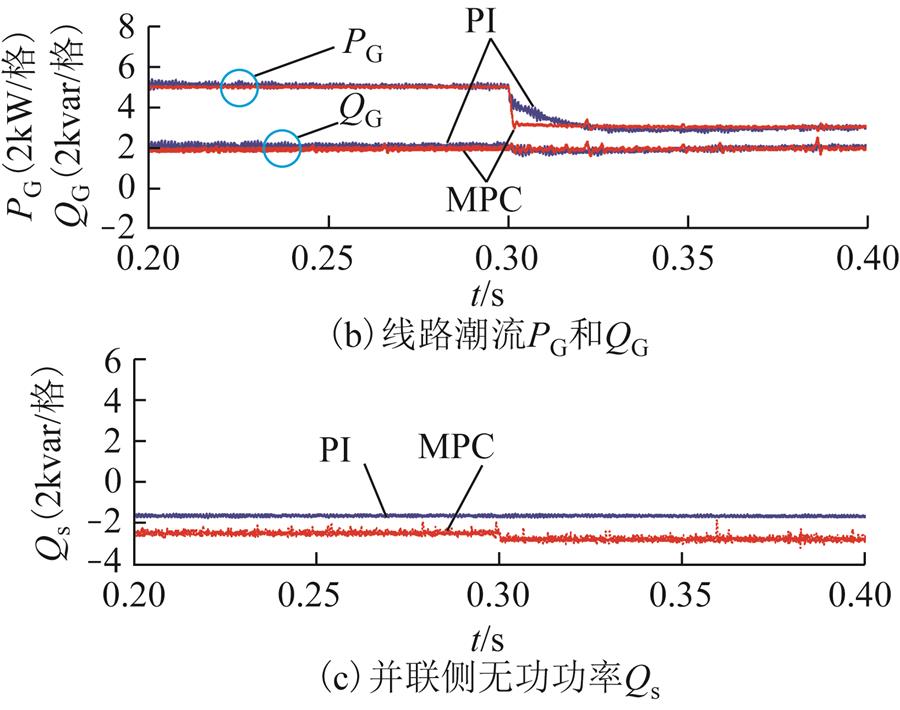
图7 MPC与PI策略下IMC-UPFC系统响应(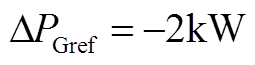 )
)
Fig.7 The response of IMC-UPFC with MPC and conventional SVM method(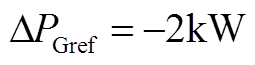 )
)
依据图7a和图7c可得,在相同运行状态下,MPC控制策略下的并联侧相电流幅值与无功均要大于采用PI控制策略的情况;由图7b可知,采用两种不同策略所产生的线路潮流响应均能稳定至其参考值,两种策略下的有功功率和无功功率波形曲线基本重合,同时MPC策略下的线路潮流暂态性能更好。
同理,假定线路潮流初始参考值不变,0.3s时线路潮流无功功率变化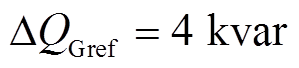 ,可得两种控制策略下系统响应。图8a为PI与MPC控制策略的并联侧A相电流波形,图8b为两种策略下节点G流向线路的有功功率和无功功率波形曲线,图8c为两种策略下系统的并联侧无功功率波形曲线。
,可得两种控制策略下系统响应。图8a为PI与MPC控制策略的并联侧A相电流波形,图8b为两种策略下节点G流向线路的有功功率和无功功率波形曲线,图8c为两种策略下系统的并联侧无功功率波形曲线。
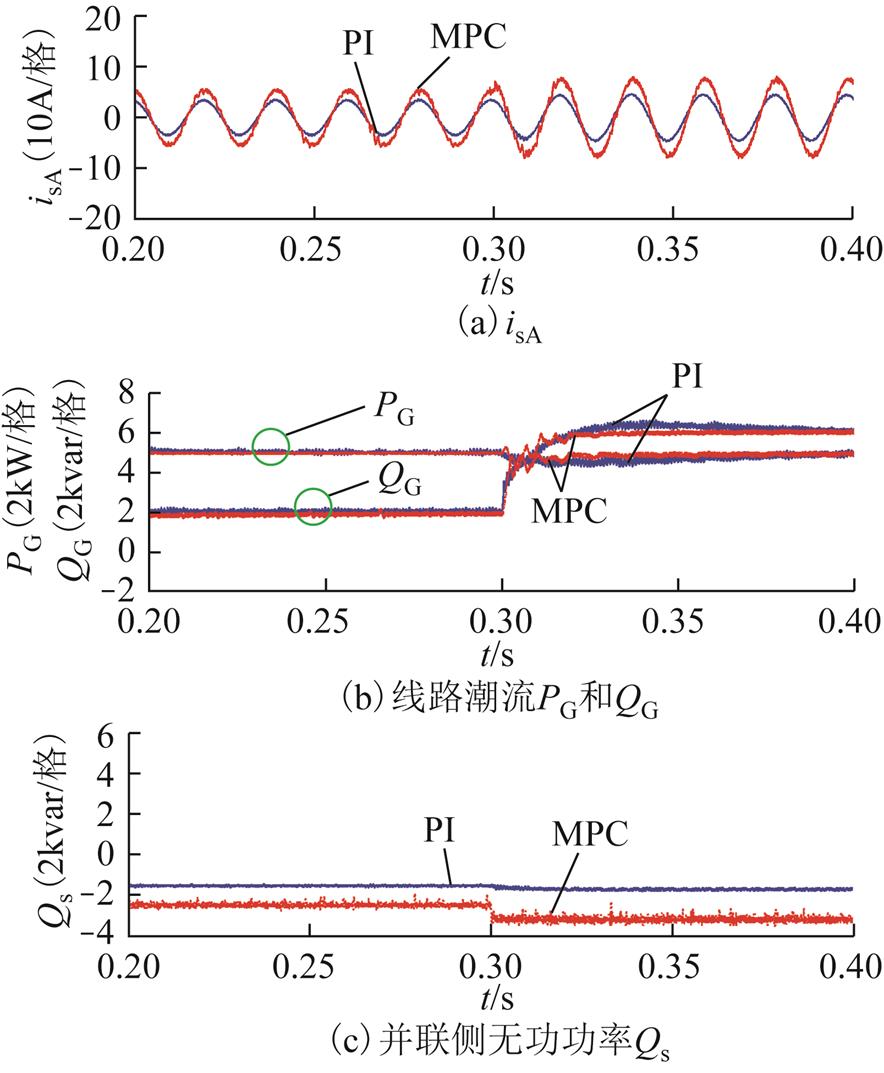
图8 MPC与常规SVM策略下IMC-UPFC系统响应(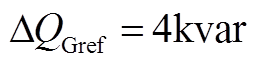 )
)
Fig.8 The response of IMC-UPFC with MPC and conventional SVM method(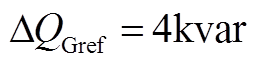 )
)
从图8a和图8c可得,相同条件下,MPC控制策略下的并联侧相电流幅值与无功功率均要大于采用PI策略的情况;由图8b可知,两种策略下节点G传输的有功功率和无功功率波形基本一致,且都能达到参考值,同时MPC策略下的系统潮流能更快速稳定至其参考值。
进一步分析MPC控制策略对IMC-UPFC并联侧无功范围的影响,依据仿真结果画出PI与MPC控制策略下IMC-UPFC并联侧无功随线路潮流变化的曲线如图9所示(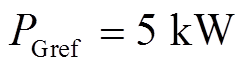 恒定,
恒定,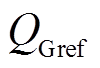 递增)。由图9可以看出, MPC控制策略下的并联侧无功可以达到并大于PI控制策略下的并联侧输入无功最大值
递增)。由图9可以看出, MPC控制策略下的并联侧无功可以达到并大于PI控制策略下的并联侧输入无功最大值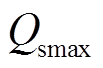 。
。
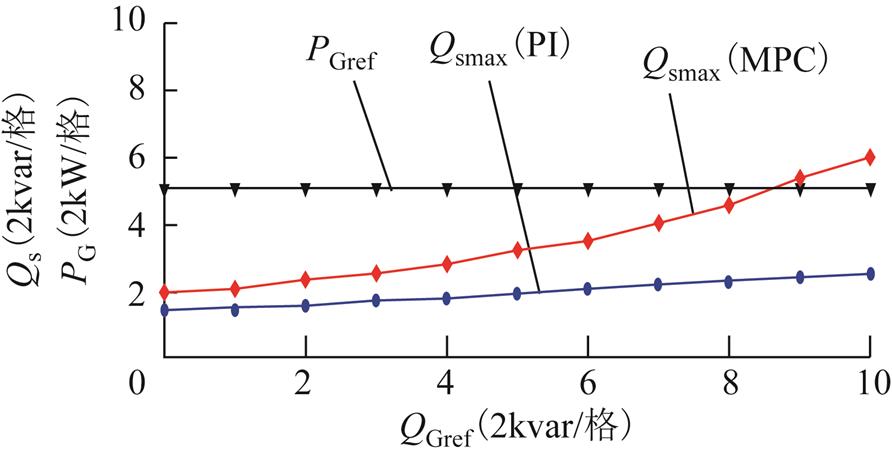
图9 两种策略下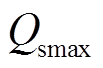 随线路潮流变化曲线
随线路潮流变化曲线
Fig.9 Curves of 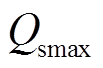 variation with power flow under two strategies
variation with power flow under two strategies
为了分析系统发生故障时的暂态响应,考虑0.25s时节点L发生A相短路接地故障,0.26s故障切除(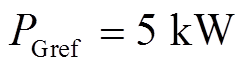 ,
,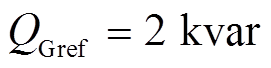 )。图10a、图10b为两种策略下节点G流向线路的有功功率和无功功率波形曲线,图10c、图10d为两种策略下系统的并联侧有功功率、无功功率波形曲线。
)。图10a、图10b为两种策略下节点G流向线路的有功功率和无功功率波形曲线,图10c、图10d为两种策略下系统的并联侧有功功率、无功功率波形曲线。
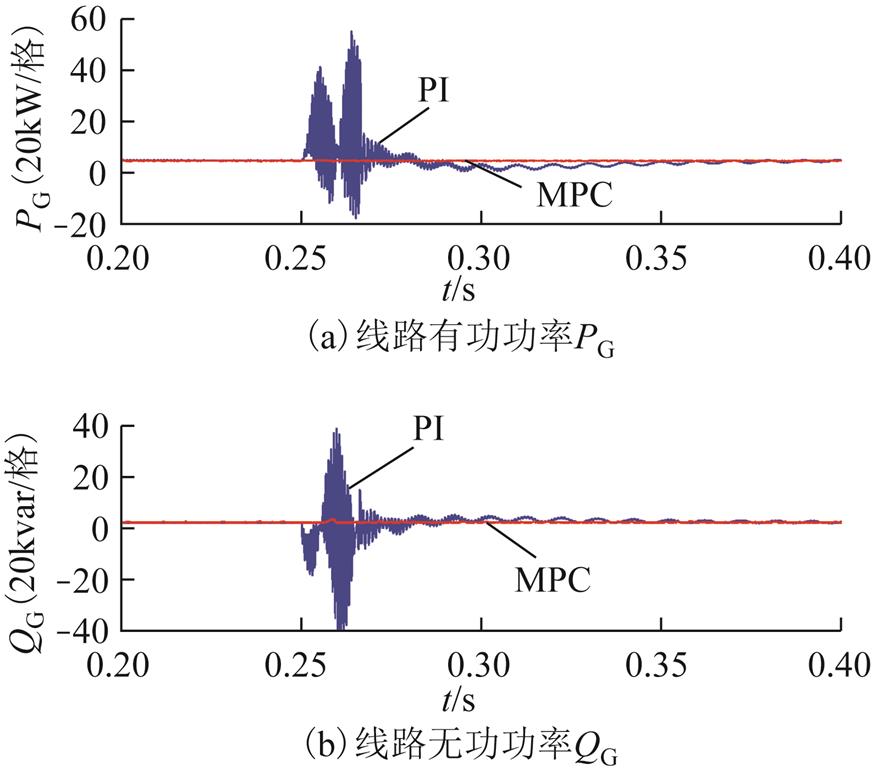
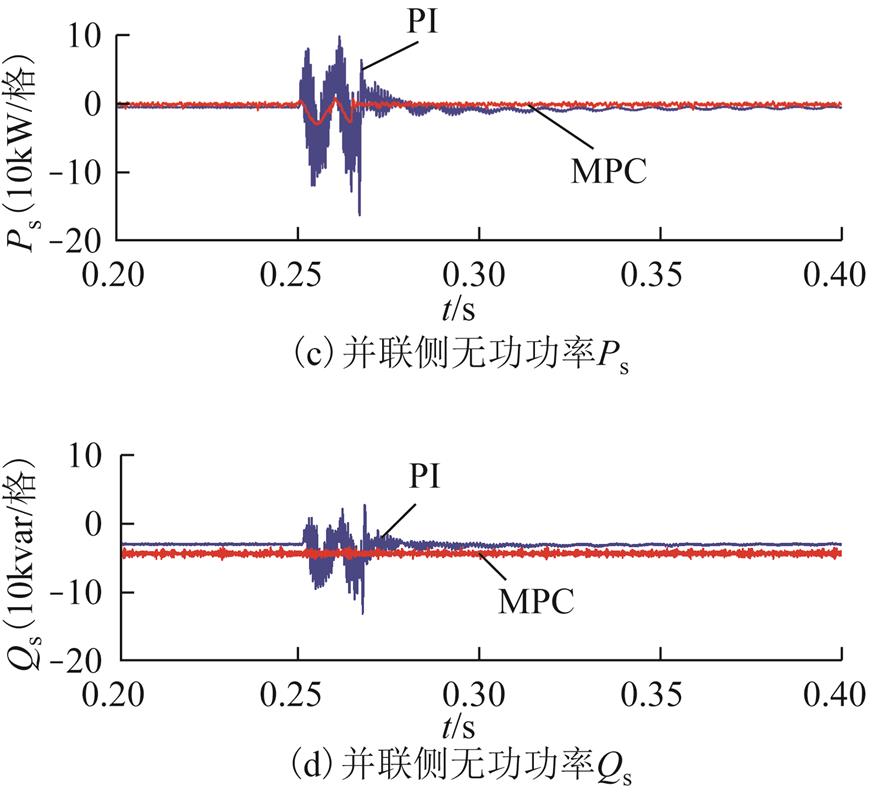
图10 MPC与PI策略下IMC-UPFC系统暂态响应
Fig.10 The transient response of IMC-UPFC with MPC and conventional SVM method
由图10a、图10b和图10d可知,相同L节点处单相故障条件下,MPC策略下线路有功功率、无功功率和并联侧无功功率在故障期间和故障恢复过程基本和故障前保持一致,而PI控制下的有功功率、无功功率和并联侧无功功率均产生较大波动和振荡;由图10c可知,MPC策略下并联侧有功功率响应波动和振荡更小。这进一步证实了所提MPC策略的优越的暂态性能。
从上述分析可知,在相同条件下,与PI控制策略相比较:稳态条件下,MPC控制策略下的IMC-UPFC的并联侧无功的范围更大,线路潮流保持稳定;暂态条件下,MPC控制策略下的IMC-UPFC暂态性能更优越。
本文针对IMC-UPFC提出一种基于模型预测控制的并联侧无功扩展方案。该方案不仅算法简单明了,而且克服了IMC输入无功控制范围受限于调制规则的问题,可有效提高IMC-UPFC的潮流控制能力。通过建立两节点低压网络的IMC-UPFC仿真模型与常规算法展开对比分析,结果表明文中所提方案在维持线路潮流稳定的同时还可获得更大的并联侧无功范围,这在一定程度上提升了IMC-UPFC对电力系统的补偿能力。
此外,所提方法还可十分方便地与系统级控制方法相结合,为电力系统提供更多支撑,如抑制电力系统的次同步振荡和提升风机并网低压穿越能力等。
附 录
附表1 整流级开关状态
App.Tab.1 Switching states of rectifier stage
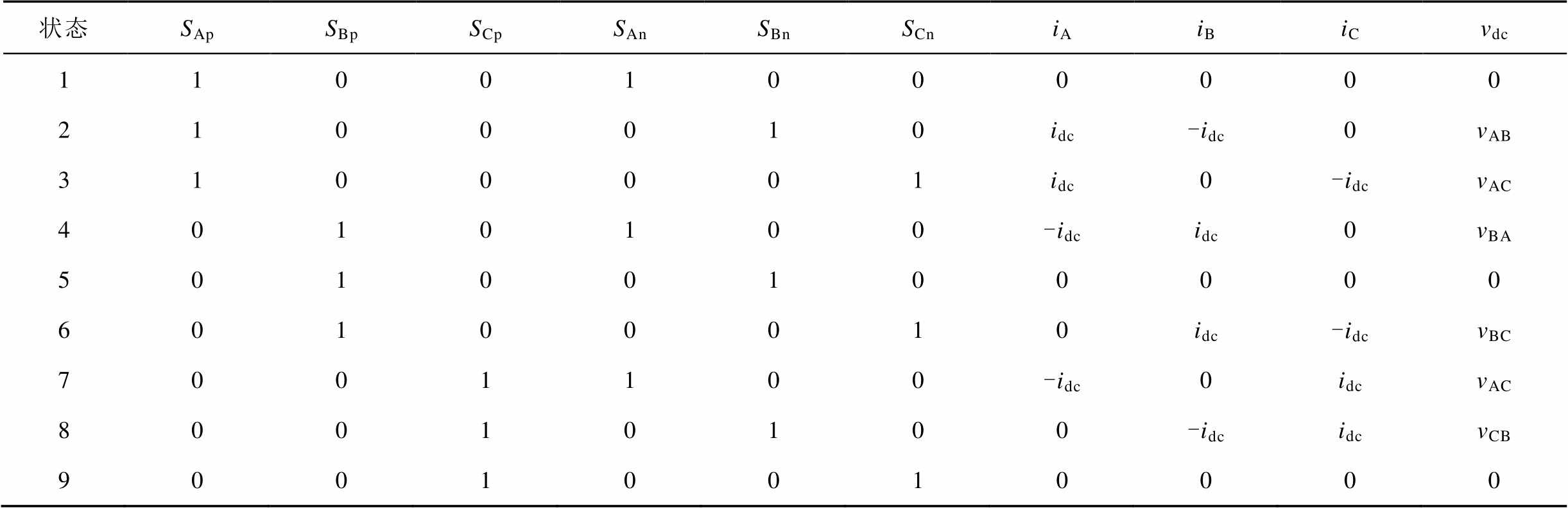
状态SApSBpSCpSAnSBnSCniAiBiCvdc 11001000000 2100010idc-idc0vAB 3100001idc0-idcvAC 4010100-idcidc0vBA 50100100000 60100010idc-idcvBC 7001100-idc0idcvAC 80010100-idcidcvCB 90010010000
附表2 逆变级开关状态
App.Tab.2 Switching states of inverter stage
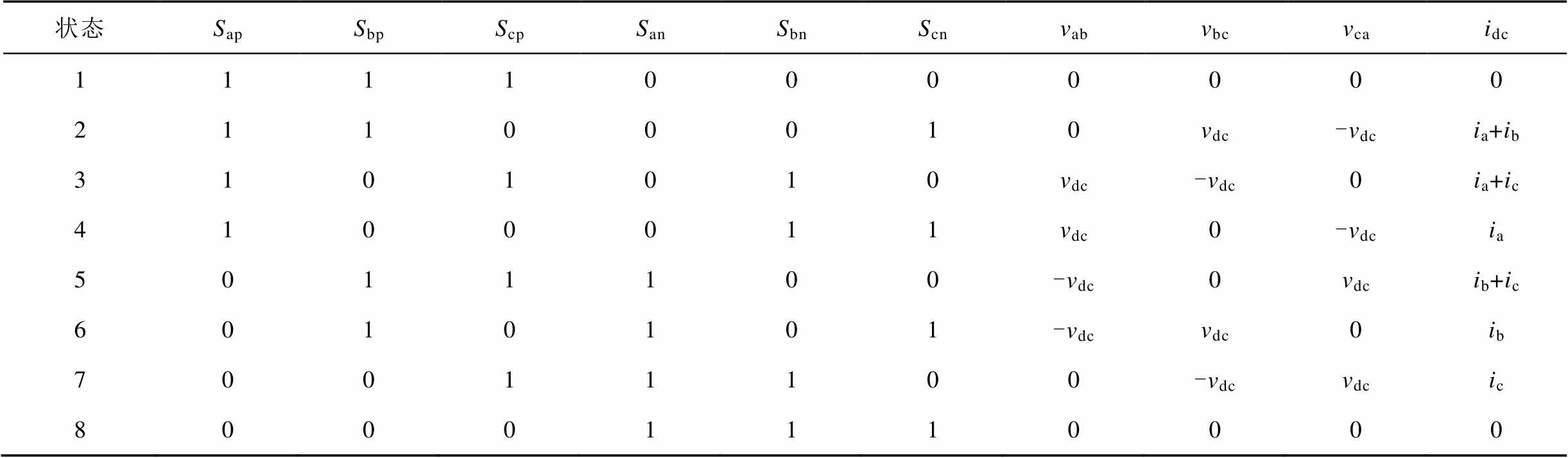
状态SapSbpScpSanSbnScnvabvbcvcaidc 11110000000 21100010vdc-vdcia+ib 3101010vdc-vdc0ia+ic 4100011vdc0-vdcia 5011100-vdc0vdcib+ic 6010101-vdcvdc0ib 70011100-vdcvdcic 80001110000
附表3 IMC-UPFC仿真参数
App.Tab.3 Simulation parameters of IMC-UPFC

参数数值 节点G相电压幅值VG/V311 节点R相电压幅值VR/V311 电压相角/(°)0 电压相角/(°)20 输入滤波器电阻/Ω4.8 输入滤波电感/ mH1 输入滤波电容/μF30 输出滤波器电阻/Ω2 输出滤波电感/mH3 输出滤波电容/μF30 采样周期/ms20
仿真参数选取依据:
1)滤波电容的选取主要依据其吸收的无功功率来确定,一般限定其吸收的无功功率低于额定输出功率的10%。
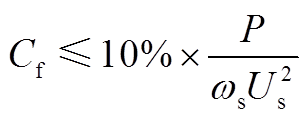 (A1)
(A1)式中,Us为滤波器输入电压有效值;ws为电网角频率;P为IMC额定输出功率。本文选取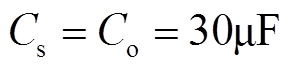 。
。
2)滤波电感的选取主要是确保输出电压尽可能大、电感两端电压降尽可能小(一般不大于电源电压的10%)。
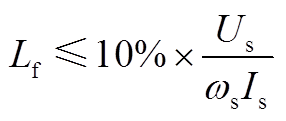 (A2)
(A2)式中,Is为滤波器输入电流有效值。本文选取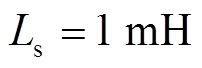 ,
,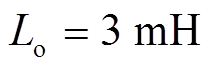 。
。
为了不使LCR滤波器的谐振峰出现在低频或者高频段,故应限制其截止频率在电网频率的10倍以上,开关频率的一半以下。
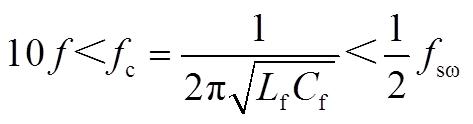 (A3)
(A3)通过计算可知,输入/输出滤波器的截止频率都满足式(A3)要求。
参考文献
[1] 任必兴, 杜文娟, 王海风. UPFC与系统的强动态交互对机电振荡模式的影响[J]. 电工技术学报, 2018, 33(11): 2520-2534. Ren Bixing, Du Wenjuan, Wang Haifeng. Impact of strong dynamic interaction between UPFC and system on electromechanical oscillation model[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2520-2534.
[2] 陈勇, 曹伟炜, 柏彬, 等. MMC-UPFC单相接地故障下运行特性分析及整体保护策略设计[J]. 电工技术学报, 2019, 34(3): 599-610. Chen Yong, Cao Weiwei, Bai Bin, et al. Operation characteristics analysis under single-phase grounding fault and overall protection scheme design of MMC-UPFC device[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 599-610.
[3] 姜涛, 张明宇, 崔晓丹, 等. 电力系统静态电压稳定域边界快速搜索的优化模型[J]. 电工技术学报, 2018, 33(17): 4167-4179. Jiang Tao, Zhang Mingyu, Cui Xiaodan, et al. A novel optimization model to explore static voltage stability region boundary in bulk power systems[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4167-4179.
[4] 胡亚辉, 张卫东, 张雷, 等. UPFC换流阀IGBT模块近场电磁骚扰分布特性研究[J]. 电气技术, 2015, 16(9): 1-6. Hu Yahui, Zhang Weidong, Zhang Lei, et al. The research on IGBT near-field electromagnetic disturbance characteristic of UPFC converter valves[J]. Electrical Engineering, 2015,16(9): 1-6.
[5] 李林, 宋宗勋, 李峰, 等. 抑制区域间低频振荡的UPFC 模糊滑模控制器[J]. 电力系统保护与控制, 2017, 45(10): 104-109. Li Lin, Song Zongxun, Li Feng, et al. UPFC fuzzy sliding mode controller for damping inter-area low frequency oscillation[J]. Power System Protection and Control, 2017, 45(10): 104-109.
[6] Liu Yang, Yang Shuitao, Wang Xiaorui, et al. Application of transformer-less UPFC for interconnecting two synchronous AC grids with large phase difference[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6092-6103.
[7] Yang Shuitao, Liu Yang, Wang Xiaorui, et al. Modulation and control of transformer-less UPFC[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1050-1063.
[8] 余梦泽, 李俭, 刘雷, 等. 电磁混合式统一潮流控制器的拓扑结构与控制策略优化[J]. 电工技术学报, 2015, 30(增刊2): 169-175. Yu Mengze, Li Jian, Liu Lei, et al.Topology structure and control strategy optimization of electromagnetic hybrid unified power flow controller[J]. Transactions of China Electrotechnical Society, 2015, 30(S2): 169-175.
[9] Liu Liming, Zhu Pengcheng, Kang Yong, et al. Power-flow control performance analysis of a unified power-flow controller in a novel control scheme[J]. IEEE Transactions on Power Delivery, 2007, 22(3): 1613-1619.
[10] Monteiro J, Silva J F, Pinto S F, et al. Matrix converter-based unified power-flow controllers: Advanced direct power control method[J]. IEEE Transactions on Power Delivery, 2011, 26(1): 420-430.
[11] Monteiro J, Silva J F, Pinto S F, et al. Linear and sliding-mode control design for matrix converter-based unified power flow controllers[J]. IEEE Transactions on Power Electronics, 2014, 29(7): 3357-3367.
[12] 林崎, 毕睿华, 李先允, 等. 双级矩阵变换器在统一潮流控制器中的应用研究[J]. 电力系统保护与控制, 2011, 39(9): 65-71, 76. Lin Qi, Bi Ruihua, Li Xianyun, et al. Study of the application of matrix converter in unified power flow controller[J]. Power System Protection and Control, 2011, 39(9): 65-71, 76.
[13] 章勇高, 康勇, 刘黎明, 等. 统一潮流控制器并联变换器的改进型双环控制系统[J]. 中国电机工程学报, 2007, 27(4): 40-46. Zhang Yonggao, Kang Yong, Liu Liming, et al. Improved double close-loop control system for shunt inverter of UPFC[J]. Proceedings of the CSEE, 2007, 27(4): 40-46.
[14] 刘黎明, 康勇, 陈坚, 等. UPFC的交叉耦合控制及潮流调节能力分析[J]. 中国电机工程学报, 2007, 27(10): 42-48. Liu Liming, Kang Yong, Chen Jian, et al. Cross-coupling control scheme and performance analysis for power flow control of UPFC[J]. Proceedings of the CSEE, 2007, 27(10): 42-48.
[15] Albatsh F M, Mekhilef S, Ahmad S, et al. Fuzzy logic based UPFC and laboratory prototype validation for dynamic power flow control in transmission lines[J]. IEEE Transactions on Industrial Electronics, 2017, 64(12): 9538-9548.
[16] 孙海顺, 马凡, 刘黎明, 等. 一种UPFC模糊PI自整定控制[J]. 电工技术学报, 2007, 22(9): 136-142. Sun Haishun, Ma Fan, Liu Liming, et al.An UPFC fuzzy PI self-tuning control strategy[J]. Transactions of China Electrotechnical Society, 2007, 22(9): 136-142.
[17] 阎博, 汪可友, Mariesa L.Crow, 等. UPFC状态反馈精确线性化潮流控制策略[J]. 中国电机工程学报, 2012, 32(19): 42-48. Yan Bo, Wang Keyou, CROW M L, et al. UPFC power flow control strategy based on exact linearization via feedback[J]. Proceedings of the CSEE, 2012, 32(19): 42-48.
[18] 邓文浪, 余帅, 郭有贵, 等. 双级矩阵变换器-统一潮流控制器预测控制策略研究[J]. 电气工程学报, 2015, 10(6): 27-32. Deng Wenlang, Yu Shuai, Guo Yougui, et al. Predictive control study on unified power flow controller based on two-stage matrix converter[J]. Journal of Electrical Engineering, 2015, 10(6): 27-32.
[19] Li Xing, Su Mei, Sun Yao, et al. Modulation strategy based on mathematical construction for matrix converter extending the input reactive power range[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 654-664.
[20] Li Xing, Sun Yao, Zhang Jianxin, et al. Modulation methods for indirect matrix converter extending the input reactive power range[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4852-4863.
[21] 李幸. 矩阵变换器的无功特性及控制研究[D]. 长沙: 中南大学, 2014.
[22] Lei Jiaxing, Zhou Bo, Wei Jiadan, et al. Predictive power control of matrix converter with active damping function[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4550-4559.
[23] 柳志飞, 杜贵平, 杜发达. 有限集模型预测控制在电力电子系统中的研究现状和发展趋势[J]. 电工技术学报, 2017, 32(22): 58-69. Liu Zhifei, Du Guiping, Du Fada.Research status and development trend of finite control set model predictive control in power electronics[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 58-69.
[24] 肖智明, 陈启宏, 张立炎. 电动汽车双向DC-DC变换器约束模型预测控制研究[J]. 电工技术学报, 2018, 33(增刊2): 489-498. Xiao Zhiming, Chen Qihong, Zhang Liyan. Constrained model predictive control for bidirectional DC-DC converter of electric vehicles[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 489-498.
[25] Vargas R, Rodriguez J, Ammann U, et al. Predictive current control of an induction machine fed by a matrix converter with reactive power control[J]. IEEE Transactions on Industrial Electronics, 2008, 55(12): 4362-4371.
Extending the Reactive Power Range of Shunt Side for Unified Power Flow Controllers Based on Indirect Matrix Converters
Abstract Considering the intrinsic limitations of reactive power range of shunt side for the unified power flow controllers based on indirect matrix converters (IMC-UPFC),a model predictive control (MPC)strategy is proposed to enlarge the reactive power range of the shunt side in this paper. The prediction model of line current for series side and the reactive power of shunt side for IMC-UPFC were deduced, and a comprehensive cost function was formed to control the power flow in the transmission line and extend the reactive power range of shunt side. Then, the optimal switching state of IMC with minimum cost function was synthesized to achieve the control objectives. MPC control strategy has the advantages of simple algorithm and no additional modulation rules. And the Matlab/Simulink simulation results for IMC-UPFC in two-bus network show that the proposed MPC control strategy can effectively enlarges the reactive power range of IMC-UPFC in shunt side, and further proves the rationality and correctness of the scheme.
keywords:Indirect matrix converters (IMC), unified power flow controllers (UPFC), model predictive control (MPC), extending the reactive power range of shunt side
DOI:10.19595/j.cnki.1000-6753.tces.190175
中图分类号:TM712
韩 建 男,1993年生,博士研究生,研究方向为现代电力电子系统控制与优化、FACTS技术。E-mail:hjhnu29@163.com
李 幸 女,1988年生,副教授,博士生导师,研究方向为现代电力电子系统控制与优化、新能源发电和微电网。E-mail:lxhnu@hnu.edu.cn(通信作者)
国家自然科学基金项目(51607063)和中国留学基金项目(201806135013)资助。
收稿日期2019-02-25
改稿日期 2019-04-25
(编辑 赫蕾)