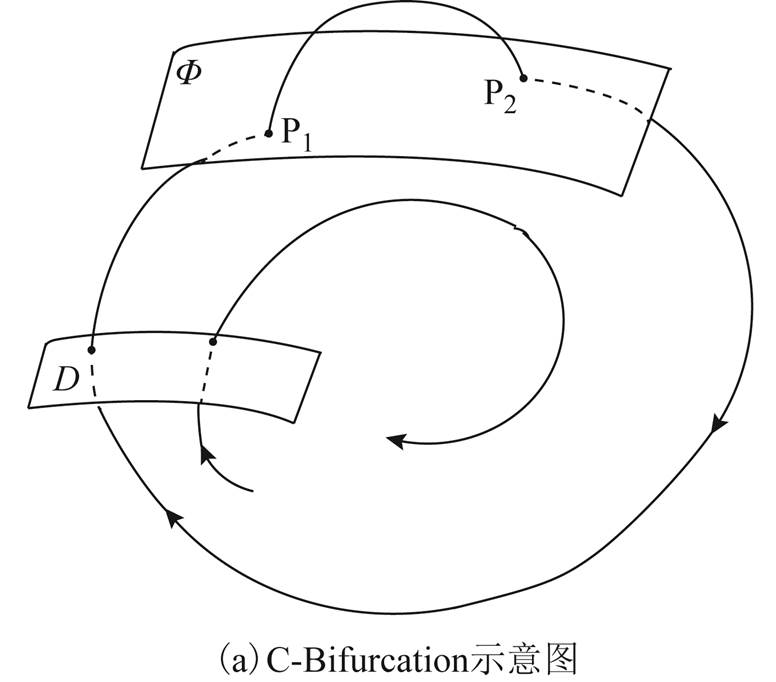
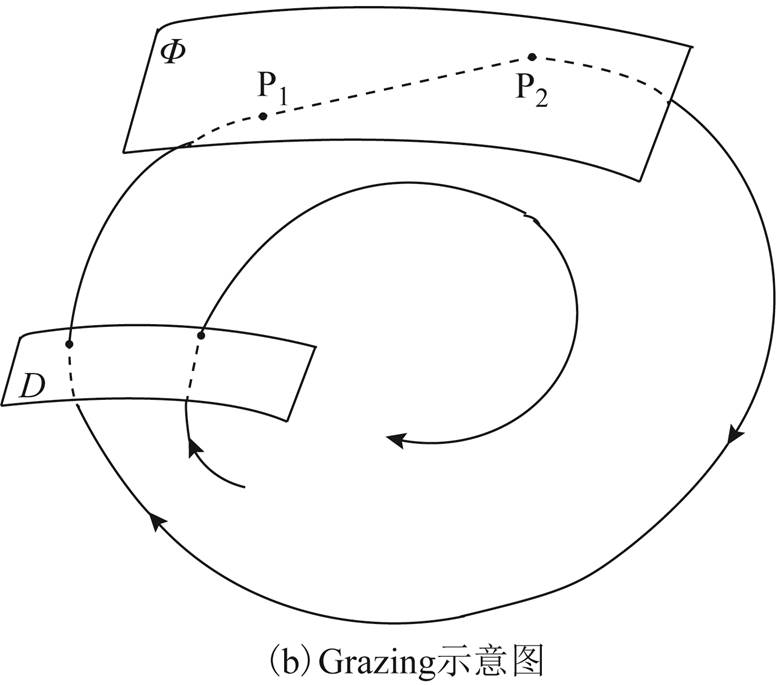
图1 非光滑分岔示意图
Fig.1 Non-smooth bifurcation diagram
摘要 针对单水电机组的电力系统,结合相图法分析水电机组调速系统限幅对超低频频率振荡的影响,揭示其发生超低频频率振荡的数学机理之一是非光滑分岔。首先,介绍限幅环节饱和导致的非光滑系统的振荡现象,说明了一般动力系统振荡的原因之一是限幅环节饱和相关的非光滑分岔;其次,给出含限幅环节的单水电机组电力系统的简单数学模型、状态方程及其平衡点特性;再次,分析不同初始条件、有/无限幅时,系统相图有/无极限环的动力学特性,说明了调速系统限幅环节作用和足够大的初值是系统发生超低频频率振荡的原因之一,揭示了系统对初值的非光滑分岔特性;最后,分析了不同系统参数对系统有/无极限环的动力学性质影响,揭示了在一定初值下的单水电机组电力系统的参数非光滑分岔特性。
关键词:非光滑分岔 超低频频率振荡 极限环 限幅 调速系统
超低频振荡频率低、振荡周期长,是限制电力输送能力、威胁电网安全运行的重要因素之一。
传统上,超低频振荡主要是大型电网联网时出现的联络线功率的超低频段振荡,相应的低频振荡的机理、分析方法、抑制手段研究已经比较成熟[1-6]。然而,近年来,水电机组高占比电网中发生了多次超低频频率振荡,和传统的低频振荡有本质区别[7-8]。
目前,对于超低频频率振荡问题,在机理和分析方法上已经有较多研究成果[9-17]。文献[9]通过对振荡模式的排查和分析,指出了超低频频率振荡是调速系统引起的机械振荡模式。文献[10]通过大量现场试验数据分析,得出水电机组调速系统提供负阻尼是造成云南电网超低频频率振荡的直接原因。文献[11]总结了特高压直流孤岛运行时,超低频频率振荡发生的条件与特性。文献[12-13]认为,超低频频率振荡是类强迫振荡,在起振阶段,系统表现为负阻尼振荡,在振荡持续阶段,系统以共振形式发生频率振荡。文献[14]分析了水电机组调速器不同参数对系统阻尼比的影响,并给出了超低频频率振荡的抑制措施。文献[15]基于直流调制层面,使用频率限制控制器(Frequency Limit Controller, FLC)提高了西南电网的频率稳定水平。文献[16-17]分别针对土耳其和哥伦比亚的超低频频率振荡,通过优化调速器参数和增加火电开机容量来抑制振荡。上述研究一是针对具体振荡案例提出控制措施,二是从调速系统负阻尼角度分析了超低频频率振荡的机理。
值得注意的是,实际大电网在仿真中出现超低频频率振荡现象,虽然有水电机组调速系统呈现负阻尼特性的原因,但该超低频频率振荡仅在某些故障条件下出现[18-19]。
另一方面,除负阻尼外,系统中特殊的非线性环节如限幅环节也会造成系统发生振荡。如文献[20-23]探讨了励磁限幅环节引起的单机无穷大系统的振荡现象。文献[24]探讨了再热式汽轮机在大扰动下限幅起作用,系统将产生稳定的极限环,发生不衰减的振荡。文献[25]利用非光滑系统的分岔理论,探讨了限幅环节引起的低频振荡问题。文献[26]分析了混合发电系统非线性行为造成的分岔现象及稳定边界问题。文献[27-28]分析认为超低频振荡与电力系统的非线性特性相关。
鉴于此,本文根据限幅环节引起振荡的现象,探讨超低频频率振荡的另一种数学机理。通过单水电机组电力系统的动力学特性,即一定的初始条件下系统状态会由于限幅的存在而收敛到稳定的极限环(在物理上对应着超低频频率振荡)的特性,说明超低频频率振荡是足够大的初值和限幅环节作用的共同结果;通过系统参数对动力学性质的影响分析,表明超低频频率振荡对应着非光滑分岔。上述工作是对电网超低频频率振荡机理的有益补充。
数学上,含有限幅的微分动力系统属于非光滑系统(如切换微分动力系统)。对于非光滑系统,因其限幅或切换界面的存在,其动力学特征复杂,系统是振荡发散还是发生等幅振荡,与是否有限幅环节作用存在明显关联。如考虑励磁系统限幅的单机无穷大系统因为限幅环节起作用将出现稳定的持续振荡[20-25]。
从分岔角度看,上述持续振荡特性也和非光滑系统分岔相关。非光滑分岔主要有C-分岔(Corner-collision Bifurcation, C-Bifurcation)和擦边分岔(Grazing Bifurcation)等,分别如图1所示。对于C-分岔,轨线会越过非光滑切换面(限幅环节),而后其轨迹将完全变成另一种状态方程的形式。而对于擦边分岔,当轨线和非光滑切换面(限幅环节)相交时,轨线会停留在曲面上一定时间后再离开。同时,在轨线和曲面相交处,轨线虽然具有连续性,但交点不是光滑的。如图中的P点,其可视为轨线和非光滑切换面相交(即限幅起作用)的标志之一。


图1 非光滑分岔示意图
Fig.1 Non-smooth bifurcation diagram
图1中D为Poincare映射截面,当Poincare映射截面存在不动点(特征根小于1)时,系统出现稳定的极限环,即在适当的参数、初值条件下,系统出现稳定的振荡(即为稳定的极限环)。
下文将结合相图和单水电机组电力系统的数学模型分析超低频频率振荡现象与其限幅环节的关系。
鉴于超低频频率振荡和水轮机调速系统相关[10],本文研究单水轮发电机供电的电力系统。水轮发电机受调速系统控制,调速系统由调节系统、电液伺服系统、水轮机组成,其简化模型如图2所示。
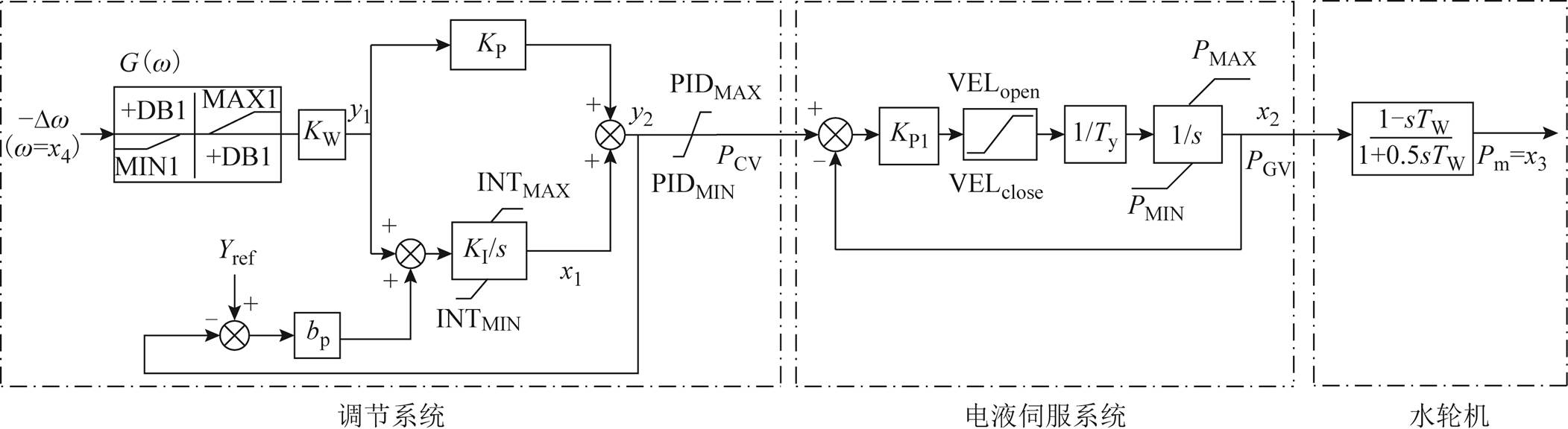
图2 调速系统的数学模型
Fig.2 The mathematical model of governor system
调节系统是水轮机调速系统的主要控制部分,其中包含频率死区环节、PID控制模块、限幅环节等。调节系统采集得到的发电机组频率偏差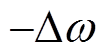 经过一次调频死区、限幅环节后放大,与功率或开度偏差一起经过PID控制调节输出调门信号PCV。图2中,KW、KP、KI、bp分别为频率偏差放大倍数、PID控制模块中比例、积分环节的放大倍数和永态转差系数。
经过一次调频死区、限幅环节后放大,与功率或开度偏差一起经过PID控制调节输出调门信号PCV。图2中,KW、KP、KI、bp分别为频率偏差放大倍数、PID控制模块中比例、积分环节的放大倍数和永态转差系数。
电液伺服系统模型对应着调速器中的执行机构,将调节系统发出的调门指令PCV经过电液转换等环节放大转换为控制水轮机的导叶开度信号PGV。图2中,KP1为电液转换模块的放大倍数;VELopen、VELclose分别是过速开启、关闭系数;Ty为接力器时间常数;PMAX、PMIN根据参数类型可设为1(pu)和0(pu)。
水轮机模型反映了输出机械功率Pm和导叶开度信号PGV的数学关系,其经典模型如图2所示,TW为水锤效应时间常数,指在额定水头下,过水管道内的流量由零增大至额定流量所需要的时间,满载时TW在0.5~4.0s之间。在动态过程中,水轮机导叶开启或关闭,由于水锤效应短时间内都会产生与控制目标相反的逆向调节[29]。若水轮机导叶开启或关闭频繁,将给系统的动态稳定和响应特性带来不利影响,成为引发系统不稳定的关键因素。
图2中调速系统的数学模型包括一次调频限幅、PID环节输出限幅、过速关闭/开启限幅、调门开度限幅多个限幅环节。本文主要研究该一次调频死区和一次调频限幅非线性环节对频率振荡的影响。该非线性环节的数学输入-输出描述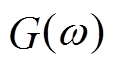 如下。
如下。
当无一次调频限幅时
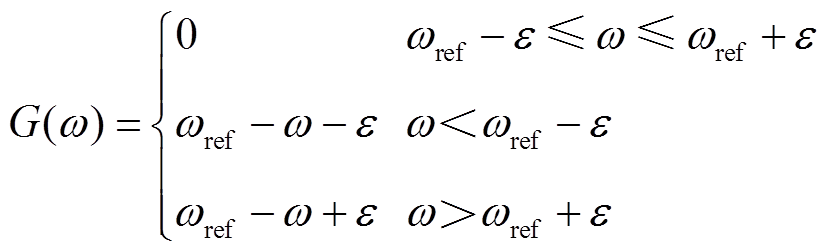 (1)
(1)当存在一次调频限幅时
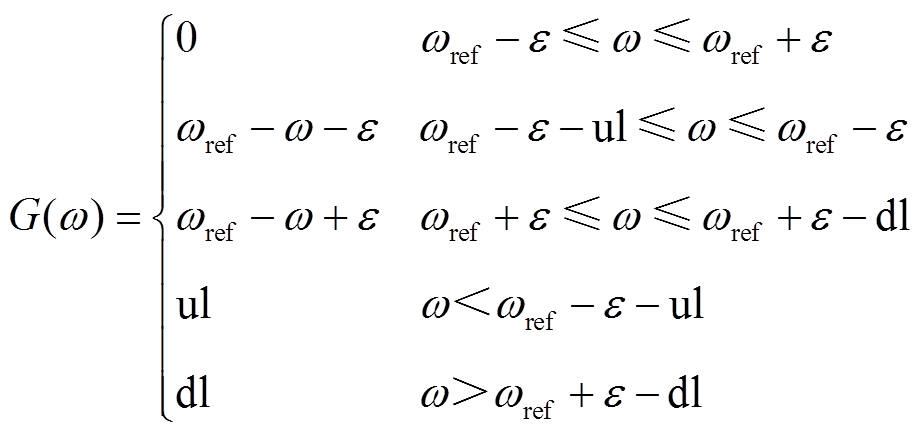 (2)
(2)
式中,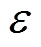 、ul、dl分别为该环节的死区、上限和下限值。
、ul、dl分别为该环节的死区、上限和下限值。
图2中x1、x2、x3、x4、y1、y2表示调速系统模型的输入、输出以及中间变量。忽略网损且只计及负荷的频率调节效应时,根据发电机转子的运动方程有
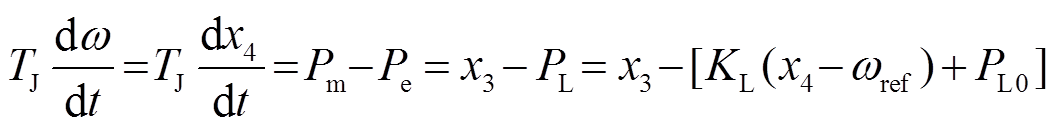 (3)
(3)式中,TJ为发电机转动惯量;KL为负荷的单位调节功率;PL0为负荷的初始值;Pe为电磁功率。
综合式(3)和图2中的微分环节,单水轮发电机供电的电力系统的简化微分-代数方程为
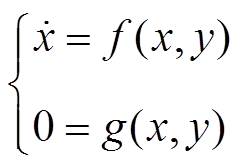 (4)
(4)可描述为
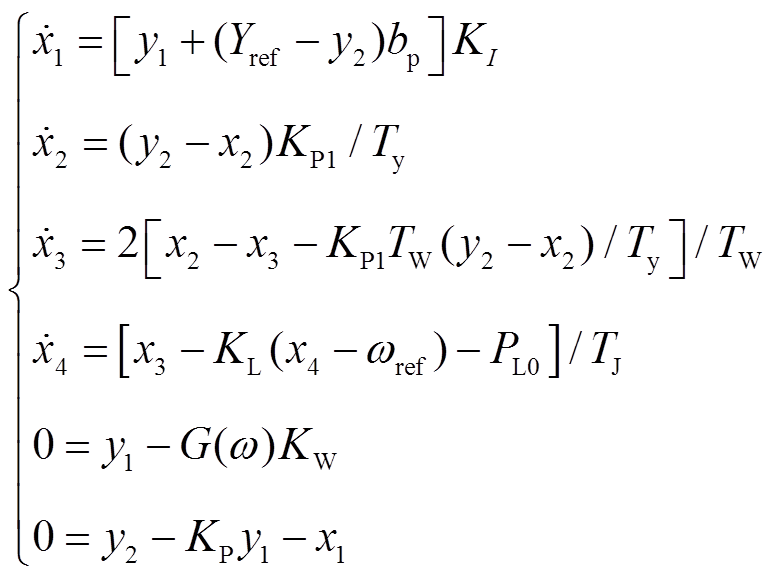 (5)
(5)
结合电力系统运行特性,可设调速系统模型中各参考量为ωref=1(pu)、Yref=1(pu),同时假定系统的初始负荷为额定值,即PL0=1(pu)。
根据方程组(5)和平衡点定义,可由
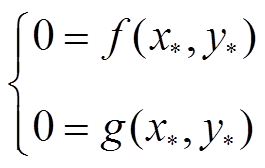 (6)
(6)获得平衡点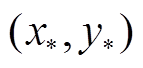 。具体地,根据有无一次调频限幅和频率初值代入不同的
。具体地,根据有无一次调频限幅和频率初值代入不同的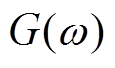 ,可求解平衡点。
,可求解平衡点。
无一次调频限幅时,三段区间内平衡点的求解分别如下。
1)当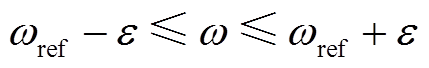 时,将
时,将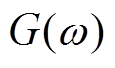 =0代入方程组求解得
=0代入方程组求解得
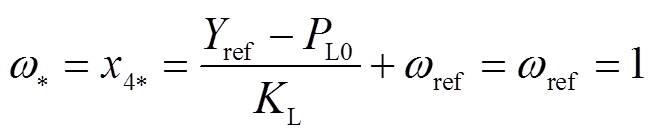
状态量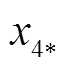 满足要求。进一步,可得平衡点处其他状态量的取值为
满足要求。进一步,可得平衡点处其他状态量的取值为
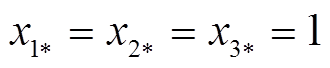
2)当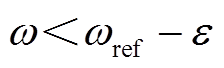 时,将
时,将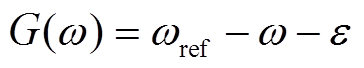 代入方程组求解得
代入方程组求解得
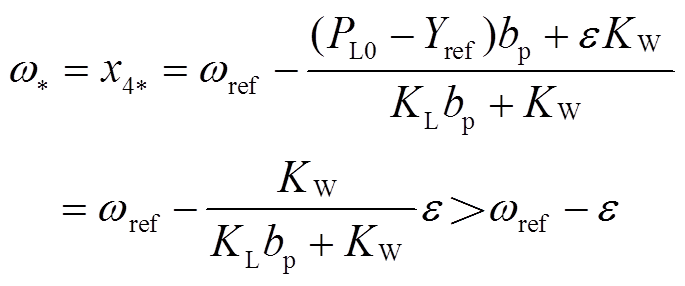
故状态量x4*不满足要求,即该区间内不存在平衡点。
3)当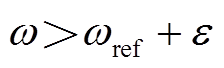 时,将
时,将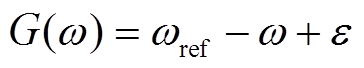 代入方程组求解得
代入方程组求解得
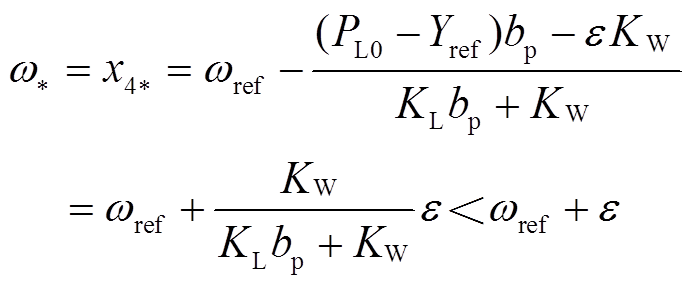
该区间内不存在平衡点。
综上,无一次调频限幅时,简化系统存在唯一的平衡点,即(1,1,1,1)。
有一次调频限幅时,按照相同的方法,可得在式(2)所对应的五个区间段内,仅在死区内存在唯一的平衡点(1,1,1,1)。
将方程组(5)在平衡点处线性化,得到
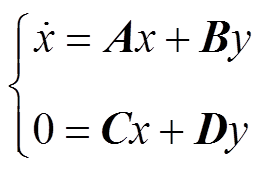 (7)
(7)其中
A=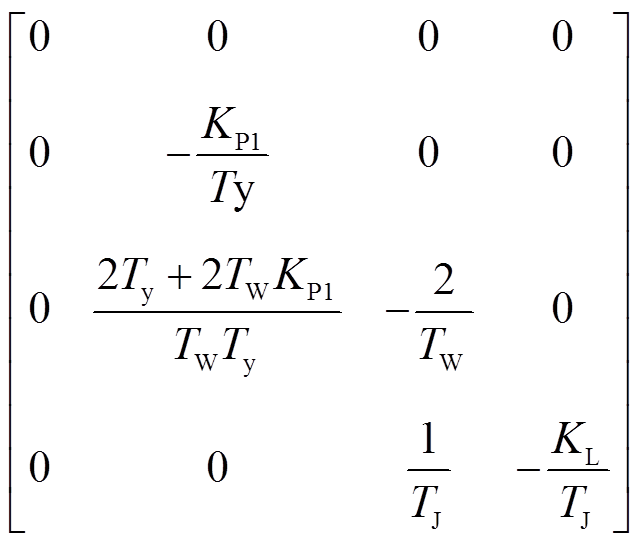 B=
B=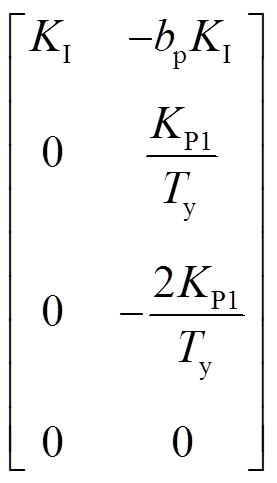
C=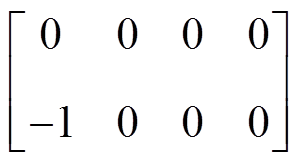 D=
D=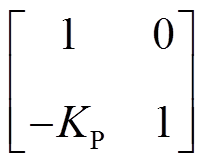
从而雅可比矩阵J为
J=A-BD-1C=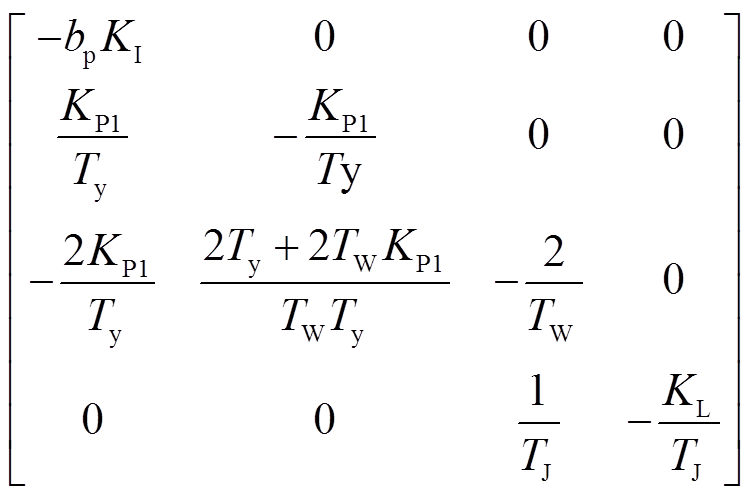
相应的四个特征根分别为: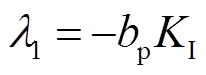 ,
,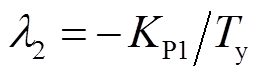 ,
,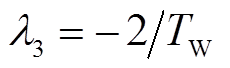 ,
,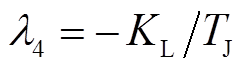 。四个特征根均为负实数,表明在局部范围(死区范围内),该平衡点是稳定的。
。四个特征根均为负实数,表明在局部范围(死区范围内),该平衡点是稳定的。
本节考虑在不同的初值(1, 1, 1, x4(0))下(即频率具有不同偏差作为初始值时),系统在有/无一次调频限幅时的动力学特性。
本文采用典型电力系统参数:KL=1.5,ε=0.000 8,ul=0.11,dl=-0.11,KW=1.1,KP=5,KI=1,bp=0.03,KP1=40,Ty=13.86,TW=1.6s,TJ=10。
在单机系统的初始频率偏差较小时,有/无一次调频限幅时状态方程的角频率x4-积分环节输出x1的相图如图3所示。
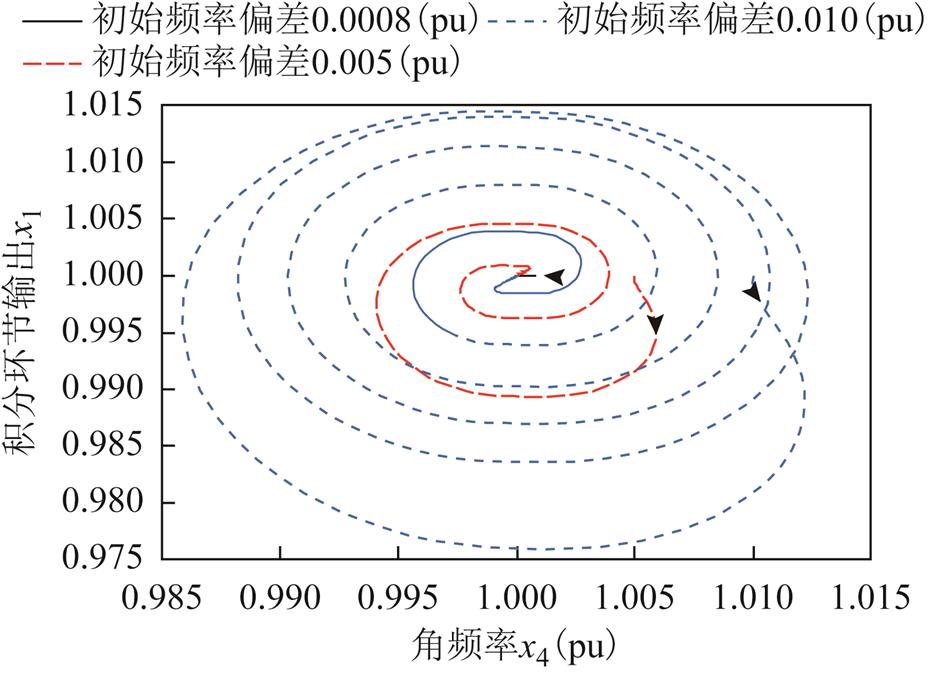
图3 初始频率偏差较小的x4-x1相图
Fig.3 The x4-x1 phase portrait under small initial frequency deviation
图3表明,单机系统的初始频率偏差较小时,系统状态会随着时间推移,逐步收敛到稳定的平衡点,即单机系统经过调速系统的调节作用,系统频率恢复稳定;且有/无一次调频限幅时,系统的状态响应过程基本相同。
进一步分析表明,当初始频率偏差小于0.015 7(pu)时,有/无一次调频限幅,系统状态均会收敛到稳定的平衡点,且收敛过程基本相同,这与上节平衡点在局部是稳定的结论一致。
在初始频率偏差为0.015 8(pu)时,有/无一次调频限幅时状态方程的相图如图4所示。
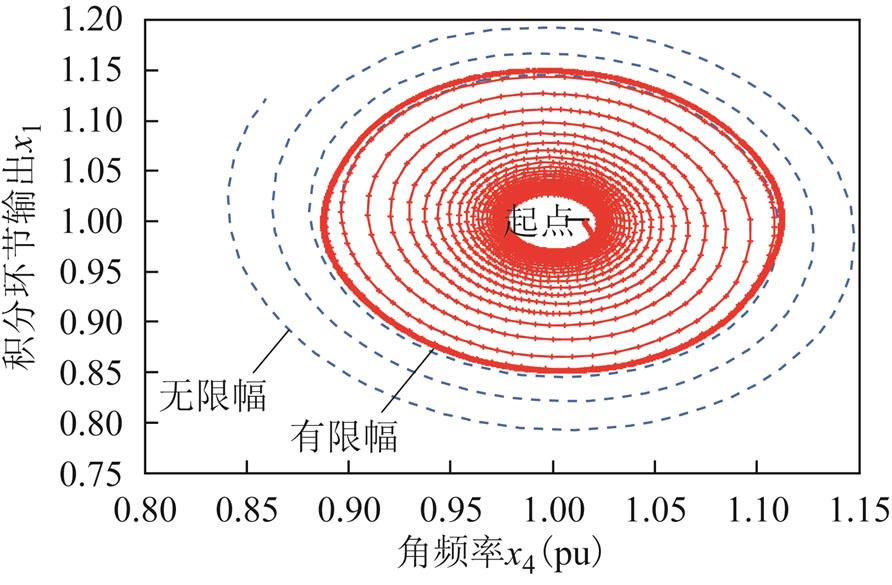
图4 初始频率偏差为0.015 8(pu)的x4-x1相图
Fig.4 The x4-x1 phase portrait under the initial frequency deviation of 0.015 8(pu)
图4表明,在初始频率偏差为0.015 8(pu)时,若无一次调频限幅,单机系统的状态响应会振荡发散,如图4中虚线所示;若有一次调频限幅,状态方程的轨线会收敛到一个稳定的极限环,如图4中实线所示。
进一步分析表明,在大于0.015 7(pu)的初始频率偏差下,若无一次调频限幅,系统的状态响应均会振荡发散;若有一次调频限幅,系统的轨线会收敛到稳定的极限环,对应着单机系统形成持续的等幅频率振荡。因此,一次调频限幅起作用是造成系统频率振荡的原因之一。
考察具有一次调频限幅且初始频率偏差大于0.015 7(pu)时(选取状态变量x4的初值为偏离平衡点0.06(pu)和0.13(pu)),系统形成的极限环。此时,状态变量x4即系统频率的时域变化如图5所示。相应的,角频率x4-积分环节输出x1的相图如图6所示。
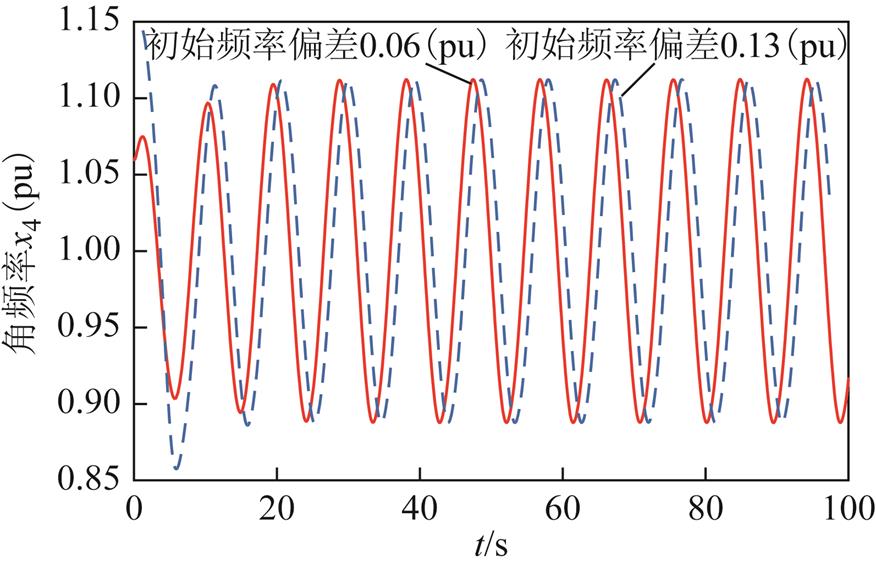
图5 不同初始频率偏差下的系统频率
Fig.5 The system frequency under different initial frequency deviation
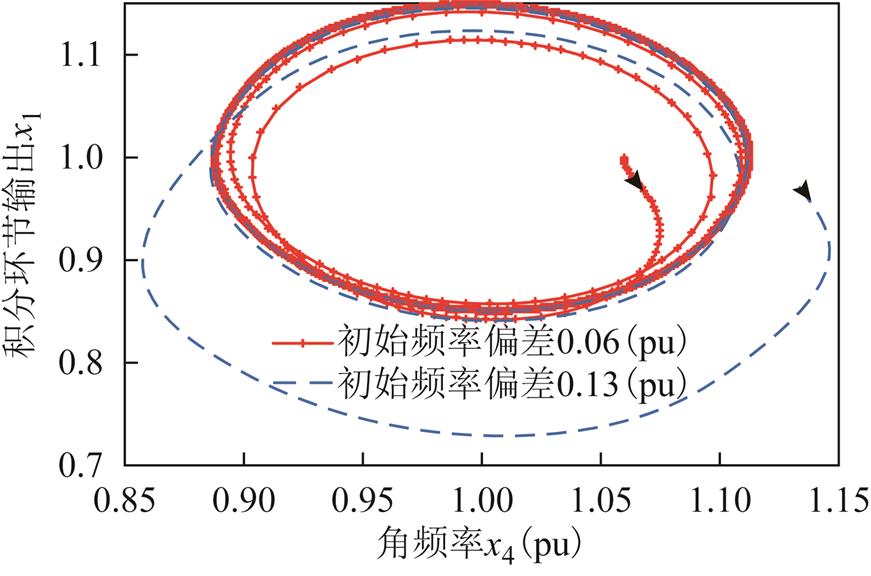
图6 不同初始频率下的x4-x1相图
Fig.6 The x4-x1 phase portrait under different initial frequency deviation
图5表明,不同初值下,单机系统最终形成振荡幅度相等的频率振荡,且其振荡频率约为0.106 7Hz,属于超低频频率振荡范畴。
进一步,图3、图4和图6对比说明,虽然系统具有稳定的平衡点,但是当初值足够大(初值也一种是参数)时,一次调频限幅起作用,且在限幅的作用下,系统会收敛到稳定的极限环,发生振荡,即系统针对初值参数,出现非光滑分岔。
在电力系统中,对应不同故障导致系统承受的冲击不同,进而导致故障切除后系统的初值不同,不同的初值决定限幅环节是否起作用。系统中足够大的冲击导致的偏离平衡点较大的初值和限幅的互相作用可能导致稳定的极限环的产生,在物理上表现为等幅的超低频频率振荡。
进一步,状态变量x4的初值为偏离平衡点0.06(pu)时,该系统最终形成的极限环中,经过一次调频限幅环节后的中间代数量y1和积分环节输出x1的相图如图7所示。
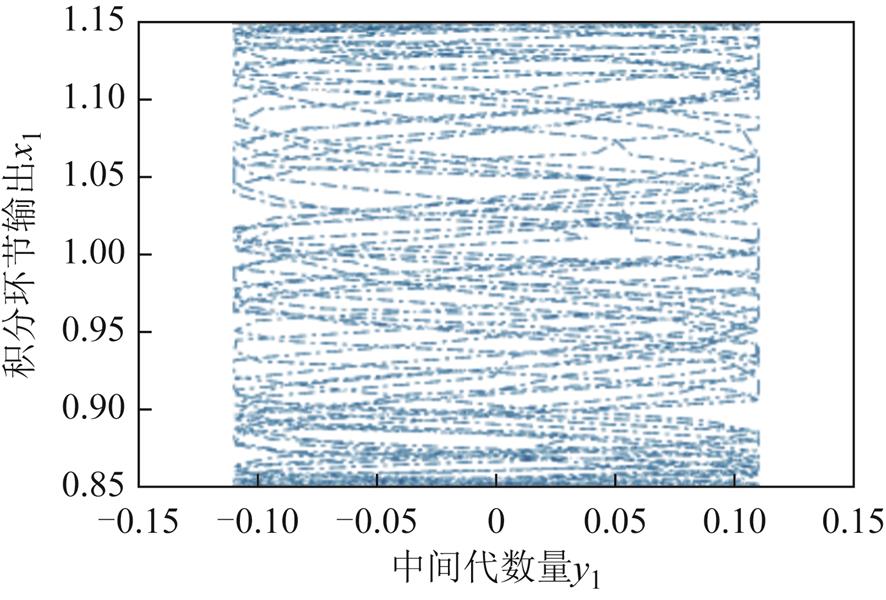
图7 初始频率偏差为0.06(pu)的y1-x1相图
Fig.7 The y1-x1 phase portrait under the initial frequency deviation of 0.06(pu)
图7表明,中间代数量的值y1在-0.11和0.11之间波动,即一次调频限幅起作用。结合图1可知,从中间代数量y1的角度看,此时限幅饱和的作用和非光滑分岔中的擦边分岔类似。
第4节研究表明,状态量的初值(实质上也是一个参数)的大小对系统动力学特性存在影响。本节研究调节系统PI控制环节的KP、KI参数对动力学特性的影响,即系统的非光滑分岔特性。
考虑图2所示的单机系统,状态变量x4的初值为偏离平衡点0.5(pu)时,取KP=4,KI=1,有/无一次调频限幅的角频率x4-积分环节输出x1的相图如图8所示。
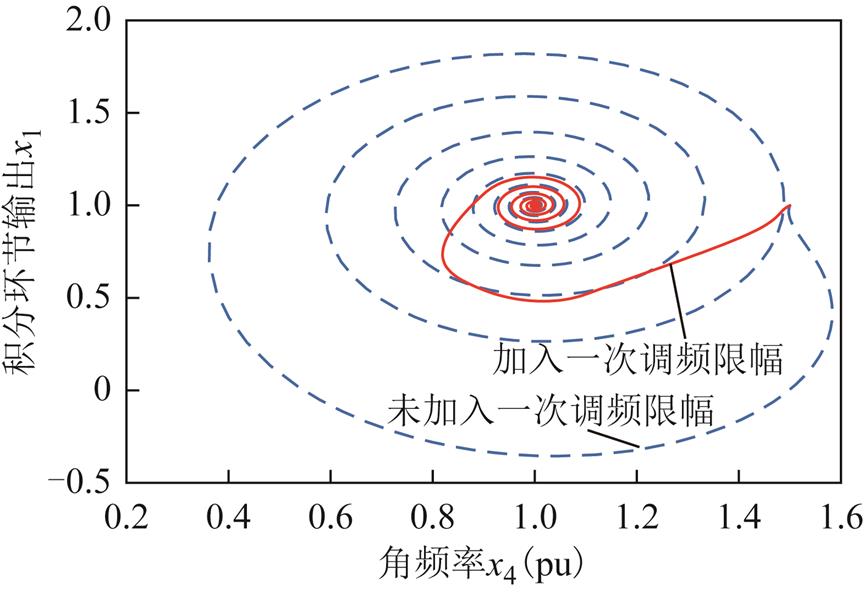
图8 有/无限幅对比
Fig.8 Contrast of with/without limit
图8表明,在KP参数较小时,系统会收敛到稳定的平衡点,且限幅环节起作用能加快系统轨线的收敛速度。
当调节系统模型带有一次调频限幅,状态变量x4的初值为偏离平衡点0.02(pu),取较大的PI参数分别为KP=5、KI=1,KP=5、KI=2,KP=7、KI=6.94时,角频率x4-积分环节输出x1的相图如图9所示。
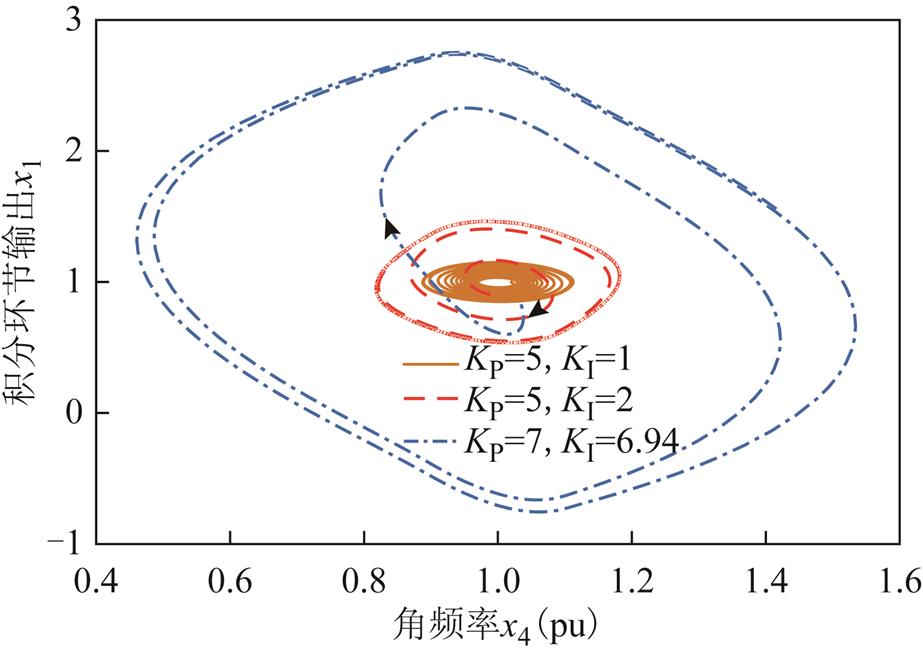
图9 不同PI参数下的极限环
Fig.9 The limit cycles under different PI parameters
图9和各状态变量的结果数据表明,PI参数越大,形成的极限环越大,即振荡幅度越大,同时振荡周期越长,振荡频率越低。
进一步,上述参数下取不同的初始频率偏差时,其动力学性质和振荡特性见表1。
表1 不同PI参数下的动力学性质
Tab.1 The dynamic characteristics under different PI parameters

参数不同初始频率偏差下的动力学性质振荡频率/Hz振荡幅度(pu) KP=4,KI=1任何初始频率下都收敛到稳定的平衡点—— KP=5,KI=10~0.015 7(pu)收敛到ω=1(pu);0.015 7(pu)外收敛到稳定的极限环0.106 70.112 KP=5,KI=20~0.002 3(pu)收敛到ω=1(pu);0.002 3(pu)外收敛到稳定的极限环0.082 70.182 KP=7,KI=6.940~0.001 1(pu)收敛到ω=1(pu);0.001 1(pu)外收敛到稳定的极限环0.067 50.539
表1表明,增加KP、KI参数,系统在初值偏离平衡点足够大时,会出现稳定的极限环,即发生振荡。随着PI参数的增大,发生振荡的初始频率偏差由0.015 7(pu)减小到0.001 1(pu),振荡频率由0.106 7Hz减小到0.067 5Hz,振荡幅度由0.112(pu)增大到0.539(pu)。该现象对应着电力系统中水电机组调速系统的PI参数过大,由水锤效应导致的反调作用明显,易造成系统频率不稳定,发生持续的等幅频率振荡。
选取状态变量x4的初值为偏离平衡点0.004(pu),改变系统的PI参数,得到系统动力学性质发生变化的参数域如图10所示。
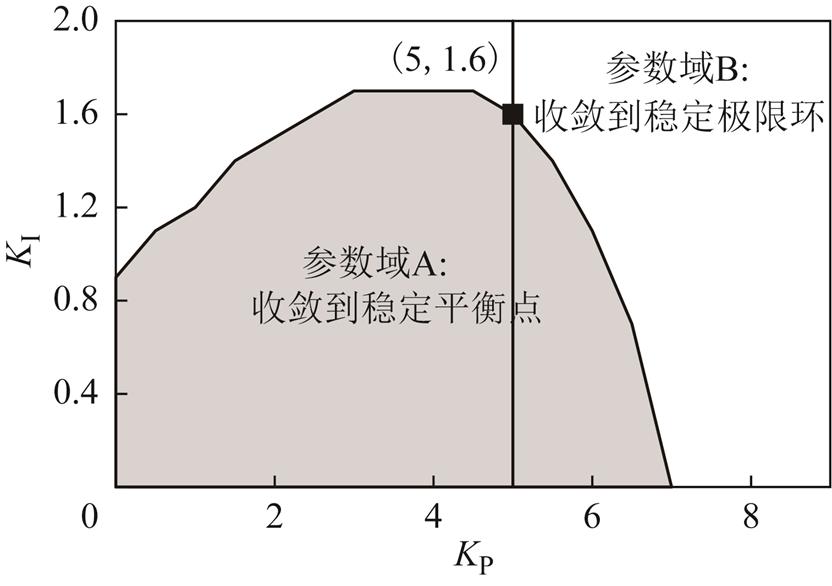
图10 固定初值下发生分岔的参数域
Fig.10 Parametric domain of bifurcation under fixed initial value
图10表明,在某一固定的初值下,系统的动力学性质在不同的PI参数下存在非光滑分岔点。例如,若系统的初始频率偏差为0.004(pu),固定KP=5,当KI<1.6时,则系统的状态响应都会收敛到稳定的平衡点;当KI≥1.6时,则系统轨线都会收敛到稳定的极限环。此时,KI变化中,系统即经历了非光滑分岔。
另一方面,当初始频率偏差较小(在死区内)时,系统频率的时域响应都会收敛到稳定的平衡点;此时系统不存在参数空间的非光滑分岔。而初始频率偏差较大(在死区外),状态变量x4的轨迹与系统是否会出现图10所示的非光滑分岔息息相关。如果系统参数正好落在收敛到平衡点的区域A(图中阴影区域)内,则系统收敛到平衡点,不出现极限环,即不发生振荡;但若系统发生非光滑分岔,系统参数正好落在出现极限环的区域B(图中空白区域)内,则在限幅作用下,系统出现极限环,即发生超低频频率振荡。
本文分析了单水电机组电力系统超低频频率振荡现象与其限幅环节的关系,揭示了超低频频率振荡发生的数学机理之一是系统出现非光滑分岔。主要结论如下:
1)存在限幅时,系统的动力学性质在初值参数角度具有非光滑分岔特性,表现为限幅环节起作用和足够大的初值,是导致系统发生超低频频率振荡的原因之一。
2)存在限幅时,系统的动力学性质在调速系统PI参数上存在非光滑分岔特性,即不同的PI参数将对振荡特性产生不同的效果。
参考文献
[1] 倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.
[2] 谢剑, 成业, 王晓茹. 基于NExT和PRCE方法的低频振荡分析[J]. 电工技术学报, 2018, 33(1): 121-130. Xie Jian, Cheng Ye, Wang Xiaoru. Estimation of electromechanical oscillation modes based on NExT-PRCE method[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 121-130.
[3] 赵妍, 李志民, 李天云. 低频振荡模态参数辨识的共振稀疏分解SSI分析方法[J]. 电工技术学报, 2016, 31(2): 136-144. Zhao Yan, Li Zhimin, Li Tianyun. Low frequency oscillation modal parameter identification using resonance-based sparse signal decomposition and SSI method[J]. Transactions of China Electrotechnical Society, 2016, 31(2): 136-144.
[4] 陈月辉, 张文朝, 徐遐龄, 等. 基于前K最短路径的电力系统低频振荡源定位方法[J]. 电力系统保护与控制, 2017, 45(13): 117-123. Chen Yuehui, Zhang Wenchao, Xu Xialing, et al. Locating method of low frequency oscillation source based on K shortest paths[J]. Power System Protection and Control, 2017, 45(13): 117-123.
[5] 龚鸿, 江伟, 王渝红, 等. 基于静止同步补偿器与直流调制协调控制的低频振荡抑制方法[J]. 电工技术学报, 2017, 32(6): 67-75. Gong Hong, Jiang Wei, Wang Yuhong, et al. A survey on damping low frequency oscillation based on coordination strategy of static synchronized compensator modulation[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 67-75.
[6] Butti D, Mangipudi S, Rayapudi S. Interconnected multi-machine power system stabilizer design using whale optimization algorithm[J]. Protection and Control of Modern Power Systems, 2019, 4(4): 13-23.
[7] 周靖皓, 江崇熙, 甘德强, 等. 基于值集法对云南电网超低频振荡的稳定分析[J]. 电网技术, 2017, 41(10): 3147-3152. Zhou Jinghao, Jiang Chongxi, Gan Deqiang, et al. Stability analysis of ultra-low frequency oscillation of Yunnan power grid based on value set approach[J]. Power System Technology, 2017, 41(10): 3147-3152.
[8] 路晓敏, 陈磊, 陈亦平, 等. 电力系统一次调频过程的超低频振荡分析[J]. 电力系统自动化, 2017, 41(16): 64-70. Lu Xiaomin, Chen Lei, Chen Yiping, et al. Ultra-low-frequency oscillation of power system primary frequency regulation[J]. Automation of Electric Power Systems, 2017, 41(16): 64-70.
[9] 王官宏, 于钊, 张怡, 等. 电力系统超低频振荡模式排查及分析[J]. 电网技术, 2016, 40(8): 2324-2330. Wang Guanhong, Yu Zhao, Zhang Yi, et al. Troubleshooting and analysis of ultra-low frequency oscillation mode in power system[J]. Power System Technology, 2016, 40(8): 2324-2330.
[10] 刘春晓, 张俊峰, 陈亦平, 等. 异步联网方式下云南电网超低频振荡的机理分析与仿真[J]. 南方电网技术, 2016, 10(7): 29-34. Liu Chunxiao, Zhang Junfeng, Chen Yiping, et al. Mechanism analysis and simulation on ultra-low frequency oscillation of Yunnan power grid in asynchronous interconnection mode[J]. Southern Power System Technology, 2016, 10(7): 29-34.
[11] 肖湘宁, 李伟, 罗超, 等. 特高压直流孤岛运行特性与稳定控制研究综述[J]. 电工技术学报, 2017, 32(10): 1-11. Xiao Xiangning, Li Wei, Luo Chao, et al. Survey on operational characteristics and stability control of ultra-HVDC transmission system in islanded mode[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 1-11.
[12] 陈怡君. 由局部控制器失稳引发的类强迫超低频振荡辨识及抑制[D]. 北京: 清华大学, 2018.
[13] Yijun Chen, Feng Liu, Chen Shen, et al. Mitigating a class of ultra-low-frequency oscillations in hydro-turbine dominant power systems[C]//2018 Biennial International Conference on Power and Energy Systems: Towards Sustainable Energy(PESTSE), Bangalore, 2018.
[14] 张建新, 刘春晓, 陈亦平, 等. 异步联网方式下云南电网超低频振荡的抑制措施与试验[J]. 南方电网技术, 2016, 10(7): 35-39. Zhang Jianxin, Liu Chunxiao, Chen Yiping, et al. Countermeasures and experiments on ultra-low frequency oscillation of Yunnan power grid in asynchronous interconnection mode[J]. Southern Power System Technology, 2016, 10(7): 35-39.
[15] 王菲, 刘建琴, 韩丰, 等. 应用直流调制改善水电能源基地交流电网运行特性[J]. 电网技术, 2017, 41(12): 3911-3916. Wang Fei, Liu Jianqin, Han Feng, et al. Application of DC modulation to improving operation characteristics of hydropower base grid[J]. Power System Technology, 2017, 41(12): 3911-3916.
[16] Gencoglu C, Tor O B, Cebeci E, et al. Assessment of the effect of hydroelectric power plants' governor settings on low frequency inter area oscillations[C]// IEEE International Conference on Power System Technology, Hangzhou, 2010: 1-8.
[17] Villegas H N. Electromechanical oscillations in hydro-dominant power systems: an application to the Colombian Power System [D]. Ames, lowa: Lowa State University, 2011.
[18] 付超, 柳勇军, 涂亮, 等. 云南电网与南方电网主网异步联网系统试验分析[J]. 南方电网技术, 2016, 10(7): 1-5, 12. Fu Chao, Liu Yongjun, Tu Liang, et al. Experiment and analysis on asynchronously interconnected system of Yunnan power grid and main grid of China Southern power grid[J]. Southern Power System Technology, 2016, 10(7): 1-5, 12.
[19] 陈刚, 丁理杰, 李旻, 等. 异步联网后西南电网安全稳定特性分析[J]. 电力系统保护与控制, 2018, 46(7): 76-82. Chen Gang, Ding Lijie, Li Min, et al. Stability characteristics of southwest China power grid after asynchronous interconnection[J]. Power System Protection and Control, 2018, 46(7): 76-82.
[20] Ji W, Venkatasubramanian V. Hard-limit induced chaos in a single-machine-infinite-bus power system[C]//Proceedings of the IEEE Conference on Decision and Control, New Orleans, LA, 1995(4): 3465-3470.
[21] Ji W, Venkatasubramanian V. Hard-limit induced chaos in a fundamental power system model[J]. International Journal of Electronics Power and Energy System, 1996, 18(5): 279-295.
[22] Jiang X, Venkatasubramanian V, Schattler H, et al. Hardlimit related stability phenomena in the power system[C]//Proceedings of International Conference on Control Applications, Albany, NY, 1995: 63-72.
[23] Venkatasubramanian V. Stability boundary analysis of nonlinear dynamics subject to state limits[C]//Hawaii International Conference on System Sciences, IEEE Computer Society, Maui, HI, 2001: 2024.
[24] 戴义平, 张镇一, 蔡元基, 等. 非线性因素与中间再热透平调节系统的稳定性[J]. 汽轮机技术, 1991(1): 8-14, 56.Dai Yiping, Zhang Zhenyi, Cai Yuanji, et al. Nonlinear factors and stability of intermediate reheat turbine regulation system[J]. Turbine Technology, 1991(1): 8-14, 56.
[25] Donde V, Hiskens I A. Dynamic performance assessment: grazing and related phenomena[J]. IEEE Transactions on Power Systems, 2005, 20(4): 1967-1975.
[26] 韦李军, 黄萌, 孙建军, 等. 带恒功率负载的光伏-储能混合发电系统非线性行为分析[J]. 电工技术学报, 2017, 32(7): 128-137.Wei Lijun, Huang Meng, Sun Jianjun, et al. Nonlinear analysis of photovoltaic battery hybrid power system with constant power loads[J]. Transactions of China Electrotechnical Society, 2017, 32(7): 128-137.
[27] 赵雅博, 张毅威, 陈磊, 等. 电力系统机电振荡的非线性现象[J]. 电网技术, 2012, 36(10): 172-177.Zhao Yabo, Zhang Yiwei, Chen Lei, et al. Study on nonlinearity in power system electro-mechanical oscillation[J]. Power System Technology, 2012, 36(10): 172-177.
[28] 邓集祥, 纪晶, 邓斌. 基于复合模式的电力系统超低频振荡产生机理[J]. 电工技术学报, 2007, 22(8): 84-89.Deng Jixiang, Ji Jing, Deng Bin. The generation mechanism of ultra-low frequency oscillation in power systems based on combination modes[J]. Transactions of China Electrotechnical Society, 2007, 22(8): 84-89.
[29] 潘道明. 柬埔寨达岱电厂基于自适应控制策略的调速器系统分析[J]. 电气技术, 2016, 17(7): 87-92.Pan Daoming. The governor systems analysis based on adaptive control strategy in DadaiHydropower Station of Cambodia[J]. Electrical Engineering, 2016, 17(7): 87-92.
Mechanism Analysis of Ultra-Low Frequency Oscillation of Single Hydropower System Based on Non-Smooth Bifurcation
Abstract To the power system of single hydropower unit, this paper analyses the influence of limit of governor system on ultra-low frequency oscillations (ULFO) by the phase portrait method, and reveals that one of the mathematical mechanisms of ULFO is non-smooth bifurcation. In detail, firstly, the oscillation phenomenon of non-smooth system caused by the saturation of limit is analyzed, illustrating that one of the reasons for the oscillation of general dynamic systems is the non-smooth bifurcation associated with the saturation of limit. Secondly, a simple mathematical model, state equation and balance point characteristics of the power system of single hydropower unit with limiting link are given. And then, the dynamic characteristics of the system phase portrait with/without limit cycle under different initial conditions and with/without limit are analyzed, which show that the saturation of the limit of governor system and the large enough initial value are one of the reasons for the system ULFO and reveal the non-smooth bifurcation characteristics of the system for initial values. Finally, the influence of different system parameters on the dynamic characteristics of the system with/without limit cycle is analyzed, and the non-smooth bifurcation characteristics of system parameters under certain initial values are revealed.
keywords:Non-smooth bifurcation, ultra-low frequency oscillation, limit cycle, limit, governor system
DOI:10.19595/j.cnki.1000-6753.tces.190448
中图分类号:TM712
薛安成 男,1979年生,教授,博士生导师,研究方向为模型和数据驱动的电力系统稳定分析和安全防御、二次设备评估。E-mail:acxue@ncepu.edu.cn(通信作者)
王嘉伟 男,1996年生,博士研究生,研究方向为电力系统频率振荡的分析和控制。E-mail:15650759520@163.com
国家重点研发计划项目(2017YFB0902000)和国家自然科学基金项目(51477050, 50707035)资助。
收稿日期 2019-04-19
改稿日期 2019-09-03
(编辑 赫蕾)