 (1)
(1)摘要 精确、可靠的发电机动态状态量对电力系统的实时监测和控制至关重要。信息攻击的出现给发电机状态估计带来了新的挑战。其中,虚假数据注入(FDI)攻击通过对量测装置注入虚假数据,恶化了状态估计的精度。为此,该文提出一种针对发电机动态状态估计的FDI攻击模型。首先,采用泰勒公式将发电机量测方程线性化;其次,根据FDI攻击前后量测残差不变的原理,建立攻击向量的表达式,将其施加在量测量中,从而躲避常规的不良数据检测,成功实施FDI攻击;然后,根据攻击程度分别设定三种攻击情形,通过容积卡尔曼滤波(CKF)和抗差容积卡尔曼滤波(RCKF)对所提的三种不同情形的FDI攻击进行验证;最后,IEEE 9节点系统和新英格兰16机68节点系统的仿真结果验证了所提FDI攻击的有效性。
关键词:动态状态估计 信息攻击 发电机 容积卡尔曼滤波 虚假数据注入攻击 PMU数据
精确、可靠的发电机动态状态量对电力系统的实时监测和控制至关重要[1-3]。作为一个典型的信息物理系统,电力系统已经出现并运行了一百多年,但是日益增多的信息攻击、自然灾害和对通信控制的依赖导致了新型故障源的产生和连锁故障的发生。同时,随着可再生能源的大量接入,电力系统运行的不确定性也随之增大[4]。所有这些转变都给维持系统安全、可靠运行带来了新的挑战。同步相量测量单元(Phasor Measurement Unit, PMU)作为电力系统状态估计与动态监视的重要部分,在电力系统安全稳定评估和监控中发挥了重要作用[5-6]。
当前电力系统的运行面临着严峻的信息攻击威胁,其中虚假数据注入(False Data Injection, FDI)攻击就是信息攻击的一种典型代表。该攻击对电力系统中量测装置产生的量测数据进行虚假数据注入,且具有避开不良数据检测的能力,使估计结果较正常结果偏差较大,从而影响电力系统在线安全评估,使安全约束经济调度方案偏离最优解,增加系统运行成本,甚至造成大范围甩负荷的事件发生。2015年12月23日,乌克兰国家电网突发停电事故就是FDI攻击电力系统的现实案例[7]。
近年来,国内外对FDI攻击和发电机状态估计的研究取得了一定进展。就FDI攻击而言,针对攻击的建模、检测及防御已有大量文献对此进行了研究。其中,文献[8]通过引入攻击向量的松弛误差建立了一种FDI攻击模型;文献[9]使用主成分分析法对FDI攻击进行建模,并验证了所提攻击的隐蔽性;文献[10-11]分别基于网络拓扑结构建立了针对直流潮流和交流潮流的FDI攻击模型;而文献[12]又将直流模型扩展为更一般的线性模型,推导出了基于该模型的FDI攻击;文献[13]则依靠量测矩阵的低秩特征和攻击矩阵的稀疏性对FDI攻击进行检测;文献[14]提出了一种动态估计的风险缓解策略以消除FDI攻击的威胁;文献[15]研究了在FDI攻击下卡尔曼滤波器对电力系统动态估计的影响。在发电机动态状态估计领域,各文献也使用了很多非线性滤波的方法来解决此问题。文献[1,16-17]分别采用容积卡尔曼滤波(Cubature Kalman Filter, CKF)、无迹卡尔曼滤波(Unscented Kalman Filter, UKF)和扩展卡尔曼滤波(Extended Kalman Filter, EKF)的方法进行发电机动态状态估计;其中EKF通过泰勒公式展开将非线性问题线性化,但由于忽略了泰勒展开式中的高次项,进而对估计精度产生了一定的影响[18];UKF利用无迹变换来解决非线性问题,无需进行雅克比公式的计算,但其估计精度在很大程度上取决于sigma点的分布情况和状态维数,这也在一定程度上限制了UKF的应用[19];CKF则采用球面-径向准则生成一组等权值的容积点,进而解决了发电机动态状态估计中的非线性滤波问题,其在处理估计偏差和状态维度的问题上优于EKF和UKF。综上,在状态估计领域内,多数文献研究了基于电力系统稳态潮流模型的FDI攻击,迄今尚未见有在发电机动态状态估计中施加FDI攻击的相关研究报道。
本文提出了一种新的针对发电机动态状态估计的虚假数据注入攻击方法。首先,采用泰勒公式将发电机量测方程线性化;其次,根据FDI攻击前后量测残差不变的原理,建立了攻击向量的表达式,将其施加在量测量中,从而躲避常规的不良数据检测,成功实施FDI攻击;然后,根据攻击程度设定了三种攻击情形,通过容积卡尔曼滤波和抗差容积卡尔曼滤波(Robust CKF, RCKF)对所提的不同情形的FDI攻击进行验证;最后,IEEE 9节点系统和新英格兰16机68节点系统的仿真结果验证了所提FDI攻击的有效性。
建立非线性动态系统数学模型是对发电机动态状态估计研究的前提,其状态方程和量测方程为[1]
 (1)
(1)式中,x、u、z分别为状态向量、控制向量和量测向量;v和w分别为系统噪声向量和量测噪声向量,其分别服从均值为0、误差方差阵为Q和R的正态分布,其中Q为系统噪声方差矩阵,R为量测噪声方差矩阵;k为时刻。
发电机动态状态估计的状态方程为[20-21]
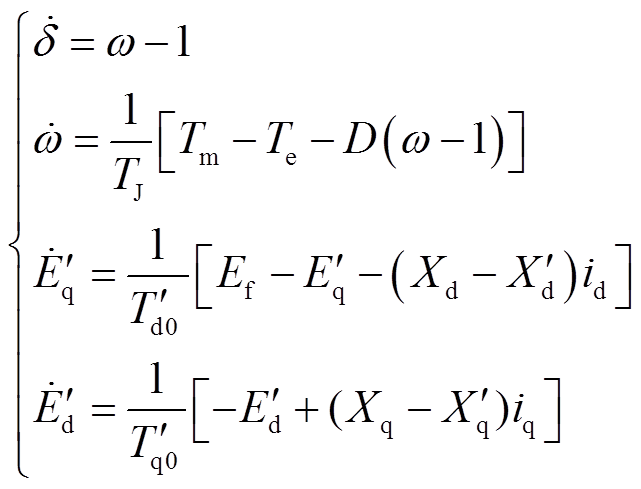 (2)
(2)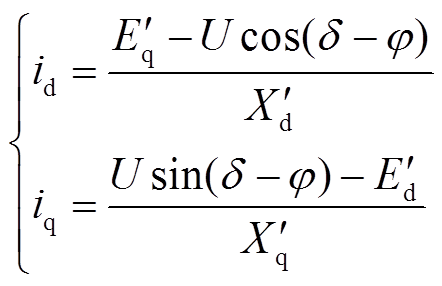 (3)
(3)
式中, 为发电机d轴暂态电动势;
为发电机d轴暂态电动势;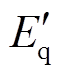 为发电机q轴暂态电动势;
为发电机q轴暂态电动势;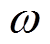 为电角速度标幺值;
为电角速度标幺值;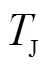 为惯性时间常数;
为惯性时间常数;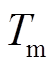 为发电机机械转矩;
为发电机机械转矩; 为励磁电动势;
为励磁电动势;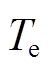 为发电机电磁转矩;
为发电机电磁转矩;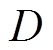 为阻尼系数;
为阻尼系数;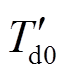 为发电机d轴暂态时间常数;
为发电机d轴暂态时间常数; 为发电机d轴电抗;
为发电机d轴电抗;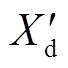 为发电机d轴暂态电抗;
为发电机d轴暂态电抗;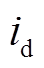 为发电机d轴输出电流分量;
为发电机d轴输出电流分量;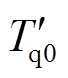 为发电机q轴暂态时间常数;
为发电机q轴暂态时间常数;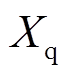 为发电机q轴电抗;
为发电机q轴电抗;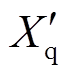 为q轴暂态电抗;
为q轴暂态电抗;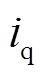 为发电机q轴输出电流分量;
为发电机q轴输出电流分量;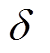 为功角;
为功角;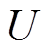 和
和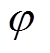 分别为发电机出口电压幅值和相角。
分别为发电机出口电压幅值和相角。
量测变量包括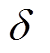 、
、 和
和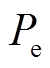 ,量测方程为[3]
,量测方程为[3]
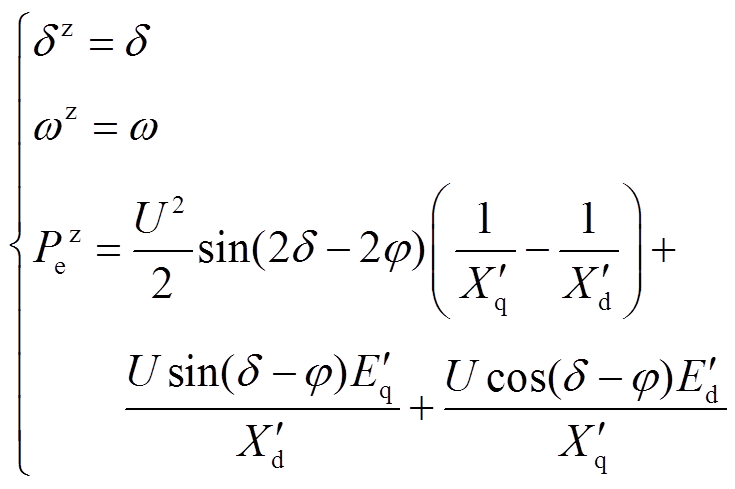 (4)
(4)式中,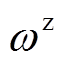 和
和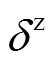 分别为发电机角速度和功角的量测量;
分别为发电机角速度和功角的量测量;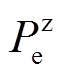 为发电机电磁功率量测量。
为发电机电磁功率量测量。
发电机量测误差方差矩阵Rk+1表示为
 (5)
(5)式中, 、
、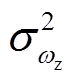 、
、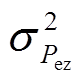 分别为功角量测方差、角速度量测方差和电磁功率量测方差,
分别为功角量测方差、角速度量测方差和电磁功率量测方差,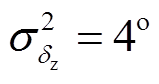 ,
,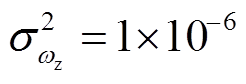 。
。
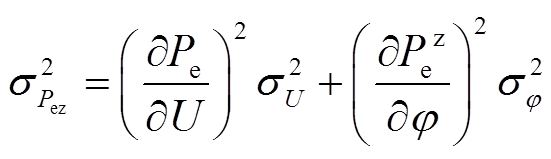 (6)
(6)
式中,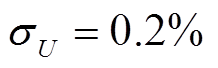 ,
,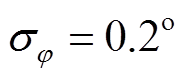 。
。
在发电机模型中,状态量、量测量和控制量分别为
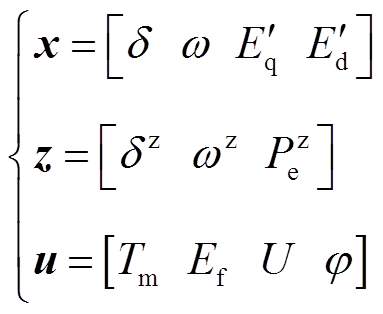 (7)
(7)在发电机动态状态估计中,状态变量统一表示为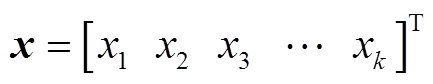 ,量测量统一表示为
,量测量统一表示为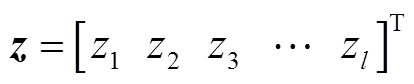 。量测方程为
。量测方程为
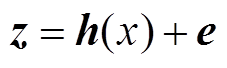 (8)
(8)其中
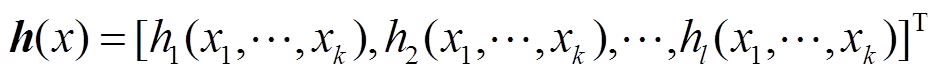 (9)
(9)
表示状态量和量测量之间的非线性关系,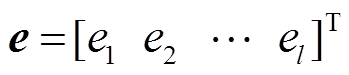 表示量测误差。
表示量测误差。
以h1函数为例,使用泰勒公式对h1函数进行扩展,由于发电机各状态量参数在机电暂态过程中不能突变,h1函数中的高次项可以被忽略,因此能够对发电机量测方程线性化,具体为

式中,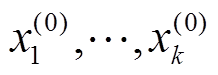 为接近状态量
为接近状态量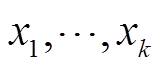 的设置初始值;
的设置初始值;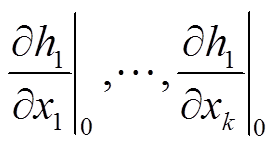 为将
为将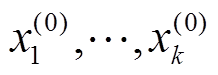 代入偏导数公式后的计算结果;
代入偏导数公式后的计算结果;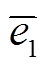 为常数。因此,式(8)可进一步表示为
为常数。因此,式(8)可进一步表示为
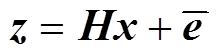 (11)
(11)
 (12)
(12)式中,H为雅克比矩阵;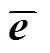 可被视为新的量测误差。将式(4)代入式(12),可得
可被视为新的量测误差。将式(4)代入式(12),可得
 (13)
(13)
式中,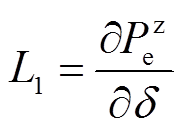 ;
;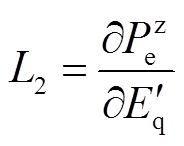 ;
;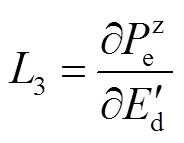 。
。
在发电机实际运行中,不良数据时常出现,严重影响电力系统状态估计精度[19]。残差方程的应用在很大程度上消除了不良数据的影响。因此,文中将基于残差的检测法应用于对量测数据的检测。
定义残差方程为[22]
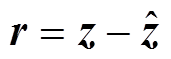 (14)
(14)式中,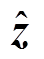 为量测量z的估计值,
为量测量z的估计值,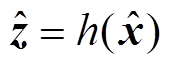 。
。
依据残差的定义并结合式(8)~式(13),式(14)可改写为
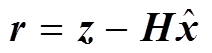 (15)
(15)若用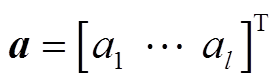 表示攻击者在量测值中注入的虚假数据向量,则实际的量测数据为
表示攻击者在量测值中注入的虚假数据向量,则实际的量测数据为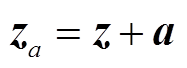 ;
;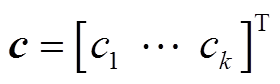 表示状态变量中由FDI攻击而带入的误差向量,其可服从均值为零、不同标准差的高斯分布[23],进而状态变量估计值变为
表示状态变量中由FDI攻击而带入的误差向量,其可服从均值为零、不同标准差的高斯分布[23],进而状态变量估计值变为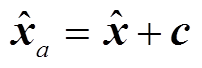 。因此,FDI攻击后的量测残差为[9]
。因此,FDI攻击后的量测残差为[9]
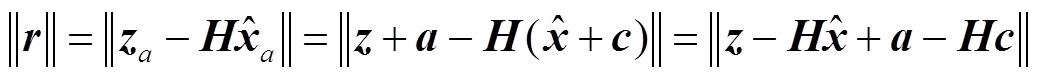 (16)
(16)
显然,当 ,有式(17)成立,结果显示在FDI攻击前后的量测残差相等,导致在以残差方程为根据的基础上,不良数据检测无法识别虚假数据,因此量测数据被成功引入FDI攻击,攻击下的量测数据比真实值偏差较大,将直接破坏电力系统安全稳定运行[22]。
,有式(17)成立,结果显示在FDI攻击前后的量测残差相等,导致在以残差方程为根据的基础上,不良数据检测无法识别虚假数据,因此量测数据被成功引入FDI攻击,攻击下的量测数据比真实值偏差较大,将直接破坏电力系统安全稳定运行[22]。
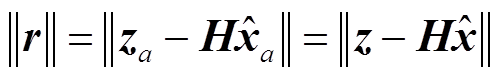 (17)
(17)若进一步将虚假数据误差考虑在内,攻击前后的量测残差将不再相等[18],如式(18)所示。
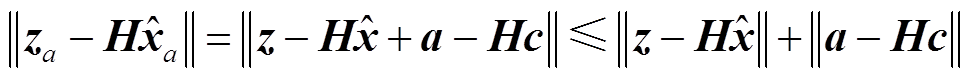 (18)
(18)
然而,如果量测数据的残差值小于不良数据的检测阈值,FDI攻击仍然可以成功实施。在基于残差的不良数据检测中,将正常情况下最大估计偏差值增加一定的冗余度,形成检测阈值 。其检测过程为
。其检测过程为
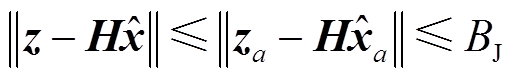 (19)
(19)即如果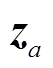 满足式(19),FDI攻击将会被成功引入发电机动态状态估计中。
满足式(19),FDI攻击将会被成功引入发电机动态状态估计中。
CKF算法采用球面-径向准则生成一组等权值的容积点,进而解决了发电机动态状态估计中的非线性滤波问题,其具体分为两部分:
1)预报步。CKF根据球面-径向准则产生一组等权值的状态量容积点,之后利用状态方程获得下一时刻状态量的预报值,并计算状态量预报误差方差矩阵。其具体步骤如下:
利用k时刻状态量的估计误差方差矩阵得到其平方根矩阵Pk/k为
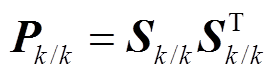 (20)
(20)生成状态量的容积点为
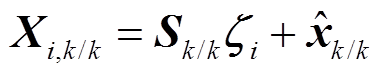 (21)
(21)
式中,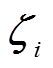 为容积点权值矩阵
为容积点权值矩阵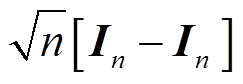 的第i列,
的第i列,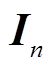 为单位阵,n为状态量数量;
为单位阵,n为状态量数量;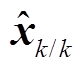 为k+1时刻状态量估计值。
为k+1时刻状态量估计值。
经状态方程计算得到状态量容积点预报值为
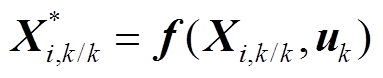 (22)
(22)对式(22)结果进行加权求和计算,进一步得到状态量预报值为
 (23)
(23)
计算获取状态量预报误差方差矩阵
 (24)
(24)2)滤波步。通过量测量完成对状态量预报值的修正,得到更为准确的估计值。其具体过程如下:
(1)计算状态量预报误差方差矩阵的平方根矩阵。
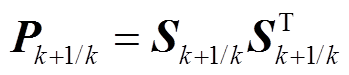 (25)
(25)(2)计算状态量预报值的容积点。
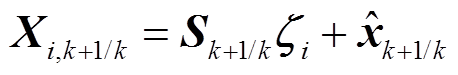 (26)
(26)
(3)通过量测方程计算量测量预报值容积点。
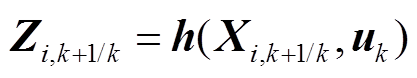 (27)
(27)对式(27)结果进行加权求和计算,进一步得到量测量预报值为
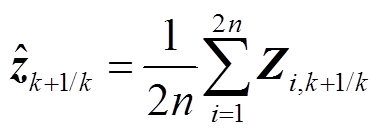 (28)
(28)
(4)建立量测量误差方差矩阵。
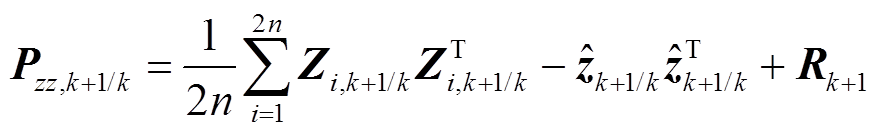 (29)
(29)(5)计算交叉误差方差矩阵。
 (30)
(30)
(6)计算滤波增益。
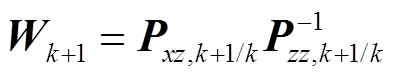 (31)
(31)(7)计算k+1时刻状态量估计值。
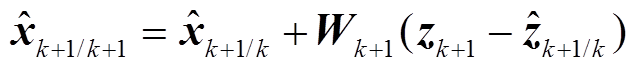 (32)
(32)
(8)计算下一时刻状态量估计误差方差矩阵。
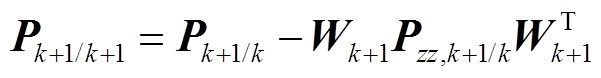 (33)
(33)RCKF算法是抗差估计理论中的中位数估计方法和CKF算法的融合。在抗差估计理论中,M估计是经典极大似然估计的推广,又称为广义似然估计,在电力系统中应用极为广泛。给定量测方程为
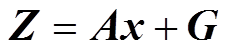 (34)
(34)式中,A为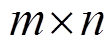 阶系数矩阵;x为状态向量;Z为量测向量;G为Z的残差向量。
阶系数矩阵;x为状态向量;Z为量测向量;G为Z的残差向量。
残差向量G的M估计准则函数为
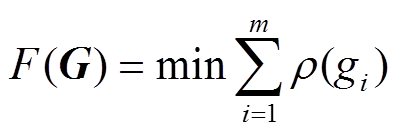 (35)
(35)式中,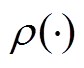 为适当选择的凸函数;量测残差
为适当选择的凸函数;量测残差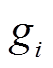 为G的第i个元素。
为G的第i个元素。
作为M估计中的一种估计方法,中位数估计方法通过设置残差的中位数来滤除量测量中的粗差,与其他的传统最小二乘抗差方法相比,能够避免更多的量测不良数据对估计结果的影响,具有良好的抗差性能。在中位数估计中,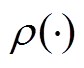 函数和等价权因子
函数和等价权因子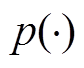 分别为
分别为
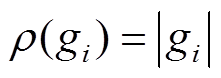 (36)
(36)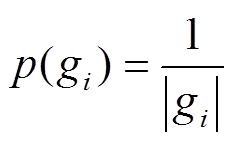 (37)
(37)
式中,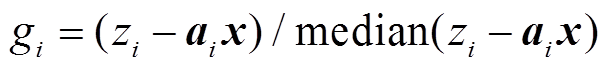 ,
,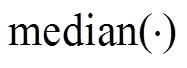 表示取中位数,ai为矩阵A的第i行。
表示取中位数,ai为矩阵A的第i行。
经上述方法,首先根据中位数估计方法确定预测残差中误差,并计算标准化残差;然后基于标准化残差绝对值,通过两段函数获得量测噪声的抗差协方差矩阵;最后用其替换原来的量测误差方差矩阵。因此,在算法计算过程中,量测量误差方差矩阵被不断修正,进而形成RCKF算法[24]。其具体过程如下:
(1)计算量测量的预测残差向量。
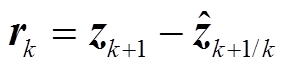 (38)
(38)(2)计算预测残差中误差。
 (39)
(39)
(3)计算标准化残差。
 (40)
(40)(4)计算抗差协方差矩阵。
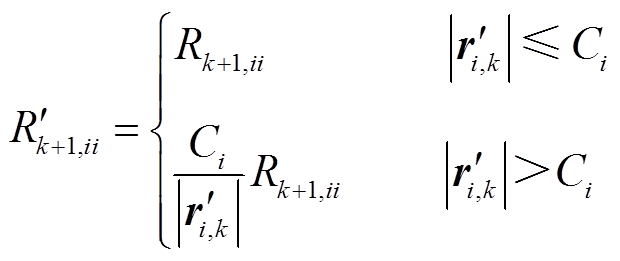 (41)
(41)
式中,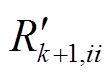 和
和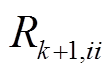 分别为
分别为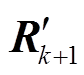 和
和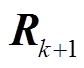 的第i个对角元素,非对角元素为零;
的第i个对角元素,非对角元素为零;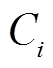 为先验阈值(即检测量测数据异常的阈值),常数。由于RCKF是以CKF为基础的算法,因此需要通过CKF算法计算的标准化残差值来确定
为先验阈值(即检测量测数据异常的阈值),常数。由于RCKF是以CKF为基础的算法,因此需要通过CKF算法计算的标准化残差值来确定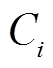 。具体步骤为:①在确定的系统中预先设置线路或母线故障,对于给定的发电机进行基于CKF算法的动态状态估计,通过式(32)计算得到量测量的标准化残差随时间的变化曲线。②根据曲线的分布情况确定阈值:如果曲线收敛,则取其收敛值作为RCKF算法中的先验阈值;否则,取介于最大值和最小值的中间值作为先验阈值。
。具体步骤为:①在确定的系统中预先设置线路或母线故障,对于给定的发电机进行基于CKF算法的动态状态估计,通过式(32)计算得到量测量的标准化残差随时间的变化曲线。②根据曲线的分布情况确定阈值:如果曲线收敛,则取其收敛值作为RCKF算法中的先验阈值;否则,取介于最大值和最小值的中间值作为先验阈值。
(5)更新量测量误差方差矩阵。
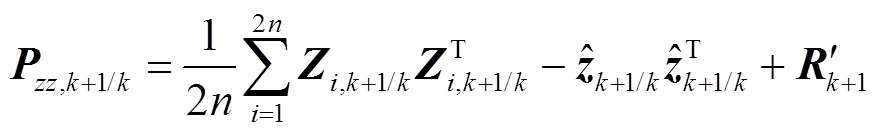 (42)
(42)将式(42)替换式(29),进而形成RCKF算法。
FDI攻击场景下,本文中发电机动态状态估计的步骤如下:
1)建立发电机状态方程,将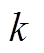 时刻状态量的估计值和由PMU实时测得的发电机出口电压幅值U及相角
时刻状态量的估计值和由PMU实时测得的发电机出口电压幅值U及相角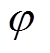 代入发电机状态方程,进行预报步的计算,从而得到
代入发电机状态方程,进行预报步的计算,从而得到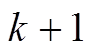 时刻状态量的预报值。
时刻状态量的预报值。
2)建立发电机量测方程,根据量测方程求出联系量测量和状态量之间的雅克比矩阵。分别建立服从不同标准差高斯分布的状态量误差向量。将两者相乘形成攻击向量,让其施加在由PMU测得的量测数据中,并进一步对量测数据进行不良数据检测。
3)在发电机量测方程和更新后量测值的基础上,通过CKF算法或RCKF算法的滤波阶段,进一步得到该攻击场景下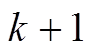 时刻状态量的估计值。
时刻状态量的估计值。
4)判断仿真时间是否结束,如果结束则停止估计过程;否则将此估计值代入步骤1)进行下一时刻的状态估计。
FDI攻击场景下,本文中发电机动态状态估计的流程如图1所示。

图1 状态估计流程
Fig.1 Flow chart of the state estimation
在Matlab环境下,采用Power System Toolbox(PST)为仿真工具。所有仿真均在配置为Intel Core i5-45903.3 GHz处理器、8 GB内存的PC上实现。仿真基准频率为50Hz,采样步长为0.02s;PMU量测误差服从如下正态分布:均值为零,发电机功角标准差是2°,角速度标准差是0.1%,出口电压的相角和幅值标准差是0.1°和0.1%[1]。
结合文献[23]中基于FDI攻击下状态量的误差向量c的选取结果,为了进一步研究更大程度的攻击对估计结果的影响,因此,在本文的仿真分析中,根据FDI攻击程度由弱到强共设计了三种攻击情形,见表1。
表1 虚假数据注入攻击情形
Tab.1 False data injection attack situation

攻击情形状态量的误差向量 Case 1 Case 2 Case 3
在表1中,Case1、Case2和Case3分别表示在此三种攻击情形下,状态量的误差向量分别服从均值为零,标准差为0.01、0.1和1的高斯分布。
建立发电机动态状态估计的量化评估指标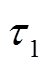 和总估计误差方差
和总估计误差方差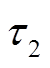 ,具体计算公式为[1]
,具体计算公式为[1]
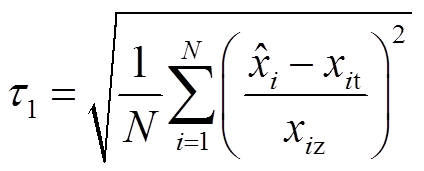 (43)
(43)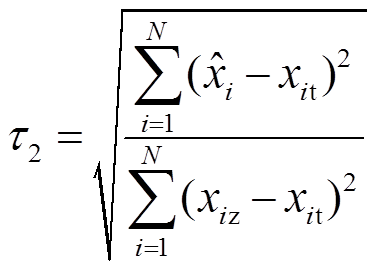 (44)
(44)
式中,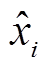 和
和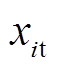 分别为估计值和真实值;
分别为估计值和真实值;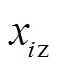 为量测值;
为量测值; 为采样点数。评估指标
为采样点数。评估指标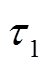 可衡量基于同一估计方法在不同攻击场景下的滤波性能;
可衡量基于同一估计方法在不同攻击场景下的滤波性能;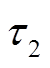 可评价在同一信息攻击下不同估计方法的滤波性能。
可评价在同一信息攻击下不同估计方法的滤波性能。
将所提算法用于IEEE 9节点系统进行仿真,仿真设置如下:t=1.2s时在节点5设置三相金属性短路故障,随后故障被断路器切除,仿真持续时间20s。经过多次仿真测试,设置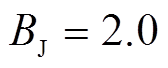 。在此情况下,不良数据检测能够检测到不良数据但是检测不到注入的虚假数据。
。在此情况下,不良数据检测能够检测到不良数据但是检测不到注入的虚假数据。
以发电机1为例,图3所示为基于CKF算法的三个量测量标准化残差的变化情况。
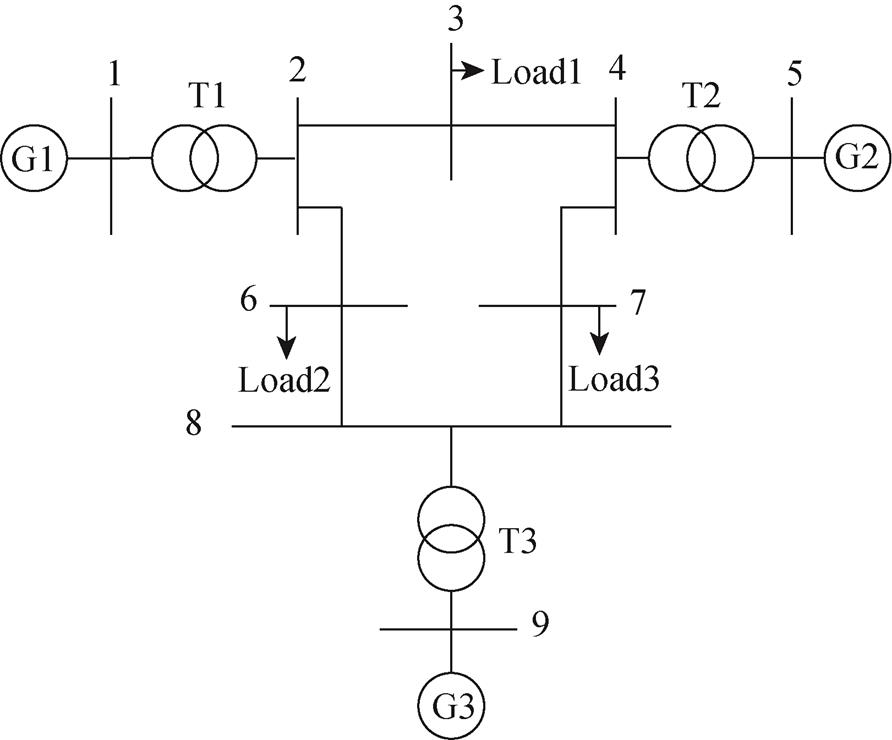
图2 IEEE 9节点系统
Fig.2 IEEE 9-bus system
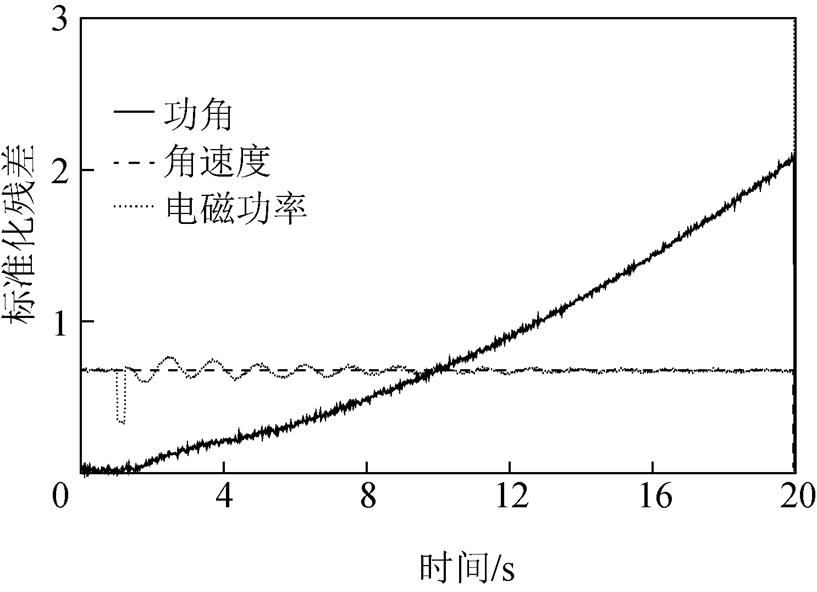
图3 基于CKF算法的标准化残差
Fig.3 Standardized residuals based on CKF algorithm
由图3可得,由于量测异常值的存在,CKF计算下的标准化残差变化不一,其中功角的标准化残差逐渐增大,角速度的标准化残差比较稳定,电磁功率的标准化残差在前期虽存在跳变,但后期主体趋势逐渐稳定,故对三个先验阈值分别取值1、0.7和0.7。
以发电机1为例,分别在上述三种攻击情形下,进行基于RCKF和CKF的发电机动态状态估计,得到以下发电机功角和角速度的仿真图形。在无攻击情形和三种不同攻击情形下的发电机功角和角速度的仿真结果分别如图4~图11所示。
1)无攻击情形

图4 无攻击情形下的发电机功角
Fig.4 Generator’s power angle without attack
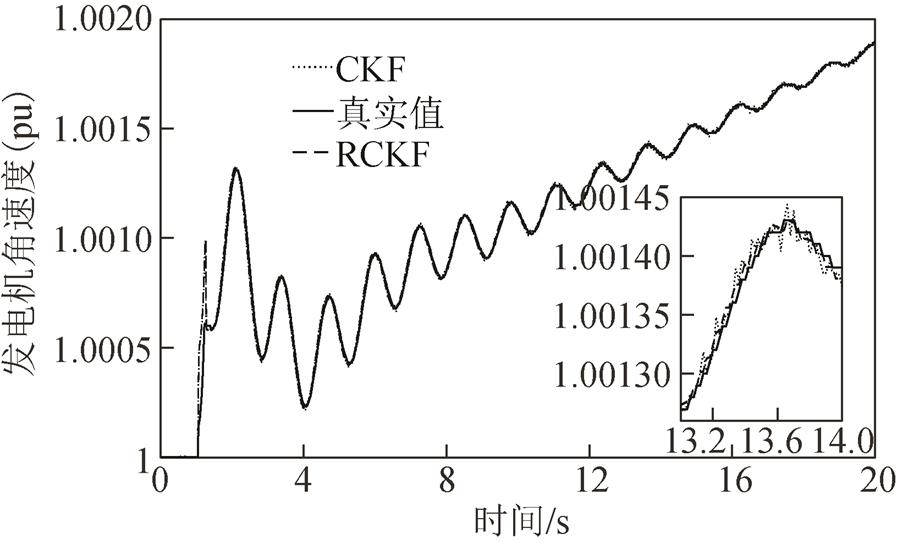
图5 无攻击情形下的发电机角速度
Fig.5 Generator’s angular velocity without attack
2)Case1
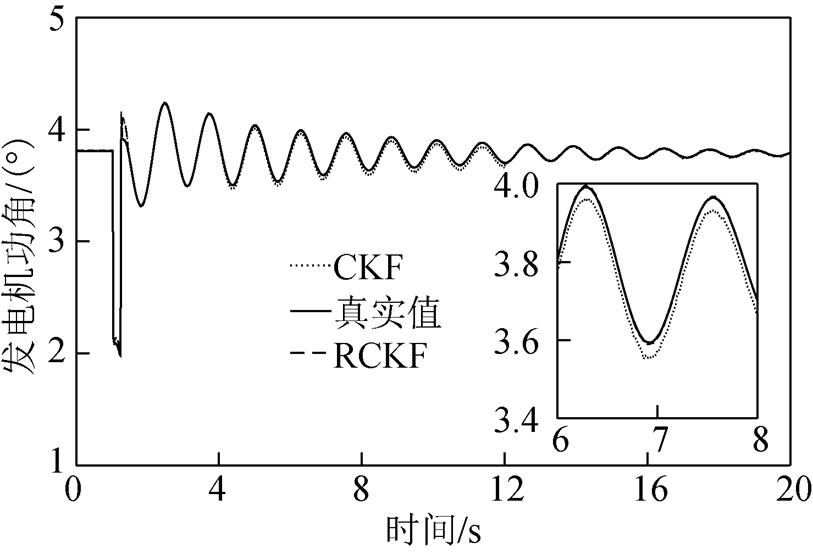
图6 情形1下的发电机功角
Fig.6 Generator’s power angle under Case 1
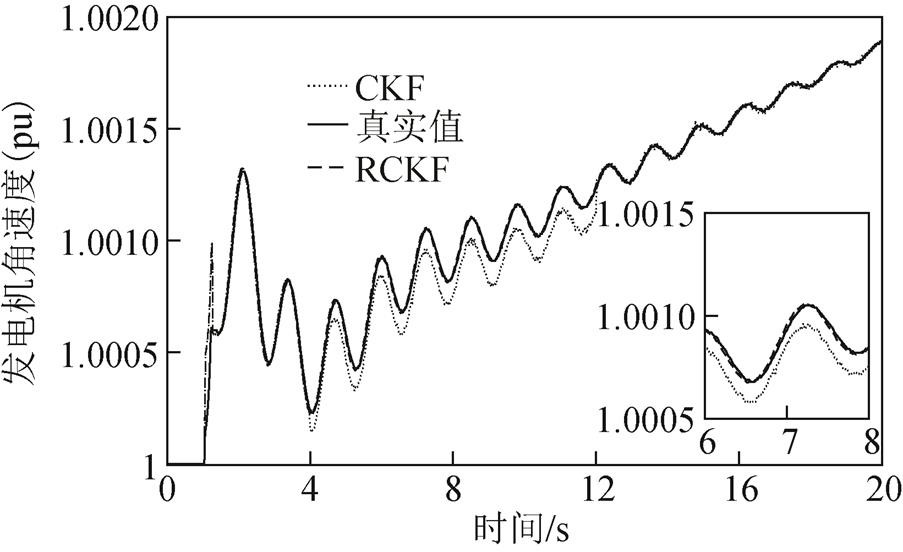
图7 情形1下的发电机角速度
Fig.7 Generator’s angular velocity under Case 1
3)Case2
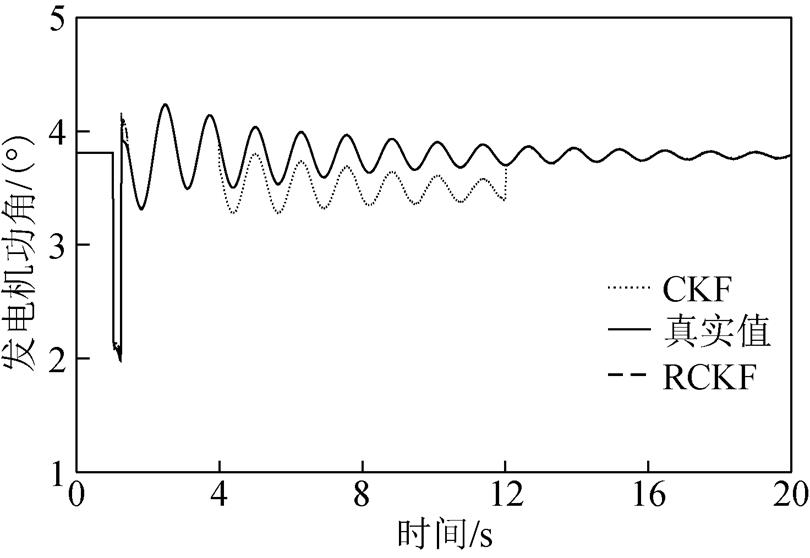
图8 情形2下的发电机功角
Fig.8 Generator’s power angle under Case 2
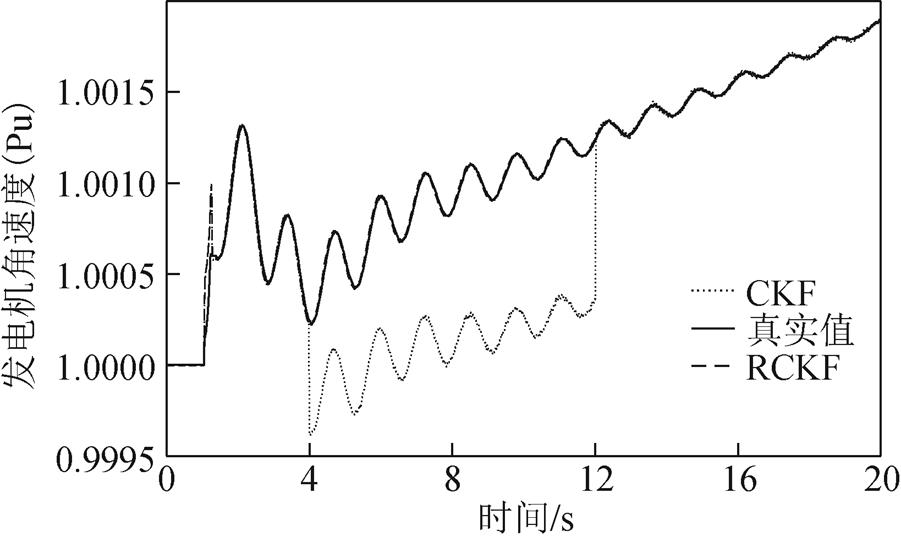
图9 情形2下的发电机角速度
Fig.9 Generator’s angular velocity under Case 2
4)Case3
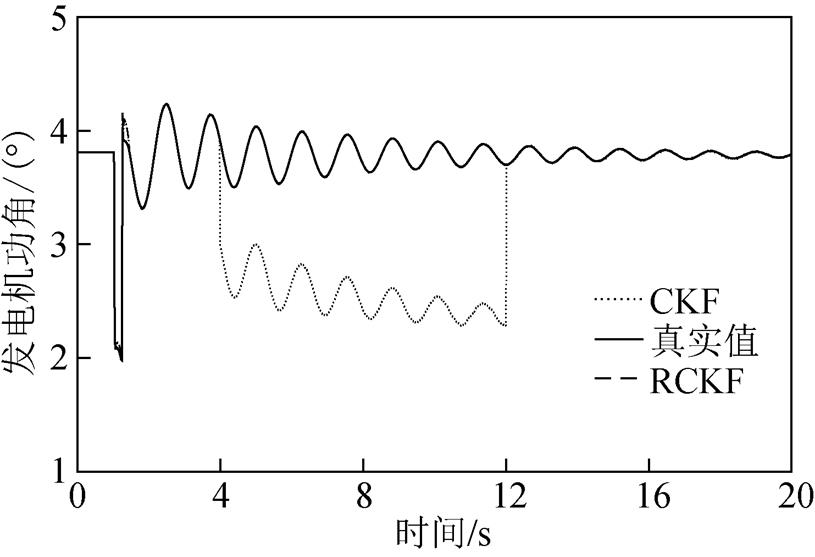
图10 情形3下的发电机功角
Fig.10 Generator’s power angle under Case 3
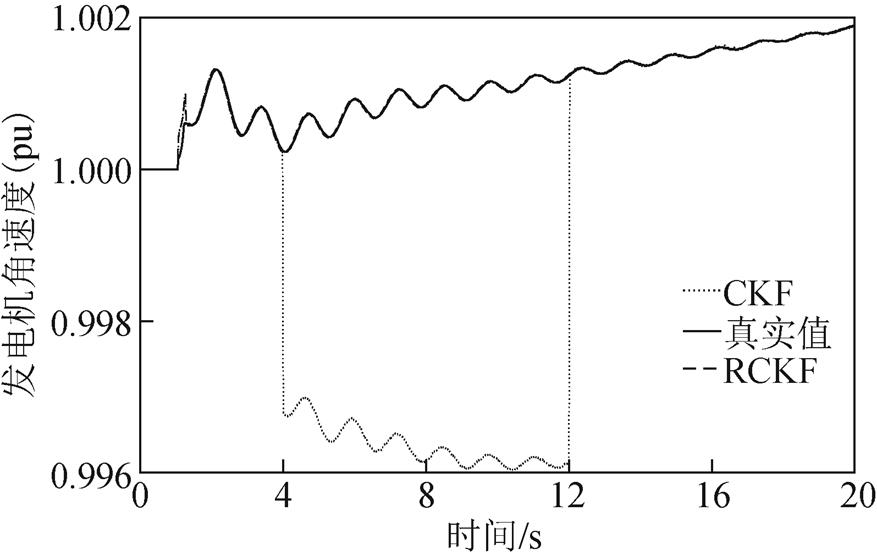
图11 情形3下的发电机角速度
Fig.11 Generator’s angular velocity under Case 3
图4和图5显示了无攻击情形下分别基于CKF和RCKF的发电机功角和角速度的估计结果;图6、图8、图10分别显示了在三种FDI攻击场景下,发电机功角的估计结果;图7、图9、图11分别显示了在三种FDI攻击场景下,发电机角速度的估计结果。可以看出在4~12s的攻击时段内,与无攻击情形相比,随着攻击强度的增加,CKF的估计值逐渐偏离真实值,从而验证了所提FDI攻击对基于CKF算法的发电机动态状态估计的有效性。随着攻击情形的变化,RCKF算法对攻击具有一定的抵抗能力,其估计值未明显偏移。
5)状态估计指标对比
发电机1的状态估计指标见表2。
表2 发电机1的动态状态估计指标
Tab.2 Dynamic state estimation index of generator 1
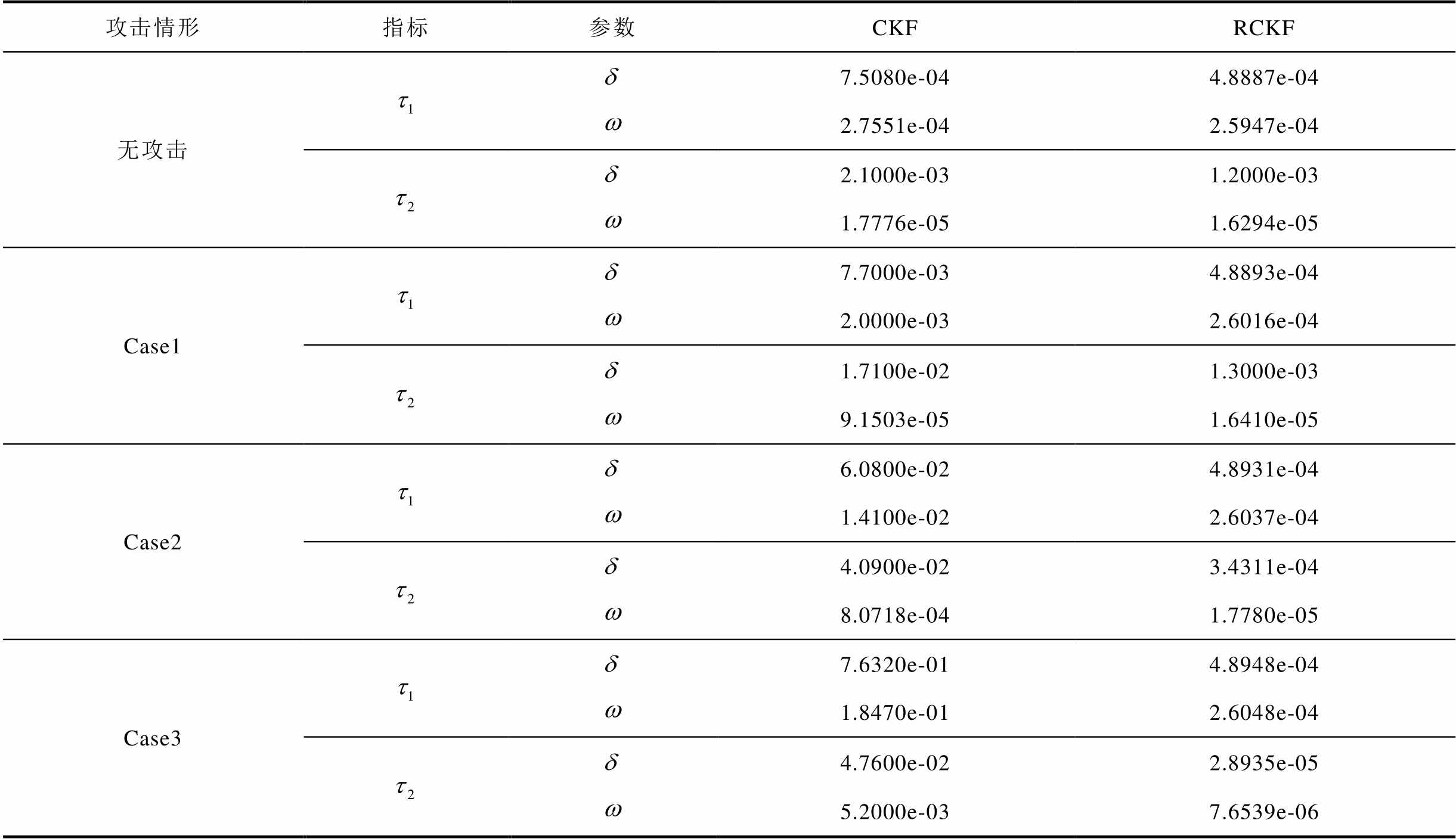
攻击情形指标参数CKFRCKF 无攻击7.5080e-044.8887e-04 2.7551e-042.5947e-04 2.1000e-031.2000e-03 1.7776e-051.6294e-05 Case17.7000e-034.8893e-04 2.0000e-032.6016e-04 1.7100e-021.3000e-03 9.1503e-051.6410e-05 Case26.0800e-024.8931e-04 1.4100e-022.6037e-04 4.0900e-023.4311e-04 8.0718e-041.7780e-05 Case37.6320e-014.8948e-04 1.8470e-012.6048e-04 4.7600e-022.8935e-05 5.2000e-037.6539e-06
由表2可知:在无攻击和三种不同攻击情形下,基于CKF和RCKF的各指标值均有所变化。①基于状态指标值 ,在分别面对无攻击和三种逐渐增强的攻击时,CKF的功角指标值和角速度指标值逐渐增加且增幅很大,与此同时,RCKF的功角指标值和角速度指标值也逐渐增加,说明RCKF虽具有抗差能力,但在面对逐渐增强的FDI攻击时,其状态估计精度仍有所下降,即验证了所提FDI攻击对基于CKF和RCKF的发电机动态状态估计的有效性。②基于状态指标值
,在分别面对无攻击和三种逐渐增强的攻击时,CKF的功角指标值和角速度指标值逐渐增加且增幅很大,与此同时,RCKF的功角指标值和角速度指标值也逐渐增加,说明RCKF虽具有抗差能力,但在面对逐渐增强的FDI攻击时,其状态估计精度仍有所下降,即验证了所提FDI攻击对基于CKF和RCKF的发电机动态状态估计的有效性。②基于状态指标值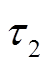 ,在面对无攻击和三种攻击情形时,RCKF的滤波精度均大于CKF。因为在无攻击情形下,结合了中位数估计方法的RCKF有效滤除了量测噪声,因此其抗噪性能优于CKF;在面对三种逐渐增强的攻击时,由于具有抗差能力,RCKF在一定程度上削弱了攻击向量对其估计精度的影响,因而RCKF的滤波能力优于CKF。
,在面对无攻击和三种攻击情形时,RCKF的滤波精度均大于CKF。因为在无攻击情形下,结合了中位数估计方法的RCKF有效滤除了量测噪声,因此其抗噪性能优于CKF;在面对三种逐渐增强的攻击时,由于具有抗差能力,RCKF在一定程度上削弱了攻击向量对其估计精度的影响,因而RCKF的滤波能力优于CKF。
该系统为状态估计领域的经典测试算例[16],由16台同步发电机,68条母线,86条传输线路组成。t=1s时在节点6设置三相金属性短路故障,1.05s时切除节点1的近端故障,1.1s时切除节点54的远端故障,仿真持续时间10s。与在IEEE 9节点系统中对BJ的设置方法一样,在新英格兰16机68节点系统中设置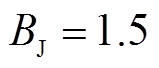 。
。
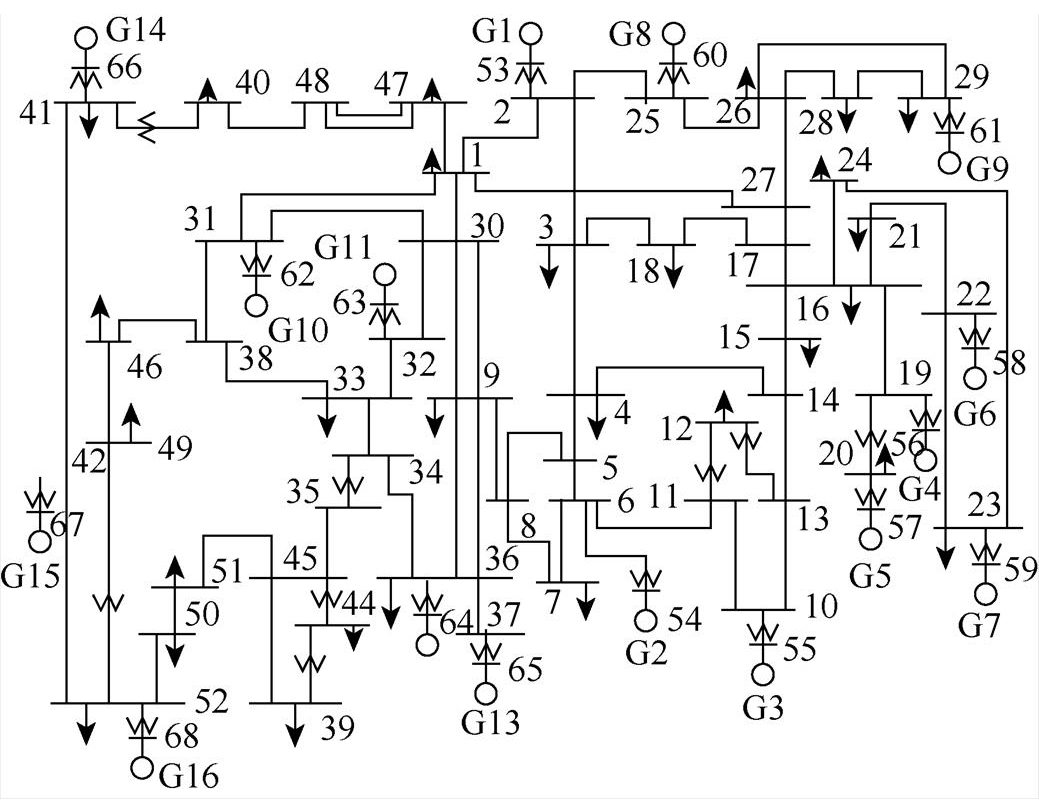
图12 新英格兰16机68节点系统
Fig.12 New England 16-machine-68-bus system
采用CKF算法时,量测量的残差变化情况如图13所示。
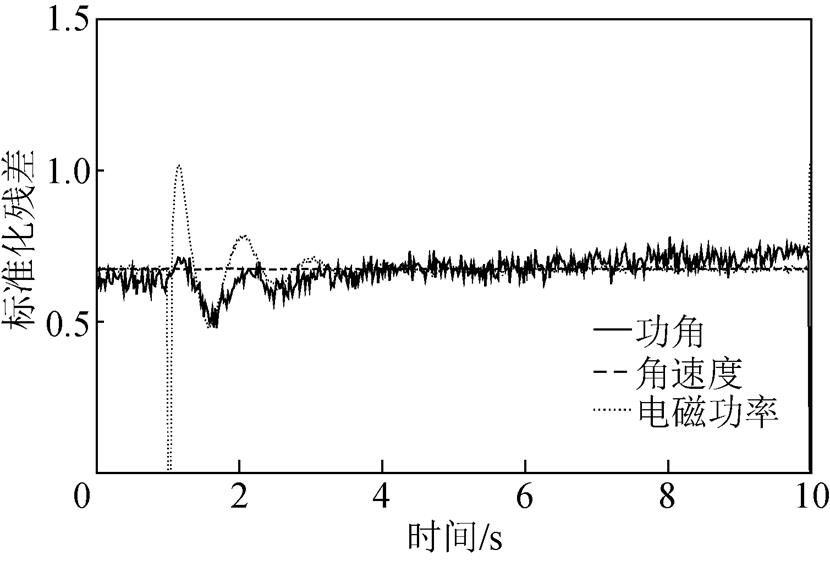
图13 基于CKF算法的标准化残差
Fig.13 Standardized residuals based on CKF algorithm
由图13可知,由于PMU量测异常值的存在,CKF算法下三个量测量的标准化残差仍然存在大量的跳变,但主体趋势稳定,故在此系统下对三个先验阈值均取0.67。
与IEEE 9节点系统的攻击情形设置相同,以发电机1为例,在无攻击情形和三种攻击情形下,基于上述两种算法的仿真结果分别如图14~图21所示。
1)无攻击情形
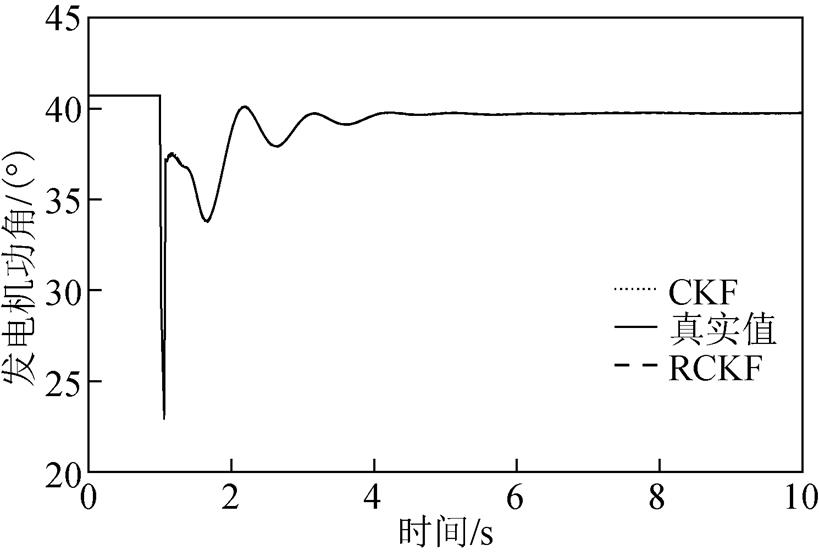
图14 无攻击情形下的发电机功角
Fig.14 Generator’s power angle without attack
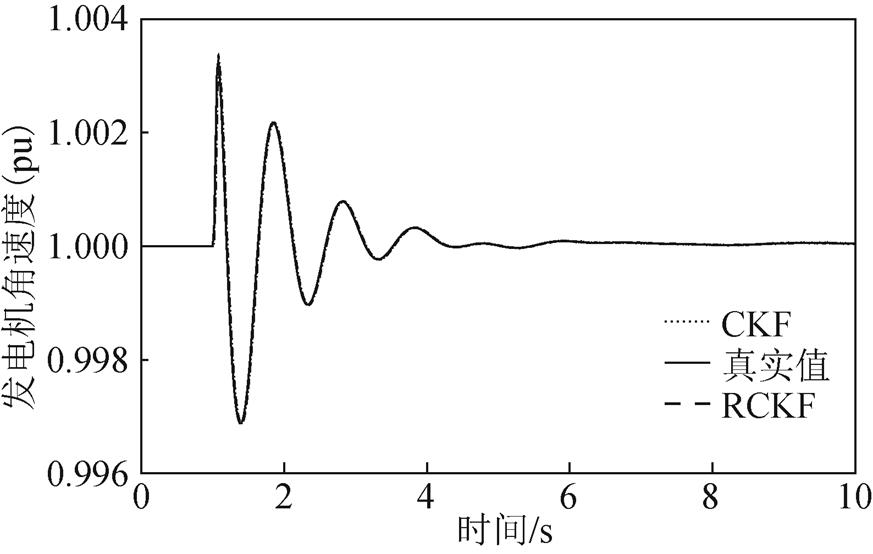
图15 无攻击情形下的发电机角速度
Fig.15 Generator’s angular velocity without attack
2)Case1
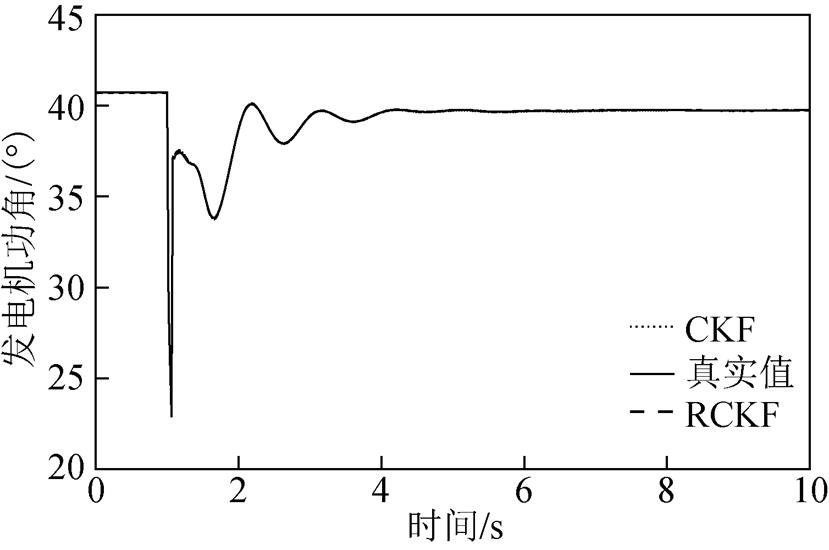
图16 情形1下的发电机功角
Fig.16 Generator’s power angle under Case 1

图17 情形1下的发电机角速度
Fig.17 Generator’s angular velocity under Case 1
3)Case2

图18 情形2下的发电机功角
Fig.18 Generator’s power angle under Case 2
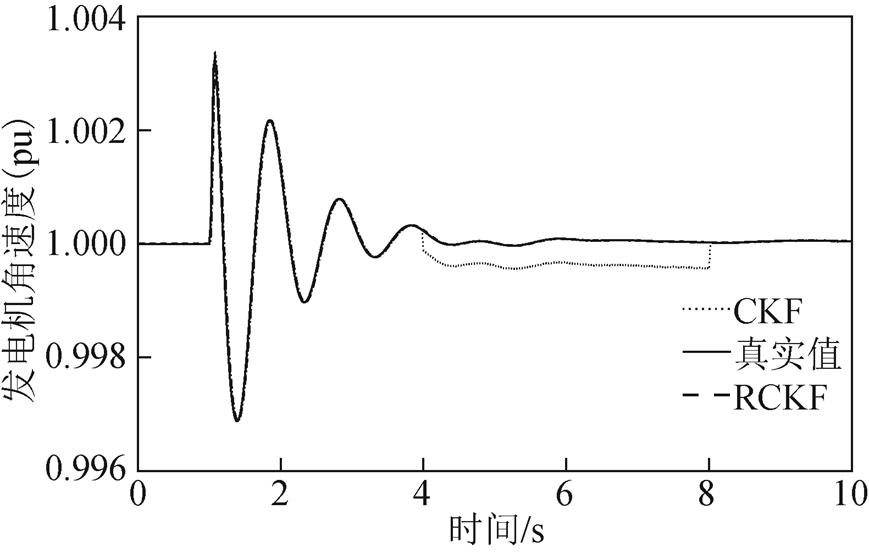
图19 情形2下的发电机角速度
Fig.19 Generator’s angular velocity under Case 2
4)Case3

图20 情形3下的发电机功角
Fig.20 Generator’s power angle under Case 3
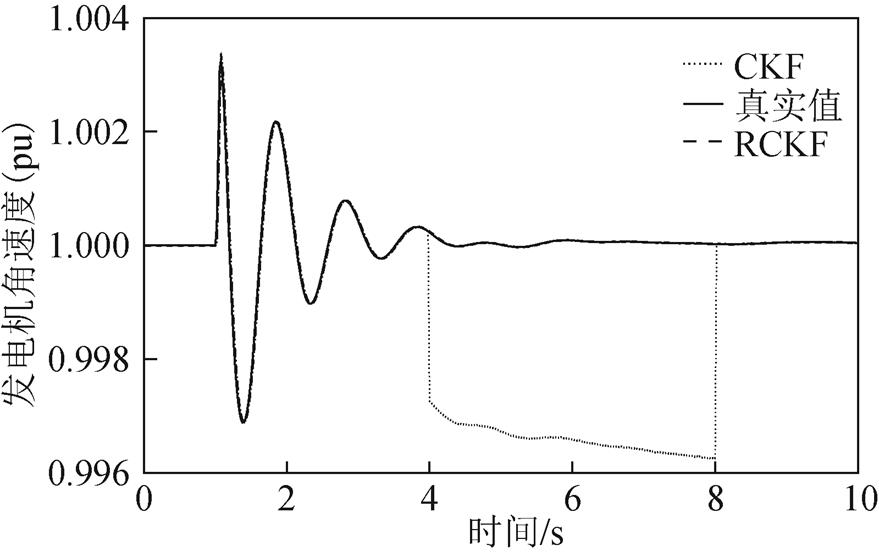
图21 情形3下的发电机角速度
Fig.21 Generator’s angular velocity under Case 3
图14和图15分别显示了无攻击下的发电机功角和角速度的估计结果;图16、图18、图20分别显示了在三种攻击情形下发电机功角的估计结果;图17、图19、图21分别显示了三种攻击情形下发电机角速度的估计结果。可以看出,在4~8s的攻击时间内,面对无攻击情形和三种逐渐增强的攻击时,CKF的估计值越来越偏离真实值,因此验证了所提FDI攻击在较大规模系统中对基于CKF的发电机动态状态估计的有效性。与此同时,随着攻击情形的变化,RCKF算法对攻击具有一定的抵抗能力,估计值未出现明显偏移。
5)状态估计指标对比
发电机1的状态估计指标见表3。
表3 发电机1的动态状态估计指标
Tab.3 Dynamic state estimation indicators of generator 1
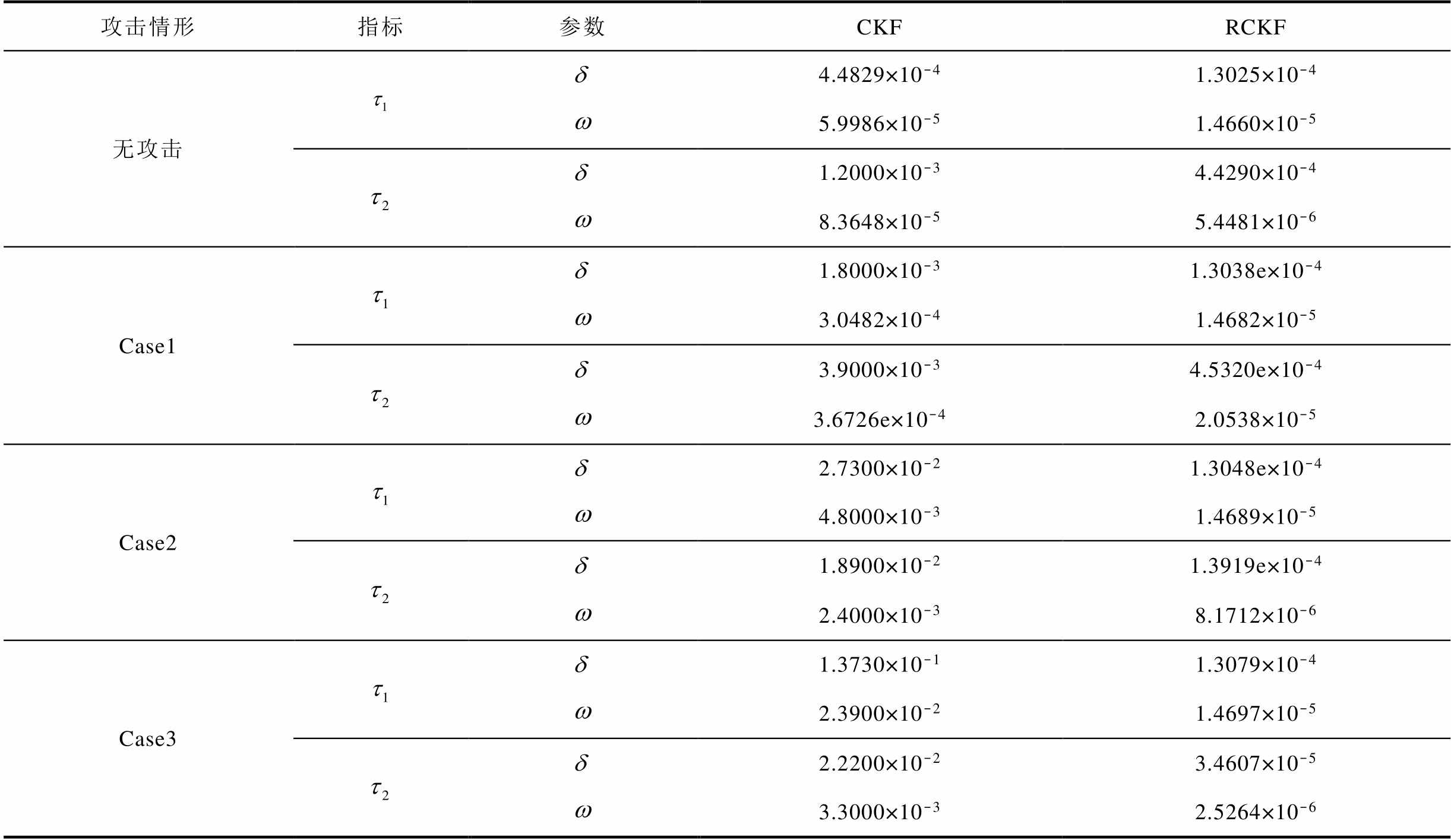
攻击情形指标参数CKFRCKF 无攻击4.4829×10-41.3025×10-4 5.9986×10-51.4660×10-5 1.2000×10-34.4290×10-4 8.3648×10-55.4481×10-6 Case11.8000×10-31.3038e×10-4 3.0482×10-41.4682×10-5 3.9000×10-34.5320e×10-4 3.6726e×10-42.0538×10-5 Case22.7300×10-21.3048e×10-4 4.8000×10-31.4689×10-5 1.8900×10-21.3919e×10-4 2.4000×10-38.1712×10-6 Case31.3730×10-11.3079×10-4 2.3900×10-21.4697×10-5 2.2200×10-23.4607×10-5 3.3000×10-32.5264×10-6
由表3可知,面对不同的攻击情形时,CKF和RCKF的指标值均有所变化:①对于指标 ,随着攻击程度的逐渐增强,基于RCKF的发电机功角和角速度的指标值均逐渐递增,而基于CKF的发电机功角和角速度的指标值大幅增加,表明了基于CKF和RCKF的估计结果精度均受到FDI攻击的影响,从而验证了在新英格兰16机68节点系统中,所提FDI攻击对基于这两种算法的发电机动态状态估计的有效性。②对于指标
,随着攻击程度的逐渐增强,基于RCKF的发电机功角和角速度的指标值均逐渐递增,而基于CKF的发电机功角和角速度的指标值大幅增加,表明了基于CKF和RCKF的估计结果精度均受到FDI攻击的影响,从而验证了在新英格兰16机68节点系统中,所提FDI攻击对基于这两种算法的发电机动态状态估计的有效性。②对于指标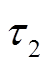 ,在面对无攻击和三种攻击情形时,RCKF的滤波精度均大于CKF。因为在无攻击情形下,RCKF滤除了量测量中存在的噪声;在面对三种逐渐增强的攻击时,由于RCKF具有抗差能力,其一定程度上削弱了量测量中攻击向量对估计精度的影响,所以RCKF的滤波性能优于CKF。
,在面对无攻击和三种攻击情形时,RCKF的滤波精度均大于CKF。因为在无攻击情形下,RCKF滤除了量测量中存在的噪声;在面对三种逐渐增强的攻击时,由于RCKF具有抗差能力,其一定程度上削弱了量测量中攻击向量对估计精度的影响,所以RCKF的滤波性能优于CKF。
对比表2和表3,可得:①对于 ,在两个测试算例中,面对不同攻击情形,RCKF的指标值和CKF的指标值均有不同程度的增加,验证了本文所提的FDI攻击对基于这两种算法的发电机动态状态估计的有效性;②对于
,在两个测试算例中,面对不同攻击情形,RCKF的指标值和CKF的指标值均有不同程度的增加,验证了本文所提的FDI攻击对基于这两种算法的发电机动态状态估计的有效性;②对于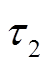 ,两种测试系统的仿真结果表明,基于RCKF的指标值均小于CKF,证实了RCKF较CKF具有良好的滤波性能。
,两种测试系统的仿真结果表明,基于RCKF的指标值均小于CKF,证实了RCKF较CKF具有良好的滤波性能。
以上测试中,两种算法的计算时间见表4。
表4 计算时间
Tab.4 Calculating time
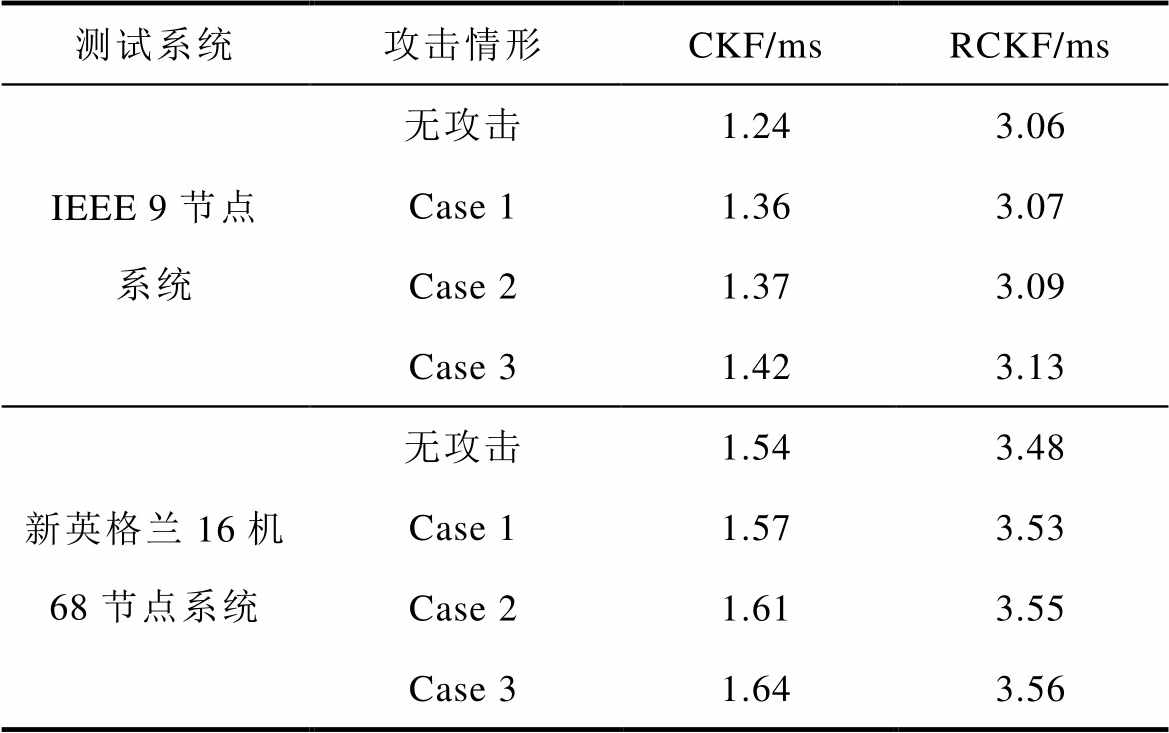
测试系统攻击情形CKF/msRCKF/ms IEEE 9节点系统无攻击1.243.06 Case 11.363.07 Case 21.373.09 Case 31.423.13 新英格兰16机 68节点系统无攻击1.543.48 Case 11.573.53 Case 21.613.55 Case 31.643.56
由表4可知,因为需要经过抗差计算处理,因此算法的计算时间略长于CKF算法,但仍远小于PMU采样间隔(20ms)。故而,RCKF仍能满足发电机动态状态估计对实时性的应用需求。
本文提出了一种发电机动态状态估计的虚假数据注入攻击方法。该方法首先建立了FDI攻击模型,并将攻击向量施加在量测量中,然后根据攻击程度分别设定三种攻击情形,最后,在此基础上分别进行基于CKF和RCKF的发电机动态状态估计仿真。两个仿真系统的测试结果表明:①所提FDI攻击均不同程度地恶化了基于两种算法的发电机动态状态估计结果,验证了所提方法的有效性;②在无攻击情形和所提FDI攻击场景下,RCKF的滤波性能优于CKF。
文中仅考虑了虚假数据注入攻击,下一步将研究其他类型信息攻击场景下的发电机状态估计。文中不良数据检测阈值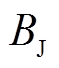 是基于经验、经过多次仿真测试确定的。后续研究中将进一步设计一种通用的阈值选取方法。此外,将所提方法扩展至整个电力系统的状态估计也是值得研究的课题[25-28]。
是基于经验、经过多次仿真测试确定的。后续研究中将进一步设计一种通用的阈值选取方法。此外,将所提方法扩展至整个电力系统的状态估计也是值得研究的课题[25-28]。
参考文献
[1] 陈亮, 毕天姝, 李劲松, 等. 基于容积卡尔曼滤波的发电机动态状态估计[J]. 中国电机工程学报, 2014, 34(16): 2706-2713. Chen Liang, Bi Tianshu, Li Jinsong, et al. Dynamic state estimator for synchronous machines based on cubature Kalman filter[J]. Proceedings of CSEE, 2014, 34(16): 2706-2713.
[2] 毕天姝, 陈亮, 薛安成, 等. 基于鲁棒容积卡尔曼滤波器的发电机动态状态估计[J]. 电工技术学报, 2016, 31(4): 163-169. Bi Tianshu, Chen Liang, Xue Ancheng, et al. Dynamic state estimator for synchronous-machines based on robust cubature Kalman filter[J]. Transactions of China Electrotechnical Society, 2016, 31(4): 163-169.
[3] 安军, 杨振瑞, 周毅博, 等. 基于平方根容积卡尔曼滤波的发电机动态状态估计[J]. 电工技术学报, 2017, 32(12): 234-240. An Jun, Yang Zhenrui, Zhou Yibo, et al. Dynamic state estimation for synchronous-machines based on square root cubature Kalman filter[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 234-240.
[4] Li Yang, Yang Zhen, Li Guoqing, et al. Optimal scheduling of an isolated microgrid with battery storage considering load and renewable generation uncertainties[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1565-1575.
[5] 罗深增, 李银红, 石东源. 广域测量系统可观性概率评估及其在PMU优化配置中的应用[J]. 电工技术学报, 2018, 33(8): 1844-1853. Luo Shenzeng, Li Yinhong, Shi Dongyuan. Wide area monitoring system observability probabilistic evaluation and it’s application in optimal PMU placement[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1844-1853.
[6] 肖湘宁, 廖坤玉, 唐松浩, 等. 配电网电力电子化的发展和超高次谐波新问题[J]. 电工技术学报, 2018, 33(4): 707-720. Xiao Xiangning, Liao Kunyu, Tang Songhao, et al. Development of power-electronized distribution girds and the new supraharmonics issues[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 707-720.
[7] 赵俊华, 梁高琪, 文福拴, 等. 乌克兰事件的启示: 防范针对电网的虚假数据注入攻击[J]. 电力系统自动化, 2016, 40(7): 149-151. Zhao Junhua, Liang Gaoqi, Wen Fushuan, et al. Lessons learnt from Ukrainian blackout: protecting power grids against false data injection attacks[J]. Automation of Electric Power Systems, 2016, 40(7): 149-151.
[8] Zhao Junbo, Zhang Gexiang, Dong Zhaoyang, et al. Forecasting-Aided imperfect false data injection attacks against power system nonlinear state estimation[J]. IEEE Transactions on Smart Grid, 2015, 7(1): 6-8.
[9] Yu Zonghan, Chin W L. Blind false data injection attack using PCA approximation method in smart grid[J]. IEEE Transactions on Smart Grid, 2015, 6(3): 1219-1226.
[10] Liu Yao, Ning Peng, Reiter M K. False data injection attacks against state estimation in electric power grids[J]. ACM Transactions on Information and System Security, 2011, 14(1): 1-33.
[11] Liu Xuan, Li Zuyi. False data attacks against AC state estimation with incomplete network information[J]. IEEE Transactions on Smart Grid, 2016, 8(5): 2239-2248.
[12] Zhao Junbo, Zhang Gexiang, Scala M L, et al. Short-term state forecasting-aided method for detection of smart grid general false data injection attacks[J]. IEEE Transactions on Smart Grid, 2015, 8(4): 1580-1590.
[13] Li Boda, Ding Tao, Huang Can, et al. Detecting false data injection attacks against power system state estimation with fast Go-Decomposition (GoDec) approach[J]. IEEE Transactions on Industrial Informatics, 2019, 15(5): 2892-2904.
[14] Taha A F, Qi Junjian, Wang Jianhui, et al. Risk mitigation for dynamic state estimation against cyber attacks and unknown inputs[J]. IEEE Transactions on Smart Grid, 2016, 9(2): 886-899.
[15] Qi Junjian, Taha A F, Wang Jianhui. Comparing Kalman filters and observers for power system dynamic state estimation with model uncertainty and malicious cyber attacks[J]. IEEE Access, 2018, 6: 77155-77168.
[16] 孙国强, 黄蔓云, 卫志农, 等. 基于无迹变换强跟踪滤波的发电机动态状态估计[J]. 中国电机工程学报, 2016, 36(3): 615-623. Sun Guoqiang, Huang Manyun, Wei Zhinong, et al. Dynamic state estimation for synchronous machines based on unscented transformation of strong tracking filter[J]. Proceedings of the CSEE, 2016, 36(3): 615-623.
[17] Ghahremani E, Kamwa I. Dynamic state estimation in power system by applying the extended Kalman filter with unknown inputs to phasor measurements[J]. IEEE Transactions on Power Systems, 2011, 26(4): 2556-2566.
[18] Gultekin S, Paisley J. Nonlinear Kalman filtering with divergence minimization[J]. IEEE Transactions on Signal Processing, 2017, 65(23): 6319-6331.
[19] 马安安, 江全元, 熊鸿韬, 等. 考虑量测坏数据的发电机动态状态估计方法[J]. 电力系统自动化, 2017, 41(14): 140-146. Ma Anan, Jiang Quanyuan, Xiong Hongtao, et al. Dynamic state estimation method for generator considering measurement of bad data[J]. Automation of Electric Power Systems, 2017, 41(14): 140-146.
[20] Zhou Ning, Meng Da, Lu Shuai. Estimation of the dynamic states of synchronous machines using an extended particle filter[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4152-4161.
[21] Ghahremani E, Kamwa I. Online state estimation of a synchronous generator using unscented Kalman filter from phasor measurements units[J]. IEEE Transactions on Energy Conversion, 2011, 26(4): 1099-1108.
[22] 王先培, 田猛, 董政呈, 等. 输电网虚假数据攻击研究综述[J]. 电网技术, 2016, 40(11): 3406-3414. Wang Xianpei, Tian Meng, Dong Zhengcheng, et al. A survey of research on false data attacks in transmission network[J]. Power System Technology, 2016, 40(11): 3406-3414.
[23] 田猛, 王先培, 董政呈, 等. 基于拉格朗日乘子法的虚假数据攻击策略[J]. 电力系统自动化, 2017,41(11): 32-38. Tian Meng, Wang Xianpei, Dong Zhengcheng, et al. Injected attack strategy for false data based on lagrange multipliers method[J]. Automation of Electric Power Systems, 2017, 41(11): 32-38.
[24] 陶叶青, 高井祥, 姚一飞. 基于中位数法的抗差总体最小二乘估计[J]. 测绘学报, 2016, 45(3): 297-301. Tao Yeqing, Gao Jingxiang, Yao Yifei. Robust total least squares estimation based on median method[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 297-301.
[25] 蔡永智, 陈皓勇, 万楚林. 基于局部信息融合和估计投影法的多区域电力系统状态估计[J]. 电工技术学报, 2017, 32(1): 69-77. Cai Yongzhi, Chen Haoyong, Wan Chulin. Multi-region power system state estimation based on local information fusion and estimated projection method[J]. Transactions of China Electrotechnical Society, 2017, 32(1): 69-77.
[26] 肖润龙, 王刚, 李子梦. 中压直流输电直流区域配电综合电力系统静态状态估计方法研究[J]. 电工技术学报, 2018, 33(13): 3023-3033. Xiao Runlong, Wang Gang, Li Zimeng. Static estimation of the integrated power system with medium voltage DC and DC zonal distribution system[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3023-3033.
[27] 怀全, 候小虎, 何良策. 一种含分布式电源的中低压配电网状态估计方法研究[J]. 电力系统保护与控制, 2018, 46(21): 75-83. Huai Quan, Hou Xiaohu, He Liangce. A method of state estimation for middle voltage and low voltage distribution network with distributed generations[J]. Power System Protection and Control, 2018, 46(21): 75-83.
[28] 胡春潮, 何杰, 马凯. 基于信息冗余的电力系统分布式状态估计[J]. 电力系统保护与控制, 2017, 45(16): 111-115. Hu Chunchao, He Jie, Ma Kai. Power system distributed state estimation based on information redundancy of secondary system[J]. Power System Protection and Control, 2017, 45(16): 111-115.
A False Data Injection Attack Method for Generator Dynamic State Estimation
Abstract Accurate and reliable dynamic state quantities of generators are very important for real-time monitoring and control of the power system. The emergence of cyber attacks has brought new challenges to the state estimation of generators. Especially, false data injection (FDI) attacks deteriorate the accuracy of state estimation by injecting the false data into the measurement device. In this regard, this paper proposes for the first time an FDI attack model based on the dynamic state estimation of generators. Firstly, Taylor's formula was used to linearize the generator's measurement equation. Secondly, according to the principle that the measurement residuals before and after the FDI attack are equal, the expressions of the attack vectors were established, and they were applied to the measurement quantities to avoid the conventional bad data detection. Thereby, the FDI attacks were successfully implemented. Then, three attack scenarios were set according to the degree of the FDI attacks, and they were tested by the cubature Kalman filter (CKF) and the robust cubature Kalman filter (RCKF). Finally, the simulation results of the IEEE 9-bus system and the New England 16-machine 68-bus system verify the effectiveness of the proposed FDI attacks.
keywords:Dynamic state estimation, cyber attacks, generator, cubature Kalman filter, false data injection attacks, PMU data
DOI:10.19595/j.cnki.1000-6753.tces.190580
中图分类号:TM71
李 扬 男,1980年生,博士,副教授,研究方向为电力系统运行分析与控制。E-mail:liyang@neepu.edu.cn (通信作者)
李 智 男,1994年生,硕士研究生,研究方向为电力系统运行分析与控制。E-mail:1782798766 @qq.com
国家重点研发计划(2017YFB0902401)和国家自然科学基金(51677023)资助。
收稿日期2019-05-14
改稿日期2019-08-14
(编辑 赫蕾)