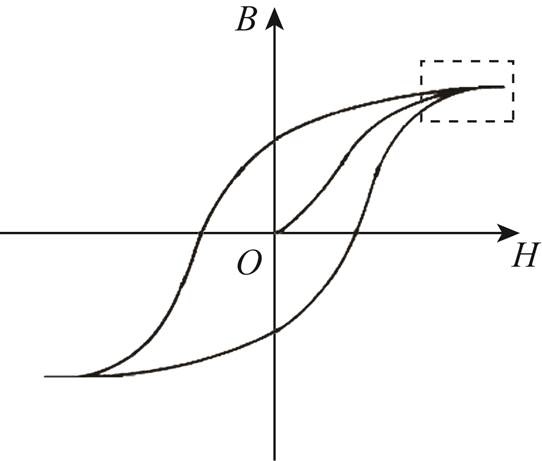
图1 理论上变压器磁化曲线
Fig.1 Theoretical magnetization hysteresis loop
摘要 提出一种基于等效磁化曲线智能识别的变压器保护原理。铁心的动态行为能够从本质上反应变压器的运行状态,磁化曲线的几何特征是变压器铁心动态行为的外在表现。首先,在研究磁化曲线几何特性的基础上,构建基于励磁支路电压-差动电流(U-I)的等效磁化曲线,并分析等效磁化曲线与变压器运行状态的对应关系;其次,构建以等效磁化曲线倾斜角度、椭圆率以及长轴数值为输入,以变压器运行状态为输出的BP神经网络模型,生成基于BP神经网络的变压器内部故障识别算法;最后,利用大量数字仿真和动模实验数据对所提算法进行验证,结果表明,保护方案从铁心动态行为出发,利用少量数据并结合传统的监督学习算法即可准确地判断变压器运行状态,仿真及动模实验数据的正确动作率均达到了100%。特别地,该方法具有良好的泛化能力,对CT饱和等场景具有良好的适应性,可以直接作为由铁磁材料构成的电力变压器的主保护,具有良好的应用前景。
关键词:变压器保护 等效磁化曲线 BP神经网络 数据融合 泛化能力
变压器是电力系统重要的电力设备之一,其在电能的传输、分配和应用中发挥着重要作用,快速、灵敏、可靠地识别并隔离变压器故障对于保证电力系统的安全运行具有重要意义。目前,电力变压器保护大多采用带有励磁涌流制动/闭锁的电流差动保护原理,大型电力变压器铁心的工作点普遍较低,同时考虑到交直流混联电力系统的电磁暂态过程日趋复杂,以二次谐波制动[1]、间断角原理[2]为代表的励磁涌流识别判据已经不能满足变压器保护的要求。近年来,研究者们在基于变压器等效回路参数识别的保护原理[3-7]、基于漏磁场及油流速度等非电气量的保护技术以及利用先进数据工具挖掘波形特征[8-11]等方面取得了较大的进展,但是这些方法和判据均基于单一故障特征信息,在某些运行工况下性能欠佳或存在死区。取长补短,综合利用多种故障特征信息的变压器保护原理和技术是未来变压器保护新的发展方向。
神经网络、支持向量机等人工智能(Artificial Intelligence, AI)技术是多源信息融合的常用工具,在电力系统继电保护领域,AI技术也得到了广泛应用。文献[12]利用人工神经网络(Artificial Neural Network, ANN)识别差动电流故障特征,通过递归神经网络对CT饱和电流进行修正,进一步提高了故障正确识别率;文献[13]利用模糊逻辑、ANN和遗传算法(Genetic Algorithms, GA)开发了一种内部故障识别方案,ANN同样用于补偿饱和电流信号,使用GA估计基波分量和谐波,最终利用模糊逻辑进行故障识别;文献[14]利用概率神经网络识别差动电流故障特征,受谐波影响较小、训练速度更快;文献[15]利用随机森林分析差动电流故障特征,可不受CT饱和的影响;文献[16]将三相电压、电流作为输入,利用三个层级的ANN组成混合系统,实现了从变压器故障诊断到故障位置、类型的判断;文献[17]以差动电流作为输入矢量,利用自适应小波神经网络识别励磁涌流和内部故障;文献[18]利用ANN逼近变压器的电磁关系,在线识别变压器的内部参数,利用该ANN模型实现变压器保护;文献[19]选择二次谐波含量、间断角作为最小二乘支持向量机(Least Squares-Support Vector Machine, LS-SVM)的输入,基于高斯核函数建立LS-SVM分类模型,识别励磁涌流和内部故障;文献[20]利用数学形态谱对变压器短路电流和励磁涌流进行变换,其谱值作为LS-SVM的输入特征量,识别变压器的运行状态;文献[21]采用二次谐波、波形相关系数、铁心饱和点数、变压器励磁侧的电压值作为输入,训练变压器运行状态的SVM分类模型。此外,利用变压器油中溶解气体的特点,大量的海内外学者基于小波神经网络、深度置信网络等对变压器故障诊断展开了研究。基于仿真数据,上述方案均取得了较好的识别效果。但由于上述方案仅从仿真数据特征出发且电力系统多变的运行方式对分类模型的输入影响较大,无法保证模型的泛化能力,在实际工程中的应用效果有待检验。另外,基于多场景的大量训练样本是上述分类模型性能的保证,但仿真样本获取工作繁琐、实际工程样本量小的特点,进一步限制了其在工程中的应用。可见,分类模型的泛化能力及工程实用性制约了AI在变压器保护领域内的应用。如何充分利用AI技术,结合变压器保护的特点并借鉴其他电力领域的最新研究成果[22-27],构建融合多故障特征的实用化继电保护,是本领域目前迫切需要解决的问题。
实际上,变压器磁化曲线形状特征能够从本质上反映铁心的运行状态,基于励磁支路等效电压和差动电流关系构建的等效磁化曲线与磁化曲线具有对应关系,其同样能够反映变压器的工作状态。本文在分析等效磁化曲线特征的基础上,提取了椭圆率、斜率及长轴短轴特征最为明显的特征量,利用BP神经网络构建融合其特征的分类模型,提出了一种基于等效磁化曲线智能识别的变压器保护原理。本文通过等效磁化曲线的拟合模型、PSCAD仿真分别生成训练、测试样本集,并提取等效磁化曲线的若干种几何特征作为BP神经网络的输入矢量,训练得到最优的励磁涌流及内部故障的分类模型。本文在不同的变压器内、外部运行条件下,利用大量的仿真及动模实验样本验证了本文分类模型的有效性,分类效果均达100%。由于等效磁化曲线在不同的变压器、运行场景之间具有一定的通用性,基于小规模的样本集即可获得泛化能力较强的分类模型,又由于分类模型的输入为等效磁化曲线的形状特征,系统谐波对其影响较小,不同运行条件下的仿真样本证明了本文的算法具有较强的工程实用性价值。
变压器铁心通过交变磁通后,磁感应强度B滞后于磁场强度H,经过反复磁化,形成比较稳定的闭合曲线,如图1所示。实际电路中的工频交流电压变化较快,且磁通往往滞后于电压,实际的磁通往往无法达到图1虚线框内的轨迹[28],因此,磁化曲线往往近似于图2。当变压器正常运行、内部故障、外部故障时,磁化曲线均近似于较扁平的椭圆,其切线斜率反映了变压器励磁支路实时的阻抗值;但若内部故障、外部故障导致励磁支路电压降低,B-H轨迹将成为比原曲线更小的椭圆,如图2a所示。由变压器合闸引起的电压突增使铁心发生饱和,导致励磁支路的阻抗值周期性地在极大值与极小值之间发生变化,B-H曲线呈现单边饱和特征,如图2b所示。

图1 理论上变压器磁化曲线
Fig.1 Theoretical magnetization hysteresis loop
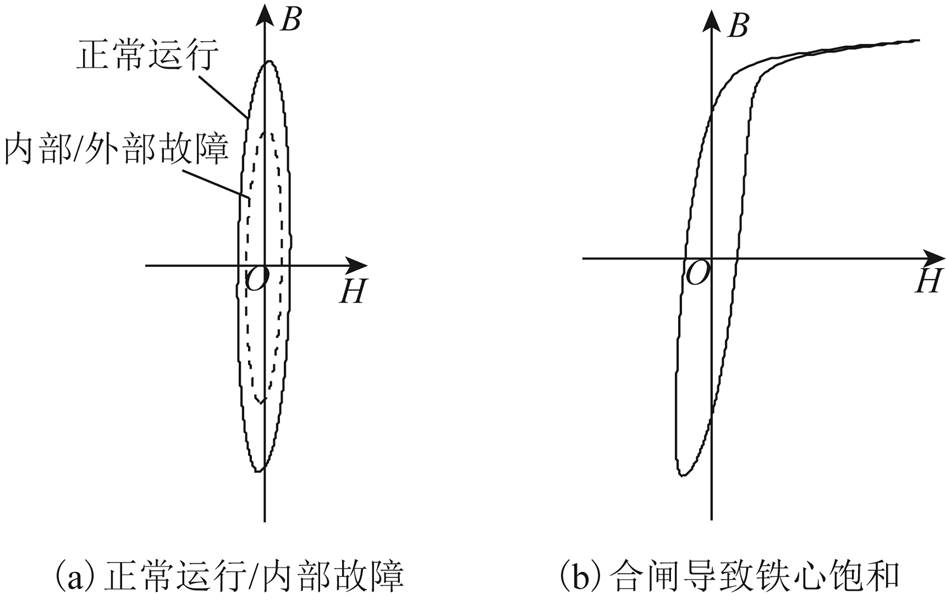
图2 变压器实际的磁化曲线
Fig.2 Practical magnetization hysteresis loop
B-H曲线的形状可以可靠地反映变压器的运行状态,可用于变压器内部故障、励磁涌流的分类识别。但B、H无法直接测量,直接利用B-H曲线构建变压器保护方案存在困难。实际上,当变压器正常运行/外部故障时,H、B分别与差动电流I、励磁支路的电压U成正比,此时,等效磁化曲线(励磁支路电压U-差动电流I)具有和B-H曲线相似的特征;当变压器发生内部故障时,故障电流、励磁电流均为差动电流I的一部分,而B-H曲线仅和励磁电流有关,因此,等效磁化曲线的故障特征更明显,与正常运行的等效磁化曲线差异性更大;无论变压器是否存在内部故障,变压器合闸造成的铁心饱和可使励磁电流(正常变压器)或差动电流(故障变压器)发生畸变。因此,在正常运行、外部故障、励磁涌流等工况下,变压器等效磁化曲线与B-H曲线具有对应关系,但当变压器发生内部故障时,曲线轨迹则存在很大不同,等效磁化曲线的故障特征更加明显,将其用于变压器正常运行/外部故障、内部故障、励磁涌流等工况的分类识别是可行的。基于此,本文提出了一种基于等效磁化曲线的变压器保护方案。
具体地,图3a所示为变压器不同工况下典型差动电流波形,其对应等效磁化曲线形状如图3b所示。由图3可知变压器等效磁化曲线特征包括:①变压器正常运行时,等效磁化曲线为一关于原点对称的扁平椭圆,曲线的绝大数区域几乎垂直于横轴,且较小的差动电流使长轴接近于电压值;②变压器发生内部故障时,等效磁化曲线仍为关于原点对称的椭圆,但曲线整体的倾斜程度更小、椭圆长宽比减小,较大的电流成分使长轴增大;③变压器空载合闸时,无论变压器存在故障与否,铁心将周期性地进入和退出饱和区,等效磁化曲线呈现单边饱和特征,当铁心工作点位于非饱和区时,等效磁化曲线特征与正常运行/内部故障相同。
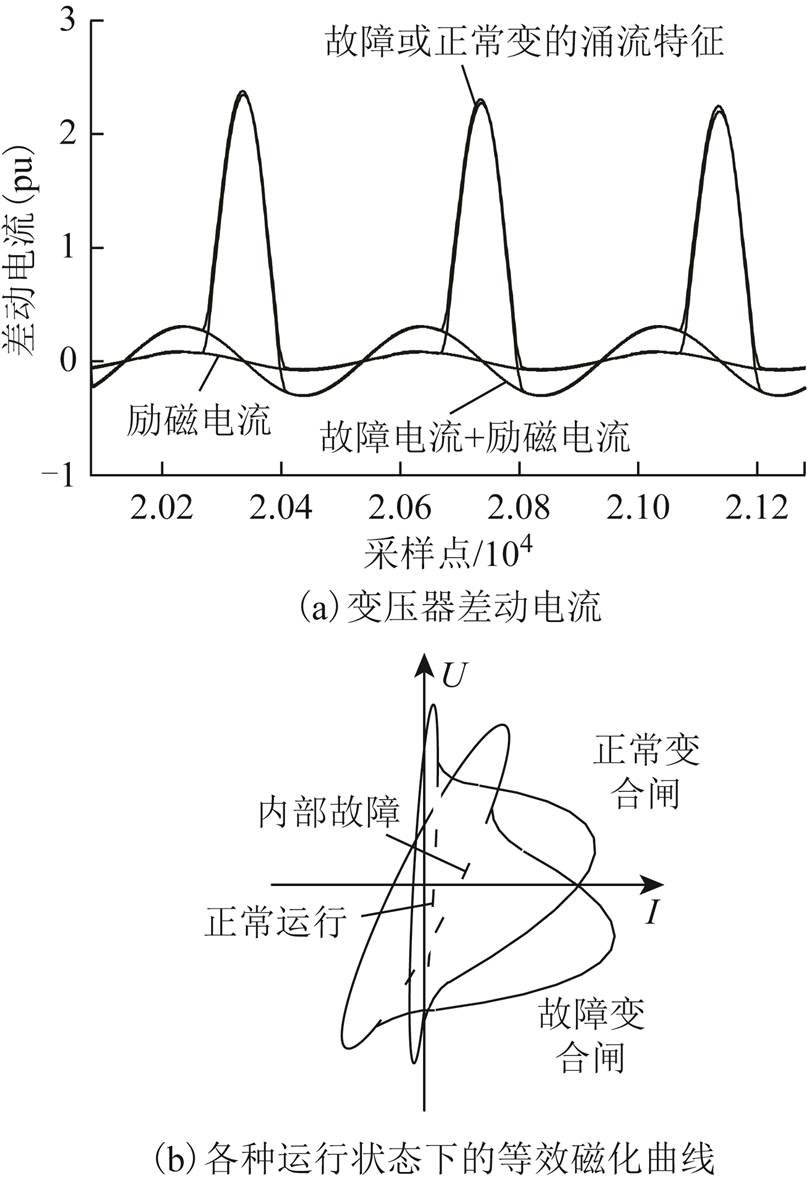
图3 差动电流及其对应的等效磁化曲线
Fig.3 Differential current and U-I curves
运行状态的变化改变了等效磁化曲线面积、长短轴、椭圆率等全局特征,以及曲率、斜率等局部特征,如图4所示。本文通过倾斜角度、长轴/短轴以及椭圆率等描述等效磁化曲线的图形特征。
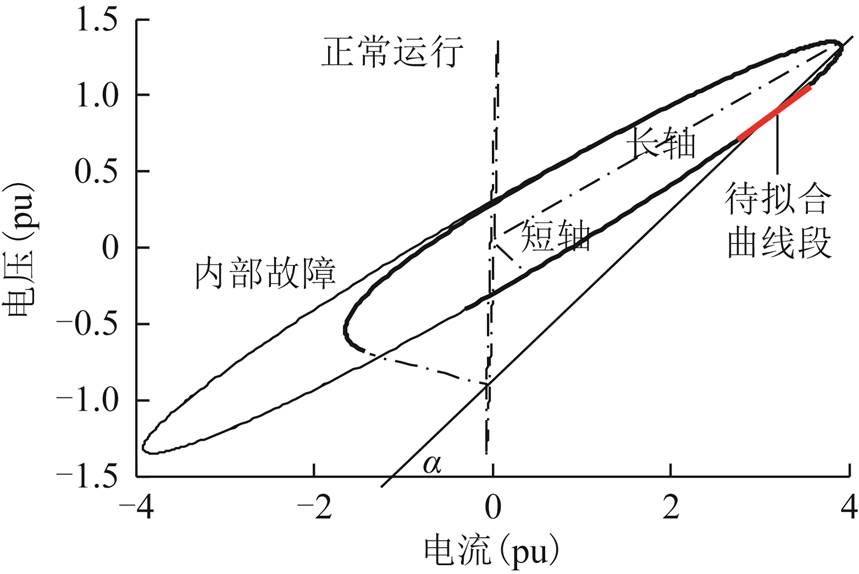
图4 等效磁化曲线的几何特征
Fig.4 Geomatric features of U-I curve
1.2.1 倾斜角度
倾斜角度θ定义为:等效磁化曲线各曲线段的线性拟合曲线与横轴夹角α的最大值,其在客观上反应了变压器励磁电感的数值变化。倾斜角度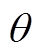 表达式为
表达式为
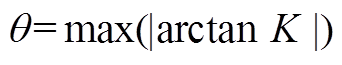 (1)
(1)式中,K为拟合曲线斜率序列。考虑在不计剩磁的情况下,变压器铁心饱和时间不会超过10ms,只要变压器未发生故障,在一个工频周期内,总是存在倾斜角度接近90°的曲线段;发生内部故障时,励磁支路电压降低,励磁电流的增大,将使等效磁化曲线整体的倾斜角度显著下降。
1.2.2 长轴、短轴
长轴L、短轴l分别定义为:原点(0,0)与等效磁化曲线的非饱和部分(即椭圆部分)采样点间的距离最大值、最小值,如式(2)及图4所示。
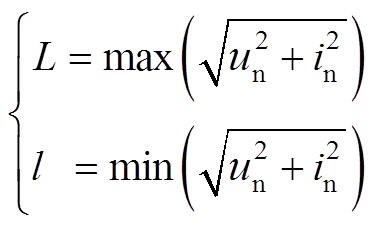 (2)
(2)式中,un、in分别为一个工频周期内等效磁化曲线非饱和部分的电压、电流序列。变压器正常运行/外部故障时,椭圆长轴L的最大值为
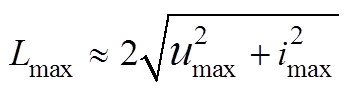 (3)
(3)
式中,umax、imax分别为序列un、in绝对值的最大值。变压器正常运行时,由于励磁电流远小于电压,因此,等效磁化曲线的长轴较小;发生内部故障时,故障电流成为差动电流的一部分,长轴增大,一般大于Lmax;发生外部故障时,变压器端口电压存在降低的可能性,长轴减小,一般小于等于Lmax。
1.2.3 椭圆率
椭圆率E定义为:等效磁化曲线短轴与长轴的比值,用于描述椭圆的扁平程度,等效磁化曲线椭圆率为
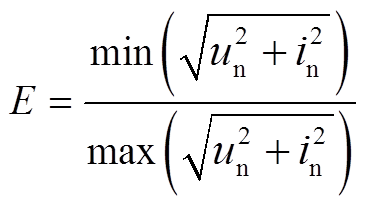 (4)
(4)变压器正常运行时,差动电流一般为0.02(pu)~ 0.10(pu),远小于1.0(pu)的电压,因此,椭圆率较小;发生内部故障时,差动电流增大,使椭圆率增大。
综上,等效磁化曲线的图形信息与运行状态的对应关系见表1,显然,单一故障特征无法可靠地识别内部故障和励磁涌流。例如,当变压器发生内部故障时,等效磁化曲线椭圆率增大,但对于严重的外部故障,端口电压的下降将造成长轴下降,进而使椭圆率增大,具备内部故障特征,可见,单一的椭圆率特征并不能可靠地识别变压器内、外部故障。因此,构建多源数据融合算法,实现对等效磁化曲线特征的综合利用,是构建基于等效磁化曲线特征的变压器保护的必然选择。
表1 等效磁化曲线几何特征总结
Tab.1 Summary of U-I curve geometric characteristics

运行状态倾斜角度椭圆率长轴 正常运行处处接近90°非常小不超过2.842 5 外部故障可能增大 正常变合闸部分区域接近90°可能增大不超过2.842 5 内部故障存在接近90°曲线的可能性增大超过2.842 5 故障变压器合闸一般不存在近似90°的直线增大可能小于2.842 5
基于等效磁化曲线的智能识别算法将融合等效磁化曲线的倾斜角度、长轴、椭圆率三种几何特征,并作为输入,训练BP神经网络。
首先,本文构建了基于励磁支路电压、差动电流故障分量的启动判据。
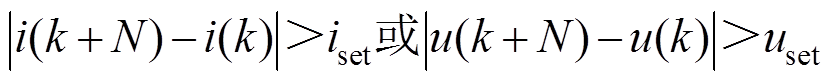 (5)
(5)式中,iset、uset为启动判据阈值;N为一个周期内的采样点数;u、i分别为一个工频周期内等效磁化曲线的电压序列、电流序列;k为电压、电流序列的第k个采样点。若变压器保护满足启动条件式(5),算法将提取变压器A、B、C三相等效磁化曲线的倾斜角度、长轴、椭圆率共9个特征值,构建BP神经网络的输入矢量为
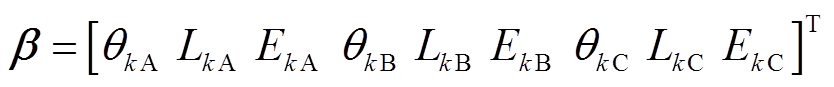
式中,θk*、Lk*、Ek*分别为A、B、C三相等效磁化曲线的倾斜角度、长轴、椭圆率。
最后,以矢量β作为输入,利用BP神经网络进行变压器内部故障的识别,本文算法的输出为:正常变压器(正常运行/外部故障/正常变合闸)、故障变压器(内部故障/故障变合闸)。基于等效磁化曲线智能识别的变压器保护算法如图5所示。
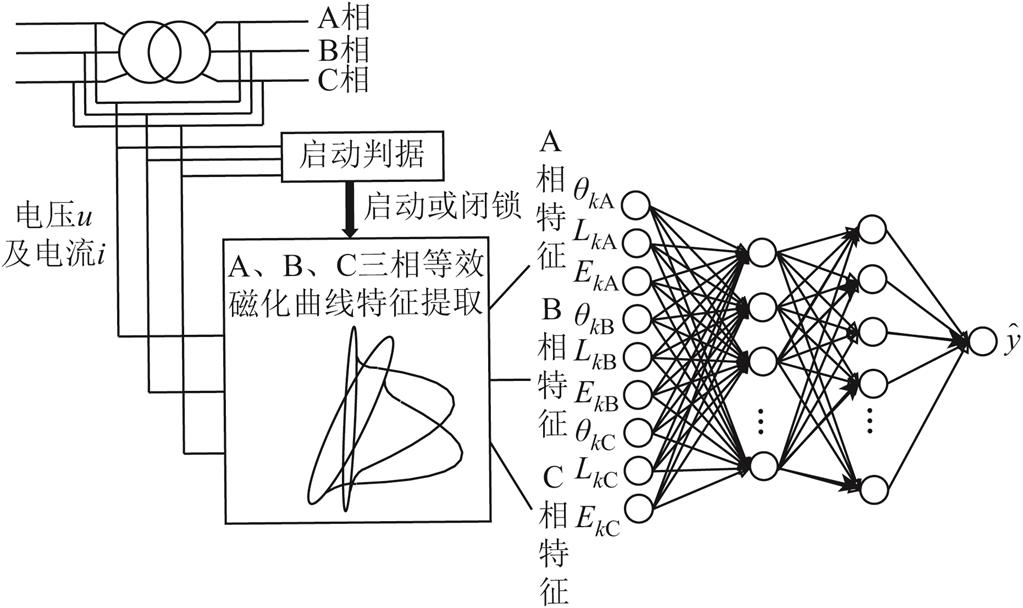
图5 等效磁化曲线智能识别变压器保护算法示意图
Fig.5 Illustration of U-I curve-based identification
2.2.1 基于等效磁化曲线拟合模型的样本生成
从形状上,变压器的等效磁化曲线总是关于原点对称的椭圆,或者由部分椭圆段和不规则饱和段组成,其特征具有通用性,不同变压器等效磁化曲线仅存在几何特征参数的差异。为提高本文算法的泛化能力,拟通过圆锥曲线与高斯函数建立典型等效磁化曲线的拟合模型,并通过随机调整模型参数的方式生成BP神经网络的训练集数据,拟合模型为
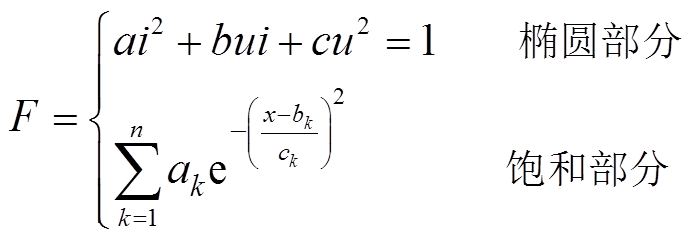 (6)
(6)式中,a、b、c、ak、bk、ck为模型可调参数。基于拟合模型的等效磁化曲线生成过程应满足如下约束条件。
1)椭圆拟合的约束条件
由变压器电气量约束关系,变压器正常运行或外部故障时,等效磁化曲线椭圆部分的电压、电流有效值约束条件为i∈[-0.1,0.1],u∈[-1,1];内部故障时,约束条件为|i|∈(0.1,∞),u∈[-1,1]。
2)高斯函数拟合的约束条件
无论变压器故障与否,拟合样本的饱和部分应偏向于时间轴一侧,呈现尖顶波特征。
基于拟合模型式(6)及其约束条件,共生成正常/故障变压器空载合闸数据各200组;正常运行/外部故障、内部故障曲线各200组,作为训练集对BP神经网络进行训练。图6为实际的正常变压器空载合闸的等效磁化曲线饱和部分的拟合情况。从图中可以看出,本文通过随机调整拟合模型参数并结合物理背景生成等效磁化曲线是可行的。
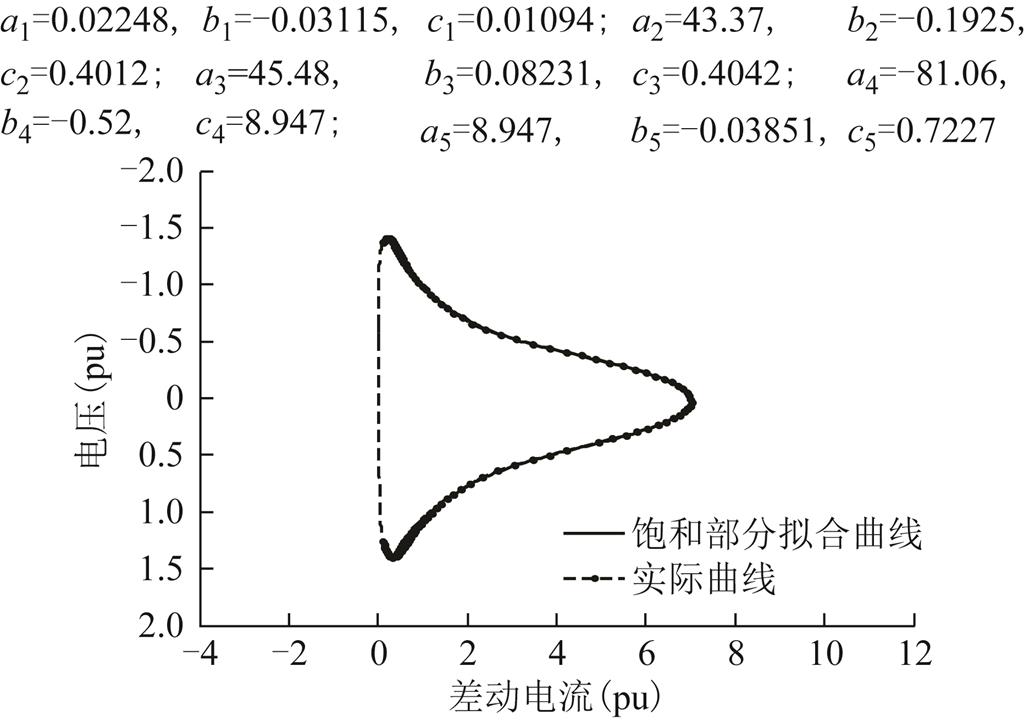
图6 正常变压器合闸时的等效磁化曲线及其拟合情况
Fig.6 U-I curve of energized normal transformer and fitting results
2.2.2 基于电磁暂态仿真的测试集样本生成
不同于训练集,测试集通过PSCAD仿真获取,以验证基于等效磁化曲线智能识别的变压器保护的可行性。测试集的选取应充分考虑铁心类型、合闸角度、故障角度、故障匝数等外部特性对等效磁化曲线的影响,PSCAD仿真模型如图7所示。测试样本分为两部分:①变压器Yd11接线,电压比230kV/11kV,一、二次侧漏电抗均为0.1(pu),采样频率20kHz,铜损0.005(pu),铁损分别为0.05(pu)、0.07(pu)、0.10(pu),铁心膝点0.72%(1.1(pu)),铁心性能曲线见表2;②铁心膝点0.50%(1.1(pu)),铁心特性曲线见表3,电压比为230kV/35kV,其他条件与①相同。
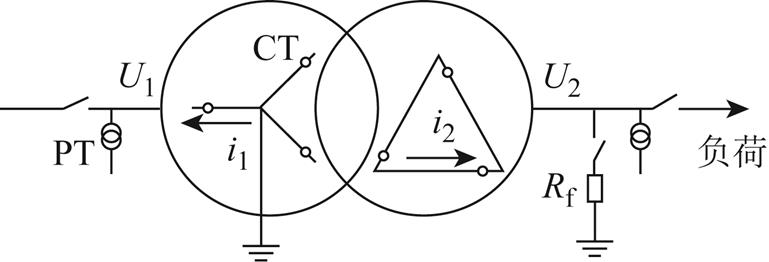
图7 PSCAD仿真模型
Fig.7 Simulation model on PSCAD
表2 测试集铁心特性曲线1
Tab.2 First magnetization curve of test set
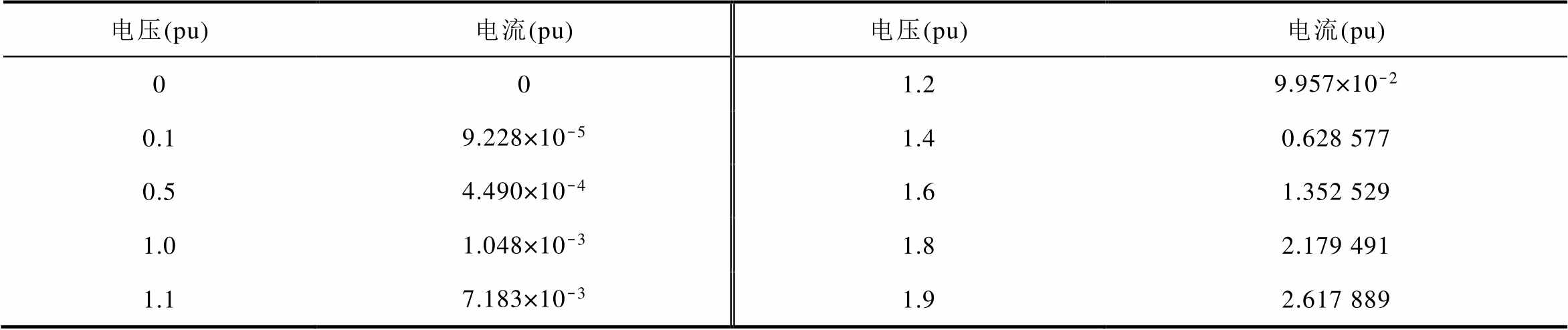
电压(pu)电流(pu)电压(pu)电流(pu) 001.29.957×10-2 0.19.228×10-51.40.628 577 0.54.490×10-41.61.352 529 1.01.048×10-31.82.179 491 1.17.183×10-31.92.617 889
表3 测试集铁心特性曲线2
Tab.3 Second magnetization curve of test set
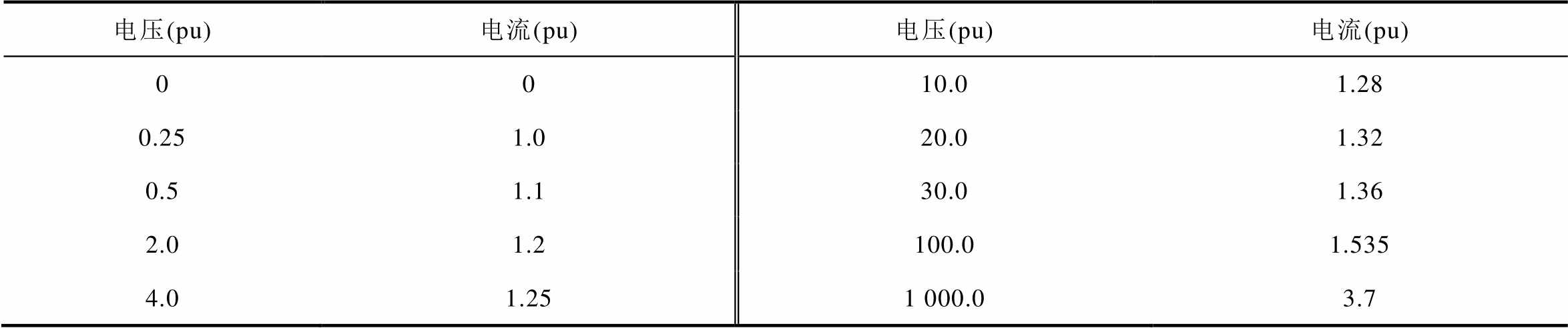
电压(pu)电流(pu)电压(pu)电流(pu) 0010.01.28 0.251.020.01.32 0.51.130.01.36 2.01.2100.01.535 4.01.251 000.03.7
测试集的仿真场景见表4,共1 520组。对于采用等效磁化曲线拟合模型生成的训练集,其正常未饱和时的励磁电流与测试变压器发生微弱故障时的差动电流相差不大,二者的等效磁化曲线差异较小,有利于保证BP神经网络的分类能力。
表4 测试集仿真场景选择
Tab.4 Operation scenes simulated on PSCAD
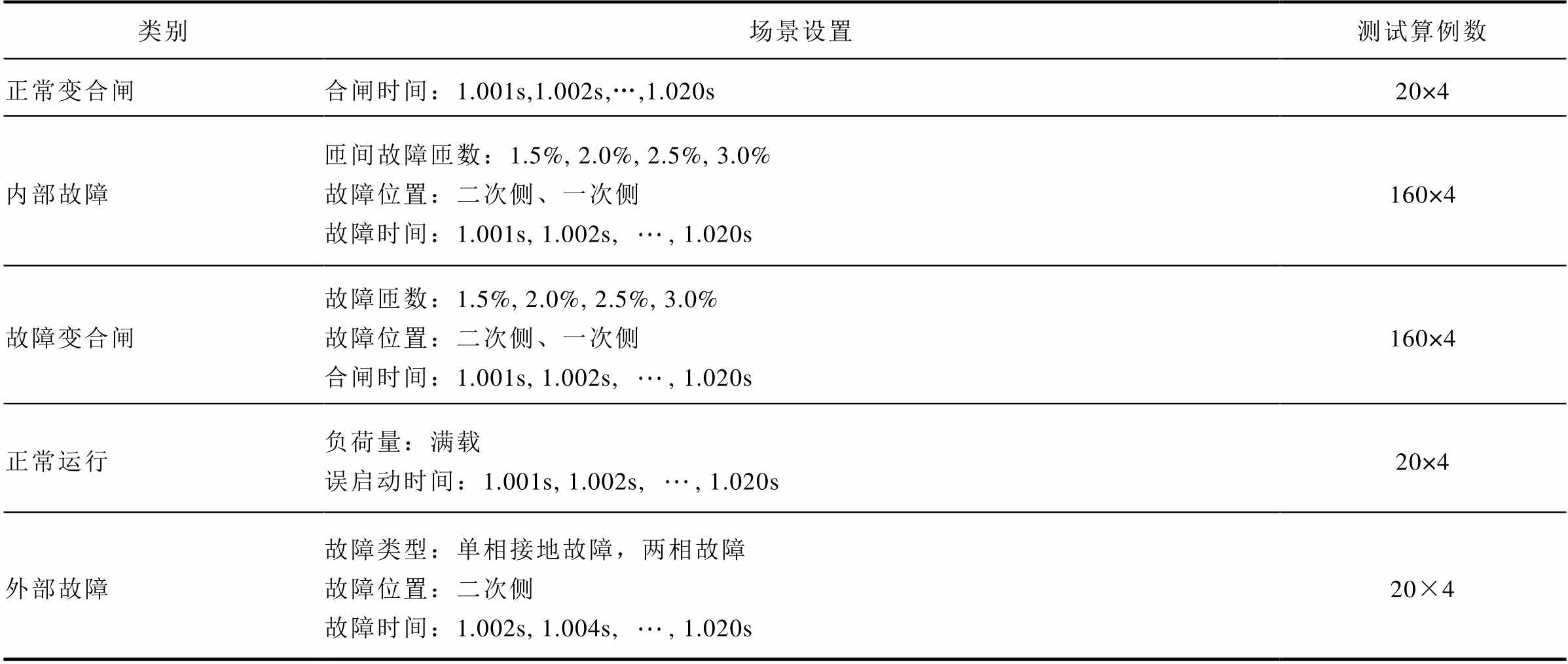
类别场景设置测试算例数 正常变合闸合闸时间:1.001s,1.002s,…,1.020s20×4 内部故障匝间故障匝数:1.5%, 2.0%, 2.5%, 3.0%故障位置:二次侧、一次侧故障时间:1.001s, 1.002s, , 1.020s160×4 故障变合闸故障匝数:1.5%, 2.0%, 2.5%, 3.0%故障位置:二次侧、一次侧合闸时间:1.001s, 1.002s, , 1.020s160×4 正常运行负荷量:满载误启动时间:1.001s, 1.002s, , 1.020s20×4 外部故障故障类型:单相接地故障,两相故障故障位置:二次侧故障时间:1.002s, 1.004s, , 1.020s20×4
2.3.1 输入量的处理
1)倾斜角度
在某些合闸角度下,铁心在很短时间内即可发生饱和,或磁通积累较长时间才可使铁心发生饱和。但只要选择足够长的数据窗,即可保证数据窗内含有曲线未饱和部分。
本文数据窗长为13ms,利用一次多项式拟合数据窗内的7个曲线段,分别为数据窗内第1ms、3ms、5ms、7ms、9ms、11ms、13ms对应的曲线段,并得到倾斜角度θ。
2)长轴
对于等效磁化曲线而言,本文采用的13ms数据窗中至多包含10ms的饱和部分,可采用以下方法确定长轴数值。
首先计算数据窗内采样点与原点(0,0)间距离,并得到数据对(L1, u1), (L2, u2),×××,(Lk, uk),×××(Ln, un),其中,Lk为等效磁化曲线第k个采样点与原点间的距离;uk为该采样点的纵坐标,即电压值;n为13ms数据窗中采样点数,取uk绝对值最大时的距离Lk为长轴数值L。13ms数据窗内的等效磁化曲线长轴数值确定方法如图8所示。
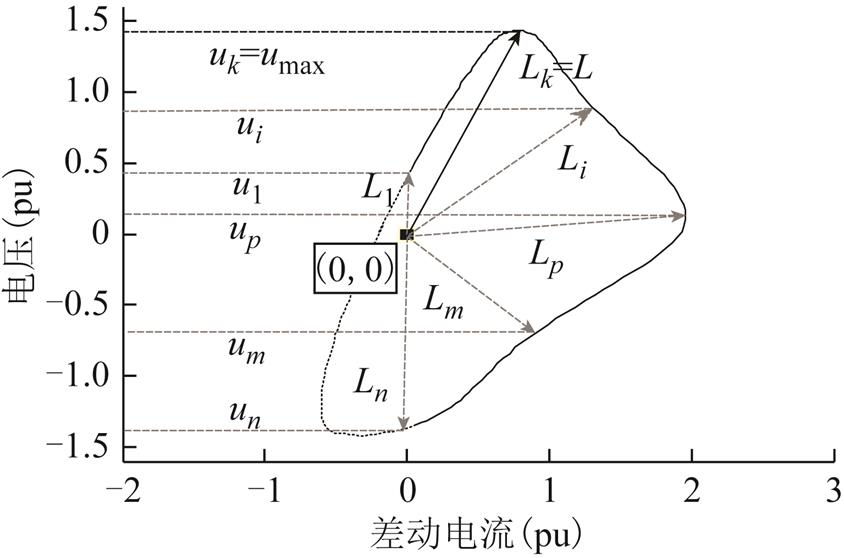
图8 等效磁化曲线长轴计算
Fig.8 Calculation of major axis
3)椭圆率
根据长轴数值L、长轴对应向量的方向以及椭圆段任意几点的采样点(u, i),可近似确定椭圆方程并得到椭圆短轴值。最后,结合长轴真实值L计算短长轴之比即椭圆率E。
2.3.2 最优模型参数的确定
本文BP神经网络的各层激活函数采用Log-sigmoid型函数,其函数映射值无法达到0和1,输出值越接近于0和1,激活函数的导数值越小,从一定程度上影响下降速度。Log-sigmoid函数曲线如图9所示,当输出值位于0.9或者0.1左右时,曲线的导数值较大,因此,故障变压器的期望输出Q1设为0.9,若网络的实际输出Q1≥0.5,视判断正确;正常变压器的期望输出Q2设为0.1,若实际输出Q2<0.5,视判断正确。
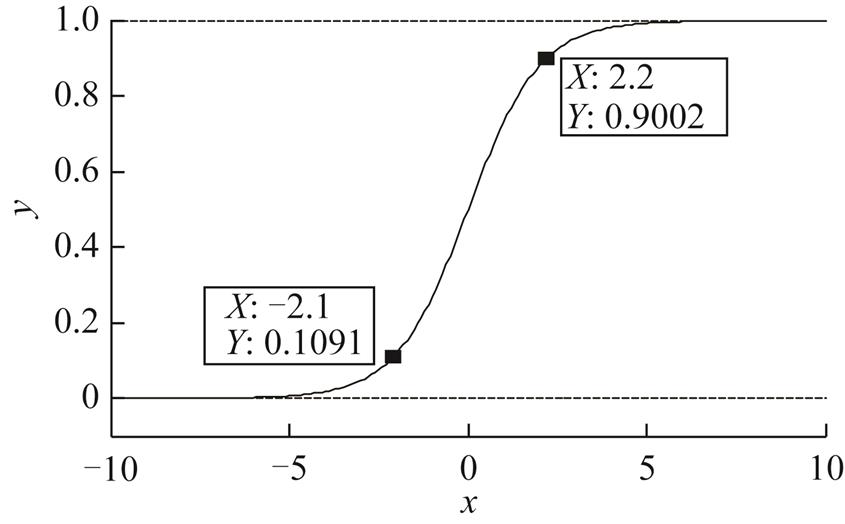
图9 Log-sigmoid函数曲线
Fig.9 Log-sigmoid function
神经网络采用双隐层结构,输入节点数为9,隐含层节点数一般不多于输入节点数,BP神经网络的迭代优化过程以损失值即期望输出值与实际输出值之间的距离最小为目标。通过枚举法,对不同的神经网络结构随机初始化各30次,选取训练集、测试集的分类准确率均达到99%以上的网络结构,并分析测试集误差均值及方均误差,统计结果如图10所示,误差定义为测试样本的期望输出与实际输出的差。图中,横坐标(m, n)代表第一、二隐含层的节点数分别为m、n时的BP神经网络,不同色块对应BP神经网络每次随机初始后的方均误差、误差均值。由图10可知,六种网络结构的误差较小且分布相对均匀,表明利用拟合模型生成的小规模样本集,训练得到的BP神经网络具有良好的内部故障识别能力。当第一、二隐含层节点数分别为4、7时,神经网络的输出误差方均值、均值均最小,分类模型的泛化能力更强、稳定性更高。此时,训练集、测试集的准确率均为100%。因此,确定BP神经网络最佳结构为:第一、二隐藏层的节点数分别为4、7。对网络再次随机初始化,选择使训练集、测试集分类准确率最高、测试集输出误差较小的神经网络。
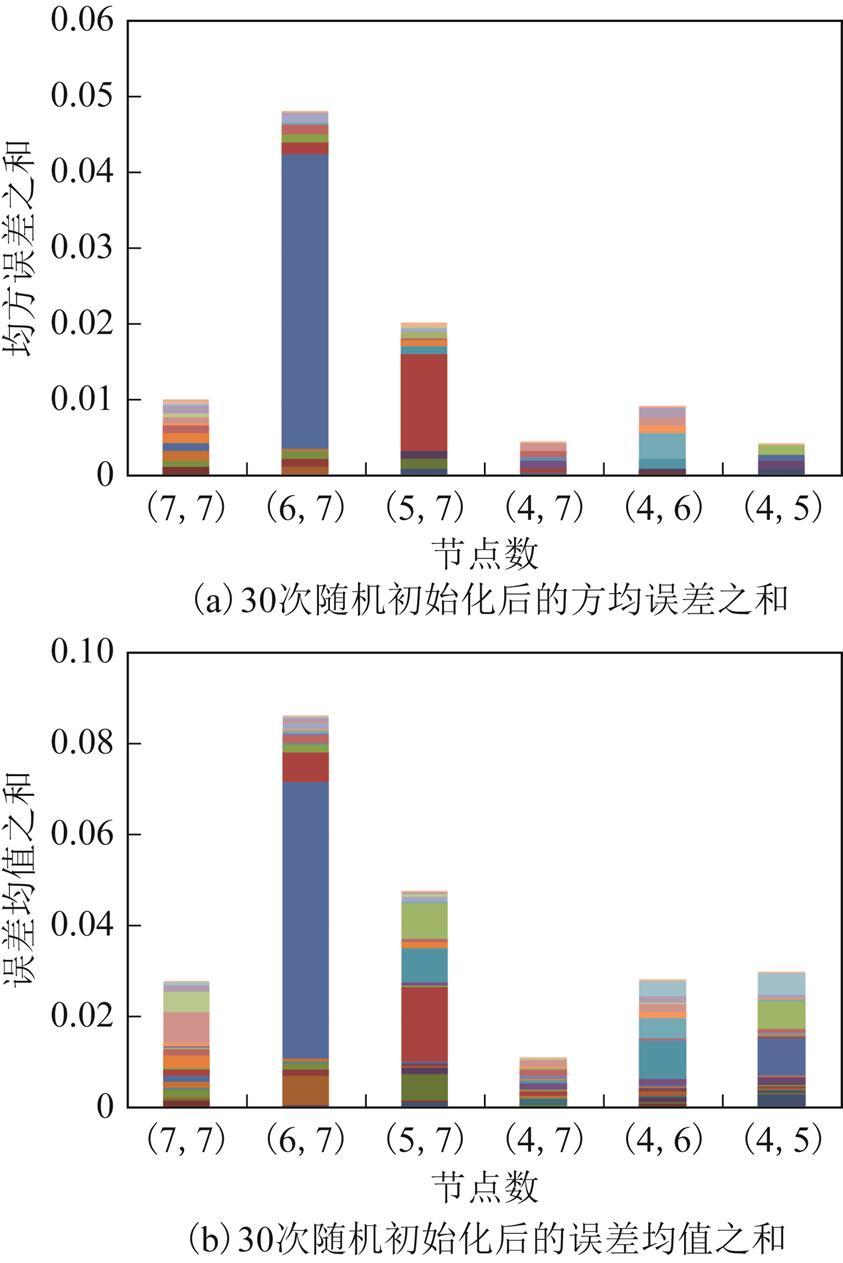
图10 测试集对应的输出误差情况
Fig.10 Output error of testing set
为了进一步证明本文算法的有效性及其泛化能力,建立了与2.2.2节中参数完全不同的变压器电磁暂态仿真模型,并利用动模变压器生成的实验数据对本文算法进行验证。
仿真中采用的变压器参数如下:额定容量为250MV·A的三相三绕组升压变压器,电压比为35/220/500kV,漏电抗0.1(pu),铜损和铁损分别为0.005(pu)、0.06(pu),仿真中变压器的联结方式为dYY11,变压器铁心特性曲线见表5。仿真场景的选择见表6,本文算法能够正确识别内部故障,正确动作率为100%。
表5 PSCAD仿真变压器铁心特性曲线
Tab.5 Magnetization curve of the transformer on PSCAD
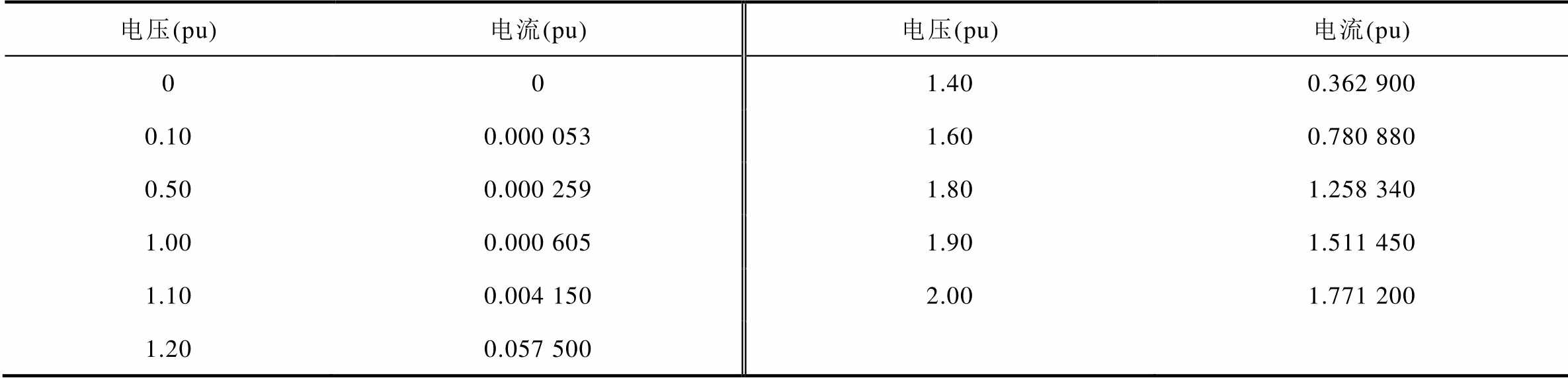
电压(pu)电流(pu)电压(pu)电流(pu) 001.400.362 900 0.100.000 0531.600.780 880 0.500.000 2591.801.258 340 1.000.000 6051.901.511 450 1.100.004 1502.001.771 200 1.200.057 500
表6 数字仿真情况下的算法性能
Tab.6 Operation scenes simulated on PSCAD
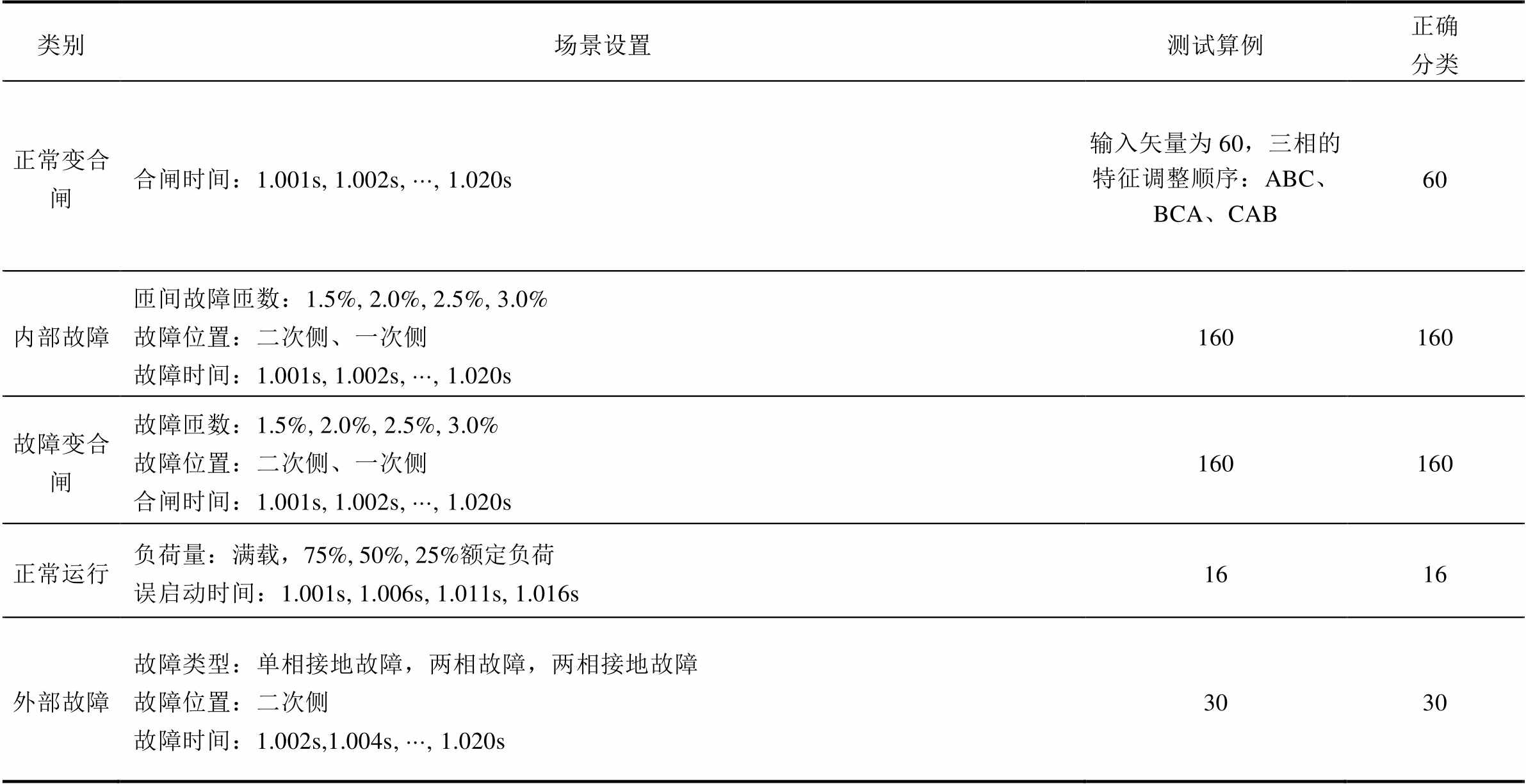
类别场景设置测试算例正确分类 正常变合闸合闸时间:1.001s, 1.002s,×××, 1.020s输入矢量为60,三相的特征调整顺序:ABC、BCA、CAB60 内部故障匝间故障匝数:1.5%, 2.0%, 2.5%, 3.0%故障位置:二次侧、一次侧故障时间:1.001s, 1.002s, ×××, 1.020s160160 故障变合闸故障匝数:1.5%, 2.0%, 2.5%, 3.0%故障位置:二次侧、一次侧合闸时间:1.001s, 1.002s, ×××, 1.020s160160 正常运行负荷量:满载,75%, 50%, 25%额定负荷误启动时间:1.001s, 1.006s, 1.011s, 1.016s1616 外部故障故障类型:单相接地故障,两相故障,两相接地故障故障位置:二次侧故障时间:1.002s,1.004s, ×××, 1.020s3030
动模变压器是由三台220V的单相变压器组成的三相双绕组变压器,联结方式为Yd11,额定容量2kV·A。空载实验和短路实验测得的空载电流i0=1.17%,空载损耗p0=0.7%,短路电压uk%=11.2%,短路损耗pk%=1.0%。实验运行场景见表7,本文算法具有较好的性能,实验样本正确识别率为100%(202/202)。
表7 动模实验中的算法性能
Tab.7 Operation scenes of dynamic-model experiment
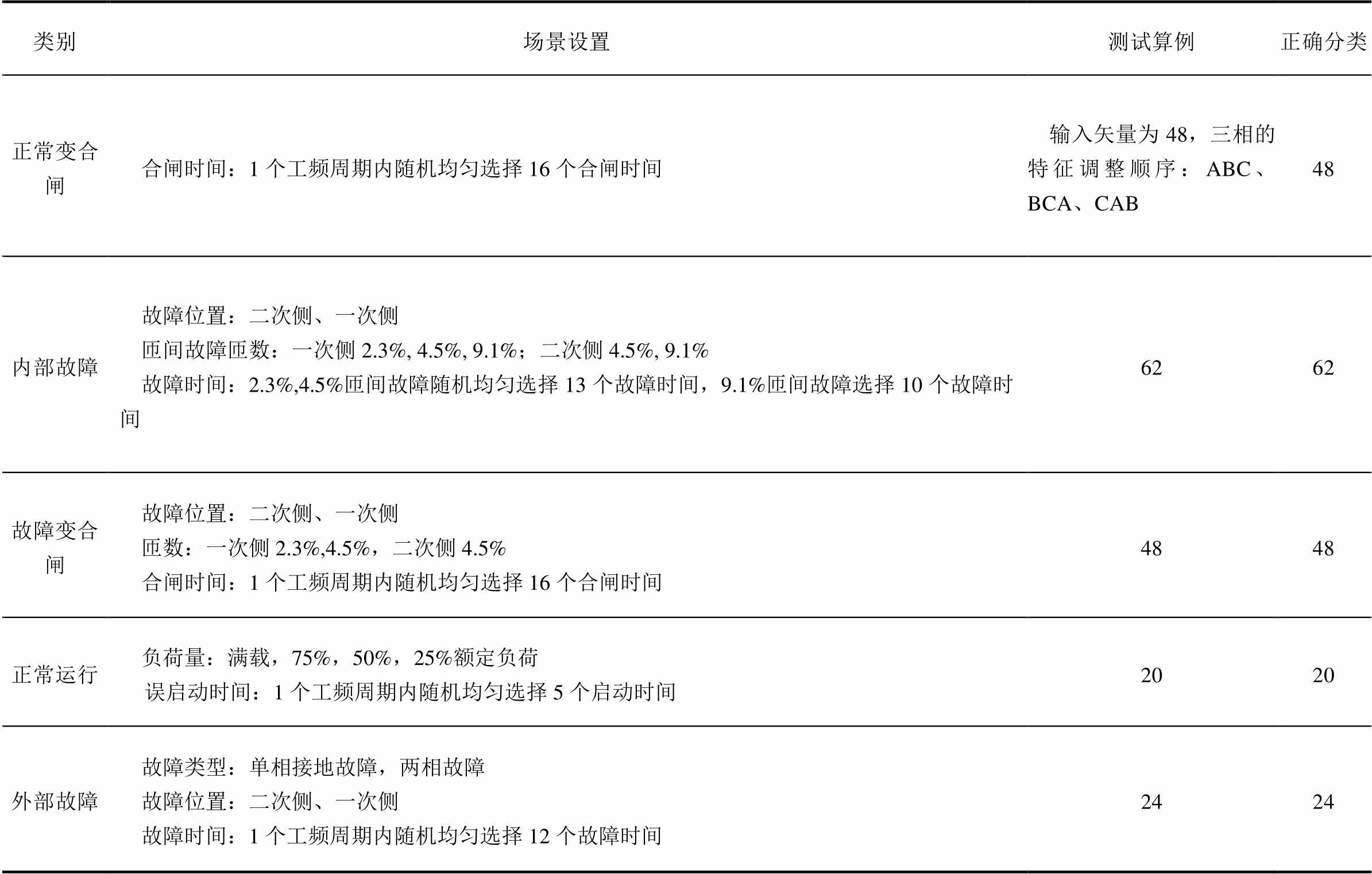
类别场景设置测试算例正确分类 正常变合闸合闸时间:1个工频周期内随机均匀选择16个合闸时间输入矢量为48,三相的特征调整顺序:ABC、BCA、CAB48 内部故障故障位置:二次侧、一次侧匝间故障匝数:一次侧2.3%, 4.5%, 9.1%;二次侧4.5%, 9.1%故障时间:2.3%,4.5%匝间故障随机均匀选择13个故障时间,9.1%匝间故障选择10个故障时间6262 故障变合闸故障位置:二次侧、一次侧匝数:一次侧2.3%,4.5%,二次侧4.5%合闸时间:1个工频周期内随机均匀选择16个合闸时间4848 正常运行负荷量:满载,75%,50%,25%额定负荷误启动时间:1个工频周期内随机均匀选择5个启动时间2020 外部故障故障类型:单相接地故障,两相故障故障位置:二次侧、一次侧故障时间:1个工频周期内随机均匀选择12个故障时间2424
根据实验样本的分类结果,得出以下结论:①虽然训练集并非实际变压器的实测数据,但由等效磁化曲线拟合模型的通用性,本文算法仍具有较强的泛化能力;②动模实验数据含有丰富的谐波,能够反映变压器保护现场恶劣的运行情况,但其只影响了等效励磁曲线的粗糙程度,并未影响倾斜角度、长轴、椭圆率等形状特征,算法性能未受影响。
为探究模型对特殊运行场景的适应性,本节在PSCAD仿真环境中,研究了CT饱和、过励磁及仅配置线路CT等情况下算法的性能。
3.3.1 过励磁
过励磁工况中的变压器铁心饱和通常为弱饱和,过电压水平不会超过1.4(pu),仿真场景选择见表8。本文算法可以将其正确分类,准确率为100%,变压器保护不会误动作。
表8 过电压情况下的算法性能
Tab.8 Performance of model on over-excitation

过电压水平(pu)发生时间测试算例数正确分类 1.21.001s, 1.002s, , 1.020s2020 1.32020 1.42020
过励磁工况下,铁心饱和时刻总是滞后于过电压发生时刻,且这种情况下的铁心饱和具有弱饱和特征,即:在一个工频周期内,饱和时间总是小于10ms,这种情况下的等效磁化曲线必含有充分的非饱和部分。过励磁工况下的差动电流及等效磁化曲线如图11所示。由图11可知,变压器在1.018s(A)处发生过电压1.2(pu);在1.022s(B)发生饱和并在1.026s(C)退出饱和,饱和持续时间为4ms;铁心在1.032s(D)再次发生饱和,铁心正常运行时间为6ms。
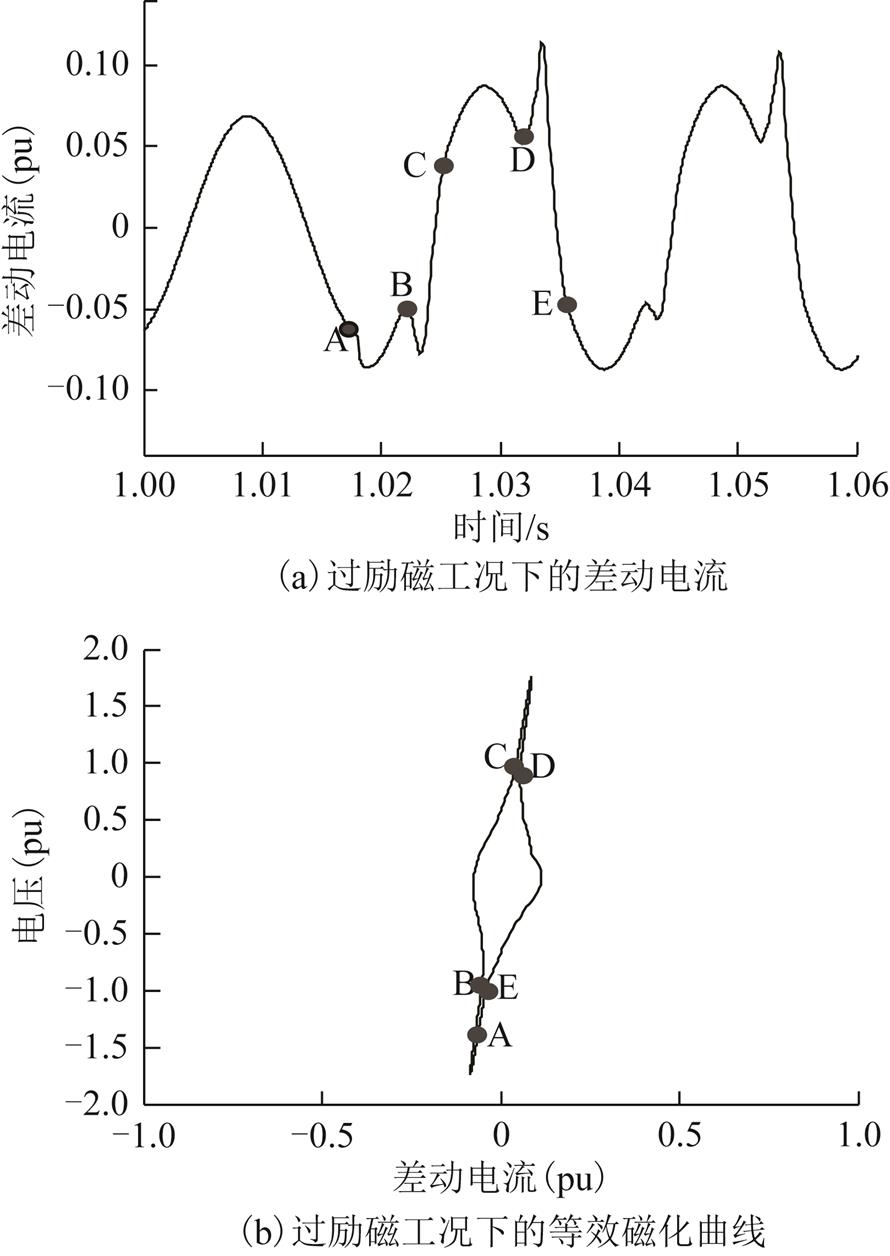
图11 过励磁工况下的差动电流及等效磁化曲线
Fig.11 Differential current and U-I curve of over-excitation
事实上,过励磁工况下的等效磁化曲线形状与正常变压器合闸相似,由于本文的特征融合算法关注的是等效磁化曲线的形状特征而非具体的数值特征,因此,虽然分类模型的训练过程未考虑过励磁场景,但本文算法仍能将其正确判断为正常变压器。
3.3.2 CT饱和
CT饱和场景见表9。本文算法可以将其正确分类,准确率为100%,不会产生误动作。一般情况下,CT饱和发生时刻总是滞后于故障发生时刻3~5ms[29],该时间段内,CT仍能正常传变电流。外部故障致CT饱和时的差动电流和等效磁化曲线如图12所示。由图12可知变压器在1.001s(A)发生外部单相接地故障,在1.007s(B)发生CT饱和,差动电流增大。故障发生与CT铁心发生饱和相隔时间6.0ms。CT饱和前,等效磁化曲线展现了与正常运行/外部故障相同的特点。
表9 CT饱和情况下的算法性能
Tab.9 Performance of model on CT saturation

故障类型发生时间测试算例数正确分类 5.0%匝间故障7.5%匝间故障1.001s 1.002s1.020s4040 外部单相接地故障外部两相故障4040
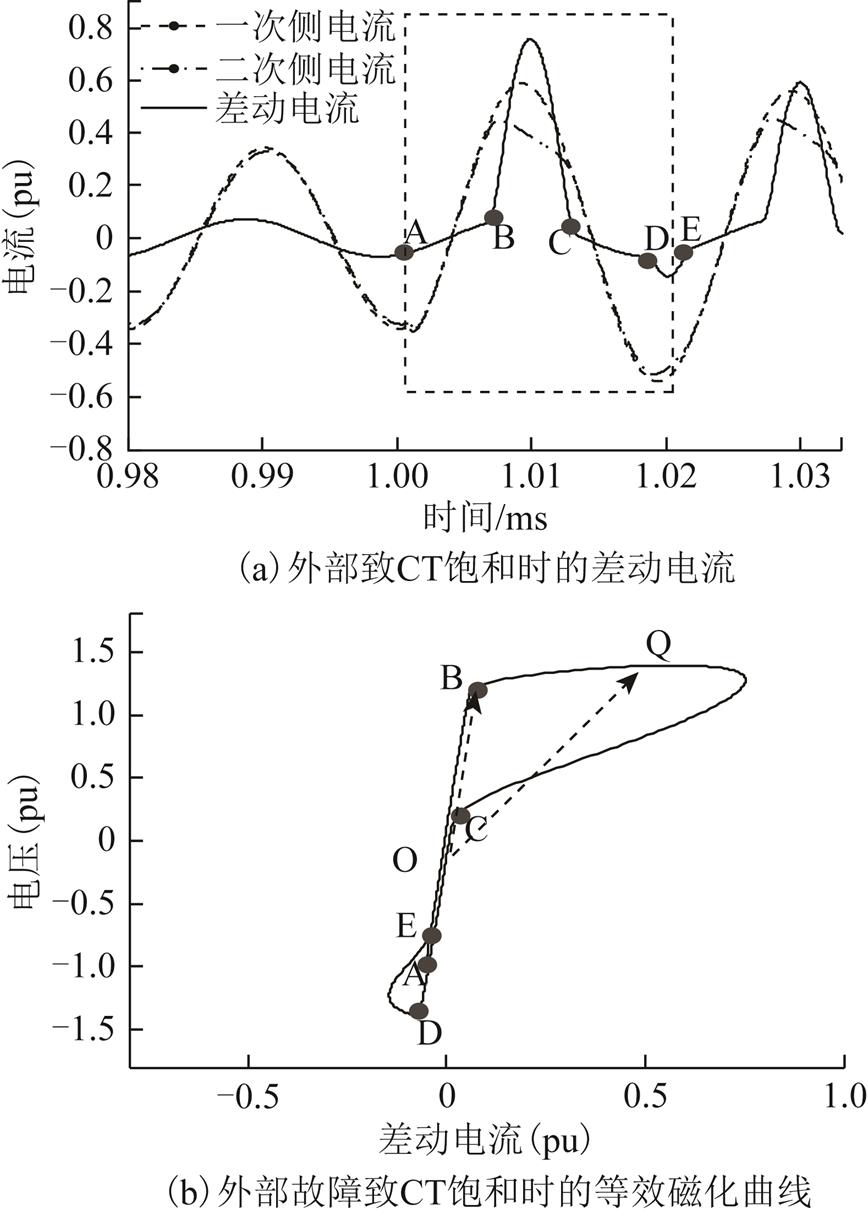
图12 外部故障致CT饱和时的差动电流和等效磁化曲线
Fig.12 Differential current and U-I curve of CT saturation
事实上,对于变压器内外部故障引起的CT饱和,变压器励磁支路电压绝对值的最大值有可能发生于CT饱和阶段,因此本文算法计算得到的长轴并非等效磁化曲线的真实值。如图12b所示,等效磁化曲线的真实长轴为OB,但根据本文算法计算得到的长轴为OQ,即便如此,由于分类模型融合了等效磁化曲线的多种几何特征,分类模型仍能根据曲线的倾斜角度判断变压器故障与否。
3.3.3 仅配置线电流CT
对于三相一体式变压器,三角形联结内无法加装CT,为此,本文研究了CT置于三角形联结外部时的等效磁化曲线可分类性。当CT加装于三角形绕组外侧时,对于变压器空载合闸,至多有一相差动电流波形呈现对称涌流特征;当变压器发生匝间故障时,至少两相线电流含有故障信息。因此,基于线电流的等效磁化曲线仍具有明显的可分类特征。由于此场景下的BP神经网络输入矢量的数值特征与配置绕组CT时不同,由2.3节得到的BP神经网络并不适用于本节等效磁化曲线的识别。因此,当CT加装于三角形绕组外侧时,需要针对线电流CT的智能变压器进行重新训练。等效磁化曲线的U、I由式(7)得到。
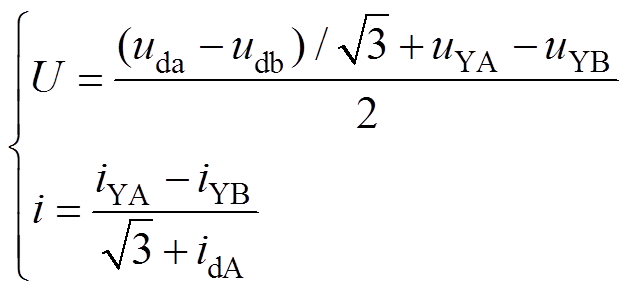 (7)
(7)式中,uda、udb分别为三角形侧A、B相相电压;uYA、uYB分别为星形侧A、B相相电压;idA为三角形侧A相线电流;iYA、iYB为星形侧相电流。
训练集采用Yd11联结,电压比230kV/11kV,漏电抗0.1(pu),铜损、铁损分别为0.005(pu)、0.05(pu),铁心性能曲线数据见表2;测试集采用dYY11联结,电压比35kV/220kV/500kV,漏电抗、铜损及铁损与训练集相同,铁心性能曲线数据见表5。训练集、测试集均含440个样本,见表10。BP神经网络的训练过程同2.3节,最终训练集、测试集的分类准确率均为100%。进一步证明了本文研究思路的可行性。
表10 仿真场景选择
Tab.10 Operation scenes simulated on PSCAD
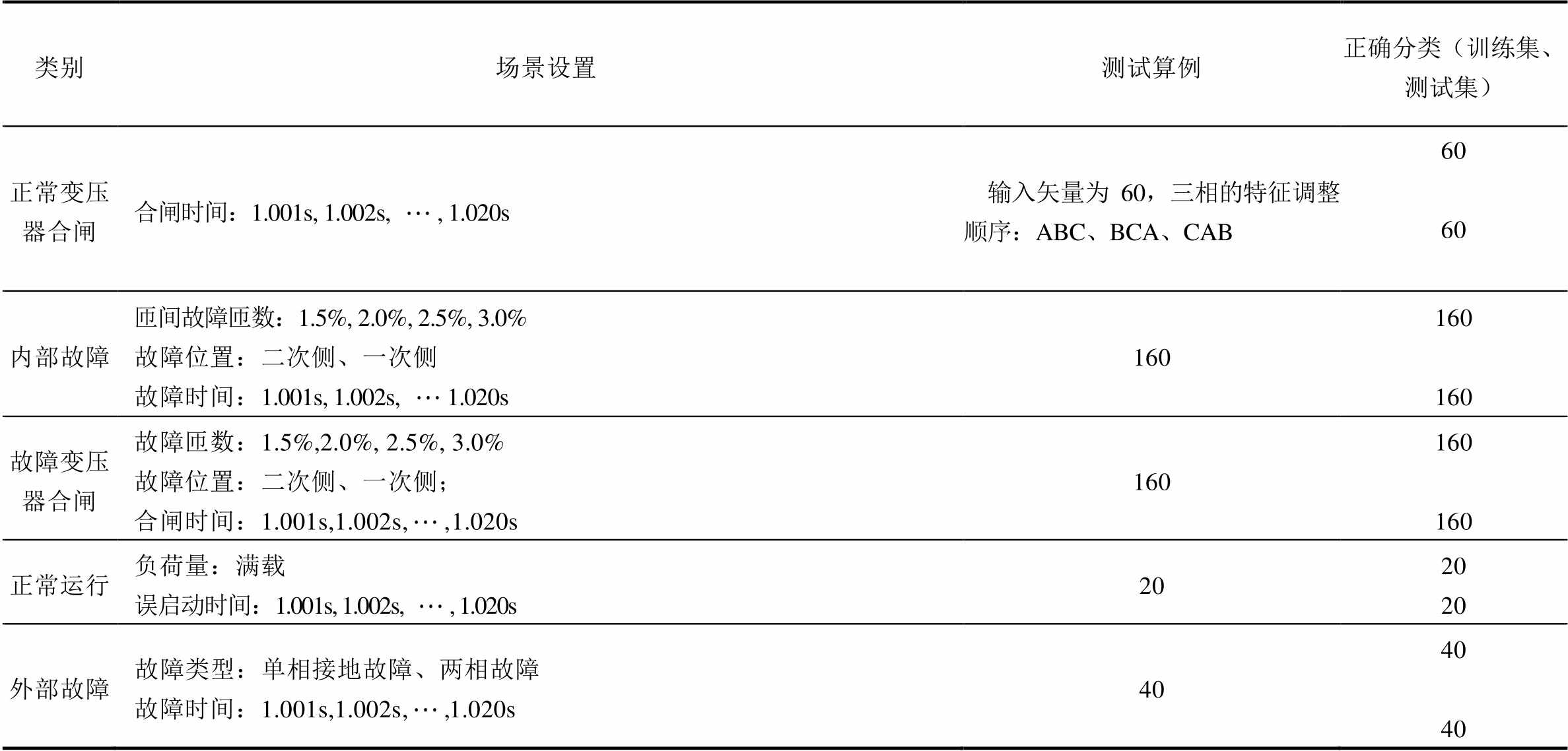
类别场景设置测试算例正确分类(训练集、测试集) 正常变压器合闸合闸时间:1.001s, 1.002s, , 1.020s输入矢量为60,三相的特征调整顺序:ABC、BCA、CAB6060 内部故障匝间故障匝数:1.5%, 2.0%, 2.5%, 3.0%故障位置:二次侧、一次侧故障时间:1.001s, 1.002s, 1.020s160160160 故障变压器合闸故障匝数:1.5%,2.0%, 2.5%, 3.0%故障位置:二次侧、一次侧;合闸时间:1.001s,1.002s,,1.020s160160160 正常运行负荷量:满载误启动时间:1.001s, 1.002s, , 1.020s202020 外部故障故障类型:单相接地故障、两相故障故障时间:1.001s,1.002s,,1.020s404040
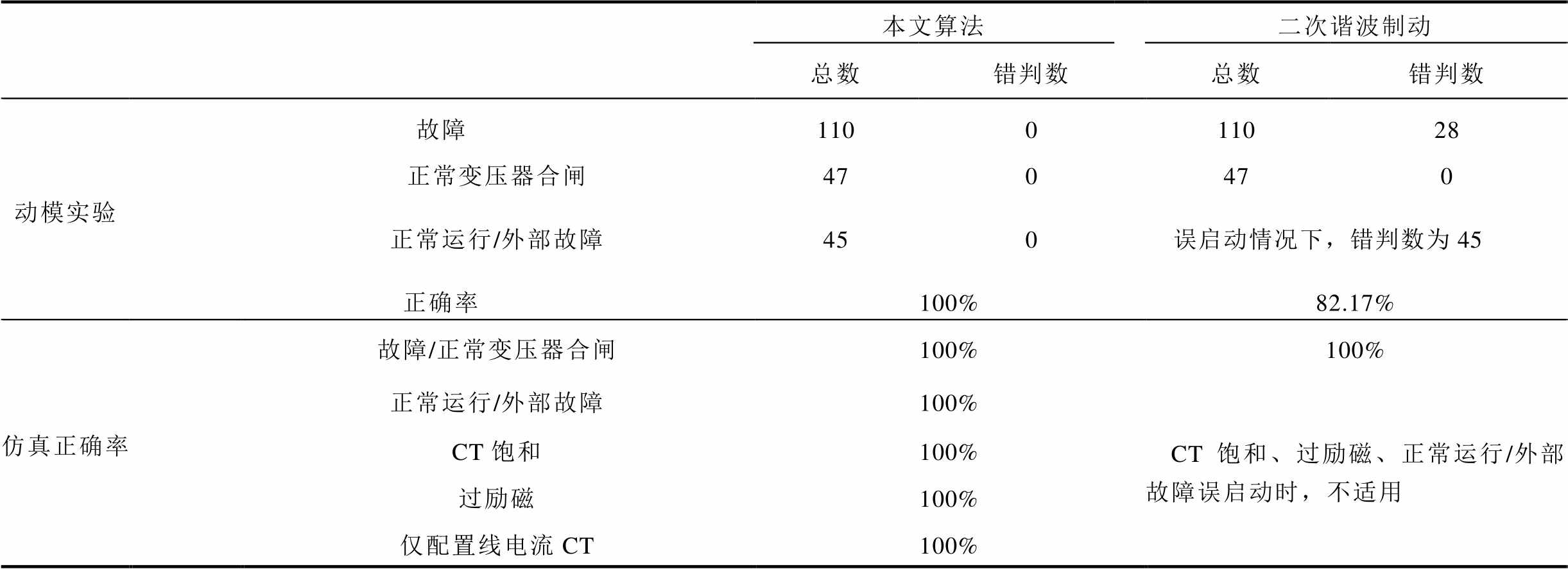
为进一步验证本文算法的性能,本节进行本文算法与带二次谐波制动的电流差动保护的比较研究,其结果见表11。由表11,对于动模实验数据,相比于传统的二次谐波制动的励磁涌流闭锁方案,本文提出的算法准确率更高,准确率达到了100%;由于实验变压器差动电流谐波较高,当变压器发生内部故障时,基于二次谐波制动的变压器保护存在较高的拒动风险。对于PSCAD仿真算例,本文算法及二次谐波制动方案的准确率均达到100%。
综上,基于等效磁化曲线智能识别的变压器保护受谐波等外部运行因素影响小、泛化能力强,能够可靠地识别变压器内部故障、励磁涌流,且不受CT饱和、过励磁的影响。
表11 算法的比较研究结果统计
Tab.11 Statistical table of classification results
本文算法二次谐波制动 总数错判数总数错判数 动模实验故障110011028 正常变压器合闸470470 正常运行/外部故障450 误启动情况下,错判数为45 正确率100%82.17% 仿真正确率故障/正常变压器合闸100%100% 正常运行/外部故障100%CT饱和、过励磁、正常运行/外部故障误启动时,不适用 CT饱和100% 过励磁100% 仅配置线电流CT100%
人工智能的发展对继电保护技术革新具有指导意义,但大规模的训练样本是决定模型性能的重要因素之一,阻碍了人工智能技术在电力系统中的应用,需要结合本质的物理问题进行研究。本文在分析变压器各运行状态下的磁化曲线形状特征的基础上,提出了一种融合等效磁化曲线多图形特征的变压器保护原理,通过构建BP神经网络识别变压器内部故障。利用等效磁化曲线拟合模型、电磁暂态仿真和动模实验等方法,生成了训练集和测试集样本库,对神经网络进行了优化,并着重验证了本文算法的泛化能力以及对过励磁、CT饱和和不同CT配置等场景的适应性。结果表明:本文算法基于小规模样本集,对不同运行环境下的PSCAD仿真、动模实验样本表现出了较强的泛化能力,不受谐波等外部条件的影响,样本分类准确率为100%;当内外部故障引起CT饱和或变压器发生过励磁时,算法表现出很强的适应能力。基于等效磁化曲线智能识别的变压器保护原理,训练简单,泛化能力强,适应能力强,具有良好的应用前景。
参考文献
[1] Sharp R L, Glassburn W E. A transformer differential relay with second-harmonic restraint[J]. Transactions of the American Institute of Electrical Engineers Part III Power Apparatus & Systems, 2008, 77(3): 913-918.
[2] 朱亚明, 郑玉平, 叶锋, 等. 间断角原理的变压器差动保护的性能特点及微机实现[J]. 电力系统自动化, 1996, 20(11): 36-40. Zhu Yaming, Zheng Yuping, Ye Feng, et al. Performance and digital realization of transformer differential relay based on dead angle philosophy[J]. Automation of Electric Power Systems, 1996, 20(11): 36-40.
[3] 马静, 王增平, 王雪. 基于等效瞬时漏电感的变压器保护新原理[J]. 电力系统自动化, 2006, 30(23): 64-68. Ma Jing, Wang Zengping, Wang Xue. Novel principle of power transformer protection based on equivalent instantaneous leakage inductance[J]. Automation of Electric Power Systems, 2006, 30(23): 64-68.
[4] 郝治国, 张保会, 褚云龙, 等. 基于等值回路平衡方程的变压器保护原理[J]. 中国电机工程学报, 2006, 26(10): 67-72. Hao Zhiguo, Zhang Baohui, Chu Yunlong, et al. Study on transformer protection principle based on equivalent circuit equilibrium equation[J]. Proceedings of the CSEE, 2006, 26(10): 67-72.
[5] 焦在滨, 马涛, 屈亚军, 等. 基于励磁电感参数识别的快速变压器保护[J]. 中国电机工程学报, 2014, 34(10): 1658-1666. Jiao Zaibin, Ma Tao, Qu Yajun, et al. A novel excitation inductance-based power transformer protection scheme[J]. Proceedings of the CSEE, 2014, 34(10): 1658-1666.
[6] Ge Baoming, Almeida A T D, Zheng Qionglin, et al. An equivalent instantaneous inductance-based technique for discrimination between inrush current and internal faults in power transformers[J]. IEEE Transactions on Power Delivery, 2005, 20(4): 2473-2482.
[7] 黎功华, 罗建, 杨浩. 基于绕组不平衡参数回路方程的变压器保护原理[J]. 电力系统自动化, 2008, 32(6): 91-94. Li Gonghua, Luo Jian, Yang Hao. A new transformer protection principle based on winding unbalanced parameter loop equation[J]. Automation of Electric Power Systems, 2008, 32(6): 91-94.
[8] Barbosa D, Netto U C, Coury D V, et al. Power transformer differential protection based on clarke's transform and fuzzy systems[J]. IEEE Transactions on Power Delivery, 2011, 26(2): 1212-1220.
[9] Medeiros R P, Costa F B, Silva K M. Power transformer differential protection using the boundary discrete wavelet transform[J]. IEEE Transactions on Power Delivery, 2016, 31(5): 2083-2095.
[10] 吴青华, 张东江. 形态滤波技术及其在继电保护中的应用[J]. 电力系统自动化, 2003, 27(7): 45-49. Wu Qinghua, Zhang Dongjiang. Morphological filtering techniques and applications in protection relaying[J]. Automation of Electric Power Systems, 2003, 27(7): 45-49.
[11] 翁汉琍, 王胜, 林湘宁, et al. 基于波形相似度的抗电流互感器饱和变压器相位差动保护[J]. 电力系统自动化, 2019, 43(4): 132-138. Weng Hanli, Wang Sheng, Lin Xiangning, et al. Waveform similarity based transformer phase differential protection against current transformer saturation[J]. Automation of Electric Power Systems, 2019, 43(4): 132-138.
[12] Segatto E C, Coury D V. A differential relay for power transformers using intelligent tools[J]. IEEE Transactions on Power Systems, 2006, 21(3): 1154-1162.
[13] Barbosa D, Coury D V, Oleskovicz M. New approach for power transformer protection based on intelligent hybrid systems[J]. IET Generation Transmission & Distribution, 2012, 6(10): 1009-1018.
[14] Tripathy M, Maheshwari R P, Verma H K. Power transformer differential protection based on optimal probabilistic neural network[J]. IEEE Transactions on Power Delivery, 2010, 25(1): 102-112.
[15] Shah A M, Bhalja B R. Fault discrimination scheme for power transformer using random forest technique[J]. IET Generation Transmission & Distribution, 2016, 10(6): 1431-1439.
[16] Mohamed E A, Abdelaziz A Y, Mostafa A S. A neural network-based scheme for fault diagnosis of power transformers[J]. Electric Power Systems Research, 2005, 75(1): 29-39.
[17] 李海锋, 王钢, 李晓华, 等. 电力变压器励磁涌流判别的自适应小波神经网络方法[J]. 中国电机工程学报, 2005, 25(7): 144-150. Li Haifeng, Wang Gang, Li Xiaohua, et al. Distinguish between inrush and internal fault of transformer based on adaptive wavelet neural network[J]. Proceedings of the CSEE, 2005, 25(7): 144-150.
[18] 黎功华. 基于人工神经网络模型的变压器保护原理[J]. 电力系统保护与控制, 2010, 38(10): 26-30. Li Gonghua. Transformer protection principle based on the artificial neural network model[J]. Power System Protection and Control, 2010, 38(10): 26-30.
[19] 黄永红, 马锋, 沈敏. 基于最小二乘支持向量机的变压器励磁涌流识别方法研究[J]. 电力系统保护与控制, 2010, 38(23): 93-96. Huang Yonghong, Ma Feng, Shen Min. Research of magnetizing inrush current identification method based on LS-SVM[J]. Power System Protection and Control, 2010, 38(23): 93-96.
[20] 祝磊, 丘毅昌, 张蓉蓉, 等. 基于数学形态谱和LS-SVM的变压器励磁涌流和短路电流识别方法[J]. 电网技术, 2008, 32(增刊1): 87-89. Zhu Lei, Qiu Yichang, Zhang Rongrong, et al. Recognition of inrush current and fault current based on pattern spectrum and LS-SVM[J]. Power System Technology, 2008, 32(S1): 87-89.
[21] 王世勇, 孙鸣, 丁中奎. 一种基于支持向量机的变压器励磁涌流判别新方法[J]. 继电器, 2008, 36(5): 1-6. Wang Shiyong, Sun Ming, Ding Zhongkui. A new scheme to distinguish between inrush current and internal fault of transformer based on support vector machine[J]. Relay, 2008, 36(5): 1-6.
[22] 李臻, 罗林根, 盛戈皞, 等. 基于压缩感知的特高频局部放电定位法[J]. 电工技术学报, 2018, 33(1): 202-208. Li Zhen, Luo Lingen, Sheng Gehao, et al. Ultrahigh frequency partial discharge localization methodology based on compressed sensing[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 202-208.
[23] 左曙光, 刘洋, 邓文哲. 轴向磁通轮毂电机电磁力波灵敏度分析和优化[J]. 电工技术学报, 2018, 33(11): 2423-2430. Zuo Shuguang, Liu Yang, Deng Wenzhe. Sensitivity analysis and optimization of electromagnetic force wave of an axial-flux in-wheel motor[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2423-2430.
[24] 彭道刚, 陈跃伟, 钱玉良, 等. 基于粒子群优化-支持向量回归的变压器绕组温度软测量模型[J]. 电工技术学报, 2018, 33(8): 1742-1749. Peng Daogang, Chen Yuewei, Qian Yuliang, et al. Transformer winding temperature soft measurement model based on particle swarm optimization-support vector regression[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1742-1749.
[25] 赵希梅, 吴勇慷. 基于自适应修正拉盖尔递归神经网络的永磁直线同步电机反推控制[J]. 电工技术学报, 2018, 33(10): 2392-2399. Zhao Ximei, Wu Yongkang. Backstepping control based on adaptive modified laguerre recurrent neural network for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(10): 2392-2399.
[26] 程学珍, 朱晓林, 杜彦镔, 等. 基于神经模糊Petri网的高压断路器故障诊断研究[J]. 电工技术学报, 2018, 33(11): 137-146. Cheng Xuezhen, Zhu Xiaolin, Du Yanbin, et al. High voltage circuit breaker fault diagnosis based on neural fuzzy Petri nets[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 137-146.
[27] 朱元振, 刘玉田. 基于深度学习直流闭锁判断的高风险连锁故障快速搜索[J]. 电力系统自动化, 2019, 43(22): 59-67. Zhu Yuanzhen, Liu Yutian. Fast search for high-risk cascading failures based on deep learning DC blocking judgment[J]. Automation of Electric Power Systems, 2019, 43(22): 59-67.
[28] 赵晓坦, 柴建云, 苏鹏声, 等. 利用磁通轨迹特征识别变压器励磁涌流[J]. 继电器, 2004, 32(2): 1-5. Zhao Xiaotan, Chai Jianyun, Su Pengsheng, et al. Identification of magnetizing inrush current of power transformer based on features of flux locus[J]. Relay, 2004, 32(2): 1-5.
[29] Etumi A A, Anayi F. The application of correlation technique in detecting internal and external faults in three-phase transformer and saturation of current transformer[J]. IEEE Transactions on Power Delivery, 2016, 31(5): 2131-2139.
Equivalent Magnetization Curve Intelligent Recognition Based Transformer Protection
Abstract This paper proposed an equivalent magnetization curve-based transformer protection. The transformer operation states are essentially affected by iron core and intuitively demonstrated by magnetization hysteresis loop. Firstly, based on the analysis of magnetization hysteresis loop, the correspondence between equivalent magnetization curves and operation states was shown in this paper. Secondly, several extracted geometric characteristics were used as input to BP neural network, which was trained with a small amount of training data to identify transformer operation states. Finally, digital simulation and dynamic-model experiments were conducted to verify the proposed scheme. The results of 100% showed that the classification model with a small amount of training data could accurately identify transformer operation states. Moreover, this classification model had higher generalization ability, not affected by CT saturation and over-excitation. The proposed scheme solves effectively the poor performance of AI technique in power system, which has a great application value.
keywords:Transformer protection, equivalent magnetization curve, BP neural network, data fusion, generalization ability
DOI:10.19595/j.cnki.1000-6753.tces.190511
中图分类号:TM40
李宗博 男,1992年生,博士研究生,研究方向为基于人工智能的继电保护新原理与新技术。E-mail:lizongbo1992@163.com
焦在滨 男,1976年生,副教授,博士生导师,研究方向为电力系统新型继电保护、交直流混联直流配电系统的运行与控制、人工智能在电力系统故障处理中的应用。E-mail:jiaozaibin@mail.xjtu.edu.cn(通信000作者)
国家自然科学基金资助项目(51877167, 51377129)。
收稿日期2019-04-30
改稿日期 2019-08-30
(编辑 赫蕾)