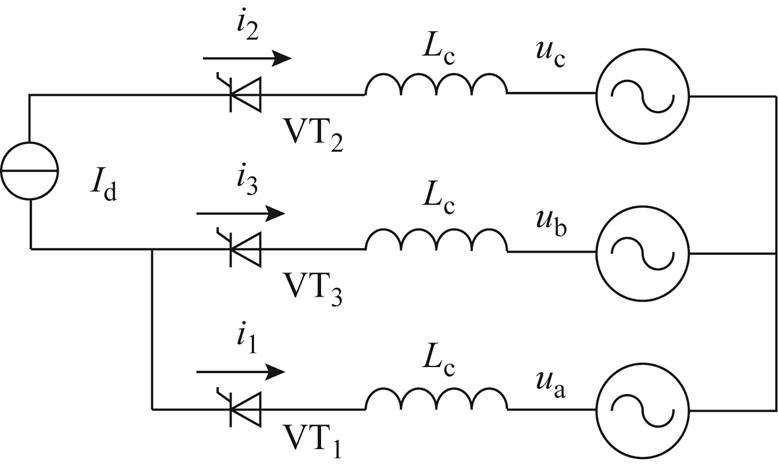
图1 换相等效电路
Fig.1 Equivalent circuit of commutation
摘要 为减少高压直流输电系统换相失败的发生概率，从换相失败机理出发，提出了一种基于电压波形拟合的换相失败快速预测与抑制措施。首先，以换相电压-时间面积为理论基础，推导出换相需求面积和可供应最小换相面积的数学解析并以此为换相失败预测判据，通过三点法对故障前后电压波形进行拟合，从而实现所提换相失败预测方法的实时量化分析。然后，提出一种基于临界换相面积的提前触发控制策略，可根据临界换相面积动态变化来调节提前触发的角度。最后，基于CIGRE标准测试模型的仿真结果表明，所提方法不但可以实现换相失败的快速预测，同时还能在一定程度上抑制换相失败的发生，改善系统的故障恢复性能。
关键词：高压直流输电换相失败换相面积曲线拟合提前触发
传统的高压直流输电（High Voltage Direct Current，HVDC）凭借输送容量大、功率调节能力强、造价相对较低等特点[1]，在我国“南北互供”、“西电东送”以及“全国联网”等国家电网发展战略中扮演了重要的角色[2-3]。我国目前已有30多条高压直流输电工程建成并投入运行，已成为拥有直流输电工程最多、输送容量最大、输送线路最长的国家[4]。然而该输电技术的核心元件晶闸管却没有自关断能力，这导致其在逆变侧交流系统电压支撑不足的情况下极易发生换相失败[5-7]。换相失败不仅会引发直流电流激增、导致换流阀受到冲击，还会造成直流功率的大幅度波动，严重情况甚至导致直流系统闭锁，该功率波动将给直流系统的送、受端电网安全稳定运行带来更为严峻的考验[8]。
虽然传统高压直流输电技术有与生俱来的换相失败缺陷，但其在输送能力、输送距离、造价等方面的显著优点使其工程应用依旧广泛。因此，国内外学者针对换相失败的预防研究已经开展了大量的工作，其预防措施主要分为拓扑结构改进和控制策略优化两个方面。然而拓扑结构的改进虽然能从换相机理上消除换相失败[9-10]，但改进成本过高，同时工程实施难度较大。
在控制策略优化方面，为实现换相失败的快速预防，其研究思路主要分为两个步骤：首先是换相失败的快速检测，其次是换相失败的快速抑制。目前应用于直流输电系统的换相失败检测分为实测型和预测型两大类。
1）实测型，是通过量测各换流阀换相结束时刻与对应的换相电压过零时刻的间隔，并将其转换为角度量从而获得熄弧角，通过与最小熄弧角的比较判断是否发生换相失败[11]。首先实测型是对已经发生的换相失败进行检测，所以其后续采取的控制措施都在换相失败发生后，会导致控制系统的响应速度降低，其次因为直流工程中一个换流桥臂的晶闸管数量太多，故晶闸管的熄弧角不易测量[12]。
2）预测型，是在逆变侧交流母线对三相电压提取零序分量或ab变换，从而预测单相故障和三相对称故障所引发的换相失败。在此基础上，文献[13]针对电压过零点启动慢的缺点，提出了增加正弦-余弦分量的检测方法。虽然预测法在检测速度上大大提高，为抑制换相失败发生争取了更多的时间，但现有预测法针对换相失败是否发生的判据主要依赖仿真计算[14]，无法建立换相失败与预测判据之间的物理关系，缺乏理论依据，需针对各个工况进行仿真，普适性有待提高。
目前针对换相失败的抑制措施主要为提前触发，增大换相裕度。文献[15-16]均采用了模糊控制器，设计了综合各有关电气量的模糊控制方案来计算提前触发角度，以实现换相失败的抑制。文献[17]在现有的换相失败预测控制的基础上提出了将零序电压分量和旋转矢量所检测的最大值转换为提前触发的角度。文献[17-18]认为提前触发过大会导致无功需求增大，直流电流增大，这将更不利于换相过程。提前触发角度过大的主要原因是现有方法并未将提前触发角度与换相失败的边界条件建立物理关系，这也恰恰导致提前触发控制存在超调的可能性。
综合上述研究成果，本文从换相失败的物理判据出发，以换相需求面积和可供应最小换相面积之间的关系作为换相失败判断标准，利用三点法对故障前后的换相线电压波形进行拟合，从而实现对换相失败的快速预测；并在此基础上，通过换相失败的边界条件，借助换相面积理论求解出控制器的最大触发延迟角，增大换相裕度以实现对换相失败的快速抑制。基于CIGRE直流输电标准模型，对本文所提换相失败快速预测及抑制措施进行仿真验证，仿真结果表明本方法可以实现对换相失败的准确、快速预测，并在一定程度上抑制HVDC系统发生换相失败。
换相失败是指当换流桥两个桥臂之间换相结束后，刚退出导通的换流阀在反向电压作用的一段时间内，如果未能恢复阻断能力或者在反向电压期间换相过程一直未能完成，此时，阀电压转变为正向时被换相的阀将向原来预定退出导通的阀进行倒换相[17]。
换相等效电路如图1所示。以VT1向VT3换相为例，i1、i2、i3分别为换流阀1、2、3的阀电流，
图1 换相等效电路
Fig.1 Equivalent circuit of commutation
计及换流变压器的等值电抗Lc，且uba=ub-ua为换相电压，根据基尔霍夫电压定律有
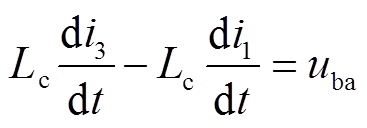（1）设t1和t2分别为换相开始时刻与换相结束时刻，换相过程中i1=Id-i3，将其代入式（1）并对等式两端同时积分可得
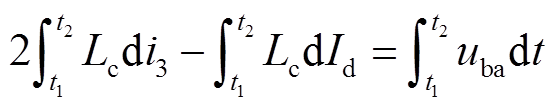（2）
根据换相过程可知，i3(t1)=0，i3(t2)=Id(t2)，将时域形式转换成电角度形式，可得
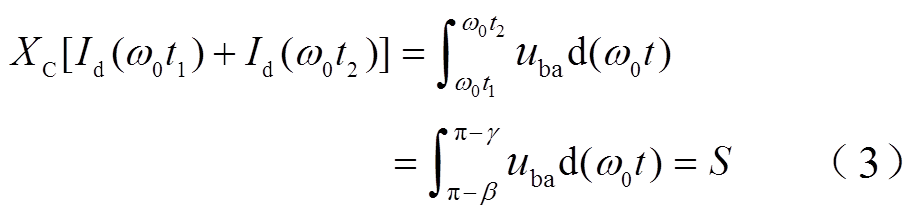
式中，XC为逆变侧等值换相电抗；b为越前触发角；γ为关断角。由式（3）可知，LCC-HVDC的换相过程需要一定的换相电压时间面积，且该面积与直流电流大小呈正相关，故简称S为换相面积。
然而上述对于换相面积的推导是基于三相对称系统场景，虽然可将其推广至交流系统三相对称故障，但未考虑三相不对称故障而引发线电压换相点偏移的影响。
考虑电压换相点偏移的换相电压面积如图2所示。考虑线电压换相点偏移产生的换相偏移角Δφ后，将式（3）修正后，可得
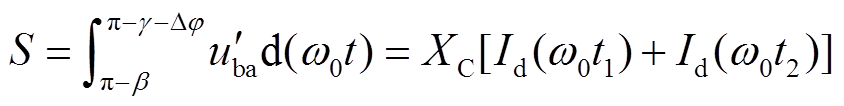（4）
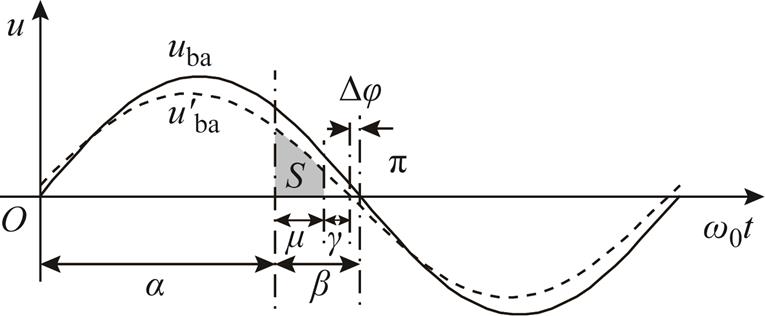
图2 考虑电压换相点偏移的换相电压面积
Fig.2 Commutation voltage area considering voltage commutation point offset
由上述分析可知，换相面积与直流电流Id、越前触发角β、换相点偏移角Δφ以及受端电网交流母线线电压有密切关系，且该关系可以通过数学推导表征，因此利用换相面积作为换相失败快速预测判据是具备理论支撑的。同时换相面积的数学推导充分考虑了交流系统故障后的直流电流、换相点偏移以及交流电压的降低，实现了对交流故障情况下换相过程的精细刻画，为换相失败的准确、快速预测提供了理论支撑。
根据换相面积理论，决定换相过程成功与否的关键是两个换相面积指标，分别将其定义为：Sneed为换相需求面积，Smin为可供应最小换相面积。因此换相失败的判据为：当Smin≥Sneed时，逆变器不会发生换相失败；当Smin＜Sneed时，逆变器会发生换相失败。因此，Sneed和Smin的准确计算至关重要。
由式（4）可知，考虑直流电流的变化情况，换相需求面积Sneed不再恒定，然而本文所述方法是针对故障发生后第一次换相失败发生的预测，由于换相失败发生前直流电流的变化速度较慢，同时直流侧的平波电抗器也会降低直流电流的增加速度，因此采样得到换相起始时刻t0所对应的直流电流Id(ω0t0)，据此可将换相需求面积Sneed定义为
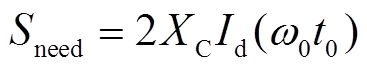（5）依据换相面积理论，可供应最小换相面积Smin的大小主要取决于故障后的线电压曲线。假设故障后交流角速度ω0保持不变且仍为正弦波，故可将故障后的线电压曲线定义为
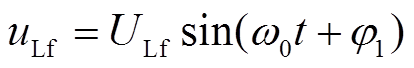（6）
式中，ULf为故障后线电压峰值；φ1为故障后线电压初相位。针对故障后的所有线电压波形，由式（4）和式（6）求得各个换相电压所能提供的换相面积为
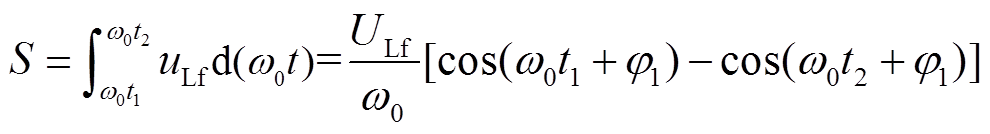（7）可供应最小换相面积Smin即为上述各线电压所对应换相面积的最小值。
由式（5）和式（7）可知，在Smin和Sneed的数值求解过程中，需要对换相起始时刻t1和换相终止时刻t2进行求解，如图3所示。
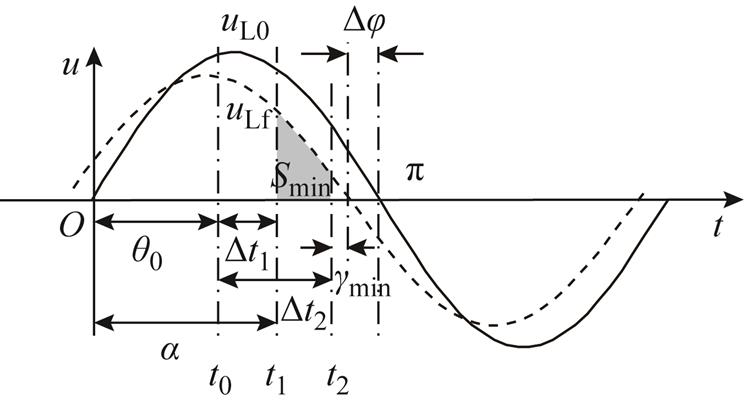
图3 故障后系统可供应最小面积
Fig.3 Minimum supplied area after fault
图3中，t0为采样时刻，α为逆变侧触发延迟角，θ0为系统正常运行时线电压曲线t0时刻的电压相角，θ0=ω0t0+α0。换相起始时间t1由图3得
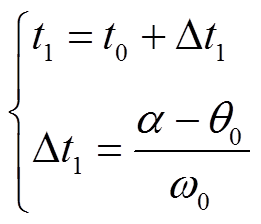（8）系统故障前正常运行时线电压为
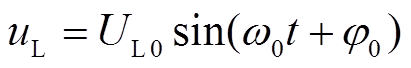（9）
依据换相过程的物理特性，使采样时刻t0的取值范围为各换相线电压正半周期中（0, 90°）的区间，可保证对故障后下一次换相实现准确预测，将采样时刻t0代入式（9），可解得θ0为
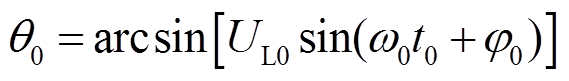（10）由图3可得换相终止时间t2为
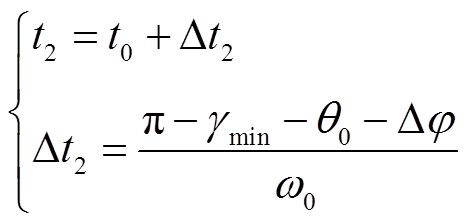（11）
式中，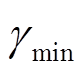
为最小关断角，可由故障前线电压曲线和故障后线电压曲线的初相位求得换相点偏移角
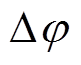为
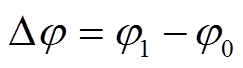（12）由式（8）~式（12），可以求得换相起始时间t1和换相终止时间t2。由式（6）和式（9）可求得换相需求面积Sneed和可供应最小换相面积Smin。即可通过比较Sneed和Smin的大小，从而实现在故障后很短的采样时间内预测换相失败的发生。
由上述分析可知，本文所提方法在Sneed和Smin求解过程中的所需参数基本都已求解，仅有故障后的线电压曲线uLf仍是未知的，因此在后文中将对uLf进行求解。
本文所提出的换相失败预测方法的可靠性和快速性主要取决于拟合电压曲线的准确性和快速性。而影响电压曲线拟合准确性的主要因素有系统采样频率、拟合曲线的计算方法以及受端系统的强度。其中受端系统越强则故障后受端系统的频率偏差越小，电压波形越接近正弦，换相失败预测的准确性越高。本预测方法的快速性主要受所需电压采样点数量的影响，因此采样点越少，预测速度越快。基于上述要求，本文采用了基于三点法[19]的电压波形预测拟合算法。
2.2.1 基于三点法的电压曲线预测拟合
三点法的原理是通过正弦曲线的三个采样点，计算出正弦曲线幅值、频率、相角。假设故障后交流系统频率不变，仍为工频频率50Hz，角频率为ω0=2π×50rad/s，则通过两个采样点可求出电压曲线的幅值和相角，就可以确定电压曲线。设故障后交流侧线电压为
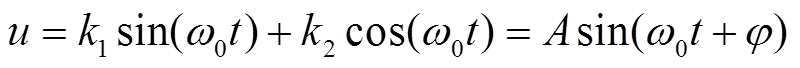（13）逆变侧交流母线线电压两个采样点分别为(t1,u1)和(t2,u2)，则有
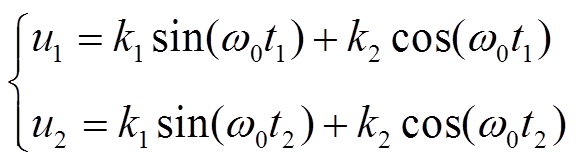（14）
为使式（14）表达更简略，构造矩阵
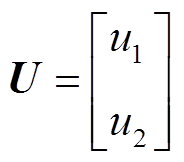
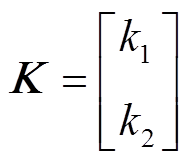
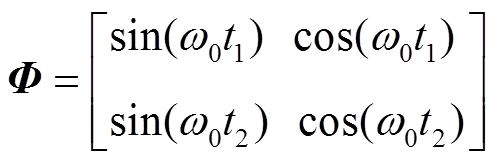
则式（14）可以表达为
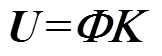（15）
可求出系数矩阵K为
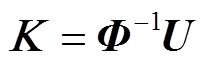（16）通过电压曲线的系数矩阵，可进一步求得电压曲线的幅值及相位为
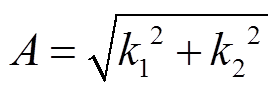（17）
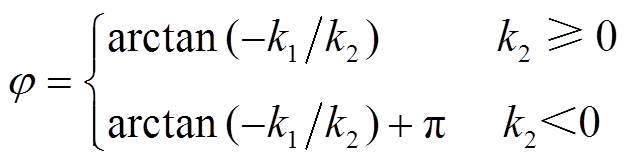（18）即可确定故障后工频电压曲线的表达式。
基于三点法拟合正弦曲线的方法属于直接求解法，采样点数量与电压曲线未知量个数相同，所需采样点数量最少，采样时间最短，计算量最小，具有快速性的优点。通过仿真分析与理论计算对比，三点法拟合的电压曲线与系统电压变化的趋势基本一致，并能够更快速地响应故障后电压的降落，三点法输出的电压幅值响应电压降落的速度均比所测电压有效值的响应速度快，克服了电压有效值测量无法满足控制系统调节快速性的要求。
2.2.2 基于电压波形拟合的换相失败预测模型
基于上文的分析，可以通过三点法预测故障后的交流电压波形，并且实时采样直流电流值，实现对LCC-HVDC型直流输电系统换相需求面积Sneed和可供应最小换相面积Smin的数值解析，从而实现换相失败的快速预测，具体预测方案实施如图4所示。
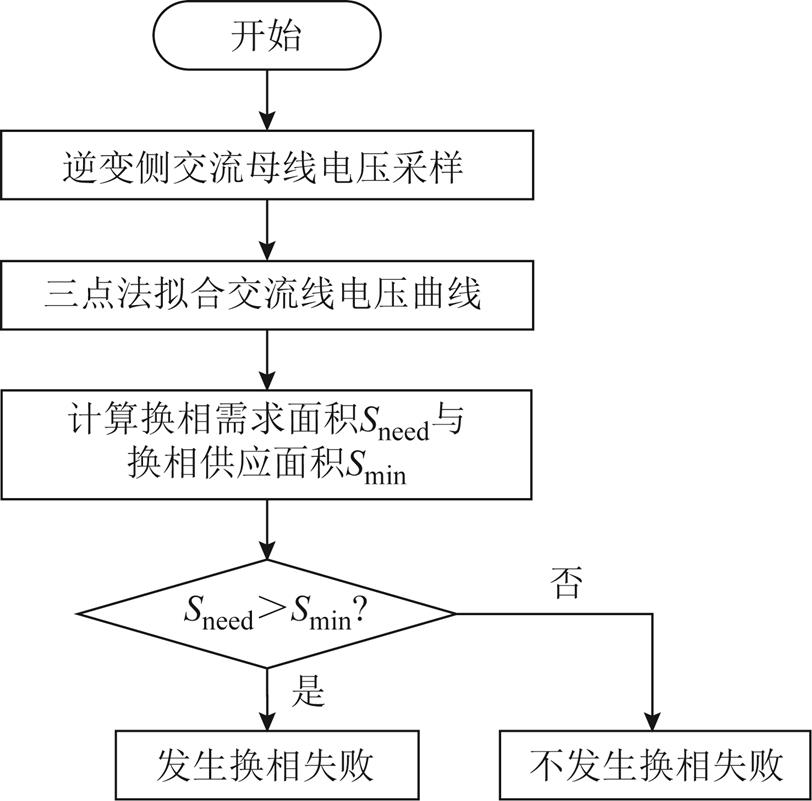
图4 换相失败预测示意图
Fig.4 Commutation failure prediction diagram
在逆变侧交流母线处获得故障后线电压的采样值，通过三点法计算出当前采样时刻的线电压幅值和相角，同时通过三点法拟合故障后的线电压参数，并将逆变侧触发延迟角、直流电流、采样时间等参数均输入到换相面积计算单元，其输出为系统换相需求面积Sneed和可供应最小面积Smin的差值，当此差值大于0时，判断逆变器即将发生换相失败。
然而由于采用三点法拟合故障后的换相电压，仅利用故障后的两个采样点，窗长较短。在实际工程中，如果出现暂态扰动或者数据异常，很容易导致所提方法出现误触发的问题。为增强本文所提方法的鲁棒性与实用性，参考微机保护原理的相关设计[20]，对基于电压波形拟合的换相失败预测模型进行完善。以两个采样点为窗长计算换相面积，设k的初始值为0，当满足Sneed(k)-Smin(k)＞0，k逐次加1递进，连续5次换相面积满足Sneed(k)-Smin(k)＞0时，即k≥5，换相失败预测信号（Commutation Failure Prediction Signal, CFPS）输出为1；当差值小于等于0时，判断逆变器不会发生换相失败，k归0，同时换相失败预测信号CFPS输出为0。具体的控制结构如图5所示。
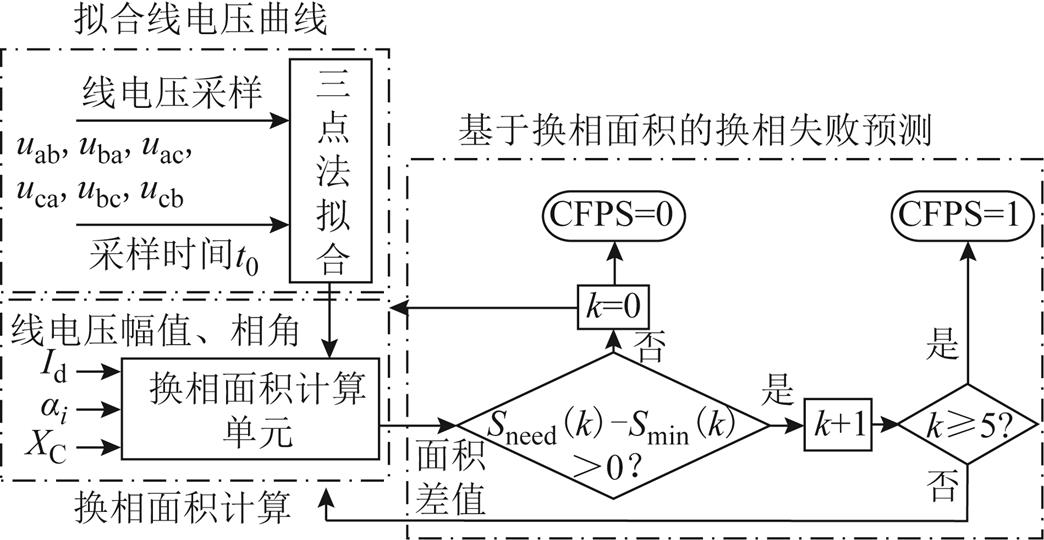
图5 控制结构框图
Fig.5 Control block diagram
以往的换相失败预测控制是以不对称接地故障的零序电压和三相对称故障的ab电压值作为换相失败的判断标准。不同故障类型的换相失败判断标准就不相同，而相同故障类型的故障电压受故障时间和故障距离的影响，也无法完全统一。这导致现有的换相失败预测控制存在不足，主要体现在其预测判据过度依赖仿真，缺乏理论层面的定量分析，同时该控制对触发延迟角的减小很可能超调，导致无功消耗增大，不利于对换相失败的抑制[15-16]。
然而本文所提的方法不受故障类型、故障时间以及故障距离等因素的影响，使得换相失败的判断标准达到统一。因此在本文所提基于电压波形拟合的换相失败快速预测方法的理论基础上，在不同故障类型和程度下，借助换相成功时的临界换相面积，实时采样计算得出相应的触发延迟角，实现提前触发，从而抑制换相失败的发生。
由上述分析可知，若换相失败不发生，即Sneed≤Smin，γmin一般取7°~10°，本文取γmin=7°。当Sneed=Smin时可以求得满足换相成功条件的逆变侧最大触发延迟角αimax。
由图3可得
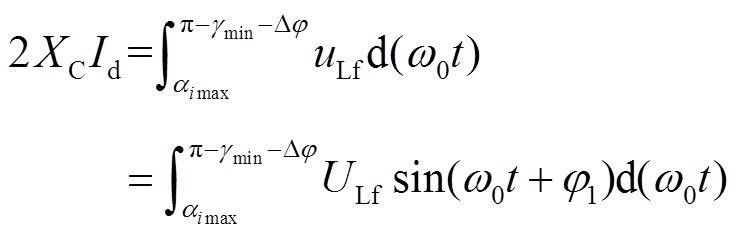（19）求得逆变侧最大触发延迟角αimax为
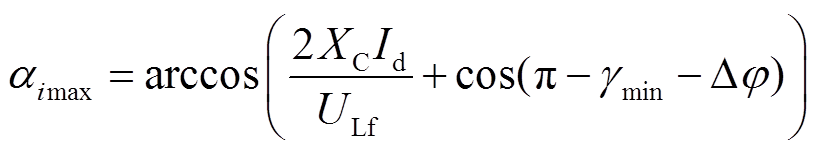（20）
式中，ULf和Δφ由三点法拟合曲线求得。
由式（20）可知，故障后逆变侧触发延迟角可以通过换相面积量化，不再依靠经验值给出，具有较强的普适性，可以满足不同运行和故障条件下对触发延迟角的动态调节需求。
换相失败快速抑制方法控制模块通过换相失败预测模块输出的换相失败预测信号（CFPS）触发，最后与原控制系统定关断角控制和定电流控制等输出的触发延迟角比较，取它们的最小值作为逆变侧最终的触发延迟角。该抑制措施的控制结构如图6所示。
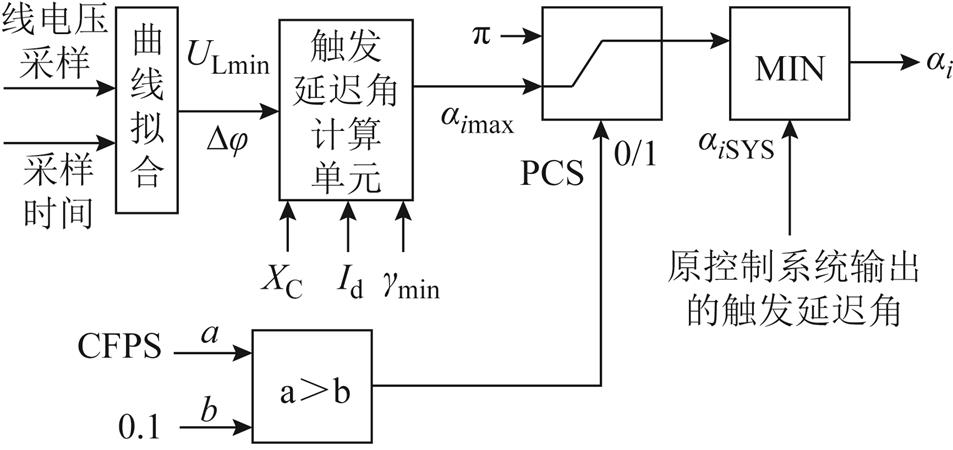
图6 基于换相面积的触发角控制框图
Fig.6 Trigger angle control block diagram based on commutation area
当直流系统正常运行时，换相失败预测模块输出的CFPS始终为0，预测控制信号PCS也始终为零，这时逆变侧的触发延迟角αi为原控制系统输出的触发延迟角αiSYS和π两者中的最小值，由于逆变侧触发延迟角的取值范围为π/2~π，因此，在这种情况下逆变侧的触发延迟角αi一定为αiSYS，确保基于换相面积的换相失败控制策略不会影响直流系统的正常运行。当换相失败预测模块输出的CFPS从0变为1后，预测控制信号PCS为1，逆变侧的触发延迟角αi为原控制系统输出的触发延迟角αiSYS和基于换相面积求得的αimax两者中的最小值。
为了检验本文所提出方法的有效性，在PSCAD/EMTDC中基于CIGRE直流输电标准模型建立测试系统，仿真步长为20ms，实现了所提出的换相失败快速预测与抑制措施。信号采样频率为20kHz，最小关断角γmin选取7°，模型的其他控制参数、故障设置与原标准系统均完全相同。
4.2.1 单相接地故障的换相失败预测
设置5.001s时刻逆变侧交流母线发生A相经Lf=0.88H过渡电阻接地故障，故障持续时间为50ms，其中Sneed-Smin为换相面积计算单元输出的换相面积差值；CFPS为换相失败预测信号，其值从0变为1，预测系统即将发生换相失败；γ为逆变侧实际测得的关断角, 仿真结果如图7所示。
由图7可知，本文换相失败预测算法在直流系统正常运行情况下，Sneed-Smin始终小于0，判断不发生换相失败，并留有一定的裕度，即使存在波动也不会发生误判；发生单相故障时，Sneed-Smin明显增加，而此时直流电流、触发延迟角均未发生变化，故此时换相面积差值增大主要是母线电压骤降和电压换相点偏移导致的。发生换相失败后，Sneed-Smin快速增加，是由直流系统短路导致直流电流骤增引起的。故障后实际电压中的谐波导致换相失败面积差值存在波动，但不影响对换相失败的准确预测。
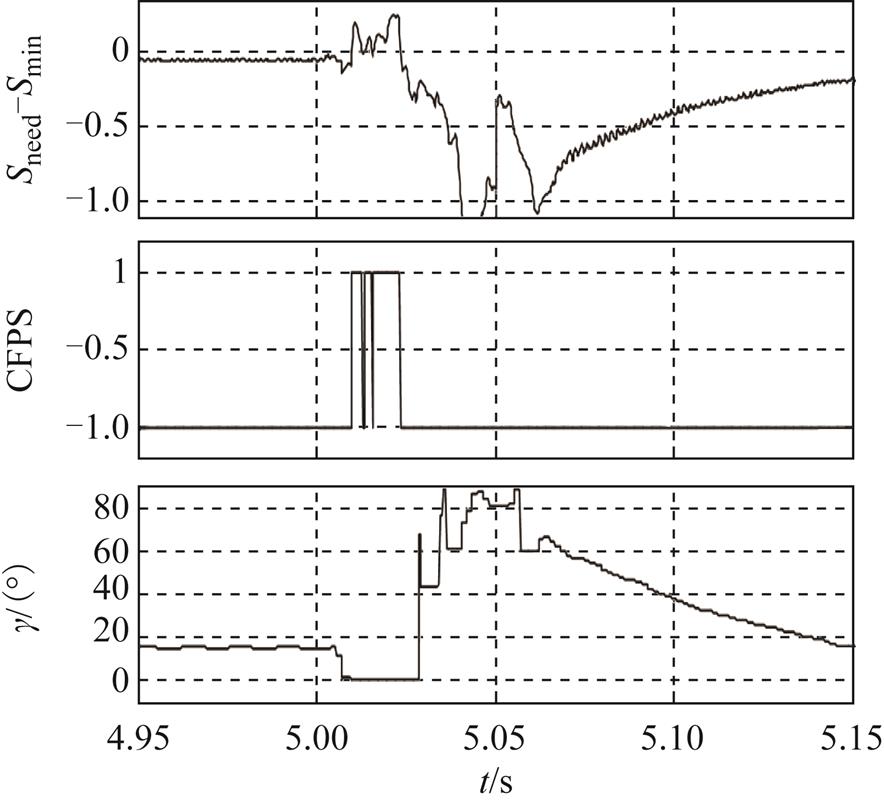
图7 单相接地故障时换相失败预测模块响应波形
Fig.7 Commutation failure prediction module response waveforms in single-phase ground fault
为对本文所提方法性能进行更为全面的测试，设置故障在5~5.009s，间隔0.001s，设置0~0.92H的接地电感，模拟不同时刻不同程度的故障，故障持续时间均为50ms，统计换相失败实际和预测发生的情况，如图8所示。
图8 单相故障条件下换相失败预测与实际情况对比
Fig.8 Comparison of commutation failure prediction and actual situation under single-phase fault conditions
如图8所示，基于换相面积的换相失败预测方法预测结果与实际情况完全一致，能够准确地预测单相故障时换相失败的发生，并且不同故障时刻对换相失败预测效果影响不大。
4.2.2 三相对称接地故障的换相失败预测
在5.001s时刻，仿真直流系统发生临界换相失败，换相失败预测模块响应波形如图9所示。
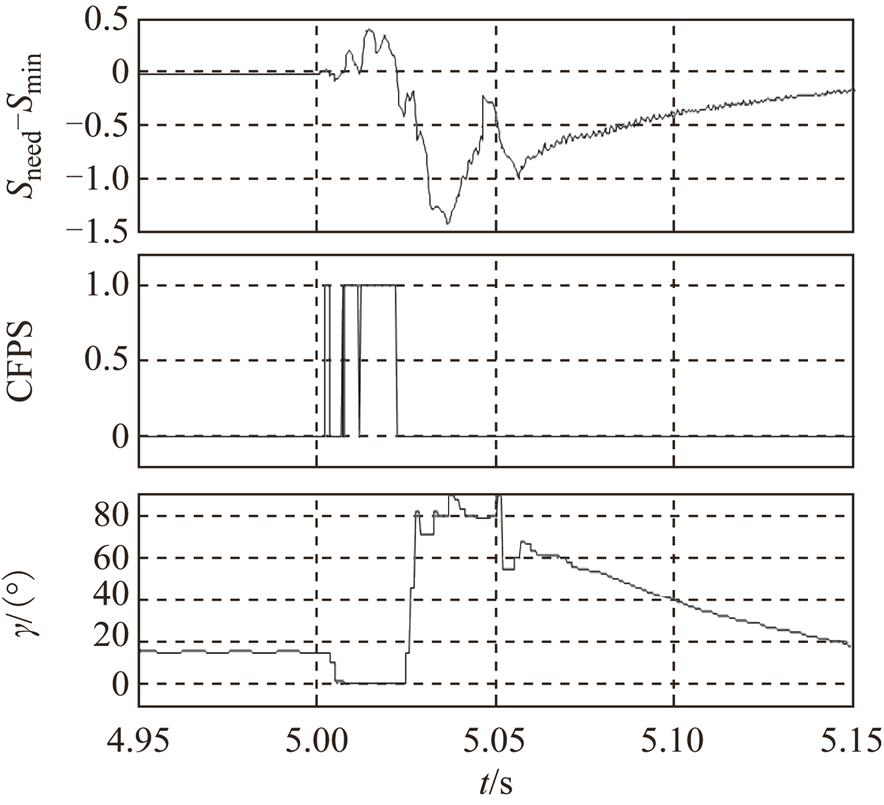
图9 临界换相失败时系统响应波形(Lf=1.18H)
Fig.9 System response waveform when critical commutation fails (Lf=1.18H)
由图9可知，本方法针对三相对称故障所引发的换相失败也能实现快速预测，同时换相面积差值的波动较非对称故障大大减小，判断结果更为可靠。
设置故障在5.000~5.009s，间隔0.001s，模拟不同时刻不同程度的故障，故障持续时间均为50ms，统计换相失败实际和预测发生的情况如图10所示。
图10 三相故障条件下换相失败预测与实际情况对比
Fig.10 Comparison of commutation failure prediction and actual situation under three-phase fault conditions
由图10可知，换相失败预测模块可以在交流系统发生三相故障后快速预测换相失败，为控制系统快速调节抑制换相失败提供了时间。
4.3.1 抑制换相失败效果分析
分别在逆变侧换流母线上设置单相接地故障、相间故障和三相故障，统计不同时刻和不同程度的故障条件下，统计CIGRE标准测试模型和基于临界换相面积的预测控制模型发生换相失败的情况。其中单相接地故障以A相接地故障为例；相间短路故障以B、C两相短路为例。统计结果如图11所示。
图11 不同类型故障下换相失败控制策略抑制结果
Fig.11 Commutation failure control strategy suppression result under different types of fault conditions
由图11可知，在不同类型交流侧故障下，该预测控制模型降低了临界换相失败的接地电感值，说明基于换相面积的触发角控制策略可有效抑制换相失败的发生。由数据看出，单相故障时临界电感值最高减小0.2H，三相故障时减小0.12H，相间故障时减小0.8H，系统抵御换相失败的性能有了明显提升。
4.3.2 基于换相失败免疫因子（CFII）的换相失败抵御能力评价指标
为更加直观地观察系统抵御换相失败的能力，引入换相失败免疫因子（Commutation Failure Immunity Index，CFII）[7]，将其作为系统抵御换相失败能力的评价指标。CFII的计算公式为
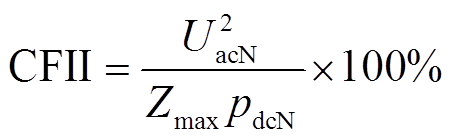（21） 式中，UacN为逆变侧换流母线额定电压值；Zmax为换相失败临界阻抗；pdcN为直流线路额定功率。CFII值越大说明故障临界阻抗越小，引起换相失败的故障越严重，系统抵御换相失败的能力越强。由图11提供的换相失败临界电感可计算出不同故障类型、不同故障时刻的换相失败免疫因子CFII，如图12所示。
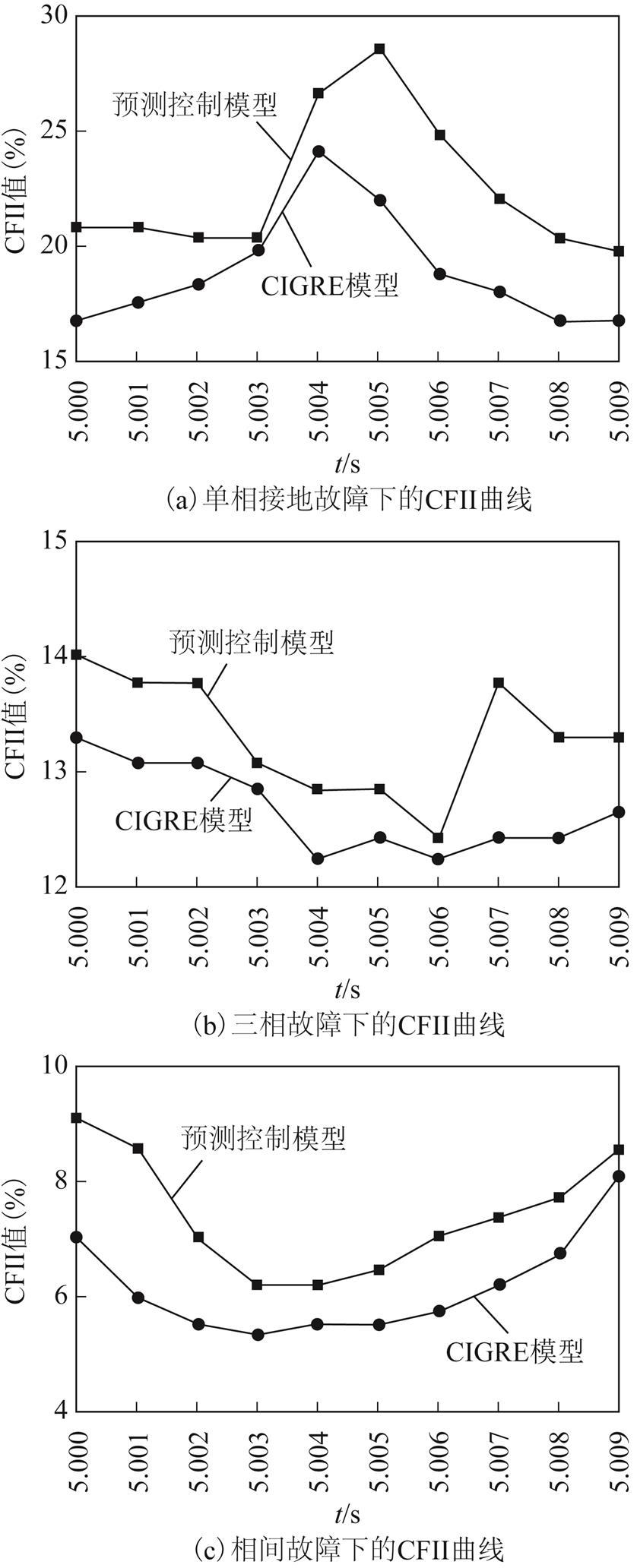
图12 不同故障类型下的CFII曲线
Fig.12 CFII curves under different fault types
可以看出，交流系统发生不同类型故障时，基于换相失败面积的量化触发角控制模型抵御换相失败的能力均高于CIGRE标准模型，尤其在单相接地和相间故障下，系统对换相失败的抵御能力有明显提升；三相故障下，抵御能力提升相对较小，是因为三相故障一般较严重，交流母线电压下降剧烈，不利于换相失败的抑制。
此外，本文所提方法的验证均是在数字仿真环境下进行的，因此其仿真步长对测试结果有一定的影响，故在附录中予以解释说明。
本文从换相失败机理层面——换相电压-时间面积出发，提出了一种基于电压波拟合的换相失败快速预测方法，并在此基础上延伸出了一种基于临界换相面积的量化触发角控制策略。通过理论分析和大量仿真验证，获得如下结论：
1）换相失败机理层面的原因是可供应最小换相面积小于换相需求面积，两者之间的关系可用来作为换相失败的检测判据，且物理意义清晰。
2）利用三点法快速拟合故障后的电压波形，可以完成换相失败的快速预测，且该预测不受故障类型、故障时间以及故障位置等因素的影响，且启动判据不依赖仿真，具有明晰的物理意义，保证预测的可靠性。
3）基于临界换相面积的量化触发角控制策略，可以实现更为精准的提前触发，不但能降低换相失败的发生风险，还能避免过度超前触发所引起的连续换相失败，从而有利于系统的故障恢复。
附录 仿真系统步长参数说明
本文所提方法在数字仿真的测试环境下对仿真的步长有一定的要求。为完善验证分析，分别对10 ms、20ms、30 ms、40ms、50ms、60ms、70ms和80ms的仿真步长进行测试，观察单相接地故障下的CFII平均值的变化趋势，见附表1。
通过上述仿真分析可以得出以下三个结论：
1）当仿真步长从20ms缩短至10ms时，本文方法在10kHz采样频率下的效果并未发生变化，其原因是其采样频率较低，对仿真步长变小的感知不明显。而在15kHz和20kHz下，本方法在个别故障发生时刻与换相时刻临近点的换相失败免疫能力有所下降，其原因是仿真步长的缩短导致其暂态信息更加丰富，因此换相失败判别时间可能增大，且故障时刻与换相时刻太近，从而错过最佳提前触发机会。但总体来说，仿真步长的缩短对本方法在个别故障时刻有轻微的影响，但总体影响不大。
附表1 不同仿真步长下的单相故障CFII值
App.Tab.1 CFII values under single-phase fault in different simulation step size
仿真步长/msCFII（%） 10kHz15kHz20kHz 1021.0522.1023.32 2021.0522.1323.39 3021.3022.4623.39 4021.4822.6323.39 5021.0122.2323.17 6020.5921.6722.26 7020.2621.0221.54 8020.0120.5620.75
2）当仿真步长从20ms增大到40ms时，在10kHz和15kHz下本文所提方法的效果有轻微提升，其原因主要是随着仿真步长的增大，其暂态信息确实存在一定程度的遮蔽现象。暂态干扰减小，使控制的动作更加迅速，因此在个别故障时刻的免疫能力有轻微的增强。
3）当仿真步长从40ms增大到80ms时，其暂态信息遮蔽现象较为严重，随着仿真步长的增大，三种采样频率下，其换相失败免疫能力均有所降低，同时三者之间换相失败免疫能力的差距也在不断缩短，其原因是较大的仿真步长导致高采样频率的优势丧失。
综上所述，在数字仿真的场景下，仿真步长确实对方法的效果有一定的影响。在保持高采样频率和较短仿真步长的情况下，本方法能提高直流系统的换相失败免疫能力。
参考文献
[1] 浙江大学发电教研组直流输电科研组. 直流输电[M]. 北京: 水利电力出版社, 1985: 6-16.
[2] 刘振亚, 张启平, 董存, 等. 通过特高压直流实现大型能源基地风、光、火力大规模高效率安全外送研究[J]. 中国电机工程学报, 2014, 34(16): 2513-2522. Liu Zhenya, Zhang Qiping, Dong Cun, et al. Efficient and security transmission of wind, photovoltaic and thermal power of large-scale energy resource bases through UHVDC projects[J]. Proceedings of the CSEE, 2014, 34(16): 2513-2522.
[3] 王玲, 文俊, 司瑞华, 等. UHVDC分级分层接入方式及其运行特性[J]. 电工技术学报, 2018, 33(4): 730-738. Wang Lin, Wen Jun, Si Ruihua, et al. The connection mode and operation characteristics of UHVDC with hierarchical connection by pole[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 730-738.
[4] 汤广福, 庞辉, 贺之渊. 先进交直流输电技术在中国的发展与应用[J]. 中国电机工程学报, 2016, 36(7): 1760-1771. Tang Guangfu, Pang Hui, He Zhiyuan. R&D and application of advanced power transmission technology in China[J]. Poceedings of the CSEE, 2016, 36(7): 1760-1771.
[5] 程佩芬, 李崇涛, 傅闯, 等. 基于状态空间法的高压直流输电系统电磁暂态简化模型的解析算法[J]. 电工技术学报, 2019, 34(6): 1230-1239. Cheng Peifen, Li Chongtao, Fu Chuang, et al. An analytic solution for simplified electromagnetic transient model of HVDC transmission system based on state space method[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1230-1239.
[6] 杨之翰, 李梦柏, 向往, 等. 基于无闭锁直流自耦变压器的LCC-HVDC与VSC-HVDC互联系统[J]. 电工技术学报, 2018, 33(2): 499-510. Yang Zhihan, Li Mengbo, Xiang Wang, et al. Research on the interconnection system of VSC-HVDC and LCC-HVDC based on un-interrupted DC-DC autotransformer[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 499-510.
[7] 曹文远, 韩民晓, 谢文强, 等. 交直流配电网逆变器并联控制技术研究现状分析[J]. 电工技术学报, 2019, 34(20): 4226-4241. Cao Wenyuan, Han Minxiao, Xie Wenqiang, et al. Analysis on research status of parallel inverters control technologies for AC/DC distribution network[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4226-4241.
[8] 王增平, 刘席洋, 李林泽, 等. 多馈入直流输电系统换相失败边界条件[J]. 电工技术学报, 2017, 32(10): 12-19. Wang Zengping, Liu Xiyang, Li Linze, et al. The research on boundary conditions of commutation failure in multi-infeed HVDC systems[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 12-19.
[9] Xue Ying, Zhang Xiaoping, Yang Conghuan. Elimination of commutation failures of LCC HVDC system with controllable capacitors[J]. IEEE Transactions on Power Systems, 2015, 31(4): 3289-3299.
[10] Guo Chunyi, Li Chunhua, Zhao Chengyong, et al. An evolutional line-commutated converter integrated with thyristor-based full-bridge module to mitigate the commutation failure[J]. IEEE Transactions on Electronics, 2016, 32(2): 967-976.
[11] 李楠, 张亚琼, 郭虎锋, 等. HCM3000中预测性熄弧角控制算法的实现[J]. 电力系统保护与控制, 2015, 43(17): 119-124. Li Nan, Zhang Yaqiong, Guo Hufeng, et al. Design of predictive extinction angle control algorithm used in HCM3000[J]. Power System Protection and Control, 2015, 43(17): 119-124.
[12] 赵畹君. 高压直流输电工程技术[M]. 北京: 中国电力出版社, 2004: 124-126.
[13] 陈树勇, 李新年, 余军, 等. 基于正余弦分量检测的高压直流换相失败预防方法[J]. 中国电机工程学报, 2005, 25(14): 1-6. Chen Shuyong, Li Xinnian, Yu Jun. A method based on the sin-cos components detection mitigates commutation failure in HVDC[J]. Proceedings of the CSEE, 2005, 25(14): 1-6.
[14] 王玉, 侯玉强, 刘福锁, 等. 考虑多直流协调恢复的换相失败预测控制启动值优化方法[J]. 电力系统自动化, 2018, 22(44): 85-90. Wang Yu, Hou Yuqiang, Liu Fusuo, et al. Optimization method for startup threshold of commutation failure prediction control considering coordinated recovery of multi-infeed HVDC systems[J]. Automation of Electric Power Systems, 2018, 22(44): 85-90.
[15] Bauman J, Kazerani M. Commutation failure reduction in HVDC systems using adaptive fuzzy logic controller[J]. IEEE Transactions on Power Systems, 2007, 22(4): 1995-2002.
[16] Sun Yuanzhang, Peng Ling, Ma Feng, et al. Design a fuzzy controller to minimize the effect of HVDC commutation failure on power system[J]. IEEE Transactions on Power Systems, 2008, 23(1): 100-107.
[17] 李新年, 陈树勇, 庞广恒, 等. 华东多直流馈入系统换相失败预防和自动恢复能力的优化[J]. 电力系统自动化, 2015, 39(6): 134-140. Li Xinnian, Chen Shuyong, Pang Guangheng, et al. Optimization of commutation failure prevention and automatic recovery for east china multi-infeed high voltage direct current system[J]. Automation of Electric Power Systems, 2015, 39(6): 134-140.
[18] 袁阳, 卫志农, 王华伟, 等. 基于直流电流预测控制的换相失败预防方法[J]. 电网技术, 2014, 38(3): 565-570. Yuan Yang, Wei Zhinong, Wang Huawei, et al. A DC Current predictive control based method to decrease probability of commutation failure[J]. Power System Technology, 2014, 38(3): 565-570.
[19] IEEE Standards Board. IEEE standard of digitizing waveform recorders[S]. New York, IEEE, 1994.
[20] 杨奇逊, 黄少锋. 微型机继电保护基础[M]. 3版. 北京: 中国电力出版社, 2007.
The Research on Fast Prediction and Suppression Measures of Commutation Failure Based on Voltage Waveform Fitting
Abstract In order to reduce the probability of commutation failure of HVDC transmission system, a commutation failure fast prediction and suppression measure based on voltage waveform fitting is proposed. Firstly, based on the theory of commutation voltage-time area, the mathematical analysis of the commutation demand area and the minimum supplied area can be derived and used as the commutation failure prediction criterion. The voltage waveform before and after the fault is fitted by the three-point method, therefore realizing real-time quantitative analysis of the proposed commutation failure prediction method. Then, an advanced firing control strategy based on the critical commutation area is proposed, and the angle of the advanced firing can be adjusted according to the dynamic change of the critical commutation area. Finally, the simulation results based on the CIGRE standard test model show that the proposed method can not only achieve fast prediction of commutation failure, but also suppress the occurrence of commutation failure to some extent and improve the system's fault recovery performance.
keywords：HVDC transmission, commutation failure, commutation area, curve fitting, advanced firing
DOI:10.19595/j.cnki.1000-6753.tces.190759
中图分类号：TM721.1
王增平 男，1964年生，教授，博士生导师，研究方向为继电保护、变电站综合自动化、系统安全保护等。E-mail：wangzp1103@sina.com
刘席洋 男，1991年生，博士研究生，研究方向为换相失败、交直流系统交互机理等。E-mail：ncepulxy@126.com（通信000作者）
国家重点研发计划智能电网技术与装备重点专项（2016YFB0900604）、国家自然基金重点项目（51637005）和国家电网公司科技项目（52094017000W）资助。
收稿日期 2019-06-25
改稿日期2019-12-06
（编辑 赫蕾）