 N)获取M ×1维观测数据向量y。由于系统发生扰动后,整个系统都会受到扰动带来的影响,离扰动点越近,系统受到的影响也就越大[13-14],因此各个PMU节点所观测到的电气量变化程度也有所不同,因此向量y中隐含扰动源的位置信息。
N)获取M ×1维观测数据向量y。由于系统发生扰动后,整个系统都会受到扰动带来的影响,离扰动点越近,系统受到的影响也就越大[13-14],因此各个PMU节点所观测到的电气量变化程度也有所不同,因此向量y中隐含扰动源的位置信息。摘要 电力系统扰动发生后,迅速准确地进行扰动源的定位是实施及时有效的电力系统安全稳定控制措施的重要前提。由于扰动不会大范围同时出现,因此扰动源在空间分布上具有稀疏特性,如何利用系统中配置的数量有限的同步相量测量装置感知电力系统中的扰动是一个重要的研究课题。提出一种基于过完备字典设计的电力系统扰动定位方法,其创新之处在于根据扰动后系统拓扑结构或电气参数的变化构造过完备字典,结合压缩感知重构算法从低维同步相量测量装置的观测数据中恢复出具有稀疏特性的高维扰动定位数据,完成电力系统扰动的定位。以切机与切负荷扰动为例,大量仿真结果表明,该方法能以很高的准确率完成扰动源位置的定位,对其他类型扰动定位也有重要的借鉴意义。
关键词:扰动定位 过完备重构字典 稀疏特性 切机 切负荷
电力系统扰动发生后,为防止扰动扩大对系统造成的负面影响,需及时、准确地定位扰动源的位置,这对实施紧急控制、维护电力系统的正常运行至关重要。文献[1-2]试图通过扰动后潮流分布模式来识别断线支路,由于数据采集与监视控制系统(Supervisory Control And Data Acquisition, SCADA)观测的扰动数据不同步,因此带来了不小的误差。同步相量测量装置(Phasor Measurement Unit, PMU)作为广域检测系统的核心,利用全球定位系统(Global Position System, GPS),以统一的时标测量包含相角的相量数据,在很大程度上克服了数据不同步的问题[3-4]。在电力系统所有节点配置PMU可对系统进行整体的实时观测,但预算费用高,而且也没有必要。压缩感知技术[5-6]的出现可实现以少量PMU测量数据观测整个电力系统运行状态的目的。文献[7]分析了不同类型扰动的原理并实现了扰动定位,相比以压缩感知进行计算而言,步骤复杂且计算量庞大,定位准确度受误差影响较大。文献[8]以配电网故障区段定位技术为基础,针对现有矩阵算法容错性差、优化算法定位速度慢的问题,提出一种矩阵算法和优化算法相结合的配电网故障定位方法。文献[9]通过收集扰动前后节点电压与节点注入电流间的变化量并建立两者之间的联系,对短路扰动进行定位。文献[10]通过对行波自然频率的分析进行输电线路短路扰动的定位。文献[11]通过压缩感知重构算法结合电力系统潮流计算对无故障跳闸扰动进行了分析与定位。文献[12]利用外加扰动信号追踪的方式,建立了小电流接地系统等值电路,根据扰动信号注入不同非故障相后单相接地故障电流的变化规律后进行扰动定位。
本文利用压缩感知理论,将不同类扰动的定位体现为系统节点中扰动节点稀疏向量的重构,将扰动后系统拓扑结构及系统参数的变化体现为过完备字典的设计。以切机与切负荷扰动为例,通过PMU收集扰动发生前后支路正序电流、支路有功功率等向量作为压缩感知算法中的观测数据,对切机、切负荷扰动进行定位,并计算出切负荷扰动的切除容量。同时为验证本文扰动定位方法的抗噪能力,进行对比实验,在包含测量误差的PMU观测数据中添加信噪比为30dB的高斯白噪声,通过仿真及数据说明本文方法的有效性及抗噪能力。
电力系统中扰动不会大范围同时出现,因此扰动源在空间分布上具有稀疏特性。由于系统中可利用的PMU测量装置有限,因此本文要解决的主要问题是如何利用少数测量点的数据定位各种扰动,其本质上是从低维观测数据中恢复出具有稀疏特性的高维数据的过程,这也是压缩感知重构算法理论研究的主要范畴。电力系统扰动源在空间上分布的稀疏特性说明,表征各类扰动位置的向量是稀疏的,故可采用压缩感知重构算法进行扰动源的定位。
设系统中PMU观测数据为y∈RM×1,表征扰动源位置的稀疏向量为s∈RN×1,N为扰动定位稀疏向量的维度,亦即系统节点数。对扰动定位稀疏向量s进行压缩感知算法重构流程如下。
1)扰动特征收集及处理。根据压缩感知重构算法的相关描述,在N个节点的电力系统中,首先需要通过在M个节点处配置PMU设备(M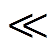 N)获取M ×1维观测数据向量y。由于系统发生扰动后,整个系统都会受到扰动带来的影响,离扰动点越近,系统受到的影响也就越大[13-14],因此各个PMU节点所观测到的电气量变化程度也有所不同,因此向量y中隐含扰动源的位置信息。
N)获取M ×1维观测数据向量y。由于系统发生扰动后,整个系统都会受到扰动带来的影响,离扰动点越近,系统受到的影响也就越大[13-14],因此各个PMU节点所观测到的电气量变化程度也有所不同,因此向量y中隐含扰动源的位置信息。
2)构建过完备重构字典。由于多数母线节点处观测数据的缺失,仅获取到M个PMU节点的观测数据并不能达到扰动定位的目的。为了从低维观测数据中恢复出具有稀疏特性的高维原始信号,需要进行过完备扰动传感矩阵,即M×N维过完备字典Λ的设计。电力系统扰动发生后,系统拓扑结构及系统线路参数将发生变化,可从该角度出发建立起低维PMU观测向量y与高维扰动源稀疏向量s间的联系,即
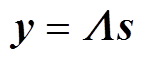 (1)
(1)式中,y为PMU观测向量;Λ为扰动过完备字典;s为扰动源稀疏向量。
3)稀疏重构算法。压缩感知算法中向量重构的核心问题是利用过完备字典Λ中的原子对接收到的PMU观测向量y进行匹配。y为M×1维向量,有M个原子;Λ中有N个M×1维向量,即
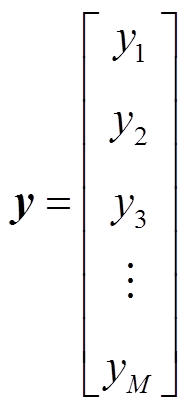
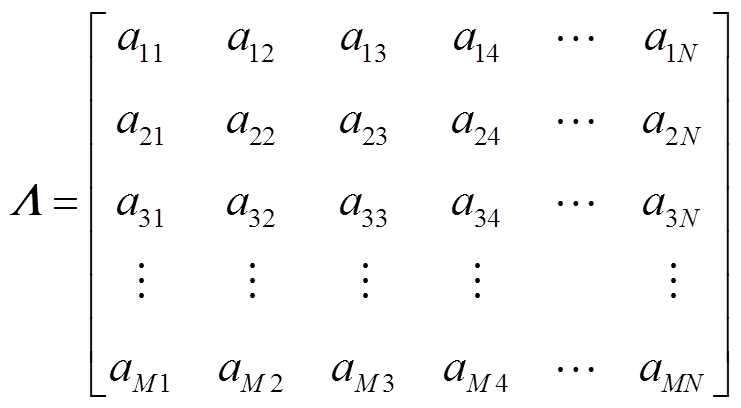 (2)
(2)式中,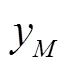 为y中第M个原子;
为y中第M个原子;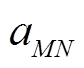 为Λ中第N个向量的第M个原子。匹配跟踪(Matching Pursuit, MP)类算法利用两向量的内积γ表征原子的相似度,即
为Λ中第N个向量的第M个原子。匹配跟踪(Matching Pursuit, MP)类算法利用两向量的内积γ表征原子的相似度,即
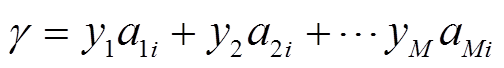 (3)
(3)
匹配跟踪本质是计算观测向量y与过完备字典Λ中每列向量及夹角余弦值的乘积,其中i=1,2,…,N,余弦值越大则两个向量在空间上构成的夹角越小,向量相似度越高。在压缩感知重构算法中,观测向量y需与Λ中的所有列作内积运算,算出Λ中与y内积最大的K列,K为向量的稀疏值。这些列的编号即为稀疏向量s中稀疏值所在的编号。由PMU观测向量y及过完备字典Λ重构出原始向量s,利用重构算法求解最优问题,即
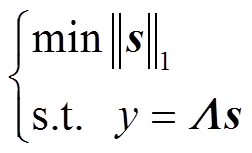 (4)
(4) 式中,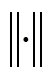 表示信号的范数。基于过完备字典设计的电力系统扰动定位方法原理如图1所示。
表示信号的范数。基于过完备字典设计的电力系统扰动定位方法原理如图1所示。
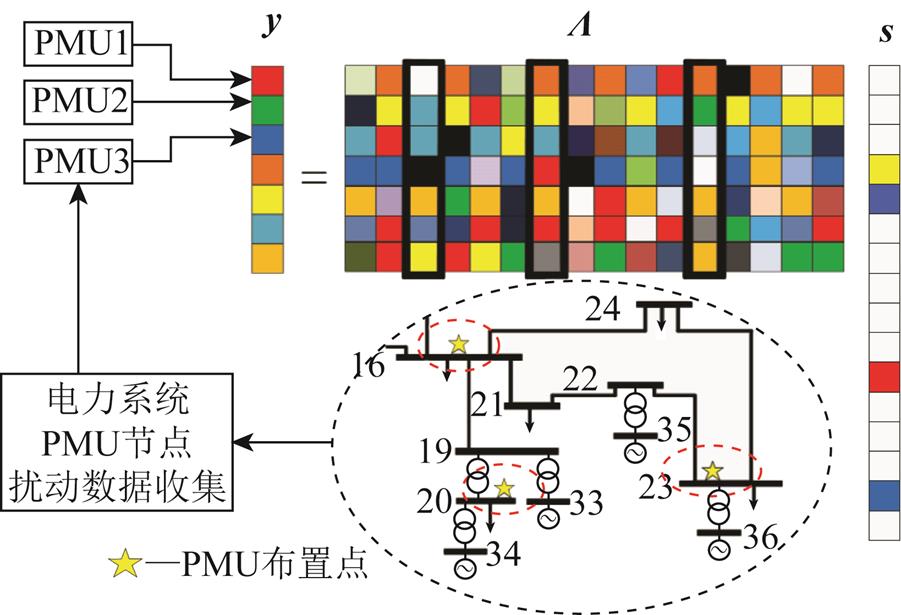
图1 扰动向量重构算法原理
Fig.1 Principle of disturbance vector reconstruction algorithm
通过压缩感知重构算法,可恢复出表征系统中扰动源位置的稀疏向量,稀疏值所对应的节点编号即为扰动源的位置。本文收集电力系统扰动前后PMU配置节点的观测数据并预处理得到y,根据预先设计的过完备扰动字典使用压缩感知重构算法对表征扰动位置的稀疏信号进行重构,达到扰动定位的目的,扰动定位流程如图2所示。该流程中的核心部分为电力系统扰动的过完备字典设计,本文方法依据扰动发生后系统拓扑结构及系统线路参数的变化构造出的电力系统扰动定位的过完备字典,具体构造方法将在下文中具体阐述。
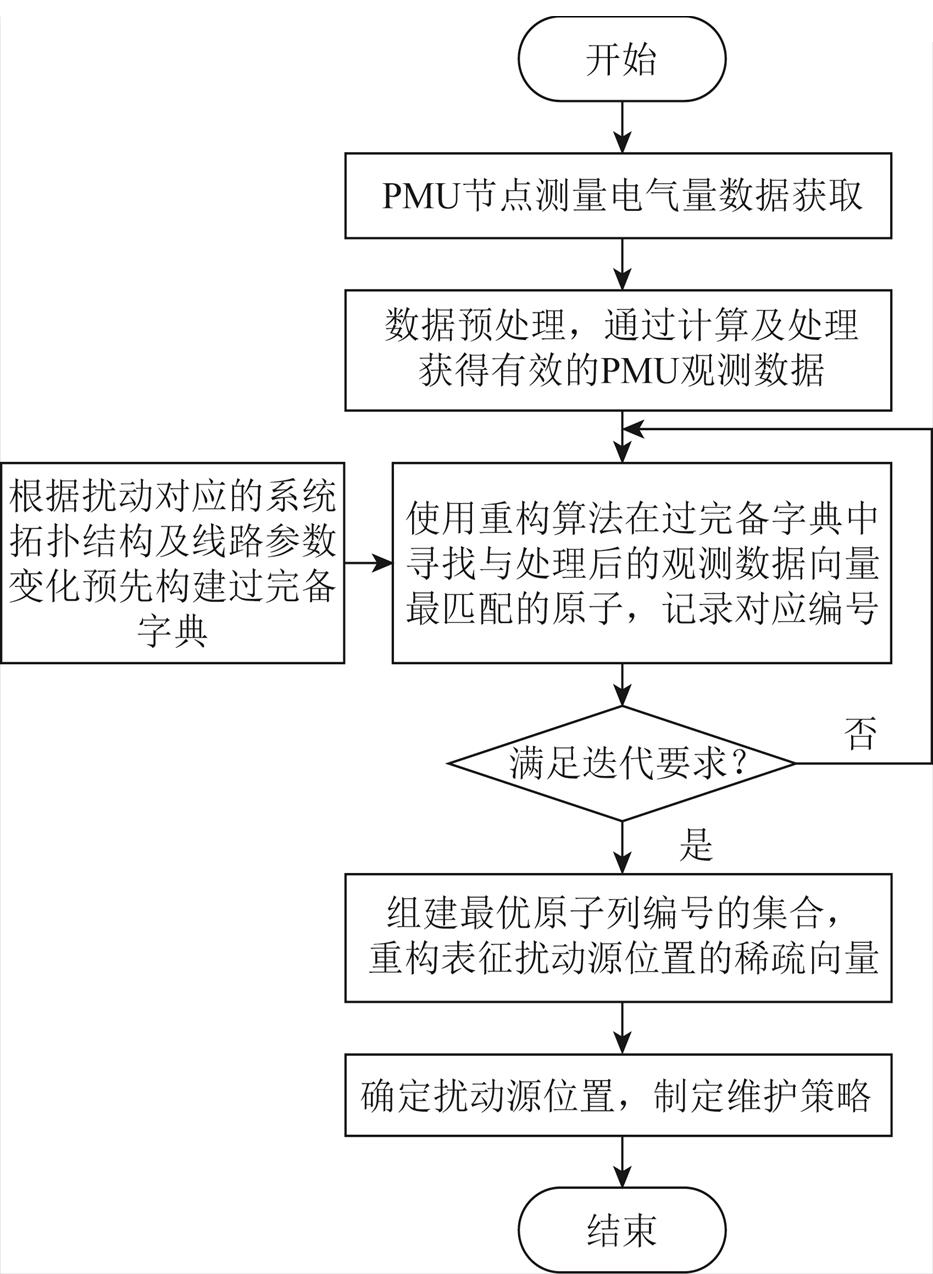
图2 扰动定位流程
Fig.2 Flow chart of disturbance location
PMU作为一种电力系统测量装置,通过利用全球定位系统GPS提供的时标来实现数据的相量量测。相对于SCADA系统,PMU能够获得安装节点处的电压相量和与之相连的所有支路的电流相量,且相对于传统量测的支路功率和电压幅值,PMU具有较高的量测频率和精度。
一般来说,可以假设PMU配置满足以下四个条件:①配置了PMU的母线,其电压及连接到该母线的所有支路的电流均能被测量;②若线路的一侧母线电压及线路电流已知,则另一侧的节点电压能通过欧姆定理计算得知;③若线路两侧母线电压已知,则该线路电流能通过欧姆定理计算得到;④除一条线路外,若其他与某节点相连的所有线路的电流已知,则该线路上的电流可以利用基尔霍夫电流定理计算得到。
由以上四点可知,系统中PMU配置越多、配置位置越合适,通过计算后对系统运行的实时参数检测的效果就越好、对系统感知的范围就越大。然而由于PMU设备昂贵,一次性在系统的所有节点均配置PMU并不现实,因此应尽量利用最少的PMU对系统进行最大范围的扰动识别与定位。在本文切机与切负荷扰动定位中,PMU观测数据y为支路正序电流与功率,因此若PMU数量有限,在上述四个条件应用背景下仍不能对系统进行全局观测时,应尽量将有限的PMU设备配置在连接支路较多的母线处。观测到的支路数据量越多,扰动定位的准确率也就越高。
电力系统扰动发生后,系统拓扑结构及线路参数将发生变化,不同类型的扰动对系统造成的拓扑结构及参数的变化一般不同。扰动过完备字典设计思路如下:若要从PMU观测向量y中重构出表征扰动源位置的稀疏向量s,所设计的过完备字典须包含以下某一个或几个部分:①系统拓扑结构信息;②发电机、负荷、线路等设施的电气参数;③扰动对系统的影响信息。本文根据以上三点原则设计出扰动识别过完备字典,以切机与切负荷扰动为例,设计方法如下。
发电机切机时突然从电网中退出,与系统之间没有能量交换,输出电磁功率为0,若负荷不变,会导致系统电压与频率的降低。所以当切机扰动发生时,可以选取电网的电压、频率变化作为扰动特征。本文使用节点电压作为表征切机扰动位置的稀疏向量。节点电压方程为
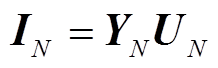 (5)
(5)式中,IN为节点注入电流;UN为节点注入电压;YN为系统的节点导纳矩阵,且
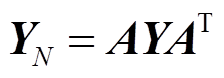 (6)
(6)
式中,A为系统的节点关联矩阵;Y为系统的支路导纳矩阵;AT为节点关联矩阵的转置,则支路导纳矩阵为
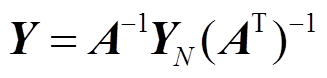 (7)
(7)建立支路电流与节点电压之间的关系为[15-16]
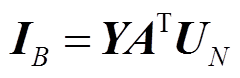 (8)
(8)
式中,IB为支路电流。由于任何状态下支路电流的正序分量均存在,故使用支路电流正序分量作为收集的扰动数据,三相各相量与三组序分量的关系为
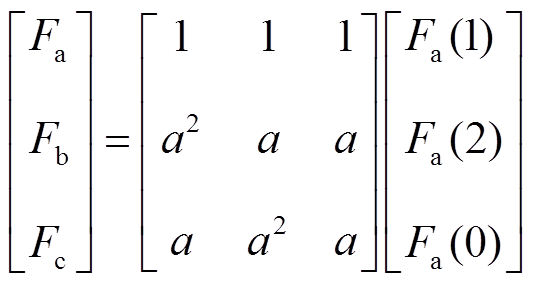 (9)
(9)式中,Fa、Fb、Fc分别代表a、b、c相的相量数据;Fa(1)为a相正序分量;Fa(2)为a相负序分量;Fa(0)为a相零序分量;a为旋转因子,a=1∠120°。式(9)通过变换可得
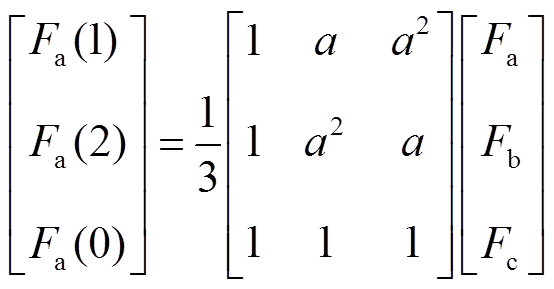 (10)
(10)
同时为了简化计算、降低收集到的电流向量相角引入的误差,本文对收集到的正序支路电流作绝对值运算。仿真结果显示,取绝对值后对扰动的定位结果没有影响,只是重构的幅值大小不再代表发电机节点在切机扰动后的电压变化量,则切机扰动的压缩感知数学模型为
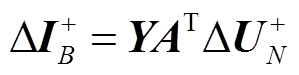 (11)
(11)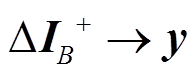
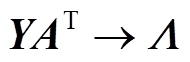
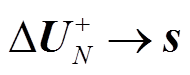
式中,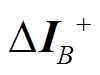 为收集到的正序支路电流作绝对值处理后的向量;
为收集到的正序支路电流作绝对值处理后的向量;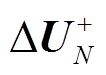 为正序节点电压的重构值。对于一个N节点L条支路的电力系统而言,A为N×L阶。通过大量数据重构效果的对比,压缩感知重构算法中取迭代次数t=2最为合适,迭代次数即稀疏向量的稀疏度。
为正序节点电压的重构值。对于一个N节点L条支路的电力系统而言,A为N×L阶。通过大量数据重构效果的对比,压缩感知重构算法中取迭代次数t=2最为合适,迭代次数即稀疏向量的稀疏度。
突然变化的负荷将打破电网中有功与无功间的平衡。在切负荷扰动发生后,经过各发电机组的调节,负荷将在机组间重新分配,此过程将导致系统中各节点的频率波动,而有功的输送需要无功的支撑,同时也导致了电压的波动。以系统中某负荷节点突然切负荷(-ΔP)为例,由于-ΔP的作用,打破了系统原有的功率平衡。系统中电源机组将按照各自的同步功率系数来分担负荷增量-ΔP。由于负荷减少、原动机功率不变,转子储存的动能增加,以维持系统的能量均衡。转子动能增加使机组转速上升,频率会相应升高。此外,切负荷扰动所引起的节点频率变化还与系统容量有关,系统电源运行容量越大,相对于系统发电容量的负荷变化越小,频率偏差也越小。系统静态频率特性为
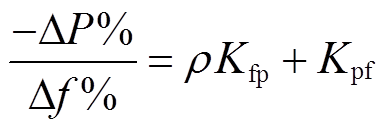 (12)
(12)式中,ΔP为相对于系统发电容量的负荷变化;Δf为相对于节点正常频率的频率偏差;ρ为备用容量系数,等于系统发电容量与总负荷之比;Kfp为系统发电机原动机调速系统频率静态特性的平均斜率;Kpf为负荷的静态频率特性调节系数。由式(12)可知,系统电源运行容量越大,相对于系统发电容量的负荷变化越小,因此频率偏差Δf也就越小。本文使用各节点频率变化量作为表征切负荷扰动位置的稀疏变量,借鉴负荷功率方程进行切负荷压缩感知过完备字典的构造。
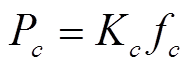 (13)
(13)
式中,Pc为节点c处负荷吸收的有功功率;Kc为节点c处的负荷静态频率特性调节系数;fc为节点c处的频率。设在一个有i个母线节点的电力系统中,有j个负荷母线节点。由于PMU可以检测母线及与母线相连传输线的各运行参数,通过借鉴负荷功率方程构造切负荷时切负荷压缩感知重构方程为
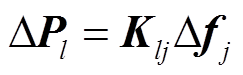 (14)
(14)式中,ΔPl为所有PMU可检测到的l条支路发生切负荷扰动前后的功率变化量;Klj为构造的l×j维过完备字典,其第α行(α =1,2, ,l)的内容为j个负荷分别发生切负荷扰动时第α条传输线上有功功率与负荷节点频率变化量进行单位化处理后的变量;Δfj为j个负荷节点处的频率变化量。
,l)的内容为j个负荷分别发生切负荷扰动时第α条传输线上有功功率与负荷节点频率变化量进行单位化处理后的变量;Δfj为j个负荷节点处的频率变化量。
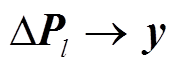
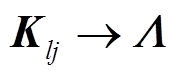
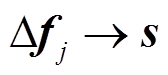
其中最为重要的就是切负荷扰动时在压缩感知重构算法中过完备字典的构造,切负荷过完备字典构造流程如下:
1)在共i条母线的系统中,将连接了负荷的j条母线作为处理对象,逐条进行切负荷处理,测量每次切负荷前后该条母线处的频率变化量Δfb(b=1,2,…, j)。
2)逐条记录第b条负荷母线切负荷时所有PMU可测共l条支路的有功功率变化量ΔPlb,并作单位化处理:ΔPlb/Δfb。
3)根据步骤1)、步骤2)构造出l×j维的切负荷过完备字典Klj。其行代表切负荷前后PMU所有可测支路的有功功率变化量,列代表所有负荷节点切负荷前后频率变化量。
4)设计切负荷过完备字典Klj。若电网拓扑结构不变,Klj可离线求解。在实际应用中,收集l条支路发生切负荷扰动前后的功率变化量ΔPl作为压缩感知重构算法中的观测量y,切负荷过完备字典Klj作为过完备字典,重构结果中,横轴代表含负荷的母线编号,纵轴代表切负荷前后频率变化的幅值。通过重构频率幅值与原始频率Δfb的比例关系,可高精度估算出切除负荷的容量占系统总容量的比例。
本文设计了扰动定位的过完备字典,与切机及切负荷扰动类似,通过本文所提思路可以构造出短路与断线扰动的扰动定位过完备字典,本文中不再赘述。
本文选择IEEE 39节点系统作为仿真模型进行切机、切负荷扰动的扰动源定位测试,利用PSCAD4.5X仿真软件作为扰动设定与数据收集工具,使用Matlab 2016a进行数据的相关算法运算。首先为模拟真实情况下的PMU数据,对收集的PMU观测数据引入测量误差,幅值测量误差极限0.2%,相角误差测量极限0.5°[17]后,进行计算分析获取定位重构结果。然后为了验证本文方法的抗噪性能,在引入测量误差的PMU数据中加入信噪比为30dB的高斯白噪声后进行定位重构分析,通过两次重构的结果对比说明本文方法的扰动定位准确程度及抗噪性能。
根据PMU设备的数据测量特点,在安装PMU的节点可直接测量该节点的母线电压和与其相连的所有相关支路的电流向量与功率变化情况,而且由于与该节点的相邻线路阻抗已知,可以计算出与该节点相邻的电压向量。PMU设备布点情况如图3所示。
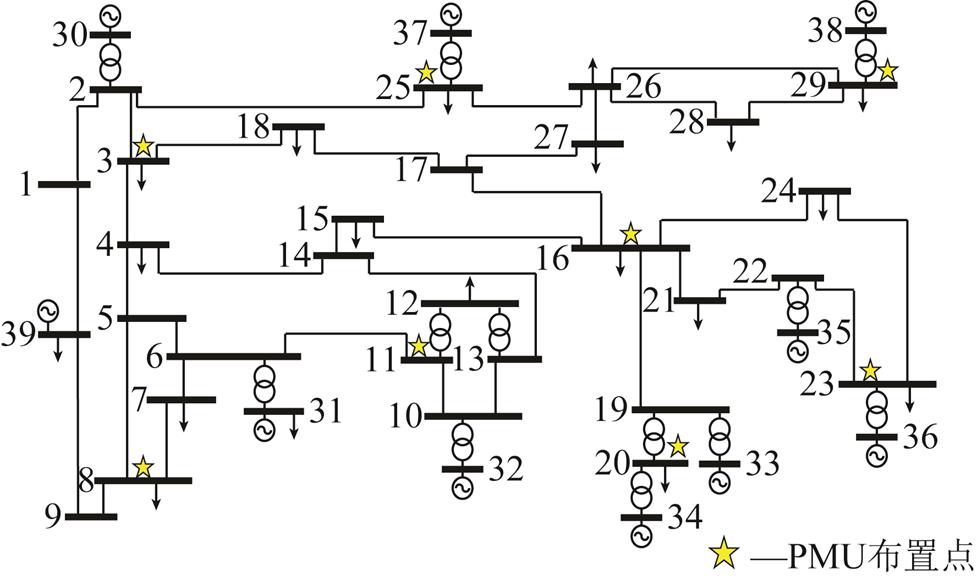
图3 IEEE 39节点系统PMU布点
Fig.3 Place figure of PMU in IEEE 39 system
以图中的配置情况安装PMU装置,能以较少的PMU配置数量达到令人满意的系统状态感知目的[18],与PMU配置母线节点相连的支路数共25条,可观测范围占总支路数的54.3%,并在此条件下完成基于过完备字典设计的电力系统扰动定位工作。
首先进行切机扰动的定位工作。以IEEE 39节点系统中30号发电机切机为例,观测数据y的观测与字典的构建后,通过正交匹配跟踪(Orthogonal Matching Pursuit, OMP)算法重构,设置迭代次数t=2得到稀疏值对应母线编号为4和23,结果如图4所示。
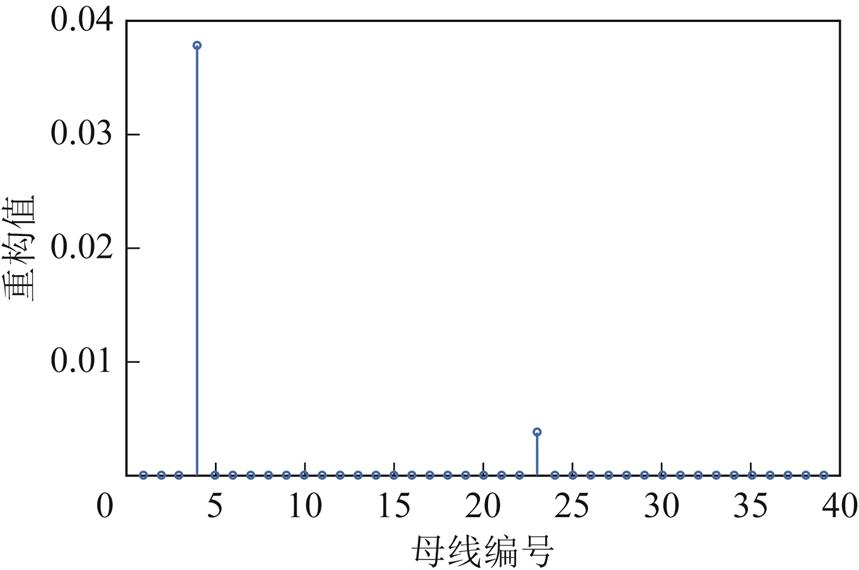
图4 30号发电机切机后重构结果
Fig.4 Reconstruction result of No.30 generator after shedding
本文将稀疏值对应的两个母线称为扰动近域母线。得到扰动近域母线编号后,在系统拓扑结构中寻找在地域上与扰动近域母线节点最近的PMU配置点,在拓扑结构中可知,与节点4最近的PMU配置点为节点3;与节点23最近的PMU配置节点为节点23,结果如图5所示。

图5 重构节点最近PMU匹配结果
Fig.5 Match Result between reconstruction node and its’ closest PMU
分别收集扰动前后节点3与节点23两处PMU的可测支路中最大正序电流相位变化扰动分量进行对比,结果如图6所示。由图6可看出,在0.6s发生扰动时,母线3处电流相位变化较大,其扰动近域母线为母线4,说明在所有的发电机中,离母线4最近的发电机发生切机扰动的可能性最大,本文将该扰动近域母线称为扰动定位母线,与其最近的发电机节点为节点30,故定位在发电机30处,符合假设情况,定位准确。

图6 两PMU测量相位变化情况
Fig.6 Measures phase change by 2PMUs
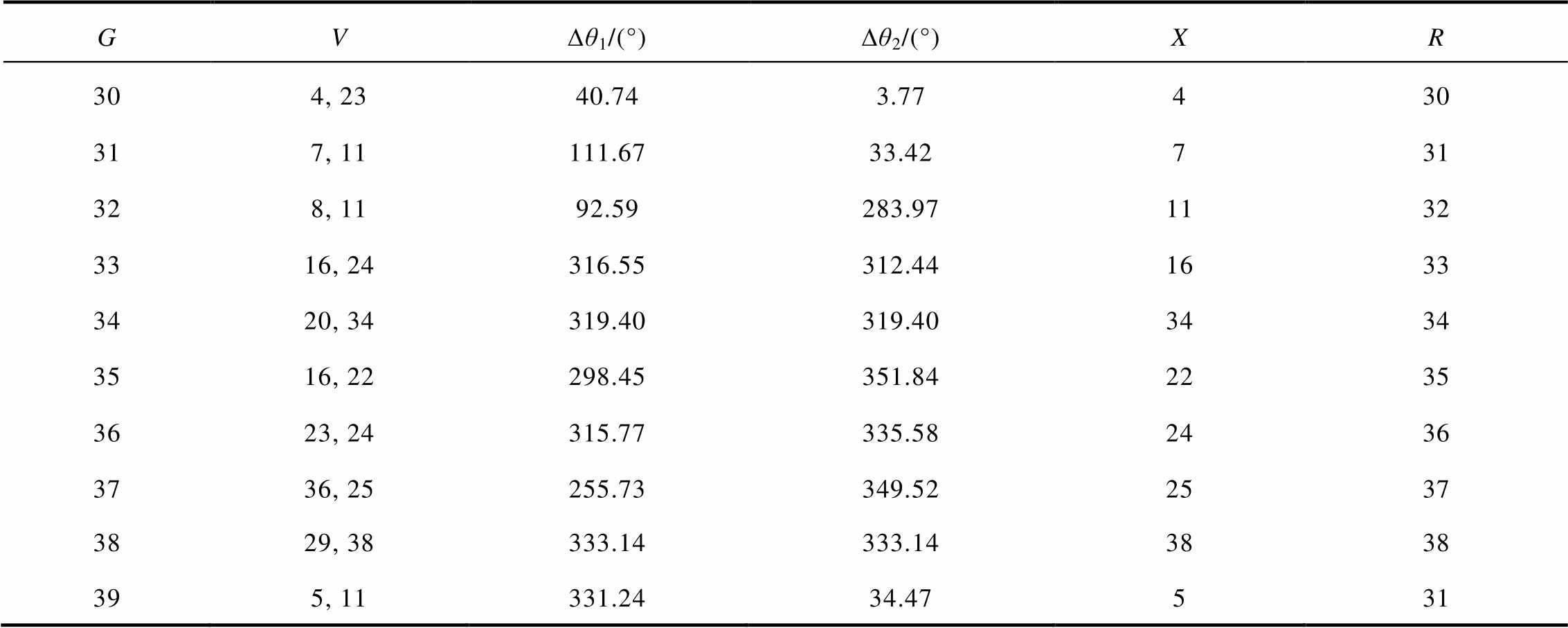
本文对系统中所有的发电机都进行了切机扰动的定位,定位情况见表1,其中∆θ1为离第一个扰动近域母线最近的PMU所能测量到的最大支路电流相位变化量,∆θ2为离第二个扰动近域母线最近的PMU所能测量到的最大支路电流相位变化量。从表1中可知,本文所提出的基于过完备字典设计的切机扰动定位方法在IEEE 39节点系统中对发电机切机的定位准确程度达到了系统中全部发电机的90%。表中符号内涵如下:G为切机发电机节点编号;V为扰动近域母线编号;X为扰动定位母线编号;R为切机发电机定位结果编号。
表1 切机扰动辨识结果
Tab.1 Disturbance identification results of generator shedding
GV∆θ1/(°)∆θ2/(°)XR 304, 2340.743.77430 317, 11111.6733.42731 328, 1192.59283.971132 3316, 24316.55312.441633 3420, 34319.40319.403434 3516, 22298.45351.842235 3623, 24315.77335.582436 3736, 25255.73349.522537 3829, 38333.14333.143838 395, 11331.2434.47531
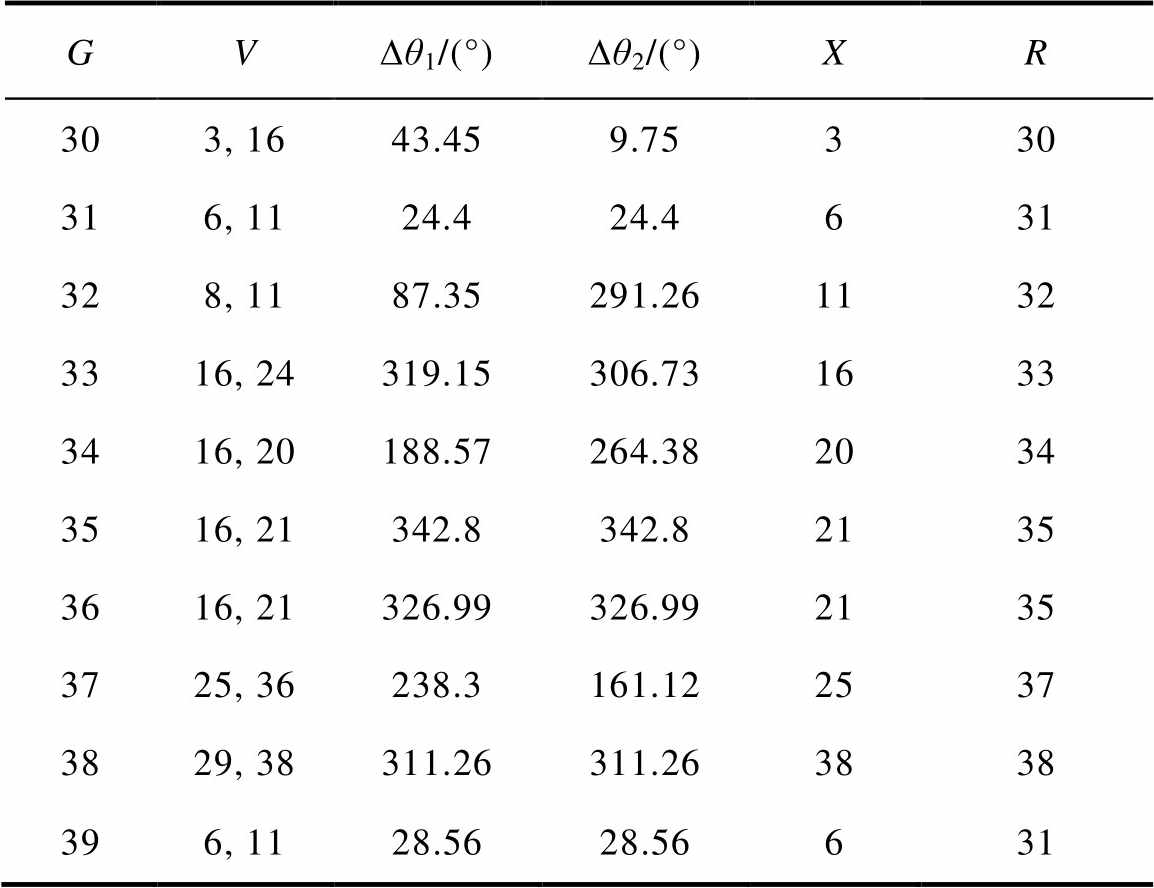
为验证切机扰动定位的抗噪性能,本文在所有PMU可观测的支路中加入信噪比为30dB的高斯白噪声,并在含噪情况下计算支路电流的正序分量,然后进行切机扰动定位分析,结果见表2。由表2可知,引入噪声后,本文所提方法在IEEE 39节点系统中对发电机切机的定位准确程度达到了系统中全部发电机的80%。噪声的影响略微降低了定位准确率。在36号发电机切机时,定位结果为35号发电机,虽然定位错误,但可以看到在IEEE 39节点拓扑结构中36号发电机与35号发电机距离相隔很近。
表2 切机扰动辨识结果(含噪声)
Tab.2 Disturbance identification results of generator shedding (with noise)
GV∆θ1/(°)∆θ2/(°)XR 303, 1643.459.75330 316, 1124.424.4631 328, 1187.35291.261132 3316, 24319.15306.731633 3416, 20188.57264.382034 3516, 21342.8342.82135 3616, 21326.99326.992135 3725, 36238.3161.122537 3829, 38311.26311.263838 396, 1128.5628.56631
在重构过程中,由于观测数据y为支路电流向量,切机过完备字典中包含支路导纳矩阵,数据均包含实部与虚部,在数据收集过程中会产生相位的误差。在重构过程中由于相位误差的引入将导致重构的偏差,通过各种常见重构算法的重构对比发现,常用的几种重构算法定位效果差异不大,因此选择较简单常用的OMP算法进行切机扰动的定位工作,以减少计算量,降低运算复杂度。
在切负荷扰动的定位重构中,本文收集PMU配置节点的所有可观测支路扰动前后的功率变化量作为观测数据y,通过对切负荷扰动的过完备字典的设计完成切负荷扰动的定位工作。
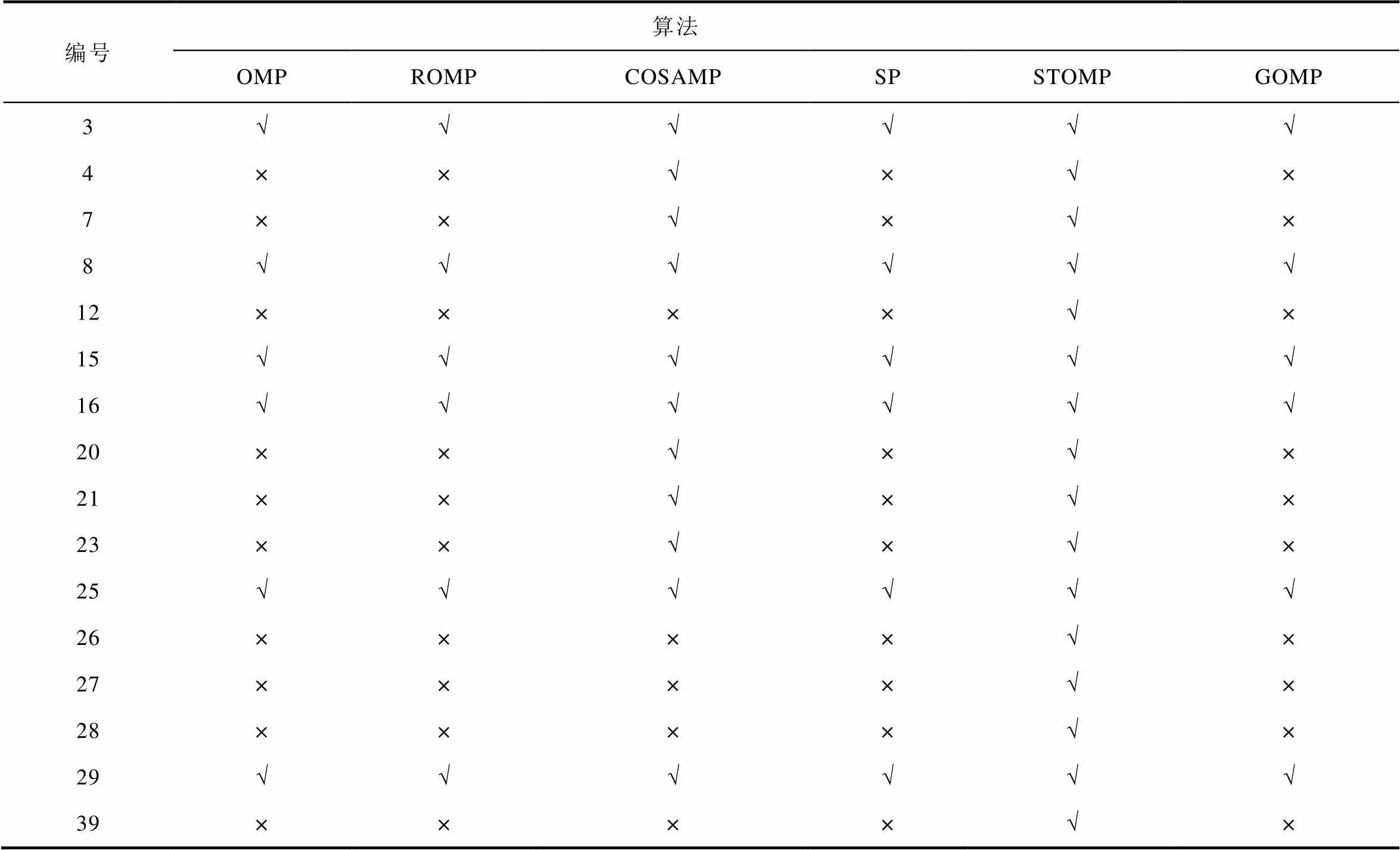
压缩感知常用的OMP算法利用内积表征原子的相似度。由于当切负荷扰动发生后,扰动观测数据y与重构字典Λ中的某列极为相似,两者相差较小,通过大量的计算发现,与重构字典中的所有列求向量求内积后,观测向量与之极其相似的重构字典中列向量求内积的结果并不一定是最大的,因此传统的OMP算法并不能准确重构出扰动的位置,且误差可能极大,因此本文对常见的六种压缩感知重构算法做切负荷定位的对比分析,除常规的OMP算法外,其余五种重构算法分别为:正则化正交匹配追踪(Regularized OMP, ROMP)、压缩采样匹配追踪(Compressive Sampling MP, COSAMP)、子空间追踪(Subspace Pursuit, SP)、分段正交匹配追踪(Stagewise OMP, STOMP)、广义正交匹配追踪(Generalized OMP, GOMP)。不同重构算法的重构定位结果见表3。表中“√”代表定位正确,“×”代表定位错误。
表3 不同重构算法的定位结果
Tab.3 Localization results of different algorithms
编号算法OMPROMPCOSAMPSPSTOMPGOMP 3√√√√√√ 4××√×√× 7××√×√× 8√√√√√√ 12××××√× 15√√√√√√ 16√√√√√√ 20××√×√× 21××√×√× 23××√×√× 25√√√√√√ 26××××√× 27××××√× 28××××√× 29√√√√√√ 39××××√×
通过对比可以发现,在IEEE 39节点系统中对16个负荷节点分别切负荷操作后进行定位,常用的OMP重构算法进行切负荷扰动的定位,在16个负荷节点中仅有6个负荷节点定位正确,准确度只有37.5%,而分段正交匹配追踪(Stagewise Orthogonal Matching Pursuit, STOMP)算法则达到了100%,后续容量估算使用STOMP算法进行。
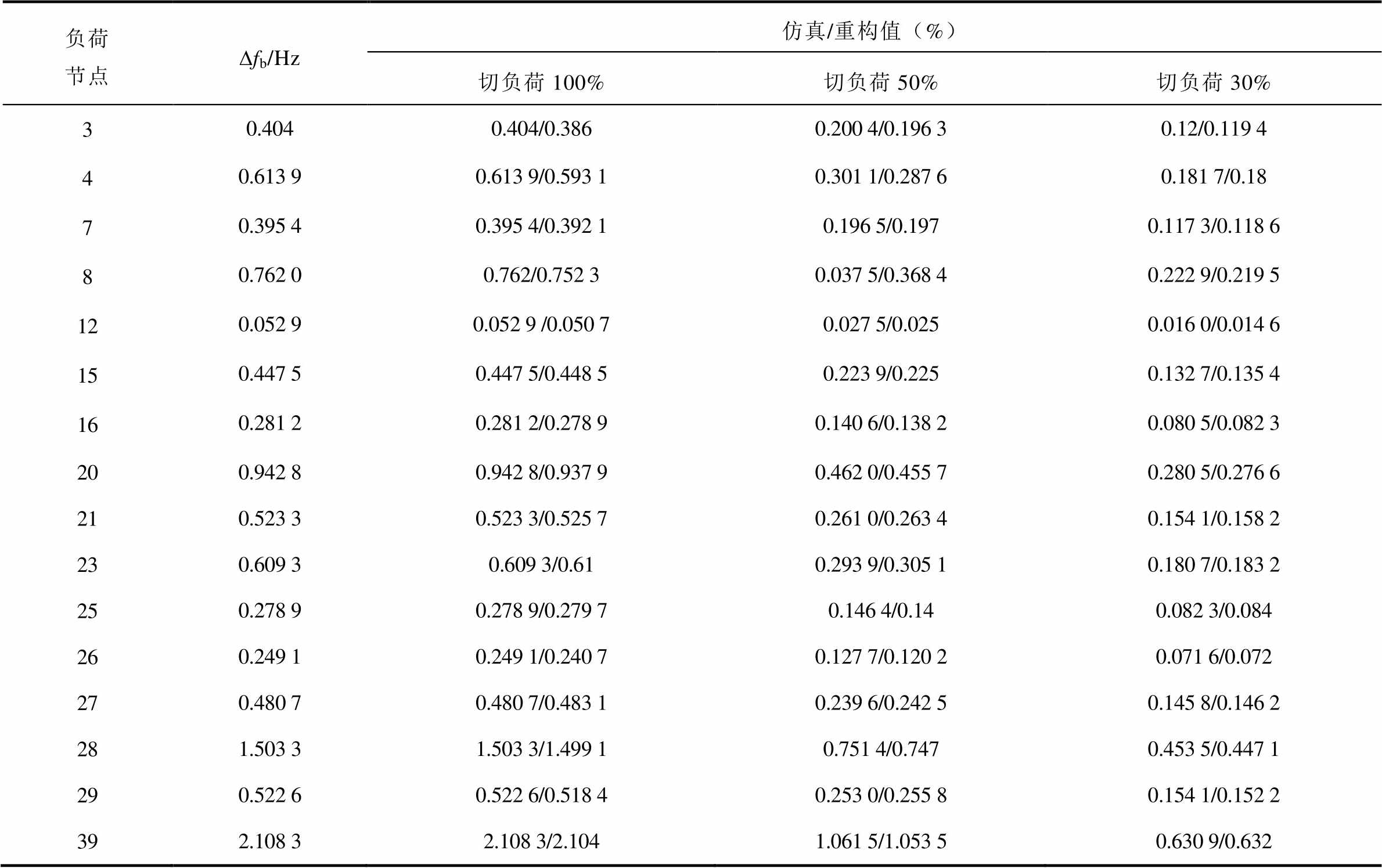
切负荷扰动的重构数据不仅可以定位扰动源的位置,而且可以高精度地估算出所切负荷量占系统总负荷量的百分比。本文对IEEE 39节点中16个负荷节点切负荷的容量进行高精度估算,分别切除各负荷节点负荷容量的100%、50%、30%,以重构的幅值与理论值对比,其中Δfb代表该负荷节点切除100%容量时的节点频率变化,结果见表4、表5。
表4 切负荷容量估算结果
Tab.4 Estimate of load shedding capacity
负荷节点∆fb/Hz仿真/重构值(%)切负荷100%切负荷50%切负荷30% 30.4040.404/0.3860.200 4/0.196 30.12/0.119 4 40.613 90.613 9/0.593 10.301 1/0.287 60.181 7/0.18 70.395 40.395 4/0.392 10.196 5/0.1970.117 3/0.118 6 80.762 00.762/0.752 30.037 5/0.368 40.222 9/0.219 5 120.052 90.052 9 /0.050 70.027 5/0.0250.016 0/0.014 6 150.447 50.447 5/0.448 50.223 9/0.2250.132 7/0.135 4 160.281 20.281 2/0.278 90.140 6/0.138 20.080 5/0.082 3 200.942 80.942 8/0.937 90.462 0/0.455 70.280 5/0.276 6 210.523 30.523 3/0.525 70.261 0/0.263 40.154 1/0.158 2 230.609 30.609 3/0.610.293 9/0.305 10.180 7/0.183 2 250.278 90.278 9/0.279 70.146 4/0.140.082 3/0.084 260.249 10.249 1/0.240 70.127 7/0.120 20.071 6/0.072 270.480 70.480 7/0.483 10.239 6/0.242 50.145 8/0.146 2 281.503 31.503 3/1.499 10.751 4/0.7470.453 5/0.447 1 290.522 60.522 6/0.518 40.253 0/0.255 80.154 1/0.152 2 392.108 32.108 3/2.1041.061 5/1.053 50.630 9/0.632
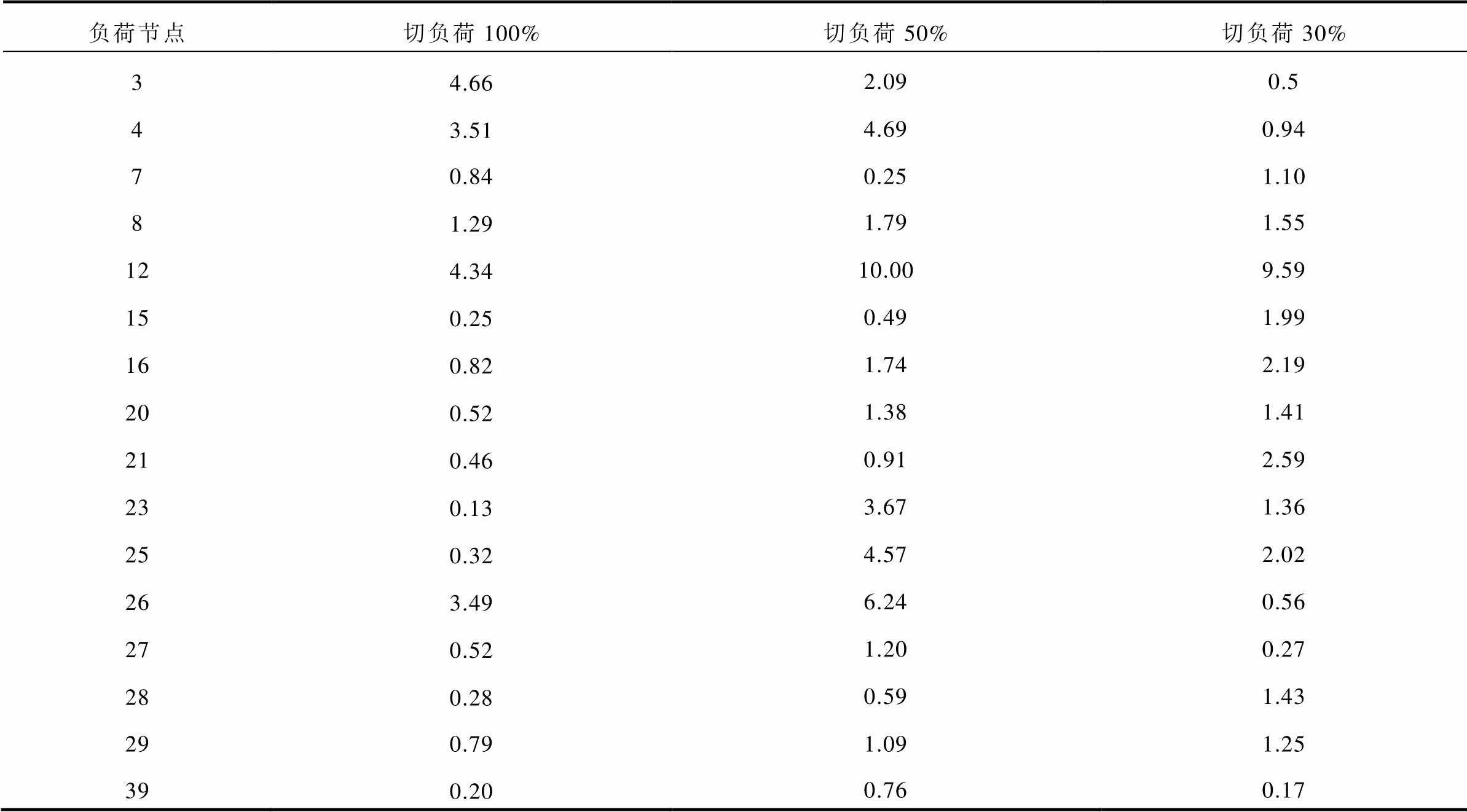
表5 切负荷容量估算误差
Tab.5 Load shedding capacity estimation accuracy (%)
负荷节点切负荷100%切负荷50%切负荷30% 34.662.090.5 43.514.690.94 70.840.251.10 81.291.791.55 124.3410.009.59 150.250.491.99 160.821.742.19 200.521.381.41 210.460.912.59 230.133.671.36 250.324.572.02 263.496.240.56 270.521.200.27 280.280.591.43 290.791.091.25 390.200.760.17
通过上述分析,本文方法对切负荷扰动的定位与切除容量估算均有较高准确度。
为验证切负荷扰动定位的抗噪性能,本文在所有PMU可观测的支路中加入信噪比为30dB的高斯白噪声,然后进行切负荷扰动定位分析,定位结果及切负荷量准确度结果见表6、表7。
表6 切负荷容量估算结果(含噪声)
Tab.6 Estimate of load shedding capacity(with noise)

负荷节点∆fb/Hz仿真/重构值(%) 切负荷100%切负荷50%切负荷30% 30.4040.404/0.402 30.200 4/0.199 70.12/0.119 5 40.613 90.613 9/0.618 80.301 1/0.310 40.181 7/0.187 2 70.395 40.395 4/0.392 30.196 5/0.197 10.117 3/0.118 1 80.762 00.762/0.759 80.375/0.377 20.222 9/0.225 3 120.052 90.052 9/0.050 60.027 5/0.025 40.016 0/0.014 5 150.447 50.447 4/0.448 40.223 9/0.225 10.132 7/0.135 3 160.281 20.281 2/0.278 80.140 6/0.138 20.080 5/0.081 8 200.942 80.942 8/0.937 10.462 0/0.455 40.280 5/0.277 210.523 30.523 3/0.525 60.261 0/0.263 10.154 1/0.158 230.609 30.609 2/0.609 90.293 9/0.305 20.180 7/0.183 1 250.278 90.278 8/0.279 70.146 4/0.139 80.082 3/0.084 4 260.249 10.249 1/0.241 40.127 7/0.119 80.071 6/0.074 270.480 70.480 6/0.483 40.239 6/0.242 80.145 8/0.146 5 281.503 31.503 3/1.500 40.751 4/0.745 10.453 5/0.446 7 290.522 60.522 5/0.518 40.253 0/0.255 70.154 1/0.152 5 392.108 32.108 3/2.104 81.061 5/1.053 50.630 9/0.632
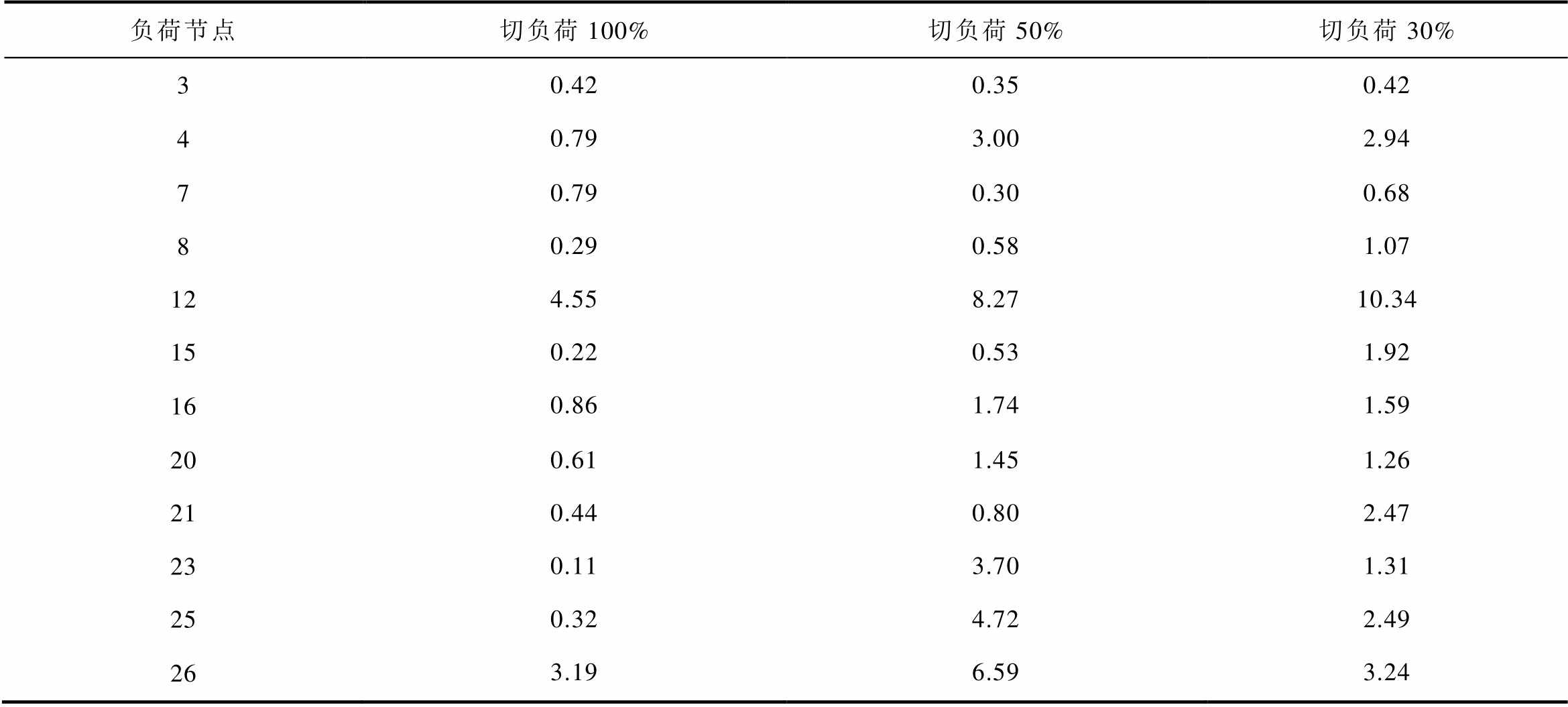
表7 切负荷容量估算误差(含噪声)
Tab.7 Load shedding capacity estimation accuracy (with noise) (%)
负荷节点切负荷100%切负荷50%切负荷30% 30.420.350.42 40.793.002.94 70.790.300.68 80.290.581.07 124.558.2710.34 150.220.531.92 160.861.741.59 200.611.451.26 210.440.802.47 230.113.701.31 250.324.722.49 263.196.593.24
(续)

负荷节点切负荷100%切负荷50%切负荷30% 270.581.320.48 280.190.851.52 290.791.061.05 390.170.760.17
通过表6、表7可以发现,在引入噪声的切负荷扰动定位与负荷投切量估算中,对切负荷扰动定位的正确率没有任何影响,在IEEE 39节点中,切负荷扰动定位正确率仍为100%。切负荷投切量估计中,相比未引入噪声时的切负荷投切量估算,在引入噪声后,切负荷投切量估算准确率将产生波动,部分估算准确率将提高,部分估算准确率会降低,但变动幅度均不大,且切负荷比例不同时,估算准确度的差异与切负荷量无关,没有规律。
本文提出了一种基于过完备字典设计的电力系统扰动定位方法,通过收集扰动观测数据及设计过完备位字典,可对电网中的各类扰动进行定位。本文以切机与切负荷扰动定位为例,不仅成功定位切机与切负荷扰动源的位置,并且可以计算切负荷扰动中所切负荷量。在观测数据具有测量误差及传输噪声的情况下,本文方法对IEEE 39节点系统的切机扰动的定位准确率超过了80%,对切负荷扰动的定位准确率达到了100%,同时切负荷容量计算正确率也达到了90%以上,在电力系统扰动定位中本文所提方法具有借鉴意义。
参考文献
[1] 韩学军, 石磊, 赵凤英. 连锁过载识别方法的比较[J]. 电网技术, 2007, 31(21): 37-40, 60. Han Xuejun, Shi Lei, Zhao Fengying. Comparative research on identifying method of cascading overload[J]. Power System Technology, 2007, 31(21): 37-40, 60.
[2] 陈彬, 于继来. 基于电网潮流分布特征的在线故障智能诊断[J]. 电力系统自动化, 2007, 31(16): 29-34. Chen Bin, Yu Jilai. Online fault intelligent diagnosis based on distributed characteristics of power flow with outage of electric power network[J].Automation of Electric Power Systems, 2007, 31(16): 29-34.
[3] 金涛, 陈毅阳, 段小华, 等.基于改进DFT的电力系统同步相量测量算法研究[J].电工技术学报, 2017, 32(17): 1-10. Jin Tao, Chen Yiyang, Duan Xiaohua, et al. Research on synchronous phasor measurement algorithm of power system based on improved DFT[J]. Transactions of China Electrotechnical Society, 2017, 32(17): 1-10.
[4] 罗深增, 李银红, 游昊, 等. 基于同步相量测量单元的串联补偿线路自适应故障定位算法[J]. 电工技术学报, 2017, 32(5): 143-151. Luo Shenzeng, Li Yinhong, You Hao, et al. An adaptive fault location algorithm based on PMU measurement for series compensated transmission lines[J]. Transactions of China Electrotechnical Society, 2017, 32(5): 143-151.
[5] 陈雷, 郑德忠, 廖文喆. 基于压缩感知的含扰动电能质量信号压缩重构方法[J]. 电工技术学报, 2016, 31(8): 163-171. Chen Lei, Zheng Dezhong, Liao Wenzhe. Method based on compressed sensing for compression and reconstruction of power quality signals with disturbances[J]. Transactions of China Electrotechnical Society, 2016, 31(8): 163-171.
[6] 刘嫣, 汤伟, 刘宝泉. 基于压缩感知的电能质量扰动数据稀疏分析与改进重构算法[J]. 电工技术学报, 2018, 33(15): 3461-3470. Liu Yan, Tang Wei, Liu Baoquan. Datasparseanalysisandimprovedreconstructionalgorithmofpowerqualitydisturbancebasedoncompressedsensing[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3461-3470.
[7] 秦晓辉, 毕天姝, 杨奇逊. 基于广域同步量测的电力系统扰动识别与定位方法[J]. 电网技术, 2009, 33(12): 35-41. Qin Xiaohui, Bi Tianshu, Yang Qixun. WAMS based power system disturbance identification and location approach[J]. Power System Technology, 2009, 33(12): 35-41.
[8] 徐彪, 尹项根, 张哲, 等. 矩阵算法和优化算法相结合的配电网故障定位[J]. 电力系统自动化, 2019, 43(05): 152-161. Xu Biao, Yin Xianggen, Zhang Zhe, et al. Fault location for distribution network based on matrix algorithm and optimization algorithm[J]. Automation of Electric Power Systems, 2019, 43(05): 152-161.
[9] Majidi M, Etezadi-Amoli M, Fadali M S. A sparse-data-driven approach for fault location in transmission networks[J]. IEEE Transactions on Smart Grid, 2017, 8(2): 548-556.
[10] 于华楠, 马聪聪, 王鹤. 基于压缩感知估计行波自然频率的输电线路故障定位方法研究[J]. 电工技术学报, 2017, 32(23): 140-148. Yu Huanan, Ma Congcong, Wang He. Transmission line fault location method based on compressed sensing estimation of traveling wave natural frequencies[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 140-148.
[11] Zhu Hao, Giannakis G B. Sparse overcomplete representations for efficient identification of power line outages[J]. IEEE Transactions on Power Systems, 2012, 27(4): 2215-2224.
[12] 齐郑, 庄舒仪, 刘自发, 等. 基于并联电阻扰动信号的配电网故障定位方法分析[J]. 电力系统自动化, 2018, 42(09): 195-200. Qi Zheng, Zhuang Shuyi, Liu Zifa, et al. Analysis on distribution network fault location method based on parallel resistance disturbed signal injection[J]. Automation of Electric Power Systems, 2018, 42(09): 195-200.
[13] Xu Yan, Liu Jingyan.Reasearch of fault line selection and fault type recognition method of DC system based on graph theory[J]. Protection and Control of Modern Power Systems, 2018, 39(8): 2279-2286.
[14] Denegri C B, Invernizzi M, Serra P. Perturbation identification via voltage phasor monitoring in transmission systems[C]//2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 2004: 23-26.
[15] 马静, 李金龙, 杨奇逊. 基于故障模型的广域故障定位新方法[J]. 电力系统保护与控制, 2010, 38(20): 74-78. Ma Jing, Li Jinlong, Yang Qixun. Anovelwide-areafaultlocationalgorithmbasedonfaultmodel[J]. PowerSystemProtectionandControl, 2010, 38(20): 74-78.
[16] 徐慧明, 毕天姝. 计及暂态过程的多支路切除潮流转移识别算法研究[J]. 中国电机工程学报, 2007, 27(16): 24-30.Xu Huiming, Bi Tianshu. Flowtransferringidentificationalgorithmformulti-branchesremovaleventwithconsiderationoftransientphenomena[J]. ProceedingsoftheCSEE, 2007, 27(16): 24-30.
[17] 国家电网有限公司. Q/GDW10131-2017电力系统实时动态监测系统技术规范[S]. 2017.
[18] Aminifar F, Khodaei A, Fotuhi-Firuzabad M A. Contingency-constrainedPMU placement in power networks[J]. IEEE Transactions on Power System, 2010, 25(1): 516-523.
Disturbance Location Method of Power System Based on Over-Complete Reconstruction Dictionary Design
Abstract Disturbance location of power system quickly and accurately is an important precondition to implement safety and stability control measures of power system. The disturbance source has sparse characteristics in the spatial distribution since the disturbance will not occur in a large range at the same time. How to use the limited number of phasor measurement unit devices to perceive the disturbance in the power system is an important research topic. This paper presented a power system disturbance positioning based on a overcomplete dictionary design, its innovation is based on the changes of the system topology or electrical parameters of the disturbance to construct a overcomplete dictionary, in combination with compressed sensing reconstruction algorithm to recover from low dimensional phasor measurement unit observation data of the sparse characteristics to high dimensional disturbance location data, then the disturbance of power system got located. The generator shedding and the load shedding disturbance are taken as examples. A large number of simulation results show that the method proposed in this paper can locate the disturbance source with high accuracy, and it has important reference significance for other types of disturbance location.
keywords:Disturbance location, overcomplete dictionary, sparse features, generator shedding, load shedding
DOI:10.19595/j.cnki.1000-6753.tces.190451
中图分类号:TM744
于华楠 女,1981年生,博士,副教授,研究方向为压缩感知在电力系统中的应用、电能质量信号检测与分析。E-mail:yhn810117@163.com(通信作者)
李永鑫 男,1994年生,硕士研究生,研究方向为压缩感知在电力系统扰动定位中的应用。E-mail:542426856@qq.com
国家重点研发计划(2016YFB0901200)和吉林省科技厅项目(20160520089JH)资助。
收稿日期2019-04-22
改稿日期 2019-09-08
(编辑 赫蕾)